5.2.1. Метод Ньютона–Рафсона
Идея метода заключается в линеаризации уравнений системы (5.1), что позволяет свести исходную задачу решения СНУ к многократному решению системы линейных уравнений.
Рассмотрим, как были получены расчетные зависимости метода.
Пусть известно приближение xi(k) решения системы нелинейных уравнений xi*. Введем в рассмотрение поправку Dxi как разницу между решением и его приближением:
,
Подставим полученное выражение для xi* в исходную систему.
…
Неизвестными в этой системе нелинейных уравнений являются поправки Dxi. Для определения Dxi нужно решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако эту систему можно Линеаризовать, и, решив ее, получить Приближенные значения поправок Dxi для данного приближения, т. е. Dxi(k). Эти поправки не позволяют сразу получить точное решение , но дают возможность приблизиться к решению, – получить новое приближение решения
, (5.
Для линеаризации системы следует разложить функцию fi в ряды Тейлора в окрестности xi(k), ограничиваясь первыми дифференциалами.
Полученная система имеет вид:
, (5.15)
Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения xi(k). Для решения системы линейных уравнений (5.15) при n=2,3 можно использовать формулы Крамера, при большей размерности системы n – метод исключения Гаусса.
Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности e, расчет завершается. Таким образом, условие окончания расчета:
δ =
Можно использовать и среднее значение модулей поправок:
В матричной форме систему (5.15 ) можно записать как:
(5.16)
Где:
, – матрица Якоби (производных),
– вектор поправок
– вектор-функция
W(X(k)) – матрица Якоби, вычисленная для очередного приближения.
F(X(k)) – вектор-функция, вычисленная для очередного приближения.
Выразим вектор поправок ∆X(k) из (5.16):
Где W-1 – матрица, обратная матрице Якоби.
Окончательно формула последовательных приближений метода Ньютона решения СНУ в матричной форме имеет вид:
(5.17)
Достаточные условия сходимости для общего случая имеют очень сложный вид, и на практике проверяются редко. Нужно отметить, что метод сходится очень быстро (за 3 – 5 итераций), если det|W| ¹ 0 и начальное приближение X(0) выбрано близким к решению (отличаются не более чем на 10%).
Алгоритм решения СНУ методом Ньютона состоит в следующем:
1. Задается размерность системы n, требуемая точность ε, начальное приближенное решение X = (xi)n.
2. Вычисляются элементы матрицы Якоби W = (¶¦i ¤ ¶xj)n, n.
3. Вычисляется обратная матрица W-1.
4. Вычисляется вектор функция F=(fi)n, , .
5. Вычисляются вектор поправок
6. Уточняется решение
7. Оценивается достигнутая точность δ= или
8. Проверяется условие завершения итерационного процесса
δ≤ε
Если оно не соблюдается, алгоритм исполняется снова с пункта 2.
Для уменьшения количества арифметических действий Рафсон предложил не вычислять обратную матрицу W-1, а вычислять поправки как решение СЛУ (5.15)
Схема алгоритма метода Ньютона – Рафсона представлена на рис.5.2. При разработке схемы учтена необходимость защиты итерационного цикла от зацикливания: введен счетчик итераций k и ограничение на число итераций kmax (на практике не более 100).
Рис 5.5. Схема алгоритма решения СНУ методом Ньютона – Рафсона.
Достоинством методов Ньютона является быстрая сходимость, недостатками – сложность расчетов (вычисление производных, многократное решение системы линейных уравнений), сильная зависимость от начального приближения.
Пример 5.3. Требуется методом Ньютона-Рафсона уточнить одно из решений системы
x12+x22=1
Ln x1+2×2= –1
Заданная точность ε=0,001. Решения отделены ранее (пример 5.1)
Запишем уравнения в стандартном виде:
Начальное приближение Х(0)=(0,9;-0,4).
Первая итерация.
Элементы матрицы Якоби W=(wi, j)2,2
W1,1=
W1,2=
W2,1=
W2,2=
Значение функций
F1(0,9;-0,4) = 0,92 + 0,42 – 1 = 0,81+ 0,16 – 1 = -0,03
F2(0,9;-0,4) = ln(0,9) + 2*(-0,4) + 1 = -0,1054 + 0,2 + 1 = 0,0946
Для вычисления поправок нужно решить систему
1,8×∆x1 – 0,8×Dx2= -(-0,03)
1,1111×∆x1 + 2×∆x2= –0,0946
По формулам Крамера
DetW≠0 – система обусловлена.
Первое приближение решения
Х1 = х1 + ∆х1 = 0,9+(-0,0035) = 0,8965
Х2 = х2 + ∆х2 = -0,4 + (-0,0454) = -0,4454
Оценка достигнутой точности
Нужно продолжить итерационный процесс т. к. δ>ε.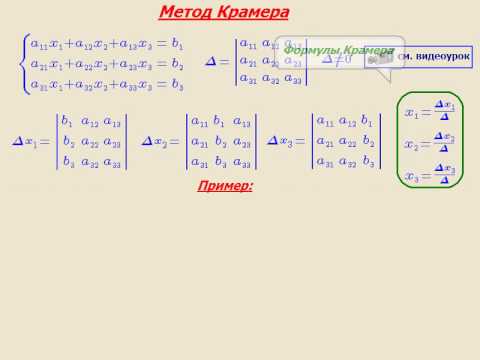
После второй итерации требуемая точность достигается, х1=0,8995 х2=-0,4449, d » 0,001.
| < Предыдущая | Следующая > |
|---|
| Бесплатные онлайн-инструменты для решения системы уравнений
Интересно, как понять базовый уровень понятий линейных уравнений за считанные секунды. Это не проблема, поскольку мы создали концептуальные калькуляторы линейных уравнений. Эти калькуляторы для решения линейных уравнений бесплатны и удобны. Это помогает детям, а также учителям найти точный результат предоставленных линейных уравнений в течение нескольких секунд. Перейдите на эту страницу и воспользуйтесь возможностью использовать бесплатные онлайн-инструменты для расчета линейных уравнений.
Быстрый подход к решению вычислений линейных уравнений, таких как линейные уравнения с одной переменной, линейные уравнения с двумя переменными, графическое построение линейных уравнений и т.
д., заключается в использовании калькуляторов линейных уравнений. Список бесплатных онлайн-калькуляторов по линейным уравнениям представлен здесь по быстрым ссылкам. Перейдите по этим доступным ссылкам калькулятора и с легкостью решите вычисления линейных уравнений.
Калькулятор решения линейных уравнений
- Калькулятор решения линейных уравнений
- Линейные уравнения в калькуляторе с одной переменной
- Калькулятор линейных уравнений с двумя переменными
- Калькулятор линейных уравнений с тремя переменными
- Графический калькулятор линейных уравнений
- Решение линейного уравнения с использованием правила Крамерса (3 переменные)
- Решение линейных уравнений с помощью обратной матрицы (2 переменные)
- Решение линейных уравнений с помощью обратной матрицы (4 переменные)
- Решение линейных уравнений с использованием операций со строками (2 переменные)
- Решение линейных уравнений с использованием расширенной матрицы (2 переменные)
- Калькулятор нелинейных уравнений
- Линейные уравнения с помощью калькулятора подстановок
- Линейные уравнения с калькулятором дробей
- Калькулятор линейных уравнений и неравенств
- Решение линейного уравнения с использованием правила Крамерса (4 переменные)
- Решение линейного уравнения с использованием правила Крамерса (2 переменные)
- Решение линейных уравнений с помощью обратной матрицы (3 переменные)
- Решение линейных уравнений методом подстановки (2 переменные)
- Решение линейных уравнений с использованием операций со строками (3 переменные)
- Решение линейных уравнений с использованием расширенной матрицы (3 переменные)
Наши решения класса 6 в Раджастхане Вопросы и ответы
Наши решения класса 6 в Раджастхане Вопросы и ответы
- Глава 1 Раджастхан.
Введение - Глава 2 История Раджастхана
- Глава 3 Источники истории
- Глава 4 Места древней цивилизации в Раджастхане
- Глава 5 Форма правления до обретения независимости
- Глава 6 Физическое формирование Раджастхана
- Глава 7 Водные ресурсы и сохранение
- Глава 8 Основные средства к существованию
- Глава 9 Основные услуги в Раджастхане
- Глава 10 Народная культура и искусство
ВведениеНаши решения класса 7 в Раджастхане Вопросы и ответы
Наши решения класса 7 в Раджастане Вопросы и ответы
- Глава 1 Леса, дикая природа и ее охрана
- Глава 2 Минеральные и энергетические ресурсы
- Глава 3 Сельское хозяйство и ирригация
- Глава 4 Сельскохозяйственный маркетинг в Раджастане
- Глава 5 Торговля в Раджастане
- Глава 6.
- Глава 7 Движение за независимость и Раджастхан
- Глава 8 Социальные и образовательные реформы в Раджастане до обретения независимости
- Глава 9 Вклад Раджастхана в создание Конституции
Наши решения класса 8 в Раджастхане Вопросы и ответы
Наши решения класса 8 в Раджастане Вопросы и ответы
- Глава 1 Леса, дикая природа и их охрана
- Глава 2 Минеральные и энергетические ресурсы
- Глава 3 Сельское хозяйство и ирригация
- Глава 4 Сельскохозяйственный маркетинг в Раджастане
- Глава 5 Торговля в Раджастане
- Глава 6. Выдающиеся правители Раджастхана
- Глава 7 Движение за независимость и Раджастхан
- Глава 8 Социальные и образовательные реформы в Раджастане до обретения независимости
- Глава 9 Вклад Раджастхана в создание Конституции
Калькулятор дробей
- Сложение дробей
- Вычитание дроби
- Умножение дроби
- Дробный отдел
- Упрощение дробей
- Эквивалент дроби
- Десятичная дробь
- Проценты в дроби
- Дробь до десятичной дроби
- Доля в процентах
Калькулятор решения линейных уравнений
Решение линейных уравнений вида Ax+By=C представляет собой слияние двух переменных и константы.
Здесь x и y — переменные, а A, B и C — константы. Этот бесплатный онлайн-калькулятор точно вычисляет значения переменных.
Например, 2x+6y=4 и 5x+1y=2 являются линейными уравнениями
Калькулятор линейных уравнений с одной переменной
Уравнение, имеющее одну переменную со степенью один, называется линейным уравнением с одной переменной. Стандартное уравнение линейного уравнения с одной переменной записывается в виде ax+b=0, где x — переменная, а a, b — константы. Он дает решение для одной переменной.
Например, 3x-5=10 — это линейные уравнения с одной переменной. Следовательно, х=5.
Калькулятор линейных уравнений с двумя переменными
Линейное уравнение с двумя переменными является решением переменных Стандартная форма уравнения, т. е. ax+by+c=0, называется линейным уравнением с двумя переменными x и y, где мы получаем решение для двух переменных. Если a,b,c — действительные числа и они равны 0, то линейное уравнение с двумя переменными имеет вид ax+by=c.
Например, x + 2y = 10, 2x + y = 20 — линейное уравнение с двумя переменными, а значит, x = -3 и y = 26 — решения данного линейного уравнения с двумя переменными.
Калькулятор построения графиков линейных уравнений
A Графики линейных уравнений представляют собой графическое представление линейных уравнений. Для решения системы линейных уравнений мы используем различные методы, одним из которых является построение линейных уравнений в виде графика, в результате которого получается прямая линия.
Например, y=mx+b является графическим примером линейных уравнений.
Калькулятор нелинейных уравнений
Нелинейное уравнение — это уравнение, в котором переменная имеет степень 2 или более двух. Стандартная форма нелинейного уравнения: ax² + by² = c, где a, b, c — константы, а x и y — переменные. Нелинейное уравнение на графике представляет собой кривую и имеет переменное значение наклона.
Например, 2x² – 4y² = 1 и 3x² + 2x + 1 = 0 являются двумя экземплярами системы нелинейных уравнений.
Калькулятор линейных уравнений методом подстановки
Решение системы уравнений методом подстановки — самый простой способ решения вычислений линейных уравнений. Калькулятор линейных уравнений с помощью подстановки находит значения переменных для заданной пары уравнений.
Например, решая линейные уравнения x-3y=4, x+2y=1 с помощью подстановки, получаем x=11/5, y=-3/5.
Калькулятор линейных уравнений с дробями
Линейное уравнение с дробями — это уравнение, содержащее дробные члены в числителе/знаменателе. Онлайн-калькулятор линейных уравнений с дробями сначала решает выражение, исключая знаменатели, а затем продолжает тот же процесс решения линейных уравнений.
Например: (2x+2y)/(x-y) — это линейное уравнение с дробями, и его решение равно 2(x+y)/(x-y).
Калькулятор линейных уравнений и неравенств
Линейные функции, включенные в такие неравенства, как меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) символов, легко вычисляются с помощью линейных уравнений с помощью калькулятора неравенств.
Например, 2x-5/3 > 3x+3/4 является примером функции линейного неравенства. следовательно, решение уравнения x < -29.
Различные формы линейных уравнений с примерами
| Линейное уравнение | Общая форма | Пример |
| Форма пересечения склона | у = мх + б | у + 2х = 3 |
| Точечно-наклонная форма | у – у1 = м(х – х1) | у – 3 = 6(х – 2) |
| Общая форма | Топор + В + С = 0 | 2х + 3у – 6 = 0 |
| Форма запроса | х/а + у/б = 1 | х/2 + у/3 = 1 |
Методы решения линейных уравнений с двумя переменными
Для решения линейных уравнений с двумя переменными существуют различные методы, и они следующие:
- Метод подстановки
- Метод перекрестного умножения
- Метод устранения
- Графический метод
Стандартная форма формулы линейного уравнения?
Стандартная форма формулы линейного уравнения состоит из переменной и константы.
Формула линейного уравнения: ax + b = 0, где a ≠ 0, а x — переменная.
- Что такое определение и пример линейного уравнения?
Алгебраическое уравнение, в котором каждый член имеет показатель степени, равный единице, а графическое изображение уравнения представляет собой прямую линию, является определением линейного уравнения. Примером линейного уравнения является y=mx + b.
- Каковы 5 различных форм линейных уравнений?
Стандартная форма, Форма пересечения наклона, Форма точки-наклона, Форма с двумя точками и Форма с двумя пересечениями — это пять различных форм линейного уравнения.
- Где я могу получить бесплатный онлайн калькулятор для решения линейных уравнений?
Вы можете бесплатно получить онлайн-калькулятор решения линейных уравнений на сайте linearequationscalculator.com
- Что такое калькулятор формул линейных уравнений?
Калькулятор формул для линейных уравнений — это бесплатный онлайн-инструмент, который помогает учащимся легко и быстро решать системы уравнений.
▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно. Пройдите курсы по математике, естественным наукам и бизнесу
Подготовка к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.
— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—
| 95% купили больше ПРИЛОЖЕНИЙ. | 97% сообщили об улучшении результатов. | Рейтинг: 4,89из 5 звезд. | Доступно 46 ПРИЛОЖЕНИЙ. |
КОВИД СПЕЦИАЛЬНЫЙ
Купите 3 приложения Made Easy по цене 2 приложений.
Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenie ur Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyPhysik Leicht EasyPhysik Research Made EasyPhysik Research Made Easy GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometr ia de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.
Находится в разделе 5:Настройки → 4:Статус → О программе
ID может выглядеть так: 1008000007206E210B0 BD92F455 .
ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.
или на международном уровне:
В конце оплаты через PayPal вам будет отправлено электронное письмо с вашим ключом и программным обеспечением.
Хотите купить TI-калькулятор?
Получите самые низкие цены на TI-Calculators
(со сравнением цен)
СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.
Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Установите оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, отремонтированные, подержанные калькуляторы.
Посмотрите обучающие видео и прочитайте руководства по калькуляторам.
Читайте последние новости о калькуляторах в Интернете.
БЕСПЛАТНАЯ загрузка:
Решатель квадратных уравнений (шаг за шагом)
Загрузите пошаговый решатель квадратных уравнений
. Этот решатель является частью приложения Algebra Made Easy.
– Загрузите бесплатные пробные версии здесь.
– Срок действия пробных и платных приложений не ограничен.
– Будущие обновления бесплатны – навсегда!
Онлайн-репетиторство по математике
Получите онлайн-репетиторство.
Репетиторы с отличными оценками по математике будут рады помочь вам.
Получите индивидуальную помощь по математике.
Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.