Решение задач по химии 9: Решение задач по химии. 9 класс - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Экспериментальное решение задач по химии. 8–9 классы. Программа элективного курса

Рабочие программы

Основное общее образование

Химия

Программа курсов по выбору “Экспериментальное решение задач по химии. 8–9 классы” предназначена для предпрофильной подготовки. В данном сборнике представлены шестнадцать программ элективных курсов по химии. Курсы прошли апробацию в средних общеобразовательных учреждениях.

Программы для учащихся 8 классов:
1. Алхимия: мифы и реальность
2. Химическая мозаика
3. Химия и медицина

Программы для учащихся 9 классов:
1. Экспериментальное решение задач по химии
2. Химия в сельском хозяйстве
3. Химия как инструмент творчества в теории решения изобретательских задач
4. Введение в неорганический синтез
5. Знакомство с работой лаборанта в кабинете химии
6. Вещества и материалы в нашем доме
7. Геохимические циклы в природе: вечное движение химических элементов на Земле

8. Химия – наука экспериментальная. Практикум
9. Я – хозяин своей планеты
10. Информационные ресурсы по химии и работа с ними
11. Химия в быту
12. Химические секреты агронома
13. Роль неорганических веществ в жизнедеятельности организмов

Хотите сохранить материал на будущее? Отправьте себе на почту

в избранное

Только зарегистрированные пользователи могут добавлять в избранное.

Войдите, пожалуйста.

Учебные издания по теме

977
Купить
278
Купить
293
Купить
293
Купить

216
Купить
977
Купить
271
Купить
278
Купить
278
Купить

Оценка разработки

Для оценки работы вам необходимо авторизоваться на сайте

Войти или зарегистрироваться

Ограничение доступа

Для доступа к материалу требуется регистрация на сайте

Войти или зарегистрироваться

Нужна помощь?

Задачи по химии и способы их решения.

8-9 кл. (Олег Габриелян)

Купить офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 254 магазинах. Смотреть на карте

В пособии подробно рассмотрены способы решения задач в объеме школьной программы для 8—9 классов и приведены задачи для самостоятельного решения. Большое внимание уделено решению комбинированных задач.
Данное пособие поможет научиться правильно решать расчетные задачи по химии и будет полезным как для учащихся 8 и 9 классов, так и для преподавателей химии.

Описание

Характеристики

Дрофа

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя.

Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Задачник по химии для 8-9 классов с разбором решений

Плюсы

На мой взгляд, в сборнике встречаются довольно разноплановые задачи, некоторые из них могут показаться даже нестандартными для школьной программы общеобразовательных учреждений.

Книга «Задачи по химии и способы их решения. 8-9 кл.» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Олег Габриелян «Задачи по химии и способы их решения. 8-9 кл.» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

2.9: PSS.9 – Решение проблем модульного анализа

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 69073

Цель обучения

Преобразование одной единицы измерения в другую единицу того же типа.

В разделе 2.2 мы показали несколько примеров того, как заменить исходные единицы другими единицами того же типа, чтобы получить числовое значение, которое легче понять. В этом разделе мы формализуем процесс.

Рассмотрим простой пример: сколько футов в 4 ярдах? Большинство людей почти автоматически ответят, что в 4 ярдах 12 футов. Как вы приняли это решение? Итак, если в 1 ярде 3 фута, а в 4 ярдах, то в 4 ярдах 4 × 3 = 12 футов.

Это, конечно, правильно, но неформально. Давайте формализуем его так, чтобы его можно было применять в более общем виде. Мы знаем, что 1 ярд (ярд) равен 3 футам (футам):

\[1\, ярды = 3\, футы\не число \]

В математике это выражение называется равенством . Правила алгебры гласят, что вы можете изменить (то есть умножить или разделить, добавить или вычесть) равенство (при условии, что вы не делите на ноль), и новое выражение все равно будет равенством. Например, если мы разделим обе части на 2, мы получим:

\[\dfrac{1}{2}\,yd= \dfrac{3}{2}\, ft\nonumber \]

Мы видим, что половина ярда равна 3/2, или один и половина, футы — что-то, что мы также знаем, чтобы быть правдой — так что приведенное выше уравнение по-прежнему является равенством. Возвращаясь к исходному равенству, предположим, что мы делим обе части уравнения на 1 ярд (число и единиц):

\[\dfrac{1\,yd}{1\,yd}= \dfrac{3\ ,ft}{1\,yd}\nonumber \]

Выражение по-прежнему является равенством по правилам алгебры.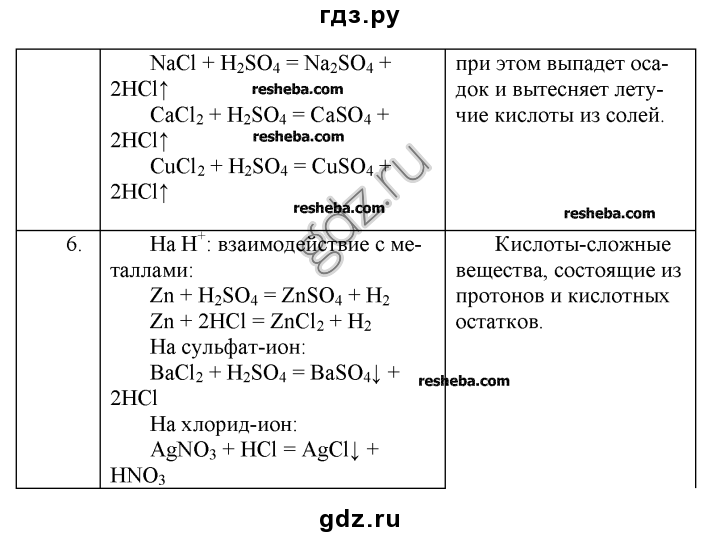 Левая дробь равна 1. У нее одинаковое количество в числителе и знаменателе, поэтому она должна быть равна 1. Величины в числителе и знаменателе сокращаются, оба числа и единица:

\[\dfrac{1\,yd}{1\,yd}= \dfrac{3\,ft}{1\,yd}\nonumber \]

Когда все отменяется в дробь, дробь сводится к 1:

\[1= \dfrac{3\,ft}{1\,yd}\nonumber \]

Коэффициенты преобразования

У нас есть выражение, равное 1.

\[ \dfrac{3\,ft}{1\,yd}=1\nonumber \]

Это странный способ записи 1, но он имеет смысл: 3 фута равны 1 ярду, поэтому величины в числителе и знаменателе это одна и та же величина, просто выраженная в разных единицах.

Выражение

\[\dfrac{3\,ft}{1\,yd}\nonumber \]

называется переводным коэффициентом и используется для формального преобразования единицы количества в другую единицу. (Процесс преобразования единиц таким формальным образом иногда называют анализом измерений или методом маркировки факторов . )

Чтобы увидеть, как это происходит, начнем с исходного количества: 4 ярда.

Теперь давайте умножим это количество на 1. Когда вы умножаете что-либо на 1, вы не меняете значение количества. Вместо того, чтобы умножать только на 1, давайте запишем 1 как:

\[\dfrac{3\,ft}{1\,yd}\nonumber \]

\[4\,yd\times \dfrac{3\,ft}{1\,yd}\nonumber \]

Термин 4 ярда можно рассматривать как 4 ярда/1; то есть его можно рассматривать как дробь с 1 в знаменателе. По сути, мы умножаем дроби. Если в числителе и знаменателе дроби встречается одно и то же, они сокращаются. В этом случае отменяется единица измерения ярдов :

\[4\,yd\times \dfrac{3\,ft}{1\,yd}\nonumber \]

Это все, что мы можем отменить . Теперь умножьте и разделите все числа, чтобы получить окончательный ответ:

\[\dfrac{4\times 3\, ft}{1}= \dfrac{12\,ft}{1}= 12\,ft\nonumber \]

Снова получаем ответ 12 ft , как мы это делали изначально. Но в данном случае мы использовали более формальную процедуру, применимую к множеству задач.

Сколько миллиметров в 14,66 м? Чтобы ответить на этот вопрос, нам нужно построить коэффициент преобразования между миллиметрами и метрами и правильно применить его к исходной величине. Начнем с определения миллиметра, а именно:

\[1\,mm= \dfrac{1}{1000\,m}\nonumber \]

1/1000 означает префикс милли-. Большинству людей удобнее работать без дробей, поэтому мы перепишем это уравнение, подставив 1000 в числитель другой части уравнения:

\[1000\,mm=1\,m\nonnumber \]

Теперь мы строим переводной коэффициент, разделив одну величину на обе части. Но теперь возникает вопрос: на какое количество мы делим? Получается, что у нас есть два варианта, и два варианта дадут нам разные коэффициенты преобразования, оба равны 1:9.0030

\[\dfrac{1000\,мм}{1000\,мм}= \dfrac{1\,m}{1000\,мм} \номер \]

или

\[\dfrac{1000\, мм}{1\,m}= \dfrac{1\,m}{1\,m}\nonumber \]

\[1=\dfrac{1\,m}{1000\,mm}\nonumber \ ]

или

\[\dfrac{1000\,mm}{1\,m}=1\nonnumber \]

Какой коэффициент преобразования мы используем? Ответ основан на том, от какой единицы вы хотите избавиться в исходном количестве . Исходной единицей нашего количества являются метры, которые мы хотим преобразовать в миллиметры. Поскольку предполагается, что исходная единица находится в числителе, чтобы избавиться от нее, мы хотим, чтобы метр был в знаменатель ; потом отменят. Поэтому воспользуемся вторым коэффициентом преобразования. Сокращая единицы измерения и выполняя математические вычисления, мы получаем:

\[14.66m\times \dfrac{1000\,mm}{1\,m}= 14660\,mm\nonumber \]

Обратите внимание, как \(m\) отменяется, оставляя \(мм\), что является единицей измерения.

Способность создавать и применять правильные коэффициенты преобразования — очень мощный математический прием в химии. Вам необходимо освоить эту технику, если вы собираетесь добиться успеха в этом и будущих курсах.

Пример \(\PageIndex{1}\)

Преобразование 35,9 кл в литры.
Перевести 555 морских миль в метры.

Решение

Мы будем использовать тот факт, что 1 кЛ = 1000 л. Из двух коэффициентов преобразования, которые можно определить, будет работать тот, который равен 1000 л/1 кл. Применяя этот коэффициент пересчета, получаем:

\[35.9\, kL\times \dfrac{1000\,L}{1\,kL}= 35 900\, L \nonumber \nonumber \]

Будем использовать тот факт, что 1 нм = 1/1 000 000 000 м, что мы перепишем как 1 000 000 000 нм = 1 м, или 10 9{-7}\,m \nonumber \nonumber \]
На последнем шаге мы выразили ответ в экспоненциальном представлении.
Упражнение \(\PageIndex{1}\)
1. Преобразование 67,08 мкл в литры.
2. Перевести 56,8 м в километры.
Ответить на
6,708 × 10 ⁻⁵ л
Ответ b
5,68 × 10 ⁻² км
Что делать, если у нас есть производная единица, являющаяся произведением более чем одной единицы, например m ² ? Предположим, мы хотим преобразовать квадратные метры в квадратные сантиметры? Важно помнить, что m ² означает m × m, что означает, что у нас есть два метра в нашей производной единице. Это означает, что мы должны включить в число два коэффициента преобразования , по одному на каждую единицу. Например, чтобы перевести 17,6 м ² в квадратные сантиметры, мы выполняем преобразование следующим образом:
9{3}\nonumber \]
Вы должны продемонстрировать себе, что трехметровые единицы действительно сокращаются.
Упражнение \(\PageIndex{2}\)
Сколько кубических миллиметров содержится в 0,0923 м ³ ?
Ответить
9,23 × 10 ⁷ мм ³
Предположим, единица измерения, которую вы хотите преобразовать, находится в знаменателе производной единицы — что тогда? Затем в коэффициенте преобразования единица, которую вы хотите удалить, должна быть в числитель . Это отменит исходную единицу в знаменателе и введет новую единицу в знаменателе. Следующий пример иллюстрирует эту ситуацию.
Пример \(\PageIndex{3}\)
Преобразование 88,4 м/мин в метры/секунду.
Решение
Мы хотим изменить единицу измерения в знаменателе с минут на секунды. Поскольку в 1 минуте 60 секунд (60 секунд = 1 минута), мы создаем коэффициент преобразования, чтобы единица измерения, которую мы хотим удалить, минуты, находилась в числителе: 1 минута/60 секунд. Применить и выполнить математику:
\[\dfrac{88.4m}{min}\times \dfrac{1\,min}{60\,s}= 1.47\dfrac{m}{s}\nonumber \]
Обратите внимание, что 88.4 автоматически входит в числитель. Это потому, что любое число можно рассматривать как числитель дроби, деленной на 1.
Упражнение \(\PageIndex{3}\)
Преобразовать 0,203 м/мин в метры/секунду.
Ответить
0,00338 м/с
или
3,38 × 10 ⁻³ м/с
Иногда возникает необходимость преобразовать одну единицу с одним числовым префиксом в другую единицу с другим числовым префиксом. Как мы обрабатываем эти преобразования? Ну, вы могли бы запомнить коэффициенты преобразования, которые связывают между собой все числовые префиксы. Или вы можете пойти по более простому пути: сначала преобразовать количество в базовую единицу — единицу без числового префикса — используя определение исходного префикса. Затем преобразуйте количество в базовой единице в нужную единицу, используя определение второго префикса. Вы можете выполнить преобразование в два отдельных шага или как один длинный алгебраический шаг. Например, чтобы преобразовать 2,77 кг в миллиграммы: 9{6}\,mg \end{align}\nonumber \]
Вы получите один и тот же ответ в любом случае.
Пример \(\PageIndex{4}\)
Сколько наносекунд составляет 368,09 мкс?
Решение
Вы можете сделать это как одношаговое преобразование из микросекунд в наносекунды или сначала преобразовать в базовую единицу, а затем в конечную желаемую единицу. Здесь мы будем использовать второй метод, показывая два шага в одной строке. Используя определения префиксов микро- и нано-9{5}\,ns\nonumber \]
Упражнение \(\PageIndex{4}\)
Сколько миллилитров содержится в 607,8 кЛ?
Ответить
6,078 × 10 ⁸ мл
При рассмотрении значащих цифр окончательного числового ответа при преобразовании есть один важный случай, когда число не влияет на количество значащих цифр в окончательном ответе: так называемое точное число . Точное число — это число из определенного соотношения, а не измеренное. Например, префикс кило- означает 1000- ровно 1000, не больше и не меньше. Таким образом, при построении коэффициента пересчета:
\[\dfrac{1000\,g}{1\,kg}\number \]
ни 1000, ни 1 не учитываются при рассмотрении значащих цифр. Числа в числителе и знаменателе точно определяются тем, что означает префикс кило-. Другой способ думать об этом состоит в том, что эти числа можно рассматривать как имеющие бесконечное количество значащих цифр, например:
\[\dfrac{1000.0000000000 \dots \,g}{1.0000000000 \ldots \,kg}\nonumber \]
Другие числа в расчете будут определять количество значащих цифр в окончательном ответе.
Пример \(\PageIndex{5}\)
Прямоугольный участок в саду имеет размеры 36,7 см на 128,8 см. Какова площадь садового участка в квадратных метрах? Выразите ответ в нужном количестве значащих цифр.
Решение
Площадь определяется как произведение двух измерений, которые затем мы должны преобразовать в квадратные метры и выразить наш окончательный ответ правильным числом значащих цифр, которых в данном случае будет три. 9{2}\nonumber \]
Значения 1 и 100 в коэффициентах преобразования не влияют на определение значащих цифр, так как это точные числа, определяемые префиксом санти-.
Упражнение \(\PageIndex{5}\)
Каков объем блока в кубических метрах с размерами 2,1 см × 34,0 см × 118 см?
Ответить
0,0084 м ³
Химия повсюду: планер Гимли
23 июля 1983 года самолету Air Canada Boeing 767 пришлось совершить аварийную посадку в аэропорту промышленного парка Гимли в Гимли, Манитоба, поскольку во время полета у него неожиданно закончилось топливо. Людей в ходе аварийной посадки не было, только легкие травмы, частично связанные с эвакуацией корабля после приземления. До конца срока службы (самолет был списан в 2008 г.) самолет получил прозвище «планер Гимли».
Планер Гимли — это Боинг 767, у которого закончилось топливо, и он направился в безопасное место в аэропорту Гимли. У самолета закончилось топливо из-за путаницы в единицах измерения количества топлива. Источник: Фото предоставлено Уиллом Ф. (CC BY-SA 2.5; Aero Icarus).
Боинг 767 вылетел из Монреаля в Оттаву и в конечном итоге направился в Эдмонтон, Канада. Примерно в середине полета все двигатели самолета начали глохнуть из-за нехватки топлива. Когда последний двигатель отключился, все электричество (которое вырабатывалось двигателями) было потеряно; самолет стал, по сути, бессильным планером. Капитан Роберт Пирсон был опытным пилотом-планеристом, хотя он никогда не летал на планере размером с Боинг-767. Первый офицер Морис Куинтал быстро определил, что самолет не сможет долететь до Виннипега, следующего крупного аэропорта. Он предложил свою старую базу Королевских ВВС на станции Гимли, одна из взлетно-посадочных полос которой все еще использовалась как общественный аэропорт. Благодаря усилиям пилотов и летного экипажа им удалось благополучно посадить самолет на землю (хотя и с пристегнутым шасси) и благополучно покинуть всех пассажиров.
Что случилось? В то время Канада переходила от старой английской системы к метрической системе. Боинг 767 был первым самолетом, датчики которого были откалиброваны в метрической системе единиц (литры и килограммы), а не в английской системе единиц (галлоны и фунты). Таким образом, когда указатель уровня топлива показывал 22 300, он означал килограммы, но наземная команда по ошибке заправила самолет 22 300 фунтов топлива. В итоге это составило чуть меньше половины топлива, необходимого для поездки, в результате чего двигатели остановились примерно на полпути к Оттаве. Сообразительность и экстраординарное мастерство спасли жизни 61 пассажиру и 8 членам экипажа — инцидента, которого бы не произошло, если бы люди следили за своими подразделениями.
Ключевые выводы
Единицы могут быть преобразованы в другие единицы с использованием соответствующих коэффициентов преобразования.
Коэффициенты пересчета строятся из равенств, связывающих две разные единицы.
Преобразования могут быть одноэтапными или многоэтапными.
Преобразование единиц измерения — это мощная математическая техника в химии, которую необходимо освоить.
Точные числа не влияют на определение значащих цифр.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Показать страницу TOC
№ на стр.
Теги
На этой странице нет тегов.
Задачи и решение задач в химическом образовании
Содержание страницы
Задачи и решение задач в химическом образовании: анализ данных, поиск закономерностей и выводы
Под редакцией Georgios Tsaparlis , Университет Иоаннины , Греция
Счет Содержание:
ГЛАВА 1. ВВЕДЕНИЕ 􏰂- бесплатный образец на https://pubs.rsc.org/en/content/ebook/978-1-83916-218-3]
1.1 Проблемы и решение проблем
1.2 Типы и виды проблем
1.3 Новичок по сравнению с экспертами-решателями проблем/эвристикой решения проблем
1.4 Chemistry Problems
1.5 The Present Volume
Part I: General Issues in Problem Solving in Chemistry Education
Chapter 2. Qualitative Reasoning in Problem-solving in Chemistry
Vicente Talanquer
2.1 Introduction
2. 2 Качественное обоснование
2.3 Качественное химическое обоснование
2.4 Трудности в рассуждении
2.5 Образовательные последствия
2.6 Conclusions
Chapter 3. Scaffolding Metacognition and Resource Activation During Problem Solving: A Continuum Perspective
Nicole Graulich, Axel Langner, Kimberly Vo and Elizabeth Yuriev
3.1 Introduction
3.2 Case Studies of Two Леса
3.3 Обсуждение
3.4 Выводы
Глава 4. Деконструкция процесса решения проблем: ниже назначенных баллов и за пределами традиционной оценки
Ozcan Gulacar, Charlie Cox и Herb Fynewever
4.1 Введение
4.2 Обоснование и теоретические рамки
4.3. углубленный анализ задач учащихся: COSINE (система кодирования для исследования подзадач и сетей)
4.5 Изучение успехов и неудач учащихся с помощью кодов и формул COSINE
4. 6 Косинус-коды и успеваемость учащихся по курсу химии
4.7 Коды и метапознание
4.8 Выводы
и ее ограничения
Георгиос Цапарлис
5.1. Введение
5.2. Требования к умственной задаче и ее логическая структура0010
5.4 Проверка достоверности модели для задач органического синтеза с более высоким спросом M
5.5 Выводы и дальнейшие вопросы
Формализм толкания
Гаутам Бхаттачарья
6.1 Введение
6.2 MR EPF: уникальная форма рассуждения
6.3 Подходы учащихся к изучению механизмов EPF
6.4 Оценка
6.5 Заключительные мысли
Глава 7. Навыки синтеза каркасов в органической химии
Элисон Б. Флинн
7.1. Внедрение
7.2 Фаза 1 –Oirtation: Ascient: Ascient: Ascient: Ascient: Ascient. 2 – Исследование: рассмотрение вариантов
7. 4 Этап 3 – Исследование: предложение синтеза (выбор возможных шагов)
7.5 Этап 4 – Проверка: выявление конкурирующих реакций
7.6 Выводы
Глава 8. Решение проблем с использованием ЯМР и ИК -спектроскопии для структурной характеристики при органической химии
Меган С. Коннор и имбирь В. Шульц
8.1. Роль Спектропный анализ в Органе Синтез
8.1.
8.3 Инновации в обучении
8.4. Значение
8.5. Выводы 194
0024
Jon-Marc G. Rodriguez, Sven J. Philips, Nicholas P. Hux и Marcy H. Towns
9,1 Введение
9.2 Теоретические перспективы
9,3 Методы
9.4 Находящие
9.5 9.5.
Часть III: Решение задач по химии в особых условиях
Глава 10. Решение задач в учебной лаборатории по химии: происходит ли такое?
Ян Хокинс, Вичуда К. Хантер, Майкл Дж. Сэнгер и
Эми Дж. Фелпс
10.1 Введение
10.2
10.6 Последствия для решения задач в лаборатории
10.7 Выводы
Глава 11. Задачи и решение задач в свете контекстно-ориентированной химии
Karolina Broman
11.1 Проблемы и решение проблем
11.2 Подходы на основе контекста. Восприятие учащимися проблем, связанных с контекстом
11.6 Стратегии решения проблем учащимися
11.7 Проблемы, связанные с контекстом – как нам двигаться дальше?
Глава 12. Использование группового обучения для содействия решению проблем посредством активного обучения
Натали Дж. Капел, Лаура М. Хэнкок, Хлоя Хоу, Грэм Р. Джонс, Тесс Р. Филлипс и Даниэла Плана
12.1 Введение
12.2 Групповое обучение
12.3 Обзор группового обучения в области физических и математических наук
12. 4 Сравнение командного обучения и других подходов к совместному обучению
12.5 Групповое обучение по химии в Килском университете
12.6 Примеры из практики
12.7 Заключение
Часть IV. Новые технологии в решении задач по химии
Джек Д. Полифка, Джон Ю. Балют и Томас А. Холм
13.1 Введение
13.2 Методы
13.3 Результаты
13.4 Limitations, Conclusions and Teaching Implications
Chapter 14. An Educational Software for Supporting Students’ Learning of IR Spectral Interpretation
Maria Limniou, Nikos Papadopoulos, Dimitris Gavril, Aikaterini Touni and Markella Chatziapostolidou
14.1 Introduction
14.2 Программное обеспечение для интерпретации ИК-спектров
14.3 Результаты
14.4 Обсуждение и заключение
Глава 15. Изучение проблем с химии с вычислительными

инструментами квантовой химии в учебной программе по химии бакалавриата
Майкл П. Сигалас
15.1 Введение
15.2 Знание к квантовой хитюме из высшего второго курса.
15.2. и решение задач в программе бакалавриата по химии
15.4 Заключение
Часть V: Новые перспективы решения задач в химическом образовании
Глава 16. Методологические и эпистемологические проблемы в научном образовании. Исследование решений проблем: линейные и нелинейные парадигмы
Dimitrios Stamovlasis и Julie Vaiopoulou
16.1 Введение
16.2. Подходы к решению проблем
16.4 Поиск и разработка теорий: следующая фаза
16.5 Решение проблем и концептуальное понимание
16.6 Методологические проблемы
16,7 Эпистемологические проблемы: за пределами линейного режима
16,8 Теория катастроф в решении проблем
16,9 Нелинейная динамика и сложность в решении проблем
16.10 Заключительные замечания
9
.