Решение задач по механике: Примеры решения задач теоретической механики

Расчет траектории, скорости, ускорения и пути точки

Пример решения задачи по определению траектории равноускоренного движения точки, заданного уравнениями, скорости и ускорения в некоторые моменты времени, координаты начального положения точки, а также путь, пройденный точкой за время t.

Задача

Движение точки A задано уравнениями:

где x и y – в см, а t – в с. Определить траекторию движения точки, скорость и ускорение в моменты времени t₀=0 с, t₁=1 с и t₂=5 с, а также путь, пройденный точкой за 5 с.

Другие примеры решений >
Помощь с решением задач >

Решение

Расчет траектории

Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:

3x=6t²+6
-4y=-6t²-4
————
3x-4y=2

Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.

5).

Наш видеоурок по теме:

Для того, чтобы определить координаты начального положения точки A₀, подставим в заданные уравнения значения t₀=0; из первого уравнения получим x₀=2 см, из второго y₀=1 см. При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A₀ (2; 1).

Рисунок 1.5

Расчет скорости

Определяем скорость движения точки, найдя сначала ее проекции на оси координат:

тогда

При t₀=0с скорость точки v₀=0, при t₁=1с – v₁=5 см/с, при t₂=5с – v₂=25см/с.

Расчет ускорения

Определяем ускорение точки. Его проекции на оси координат:

Проекции ускорения не зависят от времени движения,

т. е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.

С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:

Определение пути

Определяем путь, пройденный точкой за первые 5с движения. Выразим путь как функцию времени:

Проинтегрируем последнее выражение:

Если t=t₀=0, то C=s₀; в данном случае s₀=0, поэтому s=2,5t². Находим, что за 5с точка проходит расстояние

s|_t=5с=2,5∙5²=62,5 см.

Другие примеры решения задач >>

Заказать решение задач по теоретической механике в Минске недорого, цена от 5 руб.

Оплатить выбранные товары вы можете следующим способом:

Зарегистрируйтесь. Перейдите в личный кабинет в раздел “Баланс” -> “Пополнить баланс”.

Введите сумму для пополнения и нажмите “Пополнить”.

После нажатия кнопки «Пополнить» вы перейдете на специальную защищенную платежную страницу процессинговой системы bePaid

На платежной странице будет указан номер заказа и сумма платежа. Для оплаты вам необходимо ввести свои карточные данные и подтвердить платеж, нажав кнопку «Оплатить».

Если ваша карта поддерживает технологию 3-D Secure, системой ваш будет предложено пройти стандартную одноминутную процедуру проверки владельца карты на странице вашего банка (банка, который выдал вашу карту).

После оплаты наш менеджер свяжется с вами для уточнения деталей по доставке.

Обращаем ваше внимание, что после проведения платежа на указанный вами электронный адрес придет подтверждение оплаты. Просим вас сохранять данные оплат.

Мы принимаем платежи по следующим банковским картам: Visa, Visa Electron, MasterCard, Maestro, Белкарт.

Платежи по банковским картам осуществляются через систему электронных платежей bePaid. Платежная страница системы bePaid отвечает всем требованиям безопасности передачи данных (PCI DSS Level 1). Все конфиденциальные данные хранятся в зашифрованном виде и максимально устойчивы к взлому. Доступ к авторизационным страницам осуществляется с использованием протокола, обеспечивающего безопасную передачу данных в Интернетe (SSL/TLS).

Возврат денежных средств осуществляется на карту, с которой ранее была произведена оплата. Срок поступления денежных средств на карту от 3 до 30 дней с момента осуществления возврата Продавцом.

Решение задач по 📝 теоретической механике в Киеве

Теоретическая механика для студентов физико-математического факультета входит в список основных предметов. В большинстве случаев, студентам приходиться изучать множество дисциплин, из них половина дается очень тяжело. Такое происходит из-за того, что для подготовки одного домашнего задания уходит достаточно времени.

И тогда или все изучается поверхностно, или вы засиживаетесь над учебниками до полуночи. Знакома такая ситуация? Студенты не понаслышке знают, что такое бессонные ночи.

Если вы учите теоретическую механику…

Каким бы интересным не был период студенчества, а всегда есть такие задания, над которыми приходиться думать часами. Конечно же, в теормехе множество аксиом и законов, которые нужно знать. Но иногда для задач недостаточно изученного, ведь пройденный материал еще не систематизирован. А значит, нужна постоянная практика. Решение задач по теоретической механике в Киеве оценило уже множество студентов. К тому же, консультанты помогли учащимся разобраться в сложном материале. Это объясняет, почему даже те, у которых хорошие отметки, иногда обращаются за помощью к специалистам.

Ну а что делать, если вы пропустили или не поняли какую-то тему, а по ней нужно сделать задание? С сервисом «Все Сдал!» у вас появляется возможность наверстать упущенное и прийти на пары с подготовленной домашней работой. Более того, вы не рискуете ни денежными средствами, ни временем.

В чем преимущества обращения к специалистам?

Дело в том, что в институте задают много заданий. Возможно, таким образом, преподаватели стараются уместить всю программу в заданные сроки. Подразумевается, что человек впоследствии практики будет развиваться в своей профессии, а также научится правильно распределять время на выполнение заданий.

Но на самом деле, получается так, что и с домашними делами справиться надо, и с учебными, и позволить себе побыть настоящим студентом. Решение задач по теоретической механике в Киеве на сервисе “Все Сдал!” предоставляют специалисты своего профиля. Наши работники окончили институт с высокими отметками.  Если вы мечтаете про достойные оценки и успешно сдать задания, обращайтесь!  Сотрудники сервиса, овладевшие предметом от «А» до «Я», могут поделиться с вами своим опытом. Причем стоимость решения низкая, минимально – 15 грн. Все потому, что мы работаем без посредников.

Решение задач по теоретической механике в Киеве может быть выполнено по:

• статике;
• кинематике;
• динамике.

Как оставить заявку на решение?

Сервис «Все сдал!» создан для студентов, которым нужно уделить время не только учебе. Каждый из нас, естественно, за время получения профессии, сдавал множество контрольных, экзаменов и самостоятельных. Поэтому понимание важности и срочности выполнения задания также учитывается работниками ресурса. Обратите внимание, что система оплаты позволяет не переживать о своих деньгах. Любая сумма, внесенная за работу, будет сберегаться на счету до полной проверки задания преподавателем.

РЕШЕНИЕ ЗАДАЧ МЕХАНИКИ – Энциклопедия по машиностроению XXL

Влияние предыстории движения на силу /, действующую на частицу, существенно осложняет решение задач механики дисперс-  [c.178]

Решать задачи статики можно или путем соответствующих геометрических построений (геометрический и графический методы), или с помощью численных расчетов (аналитический метод). В курсе будет главным образом применяться аналитический метод, однако следует иметь в виду, что наглядные геометрические построения играют при решении задач механики чрезвычайно важную роль.  

[c.11]

Правильное определение направлений реакций связей играет при решении задач механики очень важную роль. Рассмотрим по-  [c.15]

Для решения задач механики удобнее задавать силу ее проекциями F , Fy, F на координатные оси. Зная эти проекции, можно определить модуль силы и углы, которые она образует с координатными осями, по формулам  [c.22]

Введенное в 3 понятие о связях охватывает не все их виды. Поскольку рассматриваемые ниже методы решения задач механики применимы вообще к системам не с любыми связями, рассмотрим вопрос о связях и об их классификации несколько подробнее.  

[c.357]

При решении задач механики требуется учитывать основные параметры приводов, их влияние на динамику управляемых ими механизмов. Проблема разработки приводов и систем управления роботами, манипуляторами, шагающими и другими машинами является одной из важнейших в создании машин подобного типа. При решении этих проблем возникают вопросы создания систем с большой надежностью, оптимальными габаритами, малой инерционностью, обладающих широкими диапазонами скоростей.  [c.12]

При небольших скоростях скольжения сила трения скольжения Rf очень близка к шах Rp, кроме того, / почти не изменяется с изменением скорости скольжения. Поэтому при решении задач механики обычно используют формулу (1.42).  [c.53]

При решении задач механики используют чаще последние формулы.  [c.71]

При решении задач механики часто приходится суммировать векторы. Алгоритм определения величины и направления вектора I суммы двух других векторов и реализуется операторной функцией  [c.49]

Нам представлялось необходимым дать читателям понятие о разнообразных способах решения задач механики. Поэтому, в частности в кинематике, мы рассматриваем, впервые в учебнике теоретической механики, некоторые приложения комплексного представления векторных функций на плоскости, а также кратко останавливаемся на вопросах синтеза механизмов согласно П. Л. Чебышеву.  [c.13]

Наконец, заметим, что третий закон Ньютона позволяет отличить реальные силы, приложенные к точке, от фиктивных, которые могут появиться при математическом решении задач механики, например при разложении действующей силы на две составляющие.  [c.232]

Возникает обратная проблема не являются ли некоторые силовые поля, с которыми приходится встречаться при решении задач механики, результатом  [c.443]

Найдем моменты инерции некоторых тел простейшей формы, встречающихся при решении задач механики.  [c.59]

Теоремы о движении центра инерции, об изменении количества движения системы и об изменении кинетического момента системы позволяют исключить из решения задач механики внутренние силы. Этим иногда удается упростить математическое решение механической задачи, однако одновременно с этим теряется возможность глубже проникнуть во внутренние физические связи между составными частями системы, утрачивается возможность иметь более глубокие и полные представления о том физическом явлении, которое составляет смысл задачи механики. Этот недостаток отсутствует в теореме об изменении кинетической энергии.  [c.93]

Мы ограничимся этими далеко ие полными общими замечаниями о применении теорем динамики. В следующей части курса рассматриваются более совершенные методы решения задач механики.  [c.106]

Мы не останавливаемся на этих вопросах, так как канонические уравнения с избыточными координатами применяются при решении задач механики сравнительно редко.  [c.148]

Книга написана на базе специальных курсов, читаемых авторами в течение ряда лет студентам факультета прикладной математики Московского института электронного машиностроения, специализирующимся в области применения ЭВМ для решения инженерных задач, в частности для решения задач механики деформируемого твердого тела.  [c.3]

Отметим, что матрица жесткости имеет структуру, близкую к ленточной, т. е. все ее ненулевые элементы сосредоточены вблизи главной диагонали. Именно это свойство обеспечило широкое распространение описанного выше метода для решения задач механики сплошных сред, так как нули матрицы [/С] хранить в памяти не нужно, а при решении системы (3.74) матрицу [/ J можно обрабатывать блоками, вызывая их поочередно из внешней памяти машины следовательно, при помощи ЭВМ даже со сравнительно небольшой оперативной памятью можно добиться высокой точности расчетов.  [c.143]

Литература, в том числе учебная, в которой излагаются приближенные методы решения экстремальных задач, в настоящее время насчитывает десятки книг л монографий, поэтому здесь будет приведено описание только некоторых методов, фактически применяемых для решения задач механики деформируемого твердого тела используются материалы работ [30], [31], [36—38].  [c.340]

При решении задач механики, связанных с вращательным движением тел, их формой и размерами пренебрегать нельзя. В таких случаях тела рассматриваются как абсолютно твердые, их форма и размеры принимаются неизменяемыми при любых воздействиях со стороны других тел. Иначе говоря, в абсолютно твердых телах расстояния между двумя любыми точками остаются постоянными.  [c.7]

Численные методы решения задач механики деформируемого твердого тела успешно используются как в научных исследованиях, так и в инженерных расчетах в связи с широким развитием быстродействующих ЭВМ. С их помощью можно проводить  [c.104]

Таким образом, принцип Гамильтона-Остроградско] о (42. Ij принимает конкретную формулу, пригодную для решения задач механики разрушения ”  [c.326]

Ряд важнейших исследований по аналитическим методам решения задач механики принадлежит знаменитому русскому математику и механику М. В. Остроградскому (1801 —1861). Он установил очень важный вариационный принцип динамики — принцип наименьшего действия, позволяющий сводить изучение движения механических систем к некоторой экстремальной задаче. Этот принцип называется принципом Остроградского — Гамильтона, так как независимо от Остроградского и в несколько менее общем виде он одновременно также был дан английским ученым Гамильтоном (1805— 1865). М. В. Остроградский решил также много частных механических задач в области гидростатики, гидродинамики, теории упругости, теории притяжения и баллистики.  [c.16]

До сих пор мы рассматривали движение точки по отношению к одной заданной системе отсчета, которую считали условно неподвижной. Однако в ряде случаев при решении задач механики оказывается удобным рассматривать движение точки одновременно по отношению к двум системам отсчета, из которых одна принимается за неподвижную, а другая определенным образом движется по отношению к первой.  [c.309]

При решении задач механики весьма существенно обходиться без определения реакций связей или определять только те реакции, которые требуются в задаче. Другой, не менее важной  [c. 337]

Функции (19), (20) есть общее решение задачи механики при произвольных а,. Из (18)  [c.285]

Механика разрушения как наука о равновесии и распространении трещин в деформируемых телах бурно развивается под влиянием все более глубокого проникновения в ее арсеналы численных методов решения задач механики, с одной стропы, и привлечения результатов, полученных в физике твердого тела,— с другой. Здесь актуальными являются проблемы зарождения и развития усталостных трещин, долговечность конструкций в агрессивных средах, распространение трещин в композитных материалах и др.  [c.389]

В общем случае положение и форма межфазных границ в многофазных системах не могут быть определены заранее. Этим гетеро-фазные системы принципиально отличаются от гомогенных, для которых границы области протекания процесса, как правило, бывают известны (твердые ограничивающие поверхности), и на них задаются граничные условия — условия однозначности математического описания процесса. В многофазных (в частности, в двухфазных газожидкостных) системах эволюция межфазных границ могла бы быть определена только в процессе рещения задачи. Это означает, что в исходном математическом описании условия совместности могут быть записаны для границ раздела неизвестной формы. В настоящее время имеются лишь единичные примеры численного решения задач механики газожидкостных систем в такой строгой постановке, когда форма межфазной границы не задается, а определяется в процессе решения. При этом речь идет о достаточно простых задачах, например о росте одиночного парового пузырька на твердой обогреваемой поверхности в первоначально неподвижной жидкости.  [c.16]

При решении задач механики реагирующих газов обычно используют р — V — 1 уравнений неразрывности для компонентов, V уравнений неразрывности для элементов и уравнение неразрывности для смеси газов. Часто для расчета диффузионных потоков оказывается удобным использовать соотношения Стефана—Максвелла (3.6.22). В этом случае ] представляют собой дополнительные искомые  [c.183]

Решение задач механики деформируемого тела для областей с разрезами (трещинами) связано с известными математическими трудностями вследствие наличия особых (сингулярных) точек. Большинство этих задач эффективно может быть решено только с применением ЭВМ. Среди вычислительных методов в задачах механики разрушения в настоящее время наиболее широкое распространение получил метод конечных элементов (МКЭ). Произошло это вследствие универсальности метода, хорошо разработанной теории и наличия значительного количества вычислительных программ, реализующих МКЭ. Немаловажным обстоятельством является то, что конечный элемент представляет собой объект хорошо понятный инженеру, что особенно полезно при моделировании таких явлений, как развитие трещины.  [c.82]

Не безынтересно дополнительно отметить, что А. Н. Боголюбов (см. предыдущую сноску) пишет Развитие механики в Западной Европе в течение 1000 лет происходит двумя различными путями, которые почти не пересекаются. .. Такое положение, если относить его к современным условиям, по-видимому, должно свидетельствовать о наличии принципиально различных подходов к решению задач механики жидкости (см. рис. 1-12), с одной стороны, у инженеров-ученых, формирующих технические науки,  [c.31]

Другая форма обобщенного закона Гука, В качестве основных неизвестных при решении задач механики деформируемого твердого тела можно  [c.172]

При подготовке четвертого издания авторы уточнили некоторые положения, внесли дополнения, продиктованные динакйчным развитием учения о прочности и новыми тенденциями в методике преподавания в высшей школе. В частности, авторы сочли необходимым включить параграф о малоцикловой усталости, имея в виду практическую важность этой характеристики материалов при решении задач механики деформируемого твердого тела. Авторам представлялось важным в курсе сопротивления материалов осветить современные проблемы прочности, которые могут заинтересовать учащуюся молодежь, приобщающуюся к научной работе со 2—3-го года обучения в институте.  [c.4]

С. В. Ковалевская (1850—1891), решившая одну из труднейших задач динамики твердого тела А. М. Ляпунов (1857—1918), который дал строгую постановку одной из фундаментальных задач механики и всего естествознания — задачи об устойчивости равновесия и движения.и разработал наиболее общие методы ее решения И. В. Ме-ш,ерский (18Й—1935), внесший большой вклад в решение задач механики тел переменной массы К. Э. Циолковский (1857—1935), автор ряда фундаментальных исследований по теории реактивного движения А. Н. Крылов (1863—1945), разработавший теорию корабля и много внесший в развитие теории гироскопа и гироскопических приборов.  [c.8]

Методы решения задач механики, которые до сих пор рассматривались, основываются на уравнениях, вытекающих или непосредственно и.з законов Ньютона, или же из общих теорем, являющихся следствием этих законов. Однако этот путь не является единственным. Оказывается, что уравнейия движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Да.шмбера.  [c.344]

Развитие кинематики в XVIII в. связано с работами Леонарда Эйлера (1707—1783). Эйлер заложил основы кинематики твердого тела, создал аналитические методы решения задач механики.  [c.154]

Перейдем к изучению наиболее общих методов решения задач механики. Эти методы основываются на общем принципе — принципе возможных перемеицений, или принципе Лагранжа, так как Ж. Лагранж первый придал этому принципу законченную форму и положил его в основу статики. Обч единнв этот принцип с принципом Даламбера, Ж. Лагранж получил общее уравнение динамики, из которого вытекают основные дифференциальные уравнения движения материальной системы и основные теоремы динамики ).  [c.107]

Общим уравненпем динамики можно также пользоваться для непосредственного решения задач механики.  [c.120]

Влияние других факторов на величину коэф]5ициента трения мало и при решении задач механики не рассматривается. Считается, правда, что с увеличением скорости скольжения одного тела по отношению к другому величина коэффициента трения несколько уменьшается. Исключением являются случаи, когда одним из тел является тело из резины или кожи. Но во всех случаях при решении учебных задач механики зависимость коэффициента трения от каких-либо факторов при движении тела не учитывается.  [c.35]

Что понимается под механической системой Какие две инерционные характеристики тела исполыуются при решении -задач механики  [c.183]

Приступая к решению задач механики, необходимо прежде всего рассмотреть методы описания движений. Раздел механики, в котором рассматриваются только методы описания движений, но не ставятся вопросы о законах движения, называется кинематикой. Законы дви-же1шя и их применение к отдельным конкретным задачам изучает динамика. Динамика в виде частного случая включает в себя статику, изучающую условия, при которых тела остаются в покое. В зависимости от свойств тел, движение которых изучается, характера изучаемых движений и содержания вопросов, на которые должен быть получен ответ, механика делится на механику точки, механику твердых (недеформируемых) тел и механику упругих тел (последняя включает в себя механику жидкостей и газов).  [c.12]

В последнее время все более широкое распространение в теории упругости получает метод граничных интегральных уравнений (МГИУ). Эффективность метода позволяет применить его и для решения задач механики разрушения. Сущность этого метода заключается в сведении соответствующей задачи теории упругости к решению интегрального уравнения, а основное его преимущество по сравнению с другими численными методами состоит в том, что он понижает размерность задачи. Остановимся вкратце на выводе интегральных уравнений основных пространственных задач теории упругости и методах их решения [231]. Пусть S — некоторая достаточно гладкая замкнутая поверхность, а и D — области, расположенные внутри и вне ее ( ) = )+ + ) ). Если однородное изотропное упругое тело занимает конечный объем D , то задача называется внутренней. Если же тело занимает бесконечный объем D , то задача называется внешней. Требуется найти регулярное решение уравнения статики упругого тела (2.2)  [c.100]

Использование аналитико-машинного метода для решения задач механики весьма перспективно. При этом разрабатывается и формулируется алгоритм решения—рациональная последовательность арифметических и логических операций, которые необходимо выполнить, руководствуясь исходными данными и результатами промежуточных вычислений.  [c.488]

---

Как решать задачи по механике … ??

Поскольку все мы знаем, насколько важна механика в физике, вот еще несколько советов по дальнейшему решению проблем. Хотя в механике требуется интенсивная практика, важно также знать, как решать проблемы….

Вот несколько способов решения проблем в механике…

В САМОЛЕТЕ:

1. Проблемы, связанные с движением в двумерной плоскости : В задачах такого типа выполните следующие действия:

и. Самый первый необходимый шаг – выбрать систему координат и разложить вектор скорости на отдельные компоненты x и y.

ii. Затем найдите соответствующее ускорение в каждом направлении и решите в соответствии с уравнением прямолинейного движения.

iii. Теперь, если вы обнаружите ускорение только в вертикальном направлении, следуйте методам решения задач с постоянным ускорением для анализа вертикального движения. Движение по x и y имеет одинаковое время полета t.

iv. Если есть какая-либо проблема, связанная с траекторией, найдите движения в направлении x и y относительно времени из предыдущей точки и из одного уравнения, найдите значение t и подставьте его в другое уравнение, чтобы найти уравнение траектория.

2. Проблемы, связанные с Движение на трехмерной плоскости : i . Чтобы решить такие проблемы, просто выберите одну систему координат и разрешите скорость в направлениях x, y и z.

ii. Ускорение в каждом направлении может быть определено и решено в соответствии с уравнением прямолинейного движения.

3. Задачи, связанные с равномерным круговым движением: i . Чтобы подойти к любой проблеме, первое, что нужно сделать, – это нарисовать аккуратную схему системы.

ii. Затем рассмотрите все силы и их происхождение на каждом объекте. Узнайте силы, действующие на каждый объект. Запишите все контактные силы везде, где есть контакт.

iii. Рассчитайте центростремительную силу, необходимую для кругового движения.

Скорость определяется соответственно центростремительной силой = mv² / R.

Решение задач в механике Ньютона

Оллвуд К. М. (1984), «Процессы обнаружения ошибок при решении статистических задач», Когнитивная наука 8: 413–437.

Google ученый

Банди, А., Берд, Л., Люгер, Г., Меллиш, К. и Палмер, М. (1979). «Решение проблем механики с использованием метауровневого вывода», доклад, представленный на 6-й конференции Совместной международной конференции по искусственному интеллекту, Токио, Япония.

Чи М., Фельтович П. и Глейзер Р. (1981). «Категоризация и представление физических проблем экспертами и новичками», Cognitive Science 5: 121–153.

Google ученый

Файкс Р.Э. и Нильссон Н. Дж. (1971). «STRIPS: новый подход к применению доказательства теорем для решения задач», Искусственный интеллект 2: 189–209.

Google ученый

Хинсли Д., Хейс Дж. И Саймон Х. (1977). «Когнитивные процессы в понимании», Джаст и Карпентер (ред. ), Когнитивные процессы в понимании . Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.

Google ученый

Ларкин Дж.(1979). «Приобретение навыков решения физических задач», C.I.P. № 409, факультет психологии, Университет Карнеги-Меллон, Питтсбург.

Google ученый

Ларкин, Дж. (1979). «Модели стратегии решения физических задач», доклад, представленный на ежегодном собрании Американской ассоциации исследований в области образования, Сан-Франциско, Калифорния.

Ларкин Дж. (1980). «Познание изучения физики», Документ по прикладной когнитивной психологии №1, факультет психологии Университета Карнеги-Меллон, Питтсбург.

Google ученый

Ларкин Дж. Макдермотт Дж., Саймон Д. и Саймон Х. (1979). «Модели конкуренции при решении физических задач», C.I.P. № 408, факультет психологии, Университет Карнеги-Меллон, Питтсбург.

Google ученый

Люгер Г. (1977) «Использование протоколов и представление семантической информации в задачах шкива», Отчет DAI Research No.36, факультет искусственного интеллекта, Эдинбургский университет, Эдинбург.

Google ученый

Ньюэлл А. и Саймон Х. А. (1972). Решение человеческих проблем . Энглвуд Клиффс, штат Нью-Джерси: Прентис-Холл.

Google ученый

Новак Г. (1977). «Представление знаний в программе для решения физических задач», доклад, представленный на 5-й конференции Международной совместной конференции по искусственному интеллекту, Массачусетс.

Пейдж Г. и Саймон Х. (1974). «Когнитивные процессы при решении задач по алгебре», в Б. Кляйнмутц (ред.), Решение задач: исследования, метод и теория . Нью-Йорк: Кригер.

Google ученый

Скэнлон, Э. , Хокридж, К. и Эверц, Р. (1983a). «Моделирование решения физических задач: модели производственных правил для двух задач», Технический отчет Группы CAL Открытого университета № 39, Милтон Кейнс.

Скэнлон, Э., Хокридж, К. и О’Ши, Т. (1983b). «Моделирование решения физических задач: сценарии и производственные правила», Технический отчет № 36 Группы CAL Открытого университета, Милтон Кейнс.

Обход решения обратных задач в механике с помощью глубокого обучения: применение к визуализации упругости

Способность определять упругую неоднородность и нелинейность по отклику образца важна в таких областях, как неразрушающий контроль и оценка, а в последнее время , в медицинской визуализации.В медицинской визуализации традиционные методы визуализации, такие как ультразвук, оптическая когерентная томография (ОКТ) и магнитно-резонансная томография (МРТ), могут использоваться для измерения данных смещения в ткани по мере ее деформации [1], [2], [3], [4] ]. Эти данные затем используются вместе с законами механики для вывода пространственного распределения упругих свойств [5], [6], [7], [8].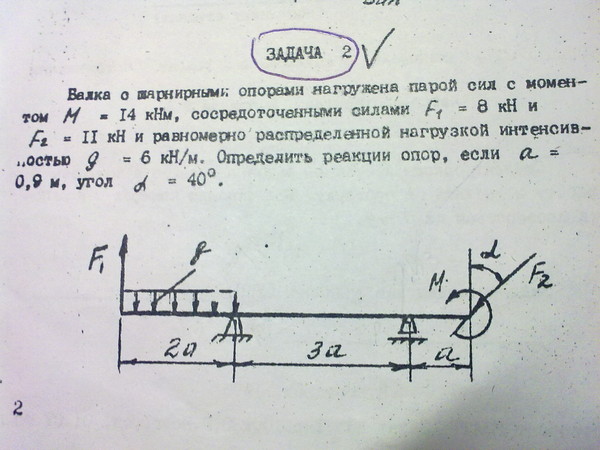 После того, как эти свойства определены, они исследуются, чтобы определить особенности, которые могут быть полезны при постановке диагноза. Например, в контексте рака груди недавние результаты показали, что степень неоднородности сдвига или модуля Юнга и степень нелинейной эластической реакции связаны со злокачественным диагнозом [9], [10], [11] .В частности, злокачественные новообразования имеют тенденцию к пространственно неоднородному распределению модуля Юнга, а также имеют тенденцию к более быстрому затвердеванию с увеличением общей деформации, чем их доброкачественные аналоги.

Процесс определения того, является ли данный образец упруго неоднородным или имеет значительную упругую нелинейность, включает следующие этапы:

1.

Получите изображение образца с помощью обычного фазочувствительного метода визуализации, такого как ультразвук, МРТ или ОКТ, как деформируется.

2.

Используйте кросс-корреляцию изображений или метод отслеживания фазы для определения смещений внутри ткани.

3.

Используйте данные о смещении и физические законы механики, чтобы вывести пространственное распределение механических свойств образца путем решения обратной задачи.

4.

Определите количественно значение целевой характеристики в пределах этих распределений (неоднородность / нелинейность).

5.

Используйте эту функцию, чтобы классифицировать образец (например, злокачественный или доброкачественный).

Этот рабочий процесс, который представляет текущее состояние дел, показан на рис. 1. Среди этапов рабочего процесса этап решения обратной задачи упругости для определения пространственного распределения механических свойств ( Шаг 3) и этап определения и количественной оценки соответствующих характеристик из этих распределений (Шаг 4) являются особенно сложными. Шаг 3 требует решения некорректно поставленной задачи, что является сложной задачей.Кроме того, как только обратная задача решена и получено распределение модулей, определение полезных свойств и соответствующих мер для количественной оценки этих характеристик для данной проблемы также становится сложной задачей.

Учитывая, что механические свойства, полученные в результате решения обратной задачи, исследуются на предмет соответствующих характеристик, и что эти характеристики используются для диагностики, возникает интригующий вопрос, нужно ли вообще решать обратную задачу. Или, другими словами, можно ли перейти непосредственно от измеренных перемещений к желаемому диагнозу? Учитывая, что алгоритмы глубокого обучения хороши для извлечения полезных функций из данных, а затем использования их для данной задачи, мы спрашиваем, можно ли использовать возможности этих моделей на основе данных в стандартном рабочем процессе, основанном на физике.

Благодаря своей способности обнаруживать сложную структуру в данных большой размерности, наряду с улучшенными вычислительными ресурсами и доступностью большого объема данных, алгоритмы глубокого обучения позволили добиться значительных успехов в различных областях, от распознавания изображений [12], [13] от обработки естественного языка [14], обучения с подкреплением [15] до физики высоких энергий [16], вычислительной химии [17] и медицинской визуализации [18]. Эти алгоритмы могут выполнять множество задач анализа данных, включая решение задач классификации, цель которых состоит в том, чтобы разделить набор входных данных на две или более группы [19].Вход в эти проблемы может быть иерархическим, например, аудио, изображения, текст и видео, или неиерархическим, например, общие табличные данные. Сверточные нейронные сети (CNN) разработаны специально для эффективного изучения различных уровней абстракции иерархических данных и в настоящее время широко используются в различных задачах компьютерного зрения, таких как обнаружение объектов, распознавание изображений и сегментация изображений [12], [20] , [21]. Эти сети состоят из нескольких уровней пространственно-локальных операторов свертки, которые работают с данными изображения для извлечения соответствующих характеристик из изображений.Сверточные слои обычно сопровождаются полностью связанными слоями, где извлеченные объекты обрабатываются в многомерном пространстве признаков и передаются на последний слой, который выполняет задачу классификации.

В этой рукописи мы рассматриваем следующий вопрос: можем ли мы обучить CNN, чтобы она могла успешно идентифицировать механические особенности, используя данные смещения в качестве входных? В частности, можно ли его использовать для классификации образцов как упруго неоднородных или упруго-нелинейных на основе их реакции на смещение? Полезность сети, которая может выполнить эту задачу, становится очевидной, если рассмотреть рабочий процесс, изображенный на рис.1. В случае успеха можно обойти следующие этапы: (а) решение сложной обратной задачи для определения распределений механических свойств, (б) идентификация и извлечение соответствующих характеристик и (в) классификация на основе этих характеристик. Вместо рабочего процесса, показанного на рис. 1, это привело бы к гораздо более простому рабочему процессу, основанному на обучении, изображенному на рис. 2, где эти шаги объединены в один этап обучения CNN.

Чтобы ответить на этот вопрос, мы генерируем большой набор распределений свойств материала, которые принадлежат к «злокачественным» и «доброкачественным» классам.По сравнению с доброкачественным классом, распределение модуля Юнга в злокачественном классе более неоднородно, а параметр нелинейной упругости повышен. После этого мы решаем прямые задачи упругости, чтобы определить поле смещения для этих образцов в ответ на сжимающую нагрузку. Эти данные о смещении и соответствующая метка (доброкачественная или злокачественная) используются для обучения простой CNN, производительность которой затем проверяется на другом наборе данных о смещении. Обнаружено, что обученная CNN способна правильно классифицировать поражение как злокачественное или доброкачественное с замечательной точностью (≈99%) даже при наличии значительного шума в поле смещения.

После обучения CNN мы исследуем веса ее сверточных слоев, чтобы лучше понять, почему она успешна и что она извлекла из данных. Поскольку свертки являются пространственно локальными операторами, они предлагают прямую интерпретацию как дискретные локальные операторы [22]. Вообще говоря, мы наблюдаем, что свертки в первом слое ведут себя как фильтры нижних частот, которые сглаживают входные данные смещения, в то время как свертки в следующих слоях ведут себя как операторы конечных разностей, которые извлекают особенности в изображениях смещения путем вычисления дискретных пространственных производных.Это неудивительно, учитывая, что несколько методов, которые в настоящее время используются в эластографии, вычисляют различные меры деформации (производные смещений), чтобы сделать вывод о нижележащих распределениях упругих свойств [1], [23].

Наконец, мы применяем обученный нелинейный классификатор эластичности к данным смещения, полученным при поражениях груди у десяти человек. Отметим, что классификатор обучается только на данных моделирования и тестируется на реальных данных. Примечательно, что даже в этом случае он может правильно классифицировать восемь поражений из десяти.Эта идея иллюстрирует, как можно использовать основанные на физике модели для генерации данных для обучения алгоритмов машинного обучения (ML), которые затем можно применять к задачам, включающим «реальные» данные. В контексте номенклатуры машинного обучения это форма трансфертного обучения [24], [25], [26], когда модель обучается одной задаче и использует знания, полученные в результате этой задачи, для выполнения другой задачи. Что примечательно в нашем подходе, так это то, что мы используем основанную на физике модель для генерации обучающих данных, которые кодируют ценные знания в нашей модели.После этого мы применяем эту модель к реальным данным. Подобные идеи недавно были исследованы в [27] в контексте обучения робота в смоделированных средах для выполнения определенных задач, а затем тестирования его производительности в реальных условиях. Можно также думать об этом подходе как о форме увеличения данных, которая использует лежащую в основе физику для увеличения обучающих данных [19], [28], [29]. Это увеличение данных физически непротиворечиво, а также является «экстремальным» в том смысле, что при обучении сети используются только расширенные данные.Мы считаем, что подобные идеи могут оказаться полезными в приложениях с ограниченным объемом данных, таких как медицинская диагностика.

Формат оставшейся части этого документа следующий. Раздел 2 посвящен вычислительным методам, используемым в этом исследовании, и включает описание текущих и предлагаемых рабочих процессов для решения задачи классификации, процесса генерации обучающих и тестовых данных смещения, а также архитектуры сверточной нейронной сети. Раздел 3 посвящен результатам и анализу.В частности, мы количественно оцениваем точность CNN на зашумленных данных, анализируем некоторые из изученных фильтров свертки, а также тестируем производительность CNN на небольшом наборе экспериментальных данных / данных пациентов. Мы заканчиваем заключительными замечаниями в разделе 4.

Решение задач с векторами

Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.

Скорость:

Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина – скоростью.

Пример :

Мяч брошен с начальной скоростью 70 футов в секунду., под углом 35 год ° с горизонтальным. Найдите вертикальную и горизонтальную составляющие скорости.

Позволять v представлять скорость и использовать данную информацию для записи v в форме единичного вектора:

v знак равно 70 ( потому что ( 35 год ° ) ) я + 70 ( грех ( 35 год ° ) ) j

Упростим скаляры, получим:

v ≈ 57.34 я + 40,15 j

Поскольку скаляры являются горизонтальной и вертикальной составляющими v ,

Следовательно, горизонтальная составляющая равна 57,34 футов в секунду, а вертикальная составляющая 40,15 футов в секунду.

Сила:

Сила также представлена ​​вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, является векторной суммой этих сил.

Пример :

Две силы F 1 а также F 2 с величинами 20 а также 30 фунт соответственно воздействуют на объект в точке п как показано. Найдите равнодействующие силы, действующие в п .

Сначала мы пишем F 1 а также F 2 в компонентном виде:

v ≈ 57.34 я + 40,15 j

Упростим скаляры, получим:

F 1 знак равно ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) j знак равно 20 ( 2 2 ) я + 20 ( 2 2 ) j знак равно 10 2 я + 10 2 j F 2 знак равно ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) j знак равно 30 ( – 3 2 ) я + 30 ( 1 2 ) j знак равно – 15 3 я + 15 j

Итак, равнодействующая сила F является

F знак равно F 1 + F 2 знак равно ( 10 2 я + 10 2 j ) + ( – 15 3 я + 15 j ) знак равно ( 10 2 – 15 3 ) я + ( 10 2 + 15 ) j ≈ – 12 я + 29 j

Работа:

Работа W сделано силой F в движении по вектору D является W знак равно F ⋅ D .

Пример :

Сила задается вектором F знак равно 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9 ) . Найдите проделанную работу.

Сначала мы находим Displacement.

Вектор смещения

D знак равно 〈 5 – 1 , 9 – 3 〉 знак равно 〈 4 , 6 〉 .

Используя формулу, проделанная работа

W знак равно F ⋅ D знак равно 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 знак равно 26 год

Если единицей силы являются фунты, а расстояние измеряется в футах, то выполненная работа 26 год фут-фунт

Как решать физические задачи: метод и примеры – видео и стенограмма урока

Система GUESS

GUESS – это аббревиатура стратегии, которую мы будем использовать для решения любых физических задач. Буквы обозначают:

• Дано
• Неизвестно
• Уравнение (а)
• Замена
• Решить

Давайте рассмотрим каждый из этих шагов более подробно.

1. Дано

Проблемы с физикой, как правило, представляют собой страшные словесные задачи. Вы не можете прочитать задачу по физике, как если бы читали газетную статью или роман. Предложения в задачах по физике содержат много информации. Вы внимательно читаете каждое слово в предложении и делаете паузу, когда получаете новый фрагмент информации, чтобы записать его.

Часть данного включает набросок сценария. Это должен быть простой набросок, на котором такие объекты, как автомобили или люди, представлены в виде точек или квадратов.Рисование эскиза также может помочь вам определить информацию, имеющую отношение к сценарию, которая явно не выражена в проблеме, например ускорение свободного падения.

2. Неизвестно

В пространстве отдельно от данного или в самом эскизе запишите то, что вы ищете, поставив после него вопросительный знак. Например, если в задаче о силе требуется указать массу объекта, мы должны написать: масса? Это может показаться ненужным, но это действительно помогает сохранить организованность и сосредоточенность на решении проблемы.

3. Уравнение (а)

Эта часть процесса решения проблемы включает выбор подхода к проблеме с точки зрения содержания. Стоит ли использовать энергетический подход? Это проблема сил? Как только вы выберете подход, вам нужно будет искать уравнения, которые содержат переменные в заданных и неизвестных, которые вы уже записали. Часто потребуется несколько уравнений, а это значит, что вам нужно будет подключить одно к другому. Лучше всего провести алгебру с переменными и найти переменную, которую вы ищете.Таким образом, если вы допустили ошибку, ее будет легче найти. Просеивая числа, находить ошибки намного труднее.

4. Подстановка

После того, как вы решите соответствующие уравнения для переменной, которую вас просят решить, пора подставить данные значения. Убедитесь, что вы выполнили все необходимые преобразования единиц, прежде чем вводить данные значения. Например, если вы работаете над проблемой кинематики и скорость указывается в км / час, а ваше ускорение – в м / с2, вам необходимо преобразовать единицы времени и расстояния, чтобы они совпадали.

Остался один шаг – решить проблему!

5. Решить

Решение проблемы включает выполнение окончательных расчетов. Когда вы придете к ответу, ваш последний шаг – подумать над ним. Имеет ли смысл ценность? Например, если ваша проблема связана с вычислением ускорения автомобиля и вы достигли скорости 1000 м / с2, скорее всего, вы где-то ошиблись. 1000 м / с2 – нереальное ускорение для автомобиля. К сожалению, при решении физических задач ошибки случаются, и вам нужно вернуться к началу, чтобы найти ошибку.Ошибки допускают даже лучшие физики!

Давайте рассмотрим пример задачи, в которой мы реализуем метод GUESS для ее решения.

Пример задачи

Вот наша подсказка:

Человек роняет камень с моста высотой 115 м. Какова конечная скорость камня прямо перед тем, как он упадет в воду?

Вот наше решение:

В нашем примере показано, как использовать метод GUESS для решения этой проблемы:

Это показывает нам, что, пройдя наши шаги, мы приходим к решению 47.5 м / с. Как говорится рядом с ответом, это очень разумный ответ.

Краткое содержание урока

Физика – это предмет, требующий обширных навыков решения проблем. Для правильного и эффективного решения любой проблемы очень важно оставаться организованным и идти в ногу со временем. Аббревиатура GUESS означает:

• Учитывая
.
• Неизвестно
• Уравнение (а)
• Замена
• Решить

и является эффективным методом решения любых вопросов физики.

Запись данного и неизвестного помогает упростить язык словесной проблемы и включает схему сценария. Часть уравнения фокусируется на сборе соответствующих уравнений и решении для заданной переменной. Этап подстановки включает в себя вставку заданных значений и получение ответа. На этапе решения ответ оценивается, чтобы определить его реалистичность.

Как решить вирусную математическую задачу 2019

Вот оно появилось в Твиттере, как жестокая насмешка:

Этот контент импортирован из Twitter.Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

Каждые несколько месяцев Интернет пожирает себя какой-нибудь вирусной загадкой или иллюзией, каждая из которых выводит из себя больше, чем предыдущая. И так, как по маслу, эта сводящая с ума математическая задача стала вирусной, следуя великой традиции таких травмирующих событий, как «Платье» и «Янни / Лорел».

Загадки такого рода преднамеренно созданы для того, чтобы разделять и подчинять, и, как и ожидалось, кажущаяся простая проблема, поставленная в оскорбительном твите – 8 ÷ 2 (2 + 2) – на практике вызвала гражданскую войну в офисе Popular Mechanics . которыми мы также делимся с нашими (бывшими) друзьями в журналах Runner’s World и Bicycling .

➗ Вы любите сложные математические задачи. И мы тоже. Решим их вместе.

Естественно, мы обратились к Slack, чтобы выявить наши различия. Вот горячая беседа между редакторами, которые перестали делать хоть какое-то подобие реальной работы в течение дня, чтобы решить уравнение, созданное, чтобы сбить с толку четвероклассников – и нажить много врагов в процессе, – за которым следует понимание реальных математиков и физиков, которые неохотно откликнулись на нашу просьбу за комментарий, чтобы раз и навсегда разрешить яростные математические дебаты.

The Slack War, часть I

Дерек Колл, продюсер видео: 8 разделить на 8 равно 1.

Джефф Денгейт, Runner’s World Главный бегун: PEMDAS. 16.

Бобби Ли, редактор тестов (и трехкратный олимпийский велосипедист): i ride bikes

Пэт Хайне, продюсер видео: … она записывает PEMDAS, а затем PEDMAS

Matt: Вы явно не слушали

Pat: Я не слушал…я была занята исправлением своей математики.

Дерек: Когда они изобретают математику заново?

Мэтт: хорошо, Дерек, видео для вас

Пат: если вы получили 16, это потому, что вы не знаете разницы между скобками и скобками.

Википедия

Морган Петруни, редактор тестирования: Я согласен с Дереком и не согласен с YouTube. Что, если вы хотите проделать долгий путь и использовать свойство распределения, а сначала распространить 2? Вы бы сделали: 8 / (4 + 4) = 1.

Или дистрибутивное свойство вдруг перестало действовать?

Это то, что я бы сказал, доказывает, что 1 правильный.

Дерек: Я доверяю Морган, потому что в это десятилетие у нее был урок математики.

Pat: Википедия говорит, что вы ненавидите Америку, если получаете 16.

Википедия

Дэн Роу, редактор теста: Верно, но это умножение / деление, а не умножение, а затем деление

Морган: НО умножение с круглыми скобками превосходит деление.Так что у вас все еще остается 8/2 (4). Так что сначала вам нужно сделать 2х4. По крайней мере, так меня учили.

Дэн: умные люди из Беркли говорят, что это слишком двусмысленно; PEMDAS – это не столько математическое соглашение, сколько метод обучения

Pat: умножение / деление :: правильно / неправильно

Тейлор Ройек, помощник редактора функций: Главный вывод не в том, что кто-то плохо разбирается в математике, но этот человек не умеет писать четкие уравнения

Билл Стрикленд, редакторский директор : СДЕЛАЙТЕ ЭТО СОДЕРЖАНИЕ!

инстаграм-история, в которой наши сотрудники обсуждают?

можно назвать известного математика?

Бобби: Это похоже на разговор, который относится к сегменту «Не моя работа» Подожди, подожди, не говори мне

Кэти Фогель, редактор социальных сетей: сейчас опрашивает нашу аудиторию IG по этому поводу…

Pat: Уравнение написано не в соответствии со стандартами ISO, что оставляет неоднозначность интерпретации, и настоящий ответ заключается в том, что нам нужно научить лучше писать математику.

Неоднозначный PEMDAS

Неоднозначные проблемы, порядок операций, PEMDAS, BEMDAS, BEDMAS

он же … то, что сказал Тейлор, но из Гарварда

Морган: он же … научить распределительному свойству вместо случайных сокращений

Pat: Если написано в соответствии со стандартом ISO, ответ – 1.

Пэт Хайне

Эндрю Дэниэлс, редактор с практическими рекомендациями: честно, мы могли бы опубликовать эту слабую ветку слово в слово, а затем попросить ученого присоединиться к нам и обучить нас

Кэти Фогель: Из нашей аудитории IG …

Кэти Фогель / Instagram

Кит Фокс, редактор специальных проектов: Не возникает ли вопрос и двусмысленность, когда исчезают круглые скобки? Мол, остаются ли парены после того, как вы сделаете 2 + 2? Или они исчезнут, как только вы сначала решите мини-уравнение внутри скобок.Я говорю, что они никуда не денутся. Я в команде 1

Я также не посещал математические классы более 10 лет

Тревор Рааб, фотограф: Мой вопрос в том, к какому сценарию реального мира это применимо к

Брэд Форд, редактор теста: Класс математики?

Тревор: ах, классический учись математике, чтобы научиться больше заниматься математикой

Бобби: школа – не реальный мир

Морган: Создание горячих и поляризующих офисных дискуссий

Брэд: Бобби, скажи это шестикласснику.

Бобби: Я буду работать над подготовкой моего аргумента сейчас

Тейлор: У вас есть, что, 11 лет, чтобы усовершенствовать его

Бобби: время на моей стороне

это код для: Я могу отложить это на очень долгое время

Пат: , который является кодом для «спроси свою мать»

Бобби: она любит утверждать, что она хороша в математике. Она может пожалеть о том дне, когда хвасталась этим

Pat: «Это не поможет мне выиграть миллионы долларов в Fortnite, хотя»

Краткое заявление Майка Брина, сотрудника по общественной осведомленности Американского математического общества , Чья работа – «рассказывать людям, насколько хороша математика»

В соответствии с порядком операций вы сначала решаете то, что указано в скобках.Это дает вам 4. Затем в PEMDAS умножение и деление имеют равный приоритет, поэтому вы должны делать первое, что происходит слева направо. Итак, сначала нужно разделить 8 на 2, то есть 4. Таким образом, получится 16 в соответствии с классическим порядком операций.

Но как написано, неоднозначно. В математике очень часто возникают двусмысленности. Математики стараются делать правила как можно точнее. По строгому порядку действий вы получите 16, но я бы не стал бить кого-нибудь линейкой по запястью, если он скажет 1.

The Slack War, часть II

Эндрю: ууууу мальчик

я только что разговаривал по телефону с американским математическим обществом

какие американские горки это оказывается

мой человек микрофон с AMS, чья работа состоит в том, чтобы прямо отвечать на подобные вопросы, говорит, что ответ такой …

Брэд: 42

Тайлер Дасвик, помощник редактора функций: тайно лучший ответ здесь

Эндрю: ШЕСТНАДЦАТЬ

Эндрю, минут спустя: , почему никто не реагирует должным образом на эту новость

Брэд: Потому что он неправ.

Тревор: , но разве это не противоречит PEMDAS?

Эндрю: он говорит (и мне придется вернуться к стенограмме), что при использовании * традиционного * порядка операций ответ будет 16

Мэтт Филлипс, старший редактор тестирования: Эндрю, у моего брата есть имеет степень доктора теоретической физики и пишет статьи с такими названиями, как… «Угловая зависимость для ν ‘, j’-разрешенных состояний в реактивном рассеянии F + h3 → HF (ν’, j ‘) + H с использованием нового источника пучка атомного фтора» I может посмотреть, хочет ли он взвесить…

Андрей: да! пожалуйста, сделайте [Примечание редактора: брат Мэтта не ответил.]

Тейлор: есть ли способ, которым 1 также является правильным ответом на этот вопрос?

Тревор: PEMDAS

Эндрю: Я также отправлю запрос своему физику, который также только что ответил на вопрос POP о том, как прыгнуть с движущегося поезда

Тейлор: tbh, это было бы было бы здорово, если бы мы смогли найти экспертов, которые не согласны

Тревор: подождите, вернул мою интерпретацию PEMDAS обратно к 16

вот почему я пошел в художественную школу

Тейлор: Я спросил своего друга [УДАЛЕНО], кто он собирается закончить университет с докторской степенью по статистике из [УДАЛЕНО], имеет три или четыре степени магистра математики

, и я так рад сообщить, что она на моей стороне

Тейлор Ройек

Дерек: [УДАЛЕНО] выигрывает

Эндрю: но что [УДАЛЕНО] было ответом ??!

Тейлор: нет ответа, фальшивый вопрос, созданный для разжигания возмущения

Билл: , может быть, наш умный подход таков: математика не субъективна, никто не пишет математику так, вот что не так

Тейлор: она только начинает

Тейлор Ройек

Комплект: Похоже, [УДАЛЕНО] нужно написать потную математику. Take

Эндрю: daaaaang [УДАЛЕНО]

go off

Бобби: нет, мы что-то поняли!

Прощальный выстрел от Ретта Аллена, доктора философии.D., доцент кафедры физики Университета Юго-Восточной Луизианы, вынесший окончательный вердикт и решительно закрыл нас всех

Это математическая версия: «Какого цвета это платье? Синий и черный или золотой и белый? »Я отвечу, что сначала вы ставите скобки, так что получается:

8/2 * 4

Затем вы идете слева направо.

8/2 равно 4, поэтому это

4 * 4

Теперь вы получаете 16.

Конечно, это не математика. Это условность.У нас есть соглашения о том, как писать эти вещи, точно так же, как у нас есть соглашения о том, как писать что-то по буквам. Но все же есть разные условности. Некоторые люди пишут это как «серый», а другие как «серый». Мы все еще понимаем, что происходит. Что касается меня, я бы написал это более подробно, чтобы не было путаницы. Вот так:

8 / (2 * (2 + 2)), если это то, что вы пытаетесь сделать. Таким образом, никто не ошибется.

Футболки Popular Mechanics на Amazon

Футболка с обложки Popular Mechanics, апрель 1940 г.

Футболка на обложке Popular Mechanics, январь 1951

Футболка с обложкой журнала Popular Mechanics, июль 1982 года

Футболка с обложкой Popular Mechanics, октябрь 1943 г.

Футболка на обложке Popular Mechanics, март 1936 года

Футболка с обложкой журнала Popular Mechanics, июнь 1935 года

Футболка с обложкой Popular Mechanics, ноябрь 1923

Футболка с обложкой Popular Mechanics, ноябрь 1922

Футболка с обложкой Popular Mechanics, январь 1994

Футболка на обложке Popular Mechanics, апрель 1915 года

Футболка с обложкой Popular Mechanics, январь 1931

Футболка с обложкой журнала Popular Mechanics, июнь 1926 года

Эндрю Дэниелс Эндрю Дэниэлс – старший редактор журнала Popular Mechanics.