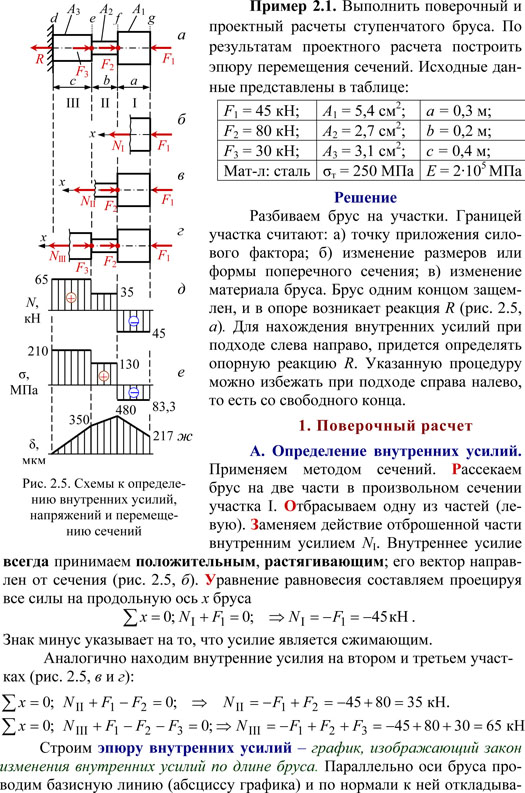
Примеры решения задач по строительной механике(расчет составной балки)
Задача 32 (300).
Для балки требуется :
1. Используя индивидуальный шифр выбрать : расчётную схему балки, её размеры, действующую нагрузку.
2. Провести кинематический анализ балки, построив её этажную схему.
3. Рассчитать отдельные простые балки и построить для них эпюры М и Q.
4. Построить эпюры усилий для исходной составной балки.
5. Построить линии влияния : двух опорных реакций (по собственному выбору), двух изгибающих моментов Mi, Mk и двух поперечных сил Qi, Qk (номера точек i, k даются в таблице).
6. Загрузить одну из линий влияния (по выбору) заданной нагрузкой, определить по ней соответствующие усилие и сравнить его со значением, полученным в п. 3.
Дано :
|
№ схемы |
№ загружения |
L1 , |
L2 , м |
L3, м |
а, м |
F1, кН |
F2, кН |
q, кН/м |
i |
k |
|
3 |
0 |
6 |
4. |
5.1 |
2 |
|
28 |
10 |
3 |
8 |
Решение.
1. Составляем расчётную схему балки.
2. Кинематический анализ схемы, построение её этажной схемы.
Степень свободы балки по формуле :
W=3Д-2Ш-С0
где Д – число дисков ; Ш – число простых шарниров ; C0 – число опорных связей.
В нашем случае : Д=3 ; Ш=2 ; C0=5.
Тогда степень свободы балки :
W=3×3-2×2-5=9-4-5=0
На рисунке 1 построена поэтажная схема. Составная балка состоит из трёх дисков : DN – основная балка, к которой присоединены второстепенные – AD и NH.
Таким образом, балка не подвижна, геометрически неизменяема и статически определима.
3. Рассчитаем отдельные простые балки и построим эпюры М и Q.
Балка NH. Определим опорные реакции :
ΣmL=0 ; –
RN= кН
ΣmN=0 ;
RL= кН
Контроль :
ΣY=RL+RN-q(2L3/3+a)=11.12+42.88-10×(3.4+2)=0
Запишем выражения Q и М для каждого участка.
Участок NL : 0<x1<3.4 м (ход слева)
Q1=RN-qx1 ; M1=RNx1-0.5qx12
Участок LH : 0<x2<2 м (ход справа)
Q2=qx2 ; M2=-0.5qx22
Находим значения Q и М в характерных точках балки.
Участок NL : при x1=0
QN=RN=11.12 кН ; MN=0
при x1=3.4 м
QLл=RN-3.4q=11.12-3.4×10=-22.88 кН ;
MLл=3.4RN-0.5q·3.42=3.4×11.12-0.5×10×3.42= -20 кН·м
На участке NL эпюра М ограничена параболой, имеющей экстремум.
Значение экстремального момента :
Mэкс=RNx0-0.5qx02=11.12×1.1-0.5×10×1.12=6.2 кН·м
Участок LH : при x2=2 м
QLпр=2q=2×10=20 кН ; MLпр=-0.5q·22=-0.5×10×22=-20 кН·м
при x2=0
QH=0 ; MH=0
На основании вычислений эпюры Q и М построены на рисунке 2.
Балка AD. Определим опорные реакции.
ΣmD=0 ;
RB= кН
ΣmB=0 ;
RD= кН
Контроль :
ΣY=RB+RD-F1-qa=50+20-50-10×2=0
Запишем выражения Q и М для каждого участка.
Участок AB : 0<x1<2 (ход слева).
Q1= -qx1 ; M1=-0.5qx12
Участок BC : 2<x2<4 (ход лева).
Q2=-qa+RB ; M2=-qa(x2-0.5a)+RB(x2-a)
Участок CD : 0<x3<2 (ход справа).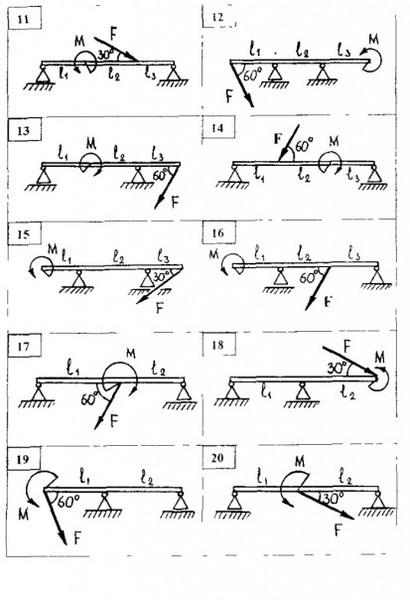
Q3=-RD ; M3=RDx3
Находим Q и М в характерных точках балки.
Участок AB : при x1=0
QA=0 ; MA=0
при x1=2 м
QBл=-2q=-2×10= -20 кН ; MBл=-0.5q·22=-0.5×10×4= -20 кН·м
Участок BC : при x2=2
QBпр=-qa+RB=-10×2+50=30 кН ;
MBпр=-qa(2-0.5a)+RB(2-a)=-10×2×1=-20 кН·м
при x2=4
QCл=-qa+RB=-10×2+50=30 кН ;
MCл=-qa(4-0.5a)+RB(4-a)=-10×2×(4-1)+50×(4-2)=40 кН·м
Участок CD : при x3=2
QCпр=-RD=-20 кН ; MCпр=2RD=2×20=40 кН·м
при x3=0
QD=-RD=-20 кН ; MD=0
Эпюры Q и М построены на рисунке 2.
Балка DN. Определим опорные реакции.
ΣmM=0 ;
RE=
кН
ΣmE=0 ;
RM=
кН
Контроль :
ΣY=-RD+RE-F2+RM-1.
7q-RN= -20+40.14-28+35.98-1.7×10-11.12=0
Запишем выражения Q и М для каждого участка.
Участок DE : 0<x1<2 (ход слева)
Q1= -RD ; M1=-RDx1
Участок EF : 2<x2<3.5 (ход слева)
Q2=-RD+RE ; M2=-RDx2+RE(x2-L1/3)
Участок FM : 1.7<x3<4.7 (ход справа)
Q3=qL3/3+RN-RM ; M3=-RNx3-q(L3/3)(x3-0.5L3/3)+RM(x3-L3/3)
Участок MN : 0<x4<1.7
Q4=qx4+RN ; M4=-0.5qx42-RNx4
Находим Q и М в характерных точках балки.
Участок DE : при x1=0
QD=-RD=-20 кН ; MD=0
при x1=2 м
QEл=-RD=-20 кН ; MEл=-2RD=-2×20=-40 кН·м
Участок EF : при x2=2 м
QEпр=-RD+RE=-20+40.14=20.14 кН ;
MEпр=-2RD+RE(2-2)=-2×20=-40 кН
при x2=3.5 м
QFл=-RD+RE=-20+40.14=20.14 кН
MFл=-3.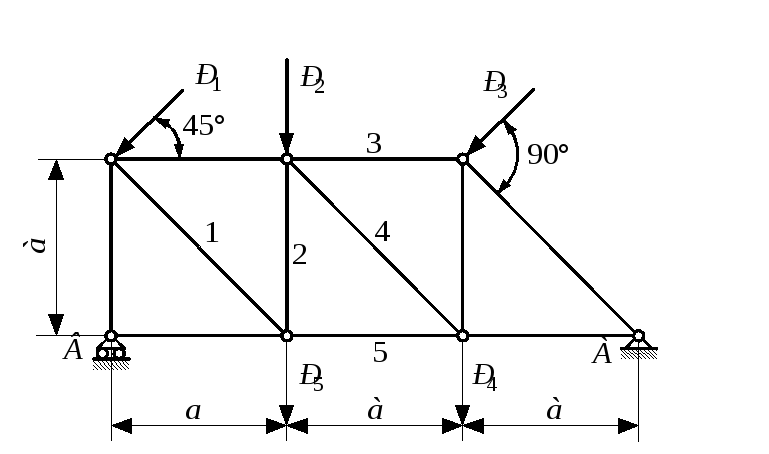
5RD+RE(3.5-2)=-3.5×20+40.14×1.5=-9.79 кН·м
Участок FM : при x3=4.7 м
QFпр=qL3/3+RN-RM=10×1.7+11.12-35.98= -7.86 кН
MFпр=-4.7RN-q(L3/3)(4.7-0.5L3/3)+RM(4.7-L3/3)=
=-4.7×11.12-1.7×10×(4.7-0.5×1.7)+35.98×(4.7-1.7)= -9.77 кН·м
при x3=1.7 м
QMл=qL3/3+RN-RM=10×1.7+11.12-35.98=-7.86 кН
MMл=-1.7RN-q(L3/3)(1.7-0.5L3/3)+RM(1.7-L3/3)=
=-1.7×11.12-10×1.7×(1.7-0.5×1.7)= -33.35 кН·м
Участок MN : при x4=1.7
QMпр=1.7q+RN=1.7×10+11.12=28.12 кН
MMпр=-0.5q·1.72-1.7RN=-0.5×10×1.72-1.7×11.12=-33.35 кН·м
при x4=0
QN=RN=11.12 кН
MN=0
Эпюры Q и М построены на рисунке 2.
4.
Эпюры Q и М для исходной составной балки.
Объединяя эпюры Q и М, построенные для каждой простой балки в одну, получим эпюры Q и М для исходной составной балки.
Эпюры Q и М для составной балки построены на рисунке 3.
5. Построение линий влияния.
Построение линии влияния реакции RB.
Располагаем начало координат в точке B. Пусть сила P=1 движется по балке AD. Тогда уравнение равновесия балки :
ΣMD=0 ; -4RB+P(4-x)=0
Отсюда уравнение линии влияния RB на участке AD имеет вид :
RB==1-x/4
Строим линию влияния RB по двум точкам :
при x=0 (сила P располагается в точке B) – RB=1
при x=4 (сила P располагается в точке D) – RB=0
Найдём ординату линии влияния в точке А :
при x=-2 (сила P располагается в точке А) – RB=1.5
При движении силы P=1 по участкам DN и NH RB=0, так как при положениях груза P=1 на этих участках балка AD не работает.
Построение линии влияния RE.
При расположении силы P=1 на участке DN уравнение линии влияния RE найдём из уравнения равновесия балки :
ΣMM=0 ; -4.5RE+P(10.5-x)=0
RE=
Эту линию строим по двум точкам :
при x=6 (сила P располагается в точке Е) – RE=1 ;
при x=10.5 (сила P располагается в точке М) – RE=0
Определим ординаты линии влияния RE в точках D и N :
при x=4 (сила P находится в точке D) – RE=1.4
при x=12.2 (сила P находится в точке N) – RE=-0.4
Линию влияния RE на участке AD строим по двум точкам. В точке D ордината линии влияния участка AD совпадает с ординатой линии влияния участка DN. В точке B – RE=0. Через эти точки проводим линию влияния RE на участке AD.
Определим ординату линии влияния в точке А.
RE=1.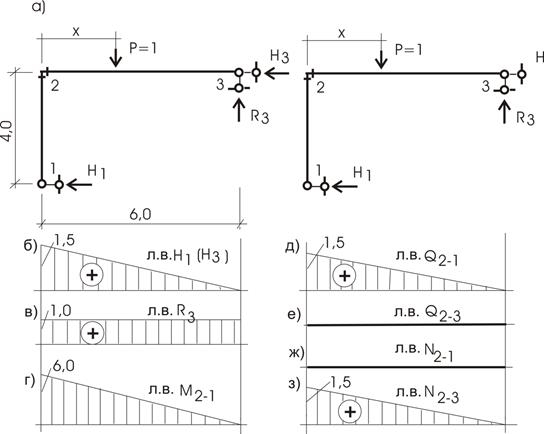
4RD, где RD – реакция в точке D. Определим её из уравнения равновесия балки AD :
4RD-Px=0 ; RD=x/4
Тогда уравнение линии влияния на участке AD имеет вид :
RE= ; при x=-2 (сила P располагается в точке А) – RE=-0.7
Аналогично строим линию влияния на участке NH. В точке N – RE=-0.4 ; в точке L – RE=0. Найдём ординату линии влияния в точке H.
RE=-0.4RN , где RN – реакция в точке N. Определим её из уравнения равновесия балки NH :
-3.4RN+P(15.6-x)=0 ; RN= – уравнение линии влияния на участке NH.
при x=17.6 (сила P располагается в точке H) – RE=
Линия влияния RE построена на рисунке 4.
Построение линии влияния изгибающего момента в сечении 3 (левее точки Е, бесконечно близко к ней).
При движении P=1 по участку DE левее точки 3, рассматривая равновесие левой отсечённой части (относительно точки 3) балки DN, имеем :
M3=-P(2-x)=-(2-x)
при x=0 (точка D) – M3=-2 м ; при x=2 м (точка Е) – M3=0.
По этим точкам строим линию влияния М3 на участке DE.
При движении P=1 по участку ED правее точки 3, рассматривая равновесие левой отсечённой части балки DN, имеем :
M3=0
При движении P=1 по участку EN балки DN и по балки NH, рассматривая равновесие левой отсечённой части балки DN, также получим : M3=0. Т.е. на участках EN и NH линия влияния совпадает с осью абсцисс.
При движении P=1 по балке AD М3=-2RD, где RD находим из уравнения равновесия балки AD :
ΣmB=0 ; -P(-4-x)-4RD=0 ; RD=
Тогда уравнение линии влияния М3=
при x=0 (точка D) – M3=-2 м ; при x=-4 м (точка B) – M3=0 ; при x=-6 м (точка А) – М3=1 м.
Линия влияния М3 построена на рисунке 5.
Построение линии влияния поперечной силы Q3 в сечении 3 (левее точки Е, бесконечно близко к ней).
Линия влияния Q3 строится аналогично линии влияния М3.
При движении P=1 по участку DE левее точки 3, рассматривая равновесие левой отсечённой части (относительно точки 3) балки DN, имеем :
Q3=-P=-1
Т.
е. на участке DE линия влияния Q3 параллельна оси абсцисс.
Для построения л.в. на участке AD поступим следующим образом : ординату точки D (y=-1) соединим с ординатой точки B (y=0) и продолжим до пересечения с ординатой точки А. Ординату точки А найдём из подобия треугольников : yA=2×1/4=0.5
При движении P=1 по участку DE, правее точки 3, а также по участкам EN и NH, рассматривая равновесие левой отсечённой части балки DN, имеем Q3=0
Линия влияния Q3 построена на рисунке 5.
Построение линии влияния изгибающего момента М8 в сечении 8 (левее точки М, бесконечно близко от неё).
При движении P=1 по участку DM левее точки 8 и по участку AD – М8=0 (линия влияния совпадает с осью абсцисс). Это следует из рассмотрения равновесия правой отсечённой части MN :
M8=MM=RM·0=0
При движении P=1 по участку MN правее точки 8, рассматривая равновесие правой отсечённой части MN балки DN, имеем :
M8=RM·0-Px=-x
при x=0 (точка М) – М8=0 ; при x=1. 7 м (точка N) – M8=-1.7 м
При движении P=1 по участку NH, рассматривая равновесие правой отсечённой части MN балки DN, имеем :
M8=-1.7RN
где RN находим, рассматривая равновесие участка NH.
ΣmL=0 ; -3.4RN+P(5.1-x)=0 ; RN=
M8=
при x=1.7 (точка N) – M8=-1.7 м ; при x=5.1 (точка L) – M8=0 ; при x=7.1 м (точка H) – M8=1 м.
Линия влияния М8 построена на рисунке 6.
Построение линии влияния поперечной силы Q8 в сечении 8 (левее точки М, бесконечно близко к ней).
Линия влияния Q8 строится аналогично линии влияния М8.
При движении P=1 по участку DM (с лево от точки 8), рассматривая равновесие правой отсечённой части (MN) балки DN, имеем :
Q8=-RM=
где RM находим из уравнения равновесия, составленного для балки DN :
ΣME=0 ; -P(x-2)+4.5RM=0 ; RM=
при x=0 (точка D) – Q8=0. 4 ; при x=2 м (точка Е) – Q8=0 ; при x=6.5 м (точка M) – Q8=-1 ; при x=8.2 м (точка N) – Q8=-1.4
По полученным данным строим левую прямую л.в. Q8, при движении P=1 по балке DM.
Для построения л.в., при движении P=1 по балке AD поступаем следующим образом : соединяем ординату точки D (0.4) с ординатой точки B (y=0) и, продолжаем эту прямую до пересечения с ординатой точки А. Ординату точки А находим из подобия треугольников : ; yA=2×0.4/4=0.2. Таким образом, левая прямая л.в. построена.
При движении P=1 по участку MN (с право от точки 8), рассматривая равновесие левой отсечённой части (DM), балки DN, имеем :
Q8=-RE=
где RE находим из уравнения равновесия, составленного для балки DN :
ΣmM=0 ; -P(x-6.5)+4.5RE=0 ; RE=
при x=0 (точка D) – Q8=1.4 ; при x=6.5 м (точка М) – Q8=0 ; при x=8.2 м (точка N) –
Q8= -0.4.
По полученным данным строим правую прямую л.в. Q8, при движении P=1 по участку MN. Для построения л.в., при движении P=1 по балке NH поступаем следующим образом : соединяем ординату точки N (-0.4) с ординатой точки L (y=0) и, продолжаем эту прямую до пересечения с ординатой точки H. Ординату точки H найдём из подобия треугольников : yH=2×0.4/3.4=0.24. Таким образом, правая прямая л.в. Q8 – построена. Линия влияния Q8 приведена на рисунке 6.
6. Определение поперечной силы QE в сечении Е по линии влиянии от заданно нагрузки.
QE=
где y – ордината линии влияния под сечением с сосредоточенной нагрузкой P ; ω – площадь участка линии влияния под нагрузкой q ; α – угол наклона линии влияния в месте приложения сосредоточенного момента.
Тогда (см. рисунок 7) :
QE= кН
На эпюре Q, при движении слева : QE=-20 кН
Заказать решение задач по строительной механике в Москве, помощь в решении задач по строительной механике на заказ, цена
Как мы пишем работы
Оформить заявку
Гарантии выполнения заказа
На протяжении выбранного вами гарантийного срока вы можете вернуть потраченные деньги, если качество написанной под заказ студенческой работы вас не устроит или не будет соответствовать требованиям учебного заведения.
Перед сдачей клиенту, каждая работа проходит тщательную проверку на плагиат по выбранному вами сервису.
Написанием работ занимаются только опытные авторы, которые хорошо знают тонкости учебной дисциплины и имеют практический опыт в отрасли.
Мы строго храним тайну сотрудничества между агентством по написанию студенческих работ и клиентом.
Отзывы авторов
Узнать стоимость работы за 1 минутуОтзывы наших клиентов
Узнайте почему выбирают студенты:
Rodion
Когда совмещаешь учебу с работой, сложно всё успевать.
Периодически пользуюсь услугами студенческого сервиса FastFine. Решение задач заказывал дважды, оба раза получал на руки качественно выполненную работу. Рекомендую сотрудников сервиса фастфайн как ответственных исполнителей.Обратилась в компанию FASTFINE за помощью в решении задач по статистике. Могу сказать, что компания оставила очень приятное впечатление о себе. Очень вежливые и предупредительные сотрудники, грамотные исполнители. Решение каждой задачи было расписано самым подробным образом, так что я смогла разобраться в теме, и уже на экзамене самостоятельно решать подобные задания. Разумеется, я теперь буду пользоваться услугами фастфайн ру, если опять будут проблемы с учебой.
Пропустила практические занятия по высшей математике из-за болезни, самостоятельно разобраться с материалом не получилось.
Надо было решить большое количество задач, а там такие дебри, что мне самой не справиться. Попросила подругу помочь, она сослалась на сильную занятость и кинула мне ссылку на сайт fastfine.ru. Сказала, что там мне помогут. Оказалось, что можно заказать решение задач у специалистов. В моей ситуации это действительно был выход. Благодарю сотрудников ФастФайна за квалифицированную помощь!
Предлагаем заказать решение задач по строительной механике быстро и недорого
Строительная механика относится к одной из наиболее сложных учебных дисциплин, которые приходится изучать студентам инженерных и технических специальностей. Чтобы справиться с поставленными преподавателем условиями, нужно не просто иметь глубокий уровень теоретической подготовки, но и хорошо понимать практическую суть выполняемых действий. Научиться этому можно, но без должного опыта некоторые задачи будут представлять существенную проблему. Перед студентом возникает непростой выбор: полагаться только на собственные силы и удачу, доверить выполнение практических заданий своим однокурсникам или более опытным обучающимся старших курсов, ну или попытаться найти компетентного исполнителя на стороне. Третий вариант выглядит наиболее перспективным, вот только профессионалов, способных относительно быстро и за приемлемые деньги решить большое количество задач по строительной механике, на самом деле немного. Таких можно найти на универсальных биржах контента, но это редкость и большое везение. Лучше не полагаться на удачу, а сразу обратиться за помощью к тому, кто является признанным экспертом в своей отрасли знаний. Только в таком случае реально претендовать на высокую оценку, допуск к защите письменной работе с первого раза, успешную сдачу экзамена и переход на следующий курс.
Сервис по написанию студенческих работ готов оказать посильную помощь и своевременные консультации по выполнению широкого спектра поставленных задач по данной учебной дисциплине. Мы привлекаем к сотрудничеству только опытных практиков, которые могут и решить предложенный объем заданий, и дать по ним подробные пояснения. Только в таком случае вы сможете ответить на самый каверзный вопрос и получить высокую оценку за работу. Чтобы понять, как работает наша компания, можно познакомиться с отзывами клиентов или обратить внимание на основные этапы оформления заказа в FastFine:
- Прохождение регистрации на сервисе, получение доступа к личному кабинету;
- Подача заявки в режиме онлайн и оценка предоставленной информации нашими специалистами;
- Согласование цены, подписание договора и внесение предоплаты за заказ;
- Отправка готовой работы клиенту, внесение правок при необходимости.
Помощь в написании учебной работы по предметам
- Техническая механика
- Теоретическая механика
Посмотреть все предметы
Обратные задачи нестационарной структурной акустики.
(Конференция)- Полная запись
- Другое связанное исследование
Аннотация не предоставлена.
- Авторов:
- Уолш, Тимоти
- Дата публикации:
- Исследовательская организация:
- Национальная лаборатория Сандия. (SNL-NM), Альбукерке, Нью-Мексико (США)
- Организация-спонсор:
- Национальная администрация по ядерной безопасности Министерства сельского хозяйства США (NNSA)
- Идентификатор ОСТИ:
- 1258242
- Номер(а) отчета:
- ПЕСОК2015-3848К
583972
- Номер контракта с Министерством энергетики:
- АК04-94АЛ85000
- Тип ресурса:
- Конференция
- Отношение ресурсов: Конференция
- : предложена для презентации на собрании Американского акустического общества, которое состоится 18–21 мая 2015 г. в Питтсбурге, штат Пенсильвания.
- Страна публикации:
- США
- Язык:
- Английский
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Уолш, Тимоти. Обратные задачи нестационарной структурной акустики. . США: Н. П., 2015.
Веб.
Копировать в буфер обмена
Уолш, Тимоти. Обратные задачи нестационарной структурной акустики. . Соединенные Штаты.
Копировать в буфер обмена
Уолш, Тимоти. 2015.
«Обратные задачи нестационарной структурной акустики». Соединенные Штаты. https://www.osti.gov/servlets/purl/1258242.
Копировать в буфер обмена
@статья{osti_1258242,
title = {Обратные задачи нестационарной структурной акустики.},
автор = {Уолш, Тимоти},
abstractNote = {Аннотация не предоставлена.},
дои = {},
URL-адрес = {https://www.osti.gov/biblio/1258242},
журнал = {},
номер =,
объем = ,
место = {США},
год = {2015},
месяц = {5}
}
Копировать в буфер обмена
Посмотреть конференцию (1,43 МБ)
Дополнительную информацию о получении полнотекстового документа см. в разделе «Доступность документа». Постоянные посетители библиотек могут искать в WorldCat библиотеки, в которых проводится эта конференция.
Экспорт метаданных
Сохранить в моей библиотеке
Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.
Аналогичных записей в сборниках OSTI.GOV:
- Аналогичные записи
Численный алгоритм решения нелинейных задач строительной механики на основе метода продолжения в сочетании с методом динамической релаксации
Открытый доступ
| Проблема | Веб-конференция MATEC. Том 86, 2016 5 -я Международная научная конференция «Интеграция, партнерство и инновации в строительной науке и образовании» | |
|---|---|---|
| Номер статьи | 01006 | |
| Количество страниц) | 6 | |
| Раздел | 1 Строительная механика | |
| DOI | https://doi. org/10.1051/matecconf/20168601006 | |
| Опубликовано онлайн | 28 ноября 2016 г. | |
MATEC Web of Conferences 86 , 01006 (2016)
Численный алгоритм решения нелинейных задач строительной механики на основе метода продолжения в сочетании с методом динамической релаксации
Сергей Трушин *
НСУМГ , кафедра строительной и теоретической механики, Ярославское ш. 26, 129337 Москва, Россия * Автор, ответственный за переписку: [email protected]
Abstract
Предложен численный алгоритм расчета прочности и устойчивости нелинейно-деформируемых стержневых систем и тонкостенных пространственных конструкций. Численный метод основан на методе продолжения и методе динамической релаксации. При использовании метода динамической релаксации состояние статического равновесия конструкций определяют после затухающих колебаний путем интегрирования по ведущему параметру.