Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание.
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание.
Вычислить $A B$ и $B A$,
если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$
Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Калькулятор онлайн – Операции над матрицами: сложение, вычитание, умножение, деление, возведение в степень.
Вычисление определителя матрицы, обратной матрицы, ранга матрицы
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Матрицы и операции над ними
Виды матриц
Определение 1.Матрицей размера
Как правило, их обозначают строчной буквой с двумя индексами, например \(a_{ij}\), где \(i\) — номер строки ( \(i=\overline{1,m} \) ), \(j\) — номер столбца ( \(j=\overline{1,n} \) ), в которых расположен этот элемент.
Матрицу записывают так:
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} $$
Если по тексту ясно, в каких пределах изменяются индексы \(i\) и \(j\), то сокращённо матрицу можно записать так: \( \left(a_{ij} \right) \).
Матрицу как единый объект обозначают прописной буквой: \(A\), \(B\) и т.д.
Элементами матриц могут быть не только действительные числа, но и комплексные, и даже другие математические объекты. Например, элементами матриц могут быть многочлены или матрицы.
Матрицу называют матрицей-строкой, если матрица имеет размер \(1 \times n \), т.е. если у матрицы всего одна строка. Число элементов в матрице-строке называют её
\(A=(a_1, \; …,\; a_n) \)
Матрицу называют матрицей-столбцом, если матрица имеет размер \(m \times 1 \), т.е. если у матрицы один столбец. Число элементов
в матрице-столбце называют её высотой.
\(A = \begin{pmatrix}
a_{1} \\
\vdots \\
a_{m} \\
\end{pmatrix} \)
Матрицу называют квадратной порядка \(n\), если \( m=n\), т.е. когда матрица имеет столько же столбцов, сколько и строк :
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix} $$
а если \(m \neq n \) —
У квадратных матриц выделяют последовательности элементов \( a_{11}, \; a_{22}, \; …, \; a_{nn} \) — главную диагональ, и \( a_{n1}, \; a_{n-1,2}, \; …, \; a_{1n} \) — побочную диагональ. Элементы главной диагонали называют диагональными. Понятия диагонального элемента и главной диагонали распространяют и на прямоугольные матрицы.
Если в квадратной матрице порядка \(n\) все элементы, стоящие вне главной диагонали, равны нулю, т.е. если матрица имеет вид
$$ \begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
0 & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{pmatrix} $$,
то её называют диагональной к обозначают \( \text{diag} (a_{11}, \; …, \; a_{nn} ) \).
Если в диагональной матрице порядка \(n\) на
диагонали стоят единицы, то её называют единичной и обозначают обычно \(E\) :
$$ E = \begin{pmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 \\
\end{pmatrix} $$,
Матрицу размера \(m \times n \), все элементы которой равны нулю, называют нулевой матрицей соответствующего размера и обозначают
буквой \(\Theta\) или цифрой 0.
Часто используют матрицы и других видов, например верхние треугольные матрицы
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{pmatrix} $$
у которых элементы, расположенные под главной диагональю, равны нулю, и нижние треугольные матрицы, у которых, наоборот,
элементы над главной диагональю равны нулю:
$$ \begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
a_{21} & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix} $$
Ступенчатой матрицей (матрицей ступенчатого вида) называют матрицу размера \(m \times n \), если для любой её строки выполнено
следующее условие: под первым слева ненулевым элементом строки и предшествующими ему нулевыми элементами строки все элементы матрицы
равны нулю.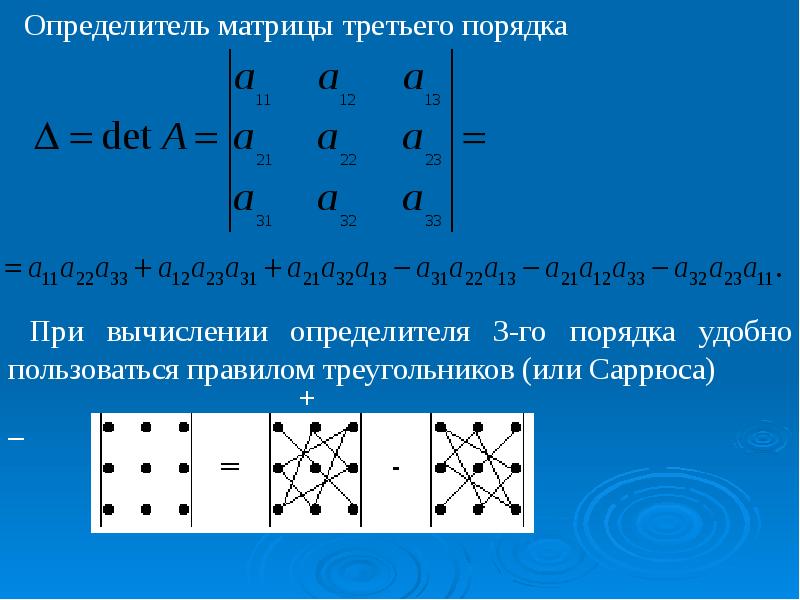
Следующие матрицы имеют ступенчатый вид:
\( \begin{pmatrix}
0 & 2 & 3 & 0 \\
0 & 0 & -1 & 1 \\
0 & 0 & 0 & 3 \\
\end{pmatrix} \)
\( \begin{pmatrix}
3 & 1 & 3 & 3 \\
0 & 0 & 2 & 1 \\
0 & 0 & 0 & 0 \\
\end{pmatrix} \)
\( \begin{pmatrix}
1 & 1 & 3 & 3 \\
0 & 3 & 0 & 1 \\
0 & 0 & 1 & -1 \\
\end{pmatrix} \)
Линейные операции над матрицами
Определение 2.
Две матрицы называют равными, если они имеют один и тот же размер и если у них совпадают соответствующие элементы.
Определение 3.
Суммой матриц \( A=(a_{ij}) \) и \( B=(b_{ij}) \) размера \(m \times n \) называют матрицу \( C=(c_{ij}) \) того же размера с элементами
\( c_{ij} = a_{ij} + b_{ij}, \; i=\overline{1,m} , \; j=\overline{1,n} \)
В подробной записи:
\( A+B = \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} + \)
\( \begin{pmatrix}
b_{11} & b_{12} & \cdots & b_{1n} \\
b_{21} & b_{22} & \cdots & b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
b_{m1} & b_{m2} & \cdots & b_{mn} \\
\end{pmatrix} = \)
\( \begin{pmatrix}
a_{11}+b_{11} & a_{12}+b_{12} & \cdots & a_{1n}+b_{1n} \\
a_{21}+b_{21} & a_{22}+b_{22} & \cdots & a_{2n}+b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1}+b_{m1} & a_{m2}+b_{m2} & \cdots & a_{mn}+b_{mn} \\
\end{pmatrix} = C \)
Сумма определена только для матриц одного размера.
Определение 4.
Произведением матрицы \( A=(a_{ij}) \) размера \(m \times n \) на число \( k \in \mathbb{R}\) называют матрицу
\( C=(c_{ij}) \) размера \(m \times n \) с элементами \( c_{ij} = k \cdot a_{ij} \).
Подробно это произведение выглядит так:
\( k \cdot \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} = \)
\( \begin{pmatrix}
k \cdot a_{11} & k \cdot a_{12} & \cdots & k \cdot a_{1n} \\
k \cdot a_{21} & k \cdot a_{22} & \cdots & k \cdot a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
k \cdot a_{m1} & k \cdot a_{m2} & \cdots & k \cdot a_{mn} \\
\end{pmatrix} \)
Замечание. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами.
{n+m}\).
Элементарные преобразования матриц
Следующие три операции называют элементарными преобразованиями строк матрицы :1. Умножение строки матрицы на число не равное нулю.
2. Перестановка двух строк матрицы.
3. Суммирование одной строки с другой строкой, умноженной на число.
Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов.
Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование, которое преобразованную матрицу превращает в исходную.
Теорема. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду.
Определители
Определители n-го порядка
В теории определителей n-го порядка используются понятия перестановки, подстановки и их четности.
Всякое расположение чисел \( 1,\; 2,\; 3,\; …,\; n \) в определенном порядке называют перестановкой из \(n\) чисел.
Из \(n\) чисел можно образовать \(n!\) различных перестановок.
В общем случае перестановку записывают в виде матрицы-строки \( \alpha = (\alpha_1,\; \alpha_2,\; …,\; \alpha_n ) \)
Перестановку \( (1,\; 2,\; 3,\; …,\; n) \) называют нормальной.
Два числа \(\alpha_i\) и \(\alpha_j\) в перестановке \( \alpha = (\alpha_1,\; …,\; \alpha_n ) \) образуют инверсию,
если \(\alpha_j > \alpha_i \) но при этом \(\alpha_i\) стоит в перестановке правее \(\alpha_j\) (т.е. \(i>j\) ).
Общее количество инверсий в перестановке \(\alpha \) обозначают \( |\alpha | \), и если это число четное, то перестановку называют
четной, а если оно нечетное — нечетной.
Транспозицией перестановки называют такое её преобразование, при котором в ней меняются местами какие-либо два элемента,
а другие остаются на своих местах.
Теорема. Любая транспозиция меняет четность перестановки.
Из двух перестановок \( ( \alpha_1,\; …,\; \alpha_n ) \) и \( ( \beta_1,\; …,\; \beta_n ) \) одних и тех же чисел можно
составить новый объект
$$ \sigma = \begin{pmatrix}
\beta_1 & \beta_2 & \cdots & \beta_n \\
\alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} , \tag{1} $$
который называют подстановкой n-й степени.
Подстановку называют четной, если перестановки, из которых она состоит, имеют одинаковую четность, и нечетной в
противоположном случае.
Четность подстановки \( (1) \) совпадает с четностью числа \( |\beta|+|\alpha| \) — общего количества инверсий
в строках подстановки, которое обозначают \( |\sigma| \).
Транспозицией подстановки называют любую перестановку её столбцов. Поскольку транспозиция подстановки вызывает
транспозиции и в образующих её перестановках, то, согласно предыдущей теореме, очевидно, что транспозиция подстановки не меняет
её четность.
Каждая подстановка вида \( (1) \) задает взаимно однозначное отображение множества чисел \( 1,\; 2,\; 3,\; …,\; n \) на себя,
при котором \( \beta_1 \) отображается в \( \alpha_1 \; , \; \beta_2 \) — в \( \alpha_2\) и т.д.
В соответствии с интерпретацией подстановок как отображений две подстановки считают равными, если они отличаются только
порядком записи своих столбцов.
Например, подстановки
\( \begin{pmatrix}
1 & 3 & 4 & 2 \\
2 & 4 & 1 & 3 \\ \end{pmatrix}
\;\; и \;\;
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 3 & 4 & 1 \\ \end{pmatrix} \)
равны, так как вторая получается из первой перестановкой столбцов.
Соглашение о равенстве подстановок позволяет записать любую подстановку так, чтобы первая строка являлась нормальной перестановкой. Поэтому различных подстановок \(n\)-й степени имеется ровно \(n!\)
Определение.
{|\sigma|} a_{1\alpha_1} a_{2\alpha_2} … a_{n\alpha_n} \tag{3} $$
которая берется по всевозможным подстановкам вида
\( \sigma = \begin{pmatrix}
1 & 2 & \cdots & n \\
\alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} \)
Определитель матрицы \(A\) часто называют просто определителем, или детерминантом, и обозначают
\( \begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{vmatrix} \)
или \( \det A\), называя \(A\) матрицей этого определителя.
Свойства определителей
Поскольку определители соответствуют квадратным матрицам, в их теорию легко переносится матричная терминология
(порядок, элементы, строки, столбцы, диагональ, диагональные элементы, виды матриц и определителей,
транспонирование, элементарные преобразования строк и столбцов, линейные комбинации строк и столбцов
и др.
T \right| \)
Свойство 2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
Свойство 3. Если все элементы \(j\)-го столбца определителя представлены в виде суммы двух слагаемых, то определитель равен
сумме двух определителей, у которых все столбцы, кроме \(j\)-го, такие же, как и в данном определителе, а \(j\)-й столбец
первого определителя состоит из первых слагаемых \(j\)-го столбца данного определителя, а второго — из вторых слагаемых :
\( \begin{vmatrix}
a_{11} & \cdots & \alpha_{1j} + \beta_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \alpha_{2j} + \beta_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \alpha_{nj} + \beta_{nj} & \cdots & a_{nn} \end{vmatrix} = \)
\( \begin{vmatrix}
a_{11} & \cdots & \alpha_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \alpha_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \alpha_{nj} & \cdots & a_{nn} \end{vmatrix} + \)
\( \begin{vmatrix}
a_{11} & \cdots & \beta_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \beta_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \beta_{nj} & \cdots & a_{nn} \end{vmatrix} \)
Аналогично для строки.
Свойство 4. Общий множитель элементов строки или столбца может быть вынесен за знак определителя.
Для умножения определителя на число достаточно умножить на это число элементы любой строки или любого столбца.
Свойство 5. Определитель равен нулю, если он имеет :
1) нулевую строку (столбец)
2) хотя бы две одинаковые строки (столбца)
3) хотя бы две строки (столбца), элементы которых пропорциональны
4) хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).
Свойство 6. Определитель не изменится, если к любой его строке (столбцу) прибавить другую строку (столбцец), умноженную на число.
В матрице \(A\) вычеркнем \(i\)-ю строку и \(j\)-й столбец, в которых стоит элемент \(a_{ij}\). Из оставшихся элементов можно
составить новую квадратную матрицу (n-1)-го порядка, сдвинув строки и столбцы после вычеркивания.
Определитель построенной матрицы обозначают через \( M_{ij} \) и называют минором (матрицы \(A\) и её определителя
\(\Delta\) ), соответствующим элементу \(a_{ij}\).
{i+j} a_{ij} M_{ij} \tag{5} $$
( разложение по \(j\)-му столбцу )
Разложения по строке (4) и столбцу (5) дают правила, в соответствии с которыми определитель n-го порядка сводится к n
определителям (n-1)-го порядка, раскладывая которые получим n(n-1) определителей (n-2)-го порядка и т.д.
Эти вычисления получаются громоздкими, однако процесс упрощается, если среди элементов определителя имеется много нулей.
Целесообразно раскладывать определитель по тому ряду (строке, столбцу), в котором больше нулей.
Если же в этом смысле некоторые ряды одинаковы, то удобнее выбирать тот из них, в котором элементы имеют большие значения
по абсолютной величине, поскольку это упрощает выполнение арифметических вычислений.
Свойство 8. Определитель верхней (нижней) треугольной матрицы равен произведению элементов её главной диагонали,
т.е.
$$ \begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{vmatrix} = $$
$$ \begin{vmatrix}
a_{11} & 0 & \cdots & 0 \\
a_{21} & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{vmatrix} = $$
$$ a_{11}a_{22}.
n a_{ii} $$
С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы легко найти по свойству 8. В алгоритме приведения к ступенчатому виду используется перестановка строк, при которой определитель матрицы меняет знак. Изменение знака можно учесть, например, дополнительным умножением определителя или одной из строк на —1. Следовательно, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением значения её определителя.
Свойство 9. Определитель произведения двух квадратных матриц A, B равен произведению их определителей, т.е. \( |АВ| = |A||B| \).
Свойство 10. Определитель обратной матрицы: \( \left| А^{-1} \right| = \frac{1}{|A|} \)
Свойство 11.
{1+3} a_{13} M_{13} = $$
$$ a_{11} \begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \end{vmatrix}
– a_{12} \begin{vmatrix}
a_{21} & a_{23} \\
a_{31} & a_{33} \end{vmatrix}
+ a_{13} \begin{vmatrix}
a_{21} & a_{22} \\
a_{31} & a_{32} \end{vmatrix} = $$
$$ a_{11}a_{22}a_{33} – a_{11}a_{23}a_{32} – a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} – a_{13}a_{22}a_{31} $$
Чтобы запомнить, какие произведения элементов берутся со знаком \( “+” \), а какие со знаком \( “-” \) можно
использовать следующее правило треугольников.
Произведения элементов, стоящих на зелёных точках складываются, а на
синих – вычитаются :
Также для вычисления определителя 3-го порядка существует правило Саррюса.
Первый и второй столбцы матрицы записываются справа от основной матрицы.
Произведения элементов, стоящих на зелёных линиях складываются, а на
синих – вычитаются :
Обратная матрица и её свойства
Определение.
{-1}\), обратную к \(A\), фактически надо решить матричное уравнение \(AX=E\).
Отметим, что если над матрицей \(A\) выполняется какое-либо элементарное преобразование строк, то это же
преобразование осуществляется и над матрицей \(AX\), поскольку любое элементарное преобразование строк матрицы
эквивалентно умножению её слева на соответствующую матрицу специального вида. Таким образом, если в уравнении
\(AX=E\) над матрицами \(A\) и \(E\) одновременно выполнить какое-либо элементарное преобразование строк, т.е.
домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное
уравнение \(A_1X=B_1\). Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное
преобразование строк имеет обратное элементарное преобразование строк.
Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица \(A\)
превратилась в единичную матрицу.
В результате этих s шагов получается уравнение \(A_sX=B_s\), где \(A_s=E\), т.
{-1}\).
Ранг матрицы
Определение.Рангом матрицы называют число, которое равно максимальному порядку среди её ненулевых миноров.
Для ранга матрицы \(A\) используют обозначение \(\text{rang}A\).
Если квадратная матрица порядка n невырождена, то её ранг равен её порядку n : ненулевым является единственный
минор максимального порядка n, совпадающий с определителем матрицы.
В частности, ранг единичной матрицы \(E\) порядка n равен n.
Если квадратная матрица вырождена, то её ранг меньше её порядка : единственный минор максимального
порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок.
Ранг нулевой матрицы полагают равным нулю.
Ранг диагональной матрицы равен количеству её ненулевых диагональных элементов.
Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его
характеризующее.
T = \text{rang} A \)
Теорема. Ранг матрицы не меняется при элементарных преобразованиях её строк и столбцов.
Теорема о базисном миноре
Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.
Определение.
Минор \(M\) матрицы \(M\) называют базисным, если выполнены два условия:
1) он не равен нулю
2) его порядок равен рангу матрицы А
Матрица \(A\) может иметь несколько базисных миноров. Строки и столбцы матрицы \(A\), в которых расположен выбранный базисный минор, называют базисными.
Теорема о базисном миноре. Базисные строки (столбцы) матрицы \(A\), соответствующие любому её базисному минору \(M\), линейно независимы. Любые строки (столбцы) матрицы \(A\), не входящие в \(M\), являются линейными комбинациями базисных строк (столбцов).
Следствие. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы её
строки (столбцы) были линейно независимы.
Теорема. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).
Теорема. Для любой матрицы её ранг равен максимальному количеству её линейно независимых строк (столбцов).
Следствие. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.
Вычисление ранга матрицы
Метод окаймляющих миноров
Минор \(M’\) матрицы \(A\) называют окаймляющим для минора \(M\), если он получается из последнего
добавлением одной новой строки и одного нового столбца матрицы \(A\).
Ясно, что порядок окаймляющего минора \(M’\) на единицу больше, чем порядок минора \(M\).
Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем.
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы).
К очередному ненулевому минору
последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого
сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот
процесс рано или поздно закончится из-за ограниченных размеров матрицы.
Теорема. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.
Метод элементарных преобразований
При элементарных преобразованиях строк (столбцов) матрицы её ранг не меняется. С помощью этих преобразований можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.
Например с помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг
же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на
пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк.
Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его
окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных
преобразований строк позволяет вычислить ранг матрицы.
Приведенные два метода существенно отличаются друг от друга.
При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество
вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до
минимального из размеров матрицы. Однако в результате будет найден не только ранг матрицы, но и один из её
базисных миноров.
При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений.
Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением её вида. Но этот метод
позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных
преобразований.
Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже
известного ранга матрицы.
Онлайн калькуляторы матриц
В данном разделе содержатся онлайн калькуляторы для работы с матрицами. С помощью калькуляторов можно выполнять все основные действия над матрицами: сложение, умножение, находить определитель, обратную матрицу и др. Для каждого калькулятора доступно подробное решение задачи на русском языке.
Операции над матрицами 12
Сложение матриц Калькулятор позволяет сложить две матрицы. Подробное решение также доступно.
Вычитание матриц
Калькулятор находит разность двух матриц с описанием подробного хода решения на русском языке.
Умножение матриц Калькулятор позволяет найти произведение двух матриц. Подробное решение также присутствует.
Возведение матрицы в степень Калькулятор позволяет возвести матрицу в степень натурального числа. Подробное решение доступно на русском языке.
Вычисление ранга матрицы Калькулятор вычисляет ранг матрицы. Описание подробного хода решения представлено на русском языке.
Калькулятор матриц — простой, удобный и совместим со старыми смартфонами
Приближается новый учебный год, и многие студенты уже начали к нему готовиться, несмотря на солнечную погоду, которая настраивает скорее на развлечения, чем на серьезные занятия.
Среди того, что нужно современному студенту, — не только талант к математике, учебники, тетради и ручки, но и набор программных инструментов, который поможет в решении даже самых сложных задач. Одним из таких приложений является Калькулятор матриц от разработчика Koliuzhnov Viacheslav, которое можно загрузить из Google Play.
Приложение не только позволяет выполнять над матрицами различные действия, но и шаг за шагом последовательно отображает процесс выполняемых вычислений. Матрицы в рассматриваемом калькуляторе можно не только складывать и вычитать, но также умножать и возводить в степень. Матрица может быть также умножена на определенное число.
Кроме того, как следует из описания рассматриваемого приложения, с его помощью может быть найден детерминант матрицы или осуществлено ее транспортирование. Данный калькулятор предназначен в том числе и для решения систем линейных алгебраических уравнений (СЛАУ) методами Крамера и Гаусса.
Калькулятор дает возможность задать значения матриц (A, B) и указать их размерность (по умолчанию 3×3).
Матрица C — результат произведенных вычислений. В приложении, воспользовавшись специальными экранными кнопками, можно поменять матрицы местами (к примеру, [A⇿B]).
В настройках приложения (Настройки) могут быть заданы точность вычислений, размер шрифта математических формул и возможность не отключать экран в процессе работы приложения.
Умножение матрицы в данном приложении может осуществляться как на вещественное число, так и на простую дробь.
В дизайне приложения преобладает светло-серый цвет, удобный для зрительного восприятия и психологически настраивающий на то, что приложение предназначено для решения сложных математических задач и пользователю необходимо сосредоточиться на правильном вводе значений, не отвлекаясь на красочные элементы интерфейса. Страницы вычислений стилизованы под привычную студенческую тетрадь в клетку.
Отсутствие эстетических излишеств в значительной мере упрощает использование приложения, делая его интерфейс понятным даже для тех пользователей, которые не считают высшую математику своей сильной стороной.
Такой дизайнерский подход также позволяет осуществлять столь сложные вычисления даже на телефонах, которые помогают своим пользователям уже не первый год.
Приложением смогут воспользоваться обладатели девайсов под управлением операционных систем Android начиная с версии 2.3.3. Таким образом, рассматриваемый «Калькулятор матриц» доступен даже тем пользователям операционной системы Android, которые не считают нужным часто менять смартфон.
В Google Play присутствует также простой калькулятор интегралов и дифференциальных уравнений. Обладатели Android-устройств могут одним касанием решать квадратные уравнения и системы линейных уравнений. Рассмотренное приложение в очередной раз показывает, что смартфон — не только замена игровой консоли, но и мощный инструмент, помогающий достигать успехов в учебе.
Стало ли студентам с появлением Android-девайсов проще изучать точные науки?
- Приложение: Калькулятор матриц
- Разработчик: Koliuzhnov Viacheslav
- Категория: Образование
- Версия: 1.
5 - Цена: Бесплатно
- Скачать: Google Play
- Приложением уже заинтересовались: 262 человека
5Онлайн калькулятор: Приведенные ступенчатые матрицы
Этот онлайн калькулятор проводит пошаговое преобразование заданной матрицы к приведенному ступенчатому виду. Помимо решения – приведенной ступенчатой матрицы – калькулятор также показывает использованные на каждом шаге элементарные преобразования строк. Определения терминов, для тех, кто забыл, приведены, как обычно, под калькулятором.
Приведенные ступенчатые матрицы
1 2 0 1 0 0 0 0 0 3 0 0 0 0 1 3 1 0Точность вычисленияЗнаков после запятой:
Приведенный ступенчатый вид
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
content_copy Ссылка save Сохранить extension Виджет
Ступенчатая матрица
Ступенчатой матрицей, или матрицей ступенчатого вида по строкам, называется матрица, такая что
- все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками
- ведущий элемент (первый, считая слева направо, ненулевой элемент строки) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
Примеры ступенчатых матриц:
- нулевая матрица
- однострочная матрица
- единичная матрица
- верхнетреугольная матрица
Матрица, приведенная ниже, также является ступенчатой матрицей:
Приведенная ступенчатая матрица
Ступенчатая матрица называется приведенной, если матрица, составленная из всех ее основных столбцов, является единичной матрицей (столбец матрицы называется основным, если он содержит ведущий элемент какой-либо строки матрицы).
То есть, приведенная ступенчатая матрица не имеет нулевых строк, и все ведущие элементы ее строк равны единице. При этом все элементы основных столбцов, помимо ведущих элементов, являются нулями.
Матрица, приведенная ниже, является приведенной ступенчатой матрицей:
Преобразование матрицы к приведенному ступенчатому виду по строкам (каноническому виду по строкам)
Для приведения матрицы к ступенчатому или приведенному ступенчатому виду используются элементарные преобразования строк.
Каждая матрица может быть преобразована к уникальному приведенному ступенчатому виду.
Элементарные преобразования строк:
- перестановка местами любых двух строк матрицы
.
- умножение любой строки матрицы на ненулевую константу
- прибавление к любой строке матрицы другой строки, умноженной на некоторую ненулевую константу
.
Эти преобразования и используются калькулятором выше для приведения матрицы к каноническому виду по строкам.
RTI Доставка Матричные решения HDMI 2.0
Поддерживая видео 4K UHD, матрицы 4×4 и 8×8 обеспечивают HDMI, двунаправленный ИК-порт и PoC на расстоянии до 229 футов.
Персоналом RS
«VX44-18G-Kit, VX88-18G и VRX70-18G дополняют расширяющийся портфель решений RTI для распределения видео для поддержки стандарта HDBaseT 18 Гбит / с», – говорит Нил Эллсворт, директор RTI по управлению продуктами, AV. «Они изначально интегрируются в среду управления RTI с драйвером, встроенным в последнюю версию программного обеспечения RTI Integration Designer APEX, чтобы сэкономить время при каждой установке. Для конечных пользователей управление полностью находится в системе управления RTI, что обеспечивает простое и интуитивно понятное управление.”
Решения RTI с полной полосой пропускания поддерживают разрешение 4K UHD с частотой обновления 60 Гц и дискретизацией цветности 4: 4: 4, чтобы обеспечить четкое качество изображения и устранить размытость в боевиках. Устройства совместимы с HDCP 2.2 и поддерживают все известные аудиоформаты HDMI, включая Dolby TrueHD, Dolby Atmos, Dolby Digital Plus и DTS-HD Master Audio.
Матрицы VX44-18G-Kit и VX88-18G имеют четыре и восемь входов HDMI, соответственно, которые можно независимо направлять на четыре и восемь выходов HDBaseT.
Кроме того, каждое устройство предлагает одновременный выход HDBaseT / HDMI. Устройства обеспечивают понижающее преобразование видео для дисплеев с низким разрешением, а модуль интерфейса веб-браузера предлагает простую настройку.
Матрицы могут быть спарены с приемником VXR70-18G – VX44-18G-Kit поставляется в комплекте с четырьмя – который поддерживает повторную синхронизацию HDMI для решения проблем с HDMI HDCP, совместимостью и квитированием, а также поддерживает сквозную передачу ИК-сигналов на совместимые устройства HDBaseT. Для упрощения установки приемник питается от матриц через кабель Power over (PoC), что устраняет необходимость в дополнительных источниках питания.
Для получения дополнительной информации посетите www.rticorp.com.
Подписка
Чтобы получать больше подобных новостей и быть в курсе всех наших ведущих новостей, функций и аналитических материалов, подпишитесь на нашу рассылку новостей здесь.
Этот сайт использует файлы cookie для повышения производительности.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку “Назад” и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.
Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Matrix Solutions: внедрение национального процесса продаж медийной рекламы
Matrix внедряет национальный рабочий процесс продаж медийной рекламы
«Наш национальный рабочий процесс продаж рекламы демонстрирует нашу миссию, которой мы гордимся, учитывая нашу приверженность унификации разрозненных источников данных и развертыванию более автоматизированных процессов и рабочих процессов», – поделился Марк Горман, генеральный директор Matrix.
ПИТТСБУРГ (PRWEB)
26 января 2021 г.
Matrix, единственная глобальная платформа для продажи рекламы, созданная для СМИ, объявляет о новом рабочем процессе, который теперь доступен в рамках их платформы продаж медиа-рекламы Monarch для продавцов национальной медиа-рекламы. Устраняя необходимость собирать информацию воедино, национальный рабочий процесс автоматически агрегирует и доставляет необходимую информацию из нескольких источников в экосистеме продаж, что позволяет повысить эффективность прогнозирования будущих покупок рекламы на основе правильной информации в реальном времени.В свою очередь, это обеспечивает более надежное планирование и точность прогнозов для портфеля национальных продавцов.
Рабочий процесс продаж национальной рекламы, доступный в виде модуля для Monarch, позволяет продавцу прогнозировать доход, рыночный бюджет и обмениваться данными на платформе. Объединение информации позволяет системе лучше использовать эти данные, чтобы предупреждать продавцов о ключевых выводах и действиях, когда они отслеживают прогнозы относительно ожидаемых будущих расходов.
Monarch предлагает чистое объединение данных по всей национальной сбытовой организации, позволяя при необходимости выполнять более детальную детализацию.Используя интегрированные данные при поиске и переговорах, национальные продавцы могут прогнозировать более разумно и более эффективно.
Помимо агрегированных данных, национальные продавцы экономят время за счет автоматического создания сделок, определяемых интеграцией запросов предложений и предложений, которые затем автоматически сверяются с ожидающими и зарегистрированными долларами. Преимущества этого нового рабочего процесса распространяются на общую эффективность платформы Monarch как для национальной группы продаж, так и для всей организации, занимающейся продажами средств массовой информации.
«Наши усилия по развитию являются целенаправленными, целенаправленными и дальновидными, поэтому мы, как организация, остаемся верными нашей миссии и мантре« Мы имеем в виду СМИ », – поделился генеральный директор Matrix Марк Горман.
«Наш национальный рабочий процесс продаж рекламы демонстрирует нашу миссию, которой мы гордимся, учитывая нашу приверженность объединению разрозненных источников данных и развертыванию более автоматизированных процессов и рабочих процессов, чтобы не только дать нашим клиентам возможность продавать более эффективно и результативно, но и помочь целостно продвигать отрасль вперед.”
Для получения дополнительной информации о Matrix посетите matrixformedia.com, а для получения дополнительной информации о рабочем процессе свяжитесь с [email protected].
О Матрице
Matrix делает медиа реальностью, обеспечивая эффективность и работая над раскрытием доходов, чтобы медиа-компании могли создавать контент, развлекать и информировать. Его флагманский продукт, Monarch, – это единственная глобальная платформа для продаж рекламы, созданная для СМИ, которая преобразует хаотичные данные в действенную информацию о продажах, которая дает понимание, необходимое для поиска, управления, оценки и закрытия бизнеса.
Компания управляет доходом от медиа-рекламы на сумму более 13 миллиардов долларов, предлагая лучшую в своем классе аналитику, аналитику продаж, специализированные CRM для СМИ и инструменты продаж более чем 10 000 продавцов СМИ для более эффективного управления их рабочим процессом. Для получения дополнительной информации посетите http://www.matrixformedia.com.
Поделиться статьей в социальных сетях или по электронной почте:
Matrix Solutions Профиль компании: Финансирование и инвесторы
Обзор матричных решений
Обновите этот профиль- Тип последней сделки
- Выкуп / LBO
Matrix Solutions Общая информация
Описание
Разработчик программного обеспечения для управления взаимоотношениями с клиентами и аналитики, предназначенного для медиа-продаж.Компания специализируется на платформе CRM, данных и отчетности для СМИ и сетевых торговых организаций в Северной Америке.
Он преобразует данные в полезную информацию о продажах и обеспечивает рабочий процесс продаж в СМИ, чтобы предоставить точную информацию, необходимую для поиска, управления, оценки и закрытия бизнеса.
Контактная информация
Хотите покопаться в этом профиле?
Мы поможем вам найти то, что вам нужно
Учить большеMatrix Solutions Оценка и финансирование
| Тип сделки | Дата | Количество | Оценка / EBITDA | Пост-Вал | Статус | Долг |
|---|
Эта информация доступна на платформе PitchBook.Чтобы изучить полный профиль Matrix Solutions, запросите доступ.
Запросить бесплатную пробную версиюСравнение матричных решений
Описание
Первичная
Промышленность
Расположение штаб-квартиры
Сотрудников
Всего собрано
Постоценка
Подробная информация о последнем финансировании
Разработчик программного обеспечения для управления взаимоотношениями с клиентами и аналитики, предназначенного для медиа-продаж.
Компания специализируется на i
Программное обеспечение для бизнеса / повышения производительности
Питтсбург, Пенсильвания
110 По состоянию на 2014 г.
0.00 0000-00-00
000000000000
00000
аликва. Ut enim ad minim veniam, quis nostrud упражнения ullamco labouris nisi ut aliquip ex ea co
000000000000000000000 00000000
Маунтин-Вью, CA
0000
000000 и 0 0000
00000000
s aute irure dolor в репрезендерите в сладострастном velit esse cillum dolore eu fugiat nulla pariatur.
00000 000 00000000000 00000000 (000)
Сан-Франциско, Калифорния
000 По состоянию на 0000
0000
000000000 – 0000
Добавить сравнение Функция сравнения PitchBook дает вам параллельный обзор ключевых показателей для аналогичных компаний.Персонализируйте, какие точки данных вы хотите видеть, и мгновенно создавайте визуализации.
Matrix Solutions Конкуренты (29)
| Название компании | Статус финансирования | Расположение | Сотрудников | Всего собрано | Дата последнего финансирования / Тип | Сумма последнего финансирования |
|---|---|---|---|---|---|---|
| Вывод | Корпоративная поддержка или приобретение | Mountain View, CA | 0000 | 000000 и 0 | 0000 | |
| 000000000 | Обеспечение венчурным капиталом | Сан-Франциско, Калифорния | 000 | 0000 | 000000000 – | 0000 |
| 0000000000 | Обеспечение венчурным капиталом | Беркли, Калифорния | 000 | 000. 00 | 000000000 – | 000,00 |
| 000000000 | Обеспеченный частным капиталом | Нью-Йорк, NY | 000 | 000,00 | 000000000000 | 000,00 |
| 000-00 00000000 | Обеспеченный частным капиталом | Портленд, ИЛИ | 000 | 00000 | 0000000 0000 | 00000 |
Команда руководителей Matrix Solutions (6)
Обновите этот профиль| Имя | Название | Сиденье для борта | Контактная информация |
|---|---|---|---|
| Марк Горман JD | Главный исполнительный директор | ||
| Адам Готлиб | Главный технический директор | ||
| Бренда Хетрик | Директор по доходам | ||
| Бирен Бхаруча | Вице-президент по корпоративным продажам | ||
| Курт Эмерик | Вице-президент по операциям |
Получить полный список »Сигналы матричных решений
Скорость роста
0,80%
Еженедельный рост на
Еженедельный рост 0,80%, 93% ile
-35,5%. 530%
Множественный размер
219x Медиана
Множественный размер 219x, 100% ile
0,00x 0,95x. 413Kx
Ключевые точки данных
подписчиков на Twitter
5.5k
Similarweb Уникальные посетители
15.0K
Величественные ссылающиеся домены
314
Нефинансовые показателиPitchBook помогают оценить динамику роста компании и ее рост, используя присутствие в Интернете и социальные сети.
Запросить бесплатную пробную версиюMatrix Solutions Investors
| Имя инвестора | Тип инвестора | Холдинг | Инвестор с | Раундов участников | Контактная информация |
|---|
Эта информация доступна на платформе PitchBook.
Чтобы изучить полный профиль Matrix Solutions, запросите доступ.
Решение систем линейных уравнений с использованием матриц
Привет! Эта страница будет иметь смысл только тогда, когда вы немного знаете о системах линейных уравнений и матриц, поэтому, пожалуйста, пойдите и узнайте о них, если вы их еще не знаете!
Пример
Одним из последних примеров систем линейных уравнений был этот:
Пример: Решить
- х + у + г = 6
- 2y + 5z = −4
- 2x + 5y – z = 27
Затем мы решили его, используя метод «исключения»… но мы можем решить это с помощью Матриц!
Использование матриц упрощает жизнь, потому что мы можем использовать компьютерную программу (например, Матричный калькулятор), чтобы выполнять всю «обработку чисел».
Но сначала нам нужно написать вопрос в матричной форме.
в матричной форме?
ОК. Матрица – это массив чисел, верно?
Матрица
Ну, подумайте об уравнениях:
| x | + | y | + | z | = | 6 |
| 2 года | + | 5z | = | −4 | ||
| 2x | + | 5лет | – | z | = | 27 |
Их можно было бы превратить в таблицу чисел вот так:
| 1 | 1 | 1 | = | 6 | ||
| 0 | 2 | 5 | = | −4 | ||
| 2 | 5 | -1 | = | 27 |
Мы могли бы даже разделить числа до и после “=” на:
| 1 | 1 | 1 | 6 | |
| 0 | 2 | 5 | и | −4 |
| 2 | 5 | -1 | 27 |
Теперь похоже, что у нас есть 2 матрицы.
На самом деле у нас есть третий, это [x y z]:
Почему [x y z] идет туда? Потому что, когда мы умножаем матрицы, левая часть становится:
Это исходная левая часть приведенных выше уравнений (вы можете это проверить).
Матричное решение
Мы можем написать это:
как это:
AX = B
где
- A – это матрица 3×3 коэффициентов x, y и z
- X – это x, y и z, и .
- B – это 6, −4 и 27
Тогда (как показано на странице инверсии матрицы) решение следующее:
X = A -1 B
Что это значит?
Это означает, что мы можем найти значения x, y и z (матрица X), умножив , инверсную матрицу A , на матрицу B .
Итак, давайте продолжим и сделаем это.
Во-первых, нам нужно найти , обратную матрице A (при условии, что она существует!)
Используя Матричный калькулятор, получаем:
(я оставил определитель 1 / вне матрицы, чтобы упростить числа)
Затем умножьте A -1 на B (мы снова можем использовать Матричный калькулятор):
И готово! Решение:
x = 5,
y = 3,
z = −2
Как и на странице Системы линейных уравнений.
Довольно изящный и элегантный, человек думает, а компьютер производит вычисления.
Просто для удовольствия … Сделай это снова!
Для развлечения (и для того, чтобы помочь вам учиться), давайте сделаем все это снова, но сначала поставим матрицу «X».
Я хочу показать вам этот путь, потому что многие люди думают, что решение, приведенное выше, настолько изящно, что это, должно быть, единственный способ.
Так что решим так:
XA = B
И из-за способа умножения матриц нам нужно настроить матрицы по-другому.Строки и столбцы необходимо поменять местами («транспонировать»):
И XA = B выглядит так:
Матричное решение
Тогда (также показано на странице инверсии матрицы) решение следующее:
X = BA -1
Это то, что мы получаем для A -1 :
На самом деле он похож на инверсию, которую мы получали раньше, но транспонированную (строки и столбцы меняются местами).
Затем умножаем B на A -1 :
И решение то же:
x = 5, y = 3 и z = −2
Это не выглядело так красиво, как предыдущее решение, но оно показывает нам, что существует более одного способа составления и решения матричных уравнений.Только будьте осторожны со строками и столбцами!
Покрытия для адгезии клеток| Факторы привязанности | ECM | Ламинин | Коллаген | Фибронектин | PDL
2017
2016
2015
2014
Камос, С., К. Губерн, М. Собрадо, Р. Родригес, В. Ромера, М. Моро, И. Лизасоайн, Х. Серена, Дж. Маллолас и М. Кастелланос. 2014. Фактор транскрипции I-Y группы высокой подвижности участвует в ишемии головного мозга и модулирует экспрессию ангиогенных белков.Неврология, 269: 112-130. Узер, Г., С. Понгкитвитун, К. Ян, У. Томпсон, Дж. Рубин, М. Чан и С. Джудекс. 2014.
Связь по щелевому соединению в остеоцитах усиливается вибрациями низкой интенсивности in vitro. PLoS ONE, 10 марта.
2012
ДеКостер М., Дж. Макнамара, К. Коттон, Д. Грин, К. Джеясанкар, Р. Идову, К. Эванс, З. Син и Ю. Львов. Бионанокомпозиты для многомерной передачи сигналов в клетках мозга. Гл. 8. У Томаса, С., Н. Нинана, С. Мохана и Э. Фрэнсиса.2012. Природные полимеры, биополимеры, биоматериалы, композиты, смеси и IPNS. Успехи материаловедения, Том 2.
Лю, Б. 2012. Роль GRK2 в артериальной гипертензии и регуляции GPR30. Магистерская диссертация, Университет Западного Онтарио.
Нотон, Г., Дж. Мэнсбридж, Р. Пинни и Дж. Зелтингер. 2012. Методы использования трехмерной стромальной ткани для стимуляции ангиогенеза. Патент США 8128924 B2.
Узер, Г. 2012. Роль жидкостной модуляции сдвига на метаболизм костных клеток во время высокочастотных колебательных колебаний.Докторская диссертация, Stony Brook U.
2010
Шейх-Али, М.
, С. Султан, А.-Р. Аламир, М.Дж. Хаас и А.Д. Мурадян. 2010a. Влияние антиоксидантов на оксидативный стресс, вызванный глюкозой, и стресс эндоплазматического ретикулума в эндотелиальных клетках. Исследования и клиническая практика диабета. 87: 161-166.
Шейх-Али, М., С. Султан, А.-Р. Аламир, М.Дж. Хаас и А.Д. Мурадян. 2010b. Стресс эндоплазматического ретикулума в эндотелиальных клетках, вызванный гипергликемией. Питание.26: 1146-1150.
2009
Хендрикс-Балк, М., Дж. Унен, Х. Берт и Дж. Батлер. 2009. Исчезновение внеклеточного S1P: влияние на сигнальную активность. Источник: Balk, M. 2009. Регулирование сердечно-сосудистой передачи сигналов GPCR. Кандидатская диссертация, Университет Амстердама.
патентов присвоено CONCEPT MATRIX SOLUTIONS
Номер публикации: 201
Abstract: Пленки (ODF), содержащие растительные экстракты, представлены, а также способы их изготовления и использования.
Тип: Заявление
Зарегистрирован: 25 апреля 2019 г.,
Дата публикации: 5 сентября 2019 г.,
Заявитель: Концептуальные матричные решения
Изобретателей: Эрик Аллен, Роберт Дэвидсон, Тони ЛаРоса, Дэвид Рид
.