Решетка шифр: Кабинет Информатики – Шифр «Решетка Кардано»

Кабинет Информатики – Шифр «Решетка Кардано»

Шифр «Решетка Кардано»

 Даже если вы не разбираетесь в автомобилестроении, то наверняка слышали о каком-то карданном вале. Это такая деталь, которая передает крутящий момент от коробки передач или раздаточной коробки к редуктору переднего или заднего моста. Джероламо придумал этот шарнирный механизм, но, помимо «автомобильного» изобретения, у Кардано было много других блестящих идей, например о пользе переливания крови. Еще одно изобретение Кардано – шифрование по трафарету или решётке.

 «Решётка Кардано» знакома каждому, кто хоть раз смотрел бессмертный советский сериал с Василием Ливановым в роли Шерлока Холмса. В заглавных титрах одной из серий этого фильма показана идея шифрования решёткой Кардано – из массы бессмысленных символов сквозь прорези в нужных местах решётки как будто проступал осмысленный текст.

 «Решётка Кардано» может быть двух видов – простая и симметрично-поворотная.

В первом случае для шифрования применяется трафарет с отверстиями, через которые «фильтруется» полезный текст. Другой вариант решетки, более интересный, состоит в том, чтобы использовать симметричный (квадратный) трафарет, который можно применять несколько раз, просто поворачивая его вокруг центра. Поворотная решётка Кардано позволяет записать текст массивом символов так, что результат будет выглядеть совершенно нечитаемым.

 «Решётка Кардано» – инструмент кодирования и декодирования, представляющий собой специальную прямоугольную (в частном случае – квадратную) таблицу-карточку, часть ячеек которой вырезана.

 Решётка не имеет жесткого шаблона, она сделана из листа картона или пергамента, или же из тонкого металла. Чтобы обозначить линии письма, бумагу разлиновывают, и между этими линиями вырезают прямоугольные области через интервалы произвольной длины.

 Шифратор помещает решетку на лист бумаги и пишет сообщение в прямоугольных отверстиях, в которых помещается отдельный символ, слог или целое слово. Исходное сообщение оказывается разделенным на большое число маленьких фрагментов. Затем решетка убирается, и пустые места на бумаге заполняются посторонним текстом так, чтобы скрываемый текст стал частью другого текста. Такое заполнение требует известного литературного таланта.

 Для расшифровки у получателя сообщения должна быть такая же решетка.

---

Текст записки: Сэр Джон высоко ценит Вас и снова повторяет, что все, что доступно ему, теперь ваше, навсегда. Может ли он заслужить прощение за свои прежние промедления посредством своего обаяния.

Шифрованное послание: В мае Испания направит свои корабли на войну.

---

 Шифрование с помощью решёток применяется для защиты информации, представляющую ценность в течение ограниченного времени (несколько часов). Этот шифр также является перестановочным, т.е. криптограммы этого шифра представляют собой анаграммы открытого текста. Данный метод шифрования активно применялся во время второй мировой войны, и до сих пор используется в качестве армейского шифра.

2:

 Поворачиваем квадрат на 90 градус по часовой стрелке и приписываем справа от исходного квадрата:

1	2	3	7	4	1
4	5	6	8	5	2
7	8	9	9	6	3

 Поворачивая на 90 градусов по часовой стрелки и добавляя полученный квадрат сначала снизу, а затем слева от предыдущего, получим следующий квадрат со стороной 2k:

1	2	3	7	4	1
4	5	6	8	5	2
7	8	9	9	6	3
3	6	9	9	8	7
2	5	8	6	5	4
1	4	7	3	2	1

 В этом квадрате закрасим произвольным образом все цифры, причем каждая цифра может быть закрашена только один раз.

Вот например:

1	2	3	7	4	1
4	5	6	8	5	2
7	8	9	9	6	3
3	6	9	9	8	7
2	5	8	6	5	4
1	4	7	3	2	1

 Это и будет решёткой для шифрования. Код для шифрования представляет последовательность k цифр от 1 до 4, i-тая цифра обозначает в каком подквадрате (нумеруются в порядке создания) закрашивать число i(например, для этой таблицы код решетки имеет вид: 242431134). Асимптотическая сложность шифра – 4^k^2(для этой решетки – 262144). 2. Решетка накладывается на пустой лист бумаги, закрашиваемые клетки вырезаются. Для первой подстроки ее i-ый символ записывается в вырезанное i-ое число решетки. Повторяем процесс еще 3 раза, поворачивая перед этим решетку на 90 градусов по часовой стрелке. В результате получаем таблицу, составляющую из символов открытого текста. Криптограмма из этой таблицы получается путем построчного выписывания символов или применения приемов маршрутного шифрования.

Пример
 Пусть задан открытый текст: ТЕКСТ ПОСЛЕ ШИФРОВАНИЯ СТАНЕТ НЕПОНЯТНЫМ
 В качестве кодирующей решетки возьмем выше взятый пример. В результате запись первого блока (ТЕКСТПОСЛ) запишется с помощью решетки так:

					Т
		П
О					К
		Л		С
Е				Т
	С

 Повторив эту операцию для других трех блоков, повернув перед каждой операции решетку на 90 градусов по часовой стрелки, получим итоговую таблицу:

Е	Ш	О	В	Т	Т
Ф	А	П	Ы	Я	Я
О	Т	Н	Н	О	К
С	Т	Л	М	С	Е
Е	Р	А	Н	Т	Н
И	С	Н	И	П	Е

 Из этой таблицы криптограмма получается выписыванием символов по любому маршруту.

 

 Остаётся добавить, что применение решёток Кардано обеспечивает сравнительно высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано неподготовленным незаконным пользователем. Однако для специалиста взлом такого шифра не представляет особых трудностей.
 

 Чтобы вам было легче разобраться с принципом построения решётки, скачайте приложение Владимира Беглецова «Шифратор решетки Кардано». С помощью этой программы можно генерировать решетку разной размерности, а также кодировать и расшифровывать текстовое сообщение.

Поворотная решётка | kriptografia

Шифр “Поворотная решетка”

Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера 2m*2k клеток. В трафарете вырезано m*k клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа. Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке.

 

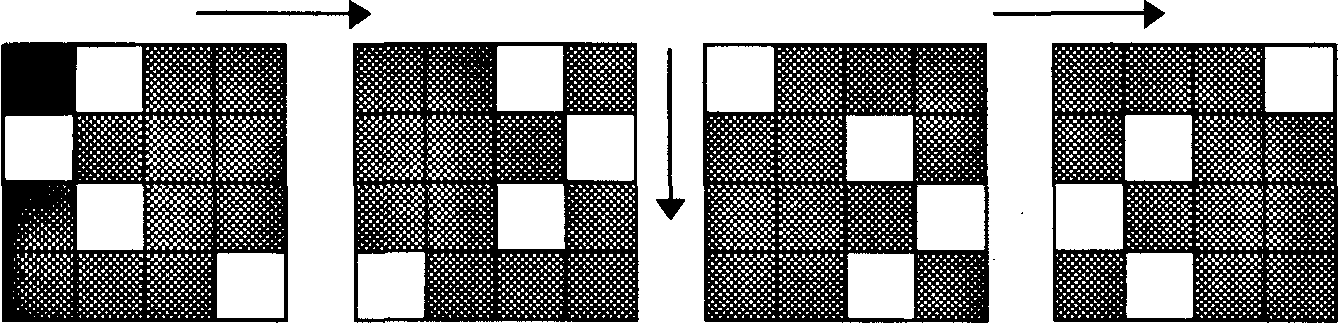
Поясним процесс шифрования на примере. Пусть в качестве ключа используется решетка 6*10, приведенная на рис.1:

 

 

 

 

 

 

 

 

 

Зашифруем с ее помощью текст:

 

ШИФРРЕШЕТКАЯВЛЯЕТСЯЧАСТНЫМСЛУЧАЕМШИФРАМАРШРУТНОЙПЕРЕСТАНОВКИ

 

Наложив решетку на лист бумаги, вписываем первые 15 (по числу вырезов) букв сообщения: ШИФРРЕШЕТКАЯВЛЯ…. Сняв решетку, мы увидим текст, представленный на рис. 2. Поворачиваем решетку на 180 градусов. В окошечках появятся новые, еще не заполненные клетки. Вписываем в них следующие 15 букв. Получится запись, приведенная на рис. 3. Затем переворачиваем решетку на другую сторону и зашифровываем остаток текста аналогичным образом (рис. 4, 5).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получатель сообщения, имеющий точно такую же решетку, без труда прочтет исходный текст, наложив решетку на шифртекст по порядку четырьмя способами.

 

Можно доказать, что число возможных трафаретов, то есть количество ключей шифра “решетка”, составляет T=4mk (см. задачу 1). Этот шифр предназначен для сообщений длины n=4mk . Число всех перестановок в тексте такой длины составит (4mk)! , что во много раз больше числа T. Однако, уже при размере трафарета 8*8 число возможных решеток превосходит 4 миллиарда.

 

Широко распространена разновидность шифра маршрутной перестановки, называемая “шифром вертикальной перестановки” (ШВП). В нем снова используется прямоугольник, в который сообщение вписывается обычным способом (по строкам слева направо). Выписываются буквы по вертикали, а столбцы при этом берутся в порядке, определяемом ключом. Пусть, например, этот ключ таков: (5,4,1,7,2,6,3), и с его помощью надо зашифровать сообщение:

 

ВОТПРИМЕРШИФРАВЕРТИКАЛЬНОЙПЕРЕСТАНОВКИ

 

Впишем сообщение в прямоугольник, столбцы которого пронумерованы в соответствии с ключом:

 

 

 

 

 

 

 

 

Теперь, выбирая столбцы в порядке, заданном ключом, и выписывая последовательно буквы каждого из них сверху вниз, получаем такую криптограмму:

 

ОРЕЬЕКРФИЙА-МААЕО-ТШРНСИВЕВЛРВИРКПН-ПИТОТ-

 

Число ключей ШВП не более m!, где m – число столбцов таблицы.

Как правило, m гораздо меньше, чем длина текста n (сообщение укладывается в несколько строк по m букв), а, значит, и m! много меньше n!.

 

Пользуясь приведенной выше формулой Стирлинга при больших m и n, попытайтесь оценить, во сколько раз число возможных перестановок ШВП с m столбцами меньше числа всех перестановок на тексте длины n, кратном m. В случае, когда ключ ШВП не рекомендуется записывать, его можно извлекать из какого-то легко запоминающегося слова или предложения. Для этого существует много способов. Наиболее распространенный состоит в том, чтобы приписывать буквам числа в соответствии с обычным алфавитным порядком букв. Например, пусть ключевым словом будет ПЕРЕСТАНОВКА. Присутствующая в нем буква А получает номер 1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает номер 2. Поскольку буквы Б в этом слове нет, то буква В получает номер 3 и так далее. Процесс продолжается до тех пор, пока все буквы не получат номера.

Таким образом, мы получаем следующий ключ:

 

П  Е   Р   Е   С   Т   А  Н  О  В  К  А

9  4  10  5  11 12  1  7   8  3   6  2

 

Перейдем к вопросу о методах вскрытия шифров перестановки. Проблема, возникающая при восстановлении сообщения, зашифрованного ШП, состоит не только в том, что число возможных ключей велико даже при небольших длинах текста. Если и удастся перебрать все допустимые варианты перестановок, не всегда ясно, какой из этих вариантов истинный. Например, пусть требуется восстановить исходный текст по криптограмме АОГР, и нам ничего не известно, кроме того, что применялся шифр перестановки. Какой вариант “осмысленного” исходного текста признать истинным: ГОРА или РОГА? А может быть АРГО? Приведем пример еще более запутанной ситуации. Пусть требуется восстановить сообщение по криптограмме

 

ААНИНК-ТЕОМЛ,З.ЬЬЗИВТЛП-ЬЯО,

 

полученной шифром перестановки. Возможны, как минимум, два варианта исходного сообщения:

 

КАЗНИТЬ,-НЕЛЬЗЯ-ПОМИЛОВАТЬ.

и

КАЗНИТЬ-НЕЛЬЗЯ,-ПОМИЛОВАТЬ.

 

У этих вариантов прямо противоположный смысл, и в имеющихся условиях у нас нет возможности определить, какой из вариантов истинный.

Классические шифры перестановки. Шифр вертикальной перестановки[править

Шифры подстановки (замены) основаны на алгебраической операции, называемой подстановкой. Подстановкой называется взаимно-однозначное отображение конечного множества M на себя. Число N элементов множеств называется степенью подстановки. Количество n чисел действительно перемещаемых подстановкой называется длиной цикла подстановки.

Шифры перестановки – это шифр, преобразование из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих.

Слабость шифров замены. Если в открытом сообщении часто встречается какой-то символ, то в шифрованном сообщении с такой же частотой встречается соответствующий символ. При больших объемах текста это приводит к успешному криптоанализу. Таким образом, на одном ключе нельзя шифровать достаточно длинные сообщения.

Сети (как элемент шифрования) – любой блочный шифр является комбинацией первых двух схем. Использование понятия «сети» в блочном шифровании заключается в многократном повторении исходных операций (повторения – циклы или раунды, а сами операции – слоями). Некоторые из слоев могут содержать ключи. Это позволяет:

1. Сделать шифр легко усложняемым (за счет увеличения количества раундов)
2. Сократить размера программного кода
3. Унифицировать алгоритмическую формулу шифрования

Сеть Фейсиля (Файсиля) – Feistel – это способ построения цикла шифрования в алгоритмах шифрования итеративных на основе регистра сдвига, с функцией обратной связи, зависящей от раундового ключа (оптимальное число раундов от 8 до 32)

DES – федеральный стандарт шифрования США (1997-2001).

Архитектура – классическая, сбалансированная сеть Фейсиля с начальными и конечными битовыми перестановками общего вида. Размер ключа – 56 бит. На его основе – международный стандарт ISO 8372-87. Алгоритм предназначен для шифрования данных 64-битовыми блоками.

DES представляет собой комбинацию двух основных методов:

1. Подстановка
2. Перестановка.

К тексту применяется единичная комбинация этих двух методов.

DES включает 16 раундов, то есть одна и та же комбинация методов применяется к открытому тексту 16 раз.

Наложение ключа-раунда производится операцией XOR

Исходный текст=>Начальная перестановка=>Шифрование * 16(Конечная перестановка=>шифротекст

Цель начальной перестановки – равномерно распределить по блокам рядом стоящие биты.

Для зашифрования и расшифрования можно использовать одну и ту же функцию, но ключи используются в обратном порядке.

DES предусматривает 4 типа работы:

1. ECB-электронный шифр-блокнот. Открытый текст обрабатывается блоками по 64 бит, шифруемых одним ключом
2. CBC – цепочка блоков. Устраняет недостаток первого режима. Входное значение алгоритма зашифрования задается равным XOR-разности текущего блока открытого текста и полученного на предыдущем шаге блока шифрованного текста. Таким образом, все блоки исходного текста оказывается связанными (текст=>зашифрованный текст=>XOR=>текст=>зашифрованный текст)
3. CFB – обратная связь по шифро-тексту. Алгоритм преобразуется в поточный шифр, то есть каждый символ можно зашифровать и сразу передавать получателю
4. OFB – обратная связь по выходу. В регистр сдвига подается порция зашифрованного текста. Для каждого сеанса шифрования используется новое начальное состояние регистра.

Считается, что четырех режимов достаточно, чтобы использовать DES в практически любой области, для которой этот алгоритм подходит

Аппаратная реализация алгоритма на отдельной микросхеме позволяет достичь высокой скорости шифрования при незначительных габаритах устройства.

AES-федеральный стандарт шифрования США, используемый в настоящее время.

AES – улучшенный стандарт шифрования.

Требования:

1. Шифр должен быть блочным
2. Шифр должен иметь длину блока, равную 128 битам
3. Шифр должен поддерживать ключи длиной 128, 192, 256 бит

Алгоритм является нетрадиционным блочным шифром, поскольку не использует сеть Фейштеля для криптопреобразований.

Алгоритм представляет каждый блок кодируемых данных в виде двумерного массива байтов размером 4х4, 4х6 или 4х8 в зависимости от установленной длины блока.

Алгоритм состоит из определенного количества раундов (от 10 до 14 – это зависит от размера блока и длины ключа).

ГОСТ 28147089 – стандарт РФ на шифрование и имитозащиту данных.

Алгоритм предназначен для аппаратной и программной реализации, удовлетворяет необходимым криптографическим требования и не накладывает ограничений на степень секретности защищаемой информации.

Алгоритм реализует шифрование 64-битовых блоков данных с помощью 256-битового ключа, состоящего из восьми 32-битовых подключей.

На каждом i-м раунде используется K­ i -й подключ.

Алгоритмы шифрования ГОСТ 28147-89 обладают достоинствами других алгоритмов для симметричных систем и превосходят их своими возможностями.

На каждом i-м раунде алгоритма ГОСТ выполняется следующие операции:

L i =R i -1 , R i =L i -1 (плюсвкружочке)f(R i -1 , K i)

После выполнения этих 32 операций реализация алгоритма шифрования будет завершена.

Достоинством ГОСТ является наличие защиты от навязывания ложных данных (режим имитовставки), а также одинаковый цикл шифрования во всех 4 режимах (алгоритмах) ГОСТ.

Высокая криптостойкость обеспечивается за счет большой длины ключа (256 бит) и 32 раундов преобразования.

Стандарт включает режимы (алгоритмы):

1. Режим простой замены
2. Режим гаммирования
3. Режим гаммирования с обратной связью
4. Режим выработки имитовставки

Асимметричные алгоритмы шифрования.

В асимметричных алгоритмах шифрования (или криптографии с открытым ключом) для зашифрованной информации используют один ключ (открытый), а для расшифровывания – другой (секретный)

Эти ключи различны и не могут быть получены один из другого.

Схема обмена информацией:

1. Получатель вычисляет открытый и секретный ключи секретный ключ хранит в тайне, открытый же делает доступным (сообщает отправителю, группе пользователей сети, публикует)
2. Отправитель, используя открытый ключ получателя, зашифровывает сообщение, которое пересылается получателю
3. Получатель получает сообщение и расшифровывает его, используя свой секретный ключ

Использование асимметричного метода шифрования

Применение таких шифров стало возможным благодаря К. Шеннону, предложившему строить шифр таким способом, чтобы его раскрытие было эквивалентно решению математической задачи, требующей выполнения объемов вычислений, превосходящих возможности современных ЭВМ (например, операции с большими простыми числами и их произведениями; нахождение значения произведения P=x*y)

Криптосистема шифрования данных RSA.

В настоящее время наиболее развитым методом криптографической защиты информации с известным ключом является RSA, названный так по начальным буквам фамилий её изобретателей (Rivest, Shamir, Adleman)

Чтобы использовать алгоритмы RSA, надо сначала сгенерировать открытый и секретный ключи, выполнив следующие шаги:

1. Выбрать два очень больших простых числа p и q и определить n как результат умножения p на q (n=p*q)
2. Выбрать большое случайное число d. Это число должно быть взаимно простым с m результатом умножения (p-1)(q-1)
3. Определить такое число e, для которого является истинным следующее соотношения (e*d)mod(m)=1 или e=(1mod(m))/d
4. Открытым ключом будут числа e,n, а секретным ключом – числа d,n

Красным выделено создание ключа.

Асимметрические криптосистемы на базе эллиптических кривых.

На базе эллиптических кривых Е можно реализовать не только криптоалгоритмы асимметричного шифрования, но и выработки общего секретного ключа для симметричного шифрования.

Криптосистемы на базе эллиптических кривых позволяют использовать существенно меньшие размеры ключей по сравнению с другими криптоалгоритмами при сохранении одинакового уровня криптостойкости.

Для перечисленных выше реализаций используются эллиптические кривые над полями Галуа GF(p) конечным числом p элементов двух видов:

1. Эллиптическая кривая над конечным полем типа E(GF(p)), где р – некоторое простое число
2. Эллиптическая кривая над конечным полем типа E(GF(2m)), где p=2m

Пример: Алгоритм асимметричного шифрования на базе эллиптических кривых ECES (Elliptic Curve Encryption Scheme)

Алгоритм Эль-Гамаля.

Система Эль-Гамаля – это криптосистема с открытым ключом, основанная на проблеме вычисления логарифма. Данный алгоритм используется как для шифрования, так и для цифровой подписи.

Множество параметров системы включает простое число p и целое g, степени которого по модулю p порождают большое число элементов Z p

Методы замены.

Шифр замены замещает одни символы другими, но сохраняет порядок их следования в сообщении.

4 типа замены (подстановки):

1. Моноалфавитная. Формула = Y i =k 1 X i +k 2 (modN), где Y i – i-символ алфавита, k 1 , k 2 – константы, Х i – i-символ открытого текста, N – длина используемого алфавита.

Пример. Замена – открытый текст, Ключ – Ключ

1. Гомофоническая замена – замена одному символу открытого текста ставит в соответствие несколько символов шифртекста. Этот метод применяется для искажения статистических свойств шифротектста. Используется подстановка таблицей. Значения используются поочередно из столбца.

1. Полиалфавитная замена – использование нескольких алфавитов. Смена алфавита идет на каждом шаге шифрования. Используется ступеньчатая замена букв по таблице.
2. Полиграммная замена – формируется из одного алфавита с помощью специальных правил. Шифр располагается в матрице, а открытый текст разбивается на пары символов XiXi+1

Шифры перестановки.

Отличие шифра перестановки – изменяется только порядок следования символов сходного текста, но не изменяют их самих.

Пример. Текст «Грузите апельсины бочками Братья Карамазовы»

Шифротекст «Птр_аезгуионл_бысеьит_крабмчаизрямаакь_а__в____оы»

Шифр перестановки «скитала». В V в. до н.э. правители греческого государства Спарты имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью скитала, первого простейшего криптографического устройства, реализующего метод простой перестановки (рис. 1.6).

Рис. 1.6.

Шифрование выполнялось следующим образом. На стержень цилиндрической формы, который назывался скитала, наматывали спиралью (виток к витку) полоску кожи и писали на ней вдоль стержня несколько строк текста сообщения. Затем снимали со стержня полоску – буквы на ней оказывались расположенными вразнобой.

Вестник обычно прятал сообщение, используя кожаную полосу как пояс, т.е. кроме шифрования применяли также и стеганографию. Чтобы получить исходное сообщение, полоску кожи надо намотать вокруг скиталы того же диаметра. Ключом этого шифра является диаметр стержн я – с к итал ы. Зная только вид шифра, но не имея ключа, расшифровать сообщение непросто. Шифр «скитала» многократно совершенствовался в последующие времена.

Способ взлома этого шифра предложен Аристотелем. Надо изготовить длинный конус и, начиная с основания, обертывать его лентой с шифрованным сообщением, постепенно сдвигая к вершине. В какой-то момент начнут просматриваться куски сообщения. Диаметр конуса в этом месте соответствует диаметру скиталы.

Шифрующие таблицы. Одним из самых примитивных табличных шифров перестановки является простая перестановка, для которой ключом служит размер таблицы. Этот метод шифрования в простейшем варианте сходен с шифром «скитала». Например, текст сообщение записывается в таблицу определенного размера в столбик, а считывается но строкам.

Запишем фразу «Терминатор прибывает седьмого в полночь» в таблицу размером 5×7 (рис. 1.7) но столбцам. Выписав текст из таблицы построчно, получим шифр: «тннвеглеарадонртиеьвомобтмнчирысооь».

Рис. 1.7.

Отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. При расшифровке действия выполняют в обратном порядке (построчная запись, чтение по столбцам).

Этот шифр может быть несколько усложнен: например, столбцы могут быть переставлены в некоторой последовательности, определяемой ключом. Возможна двойная перестановка – столбцов и строк.

Решетка Кардано. Решетка Кардано (поворотная решетка) – это прямоугольная или квадратная карточка с четным числом строк и столбцов 2k X 2т. В ней проделаны отверстия таким образом, что при последовательном отражении или поворачивании и заполнении открытых клеток карточки постепенно будут заполнены все клетки листа.

Карточку сначала отражают относительно вертикальной оси симметрии, затем – относительно горизонтальной оси, и снова – относительно вертикальной (рис. 1.8).

Если решетка Кардано – квадратная, то возможен и другой вариант ее преобразований – поворот на 90° (рис. 1.9).

Рис. 1.8.

Рис. 1.9.

При записи обычным способом (слева направо и сверху вниз) словосочетания «шифрование текста» (без пробелов) в свободные клетки поворотной решетки, изображенной на рис. 1.9, получим текст в виде таблицы (рис. 1.10), или, записав текст в одну строку, – «кшииоесвтафатрен».

Рис. 1.10.

Получатель должен знать трафарет и наложить его в той же последовательности, что и при шифровании. Ключом является выбранный тип перемещения решетки (отражение или поворот) и трафарет – расположение отверстий, которые для квадратной решетки размером 2т х 2к могут быть выбраны 4″”* способами (с учетом начальной ориентации трафарета). В этом случае среди трафаретов, считающихся различными, будут встречаться такие, которые являются зеркальным отражением или поворотами других трафаретов, т.е. трафареты, различающиеся только начальным расположением (ориентацией). Если пренебречь начальным расположением трафарета, то, очевидно, различных трафаретов будет в 4 раза меньше – 4″”*”

Например, для решеток размером 4X4 существует 256 возможных вариантов трафарета (с учетом начальной ориентации) или всего 64 различных трафаретов.

Несмотря на то, что число трафаретов для больших решеток достаточно велико (порядка 4 млн (4- 10 е)), оно все же существенно меньше, чем случайных перестановок элементов таблицы, число которых равно (2т? 2k).

Например, для таблицы размером 4×4 число случайных перестановок составляет порядка 2 ? 10 13 , а для таблиц размером 8×8 – около 10 89 .

Решетки Кардано, так же как и шифрующие таблицы, являются частными случаями шифра маршрутной перестановки.

Этот метод заключается в том, что символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока символов, т.е. преобразования приводят к изменению только порядка следования символов исходного сообщения. Рассмотрим некоторые наиболее часто встречающиеся разновидности этого метода – простую, усложненную по таблице и усложненную по маршрутам перестановку.

Шифрование простой перестановкой (вертикальной перестановкой) осуществляется следующим образом:

1) выбирается ключевое слово с неповторяющимися символами;

2) шифруемый текст записывается последовательными строками под символами ключевого слова;

3) зашифрованный текст выписывается колонками в той последовательности, в которой располагаются в алфавите буквы ключа (или в порядке следования цифр в натуральном ряду, если ключ цифровой).

В качестве иллюстрации приведем пример шифрования способом простой перестановки сообщения: «БУДЬТЕ ОСТОРОЖНЫ С ПРЕДСТАВИТЕЛЕМ ФИРМЫ “ФЕНИКС”. При этом применим цифровой ключ 5 – 8 – 1 – 3 – 7 – 4 – 6 – 2. В исходном тексте вместо пробелов используется буква а.

Б	У	Д	Ь	Т	Е	а	О
С	Т	О	Р	О	Ж	Н	Ы
А	С	а	П	Р	Е	Д	С
Т	А	В	И	Т	Е	Л	Е
М	а	Ф	И	Р	М	Ы	а
Ф	Е	Н	И	К	С	а	а

Выписывая текст по колонкам и группируя символы по пять, получаем зашифрованный текст в виде:

ДО ВФ НОЫСЕ ЬРП ИИИЕЖ ЕЕМСБ С ТМФ НДЛЫ TOPT РКУТС A E .

Расшифрование выполняется в следующем порядке:

1) подсчитываем число знаков в зашифрованном тексте и делим на число знаков ключа;

2) выписываем ключевое слово и под его знаками в соответствующей последовательности выписываем символы зашифрованного текста в определенном выше количестве;

3) по строкам таблицы читаем исходный текст.

Число ключей не более m!, где m – число столбцов таблицы.

Слабость шифрования простой перестановкой обуславливается тем, что при большой длине шифруемого текста в зашифрованном тексте могут проявиться закономерности символов ключа. Для устранения этого недостатка можно менять ключ после зашифровки определенного числа знаков. При достаточно частой смене ключа стойкость шифрования можно существенно повысить. При этом, однако, усложняется организация процесса шифрования и расшифрования.

Для получения и запоминания числового ключа существуют различные методы. Один из самых распространенных состоит в том, чтобы приписывать буквам числа в соответствии с алфавитным порядком букв. Возьмем, например, слово ПЕРЕСТАНОВКА. Присутствующая в нем буква А получает №1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает №2. Буквы Б в этом слове нет, то буква В получает №3, и т.д.:

П	Е	Р	Е	С	Т	А	Н	О	В	К	А

Усложнение перестановки по таблице заключается в том, что для записи символов шифруемого текста используется специальная таблица, в которую введены некоторые усложняющие элементы. Усложнение состоит в том, что определенное число клеток таблицы не используется (на рисунке они пусты). Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования. Шифруемый текст блоками по m х n – s элементов (m х n – размеры таблицы,s – число неиспользуемых элементов) записывается в таблицу. Далее шифрование аналогична простой перестановке.

Б	У	Д		Ь	Т	Е	а	О	С
	Т	О	Р	О	Ж	Н		Ы	а
С	а	О	Р	Е	Д	С	Т		А
В	И		Т	Е	Л	Е	М	а	Ф
И		Р	М	Ы	а	Ф	Е	Н	И
К	С	а	а	а		а	А	а	а

Зашифрованный текст будет выглядеть так: ДОПР БСВИК РРТМ ОЫ Н ЕНСЕФ УТ И СС АФ И ЬОЕ ЕЫ Т МЕ ТЖ ДЛ .

При расшифровании знаки зашифрованного текста записываются столбцами таблицы в последовательности знаков ключа с пропуском неиспользуемых элементов. Исходный текст считывается по строкам. Варьируя размерами таблицы, последовательностью символов ключа, количеством и расположением неиспользуемых элементов, можно получить требуемую стойкость зашифрованного текста.

Еще один вариант – шифр “Поворотная решетка” . предназначен для сообщений длины 4mk. Берется трафарет размером 2m*2k клеток, вырезается m*k клеток так, что при наложении его на лист бумаги того же размера 4 различными способами (поворачивая на 90°) его вырезы полностью покрывают всю площадь листа. Буквы сообщения последовательно вписываются в вырезы трафарета по строкам, в каждой строке слева направо, при каждом из 4-х его возможных положений в заранее установленном порядке. Число возможных трафаретов, т.е. количество ключей этого шифра составляет 4 mk (при размере трафарета 8*8 число вариантов превосходит 4 миллиарда).

Весьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется несколько различных маршрутов. Для примера рассмотрим шифрование по маршругам Гамильтона при n =3. Структура и три маршрута показаны на Рис. 7, а пример шифрования – на Рис. 8.

Широкое применение получили так называемые мар­шрутные перестановки, основанные на некоторой геометри­ческой фигуре. Отрезок открытого текста записывается в та­кую фигуру по некоторой траектории. Шифрованным текстом является последовательность, полученная при выписывании текста по другой траектории. Например, можно записывать сообщение в прямоугольную таблицу, выбрав такой маршрут: будем двигаться по горизонтали, начиная с левого верхнего угла, поочередно слева направо и справа налево. Списывать же сообщение будем по другому маршруту: по вертикалям, начиная с верхнего правого угла и двигаясь поочередно свер­ху вниз и снизу вверх.

Пример (маршрутной перестановки)

Зашифруем указанным выше способом фразу пример маршрутной перестановки, используя прямоугольную табли­цу размером 4х7:

п	р	и	м	е	р	м
н	т	у	р	ш	р	а
о	й	п	е	р	е	с
и	к	в	о	н	а	т

Зашифрованная фраза выглядит следующим образом:

мастаеррешрноермиупвкйтрпнои

Обращение описанных шагов при расшифровании не представляет труда.

Широкое распространение получила разновидность мар­шрутной перестановки, называемая вертикальной переста­новкой. В этой системе также используется прямоугольная таблица, в которую сообщение записывается обычным обра­зом (по строкам слева направо). Выписывается же сообщение по вертикалям (сверху вниз), при этом столбцы выбираются в порядке, определяемом числовым ключом.

Пример (вертикальной перестановки)

Зашифруем фразу вот пример шифра вертикальной пере­становки, используя прямоугольник размером 6 х 7 и число­вой ключ (5,1,4,7,2,6,3).

Отметим, что нецелесообразно заполнять последнюю строку прямоугольника “нерабочими” буквами, так как это дало бы противнику, получившему в свое распоряжение дан­ную криптограмму, сведения о длине числового ключа. В са­мом деле, в этом случае длину ключа следовало бы искать среди делителей длины сообщения.

Теперь, выписывая буквы по столбцам в порядке, указан­ном числовым ключом, получим такую криптограмму:

ореьекрфийамааеотшрнсивевлрвиркпнпитот

При расшифровании, в первую очередь, надо определить число длинных столбцов, то есть число букв в последней строке прямоугольника. Для этого нужно разделить число букв в сообщении на длину числового ключа. Ясно, что оста­ток от деления и будет искомым числом. Когда это число оп­ределено, буквы криптограммы можно водворить на их соб­ственные места, и сообщение будет прочитано естественным образом.

В нашем примере 38=7×5+3, поэтому в заполненной таблице имеется 3 длинных и 4 коротких столбца.

Более сложные маршрутные перестановки могут исполь­зовать другие геометрические фигуры и более “хитрые” мар­шруты, как, например, при обходе шахматной доски “ходом коня”, пути в некотором лабиринте и т.п. Возможные вариан­ты зависят от фантазии составителя системы и, конечно, есте­ственного требования простоты ее использования.

История

Точное время появления шифра перестановки не известно. Вполне возможно, что писцы в древности переставляли буквы в имени своего царя ради того, чтобы скрыть его подлинное имя или в ритуальных целях.

Одно из древнейших известных нам шифровальные устройство – Скитала. Бесспорно известно, что скитала использовалась в войне Спарты против Афин в конце V века до н. э.

Прародителем анаграммы считают поэта и грамматика Ликофрона, который жил в Древней Греции в III веке до н. э. Как сообщал византийский автор Иоанн Цец, из имени царя Птоломея он составил первую из известных нам анаграмм: Ptolemaios – Аро Melitos, что в переводе означает «из мёда», а из имени царицы Арсинои – как «Ion Eras » (фиалка Геры).

Шифры простой перестановки

Как правило, при шифровании и дешифровании шифра простой перестановки используется таблица перестановок:

1 {\displaystyle 1}	2 {\displaystyle 2}	3 {\displaystyle 3}	…	n {\displaystyle n}
I 1 {\displaystyle I_{1}}	I 2 {\displaystyle I_{2}}	I 3 {\displaystyle I_{3}}	…	I n {\displaystyle I_{n}}

Первая строка – позиция символа в открытом тексте, вторая строка – позиция в шифрограмме. Таким образом, при длине сообщения n {\displaystyle n} символов существует ровно n ! {\displaystyle n!\ } ключей.

Шифры маршрутной перестановки

Широкое распространение получили так называемые маршрутные перестановки, использующие некоторую геометрическую фигуру (плоскую или объемную). Преобразования состоят в том, что отрезок открытого текста записывается в такую фигуру по некоторой траектории, а выписывается по другой траектории. Пример данного шифра – шифр Скиталы.

Шифр табличной маршрутной перестановки

Наибольшее распространение получили маршрутные шифры перестановки, основанные на прямоугольниках (таблицах). Например, можно записать сообщение в прямоугольную таблицу по маршруту: по горизонтали, начиная с верхнего левого угла, поочередно слева направо. Сообщение будем списывать по маршруту: по вертикалям, начиная с верхнего правого угла, поочередно сверху вниз.

п	р	и	м	е
р	м	а	р	ш
р	у	т	н	о
й	п	е	р	е
с	т	а	н	о
в	к	и

КРИПТОГРАММА: ешоеомрнрниатеаирмупткпррйсв

Обращение описанных шагов не представит труда при расшифровании.

Шифр вертикальной перестановки

Широкое распространение получила разновидность маршрутной перестановки – вертикальная перестановка. В этом шифре также используется прямоугольная таблица, в которую сообщение записывается по строкам слева направо. Выписывается шифрограмма по вертикалям, при этом столбцы выбираются в порядке, определяемом ключом.

ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки

КЛЮЧ: (3, 1, 4, 2, 5)

п	р	и	м	е
р	м	а	р	ш
р	у	т	н	о
й	п	е	р	е
с	т	а	н	о
в	к	и

КРИПТОГРАММА: рмупткмрнрнпррйсвиатеаиешоео

Заполнять последнюю строку таблицы «нерабочими» буквами нецелесообразно, так как криптоаналитик, получивший данную криптограмму, получает сведения о длине числового ключа.

Шифр «поворотная решётка

В 1550 году итальянский математик Джероламо Кардано (1501-1576) в книге «О тонкостях» предложил новую технику шифрования сообщений – решётку.

Изначально решётка Кардано представляла собой трафарет с отверстиями, в которые записывали буквы, слоги или слова сообщения. Затем трафарет убирали, а свободное место заполняли более или менее осмысленным текстом. Такой метод сокрытия информации относится к стеганографии.

Позднее был предложен шифр «поворотная решётка» – первый транспозиционный (геометрический) шифр. Несмотря на то, что существует большая разница между изначальным предложением Кардано и шифром «поворотная решётка», методы шифрования, основанные на трафаретах, принято называть «решётками Кардано».

Для шифрования и дешифрования с помощью данного шифра изготовляется трафарет с вырезанными ячейками. При наложении трафарета на таблицу того же размера четырьмя возможными способами, его вырезы полностью должны покрывать все клетки таблицы ровно по одному разу.

При шифровании трафарет накладывают на таблицу. В видимые ячейки по определённому маршруту вписывают буквы открытого текста. Далее трафарет переворачивают три раза, каждый раз проделывая операцию заполнения.

Шифрограмму выписывают из получившейся таблицы по определённому маршруту. Ключом являются трафарет, маршрут вписывания и порядок поворотов.

Данный метод шифрования использовался для передачи секретной информации нидерландскими правителями в 1740-х годах. Во время Первой мировой войны армия кайзера Вильгельма использовала шифр «поворотная решётка». Немцы использовали решётки разных размеров, однако очень недолго (четыре месяца), к огромному разочарованию французских криптоаналитиков, которые только-только начали подбирать к ним ключи. Для решёток разных размеров французы придумали собственные кодовые имена: Анна (25 букв), Берта (36 букв), Дора (64 буквы) и Эмиль (81 буква).

от сцитала до RSA / Хабр

Красота математики в современном шифровании выражается в том, что когда у вас есть зашифрованное сообщение и открытый ключ, которым его шифровали, на расшифровку современными вычислительными мощностями может уйти бесконечность. При этом расшифровка со вторым (секретным) ключом пройдет практически мгновенно. Но эта революция произошла относительно недавно, а до этого столетиями использовали другие принципы.

Под катом несколько исторических примеров систем шифрования, а также математические принципы, заложенные в современных алгоритмах с открытым и закрытым ключом. А поскольку все гениальное просто, в статье не будет сложных формул и чрезмерного занудства.

Этот пост — адаптация лекции Евгения Бережного, доктора физико-математических наук и профессора математического факультета ярославского Демидовского университета, которая прошла в Точке кипения ЯрГУ.

Давайте на примерах рассмотрим общие принципы криптографии, существовавшие до эпохи вычислительных машин.

Шифрование в древности: несколько примеров

Натан Ротшильд когда-то сказал легендарную фразу, что тот, кто владеет информацией — владеет миром. 

И хотя с тех пор никто нам внятно так и не объяснил, зачем нужно этим миром владеть, информация в цене только растет.

Когда у человека появились ценные сведения, возникла потребность в ограничении доступа к ним. Это означает, что одна группа людей должна понимать сообщение, а для другой группы эта информация должна быть закрытой. 

Первые попытки закрыть информацию были, по теперешним меркам, наивно-примитивны: часть информации просто писали на другом языке. 

Например, вместо греческого языка текст писали на латинском. Это делали для той части греков, которые не знали латынь.

Пример текста диалога Платона и Евтифрона на греческом и латинском языках под редакцией Роберта Этьена (репринт 1578 года)

Современная криптография работает по похожему принципу — изобретается некий «язык», который недоступен основной массе.

Сцитала — первый механический шифр

Одна из первых криптографических систем и первых попыток изобрести свой секретный язык — шифросистема сцитала (другое название — скитала). 

Главная деталь такой системы — стержень или конус определенного диаметра. На него наматывали длинную полоску бумаги, на витках которой записывали текст. Затем бумагу снимали и отправляли, скажем, в другой город, где получатель имел цилиндр или конус аналогичной формы. Намотав такую бумагу на такой стержень, человек мог прочитать послание.

 Чтобы такая система работала, необходимо, чтобы и на передаче, и на приёме для восстановления информации использовали один и тот же цилиндр. Это был один из самых первых известных нам механических шифров. И, если говорить современным языком, он был не очень криптостойким.

Шифр Цезаря

Следующие шифросистемы были более хитрыми. Например, стоит упомянуть так называемый «шифр Цезаря». Суть шифра состояла в подмене значений. Предположим, у нас есть алфавит, неважно какой — латинский, русский, цифровой. И есть цифры — от единицы до пяти. Каждой цифре соответствует другая цифра, например, единице — тройка, двойке — пятерка, тройке — четверка, четверке — двойка, пятерке — единица. Таким образом, если необходимо было передать сообщение в виде последовательности цифр 1, 2, 3, 4, 5, информацию кодируют как 3, 5, 4, 2, 1. Для восстановления исходной информации на приеме используют табличку с теми же соответствиями символов.

Подмену символов делали разными способами. Например, одному символу могли соответствовать сразу несколько символов алфавита. Для упрощения дешифровки использовали сдвиг алфавита на заданное число символов. Все эти типы шифров — вариации шифра Цезаря. В каждом таком случае для шифрования информации на передаче и дешифровки на приеме использовали один и тот же ключ — табличку с сопоставленными исходными и подменяемыми символами.

Поворотная решетка: надежный механический шифр

Совершенствуя навыки тайнописи, человек создавал все более экзотические шифры. Один из них — поворотная решетка. Как и в случае со сциталой, это механический шифр. Для него необходим специальный инструмент: некий квадратный трафарет с вырезанными отверстиями-окошечками. В этих отверстиях писали текст сообщения. Далее решетку поворачивали на 90 градусов относительно центра, и отверстия попадали на чистые поля бумаги, где можно было продолжать текст. Потом решётку поворачивали еще два раза. Когда текст сообщения заканчивался, оставшиеся пустые места заполняли случайными буквами. 

В результате написанный текст образовывал некий массив бессвязных символов. Для восстановления информации, то есть на приеме, использовали аналогичную поворотную решетку с тем же набором отверстий. Криптостойкость такой системы зависила от числа ячеек в решетке. Чем больше окошечек, тем выше стойкость шифрования поворотной решеткой.

Обычно под криптостойкостью понимают количество идентичных шифров, похожих на данный. Если вернуться к шифру Цезаря и нашему примеру с цифрами от единицы до пяти, то всего количество перестановок будет 5!. Поэтому криптостойкость нашего примера шифрования будет 1/5!. Это, конечно, не очень большое число, но если у нас 32 элемента в алфавите, то вероятность того, что мы угадаем шифр, уже будет 1/32!.

Если число элементов поворотной решетки вдоль одной стороны будет 4n, то криптостойкость метода составит 4²ⁿ.

По мере развития криптографии появлялось все больше и больше «секретов», в то время как главный принцип — замещения — оставался неизменным.

Криптографические приемы нашли место во многих литературных произведениях, особенно в детективах. В рассказе «Пляшущие человечки» Конан Дойл описал шифр, где использовали принцип замещения — каждой букве присваивали свой рисунок человечка. Шерлок Холмс блестяще справился с разгадкой этого шифра, используя простую логику и принципы построения фраз. 

Оригинальный шифр из книги Артура Конан Дойла. Человечки с флагами работают пробелами

Переход в эпоху вычислительной техники и создание несимметричного шифра

Промышленные криптосистемы появились позже, когда возникла необходимость скрывать большие объемы данных и ограничивать доступ к информации государственной важности. Во вторую мировую войну наибольшую известность обрела немецкая шифровальная машина «Энигма», историю которой все знают по фильмам «U-571», «Игра в имитацию» и других. В легендарной немецкой шифровальной машине тоже использовали  шифр, основанный на шифре Цезаря, многократно усложненный.

Подробнее об алгоритме работе «Энигмы» можно узнать из этого ролика (eng.)

С появлением электроники криптографические системы заметно изменились. Метод закрытия информации стал иным: передаваемое сообщение в виде последовательного набора цифр 1, 2, 3, 4, 5 складывали с так называемой псевдослучайной последовательностью, генерируемой вычислительными машинами. На приеме для получения исходного сообщения эту избыточную информацию вычитали с помощью тех же вычислительных машин. 

Еще лет пятьдесят назад подобные способы закрытия данных считали относительно надежными: их, например, широко использовали вооруженные силы. Ключевой момент таких систем шифрования в том, что и на передаче сообщения, и на приеме используют, грубо говоря, одну «перфокарту», которая содержит псевдослучайную последовательность —  один пароль.

RSA — имея зашифрованное сообщение и шифровальный ключ, расшифровать практически нереально

К середине восьмидесятых годов прошлого века никаких новых методов закрытия информации не появилось, и многие сочли криптографию устаревшей наукой. 

Даже в опубликованной в 1988 году советской брошюре по криптографии было написано, что эта тема себя исчерпала и не может содержать ничего нового.

Автор брошюры ошибался. В это же время в Массачусетском технологическом институте трое сотрудников — Рональд Ривест, Ади Шамир и Леонард Адлеман — придумали новую шифросистему с высокой криптостойкостью, которая базировалась на принципах, отличных от тех, что использовались ранее. 

Ади Шамир, Рональд Ривест и Леонард Адлеман — создатели алгоритма несимметричного шифрования

Для взлома этой системы на то время понадобилось бы примерно 10 тысяч лет.

До ее изобретения все шифровальные методы основывались на целочисленной арифметике и использовали все множество целых чисел. Уникальность нового метода в том, что он использовал также и арифметику остатков.

Предположим, у нас есть произвольное целое число n. И давайте возьмем m=5. Произвольное число n можно поделить на пять, в результате чего получится частное плюс остаток. Остаток может принимать значение 0, 1, 2, 3, 4. Оказывается, эти остатки могут вести себя как обычные числа. Запишем две таблицы — таблицу сложения для остатков и таблицу умножения для остатков. 

Таблицы остатков от сложения и деления (плюс в карму тому, кто первый найдет у лектора ошибку, сделанную по невнимательности)

Имея на руках такие таблицы, можно опять получить новую арифметику. Объекты с такой новой арифметикой обозначаются как Z(m). Остаток от деления числа a на m записывается следующим образом: a mod m = b. Мы записали таблицы для числа пять — Z(5). Аналогичным образом можно записать такие таблицы для любого натурального числа Z(m).

Пример

Предположим, мы имеем исходное сообщение, которое необходимо закрыть — x. Нам необходимо придумать некоторое число m — основание для создания Z(m), а также придумать число a. Эти два числа находятся в открытом доступе, известны всем. Кроме того известно, что m=m₀ × m₁, где m₁ и m₀ — простые числа (которые делятся только на себя и единицу).

Далее согласно алгоритму шифрования создаем уравнение: x^amod m = b, где b (остаток от деления x^a на m) — наше зашифрованное сообщение. Таким образом, a,b,m — известны, и необходимо вычислить x. Для решения этой задачи нужно найти разложение m = m₀ × m₁. Как только m₁и m₀ будут найдены, расшифровать сообщение можно будет достаточно быстро через специальную систему уравнений.

Криптостойкость зависит от того, насколько большими будут числа m0 и m1 . А m, по сути, является открытым ключом, который передает отправителю получатель для шифровки сообщения

Изобретатели нового шифра зашифровали фразу, где в качестве a было взято число 1007, m₀ и m_{1содержали примерно по 65 знаков в десятичной системе. Математики озвучили публичные а, зашифрованную фразу и m, предлагая всем желающим расшифровать секретную фразу. Также был опубликован алгоритм, как взломать эту систему. Вся криптостойкость определялась разложением m = m0 × m1.} 

История длилась 17 лет, пока с появлением интернета у пользователей не появилась возможность задействовать сеть компьютеров с распределенными вычислениями. За 220 дней около 1600 компьютеров смогли восстановить исходную информацию, разложив m на два простых числа. Это событие показало, что криптография как наука жива. 

Также это доказало непостижимую эффективность математики при решении реальных задач. Сама же система получила название RSA — по именам своих создателей.

Практическое применение криптографии

С появлением интернета возник целый класс задач, для решения которых снова и снова приходится прибегать к математике. В частности, речь идет об удаленных и защищенных действиях. Используя интернет и инструменты для закрытия информации можно, скажем, открыть счет в банке, провести платеж без личного присутствия человека. Требования к таким криптосистемам отличаются от классических, присутствовавших в жизни человека раньше. 

Если при зарождении криптографии на передаче и на приеме была одна и та же шифросистема — поворотная решетка, сцитала и т. д., — то теперь ситуация кардинально иная. На передаче и приеме в новых криптосистемах применяют совершенно разные методы обработки информации. 

На передаче используют простые алгоритмы, чтобы закрыть информацию (в нашем случае — возвести x в степень a), а на приеме происходит быстрое восстановление (если вам заранее известно разложение m на m₀ и m₁). Получается несимметричная система шифрования, которая удобна и надежна. 

По сравнению с симметричными системами шифрования, предложенный вариант не годится для передачи данных сверхбольшого объема ввиду ресурсоемкости операций. Зато в случае несимметричного шифра отпадает необходимость в передаче секретного ключа, что весьма удобно, если необходимо использовать сеансовый пароль.

Новые принципы криптографии привели к созданию цифровой подписи — механизму, который подтверждает аутентификацию пользователя.

Им можно подписывать документы и заверять свою личность — например, в финансовых документах. 

Наш ГОСТ и американский стандарт цифровой подписи основаны на эллиптических кривых и решении логарифмических уравнений. Математика, которую там используют, очень сложна, и сегодня мы опустим эти математические выкладки.

Иногда криптографию применяют в неожиданных сферах, где требуется подтверждение достоверности информации. Например, если вы, расслабившись в конце рабочего дня, сядете играть в карты, то вы можете быть уверены в честной игре, даже не имея на руках реальных карт. Скрытую информацию с помощью описанных алгоритмов всегда можно восстановить и проверить. Тем же способом же можно организовывать честное голосование без необходимости физического присутствия человека на избирательном участке. 

Математика позволяет решать самые разные и сложные задачи обеспечения информационной безопасности. И по мере развития вычислительных систем алгоритмы будут только усложняться.

(PDF) Cardan grilles

58

Потенциал. Математика. Физика. Информатика № 01 (157) 2018Потенциал. Математика. Физика. Информатика № 07 (175) 2019

Информатика

Само собой разумеется, что крайне

желательно, чтобы распределение

частот этих случайных символов

совпадало с таковым распределе-

нием букв того языка, сообщение

на котором шифруется.

Методы атаки

Давайте теперь подумаем, ка-

кими методами может восполь-

зоваться криптоаналитик для де-

шифровки шифрограммы, смысл

которой скрыт при помощи решёт-

ки Кардано. Как обычно, необходи-

мо решить следующие задачи:

1. Определить тип шифра, то есть

в рассматриваемом случае —

определить, что это действи-

тельно шифр Кардано.

2. Определить параметры шифро-

вания. В рассматриваемом слу-

чае – размеры использованных

решёток и их количество.

3. Собственно, дешифровать

сообщение.

С решётками Кардано есть про-

блема – очень сложно понять, что

шифрограмма построена на их ос-

нове. Перемешивание символов

исходного текста не меняет ча-

стотность символов. Но вот такие

намёки могут дать подсказку:

1. Если в шифрограмме исполь-

зуются те же самые символы,

что и символы открытого текста

(это очень слабый намёк).

2. Если в шифрограмме частот-

ность символов абсолютно такая

же, как и частотность открытых

текстов на заданном языке, но

при этом разгадать шифрограм-

му методом частотного анализа

не представляется возможным.

3. Если в шифрограмме часто

встречаются последователь-

ности одинаковых букв, стоя-

щих вместе, то в совокупности

с неизменённой частотностью

это, скорее всего, намекает, что

перед криптоаналитиком пере-

становочный шифр.

4. Наконец, если количество сим-

волов в шифрограмме можно

выразить как kn2, то есть как

целое число квадратов, то это

очень сильный намёк на исполь-

зование решёток Кардано.

Если получена шифрограмма,

которая так или иначе совпадает

с перечисленными четырьмя кри-

териями (особенно с четвёртым),

то можно предположить, что перед

нами шифрограмма, зашифрован-

ная при помощи решёток Кардано.

Но что делать дальше? А дальше,

кроме как методом подбора, вряд

ли что-то получится сделать.

Давайте посмотрим, как можно

осуществить перебор. Для ква-

дратной матрицы со сторо-

ной (2m)2 необходимо выбрать

(2m)2/4 = m2 закрашенных позиций.

Комбинаторика даёт нам ответ –

это число сочетаний из (2m)2 по m2,

то есть:

.

Это довольно большое число при

возрастающем m. Его, конечно ещё

надо разделить на 4, так как не

требуются сочетания, переводимые

друг в друга поворотами. Но тем

не менее. Чтобы понять проблему,

давайте посмотрим, чем равно это

число для m от 1 до 5, что соответ-

ствует матрицам Кардано с чётны-

ми сторонами от 2 до 10:

Криптография. Возникновение криптографии – презентация онлайн

1. КРИПТОГРАФИЯ

ЛЕКЦИЯ №1
ЛЕКТОР: ИЩУКОВА ЕВГЕНИЯ АЛЕКСАНДРОВНА, К.Т.Н.,
ДОЦЕНТ КАФЕДРЫ БЕЗОПАСНОСТИ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

2. ВОЗНИКНОВЕНИЕ КРИПТОГРАФИИ

История криптографии насчитывает несколько
тысячелетий. Первые письменные источники
относятся к 1900-м годам до н. э. Именно этим
периодом датируются найденные в Египте
свитки, в которых использованы
видоизмененные иероглифы, по-видимому
применявшиеся для тайного обмена
сведениями.

3. Запись на неизвестном языке – тайная запись

Японские иероглифы
Иероглифы индейцев Майя
Египетские иероглифы
Греческие иероглифы

4. Зачем нужна криптография

Как передать нужную информацию нужному адресату в тайне от
других?
1. Создать абсолютно надежный, недоступный для
других канал связи между абонентами.
2. Использовать общедоступный канал связи, но
скрыть сам факт передачи информации.
3. Использовать общедоступный канал связи, но
передавать
по
нему
информацию
в
преобразованном виде, чтобы восстановить ее мог
только адресат.

5. Зачем нужна криптография

6. До сих пор не разгаданные шифры Манускрипт Войнича

Это 240-страничная книга,
написанная на абсолютно
неизвестном языке с цветными
рисунками и странными
диаграммами, изображениями
невероятных событий и
растений, которые не похожи ни
на один известный вид.

7. До сих пор не разгаданные шифры Криптос

Скульптура, созданная
художником Джимом
Санборном, которая
расположена перед штабквартирой Центрального
разведывательного управления в
Лэнгли, Вирджиния. Скульптура
содержит в себе четыре
шифровки, вскрыть код
четвёртой не удаётся до сих пор.
В 2010 году было раскрыто, что
символы 64-69 NYPVTT в
четвёртой части означают слово
БЕРЛИН

8. До сих пор не разгаданные шифры Шифр Бэйла

Шифр Бэйла —
три зашифрованных сообщения,
которые, как предполагается, содержат
сведения о местонахождении клада из
двух фургонов золота, серебра и
драгоценных камней, зарытого в 1820-х
годах под Линчбергом, что в округе
Бедфорд, штат Виргиния, партией
золотоискателей под предводительством
Томаса Джефферсона Бейла. Цена не
найденного доныне клада в пересчете на
современные деньги должна составлять
около 30 млн долларов. Загадка
криптограмм не раскрыта до сих пор, в
частности, спорным остается вопрос о
реальном существовании клада. Одно из
сообщений расшифровано – в нем
описан сам клад и даны общие указания
на его местоположение. В оставшихся
нераскрытыми письменах, возможно,
содержатся точное место закладки и
список владельцев клада.

9. Тайна головы раба

Один из способой защиты информации получил название
“стеганография” латино-греческое сочетание слов, означающих в
совокупности “тайнопись”). Он заключался в сокрытии самого
факта наличия информации. В данном случае использовались так
называемые симпатические чернила. При соответствующем
“проявлении” бумаги текст становится видимым. Один из
примеров сокрытия информации приведен в трудах
древнегреческого историка Геродота. На голове раба, которая
брилась наголо, записывалось нужное сообщение. И когда волосы
его достаточно отрастали, раба отправляли к адресату, который
снова брил его голову и считывал полученное сообщение.
использования.

10. Таблица Энея

На небольшой таблице горизонтально располагался алфавит, а
по ее боковым сторонам имелись выемки для наматывания нити.
При зашифровани нить закреплялась у одной из сторон таблицы и
наматывалась на нее. На нити делались отметки (например,
узелки) в местах, которые находились напротив букв данного
текста. По алфавиту можно было двигаться лишь в одну сторону,
то есть делать по одной отметке на каждом витке. После
зашифрования нить сматывалась и передавалась адресату. Этот
шифр представлял собой шифр замены букв открытого текста
знаками, которые означали расстояния между отметками нити.
Ключом являлись геометрические размеры таблицы и порядок
расположения букв алфавита.

11. Диск Энея

12. Шифр Сцитала

13. Шифр Скитала – мой вариант

В качестве основы мы с мамой взяли рулон бумаги, намотали на него полоску
бумаги. Я написал сообщение «Спасите». А остальные буквы написал в
произвольном порядке

14. Азбука Морзе

15. Шифры замены

Шифрами замены называются
такие
шифры,
преобразования в которых
приводят к замене каждого символа
открытого сообщения на другие символы шифробозначения,
причем
порядок
следования шифробозначений совпадает с
порядком следования соответствующих им
символов открытого сообщения.

16. Шифры Темура и Атбаш

В 600 – 500 годы до н. э. на Ближнем Востоке древними евреями был
разработан один из первых систематических шифров; этот метод
называется темура — «обмен». Буквы еврейского алфавита делились на
две части, причем одна помещалась над другой; затем верхние буквы
заменялись на нижние или наоборот. При этом можно было составлять
всевозможные комбинации в зависимости от места разделения алфавита и
направления перемещаемых букв. Самый простой способ заключался в
разделении алфавита посередине так, чтобы первые две буквы, А (Алеф)
и Б (Бет), совпадали с двумя последними, Т (Тае) и Ш (Шин). Эти буквы и
дали название методу шифровки — «Атбаш». В России система
шифрования «Атбаш» получила широкое распространение в 16-18 веках и
название «тарабарская грамота».

17. Шифр Полибия

Греческий писатель Полибий использовал систему
сигнализации, которая была широко принята как
метод шифрования. Он записывал буквы алфавита в
квадратную таблицу и заменял их парой чисел,
которые указывали соответственно на номер строки
и номер столбца, на пересечении которых
находилась зашифровываемая буква.
При передачи сообщений между сторожевыми
вышками тех времен использовались факелы. Так,
чтобы передать букву В необходимо было взять 4
факела в правую руку и 3 – в левую. Полибий
использовал это для шифрования сообщений и стал
записывать каждую букву парой координат.

18. Шифр Полибия

В нашей стране принцип использования таблицы
Полибия нашел широкое применение в 19 веке в
среде революционеров, находящихся в тюремном
заключении. Революционерами использовались
различные наборы алфавитов (то есть опускалось
различное число редко встречающихся букв
русского языка) и различные размеры таблиц для
перестукивания друг с другом через стены камер.
Такие системы получили название «тюремных
шифров».

19. Квадрат Полибия

20. Квадрат Полибия

21. Квадрат Полибия

22. Квадрат Полибия

23. Шифр Цезаря

24. Шифр Цезаря

25. Шифр Цезаря

26. Шифр равнозначной замены

27. Шифр равнозначной замены

Расшифруйте сообщение
733298131911

28. Пример шифров замены

29. Пример шифров замены

30. Анализ шифров простой замены

31. Анализ шифров простой замены

32. Липограмма

В романе французского писателя и режиссёра Жоржа Перека «Исчезание»
отсутствует одна из букв. Во французском варианте в «Исчезании» нет ни одной
буквы «е» — наиболее часто встречающейся в этом языке. В русском же
варианте, благодаря переводу лауреата премии Мориса Ваксмахера Валерия
Кислова, отсутствует буква «о», без которой тоже сложно представить
подавляющее большинство слов.
Верси-Ярн раскрыл сумку и вытащил из неё чёрную глиняную шкатулку с белыми
письменами на крышке. Некий умелый мастер не выписал, а вырезал их
мастихинами, заимствуя у Жержека приём, мультиплицирующий фигурки
«Жилей» («Жиль» — грустный Белый Шут с картины мастера «галантных
сцен»). В результате на выцарапанных местах верхний страт (чёрная индийская
тушь) был удалён, а нижний (белая глиняная глазурь) выявился, причём
филигранью, в мельчайших чертах, имитируя надписи, встречающиеся в нижней
части нихандзийских акварелей.

33. Шифры перестановки

Шифр, преобразования которого изменяют
только порядок следования символов
исходного текста, но не изменяют их самих,
называется шифром перестановки.

34. Понятие шифра перестановки

35. Простой шифр перестановки

36. Шифр маршрутной перестановки

37. Шифр вертикальной перестановки

38. Шифр вертикальной перестановки

39. Шифр поворотная решетка

40. Шифр поворотная решетка

41. Шифр поворотная решетка

42. Шифр поворотная решетка

43. Шифр Ришелье (объединение криптографии и стеганографии)

44. Шифры многозначной замены

45. Упражнения

https://learningapps.org/460431
https://learningapps.org/2978300
https://learningapps.org/2752735

46. Домашнее задание Задача №1

47. Домашнее задание Задача №2

Шифрование методом перестановки. Виды и способы шифров

Аатбаш, шифр Сцитала, решетка Кардано – известные способы скрыть информацию от чужих глаз. В классическом смысле шифр перестановки представляет собой анаграмму. Его суть заключается в том, что буквы открытого текста меняются по определенному правилу позициями. Иными словами, ключом шифра является смена очередности следования символов в открытом сообщении. Однако зависимость ключа от длины шифруемого текста породила множество неудобств для использования этого вида шифров. Но умные головы нашли интересные хитрые решения, которые описываются в статье.

Перевернутые группы

Для ознакомления с шифрованием методом перестановки упомянем один из простейших примеров. Алгоритм его заключается в разделение сообщения на n блоков, которые затем переворачиваются задом наперед и меняются местами. Рассмотрим пример.

• “День уходил, и неба воздух темный”.

Разделим это сообщение на группы. В данном случае n = 6.

• “Деньух одили небав озд ухтем ный”.

Теперь развернем группы, записав каждую с конца.

• “хуьнед вабен дзо метху йын”.

Переставим определенным образом местами.

• “илидо метху йын хуьнед вабен дзо”.

Для незнающего человека в таком виде сообщение представляет собой не более чем белиберду. Но, разумеется, тот, кому адресовано сообщение, ведает алгоритмом расшифровки.

Серединная вставка

Алгоритм данного шифрования немного сложнее шифрования методом перестановки:

1. Разделить сообщение на группы с четным количеством символов.
2. В середину каждой группы вставить дополнительные буквы.

Рассмотрим на примере.

1. “Земные твари уводил ко сну”.

2. “Земн ыетв ариу води лкосну”.

3. “Зеамн ыеабтв араиу воабди лкоасну”.

В данном случае в середину групп были вставлены чередующиеся буквы “а”и “аб”. Вставки могут быть разными, в разном количестве и не повторяться. Помимо этого, можно развернуть каждую группу, перемешать их и т.д.

Шифрограмма “Сэндвич”

Еще один занимательный и простой пример шифрования методом перестановки. Для его использования нужно открытый текст разделить на 2 половины и одну из них посимвольно вписать между букв другой. Покажем на примере.

• “От их трудов; лишь я один, бездомный”.

Разделим на половины с равным количеством букв.

• “Отихтрудовлишь яодинбездомный”.

Теперь запишем первую половину сообщения с большим интервалом между буквами.

• “О т и х т р у д о в л и ш ь”.

И в этих промежутках разместим буквы второй половины.

• “Оятоидхитнрбуедзодволминшыьй”.

Наконец сгруппируем буквы в своего рода слова (необязательная операция).

• “Оятои дхи тнрбуе дзодвол миншыьй”.

Зашифровать текст этим методом очень легко. Полученную строку-белиберду непосвященному придется разгадывать некоторое время.

Перестановки по “маршруту”

Такое название получили шифры, широко применявшиеся в древности. Маршрутом в их построении выступала какая-либо геометрическая фигура. Открытый текст записывался в такую фигуру по определенной схеме, а извлекался по обратной ей. Например, одним из вариантов может быть запись в таблицу открытого текста по схеме: змейка ползает в ячейках по часовой стрелке, а зашифрованное сообщение составляется путем списывания столбцов в одну строку, с первого по последний. Это также является шифрованием методом перестановки.

Покажем на примере, как зашифровать текст. Попробуйте сами определить маршрут записи и маршрут составления шифрограммы.

Будем записывать сообщение в таблицу размерами 3×9 клеток. Размерность таблицы можно определить, исходя из длины сообщения, или использовать некоторую фиксированную таблицу несколько раз.

п	р	и	г	о	т	о	в	л
р	е	д	ы	в	я	с	л	я
ж	а	т	ь	в	о	й	н	у

Шифр будем составлять, начиная с правого верхнего угла таблицы.

• “Ляунлвосйоятоввьыгидтаерпрж”.

Обращение описанных шагов не представляет труда. Достаточно просто сделать все наоборот. Данный способ является крайне удобным, потому что позволяет легко запомнить процедуру шифрования и расшифровки. А также он является интересным, потому что использовать для шифра можно любую фигуру. Например, спираль.

Вертикальные перестановки

Этот вид шифров также является вариантом маршрутной перестановки. Интересен он в первую очередь наличием ключа. Данный способ был широко распространен в прошлом и также использовал таблицы для шифрования. Сообщение записывается в таблицу обычным образом – сверху вниз, а шифрограмма выписывается по вертикалям, при этом соблюдается порядок, указанный ключом или паролем. Посмотрим на образец такого шифрования.

Используем таблицу размерностью 4х8 клеток и запишем в нее наше сообщение обычным образом. А для шифровки используем ключ 85241673.

и	с	т	я	г	о	с	т
н	ы	м	п	у	т	е	м
и	с	с	о	с	т	р	а
д	а	н	ь	е	м

Ключ приведен ниже.

Теперь, используя ключ в качестве указания на порядок следования, выпишем столбцы в строку.

• “Гусетмснтмаяпоьсысаоттмсеринид”.

Важно заметить, что при этом способе шифрования пустые ячейки в таблице не следует заполнять случайными буквами или символами, надеясь, что это усложнит шифрограмму. На самом деле, наоборот, такое действие даст врагам подсказку. Потому что длина ключа окажется равной одному из делителей длины сообщения.

Обратная расшифровка вертикальной перестановки

Вертикальная перестановка представляет интерес тем, что расшифровка сообщения не является простым следованием алгоритму от обратного. Тому, кто знает ключ, известно, сколько в таблице столбцов. Чтобы дешифровать сообщение, нужно определить число длинных и коротких строк в таблице. Это позволит определить начало, откуда начинать записывать шифрограмму в таблицу, чтобы прочитать открытый текст. Для этого разделим длину сообщения на длину ключа и получим 30/8=3 и 6 в остатке.

Таким образом, нам стало известно, что в таблице 6 длинных столбцов и 2 коротких, заполненных буквами не до конца. Посмотрев на ключ, мы видим, что шифрование началось с 5-го столбца, и он должен быть длинным. Так мы находим, что первые 4 буквы шифрограммы соответствуют пятому по счету столбцу таблицы. Теперь можно записать все буквы по местам и прочесть тайное послание.

Решетка Кардано

Данный тип относится к так называемым трафаретным шифрам, но по своей сути является шифрованием методом перестановки символов. В роли ключа выступает трафарет в форме таблицы с прорезанными отверстиями в нем. На самом деле трафаретом может быть любая фигура, но чаще всего используется квадрат или таблица.

Трафарет Кардано изготавливается по следующему принципу: вырезанные ячейки при повороте на 90° не должны перекрывать друг друга. То есть после 4 поворотов трафарета вокруг своей оси прорези в нем не должны совпадать ни разу.

Используем для примера простую решетку Кардано (на рисунке ниже).

Используя этот трафарет, зашифруем фразу “О Музы, к вам я обращусь с воззваньем”.

–	О	–	М	–	–
		У
	З				Ы
		К
	В				А
М

Заполняем ячейки трафарета буквами по правилу: сначала справа налево, а затем сверху вниз. Когда ячейки кончатся, поворачиваем трафарет на 90° по часовой стрелке. Таким способом получаем следующую таблицу.

Я	–	–	–	–	–
	О		Б		Р
		А		Щ
					у
	С		Ь

И еще раз поворачиваем на 90°.

–	–	–	–	–	С
В				О
			З
В				А
			Н
		Ь		Е

И последний поворот.

После объединения 4 таблиц в одну получаем итоговое зашифрованное послание.

Я	О	М	М	Г	С
В	О	У	Б	О	Р
Г	З	А	З	Щ	Ы
В	Г	К	Г	А	У
Г	В	Г	Н	Г	А
М	С	Ь	Ь	Е	Г

Хотя послание может остаться и таким, но для передачи удобнее будет получить привычную на вид шифрограмму. Для этого пустые ячейки можно заполнить случайными буквами и выписать столбцы в одну строку:

• “ЯВГВГМ ООЗГВС МУАКГЬ МБЗГНЬ ГОЩАГЕ СРЫУАГ”

Для того чтобы расшифровать это послание, получатель должен обладать точной копией трафарета, который был использован для шифрования. Данный шифр долгое время считался достаточно устойчивым. Также у него существует множество вариаций. Например, применение сразу 4 решеток Кардано, каждая из которых вращается своим образом.

Анализ шифров перестановки

Все перестановочные шифры уязвимы против частотного анализа. Особенно в случаях, когда длина сообщения сопоставима с длиной ключа. И этот факт не может быть изменен многократным применением перестановок, какими бы сложными они ни были. Поэтому в криптографии устойчивыми могут быть только те шифры, которые используют сразу несколько механизмов, помимо перестановки.

Что такое криптография на основе решеток и почему вам это должно быть небезразлично | от Wickr | Блог Wickr Crypto + Privacy

В последнее время все более актуальным становится вопрос о том, насколько мы близки к тому, чтобы квантовые вычисления (QC) стали мейнстримом. Очевидно, что по мере нашего приближения разумно и даже срочно повысить устойчивость наших систем к постквантовым атакам, некоторые из которых, как мы теперь можем себе представить, будут использовать будущие возможности контроля качества для расшифровки данных, собранных сегодня. При этом криптография на основе решеток часто упоминается в новостях.Так что же это такое и каков его потенциал для нашего постквантового будущего?

Криптография бывает разных видов. В течение долгого времени, по крайней мере, еще со времен Юлия Цезаря, схемы шифрования и другие криптографические инструменты в основном следовали специальным проектам. Безопасность в основном основывалась на интуиции и эвристике. Однако в конце 1970-х – начале 1980-х годов появилась новая, более принципиальная и строгая методология.

Основная идея заключается в следующем. Область математики полна очень-очень сложных проблем, которые человечество коллективно не смогло решить, несмотря на многие десятилетия, столетия или даже тысячелетия попыток.А теперь представьте, что мы могли бы построить схему шифрования таким образом, чтобы взлом ее безопасности потребовал решения одной из этих очень сложных проблем. Это превратит все, казалось бы, напрасные усилия, посвященные этой проблеме нынешними и прошлыми математиками, в свидетельство безопасности нашей недавно проверенной схемы шифрования. Фактически, все эти неудачные попытки теперь можно рассматривать как попытки взломать систему шифрования.

Конечно, это легче сказать, чем сделать. Действительно, одна из самых сложных задач здесь – найти подходящую нерешенную математическую задачу.С одной стороны, чтобы вселить в нас желаемую уверенность в своей сложности, проблема должна быть как можно более широко известна и хорошо изучена. Но он также должен быть достаточно гибким, чтобы мы могли превратить проблему во что-то полезное.

Оказывается, большой источник сложных проблем – это раздел математики, называемый теорией чисел. Во-первых, это один из старейших разделов математики. Например, Евклид, Пифагор и другие древние греки были заядлыми теоретиками чисел; даже вавилоняне работали над некоторой базовой теорией чисел.

Несмотря на свой возраст, теория чисел полна очень простых и очень гибких (и поэтому с ними легко работать), но все еще нерешенных проблем. Фактически, небольшая группа тесно связанных проблем сыграла решающую роль в современной криптографии с открытым ключом. Вероятно, самая простая из этих задач, которую можно описать в терминах базовой школьной математики, – это задача Factoring .

За последние четыре десятилетия многие широко используемые криптографические схемы с открытым ключом были разработаны на основе сложности факторинга и других подобных проблем.Это включает RSA, обмен ключами Диффи-Хеллмана, ECDH, ECDSA, Ed448, Ed25519. Эти схемы сейчас используются в большинстве наших повседневных приложений безопасности более высокого уровня, включая Wickr, SSH, TLS, HTTPS, Биткойн, PGP и VPN.

Каждая из этих базовых схем снабжена «доказательством безопасности», которое представляет собой формальное математическое доказательство, показывающее, что взломать систему безопасности схемы не менее сложно, чем решить одну из фундаментальных математических задач, например, разложение на множители. Такие доказательства играют решающую роль, помогая нам создать необходимую уверенность в безопасности этих самых основных криптографических строительных блоков.Поскольку безопасность большей части нашей цифровой инфраструктуры, помимо прочего, зависит от водонепроницаемости этих строительных блоков, уверенность в ее доказательствах жизненно важна. рушится. Хотя мы еще не построили его, мы уже знаем, как можно использовать квантовые вычисления. Более того, одна из первых новых вещей, которые мы осознали, что можем сделать с помощью QC, – это решение задач факторизации с использованием метода, называемого Алгоритм Шора .Фактически, практически любая другая теоретико-числовая математическая задача, которую мы использовали за последние 40 лет в качестве основы для нашей безопасности, оказывается легко решаемой на крупномасштабном квантовом компьютере, обычно с использованием некоторого варианта алгоритма, называемого Обыск Гровера . Другими словами, если злоумышленник имеет доступ к такому устройству, доказательства безопасности становятся совершенно бессмысленными. В конце концов, какой смысл доказывать, что схема, по крайней мере, так же безопасна, как какая-то математическая задача, если эту проблему теперь легко решить?

Теперь вы можете подумать: «Погодите, просто потому, что доказательства бессмысленны, это не означает, что нет какого-то другого нового доказательства, которое все еще показывает, что схемы безопасны.Увы, почти во всех случаях довольно легко увидеть, как квантовый компьютер действительно может быть использован для взлома криптографической схемы. Другими словами, никогда не будет доказательств безопасности, потому что схемы просто не защищены от злоумышленников с помощью квантовых компьютеров.

Вот что это сводится к следующему: то, что сейчас нужно миру, – это новый урожай математических задач и соответствующие криптографические схемы, которые трудно решить (и, следовательно, безопасно) даже перед лицом квантовых вычислений.

К счастью, за последнее десятилетие криптографы и математики усердно работали над поиском таких проблем и превращением их в полезные криптографические схемы. Фактически, в настоящее время исследуются несколько различных семейств математических задач, каждое из которых взято из разных разделов математики.

В рамках этого поста я сосредоточусь на семействе проблем, используемом в том, что обычно называют криптографией на основе решетки . Название происходит от того факта, что криптографические схемы в этой области снабжены доказательствами безопасности, которые связывают их безопасность со сложными математическими задачами, связанными с решетками.Позвольте мне описать две наиболее важные проблемы криптографии на основе решеток. Также я поделюсь парой полезных терминов.

L атлас: Так что же такое решетки? Решетку можно представить как любую равномерно распределенную сетку точек, простирающуюся до бесконечности. Например, вот две разные двумерные решетки.

V ector: Вектор – это не что иное, как причудливое имя для точки, набор чисел, называемый координатами вектора.Итак, (2, 3) – это конкретный двумерный вектор, поскольку он имеет 2 координаты, а решетка – это набор равномерно распределенных векторов. Особый интерес представляет вектор origin , который является вектором со всеми координатами, установленными в 0. Например, в трех измерениях начало координат равно (0, 0, 0). Мы говорим, что вектор имеет длину , если он находится далеко от начала координат. И наоборот, вектор короче , если он близок к началу координат.

B asis: Решетки – это бесконечно большие объекты, но компьютеры имеют ограниченный объем памяти для работы.Поэтому нам понадобится краткий способ представления решеток, если мы собираемся использовать их в криптографии. Для этого мы используем то, что называется базисом решетки. Базис – это небольшой набор векторов, который можно использовать для воспроизведения любой точки сетки, образующей решетку.

Давайте посмотрим на случай двумерной решетки, сетки точек на плоской поверхности, такой как лист бумаги. Сначала выберите еще две точки, которые не должны лежать на одной линии, проходящей через начало координат.Например, мы могли бы выбрать (2,0) и (0,2). Вот как эти точки могут быть использованы для создания третьей точки:

• Сначала мы выбираем два целых числа; скажем, 3 и -1.
• Мы умножаем координаты первой точки на 3, чтобы получить точку (6,0), и координаты второй точки на -1, чтобы получить (0, -2).
• Теперь мы складываем результаты вместе, чтобы получить нашу новую точку (6, -2).

Используя этот метод, мы можем использовать (2,0) и (0,2), чтобы сгенерировать всю сетку из равномерно расположенных точек, а именно всех точек с координатами (x, y), так что и x, и y являются четными числами. где мы также считаем 0 четным числом.Другими словами, базис , состоящий из векторов (2,0) и (0,2), генерирует точки решетки с четными координатами. Идея состоит в том, что, выбирая базис, мы фактически выбрали целую решетку, а именно ту, точки которой порождаются векторами в базисе. Важно отметить, что в отличие от бесконечной сетки точек, базис – это простой конечный объект, который мы можем представить в памяти компьютера.

Рисунок 1

Важно отметить, что любая заданная решетка не имеет только одного основания.На самом деле у него , много баз. Например, вместо использования (2,0) и (0,2) выше мы могли бы с таким же успехом выбрать (-2,0) и (0, -2) или даже (4, 2) и (2, 2). ). В каждом случае они создают одну и ту же сетку точек.

Рисунок 2

Мы говорим, что базис – это короткий , если он состоит из коротких векторов (см. Синий базис на рисунке 1 ниже). И наоборот, мы говорим, что базис равен long , если он состоит только из длинных векторов (см. Зеленый базис на рисунке 2 ниже).Оказывается, короткие базисы гораздо более полезны, чем длинные, когда дело доходит до решения типов задач жесткой решетки, которые интересуют криптографов.

Так как же будет выглядеть задача жесткой решетки ? Оказывается, что, учитывая то, что мы узнали до сих пор, эти проблемы теперь очень просто понять. Например, вот «проблема коротких векторов», которая, вероятно, является самой важной проблемой в криптографии на основе решеток.

На первый взгляд может показаться, что решить эту проблему относительно легко.Однако обратите внимание, что базис, который нам дан, состоит из длинных векторов. Поэтому не сразу понятно, как их можно объединить для создания точки с небольшими координатами, а именно короткого вектора. Более того, когда дело доходит до криптографии, мы действительно говорим о решетках в гораздо более высоких измерениях (например, 10 000 вместо двух, как в наших примерах выше). Это означает, что наши точки на самом деле имеют 10 000 координат, а не 2 координаты. Таким образом, найти комбинацию базисных векторов, при которой одновременно делает малыми все 10000 сгенерированных координат, оказывается довольно сложно, настолько, что мы не знаем, как быстро решить проблему даже с помощью квантового компьютера, не говоря уже о традиционном один.

Вот еще две важные и очень тесно связанные проблемы жесткой решетки, используемые криптографами для создания безопасности:

Хитрое шифрование, которое может поставить в тупик квантовые компьютеры

Однако, опять же, казалось, что существует компромисс между безопасностью и эффективностью. и досадная невозможность иметь и то, и другое. У Ring-LWE были лучшие гарантии безопасности, чем у NTRU, и он был гораздо более универсальным, но не столь эффективным. Некоторые исследователи полагали, что у них получится лучше. С 2007 года они рассматривают криптографические схемы, основанные на «решетках главных идеалов», которые генерируются одним вектором, почти так же, как набор целых чисел {…, -6, -3, 0, 3, 6, 9,…} может быть сгенерировано кратным целому числу 3.

«Они были жадными; они были недовольны существующей эффективностью », – сказал Регев.

Cat and Mouse

По мере того, как академические криптографы разрабатывали криптографические схемы, основанные на принципиальных идеальных решетках, то же самое делали и люди из-за кулис в GCHQ. Их секретная схема, получившая название Soliloquy, использовала методы теории чисел для уменьшения размера открытого ключа с матрицы больших чисел до одного простого числа. В основной задаче решетки это эквивалентно созданию решетки с одним очень коротким вектором.«К сожалению, для этого использовалась ахиллесова пята», – сказал представитель GCHQ в электронном письме.

В своей статье, опубликованной в октябре прошлого года, под названием «Монолог: предостерегающий рассказ» исследователи GCHQ показали, что они изобрели монолог, а затем отказались от работы над ним в 2013 году, обнаружив квантовую атаку, которая могла его сломать. В документе был представлен лишь расплывчатый набросок атаки, однако оставался открытым вопрос о том, как она работает и какие другие схемы на основе решеток могут быть затронуты.Казалось, что в погоне за эффективностью была пересечена красная черта. Но где была линия?

«Первоначально предполагалось, что эта атака может быть шире и, возможно, будет связана со всей криптографией на основе решеток», – сказал Пайфер. Другие скептически относились к тому, что атака вообще сработала.

Криптографы потратили почти год на определение масштабов атаки Soliloquy. «Люди стали одержимы», – сказал Хоффштейн. «Было безумие». Оказалось, что команда GCHQ сама не проработала многие детали, а просто имела «достаточно веские доказательства того, что атака может быть разработана и, следовательно, что Soliloquy не может быть рекомендован для использования в реальном мире», как выразился представитель Эл. адрес.В мартовской статье Регев, Пайкерт, Крамер и Лео Дука из CWI разработали ту часть атаки, для которой требовался только обычный компьютер; На прошлой неделе Жан-Франсуа Биасс и Фанг Сонг из Университета Ватерлоо в Онтарио изложили квантовые шаги.

Помимо Soliloquy, результаты показали, что другие схемы, основанные на решетках главных идеалов, генерируемых одним коротким вектором, также не работают, тогда как схемы, основанные на более общих идеальных решетках, такие как Ring-LWE и NTRU, не затрагиваются.«Похоже, что на начальном этапе есть некоторые технические препятствия для переноса этих методов на другие важные схемы», – сказал Крамер, добавив, что это требует дальнейшего изучения.

Что касается континуума безопасности и эффективности, криптографы зашли слишком далеко в сторону эффективности. В их стремлении найти лучшие квантово-устойчивые схемы для банков, правительств и остальной части защищенного Интернета атака Soliloquy вынудила их вернуться к схемам, которые несколько менее эффективны, но более прочно основаны на проблемах жесткой решетки.То есть предполагаемые проблемы с жесткой решеткой.

Нет никаких доказательств того, что квантовые компьютеры не могут ориентироваться в решетках. «Может быть, все эти проблемы на самом деле легкие», – сказал Пайкерт. «Но это кажется маловероятным, учитывая то, что мы знаем».

Что касается того, почему чрезвычайная эффективность и идеальная безопасность кажутся столь диаметрально противоположными, Хоффштейн сказал: «Вселенная – раздражающее место, и это всего лишь еще один пример этого».

Исправление: Эта статья была отредактирована сент.8, 2015, чтобы уточнить, что схемы, нарушаемые атакой Soliloquy, основаны на решетках главных идеалов, порожденных одним коротким вектором, а не схемах, основанных на решетках главных идеалов, порожденных более чем одним коротким вектором.

Оригинальный рассказ перепечатан с разрешения Quanta Magazine, редакционно независимого издания Фонда Саймонса, чья миссия состоит в том, чтобы улучшить понимание науки общественностью путем освещения исследований и тенденций в математике, а также в физических науках и науках о жизни.

Введение в решетчатые алгоритмы и решеточную криптографию

Введение в решетчатые алгоритмы и решеточную криптографию

Курс: Введение в решеточные алгоритмы и криптографию
Время: вторник, 14: 45 (неделя 6-21)
Расположение: Утрехтский университет, Buys-Ballotgebouw, комната 023

Описание курса:

Геометрия и структура евклидовых решеток изучались веками, чтобы понять геометрию периодических структур, таких как плотные упаковки сфер.Гораздо позже решетки занимали центральное место в разработке криптографических схем, которые считаются гораздо более безопасными, чем теоретико-числовые схемы, такие как RSA, которые могут быть скомпрометированы, если когда-либо будут построены эффективные квантовые компьютеры. Цель этого курса – дать четкое представление о геометрии решеток, алгоритмах решения центральных вычислительных задач на решетках и их приложениях в криптографии на основе решеток. Примеры тем включают: Первая и Вторая теоремы Минковского, теоремы переноса в геометрии чисел, алгоритмы для кратчайших (SVP) и ближайших векторных задач (CVP), обучение с ошибками (LWE), криптографическая схема с открытым ключом на основе LWE Регева, на основе решетки. подписи, NTRU, сокращение от худшего до среднего и дискретная гауссова выборка.

Схема оценок:

Домашние задания (3x): 40% Финальный экзамен: 60%

Преподаватели:

Даниил Дадуш : [email protected].
Лео Дука : [email protected].

Новостей:

• 06/02: Добро пожаловать на курс!

Домашних работ:

Расписание:

Дата	Тема	Ресурсы
1.06/02	Решетки и основания
2. 13/02	Детерминанты, упаковка и покрытие и теоремы Минковского
3. 20/02	Теорема двух квадратов, ортогонализация Грама Шмидта и Фундаментальные владения Бабая
4. 27/02	Ближайшая плоскость Бабая и алгоритм LLL
5.06/03	Свойства баз LLL, двойственность, алгоритмы перечисления
6. 13/03	Теоремы переноса, основы HKZ, формула суммирования Пуассона
7. 20/03	Периодический гауссовский, дискретный гауссовский и перенос
8. 27/03	Конец переноса, сложность проблем решетки
9.03/04	Проблема решения коротких целых чисел (SIS), коллизия устойчивые функции, односторонние функции
10. 10/04	Плавность SIS, схемы обязательств из SIS
11. 17/04	Обучение с ошибками и шифрованием с открытым ключом	Конспект лекций: Скоро.
12.24/04	Приложения LLL	Конспект лекций: Скоро.
13. 01/05	От худшего случая до среднего снижения Часть I	Конспект лекций: Скоро.
14. 08/05	Снижение от худшего до среднего: Часть II	Конспект лекций: Скоро.
15. 15/05	Полностью гомоморфное шифрование	Конспект лекций: Скоро.
16. 22/05	Алгоритм просеивания AKS для SVP	Конспект лекций: Скоро.

Другие решетки:

• Курс Одеда Регева «Решетки в информатике»: ссылка.
• Курс Даниэле Миччианчио «Решеточные алгоритмы и приложения»: ссылка
• Курс Криса Пайкерта “Решетки в криптографии”: ссылка
• Курс Винода Вайкунтанатана «Решетки в криптографии»: ссылка

Предисловие к специальной теме по криптографии на основе решеток | Национальный научный обзор

Классическая криптография существует уже давно в документированной истории человечества, но большинство классических шифров было взломано и даже решено вручную.Шеннон ввел понятие полной секретности, которое формально определяет конфиденциальность в теоретико-информационном смысле, что возможно только в ограниченных сценариях, когда длина сообщения не превышает длину ключа шифрования. Изобретение криптографии с открытым ключом (протокол обмена ключами Диффи-Хеллмана в 1976 году и криптосистема RSA в 1977 году) знаменует рождение современной криптографии, позволяющей сторонам безопасно обмениваться сообщениями без предварительного разглашения каких-либо секретов. Кроме того, он обеспечивает вычислительную безопасность, основанную на предполагаемой сложности математических задач, таких как факторизация и дискретный логарифм.Криптография с открытым ключом нашла множество применений в Интернете, финансовой и банковской сфере, а также в блокчейнах и играет решающую роль в защите информации и безопасности активов. К сожалению, в 1990-х годах Шор предложил эффективные квантовые алгоритмы, решающие теоретико-числовые задачи, включая факторизацию и дискретные логарифмы за полиномиальное время. Как только квантовый компьютер определенного масштаба станет реальностью, он нанесет сокрушительный удар по существующей инфраструктуре открытых ключей.Чтобы справиться с таким «квантовым кризисом», академические круги и промышленность изучают разработку, анализ и стандартизацию криптографических алгоритмов, которые могут противостоять квантовым компьютерам, именуемым постквантовой криптографией (PQC). Национальный институт стандартов и технологий (NIST) с 2016 года запрашивает предложения по постквантовым алгоритмам с открытым ключом. Совсем недавно Китайская ассоциация криптологических исследований (CACR) провела конкурс на разработку криптографических алгоритмов, чья криптография с открытым ключом трек, посвященный постквантовым криптографическим алгоритмам.Криптография на основе решеток рассматривается большинством как основной технический путь постквантовой криптографии, что отражается в количестве предложений (и их процентной доле от общего числа), полученных в процессе NIST PQC.

Чтобы отразить статус-кво постквантовой криптографии, мы приглашаем ведущих экспертов в этой области поделиться тремя техническими перспективами, которые призваны помочь читателям понять алгоритмы, лежащие в основе базовые методы и различные технические пути достижения квантовой устойчивости.

Первая перспектива, представленная Лу и Чжаном, представляет криптографические алгоритмы с открытым ключом, квантовая безопасность которых сводится к предполагаемой квантовой твердости решеточных задач. В частности, они в основном сосредоточены на шифровании с открытым ключом (PKE) и механизме инкапсуляции ключей (KEM), которые являются важными строительными блоками для обеспечения конфиденциальности связи без предварительного совместного использования секретов. Оба типа криптосистем требуют стандартизации NIST PQC и конкурса разработки алгоритмов CACR.Эта перспектива дает всесторонний обзор практических PKE / KEM на основе решеток и их наиболее известных квантовых и классических атак.

Другой важной постквантовой криптосистемой является цифровая подпись, которая обеспечивает достижение трех целей информационной безопасности, помимо конфиденциальности, а именно целостности, аутентификации и неотказуемости. Вторая точка зрения – решетчатая подпись Любашевского. С этой точки зрения он рассматривает различные методы построения постквантовых криптосистем на основе решеток, обсуждает проблемы, связанные с преодолением проблем с производительностью, и дает нам современные схемы цифровой подписи.

Помимо обеспечения «статической» безопасности информации при хранении и передаче, усовершенствованные криптографические алгоритмы и протоколы могут гарантировать информационную безопасность во время процесса вычислений (возможно, между несколькими сторонами), называемого вычислением с сохранением конфиденциальности. Криптографические методы, используемые для вычислений с сохранением конфиденциальности, включают безопасные многосторонние вычисления, доказательство с нулевым разглашением и полностью гомоморфное шифрование. Настоятельно необходимо перенести их в постквантовую эру.Третья перспектива, представленная Ю и Се, представляет собой практическое воплощение этих алгоритмов и обсуждает возможные способы их миграции на их квантово-устойчивые аналоги.

Подводя итог, постквантовая криптография получила широкое внимание и в последние годы добилась значительного прогресса. Некоторые постквантовые криптографические алгоритмы, такие как кандидат на основе решетки, также имеют другие преимущества (например, вычислительную эффективность и полный гомоморфизм) по сравнению с их классическими аналогами.Криптография на основе решеток – это развивающаяся область с высокой теоретической ценностью и широким применением, и мы поощряем молодых исследователей войти и изучить эту новую и захватывающую область.

© Автор (ы) 2021. Опубликовано Oxford University Press от имени China Science Publishing & Media Ltd.

Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (https://creativecommons.org/ лицензии / by / 4.0 /), что разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.

PALISADE Homomorphic Encryption Software Library – Библиотека программного обеспечения Lattice Crypto с открытым исходным кодом

Рост сообщества: Мы всегда рады новым участникам сообщества PALISADE. Пожалуйста, отправьте электронное письмо по адресу [email protected] с вопросами о конкретном проекте, который может вас заинтересовать, который улучшает и основывается на проекте PALISADE.

PALISADE – это проект с открытым исходным кодом, который обеспечивает эффективную реализацию строительных блоков решетчатой ​​криптографии и ведущих схем гомоморфного шифрования.

PALISADE разработан для удобства использования, предлагая более простые API, модульность, кроссплатформенную поддержку и интеграцию аппаратных ускорителей. PALISADE соответствует стандартам безопасности HomomorphicEncryption.org для гомоморфного шифрования. Мы предлагаем PALISADE в соответствии с лицензией BSD с открытым исходным кодом, состоящей из двух пунктов, что упрощает упаковку и распространение PALISADE в продуктах.

PALISADE теперь поддерживает схемы BGV, BFV, CKKS и FHEW и более безопасный вариант схемы TFHE, включая самозагрузку.У нас есть более эффективные схемы начальной загрузки, которые находятся в активной разработке. PALISADE также обеспечивает постквантовое шифрование с открытым ключом, повторное шифрование прокси, пороговое FHE для многосторонних вычислений, шифрование на основе идентичности, шифрование на основе атрибутов и поддержку цифровой подписи.

Основываясь на сотрудничестве сообщества PALISADE с профессором Даниэле Миччансио из UCSD и его аспирантом Байю Ли, мы разработали усовершенствование CKKS, которое учитывает их недавно опубликованное наблюдение (https: // eprint.iacr.org/2020/1533), что модель IND-CPA может быть недостаточно сильной для некоторых специальных практических приложений, использующих приближенные гомоморфные схемы шифрования, такие как CKKS. Вы можете прочитать наше более подробное обсуждение этой темы здесь, о том, как наше усовершенствование CKKS было выпущено в PALISADE v1.10.6 и совместно с другими основными библиотеками FHE с открытым исходным кодом.

Разработка

PALISADE продолжает щедро поддерживать DARPA, IARPA, Sloan Foundation и другие. Основными участниками PALISADE являются инженеры и ученые из ведущих оборонных подрядчиков, стартапов и университетов.

PALISADE официально входит в состав NumFocus стабильных проектов программного обеспечения с открытым исходным кодом.

Команда PALISADE регулярно проводит вебинары по FHE и PALISADE. Вы можете узнать о предстоящих вебинарах и посмотреть предыдущие записи на странице вебинаров.

У нас также есть группа объявлений Google, к которой может присоединиться любой желающий: https://groups.google.com/a/palisade-crypto.org/d/forum/announcements

(на основе идентичности) двойное шифрование приемника из программируемых хэш-функций на основе решетки с высокой минимальной энтропией | Cybersecurity

В этом разделе мы дадим общую конструкцию IB-DRE с использованием программируемых хэш-функций на основе решетки, а также предоставим выбор параметров и подтверждение безопасности схемы.{п \ раз п} \). Наконец, вывод P P = ( n , m , q , A , K ₁ , K ₂ , U ) и M s k = T _A .

\ (\ mathsf {KeyGen} _ {\ mathsf {ID}} (PP, Msk, \ mathbf {id} _ {1st}, \ mathbf {id} _ {2nd} \ in \ mathcal {ID}): \ ) Учитывая общедоступные параметры PP , мастер-ключ Msk и идентификаторы i d _{1 s t} , i d _{2 n d вычислить}

$$ \ mathbf {A} _ {\ mathbf {id} _ {1}} = \ mathcal {H}.{2m \ times n} \), удовлетворяющее \ (\ left [\ mathbf {A} | \ mathbf {A} _ {\ mathbf {id} _ {1}} \ right] \ cdot \ mathbf {E} _ {\ mathbf {id} _ {1}} = \ mathbf {U} \ phantom {\ dot {i} \!} \). Точно так же получите \ (\ phantom {\ dot {i} \!} Sk _ {\ mathbf {id} _ {2nd}} = \ mathbf {E} _ {\ mathbf {id} _ {2}} \) такое, что \ (\ left [\ mathbf {A} | \ mathbf {A} _ {\ mathbf {id} _ {2}} \ right] \ cdot \ mathbf {E} _ {\ mathbf {id} _ {2}} = \ mathbf {U} \).

Enc _ID ( P P , i d _{1 s t} , i d 9044 904 904 904 904 904 m ): вычислить \ (\ mathbf {A} _ {\ mathbf {id} _ {1}}, \ mathbf {A} _ {\ mathbf {id} _ {2}} \ phantom {\ dot {i} \!}\) как указано выше.{n} _ {q} \). Установите ( m ) _i = 1, если \ (\ left | (\ mathbf {b}) _ {i} – \ lceil \ frac {q} {2} \ rceil \ right | <\ lceil \ frac {q} {4} \ rceil \); в противном случае установите ( m ) _i = 0, где i ∈ {1, ⋯, n }. Наконец, он возвращает открытый текст m = (( m ) ₁ , ⋯, ( m ) _n ) ^⊤ .

Правильность и выбор параметров

Выбор параметров.{\ prime} q \ sqrt {2m} \ leq q / 4. \ end {align}} $$

алгоритм TrapGen может работать (т.е. м ≥6 n log q )

Алгоритмы SampleLeft могут работать (т.е. \ (\ sigma \ geq \ | \ widetilde {\ mathbf {T_ {A}}} \ | \ cdot \ omega \ left (\ sqrt {\ log {m}} \ right) = \ mathcal {O} \ left (\ sqrt {n \ log {q}} \ right) \ left.{*} _ {2}} \ right) \ leq 1 + 2 \ beta \) и \ (\ alpha q> \ max \ left \ {\ omega \ left (\ sqrt {\ log {m}} \ right ), \ omega \ left (\ sqrt {\ log {3m}} \ right) \ right \} = \ left. \ omega \ left (\ sqrt {\ log {3m}} \ right) \ right) \)

работает сокращение от худшего случая к среднему (т. {n \ times m} _ {q} \), где γ = negl ( λ ) и δ > 0.Тогда, если выполняется предположение DLWE _{q , n , n + m , α} , то приведенная выше схема \ (\ mathcal {IB} – \ mathcal {DRE} \) представляет собой безопасную схему IB-DRE против атак с выбранным открытым текстом и адаптивно выбранной идентичностью.

Доказательство (теоремы 2). Мы показываем, что при наличии злоумышленника PPT \ (\ mathcal {A} \) может нарушить нашу \ (\ mathcal {IB} – \ mathcal {DRE} \) схему с не- незначительное преимущество ε (т.{i} \ right) _ {i \ in [Q]} \ right \} \) набор идентификаторов задач и идентификаторов для ключевых запросов. Мы докажем теорему с помощью последовательностей игр, в которых первая игра является реальной игрой IND-ID-CPA в таблице 4, а в последней игре противник имеет нулевое преимущество. В каждой игре претендент \ (\ mathcal {C} \) выбирает однородную монету \ (b \ overset {\ $} {\ leftarrow} \ {0,1 \} \) в фазе вызова, а наконец \ ( \ mathcal {A} \) возвращает претенденту бит предположения b ^′ для b . {i } _ {2}} \ in {\ mathbf {Inv}} _ {\ mathbf {n}}, \\ 1, & \ text {в противном случае}, \ end {array} \ right.{3m} _ {q} \). В этой игре преимущество противника равно нулю. А именно \ (\ Pr [X_ {7}] = \ frac {1} {2} \). По определению Γ ₇ , мы имеем Γ ₇ = 0.

Анализ игр.

Лемма 8

Если \ (\ mathcal {H} \) – LPHF с высокой мин-энтропией, то | Pr [ X ₁ ] – Pr [ X ₀ ] | ≤ пренебрежение ( λ ).

Доказательство Эту лемму можно доказать с помощью свойства статистически закрытых секретных ключей LPHF из определения 3.

Для i ∈ {2,3,4,5,6,7} пусть \ (\ widetilde {p_ {i}} \) – вероятность того, что претендент не прервет этап проверки прерывания в G a m e _i , и вероятность на этапе искусственного прерывания в G a m e _i определяется как \ (p_ {i} = \ Pr \ left [\ mathbf {\ tau} \ left (\ widehat {td_ {1}}, \ widehat {td_ {2}}, \ widehat {K ^ {\ prime} _ {1}}, \ widehat {K ^ {\ prime} _ {2}}, I ^ {*} \ right) = 0 \ right] \). {2} – \ Gamma _ {2}).\)

Чтобы не прерывать доказательство теоремы 2, мы пока опускаем доказательство леммы 9.

Лемма 10

Если \ (\ mathcal {H} \) является (1, v , β , γ , δ ) -LPHF, и Q ≤ v , то | Pr [ X ₃ ] – Pr [ X ₂ ] | ≤ пренебрежение ( λ ) и | Γ ₃ – Γ ₂ | ≤ пренебрежение ( λ ).{i} _ {j}} \), i ∈ [ Q ], j = 1,2, использование SampleRight вместо SampleLeft дает лишь незначительную разницу. В заключение | Pr [ X ₃ ] – Pr [ X ₂ ] | ≤ пренебрежение ( λ ) и | Γ ₃ – Γ ₂ | ≤ пренебрежение ( λ ).

Лемма 11

Если \ (\ mathcal {H} \) является (1, v , β , γ , δ ) -LPHF, и Q ≤ v , то | Pr [ X ₄ ] – Pr [ X ₃ ] | ≤ пренебрежение ( λ ) и | Γ ₄ – Γ ₃ | ≤ пренебрежение ( λ ).

Доказательство Эту лемму можно доказать с помощью свойства ReRand из леммы 17.

Лемма 12

Предположим, что выполнено предположение DLWE _{n , q , n + m , α} , тогда | Pr [ X ₅ ] – Pr [ X ₄ ] | ≤ DLWE _{n , q , n + m , α} и | Γ ₅ – Γ ₄ | ≤ DLWE _{n , q , n + m , α} .

Доказательство , которое мы можем построить противник \ (\ mathcal {B} \) против DLWE _{n , q , n + m , α} задача, используя способность \ (\ mathcal {A} \), где \ (\ mathcal {A} \) – противник в G a m e ₄ или G a m е ₅ . {n + m}, \ alpha q } \).{n + m} _ {q} \), то вид противника \ (\ mathcal {A} \) такой же, как в G a m e ₅ . Таким образом, преимущество \ (\ mathcal {B} \) | Pr [ X ₅ ] – Pr [ X ₄ ] |, согласно предположению DLWE , | Pr [ X ₅ ] – Pr [ X ₄ ] | ≤ DLWE _{n , q , n + m , α} и | Γ ₅ – Γ ₄ | ≤ DLWE _{n , q , n + m , α} .

Лемма 13

| Pr [ X ₆ ] – Pr [ X ₅ ] | ≤ пренебрежение ( λ ) и | Γ ₆ – Γ ₅ | ≤ пренебрежение ( λ ).

Доказательство Эта лемма может быть доказана в соответствии со свойством ReRand из леммы 17.

Лемма 14

Если \ (\ mathcal {H} \) – LPHF с высокой мин-энтропией, то | Pr [ X ₇ ] – Pr [ X ₆ ] | ≤ пренебрежение ( λ ) и | Γ ₇ – Γ ₆ | ≤ пренебрежение ( λ ).{2} \ epsilon} {3} – \ mathsf {negl} (\ lambda). \)

Чтобы завершить доказательство теоремы 2, нам нужно доказать лемму 9, используя лемму 28 в полной мере. из Agrawal et al. (2010), который описывается следующим образом.

Лемма 15

(лемма 28 в Agrawal et al. (2010)) Пусть I ^∗ будет ( Q +1) -ID кортежом { i d ^∗ , { i d _j } _{j ∈ [ Q ]} } обозначает идентификатор задачи вместе с запрошенными идентификаторами, а η ( I ^∗ ) вероятность того, что прерывание не произойдет в G a m e ₂ .Пусть η _max = max η ( I ^∗ ) и η _min = min η ( I ^∗ ). Для i = 1,2, мы устанавливаем X _i как событие, что \ (\ hat {b} = b \) в конце G a m e ₁ . потом

$$ \ left | \ Pr [X_ {2}] – \ frac {1} {2} \ right | \ geq \ eta_ {min} \ left | \ Pr [X_ {1}] – \ frac {1} {2} \ right | – \ frac {1} {2} (\ eta_ {max} – \ eta_ {min}).{\ prime} \ leq p_ {2} \ left (1 – \ frac {\ epsilon} {8} \ right) \ right] \ leq \ lambda \ frac {\ epsilon} {8} \). Потом,

$$ {\ begin {align} \ eta_ {max} & \ leq \ left (1 – \ lambda \ frac {\ epsilon} {8} \ right) \ widetilde {p_ {2}} \ frac {\ lambda } {p_ {2} \ left (1 – \ frac {\ epsilon} {8} \ right)}, ~ \\ \ eta_ {min} & \ geq \ left (1 – \ lambda \ frac {\ epsilon} { 8} \ right) \ widetilde {p_ {2}} \ frac {\ lambda} {p_ {2} (1 + \ frac {\ epsilon} {8})} \ geq \ frac {7 \ lambda \ widetilde {p_ {2}}} {9p_ {2}} \\ \ eta_ {max} – \ eta_ {min} & \ leq \ left (1 – \ lambda \ frac {\ epsilon} {8} \ right) \ frac {\ лямбда \ epsilon \ widetilde {p_ {2}}} {4 (1- \ frac {\ epsilon ^ {2}} {64}) p_ {2}} \ leq \ frac {16 \ lambda \ epsilon \ widetilde {p_ {2}}} {63p_ {2}} \ end {align}} $$

Подставляя их и значение λ в неравенство в лемме 15, мы можем получить

$$ {{} \ begin {align} \ left | \ Pr [X_ {2}] – \ frac {1} {2} \ right | & \ geq \ frac {7 \ lambda \ widetilde {p_ {2}}} {9p_ {2}} \ cdot \ epsilon – \ frac {1} {2} \ cdot \ frac {16 \ lambda \ epsilon \ widetilde { p_ {2}}} {63p_ {2}} \\ & \! \ geq \! \ frac {\ lambda \ epsilon (p_ {2} – \ Gamma_ {2})} {2p_ {2}} \! \ geq \! \ frac {1} {2} \ epsilon (\ lambda \, – \, \ Gamma_ {2}) \, = \, \ frac {1} {2} \ epsilon \ left (\ delta ^ {2} – \ Гамма_ {2} \ справа).\ end {align}} $$

Его приложения, области интересов и будущие масштабы

● Задача кратчайшего вектора (SVP)



:



Для заданного базиса решетки

другой создается базис XLX ′

такой, что векторы, где LX = LX ′ X ′

являются самыми короткими для любой нормы [8].

● Задача приближенного кратчайшего вектора (

𝞪

-SVP)



:

Для данной решетки проблема решается с помощью L

, находящего ненулевой вектор ‘x’, где

[8].x ε L, ∀ yε L, || x || ≤ α || y ||

● Задача кратчайшего независимого вектора (SIVP).

● Проблема ближайшего вектора (CVP).

● Задача приблизительного ближайшего вектора (

𝞪

-CVP).

● Декодирование с ограниченным расстоянием (BDD).

● Задача кратчайшего целочисленного решения (SIS)



.

Различные алгоритмические решения для этих проблем с решеткой

включают ориентацию Грама-Шмидта, алгоритм LLL,

, который является наиболее известным алгоритмом полиномиального времени,

BKZ и наиболее широко используемый алгоритм

Бабая, алгоритм округления [ 8], который доказал, что CVP в Rn

может быть аппроксимирована.2н

II. РЕШЕТКАЯ КРИПТОСИСТЕМА

Поскольку все мы знаем недостатки классической криптосистемы

, которая включает RSA.

RSA использует большие конечные абелевы группы [5]. В Z / NZ) G = (x

, чтобы ускорить процесс, мы ввели:

● Криптография на основе эллиптических кривых, которая использует меньшие группы

, операции которых более дороги [8].

● Криптография на основе решеток, которая использует более крупные группы

, работа которых значительно дешевле [8].

Криптография на основе решеток использует многомерные геометрические структуры

для сокрытия информации, создавая

проблем, которые невозможно решить без ключа

даже универсальными отказоустойчивыми квантовыми компьютерами

.

Чтобы сделать такую ​​криптографию возможной, прежде всего,

, нам нужно построить прототип системы и протестировать его

в нескольких жестких условиях.Поскольку до сих пор мы ясно знаем о Решетках и их теории. Мы хорошо осведомлены о том, что эта криптосистема

полностью полагается на серьезность проблемы.

Считая его кандидатом на постквантовую криптографию

, рассматриваемая сложная задача должна быть достаточно сложной

, чтобы обмануть и схемы квантовых вычислений

.[8].

Различные криптосистемы, которые реализованы в настоящее время

, используют SVP / CVP / BDD в качестве жесткости, используемой в тех задачах

, используя концепции Lattice Equality как

односторонней функции лазейки.

Некоторые обычно используемые криптосистемы: –

● GGH.

● Кольцо Пикерта – обучение с ошибками (кольцо

LWE) Обмен ключами.

● NTRUEncrypt.

● Криптосистема Micciancio.

● Другие криптосистемы на основе CVP.

III. ПРИЛОЖЕНИЯ

С появлением различных компьютерных парадигм необходимость содержать определения безопасности

стала реальной угрозой для компьютерных ученых. Как

технологических услуг, таких как облачные вычисления,

высокопроизводительных (в реальном времени) виртуализированных сред,

Интернета вещей, квантовых вычислений и т. Д.требуют

программно-определяемых сетей с высоким уровнем защиты / шифрования для

их связи.

В IoT классические криптографические меры, похоже, не работают

, потому что пространство IoT требует увеличенного числа ключей

. Чтобы справиться с этой увеличенной генерацией ключа

с помощью классических криптографических мер, потребовалась разработка некоторых стандартных облегченных криптографических схем

и шифров с повышенной маневренностью и производительностью

.Эта разработка требует криптосистемы с открытым ключом

на основе решеток и, следовательно, становится областью интереса

для ее реализации / применения.

Аналогично, для облачных вычислений канал или программно-определяемая сеть

, которая ему требуется, должна иметь

высокой маневренности и производительности, должна быть энергоэффективной

Труды Третьей Международной конференции по методологиям вычислений и коммуникации ( ICCMC 2019)

Номер детали IEEE Xplore: CFP19K25-ART; ISBN: 978-1-5386-7808-4

978-1-5386-7808-4 / 19/31 доллар США.