Слу метод крамера. Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$.

- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус.
 B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.
B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель.

- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
Навигация по странице.
Метод Крамера – вывод формул.
Пусть нам требуется решить систему линейных уравнений вида
Где x 1 , x 2 , …, x n – неизвестные переменные, a i j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b 1 , b 2 , …, b n – свободные члены. Решением СЛАУ называется такой набор значений x 1 , x 2 , …, x n при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B
, где – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, – матрица – столбец свободных членов, а – матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x 1 , x 2 , …, x n
, матрица становится решением системы уравнений и равенство A ⋅ X = B
обращается в тождество .
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).
Метод Крамера основывается на двух свойствах определителя матрицы:
Итак, приступим к нахождению неизвестной переменной x 1
. Для этого умножим обе части первого уравнения системы на А 1 1
, обе части второго уравнения – на А 2 1
, и так далее, обе части n-ого
уравнения – на А n 1
(то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А
):
Если обратиться к озвученным ранее свойствам определителя, то имеем
и предыдущее равенство примет вид
откуда
Аналогично находим x 2
. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А
:
Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А
:
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x 1 , x 2 , …, x n и применяем свойства определителя:
Откуда
.
Аналогично находятся оставшиеся неизвестные переменные.
Если обозначить
То получаем формулы для нахождения неизвестных переменных по методу Крамера .
Замечание.
Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера .
Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .
Решение.
Основная матрица системы имеет вид . Вычислим ее определитель по формуле :
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .
Вычисляем эти определители:
Находим неизвестные переменные x 1
и x 2
по формулам :
Выполним проверку. Подставим полученные значения x 1
и x 2
в исходную систему уравнений:
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера .
Решение.
Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле
Имеем
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :
Таким образом,
Ответ:
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x 1 , x 2 , …, x n . Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x , y и z вместо x 1 , x 2 и x 3 ). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:
Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:
Осталось найти неизвестные переменные по формулам :
Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите раздел ):
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3
.
Пример.
Решите методом Крамера систему линейных уравнений , где a и b – некоторые действительные числа.
Решение.
Ответ:
Пример.
Найдите решение системы уравнений методом Крамера, – некоторое действительное число.
Решение.
Вычислим определитель основной матрицы системы: . выражения есть интервал , поэтому при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем и :
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений,
сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т. е. коэффициенты при неизвестных и свободные члены пропорциональны.
е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8..png)
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Проверить совместимость системы уравнений онлайн методом крамера. Линейные уравнения
Габриэль Крамер – швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры.
Крамер рассмотрел систему произвольного количества линейных уравнений с квадратной матрицей. Решение системы
он представил в виде столбца дробей с общим знаменателем – определителем матрицы. Метод Крамера основан на
использовании определителей в решении систем линейных уравнений, что позволяет существенно ускорить процесс
решения. Данный метод может быть применен в решении системы стольких линейных уравнений, сколько в каждом
уравнении неизвестных. Главное, чтобы определитель системы не был равен “0”, тогда метод Крамера может быть
использован в решении, если “0” – данный метод использовать нельзя. Также данный метод может быть применен
для решения систем линейных уравнений с единственным решением.
Решение системы
он представил в виде столбца дробей с общим знаменателем – определителем матрицы. Метод Крамера основан на
использовании определителей в решении систем линейных уравнений, что позволяет существенно ускорить процесс
решения. Данный метод может быть применен в решении системы стольких линейных уравнений, сколько в каждом
уравнении неизвестных. Главное, чтобы определитель системы не был равен “0”, тогда метод Крамера может быть
использован в решении, если “0” – данный метод использовать нельзя. Также данный метод может быть применен
для решения систем линейных уравнений с единственным решением.
Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно
единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель
системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при
этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого
порядка.
Допустим, дано СЛАУ такого вида:
\[\left\{\begin{matrix} 3x_1 + 2x_2 =1\\ x_1 + 4x_2 = -3 \end{matrix}\right.\]
Согласно теореме Крамера получаем:
Ответ: \
Где можно решить уравнение методом Крамера онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1. 5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1. 8. Найти, если это возможно, произведение матриц AB и BA :
8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A – 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A – 1 , мы получим решение системы:
14) слева на A – 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).
18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
…………………………………………………………………. . . | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
…………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = – 3 + 2t
x 2 = – 1 – 3t
x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами.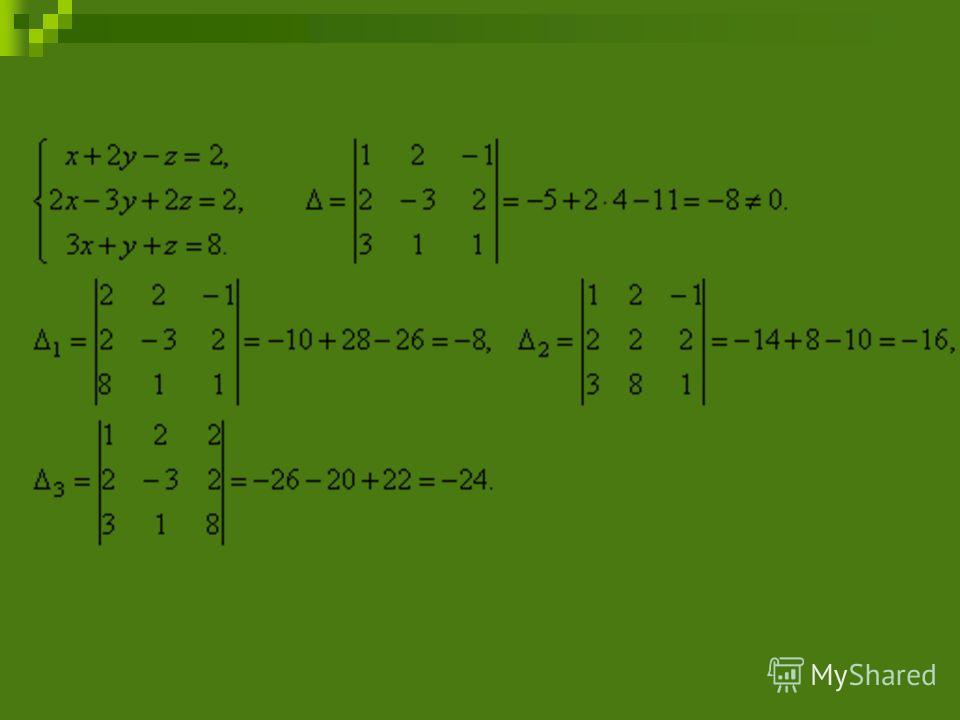 Эта теорема имеет место для системы линейных уравнений любого порядка.
Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Решение линейных уравнений по правилу крамера. Метод крамера решения систем линейных уравнений. Решение систем линейных уравнений методом обыкновенных жордановых исключений
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т. е. коэффициенты при неизвестных и свободные члены пропорциональны.
е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.
К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Решение СЛАУ матричным методом – презентация онлайн
1. Решение СЛАУ матричным методом
2. Матричный метод решения СЛАУ
Матричный метод – это метод решениячерез обратную матрицу квадратных
(с числом уравнений, равным числу
неизвестных) систем линейных
алгебраических уравнений с
ненулевым определителем.
3. Пусть дана система линейных уравнений с n неизвестными
Пусть дана система линейных уравнений с n неизвестнымиЗапишем ее в матричной форме:
A — основная матрица системы, состоящая из
коэффициентов при неизвестных.

B — вектор – столбец свободных членов (слагаемых)
X — вектор – столбец решений системы
4. Запишем СЛАУ в виде матричного уравнения и решим его
AX = BУмножим это матричное уравнение слева на A − 1 — матрицу,
обратную матрице A:
Так как A − 1A = E по определению обратной матрицы, получаем
E X = A − 1B
X = A − 1B
где A – 1=1/∆ (A*)Т ,
∆≠0
(A*)Т – транспонированная матрица алгебраических дополнений
соответствующих элементов матрицы A.
5. Пример Решить СЛАУ матричным методом:
Сначала убедимся в том, что определитель матрицы изкоэффициентов при неизвестных СЛАУ не равен нулю.
6. Вычислим алгебраические дополнения для элементов основной матрицы
Вычислим алгебраические дополнения дляэлементов основной матрицы
7. Найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы
Найдём союзную матрицу, транспонируем её и подставимв формулу для нахождения обратной матрицы
8.
 Найдем неизвестные, перемножив обратную матрицу и столбец свободных членов Найдем неизвестные, перемножив обратную
Найдем неизвестные, перемножив обратную матрицу и столбец свободных членов Найдем неизвестные, перемножив обратнуюматрицу и столбец свободных членов
Ответ: x=2; y=1; z=4.
10. Самостоятельная работа
1 вариант2 вариант
Решить СЛАУ:
Решить СЛАУ:
2 x1 3 x2 x3 7
3 x1 2 x2 x3 5
4 x 7 x 3 x 4
2
3
1
x1 2x 2 – x 3 4
3×1 2 x 3 8
4x – 2x 5x 0
1
2
3
11. Домашнее задание
Решить СЛАУ:Решение с помощью формул крамера. Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений,
сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
| 1 | Упростить | квадратный корень s квадратный корень s^7 | |
| 2 | Упростить | кубический корень 8x^7y^9z^3 | |
| 3 | Упростить | arccos(( квадратный корень 3)/2) | |
| 4 | Risolvere per ? | sin(x)=1/2 | |
| 5 | Упростить | квадратный корень s квадратный корень s^3 | |
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град.2+n-72)=1/(n+9) |
Найти определитель матрицы онлайн методом Крамера. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера
Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера можно использовать для решения системы линейных уравнений, количество которых равно количеству неизвестных в каждом уравнении. Если определитель системы не равен нулю, то в решении можно использовать метод Крамера, если он равен нулю, то нельзя.Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.
Определение … Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Детерминанты
получаются заменой коэффициентов соответствующими неизвестными свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, а неизвестное равно отношению определителей.В знаменателе стоит определитель системы, а в числителе – определитель, полученный из определителя системы заменой коэффициентов в этой неизвестной свободными членами. Эта теорема верна для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн калькулятор, метод Крамера.
Три случая при решении систем линейных уравнений
Как видно из теорем Крамера , при решении системы линейных уравнений могут иметь место три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система непротиворечивая и определенная)
Второй случай: система линейных уравнений имеет бесконечное число решений
(система непротиворечивая и неопределенная)
** ,
т.е.коэффициенты при неизвестных и свободных членах пропорциональны.
Третий случай: система линейных уравнений не имеет решений
(система несовместима)
Итак, система m линейных уравнений с n переменными называется несовместной , если она не имеет решений, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется некоторым , а более одного – неопределенным .
Примеры решения систем линейных уравнений методом Крамера
Пусть системе дано
.
На основании теоремы Крамера
………….
,
где
–
. Остальные определители получаем заменой в столбце коэффициентов соответствующей переменной (неизвестной) со свободными членами:
Пример 2.
Следовательно, система определена.Чтобы найти ее решение, вычислим определители
По формулам Крамера находим:
Итак, (1; 0; -1) — единственное решение системы.
Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, решающим метод Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие элементы равны нулю! Это следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Раствор. Находим определитель системы:
Посмотрите внимательно на систему уравнений и определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычислим определители для неизвестных
По формулам Крамера находим:
Итак, решение системы равно (2; -1; 1).
Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, решающим метод Крамера.
Вернуться к началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители неизвестных не равны нулю, то система несовместна, то есть не имеет решений. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Раствор. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определена, либо несовместна, то есть не имеет решений. Для большей точности вычислим определители для неизвестных
Определители неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, решающим метод Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть еще и другие буквы. Эти буквы обозначают определенное число, чаще всего действительное число. На практике к таким уравнениям и системам уравнений приводят задачи поиска общих свойств некоторых явлений и объектов.То есть вы изобрели какой-то новый материал или устройство, и для описания его свойств, общих вне зависимости от размера или номера экземпляра, вам нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных стоят буквы. За примерами далеко ходить не надо.
Следующий пример для аналогичной задачи, только увеличивается количество уравнений, переменных и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Раствор.Находим определитель системы:
Найти определители неизвестных
Габриэль Крамер — швейцарский математик, ученик и друг Иоганна Бернулли, одного из основоположников линейной алгебры. Крамер рассмотрел систему произвольного числа линейных уравнений с квадратной матрицей. Он представил решение системы в виде столбца дробей с общим знаменателем – определителем матрицы. Метод Крамера основан на использовании определителей при решении систем линейных уравнений, что позволяет значительно ускорить процесс решения.Этот метод можно применять при решении системы линейных уравнений, количество которых равно количеству неизвестных в каждом уравнении. Главное, чтобы определитель системы не был равен “0”, тогда в решении можно использовать метод Крамера, если “0” – этот метод использовать нельзя. Также этот метод можно использовать для решения систем линейных уравнений с единственным решением.
Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, а неизвестное равно отношению определителей.В знаменателе стоит определитель системы, а в числителе – определитель, полученный из определителя системы заменой коэффициентов в этой неизвестной свободными членами. Эта теорема верна для системы линейных уравнений любого порядка.
Предположим, что задана СЛАУ этого типа:
\[\влево\(\начало(матрица)3x_1+2x_2=1\x_1+4x_2=-3\конец(матрица)\вправо.\]
По теореме Крамера получаем:
Ответ: \
Где можно решить уравнение методом Крамера с помощью онлайн-решателя?
Решить уравнение можно на нашем сайте https://сайт.Бесплатный онлайн-решатель позволит решить онлайн уравнение любой сложности за считанные секунды. Все, что вам нужно сделать, это просто ввести свои данные в решатель. Вы также можете посмотреть видео-инструкцию и научиться решать уравнение на нашем сайте. А если у вас остались вопросы, вы можете задать их в нашей группе Вконтакте http://vk.com/pocketteacher. Присоединяйтесь к нашей группе, мы всегда рады вам помочь.
2. Решение систем уравнений матричным методом (с использованием обратной матрицы).
3. Метод Гаусса для решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений ( СЛАУ ).
Формулы на примере системы двух уравнений с двумя переменными.
Дано: Решить систему методом Крамера
Переменные NS и at .
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы Вычисление определителей.:
Применяем формулы Крамера и находим значения переменных:
и .
Пример 1:
Решите систему уравнений:
относительно переменных NS и на .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Проделаем аналогичное действие, заменив в первом определителе второй столбец:
Применимы формулы Крамера и найдем значения переменных:
и .
Ответ:
Комментарий: Этот метод можно использовать для решения систем больших размерностей.
Комментарий: Если оказывается, что и делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система либо имеет бесконечно много решений, либо вообще не имеет решений.
Пример 2 (бесконечное количество решений):
Решите систему уравнений:
относительно переменных NS и на .
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы:
Решение систем методом подстановки.
Первым из уравнений в системе является равенство, которое верно при любых значениях переменных (потому что 4 всегда равно 4). Так что осталось только одно уравнение. Это уравнение связи между переменными.
Получено, решением системы является любая пара значений переменных, связанных друг с другом равенством.
Общее решение запишется так:
Частные решения можно определить, выбрав произвольное значение y и вычислив x, используя это равенство связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (нет решений, система несовместима):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы:
Формулы Крамера неприменимы.Решим эту систему методом подстановки
Вторым уравнением системы является равенство, что неверно ни при каких значениях переменных (разумеется, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то вся система не имеет решений.
Ответ: нет решений
Методы Kramer и Gauss – одни из самых популярных методов решения СЛАУ …Кроме того, в ряде случаев целесообразно использовать специфические методы. Сессия подошла к концу, и сейчас самое время вернуться к ним или освоить их с нуля. Сегодня мы имеем дело с решением методом Крамера. Ведь решение системы линейных уравнений по методу Крамера — очень полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – это система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, а и б – реальные коэффициенты.Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (х) в СЛАУ может быть гораздо больше двух, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнения с n неизвестно.
Такую систему можно переписать в матричной форме
Здесь А – основная матрица системы, Х и В соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ по методу Крамера
Если определитель главной матрицы отличен от нуля (матрица невырожденная), то система может быть решена методом Крамера.
По методу Крамера решение находится по формулам:
Здесь дельта Является определителем основной матрицы, а дельта х n-й – определитель, полученный из определителя основной матрицы заменой n-го столбца на столбец свободных членов.
В этом весь смысл метода Крамера. Подставив найденные значения по приведенным выше формулам х в нужную систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы вы быстрее вникли в суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у вас не получится с первого раза, не расстраивайтесь! Немного потренировавшись, вы начнете переворачивать SLAU, как орехи.К тому же теперь совершенно необязательно корпеть над тетрадью, решая громоздкие вычисления и выписывая штангу. Вы легко сможете решить СЛАУ методом Крамера онлайн, только подставив коэффициенты в готовую форму. Вы можете попробовать онлайн-калькулятор решения по методу Крамера, например, на этом сайте.
А если система окажется упрямой и не сдастся, вы всегда можете обратиться за помощью к нашим авторам, например, к . Если в системе будет хотя бы 100 неизвестных, мы обязательно решим ее правильно и в срок!
Cramer – Программное обеспечение для сборки
Введение
Этот метод находит все решения системы линейных уравнений.Мы определяем систему линейных уравнений как n наборов уравнений в форме: Эти системы могут быть представлены как произведение матриц, таких как следующие:
Что также может быть представлено как:
Решениями этой задачи являются наборы значений от x1 до xn, которые удовлетворяют уравнениям.
Система линейных уравнений состоит из двух частей: обратимой матрицы размера nxn (квадрата), которая содержит коэффициенты каждого уравнения, и матрицы размера nx1 (столбца), которая содержит независимые члены каждого уравнения.
Метод
Метод Крамера основан на определителях. Определитель — это числовое значение матрицы, которое можно вычислить несколькими способами. Более подробную информацию об определителях, их свойствах и способах их расчета можно найти здесь.
Правило Крамера следующее:
Где A_j — исходная матрица с j-й строкой, измененной с помощью b.
Примеры
- А = [7., 2.; -21., -5.], В = [16.; 50.], R = [-25,7; 98.]
- А = [2., -3.; 4., 1.], В = [-2.; 24.], р = [5.; 4.]
- А = [3., -0,1, -0,2; 0,1, 7, -0,3; 0,3, -0,2, 10.], В = [7,85; -19,3; 71,4], Р = [3.; -2,5; 7.]
- А = [0,3, 0,52, 1.; 0,5, 1, 1,9; 0,1, 0,3, 0,5], В = [-0,01; 0,67; -0,44], R=[-14,9; -29,5; -19,8]
Особенности
Этот метод не является итеративным. Несмотря на то, что он реализует вычисления с итерациями, эти итерации определяются размером матрицы, а не ее содержимым.Итерационный метод реализует неизвестные итерации и останавливается до тех пор, пока не будет достигнут заданный критерий ошибки. Из-за этого итерационный метод может расходиться. С другой стороны, неитерационная ошибка делает фиксированное количество итераций. Он может иметь ужасную сложность, но он конечен. Не расходится, не проваливается.
Вычисление определителя матрицы — очень тяжелая операция. Это требует много памяти и времени. Попытка решить большие системы уравнений может стать сложной задачей, поскольку разложение детерминанта Лапласа требует O (n!).
Блок-схема
Код
Выводы
Метод Крамера действительно прост для понимания и программирования (учитывая, что у нас есть функция для получения определителя матрицы, так как это не так просто реализовать). Но он имеет свой потенциал только с небольшими системами. Более крупные системы требуют большего вычислительного времени и места.
Нравится:
Нравится Загрузка…
Борис Крамер – UCSD
Аннотация
Эта диссертация посвящена проблемам проектирования, оптимизации и управления сложными крупномасштабными динамическими системами с разных точек зрения.Цель состоит в том, чтобы разработать новые алгоритмы и методы, которые более эффективно решают реальные проблемы, а также обеспечить математическое понимание успеха этих методов. В диссертации есть три основных вклада. В главе 3 мы предлагаем новый метод решения крупномасштабных алгебраических уравнений Риккати, возникающих при оптимальном управлении, фильтрации и редукции моделей. Мы представляем основанный на проекциях алгоритм, использующий правильную ортогональную декомпозицию, которая продемонстрировала высокую точность решений при низком ранге.Этот метод можно распараллелить, его легко реализовать для практиков, и он является первым шагом к безматричному подходу к решению ARE. Представлены численные примеры для n >= 100 000 неизвестных. В главе 4 мы разрабатываем метод идентификации системы, основанный на тангенциальной интерполяции. Это решает проблему подгонки линейных неизменных во времени систем к характеристикам входа-выхода сложной динамики, где количество входов и выходов относительно велико.Этот метод снижает вычислительную нагрузку, связанную с полным разложением по сингулярным числам, за счет тщательного выбора направлений, на которые следует проецировать импульсную характеристику до сборки матрицы Ганкеля. Шаг идентификации и редукции модели следует из алгоритма реализации собственной системы. Мы представляем три численных примера, систему с массовым пружинным демпфером, задачу теплообмена и гидродинамическую систему. Получены оценки погрешности и результаты устойчивости для этого метода. В главе 5 рассматривается проектирование управления и наблюдения для динамических систем, зависящих от параметров.Мы решаем эту проблему, используя локальные параметрические модели пониженного порядка, которые можно использовать онлайн. Данные, полученные в результате моделирования системы в различных конфигурациях (параметры, граничные условия), используются для извлечения разреженной основы для представления динамики (путем декомпозиции по динамическим модам). Впоследствии был разработан новый алгоритм классификации на основе сжатых измерений, который включает извлеченную динамическую информацию в основу измерений. Мы показываем, что эта расширенная классификационная основа делает метод более устойчивым к шуму и обеспечивает превосходную идентификацию правильного параметра.Численные примеры состоят из приложения потока Навье-Стокса, а также приложения потока Буссинеска.
Бибтекс
@phdthesis{kramer15thesisMOR,
title={Модель и обработка данных для управления, идентификации и сжатого зондирования},
автор={Борис Крамер},
year={2015},
school={Virginia Tech},
url = { http://hdl.handle.net/10919/75179}
}
Стивен Н. Крамер, доктор философии, ЧП.
Стивен Н. Крамер, доктор философии, ЧП
Профессор Emeritus
Отдел механических, промышленных и производственных инженерных,
Nitschke Hall 4039
Университет ToLEDO
TOLEDO, OH 43606
Mail STOP 312
Телефон: (419) 874-6535
Факс: (419) 874-2157
Электронная почта: Стивен[email protected]
2005 г., советник факультета ASME
Биография
Доктор Стивен Н. Крамер является почетным профессором механики, промышленности и производства. инженерного дела в университете Толедо. Доктор Крамер получил степень доктора философии в Rensselaer. Политехнический институт в 1973 году и с тех пор находится в ТУ. Его промышленный опыт включает IBM Corporation, Outboard Marine Corporation, Dunham Tool Company, Олбани. International Corporation, а также консультировал Owens-Illinois Corporation.
Исследовательская деятельность доктора Крамера включает CAD плоских и пространственных механизмов, а также различные приложения для робототехники и проекты моделирования, финансируемые местной промышленностью. Он опубликовал более 90 статей в различных материалах конференций и архивных журналах.
Доктор Крамер получил несколько наград и наград. В 1984 году он получил выдающийся Преподавательская премия в Университете Толедо, а в 1985 году он получил национальную премию Ральфа. Р.Премия Teetor за выдающиеся достижения от Общества автомобильных инженеров. Также в том года, он также был выбран «Инженером-механиком года» на Северо-Западе. Секция Огайо Американского общества инженеров-механиков. В 1986 году доктор Крамер получил Премия преподавателя ASME для пятого региона, а в 1988 году он был выбран как выдающийся Преподаватель инженерного дела в штате Огайо Общества профессиональных инженеров Огайо.В 1991 году доктор Крамер стал лауреатом премии South-Pointing Chariot Research Award. в области прикладных механизмов и робототехники. В 1994 году он получил почётную грамоту. Премия советника в Университете Толедо. В 1999 году он получил первый университет Премии Толедо «Профессор года» по программе UT Honors Program. Доктор Крамер единственный человек в истории Толедского университета, получивший выдающуюся преподавание, выдающееся консультирование и награды «Профессор года».
Доктор Крамер является активным членом Американского общества инженеров-механиков (ASME). У него есть работал председателем Национального комитета по наградам и наградам за дизайн. инженерного отдела, в качестве председателя группы по образованию пятого региона и в качестве член регионального операционного совета ASME. Он также является членом исполнительного совета секции Северо-Западного Огайо ASME и является членом Комитета по автоматизации проектирования. в конструкторско-технологическом отделе.В 1987 году он был избран научным сотрудником ASME. – уровень членства, ограниченный менее чем одной десятой процента его членства. Доктор Крамер также является советником факультета ASME в UT.
В Университете Толедо доктор Крамер работал в многочисленных комитетах колледжа. и университетского уровня. Он работал советником факультета в студенческой секции Общества. женщин-инженеров с 1977 по 1990 год, а также в качестве советника факультета студенческой секции ASME. с 1979 по 1986 год и с 1995 года по настоящее время.Доктор Крамер был членом Инженерного Комитет по академическим кадрам с 1980 по 1985 год и член университетского комитета. по академическим кадрам с 1985 по 1987 год.
Научные интересы
КОМПЬЮТЕРНОЕ ПРОЕКТИРОВАНИЕ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ МЕХАНИЗМОВ проектирование и оптимизация плоскостных и пространственных механизмов для развития взаимоотношений для перемещения, скорости и ускорения плоскостных и пространственных механизмов с использованием различные методы.Наиболее популярным и универсальным методом является метод комплексных чисел. механизма синтеза. Другие методы включают алгебраические, матричные и двойные числа. метод.
ИССЛЕДОВАНИЕ ДОПУСКОВ И УГЛОВ ПЕРЕДАЧИ В МЕХАНИЗМАХ В качественном смысле, существует общее мнение, что вариации длин звеньев механизма (из-за производственных допусков) больше влияют на механическую ошибку при передаче углы плохие, чем когда они близки к оптимальным значениям.Никто не проводил исчерпывающую количественное исследование этого. Это отличный проект уровня мастеров для кого-то интересует планарные механизмы.
ЧУВСТВИТЕЛЬНОСТЬ К ДОПУСКАМ КАК ИНСТРУМЕНТ ПРОЕКТИРОВАНИЯ Многие люди проводили анализ допусков на механизмах, но необходимо иметь чувствительность к допускам в качестве инструмента проектирования. Это позволило бы разработчикам механизмов проектировать механизмы, которые работают выше определенного заданный уровень производительности при наличии допусков.
ПРИМЕНЕНИЕ МЕТОДОВ ОПТИМИЗАЦИИ ДЛЯ РЕШЕНИЯ ЗАДАЧ МЕХАНИЧЕСКОГО ПРОЕКТИРОВАНИЯНелинейный методы оптимизации с ограничениями применялись и могут применяться к решению важных проблем механического проектирования. В настоящее время доступны методы оптимизации для непрерывных и дискретных задач, и их можно использовать для решения многих задач в области дизайна.
Публикации
Журнальные публикации
- «Конечный кинематический синтез циклоидального кривошипно-шатунного механизма для генерации функций», ASME Transactions, Журнал машиностроения для промышленности, серия B, Vol. 92, № 3, август 1970, стр. 531-536. С Г. Н. Сандором.
- «Анализ прогиба и напряжения в высокоскоростных планарных механизмах с эластичными звеньями», ASME Сделки, Журнал техники для промышленности; Серия Б, Том.95; Май 1973 г., стр. 541-548. С И. Имамом и Г. Н. Сандором.
- «Селективный прецизионный синтез — общий метод оптимизации планарных механизмов», ASME Transactions, Журнал машиностроения для промышленности, серия B, Vol. 97, № 2, май 1975 г., стр. 689-701. С Г. Н. Сандором.
- «Выборочный прецизионный синтез четырехтактного генератора движения с заданным входом Сроки “, ASME Transactions, Journal of Mechanical Design, Vol.101, № 4, октябрь 1979, стр. 614-618.
- «Селективный прецизионный синтез механизма, удовлетворяющего ограничениям по положению и скорости», Международный Журнал теории механизмов и машин, Vol. 14, № 3, 1979, стр. 161-170. С Р. С. Шефер.
- «Синтез комплексных чисел четырехтактных механизмов генерации путей, регулируемых для нескольких Тангенциальные дуги окружности.” ASME Transactions, Journal of Mechanical Design, Vol. 104, № 1, январь 1982 г., стр. 185–191. С Л. Хьюстоном.
- «Разработка транссимметричного движения с переменной скоростью с дискретно исчезающим скачком», ASME Transactions, Журнал механизмов, трансмиссий и автоматизации в дизайне, Vol. 106, № 1, март 1984 г., стр. 109-113.
- «Кинематический синтез и анализ зубчато-реечного механизма для генерации функций», Международный Журнал теории механизмов и машин, Vol.19, № 3, 1984, стр. 369-376. С Д. Гибсон.
- “Символическое обозначение и кинематические уравнения движения планетарной системы двадцати двух шпор”. Зубчатые передачи», Транзакции ASME, Журнал механизмов, трансмиссий и автоматизации. в дизайне, Vol. 106, № 3, сентябрь 1984 г., стр. 333-340. С Д. Гибсоном.
- «Обнаружение и устранение дефектов механизма селективного прецизионного синтеза плоских механизмов», Международный журнал теории механизмов и машин, Vol.20, № 6, 1985, стр. 521-535. С А. Байпаем.
- «Кинематический синтез и анализ реечного механизма для четырехточечной траектории». Генерация с заданным временем ввода», Транзакции ASME, Журнал механизмов, Трансмиссии и автоматизация в проектировании, Vol. 108, № 1, март 1986 г., стр. 10-14. С участием М. Клаудио.
- «Техника автоматизированного проектирования для оптимального синтеза пути генерации RRSS Пространственные механизмы с заданным временем ввода», Транзакции ASME, Журнал механизмов, Трансмиссии и автоматизация в дизайне, Vol.108, № 4, декабрь 1986 г., стр. 538-542. С П. Премкумаром.
- «Кинематический синтез и анализ реечного механизма для плоского пути». Генерация и генерация функций для шести условий точности», Международный журнал теории механизмов и машин, том 22, № 6, 1987, стр. 563-568. С П. Душлем.
- «Разработка трехуровневой траектории переменной скорости с дискретно исчезающим скачком для оптимального проектирования», Транзакции ASME, Журнал механизмов, трансмиссий и автоматизации. в дизайне, Vol.110, № 1, март 1988 г., стр. 88-92. С Р. Курраном.
- «Компьютерное проектирование функции формирования пространственного механизма РССР с использованием Метод селективного прецизионного синтеза», ASME Transactions, Journal of Mechanisms, Transmissions и автоматизация в дизайне, Vol. 110, № 4, декабрь 1988 г., стр. 378-382. С С. Дхолл.
- «Компьютерный метод проектирования для оптимального синтеза плоских четырехзвенных механизмов». Удовлетворение заданным кинематическим и динамическим условиям», Транзакции ASME, журнал механизмов, трансмиссий и автоматики в конструкции.110, № 3, сентябрь, 1988, стр. 263-268. С Г. Ригельманом.
- «Селективный прецизионный синтез кривошипно-шатунного механизма с пространственным ползунком для траектории и Генерация функций», Транзакции ASME, Журнал механизмов, трансмиссий и Автоматизация в дизайне, Vol. 110, № 3, сентябрь 1988 г., стр. 295-302. С П. Премкумаром и С. Дхолл.
- “Синтез положения, скорости и ускорения пространственного пути RRSS, генерирующего Механизм с использованием метода селективного прецизионного синтеза», ASME Transactions, Journal механизмов, трансмиссий и автоматики в конструкции.111 № 1, март 1989 г., стр. 54-58. С П. Премкумаром.
- «Обобщенная оболочка экспертной системы для реализации приложений механического проектирования: Обзор, введение и основные концепции», ASME Transactions, Journal of Mechanisms, Трансмиссии и автоматизация в дизайне, Vol. 111, № 3, сентябрь 1989 г., стр. 439-442. С участием П. Премкумар.
- “Синтез многоконтурных пространственных механизмов методом итеративного анализа: путь РССР-СС” Генератор», ASME Transactions, Journal of Mechanical Design, Vol.112, № 1, март, 1990, стр. 69-73. С П. Премкумаром.
- «Проектирование и анализ пространственных механизмов HCCC, RCCC и PCCC для генерации функций», ASME Transactions, Journal of Mechanical Design, Vol. 112, № 1, март 1990 г., стр. 74-78. С С. Дхолл.
- «Прямое и обратное кинематическое решение фермы с переменной геометрией на основе робота на ферме N-Celled Tetrahedron-Tetrahedron», ASME Transactions, Journal of Mechanisms, Трансмиссии и автоматизация в дизайне, Vol.112, № 1, март 1990 г., стр. 16-22. С участием С. Джейн.
- «Анализ чувствительности уравнений Бюрместера плоского движения», ASME Transactions, Журнал механического дизайна. Том. 112, № 3, сентябрь 1990 г., стр. 299-306. С С. Махаблешваркар.
- «Кинематический синтез и анализ реечного многоцелевого механизма», ASME Transactions, Журнал механического проектирования.Том. 114, № 3, сентябрь 1992 г., стр. 428-432. С Г.К. Анантасуреш.
- «Решение обратной кинематики манипулятора фермы с изменяемой геометрией на основе тетраэдра», ASME Transactions, Журнал механического проектирования. Том. 114, № 3, сентябрь 1992 г., стр. 433-437. С М. Субраманиам.
- «Проблемы автономного моделирования задач и загрузки кода движения в промышленных роботов», Журнал прикладных механизмов и робототехники, Vol.1, № 1, 1993. Совместно с Г. Наганатаном.
- «Анализ и оптимальный синтез пространственного механизма RSCR», ASME Transactions, Журнал механического дизайна. Том. 116, № 1, март 1994 г., стр. 174-181. С Г.К. Анантасуреш.
- «Метод расширенного множителя Лагранжа для смешанной целочисленной дискретной непрерывной оптимизации» и его применение в механическом проектировании», ASME Transactions, Journal of Mechanical Дизайн, Том.116, № 2, июнь 1994 г., стр. 405-411. С Б.К. Каннаном.
- «Простой и точный метод определения больших прогибов в податливых механизмах». Под действием конечных сил и моментов», ASME Transactions, Journal of Mechanical Design, Том. 120, № 4, сентябрь 1998 г., стр. 392-400. С Анупамом Саксеной.
Публикации в материалах конференции
- «Циклоидный кривошипный механизм», Материалы Первой конференции по прикладным механизмам, Государственный университет Оклахомы, октябрь 1969 г., статья No.16. С Г. Н. Сандором.
- «Кинематический синтез механизма Ватта», Материалы одиннадцатого ASME Механизмы Конференция, Колумбус, Огайо, ноябрь 1970 г., документ № 70-Мех-50.
- «Шестистержневая конструкция с редуктором», Материалы второй конференции по прикладным механизмам, Государственный университет Оклахомы, октябрь 1971 г., документ № 25.
- «Использование метода избирательного прецизионного синтеза для оптимизации планарных механизмов», Материалы четвертой конференции по прикладным механизмам, Чикагский университет, ноябрь. 1975, Бумага №.14.
- «Обнаружение и устранение дефектов механизма селективного прецизионного синтеза планарных механизмов», Труды восьмой конференции по прикладным механизмам, Санкт-Петербург. Луи, сентябрь 1983 г., документ № 10. Совместно с А. Баджпаем.
- “Модель нелинейного программирования для синтеза планарных механизмов, удовлетворяющих произвольным Комбинации ограничений положения, скорости и ускорения», Труды Восьмая конференция по прикладным механизмам, г.Луи, сентябрь 1983 г., документ № 43. С А. Байпай.
- «Кинематический синтез, анализ и оптимизация путем точного изменения расстояния между точками Механизм генерации функций зубчатой рейки», Конференция по механизмам ASME, Бостон, Октябрь 1984 г., Документ 84-DET-134. С К. Хофмайстером.
- «Компьютерное проектирование механизмов в Университете Толедо», Труды Конференция ASME Computers in Engineering, Лас-Вегас, август 1984 г., том 2, стр.44-47.
- «Как избавиться от прокрастинации и улучшить презентации учащихся в старших классах». Уровень курса проектирования машиностроения», Труды ASEE Computer Aided Инженерная конференция, Атланта, июнь 1985 г.
- «Реализация автономного программирования роботов с помощью системы компьютерного зрения CAD / CAM», Материалы Девятой конференции по прикладным механизмам, Канзас-Сити, октябрь 1985 г., документ No.16. С Р. Бхаргавой и П. Уайтом.
- «Определение параметров поперечного сечения манипуляторов роботов-манипуляторов со стандартными Сформируйте сегменты для минимального крутящего момента или минимального времени на основе динамических характеристик», Материалы конференции «Кинематика, динамика и управление механизмами и манипуляторами», Трой, Нью-Йорк, июнь 1986 г. С П. Дастидаром.
- «Партнерство между университетами и промышленностью в применении робототехники в производстве». Процессы», Конференция по автоматизации проектирования ASME, Колумбус, октябрь 1986 г., документ 86-DET-108.С П. Дастидаром, Л. Хо и С. Даллом.
- «Метод компьютерного проектирования для оптимального синтеза пути генерации RRSS Пространственные механизмы с заданным временем ввода», Конференция по механизмам ASME, Колумбус, Октябрь 1986 г., Документ 86-DET-13. С П. Премкумаром.
- «Применение робототехники и производственных технологий — университетско-промышленное партнерство», Материалы конференции по прикладной робототехнике и автоматизации производства, Санкт-Петербург.Луи, ноябрь 1986, Бумага № 1. Совместно с Р. Амиредди.
- «Селективный прецизионный синтез — общий метод проектирования плоских и пространственных механизмов», Материалы 7-го Всемирного конгресса – Теория машин и механизмов, Vol. 1, стр. 275–278. Севилья, Испания, сентябрь 1987 г.
- «Компьютерное проектирование функции формирования пространственного механизма РССР с использованием Селективный прецизионный метод синтеза», Труды ASME Advances in Design Конференция по автоматизации, Vol.2, стр. 203-208. Бостон, сентябрь 1987 г. С С. Дхоллом.
- «Компьютерный метод проектирования для оптимального синтеза плоских четырехзвенных механизмов». Удовлетворение заданным кинематическим и динамическим условиям», Труды ASME Advances на конференции по автоматизации проектирования, Vol. 2, стр. 209-214. Бостон, сентябрь 1987 г. С Г. Ригельман.
- «Селективный прецизионный синтез кривошипно-шатунного механизма с пространственным ползунком для траектории и Генерация функций», Материалы конференции ASME Advances in Design Automation, Том.2, стр. 161-168. Бостон, сентябрь 1987 г. С П. Премкумаром и С. Дхоллом.
- “Синтез положения, скорости и ускорения пространственного пути RRSS, генерирующего Механизм с использованием метода селективного прецизионного синтеза», Труды Десятого Конференция по прикладным механизмам, Vol. 3, Сессия 8A, стр. 5.1-5.5. Новый Орлеан, декабрь. 1987. С П. Премкумаром.
- «Применение метода выборочного прецизионного синтеза к механизмам, генерирующим пространственное движение», Материалы Десятой конференции по прикладным механизмам, Vol.2, Сессия 4А, стр. 4.1-4.6, Новый Орлеан, декабрь 1987 г. С П. Премкумаром.
- «Проблемы производительности при реализации промышленных манипуляторов», Труды Десятого Конференция по прикладным механизмам, Vol. 3, сессия 7B, стр. 2.1-2.7, Новый Орлеан, декабрь 1987. С Р. Амиредди и Г. Наганатаном.
- «Анализ и селективный прецизионный синтез механизма генерации функций HCCC», Материалы Десятой конференции по прикладным механизмам, Vol.3, Сессия 8A, стр. 1.1-1.7. Новый Орлеан, декабрь 1987 г. С С. Даллом.
- “KANTHI: Экспертная система для настройки механизмов создания трехмерных Движение», Материалы второй ежегодной конференции и выставки экспертных систем, стр. 341-350, Детройт, апрель 1988 г. Повторно представлено и опубликовано по приглашению на Первая национальная конференция по прикладным механизмам и робототехнике, ноябрь 1989 г., документ 3C-5.С П. Премкумаром.
- «Проектирование ферменного робота с изменяемой геометрией на основе N-клеточного тетраэдра-тетраэдра» Ферма», Материалы ASME «Тенденции и разработки в области механизмов, машин и Конференция по робототехнике, Орландо, Vol. 3, сентябрь 1988 г., стр. 119-124. С С. Джайном.
- «Обобщенная оболочка экспертной системы для реализации приложений механического проектирования: Обзор, введение и основные концепции», Труды ASME Advances in Конференция по автоматизации проектирования, Орландо, сентябрь 1988 г., стр. 309–314.С П. Премкумаром.
- “Синтез многоконтурных пространственных механизмов методом итеративного анализа: путь РССР-СС” Генератор», Материалы ASME Тенденции и разработки в области механизмов, машин и конференция по робототехнике, Орландо, Vol. 1, сентябрь 1988 г., стр. 457-462. С П. Премкумаром.
- «Автоматический сбор знаний в области механического проектирования», Материалы Третья ежегодная конференция по экспертным системам, апрель 1989 г., Детройт.С П. Премкумаром.
- «Анализ чувствительности уравнений Бюрместера плоского движения», Достижения в области дизайна. Автоматизация – 1989, Материалы Технической конференции по проектированию ASME, Vol. 3 сентября, стр. 379-386. С С. Махаблешваркаром.
- “Прямая и обратная кинематика фермы с изменяемой геометрией тетраэдра-тетраэдра” Манипулятор», Материалы Первой национальной конференции по прикладным механизмам и робототехнике, Ноябрь 1989 г., документ 4A-2.С Р. Сомшетти.
- «Планирование и выполнение полиномиальных совместных траекторий кубических сплайнов для промышленного Манипулятор», Материалы Первой национальной конференции по прикладным механизмам и робототехнике, Ноябрь 1989 г., документ 8C-3. С Р. Рао и Г. Наганатаном.
- «Координатно-винтовой подход к управлению роботизированными манипуляторами в реальном времени», Материалы Первой национальной конференции по прикладным механизмам и робототехнике, ноябрь 1989 г., доклад 8Б-6.С К. Девасией и Г. Наганатаном.
- «Математическое моделирование и компьютерное графическое моделирование реального производства». Альтернативы», Материалы Первой национальной конференции по прикладным механизмам и робототехнике, Ноябрь 1989 г., документ 6C-5. С Г. Наганатаном и семью аспирантами.
- «Кинематический синтез и анализ реечного многоцелевого механизма», Материалы конференции ASME по дизайну кулачков, зубчатых колес, роботов и механизмов: том 26, стр. 41-46, Чикаго, сентябрь 1990 г.С Г.К. Анантасуреш.
- «Интеграция компьютеров в учебную программу ME в Университете Толедо», Представлено на конференции UPCAEDM 1990 г., Анн-Арбор, 13-14 августа, опубликовано в материалах конференции, 6 страниц. С Г. Наганатаном.
- «Анализ и оптимальный синтез пространственного механизма RSCR», Материалы 1991 Конференция по автоматизации проектирования ASME.DE-Vol. 32-2. стр. 371-381. С Г.К. Анантасуреш.
- Алгоритм обхода препятствий и планирования пути для мобильных роботов в реальном времени». Материалы конференции по автоматизации проектирования 1991 года. DE-Vol. 32-2. стр. 507-514.
- Для публикации в ASME Transactions, Journal of Mechanical Design. С Ю. Л. Шринивасом.
- «Компьютерное проектирование и анализ реечного механизма», Труды конференции по механизмам ASME 1992 г., проектирование и синтез механизмов, DE-Vol.46, стр. 275-279, Феникс, сентябрь 1992 г. Совместно с Д. Шринивасом.
- «Динамические уравнения движения и схема срабатывания для переменной на основе тетраэдра Манипулятор фермы геометрии », Материалы конференции по механизмам ASME 1992 г., Механизм Дизайн и синтез, DE-Vol. 45, стр. 173–178, Феникс, сентябрь 1992 г. Совместно с Р. Сармой. и В. Рамамурти.
- «Метод на основе расширенного множителя Лагранжа для смешанных целочисленных дискретных непрерывных Оптимизация и ее приложения к механическому проектированию», Достижения ASME в области автоматизации проектирования, Альбукерке, сентябрь 1993 г.DE Том. 65-2, стр. 103-112. С Б.К. Каннаном.
- «Общее символическое обозначение для кинематического анализа планетарных зубчатых передач», Материалы Третьей национальной конференции по прикладным механизмам и робототехнике, ноябрь 1993, Цинциннати. С Майклом Дж. Твинингом. Бумага № АМР-93-087.
- «Нечеткий синтез механизмов», Труды Третьего национального прикладного механизма. и конференция по робототехнике, ноябрь 1993 г., Цинциннати.С С. Кришнамурти и К. Кришной. Бумага № АМР-93-094.
- «Применение теории нечетких множеств к проектированию плоских и пространственных механизмов», Труды конференции по механизмам ASME, Миннеаполис, сентябрь 1994 г. DE-Vol. 70, стр. 153-160. С К. Кришной и С. Кришнамурти.
- «Конструкция коленного механизма для протеза экзартикуляции коленного сустава», Труды Конференция по механизмам ASME, Миннеаполис, сентябрь 1994 г.DE-Vol. 71, стр. 455-462. С С. Шринивасаном.
Публикации – прочее
- «Выборочный прецизионный синтез планарных механизмов, удовлетворяющих практическим требованиям проектирования», Докторская диссертация, август 1973 г.; Политехнический институт Ренсселера; Университетские микрофильмы, Анн-Арбор, Мичиган, 74-12786.
- «Материалы конференции по робототехнике и гибкой автоматизации», главный редактор, университет. Толедо, февраль 1984 г.
- «Разработка роботизированной системы на основе машинного зрения для погрузочно-разгрузочных работ», Научный журнал Огайо, тезисы, Vol. 85, № 2, апрель 1985 г. Совместно с Р. Бхаргавой.
- «Проектирование и изготовление системы поддержки лазерного доплеровского измерителя скорости», механический Инженерные новости, Подразделение машиностроения ASEE, Vol. 23, нет.1 февраля 1986, стр. 7-12. С М. Томпсоном.
- «От свалки до шоссе: два двигателя получают новую жизнь», женщина из США. инженер, журнал Общества женщин-инженеров, май/июнь 1989 г., стр. 21–22, Нью-Йорк.
- Редактор главы 4 изданной книги “Первые сорок лет современной кинематики” Джон Уайли, 1993.Отредактировал 38-страничную главу.
Консалтинг
Стивен Н. Крамер, доктор философии, ЧП.
Специалист по реконструкции дорожно-транспортных происшествий и эксперт по безопасности и
Почетный профессор машиностроения, промышленности и производства.
Доктор Стивен Крамер является почетным профессором механики, промышленности и производства. инженерного дела в университете Толедо.Он преподавал в университете г. Толедо с 1973 года и вышел на пенсию в мае 2008 года. Помимо преподавания машиностроения и проводит исследования в области кинематики, динамики, механического проектирования, автоматизированного проектирования, и робототехники, он помогал адвокатам в районе Толедо, на северо-западе Огайо и юго-востоке Мичиган в случаях реконструкции дорожно-транспортных происшествий и ответственности за качество продукции. Он ему понравилось это занятие, и ему много раз говорили, что он очень помогает.
С 1979 года д-р Крамер выполнил реконструкцию более 200 несчастных случаев; о две трети для истца и одна треть для защиты. Он дал многочисленные показания, несколько раз давал показания в суде и был принят в качестве эксперта по всем эти случаи. Среди местных адвокатов, с которыми работал доктор Крамер, были Уиллис Джонс, Боб Бахрет, Джозеф Альбрехта, Марк Уильямс-Янг, Пит Мангер, Марти Холмс, Томас и Деннис Мюррей, и Билл Кронке, чтобы назвать некоторых.Сильные стороны доктора Крамера в аварии реконструкция включает его знание сил, ударов и движения транспортных средств, его умение эффективно общаться с аудиторией разного происхождения, его понимание судебного процесса, его доступность в кратчайшие сроки, его оперативность и заинтересованность в оказании помощи адвокатам в этой деятельности. С любым из этих адвокатов можно связаться в качестве ссылки для доктора Крамера.
Знания доктора Крамера о реконструкции дорожно-транспортных происшествий происходят из его инженерных знания (степень доктора наук Политехнического института Ренсселера), прочитав несколько ключевых руководств по реконструкции аварий, а также из своего опыта, полученного в ходе предыдущих случаи. Кроме того, у доктора Крамера есть коллекция из примерно двадцати автомобильных обществ. Пособия и справочники инженеров (SAE) по данной теме.У доктора Крамера также есть камера, которую можно использовать на месте аварии или при осмотре транспортных средств. Доктор Крамер обучает студентов инженерных специальностей законам об ответственности за качество продукции в Огайо и хорошо осведомлен во всех частях ORC-2307 и CFR.
Если вы считаете, что доктор Крамер может помочь вам в реконструкции дорожно-транспортного происшествия или в случае ответственности за качество продукции, не стесняйтесь обращаться к нему по адресу: [email protected] или по телефону: 419-874-6535.
10.3 – Чувствительность, специфичность, положительное прогностическое значение и отрицательное прогностическое значение
В этом примере две колонки указывают фактическое состояние субъектов, больных или здоровых. В строках указаны результаты теста, положительные или отрицательные.
Ячейка A содержит истинно положительные результаты, субъектов с заболеванием и положительными результатами тестов.Субъекты клетки D не имеют заболевания, и тест дает результаты.
Хороший тест будет иметь минимальные числа в ячейках B и C. Ячейка B идентифицирует людей без болезни, но для которых тест показывает «болезнь». Это ложные срабатывания. Ячейка C имеет ложноотрицательные результаты.
Если это результаты популяционного исследования, распространенность можно рассчитать следующим образом:
Распространенность заболеваний = \(\dfrac{T_{\text{заболевание}}}{\text{Всего}} \times 100\)
Популяция, используемая для исследования, влияет на расчет распространенности.
Чувствительность — это вероятность того, что тест укажет на «заболевание» среди больных:
Чувствительность: A/(A+C) × 100
Специфичность — это доля здоровых людей, у которых будет отрицательный результат теста:
Специфичность: D/(D+B) × 100
Чувствительность и специфичность являются характеристиками теста . Население не влияет на результаты.
У клинициста и пациента другой вопрос: какова вероятность того, что человек с положительным тестом действительно болен? Если субъект находится в первой строке таблицы выше, какова вероятность того, что он окажется в ячейке А по сравнению с ячейкой В? Клиницист вычисляет по ряду следующим образом:
Положительная прогностическая ценность: A/(A+B) × 100
Отрицательное прогностическое значение: D/(D+C) × 100
Положительные и отрицательные прогностические значения зависят от распространенности заболевания в тестируемой популяции.Если мы тестируем в условиях высокой распространенности, более вероятно, что люди с положительным результатом теста действительно больны, чем если бы тест проводился в популяции с низкой распространенностью..
Давайте посмотрим, как это работает с некоторыми числами…
Гипотетический пример 1 – Отборочный тест A
100 человек проверены на заболевание. 15 человек имеют заболевание; 85 человек не больны. Итак, распространенность составляет 15%:
- Распространенность заболеваний:
\(\dfrac{T_{\text{disease}}}{\text{Total}} \times 100\),
15/100 × 100 = 15%
Чувствительность составляет две трети, поэтому тест способен выявить две трети людей с заболеванием.Тест пропускает одну треть людей, у которых есть заболевание.
- Чувствительность:
A/(A + C) × 100
10/15 × 100 = 67%
Специфичность теста составляет 53%. Другими словами, 45 человек из 85 человек с отрицательными результатами действительно отрицательные, а 40 человек дали положительный результат на заболевание, которого у них нет.
- Специфичность:
D/(D + B) × 100
45/85 × 100 = 53%
Чувствительность и специфичность являются характеристиками этого теста.Однако для клинициста важным фактом является то, что среди людей с положительным результатом теста только 20% действительно болеют этим заболеванием.
- Положительное прогностическое значение:
A/(A + B) × 100
10/50 × 100 = 20%
Среди тех, у кого тест отрицательный, 90% не имеют заболевания.
- Отрицательное прогностическое значение:
D/(D + C) × 100
45/50 × 100 = 90%
Теперь изменим распространенность..
Гипотетический пример 2 — повышенная распространенность, тот же тест
На этот раз мы используем тот же тест, но в другой популяции с распространенностью заболевания 30%.
- Распространенность болезней:
- \(\dfrac{T_{\text{болезнь}}}{\text{Всего}} \умножить на 100\)
30/100 × 100 = 30%
Мы сохраняем ту же чувствительность и специфичность, поскольку они характерны для этого теста.
- Чувствительность:
A/(A + C) × 100
20/30 × 100 = 67%
- Специфичность:
D/(D + B) × 100
37/70 × 100 = 53%
Теперь посчитаем прогнозные значения:
- Положительное прогностическое значение:
A/(A + B) × 100
20/53 × 100 = 38%
- Отрицательное прогностическое значение:
D/(D + C) × 100
37/47 × 100 = 79%
Использование того же теста в популяции с более высокой распространенностью повышает положительную прогностическую ценность.И наоборот, увеличение распространенности приводит к снижению отрицательной прогностической ценности. При рассмотрении прогностических значений диагностических или скрининговых тестов учитывайте влияние распространенности заболевания . На приведенном ниже рисунке показана взаимосвязь между распространенностью заболевания и прогностической ценностью теста с чувствительностью 95% и специфичностью 95%:
Связь между распространенностью заболевания и прогностической ценностью теста с чувствительностью 95% и специфичностью 85%.
(Из Mausner JS, Kramer S: Mausner and Bahn Epidemiology: An Introductory Text. Philadelphia, WB Saunders, 1985, p. 221.)
Попробуйте!
При каких обстоятельствах вы действительно хотели бы свести к минимуму количество ложных срабатываний?
ОтвечатьСведение к минимуму ложноположительных результатов важно, когда затраты или риски последующего лечения высоки, а само заболевание не угрожает жизни… Одним из примеров является рак предстательной железы у пожилых мужчин; с другой стороны, акушеры должны учитывать потенциальный вред от ложноположительного теста на АФП в сыворотке матери (который может сопровождаться амниоцентезом, ультразвуковым исследованием и усиленным наблюдением за плодом, а также вызывать беспокойство у родителей и маркировку будущего ребенка) в сравнении с потенциальной пользой. .
Попробуйте!
Когда вы хотите свести к минимуму количество ложных срабатываний?
ОтвечатьНам не нужно много ложноотрицательных результатов, если болезнь часто протекает бессимптомно и
- является серьезным заболеванием, быстро прогрессирует и может более эффективно лечиться на ранних стадиях ИЛИ
- легко передается от одного человека к другому
Что такое хороший тест в популяции? На самом деле все тесты имеют свои преимущества и недостатки, так что ни один тест не идеален.Бесплатных обедов в скрининге и раннем выявлении заболеваний не бывает.
Творчество под прицелом
Кратко об идее
Ваши самые творческие сотрудники генерируют свои лучшие идеи в сжатые сроки, верно? Неправильный. В то время как нехватка времени может заставить людей чувствовать себя более творческими, это обычно мешает им действительно мыслить творчески — жонглировать новыми идеями, пока они не столкнутся оригинальными и в конечном итоге прибыльными способами. Когда креативность находится под прицелом, ее обычно убивают.
Что делать менеджеру? Способность вашей компании разрабатывать продукты и услуги завтрашнего дня зависит от высочайшего уровня творчества. Но цейтнот и отвлекающие факторы обычно берут верх. В дни наибольшего напряжения большинство людей на 45% 90 504 меньше 90 505 склонны мыслить творчески, чем в дни с меньшим давлением.
Тем не менее, в некоторых организациях творческие способности процветают, несмотря на жесткие сроки. Как? Менеджеры минимизируют потери времени и используют их, чтобы вдохновить на новое мышление.Они позволяют людям оставаться погруженными в важную работу, не отвлекаясь. И они кристально ясно дают понять, что срочность законна.
Идея на практике
Защита творчества
Творчество может расцвести или угаснуть под любым давлением времени. Вот в чем разница:
На задании: Напряженные творческие дни наполнены сосредоточенностью и значимой срочностью. Люди концентрируются на одном проекте большую часть дня, чувствуют себя вовлеченными в свою работу и понимают, почему их проект имеет решающее значение.Если они и сотрудничают, то обычно один на один.
На беговой дорожке: В дни высокого напряжения и низкой творческой активности люди чувствуют, что бегут быстрее, но отстают еще сильнее. Их тянут в разные стороны, они чувствуют себя растерянными, сбитыми с толку и застрявшими на групповых собраниях.
В экспедиции: Дни с низким уровнем стресса способствуют творчеству, когда люди больше сосредотачиваются на изучении идей, чем просто на выявлении проблем, и когда они сотрудничают один на один, а не в группах.
На автопилоте: Дни низкого давления не генерируют творчества, когда люди выполняют свою работу без участия. Менеджеры мало поощряют мыслить по-новому, а сотрудники томятся на многочисленных совещаниях.
Активизация творчества под давлением
Чтобы помочь сотрудникам почувствовать, что они находятся в миссии или экспедиции, а не на беговой дорожке или на автопилоте:
- Не поддавайтесь иллюзии, что давление стимулирует творчество. Обычно нет.В Bell Labs компании AT&T философия, согласно которой «большие идеи требуют времени», привела к революционным инновациям — транзистору, лазерному лучу — за что исследователи получили семь Нобелевских премий.
- В дни низкого давления поощряйте людей экспериментировать с идеями и разрабатывать что-то новое. Известно, что компания 3M поощряет ученых посвящать 15 % своей рабочей недели творческим начинаниям — даже тем, которые далеки от их основной работы.
- Формулируйте реалистичные цели. Чтобы стимулировать творческие идеи, которые направляют проект к захватывающим решениям, разработайте осуществимые планы проекта, которые отражают реальные требования к успеху.
- Защитите креативных мыслителей, которым не хватает времени, от отвлекающих факторов и посторонних требований. В одном исследовании инженеры, которые давали друг другу непрерывную тишину в определенные промежутки времени каждый день, добивались большего и чувствовали себя лучше в своей работе.
- Объясните, почему необходимы сжатые сроки. Сотрудники чувствуют свою миссию, когда понимают настоятельную необходимость их работы. Они чувствуют, что находятся на беговой дорожке , если подозревают, что вы установили произвольные сроки только для того, чтобы заставить их работать быстрее.
- Поощряйте сотрудничество один на один. Слишком много обязательных групповых встреч порождают чувство раздробленности и напрасной траты времени.
- Сведите к минимуму внезапные изменения расписания. Вы уменьшите неопределенность, помогая людям сосредоточиться на своей реальной работе.
По-настоящему прорывные идеи редко рождаются за одну ночь. Возьмем, к примеру, теорию эволюции Чарльза Дарвина, у которой была собственная длительная эволюция. Дарвин провел десятилетия, читая научную литературу, совершая путешествия на корабле HMS Beagle к Галапагосским островам и другим экзотическим направлениям, выполняя кропотливо подробные наблюдения и создавая тысячи страниц заметок об этих наблюдениях и своих идеях для их объяснения. Немыслимо, чтобы его прорыв произошел, если бы он попытался поторопиться.В бизнесе тоже есть поразительные примеры ценности относительно неструктурированного, свободного времени для создания и развития новых идей. Ученые, работающие в легендарной лаборатории Bell Labs компании AT&T, руководствуясь корпоративной философией, согласно которой большие идеи требуют времени, создали революционные инновации, включая транзистор и лазерный луч. Их изобретательность принесла исследователям несколько Нобелевских премий. У них, как и у Дарвина, было время мыслить творчески.
Но мы все можем указать на примеры, когда творчество, казалось, пробудилось из-за крайнего дефицита времени.В 1970 году во время полета «Аполлона-13» на Луну на борту произошел разрушительный взрыв, повредивший систему фильтрации воздуха и приведший к опасному накоплению углекислого газа в салоне. Если бы систему нельзя было починить или заменить, астронавты погибли бы в течение нескольких часов. Вернувшись в центр управления полетами НАСА в Хьюстоне, практически все инженеры, ученые и техники немедленно сосредоточили свое внимание на проблеме. Работая с набором материалов, идентичных тем, что находятся на борту космического корабля, они отчаянно пытались создать систему фильтрации, которую астронавты могли бы воспроизвести.Были рассмотрены все мыслимые материалы, в том числе обложка руководства по процедурам полетов. Имея мало свободного времени, они придумали что-то уродливое, неэлегантное и далекое от совершенства, но казалось, что это просто могло бы сработать. Инженеры быстро передали конструкцию с достаточной ясностью, чтобы астронавты с когнитивными нарушениями, почти невероятно, смогли построить фильтр. Это сработало, и три жизни были спасены.
Бизнес-примеры креативности под давлением явно менее драматичны, но их тоже предостаточно.Прославленная дизайнерская фирма Ideo внесла свои новшества в персональные компьютеры, медицинское оборудование, автомобильную электронику, игрушки и даже аниматронных роботов для фильмов — и многие из новых проектов для этих продуктов были разработаны менее чем за три месяца. Если вы похожи на большинство менеджеров, вы почти наверняка работали с людьми, которые клянутся, что выполняют свою самую творческую работу в сжатые сроки. Вы можете использовать давление как метод управления, полагая, что это подтолкнет людей к большим скачкам понимания.Вы даже можете управлять собой таким образом. Если да, то вы правы?
Согласно нашим исследованиям, короткий ответ — «нет». Когда творчество находится под прицелом, его обычно убивают. Хотя нехватка времени может побуждать людей работать больше и делать больше и даже может заставить их чувствовать себя более творческими, на самом деле это заставляет их мыслить менее творчески. Конечно, короткий ответ — это еще не все. Давайте посмотрим, что такое цейтнот, что он чувствует, когда люди испытывают его на работе, и как им можно управлять для повышения креативности.
Борьба с часами
Мария была разработчиком программного обеспечения в команде, которой было поручено создать онлайн-систему, через которую медицинские работники могли получить доступ к жизненно важной информации о некоторых пациентах с высоким риском. Было крайне важно, чтобы новая система была защищена от ошибок, поскольку целевыми пациентами были пожилые люди или люди с тяжелыми формами инвалидности; в ситуациях, угрожающих жизни, точная информация о них должна была сообщаться мгновенно. К сожалению, первоначальный контракт на проект сильно недооценивал время, необходимое для его разработки.В результате Мария и ее команда оказались в крайнем дефиците времени по мере приближения крайнего срока. (Личность Марии, как и все личности, проекты и компании в этой статье, была замаскирована.)
Команда работала почти круглосуточно, хотя с каждым днем становилось все яснее, что сложные технические проблемы, с которыми она сталкивалась, просто не могли быть адекватно решены в исходные сроки. Тем не менее, высшее руководство, а также руководитель проекта настаивали на том, чтобы команда уложилась в срок, несмотря ни на что.Свои переживания за это время Мария записала в ежедневник:
.«Сегодня в 7:30 утра руководитель моей группы спросил меня, каков мой план игры на день и могу ли я быть доступен для совещания по внедрению. Я написал на флип-чарте, что, по моему мнению, нужно сделать сегодня, посмотрел на список и сказал ему, что это два или три дня работы. Теперь, когда я вымотался и готовлюсь к отъезду, я смотрю на флипчарт и понимаю, что в лучшем случае 20% работы выполнено. Этот однодневный список на самом деле является четырех- или пятидневным списком.Больше всего за весь день мне запомнился этот чертов флипчарт, на котором так мало вычеркнуто».
Несколько дней спустя Мария казалась еще ближе к концу своей веревки:
«Я сказал своему руководителю, что часы, которые я работаю, совершенно неприемлемы, и что я планирую покинуть компанию, если это будет оставаться нормой для проектов здесь. Выражение его лица было немного ошеломленным. Был ли он действительно потрясен? Может ли это быть сюрпризом? Весь день я чувствовал себя физически истощенным, как будто у меня был низкий уровень сахара в крови.Прошлой ночью я очень плохо спал, несколько часов не спал среди ночи. Прямо сейчас я снова чувствую себя физически истощенным — отсутствие ясности ума, отсутствие мотивации в отношении проекта».
Мария была не одинока в своем ощущении крайнего дефицита времени, в котором работала группа. Ричард, еще один член команды, в этот период вел свой дневник и сказал следующее:
«Руководитель группы объявил, что основные часы проекта — когда все должны быть в офисе и работать — были продлены: «Сейчас они с 8 утра до 7 вечера, и не строят социальных планов на следующие три выходных». , поскольку мы, вероятно, будем работать.Теперь этот проект официально стал для меня маршем смерти. Я не могу понять, сколько работы у нас осталось, как сильно мы недооценили этот проект и насколько сложной стала эта собака. На каждом шагу мы обнаруживаем больше нерешенных, незавершенных или гораздо более сложных вещей, чем мы когда-либо думали».
Мы собрали более 9000 таких дневниковых записей в ходе недавнего исследования 177 сотрудников семи американских компаний. Наша цель состояла в том, чтобы глубоко изучить, как люди ежедневно испытывают дефицит времени, работая над проектами, требующими высокого уровня изобретательности, а также измерить их способность творчески мыслить в условиях такого дефицита.В частности, мы попросили каждого из участников, большинство из которых были высокообразованными работниками умственного труда, заполнить онлайн-форму дневника, в которой они оценили некоторые аспекты своей работы и рабочей среды в тот день, в том числе то, насколько сильно они ощущали нехватку времени. В отдельном разделе формы мы также попросили их описать что-то, что запомнилось им в тот день, и тщательно проанализировали эти короткие записи на наличие признаков творческого мышления. (См. врезку «Ловушка творчества в дикой природе» для подробного описания нашего метода исследования, включая конкретное определение нашего исследования «творческого мышления».»)
То, что мы увидели в этих дневниковых записях, было одновременно захватывающим и отрезвляющим. Многие участники нашего исследования сообщали об опыте, похожем на опыт Марии: они часто чувствовали себя переутомленными, раздробленными и выгоревшими. Таким образом, на самом базовом уровне мы нашли подтверждение недавним наблюдениям популярной прессы о том, что американцы испытывают нехватку времени на работе, создавая то, что один репортер Newsweek назвал нацией «быстрых или смертельно уставших». Проблема была с нами в течение некоторого времени.Еще в 1995 году U.S. News & World Report описал общенациональный опрос, показывающий, что более половины американцев хотели бы иметь больше свободного времени, даже если это означало меньше денег. А в 1996 году, согласно опросу Wall Street Journal — NBC News , 75% людей, зарабатывающих более 100 000 долларов в год, назвали управление своим временем более серьезной проблемой, чем управление своими деньгами.
Нехватка времени стала фактом жизни американского рабочего. В обычный день участники нашего исследования сообщали о том, что чувствуют «умеренный» дефицит времени — и это было среднее значение.Рабочий день многих участников характеризовался «чрезвычайно» высоким уровнем нехватки времени. «Сегодня я понял, что у нас почти не осталось времени на подготовку к предстоящим презентациям», — написал один из участников в довольно типичной записи. Другой сотрудник другой компании пожаловался: «За одну ночь мне пришлось составить подробный план оставшейся части этапа разработки, чтобы мы знали, насколько мы отстали».
Возможно, это неудивительно, хотя наши участники сказали, что временной дефицит большую часть времени был довольно высоким, мы заметили тенденцию, согласно которой нехватка времени, казалось, нарастала по мере того, как рабочие проекты переходили от ранних к более поздним стадиям; как и в случае с проектом Марии, люди чувствовали себя все более и более ограниченными во времени по мере приближения крайних сроков.Интересно, что мы также наблюдали небольшую тенденцию изменения нехватки времени в течение недели: нехватка времени начиналась относительно низко по понедельникам, увеличивалась в течение недели до пика по четвергам и уменьшалась по пятницам. Это может быть связано с тем, что ожидания менеджеров в отношении производительности несколько ниже по понедельникам и пятницам. Или, возможно, дело просто в том, что в дни, предшествующие выходным, люди уже (или все еще) настроены на выходные и менее подвержены ощущению существующего дефицита времени.Мы также обнаружили, что люди чаще сообщали о сильном дефиците времени в те дни, когда они были в командировках или работали вне офиса. Вполне возможно, что в такие дни люди стараются уложить больше работы, чтобы свести к минимуму общее время, проведенное вне офиса. И, конечно же, многочисленные хлопоты самого путешествия, несомненно, способствуют ощущению зажатости.
Энергия и разочарование
Как описано в дневниках, дни, когда участники нашего исследования чувствовали крайнюю нехватку времени, заметно отличались от дней, когда они чувствовали меньше времени.Люди, как правило, работали больше часов и были вовлечены в большее количество дел, им приходилось чаще переключать передачи в дни нехватки времени. Это дает нам первую подсказку о том, как нехватка времени может повлиять на творчество, — подсказку, к которой мы вернемся позже.
Люди испытывали разные чувства по мере увеличения нехватки времени, но мы не можем просто сказать, что они чувствовали себя лучше или хуже. Это был смешанный пакет. Поначалу люди чувствовали себя более вовлеченными в свою работу и вызывали ее: «Я испытываю сильное давление, чтобы запустить производственную машину для нашего нового продукта на этой неделе… Я был действительно счастлив бежать в хозяйственные магазины за фитингами для шлангов и болтами. .Впервые я чувствую, что мы действительно добились реального прогресса». И, в отличие от реакции Марии на чувство истощения, люди обычно чувствовали себя более энергичными под высоким давлением. Как сообщил один автор дневника: «Мы прошли три четверти пути! Мне очень нравится видеть, как команда сплачивается».
Но некоторые люди также испытывали глубокое разочарование по мере увеличения дефицита времени: «Мне часто кажется, что я плыву против течения в этом проекте и всегда погребен под работой». В частности, они, казалось, были разочарованы тем, что другие члены команды постоянно отвлекали их в дни дефицита времени.Один из участников нашего исследования рассказал особенно яркую историю о своем разочаровании коллегой:
«У нас было совещание о том, что не так с программой фильтрации и как выйти на приемлемый уровень понимания и сбора информации. Как обычно, Пол, Эмилио, Сара и я шли с головокружительной скоростью, пытаясь убедиться, что мы все справляемся. Но Радж мог только неоднократно повторять: «Но какую часть моей работы вы не хотите, чтобы я делал, если вы ожидаете, что я буду делать это?» Он был спорщиком и негативным, и все, что я мог думать, было: «Прекрати!» Я смогла совладать с собой и не закричала на него, но была рядом.
Когда мы смотрим на общую картину того, как люди испытывали нехватку времени, кажется, что они много работали, проводили долгие часы на работе и иногда чувствовали себя окрыленными тем, что они делали. Но в то же время было много разочарований — еще одна подсказка, которая поможет нам понять влияние нехватки времени на креативность.
Ловушка давления
Наше исследование показывает, что чем больше времени люди испытывают в данный день, тем меньше вероятность того, что они будут мыслить творчески.Удивительно, однако, что люди, кажется, в значительной степени не знают об этом явлении. В своих ежедневных оценках собственной креативности участники нашего исследования в целом считали себя творческими на 90 504 более 90 505 в условиях жесткого дефицита времени. К сожалению, их дневники опровергли эти самооценки. Очевидно, что по мере того, как цейтнот увеличивался, творческого мышления было все меньше и меньше.
Более того, падение творческого мышления было наиболее очевидным, когда нехватка времени была наибольшей.В форме ежедневного дневника участников просили оценить давление времени, которое они ощущали, по шкале от одного до семи, где семь — самый высокий уровень давления. В дни, оцененные в семь баллов, люди были на 45% менее склонны к творческому мышлению, чем в любой из дней с более низким уровнем стресса.
Руководители могут подумать, что случайный нетворческий день — это просто цена, уплаченная за то, чтобы работать в соответствии с высокопродуктивным графиком. Они могут возразить, что если ваши творческие способности замерзают в особенно загруженный четверг, вы сможете вернуться к творчеству в пятницу, когда спрос немного снизится.А может и нет. К нашему удивлению, большая нехватка времени в определенный день означала меньше творческого мышления в этот день, на следующий день, и на следующий день. Другими словами, то ли из-за истощения, то ли из-за стойкого когнитивного паралича после стресса, участники нашего исследования, похоже, испытывали «похмелье от стресса», которое длилось как минимум пару дней.
Этот затянувшийся эффект нехватки времени проявлялся независимо от того, исследовали ли мы нехватку времени изо дня в день или в течение более длительных периодов времени. Чем выше общее ощущение нехватки времени, которое участники испытывали в течение первой недели своих проектов, тем ниже уровень творческого мышления, который мы наблюдали у них в течение первой половины их проектов (период, который варьировался от трех недель до четырех месяцев).И чем выше общее ощущение цейтнота в середине, тем ниже уровень творческого мышления во второй половине.
Почему нехватка времени так тормозит творчество? Психологические исследования за последние 30 лет, наряду с теориями о том, как возникает творчество, могут помочь в объяснении. Психологи долгое время считали, что творчество является результатом формирования в уме большого количества ассоциаций с последующим отбором ассоциаций, которые могут быть особенно интересными и полезными.В некотором смысле это как если бы разум бросал кучу мячей в когнитивное пространство, жонглируя ими, пока они не столкнутся интересным образом. В этом процессе есть определенная игривость; на самом деле Эйнштейн однажды назвал творчество «комбинаторной игрой». Если ассоциации возникают между понятиями, которые редко сочетаются друг с другом, то есть если шары, которые обычно не приближаются друг к другу, сталкиваются, то окончательная новизна решения будет выше.
Значительные исследования, основанные на экспериментах и наблюдениях за творческой деятельностью, подтверждают этот взгляд на творческий процесс.И некоторые недавние исследования показывают, что успех комбинаторного процесса зависит как от наличия достаточного времени для создания мячей для жонглирования — изучения концепций и изучения вещей, которые могут быть так или иначе полезны, — так и от наличия достаточного количества времени, чтобы посвятить себя жонглированию. Например, одно исследование, проведенное нами и нашими коллегами, показало, что люди, которые уделяют больше времени исследовательскому поведению при выполнении задачи, производят работу, которую эксперты оценивают как более творческую. Другое исследование показало, что простое наличие нескольких минут на обдумывание задачи — изучение материалов, игра с ними — может привести к большему творчеству, чем необходимость погрузиться в задачу на холостом ходу.Так что у нас есть еще больше подсказок о том, как нахождение под прицелом может повлиять на творческий процесс.
Защита творчества
Несмотря на то, что нехватка времени, кажется, подрывает творческое мышление в целом, есть поразительные исключения. Мы знаем из нашего собственного исследования и из анекдотических свидетельств, что люди могут и действительно находят гениальные решения в отчаянно короткие сроки. В чем разница? Пришло время собрать подсказки.
Когда мы сравнили записи в дневнике тех дней, в которые не хватало времени, когда возникало творческое мышление, с записями в те дни, когда не было творческого мышления, мы обнаружили, что творческие дни характеризовались особым — и довольно редким — набором условий труда. .Прежде всего, эти дни были отмечены чувством сосредоточенности. Люди смогли сконцентрироваться на одной работе в течение значительной части дня. Как радостно заявил один автор дневника: «Событием дня было то, что у меня не было выдающихся событий. Я смог сосредоточиться на текущем проекте, не отвлекаясь». Этот фокус часто был достигнут с трудом, поскольку отдельные лица или их менеджеры шли на многое, чтобы защитить свою работу от прерываний и других помех: «Было так много перерывов для болтовни, что я не мог выполнить ни одной приличной работы.В конце концов мне пришлось работать очень тихо в другой комнате, чтобы сделать часть этого».
В самом деле, это ощущение сосредоточенности предполагает некоторую степень изоляции. В дни нехватки времени, которые все еще давали возможность творческого мышления, мы отмечали, что сотрудничество было ограниченным. Когда это случалось, скорее всего, это делалось сосредоточенно — например, работая с другим человеком, а не в группе: «В конце дня у меня была возможность поговорить со Сьюзен. Она помогла подтвердить, что путь, по которому я пошел, был правильным, и помогла мне разобраться в некоторых различиях в кодах.Ее помощь поможет мне двигаться вперед».
Другим ключевым условием достижения творческого потенциала в трудные дни была интерпретация цейтнота как значимой срочности. Люди понимали, почему решение проблемы или завершение работы имели решающее значение, и верили в эту срочность, чувствуя себя на задании . (См. выставку «Матрица нехватки времени/творчества» для краткого изложения условий работы, в которых участвовали участники нашего исследования.) Они были вовлечены в свою работу и чувствовали, что она бросает вызов.Чувство безотлагательности и способность сосредоточиться, вероятно, связаны по двум причинам. Если люди считают, что их работа жизненно важна, они могут с большей готовностью и способностью игнорировать различные отвлекающие факторы в течение рабочего дня. Между тем, менеджеры, разделяющие чувство срочности, могут освободить людей от менее важных задач. Это явно имело место в миссии «Аполлон-13»: вся второстепенная работа была прекращена до тех пор, пока не была решена проблема фильтрации воздуха и астронавты благополучно не вернулись домой.
Матрица нехватки времени/творчества Наше исследование показывает, что нехватка времени влияет на креативность по-разному в зависимости от того, позволяет ли окружающая среда людям сосредоточиться на своей работе, вызывает ли у них ощущение значимой срочности выполнения поставленных задач, стимулирует или подрывает творческое мышление. другими способами.
Но когда этот защищенный фокус отсутствовал в дни дефицита времени — а это очень часто случалось — люди больше чувствовали себя на беговой дорожке . В эти дни наши авторы дневников сообщали о более сильном дефиците времени, хотя они не работали больше часов, и они чувствовали себя гораздо более рассеянными.При записи количества различных действий, которые они выполняли, они, скорее всего, использовали такие слова, как «несколько», «много» и «слишком много, чтобы сосчитать». Их тянуло в слишком многих направлениях, они не могли сосредоточиться на одном виде деятельности в течение какого-либо значительного периода времени. Один автор дневника, перефразируя часто повторяемый плач, сказал: «Чем быстрее я бегу, тем отстаю».
Наша первая подсказка о том, что людям, возможно, придется чаще переключать передачи в условиях нехватки времени, лежит в основе этого состояния беговой дорожки; многие вещи требуют внимания людей одновременно.Помните также нашу подсказку о том, что чувство нехватки времени связано с разочарованием, особенно с разочарованием по отношению к другим членам команды. Мы подозреваем, что прерывания способствуют этому разочарованию. Другие свидетельства дополняют картину отвлеченной, взволнованной, запутанной обстановки в дни беговой дорожки. У людей было гораздо больше встреч и дискуссий с группами, чем с отдельными людьми. Более того, им часто приходилось справляться с внесением изменений в расписания и планы в последнюю минуту. Во многих отношениях они, казалось, работали в условиях большей неопределенности: «На собрании мы обнаружили, что работу, которую мы проделали до сих пор, возможно, придется полностью переделать из-за решения, принятого высшим руководством, изменить то, как новая система будет работать. обрабатывать заказы клиентов.«В эти дни с низкой концентрацией внимания и дефицитом времени люди вряд ли считали то, что они делают, важным или чувствовали значимое чувство срочности для завершения проекта или задачи.
Гарантировало ли отсутствие цейтнота, что люди будут более творческими? Конечно нет. При любом уровне нехватки времени, низком или сильном, сообщения о творческом мышлении были относительно редки; они фигурировали лишь в 5% из более чем 9000 ежедневных дневниковых отчетов. В условиях нехватки времени разница в том, произошло ли творчество или нет, похоже, заключается в том, как люди проводят свои дни.Наиболее заметно, что когда люди проявляли творческий подход в отсутствие дефицита времени, они были больше ориентированы на исследование и генерирование новых идей, чем на выявление проблем, которые необходимо было решить. (Вспомните нашу подсказку из психологической литературы о комбинаторной игре.) Люди вели себя так, как если бы они были в экспедиции . Кроме того, если люди в этом состоянии работали с кем-то еще, они, как правило, проводили день (или его часть), сотрудничая только с одним другим человеком; сотрудничество со многими людьми было редкостью.Наличие единого фокуса, от которого можно отталкиваться от новых идей, может помочь людям оставаться ориентированными на работу в эти более спокойные дни, в отличие от множества «товарищей по играм» одновременно.
Наконец, конечно, были дни, когда люди не чувствовали сильного дефицита времени и не проявляли никаких признаков творческого мышления. Казалось, они делали свою работу, ставя одну ногу впереди другой, не слишком углубляясь в происходящее. Они вели себя так, как если бы они были на автопилоте .В эти дни в целом уровень совместной работы был низким, хотя было больше встреч и дискуссий, в которых участвовали группы, а не отдельные лица. И люди чувствовали наименьшее поощрение со стороны высшего руководства к творческой работе. Возможно, если бы больше поощрялось творчество, эти люди могли бы лучше использовать свои относительно спокойные дни.
Уроки управления и самоуправления
Наше исследование было сосредоточено на работниках умственного труда — людях, которые, по словам исследователя Лесли Перлоу, чаще всего страдают от «временного голода» в современных американских организациях.Это люди, от которых мы нуждаемся и ожидаем высочайшего уровня творчества; они разрабатывают продукты, услуги и организации завтрашнего дня. Они также являются людьми, которые наиболее ограничены в своем стремлении к творчеству.
Нет никаких сомнений в том, что творческое мышление возможно в условиях сильного — даже экстремального — дефицита времени. Но это кажется вероятным только в ситуации, которая, как показывают исследования, не является нормой в современных организациях: способность глубоко погрузиться и оставаться глубоко погруженным в важную, неотложную проблему.Учитывая требования большинства организаций к коммуникациям и проверкам процессов, а также преобладание сильно взаимозависимых рабочих ролей, защищенное время творчества не возникает естественным образом. Что же тогда могут сделать менеджеры, чтобы свести к минимуму негативные последствия цейтнота и правильно использовать его на службе творчества? Что каждый из нас может сделать, чтобы сохранить свою креативность в сегодняшних организациях, испытывающих давление?
Наше первое предложение очевидно: по возможности избегайте чрезмерного дефицита времени, особенно если вы стремитесь к высокому уровню обучения, исследований, генерации идей и экспериментов с новыми концепциями.Не обманывайте себя, думая, что нехватка времени сама по себе будет стимулировать творчество. Это мощная иллюзия, но, тем не менее, иллюзия. Сложная когнитивная обработка требует времени, а без разумного времени для этой обработки творчество практически невозможно.
Не обманывайте себя, думая, что нехватка времени сама по себе будет стимулировать творчество. Это мощная иллюзия, но, тем не менее, иллюзия.
Конечно, было бы глупо думать, что идеалом для творчества является полное отсутствие цейтнота на тот или иной рабочий проект.Учитывая требования, которые современная жизнь предъявляет к людям, слишком вероятно, что другие вещи отвлекут внимание от проекта — срочное вытеснит важное — и ничего не будет достигнуто. Более того, людям было бы легко перейти в режим автопилота, если бы не было ощущения срочности. Наше исследование показывает, что нехватка времени не обязательно способствует творческому мышлению, но это может произойти, когда людей поощряют учиться, экспериментировать с идеями и разрабатывать что-то действительно новое.Рассмотрим методы защиты творчества в 3M. В течение многих лет этот центр инноваций имеет традицию выделять 15% рабочей недели для творческих начинаний. Все его ученые-исследователи посвящают это время изучению любых новых идей или любимых проектов, которые больше всего интересуют их лично, даже если эти идеи и проекты далеки от их назначенной работы.
Для большинства компаний лучший способ избежать чрезмерного дефицита времени — сформулировать цели на всех уровнях организации, реалистичные и тщательно спланированные, избегая пристрастия к оптимизму, от которого страдает корпоративное планирование.Объявление о том, что в предстоящем году будет разработано определенное количество новых продуктов, без представления о достижимости этой цели, вероятно, вызовет крайнюю нехватку времени в организации — вплоть до людей, которые на самом деле должны прийти. с идеями для этих продуктов. Подписание контракта, который обещает доставить товары клиенту к определенной дате, без тщательного определения того, что, вероятно, будет включать в себя проект, может привести к менталитету беговой дорожки, который мы видели в команде Марии.Люди могут продолжать продвигать работу, но у них не будет творческих идей, которые заставят проект совершить скачок вперед к действительно интересным решениям.
Подписание контракта, который обещает доставить товары клиенту к определенной дате, без тщательного определения того, что, вероятно, будет включать в себя проект, может привести к менталитету беговой дорожки.
В ситуациях, когда невозможно избежать нехватки времени, менеджеры должны сосредоточиться на защите людей, которым не хватает времени, которые должны заниматься творческой работой, от помех, отвлекающих факторов и посторонних требований в течение значительной части каждой рабочей недели.Эта концентрация на «настоящей работе» может уменьшить фрагментацию времени, которую мы видели в ежедневных дневниках многих наших участников.
Исследование Перлоу в высокотехнологичной фирме, как сообщается в ее книге В поисках времени: как корпорации, отдельные лица и семьи могут извлечь выгоду из новых методов работы (Cornell University Press, 1997), показало, что инженеры, которые согласились дать друг другу такое непрерывное время тишины в определенные периоды каждый день смогли сделать больше по своим проектам и лучше себя чувствовали в течение рабочего дня.Ее исследование также показало, к сожалению, что трудно поддерживать такие серьезные изменения в нормах рабочего дня без глубоких культурных изменений в организации.
Креативность также можно поддерживать в условиях нехватки времени, если менеджеры могут помочь людям понять, почему необходимы сжатые временные рамки. Гораздо легче почувствовать, что вы выполняете миссию, если вы признаете, что существует важная, настоятельная потребность в работе, которую вы делаете, а не чувствуете, что произвольный срок был установлен просто для того, чтобы заставить вас бежать еще быстрее по своей беговой дорожке. -мельница.Наше исследование показывает, что менеджеры также должны поощрять сотрудничество и обсуждения один на один, избегая чрезмерного количества обязательных групповых встреч, которые могут способствовать возникновению чувства фрагментации и напрасной траты времени. Наконец, люди смогут лучше сосредоточиться на своей работе, если менеджеры сведут к минимуму резкие изменения запланированных действий и планов.• • •
Короче говоря, ключ к защите творческой деятельности, в том числе вашей собственной, заключается в том, чтобы компенсировать последствия крайнего дефицита времени. Очевидный способ сделать это — уменьшить нехватку времени.Но в тех случаях, когда это неизбежно, его негативные последствия можно несколько смягчить, настроив своих людей и себя на выполнение миссии, разделив чувство жизненной важности работы и обоснованности срочности. Это также означает безжалостную охрану защищенных блоков рабочей недели, ограждение персонала от отвлекающих факторов и прерываний, которые являются нормальным состоянием организационной жизни. Лучшая ситуация для творчества — не быть под прицелом. Но если вы не можете справиться с этим, по крайней мере, научитесь уворачиваться от пуль.
Версия этой статьи появилась в выпуске Harvard Business Review за август 2002 года.Произошла ошибка при настройке пользовательского файла cookie
Произошла ошибка при настройке пользовательского файла cookieЭтот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно.Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.


 B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.
B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.