Примеры решения системы линейных алгебраических уравнений 4-ого порядка методом Гаусса, пример № 4
СЛАУ 3-его порядка:
1 –
2 –
3 –
4 –
5 –
6 –
7 –
8 –
9 –
10 –
11 –
12
СЛАУ 4-ого порядка:
1 –
2 –
3 –
4 –
5 –
6 –
7 –
8 –
9 –
10 –
11 –
12
Условие
|
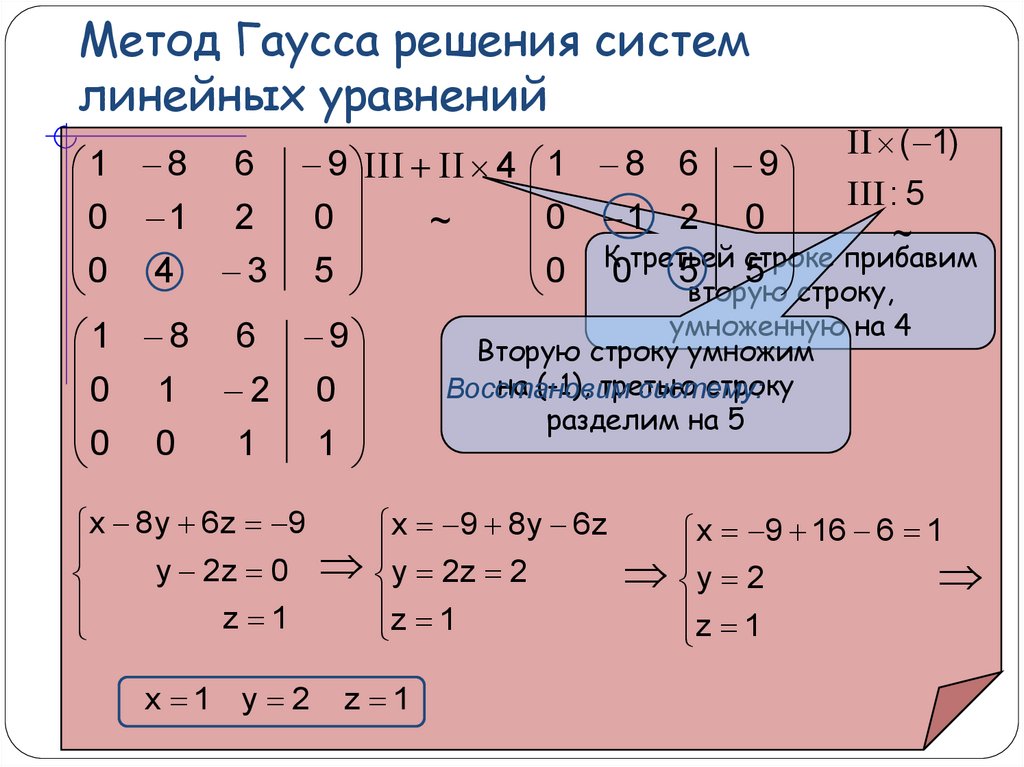
Решение системы линейных алгебраических уравнений методом Гаусс
Для проверки ответов можете воспользоваться нашим онлайн сервисом –
Решение системы линейных уравнений методом Гаусса.
Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.
Проведём следующие действия:
- Поменяем местами строку № 1 и строку № 4
Получим:
Проведём следующие действия:
- Из строки № 2 вычтем строку № 1 умноженную на 2 (Строка 2 – 2 × строка 1)
- Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 – 2 × строка 1)
- Из строки № 4 вычтем строку № 1 умноженную на 3 (Строка 4 – 3 × строка 1)
Получим:
Проведём следующие действия:
- Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)
- Поменяем местами строку № 2 и строку № 3
Получим:
Проведём следующие действия:
- К строке № 3 прибавим строку № 2 умноженную на 3 (Строка 3 + 3 × строка 2)
- К строке № 4 прибавим строку № 2 умноженную на 2 (Строка 4 + 2 × строка 2)
Получим:
Проведём следующие действия:
- Строку № 4 поделим на -3 (
- Поменяем местами строку № 3 и строку № 4
Получим:
Проведём следующие действия:
- К строке № 4 прибавим строку № 3 умноженную на 7 (Строка 4 + 7 × строка 3)
Получим:
Проведём следующие действия:
- Строку № 4 поделим на 55 (Строка 4 = строка 4 / 55)
- Из строки № 3 вычтем строку № 4 умноженную на 6 (Строка 3 – 6 × строка 4)
- Из строки № 2 вычтем строку № 4 умноженную на 5 (
- Из строки № 1 вычтем строку № 4 умноженную на 2 (Строка 1 – 2 × строка 4)
Получим:
Проведём следующие действия:
- К строке № 2 прибавим строку № 3 умноженную на 5 (Строка 2 + 5 × строка 3)
- К строке № 1 прибавим строку № 3 умноженную на 3 (Строка 1 + 3 × строка 3)
Получим:
Проведём следующие действия:
- Из строки № 1 вычтем строку № 2 (
Получим:
В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
В правом столбце получаем решение:
х1 = 0
х2 = 0
х3 = 1
х4 = 0
Вы поняли, как решать? Нет?
Другие примеры
Mathway | Популярные задачи
Популярные задачи
Элемент. математикаОсновы алгебрыАлгебраТригонометрияОсновы мат. анализаМатематический анализКонечная математикаЛинейная алгебраХимияPhysics
| Рейтинг | Тема | Задача | Форматированная задача |
|---|---|---|---|
| 1 | Решить, используя обратную матрицу | x+2y=1 , 4x+5y=13 | , |
| 2 | Перемножить матрицы | [[1/( квадратный корень из 17),-4/( квадратный корень из 17)]][[1/( квадратный корень из 17)],[-4/( квадратный корень из 17)]] | |
| 3 | Найти область определения | ||
| 4 | Найти область определения | x-y=3 | |
| 5 | Найти область определения | y=-2x+3 | |
| 6 | Найти область определения | y=2x+1 | |
| 7 | Записать в виде векторного равенства | x=x^2+9x+3 , x=x+2 | , |
| 8 | Найти область определения | y=2x | |
| 9 | Найти область определения | y=-3x | |
| 10 | Найти область определения | y=3x-2 | |
| 11 | Найти область определения | y=4x | |
| 12 | Найти область определения | 3x+2y=6 | |
| 13 | Trovare la 5×5 Matrice Identità | 5 | |
| 14 | Trovare la 6×6 Matrice Identità | 6 | |
| 15 | Trovare la 4×4 Matrice Identità | 4 | |
| 16 | Решить, используя обратную матрицу | 2x+y=-2 , x+2y=2 | , |
| 17 | Решить, используя обратную матрицу | 4x+4=y , y=6x | , |
| 18 | Решить, используя обратную матрицу | 4x+2=5y-3 , y=3x-1 | , |
| 19 | Найти степенное множество | (3,4) | |
| 20 | Вычислить | кубический корень из 216 | |
| 21 | Найти степенное множество | (1,3) | |
| 22 | Найти область определения | 3x-2y=12 | |
| 23 | Найти область определения | y=5x+2 | |
| 24 | Найти область определения | y=2x-3 | |
| 25 | Найти область определения | y=2x-4 | |
| 26 | Найти область определения | y=2x+5 | |
| 27 | Найти область определения | y=1/2x | |
| 28 | Найти область определения | y=1/2x-3 | |
| 29 | Найти область определения | y=2/3x-2 | |
| 30 | Найти область определения | x=2y | |
| 31 | Найти область определения | x-2y=2 | |
| 32 | Найти область определения | x-2y=6 | |
| 33 | Найти область определения | 2y+x | |
| 34 | Найти область определения | 2x+y=0 | |
| 35 | Найти область определения | y=5x+6 | |
| 36 | Найти область определения | y=x+3 | |
| 37 | Solve Using a Matrix by Elimination | y=4x+3x-2 , y=6 | , |
| 38 | Проверить линейную зависимость | B={[[-10,2],[5,-2. 5]]} 5]]} | |
| 39 | Сложение | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | |
| 40 | Проверить линейную зависимость | B={[[-1,2],[0,-2.5]]} | |
| 41 | Перемножить матрицы | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | |
| 42 | Найти область определения | y=5x | |
| 43 | Найти область определения | y=7x | |
| 44 | Найти область определения | y=-x-2 | |
| 45 | Найти область определения | y=x-2 | |
| 46 | Найти область определения | y=x-3 | |
| 47 | Привести матрицу к ступенчатому виду по строкам | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | |
| 48 | Записать в виде векторного равенства | x+y+z=2 , 4x+5y+z=12 , 2x=-4 | , , |
| 49 | Найти определитель | [[0,-1,a],[3,-a,1],[1,-2,3]] | |
| 50 | Найти область определения | y=-x+2 | |
| 51 | Найти определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | |
| 52 | Найти определитель | [[7,5,0],[4,5,8],[0,-1,5]] | |
| 53 | Найти обратный элемент | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | |
| 54 | Найти обратный элемент | [[1,2,3],[2,5,7],[3,7,9]] | |
| 55 | Привести матрицу к ступенчатому виду по строкам | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | |
| 56 | Привести матрицу к ступенчатому виду по строкам | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | |
| 57 | Привести матрицу к ступенчатому виду по строкам | [[1,2,3],[4,5,6],[7,8,9]] | |
| 58 | Привести матрицу к ступенчатому виду по строкам | [[7,8]] | |
| 59 | Найти область определения | 2x+y=1 | |
| 60 | Записать в виде векторного равенства | 2x+y=-2 , x+2y=2 | , |
| 61 | Найти область определения | x-2y=4 | |
| 62 | Найти область определения | x-y=-1 | |
| 63 | Найти область определения | x+y=5 | |
| 64 | Найти область определения | x=-3y-8 | |
| 65 | Найти область определения | x=-2y-8 | |
| 66 | Найти область определения | x+y=6 | |
| 67 | Найти область определения | x+y=4 | |
| 68 | Найти область определения | x+2y=4 | |
| 69 | Найти область определения | x+y | |
| 70 | Найти область определения | y=7x+9 | |
| 71 | Найти область определения | y=1/2x-5 | |
| 72 | Найти область определения | ||
| 73 | Найти область определения | y=1/2x+3 | |
| 74 | Найти область определения | x-y=-3 | |
| 75 | Найти область определения | x-y=4 | |
| 76 | Найти область определения | y=-2x | |
| 77 | Найти область определения | y=-2x+1 | |
| 78 | Найти область определения | y=2^(x+9) | |
| 79 | Найти область определения | y=10-x^2 | |
| 80 | Найти область определения | y=2x-6 | |
| 81 | Найти область определения | y=-2x-3 | |
| 82 | Найти область определения | y=3x-8 | |
| 83 | Найти область определения | y=3x | |
| 84 | Найти область определения | y=-3x+1 | |
| 85 | Найти область определения | y=4x+3 | |
| 86 | Найти область определения | y=3x-4 | |
| 87 | Найти область определения | y=4x-2 | |
| 88 | Найти область определения | y=-6x | |
| 89 | Найти область определения | y=x-4 | |
| 90 | Найти область определения | 7 корень четвертой степени из 567y^4 | |
| 91 | Найти область определения | c=5/9*(f-32) | |
| 92 | Найти область определения | f=9/5c+32 | |
| 93 | Вычислить | квадратный корень из 4 | |
| 94 | Привести матрицу к ступенчатому виду по строкам | [[-6,7],[2,6],[-4,1]] | |
| 95 | Найти собственные значения | [[2,1],[3,2]] | |
| 96 | Найти собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | |
| 97 | Найти степенное множество | A=(2,3,4,5) | |
| 98 | Найти мощность | (2,1) | |
| 99 | Решить, используя обратную матрицу | -3x-4y=2 , 8y=-6x-4 | , |
| 100 | Решить, используя обратную матрицу | 2x-5y=4 , 3x-2y=-5 | , |
Исключение Гаусса в Python — Javatpoint
следующий → ← предыдущая Практически во всех областях численного моделирования используются линейные и полиномиальные уравнения. При моделировании линейных систем генерируются математические уравнения вида Ax = b, где x — входная матрица, а b — вектор отклика системы. Внутренние свойства системы отражаются в A, называемой матрицей коэффициентов, независимой от входного вектора. Если ввод изменен, система линейных уравнений, которую мы хотим оценить, по-прежнему будет содержать точную матрицу коэффициентов A, но отдельный вектор отклика b. Методы решения систем линейных уравнений Наряду с итерационными процедурами существуют так называемые прямолинейные подходы, которые мы здесь обсуждать не будем. Объединяет их стремление преобразовать исходные уравнения в систему, эквивалентную по свойствам исходной системе, но более простую для решения. Мы можем использовать три основные операции для достижения этого преобразования:
Эти процедуры, конечно, не влияют на решения системы, которые остаются неизменными, но могут повлиять на матрицу коэффициентов A и ее определитель. Три основных прямых способа решения собраны в следующей таблице:
Метод исключения Гаусса Сокращение строк — это еще одно название исключения Гаусса.
Эти процедуры выполняются до тех пор, пока необходимо заполнить нижнюю левую часть матрицы коэффициентов нулями. Алгоритм исключения Гаусса в PythonЧто касается ручного процесса, есть два возможных подхода: первый заключается в том, что строки преобразуются путем вычитания, а не суммирования, а другой заключается в том, что преобразованные строки не заменяются исходными строками матрицы A, а только компоненты характерны для верхней треугольной матрицы. В действительности на вычисление решений не влияют элементы, не принадлежащие U (модифицированная матрица). Код # Программа на Python для поиска решения системы линейных уравнений с использованием метода исключения Гаусса. Вывод: 3 3 4 -1 5 -2 1 2 -2 1 8 4 1 ['8', '4', '1'] 3 | 4 | -1 | 8 | 5 | -2 | 1 | 4 | 2 | -2 | 1 | 1 | Результат: 1 2 3 Если мы дадим набор уравнений, не имеющих решения, вывод будет следующим: Выход 3 1 1 1 0 1 -3 2 1 5 2 1 0 ['2', '1', '0'] 1 | 1 | 1 | 2 | 0 | 1 | -3 | 1 | 2 | 1 | 5 | 0 | -------------------------------------------------- ------------------------- ZeroDivisionError Traceback (последний последний вызов) в 75 76 # Вычисление решения матрицы ---> 77 x = gauss_elem(A_mat) 78 79# Печать результата ________________________________________ 3 кадра ________________________________________ /usr/lib/Python3. |

 Но область анализа линейных систем уравнений — это то место, где они наиболее естественно используются в технике. Конструкции, упругие вещества, тепловые потоки, электромагнетизм, электрические цепи и многое другое подпадают под общую категорию линейных систем.
Но область анализа линейных систем уравнений — это то место, где они наиболее естественно используются в технике. Конструкции, упругие вещества, тепловые потоки, электромагнетизм, электрические цепи и многое другое подпадают под общую категорию линейных систем.
 Это линейный алгебраический метод решения линейной системы уравнений. По сути, матрица коэффициентов подвергается ряду процессов. Это действия, которые задействованы:
Это линейный алгебраический метод решения линейной системы уравнений. По сути, матрица коэффициентов подвергается ряду процессов. Это действия, которые задействованы: # Создание функции для печати расширенной матрицы с заданным набором линейных уравнений
защита print_aug (мат):
нет = лен (мат)
для i в диапазоне (0, нет):
л = “”
для k в диапазоне (0, n + 1):
l += str(mat[i][k]) + “\t”
если j == нет – 1:
л += “| ”
печать (л)
Распечатать(“”) # Создание функции для выполнения исключения Гаусса на заданной матричной матрице
защита gauss_elem (мат):
число = длина (мат) для я в диапазоне (0, число):
# Поиск максимального значения определенного столбца
max_el = абс (мат [я] [я])
# Строка с элементом максимального значения
максимальная_строка = я
для k в диапазоне (i + 1, число):
если abs(mat[k][i]) > max_el:
max_el = абс (мат [k] [i])
максимальная_строка = к # Замена максимальной строки на текущую строку
для k в диапазоне (i, n + 1):
темп = мат[max_row][k]
мат[max_row][k] = мат[i][k]
мат[i][k] = температура # Изменение значения строк ниже текущей строки на 0
для k в диапазоне (i + 1, n):
текущий = -мат [к] [я] / мат [я] [я]
для j в диапазоне (i, n + 1):
если я == j:
мат [к] [j] = 0
еще:
мат[k][j] += текущий * мат[i][j] # Решение уравнения Ax = b для созданной верхней треугольной матрицы mat
l = [0 для i в диапазоне (n)]
для j в диапазоне (n – 1, -1, -1):
l[j] = мат[j][n] / мат[j][j]
для k в диапазоне (j – 1, -1, -1):
мат[k][n] -= мат[k][j] * l[j]
вернуть л если __name__ == “__main__”:
из дробей импорт дроби п = интервал (ввод ()) A_mat = [[0 для j в диапазоне (n + 1)] для i в диапазоне (n)] # Чтение входных коэффициентов линейных уравнений
для j в диапазоне (0, n):
l = карта (Дробь, ввод ().
# Создание функции для печати расширенной матрицы с заданным набором линейных уравнений
защита print_aug (мат):
нет = лен (мат)
для i в диапазоне (0, нет):
л = “”
для k в диапазоне (0, n + 1):
l += str(mat[i][k]) + “\t”
если j == нет – 1:
л += “| ”
печать (л)
Распечатать(“”) # Создание функции для выполнения исключения Гаусса на заданной матричной матрице
защита gauss_elem (мат):
число = длина (мат) для я в диапазоне (0, число):
# Поиск максимального значения определенного столбца
max_el = абс (мат [я] [я])
# Строка с элементом максимального значения
максимальная_строка = я
для k в диапазоне (i + 1, число):
если abs(mat[k][i]) > max_el:
max_el = абс (мат [k] [i])
максимальная_строка = к # Замена максимальной строки на текущую строку
для k в диапазоне (i, n + 1):
темп = мат[max_row][k]
мат[max_row][k] = мат[i][k]
мат[i][k] = температура # Изменение значения строк ниже текущей строки на 0
для k в диапазоне (i + 1, n):
текущий = -мат [к] [я] / мат [я] [я]
для j в диапазоне (i, n + 1):
если я == j:
мат [к] [j] = 0
еще:
мат[k][j] += текущий * мат[i][j] # Решение уравнения Ax = b для созданной верхней треугольной матрицы mat
l = [0 для i в диапазоне (n)]
для j в диапазоне (n – 1, -1, -1):
l[j] = мат[j][n] / мат[j][j]
для k в диапазоне (j – 1, -1, -1):
мат[k][n] -= мат[k][j] * l[j]
вернуть л если __name__ == “__main__”:
из дробей импорт дроби п = интервал (ввод ()) A_mat = [[0 для j в диапазоне (n + 1)] для i в диапазоне (n)] # Чтение входных коэффициентов линейных уравнений
для j в диапазоне (0, n):
l = карта (Дробь, ввод (). Разделить («»))
для i элемент в enumerate(l):
A_mat[j][i] = элемент л = ввод().разделить(” “)
печать (л)
последний = список (карта (дробь, л))
для j в диапазоне (0, n):
A_mat[j][n] = последний[j] # Печать расширенной матрицы из входных данных
print_aug(A_mat) # Вычисление решения матрицы
x = gauss_elem (A_mat) # Печать результата
л = “Результат:\t”
для j в диапазоне (0, n):
л += ул(х[j]) + “\t”
печать (л)
Разделить («»))
для i элемент в enumerate(l):
A_mat[j][i] = элемент л = ввод().разделить(” “)
печать (л)
последний = список (карта (дробь, л))
для j в диапазоне (0, n):
A_mat[j][n] = последний[j] # Печать расширенной матрицы из входных данных
print_aug(A_mat) # Вычисление решения матрицы
x = gauss_elem (A_mat) # Печать результата
л = “Результат:\t”
для j в диапазоне (0, n):
л += ул(х[j]) + “\t”
печать (л)