Решить онлайн метод гаусса: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Решение системы линейных уравнений методом Гаусса с нахождением общего решения

УчебаМатематика

Решает систему линейных алгебраических уравнений методом Гаусса. Умеет выводить решение для совместных неопределенных систем линейных уравнений. Кроме того, выводит результат в формате с плавающей точкой и в формате дроби.

Вообще говоря, на сайте уже есть один калькулятор, решающий СЛАУ методом Гаусса — Решение системы линейных алгебраических уравнений методом Гаусса. Он даже расписывает решение пошагово.

Однако, у него есть некоторые недостатки, которые будет решать новый калькулятор из этой статьи:

Во-первых, предыдущий калькулятор выдает решение в формате с плавающей запятой, тогда как во многих задачниках ответ обычно дается в виде дроби.

Во-вторых, предыдущий калькулятор только определяет факт наличия бесконечного множества решений (неопределенная система), но не выдает решение в общем виде.

В-третьих, предыдущий калькулятор работает только в случае когда число уравнений совпадает с числом неизвестных, и таким образом, не может решать недоопределенных (число неизвестных больше числа уравнений) и переопределенных систем (число неизвестных меньше числа уравнений).

Что касается, второго и третьего пунктов, то универсальность метода Гаусса состоит в том, что на самом деле он годится для систем линейных уравнений с любым числом уравнений и неизвестных, просто это не было использовано.

Описание самого метода Гаусса можно посмотреть по ссылке выше, а под калькулятором подробнее рассмотрены разные случаи (виды систем).

Сам калькулятор, помимо нахождения единственного решения, может находить и общее решение в случае неопределенной системы уравнений.
Матрица уравнений из случая 2 ниже (совместная неопределенная система линейных уравнений) использована в нем в качестве входных данных по умолчанию:

Решение системы линейных уравнений методом Гаусса для любого числа уравнений и неизвестных

1 2 -3 5 1 1 3 -13 22 -1 3 5 1 -2 5 2 3 4 -7 4

СЛАУ в матричном виде

Количество решений

 

Коэффициенты решения

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.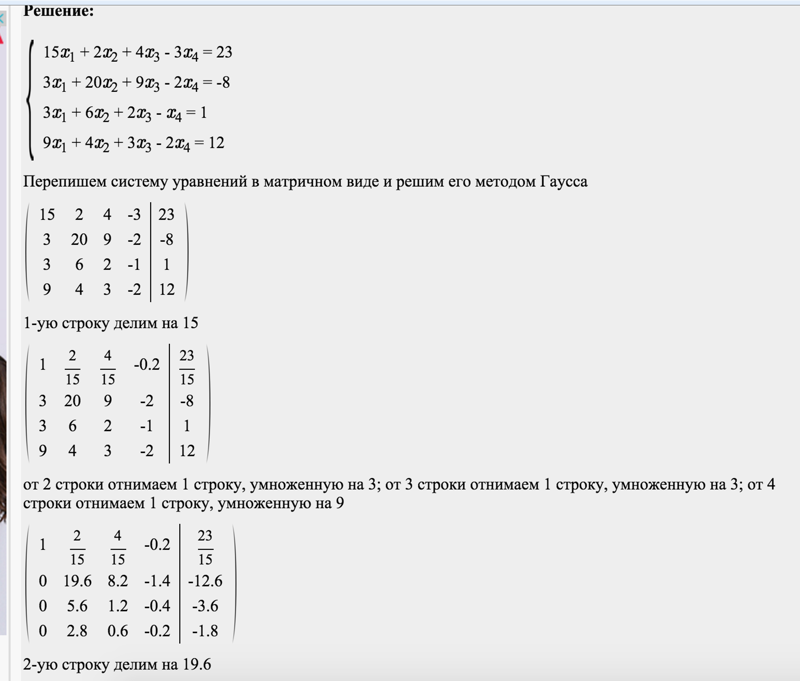

1. Совместная определенная система линейных уравнений (имеющая одно решение)

Пример: пусть дана система линейных уравнений

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Откуда обратным ходом находим единственное решение:

Система совместна и определена.

2. Совместная неопределенная система линейных уравнений (имеющая бесконечное множество решений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

В результате приходим к системе:

Последние два уравнения верны при любых значениях переменных:

поэтому их можно отбросить.

Чтобы найти решения оставшихся двух уравнений, x1 и x2 можно выразить через x3 и x4.

При этом сами x3 и x4 могут принимать любые значения

Полученная эквивалентная система совместна, но неопределена. Формулы:
;
при произвольных x3 и x4 описывают бесконечное множество решений заданной системы.

3. Несовместная система линейных уравнений (не имеющая решений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Полученная эквивалентная система несовместна, так как последнее уравнение:

не может быть удовлетворено никакими значениями неизвестных.
Эта система несовместна, т. е. не имеет решения.

4. Переопределенная система линейных уравнений (число неизвестных меньше числа уравнений)

Пример: пусть дана система линейных уравнений

После приведения матрицы к трапециевидной форме методом Гаусса получим

Как видим, в данном случае «лишнее» уравнение можно просто отбросить. Также в результате преобразований можно получить одинаковые строки, «лишние» из которых тоже можно отбросить — после чего задача сводится к случаям 1 или 2.

5. Недоопределенная система линейных уравнений (число неизвестных больше числа уравнений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Полученная эквивалентная система имеет вид:

Как видно, в ней отсутствуют уравнения, дающие однозначные значения для x3 и x4, что равносильно появлению уравнений вида:

которые можно отбросить.

Таким образом этот случай сводится к случаю 2 с бесконечным множеством решений, которые описываются следующими формулами:

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Решение системы линейных алгебраических уравнений методом Гаусса с сохранением дробей
• • Решение неоднородной системы линейных алгебраических уравнений матричным методом
• • Решение системы линейных алгебраических уравнений методом Гаусса
• • Метод Крамера с подробным решением
• • Линейные диофантовы уравнения с двумя переменными
• • Раздел: Математика ( 264 калькуляторов )

 Гаусс дроби Математика метод Гаусса недоопределенная система линейных уравнений неопределенная система линейных уравнений несовместная система линейных уравнений определенная система линейных уравнений Система линейных уравнений СЛАУ совместная система линейных уравнений

 PLANETCALC, Решение системы линейных уравнений методом Гаусса с нахождением общего решения

Timur2020-11-03 14:19:33

Решение уравнений методом Гаусса онлайн калькулятор

Карл Фридрих Гаусс – немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса позволяет максимально легко и быстро решить систему линейных алгебраических уравнений (СЛАУ). Успех данного метода заключается в последовательном исключении неизвестных из уравнений. Сегодня решить систему алгебраических уравнений онлайн методом Гаусса можно с помощью специальных решательов, но ниже мы разберем решение системы линейных уравнений, чтобы наглядно на примере увидеть все его достоинства.

Так же читайте нашу статью “Решить уравнение матричным способом онлайн решателем”

Допустим, дана система линейных уравнений:

\[\left\{\begin{matrix} 2\cdot x_1+4\cdot x_2+1\cdot x_3 = 36\\ 5\cdot x_1 + 2 \cdot x_2 +1 \cdot x_3 =47\\ 2\cdot x_1 + 3\cdot x_2 + 4 \cdot x_3 = 37 \end{matrix}\right. \]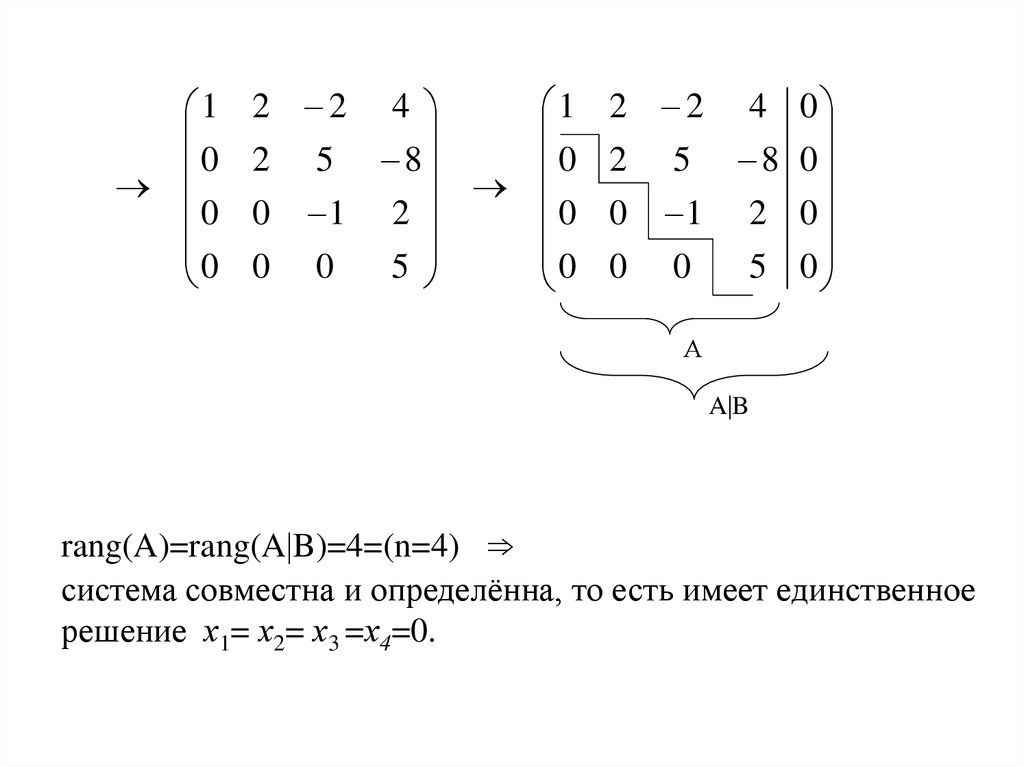

Представим ее в матричной форме:

\[\begin{bmatrix} 2 & 4 & 1\\ 5 & 2 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 36\\ 47\\ 37 \end{bmatrix}\]

Выберем строку с максимальным коэффициентом \[a_i1\] и меняем ее с первой.

\[\begin{bmatrix} 5 & 2 & 1\\ 2 & 4 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 47\\ 36\\ 37 \end{bmatrix}\]

Нормируем уравнения относительно коэффициента при \[x_1\]:

\[\begin{bmatrix} 1 & \frac{2}{5} & \frac{1}{5}\\ 2 & \frac{4}{2} & \frac{1}{2}\\ 2 & \frac{3}{2} & \frac{4}{2} \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} \frac{47}{5}\\ \frac{36}{2}\\ \frac{37}{2} \end{bmatrix} \]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 1 & 2 & 1\\ 1 & 1.5 & 2 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.

4\\ 9.6\\ 9.1 \end{bmatrix}\]

Вычитаем 1 уравнение из 2 и 3:

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Выбираем строку с наибольшим коэффициентом при \[a_i2\] (уравнение 1 не рассматривается) и перемещаем ее на место 2.

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Нормируем 2 и 3 уравнения относительно коэффициента при \[x_2\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 1 & 1.636 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 8.272 \end{bmatrix}\]

Вычитаем уравнение 2 из 3

\[\begin{bmatrix} 1 & 0.4 & 0. T\].

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Тесты по теме “Системы уравнений” онлайн

• Решение рациональных уравнений и неравенств

  01.12.2020 318 0

  Тест предназначен для проверки умения решать постейшие рациональные уравнения и неравенства и их системы

• 7_Решение систем уравнений

  20. 04.2020 7603

  Данный тест предназначен для проверки знаний по алгебре учащихся 7-х классов,  которые изучили тему “Системы линейных уравнений с двумя переменными”.     Тест состоит из 20 заданий разной степени трудности, в том числе, и заданий с множественным выбором ответа, заданий на соответствие, заданий на знание терминов и рассчитан на 90 минут выполнения.

• Решение систем уравнений

  28.05.2020 4000 0

  Тест предназначен для проверки умения решать системы уравнения методом подстановки и методом сложения..

• Решение задач с помощью систем уравнений

  17.

  04.2020 5324 0

  Данная работа предназначена для закрепления знаний по теме “Решение задач с помощью систем линейных уравнений” и рассчитана на 40 минут. 

• Системы уравнений

  19.04.2020 3602

  Тест соответствует учебнику “Алгебра. 7 класс” под редакцией С.А. Теляковского. 

• Тест “Система линейных уравнений” по алгебре 7 класс

  24.11.2020 1850 0

  Материал представляет  зачетную работу в 7классе по  теме “Система линейных уравнений”.

• Системы уравнений

  24. 04.2020 2019

  Данная работа предназначена для закрепления знаний по теме “Системы уравнений” и рассчитана на 30 минут. 

• Системы показательных и логарифмических уравнений

  28.05.2020 325 0

  Тест предназначен для проверки умения решать системы показательных и логарифмических уравнений

• Линейное программирование

  12.06.2020 568 0

  Тест предназначен для проверки знания понятий линейного программирования, умения составлять математические модели, применять графический и симплексный методы решения задач линейного программирования, решать транспортные задачи.

• Итоговый тест по теме «Системы линейных уравнений»

  03.08.2020 661 0

  Тест предназначен для проверки знаний и умений, полученных вами при изучении темы “Системы линейных уравнений”

• Тест по модулю 2

  20.08.2020 10 0

  Привет, ребята! Пришло время показать свои знания на практике. 

• 9 класс. Повторение. Системы рациональных уравнений. Подготовка к ОГЭ.

  04. 04.2022 171 0

  Для успешного прохождения теста повторите алгоритмы решений систем методом подстановки, методом сложения и графическим способом.

Калькулятор исключения Гаусса

Что говорят наши клиенты…

Тысячи пользователей используют наше программное обеспечение, чтобы справиться со своими домашними заданиями по алгебре. Вот некоторые из их опыта:

Я ценю, что это основа. Это очень помогло мне

Рик Паркер, Миссури

Я был так горд, когда мой сын решил сдать экзамен с отличием по алгебре, но я был обескуражен, когда понял, что могу не помогать ему с домашним заданием. Я не изучал алгебру со школы и просто не помнил, как выполнять некоторые проекты. Алгебратор позволил нам пройти каждый шаг вместе. Спасибо за создание программы, которая позволяет мне помочь моему сыну!

Джим Хендри, Коннектикут.

Существует так много программ по алгебре. Я не знаю, как я застрял с вашим, но академически говоря, это лучшее, что когда-либо случалось со мной!

Сара Джонс, Калифорния

Я учусь в 9-м классе, и мне всегда было интересно, как некоторые ученики всегда получают хорошие оценки по математике, но никогда не могли представить, что я буду одним из них. Снимаю шляпу перед Алгебратором! Теперь я хорошо разбираюсь в алгебре, и мой подход к решению задач стал более методичным.

Alexis Stratton, FL

Больше всего мне нравится в этом программном обеспечении возможность настройки в соответствии с требованиями пользователя. Сопоставьте свой ответ или проверьте свои шаги или обратитесь за объяснением – это ваша собственная воля. Это дает вам практическое и четкое понимание проблемы.

Алекс Мартин, NH

Поисковые фразы, использованные 27 мая 2011 г.:

Студенты, борющиеся со всевозможными задачами по алгебре, обнаруживают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?

• Глава 4 умножение и деление десятичных дробей
• математические степени числа 8
• КАК ИЗМЕНИТЬ ДРОБЬ НА ЦЕЛОЕ ИЛИ СМЕШАННОЕ ЧИСЛО
• преобразовать десятичное число в целое число
• “Бесплатные рабочие листы по математике для третьего класса”
• стихотворения об элементарной алгебре
• график данных квадратного уравнения
• от шаблона к тесту по алгебре
• Алгебра 2 Глава 6 Практические листы
• решить нелинейные уравнения ti-83
• умножающий биномиальный калькулятор
• С++ наибольший общий делитель
• лог2 ти 89
• Калькулятор gcf
• Рабочий лист решения триггерных уравнений
• Решатель уравнений третьего порядка
• алгебраический тест терминов
• KS3 онлайн-тест по математике и естественным наукам бесплатно
• математика + урок + логарифм + swf
• калькулятор наименьшего общего знаменателя
• При графическом отображении линейного неравенства, как узнать, представляет ли неравенство площадь над линией
• десятичная до ближайшей дроби
• Алгебра 10 класс
• средний на Ti 83
• образование воды (химическое уравнение)
• алгебра квадратный корень кратный
• учебное пособие cpt алгебра примеры
• Рабочие листы порядка операций
• тригонометрический калькулятор
• математические упражнения 11 класс
• бесплатный онлайн-решатель сложных математических задач
• преобразование десятичной дроби в квадратные ярды
• строка Java удалить пунктуацию
• Структура алгебры читов и книга методов 1 ответы
• лист с подсказками по алгебре и математике
• ответы на домашнее задание 8 класса
• формула для расчета наклона x y
• растворяющие радикалы
• mcdougal littell inc глава 4 ресурсная книга ответы
• найти корни полиномиального калькулятора
• Почему GCM используется в задачах на дроби
• переменные и показатели
• такс вопрос с уклоном
• рабочие листы времени на вычитание, 6 класс
• уроки алгебры по структуре и методике
• формулы концептуальной физики
• преобразование вершины функции в стандартную
• символ квадратного корня из трех над двумя
• триггерный решатель уравнений
• преобразование десятичной дроби в дробную
• квадратный корень из десятичной дроби не менее 1
• Калькулятор наименьших общих кратных
• TI-83plus как набирать комплексные числа
• Т1 калькулятор онлайн
• экзамен по алгебре в колледже
• Рунге кутта матлаб одновременный
• функция в кубе
• 4 шага к составлению сбалансированного химического уравнения
• «бесплатные математические рабочие листы», описывающие шаблоны в формуле
• смешанное число как десятичное
• как создать хороший выпускной экзамен по алгебре 2
• решение систем линейных уравнений на ти-83+
• тесты по алгебре онлайн ks3
• БЕСПЛАТНАЯ студенческая алгебра для чайников
• Онлайн-справка по алгебре1
• как делить дроби вычитанием
• чит на сложение и вычитание дробей
• Возраст для начинающих
• тест системы уравнений
• примеры нелинейных задач
• бесплатные контрольные работы для средних школ Сингапура
• Глава 4 Практические вопросы по алгебре для восьмого класса
• Бесплатное ПО “KS3 Mental Maths”
• калькулятор порядка десятичных дробей от наименьшего к наибольшему
• решение квадратных уравнений методом квадратного корня
• Рабочие листы делимости для пятого класса
• квадратный корень из многочлена
• Рабочий лист по квадрату, завершающий квадрат
• КУБИЧЕСКИЙ КОРЕНЬ НА КАЛЬКУЛЯТОРЕ
• ти-83 фактор
• рабочие листы делимости
• даже ответы на прентис холл
• когнитивный репетитор по алгебре 1 скачать бесплатно
• Расширенный трехчленный рабочий лист
• сложные математические коэффициенты
• математическая задача Словер
• какая формула для расчета процентов
• упростить рабочий лист корней
• Метод наибольшего общего делителя

Предыдущий

Далее

Академия математического образования Гаусса

Добро пожаловать в Академию математического образования Гаусса!

Gauss Math предлагает внешкольную программу повышения квалификации по математике , разработанную, чтобы помочь детям улучшить свое логическое и абстрактное мышление, добиться успеха в многочисленных конкурсах, стандартизированных тестах и приобрести интерес к математике и естественным наукам на всю жизнь.

Предстоящие события в Gauss:
​

• Gauss 2022-2023 учебный год Регистрация начинается 1 июля. Скидка 5% при раннем бронировании будет действовать 25 июля. См.  2022/23 Регистрация  чтобы ознакомиться с расписанием занятий. Пожалуйста, заполните регистрационную форму: forms.gle/zusCDVTmzQ1SvNPJ9
• Регистрация на летнюю онлайн-программу Gauss 2022 начнется 1 марта. См. Лето 2022​. Ознакомьтесь с информацией о классе и заполните регистрационную форму. аут: Математический турнир Гаусса
• Logistem Science Challenger состоится в субботу, 18 июня. Пожалуйста, ознакомьтесь: Конкурс Science Challenger
• Обсуждение Gauss Senior Panel состоится в субботу, 18 июня. Пожалуйста, ознакомьтесь: Gauss 2022 Senior Panel

Почему математика Гаусса?

Школьное математическое образование теперь ежедневно обсуждается в редакционных статьях, на радио и телевидении и даже в залах Конгресса.
Причин тому может быть много, но самые очевидные из них:

• Школьная программа США описывается как «ширина в милю и глубина в дюйм»;
• В начальной школе не уделяется особого внимания созданию прочной основы базовых математических и естественных понятий;
• Отсутствует многоуровневый подход к преподаванию сложной математики или физики в средней школе
• Лишь ограниченное число учащихся (менее 20%) достигают продвинутого уровня математики и изучают любую физику в средней школе
• Существует небольшая корреляция и преемственность между учебными программами по математике и естественным наукам и учебниками начальной, средней и старшей школы.

Что мы (родители и педагоги) можем сделать, чтобы помочь нашим детям добиться успехов в математике и физике? И почему мы должны делать упор на математику и физику из всех школьных предметов? Ответ очень простой. Потому что математику считают «экономикой информации», а физику всегда называют «логикой технологической революции». Все мы понимаем, что нашим детям предстоит жить и работать в 21 веке, и наш долг помочь им не только добиться успеха во всем, чем они хотят заниматься в жизни, но и помочь им быть счастливыми и гордиться собой. и их достижений. И что может быть лучше для родителей, чтобы помочь своим детям добиться успеха, чем познакомить их с хорошей, структурированной, веселой и свободной от стресса, но сложной программой по математике и физике на самой ранней стадии. И в этом вся суть ИГРЫ.

Наши методики

• Наша учебная программа дополняет стандартную школьную программу, но также предлагает более сложные задачи и задания, чем обычно ожидается в классе. Наша учебная программа разработана таким образом, чтобы соответствовать и превосходить требования по математике на экзаменах SAT, ACT и AP. Наша олимпиадная учебная программа по математике имеет собственную систему, направленную на достижение наивысших стандартов математического мастерства.
• Математические рассуждения и их применение являются важным компонентом нашей учебной программы. Мы фокусируемся на уникальных темах для каждого уровня, в которых ранее изученные навыки и методы будут укрепляться и развиваться на каждом этапе. Особое внимание уделяется аргументации и применению.
• Строгие и интуитивные:  Математика – довольно строгая и строгая дисциплина, и, хотя мы не можем переоценить важность строгих математических рассуждений, чрезвычайно важно научить учащихся использовать правдоподобные рассуждения для решения сложных задач. В конечном счете, для студентов крайне важно развивать математическую интуицию, которая станет жизненно важной, когда они будут работать над сложными математическими сценариями в будущем.
• Понимание против запоминания : Само собой разумеется, чтобы освоить математику, нужно запомнить некоторые факты, формулы и теоремы. Однако, что действительно важно для успеха детей в математике, так это понимание значения математических задач и их решений. Таким образом, дети могут интуитивно получить много замечательных, но простых ответов.
• Повторение против творчества:  Повторение является неотъемлемой частью процесса обучения для маленьких детей, следовательно, «практика делает совершенным». Однако не менее важно поощрять детей к поиску творческих решений. Например, детей следует с самого раннего возраста учить думать о том, как изменить данную математическую задачу, чтобы получить новое (или другое) решение.
• Геометрический и алгебраический методы: Алгебраические и геометрические методы во многом дополняют друг друга. Наша учебная программа предназначена для развития у учащихся способности решать задачи с помощью наиболее эффективных инструментов, имеющихся в их распоряжении.
  

Калькулятор нормального распределения вероятность при заданной нормальной случайной величине; наоборот. За помощью в использовании калькулятор, прочтите часто задаваемые вопросы или просмотрите примеры задач.

Чтобы узнать больше о нормальном распределении, посетите Stat Trek’s учебник по нормальному распределению.

• Введите значение в три из четырех текстовых полей.
• Оставьте четвертое текстовое поле пустым.
• Нажмите кнопку Вычислить , чтобы вычислить значение для четвертого текстового поля.

Стандартный счет: z
Вероятность: P(Z≤z)	363
Стандартное отклонение

большинство статистических текстов основано на стандартное нормальное распределение, имеющее среднее значение 0 и стандартное отклонение 1. Для получения выходных данных из стандартного нормального распределения с помощью этого калькулятора, установите среднее значение равным 0, а стандартное отклонение равным 1.

Реклама

Часто задаваемые вопросы

Калькулятор | Пример задачи

Инструкции: Чтобы найти ответ на часто задаваемый вопрос, просто нажмите на вопрос.

Почему нормальное распределение так важно?

Нормальное распределение важно, поскольку оно описывает статистическое поведение многих реальных событий. Форма в норме распределение полностью описывается средним значением и стандартным отклонением.

Таким образом, зная среднее значение и стандартное отклонение, вы можете использовать свойства нормального распределения для быстрого вычисления кумулятивного вероятность любого значения. Этот процесс проиллюстрирован в примерах задач ниже.

Что такое стандартное нормальное распределение?

Существует бесконечное количество нормальных распределений. Несмотря на то что каждое нормальное распределение имеет колоколообразную кривую, некоторые нормальные распределения иметь высокую и узкую кривую; в то время как другие имеют короткую кривую и широкий.

Точная форма нормального распределения определяется его среднее значение и его стандартное отклонение. Стандартное нормальное распределение — это нормальное распределение, имеющее среднее значение, равное нулю, и стандартное отклонение, равное единице.

Нормальный случайная величина стандартного нормального распределения называется стандартом оценка или z-оценка . Нормальная случайная величина X из любого нормального распределения можно преобразовать в z-оценку из стандартное нормальное распределение с помощью следующего уравнения:

z = ( X – μ) / σ

, где X — нормальная случайная величина, μ — среднее значение, σ — стандартное отклонение.

Поскольку любую нормальную случайную величину можно «преобразовать» в z-значение, стандартное нормальное распределение обеспечивает полезную систему отсчета. На самом деле, это нормальное распределение, которое обычно приводится в приложении. учебников по статистике.

Что такое нормальная случайная величина?

Нормальное распределение определяется следующим уравнением:

Нормальное уравнение . Значение случайной величины Y равно:

Y = { 1/[ σ * sqrt(2π) ] } * e ^{-(x – μ) 2 /2σ 2}

, где X — нормальная случайная величина, μ — среднее значение, σ — стандартное отклонение, π — приблизительно 3,14159, а e — приблизительно 2,71828.

В этом уравнении случайная величина X называется нормальной случайной величиной. Уникальный кумулятивная вероятность может быть связана с каждой нормальной случайной величиной. Учитывая нормальную случайную величину, стандартное отклонение нормального распределение и среднее значение нормального распределения, мы можем вычислить кумулятивная вероятность (т. е. вероятность того, что случайный выбор из нормальное распределение будет меньше или равно нормальной случайной величине.)

Что такое z-оценка?

Z-оценка (также известная как стандартная оценка) нормальная случайная величина из стандартное нормальное распределение.

Для преобразования обычной случайной величины (x) в эквивалентную z-значение (z), используйте следующую формулу:

z = ( x – μ) / σ

, где μ — среднее значение, а σ — стандартное отклонение.

Что такое вероятность?

Вероятность – это число, выражающее вероятность того, что конкретное произойдет событие. Это число может принимать любое значение от 0 до 1. Вероятность 0 означает, что вероятность того, что событие произойдет, равна нулю; вероятность 1 означает, что событие обязательно произойдет.

Количественное определение чисел от 0 до 1 неопределенность, связанная с событием. Например, вероятность подбрасывание монеты, в результате которого выпадет орел (а не решка), будет равно 0,50. Пятьдесят процентов в то время при подбрасывании монеты выпадал орел; и пятьдесят процентов время, это приведет к хвостам.

Что такое кумулятивная вероятность?

Кумулятивная вероятность представляет собой сумму вероятностей. В связи при нормальном распределении кумулятивная вероятность относится к вероятность того, что случайно выбранный результат будет меньше или равен заданное значение, называемое нормальной случайной величиной.

Предположим, например, что у нас есть школа со 100 первоклассники. Если мы спросим о вероятности того, что случайно выбранный первый грейдер весит ровно 70 фунтов, мы спрашиваем о простой вероятности – не кумулятивная вероятность.

Но если мы спросим о вероятности того, что случайно выбранный первоклассник на меньше или равен до 70 фунтов, мы действительно спрашиваем о сумме вероятностей (т. е. вероятности того, что студент точно 70 фунтов плюс вероятность того, что ему 69 лет.фунтов плюс вероятность что он/она весит 68 фунтов и т. д.). Таким образом, мы спрашиваем о совокупном вероятность.

Что такое средний балл?

Средний балл — это средний балл. это сумма индивидуальных баллы разделить на количество человек.

Что такое стандартное отклонение?

Стандартное отклонение — это числовое значение, используемое для указания того, как широко оценки в наборе данных варьируются. Это мера среднего расстояния индивидуальные наблюдения от среднего значения группы.

Пример задачи

Калькулятор | Часто задаваемые вопросы

1. Компания Acme Light Bulb Company обнаружила, что средняя лампочка служит 1000 часов. часов со стандартным отклонением 100 часов. Предположим, что срок службы лампы в норме распределенный. Какова вероятность того, что случайно выбранная лампочка выгорают за 1200 часов или меньше?

   Решение:

   Мы знаем следующее:

   • Средний балл равен 1000.
   • Стандартное отклонение равно 100.
   • Необработанная оценка, для которой мы хотим найти кумулятивную вероятность, равно 1200.
   
   Поэтому мы подставляем эти числа в Нормальный Калькулятор распределения и нажмите кнопку «Рассчитать».

   Калькулятор сообщает, что кумулятивный вероятность равна 0,97725. Таким образом, вероятность того, что Acme Light Лампа перегорит в течение 1200 часов.

2. Билл утверждает, что он может сделать больше отжиманий, чем 90% мальчиков в его школе.