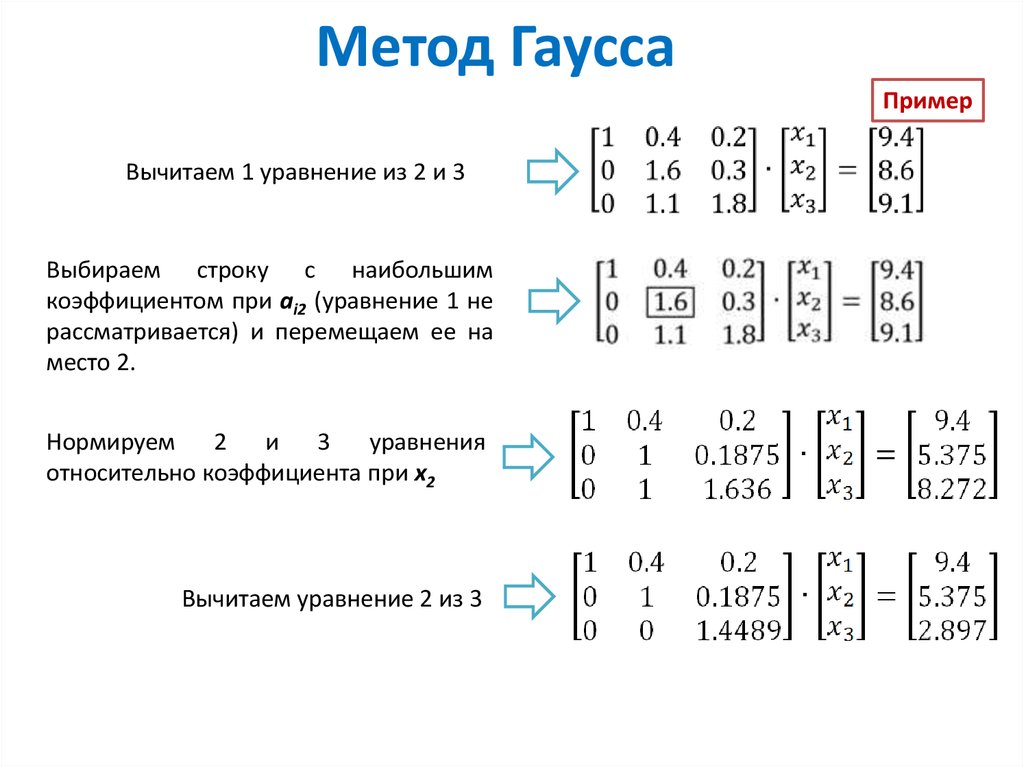
Мэтуэй | Популярные задачи
Популярные задачи
Базовая математикаПредварительная алгебраАлгебраТригонометрияПредварительный исчислениеИсчислениеКонечная математикаЛинейная алгебраХимияФизика
| Ранг | Тема | Проблема | Проблема с форматированием | |
|---|---|---|---|---|
| 1 | Решение с использованием обратной матрицы | х+2у=1 , 4х+5у=13 | , | |
| 2 | Умножение матриц | [[1/(квадратный корень из 17),-4/(квадратный корень из 17)]][[1/(квадратный корень из 17)],[-4/(квадратный корень из 17)]] | ||
| 3 | Найти домен | |||
| 4 | Найти домен | х-у=3 | ||
| 5 | Найти домен | у=-2х+3 | ||
| 6 | Найти домен | у=2х+1 | ||
| 7 | Записать как векторное равенство | 92+9х+3 , х=х+2, | ||
| 8 | Найти домен | у=2х | ||
| 9 | Найти домен | г=-3x | ||
| 10 | Найти домен | у=3х-2 | ||
| 11 | Найти домен | у=4х | ||
| 12 | Найти домен | 3x+2y=6 | ||
| 13 | Найдите матрицу идентичности 5×5 | 5 | ||
| 14 | Найдите матрицу идентичности 6×6 | 6 | ||
| 15 | Найдите матрицу идентичности 4×4 | 4 | ||
| 16 | Решение с использованием обратной матрицы | 2х+у=-2, х+2у=2 | , | |
| 17 | Решение с использованием обратной матрицы | 4х+4=у, у=6х | , | |
| 18 | Решение с использованием обратной матрицы | 4х+2=5у-3, у=3х-1 | , | |
| 19 | Найдите силовой набор | (3,4) | ||
| 20 | Оценка | кубический корень из 216 | ||
| 21 | Найдите силовой набор | (1,3) | ||
| 22 | Найти домен | 3x-2y=12 | ||
| 23 | Найти домен | у=5х+2 | ||
| 24 | Найти домен | у=2х-3 | ||
| 25 | Найти домен | у=2х-4 | ||
| 26 | Найти домен | у=2х+5 | ||
| 27 | Найти домен | у=1/2х | ||
| 28 | у=1/2x-3 | |||
| 29 | Найти домен | у=2/3х-2 | ||
| 30 | Найти домен | х=2у | ||
| 31 | Найти домен | х-2у=2 | ||
| 32 | Найти домен | х-2у=6 | ||
| 33 | Найти домен | 2г+х | ||
| 34 | Найти домен | 2х+у=0 | ||
| 35 | Найти домен | у=5х+6 | ||
| 36 | Найти домен | у=х+3 | ||
| 37 | Решить с помощью матрицы путем исключения | у=4х+3х-2, у=6 | , | |
| 38 | Определить, является ли линейно зависимым | В={[[-10,2],[5,-2,5]]} | ||
| 39 | Добавить | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | ||
| 40 | Определить, является ли линейно зависимым | В={[[-1,2],[0,-2,5]]} | ||
| 41 | Умножение матриц | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1, 1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | ||
| 42 | у=5х | |||
| 43 | Найти домен | у=7х | ||
| 44 | Найти домен | у=-х-2 | ||
| 45 | Найти домен | у=х-2 | ||
| 46 | Найти домен | у=х-3 | ||
| 47 | Найти сокращенную форму эшелона строк | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | ||
| 48 | Записать как векторное равенство | х+у+г=2, 4х+5у+г=12, 2х=-4 | , , | |
| 49 | Найти определитель | [[0,-1,а],[3,-а,1],[1,-2,3]] | ||
| 50 | Найти домен | у=-х+2 | ||
| 51 | Найдите определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | ||
| 52 | Найти определитель | [[7,5,0],[4,5,8],[0,-1,5]] | ||
| 53 | Найдите обратное | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | ||
| 54 | Найдите обратное | [[1,2,3],[2,5,7],[3,7,9]] | ||
| 55 | Найти сокращенную форму Echelon Row | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | ||
| Найти сокращенную форму эшелона строк | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | |||
| 57 | Найти сокращенную форму эшелона строк | [[1,2,3],[4,5,6],[7,8,9]] | ||
| 58 | Найти сокращенную форму эшелона строк | [[7,8]] | ||
| 59 | Найти домен | 2х+у=1 | ||
| 60 | Записать как векторное равенство | 2х+у=-2, х+2у=2 | , | |
| 61 | Найти домен | х-2у=4 | ||
| 62 | Найти домен | х-у=-1 | ||
| 63 | Найти домен | х+у=5 | ||
| 64 | Найти домен | х=-3у-8 | ||
| 65 | Найти домен | х=-2у-8 | ||
| 66 | Найти домен | х+у=6 | ||
| 67 | Найти домен | х+у=4 | ||
| 68 | Найти домен | х+2у=4 | ||
| 69 | Найти домен | х+у | ||
| 70 | Найти домен | у=7х+9 | ||
| 71 | Найти домен | у=1/2x-5 | ||
| 72 | Найти домен | у=1/2х+2 | ||
| 73 | Найти домен | у=1/2х+3 | ||
| 74 | Найти домен | х-у=-3 | ||
| 75 | Найти домен | х-у=4 | ||
| 76 | Найти домен | г=-2x | ||
| 77 | Найти домен | у=-2х+1 | 92 | |
| 80 | Найти домен | у=2х-6 | ||
| 81 | Найти домен | у=-2x-3 | ||
| 82 | Найти домен | у=3х-8 | ||
| 83 | Найти домен | у=3х | ||
| 84 | Найти домен | у=-3х+1 | ||
| 85 | Найти домен | у=4х+3 | ||
| 86 | Найти домен | у=3х-4 | ||
| 87 | Найти домен | у=4х-2 | ||
| 88 | Найти домен | у=-6х | ||
| 89 | Найти домен | у=х-4 | 94||
| 91 | Найти домен | с=5/9*(ф-32) | ||
| 92 | Найти домен | ф=9/5с+32 | ||
| 93 | Оценка | квадратный корень из 4 | ||
| 94 | Найти сокращенную форму эшелона строк | [[-6,7],[2,6],[-4,1]] | ||
| 95 | Найдите собственные значения | [[2,1],[3,2]] | ||
| 96 | Найдите собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | ||
| 97 | Найдите силовой набор | А=(2,3,4,5) | ||
| 98 | Найти мощность | (2,1) | ||
| 99 | Решение с использованием обратной матрицы | -3x-4y=2 , 8y=-6x-4 | , | |
| 100 | Решение с использованием обратной матрицы | 2x-5y=4 , 3x-2y=-5 | , |
Калькулятор линейных комбинаций | Шаги
Создано Анной Щепанек, доктором философии
Рецензировано Домиником Черниа, доктором философии и Джеком Боуотером
Последнее обновление: 15 февраля 2022 г.
- Что такое система линейных уравнений?
- Что такое метод линейной комбинации?
- Как пользоваться этим калькулятором линейных комбинаций?
- Как использовать метод линейной комбинации?
- Примеры метода линейной комбинации
Наш калькулятор линейной комбинации находится здесь всякий раз, когда вам нужно решить систему уравнений, используя метод линейной комбинации (также известный как метод исключения). Если вы хотите узнать, что такое метод линейной комбинации или как использовать метод линейной комбинации, ознакомьтесь со статьей ниже.
Мы объясняем, что означает комбинирование линейных уравнений и как использовать метод линейного комбинирования для решения систем линейных уравнений. Самое главное, мы покажем вам несколько очень подробных пошаговых примеров систем, решенных методом линейной комбинации.
Что такое система линейных уравнений?
Чтобы уравнение было линейным , все его переменные должны быть в первой степени: их нельзя возводить в квадрат/куб, ни под корнем, ни помещать в знаменатель. Если некоторые числа удовлетворяют сразу нескольким линейным уравнениям, мы говорим, что эти числа являются решением система тех линейных уравнений .
Если некоторые числа удовлетворяют сразу нескольким линейным уравнениям, мы говорим, что эти числа являются решением система тех линейных уравнений .
В школе чаще всего встречаются системы двух линейных уравнений с двумя переменными . В целом, такая система принимает форму:
A 1 x + B 1 Y = C 1
A 2 X + B 2 y = C
2 9. где:
-
x и y - переменные; -
а 1 , б 1 , c 1 — коэффициенты первого уравнения; и -
a 2 , b 2 , c 2 — коэффициенты второго уравнения.
Что такое метод линейной комбинации?
Линейная комбинация уравнений — это метод решения систем линейных уравнений . Ключевая идея состоит в том, чтобы объединить уравнения в систему меньшего количества и более простых уравнений . Если мы имеем дело с двумя линейными уравнениями с двумя переменными, мы хотим объединить эти уравнения в одно уравнение с одной переменной.
Ключевая идея состоит в том, чтобы объединить уравнения в систему меньшего количества и более простых уравнений . Если мы имеем дело с двумя линейными уравнениями с двумя переменными, мы хотим объединить эти уравнения в одно уравнение с одной переменной.
Под объединением линейных уравнений мы подразумеваем умножение одного или обоих уравнений на подходящие числа и последующее сложение уравнений вместе. Множители должны допускать операцию сложения, чтобы одна из переменных обращалась в нуль. В итоге мы получим одно уравнение с одной переменной, которое легко решим. Как только мы решили это уравнение, мы подставляем найденное значение в одно из исходных уравнений. Это приводит к другому уравнению с одной переменной , которую мы быстро решаем. Таким образом, мы решили систему с помощью линейной комбинации!
Существуют ли другие методы решения систем линейных уравнений ? Конечно! Вы наверняка слышали о методе подстановки. Существует также метод исключения Гаусса и правило Крамера.
Существует также метод исключения Гаусса и правило Крамера.
Как пользоваться этим калькулятором линейных комбинаций?
Если вы хотите быстро решить систему уравнений с помощью линейной комбинации, наш инструмент — лучший выбор! Чтобы использовать его, выполните следующие действия:
- Сообщите нам коэффициенты вашей системы : введите их в соответствующие поля.
- Наш калькулятор линейных комбинаций решает систему методом линейных комбинаций ...
- ...и показывает и объясняет все промежуточных шагов !
- Перейдите в расширенный режим
калькулятора линейных комбинаций, если вы хотите вычислить решение с большей точностью (с большим числом цифр). По умолчанию наш калькулятор линейных комбинаций использует шесть цифр.
Как использовать метод линейной комбинации?
For the system of equations:
a 1 x + b 1 y = c 1
a 2 x + b 2 y = c 2
мы всегда можем использовать наименьшее общее кратное 1 и 2 . А именно, положим:
А именно, положим:
m 1 := LCM(a 1 , a 2 ) / a 1
m 2 := LCM(a 1 , a 2 ) / a 2
and multiply the first equation by m 1 а второе уравнение на -m 2 . Это приводит к следующей системе:
НОК(a 1 , a 2 )x + [LCM(a 1 , a 2 )b 1 /a 1CM ( 1 , 2 ) C 1 /A 1
-LCM (A 1 , A 2 ) X - [LCM (A 1 , A 2 979). 2 ]y = -LCM(a 1 , a 2 )c 2 /a 2
Мы создали противоположных коэффициентов для переменной x6 ! Все, что нам нужно сделать, это сложить эти уравнения вместе: мы получим уравнение только с переменной y .
В некоторых конкретных ситуациях этот подход LCM сводится к элементарным операциям:
Когда коэффициенты одной переменной равны напротив чисел , оба множителя равны 1 .
Когда коэффициенты одной переменной равны, один множитель равен 1 , а другой -1 .
Иногда может случиться так, что вы исключите обе переменные сразу. Прежде всего, не паникуйте. Вы пришли к утверждению о числах. В зависимости от того, верно ли полученное вами утверждение, например:
0 = 0 или 7 = 7 ,
или ложь, например,:
0 = 1 или 5 = 7 ,
. Нарисуйте выводы около системы :
. Около системы :
. Если утверждение неверно, то система не имеет решения .
Если последнее утверждение верно, то система имеет бесконечно много решений .
Примеры метода линейной комбинации
Ух ты, мы многое узнали о методе линейной комбинации! Пришло время решить несколько систем линейных уравнений с помощью линейных комбинаций.
Рассмотрим систему уравнений:
х - 4г = 1
-2x + 4y = 2
и решить его с помощью линейной комбинации.
Сложите два уравнения вместе:
-х = 3
Решить для x :
х = -3
Подставляем x = -3 в первое уравнение:
-3 - 4 года = 1
Найти y :
-4г = 4
г = -1
Решение: х = -3, у = -1
Решите, используя линейную комбинацию:
2х + 3у = 3
2х - у = -3
Сначала умножьте первое уравнение на -1 :
-2x - 3y = -3
2х - у = -3
Сложите уравнения, что приведет к удалению x :
-4г = -6
Найти y :
г = 1,5
Подставляем y = 1,5 во второе уравнение:
2x - 1,5 = -3
Решить для x :
2x = -1,5
х = -0,75
Решение: х = -1,5, у = -0,75
Решите систему с помощью линейной комбинации:
3x - 7y = 1
4x + 4y = -2
Используйте подход LCM: найдите вычисление наименьшей общей кратности 3 и 4 :
НОК(3, 4) = 12 .

 Ключевая идея состоит в том, чтобы объединить уравнения в систему меньшего количества и более простых уравнений . Если мы имеем дело с двумя линейными уравнениями с двумя переменными, мы хотим объединить эти уравнения в одно уравнение с одной переменной.
Ключевая идея состоит в том, чтобы объединить уравнения в систему меньшего количества и более простых уравнений . Если мы имеем дело с двумя линейными уравнениями с двумя переменными, мы хотим объединить эти уравнения в одно уравнение с одной переменной. Существует также метод исключения Гаусса и правило Крамера.
Существует также метод исключения Гаусса и правило Крамера.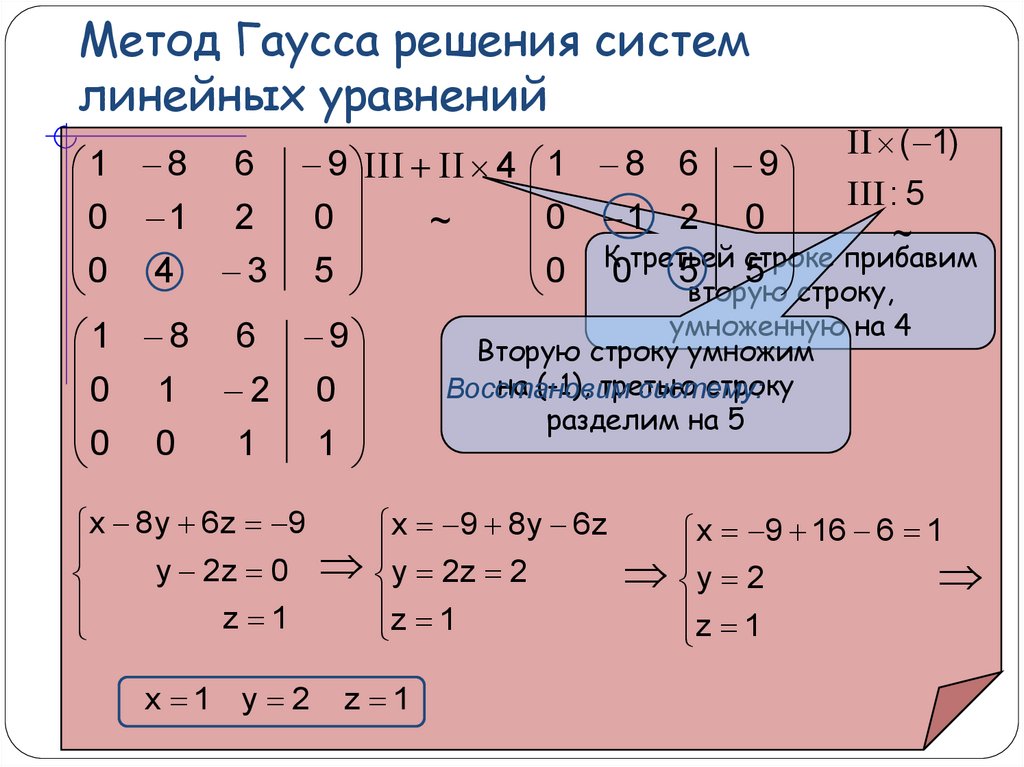 А именно, положим:
А именно, положим: