Решить онлайн уравнение методом крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решить уравнение по крамеру. Решение линейных уравнений методом крамера по математике

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется

определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы.

За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .

Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.

Ответ: решений нет

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.

Навигация по странице.

Метод Крамера – вывод формул.

Пусть нам требуется решить систему линейных уравнений вида

Где x 1 , x 2 , …, x n – неизвестные переменные, a i j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b 1 , b 2 , …, b n – свободные члены. Решением СЛАУ называется такой набор значений x 1 , x 2 , …, x n при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B , где – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, – матрица – столбец свободных членов, а – матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x 1 , x 2 , …, x n , матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

Итак, приступим к нахождению неизвестной переменной x 1 . Для этого умножим обе части первого уравнения системы на А 1 1 , обе части второго уравнения – на А 2 1 , и так далее, обе части n-ого уравнения – на А n 1 (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А ):

Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x 1 , x 2 , …, x n , и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем

и предыдущее равенство примет вид

откуда

Аналогично находим x 2 . Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А :

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x 1 , x 2 , …, x n и применяем свойства определителя:

Откуда
.

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить

То получаем формулы для нахождения неизвестных переменных по методу Крамера .

Замечание.

Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .

Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера .

Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.

Пример.

Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель по формуле :

Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .

Вычисляем эти определители:

Находим неизвестные переменные x 1 и x 2 по формулам :

Выполним проверку. Подставим полученные значения x 1 и x 2 в исходную систему уравнений:

Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.

Пример.

Найдите решение системы линейных уравнений методом Крамера .

Решение.

Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле

Имеем

Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :

Таким образом,

Ответ:

Обозначения неизвестных переменных в уравнениях системы могут отличаться от x 1 , x 2 , …, x n . Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.

Пример.

Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .

Решение.

В данном примере неизвестные переменные имеют другое обозначение (x , y и z вместо x 1 , x 2 и x 3 ). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:

Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:

Осталось найти неизвестные переменные по формулам :

Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите раздел ):

В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.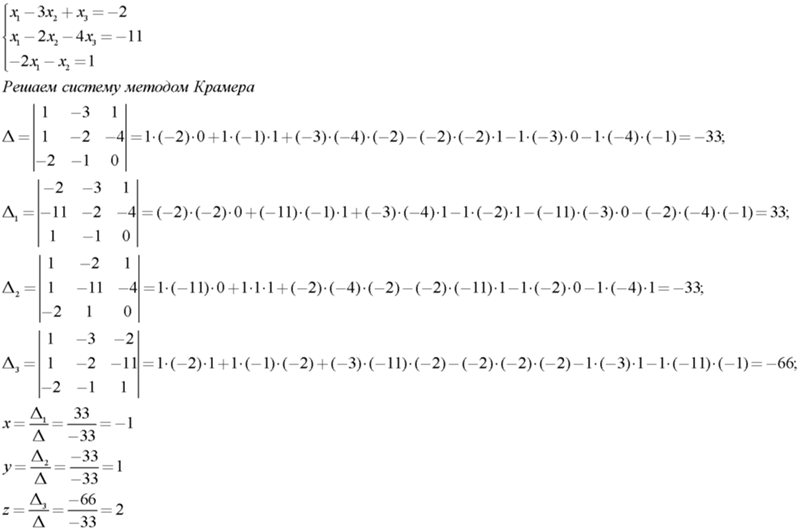

Ответ:

x = 0, y = -2, z = 3 .

Пример.

Решите методом Крамера систему линейных уравнений , где a и b – некоторые действительные числа.

Решение.

Ответ:

Пример.

Найдите решение системы уравнений методом Крамера, – некоторое действительное число.

Решение.

Вычислим определитель основной матрицы системы: . выражения есть интервал , поэтому при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем и :

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1. 5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1. 16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1. 21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21 -26 -13 -37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Метод Крамера – решение систем линейных уравнений, примеры – смотреть онлайн видео урок бесплатно! Автор: alWEBra – Линейная алгебра

В этом видео рассказывается о методе Крамера – решение систем линейных уравнений, примеры. Это один из методов решения систем алгебраических уравнений, его еще называют методом определителей. Метод Крамера достаточно прост в использовании и позволяет быстро найти искомое решение, хотя и имеет ряд недостатков. Стоит отметить, что система уравнений называется линейной в том случае, если неизвестные между собой не перемножаются и не возводятся в степень. Именно для решения таких систем можно использовать метод Крамера. Решить систему – это значит найти все такие значения неизвестных, которые обращают каждое уравнение системы в тождество. Для решения системы линейных уравнений методом Крамера, сначала вычисляют определитель матрицы, составленных из коэффициентов при неизвестных. Если этот определитель не равен нулю, то система имеет единственное решение и метод крамера можно использовать, а если он равен нулю, то для решения данной системы уравнений необходимо использовать другой метод, например метод Гаусса. В этом уроке будет изучены все формулы метода Крамера и рассмотрен пример решения системы уравнения. Видео урок «Метод Крамера – решение систем линейных уравнений, примеры» вы можете смотреть онлайн абсолютно бесплатно в любое удобное время. Успехов!

Автор: alWEBra
Длительность: 4:19
Дата: 20.11.2013
Смотрели: 537
Рейтинг: 5. 0/1

Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.

5 метод крамера решения систем линейных уравнений. Правило Крамера

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Навигация по странице.

Метод Крамера – вывод формул.

Пусть нам требуется решить систему линейных уравнений вида

Метод Крамера основывается на двух свойствах определителя матрицы:

Откуда
.

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить

То получаем формулы для нахождения неизвестных переменных по методу Крамера .

Замечание.

Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера .

Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.

Пример.

Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель по формуле :

Вычисляем эти определители:

Находим неизвестные переменные x 1 и x 2 по формулам :

Выполним проверку. Подставим полученные значения x 1 и x 2 в исходную систему уравнений:

Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

Пример.

Найдите решение системы линейных уравнений методом Крамера .

Решение.

Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле

Имеем

Таким образом,

Ответ:

Пример.

Решение.

Осталось найти неизвестные переменные по формулам :

В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.

Ответ:

x = 0, y = -2, z = 3 .

Пример.

Решите методом Крамера систему линейных уравнений , где a и b – некоторые действительные числа.

Решение.

Ответ:

Пример.

Найдите решение системы уравнений методом Крамера, – некоторое действительное число.

Решение.

. (1.6)

(j = 1, 2, …, n ). (1.7)

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

, (1.13)

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

1) Найдем алгебраические дополнения A ij :

где

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

, откуда

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Пример 1.11.

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Пусть дана система линейных форм (уравнений):

Мы получим следующую систему:

. (1.21)

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

После приведения подобных членов, получим:

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

-21 -26 -13 -37

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

Метод Крамера: что это такое, пример решения и как вычислить определитель

Метод Крамера — это метод решения систем линейных алгебраических уравнений (СЛАУ) с одинаковым количеством уравнений и переменных.

Метод Крамера нельзя использовать, когда определитель основной матрицы равен 0 (в этом случае применяется метод Гаусса).

Как решить систему линейных уравнений методом Крамера

Пример

Нужно решить систему линейных уравнений:

2x + 1y + 1z = 3

1x – 1y – 1z = 0

1x + 2y + 1z = 0

1. Нужно найти главный определитель

2. Теперь заменяем по очереди каждый из столбцов на столбец ответов:

В первую колонку, для x и вычисляем определитель:

Во вторую колонку, для y и вычисляем определитель:

В третью колонку, для z и вычисляем определитель:

Последний шаг: нужно разделить каждый на главный определитель.

То есть:

x = Δx ÷ Δ = 3 ÷ 3 = 1

y = Δy ÷ Δ = (-6) ÷ 3 = -2

z = Δz ÷ Δ = 9 ÷ 3 = 3

Как вычислить определитель?

Матрицы 2 × 2

Матрицы 3 × 3

Существует несколько способов вычисления определителя матрицы 3 × 3. Этот способ, под названием правило Саррюса, выглядит наиболее простым.

Нужно найти определитель матрицы 3 × 3

1. Дополнить матрицу первыми двумя столбцами (т. е. скопировать первые 2 столбца и дополнить её):

2. Умножить и сложить по диагоналям вниз:

3. Умножить и сложить по диагоналям вверх:

4. Из первой суммы (зелёной, по диагонали вниз) вычесть вторую (красную, по диагонали вверх): 8 – 2 = 6, т. е. det (A) = 6.

Узнайте про Интегралы, Логические операции и Корреляции.

Дата обновления 24/07/2020.

Другие значения и понятия, которые могут вас заинтересовать

Правило крамера примеры решения. Правило Крамера

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

, (1.13)

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

1) Найдем алгебраические дополнения A ij :

где

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

, откуда

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

Пример 1.11.

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Пусть дана система линейных форм (уравнений):

Мы получим следующую систему:

. (1.21)

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

-21 -26 -13 -37

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Метод крамера описание метода. Линейные уравнения

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

решений систем линейных алгебраических уравнений (СЛАУ)

2. Решение систем уравнений матричным методом (с использованием обратной матрицы).
3. Метод Гаусса для решения систем уравнений.

Метод Крамера.

Метод Крамера используется для решения систем линейных алгебраических уравнений ( SLAU ).

Формулы для примера системы двух уравнений с двумя переменными.
Дано: Решите систему методом Крамера

Переменные NS и в .
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы Вычисление определителей. :

Применяем формулы Крамера и находим значения переменных:
и.
Пример 1:
Решите систему уравнений:

относительно переменных NS и в .
Решение:

Замените первый столбец в этом определителе столбцом коэффициентов из правой части системы и найдите его значение:

Проделаем аналогичное действие, заменив второй столбец в первом определителе:

Применимые формулы Крамера и найдем значения переменных:
и.
Ответ:
Комментарий: Этот метод можно использовать для решения систем более высоких измерений.

Комментарий: Если оказывается, что и на ноль делить нельзя, то говорят, что в системе нет единого решения. В этом случае у системы либо бесконечно много решений, либо их нет вовсе.

Пример 2 (бесконечное количество решений):

Решите систему уравнений:

относительно переменных NS и в .
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы:

Решение систем методом подстановки.

Первым из уравнений системы является равенство, которое верно для любых значений переменных (поскольку 4 всегда равно 4). Итак, осталось только одно уравнение. Это уравнение взаимосвязи между переменными.
Получается, что решением системы является любая пара значений переменных, связанных равенством.
Общее решение будет записано так:
Частные решения могут быть определены путем выбора произвольного значения y и вычисления x с использованием этого равенства связи.

и т. Д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместима):

Решите систему уравнений:

Решение:
Найдем определитель матрицы, составленной из коэффициентов системы:

Формулы Крамера применить нельзя.Решим эту систему методом подстановки

Второе уравнение системы – это равенство, что неверно ни при каких значениях переменных (разумеется, поскольку -15 не равно 2). Если одно из уравнений системы не выполняется ни при каких значениях переменных, то вся система не имеет решений.
Ответ: решений нет

В первой части мы рассмотрели небольшой теоретический материал, метод подстановки, а также метод почленного сложения для уравнений системы.Рекомендую всем, кто зашел на сайт через эту страницу, прочитать первую часть. Возможно, некоторые посетители сочтут материал слишком простым, но в процессе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А теперь разберем правило Крамера, а также решение системы линейных уравнений с использованием обратной матрицы (матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут узнать, как решать системы указанными выше способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшая система решается школьным методом, заочно!

Дело в том, что даже иногда, но есть такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложных случаев – систем трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом этапе вычисляем определитель, он называется главным определителем системы .

Метод Гаусса.

Если, то система имеет единственное решение, и чтобы найти корни, мы должны вычислить еще два определителя:
и

На практике вышеуказанные детерминанты также можно обозначать латинскими буквами.

Находим корни уравнения по формулам:
,

Пример 7

Решите систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно большие, с правой стороны стоят десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, я взял эту систему из эконометрической задачи.

Как решить такую систему? Вы можете попробовать выразить одну переменную через другую, но в этом случае вы, вероятно, получите ужасные причудливые дроби, с которыми крайне неудобно работать, и дизайн решения будет выглядеть просто ужасно.Вы можете умножить второе уравнение на 6 и вычесть член за членом, но здесь будут отображаться те же дроби.

Что делать? В таких случаях на помощь приходят формулы Крамера.

;

Ответ :,

Оба корня имеют бесконечные хвосты и находятся приблизительно, что вполне приемлемо (и даже часто) для эконометрических задач.

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс.При использовании этого метода обязательный фрагментом задания будет следующий фрагмент: «Что означает, что в системе есть только одно решение» … В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Не лишним будет проверить, что удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В результате с небольшой ошибкой вы должны получить числа, которые находятся в нужных частях.

Пример 8

Ответ – представить в обычных неправильных дробях … Сделайте чек.

Это пример для самостоятельного решения (пример окончания и ответ в конце урока).

Теперь перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Найдите главный определитель системы:

Если, то система имеет бесконечно много решений или противоречива (не имеет решений).В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.

Если, то система имеет единственное решение, и чтобы найти корни, мы должны вычислить еще три определителя:
“

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально не отличается от случая «два на два», столбец свободных членов последовательно «ходит» слева направо по столбцам главного определителя.

Пример 9

Решите систему, используя формулы Крамера.

Решение : Давайте решим систему, используя формулы Крамера.

, что означает, что система имеет уникальное решение.

Ответ :.

Собственно, и здесь комментировать особо нечего, учитывая, что решение принимается по готовым формулам.Но следует отметить несколько моментов.

Бывает, что в результате вычислений получаются “плохие” несократимые дроби, например :.
Рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, сделаем так:

1) Возможна ошибка в расчетах. Как только вы столкнулись с «плохой» дробью, вам следует немедленно проверить , правильно ли переписано условие … Если условие переписано без ошибок, то необходимо пересчитать определители, используя разложение по другой строке ( столбец).

2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задачи была опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решаем задачу до конца, а потом обязательно проверяем и оформляем на чистую копию после решения. Конечно, проверка дробного ответа – занятие неприятное, но это будет обезоруживающий аргумент для учителя, который, ну, очень любит ставить минус любому лайку бяки. Как работать с дробями, подробно описано в ответе к примеру 8.

Если под рукой есть компьютер, то для его проверки воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение матричного метода системы.

Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении нет переменной, во втором нет переменной.В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, детерминанты с нулями рационально открывать по той строке (столбцу), в которой стоит ноль, так как вычислений гораздо меньше.

Пример 10

Решите систему, используя формулы Крамера.

Это пример самостоятельного решения (образец отделки и ответ в конце урока).

Для случая системы из 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно найти в уроке Determinant Properties. Понижение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задание уже довольно напоминает сапог профессора на груди удачливого ученика.

Решение системы с использованием обратной матрицы

Метод обратной матрицы – это, по сути, частный случай матричного уравнения (см. Пример № 3 указанного урока).

Для изучения этого раздела вы должны уметь расширять определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут предоставлены по пути.

Пример 11

Решите систему матричным методом

Решение : Запишем систему в матричной форме:
, где

Обратите внимание на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю, все понимают.Единственный комментарий: если бы в уравнениях отсутствовали какие-то переменные, то в соответствующие места в матрице пришлось бы поставить нули.

Находим обратную матрицу по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы.

Сначала разберемся с определителем:

Здесь квалификатор раскрывается на первой строке.

Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно.В этом случае система решается методом исключения неизвестных (метод Гаусса).

Теперь нам нужно вычислить 9 миноров и записать их в матрицу миноров

Артикул: Полезно знать значение двойных индексов в линейной алгебре. Первая цифра – это номер строки, в которой расположен этот элемент. Вторая цифра – это номер столбца, в котором расположен этот элемент:

То есть двойной нижний индекс указывает, что элемент находится в первой строке, третьем столбце, и, например, элемент находится в строке 3, столбце 2

С количеством уравнений, равным количеству неизвестных с главным определителем матрицы, который не равен нулю, коэффициенты системы (для таких уравнений есть решение и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы отличен от нуля, это означает, что система непротиворечива и имеет одно решение, и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в которой вместо i -й столбец содержит столбец правых частей.

Когда определитель системы равен нулю, это означает, что система может стать совместной или несовместимой.

Этот метод обычно используется для небольших систем с большими вычислениями и когда необходимо определить одно из неизвестных. Сложность метода состоит в том, что необходимо вычислить множество детерминант.

Описание метода Крамера.

Имеется система уравнений:

Систему трех уравнений можно решить методом Крамера, который был рассмотрен выше для системы из двух уравнений.

Составим определитель из коэффициентов неизвестных:

Это будет системный идентификатор … Когда D ≠ 0 , значит система совместима. Теперь составим 3 дополнительных определителя:

Решаем систему формул Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Учитывая систему:

Решим его методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Поскольку Δ ≠ 0, следовательно, по теореме Крамера система непротиворечива и имеет одно решение.Вычисляем дополнительные детерминанты. Определитель Δ 1 получается из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же образом получим определитель Δ 2 из определителя матрицы системы, заменив второй столбец столбцом свободных коэффициентов:

Методы Kramer и Gauss – одни из самых популярных методов решения SLAU … Кроме того, в некоторых случаях желательно использовать именно определенные методы … Сессия близка, и сейчас самое время пересмотреть или освоить их с нуля. Сегодня мы имеем дело с решением по методу Крамера. Ведь решение системы линейных уравнений методом Крамера – очень полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – это система уравнений вида:

Набор значений x , при котором уравнения системы превращаются в тождества, называется решением системы, a и b – реальные коэффициенты.Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразив одну переменную через другую. Но переменных (x) в СЛАУ может быть намного больше двух, и здесь нельзя делать простые школьные манипуляции. Что делать? Например, решайте СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестно.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, столбцы матриц неизвестных переменных и свободных членов.

Решение SLAE методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), система может быть решена методом Крамера.

По методу Крамера решение находится по формулам:

Здесь дельта – определитель основной матрицы, а дельта x n-й – определитель, полученный из определителя основной матрицы заменой n-го столбца на столбец свободных элементов.

В этом весь смысл метода Крамера. Подставляя значения, найденные по приведенным выше формулам x в желаемую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы вы быстрее уловили суть, мы приводим пример ниже. детальное решение СЛАУ по методу Крамера:

Даже если вы проиграете с первого раза, не расстраивайтесь! Немного потренировавшись, вы начнете переворачивать SLAU, как орехи. Тем более, что теперь совершенно не нужно копаться в тетради, решая громоздкие вычисления и выписывая стержень.Вы можете легко решить СЛАУ методом Крамера онлайн, только подставив коэффициенты в готовом виде. Попробовать решения онлайн-калькулятора по методу Крамера можно, например, на этом сайте.

И если система оказалась упорной и не сдается, вы всегда можете обратиться за помощью к нашим авторам, например, к. Если в системе не менее 100 неизвестных, мы обязательно решим правильно и в срок!

Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е.е. имеет вид

Такие системы линейных уравнений называются квадратичными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Обозначим его греческой буквой D. Таким образом,

. (1,6)

Если главным определителем является произвольный ( j -й) столбец, заменим его столбцом свободных членов системы (1.5), то мы можем получить еще n вспомогательных определителей:

( j = 1, 2,…, n ).(1,7)

Правило Крамера Решение квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:

(1,8)

Пример 1.5. Использование метода Крамера для решения системы уравнений

Вычислим главный определитель системы:

Поскольку D¹0, система имеет единственное решение, которое находится по формулам (1.8):

Таким образом,

Матричные операции

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Чтобы умножить матрицу на число, нужно умножить все ее элементы на это число. То есть

. (1,9)

Пример 1.6. .

Добавление матриц.

Эта операция вводится только для матриц одного порядка.

Чтобы сложить две матрицы, необходимо добавить соответствующие элементы другой матрицы к элементам одной матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если количество столбцов матрицы A совпадает с количеством строк матрицы V , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы A габаритами м ´ n на матрицу V габаритами n ´ k мы получим матрицу С размером м ´ k … Причем элементы матрицы СО вычисляются по формулам:

Задача 1.8. Найдите, если возможно, произведение матриц AB и BA :

Решение. 1) Чтобы найти работу AB , нужно строки матрицы A умножить на столбцы матрицы B :

2) Графическое изображение BA не существует, поскольку количество столбцов в матрице B не совпадает с количеством строк в матрице A .

Обратная матрица. Матричное решение систем линейных уравнений

Матрица A – 1 называется обратной квадратной матрицы A , если выполняется равенство:

, где через I обозначена единичная матрица того же порядка, что и матрица A :

Для того чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы ее определитель был ненулевым. Обратная матрица находится по формуле:

, (1.13)

, где A ij – алгебраические дополнения к элементам a ij матрицы A (обратите внимание, что алгебраические дополнения к строкам матрицы A, расположены в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Находим обратную матрицу по формуле (1.13), которая для случая n = 3 имеет вид:

Найти дет. A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Поскольку определитель исходной матрицы отличен от нуля, обратная матрица существует.

1) Найдите алгебраические дополнения A ij :

Для удобства поиска обратной матрицы мы поместили алгебраические добавления к строкам исходной матрицы в соответствующие столбцы.

Из полученных алгебраических дополнений составляем новую матрицу и делим ее на определитель det A … Таким образом, получаем обратную матрицу:

Квадратичные системы линейных уравнений с ненулевым главным определителем могут быть решены с помощью обратной матрицы. Для этого система (1.5) записывается в матричном виде:

где

Умножая обе части равенства (1.14) слева на A – 1, получаем решение системы:

, где

Таким образом, чтобы найти решение квадратной системы, нужно найти матрицу, обратную основной матрице системы, и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решите систему линейных уравнений

с использованием обратной матрицы.

Решение. Запишем систему в матричном виде :,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Поскольку основной определитель системы, то основная матрица системы A, имеет обратную матрицу A, -1. Чтобы найти обратную матрицу A -1, вычислим алгебраические дополнения ко всем элементам матрицы A :

Из полученных чисел составляем матрицу (причем алгебраические дополнения к строкам матрицы A записываем в соответствующие столбцы) и делим ее на определитель D.Таким образом, мы нашли обратную матрицу:

Находим решение системы по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обычных жордановых исключений

Пусть дана произвольная (не обязательно квадратичная) система линейных уравнений:

(1,16)

Требуется найти решение системы, т.е. набор переменных, удовлетворяющий всем равенствам системы (1.16). V система общего случая (1.16) может иметь не только одно решение, но и бесчисленное множество решений. У нее также может вообще не быть решений.

При решении таких задач применяется известный из школьного курса метод исключения неизвестных, который еще называют методом обычных исключений Джордана. Суть этого метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы.В результате получается система, которая содержит на одно уравнение и на одну переменную меньше, чем исходная система. Запоминается уравнение, из которого была выражена переменная.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестных некоторые уравнения могут превратиться в истинные тождества. Такие уравнения исключаются из системы, так как они выполняются при любых значениях переменных и, следовательно, не влияют на решение системы.Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может быть выполнено ни при каких значениях переменных (например), то мы заключаем, что система не имеет решения.

Если в процессе решения не возникло противоречивых уравнений, то одна из оставшихся в нем переменных находится из последнего уравнения. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются другие переменные, то они считаются параметрами, и переменная, выраженная через них, будет функцией этих параметров.Потом так называемый «реверс». Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запомненное уравнение, и находится третья переменная, и так далее до первого запомненного уравнения.

В результате получаем решение системы. Это решение будет уникальным, если найденные переменные будут числами. Если первая найденная переменная, а затем все остальные зависят от параметров, то система будет иметь бесконечное количество решений (каждому набору параметров соответствует новое решение).Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.

Пример 1.11.

Запомнив первое уравнение и сократив аналогичные члены во втором и третьем уравнениях, мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Вспомним второе уравнение, и из первого находим z :

Делая обратный ход, последовательно находим y и z … Для этого сначала подставляем в последнее запомненное уравнение, откуда находим y :

Затем подставляем в первое запомненное уравнение, откуда находим x :

Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Давайте вспомним первое уравнение

В этой системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получаем, что 14 = 17. Это равенство не выполняется ни при каких значениях переменных x , y и z … Следовательно, система (1.17) несовместима. , то есть не имеет решения.

Предлагаем читателям самостоятельно проверить, что основной детерминант исходной системы (1.17) равен нулю.

Рассмотрим систему, которая отличается от системы (1.17) только одним свободным членом.

Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:

. (1.18)

Решение. Как и раньше, мы выражаем из первого уравнения переменную x и подставляем ее во второе и третье уравнения:

Давайте вспомним первое уравнение и дадим аналогичные члены во втором и третьем уравнениях.Заходим в систему:

Выражая y из первого уравнения и подставляя его во второе уравнение, получаем тождество 14 = 14, которое не влияет на решение системы, а значит, может быть исключено из системы.

В последнем запомненном равенстве переменная z будет считаться параметром. Мы верим. Тогда

Подставьте y и z в первое запомненное равенство и найдите x :

Таким образом, система (1.18) имеет бесконечное множество решений, и любое решение можно найти по формулам (1.19), выбрав произвольное значение параметра t :

(1.19)
Итак, решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. Д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений кажется громоздким.Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в общем виде и сформулировать решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где xj – независимые (искомые) переменные, a ij – постоянные коэффициенты
( i = 1, 2,…, m ; j = 1, 2,…, № ).Правая часть системы y i ( i = 1, 2,…, m ) может быть как переменными (зависимыми), так и константами. Требуется найти решения этой системы, исключив неизвестные.

Рассмотрим следующую операцию, в дальнейшем называемую «один шаг обычных исключений Джордана». Из произвольного ( r -го) равенства выражаем произвольную переменную ( x s ) и подставляем во все остальные равенства. Конечно, это возможно только при и 0.Коэффициент и RS называют разрешающим (иногда руководящим или основным) элементом.

Получим такую систему:

. (1,21)

Из s -го равенства системы (1.21) впоследствии находим переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем исключается из системы. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты получившейся системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть так:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1,23)
Теперь вычислим новые коэффициенты b ij ( i ¹ r ) по произвольному уравнению… Для этого подставим переменную, выраженную в (1.22) x s v i -ое уравнение системы (1.20):

Приведя аналогичные термины, получаем:

(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обычных жордановых исключений формализуется в виде таблиц (матриц).Эти таблицы называются «жордановы».

Таким образом, задача (1.20) связана со следующей таблицей Иордании:

Таблица 1.1

	x 1	x 2	…	x	…	х	…	x n
y 1 =	а 11	а 12		a 1 j		а 1 с		a 1 n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		а это		а дюйм
………………………………………………………………… ..
г =	и 1	и 2		RJ		а RS		а рн
………………………………………………………………….
да n =	а м 1	а м 2		a mj		а мс		а мин

Jordan Таблица 1.1 содержит левый столбец заголовка, в котором записаны правые части системы (1.20), и верхний ряд заголовка, в котором записаны независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если мы умножим матрицу A на матрицу, состоящую из элементов верхней строки заголовка, то вы получите матрицу, состоящую из элементов левого столбца заголовка. То есть, по сути, жорданова таблица – это матричная запись системы линейных уравнений:. Система (1.21) в этом случае соответствует следующей жордановой таблице:

Таблица 1.2

	x 1	x 2	…	x	…	г	…	x n
y 1 =	б 11	б 12		b 1 j		b 1 с		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		б в
………………………………………………………………… ..
x s =	b r 1	b r 2		b rj		BS		млрд рн
………………………………………………………………….
да n =	мм 1	мм 2		b mj		б мс		млрд мин

Разрешающий элемент a RS выделим жирным шрифтом. Напомним, что для того, чтобы имел место один шаг жордановых исключений, разрешающий элемент должен быть ненулевым. Строка таблицы, содержащая разрешающий элемент, называется разрешающей строкой.Столбец, содержащий разрешающий элемент, называется разрешающим столбцом. При переходе от этой таблицы к следующей таблице одна переменная ( xs ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( yr ) из левый верхний столбец таблицы перемещается в верхний верхний ряд.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), что следует из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным:

2. Остальные элементы разрешительной линии разделяются разрешающим элементом и меняют знак на противоположный:

3. Остальные элементы разрешающей колонки делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последнюю формулу легко запомнить, если вы заметите, что элементы, составляющие дробь, находятся на пересечении i -й и r -ой строк и j -го и s -го столбца (разрешающая строка, разрешающий столбец, а также строка и столбец, на пересечении которых находится пересчитываемый элемент).Точнее, при запоминании формулы может использоваться следующая диаграмма:

-21 -26 -13 -37

Принимая первый шаг исключения Jordan, любой элемент таблицы 1.3, расположенный в столбцах x 1,…, x 5 (все указанные элементы не равны нулю). Вы должны не только выбирать разрешающий элемент в последнем столбце, потому что вам нужно найти независимые переменные x 1,…, x 5.Выберем, например, коэффициент 1 с переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент выделен жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней строки заголовка заменяется константой 0 левого столбца (третья строка). В этом случае переменная x 3 выражается через остальные переменные.

Строка x 3 (Таблица 1.4) после запоминания может быть исключена из Таблицы 1.4. Третий столбец с нулем в верхней строке заголовка также исключен из таблицы 1.4. Дело в том, что независимо от коэффициентов этого столбца b i 3 все соответствующие члены каждого уравнения 0 b i 3 системы будут равны нулю. Поэтому эти коэффициенты можно не указывать. Исключая одну переменную x 3 и запоминая одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с перечеркнутой линией x 3). Выбор по таблице 1.4 как разрешающий элемент b 14 = -5, перейти к таблице 1.5. В таблице 1.5 мы запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2 x 5.

Последовательно подставляя уже найденные переменные в сохраненные строки, находим оставшиеся переменные:

Таким образом, в системе есть бесчисленное множество решений. Переменной x 5 можно присвоить произвольные значения.Эта переменная действует как параметр x 5 = t. Мы доказали совместимость системы и нашли ее общее решение:

x 1 = – 3 + 2 т

x 2 = – 1-3 т

x 3 = – 2 + 4 т . (1,27)
x 4 = 4 + 5 т

x 5 = т

Придавая параметру t различные значения, мы получаем бесчисленное множество решений для исходной системы.Так, например, решение системы – это следующий набор переменных (- 3; – 1; – 2; 4; 0).

Решатель линейных уравнений

Система m линейных уравнений от n неизвестных имеет решение тогда и только тогда, когда ранг r расширенной матрицы равен рангу матрицы коэффициентов.
Если две матрицы имеют одинаковый ранг r и r = n, решение уникально.
Если две матрицы имеют одинаковый ранг r и r

Общий вид линейной системы уравнений можно представить формулой: A x _i = B _i
Матрица коэффициентов	– это матрица, которая содержит коэффициенты переменных (матрица в формуле).
Постоянная матрица	– это массив значений свободных столбцов (векторный массив B _i).
Расширенная матрица	– это комбинированная матрица, которая содержит рядом матрицу коэффициентов и матрицу констант (матрица AB _i).

Другой способ решения линейной системы уравнений – это правило Крамера, которое включает только детерминанты. Рассмотрим систему уравнений:

Решение дается уравнением:

D _i	– это определитель, установленный путем замены i-го столбца столбцом свободных значений b _i
D	– определитель матрицы коэффициентов.

Поскольку r n = 4 2 = 2, две переменные зависят от двух других переменных, и мы должны выбрать определенные значения для двух переменных
например: w = a и y = b (a, b – любое число), тогда:

z = 1 + 2a

x = 4 2b + a

Вектор пространства решений равен (4 + a 2b, b, 1 + 2a, a)
например, если мы выберем: a = 1 b = 1, то решение будет:
(7, 1, 3, 1).

Используйте правило Крамера, чтобы решить: 3x-5y = 21 и 4x + 2y = 2

(10 баллов) Решите следующую систему, используя либо правило Крамера, либо матрицы (3x – 2y + …

(10 баллов) Решите следующую систему, используя либо правило Крамера, либо матрицы (3x – 2y + 5z = -5 x – y + 3z = -4 4x + y + z = 5

O СИСТЕМЫ УРАВНЕНИЙ И МАТРИЦ Использование правила Крамера для решения 3x … Español Используйте …

O СИСТЕМЫ УРАВНЕНИЙ И МАТРИЦ Использование правила Крамера для решения 3x… Español Используйте правило Крамера, чтобы найти значение y, удовлетворяющее уравнениям. 5y + z = 0 3x + 5y + 2z = -5 – 5x + y-2z = 0 Определитель матрицы коэффициентов равен D = Aa y D

Использовать Правило Крамера для решения системы. Используйте правило Крамера, чтобы решить систему. 9x + …

Использовать Правило Крамера для решения системы. Используйте правило Крамера, чтобы решить систему. 9x + 5y 4x – 4y = = -11-36 <- и y = +

3. Используйте правило Крамера для решения следующих систем уравнений: (a) 8×1 – x2 = 16…

3. Используйте правило Крамера для решения следующих систем уравнений: (a) 8×1 – x2 = 16 (©) 4x + 3y – 2z = 1 2×2 + 5×3 = 5 x + 2y = 6 2X1 + 3×3 = 7 3x + Z = 4 (6) – X1 + 3×2 + 2×3 = 24 (d) -x + y + 7 = a X, + x3 = 6 x-y + z = b Sx2 – X + Y-7 = C X3 = 8

Борюсь с этими двумя. Помоги мне, пожалуйста Используйте правило Крамера, чтобы решить (если возможно) систему …

Борюсь с этими двумя. Помоги мне, пожалуйста Используйте правило Крамера для решения (если возможно) системы линейных уравнений.(Если невозможно, введите НЕВОЗМОЖНО.) 4x – 2y + 32 = -7 2x + 2y + 5z – 13 8x – 5y – 22 = 1 (x, y, z) = (НЕВОЗМОЖНО *) Нужна помощь? Прочтите это Поговорите с преподавателем Отправить ответ Практика Другая версия 12. -14 баллов LarlinAlg8 3.4.027. Мои заметки Попросите учителя Воспользуйтесь правилом Крамера, чтобы решить …

Воспользуйтесь правилом Крамера, чтобы решить систему 2y + z = 0 2 + y – 26 5y +, 32 …

Используйте правило Крамера для решения системы \ (2 x-y + z = 0 \) \ (x + yz = 6 \) \ (4 x-5 y + 3 z = 28 \). Любой другой метод не будет оцениваться ! Обосновать ответ!

Решить, используя правило Крамера X – 2y + z = 7 2x + y – z = 0 3x + 2y -…

Решить, используя правило Крамера X – 2y + z = 7 2x + y – z = 0 3x + 2y – 2z = -2 O (1, -2,0) O (2, -1,3) O (1, -1 , 1) Нет решения

Правило Крамера: 5. Используйте правило Крамера, чтобы найти x, y и z для следующей системы …

Правило Крамера: 5. Используйте правило Крамера, чтобы найти x, y и z для следующей системы уравнений. Х 2 7x + 2y – z = -1។ 6x + 5y + z = 16 -5x – 4y + 3z = -5 2: 2 a. Сначала напишите матрицу коэффициентов для указанной выше системы. Назовите это матрицей D. 7 2 5 L-8-4 3 1 14] = 0 b.Найдите определитель матрицы коэффициентов (det (D)).

8. (8 баллов) Используя правило Крамера, решите 4x – 2y = 10 3c – 5y11 относительно …

8. (8 баллов) Используя правило Крамера, решите 4x – 2y = 10 3c – 5y11 только для y.

2x y5z 2 5x y 4x y 2z = – Используйте правило Крамера, чтобы решить систему уравнений справа. Если D 0, используйте другой метод …

2x y5z 2 5x y 4x y 2z = – Используйте правило Крамера, чтобы решить систему уравнений справа.Если D 0, воспользуйтесь другим методом для завершения решения. Z = -4 L 8 Запишите дроби, используя правило Крамера в виде определителей. det det det det det y = Z = X = det 2x y5z 2 5x y 4x y 2z = – Используйте правило Крамера, чтобы решить систему уравнений справа. Если D 0, используйте другой …

Решения

с использованием детерминантов с двумя переменными

Линейные уравнения: решения с использованием определителей с двумя переменными

Квадратный массив чисел или переменных, заключенный между вертикальными линиями, называется определителем . Определитель отличается от матрицы тем, что определитель имеет числовое значение, а матрица – нет. Следующий определитель имеет две строки и два столбца.

Значение этого детерминанта определяется путем нахождения разницы между продуктом по диагонали вниз и продуктом по диагонали вверх:

Пример 1

Оцените следующий определяющий фактор.

Пример 2

Решите следующую систему, используя определители.

Для решения этой системы созданы три определителя. Один называется определителем знаменателя и обозначен как D; другой – определитель числителя x , помеченный как D _x; , а третий – определитель числителя y , обозначенный как D _y .

Определитель знаменателя, D , формируется путем взятия коэффициентов x и y из уравнений, записанных в стандартной форме.

Определитель числителя x формируется путем взятия постоянных членов из системы и размещения их в положениях с коэффициентами x с сохранением коэффициентов y .

Определитель числителя y формируется путем взятия постоянных членов из системы и помещения их в позиции коэффициентов y и сохранения коэффициентов x .

Ответы для x и y следующие:

Чек остается на ваше усмотрение.Решение: x = –5, y = –2.

Часто поиск решений с использованием определителей упоминается как Правило Крамера , названное в честь математика, который разработал этот метод. Правило Крамера вряд ли можно считать «сокращением», но это довольно изящный способ решения систем уравнений с использованием определителей.

Пример 3

Используйте правило Крамера, чтобы решить эту систему.

Чек остается на ваше усмотрение. Решение -.

Правило Крамерса

метод решения линейное уравнение по определителям называется правилом Крамера. Это правило для линейных уравнений с 3 неизвестными является методом решения определители – следующие уравнения для x , y , z a ₁ x + b ₁ y + c ₁ z = d ₁
a ₂ x + b ₂ y + c ₂ z = d ₂
a ₃ x + b ₃ y + c ₃ z = d ₃

Если мы аналитически решать из приведенных выше уравнений получаем

Если

является определителем коэффициентов из x , y , z и предполагается, что

не равно нулю, тогда мы можем переписать значения как

Решение с детерминантами, легко запомнить, если помнить об этих просто идей:

Знаменатели даны как определитель, в котором элементы являются коэффициентами x , y и z , расположенные как в оригинале данные уравнения.

Числитель в решении для любой переменной совпадает с определителем коэффициентов ∆ за исключением того, что столбец коэффициентов неизвестного, подлежащего определению, заменяется на столбец констант справа от оригинала уравнения.

То есть, для первой переменной вы подставляете первый столбец определитель с константами справа; на второй переменной, вы подставляете второй столбец константами справа и так далее…

Пример:

Решить эта система использует правило Крамера

2 x + 4 y – 2 z = -6
6 x + 2 y + 2 z = 8
2 x – 2 y + 4 z = 12

Для x , возьмите определитель выше и замените первый столбец константами справа от системы. Потом, разделите это на определитель:

Для y , замените второй столбец на константы справа от системы.Затем разделите его на определитель:

Для z , замените третий столбец на константы справа от системы. Затем разделите его на определитель:

You только что решил эту систему!

дюйм Матлаб, это даже Полегче. Вы можете решить систему с помощью всего одной инструкции.

Let D быть матрицей только коэффициентов при переменных:

D = [2 4 -2;
6 2 2;
2 -2 4];

Let b быть вектор-столбец констант в правой части системы:

b = [-6 8 12] ‘; % Апостроф используется для транспонирования вектор

Найдите вектор-столбец неизвестных на ‘ слева разделительный ‘ D по b (используйте обратная косая черта), например:

переменных = D \ b

А также Ответ Matlab:

переменных =
1.0000
-1,0000
2,0000

От правила Крамерса к дому

От правила Крамерса к линейному Алгебра ‘

Решите систему – уравнения с несколькими неизвестными

Описание:

Функция Solve_system позволяет решать уравнения с несколькими неизвестными: уравнение 2 неизвестных систем, системы уравнений с 3 неизвестными от n неизвестных систем.

решить_system онлайн

Описание:

Решение уравнений с несколькими неизвестными другими словами, Решение системы уравнений онлайн это возможно благодаря использованию функции решающего_система калькулятора.Калькулятор разрешает систему онлайн нескольких типов, это возможно:

– решать системы уравнений с двумя неизвестными онлайн ,
по решать системы уравнений с тремя неизвестными в режиме онлайн ,
и, в более общем смысле, разрешение онлайн-системного уравнения с несколькими неизвестными.

Обладая способностями к алгебре, калькулятор может решать уравнения с двумя неизвестными или решать уравнения с 3 неизвестными с использованием букв (буквальное вычисление).

Калькулятор представляет собой средство решения системы уравнений , которое использует очень простой синтаксис для решения систем линейных уравнений, допускающих единственное решение.

Решение системы двух уравнений с двумя неизвестными

Существует несколько методов решения системы из двух уравнений с двумя неизвестными: метод замены , метод комбинации , графический метод , метод Крамера .

Метод комбинирования заключается в исключении одной из переменных благодаря арифметическим операциям с уравнениями;
Метод замены состоит в выражении одной из переменных как функции другой и последующей замене для получения уравнения с одним неизвестным;
Метод графического решения позволяет предположить решение, которое должно быть проверено расчетом, графический метод заключается в изображении прямых линий, соответствующих уравнениям, затем «считывании» координат точки пересечения, графический калькулятор позволяет выполнять этот тип операций;
Метод Крамера использует определители.

Калькулятор может использовать эти методы для решения уравнений с двумя неизвестными

Чтобы решить систему 2 уравнений с 2 неизвестными согласно x + y = 18 и 3 * y + 2 * x = 46, необходимо ввести решить_system (`[x + y = 18; 3 * y + 2 * x = 46]; [x; y]`), после вычисления возвращается результат [x = 8; y = 10].

Решение системы трех уравнений с тремя неизвестными

Для найти решения системы 3 уравнений с 3 неизвестными калькулятор может использовать метод подстановки, метод комбинации или метод Крамера.

Таким образом, например, чтобы решить линейную систему уравнений согласно x + y + z = 1, x-y + z = 3, x-y-z = 1, необходимо ввести решить_system (`[x + y + z = 1; x-y + z = 3; xyz = 1]; [x; y; z]`), после вычисления результат [x = 1; y = -1; z = 1] возвращается.

Функция resolve_system позволяет решать уравнения с несколькими неизвестными: уравнение 2 неизвестных систем, системы уравнений с 3 неизвестными от n неизвестных систем.

Синтаксис:

решить_система ([уравнение1; уравнение2 ;…; уравнениеN]; [переменная1; переменная2 … переменнаяN])

Примеры:

solution_system (`[x + y = 18; 3 * y + 2 * x = 46]; [x; y]`), возвращает [x = 8; y = 10] Расчет онлайн с помощью resolve_system (решение системы линейных уравнений)

Применение определителя к системам: правило Крамера

Мы видели, что определитель может быть полезен при нахождении обратной матрицы невырожденной матрицы.Мы можем использовать эти результаты при решении линейных систем, для которых матричный коэффициент невырожден (или обратим).

Рассмотрим линейную систему (в матричной форме)

A X = B

где A – матричный коэффициент, B – неоднородный член и X – неизвестная матрица-столбец. У нас есть:

Теорема. Линейная система AX = B имеет уникальное решение тогда и только тогда, когда A является обратимым.В этом случае решение дается так называемыми формулами Крамера :

где x _i – неизвестные системы или записи X , а матрица A _i получается из A путем замены i ^th столбец по столбцу B . Другими словами, у нас есть

где b _i – это записи B .

В частности, если линейная система AX = B однородна, то есть , тогда, если A обратимо, единственное решение – тривиальное, то есть . Итак, если мы ищем ненулевое решение системы, матричный коэффициент A должен быть сингулярным или необратимым. Мы также знаем, что это произойдет тогда и только тогда, когда . Это важный результат.

Пример. Решите линейную систему

Ответ. Прежде всего отметим, что

откуда следует обратимость матричного коэффициента. Итак, мы можем использовать формулы Крамера. У нас есть

Подробности оставляем читателю, чтобы он узнал

Обратите внимание, что легко видеть, что z = 0. Действительно, определитель, который дает z , имеет две идентичные строки (первую и последнюю). Мы настоятельно рекомендуем вам проверить, что значения, найденные для x , y и z , действительно являются решением для данной системы.

Замечание. Помните, что формулы Крамера действительны только для линейных систем с обратимым матричным коэффициентом.

[Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]

S.O.S MATH: Домашняя страница

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.