Решить систему линейных уравнений онлайн методом гаусса: Решение системы линейных уравнений (СЛАУ) онлайн - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решение систем линейных уравнений методом Гаусса

1. Решение систем линейных уравнений методом Гаусса

2. Метод Гаусса – это метод последовательного исключения переменных

• Систему уравнений приводят к
эквивалентной ей системе с
треугольной матрицей. Это называется
прямым ходом.
• Из полученной треугольной системы
переменные находят с помощью
последовательных подстановок. Это
называется обратным ходом.

3. При выполнении прямого хода используют следующие преобразования:

1. Умножение или деление коэффициентов
свободных членов на одно и то же число;
2. Сложение и вычитание уравнений;
3. Перестановка уравнений системы;
4. Исключение из системы уравнений, в
которых все коэффициенты при
неизвестных и свободные члены равны
нулю.

4. Решить систему уравнений методом Гаусса

x y 5
2 x y 7
Нужно записать расширенную матрицу системы
1 1 5
2 1 7
Вертикальная черта внутри матрицы не несёт
никакого математического смысла – это
просто отчеркивание для удобства
оформления.

Матрица системы – это матрица,
составленная только из
коэффициентов при неизвестных.
Расширенная матрица системы – это
та же матрица системы плюс
столбец свободных членов, в
данном случае.

6. Решение. Умножим первую строку на (-2)

1 1 5
2 1 7
2 2 10
2 1 7

7. ко второй строке прибавим первую строку умноженную на -2

1 1 5
2 1 7
2 2 10
0 3 3
2 2 10
2 1 7

8. Разделим опять первую строку на (-2)

1 1 5
2 1 7
2 2 10
0 3 3
2 2 10
2 1 7
1 1 5
0 3 3
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

9. Цель элементарных преобразований –

Цель элементарных преобразований
–
привести матрицу к ступенчатому виду.
Сам термин «ступенчатый вид» не
вполне теоретический, в научной и
учебной литературе он часто
называется трапециевидный

вид или треугольный

10.

В результате элементарных преобразований получена эквивалентная исходной система уравнений В результате элементарных преобразований
получена эквивалентная исходной система уравнений
x y 5
2 x y 7
x y 5
y 1
Выполняем обратный ход, т.е. подстановку в первое
уравнение вместо у,
х =-5+у
х=-5+1
х=-4
Ответ: (-4; 1)

11. Решить систему уравнений методом Гаусса

3 x 2 y z 4
2 x y 3z 9
x 2 y 2z 3
Решение.
Переставим третье уравнение на место первого и запишем расширенную
матрицу:
x 2 y 2z 3
3 x 2 y z 4
2 x y 3z 9
1 2 2 3
3 2 1 4
2 1 3 9

12. Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на 3, а затем на 2 и вычтем результаты из 2-й и 3-й строк

1 2 2 3
3 2 1 4
2 1 3 9
1 2 2 3
0 8 7 5
0 3 1 3

13. Разделим 2-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки

1 2 2 3
3 2 1 4
2 1 3 9
1 2 2 3
0 1 7 5
8 8
0 3 1 3
1 2 2 3
0 8 7 5
0 3 1 3
1 2 2 3
0 3 21 15
8
8
0 3 1 3
1 2 2
3
21
15
0
3
8
8
39
0 0 13
8
8

14.

Запишем новую эквивалентную систему с учетом расширенной матрицы x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
Выполняем обратный ход, с помощью
последовательных подстановок находим
неизвестные
13
39
z
z 3
8
8
7
5
5 21 16
y 3
y
2
8
8
8 8
8
x 2 2 2 3 3 x 3 4 6 1
Ответ: (1; 2; 3)

Решение системы линейных уравнений методом гаусса-жордана

метод Гаусса–Жордана – один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком, что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.

Алгоритм метода Гаусса

На основании системы линейных уравнений составляем расширенную матрицу системы;

Приводим матрицу к “треугольному” виду;
Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;

Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

Рассматриваем строку i(начиная с первой). Если, элемент a i i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a 1 1 отличен от нуля – переходим к следующему шагу;

Для каждой строки j, ниже i-й находим значение коэффициента K j =a j i /a i i ;
Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a j k нов.=a j k -K j *a i k ; После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n – размерность матрицы A
В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пa i i , которое и будет являтся определителем;

Другими словами, суть метода можно сформулировать следующим образом.

Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце. Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк. Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн

больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

Записываем расширенную матрицу.

Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.

Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…

Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.

На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?

…да, такое бывает только по любви =)

Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий.

Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:

Ну, и совсем замечательно, если отработано понижение порядка определителя .

Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .

Не мудрствуя лукаво:

Пример 1

Решить систему методом Гаусса-Жордана

Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:

Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .

Идеальный с точки зрения простоты случай:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) К первой строке прибавили вторую строку, умноженную на –2.

Не могу удержаться от иллюстрации итоговой системы:

Ответ :

Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.

Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:

Пример 2

Решить систему линейных уравнений методом Гаусса-Жордана.

Решение : первая часть задания хорошо знакома:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.

(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.

(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7

(4) Третью строку разделили на 2.

Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .

Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:

Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т. е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:

(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.

(8) К первой строке прибавили вторую.

(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!

В результате элементарных преобразований получена эквивалентная исходной система:

Элементарно выражаем базисные переменные через свободную:

и записываем:

Ответ : общее решение:

В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.

И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .

Для самостоятельного решения:

Пример 3

Найти базисное решение с помощью элементарных преобразований

Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.

Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.

Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!

Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .

Продолжаем совершенствовать свои навыки на следующей прикладной задаче:

Как найти обратную матрицу методом Гаусса?

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.

Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

(Понятно, что обратная матрица должна существовать)

Демо-пример 4

Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:

(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Ответ :

Сверьтесь с ответом первого примера урока Как найти обратную матрицу?

Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:

Пример 5

Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :

(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».

(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.

(3) К 3-й строке прибавили 2-ю строку, умноженную на –1

Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.

К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.

(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:

(5) К 1-й и 2-й строкам прибавили третью строку.

(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.

(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.

(8) К первой строке прибавили вторую строку.

(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.

(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4).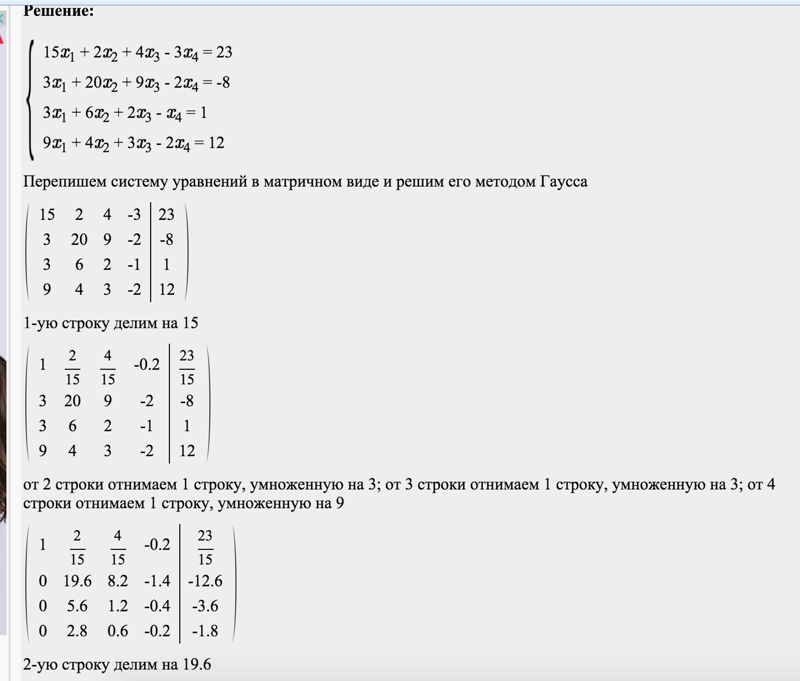 Совершенно понятно, что это число 44. Третью строку умножаем на 11.

(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!

Таким образом, обратная матрица:

Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.

Ответ :

Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .

Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.

Аналогичное задание для самостоятельного решения:

Пример 6

Найти обратную матрицу методом Гаусса-Жордана.

Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .

Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .

На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».

И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .

Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:

Пример 7

Найти обратную матрицу с помощью элементарных преобразований

Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.

И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)

Желаю успехов!

Решения и ответы:

Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:

(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :

Ответ : общее решение:

Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:

(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.

(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :

Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:

(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :

Березнёва Т. Д.

Тема 7

«СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

МЕТОД ГАУССА – ЖОРДАНА.»

(Учебная дисциплина “Введение в линейную алгебру и аналитическую геометрию”)

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

МЕТОД ГАУССА – ЖОРДАНА.

Основные понятия

Уравнение с n переменными называется линейным , если все переменные (x 1 , x 2 , … x n ) входят в него в степени 1. Общий вид такого уравнения формально записывается следующим образом:

a 1 x 1 + a 2 x 2 + … a j x j + … a n x n = b , (*)

= b .

Величины a j , j = 1,…, n , и b являются известными (заданными). Величиныa j называются коэффициентами при переменных (при неизвестных), а b – свободным членом .

Решением линейного уравнения (*) ,,…,) значений переменных, который при подстановке в уравнение (т.е. при заменеx j на при всехj от 1до n обращает его в тождество. Подчеркнем, что решение уравнения с n переменными всегда есть набор из n чисел и каждый такой набор из n чисел представляет собой одно решение. Очевидно, что если хотя бы один коэффициент при переменных не равен 0, то уравнение (*) имеет решение. В противном случае решение существует только при b = 0, и это все произвольные наборы из n чисел.

Рассмотрим одновременно m уравнений вида (*), т.е. систему m линейных алгебраических уравнений с n переменными . Пусть каждое i – е уравнение, i = 1,2,…,m, задается коэффициентами при переменных a i 1 , a i 2 , …, a in и свободным членом b i , т.е. имеет вид

a i1 x 1 + a i2 x 2 + … + a ij x j + … + a in x n = b i .

Тогда в общем виде система m линейных алгебраических уравнений с n переменными может быть записана в виде:

a 11 x 1 + a 12 x 2 + … + a 1j x j + … + a 1n x n = b 1

a 21 x 1 + a 22 x 2 + … + a 2j x j + … + a 2n x n = b 2

………………………………………………………………………………

a i1 x 1 + a i2 x 2 + … + a ij x j + … + a in x n = b i (1)

…………………………………………………

a m1 x 1 + a m2 x 2 + … + a mj x j + … + a mn x n = b m

или, что то же самое,

= b i , i = 1,…, m .

Если все свободные члены равны нулю, то система (1) называется однородной , т.е. имеет вид

= 0, i = 1,…, m, (1 0 )

в противном случае – неоднородной . Система (1 0 ) является частным случает общей системы (1) .

Решением системы уравнений (1) называется упорядоченный набор (,,…,) значений переменных, который при подстановке в уравнения системы (1) (т.е. при заменеx j на , j = 1,…,n) все эти уравнения обращает в тождества, т.е.
=b i при всех i = 1,…,m.

Система уравнений (1) называется совместной, если у нее существует хотя бы одно решение. В противном случае система называется несовместной .

Совокупность всех решений системы уравнений (1) мы будем называть множеством ее решений и обозначать X b (X 0 , если система однородная). Если система несовместна, то X b = .

Основная задача теории систем линейных алгебраических уравнений состоит в том, чтобы выяснить, совместна ли система (1), и, если совместна, то описать множество всех её решений. Существуют методы анализа таких систем, которые позволяют описывать множество всех решений в случае совместных систем или убеждаться в несовместности в противном случае. Одним из таких универсальных методов является метод последовательного полного исключения неизвестных, или метод Гаусса – Жордана , который мы будем подробно изучать.

Прежде, чем переходить к описанию метода Гаусса – Жордана, приведем ряд полезных для дальнейшего определений и утверждений.

Две системы уравнений называются эквивалентными , если они имеют одно и то же множество решений. Другими словами, каждое решение одной системы является решением другой, и наоборот. Все несовместные системы считаются эквивалентными между собой.

Из определений эквивалентности и множества решений систем вида (1) сразу же вытекает справедливость следующих утверждений, которые мы сформулируем в виде теоремы.

Теорема 1. Если в системе (1) имеется уравнение с номером k , 1k m , такое, что a kj = 0 j , то

Справедливость утверждений теоремы становится очевидной, если заметить, что k – е уравнение имеет вид

0 x 1 + 0 x 2 + … + 0 x j + … + 0 x n = b k .

Теорема 2. Если к одному уравнению системы (1) прибавить другое уравнение этой же системы, умноженное на любое число, то получится система уравнений, эквивалентная исходной системе.

Доказательство. Умножим, например, второе уравнение системы (1) на некоторое число и прибавим его к первому уравнению. В результате этого преобразования получим систему (1’), в которой все уравнения, начиная со второго, не изменились, а первое имеет следующий вид

= b 1 + b 2 .

Очевидно, если какой-нибудь набор (,,…,) значений переменных обращает в тождества все уравнения системы (1), то он обращает в тождества и все уравнения системы (1’). Наоборот, решение (x’ 1 ,x’ 2 ,…,x’ j , … ,x’ n) системы (1’) является также решением системы (1), так как система (1) получается из системы (1’) с помощью аналогичного преобразования, когда к первому уравнению системы (1’) прибавляется второе уравнение системы (1’), умноженное на число (-).

Точно также доказывается и следующее утверждение.

Теорема 2’ . Умножение произвольного уравнения системы (1) на любое число, отличное от нуля, переводит систему (1) в эквивалентную ей систему уравнений .

Теоремы 2 и 2’ дают два вида преобразований, которым подвергалась система (1), оставаясь эквивалентной:

а) умножение (или деление) произвольного уравнения системы (1) на любое число, отличное от нуля;

б) прибавление (или вычитание) к одному уравнению другого, умноженного на некоторое число.

Такие преобразования а) и б) называются элементарными преобразованиями системы уравнений (1).

Если к системе уравнений (1) несколько раз применить элементарные преобразования, то полученная в результате система, очевидно, также будет эквивалентна первоначальной.

Систему уравнений (1) можно записать в табличной форме:

Прямоугольная таблица чисел, составленная из коэффициентов a ij при неизвестных системы (1), называется матрицей системы (1) и обозначается A (в ней m строк и n столбцов), столбец свободных членов обозначается b. Прямоугольная таблица, составленная из коэффициентов a ij при неизвестных и из столбца свободных членов b системы (1), называется расширенной матрицей системы (1) и обозначается (в нейm строк и (n+1) столбцов), т.е = (A, b). В i – ой строке матрицы содержатся всеизвестные параметры, характеризующие i – ое уравнение системы (1), i = 1,…, m. В j – м столбце матрицы A содержатся все коэффициенты при неизвестном x j , встречающиеся в системе (1).

Числа a ij называются элементами матрицы А. Элемент a ij находится в i – ой строкеи в j – м столбце матрицы А. Принято говорить, что элементa ij находится на пересечении i – ой строки и j – го столбца матрицы А. Если все элементы строки (столбца) матрицы А (кроме одного) равны нулю, а ненулевой элемент равен единице, то такая строка (столбец) называется единичной (единичным).

Элементарным преобразованиям системы (1) соответствуют следующие элементарные преобразования таблицы (2):

а) умножение (или деление) всех элементов произвольной строки таблицы (2) на любое число, отличное от нуля ,

б) прибавление (или вычитание) к одной строке (поэлементно) другой строки, умноженной на некоторое число.

В результате любого элементарного преобразования получается новая таблица , в которой вместо той строки, к которой прибавляли (или умножали на любое число, отличное от нуля), пишется новая строка , а остальные строки (в том числе и та, которую прибавляли) пишутся без изменения . Новая таблица соответствует системе уравнений, эквивалентной исходной системе .

Применяя элементарные преобразования можно таблицу (2) и соответственно систему (1) упростить так, что решить исходную систему становится просто. На этом и основан предлагаемый метод.

Метод последовательного полного исключения неизвестных

(Метод Гаусса – Жордана)

Метод последовательного полного исключения неизвестных, или метод Гаусса – Жордана , является универсальным методом анализа любых (заранее неизвестно, каких – совместных или несовместных) систем линейных алгебраических уравнений. Он позволяет решать совместные системы или убеждаться в несовместности несовместных систем.

Отметим принципиальное отличие предлагаемого метода решения систем линейных алгебраических уравнений от метода решения, скажем, стандартного квадратного уравнения. Оно решается с помощью хорошо известных формул, в которых неизвестные выражаются через коэффициенты уравнения. В случае общих систем линейных алгебраических уравнений мы таких формул не имеем и используем для отыскания решения метод итераций , или итеративный метод , или итерационный метод . Такие методы задают не формулы, а последовательность действий.

Метод Гаусса – Жордана представляет собой последовательную реализацию ряда однотипных больших шагов (или итераций ). Это конкретный итерационный метод – один из многих методов итераций, предложенных для решения систем линейных алгебраических уравнений вида (1). Он состоит из начального этапа, основного этапа и заключительного этапа . Основной этап содержит повторяющиеся итерации – наборы однотипных действий.

Пусть задана конкретная система линейных алгебраических уравнений (1). Это значит, что известны n , m , a ij , b i , i = 1,…, m ; j = 1,…, n . Опишем предлагаемый метод решения этой системы.

Начальный этап включает в себя построение таблицы I (0) вида (2) и выбор в ней ведущего элемента – любого ненулевого коэффициента при переменных из таблицы (2). Столбец и строка, на пересечении которых стоит ведущий элемент, называются ведущими . (Пусть выбран элемент a i 0 j 0 . Тогда i 0 – ая строка ведущая, j 0 – й столбец ведущий.) Переходим к основному этапу. Заметим, что часто ведущий элемент называют разрешающим .

Основной этап состоит из повторяющихся однотипных итераций с номерами k = 1, 2,…. Опишем подробно итерации метода Гаусса – Жордана.

К началу каждой итерации известна некоторая таблица I вида (2), в ней выбран ведущий (разрешающий) элемент и, соответственно, ведущий столбец и ведущая строка. Кроме того, имеется информация о том, какие строки и столбцы уже были ведущими. (Так, например, после начального этапа, т.е. на итерации 1 известны I (0) , ведущий (разрешающий) элемент a i 0 j 0 и i 0 – ая строка ведущая, j 0 – ой столбец ведущий.)

Итерация(с номером k ) состоит из следующих действий.

Преобразование ведущего столбца (т.е. столбца, содержащего ведущий элемент) в единичный с 1 на месте ведущего элемента путем последовательного поэлементного вычитания ведущей строки (т.е. строки, содержащей ведущий элемент), умноженной на некоторые числа, из остальных строк таблицы. Сама ведущая строка преобразуется путем поэлементного деления ее на ведущий элемент.

Выписывается новая таблица I (k) , (k – номер итерации), в которой все столбцы, которые были когда-либо ведущими, – единичные .

Проверяется, можно ли в таблице I (k) выбрать новый ведущий (разрешающий) элемент . По определению это любой ненулевой элемент, который стоит на пересечении строки и столбца, которые еще не были ведущими .

Если такой выбор возможен, то столбец и строка, на пересечении которых стоит ведущий (разрешающий) элемент, называются ведущими . Затем итерация повторяется с новой таблицей I (k) , т.е. действия 1 – 3 повторяются с новой таблицей I (k) . При этом строится новая таблица I (k +1) .

Если нельзя выбрать новый ведущий элемент, то переходим к заключительному этапу.

Заключительный этап. Пусть проделано r итераций, получена таблица I (r) , состоящая из матрицы коэффициентов при переменных A (r) и столбца свободных членов b (r) , и в ней нельзя выбрать новый ведущий элемент, т.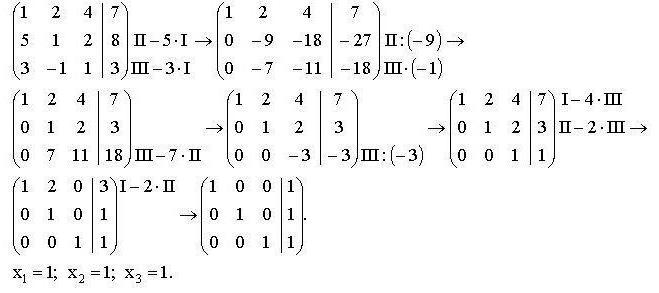 е. метод остановился . Заметим, что метод обязательн о остановится за конечное число шагов , т.к. r не может быть больше min{m,n}.

Каковы варианты остановки метода? Что значит «нельзя выбрать новый ведущий элемент»? Это значит, что после r – ой итерации в матрице A (r) новой системы, эквивалентной системе (1), либо

а) все строки A (r) были ведущими, т.е. в каждой строке стоит одна и ровно одна единица, которая не стоит больше не в какой другой строке,

б) остались строки в A (r) , состоящие только из нулей.

Рассмотрим эти варианты.

а) В этом случае r = m, m n. Переставив строки и перенумеровав переменные (т.е. переставив столбцы), можно таблицу I (r) представить в виде

Подчеркнем, что в таблице (3) каждая переменная с номером i, не превосходящим r, встречается только в одной строке. Таблица (3) соответствует системе линейных уравнений вида

x 1 +
=b (r) 1 ,

x 2 +
=b (r) 2 ,

………………………, (4)

x r +
=b (r) r ,

в которой каждая переменная с номером i, не превосходящим r , однозначно выражается через переменные x r +1 , … ,x n , коэффициенты матрицы a (r) ij , j = r+1,…,n, и свободный член b (r) i , представленные в таблице (3). На переменные x r +1 , … , x n не накладываются никакие ограничения , т.е. они могут принимать любые значения . Отсюда произвольное решение системы, описываемой таблицей (3), или, что то же самое, произвольное решение системы (4), или, что то же самое, произвольное решение системы (1) имеет вид

x i = b (r) i – a (r) ij x j , i = 1,…,r = m; x j – любое при j = (r+1),…,n. (5)

Тогда множество решений системы (1) можно записать как

X b = {x=(x 1 , … ,x n) : x i = b (r) i – a (r) ij x j при i = 1,…, r = m; x j – любое при j =(r+1),…,n.}.

б) В этом случае r r, (предполагаем, что сделана перестановка строк и столбцов такая же, как в пункте а)) такая, что a (r) kj = 0 при всех j. Тогда, если соответствующий свободный член b (r) k не равен 0, то k – е уравнение не имеет решения, и, следовательно, вся система не имеет решения, т.е. система (1) несовместна .

Если же соответствующий b (r) k равен 0, то k – ое уравнение является лишним и его можно отбросить. Отбросив все такие уравнения, получим, что система (1) эквивалентна системе изr уравнений с n переменными, которая через r шагов записывается с помощью таблицы вида (3), в которой все строки были ведущими. Таким образом, мы пришли к рассмотренному выше случаю а) и можем выписать решение вида (5).

Метод Гаусса – Жордана описан полностью. За конечное число итераций система линейных алгебраических уравнений будет решена (если она совместна) или будет очевидно, что она несовместна (если она действительно несовместна).

Переменные, соответствующие ведущим (разрешающим) элементам , или стоящие в ведущих столбцах, принято называть базисными , а остальные переменные –свободными .

Обратим внимание на следующее.

1) Когдамы начинаем решать систему методом Гаусса – Жордана, мы можем не знать, совместна эта система или нет. Метод Гаусса – Жордана за конечное число итераций r даст ответ на этот вопрос. В случае совместной системы на основании последней таблицы выписывается общее решение исходной системы. В этом случае число базисных переменных обязательно равно номеру r последней итерации, т.е. числу выполненных итераций. Число r всегда не превосходит min{m,n},гдеm – число уравнений системы,а n – число переменных системы. Если r , то ( n – r) равно числу свободных переменных.

2) При записи общего решения не нужно перенумеровывать переменные, как это делалось для простоты понимания при описании Заключительного этапа. Это сделано для более ясного понимания.

3) При решении системы (1) методом Гаусса – Жордана базисными переменными будут только переменные, соответствующие столбцам, которые на каких-то итерациях выступали в роли ведущих , и наоборот, если на какой-то итерации столбец выступал в качестве ведущего, соответствующая ему переменная обязательно будет в числе базисных.

4) Если общее решение системы (1) содержит хотя бы одну свободную переменную, то эта система имеет бесконечно много частных решений, если же свободных переменных нет, то система имеет единственное решение, которое совпадает с общим решением.

5) Ведущие элементы могут быть выбраны на каждой итерации различным способом. Важно только то, что это ненулевые коэффициенты, стоящие на пересечении строки и столбца, которые до этого не были ведущими. Различный выбор ведущих элементов может дать различные записи множества решений. Однако, само множество решений при любой записи одно и то же.

Поясним работу метода на примерах.

Пример I. Решить следующую систему линейных алгебраических уравнений

2 x 1 – 3 x 2 + 3 x 3 + 5 x 4 = -1,

3 x 1 + 4 x 2 – 2 x 3 + 6 x 4 = 2, (6)

5 x 1 – 4 x 2 + 6 x 3 + 10 x 4 = 2

методом последовательного полного исключения неизвестных (методом Гаусса – Жордана).

Начальный этап. Сначала выпишем систему уравнений (6) в более удобной форме – в виде таблицы I (0) .

Каждой системе линейных уравнений поставим в соответствие расширенную матрицу , полученную присоединением к матрице А столбца свободных членов:

Метод Жордана–Гаусса применяется для решения системы m линейных уравнений с n неизвестными вида:

Данный метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений с матрицей определенного вида.

Над строками расширенной матрицы осуществляем следующие элементарные преобразования:

1. перестановка двух строк ;

2. умножение строки на любое число, отличное от нуля ;

3. прибавление к одной строке другой строки, умноженной на некоторое число ;

4. отбрасывание нулевой строки (столбца) .

Пример 2.11. Решить методом Жордана–Гаусса системы линейных уравнений:

а ) Х 1 + Х 2 + 2Х 3 = -1

2Х 1 – Х 2 + 2Х 3 = -4

4Х 1 + Х 2 + 4Х 3 = -2

Решение: Составим расширенную матрицу:

Итерация 1

В качестве направляющего элемента выбираем элемент . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на (-2) и (-4). Получим матрицу:

На этом первая итерация закончена.

Итерация 2

Выбираем направляющий элемент . Так как , то делим вторую строку на -3. Затем умножаем вторую строку соответственно на (-1) и на 3 и складываем соответственно с первой и третьей строками. Получим матрицу

Итерация 3

Выбираем направляющий элемент . Так как , то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку соответственно на (-4/3) и на (-2/3) и складываем соответственно с первой и второй строками. Получим матрицу

откуда Х 1 = 1, Х 2 = 2, Х 3 = -2.

Закончив решение, на этапе обучения необходимо выполнять проверку, подставив найденные значения в исходную систему, которая при этом должна обратиться в верные равенства.

б ) Х 1 – Х 2 + Х 3 – Х 4 = 4

Х 1 + Х 2 + 2Х 3 +3Х 4 = 8

2Х 1 +4Х 2 + 5Х 3 +10Х 4 = 20

2Х 1 – 4Х 2 + Х 3 – 6Х 4 = 4

Решение: Расширенная матрица имеет вид:

Применяя элементарные преобразования, получим:

Исходная система эквивалентна следующей системе уравнений:

Х 1 – 3Х 2 – 5Х 4 = 0

2Х 2 + Х 3 + 4Х 4 = 4

Последние две строки матрицы A (2) являются линейно зависимыми.

Определение. Строки матрицы e 1 , e 2 ,…, e m называются линейно зависимыми , если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

где 0 =(0, 0…0). Строки матрицы являются линейно независимыми , когда комбинация этих строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю.

В линейной алгебре очень важно понятие ранга матрицы , т.к. оно играет очень большое значение при решении систем линейных уравнений.

Теорема 2.3 (о ранге матрицы). Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).

Ранг матрицы A (2) равен 2, т.к. в ней максимальное число линейно независимых строк равно 2 (это первые две строки матрицы).

Теорема 2.4 (Кронекера–Капели). Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.

2. Если ранг матрицы системы меньше числа переменных, т.е. r

В данном случае система имеет 4 переменных, а её ранг равен 2, следовательно, она имеет бесконечное множество решений.

Определение. Пусть r n , r переменных x 1 , x 2 ,…, x r называются базисными , если определитель матрицы из коэффициентов при них (базисный минор ) отличен от нуля. Остальные n – r переменных называются свободными .

Определение. Решение системы, в котором все n – r свободных переменных равны нулю, называется базисным .

Совместная система m линейных уравнений с n переменными (m ) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где .

В нашем случае , т. е. система имеет не более 6 базисных решений.

Общее решение имеет вид:

Х 1 = 3Х 2 +5Х 4

Х 3 = 4 – 2Х 2 – 4Х 4

Найдем базисные решения. Для этого полагаем Х 2 = 0, Х 4 = 0, тогда Х 1 =0, Х 3 = 4. Базисное решение имеет вид: (0, 0, 4, 0).

Получим другое базисное решение. Для этого в качестве свободных неизвестных примем Х 3 и Х 4 . Выразим неизвестные Х 1 и Х 2 через неизвестные Х 3 и Х 4:

Х 1 = 6 – 3/2Х 2 – Х 4

Х 2 = 2 – 1/2Х 3 – 2Х 4 .

Тогда базисное решение имеет вид: (6, 2, 0, 0).

Пример 2.12. Решить систему:

X 1 + 2X 2 – X 3 = 7

2X 1 – 3X 2 + X 3 = 3

4X 1 + X 2 – X 3 = 16

Решение.Преобразуем расширенную матрицу системы

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = –1, следовательно, данная система несовместна. Данный вывод можно также получить, если заметить, что ранг матрицы системы равен 2, тогда как ранг расширенной матрицы системы равен 3.

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)

Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)

Пример из видеоурока в рукописном виде:

Пример 2.

Запишем систему в виде:

1	-2	2	-1	-1	2	4
0	-1	1	3	-1	2	-2
-2	4	-4	-2	-2	1	1
-1	1	0	-1	1	1	-2

Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ – (А*В)/РЭ, где РЭ – разрешающий элемент (1), А и В – элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.

1	-2	2	-1	-1	2	4
0	-1	1	3	-1	2	-2
0	0	0	-4	-4	5	9
0	-1	2	-2	0	3	2

Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	-7	1	-2	8
0	1	-1	-3	1	-2	2
0	0	0	-4	-4	5	9
0	0	1	-5	1	1	4

Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	-7	1	-2	8
0	1	0	-8	2	-1	6
0	0	1	-5	1	1	4
0	0	0	-4	-4	5	9

Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	0	8	-10.75	-7.75
0	1	0	0	10	-11	-12
0	0	1	0	6	-5. 25	-7.25
0	0	0	1	1	-1.25	-2.25

Теперь исходную систему можно записать как:
x1 = -7.75 – 8×5 – 10.75×6
x2 = -12 – 10×5 – 11×6
x3 = -7.25 – 6×5 – 5.25×6
x4 = -2.25 – x5 – 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.

Решение уравнений методом Гаусса | matematicus.

С помощью метода Гаусса можно решить любую систему линейных уравнений с различным числом уравнений и неизвестных переменных. И именно этим свойством этот метод превосходит матричный метод и метод Крамера.

Суть метода состоит в приведении системы линейных уравнений к ступенчатому (треугольному) виду за счет последовательного исключения неизвестных. Затем её решения с помощью обратной подстановки.

Допустимые преобразования матрицы:

Перестановка местами двух строк или двух столбцов;
Умножение строки на число, которое не равно 0;
Прибавление одной строки к другой.
Исключение или добавление нулевой строки

Допустим, дана система линейных алгебраических уравнений с четырьмя уравнениями и четырьмя неизвестными.

Составим расширенную матрицу СЛАУ:

Затем первое уравнение СЛАУ делим на a₁₁. При этом a₁₁≠0, если равно нуля, то переставляем две строки или два столбца местами так, чтобы избавится от нуля. После полученное уравнение умножаем на a₂₁ и вычитаем из второго уравнения, дальше, умножаем на a₃₁ и вычитаем из третьего уравнения и т.д.

Также поступаем и с оставшемся уравнениями, т.е. со вторым, третьем и четвёртым. В итоге должна получится матрица ступенчатого или треугольного вида.

Система уравнений примет вид

Такую систему элементарно решить обратным ходом, т.е. последовательным решением уравнений от нижнего к верхнему.

Рассмотрим наиболее подробно метод Гаусса при решении СЛАУ на практике.

Пример 1

Решить методом Гаусса систему уравнений

Решение

Составим расширенную матрицу системы уравнений:

Первую строку разделим на a₁₁, но так как в этой строке a₁₁=0, то необходимо поменять строку у которой первый элемент не равен нулю. Выберем по модулю наибольшей элемент, это a₄₁=2 Поэтому поменяем первую и четвёртую строки местами.

Получаем:

Первую строку разделим на a₁₁=2. Получим матрицу:

Умножаем элементы первой строки на -1 и прибавляем к элементам второй строк. Получим матрицу:

Умножаем элементы первой строки на -1 и прибавляем к элементам третьей строки.

Четвёртую строку оставляем без изменений, так как её первый элемент равен нулю.

Теперь первый столбец не трогаем.

Начинаем повторять действия, которые применяли ранее.

Второе уравнение разделим на a₂₂=-1/2, тогда

Умножаем элементы второй строки на -1/2 и прибавляем к элементам третьей строки.

Умножаем элементы второй строки на -1 и прибавляем к элементам четвёртой строки.

Первый и второй столбец не трогаем.

Третьей столбец разделим на 2.

Умножаем элементы третьей строки на -1 и прибавляем к элементам четвёртой строки.

Получаем ступенчатую систему алгебраических уравнений:

Отсюда, решая систему снизу вверх, получаем корни системы уравнений

Приведём простой пример краткой записи решения СЛАУ методом Гаусса

Пример 2

Решить систему линейных уравнений с тремя неизвестными методом Гаусса.

Решение

Составим расширенную матрицу системы линейных уравнений .

Следовательно, искомая система может быть представлена в ступенчатом виде:

Решая последовательно уравнение, получаем:

Ответ: z = 3; y = 2; x = 1

Система комплексных линейных уравнений

Вы ввели следующую систему уравнений

Решение системы следующее

Решение системы линейных уравнений

Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:

– иметь только одно верное решение;

– иметь бесконечное множество корней;

– иметь несовместный тип (когда решений быть не может).

Метод Гаусса, используемый нашим АБАК-ботом – самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.

Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т.н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами – ровно то же самое, что и элементарные преобразования матриц в переложении для строк.

Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!

Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей а также в множестве специализированных задач.

Данный сервис позволяет решать неограниченную по размерам систему линейных уравнений с комплексными коэффициентами.

Практическое применение:

Ну, раз бот умеет считать решения комплексных систем, то для него не составит труда считать частный случай, когда элементы системы являются вещественные числа.

Второе, в школе Вам это наверняка не понадобится, но вот в институте, особенно институтах связи, при расчетах токов в сложных контурах в электротехнике, наверняка пригодится.

Синтаксис

Для пользователей XMPP клиентов: linur_i <список элементов системы>

список элементов системы – является список значений перечисленных в одну или несколько строк разделенными пробелами между собой

linur_i 5:2 3 10 2 -11:3 0:-30

Примеры

linur_i 5:2 3 10 2 -11:3 0:-30

Корни системы линейных уравнений равны следующим значениям.

Переменные считаются слева направо

1.4389598942265:-1.941383869546

-0.3591890700749:2.2763331864257

то есть x1=1.4389598942265 – 1.941383869546 i

x2=-0.3591890700749+2.2763331864257 i

Рассчитаем комплексную систему линейных уравнений

такого вида

Записываем все элементы в поле ввода. Как видите, данные могут быть не только числовые но и быть произвольным выражением, включающее в себя комплексные числа.

И получаем следующий результат.

Вы ввели следующую систему уравнений

Решение системы следующее

Успехов в расчетах !

Скалярное произведение двух матриц >>

Метод Гаусса для решения систем линейных уравнений | Математика

Пусть задана система из линейных уравнений с неизвестными:

(1.

27)

Допустим, что в системе коэффициент при в первом уравнении Разделив обе части этого уравнения на , получим равносильную данной систему:

(1.28)

где

Получить решение

Исключим с помощью первого уравнения системы (1.28) неизвестное из всех оставшихся уравнений этой системы. Для этого умножим первое уравнение этой системы последовательно на и в том же порядке вычтем полученное из второго, третьего и последующих уравнений системы (1.28). В результате получим равносильную систему вида

(1.29)

где

Допустим, что коэффициент при во втором уравнении системы (1.29) отличен от нуля. В противном случае переставим местами уравнения этой системы, записав вторым другое уравнение с подходящим вторым коэффициентом.

Исключим неизвестное с помощью второго уравнения из всех последующих уравнений. Для этого разделам второе уравнение на . Затем умножим последовательно полученное второе уравнение на и вычтем эти результаты из третьего, четвертого и всех оставшихся уравнений.

В итоге получим очередную систему уравнений:

где

Продолжая этот процесс исключения неизвестных, получим либо несовместную, либо совместную систему уравнений. В первом случае в системе будет содержаться уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, т.е. уравнение вида , где . Во втором случае получим либо систему треугольной формы

(1.30)

либо систему трапециевидной (ступенчатой) формы

(1.31)

В случае треугольной системы из последнего уравнения (1. 30) следует, что Подставляя это значение в предпоследнее уравнение системы (1.30), найдем неизвестное . Подставляя значения и в предыдущее уравнение, найдем значение неизвестного и т.д.

Таким образам, если данная система (1.27) с помощью элементарных преобразований приводится к системе треугольной формы, то система имеет единственное решение (т.е. система совместна и определенна).

В случае системы ступенчатой формы (1.31), перенося все слагаемые, содержащие неизвестные в правую часть уравнений, получим систему вида

(1.32)

Из (1.32) следует, что значения неизвестных выражаются через значения неизвестных . Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.32), а вместе с ней и данная система (1.27), имеет бесконечное множество решений.

Итак, если данная система приводится к трапециевидной форме, то она имеет бесконечное множество решений (т. е. система совместна и неопределенна). Найденные решения, записанные в форме

где любые числа, называются общими решениями системы. Решения, полученные из общих решений при конкретных значениях свободных неизвестных , называются частными решениями.

Заключение

Матричный способ решения систем линейных уравнений, как и решение методом Крамера, применим только для особых систем линейных уравнений, в которых количество неизвестных совпадает с количеством уравнений. Метод Гаусса применим для решения произвольных систем линейных уравнений и, следовательно, является универсальным методом. Этот метод позволяет существенно упростить и сам процесс поиска решений, если все промежуточные преобразования осуществить над специальной матрицей составленной из коэффициентов системы (1.27) и ее свободных членов.

Матрица В называется расширенной матрицей системы. Она позволяет заменить элементарные преобразования системы уравнений на соответствующие элементарные преобразования над своими строками, что существенно сокращает процесс поиска решении.

Примеры решения методом Гаусса

ПРИМЕР 1.1.15

Решить систему уравнений методом Гаусса.

Построим расширенную матрицу системы

Исключая с помощью первой строки неизвестное из всех оставшихся строк матрицы , получим

где символ есть символ элементарного преобразования матрицы.

Исключая с помощью второй строки неизвестное из всех последующих строк матрицы , получим

Исключая с помощью третьей строки неизвестное из четвертой строки, получим:

Матрица имеет треугольную форму. Следовательно, заданная система эквивалентна системе

Последовательно вычисляя из последнего уравнения, далее из третьего, из второго и из первого уравнения этой системы найдем, что =2, =1, =0, =1. Итак, заданная система имеет единственное решение =1, =0, =1, =2.

ПРИМЕР 1.1.16

Решить систему уравнений

Построим расширенную матрицу системы

Таким образом, заданная система эквивалентна системе,

которая имеет ступенчатый вид, и, следовательно, имеет бесконечное множество решений. Выразим переменные через :

;

Итак, общим решением данной системы будет

любое число.

Полагая, в частности, найдем, что . Тогда , будет одним из частных решений системы.

в чем суть, решение системы уравнений, примеры с объяснением

Благодаря великим ученым было открыто множество эффективных теорем для работы со сложными математическими задачами. Один из таких примеров — метод Гаусса.

Метод Гаусса — что это такое

Метод Гаусса представляет собой методику эквивалентного преобразования исходной системы линейных уравнений в систему, решаемую существенно проще, чем исходный вариант.

Метод Гаусса используют для решения систем линейных алгебраических формул. Такой способ обладает рядом важных преимуществ:

Нет необходимости сравнивать уравнения для оценки совместимости.
Решение систем равенств, в которых число определителей совпадает или не совпадает с количеством неизвестных переменных.
Поиск решений для уравнений с нулевым определителем.
Сравнительно небольшое количество вычислительных операций для получения результата.

Основные определения и обозначения

Матрицы: определение и свойства

Такие системы являются наиболее удобным способом представления данных, с которыми впоследствии производят манипуляции. Матрица имеет вид прямоугольника для удобства расчетов. При использовании метода Гаусса работа осуществляется с треугольными матрицами, при записи которых применяется прямоугольник с нулями на тех местах, где числа отсутствуют. Часто нули не записывают, а только подразумевают.

Важным параметром матрицы является размер:

ширина — это количество строк, обозначают буквой m;
длину выражают числом столбцов, записывают буквой n.

Источник: bigpicture.ru

Размер матрицы будет записан в формате А m*n. В случае, когда m=n, матрица является квадратной, а m=n служит ее порядком. Номера строк и столбцов изменяются.

Определитель

Матрица обладает крайне важной характеристикой. Таким параметром является определитель. Данную величину рассчитывают с помощью диагонали. Для этого в матрице необходимо провести воображаемые диагональные линии. Затем следует найти произведение элементов, которые располагаются на этих диагоналях, а полученные значения суммировать таким образом:

Если диагональ обладает наклоном в правую сторону, то знак «+».
Для диагоналей, наклоненных влево, знак «–».

Источник: wp.com

Рассчитать определитель представляется возможным лишь в случае работы с квадратной матрицей.

Если необходимо определить данный параметр для прямоугольной матрицы, то следует выполнить следующие манипуляции:

из числа строк и числа столбцов выбрать наименьшее и обозначить его k;
отметить в матрице произвольным образом k столбцов и k строк.

Элементы, которые расположены на пересечении отмеченных столбцов и строк, образуют новую квадратную матрицу. В случае, когда определитель является числом, не равным нулю, то данный параметр будет обозначен как базисный минор первоначальной прямоугольной матрицы. Перед решением систем уравнений методом Гаусса полезно рассчитать определитель. Если данная характеристика равна нулю, то матрица имеет бесконечное множество решений либо не имеет их вовсе. В таком случае потребуется определить ранг матрицы.

Классификация систем

Ранг матрицы является распространенным понятием. Он обозначает максимальный порядок ее определителя, который не равен нулю. По-другому можно сказать, что ранг матрицы представляет собой порядок базисного минора. Исходя из данного критерия, СЛАУ классифицируют на несколько типов. В совместных системах, которые состоят лишь из коэффициентов, ранг основной матрицы совпадает с рангом расширенной. Для подобных систем характерно одно или множество решений. По этой причине совместные системы подразделяют на следующие типы:

определенные, обладающие одним решением, в которых наблюдается равенство ранга матрицы и количество неизвестных;
неопределенные;
обладающие бесконечным числом решений с рангом матрицы, который меньше количества неизвестных.

В несовместных системах ранги, характеризующие основную и расширенную матрицы, отличаются. С помощью метода Гаусса в процессе решения можно прийти либо к однозначному доказательству несовместности системы, либо к решению общего вида для системы, обладающей бесконечным количеством решений.

Источник: asiaplustj.info

Основные правила и разрешаемые преобразования при использовании метода Гаусса

Перед тем, как решать систему, необходимо ее упростить. На данном этапе выполняют элементарные преобразования, которые не влияют на конечный результат. Определенные манипуляции справедливы лишь в случае матриц, исходниками которых являются СЛАУ. Список элементарных преобразований:

Перестановка строк. При перемене записей в системе местами ее решение не меняется. Можно менять место строк в матрице, учитывая столбец со свободными членами.
Произведение всех элементов строк и некоторого коэффициента. Сокращаются большие числа в матрице, и исключаются нули. При этом множество решений сохраняется без изменений, а дальнейшие манипуляции существенно упрощаются. Важным условием является отличие от нуля коэффициента.
Удаление строк, которые содержат пропорциональные коэффициенты. Данное преобразование следует из предыдущего пункта. При условии, что две или более строк в матрице обладают пропорциональными коэффициентами, то при произведении или делении одной из строк на коэффициент пропорциональности получают две или более абсолютно одинаковые строки. В этом случае лишние строки исключают, оставляя только одну.
Удаление нулевой строки. Бывают случаи, когда в процессе манипуляций с уравнениями возникает строка, все элементы которой, в том числе свободный член, равны нулю. Нулевую строку допустимо исключать из матрицы.
Суммирование элементов одной строки с элементами другой, умноженными на некоторый коэффициент, в соответствующих столбцах. Данное преобразование имеет наиболее важное значение из всех перечисленных.

Особенности использования метода Гаусса для решения СЛАУ

На первом этапе система уравнений записывается в определенном виде. Пример выглядит следующим образом:

Источник: wp.com

Коэффициенты необходимо представить в виде таблицы. С правой стороны в отдельном столбце записаны свободные члены. Данный блок отделен для удобства решения. Матрицу со столбцом со свободными членами называют расширенной.

Источник: wp.com

Затем основная матрица с коэффициентами приводится к верхней треугольной форме. Данное действие является ключевым моментом при решении системы уравнений с помощью метода Гаусса. По итогам преобразований матрица должна приобрести такой вид, чтобы слева внизу находились одни нули:

Источник: wp.com

При записи новой матрицы в виде системы уравнений можно отметить, что последняя строка уже содержит значение одного из корней, которое в дальнейшем подставляется в уравнение выше для нахождения следующего корня и так далее. Подобное описание позволяет разобраться в методе Гаусса в общих чертах.

Обратный и прямой ход метода Гаусса

В первом случае необходимо представить запись расширенной матрицы системы. При выполнении обратного метода Гаусса далее в главную матрицу добавляют столбец со свободными членами.

Источник: wp.com

Суть такого способа заключается в выполнении элементарных преобразований, по итогам которых данная матрица приводится к ступенчатому или треугольному виду. В этом случае над или под главной диагональю матрицы располагаются только нули.

Источник: wp.com

Варианты дальнейших действий:

перемена строк матрицы местами, при наличии одинаковых или пропорциональных строк их можно исключить, кроме одной;
деление либо умножение строки на любое число, не равное нулю;
удаление нулевых строк;
добавление строки, умноженной на число, не равное нулю, к другой строке.

Имея преобразованную систему с одной неизвестной Xn, которая становится известной, можно выполнить поиск в обратном порядке остальных неизвестных с помощью подстановки известных х в уравнения системы, вплоть до первого. Данный способ называют обратным методом Гаусса.

Примеры решений с объяснением

Пример 1

Требуется решить с помощью метода Гаусса систему линейных уравнений, которая выглядит следующим образом:

Источник: wp.com

Решение

Необходимо записать расширенную матрицу:

Источник: wp.com

Затем нужно выполнить преобразования. В результате матрица должна приобрести треугольный вид. Для этого следует умножить первую строку на (3) и умножить вторую строку на (-1). В результате суммирования второй и первой строк получается следующее:

Источник: wp.com

Далее следует умножить третью строку на (-1). После добавления третьей строки ко второй получаем следующие преобразования:

Источник: wp.com

После этого необходимо умножить первую строку на (6) и вторую строку на (13). Далее следует добавить вторую строку к первой:

Источник: wp.com

После того, как система преобразована, остается вычислить неизвестные:

$x_{3}=\frac{98}{49}=2$

$x_{2}=\frac{14-7x_{3}}{6}=\frac{14-7*2}{6}=0$

$x_{3}=\frac{-9+5x_{2}+6x_{3}}{3}=\frac{-9+5*0+6*2}{3}=1$

Данный пример демонстрирует единственное решение системы.

Источник: supertics.com

Пример 2

Необходимо решить систему уравнений, которая выглядит следующим образом:

Источник: wp.com

Решение

Необходимо составить матрицу:

Источник: wp.com

Согласно методу Гаусса уравнение первой строки по итогам преобразований не меняется. Удобнее, когда левый верхний элемент матрицы обладает наименьшим значением. В таком случае первые элементы остальных строк после преобразований будут равны нулю. Таким образом, составленная матрица будет решаться проще, если на место первой строки поставить вторую:

вторая строка:

$k = (-a_{21} /a_{11}) = (-3/1) = -3$

$a”_{21} = a_{21} + k×a_{11} = 3 + (-3)×1 = 0$

$a” _{22} = a_{22} + k×a _{12} = -1 + (-3)×2 = -7$

$a”_{ 23} = a_{23} + k×a_{13} = 1 + (-3)×4 = -11$

b” 2 = b 2 + k×b 1 = 12 + (-3)×12 = -24

третья строка:

$k = (-a_{31} /a_{11}) = (-5/1) = -5$

$a”_{31} = a_{31} + k×a_{11} = 5 + (-5)×1 = 0$

$a”_{32} = a_{32} + k×a_{12} = 1 + (-5)×2 = -9$

$ a”_{33} = a_{33} + k×a_{13} = 2 + (-5)×4 = -18$

$ b”_3 = b_3 + k×b_1 = 3 + (-5)×12 = -57$

Матрица с промежуточными результатами манипуляций будет иметь следующий вид:

Источник: wp.com

Благодаря некоторым операциям можно придать матрице наиболее удобный вид. К примеру, вторую строку можно избавить от всех «минусов» путем умножения каждого элемента на «-1». Можно заметить, что для третьей строки характерны все элементы, кратные трем. В этом случае строка сокращается с помощью произведения каждого элемента на «-1/3». Минус позволит удалить отрицательные значения.

Источник: wp.com

Далее следует приступить к манипуляциям со второй и третьей строками. Необходимо суммировать третью и вторую строки. Вторая строка при этом умножается на такой коэффициент, при котором элемент а 32 будет равен нулю.

$k = (-a_{32} /a_{22}) = (-3/7) = -3/7$

В случае, когда некоторые преобразования приводят в результате к получению не целого числа, следует оставить его в этом виде. Таким образом, вычисления будут более точными. Затем при получении ответов можно определиться с его дальнейшем округлением или переводом в другую форму записи.

$a”_{32} = a_{32} + k×a_{22} = 3 + (-3/7)×7 = 3 + (-3) = 0$

$a”_{33} = a_{33} + k×a_{23} = 6 + (-3/7)×11 = -9/7$

$b”_3 = b_3 + k×b_2 = 19 + (-3/7)×24 = -61/7$

Преобразованная матрица будет иметь следующий вид:

Матрица обладает ступенчатым видом. Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».

Источник: wp.com

Затем необходимо представить запись матрицы в виде системы уравнений для вычисления корней.

x + 2y + 4z = 12 (1)

7y + 11z = 24 (2)

Найти корни можно обратным методом Гаусса. Уравнение (3) содержит значение z:

y = (24 – 11×(61/9))/7 = -65/9

С помощью первого уравнения можно определить х:

x = (12 – 4z – 2y)/1 = 12 – 4×(61/9) – 2×(-65/9) = -6/9 = -2/3

Подобная система является совместной и определенной, для которого характерно единственное решение. Ответ будет следующим:

x 1 = -2/3, y = -65/9, z = 61/9.

Метод Гаусса предполагает последовательное исключение неизвестных. Методика справедлива в случае решения квадратных систем линейных алгебраических уравнений. Несмотря на простоту метода, многие студенты сталкиваются с некоторыми трудностями в процессе поиска правильного решения. Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.

Дифференциальные уравнения – Обзор: Системы уравнений

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с “узкой” шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-1: Обзор: Системы уравнений

Поскольку мы собираемся работать почти исключительно с системами уравнений, в которых количество неизвестных равно количеству уравнений, мы ограничим наш обзор этими типами систем.

Все, что мы здесь будем делать, можно легко распространить на системы с большим количеством неизвестных, чем уравнений, или большим количеством уравнений, чем неизвестных, если потребуется.

Начнем со следующей системы уравнений \ (n \) с \ (n \) неизвестными, \ (x_ {1} \), \ (x_ {2} \),…, \ (x_ {n} \ ).

\ [\ begin {уравнение} \ begin {выровнено} {a_ {11}} {x_1} + {a_ {12}} {x_2} + \ cdots + {a_ {1n}} {x_n} & = {b_1} \ \ {a_ {21}} {x_1} + {a_ {22}} {x_2} + \ cdots + {a_ {2n}} {x_n} & = {b_2} \\ \ vdots \ hspace {0.8in} & \\ {a_ {n1}} {x_1} + {a_ {n2}} {x_2} + \ cdots + {a_ {nn}} {x_n} & = {b_n} \ end {выровнено} \ label { уравнение: уравнение1} \ end {уравнение} \]

Обратите внимание, что в нижних индексах коэффициентов в этой системе, \ (a_ {ij} \), \ (i \) соответствует уравнению, в котором находится коэффициент, а \ (j \) соответствует неизвестному, которое является умноженный на коэффициент.

Чтобы использовать линейную алгебру для решения этой системы, мы сначала запишем расширенную матрицу для этой системы.Расширенная матрица – это просто все коэффициенты системы и числа для правой части системы, записанные в матричной форме. Вот расширенная матрица для этой системы.

\ [\ left ({\ begin {array} {* {20} {r}} {{a_ {11}}} & {{a_ {12}}} & \ cdots & {{a_ {1n}}}} & {{b_1}} \\ {{a_ {21}}} & {{a_ {22}}} & \ cdots & {{a_ {2n}}} и {{b_2}} \\ \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ {{a_ {n1}}} и {{a_ {n2}}} & \ cdots & {{a_ {nn}}} & {{b_n}} \ end {array} } \верно)\]

Для решения этой системы мы будем использовать элементарные операции со строками (которые мы определим позже), чтобы переписать расширенную матрицу в треугольной форме.Матрица будет иметь треугольную форму, если все элементы ниже главной диагонали (диагональ, содержащая \ (a_ {11} \), \ (a_ {22} \),…, \ (a_ {nn} \)) равны нулю. .

Как только это будет сделано, мы можем вспомнить, что каждая строка в расширенной матрице соответствует уравнению. Затем мы преобразуем нашу новую расширенную матрицу обратно в уравнения, и на этом этапе решение системы станет очень простым.

Прежде чем работать с примером, давайте сначала определим элементарные операции со строками.Их трое.

Поменять местами два ряда. Это именно то, что написано. Мы заменим строку \ (i \) строкой \ (j \). Обозначение, которое мы будем использовать для обозначения этой операции: \ ({R_i} \ leftrightarrow {R_j} \)
Умножить строку \ (i \) на константу \ (c \). Это означает, что каждая запись в строке \ (i \) будет умножена на константу \ (c \). Обозначение для этой операции: \ (c {R_i} \)
Добавить строку \ (i \), кратную строке j. В уме мы умножим строку \ (i \) на соответствующую константу, а затем добавим результаты в строку \ (j \) и поместим новую строку обратно в строку \ (j \), оставив строку \ (i \) в матрица без изменений. Обозначение для этой операции: \ (c {R_i} + {R_j} \)

Всегда немного легче понять эти операции, если мы увидим их в действии. Итак, давайте решим пару систем.

Пример 1 Решите следующую систему уравнений. \ [\ begin {align *} – 2 {x_1} + {x_2} – {x_3} & = 4 \\ {x_1} + 2 {x_2} + 3 {x_3} & = 13 \\ 3 {x_1} + { x_3} & = – 1 \ end {align *} \] Показать решение

Первый шаг – записать расширенную матрицу для этой системы.Не забывайте, что коэффициенты отсутствующих членов равны нулю.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} – 2} & 1 & {- 1} & 4 \\ 1 & {\ color {Red} 2 } & 3 & {13} \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \]

Теперь мы хотим, чтобы записи ниже главной диагонали были равны нулю. Основная диагональ окрашена в красный цвет, поэтому мы можем отслеживать ее в первом примере. По причинам, которые в конечном итоге станут очевидными, мы бы предпочли, чтобы все записи по главной диагонали тоже были единицами.

Мы можем получить единицу в самом верхнем месте, заметив, что если мы поменяем местами первый и второй ряды, мы получим единицу в самом верхнем месте бесплатно. Так что давай сделаем это.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} – 2} & 1 & {- 1} & 4 \\ 1 & {\ color {Red} 2 } & 3 & {13} \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} \ leftrightarrow {R_2}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ {- 2} & {\ color {Red} 1} & {- 1} & 4 \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \]

Теперь нам нужно, чтобы последние две записи (-2 и 3) в первом столбце были равны нулю.Мы можем сделать это с помощью операции третьей строки. Обратите внимание, что если мы возьмем 2 раза первую строку и добавим ее ко второй строке, мы получим ноль во второй записи в первом столбце, а если мы возьмем -3 раза первую строку для третьей строки, мы получим 3 для быть нулем. Мы можем выполнять обе эти операции одновременно, так что давайте сделаем это.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ {- 2} & {\ color {Red}} 1} & {- 1} & 4 \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \ begin {array} {* {20} {c}} {2 { R_1} + {R_2}} \\ {- 3 {R_1} + {R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 5} & 5 & {30} \\ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {массив }} \верно)\]

Прежде чем переходить к следующему шагу, давайте убедимся, что вы следовали тому, что мы только что сделали.Давайте посмотрим на первую операцию, которую мы выполнили. Эта операция требует умножить запись в строке 1 на 2 и добавить ее к соответствующей записи в строке 2, а затем заменить старую запись в строке 2 этой новой записью. Ниже приведены четыре отдельные операции, которые мы выполнили для этого.

\ [\ begin {align *} 2 \ left (1 \ right) + \ left ({- 2} \ right) & = 0 \\ 2 \ left (2 \ right) + 1 & = 5 \\ 2 \ left (3 \ right) + \ left ({- 1} \ right) & = 5 \\ 2 \ left ({13} \ right) + 4 & = 30 \ end {align *} \]

Хорошо, следующий шаг необязателен, но опять же удобен.Технически 5 во втором столбце можно оставить. Однако, если это 1. Мы можем использовать операцию второй строки, чтобы решить эту проблему в будущем, это упростит нашу жизнь. Мы можем разделить всю строку на 5. Это дает

. \ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 5} & 5 & { 30} \\ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array}} \ right) \ begin {array} {* {20} {c}} {\ frac {1} {5} {R_2}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \ \ 0 & {\ color {Red} 1} & 1 & 6 \\ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array}} \ right) \]

Следующий шаг – использовать операцию третьей строки, чтобы превратить -6 во втором столбце в ноль.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 1} & 1 & 6 \ \ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array}} \ right) \ begin {array} {* {20} {c}} {6 {R_2} + {R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color { Красный} 1} & 1 & 6 \\ 0 & 0 & {\ color {Red} – 2} & {- 4} \ end {array}} \ right) \]

Итак, официально мы закончили, но опять же, довольно удобно разместить все на главной диагонали, поэтому мы сделаем последний шаг.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 1} & 1 & 6 \ \ 0 & 0 & {\ color {Red} – 2} & {- 4} \ end {array}} \ right) \ begin {array} {* {20} {c}} {- \ frac {1} {2} { R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red } 1} & 1 & 6 \\ 0 & 0 & {\ color {Red} 1} & 2 \ end {array}} \ right) \]

Теперь мы можем преобразовать обратно в уравнения.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 1} & 1 & 6 \ \ 0 & 0 & {\ color {Red} 1} & 2 \ end {array}} \ right) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ begin {align} {x_1} + 2 {x_2} + 3 { x_3} & = 13 \\ {x_2} + {x_3} & = 6 \\ {x_3} & = 2 \ end {выровнено} \]

На данный момент решение довольно просто. Мы получаем \ (x_ {3} \) бесплатно, и как только мы получим это, мы можем вставить это во второе уравнение и получить \ (x_ {2} \).Затем мы можем использовать первое уравнение, чтобы получить \ (x_ {1} \). Также обратите внимание, что наличие единиц по главной диагонали несколько помогло в этом процессе.

Решение этой системы уравнений:

\ [{x_1} = – 1 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} {x_2} = 4 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} {x_3} = 2 \]

Процесс, используемый в этом примере, называется Исключение Гаусса . Давайте посмотрим на другой пример.

Пример 2 Решите следующую систему уравнений.\ [\ begin {align *} {x_1} – 2 {x_2} + 3 {x_3} & = – 2 \\ – {x_1} + {x_2} – 2 {x_3} & = 3 \\ 2 {x_1} – {x_2} + 3 {x_3} & = 1 \ end {align *} \] Показать решение

Сначала запишите расширенную матрицу.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ {- 1} & 1 & {- 2} & 3 \\ 2 & {- 1} & 3 & 1 \ end {array}} \ right) \]

При работе с этим примером мы не будем вкладывать столько слов.Вот как работает эта расширенная матрица.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ {- 1} & 1 & {- 2} & 3 \\ 2 & {- 1} & 3 & 1 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} + {R_2}} \\ {- 2 {R_1} + {R_3}} \\ \ to \ конец {массив} \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & {- 1} & 1 & 1 \\ 0 & 3 & {- 3} & 5 \ end {array}} \ right) \] \ [\ begin {array} {* {20} {r}} {- {R_2}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 3 & {- 3} & 5 \ end {array}} \ right) \ begin {array} {* {20} {c }} {- 3 {R_2} + {R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 8 \ end {array}} \ right) \]

В этом примере мы не пойдем дальше.Давайте вернемся к уравнениям, чтобы понять, почему.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 8 \ end {array}) } \ right) \ Rightarrow \ begin {align} {x_1} – 2 {x_2} + 3 {x_3} & = – 2 \\ {x_2} – {x_3} & = – 1 \\ 0 & = 8 \ end { выровнено} \]

Последнее уравнение должно вызвать некоторые опасения. Здесь есть один из трех вариантов. Во-первых, нам каким-то образом удалось доказать, что 0 равно 8, и мы знаем, что это невозможно.Во-вторых, мы допустили ошибку, но после того, как мы вернулись к нашей работе, не оказалось, что мы сделали ошибку.

Остается третий вариант. Когда мы получаем что-то вроде третьего уравнения, которое просто не имеет смысла, мы сразу понимаем, что решения нет. Другими словами, не существует набора из трех чисел, который одновременно выполнял бы все три уравнения.

Давайте рассмотрим другой пример. Мы собираемся получить систему для этого нового примера, внеся очень небольшое изменение в систему из предыдущего примера.

Пример 3 Решите следующую систему уравнений. \ [\ begin {align *} {x_1} – 2 {x_2} + 3 {x_3} & = – 2 \\ – {x_1} + {x_2} – 2 {x_3} & = 3 \\ 2 {x_1} – {x_2} + 3 {x_3} & = – 7 \ end {align *} \] Показать решение

Итак, единственная разница между этой системой и системой из второго примера состоит в том, что мы изменили 1 в правой части знака равенства в третьем уравнении на -7.

Теперь запишите расширенную матрицу для этой системы.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ {- 1} & 1 & {- 2} & 3 \\ 2 & {- 1} & 3 & {- 7} \ end {array}} \ right) \]

Шаги для решения этой проблемы идентичны шагам для второй задачи, поэтому мы не будем записывать их все. Выполнив те же действия, мы приходим к следующей матрице.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 \ end {array}) } \верно)\]

На этот раз последнее уравнение сводится к

\ [0 = 0 \]

и в отличие от второго примера это не проблема.Ноль на самом деле равен нулю!

Мы могли бы остановиться на этом и вернуться к уравнениям, чтобы получить решение, и в этом случае решение есть. Однако, если мы сделаем еще один шаг и получим ноль над единицей во втором столбце, а также под ним, наша жизнь станет немного проще. Это дает

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 \ end {array} } \ right) \ begin {array} {* {20} {c}} {2 {R_2} + {R_1}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20 } {r}} 1 & 0 & 1 & {- 4} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 \ end {array}} \ right) \]

Если мы теперь вернемся к уравнению, мы получим следующие два уравнения.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & 0 & 1 & {- 4} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 & 0 \ end {array}} \ right) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ begin {array} {* {20} {r}} {{x_1} + {x_3} = – 4} \\ {{x_2} – {x_3} = – 1} \\ {} \ end {массив} \]

У нас есть два уравнения и три неизвестных. Это означает, что мы можем найти две переменные в терминах оставшейся переменной. Поскольку \ (x_ {3} \) присутствует в обоих уравнениях, мы будем решать в терминах этого.

\ [\ begin {align *} {x_1} & = – {x_3} – 4 \\ {x_2} & = {x_3} – 1 \ end {align *} \]

Это решение означает, что мы можем выбрать значение \ (x_ {3} \), которое нам нужно, а затем найти значения \ (x_ {1} \) и \ (x_ {2} \ ). В этих случаях мы обычно пишем решение следующим образом:

\ [\ begin {align *} {x_1} & = – t – 4 \\ {x_2} & = t – 1 \ hspace {0,25 дюйма} \ hspace {0.25 дюймов} t = {\ mbox {любое действительное число}} \\ & {x_3} = t \ end {align *} \]

Таким образом мы получаем бесконечное количество решений, по одному для каждого значения \ (t \).

Эти три примера приводят нас к интересному факту о системах уравнений.

Факт

Учитывая систему уравнений, \ (\ eqref {eq: eq1} \), у нас будет один из трех возможных вариантов количества решений.

Нет решения.
Ровно одно решение.
Бесконечно много решений.

Прежде чем перейти к следующему разделу, нам нужно взглянуть на еще одну ситуацию. Система уравнений в \ (\ eqref {eq: eq1} \) называется неоднородной системой, если хотя бы одна из b _i ’ s не равна нулю. Если, однако, все \ (b_ {i} \) равны нулю, мы называем систему однородной, и система будет,

\ [\ begin {уравнение} \ begin {выровнено} {a_ {11}} {x_1} + {a_ {12}} {x_2} + \ cdots + {a_ {1n}} {x_n} & = 0 \\ { a_ {21}} {x_1} + {a_ {22}} {x_2} + \ cdots + {a_ {2n}} {x_n} & = 0 \\ \ vdots \ hspace {0.8in} & \\ {a_ {n1}} {x_1} + {a_ {n2}} {x_2} + \ cdots + {a_ {nn}} {x_n} & = 0 \ end {выровнено} \ label {eq: eq2} \ end {уравнение} \]

Теперь обратите внимание, что в однородном случае мы гарантированно получаем следующее решение.

\ [{x_1} = {x_2} = \ cdots = {x_n} = 0 \]

Это решение часто называют тривиальным решением .

Для однородных систем приведенный выше факт может быть изменен на следующее.

Факт

Учитывая однородную систему уравнений, \ (\ eqref {eq: eq2} \), у нас будет один из двух возможных вариантов количества решений.

Ровно одно решение, тривиальное решение
Бесконечно много ненулевых решений в дополнение к тривиальному решению.

Во втором варианте мы можем сказать ненулевое решение, потому что, если будет бесконечно много решений и мы знаем, что одно из них является тривиальным решением, тогда все остальные должны иметь хотя бы одно из \ (x_ {i} \) не равны нулю, и, следовательно, мы получаем ненулевое решение.

Используйте метод исключения Гаусса для решения следующей системы линейных уравнений.7x + 10y + 5: -4 13x + 6y +2: -31 Ilx + 14 …

1 (a) Используйте метод исключения Гаусса для решения системы линейных уравнений x + 2y …

1 (a) Используйте метод исключения Гаусса для решения системы линейных уравнений x + 2y + 22 = 4, 2x + y- z = -1 (b) Сформулируйте правило Крамера для решения систем линейных уравнений и используйте это для вычисления решения системы уравнений в (а)

2,3, 6, 7 1. Без матриц решите следующую систему, используя метод исключения Гаусса +…

2,3, 6, 7 1. Без матриц решите следующую систему, используя метод исключения Гаусса + 1 + HP 6x – Sy- -2 2. Рассмотрите следующую линейную систему уравнения 3x 2 Sy- (a) Запишите расширенную матрицу для этой линейной системы (b ) Используйте операции со строками, чтобы преобразовать расширенную матрицу в форму row.echelon (пометьте все шаги) (c) Используйте обратную подстановку для решения линейной системы. (найти x и y) x + 2y 2x = 5 3. Рассмотрим …

3 Линейные системы 18.Решите линейную систему уравнений, используя метод исключения наивного Гаусса …

3 Линейные системы 18. Решите линейную систему уравнений, используя метод исключения Гаусса x, + x: + x) = 1 + 2x, + 4×1 x 19. Решите линейную систему уравнений, используя метод исключения Гаусса с частичным поворотом 12×1. + 10×2-7×3 = 15 6x, + 5×2 + 3×3 = 14 24x, -x2 + 5x, = 28 20. Найдите LU-разложение для следующей системы линейных уравнений 6x, + 2x, +2, 2 21. Найдите приближенное решение следующей линейной системы уравнений…

Используйте метод исключения Гаусса для решения каждой из следующих систем линейных уравнений. В…

Используйте метод исключения Гаусса для решения каждой из следующих систем линейных уравнений. В каждом случае укажите, является ли система последовательной или непоследовательной. Приведите полный набор решений, и, если набор решений бесконечен, укажите три конкретных решения. 1-5×1 – 2×2 + 2×3 = 14 * (a) 3×1 + x2 – x3 = -8 2×1 + 2×2 – x3 = -3 3×1 – 3×2 – 2×3 = (b) -6×1 + 4×2 + 3×3 = -38 1-2×1 +…

2. (10 баллов) Используйте метод исключения Гаусса, чтобы решить следующую систему уравнений: 6x + y-z = 5-40-y + z = …

2. (10 баллов) Используйте метод исключения Гаусса, чтобы решить следующую систему уравнений: 6x + y-z = 5-40-y + z = -3 2x – z = -1

Решить методом замены или исключения: 3х – 2у = 26 -7x + 3y = -49 2

1. Решите методом замены или исключения: 3х – 2у = 26 -7x + 3y = -49 2. Решите методом замены или исключения: 4х – 5лет = 14 -12x + 15y = -42 3.Решить методом замены или исключения: -2x + 6y = 19 10x – 30 лет = -15 Второй набор проблем: 1. Постройте график уравнений 2x – 3y = 5 и 4x – 6y = 21 и интерпретируйте результат. 2. Постройте …

решить относительно x и y линейные уравнения методом исключения 2х + 6у = -2 5x-3y = 3 и -9x + 3y = 5 9х + 4у = -6 …

решить относительно x и y линейные уравнения методом исключения 2х + 6у = -2 5x-3y = 3 и -9x + 3y = 5 9х + 4у = -6 является ли следующая система зависимой, несовместимой или имеет уникальное решение? почему это так? х-8у = 9 6x-48y = 36

1) Решите следующую систему линейных уравнений, используя метод исключения Гаусса (5 баллов) 5×1…

1) Решите следующую систему линейных уравнений, используя метод исключения Гаусса (5 баллов) 5×1 + 5×2 + 3×3 = 10 3×1 + 8×2 – 3×3 = -1 4×1 + 2×2 + 5×3 = 4

Решите систему уравнений методом исключения Гаусса. (Если система зависимая, введите …

Решите систему уравнений методом исключения Гаусса. (Если система зависимая, введите общее решение в терминах c. Если решения нет 3y + 2z = 1 3x – 4y – 32-11 3x + Y Z-12 2x –

Решите систему уравнений с помощью матриц.Используйте метод исключения Гаусса с обратной подстановкой. х + …

Решите систему уравнений с помощью матриц. Используйте метод исключения Гаусса с обратной подстановкой. x + 4y 0 x + 5y + z = 4x y – z = – 33 Множество решений – {(DDD)}. (Упростите свои ответы.)

Система линейных уравнений – линейная алгебра с приложениями

Практические задачи во многих областях науки, таких как биология, бизнес, химия, информатика, экономика, электроника, инженерия, физика и социальные науки, часто можно свести к решению системы линейных уравнений.Линейная алгебра возникла в результате попыток найти систематические методы решения этих систем, поэтому естественно начать эту книгу с изучения линейных уравнений.

Если, и – действительные числа, график уравнения вида

– прямая линия (если и не равны нулю), поэтому такое уравнение называется линейным уравнением в переменных и. Однако часто удобно записывать переменные как, особенно когда задействовано более двух переменных.Уравнение вида

называется линейным уравнением в переменных. Здесь обозначают действительные числа (называемые коэффициентами соответственно), а также число (называемое постоянным членом уравнения). Конечный набор линейных уравнений с переменными называется системой линейных уравнений с этими переменными. Следовательно,

– линейное уравнение; коэффициенты при, и равны, и, а постоянный член равен.Обратите внимание, что каждая переменная в линейном уравнении встречается только в первой степени.

Для линейного уравнения последовательность чисел называется решением уравнения, если

, то есть, если уравнение удовлетворяется при выполнении замен. Последовательность чисел называется решением системы уравнений, если она является решением каждого уравнения в системе.

Система может не иметь решения вообще, может иметь уникальное решение или может иметь бесконечное семейство решений.Например, система не имеет решения, потому что сумма двух чисел не может быть одновременно 2 и 3. Система, у которой нет решения, называется несовместимой ; система с хотя бы одним решением называется согласованная .

Покажите, что для произвольных значений и

– это решение системы

Просто подставьте эти значения,, и в каждое уравнение.

Поскольку оба уравнения удовлетворяются, это решение для всех вариантов и.

Величины и в этом примере называются параметрами, , а набор решений, описанный таким образом, считается заданным в параметрической форме и называется общим решением для системы. Оказывается, что решения для каждой системы уравнений (если – это решений) могут быть заданы в параметрической форме (то есть, переменные задаются в терминах новых независимых переменных и т. Д. .).

Когда задействованы только две переменные, решения систем линейных уравнений могут быть описаны геометрически, потому что график линейного уравнения представляет собой прямую линию, если оба они не равны нулю. Более того, точка с координатами и лежит на прямой тогда и только тогда, когда – то есть когда, является решением уравнения. Следовательно, решения системы линейных уравнений соответствуют точкам, которые лежат на всех рассматриваемых линиях.

В частности, если система состоит только из одного уравнения, должно быть бесконечно много решений, потому что на прямой бесконечно много точек. Если система имеет два уравнения, есть три возможности для соответствующих прямых:

Линии пересекаются в одной точке. Тогда в системе есть уникальное решение , соответствующее этой точке.
Линии параллельны (и четкие) и не пересекаются. Тогда в системе нет решения .
Строки идентичны. Тогда в системе будет бесконечно много решений – по одному для каждой точки на (общей) прямой.

С тремя переменными график уравнения может быть показан как плоскость и, таким образом, снова дает «картину» множества решений. Однако у этого графического метода есть свои ограничения: когда задействовано более трех переменных, физическое изображение графов (называемых гиперплоскостями) невозможно. Необходимо обратиться к более «алгебраическому» методу решения.

Перед описанием метода мы вводим понятие, упрощающее вычисления. Рассмотрим следующую систему

трех уравнений с четырьмя переменными. Массив чисел

, встречающееся в системе, называется расширенной матрицей системы. Каждая строка матрицы состоит из коэффициентов переменных (по порядку) из соответствующего уравнения вместе с постоянным членом. Для наглядности константы разделены вертикальной линией.Расширенная матрица – это просто другой способ описания системы уравнений. Массив коэффициентов при переменных

называется матрицей коэффициентов системы, а
называется постоянной матрицей системы.

Элементарные операции

Алгебраический метод решения систем линейных уравнений описывается следующим образом. Две такие системы называются эквивалентами , если они имеют одинаковый набор решений.Система решается путем написания серии систем, одна за другой, каждая из которых эквивалентна предыдущей системе. Каждая из этих систем имеет тот же набор решений, что и исходная; цель состоит в том, чтобы получить систему, которую легко решить. Каждая система в серии получается из предыдущей системы простой манипуляцией, выбранной так, чтобы она не меняла набор решений.

В качестве иллюстрации мы решаем систему таким образом. На каждом этапе отображается соответствующая расширенная матрица.Исходная система –

Сначала вычтите дважды первое уравнение из второго. В результате получается система

.
, что эквивалентно оригиналу. На этом этапе мы получаем, умножив второе уравнение на. В результате получается эквивалентная система
.
Наконец, мы дважды вычитаем второе уравнение из первого, чтобы получить другую эквивалентную систему.
Теперь эту систему легко решить! И поскольку он эквивалентен исходной системе, он обеспечивает решение этой системы.
Обратите внимание, что на каждом этапе в системе (и, следовательно, в расширенной матрице) выполняется определенная операция для создания эквивалентной системы.
Следующие операции, называемые элементарными операциями , могут в обычном порядке выполняться над системами линейных уравнений для получения эквивалентных систем.
Поменять местами два уравнения.
Умножьте одно уравнение на ненулевое число.
Добавьте одно уравнение, кратное одному, к другому уравнению.
Предположим, что последовательность элементарных операций выполняется над системой линейных уравнений. Тогда полученная система имеет тот же набор решений, что и исходная, поэтому две системы эквивалентны.
Элементарные операции, выполняемые над системой уравнений, производят соответствующие манипуляции с строками расширенной матрицы. Таким образом, умножение строки матрицы на число означает умножение каждой записи строки на.Добавление одной строки к другой означает добавление каждой записи этой строки к соответствующей записи другой строки. Аналогично производится вычитание двух строк. Обратите внимание, что мы считаем две строки равными, если соответствующие записи совпадают.
В ручных вычислениях (и в компьютерных программах) мы манипулируем строками расширенной матрицы, а не уравнениями. По этой причине мы переформулируем эти элементарные операции для матриц.
Следующие операции называются операциями с элементарной строкой матрицы.
Поменять местами два ряда.
Умножить одну строку на ненулевое число.
Добавить кратное одной строки в другую строку.
На иллюстрации выше серия таких операций привела к матрице вида
, где звездочки обозначают произвольные числа. В случае трех уравнений с тремя переменными цель состоит в том, чтобы получить матрицу вида
Это не всегда происходит, как мы увидим в следующем разделе.Вот пример, в котором это действительно происходит.
Решение:
Расширенная матрица исходной системы –
Чтобы создать в верхнем левом углу, мы можем умножить строку с 1 на. Однако можно получить без введения дробей, вычтя строку 2 из строки 1. Результат:
Верхний левый угол теперь используется для «очистки» первого столбца, то есть для создания нулей в других позициях в этом столбце.Сначала отнимите строку 1 от строки 2, чтобы получить
.
Следующее умножение на строку 1 из строки 3. Результат:
.
Это завершает работу над столбцом 1. Теперь мы используем во второй позиции второй строки, чтобы очистить второй столбец, вычитая строку 2 из строки 1 и затем добавляя строку 2 к строке 3. Для удобства обе операции со строками сделано за один шаг. Результат
Обратите внимание, что две последние манипуляции не повлияли на первый столбец (во второй строке там стоит ноль), поэтому наши предыдущие усилия там не были подорваны.Наконец, мы очищаем третий столбец. Начните с умножения строки 3 на, чтобы получить
.
Теперь вычтите умножение строки 3 из строки 1, а затем прибавьте умножение строки 3 к строке 2, чтобы получить
.
Соответствующие уравнения:, и, которые дают (единственное) решение.
Алгебраический метод, представленный в предыдущем разделе, можно резюмировать следующим образом: Для данной системы линейных уравнений используйте последовательность элементарных операций со строками, чтобы преобразовать расширенную матрицу в «красивую» матрицу (что означает, что соответствующие уравнения легко решить. ).В примере 1.1.3 эта красивая матрица приняла вид
.
Следующие определения идентифицируют хорошие матрицы, возникающие в этом процессе.
Матрица, как говорят, находится в форме эшелон строки (и будет называться матрицей эшелон строки , если она удовлетворяет следующим трем условиям:
Все нулевые строки (полностью состоящие из нулей) находятся внизу.
Первая ненулевая запись слева в каждой ненулевой строке – это a, называемая ведущей для этой строки.
Каждый ведущий находится справа от всех ведущих в строках над ним.
Матрица строка-эшелон называется сокращенной строкой-эшелонной формой (и будет называться сокращенной матрицей строки-эшелон, если, кроме того, она удовлетворяет следующему условию:
4. Каждый ведущий элемент – это единственная ненулевая запись в своем столбце.
Матрицы «строка-эшелон» имеют форму «ступеньки», как показано в следующем примере (звездочки указывают произвольные числа).
Ведущие элементы проходят через матрицу «вниз и вправо». Записи выше и справа от ведущих s произвольны, но все записи ниже и слева от них равны нулю. Следовательно, матрица в виде эшелона строк находится в сокращенной форме, если, кроме того, все элементы непосредственно над каждым ведущим равны нулю. Обратите внимание, что матрица в форме эшелона строк может с помощью нескольких дополнительных операций со строками быть приведена к сокращенной форме (используйте операции со строками, чтобы последовательно создавать нули над каждой ведущей единицей, начиная справа).
Важность матриц «строка-эшелон» вытекает из следующей теоремы.
Каждая матрица может быть приведена к (сокращенной) форме строки-эшелона последовательностью элементарных операций со строками.
Фактически, мы можем дать пошаговую процедуру для фактического нахождения матрицы ряда строк. Обратите внимание: несмотря на то, что существует множество последовательностей операций со строками, которые приведут матрицу к форме ряда строк, та, которую мы используем, является систематической и ее легко программировать на компьютере. Обратите внимание, что алгоритм имеет дело с матрицами в целом, возможно, со столбцами нулей.
Шаг 1. Если матрица полностью состоит из нулей, остановитесь – она уже в виде эшелона строк.
Шаг 2. В противном случае найдите первый столбец слева, содержащий ненулевую запись (назовите его), и переместите строку, содержащую эту запись, в верхнюю позицию.
Шаг 3. Теперь умножьте новую верхнюю строку на, чтобы создать интерлиньяж.
Шаг 4. Вычитая кратные числа этой строки из строк под ней, сделайте каждую запись ниже начального нуля. Это завершает первую строку, и все дальнейшие операции со строками выполняются с оставшимися строками.
Шаг 5. Повторите шаги 1–4 для матрицы, состоящей из оставшихся строк.
Процесс останавливается, когда либо на шаге 5 не остается строк, либо оставшиеся строки состоят полностью из нулей.
Обратите внимание на то, что гауссовский алгоритм является рекурсивным: когда получен первый ведущий, процедура повторяется для оставшихся строк матрицы. Это упрощает использование алгоритма на компьютере. Обратите внимание, что в решении примера 1.1.3 не использовался гауссовский алгоритм в том виде, в каком он был написан, потому что первый ведущий не был создан путем деления строки 1 на.Причина этого в том, что он избегает дробей. Однако общий шаблон ясен: создайте ведущие слева направо, используя каждый из них по очереди, чтобы создать нули под ним. Вот один пример.
Решение:
Соответствующая расширенная матрица –
Создайте первую ведущую, поменяв местами строки 1 и 2
Теперь вычтите умноженную строку 1 из строки 2 и вычтите умноженную строку 1 из строки 3.Результат
Теперь вычтите строку 2 из строки 3, чтобы получить
.
Это означает, что следующая сокращенная система уравнений
эквивалентен исходной системе. Другими словами, у них одинаковые решения. Но эта последняя система явно не имеет решения (последнее уравнение требует этого и удовлетворяет, а таких чисел не существует). Следовательно, исходная система не имеет решения.
Для решения линейной системы расширенная матрица преобразуется в сокращенную форму строки-эшелон, а переменные, соответствующие ведущим, называются ведущими переменными .Поскольку матрица представлена в сокращенной форме, каждая ведущая переменная встречается ровно в одном уравнении, поэтому это уравнение может быть решено для получения формулы для ведущей переменной в терминах не ведущих переменных. Принято называть нелидирующие переменные «свободными» переменными и маркировать их новыми переменными, называемыми параметрами . Каждый выбор этих параметров приводит к решению системы, и каждое решение возникает таким образом. Эта процедура в целом работает и получила название
.
Для решения системы линейных уравнений выполните следующие действия:
Перенести расширенную матрицу \ index {расширенную матрицу} \ index {матрица! Расширенная матрица} в сокращенную матрицу-эшелон строк, используя элементарные операции со строками.
Если возникает строка, система несовместима.
В противном случае присвойте не ведущие переменные (если они есть) в качестве параметров и используйте уравнения, соответствующие сокращенной матрице строки-эшелон, чтобы найти ведущие переменные в терминах параметров.
Существует вариант этой процедуры, в котором расширенная матрица переносится только в строчно-эшелонированную форму. Не ведущие переменные, как и раньше, назначаются как параметры. Затем последнее уравнение (соответствующее форме строки-эшелона) используется для решения последней ведущей переменной в терминах параметров.Эта последняя ведущая переменная затем подставляется во все предыдущие уравнения. Затем второе последнее уравнение дает вторую последнюю ведущую переменную, которая также подставляется обратно. Процесс продолжает давать общее решение. Эта процедура называется обратной заменой . Можно показать, что эта процедура численно более эффективна и поэтому важна при решении очень больших систем.
Рейтинг
Можно доказать, что уменьшенная строка-эшелонированная форма матрицы однозначно определяется.То есть, независимо от того, какая серия операций со строками используется для переноса в сокращенную матрицу эшелонов строк, результатом всегда будет одна и та же матрица. Напротив, это неверно для матриц ряда строк: разные серии операций со строками могут переносить одну и ту же матрицу в разные матрицы ряда строк. В самом деле, матрица может быть перенесена (с помощью одной строковой операции) в матрицу-эшелон строк, а затем с помощью другой строковой операции в (сокращенную) матрицу-эшелон. Однако – это , правда, что количество ведущих единиц должно быть одинаковым в каждой из этих матриц строки-эшелон (это будет доказано позже).Следовательно, количество зависит только от того, каким образом приведено в строй.
Ранг матрицы – это количество ведущих s в любой матрице строка-эшелон, к которой могут быть перенесены операции со строками.
Вычислить ранг.
Решение:
Приведение к строчной форме
Так как эта матрица эшелонов строк имеет два ведущих s, rank.
Предположим, что ранг, где – матрица со строками и столбцами.Тогда потому что ведущие s лежат в разных строках, и потому что ведущие s лежат в разных столбцах. Более того, у ранга есть полезное приложение к уравнениям. Напомним, что система линейных уравнений называется непротиворечивой, если она имеет хотя бы одно решение.
Проба:
Тот факт, что ранг расширенной матрицы равен, означает, что есть ровно ведущие переменные и, следовательно, точно не ведущие переменные. Все эти нелидирующие переменные назначаются как параметры в гауссовском алгоритме, поэтому набор решений включает в себя именно параметры.Следовательно, если существует хотя бы один параметр, а значит, и решений бесконечно много. Если, нет параметров и поэтому единственное решение.
Теорема 1.2.2 показывает, что для любой системы линейных уравнений существуют ровно три возможности:
Нет решения . Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система несовместима.
Уникальное решение . Это происходит, когда каждая переменная является ведущей переменной.
Бесконечное множество решений . Это происходит, когда система согласована и есть хотя бы одна не ведущая переменная, поэтому задействован хотя бы один параметр.
https://www.geogebra.org/m/cwQ9uYCZ
Пожалуйста, ответьте на эти вопросы после открытия веб-страницы:
1. Что представляет собой каждая из них для данной линейной системы?
2. Исходя из графика, что можно сказать о решениях? Есть ли у системы одно решение, нет решения или бесконечно много решений? Почему
3.Измените постоянный член в каждом уравнении на 0, что изменилось на графике?
4. Для следующей линейной системы:
Можете ли вы решить это методом исключения Гаусса? Что вы наблюдаете, глядя на график?
Многие важные проблемы связаны с линейными неравенствами , а не с линейными уравнениями Например, условие для переменных и может принимать форму неравенства, а не равенства.Существует метод (называемый симплексным алгоритмом ) для поиска решений системы таких неравенств, который максимизирует функцию вида где и являются фиксированными константами.
Система уравнений с переменными называется однородной , если все постоянные члены равны нулю, то есть если каждое уравнение системы имеет вид
Очевидно, решение такой системы; это называется тривиальным решением .Любое решение, в котором хотя бы одна переменная имеет ненулевое значение, называется нетривиальным решением .
Наша главная цель в этом разделе – дать полезное условие, при котором однородная система имеет нетривиальные решения. Следующий пример поучителен.
Покажите, что следующая однородная система имеет нетривиальные решения.
Решение:
Приведение расширенной матрицы к сокращенной форме эшелона строк описано ниже.
Ведущими переменными являются,, и, например, назначается как параметр.Тогда общее решение:,,,. Отсюда, взяв (скажем), получаем нетривиальное решение:,,,.
Существование нетривиального решения в примере 1.3.1 обеспечивается наличием параметра в решении. Это связано с тем, что существует не ведущая переменная (в данном случае). Но здесь должно быть не ведущей переменной, потому что есть четыре переменных и только три уравнения (и, следовательно, не более три ведущие переменные).Это обсуждение обобщает доказательство следующей основной теоремы.
Если однородная система линейных уравнений имеет больше переменных, чем уравнений, то она имеет нетривиальное решение (фактически бесконечно много).
Проба:
Предположим, что есть уравнения в переменных, где, и пусть обозначают сокращенную строчно-эшелонированную форму расширенной матрицы. Если есть ведущие переменные, есть не ведущие переменные и, следовательно, параметры. Следовательно, достаточно показать это.Но потому что имеет ведущие единицы и строки, и по гипотезе. Итак, что дает.
Обратите внимание, что обратное утверждение теоремы 1.3.1 неверно: если однородная система имеет нетривиальные решения, она не должна иметь больше переменных, чем уравнения (система имеет нетривиальные решения, но.)
Теорема 1.3.1 очень полезна в приложениях. В следующем примере представлена иллюстрация из геометрии.
Мы называем график уравнения конической , если числа, и не все равны нулю.Покажите, что есть хотя бы одна коника, проходящая через любые пять точек на плоскости, которые не все лежат на одной прямой.
Решение:
Пусть координаты пяти точек будут,,, и. График проходов if
Это дает пять уравнений, по одному для каждого, линейных по шести переменным,,,,, и. Следовательно, по теореме 1.1.3 существует нетривиальное решение. Если все пять точек лежат на линии с уравнением, вопреки предположению. Следовательно, один из “ отличен от нуля.
Линейные комбинации и базовые решения
Что касается строк, два столбца считаются равными , если они имеют одинаковое количество записей и соответствующие записи одинаковы. Позвольте и быть столбцами с одинаковым количеством записей. Что касается операций с элементарными строками, их сумма получается путем сложения соответствующих записей, и, если это число, скалярное произведение определяется путем умножения каждой записи на. Точнее:
Сумма скалярных кратных нескольких столбцов называется линейной комбинацией этих столбцов.Например, это линейная комбинация и для любого выбора чисел и.
Решение:
Для, мы должны определить, существуют ли числа, и такие, что, то есть
Приравнивание соответствующих элементов дает систему линейных уравнений,, и для,, и. Путем исключения Гаусса решение есть, и где – параметр. Взяв, мы видим, что это линейная комбинация, и.
Обращаясь к, снова ищем, и такие, что; то есть
, что приводит к уравнениям,, и для действительных чисел, и.Но на этот раз, как может проверить читатель, нет решения , равно как и , а не , линейная комбинация, и.
Наш интерес к линейным комбинациям проистекает из того факта, что они предоставляют один из лучших способов описания общего решения однородной системы линейных уравнений. Когда
решает такую систему с переменными, запишите переменные в виде матрицы столбцов:. Обозначается тривиальное решение. В качестве иллюстрации, общее решение в
Пример 1.3.1 – это,, и, где – параметр, и теперь мы могли бы выразить это как
, говоря, что общее решение -, где произвольно.
Теперь пусть и – два решения однородной системы с переменными. Тогда любая линейная комбинация этих решений снова оказывается решением системы. В более общем плане:
Фактически, предположим, что типичное уравнение в системе имеет вид, и предположим, что
, являются решениями. Потом и
.
Следовательно, это тоже решение, потому что
Аналогичный аргумент показывает, что Утверждение 1.1 верно для линейных комбинаций более двух решений.
Примечательно то, что каждое решение однородной системы представляет собой линейную комбинацию определенных частных решений, и, фактически, эти решения легко вычисляются с использованием гауссовского алгоритма. Вот пример.
Решить однородную систему с матрицей коэффициентов
Решение:
Приведение дополненной матрицы к уменьшенной форме –
, поэтому решениями являются,, и методом исключения Гаусса.Следовательно, мы можем записать общее решение в матричной форме
Вот и частные решения, определяемые гауссовским алгоритмом.
Решения и в примере 1.3.5 обозначены следующим образом:
Алгоритм Гаусса систематически выдает решения для любой однородной линейной системы, называемые базовыми решениями , по одному для каждого параметра.
Кроме того, алгоритм дает стандартный способ выразить каждое решение как линейную комбинацию базовых решений, как в Примере 1.3.5, где общее решение принимает вид
Следовательно, вводя новый параметр, мы можем умножить исходное базовое решение на 5 и таким образом исключить дроби.
По этой причине:
Любое ненулевое скалярное кратное базового решения будет по-прежнему называться базовым решением.
Таким же образом алгоритм Гаусса выдает базовые решения для в каждой однородной системе, по одному для каждого параметра ( нет базовых решений, если система имеет только тривиальное решение).Более того, каждое решение задается алгоритмом как линейная комбинация
этих базовых решений (как в Примере 1.3.5). Если имеет ранг, теорема 1.2.2 показывает, что есть ровно параметры, а значит, и базовые решения. Это доказывает:
Найдите основные решения однородной системы с матрицей коэффициентов и выразите каждое решение как линейную комбинацию основных решений, где
Решение:
Приведение расширенной матрицы к сокращенной форме строки-эшелона равно
, поэтому общее решение – это,,,, и где, и – параметры.В матричной форме это
Отсюда базовые решения –
Я занимаюсь математикой · Программа для решения одновременных линейных уравнений
См. Также: матрица, исключение Гаусса-Жордана, геометрическое линейное преобразование
Калькулятор, представленный ниже, решит одновременные линейные уравнения с двумя, тремя и до 10 переменными, если система уравнений имеет единственное решение.
Для систем уравнений с множеством решений используйте метод исключения Гаусса-Жордана.
Прокрутите вниз, чтобы прочитать о различных методах решения одновременных линейных уравнений.
Программа для решения одновременных линейных уравнений
Выберите размер системы.
загрузка. . .
Расчет. . .

Сообщайте о любых ошибках на [адрес электронной почты]

Методы решения одновременных линейных уравнений
Существует как минимум пять методов решения одновременных линейных уравнений.
Например, давайте попробуем найти решение для следующего набора одновременных линейных уравнений с 3 переменными
{x & plus; y − z = 1 (1) 8⁢x & plus; 3⁢y − 6⁢z = 1 (2) −4⁢x − y & plus; 3⁢z = 1 (3)
Метод исключения
Как следует из названия, этот метод пытается исключить переменные, пока не останется только 1 переменная.
Во-первых, посмотрите на уравнения и попытайтесь найти 2 уравнения с одинаковым коэффициентом (плюс или минус) для одинаковых переменных. Например, см. Уравнения (1) и (3). Коэффициент для y равен 1 и -1 соответственно. Мы можем сложить два уравнения, чтобы исключить y, и мы получим уравнение (4).
x & plus; y − z = 1 (1) −4⁢x − y & plus; 3⁢z = 1 (3) ———————— & plus ; −3⁢x & plus; 0 & plus; 2⁢z = 2 (4)
Обратите внимание, что уравнение (4) состоит из переменных x и z. Теперь нам нужно другое уравнение, которое имеет те же переменные, что и уравнение (4).Чтобы получить это, мы исключим y из уравнений (1) и (2). В уравнениях (1) и (2) коэффициенты при y равны 1 и 3 соответственно. Чтобы исключить y, мы умножаем уравнение (1) на 3, а затем вычитаем уравнение (2) из уравнения (1).
x & plus; y − z = 1 (1) × 3 8⁢x & plus; 3⁢y − 6⁢z = 1 (2)
3⁢x & plus; 3⁢y − 3⁢z = 3 (1) 8⁢x & plus; 3 ⁢Y − 6⁢z = 1 (2) ———————— −−5⁢x & plus; 0⁢y & plus; 3⁢z = 2 (5)
Теперь, используя уравнения (4) и (5), мы можем исключить z.
−3⁢x & plus; 2⁢z = 2 (4) × 3 −5⁢x & plus; 3⁢z = 2 (5) × 2
−9⁢x & plus; 6⁢z = 6 (4) −10⁢x & plus; 6 ⁢Z = 4 (5) ———————— – & plus; 01⁢x & plus; 0⁢z = 2 (6)
Из уравнения ( 6) получаем x = 2.Теперь мы можем подставить это значение x в уравнение (4), чтобы получить значение z.
−3⁢ (2) & plus; 2⁢z = 2 (4) −6 & plus; 2⁢z = 22⁢z = 2 & plus; 62⁢z = 8z = 8 ÷ 2z = 4
Наконец, мы можем подставить значения x и z в уравнение (1), чтобы получить y.
2 & plus; y − 4 = 1 (1) y = 1−2 & plus; 4y = 3
Следовательно, решение системы линейных уравнений имеет вид х = 2, у = 3, г = 4.
Метод замещения
Во-первых, давайте перегруппируем уравнение (1) так, чтобы только 1 переменная находилась в левой части.
x = 1 − y & plus; z (1)
Теперь давайте подставим этот x в уравнение (2).
8⁢ (1 − y & plus; z) & plus; 3⁢y − 6⁢z = 1 (2) 8−8⁢y & plus; 8⁢z & plus; 3⁢y − 6⁢z = 1−5⁢y & plus; 2⁢z = 1−8−5⁢y & plus; 2⁢z = −7 (4)
Аналогичным образом подставим x в уравнение (3).
−4⁢ (1 − y & plus; z) −y & plus; 3⁢z = 1 (3) −4 & plus; 4⁢y − 4⁢z − y & plus; 3⁢z = 13⁢y − z = 1 & plus; 43⁢y− z = 5 (5)
Теперь давайте перегруппируем уравнение (5) так, чтобы только 1 переменная находилась в левой части.
z = 3⁢y − 5 (5)
Затем подставляем это значение z в уравнение (4).
−5⁢y & plus; 2⁢ (3⁢y − 5) = – 7 (4) −5⁢y & plus; 6⁢y − 10 = −7y = −7 & plus; 10y = 3
Теперь, когда мы нашли y, мы можем подставьте это в уравнение (5), чтобы найти z.
z = 3⁢ (3) −5 (5) z = 9−5z = 4
Наконец, мы можем подставить значение y и z в уравнение (1), чтобы получить значение x.
х = 1-3 & плюс; 4 (1) х = 2

Графический метод
Решение системы линейных уравнений с использованием графического метода выполняется путем рисования линий или плоскостей, которые представляют каждое уравнение.Решение – это координаты пересечения линий или плоскостей.
Для простоты рассмотрим систему линейных уравнений с двумя переменными.
{x & plus; y = 32⁢x − y = −3
Постройте линии этих двух уравнений.
Как показано на графике, две прямые пересекаются в точке (0,3). Это решение системы линейных уравнений, т.е. x = 0, у = 3.
Для системы линейных уравнений с тремя переменными решением является точка пересечения трех плоскостей, представляющих каждое уравнение.
Метод обратной матрицы
Система линейных уравнений, определяемая уравнениями (1), (2) и (3), может быть выражена в матричной форме следующим образом.
A⁢B = C12−183−6−4−13⁢xyz = 111
Множеством решений является матрица B. Чтобы выделить только B на одной стороне уравнения, мы умножаем обе части уравнения на матрицу, обратную матрице A
A − 1⁢A⁢B = A − 1⁢CB = A − 1⁢C
Теперь, чтобы найти B, нам нужно найти A − 1. Пожалуйста, проверьте страницу матрицы, чтобы узнать, как найти обратную матрицу.
A − 1 = −323012−435B = −323012−435⁢111B = 234
Следовательно, множество решений х = 2, у = 3, г = 4.
Исключение Гаусса / Исключение Гаусса-Джордана
Система линейных уравнений, определяемая уравнениями (1), (2) и (3), может быть выражена в форме расширенной матрицы следующим образом.
A = 11−1 | 183−6 | 1−4−13 | 1
Выполняя серию операций со строками (исключение Гаусса), мы можем привести указанную выше матрицу к ее эшелонированной форме по строкам.
A = 10,375−0,75 | 0,12501−0,4 | 1.4001 | 4
Затем мы можем выполнить обратную подстановку, чтобы получить значения всех неизвестных / переменных, или мы можем выполнять дальнейшие операции со строками, пока матрица приведена в виде приведенного ряда строк (с использованием метода исключения Гаусса-Жордана).
A = 100 | 2010 | 3001 | 4
Выполняя исключение Гаусса-Жордана, мы получаем решение системы уравнений в последнем столбце: x = 2, у = 3, г = 4.
Чтобы просмотреть пошаговые операции со строками, см. Страницу исключения Гаусса-Джордана.
Запутались, есть вопросы? У нас есть ответы.С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области.
Джимми Си
См. Также: матрица, исключение Гаусса-Жордана, геометрическое линейное преобразование

Исключение по Гауссу – Предварительное вычисление | Сократик

ПРИМЕР:
Используйте метод исключения Гаусса для решения следующей системы уравнений.
# x + 2y + 3z = -7 #
# 2x-3y-5z = 9 #
# -6z-8y + z = -22 #
Решение:
Настроить расширенную матрицу формы.
# ((1,2,3, |, -7), (2,3, -5, |, 9), (- 6, -8,1, |, 22)) #
Цель 1. Получите 1 в верхнем левом углу.
Уже сделано.
Цель 2a: Получите ноль под 1 в первом столбце.
Умножьте строку 1 на # -2 #, чтобы получить
# ((- 2, -4, -6, |, 14)) #
Добавьте результат в строку 2 и поместите результат в строку 2.
Обозначим операции как # -2R_2 + R_1 → R_2 #.
# ((1,2,3, |, -7), (2,3, -5, |, 9), (- 6, -8,1, |, 22)) stackrel (-2R_1 + R_2 → R_2) (→) ((1,2,3, |, -7), (0, -7, -11, |, 23), (- 6, -8,1, |, 22)) #
Цель 2b: Получите еще один ноль в первом столбце.
Для этого нам понадобится операция # 6R_1 + R_3 → R_3 #.
# ((1,2,3, |, -7), (0, -7, -11, |, 23), (- 6, -8,1, |, 22)) stackrel (6R_2 + R_3 → R_3) (→) ((1,2,3, |, -7), (0, -7, -11, |, 23), (0,4,19, |, -64)) #
Цель 2c. Получите оставшийся ноль.
Умножьте строку 2 на # -1 / 7 #.
# ((1,2,3, |, -7), (0, -7, -11, |, 23), (0,4,19, |, -64)) stackrel (- (1/7 ) R_2 → R_2) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,4,19, |, -64 )) #
Теперь используйте операцию # -4R_2 + R_3 → R_3 #.
# ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,4,19, |, -64)) stackrel (-4R_2 + R_3 → R_3) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,0,89 / 7, |, -356/7)) #
Умножьте третью строку на # 7/89 #.
# ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,0,89 / 7, |, -356 / 7)) stackrel (7 / 89R_3 → R_3) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,0,1, | , -4)) #
Цель 3. Используйте обратную замену, чтобы получить значения # x #, # y # и # z #.
Цель 3а. Рассчитайте # z #.
#z = -4 #
Цель 3b. Вычислить # y #.
# y + 11 / 7z = -23 / 7 #
# y-44/7 = -23 / 7 #
# y = 44 / 7-23 / 7 = 21/7 #
# у = 3 #
Цель 3c. Вычислить x.
# x + 2y + 3z = -7 #
# x + 6-12 = -7 #
# x-6 = -7 #
# х = 1 #
Решение: # x = 1, y = 3, z = -4 #
Форма эшелона строк и форма сокращенного эшелона строк

Содержание (Щелкните, чтобы перейти к этому разделу:
Что такое форма эшелона?
Форма ступенчатого эшелона
Форма ступенчатого редуктора
Исключение по Гауссу
Ранг матрицы
Посмотрите видео с определениями эшелонов, рядов и пониженных рядов:

Не можете посмотреть видео? Кликните сюда.
Что такое форма эшелона?
Форма
Echelon означает, что матрица находится в одном из двух состояний:
Рядная форма эшелона.
Уменьшенная форма эшелона строки.
Это означает, что матрица удовлетворяет следующим трем требованиям:
Первое число в строке (называемое ведущим коэффициентом) – 1. Примечание: некоторые авторы не требуют, чтобы ведущий коэффициент был равен 1; это могло быть любое число. Вы можете узнать у своего инструктора, какой версии этого правила они придерживаются).
Каждая ведущая единица находится справа от первой.
Любые ненулевые строки всегда находятся над строками со всеми нулями.
Следующие примеры представляют собой матрицы в эшелонированной форме:
Следующие примеры представляют собой , а не в эшелонированной форме:

Матрица A не имеет строк со всеми нулями ниже ненулевых строк.
Матрица B имеет 1 на второй позиции в третьей строке. Для формы эшелона строки он должен быть справа от ведущего коэффициента над ним.Другими словами, он должен быть на четвертой позиции вместо 3.
Matrix C имеет 2 в качестве ведущего коэффициента вместо 1.
Matrix D имеет -1 в качестве ведущего коэффициента вместо 1.
Другой способ думать о матрице в форме эшелона – это то, что матрица подверглась гауссовскому исключению, которое представляет собой серию операций со строками.
Уникальность и формы эшелона
Эшелонированная форма матрицы не уникальна, что означает, что при сокращении строк возможно бесконечное количество ответов.Уменьшенная форма эшелона строки находится на другом конце спектра; уникальна на , что означает, что сокращение строк в матрице даст один и тот же ответ независимо от того, как вы выполняете одни и те же операции со строками.
Вернуться к началу.
Что такое форма эшелона строк?
Матрица находится в форме эшелона строк, если она соответствует следующим требованиям:
Первое ненулевое число слева («ведущий коэффициент») всегда находится справа от первого ненулевого числа в строке выше.
Строки, состоящие из всех нулей, находятся внизу матрицы.
Форма рядного эшелона. «А» может представлять любое число.

Технически ведущий коэффициент может быть любым числом. Однако в большинстве учебников линейной алгебры утверждается, что ведущим коэффициентом должно быть число 1. Чтобы добавить путаницы, некоторые определения формы эшелона строк утверждают, что должны быть нули как выше , так и на ниже ведущего коэффициента. Поэтому лучше всего следовать определению, данному в учебнике, которому вы следуете (или тому, что дал вам ваш профессор).Если вы не уверены (то есть сейчас воскресенье, у вас должна быть домашняя работа, и вы не можете связаться с профессором), безопаснее всего использовать 1 в качестве ведущего коэффициента в каждой строке.
Если ведущим коэффициентом в каждой строке является ненулевое число только в этом столбце, матрица называется уменьшенной эшелонированной строкой.
Матрица 3 × 5 в сокращенной форме эшелона строк.
Строковые формы эшелона обычно встречаются в линейной алгебре, когда вас иногда просят преобразовать матрицу в эту форму.Форма эшелона строк может помочь вам увидеть, что представляет собой матрица, а также является важным шагом к решению систем линейных уравнений.

Онлайн-калькулятор формы эшелона строк
Этот онлайн-калькулятор преобразует любую матрицу, и предоставляют операции со строками, которые помогут вам от шага к шагу. На следующем изображении (из калькулятора Университета Старого Доминиона показано, как матрица [01, 00, 59] приводится к форме эшелона строк с помощью двух простых операций со строками:

Back to Top.
Что такое форма сокращенного эшелона строк?
Уменьшенная форма эшелона строк – это тип матрицы, используемой для решения систем линейных уравнений. Форма пониженного ряда имеет четыре требования:
Первое ненулевое число в первой строке (, ведущая запись ) – это число 1.
Вторая строка также начинается с цифры 1, которая находится правее первой записи в первой строке. В каждом последующем ряду цифра 1 должна быть правее.
Начальная запись в каждой строке должна быть единственным ненулевым числом в ее столбце.
Любые ненулевые строки помещаются внизу матрицы.
Матрица 3 × 5 в сокращенной форме эшелона строк.
Преобразование матрицы в форму сокращенного эшелона строк
Любая матрица может быть преобразована в сокращенную форму эшелона строк с помощью метода, называемого исключением по Гауссу. Это особенно полезно для решения систем линейных уравнений. Большинство графических калькуляторов (например, TI-83) имеют функцию rref, которая преобразует матрицу в сокращенную форму эшелона строк.См. Эту статью на веб-сайте Университета штата Колорадо, где приведены инструкции по использованию TI-89 и TI-83 для расчета формы сокращенного эшелона строки.
Этот онлайн-калькулятор на веб-сайте Old Dominion University преобразует вводимую вами матрицу в сокращенную форму эшелона строк.
Для ручного расчета требуется знание элементарных операций со строками, а именно:
Поменять местами один ряд другим.
Умножить одну строку на ненулевую константу.
Заменить одну строку на: одну строку плюс константу, умноженную на другую строку.
Кроме того, недостаточно просто знать правила, вы должны уметь взглянуть на матрицу и принять логическое решение о том, какое правило вы собираетесь использовать и когда. Вы пытаетесь преобразовать матрицу в сокращенный ряд строк, поэтому вам также необходимо выполнить четыре требования, приведенные в начале этой статьи. Если вам нужно вручную преобразовать матрицу в сокращенную форму эшелона строк, рекомендуется использовать один из приведенных выше калькуляторов, чтобы проверить свою работу. Фактически, если вы используете онлайн-калькулятор ODU, он даже предоставит вам операции со строками.На изображении ниже показано преобразование калькулятором матрицы [204,923]:

Вернуться к началу.
Что такое метод исключения Гаусса?
Метод исключения Гаусса – это способ найти решение системы линейных уравнений. Основная идея состоит в том, что вы выполняете математическую операцию над строкой и продолжаете, пока не останется только одна переменная. Например, некоторые возможные операции со строками:
Поменять местами любые два ряда
Сложите две строки вместе.
Умножьте одну строку на ненулевую константу (т.е. 1/3, -1, 5)
Вы также можете выполнять более одной строковой операции одновременно. Например, умножьте одну строку на константу, а затем добавьте результат к другой строке.
После этого цель состоит в том, чтобы получить матрицу в сокращенной форме эшелона строк, где ведущий коэффициент, 1, в каждой строке находится справа от ведущего коэффициента в строке над ней. Другими словами, вам нужно получить 1 в верхнем левом углу матрицы. В следующей строке должен быть 0 в позиции 1 и 1 в позиции 2.Это дает вам решение системы линейных уравнений.
Пример исключения по Гауссу
Решите следующую систему линейных уравнений методом исключения Гаусса:
х + 5у = 7
-2x – 7y = -5
Шаг 1. Преобразуйте уравнение в форму матрицы коэффициентов . Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:

Шаг 2. Превратите числа в нижней строке в положительные, прибавив 2 раза первую строку:

Шаг 3: Умножьте вторую строку на 1/3.Это дает вам второй ведущий 1:

Шаг 4: Умножьте строку 2 на -5, а затем добавьте это к строке 1:
Вот и все!
В первой строке у вас x = -8, а во второй строке y = 3. Обратите внимание, что x и y находятся в тех же положениях, что и при преобразовании уравнения на шаге 1, поэтому все, что вам нужно сделать, это прочтите решение:
Вернуться к началу.
Что такое ранг матрицы?
Ранг матрицы равен количеству линейно независимых строк.Линейно независимая строка – это строка, которая не является комбинацией других строк.
Следующая матрица имеет две линейно независимых строки (1 и 2). Однако, когда в смесь добавляется третья строка, вы можете видеть, что первая строка теперь равна сумме второй и третьей строк. Следовательно, ранг этой конкретной матрицы равен 2, так как есть только две линейно независимых строки.
Ранг матрицы всегда будет на меньше, чем – количество ненулевых строк или количество столбцов в матрице.Если все строки в матрице линейно независимы, матрица имеет ранг , полный ранг строки . Для квадратной матрицы она имеет полный ранг только в том случае, если ее определитель не равен нулю.
Выяснить ранг матрицы, пытаясь определить на глаз, сколько строк или столбцов линейно независимы, может быть практически невозможно. Более простой (и, возможно, очевидный) способ – преобразовать в форму эшелона строк.
Как найти матрицу Рейтинг
Найти ранг матрицы просто, если вы знаете, как найти матрицу эшелона строк.Чтобы найти ранг любой матрицы:
Найдите матрицу эшелонов строк.
Подсчитать количество ненулевых строк.
Преобразование матрицы в форму эшелона строк.

Вышеупомянутая матрица была преобразована в форму эшелона строк с двумя ненулевыми строками. Следовательно, ранг матрицы равен 2.
Вы также можете найти отличный инструмент для конвертации на сайте Old Dominion University.
Вернуться к началу.
Список литературы
Эверитт, Б.S .; Скрондал, А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Сирл, С. (2017). Матричная алгебра, полезная для статистики (серия Уайли по вероятности и статистике), 2-е издание. Вайли.
————————————————– —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Метод исключения Гаусса (Введение в линейные системы)
Метод исключения Гаусса – это процедура решения систем линейных уравнений. Его можно описать как последовательность операций, выполняемых над соответствующей матрицей коэффициентов. Мы мотивируем исключение Гаусса и исключение Гаусса – Жордана несколькими примерами с упором на понимание операций со строками.

Введение в системы линейных уравнений
Система линейных уравнений с двумя переменными $ x $ и $ y $ имеет вид $$ \ begin {cases} ax + by = c \\ d x + ey = f \ end {ases} $$ где $ a, b , c, d, e, f $ заданы числа, такие как действительные или комплексные числа. Иногда система линейных уравнений также записывается с использованием индексов \ begin {equal} \ label {2by2sys} \ begin {cases} a_ {11} x + a_ {12} y = b_1 \\ a_ {21} x + a_ {22} y = b_2 \ end {case} \ end {формула}, чтобы уменьшить количество используемых букв.Для простоты давайте временно предположим, что коэффициенты являются ненулевыми действительными числами, и зададимся вопросом: сколько решений может быть у системы $ 2 \ times 2 $? Ключевая идея состоит в том, чтобы понять, что каждое линейное уравнение представляет собой линию в декартовой плоскости. Если мы рассмотрим возможные способы пересечения прямых на плоскости, мы приходим к выводу, что не должно быть решений, одно единственное решение или бесконечно много точек $ (x, y) $, которые решают систему.
Пример .Определите, соответствует ли система линейных уравнений \ begin {уравнение} \ label {consys} \ begin {cases} 2x + 3y = 0 \\ 4x + 5y = 0. \ end {ases} \ end {Equation} не имеет решений, ровно одно решение или бесконечно много решений. Если мы умножим первое уравнение, а именно $ 2x + 3y = 0 $, на 2 и вычтем из второго уравнения $ 4x + 5y = 0 $, мы получим $ y = 0. $ Следовательно, решение является единственным и имеет вид $ (x , y) = (0,0). $
Система линейных уравнений $ 3 \ times 3 $ имеет вид \ begin {уравнение} \ label {3by3sys} \ begin {cases} a_ {11} x + a_ {12} y + a_ {13} z = b_1 \\ a_ {21} x + a_ {22} y + a_ {23} z = b_2 \\ a_ {31} x + a_ {32} y + a_ {33} z = b_3 \\ \ end {case} \ end { уравнение}, где $ a_ {ij} $ и $ b_1, b_2, b_3 $ – числа, а $ x, y, z $ – переменные.Геометрически линейные уравнения с тремя переменными – это просто плоскости в трех измерениях. Итак, каковы различные типы наборов решений для системы? Рассматривая возможные способы пересечения трех плоскостей в трех измерениях, мы приходим к выводу, что не должно быть решений, одно единственное решение или бесконечно много точек $ (x, y, z) $, которые решают систему.
Пример . Определите, соответствует ли система линейных уравнений \ begin {уравнение} \ label {linesysex1} \ begin {cases} x + 2y + 3z = 0 \\ 4x + 5y + 6z = 3 \\ 7x + 8y + 9z = 0 \ end { case} \ end {equal} не имеет решений, ровно одно решение или бесконечно много решений.Умножьте первое уравнение на $ -2 $ и добавьте ко второму уравнению, получив уравнение $ 2x + y = 3. $ Удалив $ z $ из первого и третьего уравнений, мы получим $ 4x + 2y = 0 $, умножив первое уравнение. на $ -3 $ и добавив к третьему уравнению. $ X $ и $ y $, удовлетворяющие системе, также должны удовлетворять системе \ begin {уравнение} \ begin {cases} 2x + y = 3 \\ 4x + 2y = 0. \ end {ases} \ end {Equation} Умножение первого уравнения на $ 2 $ дает $ 4x + 2y = 6. $ Обратите внимание, что нет $ x $ и $ y $, которые удовлетворяют как $ 4x + 2y = 6 $, так и $ 4x + 2у = 0.$ Таким образом, у системы нет решений; поэтому исходная система также не имеет решений.
Пример . Для чисел $ a, b $ и $ c $ покажите, что система линейных уравнений $$ \ begin {cases} x + 2y + 3z = a \\ x + 3y + 8z = b \\ x + 2y + 2z = c \ end {case} $$ либо не имеет решений, либо ровно одно решение, либо бесконечно много решений. Мы выбираем сначала удалить $ x $ и получаем систему $$ \ begin {cases} -y-5z = a-b \\ z = a-c. \ end {ases} $$ Затем мы исключаем $ z $, получая $ y = -6a + b + 5c.$ Следовательно, единственное решение – $$ (x, y, z) = (10a-2b-7c, -6a + b + 5c, a-c).
$
Давайте рассмотрим набор линейных уравнений, который включает $ n $ неизвестных величин, представленных $ x_1, x_2, \ ldots, x_n. $ Пусть $ a_ {ij} $ представляет число, которое является коэффициентом $ x_j $ в $ i $ -ое уравнение. Пусть даны числа $ b_1, b_2, \ ldots, b_m $. Система линейных уравнений уравнений \ begin {equal} \ label {syseq} \ begin {cases} a_ {11} x_1 + a_ {12} x_2 + \ cdots + a_ {1n} x_n = b_1 \\ a_ {21} x_1 + a_ {22} x_2 + \ cdots + a_ {2n} x_n = b_2 \\ \ hfill \ vdots \ hfill \\ a_ {m1} x_1 + a_ {m2} x_2 + \ cdots + a_ {mn} x_n = b_m \\ \ end {case} \ end {уравнение} называется системой одновременных линейных алгебраических уравнений .
Решение этой системы – это упорядоченный набор из $ n $ чисел, который удовлетворяет каждому из операторов $ m $ в системе. Система линейных уравнений без решения называется несовместимой , а система по крайней мере с одним решением называется непротиворечивой . Массив $$ \ left [\ begin {array} {l | l} \ begin {matrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\ & & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \\ \ end {matrix} & \ begin {matrix} b_1 \\ b_2 \\ \ vdots \\ b_m \ end {matrix} \ end {array} \ right] $$ называется расширенной матрицей , соответствующей системе линейных уравнений.
Например, система линейных уравнений выше оказалась непротиворечивой, а другая система линейных уравнений выше оказалась непоследовательной. Дополненные матрицы для этих систем следующие. $$ \ left [\ begin {array} {l | l} \ begin {matrix} 2 & 3 \\ 4 & 5 \ end {matrix} & \ begin {matrix} 0 \\ 0 \ end {matrix} \ end {массив} \ right] \ qquad \ text {and} \ qquad \ left [\ begin {array} {l | l} \ begin {matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \ end {matrix} & \ begin {matrix} 0 \\ 3 \\ 0 \ end {matrix} \ end {array} \ right] $$
Пример .Найдите все решения следующей системы линейных уравнений. % $ \ begin {case} -150 x + 500y-z = 0 \\ 50x + 100y + z = 200. \ end {ases} $$ Сложение этих уравнений дает $ -100x + 600y = 200. $ Поскольку у нас есть одно уравнение с двумя переменными, одна из переменных свободна. Мы решили позволить $ y $ быть свободным. Пусть $ y = t $ для произвольного числа $ t. $ Тогда, решая для $ x $, мы получаем $ -100x = 200y-600y $, или, что то же самое, $ x = -2 + 6t.$ Подставляя в исходную систему, находим $$ z = -150 (-2 + 6t) + 500t = 300-400t. $$ Следовательно, существует бесконечно много решений, которые можно представить в виде множества $$ \ {(x, y, z) \ mid x = -2 + 6t, y = t, z = 300-400t \ text { где $ t \ in \ mathbb {R} $} \}.
$
Другая расширенная матрица для этой системы линейных уравнений – $$ \ left [\ begin {array} {l | l} \ begin {matrix} -150 & 500 & -1 \\ 50 & 100 & 1 \ end {matrix} & \ begin {matrix} 0 \\ 200 \ end {matrix} \ end {array} \ right] $$ Как вы думаете, возможно ли решить, проверяя расширенную матрицу, соответствует ли соответствующая система линейных уравнений будет последовательным или непоследовательным?
Операции со строками: решение систем линейных уравнений
До сих пор в наших примерах мы видели системы линейных уравнений, не имеющие решений, единственное решение или, возможно, бесконечное количество решений.Эти примеры предлагают следующее определение.
Определение . Две системы линейных уравнений называются эквивалентными , если они имеют одинаковый набор решений.
Пример . Найдите систему линейных уравнений с тремя неизвестными $ x, y, z $, решениями которой являются $ x = 6 + 5t $, $ y = 4 + 3t $, $ z = 2 + t $, где $ t $ произвольно. Мы хотим исключить $ t. $ Решение для $ t $ дает $ t = z-2. $ Путем подстановки $ x = 6 + 5 (z-2) $ и $ y = 4 + 3 (z-2). $ Таким образом, у нас есть система линейных уравнений $$ \ begin {ases} x-5z = -4 \\ y-3z = -2 \ end {ases} $$, которая имеет бесконечно много решений.
Теорема . Системы линейных уравнений эквивалентны, если каждая может быть получена из другой с помощью одной или нескольких следующих операций.
Поменяйте порядок уравнений.
Умножьте (или разделите) одно уравнение на ненулевой скаляр.
Добавьте одно уравнение, кратное одному, к другому.
Доказательство . Если мы рассматриваем набор решений как геометрический объект, должно быть очень легко понять, что способ, которым мы пишем уравнения, представляющие объект, не меняет объект.Таким образом, должно быть очевидно, что изменение порядка уравнений не изменит решений системы линейных уравнений. Также не будет умножения (или деления) обеих частей уравнения на ненулевую константу.
Пусть система $ A $ будет системой $ m \ times n $, представленной \ begin {equal} \ label {syseqA} \ begin {cases} a_ {11} x_1 + a_ {12} x_2 + \ cdots + a_ {1n} x_n = b_1 \\ \ hfill \ vdots \ hfill \\ a_ {i1} x_1 + a_ {i2} x_2 + \ cdots + a_ {in} x_n = b_i \\ \ hfill \ vdots \ hfill \\ a_ {m1} x_1 + a_ {m2} x_2 + \ cdots + a_ {mn} x_n = b_m & \\ \ end {cases} \ end {equal} Рассмотрим систему $ B $, полученную из системы $ A $ добавлением $ k $ умноженного на $ i $ уравнения в уравнение $ j $ следующим образом: \ begin {Equation} \ label {syseqB} \ begin {cases} a_ {11} x_1 + a_ {12} x_2 + \ cdots + a_ {1n} x_n = b_1 \\ \ qquad \ qquad \ vdots \ qquad \ qquad \ qquad \ vdots \\ (a_ {j1} + k a_ {i1}) x_1 + (a_ {j2} + k a_ {i2}) x_2 + \ cdots + (a_ {jn} + k a_ {in }) x_n = b_j + k b_i \\ \ qquad \ qquad \ vdots \ qquad \ qquad \ qquad \ vdots \\ a_ {m1} x_1 + a_ {m2} x_2 + \ cdots + a_ {mn} x_n = b_m \\ \ end {cases} \ end {Equation} Пусть $ S_A $ и $ S_B $ – множества решений систем $ A $ и $ B $ соответственно.Мы покажем $ S_A = S_B. $
.
Пусть $ x_0 = (x_1, x_2, \ ldots, x_n) $ – решение системы $ A. $ Таким образом, $ x_0 $ удовлетворяет всем линейным уравнениям. Итак, $ x_0 $ удовлетворяет всем уравнениям в системе B, кроме, возможно, $ j $ -го уравнения. Работая с $ j $ -м уравнением в системе $ B $, находим
\ begin {align} & (a_ {j1} + k a_ {i1}) x_1 + (a_ {j2} + k a_ {i2}) x_2 + \ cdots + (a_ {jn} + k a_ {in}) x_n \ \ & \ qquad = a_ {j1} x_1 + \ cdots + a_ {jn} x_n + k (a_ {i1} x_1 + \ cdots a_ {jn} x_n) \\ & \ qquad = b_j + k b_i.\ end {align}
Это показывает, что $ x_0 $ также удовлетворяет $ j $ -му уравнению системы $ B. $ Поскольку $ x_0 $ удовлетворяет каждому уравнению, $ x_0 $ также является членом $ S_B. $ До сих пор мы показали $ S_A \ substeq S_B . $ И наоборот, предположим, что $ x_0 $ является решением любого уравнения второй системы линейных уравнений. Работая с $ j $ -м уравнением системы $ A $, находим,
\ begin {align} & a_ {j1} x_1 + a_ {j2} x_2 + \ cdots + a_ {jn} x_n = b_j \ notag \\ \ Longleftrightarrow \ quad & a_ {j1} x_1 + (k a_ {i1} -ka_ {i1}) x_1 + \ cdots + a_ {jn} + (k a_ {i1} -ka_ {i1}) x_n = b_j \ notag \\ \ Longleftrightarrow \ quad & (a_ {j1} + k a_ {i1}) x_1 + (a_ {j2} + k a_ {i2}) x_2 + \ cdots + (a_ {jn} + k a_ {in}) x_n = b_j + k b_i.\ label {eqsys} \ end {align}
Следовательно, поскольку $ x_0 $ удовлетворяет системе $ B $; и, таким образом, $ x_0 $ удовлетворяет $ j $ -му уравнению системы $ A. $ Следовательно, $ S_A = S_B $, как и нужно.
Прорабатывая детали следующих двух примеров, обратите внимание на то, как используются операции в Row Operations.
Пример . Пусть $ a, b $ и $ c $ – константы. Решите систему линейных уравнений $$ \ begin {cases} y + z = a \\ x + z = b \\ x + y = c. \ end {ases} $$ Исключая $ z $ из первого и второго уравнений, получаем систему $$ \ begin {ases} xy = ba \\ x + y = c \ end {ases} $$ Решение для $ x $ дает $ x = (c + ba) / 2.$ Используя исходную систему, мы находим, что $ y $ и $ z $ равны $$ y = cx = c- (c + ba) / 2 = (c-b + a) / 2 $$ $$ z = ay = a – (c-b + a) / 2 = (a + bc) / 2 $$ Следовательно, решение системы: $$ (x, y, z) = \ left (\ frac {c + ba} {2 }, \ frac {a + cb} {2}, \ frac {a + bc} {2} \ right).
$
Пример . Найдите наименьшее натуральное число $ C $ такое, что $ x, y, z $ являются целыми числами и удовлетворяют системе линейных уравнений уравнений $$ \ begin {cases} 2x + y = C \\ 3y + z = C \\ x + 4z = C \ end {cases} $$ Умножьте третье уравнение на $ -2 $ и добавьте к первому уравнению, получив $ y-8z = -C.$ Умножая второе уравнение на 8 и прибавляя к $ y-8z = -C $, получаем $ 25y = 7C. $ Решая $ y $, получаем $ y = (7/25) C. $ Подстановкой $ x = (9/25) C $ и $ z = (4/25) C. $ Следовательно, 25 – наименьшее целое число $ C $ такое, что $ x, y, z $ являются целыми числами и решает систему.
Исключение по Гауссу
Мы будем решать систему линейных уравнений, используя элементарные операции со строками над матрицами, используя процедуру, известную как Исключение Гаусса . Набор решений будет набором векторов.
Определение . Следующие операции известны как операции с элементарной строкой .
(1) Поменяйте местами два ряда.
(2) Умножьте строку на ненулевой скаляр.
(3) Добавить строку из другой строки, кратную строке.
Из операций со строками очевидно, что применение элементарных операций со строками к системе линейных уравнений приводит к эквивалентной системе. Редукция системы линейных уравнений при сохранении множества решений – чрезвычайно полезная идея, которую мы будем активно развивать.
Например, мы обнаруживаем, что система линейных уравнений \ begin {equal} \ label {refex} \ begin {cases} x + 2y + z = 3 \\ 2x + 5y-z = -4 \\ 3x-2y- z = 5 \ end {case} \ qquad \ qquad \ begin {cases} x = 2 \\ y = -1 \\ z = 3 \ end {case} \ end {уравнение} эквивалентны. Мы покажем, как применить элементарные операции со строками, чтобы получить систему справа. В то время как система слева может быть заданной системой линейных уравнений, система справа решена.
Определение .Считается, что матрица находится в эшелоне строки формы , если она удовлетворяет всем следующим условиям.
(1) Все строки с хотя бы одним ненулевым коэффициентом находятся над любыми строками со всеми нулями.
(2) Первое ненулевое число слева (называемое ведущим коэффициентом ) ненулевой строки всегда находится строго справа от ведущего коэффициента строки над ней.
(3) Все записи в столбце под ведущим коэффициентом нулевые.
Кроме того, говорят, что матрица находится в форме сокращенного эшелона строк , если она находится в форме эшелона строк и выполняется дополнительное условие: каждый ведущий коэффициент равен 1 и является единственной ненулевой записью в своем столбце.
Например, расширенные матрицы для системы линейных уравнений выше: $$ \ begin {bmatrix} \ begin {array} {ccc | c} 1 & 2 & 1 & 3 \\ 2 & 5 & -1 & -4 \\ 3 & -2 & -1 & 5 \ end {array} \ end {bmatrix} \ qquad \ qquad \ begin {bmatrix} \ begin {array} {ccc | c} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 3 \ end {array} \ end {bmatrix}.$$ Проверив эти четыре условия, мы увидим, что матрица справа имеет вид сокращенного ряда строк. Для получения дополнительных примеров рассмотрим следующие матрицы. $$ A = \ begin {bmatrix} 0 & 5 \\ 2 & 3 \ end {bmatrix} \ qquad B = \ begin {bmatrix} 1 & 0 \\ 1 & 0 \ end {bmatrix} \ qquad C = \ begin {bmatrix} 0 & 0 \\ 0 & 1 \ end {bmatrix} $$ $$ D = \ begin {bmatrix} 0 & 1 \\ 0 & 0 \ end {bmatrix} \ qquad E = \ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix} \ qquad F = \ begin {bmatrix} 1 & 2 \\ 0 & 1 \ end {bmatrix} $$ Обратите внимание, что матрицы $ D $ и $ E $ находятся в уменьшенной строке форма эшелона, а остальные нет.
Пример . Используйте метод исключения Гаусса-Жордана для решения системы линейных уравнений. $$ \ begin {cases} x + 2y + z = 3 \\ 2x + 5y-z = -4 \\ 3x-2y-z = 5 \ end {cases} $$ Используя операции со строками в расширенной матрице, мы получаем уменьшенная форма рядного эшелона.
\ begin {align *} & \ begin {bmatrix} \ begin {array} {ccc | c} 1 и 2 и 1 и 3 \\ 2 и 5 и -1 и -4 \\ 3 и -2 и -1 и 5 \ end {массив} \ end {bmatrix} \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_1 + R_2} \\ \ stackrel {\ longrightarrow} {\ scriptstyle -3R_1 + R_3} \ end {массив} \ begin {bmatrix} \ begin {array} {ccc | c} 1 и 2 и 1 и 3 \\ 0 & 1 & -3 & -10 \\ 0 & -8 & -4 & -4 \ end {массив} \ end {bmatrix} \\ & \ qquad \ qquad \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle 8 R_2 + R_3} \ end {массив} \ begin {bmatrix} \ begin {array} {ccc | c} 1 и 2 и 1 и 3 \\ 0 & 1 & -3 & -10 \\ 0 & 0 & -28 & -84 \ end {массив} \ end {bmatrix} \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle – \ frac {1} {28} R_3} \ end {массив} \ begin {bmatrix} \ begin {array} {ccc | c} 1 и 2 и 1 и 3 \\ 0 & 1 & -3 & -10 \\ 0 и 0 и 1 и 3 \ end {массив} \ end {bmatrix} \\ & \ qquad \ qquad \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle 3R_3 + R_2} \\ \ stackrel {\ longrightarrow} {\ scriptstyle -R_3 + R_1} \ end {массив} \ begin {bmatrix} \ begin {array} {ccc | c} 1 и 2 и 0 и 0 \\ 0 & 1 & 0 & -1 \\ 0 и 0 и 1 и 3 \ end {массив} \ end {bmatrix} \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_2 + R_1} \ end {массив} \ begin {bmatrix} \ begin {array} {ccc | c} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & -1 \\ 0 и 0 и 1 и 3 \ end {массив} \ end {bmatrix}.\ end {align *}
Следовательно, единственное решение – $ x = 2 $, $ y = -1 $ и $ z = 3. $
Пример . Используйте метод исключения Гаусса-Жордана для решения следующей системы линейных уравнений. \ begin {уравнение} \ label {gjee1} \ begin {cases} x + y -2z + 4t = 5 \\ 2x + 2y-3z + t = 3 \\ 3x + 3y-4z-2t = 1 \ end {case } \ end {уравнение} Используя операции со строками над расширенной матрицей, мы получаем сокращенную форму эшелона строк.
\ begin {align *} \ begin {bmatrix} \ begin {array} {cccc | c} 1 и 1 и -2 и 4 и 5 \\ 2 и 2 и -3 и 1 и 3 \\ 3 и 3 и -4 и -2 и 1 \ end {массив} \ end {bmatrix} & \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_1 + R_2} \\ \ stackrel {\ longrightarrow} {\ scriptstyle -3R_1 + R_3} \ end {массив} \ begin {bmatrix} \ begin {array} {cccc | c} 1 и 1 и -2 и 4 и 5 \\ 0 & 0 & 1 & -7 & -7 \\ 0 & 0 & 2 & -14 & -14 \ end {массив} \ end {bmatrix} \\ & \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_2 + R_3} \\ \ stackrel {\ longrightarrow} {\ scriptstyle 2R_2 + R_1} \ end {массив} \ begin {bmatrix} \ begin {array} {cccc | c} 1 и 1 и 0 и -10 и -9 \\ 0 & 0 & 1 & -7 & -7 \\ 0 & 0 & 0 & 0 & 0 \ end {массив} \ end {bmatrix} \ end {align *}
Эта система эквивалентна $$ \ begin {cases} x + y-10t = -9 \\ z-7t = -7 \ end {ases} \ quad \ text {или, проще говоря} \ quad \ begin {cases} х = -9-у + 10т \\ г = -7 + 7т.4 \ mid x = -9-y + 10t, y = s, z = -7 + 7t, w = t, \ text {for} s, t \ in \ mathbb {R} \}. $$ – это набор решений.
Пример . Используйте метод исключения Гаусса-Жордана для решения следующей системы линейных уравнений. $$ \ begin {case} x_1 + x_2-2x_3 + 3x_4 = 4 \\ 2x_1 + 3x_2 + 3x_3-x_4 = 3 \\ 5 x_1 + 7 x_2 + 4 x_3 + x_4 = 5 \ end {cases} $$ Использование строки операций над расширенной матрицей мы получаем приведенную форму эшелона строк.
\ begin {align *} \ begin {bmatrix} \ begin {array} {cccc | c} 1 и 1 и -2 и 3 и 4 \\ 2 и 3 и 3 и -1 и 3 \\ 5 и 7 и 4 и 1 и 5 \ end {массив} \ end {bmatrix} & \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_1 + R_2} \\ \ stackrel {\ longrightarrow} {\ scriptstyle -5R_1 + R_3} \ end {массив} \ begin {bmatrix} \ begin {array} {cccc | c} 1 и 1 и -2 и 3 и 4 \\ 0 и 1 и 7 и -7 и -5 \\ 0 и 2 и 14 и -14 и 15 \ end {массив} \ end {bmatrix} \\ & \ begin {массив} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_2 + R_3} \ end {массив} \ begin {bmatrix} \ begin {array} {cccc | c} 1 и 1 и -2 и 3 и 4 \\ 0 и 1 и 7 и -7 и -5 \\ 0 & 0 & 0 & 0 & 25 \ end {массив} \ end {bmatrix} \ end {align *}
Обратите внимание, что последняя строка соответствует уравнению $ 0x_1 + 0x_2 + 0x_3 + 0x_4 = 25.2 $ – такой многочлен. Используя данные точки, мы настраиваем систему и решаем.
\ begin {align *} & \ left [\ begin {array} {c | c} \ begin {matrix} а & b & c \\ а & 2b & 4c \\ a, 3b и 9c \ end {matrix} & \ begin {matrix} -1 \ 3 \ 13 \ end {матрица} \ end {array} \ right] \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -R_1 + R_2} \\ \ stackrel {\ longrightarrow} {\ scriptstyle -R_1 + R_3} \ end {массив} \ left [\ begin {array} {c | c} \ begin {matrix} а & b & c \\ 0 & b & 3c \\ 0 и 2b и 8c \ end {matrix} & \ begin {matrix} 1 \ 4 \ 14 \ end {матрица} \ end {array} \ right] \\ & \ qquad \ qquad \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -2R_2 + R_3} \ end {массив} \ left [\ begin {array} {c | c} \ begin {matrix} а & б & с \\ 0 & b & 3c \\ 0 и 0 и 2c \ end {matrix} & \ begin {matrix} -1 \ 4 \ 6 \ end {matrix} \ end {array} \ right] \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle \ frac {1} {2} R_3} \ end {массив} \ left [\ begin {array} {c | c} \ begin {matrix} а & б & с \\ 0 & b & 3c \\ 0 & 0 & c \ end {matrix} & \ begin {matrix} -1 \ 4 \ 3 \ end {матрица} \ end {array} \ right] \\ & \ qquad \ qquad \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -3R_3 + R_2} \ end {массив} \ left [\ begin {array} {c | c} \ begin {matrix} а & b & c \\ 0 & b & 0 \\ 0 & 0 & c \ end {matrix} & \ begin {matrix} -1 \ -5 \ 3 \ end {матрица} \ end {array} \ right] \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -R_2 + R_1} \ end {массив} \ left [\ begin {array} {c | c} \ begin {matrix} а & 0 & с \\ 0 & b & 0 \\ 0 & 0 & c \ end {matrix} & \ begin {matrix} 4 \ -5 \ 3 \ end {матрица} \ end {array} \ right] \\ & \ qquad \ qquad \ begin {array} {c} \ stackrel {\ longrightarrow} {\ scriptstyle -R_3 + R_1} \ end {массив} \ left [\ begin {array} {c | c} \ begin {matrix} а & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \ end {matrix} & \ begin {matrix} 1 \ -5 \ 3 \ end {матрица} \ end {array} \ right].2-5 лет + 1. $
Упражнения по системе линейных уравнений
Упражнение . Убедитесь, что $ (2,3, -1) $ является решением системы линейных уравнений.
$ \ begin {cases} x + 2y + z = 7 \\ xy = -1 \\ 4x + y + z = 10 \ end {cases} $
$ \ begin {cases} x + y = 5 \ \ xz = 3 \\ y + z = 2 \ end {cases} $
Упражнение . Убедитесь, что каждая тройка вида $ (7-2k, 8 + 6k, k) $ является решением системы линейных уравнений.
$ \ begin {cases} x_1 + 2x_3 = 7 \\ x_2-6x_3 = 8 \ end {cases} $
$ \ begin {cases} 2x_1 + 4x_3 = 14 \\ x_1 + 3x_2-16x_3 = 31 \ end {кейсы}
$
Упражнение .У следующих систем нет решений, ровно одно решение или бесконечно много решений? Обосновать ответ.
$ \ begin {case} x + y = 1 \\ x + 2y = 1 \ end {cases} $
$ \ begin {cases} 3x + y = 1 \\ y = -2 \ end {case} $
$ \ begin {case} x + y = 1 \\ 2x + 2y = 2 \ end {cases} $
$ \ begin {cases} 3x + y = 2 \\ 6x + 2y = 4 \ end { case} $
Exercise . Нарисуйте график каждого уравнения системы линейных уравнений и решите, нет ли у него решений, ровно одно решение или бесконечно много решений.
$ \ begin {cases} x + y = 2 \\ 2x + 3y = 0 \ end {cases} $
$ \ begin {cases} -x + 3y = 2 \\ 2x-6y = -4 \ end {кейсы}
$
Упражнение . Найдите решения, если таковые имеются, следующей системы линейных уравнений без использования матриц. Если уравнение имеет более одного решения, напишите общее решение.
$ \ begin {case} 3x-2y = 7 \\ 2x + y = 15 \ end {cases} $
$ \ begin {cases} x + y = 7 \\ 3x + 4y = 12 \ end {случаях } $
$ \ begin {case} 2x_1-3x_2 = 1 \\ 4x_1-6x_2 = -2 \\ x_1 + x_2 = 1 \ end {cases} $
$ \ begin {cases} 2x_1-5x_2 = 12 \ end {case} $
$ \ begin {cases} i x_1-3ix_2 = 1 \\ (2 + i) x_1-x_2 = -1 \ end {cases} $
$ \ begin {cases} (1 + i ) x_1-2ix_2 = 2 \\ 2x_1-3i x_2 = 4-3i \ end {cases} $
Упражнение .Если возможно, найдите точки пересечения.
$ x-4y = 11 $ и 7x-2y = 9 $
$ x-4y + 3z = 11 $, 7x-2y-z = -1 $, 7x-2y + z = -2 $
Упражнение . Пусть $ u = (1,1,2, -1) $ и $ v = (1,1,1,0). $ Для каких скаляров $ a $ и $ b $ верно, что $ a u + bv $ это решение следующей системы?
$ \ begin {cases} 4x-2y-zw = 1 \\ x + 3y-2z-2w = 2 \ end {cases} $
$ \ begin {cases} x-4y-z-2w = 4 \ \ 7x + y-5z-2w = 12 \ end {cases} $
Упражнение .Найдите все решения, если таковые существуют, следующей системы линейных уравнений.
$ \ begin {case} xy = 1 \\ 2x = 4 \ end {cases} $
$ \ begin {cases} 2x + 3y-z = 19 \\ 3x-2y + 3z = 7 \ end {case } $
$ \ begin {case} x-3y = 2 \\ -2x + 6y = -4 \ end {cases} $
$ \ begin {cases} x-y + 2z-2w = 1 \\ 2x + y + 3w = 4 \\ 2x + y + 3w = 6 \ end {cases} $
Упражнение . Найдите все решения, если таковые существуют, следующей системы линейных уравнений.
$ \ begin {cases} 2x-z = -1 \\ x + yz = 0 \\ 2x-y + 2z = 3 \ end {cases} $
$ \ begin {cases} 2x-3y + 2z = 1 \\ x-6y + z = 2 \\ -x-3y-z = 1 \ end {cases} $
Упражнение .Найдите все решения, если таковые существуют, следующей системы линейных уравнений.
$ \ begin {cases} x_1 + 2x_2-x_3 = 0 \\ 2x_1 + 5x_2 + 5x_3 = 0 \\ x_1 + 4x_2 + 7x_3 = 0 \\ x_1 + 3x_2 + 3x_3 = 0 \ end {cases} $
$ \ begin {case} x + y + z + w = 1 \\ 2x-2y + z + 2w = 3 \\ 2x + 6y + 3z + 2w = 1 \\ 5x-3y + 3z + 5w = 8 \ end {кейсы}
$
Упражнение . При каких значениях константы $ k $ у систем нет решения, ровно одно решение или бесконечное множество решений.
$ \ begin {case} x + y = 1 \\ 3x + 3y = k \ end {cases} $
$ \ begin {cases} x + ky = 1 \\ 2x-y = k \ end {случаях } $
Exercise .2 + 2} + \ frac {c} {2x-1}.
$
Упражнение . Пусть $ a $ и $ b $ – произвольные постоянные. Найдите все решения системы линейных уравнений.
$ \ begin {case} x + 2y = a \\ 3x + 5y = b \ end {cases} $
$ \ begin {cases} a x + 2y = 1 \\ 3x + by = 4 \ end { case} $
Exercise .
Пусть $ a $ и $ b $ – произвольные постоянные. Найдите все решения системы линейных уравнений.
$ \ begin {case} x + 2y + 3z = a \\ x + 3y + 8z = b \\ x + 2y + 2z = c \ end {cases} $
$ \ begin {cases} x-2y + 4z = a \\ x-3y + 5z = b \\ x-2y + 6z = c \ end {cases} $
Упражнение .Система линейных уравнений, все постоянные члены которой равны нулю, называется однородной системой
.
Покажите, что в однородной системе всегда есть хотя бы одно решение.
Приведите примеры, показывающие, что гомогенная система может иметь более одного решения или только одно решение.
Упражнение . Напишите систему, соответствующую каждой расширенной матрице.
$ \ left [\ begin {array} {ccc | c} 1 & 2 & 1 & 1 \\ 0 & 4 & 0 & 1 \\ 0 & 0 & 3 & 3 \ end {array} \ right] $
$ \ left [\ begin {array} {cccc | c} 1 & 0 & 0 & 0 & 0 \ end {array} \ right] $
$ \ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ end {array} \ right] $
$ \ left [\ begin {array} {c | c} 2 & 1 \\ 0 & 1 \\ 1 & 2 \ end {array} \ right] $
$ \ left [\ begin {array} {c | c} 1 & 1 \\ 1 & 0 \ end {массив } \ right] $
$ \ left [\ begin {array} {cccc | c} 1 & 1 & 1 & 1 & 0 \ end {array} \ right] $
Упражнение .Какие из следующих матриц представлены в виде сокращенного ряда строк?
$ \ begin {bmatrix} 0 & 1 & 2 & 0 & 3 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \ end {bmatrix} $
$ \ begin {bmatrix} 1 & 0 & 0 & 2 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \ end {bmatrix} $
$ \ begin {bmatrix} 1 & 1 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \ end {bmatrix} $
$ \ begin {bmatrix} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ \ end {bmatrix} $
Упражнение .Какие из следующих матриц представлены в виде сокращенного ряда строк?
$ \ begin {bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \ end {bmatrix} $
$ \ begin {bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \ end {bmatrix} $
$ \ begin {bmatrix} 1 & 0 & 0 & 3 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \ end {bmatrix} $
$ \ begin {bmatrix} 1 & 0 & 2 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \ end {bmatrix } $
Exercise .Найти все решения системы линейных уравнений методом исключения Гаусса-Жордана.
$ \ begin {cases} x_2 + 2x_4 + 3x_5 = 0 \\ 4x_4 + 8x_5 = 0 \ end {cases} $
$ \ begin {cases} 3x + 4y = 0 \\ -2x + 7y = 0 \ конец {кейсы} $
Упражнение . Найти все решения системы линейных уравнений методом исключения Гаусса-Жордана.
$ \ begin {cases} x_4 + 2x_5-x_6 = 2 \\ x_1 + 2x_2 + x_5-x_6 = 0 \\ x_1 + 2x_2 + 2x_3-x_5 + x_6 = 2 \ end {cases} $
$ \ begin {case} 3x_1 + 3x_2-4x_3 + x_4 = 2 \\ x_1 + x_2-x_3-x_4 = 5 \ end {cases} $
$ \ begin {cases} 2 x_1 + 3x_2 + 4x_3 = 6-x_4 \\ 3x_1 -2x_2-x_4 = 1 + 4x_3 \\ 3x_1 + 3x_3 + x_4 = 4-x_2 \\ x_2 + x_3-4x_4 = -3-4x_1 \ end {cases} $
$ \ begin {cases} 4x_1 + 3x_2 + 2x_3 -x_4 = 4 \\ 5x_1 + 4x_2 + 3x_3-x_4 = 4 \\ -2x_1-2x_2-x_3 + 2x_4 = -3 \\ 11x_1 + 6x_2 + 4x_3 + x_4 = 11 \ end {case} $
$ \ begin {case} 2x_1-3x_2 + x_3 = 5 \\ x_1 + x_2-x_3 = 3 \\ 4x_1-x_2-x_3 = 1 \ end {cases} $
$ \ begin {cases} x_1-x_2 = 4 \\ 2x_1 + x_2 = 7 \\ 5x_1-2x_2 = 19 \ end {case} $
Упражнение .Найдите все матрицы размером $ 4 \ times 1 $ в приведенной форме эшелона строк.
Упражнение . Сколько существует типов матриц размером $ 3 \ times 2 $ в приведенной строчной форме? Сколько существует типов матриц размером $ 2 \ times 3 $ в приведенной строчной форме?
Упражнение . Опишите возможные формы сокращенного эшелона строк для матрицы с двумя строками и двумя столбцами. Опишите возможные формы сокращенного эшелона строк для матрицы с тремя строками и тремя столбцами.
Упражнение .Найдите многочлен степени 3, график которого проходит через точки
$ (0,1) $, $ (1,0) $, $ (- 1,0) $ и $ (2, -15). $ Нарисуйте эскиз график этой кубики.
Упражнение . Найдите многочлен степени 4, график которого проходит через точки $ (1,1) $, $ (2, -1) $, $ (3, -59) $ и $ (- 2, -29). $ Sketch график этой квартики.
Упражнение . Найдите значения $ k $, если они есть, для которых система имеет: только одно решение, никаких решений, бесконечное количество решений.