Резонанс – друг и враг
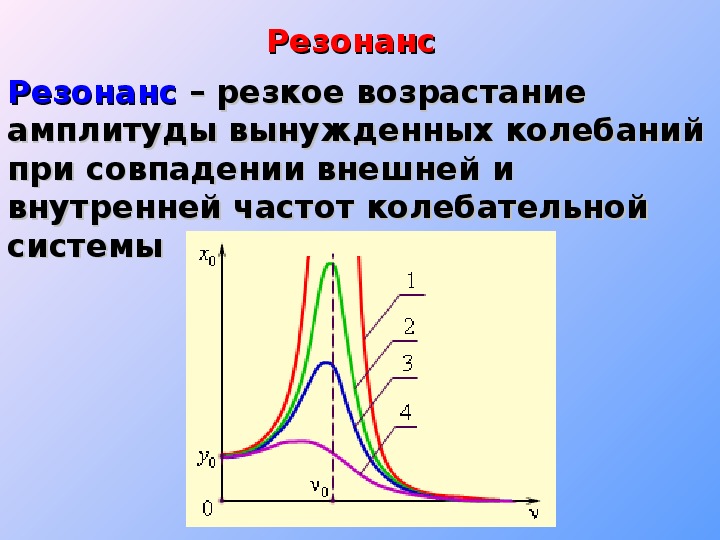
Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний системы, которое наступает при приближении частоты внешнего воздействия к определенным значениям (резонансных частот), обусловленным свойствами системы. Таким образом, причиной резонанса является совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы.
Резонанс встречается в механике, электронике, оптике, акустике, астрофизике.
Явление резонанса лежит в основе проектирования музыкальных инструментов: рояля, скрипки, флейты …
Используется явление резонанса и в электронике. Колебательный контур, состоящий из емкости и индуктивности, используется в элементах настройки и электрических фильтрах. Однако резонанс может быть и вредным, если он вызывает искажение сигнала или паразитные шумы.
Наблюдается резонанс и в космосе, когда два небесных тела, которые имеют периоды обращения, относящихся друг с другом как небольшие целые числа, делают регулярное гравитационное воздействие друг на друга, которое может стабилизировать их орбиты (орбитальный резонанс в небесной механике).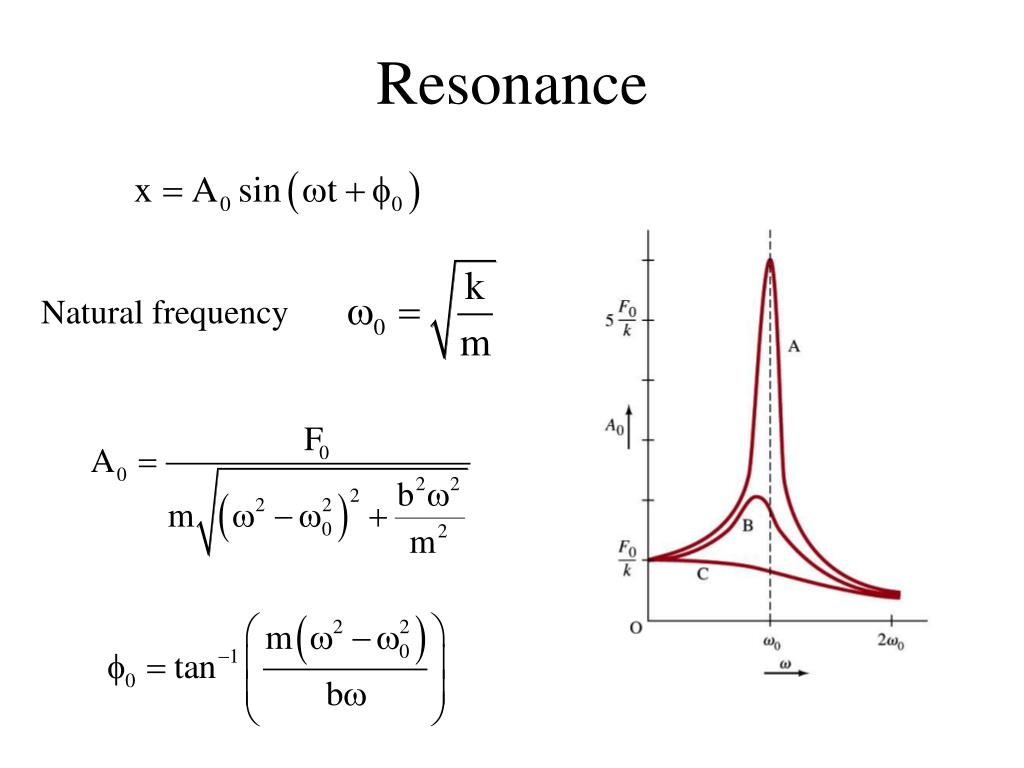
Однако наиболее часто резонанс бывает в классической и строительной механике, а также гидро- и аэромеханике. И, к сожалению, во многих случаях именно тогда, когда он совершенно нежелателен.
… Известно, что военным подразделениям при прохождении мостов приписывается “сбивать ногу” и идти не строевым, а свободным шагом. Горький опыт некоторых катастроф научил военнослужащих в подобных ситуациях отходить от многовековых традиций.
Так, 12 апреля 1831 разрушился Бротонский подвесной мост через реку Ирвелл в Англии, когда по нему шел военный отряд. Частота шагов воинов, шагавших в ногу, совпала с частотой собственных колебаний моста, через которые амплитуда резко возросла, цепи оборвались, и мост рухнул в реку. Именно этот случай, в результате которого два десятка человек были травмированы, способствовал принятию в британской армии правила “идти не в ногу” при прохождении войсками мостов. По той же причине в 1850 году неподалеку от французского города Анже был разрушен подвесной цепной мост над рекой Мин длиной более ста метров, что привело к многочисленным жертвам.
Причиной разрушения мостов из-за резонанса могут стать не только пешеходы, но и железнодорожные поезда. Для исключения резонанса моста поезд может двигаться или медленно, или на максимальной скорости (вспомните, как замедляют ход поезда метрополитена во время их движения через мост Метро в Киеве). Это обычно делается для исключения совпадения частоты ударов колес по стыкам рельсов с собственной частотой колебаний моста (по этой же причине участок рельсов на мосту часто выполняют сплошной, т.е. без стыков).
Катастрофические последствия для мостов могут послужить также и от воздействия ветра. Так, 7 ноября 1940 через игнорирование действия ветровой нагрузки на мост при его проектировании и вследствие возникновения резонанса разрушился Такомский подвесной мост общей длиной 1800 м и длиной центрального пролета 850 м (США).
С резонансом можно столкнуться не только на суше, но и на море и в воздухе. Так, при некоторых частотах вращения гребного вала в резонанс входили даже корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания элементов самолета, что он полностью разрушался в воздухе.
Причиной резонанса элементов летательных аппаратов и их разрушение может стать и флаттер – сочетание самовозбуждающиеся незатухающих изгибающих и крутильных автоколебаний элементов конструкции (главным образом крыла самолета или несущего винта вертолета). Одним из путей борьбы с этим явлением является использование так называемых протифлатерных грузов.
Интересно, что крепления двигателей на пилонах крыльев самолетов – это не прихоть конструкторов и дизайнеров, а насущная необходимость, поскольку двигатели демпфирующие колебания крыла в полете воздушного судна, будучи при этом своеобразным протифлатерним грузом.
Также известны случаи, когда во время выступлений знаменитого русского певца Федора Ивановича Шаляпина часто лопались плафоны в люстрах. И происходило это опять же через резонанс, когда частота собственных колебаний стекла совпадала с частотой акустических волн, воспроизводимых певцом.
И происходило это опять же через резонанс, когда частота собственных колебаний стекла совпадала с частотой акустических волн, воспроизводимых певцом.
Еще более интересным фактом является то, что во время Великой Отечественной войны все тот же резонанс едва не поставил под угрозу существование единой ниточки, проходившей по льду Ладожского озера и связывала блокадный Ленинград с “большой землей”.
… Во время наведения участка Дороги жизни по Ладожскому озеру защитники Ленинграда неожиданно столкнулись с необычным явлением, когда после нормального прохождения по льду тяжелого грузовика, легкая машина, которая шла по тому же пути, нередко проваливалась под лед.
Перед учеными была поставлена задача срочно разобраться с ситуацией, сложившейся и предоставить рекомендации по преодоления автомобилями ледяного покрова. В южной части Ладожского озера, под артиллерийским и минометным огнем врага гидрограф и гидротехники проводили эксперименты по определению предельных нагрузок на лед. Все выводы ученых поступали в Ледовую службу Морской обсерватории. Было изучено деформационную устойчивость льда под статической нагрузкой и данные про упругие деформации льда при распространении по льду взрывной волны. При проведении автоколонн по Ладоге наблюдались и неизвестные ранее колебания ледяного покрова: водяной волна, образовавшаяся под льдом проседала, двигалась с постоянной для определенной толщины льда и глубины водоема скоростью. Она могла опережать приложенную нагрузку или отставать от нее, но опасным было совпадения этих скоростей – тогда вода прекращала поддержку ледяного покрова, и поддержка обеспечивалась только упругими свойствами льда. При этом наступал резонанс, что приводило к разрушению льда. Это проявление резонанса было названо изгибно-гравитационной волной.
Все выводы ученых поступали в Ледовую службу Морской обсерватории. Было изучено деформационную устойчивость льда под статической нагрузкой и данные про упругие деформации льда при распространении по льду взрывной волны. При проведении автоколонн по Ладоге наблюдались и неизвестные ранее колебания ледяного покрова: водяной волна, образовавшаяся под льдом проседала, двигалась с постоянной для определенной толщины льда и глубины водоема скоростью. Она могла опережать приложенную нагрузку или отставать от нее, но опасным было совпадения этих скоростей – тогда вода прекращала поддержку ледяного покрова, и поддержка обеспечивалась только упругими свойствами льда. При этом наступал резонанс, что приводило к разрушению льда. Это проявление резонанса было названо изгибно-гравитационной волной.
По результатам исследований для автомобилей, которые двигались по льду, были установлены определенные скорости и дистанции. Ежедневно по ледяному покрову в обе стороны перевозилось около 6 тыс. Тонн грузов, а общее количество доставленных в Ленинград по Дороге жизни грузов за весь период ее существования составила более 1 млн 615 тыс.
С учетом приобретенного опыта позже был разработан резонансный метод разрушения льда, энергоемкость которого в несколько раз меньше энергоемкости традиционного разрушения ледяного покрова с помощью ледоколов и ледокольного навесного оборудования.
Как видим, резонанс может быть достаточно коварным, но укротить его и вернуть на пользу человеку вполне по силам!
понятное объяснение, примеры, польза и вред
Слышали ли вы о том, что отряд солдат, переходя мост, должен перестать маршировать? Солдаты, идущие до этого в ногу, перестают это делать и начинают идти свободным шагом.
Такой приказ отдается командирами вовсе не с целью дать солдатам возможность полюбоваться местными красотами. Это делается для того, чтобы солдаты не разрушили мост. Какая тут связь? Очень простая. Чтобы это понять, надо ознакомиться с явлением резонанса.
Что такое явление резонанса: частота колебаний
Чтобы проще понять, что такое резонанс, вспомните такую нехитрую и приятную забаву, как катание на подвесных качелях. Один человек сидит на них, а второй раскачивает.
Один человек сидит на них, а второй раскачивает.
И прикладывая совсем небольшие силы, даже ребенок может очень сильно раскачать взрослого. Как он этого добивается? Частота его раскачиваний совпадает с частотой качающегося, возникает резонанс, и амплитуда раскачиваний сильно возрастает. Как-то так. Но обо всем по порядку.
Частота колебаний это количество колебаний за одну секунду. Измеряется она при этом не в разах, а в герцах (1 Гц). То есть, частота колебаний в 50 герц означает, что тело совершает 50 колебаний в секунду.
В случае вынужденных колебаний всегда есть самоколеблющееся (или в нашем случае качающееся) тело и вынуждающая сила. Так вот эта сторонняя сила действует с определенной частотой на тело.
И если его частота будет сильно отличаться от частоты колебаний самого тела, то сторонняя сила будет слабо помогать телу колебаться или, говоря научно, слабо усиливать его колебания.
Например, если пытаться раскачать человека на качелях, толкая его в момент, когда он летит на вас, вы можете отбить себе руки, скинуть человека, но вряд ли сильно его раскачаете.
А вот если раскачивать его, толкая в направлении движения, то нужно совсем немного усилий, чтобы добиться результата. Вот это и есть совпадение частоты или резонанс колебаний. При этом сильно возрастает их амплитуда.
Примеры резонансных колебаний: польза и вред
Так же и при катании на другом варианте качелей в виде доски на подставке проще и эффективнее отталкиваться ногами от земли, когда ваша сторона качелей уже поднимается, а не когда она опускается.
По этой же причине застрявшую в ямке машину постепенно раскачивают и толкают вперед в моменты, когда она сама двигается вперед. Так значительно повышают ее инерцию, усиливая амплитуду колебаний.
Можно приводить множество подобных примеров, которые говорят о том, что мы на практике очень часто применяем явление резонанса, только делаем мы это интуитивно, не догадываясь, что применяем правила физики.
Выше говорилось о полезности явления резонанса. Однако, резонанс может и вредить. Иногда возникающее увеличение амплитуды колебаний может быть очень вредным.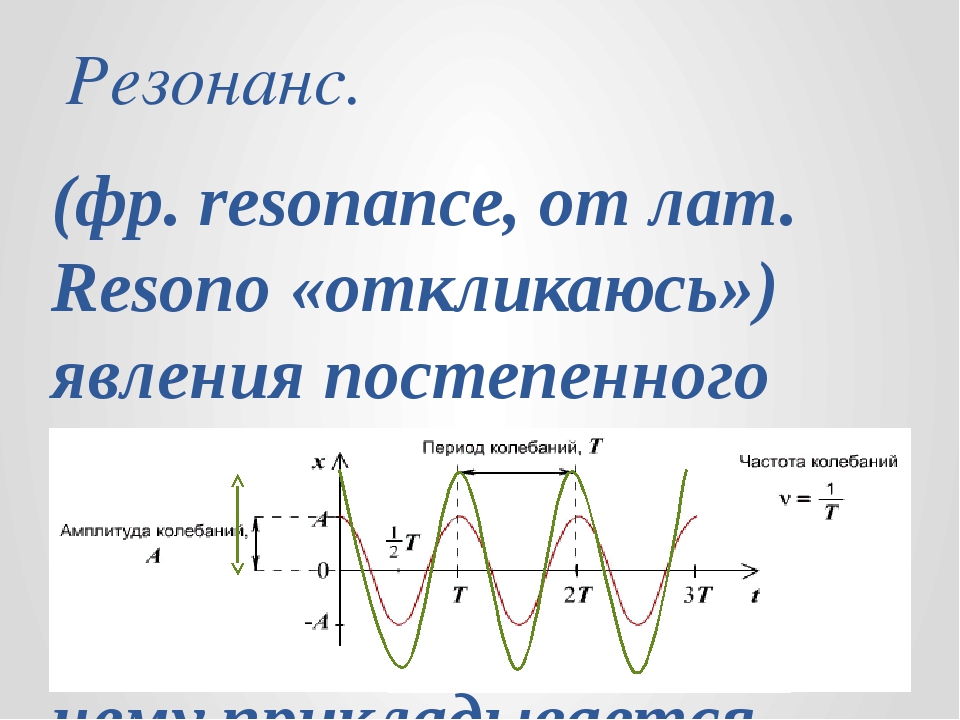
Так вот были несколько случаев в истории, когда под шагами солдат реально разрушались и падали в воду мосты. Последний из них произошел около ста лет назад в Петербурге. В таких случаях частота ударов солдатских сапог совпадала с частотой колебаний моста, и мост рушился.
Именно поэтому, на основе горького опыта, было введено правило для солдат сбрасывать шаг, заходя на мост.
Нужна помощь в учебе?
Предыдущая тема: Превращения энергии при колебаниях: затухающие и вынужденные колебания
Следующая тема:   Распространение колебаний в среде и волны: продольные и поперечные
Вынужденные колебания. | |||||
Вынужденными колебаниями наз. незатухающие колебания системы, которые вызываются действием внешней периодической силы. |
| ||||
Если сила не будет периодической, то не возникнет и периодических колебаний. Например, если сила постоянна, то возникает статическое отклонение системы. Примеры: колебания гребных винтов, лопаток турбины, качелей при раскачивании, мостов и балок при ходьбе и т.д. |
| ||||
Сила, вызывающая вынужденные колебания, наз. вынуждающей (возмущающей) силой. |
| ||||
Если внешняя вынуждающая сила изменяется по гармоническому закону , то в системе устанавливаются гармонические колебания с частотой внешней вынуждающей силы (процесс установления колебаний изображен на рисунке: вынужденные колебания накладываются на свободные затухающие колебания; после того, как свободные колебания прекращаются, остаются только вынужденные). | |||||
Резонанс. | |||||
Явление возрастания амплитуды колебаний при приближении частоты вынуждающей силы ω к собственной частоте колебательной системы ω0, называется резонансом. |
| ||||
Соответственно данная частота наз. резонансной частотой. | |||||
При наличии трения резонансная частота несколько меньше собственной частоты колебательной системы. С энергетической точки зрения при резонансе создаются наилучшие условия для передачи энергии от внешнего источника к колебательной системе. | |||||
Резонанс применяется для измерения частоты (частотомеры) вибраций, в акустике. Резонанс необходимо учитывать при расчете балок, мостов, станков и т.д. |
| ||||
Автоколебания. | |||||
Колебательная система, совершающая незатухающие колебания за счет действия источника энергии, не обладающего колебательными свойствами (периодичностью), наз. |
| ||||
Примеры: часы, орган, духовые инструменты, сердечно-сосудистая система, паровые машины и двигатели внутреннего сгорания и т.д. |
| ||||
Любая автоколебательная система состоит из 4 частей:
| |||||
Примером механической автоколебательной системы могут быть часы с анкерным ходом. | |||||
| Часы с маятником | Ручные часы | |||
Колебательная система | Маятник | Балансир (маховик) | |||
Источник энергии | Поднятая гиря | Заведенная пружина | |||
Клапан | Анкер | ||||
Обратная связь | Взаимодействие анкера с ходовым колесом | ||||
РЕЗОНАНС • Большая российская энциклопедия
В книжной версии
Том 28.
 Москва, 2015, стр. 336-337
Москва, 2015, стр. 336-337Скопировать библиографическую ссылку:
Авторы: В. В. Клиньшов, В. И. Некоркин
РЕЗОНА́НС (франц. resonance, от лат. resono – откликаться), избирательный отклик колебат. системы на внешнее периодич. воздействие определённой частоты. Явление Р. происходит при приближении частоты внешнего воздействия ω к частоте собств. колебаний системы ω0 и заключается в резком возрастании амплитуды её вынужденных колебаний. В этом случае частота воздействия называется резонансной (ωр). Её величина определяется свойствами колебат. системы. Впервые Р. описан Г. Галилеем для механич. систем. От Р. при внешнем воздействии следует отличать параметрический резонанс, возникающий при периодич. изменении параметров колебат. системы.
систем. От Р. при внешнем воздействии следует отличать параметрический резонанс, возникающий при периодич. изменении параметров колебат. системы.
Суть эффекта Р. можно понять на примере раскачивания качелей путём их периодич. подталкивания. Для эффективного раскачивания качелей частота внешнего подталкивания должна совпадать с частотой их собств. колебаний. В этом случае каждый толчок происходит в одной и той же фазе движения качелей, способствуя увеличению размаха колебаний. При неправильно выбранной частоте подталкивания толчки происходят в разных фазах движения, то ускоряя, то замедляя качели, и существенной раскачки колебаний не происходит.
Рис. 1. Резонансная кривая линейной системы.
Осн. свойства Р. можно наблюдать при воздействии внешнего гармонич. сигнала на линейную систему с одной степенью свободы, такую как колебат. контур или математич. маятник. Зависимость амплитуды A вынужденных колебаний такой системы от частоты внешнего сигнала ω (резонансная кривая) имеет чётко выраженный максимум на резонансной частоте ωр (рис. 1). Для описания резонансных свойств линейной колебат. системы часто используют понятие добротности, характеризующее степень затухания колебаний в системе. Величина добротности определяет форму резонансной кривой: чем больше добротность, тем меньше ширина пика резонансной кривой, т. е. тем более избирательной является колебат. система. С ростом добротности увеличивается высота пика и уменьшается разница между резонансной и собств. частотами.
сигнала на линейную систему с одной степенью свободы, такую как колебат. контур или математич. маятник. Зависимость амплитуды A вынужденных колебаний такой системы от частоты внешнего сигнала ω (резонансная кривая) имеет чётко выраженный максимум на резонансной частоте ωр (рис. 1). Для описания резонансных свойств линейной колебат. системы часто используют понятие добротности, характеризующее степень затухания колебаний в системе. Величина добротности определяет форму резонансной кривой: чем больше добротность, тем меньше ширина пика резонансной кривой, т. е. тем более избирательной является колебат. система. С ростом добротности увеличивается высота пика и уменьшается разница между резонансной и собств. частотами.
Рис. 2. Резонансная кривая нелинейной системы.
В нелинейных системах Р. имеет существенные особенности по сравнению с линейными. Во-первых, резонансная частота нелинейной системы зависит от амплитуды внешнего воздействия. Во-вторых, при достаточно сильных воздействиях исчезает однозначное соответствие амплитуды вынужденных колебаний параметрам внешнего сигнала. При одной и той же частоте внешней силы возможны режимы колебаний с разл. амплитудами (рис. 2). Штриховой кривой на рисунке показана ветвь, соответствующая неустойчивому режиму колебаний. Переключение между разл. режимами при перестройке частоты происходит в виде скачков амплитуды и имеет гистерезисный характер.
имеет существенные особенности по сравнению с линейными. Во-первых, резонансная частота нелинейной системы зависит от амплитуды внешнего воздействия. Во-вторых, при достаточно сильных воздействиях исчезает однозначное соответствие амплитуды вынужденных колебаний параметрам внешнего сигнала. При одной и той же частоте внешней силы возможны режимы колебаний с разл. амплитудами (рис. 2). Штриховой кривой на рисунке показана ветвь, соответствующая неустойчивому режиму колебаний. Переключение между разл. режимами при перестройке частоты происходит в виде скачков амплитуды и имеет гистерезисный характер.
Для линейных систем с несколькими степенями свободы и для распределённых систем, в которых собств. колебания могут происходить на разных частотах, Р. наблюдается при приближении частоты внешнего сигнала к одной из этих частот. В этом случае резонансная кривая характеризуется наличием нескольких максимумов, и внешнее воздействие распределяется по отд. координатам системы.
В этом случае резонансная кривая характеризуется наличием нескольких максимумов, и внешнее воздействие распределяется по отд. координатам системы.
Р. играет важную роль в природе, науке и технике. В некоторых случаях он является нежелательным, т. к. приводит к негативным последствиям. Напр., при совпадении частоты набегающих на корабль волн с собств. частотой килевой качки возникает резкое увеличение амплитуды колебаний корабля, при которых его нос «зарывается» в волну. Р. может вызывать сильные колебания и последующие разрушения при работе вибрирующих станков, машин, двигателей внутр. сгорания. Известны случаи разрушения мостов под действием ритмич. толчков от проходящих по ним войск. С др. стороны, на явлении Р. основана работа мн. приборов и устройств. Напр., настройка частоты колебат. контура радиоприёмника на частоту электромагнитного сигнала позволяет осуществлять его приём.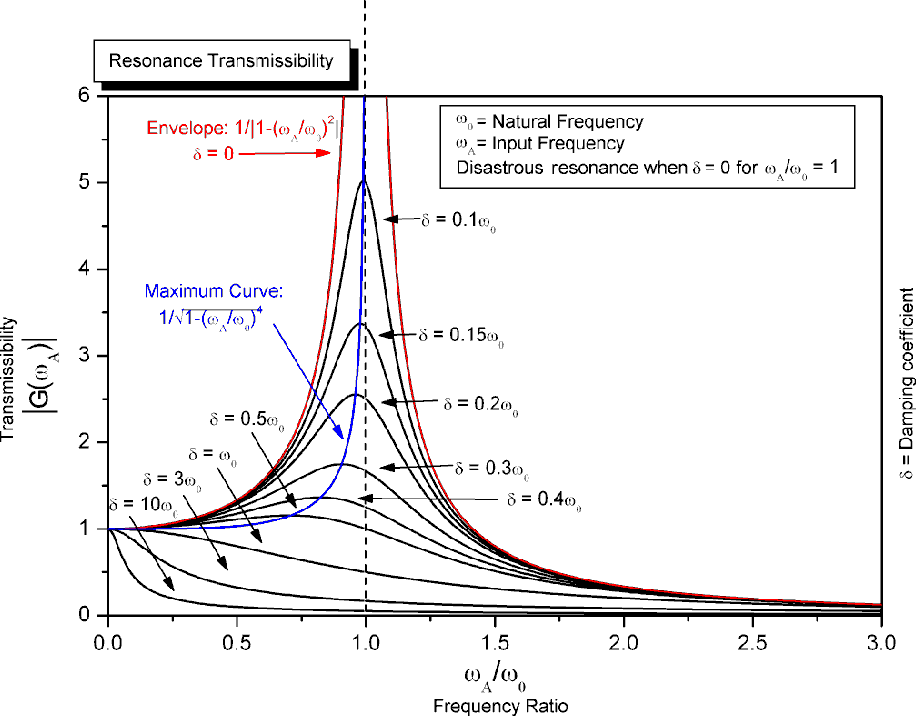 Явление Р. лежит в основе принципа действия СВЧ электронных приборов, напр. клистронов, использующих высокодобротные объёмные резонаторы для усиления СВЧ-сигналов.
Явление Р. лежит в основе принципа действия СВЧ электронных приборов, напр. клистронов, использующих высокодобротные объёмные резонаторы для усиления СВЧ-сигналов.
Microsoft Word – Физ-10_2_52.doc
%PDF-1.6 % 1 0 obj > endobj 5 0 obj >/Font>>>/Fields[]>> endobj 2 0 obj >stream 2014-05-02T21:05:51+04:002014-05-02T21:05:51+04:002014-05-02T21:05:51+04:00PScript5.dll Version 5.2.2application/pdf
 xLVD8Taø”34l;=F$EAN4nV{y-DG;).r
:yu_уOx9Z
xLVD8Taø”34l;=F$EAN4nV{y-DG;).r
:yu_уOx9Z| Адроны | msimagelist>|
| Альфа-распад | msimagelist>|
| Альфа-частица | msimagelist>|
| Аннигиляция | msimagelist>|
| Антивещество | msimagelist>|
| Антинейтрон | msimagelist>|
| Антипротон | msimagelist>|
| Античастицы | msimagelist>|
| Атом | msimagelist>|
| Атомная единица массы | msimagelist>|
| Атомная электростанция | msimagelist>|
| Барионное число | msimagelist>|
| Барионы | msimagelist>|
| Бета-распад | msimagelist>|
| Бетатрон | msimagelist>|
| Бета-частицы | msimagelist>|
| Бозе – Эйнштейна статистика | msimagelist>|
| Бозоны | msimagelist>|
| Большой адронный коллайдер | msimagelist>|
| Большой Взрыв | msimagelist>|
Боттом. Боттомоний Боттомоний | msimagelist>|
| Брейта-Вигнера формула | msimagelist>|
| Быстрота | msimagelist>|
| Векторная доминантность | msimagelist>|
| Великое объединение | msimagelist>|
| Взаимодействие частиц | msimagelist>|
| Вильсона камера | msimagelist>|
| Виртуальные частицы | msimagelist>|
| Водорода атом | msimagelist>|
| Возбуждённые состояния ядер | msimagelist>|
| Волновая функция | msimagelist>|
| Волновое уравнение | msimagelist>|
| Волны де Бройля | msimagelist>|
| Встречные пучки | msimagelist>|
| Гамильтониан | msimagelist>|
| Гамма-излучение | msimagelist>|
| Гамма-квант | msimagelist>|
| Гамма-спектрометр | msimagelist>|
| Гамма-спектроскопия | msimagelist>|
| Гаусса распределение | msimagelist>|
| Гейгера счётчик | msimagelist>|
| Гигантский дипольный резонанс | msimagelist>|
| Гиперядра | msimagelist>|
| Глюоны | msimagelist>|
| Годоскоп | msimagelist>|
| Гравитационное взаимодействие | msimagelist>|
| Дейтрон | msimagelist>|
| Деление атомных ядер | msimagelist>|
| Детекторы частиц | msimagelist>|
| Дирака уравнение | msimagelist>|
| Дифракция частиц | msimagelist>|
| Доза излучения | msimagelist>|
| Дозиметр | msimagelist>|
| Доплера эффект | msimagelist>|
| Единая теория поля | msimagelist>|
| Зарядовое сопряжение | msimagelist>|
| Зеркальные ядра | msimagelist>|
| Избыток массы (дефект массы) | msimagelist>|
| Изобары | msimagelist>|
| Изомерия ядерная | msimagelist>|
| Изоспин | msimagelist>|
| Изоспиновый мультиплет | msimagelist>|
| Изотопов разделение | msimagelist>|
| Изотопы | msimagelist>|
| Ионизирующее излучение | msimagelist>|
| Искровая камера | msimagelist>|
| Квантовая механика | msimagelist>|
| Квантовая теория поля | msimagelist>|
| Квантовые операторы | msimagelist>|
| Квантовые числа | msimagelist>|
| Квантовый переход | msimagelist>|
| Квант света | msimagelist>|
| Кварк-глюонная плазма | msimagelist>|
| Кварки | msimagelist>|
| Коллайдер | msimagelist>|
| Комбинированная инверсия | msimagelist>|
| Комптона эффект | msimagelist>|
| Комптоновская длина волны | msimagelist>|
| Конверсия внутренняя | msimagelist>|
| Константы связи | msimagelist>|
| Конфайнмент | msimagelist>|
| Корпускулярно волновой дуализм | msimagelist>|
| Космические лучи | msimagelist>|
| Критическая масса | msimagelist>|
| Лептоны | msimagelist>|
| Линейные ускорители | msimagelist>|
| Лоренца преобразования | msimagelist>|
| Лоренца сила | msimagelist>|
| Магические ядра | msimagelist>|
| Магнитный дипольный момент ядра | msimagelist>|
| Магнитный спектрометр | msimagelist>|
| Максвелла уравнения | msimagelist>|
| Масса частицы | msimagelist>|
| Масс-спектрометр | msimagelist>|
| Массовое число | msimagelist>|
| Масштабная инвариантность | msimagelist>|
| Мезоны | msimagelist>|
| Мессбауэра эффект | msimagelist>|
| Меченые атомы | msimagelist>|
| Микротрон | msimagelist>|
| Нейтрино | msimagelist>|
| Нейтрон | msimagelist>|
| Нейтронная звезда | msimagelist>|
| Нейтронная физика | msimagelist>|
| Неопределённостей соотношения | msimagelist>|
| Нормы радиационной безопасности | msimagelist>|
| Нуклеосинтез | msimagelist>|
| Нуклид | msimagelist>|
| Нуклон | msimagelist>|
| Обращение времени | msimagelist>|
| Орбитальный момент | msimagelist>|
| Осциллятор | msimagelist>|
| Отбора правила | msimagelist>|
| Пар образование | msimagelist>|
| Период полураспада | msimagelist>|
| Планка постоянная | msimagelist>|
| Планка формула | msimagelist>|
| Позитрон | msimagelist>|
| Поляризация | msimagelist>|
| Поляризация вакуума | msimagelist>|
| Потенциальная яма | msimagelist>|
| Потенциальный барьер | msimagelist>|
| Принцип Паули | msimagelist>|
| Принцип суперпозиции | msimagelist>|
| Промежуточные W-, Z-бозоны | msimagelist>|
| Пропагатор | msimagelist>|
| Пропорциональный счётчик | msimagelist>|
| Пространственная инверсия | msimagelist>|
| Пространственная четность | msimagelist>|
| Протон | msimagelist>|
| Пуассона распределение | msimagelist>|
| Пузырьковая камера | msimagelist>|
| Радиационный фон | msimagelist>|
| Радиоактивность | msimagelist>|
| Радиоактивные семейства | msimagelist>|
| Радиометрия | msimagelist>|
| Расходимости | msimagelist>|
| Резерфорда опыт | msimagelist>|
| Резонансы (резонансные частицы) | msimagelist>|
| Реликтовое микроволновое излучение | msimagelist>|
| Светимость ускорителя | msimagelist>|
| Сечение эффективное | msimagelist>|
| Сильное взаимодействие | msimagelist>|
| Синтеза реакции | msimagelist>|
| Синхротрон | msimagelist>|
| Синхрофазотрон | msimagelist>|
| Синхроциклотрон | msimagelist>|
| Система единиц измерений | msimagelist>|
| Слабое взаимодействие | msimagelist>|
| Солнечные нейтрино | msimagelist>|
| Сохранения законы | msimagelist>|
| Спаривания эффект | msimagelist>|
| Спин | msimagelist>|
| Спин-орбитальное взаимодействие | msimagelist>|
| Спиральность | msimagelist>|
| Стандартная модель | msimagelist>|
| Статистика | msimagelist>|
| Странные частицы | msimagelist>|
| Струи адронные | msimagelist>|
| Субатомные частицы | msimagelist>|
| Суперсимметрия | msimagelist>|
| Сферическая система координат | msimagelist>|
| Тёмная материя | msimagelist>|
| Термоядерные реакции | msimagelist>|
| Термоядерный реактор | msimagelist>|
| Тормозное излучение | msimagelist>|
| Трансурановые элементы | msimagelist>|
| Трек | msimagelist>|
| Туннельный эффект | msimagelist>|
| Ускорители заряженных частиц | msimagelist>|
| Фазотрон | msimagelist>|
| Фейнмана диаграммы | msimagelist>|
| Фермионы | msimagelist>|
| Формфактор | msimagelist>|
| Фотон | msimagelist>|
| Фотоэффект | msimagelist>|
| Фундаментальная длина | msimagelist>|
| Хиггса бозон | msimagelist>|
| Цвет | msimagelist>|
| Цепные ядерные реакции | msimagelist>|
| Цикл CNO | msimagelist>|
| Циклические ускорители | msimagelist>|
| Циклотрон | msimagelist>|
Чарм. Чармоний Чармоний | msimagelist>|
| Черенковский счётчик | msimagelist>|
| Черенковсое излучение | msimagelist>|
| Черные дыры | msimagelist>|
| Шредингера уравнение | msimagelist>|
| Электрический квадрупольный момент ядра | msimagelist>|
| Электромагнитное взаимодействие | msimagelist>|
| Электрон | msimagelist>|
| Электрослабое взаимодействие | msimagelist>|
| Элементарные частицы | msimagelist>|
| Ядерная физика | msimagelist>|
| Ядерная энергия | msimagelist>|
| Ядерные модели | msimagelist>|
| Ядерные реакции | msimagelist>|
| Ядерный взрыв | msimagelist>|
| Ядерный реактор | msimagelist>|
| Ядра энергия связи | msimagelist>|
| Ядро атомное | msimagelist>|
| Ядерный магнитный резонанс (ЯМР) | msimagelist>
Урок физики в 9 классе по теме “Резонанс”
Урок физики
Тема: Резонанс
Класс: 9 класс
Учитель: Белова М. И.
И.
В тематическом планировании данный урок по теме «Механические колебания» пятый.
Тип урока: Урок изучения нового материала.
Цели обучения:
1.Научиться объяснять, в чем заключается явление резонанса;2.Приводить примеры полезных и вредных проявлений резонанса и пути устранения последних.
1. Осознанное, уважительное и доброжелательное отношение к другому человеку
2. Готовность и способность вести диалог с другими людьми и достигать в нем взаимопонимания.
1.Извлекать информацию из прочитанного текста.
2.Строят логические рассуждения.
3. Анализировать полученные результаты.
1. Целеполагание, планирование своей деятельности
1.Выражают свои мысли понятно и точно.
2.Слушают и вступают в диалог, добывают недостающую информацию с помощью вопросов
Структура урока:
.
Деятельность обучающихся
Познавательная
Коммуникативная
Регулятивная
1. Постановка учебной задачи
Постановка учебной задачи
Создание проблемной ситуации. Фиксация новой учебной задачи
Организовывает погружение в проблему, создает ситуацию разрыва.
Пытаются решить задачу. Фиксируют проблему.
Слушают учителя. Строят понятные для собеседника высказывания
Принимают и сохраняют учебную цель и задачу.
2. Совместное исследование проблемы.
Поиск решения учебной задачи.
Организовывает устный коллективный анализ учебной задачи. Фиксирует выдвину-тые ученииками гипотезы, организует их обсуждение.
Анализируют, аргументируют свою точку зрения
Осознанно строят речевые высказывания, рефлексия своих действий
Исследуют условия учебной задачи, обсуждают предметные способы решения
3. Моделирование
Составление плана действий по решению учебной задачи
Организует учебное взаимодействие учеников (группы) и следующее обсуждение составленных моделей планирования.
Проводят актуализацию знаний. Фиксируют формулы, знания, необходимые действия для решения учебной задачи
Фиксируют формулы, знания, необходимые действия для решения учебной задачи
Воспринимают и обсуждают варианты моделей планов обучающихся
Осуществляют самоконтроль Принимают и сохраняют учебную цель и задачу.
4. Этап решения учебной задачи.
Первичный контроль за правильностью выполнения плана действий.
Диагностическая работа , оценивает выполнение каждого действия.
Осуществляют работу по выполнению отдельных действий.
Учатся формулировать собственное мнение и позицию, оказывают помощь друг другу
Осуществляют самоконтроль, взаимоконтроль
6. Промежуточный контроль
Осмысление действий по решению учебной задачи.
Отработка операций, в которых допущены ошибки. Организует коррекционную работу, самостоятельную коррекционную работу.
Исправляют ошибки.
Строят рассуждения, понятные для собеседника.
Взаимопроверка. Осуществляют пошаговый контроль по результату
7. Контроль на этапе окончания учебной темы.
Контроль на этапе окончания учебной темы.
Контроль. Осознание результатов работы
Диагностическая работа (на выходе):
– контрольно-оценивающая деятельность.
Выполняют работу, анализируют, контролируют и оценивают результат.
Рефлексия своих действий
Осуществляют пошаговый контроль по результату
Учебная задача:
Посмотрите часть мультфильма и ответьте на вопросы
1.Есть ли связь между видеороликом и изучаемой темой?
2.Что случилось с птицей? Что в это время делала девушка?
Видеоролик (из мультфильма «Шрек»)
3.Почему птица увеличилась в размерах и лопнула как воздушный шарик?
Конспект урока
Тема: Резонанс.
1.Орг момент.
2.Актуализация опорных знаний.
Какую тему изучали на предыдущем уроке?
Повторим основные понятия темы:
Вопросы на слайде. Отвечаем по очереди.
Отвечаем по очереди.
1.Какие движения называются колебаниями?
2.Какие колебания называют свободными?
3.Какие колебания называют вынужденными?
4.Что является источником колебаний?
5.Является ли звук колебанием?
6. Что называют амплитудой колебаний?
7.Что называют частотой колебаний?
8.Что называют периодом колебаний?
9.От чего зависит частота колебаний нитяного маятника?
Если вы правильно ответили на вопрос, поставьте себе 1 балл за это в лист оценивания (колонка Этап актуализации знаний. Ответы на вопросы), если неправильно или вообще не ответили, то 0 баллов
3.Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Посмотрите часть мультфильма и ответьте на вопросы
1.Есть ли связь между видеороликом и изучаемой темой?
2.Что случилось с птицей? Что в это время делала девушка?
Видеоролик (из мультфильма «Шрек»
3. Почему птица увеличилась в размерах и лопнула как воздушный шарик?
Почему птица увеличилась в размерах и лопнула как воздушный шарик?
Выскажите предположения.
Эта ситуация слишком преувеличенная, но основывается она на одном из механических явлений, которое нам предстоит сегодня изучить.
Следующий видеоролик поможет определить тему сегодняшнего урока. При озвучивании комментатор назовёт механическое явление, название которого и будет темой сегодняшнего урока. Посмотрите и запомните название этого явления.
Видеоролик. (перемещение глыб)
Назовите механическое явление.
Если не назовут, то ещё один видеоролик (обрушение мостов)
Итак тема сегодняшнего урока «Резонанс»
Скажите, что конкретно мы должны узнать на уроке о резонансе?
-определение;
-условия возникновения;
-польза;
-вред.
4. Первичное усвоение новых знаний.
Будем работать в парах. Каждой паре будет дано задание.
Задание для группы 1.
Резонанс – это резкое увеличинение амплитуды колебаний.
Соедините 2 штатива толстой ниткой. К ней присоедините несколько (3-4) маятников на нити. Раскачайте один из маятников. Внимательно наблюдайте за остальными. Возьмите ещё один маятник и прикрепите его к нити так, чтобы его длина была равна длине первого маятника, который вы раскачиваете сами. Раскачайте его. Как ведут себя остальные маятники? У какого маятника наблюдается явление резкого увеличения амплитуды колебаний, резонанса? Сравните характеристики колебаний маятников, у которых наблюдается резкое увеличение амплитуды колебаний. При каком условии наблюдается резонанс?
Задание для группы 2.
Прочитайте учебник стр.105-107 “Резонанс “.
Сделайте вывод:
1) в чем заключается явление, называемое резонансом,
2) от какой физической величины, характеризующей колебания, зависит возникновение явления резонанса,
3) к каким колебаниям –свободным или вынужденным – применимо понятие резонанса.
Задание для группы 3.
Прочитайте учебник стр.105-107 “Резонанс “.
Используя Интернет найдите примеры пользы и вреда резонанса (по 3 примера)
5. Первичная проверка понимания
Заслушиваем отчёты о выполнении заданий каждой группы.
Оцените свою работу (2.колонка. Работа в группах. Изучение нового материала): 5 баллов, если всё сделано правильно и ответы даны на все вопросы. 4 балла, если были недочёты; 3 балла, если вы сделали половину; 2 балла, если сделали хоть что-то,; 1 балл, если пытались, но ничего сделать не удалось.
6. Первичное закрепление.
Основная информация о резонансе получена. Попробуем применить знания для решения заданий.
(Каждая группа получает 1 задание, объяснение которого требует знаний по теме «Резонанс»)
Задание для группы 1.
Вода, которую мальчик несёт в ведре, начинает сильно расплёскиваться. Что нужно сделать мальчику, чтобы вода перестала расплёскиваться?
Задание для группы 2.
Как должен идти кавалерийский полк по мосту, чтобы он не разрушился?
Задание для группы 3.
Вспомните видеоролик в начале урока. Скажите что случилось с птицей во время пения девушки? Объясните явление.
Оцените свою работу: (Колонка в таблице 3.Работа в группах. Применение знаний) 1 балл, если ответили правильно, 0 если неправильно.
Выслушиваем ответы каждой группы.
7.Контроль на этапе окончания учебной темы.
Тест с самопроверкой по слайду.
1. Явление резонанса может наблюдаться в
1) любой колебательной системе
2) системе, совершающей свободные колебания
3) автоколебательной системе
4) системе, совершающей вынужденные колебания
2. Резонанс возникает, когда собственная частота колебательной системы совпадает с
А. амплитудой вынуждающей силы
Б. частотой вынуждающей силы
Верно(-ы) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Примером вредного проявления резонанса может быть
Примером вредного проявления резонанса может быть
А. сильное раскачивание железнодорожного вагона
Б. сильное раскачивание кораблей на волнах
Верно(-ы) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
4. Примером полезного проявления резонанса может быть
А. дребезжание стекол в автобусе
Б. постепенное раскачивание тяжелого языка колокола
Верно(-ы) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
5. На рисунке представлен график зависимости амплитуды А вынужденных колебаний от частоты v вынуждающей силы. Резонанс происходит при частоте
1) 0 Гц
2) 10 Гц
3) 20 Гц
4) 30 Гц
Проверьте ответы по слайду. Поставьте за каждый правильный ответ 1 балл.
Урок окончен, всем спасибо.
Учебное пособие по физике: Резонанс
Цель урока 11 учебного курса по физике – развить понимание природы, свойств, поведения и математики звука и применить это понимание к анализу музыки и музыкальных инструментов. До сих пор в этом модуле принципы звуковых волн применялись к обсуждению ударов, музыкальных интервалов, акустики концертного зала, различий между шумом и музыкой, а также воспроизведения звука музыкальными инструментами.В Уроке 5 основное внимание будет уделено применению математических соотношений и концепций стоячей волны к музыкальным инструментам. Будут исследованы три основные категории инструментов: инструменты с вибрирующими струнами (которые будут включать струны гитары, струны скрипки и струны фортепиано), инструменты с открытой воздушной колонной (которые будут включать медные инструменты, такие как тромбон, и деревянные духовые инструменты, такие как флейта и блок-флейта), а также инструменты с воздушной колонной закрытого типа (которые будут включать в себя органную трубу и флаконы поп-бутылочного оркестра ).Четвертая категория – вибромеханические системы (в которую входят все ударные инструменты) – обсуждаться не будет. Эти категории инструментов могут быть необычными для некоторых; они основаны на общности их моделей стоячих волн и математических соотношениях между частотами, производимыми инструментами.
До сих пор в этом модуле принципы звуковых волн применялись к обсуждению ударов, музыкальных интервалов, акустики концертного зала, различий между шумом и музыкой, а также воспроизведения звука музыкальными инструментами.В Уроке 5 основное внимание будет уделено применению математических соотношений и концепций стоячей волны к музыкальным инструментам. Будут исследованы три основные категории инструментов: инструменты с вибрирующими струнами (которые будут включать струны гитары, струны скрипки и струны фортепиано), инструменты с открытой воздушной колонной (которые будут включать медные инструменты, такие как тромбон, и деревянные духовые инструменты, такие как флейта и блок-флейта), а также инструменты с воздушной колонной закрытого типа (которые будут включать в себя органную трубу и флаконы поп-бутылочного оркестра ).Четвертая категория – вибромеханические системы (в которую входят все ударные инструменты) – обсуждаться не будет. Эти категории инструментов могут быть необычными для некоторых; они основаны на общности их моделей стоячих волн и математических соотношениях между частотами, производимыми инструментами.
Как упоминалось в Уроке 4, музыкальные инструменты приводятся в колебательное движение с их естественной частотой, когда человек ударяет, ударяет, звенит, щиплет или как-то мешает объекту.Каждая собственная частота объекта связана с одним из множества паттернов стоячих волн, с помощью которых этот объект может вибрировать. Собственные частоты музыкального инструмента иногда называют гармониками инструмента. Инструмент можно заставить вибрировать на одной из своих гармоник (с одной из его моделей стоячих волн), если другой взаимосвязанный объект толкает его с одной из этих частот. Это известно как резонанс – когда один объект вибрирует с той же собственной частотой, что и второй объект, заставляет этот второй объект совершать колебательные движения.
Слово «резонанс» происходит от латинского и означает «звучать» – звучать вместе с громким звуком. Резонанс – частая причина звукоизвлечения музыкальных инструментов. Одна из наших лучших моделей резонанса в музыкальном инструменте – это резонансная трубка (полая цилиндрическая трубка), частично заполненная водой и вызываемая вибрацией с помощью камертона. Камертон – это объект, который заставил воздух внутри резонансной трубки войти в резонанс. Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые сталкиваются с отверстием резонансной трубки.Эти падающие звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Таким образом, если частота, на которой вибрирует камертон, не идентична одной из собственных частот воздушного столба внутри резонансной трубки, резонанса не произойдет, и два объекта не будут издавать звук вместе с громким звуком.
Одна из наших лучших моделей резонанса в музыкальном инструменте – это резонансная трубка (полая цилиндрическая трубка), частично заполненная водой и вызываемая вибрацией с помощью камертона. Камертон – это объект, который заставил воздух внутри резонансной трубки войти в резонанс. Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые сталкиваются с отверстием резонансной трубки.Эти падающие звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Таким образом, если частота, на которой вибрирует камертон, не идентична одной из собственных частот воздушного столба внутри резонансной трубки, резонанса не произойдет, и два объекта не будут издавать звук вместе с громким звуком. Но расположение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха. Как мы узнали ранее, увеличение длины колебательной системы (здесь воздух в трубке) увеличивает длину волны и снижает собственную частоту этой системы. И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, повышая и понижая уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон.Когда согласование достигается, камертон заставляет столб воздуха внутри резонансной трубки вибрировать с собственной частотой, и достигается резонанс. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Но расположение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха. Как мы узнали ранее, увеличение длины колебательной системы (здесь воздух в трубке) увеличивает длину волны и снижает собственную частоту этой системы. И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, повышая и понижая уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон.Когда согласование достигается, камертон заставляет столб воздуха внутри резонансной трубки вибрировать с собственной частотой, и достигается резонанс. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Еще одна распространенная физическая демонстрация, которая служит отличной моделью резонанса, – это знаменитая демонстрация «поющего жезла». В центре держится длинный полый алюминиевый стержень.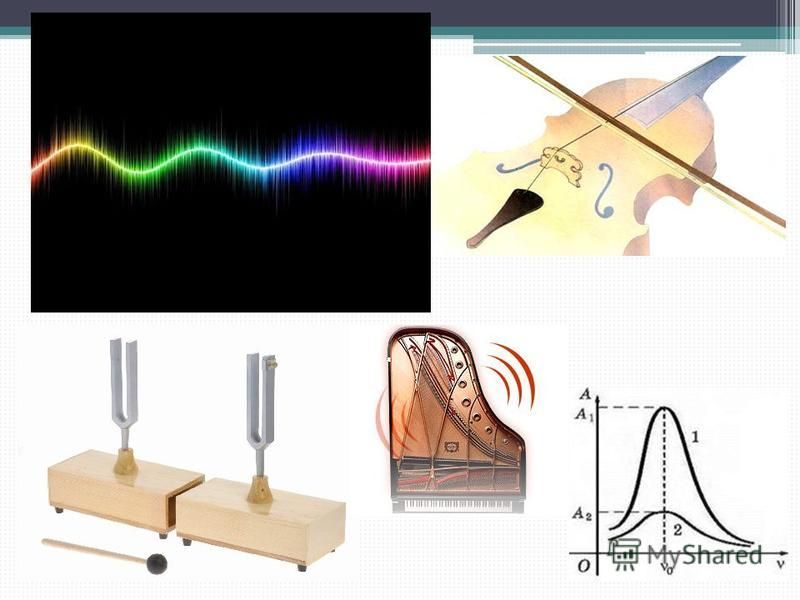 Будучи профессиональным музыкантом, учитель достает канифольный пакет, чтобы подготовиться к мероприятию.Затем с большим энтузиазмом он / она медленно проводит рукой по длине алюминиевого стержня, заставляя его издавать громкий звук. Это пример резонанса. Когда рука скользит по поверхности алюминиевого стержня, трение между рукой и стержнем вызывает колебания алюминия. Колебания алюминия заставляют воздушный столб внутри стержня колебаться с собственной частотой. Соответствие колебаний столба воздуха одной из собственных частот поющего стержня вызывает резонанс.Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Будучи профессиональным музыкантом, учитель достает канифольный пакет, чтобы подготовиться к мероприятию.Затем с большим энтузиазмом он / она медленно проводит рукой по длине алюминиевого стержня, заставляя его издавать громкий звук. Это пример резонанса. Когда рука скользит по поверхности алюминиевого стержня, трение между рукой и стержнем вызывает колебания алюминия. Колебания алюминия заставляют воздушный столб внутри стержня колебаться с собственной частотой. Соответствие колебаний столба воздуха одной из собственных частот поющего стержня вызывает резонанс.Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Знакомый шум моря , который слышен, когда морская ракушка подносится к уху, также объясняется резонансом. Даже в кажущейся тихой комнате есть звуковые волны с разными частотами. Эти звуки в основном неслышны из-за их низкой интенсивности. Этот так называемый фоновый шум наполняет морскую ракушку, вызывая вибрацию внутри ракушки. Но у морской ракушки есть набор собственных частот, на которых она будет вибрировать. Если одна из частот в комнате заставляет воздух внутри ракушки вибрировать с собственной частотой, возникает резонансная ситуация. И всегда результатом резонанса является сильная вибрация, то есть громкий звук. На самом деле звук достаточно громкий, чтобы его можно было услышать. Поэтому в следующий раз, когда вы услышите звук моря в морской раковине, помните, что все, что вы слышите, – это усиление одной из многих фоновых частот в комнате.
Но у морской ракушки есть набор собственных частот, на которых она будет вибрировать. Если одна из частот в комнате заставляет воздух внутри ракушки вибрировать с собственной частотой, возникает резонансная ситуация. И всегда результатом резонанса является сильная вибрация, то есть громкий звук. На самом деле звук достаточно громкий, чтобы его можно было услышать. Поэтому в следующий раз, когда вы услышите звук моря в морской раковине, помните, что все, что вы слышите, – это усиление одной из многих фоновых частот в комнате.
Музыкальные инструменты воспроизводят выбранные звуки таким же образом. Медные инструменты обычно состоят из мундштука, прикрепленного к длинной трубке, наполненной воздухом. Трубку часто изгибают, чтобы уменьшить размер инструмента. Металлическая трубка служит лишь контейнером для столба воздуха. Именно вибрации этой колонны производят звуки, которые мы слышим. Длину вибрирующего столба воздуха внутри трубки можно регулировать, сдвигая трубку для увеличения и уменьшения ее длины или открывая и закрывая отверстия, расположенные вдоль трубки, чтобы контролировать, где воздух входит и выходит из трубки. Медные духовые инструменты включают в себя вдувание воздуха в мундштук. Вибрации губ относительно мундштука создают диапазон частот. Одна из частот в диапазоне частот соответствует одной из собственных частот воздушного столба внутри медного инструмента.Это заставляет воздух внутри колонны испытывать резонансные колебания. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Длину вибрирующего столба воздуха внутри трубки можно регулировать, сдвигая трубку для увеличения и уменьшения ее длины или открывая и закрывая отверстия, расположенные вдоль трубки, чтобы контролировать, где воздух входит и выходит из трубки. Медные духовые инструменты включают в себя вдувание воздуха в мундштук. Вибрации губ относительно мундштука создают диапазон частот. Одна из частот в диапазоне частот соответствует одной из собственных частот воздушного столба внутри медного инструмента.Это заставляет воздух внутри колонны испытывать резонансные колебания. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Деревянные духовые инструменты работают аналогичным образом. Только источником вибраций являются не губы музыканта, соприкасающиеся с мундштуком, а вибрация трости или деревянной полоски. Работа деревянных духовых инструментов часто моделируется на уроках физики с помощью пластиковой соломинки. Концы соломки обрезаются ножницами, образуя коническую трость . Когда воздух проходит через тростник, тростник вибрирует, создавая турбулентность с диапазоном частот колебаний. Когда частота вибрации язычка совпадает с частотой вибрации столба воздуха в соломе, возникает резонанс. И еще раз, результатом резонанса является сильная вибрация – язычок и столб воздуха излучаются вместе, создавая громкий звук. Как будто этого было недостаточно, длину соломинки обычно сокращают, отрезая небольшие кусочки от противоположного конца. По мере того как соломинка (и столб воздуха, который в ней содержится) укорачивается, длина волны уменьшается, а частота увеличивается.По мере укорачивания соломы наблюдаются все более высокие шаги. Деревянные духовые инструменты издают звуки, похожие на соломенную демонстрацию. Вибрирующий язычок заставляет столб воздуха вибрировать на одной из собственных частот. Только для духовых инструментов длина столба воздуха регулируется путем открытия и закрытия отверстий в металлической трубе (поскольку трубы немного трудно разрезать и их слишком дорого заменять каждый раз, когда их разрезают).
Когда воздух проходит через тростник, тростник вибрирует, создавая турбулентность с диапазоном частот колебаний. Когда частота вибрации язычка совпадает с частотой вибрации столба воздуха в соломе, возникает резонанс. И еще раз, результатом резонанса является сильная вибрация – язычок и столб воздуха излучаются вместе, создавая громкий звук. Как будто этого было недостаточно, длину соломинки обычно сокращают, отрезая небольшие кусочки от противоположного конца. По мере того как соломинка (и столб воздуха, который в ней содержится) укорачивается, длина волны уменьшается, а частота увеличивается.По мере укорачивания соломы наблюдаются все более высокие шаги. Деревянные духовые инструменты издают звуки, похожие на соломенную демонстрацию. Вибрирующий язычок заставляет столб воздуха вибрировать на одной из собственных частот. Только для духовых инструментов длина столба воздуха регулируется путем открытия и закрытия отверстий в металлической трубе (поскольку трубы немного трудно разрезать и их слишком дорого заменять каждый раз, когда их разрезают).
Резонанс – причина образования звука в музыкальных инструментах.В оставшейся части Урока 5 математика стоячих волн будет применена для понимания того, как резонирующие струны и воздушные колонны создают свои определенные частоты.
14.4 Звуковые помехи и резонанс – Физика
Задачи обучения разделу
К концу этого раздела вы сможете делать следующее:
- Опишите резонанс и биения
- Определение основной частоты и гармонического ряда
- Контрастность резонатора открытого и закрытого типа
- Решение проблем, связанных с гармоническими сериями и частотой биений
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (7) Научные концепции.Студент знает характеристики и поведение волн.
 Ожидается, что студент:
Ожидается, что студент:- (D) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
Кроме того, в Руководстве по лаборатории физики средней школы рассматривается содержание этого раздела лаборатории под названием «Звуковые волны», а также следующие стандарты:
- (7) Научные концепции. Студент знает характеристики и поведение волн.Ожидается, что студент:
- (D) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
Раздел Основные термины
| удар | частота биений | демпфирование | основной | гармоник |
| собственная частота | обертонов | резонанс | резонировать |
Поддержка учителя
Поддержка учителя
[BL] Перед началом этого раздела было бы полезно рассмотреть свойства звуковых волн и то, как они связаны друг с другом, стоячие волны, суперпозиция и интерференция волн.
Резонанс и удары
Сядьте как-нибудь перед пианино и спойте на нем короткую громкую ноту, нажимая на педаль сустейна. Он пропоет вам ту же ноту – струны, которые имеют те же частоты, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Это хороший пример того факта, что объекты – в данном случае струны фортепиано – можно заставить колебаться, но лучше всего они колеблются на своей собственной частоте.
Движущая сила (например, ваш голос в примере) вводит энергию в систему на определенной частоте, которая не обязательно совпадает с собственной частотой системы.Со временем энергия рассеивается, а амплитуда постепенно уменьшается до нуля – это называется затуханием. Собственная частота – это частота, с которой система будет колебаться, если бы не было движения и демпфирующей силы. Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
Большинство из нас играли с игрушками, в которых объект подпрыгивает на резинке, что-то вроде шарика, подвешенного на пальце на рисунке 14.18. Сначала вы держите палец неподвижно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете. По мере того, как частота возбуждения постепенно становится выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.
Рис. 14.18 Шарик на резиновой ленте перемещается в ответ на палец, поддерживающий его. Если палец движется с собственной частотой мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он реагирует колебаниями с меньшей амплитудой.
На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он реагирует колебаниями с меньшей амплитудой.
Другой пример: когда вы настраиваете радио, вы настраиваете его резонансную частоту так, чтобы оно колебалось только на частоте вещания желаемой радиостанции.Кроме того, ребенок на качелях приводится в движение (толкается) родителем на собственной частоте качелей для достижения максимальной амплитуды (высоты). Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.
Рисунок 14.19 В некоторых типах наушников для подавления посторонних шумов используются явления конструктивных и деструктивных помех.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Камерные вилки и трубы могут использоваться для демонстрации концепции резонанса.Используйте любую трубу или трубку, закрытую с одного конца. Закрепите его так, чтобы он стоял вертикально открытым концом вверх. Выберите камертон и ударьте по нему, чтобы он завибрировал. Поднесите его к горлышку трубы и послушайте звук. Теперь наполните трубу водой и повторите. При изменении уровня воды изменяется длина резонирующего столба воздуха. Продолжайте делать это. При достижении определенной длины звук камертона будет резонировать через колонку.
Выберите камертон и ударьте по нему, чтобы он завибрировал. Поднесите его к горлышку трубы и послушайте звук. Теперь наполните трубу водой и повторите. При изменении уровня воды изменяется длина резонирующего столба воздуха. Продолжайте делать это. При достижении определенной длины звук камертона будет резонировать через колонку.
Все звуковые резонансы вызваны конструктивными и деструктивными помехами.Только резонансные частоты конструктивно интерферируют, образуя стоячие волны, тогда как другие интерферируют деструктивно и отсутствуют. От гудка над бутылкой до узнаваемости голоса великого певца – резонанс и стоячие волны играют жизненно важную роль в звуке.
Помехи случаются со всеми типами волн, включая звуковые волны. Фактически, один из способов подтвердить, что что-то является волной , – это наблюдать эффекты интерференции. На рис. 14.19 показан набор наушников, в которых для подавления шума используется разумное использование звуковых помех. Чтобы получить деструктивную интерференцию, выполняется быстрый электронный анализ, и вводится второй звук, максимумы и минимумы которого полностью противоположны входящему шуму.
Чтобы получить деструктивную интерференцию, выполняется быстрый электронный анализ, и вводится второй звук, максимумы и минимумы которого полностью противоположны входящему шуму.
Помимо резонанса, суперпозиция волн также может создавать биения. Биения производятся наложением двух волн с немного разными частотами, но одинаковой амплитудой. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, придавая результирующей волне амплитуду, которая изменяется во времени.(См. Результирующую волну на рисунке 14.20).
Эта волна колеблется по амплитуде или биениям с частотой, называемой частотой биений. Уравнение для частоты биений:
fB = | f1 − f2 |, fB = | f1 − f2 |,14,13
, где f 1 и f 2 – частоты двух исходных волн. Если две частоты звуковых волн похожи, то мы слышим среднюю частоту, которая становится громче и тише с частотой биений.
Советы для успеха
Не путайте частоту биений с обычной частотой волны, возникающей в результате наложения.Хотя частота биений задается приведенной выше формулой и описывает частоту биений, фактическая частота волны, полученная в результате наложения, является средним значением частот двух исходных волн.
Рисунок 14.20 Биения возникают в результате наложения двух волн немного разных частот, но одинаковых амплитуд. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, придавая результирующей волне изменяющуюся во времени амплитуду.
Виртуальная физика
Волновые помехи
Для этого упражнения перейдите на вкладку «Звук». Включите параметр «Звук» и поэкспериментируйте с изменением частоты и амплитуды, а также с добавлением второго динамика и барьера.
Проверка захвата
Согласно графику, что происходит с амплитудой давления с течением времени.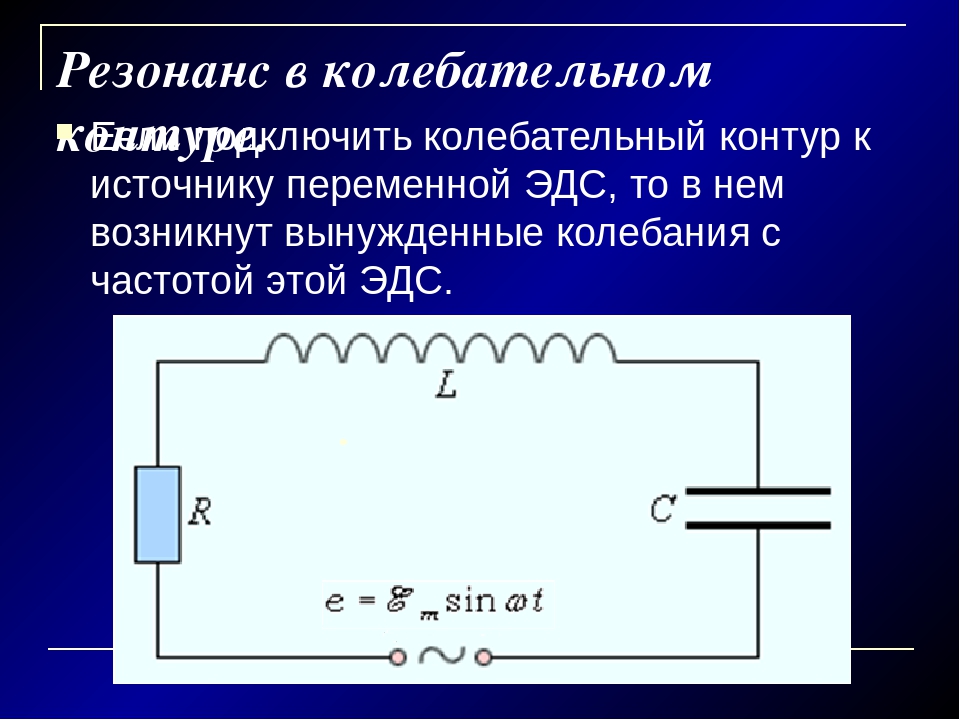 Как называется это явление и что его вызывает?
Как называется это явление и что его вызывает?
- Амплитуда со временем уменьшается. Это явление называется затуханием.Это вызвано рассеянием энергии.
- Амплитуда со временем увеличивается. Это явление называется обратной связью. Это вызвано накоплением энергии.
- Амплитуда колеблется со временем. Это явление называется эхом. Это вызвано колебаниями энергии.
Основная частота и гармоники
Предположим, мы держим камертон возле конца трубки, которая закрыта на другом конце, как показано на рисунке 14.21, Рис. 14.22 и Рис. 14.23. Если камертон имеет правильную частоту, столб воздуха в трубке громко резонирует, но на большинстве частот он очень мало вибрирует. Это означает, что столб воздуха имеет только определенные собственные частоты. На рисунках показано, как формируется резонанс на самой низкой из этих собственных частот. Возмущение распространяется по трубке со скоростью звука и отскакивает от закрытого конца. Если трубка правильной длины, отраженный звук возвращается на камертон ровно через полцикла и конструктивно мешает продолжающемуся звуку, производимому камертоном.Входящие и отраженные звуки образуют в трубке стоячую волну, как показано на рисунке.
Возмущение распространяется по трубке со скоростью звука и отскакивает от закрытого конца. Если трубка правильной длины, отраженный звук возвращается на камертон ровно через полцикла и конструктивно мешает продолжающемуся звуку, производимому камертоном.Входящие и отраженные звуки образуют в трубке стоячую волну, как показано на рисунке.
Рисунок 14.21 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение движется по трубе.
Рисунок 14.22 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение отражается от закрытого конца трубки.
Рис. 14.23 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Если длина трубки L подходящая, помеха возвращается к камертону через полцикла и конструктивно мешает продолжающемуся звуку камертона.Эта интерференция образует стоячую волну, и столб воздуха резонирует.
Стоячая волна, сформированная в трубе, имеет максимальное смещение воздуха (пучность) на открытом конце и отсутствие смещения (узел) на закрытом конце.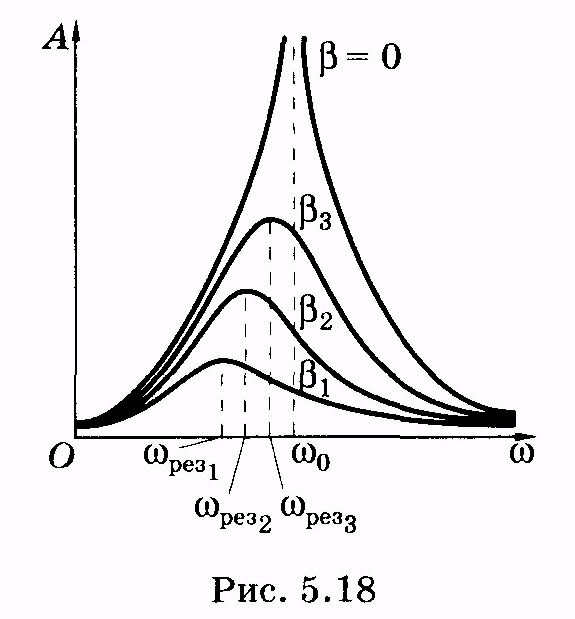 Вспомните из предыдущей главы о волнах, что движение неограничено в пучности и останавливается в узле. Расстояние от узла до пучности составляет одну четвертую длины волны, и это равно длине трубки; следовательно, λ = 4Lλ = 4L. Такой же резонанс может быть вызван вибрацией, возникающей на закрытом конце трубки или около него, как показано на рисунке 14.24.
Вспомните из предыдущей главы о волнах, что движение неограничено в пучности и останавливается в узле. Расстояние от узла до пучности составляет одну четвертую длины волны, и это равно длине трубки; следовательно, λ = 4Lλ = 4L. Такой же резонанс может быть вызван вибрацией, возникающей на закрытом конце трубки или около него, как показано на рисунке 14.24.
Рис. 14.24 Такая же стоячая волна создается в трубке из-за вибрации, вносимой около ее закрытого конца.
Поскольку максимальное смещение воздуха возможно на открытом конце, а не на закрытом, существуют другие, более короткие длины волн, которые могут резонировать в трубке (см. Рис. 14.25). Здесь стоячая волна имеет в трубке три четверти своей длины волны, или L = (3/4) λ′L = (3/4) λ ′, так что λ ′ = 4L / 3λ ′ = 4L / 3. В трубке резонирует целый ряд коротковолновых и высокочастотных звуков.
Мы используем специальные термины для обозначения резонансов в любой системе. Самая низкая резонансная частота называется основной, а все более высокие резонансные частоты – обертонами. Все резонансные частоты кратны основной и называются гармониками. Основная гармоника – это первая гармоника, первый обертон – это вторая гармоника и так далее. На рисунке 14.26 показаны основная гармоника и первые три обертона (первые четыре гармоники) в трубке, закрытой с одного конца.
Все резонансные частоты кратны основной и называются гармониками. Основная гармоника – это первая гармоника, первый обертон – это вторая гармоника и так далее. На рисунке 14.26 показаны основная гармоника и первые три обертона (первые четыре гармоники) в трубке, закрытой с одного конца.
Рис. 14.26 Основной и три нижних обертона закрытой с одного конца трубки. У всех есть максимальные вытеснения воздуха на открытом конце и нет – на закрытом конце.
Основной тон и обертоны могут присутствовать одновременно в различных комбинациях.Например, средняя до ноты на трубе звучит очень иначе, чем средняя до на кларнете, хотя оба инструмента в основном являются модифицированными версиями закрытой с одного конца трубки. Основная частота такая же (и обычно самая интенсивная), но обертоны и их сочетание интенсивностей различны. Этот микс – это то, что придает музыкальным инструментам (и человеческим голосам) их отличительные характеристики, независимо от того, есть ли у них воздушные колонны, струнные или барабанные пластинки. Фактически, большая часть нашей речи определяется формированием полости, образованной горлом и ртом, и расположением языка для регулировки основных и сочетания обертонов.
Основная частота такая же (и обычно самая интенсивная), но обертоны и их сочетание интенсивностей различны. Этот микс – это то, что придает музыкальным инструментам (и человеческим голосам) их отличительные характеристики, независимо от того, есть ли у них воздушные колонны, струнные или барабанные пластинки. Фактически, большая часть нашей речи определяется формированием полости, образованной горлом и ртом, и расположением языка для регулировки основных и сочетания обертонов.
Открытые и закрытые резонаторы
Резонансные частоты закрытой с одного конца трубки (известной как резонатор с закрытой трубкой): fn = nv4L, n = 1,3,5 …, fn = nv4L, n = 1,3,5 … ,
, где f 1 – основной тон, f 3 – первый обертон и т. Д. Обратите внимание, что резонансные частоты зависят от скорости звука v и от длины трубки L .
Другой тип трубки – открытый с обоих концов (известный как открытый резонатор).Примеры – органные трубы, флейты и гобои. Воздушные столбы в трубках, открытых с обоих концов, имеют максимальное вытеснение воздуха с обоих концов. (См. Рисунок 14.27). Стоячие волны формируются, как показано.
Рис. 14.27. Показаны резонансные частоты трубки, открытой с обоих концов, включая основной тон и первые три обертона. Во всех случаях максимальное смещение воздуха происходит на обоих концах трубы, что дает ей собственные частоты, отличные от собственных частот трубы, закрытой с одного конца.
Резонансные частоты открытого резонатора
fn = nv2L, n = 1,2,3…, fn = nv2L, n = 1,2,3 …,
, где f 1 – основной обертон, f 2 – первый обертон, f 3 – второй обертон и т. Д. Обратите внимание, что трубка, открытая с обоих концов, имеет основную частоту вдвое больше, чем она была бы, если бы закрылась с одного конца. Он также имеет другой спектр обертонов, чем трубка, закрытая с одного конца. Итак, если у вас есть две лампы с одинаковой основной частотой, но одна открыта с обоих концов, а другая закрыта с одного конца, они будут звучать по-разному при игре, потому что у них разные обертоны.
Он также имеет другой спектр обертонов, чем трубка, закрытая с одного конца. Итак, если у вас есть две лампы с одинаковой основной частотой, но одна открыта с обоих концов, а другая закрыта с одного конца, они будут звучать по-разному при игре, потому что у них разные обертоны.
Middle C будет звучать богаче при игре на открытой трубе, поскольку в ней больше обертонов. Резонатор с открытой трубкой имеет больше обертонов, чем резонатор с закрытой трубкой, потому что он имеет четные кратные основной и нечетной частоты, тогда как закрытая трубка имеет только нечетные кратные.
В этом разделе мы рассмотрели резонансные и стоячие волны для духовых инструментов, но вибрирующие струны на струнных инструментах также резонируют и имеют основы и обертоны, аналогичные таковым для духовых инструментов.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Другие инструменты также по-разному используют воздушный резонанс для усиления звука. Например, у скрипки и гитары есть звуковые коробки, но разной формы, что приводит к разным структурам обертонов. Вибрирующая струна создает звук, который резонирует в звуковой коробке, значительно усиливая звук и создавая обертоны, придающие инструменту его характерный аромат. Чем сложнее форма звуковой коробки, тем выше ее способность резонировать в широком диапазоне частот.Тип и толщина дерева или других материалов, используемых для изготовления звуковой коробки, также влияют на качество звука. Попросите учащихся привести еще несколько примеров того, как различные музыкальные инструменты используют явление резонанса.
Например, у скрипки и гитары есть звуковые коробки, но разной формы, что приводит к разным структурам обертонов. Вибрирующая струна создает звук, который резонирует в звуковой коробке, значительно усиливая звук и создавая обертоны, придающие инструменту его характерный аромат. Чем сложнее форма звуковой коробки, тем выше ее способность резонировать в широком диапазоне частот.Тип и толщина дерева или других материалов, используемых для изготовления звуковой коробки, также влияют на качество звука. Попросите учащихся привести еще несколько примеров того, как различные музыкальные инструменты используют явление резонанса.
Решение проблем, связанных с рядом гармоник и частотой биений
Рабочий пример
Определение длины трубы для замкнутого трубного резонатора
Если звук распространяется по воздуху со скоростью 344 м / с, какой длины должна быть закрытая с одного конца трубка, чтобы основная частота составляла 128 Гц?
Стратегия
Длину L можно найти, переписав уравнение fn = nv4Lfn = nv4L
.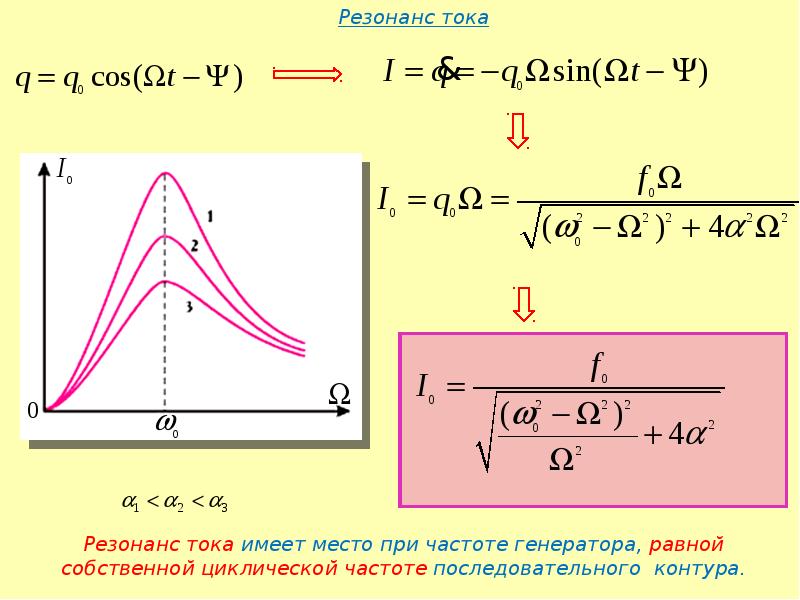
Решение
(1) Определите известных.
- Основная частота 128 Гц.
- Скорость звука 344 м / с.
(2) Используйте fn = nvw4Lfn = nvw4L, чтобы найти основную частоту ( n = 1).
(3) Решите это уравнение относительно длины.
(4) Введите значения скорости звука и частоты в выражение для L .
L = v4f1 = 344 м / с4 (128 Гц) = 0,672 мл = v4f1 = 344 м / с4 (128 Гц) = 0.672 м14,16
Обсуждение
Многие духовые инструменты представляют собой модифицированные трубки с отверстиями для пальцев, клапанами и другими устройствами для изменения длины резонирующего столба воздуха и, следовательно, частоты проигрываемой ноты. Для рожков, воспроизводящих очень низкие частоты, таких как тубы, нужны лампы такой длины, чтобы они были свернуты в петли.
Рабочий пример
Обнаружение третьего обертона в открытом резонаторе
Если трубка, открытая с обоих концов, имеет основную частоту 120 Гц, какова частота ее третьего обертона?
Стратегия
Поскольку нам уже известно значение основной частоты (n = 1), мы можем найти третий обертон (n = 4), используя уравнение fn = nv2Lfn = nv2L.
Решение
Поскольку основная частота (n = 1) равна
и
f4 = 4v2L, f4 = 4f1 = 4 (120 Гц) = 480 Гц. f4 = 4v2L, f4 = 4f1 = 4 (120 Гц) = 480 Гц.14,18
Обсуждение
Чтобы решить эту проблему, не нужно было знать длину трубки или скорость воздуха из-за взаимосвязи между основным и третьим обертоном. В этом примере был резонатор с открытой трубой; обратите внимание, что для резонатора с закрытой трубой третий обертон имеет значение n = 7 (не n = 4).
Рабочий пример
Использование частоты ударов для настройки фортепиано
Настройщики фортепиано постоянно используют биты в своей работе. Сравнивая ноту с камертоном, они прислушиваются к ударам и регулируют струну, пока удары не исчезнут (до нулевой частоты). Если тюнер пианино слышит два удара в секунду, а камертон имеет частоту 256 Гц, каковы возможные частоты фортепиано?
Стратегия
Поскольку мы уже знаем, что частота биений f B равна 2, а одна из частот (скажем, f 2 ) равна 256 Гц, мы можем использовать уравнение fB = | f1 − f2 | fB = | f1 − f2 | найти частоту фортепиано f 1 .
Решение
Так как fB = | f1 − f2 | fB = | f1 − f2 |,
мы знаем, что либо fB = f1 − f2fB = f1 − f2, либо −fB = f1 − f2 − fB = f1 − f2.
Решение для f 1 ,
f1 = fB + f2 или f1 = −fB + f2.f1 = fB + f2 или f1 = −fB + f2.14,19
Подставляя значения,
f1 = 2 + 256 Гц или f1 = −2 + 256 Гц f1 = 2 + 256 Гц или f1 = −2 + 256 Гц14,20
Итак,
f1 = 258 Гц или 254 Гц. f1 = 258 Гц или 254 Гц.14,21
Обсуждение
Настройщик пианино может изначально не определить, просто слушая, является ли частота пианино слишком высокой или слишком низкой, и должен настроить ее методом проб и ошибок, сделав настройку, а затем снова протестировав.Если после настройки ударов еще больше, то тюнер знает, что пошел в неправильном направлении.
Практические задачи
21.Две звуковые волны имеют частоты 250 Гц и 280 Гц. Какова частота биений при их наложении?
- 290 Гц
- 265 Гц
- 60 Гц
- 30 Гц

Какова длина трубы, закрытой с одного конца, с основной частотой 350 Гц? (Предположим, что скорость звука в воздухе 331 м / с.)
- 26 см
- 26 мес.
- 24 мес.
- 24 см
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащихся по целям обучения раздела. Если учащиеся борются с определенной целью, эти вопросы помогут определить ее и направить учащихся к соответствующему содержанию.
23.Что такое демпфирование?
- Со временем энергия увеличивается, а амплитуда постепенно уменьшается до нуля. Это называется демпфированием.
- Со временем энергия рассеивается, а амплитуда постепенно увеличивается.
 Это называется демпфированием.
Это называется демпфированием. - Со временем энергия увеличивается, а амплитуда постепенно увеличивается. Это называется демпфированием.
- Со временем энергия рассеивается, и амплитуда постепенно уменьшается до нуля.Это называется демпфированием.
Что такое резонанс? Когда можно сказать, что система резонирует?
- Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
- Явление возбуждения системы с частотой выше, чем ее собственная частота, называется резонансом, и система, работающая на собственной частоте, не резонирует.
- Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, и система, работающая на собственной частоте, не резонирует.

- Явление возбуждения системы с частотой выше, чем ее собственная частота, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
В эксперименте с камертоном и лампой, в случае образования стоячей волны, в какой точке трубки наблюдается максимальное возмущение от камертона? Напомним, что трубка имеет один открытый конец и один закрытый конец.
- В середине трубы
- Оба конца трубки
- На закрытом конце трубки
- На открытом конце трубки
В эксперименте с камертоном и лампой, когда столб воздуха будет издавать самый громкий звук?
- Если камертон вибрирует с частотой, вдвое превышающей собственную частоту столба воздуха.
- Если камертон вибрирует с частотой ниже собственной частоты столба воздуха.
- Если камертон вибрирует с частотой выше собственной частоты столба воздуха.
- Если камертон вибрирует с частотой, равной собственной частоте столба воздуха.

Что такое резонатор с закрытой трубой?
- Труба или цилиндрическая воздушная колонна, закрытая с обоих концов
- Труба с пучностью на закрытом конце
- Труба с узлом на открытом конце
- Труба или цилиндрическая воздушная колонна, закрытая с одного конца
Приведите два примера открытых резонаторов.
- фортепиано, скрипка
- барабан, таблица
- электрогитара, акустическая гитара
- флейта, гобой
16.7: Стоячие волны и резонанс
На протяжении этой главы мы изучали бегущие волны или волны, переносящие энергию из одного места в другое. При определенных условиях волны могут отскакивать назад и вперед через определенную область, фактически становясь стационарными. Они называются стоячими волнами .
Другой связанный эффект известен как резонанс. В книге «Колебания» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызвать движение большой амплитуды. Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды. Иногда этот резонанс хорош, например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения.В случае стоячих волн стоячие волны с относительно большой амплитудой создаются наложением составляющих волн с меньшей амплитудой.
Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды. Иногда этот резонанс хорош, например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения.В случае стоячих волн стоячие волны с относительно большой амплитудой создаются наложением составляющих волн с меньшей амплитудой.
Стоячие волны
Иногда кажется, что волны не двигаются; скорее, они просто вибрируют на месте. Например, вы можете увидеть неподвижные волны на поверхности стакана с молоком в холодильнике. Вибрация двигателя холодильника создает волны на молоке, которые колеблются вверх и вниз, но не движутся по поверхности. На рисунке \ (\ PageIndex {1} \) показан эксперимент, который вы можете попробовать дома.Возьмите миску с молоком и поставьте ее на обычный вентилятор. Вибрация вентилятора вызывает в молоке стоячие круглые волны. Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на рисунке \ (\ PageIndex {2} \) для двух идентичных волн, движущихся в противоположных направлениях. Волны проходят друг через друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией.Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на рисунке \ (\ PageIndex {2} \) для двух идентичных волн, движущихся в противоположных направлениях. Волны проходят друг через друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией.Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
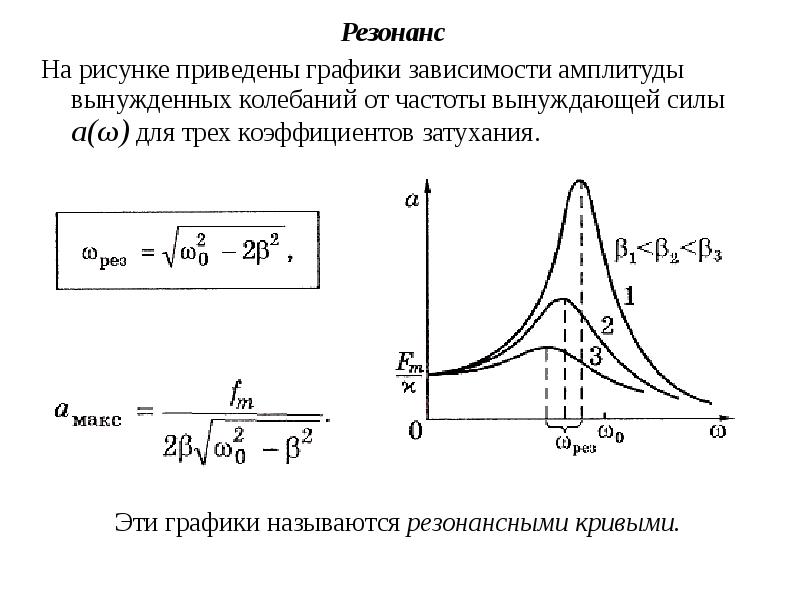 Эти точки называются фиксированными точками (узлами). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Эти точки называются фиксированными точками (узлами). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.Рассмотрим две одинаковые волны, движущиеся в противоположных направлениях. Первая волна имеет волновую функцию y 1 (x, t) = A sin (kx – \ (\ omega \) t), а вторая волна имеет волновую функцию y 2 (x, t) = A грех (кх + \ (\ омега \) т).Волны интерферируют и образуют результирующую волну
\ [\ begin {split} y (x, t) & = y_ {1} (x, t) + y_ {2} (x, t), \\ & = A \ sin (kx – \ omega t) + A \ sin (kx + \ omega t) \ ldotp \ end {split} \]
Это можно упростить с помощью тригонометрического идентификатора
\ [\ sin (\ alpha \ pm \ beta) = \ sin \ alpha \ cos \ beta \ pm \ cos \ alpha \ sin \ beta, \]
, где \ (\ alpha \) = kx и \ (\ beta \) = \ (\ omega \) t, что дает нам
\ [y (x, t) = A [\ sin (kx) \ cos (\ omega t) – \ cos (kx) \ sin (\ omega t) + \ sin (kx) \ cos (\ omega t)] – \ cos (kx) \ sin (\ omega t)], \]
, что упрощается до
\ [у (х, t) = 2A \ sin (kx) \ cos (\ omega t) \ ldotp \ label {16. 14} \]
14} \]
Обратите внимание, что результирующая волна является синусоидальной волной, которая является функцией только положения, умноженной на функцию косинуса, которая является функцией только времени. Графики y (x, t) как функции от x для различных моментов времени показаны на рисунке \ (\ PageIndex {6} \). Красная волна движется в отрицательном направлении оси x, синяя волна движется в положительном направлении оси x, а черная волна является суммой двух волн. Когда красная и синяя волны движутся друг через друга, они входят и выходят из-за конструктивной интерференции и разрушительной интерференции.
Первоначально в момент времени t = 0 две волны находятся в фазе, и в результате получается волна, которая в два раза превышает амплитуду отдельных волн. Волны также находятся в фазе в момент времени t = \ (\ frac {T} {2} \). Фактически, волны находятся в фазе в любом целом числе, кратном половине периода:
t = n \ (\ frac {T} {2} \), где n = 0, 1, 2, 3 …. (в фазе).
В другое время две волны сдвинуты по фазе на 180 ° (\ (\ pi \) радиан), и результирующая волна равна нулю. Это происходит на
t = \ (\ frac {1} {4} \) T, \ (\ frac {3} {4} \) T, \ (\ frac {5} {4} \) T ,…, \ (\ frac {n} {4} \) T, где n = 1, 3, 5 …. (не в фазе).
Обратите внимание, что некоторые x-позиции результирующей волны всегда равны нулю, независимо от фазового соотношения. Эти позиции называются узлами . Где возникают узлы? Рассмотрим решение суммы двух волн
\ [y (x, t) = 2A \ sin (kx) \ cos (\ omega t) \ ldotp \]
Нахождение позиций, в которых функция синуса равна нулю, обеспечивает положение узлов.
\ [\ begin {split} \ sin (kx) & = 0 \\ kx & = 0, \ pi, 2 \ pi, 3 \ pi, \ ldots \\ \ frac {2 \ pi} {\ lambda} x & = 0, \ pi, 2 \ pi, 3 \ pi, \ ldots \\ x & = 0, \ frac {\ lambda} {2}, \ lambda, \ frac {3 \ lambda} {2}, \ ldots = n \ frac {\ lambda} {2} \ quad n = 0, 1, 2, 3, \ ldots \ end {split} \]
Есть также положения, в которых y колеблется между y = ± A. Это пучностей . Мы можем найти их, рассмотрев, какие значения x приводят к sin (kx) = ± 1.
Это пучностей . Мы можем найти их, рассмотрев, какие значения x приводят к sin (kx) = ± 1.
\ [\ begin {split} \ sin (kx) & = \ pm 1 \\ kx & = \ frac {\ pi} {2}, \ frac {3 \ pi} {2}, \ frac {5 \ pi } {2}, \ ldots \\ \ frac {2 \ pi} {\ lambda} x & = \ frac {\ pi} {2}, \ frac {3 \ pi} {2}, \ frac {5 \ pi } {2}, \ ldots \\ x & = \ frac {\ lambda} {4}, \ frac {3 \ lambda} {4}, \ frac {5 \ lambda} {4}, \ ldots = n \ frac {\ lambda} {4} \ quad n = 1, 3, 5, \ ldots \ end {split} \]
В результате получается стоячая волна, как показано на рисунке \ (\ PageIndex {3} \), где показаны снимки результирующей волны двух идентичных волн, движущихся в противоположных направлениях.Результирующая волна выглядит как синусоидальная волна с узлами в целых кратных полуволнах. Пучности колеблются между y = ± 2A из-за члена косинуса cos (\ (\ omega \) t), который колеблется между ± 1.
Результирующая волна кажется неподвижной, без видимого движения в направлении x, хотя она состоит из одной волновой функции, движущейся в положительном направлении, тогда как вторая волна движется в отрицательном направлении x. На рисунке \ (\ PageIndex {3} \) показаны различные снимки результирующей волны.Узлы отмечены красными точками, а пучности отмечены синими точками.
На рисунке \ (\ PageIndex {3} \) показаны различные снимки результирующей волны.Узлы отмечены красными точками, а пучности отмечены синими точками.
Типичным примером стоячих волн являются волны, создаваемые струнными музыкальными инструментами.Когда струна защипывается, импульсы проходят по струне в противоположных направлениях. Концы струн фиксируются на месте, поэтому на концах струн появляются узлы – граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс, создаваемый струнным инструментом, можно смоделировать в физической лаборатории с помощью устройства, показанного на рисунке \ (\ PageIndex {4} \).
Лабораторная установка показывает струну, прикрепленную к струнному вибратору, который колеблет струну с регулируемой частотой f. Другой конец струны проходит над шкивом без трения и привязан к подвешенной массе. Величина натяжения тетивы равна весу подвешенной массы.У струны постоянная линейная плотность (масса на длину) \ (\ mu \), а скорость, с которой волна распространяется по струне, равна \ (v = \ sqrt {\ frac {F_ {T}} {\ mu}} = \ sqrt {\ frac {mg} {\ mu}} \) Уравнение 16.7. Симметричные граничные условия (узел на каждом конце) диктуют возможные частоты, которые могут возбуждать стоячие волны. Начиная с нулевой частоты и медленно увеличивая частоту, появляется первая мода n = 1, как показано на рисунке \ (\ PageIndex {5} \). Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами \ (\ lambda_ {1} \) = 2L.Основная частота , или частота первой гармоники, которая управляет этим режимом, равна
Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами \ (\ lambda_ {1} \) = 2L.Основная частота , или частота первой гармоники, которая управляет этим режимом, равна
\ [f_ {1} = \ frac {v} {\ lambda_ {1}} = \ frac {v} {2L}, \]
, где скорость волны равна v = \ (\ sqrt {\ frac {F_ {T}} {\ mu}} \). Сохранение постоянного напряжения и увеличение частоты приводит ко второй гармонике или режиму n = 2. Этот режим имеет полную длину волны \ (\ lambda_ {2} \) = L, а частота в два раза превышает основную частоту:
\ [f_ {2} = \ frac {v} {\ lambda_ {2}} = \ frac {v} {L} = 2f_ {1} \ ldotp \]
Рисунок \ (\ PageIndex {5} \): Стоячие волны, созданные на веревке длиной \ (L \).Узел находится на каждом конце строки. Узлы – это граничные условия, которые ограничивают возможные частоты, возбуждающие стоячие волны. (Обратите внимание, что амплитуды колебаний поддерживаются постоянными для визуализации.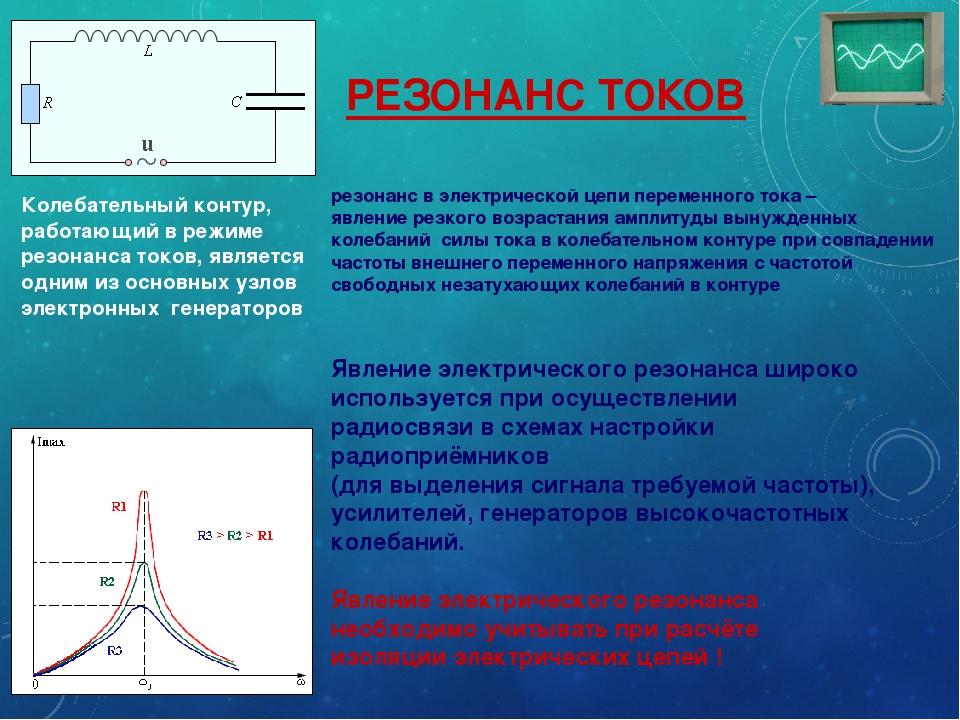 Возможные модели стоячих волн на струне известны как нормальные режимы. Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды по мере увеличения частоты.)
Возможные модели стоячих волн на струне известны как нормальные режимы. Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды по мере увеличения частоты.)Следующие два режима, или третья и четвертая гармоники, имеют длины волн \ (\ lambda_ {3} = \ frac {2} {3} \) L и \ (\ lambda_ {4} = \ frac {2} {4 } \) L, управляемый частотами f 3 = \ (\ frac {3v} {2L} \) = 3f 1 и f 4 = \ (\ frac {4v} {2L} \) = 4f 1 .Все частоты выше частоты f1 известны как обертоны . Уравнения для длины волны и частоты можно резюмировать как:
\ [\ lambda_ {n} = \ frac {2} {n} L \ quad n = 1, 2, 3, 4, 5 \ ldots \ label {16.15} \]
\ [f_ {n} = n \ frac {v} {2L} = nf_ {1} \ quad n = 1, 2, 3, 4, 5 \ ldots \ label {16.16} \]
Модели стоячей волны, которые возможны для струны, первые четыре из которых показаны на рисунке \ (\ PageIndex {5} \), известны как нормальные моды с частотами, известными как нормальные частоты. Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота нормального режима струны n = 2 – это первый обертон (или вторая гармоника). Частота нормального режима n = 3 – это второй обертон (или третья гармоника) и так далее.
Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота нормального режима струны n = 2 – это первый обертон (или вторая гармоника). Частота нормального режима n = 3 – это второй обертон (или третья гармоника) и так далее.
Решения, показанные как Equation \ ref {16.15} и Equation \ ref {16.16}, предназначены для строки с граничным условием узла на каждом конце.Когда граничные условия с обеих сторон одинаковы, говорят, что система имеет симметричные граничные условия. Уравнение \ ref {16.15} и уравнение \ ref {16.16} подходят для любых симметричных граничных условий, то есть узлов на обоих концах или пучностей на обоих концах.
Пример \ (\ PageIndex {1} \): стоячие волны на струне
Рассмотрим строку длиной L = 2,00 м. прикреплен к струнному вибратору с регулируемой частотой, как показано на рисунке \ (\ PageIndex {6} \). Волны, создаваемые вибратором, распространяются по струне и отражаются фиксированным граничным условием на шкиве. Струна, имеющая линейную массовую плотность \ (\ mu \) = 0,006 кг / м, проходит через шкив без трения с незначительной массой, а натяжение обеспечивается подвешенной массой 2,00 кг. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые струнный вибратор должен быть настроен, чтобы произвести первые три нормальные моды стоячих волн.
Струна, имеющая линейную массовую плотность \ (\ mu \) = 0,006 кг / м, проходит через шкив без трения с незначительной массой, а натяжение обеспечивается подвешенной массой 2,00 кг. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые струнный вибратор должен быть настроен, чтобы произвести первые три нормальные моды стоячих волн.
Стратегия
- Скорость волны можно найти с помощью v = \ (\ sqrt {\ frac {F_ {T}} {\ mu}} \). Натяжение обеспечивается весом подвешенной массы.
- Стоячие волны будут зависеть от граничных условий. На каждом конце должен быть узел. Первая мода будет составлять половину волны. Вторую можно найти, добавив половину длины волны. Это самая короткая длина, которая приведет к образованию узла на границах.
 Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на рисунке \ (\ PageIndex {7} \).
Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на рисунке \ (\ PageIndex {7} \). - Поскольку скорость волны равна длине волны, умноженной на частоту, частота равна скорости волны, деленной на длину волны.
Решение
- Начнем со скорости волны на струне. Натяжение равно весу подвешенной массы. Даны линейная массовая плотность и масса висящей массы: $$ v = \ sqrt {\ frac {F_ {T}} {\ mu}} = \ sqrt {\ frac {mg} {\ mu}} = \ sqrt {\ frac {(2 \; кг) (9,8 \; м / с)} {0,006 \; кг / м}} = 57.15 \; м / с \ ldotp $$
- Первая нормальная мода, имеющая узел на каждом конце, составляет половину длины волны.
 Следующие две моды находятся путем добавления половины длины волны.
Следующие две моды находятся путем добавления половины длины волны.
- Частоты первых трех мод находятся с помощью f = \ (\ frac {v_ {w}} {\ lambda} \). $$ \ begin {split} f_ {1} & = \ frac {v_ {w}} {\ lambda_ {1}} = \ frac {57.15 \; м / с} {4,00 \; m} = 14,29 \; Гц \\ f_ {2} & = \ frac {v_ {w}} {\ lambda_ {2}} = \ frac {57.15 \; м / с} {2,00 \; m} = 28,58 \; Гц \\ f_ {3} & = \ frac {v_ {w}} {\ lambda_ {3}} = \ frac {57.15 \; м / с} {1.333 \; m} = 42,87 \; Гц \ end {split} $$
Значение
Три режима стоя в этом примере были созданы путем поддержания натяжения струны и регулировки частоты возбуждения. Сохранение постоянного натяжения струны приводит к постоянной скорости. Те же самые режимы можно было бы получить, сохранив постоянную частоту и регулируя скорость волны в струне (изменяя висящую массу).
Моделирование
Посетите этот симулятор, чтобы поиграть с одномерной или двухмерной системой связанных осцилляторов массы и пружины. Варьируйте количество масс, задайте начальные условия и наблюдайте за развитием системы. См. Спектр нормальных режимов произвольного движения. См. Продольные или поперечные моды в 1-D системе.
Варьируйте количество масс, задайте начальные условия и наблюдайте за развитием системы. См. Спектр нормальных режимов произвольного движения. См. Продольные или поперечные моды в 1-D системе.
Упражнение \ (\ PageIndex {1} \)
Уравнения для длин волн и частот мод волны, создаваемой на струне:
\ [\ begin {split} \ lambda_ {n} & = \ frac {2} {n} L \ quad n = 1, 2, 3, 4, 5 \ ldots и \\ f_ {n} & = n \ frac {v} {2L} = nf_ {1} \ quad n = 1, 2, 3, 4, 5 \ ldots \ end {split} \]
были получены путем рассмотрения волны на струне, где были симметричные граничные условия узла на каждом конце.Эти режимы являются результатом двух синусоидальных волн с идентичными характеристиками, за исключением того, что они движутся в противоположных направлениях, ограниченных областью L с узлами, необходимыми на обоих концах. Будут ли работать те же уравнения при наличии симметричных граничных условий с пучностями на каждом конце? Как бы выглядели нормальные режимы для среды, которая могла бы свободно колебаться на каждом конце? Не беспокойтесь, если вы не можете представить себе такую среду, просто рассмотрите две синусоидальные волновые функции в области длиной L с пучностями на каждом конце.
Свободные граничные условия, показанные в последней проверке понимания, могут показаться трудными для визуализации. Как может быть система, которая может свободно колебаться на каждом конце? На рисунке \ (\ PageIndex {8} \) показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим). В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия. При соответствующей частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце.В части (b) стержень поддерживается в положениях, составляющих одну четверть длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При правильной частоте этот стержень также можно привести в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности. Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длину волны можно измерить между любыми двумя ближайшими идентичными точками, и рассмотрите рисунок \ (\ PageIndex {9} \).
Обратите внимание, что изучение стоячих волн может стать довольно сложным. На рисунке 16.32 (a) показана мода стоячей волны с n = 2, результатом которой является длина волны, равная L.В этой конфигурации режим n = 1 также был бы возможен с стоячей волной, равной 2L. Возможно ли получить режим n = 1 для конфигурации, показанной в части (b)? Ответ – нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия. Поскольку стержень установлен в точке, составляющей четверть длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн.Следует отметить, что когда система приводится в действие на частоте, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
На рисунке 16.32 (a) показана мода стоячей волны с n = 2, результатом которой является длина волны, равная L.В этой конфигурации режим n = 1 также был бы возможен с стоячей волной, равной 2L. Возможно ли получить режим n = 1 для конфигурации, показанной в части (b)? Ответ – нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия. Поскольку стержень установлен в точке, составляющей четверть длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн.Следует отметить, что когда система приводится в действие на частоте, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
Область машиностроения использует звук, производимый вибрирующими частями сложных механических систем, для устранения проблем с системами. Предположим, часть автомобиля резонирует с частотой двигателя автомобиля, вызывая нежелательные вибрации в автомобиле.Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, чтобы найти частоты звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте. Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Предположим, часть автомобиля резонирует с частотой двигателя автомобиля, вызывая нежелательные вибрации в автомобиле.Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, чтобы найти частоты звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте. Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Есть и другие многочисленные примеры резонанса стоячих волн в физическом мире.Воздух в трубке, например, в музыкальном инструменте, таком как флейта, может вызвать резонанс и произвести приятный звук, как мы обсуждаем в разделе «Звук».
В других случаях резонанс может вызвать серьезные проблемы. Более пристальный взгляд на землетрясения свидетельствует о наличии условий, подходящих для резонанса, стоячих волн, а также конструктивных и деструктивных помех. Здание может колебаться в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, что вызывает резонанс, в результате которого одно здание рушится, а соседние – нет.Часто здания определенной высоты разрушаются, в то время как другие более высокие здания остаются нетронутыми. Высота здания соответствует условию создания стоячей волны для данной высоты. Также важен пролет крыши. Часто можно увидеть, что спортзалы, супермаркеты и церкви страдают от повреждений, в то время как отдельным домам наносится гораздо меньший ущерб. Крыши с большой площадью поверхности, поддерживаемые только краями, резонируют с частотами землетрясений, вызывая их обрушение. Когда волны землетрясения распространяются по поверхности Земли и отражаются от более плотных горных пород, в определенных точках возникает конструктивная интерференция.Часто участки, расположенные ближе к эпицентру, не повреждаются, а участки дальше – повреждены.
Здание может колебаться в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, что вызывает резонанс, в результате которого одно здание рушится, а соседние – нет.Часто здания определенной высоты разрушаются, в то время как другие более высокие здания остаются нетронутыми. Высота здания соответствует условию создания стоячей волны для данной высоты. Также важен пролет крыши. Часто можно увидеть, что спортзалы, супермаркеты и церкви страдают от повреждений, в то время как отдельным домам наносится гораздо меньший ущерб. Крыши с большой площадью поверхности, поддерживаемые только краями, резонируют с частотами землетрясений, вызывая их обрушение. Когда волны землетрясения распространяются по поверхности Земли и отражаются от более плотных горных пород, в определенных точках возникает конструктивная интерференция.Часто участки, расположенные ближе к эпицентру, не повреждаются, а участки дальше – повреждены.
Resonance – The Physics Hypertextbook
Обсуждение
Радиопередатчики (включая телевизионные передатчики, спутниковые каналы связи и сотовые телефоны) вещают на определенной частоте или около нее. Мы плывем в море разных радиочастот как от естественных, так и от искусственных источников. Как ваше радио (телевизор, спутниковая антенна или сотовый телефон) выбирает правильную частоту среди всех остальных для декодирования?
Мы плывем в море разных радиочастот как от естественных, так и от искусственных источников. Как ваше радио (телевизор, спутниковая антенна или сотовый телефон) выбирает правильную частоту среди всех остальных для декодирования?
Еще мальчишкой я заметил, что один человек, давая эти импульсы в нужный момент, мог позвонить в такой большой колокол, что когда четверо или даже шесть мужчин схватили веревку и попытались ее остановить, их подняли с веревки. земля, все они вместе были неспособны уравновесить импульс, который один-единственный человек, должным образом рассчитав силы, придал ей.
Галилео Галилей, 1638
Это нужно перефразировать. «Примером того, как местные почвенные условия могут сильно влиять на местную интенсивность, является катастрофический ущерб в Мехико в результате землетрясения в Мексике 1985 года, MS 8.1, с центром на расстоянии около 300 км. Резонансы заполненного почвой бассейна под частями Мехико усилили колебания грунта в течение 2 секунд в 75 раз. Это сотрясение привело к выборочному повреждению зданий высотой 15-25 этажей (такой же период резонанса), что привело к потерям для зданий в размере около 4 долларов.0 миллиардов и не менее 8000 погибших ».
Это сотрясение привело к выборочному повреждению зданий высотой 15-25 этажей (такой же период резонанса), что привело к потерям для зданий в размере около 4 долларов.0 миллиардов и не менее 8000 погибших ».
Генератор гармонических колебаний
Амплитуда управляемого гармонического генератора увеличивается по мере приближения частоты возбуждения к собственной частоте. В незатухающей системе амплитуда будет бесконечной.
| А = | 1 | x = | ω | = | f | |
| √ ((1 – x 2 ) 2 + 4γ 2 x 2 ) | ω 0 | f 0 |
Падение подвесного моста Бротон, недалеко от Манчестера (1831 г.)
Похоже, что в тот день, когда произошла эта авария, 60-й полк провел боевой день на Керсалл-Мур и около 12 часов возвращался в свои помещения.
Большая часть полка дислоцировалась во временных бараках на Дайче-стрит, Сент-Джордж-роуд, и двинулась через Strangeways; но одна рота, которой командовал, как это довольно необычно, лейтенант. P.S. Фицджеральд, сын владельца моста, находившийся в казармах Солфорда, двинулся по подвесному мосту, намереваясь пройти через Пендлтон к казармам. Вскоре после того, как они подошли к мосту, мужчины, шедшие вчетвером в ряд, обнаружили, что конструкция вибрирует в унисон с размеренным шагом, с которым они шли; и поскольку эта вибрация ни в коем случае не была неприятной, они были склонны умилостивить ее своей манерой шага.По мере того, как они продолжали движение, и по мере того, как все большее число из них поднималось на мост, вибрация продолжала увеличиваться, пока голова колонны почти не достигла стороны Пендлтона реки. Затем они были встревожены громким звуком, напоминающим беспорядочный выстрел из огнестрельного оружия; и сразу одна из железных опор, поддерживающих цепи подвески, а именно.
то, что было справа от солдат и на стороне реки Бротон, упало на мост, унеся с собой большой камень с пирса, к которому он был прикреплен болтами.Конечно, этот угол моста, потеряв опору колонны, немедленно упал на дно реки, примерно на шестнадцать или восемнадцать футов; и из-за того, что дорога была сильно наклонена, почти все солдаты, находившиеся на ней, были брошены в реку, где предстала сцена великого смятения. Те из них, кто не пострадал, выбрались, как могли, одни, взобравшись на наклонную плоскость, которую представлял мост, а другие, пройдя вброд со стороны Бротона; но некоторые из них были слишком ранены, чтобы выбраться без помощи, которую немедленно оказали их товарищи.
Философские труды , 1831
вынужденных колебаний и резонанса | Физика
Цели обучения
К концу этого раздела вы сможете:
- Наблюдайте за резонансом гребного мяча на струне.
- Наблюдать за амплитудой затухающего гармонического осциллятора.

Рис. 1. Вы можете вызвать вибрацию струн пианино, просто создав звуковые волны своим голосом.(Источник: Мэтт Биллингс, Flickr)
Сядьте как-нибудь перед пианино и спойте на нем короткую громкую ноту с отключенными демпферами. Он пропоет вам ту же ноту – струны, имеющие те же частоты, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Ваш голос и струны пианино – хороший пример того факта, что объекты – в данном случае струны пианино – можно заставить колебаться, но лучше всего они колеблются на своей собственной частоте.В этом разделе мы кратко рассмотрим применение периодической движущей силы , действующей на простой гармонический осциллятор. Движущая сила вкладывает энергию в систему с определенной частотой, не обязательно такой же, как собственная частота системы. Собственная частота – это частота, с которой система будет колебаться, если бы не было движения и демпфирующей силы.
Большинство из нас играли с игрушками, в которых использовался объект, поддерживаемый на резинке, что-то вроде шарика, подвешенного на пальце на Рисунке 2. Представьте, что палец на рисунке – это ваш палец. Сначала вы держите палец ровно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете.Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом . Говорят, что система, работающая на собственной частоте, резонирует с . По мере того, как частота возбуждения постепенно становится выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.
Представьте, что палец на рисунке – это ваш палец. Сначала вы держите палец ровно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете.Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом . Говорят, что система, работающая на собственной частоте, резонирует с . По мере того, как частота возбуждения постепенно становится выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.
Рис. 2. Шарик на резиновой ленте движется в ответ на палец, поддерживающий его. Если палец движется с собственной частотой f0 мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он реагирует колебаниями с меньшей амплитудой.
Если палец движется с собственной частотой f0 мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он реагирует колебаниями с меньшей амплитудой.
На рис. 3 показан график зависимости амплитуды затухающего гармонического осциллятора от частоты движущей им периодической силы. На графике есть три кривые, каждая из которых представляет разную величину демпфирования.Все три кривые достигают пика в точке, где частота движущей силы равна собственной частоте гармонического осциллятора. Самый высокий пик или самый высокий отклик – для наименьшего количества демпфирования, потому что демпфирующая сила снимает меньше энергии.
Рис. 3. Амплитуда гармонического осциллятора как функция частоты движущей силы. Кривые представляют один и тот же генератор с одинаковой собственной частотой, но с разной степенью демпфирования. Резонанс возникает, когда частота возбуждения равна собственной частоте, а наибольший отклик – при наименьшем затухании. Самый узкий ответ также соответствует наименьшему демпфированию.
Самый узкий ответ также соответствует наименьшему демпфированию.
Интересно, что ширина резонансных кривых, показанных на рисунке 3, зависит от затухания: чем меньше затухание, тем уже резонанс. Суть в том, что если вы хотите, чтобы управляемый генератор резонировал на очень определенной частоте, вам нужно как можно меньше демпфирования. Небольшое демпфирование характерно для струн фортепиано и многих других музыкальных инструментов. И наоборот, если вам нужны колебания малой амплитуды, например, в системе подвески автомобиля, вам нужно сильное демпфирование.Сильное демпфирование снижает амплитуду, но компромисс заключается в том, что система реагирует на большем количестве частот.
Эти особенности управляемых генераторов гармоник применимы к огромному количеству систем. Например, когда вы настраиваете радио, вы настраиваете его резонансную частоту так, чтобы оно колебалось только на радиовещательной (движущей) частоте желаемой радиостанции. Чем более избирательно радио различает станции, тем меньше его демпфирование. Магнитно-резонансная томография (МРТ) – широко используемый медицинский диагностический инструмент, в котором атомные ядра (в основном ядра водорода) заставляют резонировать приходящими радиоволнами (порядка 100 МГц).Ребенок на качелях приводится в движение родителями на собственной частоте качелей для достижения максимальной амплитуды. Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.
Магнитно-резонансная томография (МРТ) – широко используемый медицинский диагностический инструмент, в котором атомные ядра (в основном ядра водорода) заставляют резонировать приходящими радиоволнами (порядка 100 МГц).Ребенок на качелях приводится в движение родителями на собственной частоте качелей для достижения максимальной амплитуды. Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.
Рис. 4. В 1940 году обрушился мост Такома-Нэрроуз в штате Вашингтон. Сильный поперечный ветер приводил мост к колебаниям на его резонансной частоте. Демпфирование уменьшалось, когда опорные тросы разрывались и начинали скользить по опорам, что увеличивало амплитуду до разрушения конструкции (кредит: PRI’s Studio 360, через Flickr)
Неровности и гравийные дороги доказывают, что даже система подвески автомобиля не застрахована от резонанса.Несмотря на тщательно спроектированные амортизаторы, которые обычно преобразуют механическую энергию в тепловую почти так же быстро, как она приходит, лежачие полицейские по-прежнему вызывают колебания большой амплитуды.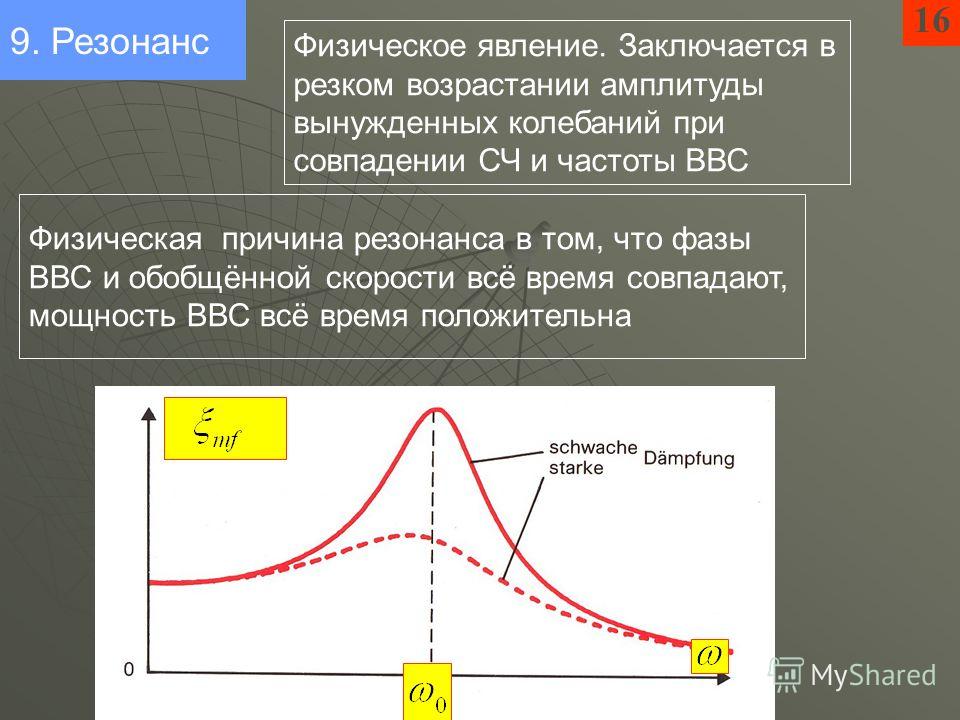 На гравийных дорогах с рифленым покрытием вы, возможно, заметили, что если вы едете с «неправильной» скоростью, неровности очень заметны, тогда как на других скоростях неровности вообще можно не почувствовать. На рис. 4 показана фотография известного примера (моста Tacoma Narrows Bridge) деструктивного воздействия возбужденного гармонического колебания.Мост Миллениум в Лондоне был закрыт на короткое время по той же причине, пока проводились проверки.
На гравийных дорогах с рифленым покрытием вы, возможно, заметили, что если вы едете с «неправильной» скоростью, неровности очень заметны, тогда как на других скоростях неровности вообще можно не почувствовать. На рис. 4 показана фотография известного примера (моста Tacoma Narrows Bridge) деструктивного воздействия возбужденного гармонического колебания.Мост Миллениум в Лондоне был закрыт на короткое время по той же причине, пока проводились проверки.
В нашем организме полость грудной клетки является ярким примером системы, находящейся в резонансе. Диафрагма и грудная стенка вызывают колебания грудной полости, в результате чего легкие раздуваются и сдуваются. Система критически демпфирована, и мышечная диафрагма колеблется с резонансным значением для системы, что делает ее высокоэффективной.
Проверьте свое понимание
В известном фокусе исполнитель поет ноту в сторону хрусталя, пока стекло не разобьется.Объясните, почему этот трюк работает с точки зрения резонанса и собственной частоты.
Решение
Исполнитель должен петь ноту, соответствующую собственной частоте стекла. Когда звуковая волна направлена на стекло, стекло резонирует с той же частотой, что и звуковая волна. Когда в систему вводится достаточно энергии, стекло начинает вибрировать и в конечном итоге разбивается.
Сводка раздела
- Собственная частота системы – это частота, с которой система будет колебаться, если на нее не действуют движущие или демпфирующие силы.
- Периодическая сила, приводящая в движение гармонический осциллятор на его собственной частоте, вызывает резонанс. Говорят, что система резонирует.
- Чем меньше демпфирование в системе, тем выше амплитуда вынужденных колебаний вблизи резонанса. Чем больше демпфирование у системы, тем более широкий отклик она имеет на изменение частот движения.
Концептуальные вопросы
- Почему солдатам обычно приказывают «шагать шагом» (идти не в ногу) через мост?
Задачи и упражнения
- Сколько энергии должны рассеять амортизаторы автомобиля массой 1200 кг, чтобы погасить отскок, изначально имеющий скорость 0.
 800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.
800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение. - Если у автомобиля есть система подвески с силовой константой 5,00 × 10 4 Н / м, сколько энергии должны отводить амортизаторы автомобиля, чтобы гасить колебания, начиная с максимального смещения 0,0750 м?
- (a) Насколько пружина с силовой константой 40,0 Н / м будет растянута объектом массой 0,500 кг, когда она неподвижно подвешена на пружине? (б) Рассчитайте уменьшение гравитационной потенциальной энергии 0.Объект весом 500 кг, когда он спускается на это расстояние. (c) Часть этой гравитационной энергии уходит в пружину. Вычислите энергию, запасенную в пружине на этом участке, и сравните ее с потенциальной энергией гравитации. Объясните, куда может уйти остальная энергия.
- Предположим, у вас есть объект весом 0,750 кг на горизонтальной поверхности, соединенный с пружиной, имеющей силовую постоянную 150 Н / м. Между объектом и поверхностью существует простое трение со статическим коэффициентом трения μ s = 0.
 100. а) Как далеко можно растянуть пружину без перемещения груза? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения составляет μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, что он начинается с максимальной амплитуды.
100. а) Как далеко можно растянуть пружину без перемещения груза? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения составляет μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, что он начинается с максимальной амплитуды. - Инженерное приложение. Подвесной мост колеблется с постоянной эффективной силы 1,00 × 10 8 Н / м. (а) Сколько энергии нужно, чтобы заставить его колебаться с амплитудой 0.100 м? (b) Если солдаты маршируют по мосту с частотой, равной собственной частоте моста, и каждую секунду передают 1,00 × 10 4 Дж энергии, сколько времени потребуется, чтобы колебания моста достигли амплитуды от 0,100 м до 0,500 м. .
Глоссарий
собственная частота: частота, с которой система будет колебаться, если бы не было движения и демпфирующих сил
резонанс: явление возбуждения системы с частотой, равной собственной частоте системы
резонирует: система работает на собственной частоте
Избранные решения проблем и упражнения
1. 384 Дж
384 Дж
3. (а). 0,123 м; (б). −0,600 Дж; (c). 0,300 Дж. Остальная энергия может уйти в тепло из-за трения и других демпфирующих сил.
5. (а) 5.00 × 10 5 Дж; (б) 1,20 × 10 3 с
4.3: Резонанс – Physics LibreTexts
Резонанс – это явление, при котором осциллятор наиболее сильно реагирует на движущую силу, которая соответствует его собственной частоте колебаний. Например, предположим, что ребенок находится на качелях на игровой площадке с собственной частотой 1 Гц.То есть, если вы вытащите ребенка из состояния равновесия, отпустите его, а затем перестанете что-либо делать на какое-то время, он будет колебаться с частотой 1 Гц. Если бы не было трения, как мы предполагали в разделе 2.5, то сумма ее гравитационной и кинетической энергии оставалась бы постоянной, а амплитуда была бы точно такой же от одного колебания к другому. Однако трение будет преобразовывать эти формы энергии в тепло, поэтому ее колебания постепенно затухнут. Чтобы этого не происходило, вы можете толкать ее один раз за цикл, т. е.е., частота ваших толчков будет 1 Гц, что совпадает с собственной частотой качания. Пока вы остаетесь в ритме, свинг реагирует довольно хорошо. Если вы начинаете качание из состояния покоя, а затем толкаете его с частотой 1 Гц, амплитуда колебания быстро нарастает, как на рисунке а, пока через некоторое время не достигнет устойчивого состояния, в котором трение снимает столько же энергии, сколько вы вкладываете в него. курс одного цикла.
е.е., частота ваших толчков будет 1 Гц, что совпадает с собственной частотой качания. Пока вы остаетесь в ритме, свинг реагирует довольно хорошо. Если вы начинаете качание из состояния покоя, а затем толкаете его с частотой 1 Гц, амплитуда колебания быстро нарастает, как на рисунке а, пока через некоторое время не достигнет устойчивого состояния, в котором трение снимает столько же энергии, сколько вы вкладываете в него. курс одного цикла.
Что будет, если вы попробуете нажать на 2 Гц? Ваш первый толчок дает некоторый импульс, \ (p \), но ваш второй толчок происходит только через половину цикла, когда колебание возвращается прямо к вам с импульсом \ (- p \)! Передачи импульса от второго толчка ровно хватит, чтобы остановить свинг.Результат – очень слабое и не очень синусоидальное движение, b.
Рисунок b: Колебание колеблется с удвоенной резонансной частотой.
Делаем математику проще
Это простой и физически прозрачный пример резонанса: качели реагируют наиболее сильно, если вы соответствуете их естественному ритму. Однако у него есть некоторые характеристики, которые математически некрасивы и, возможно, нереалистичны. Быстрые и сильные толчки известны как импульс сил, c, и они приводят к графику \ (x \) – \ (t \), который имеет недифференцируемые изломы.
Однако у него есть некоторые характеристики, которые математически некрасивы и, возможно, нереалистичны. Быстрые и сильные толчки известны как импульс сил, c, и они приводят к графику \ (x \) – \ (t \), который имеет недифференцируемые изломы.
Рисунок c: График \ (F \) – против – \ (t \) для импульсной движущей силы.
Подобные импульсные силы не только плохо работают математически, они обычно нежелательны с практической точки зрения. Например, в автомобильном двигателе инженеры очень усердно работают над тем, чтобы сила, действующая на поршни, изменялась плавно, чтобы избежать чрезмерной вибрации. В оставшейся части этого раздела мы будем предполагать, что движущая сила является синусоидальной, d, т. Е. Та, чей график \ (F \) – \ (t \) является либо синусоидальной функцией, либо функцией, отличной от синусоидальной волны. по фазе, например косинус.Сила положительна для половины каждого цикла и отрицательна для другой половины, т. Е. Есть и толкание, и тяга.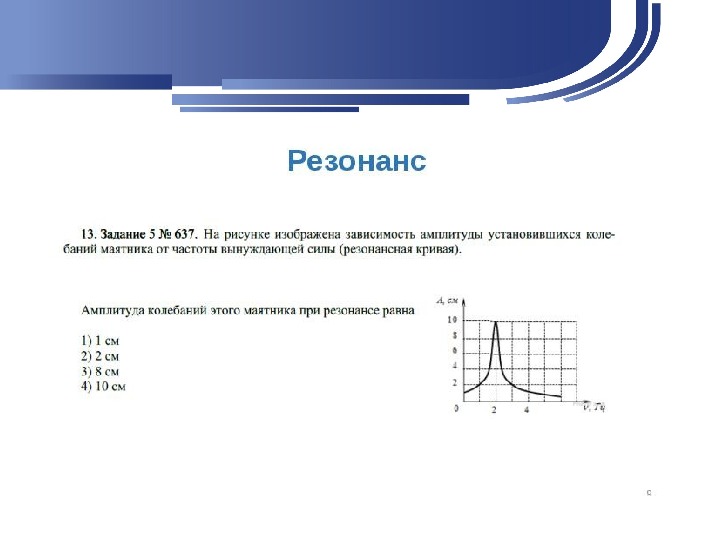 Синусоидальные функции имеют много хороших математических характеристик (мы можем дифференцировать и интегрировать их, а сумма синусоидальных функций с одинаковой частотой является синусоидальной функцией), и они также используются во многих практических ситуациях. Например, заппер моей гаражной двери излучает синусоидальную радиоволну, и приемник настроен на ее резонанс.
Синусоидальные функции имеют много хороших математических характеристик (мы можем дифференцировать и интегрировать их, а сумма синусоидальных функций с одинаковой частотой является синусоидальной функцией), и они также используются во многих практических ситуациях. Например, заппер моей гаражной двери излучает синусоидальную радиоволну, и приемник настроен на ее резонанс.
Рисунок d: Синусоидальная движущая сила.2 \). В других ситуациях, например, с газом низкой плотности или трением между твердыми поверхностями, которые были смазаны жидкостью, такой как масло, мы можем обнаружить, что сила трения имеет некоторую другую зависимость от скорости, возможно, пропорциональную \ (v \), или иметь какую-то другую сложную зависимость от скорости, которую даже нельзя выразить простым уравнением. Было бы чрезвычайно сложно рассматривать все эти различные возможности в полной мере, поэтому в оставшейся части этого раздела мы будем предполагать, что трение пропорционально скорости
\ [\ begin {уравнение *} F = -bv, \ конец {уравнение *} \]
просто потому, что полученные уравнения проще всего решить. Даже если трение не ведет себя именно так, многие из наших результатов могут быть, по крайней мере, качественно правильными.
Даже если трение не ведет себя именно так, многие из наших результатов могут быть, по крайней мере, качественно правильными.
3.3.1 Демпфирование, свободное движение
Численное моделирование
Осциллятор с трением называется демпфированным. Давайте воспользуемся численными методами, чтобы найти движение затухающего осциллятора, которое выходит из состояния равновесия, но после этого не испытывает движущей силы. Можно ожидать, что движение будет состоять из постепенно затухающих колебаний.{- ct} \ text {sin} (\ omega_ {f} t + \ delta) \).
В разделе 2.5 мы смоделировали случай без демпфирования, используя нашу испытанную функцию Python, основанную на сохранении энергии. Теперь, однако, этот подход становится немного неудобным, потому что он включает в себя разделение пути, который нужно пройти, на \ (n \) крошечные сегменты, но при наличии демпфирования каждое колебание немного короче предыдущего, и мы не знаю заранее, как далеко пойдет колебание, прежде чем развернуться. Здесь проще использовать силу, а не энергию.Второй закон Ньютона, \ (a = F / m \), дает \ (a = (- kx-bv) / m \), где мы использовали результат примера 40 для силы, оказываемой пружиной. Это станет немного красивее, если мы перепишем его в виде
Здесь проще использовать силу, а не энергию.Второй закон Ньютона, \ (a = F / m \), дает \ (a = (- kx-bv) / m \), где мы использовали результат примера 40 для силы, оказываемой пружиной. Это станет немного красивее, если мы перепишем его в виде
\ [\ begin {уравнение *} ma + bv + kx = 0, \ end {уравнение *} \]
, которое дает симметричную трактовку трех членов, включающих \ ( x \) и его первая и вторая производные, \ (v \) и \ (a \). Теперь вместо вычисления времени \ (\ Delta {} t = \ Delta {} x / v \), необходимого для перемещения на заданное расстояние \ (\ Delta {} x \), мы выбираем \ (\ Delta {} t \) и определить расстояние, пройденное за это время, \ (\ Delta {} x = v \ Delta {} t \).Кроме того, мы больше не можем обновлять \ (v \) на основе сохранения энергии, поскольку у нас нет простого способа отслеживать, сколько механической энергии было преобразовано в тепловую. Вместо этого мы пересчитываем скорость, используя \ (\ Delta {} v = a \ Delta {} t \).
импортная математика k = 39,4784 # выбрано, чтобы задать период в 1 секунду т = 1.b = 0,211 # выбрано для упрощения результатов х = 1. v = 0. т = 0. dt = 0,01 n = 1000 для j в диапазоне (n): х = х + v * dt а = (- к * х-b * v) / м если (v> 0) и (v + a * dt <0): print ("оборот в t =", t, ", x =", x) v = v + a * dt т = т + дт
оборот при t = 0.99, х = 0,899919262445 оборот при t = 1,99, x = 0,809844934046 оборот при t = 2,99, x = 0,728777519477 оборот при t = 3,99, x = 0,655817260033 оборот при t = 4,99, x = 0,5191135 оборот при t = 5,99, x = 0,531059189965 оборот при t = 6,99, x = 0,477875914756 оборот при t = 7,99, x = 0,430013546991 оборот при t = 8,99, x = 0,386940256644 оборот при t = 9,99, x = 0,348177318484
Жесткость пружины, \ (k = 4 \ pi {} = 39.4784 \) Н / м, спроектировано так, что если бы уравнение незатухания \ (f = (1/2 \ pi) \ sqrt {k / m} \) все еще было верным, частота была бы 1 Гц. Мы начинаем с того, что отметим, что добавление небольшого количества демпфирования, похоже, вообще не изменило период или, по крайней мере, не в пределах точности расчета. 10 Однако вы можете сами убедиться, что большое значение \ (b \), скажем, 5 \ (\ text {N} \! \ Cdot \! \ Text {s} / \ text {m} \) , существенно изменяет период.
10 Однако вы можете сами убедиться, что большое значение \ (b \), скажем, 5 \ (\ text {N} \! \ Cdot \! \ Text {s} / \ text {m} \) , существенно изменяет период.
Мы высвобождаем массу из \ (x = 1 \ \ text {m} \), и после одного цикла она возвращается только примерно к \ (x = 0.2 \): амплитуда снова упала ровно на 10%. Этот паттерн продолжается до тех пор, пока выполняется симуляция, например, для последних двух циклов мы имеем 0,34818 / 0,38694 = 0,89982, или снова почти точно 0,9. Это могло показаться капризным, когда я решил использовать нереалистичное уравнение \ (F = -bv \), но это результат. Только с трением \ (- bv \) мы можем получить такой математически простой экспоненциальный распад.
Поскольку затухание носит экспоненциальный характер, оно никогда не затухает полностью; это отличается от поведения, которое мы имели бы с кулоновским трением, которое в какой-то момент заставляет объекты полностью тормозиться до полной остановки.При трении, которое действует как \ (F = -bv \), \ (v \) становится меньше по мере уменьшения колебаний. Все меньшая и меньшая сила затем заставляет их умирать все медленнее и медленнее.
Все меньшая и меньшая сила затем заставляет их умирать все медленнее и медленнее.
Resonance> Лаборатория поддержки лекций по физике и астрономии> USC Dana and David Dornsife College of Letters, Arts and Sciences
W.5 (1) - Симпатический камертон
Эти камертоны (286 Гц) установлены на резонансных коробках. Размер столба воздуха выбран таким образом, чтобы он усиливал тот же звук, что и камертон.То есть коробка действует как закрытая органная труба, а длина коробки соответствует приблизительно одной четверти волны в воздухе звука, производимого вилкой. Поместите резонансные коробки выровненными так, чтобы их отверстия были обращены друг к другу. Теперь резко ударьте по вилке прилагаемым резиновым молотком. Это приводит к сильной вибрации коробки, к которой прикреплена вилка. Столб воздуха также будет вибрировать, и весь воздух вокруг него будет вибрировать. Эта вибрация создает сильную вибрацию в коробке, к которой прикреплена вилка. Этот столб воздуха во втором ящике заставляет камертон вибрировать. Таким образом, второй инструмент приводится в колебание первым инструментом.
Этот столб воздуха во втором ящике заставляет камертон вибрировать. Таким образом, второй инструмент приводится в колебание первым инструментом.
Верх
W.5 (2) -резонансный аппарат
Этот прибор используется для определения длины стоячей волны звука с помощью камертона с известной частотой и трубки, заполненной водой. Он состоит из высокой подставки, на вершине которой находится небольшой резервуар для воды, и 1.2 м пластиковая трубка, нижним концом соединенная с дном резервуара для воды. Резервуар можно перемещать вверх и вниз по подставке, чтобы можно было регулировать уровень воды в трубке. Громкий звук будет производиться, когда вибрирующая вилка поднесена к отверстию трубки и уровень воды отрегулирован в соответствии с длиной резонансной полости. Его также можно использовать для определения скорости звука в воздухе.
Верх
Вт.5 (3) - Разрушение стекла с использованием резонанса
Стакан помещается перед мощным рожковым приводом, подключенным к приемнику и функциональному генератору. С помощью пробкового шара можно продемонстрировать колебания стекла на собственной частоте. Используя стробоскоп и камеру, изображение можно проецировать на экран, чтобы показать деформации стекла и разрушение стекла при увеличении объема.
Примечание : Для настройки требуется уведомление за 48 часов!
Нажмите здесь, чтобы посмотреть видео этой демонстрации.
Верх
W.5 (4) - Демонстратор резонанса ME-311
Устройство состоит из трех пар проводов одинаковой длины, окаймленных цветными грузами.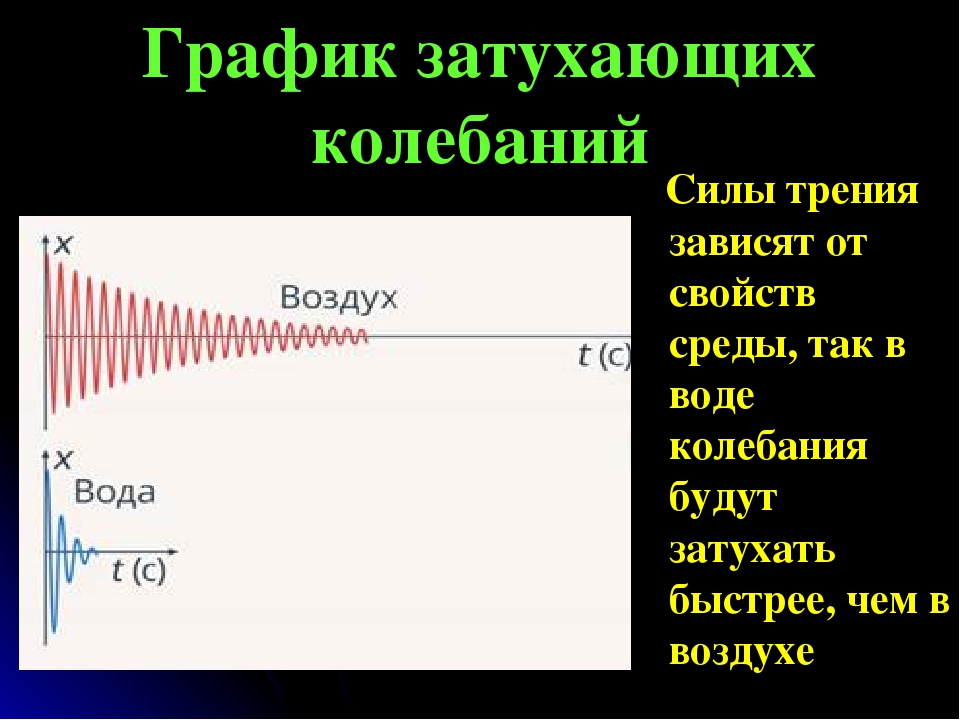



 автоколебательной.
автоколебательной.
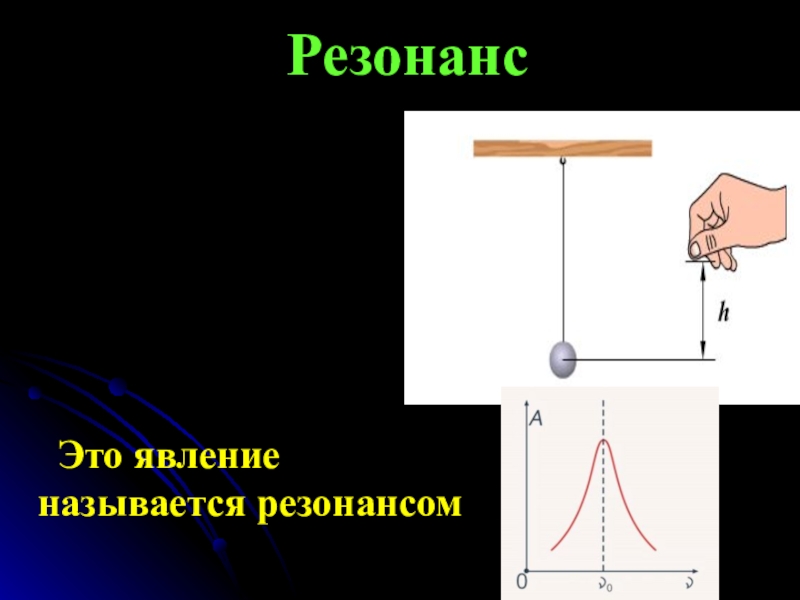 Москва, 2015, стр. 336-337
Москва, 2015, стр. 336-337 Ожидается, что студент:
Ожидается, что студент: Это называется демпфированием.
Это называется демпфированием.

 Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на рисунке \ (\ PageIndex {7} \).
Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на рисунке \ (\ PageIndex {7} \). Следующие две моды находятся путем добавления половины длины волны.
Следующие две моды находятся путем добавления половины длины волны. Большая часть полка дислоцировалась во временных бараках на Дайче-стрит, Сент-Джордж-роуд, и двинулась через Strangeways; но одна рота, которой командовал, как это довольно необычно, лейтенант. P.S. Фицджеральд, сын владельца моста, находившийся в казармах Солфорда, двинулся по подвесному мосту, намереваясь пройти через Пендлтон к казармам. Вскоре после того, как они подошли к мосту, мужчины, шедшие вчетвером в ряд, обнаружили, что конструкция вибрирует в унисон с размеренным шагом, с которым они шли; и поскольку эта вибрация ни в коем случае не была неприятной, они были склонны умилостивить ее своей манерой шага.По мере того, как они продолжали движение, и по мере того, как все большее число из них поднималось на мост, вибрация продолжала увеличиваться, пока голова колонны почти не достигла стороны Пендлтона реки. Затем они были встревожены громким звуком, напоминающим беспорядочный выстрел из огнестрельного оружия; и сразу одна из железных опор, поддерживающих цепи подвески, а именно.
Большая часть полка дислоцировалась во временных бараках на Дайче-стрит, Сент-Джордж-роуд, и двинулась через Strangeways; но одна рота, которой командовал, как это довольно необычно, лейтенант. P.S. Фицджеральд, сын владельца моста, находившийся в казармах Солфорда, двинулся по подвесному мосту, намереваясь пройти через Пендлтон к казармам. Вскоре после того, как они подошли к мосту, мужчины, шедшие вчетвером в ряд, обнаружили, что конструкция вибрирует в унисон с размеренным шагом, с которым они шли; и поскольку эта вибрация ни в коем случае не была неприятной, они были склонны умилостивить ее своей манерой шага.По мере того, как они продолжали движение, и по мере того, как все большее число из них поднималось на мост, вибрация продолжала увеличиваться, пока голова колонны почти не достигла стороны Пендлтона реки. Затем они были встревожены громким звуком, напоминающим беспорядочный выстрел из огнестрельного оружия; и сразу одна из железных опор, поддерживающих цепи подвески, а именно. то, что было справа от солдат и на стороне реки Бротон, упало на мост, унеся с собой большой камень с пирса, к которому он был прикреплен болтами.Конечно, этот угол моста, потеряв опору колонны, немедленно упал на дно реки, примерно на шестнадцать или восемнадцать футов; и из-за того, что дорога была сильно наклонена, почти все солдаты, находившиеся на ней, были брошены в реку, где предстала сцена великого смятения. Те из них, кто не пострадал, выбрались, как могли, одни, взобравшись на наклонную плоскость, которую представлял мост, а другие, пройдя вброд со стороны Бротона; но некоторые из них были слишком ранены, чтобы выбраться без помощи, которую немедленно оказали их товарищи.
то, что было справа от солдат и на стороне реки Бротон, упало на мост, унеся с собой большой камень с пирса, к которому он был прикреплен болтами.Конечно, этот угол моста, потеряв опору колонны, немедленно упал на дно реки, примерно на шестнадцать или восемнадцать футов; и из-за того, что дорога была сильно наклонена, почти все солдаты, находившиеся на ней, были брошены в реку, где предстала сцена великого смятения. Те из них, кто не пострадал, выбрались, как могли, одни, взобравшись на наклонную плоскость, которую представлял мост, а другие, пройдя вброд со стороны Бротона; но некоторые из них были слишком ранены, чтобы выбраться без помощи, которую немедленно оказали их товарищи.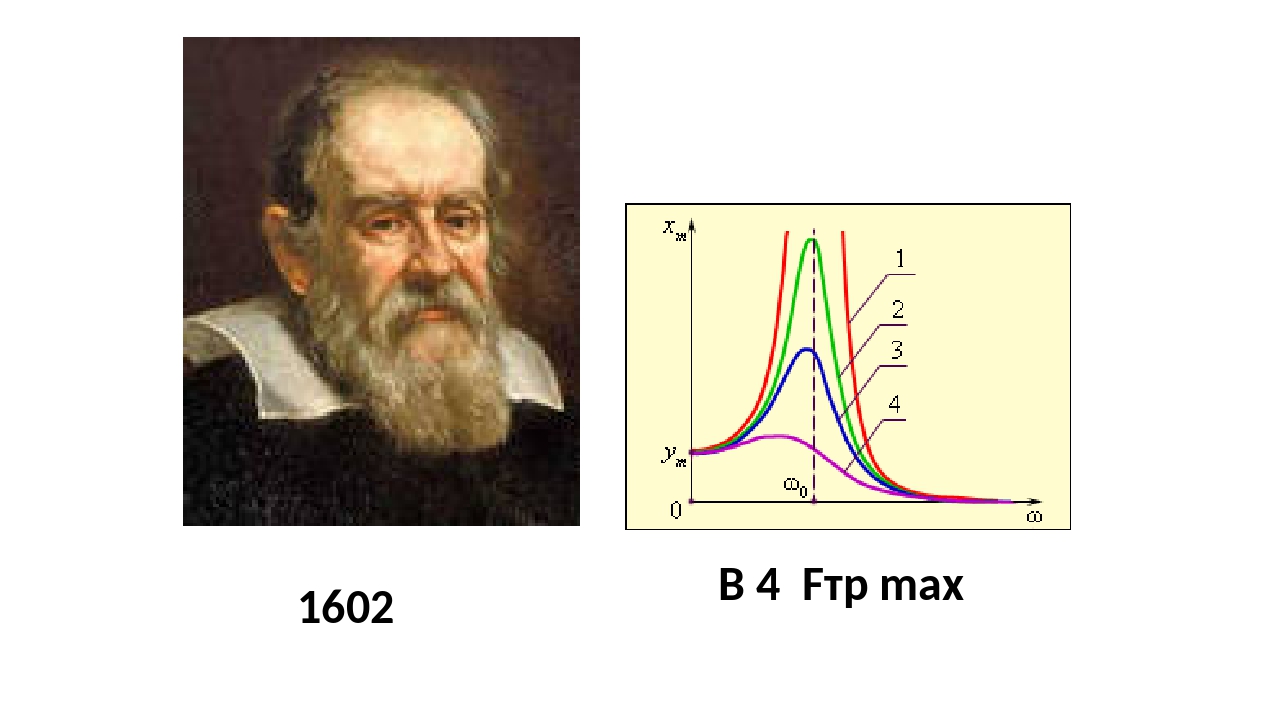
 800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.
800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.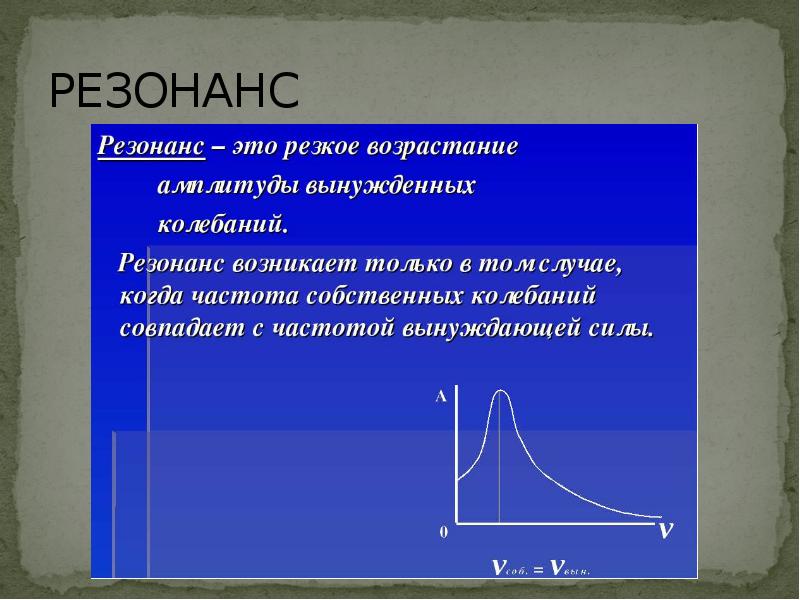 100. а) Как далеко можно растянуть пружину без перемещения груза? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения составляет μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, что он начинается с максимальной амплитуды.
100. а) Как далеко можно растянуть пружину без перемещения груза? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения составляет μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, что он начинается с максимальной амплитуды. b = 0,211 # выбрано для упрощения результатов
х = 1.
v = 0.
т = 0.
dt = 0,01
n = 1000
для j в диапазоне (n):
х = х + v * dt
а = (- к * х-b * v) / м
если (v> 0) и (v + a * dt <0):
print ("оборот в t =", t, ", x =", x)
v = v + a * dt
т = т + дт
b = 0,211 # выбрано для упрощения результатов
х = 1.
v = 0.
т = 0.
dt = 0,01
n = 1000
для j в диапазоне (n):
х = х + v * dt
а = (- к * х-b * v) / м
если (v> 0) и (v + a * dt <0):
print ("оборот в t =", t, ", x =", x)
v = v + a * dt
т = т + дт