Резонанс колебаний: Резонанс — урок. Физика, 9 класс.

Военно-техническая подготовка

1.4. Колебательный контур.

1.4.1. Свободные колебания в контуре.

Свободные (или собственные) колебания — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие).

Пусть конденсатор ёмкостью C заряжен до напряжения U0 . Энергия, запасённая в конденсаторе составляет

,

При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток I , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю.

Магнитная энергия катушки в этот (начальный) момент равна нулю.

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

,

где L — индуктивность катушки, I0

— максимальное значение тока.

После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения – U0 .

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

Рис 1. Пример: Осциллограмма LC контура во время замыкания заряженного конденсатора на катушку индуктивности.

С = 240нФ(заряженный), L = 360нГн, F0 ≈ 542кГц.

1.4.2. Вынужденные колебания в контуре.

Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:

.

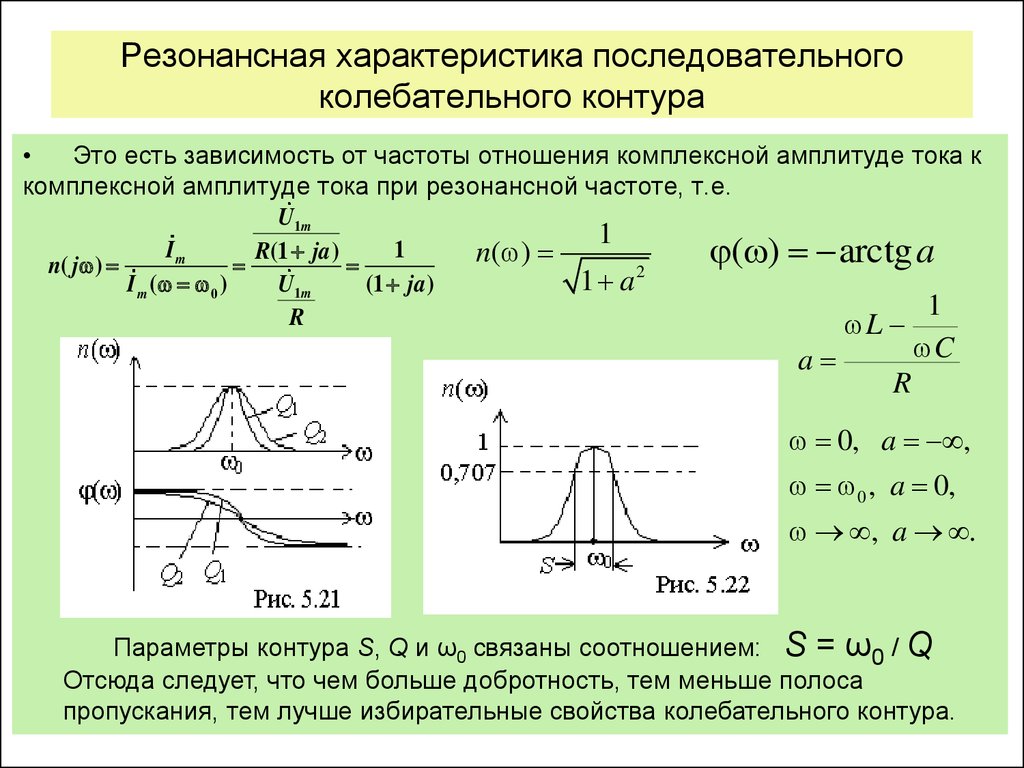
Консервативный гармонический осциллятор

Второй закон Ньютона для такого осциллятора запишется в виде:

.

Если ввести обозначения:

,

и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

,

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:

,

где A , φ — произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение.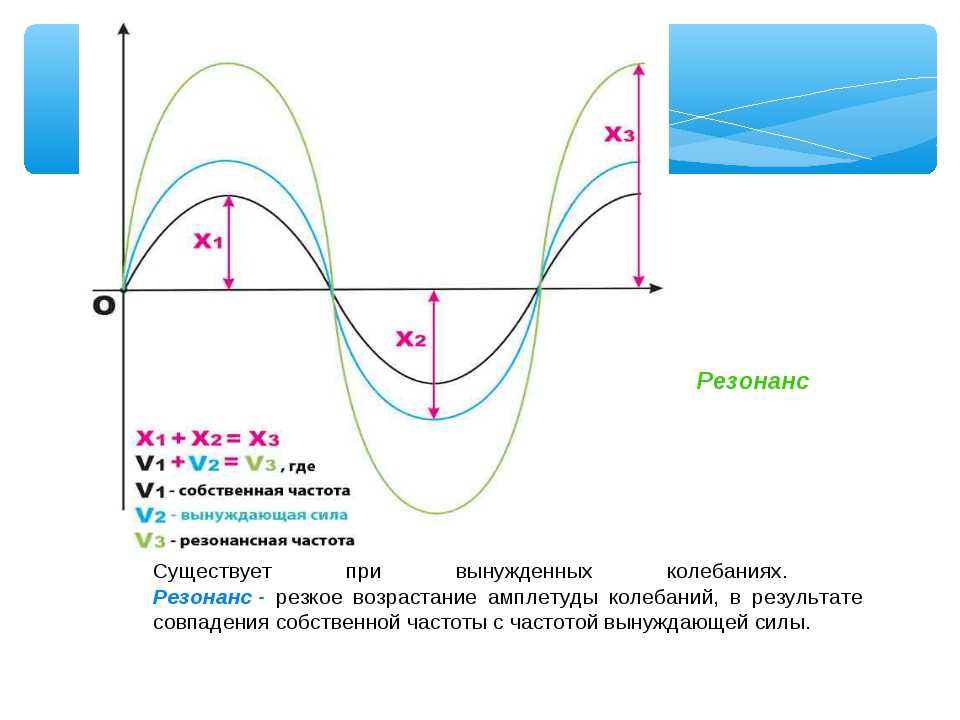

Для этого подставим в уравнение решение вида:

,

и получим значение для константы:

,

Тогда окончательное решение запишется в виде:

.

1.4.3. Резонанс в колебательном контуре.

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы.

В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

При достижении резонанса, импеданс (комплексное сопротивление двухполюсника (электрической цепи, содержащей две точки для соединения с другими цепями) для гармонического сигнала) последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов.

В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

,

где ω = 2πf ;

f — резонансная частота в герцах;

L — индуктивность в генри;

C — ёмкость в фарадах.

Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте.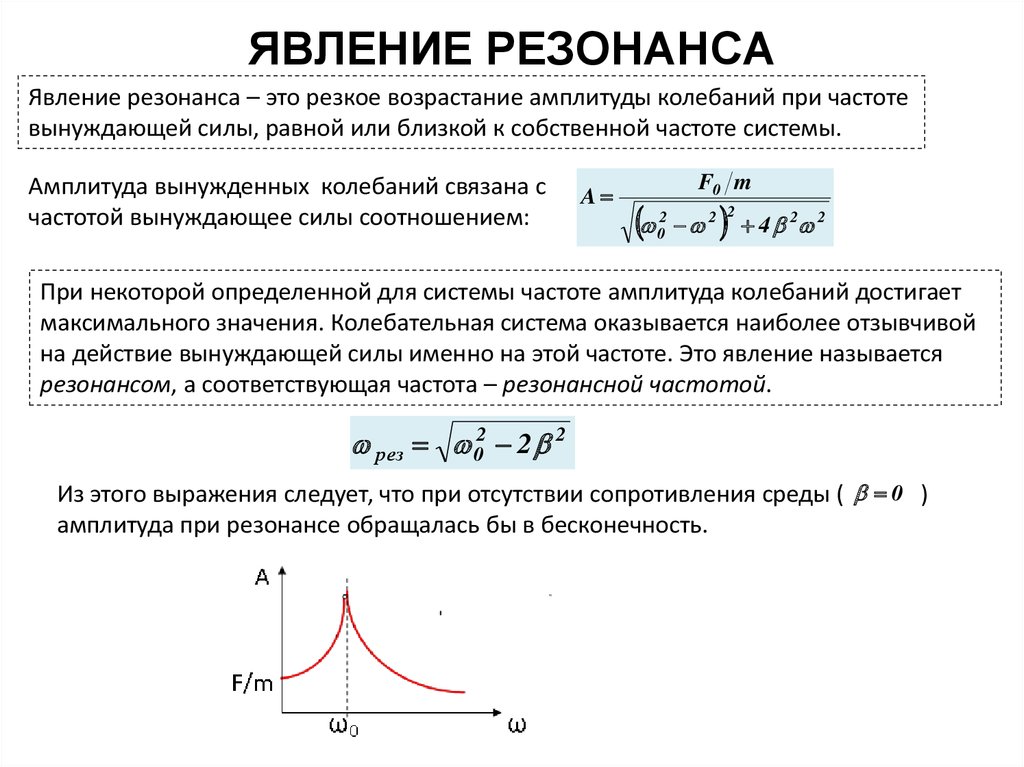

Ширина полосы пропускания определяется добротностью системы (параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.).

Рис 2. Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания.

1.4.4. Связанные цепи.

Если изменение тока в одном из элементов цепи приводит к появлению э.д.с. в другом элементе, то эти два элемента индуктивно связаны, а возникающая э.д.с. называется э.д.с. взаимной индукции.

Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи

,

где М – взаимная индуктивность элементов цепи,

L 1 и L 2 – индуктивности элементов.

При расчете цепей с взаимной индуктивностью следует на схеме отметить стрелками выбираемые положительные направления токов в ветвях (или контурных токов). Кроме того, одинаковыми условными значками (звездочками, точками, буквами и т.п.) обозначить одноименные зажимы каждой пары индуктивно связанных катушек.

Одноименными называются такие зажимы, при одинаковом положительном направлении токов относительно которых, магнитные потоки самоиндукции и взаимной индукции складываются.

1.4.5. Кварцевый резонатор.

Кварцевый резонатор — прибор, в котором пьезоэлектрический эффект и явление механического резонанса используются для построения высокодобротного резонансного элемента электронной схемы.

На пластинку, кольцо или брусок, вырезанные из кристалла кварца определённым образом, нанесены 2 и более электродов — проводящие полоски.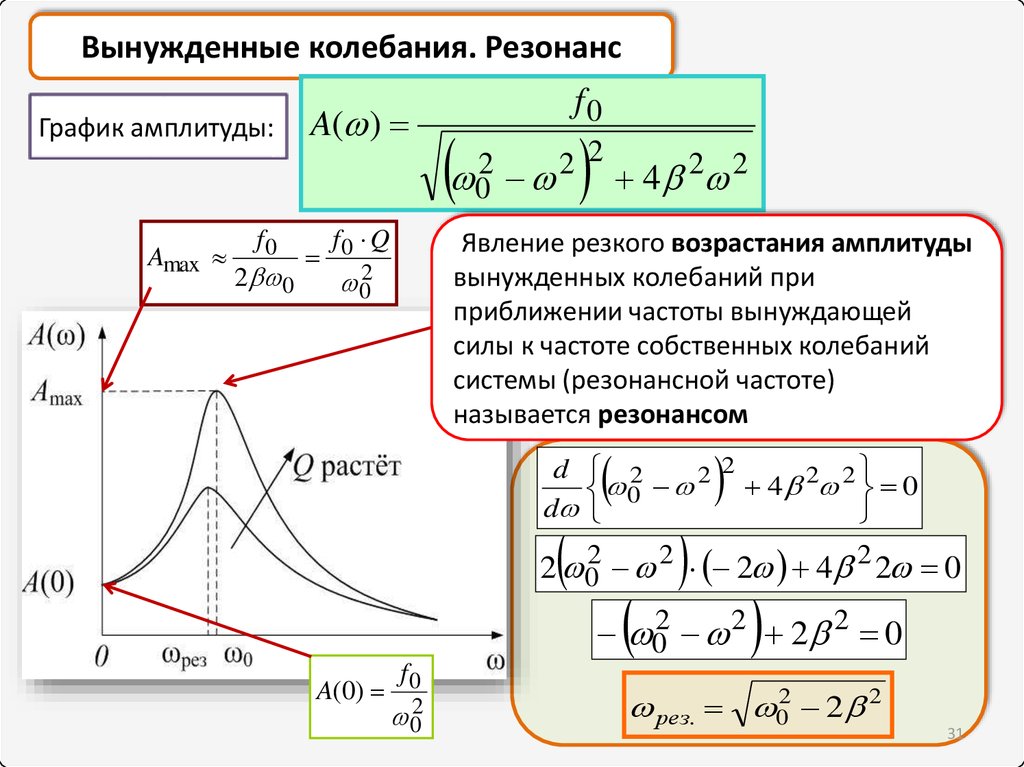

Пластинка закреплена и имеет собственную резонансную частоту механических колебаний.

При подаче напряжения на электроды благодаря пьезоэлектрическому эффекту происходит изгибание, сжатие или сдвиг в зависимости от того, каким образом вырезан кусок кристалла.

Однако колеблющаяся пластинка в результате того же пьезоэлектрического эффекта создаёт во внешней цепи противо-ЭДС, что можно рассматривать как явление, эквивалентное работе катушки индуктивности в колебательном контуре.

Если частота подаваемого напряжения равна или близка к частоте собственных механических колебаний пластинки, затраты энергии на поддержание колебаний пластинки оказываются намного ниже, нежели при большом отличии частоты. Это тоже соответствует поведению колебательного контура.

Рис 3. Эквивалентная схема.

Условное обозначение кварцевого резонатора (сверху) и его эквивалентная схема (снизу)

C0 — собственная ёмкость кристалла, образуемая кристаллодержателем и/или обкладками резонатора.

C1, L1 — эквивалентная ёмкость и индуктивность механической колебательной системы резонатора.

R1 — эквивалентное сопротивление потерь механической колебательной системы.

РЕЗОНАНС • Большая российская энциклопедия

Авторы: В. В. Клиньшов, В. И. Некоркин

РЕЗОНА́НС (франц. resonance, от лат. resono – от­кли­кать­ся), из­би­ра­тель­ный от­клик ко­ле­бат. сис­те­мы на внеш­нее пе­рио­дич. воз­дей­ст­вие оп­ре­де­лён­ной час­то­ты. Яв­ле­ние Р. про­ис­хо­дит при при­бли­же­нии час­то­ты внеш­не­го воз­дей­ст­вия ω к час­то­те собств. ко­ле­ба­ний сис­те­мы ω₀ и за­клю­ча­ет­ся в рез­ком воз­рас­та­нии ам­пли­ту­ды её вы­ну­ж­ден­ных ко­ле­ба­ний. В этом слу­чае час­то­та воз­дей­ст­вия на­зы­ва­ет­ся ре­зо­нанс­ной (ω_р). Её ве­ли­чи­на оп­ре­де­ля­ет­ся свой­ст­ва­ми ко­ле­бат. сис­те­мы. Впер­вые Р. опи­сан Г. Га­ли­ле­ем для ме­ха­нич. сис­тем. От Р. при внеш­нем воз­дей­ст­вии сле­ду­ет от­ли­чать па­ра­мет­ри­че­ский ре­зо­нанс, воз­ни­каю­щий при пе­рио­дич. из­ме­не­нии па­ра­мет­ров ко­ле­бат. сис­те­мы.

Суть эф­фек­та Р. мож­но по­нять на при­ме­ре рас­ка­чи­ва­ния ка­че­лей пу­тём их пе­рио­дич. под­тал­ки­ва­ния. Для эф­фек­тив­но­го рас­ка­чи­ва­ния ка­че­лей час­то­та внеш­не­го под­тал­ки­ва­ния долж­на сов­па­дать с час­то­той их собств. ко­ле­ба­ний. В этом слу­чае ка­ж­дый тол­чок про­ис­хо­дит в од­ной и той же фа­зе дви­же­ния ка­че­лей, спо­соб­ст­вуя уве­ли­че­нию раз­ма­ха ко­ле­ба­ний. При не­пра­виль­но вы­бран­ной час­то­те под­тал­ки­ва­ния толч­ки про­ис­хо­дят в раз­ных фа­зах дви­же­ния, то ус­ко­ряя, то за­мед­ляя ка­че­ли, и су­ще­ст­вен­ной рас­кач­ки ко­ле­ба­ний не про­ис­хо­дит.

Рис. 1. Резонансная кривая линейной системы.

Осн. свой­ст­ва Р. мож­но на­блю­дать при воз­дей­ст­вии внеш­не­го гар­мо­нич. сиг­на­ла на ли­ней­ную сис­те­му с од­ной сте­пе­нью сво­бо­ды, та­кую как ко­ле­бат. кон­тур или ма­те­ма­тич. ма­ят­ник. За­ви­си­мость ам­пли­ту­ды A вы­ну­ж­ден­ных ко­ле­ба­ний та­кой сис­те­мы от час­то­ты внеш­не­го сиг­на­ла ω (ре­зо­нанс­ная кри­вая) име­ет чёт­ко вы­ра­жен­ный мак­си­мум на ре­зо­нанс­ной час­то­те ω_р (рис.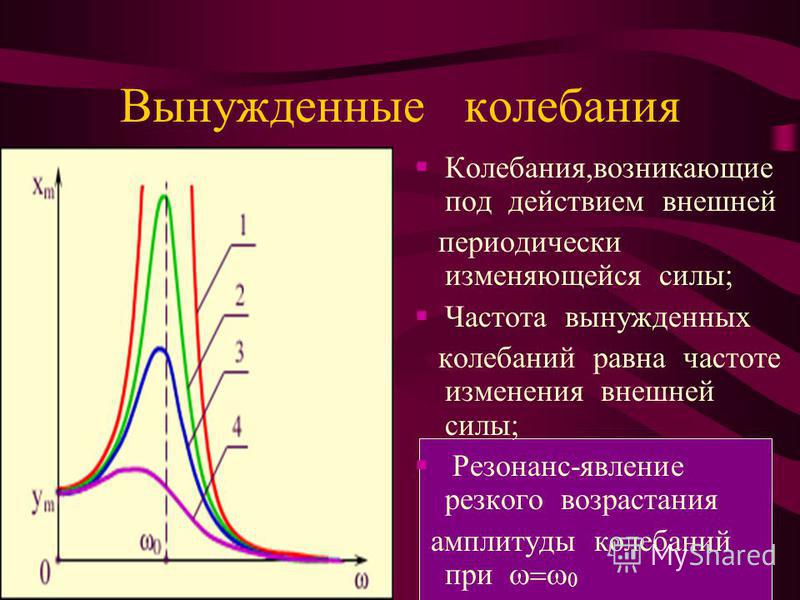  1). Для опи­са­ния ре­зо­нанс­ных свойств ли­ней­ной ко­ле­бат. сис­те­мы час­то ис­поль­зу­ют по­ня­тие доб­рот­но­сти, ха­рак­те­ри­зую­щее сте­пень за­ту­ха­ния ко­ле­ба­ний в сис­те­ме. Ве­ли­чи­на доб­рот­но­сти оп­ре­де­ля­ет фор­му ре­зо­нанс­ной кри­вой: чем боль­ше доб­рот­ность, тем мень­ше ши­ри­на пи­ка ре­зо­нанс­ной кри­вой, т. е. тем бо­лее из­би­ра­тель­ной яв­ля­ет­ся ко­ле­бат. сис­те­ма. С рос­том доб­рот­но­сти уве­ли­чи­ва­ет­ся вы­со­та пи­ка и умень­ша­ет­ся раз­ни­ца ме­ж­ду ре­зо­нанс­ной и собств. час­то­та­ми.

Рис. 2. Резонансная кривая нелинейной системы.

В не­ли­ней­ных сис­те­мах Р. име­ет су­ще­ст­вен­ные осо­бен­но­сти по срав­не­нию с ли­ней­ны­ми. Во-пер­вых, ре­зо­нанс­ная час­то­та не­ли­ней­ной сис­те­мы за­ви­сит от ам­пли­ту­ды внеш­не­го воз­дей­ст­вия. Во-вто­рых, при дос­та­точ­но силь­ных воз­дей­ст­ви­ях ис­че­за­ет од­но­знач­ное со­от­вет­ст­вие ам­пли­ту­ды вы­ну­ж­ден­ных ко­ле­ба­ний па­ра­мет­рам внеш­не­го сиг­на­ла. При од­ной и той же час­то­те внеш­ней си­лы воз­мож­ны ре­жи­мы ко­ле­ба­ний с разл. ам­пли­ту­да­ми (рис. 2). Штри­хо­вой кри­вой на ри­сун­ке по­ка­за­на ветвь, со­от­вет­ст­вую­щая не­ус­той­чи­во­му ре­жи­му ко­ле­ба­ний. Пе­ре­клю­че­ние ме­ж­ду разл. ре­жи­ма­ми при пе­ре­строй­ке час­то­ты про­ис­хо­дит в ви­де скач­ков ам­пли­ту­ды и име­ет гис­те­ре­зис­ный ха­рак­тер.

Для ли­ней­ных сис­тем с не­сколь­ки­ми сте­пе­ня­ми сво­бо­ды и для рас­пре­де­лён­ных сис­тем, в ко­то­рых собств. ко­ле­ба­ния мо­гут про­ис­хо­дить на раз­ных час­то­тах, Р. на­блю­да­ет­ся при при­бли­же­нии час­то­ты внеш­не­го сиг­на­ла к од­ной из этих час­тот. В этом слу­чае ре­зо­нанс­ная кри­вая ха­рак­те­ри­зу­ет­ся на­ли­чи­ем не­сколь­ких мак­си­му­мов, и внеш­нее воз­дей­ст­вие рас­пре­де­ля­ет­ся по отд. ко­ор­ди­на­там сис­те­мы.

Р. иг­ра­ет важ­ную роль в при­ро­де, нау­ке и тех­ни­ке. В не­ко­то­рых слу­ча­ях он яв­ля­ет­ся не­же­ла­тель­ным, т. к. при­во­дит к не­га­тив­ным по­след­ст­ви­ям. Напр., при сов­па­де­нии час­то­ты на­бе­гаю­щих на ко­рабль волн с собств. час­то­той ки­ле­вой кач­ки воз­ни­ка­ет рез­кое уве­ли­че­ние ам­п­ли­ту­ды ко­ле­ба­ний ко­раб­ля, при ко­то­рых его нос «за­ры­ва­ет­ся» в вол­ну. Р. мо­жет вы­зы­вать силь­ные ко­ле­ба­ния и по­сле­дую­щие раз­ру­ше­ния при ра­бо­те виб­ри­рую­щих стан­ков, ма­шин, дви­га­те­лей внутр. сго­ра­ния. Из­вест­ны слу­чаи раз­ру­ше­ния мос­тов под дей­ст­ви­ем рит­мич. толч­ков от про­хо­дя­щих по ним войск. С др. сто­ро­ны, на яв­ле­нии Р. ос­но­ва­на ра­бо­та мн. при­бо­ров и уст­ройств. Напр., на­строй­ка час­то­ты ко­ле­бат. кон­ту­ра ра­дио­при­ём­ни­ка на час­то­ту элек­тро­маг­нит­но­го сиг­на­ла по­зво­ля­ет осу­ще­ст­в­лять его при­ём. Яв­ле­ние Р. ле­жит в ос­но­ве прин­ци­па дей­ст­вия СВЧ элек­трон­ных при­бо­ров, напр. клис­тро­нов, ис­поль­зую­щих вы­со­ко­доб­рот­ные объ­ём­ные ре­зо­на­то­ры для уси­ле­ния СВЧ-сиг­на­лов.

Вынужденные колебания и резонанс | Физика

Цели обучения

К концу этого раздела вы сможете:

• Наблюдать резонанс гребного шарика на струне.
• Измерьте амплитуду затухающего гармонического осциллятора.

Рисунок 1. Вы можете заставить струны фортепиано вибрировать, просто производя звуковые волны своим голосом. (Фото: Matt Billings, Flickr)

Сядьте как-нибудь перед пианино и спойте громко короткую ноту, сняв демпферы со струн. Он пропоет вам ту же ноту — струны, имеющие ту же частоту, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Ваш голос и струны фортепиано — хороший пример того, что объекты — в данном случае струны фортепиано — можно заставить колебаться, но лучше всего колебаться на своей собственной частоте. В этом разделе мы кратко рассмотрим применение периодическая движущая сила , действующая на простой гармонический осциллятор. Движущая сила передает энергию в систему с определенной частотой, не обязательно такой же, как собственная частота системы. Собственная частота — это частота, с которой колебалась бы система, если бы не было ни движущей, ни демпфирующей силы.

Большинство из нас играли с игрушками, включающими объект, закрепленный на резинке, что-то вроде мяча с веслом, подвешенного к пальцу на рис. 2. Представьте, что палец на рисунке — это ваш палец. Сначала вы держите палец неподвижно, и мяч подпрыгивает вверх и вниз с небольшим затуханием. Если вы будете медленно двигать пальцем вверх и вниз, мяч будет следовать за вами, не сильно отскакивая сам по себе. По мере того, как вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мячик будет колебаться с увеличивающейся амплитудой. Когда вы ведете мяч с его собственной частотой, амплитуда колебаний мяча увеличивается с каждым колебанием до тех пор, пока вы им управляете. Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонанс . Говорят, что система, работающая на своей собственной частоте, резонирует . По мере того, как частота возбуждения становится все выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец просто будет двигаться вверх и вниз, практически не воздействуя на шар.

Рис. 2. Шарик на резиновой ленте движется в ответ на палец, поддерживающий его. Если палец движется с собственной частотой f0 шарика по резинке, то достигается резонанс, и амплитуда колебаний шарика резко возрастает. На более высоких и более низких частотах движения энергия передается мячу менее эффективно, и он отвечает колебаниями с меньшей амплитудой.

На рисунке 3 показан график зависимости амплитуды затухающего гармонического осциллятора от частоты воздействующей на него периодической силы. На графике есть три кривые, каждая из которых представляет разную величину демпфирования. Все три кривые достигают пика в точке, где частота движущей силы равна собственной частоте гармонического осциллятора. Самый высокий пик или наибольшая реакция приходится на наименьшее количество демпфирования, потому что сила демпфирования отводит меньше энергии.

Рис. 3. Амплитуда гармонического осциллятора в зависимости от частоты движущей силы. Кривые представляют один и тот же осциллятор с одинаковой собственной частотой, но с разной степенью затухания.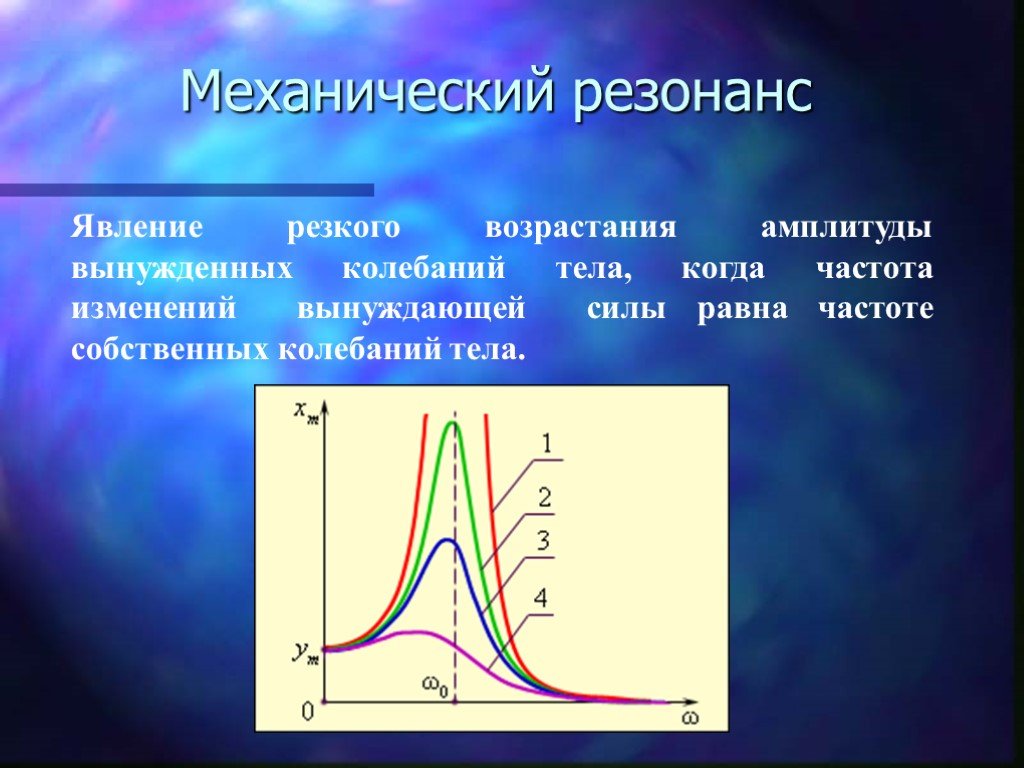 Резонанс возникает, когда частота возбуждения равна собственной частоте, а наибольший отклик достигается при наименьшем демпфировании. Самая узкая характеристика также соответствует наименьшему демпфированию.

Интересно, что ширина резонансных кривых, показанных на рисунке 3, зависит от затухания: чем меньше затухание, тем уже резонанс. Суть в том, что если вы хотите, чтобы ведомый осциллятор резонировал на очень определенной частоте, вам нужно как можно меньше демпфирования. Небольшое демпфирование характерно для струн фортепиано и многих других музыкальных инструментов. И наоборот, если вам нужны колебания малой амплитуды, например, в системе подвески автомобиля, вам нужно сильное демпфирование. Сильное демпфирование уменьшает амплитуду, но компромисс заключается в том, что система реагирует на большем количестве частот.

Эти особенности управляемых гармонических генераторов применимы к огромному разнообразию систем. Когда вы настраиваете радио, например, вы настраиваете его резонансную частоту так, чтобы оно колебалось только до частоты вещания (ведущей) желаемой станции.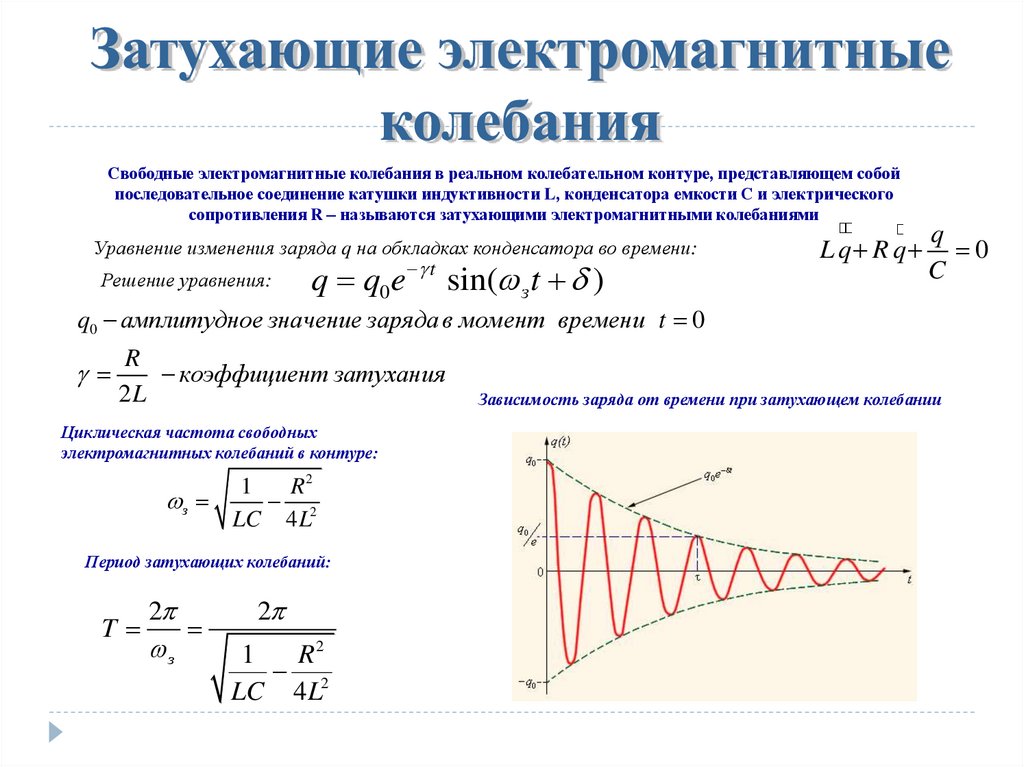 Чем более избирательно радио различает станции, тем меньше его затухание. Магнитно-резонансная томография (МРТ) — это широко используемый медицинский диагностический инструмент, в котором атомные ядра (в основном ядра водорода) заставляют резонировать с поступающими радиоволнами (порядка 100 МГц). Родитель раскачивает ребенка на качелях с естественной частотой качелей для достижения максимальной амплитуды. Во всех этих случаях эффективность передачи энергии от движущей силы к осциллятору максимальна при резонансе.

Рисунок 4. В 1940 году обрушился мост Такома-Нарроуз в штате Вашингтон. Сильный боковой ветер приводил мост в колебания на резонансной частоте. Демпфирование уменьшилось, когда опорные тросы оторвались и начали скользить по опорам, что позволяло увеличивать амплитуду до тех пор, пока конструкция не разрушилась (фото: PRI’s Studio 360, через Flickr)

Лежачие полицейские и гравийные дороги доказывают, что даже система подвески автомобиля не защищена к резонансу.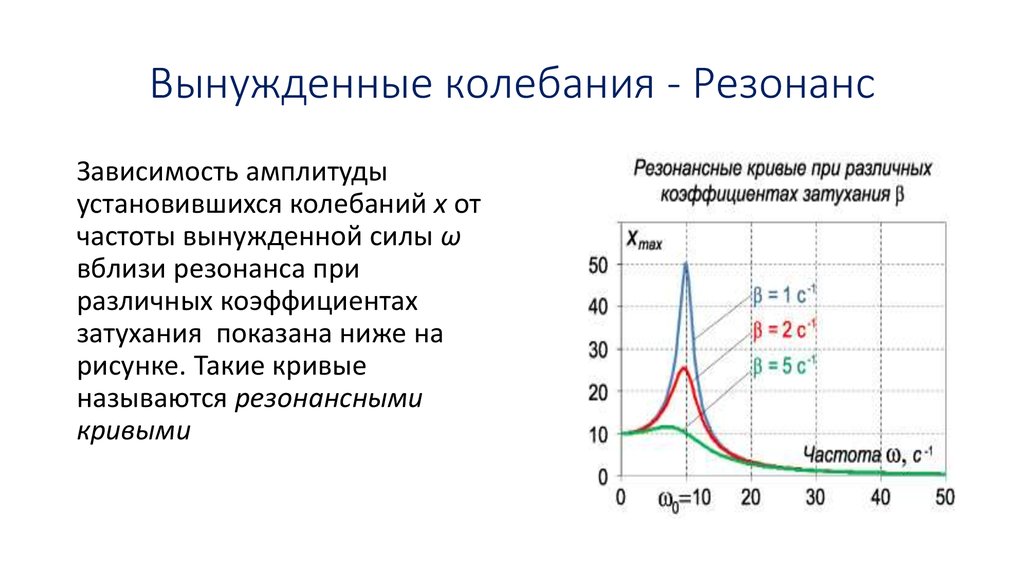 Несмотря на тонко сконструированные амортизаторы, которые обычно преобразуют механическую энергию в тепловую практически с той же скоростью, с которой она поступает, лежачие полицейские по-прежнему вызывают колебания большой амплитуды. На гравийных дорогах с волнистым покрытием вы могли заметить, что если вы едете с «неправильной» скоростью, неровности очень заметны, тогда как на других скоростях неровности практически не ощущаются. На рисунке 4 показана фотография известного примера (Мост Такома-Нарроуз) разрушительного воздействия возбуждаемых гармонических колебаний. Мост Миллениум в Лондоне был закрыт на короткое время по той же причине, пока проводились проверки.

В наших телах грудная полость является ярким примером системы, находящейся в резонансе. Диафрагма и грудная стенка вызывают колебания грудной полости, что приводит к надуванию и сдуванию легких. Система критически демпфирована, а мышечная диафрагма колеблется с резонансным значением для системы, что делает ее очень эффективной.

Проверьте свое понимание

Известный фокус состоит в том, что исполнитель поет ноту в сторону хрустального стекла, пока стекло не разбивается. Объясните, почему трюк работает с точки зрения резонанса и собственной частоты.

Решение

Исполнитель должен петь ноту, соответствующую собственной частоте стакана. Когда звуковая волна направлена ​​на стекло, стекло резонирует с той же частотой, что и звуковая волна. При достаточном количестве энергии, введенной в систему, стекло начинает вибрировать и в конце концов разбивается.

Резюме раздела

• Собственная частота системы — это частота, с которой система будет колебаться, если на нее не воздействуют движущие или демпфирующие силы.
• Периодическая сила, возбуждающая гармонический осциллятор на его собственной частоте, вызывает резонанс. Говорят, что система резонирует.
• Чем меньше демпфирование системы, тем выше амплитуда вынужденных колебаний вблизи резонанса. Чем больше демпфирование имеет система, тем шире ее отклик на различные частоты движения.

Концептуальные вопросы

1. Почему солдатам обычно приказано «перешагивать через мост» (идти не в ногу)?

Задачи и упражнения

1. Сколько энергии должны рассеять амортизаторы автомобиля массой 1200 кг, чтобы погасить отскок, скорость которого в начальном положении равновесия составляет 0,800 м/с? Предположим, что автомобиль возвращается в исходное вертикальное положение.
2. Если автомобиль имеет систему подвески с силовой константой 5,00 × 10 ⁴ Н/м, сколько энергии должны отвести амортизаторы автомобиля, чтобы погасить колебания, начиная с максимального перемещения 0,0750 м?
3. (a) Насколько пружина с постоянной силы 40,0 Н/м будет растянута объектом массой 0,500 кг, когда он неподвижно подвешен на пружине? (b) Рассчитайте уменьшение гравитационной потенциальной энергии объекта массой 0,500 кг, когда он спускается на это расстояние. (c) Часть этой гравитационной энергии уходит в пружину. Рассчитайте энергию, запасенную пружиной при этом растяжении, и сравните ее с потенциальной энергией гравитации. Объясните, куда может уйти остальная энергия.
4. Предположим, у вас есть объект массой 0,750 кг на горизонтальной поверхности, соединенный с пружиной, силовая постоянная которой равна 150 Н/м. Существует простое трение между объектом и поверхностью со статическим коэффициентом трения μ _с  = 0,100. а) Насколько можно растянуть пружину, не перемещая груз? (b) Если объект колеблется с амплитудой, вдвое превышающей расстояние, указанное в части (а), и кинетический коэффициент трения составляет μ _k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, он начинается с максимальной амплитуды.
5. Инженерное приложение. Висячий мост совершает колебания с постоянной эффективной силы 1,00 × 10 ⁸ Н/м. (а) Сколько энергии необходимо, чтобы заставить его колебаться с амплитудой 0,100 м? (b) Если солдаты маршируют по мосту с частотой, равной собственной частоте моста, и сообщают 1,00 × 10 ⁴ Дж энергии каждую секунду, сколько времени потребуется, чтобы амплитуда колебаний моста уменьшилась с 0,100 м до 0,500 м. .

Глоссарий

собственная частота:  частота, с которой система колебалась бы, если бы не было ни движущей, ни демпфирующей сил

резонанс:  явление возбуждения системы с частотой, равной собственной частоте системы

резонировать:  система, работающая на своей собственной частоте

Избранные решения задач и упражнений

1. 384 J

3. (a). 0,123 м; (б). −0,600 Дж; (с). 0,300 Дж. Остальная энергия может перейти в тепло, вызванное трением и другими демпфирующими силами.

5. (а) 5,00 × 10 ⁵ Дж; (b) 1,20 × 10 ³ с

2.6: Вынужденные колебания и резонанс

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

351

• Йиржи Лебл
• Университет штата Оклахома

Рассмотрим на примере груза на пружине. Рассмотрим теперь случай вынужденных колебаний, который мы еще не рассматривали. То есть мы рассматриваем уравнение

\[ mx” + cx’ + kx = F(t) \номер \]

для некоторого отличного от нуля \(F(t)\). Установка опять такая: \(m\) – масса, \(c\) – трение, \(k\) – постоянная пружины, а \(F(t)\) – внешняя сила, действующая на массу.

Рисунок \(\PageIndex{1}\)

Нас интересует периодическое воздействие, такое как нецентрированные вращающиеся части, или, возможно, громкие звуки или другие источники периодического воздействия. Как только мы узнаем о рядах Фурье в главе 4, мы увидим, что мы покрываем все периодические функции, просто рассматривая \(F(t) = F_0 \cos (\omega t)\) (или синус вместо косинуса, вычисления по существу одинаковый).

Незатухающее вынужденное движение и резонанс

Сначала для простоты рассмотрим незатухающее \(c = 0\) движение. У нас есть уравнение

\[ mx” + kx = F_0 \cos (\omega t) \nonumber \]

Это уравнение имеет дополнительное решение (решение ассоциированного однородного уравнения)

\[x_c = C_1 \cos ( \omega_0t ) + C_2 \sin (\omega_0t) \nonumber \]

где \(\omega_0 = \sqrt { \frac {k}{m}}\) – собственная частота (угловая), которая является частотой при которые система «хочет колебать» без внешнего вмешательства. 2} \cos ( \pi t) \nonumber \] 92} ( 2 \sin ( \frac {4 – \pi}{2}t) \sin ( \frac {4 + \pi}{2} t)) \nonumber \]

Обратите внимание, что \(x\) представляет собой высокочастотную волну, модулированную низкочастотной волной.

Теперь предположим, что \( \omega_0 = \omega \). Очевидно, что мы не можем попробовать решить \( A \cos (\omega t)\) и затем использовать метод неопределенных коэффициентов. Заметим, что \( \cos (\omega t) \) решает соответствующее однородное уравнение. Поэтому надо попробовать \( x_p = At ​​\cos (\omega t) + Bt \sin (\omega t) \). На этот раз нам нужен синус, так как вторая производная от \( t \cos (\omega t) \) содержит синусы. Пишем уравнение 92 x = \frac {F_0}{m} \cos (\omega t) \nonumber \]

Подставляя \( x_p\) в левую часть, получаем

\[ 2B \omega \cos (\omega t ) – 2A \omega \sin (\omega t) = \frac {F_0}{m} \cos (\omega t) \nonumber \]

Отсюда \( A = 0 \) и \( B = \frac { F_0}{2m \omega } \). Наше частное решение: \( \frac {F_0}{2m \omega } t \sin (\omega t) \) и наше общее решение:

\[ x = C_1 \cos (\omega t) + C_2 \sin ( \omega t) + \frac {F_0}{2m \omega } t \sin (\omega t) \nonumber \] 92_2} \), который становится все меньше и меньше пропорционально колебаниям последнего члена по мере того, как \(t\) становится больше. На рисунке \(\PageIndex{3}\) мы видим график с \(C_1 = C_2 = 0, F_0 = 2, m = 1, \omega = \pi \).

Рисунок \(\PageIndex{3}\): График \(\frac{1}{\pi}t\sin (\pi t)\).

Заставляя систему работать на нужной частоте, мы производим очень дикие колебания. Такое поведение называется резонансом или, возможно, чистым резонансом. Иногда желателен резонанс. Например, помните, когда в детстве вы могли начать раскачиваться, просто двигаясь вперед и назад на качелях с «правильной частотой»? Вы пытались добиться резонанса. Сила каждого вашего движения была небольшой, но через некоторое время она производила большие колебания. 9{1}\)

Затухание принудительного движения и практический резонанс

В реальной жизни все не так просто, как описано выше. Есть, конечно, некоторое демпфирование. Наше уравнение принимает вид

\[ \label{eq:15} mx” + cx’ + kx = F_0 \cos (\omega t), \]

для некоторого \(c > 0 \). Мы уже решали однородную задачу. Положим

\[ p = \frac {c}{2m}\quad \omega_0 = \sqrt { \frac {k}{m} } \nonumber \]

Заменим уравнение \(\eqref{eq:15 }\) с

92}} \cos (\omega t – \gamma) \nonumber \]

Если \( \omega = \omega_0\) мы видим, что \( A = 0, B = C = \frac {F_0}{2m \ омега р}, ~\rm{и} ~ \gamma = \frac {\pi}{2} \).

Точная формула не так важна, как идея. Не запоминайте приведенную выше формулу, вместо этого вы должны помнить вовлеченные в нее идеи. Для другой функции принуждения \(F\) вы получите другую формулу для \(x_p\). Так что нет смысла запоминать эту конкретную формулу. Вы всегда можете пересчитать его позже или посмотреть, если он вам действительно нужен.

По причинам, которые мы сейчас объясним, мы называем \(x_c\) переходным решением и обозначаем его \(x_{tr} \). Мы называем найденное нами \(x_p\) устойчивым периодическим решением и обозначаем его через \(x_{sp}\). Общее решение нашей задачи:

\[ x = x_c + x_p = x_{tr} + x_ {sp} \nonumber \]

Заметим, что \( x_c = x_{tr} \) стремится к нулю при \ ( t \rightarrow \infty \), так как все термины включают экспоненту с отрицательным показателем. Следовательно, для больших \(t\) эффект \(x_{tr}\) пренебрежимо мал, и мы по существу увидим только \(x_{sp}\). Отсюда и название переходный. Обратите внимание, что \(x_{sp}\) не содержит произвольных констант, и начальные условия будут влиять только на \(x_{tr} \).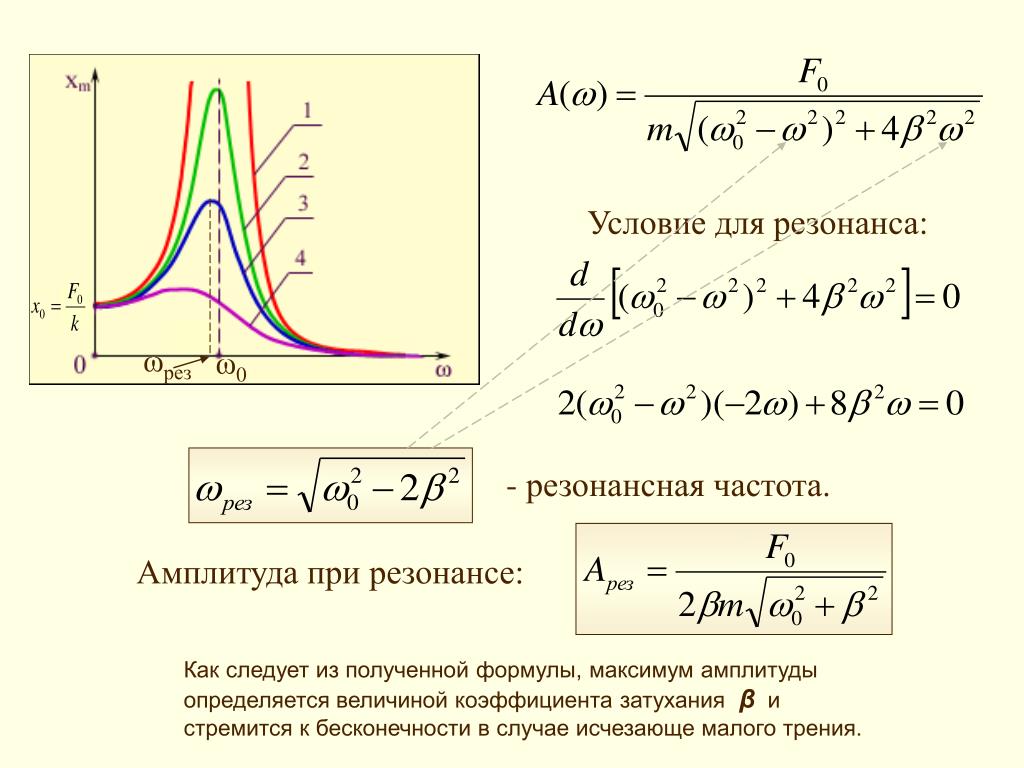 Это означает, что через некоторое время влияние начальных условий будет пренебрежимо мало. Из-за такого поведения мы могли бы также сосредоточиться на устойчивом периодическом решении и игнорировать переходное решение. См. рисунок \(\PageIndex{4}\) для графика различных начальных условий.

Рисунок \(\PageIndex{4}\): Решения с разными начальными условиями для параметров \( k = 1, m = 1, F_0 = 1, c = 0,7,\) и \( \omega = 1,1. \)

Обратите внимание, что скорость, с которой \(x_{tr}\) стремится к нулю, зависит от \(P\) (и, следовательно, \(c\)). Чем больше \(P\) (чем больше \(c\)), тем “быстрее” \(x_{tr}\) становится пренебрежимо мало. Таким образом, чем меньше затухание, тем длиннее «переходная область». Это согласуется с наблюдением, что при \(c = 0 \) начальные условия влияют на поведение на все время (т.е. бесконечная «переходная область»).

Опишем, что мы подразумеваем под резонансом при наличии демпфирования. Так как при решении с неопределенным коэффициентом конфликтов не было, то нет и члена, уходящего в бесконечность.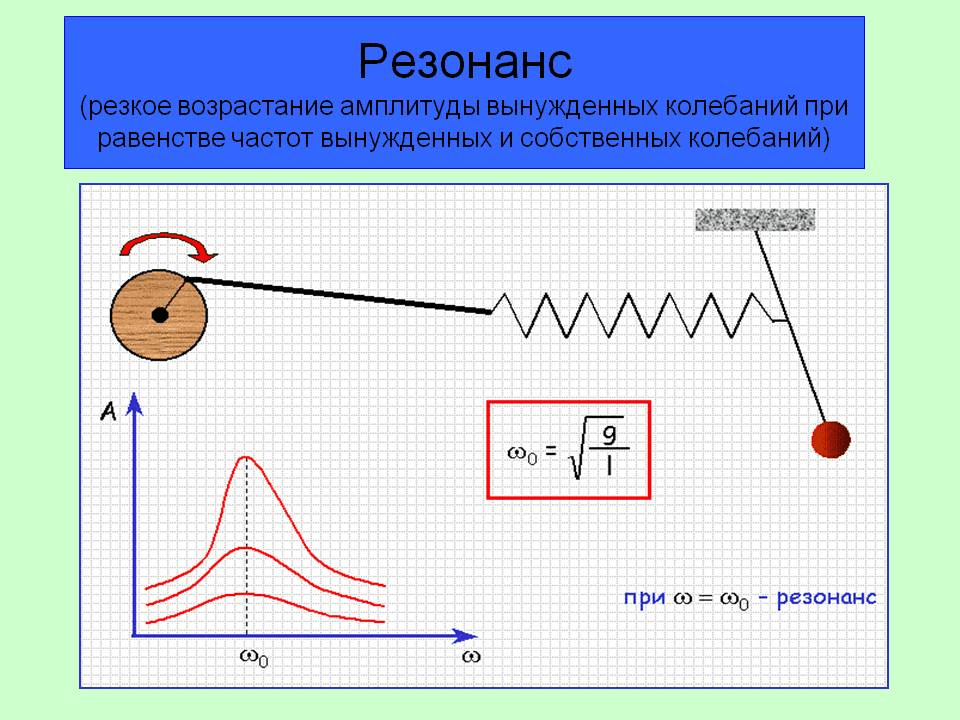 Однако мы рассмотрим максимальное значение амплитуды устойчивого периодического решения. Пусть \(C\) будет амплитудой \(x_{sp}\). Если мы построим \(C\) как функцию \(\omega \) (с фиксированными всеми остальными параметрами), мы сможем найти его максимум. Мы называем \ (\ омега \), которая достигает этого максимума, практической резонансной частотой. Мы называем максимальную амплитуду \(C(\omega)\) амплитудой практического резонанса. Таким образом, когда присутствует демпфирование, мы говорим о практическом резонансе, а не о чистом резонансе. Пример графика для трех различных значений \(c\) приведен на рисунке \(\PageIndex{5}\). Как видите, практическая амплитуда резонанса растет по мере уменьшения демпфирования, и любой практический резонанс может исчезнуть, когда демпфирование велико. 92} \) – практическая резонансная частота (то есть точка, где \( C(\omega ) \) максимальна, обратите внимание, что в этом случае \( C’ (\omega ) > 0 \) для малых \(\omega \)). Если \(\omega = 0\) является максимальным, то практического резонанса по существу нет, так как мы предполагаем, что \(\omega > 0\) в нашей системе. В этом случае амплитуда увеличивается по мере уменьшения частоты воздействия.

Если возникает практический резонанс, частота меньше \( \omega_0\). По мере того, как затухание \(c\) (и, следовательно, \(P\)) становится меньше, практическая резонансная частота достигает \(\omega_0\). Таким образом, когда затухание очень мало, \(\omega_0\) является хорошей оценкой резонансной частоты. Это поведение согласуется с наблюдением, что когда \(c = 0\), то \(\omega_0\) является резонансной частотой.

Еще одно интересное наблюдение: если \(\omega\to\infty\), то \(\omega\to 0\). Это означает, что если частота воздействия становится слишком высокой, она не может заставить массу двигаться в системе масса-пружина. Это вполне разумно интуитивно. Если мы будем очень быстро раскачиваться взад и вперед, сидя на качелях, мы вообще не заставим их двигаться, как бы сильно они ни крутились. Быстрые вибрации просто компенсируют друг друга, прежде чем масса успевает отреагировать, двигаясь в ту или иную сторону.