Резонанс | Физика
Отличительной особенностью вынужденных колебаний является зависимость их амплитуды А от частоты ν изменения внешней силы. Для изучения этой зависимости можно воспользоваться уже знакомой нам установкой, изображенной на рисунке 36. Если вращать ручку кривошипа очень медленно, то груз вместе с пружиной будет перемещаться вверх и вниз так же, как и точка подвеса О. Амплитуда вынужденных колебаний при этом будет невелика. При более быстром вращении груз начнет колебаться сильнее, и при частоте вращения, равной собственной частоте пружинного маятника (ν= νсоб), амплитуда его колебаний достигнет максимума. При дальнейшем увеличении частоты вращения ручки амплитуда вынужденных колебаний груза опять станет меньше. А очень быстрое вращение ручки оставит груз почти неподвижным: из-за своей инертности пружинный маятник, не успевая следовать изменениям внешней силы, будет просто «дрожать на месте».
Резкое возрастание амплитуды вынужденных колебаний при ν = νcoб называется резонансом.
График зависимости амплитуды вынужденных колебаний от частоты изменения внешней силы изображен на рисунке 38. Этот график называют резонансной кривой. Максимум этой кривой приходится на частоту ν, равную собственной частоте колебаний νсоб.
Явление резонанса можно продемонстрировать и с нитяными маятниками. Подвесим на рейке массивный шар 1 и несколько легких маятников, имеющих нити разной длины (рис. 39). Каждый из этих маятников имеет свою собственную частоту колебаний, которую можно определить, зная длину нити и ускорение свободного падения.
Теперь, не трогая легких маятников, выведем шар 1 из положения равновесия и отпустим. Качания массивного шара вызовут периодические изгибания рейки, вследствие которых на каждый из легких маятников начнет действовать периодически изменяющаяся сила упругости. Частота ее изменений будет равна частоте колебаний шара. Под действием этой силы маятники начнут совершать вынужденные колебания. При этом мы увидим, что маятники 2 и 3 останутся почти неподвижными. Маятники 4 и 5 будут колебаться с немного большей амплитудой. А у маятника 6, имеющего такую же длину нити и, следовательно, собственную частоту колебаний, как у шара 1, амплитуда окажется максимальной. Это и есть резонанс.
Маятники 4 и 5 будут колебаться с немного большей амплитудой. А у маятника 6, имеющего такую же длину нити и, следовательно, собственную частоту колебаний, как у шара 1, амплитуда окажется максимальной. Это и есть резонанс.
Резонанс можно наблюдать и с помощью установки, изображенной на рисунке 40. Основание маятника метронома 1 соединяют нитью 3 с нитью маятника 2. Маятник в этом опыте качается с наибольшей амплитудой тогда, когда частота колебаний метронома («дергающего» за нить маятника) совпадает с частотой свободных колебаний этого маятника.
Резонанс возникает из-за того, что внешняя сила, действуя в такт со свободными колебаниями тела, все время совершает положительную работу. За счет этой работы энергия колеблющегося тела увеличивается и амплитуда колебаний возрастает.
Явление резонанса может играть как полезную, так и вредную роль.
Известно, например, что тяжелый язык большого колокола может раскачать даже ребенок, но лишь тогда, когда будет действовать на веревку в такт со свободными колебаниями языка.
На применении резонанса основано действие язычкового частотомера. Этот прибор представляет собой набор укрепленных на общем основании упругих пластин различной длины. Собственная частота каждой пластины известна. При контакте частотомера с колебательной системой, частоту которой нужно определить, с наибольшей амплитудой начинает колебаться та пластина, частота которой совпадает с измеряемой частотой. Заметив, какая пластина вошла в резонанс, мы определим частоту колебаний системы.
С резонансом можно встретиться и тогда, когда это совершенно нежелательно. Так, например, в 1750 г. близ города Анжера во Франции через цепной мост длиной 102 м шел в ногу отряд солдат. Частота их шагов совпала с частотой свободных колебаний моста. Из-за этого размахи колебаний моста резко увеличились (наступил резонанс), и цепи оборвались. Мост обрушился в реку.
В 1830 г. по той же причине обрушился подвесной мост около Манчестера в Англии, когда по нему маршировал военный отряд.
В 1906 г. из-за резонанса разрушился и так называемый Египетский мост в Петербурге, по которому проходил кавалерийский эскадрон.
из-за резонанса разрушился и так называемый Египетский мост в Петербурге, по которому проходил кавалерийский эскадрон.
Теперь для предотвращения подобных случаев войсковым частям при переходе через мост приказывают «сбить ногу» и идти не строевым, а вольным шагом.
Если же через мост переезжает поезд, то, чтобы избежать резонанса, он проходит его либо на медленном ходу, либо, наоборот, на максимальной скорости (чтобы частота ударов колес о стыки рельсов не оказалась равной собственной частоте моста).
Собственной частотой обладает и сам вагон (колеблющийся на своих рессорах). Когда частота ударов его колес на стыках рельсов оказывается ей равной, вагон начинает сильно раскачиваться.
С резонансом можно встретиться не только на суше, но и в море и даже в воздухе. Так, например, при некоторых частотах вращения гребного вала в резонанс входили целые корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания частей самолета, что он разваливался в воздухе.
1. Что такое резонанс? При каком условии он возникает? 2. Опишите опыты, в которых можно наблюдать явление резонанса. 3. Какую роль — полезную или вредную — играет резонанс в жизни людей? Приведите примеры.
Резонанс — механический, электрический и звуковой: сообщение
Резонанс является одним из интереснейших физических явлений. И чем глубже становятся наши познания об окружающем нас мире, тем явственнее прослеживается роль этого явления, в различных сферах нашей жизни — в музыке, медицине, радиотехнике и даже на детской площадке.
Каков же смысл этого понятия, условия его возникновения и проявление?
Собственные и вынужденные колебания. Резонанс
Вспомним простое и приятное развлечение — раскачивание на подвесных качелях.
Прикладывая в нужный момент совсем незначительное усилие, ребёнок может раскачивать взрослого. Но для этого частота воздействия внешней силы должна совпасть с собственной частотой раскачивания качелей. Только в этом случае амплитуда их колебаний заметно вырастет.
Итак, резонанс это явление резкого возрастания амплитуды колебаний тела, когда частота его собственных колебаний совпадет с частотой действия внешней силы.
Прежде всего, разберемся в понятиях — собственные и вынужденные колебания. Собственные — присущи всем телам — звёздам, струнам, пружинам, ядрам, газам, жидкостям… Обычно они зависят от коэффициента упругости, массы тела и других его параметров. Такие колебания возникают под воздействием первичного толчка, осуществляемой внешней силой. Так, чтобы привести в колебания груз, подвешенный на пружине, достаточно оттянуть его на некоторое расстояние. Возникшие при этом собственные колебания будут затухающими, поскольку энергия колебаний затрачивается на преодоление сопротивления самой колебательной системы и окружающей среды.
Вынужденные колебания возникают при воздействии на тело сторонней (внешней) силы с определенной частотой. Эту стороннюю силу ещё называют вынуждающей силой. Очень важно, чтобы эта внешняя сила действовала на тело в нужный момент и в нужном месте. Именно она восполняет потери энергии и увеличивает её при собственных колебаниях тела.
Очень важно, чтобы эта внешняя сила действовала на тело в нужный момент и в нужном месте. Именно она восполняет потери энергии и увеличивает её при собственных колебаниях тела.
Механический резонанс
Очень ярким примером проявления резонанса является несколько случаев обрушения мостов, когда по ним строевым шагом проходила рота солдат.
Чеканный шаг солдатских сапог совпал с собственной частотой колебаний моста. Он стал колебаться с такой амплитудой, на которую его прочность не была рассчитана и… развалился. Тогда и родилась новая воинская команда «…не в ногу». Она звучит, когда пешая или конная рота солдат проходит по мосту.
Если вам случалось путешествовать на поезде, то самые внимательные из вас обратили внимание на заметные покачивания вагонов, когда его колеса попадают на стыки рельс. Это так вагон откликается, т. е. резонирует с колебаниями, возникающими при преодолении этих зазоров.
Корабельные приборы снабжают массивными подставками или подвешивают на мягких пружинах, чтобы избежать резонанса этих корабельных деталей с колебаниями корабельного корпуса. При запуске корабельных двигателей судно так может войти в резонанс с их работой, что это грозит его прочности.
При запуске корабельных двигателей судно так может войти в резонанс с их работой, что это грозит его прочности.
Приведенных примеров достаточно, чтобы убедиться в необходимости учитывать резонанс. Но мы иногда и используем механический резонанс, не замечая этого. Выталкивая машину, застрявшую в дорожной грязи, водитель и его добровольные помощники вначале раскачивают её, а затем дружно толкают вперёд по направлению движения.
Раскачивая тяжелый колокол, звонари тоже неосознанно используют это явление.
Они ритмично в такт с собственными колебаниями языка колокола, дергают за прикрепленный к нему шнур, всё увеличивая амплитуду колебаний.
Существуют приборы, измеряющие частоту электрического тока. Их действие основано на использовании резонанса.
Акустический резонанс
На страницах нашего сайта мы познакомили вас с важнейшими сведениями о звуке. Продолжим наш разговор, дополнив его примерами проявления акустического или звукового резонанса.
Для чего у музыкальных инструментов, особенно у гитары и скрипки такой красивый корпус? Неужели лишь для того, чтобы красиво выглядеть? Оказывается, нет. Он нужен для правильного звучания, всей издаваемой инструментом звуковой палитры. Звук, издаваемый самой гитарной струной достаточно тихий. Чтобы его усилить струны, располагают поверх корпуса, имеющего определенную форму и размеры. Звук, попадая внутрь гитары, резонирует с различными частями корпуса и усиливается.
Он нужен для правильного звучания, всей издаваемой инструментом звуковой палитры. Звук, издаваемый самой гитарной струной достаточно тихий. Чтобы его усилить струны, располагают поверх корпуса, имеющего определенную форму и размеры. Звук, попадая внутрь гитары, резонирует с различными частями корпуса и усиливается.
Сила и чистота звука зависит от качества дерева, и даже от лака, которым покрыт инструмент.
Имеются резонаторы и в нашем голосовом аппарате. Их роль выполняют самые различные воздушные полости, окружающие голосовые связки. Они-то усиливают звук, формируют его тембр, усиливая именно те колебания, частота которых близка к их собственной. Умение использовать резонаторы своего голосового аппарата — это одна из сторон таланта певца. Им в совершенстве владел Ф.И. Шаляпин.
Рассказывают, что когда этот великий артист пел во всю мощь, гасли свечи, тряслись люстры и трескались гранёные стаканы.
Т.е. явление звукового резонанса играет громадную роль в восхитительном мире звуков.
Электрический резонанс
Не миновало это явление и электрические цепи. Если частота изменения внешнего напряжения совпадет с частой собственных колебаний цепи, то может возникнуть электрический резонанс. Как всегда он проявляется в резком возрастании и силы тока и напряжения в цепи. Это чревато коротким замыкание и выходом из строя приборов, включённых в цепь.
Однако именно резонанс позволяет нам настроиться на частоту определенной радиостанции. Обычно на антенну поступает множество частот от различных радиостанций. Вращая ручку настройки, мы меняем частоту приёмного контура радиоприёмника.
Когда одна из пришедших на антенну частот совпадет с этой частотой, тогда мы и услышим эту радиостанцию.
Волны Шумана
Между поверхностью Земли и ее ионосферой существует слой, в котором очень хорошо распространяются электромагнитные волны. Этот небесный коридор называют волноводом. Рождающиеся здесь волны могут несколько раз огибать Землю. Но откуда они берутся? Оказалось, что они возникают при разрядах молний.
Но откуда они берутся? Оказалось, что они возникают при разрядах молний.
Профессор Мюнхенского технического университета Шуман рассчитал их частоту. Выяснилось, что она равна 10 Гц. Но именно с таким ритмом происходят колебания человеческого мозга! Этот удивительный факт не мог быть простым совпадением.
Т.е. для нормального самочувствия человека ритм важнейших колебаний человеческого организма должен резонировать с частотой волн Шумана.
Электромагнитный смог от работы бытовых и промышленных электроприборов искажают природные волны Земли, и разрушает наши тонкие взаимосвязи со своей планетой.
Законам резонанса подчинены все объекты Вселенной. Этим законам подчиняются даже взаимоотношения людей. Так, выбирая себе друзей, мы ищем себе подобных, с которыми нам интересно, с которыми находимся «на одной волне».
Автор: Драчёва Светлана Семёновна
Если это сообщение тебе пригодилось, буда рада видеть тебя в группе ВКонтакте. А ещё — спасибо, если ты нажмёшь на одну из кнопочек «лайков»:
Оптика и волны
В случае вынужденных колебаний система колеблется под действием периодической внешней (вынуждающей) силы. За счет работы этой силы компенсируются потери энергии системы. Частота вынужденных колебаний зависит от частоты изменения внешней силы (для краткости мы будем называть её “вынуждающей частотой”). Практически наиболее интересным является случай, когда вынуждающая сила изменяется по гармоническому закону:
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом.
|
Резонанс — это явление резкого увеличения амплитуды вынужденных колебаний при определенной частоте внешнего воздействия, называемой резонансной частотой 
|
Видео 1.21 Резонансное взаимодействие маятников
Видео 1.22 Камертоны: резонансное поглощение энергии волны
Видео 1.23 Резонанс доски с мотором
Явление резонанса используется для усиления колебаний, например электрических. Однако при конструировании машин и сооружений необходимо учитывать явление резонанса, чтобы предотвратить чаще всего нежелательные, а иногда и разрушительные последствия резонансного увеличения амплитуды вынужденных колебаний.
Для пружинного маятника уравнение вынужденного колебательного движения имеет вид:
|
|
(1.83) |
или
|
|
(1. |
где
и
Если рассматривать электрический колебательный контур, то компенсировать потери энергии в контуре можно с помощью подводимой извне периодически изменяющейся по гармоническому закону ЭДС или переменного напряжения
|
|
(1.85) |
Рис. 1.25. Вынужденные колебания в электромагнитном контуре
Уравнение колебаний в контуре (рис. 1.25) можно записать, используя закон Ома для замкнутой цепи
|
|
(1. |
или, с учетом, что
|
|
(1.87) |
где
— собственная частота контура,
— коэффициент затухания, a
Таким образом, вынужденные колебания в электрическом контуре описываются тем же самым линейным неоднородным дифференциальным уравнением второго порядка, что и в случае колебаний пружинного маятника. Предположим, что нам известно хотя бы одно решение этого уравнения — некое частное решение . Тогда разность любого другого решения q(t
 Поэтому общее решение уравнения (1.87) может быть записано как
Поэтому общее решение уравнения (1.87) может быть записано как|
|
(1.88) |
где
— частота свободных затухающих колебаний.
С течением времени из-за экспоненциального множителя роль второго слагаемого уменьшается (оно важно на начальной стадии установления колебаний). По прошествии достаточно большого времени, а именно, при
,
им можно пренебречь, сохраняя лишь первое слагаемое. Таким образом, задача исследования установившихся вынужденных колебаний сводится к нахождению хотя бы одного частного решения уравнения (1.87).
Частное решение неоднородного уравнения будем искать в виде гармонической функции, частота изменения которой совпадает с частотой вынуждающей силы:
|
|
(1. |
Подставим в виде (1.89) в уравнение (1.87):
|
|
(1.90) |
Так как функции синуса и косинуса линейно независимы, коэффициенты при них в левой части (1.90) должны быть равны нулю:
|
|
(1.91) |
Решение этой системы имеет вид:
|
|
(1. |
Решение (1.89) с коэффициентами (1.92) можно записать в стандартном виде:
|
|
(1.93) |
где
|
|
(1.94) |
и
|
|
(1. |
При знаке минус в фазе косинуса в выражении (1.93) начальная фаза имеет простой физический смысл: это отставание по фазе установившегося вынужденного колебания от гармонической вынуждающей «силы» (1.85).
Видео 1.24 Резонансный язычковый частотомер
Видео 1.25 Спектр модулированного колебания
Рассмотрим отклик системы на изменение частоты внешней силы. Под квадратным корнем в выражении для амплитуды стоит квадратичная функция частоты
Эта функция имеет минимум (а значит, амплитуда имеет максимум).
Для нахождения точки минимума дифференцируем функцию по и приравниваем производную нулю. В итоге получаем следующие выражения для резонансной частоты
|
|
(1. |
и амплитуды установившихся вынужденных колебаний при резонансе
|
|
(1.97) |
Следует отметить, что при значение резонансной частоты практически совпадает с собственной частотой колебательной системы. Поскольку стоит в знаменателе выражения для , резонансная амплитуда колебаний растет с уменьшением затухания. На графике 1.26 видно, что чем меньше затухание, тем выше и правее лежит максимум резонансной кривой.
Рис. 1.26. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы
При увеличении частоты внешнего воздействия амплитуда стремится к нулю:
Физически это понятно: система обладает некой инерционностью и не успевает следовать за быстрыми изменениями внешнего воздействия. В другом предельном случае малой внешней частоты
В другом предельном случае малой внешней частоты
мы имеем дело со статическим случаем — действием постоянной внешней силы F0 на пружинный маятник, или подсоединением контура к источнику с постоянным напряжением Um. В этом случае предельное значение амплитуды вынужденных колебаний равно
и не зависит от затухания. Последнее вполне естественно, так как затухание обусловлено действием силы сопротивления, которая пропорциональна скорости и проявляется только при движении системы, а не в статическом пределе. В случае механических колебаний
|
|
(1.98) |
что равно удлинению пружины под действием постоянной силы F0.
В случае электромагнитных колебаний в контуре
|
|
(1.99) |
что равно заряду на конденсаторе при подсоединении его к источнику постоянного напряжения Um.
Найдем отношение резонансной амплитуды к статической при малом затухании, когда :
|
|
(1.100) |
Иными словами, добротность Q характеризует также резонансные свойства колебательной системы: чем больше добротность, тем выше и относительно уже резонансный пик (см.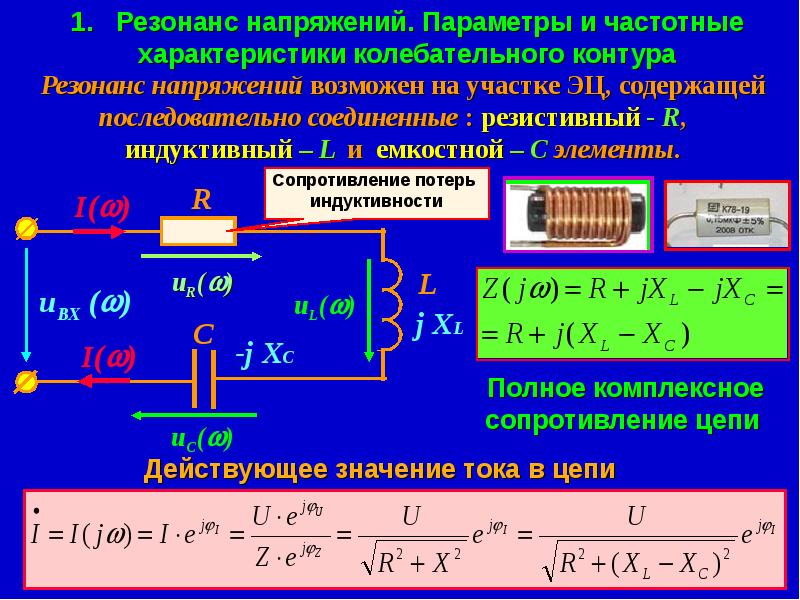 рис. 1.26).
рис. 1.26).
Автоколебательные системы. Параметрический резонанс.
Видео 1.26 Анкерный механизм механических часов
Видео 1.27 Колебания линейки под струёй воды
Видео 1.28 Спираль Роже
Видео 1.29 Параметрический резонанс
Дополнительная информация
http://class-fizika.spb.ru/index.php/slaid/193-kol – Много интересных анимаций, видео, слайд-шоу по колебаниям и волнам.
http://www.fxyz.ru/формулы_по_физике/колебания_и_волны – Основные формулы по колебаниям и волнам (см. Также раздел «подтемы» справа вверху)
http://physics-lectures.ru/category/mexanicheski-kolebaniya-i-volny/ – Лекции по колебаниям и волнам
http://www.alleng.ru/d/phys/phys105.htm – Д.В. Сивухин. Электричество, колебания и волны. Учебник.
http://www.ph5s.ru/book_ph_koleb.html – Ссылки на книги по колебаниям и волнам. Сайт бывшего преподавателя МИФИ А.Н. Варгина.
http://fmclass.ru/math.php?id=485a8e5cc78f8 – Статьи по колебаниям и оптике из журнала «Квант»
http://www. physel.ru/mainmenu-48.html – Полезные материалы по колебаниям и волнам.
physel.ru/mainmenu-48.html – Полезные материалы по колебаниям и волнам.
http://koi.tspu.ru/waves/index.htm – А.Г. Парфенов, Электронный мультимедиа-учебник по колебаниям и волнам
http://www.alleng.ru/d/phys/phys126.htm – Савельев, Курс общей физики. Т.1 – Механика, колебания и волны, молекулярная физика.
http://www.alleng.ru/d/phys/phys260.htm – А.Я. Исаков , В.В. Исакова. Колебательные и волновые процессы, руководство по самостоятельной работе.
http://lib.mexmat.ru/books/6452 – Г.С. Ландсберг. Элементарный учебник физики. Колебания и волны. Оптика. Атомная и ядерная физика.
http://elkniga.ucoz.ru/ – Г.Я. Мякишев, А.З. Синяков. Учебник по колебаниям и волнам для углубленного изучения в 11-м классе.
http://repetitor.mathematic.of.by/spravka_fizika.htm#M2 – Основные формулы по механике, в том числе – по колебаниям.
http://www.alleng.ru/d/phys/phys194.htm – Л.Н. Коршунова. Колебания и волны. Пособия по решению задач.
http://fizportal.ru/fluctuation-b – Банк задач по колебаниям и волнам с решениями.
http://www.alleng.ru/d/phys/phys127.htm – Савельев, Курс общей физики. Т.2 — Электричество и магнетизм. Волны. Оптика.
http://ligis.ru/effects/science/238/index.htm – Эффект механического резонанса.
http://schools.keldysh.ru/sch2216/students/spr_resh_zad/wob_wave/wob_wave1.htm – Задачи по колебаниям и волнам с решениями.
http://sgtnd.narod.ru/papers/TASKS.pdf – А.П. Кузнецов, А.Г. Рожнев, Д.И. Трубецков. Линейные колебания и волны. Сборник задач.
http://www.phys.kemsu.ru/viewpage.php?page_id=178 – Задачи по колебаниям и волнам повышенной сложности для старшеклассников.
http://physbook.ru/index.php/PPT._Маятник_Фуко – Маятник Фуко. История, модели.
Механический резонанс | Рефераты Физика
Скачай Механический резонанс и больше Рефераты в PDF из Физика только в Docsity! Механический резонанс – совпадение частоты собственных колебаний с частотой изменения электродинамической силы В быту Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем. В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения. Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов. Струна Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны.
Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем. В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения. Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов. Струна Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости v, с которой волна распространяется по струне: Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f[4], и т. д. Если струне придать колебание коротким воздействием (щипком f, 3f, 4f[4], и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты. В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю.
Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости v, с которой волна распространяется по струне: Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f[4], и т. д. Если струне придать колебание коротким воздействием (щипком f, 3f, 4f[4], и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты. В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением. В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора. Электроника Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником. Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален.
При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением. В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора. Электроника Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником. Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы. В электронных устройствах также применяются различные электромеханические резонансные системы. СВЧ В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями.
Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы. В электронных устройствах также применяются различные электромеханические резонансные системы. СВЧ В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями.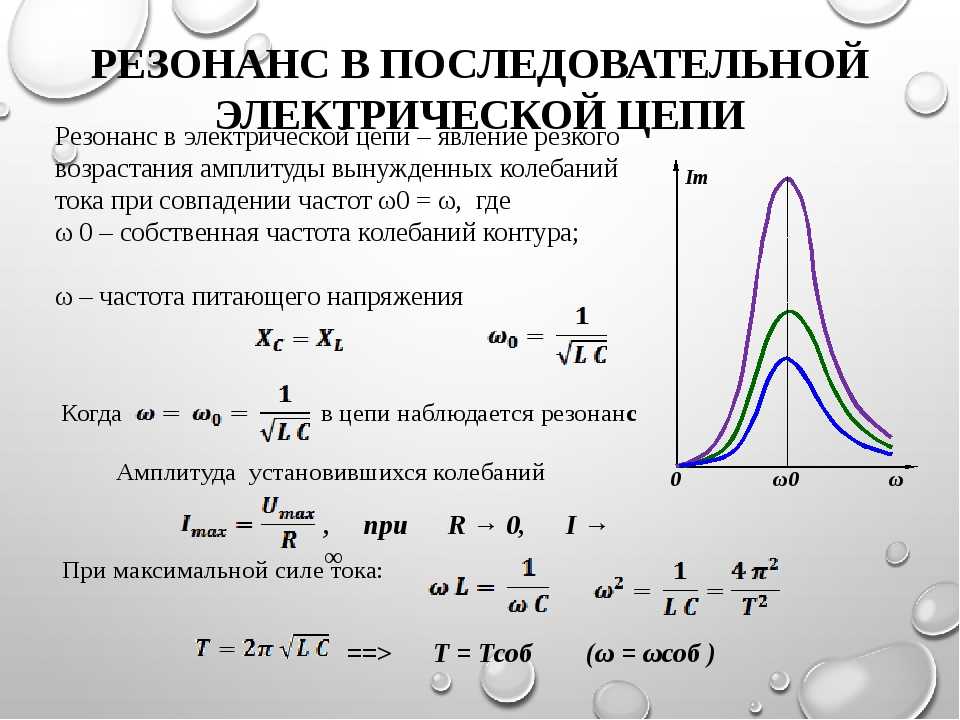 Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи. Оптика В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.
Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи. Оптика В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.
Резонанс – это что в физике
Резонанс — довольно известное и важное физическое понятие. Глубокое понимание резонанса может привести к более широкому пониманию того, как вещи вокруг вас связаны друг с другом. Такое ощущение, что резонанс похож на связь, которая скрепляет все вместе. К лучшему или к худшему, резонанс — довольно мощное присутствие. Чтобы понять резонанс, нужно начать с понимания вибрации или волн (колебаний). Вибрация является результатом излучения энергии определенным объектом наружу. Например, ребенок бросает камень в озеро, и озеро производит круговую рябь (круги по воде), и эта рябь является вибрацией.
Вибрация имеет частоту (количество колебаний в секунду), которая представляет собой количество ряби в определенном месте небольшого озера за 1 секунду. Когда вы смотрите на красивое поле, вы можете восхищаться каждой прекрасной деталью в этом поле. Это потому, что ваши глаза улавливают вибрации этих цветов (разные части ландшафта отражают разные частоты).
Все, что существует вокруг нас, излучает частоту. Вы не можете видеть, вы не можете слышать, вы ничего не можете чувствовать без разнообразия частот. Частота — это то, как вы общаетесь с миром.
Для того, чтобы понять явление резонанса надо понимать, что такое свободные и вынужденные колебания.
Содержание
Свободные колебания
В механике совокупность тел, движение которых мы рассматриваем, называют системой тел, или просто системой. Силы, действующие между телами внутри рассматриваемой системы тел, называются внутренними силами. А силы, действующие на тела системы со стороны других тел, не входящих в эту систему, называются внешними силами.
Самым простым видом колебаний являются колебания тела, возникающие в системе под действием внутренних сил после того, как она была выведена из положения равновесия. Такие движения относятся к свободным колебаниям.
Колебания, которые после возбуждения происходят без внешних воздействий, называются свободными.
Колебания груза, подвешенного на пружине или на нити, могут быть примерами свободных колебаний.
Частоту свободных колебаний называют также частотой собственных колебаний системы или собственной частотой.
Собственная частота колебаний определяется свойствами самой колебательной системы: у пружинного маятника — массой тела и жесткостью пружины, у математического — его длиной.
Итак, пружинный и математический маятники совершают свободные колебания. И не только они. Такие колебания широко распространены в природе.
Познакомившись с колебаниями маятников, нам нетрудно понять, при каких же условиях возможны свободные колебания тел.
- Во-первых, в колебательной системе должны действовать похожие друг на друга силы.
 В пружинном маятнике — это сила упругости, проекция которой на координатную ось пропорциональна деформации пружины, то есть смещению тела (). Эта сила направлена к положению равновесия. В нитяном маятнике это равнодействующая сил тяжести и упругости, проекция которой тоже пропорциональна смещению тела (), и эта сила тоже стремится к положению равновесия.
В пружинном маятнике — это сила упругости, проекция которой на координатную ось пропорциональна деформации пружины, то есть смещению тела (). Эта сила направлена к положению равновесия. В нитяном маятнике это равнодействующая сил тяжести и упругости, проекция которой тоже пропорциональна смещению тела (), и эта сила тоже стремится к положению равновесия. - Во-вторых, трение в системе должно быть достаточно мало, иначе колебания быстро прекратятся или даже не возникнут. Так как сила трения направлена в сторону, противоположную движению, то она совершает отрицательную работу, и механическая энергия снижается. С уменьшением энергии сокращается и амплитуда колебаний. Таким образом, колебания затухают. Затухающие колебания гармоническими считать нельзя, так как для гармонических колебаний характерно постоянство амплитуды.
Вынужденные колебания
Свободные колебания рано или поздно затухают. Для того, чтобы колебания были незатухающими, необходимо возмещать потери энергии на трение.
Восполнять энергию колебательной системы можно, действуя на нее внешней, периодически изменяющейся силой. Энергия системы пополняется за счет работы этой силы. Колебания тел в этом случае уже не будут свободными, они будут вынужденными. Периодическая изменяющаяся сила, вызывающая эти колебания, называется вынуждающей силой.
Вынужденными колебаниями называются колебания, совершаемые телом под действием внешней, периодически изменяющейся силы.
Подобные повторяющиеся силы вызывают периодическое движение даже таких тел, которые сами не являются колебательными системами. Вспомним, например, периодическое открывание и закрывание двери или движение иглы в швейной машине. Нетрудно заметить, что период движения (колебаний), вызванного периодически меняющейся силой равен периоду этой силы.
Резонанс
Известное явление резонанса с древности
О резонансе знали в глубокой древности. Вот изречение Эвклида о резонансе:
Резонанс — это одно из самых распространенных и частых природных явлений во Вселенной, так что в определенной степени можно даже сказать, что резонанс возникает во Вселенной у всего в мире, без резонанса не было бы мира.
Однако, впервые явление резонанса с физической точки зрения описал в 1602 году Галилео Галилей, исследовавший в то время механику музыкальных струн и математических маятников.
Определение резонанса
Явление резонанса — это свойство, присущее очень большому количеству физических объектов и систем, преимущественно поглощающих энергию, обычно в механической или электромагнитной форме, при воздействии сил, периодически меняющихся во времени.
Частота установившихся вынужденных колебаний всегда равна частоте внешних сил. Выясним теперь, как зависят от частоты амплитуда вынужденных колебаний.
Подвесим на нити два маятника. Длина маятника А не меняется, а длину маятника B можно изменять, подтягивая рукой свободный конец нити. Если привести в колебание маятник B, то он через растяжку будет действовать с некоторой периодической силой на маятник A. Вследствие этого маятник А начнет совершать вынужденные колебания.
Уменьшая длину маятника B, мы тем самым изменяем частоту его колебаний и частоту вынуждающей силы, действующей на маятник А. При этом мы заметим, что когда частота вынуждающей силы приближается к собственной частоте колебаний маятника А (длины маятников становятся равными), амплитуда колебаний маятника А резко возрастает.
При этом мы заметим, что когда частота вынуждающей силы приближается к собственной частоте колебаний маятника А (длины маятников становятся равными), амплитуда колебаний маятника А резко возрастает.
Определение резонанса
Явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты колебаний вынуждающей силы и собственной частоты колебательной системы называется резонансом.
С явлением резонанса мы часто встречаемся в повседневной жизни, но не всегда обращаем на это внимание. Например, когда мимо наших окон проезжает трамвай, трактор, поезд, грузовик стекла окон дребезжат, а в шкафу звенит посуда.
Это означает, что частота внешних колебаний совпадает с частотой собственных колебаний тел в доме, и поэтому возникает явление резонанса. Вообще всякое дребезжание обычно связано с резонансом.
Резонанс полезен или вреден
Резонанс может быть и полезным, и вредным, а иногда даже опасным. В случае, когда резонанс полезен, его стараются усилить. Например, при строительстве дорог, фундаментов домов используют специальные вибраторы-уплотнители бетона или других сыпучих материалов.
Например, при строительстве дорог, фундаментов домов используют специальные вибраторы-уплотнители бетона или других сыпучих материалов.
В случае, когда резонанс оказывает вредное воздействие, принимают специальные меры, чтобы избежать или ослабить. Например, если
Например, если электродвигатели, паровые и газовые турбины сильно закреплены на фундаменте, то их колебания полностью передаются почве, затем дому, в котором закреплена машина. Тогда вынужденные колебания могут достигать максимального значения и привести к разрушению жилых домов. В таких случаях необходимо сделать так, чтобы собственная частота колебаний не совпадала с частотой внешних сил.
Резонанс в электрической 📙 цепи
- Резонанс в электрической цепи
- Резонанс токов через реактивные элементы
- Резонанс напряжений
- Явление резонанса на практике
Разберемся сначала с важными понятиями.
Резонанс – это такое явление, в процессе которого в системе увеличивается частота своих колебаний под воздействием внешнего возбудителя.
Колебания внешнего воздействия могут усиливать даже незначительные колебания системы. Наибольший резонанс достигается при совпадении частоты колебаний внешнего воздействия с колебаниями системы.
Одним из примеров явления резонанса, есть расшатывание моста ротой солдат. Это происходит, когда частота шагов солдат, которая являются внешним воздействием, совпадает с частотой колебаний моста. Если возникнет такой резонанс, это может разрушить мост. Именно поэтому солдаты не переходят мосты стройным шагом, а идут в вольном режиме.
Часто встречаемым явлением в физике есть электрический резонанс. Без него невозможно было бы провести телетрансляцию, многие медицинские обследования и прочие важные процессы.
Востребованными резонансами в электрической цепи есть:
- резонанс напряжений;
- резонанс токов.

Резонанс в электрической цепи – это резкое возрастание амплитуды внутренних колебаний системы за счет совпадения частоты внутренних колебаний с частотой внешнего воздействия.
Схема \(RLC\) – это электрическая цепь с последовательными, параллельными или комбинированными соединениями компонентов (резисторами, индукционными катушками и конденсаторами). \(RLC\) – это сочетание сопротивления, индуктивности и емкости.
Векторная диаграмма в случае последовательного соединения \(RLC\)-цепи бывает емкостной, активной или индуктивной.
В индуктивной векторной диаграмме резонанс напряжений появляется лишь при нулевом сдвиге фаз и совпадении сопротивлений индукции и емкости.
Резонанс токов возникает при параллельном соединении реактивных сопротивлений с одинаковыми характеристиками в цепях с переменным током. Во время резонанса токов реактивная индуктивная проводимость приравнивается к реактивной емкостной проводимости, то есть \(BL=BC.\)
Колебания контура с определенной частотой совпадают с частотой колебаний источника.
Простейшим примером цепи, в которой может произойти резонанс токов, есть параллельное соединение катушки с конденсатором.
Поскольку реактивные сопротивления совпадают по модулю, то амплитуды токов конденсатора и катушки также будут совпадать и могут достичь наибольшего значения амплитуды. Согласно первому закону Кирхгофа \(IR\) равняется току источника. Иначе говоря, ток проходит лишь через резистор. Если рассмотреть параллельный контур \(LC,\) то при частоте резонанса его сопротивление будет огромным. В условиях режима гармонии при частоте резонанса в контуре будет расход тока лишь для восполнения потерь на активном сопротивлении.
Значит, в последовательной цепи \(RLC\) импеданс наименьший при частоте резонанса и равняется активному сопротивлению контура, при этом в параллельной цепи \(RLC\) импеданс наибольший при частоте резонанса и равняется сопротивлению утечки, что фактически есть активным сопротивлением контура. Это значит, что для обеспечения резонанса силы тока или напряжения в цепи необходима ее проверка с целью определения суммарного сопротивления и проводимости. 2 L}\)
2 L}\)
Частота \(ω_0\) – это резонансная величина. При постоянных напряжении и активном сопротивлении в цепи сила тока в процессе резонанса напряжения наибольшая и равняется отношению напряжения к активному сопротивлению. То есть, сила тока полностью не зависима от реактивного сопротивления. Если реактивные сопротивления индукции и емкости одинаковы и по своей величине превышают активное сопротивление, тогда на зажимах катушки и конденсатора будет напряжение, сильно превышающее напряжение на зажимах контура.
Кратность превышения напряжения на зажимах катушки и конденсатора в соотношении с напряжением контура рассчитывается так:
\(Q = {U_{C0} \over U}\)
Величина \(Q\) является добротностью контура и описывает его резонансные характеристики.
Величина, обратная добротности контура, – это затухание контура \( {1 \over Q}\).
Электрический резонансный трансформатор, который был разработан Николой Теслой в конце XIX века, является ярким примером практического применения резонанса в электрических цепях. Тесла проводил массу экспериментов при разных конфигурациях резонансных цепей.
Тесла проводил массу экспериментов при разных конфигурациях резонансных цепей.
На сегодняшний день словосочетанием «катушка Теслы» называют высоковольтные резонансные трансформаторы. Такие приспособления применяют для генерации высокого напряжения и частоты переменного тока. Если простые трансформаторы используют для передачи энергии с первичной на вторичную катушку, то резонансные – для хранения электрической энергии во временном режиме.
При помощи данного приспособления, посредством управления воздушным сердечником резонансно настроенного трансформатора, при незначительной силе тока получают высокие напряжения. При этом у каждой катушки есть собственная емкость и она работает как резонансный контур. Для создания еще большего напряжения достигают резонанса двух контуров.
Резонанс: определение, типы, частота и примеры
Всем известен старый клише, когда мощный оперный певец берет нужную ноту, и хрустальное стекло разбивается от шума, но возможно ли это на самом деле? Ситуация может показаться надуманной, как то, что вы скорее увидите в фильмах или мультфильмах, чем в реальной жизни.
На самом деле, явление резонанса означает, что это технически возможно в реальной жизни, независимо от того, создается ли резонансная частота (та, которая соответствует собственной частоте стекла) чьим-то голосом или одним или несколькими музыкальными инструментами.
Узнав больше о резонансе, вы поймете, как работает звук, принципы, лежащие в основе многих музыкальных инструментов, и как увеличить или уменьшить движение в механической системе, такой как качели или веревочный мост.
Определение резонанса
Слово резонанс первоначально происходит от латинского resonantia , что означает «эхо», и оно тесно связано с отзвуком, что означает возвращать эхо или «звук снова». Эти два определения уже относятся к звуковым волнам и дают вам общее представление о значении этого слова в физике.
Однако, более конкретно, определение резонанса в физике – это когда частота внешнего колебания или вибрации соответствует собственной частоте объекта (или полости) , и в результате либо заставляет его вибрировать, либо увеличивает его амплитуду колебаний .
В механических системах под резонансом понимается усиление, усиление или продление звука или других вибраций. Как и в приведенном выше определении, это требует приложения внешней периодической силы с частотой, равной собственной частоте движения объекта, которую иногда называют резонансной частотой.
Все объекты имеют собственную частоту или резонансную частоту, которую можно представить как частоту, с которой объект «любит» вибрировать. Например, если вы постучите ногтем по хрустальному стакану, он начнет вибрировать на своей резонансной частоте и будет издавать «звон» с соответствующей высотой звука. Частота вибрации зависит от физических свойств объекта, и вы можете довольно хорошо предсказать это для некоторых вещей, таких как натянутая струна.
Примеры резонанса – Звуковой резонанс
Изучение некоторых примеров резонанса поможет вам понять различные формы резонанса, с которыми вы сталкиваетесь в повседневной жизни. Самый распространенный и простой пример — звуковые волны, потому что, когда вы вибрируете голосовыми связками на нужной частоте (для полости рта и горла), вы можете воспроизводить речевые тона и музыкальные тона, которые могут слышать другие люди.
Самый распространенный и простой пример — звуковые волны, потому что, когда вы вибрируете голосовыми связками на нужной частоте (для полости рта и горла), вы можете воспроизводить речевые тона и музыкальные тона, которые могут слышать другие люди.
Вибрация ваших голосовых связок производит звуковые волны, которые на самом деле являются волнами давления в воздухе, состоящими из чередующихся сжатых участков (с плотностью выше средней) и разрежений (с плотностью ниже средней).
Большинство музыкальных инструментов работают одинаково. Например, в духовом инструменте вибрация губ исполнителя относительно мундштука создает начальную вибрацию, и когда она соответствует резонансной частоте (или кратной ей) для размера трубы, в которую он или она дует, возникает резонанс, а амплитуда колебаний заметно увеличивается и дает слышимый тон.
В деревянных духовых инструментах есть «трость», которая вибрирует при прохождении через нее воздуха, и снова тот же процесс резонанса и усиления превращает эту маленькую вибрацию в слышимый музыкальный тон. Струнные инструменты, такие как гитара, немного отличаются, но струны имеют резонансную частоту вибрации, и производимые звуковые волны резонируют в полости (например, в пространстве в корпусе акустической гитары), делая звук громче.
Струнные инструменты, такие как гитара, немного отличаются, но струны имеют резонансную частоту вибрации, и производимые звуковые волны резонируют в полости (например, в пространстве в корпусе акустической гитары), делая звук громче.
Более простой пример: вы роняете инструмент или тарелку на землю. Производимый лязг возникает из-за того, что инструмент или пластина вибрируют на своей резонансной частоте. Этот более простой способ создания звука используется тщательно разработанными камертонами, которые сконструированы таким образом, чтобы воспроизводить определенную высоту звука в качестве своей собственной частоты, на которую музыканты затем могут настраивать свои инструменты.
Примеры резонанса – механический резонанс
Хотя резонанс обычно используется для обозначения звуковых волн, механический резонанс в некоторых отношениях легче понять. Простой пример: ребенок впервые учится качать качели. Колебательное движение качелей имеет собственную частоту, и когда ребенок научится толкать (т. е. прикладывать периодическую силу) с собственной частотой качелей, их толкание становится намного эффективнее. В результате этого увеличивается амплитуда колебаний качелей и человек, сидящий на них, с каждым разом поднимается выше.
е. прикладывать периодическую силу) с собственной частотой качелей, их толкание становится намного эффективнее. В результате этого увеличивается амплитуда колебаний качелей и человек, сидящий на них, с каждым разом поднимается выше.
Однако попадание в естественную частоту объекта не всегда хорошо. Например, солдаты, марширующие по веревочному мосту в унисон, могут вызвать его неконтролируемую вибрацию и, возможно, даже рухнуть, если они наступят на его естественной частоте. В подобных случаях генерал может попросить их «сменить шаг», чтобы они не применяли периодическую силу с собственной частотой моста.
Даже более стабильные конструкции мостов имеют резонансные частоты, но это вызывает проблемы только в редких случаях (например, с подвесным мостом Бротон, мостом в Англии, который рухнул в 1831 году, предположительно из-за того, что солдаты шагали по мосту в ногу).
Аналоговые часы также зависят от механического резонанса и собственной частоты компонента, чтобы отсчитывать время. Например, маятниковые часы используют собственную частоту колебаний маятника для отсчета времени, и балансовое колесо работает по тому же основному принципу. Даже кварцевые часы зависят от резонансной частоты, но в этом случае кристалл регулирует колебание от электронного генератора, что приводит к значительному повышению точности по сравнению с более простыми конструкциями.
Например, маятниковые часы используют собственную частоту колебаний маятника для отсчета времени, и балансовое колесо работает по тому же основному принципу. Даже кварцевые часы зависят от резонансной частоты, но в этом случае кристалл регулирует колебание от электронного генератора, что приводит к значительному повышению точности по сравнению с более простыми конструкциями.
Другие примеры резонанса
Есть много других форм резонанса, и все они работают по одному основному принципу. Два других примера резонанса, с которыми вы будете знакомы, связаны с электромагнитными колебаниями, а не с механическими. Во-первых, это ваша микроволновка.
Волны, создаваемые микроволнами, нагревают вашу пищу, потому что их частота соответствует резонансной частоте молекул внутри пищи (например, молекул воды и жира), что заставляет их колебаться и впоследствии выделять энергию в виде тепла.
Другим примером является антенна для вашего телевизора или даже радиоантенна. Эти устройства предназначены для максимального поглощения электромагнитного излучения, и когда вы «настраиваете» антенну на определенную частоту, вы настраиваете резонансную частоту устройства. Когда частота антенны совпадает с частотой входящего сигнала, она резонирует, и ваш телевизор или радио «подхватывает» сигнал.
Эти устройства предназначены для максимального поглощения электромагнитного излучения, и когда вы «настраиваете» антенну на определенную частоту, вы настраиваете резонансную частоту устройства. Когда частота антенны совпадает с частотой входящего сигнала, она резонирует, и ваш телевизор или радио «подхватывает» сигнал.
Так как же разбить кристалл?
Теперь, когда вы понимаете ключевые моменты, касающиеся определения резонанса и того, что такое резонансная частота, вы можете понять классический пример певца, умудряющегося разбить хрустальный стакан пением в нужной тональности. Стекло имеет резонансную частоту, и если певец издает звук с соответствующей частотой, стекло начинает вибрировать. это называется симпатическая вибрация потому что до того, как певец издал звук, стекло было совершенно неподвижно.
Сначала в стекле может возникнуть небольшая вибрация, но на самом деле, чтобы разбить его, требуется устойчивый и громкий звук на нужной частоте. Если певице удается это сделать, амплитуда колебаний стакана увеличивается и в итоге начинает нарушаться структурная целостность стакана. Только в этот момент — когда нота звучит достаточно долго, чтобы вибрация стакана достигла максимальной амплитуды, которую он может выдержать, — стакан действительно разобьется.
Если певице удается это сделать, амплитуда колебаний стакана увеличивается и в итоге начинает нарушаться структурная целостность стакана. Только в этот момент — когда нота звучит достаточно долго, чтобы вибрация стакана достигла максимальной амплитуды, которую он может выдержать, — стакан действительно разобьется.
4.3: Резонанс – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 946
- Бенджамин Кроуэлл
- Колледж Фуллертона
Резонанс — это явление, при котором осциллятор наиболее сильно реагирует на движущую силу, соответствующую его собственной частоте колебаний. Например, предположим, что ребенок находится на детской площадке на качелях с собственной частотой 1 Гц. То есть, если вы выведете ребенка из состояния равновесия, отпустите его, а затем на какое-то время перестанете что-либо делать, он будет колебаться с частотой 1 Гц. Если бы не было трения, как мы предполагали в разделе 2.5, то сумма ее гравитационной и кинетической энергии оставалась бы постоянной, а амплитуда была бы точно такой же от одного колебания к другому. Однако трение будет преобразовывать эти формы энергии в тепло, поэтому ее колебания постепенно затухнут. Чтобы этого не произошло, вы можете подталкивать ее один раз за цикл, т. е. частота ваших подталкиваний будет равна 1 Гц, что совпадает с собственной частотой качания. Пока вы остаетесь в ритме, качание реагирует довольно хорошо. Если вы начнете раскачиваться из состояния покоя, а затем дадите толчок с частотой 1 Гц, амплитуда раскачивания быстро нарастает, как на рисунке а, пока через некоторое время не достигнет устойчивого состояния, при котором трение удаляет столько же энергии, сколько вы вкладываете в нее. течение одного цикла.
То есть, если вы выведете ребенка из состояния равновесия, отпустите его, а затем на какое-то время перестанете что-либо делать, он будет колебаться с частотой 1 Гц. Если бы не было трения, как мы предполагали в разделе 2.5, то сумма ее гравитационной и кинетической энергии оставалась бы постоянной, а амплитуда была бы точно такой же от одного колебания к другому. Однако трение будет преобразовывать эти формы энергии в тепло, поэтому ее колебания постепенно затухнут. Чтобы этого не произошло, вы можете подталкивать ее один раз за цикл, т. е. частота ваших подталкиваний будет равна 1 Гц, что совпадает с собственной частотой качания. Пока вы остаетесь в ритме, качание реагирует довольно хорошо. Если вы начнете раскачиваться из состояния покоя, а затем дадите толчок с частотой 1 Гц, амплитуда раскачивания быстро нарастает, как на рисунке а, пока через некоторое время не достигнет устойчивого состояния, при котором трение удаляет столько же энергии, сколько вы вкладываете в нее. течение одного цикла.
самопроверка:
Рис.
На рисунке а сравните амплитуду цикла сразу после первого нажатия с амплитудой после второго. Сравните также энергии. (ответ в конце PDF-версии книги)
Что произойдет, если вы попытаетесь нажать на 2 Гц? Ваш первый толчок создает некоторый импульс \(p\), но ваш второй толчок происходит только через половину цикла, когда замах возвращается прямо к вам с импульсом \(-p\)! Передаваемого импульса от второго толчка ровно достаточно, чтобы остановить качание. В результате получается очень слабое и не очень синусоидальное движение, б.
Рис. b: Колебание с удвоенной резонансной частотой.
Упрощение математических расчетов
Это простой и физически прозрачный пример резонанса: колебания сильнее всего реагируют, если вы соответствуете их естественному ритму. Однако у него есть некоторые характеристики, которые математически уродливы и, возможно, нереалистичны. Быстрые, сильные толчки известны как импульсов сил, c, и они приводят к графу \(x\)-\(t\), который имеет недифференцируемые перегибы.
Быстрые, сильные толчки известны как импульсов сил, c, и они приводят к графу \(x\)-\(t\), который имеет недифференцируемые перегибы.
Рисунок c: График \(F\)-\(t\) для импульсивной движущей силы.
Импульсивные силы, подобные этой, плохо себя ведут не только с математической точки зрения, они обычно нежелательны с практической точки зрения. Например, в автомобильном двигателе инженеры очень много работают над тем, чтобы сила, действующая на поршни, изменялась плавно, чтобы избежать чрезмерной вибрации. В оставшейся части этого раздела мы будем предполагать, что движущая сила является синусоидальной, т. е. той, чей график \(F\)-\(t\) является либо синусоидальной функцией, либо функцией, отличной от синусоидальной волны. в фазе, например косинус. Сила положительна для половины каждого цикла и отрицательна для другой половины, т. е. есть как толкание, так и вытягивание. Синусоидальные функции имеют много хороших математических характеристик (их можно дифференцировать и интегрировать, а сумма синусоидальных функций, имеющих одинаковую частоту, является синусоидальной функцией), и они также используются во многих практических ситуациях. Например, мой замок на двери гаража излучает синусоидальную радиоволну, и приемник настроен на резонанс с ней. 92\). В других ситуациях, например, при наличии газа с низкой плотностью или при трении между твердыми поверхностями, смазанными жидкостью, такой как масло, мы можем обнаружить, что сила трения имеет другую зависимость от скорости, возможно, пропорциональную \(v \), либо имеющие какую-то другую сложную зависимость от скорости, которую даже простым уравнением не выразить. Было бы чрезвычайно сложно рассматривать все эти различные возможности в полной общности, поэтому в оставшейся части этого раздела мы будем предполагать, что трение пропорционально скорости
Например, мой замок на двери гаража излучает синусоидальную радиоволну, и приемник настроен на резонанс с ней. 92\). В других ситуациях, например, при наличии газа с низкой плотностью или при трении между твердыми поверхностями, смазанными жидкостью, такой как масло, мы можем обнаружить, что сила трения имеет другую зависимость от скорости, возможно, пропорциональную \(v \), либо имеющие какую-то другую сложную зависимость от скорости, которую даже простым уравнением не выразить. Было бы чрезвычайно сложно рассматривать все эти различные возможности в полной общности, поэтому в оставшейся части этого раздела мы будем предполагать, что трение пропорционально скорости
\[\begin{equation*} F = -bv , \end{equation*}\]
просто потому, что получившиеся уравнения оказалось проще всего решить. Даже когда трение не ведет себя точно так же, многие из наших результатов могут быть, по крайней мере, качественно правильными.
3.3.1 Демпфированный, свободный ход
Численная обработка
Осциллятор с трением называется демпфирующим. Давайте воспользуемся численными методами, чтобы найти движение затухающего осциллятора, который выходит из равновесия, но после этого не испытывает никакой движущей силы. Можно ожидать, что движение будет состоять из колебаний, которые постепенно затухают. 9{- ct}\text{sin} (\omega_{f} t+\delta)\).
Давайте воспользуемся численными методами, чтобы найти движение затухающего осциллятора, который выходит из равновесия, но после этого не испытывает никакой движущей силы. Можно ожидать, что движение будет состоять из колебаний, которые постепенно затухают. 9{- ct}\text{sin} (\omega_{f} t+\delta)\).
В разделе 2.5 мы смоделировали незатухающий случай, используя нашу проверенную и надежную функцию Python, основанную на сохранении энергии. Однако теперь этот подход становится немного неудобным, потому что он включает в себя разбиение пути, который нужно пройти, на \(n\) крошечных сегментов, но при наличии демпфирования каждое колебание немного короче, чем предыдущее, и мы неизвестно заранее, как далеко зайдут колебания, прежде чем развернуться. Здесь проще использовать силу, а не энергию. Второй закон Ньютона \(a=F/m\) дает \(a=(-kx-bv)/m\), где мы использовали результат примера 40 для силы, действующей на пружину. Это станет немного красивее, если мы перепишем его в виде
\[\begin{equation*} ma+bv+kx = 0 , \end{equation*}\]
которое дает симметричную обработку трех членов, включающих \(x\) и его первую и вторую производные, \( v\) и \(а\). Теперь вместо расчета времени \(\Delta{}t=\Delta{}x/v\), необходимого для перемещения на заданное расстояние \(\Delta{}x\), мы выбираем \(\Delta{}t\) и определите расстояние, пройденное за это время, \(\Delta{}x=v\Delta{}t\). Кроме того, мы больше не можем обновлять \(v\) на основе сохранения энергии, поскольку у нас нет простого способа отслеживать, сколько механической энергии было преобразовано в тепловую энергию. Вместо этого мы пересчитываем скорость, используя \(\Delta{}v=a\Delta{}t\).
Теперь вместо расчета времени \(\Delta{}t=\Delta{}x/v\), необходимого для перемещения на заданное расстояние \(\Delta{}x\), мы выбираем \(\Delta{}t\) и определите расстояние, пройденное за это время, \(\Delta{}x=v\Delta{}t\). Кроме того, мы больше не можем обновлять \(v\) на основе сохранения энергии, поскольку у нас нет простого способа отслеживать, сколько механической энергии было преобразовано в тепловую энергию. Вместо этого мы пересчитываем скорость, используя \(\Delta{}v=a\Delta{}t\).
импортировать математику
k=39.4784 # выбрано для получения периода в 1 секунду
м=1.
b=0,211 # выбрано для упрощения результатов
х=1.
v=0.
т=0.
дт=.01
n=1000
для j в диапазоне (n):
х=х+v*dt
а=(-к*х-б*в)/м
если (v>0) и (v+a*dt<0):
print("оборот в t=",t,", x=",x)
v=v+a*dt
т=т+дт
оборот в t = 0,99, x = 0,8992445 оборот в t = 1,99, x = 0,809844934046 оборот при t= 2,99 , х = 0,728777519477 оборот в t = 3,99, x = 0,655817260033 оборот в t = 4,99, x = 0,5
1 оборот в t = 5,99, x = 0,5310565 оборот в t = 6,99, x = 0,477875 ">6 оборот в t = 7,99, x = 0,430013546991 оборот в t = 8,99, x = 0,386940256644 оборот в t = 9,99, x = 0,348177318484
Жесткость пружины, \(k=4\pi{}=39,4784\) Н/м, рассчитана таким образом, что если уравнение недемпфирования \(f=(1/2\pi)\sqrt{k/m}\ ) по-прежнему верно, частота будет 1 Гц. Начнем с того, что заметим, что добавление небольшого количества демпфирования, по-видимому, вообще не изменило период или, по крайней мере, не в пределах точности расчета. 10 Однако вы можете проверить сами, что большое значение \(b\), скажем, 5 \(\text{N}\!\cdot\!\text{s}/\text{m}\) , существенно меняет период.
Мы освобождаем массу от \(x=1\ \text{m}\), и после одного цикла она возвращается примерно к \(x=0,9\ \text{m}\). Я выбрал \(b=0,211\ \text{N}\!\cdot\!\text{s}/\text{m}\), повозившись, пока не получил этот результат, поскольку уменьшить ровно на 10 % легко. обсуждать. Обратите внимание, что амплитуда после двух циклов составляет около \(0,81\ \text{m}\), то есть \(1\ \text{m}\) умножить на \(0,92\): амплитуда снова упала ровно на 10%. Этот шаблон сохраняется до тех пор, пока выполняется симуляция, например, для последних двух циклов мы имеем 0,34818/0,38694 = 0,89982, или снова почти ровно 0,9. Это могло показаться капризным, когда я решил использовать нереалистичное уравнение \(F=-bv\), но это выигрыш. Только при \(-bv\) трении мы получаем такое математически простое экспоненциальное затухание.
Этот шаблон сохраняется до тех пор, пока выполняется симуляция, например, для последних двух циклов мы имеем 0,34818/0,38694 = 0,89982, или снова почти ровно 0,9. Это могло показаться капризным, когда я решил использовать нереалистичное уравнение \(F=-bv\), но это выигрыш. Только при \(-bv\) трении мы получаем такое математически простое экспоненциальное затухание.
Поскольку затухание является экспоненциальным, оно никогда не затухает полностью; это отличается от поведения, которое мы имели бы с кулоновским трением, которое заставляет объекты полностью останавливаться в какой-то момент. При трении, которое действует как \(F=-bv\), \(v\) становится меньше по мере уменьшения колебаний. Затем все меньшая и меньшая сила заставляет их вымирать со скоростью, которая становится все медленнее и медленнее.
Авторы и ссылки
Бенджамин Кроуэлл (Фуллертонский колледж). Концептуальная физика защищена авторским правом с лицензией CC-BY-SA.
Эта страница под названием 4. 3: Resonance распространяется по лицензии CC BY-SA, ее автор, ремикс и/или куратор — Бенджамин Кроуэлл.
3: Resonance распространяется по лицензии CC BY-SA, ее автор, ремикс и/или куратор — Бенджамин Кроуэлл.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Бен Кроуэлл
- Лицензия
- СС BY-SA
- Показать оглавление
- нет
- Метки
Переход в резонанс | Nature Physics
Понятие «резонанс» является одним из самых известных в науке. Два маятниковых часа в резонансе синхронизируются, звуковые волны нужной частоты вызывают сильные колебания в барабане, а фотоны, настроенные на атомные переходы, переводят атомы в возбужденное состояние. Физики элементарных частиц часто обнаруживают новые частицы по появлению резонансов в данных рассеяния. И все мы, конечно же, полагаемся на резонанс при использовании беспроводной связи.
Два маятниковых часа в резонансе синхронизируются, звуковые волны нужной частоты вызывают сильные колебания в барабане, а фотоны, настроенные на атомные переходы, переводят атомы в возбужденное состояние. Физики элементарных частиц часто обнаруживают новые частицы по появлению резонансов в данных рассеяния. И все мы, конечно же, полагаемся на резонанс при использовании беспроводной связи.
В 1965 году в своих знаменитых Лекциях по физике Ричард Фейнман предположил, что концепция резонанса стала настолько влиятельной, что каждый новый том Physical Review будет содержать по крайней мере одну резонансную кривую — характерный пик поглощения в спектральной области. область вокруг собственной внутренней частоты некоторой исследуемой колебательной системы. И все же современное знакомство с концепцией затемняет необычную историю чрезвычайно медленного распознавания, полная оценка которой заняла около 300 лет. Как отмечает Йорн Блек-Нойхаус из Бременского университета в недавнем историческом обзоре (препринт на https://arxiv. org/abs/1811.08353; 2018), лишь немногие научные идеи сопоставимой важности получили признание так медленно.
org/abs/1811.08353; 2018), лишь немногие научные идеи сопоставимой важности получили признание так медленно.
В середине семнадцатого века Галилей заметил, что один человек, правильно тянущий тяжелый маятник, может привести его в такое сильное движение, что он сможет легко поднять в воздух шесть человек. Без сомнения, другие видели подобные эффекты раньше; Галилей записал. Однако он не мог предложить никакой математической трактовки и пришел к очень неверным выводам о том, что происходит, когда периодическая сила приводит в движение систему с естественными колебаниями. В частности, он пришел к выводу, что результирующее движение никогда не может отклоняться от собственной собственной частоты колебательной системы. Эта точка зрения, по-видимому, соответствовала его вере в то, что приливы не могут быть вызваны влиянием Луны, а должны иметь какое-то другое происхождение.
Несмотря на то, что он основал классическую и небесную механику, Исаак Ньютон никогда не занимался непосредственно проблемой приводного движения неастрономической гармонической механической системы. Первое современное понимание этого вопроса — и исправление ошибки Галилея — ожидалось развитием исчисления в восемнадцатом веке, когда Леонард Эйлер решил проблему, используя дифференциальное уравнение, очень похожее на то, что мы записали бы сегодня. Он пришел к выводу, что в условиях нерезонанса движение ведомой колебательной системы без трения или демпфирования будет иметь две составляющие на разных частотах - вынужденную частоту и собственную частоту ведомой системы. Он также рассмотрел случай резонансного совпадения двух частот, заключив, что амплитуда колебаний будет увеличиваться линейно во времени и потенциально без ограничений.
Первое современное понимание этого вопроса — и исправление ошибки Галилея — ожидалось развитием исчисления в восемнадцатом веке, когда Леонард Эйлер решил проблему, используя дифференциальное уравнение, очень похожее на то, что мы записали бы сегодня. Он пришел к выводу, что в условиях нерезонанса движение ведомой колебательной системы без трения или демпфирования будет иметь две составляющие на разных частотах - вынужденную частоту и собственную частоту ведомой системы. Он также рассмотрел случай резонансного совпадения двух частот, заключив, что амплитуда колебаний будет увеличиваться линейно во времени и потенциально без ограничений.
Можно было бы ожидать, что этот прорыв в механике выдвинет явление резонанса в центр физики и техники, но этого не произошло. Возможно, как отмечает Блек-Нойхаус, это потому, что сам Эйлер рассматривал эту проблему только как математическую диковинку, не имеющую никакого практического значения. Затем результаты Эйлера игнорировались на протяжении более века, пока в девятнадцатом веке Томас Янг не вывел их снова независимо. Как ни странно, однако, Юнг рассматривал эту проблему только в связи с анализом приливов и отливов, поэтому его работа также впоследствии была проигнорирована и не оказала никакого влияния на механику в целом, ни в физике, ни в технике.
Как ни странно, однако, Юнг рассматривал эту проблему только в связи с анализом приливов и отливов, поэтому его работа также впоследствии была проигнорирована и не оказала никакого влияния на механику в целом, ни в физике, ни в технике.
Действительно, все время, вплоть до самого конца девятнадцатого века, ученые неохотно использовали термин «резонанс» в связи с чем-либо, кроме акустических явлений, откуда он и возник. Использование этого слова в других областях — особенно в механике и анализе колебаний в машинах — всегда включало некоторую оговорку, что связь была «только по аналогии», несмотря на формальную эквивалентность основных динамических уравнений.
Использование этой концепции распространилось только после признания Рэлеем и Гельмгольцем в 1860-х годах резонансоподобных эффектов в общих акустических системах, за которыми последовали эксперименты Уильяма Томсона, продемонстрировавшие естественное резонансное поведение LC-цепей. В 1885 году немецкий физик Антон Овербек озаглавил статью «О явлении с электрическими колебаниями, которое похоже на резонанс». Как оказалось, Овербек был первым ученым, записавшим знаменитую резонансную кривую, показывающую напряжение, возбуждаемое на разных частотах, и пик, обусловленный резонансным взаимодействием.
Как оказалось, Овербек был первым ученым, записавшим знаменитую резонансную кривую, показывающую напряжение, возбуждаемое на разных частотах, и пик, обусловленный резонансным взаимодействием.
Вскоре Генрих Герц связал такие резонансные явления с генерацией распространяющихся электромагнитных волн, а Гульельмо Маркони вскоре использовал их для осуществления беспроводной связи. Но все это, как оказалось, произошло до того, как инженеры действительно начали осознавать роль резонанса в более реальных механических системах. Постепенное признание резонанса как механического явления произошло только тогда, когда драматические отказы в мостах и машинах заставили инженеров болезненно осознать неадекватность статического анализа сил и необходимость учитывать неожиданные эффекты взаимодействий на аналогичных частотах.
Работая в основном с первоисточниками в Германии, Блек-Нойхаус с готовностью признает, что его история концепции резонанса ориентирована на немецких ученых. Это было интересно для меня. Мои знания об Арнольде Зоммерфельде, которые я узнал, будучи студентом-физиком в Соединенных Штатах, в основном из его упоминаний в учебниках по квантовой механике, сосредоточены на его релятивистских улучшениях боровской модели атома, сыгравших важную роль в ранней или «старой» теории атома. ' квантовая теория. Возможно, это был его самый важный вклад. Но интересно узнать, что в 1902, будучи молодым профессором ключевого технологического института в Аахене, Зоммерфельд сыграл важную роль в том, чтобы подтолкнуть инженеров к осознанию практической важности механического резонанса, тогда почти неизвестного.
Мои знания об Арнольде Зоммерфельде, которые я узнал, будучи студентом-физиком в Соединенных Штатах, в основном из его упоминаний в учебниках по квантовой механике, сосредоточены на его релятивистских улучшениях боровской модели атома, сыгравших важную роль в ранней или «старой» теории атома. ' квантовая теория. Возможно, это был его самый важный вклад. Но интересно узнать, что в 1902, будучи молодым профессором ключевого технологического института в Аахене, Зоммерфельд сыграл важную роль в том, чтобы подтолкнуть инженеров к осознанию практической важности механического резонанса, тогда почти неизвестного.
Зоммерфельд сделал это отчасти благодаря драматическому эксперименту. В ходе эксперимента он устроил шаткий стол для поддержки тяжелой машины. Увеличение подаваемой мощности может заставить машину работать быстрее, но только до определенного предела. По мере увеличения мощности машина двигалась все быстрее и быстрее, приближаясь к резонансной частоте стола, наблюдатели могли видеть, что дополнительная энергия только заставляла стол вибрировать сильнее. Зоммерфельд, как отмечает Блек-Нойхаус, «не преминул сказать, что это будет означать увеличение счета за топливо, не получая при этом ничего, кроме риска повредить машину и здание». Это явление стало известно как «эффект Зоммерфельда». Лишь позже Зоммерфельд перешел в Мюнхенский университет и основал свою чрезвычайно влиятельную школу теоретической физики.
Зоммерфельд, как отмечает Блек-Нойхаус, «не преминул сказать, что это будет означать увеличение счета за топливо, не получая при этом ничего, кроме риска повредить машину и здание». Это явление стало известно как «эффект Зоммерфельда». Лишь позже Зоммерфельд перешел в Мюнхенский университет и основал свою чрезвычайно влиятельную школу теоретической физики.
Одна из самых удивительных вещей в науке — это то, насколько очевидными могут показаться определенные принципы, однажды понятые, тогда как раньше они были совсем не очевидны. История резонанса — еще один хороший пример: сейчас эта идея очевидна для любого студента-инженера, но на протяжении более трех столетий она бросала вызов лучшим умам науки.
Определение резонанса в физике.
(существительное)
Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
Резонанс в цепях RLC
- Резонанс — это тенденция системы колебаться с большей амплитудой на одних частотах, чем на других.

- $\nu_0$ – это резонансная частота последовательной цепи RLC.
- Резонанс в цепях переменного тока аналогичен механическому резонансу , где резонанс определяется как вынужденные колебания (в данном случае вынужденные источником напряжения) на собственной частоте системы.
- Переменный конденсатор часто используется для настройки резонансной частоты для получения нужной частоты и подавления других. представляет собой график зависимости тока от частоты, иллюстрирующий резонансных пиков в Irms при $\nu_0 = f_0$.
- Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.
- Резонанс — это тенденция системы колебаться с большей амплитудой на одних частотах, чем на других.
ЯМР и МРТ
- Магнитно-резонансная томография — это метод медицинской визуализации, используемый в радиологии для детальной визуализации внутренних структур тела.
- Магнитно-резонансная томография (МРТ), также называемая ядерно-магнитно-резонансной томографией (ЯМРТ) или магнитно-резонансной томографией (МРТ), представляет собой метод медицинской визуализации, используемый в радиологии для детальной визуализации внутренних структур тела.

- МРТ использовал свойство ядерного магнитного резонанса (ЯМР) для изображения ядер атомов внутри тела.
- Это электромагнитное поле имеет правильную частоту (известную как резонансной частоты ), чтобы поглотиться, а затем обратить вращение протонов водорода в магнитном поле.
Вынужденные вибрации и резонанс
- Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом .
- Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом .
- Интересно, что ширина 9Кривые 0005 резонанса показаны в зависимости от демпфирования: чем меньше демпфирование, тем уже резонанс .
- Во всех этих случаях эффективность передачи энергии от движущей силы к осциллятору наилучшая при резонансе .
- Сильный боковой ветер привел мост в колебания на его резонансной частоте.

Стоячие волны в воздушных столбах
- Мы используем специальные термины для резонансов в любой системе.
- Самая низкая резонансная частота называется основной, а все более высокие резонансные частоты называются обертонами.
- Теперь поищем закономерность в резонансных частотах простой трубы, закрытой с одного конца.
- резонансных частот трубы, закрытой с одного конца:
- Простые резонирующие полости могут быть сделаны резонирующими со звуком гласных, например.
Стоячие волны и резонанс
- При более внимательном изучении землетрясений можно обнаружить условия, подходящие для резонанса : стоячие волны, конструктивная и деструктивная интерференция.
- Здание может вибрировать в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, создавая резонанс , в результате чего одно здание рушится, а соседние - нет.

Управляемые колебания и резонанс
- Для определенной частоты возбуждения, называемой резонансной или резонансной частотой $\!
- Этот эффект резонанса возникает только тогда, когда $\zeta
- Для систем с сильным недодемпфированием значение амплитуды может стать довольно большим вблизи резонансной частоты (см. ).
Мощность
- Например, на резонансной частоты $(\nu_0 = \frac{1}{2\pi \sqrt{LC}})$ или в чисто резистивной цепи Z=R, так что cosϕ=1.
- На других частотах средняя мощность меньше, чем при резонансе , поскольку напряжение и ток не совпадают по фазе, а Irms ниже.
- На резонансной частоте cosϕ=1.
- Амплитуда движения колес максимальна, если удары по неровностям дороги происходят на резонансной частоте.
- Масса и пружина определяют резонансная частота .

Принудительное движение с демпфированием
- Рисунок 1.9: Установка ультразвуковой спектроскопии Resonance .
- При изменении частоты мы видим характерный резонанс (см. рис. 1.8).
- Рисунок 1.8: Вот спектр резонанса для куска алюминия размером, показанным на рисунке 1.9.
- На резонансной частоте наблюдается большой скачок амплитуды.
- Квадрат амплитудного фактора вынужденного затухающего движения вблизи резонанса $\omega_0$.
Примеры и приложения
- Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
- Когда электроны проносятся мимо этих отверстий, они индуцируют резонансное высокочастотное радиополе в полости, которое, в свою очередь, заставляет электроны группироваться в группы.
- Размеры полостей определяют резонансную частоту и тем самым частоту излучаемых микроволн.

- Схема поперечного сечения резонансного магнетрона с резонатором .
Изображения режимов
- Пластина крепится винтом через отверстие посередине к резонатору .
Магнитно-резонансная физика сердечно-сосудистой системы для клиницистов: часть I | Журнал сердечно-сосудистого магнитного резонанса
- Обзор
- Открытый доступ
- Опубликовано:
- Джон П. Риджуэй 1
Журнал кардиоваскулярного магнитного резонанса том 12 , номер статьи: 71 (2010) Процитировать эту статью
87 тыс.
 обращений
обращений35 Альтметрический
Сведения о показателях
Abstract
Существует много превосходных специализированных текстов и статей, описывающих физические принципы сердечно-сосудистых методов магнитного резонанса (CMR). Есть также много текстов, написанных для клиницистов, которые представляют собой понятное, более общее введение в основные физические принципы методов и приложений магнитного резонанса (МР). Однако существует очень мало текстов или статей, в которых делается попытка дать базовое введение в физику МРТ, предназначенное для клиницистов, использующих МРТ в своей повседневной практике. Это первый из двух обзоров, которые призваны охватить основные аспекты физики CMR таким образом, чтобы он был понятен и актуален для этой группы. Он начинается с объяснения основных физических принципов МРТ, включая описание основных компонентов системы визуализации МРТ и трех типов магнитного поля, которые они генерируют. Объясняется происхождение и метод получения МР-сигнала в биологических системах, уделяя особое внимание двум свойствам релаксации намагниченности ткани (T1 и T2), которые вызывают различия в сигнале от тканей, показывая, как их можно использовать для создания контраста изображения. для характеристики тканей. Описан метод, наиболее часто используемый для локализации и кодирования эхосигналов МР-сигнала для формирования изображения поперечного сечения, в котором представлена концепция k-пространства и показано, как хранящиеся в нем данные МР-сигнала соотносятся со свойствами реконструированного изображения. Перед подробным описанием методов получения CMR вводятся основные последовательности импульсов спинового эха и градиента, определяя ключевые параметры, влияющие на контрастность изображения, включая внешний вид в присутствии текущей крови, разрешение и время получения изображения.
Он начинается с объяснения основных физических принципов МРТ, включая описание основных компонентов системы визуализации МРТ и трех типов магнитного поля, которые они генерируют. Объясняется происхождение и метод получения МР-сигнала в биологических системах, уделяя особое внимание двум свойствам релаксации намагниченности ткани (T1 и T2), которые вызывают различия в сигнале от тканей, показывая, как их можно использовать для создания контраста изображения. для характеристики тканей. Описан метод, наиболее часто используемый для локализации и кодирования эхосигналов МР-сигнала для формирования изображения поперечного сечения, в котором представлена концепция k-пространства и показано, как хранящиеся в нем данные МР-сигнала соотносятся со свойствами реконструированного изображения. Перед подробным описанием методов получения CMR вводятся основные последовательности импульсов спинового эха и градиента, определяя ключевые параметры, влияющие на контрастность изображения, включая внешний вид в присутствии текущей крови, разрешение и время получения изображения. Затем более подробно описываются основные производные этих двух импульсных последовательностей, используемых для визуализации сердца. Двумя ключевыми требованиями для CMR являются необходимость в том, чтобы сбор данных сначала был синхронизирован с ЭКГ субъекта и был достаточно быстрым, чтобы субъект мог задерживать дыхание. Поэтому методы синхронизации ЭКГ с использованием как триггерного, так и ретроспективного стробирования, а также ускоренного сбора данных с использованием турбо- или быстрого спин-эхо и импульсных последовательностей градиентного эхо-сигнала описаны более подробно. Показано, как препарат черной крови с двойной инверсией в сочетании с регистрацией последовательностей импульсов турбо- или быстрого спин-эхо используется для получения высококачественных анатомических изображений. Для функциональной визуализации сердца с использованием последовательности импульсов градиентного эхо-сигнала кинофильма две производные последовательности импульсов градиентного эхо-сигнала; сравниваются искаженное градиентное эхо и сбалансированная стационарная свободная прецессия (bSSFP).
Затем более подробно описываются основные производные этих двух импульсных последовательностей, используемых для визуализации сердца. Двумя ключевыми требованиями для CMR являются необходимость в том, чтобы сбор данных сначала был синхронизирован с ЭКГ субъекта и был достаточно быстрым, чтобы субъект мог задерживать дыхание. Поэтому методы синхронизации ЭКГ с использованием как триггерного, так и ретроспективного стробирования, а также ускоренного сбора данных с использованием турбо- или быстрого спин-эхо и импульсных последовательностей градиентного эхо-сигнала описаны более подробно. Показано, как препарат черной крови с двойной инверсией в сочетании с регистрацией последовательностей импульсов турбо- или быстрого спин-эхо используется для получения высококачественных анатомических изображений. Для функциональной визуализации сердца с использованием последовательности импульсов градиентного эхо-сигнала кинофильма две производные последовательности импульсов градиентного эхо-сигнала; сравниваются искаженное градиентное эхо и сбалансированная стационарная свободная прецессия (bSSFP). В каждом случае определены и объяснены основные важные параметры визуализации и термины, специфичные для производителя.
В каждом случае определены и объяснены основные важные параметры визуализации и термины, специфичные для производителя.
Исходная информация
Этот обзор является первым из двух, целью которых является освещение основных физических принципов, лежащих в основе наиболее часто используемых методов сердечно-сосудистого магнитного резонанса (CMR). Существует множество текстов и журнальных статей, в которых даются превосходные подробные объяснения физики МР и, в частности, физики КМР [1–5]. Этот обзор никоим образом не заменяет их, а скорее дает обзор ключевых физических принципов, лежащих в основе наиболее часто используемых методов CMR. Этот обзор начинается с основных принципов генерации МР-сигнала и формирования изображения, обрисовывает в общих чертах принципы сердечной синхронизации и быстрой визуализации на задержке дыхания. Наконец, принципы, лежащие в основе двух наиболее распространенных методов CMR; подробно описаны анатомическая визуализация с использованием двойной инверсии, последовательности импульсов спинового эхо-сигнала черной крови и функциональной кинематографической визуализации яркой крови с использованием двух последовательностей импульсов на основе градиентного эха.
Компоненты системы МРТ
Система магнитно-резонансной томографии (МРТ) состоит из трех основных электромагнитных компонентов; набор основных магнитных катушек, трех градиентных катушек и встроенной катушки радиочастотного передатчика (рис. 1а). Каждый из этих компонентов генерирует различные типы магнитного поля, которые при воздействии на пациента в комбинации создают пространственно кодированные магнитно-резонансные сигналы, которые используются для формирования МР-изображений. Три различных типа магнитного поля определяются следующим образом: Сильное постоянное магнитное поле создается основными катушками магнита. Пациент располагается для визуализации в центральном отверстии магнита (рис. 1b), где сила этого поля, обозначенная символом B или , определяет номинальную рабочую напряженность поля конкретной системы МРТ. B o измеряется в единицах Тесла (Тл), где 1 Тесла примерно в 20 000 раз превышает магнитное поле Земли. Номинальная напряженность поля варьируется от 0,2 Тл до 3,0 Тл для коммерческих систем МРТ для клинических исследований, при этом наиболее распространенная напряженность поля для визуализации сердца составляет 1,5 Тл. Базовая система координат трех ортогональных осей x, y и z используется для определения направления магнитного поля, при этом ось z выбрана параллельно направлению B или .
Базовая система координат трех ортогональных осей x, y и z используется для определения направления магнитного поля, при этом ось z выбрана параллельно направлению B или .
Компоненты системы МРТ . a) Схема, показывающая относительное расположение основных магнитных катушек, градиентных катушек x, y и z, встроенной катушки корпуса радиочастотного передатчика и катушек радиочастотного приемника. b) Типичное расположение для системы MR с цилиндрическим отверстием, показывающее отверстие магнита и опорные оси координат со статическим направлением поля B o вдоль горизонтальной оси z.
Изображение полного размера
Градиентное магнитное поле, которое можно быстро включать и выключать, создается каждой из трех градиентных катушек, установленных внутри основного магнита (рис. 1а). Каждая из этих градиентных катушек генерирует магнитное поле в том же направлении, что и B или , но с силой, которая изменяется в зависимости от положения по осям x, y или z, в зависимости от того, какая градиентная катушка используется. Это градиентное поле накладывается на магнитное поле B o , так что его напряженность увеличивается (или уменьшается) вдоль направления приложенного градиентного поля. Сила градиентного магнитного поля отражает «крутизну» его наклона и измеряется в миллитесла на метр (мТл/м).
Это градиентное поле накладывается на магнитное поле B o , так что его напряженность увеличивается (или уменьшается) вдоль направления приложенного градиентного поля. Сила градиентного магнитного поля отражает «крутизну» его наклона и измеряется в миллитесла на метр (мТл/м).
Радиочастотное (РЧ) магнитное поле создается катушкой РЧ-передатчика, установленной внутри градиентной катушки, ближайшей к пациенту (рис. 1а). Оно имеет значительно меньшую амплитуду, чем другие магнитные поля, но колеблется с характерной частотой в мегагерцовом диапазоне (отсюда и радиочастота), величина которой определяется номинальной напряженностью поля основного магнита. Радиочастотное поле часто называют B 1 поле. Статическое магнитное поле и радиочастотное поле объединяются для генерации магнитно-резонансных сигналов, которые пространственно локализованы и кодируются градиентными магнитными полями для создания МР-изображения. Для визуализации сердца обычно используется отдельная катушка РЧ-приемника, предназначенная для максимизации сигнала от сердца, для обнаружения излучаемых МР-сигналов (рис. 1а).
1а).
Генерация МР-сигналов
Происхождение МР-сигнала
Первичным источником МР-сигнала, используемого для создания изображений, является вода или жир в тканях пациента; в частности, он происходит из ядер водорода (состоящих из одного протона), содержащихся в молекулах свободной воды или липидов. Водород является одним из ряда элементов, включая 31 P, 23 Na, 13 C, ядра которых проявляют магнитно-резонансные свойства, но высокая внутренняя чувствительность и естественное содержание молекул воды и липидов делают его особенно подходящим для визуализации. Ядра водорода (отдельные протоны) обладают внутренним свойством, известным как ядерный спин, который создает небольшое магнитное поле для каждого протона, известное как магнитный момент. Обычно магнитные моменты (спины) ориентированы случайным образом, но в присутствии приложенного извне B или , они имеют тенденцию ориентироваться либо по направлению к приложенному извне магнитному полю, либо против него. Равновесное состояние быстро достигается там, где имеется небольшой избыток спинов, ориентированных по полю (обычно всего несколько на миллион), поскольку это является более энергетически выгодным направлением ориентации. Избыток магнитных моментов протонов объединяется, чтобы сформировать чистое магнитное поле или результирующую намагниченность. Этому часто присваивается символ M, и в равновесии он выравнивается вдоль положительной оси z (вдоль B o ) со значением M o . Его часто изображают стрелкой или вектором (рис. 2а).
Равновесное состояние быстро достигается там, где имеется небольшой избыток спинов, ориентированных по полю (обычно всего несколько на миллион), поскольку это является более энергетически выгодным направлением ориентации. Избыток магнитных моментов протонов объединяется, чтобы сформировать чистое магнитное поле или результирующую намагниченность. Этому часто присваивается символ M, и в равновесии он выравнивается вдоль положительной оси z (вдоль B o ) со значением M o . Его часто изображают стрелкой или вектором (рис. 2а).
Чистая намагниченность, РЧ-импульсы и угол поворота . а) В равновесии результирующая намагниченность M o находится в равновесии, ориентированном вдоль оси а. б). При подаче радиоимпульса M o образует угол с осью z, известный как угол переворота, и вращается вокруг оси в направлении изогнутой стрелки. В любой момент намагниченность можно разделить на две составляющие, M z и M xy . Вращающийся компонент M xy генерирует обнаруживаемый МР-сигнал. c) Максимальная обнаруживаемая амплитуда сигнала после одиночного РЧ-импульса возникает, когда M o полностью лежит в плоскости осей x и y, поскольку это дает наибольшую составляющую M xy . Этот импульс имеет угол поворота 90° и называется радиочастотным импульсом 90° или импульсом насыщения. d) ВЧ-импульс перефокусировки на 180° обычно применяется, когда поперечная намагниченность уже вращается в плоскости xy, и используется для мгновенного поворота поперечной составляющей намагниченности на 180° вокруг оси, также вращающейся в плоскости xy. e) Инверсионный импульс на 180° обычно применяется при равновесии и используется для поворота результирующей намагниченности на 180° от положительной к отрицательной оси z. Это также известно как импульс подготовки к намагничиванию и используется в качестве схемы подготовки к методам визуализации черной крови.
Вращающийся компонент M xy генерирует обнаруживаемый МР-сигнал. c) Максимальная обнаруживаемая амплитуда сигнала после одиночного РЧ-импульса возникает, когда M o полностью лежит в плоскости осей x и y, поскольку это дает наибольшую составляющую M xy . Этот импульс имеет угол поворота 90° и называется радиочастотным импульсом 90° или импульсом насыщения. d) ВЧ-импульс перефокусировки на 180° обычно применяется, когда поперечная намагниченность уже вращается в плоскости xy, и используется для мгновенного поворота поперечной составляющей намагниченности на 180° вокруг оси, также вращающейся в плоскости xy. e) Инверсионный импульс на 180° обычно применяется при равновесии и используется для поворота результирующей намагниченности на 180° от положительной к отрицательной оси z. Это также известно как импульс подготовки к намагничиванию и используется в качестве схемы подготовки к методам визуализации черной крови.
Полноразмерное изображение
Размер этой чистой намагниченности является одним из ключевых факторов, определяющих максимальную интенсивность сигнала, который может быть сгенерирован и использован для формирования изображений. Чем больше напряженность приложенного магнитного поля, B o , тем больше избыток протонов, выровненных с магнитным полем, и тем больше размер чистой намагниченности.
Чем больше напряженность приложенного магнитного поля, B o , тем больше избыток протонов, выровненных с магнитным полем, и тем больше размер чистой намагниченности.
Чтобы генерировать МР-сигнал из суммарной намагниченности, радиочастотное (РЧ) магнитное поле, описанное ранее, генерируется встроенной катушкой РЧ-передатчика и используется для передачи энергии популяции протонов. Это поле прикладывается на определенной частоте, известной как ларморовская частота, ω o , что определяется уравнением:
ωo=γ×Bo
Это уравнение известно как уравнение Лармора. Константа γ называется гиромагнитным отношением и имеет значение 42,6 МГц/Тесла для протона. Следовательно, ларморовская частота пропорциональна силе магнитного поля, и для 1,5 Тесла ларморовская частота составляет примерно 64 МГц. Это также известно как резонансная частота, поскольку протоны поглощают энергию (или резонируют) только на этой характерной частоте. Радиочастотное поле обычно применяется в виде короткого импульса, известного как радиочастотный импульс.
Радиочастотные импульсы и угол переворота
Перед включением радиочастотного импульса чистая намагниченность, M o , находится в равновесии, выровнена по оси z в том же направлении, что и B o (рис. 2a). При включении РЧ-импульса результирующая намагниченность начинает отклоняться от своего выравнивания с полем B o и вращаться вокруг него. Скорость этого вращательного движения, известного как прецессия, также соответствует частоте Лармора. Поэтому ларморовскую частоту также иногда называют частотой прецессии. Движение чистой намагниченности от выравнивания с B o вызвано гораздо более медленным вращением вокруг гораздо меньшего приложенного радиочастотного поля, B 1 . Это колеблющееся поле B 1 применяется как вращающееся поле под прямым углом к B o в плоскости осей x и y. Поскольку он вращается с той же частотой, что и ларморовская частота, он появляется как дополнительное статическое поле к вращающемуся суммарному вектору намагниченности. Следовательно, результирующая намагниченность вращается как вокруг полей B o , так и вокруг полей B 1 . В результате этих двух вращений результирующая намагниченность следует по спирали от своего выравнивания с B o поле (ось z) по направлению к вращательному движению в плоскости осей x и y.
Следовательно, результирующая намагниченность вращается как вокруг полей B o , так и вокруг полей B 1 . В результате этих двух вращений результирующая намагниченность следует по спирали от своего выравнивания с B o поле (ось z) по направлению к вращательному движению в плоскости осей x и y.
Помните, что результирующая намагниченность является результатом суммы многих отдельных магнитных моментов. Пока они вращаются вместе (состояние, известное как когерентность), они будут создавать общую намагниченность, которая вращается. Чем больше количество энергии, приложенной радиочастотным импульсом, тем больше угол, под которым результирующая намагниченность образует поле B o (ось z). Это зависит как от амплитуды, так и от продолжительности импульса. РЧ-импульс отключается, как только угол прецессии достигает заданного значения. Это известно как угол переворота радиочастотного импульса (рис. 2b).
После того как радиочастотный импульс заставил результирующую намагниченность составить угол с осью z, ее можно разделить на две составляющие (рис. 2b). Один компонент параллелен оси Z. Это известно как z-компонент намагниченности, M z , также известный как продольный компонент. Другая составляющая расположена под прямым углом к оси z в плоскости осей x и y и известна как x-y составляющая результирующей намагниченности, M xy , или поперечная составляющая. Поперечный компонент вращается на ларморовской частоте в плоскости xy и при вращении создает собственное небольшое колеблющееся магнитное поле, которое обнаруживается катушкой радиочастотного приемника в виде МР-сигнала. Радиочастотные импульсы обычно классифицируют как по их углу поворота, так и по их эффекту.
2b). Один компонент параллелен оси Z. Это известно как z-компонент намагниченности, M z , также известный как продольный компонент. Другая составляющая расположена под прямым углом к оси z в плоскости осей x и y и известна как x-y составляющая результирующей намагниченности, M xy , или поперечная составляющая. Поперечный компонент вращается на ларморовской частоте в плоскости xy и при вращении создает собственное небольшое колеблющееся магнитное поле, которое обнаруживается катушкой радиочастотного приемника в виде МР-сигнала. Радиочастотные импульсы обычно классифицируют как по их углу поворота, так и по их эффекту.
Радиочастотные импульсы, которые генерируют магнитно-резонансный сигнал путем передачи энергии населению спинов водорода, заставляя намагниченность отклоняться от своего равновесного положения, известны как импульсы возбуждения. ВЧ-импульс возбуждения под углом 90° обеспечивает достаточно энергии, чтобы повернуть суммарную намагниченность на 90° (рис. 2с). Это переносит всю результирующую намагниченность с оси z в плоскость xy (поперечную), не оставляя компонент намагниченности вдоль оси z сразу после импульса. Тогда говорят, что система протонов «насыщена», и 9Поэтому радиочастотный импульс 0° иногда называют импульсом насыщения. При однократном применении РЧ-импульс под углом 90° создает максимально возможную поперечную намагниченность и МР-сигнал. Этот импульс используется для первоначальной генерации сигнала для последовательностей импульсов на основе спинового эха.
2с). Это переносит всю результирующую намагниченность с оси z в плоскость xy (поперечную), не оставляя компонент намагниченности вдоль оси z сразу после импульса. Тогда говорят, что система протонов «насыщена», и 9Поэтому радиочастотный импульс 0° иногда называют импульсом насыщения. При однократном применении РЧ-импульс под углом 90° создает максимально возможную поперечную намагниченность и МР-сигнал. Этот импульс используется для первоначальной генерации сигнала для последовательностей импульсов на основе спинового эха.
ВЧ-импульсы возбуждения с малым углом поворота поворачивают результирующую намагниченность на заданный угол менее 90° (рис. 2b). Низкий флип представлен символом α или ему может быть присвоено определенное значение, например. 30°. Только часть чистой намагниченности переносится с оси z в плоскость xy, а часть остается вдоль оси z. В то время как ВЧ-импульс с малым углом переворота производит внутренне более низкий сигнал, чем 9Импульс возбуждения 0°, описанный выше, может повторяться быстрее, поскольку некоторая часть намагниченности остается вдоль оси z сразу после импульса. Этот импульс возбуждения используется для генерации сигнала в виде последовательностей импульсов градиентного эха для управления величиной намагниченности, которая передается между осью z и плоскостью xy для приложений быстрой визуализации.
Этот импульс возбуждения используется для генерации сигнала в виде последовательностей импульсов градиентного эха для управления величиной намагниченности, которая передается между осью z и плоскостью xy для приложений быстрой визуализации.
Импульс рефокусировки 180° используется в последовательностях импульсов спинового эха после импульса возбуждения 90°, где результирующая намагниченность уже перенесена в плоскость x-y. Он меняет направление намагниченности в плоскости x-y на 180°, поскольку вращается с частотой Лармора (рис. 2d). Этот импульс используется в методах, основанных на спиновом эхе, для устранения потери когерентности, вызванной неоднородностями магнитного поля (описанной в следующем разделе).
Импульсы 180° также используются для подготовки чистой намагниченности перед применением импульса возбуждения. Они известны как импульсы инверсии и используются для восстановления инверсии или последовательностей импульсов темной крови. Они применяются, когда результирующая намагниченность находится в равновесии или близка к нему, и инвертируют избыточную популяцию магнитных моментов протонов с выровненных на противоположные с полем B o (рис. 2e). Поскольку результирующая намагниченность лежит только вдоль оси z, этот импульс не приводит к детектируемому сигналу. Он используется для подготовки z-намагничивания в последовательностях импульсов восстановления инверсии и в схемах подготовки черной крови. Поэтому этот тип импульса также часто называют импульсом подготовки к намагничиванию.
2e). Поскольку результирующая намагниченность лежит только вдоль оси z, этот импульс не приводит к детектируемому сигналу. Он используется для подготовки z-намагничивания в последовательностях импульсов восстановления инверсии и в схемах подготовки черной крови. Поэтому этот тип импульса также часто называют импульсом подготовки к намагничиванию.
Характеристики МР-сигнала - релаксация T1, T2 и T2*
Сразу после РЧ-импульса спиновая система начинает возвращаться в исходное состояние равновесия. Этот процесс известен как релаксация. Существует два различных процесса релаксации, которые относятся к двум компонентам суммарной намагниченности: продольной (z) и поперечной (xy) компонентам. Первый процесс релаксации, продольная релаксация, обычно называемая релаксацией T1, отвечает за восстановление компоненты z вдоль продольной оси (z) до ее исходного значения в состоянии равновесия. Второй процесс релаксации, поперечная релаксация, отвечает за затухание компоненты xy при ее вращении вокруг оси z, вызывая соответствующее затухание наблюдаемого МР-сигнала. Продольная и поперечная релаксация происходят одновременно, однако поперечная релаксация обычно является гораздо более быстрым процессом для тканей человека. Сигнал затухает задолго до того, как спиновая система возвращается в свое равновесное состояние.
Продольная и поперечная релаксация происходят одновременно, однако поперечная релаксация обычно является гораздо более быстрым процессом для тканей человека. Сигнал затухает задолго до того, как спиновая система возвращается в свое равновесное состояние.
Релаксация T1 представляет собой экспоненциальный процесс с постоянной времени T1. Например, если импульс 90 ° (импульс насыщения) применяется в равновесии, намагниченность по оси z насыщается (уменьшается до нуля) сразу после импульса, но затем восстанавливается по оси z к своему равновесному значению, первоначально быстро, замедляется по мере приближения к равновесному значению (рис. 3). Чем короче постоянная времени Т1, тем быстрее происходит процесс релаксации и возврат к равновесию. Восстановление z-намагничивания после 9ВЧ-импульс 0° иногда называют восстановлением насыщения.
Рисунок 3 Процесс релаксации T1 . Диаграмма, показывающая процесс релаксации T1 после применения радиочастотного импульса под углом 90 ° в состоянии равновесия. Компонент z суммарной намагниченности, M z , уменьшается до нуля, но затем постепенно восстанавливается до своего равновесного значения, если не применяются дальнейшие РЧ-импульсы. Восстановление M z представляет собой экспоненциальный процесс с постоянной времени T1. Это время, когда намагниченность восстанавливается до 63% от своего значения при равновесии.
Компонент z суммарной намагниченности, M z , уменьшается до нуля, но затем постепенно восстанавливается до своего равновесного значения, если не применяются дальнейшие РЧ-импульсы. Восстановление M z представляет собой экспоненциальный процесс с постоянной времени T1. Это время, когда намагниченность восстанавливается до 63% от своего значения при равновесии.
Изображение полного размера
Поперечная релаксация может быть понята, если вспомнить, что результирующая намагниченность является результатом суммы магнитных моментов (спинов) всего населения протонов. Сразу после РЧ-импульса они вращаются вместе когерентным образом, так что при вращении они постоянно указывают в одном направлении друг с другом в плоскости xy. Угол направления, на которое они указывают в любой момент, известен как фазовый угол, а спины, имеющие одинаковые фазовые углы, на этом начальном этапе называются «синфазными» (рис. 4). Со временем, по причинам, которые мы сейчас объясним, фазовые углы постепенно расширяются, происходит потеря когерентности, и магнитные моменты больше не вращаются вместе, и говорят, что они движутся «в противофазе». Таким образом, чистая сумма магнитных моментов уменьшается, что приводит к уменьшению измеренной чистой (поперечной) намагниченности. Таким образом, сигнал, который обнаруживает приемная катушка (если не применяются дальнейшие радиочастотные импульсы или градиенты магнитного поля), рассматривается как колеблющееся магнитное поле, которое постепенно затухает (известное как затухание свободной индукции или FID). Есть две причины этой потери когерентности. Во-первых, наличие взаимодействий между соседними протонами вызывает потерю фазовой когерентности, известную как Т2-релаксация.
Таким образом, чистая сумма магнитных моментов уменьшается, что приводит к уменьшению измеренной чистой (поперечной) намагниченности. Таким образом, сигнал, который обнаруживает приемная катушка (если не применяются дальнейшие радиочастотные импульсы или градиенты магнитного поля), рассматривается как колеблющееся магнитное поле, которое постепенно затухает (известное как затухание свободной индукции или FID). Есть две причины этой потери когерентности. Во-первых, наличие взаимодействий между соседними протонами вызывает потерю фазовой когерентности, известную как Т2-релаксация.
Поперечные (T2 и T2*) процессы релаксации . Диаграмма, показывающая процесс поперечной релаксации после воздействия радиочастотного импульса под углом 90° в состоянии равновесия. Первоначально поперечная намагниченность (красная стрелка) имеет максимальную амплитуду, поскольку совокупность магнитных моментов (спинов) протонов вращается в фазе. Амплитуда результирующей поперечной намагниченности (и, следовательно, обнаруженный сигнал) затухает по мере того, как магнитные моменты протонов смещаются в противофазе друг с другом (показано маленькими черными стрелками). Результирующий затухающий сигнал известен как затухание свободной индукции (FID). Общим термином для наблюдаемой потери фазовой когерентности (расфазировки) является релаксация Т2*, которая сочетает в себе эффект релаксации Т2 и дополнительную дефазировку, вызванную локальными вариациями (неоднородностями) приложенного магнитного поля. Релаксация Т2 является результатом спин-спиновых взаимодействий и из-за случайного характера движения молекул этот процесс необратим. Релаксация T2* объясняет более быстрое затухание сигнала FID, однако дополнительное затухание, вызванное неоднородностями поля, можно обратить вспять, применив 180-градусный импульс перефокусировки. И T2, и T2* являются экспоненциальными процессами с постоянными временами T2 и T2* соответственно. Это время, когда намагниченность уменьшилась до 37% от своего начального значения сразу после 90° РЧ-импульс.
Амплитуда результирующей поперечной намагниченности (и, следовательно, обнаруженный сигнал) затухает по мере того, как магнитные моменты протонов смещаются в противофазе друг с другом (показано маленькими черными стрелками). Результирующий затухающий сигнал известен как затухание свободной индукции (FID). Общим термином для наблюдаемой потери фазовой когерентности (расфазировки) является релаксация Т2*, которая сочетает в себе эффект релаксации Т2 и дополнительную дефазировку, вызванную локальными вариациями (неоднородностями) приложенного магнитного поля. Релаксация Т2 является результатом спин-спиновых взаимодействий и из-за случайного характера движения молекул этот процесс необратим. Релаксация T2* объясняет более быстрое затухание сигнала FID, однако дополнительное затухание, вызванное неоднородностями поля, можно обратить вспять, применив 180-градусный импульс перефокусировки. И T2, и T2* являются экспоненциальными процессами с постоянными временами T2 и T2* соответственно. Это время, когда намагниченность уменьшилась до 37% от своего начального значения сразу после 90° РЧ-импульс.
Изображение в натуральную величину
Это происходит из-за того, что скорость прецессии отдельного протона зависит от магнитного поля, которое он испытывает в данный момент. Хотя приложенное магнитное поле B o является постоянным, тем не менее, магнитный момент одного протона может немного изменить магнитное поле, испытываемое соседним протоном. Поскольку протоны входят в состав атомов внутри молекул, они движутся быстро и беспорядочно, поэтому такие эффекты временны и случайны. Чистый эффект состоит в том, что ларморовская частота отдельных протонов колеблется случайным образом, что приводит к потере когерентности в популяции протонов. то есть спины постепенно приобретают разные фазовые углы, указывая в разных направлениях друг к другу, и говорят, что они движутся не в фазе друг с другом (это часто называют расфазировкой). Результирующий спад поперечной составляющей намагниченности (M xy ) имеет экспоненциальную форму с постоянной времени T2, поэтому этот вклад в поперечную релаксацию известен как релаксация T2 (рис. 4). Поскольку это вызвано взаимодействием между соседними спинами протонов, его также иногда называют спин-спиновой релаксацией. Из-за случайного характера спин-спиновых взаимодействий затухание сигнала, вызванное Т2-релаксацией, необратимо.
4). Поскольку это вызвано взаимодействием между соседними спинами протонов, его также иногда называют спин-спиновой релаксацией. Из-за случайного характера спин-спиновых взаимодействий затухание сигнала, вызванное Т2-релаксацией, необратимо.
Вторая причина потери когерентности (расфазировка) связана с локальными статическими вариациями (неоднородностями) приложенного магнитного поля, B или , которые неизменны во времени. Если это поле различается в разных местах, то меняется и ларморовская частота. Следовательно, протоны в разных пространственных положениях будут вращаться с разной скоростью, вызывая дальнейшую дефазировку, так что сигнал затухает быстрее. В этом случае, поскольку причина изменения ларморовской частоты фиксирована, результирующая расфазировка потенциально обратима. Комбинированный эффект релаксации T2 и эффекта неоднородности магнитного поля называется релаксацией T2*, и он определяет фактическую скорость затухания, наблюдаемую при измерении сигнала FID (рис. 4). Релаксация Т2* также является экспоненциальным процессом с постоянной времени Т2*.
4). Релаксация Т2* также является экспоненциальным процессом с постоянной времени Т2*.
Значение значения T1
Релаксация T1 связана с высвобождением энергии из спиновой популяции протонов, когда она возвращается в свое равновесное состояние. Скорость релаксации связана со скоростью, с которой энергия высвобождается в окружающую молекулярную структуру. Это, в свою очередь, связано с размером молекулы, содержащей ядра водорода, и, в частности, со скоростью молекулярного движения, известной как скорость падения конкретной молекулы. Когда молекулы падают или вращаются, они создают флуктуирующее магнитное поле, которое испытывают протоны в соседних молекулах. Когда это флуктуирующее магнитное поле близко к ларморовской частоте, обмен энергией более благоприятен. Например, молекулы липидов имеют размер, обеспечивающий скорость кувыркания, близкую к ларморовской частоте и, следовательно, чрезвычайно благоприятную для энергетического обмена. Поэтому жир имеет одну из самых быстрых скоростей релаксации среди всех тканей тела и, следовательно, самое короткое время релаксации T1. Более крупные молекулы имеют гораздо более низкую скорость кувыркания, что неблагоприятно для энергетического обмена, что приводит к длительному времени релаксации. Для свободной воды ее молекулы меньшего размера имеют гораздо более высокую скорость акробатики молекул, что также неблагоприятно для энергетического обмена, и поэтому она имеет большое время релаксации T1. Однако скорость кувыркания молекул воды, примыкающих к крупным макромолекулам, может быть замедлена по направлению к ларморовской частоте, что укорачивает значение T1. Таким образом, ткани на водной основе с высоким содержанием макромолекул (например, мышцы) обычно имеют более короткие значения T1. И наоборот, когда содержание воды увеличивается, например, при воспалительном процессе, значение Т1 также увеличивается.
Более крупные молекулы имеют гораздо более низкую скорость кувыркания, что неблагоприятно для энергетического обмена, что приводит к длительному времени релаксации. Для свободной воды ее молекулы меньшего размера имеют гораздо более высокую скорость акробатики молекул, что также неблагоприятно для энергетического обмена, и поэтому она имеет большое время релаксации T1. Однако скорость кувыркания молекул воды, примыкающих к крупным макромолекулам, может быть замедлена по направлению к ларморовской частоте, что укорачивает значение T1. Таким образом, ткани на водной основе с высоким содержанием макромолекул (например, мышцы) обычно имеют более короткие значения T1. И наоборот, когда содержание воды увеличивается, например, при воспалительном процессе, значение Т1 также увеличивается.
Значение значения T2
Релаксация T2 связана с величиной происходящего спин-спинового взаимодействия. Свободная вода содержит небольшие молекулы, которые находятся относительно далеко друг от друга и быстро движутся, поэтому спин-спиновые взаимодействия происходят реже, а релаксация Т2 происходит медленно (что приводит к длительному времени релаксации Т2). Молекулы воды, связанные с большими молекулами, замедляются и с большей вероятностью взаимодействуют, что приводит к более быстрой релаксации T2 и более короткому времени релаксации T2. Ткани на водной основе с высоким содержанием макромолекул (например, мышцы), как правило, имеют более короткие значения T2. И наоборот, когда содержание воды увеличивается, например, при воспалительном процессе, значение Т2 также увеличивается. Молекулы липидов имеют промежуточный размер, и существуют взаимодействия между ядрами водорода на длинных углеродных цепях (эффект, известный как J - связь), которые вызывают уменьшение постоянной времени релаксации T2 до промежуточного значения. Быстро повторяющиеся РЧ-импульсы, такие как те, которые используются в методах турбо- или быстрого спин-эхо, могут иметь эффект снижения J -связи, что приводит к увеличению времени релаксации T2 и более высокой интенсивности сигнала от жира [6].
Молекулы воды, связанные с большими молекулами, замедляются и с большей вероятностью взаимодействуют, что приводит к более быстрой релаксации T2 и более короткому времени релаксации T2. Ткани на водной основе с высоким содержанием макромолекул (например, мышцы), как правило, имеют более короткие значения T2. И наоборот, когда содержание воды увеличивается, например, при воспалительном процессе, значение Т2 также увеличивается. Молекулы липидов имеют промежуточный размер, и существуют взаимодействия между ядрами водорода на длинных углеродных цепях (эффект, известный как J - связь), которые вызывают уменьшение постоянной времени релаксации T2 до промежуточного значения. Быстро повторяющиеся РЧ-импульсы, такие как те, которые используются в методах турбо- или быстрого спин-эхо, могут иметь эффект снижения J -связи, что приводит к увеличению времени релаксации T2 и более высокой интенсивности сигнала от жира [6].
МР-эхосигналы
В то время как FID можно обнаружить как МР-сигнал, для МР-визуализации чаще всего генерируют и измеряют МР-сигнал в форме эха. Это связано с тем, что градиенты магнитного поля, которые используются для локализации и кодирования МР-сигналов в пространстве, вызывают дополнительную дефазировку, которая нарушает FID. Двумя наиболее распространенными типами эха, используемыми для МРТ, являются градиентное эхо и спиновое эхо. В следующих разделах описывается, как генерируются эти эхо-сигналы.
Это связано с тем, что градиенты магнитного поля, которые используются для локализации и кодирования МР-сигналов в пространстве, вызывают дополнительную дефазировку, которая нарушает FID. Двумя наиболее распространенными типами эха, используемыми для МРТ, являются градиентное эхо и спиновое эхо. В следующих разделах описывается, как генерируются эти эхо-сигналы.
Градиентные эхосигналы
Градиентные эхосигналы генерируются контролируемым применением градиентов магнитного поля. Градиенты магнитного поля используются для изменения напряженности поля и, следовательно, для соответствующего изменения ларморовской частоты в определенном направлении. Когда включается градиент магнитного поля, спины протонов быстро теряют когерентность или быстро дефазируются вдоль направления градиента, поскольку они прецессируют на разных частотах. Эта расфазировка приводит к быстрому падению амплитуды сигнала ПИД до нуля (рис. 5). Величину дефазировки, вызванную одним градиентом магнитного поля, можно, однако, обратить вспять, применив второй градиент магнитного поля в том же направлении с наклоном равной амплитуды, но в противоположном направлении. Если второй градиент применяется в течение того же времени, что и первый градиент, расфазировка, вызванная первым градиентом, отменяется, и снова появляется FID. Он достигает максимальной амплитуды в точке, в которой спины, дефазированные первым градиентом, возвращаются в фазу или «перефазируются». Если после этого продолжает применяться второй градиент, сигнал FID дефазируется и снова исчезает. Сигнал, который рефазируется за счет переключения направления градиента, известен как градиентное эхо. Время от точки, в которой поперечная намагниченность (ПИД) генерируется РЧ-импульсом, до точки, в которой градиентное эхо-сигнал достигает максимальной амплитуды, называется временем эхо-сигнала (сокращенно TE). Это можно контролировать, изменяя время градиентов приложенного магнитного поля. Если время эха выбрано более продолжительным, происходит более естественная дефазировка T2*, и максимальная амплитуда эха становится меньше. На практике ТЭ устанавливается оператором системы МРТ (в миллисекундах), так как он определяет, среди прочего, влияние Т2* на контрастность изображения.
Если второй градиент применяется в течение того же времени, что и первый градиент, расфазировка, вызванная первым градиентом, отменяется, и снова появляется FID. Он достигает максимальной амплитуды в точке, в которой спины, дефазированные первым градиентом, возвращаются в фазу или «перефазируются». Если после этого продолжает применяться второй градиент, сигнал FID дефазируется и снова исчезает. Сигнал, который рефазируется за счет переключения направления градиента, известен как градиентное эхо. Время от точки, в которой поперечная намагниченность (ПИД) генерируется РЧ-импульсом, до точки, в которой градиентное эхо-сигнал достигает максимальной амплитуды, называется временем эхо-сигнала (сокращенно TE). Это можно контролировать, изменяя время градиентов приложенного магнитного поля. Если время эха выбрано более продолжительным, происходит более естественная дефазировка T2*, и максимальная амплитуда эха становится меньше. На практике ТЭ устанавливается оператором системы МРТ (в миллисекундах), так как он определяет, среди прочего, влияние Т2* на контрастность изображения.
Генерация градиентного эха . На этой диаграмме показано, как изменение направления градиента магнитного поля используется для создания градиентного эха. Применение положительного градиента магнитного поля 1 st вызывает быстрое расфазирование поперечной намагниченности, M xy , и, следовательно, сигнал FID до нулевой амплитуды. Применение отрицательного градиента магнитного поля 2 nd устраняет дефазировку, вызванную первым импульсом градиента, что приводит к восстановлению сигнала FID для создания градиентного эхо-сигнала в момент эхо-сигнала TE. Увеличение продолжительности второго градиента в два раза по сравнению с первым градиентом приводит к тому, что FID смещается по фазе до нуля. Максимальная амплитуда эха зависит как от скорости релаксации T2*, так и от выбранного TE.
Полноразмерное изображение
Спиновое эхо
Спиновое эхо генерируется путем применения 180° перефокусирующего РЧ-импульса после 90° импульса возбуждения (рис. 6). В то время как дефазировка, вызванная релаксацией T2, является случайным необратимым процессом, дополнительная дефазировка, вызванная наличием неоднородностей статического магнитного поля, потенциально обратима. В определенный момент времени после начальной генерации сигнала ССИ доля относительного изменения фазы для каждого спина протона связана с локальным значением приложенного магнитного поля. Применение импульса перефокусировки на 180 ° поворачивает спины на 180 °, эффективно изменяя знак относительного изменения фазы в плоскости xy. Там, где предыдущее относительное изменение фазы было положительным из-за локального усиления поля, импульс на 180° приводит к тому, что оно становится отрицательным, и наоборот. Поскольку вариации локального поля остаются фиксированными, спины по-прежнему имеют одну и ту же ларморовскую частоту, поэтому спин в усиленном поле продолжает увеличивать фазу, а спин в уменьшающемся поле продолжает терять фазу. Поскольку знак их фазовых сдвигов был изменен на полпути импульсом перефокусировки на 180 °, все спины возвращаются в фазу, вызывая увеличение амплитуды FID, достигая максимума во время эха, TE.
6). В то время как дефазировка, вызванная релаксацией T2, является случайным необратимым процессом, дополнительная дефазировка, вызванная наличием неоднородностей статического магнитного поля, потенциально обратима. В определенный момент времени после начальной генерации сигнала ССИ доля относительного изменения фазы для каждого спина протона связана с локальным значением приложенного магнитного поля. Применение импульса перефокусировки на 180 ° поворачивает спины на 180 °, эффективно изменяя знак относительного изменения фазы в плоскости xy. Там, где предыдущее относительное изменение фазы было положительным из-за локального усиления поля, импульс на 180° приводит к тому, что оно становится отрицательным, и наоборот. Поскольку вариации локального поля остаются фиксированными, спины по-прежнему имеют одну и ту же ларморовскую частоту, поэтому спин в усиленном поле продолжает увеличивать фазу, а спин в уменьшающемся поле продолжает терять фазу. Поскольку знак их фазовых сдвигов был изменен на полпути импульсом перефокусировки на 180 °, все спины возвращаются в фазу, вызывая увеличение амплитуды FID, достигая максимума во время эха, TE. Чтобы расфазировка спина, вызванная неоднородностями поля, была полностью обращена вспять в момент времени TE, 180-градусный импульс должен быть приложен в момент времени TE/2. Сигнал, который появляется повторно (повторно фазируется) в результате применения 180-градусного РЧ-импульса перефокусировки, известен как спиновое эхо. После достижения максимальной амплитуды в момент времени ТЕ сигнал снова дефазируется из-за процесса релаксации Т2*. В целях визуализации градиенты магнитного поля также применяются во время периода расфазировки и во время измерения спинового эха.
Чтобы расфазировка спина, вызванная неоднородностями поля, была полностью обращена вспять в момент времени TE, 180-градусный импульс должен быть приложен в момент времени TE/2. Сигнал, который появляется повторно (повторно фазируется) в результате применения 180-градусного РЧ-импульса перефокусировки, известен как спиновое эхо. После достижения максимальной амплитуды в момент времени ТЕ сигнал снова дефазируется из-за процесса релаксации Т2*. В целях визуализации градиенты магнитного поля также применяются во время периода расфазировки и во время измерения спинового эха.
Генерация спинового эха . Наличие неоднородностей магнитного поля вызывает дополнительную расфазировку магнитных моментов протонов. Ларморовская частота медленнее, когда магнитное поле уменьшается, и быстрее, когда поле увеличивается, что приводит к потере или увеличению относительной фазы соответственно. После периода, равного половине времени эха, TE/2, приложение радиочастотного импульса на 180° вызывает мгновенное изменение знака фазовых сдвигов за счет вращения спинов (в данном примере) вокруг оси y. Поскольку различия в ларморовской частоте остаются неизменными, магнитные моменты протонов возвращаются в фазу в течение аналогичного периода времени, обращая вспять эффект расфазировки неоднородностей магнитного поля для создания спинового эха. В дополнение к эффекту перефокусирующего импульса на 180° применяются градиенты для дефазировки и рефазировки сигнала для целей визуализации. Обратите внимание, что для последовательностей импульсов спинового эха второй градиент имеет тот же знак, что и первый, поскольку 180-градусный импульс также меняет знак фазовых сдвигов, вызванных первым градиентом.
Поскольку различия в ларморовской частоте остаются неизменными, магнитные моменты протонов возвращаются в фазу в течение аналогичного периода времени, обращая вспять эффект расфазировки неоднородностей магнитного поля для создания спинового эха. В дополнение к эффекту перефокусирующего импульса на 180° применяются градиенты для дефазировки и рефазировки сигнала для целей визуализации. Обратите внимание, что для последовательностей импульсов спинового эха второй градиент имеет тот же знак, что и первый, поскольку 180-градусный импульс также меняет знак фазовых сдвигов, вызванных первым градиентом.
Полноразмерное изображение
Спиновое эхо по сравнению с градиентным эхом
В общем, поскольку импульс перефокусировки на 180° устраняет дефазировку, вызванную неоднородностями магнитного поля, амплитуда сигнала спинового эха больше, чем сигнала градиентного эха. На визуализацию, основанную на спин-эхо, также меньше влияет наличие неоднородностей поля, вызванных металлическими артефактами (например, стернальными проволоками или металлическим сердцем). Однако на визуализацию градиентного эха больше влияет наличие неоднородностей магнитного поля, вызванных железом, и поэтому она полезна, например, при оценке пациентов с повышенным отложением железа в сердце и печени.
Однако на визуализацию градиентного эха больше влияет наличие неоднородностей магнитного поля, вызванных железом, и поэтому она полезна, например, при оценке пациентов с повышенным отложением железа в сердце и печени.
Локализация и кодирование МР-сигналов для создания изображения
Полученные выше МР-эхо-сигналы могут быть локализованы и закодированы путем применения градиентов магнитного поля по мере их генерации для создания изображения. Это связано с тем, что приложение градиента магнитного поля приводит к тому, что сила магнитного поля и, следовательно, ларморовская частота зависят от положения в этом направлении. В следующих разделах описывается наиболее часто используемый метод построения двумерного изображения поперечного сечения (или среза изображения) с использованием комбинации РЧ-импульсов и градиентных магнитных полей.
Шаг 1. Выбор среза изображения
Во-первых, резонанс протонов ограничивается срезом ткани. Это делается путем приложения градиентного магнитного поля одновременно с передачей импульса радиочастотного возбуждения (рис. 7). Частота радиочастотного импульса соответствует ларморовской частоте в выбранной точке вдоль направления приложенного градиента. В результате резонанс возникает только для протонов в плоскости, которая пересекает эту точку под прямым углом к направлению градиента, эффективно определяя срез ткани. Этот процесс известен как выбор среза, а градиент известен как градиент выбора среза, G С . Ориентация среза определяется направлением применяемого градиента, известным как направление выбора среза (в примере на рисунке 7 это направление z). Передаваемый РЧ-импульс состоит не только из одной частоты, но из небольшого диапазона частот, известного как полоса пропускания РЧ-импульса. Это придает ломтику толщину. Толщина среза определяется комбинацией ширины полосы радиочастотного импульса и крутизны (или силы) градиента.
7). Частота радиочастотного импульса соответствует ларморовской частоте в выбранной точке вдоль направления приложенного градиента. В результате резонанс возникает только для протонов в плоскости, которая пересекает эту точку под прямым углом к направлению градиента, эффективно определяя срез ткани. Этот процесс известен как выбор среза, а градиент известен как градиент выбора среза, G С . Ориентация среза определяется направлением применяемого градиента, известным как направление выбора среза (в примере на рисунке 7 это направление z). Передаваемый РЧ-импульс состоит не только из одной частоты, но из небольшого диапазона частот, известного как полоса пропускания РЧ-импульса. Это придает ломтику толщину. Толщина среза определяется комбинацией ширины полосы радиочастотного импульса и крутизны (или силы) градиента.
Формирование изображения, шаг 1 — выбор среза . На этапе 1 процесса формирования изображения срез ткани выбирается путем применения градиента магнитного поля G S одновременно с импульсом радиочастотного возбуждения. Положение вдоль градиента (в этом примере вдоль оси z) определяет ларморову частоту, и резонанс возникает только там, где она соответствует частоте радиочастотного импульса, f 0 , определяя плоскость (срез) ткани, перпендикулярную оси z. . На практике РЧ-импульс применяется в небольшом диапазоне частот, что определяет толщину среза.
Положение вдоль градиента (в этом примере вдоль оси z) определяет ларморову частоту, и резонанс возникает только там, где она соответствует частоте радиочастотного импульса, f 0 , определяя плоскость (срез) ткани, перпендикулярную оси z. . На практике РЧ-импульс применяется в небольшом диапазоне частот, что определяет толщину среза.
Полноразмерное изображение
Шаг 2 — Фазовое кодирование
После выбора среза применяется градиент фазового кодирования G P в течение заданного периода (рис. 8). Это заставляет протоны вращаться с разной частотой в зависимости от их относительного положения вдоль градиента. Там, где градиент увеличивает магнитное поле, протоны приобретают более высокую частоту прецессии, тогда как там, где градиент уменьшает магнитное поле, протоны приобретают более низкую частоту прецессии. Поэтому протоны также постоянно меняют свою относительную фазу в зависимости от своего положения вдоль градиента. Когда градиент отключен, протоны изменят свою относительную фазу на величину, зависящую от их положения вдоль градиента. Этот процесс известен как фазовое кодирование, а направление применяемого градиента известно как направление фазового кодирования.
Этот процесс известен как фазовое кодирование, а направление применяемого градиента известно как направление фазового кодирования.
Формирование изображения, этапы 2 и 3 – кодирование фазы и частоты . Для этапа 2 процесса формирования изображения градиент фазового кодирования G P применяется в направлении вдоль выбранной плоскости изображения (в этом случае направление фазового кодирования находится вдоль направления y). Это вызывает ряд фазовых сдвигов магнитных моментов протонов, зависящих от их положения вдоль градиента, а также от наклона и продолжительности градиента. Для шага 3, после градиента фазового кодирования, градиент частотного кодирования, G F , применяется также в плоскости выбранного среза, но перпендикулярно направлению фазового кодирования. Эхо-сигнал МР измеряется в течение этого периода. Градиент частотного кодирования определяет ларморову частоту в соответствии с положением вдоль ее направления (в данном случае по оси x). Таким образом, обнаруженный МР-сигнал от среза ткани состоит из множества различных частот. Поле зрения предопределено и соответствует определенному диапазону частот, называемому полосой пропускания приемника. См. также Дополнительный файл 1.
Таким образом, обнаруженный МР-сигнал от среза ткани состоит из множества различных частот. Поле зрения предопределено и соответствует определенному диапазону частот, называемому полосой пропускания приемника. См. также Дополнительный файл 1.
Полноразмерное изображение
Шаг 3. Кодирование частоты
Вслед за градиентом фазового кодирования градиент кодирования частоты G F применяется в направлении, перпендикулярном ему, и аналогичным образом заставляет протоны вращаться. на разных частотах в соответствии с их относительным положением вдоль градиента этого направления (рис. 8). Этот градиент применяется дольше, и в то же время сигнал измеряется или дискретизируется в цифровом виде. Сигнал состоит из диапазона частот (или ширины полосы), соответствующих ларморовским частотам магнитных моментов протонов в их различных положениях вдоль градиента. Этот процесс известен как частотное кодирование, направление градиента частотного кодирования определяет направление частотного кодирования. Процессы фазового и частотного кодирования на шагах 2 и 3 дополнительно проиллюстрированы анимацией, представленной в дополнительном файле 1.
Процессы фазового и частотного кодирования на шагах 2 и 3 дополнительно проиллюстрированы анимацией, представленной в дополнительном файле 1.
Таким образом, для локализации МР-сигнала в трех измерениях применяются три отдельных градиента магнитного поля в трехэтапном процессе. Для примеров на рис. 7 и 8 эти градиенты применяются последовательно с градиентом сечения среза, G S , применяемым вдоль оси z, градиентом фазового кодирования, G P , применяемым вдоль оси y, и Градиент частотного кодирования, G F , нанесенный по оси x (рис. 9). Это определяет срез, перпендикулярный оси z, т. е. срез, ориентированный в трансаксиальной плоскости. Другие ориентации среза получаются путем переназначения каждого из градиентов на другую ось. Угловой срез получается путем объединения градиентов по двум или более осям для выполнения каждой из задач локализации. Возможность определить произвольную ориентацию среза является ключевым преимуществом магнитно-резонансной томографии, особенно для кардиологических исследований, которые требуют срезов под двойным косым углом для получения стандартных видов сердечных камер и плоскостей клапанов.
Формирование изображения – диаграмма последовательности импульсов . Диаграмма последовательности импульсов, показывающая относительную синхронизацию радиочастотных и градиентных импульсов, применяемых в рамках трехэтапного процесса локализации и кодирования МР-сигнала для формирования изображения. Частотно-кодированный эхо-сигнал MR измеряется в течение периода дискретизации с центром во времени эха, TE. Дополнительные импульсы градиента (показаны красным контуром) требуются сразу после градиента выбора среза и непосредственно перед градиентом частотного кодирования. Эти дополнительные импульсы гарантируют, что любая дефазировка поперечной намагниченности, вызванная градиентами изображения, будет отменена, как только будет достигнуто время эха, TE. Это приводит к тому, что эхо достигает максимально возможного сигнала в этой точке.
Полноразмерное изображение
Обратите внимание, что на рис. 9 показаны дополнительные импульсы градиента как после градиента выбора среза, так и перед градиентом частотного кодирования. Эти дополнительные импульсы градиента необходимы для противодействия дефазировке, вызванной этими двумя градиентами изображения, чтобы обеспечить максимально возможный сигнал в центре эхо-сигнала МР. Дополнительные импульсы градиента применяются в том же направлении, что и градиенты изображения, но с противоположным наклоном, так что поперечная намагниченность возвращается в фазу. Для градиента выбора среза дефазировка происходит только во второй половине градиента выбора среза, поскольку поперечная намагниченность генерируется только на полпути через приложенный РЧ-импульс. Поэтому за ним следует градиент перефазирования, который составляет только половину длины градиента выбора среза. Это гарантирует, что расфазировка, происходящая вдоль градиента выбора среза, будет обращена вспять. Градиенту частотного кодирования обычно предшествует дефазирующий градиент, так что при применении частотного кодирующего градиента дефазировка реверсируется первой половиной частотного кодирующего градиента, а эхо-сигнал достигает максимальной амплитуды в центре период выборки.
Эти дополнительные импульсы градиента необходимы для противодействия дефазировке, вызванной этими двумя градиентами изображения, чтобы обеспечить максимально возможный сигнал в центре эхо-сигнала МР. Дополнительные импульсы градиента применяются в том же направлении, что и градиенты изображения, но с противоположным наклоном, так что поперечная намагниченность возвращается в фазу. Для градиента выбора среза дефазировка происходит только во второй половине градиента выбора среза, поскольку поперечная намагниченность генерируется только на полпути через приложенный РЧ-импульс. Поэтому за ним следует градиент перефазирования, который составляет только половину длины градиента выбора среза. Это гарантирует, что расфазировка, происходящая вдоль градиента выбора среза, будет обращена вспять. Градиенту частотного кодирования обычно предшествует дефазирующий градиент, так что при применении частотного кодирующего градиента дефазировка реверсируется первой половиной частотного кодирующего градиента, а эхо-сигнал достигает максимальной амплитуды в центре период выборки.
Реконструкция изображения
Частотно-кодированный сигнал анализируется с помощью преобразования Фурье. Это математический инструмент, который преобразует зависящий от времени МР-сигнал в его различные частотные компоненты (рис. 10). Амплитуда каждой частотной составляющей может быть отображена на местоположение вдоль градиента частотного кодирования, чтобы определить относительную величину сигнала в каждом местоположении. Поле зрения в направлении частотного кодирования определяется оператором в мм или см. Диапазон частот в этом поле зрения известен как ширина полосы приемника и определяется амплитудой (или наклоном), необходимой для градиента частотного кодирования.
Рисунок 10 Реконструкция изображения - частотное кодирование . Частотно-кодированный сигнал анализируется с помощью преобразования Фурье для определения вклада каждой из частотных составляющих в каждую позицию вдоль градиента частотного кодирования в пределах предварительно определенного поля зрения.
Полноразмерное изображение
В то время как анализ закодированного МР-сигнала с помощью преобразования Фурье обеспечивает частотную составляющую сигнала, фазовые изменения, вызванные градиентом фазового кодирования, не могут быть декодированы с помощью аналогичного процесса. Преобразование Фурье может анализировать только сигнал, который изменяется во времени. Чтобы сделать это возможным, несколько эхо-сигналов генерируются путем повторения описанного выше трехэтапного процесса (выбор среза, фазовое кодирование и частотное кодирование), каждый раз применяя один и тот же градиент выбора среза и частотного кодирования, но разное количество фазового кодирования ( Рисунок 11). Это делается путем увеличения силы (или наклона) градиента фазового кодирования для каждого повторения на равные приращения или шаги. Для каждого шага фазового кодирования эхо-сигнал измеряется, оцифровывается и сохраняется в матрице необработанных данных. Интервал времени между каждым повторением известен как время повторения, TR. Как только все сигналы для заданного числа шагов фазового кодирования будут получены и сохранены, они анализируются вместе с помощью двумерного (2D) преобразования Фурье для декодирования информации о частоте и фазе (рис. 12).
Как только все сигналы для заданного числа шагов фазового кодирования будут получены и сохранены, они анализируются вместе с помощью двумерного (2D) преобразования Фурье для декодирования информации о частоте и фазе (рис. 12).
Шаги фазового кодирования и время повторения, TR . Чтобы получить достаточную информацию для реконструкции изображения, последовательность импульсов повторяется несколько раз, при этом каждый раз применяется приращение силы (или наклона) градиента фазового кодирования. В этом примере используются 7 значений наклона градиента фазового кодирования (показаны пунктирными линиями). Обратите внимание, что по мере увеличения силы градиента фазового кодирования это увеличивает величину дефазировки вдоль градиента. Когда сила (или наклон) градиента фазового кодирования равна нулю (шаг 4), расфазировка отсутствует и сигнал имеет максимально возможную амплитуду. Интервал времени между каждым повторением известен как время повторения, TR.
Полноразмерное изображение
Рисунок 12 Реконструкция изображения, k-пространство и пространство изображения . Сигналы MR, полученные на каждом этапе фазового кодирования, сохраняются в матрице необработанных данных, известной как k-пространство. Двумерное преобразование Фурье этой матрицы приводит к восстановлению изображения. Количество шагов фазового кодирования определяет количество пикселей в изображении вдоль направления фазового кодирования. Координатами изображения являются пространственные координаты x и y. Распределение компонентов МР-сигнала в изображении определяется их частотой по направлению частотного кодирования (в данном случае x) и их изменением по фазе с каждым шагом фазового кодирования по направлению фазового кодирования (в данном случае y). Координатами k-пространства являются пространственные частоты k x = 1/x и k y = 1/y. Таким образом, точки данных в k-пространстве (дискретизированные сигналы MR) представляют содержание пространственных частот изображения. При декартовом сборе данных точки данных сохраняются строка за строкой вдоль направления k x , причем каждая строка соответствует отдельно выбранному МР-сигналу. Положение вдоль k x зависит от момента времени в течение периода выборки. Расположение каждой строки точек данных в направлении k y определяется амплитудой и длительностью направления фазового кодирования на каждом этапе фазового кодирования.
При декартовом сборе данных точки данных сохраняются строка за строкой вдоль направления k x , причем каждая строка соответствует отдельно выбранному МР-сигналу. Положение вдоль k x зависит от момента времени в течение периода выборки. Расположение каждой строки точек данных в направлении k y определяется амплитудой и длительностью направления фазового кодирования на каждом этапе фазового кодирования.
Полноразмерное изображение
Время повторения и время получения изображения
Время повторения TR — еще один важный параметр, который может быть установлен оператором в миллисекундах. Как мы увидим позже, это не только определяет скорость получения МР-изображений, но и влияет на контрастность изображения. Количество пикселей в направлении фазового кодирования реконструированного изображения определяется количеством используемых шагов фазового кодирования, N P . Таким образом, пространственное разрешение изображения также зависит от количества шагов фазового кодирования и, как следствие, часто ограничено временем получения изображения, как
Время получения изображения = TR×NP
Если требуется более высокое пространственное разрешение в направлении фазового кодирования (для фиксированного поля зрения), количество пикселей в этом направлении (иногда называемое размером матрицы полученного изображения) должно быть увеличено. Это требует большего количества повторений и, следовательно, более длительного времени получения изображения.
Это требует большего количества повторений и, следовательно, более длительного времени получения изображения.
k-space
То, как генерируются и кодируются МР-сигналы с использованием градиентов магнитного поля, приводит к особой взаимосвязи между точками данных в сигнале и на изображении. Одна точка данных в сигнале MR вносит определенный атрибут во все изображение. И наоборот, один пиксель на изображении может иметь вклад от всех собранных МР-сигналов. Точно так же, как каждый пиксель занимает уникальное место в пространстве изображения, каждая точка эха МР-сигнала принадлежит определенному местоположению в связанном пространстве, известном как k-пространство [7]. Существует обратная зависимость между пространством изображения и k-пространством (рис. 12). В то время как координаты изображения представляют пространственное положение (x и y), координаты k-пространства представляют 1/x и 1/y, иногда называемые пространственными частотами, k x и k y . Значение каждой точки в k-пространстве представляет, сколько конкретной пространственной частоты содержится в соответствующем изображении.
Значение каждой точки в k-пространстве представляет, сколько конкретной пространственной частоты содержится в соответствующем изображении.
Пространственную частоту сложно изобразить. Изображение, состоящее из одной пространственной частоты, выглядит как волна, распространяющаяся по изображению с яркими и темными пиками и впадинами (рис. 13). Низкая пространственная частота (исходящая из точки, близкой к центру k-пространства) имеет пики и впадины далеко друг от друга и, таким образом, вносит основной вклад в содержание сигнала и контрастность изображения. Высокая пространственная частота (возникающая из точки вблизи края k-пространства) имеет пики и впадины близко друг к другу и, таким образом, вносит мелкие детали или края, эффективно определяя пространственное разрешение изображения. Для создания изображения, полностью точно отображающего отображаемый объект, важно, чтобы был получен весь диапазон пространственных частот (вплоть до максимума, определяющего пространственное разрешение изображения), т. е. чтобы все k-пространство покрыт. Для стандартной визуализации это делается путем заполнения k-пространства равноотстоящими параллельными строками данных сигнала, строка за строкой, вдоль k x направление. Это известно как декартово приобретение (рис. 12). Градиент фазового кодирования определяет положение линии, заполняемой в направлении k y . Обычно амплитуда градиента фазового кодирования увеличивается ступенчато, так что следующая соседняя строка в k-пространстве заполняется при каждом последующем повторении, начиная с одного края k-пространства и заканчивая противоположным краем. Это известно как линейный порядок фазового кодирования (рис. 14). Выбор другого порядка шагов фазового кодирования особенно важен в некоторых динамических приложениях, таких как ангиография с контрастным усилением, где важно получать информацию о контрасте сразу в начале получения данных изображения, когда контрастное вещество достигает определенного сегмента сосуда. В этом случае градиент фазового кодирования увеличивается от нуля, но с чередующимся знаком, начиная с центра k-пространства и двигаясь наружу к краям k-пространства, что известно как центральный или низкий-высокий порядок k-пространства (рис.
е. чтобы все k-пространство покрыт. Для стандартной визуализации это делается путем заполнения k-пространства равноотстоящими параллельными строками данных сигнала, строка за строкой, вдоль k x направление. Это известно как декартово приобретение (рис. 12). Градиент фазового кодирования определяет положение линии, заполняемой в направлении k y . Обычно амплитуда градиента фазового кодирования увеличивается ступенчато, так что следующая соседняя строка в k-пространстве заполняется при каждом последующем повторении, начиная с одного края k-пространства и заканчивая противоположным краем. Это известно как линейный порядок фазового кодирования (рис. 14). Выбор другого порядка шагов фазового кодирования особенно важен в некоторых динамических приложениях, таких как ангиография с контрастным усилением, где важно получать информацию о контрасте сразу в начале получения данных изображения, когда контрастное вещество достигает определенного сегмента сосуда. В этом случае градиент фазового кодирования увеличивается от нуля, но с чередующимся знаком, начиная с центра k-пространства и двигаясь наружу к краям k-пространства, что известно как центральный или низкий-высокий порядок k-пространства (рис. 14).
14).
k-пространство и пространственные частоты . Одна точка в k-пространстве определяет пространственную частоту, которую можно представить как волну в пространстве изображения. Точка, близкая к центру k-пространства, дает низкую пространственную частоту, представленную волной с широкими пиками и впадинами. Это обеспечивает содержание сигнала для больших областей однородного сигнала в изображении и, следовательно, контрастность изображения. Точка на краю k-пространства вносит вклад в высокую пространственную частоту и представлена тонкой волной «зубчатый гребень». Максимальное содержание пространственной частоты определяет предел пространственного разрешения изображения.
Полноразмерное изображение
Рисунок 14 Порядок k-пространства . Сбор стандартных декартовых данных МРТ заполняет k-пространство, начиная с одного края k-пространства, увеличивая строку за строкой, пока не будет достигнут противоположный край k-пространства. Это известно как линейный порядок k-пространства. «Центральный» или «лоу-хай» порядок k-пространства начинается в центре k-пространства и заполняет линии k-пространства наружу к обоим краям попеременно.
Это известно как линейный порядок k-пространства. «Центральный» или «лоу-хай» порядок k-пространства начинается в центре k-пространства и заполняет линии k-пространства наружу к обоим краям попеременно.
Полноразмерное изображение
Последовательности импульсов и контраст изображения
Контрастность и взвешивание изображения
Одним из наиболее важных преимуществ МРТ перед другими методами визуализации является возможность создания контраста между различными типами мягких тканей. Это связано с тем, что разные типы мягких тканей имеют разные характерные времена релаксации Т1 и Т2. Зависимость МР-сигнала конкретной ткани от ее релаксационных свойств регулируется выбором параметров импульсной последовательности. Для последовательностей импульсов спинового эха угол поворота возбуждения фиксируется на 9°.0° и выбор TR и TE контролируют только влияние времени релаксации ткани T1 и T2 на сигнал. Для последовательностей импульсов градиентного эха TR, TE и угол поворота контролируют влияние времени релаксации ткани T1 и T2* на сигнал.
Контраст и взвешивание спинового эха
Для последовательностей импульсов спинового эха добавление импульса перефокусировки на 180° устраняет эффект Т2*-релаксации и определяет, что на амплитуду спинового эха влияет только Т2-релаксация. TR и TE выбираются для взвешивания контраста изображения таким образом, чтобы он либо в первую очередь зависел от различий во временах релаксации T1 (T1-взвешенный), либо в основном зависел от различий во временах релаксации T2 (T2-взвешенный). Если параметры выбраны таким образом, что на контрастность изображения не влияют ни различия T1, ни T2, говорят, что тканевый сигнал в первую очередь взвешен по «плотности протонов». TR управляет взвешиванием T1, а TE управляет взвешиванием T2.
Т1-взвешенное спиновое эхо
Выбор параметра для Т1-взвешенного спинового эха — короткий TR и короткий TE (рис. 15). Выбор короткого ТР определяет, что ткани с длинным Т1 (например, жидкость) будут восстанавливаться меньше, чем ткани с коротким Т1 (например, жир)). Это определяет начальное значение поперечной намагниченности M xy при подаче следующего РЧ-импульса. Ткани, которые восстанавливаются медленнее, будут иметь меньшую продольную намагниченность перед следующим РЧ-импульсом, что приведет к меньшей поперечной намагниченности после РЧ-импульса. Короткий TE ограничивает влияние различных скоростей затухания T2. Таким образом, результирующий контраст называется Т1-взвешенным. Т1-взвешенные спиновые эхо-изображения обычно характеризуются ярким сигналом от жира и слабым сигналом от жидкости и полезны для анатомической визуализации, где требуется высокий контраст между жиром, мышцами и жидкостью. При визуализации сердца последовательность импульсов синхронизируется с сердечным циклом, поэтому TR определяется частотой сердечных сокращений пациента. Для Т1-взвешенной визуализации TR устанавливается на один интервал RR, а TE устанавливается на короткое значение, чтобы минимизировать взвешивание T2.
Это определяет начальное значение поперечной намагниченности M xy при подаче следующего РЧ-импульса. Ткани, которые восстанавливаются медленнее, будут иметь меньшую продольную намагниченность перед следующим РЧ-импульсом, что приведет к меньшей поперечной намагниченности после РЧ-импульса. Короткий TE ограничивает влияние различных скоростей затухания T2. Таким образом, результирующий контраст называется Т1-взвешенным. Т1-взвешенные спиновые эхо-изображения обычно характеризуются ярким сигналом от жира и слабым сигналом от жидкости и полезны для анатомической визуализации, где требуется высокий контраст между жиром, мышцами и жидкостью. При визуализации сердца последовательность импульсов синхронизируется с сердечным циклом, поэтому TR определяется частотой сердечных сокращений пациента. Для Т1-взвешенной визуализации TR устанавливается на один интервал RR, а TE устанавливается на короткое значение, чтобы минимизировать взвешивание T2.
Т1-взвешенное спиновое эхо . Кривые релаксации T1 и T2 для T1-взвешенной последовательности импульсов спинового эха (импульс 180° не показан) для двух периодов повторения и для трех разных тканей. Короткий TR приводит к разной степени восстановления z-намагничивания для трех тканей, что приводит к контрасту на основе T1. Короткий TE минимизирует различия из-за различий в релаксации T2. Т1-взвешенные изображения характеризуются ярким жиром и низкой интенсивностью сигнала от статической жидкости.
Кривые релаксации T1 и T2 для T1-взвешенной последовательности импульсов спинового эха (импульс 180° не показан) для двух периодов повторения и для трех разных тканей. Короткий TR приводит к разной степени восстановления z-намагничивания для трех тканей, что приводит к контрасту на основе T1. Короткий TE минимизирует различия из-за различий в релаксации T2. Т1-взвешенные изображения характеризуются ярким жиром и низкой интенсивностью сигнала от статической жидкости.
Полноразмерное изображение
Т2-взвешенное спиновое эхо
Выбор параметра для Т2-взвешенного спинового эха — длинный TR и длинный TE (рис. 16). Выбор длинного TR позволяет восстановить z-намагниченность, близкую к равновесным значениям для большинства тканей, тем самым уменьшая влияние различий во времени релаксации T1. Однако более длительное время эха допускает большее затухание xy-компонента намагниченности. Различная скорость распада между тканью с коротким T2 (например, мышцей) и тканью с длинным T2 (например, жидкостью) приводит к различию в сигнале, который называется T2-взвешенным. Короткий Т2 приводит к уменьшению интенсивности сигнала, а длинный Т2 приводит к увеличению интенсивности сигнала. Эти изображения характеризуются яркой жидкостью и полезны для изображения скоплений жидкости и характеристики сердечных образований и отеков. Для Т2-взвешенных изображений с сердечной синхронизацией TR устанавливается равным двум или трем интервалам RR, в зависимости от частоты сердечных сокращений, чтобы обеспечить длительное TR и минимизировать T1-взвешивание.
Короткий Т2 приводит к уменьшению интенсивности сигнала, а длинный Т2 приводит к увеличению интенсивности сигнала. Эти изображения характеризуются яркой жидкостью и полезны для изображения скоплений жидкости и характеристики сердечных образований и отеков. Для Т2-взвешенных изображений с сердечной синхронизацией TR устанавливается равным двум или трем интервалам RR, в зависимости от частоты сердечных сокращений, чтобы обеспечить длительное TR и минимизировать T1-взвешивание.
Т2-взвешенное спиновое эхо . Кривые релаксации Т1 и Т2 для последовательности импульсов Т2-взвешенного спинового эха (импульс 180° не показан) для трех разных тканей. Длинный TR минимизирует различия из-за различий в релаксации T1. Длинный TE приводит к различному ослаблению намагниченности xy для трех тканей, что приводит к контрасту на основе T2. Т2-взвешенные изображения характеризуются яркой жидкостью и низкой интенсивностью сигнала от мышц.
Полноразмерное изображение
Спиновое эхо, взвешенное по плотности протонов
Выбор параметра для спинового эха, взвешенного по плотности протонов, представляет собой короткий TR и короткий TE (рис. 17). Выбор длинного TR позволяет восстановить z-намагниченность для большинства тканей, тем самым уменьшая влияние различий во времени релаксации T1, а 90-градусный импульс возбуждения, таким образом, передает одинаковую величину сигнала в плоскость xy для всех тканей. Выбор короткого TE ограничивает количество распада T2 для любой ткани во время измерения. Это приводит к высокому сигналу от всех тканей с небольшой разницей между ними. Таким образом, на амплитуду сигнала не сильно влияют релаксационные свойства T1 или релаксационные свойства T2. Таким образом, первичным фактором, определяющим амплитуду сигнала, является равновесная намагниченность ткани, а контраст изображения считается взвешенным по плотности протонов. Этот тип взвешивания полезен, когда требуется изображение анатомической структуры без необходимости введения контраста мягких тканей.
17). Выбор длинного TR позволяет восстановить z-намагниченность для большинства тканей, тем самым уменьшая влияние различий во времени релаксации T1, а 90-градусный импульс возбуждения, таким образом, передает одинаковую величину сигнала в плоскость xy для всех тканей. Выбор короткого TE ограничивает количество распада T2 для любой ткани во время измерения. Это приводит к высокому сигналу от всех тканей с небольшой разницей между ними. Таким образом, на амплитуду сигнала не сильно влияют релаксационные свойства T1 или релаксационные свойства T2. Таким образом, первичным фактором, определяющим амплитуду сигнала, является равновесная намагниченность ткани, а контраст изображения считается взвешенным по плотности протонов. Этот тип взвешивания полезен, когда требуется изображение анатомической структуры без необходимости введения контраста мягких тканей.
Спиновое эхо-взвешенное по плотности протонов . Кривые релаксации Т1 и Т2 для взвешенной по плотности протонов последовательности импульсов спинового эха (импульс 180° не показан) для трех разных тканей. Длинный TR минимизирует различия из-за различий в релаксации T1, в то время как короткий TE минимизирует различия из-за различий в релаксации T2, что приводит к контрасту на основе T2. Изображения, взвешенные по плотности протонов, характеризуются высокой интенсивностью сигнала от большинства тканей и низким контрастом тканей.
Длинный TR минимизирует различия из-за различий в релаксации T1, в то время как короткий TE минимизирует различия из-за различий в релаксации T2, что приводит к контрасту на основе T2. Изображения, взвешенные по плотности протонов, характеризуются высокой интенсивностью сигнала от большинства тканей и низким контрастом тканей.
Полноразмерное изображение
Контраст черной крови в последовательностях импульсов спинового эха
Последовательность импульсов спинового эха создает изображения, которые имеют собственный контраст черной крови при визуализации быстро движущейся крови, протекающей через срез изображения [8]. Это связано с тем, что он использует два импульса, 90 ° и 180 °, для создания сигнала спинового эха. Оба этих импульса селективны по срезам, но разделены временем, равным половине времени эха (рис. 18). Поперечная намагниченность крови, протекающей через срез, которая выходит из среза между двумя импульсами, не перефокусируется 180-градусным импульсом и не способствует генерации спинового эха. Если поток достаточно быстрый для всей крови, получающей 90° импульс для выхода из среза, это приводит к потере сигнала. Этот эффект также известен как эффект вымывания спина, который описывает «вымывание» спинов протонов из среза изображения, которые в противном случае были бы перефокусированы и вносили вклад в сигнал спинового эха. При значительном кровотоке от 90 237 до 90 238 срезов этот внешний вид «черной крови» обеспечивает высокий внутренний контраст между пулом крови и стенками сердца и кровеносных сосудов, что на ранних этапах МРТ сердца приводило к появлению спинового эха в последовательности импульсов. выбор для анатомической визуализации. Однако эффект вымывания при вращении уменьшается, когда кровь медленно движется через плоскость среза изображения или внутри нее. Это приводит к потере контраста темной крови и высокому остаточному сигналу крови, что может привести к значительным артефактам двоения. Поэтому подход, основанный на спиновом эхе, был модифицирован для широкого клинического применения путем добавления схемы подготовки к намагничиванию черной крови [9].
Если поток достаточно быстрый для всей крови, получающей 90° импульс для выхода из среза, это приводит к потере сигнала. Этот эффект также известен как эффект вымывания спина, который описывает «вымывание» спинов протонов из среза изображения, которые в противном случае были бы перефокусированы и вносили вклад в сигнал спинового эха. При значительном кровотоке от 90 237 до 90 238 срезов этот внешний вид «черной крови» обеспечивает высокий внутренний контраст между пулом крови и стенками сердца и кровеносных сосудов, что на ранних этапах МРТ сердца приводило к появлению спинового эха в последовательности импульсов. выбор для анатомической визуализации. Однако эффект вымывания при вращении уменьшается, когда кровь медленно движется через плоскость среза изображения или внутри нее. Это приводит к потере контраста темной крови и высокому остаточному сигналу крови, что может привести к значительным артефактам двоения. Поэтому подход, основанный на спиновом эхе, был модифицирован для широкого клинического применения путем добавления схемы подготовки к намагничиванию черной крови [9]. ], что обеспечивает более надежный контраст черной крови (см. далее).
], что обеспечивает более надежный контраст черной крови (см. далее).
Контраст черной крови из последовательностей импульсов спин-эхо . Появление черной крови при использовании последовательностей импульсов спинового эха вызвано движением крови через срез изображения между импульсами 90° и 180°. Импульс 90° вызывает резонанс во всей ткани внутри среза, однако сигнал спинового эха возникает только тогда, когда та же самая ткань и кровь также получают импульс рефокусировки 180°. Кровь, которая выходит из среза в течение времени между 9Импульсы 0° и 180° не создают спин-эхо, что приводит к пропаданию сигнала, как видно в крупных сосудах на примере изображения спин-эхо черной крови.
Полноразмерное изображение
Градиент-эхо-контраст и взвешивание
Существует несколько типов последовательности импульсов градиент-эхо, каждый из которых имеет совершенно разные характеристики контрастности [10]. Два основных типа последовательности импульсов градиентного эха, используемых для киновизуализации сердца, имеют общие названия: испорченное градиентное эхо и сбалансированная устойчивая свободная прецессия (bSSFP). Производители MR также имеют собственные названия для этих импульсных последовательностей, которые также приведены в следующих разделах:
Производители MR также имеют собственные названия для этих импульсных последовательностей, которые также приведены в следующих разделах:
Spoiled gradient echo
Siemens: FLASH F ast L ow A ngle Sh ot
Philips: T1 FFE T1 -weighted F ast F ield E cho
GE: SPGR SP смазанного маслом GR ( G Radient R ECALLED
A CQUISITIO короткие значения TR (<10 миллисекунд), что приводит к более сложному поведению контраста. Используемые значения TR намного короче, чем времена релаксации T2 крови и миокарда. Это означает, что если поперечная намагниченность, создаваемая каждым РЧ-импульсом, не разрушается после его выборки, она все еще будет существовать при приложении следующего РЧ-импульса. Это может потенциально способствовать или мешать сигналу во время следующего TR. В испорченном градиентном эхо этот сигнал дефазируется (или искажается) либо с помощью градиента спойлера в конце каждого периода TR, либо с помощью метода, известного как искажение rf [11], так что его вклад в последующие периоды TR подавляется. .
.
Импульсные последовательности испорченного градиентного эхо-сигнала следуют контрастному поведению, аналогичному описанному для спин-эхо, однако есть некоторые ключевые отличия. Для последовательностей импульсов градиентного эха отсутствие импульса перефокусировки на 180° определяет, что на амплитуду градиентного эха в TE влияет релаксация T2*. Кроме того, переменный угол поворота импульса возбуждения, а также TR и TE используются для управления контрастом изображения. Эти три параметра могут быть выбраны для взвешивания контраста изображения таким образом, чтобы он либо в первую очередь зависел от различий во временах релаксации T1 (T1-взвешенный), либо в основном зависел от различий во временах релаксации T2* (T2*-взвешенный). Использование малого угла поворота важно для методов искаженного градиентного эха [12, 13], поскольку это позволяет снизить TR до гораздо более низких значений, чем это возможно для методов спинового эха (рис. 19).). Низкий угол поворота, α, обычно выбирается менее 90° (обычно 30° или менее). Хотя это первоначально приводит к меньшей поперечной намагниченности (и, следовательно, к сигналу), поскольку только часть намагниченности по оси z переносится в плоскость xy, намагниченность, которая остается вдоль оси z, возвращается к своему равновесному значению раньше, что позволяет повторение время сократить. В этом случае достигается гораздо большая поперечная намагниченность, следующая за последующими импульсами с малым углом переворота, по сравнению с генерируемой серией из 9импульсы 0° в сочетании с таким же очень коротким TR. Это известно как визуализация с малым углом переворота, и оно формирует основную основу, с помощью которой последовательности испорченных импульсов градиентного эха используются для быстрой визуализации.
Хотя это первоначально приводит к меньшей поперечной намагниченности (и, следовательно, к сигналу), поскольку только часть намагниченности по оси z переносится в плоскость xy, намагниченность, которая остается вдоль оси z, возвращается к своему равновесному значению раньше, что позволяет повторение время сократить. В этом случае достигается гораздо большая поперечная намагниченность, следующая за последующими импульсами с малым углом переворота, по сравнению с генерируемой серией из 9импульсы 0° в сочетании с таким же очень коротким TR. Это известно как визуализация с малым углом переворота, и оно формирует основную основу, с помощью которой последовательности испорченных импульсов градиентного эха используются для быстрой визуализации.
Использование низких углов поворота с последовательностями импульсов градиентного эха . Последовательности градиентного эха могут использовать переменный (низкий) угол поворота для импульса возбуждения, что позволяет использовать гораздо более короткие значения TR без потери слишком большого количества сигнала. Когда используется РЧ-импульс под углом 90° (верхний ряд), короткий TR обеспечивает очень небольшое восстановление между РЧ-импульсами. Намагниченность по оси z быстро уменьшается, что приводит к низкой амплитуде сигнала при его переносе в плоскость xy. Использование малого угла поворота (в данном случае 30 °, нижний ряд) позволяет намагниченности по оси z оставаться намного ближе к ее равновесному значению. Это, при переносе в плоскость xy, приводит к гораздо большему сигналу по сравнению.
Когда используется РЧ-импульс под углом 90° (верхний ряд), короткий TR обеспечивает очень небольшое восстановление между РЧ-импульсами. Намагниченность по оси z быстро уменьшается, что приводит к низкой амплитуде сигнала при его переносе в плоскость xy. Использование малого угла поворота (в данном случае 30 °, нижний ряд) позволяет намагниченности по оси z оставаться намного ближе к ее равновесному значению. Это, при переносе в плоскость xy, приводит к гораздо большему сигналу по сравнению.
Полноразмерное изображение
T1-взвешенное искаженное градиентное эхо
Для искаженного градиентного эха T1-контраст управляется как TR, так и углом поворота.
Кинематографическая визуализация сердца требует использования очень короткого времени повторения, поэтому результирующая последовательность искаженных градиентных эхо-сигналов с коротким TR (<10 мс) и TE (<5 мс) в сочетании с углом поворота около 30° по существу ведет себя как T1-взвешенная последовательность импульсов. Поскольку используется очень короткий TR, миокардиальная ткань или кровь, которые остаются в срезе, становятся насыщенными. Таким образом, эта последовательность зависит от потока крови для создания контраста.
Поскольку используется очень короткий TR, миокардиальная ткань или кровь, которые остаются в срезе, становятся насыщенными. Таким образом, эта последовательность зависит от потока крови для создания контраста.
T2*-взвешенное искаженное градиентное эхо-сигнал
Взвешивание T2* с последовательностями импульсов искаженного градиентного эхо-сигнала достигается путем увеличения TR и TE до относительно длинных значений. Поскольку значения T2* для тканей короче, чем значения T2, время эхо-сигнала, выбранное для достижения взвешивания T2* с помощью градиентного эхо, также намного короче, чем время эхо-сигнала, необходимое для достижения взвешивания T2 с помощью последовательностей спин-эхо. Для Т2*-взвешенного градиентного эха на контрастность изображения сильно влияет наличие эффектов магнитной восприимчивости, и его можно использовать для обнаружения присутствия железа, например, при кровоизлиянии или нагрузке железом на ткань [14].
Balanced steady state free precession (bSSFP)
GE: FIESTA F ast I maging E mploying S teady s T ate A cquisition
Philips: bFFE b alanced F AST F IELD E CHO
SIEMENS: True FISP True F AST I Maging с S Teady P с S TEADY P Secessient
5 Seace Secencient9 DANGINDINGSIENT SEGINDIENT ARESTIENT AREDESTIENT AREDENTIENT AREDESTIENT ARESTIENTIENT
. не портится, а возвращается в фазу в конце каждого периода TR при подаче следующего РЧ-импульса. Затем это переносится в следующее повторение и накладывается на поперечную намагниченность, генерируемую этим РЧ-импульсом. После ряда повторений это приводит к установившемуся состоянию, когда поперечная намагниченность от двух или трех последовательных периодов повторения объединяется, чтобы дать гораздо больший сигнал [15, 16].
не портится, а возвращается в фазу в конце каждого периода TR при подаче следующего РЧ-импульса. Затем это переносится в следующее повторение и накладывается на поперечную намагниченность, генерируемую этим РЧ-импульсом. После ряда повторений это приводит к установившемуся состоянию, когда поперечная намагниченность от двух или трех последовательных периодов повторения объединяется, чтобы дать гораздо больший сигнал [15, 16].
Контрастное поведение последовательностей bSSFP сильно отличается от поведения испорченных последовательностей градиентного эха. Контрастность SSFP связана с соотношением T2/T1 ткани, при этом жидкость и жир, в частности, выглядят ярче, чем другие ткани. Поскольку поперечная намагниченность, возникающая из нескольких TR, объединяется, амплитуда сигнала MR для bSSFP намного больше по сравнению с искаженным градиентным эхом. Увеличенный сигнал позволяет использовать более широкую полосу пропускания приемника, что приводит к более коротким TE и TR по сравнению с последовательностями импульсов с искаженным градиентным эхом и, следовательно, к повышению эффективности визуализации. Однако, если магнитное поле не является однородным, поперечная намагниченность от разных TR может деструктивно компенсировать, а не суммироваться в областях неоднородности магнитного поля, что делает метод SSFP склонным к артефактам темных полос по всему изображению [16]. Поэтому очень важно обеспечить, чтобы магнитное поле было как можно более однородным в интересующей области, чтобы получить изображения без артефактов полос. Это достигается с помощью индивидуального для пациента процесса, называемого динамическим шиммированием, в котором используются градиенты магнитного поля для коррекции неоднородностей поля, создаваемых пациентом. Сохранение TR как можно короче также помогает свести к минимуму артефакты полос, наблюдаемые при визуализации bSSFP.
Однако, если магнитное поле не является однородным, поперечная намагниченность от разных TR может деструктивно компенсировать, а не суммироваться в областях неоднородности магнитного поля, что делает метод SSFP склонным к артефактам темных полос по всему изображению [16]. Поэтому очень важно обеспечить, чтобы магнитное поле было как можно более однородным в интересующей области, чтобы получить изображения без артефактов полос. Это достигается с помощью индивидуального для пациента процесса, называемого динамическим шиммированием, в котором используются градиенты магнитного поля для коррекции неоднородностей поля, создаваемых пациентом. Сохранение TR как можно короче также помогает свести к минимуму артефакты полос, наблюдаемые при визуализации bSSFP.
Яркий контраст крови последовательностей импульсов градиентного эха
В отличие от последовательности импульсов спинового эха, последовательность градиентного эха использует только один РЧ-импульс для генерации сигнала, поэтому эффект вымывания спина не применяется, и сигнал от текущей крови обычно видимый. Действительно, вместо того, чтобы страдать от снижения сигнала, текущая кровь часто появляется с явно повышенным сигналом по сравнению с окружающими тканями [17]. Поэтому последовательность импульсов градиентного эха обычно называют методом визуализации яркой крови.
Действительно, вместо того, чтобы страдать от снижения сигнала, текущая кровь часто появляется с явно повышенным сигналом по сравнению с окружающими тканями [17]. Поэтому последовательность импульсов градиентного эха обычно называют методом визуализации яркой крови.
Очень короткое TR (TR < 10 мс), используемое для быстрой визуализации, означает, что намагниченность ткани, которая остается в срезе изображения, становится частично насыщенной, поскольку РЧ-импульсы быстро воздействуют на ту же ткань, так как времени мало. для восстановления z-намагничивания между импульсами (рис. 20). Это приводит к уменьшению сигнала от неподвижной ткани или крови, которые остаются в срезе. Однако текущая кровь, которая движется в срез, не получала никаких предыдущих импульсов, и поэтому популяция спинов полностью намагничена. Таким образом, движущаяся кровь способна генерировать гораздо более высокий сигнал, чем окружающая ткань, поэтому сигнал крови кажется усиленным или ярким. Этот эффект известен как усиление притока и особенно важен для испорченных последовательностей импульсов градиентного эха, для которых большую роль играет насыщение сигнала крови. При значительном кровотоке через срез яркий сигнал крови обеспечивает хороший внутренний контраст между пулом крови и стенками сердца и кровеносных сосудов. Эффект усиления потока в методах испорченного градиентного эха также используется в качестве основы для времяпролетной МР-ангиографии (TOF MRA). Когда кровь течет медленно через срез или в направлении внутри плоскости среза изображения, усиление притока уменьшается, а яркий контраст крови уменьшается. Усиление притока играет меньшую роль в импульсных последовательностях bSSFP, поскольку яркий сигнал крови в основном возникает из-за внутреннего контраста, основанного на более высоком соотношении T2/T1 для крови по сравнению с таковым для миокарда и стенок сосудов.
При значительном кровотоке через срез яркий сигнал крови обеспечивает хороший внутренний контраст между пулом крови и стенками сердца и кровеносных сосудов. Эффект усиления потока в методах испорченного градиентного эха также используется в качестве основы для времяпролетной МР-ангиографии (TOF MRA). Когда кровь течет медленно через срез или в направлении внутри плоскости среза изображения, усиление притока уменьшается, а яркий контраст крови уменьшается. Усиление притока играет меньшую роль в импульсных последовательностях bSSFP, поскольку яркий сигнал крови в основном возникает из-за внутреннего контраста, основанного на более высоком соотношении T2/T1 для крови по сравнению с таковым для миокарда и стенок сосудов.
Яркий контраст крови из последовательностей импульсов градиентного эха . Последовательности импульсов градиентного эха часто используют очень короткое время повторения, чтобы обеспечить быструю визуализацию. Это приводит к ограниченному восстановлению намагниченности ткани между импульсами. Таким образом, ткань, которая остается в пределах среза, имеет уменьшенный сигнал. Кровь, которая течет через срез изображения, постоянно заменяется полностью намагниченной кровью, которая способна генерировать гораздо более высокий сигнал при подаче импульса возбуждения, что приводит к яркому внешнему виду крови. Усиление, связанное с кровотоком, можно четко увидеть в восходящей и нисходящей аорте на примере градиентного эхо-изображения с яркой испорченной кровью. Обратите внимание, что в основной легочной артерии и предсердиях усиление, связанное с потоком, меньше, поскольку кровь не течет через срез изображения и, следовательно, частично насыщается.
Это приводит к ограниченному восстановлению намагниченности ткани между импульсами. Таким образом, ткань, которая остается в пределах среза, имеет уменьшенный сигнал. Кровь, которая течет через срез изображения, постоянно заменяется полностью намагниченной кровью, которая способна генерировать гораздо более высокий сигнал при подаче импульса возбуждения, что приводит к яркому внешнему виду крови. Усиление, связанное с кровотоком, можно четко увидеть в восходящей и нисходящей аорте на примере градиентного эхо-изображения с яркой испорченной кровью. Обратите внимание, что в основной легочной артерии и предсердиях усиление, связанное с потоком, меньше, поскольку кровь не течет через срез изображения и, следовательно, частично насыщается.
Полноразмерное изображение
Спиновое эхо и градиентное эхо
Импульс возбуждения под углом 90°, используемый последовательностью импульсов спинового эха, переносит всю доступную намагниченность по оси z в поперечную плоскость. Это в сочетании с импульсом перефокусировки на 180 ° дает максимально возможный сигнал при условии, что намагниченность достаточно восстанавливается между повторениями. Эти два атрибута делают метод спинового эха идеально подходящим, когда основной целью является получение изображений с высоким отношением сигнал/шум и пониженной чувствительностью к артефактам, вызванным неоднородностями магнитного поля. Последовательности быстрых импульсов градиентного эха используются там, где скорость визуализации важнее качества изображения. Отсутствие перефокусирующего импульса на 180° в последовательности градиентного эха приводит к потере сигнала при наличии эффектов магнитной восприимчивости и на границе между водными и жировыми тканями. Текущая кровь также выглядит по-разному между двумя последовательностями: спиновое эхо дает характерный вид черной крови, а последовательности импульсов градиентного эха дают характерный вид яркой крови. Ключевые различия между градиентным эхо и методами, основанными на вращении, приведены в таблице 1.
Эти два атрибута делают метод спинового эха идеально подходящим, когда основной целью является получение изображений с высоким отношением сигнал/шум и пониженной чувствительностью к артефактам, вызванным неоднородностями магнитного поля. Последовательности быстрых импульсов градиентного эха используются там, где скорость визуализации важнее качества изображения. Отсутствие перефокусирующего импульса на 180° в последовательности градиентного эха приводит к потере сигнала при наличии эффектов магнитной восприимчивости и на границе между водными и жировыми тканями. Текущая кровь также выглядит по-разному между двумя последовательностями: спиновое эхо дает характерный вид черной крови, а последовательности импульсов градиентного эха дают характерный вид яркой крови. Ключевые различия между градиентным эхо и методами, основанными на вращении, приведены в таблице 1.
Полноразмерная таблица
МР сердечно-сосудистых заболеваний
Синхронизация с сердечным циклом
Для получения изображения сердца, на которое не влияет движение, необходимо, чтобы изображение приобретается всего за несколько десятков миллисекунд. Это означает как ограничение количества шагов фазового кодирования (и, следовательно, пространственного разрешения), так и максимально возможное сокращение TR. Хотя это можно сделать, это происходит за счет значительного снижения качества изображения. С другой стороны, для достижения приемлемого качества изображения время получения изображения становится слишком большим, чтобы «заморозить» движение сердца. Таким образом, для рутинной МРТ МР-сигналы получают в течение нескольких сердечных сокращений, синхронизируя последовательность импульсов и, следовательно, получение сигнала с определенным моментом времени в сердечном цикле. Сердечная синхронизация достигается за счет использования сигнала ЭКГ пациента, полученного путем наложения электродов и электродов ЭКГ на грудную клетку пациента (рис. 21). Программное обеспечение используется для обнаружения зубца R на ЭКГ и для генерации синхронизирующего импульса, который затем используется для синхронизации сбора данных МРТ [18]. Это позволяет получать изображения бьющегося сердца либо в один момент времени (неподвижное изображение), либо в несколько моментов времени в течение сердечного цикла (киносъемка).
Это означает как ограничение количества шагов фазового кодирования (и, следовательно, пространственного разрешения), так и максимально возможное сокращение TR. Хотя это можно сделать, это происходит за счет значительного снижения качества изображения. С другой стороны, для достижения приемлемого качества изображения время получения изображения становится слишком большим, чтобы «заморозить» движение сердца. Таким образом, для рутинной МРТ МР-сигналы получают в течение нескольких сердечных сокращений, синхронизируя последовательность импульсов и, следовательно, получение сигнала с определенным моментом времени в сердечном цикле. Сердечная синхронизация достигается за счет использования сигнала ЭКГ пациента, полученного путем наложения электродов и электродов ЭКГ на грудную клетку пациента (рис. 21). Программное обеспечение используется для обнаружения зубца R на ЭКГ и для генерации синхронизирующего импульса, который затем используется для синхронизации сбора данных МРТ [18]. Это позволяет получать изображения бьющегося сердца либо в один момент времени (неподвижное изображение), либо в несколько моментов времени в течение сердечного цикла (киносъемка).
ЭКГ-синхронизация последовательностей импульсов визуализации . Сердечная синхронизация достигается путем получения сигнала ЭКГ от пациента с использованием электродов и отведений ЭКГ, совместимых с МРТ. Затем используется программный алгоритм для обнаружения комплекса QRS и генерации импульса синхронизации. Это инициирует контроллер последовательности импульсов для создания высокочастотных и градиентных импульсных сигналов, которые усиливаются для управления высокочастотным передатчиком и градиентными катушками. Затем это повторяется, при этом каждый сердечный цикл запускает новое повторение последовательности импульсов.
Полноразмерное изображение
Работа с дыхательными движениями
Для традиционных методов визуализации спинового и градиентного эха градиент фазового кодирования увеличивается с каждым последующим сердечным сокращением, получая одну линию k-пространства при каждом сердечном сокращении и в результате получая визуализацию. раз в несколько минут. Это означает, что изображения с использованием этих методов ухудшаются из-за дыхательных движений. Ухудшение изображения, вызванное дыхательным движением, можно уменьшить, используя один из трех возможных подходов, а именно методы компенсации дыхания (респираторный стробирование), синхронизированные с сердцем методы быстрой визуализации в сочетании с задержкой дыхания пациента или сверхбыстрые (однократные) методы визуализации ( так называемые методы визуализации в реальном времени, описанные ниже). На практике большинство изображений сердца выполняется с задержкой дыхания пациента в сочетании с методами быстрой визуализации, которые описаны в следующем разделе.
раз в несколько минут. Это означает, что изображения с использованием этих методов ухудшаются из-за дыхательных движений. Ухудшение изображения, вызванное дыхательным движением, можно уменьшить, используя один из трех возможных подходов, а именно методы компенсации дыхания (респираторный стробирование), синхронизированные с сердцем методы быстрой визуализации в сочетании с задержкой дыхания пациента или сверхбыстрые (однократные) методы визуализации ( так называемые методы визуализации в реальном времени, описанные ниже). На практике большинство изображений сердца выполняется с задержкой дыхания пациента в сочетании с методами быстрой визуализации, которые описаны в следующем разделе.
Быстрые методы визуализации
Традиционные методы визуализации получают только один шаг фазового кодирования (одну строку k-пространства) за одно сердцебиение. Таким образом, TR для этих последовательностей импульсов определяется частотой сердечных сокращений пациента и равен интервалу R-R. Поэтому неизменно требуется несколько минут, чтобы получить набор данных анатомического изображения с обычным спиновым эхо (SE) или набор данных кинофильма с обычными последовательностями градиентного эха (испорченное градиентное эхо или последовательности импульсов bSSFP). Чтобы преодолеть это ограничение и добиться более короткого времени получения изображения, методы быстрой визуализации получают более одной строки k-пространства при каждом сердечном сокращении [19].]. Это быстрее заполняет k-пространство, что приводит к сокращению времени получения изображения. Последовательности импульсов спинового эха и градиентного эха, в которых используется этот принцип, известны как последовательности турбо или быстрых импульсов.
Поэтому неизменно требуется несколько минут, чтобы получить набор данных анатомического изображения с обычным спиновым эхо (SE) или набор данных кинофильма с обычными последовательностями градиентного эха (испорченное градиентное эхо или последовательности импульсов bSSFP). Чтобы преодолеть это ограничение и добиться более короткого времени получения изображения, методы быстрой визуализации получают более одной строки k-пространства при каждом сердечном сокращении [19].]. Это быстрее заполняет k-пространство, что приводит к сокращению времени получения изображения. Последовательности импульсов спинового эха и градиентного эха, в которых используется этот принцип, известны как последовательности турбо или быстрых импульсов.
Неподвижное изображение (анатомическое изображение черной крови)
Метод синхронизации ЭКГ, используемый для неподвижного изображения, известен как запуск. Импульс синхронизации используется в качестве триггера для запуска последовательности импульсов в определенный момент времени после зубца R в каждом сердечном цикле. Эта временная точка называется задержкой триггера и выбирается системным оператором для определения точки сердечного цикла, в которой сердце должно быть визуализировано. Этот подход к неподвижной визуализации можно использовать для оценки жизнеспособности миокарда или анатомической визуализации коронарной ангиографии, но наиболее рутинным применением является использование его в сочетании с последовательностью импульсов быстрого или турбо-спинового эха для получения изображений черной крови для анатомической визуализации.
Эта временная точка называется задержкой триггера и выбирается системным оператором для определения точки сердечного цикла, в которой сердце должно быть визуализировано. Этот подход к неподвижной визуализации можно использовать для оценки жизнеспособности миокарда или анатомической визуализации коронарной ангиографии, но наиболее рутинным применением является использование его в сочетании с последовательностью импульсов быстрого или турбо-спинового эха для получения изображений черной крови для анатомической визуализации.
Turbo (or fast) spin echo
Philips, Siemens TSE T urbo S pin E cho
GE FSE F ast S pin E cho
The conventional spin echo ( SE) последовательность импульсов генерирует один сигнал спинового эха за счет использования импульса возбуждения, за которым следует импульс рефокусировки на 180°. Последовательность импульсов турбо- или быстрого спинового эха [20, 21] генерирует множественные эхо-сигналы, применяя несколько 180-градусных импульсов после начальных 9 импульсов. импульс 0° (рис. 22). Каждый раз, когда спиновое эхо дефазируется из-за наличия неоднородностей магнитного поля, дефазировка реверсируется приложением дополнительного 180-градусного импульса, генерируя дополнительный соответствующий спиновый эхо. Каждое эхо используется для заполнения новой строки k-пространства путем применения различного количества фазового кодирования к каждому эху перед выборкой данных. Количество эхо-сигналов, полученных для каждого импульса возбуждения, известно как длина последовательности эхо-сигналов (ETL) или «турбофактор». Это эффективно определяет коэффициент, на который ускоряется последовательность импульсов. Например, если выбрано значение ETL, равное 2, в каждом TR заполняется четыре строки k-пространства, а не одна. Обычно используются эхо-последовательности длиной 15 или 16, чтобы сократить время визуализации до периода задержки дыхания. Обратите внимание, что каждый последующий эхо-сигнал в последовательности эхо-сигналов имеет разное время эхо-сигнала, при этом амплитуда каждого эхо-сигнала уменьшается по мере увеличения времени эхо-сигнала в соответствии с затуханием T2.
импульс 0° (рис. 22). Каждый раз, когда спиновое эхо дефазируется из-за наличия неоднородностей магнитного поля, дефазировка реверсируется приложением дополнительного 180-градусного импульса, генерируя дополнительный соответствующий спиновый эхо. Каждое эхо используется для заполнения новой строки k-пространства путем применения различного количества фазового кодирования к каждому эху перед выборкой данных. Количество эхо-сигналов, полученных для каждого импульса возбуждения, известно как длина последовательности эхо-сигналов (ETL) или «турбофактор». Это эффективно определяет коэффициент, на который ускоряется последовательность импульсов. Например, если выбрано значение ETL, равное 2, в каждом TR заполняется четыре строки k-пространства, а не одна. Обычно используются эхо-последовательности длиной 15 или 16, чтобы сократить время визуализации до периода задержки дыхания. Обратите внимание, что каждый последующий эхо-сигнал в последовательности эхо-сигналов имеет разное время эхо-сигнала, при этом амплитуда каждого эхо-сигнала уменьшается по мере увеличения времени эхо-сигнала в соответствии с затуханием T2. Эффективное время эхо-сигнала определяется как время эхо-сигнала, полученного ближе всего к центру k-пространства (с наименьшим градиентом фазового кодирования), поскольку это эхо-сигнал оказывает наибольшее влияние на контрастность изображения. По сравнению с обычной спиновой эхо-визуализацией, изображения, полученные с использованием импульсных последовательностей турбо- или быстрого спин-эхо, характеризуются высокой интенсивностью сигнала от жира, несмотря на его промежуточное значение T2 [6]. Это увеличение сигнала связано с применением быстро повторяющихся 180-градусных РЧ-импульсов, которые разрушают взаимодействие, известное как J – связь, присутствующая между ядрами водорода в молекулах с длинными углеродными цепями. Это взаимодействие приводит к уменьшению времени Т2-релаксации и, следовательно, интенсивности сигнала в обычных спин-эхо-изображениях. Для визуализации сердца обычно используются последовательности импульсов турбо- или быстрого спин-эхо в сочетании со схемой подготовки намагничивания «черная кровь» с двойной инверсией для получения анатомических изображений сердца и крупных сосудов.
Эффективное время эхо-сигнала определяется как время эхо-сигнала, полученного ближе всего к центру k-пространства (с наименьшим градиентом фазового кодирования), поскольку это эхо-сигнал оказывает наибольшее влияние на контрастность изображения. По сравнению с обычной спиновой эхо-визуализацией, изображения, полученные с использованием импульсных последовательностей турбо- или быстрого спин-эхо, характеризуются высокой интенсивностью сигнала от жира, несмотря на его промежуточное значение T2 [6]. Это увеличение сигнала связано с применением быстро повторяющихся 180-градусных РЧ-импульсов, которые разрушают взаимодействие, известное как J – связь, присутствующая между ядрами водорода в молекулах с длинными углеродными цепями. Это взаимодействие приводит к уменьшению времени Т2-релаксации и, следовательно, интенсивности сигнала в обычных спин-эхо-изображениях. Для визуализации сердца обычно используются последовательности импульсов турбо- или быстрого спин-эхо в сочетании со схемой подготовки намагничивания «черная кровь» с двойной инверсией для получения анатомических изображений сердца и крупных сосудов.
Ускоренная спиновая эхо-томография с турбо- или быстрой спин-эхо . Обычная последовательность импульсов спинового эха (слева) применяет один импульс 180 °, следующий за импульсом 90 °, для создания одного спинового эха, заполняющего только одну строку k-пространства в каждом интервале R-R. Последовательность импульсов турбо или быстрого спинового эха (справа) применяет несколько импульсов 180°, следующих за импульсом 90°, для генерации нескольких спиновых эхо. Несколько строк k-пространства заполняются в пределах каждого интервала R-R путем применения к каждому эхо-сигналу градиента фазового кодирования с различной амплитудой. На этой диаграмме каждый градиент фазового кодирования имеет цветовую кодировку, чтобы определить, какая соответствующая строка k-пространства заполнена. Фазовое кодирование, применяемое к каждому эхо-сигналу, удаляется путем применения равных и противоположных градиентов перемотки после выборки каждого эхо-сигнала. В этом примере применяются четыре 180-градусных импульса для генерации четырех спиновых эхо-сигналов (длина серии эхо-сигналов или турбофактор = 4). Это обеспечивает четырехкратное ускорение времени сканирования.
В этом примере применяются четыре 180-градусных импульса для генерации четырех спиновых эхо-сигналов (длина серии эхо-сигналов или турбофактор = 4). Это обеспечивает четырехкратное ускорение времени сканирования.
Полноразмерное изображение
Импульсы подготовки с двойной инверсией Black Blood
Использование только эффекта вымывания для получения контраста темной крови часто приводит к противоречивым результатам из-за недостаточного кровотока. Для повышения эффективности визуализации черной крови обычно используют схему подготовки к намагничиванию черной крови в сочетании с последовательностью импульсов спинового эха [9, 22]. Схема подготовки состоит из добавления двух 180° импульсов РЧ-инверсии с последующей задержкой перед последовательностью импульсов спинового эха (рис. 23). Первый 180-градусный импульс инвертирует намагниченность всей крови и тканей в пределах досягаемости катушки радиочастотного передатчика тела. Второй 180-градусный импульс повторно инвертирует намагниченность только в срезе ткани, подлежащей визуализации. Суммарный эффект этих двух импульсов заключается в инвертировании намагниченности крови и ткани вне среза, в то время как намагниченность внутри среза остается близкой к своему равновесному значению. Затем существует временная задержка перед импульсом возбуждения (время от инверсии, TI). За это время инвертированная намагниченность крови восстанавливается за счет релаксации Т1 от своего начального отрицательного значения к своему положительному равновесному значению. TI рассчитывается равным времени, за которое инвертированная намагниченность крови проходит через ноль. В то время 9Применяется импульс возбуждения 0° последовательности импульсов турбо или быстрого спинового эха. В течение того же периода TI кровоток заставляет кровь с инвертированной намагниченностью перемещаться в срез изображения, заменяя кровь, оставшуюся в равновесии. Поскольку последовательность импульсов спинового эха применяется в тот момент, когда инвертированная намагниченность крови достигает нуля, сигнал от крови не генерируется.
Суммарный эффект этих двух импульсов заключается в инвертировании намагниченности крови и ткани вне среза, в то время как намагниченность внутри среза остается близкой к своему равновесному значению. Затем существует временная задержка перед импульсом возбуждения (время от инверсии, TI). За это время инвертированная намагниченность крови восстанавливается за счет релаксации Т1 от своего начального отрицательного значения к своему положительному равновесному значению. TI рассчитывается равным времени, за которое инвертированная намагниченность крови проходит через ноль. В то время 9Применяется импульс возбуждения 0° последовательности импульсов турбо или быстрого спинового эха. В течение того же периода TI кровоток заставляет кровь с инвертированной намагниченностью перемещаться в срез изображения, заменяя кровь, оставшуюся в равновесии. Поскольку последовательность импульсов спинового эха применяется в тот момент, когда инвертированная намагниченность крови достигает нуля, сигнал от крови не генерируется. Схема подготовки черной крови с двойным импульсом инверсии обеспечивает гораздо лучшее подавление сигнала, поскольку используемая здесь временная задержка (TI) намного больше, чем период времени (TE/2), который приводит к собственному контрасту черной крови обычной последовательности импульсов спинового эха. .
Схема подготовки черной крови с двойным импульсом инверсии обеспечивает гораздо лучшее подавление сигнала, поскольку используемая здесь временная задержка (TI) намного больше, чем период времени (TE/2), который приводит к собственному контрасту черной крови обычной последовательности импульсов спинового эха. .
Схема приготовления черной крови с двойной инверсией . В импульсной схеме приготовления черной крови с двойной инверсией используются два 180° инверсионных РЧ-импульса, чтобы сделать подавление сигнала крови более эффективным. Первый инверсионный импульс, A, не избирательен по срезам и инвертирует намагниченность всей ткани в пределах диапазона действия катушки РЧ-передатчика. Второй инверсионный импульс, B, представляет собой селективный импульс среза, который восстанавливает намагниченность ткани в пределах предполагаемого среза изображения. Чистый эффект импульсов A и B заключается в инвертировании намагниченности всей ткани за пределами предполагаемого среза изображения (показан серым цветом). После предписанного периода восстановления инверсии, TI, выбранного как время, необходимое для того, чтобы намагниченность крови достигла нуля, импульс возбуждения C применяется для генерации сигнала, который зависит от текущего значения z-намагниченности ткани и крови в пределах кусок. В течение того же периода неинвертированная кровь внутри среза (красная), вероятно, была заменена кровью снаружи среза, которая была инвертирована (серая), что привело к образованию сигнальной пустоты внутри сосуда.
После предписанного периода восстановления инверсии, TI, выбранного как время, необходимое для того, чтобы намагниченность крови достигла нуля, импульс возбуждения C применяется для генерации сигнала, который зависит от текущего значения z-намагниченности ткани и крови в пределах кусок. В течение того же периода неинвертированная кровь внутри среза (красная), вероятно, была заменена кровью снаружи среза, которая была инвертирована (серая), что привело к образованию сигнальной пустоты внутри сосуда.
Полноразмерное изображение
Анатомическая визуализация с импульсными последовательностями FSE/TSE черной крови
Наиболее часто используемая последовательность импульсов для анатомической визуализации сочетает схему подготовки черной крови с импульсной последовательностью турбо- или быстрого спин-эхо (рис. 24). Схема приготовления черной крови обеспечивает стабильно высокий контраст между стенками сердца и сосудов и кровяным пулом. Использование последовательности импульсов турбо- или быстрого спинового эхо-сигнала с длиной последовательности эхо-сигналов (турбофактором) от 15 до 20 сокращает время получения изображения, так что оно попадает в типичный период задержки дыхания. В течение каждого периода задержки дыхания обычно получают один или два среза. Регулировка порядка k-пространства в последовательности эхо-сигналов управляет эффективным временем эхо-сигнала и, следовательно, T2-взвешиванием контраста. Для взвешивания T1 выбирается короткое эффективное время эхо-сигнала, и последовательность импульсов запускается при каждом сердечном сокращении, чтобы сократить время повторения. Для взвешивания T2 используется длительное эффективное время эхо-сигнала, а последовательность импульсов запускается только через каждые два или три удара сердца для достижения длительного времени повторения. При необходимости для подавления сигнала от жира может также применяться частотно-избирательное подавление жира. Временная задержка (TI) после схемы приготовления черной крови автоматически рассчитывается программным обеспечением системы MR, чтобы обеспечить наилучшее подавление сигнала от крови. Это зависит от TR последовательности импульсов, которая определяется частотой сердечных сокращений пациента и количеством сердечных сокращений между каждым триггерным импульсом.
В течение каждого периода задержки дыхания обычно получают один или два среза. Регулировка порядка k-пространства в последовательности эхо-сигналов управляет эффективным временем эхо-сигнала и, следовательно, T2-взвешиванием контраста. Для взвешивания T1 выбирается короткое эффективное время эхо-сигнала, и последовательность импульсов запускается при каждом сердечном сокращении, чтобы сократить время повторения. Для взвешивания T2 используется длительное эффективное время эхо-сигнала, а последовательность импульсов запускается только через каждые два или три удара сердца для достижения длительного времени повторения. При необходимости для подавления сигнала от жира может также применяться частотно-избирательное подавление жира. Временная задержка (TI) после схемы приготовления черной крови автоматически рассчитывается программным обеспечением системы MR, чтобы обеспечить наилучшее подавление сигнала от крови. Это зависит от TR последовательности импульсов, которая определяется частотой сердечных сокращений пациента и количеством сердечных сокращений между каждым триггерным импульсом.
Анатомическая визуализация черной крови с турбо- или быстрым спин-эхо . Схема подготовки черной крови применяется в начале сердечного цикла с получением изображения в диастолу. Точная продолжительность инверсии Black Blood, TI Blood , рассчитывается для обеспечения наилучшего подавления крови и зависит от частоты сердечных сокращений и количества ударов сердца между каждым триггерным импульсом (обычно TI Blood = 400-600 миллисекунд). Последовательность импульсов турбо- или быстрого спин-эхо позволяет получить один или два среза за одну задержку дыхания пациента. Шесть изображений справа были получены с использованием шести отдельных задержек дыхания.
Полноразмерное изображение
Общей проблемой этой последовательности импульсов является потеря сигнала от миокарда из-за движения реинвертированной ткани миокарда за пределы среза изображения между временем схемы подготовки черной крови и временем сбор данных турбо- или быстрого спин-эхо. Этот эффект можно уменьшить, увеличив толщину среза ткани, который повторно инвертируется вторым 180-градусным импульсом схемы подготовки черной крови. Хотя толщина среза изображения обычно может составлять 6-8 мм, более подходящим значением для импульса подготовки инверсии черной крови является 20 мм. Точный выбор зависит от степени смещения миокарда через срез и требует некоторой корректировки в зависимости от задержки триггера, ориентации среза и его расположения в сердце.
Этот эффект можно уменьшить, увеличив толщину среза ткани, который повторно инвертируется вторым 180-градусным импульсом схемы подготовки черной крови. Хотя толщина среза изображения обычно может составлять 6-8 мм, более подходящим значением для импульса подготовки инверсии черной крови является 20 мм. Точный выбор зависит от степени смещения миокарда через срез и требует некоторой корректировки в зависимости от задержки триггера, ориентации среза и его расположения в сердце.
Кинематографическая визуализация
Кинематографическая визуализация требует использования очень короткого времени повторения и поэтому может быть достигнута только с использованием последовательностей импульсов на основе градиентного эха. Он включает сбор данных в несколько моментов времени, известных как сердечные фазы, на протяжении всего сердечного цикла (рис. 25). Задержка триггера для первой временной точки устанавливается на кратчайшее возможное время после зубца R, чтобы можно было получать изображения с начала сердечного цикла. Данные, полученные в рамках каждой сердечной фазы, заполняют отдельное k-пространство, что приводит к реконструкции отдельного изображения, соответствующего каждой сердечной фазе. Затем изображения для всех сердечных фаз просматриваются в виде последовательности фильмов или видеороликов, что позволяет проводить функциональную оценку сердца, движение его стенок и визуальную качественную оценку кровотока.
Данные, полученные в рамках каждой сердечной фазы, заполняют отдельное k-пространство, что приводит к реконструкции отдельного изображения, соответствующего каждой сердечной фазе. Затем изображения для всех сердечных фаз просматриваются в виде последовательности фильмов или видеороликов, что позволяет проводить функциональную оценку сердца, движение его стенок и визуальную качественную оценку кровотока.
Кинематографическая градиентная эхо-визуализация: синхронизация ЭКГ по сравнению с ретроспективным стробированием ЭКГ . Кинематографическое изображение достигается путем сбора данных для одного местоположения среза в несколько моментов времени на протяжении сердечного цикла. Затем реконструируются несколько изображений в соответствующие моменты времени, известные как фазы сердца. Затем эти изображения просматриваются как фильм, что позволяет визуализировать работу сердца и модели кровотока. Запуск ЭКГ (вверху) инициирует сбор данных о первой сердечной фазе сразу после зубца R и получает заранее определенное количество сердечных фаз. Сбор данных должен быть остановлен до окончания сердечного цикла, чтобы можно было обнаружить следующий зубец R. Это приводит к тому, что последняя часть сердечного цикла не отображается. Ретроспективное стробирование ЭКГ (внизу) непрерывно собирает данные и записывает временное положение полученных данных относительно зубца R. Сбор данных продолжается до тех пор, пока k-пространство не будет заполнено на достаточное количество временных точек, и данные не будут ретроспективно отсортированы по фазам сердца. Такой подход позволяет точно сопоставлять данные с концом сердечного цикла, обеспечивая визуализацию всего сердечного цикла.
Сбор данных должен быть остановлен до окончания сердечного цикла, чтобы можно было обнаружить следующий зубец R. Это приводит к тому, что последняя часть сердечного цикла не отображается. Ретроспективное стробирование ЭКГ (внизу) непрерывно собирает данные и записывает временное положение полученных данных относительно зубца R. Сбор данных продолжается до тех пор, пока k-пространство не будет заполнено на достаточное количество временных точек, и данные не будут ретроспективно отсортированы по фазам сердца. Такой подход позволяет точно сопоставлять данные с концом сердечного цикла, обеспечивая визуализацию всего сердечного цикла.
Полноразмерное изображение
Запуск по сравнению с ретроспективным стробированием для киносъемки
Для киносъемки синхронизация сердца может выполняться одним из двух способов: запуск по ЭКГ или стробирование по ЭКГ (рис. 25). При запуске ЭКГ используется максимально короткая задержка триггера, чтобы начать сбор данных сразу после комплекса QRS. Затем данные собираются для нескольких последовательных сердечных фаз почти до конца сердечного цикла. Затем сбор данных останавливается до тех пор, пока не будет получен синхронизирующий импульс от следующего зубца R. Этот метод требует, чтобы система оценила средний интервал R-R для визуализируемого пациента (он либо вводится оператором, либо фиксируется системой МРТ из записи ЭКГ). Затем это используется для определения средней продолжительности сердечного цикла, в течение которого могут быть получены данные, и, следовательно, количества сердечных фаз, которые могут быть получены.
Затем данные собираются для нескольких последовательных сердечных фаз почти до конца сердечного цикла. Затем сбор данных останавливается до тех пор, пока не будет получен синхронизирующий импульс от следующего зубца R. Этот метод требует, чтобы система оценила средний интервал R-R для визуализируемого пациента (он либо вводится оператором, либо фиксируется системой МРТ из записи ЭКГ). Затем это используется для определения средней продолжительности сердечного цикла, в течение которого могут быть получены данные, и, следовательно, количества сердечных фаз, которые могут быть получены.
Следствием этого подхода является наличие «слепой зоны», когда данные не собираются в конце сердечного цикла, пока система ожидает следующего запускающего импульса. Это является недостатком, если важна визуализация диастолической функции или функции митрального и трехстворчатого клапанов. Альтернативой является использование ретроспективного стробирования ЭКГ [23]. Здесь последовательность импульсов работает непрерывно с коротким TR. Импульс синхронизации используется для записи, когда повторение последовательности импульсов совпадает с зубцом «R». Затем данные МР-сигнала из этого и последующих повторений распределяются по соответствующим временным точкам сердечного цикла в конце всего сбора k-пространства. С некоторой доработкой ретроспективный гейт можно успешно использовать при визуализации пациентов с малых вариаций интервала RR от одного удара к другому. Этот метод собирает данные о каждом сердечном сокращении в целом, поэтому для сердечных сокращений разной продолжительности будет записано разное количество точек данных. В конце сбора данных средний интервал сердечных сокращений рассчитывается из всего сбора данных. Временные интервалы между точками данных, полученными при более коротких сердечных сокращениях, растягиваются, а данные о более длинных сердечных сокращениях сжимаются, чтобы соответствовать среднему интервалу сердечных сокращений, обеспечивая отображение всех точек сердечного цикла. Использование ретроспективного стробирования необходимо для таких приложений, как визуализация функции митрального или трехстворчатого клапана или сокращения предсердий.
Импульс синхронизации используется для записи, когда повторение последовательности импульсов совпадает с зубцом «R». Затем данные МР-сигнала из этого и последующих повторений распределяются по соответствующим временным точкам сердечного цикла в конце всего сбора k-пространства. С некоторой доработкой ретроспективный гейт можно успешно использовать при визуализации пациентов с малых вариаций интервала RR от одного удара к другому. Этот метод собирает данные о каждом сердечном сокращении в целом, поэтому для сердечных сокращений разной продолжительности будет записано разное количество точек данных. В конце сбора данных средний интервал сердечных сокращений рассчитывается из всего сбора данных. Временные интервалы между точками данных, полученными при более коротких сердечных сокращениях, растягиваются, а данные о более длинных сердечных сокращениях сжимаются, чтобы соответствовать среднему интервалу сердечных сокращений, обеспечивая отображение всех точек сердечного цикла. Использование ретроспективного стробирования необходимо для таких приложений, как визуализация функции митрального или трехстворчатого клапана или сокращения предсердий.
В то время как ретроспективный гейт хорошо работает при небольших вариациях интервала R-R от одного сокращения к другому, визуализация пациентов с большими вариациями от одного сокращения к другому проблематична. Для случайных аритмий обычно есть возможность отклонить точки данных, полученные от чрезмерно длинных или коротких сердечных сокращений, и получить их повторно. Это известно как отторжение аритмии. Однако в случаях, когда имеется много аритмий, отклонение данных нецелесообразно, и единственными вариантами являются возврат к триггерному сбору данных, если требуется только систолическая информация, или использование сбора данных изображения «в реальном времени», для которого синхронизация ЭКГ не требуется [24–27]. Последний подход может быть реализован только за счет временного и пространственного разрешения.
Турбо (или быстрая) последовательность импульсов градиентного эха
Ускорение киноградиентного эхо-изображения достигается простым быстрым повторением последовательности импульсов градиентного эха несколько раз для получения ряда линий k-пространства в каждой сердечной фазе (рис. 26). Каждая полученная группа линий k-пространства называется кадром. Это повторяется для каждой сердечной фазы, а затем для каждого сердечного сокращения, каждый раз приобретая другую группу линий в каждом последующем сердечном сокращении, пока не будет заполнено все k-пространство. Это известно как сегментированная градиентная эхо-визуализация в k-пространстве, поскольку k-пространство сегментировано на серию групп линий [28, 29].], и иногда его называют множественной визуализацией снимков.
26). Каждая полученная группа линий k-пространства называется кадром. Это повторяется для каждой сердечной фазы, а затем для каждого сердечного сокращения, каждый раз приобретая другую группу линий в каждом последующем сердечном сокращении, пока не будет заполнено все k-пространство. Это известно как сегментированная градиентная эхо-визуализация в k-пространстве, поскольку k-пространство сегментировано на серию групп линий [28, 29].], и иногда его называют множественной визуализацией снимков.
Ускоренная киносъемка с турбо- или быстрым градиентным эхо . В обычной последовательности импульсов градиентного эха (слева) применяется одиночный ВЧ-импульс с малым углом переворота для создания одиночного градиентного эхо-сигнала. Одна строка k-пространства заполняется каждый интервал R-R для каждой сердечной фазы. Последовательность импульсов турбо- или быстрого градиентного эхо-сигнала (справа) быстро повторяет радиоимпульс с малым углом поворота для создания нескольких градиентных эхо-сигналов. Несколько строк k-пространства заполняются в пределах каждого интервала R-R путем применения различной амплитуды градиента фазового кодирования к каждому эху. На этой диаграмме каждый градиент фазового кодирования имеет цветовую кодировку, соответствующую заполненной линии k-пространства. В этом примере четыре РЧ-импульса применяются для генерации четырех градиентных эхо-сигналов, настройка параметра, известная как турбофактор = 4 (Philips), количество сегментов = 4 (Siemens), количество просмотров на сегмент = 4 (GE). Это составляет один «выстрел». Остальные строки k-пространства заполняются путем получения нескольких снимков в течение последовательных сердечных сокращений. Это обеспечивает четырехкратное ускорение времени получения изображения.
Несколько строк k-пространства заполняются в пределах каждого интервала R-R путем применения различной амплитуды градиента фазового кодирования к каждому эху. На этой диаграмме каждый градиент фазового кодирования имеет цветовую кодировку, соответствующую заполненной линии k-пространства. В этом примере четыре РЧ-импульса применяются для генерации четырех градиентных эхо-сигналов, настройка параметра, известная как турбофактор = 4 (Philips), количество сегментов = 4 (Siemens), количество просмотров на сегмент = 4 (GE). Это составляет один «выстрел». Остальные строки k-пространства заполняются путем получения нескольких снимков в течение последовательных сердечных сокращений. Это обеспечивает четырехкратное ускорение времени получения изображения.
Полноразмерное изображение
Параметр, определяющий количество строк k-пространства, получаемых в каждом снимке, зависит от производителя следующим образом:
Philips turbofactor
Siemens количество сегментов*
GE просмотров на сегмент
(*Обратите внимание, что в интерфейсе Siemens одна строка k-пространства называется сегментом). Это определяет коэффициент ускорения для конкретной последовательности импульсов. Для функциональной визуализации он также определяет длину окна сбора данных, соответствующую каждой фазе сердечного цикла. Увеличение «турбофактора» уменьшает время сканирования (сокращает продолжительность задержки дыхания), но увеличивает окно сбора данных для каждой сердечной фазы, тем самым ограничивая количество сердечных фаз, которые могут быть отображены, что приводит к более низкой частоте кадров кино или более плохому временному показателю. разрешающая способность. Таким образом, для максимального увеличения количества сердечных фаз и минимизации периода задержки дыхания способность МР-системы достигать очень коротких значений TR является преимуществом.
Это определяет коэффициент ускорения для конкретной последовательности импульсов. Для функциональной визуализации он также определяет длину окна сбора данных, соответствующую каждой фазе сердечного цикла. Увеличение «турбофактора» уменьшает время сканирования (сокращает продолжительность задержки дыхания), но увеличивает окно сбора данных для каждой сердечной фазы, тем самым ограничивая количество сердечных фаз, которые могут быть отображены, что приводит к более низкой частоте кадров кино или более плохому временному показателю. разрешающая способность. Таким образом, для максимального увеличения количества сердечных фаз и минимизации периода задержки дыхания способность МР-системы достигать очень коротких значений TR является преимуществом.
Для визуализации киноградиентного эха с задержкой дыхания этот метод ускоренного получения изображения можно применять как к искаженным градиентным эхо, так и к импульсным последовательностям bSSFP, обычно используемым для визуализации сердца. Названия конкретных поставщиков для «турбо» или «быстрых» версий этих последовательностей приведены ниже:
Названия конкретных поставщиков для «турбо» или «быстрых» версий этих последовательностей приведены ниже:
Быстрое испорченное градиентное эхо.
Siemens TFL T urbo FL ASH
Philips T1-TFE T1- взвешенный T urbo F IELD E CHO
GE FSPGR F AST SP Смазая GR ASS
САДАННЫЙ СТАРИЧЕСКИЙ СТАВИТЬ. F ield E cho
GE FIESTA F ast I maging E mploying S teady s T ate A cquisition
Functional imaging with turbo or fast cine gradient echo pulse sequences
Визуализация сердечной функции, включая оценку движения стенок и объемную оценку, выполняется с использованием метода киноградиентного эха «яркая кровь», который получает изображения в нескольких фазах сердца, которые отображаются в виде видеоролика. Наиболее распространенным подходом к киносъемке является сочетание ретроспективного стробирования с турбо-методом или методом быстрого градиентного эха (рис. 27). Это позволяет визуализировать весь сердечный цикл в течение одного периода задержки дыхания. Выбор последовательности импульсов градиентного эха зависит от напряженности поля и конкретного применения. При 1,5 Тесла сбалансированная последовательность градиентного эха SSFP используется для большинства приложений функциональной визуализации и объемных оценок из-за высокого внутреннего контраста, который достигается между кровью и миокардом на протяжении всего сердечного цикла [30–33]. Наличие артефактов изначально ограничивало использование импульсной последовательности bSSFP при 3,0 Тл [34], хотя она успешно использовалась в клинической практике, а последние технические достижения показали, что возможны улучшения качества и надежности этого метода при 3,0 Тл. [35–37]. Последовательность испорченных импульсов градиентного эха часто используется для оценки заболеваний клапанов и струй потока из-за ее большей чувствительности к потоку. Его также часто используют вместо метода bSSFP при 3,0 Тл, поскольку он менее подвержен артефактам [34, 36].
27). Это позволяет визуализировать весь сердечный цикл в течение одного периода задержки дыхания. Выбор последовательности импульсов градиентного эха зависит от напряженности поля и конкретного применения. При 1,5 Тесла сбалансированная последовательность градиентного эха SSFP используется для большинства приложений функциональной визуализации и объемных оценок из-за высокого внутреннего контраста, который достигается между кровью и миокардом на протяжении всего сердечного цикла [30–33]. Наличие артефактов изначально ограничивало использование импульсной последовательности bSSFP при 3,0 Тл [34], хотя она успешно использовалась в клинической практике, а последние технические достижения показали, что возможны улучшения качества и надежности этого метода при 3,0 Тл. [35–37]. Последовательность испорченных импульсов градиентного эха часто используется для оценки заболеваний клапанов и струй потока из-за ее большей чувствительности к потоку. Его также часто используют вместо метода bSSFP при 3,0 Тл, поскольку он менее подвержен артефактам [34, 36]. Сравнение клинических применений методов искаженного градиентного эхо и bSSFP приведено в таблице 2.
Сравнение клинических применений методов искаженного градиентного эхо и bSSFP приведено в таблице 2.
Яркая функциональная киновизуализация крови с ретроспективно стробируемым турбо- или быстрым градиентным эхо . Для этого приложения можно использовать либо испорченный градиентный эхо-сигнал, либо сбалансированные последовательности импульсов SSFP. Количество строк k-пространства, полученных в каждой сердечной фазе (в этом примере = 4), определяет время сбора для этой последовательности (обычно в течение одного периода задержки дыхания). Увеличение количества строк (турбофактор, количество сегментов или количество просмотров на сегмент) сокращает время сбора данных, но увеличивает время между фазами сердца (интервал фаз сердца или «TR»), что приводит к ухудшению временного разрешения. Последовательности импульсов bSSFP могут достигать более короткого TR, что приводит к более коротким периодам задержки дыхания для того же пространственного и временного разрешения. Примеры изображений показывают конечную диастолическую фазу (сердечная фаза 1) для испорченного градиентного эхо (слева) и bSSFP (справа). Обратите внимание, что сигнал крови имеет большую зависимость от потока для метода испорченного градиентного эха, когда бассейн крови левого желудочка (через плоский поток) намного ярче, чем правый желудочек (плоский поток), тогда как для метода bSSFP они имеют одинаковую яркость из-за к внутреннему контрасту между кровью и миокардом по соотношению Т2/Т1. Точно так же медленно движущаяся кровь, прилегающая к границе эндокарда, частично насыщена на искаженном градиентном эхо-изображении, что приводит к ухудшению определения границы эндокарда. Это приводит к систематическим различиям в объемных измерениях между двумя методами, при этом методы bSSFP дают большие объемы и меньшие массы желудочков.
Примеры изображений показывают конечную диастолическую фазу (сердечная фаза 1) для испорченного градиентного эхо (слева) и bSSFP (справа). Обратите внимание, что сигнал крови имеет большую зависимость от потока для метода испорченного градиентного эха, когда бассейн крови левого желудочка (через плоский поток) намного ярче, чем правый желудочек (плоский поток), тогда как для метода bSSFP они имеют одинаковую яркость из-за к внутреннему контрасту между кровью и миокардом по соотношению Т2/Т1. Точно так же медленно движущаяся кровь, прилегающая к границе эндокарда, частично насыщена на искаженном градиентном эхо-изображении, что приводит к ухудшению определения границы эндокарда. Это приводит к систематическим различиям в объемных измерениях между двумя методами, при этом методы bSSFP дают большие объемы и меньшие массы желудочков.
Полноразмерное изображение
Таблица 2. Градиентное эхо с искажениями в сравнении с киноизображением bSSFP.Полноразмерная таблица
Ключевым параметром для последовательностей киноимпульсов является количество строк k-пространства, полученных в каждой фазе сердца (турбофактор, количество сегментов или количество просмотров на сегмент). Увеличение значения этого параметра сокращает время сбора данных, но также увеличивает время между сердечными фазами. Это уменьшает количество сердечных фаз в сердечном цикле и, следовательно, частоту кадров кино или «временное разрешение» получения изображения (способность разрешать более быстрое движение). Визуализация «в реальном времени» достигается за счет выбора очень высокого турбофактора [24–27], так что получение всего изображения выполняется в одной сердечной фазе при одном сердечном сокращении (однократное получение). Поскольку все этапы фазового кодирования получаются за одно сердечное сокращение, синхронизация сердца не требуется для визуализации в реальном времени. Недостатком высокого турбофактора является низкая частота кадров в кино. Приемлемая частота кадров может быть достигнута только за счет уменьшения общего количества получаемых строк в k-пространстве. Таким образом, визуализация в реальном времени страдает от плохого временного и пространственного разрешения, хотя использование параллельных изображений [38–40] может помочь сохранить пространственно-временное разрешение.
Увеличение значения этого параметра сокращает время сбора данных, но также увеличивает время между сердечными фазами. Это уменьшает количество сердечных фаз в сердечном цикле и, следовательно, частоту кадров кино или «временное разрешение» получения изображения (способность разрешать более быстрое движение). Визуализация «в реальном времени» достигается за счет выбора очень высокого турбофактора [24–27], так что получение всего изображения выполняется в одной сердечной фазе при одном сердечном сокращении (однократное получение). Поскольку все этапы фазового кодирования получаются за одно сердечное сокращение, синхронизация сердца не требуется для визуализации в реальном времени. Недостатком высокого турбофактора является низкая частота кадров в кино. Приемлемая частота кадров может быть достигнута только за счет уменьшения общего количества получаемых строк в k-пространстве. Таким образом, визуализация в реальном времени страдает от плохого временного и пространственного разрешения, хотя использование параллельных изображений [38–40] может помочь сохранить пространственно-временное разрешение.
Заключение
В этом обзоре изложены основные физические принципы, лежащие в основе наиболее часто используемых методов МРТ сердца. Были объяснены основные принципы генерации МР-сигнала и получения изображения, а также определены ключевые параметры изображения, а также объяснено их влияние на контрастность изображения, разрешение и время сбора данных. Было показано, как методы быстрой спин-эхо и градиентной эхо-визуализации могут сочетаться с методами сердечной синхронизации для обеспечения высококачественной анатомической и функциональной киновизуализации сердца в течение одного периода задержки дыхания.
Ссылки
Балабан Р.С., Питерс Д.К.: Основные принципы сердечно-сосудистого магнитного резонанса. Сердечно-сосудистый магнитный резонанс. Под редакцией: Manning WJ, Pennell DJ. 2010, Филадельфия: Сондерс, 3-18. 2
Глава Google ученый
">Финн П.Дж., Изд.: Физика МРТ. Клиники магнитно-резонансной томографии Северной Америки. 1999, 607-808.
McRobbie DW, Moore EA, Graves MJ, Prince MR: МРТ от изображения к протону. 2006, Кембридж: Издательство Кембриджского университета, 2
Книга Google ученый
Lee VS: МРТ сердечно-сосудистой системы: от физических принципов к практическим протоколам. 2005, Филадельфия: Липпинкотт Уильямс и Уилкинс
Google ученый
Constable RT, Anderson AW, Zhong J, Gore JC: Факторы, влияющие на контраст при МРТ с быстрым спиновым эхом.
 Магнитно-резонансная томография. 1992, 10: 497-511. 10.1016/0730-725Х(92)-Г.
Магнитно-резонансная томография. 1992, 10: 497-511. 10.1016/0730-725Х(92)-Г.КАС Статья пабмед Google ученый
Мезрич Р. Взгляд на k-пространство. Радиология. 1995, 195: 297-315.
КАС Статья пабмед Google ученый
Herfkens RJ, Higgins CB, Hricak H, Lipton MJ, Crooks LE, Lanzer P, Botvinick E, Brundage B, Sheldon PE, Kaufman L: Ядерно-магнитно-резонансная томография сердечно-сосудистой системы: нормальные и патологические результаты. Радиология. 1983, 147: 749-759.
КАС Статья пабмед Google ученый
Симонетти О.П., Финн Дж.П., Уайт Р.Д., Лауб Г., Генри Д.А.: "Черная кровь" Т2-взвешенное инверсионное восстановление МРТ сердца. Радиология. 1996, 199: 49-57.
КАС Статья пабмед Google ученый
">Zur Y, Wood ML, Neuringer LJ: Нарушение поперечной намагниченности в стационарных последовательностях. Магн Резон Мед. 1991, 21: 251-263. 10.1002/мрм.1
0210.КАС Статья пабмед Google ученый
Van der Meulen P, Groen JP, Cuppen JJM: Очень быстрая МРТ с эхо-сигналами поля и возбуждением под малым углом. Магнитно-резонансная томография. 1985, 3: 397-399. 10.1016/0730-725Х(85)-5.
Артикул Google ученый
Frahm J, Haase A, Matthaei D: Быстрая ЯМР-визуализация динамических процессов с использованием метода FLASH. Магн Резон Мед.
0217. 1986, 3: 321-327. 10.1002/мрм.1
1986, 3: 321-327. 10.1002/мрм.1КАС Статья пабмед Google ученый
Anderson LJ, Holden S, Davis B, Prescott E, Charrier CC, Bunce NH, Firmin DN, Wonke B, Porter J, Walker JM, Pennell DJ: Кардиоваскулярный магнитный резонанс T2-star (T2*) для раннего диагностика перегрузки миокарда железом. Европейское сердце J. 2001, 22: 2171-9. 10.1053/euhj.2001.2822.
КАС Статья пабмед Google ученый
Оппельт А., Грауманн Р., Барфусс Х., Фишер Х., Хартл В., Шайор В.: FISP: новая быстрая последовательность МРТ. Электромедика. 54: 15-18.
Шеффлер К., Ленхардт С.: Принципы и применение сбалансированных методов SSFP. Евро Радиол. 2003, 13: 2409-2418. 10.1007/s00330-003-1957-х.
Артикул пабмед Google ученый
">Lanzer P, Barta C, Botvinick EH, Wiesendanger HUD, Modin G, Higgins CB: ЭКГ-синхронизированная МРТ сердца: метод и оценка. Радиология. 1985, 155: 681-686.
КАС Статья пабмед Google ученый
Ридер С.Б., Фаранеш, Аризона: Методы сверхбыстрой последовательности импульсов для магнитно-резонансной томографии сердца. Резонансная визуализация Top Magn. 2000, 11: 312-330. 10.1097/00002142-200012000-00002.
КАС Статья пабмед Google ученый
Hennig J, Naureth A, Freiburg H: RARE-визуализация: метод быстрой визуализации для клинической МРТ. Магн Резон Мед. 1986, 3: 823-833. 10.1002/мрм.1
0602.КАС Статья пабмед Google ученый
">Эдельман Р.Р., Чиен Д., Ким Д.: Быстрая селективная МРТ черной крови. Радиология. 1991, 181: 655-660.
КАС Статья пабмед Google ученый
Ленц Г.В., Хааке Э.М., Уайт Р.Д.: Ретроспективный гейтирование сердца: обзор технических аспектов и будущих направлений. Магнитно-резонансная томография. 1989, 7: 445-455. 10.1016/0730-725С(89)-8.
КАС Статья пабмед Google ученый
Setser RM, Fischer SE, Lorenz CH: Количественная оценка функции левого желудочка с помощью магнитно-резонансных изображений, полученных в режиме реального времени. J Magn Reson Imaging. 2000, 12: 430-438. 10.
 1002/1522-2586(200009)12:3<430::AID-JMRI8>3.0.CO;2-V.
1002/1522-2586(200009)12:3<430::AID-JMRI8>3.0.CO;2-V.КАС Статья пабмед Google ученый
Плейн С., Смит В.Х.Т., Риджуэй Дж.П., Касснер К., Бикок Д.Дж., Блумер Т.Н., Сиванантан М.Ю.: Качественный и количественный анализ региональной динамики стенки левого желудочка с использованием магнитно-резонансной томографии в реальном времени. - Сравнение с обычным получением градиентного эха на задержке дыхания у добровольцев и пациентов. J Magn Reson Imaging. 2001, 14: 23-30. 10.1002/jmri.1146.
КАС Статья пабмед Google ученый
Баркхаузен Дж., Гойен М., Рум С.Г., Эггербрехт Х., Дебатин Дж.Ф., Лэдд М.Е.: Оценка функции желудочков с помощью однократной задержки дыхания в режиме реального времени в стационарном режиме со свободной прецессией. AJR Am J Рентгенол. 2001, 178: 731-735.
Артикул Google ученый
">Аткинсон Д., Эдельман Р.Р.: Киноангиография сердца на одной задержке дыхания с сегментированной последовательностью TurboFLASH. Радиология. 1991, 178: 357-360.
КАС Статья пабмед Google ученый
Sakuma H, Fujita N, Foo TK, Caputo GR, Hartiala SJ, Shimakawa J, Higgins A, B C: Оценка объема и массы левого желудочка с помощью МРТ с задержкой дыхания. Радиология. 1993, 188: 377-380.
КАС Статья пабмед Google ученый
Карр Дж.
 К., Симонетти О., Банди Дж., Ли Д., Перелес С., Финн Дж. П.: Кинематографическая МР-ангиография сердца с сегментированной истинной быстрой визуализацией с установившейся прецессией. Радиология. 2001, 219: 828-834.
К., Симонетти О., Банди Дж., Ли Д., Перелес С., Финн Дж. П.: Кинематографическая МР-ангиография сердца с сегментированной истинной быстрой визуализацией с установившейся прецессией. Радиология. 2001, 219: 828-834.КАС Статья пабмед Google ученый
Плейн С., Блумер Т.Н., Риджуэй Дж.П., Джонс Т., Бейнбридж Г., Сиванантан М.Ю. Стационарная магнитно-резонансная томография сердца со свободной прецессией: сравнение с сегментированной градиентной эхографией в k-пространстве. J Magn Reson Imaging. 2001, 14: 230-236. 10.1002/jmri.1178.
КАС Статья пабмед Google ученый
Рюм Дж., Гойен С.Г., Бак М., Лауб Т., Дебатин Г., Ф.Дж.: МРТ-оценка функции желудочков: истинная быстрая визуализация с устойчивой прецессией по сравнению с быстрой МРТ-киносъемкой под малым углом: технико-экономическое обоснование. Радиология.
 2001, 219: 264-269.
2001, 219: 264-269.Артикул пабмед Google ученый
Thiele H, Nagel E, Paetsch I, Schnackenburg B, Bornstedt A, Kouwenhoven M, Wahl A, Schuler G, Fleck E: Функциональная МРТ сердца с установившейся свободной прецессией (SSFP) значительно улучшает очертание границ эндокарда без контрастные вещества. J Magn Reson Imaging. 2001, 14: 362-367. 10.1002/jmri.1195.
КАС Статья пабмед Google ученый
Michaely HJ, Nael K, Schoenberg SO, Laub G, Reiser MF, Finn JP, Ruehm SG: Анализ сердечной функции - Сравнение магнитно-резонансной томографии сердца 1,5 Тесла и 3,0 Тесла. Инвестируйте Радиол. 2006, 41: 133-140. 10.1097/01.рли.0000192023.96494.аф.
Артикул пабмед Google ученый
Schar M, Kozerke S, Fischer SE, Boesiger P: Визуализация сердечного SSFP при 3 Тесла.
 Магн Резон Мед. 2004, 51: 799-806. 10.1002/мрм.20024.
Магн Резон Мед. 2004, 51: 799-806. 10.1002/мрм.20024.Артикул пабмед Google ученый
Келле С., Нагель Э.: МРТ сердечно-сосудистой системы при 3T. Евр Радиол Suppl. 2007, 17 (Приложение 6): F42-F47. 10.1007/с10406-007-0227-4.
Артикул Google ученый
Lee VS, Hecht EM, Taouli B, Chen Q, Prince K, Oesingmann N: МРТ тела и сердечно-сосудистой системы при 3,0T. Радиология. 2007, 244: 692-705. 10.1148/радиол.2443060582.
Артикул пабмед Google ученый
Дитрих О., Николау К., Винтерспергер Б.Дж., Флатц В., Ниттка М., Петш Р., Кифер Б., Шенберг С.О.: iPAT: Приложения для быстрой МРТ и визуализации сердечно-сосудистой системы. Электромедика. 2002, 70: 133-146.
Google ученый
">МакГи К.П., Деббинс Дж.П., Боскамп Э.Б., Блават Л., Ангелос Л., Кинг К.Ф. Параллельная магнитно-резонансная томография сердца при 3,0 Тесла: техническая осуществимость и преимущества. J Magn Reson Imaging. 2004, 19: 291-297. 10.1002/jmri.20015.
Артикул пабмед Google ученый
Sodickson DK: Клинические методы сердечно-сосудистой магнитно-резонансной томографии. Сердечно-сосудистый магнитный резонанс. Под редакцией: Manning WJ, Pennell DJ. 2002, Нью-Йорк: Черчилль Ливингстон, 3-17.
Google ученый
Бойл Г.Э., Кук Дж., Шихи Н.П., Мини Дж.Ф.: Интерактивная таксономия последовательностей изображений МРТ. Рентгенография. 2006, 26: e24-10.1148/rg.e24. викторина e24
Артикул пабмед Google ученый
Bradley WG, Waluch V, Lai KS, Fernandez EJ, Spalter C: Внешний вид быстро текущей крови на магнитно-резонансных изображениях. AJR Am J Рентгенол. 1993, 1167-1174. 143;
Эйнштейн С., Аутвотер Э., Крессель Х.Ю.: Первые принципы быстрого спинового эха. Magn Reson Q. 1992, 8: 199-244.
ПабМед Google ученый
Lee VS, Resnick D, Bundy JM, Simonetti OP, Lee P, Weinreb JC: Сердечная функция: оценка МРТ на одной задержке дыхания с истинно быстрой визуализацией в реальном времени с установившейся прецессией. Радиология. 2002, 222: 835-842. 10.1148/радиол.2223011156.
Артикул пабмед Google ученый
Ван ден Бринк Дж.С., Ватанабэ Й., Куль К.К., Чанг Т., Мутупиллай Р., Каутерен М.В., Ямада К., Дымарковски С., Богарт Дж., Маки Дж.Х., Матос С., Кассельман Дж.В., Хугевен Р.М.: Влияние SENSE MR на рутинная клиническая практика. Евр Дж Радиол. 2003, 46: 3-27. 10.1016/S0720-048X(02)00333-9.
Артикул пабмед Google ученый
Ссылки на скачивание
Благодарности
Автор выражает благодарность John Biglands за предоставленный дополнительный файл анимации.
Информация о авторе
Авторы и принадлежности
Департамент медицинской физики и инженерии, Leeds Teaching Hospitals NHS Trust, Leeds, UK
John P Ridgway
09000 9000
- 674

Вы также можете искать этого автора в PubMed Google Академия
Автор, ответственный за переписку
Джон П Риджуэй.
Дополнительная информация
Конкурирующие интересы
Автор заявляет об отсутствии конкурирующих интересов.
Вклад авторов
JPR подготовил, прочитал, отредактировал и утвердил окончательный вариант рукописи.
Электронный дополнительный материал
12968_2010_1442_MOESM1_ESM.PPTX
Дополнительный файл 1: Фазовое и частотное кодирование. Анимация PowerPoint, показывающая шаги 2 и 3 в процессе формирования изображения. Шаг 2 применяет градиент магнитного поля в направлении фазового кодирования. Это изменяет резонансную частоту спинов в этом направлении, что приводит к фазовому сдвигу, связанному с положением в этом направлении, когда градиент выключен. Шаг 3 применяет градиент магнитного поля в градиенте частотного кодирования, в результате чего получается резонансная частота, связанная с положением в этом направлении. Сигнал MR измеряется на этапе 3 и представляет собой сумму всех полученных частот. (PPTX 46 КБ)
Сигнал MR измеряется на этапе 3 и представляет собой сумму всех полученных частот. (PPTX 46 КБ)
Оригинальные файлы изображений, представленные авторами
Ниже приведены ссылки на оригинальные файлы изображений, представленные авторами.
Оригинальный файл авторов для рисунка 1
Оригинальный файл авторов для рисунка 2
Оригинальный файл авторов для рисунка 3
АВИС файл для рисунка 5
Авторский файл для рисунка 6
Оригинальный файл авторов для рисунка 7
Оригинальный файл авторов для рисунка 8
Оригинальный файл авторов для рисунка
АВТОРЫ. исходный файл для рисунка 11
Авторский оригинальный файл для рисунка 12
Авторский оригинальный файл для рисунка 13
Авторский оригинальный файл для рисунка 14
Оригинальный файл авторов для рисунка 15
Оригинальный файл авторов для рисунка 16
Оригинальный файл авторов для рисунка 17
АВТОРЫ.
 исходный файл к рис. 19
исходный файл к рис. 19Авторский исходный файл к рис. 20
Авторский исходный файл к рис. 21
Авторский исходный файл к рис. 22
Оригинальный файл авторов для рисунка 23
Оригинальный файл авторов для рисунка 24
Оригинальный файл авторов для рисунка 25
АВТОРЫ. исходный файл для рисунка 27
Авторский оригинальный файл для рисунка 28
Авторский оригинальный файл для рисунка 29
Права и разрешения
Открытый доступ Эта статья опубликована по лицензии компании BioMed Central Ltd. Эта статья находится в открытом доступе и распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 2.0 (https://creativecommons.org/licenses/by/2.0), который разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Перепечатки и разрешения
Об этой статье
16.6 Стоячие волны и резонанс - University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Описывать стоячие волны и объяснять, как они образуются
- Описать моды стоячей волны на струне
- Приведите примеры стоячих волн за пределами волн на струне
На протяжении всей этой главы мы изучали бегущие волны или волны, переносящие энергию из одного места в другое. При определенных условиях волны могут отражаться взад и вперед через определенную область, фактически становясь стационарными. Они называются стоячей волной 9.0098 с .
Другой родственный эффект известен как резонанс. В «Колебаниях» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызывать движение большой амплитуды. Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки родителя с относительно малой амплитудой могут вызвать колебания большой амплитуды. Иногда этот резонанс хорош, например, при воспроизведении музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны относительно большой амплитуды образуются в результате наложения составляющих волн меньшей амплитуды.
Иногда этот резонанс хорош, например, при воспроизведении музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны относительно большой амплитуды образуются в результате наложения составляющих волн меньшей амплитуды.
Стоячие волны
Иногда кажется, что волны не движутся; скорее, они просто вибрируют на месте. Например, вы можете увидеть неподвижные волны на поверхности стакана молока в холодильнике. Вибрации от двигателя холодильника создают волны на молоке, которые колеблются вверх и вниз, но не кажутся движущимися по поверхности. На рис. 16.25 показан эксперимент, который вы можете провести дома. Возьмите миску с молоком и поставьте ее на общий веер. Вибрации от вентилятора будут создавать круговые стоячие волны в молоке. На фото волны видны из-за отражения от лампы. Эти волны образованы суперпозицией двух или более бегущих волн, как показано на рис. 16.26 для двух одинаковых волн, движущихся в противоположных направлениях. Волны движутся сквозь друг друга, и их возмущения добавляются по мере их прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая выглядит как стоящая на месте волна и, таким образом, называется стоячей волной.
16.26 для двух одинаковых волн, движущихся в противоположных направлениях. Волны движутся сквозь друг друга, и их возмущения добавляются по мере их прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая выглядит как стоящая на месте волна и, таким образом, называется стоячей волной.
Рисунок 16.25 На поверхности чаши с молоком, стоящей на вентиляторе, образуются стоячие волны. Вибрации от вентилятора вызывают колебания поверхности молока. Волны видны из-за отражения света от лампы. (кредит: Дэвид Челтон)
Рисунок
16.26
Моментальные снимки двух синусоидальных волн. Красная волна движется в направлении − x , а синяя волна движется в направлении + x . Результирующая волна показана черным цветом. Рассмотрим результирующую волну в точках x=0m,3m,6m,9m,12m,15mx=0m,3m,6m,9m,12m,15m и обратите внимание, что результирующая волна всегда равна нулю в этих точках, независимо от времени. Эти точки известны как фиксированные точки (узлы). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Эти точки известны как фиксированные точки (узлы). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Рассмотрим две одинаковые волны, движущиеся в противоположных направлениях. Первая волна имеет волновую функцию y1(x,t)=Asin(kx−ωt)y1(x,t)=Asin(kx−ωt), а вторая волна имеет волновую функцию y2(x,t)=Asin (kx+ωt)y2(x,t)=Asin(kx+ωt). Волны интерферируют и образуют результирующую волну
y(x,t)=y1(x,t)+y2(x,t),y(x,t)=Asin(kx−ωt)+Asin(kx+ωt).y(x,t)= y1(x,t)+y2(x,t),y(x,t)=Asin(kx−ωt)+Asin(kx+ωt).
Это можно упростить, используя тригонометрическое тождество
sin(α±β)=sinαcosβ±cosαsinβ,sin(α±β)=sinαcosβ±cosαsinβ,
, где α=kxα=kx и β=ωtβ=ωt, что дает нам
y(x,t)=A[sin(kx)cos(ωt)−cos(kx)sin(ωt)+sin(kx)cos(ωt)+cos(kx)sin(ωt)],y(x ,t)=A[sin(kx)cos(ωt)−cos(kx)sin(ωt)+sin(kx)cos(ωt)+cos(kx)sin(ωt)],
, что упрощается до
y(x,t)=[2Asin(kx)]cos(ωt). y(x,t)=[2Asin(kx)]cos(ωt).
y(x,t)=[2Asin(kx)]cos(ωt).
16.14
Обратите внимание, что результирующая волна представляет собой синусоиду, которая является функцией только положения, умноженная на косинусоидальную функцию, которая является функцией только времени. Графики зависимости х ( х , t ) от х для различных моментов времени показаны на рис. 16.26. Красная волна движется в отрицательном направлении x , синяя волна движется в положительном направлении x , а черная волна представляет собой сумму двух волн. Когда красные и синие волны проходят друг через друга, они входят и выходят из конструктивной интерференции и деструктивной интерференции.
Первоначально, в моменты времени t=0,t=0, две волны совпадают по фазе, и в результате получается волна, амплитуда которой в два раза превышает амплитуду отдельных волн. Волны также находятся в фазе в момент времени t=T2.t=T2. На самом деле волны находятся в фазе при любом целом кратном половине периода:
Волны также находятся в фазе в момент времени t=T2.t=T2. На самом деле волны находятся в фазе при любом целом кратном половине периода:
t=nT2, где n=0,1,2,3....(по фазе).t=nT2, где n=0,1,2,3....(по фазе).
В другое время две волны сдвинуты по фазе на 180°(πрадиан)180°(πрадиан), и результирующая волна равна нулю. Это происходит в
t=14T,34T,54T,...,n4T, где n=1,3,5....(в противофазе).t=14T,34T,54T,...,n4T, где n=1,3,5. ...(не в фазе).
Обратите внимание, что некоторые x -позиций результирующей волны всегда равны нулю, независимо от соотношения фаз. Эти позиции называются узлами s . Где встречаются узлы? Рассмотрим решение суммы двух волн
y(x,t)=[2Asin(kx)]cos(ωt).y(x,t)=[2Asin(kx)]cos(ωt).
Нахождение позиций, в которых синусоидальная функция равна нулю, предоставляет позиции узлов.
sin(kx)=0kx=0,π,2π,3π,...2πλx=0,π,2π,3π,...x=0,λ2,λ,3λ2,...=nλ2n=0, 1,2,3,....sin(kx)=0kx=0,π,2π,3π,. ..2πλx=0,π,2π,3π,...x=0,λ2,λ,3λ2 ,...=nλ2n=0,1,2,3,....
..2πλx=0,π,2π,3π,...x=0,λ2,λ,3λ2 ,...=nλ2n=0,1,2,3,....
Есть также позиции, где y колеблется между y=±Ay=±A. Это пучности s . Мы можем найти их, рассмотрев, какие значения x приводят к sin(kx)=±1sin(kx)=±1.
sin(kx)=±1kx=π2,3π2,5π2,...2πλx=π2,3π2,5π2,...x=λ4,3λ4,5λ4,...=nλ4n=1,3,5,. ...sin(kx)=±1kx=π2,3π2,5π2,...2πλx=π2,3π2,5π2,...x=λ4,3λ4,5λ4,...=nλ4n=1,3,5 ,....
В результате получается стоячая волна, как показано на рис. 16.27, на котором показаны снимки результирующей волны двух идентичных волн, движущихся в противоположных направлениях. Результирующая волна выглядит как синусоида с узлами на целых кратных половинах длины волны. Пучности колеблются между y=±2Ay=±2A из-за члена косинуса, cos(ωt)cos(ωt), который колеблется между ±1±1.
Результирующая волна кажется неподвижной, без видимого движения в направлении x , хотя она состоит из одной волновой функции, движущейся в положительном направлении, тогда как вторая волна движется в отрицательном направлении x - направление. На рис. 16.27 показаны различные снимки получившейся волны. Узлы отмечены красными точками, а пучности отмечены синими точками.
На рис. 16.27 показаны различные снимки получившейся волны. Узлы отмечены красными точками, а пучности отмечены синими точками.
Рисунок 16.27 Когда две одинаковые волны движутся в противоположных направлениях, результирующая волна является стоячей волной. Узлы появляются на целых кратных половинах длины волны. Пучности появляются на нечетных кратных четвертям длины волны, где они колеблются между y=±A.y=±A. Узлы отмечены красными точками, а пучности отмечены синими точками.
Типичным примером стоячих волн являются волны, создаваемые струнными музыкальными инструментами. При защипывании струны импульсы проходят по струне в противоположных направлениях. Концы струн закреплены на месте, поэтому на концах струн появляются узлы — граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс струнного инструмента можно смоделировать в физической лаборатории с помощью устройства, показанного на рис. 16.28.
Рисунок
16.28
Лабораторная установка для создания стоячих волн на струне. Струна имеет узел на каждом конце и постоянную линейную плотность. Длина между фиксированными граничными условиями равна л . Подвешенная масса обеспечивает натяжение струны, а скорость волн на струне пропорциональна квадратному корню из натяжения, деленному на линейную плотность массы.
Струна имеет узел на каждом конце и постоянную линейную плотность. Длина между фиксированными граничными условиями равна л . Подвешенная масса обеспечивает натяжение струны, а скорость волн на струне пропорциональна квадратному корню из натяжения, деленному на линейную плотность массы.
Лабораторная установка показывает струну, прикрепленную к струнному вибратору, который колеблет струну с регулируемой частотой f . Другой конец нити проходит через шкив без трения и привязан к подвешенному грузу. Величина натяжения нити равна весу подвешенного груза. Струна имеет постоянную линейную плотность (масса на длину) µµ, а скорость, с которой волна распространяется по струне, равна v=FTµ=mgµv=FTµ=mgµУравнение 16.7. Симметричные граничные условия (узел на каждом конце) определяют возможные частоты, которые могут возбуждать стоячие волны. Начиная с нулевой частоты и медленно увеличивая частоту, появляется первая мода n=1n=1, как показано на рис. 16.29.. Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами λ1=2Lλ1=2L. Основная частота или частота первой гармоники, управляющая этим режимом, равна
16.29.. Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами λ1=2Lλ1=2L. Основная частота или частота первой гармоники, управляющая этим режимом, равна
f1=vλ1=v2L,f1=vλ1=v2L,
, где скорость волны равна v=FTµ.v=FTµ. Сохранение напряжения постоянным и увеличение частоты приводит ко второй гармонике или моде n=2n=2. Эта мода представляет собой полную длину волны λ2=Lλ2=L, а частота в два раза больше основной частоты:
f2=vλ2=vL=2f1.f2=vλ2=vL=2f1.
Рисунок
16.29
Стоячие волны, созданные на струне длиной L . Узел находится на каждом конце строки. Узлы представляют собой граничные условия, ограничивающие возможные частоты, возбуждающие стоячие волны. (Обратите внимание, что амплитуды колебаний были сохранены постоянными для визуализации. Паттерны стоячих волн, возможные на струне, известны как нормальные моды. Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды по мере увеличения частоты.)
Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды по мере увеличения частоты.)
Следующие две моды, или третья и четвертая гармоники, имеют длины волн λ3=23Lλ3=23L и λ4=24L,λ4=24L, обусловленные частотами f3=3v2L=3f1f3=3v2L=3f1 и f4=4v2L=4f1. f4=4v2L=4f1. Все частоты выше частоты f1f1 известны как обертон s . Уравнения для длины волны и частоты можно резюмировать следующим образом:
λn=2nLn=1,2,3,4,5...λn=2nLn=1,2,3,4,5...
16,15
fn=nv2L=nf1n=1,2,3,4,5...fn=nv2L=nf1n=1,2,3,4,5...
16.16
Паттерны стоячих волн, которые возможны для струны, первые четыре из которых показаны на рис. 16.29, известны как нормальная мода s , а частоты известны как нормальные частоты. Таким образом, первая частота, создающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота нормальной моды n=2n=2 струны – это первый обертон (или вторая гармоника). Частотой нормальной моды n=3n=3 является второй обертон (или третья гармоника) и так далее.
Вторая частота нормальной моды n=2n=2 струны – это первый обертон (или вторая гармоника). Частотой нормальной моды n=3n=3 является второй обертон (или третья гармоника) и так далее.
Решения, представленные в уравнениях 16.15 и 16.16, относятся к строке с граничным условием узла на каждом конце. Когда граничные условия с обеих сторон одинаковы, говорят, что система имеет симметричные граничные условия. Уравнение 16.15 и уравнение 16.16 подходят для любых симметричных граничных условий, то есть узлов на обоих концах или пучностей на обоих концах.
Пример 16,7
Стоячие волны на струне
Рассмотрим строку L=2,00 м. L=2,00 м. прикреплен к струнному вибратору с регулируемой частотой, как показано на рис. 16.30. Волны, создаваемые вибратором, распространяются по струне и отражаются фиксированным граничным условием на шкиве. Струна, имеющая линейную массовую плотность µ=0,006 кг/м, µ=0,006 кг/м, пропущена по безфрикционному шкиву незначительной массы, а натяжение обеспечивается подвешенной массой 2,00 кг. а) Какова скорость волн на струне? (b) Нарисуйте первые три нормальные моды стоячих волн, которые могут быть созданы на струне, и обозначьте каждую из них длиной волны. в) Перечислите частоты, на которые должен быть настроен струнный вибратор, чтобы создавать первые три нормальные моды стоячих волн.
а) Какова скорость волн на струне? (b) Нарисуйте первые три нормальные моды стоячих волн, которые могут быть созданы на струне, и обозначьте каждую из них длиной волны. в) Перечислите частоты, на которые должен быть настроен струнный вибратор, чтобы создавать первые три нормальные моды стоячих волн.
Рисунок 16.30 Струна прикреплена к струнному вибратору с регулируемой частотой.
Стратегия
- Скорость волны можно найти, используя v=FTμ.v=FTμ. Натяжение обеспечивается весом подвешенной массы.
- Стоячие волны будут зависеть от граничных условий. На каждом конце должен быть узел. Первая мода будет половиной волны. Второй можно найти, добавив половину длины волны. Это самая короткая длина, которая приведет к узлу на границах. Например, добавление одной четверти длины волны приведет к образованию пучности на границе, а не к моде, удовлетворяющей граничным условиям.
 Это показано на рис. 16.31.
Это показано на рис. 16.31. - Поскольку скорость волны равна длине волны, умноженной на частоту, частота равна скорости волны, деленной на длину волны.
Рисунок 16.31 (a) На рисунке представлена вторая мода струны, которая удовлетворяет граничным условиям узла на каждом конце струны. (b) Эта фигура никак не может быть нормальной модой струны, потому что она не удовлетворяет граничным условиям. На одном конце есть узел, а на другом — пучность.
Решение
- Начните со скорости волны на струне. Натяжение равно весу подвешенного груза. Линейная массовая плотность и масса подвешенного груза даны:
v=FTμ=mgμ=2кг(9,8мс)0,006кгм=57,15м/с.v=FTμ=mgμ=2кг(9,8мс)0,006кгм=57,15м/с.
- Первая нормальная мода, имеющая узел на каждом конце, имеет половину длины волны. Следующие две моды находятся добавлением половины длины волны.
- Частоты первых трех мод находятся с помощью f=vwλ.
 f=vwλ.
f=vwλ.f1=vwλ1=57,15 м/с4,00 м=14,29 Гцf2=vwλ2=57,15 м/с2,00 м=28,58 Гцf3=vwλ3=57,15 м/с1,333 м=42,87 Гцf1=vwλ1=57,15 м/с4,00 м=14,29 Гцf2 =vwλ2=57,15 м/с2,00 м=28,58 Гцf3=vwλ3=57,15 м/с1,333 м=42,87 Гц
Значение
Три режима стояния в этом примере были созданы за счет поддержания натяжения струны и регулировки частоты возбуждения. Поддержание постоянного натяжения струны приводит к постоянной скорости. Те же моды можно было получить, поддерживая постоянную частоту и регулируя скорость волны в струне (путем изменения подвешенной массы).
Интерактивный
Посетите эту симуляцию, чтобы поиграть с одномерной или двумерной системой связанных пружинно-массовых осцилляторов. Меняйте количество масс, задавайте начальные условия и наблюдайте за развитием системы. См. спектр нормальных мод для произвольного движения. См. продольные или поперечные моды в системе 1D.
Проверьте свое понимание 16,7
Уравнения для длин волн и частот мод волны, создаваемой струной:
λn=2nLn=1,2,3,4,5. ..иfn=nv2L=nf1n=1,2,3,4,5...λn=2nLn=1,2,3,4,5.. .andfn=nv2L=nf1n=1,2,3,4,5...
..иfn=nv2L=nf1n=1,2,3,4,5...λn=2nLn=1,2,3,4,5.. .andfn=nv2L=nf1n=1,2,3,4,5...
были получены путем рассмотрения волны на струне с симметричными граничными условиями узла на каждом конце. Эти моды возникли в результате двух синусоидальных волн с идентичными характеристиками, за исключением того, что они двигались в противоположных направлениях и ограничивались областью L с требуемыми узлами на обоих концах. Будут ли работать те же уравнения, если бы были симметричные граничные условия с пучностями на каждом конце? Как бы выглядели нормальные моды для среды, которая могла бы свободно колебаться на каждом конце? Пока не беспокойтесь, если вы не можете представить себе такую среду, просто рассмотрите две синусоидальные волновые функции в области длиной L , с пучностями на каждом конце.
Свободные граничные условия, показанные в последней проверке вашего понимания, могут показаться сложными для визуализации. Как может существовать система, которая может свободно колебаться на каждом конце? На рис. 16.32 показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим цветом). В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия. При заданной частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, равных одной четверти длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При соответствующей частоте этот стержень также может быть приведен в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности. Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длина волны может быть измерена между любыми двумя ближайшими идентичными точками, и рассмотрите рисунок 16.33.
Как может существовать система, которая может свободно колебаться на каждом конце? На рис. 16.32 показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим цветом). В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия. При заданной частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, равных одной четверти длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При соответствующей частоте этот стержень также может быть приведен в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности. Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длина волны может быть измерена между любыми двумя ближайшими идентичными точками, и рассмотрите рисунок 16.33.
Рисунок
16.32
(a) Металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на каждом конце. При движении на правильной частоте стержень может резонировать с длиной волны, равной длине стержня с узлами на каждом конце. (b) Тот же металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца. При движении на правильной частоте стержень может резонировать с длиной волны, равной длине стержня с пучностью на каждом конце.
При движении на правильной частоте стержень может резонировать с длиной волны, равной длине стержня с узлами на каждом конце. (b) Тот же металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца. При движении на правильной частоте стержень может резонировать с длиной волны, равной длине стержня с пучностью на каждом конце.
Рисунок 16.33 Длина волны может быть измерена между двумя ближайшими повторяющимися точками. На волне на струне это означает одинаковую высоту и наклон. (а) Длина волны измеряется между двумя ближайшими точками, где высота равна нулю, а наклон максимален и положителен. (b) Длина волны измеряется между двумя одинаковыми точками, где высота максимальна, а наклон равен нулю.
Обратите внимание, что изучение стоячих волн может стать довольно сложным. На рис. 16.32(а) показана мода n=2n=2 стоячей волны, что приводит к длине волны, равной л . В этой конфигурации также была бы возможна мода n=1n=1 со стоячей волной, равной 2 L . Можно ли получить режим n=1n=1 для конфигурации, показанной в части (b)? Ответ - нет. В этой конфигурации помимо граничных условий задаются дополнительные условия. Так как стержень установлен в точке на четверть длины с каждой стороны, там должен существовать узел, а это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения рассмотреть, возможны ли другие виды стоячих волн. Следует отметить, что когда система приводится в действие на частоте, не вызывающей резонанса системы, вибрации все же могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
В этой конфигурации также была бы возможна мода n=1n=1 со стоячей волной, равной 2 L . Можно ли получить режим n=1n=1 для конфигурации, показанной в части (b)? Ответ - нет. В этой конфигурации помимо граничных условий задаются дополнительные условия. Так как стержень установлен в точке на четверть длины с каждой стороны, там должен существовать узел, а это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения рассмотреть, возможны ли другие виды стоячих волн. Следует отметить, что когда система приводится в действие на частоте, не вызывающей резонанса системы, вибрации все же могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
Область машиностроения использует звук, издаваемый вибрирующими частями сложных механических систем, для устранения проблем с системами. Предположим, что какая-то часть автомобиля резонирует на частоте двигателя автомобиля, вызывая нежелательные вибрации в автомобиле. Это может привести к преждевременному выходу двигателя из строя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют технику, называемую анализом Фурье, чтобы найти частоты звука, производимого с большой амплитудой, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте. Решение может быть таким же простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Это может привести к преждевременному выходу двигателя из строя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют технику, называемую анализом Фурье, чтобы найти частоты звука, производимого с большой амплитудой, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте. Решение может быть таким же простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Есть и другие многочисленные примеры резонанса стоячих волн в физическом мире. Воздух в трубке, такой как в музыкальном инструменте, таком как флейта, может войти в резонанс и произвести приятный звук, как мы обсуждаем в разделе «Звук».
В других случаях резонанс может вызвать серьезные проблемы. Более пристальный взгляд на землетрясения дает доказательства наличия условий, подходящих для резонанса, стоячих волн, конструктивной и деструктивной интерференции. Здание может вибрировать в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственных колебаний здания, создавая резонанс, в результате которого одно здание рушится, а соседние - нет.

 84)
84)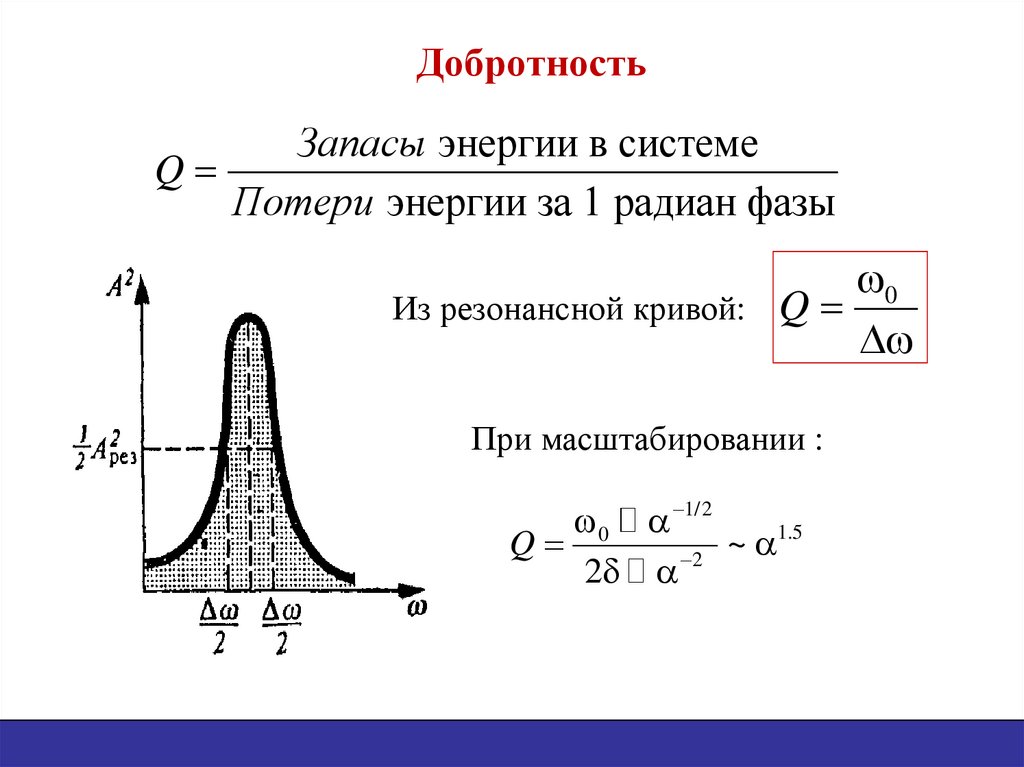 86)
86) 89)
89) 92)
92) 95)
95) 96)
96) В пружинном маятнике — это сила упругости, проекция которой на координатную ось пропорциональна деформации пружины, то есть смещению тела (). Эта сила направлена к положению равновесия. В нитяном маятнике это равнодействующая сил тяжести и упругости, проекция которой тоже пропорциональна смещению тела (), и эта сила тоже стремится к положению равновесия.
В пружинном маятнике — это сила упругости, проекция которой на координатную ось пропорциональна деформации пружины, то есть смещению тела (). Эта сила направлена к положению равновесия. В нитяном маятнике это равнодействующая сил тяжести и упругости, проекция которой тоже пропорциональна смещению тела (), и эта сила тоже стремится к положению равновесия.
