Резонансная частота контура – Справочник химика 21
Резонансная частота контура [c.53]На резонансную частоту контура активная составляющая выражения (П1.78) влияния не оказывает. Приравнивая реактивную составляющую нулю при условии резонанса, получаем выражение зависимости частоты от параметров ячейки и контура [c.144]
Следует указать, что резонансные частоты иногда хорошо заметны на диаграммах самопишущих приборов, регистрирующих работу контуров автоматического регулирования превалирующая в з аш си частота непрерывных колебаний стрелки зачастую оказывается резонансной частотой контура. [c.107]
Измерение с -ячейкой. Для определения зависимости резонансной частоты контура от величины / исследуемого раствора воспользуемся эквивалентной схемой параллельного колебательного контура, изображенного на рис. 95, б. В этом случае применяется эк- [c.144]
Принципиальная схема, реализующая резонансный метод измерения (рис. 3.40, а), состоит из генератора высокой частоты ГВЧ, измерительного колебательного контура L , содержащего образцовые и измеряемые элементы, и индикатора резонанса PV. Плавно изменяя частоту генератора, добиваются ее совпадения с резонансной частотой контура. Момент резонанса определяют с помощью индикатора PV по его максимальному показанию, а резонансную частоту % – по шкале ГВЧ. Настройку контура в резонанс можно произвести и при фиксированной частоте ГВЧ, изменением параметров образцового элемента колебательного контура (нанример, емкости С).
Приборы для измерения свойств растворов на высоких частотах конструируются на основе принципов электронных схем и имеют очень малое сходство с простым мостом для низкочастотных измерений. Обычно образец помещается между пластинами конденсатора, реже — внутри индукционной катушки таким образом, что резонансная частота контура изменяется вследствие поглощения энергии образцом. Сосуд с образцом может являться частью колебательного контура генератора. Тогда наблюдаемой величиной будет сдвиг частоты, вызываемый вве-. дением образца, или, наоборот, сосуд может входить в схему резонансного усилителя, выходное напряжение которого будет уменьшаться при изменении его резонансной частоты. Во многих конструкциях колебательный контур включает в себя калиброванный подстроечный конденсатор, используемый для компенсации изменения реа ктивного сопротивления контура.
Другими словами, резонансная частота контура ше должна превосходить наивысшие существенные частоты, колебаний в 5—10 раз. [c.108]
Изменение диэлектрической постоянной раствора не будет сказываться на показаниях прибора в силу того, что сравниваются потери в контурах, а не резонансные частоты контуров. [c.237]
Принцип автоматического балансирования использован в весах, разработанных для исследования зависимости магнитных свойств материалов от температуры При отклонении коромысла весов от положения равновесия меняется емкость конденсатора С (рис. ХУ.15), включенного в колебательный контур, питаемый током частотой 16 мгц от генератора, стабилизированного кварцем. Изменение резонансной частоты контура вызывает в оконечном
Положим теперь, что частота входного напряжения стала меньше резонансной частоты контура 2 2 Тогда его импеданс будет иметь емкостной характер, так как проводимость емкостной ветви [c.93]
Q — нормированные резонансные частоты контуров. [c.221]
Резонансные частоты контуров выбираются так, чтобы оин совпадали с полюсами функции [c.15]
Генератор зондирующих импульсов содержит два основных элемента колебательный контур, включающий в себя излучающий ЭАП (пьезопреобразователь), и электронную схему, обеспечивающую генерацию коротких радиоимпульсов той или иной формы. В колебательном контуре параллельно или последовательно пьезоэлементу включены индуктивность и активное сопротивление. Иногда применяют трансформаторную связь. Упрощенная схема показана на рис. 2.2, а. Резонансную частоту контура с помощью индуктивности Ь подбирают равной антирезонансной частоте пьезопластины (см. 1.5). Сопротивление резистора Я определяет добротность контура.
Чаще всего используют схему ударного возбуждения колебаний контура, в упрощенном виде показанную на рис. 2Л, а. Резонансную частоту контура с помощью индуктивности I подбирают равной антирезонансной частоте пьезопластины П (см. разд. 1.2.2). Сопротивление резистора К определяет добротность контура. Накопительный конденсатор С заряжают от высокого напряжения U .
Наиболее приемлемым методом измерения емкости при реализации электроемкостных методов НК является резонансный метод, поскольку, обладая небольшой емкостью, измерительные преобразователи имеют относительно высокую добротность. При включении емкостного преобразователя в колебательный контур о значении измеряемой величины можно судить по резонансной частоте контура, а о добротности конденсатора -по добротности контура. Резонансная частота контура с емкостным преобразователем равна [c.596]
После выделения параметров и характеристик объекта выбирают виды их измерений в зависимости от возможности реализации, а также от требуемой точности. При проведении измерений средства измерений взаимодействуют с объектом измерений. При этом объект и средства измерений влияют друг на друга, что может привести к некоторому изменению свойств объекта и показаний измерительного прибора. Так, входное сопротивление подключаемого средства измерений может существенно повлиять на режим работы объекта и привести к погрешности в результатах измерений. При измерениях в цепях переменного тока следует учитывать влияние на объект не только активной составляющей входного сопротивления средства измерений, подключаемого к объекту, но и реактивной. На режим работы объекта и, следовательно, на результат измерений особенно сильно воздействуют емкостные составляющие входных сопротивлений электронных вольтметров и осциллографов. Подключение вольтметра (осцил лографа) к колебательному контуру приводит к снижению резонансной частоты контура за счет входной емкости вольтметра или осциллографа и к снижению добротности контура за счет шунтирующего действия активной составляющей входного сопротивления этих приборов.
www.chem21.info
Колебательный контур | Техника радиоприёма
«Классическая» схема детекторного приемника изображена на рис. 2.1. Она повторяется во всех популярных книжках и даже школьных учебниках. Ниже мы покажем, что этот «классический» детекторный приемник сконструирован неправильно и может быть существенно улучшен, но чтобы понять, каким образом, сначала разберем его схему и назначение деталей подробнее.
Антенна WA1 и заземление присоединены непосредственно к колебательному контуру, образованному катушкой L1 и конденсатором переменной емкости (КПЕ) С1. Колебательный контур служит для выделения из всей массы принимаемых антенной сигналов лишь одного, желаемого. Радиостанции работают на разных частотах, контур также имеет свою, резонансную частоту, и если частота сигнала радиостанции совпадает с частотой настройки контура, напряжение на нем максимально.
Резонансная частота (частота настройки) колебательного контура определяется формулой Томсона: f0 = 1/2π(LС)1/2. Для изменения частоты настройки можно изменять как индуктивность, так и емкость. Чаще всего для настройки в пределах диапазона изменяют емкость (используют КПЕ), а для переключения диапазонов изменяют индуктивность, подключая разные катушки или переключая отводы обмотки.
На резонансной частоте f0 индуктивное сопротивление катушки в точности равно емкостному сопротивлению конденсатора, и оба они носят название характеристическое сопротивление контура ρ: XL = Хс = ρ. Для тех, кто подзабыл, что такое реактивные сопротивления, напомним, что индуктивное сопротивление прямо пропорционально частоте: X
Знак j в математике указывает на мнимую величину, и в электротехнике соответствует реактивному характеру сопротивлений. Реактивные сопротивления не рассеивают мощности, поскольку ток в них сдвинут по фазе относительно напряжения на 90°, в индуктивности ток отстает, а в емкости опережает напряжение.
Если бы в контуре не было больше никаких сопротивлений, кроме равных друг другу индуктивного и емкостного, то свободные колебания тока в контуре на частоте f
Реально всегда имеется активное сопротивление, хотя бы сопротивление провода катушки, показанное на эквивалентной схеме (рис. 2.3а), в виде последовательного сопротивления r. В активном сопротивлении r выделяется мощность, поэтому свободные колебания будут затухать, как показано на рис. 2.4.
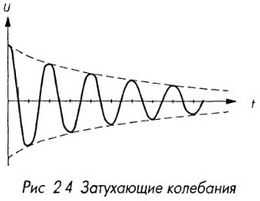
Скорость затухания колебаний определяется добротностью – отношением реактивного сопротивления ρ к активному r: Q = ρ / r. Число свободных колебаний в контуре до их практического прекращения (уменьшения амплитуды примерно до 0,05 от начальной) как раз и равно добротности. Величину, ей обратную, иногда называют затуханием контура. Затухание может вноситься не только последовательным, но и параллельно подключенным сопротивлением R, например входным сопротивлением детектора, который также потребляет мощность (на этот раз с полезными целями), см. рис. 2.3б. Добротность в этом случае равна Q = R / ρ. Для облегчения анализа удобно пересчитывать параллельное сопротивление в последовательное и наоборот, это легко сделать при не слишком малой добротности контура (от десятков и выше): R = ρ
От добротности зависит амплитуда вынужденных колебаний в контуре, создаваемых полезным сигналом. Реакция контура на возбуждение сигналами разных частот дается резонансной кривой (рис. 2.5). По вертикали отложены значения тока в контуре, или практически пропорционального ему напряжения на катушке, по горизонтали – частота сигнала. Кривые построены для трех значений добротности. Видно, что чем выше добротность, тем острее резонансная кривая и выше селективность приемника.
Если в цепь (рис. 2.3а) последовательно включить некоторый источник ЭДС, изменять частоту его колебаний и измерять напряжение на катушке высокочастотным вольтметром, то мы и получим резонансную кривую (рис. 2.5). Напряжение на катушке при резонансе в Q раз превосходит значение вводимой в контур внешней ЭДС. Как же так? Разве могут напряжения в цепи превосходить напряжение источника? В резонансных цепях могут. Посмотрим на рис. 2.6.
На резонансной частоте реактивные сопротивления катушки и конденсатора равны и противоположны по знаку, поэтому компенсируются, и полное сопротивление цепи активно и равно r. Ток максимален и равен ε/r. Но этот ток протекает через реактивные сопротивления катушки и конденсатора, которые в Q раз больше, следовательно, и напряжения на них во столько же раз больше. При расстройке источника вниз по частоте возрастает емкостное сопротивление конденсатора, а при расстройке вверх – индуктивное сопротивление катушки. В любом случае ток в цепи падает в соответствии с резонансной кривой.
Пересчитав входное сопротивление детектора – полезной нагрузки – R в последовательное rд и обозначив общее сопротивление потерь контура rп, мы получим эквивалентную схему контура, позволяющую рассчитать его КПД и показанную на рис 2.7. Поскольку один и тот же ток проходит через оба сопротивления, КПД контура оказывается равным отношению приведенного сопротивления детектора к общему: КПД = rд / (rд + rп).
Из формулы видно, что для повышения КПД сопротивление потерь контура должно быть малым. Полезно ввести понятие собственной добротности контура. В хорошо спроектированном приемнике собственная добротность контура должна быть как можно выше. А какой должна быть нагруженная добротность? Оптимальной. Если мы сделаем ее слишком высокой, то селективность приемника возрастет, но будут ослаблены высокие звуковые частоты, поскольку полоса пропускаемых контуром частот окажется уже спектра принимаемого сигнала. Если же нагруженная добротность мала, то при высоком КПД получится низкая селективность: вместе с полезным сигналом могут прослушиваться соседние по частоте станции.
В принципе, проблему решают многоконтурные фильтры. При высокой собственной добротности контуров в них удается получить и широкую полосу пропускания, и высокую селективность, и малые потери, то есть высокий КПД. Любопытно, что впервые трехконтурные фильтры, содержащие антенный, детекторный и промежуточный контуры, были предложены еще в доламповый период развития радиотехники, в 1907 г., Франклином и Стоуном независимо друг от друга.
Полосу пропускания контура (как, впрочем, и других устройств – усилителей, радиоприемников) отсчитывают по точкам на резонансной кривой, где амплитуда колебаний уменьшается до 0,7 от максимальной, при этом мощность колебаний падает в два раза. Требуемая при этом расстройка (рис. 2.8) обозначена как Δf, а полная ширина полосы получается 2Δf. Полоса пропускания 2Δf, частота настройки f0 и добротность Q связаны простым соотношением: 2Δf = f0/Q. Это соотношение часто используют при измерении добротности, поскольку полосу пропускания определить очень легко, подключив к контуру генератор стандартных сигналов и высокочастотный вольтметр или осциллограф.
Читать дальше – Детектирование
amfan.ru
Резонансная частота, добротность последовательного контура
⇐ ПредыдущаяСтр 3 из 7Следующая ⇒
Выведем формулу резонансной частоты:
Вывод: резонанс напряжений наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура .
Настроить контур в резонанс можно:
1) изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения;
2) можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура.
Т. к. , то можно записать, что .
Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура.
Формула добротности:
Вывод:добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса.
Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной
Расстройка — отклонение частоты от резонансной. Различают:
1) Абсолютная расстройка — разность текущей частоты и резонансной:
Расстройка может и положительной и отрицательной.
2) Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:
3) Обобщённая расстройка — отношение реактивного сопротивления x к резистивному:
Обычно входные характеристики строят от расстройки.
Входные АЧХ и ФЧХ последовательного контура
, где
— формула входной АЧХ последовательного контура
(на резонансной частоте все расстройки равны 0)
Вывод: на резонансной частоте сопротивление последовательного контура имеет наименьшее значение . По мере увеличения расстройки сопротивление контура возрастает.
ФЧХ:
— формула входной ФЧХ последовательного контура
Вывод: на резонансной частоте последовательный контур имеет чисто активное сопротивление: . На частотах меньше резонансной характер сопротивления активно-емкостной, т. к. . На частотах больше резонансной характер сопротивления активно-индуктивный: .
Передаточные АЧХ и ФЧХ последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать
— передаточная АЧХ последовательного контура в абсолютных координатах
Вывод: на резонансной частоте коэффициент передачи последовательного контура максимальный: .
ФЧХ:
На выходе стоит конденсатор, поэтому напряжение выхода отстаёт от тока на 90°. Угол практически равен углу выходного напряжения, поэтому характеристику сдвигаем на 90° вниз:
Передаточная ФЧХ имеет линейный участок при расстройках от до .
Прохождение через колебательный контур сигналов негармонической формы. Избирательные свойства последовательного контура
Избирательность — способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды.
На выходе амплитуда сигнала не резонансной частоте будет максимальной, т. к. , и на этой частоте самый большой коэффициент передачи.
Вывод: последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.
Полоса пропускания контура — область частот, на границах которой модуль комплексного коэффициента передач уменьшается в раз по сравнению с резонансным.
На уровне полосы пропускания коэффициент обозначается :
Нарисуем передаточную характеристику :
Вывод: чем выше добротность, тем уже полоса пропускания контура.
1)
2)
Кривые тока и напряжения такого вида называются резонансными.
Примечание:
При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:
Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность
Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.
В параллельном контуре может возникнуть резонанс токов, когда напряжение и ток на входе совпадают по фазе: .
— условие резонанса токов
Проводимость индуктивная равна проводимости емкостной.
При резонансе токов сопротивление параллельного контура максимально.
Свойства цепи при резонансе токов:
1. Ток в момент резонанса:
При резонансе токов общий ток минимальный.
2. На практике ,
При резонансе токов токи ветвей приблизительно равны.
3. Построим векторную диаграмму для резонанса токов:
Если бы (контур идеальный), то токи , и общий ток был бы равен 0, но т. к. есть небольшое , то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.
4. Выведем формулу резонансной частоты. Для этого
Вывод: резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура.
Получить резонанс токов можно, изменяя L или C, или частоту питающего напряжения.
5. Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:
Рассчитаем токи в момент резонанса:
Вывод: добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.
Рекомендуемые страницы:
lektsia.com
РЕЗОНАНС НАПРЯЖЕНИЙ в колебательном контуре
Имеются два случая резонанса в колебательных контурах: резонанс напряжений и резонанс токов.
Резонанс напряжений, или последовательный резонанс, наблюдается в случае, когда генератор переменной эдс нагружен
Рис.1 — Схема и резонансные кривые для резонанса напряжений
на соединенные последовательно L и С контура (рис.1 а), т.е. включен внутри контура.
В такой цепи имеется активное сопротивление г и общее реактивное сопротивление х, равное
Разность хL, и xC берется потому, что индуктивное и емкостное сопротивления оказывают противоположные влияния на ток. Первое вызывает отставание по фазе тока от напряжения, а второе, наоборот, создает отставание напряжения от тока.
Для собственных колебаний xL и хс равны друг другу. Если частота генератора равна частоте контура, то для тока, создаваемого генератором, xL и хC также одинаковы. Тогда общее реактивное сопротивление х станет равным нулю и полное сопротивление цепи для генератора равно только одному активному сопротивлению, которое в контурах имеет сравнительно небольшую величину. Благодаря этому ток значительно возрастает и устраняется сдвиг фаз между напряжением генератора и током.
Резонанс напряжений выражается в том, что полное сопротивление контура становится наименьшим и равным активному сопротивлению, а ток становится максимальным.
Условием резонанса напряжений является равенство частот генератора и контура f = fo, или равенство индуктивного и емкостного сопротивлений для тока генератора: xL = хC.
Когда частота генератора больше частоты контура, индуктивное сопротивление преобладает над емкостным и контур представляет для генератора сопротивление индуктивного характера.
Если частота генератора меньше частоты контура, то емкостное сопротивление больше индуктивного и контур для генератора является сопротивлением емкостного характера. В любом из этих случаев при отклонении от резонанса полное сопротивление контура возрастает по сравнению а его величиной при резонансе.
На (рис.1 б) показаны графики изменения полного сопротивления контура z и тока I при изменении частоты генератора f.
Для расчета сопротивления контура и тока при резонансе напряжений служат простые формулы:
Таким образом, напряжение генератора U равно падению напряжения на активном сопротивлении (г).
Большой ток в контуре при резонансе создает на индуктивном и емкостном сопротивлениях напряжения, значительно превышающие напряжение генератора. Они равны:
Так как хL = хC = р, то эти напряжения равны, но они противоположны по фазе и взаимно компенсируют друг друга. Действительно, напряжение на катушке опережает ток на 90°, а напряжение на конденсаторе отстает от тока на 90°. Ясно, что между этими напряжениями сдвиг фаз равен 180°.
Кривая резонанса для тока, приведенная на (рис.1 6), при небольшом Изменении частоты показывает также изменение напряжения UL и Uс (только в ином масштабе). Это следует из того, что при изменении частоты вблизи резонанса ток меняется сильно, а сопротивления xL и хC — сравнительно мало.
Например, если fpeз — 1000 кгц и частота изменяется на 20 кгц, т.е. на 2%, то сопротивления xL и хС изменяются каждое также только на 2%. В результате напряжения UL = IxL и Uc = IxС изменяются почти точно пропорционально току.
При резонансе напряжение на катушке или на конденсаторе в Q раз больше, чем напряжение генератора, равное U — Ir. Напряжение на L или С равно UL = Uc = р. Поэтому
Чем выше добротность контура Q, тем больше увеличение напряжения при резонансе.
Повышение напряжения на катушке и на конденсаторе характерно для резонанса напряжений, само название которого подчеркивает увеличение напряжения в момент резонанса.
Большие напряжения на катушке и конденсаторе получаются за счет постепенного накопления энергии в контуре в процессе возникновения в нем колебаний. Эдс генератора возбуждает в контуре колебания, амплитуда которых нарастает до тех пор, пока энергия, даваемая генератором, не станет равна потерям энергии в активном сопротивлении контура. После этого в контуре происходят мощные колебания, характеризующиеся большой величиной тока и большими напряжениями, а генератор расходует небольшую мощность только для компенсации потерь энергии.
Подобно этому можно, раскачивая тяжелый маятник легкими движениями руки с частотой, равной его собственной частоте, постепенно довести амплитуду колебаний маятника до значительной величины, во много раз превышающей амплитуду колебаний руки, играющей роль генератора.
Резонанс напряжений применяется в радиотехнике для получения максимального тока и напряжения в контуре.
Например, антенный контур радиопередатчика настраивают на резонанс напряжений для того, чтобы ток в антенне был максимальным. Тогда дальность действия передатчика будет наибольшей. Входной контур приемника также настраивают на резонанс напряжений для того, чтобы получить усиление напряжения сигналов той радиостанции, на частоту которой настроен контур. Напряжения сигналов других радиостанций, частоты которых отличаются от резонансной частоты приемного контура, усиливаются незначительно.
При резонансе напряжений в величину активного сопротивления контура входит внутреннее сопротивление генератора. Если оно велико, то качество контура может стать низким и резонансные свойства его будут выражены слабо. Поэтому для резонанса напряжений генератор, питающий контур, должен иметь малое внутреннее сопротивление.
www.radioingener.ru
Колебательный контур. Резонанс. Определение, примеры.
ВСЕ О КОЛЕБАТЕЛЬНОМ КОНТУРЕ В РАДИОТЕХНИКЕ 1. Электрические колебания 2. Способы настройки контуров 3. Автотрансформаторная связь 4. ЕМКОСТНАЯ СВЯЗЬ — колебательных контуров 5. Индуктивная или трансформаторная…
Электрические колебанияВажнейшими частями радиопередатчиков и радиоприемников являются колебательные контуры, в которых возбуждаются электрические колебания, т. е. переменные токи высокой частоты. Для…
АМПЛИТУДА И ЧАСТОТА СВОБОДНЫХ КОЛЕБАНИЙ В КОНТУРЕАмплитуды напряжения и тока свободных электрических колебаний в данном контуре зависят от начального запаса энергии. Чем больше напряжение первоначального заряда…
ЗАТУХАЮЩИЕ И НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯМы рассматривали идеальный контур, который состоит только из емкости и индуктивности, являющихся реактивными сопротивлениями и не вызывающих потерь энергии. При…
РЕЗОНАНС НАПРЯЖЕНИЙ в колебательном контуреИмеются два случая резонанса в колебательных контурах: резонанс напряжений и резонанс токов. Резонанс напряжений, или последовательный резонанс, наблюдается в случае,…
РЕЗОНАНС ТОКОВ в колебательном контуреРезонанс токов, или параллельный резонанс, получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор…
ПОЛОСА ПРОПУСКАНИЯ КОЛЕБАТЕЛЬНОГО КОНТУРАВо время передачи тех или иных сигналов ток высокой частоты в антенне радиопередатчика состоит из нескольких токов различной частоты. Такой…
ИНДУКТИВНАЯ ИЛИ ТРАНСФОРМАТОРНАЯ СВЯЗЬЕсли энергия колебаний переходит из одного контура в другой, то такие контуры называются связанными. Иначе говоря, контуры являются связанными в…
ЕМКОСТНАЯ СВЯЗЬ — колебательных контуровЭта связь осуществляется с помощью конденсатора связи Ссв (рис.1) и, следовательно, энергия переходит из первичного контура во вторичный через электрическое…
www.radioingener.ru
Резонансная частота Википедия
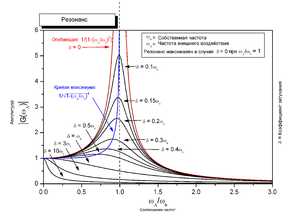Эффект резонанса для разных частот внешнего воздействия и коэффициентов затуханияРезона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы[1].
Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.[2][3]
Механика[ | ]
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:
- f=12πgL{\displaystyle f={1 \over 2\pi }{\sqrt {g \over L}}},
где g — это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна и включает эллиптический интеграл.) Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем.
В основе работы механических резонаторов лежит преобразование потенциальной энерг
ru-wiki.ru
Колебательные контуры – RadioRadar
Документация
Главная Справочник Документация
“Документация” – техническая информация по применению электронных компонентов, особенностях построения различных радиотехнических и электронных схем, а также документация по особенностям работы с инженерным программным обеспечением и нормативные документы (ГОСТ).
Оглавление
Материал предоставлен журналом Радиолюбитель
Последовательный колебательный контур
Как известно, простейшими резонансными (или колебательными) цепями являются последовательный и параллельный колебательные контуры. Рассмотрим цепь, состоящую из последовательно включенных катушки индуктивности и конденсатора (рис. 1). При воздействии на такую цепь переменного (в простейшем случае гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина (амплитуда) которого может быть вычислена согласно закону Ома: I = U/|ХΣ| , где |ХΣ| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора. На рис. 2 приведены зависимости реактивных сопротивлений катушки XL и конденсатора ХC от круговой частоты ω, а также график зависимости от частоты ω их алгебраической суммы ХΣ Последний график, по сути, показывает зависимость от частоты общего реактивного сопротивления цепи, изображенной на рис. 1. Из этого графика видно, что на некоторой частоте ω=ωр , на которой реактивные сопротивления катушки и конденсатора равны по модулю, общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи, а саму цепь, изображенную на рис. 1, принято называть последовательным колебательным контуром. Также из рис. 2 видно, что на частотах ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах – индуктивный. Что касается самой резонансной частоты, то она может оыть вычислена при помощи известной формулы Томсона: ωр = 1/√(LC).
Рис. 1
Последовательный колебательный контур
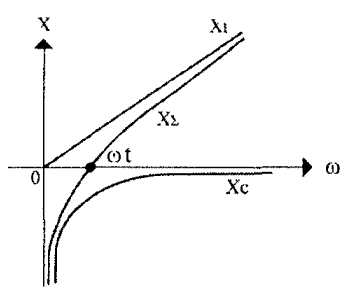
Рис. 2
Зависимости реактивных сопротивлений катушки XL и конденсатора ХC от круговой частоты ω
На рис.3 изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь r, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Модуль полного сопротивления (импеданса) такой цепи определяется следующим образом: |z| = √(r2+|XΣ|2), где |XΣ| = ωL-1/ωC. Очевидно, что на резонансной частоте, когда величины реактивных сопротивлений катушки XL = jωL и конденсатора ХC= -j/ωС равны по модулю, величина |XΣ| обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/r. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение UL=UC=I|XL|=I|XC|. На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы – они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений |XL| и |XC| .Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. С учетом приведенной записи для импеданса цепи можно привести часто встречающееся определение резонансной частоты: резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер.
Рис. 3
Эквивалентная схема последовательного резонансного контура
Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое сопротивление ρ и добротность Q. Характеристическим сопротивлением контура ρ называется величина модуля реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = |ХL| =|ХC| при ω =ωр . В общем случае характеристическое сопротивление может быть вычислено следующим образом: ρ = √(LC). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура – катушкой (энергия магнитного поля) WL= (LI2)/2 и конденсатором (энергия электрического поля) WC=(CU2)/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает “качество”. Величину, обратную добротности d=1/Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q=ρ/r, где r-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р=I2r. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Рис.4 а
Рис.4 б
| Рис. 5 а | Рис. 5 б |
Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ). На рис. 4а и рис. 4б представлены два простейших четырехполюсника, содержащих последовательный колебательный контур. АЧХ этих цепей приведены (показаны сплошными линями) на рис. 5а и рис. 5б соответственно. По вертикальной оси отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному. Для пассивных цепей (не т.е. содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Очевидно, что сопротивление цепи на рис. 4а переменному току будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля. При резонансе в цепи, изображенной на рис. 4б, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. Чаще всего за полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение – в зависимости от вида цепи) коэффициента передачи относительного его значения на резонансной частоте, не превышает величины 0,707 (3дБ).
Пунктирными линиями на рис. 5а и рис. 5б показаны АЧХ точно таких же цепей, как на рис. 4а и рис. 4б соответственно, колебательные контуры которых имеют такие же резонансные частоты, как и для случая рассмотренного выше, но обладающие меньшей добротностью (например, катушка индуктивности намотана проводом, обладающим большим сопротивлением постоянному току). Как видно из рис. 5а и рис. 5б, при этом расширяется полоса пропускания цепи и ухудшаются ее селективные (избирательные) свойства. Исходя из этого, при расчете и конструировании колебательных контуров нужно стремиться к повышению их добротности. Однако, в ряде случаев, добротность контура, наоборот, приходится занижать (например, включая последовательно с катушкой индуктивности резистор небольшой величины сопротивления), что позволяет избежать искажений широкополосных сигналов. Хотя, если на практике требуется выделить достаточно широкополосный сигнал, селективные цепи, как правило, строятся не на одиночных колебательных контурах, а на более сложных связанных (многоконтурных) колебательных системах, в т.ч. многозвенных фильтрах.
Параллельный колебательный контур
В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рис. 6 приведена принципиальная схема параллельного колебательного контура Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя – можно лишь складывать проводимости На рис. 7 приведены графические зависимости реактивных проводимостей катушки индуктивности BL = j/ωL, конденсатора ВC = -jωC, а также суммарной проводимости ВΣ, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току. Действительно, если построить зависимость реактивного сопротивления контура от частоты XΣ=1/BΣ, эта кривая (рис. 8) в точке ω = ωр будет иметь разрыв второго рода. Сопротивление реального параллельного колебательного контура (т.е с потерями), разумеется, не равно бесконечности – оно тем меньше, чем больше омическое сопротивление потерь в контуре, т.е уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический смысл понятий добротности, характеристического сопротивления и резонансной частоты колебательного контура, а также их расчетные формулы, справедливы как для последовательного, так и для параллельного колебательного контура.
Рис. 6
Параллельный колебательный контур
Рис. 7
Зависимости реактивных поводимостей катушки и конденсатора и суммарная проводимость этих двух элементов
Рис. 8
Зависимость реактивного сопротивления контура от частоты
Рассмотрим цепь, состоящую из генератора гармонических колебаний и параллельного колебательного контура. В случае, когда частота колебаний генератора совпадает с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут одинаковыми. В этом случае говорят, что в цепи имеет место резонанс токов. Как и в случае последовательного колебательного контура, реактивности катушки и конденсатора компенсируют друг друга, и сопротивление контура протекающему через него току становится чисто активным (резистивным). Величина этого сопротивления, часто называемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление Rэкв=Q·ρ. На частотах, отличных от резонансной, сопротивление контура уменьшается и приобретает реактивный характер (рис. 8) на более низких частотах – индуктивный (поскольку реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких – наоборот, емкостной (т к реактивное сопротивление емкости падает с ростом частоты). В процессе работы контура, дважды за период колебаний, происходит энергетический обмен между катушкой и конденсатором (рис. 9). Энергия поочередно накапливается то в виде энеогии электрического поля заряженного конденсатора, то в виде энергии магнитного поля катушки индуктивности. При этом в контуре протекает собственный контурный ток Iк, превосходящий по величине ток во внешней цепи I в Q раз. В случае идеального контура (без потерь), добротность которого теоретически бесконечна, величина контурного тока также будет бесконечно большой.
Рис. 9
Процесс работы контура
| Рис. 10 а | Рис. 10 б |
Рассмотрим, как изменяются коэффициенты передачи четырехполюсников, аналогичных приведенным на рис. 4а и рис. 4б, от частоты, при включении в них не последовательных колебательных контуров, а параллельных. Четырехполюсник, изображенный на рис. 10а, на резонансной частоте контура представляет собой огромное сопротивление току, поэтому при ω=ωр его коэффициент передачи будет близок к нулю (с учетом омических потерь). На частотах, отличных от резонансной, сопротивление контура будет уменьшатся, а коэффициент передачи четырехполюсника – возрастать. Этот случай соответствует графику АЧХ, приведенному на рассмотренном ранее рис. 5б. Для четырехполюсника, приведенного на рис. 10б, ситуация будет противоположной – на резонансной частоте контур будет представлять собой очень большое сопротивление и практически все входное напряжение поступит на выходные клеммы (т.е коэффициент передачи будет максимален и близок к единице). При значительном отличии частоты входного воздействия от резонансной частоты контура, источник сигнала, подключаемый к входным клеммам четырехполюсника, окажется практически закороченном накоротко, а коэффициент передачи будет близок к нулю. АЧХ такого четырехполюсника соответствует изображенной на рис. 5а.
В заключении настоящего экскурса отметим тот факт, что достаточно часто в реальной радиоэлектронной аппаратуре приходится сталкиваться с необходимостью перестройки колебательных контуров – например, в приемнике, для обеспечения возможности приема радиостанций, работающих на разных частотах В этом случае емкостные элементы контуров выполняются в виде конденсаторов переменной емкости, либо специальных диодов – варикапов, обладающих большой барьерной емкостью, зависящей от приложенного к ней запирающего напряжения В ряде случаев применяют и перестраиваемый катушки индуктивности – вариометры.
Дата публикации: 09.09.2003
Оглавление
Мнения читателей
- Павел / 12.01.2017 – 09:20
Спасибо! - Поиск / 14.01.2016 – 21:21
подскажите как вычислить частоту контура, если включить катушку параллельно последовательному контуру? - Кирилл / 18.02.2014 – 22:22
Мужики дайте схему подключения аудиомодуляции к первичке тесла? Хочу переделать Ионофон под поющий транс тесла. Или подскажите где такие схемы найти если они есть? Пожалуйста и заранее спасибо! - николай / 21.10.2013 – 07:32
подскажите как вычислить частоту контура, если включить конденсатор параллельно последовательному контуру - sad / 10.07.2013 – 13:22
Ыыыы!!! - Денис / 20.06.2013 – 09:43
Как изменится период колебаний контура, если пластины конденсатора, включенного в контур сблизить между собой: а) уменьшится ; б) увеличится Дать математически обоснованный ответ. Помогите я в физике дуб дубом.. 🙁 Зарание спасибо - витя / 19.04.2013 – 11:51
спасибо за информацию - Влад… / 23.11.2012 – 17:41
Спасибо, очень доходчиво написано. - ааааааа / 04.10.2012 – 10:24
ааааааа - Света / 18.09.2012 – 15:06
колебательній контур состоит из конденсатора емкостью 2 Пф и катушки с индуктивностью 0,50 мкГн,какова частота колебаний в контуре - серегей / 15.09.2012 – 11:51
помогите пожалуста .как отличается зависимость полного сопротивления от частоты для последовательного и параллельного контуров? - Срез умоляю помогите / 05.06.2012 – 05:57
колебательный контур излучает в воздухе электромагнитные войны длиной 150м. Какая емкость включена в контур, если его индуктивноть равна 0,25 мГн? Активным сопротивлением пренебречь - Денис / 13.05.2012 – 19:09
ребят, подскажите плиз) эт вопрос на билет к экзамену( не могу нигде найти( Реальный колебательный контур.Свободные колебание в контуре с потерями. Характеристики оценивающие реальный колебательный контур. - Денис / 13.05.2012 – 19:00
ребят, подскажите плиз) эт вопрос на билет к экзамену( не могу нигде найти( Реальный колебательный контур.Свободные колебание в контуре с потерями. Характеристики оценивающие реальный колебательный контур. - Ann / 11.05.2012 – 15:31
как изменится форма резонансной кривой,если в колебательный контур включить резистор? - Ann / 11.05.2012 – 15:29
как изменится форма резонансной кривой,если в колебательный контур включить резистор? - василий / 16.04.2012 – 10:11
обьясните пожалуста как рабтает колебательный контур ? - Сергей,Ужгород / 10.02.2012 – 13:33
Спасибо автору. Простое и понятное объяснение без заумной теории и формул. Кому надо более глубокий анализ – изучайте курс ЛРТУ (линейные радиотехнические устройства). А всякие придирки типа “Скажите, где вы видите контур на рис.1. Лично я вижу там двухполюсник” – чепуха, игра слов. Все изожено просто и понятно. - Саша / 19.12.2011 – 09:35
Ну что,могу сказать только одно,отличный сайт!Очень познавательный,вот только если б кто подкрепил теорию вечного двигателя основанного на резонансе,практикой,и выложил бы материалы на сайт,я думаю было бы ещё интересней.должен же кто нибудь когда нибудь до этого дойти.Я поддерживаю идею этого,по сути простейшего,вечного двигателя.И Теслу уважаю,он был прав на счет всего о чем сейчас ведутся разговоры.Его ещё вспомнят!Я считаю,что от наших разговоров о резонансе и получении на выходе мощности больше чем на входе,закон сохранения энергии уже канул в лето,вопреки всему,свободная энергия существует!!!:)как сказал один … :”и всё таки она вертится!”,только в нашем случае:”и всё таки она существует!!!” - Алекс / 16.09.2011 – 12:16
Здравствуйте. Характеристическое сопротивление равно корень квадратный из отношения L/С (а не произведения LC)
Вы можете оставить свой комментарий, мнение или вопрос по приведенному вышематериалу:
www.radioradar.net