Резонанс в последовательном и параллельном LC контуре. » Хабстаб
Чтобы понять причину возникновения резонанса необходимо разобраться как течёт ток через конденсатор и катушку индуктивности.
При протекании тока через катушку индуктивности напряжение опережает ток. Давайте рассмотрим этот процесс подробнее, когда напряжение на концах катушки максимально, ток через катушку не течет, по мере уменьшения напряжения, ток увеличивается и когда напряжение на концах катушки равно нулю, ток через катушку максимален. Далее, напряжение уменьшается и достигает минимума, ток при этом равен нулю. Из этого можно сделать вывод, что ток через катушку максимален, когда напряжение на её концах равно нулю и ток равен нулю, когда напряжение на её концах максимально. Таким образом, если сопоставить графики изменения напряжения и тока , создаётся впечатление, что напряжение опережает ток на 90 градусов. Это можно увидеть на рисунке ниже.
Совсем противоположно катушке индуктивности ведет себя конденсатор.
Когда напряжение на концах конденсатора равно нулю, ток через него максимален, по мере зарядки конденсатора ток через него уменьшается, это связано с тем, что разность потенциалов между конденсатором и источником напряжения уменьшается, а чем меньше разность потенциалов, тем меньше ток. Когда конденсатор полностью заряжен ток через него не течет так, как нет разности потенциалов. Напряжение начинает уменьшаться и становится равно нулю, при этом ток максимален только течет в другом направлении, далее напряжение достигает минимума и ток через конденсатор снова не течет. Делаем вывод, что ток через конденсатор максимальный когда напряжение на его обкладках равно нулю и ток равен нулю когда напряжение на конденсаторе минимально. Если сопоставить графики изменения тока и напряжение, создается впечатление, что ток опережает напряжение на 90 градусов. Это можно увидеть на рисунке ниже.
На резонансной частоте для контура, состоящего из конденсатора и катушки индуктивности, неважно параллельный он или последовательный, их сопротивления равны и сдвиг фаз между напряжением и током равен нулю.
Ведь действительно если подумать, то в конденсаторе ток опережает напряжение на 90 градусов, то есть +90 градусов, а в катушке индуктивности ток отстает от напряжения на 90 градусов, то есть -90 градусов и если сложить их получится нуль. Для пары, конденсатор и катушка индуктивности параллельный и последовательный резонанс возникают на одной и той же частоте.
Давайте рассмотрим резонанс в последовательном колебательном контуре.
На верхнем графике изображена зависимость тока от времени, протекающего через контур, ниже два графика это напряжения, на конденсаторе и катушке, самый нижний это сумма напряжений на катушке и конденсаторе. Видно, что суммарное напряжение на конденсаторе и катушке индуктивности равно нулю, также говорят, что сопротивление последовательного колебательного контура на резонансной частоте стремится к нулю.
Давайте соберем простую схему, изображенную на рисунке.
Сопротивление резистора должно быть больше выходного сопротивления генератора, то есть больше 50 Ohm, я взял первый попавшийся.
Расчетная резонансная частота такого контура 270 KHz, но так как номиналы имеют определенный допуск, который обычно указывается в процентах, придется ее подобрать. Подбирать будем исходя из того, что сопротивления катушки индуктивности и конденсатора на резонансной частоте равны, а так как они соединены последовательно, то равны и падения напряжений. Первый канал показывает напряжение на контуре, второй канал напряжение на катушке, канал Math показывает разность между первым и вторым каналом, а по сути напряжение на конденсаторе. Причина по которой, я не подключил щуп осциллографа параллельно конденсатору, будет подробно описана в следующей статье. Если кратко, то есть правило подключать земляной крокодил только к земле, если осциллограф и исследуемая схема питаются от бытовой сети и имеют заземление. Делается это, для того чтобы не спалить исследуемую схему и осциллограф.
На осциллограммах видно, что на резонансной частоте падение напряжения на катушке и конденсаторе равны и противоположны по знаку, а суммарное падение напряжения на контуре стремится к нулю.
В последовательном колебательном контуре на резонансной частоте напряжение на катушке и конденсаторе выше чем на генераторе. Давайте увеличим частоту и посмотри что изменится.
Видим, что напряжение на катушке увеличилось потому, что увеличилось её сопротивление, так как оно прямо пропорционально зависит от частоты. Напряжение на конденсаторе уменьшилось потому, что его сопротивление с ростом частоты уменьшается. Теперь уменьшим частоту.
Видим, что напряжение на конденсаторе увеличилось, а на катушке уменьшилось, также надо отметить, что разность фаз между сигналами равна 180 градусам.
Давайте теперь рассмотрим резонанс в параллельном контуре, ситуация аналогичная с последовательным контуром, только в последовательном мы рассматривали напряжения, а в параллельном будем рассматривать токи.
Видим, что токи сдвинуты относительно друг друга на 180 градусов, а их сумма равна нулю, то есть ток через контур не течет, а его сопротивление стремится к бесконечности.
Параллельный колебательный контур используют как полосно-заграждающий фильтр, радиолюбители называют его фильтр- пробка. Он не пропускает напряжение частота которого равна его резонансной частоте. Давайте соберем простую схему, изображенную на картинке ниже и посмотрим как будет изменяться напряжение на концах контура в зависимости от частоты.
Так как конденсатор и индуктивность те же, что и в прошлом эксперименте резонансная частота контура та же.
На резонансной частоте сопротивление контура стремится к бесконечности, следовательно и напряжение будет максимально. Давайте уменьшим частоту.
Видим, что напряжение на контуре уменьшилось, произошло это потому, что сопротивление катушки уменьшилось и она зашунтировала конденсатор.
Теперь давайте увеличим частоту.
С ростом частоты сопротивление конденсатора уменьшилось и он зашунтировал катушку.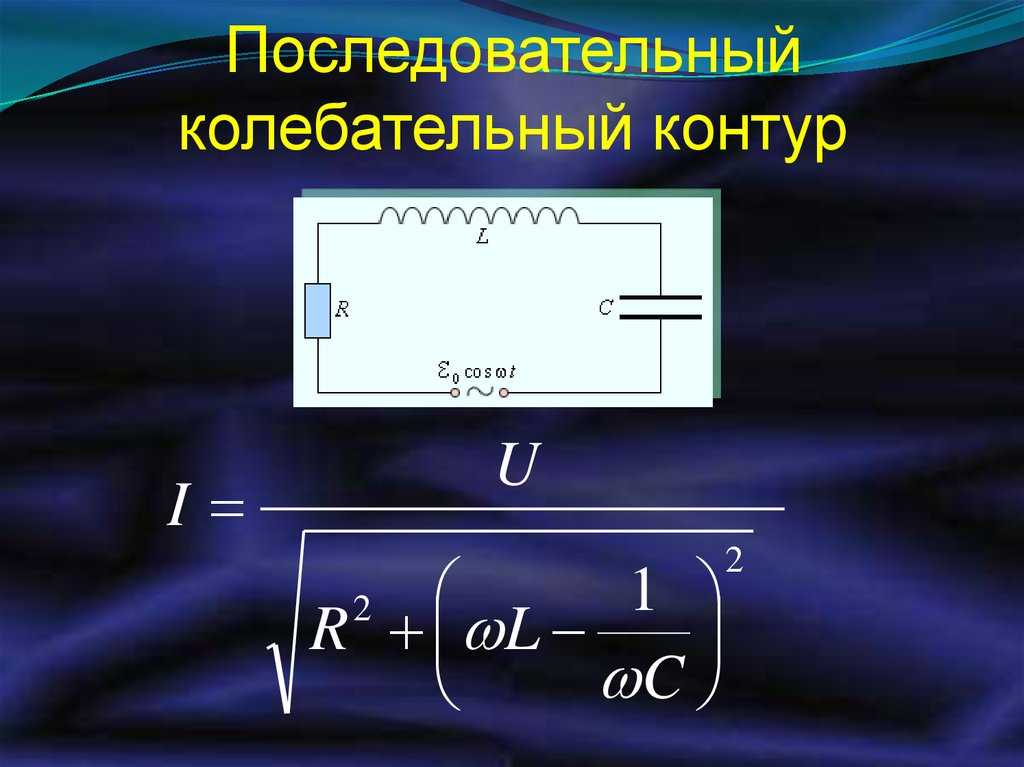
Пожалуй, это всё, что хотелось рассказать про резонанс.
Колебательный LC контур: определение, принцип действия, расчет
Сегодня нас интересует простейший колебательный контур, его принцип работы и применение.
За полезной информацией по другим темам переходите на наш телеграм-канал.
Колебания – процесс, повторяющийся во времени, характеризуется изменением параметров системы около точки равновесия.
Первое, что приходит на ум – это механические колебания математического или пружинного маятников. Но ведь колебания бывают и электромагнитными.
По определению колебательный контур (или LC-контур) – это электрическая цепь, в которой происходят свободные электромагнитные колебания.
Такой контур представляет собой электрическую цепь, состоящую из катушки индуктивностью L и конденсатора емкостью C.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Принцип действия колебательного контура
Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.
Колебания, которые происходят в контуре – свободные затухающие колебания.
То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.
Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.
Еще одна важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.
Резонанс LC-контура
Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс – в нашей отдельной статье.
Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура).
Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу:
Применение колебательного контура
Колебательный контур широко применяется на практике. На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис. Качественная и быстрая помощь в решении любых задач не заставит себя ждать!
Автор: Иван
Иван Колобков, известный также как Джони.
Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Калькулятор резонансной частоты – все RF
Резонансная частота LC-контура – это частота, при которой индуктивное и емкостное сопротивления LC-контура равны.
Этот онлайн-калькулятор резонансной частоты разделен на три калькулятора.
Калькулятор 1: Рассчитывает резонансную частоту LC-контура путем ввода значений индуктивности и емкости.
Калькулятор 2: Рассчитывает значение индуктивности LC-контура для заданной частоты и значения емкости.
Калькулятор 3: Рассчитывает значение емкости контура LC Tank для заданной частоты и значения индуктивности.
Калькулятор резонансной частоты
В LC-цепи резонансной частотой называется частота, при которой возникает резонанс, т.
е. при этой частоте индуктивное и емкостное сопротивления LC-цепи равны.
Этот онлайн-калькулятор резонансной частоты вычисляет резонансную частоту LC-контура, вводя значения индуктивности (нГн) и емкости (пФ).
Этот онлайн-калькулятор также предоставляет следующие дополнительные калькуляторы:
- Для расчета индуктивности (нГн) путем ввода значения емкости (пФ) и частоты (ГГц).
- Чтобы рассчитать емкость (пФ), введите значение индуктивности (нГн) и частоты (ГГц).
Какова резонансная частота LC-контура? Пожалуйста, укажите еще пару моментов для резонансной частоты. Почему это важно, что такое резонансные цепи, как это влияет на цепь
В LC-цепи резонансной частотой называется частота, при которой возникает резонанс, т. е. на этой частоте индуктивное сопротивление и емкостная реактивность LC-цепи равны равный.
Как рассчитать резонансную частоту LC-контура?
Следующая формула используется для расчета резонансной частоты LC-контура.
- Где:
- L = индуктивность LC-контура (LC-бак) в нГн
- C= Емкость LC-цепи в пФ
- F = Резонансная частота контура.
Как рассчитать индуктивность по частоте и емкости?
Напишите пожалуйста пару пунктов по индуктивности. Почему это важно, что такое резонанс контуров, как он влияет на контур
Следующая формула используется для расчета индуктивности по частоте и емкости.
Как рассчитать емкость по частоте и индуктивности?
Пожалуйста, напишите 2 предложения о емкости. как это влияет на LC-цепь
Следующая формула используется для расчета емкости по частоте и индуктивности.
- Где:
- L = индуктивность LC-контура (LC-бак) в нГн
- C= Емкость LC-цепи в пФ
- F = Частота
LC Circuit: уравнения, частота и мощность
Представьте, что вы стоите на пляже и смотрите на волны, набегающие и отходящие от берега в идеальном равновесии.
Волны, кажется, выходят и отступают в точное и одинаковое время, демонстрируя волнообразное поведение, подобное тем, которые мы наблюдаем в тригонометрических функциях в математике. Феномен синусоидальных волн мы наблюдаем во всех областях физики, одним из примеров, которые мы рассмотрим сегодня, являются цепи индуктивности и конденсатора, также называемые 9.0009 Цепь LC. Вы можете быть знакомы с индукторами из предыдущих курсов; они состоят из проводящих материалов, которые позволяют индуцировать токи посредством изменяющегося магнитного поля. С другой стороны, у нас есть конденсаторы, которые хранят электрическую энергию. эти два электрических компонента дополняют друг друга и позволяют LC-цепям проявлять волнообразное поведение частоты тока. Продолжайте читать, чтобы узнать больше!
Рис. 1. Волнообразное поведение наблюдается во всех областях физики, включая схемы.
Уравнения LC-цепи
Прежде чем мы подробно расскажем об уравнениях и частоте в LC-цепях, давайте более подробно рассмотрим настройку схемы.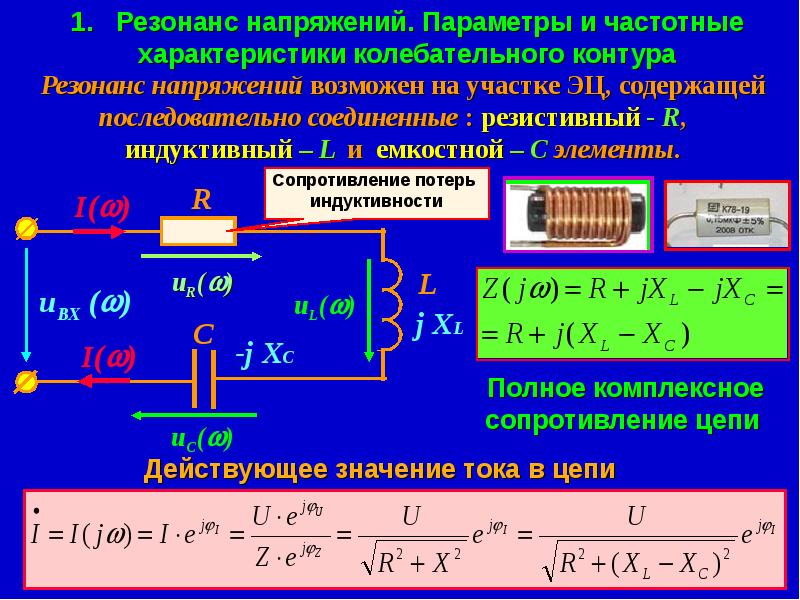
Ссылаясь на рисунок ниже, у нас есть заряженный конденсатор емкостью \(C\), подключенный к соленоиду с индуктивностью \(L\).
Рис. 2. Структура LC-цепи с заряженным конденсатором, подключенным к соленоиду
Если вы знакомы с конденсаторами, то должны знать, что эти электрические компоненты накапливают электрическую энергию за счет разделения заряда между их параллельными пластинами. Вы можете ознакомиться с другими нашими статьями о конденсаторах, чтобы узнать больше! Эти конденсаторы с параллельными пластинами заряжаются путем подключения их к источнику питания в цепи, что позволяет электронам накапливаться на одной стороне пластины. Это разделение заряда создает электрическое поле между пластинами, накапливая в нем энергию.
Теперь, когда у нас есть заряженный конденсатор, мы подключаем его к катушке индуктивности, которая в данном случае является соленоидом. Поскольку к конденсатору больше не подключен источник питания, нет электрического потенциала, удерживающего электроны на одной из параллельных пластин.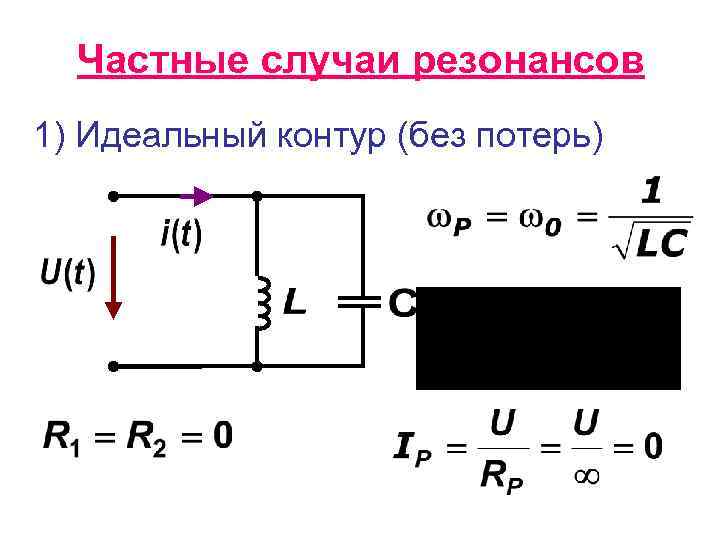
Таким образом, конденсатор разряжается и генерирует ток, который течет по цепи, а также через соленоид. Пропуская ток через соленоид, мы теперь имеем магнитное поле, окружающее катушку. Однако по мере того, как у конденсатора заканчивается электрическая энергия для разряда, магнитное поле становится все слабее и слабее. С другой стороны, это ослабление магнитного поля приводит к изменению магнитного потока, который затем индуцирует ток в соленоиде посредством явления электромагнитной индукции. Затем этот ток заряжает конденсатор до тех пор, пока магнитное поле не достигнет нуля, и мы вернемся к началу!
Теперь мы можем видеть, что катушка индуктивности и конденсатор работают вместе в идеальном балансе друг с другом. Электрическая энергия, запасенная в каждом компоненте, колеблется между собой, подобно колебаниям синусоидальной волны. Теперь, когда мы качественно разобрались в LC-цепях. Выразим это количественно через математическое выражение.
Во-первых, нам нужно установить общее напряжение в цепи.
Поскольку компоненты соединены последовательно, мы можем суммировать их индивидуальные напряжения, чтобы получить
\[ V_{\text{T}} = V_{\text{L}} + V_{\text{C}} ,\]
где \(V_{\text{T}}\) общее напряжение, \(V_{\text{L}}\) – напряжение катушки индуктивности, а \(V_{\text{C}}\) – напряжение конденсатора. Все они измеряются в вольтах \(\mathrm{V}\). Теперь вернемся к нашим знаниям о конденсаторах и катушках индуктивности и вспомним их уравнения, связывающие их с напряжением. Для индуктора это определяется как
\[ V_{\text{L}} = L \frac{\mathrm{d} I}{\mathrm{d} t},\]
где \(L\) – индуктивность, измеренная в генри \(\mathrm{H}\), \(I\) – ток, измеренный в амперах \(\mathrm{A}\), и \( t\) – время, измеряемое в секундах \(\mathrm{s}\). Аналогично, для конденсатора уравнение имеет вид емкости конденсатора, измеренной в кулонах \(\mathrm{C}\), а \(C\) – емкость конденсатора, измеренная в фарадах \(\mathrm{F}\). Теперь мы можем подставить их в наше выражение для полного напряжения в цепи,
\[ V_{\text{T}} = L \frac{\mathrm{d} I}{\mathrm{d} t} + \frac{Q}{C} .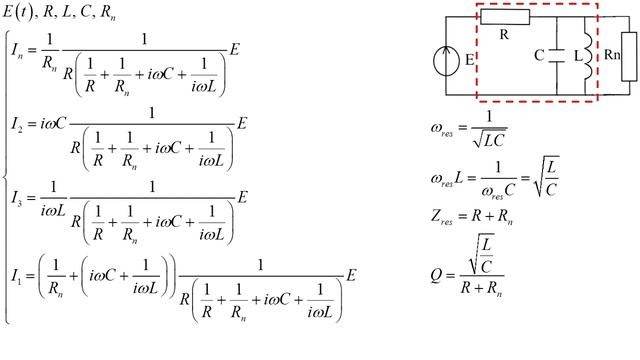
\]
Резонансная частота LC Контур
Теперь, когда у нас есть уравнение LC-контура, мы можем использовать его для получения резонансной частоты системы. Мы можем определить резонансную частоту следующим образом.
Резонансная частота системы — это собственная частота, которую она проявляет, когда на нее не действует внешняя сила.
Поскольку наш LC-контур не подключен к внешнему источнику питания, мы можем сказать, что колебания, которые он демонстрирует, имеют его собственную или резонансную частоту. Теперь, используя уравнение LC-цепи, мы можем взять его производную по времени как 92} + \frac{1}{C} I. \end{align} \]
Теперь распаковываем то, что мы получили выше. В первой строке мы взяли производную по времени от обеих компонент в правой части. Это включает только ток \(I\) и заряд \(Q\), поскольку они являются единственными компонентами, зависящими от времени, в то время как индуктивность \(L\) и емкость \(C\) являются постоянными.
Впоследствии мы можем переписать производную по времени от заряда \( \frac{\mathrm{d} Q}{\mathrm{d} t} \) как ток \(I\), благодаря тому, что ток – это скорость потока заряда. Наконец, в последней строке мы заменяем производную полного напряжения по времени на ноль. Это потому, что мы знаем, что общее напряжение \(V_{\text{T}}\) в цепи остается постоянным, так как нет внешнего источника питания.
Теперь вы можете распознать это уравнение как однородное дифференциальное уравнение второго порядка, которое мы можем решить, чтобы определить частоту системы. Мы проведем полный вывод частоты, но сначала мы можем определить ее как
\[ \omega_0 = \frac{1}{\sqrt{LC}},\]
, где \(\omega_0\) резонансная частота измеряется в единицах \ (\ mathrm {\ frac {rad} {s}} \).
Частота контура LC
При решении дифференциальных уравнений второго порядка мы сначала используем общее решение, которое мы можем подставить в уравнение. Это дается 9{-i \omega_0 t} ,\]
где \(c_1\) и \(c_2\) — константы, которые необходимо определить.
Однако мы знаем, что текущий \(I\) является действительной наблюдаемой величиной, поэтому мы можем отбросить мнимую часть функции, если сможем отделить ее от действительной части. Это делается путем подстановки в уравнение Эйлера, чтобы получить
\[ \begin{align} I(t) &= c_1 \left( \cos(\omega_0 t) + i \sin(\omega_0 t) \right) + c_2 \left( \cos(\omega_0 t) – i \sin(\omega_0 t) \right) \\ I(t) &= (c_1 + c_2) \cos(\omega_0 t) + i(c_1 – c_2) \sin(\omega_0 т) . \end{выравнивание} \]
Отбрасывая мнимую часть, мы остаемся с
\[ I(t) = A\cos(\omega_0 t ).\]
Где мы заменили \(c_1 + c_2\) на \(A\) поскольку они обе являются просто константами, которые можно переписать как другую константу. Теперь, чтобы решить для \(A\), нам нужно рассмотреть начальное условие, в момент времени \(t = 0 \, \mathrm{s}\), когда катушка индуктивности впервые подключена к конденсатору, мы знаем, что ток в цепи есть \(I_0\), начальный ток. Таким образом,
\[ I( t = 0\, \mathrm{s} ) = I_0 .
\]
Наконец, наше выражение для тока в LC-цепи:
\[ I(t) = I_0 \cos(\omega_0 t) .\]
действительно резонансная частота LC-контура. Мы можем преобразовать эту угловую частоту в частоту в герцах, используя уравнение
\[ \begin{align} \omega_0 &= 2 \pi f \\ \frac{1}{\sqrt{LC}} &= 2 \pi f \\ f &= \frac{1}{\sqrt{LC} \, 2 \pi } , \end{align} \]
где \(f\) – измеряемая частота тока в LC-цепи в герцах \(\mathrm{Гц}. \)
Теперь давайте рассмотрим пример, используя уравнения, которые мы вывели выше. Рассмотрим LC-контур с катушкой индуктивности \(L = 1,5 \, \mathrm{\mu H} \) и конденсатором с емкостью \(6,4 \, \mathrm{n F} \). Начальный ток в цепи равен \( I_0 = 2,5 \, \mathrm{A}\).
- Какова частота тока в цепи?
- Каково значение тока в момент времени \(t = 0,7 \, \mathrm{s}\)?
1. Чтобы найти частоту, мы можем подставить наши значения индуктивности и емкости, чтобы найти 9{7} \, \mathrm{\frac{rad}{s}} \times 0,7 \, \mathrm{s} ) \\ I( t = 0,7 \, \mathrm{s} ) &= -2,0 \, \ матрм{А} .
\end{align}\]
Здесь мы видим, что наш текущий в момент времени \(t = 0.7 \, \mathrm{s}\) отрицателен. Это указывает на то, что ток течет в направлении, противоположном его первоначальной ориентации.
Постоянная времени LC-цепи
Во-первых, давайте определим, что такое постоянная времени.
Постоянная времени в физической системе — это время, за которое система достигает 0,632 от своего начального или конечного значения, в зависимости от того, увеличивается или уменьшается система.
Какие типы систем имеют постоянные времени? Это системы, которые развиваются с течением времени и в конечном итоге достигают устойчивого состояния, что не приводит к изменению системы с течением времени. Примером такого типа системы в цепях может быть цепь резистор-конденсатор, также называемая RC-цепью. Когда заряженный конденсатор подключен к резистору, он со временем разряжается, позволяя току проходить через резистор. Однако, как только заряд на конденсаторе истощается, в цепи не остается тока для повторной зарядки конденсатора, в отличие от LC-цепи, таким образом достигается устойчивое состояние.
Рис. 3. Резистивно-емкостная цепь достигает устойчивого состояния, когда конденсатор полностью разряжен.
Если мы сравним это с LC-контуром, который мы рассматривали ранее, должно быть ясно, что LC-контур не достигает устойчивого состояния, поскольку ток постоянно изменяется из-за обмена электрической энергией между катушкой индуктивности и конденсатором. . Следовательно, LC-цепь не имеет постоянной времени.
Максимальный ток цепи LC
Наконец, мы хотим определить значение максимального тока, протекающего через цепь, и при каких значениях времени он возникает. Поскольку у нас есть уравнение для тока, мы можем продифференцировать его по времени, чтобы найти максимальный ток. Однако, исходя из наших знаний о синусоидальных функциях, мы также можем прочитать амплитуду функции как \(I_0\). Это говорит нам о том, что максимальный ток в LC-цепи равен начальному току в момент времени \(t = 0 \, \mathrm{s} \).
Теперь давайте продифференцируем функцию, чтобы найти значения времени, при которых возникает максимальный ток.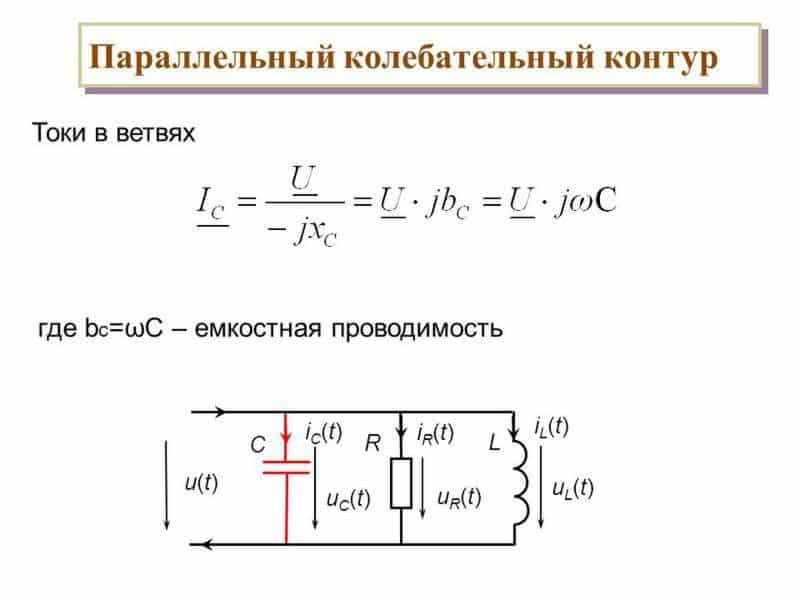
Это дает нам
\[ \frac{\mathrm{d} I}{\mathrm{d} t} = -I_0 \omega_0 \sin(\omega_0 t) .\]
Приравняв эту функцию к нулю, мы находим
\[ \begin{align} -I_0 \omega_0 \sin(\omega_0 t) &= 0 \\ \sin(\omega_0 t) &= 0 \\ \omega_0 t &= 0, \pi, 2\pi \\ t &= 0, \frac{\pi}{\omega_0} , \frac{2\pi}{\omega_0} . \end{align} \]
Таким образом, у нас есть максимальный ток и время, в которое он возникает.
LC-цепь — основные выводы
- LC-цепь состоит из катушки индуктивности (соленоида) и заряженного конденсатора.
- Заряженный конденсатор со временем разряжает свою электрическую энергию, позволяя току проходить через соленоид.
- Затем соленоид создает магнитное поле.
- По мере того, как в конденсаторе заканчивается электрическая энергия, сила магнитного поля уменьшается, что приводит к возврату тока в цепь за счет электромагнитной индукции.
- Резонансная частота контура определяется выражением \(\omega_0 = \frac{1}{\sqrt{LC}} \).
