Резонансные колебания: РЕЗОНАНСНЫЕ КОЛЕБАНИЯ С ПРЕДЕЛЬНОЙ АМПЛИТУДОЙ В ВИБРАЦИОНОМ ЭЛЕКТРОМАГНИТНОМ АКТИВАТОРЕ

Содержание

РЕЗОНАНСНЫЕ КОЛЕБАНИЯ С ПРЕДЕЛЬНОЙ АМПЛИТУДОЙ В ВИБРАЦИОНОМ ЭЛЕКТРОМАГНИТНОМ АКТИВАТОРЕ

Том 330 № 1 (2019)

DOI https://doi.org/10.18799/24131830/2019/1/70

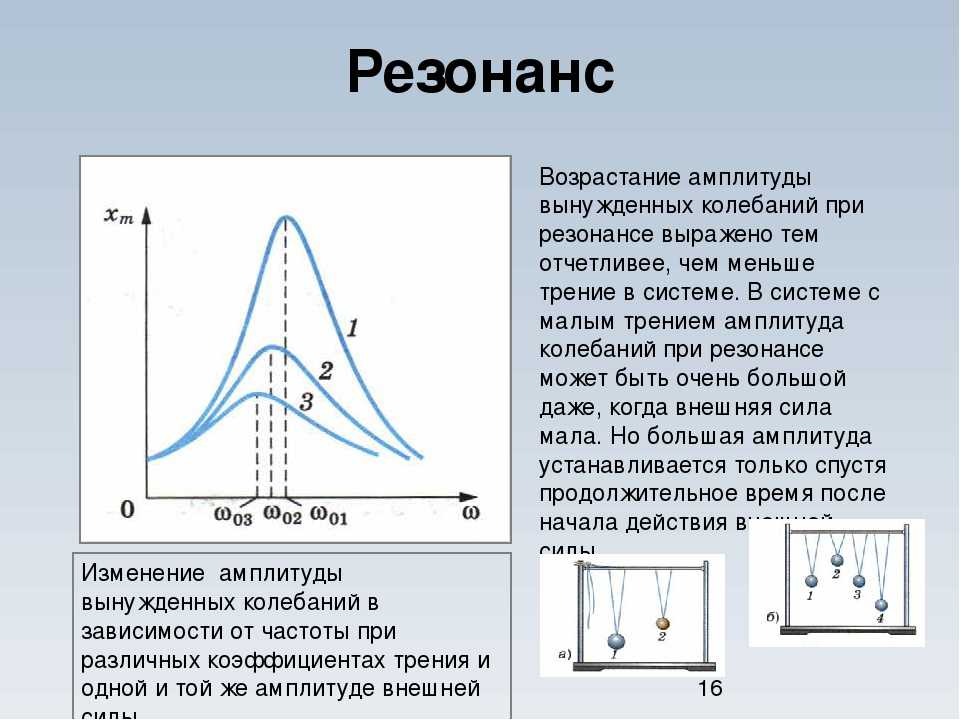
Актуальность исследования обусловлена тем, что вибрационные электромагнитные активаторы являются перспективными для применения в различных технологиях, связанных с добычей и транспортировкой георесурсов, в том числе при приготовлении буровых растворов и разжижении вязких нефтепродуктов. Вибрационный электромагнитный активатор представляет собой электрическую машину возвратно-поступательного движения с якорем-активатором, образующим в жидкой обрабатываемой среде турбулентные затопленные струи. В первом попупериоде якорь-активатор притягивается к стенке за счет импульса тока в катушках, при этом в упругой пружине накапливается потенциальная энергия. Этот режим является режимом вынужденных колебаний в механической системе вибрационного электромагнитного активатора. Во втором полупериоде ток в катушках отсутствует, а якорь-активатор отталкивается от стенок за счет энергии пружины – это режим свободных колебаний в механической системе. С точки зрения улучшения энергоэффективности следует настраивать вибрационный электромагнитный активатор на резонансную частоту. Резонансная частота не является постоянной и зависит от свойств обрабатываемой жидкости. Форма вынуждающей колебания силы должна быть такой, чтобы обеспечивать колебания в механической системе на резонансной частоте с предельной амплитудой, что обеспечит повышение энергоэффективности и производительности вибрационного электромагнитного активатора.

Цель: провести аналитические исследования, позволяющие обеспечивать резонансные колебания с предельной амплитудой в вибрационном электромагнитном активаторе.

Методы исследования основаны на использовании обыкновенных дифференциальных уравнений, преобразования Лапласа, амплитудно-частотных характеристик, систем нелинейных алгебраических уравнений, спектрального анализа, сопоставления аналитических и экспериментальных характеристик. Результаты. На основе линеаризованной математической модели механической системы вибрационного электромагнитного активатора рассмотрен режим свободных колебаний якоря-активатора с предельной амплитудой. Режим вынужденных колебаний предлагается рассматривать как естественное дополнение к режиму свободных колебаний с вынуждающей силой, действующей половину периода и имеющей специальную форму. Показано, что режимы свободных и вынужденных колебаний существенно зависят от параметров механической системы, которые определяются свойствами обрабатываемой жидкой среды. Проведен спектральный анализ вынуждающей силы, обеспечивающей резонансные колебания с предельной амплитудой в механической системе вибрационного электромагнитного активатора.

Предложено техническое решение, обеспечивающее управление вибрационным электромагнитным активатором с автоматической настройкой на резонансную частоту и предельную амплитуду колебаний якоря-активатора. Такой режим обеспечивает максимизацию энергоэффективности и производительности процессов перемешивания жидких обрабатываемых сред. На основе сопоставления аналитических и экспериментальных частотных характеристик подтверждена гипотеза о допустимости линеаризации математической модели механической системы вибрационного электромагнитного активатора при аналитическом исследовании вынуждающей силы оптимальной формы.

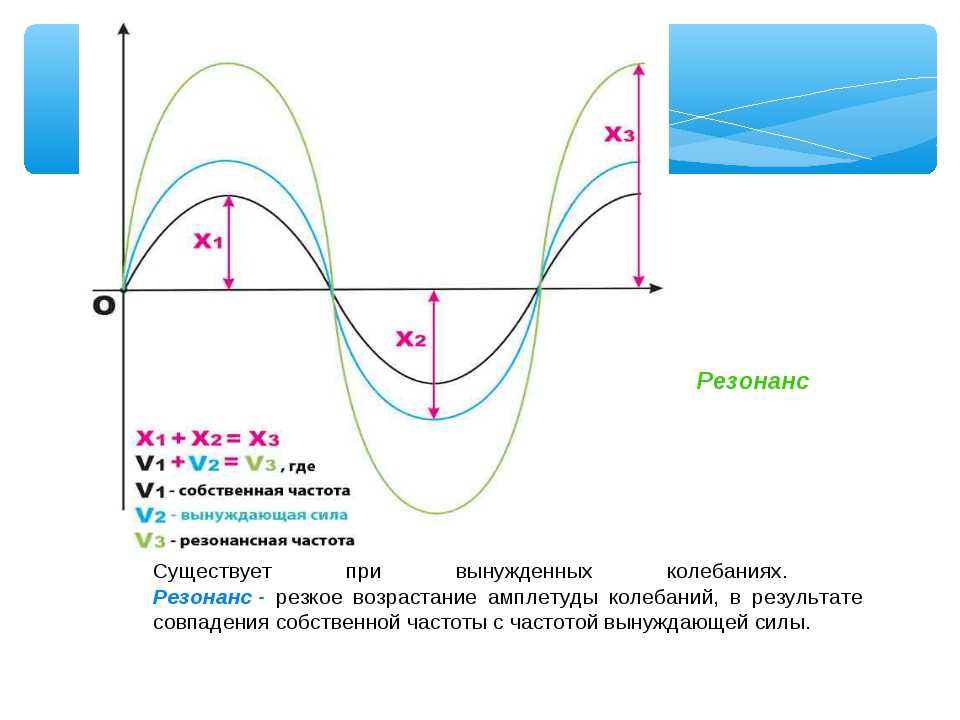
Ключевые слова:

Буровой раствор, высоковязкий нефтепродукт, вибрационный электромагнитный активатор, резонанс, вынуждающая колебания сила, свободные колебания, вынужденные колебания, спектральный анализ, настройка на резонансную частоту, оценка погрешности

Авторы:

Алексей Николаевич Гаврилин

Евгений Владимирович Боловин

Александр Савельевич Глазырин

Сергей Николаевич Кладиев

Владимир Иосифович Полищук

Скачать PDF

Резонансные колебания при движении автотранспортного средства по виброполосе

Библиографическое описание:

Кычкин, В. И. Резонансные колебания при движении автотранспортного средства по виброполосе / В. И. Кычкин, В. С. Юшков. — Текст : непосредственный // Молодой ученый. — 2013. — № 3 (50). — С. 65-68. — URL: https://moluch.ru/archive/50/6401/ (дата обращения: 17.02.2023).

Проблема аварийности на автотранспорте имеет важную роль в последнее десятилетие в связи с несоответствием существующей дорожно-транспортной инфраструктуры потребностям общества и государства в безопасном дорожном движении, недостаточной эффективностью функционирования системы обеспечения безопасности дорожного движения, крайне низкой дисциплиной участников дорожного движения [1, 10, 11].

Мероприятия, позволившие добиться снижение аварийности на автомобильных дорогах, связаны с внедрением, прежде всего, с принудительным ограничением скорости автотранспортных средств (АТС) в местах повышенной опасности [2]. Одним из путей решения этой проблемы является создание конструктивных элементов на дорожной одежде, способствующих генерации колебаний транспортных средств в режимах некомфортного восприятия водителем условий движения, что ведет к изменению параметров движения по направлению и скорости.

Для выбора оптимальных параметров такой конструкции необходимы математические модели, включающие в себя особенности тактильного восприятия водителем наличия виброполосы, характеристики автотранспортных средств, скорость движения, общую длину полосы, глубину, ширину и шаг неровностей, материалы элементов конструкции виброполосы, дорожного покрытия и основания [3].

Виброполоса является конструктивным элементом дороги и в свою очередь определяет совокупные транспортно — эксплуатационные характеристики участка ее расположения, на котором этот элемент является средством снижения риска возможного дорожно-транспортного происшествия.

При наличии неровностей на поверхности автомобильной дороги в виде виброполосы, проведенные нами исследования позволяют определить основные ее параметры при движении АТС со скоростью 60 км/ч и шагом неровностей виброполосы 200 мм: глубина конструктивного элемента виброполосы 20…30 мм, ширина полосы может быть принята 150…200 мм, длина виброполосы выбирается в зависимости от продольного и поперечного профилей автомобильной дороги.

С ростом скорости движения автомобиля и уменьшением длины волны неровностей существенного влияния глубины конструктивного элемента не наблюдается, что позволяет принять этот параметр на уровне 40 мм. При этом достигаются виброускорения в пределах 2,1 м/с².

На следующем этапе рассматривается вибронагружение дорожной конструкции в следствие движения АТС по виброполосе. Принимая принципы расчета линейных упругих систем, рассмотрим динамическую модель дорожной конструкции и виброполосы с одной степенью свободы, с учетом вязко — упругих свойств материалов конструкции. Диссипативные силы принимаются пропорциональными скоростям. Ударный импульс представлен в форме полуволны синусоиды и из спектра нагрузки выделены частоты 8…20 Гц.

Действующие нагрузки являются квазистационарными с полимодальным распределением вероятностей. Накопленные остаточные деформации не определяются какой-либо одной нагрузкой, и характеризуются всей их совокупностью с учетом стохастичности.

В связи с этим требуется разработка методики учета всех разновидностей режимов нагружения по долям их участия в формировании основных статистик распределения вероятности воздействий в каждом сегменте пути [4].

Определим единичное перемещение основания по зависимости [5]:

где P₀_{, —}параметры нагрузки; Q, ξ, ,

— параметры процесса; t — время; m — активная масса.

, , , , ,

где — коэффициент поглощения строительных материалов 0,25; — частота внешней силы; — собственная частота; С — жесткость; К — коэффициент согласования 1,13; F — площадь штампа.

По разработанной математической модели были проведены имитационные расчеты перемещений дорожного покрытия (рис. 1). Колебания носят затухающий характер при расчетном коэффициенте затухания. Максимальное значение амплитуды перемещения наблюдается при t = 0,02–0,03 с.

Рис. 1. График зависимости динамического прогиба от времени при Е = 200 кг/см²

Полимодальное действие внешней нагрузки представлено на рис. 2, 3. По результатам расчетов отметим, что в системе имеет место резонанс, например, при Е = 200 кг/см²и^{t
= 0,01 с резонанс наступает при частоте 14 Гц. При Е = 500
кг/см²резонанс
смещается в сторону увеличения частоты и наблюдается при
частоте 21 Гц.}

Рис. 2. График зависимости динамического прогиба от частоты нагружения при Е = 200 кг/см2

Рис. 3. График зависимости динамического прогиба от частоты нагружения при Е = 500 кг/см²

Проведены также расчеты статического модуля упругости по формуле:

где Р — давление в месте контакта; D — диаметр эквивалентного штампа; — коэффициент Пуассона материала основания; y — прогиб.

Результаты расчетов приведены на рис. 4. В качестве примера рассмотрено отношение динамического модуля к статическому при действии нагрузки 25 кН с частотой 8 Гц. Это отношение составило . В работе [6] указано, что с ростом скорости движения с 10 до 130 км/ч динамический модуль упругости может вырасти в 12 раз, а напряжение сжатия на поверхности основания могут увеличиться больше, чем на 20 %.

Рис. 4. Статический модуль основания в функции прогиба

В работе также рассмотрена двухмассовая модель дорожной конструкции для динамической идентификации деформационного состояния дорожной конструкции при свободных колебаниях [7, 8, 9]:

где m₁и_{m_{2 —}массы
верхнего и нижнего слоя; С₁
и С_{2 —}коэффициент
жесткости дорожного покрытия и основания; у₁
и у₂ —
перемещение первой и второй масс.}

Если виброперемещения представить в виде у₁=А₁sin(ωt+φ₁) и у₂=А₂sin(ωt+φ₂), то соответствующие преобразования дают соотношение для определения собственных частот:

, с^-1

Методика расчета реализована при допущении: формирование жесткостей слоев С₁ и С₂ до расчетного значения происходит во времени намного большее, чем время действия штатной или тестовой нагрузки.

Для определения амплитуд колебаний двухмассовой системы без учета затухания представим решения дифференциальных уравнений движения в виде:

где - амплитуды колебаний по обеим гармоникам; - фазы колебаний.

Для определения коэффициентов _{воспользуемся
отношением амплитуд составляющих гармоник, соответственно для первой
и второй частоты:}

, , , , , .

Для исследование влияния параметров состояния слоев основания дороги на спектр собственных колебаний конструкций воспользуемся пакетом программ Mathcad.

Результаты моделирования колебаний дорожного покрытия и слоев основания с учетом динамической жесткости дорожной конструкции приведены на рис. 5, из которого видно, что перемещение слоев происходит в противофазе (относительная влажность w/w₀ = 0,5 %, Е_у — модуль упругости основания).

Рис. 5. Результаты расчетов вибрационных перемещений слоев дорожной конструкции

Математическая модель и результаты расчетов являются составной частью программного обеспечения диагностических процедур оценки динамического модуля материалов дорожной конструкции в режимах их нагружения АТС движущихся по виброполосе [12]. Это является основой разработки метода оценки, прогнозирования и повышения эффективности функционального назначения виброполосы для достижения цели снижения ДТП при анализе деформативности дорожной конструкции.

Литература:

Кычкин В. И., Юшков В. С. Математическая модель создания некомфортных условий при движении автомобиля по виброполосе // «Инновации в науке». Часть I г. Новосибирск 2012 г. С 73–80.
Илиополов С. К., Селезнев М. Г., Углова Е. В. Динамика дорожных конструкций. Ростов Н/Д: Рост. гос. строит. ун-т, 2002. — 258 с.
Смирнов А. В., Андреева Е. В., Кузин Н. В. Гашение колебаний и резонанс в дорожных конструкциях // М.: Наука и техника в дорожной отрасли. № 3–2006. С. 39–41.
Кычкин В. И., Мунасипов И. И. Разработка и исследование математической модели вибродиагностики подшпального основания трамвайных путей // Вестник ПНИПУ. — 2012 № 1. — С. 119–127.
Саргсян А. Е. Строительная механика. Механика инженерных конструкций: Учеб. для вузов / А. Е. Саргсян. — М.: Высш. шк. , — 462 с.
Zhao Yan — ging, Yu Xin, Tan Yi — giu Beijing gongye daxue xuebao // J. Beijing Univ. Technol. 2010. 36, № 9, с. 1253–1257.
Кычкин В. И., Юшков В. С. Перспективный метод отраслевой системы вибродиагностики автомобильных дорог // Журнал «Молодой ученый» № 11 Чита 2012 г. С. 65–68.
Кычкин В. И., Юшков В. С. Неразрушающий динамический метод контроля дорожных одежд // Интернет-журнал «Науковедение». 2013 № 1 (14) [Электронный ресурс].- М. 2013. — Режим доступа: http://naukovedenie.ru/sbornik14/34tvn113.pdf.
Юшков Б. С., Юшков В. С., Кычкин В. И. Конструктивные особенности виброполосы в качестве дорожной разметки // Журнал «Народное хозяйство. Вопросы инновационного развития». Изд-во МИИ наука Москва № 2 2012 г. С. 71–75.
Юшков В. С. Новые подходы по нанесению горизонтальной дорожной разметки // Приволжский научный вестник № 2. Издательский центр Научного просвещения. Ижевск 2012 г. С. 17–19.
Юшков В. С. Шумовые полосы для снижения аварийности на автомобильных дорогах // Журнал «Молодой ученый» № 3 Чита 2012 г. С. 86–87.
Юшков Б. С., Кычкин В. И., Юшков В. С., Отчик Е. А. Разработка математической модели взаимодействия автомобиля и шумовой полосы // Вестник ПНИПУ «Охрана окружающей среды, транспорт, безопасность жизнедеятельности» № 2 Пермь 2012 г. С. 79–85.

Что такое вибрационный резонанс?

Вибрационный резонанс возникает, когда оборудование или изделие подвергается воздействию внешней вынужденной вибрации, возникающей на одной или нескольких собственных частотах. Возникающая в результате вибрация отклика продукта усиливается и может быть огромной! Вибрационные резонансы могут нанести серьезный ущерб изделиям и значительно сократить срок их службы.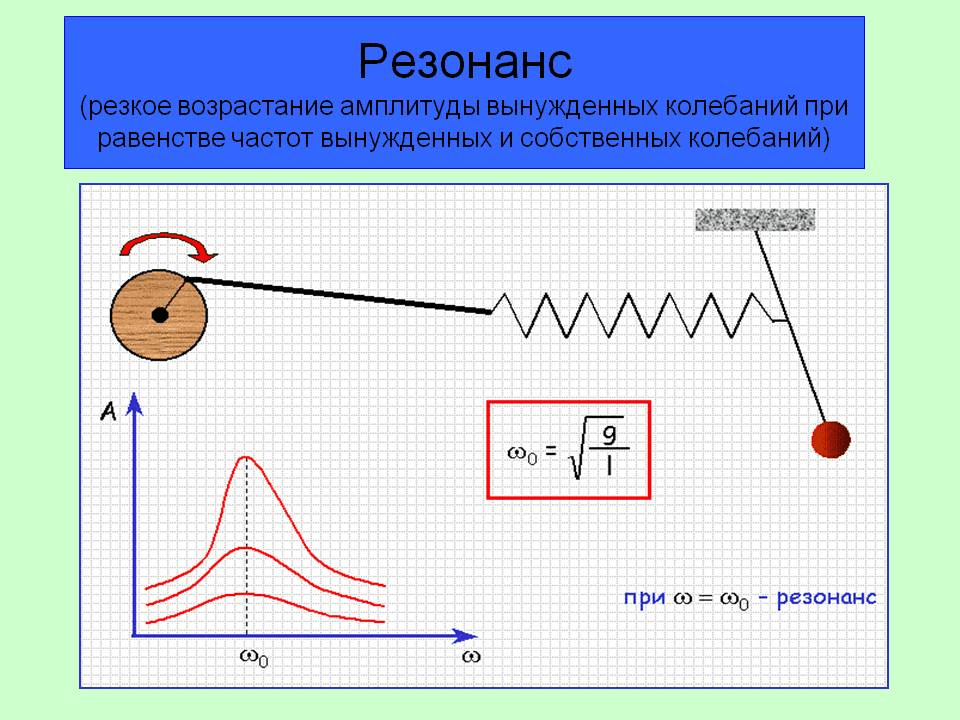 Примеры вибрационных резонансов можно увидеть ниже и на нашей странице с видео.

A собственная частота — это частота, с которой система будет колебаться после того, как внешняя сила будет приложена, а затем удалена. Все объекты имеют естественную частоту, с которой они вибрируют. Большинство продуктов имеют много собственных частот.

При вибрационных испытаниях с использованием вибровибраторов для изучения резонансов в изделиях используется синусоидальное виброрезонансное сканирование или поиск резонанса. При выполнении резонансного сканирования вибрационный стол подвергает продукт контролируемым вынужденным вибрациям в диапазоне частот, чтобы изучить ответные вибрации продукта. Уровни вынужденной вибрации низкие (обычно ½ G) и считаются неповреждающими. Ускорения реакции продукта сравниваются с ускорениями контролируемого стола. Любое усиление, равное или превышающее 2 к 1, обычно считается резонансом. Частота, с которой это происходит, называется резонансная частота . DES видел очень серьезные резонансные пики, превышающие 20 к 1! Типичный график резонансного сканирования показан ниже. Например, ускорение отклика продукта (ИУ) составляет 2,288 G при частоте 688,1 Гц. Ускорения стола (управление) составляют ½ G при 688,1 Гц. Таким образом, 688,1 Гц считается резонансной частотой, поскольку отношение ускорения продукта к столу составляет 2,288G/0,5G = 4,576, что больше, чем 2 к 1.

Условия и процедуры испытаний бортового оборудования) требуют сканирования резонанса синусоидальной вибрации до и после испытания по каждой оси. Любое существенное изменение результатов резонансного сканирования может быть признаком повреждения или отказа продукта.

Самым известным отказом из-за резонанса было катастрофическое обрушение моста Tacoma Narrows Bridge, описанное в статье нашего блога Vibration Response of Products. Когда изделия подвергаются вибрации, близкой к их собственной частоте, могут возникнуть усталостные разрушения из-за вибрационного резонанса. Компрессоры и двигатели являются примерами оборудования, которое может генерировать значительные вибрации. Продукты, установленные рядом с таким оборудованием, не должны иметь собственные частоты, близкие к их рабочей скорости.

Чтобы предотвратить преждевременные усталостные разрушения вашего продукта, DES может протестировать и проанализировать реакцию вашего продукта на вибрацию, используя свои обширные знания и программное обеспечение для анализа вибрации.

Опубликовано 22 июня 2015 г. 23 июня 2015 г. Автор DESCategories Вибрационные и ударные испытанияТеги Испытание на синусоидальную вибрацию, Испытание на вибрацию

Роль резонансных колебаний в электронной передаче энергии

. 2016 4 мая; 17 (9): 1356-68.

doi: 10.1002/cphc.201500965. Epub 2016 22 марта.

Павел Малый ^{1
2} , Оскар Дж. Г. Сомсен ³ , Владимир I Новодережкин ⁴ , Томаш Манчал ² , Ринк ван Грондель ¹

Принадлежности

¹ Кафедра физики и астрономии, Свободный университет Амстердама, De Boelelaan 1081, 1081 HV, Амстердам, Нидерланды.
² Институт физики Карлова университета в Праге, Ke Karlovu 5, 12116, Прага, Чехия.
³ Академия обороны Нидерландов, P.O. Box 10000, 1780 CA, Ден-Хелдер, Нидерланды.
⁴ Институт физико-химической биологии им. А. Н. Белозерского Московского государственного университета, Ленинские горы, 119992, Москва, Россия.

PMID: 26910485
PMCID: PMC5021137
DOI: 10.1002/cphc.201500965

Бесплатная статья ЧВК

Павел Малый и др. Химфиз. 2016 .

Бесплатная статья ЧВК

. 2016 4 мая; 17 (9): 1356-68.

doi: 10.1002/cphc.201500965. Epub 2016 22 марта.

Авторы

Павел Малый ^{1
2} , Оскар Дж. Г. Сомсен ³, Владимира Новодережкина ⁴ , Томаш Манчал ² , Ринк ван Грондель ¹

Принадлежности

¹ Кафедра физики и астрономии, Свободный университет Амстердама, De Boelelaan 1081, 1081 HV, Амстердам, Нидерланды.
² Институт физики Карлова университета в Праге, Ke Karlovu 5, 12116, Прага, Чехия.
³ Академия обороны Нидерландов, P.O. Box 10000, 1780 CA, Ден-Хелдер, Нидерланды.
⁴ Институт физико-химической биологии им. А. Н. Белозерского Московского государственного университета, Ленинские горы, 119992, Москва, Россия.

PMID: 26910485
PMCID: PMC5021137
DOI: 10.1002/cphc.201500965

Абстрактный

Колебания ядер играют важную роль в спектроскопии и динамике электронных систем. Как показывают недавние экспериментальные и теоретические исследования, это может быть еще более значимым, когда колебательные частоты находятся в резонансе с переходами между электронными состояниями. Здесь представлена вибронная многоуровневая модель Редфилда для экситонно-связанных электронных двухуровневых систем с несколькими явно включенными колебательными модами, взаимодействующими с фононной ванной. С помощью численного моделирования проиллюстрировано влияние квантованных колебаний на динамику передачи энергии и когерентность в модельном димере. Резонанс между частотой колебаний и энергетическим зазором между узлами приводит к большой делокализации вибронных состояний, что затем приводит к более быстрой передаче энергии и более долгоживущим смешанным когерентностям.

Ключевые слова: передача энергии; резонансные колебания; спектроскопия с временным разрешением; двумерная электронная спектроскопия; Вибронная динамика.

Цифры

Рисунок 1

Пространство конфигурации с…

Рисунок 1

Конфигурационное пространство с параболическими потенциалами земли (0) и возбужденных…

Рисунок 1

Конфигурационное пространство с параболическими потенциалами основного (0) и возбужденного состояний пигментов. Возбужденные состояния смещены от основного состояния по соответствующим обобщенным координатам.

Рисунок 2

Результаты для несвязанных пигментов: A)…

Рисунок 2

Результаты для несвязанных пигментов: A) спектр поглощения, B) динамика вибронной популяции, C) когерентность…

фигура 2

Результаты для несвязанных пигментов: A) спектр поглощения, B) динамика вибронной популяции, C) динамика когерентности и D) межсайтовая когерентность. Муфта: J = 0 см ^-1 ; остальные параметры приведены в Таблице 1.

Рисунок 3

Результаты для связанных пигментов. В…

Рисунок 3

Результаты для связанных пигментов. Свойства системы рассчитаны для трех…

Рисунок 3

Результаты для связанных пигментов. Свойства системы рассчитаны для трех различных энергетических щелей, ∆ Е ; остальные параметры приведены в таблице 1. A–C) Спектр поглощения, состояния отсортированы по энергии. г – Е) Динамика заселенности вибронных состояний. G–I) Вибронная динамика когерентности, упорядоченная по их начальной амплитуде. J – L) Динамика межсайтовой когерентности. M–O) Динамика населения участка.

Рисунок 4

A) Наличие общей амплитуды когерентности…

Рисунок 4

A) Суммарная амплитуда когерентности в системе, рассчитанная для четырех различных энергий…

Рисунок 4

A) Полная амплитуда когерентности, присутствующая в системе, рассчитана для четырех различных расстроек энергии. Б) Сравнение «векового» и полного расчетов Редфилда зависимости времени передачи от расстройки энергии.

Рисунок 5

Влияние расстройки на передачу…

Рисунок 5

Влияние расстройки на время передачи: роль резонанса. Зависимость…

Рисунок 5

Влияние расстройки на время передачи: роль резонанса. Зависимость рассчитана для четырех различных смещений состояния 1 и для связей А) 120 и Б) 60 см ⁻¹ . Черными вертикальными линиями отмечены резонансные ΔE=kΩ. энергетические пробелы.

Рисунок 6

Зависимость передачи…

Рисунок 6

Зависимость времени передачи от энергетической расстройки. А) Сравнение…

Рисунок 6

Зависимость времени передачи от энергетической расстройки. A) Сравнение BO и плоской спектральной плотности для двух различных смещений состояния 1. Стрелки указывают на смещение минимумов резонанса от плоского к случаю спектральной плотности БО. B) Возникновение множественных резонансов для более высокой энергетической щели, как рассчитано с плоской спектральной плотностью (33). Черными вертикальными линиями отмечены резонансные ΔE=kΩ. энергетические пробелы.

Рисунок 7

Зависимость передачи…

Рисунок 7

Зависимость времени передачи от энергетической расстройки. Влияние…

Рисунок 7

Зависимость времени передачи от энергетической расстройки. Влияние силы связи A) электронной и B) вибрационной ванн рассчитано для четырех различных смещений состояния 1. Стрелками показано смещение минимумов резонанса при увеличении силы связи с соответствующей ванной.

Рисунок 8

Моментальные снимки движения…

Рисунок 8

Снимки движения вибронного волнового пакета при различных энергетических расстройках. Черный…

Рисунок 8

Моментальные снимки движения вибронного волнового пакета при различных энергетических расстройках. Черные цифры обозначают минимумы соответствующих состояний ПЭС, см. рисунок 1. В T =0 fs, после перехода Франка–Кондона волновой пакет имеет положение и форму, которые он имел в равновесии в основном состоянии. В более поздние моменты времени возбуждение когерентно колеблется вокруг минимумов состояний 2 и 1, просачиваясь через потенциальные пересечения, в конечном итоге релаксируя до более низкого энергетического состояния 1.

См. это изображение и информацию об авторских правах в PMC

Цитируется

Точное моделирование комплексов пигмент-белок раскрывает вибронную перенормировку электронных параметров в сверхбыстрой спектроскопии.
Кайседо-Солер Ф., Маттиони А. , Лим Дж., Ренгер Т., Уэльга С.Ф., Пленио М.Б. Кайседо-Солер Ф. и др. Нац коммун. 2022 25 мая; 13 (1): 2912. doi: 10.1038/s41467-022-30565-4. Нац коммун. 2022. PMID: 35614049 Бесплатная статья ЧВК.
Скрытая вибронная и экситонная структура и передача вибронной когерентности в бактериальном реакционном центре.
Полихт В.Р., Нидрингхаус А., Уиллоу Р., Лайбл П.Д., Боциан Д.Ф., Кирмайер С., Холтен Д., Манчал Т., Огилви Д.П. Полихт В.Р. и др. Научная реклама 2022 7 января; 8 (1): eabk0953. doi: 10.1126/sciadv.abk0953. Epub 2022 5 января. Научная реклама 2022. PMID: 34985947 Бесплатная статья ЧВК.
Фотосинтез настраивает квантово-механическое смешение электронных и колебательных состояний, чтобы управлять передачей энергии экситона.
Хиггинс Дж.С., Ллойд Л.Т., Сохейл С.Х., Аллоди М.А., Отто Дж.П., Саер Р.Г., Вуд Р.Э., Мэсси С.К., Тинг П.С., Бланкеншип Р.Э., Энгель Г.С. Хиггинс Дж.С. и др. Proc Natl Acad Sci U S A. 2021 Mar 16;118(11):e2018240118. doi: 10.1073/pnas.2018240118. Proc Natl Acad Sci U S A. 2021. PMID: 33688046 Бесплатная статья ЧВК.
Асимметрия в спектрах флуоресценции и поглощения Q _y хлорофилла a , относящаяся к динамике экситонов.
Reimers JR, Rätsep M, Freiberg A. Реймерс Дж. Р. и соавт. Фронт хим. 2020 2 декабря; 8: 588289. doi: 10.3389/fchem.2020.588289. Электронная коллекция 2020. Фронт хим. 2020. PMID: 33344415 Бесплатная статья ЧВК.
Установление спектра поглощения Q _y хлорофилла a , распространяющегося на ближний инфракрасный диапазон.
Лейгер К., Линнанто Дж.М., Фрайберг А. Лейгер К. и др. Молекулы. 2020 авг. 20;25(17):3796. doi: 10,3390/молекулы 25173796. Молекулы. 2020. PMID: 32825445 Бесплатная статья ЧВК.

Просмотреть все статьи “Цитируется по”

РЕЗОНАНСНЫЕ КОЛЕБАНИЯ С ПРЕДЕЛЬНОЙ АМПЛИТУДОЙ В ВИБРАЦИОНОМ ЭЛЕКТРОМАГНИТНОМ АКТИВАТОРЕ

Том 330 № 1 (2019)

DOI https://doi.org/10.18799/24131830/2019/1/70

Ключевые слова:

Авторы:

Алексей Николаевич Гаврилин

Евгений Владимирович Боловин

Александр Савельевич Глазырин

Сергей Николаевич Кладиев

Владимир Иосифович Полищук

Резонансные колебания при движении автотранспортного средства по виброполосе

Что такое вибрационный резонанс?

Роль резонансных колебаний в электронной передаче энергии

Принадлежности

Авторы

Принадлежности

Абстрактный

Цифры

Похожие статьи

Цитируется

Рекомендации

Оставить комментарий Отменить ответ