Второй закон ньютона рисунок простой (50 фото) » Рисунки для срисовки и не только
Законы Ньютона 1.2.3 формулы
СкачатьВторой закон Ньютона
СкачатьРисунок второго закона Ньютона
СкачатьНьютон закон три закона движения
СкачатьСхема второго закона Ньютона
СкачатьФормула второго закона Ньютона
СкачатьФормула 2 закон Ньютона в физике
СкачатьЗаконы Ньютона рисунки
Скачать2 Закон Ньютона чертеж
Скачать3 Закон Ньютона схема
СкачатьВторой закон Ньютона рисунок
СкачатьЗаконы Ньютона 1.2.3 формулы
Скачать2 Закон Ньютона примеры
Скачать2 Закон Ньютона
Скачать2 Закон Ньютона иллюстрация
СкачатьВторой закон Ньютона рисунок
СкачатьРисунок второго закона Ньютона
СкачатьВторой закон Ньютона
СкачатьЗадачи по физике третий закон Ньютона 9 кл.
1 Закон Ньютона рисунок
СкачатьПервый закон Ньютона 7 класс физика
Скачать1 2 И 3 законы Ньютона формулировка и формулы
Скачать2 Закон Ньютона чертеж
СкачатьУскорение из второго закона Ньютона
СкачатьСила действия равна силе противодействия 3 закон
СкачатьРисунок 1 закона Ньютона 2 закона Ньютона 3 закона Ньютона
СкачатьВторой закон Ньютона рисунок
СкачатьФормула первого закона Ньютона
СкачатьРисунок 1 закона Ньютона 2 закона Ньютона 3 закона Ньютона
СкачатьВторой закон Ньютона 9 класс физика
СкачатьТри закона Ньютона 9 класс физика
Скачать2 Закон Ньютона примеры
СкачатьЗаконы Ньютона рисунки
СкачатьПервый и второй закон Ньютона
СкачатьФормула третьего закона Ньютона в физике 9 класс
СкачатьТретий закон Ньютона
СкачатьТретий закон Ньютона рисунок схема
СкачатьЗакон Ньютона сила действия равна силе противодействия
СкачатьОпыты по 2 закону Ньютона
СкачатьПримеры применения закона на практике второй закон Ньютона
СкачатьФормулировка третьего закона Ньютона 9 класс
СкачатьВторой закон Ньютона формула физика 9 класс
СкачатьТри закона Ньютона картинки
СкачатьТретий закон Ньютона
СкачатьВторой закон Ньютона 9 класс физика
Скачать3 Закон Ньютона примеры
СкачатьСкачать
Скачать
Скачать
Второй закон Ньютона • 9 класс • Физика
Содержание
На прошлом уроке мы познакомились с первым законом Ньютона.
Согласно этому закону, существуют такие системы отсчета, в которых тело находится или в состоянии покоя, или двигается прямолинейно и равномерно, если на него не действуют никакие силы или их действие компенсируется.
А что должно произойти, чтобы тело начало изменять свою скорость (приобрело некое ускорение)? Чтобы ответить на этот вопрос, нам нужно будет вспомнить о том, что является следствием взаимодействием тел, а что — причиной. Разобравшись с этими вопросами и проведя несколько интересных опытов, мы с вами на данном уроке сформулируем второй закон Ньютона.
Причина возникновения ускорения
Из курса 7 класса нам уже известно, что скорость тела (и ее направление, и численное значение) может измениться только под действием другого тела. Иными словами, изменение скорости — это результат взаимодействия нашего тела с каким-то другим телом. Мерой этого взаимодействия является сила ($\vec F$).
Например, яблоко падает на землю под действием силы тяжести (рисунок 1, а).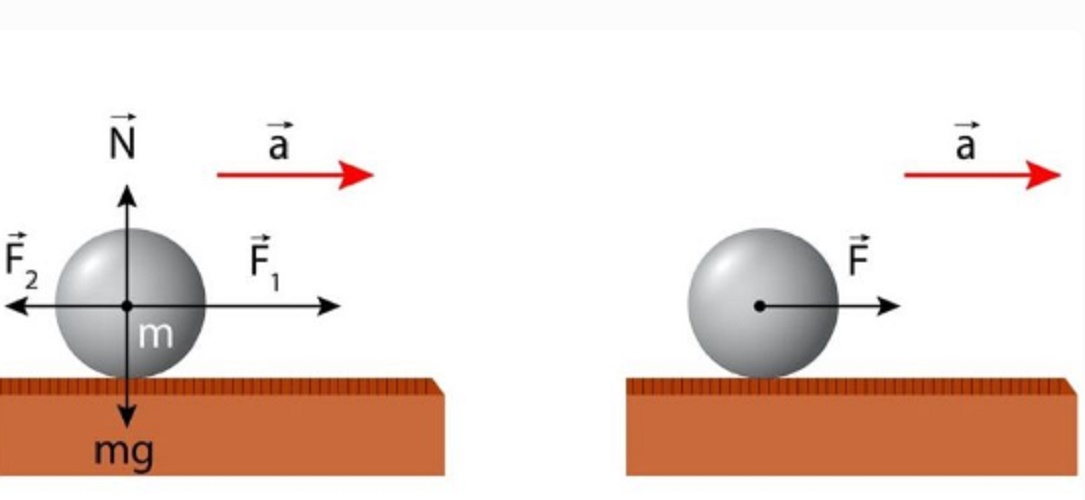
Мы можем сказать, что сама Земля действует на яблоко с силой $\vec F_{тяж} = m \vec g$.
Или Образавр толкает перед собой тележку с продуктами (рисунок 1, б). Тележка движется, потому что Образавр действует на нее с какой-то силой $\vec F$.
Рисунок 1. Движение тел под воздействием некоторых силИтак, скорость тела изменяется. Она либо возрастает, либо уменьшается. Это означает, что в этот момент тело движется с некоторым ускорением.
Что является причиной ускоренного движения тел?
Причиной ускоренного движения тела является действие на это тело других тел с некоторой силой.
{"questions":[{"content":"Тело движется с некоторым ускорением. Это говорит нам о том, что[[choice-23]]","widgets":{"choice-23":{"type":"choice","options":["на тело действуют другие тела с какой-то силой","равнодействующая всех сил равна нулю","на него не действуют никакие другие тела"],"answer":[0]}}}]}Равнодействующая сил и ускорение
Вспомним, какую физическую величину мы называем равнодействующей сил (рисунок 2).
Рисунок 2. Равнодействующая двух сил, направленных по одной прямойРавнодействующая сил — это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Если равнодействующая всех сил, действующих на тело, будет равна нулю, то в силу вступает первый закон Ньютона. Рассматриваемое тело будет или покоиться, или двигаться равномерно и прямолинейно.
А вот если равнодействующая сил не равна нулю, то скорость тела будет изменяться — тело будет двигаться с неким ускорением.
{"questions":[{"content":"Соотнесите утверждения о равнодействующей сил и поведение физического тела.[[grouper-26]]","widgets":{"grouper-26":{"type":"grouper","labels":["Равнодействующая сил равна нулю","Равнодействующая сил не равна нулю"],"items":[["Тело покоится","Тело двигается равномерно и прямолинейно"],["Тело двигается с некоторым ускорением"]]}}}]}Ускорение и действующая сила
Получается, что ускорение — это результат действия на тело какой-то силы.
Логично предположить, что между этими двумя величинами есть какая-то взаимосвязь.
Давайте приведем примеры из жизни, свидетельствующие о том, что чем больше приложенная к телу сила, тем больше сообщаемое этой силой ускорение.
Например, чем сильнее пнуть лежачий мяч, тем большее ускорение он приобретет. При этом он успеет набрать намного большую скорость за те доли секунды, что взаимодействует с ногой игрока, чем при слабом ударе. Об этой скорости мы можем судить, если посмотрим на расстояние, которое мяч пролетает после удара.
Чем сильнее мы оттолкнемся, катаясь на коньках, тем большее ускорение мы получим и тем большее расстояние мы проедем. Чем сильнее мы толкнем мяч для боулинга, тем большую скорость он сможет набрать до того, как встретится с кеглями.
Также можно провести простой опыт, который даст нам тот же результат, что и предыдущие размышления.
Прикрепим тележку к динамометру. На саму тележку установим специальную конструкцию с подвешенным шариком.
Остановим тележку. Снова потянем за динамометр, но на этот раз сильнее. Динамометр покажет нам большее значение, чем в первый раз. Тележка пришла в движение. Подвешенный шарик отклонился на большее расстояние (рисунок 3, б).
Зафиксируем вывод.
Ускорение, которое тело приобретает в результате действия на него силы, прямо пропорционально величине этой силы.
{"questions":[{"content":"Ускорение тела и величина силы, приложенной к этому телу,[[choice-29]]","widgets":{"choice-29":{"type":"choice","options":["прямо пропорциональны друг другу","обратно пропорциональны друг другу","равны друг другу","никак не связаны друг с другом"],"answer":[0]}}}]}Ускорение и масса тела
Теперь давайте рассмотрим, как связаны между собой масса тела и его ускорение.
Опыт №1
Для начала проведем более простой и наглядный опыт. Возьмем два идентичных воздушных шарика. В один из них положим маленькую бусинку, чей вес все же позволит шару взлететь. Наполним шары гелием до одинакового объема.
Теперь запустим эти два шарика с одинаковой высоты (рисунок 4, а). Посмотрим, какой из них быстрее достигнет потолка.
Мы увидим, что шарик без бусинки достигнет потолка первым (рисунок 4, б).
Рисунок 4. Опыт с воздушными шарикамиНа шарики действовали одинаковые равнодействующие сил $F$ (рисунок 5). Эта равнодействующая в обоих случаях равна разности архимедовой силы и силы сопротивления воздуха: $F = R = F_А \space − \space F_{сопр}$.
Рисунок 5. Силы, действующие на шарикиПолучается, что под действием одной и той же равнодействующей сил шарик без груза внутри получил большее ускорение.
Как мы можем здесь судить о величине ускорения? Шарик без груза прошел фиксированное расстояние за меньшее время, чем шарик с грузом внутри, масса которого больше.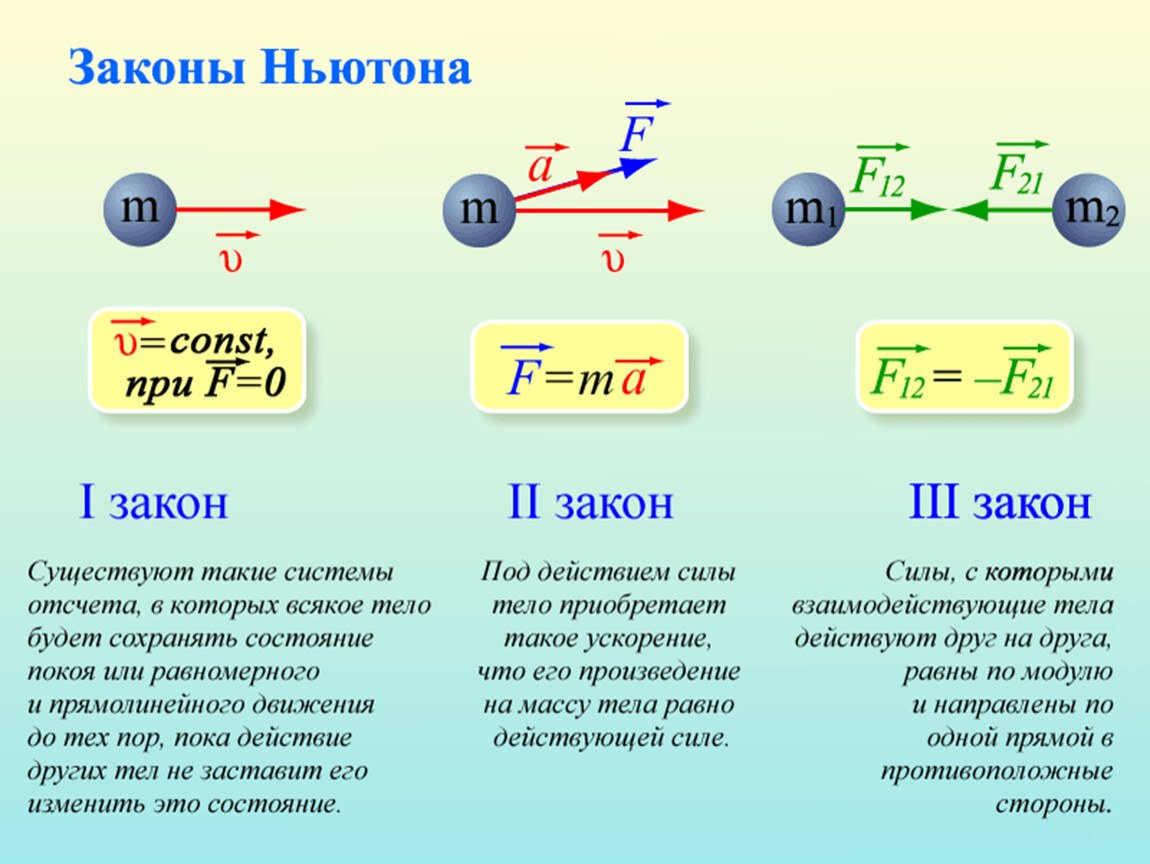
Это значит, что скорость шарика без груза возрастала быстрее. То есть он имел большее ускорение, чем шарик большей массы.
{"questions":[{"content":"Если равнодействующие сил, действующих на два разных тела, равны друг другу, то ускорения этих тел[[choice-36]]","widgets":{"choice-36":{"type":"choice","options":["могут различаться по величине","всегда будут одинаковы по величине","равны нулю"],"answer":[0]}}}]}Опыт №2
Перейдем к следующему опыту.
Возьмем легкую тележку. Установим на ней маленькую капельницу и два вентилятора. Масса этой конструкции равна $0.4 \space кг$.
Теперь возьмем нить. Один ее конец привяжем к тележке. Другой конец перекинем через блок и привяжем к нему груз. Он скомпенсирует силу трения, которая будет действовать на тележку при движении.
Вдоль линии движения тележки положим бумажную ленту. На ней будут оставаться капли из капельницы, чтобы мы могли фиксировать пройденное тележкой расстояние.
Открываем кран и включаем вентиляторы.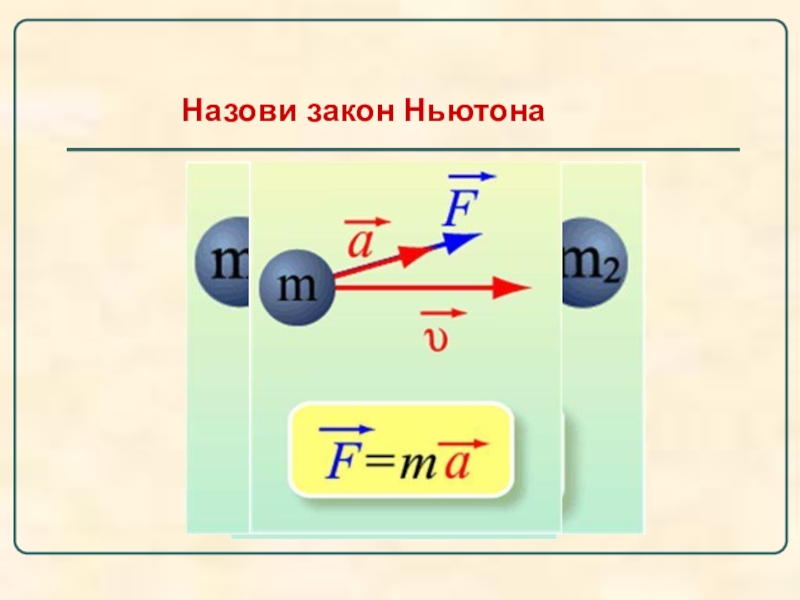
Они начинают толкать тележку с постоянной силой. На бумажной ленте остаются следы капель, которые падают через равные промежутки времени $t = 1 \space с$ (рисунок 6).
После того, как тележка упрется в ограничитель, выключим вентиляторы. Измерим расстояния между соседними каплями на ленте:
$s_2 = 6 \space см$,
$s_3 = 10 \space см$,
$s_4 = 14 \space см$,
$s_5 = 18 \space см$.
Получается, что эти расстояния относятся как ряд нечетных последовательных чисел:
$s_1 : s_2 : s_3 : s_4 : s_5 = 1 : 3 : 5 : 7 : 9$.
Как вы помните, это одна из закономерностей равноускоренного движения. Значит, наша тележка двигалась равноускоренно.
Все движение тележки заняло ровно $5 \space с$. Расстояние, которое она прошла с начала движения, равно $0.5 \space м$.
Теперь запишем формулу для модуля перемещения при равноускоренном прямолинейном движении без начальной скорости:
$s = \frac{at^2}{2}$.
2}} = 2$.
Получается, что при действии одной и той же силы система тел, масса которой стала вдвое больше, приобрела в 2 раза меньшее ускорение, то есть $\frac{a}{2}$.
Сделаем вывод.
Ускорения, сообщаемые телам одной и той же постоянной силой, обратно пропорциональны массам этих тел.
{"questions":[{"content":"Ускорение, приобретенное телом в результате действия на него силы, и масса этого тела[[choice-39]]","widgets":{"choice-39":{"type":"choice","options":["обратно пропорциональны друг другу","прямо пропорциональны друг другу","никак не связаны друг с другом"],"answer":[0]}}}]}Второй закон Ньютона
Как вы уже догадываетесь, этот закон как раз и отражает количественную взаимосвязь между массой тела, ускорением, с которым оно движется, и равнодействующей приложенных к телу сил, вызывающих это ускорение.
Сформулируем второй закон Ньютона.
Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
Точно так же, как и в первом законе Ньютона, здесь под телом мы подразумеваем материальную точку, а ее движение мы рассматриваем в инерциальной системе отсчета.
Какой математической формулой выражается второй закон Ньютона?
$\vec a = \frac{\vec F}{m}$.
Что можно сказать о направлении вектора ускорения и вектора равнодействующей приложенных к телу сил?
Из этой формулы мы видим, что вектор ускорения будет совпадать по направлению с вектором равнодействующей приложенных к телу сил.
Запишем второй закон Ньютона в скалярной форме.
$a_x = \frac{F_x}{m}$ или $a = \frac{F}{m}$,
где $a_x$ и $F_x$ — это проекции векторов ускорении и силы на ось OX,
$a$ и $F$ — модули этих векторов.
{"questions":[{"content":"Выберите правильную математическую формулировку второго закона Ньютона.[[choice-42]]","widgets":{"choice-42":{"type":"choice","options":["$\\vec a = \\frac{\\vec F}{m}$","$\\vec F = \\frac{\\vec a}{m}$","$m = \\vec F \\vec a$","$\\vec a = \\vec Fm$"],"answer":[0]}}}]}Единицы измерения силы
В СИ сила всегда измеряется в ньютонах ($Н$).
2}} = 9.6 \space Н$.
Ответ: $F_1 \neq F_2$, $F_2 = 9.6 \space Н$.
Упражнение №4
С каким ускорением будет всплывать находящийся под водой мяч массой $0.5 \space кг$, если действующая на него сила тяжести равна $5 \space Н$, архимедова сила — $10 \space Н$, а средняя сила сопротивления движению — $2 \space Н$?
Рисунок 8. Чертеж к упражнению №4Дано:
$m = 0.5 \space кг$
$F_{тяж} = 5 \space Н$
$F_А = 10 \space Н$
$F_{сопр} = 2 \space Н$
$a_x — ?$
Для наглядности удобно использовать чертеж (рисунок 8), на котором мы обозначили все силы, действующие на мяч, и их равнодействующую. Ось OX мы направили наверх по ходу движения мяча.
Посмотреть решение и ответ
Скрыть
Решение:
Запишем формулу для равнодействующей всех сил, действующих на всплывающий мяч:
$\vec F = \vec F_{тяж} \space + \space \vec F_А \space + \space \vec F_{сопр}$.
Теперь возьмем проекции на ось OX и рассчитаем равнодействующую (проекции сил будут равны их модулям с соответствующими знаками):
$F_x = F_А \space − \space F_{тяж} \space − \space F_{сопр}$,
$F_x = 10 \space Н \space − \space 2 \space Н \space − \space 5 \space Н = 3 \space Н$.
2}$.
Упражнение №5
Баскетбольный мяч, пройдя сквозь кольцо и сетку, под действием силы тяжести сначала движется вниз с возрастающей скоростью, а после удара о пол — вверх с уменьшающейся скоростью. Как направлены векторы ускорения, скорости и перемещения мяча по отношению к силе тяжести при его движении вниз; вверх?
Посмотреть ответ
Скрыть
Ответ:
После прохождения через кольцо мяч движется к полу с возрастающей скоростью. В этот момент векторы ускорения, скорости и перемещения направлены вниз (рисунок 9, а).
После удара об пол мяч движется вверх (рисунок 9, б). Значит, вверх будут направлены векторы скорости и перемещения. Но скорость мяча уменьшается. Значит, вектор ускорения направлен противоположно вектору скорости, то есть вниз.
Рисунок 9. Направление векторов ускорения, скорости и перемещения мячаУпражнение №6
Тело движется прямолинейно с постоянным ускорением. Какая величина, характеризующая движение этого тела, всегда сонаправлена равнодействующей приложенных к телу сил, а какие величины могут быть направлены противоположно равнодействующей?
Посмотреть ответ
Скрыть
Ответ:
Пользуясь вторым законом Ньютона ($\vec a = \frac{\vec F}{m}$), мы можем сказать, что ускорение у нас всегда будет сонаправлено равнодействующей сил, действующих на тело.
При этом противоположно равнодействующей могут быть направлены векторы скорости и перемещения. В этом случае тело будет двигаться в направлении, противоположном направлению векторов равнодействующей и ускорения — оно будет замедляться.
Часто задаваемые вопросы
Что является причиной ускоренного движения тел?Действие на это тело других тел с некоторой силой.
Приведите примеры из жизни, свидетельствующие о том, что чем больше приложенная к телу сила, тем больше сообщаемое этой силой ускорение.Чем сильнее ударить по мячу, тем быстрее он полетит. Чем быстрее крутить педали велосипеда, тем быстрее он разгоняется. Чем сильнее кинуть снежок, тем быстрее он достигнет цели.
Сформулируйте второй закон Ньютона. Какой математической формулой он выражается?Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе: $\vec a = \frac{\vec F}{m}$.
Что можно сказать о направлении вектора ускорения и вектора равнодействующей приложенных к телу сил?Вектор ускорения всегда будет совпадать по направлению с вектором равнодействующей приложенных к телу сил.
Второй закон Ньютона – новый взгляд
Второй закон Ньютона гласит, что ускорение объекта прямо пропорционально суммарной силе, действующей на объект, и обратно пропорционально массе объекта. Закон часто выражается в виде следующих двух уравнений.
Второй закон Ньютона использовался для анализа различных физических ситуаций. Идея заключалась в том, что если любую данную физическую ситуацию анализировать с точки зрения отдельных сил, действующих на объект, то эти отдельные силы должны складываться в виде векторов результирующей силы. Кроме того, результирующая сила должна быть равна произведению массы на ускорение. Впоследствии можно найти ускорение объекта, если известны масса объекта, а также величины и направления каждой отдельной силы. А величину любой отдельной силы можно определить, если известны масса объекта, ускорение объекта и величина других отдельных сил. Процесс анализа таких физических ситуаций с целью определения неизвестной информации зависит от способности представить физическую ситуацию с помощью диаграммы свободного тела.
Диаграмма свободного тела — это векторная диаграмма, отображающая относительную величину и направление всех отдельных сил, действующих на объект.
В этом уроке мы будем использовать принципы Модуля 2 (диаграммы свободного тела, уравнение второго закона Ньютона и т. д.) и концепции кругового движения для анализа различных физических ситуаций, связанных с движением объектов по кругу или по криволинейным траекториям. . Математические уравнения, обсуждавшиеся в уроке 1, и концепция требования центростремительной силы будут применяться для анализа американских горок и других аттракционов в парках развлечений, а также различных спортивных движений.
Круговое движение в горизонтальной плоскости
Чтобы проиллюстрировать, как можно объединить принципы кругового движения со вторым законом Ньютона для анализа физической ситуации, рассмотрим автомобиль, движущийся по горизонтальному кругу на ровной поверхности. На приведенной ниже диаграмме автомобиль изображен с левой стороны круга.
Применяя концепцию требования центростремительной силы, мы знаем, что результирующая сила, действующая на объект, направлена внутрь. Поскольку автомобиль расположен на левой стороне круга, результирующая сила направлена вправо. Анализ ситуации показал бы, что на объект действуют три силы: сила тяжести (действующая вниз), нормальная сила дорожного покрытия (действующая вверх) и сила трения (действующая внутрь или вправо). Именно сила трения обеспечивает центростремительную силу, необходимую для движения автомобиля по горизонтальному кругу. Без трения автомобиль вращал бы колеса, но не двигался бы по кругу (как это бывает на обледенелой поверхности). Этот анализ приводит к диаграмме свободного тела, показанной справа. Обратите внимание, что каждая сила представлена векторной стрелкой, указывающей конкретное направление, в котором действует сила; также обратите внимание, что каждая сила помечена в соответствии с типом (F frict , F norm и F grav ).
Такой анализ является первым шагом любой задачи, связанной со вторым законом Ньютона и круговым движением.
Теперь рассмотрим следующие две задачи, относящиеся к этому физическому сценарию поворота автомобиля на горизонтальной поверхности.
Пример задачи №1 Максимальная скорость, с которой автомобиль массой 945 кг совершает поворот на 180 градусов, составляет 10,0 м/с. Радиус окружности, по которой поворачивает автомобиль, равен 25,0 м. Определить силу трения и коэффициент трения, действующие на автомобиль. Коэффициент трения, действующий на автомобиль массой 945 кг, равен 0,850. Автомобиль совершает разворот на 180 градусов по кривой радиусом 35,0 м. Определить максимальную скорость, с которой автомобиль может совершить поворот. |
Пример задачи №1 предоставляет информацию о кинематике (v и R) и запрашивает значение отдельной силы.
Таким образом, решение проблемы потребует сначала определить ускорение и результирующую силу; тогда индивидуальное значение силы можно найти с помощью диаграммы свободного тела.
Известная и запрашиваемая информация в примере задачи №1:
Известная информация: м = 945 кг | Запрашиваемая информация: F трение = ??? |
Массу объекта можно использовать для определения силы тяжести, действующей в направлении вниз.
, где г равно 9,8 м/с/с. Зная, что вертикального ускорения автомобиля нет, можно сделать вывод, что вертикальные силы уравновешивают друг друга. Таким образом, F грав = F норма = 9261 N . Это позволяет нам определить две из трех сил, указанных на диаграмме свободного тела. Только сила трения остается неизвестной.
Поскольку сила трения является единственной горизонтальной силой, она должна быть равна суммарной силе, действующей на объект. Таким образом, если результирующую силу можно определить, то известна и сила трения. Чтобы определить результирующую силу, массу и кинематические данные (скорость и радиус) необходимо подставить в следующее уравнение:
Замена данных значений дает чистую силу 3780 ньютонов. Таким образом, сила трения равна 3780 Н .
Наконец, коэффициент трения (μ) можно определить с помощью уравнения, связывающего коэффициент трения с силой трения и нормальной силой.
Замена 3780 Н на F трение и 9261 Н на
И снова задача начинается с определения известной и запрашиваемой информации. Известная информация и запрошенная информация в примере задачи № 2:
Известная информация: м = 945 кг | Запрашиваемая информация: v = ??? |
Массу автомобиля можно использовать для определения силы тяжести, действующей в направлении вниз.
Используйте уравнение
, где g составляет 9,8 м/с/с. Зная, что вертикального ускорения автомобиля нет, можно сделать вывод, что вертикальные силы уравновешивают друг друга. Таким образом, Ф грав = Ф норма = 9261 Н . Поскольку задан коэффициент трения (μ), силу трения можно определить с помощью следующего уравнения:
Это позволяет нам определить все три силы, указанные на диаграмме свободного тела.
Суммарная сила, действующая на любой объект, представляет собой векторную сумму всех отдельных сил, действующих на этот объект. Таким образом, если известны все значения отдельных сил (как в данном случае), можно рассчитать результирующую силу. Сумма вертикальных сил равна 0 Н. Поскольку сила трения является единственной горизонтальной силой, она должна быть равна суммарной силе, действующей на объект.
Таким образом, F нетто = 7872 N .
После определения результирующей силы можно быстро рассчитать ускорение с помощью следующего уравнения.
Подстановка данных значений дает ускорение 8,33 м/с/с . Наконец, скорость, с которой автомобиль мог двигаться по повороту, можно рассчитать, используя уравнение для центростремительного ускорения:
Подставив известные значения для a и R в это уравнение и алгебраическое решение дает максимальную скорость 17,1 м/с .
Разработка правильного подхода к решению проблем
Каждая из двух приведенных выше примеров задач была решена с использованием одного и того же базового подхода к решению проблем. Подход можно резюмировать следующим образом.
|
Представьте каждую силу векторной стрелкой и пометьте силы в соответствии с типом.
И в качестве другого примера, если известны период и радиус, то можно определить ускорение.) Метод, описанный выше, хорошо послужит вам при решении задач кругового движения. Однако следует сделать одно предостережение. Каждая задача по физике отличается от предыдущей. Как такового нет волшебная формула для решения каждой. Использование соответствующего подхода к решению таких проблем (который включает в себя построение FBD, определение известной информации, определение запрашиваемой информации и использование доступных уравнений) никогда не избавит от необходимости думать, анализировать и решать проблемы .
По этой причине приложите усилия, чтобы разработать соответствующий подход к каждой проблеме; но всегда используйте свои навыки критического анализа в процессе решения. Если бы физические проблемы сводились к простому следованию надежной формуле из 5 шагов или использованию какого-то заученного алгоритма, то мы бы не называли их «задачами».
Мы хотели бы предложить… Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного равномерного кругового движения, интерактивной модели американских горок или нашего моделирования горизонтального круга. Вы можете найти эти интерактивы в разделе Physics Interactives на нашем веб-сайте. Эти интерактивы позволяют учащемуся в интерактивном режиме исследовать отношения между скоростью, ускорением и силой для объекта, движущегося по кругу или по криволинейной траектории.
Посетите: Равномерное круговое движение | Модель американских горок || Моделирование горизонтального круга
Используйте свое понимание второго закона Ньютона и принципов кругового движения, чтобы определить неизвестные значения в следующих практических задачах. Нажмите кнопку, чтобы проверить свои ответы.
1. Ведро с водой массой 1,50 кг связано веревкой и вращается по кругу радиусом 1,00 м. В верхней части круговой петли скорость ковша составляет 4,00 м/с. Определите ускорение, результирующую силу и отдельные значения силы, когда ковш находится в верхней части кругового контура.
м = 1,5 кг
а = ________ м/с/с
F нетто = _________ N
2. Ведро с водой массой 1,50 кг связано веревкой и вращается по кругу радиусом 1,00 м.
В нижней части круговой петли скорость ковша составляет 6,00 м/с. Определите ускорение, результирующую силу и отдельные значения силы, когда ковш находится в нижней части круговой петли.
м = 1,5 кг
а = ________ м/с/с
F нетто = _________ N
Следующий раздел: Перейти к следующему уроку:
Сэр Исаак Ньютон впервые представил свои три закона движения в «Principia Mathematica Philosophiae Naturalis» 1686 г. Его второй закон определяет сила равна дифференциальному изменению импульса в единицу времени, как описано математическим исчислением, которое Ньютон также развитый. Импульс определяется как масса объекта 90 385 м, умноженная на 90 386 его скорости. против . Итак, дифференциальное уравнение для силы F : F = d (м * v) / dt Если мы возьмем очень маленькие приращения времени, мы можем написать разностное уравнение из дифференциальное уравнение: F = (m1 * v1 – m0 * v0) / (t1 – t0) Если масса постоянна, используя определение ускорения a как изменение скорости со временем, второй закон сводится к более знакомому произведению массы и ускорения: F = м * а Сила, ускорение, скорость и
импульс есть у обоих величина и направление , связанное с ними. |
