7. РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MATHCAD
Информатика и вычислительная техника / Программные средства / 7. РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MATHCAD
Постановка задачи
Задача ставится следующим образом:
Пусть имеется алгебраическое уравнение с одним неизвестным х или система алгебраических уравнений
,
где f1(x1, …, xm) и fn(x1, … , xm) – некоторые функции.
Требуется решить данное уравнение или систему уравнений, т.е. найти те значения х, в которых уравнения превращаются в верное равенство.
Отыскание корней численными методами связано с несколькими задачами:
Ø Исследование существования корней в принципе, определение их количества и примерного расположения;
Ø Отыскание корней с заданной погрешностью
Всевозможные функции MathCAD нацелены на решение второй задачи, т.е. предполагается, что корни уже приблизительно локализированы. Выбор встроенных функций для решения уравнений и систем уравнений осуществляется в зависимости от специфики уравнения.
Решение одного уравнения с одним неизвестным
Рассмотрим алгебраическое уравнение f(x)=0 с одним неизвестным х, например, sin(x)=0.
Для решения таких уравнений MathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.
Мнемоника команды выглядит следующим образом:
root (f(x), x) или root (f(x), x, a, b),
где f(х) – скалярная функция, определяющая уравнение; х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root требует дополнительного задания начального значе
ния переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.
Приведем пример решения очень простого уравнения sin(x)=0, корни которого известны заранее (рис. 38).
38).
Обратите внимание, что, хотя уравнение имеет бесконечное количество корней MathCAD находит (с заданной точностью) только один из них, х0, лежащий наиболее близко к х = 0,5. Если задать другое начальное значение, например х = 3, то решением будет другой корень уравнения х
Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в область локального экстремума. В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого корня. Для решения таких уравнений лучше применять функцию Minerr.
Рис. 7.1. Функция Minerr
Примечание: Для решения уравнения с одним неизвестным применимы и градиентные методы, относящиеся в MathCAD к системам уравнений.
Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нуж
но. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Явный вид функции f(x) может быть определен непосредственно в теле функции root (рис. 39).
Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:
Ø внутри интервала [а, b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;
Ø значения f(а) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
Если уравнение не имеет действительных корней, но имеет мнимые, то их также можно найти. Например, уравнение х2+1=0, имеющее два чисто мнимых корня, решается два раза с разными начальными значениями (рис. 40).
При задании начального значения 0,5 численный метод отыскивает первый корень (отрицательную мнимую единицу –i), а при начальном значении –0,5 находится и второй корень i.
Для решения этого уравнения второй вид функции root (с четырьмя, а не с двумя аргументами) неприменим, поскольку f(х) является положительно определенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.
Нахождение корней полинома
Если функция f(x) является полиномом, то все его корни можно определить, использую встроенную функцию polyroots(v), где v – вектор, составленный из коэффициентов полинома.
Поскольку полином n-й степени имеет ровно n корней (некоторые из них могут быть кратными), вектор v должен состоять из n+1 элемента. Результатом действия функции polyroots является вектор, составленный из n корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root.
Например, найдем корни полинома четвертой степени f(x)=х4-6х3+12х2-10х+3 с
помощью функции polyroots (рис. 41).
Рис. 7.2. Функция Polyroots
Запишем коэффициенты рассматриваемого в примере полинома в виде вектора. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х1 и т.д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени x
Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х1 и т.д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени x
Совет: Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор MathCAD сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.
Далее показано действие функции polyroots. Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.
Для функции polyroots можно выбрать один из двух численных методов – метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.
Решение системы линейных алгебраических уравнений
(1)
В матричной форме СЛАУ записывается в эквивалентном виде:
А∙Х=В, (2)
где А – матрица коэффициентов СЛАУ размерности n×n; x – вектор неизвестных; В – вектор правых частей уравнений.
Рис.
7.3. Матрица
СЛАУ имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица А не очень велика.
В MathCAD СЛАУ можно решить как в более наглядной форме (1), так и в более удобной для записи форме (2). Для первого способа следует использовать вычислительный блок Given/Find, а для второго – встроенную функцию решения системы линейных уравнений lsolve.
lsoive (А, В),
где А – матрица коэффициентов системы; В – вектор правых частей.
Применение функции lsolve показано на рис. 42.
В некоторых случаях, для большей наглядности представления СЛАУ, его можно решить точно так же, как систему нелинейных уравнений. Не забывайте, что при численном решении всем неизвестным требуется присвоить начальные значения (это сделано в первой строке листинга) (рис. 43). Они могут быть произвольными, так как решение СЛАУ с невырожденной матрицей единственно.
Решение системы нелинейных уравнений
Рис. 7.4. Решение системы
Рассмотрим решение системы N нелинейных уравнений с m неизвестными
Здесь fi(x1, … , xm) – некоторые скалярные функции от скалярных переменных x1, x2, …, хm и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему можно формально переписать в виде f(x)=0, где х – вектор, составленный из переменных x1, x2, …, хm; f(x) – соответствующая векторная функция.
Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:
1) Given – ключевое слово;
2) Система, записанная логическими операторами в виде равенств и, возможно, неравенств;
3) Find (х1, …, хm) – встроенная функция для решения системы относительно переменных х1, …, хm.
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры помните, что логический знак равенства вводится сочетанием клавиш <Ctrl> + <=>. Блок Given/Find используется для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1, …, хm. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения по каждой переменной. Таким образом, число элементов вектора
Find равно числу аргументов.
Рис. 7.5. Система
В листинге (рис 44) приведен пример решения системы двух уравнений.
В первой строке листинга переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, содержащая вектор решения. Первый элемент вектора есть первый аргумент функции Find, второй элемент – ее второй аргумент.
Совет: Часто бывает очень полезно проверить точность решения уравнений, вычислив значения образующих их функций в найденных вычислительным процессором корнях.
Рис. 7.6. Точность
В листинге найдено только одно из двух решений – находящееся в правой нижней части графика (рис. 45). Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтоб они лежали ближе к другой точке пересечения графиков, например, х=–1, y=–1.
Пока мы рассмотрели пример системы из двух уравнений и таким же числом
неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х (рис. 46).
Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х (рис. 46).
Рис. 7.7. Ограничение на поиск
Обратите внимание, что, несмотря на те же начальные значения, что и в предыдущем листинге мы получили другой корень. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке.
Если предпринять попытку решить несовместную систему, MathCAD выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Примечание: Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Другая константа TOL определяет условие прекращения итераций численным алгоритмом. Значение CTOL может быть задано пользователем, так же как и TOL, например, CTOL:=0,01. По умолчанию принято, что CTOL=TOL=0,001, но по желанию можно переопределить их.
По умолчанию принято, что CTOL=TOL=0,001, но по желанию можно переопределить их.
Рис. 7.8. Переопределение
Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рас
смотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа возвращаемого функцией Find (рис 47).
Символьное решение уравнений
Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестным начальные значения нет необходимости. Рассмотрим листинги символьного решение уравнения с одним неизвестным и системы двух уравнений с двумя неизвестными.
Как видно, вместо знака равенства после функции Find в листингах (рис. 48) следует знак символьных вычислений, который можно ввести с панели Symbolic, или, нажав клавиши <Ctrl>+<. >.
>.
Рис. 7.9. Пример вычисления
Не забывайте, что сами уравнения должны иметь вид логических выражений, т.е. знаки равенства нужно вводить с помощью панели Booleans (Булевы операторы). Обратите внимание, что во втором листинге вычислены как два первых действительных корня, которые мы уже находили численным методом, так и два других мнимых корня. Эти два последних корня чисто мнимые, так как множитель
Рекомендации по использованию функции root
лаболаторная работа № 5
Решение уравнений и систем уравнений
Краткие теоретические сведения
Решение линейных и трансцендентных уравнений
Для простейших уравнений вида f(x)=0 решение в MathCad находится с помощью функции root.
root( f(х1, x2, …), х1), где
f(х1, x2, …) – функция описывающая левую часть выражения вида f(x)=0. Выражение должно возвращать скалярные значения;
х1 – имя переменной, относительно которой
решается уравнение.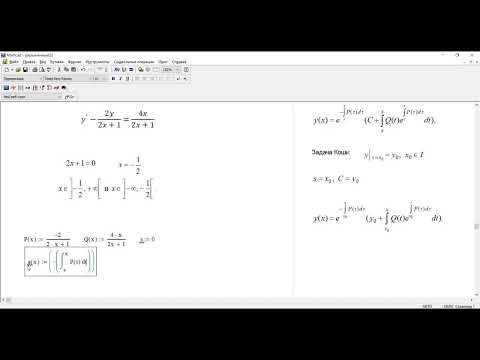
Функция реализует вычисления итерационными методами и требует предварительного задания начального приближения искомой переменной (х1). Эта переменная называется варьируемой. Функция позволяет найти как вещественные корни, так и комплексные. В этом случае начальное приближение нужно задать как комплексное число.
Приближенные значения корней (начальные приближения) могут быть:
Известны из физического смысла задачи;
Известны из решения аналогичной задачи при других исходных данных;
Найдены графическим способом.
Н
аиболее
распространен графический способ
определения начальных приближений. В
этом случае достаточно построить график
функции f(x) и отметить
точки пересечения f(x) с
осью Ох, или отметить на
оси Ох отрезки, содержащие по одному
корню. Построение графиков часто удается
сильно упростить, заменив уравнение f(x) = 0 равносильным ему
уравнением ,где
функции f1(x) и f2(x) – более простые, чем функция f(x).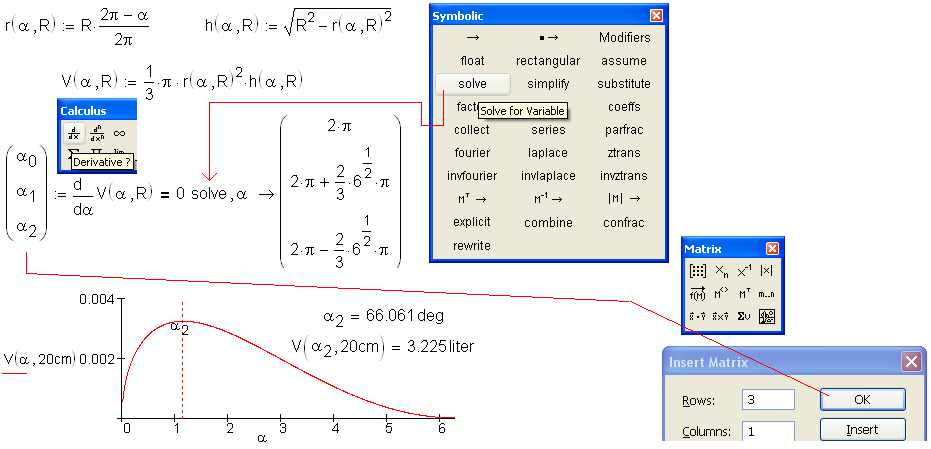 Тогда, построив графики функций у
= f1(x) и у = f2(x), искомые
корни получим как абсциссы точек
пересечения этих графиков. Для решения
уравнений вида его необходимо привести к виду .
Тогда, построив графики функций у
= f1(x) и у = f2(x), искомые
корни получим как абсциссы точек
пересечения этих графиков. Для решения
уравнений вида его необходимо привести к виду .
Часто возникает необходимость многократного решения уравнения при изменении одного из параметров.
Отсутствие сходимости функции root
Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
Уравнение не имеет корней.
Корни уравнения расположены далеко от начального приближения.
Выражение имеет локальные max и min между начальным приближением и корнями.
Выражение имеет разрывы между начальными приближениями и корнями.
Выражение имеет комплексный корень, но начальное приближение было вещественным.
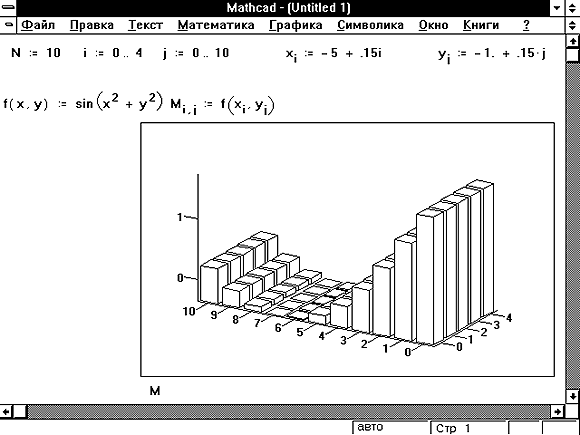
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться.
Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Значение TOL можно определить непосредственно в рабочем документе, либо в меню Math – Option . Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их.
Если функция f(x) имеет
малый наклон около искомого корня,
функция root(f(x), x) может
сходиться к значению, отстоящему от
корня достаточно далеко.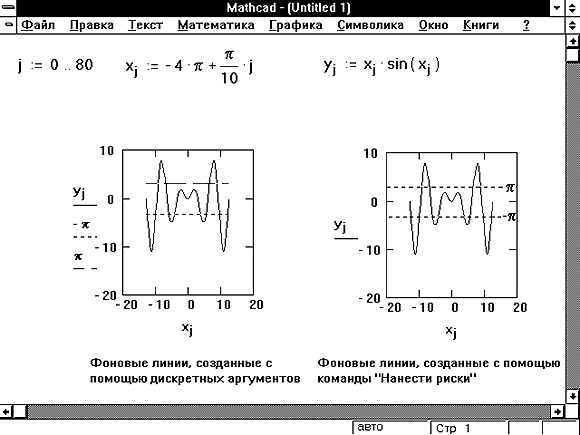 В таких случаях
для нахождения более точного значения
корня необходимо уменьшить значение TOL. Другой вариант заключается
в замене уравнения f(x) = 0 на g(x) = 0 где .
В таких случаях
для нахождения более точного значения
корня необходимо уменьшить значение TOL. Другой вариант заключается
в замене уравнения f(x) = 0 на g(x) = 0 где .
Д ля выражения f(x) с известным корнем (а) нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=f(x)/(x‑a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x) = 0, выбирая различные начальные приближения.
Нахождение корней полинома
Д
ля
нахождения корней выражения, вида используется функция polyroots. В отличие от функции root, polyroots не требует
начального приближения и возвращает
сразу все корни, как вещественные, так
и комплексные. Общий вид polyroots(v),
где v – вектор коэффициентов
полинома длины , n – степень полинома. Возвращает вектор длины n, состоящий
из корней полинома. Вектор v удобно создавать использую команду
меню Symbolics – Polynomial Cofficients.
Возвращает вектор длины n, состоящий
из корней полинома. Вектор v удобно создавать использую команду
меню Symbolics – Polynomial Cofficients.
Решение систем уравнений и неравенств
MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.
Наиболее распространенным является блочный метод. Mathcad решает систему с помощью итерационных методов. Для решения системы этим методом необходимо выполнить следующее:
Задать начальное приближение для всех неизвестных, входящих в систему уравнений;
Напечатать ключевое слово Given. Оно указывает, что далее следует система уравнений;
Введите уравнения и неравенства в любом порядке. Используйте [Ctrl] + = либо палитру, для печати символа =.
 Между левыми и правыми
частями неравенств может стоять любой
из символов <, >,
и ;
Между левыми и правыми
частями неравенств может стоять любой
из символов <, >,
и ;Введите любое выражение, которое включает функцию Find, например: .
M athcad возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных. Решающим блоком – называется част документа, расположенная между ключевыми словами Given и Find. Внутри блока недопустимы следующие символы: , дискретный переменные или выражения, содержащие дискретный аргумент в любой форме, неравенства вида a<b<c, вложенные блоки решения уравнений.
Функция, Find может возвращать результат следующими способами:
Find(var1, var2,…) =.
a := Find(x) – скаляр, var := Find(var1, var2,…) – вектор. Удобно при использовании решения системы в другом месте рабочего документа.
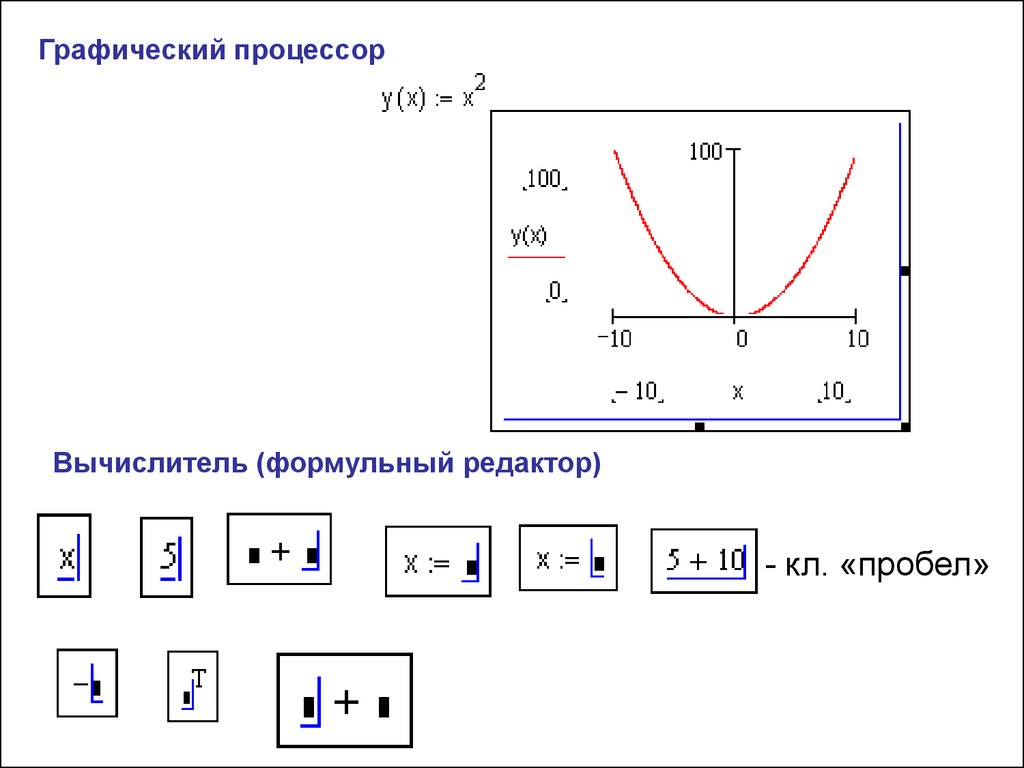
f(a, b, c, …) := Find(x, y, z, …). Определить другую функцию с помощью Find. Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений;
f (x, y, z, …) := Find(x, y, z, …). Если необходимо найти решение при различных начальных приближениях, имеет смысл определить новую функцию.
Последние два способа можно комбинировать.
[PDF] Рабочий лист MathCAD 3 – Корни, решение блоков и символьные вычисления
Рабочий лист Ph46010 MathCAD 3 Корни, блоки решения и символьная математика Цель этого рабочего листа — познакомить вас с различными методами решения в MathCAD. К концу листа вы будете знать, как: Использовать функцию root() для решения уравнений с одной переменной Использовать функцию polyroots() для поиска нескольких корней многочлена Использовать блок решения для решения более сложных систем уравнения Используйте символьный процессор для обработки и решения уравнений
Этот рабочий лист представляет собой ряд примеров, которые иллюстрируют и знакомят с этими принципами. Проработайте столько из них, сколько сможете. По крайней мере, вы должны прочитать весь лист, чтобы получить общее представление о теме.
Проработайте столько из них, сколько сможете. По крайней мере, вы должны прочитать весь лист, чтобы получить общее представление о теме.
Упражнение 1. Использование функции root() В этом упражнении мы будем использовать функцию root() для решения некоторых простых уравнений.
Запустите MathCAD и создайте новый пустой рабочий лист. Первое уравнение, для которого мы попробуем найти решение, это ex = x2. Чтобы использовать корневую функцию, она должна быть в форме f(x )=0, поэтому перепишите уравнение в этой форме и начертите его. Добавьте линии сетки на график, чтобы помочь оценить точку, в которой кривая пересекает линию y=0. Вы должны настроить пределы осей графика, чтобы увеличить область, где линия пересекает ось. Когда вы закончите, ваш график должен выглядеть так, как показано ниже:
F (x)
x
E
2
x 2
1 F (x) 0
1
1
0,5
0
0,5
x
0
0,5
x
0
0,5
x
,20051
1
Ph46010
x
MathCAD Example Sheet 3
Изучив график, вы можете увидеть, что решение будет лежать между –1 и –0,5, так как выборка и используйте корневую функцию, чтобы получить точное значение. 0,75
0,75
root( f( x) x) 0,703
Успешно решив это уравнение, используйте тот же метод для решения следующих уравнений. В каждом случае используйте график функции, чтобы найти приближенные решения, прежде чем решать с помощью root(). 1,423 x
3
2
8,114238 x 8,537238 0
sin(x) cos(x)
90 Уравнение будет иметь кубические корни. Это будет иметь много решений
7 x
Сложные корни требуют комплексного предположения
x
2
2 x 6
Упражнение 2. Влияние допуска на решения Функция root() использует итеративный метод, который использует последовательные предположения, чтобы, как мы надеемся, прийти к решению. Существует системная переменная TOL, которая определяет, насколько близка функция к 0, прежде чем mathCAD решит, что она достигла решения. Небольшое значение TOL, как правило, дает более точные решения, но для получения результата может потребоваться больше времени. В этом упражнении мы увидим, как значение TOL меняет результат решения. Следующее квадратное уравнение имеет два совпадающих корня: 9 x
В этом упражнении мы увидим, как значение TOL меняет результат решения. Следующее квадратное уравнение имеет два совпадающих корня: 9 x
2
12 x 4
Постройте квадратное уравнение и увеличьте площадь корней. Используйте следующий сегмент рабочего листа, чтобы увидеть, как изменение значения TOL меняет решения, предлагаемые MathCAD. TOL
0,0001
x
1
S OLN1 CORT (F (x) X)
S OLN1, 0,66898
F (S oln1) 4,82364 100003
x
0,5
9444 SO OLN224 SOLN224 SOLN224 SOLN 2
x
0,5
4 SH OLN222364 SOLN 2
x
0,5
944. root( f( x) x)
s oln2 0,66364
f( s oln2) 8,2614 10
5
5
Значение TOL можно изменить с помощью пункта меню в mathCAD (Математика|Опции|Встроенные переменные|TOL), но метод явная установка системной переменной на листе предпочтительнее, поскольку она показывает, что изменяется. Поскольку TOL уже определен системой, вам придется заставить систему ввести оператор присваивания, используя клавишу «:» или выбрав := в оценочной палитре.
© dpl 2002, 2005
2
Ph46010
MathCAD Пример листа 3
Упражнение 3. Использование функции Polyroots() для получения корней многочленов многочлен за одну операцию. Его преимущество заключается в том, что все корни, как действительные, так и комплексные, возвращаются сразу и нет необходимости указывать предполагаемые значения. Например, чтобы найти все корни кубического уравнения из упражнения 1, сделайте следующее: 3
x
1,423 x
2
8.114238 x
8.537238 аргумент для функции polyroots(), вставив матрицу с 4 строками и одним столбцом. Теперь используйте polyroots() для поиска решений следующих многочленов.
2 7 x 2 x 6 2 9 x 12 x 4 4 2 3 9 x 13 x 12 x 12 x 4 4 3 2 x 20 x 87 x 180 х 864
Можно ли с помощью поликорней найти 3 кубических корня из -1 и 4 корня четвертой степени из -1 ?
© dpl 2002,2005
3
Ph46010
MathCAD Пример листа 3
Упражнение 4. Использование блока решения для решения более сложных задач. Блок решения — это еще один итеративный метод, доступный в mathCAD, который позволяет решать до 50 уравнений с 50 неизвестными. Уравнения не обязательно должны быть полиномами и могут включать неравенства (,,). Каждому из неизвестных должно быть присвоено начальное предполагаемое значение. Мы начнем с нескольких простых примеров и перейдем к более сложным ситуациям. В первом примере будет использоваться блок решения для нахождения квадратного корня из 3, начиная с предполагаемого значения 2. x
Использование блока решения для решения более сложных задач. Блок решения — это еще один итеративный метод, доступный в mathCAD, который позволяет решать до 50 уравнений с 50 неизвестными. Уравнения не обязательно должны быть полиномами и могут включать неравенства (,,). Каждому из неизвестных должно быть присвоено начальное предполагаемое значение. Мы начнем с нескольких простых примеров и перейдем к более сложным ситуациям. В первом примере будет использоваться блок решения для нахождения квадратного корня из 3, начиная с предполагаемого значения 2. x
2
Дано 2
x
3 0
find( x) 1,73205
Начальное приближенное значение определяется первым завершает блок решения и возвращает решение(я)
Обратите внимание на использование полужирного знака равенства (=) или оператора «равно» в блоке решения. Это символ, отличный от оператора присваивания (:=) или оператора «вывести значение переменной» (=). Оператор «равно» широко используется в блоках решения, а также может использоваться в булевой логике. В следующем примере мы будем использовать блок решения, чтобы найти места, где единичный круг пересекается с линией x+y=0. Единичный круг (x2+y2=12) Решения
В следующем примере мы будем использовать блок решения, чтобы найти места, где единичный круг пересекается с линией x+y=0. Единичный круг (x2+y2=12) Решения
Строка x+y=0
Как и раньше, мы начинаем наш блок решения с предполагаемых значений для x- и y-
© dpl 2002,2005
4
Ph46010 x
1
MathCAD Sheet Example 3 Y
1
Значения угадания
Указано 2
x
Уравнения в решающем блоке
2
y 1
x y 0
Найти (x y)
0,70711
Найти (x y)
0,70711
() возвращает вектор решений
0,70711
возвращает значения x,y для одной из точек пересечения. Чтобы вернуть координаты другой точки, мы можем либо начать с приближенных к ней значений, либо поместить условие в блок решения для принудительного решения. x
1
Y
1
Указано 2
x
2
y 1
Дополнительное неравенство добавлено в Block
x x x 0 Найти (x y)
0,70711 0,70711
MathCAD имеет ограничения на то, что может быть записано в блоке решения (между ‘given’ и ‘find()’ ), в частности, не разрешено помещать определение переменной или функции. В приведенных выше примерах мы использовали знак равенства «вывести значение» для печати значений x и y в решении. Создав вектор для хранения результатов, мы можем установить переменные для хранения решения за один шаг, как показано ниже: xval yval
В приведенных выше примерах мы использовали знак равенства «вывести значение» для печати значений x и y в решении. Создав вектор для хранения результатов, мы можем установить переменные для хранения решения за один шаг, как показано ниже: xval yval
find( x y)
Multiple assignments in single step
xval 0.70711 yval 0.70711
© dpl 2002,2005
5
Ph46010
MathCAD Example Sheet 3
Use a solve block to solve Следующие системы уравнений: 3 x 7 y 90
2
x
7 x 2 y 25
x 2 y z 4
2
y 3
3 x 4 y 2 z
x y 1
У вас должно быть 4 точки решения
3
6 x 2 y z 4
Для первого и последнего из них вы должны проверить свой результат, используя метод обращения матрицы из предыдущего рабочего листа. В конце этой брошюры приведено упражнение, взятое из предыдущего листа с примерами Ph25010, для построения траектории пушечного ядра. Создайте это упражнение на новом рабочем листе и используйте один из приведенных выше методов решения, чтобы определить время, через которое пушечное ядро упадет на землю после выстрела.
Создайте это упражнение на новом рабочем листе и используйте один из приведенных выше методов решения, чтобы определить время, через которое пушечное ядро упадет на землю после выстрела.
Упражнение 5. Символьная математика и работа с уравнениями Наряду с методами численного решения уравнений и систем уравнений, которые мы использовали до сих пор, MathCAD включает в себя мощный символьный процессор, который может обрабатывать уравнения и решать их с помощью алгебраических методов. При работе с символьным процессором полезно вызвать символьную панель инструментов. Чтобы увидеть, как символьный процессор может символически решать уравнения и вычислять выражения, выполните следующие упражнения.
Упрощение выражений Чтобы увидеть, как символьный процессор может помочь упростить выражения, введите следующее выражение в MathCAD. 6x
2
2x a 7x 3a x
2
с полем выбора В выражении нажмите «упростить» в палитре символов и посмотрите, как mathCAD упрощает выражение, собирая общие термины и отменяя, где это возможно. 6 x
6 x
2
2 x a
7 x 3 a
© dpl 2002,2005
2
x упростить
7 x
2
5 x 4 A
6
PH46010
MathCad Пример листа 3
Используйте символический процесс, чтобы упростить следующие выражения: 3 x x x x.
7 A
2
6.5 P
2 x
6 A
2
5,7 Q
2
6.9
2
2
х
1,2 P
7 A
(2 Q)
2
2
x
2
3 3 6 3 R S n 4 3 R M n
7
3
3
7
Расширение выражений Чтобы увидеть, как символьный процессор может расширять выражения, поместите прямоугольник выбора в выражение и нажмите «расширить» в символьной палитре. После ключевого слова расширения есть заполнитель, вы должны либо заполнить переменную, которую хотите расширить, либо удалить заполнитель. Похоже, в mathCAD есть ошибка, так как кажется, что не имеет значения, что находится в заполнителе. 3
3
(g h) Расширение
3
G
3
H
3 G H
2
2 3 G H
Распределите следующие примеры: 2 y (x 7 h
. y)
3
x
(P x q) (r x s) 1,23 A
2
2 2
2 2 4.56 B 7,89 B
6.66
2.7 a
2
4.2 b
2
«Неопределяемые» переменные При символьной обработке уравнений mathCAD будет использовать числовые значения любых уже определенных переменных. В качестве примера рассмотрим следующее биномиальное разложение: x
1 2
( x y) расширить
1
2 y y
2
Здесь mathCAD использовал значение 1 вместо x перед выполнением расширения. В зависимости от вашей проблемы это не всегда может быть тем, чего вы хотите достичь.
© dpl 2002,2005
7
Ph46010
MathCAD Example Sheet 3
Чтобы отменить определение переменной, используйте оператор присваивания, чтобы установить переменную равной самой себе. MathCAD понимает это рекурсивное определение, чтобы отменить определение переменной. Это показано ниже: x
MathCAD понимает это рекурсивное определение, чтобы отменить определение переменной. Это показано ниже: x
1 2
(x y) Расширение x
1
2 y y y
2
x 2
(x y) Расширение
2
x
2 2 x y y
. Чтобы решить уравнение с помощью символьного процессора, введите уравнение, которое вы хотите решить, а затем нажмите «решить» на символьной панели инструментов. Заполните переменную, которую вы хотите найти, в заполнитель и нажмите, чтобы увидеть результат. 2
x
x 2 0 решение x
1 2
Обратите внимание, что MathCAD не может найти решение для описанного выше случая, когда x уже определен, вы должны отменить определение x, используя введенное выше рекурсивное определение. Теперь решите следующие уравнения с помощью символьного процессора: ( x 1) ( x 1) 0 2
x
1 0
2
x
1 0
( y 2) 0 y 3 z
2
2 z
8 0
© dpl 2002,2005
8
Ph46010
Math Sheet0003
Упражнение 6. Задача о консервной банке Это упражнение взято из листа с примерами для первого года обучения и показывает, как мы можем использовать символьный процессор в MathCAD для решения реальной задачи. Он представлен как проработанный пример, который вы должны скопировать и убедиться, что вы понимаете шаги для достижения решения. Производитель жестяных банок хочет максимально увеличить объем, содержащийся в банке, при минимизации количества металла, используемого для изготовления банки. Покажите, что при заданном количестве металла объем банки будет максимальным, если радиус равен половине высоты. Начните с записи выражений для объема и площади банки через радиус r и высоту h. 2 Том r ч
Задача о консервной банке Это упражнение взято из листа с примерами для первого года обучения и показывает, как мы можем использовать символьный процессор в MathCAD для решения реальной задачи. Он представлен как проработанный пример, который вы должны скопировать и убедиться, что вы понимаете шаги для достижения решения. Производитель жестяных банок хочет максимально увеличить объем, содержащийся в банке, при минимизации количества металла, используемого для изготовления банки. Покажите, что при заданном количестве металла объем банки будет максимальным, если радиус равен половине высоты. Начните с записи выражений для объема и площади банки через радиус r и высоту h. 2 Том r ч
Площадь ( 2 r h)
2 r
2
Используйте жирный знак равенства при построении этих двух уравнений, так как мы будем обрабатывать их с помощью символьного процессора. Скопируйте выражение для площади и используйте символьный решатель, чтобы получить выражение для h через площадь и r. Площадь (2 ϩ r H)
Площадь (2 ϩ r H)
2 ϩ R Solve H 2
1 2
ПЕАТЕЛЯ 2 УТАЖА и используйте символьную машину, чтобы заменить h в выражении выражением, которое вы только что получили: 2 Vol r h subs tituh
Площадь 2 ϩ r (ϩ r)
2
1 2
VOL
1 2 r Площадь 2 ϩ r
2
У нас теперь есть выражение для объема банки с точки зрения площади и радиуса. Учитывая, что площадь постоянна, dVol/dr будет равно нулю при максимальном объеме. Скопируйте и вставьте выражение для объема и используйте символическое дифференцирование, чтобы дифференцировать его относительно r. d 1 2 r Область 2 r dr 2
1 2
Область 3 r
2
Используйте символ из палитры символов или введите . Теперь у нас есть выражение для dVol/dr, мы можем найти значение r, где оно равно нулю. © DPL 2002,2005
PH46010
MathCad Пример листа 3 1
1 2
Площадь 3 ϩ R
2
0 SOLVE R
1 2 6 (. Площадь) ( 6 ) 1
Площадь) ( 6 ) 1
1 2 6 ( Площадь) (6 )
MathCAD предоставил два решения, соответствующие положительным и отрицательным значениям r. Нас интересуют положительные значения r, поэтому мы скопируем первое решение и подставим обратно выражение для площади, чтобы получить выражение для r в точке максимального объема. 1
1
1 2 6 (Область) заместителя (2 ϩ r H) (6 ϩ)
1 6 ϩ 2А (6).
2 r
2
2 r
2
2
Теперь у нас есть выражение для r через r и h, которое максимизирует объем. Итак, теперь мы можем найти r через h. 1
1 2 6 ϩ 2 ϩ r h 2 ϩ r (6 ϩ)
2
0 r s olve r
1 2
ч
Пренебрегая случаем r=0, мы теперь имеем решение, согласно которому максимальный объем достигается при r=h/2. Обратите внимание, что можно комбинировать несколько символьных операций за один шаг, как показано ниже: (6 ϩ)
Solve R 0
Заместитель (2 ϩ r H)
2 ϩ r
2
2 ϩ r
2
2
1
1 6 2rh ( 6 )
2 r
2
2
В качестве упражнения вернитесь к задаче о пушечном ядре, упомянутой ранее, и, используя символьный процессор, выведите выражение для расстояния, которое пройдет пушечное ядро, прежде чем оно попадет в цель. земли с точки зрения начальной скорости, V0 и угла пушки, . Используйте символическое дифференцирование, чтобы найти угол , который максимизирует дальность полета пушки.
земли с точки зрения начальной скорости, V0 и угла пушки, . Используйте символическое дифференцирование, чтобы найти угол , который максимизирует дальность полета пушки.
© dpl 2002,2005
10
Ph46010
Лист примеров MathCAD 3
Приложение 1. Построение пути пушечного ядра. Это упражнение взято из предыдущего курса Ph25010 и показывает, как MathCAD может прогнозировать простую траекторию пушечного ядра. До сих пор мы использовали возможности построения графиков mathCAd для построения простой функции, такой как sin(x) против x, а также видели, как мы можем построить один вектор относительно другого. Часто мы хотим построить график одной функции относительно другой, например, у нас могут быть функции, которые описывают высоту и расстояние до снаряда как функцию времени. Сопоставляя одну функцию с другой, мы можем построить траекторию снаряда. В следующем упражнении показана траектория пушечного ядра, выпущенного под определенным углом с определенной начальной скоростью.
30 DEG
Vinitial 50
M S
() VXINITIAL VINITIALCOS
SEPERATE ИСТИННАЯ ВОЗДЕЙСТВА В X-& Y-COMPONENTS
() Vyinitial Vinitialsin
. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАКЛЮЧИТЕЛЬНЫЕ ЗАКЛЮЧИТЕЛЬНЫЕ ЗАКЛЮЧИТЕЛЬНЫЕ КОЛЕВА ВАЗИНА ВАЗИНА ВАЗИНА ВАЗИНА ВАЗИНА САЙКИ ВАЗИНА ВАЗИНА ВАЗИНА САЙКИ ВАЗИЛИ САЙКИ ВАЗИНА ВАЙКИ ВАЗИНА САЙКИ САЙКИ САКОГ пушка и начальная скорость, а затем продолжает разбивать скорость на компоненты в направлениях x и y. После того, как вы создали эти операторы, можно создать две функции для описания положения пушечного ядра в направлениях X и Y, используя простые уравнения движения при постоянном ускорении. Мы пренебрегаем сопротивлением воздуха, и положение по оси x легко вычисляется по начальной скорости по оси x. Точно так же положение в направлении y может быть рассчитано с использованием встроенного значения «g» для ускорения под действием силы тяжести. Это действует вниз, тогда как наше исходное направление для оси Y вверх, отсюда и знак минус в уравнении. Позиция X(t)
Позиция X(t)
VXIinitialt
Pos Y( t )
VYInitialt
1 2 gt 2
Остается только выбрать подходящий диапазон временных шагов и построить графики функций. Хороший диапазон составляет от 0 до 6 секунд с шагом 0,1 секунды. Обратите внимание, что единицей времени должны быть секунды, и посмотрите, как это должно быть включено во все 3 условия, определяющие переменную диапазона.
© dpl 2002,2005
11
Ph46010
t
Пример листа MathCAD 3
0 S 0,1 S 6 S
40
30
20
10 Posy (T) 0
10
20
30
0
50
9 100
150
0
50 0003
100
150
0
50 0003
150
0
50 0003
0
50 0003
0
50 0003
200
250
300
PosX ( t )
Я добавил линии сетки по оси Y, которые позволяют оценить, когда пушечное ядро упадет на землю, что в данном случае будет примерно дальность 220м.
