Рупд формулы по физике: Прямолинейное равноускоренное движение. Ускорение — урок. Физика, 9 класс.

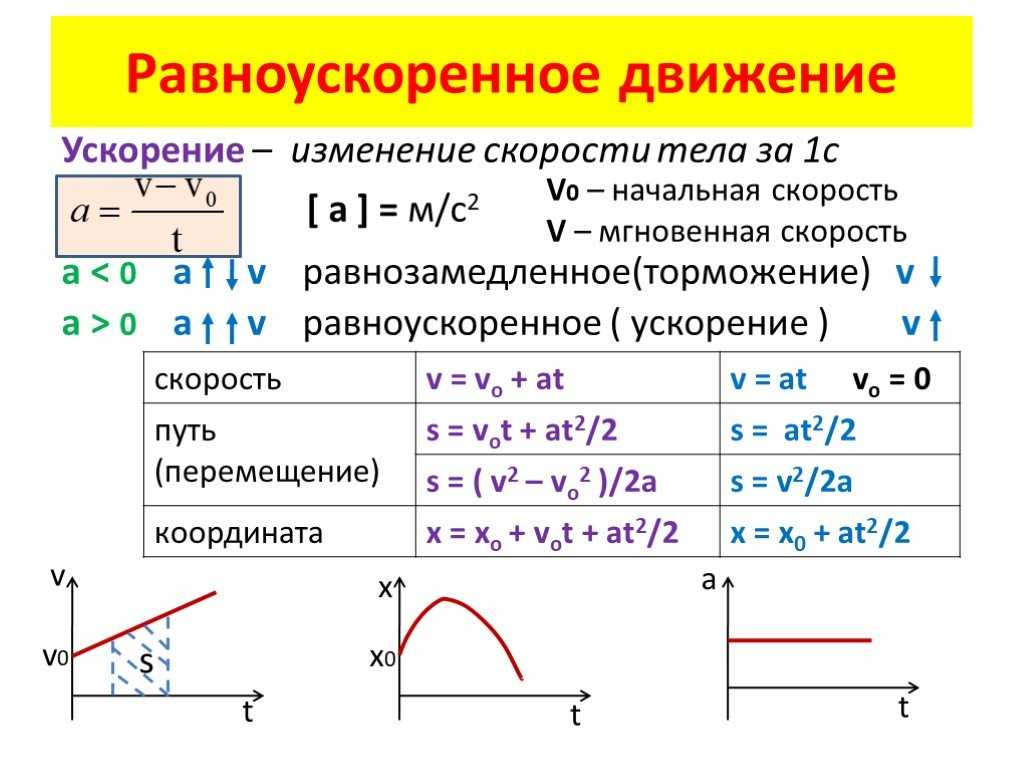
Равноускоренное движение тела – формула перемещения, примеры и определение кратко (10 класс)

4.7

Средняя оценка: 4.7

Всего получено оценок: 299.

Обновлено 28 Июля, 2021

4.7

Средняя оценка: 4.7

Всего получено оценок: 299.

Обновлено 28 Июля, 2021

Одним из видов движения, изучаемых кинематикой, является равноускоренное движение. Равноускоренное движение — это достаточно распространённый вид движения, даже большинство равномерных движений начинались с разгона и были некоторое время равноускоренными. Рассмотрим эту тему подробнее, получим формулу равноускоренного движения, приведём примеры такого движения.

Ускорение

Если некоторое тело начинает движение из состояния покоя, то его скорость изменяется от нуля до некоторого максимального значения. Следовательно, при таком движении можно указать быстроту изменения скорости.

Например, в рекламе автомобилей указывается время разгона до 100 км/ч. Ясно, что модель, достигающая такой скорости за 5 секунд, значительно резвее, чем модель со временем разгона 15 секунд, хотя конечная скорость в обоих случаях одинакова.

В чем же здесь разница, с точки зрения кинематики?

Разница в быстроте набора скорости.

Быстрота набора скорости называется ускорением. Ускорение (обозначается латинской буквой $a$) равно отношению величины набранной скорости ко времени этого увеличения:

$$\overrightarrow a={\overrightarrow {Δv}\over t}={\overrightarrow v- \overrightarrow {v_0} \over t}$$

где:

• $\overrightarrow a$ — ускорение тела;
• $\overrightarrow v$ — скорость тела в момент $t$;
• $\overrightarrow {v_0}$ — начальная скорость тела (при $t=0$).

Из данной формулы можно получить размерность ускорения. Скорость измеряется в метрах в секунду, а время — в секундах, значит, ускорение измеряется в метрах в секунду за секунду (или метров в секунду в квадрате).

В приведённом примере первый автомобиль разгоняется с ускорением 5,56 метров в секунду за секунду, а второй — с ускорением 1,85 метров в секунду за секунду.

Рис. 1. Ускорение в физике.

Равноускоренное движение

Движение, при котором ускорение тела постоянно, называется равноускоренным. При этом знак ускорения не играет роли. Движение с постоянным отрицательным ускорением также является равноускоренным, несмотря на то, что скорость уменьшается.

Наиболее частым примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё не играет большой роли. Другим примером может служить разгон автомобиля при постоянном нажатии на педаль «газа», пока не будет набрана необходимая скорость.

Рис. 2. Примеры равноускоренного движения

Формулы равноускоренного движения

Найдём формулы скорости и координаты при равноускоренном движении. Из приведённого выше определения ускорения следует, что скорость при постоянном ускорении равна:

$$\overrightarrow v= \overrightarrow {v_0} + \overrightarrow a t$$

Это — линейная зависимость. Её график представляет собой прямую, наклон которой зависит от значения $a$. Чем оно больше, тем круче поднимается график.

Из курса физики 9 класса известно, что перемещение тела равно площади под графиком скорости. 2 \over 2}$$

Это основная формула равноускоренного движения, позволяющая найти координату $\overrightarrow x$ материальной точки в момент времени $t$ при условии, что начальная координата была равна $\overrightarrow x_0$, начальная скорость — $\overrightarrow {v_0}$, а ускорение — $\overrightarrow a$. В задачах она используется, как правило, совместно с предыдущей.

Рис. 3. Формулы равноускоренного движения

Что мы узнали?

Ускорение — это физическая величина, характеризующая быстроту набора скорости материальной точкой. Движение с постоянным ускорением называется равноускоренным. Хорошим примером равноускоренного движения является свободное падение тел.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 299.

---

А какая ваша оценка?

Физика прямолинейное равноускоренное движение.

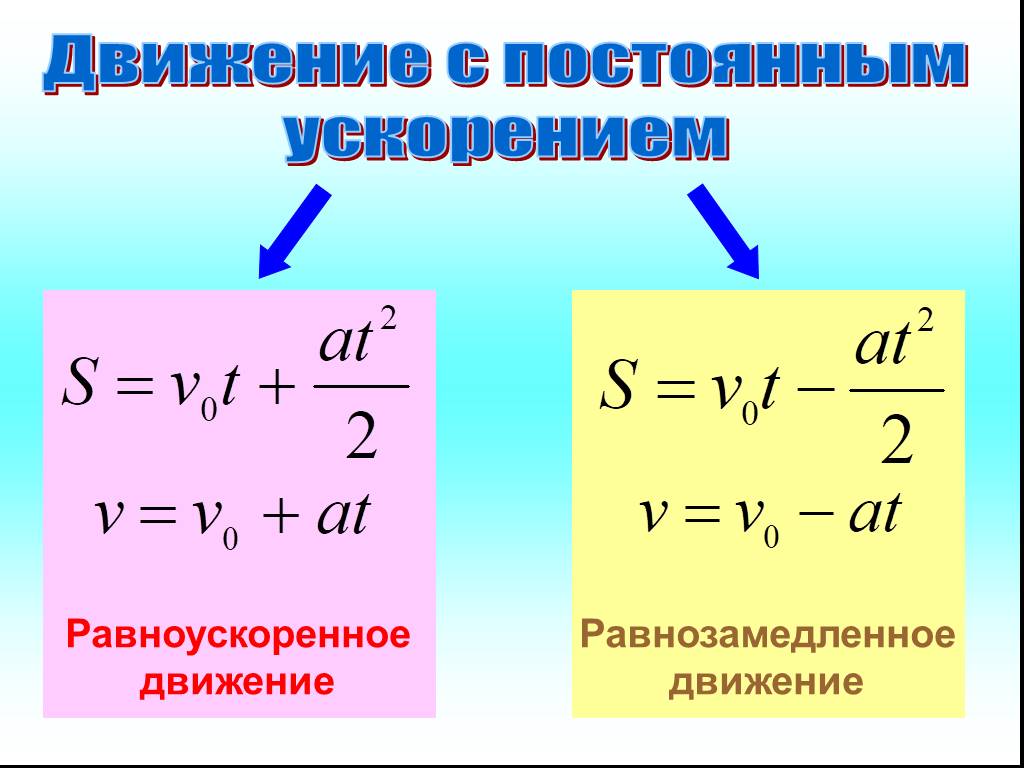Формулы прямолинейного равноускоренного движения

Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

В первую очередь это пройденный путь. Будем его обозначать буквой S. Согласно определению, путь – это расстояние, которое тело прошло вдоль траектории перемещения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S – это длина прямого отрезка на этой линии. Он в системе физических единиц СИ измеряется в метрах (м).

Скорость или как часто ее называют линейная скорость – это быстрота изменения положения тела в пространстве вдоль его траектории перемещения. Обозначим скорость буквой v. Измеряется она в метрах в секунду (м/с).

Ускорение – третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро во времени изменяется скорость тела. Обозначают ускорение символом a и определяют его в метрах в квадратную секунду (м/с 2).

Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.

Связь скорости и ускорения

Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v 0 . Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:

Здесь второе слагаемое описывает прирост скорости за каждый промежуток времени.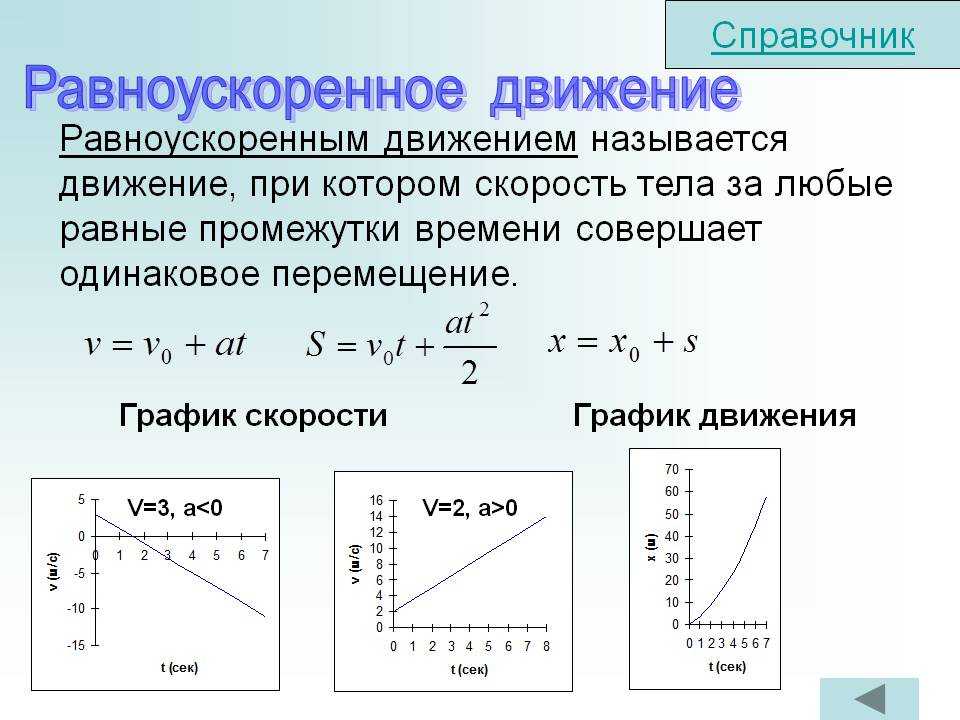 Поскольку v 0 и a являются постоянными величинами, а v и t – это переменные параметры, то графиком функции v будет прямая, пересекающая ось ординат в точке (0; v 0), и имеющая некоторый угол наклона к оси абсцисс (тангенс этого угла равен величине ускорения a).

На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v 0 , а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:

Этот вид движения называется прямолинейным равнозамедленным.

Формулы пройденного пути

На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v 0 * t + a * t 2 / 2.

Первый член соответствует равномерному движению без ускорения. Второй член – это вклад в пройденный путь чистого ускоренного движения.

В случае торможения движущегося объекта выражение для пути примет вид:

S = v 0 * t – a * t 2 / 2.

В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.

Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.

Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.

Задача на определение времени движения

Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с 2 . Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?

Расстояние, которое авто за 20 секунд пройдет, будет равно:

При этом скорость, которую он наберет за 20 секунд, равна:

Тогда искомое время движения t можно вычислить по следующей формуле:

t = (S – S 1) / v + t 1 = (S – a * t 1 2 / 2) / (a * t 1) + t 1 .

Здесь S – расстояние между A и B.

Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.

Задача на расчет пути торможения

Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.

S = v 0 * t – a * t 2 / 2.

Время торможения t и начальную скорость v 0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:

Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:

S = v 0 * t – v 0 * t / 2 = v 0 * t / 2.

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Задача на определение скорости при свободном падении

Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?

Где g = 9,81 м/с 2 .

Время падения тела определим из соответствующего выражения для пути S:

S = g * t 2 / 2;

t = √(2 * S / g).

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S / g) = √(2 * S * g).

Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.

График зависимости V(t) для этого случая показан на рис.1.2.1. Промежуток времени Δt в формуле (1.4) можно брать любой. Отношение ΔV/Δt от этого не зависит. Тогда ΔV=аΔt . Применяя эту формулу к промежутку от t о = 0 до некоторого момента t , можно написать выражение для скорости:

V(t)=V 0 + at. (1.5)

Здесь V 0 – значение скорости при t о = 0. Если направления скорости и ускорения противоположны, то говорят о равнозамедленном движении (рис. 1.2.2).

При равнозамедленном движении аналогично получаем

V(t) = V 0 – at.

Разберём вывод формулы перемещения тела при равноускоренном движении. Заметим, что в этом случае перемещение и пройденный путь – одно и тоже число.

Рассмотрим малый промежуток времени Δt . Из определения средней скорости V cp = ΔS/Δt можно найти пройденный путь ΔS = V cp Δt. На рисунке видно, что путь ΔS численно равен площади прямоугольника с шириной Δt и высотой V cp . Если промежуток времени Δt выбрать достаточно малым, средняя скорость на интервале Δt совпадет с мгновенной скоростью в средней точке. ΔS ≈ VΔt . Это соотношение тем точнее, чем меньше

Δt . Разбивая полное время движения на такие малые интервалы и учитывая, что полный путь S складывается из путей, пройденных за эти интервалы, можно убедиться, что на графике скорости он численно равен площади трапеции:

S= ½·(V 0 + V)t ,

подставляя (1.5), получим для равноускоренного движения:

S = V 0 t + (at 2 /2) (1.6)

Для равнозамедленного движения перемещение L вычисляется так:

L= V 0 t–(at 2 /2).

Разберем задачу 1.3.

Пусть график скорости имеет вид, изображенный на рис. 1.2.4. Нарисуйте качественно синхронные графики пути и ускорения от времени.

Студент: – Мне не приходилось встречаться с понятием «синхронные графики», я также не очень представляю, что значит «нарисовать качественно».

– Синхронные графики имеют одинаковые масштабы по оси абсцисс, на которой отложено время. Расположены графики один под другим. Удобны синхронные графики для сопоставления сразу нескольких параметров в один момент времени. В этой задаче мы будем изображать движение качественно, т. е. без учета конкретных числовых значений. Для нас вполне достаточно установить: убывает функция или возрастает, какой вид она имеет, есть ли у нее разрывы или изломы и т. д. Думаю, для начала нам следует рассуждать вместе.

Разделим все время движения на три промежутка ОВ , BD , DE . Скажите, какой характер носит движение на каждом из них и по какой формуле будем вычислять пройденный путь?

Студент: – На участке ОВ тело двигалось равноускоренно с нулевой начальной скоростью, поэтому формула для пути имеет вид:

S 1 (t) = at 2 /2.

Ускорение можно найти, разделив изменение скорости, т.е. длину АВ , на промежуток времени ОВ .

Студент: – На участке ВD тело движется равномерно со скоростью V 0 , приобретенной к концу участка ОВ . Формула пути – S = Vt . Ускорения нет.

S 2 (t) = at 1 2 /2 + V 0 (t– t 1).

Учитывая это пояснение, напишите формулу для пути на участке DE .

Студент: – На последнем участке движение равнозамедленное. Буду рассуждать так. До момента времени t 2 тело уже прошло расстояние S 2 = at 1 2 /2 + V(t 2 – t 1).

К нему надо добавить выражение для равнозамедленного случая, учитывая, что время отсчитывается от значения t 2 получаем пройденный путь, за время t – t 2:

S 3 =V 0 (t–t 2)–/2.

Предвижу вопрос о том, как найти ускорение a 1 . Оно равно СD/DE . В итоге получаем путь, пройденный за время t>t 2

S (t)= at 1 2 /2+V 0 (t–t 1)– /2.

Студент: – На первом участке имеем параболу с ветвями, направленными вверх. На втором – прямую, на последнем – тоже параболу, но с ветвями вниз.

– Ваш рисунок имеет неточности. График пути не имеет изломов, т. е. параболы следует плавно сопрягать с прямой. Мы уже говорили, что скорость определяется тангенсом угла наклона касательной. По Вашему чертежу получается, что в момент t 1 скорость имеет сразу два значения. Если строить касательную слева, то скорость будет численно равна tg α, а если подходить к точке справа, то скорость равна tg β. Но в нашем случае скорость – непрерывная функция. Противоречие снимается, если график построить так.

Есть еще одно полезное соотношение между S , a, V и V 0 . Будем предполагать, что движение происходит в одну сторону. В этом случае перемещение тела от начальной точки совпадает с пройденным путём. Используя (1.5), выразите время t и исключите его из равенства (1.6). Так Вы получите эту формулу.

Студент: – V(t) = V 0 + at , значит,

t = (V– V 0)/a,

S = V 0 t + at 2 /2 = V 0 (V– V 0)/a + a[(V– V 0)/a] 2 = .

Окончательно имеем:

S = . (1.6а)

История .

Однажды во время обучения в Геттингене Нильс Бор плохо подготовился к коллоквиуму, и его выступление оказалось слабым. Бор, однако, не пал духом и в заключение с улыбкой сказал:

– Я выслушал здесь столько плохих выступлений, что прошу рассматривать моё как месть.

При прямолинейном равноускоренном движении тело

1. двигается вдоль условной прямой линии,
2. его скорость постепенно увеличивается или уменьшается,
3. за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам.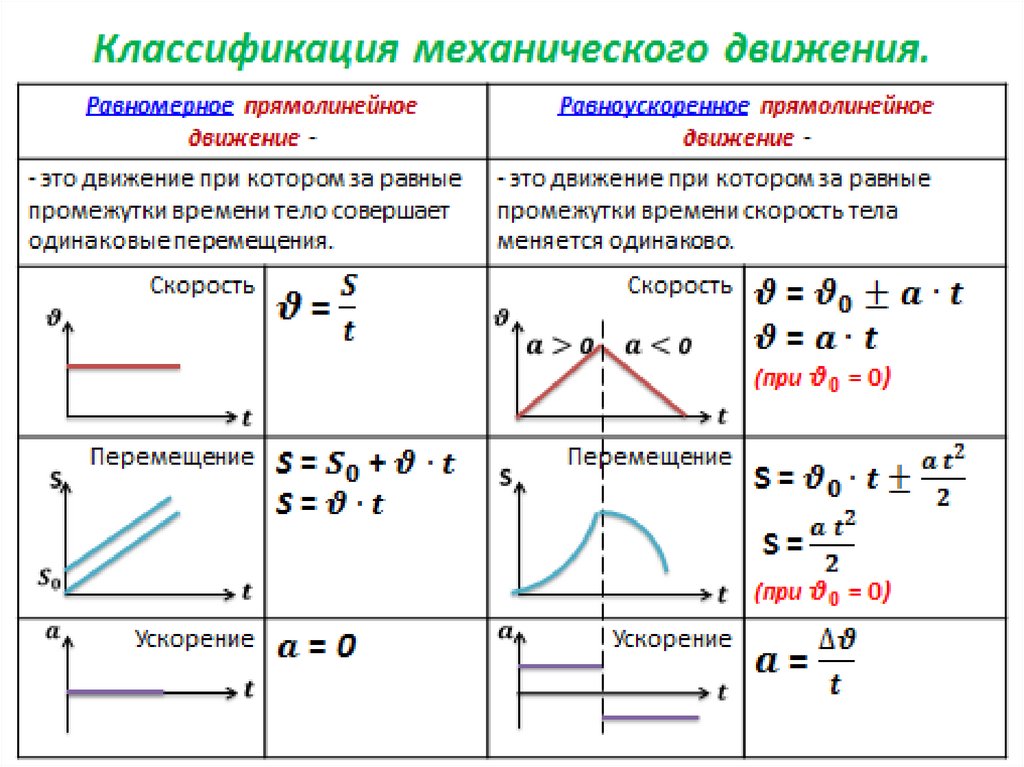 Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .

Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.

Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:

При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v 0
a = (v – v 0)/t

В случае торможения:

at = v 0 – v
a = (v 0 – v)/t

В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0.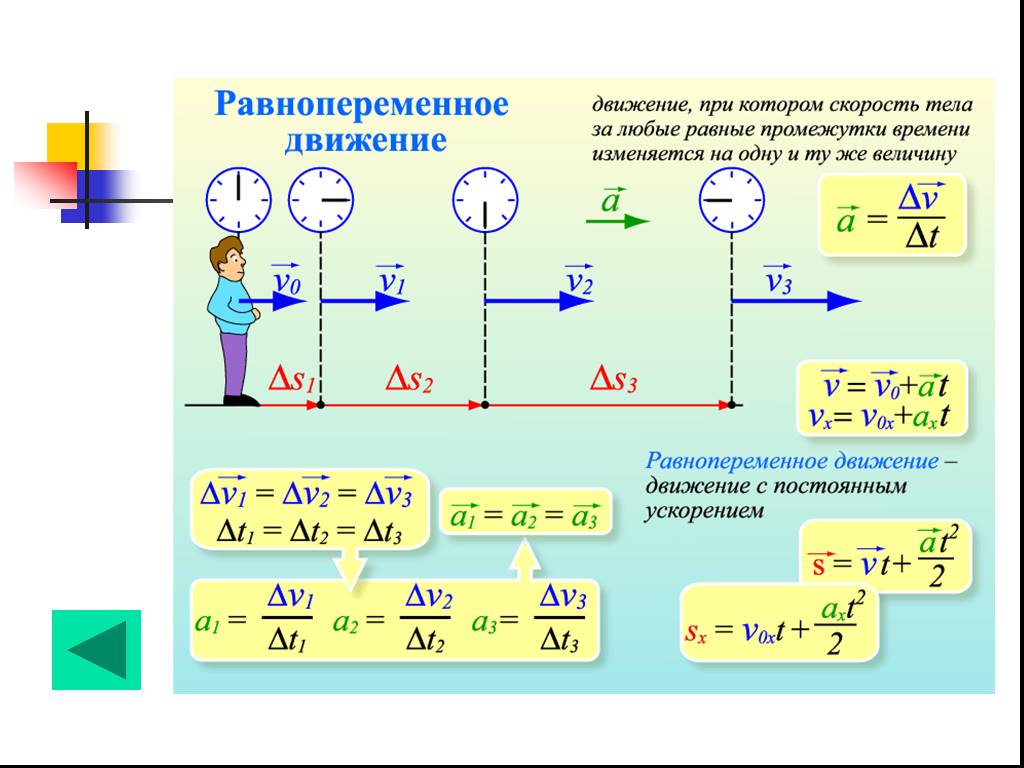 Тогда формула сокращается до такого вида:

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x – это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

s = ½ * (v 0 + v) * t

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2

Итак, пройденный путь определяется по формуле:

s = v 0 t + at 2 /2

(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)

Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.

Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать. Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.

Основные законы Динамики. Законы Ньютона – первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения – покоя, скольжения, качения + трение в жидкостях и газах.

Вы сейчас здесь: Кинематика. Основные понятия. Равномерное прямолинейное движение. Равноускоренное движение. Равномерное движение по окружности. Система отсчёта. Траектория, перемещение, путь, уравнение движения, скорость, ускорение, связь линейной и угловой скорости.

Простые механизмы. Рычаг (рычаг первого рода и рычаг второго рода). Блок (неподвижный блок и подвижный блок). Наклонная плоскость. Гидравлический пресс. Золотое правило механики

Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел

Движение по окружности. Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости

Механические колебания. Свободные и вынужденные колебания. Гармонические колебания. Упругие колебания. Математический маятник. Превращения энергии при гармонических колебаниях

Механические волны. Скорость и длина волны. Уравнение бегущей волны. Волновые явления (дифракция. интерференция…)

Гидромеханика и аэромеханика. Давление, гидростатическое давление. Закон Паскаля. Основное уравнение гидростатики. Сообщающиеся сосуды. Закон Архимеда. Условия плавания тел. Течение жидкости. Закон Бернулли. Формула Торричели

Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы – изотерма, изобара, изохора

Волновая оптика. Корпускулярно-волновая теория света. Волновые свойства света. Дисперсия света. Интерференция света. Принцип Гюйгенса-Френеля. Дифракция света. Поляризация света

Термодинамика. Внутренняя энергия. Работа. Количество теплоты. Тепловые явления. Первый закон термодинамики. Применение первого закона термодинамики к различным процессам. Уравнение теплового балланса. Второй закон термодинамики. Тепловые двигатели

Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.

Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи – последовательное и параллельное соединение. Правила Кирхгофа.

Электромагнитные колебания. Свободные и вынужденные электромагнитные колебания. Колебательный контур. Переменный электрический ток. Конденсатор в цепи переменного тока. Катушка индуктивности (“соленоид”) в цепи переменного тока.

Электромагнитные волны. Понятие электромагнитной волны. Свойства электромагнитных волн. Волновые явления

Магнитное поле. Вектор магнитной индукции. Правило буравчика. Закон Ампера и сила Ампера. Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля

Квантовая физика. Гипотеза Планка. Явление фотоэффекта. Уравнение Эйнштейна. Фотоны. Квантовые постулаты Бора.

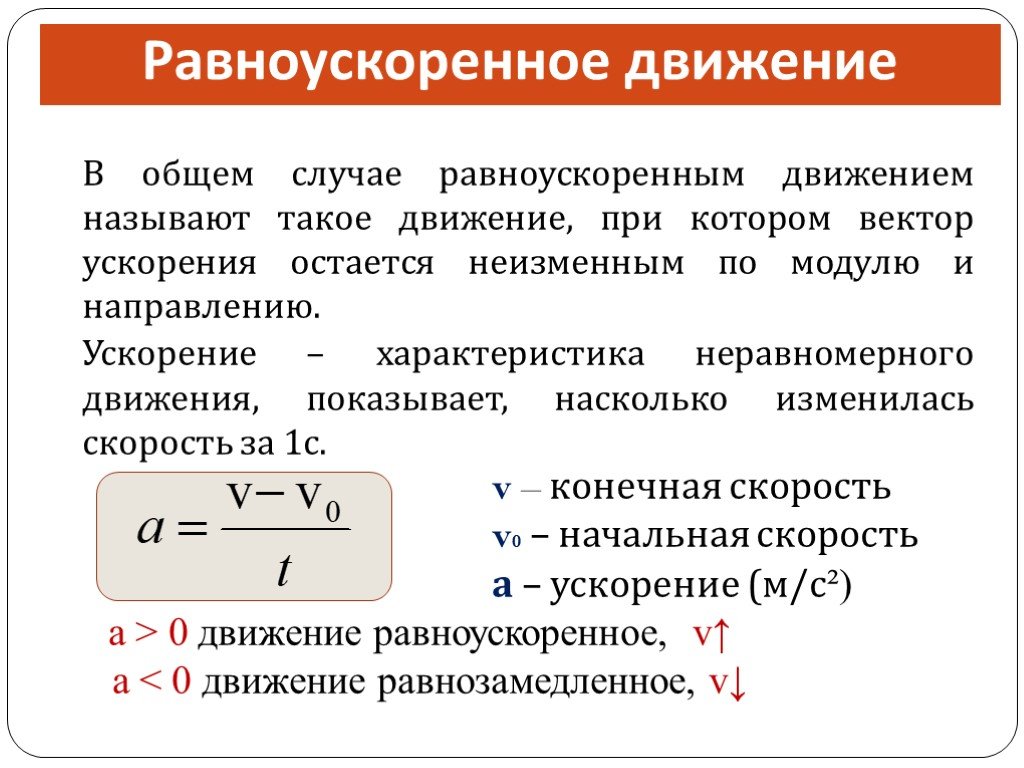Элементы теории относительности. Постулаты теории относительности. Относительность одновременности, расстояний, промежутков времени. Релятивистский закон сложения скоростей. Зависимость массы от скорости. Основной закон релятивистский динамики…

Погрешности прямых и косвенных измерений. Абсолютная, относительная погрешность. Систематические и случайные погрешности. Среднее квадратическое отклонение (ошибка). Таблица определения погрешностей косвенных измерений различных функций.

Это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т.е. ускорение постоянно.

Примерами такого движения является свободное падение тел вблизи поверхности Земли и движение под действием постоянной силы.

При равноускоренном прямолинейном движении координата тела меняется с течением времени в соответствии с законом движения:

где x 0 – начальная координата материальной точки, 0 x – проекция начальной скорости иa x – проекция ускорения точки на ось 0X .

Проекция скорости материальной точки на ось 0X в этом случае меняется по следующему закону:

При этом проекции скорости и ускорения могут принимать различные значения, в том числе и отрицательные.

Графики зависимости x (t ) иx (t ) представляют собой соответственно прямую и параболу, причем, как и в алгебре, по коэффициентам в уравнениях прямой и параболы можно судить о расположении графика функции относительно координатных осей.

На рисунке 6 приведены графики для x (t ),x (t ),s (t ) в случаеx 0 > 0, 0 x > 0,a x t ) имеет отрицательный наклон (tg =a x

3. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.

Равномерное движение по окружности происходит с постоянной по модулю скоростью, т.е.= const (рис. 7). Однако направление скорости при таком движении непрерывно изменяется, поэтому равномерное движение тела по окружности является движением с ускорением.

Для описания равномерного движения тела по окружности вводят следующие физические величины: период ,частота обращения ,линейная скорость ,угловая скорость ицентростремительное ускорение .

Период обращения T – время, за которое совершается один полный оборот.

Частота обращения – это число оборотов, совершаемых телом за 1 с. Единицей частоты обращения в СИ является с –1 .

Частота и период обращения связаны между собой соотношением .

Вектор скорости при движении точки по окружности постоянно изменяет свое направление (рис. 8).

При равномерном движении тела по окружности отрезок пути s , пройденный за промежуток времениt , является длиной дуги окружности. Отношениепостоянно во времени и называетсямодулем линейной скорости. За время, равное периоду обращенияТ , точка проходит расстояние, равное длине окружности 2R , поэтому

Скорость вращения твердых тел принято характеризовать физической величиной, называемой угловой скоростью , модуль которой равен отношению угла поворота телак промежутку времени, за которое этот поворот совершен (рис. 8):

Единицей угловой скорости в СИ является с –1 .

Так как ориентация твердого тела одинакова во всех системах отсчета, движущихся друг относительно друга поступательно, то и угловая скорость обращения твердого тела будет одинакова во всех системах отсчета, движущихся друг относительно друга поступательно.

При равномерном вращении твердого тела относительно некоторой оси любая точка этого тела движется вокруг этой же оси по окружности радиусом R с линейной скоростью, которая равна

Если начальные координаты точки равны (R ; 0), то ее координаты меняются по законуx (t ) =R cost иy (t ) =R sint .

Как рассчитать RPD | Наука

Обновлено 25 сентября 2019 г.

Автор S. Hussain Ather

Если бы вы измерили температуру жидкости, вы бы получили единственный результат для температуры. Но если вы провели несколько измерений на разных образцах, вам понадобится способ обобщить и представить их вместе.

Когда ученые проводят повторные измерения одних и тех же величин, будь то температура жидкости или нагрузка на конкретный вес, они могут использовать относительная разница в процентах (RPD) для описания этих групп или нескольких измерений.

Относительная разница между двумя точками в процентах

Вы можете рассчитать RPD между двумя точками, сначала найдя относительную разницу между двумя величинами в разных измерениях или выборках. Вычтите одно измерение из другого и возьмите абсолютное значение этой разницы.

Чтобы преобразовать эту относительную разницу в проценты, найдите сумму двух измерений и разделите ее на два, чтобы получить среднее значение. Затем разделите относительную разницу на это среднее значение, чтобы получить RPD.

Общая формула: |(x ₂ – x ₁ )|/((x ₂ + x ₁ )/2) для двух измерений x и

2 1

3

3 2 того же образца. Знаменатель ((x ₂ + x ₁ )/2 представляет среднее значение двух измерений. Имейте в виду, что 2 в знаменателе означает, что есть две величины, которые необходимо усреднить, x__ ₁ _и _x ₂ . Обратите также внимание, что формула дает вам десятичный ответ, поэтому, чтобы преобразовать в проценты, умножьте его на 100.

В качестве примера задачи представьте, что ваша арендная плата увеличилась с 900 до 1000 долларов за месяц. Тогда относительная разница в процентах равна |(1000-900)|/((900+1000)/2), что равно 0,1052 или 10,52 %.

Различия в три или более процентов

Формула RPD применяется только к двум измерениям. Если вы хотите сравнить различия между тремя или более измерениями, вы можете найти RPD каждой пары измерений. Для трех точек данных A, B и C вы найдете RPD между A и B, A и C, а также B и C.

Многократное проведение экспериментов может помочь ученым убедиться, что их точки данных более точно отражают значения, для измерения которых они предназначены. Это позволяет исследователям обнаруживать тенденции, которые они хотят наблюдать. Отслеживание значений RPD по всем наблюдениям дает им распределение различий всех их точек данных, из которых они могут делать выводы.

Если вы протестировали три разных гена на предмет экспрессии в геноме и получили четыре разных значения экспрессии для каждого из трех генов, вы должны рассчитать RPD для каждого из четырех измерений в паре друг с другом для каждого из трех генов. Это может сказать вам об относительных уровнях экспрессии этих генов таким образом, чтобы учесть все измерения в образцах.

Онлайн-калькулятор процентной разницы

Вы можете найти онлайн-калькулятор процентной разницы. Калькулятор Суп предлагает один вместе с формулой, чтобы объяснить, как рассчитывается значение. NCalculators имеет один с большей функциональностью и пояснениями о самих значениях.

Этот вычисляет -процентное изменение . Это может помочь вам сравнить относительную процентную разницу с процентным изменением. Если вы прокрутите страницу вниз, вы можете найти другой калькулятор, который работает с процентами чисел.

Используйте эти калькуляторы и онлайн-формулы, чтобы проверить свои результаты. Вы также можете использовать программное обеспечение, такое как Microsoft Excel, для отслеживания RPD, особенно в случаях, когда у вас есть много точек данных, которые необходимо проанализировать.

Вы можете использовать формулу процентной разницы в Excel, введя индексы для столбцов и строк, которые необходимо суммировать, вычитать и усреднять. Например, если вы хотите просуммировать значения в ячейках A1 и A2 , введите «СУММ(A1:A2)» в интересующую ячейку. Или вы можете написать одну формулу для RPD как “(A1-A2)/(СРЗНАЧ(A1:A2))*100”, которая использует функцию СРЗНАЧ для каждой пары точек, которые вы хотите вычислить.

Калькулятор процентной разницы

Базовый калькулятор

Калькулятор процентной разницы

\[ \dfrac{|V_1-V_2|}{\left[\dfrac{(V_1+V_2)}{2}\right]}\times100 = \; ?\]

Разница между V ₁ и V ₂

V ₁ =

В ₂ =

Ответ:

Получить виджет для этого калькулятора

© Calculator Soup

Поделиться этим калькулятором и страницей

Калькулятор Используйте

Калькулятор разницы в процентах (калькулятор разницы в процентах) найдет разницу в процентах между двумя положительными числами больше 0. Разница в процентах обычно рассчитывается, когда вы хотите узнать разницу в процентах между двумя числами. Для этого калькулятора порядок чисел не имеет значения, поскольку мы просто делим разницу между двумя числами на среднее значение двух чисел. Чтобы вычислить относительную разницу от старого числа к новому, вы должны рассчитать процентное изменение.

Соответствующие расчеты можно выполнить с помощью Калькулятор процентов, Калькулятор процентного изменения и преобразования могут быть решены с помощью Десятичная дробь в процентах, Проценты до десятичных, Дробь в процент или Проценты к дробям.

Формула разницы в процентах:

Разница в процентах равна абсолютному значению изменения стоимости, деленному на среднее значение двух чисел, умноженному на 100. Затем мы добавляем знак процента, %, для обозначения разницы в %.