Примеры решения рядов
Формулы и уравнения рядов здесь.
Пример. Исследование на сходимость и сумма ряда.
Дано: ряд
Найти: сумму ряда в случае его сходимости.
Решение.
Представим члены ряда в виде суммы двух слагаемых:
Получается, что n-я частичная сумма ряда может быть записана в виде:
Отсюда следует, что .
Ряд сходится. Сумма ряда равна .
Пример. Необходимый признак сходимости рядов.
Дано: ряд
Найти:
Проверить выполнение необходимого признака сходимости рядов.
Решение.
Необходимый признак сходимости рядов заключается в том, что если числовой ряд сходится, то
Как следствие, если ≠ 0, то ряд расходится.
Для данного в задаче числового ряда:
≠ 0. Ряд расходится.
Примеры. Достаточные признаки сходимости положительных рядов.
Дано: ряды
1)
2)
3)
4)
5)
6)
Найти:
Исследовать ряды на сходимость.
Решение.
1) Исходя из того, что ≤ при всех n и обобщенный гармонический ряд сходится, следует то, что ряд с меньшими членами сходящийся.
2) Исходя из того, что если выполняются условия: ln n ≥ 0 при n ≥ 1, то ≥ при n ≥ 1.
Обобщенный гармонический ряд расходится, следовательно, ряд с большими членами также расходится.
3) Из ряда выделим главную часть
Заданный ряд и ряд ведут себя одинаково, так как .
Геометрический ряд сходится, значит, ряд также сходится.
4) Из ряда выделим главную часть n-го члена: при n→∞ ∼ .
Порядок < 1, поэтому ряд расходится.
5) Из ряда выделяем главную часть n-го члена ряда:
при n→∞ ∼ .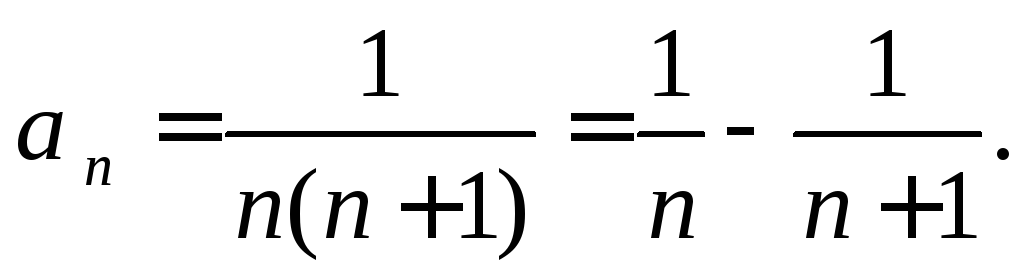
Порядок > 1, поэтому ряд сходится.
6) Из ряда выделяем главную часть n-го члена ряда:
при n→∞ ∼
Порядок , поэтому ряд расходится.
Числовые ряды. Знакоположительные ряды | Математика, которая мне нравится
Сумма называется частной суммой ряда.
Определение. Если последовательность чисел сходится к конечному пределу , то говорят, что ряд сходится и его сумма равна
Если же последовательность расходится, то говорят, что ряд расходится.
Числа называются членами ряда. Всякая конечная сумма называется отрезком ряда.
Если все числа положительны (неположительны, неотрицательны, отрицательны), ряд называется знакоположительным (знаконеположительным, знаконеотрицательным, знакоотрицательным
Пример. Рассмотрим ряд
где — некоторое фиксированное число. Частные суммы этого ряда
Если , то .
При ряд расходится, так как неограниченно возрастает.
При . Следовательно, ряд расходится.
При Следовательно, не имеет предела, и ряд расходится.
Значит, ряд сходится при , а при расходится.
Теорема (критерий Коши для ряда). Ряд
сходится тогда и только тогда, когда
В частности, если ряд сходится, то для любого . Таким образом, у сходящегося ряда — необходимое условие сходимости. Однако оно не является достаточным.
Для знаконеотрицательных рядов из ограниченности последовательности частичных сумм следует сходимость ряда.
Теорема (признак сравнения). Если знаконеотрицательный ряд сходится и существуют и : , то тогда и ряд сходится.
Доказательство. Пусть , . Тогда при
Последовательность возрастает и ограничена сверху, следовательно, она имеет предел.
Пример. Если для неотрицательного ряда
где и , то ряд сходится.
выполняется неравенство
то ряд сходится.
Если
то ряд расходится.
Доказательство. Если , то существует : начиная с некоторого номера , выполняется неравенство
Отсюда
и по признаку сравнения ряд сходится.
С именем Даламбера связан один забавный случай. Рассказывают, что, обучая математике очень тупого и очень знатного ученика и не добившись понимания доказательства, Даламбер в отчаянии воскликнул: “Ну, честное слово, сударь, эта теорема верна!” На что ученик отвечал: “Сударь, почему вы сразу так мне не сказали? Вы — дворянин, и я — дворянин; Вашего слова для меня вполне достаточно”.
Пример. Ряд
сходится, поскольку
Теорема (признак Коши).
Если для знакоположительного ряда
выполняется неравенство
то ряд сходится.
Если же
то ряд расходится.
Доказательство. Если , то существует : . Следовательно, , и по признаку сравнения ряд сходится.
Если же , то существует : . Значит, члены ряда не стремятся к нулю, и ряд расходится.
Пример.
сходится, так как
Пример. Гармонический ряд (каждый член этого ряда, начиная со второго, — среднее гармоническое двух соседних его членов: ) расходится.
Доказательство.
Частная сумма гармонического ряда может быть сделана больше чего угодно.
Математические головоломки для детей с ответами
Логическое мышление требует постоянного развития. Если вам и вашему ребенку надоело «щелкать» обычные логические задачи, попробуйте разгадать парочку математических головоломок.
Какие-то из них требуют реальных «академических» знаний, какие-то решаются при помощи находчивости и умения разбираться в причинных связях, а какие-то просто тренируют внимательность. Не упускайте шанс и устройте мозговой штурм прямо сейчас!
Что такое математические головоломки?
Головоломками принято называть задачи, требующие нестандартных решений, особенного подхода и взгляда «с другой стороны». Они тренируют разные навыки, развивают сообразительность и приносят пользу не только детям, но и взрослым.
Головоломки бывают сложные и простые, в картинках и текстовые, логические и механические (последние обычно представлены в виде «реальных» устройств: кубика Рубика, змейки Рубика и так далее). Математические головоломки традиционно считаются самым древним способом «размять» мозги и «прокачать» собственную интеллектуальную силу. Они также подразделяются по сложности и имеют приблизительный возрастной ценз: одни математические задачи дети решают самостоятельно, а другие – только при помощи взрослых.
Для чего решать головоломки?
Математические головоломки и математические игры для детей отличаются от обычных загадок на логику. Они целенаправленно воздействуют на развитие аналитического склада ума, учат детей вдумчивому счету и грамотному сопоставлению условий и решений. У дошкольников формируются усидчивость и внимательность, вырабатывается навык решения задач и расширяется кругозор. У школьников улучшаются память и настроение – головоломки куда интереснее скучных примеров, которые каждый день задает учитель.
Маленькие победы и успех в решении сложных задач помогают ребенку чувствовать себя увереннее, формируют «здоровую» самооценку и придают сил в решении реальных жизненных «кейсов». А еще они тренируют пространственное мышление и развивают воображение – это помогает ребятам успешно справляться с творческими заданиями.
7 математических головоломок
Давайте приступим к практике и попробуем решить первую головоломку из нашей сегодняшней подборки
Головоломка №1
Задание: Продавец фруктов на рынке решил взвесить яблоко, грушу и гранат.
Потом он взвесил все три фрукта вместе: весы показали цифру 26. Как ты думаешь, какую цифру показали весы, когда продавец взвесил два граната?
Подсказка: Смотри на картинку — так тебе будет легче справиться с первой задачей.
Показать ответ
Ответ: Весы показали цифру 12.
Разбираемся подробнее.
Смотрим на первую строчку. Когда продавец положил яблоко и гранат на первую чашу весов, а грушу – на вторую, весы достигли равновесия. Это значит, что вес груши равен весу яблока и граната, вместе взятых.
Смотрим на вторую строчку. Если три яблока весят 21 единицу, то одно яблоко весит 7 единиц: 21/3=7.
Смотрим на третью строчку. Если мы заменим яблоко и гранат на одну грушу (из п.1 мы помним, что они равны по весу), мы узнаем, что две груши весят 26 единиц.
Следовательно, одна груша весит 13 единиц.
Теперь мы можем узнать, сколько единиц весит один гранат. Мы знаем, что вес груши равен весу яблока и граната, вместе взятых. Если груша весит 13 единиц, а одно яблоко – 7, то один гранат весит 6 единиц (13 – 7 = 6).
Смотрим на последнюю строчку. Когда продавец взвесил два граната, весы показали цифру 12, потому что 6+6=12.
Мы надеемся, что ты быстро справился с заданием! Тебя уже ждет следующая головоломка.
Головоломка №2
Задание: Петя Чайников склеил кубик. Он несколько раз подкидывал кубик и фотографировал его на столе. А потом пришла Петина младшая сестра Галя и кубик сломала.
Петя сначала расстроился, но потом решил сделать новый кубик, точно такой же. Посмотри на развёртку кубика и на фотографии, которые успел сделать Петя. Можешь ли ты правильно раскрасить все грани кубика? Выбери из вариантов решений правильное.
Показать ответ
Ответ: Для того, чтобы решить эту задачку, тебе нужно представить, как будет выглядеть фигура, если склеить развертку (соединить все грани).
Правильный ответ – рисунок Б.
Головоломка №3
Эту задачу, которая называется «Трудное наследство», придумал итальянец по имени Тарталья. Он первым открыл способ решения кубического уравнения.
Задание: Отец оставил трем наследникам-сыновьям следующее завещание: «Поделите семнадцать лошадей, которые есть у нас в хозяйстве, в отношении 1/2 к 1/3 к 1/9». Как выполнить это условие?
Показать ответ
Ответ: Сам Тарталья предложил следующее решение.
Для того чтобы можно было разделить всех имеющихся в хозяйстве лошадей, нужно взять взаймы еще одну лошадь. После этого лошадей у братьев станет не семнадцать, а восемнадцать, и их можно будет разделить согласно завещанию: 18/2=9 лошадей одному брату; 18/3=6 лошадей другому брату, 18/9=2 лошади третьему брату.
Парадокс решения заключается в том, что после такого «деления» останется одна лишняя лошадь, которую братья вначале позаимствовали у другого владельца.
Эту лошадь нужно вернуть после раздела имущества. (9+6+2=17, а не 18).
Какой хитрый этот итальянец Тарталья! Но мы-то знаем, что ты его перехитрил вместе с взрослыми. Скорей приступай к решению четвертой головоломки.
Головоломка №4
Задание: Посмотри на ряд букв и продолжи его:
«Р, Д, Т, Ч, П, Ш, С, …».
Показать ответ
Ответ: Этот ряд – простая последовательность. Перед тобой первые буквы счета (Раз, Два, Три, Четыре, Пять, Шесть, Семь). Соответственно, следующими в ряду будут буквы В (Восемь), Д (Девять) и так далее.
Устал? Предлагаем тебе немного отдохнуть и прочитать парочку интересных фактов о головоломках.
Первая книга головоломок в Европе появилась в конце IX века. Автором сборника «Задачи для развития молодого ума» стал ирландский просветитель Алкуин.
Оказывается, умение решать головоломки может пригодиться не только в повседневной жизни, но и на настоящих соревнованиях! С 1992 года проводятся чемпионаты мира по пазлспорту — это интеллектуальный вид состязаний, в котором участники решают задачи на время.
Делу – время, а потехе – час. Сегодня тебе осталось решить две головоломки. Вперед!
Головоломка №5
Задание: Тебе нужно выбрать одну из трех дверей для того, чтобы спастись. За первой дверью – страшный пожар. За второй дверью – голодный лев, который ничего не ел целый год. За третьей дверью – безумный убийца. Какую дверь ты выберешь?
Показать ответ
Ответ: Для того чтобы выжить, нужно выбрать вторую дверь. За ней должен сидеть лев, который не ел целый год. Но это невозможно – «царь зверей» не протянет без пищи и нескольких недель, а уж год — тем более.
Ура! Мы на финишной прямой. Скорее читай осталось всего 2 головоломки.
Головоломка №6
Задание: На стоянке для автомобилей шесть мест. Одно место занято, все остальные места свободны. Каждое парковочное место имеет свой номер. Слева направо идут следующие номера: 16, 06, 68, 88, следующий номер закрывает автомобиль, 98.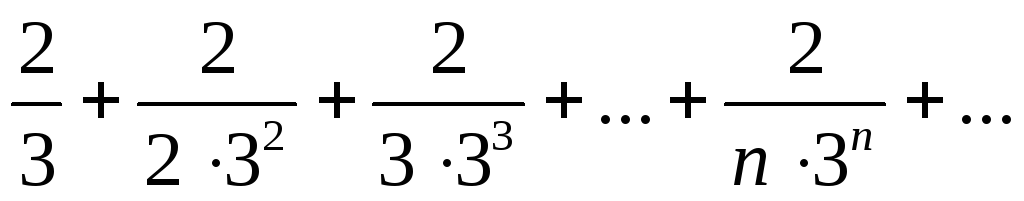
Какой номер у того парковочного места, на котором стоит автомобиль?
Подсказка: схематично изобрази условие задачи на листочке – так тебе будет проще прийти к правильному ответу.
Источник
Показать ответ
Ответ: номер парковочного места – 87. На самом деле все номера идут по порядку, просто они перевернуты.
Головоломка №7
Перед тобой несколько рядов цифр:
- 6636 / 3
- 8118 / 4
- 2242 / 0
- 3316 / ?
Как ты думаешь, что должно стоять на месте знака вопроса?
Показать ответ
Ответ: На месте знака вопроса должна стоять цифра 1. Для того чтобы получить правильный ответ, тебе нужно посчитать количество кружочков в цифрах слева от линии и написать полученный результат справа.
Мы сегодня отлично позанимались, «поломали» мозги и «прокачали» логику. Теперь ты точно справишься с самыми сложными математическими задачами.
А если возникнут трудности – приходи в Умназию и продолжай развиваться вместе с нами!
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнееПрактическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который
написал программку, уверяет, что она делает преобразование Фурье).
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
(1), где:
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
(2),
где , k-я комплексная амплитуда.
или
(3)
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
Например, на графике рис.7 исходная функция определена на отрезке {-T\2, +T\2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= к\Т, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к=3 F3=3\T;… Fk= к\Т (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени , т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)
Высшая математика «для чайников»– полезные советы по изучению
К сожалению, такая точная наука, как высшая математика, не всегда достаточно эффективно преподается в некоторых высших учебных заведениях. И это наука не случайно. Ведь высшая математика считается одной из самых сложных наук, что связано с ее теоретичностью. Однако профессионалы в данной области уверены, что получение подобных знаний – залог абстрактного мышления человека, ведь она позволяет облечь в конкретную форму практически любую концепцию. Высшую математику можно изучать самостоятельно. Однако гораздо эффективнее в этом поможет репетитор по высшей математике с многолетним опытом работы. Уверенные знания, которые получат в таком случае студенты, позволят им стать хорошими специалистами, людьми, которые могли бы поехать в Германию, Австрию, Голландию, Данию и ряд других стран на работу.
Покупка учебников, методичек и прочей обучающей литературы
В случае если вы решили самостоятельно заниматься изучением «вышки», необходимо зайти на специализированные форумы, сообщества в социальных сетях и попросить посоветовать соответствующую литературу. Начните обучающий процесс с, так называемых, книг «для чайников». Вспомните школьную программу по таким предметам, как алгебра и геометрия. Учеба в данном случае не должна сводиться к зубрежке, это будет бессмысленно.
Кроме того:
- начните обучение с тех тем, которые вам действительно интересны – скучные разделы высшей математики быстро вас утомят, и вы попросту прекратите ее изучение;
- скачайте с интернета интересные задачи, которые вам не будет скучно решать;
- ни в коем случае не погружайтесь в процесс обучения «с головой» – необходимо регулярно отвлекаться на другие предметы, заниматься выполнением физических упражнений, побольше высыпаться;
- смотрите фильмы, связанные с «вышкой».
Выбор репетитора
При выборе репетитора обязательно обратите внимание на диплом об образовании из учреждения, которое он закончил. Сегодня немало людей, толком не знающих подобный предмет, но занимающихся преподавательской деятельностью. Выбор стоит отдать людям с многолетним опытом работы в сфере образования. Желательно не соглашаться на сотрудничество по предоплате – изначально специалист обязан доказать свой профессионализм. Наконец, приступайте к обучению только после того, как репетитор составит корректируемый учебный план.
Источник: repetitor-minsk.by
ГИА-13 Математика для «чайников»
Ц е л и: устранить пробелы в знаниях по решению основных задач, обобщить знания, полученные в результате изучения тем, создание условий для осознанного и уверенного владения навыком решения, рассмотрение различных способов решения.
Задачи:
- образовательные
систематизировать знания, выработать умение выбирать рациональный способ решения, расширить и углубить представления учащихся о решении, организовать поисковую деятельность учащихся при решении и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки; навыки самостоятельной работы;
развивать устную и письменную речь учащихся;
привить любовь к предмету, желание познать новое.
- воспитательные
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
воспитывать потребность добиваться успехов в приобретении знаний; воспитание навыков самоконтроля и взаимоконтроля, развитие самостоятельности и творчества.
Тип урока: урок обобщения и систематизации знаний.
Ход урока.
1. Введение.
Организационный момент.
2. Мотивация учебной деятельности.
Предъявление темы и постановка задач урока.
Существуют два основных способа организации учебных пособий для подготовки к ГИА и ЕГЭ. В одном случае они разбиваются по номерам заданий (именно так, как это выглядит в вариантах экзамена), в другом – по темам или разделам математики.
Мне представляется, что для подготовки к ГИА-2012 (в отличие от ЕГЭ) значительно лучше подходит второй, «тематический» способ.
Это связано с тем, что во многих опубликованных сборниках вариантов ГИА нет жесткой привязки математических разделов за определенными номерами заданий.
Так как же в этом случае можно разумно готовиться к этому заданию?
3. Применение знаний в различных ситуациях.
1. «НАЙДИТЕ ТОЧКУ НА ЧИСЛОВОЙ ОСИ»
1-Й ЭТАП: РАБОТА С РИСУНКОМ, ВЫЧИСЛЕНИЯ.
В задачах такого типа практически все понятно становится из рисунка. Записав числа 8, 9, 10 в виде квадратного корня, сразу можно понять, что заданное число (точка М) находится близко от «8» и справа от нее.
1-Й ЭТАП: ВОЗВЕСТИ ИСХОДНЫЕ ЧИСЛА «В КВАДРАТ». РАСПОЛОЖИТЬ ПОЛУЧЕННЫЕ, А ЗАТЕМ ИСХОДНЫЕ ЧИСЛА В ПОРЯДКЕ, ЗАДАННОМ В УСЛОВИИ.
Итак, исходные числа таковы: √10, 2√3, 3
Получим из них другой ряд чисел: 10, 12, 9
Расположим полученные числа в порядке возрастания: 9, 10, 12
Значит, исходный ряд чисел будет расположен в таком порядке: 3,√10, 2√3
2. «НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ»
1-Й ЭТАП: ВЫБОР СПОСОБА РЕШЕНИЯ; ВЫЧИСЛЕНИЯ.
Что касается выбора способов решения подобных заданий, то их можно условно разделить на две группы:
Сразу «тупо подставить» числа вместо букв (здесь, например, вместо подставить ) и перейти к вычислениям;
Сначала как-то преобразовать исходное выражение (увидеть в нем формулу сокращенного умножения и применить ее, привести дроби к общему знаменателю и так далее), а только после этого подставлять в него числа.
3. «СРАВНИТЕ ВЫРАЖЕНИЯ»
В таких заданиях, где знак всех переменных известен проще всего вместо «буковок» сразу же подставить какие-нибудь простые числа, и дальше уже работать именно с ними.
4. ТЕКСТОВЫЕ ЗАДАЧИ «НА ПРОЦЕНТЫ»
ТЕМАТИЧЕСКОЕ ОТСТУПЛЕНИЕ: «ПРОЦЕНТЫ»
1 процент (1%) какого-либо числа – это 1/100 часть этого числа.
Чтобы найти 1% от числа, нужно это число просто разделить на 100 (напомню, что при делении на 100 десятичного числа запятая переносится влево на 2 позиции). Например:
1% от 50 равен 50/100=0,5
1% от 72 равен 72/100=0,72
1% от 12,3 равен 12,3/100=0,123
Найти какое-либо количество процентов от числа можно похожим способом. Например:
7% от 50 равно 7*50/100=3,5
20% от 72 равно 20*72/100=14,4
150% от 140 равно 150*140/100=210
300% от 12,3 равно 300*12,3/100=36,2
Существует и более короткий способ вычисления процентов, назовем его «продвинутым» способом. Он достаточно прост, и к нему можно прийти самостоятельно, внимательно просмотрев приведенные выше примеры. Покажем этот способ на тех же самых числах:
7% от 50 равно 0,07*50=3,5
20% от 72 равно 0,20*72=14,4
150% от 140 равно 1,5*140=210
300% от 12,3 равно 3*12,3=36,9
В дальнейшем мы будем, как правило, использовать для вычислений именно «продвинутый» способ.
0,06*800=48
800+48=848
5. ТЕКСТОВЫЕ ЗАДАЧИ «НА ГЕОМЕТРИЮ»
Оставшиеся текстовые задачи ГИА разделены на 2 группы заданий: текстовые задачи «на геометрию» и текстовые задачи «на движение». Поскольку они достаточно разнообразны и
отличаются по схеме решения, трудно дать некие рецепты, пригодные абсолютно для каждой задачи. Но что-то ориентирующее и полезное все же можно предложить в виде набора советов.
В задачах с отсутствующим рисунком необходимо составлять собственный.
При составлении уравнений по условию задачи необходимо это делать исходя из некоторой простой разумной идеи. Собирать же уравнения наугад (как это делают некоторые) «из чисел и буковок», мелькающих в условии, практически бесполезно.
Это приводит к тому, что ответ получается «хороший, но неправильный».
х*(х+4)=165
х2+4х-165=0
D=16-4*(-165)=676
х1=-15
х2=11
11+4=15
6. ТЕКСТОВЫЕ ЗАДАЧИ «НА ДВИЖЕНИЕ»
7. «ВЫРАЗИТЕ ИЗ ФОРМУЛЫ …»
s=s0+vt
t=(s-s0)/v
3.Домашнее задание. Работа №5 стр. 37
4.Итог урока.
Рефлексия.
Литература и ресурсы.
1. ГИА сборник заданий для подготовки к государственной итоговой аттестации в 9 классе.4-x=0
Решение Тригонометрих уравнений sin(2*x)=1
Правила ввода уравнений
В поле ‘Уравнение’ можно делать следующие операции:
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- ctg(x)
- Функция – Котангенс от x
- arcctg(x)
- Функция – Арккотангенс от x
- arcctgh(x)
- Функция – Гиперболический арккотангенс от x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- Действительные числа
- вводить в виде 7.3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- 15/7
- – дробь
Другие функции:
- asec(x)
- Функция – арксеканс от x
- acsc(x)
- Функция – арккосеканс от x
- sec(x)
- Функция – секанс от x
- csc(x)
- Функция – косеканс от x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция – округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция – гиперболический арксеканс от x
- csch(x)
- Функция – гиперболический косеканс от x
- sech(x)
- Функция – гиперболический секанс от x
- acsch(x)
- Функция – гиперболический арккосеканс от x
Постоянные:
- pi
- Число “Пи”, которое примерно равно ~3.14159..
- e
- Число e – основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности – знак для бесконечности
LaTeX Tutorial-Math Mode
Что такое математический режим?Для многих наиболее полезной частью LaTeX является возможность набора сложных математических формул. Для простоты LaTeX разделяет задачи набора математики и набора обычного текста. Это достигается за счет использования двух режимов работы: абзацного и математического. Существует также третий режим, называемый режимом LR, однако он редко используется новичками и, кроме того, обычно неявно вводится с другими командами.Здесь это не рассматривается. Режим абзаца – это режим по умолчанию для среды документа, и его не нужно вызывать явно.
Есть несколько способов войти в математический режим, но наиболее распространенным является $ …. $, где текст внутри знаков доллара находится в среде математического режима. Вы уже неосознанно использовали математический режим, используя команды \ begin {уравнение} и \ end {уравнение}.
В следующей таблице перечислены три метода и их использование для объявления математического режима.
| Метод | Особые характеристики | Использование |
|---|---|---|
| $ …. $ | Нет | Математика в строке |
| \ begin {уравнение} \ end {уравнение} | Переход к новой строке и центральному уравнению с меткой | Уравнения |
| \ […. \] | Переход к новой строке и центральному уравнению | Уравнения без этикетки |
Существуют эквивалентные способы входа в математический режим для каждого из этих методов, например $$.3} {3} = \ frac {19} {3}.
\]
\ конец {документ}
Смотреть PDF ››
Обратите внимание, что математический режим игнорирует пробелы, на самом деле весь этот код можно было бы поместить в одну строку и все же правильно скомпилировать. Еще одна вещь, на которую стоит обратить внимание, – это эффект от команды \ displaystyle. Эта команда заставляет LaTeX задать уравнению полную высоту, которую оно должно отображать, как если бы оно было на отдельной строке. Будьте осторожны при его использовании, так как он может создать документ из-за переменной высоты строки.
| College Algebra Учебник 37: Synthetic Division and Теоремы об остатке и множителях Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? |
Линейная алгебра для науки о данных
Введение
Один из наиболее частых вопросов, которые мы получаем в Analytics Vidhya:
Сколько математики мне нужно выучить, чтобы стать специалистом по данным?
Несмотря на то, что вопрос кажется простым, однозначного ответа на него нет. Обычно мы говорим, что для начала вам нужно знать основную описательную и логическую статистику.Это хорошо для начала.
Но после того, как вы изучите базовые концепции машинного обучения, вам нужно будет выучить еще немного математики. Вам это нужно, чтобы понять, как работают эти алгоритмы. Каковы их ограничения и исходят ли они от каких-либо допущений. Теперь можно было бы изучать множество областей, включая алгебру, исчисление, статистику, трехмерную геометрию и т. Д.
Если вы запутаетесь (как это сделал я) и спросите экспертов, что вам следует изучить на этом этапе, большинство из них предложит / согласится с тем, чтобы вы продолжили изучение линейной алгебры .
Но проблема не заканчивается. Следующая задача – выяснить, как изучать линейную алгебру. Вы можете потеряться в подробной математике и выводах, и их изучение не поможет! Я сам прошел через это путешествие и решил написать это подробное руководство.
Если вы столкнулись с вопросом о том, как учиться и чему учиться в линейной алгебре – вы попали в нужное место. Просто следуйте этому руководству.
И если вы хотите понять, как линейная алгебра вписывается в общую схему науки о данных, вот идеальная статья:
Содержание
- Мотивация – зачем изучать линейную алгебру?
- Представление задач линейной алгебры
2.1. Визуализация проблемы: строка
2.2. Усложняем задачу
2.3. Самолеты - Матрица
3.1 Термины, относящиеся к матрице
3.2 Основные операции с матрицей
3.3 Представление в форме матрицы - Решение проблемы
4.1. Рядный Эшелон формы
4.2. Обратная матрица
4.2.1 Нахождение инверсии
4.2.2 Мощность матриц: решение уравнений за один раз
4.2.3 Использование инверсии в науке о данных - Собственные значения и собственные векторы
5.1 Нахождение собственных векторов
5.2 Использование собственных векторов в науке о данных: алгоритм PCA - Разложение матрицы по сингулярным числам
- Конечные ноты
1. Мотивация – зачем изучать линейную алгебру?
Я хотел бы представить 4 сценария, чтобы продемонстрировать, почему изучение линейной алгебры важно, если вы изучаете Data Science и машинное обучение.
Сценарий 1:
Что вы видите, когда смотрите на изображение выше? Скорее всего, вы сказали цветок, листья – не так уж и сложно.Но если я попрошу вас написать эту логику, чтобы компьютер мог делать то же самое за вас – это будет очень трудная задача (мягко говоря).
Вы смогли идентифицировать цветок, потому что человеческий мозг прошел миллионы лет эволюции. Мы не понимаем, что находится на заднем плане, чтобы определить, красный или черный цвет на картинке. Мы каким-то образом приучили наш мозг автоматически выполнять эту задачу.
Но заставить компьютер выполнять ту же задачу – непростая задача, и это активная область исследований в области машинного обучения и информатики в целом.Но прежде чем мы займемся определением атрибутов изображения, давайте задумаемся над конкретным вопросом: как машина хранит это изображение?
Вы, наверное, знаете, что современные компьютеры предназначены для обработки только 0 и 1. Так как же изображение, подобное приведенному выше, с несколькими атрибутами, такими как цвет, может быть сохранено в компьютере? Это достигается за счет сохранения интенсивности пикселей в конструкции под названием Matrix. Затем эту матрицу можно обработать для идентификации цветов и т. Д.
Таким образом, любая операция, которую вы хотите выполнить с этим изображением, скорее всего, будет использовать линейную алгебру и матрицы в конце.
Сценарий 2:
Если вы немного знакомы с областью науки о данных, возможно, вы слышали о всемирном «XGBOOST» – алгоритме, наиболее часто используемом победителями конкурсов Data Science Competitions. Он хранит числовые данные в виде Matrix , чтобы давать прогнозы. Это позволяет XGBOOST быстрее обрабатывать данные и обеспечивать более точные результаты. Более того, не только XGBOOST, но и различные другие алгоритмы используют матрицы для хранения и обработки данных.
Сценарий 3:
Deep Learning – новое модное слово в городе использует матрицы для хранения входных данных, таких как изображение, речь или текст, чтобы дать современное решение этих проблем.Веса, полученные нейронной сетью, также хранятся в матрицах. Ниже приведено графическое представление весов, хранящихся в матрице.
Сценарий 4:
Еще одна активная область исследований в области машинного обучения связана с текстом, и наиболее распространенными используемыми методами являются «Пакет слов», «Матрица терминологического документа» и т. Д. Все эти методы очень похожим образом хранят подсчет (или что-то подобное) слов в документах и сохраняют их. эта частота подсчитывается в форме матрицы для выполнения таких задач, как семантический анализ, языковой перевод, генерация языка и т. д.
Итак, теперь вы понимаете важность линейной алгебры в машинном обучении. Мы видели изображения, текст или любые данные в целом, использующие матрицы для хранения и обработки данных. Этого должно быть достаточно, чтобы изучить приведенный ниже материал, чтобы начать изучение линейной алгебры. Это относительно длинное руководство, но оно строит линейную алгебру с нуля.
2. Представление задач линейной алгебры
Начнем с простой задачи.Предположим, что цена 1 мяча и 2 биты или 2 мячей и 1 биты составляет 100 единиц. Нам нужно узнать цену мяча и биты.
Предположим, что цена биты составляет «x» рупий, а цена мяча – «y». Значения «x» и «y» могут быть любыми в зависимости от ситуации, т.е. «x» и «y» являются переменными.
Переведем это в математическую форму –
2x + y = 100 ........... (1)
Аналогично для второго условия –
х + 2у = 100.............. (2)
Теперь, чтобы найти цены на биту и мяч, нам нужны значения «x» и «y», которые удовлетворяют обоим уравнениям. Основная проблема линейной алгебры состоит в том, чтобы найти эти значения «x» и «y», то есть решение системы линейных уравнений.
Вообще говоря, в линейной алгебре данные представлены в форме линейных уравнений. Эти линейные уравнения, в свою очередь, представлены в виде матриц и векторов.
Количество переменных, а также количество уравнений может изменяться в зависимости от условия, но представление находится в форме матриц и векторов.
2.1 Визуализируйте проблему
Обычно помогает визуализировать проблемы с данными. Посмотрим, поможет ли это в данном случае.
Линейные уравнения представляют плоские объекты. Мы начнем с самого простого для понимания, то есть с линии. Линия, соответствующая уравнению, – это совокупность всех точек, которые удовлетворяют данному уравнению. Например,
Точки (50,0), (0,100), (100/3,100/3) и (30,40) удовлетворяют нашему уравнению (1). Таким образом, эти точки должны лежать на линии, соответствующей нашему уравнению (1).Точно так же (0,50), (100,0), (100 / 3,100 / 3) – это некоторые из точек, которые удовлетворяют уравнению (2).
В этой ситуации мы хотим, чтобы выполнялись оба условия, то есть точка, которая лежит на обеих линиях. Интуитивно мы хотим найти точку пересечения обеих линий, как показано на рисунке ниже.
Давайте решим задачу с помощью элементарных алгебраических операций, таких как сложение, вычитание и подстановка.
2x + y = 100 .............(1)
х + 2у = 100 .......... (2)
из уравнения (1) –
у = (100- х) / 2
поместите значение y в уравнение (2) –
x + 2 * (100-x) / 2 = 100 ...... (3)
Теперь, поскольку уравнение (3) является уравнением с единственной переменной x, его можно решить для x , а затем для y.
Это выглядит просто – давайте сделаем еще один шаг и исследуем.
2.2 Давайте усложним задачу
Теперь предположим, что вам дан набор из трех условий с тремя переменными каждое, как указано ниже, и вас попросили найти значения всех переменных. Давайте решим проблему и посмотрим, что будет.
х + у + г = 1 ....... (4)
2x + y = 1 ...... (5)
5x + 3y + 2z = 4 ....... (6)
Из уравнения (4) получаем,
z = 1-x-y .... (7)
Подставляя значение z в уравнение (6), получаем –
5x + 3y + 2 (1-x-y) = 4
3x + y = 2..... (8)
Теперь мы можем решить уравнения (8) и (5) как случай двух переменных, чтобы найти значения « x » и « y » в приведенной выше задаче с битой и мячом. Как только мы узнаем « x » и « y », мы можем использовать (7), чтобы найти значение « z ».
Как видите, добавление дополнительной переменной значительно увеличило наши усилия по поиску решения проблемы. Теперь представьте, что у вас есть 10 переменных и 10 уравнений. Решение 10 уравнений одновременно может оказаться утомительным и трудоемким.Теперь погрузитесь в науку о данных. У нас есть миллионы точек данных. Как решить эти проблемы?
У нас есть миллионы точек данных в реальном наборе данных. Будет кошмаром найти решения с использованием упомянутого выше подхода. И представьте, что нам придется делать это снова, и снова, и снова. Пройдет много времени, прежде чем мы сможем решить эту проблему. А теперь, если я скажу вам, что это всего лишь часть битвы, что вы подумаете? Так что нам делать? Должны ли мы уйти и отпустить? Определенно нет.Потом?
Матрицаиспользуется для решения большого набора линейных уравнений. Но прежде чем мы пойдем дальше и взглянем на матрицы, давайте визуализируем физический смысл нашей проблемы. Поразмышляйте над следующей темой. Это напрямую связано с использованием матриц.
2.3 Самолеты
Линейное уравнение с 3 переменными представляет собой набор всех точек, координаты которых удовлетворяют уравнениям. Можете ли вы определить физический объект, представленный таким уравнением? Попытайтесь думать о двух переменных одновременно в любом уравнении, а затем добавьте третью.Вы должны понять, что он представляет собой трехмерный аналог линии.
По сути, линейное уравнение с тремя переменными представляет собой плоскость. С технической точки зрения плоскость – это плоский геометрический объект, простирающийся до бесконечности.
Как и в случае с линией, поиск решения линейного уравнения с тремя переменными означает, что мы хотим найти пересечение этих плоскостей. Теперь вы можете себе представить, сколькими способами может пересекаться набор из трех плоскостей? Позвольте мне помочь вам. Возможны 4 случая –
- Перекрестка нет вообще.
- Плоскости пересекаются в линию.
- Они могут пересекаться в плоскости.
- Все три плоскости пересекаются в одной точке.
Вы представляете количество решений в каждом конкретном случае? Попробуй сделать это. Вот пособие, взятое из Википедии, чтобы помочь вам визуализировать.
Итак, какой смысл в том, чтобы вы визуализировали все графики выше?
Нормальные люди вроде нас и большинство суперматематиков могут визуализировать вещи только в 3-х измерениях, а необходимость визуализировать вещи в 4-х (или 10000) измерениях сложно для смертных невозможно.Итак, как математики так эффективно справляются с данными многомерных измерений? У них есть хитрости в рукаве, и Матрицы – один из таких приемов, используемых математиками для работы с данными более высокой размерности.
Теперь перейдем к нашему главному фокусу, то есть к матрице.
3. Матрица
Matrix – это способ записать похожие вещи вместе, чтобы легко обрабатывать и манипулировать ими в соответствии с нашими требованиями. В науке о данных он обычно используется для хранения информации, такой как веса, в искусственной нейронной сети при обучении различных алгоритмов.Вы сможете понять мою точку зрения к концу этой статьи.
Технически матрица представляет собой двумерный массив чисел (насколько это касается Data Science). Например, посмотрите на матрицу A ниже.
Обычно строки обозначаются буквой «i», а столбцы – буквой «j». Элементы индексируются по строке « i » и столбцу « j ». Обозначим матрицу некоторым алфавитом, например A и его элементы через A (ij).
В вышеприведенной матрице
A12 = 2
Чтобы перейти к результату, пройдите по первой строке до второго столбца.
3.1 Термины, относящиеся к Matrix
Порядок матрицы – Если матрица имеет 3 строки и 4 столбца, порядок матрицы равен 3 * 4, то есть строка * столбец.
Квадратная матрица – Матрица, в которой количество строк равно количеству столбцов.
Диагональная матрица – Матрица, в которой все недиагональные элементы равны 0, называется диагональной матрицей.
Верхняя треугольная матрица – Квадратная матрица, в которой все элементы ниже диагонали равны 0.
Нижняя треугольная матрица – Квадратная матрица, все элементы над диагональю которой равны 0.
Скалярная матрица – Квадратная матрица, все диагональные элементы которой равны некоторой константе k.
Матрица идентичности – Квадратная матрица, в которой все диагональные элементы равны 1, а все недиагональные элементы равны 0.
Матрица столбцов – Матрица, состоящая только из 1 столбца. Иногда он используется для представления вектора.
Матрица строк – Матрица, состоящая только из строк.
Trace – это сумма всех диагональных элементов квадратной матрицы.
3.2 Основные операции с матрицей
Давайте поиграем с матрицами и реализуем возможности матричных операций.
Сложение – Сложение матриц почти аналогично простому арифметическому сложению. Все, что вам нужно, это порядок добавления всех матриц, который должен быть одинаковым.Этот момент станет очевидным, когда вы сделаете сложение матрицы самостоятельно.
Предположим, у нас есть 2 матрицы «A» и «B», а результирующая матрица после сложения – «C». Тогда
Cij = Aij + Bij
Например, возьмем две матрицы и решим их.
А =
В =
Затем,
С =
Обратите внимание, чтобы получить элементы матрицы C, я добавил A и B поэлементно, то есть от 1 до 4, от 3 до 5 и так далее.
Скалярное умножение – Умножение матрицы на скалярную константу называется скалярным умножением. Все, что нам нужно сделать при скалярном умножении, – это умножить каждый элемент матрицы на заданную константу. Предположим, у нас есть постоянный скаляр «c» и матрица «A». Тогда умножение «c» на «A» дает –
.c [Aij] = [c * Aij]
Транспонирование – Транспонирование просто означает перестановку индекса строки и столбца. Например –
A ij T = A ji
Transpose используется в векторизованной реализации линейной и логистической регрессии.
Код на Python
Код в R
Выход
[, 1] [, 2] [, 3] [1,] 11 12 13 [2,] 14 15 16 [3,] 17 18 19
т (А) [, 1] [, 2] [, 3] [1,] 11 14 17 [2,] 12 15 18 [3,] 13 16 19
Умножение матриц
Умножение матриц – одна из наиболее часто используемых операций в линейной алгебре. Мы научимся умножать две матрицы, а также рассмотрим ее важные свойства.
Прежде чем переходить к алгоритмам, следует иметь в виду несколько моментов.
- Умножение двух матриц порядков i * j и j * k приводит к матрице порядка i * k. Просто сохраните внешние индексы, чтобы получить индексы окончательной матрицы.
- Две матрицы будут совместимы для умножения, только если количество столбцов первой матрицы и количество строк второй совпадают.
- Третий момент – порядок умножения имеет значение.
Не волнуйтесь, если вы не можете получить эти баллы. Вы сможете понять к концу этого раздела.
Предположим, нам даны две матрицы A и B для умножения. Сначала я напишу окончательное выражение, а затем объясню шаги.
Я выбрал это изображение из Википедии для вашего лучшего понимания.
На первой иллюстрации мы знаем, что порядок результирующей матрицы должен быть 3 * 3. Итак, прежде всего, создайте матрицу порядка 3 * 3.Чтобы определить (AB) ij, умножьте каждый элемент i-й строки A на j-й столбец B по одному и сложите все члены. Чтобы помочь вам понять поэлементное умножение, взгляните на приведенный ниже код.
импорт numpy as np
A = np.arange (21,30) .reshape (3,3)
B = np.arange (31,40) .reshape (3,3)
A. точка (B)
AB = массив ([[2250, 2316, 2382], [2556, 2631, 2706], [2862, 2946, 3030]])B.точка (A)
BA = массив ([[2310, 2406, 2502],
[2526, 2631, 2736],
[2742, 2856, 2970]]) Итак, как мы получили 2250 в качестве первого элемента матрицы AB? 2250 = 21 * 31 + 22 * 34 + 23 * 37. Аналогично и по остальным элементам.
Код в R
А * В [, 1] [, 2] [, 3] [1,] 220 252 286 [2,] 322 360 400 [3,] 442 486 532
Обратите внимание на разницу между AB и BA.
Свойства умножения матриц
- Умножение матриц является ассоциативным при условии, что данные матрицы совместимы для умножения, т. Е.
ABC = (AB) C = A (BC)
import numpy as np
A = np.arange (21,30) .reshape (3,3)
B = np.arange (31,40) .reshape (3,3)
C = np.arange (41,50) .reshape (3,3)
temp1 = (A. точка (B)). Точка (C)
массив ([[306108, 313056, 320004],
[347742, 355635, 363528],
[389376, 398214, 407052]]) temp2 = A.точка ((B.dot (C)))
массив ([[306108, 313056, 320004],
[347742, 355635, 363528],
[389376, 398214, 407052]]) 2. Умножение матриц не коммутативно, т.е. AB и BA не равны. Мы проверили этот результат выше.
Умножение матриц используется в линейной и логистической регрессии, когда мы вычисляем значение выходной переменной параметризованным векторным методом. Поскольку мы изучили основы матриц, пора применить их.
3.3 Представление уравнений в матричной форме
Позвольте мне сделать для вас что-нибудь интересное. Воспользуйтесь ручкой и бумагой и попытайтесь найти значение матричного умножения, показанное ниже
.Очень легко проверить, что выражение содержит наши три уравнения. Мы назовем наши матрицы «A», «X» и «Z».
Он явно подтверждает, что мы можем записать наши уравнения вместе в одном месте как
AX = Z
Следующим шагом должны быть методы решения.Мы рассмотрим два метода, чтобы найти решение.
4. Решение проблемы
Теперь мы подробно рассмотрим два метода решения матричных уравнений.
- Форма ступенчатого эшелона
- Обращение матрицы
4.1 Рядный эшелон формы
Теперь вы визуализировали, что представляет собой уравнение с 3-мя переменными, и немного разобрались с матричными операциями. Давайте найдем решение данной системы уравнений, чтобы понять наш первый интересующий метод, и подробно исследуем его позже.
Я уже показал, что решение уравнений методом подстановки может оказаться утомительным и трудоемким. Наш первый метод знакомит вас с более аккуратным и систематическим методом выполнения работы, в котором мы систематически манипулируем нашими исходными уравнениями, чтобы найти решение. Но что это за действительные манипуляции? Есть ли какие-либо квалификационные критерии, которым они должны соответствовать? Ну да. Есть два условия, которым должна соответствовать любая манипуляция.
- Манипуляция должна сохранять раствор, т.е. раствор не должен изменяться при наложении манипуляции.
- Манипуляции должны быть обратимыми.
Итак, что это за манипуляции?
- Мы можем поменять порядок уравнений.
- Мы можем умножить обе части уравнения на любую ненулевую константу «c».
- Мы можем умножить уравнение на любую ненулевую константу, а затем добавить к другому уравнению.
Эти моменты станут более ясными, если вы пройдетесь по алгоритму и попрактикуетесь в нем.Основная идея состоит в том, чтобы очистить переменные в последовательных уравнениях и сформировать верхнюю треугольную матрицу. Имея все необходимое, давайте приступим. Но перед этим настоятельно рекомендуется пройти по этой ссылке для лучшего понимания.
Я решу нашу исходную задачу в качестве иллюстрации. Давайте сделаем это поэтапно.
- Сделайте расширенную матрицу из матриц «A» и «Z».
Я только что соединил две матрицы.Расширенная матрица просто сообщает, что элементы в строке являются коэффициентами «x», «y» и «z», а последний элемент в строке является правой частью уравнения.
- Умножьте строку (1) на 2 и вычтите из строки (2). Аналогичным образом умножьте уравнение 1 на 5 и вычтите из строки (3).
- Чтобы получить верхнюю треугольную матрицу, умножьте строку (2) на 2, а затем вычтите из строки (3).
Не забудьте сделать каждый ведущий коэффициент, также называемый опорным элементом, равным 1, с помощью подходящих манипуляций; в этом случае умножение строки 2 на -1.Кроме того, если строка состоит только из 0, она должна быть ниже каждой строки, которая содержит ненулевую запись. Полученная форма матрицы называется формой эшелона строк. Обратите внимание, что плоскости, соответствующие новым уравнениям, сформированным в результате манипуляции, не эквивалентны. Выполняя эти операции, мы просто сохраняем решение уравнений и пытаемся добраться до него.
- Теперь мы упростили нашу работу, давайте найдем модифицированные уравнения. Мы начнем с самого простого, то есть с минимального количества оставшихся переменных.Если вы будете следовать проиллюстрированной процедуре, вы обнаружите, что последнее уравнение оказывается самым простым.
0 * x + 0 * y + 1 * z = 1
z = 1
Теперь найдите уравнение (2) и введите в него значение «z», чтобы найти «y». Сделайте то же самое для уравнения (1).
Разве это не довольно просто и чисто?
Давайте поразмышляем над еще одним моментом. Всегда ли мы сможем составить верхнетреугольную матрицу, дающую уникальное решение? Возможны ли разные случаи? Напомним, что самолеты могут пересекаться разными способами.Не торопитесь, чтобы понять это, а затем продолжайте дальше.
Различные возможные случаи –
- Возможно, мы получим уникальное решение, как показано в примере выше. Это означает, что все три плоскости пересекаются в одной точке.
- Мы можем получить корпус, как показано ниже
Обратите внимание, что в последнем уравнении 0 = 0, что всегда верно, но похоже, что у нас есть только 2 уравнения. Одно из уравнений является избыточным. Во многих случаях также возможно, что количество повторяющихся уравнений больше одного.В этом случае количество решений бесконечно.
- Есть еще один случай, когда матрица Echelon выглядит так, как показано ниже
Давайте найдем последнее уравнение.
0 * х + 0 * у + 0 * г = 4
0 = 4
Возможно ли это? Очень четкая интуиция – НЕТ. Но означает ли это что-то? Это аналогично утверждению, что решение найти невозможно, и это действительно так. Мы не можем найти решение для такой системы уравнений.Вы можете подумать, что на самом деле происходит с самолетами? Вернитесь в раздел, где мы видели пересекающиеся самолеты, и выясните это.
Обратите внимание, что этот метод эффективен для набора из 5-6 уравнений. Хотя метод довольно прост, если набор уравнений становится больше, количество манипуляций с уравнениями становится чрезвычайно большим, и метод становится неэффективным.
Ранг матрицы – Ранг матрицы равен максимальному количеству линейно независимых векторов-строк в матрице.
Набор векторов является линейно зависимым, если мы можем выразить хотя бы один из векторов как линейную комбинацию оставшихся векторов в наборе.
4.2 Обращение матрицы
Для решения большого количества уравнений за один прием используется обратное. Не паникуйте, если вы не знакомы с обратным. Мы хорошо проработаем все необходимые концепции. Начнем с нескольких терминов и операций.
Определитель матрицы – Концепция определителя применима только к квадратным матрицам.Я приведу вас к обобщенному выражению определителя по шагам. Для начала возьмем матрицу 2 * 2 A.
А пока остановимся на матрице 2 * 2. Выражение определителя матрицы A будет:
det (A) = a * d-b * c
Обратите внимание, что det (A) – стандартное обозначение определителя. Обратите внимание, что все, что вам нужно сделать, чтобы найти определитель в этом случае, – это перемножить диагональные элементы вместе и поставить перед ними положительный или отрицательный знак.Для определения знака просуммируйте индексы конкретного элемента. Если сумма четное число, поставьте знак плюс перед умножением, а если сумма нечетная, поставьте знак минус. Например, сумма индексов элемента «a11» равна 2. Точно так же сумма индексов элемента «d» равна 4. Таким образом, мы ставим положительный знак перед первым членом в выражении. Сделайте то же самое для второго срока самостоятельно.
Теперь возьмите матрицу «B» 3 * 3 и найдите ее определитель.
Сначала я напишу выражение, а затем пошагово объясню процедуру.
Каждый член в основном состоит из двух частей, то есть подматрицы и коэффициента. Прежде всего, выберите константу. Обратите внимание, что коэффициенты выбираются только из первой строки. Для начала я выбрал первый элемент первого ряда. Вы можете начать где угодно. После того, как вы выбрали коэффициент, просто удалите все элементы в строке и столбце, соответствующие выбранному коэффициенту. Далее составляем матрицу из оставшихся элементов; каждый из них в исходном положении после удаления строки и столбца и найти определитель этой подматрицы.Повторите ту же процедуру для каждого элемента в первой строке. Теперь, чтобы определить знак терминов, достаточно добавить индексы элемента коэффициента. Если он четный, поставьте знак плюс, если нечетный – знак минус. Наконец, сложите все члены, чтобы найти определитель. Теперь давайте возьмем матрицу «C» более высокого порядка и обобщим концепцию.
Попробуйте связать выражение с тем, что мы уже сделали, и придумайте окончательное выражение.
Код на Python
import numpy as np
# создать матрицу 4 * 4
arr = np.оранжевый (100,116) .reshape (4,4)
массив ([[100, 101, 102, 103],
[104, 105, 106, 107],
[108, 109, 110, 111],
[112, 113, 114, 115]]) # найти определитель
np.linalg.det (arr)
Код в R
[, 1] [, 2] [, 3]
[1,] -0,16208333 -0,1125 0,17458333
[2,] -0,077 0,1250 -0,04583333
[3,] 0,207 -0,0125 -0,09541667
# Детерминант
-0.0004166667 Минор матрицы
Возьмем квадратную матрицу A. Тогда минор, соответствующий элементу A (ij), является определителем подматрицы, образованной удалением «i-й строки» и «j» -го столбца матрицы. Надеюсь, вы понимаете то, что я уже объяснил в разделе, посвященном определителям. Возьмем пример.
Чтобы найти второстепенный элемент, соответствующий элементу A11, удалите первую строку и первый столбец, чтобы найти подматрицу.
Теперь найдите определитель этой матрицы, как уже объяснялось. Если вычислить определитель этой матрицы, то получится 4. Если минор обозначить M11, то
M11 = 4
Аналогично можно поступить и с другими элементами.
Кофактор матрицы
В приведенном выше обсуждении миноров, если мы рассматриваем знаки младших членов, полученный результат называется кофактором матрицы. Чтобы присвоить знак, просто просуммируйте индексы соответствующего элемента.Если он окажется четным, поставьте знак плюс. Остальное присваиваем отрицательному. В качестве примера возьмем иллюстрацию выше. Если мы сложим индексы, то есть 1 + 1 = 2, значит, мы должны поставить положительный знак. Скажем, C11. Тогда
C11 = 4
Вы должны сами найти кофакторы, соответствующие другим элементам, для хорошей практики.
Матрица сомножителей
Найдите сомножитель, соответствующий каждому элементу. Теперь в исходной матрице замените исходный элемент соответствующим кофактором.Найденная таким образом матрица называется кофакторной матрицей, соответствующей исходной матрице.
Например, возьмем нашу матрицу A. Если вы нашли кофакторы, соответствующие каждому элементу, просто поместите их в матрицу в соответствии с указанным выше правилом. Если вы все сделали правильно, у вас должна получиться матрица кофакторов
.Сопряжение матрицы – Наше путешествие по поиску инверсии почти подошло к концу. Просто задержите статью на пару минут, и мы будем там.Итак, теперь мы найдем сопряженный к матрице.
Предположим, нам нужно найти сопряженный к матрице A. Мы сделаем это в два этапа.
На шаге 1 найдите матрицу сомножителей A.
На шаге 2 просто транспонируйте матрицу сомножителей.
Результирующая матрица является сопряженной к исходной матрице. Для иллюстрации, давайте найдем сопряженный к нашей матрице A. У нас уже есть матрица кофакторов C. Транспонирование матрицы кофакторов должно быть
Наконец, в следующем разделе мы найдем обратное.
4.2.1 Нахождение обратной матрицы
Вы помните понятие обратного числа в элементарной алгебре? Что ж, если существуют два числа, умножение которых дает 1, то эти два числа называются обратными друг другу. Аналогично в линейной алгебре, если существуют две матрицы, умножение которых дает единичную матрицу, то матрицы называются обратными друг другу. Если вы не можете понять то, что я объяснил, просто прочтите статью.Это придет к вам интуитивно. Лучший способ учиться – учиться на практике. Итак, давайте сразу перейдем к алгоритму нахождения обратной матрицы A. Мы снова сделаем это в два этапа.
Шаг 1 : Найдите сопряженное матрице A с помощью процедуры, описанной в предыдущих разделах.
Шаг 2: Умножьте сопряженную матрицу на матрицу, обратную определителю матрицы A. Полученная матрица обратна матрице A.
Например, возьмем нашу матрицу A и найдем ее обратной.Сопряженная матрица у нас уже есть. Определитель матрицы A оказывается равным -2. Таким образом, его обратное значение будет
.Теперь предположим, что определитель оказывается равным 0. Что происходит, когда мы инвертируем определитель, то есть 0? Есть ли в этом смысл? Это ясно указывает на то, что мы не можем найти инверсию такой матрицы. Следовательно, эта матрица необратима. Более технически этот тип матрицы называется сингулярной матрицей.
Имейте в виду, что результат умножения матрицы на обратную ей является единичной матрицей.Это свойство будет широко использоваться при решении уравнений.
Обратный используется для нахождения вектора параметров, соответствующего функции минимальной стоимости в линейной регрессии.
4.2.2 Мощность матриц
Что происходит, когда мы умножаем число на 1? Очевидно, он остается прежним. То же самое применимо к единичной матрице, т.е. если мы умножим матрицу на единичную матрицу того же порядка, она останется такой же.
Давайте решим нашу исходную задачу с помощью матриц.Наша исходная задача, представленная в матрице, была такой, как показано ниже
AX = Z, т.е.
Что происходит, когда мы предварительно умножаем обе стороны на обратную матрицу коэффициентов, то есть A. Давайте выясним это на практике.
A -1 A X = A -1 Z
Мы можем манипулировать им как,
(A -1 A) X = A -1 Z
Но мы знаем, что умножение матрицы на обратную дает матрицу идентичности. Итак,
IX = А -1 Z
Где I – единичная матрица соответствующего порядка.
Если вы внимательно понаблюдаете, мы уже достигли решения. Умножение единичной матрицы на X не меняет ее. Таким образом, уравнение принимает вид
X = А -1 Z
Для решения уравнения нам нужно просто найти обратное. Это очень легко сделать, выполнив несколько строк кода. Разве это не действительно мощный метод?
Код для инверсии в Python
import numpy as np
# создать массив arr1
arr1 = np.оранжевый (5,21) .reshape (4,4)
# найти обратное
np.linalg.inv (arr1)
4.2.3 Применение инверсии в науке о данных
Inverse используется для вычисления вектора параметров по нормальному уравнению в линейном уравнении. Вот иллюстрация. Предположим, нам дан набор данных, как показано ниже –
| Команда | Лига | Год | RS | RA | Вт | ОБП | SLG | BA | г | OOBP | OSLG |
| ARI | NL | 2012 | 734 | 688 | 81 | 0.328 | 0,418 | 0,259 | 162 | 0,317 | 0,415 |
| ATL | NL | 2012 | 700 | 600 | 94 | 0,32 | 0,389 | 0,247 | 162 | 0,306 | 0,378 |
| BAL | AL | 2012 | 712 | 705 | 93 | 0,311 | 0,417 | 0.247 | 162 | 0,315 | 0,403 |
| БОС | AL | 2012 | 734 | 806 | 69 | 0,315 | 0,415 | 0,26 | 162 | 0,331 | 0,428 |
| CHC | NL | 2012 | 613 | 759 | 61 | 0,302 | 0,378 | 0,24 | 162 | 0.335 | 0,424 |
| CHW | AL | 2012 | 748 | 676 | 85 | 0,318 | 0,422 | 0,255 | 162 | 0,319 | 0,405 |
| CIN | NL | 2012 | 669 | 588 | 97 | 0,315 | 0,411 | 0,251 | 162 | 0,305 | 0,39 |
| CLE | AL | 2012 | 667 | 845 | 68 | 0.324 | 0,381 | 0,251 | 162 | 0,336 | 0,43 |
| COL | NL | 2012 | 758 | 890 | 64 | 0,33 | 0,436 | 0,274 | 162 | 0,357 | 0,47 |
| DET | AL | 2012 | 726 | 670 | 88 | 0,335 | 0,422 | 0.268 | 162 | 0,314 | 0,402 |
| HOU | NL | 2012 | 583 | 794 | 55 | 0,302 | 0,371 | 0,236 | 162 | 0,337 | 0,427 |
| KCR | AL | 2012 | 676 | 746 | 72 | 0,317 | 0,4 | 0,265 | 162 | 0.339 | 0,423 |
| LAA | AL | 2012 | 767 | 699 | 89 | 0,332 | 0,433 | 0,274 | 162 | 0,31 | 0,403 |
| LAD | NL | 2012 | 637 | 597 | 86 | 0,317 | 0,374 | 0,252 | 162 | 0,31 | 0,364 |
Он описывает различные переменные разных бейсбольных команд, чтобы предсказать, попадут они в плей-офф или нет.Но прямо сейчас, чтобы сделать это проблемой регрессии, предположим, что мы заинтересованы в прогнозировании OOBP по остальным переменным. Итак, «OOBP» – наша целевая переменная. Чтобы решить эту проблему с помощью линейной регрессии, нам нужно найти вектор параметров. Если вы знакомы с методом нормального уравнения, вы должны понимать, что для этого нам необходимо использовать матрицы. Давайте продолжим и обозначим наши независимые переменные ниже как матрицу «X». Эти данные являются частью набора данных, взятых из аналитического края.Вот ссылка на набор данных.
так, X =
| 734 | 688 | 81 | 0,328 | 0,418 | 0,259 |
| 700 | 600 | 94 | 0,32 | 0,389 | 0,247 |
| 712 | 705 | 93 | 0,311 | 0,417 | 0,247 |
| 734 | 806 | 69 | 0.315 | 0,415 | 0,26 |
| 613 | 759 | 61 | 0,302 | 0,378 | 0,24 |
| 748 | 676 | 85 | 0,318 | 0,422 | 0,255 |
| 669 | 588 | 97 | 0,315 | 0,411 | 0,251 |
| 667 | 845 | 68 | 0.324 | 0,381 | 0,251 |
| 758 | 890 | 64 | 0,33 | 0,436 | 0,274 |
| 726 | 670 | 88 | 0,335 | 0,422 | 0,268 |
| 583 | 794 | 55 | 0,302 | 0,371 | 0,236 |
| 676 | 746 | 72 | 0.317 | 0,4 | 0,265 |
| 767 | 699 | 89 | 0,332 | 0,433 | 0,274 |
| 637 | 597 | 86 | 0,317 | 0,374 | 0,252 |
Чтобы найти последний вектор параметров (θ), предполагая, что наша начальная функция параметризована θ и X, все, что вам нужно сделать, это найти обратное (X T X), что может быть очень легко выполнено с помощью кода, как показано ниже.
Прежде всего, позвольте мне упростить вам понимание формулировки линейной регрессии.
f θ (X) = θ T X, где θ – параметр, который мы хотим вычислить, а X – вектор-столбец функций или независимых переменных.
импортировать панды как pd
импортировать numpy как np
# Вам не о чем беспокоиться. Он просто # преобразует данные из исходного источника в матрицу
Df = pd.read_csv ("../baseball.csv")
Df1 = df.head (14)
# Мы просто берем 6 характеристик для вычисления θ.
X = Df1 [[«RS», «RA», «W», «OBP», «SLG», «BA»]]
Y = Df1 [«OOBP»]
# Преобразование X в матрицу
X = np.asmatrix (X)
# выполнение транспонирования X и присвоение его x
x = np.transpose (X)
# поиск умножения
T = x.точка (X)
#inverse of T - при условии, что он обратим, в противном случае мы используем псевдообратный
inv = np.linalg.inv (T)
#calculating θ
theta = (inv.dot (X.T)). Dot (Y)
Представьте, что вам нужно решить эту систему уравнений без использования линейной алгебры. Напомню, что этот набор данных меньше даже 1% от исходного набора дат. А теперь представьте, что вам нужно было найти вектор параметров без использования линейной алгебры. Это заняло бы много времени и усилий, а иногда даже невозможно было бы решить.
Один из основных недостатков метода обычных уравнений, когда количество функций велико, состоит в том, что он требует больших вычислительных затрат. Причина в том, что если есть «n» функций, матрица (X T X) будет иметь порядок n * n, и ее решение стоит времени порядка O (n * n * n). Обычно метод нормального уравнения применяется, когда количество функций составляет порядка 1000 или 10 000. Наборы данных с большим количеством функций обрабатываются с помощью другого метода, называемого градиентным спуском.
Далее мы рассмотрим еще одну продвинутую концепцию линейной алгебры, называемую собственными векторами.
5. Собственные значения и собственные векторы
Собственные векторы находят множество приложений в различных областях, таких как компьютерное зрение, физика и машинное обучение. Если вы изучали машинное обучение и знакомы с алгоритмом анализа главных компонентов, вы должны знать, насколько важен этот алгоритм при работе с большим набором данных. Вы когда-нибудь задумывались, что происходит за этим алгоритмом? Собственно, концепция собственных векторов составляет основу этого алгоритма.Давайте исследуем собственные векторы и собственные значения, чтобы лучше понять это.
Давайте умножим двумерный вектор на матрицу 2 * 2 и посмотрим, что произойдет.
Эта операция над вектором называется линейным преобразованием. Обратите внимание, что направления входных и выходных векторов различаются. Обратите внимание, что матрица столбцов обозначает здесь вектор.
Я проиллюстрирую свою точку зрения с помощью рисунка, как показано ниже.
На приведенном выше рисунке есть два типа векторов, окрашенных в красный и желтый цвета, и рисунок показывает изменение векторов после линейного преобразования.Обратите внимание, что при применении линейного преобразования к вектору желтого цвета его направление меняется, но направление вектора красного цвета не меняется даже после применения линейного преобразования. Вектор, окрашенный в красный цвет, является примером собственного вектора.
Точно, для конкретной матрицы; векторы, направление которых остается неизменным даже после применения линейного преобразования с матрицей, называются собственными векторами для этой конкретной матрицы. Помните, что концепция собственных значений и векторов применима только к квадратным матрицам.Еще одна вещь, которую следует знать, это то, что я взял случай двумерных векторов, но концепция собственных векторов применима к пространству любого количества измерений.
5.1 Как найти собственные векторы матрицы?
Предположим, у нас есть матрица A и собственный вектор «x», соответствующий матрице. Как уже объяснялось, после умножения на матрицу направление «x» не меняется. Допускается только изменение величины. Запишем это в виде уравнения –
Ax = сх
(A-c) x = 0 …….(1)
Обратите внимание, что в термине (A-c) «c» обозначает единичную матрицу порядка, равного «A», умноженную на скаляр «c»
У нас есть два неизвестных «c» и «x» и только одно уравнение. Можете ли вы придумать способ решить это уравнение?
В уравнении (1), если мы положим вектор «x» как нулевой вектор, это не имеет смысла. Следовательно, единственный выбор состоит в том, чтобы (A-c) была сингулярной матрицей. У сингулярной матрицы есть свойство, что ее определитель равен 0. Мы будем использовать это свойство, чтобы найти значение «c».
Det (A-c) = 0
Как только вы найдете определитель матрицы (A-c) и приравняете к 0, вы получите уравнение в «c» порядка, зависящего от данной матрицы A. все, что вам нужно сделать, это найти решение уравнения. Предположим, что мы находим решения как «c1», «c2» и так далее. Подставьте «c1» в уравнение (1) и найдите вектор «x1», соответствующий «c1». Вектор «x1», который вы только что нашли, является собственным вектором A. Теперь повторите ту же процедуру с «c2», «c3» и так далее.
Код для поиска EigenVectors в Python
импортировать numpy как np
# создать массив
arr = np.оранжевый (1,10) .reshape (3,3)
#finding собственного значения и собственных векторов arr
np.linalg.eig (arr)
Код в R для поиска собственных значений и собственных векторов:
Выход
147,737576 5,317459 -3,055035
[, 1] [, 2] [, 3] [1,] -0,3948374 0,4437557 -0,74478185 [2,] -0,5497457 -0,8199420 -0,06303763 [3,] -0,7361271 0,3616296 0,66432391
5.2 Использование собственных векторов в науке о данных
Концепция собственных векторов применяется в алгоритме машинного обучения «Анализ главных компонентов».Предположим, у вас есть данные с большим количеством функций, то есть они имеют очень высокую размерность. Возможно, в этих данных есть повторяющиеся функции. Помимо этого, большое количество функций приведет к снижению эффективности и увеличению дискового пространства. Что делает PCA, так это то, что он ограничивает некоторые менее важные функции. Но как определить эти особенности? Здесь нам на помощь приходят собственные векторы. Давайте рассмотрим алгоритм PCA. Предположим, у нас есть “n” размерные данные, и мы хотим уменьшить их до “k” измерений.Мы будем делать это поэтапно.
Шаг 1 : Данные нормализованы по среднему, а функция масштабирована.
Шаг 2: Мы находим ковариационную матрицу нашего набора данных.
Теперь мы хотим уменьшить количество элементов, то есть размеров. Но отключение функций означает потерю информации. Мы хотим минимизировать потерю информации, т.е. хотим сохранить максимальную дисперсию. Итак, мы хотим выяснить, в каких направлениях дисперсия максимальна. Мы найдем эти направления на следующем шаге.
Шаг 3: Находим собственные векторы ковариационной матрицы. Вам не нужно сильно беспокоиться о матрице ковариаций. Это продвинутая концепция статистики. Поскольку у нас есть данные в «n» измерениях, мы найдем «n» собственных векторов, соответствующих «n» собственным значениям.
Шаг 4 : Мы выберем «k» собственных векторов, соответствующих «k» наибольшим собственным значениям, и сформируем матрицу, в которой каждый собственный вектор будет составлять столбец. Мы будем называть эту матрицу U.
Пришло время найти уменьшенные точки данных. Предположим, вы хотите уменьшить точку данных «a» в наборе данных до размеров «k». Для этого вам нужно просто транспонировать матрицу U и умножить ее на вектор «a». Вы получите требуемый вектор в размерности «k».
Когда мы закончим с собственными векторами, давайте поговорим о другой продвинутой и очень полезной концепции линейной алгебры, называемой разложением по сингулярным значениям, широко известной как SVD. Его полное понимание требует строгого изучения линейной алгебры.По сути, SVD – это полноценный блог. Мы сделаем еще один блог, полностью посвященный СВД. Следите за обновлениями, чтобы получить лучший опыт. А пока я просто расскажу вам, как SVD помогает в науке о данных.
6. Разложение по сингулярным числам
Предположим, вам дана матрица признаков A. Как следует из названия, мы разлагаем нашу матрицу A на три составляющие матрицы для специальной цели. Иногда также говорят, что svd – это своего рода обобщение разложения по собственным значениям.Я не буду вдаваться в математику по уже объясненной причине и буду придерживаться нашего плана, то есть использования svd в науке о данных.
Svd используется для удаления избыточных функций в наборе данных. Предположим, у вас есть набор данных, состоящий из 1000 функций. Определенно, любой реальный набор данных с таким большим количеством функций обязательно должен содержать избыточные функции. Если вы работали с машинным обучением, вы должны быть знакомы с тем фактом, что избыточные функции вызывают множество проблем при выполнении алгоритмов машинного обучения.Кроме того, выполнение алгоритма на исходном наборе данных будет неэффективным по времени и потребует много памяти. Итак, что делать с такой проблемой? У нас есть выбор? Можем ли мы опустить некоторые особенности? Приведет ли это к потере значительного количества информации? Сможем ли мы получить достаточно эффективный алгоритм даже после исключения строк? Я отвечу на эти вопросы с помощью иллюстрации.
Посмотрите на изображения, показанные ниже, взятые по этой ссылке
Мы можем преобразовать этого тигра в черно-белое и представить его как матрицу, элементы которой представляют интенсивность пикселей как соответствующее местоположение.Проще говоря, матрица содержит информацию об интенсивности пикселей изображения в виде строк и столбцов. Но необходимо ли иметь все столбцы в матрице интенсивности? Сможем ли мы изобразить тигра с меньшим количеством информации? Следующая картинка проясняет мою точку зрения. На этом рисунке показаны разные изображения, соответствующие разным рангам с разным разрешением. А пока просто предположим, что более высокий ранг подразумевает больший объем информации об интенсивности пикселей.Изображение взято по этой ссылке
Ясно, что мы можем получить довольно хорошее изображение с 20 или 30 рангами вместо 100 или 200 рангов, и это то, что мы хотим сделать в случае сильно избыточных данных. Я хочу сказать, что для получения разумной гипотезы необязательно сохранять всю информацию, содержащуюся в исходном наборе данных. Даже некоторые функции вызывают проблему при поиске решения для лучшего алгоритма. Например, наличие избыточных функций вызывает множественную коллинеарность в линейной регрессии.Также некоторые особенности не имеют значения для нашей модели. Отсутствие этих функций помогает найти более подходящий алгоритм, а также эффективность времени и меньшее дисковое пространство. Декомпозиция по сингулярным значениям используется для избавления от избыточных функций, присутствующих в наших данных.
7. Конечные ноты
Если вы зашли так далеко – похлопайте себя по спине. В этой статье мы рассмотрели различные аспекты линейной алгебры. Я попытался предоставить достаточное количество информации, а также сохранить поток так, чтобы каждый мог понять концепции и иметь возможность выполнять необходимые вычисления.Тем не менее, если вы где-то застряли, не стесняйтесь оставлять комментарии ниже или размещать сообщения на портале обсуждения.
Учитесь, соревнуйтесь, взламывайте и получайте работу!
СвязанныеКак равномерно увеличить или уменьшить количество стежков в ряду
Когда узор говорит нам равномерно увеличивать или уменьшать стежки в ряду, это означает, что нам нужно выполнить некоторую базовую математику, чтобы выяснить, сколько стежков мы должны оставить между увеличением / уменьшением и как убедиться, что они увеличиваются / убавки более-менее центрированы, чтобы вязанное изделие выглядело симметричным.
Немного неудобно, но определенно несложно. В этом уроке я покажу вам метод, который я использую , когда я увижу инструкции, похожие на те, что выделены на этой фотографии:
Чтобы упростить задачу, давайте разделим процесс «равномерного увеличения или уменьшения количества стежков» на две части. В первой части мы разделим все петли на ровные сегменты и убедимся, что эти сегменты находятся по центру вязанного элемента.Во второй части мы фактически увеличим или уменьшим количество стежков.
ЧАСТЬ 1
Эта часть требует выполнения нескольких простых вычислений . Как вы видите на фотографии выше, образец шаблона говорит нам о равномерном уменьшении 10 петель в одном ряду, чтобы довести количество петель с 80 до 70.
1.1. РАЗДЕЛЕНИЕ СТРОЧЕК НА ЧЕТЫЕ ОТДЕЛЕНИЯ
Первое, что нужно сделать, это разделить количество петель на спицах на количество убавок плюс один.В нашем примере это будет означать:
.80 пет / (10 + 1) = 7,27 (примерно)
Вы можете спросить , почему мы прибавляем 1 к числу уменьшений . Это небольшая хитрость, чтобы убедиться, что уменьшение находится по центру. Если мы разделим количество петель на количество прибавок / убавлений, которое мы должны сделать, последнее прибавление / уменьшение будет в самом конце ряда. Это исказит одну из сторон ткани, и вязанное изделие не будет выглядеть симметричным.
Чтобы лучше понять эту концепцию, взгляните на диаграмму ниже . Стежки между увеличением / уменьшением отмечены пунктиром, а увеличение / уменьшение – точками.
Как видите, мы получаем симметричный интервал только тогда, когда у нас есть один дополнительный сегмент стежков.
Теперь, когда мы решили эту проблему, давайте вернемся к процессу равномерного увеличения / уменьшения количества стежков.
ПРИМЕЧАНИЕ: Все вышеперечисленное применимо только для равномерного увеличения / уменьшения в строке .Если вы работаете с в раунде , нет необходимости добавлять дополнительный сегмент. Просто разделите количество петель на количество прибавок / убытков, которые вы планируете сделать.
1.2. ЦЕНТРИРОВАНИЕ СЕГМЕНТОВ
Если результат вашего первого вычисления – число без остатка , вам повезло, и вы можете пропустить этот шаг и уверенно перейти к Части 2.
Но в большинстве случаев результатом первого вычисления будет число с остатком , как и в нашем примере: 80 / (10 + 1) = 7.27 (приблизительно).
Конечно, мы можем округлить это число в меньшую сторону и увеличивать / уменьшать количество стежков в пределах каждых 7 стежков. Но из дополнительных 0,27 частей будет составлять , и в зависимости от количества сегментов в проекте эти маленькие кусочки могут превратиться в довольно много стежков.
Если не учитывать их, наши прибавки / убывания будут собраны в первой части ряда, и вязанное изделие будет асимметричным . Это влияет на внешний вид ткани, но самое главное, может исказить посадку готового проекта.
Чтобы этого избежать, нам нужно сделать несколько дополнительных простых вычислений.
(а) Сначала давайте посчитаем , сколько дополнительных петель мы получим . Умножьте целое количество петель в сегменте на количество сегментов. В нашем примере это будет:
7 x (10 + 1) = 77 петель
Затем вычтите это число из исходного количества петель:
80 – 77 = 3 петли
Это означает, что те 0.Из 27 битов стежков получается 3 стежка. Не так уж и плохо, но если бы у нас было несколько сотен стежков на иглах, это количество было бы больше, а деформация ткани более существенной.
(b) Теперь давайте разделим эти лишние стежки на две и прибавим половину из них к одной стороне ткани, а другую половину – к другой стороне.
Поскольку мы не можем разделить 3 на 2 без остатка (и мы не можем проработать 1,5 петли), давайте назначим две петли в начале ряда и одну петлю в конец ряда.
Вот распределение стежков, которое мы получаем в результате:
2 дополнительных стежка + [сегмент из 7 стежков], рабочие скобки 10 раз + дополнительный сегмент из 7 стежков + 1 дополнительный стежок = 80 стежков
ПРИМЕЧАНИЕ : Если математически правильно округлить результат первого вычисления в большую сторону (например, если мы получим 7,72 вместо 7,27), то у нас есть , два варианта .
Более простой, но менее точный способ – узнать количество дополнительных петель и провязать половину из них в начале ряда, а другую половину в конце ряда, как мы это делали в нашем примере.Это приведет к получению более широких сегментов по бокам изделия, но не исказит внешний вид и форму ткани.
Более точный способ, – распределить эти лишние стежки между сегментами. В нашем примере мы бы чередовали сегменты по 7 петель с сегментами по 8 петель. Этот вариант требует более утомительных вычислений, и я не буду рассматривать его в этом руководстве, чтобы упростить работу.
Теперь, когда наши стежки сегментированы более или менее равномерно, пришло время увеличить или уменьшить количество стежков.
ЧАСТЬ 2
После всей математики, которую мы только что прошли, эта часть будет легкой.
Чтобы увеличить количество стежков , добавьте новый стежок после каждого сегмента стежков (кроме «дополнительного сегмента»).
В нашем примере это будет выглядеть так:
работа 2 петли + [провяжите 7 петель, прибавка], рабочие скобки 10 раз + провяжите 7 петель + провяжите 1 петлю = 90 петель
Не стесняйтесь использовать любой тип увеличения. – пряжу поверх, «сделать 1» прибавку или любой другой способ добавить новую строчку к проекту, рекомендованному в шаблоне, которому вы следуете.
Для уменьшения петель, довяжите до последних двух петель каждого сегмента (кроме «дополнительного сегмента»), затем провяжите 2 петли вместе, сделайте уменьшение SSK или убавьте одну петлю любым другим способом.
В нашем примере мы будем работать следующим образом:
работа 2 петли + [провяжите 5 петель, убавка], рабочие скобки 10 раз + провяжите 7 петель + провяжите 1 петлю = 70 петель
Фактически, этот пример взят из шаблона для проекта, над которым я работаю прямо сейчас (Lou Sweater от Phidar).Я использовал те же самые вычисления, чтобы уменьшить количество стежков, когда я перешел от резинки к основному рисунку и получил 10 равномерно расположенных убавок.
Я надеюсь, что этот урок поможет вам равномерно увеличивать или уменьшать количество стежков в ваших проектах, чтобы делать идеально симметричные, хорошо сидящие трикотажные изделия. Счастливое вязание 🙂
Используйте Excel в качестве калькулятора в Excel для Mac
Вместо того, чтобы тянуться к калькулятору, используйте Excel для вычислений!
На листе вы можете вводить простые формулы для сложения, вычитания, умножения и деления двух или более числовых значений.Создав формулу, вы можете заполнить ее соседними ячейками – не нужно создавать одну и ту же формулу снова и снова. Вы также можете ввести формулу, которая использует функцию СУММ для быстрого суммирования ряда значений без необходимости вводить какое-либо из них вручную в формулу.
Выполните одно из следующих действий:
Используйте простую формулу для сложения, вычитания, умножения или деления числовых значений
Чтобы создать простую формулу, вы вводите значения и математические операторы в ячейку или в строку формул, чтобы получить результат.Вместо того, чтобы вводить значения непосредственно в формулу, вы также можете ссылаться на ячейки, содержащие значения, которые вы хотите вычислить. Использование ссылки на ячейку в формуле гарантирует, что результат будет обновлен при изменении значений.
Введите в ячейки несколько значений.
Например, в ячейке A1 введите 5 , а в ячейке B1 введите 20 .
Щелкните любую пустую ячейку и введите знак равенства ( = ), чтобы начать формулу.
После знака равенства (=) вы можете ввести два числа и математический оператор, чтобы создать простую формулу.
Например, вы можете просто ввести = 5 + 20 или = 5 * 20 . Но чтобы создать формулу, которую вам не нужно было бы изменять, даже если вы измените одно из значений, введите ссылку на ячейку и математический оператор. Например, A1 + B1 .
После того, как вы попробовали формулу со знаком плюс (+), введите знак минус (-) для вычитания значений, звездочку (*) для умножения значений и косую черту (/) для разделения значений.
Если вы используете числа из примера, результаты будут 25, -15, 100 и 0,25
Примечание: Вы можете использовать варианты этой формулы для всех основных математических вычислений в Excel.
Добавить формулу в соседние ячейки
После создания формулы ее можно легко перетащить в соседние ячейки в строке или столбце.После этого формула автоматически корректируется для вычисления значений в соответствующей строке или столбце.
Щелкните ячейку, содержащую формулу.
Контур ячейки показывает квадрат в правом нижнем углу, называемый маркером заполнения.
Перетащите маркер заполнения в соседнюю ячейку.
Формула копируется туда и автоматически корректирует ссылки на ячейки.
Используйте функцию СУММ для суммирования числовых значений в столбце или строке
Чтобы вычислить сумму ряда числовых значений в строке или столбце, вам не нужно вручную вводить все эти значения в формулу. Вместо этого вы можете использовать предопределенную формулу, в которой используется функция СУММ.
На листе введите три числа в ряд.
Например, в ячейке A1 введите 5 , в ячейке B1 введите 20 , а в ячейке C1 введите 8 .
Щелкните пустую ячейку справа от введенных значений.
Например, щелкните ячейку D1.
На вкладке Формулы в разделе Функция щелкните Автосумма .
Excel выделяет ячейки, которые будут включены в результат.
Нажмите RETURN.
Если вы используете числа, указанные на первом шаге, результат будет 33.
См. Также
Создайте простую формулу
Введите формулу
Умножайте и делите числа
Сложить и вычесть числа
Операторы расчета и порядок действий
Операции со строками матрицы
Матрица Операции со строками (стр. 1 из 2)
«Операции» математик для “процедур”.Четыре основных операции “над числами – сложение, вычитание, умножение, и деление. Для матриц есть три основных операции со строками; что есть три процедуры, которые вы можете проделать со строками матрицы.
Первая операция переключение строк. Например, учитывая матрицу:
… можно переключать ряды вокруг, чтобы поместить матрицу в более удобное расположение строк, например:
Переключение строк часто обозначено стрелками, например:
При переключении рядов, будьте осторожны, чтобы правильно скопировать записи.
Вторая операция умножение строк. Например, учитывая следующую матрицу:
… вы можете умножить первый ряд на 1 получить положительное лидерство значение в первой строке:
Умножение этой строки часто обозначается стрелкой с указанием умножения вверху из этого, вот так:
“1 R 1 ” указывает на фактическую операцию.”1″ говорит, что мы умножили на отрицательный; “ R 1 ” говорит, что мы работали с первым рядом. Обратите внимание, что второй и третьи строки были скопированы без изменений во вторую матрицу. Умножение применяется только к первой строке, поэтому записи для двух других строк были просто унесены без изменений.
Умножить можно на что угодно тебе нравится. Например, чтобы получить ведущую 1 в третьей строке предыдущей матрицы можно умножить третью строку на отрицательную половину:
Поскольку вы не делали что-либо с первой и второй строками, эти записи были просто скопированы без изменений в новую матрицу.
Вы можете сделать больше одного умножение строк за один шаг, чтобы вы могли выполнить два вышеуказанные шаги всего за один шаг, например:
Это хорошая идея использовать некоторая форма записи (например, стрелки и нижние индексы выше), чтобы вы может отслеживать вашу работу. Матрицы очень беспорядочные, особенно если вы выполняя их вручную, а заметки могут упростить проверку вашей работы позже.Это также произведет впечатление на вашего учителя.
Операция последней строки это добавление строк. Сложение строк аналогично методу «сложение». для решения системы линейных уравнений. Предположим, у вас есть следующая система уравнений:
Вы можете приступить к решению эта система, добавляя столбцы, чтобы получить 4 y = 4:
Можно сделать нечто подобное с матрицами.Например, учитывая следующую матрицу:
… можно “уменьшить”
(добавьте больше нулей в начале) во вторую строку, добавив первую строку к
это (общая цель с матрицами на этом этапе – получить “1”
или “0”
а затем “1”
в начале каждой строки матрицы). Когда вы сокращали два уравнения
линейной системы, добавив, вы нарисовали полосу “равно” поперек
снизу и добавлен.Когда вы используете сложение в матрице, вы
нужно захватить бумагу для заметок, потому что вы не хотите пытаться
работать внутри матрицы. Так что добавьте две строки на бумаге для заметок:
Царапины |
Это ваша новая секунда ряд; вы напишете его вместо старой второй строки.Результат будет выглядят так:
В данном случае « R 1 + R 2 ” на стрелке означает “Я добавил строку один ко второй строке, и это результат Я получил “. Поскольку первая строка на самом деле не изменилась, а поскольку мы не делать что-нибудь с третьей строкой, эти строки копируются в новую матрицу без изменений.
Верх | 1 | 2 | Возвращение к указателю Вперед >>
Цитируйте эту статью как: | Стапель, Елизавета.«Матричные операции со строками». Purplemath . Доступный
из |
Стойка для номеров | Центр обучения математике
Стойки с цифрами (также известные как рекенрексы) способствуют естественному развитию у детей чувства числа. В приложении Number Rack ряды подвижных цветных бусинок побуждают учащихся думать группами по 5 и 10, помогая им исследовать и открывать для себя различные стратегии сложения и вычитания.Отобразите до 10 рядов по 10 бусин в каждом, чтобы работать с числами до 100.
Эта виртуальная версия манипулятора представляет собой открытый образовательный инструмент, идеально подходящий для начальных классов и других учебных сред, в которых используются ноутбуки, iPad или Chromebook.
Стойка с номерами – ключевой компонент второго издания «Мосты по математике». Доступен онлайн-предварительный просмотр.
Функции приложения
- Сдвигайте бусинки по одной или группами в ряд.
- Покажите от 1 до 10 рядов бисерин, по 10 бисеринок в ряду.
- Поменяйте местами цвета рядов с 6 по 10, чтобы различать (или нет) группы из 25 бусинок.
- Скрывайте бусинки с крышками изменяемого размера, чтобы создавать проблемы и играть в игры.
- Поделитесь своей работой, сохранив изображение или создав 8-значный код и ссылку для отправки другим.
Получите больше от этого приложения
Книга для педагогов
Эта книга предлагает учителям теоретические основы и практические знания по использованию числовой стойки или рекенрека в качестве мощного математического инструмента.Основываясь на идее, что дети должны уметь «видеть» числа в других числах (например, 7 можно представить как «5 плюс еще 2»), стойка с цифрами помогает детям распознавать числовые комбинации 5 и 10, развивать богатое понимание чисел от 0 до 20 и создание мощного набора интуитивно понятных стратегий для сложения и вычитания как однозначных, так и двузначных чисел.
Скачать английский Скачать испанский
Дополнительная тетрадь
Этот сборник готовых для учеников заданий основывается на контекстах и целях обучения в разделе «Обучение математическому мышлению с помощью Rekenrek» (перечислено выше).Учащиеся решают мыслимые и доступные проблемы, включая количество элементов, отношения один-к-одному, отношения «часть-часть-целое» и субитизацию.
Скачать
Рабочая тетрадь
Десять занятий и введение в использование рекенрека или стойки с номерами. Включает соответствие Общим основным государственным стандартам.
Скачать
Создайте собственную стойку для номеров
Необходимые материалы
- 1 кусок матовой доски, 6 “x 3”
- 2 черных очистителя труб
- 10 красных бусинок
- 10 белых бусинок
- Лента
Инструкции
Вдоль короткой стороны матовой доски сделайте две небольшие выемки на расстоянии 2,5 см от каждого края.Нанижите пять белых бусинок, а затем пять красных бусинок на каждый очиститель труб. Поместите каждый очиститель труб на переднюю часть матовой доски и загните концы в выемки и поверните их назад. Закрепите концы очистителя труб лентой.
Благодарности
Приложение Number Rack стало возможным благодаря щедрому пожертвованию доктора Дэвида Мурсунда.
Техническая поддержка и обратная связь
Это приложение было разработано Clarity Innovations: «Мы улучшаем преподавание и обучение, создавая решения, которые сочетают перспективные технологии с потребностями образования.