Напишем и поймем Decision Tree на Python с нуля! Часть 5. Информационная энтропия / Хабр
Данная статья — пятая в серии. Ссылки на предыдущие статьи: первая, вторая, третья, четвертая5.1 Информационная энтропия (Средний объем информации)
При создании дерева решений из данных алгоритм ID3 использует индекс, называемый информационной энтропией, чтобы определить, какой атрибут следует использовать для ветвления с наиболее эффективным распределением данных.
В начале, определимся с понятием объем информации. Интуитивно понятно, что объем данных = сложность, запутанность данных. Дерево решений собирает данные с одинаковыми значениями классов с каждого ветвления, таким образом снижая степень запутанности значений класса. Следовательно, при выборе атрибута, согласно которому лучше всего проводить ветвление, опираться стоит на то, насколько простыми стали данные после разветвления.
5.1.1 Определяем понятие объем информации
Объем данных, по сути, это ценность полученной информации.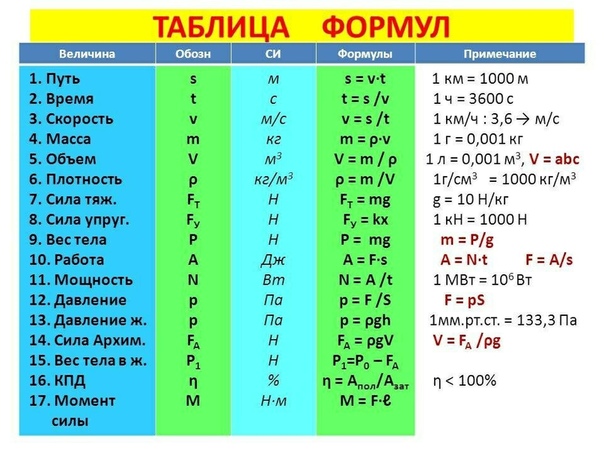
Предположим, что информация о явлениях с низкой вероятностью возникновения (например, данные, согласно которым произойдет то или иное явление), встречается гораздо чаще, чем информация о событиях, которые произойдут с высокой вероятностью.
Например, знание правильного ответа из пяти предложенных вариантов, по объему информации больше, чем знание правильного ответа из двух вариантов.
И для того, чтобы передать это знание другому человеку, представим, что оно закодировано как двоичное число и отправлено по каналу связи. В данном случае объем такого сообщения (длина в битах) и будет определяться как объем информации.
Когда вероятность того, что событие E произойдет, равна P (E), объем информации I (E), который знает, что событие E произошло, определяется следующим образом.
I(E)=log2(1/P(E))=−log2P(E)
5.1.2 Что такое информационная энтропия (средний объем информации)
У любого атрибута есть несколько значений. Например атрибут “Погода” представлен в 3 вариантах: “Ясно”, “Облачно”, “Дождь”.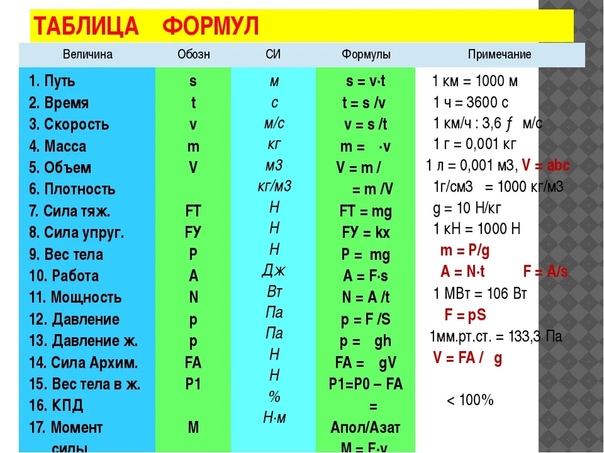
В следующей формуле она представления буквой Н.
H=−∑E∈ΩP(E)log2P(E)
Например, рассчитать значение энтропии 2-ух представленных на рисунке атрибутов, можно следующим образом. Более смешанная, хаотичная левая сторона имеет высокое значение энтропии, по сравнению с черной правой стороной, имеющей низкое значение энтропии.
Однако, даже не используя запутанные формулы, из примера сверху можно понять, что правой стороне не хватает сложности, если посмотреть на количество черных точек. Можно, например, рассмотреть случай с добавлением желтой точки, создав тем самым ситуацию с 3 значениями. Информационную энтропию можно вычислить одинаковым образом как для двух значений, так и для трех значений, что делает ее, можно сказать, унифицированной и простой в обращении.
В примере ниже, несмотря на одинаковое количество черных точек с обеих сторон, значение энтропии будет выше на стороне, где присутствуют желтый и красный цвет, нежели чем на стороне, где оставшиеся точки только красные.
И алгоритм ID3 ищет значения атрибутов, которые разделяют данные на группы с более низкой энтропией.
5.2 Вычисление информационной энтропии
Информационная энтропия может быть вычислена с помощью следующего лямбда-выражения с DataFrame в качестве ввода и значением энтропии в качестве вывода.
entropy = lambda df:-reduce(lambda x,y:x+y,map(lambda x:(x/len(df))*math.log2(x/len(df)),df.iloc[:,-1].value_counts()))Так как в данном лямбда-выражении уже присутствует другое лямбда-выражение, можно все немного упорядочить, и получится следующее:
entropy = lambda df:-reduce( #4.reduce создает одно значение из всех элементов массива.
lambda x,y:x+y,#5.Складываем значения энтропии, полученные из индивидуальных значений (9,5).
map( #2.Преобразовываем число (9,5) частотного массива (["○": 9, "×": 5]) в энтропию согласно следующему лямбда-выражению
lambda x:(x/len(df))*math.log2(x/len(df)),#3.Вычисляем P(E)log2(P(E))
df.
iloc[:,-1].value_counts() #1.Частота последнего столбца DataFrame(например:["○":9,"×":5])
)
)Данное выражение можно упорядочить следующим образом:
- df.iloc[:,-1]извлекает последний столбец DataFrame, а value_counts дает его частотное распределение (пример частотного распределения: [“○”: 9, “×”: 5])
- map преобразует каждое из значений частотного распределения (например, 9,5) в значения энтропии.
- (x / len (df)) * math.log2 (x / len (df)) вычисляет формулу P (E) log2P (E) для одного значения энтропии.
- reduce используется для создания единого значения из всех элементов массива. Например, его можно использовать для расчета сумм, средних значений и т. д.
- Лямбда-выражение x, y: x + y дает сумму двух аргументов (x, y), то есть сумму массивов. Это часть с “сигмой” в формуле энтропии (−∑E∈ΩP(E)log2P(E)). Так как выражение имеет минус в начале, оно также имеет минус перед reduce в программе.
5.
 2.1 Вычисление информационной энтропии
2.1 Вычисление информационной энтропииd = {"Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"]}
# Энтропия равна 0.9402859586706309С другой стороны, в случае, если первые два x изменяются на ○, ○ станут доминирующими данными (сложность снизится), то энтропия будет равна 0,74959525725948.
d = {"Гольф":["○","○","○","○","○","×","○","×","○","○","○","○","○","×"]}
# Энтропия равна 0.74959525725948Ниже приведен список всех программ, вычисляющих информационную энтропию.
import pandas as pd from functools import reduce import math d = {"Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"]} df0 = pd.DataFrame(d) entropy = lambda df:-reduce( lambda x,y:x+y, map( lambda x:(x/len(df))*math.log2(x/len(df)), df.iloc[:,-1].value_counts() ) ) print(entropy(df0)) # Вывод 0.9402859586706309
Спасибо за прочтение!
Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна?
Мощность (физика) – это.
 .. Что такое Мощность (физика)?
.. Что такое Мощность (физика)?Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т.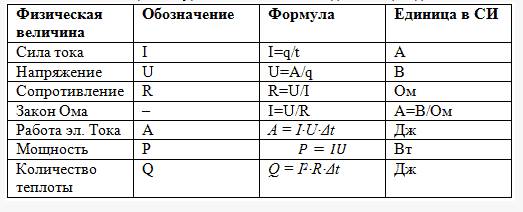
| — средняя мощность |
| — мгновенная мощность |
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
Единицы измерения
В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Другой распространённой единицей измерения мощности является лошадиная сила.
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с. |
|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10-3 | 10-6 | 0,102 | 107 | 1,36·10-3 |
| 1 киловатт | 103 | 1 | 10-3 | 102 | 1010 | 1,36 |
| 1 мегаватт | 106 | 103 | 1 | 102·103 | 1013 | 1,36·103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10-3 | 9,81·10-6 | 1 | 9,81·107 | 1,33·10-2 |
| 1 эрг в секунду | 10-7 | 10-10 | 10-13 | 1,02·10-8 | 1 | 1,36·10-10 |
| 1 лошадиная сила[2] | 735,5 | 735,5·10-3 | 735,5·10-6 | 75 | 7,355·109 | 1 |
Мощность в механике
 Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
M — момент, — угловая скорость, — число пи, n — частота вращения (об/мин).
Электрическая мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
S=P+jQ
S — Полная мощность, ВА
P — Активная мощность, Вт
Q — Реактивная мощность, ВАр
Приборы для измерения мощности
Примечания
- ↑ Большая Советская энциклопедия
- ↑ «метрическая лошадиная сила»
См. также
Ссылки
Wikimedia Foundation. 2010.
Физика 8 класс.
 Электрическое сопротивление. Удельное сопротивление :: Класс!ная физика
Электрическое сопротивление. Удельное сопротивление :: Класс!ная физикаФизика 8 класс. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ
Электрическое сопротивление ( R ) – это физическая величина, численно равная отношению
напряжения на концах проводника к силе тока, проходящего через проводник.
Величину сопротивления для участка цепи можно определить из формулы закона Ома для участка цепи.
Однако, сопротивление проводника не зависит от силы тока в цепи и напряжения, а определяется только формой, размерами и материалом проводника.
где l – длина проводника ( м ), S – площадь поперечного сечения (кв.м ),
r ( ро) – удельное сопротивление (Ом м ).
Удельное сопротивление
– показывает, чему равно сопротивление проводника, выполненного из данного вещества,
длиной в 1м и с поперечным сечением 1 м кв.
Единица измерения удельного сопротивления в системе СИ: 1 Ом м
Однако, на практике толщина проводов значительно меньше 1 м кв,
поэтому чаще используют внесистемную единицу измерения удельного сопротивления:
Единица измерения сопротивления в системе в СИ:
[R] = 1 Ом
Сопротивление проводника равно 1 Ом, если при разности потенциалов на его концах в 1 В,
по нему протекает ток силой 1 А.
___
Причиной наличия сопротивления у проводника является взаимодействие движущихся электронов с ионами кристалической решетки проводника. Из-за различия в строении криталической решетки у проводников, выполненных из различных веществ, сопротивления их отличаются друг от друга.
ЗАПОМНИ !
Существует физическая величина обратная сопротивлению – электрическая проводимость.
R – это сопротивление проводника,
1/R – это электрическая проводимость проводника
___
Величины проводимости проводников и изоляторов различаются в большое число раз,
измеряемое единицей с двадцатью двумя нулями!
ЗНАЕШЬ ЛИ ТЫ ?
… что сопротивления кожи человека обычно изменяется от 1 кОм ( для влажной кожи )
до 500 кОм ( для сухой кожи ). Сопротивление других тканей тела равно от 100 до 500 Ом.
Устали? – Отдыхаем!
Интервью с Аркадием Цейтлиным: «Вселенная вибрирующих струн»
Публикуем интервью «Русского репортера» и Expert.online с Аркадием Цейтлиным (д.ф.-м.н., профессор Физического института им. П. Н. Лебедева РАН, директор Института теоретической и математической физики МГУ, член Научного совета Фонда развития теоретической физики и математики «БАЗИС», professor of Imperial College London).
В МГУ начал работу Институт теоретической и математической физики. Мы поговорили о природе реальности и крупнейших достижениях современной физики с директором института Аркадием Цейтлиным, профессором теоретической физики Имперского колледжа Лондона, занимающим одно из первых мест в списке российских физиков по индексу Хирша. Цейтлин — один из крупнейших в мире специалистов по теории струн, согласно которой фундаментальная реальность — это вибрирующие струны энергии, ультрамикроскопические и бесконечно тонкие.
«Теория струн утверждает, что элементарный объект нашего мира — это струна, у нее уже нет никакой структуры, она не состоит из каких-то частей, а является фундаментальным элементом. Все элементарные частицы — возбуждения, состояния этой струны»
— Насколько современная физика близка к пониманию подлинного мироустройства? Иногда кажется, что все главное уже открыто. Писали, что Хокинг называл открытие бозона Хиггса на Большом адронном коллайдере «скучным открытием, больше похожим на закрытие» — ведь обнаружили лишь то, что давно было предсказано.
— Окончательной картины мира у нас, наверное, не будет никогда, а сейчас в физике и вовсе назревает «революционная ситуация». Мы многое знаем о том, как устроен мир — теория, Стандартная модель, хорошо описывает все данные о частицах, которые мы получаем на ускорителях (Стандартная модель — фундаментальная физическая модель, описывающая все известные элементарные частицы, поля и их взаимодействия; что-то вроде таблицы Менделеева для элементарных частиц. — «РР») . И при этом у нас большие проблемы с пониманием, почему мир устроен именно так, а не иначе. Почему например, Вселенная все быстрее расширяется? Загадок очень много: темная энергия, темная материя… Возможно, мы стоим у начала новой эры в космологии (науки о происхождении Вселенной как целого. — «РР»), связанной с изучением черных дыр, гравитационных волн, реликтового излучения — много чего сейчас в этой области науки происходит. А в физике элементарных частиц прогресс видимо зависит от строительства новых, еще более мощных и дорогих ускорителей, чем БАК. Но, может быть, главный прорыв ждет нас именно в понимании того, как связаны данные космологии, результаты наблюдений Вселенной в самых больших масштабах, с физикой элементарных частиц.
— «РР») . И при этом у нас большие проблемы с пониманием, почему мир устроен именно так, а не иначе. Почему например, Вселенная все быстрее расширяется? Загадок очень много: темная энергия, темная материя… Возможно, мы стоим у начала новой эры в космологии (науки о происхождении Вселенной как целого. — «РР»), связанной с изучением черных дыр, гравитационных волн, реликтового излучения — много чего сейчас в этой области науки происходит. А в физике элементарных частиц прогресс видимо зависит от строительства новых, еще более мощных и дорогих ускорителей, чем БАК. Но, может быть, главный прорыв ждет нас именно в понимании того, как связаны данные космологии, результаты наблюдений Вселенной в самых больших масштабах, с физикой элементарных частиц.
— Это углубит наши знания о далеких мирах, невообразимо маленьких или больших масштабах, но ведь знания об окружающих нас звездах и галактиках уже мало изменятся?
— Возможно, мы застряли в иллюзии о том, что понимаем, как устроен мир: что есть звезды, галактики и так далее. А может оказаться, что эти представления не так уж отличаются от уровня средних веков, когда люди думали, что Земля плоская, а мир ограничен Солнечной системой! Может оказаться, что наша Вселенная возникла в сингулярности черной дыры, или что мы живем лишь в одной из множества вселенных. Теория струн предсказывает, что может быть очень много разных вариантов устройства мира. Из теории струн можно вывести описание элементарных частиц, очень похожее на Стандартную модель, — но лишь как один из множества вариантов устройства мира. А вот почему реализован именно он, теория струн не объясняет. Почему наш мир устроен именно таким, каким мы его видим? Возможный ответ – мы живем в таком мире, где жизнь возможна; это называют антропным принципом.
А может оказаться, что эти представления не так уж отличаются от уровня средних веков, когда люди думали, что Земля плоская, а мир ограничен Солнечной системой! Может оказаться, что наша Вселенная возникла в сингулярности черной дыры, или что мы живем лишь в одной из множества вселенных. Теория струн предсказывает, что может быть очень много разных вариантов устройства мира. Из теории струн можно вывести описание элементарных частиц, очень похожее на Стандартную модель, — но лишь как один из множества вариантов устройства мира. А вот почему реализован именно он, теория струн не объясняет. Почему наш мир устроен именно таким, каким мы его видим? Возможный ответ – мы живем в таком мире, где жизнь возможна; это называют антропным принципом.
— То есть мы здесь, потому что именно наш мир жизнеспособен, а миры с другими базовыми настройками будут гораздо проще и не смогут породить разум?
— Да, именно так. Антропный принцип говорит, что наш мир устроен с такими, а не иными базовыми физическими константами, потому что здесь живем мы. Многим физикам, впрочем, антропный принцип не нравится — они считают его антинаучным. Они пытаются вывести эти константы математически и таким образом показать, почему мир имеет именно такие базовые настройки.
Многим физикам, впрочем, антропный принцип не нравится — они считают его антинаучным. Они пытаются вывести эти константы математически и таким образом показать, почему мир имеет именно такие базовые настройки.
— Теория струн может связать «микромир» с «макромиром»? Что это за струны, из которых все состоит?
— Изначально, в 1960-70-х, под струной понималось свернутое в трубку поле — но не электромагнитное, а поле, связанное с так называемыми сильными взаимодействиями, которые склеивают кварки в составные частицы, такие как протон и нейтрон. А потом развитие математического аппарата привело к тому, что мы стали смотреть на любую частицу как на колебания квантовой струны. Эта струна фундаментальна, то есть не имеет «микроструктуры», а различные моды колебаний струны (это как отдельные ноты или звуки гитарной струны) выступают для нас как та или иная частица. Параметры этих колебаний определяют массу и другие характеристики любой частицы. Даже еще не открытый гравитон (гипотетическая частица, передающая гравитационные взаимодействия. — «РР») можно мыслить как определенный вид колебаний все той же струны.
Даже еще не открытый гравитон (гипотетическая частица, передающая гравитационные взаимодействия. — «РР») можно мыслить как определенный вид колебаний все той же струны.
— То есть мир на самом деле — вибрация струн? Звучит очень музыкально…
— Теория струн шире, чем только «теория, возможно описывающая истинное устройство мира». Этим занимается фундаментальная теория струн, но кроме нее есть и прикладная — это математический аппарат, который точно описывает физические поля. Теория струн приводит к новым идеям в физике, даже к новым парадигмам. Одна из таких идей заключается в том, что на фундаментальном уровне существуют не только одномерные струны, но и двумерные мембраны и трехмерные «трибраны», как наш мир. Возможно, трибрана, на которой мы живем, окружена большим числом измерений — может быть, их целый десяток.
— А они как-то влияют на наш мир?
— Предполагают, что мы их не видим, потому что они очень маленькие, а чтобы их «пощупать», нужны очень высокие энергии. Трудно предсказать, когда это может случиться — физика развивается очень нелинейно. Еще сравнительно недавно никто не ожидал, что мы откроем гравитационные волны и что полученные с их помощью данные об устройстве черных дыр будут буквально совпадать с теми описаниями черных дыр, которые нам давала теория Эйнштейна. Может быть, следующий прорыв в области теории струн даст обнаружение частиц темной материи.
Трудно предсказать, когда это может случиться — физика развивается очень нелинейно. Еще сравнительно недавно никто не ожидал, что мы откроем гравитационные волны и что полученные с их помощью данные об устройстве черных дыр будут буквально совпадать с теми описаниями черных дыр, которые нам давала теория Эйнштейна. Может быть, следующий прорыв в области теории струн даст обнаружение частиц темной материи.
«В физике назревает “революционная ситуация”. Мы многое знаем о том, как устроен мир. И при этом у нас большие проблемы с пониманием, почему мир устроен именно так, а не иначе. Почему, например, Вселенная все быстрее расширяется? Загадок очень много: темная энергия, темная материя…»
— И эти частицы — тоже вибрации струн? Значит, поиск элементарных частиц, неделимых далее, завершится нахождением элементарных струн?
— Теория струн утверждает, что да, элементарный объект нашего мира — это струна, у нее уже нет никакой структуры, она не состоит из каких-то частей, а является фундаментальным элементом. Все элементарные частицы — возбуждения, состояния этой струны.
Все элементарные частицы — возбуждения, состояния этой струны.
— Какие еще фундаментальные вопросы сейчас более всего актуальны для теоретической физики?
— Нужно ли модифицировать теорию Эйнштейна, чтобы включить в нее темную энергию и темную материю и понять, почему они есть и как устроены. Многие сейчас работают над этим, пытаются выстроить фундаментальную теорию «снизу», придумывая эффективные способы расширить старые теории так, чтобы они описывали и новые наблюдаемые явления. Есть резоны предполагать, что теория Эйнштейна справедлива для тех масштабов, на которых мы ее до сих пор исследовали, а для больших, «галактических» масштабов — уже нет.
Очень интересен вопрос о существовании суперсимметрии — симметрии между бозонами и фермионами, которая следует из теории струн, но почему-то пока не наблюдается в реальном мире (согласно Стандартной модели, частицы делятся на два типа. Фермионы, например кварк или электрон, — это «кирпичики», из которых состоит материя. А бозоны передают взаимодействия между фермионами — например, фотон переносит электромагнитные взаимодействия. — «РР»).
Фермионы, например кварк или электрон, — это «кирпичики», из которых состоит материя. А бозоны передают взаимодействия между фермионами — например, фотон переносит электромагнитные взаимодействия. — «РР»).
— Возможно ли экспериментально проверить теорию струн?
— Мы надеемся, что да. Но как именно, пока не известно. Мы могли бы получить ответ при анализе данных с более мощного ускорителя, чем БАК, ну а если ускорителей строить больше не будут, — при анализе данных космологии, связанных с темной энергией, темной материей, рождением Вселенной.
— БАК же вроде бы никакого великого прорыва в физике не дал. А что может дать более мощный коллайдер?
— На БАК возлагали надежды, что он, в частности, откроет так называемые суперпартнеры — новые типы частиц, которые предсказываются теорией суперсимметрии; у каждой частицы должен быть такой партнер. Тогда была бы экспериментально подтверждена теория суперсимметрии. Но этого не произошло, и сейчас есть большой скептицизм по поводу того, существует ли вообще суперсимметрия как симметрия нашего мира. Но все быстро меняется, и через 5–10 лет вполне может оказаться, что эта теория верна — просто при более высоких энергиях.
Но этого не произошло, и сейчас есть большой скептицизм по поводу того, существует ли вообще суперсимметрия как симметрия нашего мира. Но все быстро меняется, и через 5–10 лет вполне может оказаться, что эта теория верна — просто при более высоких энергиях.
«Мы застряли в иллюзии о том, что понимаем, как устроен мир: что есть звезды, галактики и так далее. А может оказаться, что эти представления не так уж отличаются от уровня Средних веков, когда люди думали, что Земля плоская, а мир ограничен Солнечной системой!»
— Какие физические мегапроекты вам представляются самыми важными?
— Прежде всего, это все-таки строительство нового ускорителя. Называют суммы в десятки миллиардов долларов, но в контексте того, на что государства обычно тратят такие деньги, это совсем не так уж много, если в проекте будут участвовать несколько стран. Если сейчас остановиться, это все равно что идти по большому полю, ничего не найти и повернуть назад — а потом окажется, что на границе этого поля были залежи золота. Чудеса в мире еще могут быть, просто пока мы их не видим и не знаем!
Чудеса в мире еще могут быть, просто пока мы их не видим и не знаем!
— Как возникла идея создать Институт теоретической и математической физики?
— Институт создан по инициативе фонда «БАЗИС», при его финансовой и организационной поддержке. «БАЗИС» — российский фонд поддержки и развития теоретической физики и математики, он дает гранты на исследования и участие в научных программах, организует сезонные международные тематические школы и конференции, выделяет стипендии для талантливых студентов и аспирантов, гранты для преподавателей.
Другую часть денег и помещение дает МГУ. То, что у нас два независимых источника финансирования, дает нам дополнительную свободу.
Цель института — заниматься фундаментальной наукой на высоком уровне и готовить магистров и докторов. Будем привлекать для этого известных физиков из-за границы. Многие из наших соотечественников, работающих на Западе, заинтересованы в том, чтобы приезжать и читать здесь лекции.
— Но почему решили сделать упор именно на теоретическую физику, а не прикладные области?
— Это теоретическая база, которая очень важна и для подготовки сильных практических специалистов, умеющих логически мыслить, формулировать задачи и находить нетривиальные решения. Это совершенно ключевые навыки мышления, и в западных университетах люди, которые заканчивают магистратуру по фундаментальной физике не обязательно остаются в науке, а работают, например, в финансовой индустрии, добиваются успеха в самых разных сферах.
— Но вы же их все-таки не в инвесторы готовите…
— В Имперском колледже Лондона, где я работаю, доля аспирантов, которые защищают диссертации и остаются в науке, тоже невелика — ну, может быть, это каждый пятый. И даже из них немногие в конечном счете становятся профессорами, получают постоянную позицию в вузах. Там очень серьезный отбор.
— То есть для большинства это просто школа мышления?
— Да, абсолютно так. Хороший пример – Олег Дерипаска, предприниматель, создатель крупнейших в России промышленных предприятий. Он выпускник физфака, теоретик по специализации. Юрий Мильнер, технологический предприниматель, ставший миллиардером, тоже закончил физфак МГУ и тоже изучал теоретическую физику.
Хороший пример – Олег Дерипаска, предприниматель, создатель крупнейших в России промышленных предприятий. Он выпускник физфака, теоретик по специализации. Юрий Мильнер, технологический предприниматель, ставший миллиардером, тоже закончил физфак МГУ и тоже изучал теоретическую физику.
— А чем отличается мышление физика?
— Трудно сказать. Физики не обязательно самые «умные», с самым высоким IQ, совсем нет. Тут какая-то сложная комбинация разных навыков: например, очень важен сильный интерес к тому, как мир устроен, желание разобраться. А чтобы понять, как все устроено, нужно мыслить на шаг вперед и глубже.
S – это общая основа. Квантовый ум [Грань между физикой и психологией]
Читайте также
б) Выражение — это основа
б) Выражение — это основа
Двусмысленность проявления преодолевается через Выражение, представление мне иного, что является изначальным событием «означения» (signification). Понять значение не предполагает двигаться от одного члена отношения к другому либо узреть внутри того,
Понять значение не предполагает двигаться от одного члена отношения к другому либо узреть внутри того,
Мозг как основа тождественности
Мозг как основа тождественности Согласно этой теории мозг — основа самотождественности. Кроме мозга у человека есть еще другие органы и части тела, но они, в аристотелевском смысле, имеют акцидентальные черты: можно лишиться любого органа или части тела, сохранив при
5. Основа
5. Основа — Во всяком особенном существовании я задаю вопрос о его основе, мысля тотальность (Allheit) существования, я хочу еще раз спросить об основе. С этим вопросом я трансцендирую от существования к бытию (via causalitatis). И все же этот путь не приводит ни к какому результату,
9.
 Основа нормального правосознания
Основа нормального правосознания
9. Основа нормального правосознания Сущность правосознания состоит в том, что душа человека, слагая в себе мотивы для жизненного действования, почерпает их в предметном переживании идеи права. Содержание этой идеи полагается ею, далее, и в основание положительного права,
2. Милосердие как основа гуманизма
2. Милосердие как основа гуманизма Милосердие было нужно людям всегда. Что же это такое? Чувство? Мысль? Слово? Действие? Или общественное событие, которое можно организовать и которым можно управлять?Попытаемся заглянуть за ширму внешней суеты вокруг явления, которое
§1. Основа
§1. Основа 1. Структурность
Выражающие моменты отличны от выражаемых. Следовательно, они являются в отношении их инобытием. Но это инобытие не может допускаться только в полном отличии от выражаемой предметности и только в полном разрыве с нею. Наоборот, выражающие
Следовательно, они являются в отношении их инобытием. Но это инобытие не может допускаться только в полном отличии от выражаемой предметности и только в полном разрыве с нею. Наоборот, выражающие
Где конкретно основа бытия?
Где конкретно основа бытия? Где нам следует помещать Дух? Что нам действительно можно признавать Священным? Где конкретно искать основу бытия? В младенчестве? В матриархате? В Просветлении? В Гее? В некоторой отдаленной, но, возможно, быстро приближающейся Точке Омега? Где
ОСНОВА ЖИЗНИ ЧЕЛОВЕЧЕСТВА
ОСНОВА ЖИЗНИ ЧЕЛОВЕЧЕСТВА Люди утратили великое знание того, что каждое совокупление мужчин и женщин, являющееся основой жизни человечества, только внешне похоже одно на другое. Нет двух одинаковых совокуплений, одно от другого может разниться буквально, как небо и
Основа нашего бытия
Основа нашего бытия ГЛУБИНА В СРЕДОТОЧИИ ЖИЗНИ Тот разрыв с традиционным мышлением, к которому, как мне кажется, мы теперь призваны, значительно более радикален, чем предыдущий, позволивший христианской теологии отказаться от буквальной веры в Бога, локализованного на
2.
 2.1. Основа «привычного» мировоззрения
2.1. Основа «привычного» мировоззрения
2.2.1. Основа «привычного» мировоззрения Современное «усреднённое» мировоззрение большинства людей практически всех религиозных и идеологических систем (в том числе и тех, которые считаются атеистическими, либо людей, которые вообще не думают о религиях) основывается на
2.2.4. Основа правильного мировоззрения
2.2.4. Основа правильного мировоззрения Мозаичное мировоззрение тоже может различаться по принципам организации направленности построения взаимосвязей смысловых единиц в мозаичной картине мира — мысленном древе. Ранее была приведена система предельных обобщений и
Хлебников В. Наша основа
Хлебников В.
Наша основа Хлебников Велимир (настоящее имя – Виктор Владимирович; 1885–1922) – поэт, основатель русского футуризма, теоретик литературного авангарда. Родился в Зимней Ставке б. Астраханской губ. в семье ученого-естественника, орнитолога и лесовода; в год
Родился в Зимней Ставке б. Астраханской губ. в семье ученого-естественника, орнитолога и лесовода; в год
Пространство-время и общая основа взаимопонимания в соОБЩЕСТВЕ
Пространство-время и общая основа взаимопонимания в соОБЩЕСТВЕ Я никогда не встречался с доном Хенаро, но имел опыт общения со сходными традиционными шаманами в Африке, Австралии и Южной Америке, нередко в групповой обстановке. У меня всегда было чувство, что шаманами,
Fortnite для Xbox Series X|S и PS5 выйдет уже на следующей неделе
ОБНОВЛЕНИЕ (17 декабря 2020 г.)
Мы выпустили техническое обновление игры для PlayStation 5, чтобы решить проблему, из-за которой при отключённом режиме «120 кадров в секунду» на отдельных дисплеях Fortnite работал с разрешением 1080p вместо 4K.
С выходом этого обновления режим «120 кадров в секунду» появится в настройках, только если в параметрах консоли включён режим быстродействия (Сохранённые данные и настройки игр/приложений > Предустановки игр > Режим быстродействия).
Игроки, которые предпочитают играть с разрешением 4K, а не с частотой 120 кадров в секунду, должны убедиться, что в настройках консоли PS5 режим быстродействия не включён.
ОБНОВЛЕНИЕ (15 декабря 2020 г.)
С выходом обновления 15.10 в Fortnite появилась поддержка частоты 120 кадров в секунду в «Королевской битве» и творческом режиме как на PlayStation 5, так и на Xbox Series X|S!
Для того чтобы играть в «Королевской битве» и творческом режиме на новых консолях с частотой 120 кадров в секунду, откройте параметры графики в Fortnite и включите режим «120 кадров в секунду». Чтобы частота достигала стабильных 120 кадров в секунду, максимальное разрешение на Xbox Series X и PS5 в этом режиме уменьшено с 4K до 1440p. Качество теней и постобработки, а также дальность потоковой загрузки слегка уменьшены, однако такие параметры, как объёмные облака, контурное освещение объектов и высококачественные шейдеры, остались включёнными.
Качество теней и постобработки, а также дальность потоковой загрузки слегка уменьшены, однако такие параметры, как объёмные облака, контурное освещение объектов и высококачественные шейдеры, остались включёнными.
На Xbox Series S режим «120 кадров в секунду» работает при разрешении 1080p. (Если режим «120 кадров в секунду» отключён, максимальное разрешение будет увеличено с 1080p до 1200p во всех игровых режимах.) При включённом режиме «120 кадров в секунду» на Xbox Series S разрешение теней и прочие параметры будут снижены, а объёмные облака — отключены.
Обратите внимание, что для работы режима «120 кадров/с» требуется экран с частотой обновления 120 Гц. Если вы играете на Xbox Series X|S, убедитесь, что в настройках экрана на консоли включена частота обновления 120 Гц.
ОРИГИНАЛЬНАЯ ПУБЛИКАЦИЯ (2 ноября 2020 г.)
Новое поколение — уже на следующей неделе! Когда вы распакуете коробку с новенькой Xbox или PlayStation (или обе коробки, если вам крупно повезло) и вдоволь надышитесь ароматом свежей консоли, вас уже будет ждать версия Fortnite для нового поколения. Fortnite для Xbox Series X|S и PS5 — это не просто слегка улучшенные версии предыдущего поколения. Это новые приложения, использующие возможности новых консолей на полную катушку!
Fortnite для Xbox Series X|S и PS5 — это не просто слегка улучшенные версии предыдущего поколения. Это новые приложения, использующие возможности новых консолей на полную катушку!
Давние поклонники Fortnite смогут продолжить свои приключения с того места, на котором остановились, а если вы ещё не играли в Fortnite — это отличный повод познакомиться с игрой. И ветераны, и новички смогут загрузить игру на своей новой консоли прямо в день её выхода и насладиться возможностями «нового поколения», доступными в Fortnite.
Вот чем Fortnite порадует вас на консолях нового поколения!
Fortnite для Xbox Series X|S
10 ноября в продажу поступят сразу две новых консоли Xbox, на которых можно играть в Fortnite. Улучшения Fortnite, доступные в день выхода Xbox Series X|S:
Разрешение 4K со скоростью 60 кадров/сек. на Series X
Fortnite для Xbox выглядит ещё лучше прежнего на Xbox Series X в умопомрачительном разрешении 4K с плавными 60 кадрами в секунду.
Зрелищная графика и физика на Series X
Откройте более живой и интерактивный мир, где трава и деревья реагируют на взрывы, с улучшенной симуляцией текучей среды для дыма и жидкостей (эффекты дыма и жидкостей выглядят гораздо круче), а также абсолютно новыми эффектами Бури и облаков.
Разрешение 1080p со скоростью 60 кадров/сек. на Series S
Запускайте любой режим и наслаждайтесь плавной игрой в разрешении 1080p со скоростью 60 кадров в секунду. Xbox Series S поддерживает большинство визуальных улучшений, доступных на Series X.
Ускоренный запуск матчей
Скорость загрузки данных значительно возросла, и это затронуло не только загрузку текстур — теперь вы сможете быстрее попасть в матч сразу после запуска игры.
Улучшенный режим разделённого экрана
Режим разделённого экрана поддерживает 60 кадров в секунду на Xbox Series X|S.
Fortnite для PlayStation 5
PlayStation 5 поступит в продажу 12 или 19 ноября в зависимости от вашего региона. Улучшения Fortnite, доступные в день выхода PS5:
Улучшения Fortnite, доступные в день выхода PS5:
Разрешение 4K со скоростью 60 кадров/сек.
Fortnite для PlayStation выглядит ещё лучше прежнего на PlayStation 5 в умопомрачительном разрешении 4K с плавными 60 кадрами в секунду.
Зрелищная графика и физика
Откройте более живой и интерактивный мир, где трава и деревья реагируют на взрывы, с улучшенной симуляцией текучей среды для дыма и жидкостей (эффекты дыма и жидкостей выглядят гораздо круче), а также абсолютно новыми эффектами Бури и облаков.
Погрузитесь в игру с контроллером DualSense
Благодаря тактильной отдаче вы почувствуете, будто держите в руках пистолет-пулемёт с глушителем или снайперскую винтовку со скользящим затвором. В дополнение к отличным эффектам отдачи мы включили поддержку тактильной отдачи для стрелкового оружия на новом контроллере DualSense.
Выберите любимый режим на начальном экране PS5
Fortnite поддерживает события PS5. Вы сможете перейти сразу в лобби «Королевской битвы» для одиночек, пар или отрядов. Оказавшись в лобби, просто встаньте в очередь нужного вам режима!
Оказавшись в лобби, просто встаньте в очередь нужного вам режима!
Ускоренный запуск матчей
Скорость загрузки данных значительно возросла, и это затронуло не только загрузку текстур — теперь вы сможете быстрее попасть в матч сразу после запуска игры.
Улучшенный режим разделённого экрана
Режим разделённого экрана поддерживает 60 кадров в секунду на PS5.
Играйте с того места, на котором остановились
Неважно, на какой платформе вы играли в Fortnite раньше (или будете играть дальше на новых консолях), вам по-прежнему доступна кроссплатформенная игра. Ваш прогресс и все косметические предметы будут перенесены на новые платформы.
На Xbox Series X|S, если вы перенесли свой профиль с Xbox One, просто загрузите версию игры для Xbox Series X|S и продолжайте с того места, на котором остановились. На PlayStation 5 просто загрузите Fortnite из PlayStation Store и войдите в игру со своей учётной записью Epic или PlayStation Network.
Ностальгический бонус
Мы смотрим в будущее, но не забываем о прошлом, поэтому мы дарим всем поклонникам Fortnite, на какой бы поддерживаемой платформе они ни играли, бесплатную «Первую кирку». Начиная с 4 ноября все желающие смогут получить классическую стандартную кирку из 1-й главы Fortnite прямо в игре или в PlayStation Store. Она будет доступна до 31 января 2021 года (20:00 по московскому времени) включительно.
Это только начало!
Как и всем вам, нам тоже не терпится поближе познакомиться с Xbox Series X|S и PlayStation 5. По мере изучения этих консолей мы будем искать новые способы выжать максимум возможностей из каждой!
Электричество и магнетизм
Таким образом, скорость в выражении (4.7) — это дрейфовая скорость носителей тока в присутствии внешнего электрического поля или любого другого силового поля, обуславливающего направленное (упорядоченное) движение носители заряда. Если в веществе возможно движение зарядов разного знака, то полная плотность тока определяется векторной суммой плотностей потоков заряда каждого знака.
Как уже указывалось, в отсутствие электрического поля движение носителей заряда хаотично и не создает результирующего тока. Если, приложив электрическое поле, сообщить носителям заряда даже малую (по сравнению с их тепловой скоростью) скорость дрейфа, то, из-за наличия в проводниках огромного количества свободных электронов, возникнет значительный ток.
Поскольку дрейфовая скорость носителей тока создается электрическим полем, логично предположить пропорциональность
так что и плотность тока будет пропорциональна вектору напряженности (рис. 4.4)
|
|
(4.9) |
Более подробно этот вопрос обсуждается в Дополнении
Входящий в соотношение (4.9)
|
Коэффициент пропорциональности называется проводимостью вещества проводника. |
Проводимость связывает напряженность поля в данной точке с установившейся скоростью «течения» носителей заряда. Поэтому она может зависеть от локальных свойств проводника вблизи этой точки (то есть от строения вещества), но не зависит от формы и размеров проводника в целом. Соотношение (4.9) носит название закона Ома для плотности тока в проводнике (его называют также законом Ома в дифференциальной форме).
Рис. 4.4. Силовые линии электрического поля совпадают с линиями тока
Чтобы понять порядки величин, оценим дрейфовую скорость носителей заряда в одном из наиболее распространенных материалов — меди. Возьмем для примера силу тока I = 1 А, и пусть площадь поперечного сечения провода составляет
1 мм2 = 10–6 м2. Тогда плотность тока равна j = 106 А/м2. Теперь воспользуемся соотношением (4.7)
Теперь воспользуемся соотношением (4.7)
Носителями зарядов в меди являются электроны (е = 1.6·10-19 Кл), и нам осталось оценить их концентрацию . В таблице Менделеева медь помещается в первой группе элементов, у нее один валентный электрон, который может быть отдан в зону проводимости. Поэтому число свободных электронов примерно совпадает с числом атомов. Берем из справочника плотность меди — r Cu=8,9·103 кг/м3. Молярная масса меди указана в таблице Менделеева — MCu = 63,5·10–3 кг/моль. Отношение
— это число молей в 1 м3. Умножая на число Авогадро Na = 6,02·1023 моль–1, получаем число атомов в единице объема, то есть концентрацию электронов
Теперь получаем искомую оценку дрейфовой скорости электронов
Для сравнения: скорости хаотического теплового движения электронов при 20°С в меди по порядку величины составляют 106 м/с, то есть на одиннадцать порядков величины больше.
Возьмем произвольную воображаемую замкнутую поверхность S, которую в разных направлениях пересекают движущиеся заряды. Мы видели, что полный ток через поверхность равен
где dq — заряд, пересекающий поверхность за время dt. Обозначим через q ‘ заряд, находящийся внутри поверхности. Его можно выразить через плотность заряда , проинтегрированную по всему объему, ограниченному поверхностью
Из фундаментального закона природы – закона сохранения заряда — следует, что заряд dq, вышедший через поверхность за время dt, уменьшит заряд q ‘ внутри поверхности точно на эту же величину, то есть dq ‘ = –dq или
Подставляя сюда написанные выше выражения для скоростей изменения заряда внутри поверхности , получаем математическое соотношение, выражающее закон сохранения заряда в интегральной форме
|
|
(4. |
Напомним, что интегрирования ведутся по произвольной поверхности S и ограниченному ею объему V.
2.5 Графический анализ одномерного движения – Физика Дугласского колледжа 1104 Пользовательский учебник – Зима и лето 2020
Сводка
- Опишите прямолинейный график с точки зрения его наклона и точки пересечения по оси Y.
- Определите среднюю или мгновенную скорость по графику положения в зависимости от времени.
- Определите среднее или мгновенное ускорение по графику зависимости скорости от времени.
- Постройте график зависимости скорости от времени из графика зависимости положения от времени.время.
- Постройте график зависимости ускорения от времени из графика зависимости скорости от времени.
График, как и рисунок, лучше тысячи слов. Графики содержат не только числовую информацию; они также раскрывают отношения между физическими величинами. В этом разделе используются графики перемещения, скорости и ускорения в зависимости от времени, чтобы проиллюстрировать одномерную кинематику.
В этом разделе используются графики перемещения, скорости и ускорения в зависимости от времени, чтобы проиллюстрировать одномерную кинематику.
PHET EXPLORATIONS: Моделирование, чтобы помочь вам понять концепцию
График угла наклона
График пересечения наклона.Прямая ссылка: https://phet.colorado.edu/en/simulation/graphing-slope-intercept
Построение прямых линий
Построение прямых линий.Прямая ссылка: https://phet.colorado.edu/en/simulation/graphing-lines
ГРАФИК УРАВНЕНИЙ
Узнайте о графических полиномах. Форма кривой изменяется по мере настройки констант. Просмотрите кривые для отдельных членов (например, y = bx ), чтобы увидеть, как они складываются для создания полиномиальной кривой.Обратите внимание, что здесь используется Flash, поэтому он может работать не на всех компьютерах.
Рис. 14. График уравнений. Сюда встроены две модели PHET, упомянутые в предыдущей главе, так что вы можете поиграть с ними сейчас.
Прежде всего, обратите внимание, что графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная. Когда две физические величины нанесены друг на друга на таком графике, горизонтальная ось обычно рассматривается как независимая переменная , а вертикальная ось – как зависимая переменная .Если мы назовем горизонтальную ось x – осью, а вертикальную ось – осью y , как на рисунке 1, прямолинейный график будет иметь общий вид
y = mx + b
Здесь м – это уклон , определяется как подъем, разделенный на пробег (как показано на рисунке) прямой линии. Буква b используется для точки пересечения y , которая является точкой, в которой линия пересекает вертикальную ось.
Рис. 1. Прямолинейный график. Уравнение прямой: y = mx + b.
Уравнение прямой: y = mx + b. Время обычно является независимой переменной, от которой зависят другие величины, такие как смещение. График смещения в зависимости от времени, таким образом, будет иметь x по вертикальной оси и t по горизонтальной оси. Рисунок 2, показанный ниже, представляет собой именно такой прямолинейный график.На нем показан график перемещения в зависимости от времени для реактивного автомобиля на очень плоском высохшем дне озера в Неваде, .
Рис. 2. График перемещения от времени для реактивного автомобиля на соляных равнинах Бонневиль. Используя взаимосвязь между зависимыми и независимыми переменными, мы видим, что наклон на приведенном выше графике – это средняя скорость или [латекс] \ boldsymbol {\ bar {v}} [/ latex], а точка пересечения – это смещение в нулевой момент времени, то есть , x 0 . Подставляя эти символы в y = mx + b , получаем
Подставляя эти символы в y = mx + b , получаем
x = (средняя скорость) + x o
Таким образом, график смещения в зависимости от времени дает общую взаимосвязь между смещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации.
НАКЛОН X VS. Т
Наклон графика перемещения x от времени t – это скорость v .
наклон = подъем / ход = Δx / Δt = v в среднем или v бар (по определению)
Обратите внимание, что это уравнение совпадает с уравнением, полученным алгебраически из других уравнений движения в предыдущем разделе.
Из рисунка видно, что автомобиль имеет водоизмещение 25 м за 0,50 с и 2000 м за 6,40 с. Его смещение в остальное время можно увидеть на графике; кроме того, информация о его скорости и ускорении также может быть получена из графика.
Пример 1: Определение средней скорости по графику смещения в зависимости от времени: Реактивный автомобиль
Найдите среднюю скорость автомобиля, положение которого показано на Рисунке 2 выше.
Стратегия
Наклон графика x по сравнению с t – это средняя скорость, поскольку наклон равен подъему за пробег. В данном случае подъем = изменение рабочего объема, а бег = изменение во времени, так что
наклон = подъем / спуск = Δx / Δt = v среднее значение
Поскольку наклон здесь постоянный, любые две точки на графике могут использоваться для определения наклона.(Вообще говоря, наиболее точно использовать две широко разнесенные точки на прямой. Это связано с тем, что любая ошибка при чтении данных с графика пропорционально меньше, если интервал больше.)
Решение
1. Выберите две точки на линии. В этом случае мы выбираем точки, помеченные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Учтите, однако, что вы можете выбрать любые две точки.)
(Учтите, однако, что вы можете выбрать любые две точки.)
2. Подставьте значения x и t выбранных точек в уравнение.Помните, что при вычислении изменения ( Δ ) мы всегда используем конечное значение минус начальное значение.
наклон = подъем / спуск = Δx / Δt = v в среднем = (2000 м / с – 525 м / с) / (6,4 – 0,50 с)
дает среднюю скорость = 250 м / с
Обсуждение
Это впечатляюще большая сухопутная скорость (900 км / ч или около 560 миль / ч): намного больше, чем типичное ограничение скорости на шоссе в 60 миль / ч (27 м / с или 96 км / ч), но значительно скромнее. рекорда 343 м / с (1234 км / ч или 766 миль / ч), установленного в 1997 году.
Графики на Рисунке 3 ниже представляют движение автомобиля с реактивным двигателем, когда он набирает максимальную скорость, но только в то время, когда его ускорение является постоянным. Время для этого движения начинается с нуля (как если бы оно измерялось секундомером), а смещение и скорость изначально составляют 200 м и 15 м / с соответственно.
Время для этого движения начинается с нуля (как если бы оно измерялось секундомером), а смещение и скорость изначально составляют 200 м и 15 м / с соответственно.
График смещения от времени на Рисунке 3 (а), показанный выше, представляет собой кривую, а не прямую линию. Наклон кривой становится более крутым с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости смещения от времени – это мгновенная скорость в этой точке. Его можно найти, проведя прямую касательную к кривой в интересующей точке и взяв наклон этой прямой.Касательные линии показаны выше для двух точек на Рисунке 3 (а). Если это делается в каждой точке кривой и значения наносятся в зависимости от времени, то получается график зависимости скорости от времени, показанный на рисунке 3 (b). Кроме того, наклон графика зависимости скорости от времени – это ускорение, которое показано на Рисунке 3 (c).
Наклон кривой становится более крутым с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости смещения от времени – это мгновенная скорость в этой точке. Его можно найти, проведя прямую касательную к кривой в интересующей точке и взяв наклон этой прямой.Касательные линии показаны выше для двух точек на Рисунке 3 (а). Если это делается в каждой точке кривой и значения наносятся в зависимости от времени, то получается график зависимости скорости от времени, показанный на рисунке 3 (b). Кроме того, наклон графика зависимости скорости от времени – это ускорение, которое показано на Рисунке 3 (c).
Пример 2: Определение мгновенной скорости по уклону в точке: Реактивный автомобиль
Рассчитайте скорость реактивного автомобиля за время 25 с, найдя наклон x vs. t график на графике ниже.
Рис. 5. Наклон графика x против t – это скорость. Это показано в двух точках. Мгновенная скорость в любой точке – это наклон касательной в этой точке.
Это показано в двух точках. Мгновенная скорость в любой точке – это наклон касательной в этой точке.Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке. Этот принцип проиллюстрирован на рисунке, показанном выше, где Q – точка при t = 25 с .
Решение
1. Найдите касательную к кривой при t = 25 с .
2. Определите конечные точки касательной. Они соответствуют позиции 1300 м за 19 с и позиции 3120 м за 32 с.
3. Подставьте эти конечные точки в уравнение для определения наклона: v .
v Q = Δx Q / Δt Q = (3120 м – 1300 м) / (32 с – 19 с)
Таким образом, v Q = (1820 м) / (13 с) = 140 м / с
Обсуждение
Это значение, приведенное в таблице этого рисунка для v при t = 25 с . Значение 140 м / с для v Q показано на рисунке 5 (b). Таким образом можно получить весь график v против t .
Значение 140 м / с для v Q показано на рисунке 5 (b). Таким образом можно получить весь график v против t .
Продолжая этот шаг дальше, отметим, что наклон графика зависимости скорости от времени – это ускорение. Склон делится на подъем, разделенный бегом; на графике v vs. t , подъем = изменение скорости Δ v и бег = изменение во времени Δ t .
СКЛОН V VS. Т
Наклон графика зависимости скорости v от времени t – это ускорение a .
крутизна = среднее ускорение = Δv / Δt
Поскольку график зависимости скорости от времени на рис. 3 (b) представляет собой прямую линию, ее наклон везде одинаковый, что означает, что ускорение является постоянным. Ускорение в зависимости от времени показано на Рисунке 3 (c)
Ускорение в зависимости от времени показано на Рисунке 3 (c)
Дополнительную общую информацию можно получить из рисунка 6 и выражения для прямой линии y = mx + b .
В данном случае вертикальная ось y равна V , точка пересечения b равна v 0 , наклон м составляет a , а горизонтальная ось x – t . Подстановка этих символов дает
v = a t + v o или часто записывается v = v o + a t
Общая зависимость скорости, ускорения и времени снова была получена из графика.Обратите внимание, что это уравнение также было выведено алгебраически из других уравнений движения в предыдущих разделах.
Неслучайно те же уравнения получаются графическим анализом и алгебраическими методами. Фактически, важный способ обнаружить физические взаимосвязи – это измерить различные физические величины, а затем построить графики одной величины относительно другой, чтобы увидеть, коррелированы ли они каким-либо образом. Корреляции подразумевают физические отношения и могут быть показаны в виде гладких графиков, подобных приведенным выше.Из таких графиков иногда можно постулировать математические отношения. Затем проводятся дальнейшие эксперименты для определения достоверности предполагаемых соотношений.
Фактически, важный способ обнаружить физические взаимосвязи – это измерить различные физические величины, а затем построить графики одной величины относительно другой, чтобы увидеть, коррелированы ли они каким-либо образом. Корреляции подразумевают физические отношения и могут быть показаны в виде гладких графиков, подобных приведенным выше.Из таких графиков иногда можно постулировать математические отношения. Затем проводятся дальнейшие эксперименты для определения достоверности предполагаемых соотношений.
Теперь рассмотрим движение реактивного автомобиля от 165 м / с до максимальной скорости 250 м / с, как показано на Рисунке 6 ниже. Время снова начинается с нуля, а начальное смещение и скорость составляют 2900 м и 165 м / с соответственно. (Это были окончательное смещение и скорость автомобиля в движении, показанные на Рисунке 3.Ускорение постепенно уменьшается с 5,0 м / с 2 до нуля, когда автомобиль достигает скорости 250 м / с. Наклон графика x по сравнению с t увеличивается до t = 55 с , после чего наклон остается постоянным. Точно так же скорость увеличивается до 55 с, а затем становится постоянной, поскольку ускорение уменьшается до нуля на 55 с и остается нулевым после этого.
Точно так же скорость увеличивается до 55 с, а затем становится постоянной, поскольку ускорение уменьшается до нуля на 55 с и остается нулевым после этого.
Пример 3: Расчет ускорения по графику зависимости скорости от времени
Рассчитайте ускорение реактивного автомобиля за время 25 с, найдя наклон v vs. t график на рисунке 6 (б).
Стратегия
Наклон кривой в точке t = 25 с равен наклону касательной прямой в этой точке, как показано на рисунке 6 (b)
Решение
Определите конечные точки касательной по рисунку, а затем подставьте их в уравнение для определения наклона: a .
уклон = Δv / Δ t = (260 м / с – 210 м / с) / (51 – 1.0 с) = 1,0 м / с 2
Обсуждение: Обратите внимание, что это значение для a согласуется со значением, нанесенным на рисунок 6 (c) при t = 25 с .
График перемещения в зависимости от времени можно использовать для построения графика зависимости скорости от времени, а график зависимости скорости от времени можно использовать для построения графика зависимости ускорения от времени. Мы делаем это, находя наклон графиков в каждой точке. Если график линейный (т.е., линия с постоянным наклоном), легко найти наклон в любой точке, и у вас есть наклон для каждой точки. Графический анализ движения может использоваться для описания как частных, так и общих характеристик кинематики. Графики также можно использовать для других тем по физике. Важным аспектом изучения физических отношений является их графическое отображение и поиск лежащих в основе отношений.
Проверьте свое понимание
1: График зависимости скорости от времени захода корабля в гавань показан ниже.(а) Опишите движение корабля на основе графика. б) Как будет выглядеть график ускорения корабля?
Рисунок 7.- Графики движения можно использовать для анализа движения.
- Графические решения дают идентичные решения математическим методам вывода уравнений движения.
- Наклон графика смещения x от времени t – это скорость v .
- Наклон графика зависимости скорости от отвремя t график – ускорение a .
- Средняя скорость, мгновенная скорость и ускорение могут быть получены путем анализа графиков.
Концептуальные вопросы
1: (a) Объясните, как можно использовать график положения в зависимости от времени на Рисунке 8 ниже o описать изменение скорости во времени. Определите (b) время ( t a , t b , t c , t d или t e ), в которое мгновенная скорость является наибольшей, (c) время при котором он равен нулю, и (d) момент времени, когда он отрицательный.
Определите (b) время ( t a , t b , t c , t d или t e ), в которое мгновенная скорость является наибольшей, (c) время при котором он равен нулю, и (d) момент времени, когда он отрицательный.
2: (a) Изобразите график зависимости скорости от времени, соответствующий графику перемещения от времени, приведенному на рисунке 9 ниже (b) Определите время или времена ( t a , t b , t c , и т. д.), при которой мгновенная скорость максимальна. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
Рисунок 9.3: (a) Объясните, как можно определить ускорение с течением времени по графику зависимости скорости от времени, например, на рисунке 10 ниже.(b) Как видно из графика, как ускорение изменяется с течением времени?
Рисунок 10.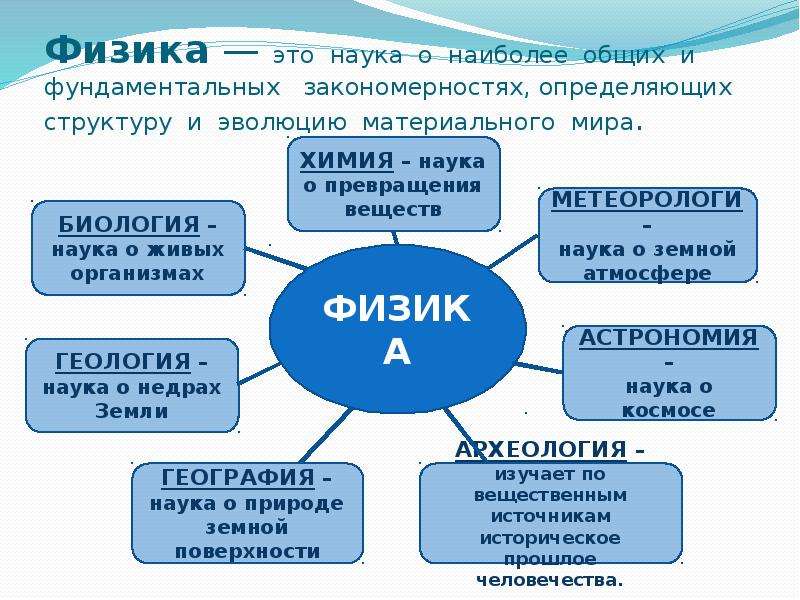
4: (a) Изобразите график зависимости ускорения от времени, соответствующий графику зависимости скорости от времени, представленному на рисунке 11 ниже. (b) Определите время или моменты времени ( t a , t b , t c , и т. д.), в которые ускорение является наибольшим. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
Рисунок 11. 5: Рассмотрим график зависимости скорости человека в лифте от времени, показанный на рисунке 12. Предположим, лифт изначально находится в состоянии покоя. Затем он ускоряется в течение 3 секунд, поддерживает эту скорость в течение 15 секунд, затем замедляется на 5 секунд, пока не остановится. Ускорение для всей поездки не является постоянным, поэтому мы не можем использовать уравнения движения, которые вы использовали ранее в этой главе, для всей поездки. (Однако мы могли бы использовать их в трех отдельных разделах, где ускорение является постоянным. ) Нарисуйте графики (а) положения в зависимости от времени и (б) ускорения в зависимости от времени для этой поездки.
) Нарисуйте графики (а) положения в зависимости от времени и (б) ускорения в зависимости от времени для этой поездки.
6: На цилиндр толкают, а затем он скатывается по наклонной плоскости. Если начало координат является начальной точкой, нарисуйте положение, скорость и ускорение цилиндра в зависимости от времени, когда он поднимается, а затем опускается по плоскости.
Задачи и упражнения
Примечание: всегда есть неопределенность в числах, взятых из графиков. Если ваши ответы отличаются от ожидаемых значений, проверьте их, чтобы увидеть, находятся ли они в пределах оцененных вами неопределенностей извлечения данных.
1: (a) Взяв наклон кривой на Рисунке 13 ниже, убедитесь, что скорость реактивного автомобиля составляет 115 м / с при t = 20 с. (b) Взяв наклон кривой в любой точке на Рисунке 14. убедитесь, что ускорение реактивного автомобиля составляет 5,0 м / с 2 .
2: Используя приблизительные значения, вычислите наклон кривой на Рисунке 15 ниже, чтобы убедиться, что скорость при t = 10,0 с равна 0.208 м / с. Предположим, что все значения известны с 3 значащими цифрами.
Рисунок 15.3: Используя приблизительные значения, вычислите наклон кривой на Рисунке 15 выше, чтобы убедиться, что скорость при t = 30,0 с составляет 0,238 м / с. Предположим, что все значения известны с 3 значащими цифрами.
4: Взяв наклон кривой на Рисунке 16 ниже, убедитесь, что ускорение составляет 3,2 м / с 2 при t = 10 с.
Рисунок 16. 5: Постройте график смещения для маршрутного поезда метро, как показано в предыдущем разделе, Глава 2.7, Рисунок 7 (a). Ваш график должен показывать положение поезда в километрах от t = 0 до 20 с. Вам нужно будет использовать информацию об ускорении и скорости, приведенную в примерах к этому рисунку.
Вам нужно будет использовать информацию об ускорении и скорости, приведенную в примерах к этому рисунку.
6: (a) Взяв наклон кривой на Рисунке 17 ниже, найдите скорость бегуна при t = 2,5 с. (b) Повторить через 7,5 с. Эти значения должны соответствовать графику на Рисунке 18, также ниже.
Рисунок 17. Рисунок 18. Рисунок 19.7: График v (t) , показанный для бегуна мирового класса в беге на 100 м, показан ниже на рисунке 20. Какова средняя скорость бегуна (а) в течение первых 4 с. ? (б) мгновенная скорость при t = 5 с? (c) среднее ускорение от 0 до 4 с? г) ускорение при t = 5 с? (д) время для гонки?
Рисунок 20.8: На рисунке 21 ниже показан график смещения частицы за 5 с.Нарисуйте соответствующие графики скорости и ускорения.
Рисунок 21.Глоссарий
- независимая переменная
- переменная, относительно которой измеряется зависимая переменная; обычно наносится по оси x –
- зависимая переменная
- переменная, которая измеряется; обычно наносится по оси y –
- уклон
- разница в y -значение (подъем), деленное на разницу в x -значение (разбег) двух точек на прямой
- Y-перехват
- значение y , когда x = 0 , или когда график пересекает ось y
Решения
Проверьте свое понимание
1: (a) Корабль движется с постоянной скоростью, а затем начинает замедляться с постоянной скоростью. В какой-то момент скорость его замедления снижается. Он поддерживает эту более низкую скорость замедления до тех пор, пока не перестанет двигаться.
В какой-то момент скорость его замедления снижается. Он поддерживает эту более низкую скорость замедления до тех пор, пока не перестанет двигаться.
(b) График ускорения в зависимости от времени покажет нулевое ускорение на первом отрезке, большое и постоянное отрицательное ускорение на втором отрезке и постоянное отрицательное ускорение.
Рис. 22.Вопросы концепции
1: (b) t a 1 (c) t d 1 (d) t e
2: (b) t a and or t d 1 (c) t c t e t g 1d) t a t b t f
4: (c) t d t e t h
Задачи и упражнения
1: (а) 115 м / с (б) 5.0 м / с 2
3: v = (11,7 – 6,95) x 10 3 м / (40,0 x – 20,0 с) = 238 м / с
5:
Рисунок 23.
6: Графики плохо читаются. Примерно a) v 2,5 = (18 м / 5 с) = + 3,6 м / с b) v 7,5 = (2-18 м) / (10-5 с) = – 2,8 м / с Эти значения являются в соответствии с графиками.
7: (а) 6 м / с (б) 12 м / с в) 3 м / с 2 г) 0 м / с 2 д) 10 с
8: От t = 0 до t = 2 секунды, средняя скорость = 1 м / с и ускорение равно нулю.
От t = 2 до t = 3 секунды средняя скорость составляет -5 м / с, а ускорение равно нулю.
От t = 3 до t = 5,0 секунды средняя скорость = 0 м / с и ускорение = 0 м / с.
От t = 5 до t = 6 секунд средняя скорость составляет + 1 м / с. Оно постоянно в это время, а ускорение равно нулю.
Ускорение равно нулю для всех отрезков прямой. За очень короткое время, необходимое для изменения скорости, произошло бесконечно большое ускорение.
3.4 Движение с постоянным ускорением – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.

- Используйте соответствующие уравнения движения для решения задачи о преследовании двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, получившее название задачи преследования двух тел .
Обозначение
Прежде всего, сделаем несколько упрощений в обозначениях.Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Так как прошло время
, принимая
означает, что
, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть
Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть
– начальная позиция и
– начальная скорость .Мы не ставим индексы на окончательные значения. То есть t – это конечный момент времени , x – конечная позиция , а v – конечная скорость . Это дает более простое выражение для прошедшего времени:
. Это также упрощает выражение для смещения x , которое теперь составляет
. Кроме того, это упрощает выражение для изменения скорости, которое теперь составляет
. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь сделаем важное предположение, что ускорение постоянно . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
Таким образом, мы можем использовать обозначение a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения.Во-первых, ускорение равно постоянному в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена
упрощенным обозначениеми
дает
Решение для x дает нам
со средней скоростью
Уравнение
отражает тот факт, что при постоянном ускорении v – это просто среднее значение начальной и конечной скоростей. (Рисунок) графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость на 1-часовом интервале от 40 км / ч до 80 км / ч составляет 60 км / ч:
(Рисунок) графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость на 1-часовом интервале от 40 км / ч до 80 км / ч составляет 60 км / ч:
В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рис. 3.18. (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости.Средняя скорость –
. (b) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не указана в
, но больше 60 км / ч.
Решение окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Замена
упрощенным обозначениеми
дает нам
Решение для v дает
Пример
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70. 0 м / с, а затем замедляется со скоростью 1,50 м / с 2 в течение 40,0 с. Какова его конечная скорость?
0 м / с, а затем замедляется со скоростью 1,50 м / с 2 в течение 40,0 с. Какова его конечная скорость?
Стратегия
Сначала мы идентифицируем известные:
.
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость
.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя (Рисунок),
.
Решение
[Показать-ответ q = ”287818 ″] Показать ответ [/ Показать-ответ]
[hidden-answer a =” 287818 ″] Подставить известные значения и решить:
(рисунок) – это эскиз, на котором показаны векторы ускорения и скорости. [/ Hidden-answer]
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.
Уравнение
не только помогает при решении задач.дает нам представление о взаимосвязи между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление
в каждую сторону этого уравнения и деление на 2 дает
С
для постоянного разгона, у нас
Теперь подставим это выражение вместо
.в уравнение перемещения,
, давая
Пример
Расчет смещения ускоряющегося объекта
Dragsters может развивать среднее ускорение 26.0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя в течение 5,56 с (рисунок). Как далеко он пролетит за это время?
Рисунок 3. 20. Пилот Top Fuel американской армии Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фотография предоставлена армией США.)
20. Пилот Top Fuel американской армии Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фотография предоставлена армией США.)Стратегия
Сначала нарисуем эскиз (рисунок). Нас просят найти смещение, которое составляет x , если мы возьмем
равняется нулю.(Подумайте о
как стартовая линия гонки. Он может быть где угодно, но мы называем его нулем и измеряем все остальные положения относительно него.) Мы можем использовать уравнение
, когда мы идентифицируем
,
, и т. из постановки задачи.
Рис. 3.21 Эскиз разгоняющегося драгстера.Решение
[show-answer q = ”9 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 9 ″] Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что
, a равно 26,0 м / с2, а t равно 5,56 с.
Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений a и t дает
[/ hidden-answer]
Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга.Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.
Что еще мы можем узнать, исследуя уравнение
Мы видим следующие отношения:
- Смещение зависит от квадрата прошедшего времени, когда ускорение не равно нулю.
 На (Рис.) Драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
На (Рис.) Драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени. - Если ускорение равно нулю, то начальная скорость равна средней скорости.
и
Решение окончательной скорости с расстояния и ускорения
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим
за т , получаем
Подставляя это и
в
, получаем
Пример
Расчет конечной скорости
Рассчитайте окончательную скорость драгстера на (Рисунок) без использования информации о времени.
Стратегия
Уравнение
идеально подходит для этой задачи, поскольку он связывает скорости, ускорение и смещение и не требует информации о времени.
Решение
[show-answer q = ”350935 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 350935 ″] Сначала мы идентифицируем известные значения. Мы знаем, что v0 = 0, поскольку драгстер стартует из состояния покоя. Мы также знаем, что x – x0 = 402 м (это был ответ на (Рисунок)).Среднее ускорение составило a = 26,0 м / с2.
Мы знаем, что v0 = 0, поскольку драгстер стартует из состояния покоя. Мы также знаем, что x – x0 = 402 м (это был ответ на (Рисунок)).Среднее ускорение составило a = 26,0 м / с2.
ПЕРЕРЫВ Во-вторых, мы подставляем известные в уравнение
и решите для v:
ПЕРЕРЫВ
Таким образом, BREAK
[/ hidden-answer]
Значение
Скорость 145 м / с составляет около 522 км / ч, или около 324 миль / ч, но даже эта головокружительная скорость отстает от рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.
Исследование уравнения
может дать дополнительную информацию об общих отношениях между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии.
 Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (постоянная a )
Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя (рисунок), получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико и приближается к нулю в том пределе, когда начальная и конечная скорости равны. Напротив, в пределах
Напротив, в пределах
для конечной разницы между начальной и конечной скоростями ускорение становится бесконечным.
Аналогичным образом, переставляя (рисунок), мы можем выразить ускорение в терминах скоростей и смещения:
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю.Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример
Как далеко уезжает машина?
На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции, равное 0.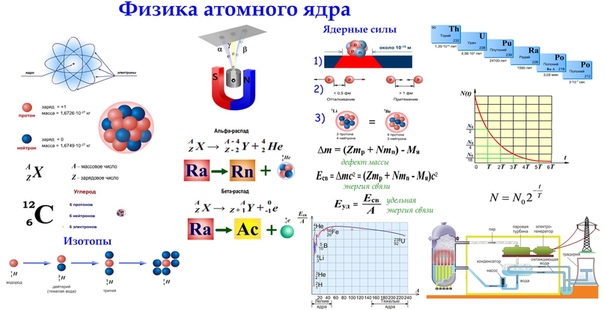 500 с, чтобы нажать на педаль тормоза.
500 с, чтобы нажать на педаль тормоза.
Стратегия
Для начала нам нужно нарисовать эскиз (рисунок). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рис. 3.22 Образец эскиза для визуализации замедления и тормозного пути автомобиля.Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30.0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости). Примем x 0 равным нулю. Ищем перемещение
или x – x 0 . Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования –
Это уравнение лучше всего, потому что оно включает только одно неизвестное, x .Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x :
и подставляем известные значения:
Таким образом,
- Эта часть может быть решена точно так же, как (а).Единственное отличие состоит в том, что ускорение составляет -5,00 м / с 2 . Результат
- [Показать-ответ q = ”175639 ″] Показать ответ [/ Показать-ответ]
[hidden-answer a =” 175639 ″] Когда водитель реагирует, тормозной путь такой же, как в пунктах (а) и ( б) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.Для этого мы, опять же, определяем известные и то, что мы хотим решить. Мы знаем это,
и
. Берем
равняется нулю. Ищем
. Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В данном случае
работает хорошо, потому что единственное неизвестное значение – это x, которое мы и хотим найти.В-третьих, мы подставляем известные, чтобы решить уравнение:
Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции. Наконец, мы добавляем смещение во время реакции к смещению при торможении ((Рисунок)),
и находят (а) равным 64,3 м + 15,0 м = 79,3 м в сухом состоянии и (б) равным 90,0 м + 15,0 м = 105 м во влажном состоянии.[/ hidden-answer]
Значение
Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример
Время расчета
Предположим, автомобиль выезжает на автомагистраль на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с 2 , сколько времени потребуется машине, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)
Стратегия
Сначала рисуем эскиз (рисунок). Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t .)
Рис. 3.24 Эскиз автомобиля, ускоряющегося на съезде с автострады.Решение
[раскрыть-ответ q = ”712029 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 712029 ″] Опять же, мы определяем известные знания и то, что мы хотим решить. Мы знаем, что
, и x = 200 м.
Нам нужно решить за t. Уравнение
работает лучше всего, потому что единственная неизвестная в уравнении – это переменная t, которую нам нужно решить.Из этого понимания мы видим, что, вводя известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t, а затем подставить известные значения в уравнение:
Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t – величина времени, а s – единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t,
, что дает два решения: t = 10.0 и t = -20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
[/ hidden-answer]
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.
Проверьте свое понимание
Пилотируемая ракета ускоряется со скоростью 20 м / с 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
[показывать-ответ q = ”fs-id1168329484424 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168329484424 ″]
Чтобы ответить на этот вопрос, выберите уравнение, которое позволяет нам решить для времени t , учитывая только a , v 0 и v :
Переставить, чтобы решить для т :
[/ hidden-answer]
Пример
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне.Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа. Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.
Решение
[show-answer q = ”835228 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 835228 ″] Сначала мы решаем
с использованием
Затем подставляем
в
, чтобы найти окончательную скорость:
[/ hidden-answer]
Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении.Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть нелегкими, например простой заменой в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.
Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений.Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче о преследовании двух тел движения объектов связаны – это означает, что неизвестное, которое мы ищем, зависит от движения обоих объектов.Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это проиллюстрировано на (Рисунок).
Рис. 3.25 Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением. Автомобиль 1 догонит автомобиль 2 позже.Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1.Чтобы найти эти неизвестные, необходимо решить кинематические уравнения, описывающие движение обеих машин.
Рассмотрим следующий пример.
Пример
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с. В момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?
Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему.Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, – это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку они оба начинаются с
, их водоизмещения такие же, в более позднее время т. , когда гепард догоняет газель.Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем приравнять уравнения друг к другу и решить неизвестное, то есть время.
Решение
- [показать-ответ q = ”699945 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 699945 ″] Уравнение для газели: газель имеет постоянную скорость, которая является ее средней скоростью, поскольку это не ускоряется. Поэтому мы используем (рисунок) с:
Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем (рисунок) с
.и
:
Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение.В этом случае мы решаем для t:
Газель имеет постоянную скорость 10 м / с, что является ее средней скоростью. Ускорение гепарда составляет 4 м / с2. Оценивая t, время, за которое гепард достигает газели, получаем
[/ hidden-answer]
- [Показать-ответ q = ”316146 ″] Показать ответ [/ Показать-ответ]
[Скрытый-ответ a =” 316146 ″] Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку они оба должны дать одинаковый ответ.Вытеснение гепарда:Водоизмещение газели:
Мы видим, что оба смещения равны, как и ожидалось. [/ Hidden-answer]
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.
Проверьте свое понимание
Велосипед имеет постоянную скорость 10 м / с. Человек стартует с отдыха и бежит, чтобы догнать велосипед за 30 с. Какое ускорение у человека?
[показывать-ответ q = ”fs-id1168326827870 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168326827870 ″]
.
[/ hidden-answer]
Сводка
- При анализе одномерного движения с постоянным ускорением определите известные величины и выберите соответствующие уравнения для решения неизвестных.Для решения неизвестных требуются одно или два кинематических уравнения, в зависимости от известных и неизвестных величин.
- Двухчастичные задачи преследования всегда требуют одновременного решения двух уравнений относительно неизвестных.
Концептуальные вопросы
При анализе движения отдельного объекта, какое количество известных физических переменных необходимо для решения неизвестных величин с использованием кинематических уравнений?
Укажите два сценария кинематики одного объекта, в которых три известные величины требуют решения двух кинематических уравнений относительно неизвестных.
[показывать-ответ q = ”fs-id1168326
5 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168326
5 ″]
Если ускорение, время и смещение являются известными, а начальная и конечная скорости являются неизвестными, то два кинематических уравнения должны решаться одновременно. Также, если конечная скорость, время и смещение являются известными, тогда необходимо решить два кинематических уравнения для начальной скорости и ускорения.
[/ hidden-answer]
Проблемы
Частица движется по прямой с постоянной скоростью 30 м / с.Каково его смещение между t = 0 и t = 5,0 с?
[Показать-ответ q = ”fs-id1168326
4 ″] Показать решение [/ раскрыть-ответ][скрытый-ответ a = ”fs-id1168326
4 ″]150 м
[/ hidden-answer]
Частица движется по прямой с начальной скоростью 30 м / с и постоянным ускорением 30 м / с 2 . Если на
и
, каково положение частицы при t = 5 с?
Частица движется по прямой с начальной скоростью 30 м / с и постоянным ускорением 30 м / с 2 .(а) Какое у него водоизмещение при т = 5 с? б) Какова его скорость в это же время?
[показывать-ответ q = ”fs-id1168326
2 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168326
2 ″]
а. 525 м;
г.
[/ hidden-answer]
(a) Изобразите график зависимости скорости от времени, соответствующий графику перемещения от времени, представленному на следующем рисунке. (b) Определите время или времена ( t a , t b , t c и т. д.), при которой мгновенная скорость имеет наибольшее положительное значение. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
[show-answer q = ”966010 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 966010 ″] [/ hidden-answer]
(a) Нарисуйте график зависимости ускорения от времени, соответствующий графику зависимости скорости от времени, представленному на следующем рисунке. (b) Определите время или времена ( t a , t b , t c и т. д.), при котором ускорение имеет наибольшее положительное значение. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
[раскрыть-ответ q = ”
6 ″] Показать ответ [/ раскрыть-ответ]
[hidden-answer a = ”
6 ″]
а.
г. Ускорение имеет наибольшее положительное значение на
г. Ускорение нулевое на
г. Ускорение отрицательное на
[/ hidden-answer]
Частица имеет постоянное ускорение 6.0 м / с 2 . (а) Если его начальная скорость составляет 2,0 м / с, в какое время его смещение составляет 5,0 м? б) Какова его скорость в то время?
При t = 10 с частица движется слева направо со скоростью 5,0 м / с. При t = 20 с частица движется справа налево со скоростью 8,0 м / с. Предполагая, что ускорение частицы постоянное, определите (а) ее ускорение, (б) ее начальную скорость и (в) момент, когда ее скорость равна нулю.
[показывать-ответ q = ”fs-id1168327148264 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327148264 ″]
а.
;
г.
;
г.
[/ hidden-answer]
Хорошо брошенный мяч попадает в мягкую перчатку. Если ускорение мяча
и 1,85 мс
проходит с момента первого касания мяча перчатки до остановки. Какова начальная скорость мяча?
Пуля в ружье ускоряется от камеры выстрела до конца ствола со средней скоростью
для
.Какова его начальная скорость (то есть конечная скорость)?
[показывать-ответ q = ”fs-id1168329484717 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168329484717 ″]
[/ hidden-answer]
(a) Пригородный легкорельсовый поезд ускоряется со скоростью 1,35 м / с 2 . Сколько времени нужно, чтобы достичь максимальной скорости 80,0 км / ч, начиная с состояния покоя? (b) Этот же поезд обычно замедляется со скоростью 1,65 м / с 2 .Сколько времени нужно, чтобы остановиться с максимальной скорости? (c) В аварийных ситуациях поезд может замедляться быстрее, останавливаясь на скорости 80,0 км / ч за 8,30 с. Каково его аварийное ускорение в метрах на секунду в квадрате?
При выезде на автостраду автомобиль ускоряется из состояния покоя со скоростью 2,04 м / с 2 за 12,0 с. (а) Нарисуйте набросок ситуации. (б) Перечислите известных в этой проблеме. (c) Как далеко машина уезжает за эти 12,0 с? Чтобы решить эту часть, сначала определите неизвестное, а затем укажите, как вы выбрали соответствующее уравнение для его решения.После выбора уравнения покажите свои шаги в поиске неизвестного, проверьте свои единицы и обсудите, является ли ответ разумным. (d) Какова конечная скорость автомобиля? Решите для этого неизвестного таким же образом, как в (c), явно показывая все шаги.
[показывать-ответ q = ”fs-id1168327145386 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327145386 ″]
а.
г. Знает:
и
;
г.
, ответ кажется разумным на высоте около 172,8 м; d.
[/ hidden-answer]
Необоснованные результаты В конце забега бегун замедляется со скорости 9,00 м / с со скоростью 2,00 м / с 2 . а) Как далеко она продвинется за следующие 5,00 с? б) Какова ее конечная скорость? (c) Оцените результат. Имеет ли это смысл?
Кровь ускоряется из состояния покоя до 30,0 см / с на расстоянии 1.80 см от левого желудочка сердца. (а) Сделайте набросок ситуации. (б) Перечислите известных в этой проблеме. (c) Сколько времени длится ускорение? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали соответствующее уравнение для его решения. После выбора уравнения покажите свои шаги в решении неизвестного, проверяя свои единицы. (г) Является ли ответ разумным по сравнению со временем биения сердца?
[показывать-ответ q = ”fs-id1168329325655 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168329325655 ″]
а.
г. Знает:
;
г.
;
г. да
[/ hidden-answer]
Во время удара по шлепку хоккеист разгоняет шайбу со скорости 8,00 м / с до 40,0 м / с в том же направлении. Если на этот снимок уйдет
, на каком расстоянии разгоняется шайба?
Мощный мотоцикл может разогнаться с места до 26.8 м / с (100 км / ч) всего за 3,90 с. а) Каково его среднее ускорение? б) Как далеко он пролетит за это время?
[show-answer q = ”fs-id116832
21 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id116832
21 ″]а. 6,87 с 2 ; б.
[/ hidden-answer]
Грузовые поезда могут развивать только относительно небольшие ускорения. (а) Какова конечная скорость грузового поезда, который ускоряется со скоростью
?для 8.00 мин, начиная с начальной скорости 4.00 м / с? (б) Если поезд может замедлиться со скоростью
, сколько времени потребуется, чтобы остановиться на этой скорости? (c) Как далеко он продвинется в каждом конкретном случае?
Снаряд фейерверка ускоряется из состояния покоя до скорости 65,0 м / с на расстоянии 0,250 м. (а) Рассчитайте ускорение. б) Как долго длилось ускорение?
[показывать-ответ q = ”fs-id1168326954581 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168326954581 ″]
а.
;
г.
[/ hidden-answer]
Лебедь на озере поднимается в воздух, взмахивая крыльями и бегая по воде. (a) Если лебедь должен достичь скорости 6,00 м / с для взлета и ускоряется из состояния покоя со средней скоростью
, как далеко он пролетит, прежде чем взлетит? б) Сколько времени это займет?
Мозг дятла специально защищен от сильных ускорений связками внутри черепа, похожими на сухожилия.При клевании дерева голова дятла останавливается с начальной скорости 0,600 м / с на расстоянии всего 2,00 мм. (a) Найдите ускорение в метрах в секунду в квадрате и кратно g , где g = 9,80 м / с 2 . (b) Рассчитайте время остановки. (c) Сухожилия, удерживающие мозг, растягиваются, делая тормозной путь 4,50 мм (больше, чем голова, и, следовательно, ускорение мозга меньше). Каково ускорение мозга, кратное g ?
[показывать-ответ q = ”fs-id1168326955141 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168326955141 ″]
а.
г.
;
г.
[/ hidden-answer]
Неосторожный футболист сталкивается со стойкой ворот с мягкой подкладкой при беге со скоростью 7,50 м / с и полностью останавливается, сжав подушку и свое тело на 0,350 м. а) Каково его ускорение? б) Как долго длится столкновение?
Посылка выпадает из грузового самолета и приземляется в лесу. Если предположить, что скорость посылки при ударе составляет 54 м / с (123 мили в час), то каково ее ускорение? Предположим, деревья и снег останавливают его на расстоянии 3.0 мин.
[показывать-ответ q = ”fs-id11683269 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id11683269 ″]
Знает:
. Нам нужны a , поэтому мы можем использовать это уравнение:
.
[/ hidden-answer]
Экспресс проходит через станцию. Он входит с начальной скоростью 22,0 м / с и замедляется со скоростью
м / с.как проходит.Длина станции 210,0 м. а) Как быстро он движется, когда нос покидает станцию? б) Какова длина носа поезда на станции? (c) Если длина поезда 130 м, какова скорость конца поезда, когда он уезжает? (d) Когда поезд отправляется со станции?
Неоправданные результаты Драгстеры могут развить максимальную скорость 145,0 м / с всего за 4,45 с. (а) Рассчитайте среднее ускорение для такого драгстера. (b) Найдите конечную скорость этого драгстера, начиная с состояния покоя и ускоряясь со скоростью, найденной в (a) для 402.0 м (четверть мили) без использования информации о времени. (c) Почему конечная скорость больше той, которая используется для определения среднего ускорения? ( Подсказка : подумайте, справедливо ли предположение о постоянном ускорении для драгстера. Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.)
[показывать-ответ q = ”fs-id1168329316432 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168329316432 ″]
а.
;
г.
;
г.
, потому что предположение о постоянном ускорении недействительно для драгстера. Драгстер переключает передачи и будет иметь большее ускорение на первой передаче, чем на второй, чем на третьей, и так далее. Вначале ускорение было бы максимальным, поэтому на отметке
он не разгонялся.за последние несколько метров, но существенно меньше, и конечная скорость будет меньше
.
[/ hidden-answer]
Глоссарий
- задача преследования двумя телами
- задача кинематики, в которой неизвестные вычисляются путем одновременного решения кинематических уравнений для двух движущихся объектов
S Лэнс Купер | Физика
С Лэнс КуперРайон первичных исследований
Заместитель руководителя программ магистратуры
(217) 333-2589
227B Лаборатория Лумиса
Профессор
(217) 333-2589
218 Лаборатория исследования материалов
Образование
- Тел.D. Физический университет Иллинойса, сентябрь 1988 г.
Биография
Лэнс Купер получил степень бакалавра наук. Магистр физики с отличием из Университета Вирджинии в 1982 году и докторская степень по физике в Университете Иллинойса в 1988 году. После двухлетней постдокторской работы в AT&T Bell Labs профессор Купер присоединился к преподавательскому составу UIUC в 1990 году. С 1993 по 1995 год он был членом Исследовательской группы оборонной науки (DSSG), младшим редактором отдела Physical Review Letters с 2006 по 2011 год, а также секретарем-казначеем Отдела физики конденсированных сред Американского общества физических наук. Общество 2015-2019 гг.
Группа Купера использует оптическую спектроскопию для выявления свойств и возбуждений в новых состояниях материи в сильно коррелированных материалах. Его группа накопила особый опыт в экспериментах по рассеянию света на материалах в экстремальных условиях низкой температуры, высокого давления и сильного магнитного поля. Эксперименты группы Купера по спектроскопии комбинационного рассеяния света пролили свет на поведение вещества посредством различных квантовых (T ~ 0 K) фазовых переходов, регулируемых давлением и магнитным полем.
Первым достижением группы Купера в области оптической спектроскопии в «экстремальных условиях» было исследование эволюции кристаллической решетки («фонона») и динамики атомного спина посредством разрушения под давлением изоляционного состояния слоистых рутенатных материалов. Совсем недавно его группа изучила, как высокое давление «плавит» зарядовые и орбитально-упорядоченные изолирующие состояния даже при T = 0 K, создавая новые металлические фазы. Его группа также показала, что магнитные поля могут использоваться как для управления упругими свойствами материалов (например,g., «память формы, индуцированная магнитным полем») и препятствовать дальнему порядку вплоть до T = 0 К.
Группа Cooper использовала методы плавающей зоны, переноса пара, испарения и другие методы для выращивания высококачественных монокристаллов, включая шпинели, такие как Mn 3 O 4 и CoCr 2 O 4 , материалы орбитального упорядочения такие как KCuF 3 , слоистые халькогенидные материалы, такие как TiSe 2 , и топологические изоляторы, такие как Bi 2 Se 3 .
Лэнс Купер также ведет блог студентов-физиков, в котором публикуются сведения о вакансиях, стипендиях, сроках учебы и другая информация, представляющая интерес для аспирантов; семинар по физике “Карьера”, на котором доктора наук по физике – в основном выпускники из Иллинойса – описывают свою работу и важность получения докторской степени по физике и свой опыт в аспирантуре для своей карьеры; и программа поощрения студентов, получивших диплом по физике.
Документы
Заявление об исследовании
Спектроскопия с настройкой поля и давлением магнитно-фрустрированных и прочных спин-решеточных материалов
Развитие при низких температурах некоторой формы дальнего порядка – такой как магнетизм, орбитальный порядок, зарядовый порядок или сверхпроводимость – повсеместно встречается в материалах и отражает тенденцию материала снижать вырождение своего основного состояния вблизи Т = 0 К.Мы заинтересованы в выращивании – с использованием плавающих зон и других методов выращивания – и в спектроскопическом изучении материалов, в которых структурная геометрия и конкурирующие взаимодействия вступают в сговор, препятствуя возникновению дальнего магнитного и / или орбитального порядка, даже до T = 0 К. Этот интерес мотивирован новыми низкотемпературными фазовыми свойствами, которые было предложено демонстрировать фрустрированные материалы, включая орбитальные и спин-жидкостные фазы, а также желанием выяснить связь между фрустрацией и экзотическими свойствами, такими как колоссальное магнитосопротивление и мультиферроидность. и магнитодиэлектрическое поведение.Наши текущие усилия включают использование различных методов выращивания монокристаллов для выращивания геометрически фрустрированных материалов, а затем применение зависящей от поля и давления оптической спектроскопии для изучения орбитально- и спин-неупорядоченных фаз в нескольких классах материалов, включая слоистые рутенаты, шпинели, такие как Mn 3 O 4 , иридаты, такие как Sr 2 IrO 4 , и ванадаты, такие как Ni 3 V 2 O 8 . Наши результаты выявили интересные пути, с помощью которых магнитные и орбитальные расстройства могут быть настроены с помощью поля или давления, и показали связь между орбитальными / спиновыми расстройствами и легко настраиваемыми свойствами материи.
Плавление орбитального порядка с регулировкой по полю и давлением в коррелированных материалах
Мы также заинтересованы в создании и исследовании новых орбитально-жидких фаз в различных орбитально-упорядоченных системах, таких как Ca 2 RuO 4 , Ca 3 Ru 2 O 7 и KCuF 3 . Наши результаты выявили индуцированные давлением переходы к новым квантовым жидкоподобным фазам, в которых структурные элементы флуктуируют даже при T = 0 K, а также переходы изолятор-металл, регулируемые давлением и магнитным полем, которые регулируются контролируемыми изменениями, индуцированными в орбитальной орбите. численность населения.
Квантовые фазовые переходы и сверхпроводимость в слоистых халькогенидных материалах с перестройкой давления
Мы заинтересованы в изучении того, как зарядово-упорядоченные состояния и состояния с волной зарядовой плотности (ВЗП) плавятся в неупорядоченные квантовые фазы при низких температурах, а также в исследовании новых фаз, которые, согласно прогнозам, будут развиваться в этих условиях. Для изучения этого мы используем методы роста с переносом пара для выращивания различных слоистых монокристаллов халькогенидов, включая TiSe 2 , TaSe 2 , TaS 2 , Bi 2 Se 3 и Bi 2 Te 3 , и мы изучаем квантовые (T ~ 0 K) фазовые переходы в этих материалах с помощью неупругого рассеяния света, зависящего от давления и температуры.Например, наши низкотемпературные, зависящие от давления исследования неупругого рассеяния света критической («мягкой») моды в 1T-TiSe 2 показывают, что сжатие решетки приводит к квантовому плавлению фазы ВЗП через новую несоразмерную фазу, которая может иметь гексатический порядок, и наши более поздние исследования рассеяния света мягкой моды в Cu x TiSe 2 предоставили доказательства x-зависимого смягчения квантовой моды и сосуществования флуктуирующего порядка ВЗП и сверхпроводимости в этой системе.
Главы в книгах
- S.L. Купер, Исследование магнитоструктурных фаз слоистых рутенатов с помощью комбинационного рассеяния света, глава 5 в «Границы 4d- и 5d-переходных оксидов металлов» (World Scientific Publishing, 2013).
- С.Л. Купер, П. Аббамонте, Н. Мейсон, К.С. Сноу, М. Ким, Х. Барат, Дж. Ф. Карпус, К. Чиалво, Дж. П. Рид, Ю.И. Джо, X. Чен и Д. Каса, Рамановское рассеяние как инструмент для изучения сложных материалов, Глава 6 в «Оптических методах определения характеристик материалов» (Taylor & Francis, 2011).
- С. Л. Купер, Х. Ро и К. С. Сноу. Освещение образования магнитных кластеров с неупругим рассеянием света, Глава 20 в «Наноразмерном разделении фаз и колоссальном магнитосопротивлении», изд. Э. Даготто (Springer-Verlag: Berlin, 2003).
- С. Л. Купер, Оптические спектроскопические исследования переходов металл-диэлектрик в оксидах, родственных перовскиту, в книге «Структура и связь» 98, стр. 161-219, изд. Дж. Б. Гуденаф (Springer-Verlag: Berlin-Heidelberg, 2001).
- С.Л. Купер, Магнитное и электронное комбинационное рассеяние света сверхпроводников с высоким T c , в «Справочнике по физике и химии редких земель», под ред. К. А. Г. Шнайдер-младший, Л. Эйринг и М. Б. Мэйпл (Elsevier Science, 2001), стр. 31.
- С. Л. Купер и К. Э. Грей. Анизотропия и межслойная связь в купратах с высоким T c , в «Физические свойства высокотемпературных сверхпроводников IV», изд. Д. М. Гинзберг (World Scientific: Сингапур, 1994), стр. 61-188.
Избранные статьи в журналах
- Слимак Дж. Э., Сетхи А., Колодяжный Т., Купер. Поведение в мягкой моде и доказательства магнитоструктурных эффектов, вызванных давлением, в Pr2O3. Physical Review Research 2, 043169 (2020).
- S. Buchenau, S. Scheitz, A. Sethi, J.E. Slimak, T.E. Глиэр, П. Das, T. Dankwort, L. Akinsinde, L. Kienle, A. Rusydi, C. Ulrich, S.L. Купер и М. Рубхаузен. Рамановское исследование электрон-фононных взаимодействий в тонких пленках наноструктур Bi 2 Se 3 и Bi 2 Te 3 в зависимости от температуры и магнитного поля.Physical Review B 101, 245431 (2020).
- Б. Кованен, Р. Уэр, М. Мерикл, Н. Турнипсид, Дж. П. Коулман, К. Эллиотт, Дж. Поповиц, С. Купер, Дж. Р. Галлахер, П. Прайор и Дж. Л. Зиллес. Внедрение письма как процесса в инженерное образование. Ежегодная конференция и выставка ASEE 2020 (2020).
- J.R. Gallagher, N. Turnipseed, J.Y. Ёритомо, К. Эллиот, С. Купер, Дж. Поповичс, П. Прайор и Ж.Л. Зиллес. Совместная продольная разработка для поддержки письменной педагогики факультета STEM.Technical Communication Quarterly 29, 411-426 (2020).
- А. Сетхи, Дж. Э. Слимак, Т. Колодяжный, С. Л. Купер. Эмерджентные вибронные возбуждения в магнитодиэлектрическом режиме Ce 2 O 3 . Physical Review Letters 122, 177601 (2019).
- B. Wolin, X. Wang, T. Naibert, S.L. Глисон, Г.Дж. Макдугалл, Х. Чжоу, С. Купер, Р. Будакян. Магнитное изображение мультиферроиков MnV 2 O 4 и Mn 3 O 4 в реальном пространстве.Physical Review Materials 2, 064407 (2018).
- J.Y. Ёритомо, Н. Turnipseed, S.L. Купер, К. Эллиотт, Дж.Р. Галлахер, Дж. Поповичс, П. Прайор и Дж. Зиллес. Изучение инструкций по инженерной письменной речи в большом исследовательском университете через призму письменных исследований. Ежегодная конференция и выставка ASEE 2018 (2018).
- Д. Фелан, Ф. Хан, А. Лопес-Безанилья, М. Крогстад, Ю. Гим, Ю. Ронг, Дж. Чжан, Д. Паршалл, Х. Чжэн, С.Л. Купер, М. Фейгенсон, В. Г. Ян и Ю-Шэн Чен.Структурные свойства станната бария. Журнал химии твердого тела 262, 142 (2018).
- Р. Сото-Гарридо, Ю. Ван, Э. Фрадкин, С.Л. Купер. Моды Хиггса в сверхпроводящем состоянии парной волны плотности. Physical Review B 95, 214502 (2017).
- A. Sethi, T. Byrum, R.D. McAuliffe, S.L. Глисон, Дж.Э. Слимак, Д.П. Шумейкер и С. Купер. Магноны и магнитодиэлектрические эффекты в CoCr 2 O 4 : Исследования комбинационного рассеяния света. Physical Review B 95, 174413 (2017).
- Т. Байрам, С.Л. Глисон, А. Талер, Г.Дж. Макдугалл, С.Л. Купер. Влияние магнитного поля и двойниковых доменов на смесь магнитоструктурных фаз в Mn 3 O 4 : Исследования комбинационного рассеяния света для бездвойниковых кристаллов. Physical Review B 93, 184418 (2016).
- Ю. Гим, А. Сетхи, К. Чжао, Дж. Ф. Митчелл, Г. Цао и С. Л. Купер. Изотропный и анизотропный режимы зависящей от поля спиновой динамики в Sr 2 IrO 4 : Исследования комбинационного рассеяния света.Physical Review B 93, 024405 (2016).
- S.L. Глисон, Ю. Гим, Т. Байрам, А. Когар, П. Аббамонте, Э. Фрадкин, Г.Дж. Макдугалл, Д.Дж. Ван Харлинген, К. Петрович и С.Л. Купер. Структурные вклады в перестроенную под давлением волну зарядовой плотности в сверхпроводниковый переход в ZrTe 3 : исследования комбинационного рассеяния света. Physical Review B 91, 155214 (2015).
- S-C. Вэн, Р. Сюй, А.Х. Саид, Б.М. Leu, Y. Ding, H. Hong, X. Fang, M.Y. Чжоу, А. Босак, П. Аббамонте, С.Л. Купер, Э.Фрадкин, С.-Л. Чанг и Т.-К. Чан. Антиферродистортивный фазовый переход, индуцированный давлением в SrTiO 3 : Обычное масштабирование мягкой моды в зависимости от давления и температуры. Europhysics Letters 107, 36006 (2014).
- Ю.И. Джо, X.M. Чен, П. Гэми, К.Д. Финкельштейн, Г.А. de la Pena, Y. Gan, J.C.T. Ли, С. Юань, Дж. Гек, Г.Дж. MacDougall, T.C. Чан, С.Л. Купер, Э. Фрадкин, П. Аббамонте. Возникновение доменных границ волны зарядовой плотности над сверхпроводящим куполом в TiSe 2 .Nature Physics 10, 421-425 (2014).
- S.L. Глисон, Т. Байрам, Ю. Гим, А. Талер, П. Аббамонте, Г.Дж. Макдугалл, Л. Мартин, Х. Чжоу и С. Купер. Спектры магнонов и сильная спин-решеточная связь в магнитно фрустрированном MnB 2 O 4 (B = Mn, V): исследования неупругого рассеяния света. Phys. Ред. B 89, 134402 (2014).
- S.L. Купер. Исследование магнитоструктурных фаз слоистых рутенатов с помощью комбинационного рассеяния света. Границы 4d- и 5d-оксидов переходных металлов, 99-162 (2013)
- С.Юань, М. Ким, J.T. Сили, J.C.T. Ли, С. Лал, П. Аббамонте и С.Л. Купер. Измерения неупругого рассеяния света квантовой жидкостью, индуцированной давлением в KCuF 3 , Phys. Rev. Lett. 109, 217402 (2012).
- J.T. Ли, Юань Ши, С. Лал, Джо Янг II, Ган Ю, С. Смадичи, К. Финкельштейн, Фэн, А. Русиди, П.М. Гольдбарт, С. Купер, П. Аббамонте, Двухступенчатый орбитальный порядок и динамическое нарушение спина в KCuF 3 . Nature Physics 8, 63-66, (2012) .
- М.Ким, X.M. Чен, X. Ван, К.С. Нельсон, Р. Будакян, П. Аббамонте и С.Л. Купер. Настройка давления и поля магнитоструктурных фаз Mn 3 O 4 : исследования комбинационного рассеяния света и дифракции рентгеновских лучей. Phys. Ред. B 84, 174424 (2011).
- С.Л. Купер, П. Аббамонте, Н. Мейсон, К.С. Сноу, М. Ким, Х. Барат, Дж. Ф. Карпус, К. Чиалво, Дж. П. Рид, Ю.И. Джо, X. Чен и Д. Каса. Рамановское рассеяние как инструмент исследования сложных материалов. Оптические методы определения характеристик материалов, Глава 6 (Тейлор и Фрэнсис, 2011).
- М. Ким, Х. Чен, Ю.И. Джо, Э. Фрадкин, П. Аббамонте и С. Л. Купер. Картирование магнитоструктурных квантовых фаз Mn 3 O 4 . Phys. Rev. Lett. 104, 136402 (2010).
- М. Ким, Х. Барат, С. Л. Купер, П. Аббамонте, Э. Фрадкин, М. Рубхаузен, К. Чжан и С.В. Cheong, Рамановское рассеяние исследований температурного и индуцированного полем плавления зарядового порядка в (La, Pr, Ca) MnO 3 , Phys. Ред. B 77, 134411, стр. 1-13 (2008).
- H.Барат, М. Ким, Дж.Ф. Карпус, С.Л. Купер, П. Аббамонте, Э. Фрадкин, Э. Моросан и Р.Дж. Кава, Квантовое и классическое смягчение мод вблизи перехода волна зарядовая плотность / сверхпроводник Cu x TiSe 2 . Phys. Rev. Lett. 100, 106402-1-4 (2008).
- Р. Гупта, М. Ким, Х. Барат, С. Л. Купер и Г. Цао. Фазы, индуцированные полем и давлением в Sr 4 Ru 3 O 10 : спектроскопическое исследование. Phys. Rev. Lett. 96, 067004-1-4 (2006).
- Дж. Ф. Карпус, Р. Гупта, Х. Барат, С. Л. Купер и Г. Цао. Индуцированная полем орбитальная и магнитная фазы в Ca 3 Ru 2 O 7 . Phys. Rev. Lett. 93, 167205-1-4 (2004).
- К. С. Сноу, Дж. Ф. Карпус, С. Л. Купер, Т. Э. Кидд и Т.-К. Чан. Квантовое плавление состояния с волной зарядовой плотности в 1 T-TiSe 2 . Phys. Rev. Lett. 91, 136402 (2003).
- К. С. Сноу, С. Л. Купер, Г. Цао, Дж. Э. Кроу, Х. Фукадзава, С.Накацудзи и Ю. Маэно. Коллапс состояния Мотта под давлением в Ca n +1 Ru n O 3 n +1 (n = 1,2): спектроскопические исследования комбинационного рассеяния света. Phys. Rev. Lett. 89, 226401-1-4 (2002).
- Х. Ро, К. С. Сноу, С. Л. Купер, З. Фиск, А. Коммент и Ж.-П. Ансерме. Эволюция магнитных поляронов и взаимодействий спиновых носителей через переход металл-изолятор в Eu 1- x Gd x O.Phys. Rev. Lett. 88, 127401-1-4 (2002).
с отличием
- Награда выдающегося советника инженерного совета 2011 г.
- 2008 Премия Арнольда Т. Нордсика за выдающиеся успехи в преподавании
- Премия 2006 г. за выдающиеся успехи в чтении лекций, Студенческий сенат UIUC
Исследования с отличием
- Премия выдающегося рефери Американского физического общества, 2013 г.
- Стипендиат факультета Sony, 2003-2006 гг.
- научный сотрудник Американского физического общества, 2003 г.
Недавние курсы
- PHYS 596 – Физическая ориентация для выпускников
- PHYS 598 PEN (PHYS 598 POL) – Специальные разделы по физике
Уравнение кинематики v = v_sub_o + at
Уравнение кинематики v = v_sub_o + at[Глава 2 цели]
BHS -> Персонал -> МистерСтэнбро -> Физика -> Механика -> Кинематика -> эта страница
Уравнение включает исходные и окончательные показания спидометра объекта (мгновенные скорости), v o и v , его ускорение, a , и временной интервал между исходным и финальные ситуации,. Если проблема говорит вам о любых трех из этих величин, вы можете использовать это уравнение, чтобы найти четвертое, как показано в примерах ниже.
Интересно, откуда взялось это уравнение? из? Вывод этого уравнение доступно.
Пример 1 – Определение окончательной скорости:
Автомобиль, первоначально находящийся в состоянии покоя, начинает ускоряться с 4,5 м / с 2 . Как быстро, в м / с, он будет идти в 5.0 секунды?
Решение:
Примечание : в этом решении шаги обозначены, чтобы указать шаги, необходимые для решения кинематической задачи.При решении реальная проблема, вы, как правило, не помечаете шаг 1, шаг 2, пр.
Шаг 1. Изучите проблема.
Шаг 2 – Перевести на физика:
v o = 0 м / с
a = 4,5 м / с 2
v =?
= 5.0 с
Шаг 3 – Найдите уравнение кинематики:
Уравнение кинематики, связывающее v, vo, a и является:
Шаг 4 – Решить:
В этом нет необходимости, так как уравнение уже решено для “v”.
Шаг 5 – Замена известна значения:
(Уведомление что единица секунд отменяется в правом члене, чтобы оставить м / с равным Единица.)
Шаг 6 – Сообщить ответ:
Ответ: Автомобиль будет двигаться со скоростью 23 м / с за 5,0. секунд.
Шаг 7 – Проверка:
Если автомобиль ускоряется со скоростью 4 м / с 2 , его скорость будет меняться на 4 м / с каждую секунду. Через 5 секунд это будет 20 м / с. Если бы он ускорялся со скоростью 5 м / с 2 , он бы пошел 25 м / с за 5 сек. 23 м / с кажется правильным.
Вот альтернативный решение этой проблемы.Он использует более простые уравнения, но требует больше размышлений.
Пример 2 – Определение ускорения:
Лодка, первоначально движущаяся со скоростью 20 м / с, движется только на скорости 2,0 м / с в том же направлении, спустя 25 секунд. При условии, что ускорение лодки было постоянным, каково было разгон за это время?
Решение:
v o = 20 м / с
v = 2.0 м / с
= 25 с
а =?
Уравнение кинематики, связывающее v, vo, a и это:
решение для ускорения: (Что, если я сначала подставлю ценности, тогда решать?)
заменяющий:
Ответ: Ускорение лодки равно 0.72 м / с 2 , в направлении, противоположном скорости лодки.
Это разумно? да. Если бы лодка замедлилась на 18 м / с за 24 часа. секунд (6 переходит в 18 и 24 равномерно …), величина его ускорение будет 18/24 м / с 2 = 0,75 м.с 2 .
Примечание:
В этой проблеме лодка замедляется или замедляется. Помнить что нет физического различия между ускорением и замедление – в другими словами, замедление равно ускорению.Иногда заблуждения людей делают это препятствием. Кроме того, не падай в ловушку автоматического превращения v o в меньшее значение, а v – большее значение. Внимательно прочтите проблему и понять, что происходит, прежде чем приступить к решению!
Также то, что ускорение лодки оказалось отрицательный означает, что ускорение лодки противоположное направление от скорости лодки (положительное значение).
Вот альтернативный решение для этого примера – работает довольно легко.
Пример 3 – Нахождение временного интервала:
Такси, движущееся со скоростью 28 м / с, задействует тормоза и останавливается. Если его тормоза могут замедлить его со скоростью 3,6 м / с 2 , как сколько времени нужно такси, чтобы остановиться?
Решение:
v o = 28 м / с
а = -3.6 м / с 2
v = 0 м / с
= ?
Уравнение кинематики, связывающее v, vo, a и это:
решение для: (Что, если я сначала подставлю ценности, тогда решать?)
подставляем значения из таблицы данных:
Ответ: Такси займет 7 мест.8 секунд до остановки.
Это разумный ответ? Если бы ускорение кабины было -4 м / с 2 , он будет терять 4 м / с скорости каждую секунду, поэтому потеря 28 м / с займет 7 секунд (28/4 = 7). Да ответ разумно.
Вот альтернативный решение этой проблемы.
Пример 4 – Нахождение исходной скорости:
Бейсбольный мяч движется вниз со скоростью 65 м / с. 8.5 секунд в свободном падении. Что было оригинальным бейсбольным мячом скорость?
Решение:
v o =?
a = g = 9,8 м / с 2 (вниз)
= 8,5 с
v = 65 м / с
Уравнение кинематики, связывающее v, vo, a и это:
Решениедля v o : (Что, если я подставлю, то решить?)
подставляющие значения:
Ответ: Исходная скорость бейсбольного мяча составляла 18.3 м / с снизу вверх. (Поскольку знак нисходящей скорости и нисходящей ускорение положительное, отрицательная скорость должна быть направлена вверх.)
Это разумно? Скорость бейсбольного мяча изменилась на около 10 м / с (вниз) каждую секунду в течение 8,5 секунд, поэтому он должен изменились примерно на 85 м / с (8,5 * 10) с момента запуска. 65 м / с – 85 м / с = -20 м / с. Да, разумный ответ.
Вот альтернативный решение этой проблемы.
[Глава 2 цели]
BHS -> Персонал -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница
последнее обновление 13 августа 2003 г., автор JL Stanbrough
Количественный анализ движения – Физика тела: движение к метаболизму
Теперь мы знаем, как найти среднее ускорение объекта, найдя чистую силу и применив Второй закон Ньютона.Как только ускорение известно, мы можем выяснить, как скорость и положение меняются с течением времени. Этот процесс известен как кинематика, а уравнения, которые мы используем для связи ускорения, скорости, положения и времени, известны как кинематические уравнения. Давайте рассмотрим несколько из них по очереди.
Основываясь на нашем определении ускорения как скорости изменения скорости, мы можем вычислить изменение скорости в течение временного интервала как ускорение, умноженное на длину временного интервала:
(1)
Упражнения по укреплению
Если у человека ускорение 5.0 м / с / с , насколько изменится их скорость за 2,0 с ?
Мы можем найти текущую скорость, добавив выражение для изменения скорости к начальной скорости:
(2)
Упражнения по укреплению
Если человек в предыдущем упражнении имеет начальную скорость 2,0 м / с , какова его новая скорость после 2,0 с ?
Мы можем вычислить среднюю скорость за интервал как среднее значение начальной и конечной скоростей:
(3)
Упражнения по укреплению
Какова средняя скорость человека в предыдущем упражнении?
Используя определение скорости как скорость изменения положения, мы можем вычислить изменение положения в течение временного интервала как среднюю скорость в течение интервала, умноженную на длину временного интервала.
(4)
Упражнения по укреплению
Как изменилось положение человека в предыдущих упражнениях?
Добавление приведенного выше выражения для изменения положения в исходное положение позволяет нам вычислить окончательное положение через любое время:
(5)
Упражнения по укреплению
Если человек в предыдущих упражнениях стартовал с позиции 4 м / с , какова его конечная позиция?
Мы можем объединить все из предыдущих шагов в одно уравнение, что может сэкономить время на некоторых задачах.Выглядит это так:
(6)
Чтобы получить приведенное выше уравнение, мы использовали уравнение (3), чтобы заменить среднюю скорость выражением для средней скорости:
(7)
Используя уравнение (2), мы можем заменить окончательную скорость:
(8)
После некоторого упрощения мы находимся там:
(9)
Пример на каждый день
Выйдя из квартиры друга на 3-м этаже, вы садитесь в машину и понимаете, что оставили ключи в квартире.Вы звоните своему другу и просите его бросить вам ключи в окно. Мы хотим выяснить, как долго ключи будут добираться до вас и с какой скоростью они будут падать, когда доберутся до вас. Окно третьего этажа находится на высоте примерно 35 футов над землей. Мы можем преобразовать в метры и использовать наше ранее заявленное ускорение для падающих объектов, g = 9,8 м / с / с , или мы можем придерживаться ног и использовать g = 32 фут / с / с , поэтому Давайте сделаем это.
Исходя из нашего последнего уравнения из работы, которую мы проделали выше:
Мы выбираем восходящее направление в качестве положительного направления и землю в качестве начала отсчета, поэтому наша начальная позиция – 35 футов , а наша конечная позиция – 0 футов .Клавиши выпадают из состояния покоя, поэтому наша начальная скорость равна нулю. Подставляя нули в уравнение выше, получаем:
Теперь мы можем выделить временную переменную:
(10)
Извлеките квадратный корень, чтобы найти время
(11)
Вводя наши известные значения, мы можем найти время спада. Мы будем использовать -32 ft / s / s для нашего ускорения, потому что ускорение свободного падения направлено вниз, и мы выбрали восходящее направление в качестве положительного.
(12)
Наконец, мы можем найти скорость нажатия клавиш, используя уравнение (2) выше
(13)
Конечная скорость 47 фут / с составляет около 32 миль / ч . Если клавиши будут бить вас по руке на такой скорости, будет больно. Существуют приемы, которые можно использовать для предотвращения травм в такой ситуации, и эти приемы будут темой следующего раздела.
При решении предыдущего примера мы нашли уравнение для вычисления времени, необходимого объекту с определенным ускорением, чтобы достичь конечной нулевой позиции при старте с известной начальной позиции.Помимо прочего, это позволяет нам рассчитать время, необходимое для падения на землю с определенной стартовой высоты. Это уравнение будет возникать часто, поэтому давайте запишем его здесь:
(14)
Если ускорение установлено на -9,8 м / с / с (или -g), то это уравнение вычисляет время свободного падения для выбора отрицательного значения в качестве направления вниз.
В последних нескольких главах мы узнали, что наш примерный парашютист имеет начальное ускорение 9,8 м / с / с и нулевое ускорение после достижения конечной скорости, поэтому между этими точками ускорение должно меняться.Скорость изменения ускорения известна как рывок , , но мы не будем рассматривать рывки в этом учебнике и вместо этого сосредоточимся на движении с постоянным ускорением. Однако, если мы действительно хотим проанализировать полное движение нашего парашютиста, нам нужно будет как-то справиться с изменяющимся ускорением. Об этом и пойдет речь в следующей главе.
Star Trek Warp Drive ведет к новой физике
Для Эрика Ленца все началось с Star Trek . Каждые несколько эпизодов сериала Star Trek: The Next Generation капитан Жан-Люк Пикард поднимал руку и приказывал: «Деформируйте один, вступайте в бой!» Затем звезды превратились в рывки, и световые годы пролетели с невероятной скоростью.А Ленц, еще учащийся в начальной школе, задавался вопросом, может ли варп-двигатель работать в реальной жизни.
«В какой-то момент я понял, что технологии не существует», – говорит Ленц. Он изучал физику в Вашингтонском университете, написал докторскую диссертацию. докторскую диссертацию по темной материи и вообще стал слишком занят, чтобы заниматься научной фантастикой. Но затем, в начале пандемии коронавируса, Ленц оказался один в Геттингене, Германия, где выполнял постдокторскую работу. У него внезапно появилось много свободного времени – и детские фантазии в его голове.
Ленц прочитал все, что он мог найти в научной литературе по варп-двигателям, что было не так уж и много. Затем он начал думать об этом сам. Через несколько недель с ним произошло то, что все, казалось, не заметили. Ленц изложил свою идею на бумаге и обсудил ее с более опытными коллегами. Год спустя он был опубликован в физическом журнале.
Вскоре стало ясно, что Ленц не единственный, кто мечтает о варп-двигателях. СМИ по всему миру подхватили эту историю, и десяток журналистов попросили интервью.Обсуждение на онлайн-форуме Reddit собрало 2700 комментариев и 33000 лайков. Один пользователь Интернета написал: «Кто-нибудь еще считает, что родился на 300 лет раньше срока?»
Пузырь в пространстве и времени
Нет никаких сомнений в том, что Вселенная все еще слишком велика, чтобы люди могли ее пересечь. Луч света достигает ближайшей звезды Земли Проксимы Центавра более четырех лет. Даже с лучшими доступными двигательными установками человеку потребуются десятки тысяч лет, чтобы добраться туда.Всегда можно мечтать об основании колоний в других звездных системах, но вряд ли кто-то может предпринять это путешествие.
Но, возможно, однажды удастся сократить время в пути. Есть много идей о том, как это сделать, от солнечных парусов с лазерным ускорением до ядерных двигателей. Но даже с помощью этих технологий вы не продвинетесь слишком далеко за человеческую жизнь. Галактика действительно открыта только для тех, кто путешествует со скоростью света – или быстрее.
Художник НАСА изобразил путешествие на варп-двигателе в 1998 году.Кольцо вокруг космического корабля создает поле с отрицательной энергией. С сегодняшней точки зрения, в поле отрицательной энергии больше не будет необходимости. Предоставлено: НАСА; Цифровое искусство от Les Bossinas (Cortez III Service Corp)Именно по этой причине физики с богатым воображением давно размышляли об окончательной силовой установке: пузыре в пространстве и времени, в котором космический корабль может прыгать от солнца к солнцу, точно так же, как USS Enterprise сделал. Это исследование на периферии науки: не обязательно ошибочное, но приправленное большой долей оптимизма.
Тот факт, что сегодня ученые вообще занимаются этой идеей, стал благодаря работе мексиканского физика-теоретика Мигеля Алькубьерре в 1994 году. В то время Алькубьерре был не просто страстным приверженцем Star Trek . В своей докторской диссертации в Кардиффском колледже Уэльского университета (ныне Кардиффский университет) Алькубьерре также работал над теорией относительности. Строго говоря, теория утверждает, что ничто не может двигаться быстрее света. Но проявив немного творчества, Алькубьерре обнаружил очевидную лазейку.
Для физиков теория относительности Альберта Эйнштейна состоит из двух частей: «Специальная» теория относительности, которая датируется 1905 годом, имеет дело с равномерным движением быстрых, как свет объектов. Десять лет спустя Эйнштейн обобщил эти идеи для ускоряющихся тел. Согласно «общей» теории относительности, три знакомых нам пространственных измерения (верх-низ, лево-право, перед-зад) неотделимы от времени. Каждая масса деформирует это пространство-время.
Согласно эпическому открытию Альберта Эйнштейна, мы живем в четырехмерном «пространстве-времени».«Пространство-время не статично. Как скатерть, она деформируется массивными предметами. Все, что движется по скатерти (или с по в пространстве-времени), может ускоряться только до предела скорости, установленного светом. С другой стороны, сама скатерть может деформироваться с любой скоростью, что в некоторых ситуациях показывает сама Вселенная.
В момент большого взрыва, например, исходная структура пространства-времени предположительно расширилась на долю секунды и сделала это намного быстрее, чем мог бы перемещаться любой луч света.Даже сегодня расширение продолжает отгонять очень далекие галактики со скоростью, превышающей скорость света, а это означает, что их свет больше не может достигать нас.
Основываясь на своем открытии, Алькубьерре предположил, что это будет лишь небольшой шаг к варп-движению. Если бы пространство-время было сокращено перед космическим кораблем и расширилось за ним для компенсации, можно было бы путешествовать к месту назначения со скоростью, превышающей скорость света. Корабль останется заключенным в пузырь, и экипаж не ощутит масштаб межзвездного путешествия.В лекции 2017 года Алькубьерре сравнил это с пребыванием на пассажирском конвейере в аэропорту: «Вы можете представить, что пол позади вас создается из ничего, а перед вами он разрушается, поэтому вы двигаетесь вперед».
Но формулировка этой идеи на языке общей теории относительности сразу же порождает серьезные практические проблемы. Во-первых, чтобы так радикально деформировать пространство-время, вам нужно было бы втиснуть огромную массу в пузырь, ограниченный стенкой, более тонкой, чем атомное ядро.Тогда для поддержания пузыря вам понадобятся две формы материи. Гравитация обычной массы заставила бы пространство перед пузырем сжиматься, перемещая всю конструкцию вперед. Но в то же время пространство позади пузыря должно расшириться, как поднимающееся тесто для хлеба. По словам Алькубьерре, чтобы это расширение произошло, вам потребуется некоторая форма отрицательной энергии, излучающая своего рода антигравитацию.
Проклятие отрицательной энергии
Для большинства физиков это был конец мысленного эксперимента.Энергия, которая согласно формуле Эйнштейна E = mc2 эквивалентна неограниченной массе, кажется, по определению, должна быть положительной. Но согласно квантовой теории оно действительно может иметь отрицательное значение. Однако это, кажется, происходит только в редких особых случаях – в крошечных масштабах. Например, в так называемом эффекте Казимира задействованные количества настолько ничтожны, что любое технологическое применение кажется абсурдным.
Алькубьерре, ныне профессор физики в Национальном автономном университете Мексики, соглашается с этим.С точки зрения потенциальной технологии, варп-приводов «сильно не хватает», – написали он и один из его коллег в недавнем препринте. Теперь он обратил свое внимание на известные явления, такие как черные дыры. Однако концепция варп-двигателя сохраняет свое очарование, особенно для Trekkies – и для некоторых физиков гравитации, которые время от времени публикуют вариации этой идеи.
В некоторых из этих работ показано, как уменьшить требования к массе пузыря, чтобы общая масса, необходимая для деформации пространства-времени, была меньше, чем у нашего Солнца.Но никому не удавалось обойти проблему отрицательной энергии, пока Ленц не поднял ее во время изоляции в Геттингене. В своей вынужденной изоляции Ленц нашел способ построить варп-пузырь, используя только положительную энергию. Поступая так, он, возможно, преодолел самые серьезные возражения против искривленных движений.
Что сделало возможным, так это особая особенность геометрии пространства-времени, которую Ленц обнаружил похороненной в общей теории относительности, точнее, в уравнениях поля Эйнштейна. Эти уравнения могут вычислить, как конкретное распределение материи и энергии деформирует пространство-время.Исследователи также могут использовать их, как это сделал Алькубьер, для определения массы и энергии, необходимых для создания определенной кривизны пространства.
Однако работа с динамической четырехмерной структурой, такой как пространство-время, чрезвычайно сложна. Если написать формулы Эйнштейна полностью, получится нагромождение вложенных дифференциальных уравнений с тысячами членов. В зависимости от предположений, которые вы делаете о конкретной физической ситуации, вы принимаете во внимание только некоторые из этих условий. Для теоретиков это практически безграничная игровая площадка.
Принцип движения Алькубьерре: пространство-время сжимается в передней части пузыря (справа), что соответствует деформации пространства-времени. Позади пузыря (слева) новое пространство создается из ничего, что эквивалентно растяжению пространства-времени. Предоставлено: AllenMcC Wikimedia (CC BY-SA 3.0)Ленц специально исследовал допущения, приводящие к отрицательным потребностям в энергии в работе Алькубьерре. Как и его коллега, Ленц начал с анализа пространства-времени, моделируя многомерное вещество в виде стопки очень тонких слоев.Он обнаружил, что Алькубьерре рассмотрел только сравнительно простые «линейные» отношения между уравнениями для переноса одного слоя на другой. На этом этапе выбор более сложных «гиперболических» соотношений, которые обычно выражают быстро изменяющиеся величины, приводит к другому пузырю деформации, чем тот, который был получен Алькубьерре. Он по-прежнему требует огромного количества массы и энергии, но, по расчетам Ленца, только положительных количеств. «Я был очень удивлен, что никто не пробовал это до меня», – говорит Ленц.
ПузырьЛенца отличается от пузыря, созданного Алькубьерре в 1994 году. Он состоит из ромбовидных областей измененного пространства-времени, которые напоминают стаю птиц. Создание такой геометрии пространства-времени в реальности потребовало бы сложного наслоения колец и дисков, сделанных не из твердого материала, а из чрезвычайно плотной жидкости заряженных частиц, аналогичной веществу, находящемуся внутри нейтронных звезд, говорит Ленц.
Это означает, что путешествия со скоростью, близкой к световой, все еще очень и очень далеки от прикладных технологий.Но теперь, когда нет необходимости в экзотических отрицательных плотностях энергии – по крайней мере, согласно последней работе Ленца – теоретические игры находятся в сфере устоявшейся физики. Алькубьерре описывает статью Ленца как «очень важное событие». Франсиско Лобо, исследователь из Лиссабонского университета и коллега Алькубьерре, опубликовавший учебник по варп-двигателям, также не может найти никаких очевидных ошибок. «Если это так, это может открыть новый интерес и новые направления исследований в области физики варп-двигателя», – говорит он.
ИдеяЛенца вызвала интерес даже у исследователей за пределами небольшого сообщества энтузиастов варп-двигателя, в том числе у Лавинии Гейзенберг, профессора космологии Швейцарского федерального технологического института в Цюрихе. Гейзенберг и ее ученик Шон Фелл сочли статью Ленца настолько захватывающей, что построили на ней свои собственные пузыри искривления с положительной энергией, для которых потребуется всего одна тысячная массы нашего Солнца.
«Все это гораздо менее загадочно, чем думает большинство людей», – говорит Алексей Бобрик, астрофизик из Лундского университета в Швеции.Сотрудничая с предпринимателем из Нью-Йорка Джанни Мартире, Бобрик в 2020 году придумал несколько многообещающих решений уравнений поля Эйнштейна. По словам Бобрика, все, что нужно для варп-пузыря, – это оболочка соответствующей формы из плотного материала, которая искривляет пространство-время в пространстве. в непосредственной близости от него, в то время как Вселенная, через которую движется пузырь, и пространство внутри оболочки остаются относительно нетронутыми.
Время идет так медленно
«Сравнительно» – это ключ.Алькубьерре и более поздние архитекторы варпа предполагали резкий переход между искаженным пространством-временем в стенке пузыря и гладким внутренним и внешним пространством. Но Бобрик и Мартир обнаружили, что это «усечение» гравитационного поля является причиной того, что для стабилизации искривления пространства и времени требуется большое количество отрицательной энергии.
Однако отказ от мультяшного изображения мыльного пузыря позволяет создавать варп-двигатели на основе обычной материи, утверждают они.Гравитационное поле не исчезнет просто так, если отойти от стенки оболочки. Вместо этого он постепенно распадался. Следовательно, пространство-время также будет искривлено внутри пузыря. Для путешественников на космическом корабле прямо в центре пузыря это явление будет наиболее очевидным с течением времени: их часы будут идти медленнее, чем в остальном пространстве, потому что, согласно теории относительности, на время влияет гравитация. .
Более медленное течение времени на космическом корабле может быть чем-то ценным для межзвездных путешественников.Тем не менее Бобрик и Мартир описывают и другие препятствия. Они утверждают, что пока нет известного способа ускорить образование пузыря искривления. Все предыдущие идеи по этому поводу просто предполагают, что кривизна пространства-времени уже движется с большой скоростью.
Луч света движется со скоростью 299 000 километров в секунду. Согласно специальной теории относительности Эйнштейна, это физическая константа. Скорость света – это максимальная скорость, которую может достичь любая частица, и частица может сделать это, только если у нее нет массы.Следовательно, современная физика не предлагает возможности ускорения объектов сверх скорости света. Однако при ближайшем рассмотрении этот предел применим только в четырехмерном пространстве-времени, составляющем Вселенную. В остальном возможны даже более высокие скорости.
«Ни один из физически мыслимых варп-двигателей не может разгоняться до скоростей, превышающих скорость света», – говорит Бобрик. Это потому, что вам потребуется материя, способная выбрасываться со скоростью, превышающей скорость света, но никакие известные частицы не могут перемещаться с такой скоростью.Более того, воздушным пузырем не могли управлять обитатели самого космического корабля, потому что они потеряли бы контакт с внешним миром из-за чрезвычайно сильной кривизны пространства вокруг них.
Ленц тоже считает эти возражения проблемой, но считает, что решение можно найти. Бобрик, тем временем, указывает, что к далеким звездам также можно путешествовать со скоростью, равной трети или половине скорости света, особенно если время для людей в варп-пузыре течет медленнее.Только не думайте о том, что все ваши родственники, оставшиеся на Земле, вероятно, умрут от старости до вашего возвращения. «Но, по крайней мере, идея больше не является полностью безумной», – говорит Бобрик.
От теории к практике
До сих пор ведутся споры о том, действительно ли пузыри искривления могут обойтись без отрицательной энергии. Недавно три теоретика предположили, что это утверждение верно только для наблюдателей, движущихся рядом с пузырем. Кроме того, не все, что кажется возможным согласно теории относительности, на самом деле существует – или технологически осуществимо.Например, уравнения поля Эйнштейна также можно использовать для оправдания «белых» дыр (противоположность их аналогам из черных дыр), мостов Эйнштейна-Розена (часто называемых кротовыми норами) и других экзотических изменений в пространстве-времени, которые никто никогда не наблюдал. Это могло быть потому, что законы природы, пока еще неизвестные, исключают такие явления.
Поэтому некоторые исследователи предостерегают от чрезмерных фантазий. Эксперт по космическим двигателям Мартин Таймар из Технического университета Дрездена, например, не видит практического значения для текущей работы по варп-двигателям.По его словам, задействованные огромные массы просто превосходят все, что можно испытать на Земле.
Большинство опытных исследователей варп-двигателя, несомненно, согласятся. Они рассматривают свою работу не столько как подготовку к реальным экспериментам, сколько как способ исследовать пределы теории относительности. По словам Лобо, в этом начинании полезны даже умозрительные «мысленные эксперименты».
Ленц, с другой стороны, активно работает над практическим применением своей идеи. После исследования в Геттингене он устроился на работу в ИТ-компанию.Но в свободное время он все еще думает о том, как ускорить поворот пространства-времени до скорости, превышающей скорость света, и как уменьшить энергию, необходимую для этого.
Ленц также рекомендует внимательно изучить окрестности нейтронных звезд. Возможно, эти сверхкомпактные звездные остатки выбрасывают пузыри, подобные тем, которые он описывает в своей статье. «До тех пор, пока человек не позволяет личным предубеждениям встать на пути и принимает то, что говорят вам доказательства, это область исследований, которая заслуживает такого же внимания, как и любая другая», – говорит он.
Жан-Люк Пикар, вероятно, увидел бы это точно так же.

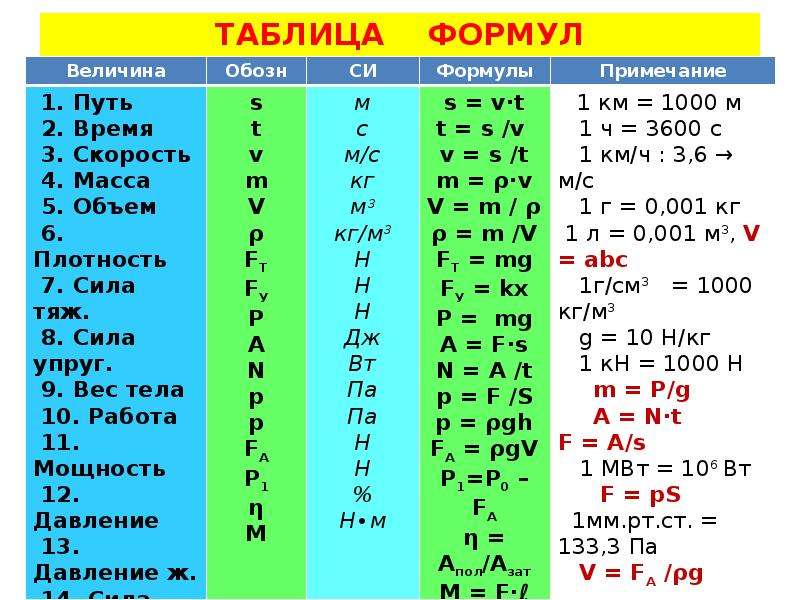

 10)
10)
 На (Рис.) Драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
На (Рис.) Драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)