25.3: Закон преломления
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2727
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять показатель преломления, зная скорость света в среде.
Заглянув в аквариум, легко заметить некоторые странности. Например, вы можете увидеть одну и ту же рыбу в двух разных местах (рис. \(\PageIndex{1}\)). Это связано с тем, что свет, идущий от рыбы к нам, меняет направление, когда покидает аквариум, и в этом случае он может идти двумя разными путями, чтобы попасть к нашим глазам. Изменение направления светового луча (обобщенно называемое искривлением), когда он проходит через изменения в материи, называется 
Преломление отвечает за огромный спектр оптических явлений, от действия линз до передачи голоса по оптическим волокнам.
Определение: ПРЕЛОМЛЕНИЕ
Изменение направления светового луча (приблизительно называемое изгибом), когда он проходит через изменения в материи, называется преломлением.
СКОРОСТЬ СВЕТА
Скорость света \(c\) не только влияет на преломление, это одно из центральных понятий теории относительности Эйнштейна. По мере повышения точности измерений скорости света оказалось, что \(с\) не зависит от скорости источника или наблюдателя. Однако скорость света точно зависит от материала, через который он проходит. Эти факты имеют далеко идущие последствия, как мы увидим в «Специальной теории относительности». Это устанавливает связи между пространством и временем и изменяет наши ожидания, например, что все наблюдатели измеряют одно и то же время для одного и того же события. Скорость света настолько важна, что ее значение в вакууме является одной из самых фундаментальных констант в природе, а также одной из четырех основных единиц СИ.
Скорость света
Ранние попытки измерить скорость света, например, сделанные Галилеем, показали, что свет движется чрезвычайно быстро, возможно, мгновенно. Первое реальное свидетельство того, что свет распространяется с конечной скоростью, было получено датским астрономом Оле Ремером в конце 17 века.
Определение: ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ
Мы определяем показатель преломления \(n\) материала как
\[n = \frac{c}{v}, \label{index}\]
где \(v\) – наблюдаемая скорость света в материале. Так как скорость света всегда меньше \(с\) в веществе и равна \(с\) только в вакууме, показатель преломления всегда больше или равен единице. То есть \(n \gt 1\).
В таблице \(\PageIndex{1}\) приведены показатели преломления некоторых репрезентативных веществ. Значения указаны для определенной длины волны света, потому что они немного меняются в зависимости от длины волны.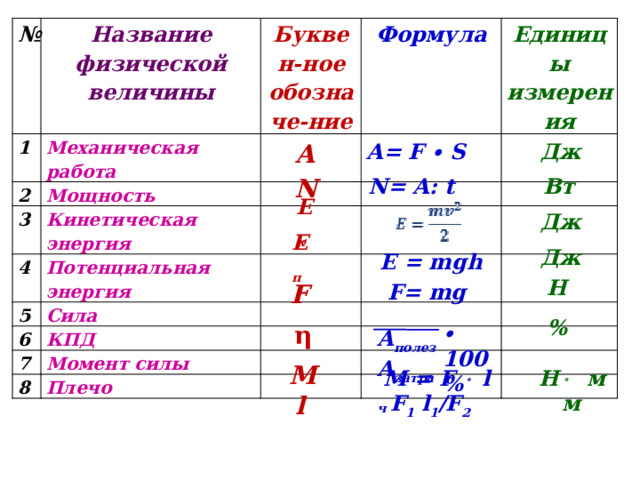
(Это может иметь важные эффекты, такие как цвета, создаваемые призмой.) Обратите внимание, что для газов \(n\) близко к 1,0. Это кажется разумным, так как атомы в газах далеко друг от друга и свет распространяется со скоростью \(с\) в вакууме между атомами. Обычно для газов принимают \(n = 1\), если не требуется большая точность. Хотя скорость света \(v\) в среде значительно отличается от ее значения \(с\) в вакууме, это все же большая скорость.
| Средний | нет |
|---|---|
| Газы при \(0ºC, 1 атм\) | |
| Воздух | |
| Углекислый газ | 1. 00045 |
| Водород | 1.000139 |
| Кислород | 1.000271 |
| Жидкости при 20ºC | |
| Бензол | 1.501 |
| Сероуглерод | 1,628 |
| Четыреххлористый углерод | 1,461 |
| Этанол | 1,361 |
| Глицерин | 1,473 |
| Вода пресная | 1,333 |
| Твердые вещества при 20ºC | |
| Алмаз | 2,419 |
| 1,434 | |
| Стекло, заводная головка | 1,52 |
| Стекло бесцветное | 1,66 |
| Лед при 20ºC | 1,309 |
| Полистирол | 1,49 |
| Оргстекло | 1,51 |
| Кварц кристаллический | 1,544 |
| Кварц, плавленый | 1,458 |
| Хлорид натрия | 1,544 |
| Циркон | 1,923 |
Пример \(\PageIndex{1}\): Скорость света в материи
Рассчитайте скорость света в цирконе, материале, используемом в ювелирных изделиях для имитации алмаза.
Стратегия:
Скорость света в материале \(v\) можно рассчитать по показателю преломления \(n\) материала с помощью уравнения \(n = c/v\) .
Обсуждение:
Эта скорость чуть больше половины скорости света в вакууме и все еще высока по сравнению со скоростями, с которыми мы обычно сталкиваемся. Единственное вещество, указанное в таблице \(\PageIndex{1}\), которое имеет больший показатель преломления, чем циркон, — это алмаз. Позже мы увидим, что большой показатель преломления циркона заставляет его сверкать больше, чем стекло, но меньше, чем алмаз.
Закон преломления
На рисунке \(\PageIndex{3}\) показано, как луч света меняет направление при переходе из одной среды в другую. Как и прежде, углы измеряются относительно перпендикуляра к поверхности в точке пересечения ее световым лучом. (Некоторая часть падающего света будет отражаться от поверхности, но сейчас мы сосредоточимся на проходящем свете.
) Изменение направления светового луча зависит от того, как изменяется скорость света. Изменение скорости света связано с показателями преломления соответствующих сред. В ситуациях, показанных на рисунке \(\PageIndex{3}\), среда 2 имеет больший показатель преломления, чем среда 1. Это означает, что скорость света в среде 2 меньше, чем в среде 1. Обратите внимание, что, как показано на Рисунок \(\PageIndex{3a}\), направление луча приближается к перпендикуляру, когда он замедляется. И наоборот, как показано на рисунке \(\PageIndex{3b}\), направление луча отклоняется от перпендикуляра, когда он ускоряется. Путь точно обратим. В обоих случаях вы можете себе представить, что происходит, если представить, как вы толкаете газонокосилку с тротуара на траву и наоборот. При переходе с тропинки на траву передние колеса замедляются и тянутся в сторону, как показано на рисунке. Это такое же изменение направления, как и для света, когда он переходит из быстрой среды в медленную. При переходе с травы на пешеходную дорожку передние колеса могут двигаться быстрее, и косилка меняет направление, как показано на рисунке.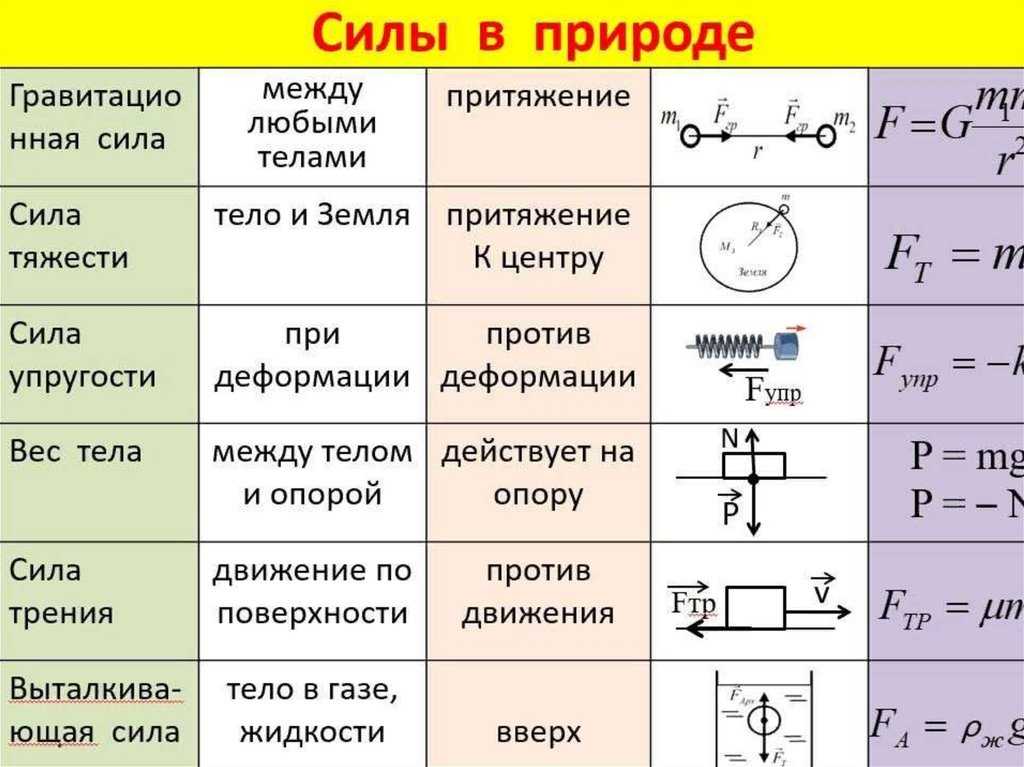
Это тоже то же изменение направления, что и при переходе света от медленного к быстрому.
Величина, на которую луч света меняет свое направление, зависит как от угла падения, так и от величины изменения скорости. Для луча под заданным углом падения большое изменение скорости вызывает большое изменение направления и, следовательно, большое изменение угла. Точное математическое соотношение представляет собой закон преломления , или «закон Снеллиуса», который формулируется в форме уравнения как
= n_{2} \sin\theta_{2}.
\label{25.4.2}\]
Здесь \(n_{1}\) и \(n_{2}\) – показатели преломления для сред 1 и 2, а \(\theta_{1}\) и \(\theta_{2} \) — это углы между лучами и перпендикуляром в средах 1 и 2, как показано на рисунке \(\PageIndex{3}\). Входящий луч называется падающим лучом, а выходящий луч — преломленным лучом, а связанные с ним углы — углом падения и углом преломления. Закон преломления также называют законом Снелла в честь голландского математика Виллеброрда Снелла (1591–1626), открывшего его в 1621 году. Эксперименты Снелла показали, что закон преломления соблюдается и что характеристический показатель преломления \(n\) может быть отнесены к определенному носителю. Снелл не знал, что скорость света различается в разных средах, но с помощью экспериментов он смог определить показатели преломления по тому, как световые лучи меняют направление.
ВОЗМОЖНЫЙ ЭКСПЕРИМЕНТ: СЛОМАННЫЙ КАРАНДАШ
Классическое наблюдение преломления происходит, когда карандаш помещают в стакан, наполовину наполненный водой.
{\circ}\). 9{\circ}}} \\[5pt] &= \frac{0,500}{0,375} \\[5pt] &=1,33. \end{align*}\]
Обсуждение
Это показатель преломления воды, и Снелл мог определить его, измерив углы и выполнив этот расчет. Затем он нашел бы, что 1,33 является подходящим показателем преломления для воды во всех других ситуациях, например, когда луч проходит из воды в стекло. Сегодня мы можем проверить, что показатель преломления связан со скоростью света в среде, напрямую измерив эту скорость. 9{\circ}\). Мы можем посмотреть показатель преломления алмаза в таблице \(\PageIndex{1}\), найдя \(n_{2} = 2,419\). Единственное неизвестное в законе Снелла — это \(\theta_{2}\), которое мы хотим определить.
Решение
Решение закона Снеллиуса (уравнение \ref{25.4.2}) для \(\sin{\theta_{2}}\) дает
\[ \sin{\theta_{2}} = \ frac{n_{1}}{n_{2}}\sin{\theta_{1}}.\]
Ввод известных значений,
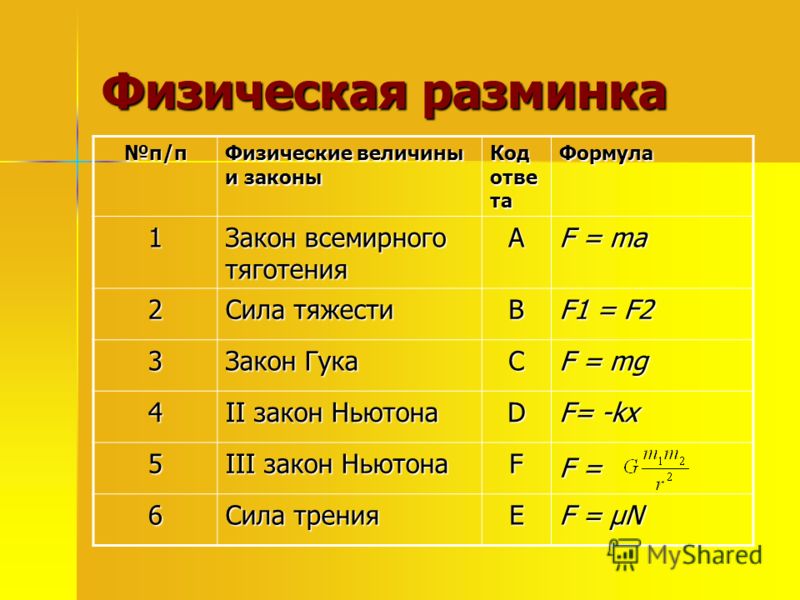
\[ \begin{align*} \sin{\theta_{2}} &= \фракция{1,00}{2,419{8} м/с\)
Глоссарий
- преломление
- изменение направления луча света при прохождении через изменения в материи
- показатель преломления
- для материала отношение скорости света в вакууме к скорости света в материале
Эта страница под названием 25.3: Закон преломления распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Вернуться к началу
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- показатель преломления
- преломление
- Закон преломления Снеллиуса
- источник@https://openstax.
org/details/books/college-physics
org/details/books/college-physicsИспользование уравнений крутящего момента — AP Physics C: Механика
Все ресурсы AP Physics C: Mechanics
2 диагностических теста 92 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics C: Справка по механике » Экзамен по механике » Движение ” Круговое и вращательное движение » Вращательное движение и крутящий момент » Использование уравнений крутящего момента
Объект выходит из состояния покоя и ускоряется до угловой скорости за три секунды при постоянном крутящем моменте . Сколько оборотов сделал объект за это время?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку он испытывает постоянный крутящий момент и постоянное угловое ускорение, угловое смещение можно рассчитать, используя:
Угловое ускорение легко рассчитать, используя угловую скорость и время:
Используя это значение, мы можем найти угловое перемещение:
Преобразование углового смещения в обороты путем погружения:
Сообщить об ошибке
Круглый диск массой 3,5 кг и радиусом 0,5.
имеет силу 25 Н, приложенную перпендикулярно его краю, заставляя его вращаться. Чему равно угловое ускорение диска?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы можем найти угловое ускорение, используя вращательное движение, эквивалентное второму закону Ньютона. При вращательном движении крутящий момент является произведением момента инерции и углового ускорения:
Момент инерции круглого диска равен:
Крутящий момент является произведением силы на расстояние (в данном случае радиус ):
Мы можем подставить их в наше первое уравнение:
Упростите и перестройте, чтобы получить уравнение для углового ускорения:
Используйте полученные значения для решения:
Сообщите об ошибке в горизонтальной плоскости, параллельной верхней части стола.
На измерительную линейку в разных местах действуют четыре силы одинаковой величины. На рисунке ниже показан вид на измерительную линейку сверху.
Можно предположить, что силы и приложены к центру измерительной палочки, а силы и приложены к концу, противоположному гвоздю.
Каково соотношение между величинами крутящих моментов на измерительной линейке, вызванных четырьмя различными силами?
Возможные ответы:
Правильный ответ:
Объяснение:
Крутящий момент определяется выражением,
Поскольку все силы равны по величине, на величину крутящего момента влияет радиус r и угол тета между радиусом и силой.
для,
для,
для,
для,
, объединяющая эту информацию. длинная однородная металлическая балка длиной .
Масса человека составляет , а масса балки – .
Какова величина чистого крутящего момента на доске относительно закрепленного конца балки? Используйте гравитацию.
Возможных ответов:
Правильный ответ:
Объяснение:
Чистый крутящий момент на балке получается путем сложения крутящих моментов, вызванных весом человека и весом самой балки, каждый на соответствующем расстоянии от конца балки:
Присвоим направление положительного крутящего момента в направлении крутящих моментов веса человека и балки, отметив, что они будут складываться, поскольку оба они указывают в одном направлении.
Мы можем еще больше упростить, скомбинировав подобные термины:
Используя заданные числовые значения,
Сообщить об ошибке таким образом, чтобы морская пила балансировала идеально горизонтально.
Дочерний элемент слева – это точка опоры.
Какова масса второго ребенка, если она сядет от оси вращения?
Возможных ответов:
Правильный ответ:
Объяснение:
Анализ крутящего момента уместен в этой ситуации из-за включения расстояний от заданной точки поворота. Как правило,
Это статическая ситуация. Есть два крутящих момента вокруг оси, вызванные весом двух детей. Заметим, что эти веса вызывают крутящие моменты в противоположных направлениях относительно оси вращения, так что
Следовательно,
Или проще,
Решение для ,
Сообщить об ошибке
Гимнастка тренируется на длинной узкой доске, поддерживаемой с обоих концов. Ее масса . Длинная доска имеет массу .
Рассчитайте силу, которую правая опора оказывает вверх, если она стоит с правого конца.
Используйте гравитацию.
Возможные ответы:
Правильный ответ:
Объяснение:
Анализ крутящего момента уместен в этой ситуации из-за включения расстояний от заданной точки поворота. Как правило,
Это статическая ситуация. Таким образом, можно выбрать любую точку разворота, относительно которой можно выполнить анализ крутящего момента. Самый быстрый способ найти неизвестную силу, указанную в вопросе, — это провести анализ крутящего момента относительно левого конца доски. Вокруг этого шарнира действуют три крутящих момента: два по часовой стрелке, вызванные весом гимнаста и самой планки, и один против часовой стрелки, вызванный силой правой опоры. Обозначая по часовой стрелке как положительное,
Следовательно,
Это упрощает до
Решение для,
Решение
ANSERSIRSING ANMERSING ARMARDS ANMERSING ARMARDS ANMERSING.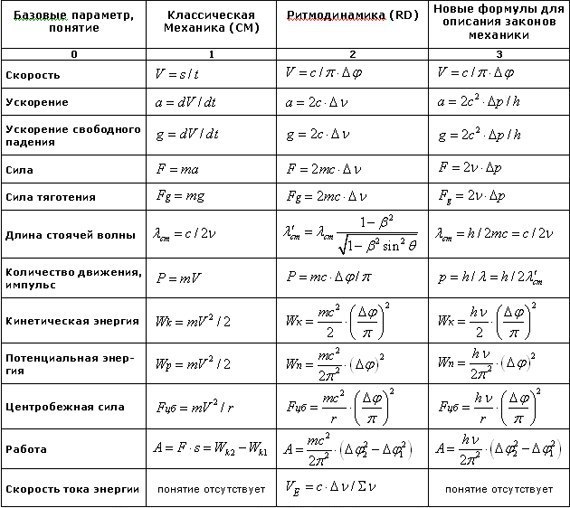
возможных осей вращения.
Какое из утверждений о соотношениях между моментами инерции верно?
Возможные ответы:
Правильный ответ:
Объяснение:
Моменты инерции для обеих осей и равны, поскольку обе эти оси проходят через центр масс.
По теореме о параллельных осях для моментов инерции (), момент инерции для оси больше, чем или
, потому что она расположена на расстоянии
от центра масс.
Сообщить об ошибке
Улавливатель ветра создается путем прикрепления четырех пластиковых чаш с массой к концам четырех легких стержней, которые затем прикрепляются к центральному стержню, который может свободно вращаться на ветру. Четыре легких стержня имеют длину , , и .
Рассчитайте момент инерции четырех чаш относительно центрального стержня.
Вы можете считать чаши точечными массами.
Возможные ответы:
Правильный ответ:
Пояснение:
Момент инерции точечной массы равен .
Чтобы рассчитать общий момент инерции, мы добавляем момент инерции для каждой части объекта, так что
Массы чашек в этой задаче равны, так что это упрощается до
Подстановка и решение с числовыми значениями,
Сообщить об ошибке
Длинный однородный тонкий стержень длиной имеет массу .
Рассчитайте момент инерции вращения вокруг оси, перпендикулярной ее длине, проходящей через точку от одного из ее концов.
Возможные ответы:
Правильный ответ:
Пояснение:
Для длинного тонкого стержня относительно центра масс:
В соответствии с теоремой о параллельных осях
ось параллельна точке, проходящей через центр масс.