Сформулируйте закон инерции первый закон ньютона: Сформулируйте закон инерции (первый закон Ньютона)

Решение задач по теме “Законы Ньютона”. 9-й класс

Цели урока:

• Образовательные: повторение законов Ньютона, закрепление и применение полученных знаний для решения качественных и количественных задач и проведения экспериментов по данной теме.
• Развивающие: развитие умений проводить наблюдения, планировать и выполнять эксперименты, выдвигать гипотезы, анализировать результаты экспериментов и делать соответствующие выводы; развитие умений быстро соображать и находить правильное решение.
• Воспитательные: воспитать любознательность, внимательность, усидчивость; содействовать формированию у школьников основных способов групповой работы.

План проведения урока

• Организационный момент
• Актуализация знаний
• Повторение
• Закрепление ранее полученных знаний
• Рефлексия
• Домашнее задание

Оборудование: Легкоподвижные тележки с магнитами, демонстрационные динамометры, лабораторные динамометры, стаканы с водой, листки бумаги, монеты.

Информационно-техническое сопровождение урока:

• Компьютерная презентация
• Компьютер, мультимедийный проектор, экран.
• Тест – Приложение 1.

ХОД УРОКА

1) Организационный момент

Здравствуйте ребята! Садитесь!

2) Актуализация знаний учащихся

Внимательно посмотрите на экран и сформулируйте тему урока.

Слайд 1

Учащиеся отвечают «Законы Ньютона». Да! Действительно сегодня на уроке мы повторим законы Ньютона, а затем перейдем к решению задач и проведению экспериментов по этой теме. Сколько законов вы знаете? Учащиеся отвечают « Три закона Ньютона».

Слайд 2

3) Повторение

Устная проверка знаний полученных на прошлых занятиях.

Фронтальный опрос по вопросам

Вопросы:

1. Сформулируйте первый закон Ньютона.
2. Каково значение первого закона Ньютона?
3.Какие системы отсчета называются инерциальными?
4. Приведите примеры инерциальных систем отсчета.
5. Сформулируйте второй закон Ньютона. Каково его значение?
6. Сформулируйте третий закон Ньютона. Каково его значение?
7. В каких системах отсчета выполняются законы Ньютона?

Слайд 3, Слайд 4, Слайд 5

Тест (по вариантам)

4) Закрепление ранее полученных знаний, решение качественных и количественных задач. Проведение экспериментов

Учитель. Как объяснить, что бегущий человек, споткнувшись, падает в направлении своего движения, а поскользнувшись, падает в направлении, противоположном направлению своего движения?

Учащиеся. Это явление легко объясняется на основании первого закона Ньютона. Бегущий человек, споткнувшись, падает в направлении своего движения. Потому что при этом ноги человека замедляют движение. А туловище сохраняет по инерции прежнее состояние движения. В то время как ноги начинают скользить вперед быстрее, потому человек падает назад.

Учитель. I закон – закон инерции. Непосредственно подтвердить экспериментально его невозможно, он аксиоматичен. Однако можно объяснить ряд опытов, что является косвенным подтверждением справедливости этого закона.

Слайд 6

Учитель. Положите листок бумаги на край стола. На листок поставьте стакан с водой. Свешивающийся конец листка возьмите в одну руку, а ребром ладони другой руки резко ударьте по нему.

(Учащиеся по группам проводят опыт. При этом листок выдергивается, а стакан остается. )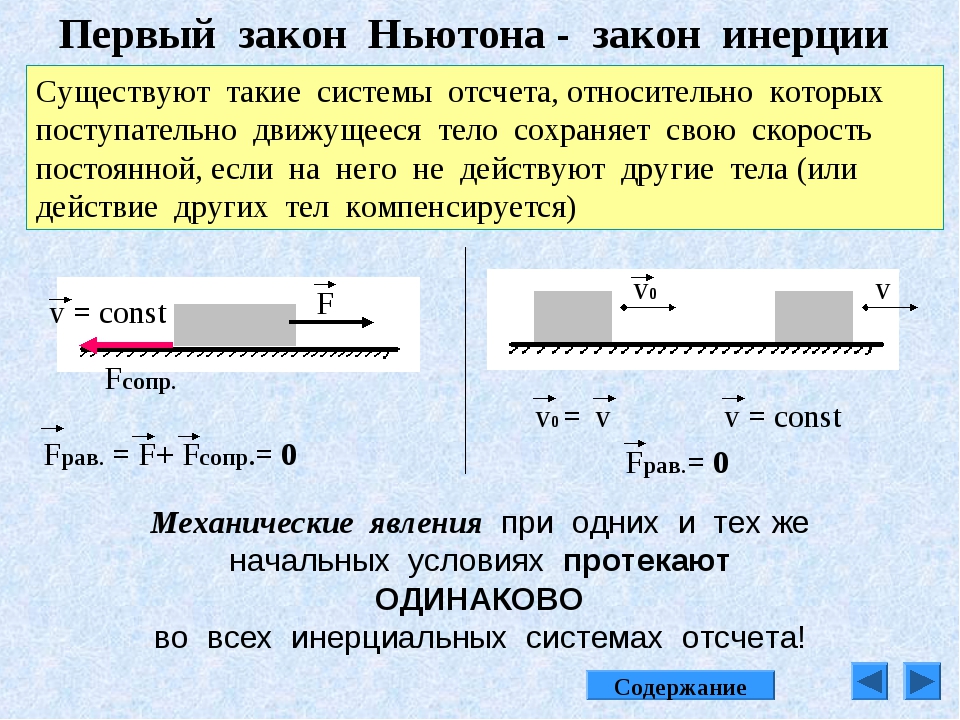

Учитель. Почему?

Учащиеся. Стакан сохраняет состояние покоя по инерции.

Слайд 7

Учитель. Положите на стакан почтовую открытку, а на открытку положите монету. Ударьте по открытке щелчком как показано на рисунке (Слайд). Почему открытка отлетает, а монета падает в стакан? (Учащиеся по группам проводят этот опыт и делают выводы).

Учащиеся. Монета сохраняет состояние покоя по инерции.

Учитель. Сформулируем проблему: если магнит действует на железо с некоторой силой, то действует ли железо на магнит и, если действует, то с какой силой?

Учащиеся ставят эксперимент.

Эксперимент. Возьмем две тележки и на одной из них закрепляем магнит, а на другой кусок железа. Затем соединяем их с динамометрами.

Учащиеся. Мы увидели, что показания этих приборов совпали. Это означает, что сила, с которой магнит притягивает к себе железо, равна по величине силе, с которой железо притягивает к себе магнит. Эти силы равны по абсолютной величине и противоположны по направлению: сила притяжения к магниту направлена влево, а сила притяжения к железу – вправо. Выполняется третий закон Ньютона.

Задача. Как направленно ускорение самолета, если на него действует 4 силы: по вертикали – сила тяжести = 200кН и подъемная сила 210кН. По горизонтали: сила тяжести мотора 20 кН и сила лобового сопротивления воздуха 10 кН. Чему равна равнодействующая всех сил?

Найдем равнодействующую всех сил, пользуясь правилом параллелограмма: R = R

Модуль силы R вычислим с помощью теоремы Пифагора: Слайд 8

Ответ: Равнодействующая всех сил направлена под углом 450 к горизонту R ~ 1,4 · 10⁴ Н

Самостоятельная работа

Задача 1. Метеорит пролетает около Земли за пределами атмосферы. В тот момент, когда вектор силы гравитационного притяжения Земли перпендикулярен вектору скорости метеорита, вектор ускорения метеорита направлен

• параллельно вектору скорости
• по направлению вектора силы
• по направлению вектора скорости
• по направлению суммы векторов силы и скорости

Решение. Направление вектора ускорения любого тела всегда совпадает с направлением равнодействующей всех сил, приложенных к телу. За пределами атмосферы на метеорит действует только сила гравитационного притяжения Земли. Поэтому направление вектора ускорения метеорита совпадает с направлением вектора силы гравитационного притяжения Земли.

Ответ: 3

Задача 2. В инерциальной системе отсчета брусок начинает скользить с ускорением вниз по наклонной плоскости.

1) mg
2) ma
3) Fтр
4) N

Решение. Направление вектора ускорения любого тела всегда совпадает с направлением равнодействующей всех сил, приложенных к телу.

Ответ: 2

Задача 3. Установите соответствие между физическими законами и физическими явлениями, которые эти законы описывают.

Ответ:

Задача 4.

Решение. Согласно второму закону Ньютона ускорение тела и равнодействующая сил имеют одинаковое направление.

Ответ: 2

5) Рефлексия

6) Домашнее задание. § 10-12. Выучить законы Ньютона.

Физика 9 класс Первый закон Ньютона, инерциальные системы отсчета

  Повторение материала с целью актуализация знаний учащихся.                 

                                       (фронтальный опрос)

 1 Что называется силой?

                               (предполагаемый ответ)

Силой в механике называют величину, являющуюся мерой взаимодействия тел.  Мы постоянно встречаемся с различными случаями взаимодействия тел друг на друга.

Просто говорят, что на тело действует сила, или к нему приложена сила. Следовательно, силу можно рассматривать как причину изменения скорости движения.

Одно тело может действовать на другое как непосредственным контактом (давление, трение), так и посредством создаваемых телами полей (гравитационное поле, электромагнитное поле).

2 Какой величиной является сила?

                               (предполагаемый ответ)

Сила является векторной величиной, и имеет не только численное значение, но и направление. Обозначается буквой , модуль силы – F. Прямая, вдоль которой направлена сила, называется линией действия силы.

Говоря о силе, действующей на тело, важно указать, к какой точке тела она приложена.

На чертеже силу изображают в виде отрезка прямой со стрелкой на конце. Точка приложения силы – начало отрезка (точка А). Длина отрезка в определенном масштабе обозначает модуль силы. Если речь об абсолютно твердом (недеформируемом) теле, то считается, что сила приложена к любой точке на линии ее действия.

Иное дело – деформируемые тела. Если пальцем надавить на кусок пластилина или ластик, он изменит свою форму (деформируется). Или другой пример –

доска, лежащая на опорах. Доска прогнется, если на нее положить груз, то есть середина доски переместится на большее расстояние, чем ее края.

Итак, результат действия силы на тело зависит от ее модуля, направления и точки приложения. Иными словами, сила – векторная величина, которая характеризуется численным значением, направлением в пространстве и точкой приложения.

  3. Сформулируйте первый закон Ньютона.

               (предполагаемый ответ с опытным обоснованием)

Единицей силы в СИ принят ньютон (Н). Один ньютон (1 Н) – это сила, которая за 1 с изменяет скорость тела массой 1 кг на 1 м/с. Часто на практике применяются килоньютоны (1 кН = 1000 Н) и миллиньютоны (1 мН = 0,001 Н).

Ньютон сформулировал закон инерции, включив его в основу механики в качестве первого из трех законов. Поэтому этот закон называют первым законом Ньютона.

Первый закон механики, или закон инерции был сформулирован Ньютоном следующим образом:

Любое тело удерживается в состоянии покоя или равномерного прямолинейного движения, пока под действием приложенных сил не изменяет это состояние.

                         ОПЫТ

Рассмотрим какое-либо покоящееся тело, не обладающее ускорением, а скорость постоянна и равна нулю.

Допустим, это будет шарик, подвешенный на резиновом шнуре. Он находится в покое относительно Земли. Около шарика множество различных тел: шнур, на котором он висит, множество предметов в комнате и других помещениях и, конечно, Земля. Однако, действие всех этих тел на шарик не одинаково. Если, например, убрать мебель в комнате, это не окажет какого-либо влияния на шарик. Но если перерезать шнур, шарик под влиянием Земли начнет падать вниз с ускорением. Но пока шнур не был перерезан, шарик находился в покое.

Этот простой опыт показывает, что из всех тел, окружающих шарик, только два заметно влияют на него: резиновый шнур и Земля. Их совместное влияние и обеспечивает состояние покоя шарика. Стоило устранить одно из этих тел — шнур, и состояние покоя нарушилось. Если бы возможно было убрать Землю, это тоже нарушило бы покой шарика: он стал бы двигаться в противоположном направлении.

Отсюда приходим к выводу, что действия на шарик двух тел — шнура и Земли, компенсируют (уравновешивают) друг друга. Когда говорят, что действия двух или нескольких тел компенсируют друг друга, то это значит, что результат их совместного действия такой же, как если бы этих тел вовсе не было.

Рассмотренный пример, как и другие подобные примеры, позволяют сделать следующий вывод: если действия тел компенсируют друг друга, то тело под влиянием этих тел находится в состоянии покоя.

4 Что называют инерциальными системами отсчета?

                               (предполагаемый ответ)

Однако, как выяснилось со временем, первый закон Ньютона выполняется только в инерциальных системах отсчета. Поэтому с точки зрения современных представлений закон Ньютона формулируют следующим образом:

Системы отсчета, относительно которых свободное тело при компенсации внешних воздействий движется равномерно и прямолинейно, называют инерциальными системами отсчета.

Закон сохранения импульса материальной точки

Мы пришли к закону сохранения импульса материальной точки в отсутствие сил импульс материальной точки сохраняется неизменным по модулю и направлению.  [c.108]

Сформулируйте закон сохранения импульса материальной точки.  [c.112]

Закон сохранения импульса материальной точки. Этот закон следует из теоремы об изменении импульса и читается так если равнодействующая сил, приложенных к материальной точке, равна нулю, вектор импульса тела остается величиной постоянной во все время движения, т. е.  [c.111]

Рассуждения, которые привели нас к закону сохранения импульса, целиком опирались на справедливость законов Ньютона. В частности, предполагалось, что материальные точки замкнутой системы взаимодействуют между собой попарно и это взаимодействие подчиняется третьему закону Ньютона. А как обстоит дело в случае систем, не подчиняющихся законам Ньютона, например в системах с электромагнитным излучением  [c.71]

Это уравнение выражает закон сохранения импульса системы материальных точек общий момент импульса системы относительно какой-либо неподвижной оси остается постоянным, если момент внешних сил относительно этой оси равен нулю.  [c.306]

В двух разных инерциальных системах отсчета одна и та же система материальных точек обладает неодинаковым импульсом, отличающимся на постоянную величину. Если же импульс системы материальных точек в одной из систем отсчета остается постоянным, то он остается постоянным и в другой системе отсчета. . Поэтому закон сохранения импульса для замкнутой системы тел справедлив для любой инерциальной системы отсчета.  [c.81]

Запишите второй закон Ньютона для материальной точки и для системы материальных точек. В чем состоит закон сохранения импульса  [c.143]

Мы пришли к закону сохранения импульса системы импульс замкнутой системы материальных точек есть величина постоянная, или, другими словами, в отсутствие внешних сил сумма импульсов всех точек системы остается постоянной, какие бы изменения внутри системы ни происходили. Это значит, что в процессе взаимодействия частицы системы лишь обмениваются импульсами, оставляя полный импульс системы неизменным.  [c.116]

Сформулируйте закон сохранения импульса системы материальных точек. Поясните, какими рассуждениями можно прийти к этому закону. От чего  [c.121]

Известно, что в ньютоновской механике закон сохранения импульса системы материальных точек справедлив для замкнутых систем. Выполняется ли указанный закон в неинерциальных системах отсчета  [c.201]

Наличие законов сохранения импульса, кинетического момента и полной энергии замкнутой системы материальных точек связано с инвариантностью уравнений Ньютона относительно группы преобразований Галилея.  [c.17]

Суммируя ЭТИ уравнения по всем материальным точкам, получим, что в силу закона сохранения импульса  [c.34]

Итак, мы нашли, что в силу закона сохранения импульса центр инерции замкнутой системы материальных точек движется прямолинейно и равномерно со скоростью V (опять в полной аналогии с радиус-вектором одной свободной материальной точки).  [c.37]

Теорема об изменении импульса системы. Закон сохранения импульса. Теоремы для системы материальных точек удобно получать, обобщая рассмотренные ранее соответствующие теоремы для одной материальной точки. Теорему об изменении импульса материальной точки в форме (9. 1) напишем для каждой /-й точки системы, подразделяя силы на внутренние и внешние  [c.135]

Пример 14.1. Применение закона сохранения импульса для вывода уравнения движения материальной точки переменной массы.  [c.140]

Если импульс материальной точки изменяется непрерывно и в некоторой инерциальной системе известна скорость передачи импульса материальной точке извне, то эту скорость передачи импульса, как и в классической механике, можно назвать силой. Если сила задана как функция координат точки пространства, скорости и времени, то, используя выражение для релятивистского импульса (4.5), можно написать равенство, выражающее закон сохранения импульса при передаче его между полем и точкой  [c.283]

Так как измерения, касающиеся светового кванта, осуществляются всегда посредством взаимодействия кванта с материальными телами, то условия (4) и (4 ), которые существенны для непротиворечивого проведения корпускулярных представлений при явлениях интерференции, позволяют, обратно, делать некоторые заключения о материальных телах. Понятие о световых квантах вводится для расчёта обмена энергией и импульсом между светом и материей (веществом). В предположении, что законы сохранения импульса и энергии при этом обмене строго выполняются, —а только этими законами энергия и импульс определяются вообще —мы получаем, как известно, что обмен будет описываться правильно, если  [c.11]

Обратимся к законам сохранения импульса и кинетического момента в пространстве. Примем какую-либо инерциальную систему за основную ( неподвижную ) и рассмотрим различные положения замкнутой системы материальных точек в один и тот же момент времени, предполагая, что расстояния между точками не изменяются. Очевидно, что это будет равносильно такому преобразованию, при котором изменяются координаты точек, но время не преобразуется. Ограничимся здесь ортогональными преобразованиями с сохранением масштаба, записывая их в векторной форме.  [c.124]

Законы сохранения импульса и кинетического момента замкнутой системы материальных точек во времени могут быть приняты в качестве основ–ных аксиом механики.  [c.124]

При решении ряда задач гидравлики применяется закон сохранения импульса, согласно которому производная по времени вектора количества движения системы материальных точек равняется главному вектору внешних сил, действующих на систему  [c.69]

Математический маятник состоит из материальной точки массой М, расположенной на нижнем конце невесомого стержня длиной L, свободно вращающегося вокруг оси, проходящей через его верхний конец (рис. 7.1). Наша задача заключается в том, чтобы найти частоту собственных колебаний маятника. Самый простой путь решения этой задачи — суметь написать в соответствующем виде второй закон динамики F = Afa. Это может быть сделано так же, как и в задаче 7.6. Однако очень поучительно попытаться решить эту задачу, исходя из закона сохранения энергии. Чтобы получить уравнения (18)—(22), можно также исходить и из сохранения момента импульса. Отклонения маятника будем измерять углом 0, который стержень об- разует с вертикалью.  [c.207]

Введение понятия эффективной потенциальной энергии полезно при рассмотрении следствий закона сохранения момента нм пульса в отношении движения материальной точки. При этом мы видим, что ес ги момент импульса остается постоянным, то при малых расстояниях г действует сила отталкивания.  [c.287]

Закон сохранения момента импульса для системы материальных точек  [c.305]

В начале докажем, что в центральном поле по отношению к центру выполняется закон сохранения момента импульса (см. 19). Из определения центрального поля следует, что сила, действующая на движущуюся в нем материальную точку, всегда проходит через центр поля. Поэтому плечо силы, а следовательно, и момент этой силы относительно центра поля равны нулю. При М = 0 из уравнения (19.6) М = – следует, что вектор момента импульса оста-  [c.116]

Таким образом, при движении материальной точки в центральном силовом поле по отношению к центру поля всегда выполняется закон сохранения момента импульса.  [c.116]

Т. е. при движении материальной точки в центральном силовом иоле ее секториальная скорость постоянна. Из этого следует, что радиус-вектор, проведенный из центра поля к движущейся материальной точке, в равные промежутки времени описывает равные площади. Это утверждение известно как второй закон Кеплера , который, по существу, является следствием закона сохранения момента импульса.  [c.117]

Закон сохранения энергии также справедлив для любой инерциальной системы координат однако это не столь очевидно, как для закона сохранения импульса. Прежде всего ясно, что потенциальная энергия данной системы точек во всех инер-циальиых системах координат одна и та же. Действительно, потенциальная энергия данной системы материальных точек зависит только от их конфигурации, т. е. от разностей координат. Поэтому потенциальная энергия данной системы материальных точек во всех инерциальных системах будет одна и та же.  [c.233]

К замкнутой системе твердых тел, так же как к замкнутой системе материальных точек, могут быть применены законы сохранения импульса и момента импульса. При суммировании уравнений движения и уравнений моментов внутренние силы, действующие между отдельными твердыми телами, исключаются (в силу третьего закона Ньютона). Поэтому, если на систему твердых тел не действуют внешние силы, то ее общий импульс остается постоянным. Точно так >ке, если сумма моментов всех внешних сил равна нулю, ю общий момент импульса системы твердых тел остается 1ЮСтоянным, Применение закона сохранения импульса к системе твердых тел ла т, по существу, то же самое, что н в случае системы материальных точек, — jaKOH движегни) центра тяжести системы тел.  [c.421]

Так как Йоз — это квант энергии моды с частотой со, то выражение (5.1а) представляет собой закон сохранения энергии для трехфононного процесса. Мода, строго говоря, не обладает механическим импульсом как материальная частица, однако величина Йq во многом сходна с импульсом. Выражение (5.16) при g = О как раз соответствует закону сохранения импульса. Взаимодействие, при котором g = О, называется нормальным процессом, а взаимодействие, при котором g =И= О, Пайерлс назвал процессом переброса. На такие процессы мы будем ссылаться как на П- и П-процессы соответственно.  [c.51]

Наоборот, можно показать, что любая материальная частица массы т должна обладать энергией причем в системе покоя частицы ее энергия есть о = Это утверждение имеет реальный смысл только тогда, когда энергию, соответствуюш,ую массе частицы, можно преобразовать з другие виды энергии, напрп.мер в кинетическую энергию других частиц. Мы не можем заранее знать, что такие аннигилящюнные процессы действительно существуют в природе, но можем показать, что если они при определенных условиях существуют и для них справедлив принцип относительности и все законы сохранения импульса и энергии, то количество высвободившейся энергии при аннигиляции массы Отд должно равняться Е — тдС .  [c.63]

Первый закон ньютона формула и формулировка – 3 закона Ньютона определения и формулы. Второй закон Ньютона формулировка. Второй закон Ньютона. Формула второго закона Ньютона

кратко и понятно о формулах и формулировках на конкретных примерах

В школьном курсе физики изучаются три закона Ньютона, являющиеся основой классической механики. Сегодня с ними знаком каждый школьник, но во времена великого ученого подобные открытия считались революционными. Законы Ньютона, кратко и понятно будут описаны ниже, они помогают не только понять основу механики и взаимодействия объектов, но и помогают записать данные в качестве уравнения.

Содержание статьи

Вводная информация

Впервые три закона Иссак Ньютон описал в труде «Математические начала натуральной философии» (1867 год), в котором были подробно изложены не только собственные выводы ученого, но все знания по этой теме открытые другими философами и математиками. Таким образом, труд стал фундаментальным в истории механики, а позднее и физики. В нем рассмотрены перемещение и взаимодействие массивных тел.

Интересно знать! Исаак Ньютон был не только талантливым физиком, математиком и астрономом, но и считался гением в механике. Занимал должность президента королевского общества Лондона.

Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).

Именно это упрощение позволило проигнорировать естественные физические явления: воздушное сопротивление, трение, температуру или другие физические показатели объекта.

Полученные данные могли быть описаны только по времени, массе или длине. Именно из-за этого формулировки Ньютона обеспечивают лишь подходящие, но приближенные значения, которые нельзя использовать для описания точной реакции крупных или изменяемых по форме объектов.

Перемещение массивных предметов, которые участвуют в определениях, принято исчислять в инерциальной системе отсчета, представленной в виде системы координат из трех измерений, и при этом она не увеличивает свою скорость и не оборачивается вокруг своей оси.

Ее часто называют системой отсчета Ньютона, но при этом ученый никогда не создавал и не использовал подобной системы, а использовал нерациональную. Именно в этой системе тела могут двигаться так, как описывает это Ньютон.

Первый закон

Называется законом инерции. Не существует его практической формулы, зато есть несколько формулировок. В учебниках по физике предлагается следующая формулировка первого закона Ньютона: есть инерциальные системы отсчета, в отношении которых объект, если он свободен от воздействия любых сил (или же они моментально компенсируется), находиться в полном покое или же двигается по прямой и с одинаковой скоростью. Что означает данное определение и как его понять?

Простыми словами первый закон Ньютона объясняется так: любое тело, если его не трогать и никоим образом не воздействовать на него, будет оставаться постоянно в состоянии покоя, то есть бесконечно стоять на месте. То же самое происходит и при его движении: оно будет равномерно двигаться по заданной траектории бесконечно, пока на него не воздействует что-либо.

Подобное утверждение озвучивал Галилео Галилей, но не смог уточнить и точно описать это явление. В этой формулировке важно правильно понять, что такое инерциальные системы отсчета. Если сказать совсем простыми словами, то это система, в которой выполняется действие данного определения.

Первый закон Ньютона

В мире можно увидеть огромное множество подобных систем, если понаблюдать за движением:

• поезда на заданном участке с одинаковой скоростью;
• Луны вокруг Земли;
• колеса обозрения в парке.

В качестве примера рассмотрим некоего парашютиста, который уже раскрыл парашют и движется прямолинейно и при этом равномерно по отношению к поверхности Земли. Движение человека не прекратиться до тех пор, пока земное притяжение будет компенсироваться движением и сопротивлением воздуха. Как только это сопротивление уменьшится, то притяжение увеличится, что приведет к изменению скорости парашютиста – его движение станет прямолинейным и равноускоренным.

Именно в отношении этой формулировки существует яблочная легенда: Исаак отдыхал в саду под яблоней и размышлял о физических явлениях, когда с дерева сорвалось спелое яблоко и упало в траву. Именно ровное падение заставило ученого изучить этот вопрос и выдать в итоге научное объяснение движению предмета в некой системе отсчета.

Интересно знать! Помимо трех явлений в механике, Исаак Ньютон также объяснил движение Луны как спутника Земли, создал корпускулярную теорию света и разложил радугу на 7 цветов.

Второй закон

Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.

Закон гласит: увеличение скорости объекта с некоторой постоянной массой в инерциальной системе отсчета прямо пропорционально силе воздействия и обратно пропорционально постоянной массе движущегося предмета.

Проще говоря, если существует некое движущиеся тело, масса которого не изменяется, и на него вдруг начнет воздействовать посторонняя сила, то оно начнет ускоряться. А вот скорость ускорения будет прямо зависеть от воздействия и обратно пропорционально зависеть от массы движущегося предмета.

Для примера можно рассмотреть снеговой шар, который катиться с горы. Если шар толкать по ходу движения, то ускорения шара будет зависеть от мощности воздействия: чем она больше, тем больше ускорение. Но, чем больше масса данного шара, тем меньше будет ускорение. Данное явление описывается формулой, в которой учитывается ускорение, или «a», равнодействующая масса всех воздействующих сил, или «F», а также масса самого предмета, или «m»:

а = F/m

Следует уточнить, что данная формула может существовать только в том случае, если равнодействующая всех сил не меньше и не равна нулю. Применяется закон только относительно тел, которые двигаются со скоростью меньше световой.

Полезное видео: первый и второй законы Ньютона

Третий закон

Многие слышали выражение: «На каждое действие есть свое противодействие». Его часто используют не только в общеобразовательных целях, но и воспитательных, объясняя, что на каждую силу найдется большая.

Эта формулировка пошла от очередного научного утверждения Исаака Ньютона, а точнее его третьего закона, который объясняет взаимодействие различных сил в природе относительно какого-либо тела.

Третий закон Ньютона определение имеет такое: предметы оказывают воздействие друг на друга с силами одинаковой природы (соединяющей массы предметов и направлены вдоль прямой), которые равны по своим модулям и при этом направлены в разные стороны. Данная формулировка звучит достаточно сложно, но простыми словами объяснить закон легко: каждая сила имеет свое противодействие или равную силу, направленную в обратную сторону.

Гораздо проще будет понять смысл закона, если в качестве примера взять пушку, из которой стреляют ядрами. Пушка воздействует на снаряд с той же силой, с которой снаряд воздействует на пушку. Подтверждением этого будет небольшое движение пушки назад во время выстрела, что подтвердит воздействие ядра на орудие. Если взять как пример тоже самое яблоко, которое падает на землю, то станет понятно, что яблоко и земля воздействуют друг на друга с равной силой.

Закон имеет также математическое определение, в котором используется сила первого тела (F1) и второго (F2):

F1 = -F2

Знак минуса сообщает о том, что векторы сил двух разных тел направлены в противоположные стороны. При этом важно помнить, что данные силы не компенсируют друг друга, поскольку направлены относительно двух тел, а не одного.

Полезное видео: 3 закона Ньютона на примере велосипеда

Вывод

Данные законы Ньютона кратко и четко необходимо знать каждому взрослому человеку, поскольку они являются основой механики и действуют в повседневной жизни, несмотря на то, что не при всех условиях данные закономерности соблюдаются. Они стали аксиомами в классической механике, и на основе их были созданы уравнения движения и энергии (сохранение импульса и сохранение механической энергии).

Вконтакте

Facebook

Twitter

Google+

znaniya.guru

9 ОКТЯБРЯ 2014 ГОДА ТЕМА УРОКА 2 ЗАКОН

9 ОКТЯБРЯ 2014 ГОДА ТЕМА УРОКА: 2 ЗАКОН НЬЮТОНА. ИНЕРТНОСТЬ Дом. задание: – § 11 читать, – на вопросы после параграфа – отвечать, – упр. 11 письменно

Самостоятельно: 1 вариант 1)Назовите тела и нарисуйте силы, действующие на тело. 2) Сформулируйте принцип относительности Галилея 2) Сформулируйте закон инерции

При взаимодействии тела могут изменять свою скорость. Причем, скорости могут меняться одинаково (т. е. а 1=а 2) или по разному (а 1=а 2). Это зависит от свойства тел, называемого инертностью. Инертность – это способность тел по-разному менять свою скорость при взаимодействии. Инертность характеризует такая физическая величина, как масса тела. Опыты показывают, что а 1 – m 2 a 2 m 1 , т. е. чем больше масса тела, тем медленнее оно меняет свою скорость, а легкие тела могут быстрее изменить свою скорость.

Причина изменения скорости тела, а значит и причина возникновения ускорения – воздействие на это тела других тел с некоторой силой. Если на тело действуют несколько сил, то их можно заменить одной силой – равнодействующей. Равнодействующая сила – это векторная сумма всех действующих на тело сил.

Чем больше равнодействующая сила, тем большее ускорение приобретет тело. Следовательно: а~F Выше мы говорили, что a ~ 1/m Исходя из этих зависимостей, получаем формулу: а = F/m – формула второго закона Ньютона

Формулировка второго закона Ньютона (стр. 46): ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.

Формулу 2 -го закона Ньютона можно записать: 1) в векторном виде а = F/m 2) в проекциях векторов ах = Fх/m 3) через модули а = F/m – для решения задач Выразим из 2 -го закона Ньютона равнодействующую силу: F = ma Отсюда: 1 Н = 1 кг * 1 м/с2 для графиков

План решения задач: Записываем данные в условие (по модулю) и переводим единицы (при необходимости). 2. Определяем, сколько сил действует на тело. 3. Если на тело действует одна сила (или на каждое тело – по одной силе), то записываем формулу 2 -го закона Ньютона по модулю и переходим к п. 4 г. Пример: 1.

Условие задачи: Найти силу, которую необходимо приложить к телу, чтобы оно из состояния покоя за 5 с приобрело скорость 5 м/с. Решение: 1) Записываем данные в условие 2) Определяем, сколько сил действует на тело 3) Записываем формулу 2 -го закона Ньютона а = F/m 4) Выражаем неизвестную величину F = ma 5) Пользуясь формулами кинематики, выражаем ускорение через скорости а = (V-V 0)/t 6) Подставляем в формулу 2 -го з. Н. F = m*(V-V 0)/t 7) Подставляем данные, производим расчет 8) Записываем ответ и оцениваем его.

4. Если на тело действует больше одной силы, то: а) Рисуем тело (в виде прямоугольника) и указываем все действующие на него силы, его скорость и ускорение. б) Выбираем ось координат (ось х, ось у или оси х, у) в) Записываем формулу 2 -го закона Ньютона в векторном виде, а затем проектируем ее на оси. г) Используя формулы кинематики, выражаем неизвестную величину. д) Подставляем данные, производим расчеты. е) Записываем ответ и оцениваем его.

4.2 Первый закон движения Ньютона: инерция – College Physics

Опыт подсказывает, что покоящийся объект будет оставаться в покое, если его оставить в покое, и что движущийся объект имеет тенденцию замедляться и останавливаться, если не прилагать каких-либо усилий, чтобы удержать его в движении. Однако первый закон движения Ньютона утверждает следующее:

Первый закон движения Ньютона

Покоящееся тело остается в покое или, если оно движется, остается в движении с постоянной скоростью, если на него не действует чистая внешняя сила.

Обратите внимание на неоднократное использование глагола «остается». Мы можем думать об этом законе как о сохранении статус-кво движения.

Вместо того, чтобы противоречить нашему опыту, первый закон движения Ньютона утверждает, что должна быть причина (которая является чистой внешней силой) , чтобы произошло какое-либо изменение скорости (изменение величины или направления) . В следующем разделе мы определим чистую внешнюю силу . Предмет, скользящий по столу или полу, замедляется из-за действующей на объект чистой силы трения.Если трение исчезнет, ​​будет ли объект по-прежнему замедляться?

Идея причины и следствия имеет решающее значение для точного описания того, что происходит в различных ситуациях. Например, рассмотрим, что происходит с объектом, скользящим по шероховатой горизонтальной поверхности. Объект быстро останавливается. Если мы распыляем на поверхность тальк, чтобы сделать поверхность более гладкой, объект скользит дальше. Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше. Экстраполируя поверхность без трения, мы можем представить себе, как объект скользит по прямой бесконечно долго. Таким образом, трение – это причина замедления (в соответствии с первым законом Ньютона). Объект вообще не замедлился бы, если бы трение было полностью устранено. Рассмотрим стол для аэрохоккея. Когда подача воздуха отключена, шайба скользит лишь на небольшое расстояние, прежде чем трение замедляет ее до полной остановки. Однако, когда воздух включен, он создает поверхность, почти не имеющую трения, и шайба скользит на большие расстояния, не замедляясь.Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, насколько быстро объект будет замедляться. Трение – это внешняя сила.

Первый закон Ньютона является полностью общим и может применяться ко всему: от объекта, скользящего по столу, до спутника на орбите и крови, перекачиваемой из сердца. Эксперименты полностью подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой. Идея общеприменимых или универсальных законов важна не только здесь – это основная черта всех законов физики.Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности. Гений Галилея, который первым разработал идею первого закона, и Ньютона, который его разъяснил, заключался в том, чтобы задать фундаментальный вопрос: «В чем причина?» Причинно-следственное мышление – это мировоззрение, коренным образом отличающееся от типичного древнегреческого подхода к таким вопросам, как «Почему у тигра полосы?» можно было бы ответить по-аристотелевски: «Такова природа зверя.Возможно, это правда, но бесполезная догадка.

Масса

Свойство тела оставаться в покое или оставаться в движении с постоянной скоростью называется инерцией. Первый закон Ньютона часто называют законом инерции. Как мы знаем по опыту, некоторые объекты обладают большей инерцией, чем другие. Очевидно, что изменить движение большого валуна сложнее, чем, например, баскетбольного мяча. Инерция объекта измеряется его массой. Грубо говоря, масса – это мера количества «вещества» (или материи) в чем-либо.Количество или количество вещества в объекте определяется количеством атомов и молекул различных типов, которые он содержит. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. На практике очень сложно подсчитать и идентифицировать все атомы и молекулы в объекте, поэтому массы не часто определяются таким способом. Оперативно массы предметов определяют путем сравнения со стандартным килограммом.

Проверьте свое понимание

Что больше по массе: килограмм ватных шариков или килограмм золота?

Решение

Они равны. Килограмм одного вещества равен по массе килограмму другого вещества. Величины, которые могут различаться между ними, – это объем и плотность.

Урок Исследование первого закона движения Ньютона – инерция

5e Модель плана урока

Многие из моих уроков естествознания основаны и преподаются с использованием модели плана урока 5E: «Вовлекать, исследовать, объяснять, разрабатывать и оценивать».Эта модель плана урока позволяет мне использовать для учащихся различные возможности и стратегии обучения. Обладая множественным опытом обучения, учащиеся могут получать новые идеи, демонстрировать мышление, делать выводы, развивать навыки критического мышления и взаимодействовать со сверстниками посредством дискуссий и практических занятий. На каждом этапе этой модели урока я выбираю стратегии, которые лучше всего подходят учащимся в отношении представленных им концепций и содержания. Эти стратегии были выбраны для этого урока, чтобы способствовать дискуссиям между коллегами, участию в групповой деятельности, практике рефлексивного обучения и ответственности за обучение.

Устройство Focus

Блок «Силы и движения» фокусируется на гравитации, которую Земля оказывает на объекты в состоянии покоя или во время движения. Имея это в виду, студенты будут исследовать типы сил и их влияние на движущиеся объекты. Они узнают, как силы могут остановить движение объекта, увеличить или уменьшить скорость движения объекта, изменить его направление и привести в движение неподвижный объект. С помощью моделей, исследований, исследований, а также в процессе проектирования и проектирования студенты узнают, что гравитация – это постоянная сила, влияющая на движение объекта.Модуль завершается со студентами, использующими процесс проектирования и проектирования для создания зиплайна, чтобы проиллюстрировать эффекты гравитационной силы.

Краткое содержание урока

В этом уроке, Первый закон движения-инерции Ньютона , я начинаю некоторое время ходить по комнате, чтобы продемонстрировать движение. Студенты делают наблюдения и делятся ими вслух. Я связываю их наблюдения с ключевой лексикой, использованной на этом уроке. Чтобы отслеживать ключевые термины, учащиеся заполняют графический органайзер. Я показываю короткое видео, в котором выделяются основные идеи и словарный запас первого закона движения Ньютона, который учащиеся добавляют в свой графический органайзер. Затем студенты исследуют этот закон движения, принимая участие в «High Dive». Мы участвуем в управляемой дискуссии и соотносим части нашей деятельности с этим законом движения-инерции. Урок завершается тем, что учащиеся применяют полученные знания, создавая плакат, на котором отображаются и объясняются три реальных примера, относящихся к закону движения-инерции Ньютона. Я собираю это и использую для формирующей оценки.

Научные стандарты нового поколения

В этом уроке будут рассмотрены и поддержаны будущие уроки по следующим стандартам NGSS:

5-ПС2-1. Поддержите аргумент, что гравитационная сила, действующая на объекты Землей, направлена ​​вниз.

Научные и инженерные практики

Студенты занимаются следующими научно-техническими практиками:

3. ) Планирование и проведение расследования. Учащиеся проводят расследование, чтобы получить доказательства Первого закона движения Ньютона, и используют свое понимание для создания плаката, демонстрирующего примеры из реального мира, которые имеют отношение к этому закону.

Общие концепции

Первый закон движения-инерции Ньютона урок будет коррелировать с другими междисциплинарными областями. Эти пересекающиеся концепции включают:

2.) Причина и следствие. Учащиеся проводят расследование, чтобы определить влияние силы, приложенной к объекту, в состоянии покоя. Они используют свои наблюдения, чтобы понять влияние силы и инерции.

Основные дисциплинарные идеи

Основные дисциплинарные идеи в рамках этого урока включают:

PS2.A – Силы и движение

PS2.B- Типы взаимодействий

______________________________________________________________________________________________________

Методы управления в классе

Важность моделирования для развития Студент

Ответственность, подотчетность и независимость

В зависимости от времени года, в которое проводится этот урок, учителя должны рассмотреть возможность моделирования того, как группы должны работать вместе; установить групповые нормы для занятий, классных дискуссий и партнерских бесед. Кроме того, важно моделировать стратегии мышления вслух. Это позволяет учащимся быть более выразительными и развивать навыки мышления во время занятия. В первой половине года я моделирую, как групповая работа и / или беседы «выглядят и звучат». Я вмешиваюсь в тот момент, когда ученики не заняты, с помощью напоминаний и перенаправления. Ко второй и последней половине года я могу спросить студентов: «Кто может дать из трех напоминаний о том, что групповая деятельность будет успешной?» Кто может сказать нам два напоминания о партнерских переговорах? » Студенты берут на себя ответственность за то, чтобы стать успешными учениками.Опять же, прежде чем проводить этот урок, примите во внимание время года, возможно, потребуется выполнить большую предварительную нагрузку, чтобы ученики в конечном итоге стали более независимыми и своевременно переходили к урокам.

В целях управления временем я использую «лабораторных крыс», где у каждого ученика есть номер на спинке стула 1,2,3,4 (ученики сидят группами по 4 человека), который отображается на доске. Для каждого вида деятельности, в которой я использую лабораторных крыс, я случайным образом меняю роли, чтобы студенты выполняли разные задачи, в том числе: директор, менеджер по материалам, репортер и техник .Это обеспечивает плавные переходы и эффективность при настройке, работе и очистке.

Закон инерции Ньютона | Texas Gateway

Этот ресурс представляет собой сборник текста, видео и других элементов, призванных создать для учащихся комплексный учебный процесс по 5E. Это предназначено для обучения Уровня I в соответствии с моделью «Реакция на вмешательство» (RtI) для 8-го класса по естественным наукам TEKS (6) (C), в частности, по закону инерции Ньютона.

Обязательно проверьте наличие необходимых знаний и навыков, а также потребности в дифференциации, проверив весь ресурс и связанные элементы, прежде чем назначать их своим ученикам или работать над ними.

Этот ресурс можно использовать для обучения по-разному.
• Использование с одним компьютером и проектором; этот ресурс можно преподавать в традиционном классе.
• Используйте с комбинацией индивидуальных компьютеров учеников, компьютера учителя и проектора (в компьютерном классе или в другой среде 1: 1).
• Назначьте ресурс учащимся в качестве работы, которую нужно выполнять вне учебного дня в рамках «перевернутого класса», чтобы можно было подавать заявки, практиковаться и получать дополнительную поддержку в течение учебного дня.
• Используйте со студентами в качестве учебных пособий.
• Поделитесь с родителями, чтобы рассказать им о том, что их ребенок изучает в школе.
• Используйте с учениками, которые не могут участвовать в традиционной учебной среде.

Engage
Студенты просматривают видео, на котором женщина чуть не упала, когда вагон метро внезапно тронулся. Это видео должно побудить учащихся задуматься о том, почему это происходит, когда транспортное средство, например вагон метро, ​​внезапно движется или останавливается.

Параметры классной комнаты
• Предложите учащимся просмотреть видео и вместе подумать о том, что происходит и какое научное явление вызывает это. Попросите учащихся записывать свои мысли в свои научные тетради.
• Попросите студентов провести мозговой штурм в других случаях, когда это происходит, а затем сравнить и сопоставить эти ситуации, чтобы объяснить, что происходит.

Исследуйте
Ученики собирают данные, просматривая видео, на котором девушка падает с лошади. Студенты заметят, что лошадь остановилась, но девушка на видео продолжала двигаться в том же направлении. Здесь учитываются ситуации, когда всадник может иметь большую или меньшую массу и возможную связь с инерцией.

Классный вариант
• Те же данные можно получить, разрешив учащимся использовать маленькие игрушечные машинки и стиральные машины разного размера, чтобы исследовать, как далеко уходит стиральная машина, когда машина внезапно останавливается. Учащиеся кладут стиральную машину на крышу игрушечной машинки, а затем внезапно останавливают машину и измеряют, насколько далеко стиральная машина перемещается от своего положения на крыше машины.

Explain I
The Explain связывает наблюдения студентов и сбор данных с помощью Engage and Explore с концепцией первого закона Ньютона, закона инерции.Важно, чтобы учащиеся использовали множество реальных приложений для понимания, поэтому также существует связь с автомобильными авариями. В разделе «Связанные элементы» есть видео, в котором подробно рассматривается закон инерции Ньютона в применении к автомобильным авариям.

Elaborate
Видео в сложном виде показывает связь с профессиональным футболом и законом инерции Ньютона. Учитель может установить любые дополнительные связи, которые сделают закон инерции актуальным для его или ее учеников.

% PDF-1.4 % 641 0 объект > эндобдж xref 641 75 0000000016 00000 н. 0000004257 00000 н. 0000004363 00000 п. 0000004492 00000 н. 0000005129 00000 н. 0000005409 00000 п. 0000008739 00000 н. 0000009138 00000 п. 0000009551 00000 п. 0000013285 00000 п. 0000013540 00000 п. 0000013652 00000 п. 0000013766 00000 п. 0000013816 00000 п. 0000014179 00000 п. 0000014481 00000 п. 0000014539 00000 п. 0000015206 00000 п. 0000015431 00000 п. 0000015840 00000 п. 0000016012 00000 п. 0000016632 00000 п. 0000017251 00000 п. 0000020604 00000 п. 0000024183 00000 п. 0000024528 00000 п. 0000027367 00000 п. 0000027598 00000 п. 0000027663 00000 п. 0000028030 00000 п. 0000028248 00000 п. 0000028549 00000 п. 0000033369 00000 п. 0000033537 00000 п. 0000033960 00000 п. 0000037485 00000 п. 0000037787 00000 п. 0000038407 00000 п. 0000038567 00000 п. 0000039187 00000 п. 0000039714 00000 п. 0000043249 00000 п. 0000043303 00000 п. 0000046248 00000 п. 0000048345 00000 п. 0000049529 00000 п. 0000050065 00000 п. 0000051247 00000 п. 0000051457 00000 п. 0000051661 00000 п. 0000052095 00000 п. 0000053273 00000 п. 0000053488 00000 п. 0000055726 00000 п. 0000058762 00000 п. 0000060748 00000 п. 0000062637 00000 п. 0000073013 00000 п. 0000085000 00000 н. 0000087529 00000 п. J` @ kA @ -`B “> , Y “ET (j-D Ժ Lg΍

ЗАКОН ИНЕРЦИИ

 

 

 
 
 Закон инерции гласит, что: 
 
  Тело будет сохранять свою скорость и направление до тех пор, пока на него не действует сила, действующая в направлении его движения.
  Например:  пакет, выброшенный из самолета, продолжит движение со скоростью самолета по горизонтальной оси (в направлении движения самолета). Поскольку на упаковку действует закон гравитации (вертикальная ось, направленная вниз), упаковка будет набирать скорость по вертикальной оси, но по горизонтальной оси ее скорость останется равной скорости самолета.
 (В этом объяснении мы не учли силу сопротивления воздуха).
 Закон инерции – основа новой физики семнадцатого века.Этот закон справедлив и для современной физики.  Галилей  открыл закон в течение первого десятилетия семнадцатого века, но на самом деле он не понимал закон в том виде, в котором мы его здесь сформулировали. Общая формулировка закона инерции была разработана учениками Галилея и  Декартом  – французским философом, математиком и физиком. Этот закон также является первым из  трех законов Ньютона .

 
 До времен Галилея считалось, что нужно приложить силу, чтобы вызвать и сохранить движение, как утверждала физика  Аристотеля .Действительно, когда мы смотрим на окружающий нас мир, мы видим, что для продолжения движения мы должны приложить силу. Так, например, чтобы сохранить скорость автомобиля, двигатель должен работать. Объекты, к которым не применяется сила для сохранения движения, в конечном итоге останавливаются. Галилей понимал, что остановку тел можно объяснить тем, что мы всегда сталкиваемся с силой трения, которая сопротивляется движению тел. Однако без такой силы сопротивления тела продолжали бы двигаться с прежней скоростью.
 Закон инерции также важен для астрономии Галилея. Он использовал этот закон, чтобы объяснить, почему мы не чувствуем движения Земли, и особенно почему объекты, падающие на поверхность земли, движутся вместе с землей. Это объяснение связано с законом относительности  , который также основан на постоянном ускорении тел. Таким образом Галилею удалось опровергнуть утверждения своих оппонентов, как в  году на примере лодки , на которой Галилей доказывает закон инерции.Галилей предложил ряд дополнительных доказательств этого закона с помощью наклонной плоскости  . Вы найдете дополнительное объяснение рядом с  глобусом  в выставочном зале.
  Лаборатория – ЗАКОН ИНЕРЦИИ 
 Первый эксперимент.
 Второй эксперимент.
 Третий эксперимент.
 Четвертый эксперимент.

 
 Первый эксперимент: 
  Выводы: 
 Предмет / мяч будет катиться вниз с нарастающей скоростью. Он начинается в состоянии покоя, т.е. его скорость равна нулю, а затем постепенно набирает скорость. Чем длиннее наклонный самолет, тем больше его скорость. Мы называем это увеличение скорости «ускорением». Противоположная ситуация, когда тело постепенно замедляется, называется «замедлением». Таким образом, мы видели, что тело, движущееся по наклонной плоскости, ускоряется вниз.
 Что будет с мячом после того, как мы толкнем его вверх?
 Скорость катящегося по наклонной плоскости шара будет постепенно уменьшаться, а скорость катящегося вниз шара будет постепенно увеличиваться.

 
 Второй эксперимент: 
 Есть ли связь между крутизной плоскости и ускорением тела, движущегося по этой плоскости?
 Между углом наклона самолета и изменением скорости тела?

 
 Третий эксперимент: 
 Есть ли разница между поездкой на велосипеде по умеренному уклону и крутым уклоном?
 
  Выводы: 
 Четвертый эксперимент: 
 Что бы произошло, если бы мы поместили движущийся шар без трения на горизонтальную плоскость, т. Е.э., самолет, не наклоненный ни вниз, ни вверх?
 Увеличит скорость – разгонится?
 Уменьшит ли скорость – замедлится?
 Сохранит ли он нынешнюю скорость?
  Выводы: 

 
  Выводы третьего эксперимента: 
 Чем более умеренный самолет, тем медленнее ускорение тела вдоль него: то есть скорость тела будет увеличиваться медленнее вверх по плоскости. Чем более умеренный наклон, тем меньше замедление тела и большее расстояние, которое оно проходит.
 Мы знаем, что сила тяжести тянет тяжелые предметы вниз, к центру Земли. По этой причине тела на наклонной плоскости тянутся вниз. Чем меньше наклон, тем меньше ускорение движущихся по плоскости тел и меньше замедление движущихся вверх по плоскости предметов.

 
  Выводы четвертого эксперимента: 
 Что-то тянет мяч вправо или влево? Сила тяжести? Любая другая сила? Будет ли мяч, поставленный на пол, двигаться сам по себе без толчка?
 Если бы самолет был несколько наклонен против направления движения мяча, мяч бы замедлился; если бы самолет был наклонен в направлении движения мяча, он бы ускорился. Следовательно, когда плоскость совсем не наклонена (т.е.это горизонтальная плоскость), мяч не будет ни ускоряться, ни замедляться, но сохранит свою текущую скорость.
 Тело, движущееся по гладкой горизонтальной плоскости без трения, не будет ни ускоряться, ни замедляться, но будет продолжать двигаться с постоянной скоростью. Такое тело остановится только тогда, когда его остановит другая сила. Фактически, это закон инерции, четко сформулированный  сэром Исааком Ньютоном  в 1687 году, более чем через восемьдесят лет после того, как Галилей начал исследовать этот закон.

 
  KNOWMAGINE  – http://muse.tau.ac.il/~vrmus
 Я никогда не был доволен первым законом Ньютона 
 Многие учебники напичканы тремя законами движения Ньютона. Для меня не очень. Во-первых, (как отмечают многие) на самом деле это идеи Ньютона о силе. Во-вторых, первый закон в значительной степени является частным случаем второго закона. Вот первые два закона (по-моему):
 Первый закон Ньютона:
 Естественное состояние объекта – постоянное движение.
 Да. Я знаю, что это не так, как обычно пишут.
 Второй закон Ньютона:
 Скорость изменения скорости объекта пропорциональна величине чистой силы, действующей на объект, и обратно пропорциональна массе объекта.
 Это также может быть записано в виде уравнения:
 Я записал ускорение и силу как векторы, потому что они таковы. Если вы не знаете, что такое вектор, просто игнорируйте символы стрелок.
 Как они такие же?
 Закон Ньютона 2  nd  гласит, что результирующая сила пропорциональна ускорению. Что, если результирующая сила равна нулю или если силы нет? Ну тогда ускорение нулевое. Что происходит с объектом с нулевым ускорением? Среднее ускорение (в одном измерении) можно записать как:
 Или вы могли бы сказать, что ускорение – это то, как изменяется скорость. Если скорость не меняется, объект либо движется по прямой с постоянной скоростью, либо находится в состоянии покоя.
 Итак, почему закон 1  st ?
 Я собираюсь предположить (или, может быть, я где-то это читал, потому что я действительно не умею догадываться), что это имеет отношение к Аристотелю. У Аристотеля были свои законы движения. Они выглядят так:
  Первый закон Артистотеля:  Если на объект нет сил, он будет оставаться в покое
  Второй закон Артистотеля:  Если вы надавите на что-то с постоянной силой, он будет двигаться со скоростью постоянная скорость
  Третий закон Артистотеля:  Если вы перестанете толкать движущийся объект, он остановится.Или … естественное состояние объекта – покой.
 Аристотель так их не формулировал, и вам не придется записывать их как три закона. Но это подводит их итог. Вы должны понять, что Аристотель был ЭТОМ человеком. То, что он сказал, было этим. Его идеи о силе долгое время считались истиной. Итак, я подозреваю, что первый закон Ньютона действительно противодействует Аристотелю. Аристотель говорит, что естественное состояние объекта – покой. Ньютон говорит, что естественное состояние объекта – постоянное движение.
 Обратите внимание, что Ньютон был не единственным, кто высказал эти идеи о силе и движении, но по какой-то причине он получил признание. Во всяком случае, дело в том, что первый закон Ньютона довольно глупый.
 Законы Ньютона 
 Первый закон Ньютона 
 Первый закон сформулирован следующим образом:
 Частица будет оставаться в покое или продолжать движение с постоянной скоростью, если на нее не воздействовать.
 внешней неуравновешенной силой.
 Пояснение 

 Каждый объект, на который не действует внешняя сила, не изменит своего состояния.Если он был в покое, он останется в покое;
 если он двигался, он продолжит двигаться с той же скоростью и в том же направлении. Ничего не меняется в
 это уважение, когда на него не действует сила. Обратите внимание на употребление в законе слова «несбалансированный»; сбалансированные силы отменить
 друг друга, в результате чего не было никакой силы.
 Примеры 
 Вертолет в зависании (на высоте нескольких футов над землей) – пример объекта.
 то есть в состоянии покоя.В горизонтальной плоскости на него не действуют никакие силы. В
 В вертикальной плоскости силы уравновешены: вес против вертикальной тяги. Вертолет
 остается в покое.
 Другой, более теоретический пример: предположим, что нет никакого трения / сопротивления;
 у вас есть
 тот же парящий вертолет, но теперь его кто-то толкает
 (не пытайтесь это
 дома!) Вертолет начнёт двигаться в том направлении, в котором он
 подталкивается и будет продолжать это делать.Это не остановит. На самом деле, однако,
 в
 вертолет перестанет двигаться, потому что на него действует другая сила: трение;
 в данном случае более известное как перетаскивание.
 Второй закон Ньютона 
 Второй закон гласит: 
. 
 F = м. 
 
 где: 
 F = Сила (Н) 
 m = Масса (кг) 
 a = Ускорение (м / с2)
 Чистая сила, действующая на объект, равна массе объекта, умноженной на
 своим ускорением.
 Пояснение 
 Этот закон гласит, что сила, необходимая для ускорения объекта, пропорциональна его величине.
 масса. Чем больше масса объекта, тем больше требуется сила (для того же
 количество ускорения). Обратите внимание, что этот закон иногда называют законом инерции. Масса объекта – это мера его инерции (инерция – это свойство
 объекта, чтобы противостоять изменению движения).
 Примеры 
 При условии, что
 вес и вертикальная тяга остались прежними, вертолет из предыдущего примера теперь хочет двигаться вперед.Для этого он должен ускориться.
 путем приложения силы, направленной вперед. Затем он начнет двигаться. Точнее разгонится на величину
 Ф / м. Чем меньше масса вертолета, тем
 тем больше ускорение (с
 такое же количество приложенной силы). Ускорение
 будет происходить до тех пор, пока прилагается сила (при условии, что нет трения и
 тяга). Когда нападающий
 сила снимается, вертолет будет двигаться вперед на
 достигнутая скорость и будет
 продолжить свое путешествие с этой скоростью.
 Теперь рассмотрим вертолет, который все еще движется с постоянной скоростью (т.к.
 к нему не прилагается прямая сила), и учитывать эффект сопротивления (трение
 вызвано движением по воздуху). Вертолет будет замедляться
 в результате сопротивления, действующего в противоположном направлении. Это замедление
 будет продолжаться, пока вертолет не остановится в воздухе; силы сопротивления
 будет
 действовать до тех пор, пока есть перетаскивание (сопротивление существует до тех пор, пока есть
 движение воздуха).
 Обратите внимание, что время, необходимое для достижения нулевой скорости, зависит от начальной скорости,
 масса вертолета и величина сопротивления. Вертолет с большим количеством
 Масса займет больше времени, чтобы достичь нулевой скорости (при том же сопротивлении).
 Третий закон Ньютона 
 Этот Закон гласит:
 Каждое действие имеет равную и противоположную реакцию.
 Пояснение 
 Этот Закон гласит, что когда на объект действует сила, всегда есть
 равная сила в противоположном направлении.Однако эта сила не работает
 на одном и том же объекте (поэтому две силы никогда не могут нейтрализовать друг друга).
 Примеры 
 Когда автомобиль останавливается, возникают силы, действующие между колесами и поверхностью автомобиля.
 дорога. На каждое колесо действует сила, а силы противоположные.
 такой же величины при работе на дорожном покрытии. 
 Когда аэродинамический профиль движется по воздуху, действуют силы трения (лобовое сопротивление).
 в теме.Силы одинаковой величины и в противоположном направлении действуют.
 в эфире. 
 Когда вертолет приземляется на вертолетную площадку, его вес ложится на плечи
 по салазкам. Там есть
 сила, работающая на салазках, удерживает вес вертолета. На поверхность вертолетной площадки действует равная и противоположная сила.
 Классическим примером в области вертолетов является крутящий момент, прилагаемый двигателем для вращения главного вала (с прикрепленными роторами). Третий закон гласит
 что в противоположном направлении должен быть равный крутящий момент.Первая сила (крутящий момент)
 действует на вал, а вторая (реакция) действует на двигатель.
 Это означает, что при работающем двигателе главный вал будет вращаться в одном направлении, а двигатель
 в противоположном. Поскольку двигатель соединен с фюзеляжем, фюзеляж начнет вращаться, потому что он не зафиксирован, а «висит».
 на свободном воздухе. Хвост
 ротор стрелы (анти
 крутящий момент ротора) существует для предотвращения вращения фюзеляжа и обеспечивает силу, с которой это не происходит.
 Комментарии отключены.
 .