Гироскоп с внутренним кардановым подвесом
ГИРОСКОП с ВНУТРЕННИМ КАРДАНОВЫМ ПОДВЕСОМ [c.252]В целях уменьшения влияния моментов трения, возникаюш их при движении гироскопа в кардановом подвесе, применяют внутренний карданов подвес. Схема гироскопа с внутренним кардановым подвесом представлена на рис. Х.1, о. [c.252]
| Рис. Х.1, Схема гироскопа с внутренним кардановым подвесом |
Гироскоп с внутренним кардановым подвесом, так же как и гироскоп, заключенный в наружном карда-новом подвесе, представляет собой механическую систему, Состоящую из трех тел ротора 8 гироскопа (наружное кольцо кардана), внутреннего кольца 3 кардана и вала 7 двигателя 10, приводящего гироскоп во вращение. [c.254]
Ротор 8 гироскопа здесь так же, как и в случае гироскопа с обычным кардановым подвесом, имеет относительно основания три степени свободы вращение вокруг осей г/1 ж Xi.
Составим уравнения движения гироскопа с внутренним кардановым подвесом. В относительном движении внутреннее кольцо 3 развивает инерционный момент М , действующий вокруг оси ри [c.255]
Х.2. Гироскоп с внутренним кардановым подвесом, имеющим идеальные опоры
Если представить себе гироскоп с внутренним кардановым подвесом, имеющим идеальные опоры, для которых [c.259]
Таким образом, гироскоп с внутренним кардановым подвесом может быть использован как измеритель угловой скорости вращения его основания. [c.266]
Формулы (Х.26) определяют вынужденное движение гироскопа с внутренним кардановым подвесом, параметры которого удовлетворяют условию (Х.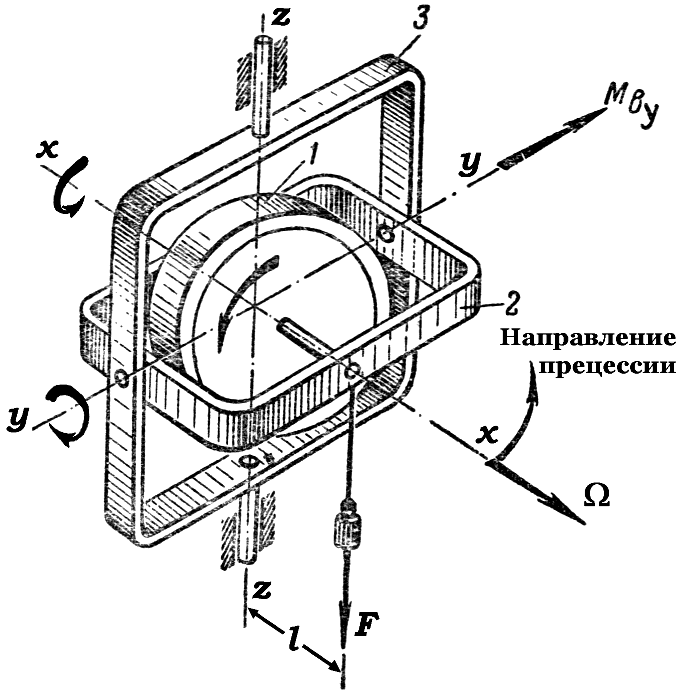 23) в относительных координатах. Абсолютные угловые скорости поворота
[c.267]
23) в относительных координатах. Абсолютные угловые скорости поворота
[c.267]
Гироскоп с внутренним кардановым подвесом при выполнении условия (Х.23) превращается в свободный гироскоп, ось г ротора которого сохраняет неизменное направление в абсолютном пространстве.
Если представить себе гироскоп с внутренним кардановым подвесом, кольца которого поворачиваются вокруг своих осей на шариковых подшипниках, то следует рассмотреть вопрос о влиянии моментов трения, непременно возникающих при поворотах колец относительно соответствующих осей. [c.268]
Х.21)] происходит по координате р,,, а при выполнении условия (Х.23) с учетом жидкостного момента трения отклонение оси z [см. (Х.ЗЗ)] происходит по координате . Моменты трения М а и М Р принуждают следить ось г ротора гироскопа с внутренним кардановым подвесом за направлением оси вращения двигателя гироскопа.
Рис.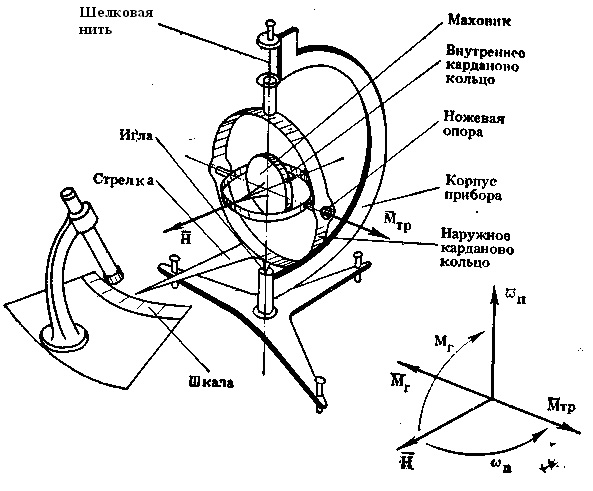 Х.З. К исследованию движения полюса Е гироскопа с внутренним кардановым подвесом Х.З. К исследованию движения полюса Е гироскопа с внутренним кардановым подвесом
|
Собственная скорость прецессии гироскопа с внутренним кардановым подвесом зависит от угловых скоро- [c.279]
Гироскоп с внутренним кардановым подвесом может стать свободным, если к =k = 0 и 2А — i = О, но при этом применение упругого подвеса становится невозможным.
Гироскопом называется твердое тело, имеющее ось динамической симметрии и закрепленное в какой-нибудь точке этой оси. Такое закрепление можно, например, осуществить, придав телу колоколообразную форму, показанную на рис. 392. В различного рода гироскопических приборах закрепление гироскопа осуществляется обычно с помощью карданова подвеса (рис. 394). Карданов подвес состоит из внешнего круглого кольца 1, могущего вращаться вокруг неподвижной оси О21, и из внутреннего круглого кольца 2, могущего вращаться вокруг оси Ох, прикрепленной к внешнему кольцу 1 и перпендику-
[c.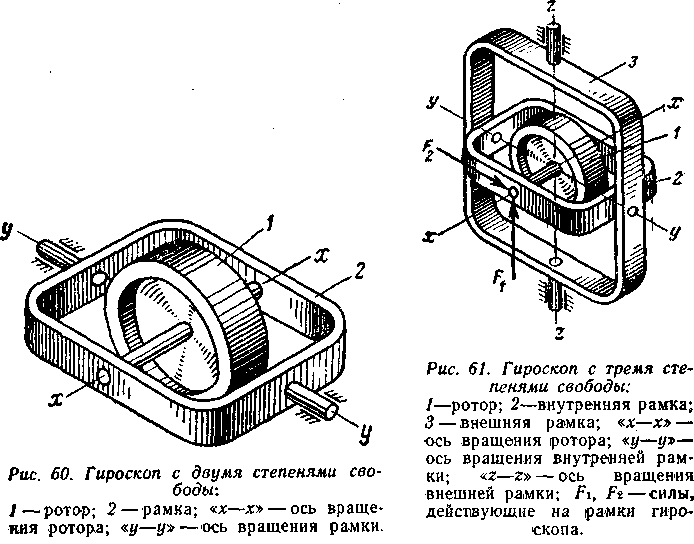
Х.4. Гироскоп с упругим внутренним кардановым подвесом [c.274]
В качестве примера рассмотрим конструктивную схему центрального датчика курса, крена и тангажа автопилота, основной частью которого является силовой трехосный гиростабилизатор с наружным кардановым подвесом (см. рис. ХХ.1). Платформа 7 служит основанием для трех гироскопов 6, 9, 18, имеющих относительно платформы две степени свободы. Карданов подвес платформы состоит из двух рамок карданова подвеса внутренней 3 и наружной 1. Установленные на платформе гироскопы 6 и 9 служат для ее стабилизации вокруг осей Х(, и г/о (в плоскости горизонта), гироскоп 18 предназначен для стабилизации платформы вокруг оси (в азимуте). На платформе 7 также расположены жидкостные маятники-переключатели 15 и 16. На прецессионной оси каждого гироскопа установлены корректирующие моментные датчики 4, 14 ш 19 и индуктивные датчики 8, 11 ж 17 углов поворота кожухов гироскопов относительно платформы. На осях рамок карданова подвеса и платформы смонтированы разгрузочные двигатели 13, 21 ж 22 с, редукторами 12, 20 и 23, сельсины-датчики 2, 5 ж 24 углов поворота платформы относительно корпуса самолета и преобразователь координат 10.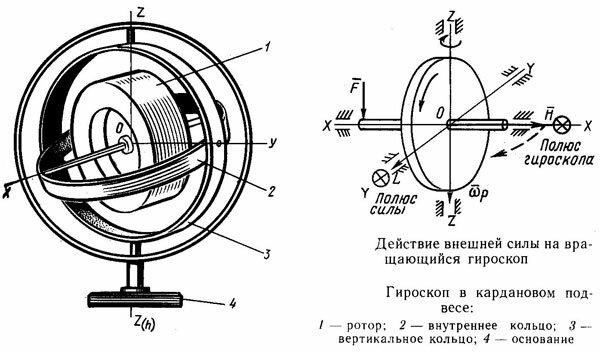
Гироскоп направления установлен в кардановом подвесе. Система координат х у г связана с внешней рамкой (ось вращения ее вертикальна), система хуг скреплена с внутренней
Схема гироскопа представлена на рис, 3.15. Начало координат выберем в точке пересечения осей карданова подвеса. Подвижную систему координат свяжем с внутренним кольцом, направив ось Ох [c.90]
Гироскоп в кардановом подвесе (см. рис. II.1) представляет собой механическую систему, состоящую из трех тел ротора 1, внутренней 3 и наружной 2 рамок карданова подвеса. При этом ротор имеет три степени свободы вращение вокруг оси z, вращение вокруг оси х ротора вместе с внутренней рамкой 3 карданова подвеса и вращение вокруг оси z/j ротора вместе с внутренней и наружной 2 рамками карданова подвеса.
По-прежнему трехгранник xyz свяжем с внутренней рамкой. Направление оси у i, совпадающей с осью наружной рамки карданова подвеса, считаем неизменным в абсолютном пространстве.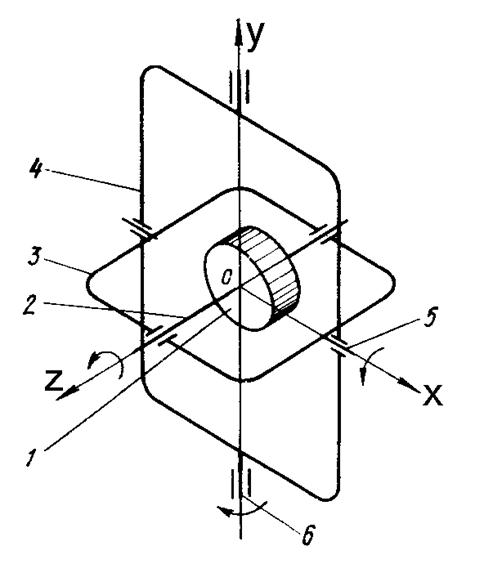 Положение гироскопа по отношению к трехграннику Xiy z определяем углами а, Р и ф (см. рис. II.1 ф — угол поворота ротора вокруг оси 2, отсчитываемый от оси х). В соответствии с этим необходимо составить три дифференциальных уравнения движения такой системы.
[c.119]
Положение гироскопа по отношению к трехграннику Xiy z определяем углами а, Р и ф (см. рис. II.1 ф — угол поворота ротора вокруг оси 2, отсчитываемый от оси х). В соответствии с этим необходимо составить три дифференциальных уравнения движения такой системы.
[c.119]
В связи с тем что ось сохраняет неизменное направление в абсолютном пространстве (корпус гироскопа установлен на неподвижном основании), уравнение моментов, действующих вокруг оси р1, для ротора, внутренней и наружной рамок карданова подвеса принимает вид
Положение гироскопа относительно системы координат, связанной с самолетом, определяется углами а и Р (см. рис. VII.1) поворота оси 2 ротора гироскопа вокруг осей /1 наружной и X внутренней рамок его карданова подвеса. [c.163]
Если I со ( гироскопический момент Л со, развиваемый гироскопом, не в состоянии преодолеть момент М трения в подшипниках оси внутренней рамки карданова подвеса.
Если гироскоп подвержен воздействию такой круговой вибрации, когда каждая точка платформы описывает окружность, лежащую в вертикальной плоскости и совпадающую с плоскостью, перпендикулярной оси х вращения подшипников внутренней рамки карданова подвеса, то скорость прецессии гироскопа, возникающая вокруг оси [c.239]
Здесь упругая связь условно представлена в виде торсиона 1, обладающего жесткостью 3 и соединяющего невесомую наружную рамку 2 карданова подвеса с маховиком 3, в котором сосредоточена масса наружной рамки карданова подвеса и стабилизируемого объекта, например оптического прицела, установленного на оси у) наружной рамки карданова подвеса. Момент инерции наружной рамки карданова подвеса и стабилизируемого объекта вокруг оси у1, которым в нашей модели гироскопа обладает маховик 3, обозначим через А2, моменты инерции внутренней рамки вместе с ротором, взятые относительно осей X и 1/1,— через Ад и Вд соответственно, кинетический момент ротора гироскопа — через Н = углы Реза-
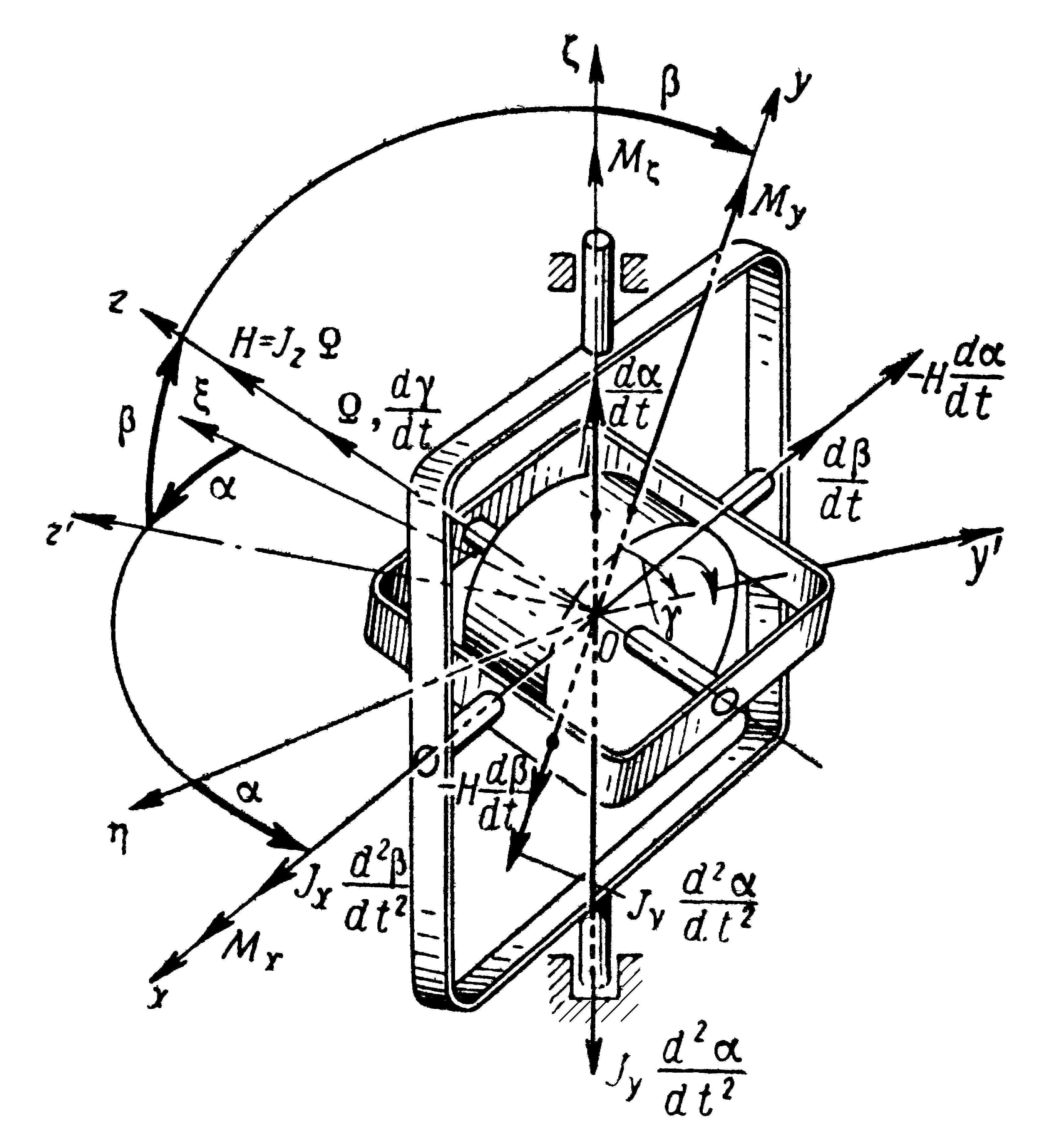 247]
247]
Х.З. Влияние моментав трения на движение гироскопа с внутренним кардановым подвесом [c.268]
Прибор Фуко представляет собой гироскоп с тремя степенями свободы, центр тяжести которого совпадает с центром карданова подвеса. Карданов подвес обеспечивает маховичку свободу вращения вокруг неподвижной точки (три степени свободы),. Он состоит из наружного 4 и внутреннего 3 колец. Маховичок 2 вращаею 1 на подшипниках относительно внутреннего кольца 3, что достигается раскручиванием его с помощью шнурка вокруг оси, перпендикулярной плоскости чертежа. Маховичок 2 вместе с внутренним кольцом 3 свободно поворачивается относительно нарущ,-ного кольца 4 вокруг горизонтальной оси X — X, л наружное кольцо 4, подвешенное на нити 1, вместе с внутренним кольцом и маховичком пово -рачивается вокруг вертикальной оси У [c.8]
Для того чтобы по возможности устранить моменты сухого и жидкостного трения, возникающие при вращении ротора в подшипниках опор карданова подвеса, можно представить себе гироскоп, подвешенный в осях внутреннего карданова подвеса с помощью плоских пружин (пендельфедоров). [c.274]
[c.274]
Рассмотрим вращающийся вокруг оси симметрии гироскоп, укрепленный на кардановом подвесе. Карданов подвес (рис. 59) устроен так, что допускает любое вращение гироскопа вокруг одной неподвижной точки О – центра подвеса, относительно которой момент сил, действующих на гироскоп со стороны подвеса, равен нулю. Он состоит из двух колец, которые могут свободно вращаться относительно осей, соответственно, 1Г и 22. Сам гироскоп укреплен во внутреннем кольце и его собственное вращение происходит вокруг оси 33. Мы рассматриваем случай, когда центр тяжести гироскопа совпадает с центром подвеса, так что момент сил тяжести относительно точки о также равен нулю. При этих условиях покоящийся гироскоп находился бы в положении безразличного равновесия, а вращающийся стремится сохранить состояние собственного вращения. Выясним, как будет вести себя гироскоп, если к его оси на расстоянии г от точки О приложена постоянная сила F (рис. 60 а). Невращаю- [c.72]
Предположим, что на борту КА, осуществляющего полет по квазикруговой орбите, устаноален гироскоп в трехстепенном кардановом подвесе, наружная ось которого параллельна оси ОУд (служащей продолжением радиуса-вектора г) орбитальной системы координат (рис. 12.4). Пусть на наружной оси установлены датчик момента ДМ и датчик угла ДУг. а на внутренней, лежащей в плоскости орбиты, размещен датчик угла ДУ При этом ДМ связан с ДУ схемой рамочной коррекции, обеспечивающей совмещение оси гироскопа с вектором угловой скорости вращения орбитальной системы координат о). Поскольку (о направлен в сторону, противоположную оси 02о рассматриваемой системы, такой гироскоп может играть роль построителя положения плоскости орбиты. Данное обстоятельство послужило основанием для введения термина гироорбита (по аналогии с терминами гирогоризонт, гировертикаль). Другим названием гиро-орбиты, более точно соответствующим ее существу, является.
[c.316]
12.4). Пусть на наружной оси установлены датчик момента ДМ и датчик угла ДУг. а на внутренней, лежащей в плоскости орбиты, размещен датчик угла ДУ При этом ДМ связан с ДУ схемой рамочной коррекции, обеспечивающей совмещение оси гироскопа с вектором угловой скорости вращения орбитальной системы координат о). Поскольку (о направлен в сторону, противоположную оси 02о рассматриваемой системы, такой гироскоп может играть роль построителя положения плоскости орбиты. Данное обстоятельство послужило основанием для введения термина гироорбита (по аналогии с терминами гирогоризонт, гировертикаль). Другим названием гиро-орбиты, более точно соответствующим ее существу, является.
[c.316]
Для более наглядного представления углов Резаля воспользуемся схемой гироскопа в кар-дановом подвесе (рис. 11.1). Карданов подвес служит для обеспечения свободы вращения ротора гироскопа вокруг неподвижной точки О и состоит из двух рамок, каждая из которых имеет свою ось вращения. Ротор 1 гироскопа вращается вокруг своей оси 2 относительно внутренней рамки 3 карданова подвеса. Внутренняя рамка 3 вместе с ротором поворачивается вокруг своей оси х относительно наружной рамки 2, а наружная рамка вместе с внутренней
[c.56]
Внутренняя рамка 3 вместе с ротором поворачивается вокруг своей оси х относительно наружной рамки 2, а наружная рамка вместе с внутренней
[c.56]
Центр тяжести элементов гироузла, включающего в себя ротор, рамки карданова подвеса и другие детали, на них установленные, не совпадает с осями внутренней и наружной рамок карданова подвеса. При этом вокруг осей карданова подвеса возникают моменты внешних сил, порождаемые весом элементов гироузла и инерционными силами, появляющимися при движении основания гироскопа с ускорением. [c.200]
Считаем, что начало О трехгранника xyz лежит на оси х внутренней рамки карданова подвеса гироскопа и вместе с самолетом движется с ускорением W = VFyj + g (см. рис. IX. 1, а). При движении точки О (проекция оси х внутренней рамки карданова подвеса на плоскость чертежа) с ускорением g, направленным в сторону положительной оси у1 вокруг оси X возникает инерционный момент 7Ир 2ц т os Р — /Пр Уц т sin Р, раВНЫЙ моменту ( р-(2ц. т os Р — — Уц.т sinP) от веса ротора. Ускорение W раскладываем на направления осей у и z
[c.242]
т os Р — — Уц.т sinP) от веса ротора. Ускорение W раскладываем на направления осей у и z
[c.242]
Моделирование динамики гироскопа | Блог COMSOL
Недавно, впервые столкнувшись с уравнениями движения вращающихся тел, один из моих сыновей вернулся домой с множеством интересных вопросов. Его вопросы вызвали воспоминание о том, как много лет назад, я испытал такое же чувство растерянности при изучении механики. В сегодняшнем топике, я представлю две модели COMSOL Multiphysics — гироскопа и волчка — иллюстрирующих примечательные свойства вращающихся тел.
Что такое гироскоп?
Гироскоп — термин, придуманный Леоном Фуко в середине 19-го века — был признан как очень полезный инструмент в области науки и техники приблизительно двести лет назад. Его предшественник, волчок, известен, начиная с древних времен, и используется как игрушка для азартных игр и как предмет с магическими и мистическими свойствами.
Как рабочий инструмент, гироскоп ценится за свою точность при измерении и сохранении ориентации. Такие свойства способствуют его использованию в самолетах, космических кораблях и подводных лодках, а также в датчиках инерциальных систем навигации.
Такие свойства способствуют его использованию в самолетах, космических кораблях и подводных лодках, а также в датчиках инерциальных систем навигации.
Копия первого гироскопа.
Классический гироскоп основан на законе сохранения момента импульса. Тело во время вращения стремится сохранить ориентацию своей оси в отсутствие моментов внешних (сил). Устойчивость к изменению ориентации при возмущении (внешнем воздействии) зависит от момента импульса, то есть произведению угловой скорости и момента инерции (тела). Если момент (сил) воздействующих на ротор не параллелен оси вращения, эффект может быть весьма неожиданным.
Примечание: В настоящее время существует несколько типов устройств, служащих той же цели, что и классический гироскоп, но они основаны на отличных физических свойствах. Последние достижения в физике и микросистемной технике сделали это возможным.
Как показано на приведенной ниже схеме, гироскоп состоит из диска, вращающегося с большой угловой скоростью вокруг своей оси.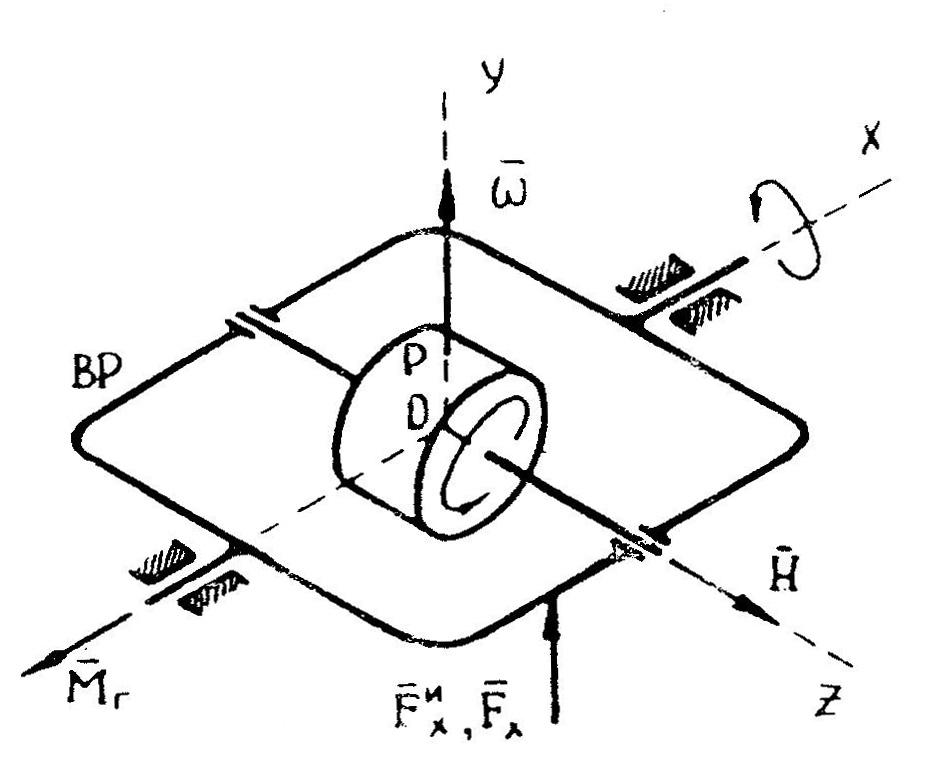 Ось соединяется с внутренним кольцом, называемым карданной подвеской (gimbal). Внутренняя подвеска прикрепляется к внешней карданной подвеске другой парой шарниров. У этих шарниров имеется ось, расположенная под прямым углом к вращающемуся валу. Третья пара шарниров прикрепляет внешнюю карданную подвеску к рамке. В результате ротор обладает тремя вращательными степенями свободы, по одной на каждую ось. Заметим, что рамка крепится к внешнему окружению (например, к сосуду).
Ось соединяется с внутренним кольцом, называемым карданной подвеской (gimbal). Внутренняя подвеска прикрепляется к внешней карданной подвеске другой парой шарниров. У этих шарниров имеется ось, расположенная под прямым углом к вращающемуся валу. Третья пара шарниров прикрепляет внешнюю карданную подвеску к рамке. В результате ротор обладает тремя вращательными степенями свободы, по одной на каждую ось. Заметим, что рамка крепится к внешнему окружению (например, к сосуду).
Если рамка вращается вокруг произвольной оси, ось ротора стремится сохранить свое направление. При этом, обе подвески вращаются.
Схема классического гироскопа.
Моделирование гироскопических эффектов в COMSOL Multiphysics
Используя модуль Динамики многотельных систем в среде COMSOL Multiphysics, мы можем смоделировать механические свойства гироскопа. Наша учебная модель «Моделирование гироскопических эффектов» ориентирована на исследования такого рода. Пример, который обсуждается далее, на самом деле включает в себя две модели: гироскоп и волчок.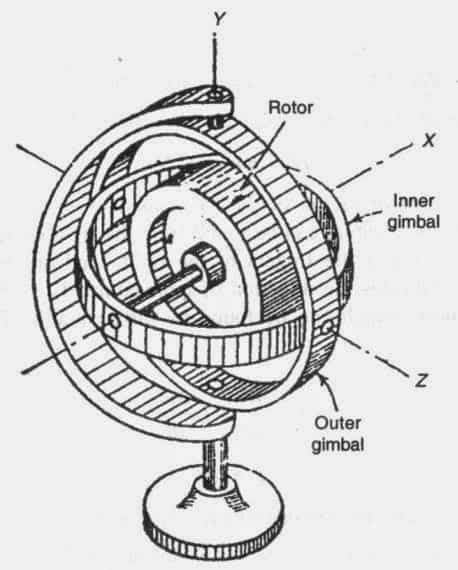
Модель гироскопа
Начнем с нашей модели гироскопа. Геометрия модели включает в себя четыре твердых тела: ротор, два карданова подвеса и рамка. Ротор изготавливается из стали, а остальные части из алюминия. Из-за такого выбора материалов, момент инерции ротора больше по сравнению с поддерживающей конструкцией. Рамке задано установленное вращение вокруг оси, ориентированной под углом 90° от оси ротора и 45° от двух кардановых подвесов винтовой оси. Вращение рамки задано гармоническим с величиной 2 радиана и частотой 2 Гц. Каждый из винтов смоделирован как шарнир.
Чтобы проиллюстрировать эффект вращения ротора на его ориентацию в ходе анализа рассмотрены две различные ситуации. В первом случае, ротор не вращается. Во втором случае, начальное значение угловой скорости ротора составляет 350 рад/с (3342 об/мин).
Первая анимация ниже демонстрирует, что если ротор не вращается, то он вынужден изменять свою ориентацию. Сила тяжести не учитывается в задаче, и кинематически, для ротора имеется возможность сохранять свою ориентацию, так что изменение в ориентации ротора вызывает динамика системы твердых тел. Во второй анимации, видно, что из-за своего вращения, ротору фактически удается сохранять свою ориентацию.
Во второй анимации, видно, что из-за своего вращения, ротору фактически удается сохранять свою ориентацию.
Ориентация ротора при вынужденном вращении рамки, с некрутящимся ротором.
Ориентация ротора при вынужденном вращении рамки, с крутящимся ротором.
На приведенном ниже графике, показано различие в стабильности угла наклона оси ротора. Угловой погрешности порядка 1°, возникающей в случае вращения (с крутящимся ротором), может оказаться все еще недостаточно для использования в высокоточных приборах. Однако изменения в конструкции могут уменьшить это отклонение. В нашем примере, скорость вращения рамки достаточно высока. Рамка поворачивается приблизительно на 115° и обратно, за 0,25 секунды, которые охватываются процессом моделирования. Для улучшения стабильности ориентации оси при таком внешнем воздействии, требуется либо повышение скорости вращения ротора или его утяжеление.
Сравнение наклона оси ротора с вращением и без.
Модель Волчка
Теперь переключим наше внимание на модель волчка. Здесь мы используем только отдельное твердое тело — ротор из предыдущего примера. Ось ротора первоначально ориентирована на 20° от вертикальной оси, а гравитационная нагрузка увеличена. Затем, ротору сообщается начальная угловая скорость вокруг собственной оси. Вместе с силой реакции опоры, сила тяжести создает момент в плоскости вращения на оси ротора и вертикальной оси.
Пара сил, действующих на волчок.
Этот момент сил вызывает угловое ускорение в направлении перпендикулярном плоскости, и волчок начинает изменять свою ориентацию. Это изменение в ориентации волчка, совместно с вращением вокруг собственной оси, вызывает гироскопический момент, действующий на волчок. Под воздействием гироскопического момента, верхушка волчка медленно описывает круговую траекторию. Такое вращение оси ротора называется прецессией. График ниже иллюстрирует траекторию движения вершины оси.
Траектория движения вершины волчка.
Как можно заметить, на широкую круговую траекторию накладываются меньшие циклические биения — движения, известного как нутация. Нутация зависит от начальных условий. Поскольку исследование волчка начинается только с закручивания вокруг оси ротора и без скорости прецессии, то начальные условия не совместимы с чисто прецессионным движением. В реальной физической системе, амплитуда нутации затухает со временем.
Заключение
При решении задач данного типа, важно правильно выбрать временной шаг для анализа. Как правило, он не должен превышать значения, соответствующего углу вращения порядка нескольких градусов за один временной шаг. В приведенных выше примерах, для временного шага используется значение 0,1 мс. Это соответствует повороту ротора вокруг своей оси на угол приблизительно 2° при каждом шаге.
Вы можете скачать учебную модель, представленную здесь, из нашей Галереи Приложений. Если вы заинтересованы в приобретении знаний о другой технологии для проектирования МЭМС гироскопов, мы рекомендуем вам также ознакомиться с нашей учебной моделью Пьезоэлектрический гиродатчик угловой скорости (Piezoelectric Rate Gyroscope tutorial model).
БК0010, MEMS гироскоп и немного Роснано / Хабр
С момента публикации предыдущего поста с вскрытыми микросхемами прошло пол года — пора рассказать, что удалось увидеть нового. Для тех кто пропустил первые 3 серии —
вот раз,
два,
три.
Toshiba TCD1201D — линейный монохромный CCD светочувствительный сенсор из 2048 элементов. Датчики такого типа применяются в факсах, считывателях штрих-кодов и даже на спутниках, фотографирующих землю. Сами светочувствительные элементы — в линии в центре кристалла. Накопленный за время облучения светом заряд постепенно «сдвигается» к краю кристалла двухфазным тактовым сигналом, где он усиливается — и далее уже может быть оцифрован, получится 1 строчка изображения.
Целый кристалл (34.8×0.8мм) в половинном разрешении. В полном разрешении он бы уже не влез в JPEG (80к+ пикселей по ширине):
Миландр 1645РТ2У — радиационно-стойкая микросхема постоянной памяти на 32k*8 бит.
Уровень поликремния, видны сами блоки памяти:
Данные хранятся в элементе antifuse — за счет пробоя тонкого диэлектрика: Здесь зеленые прямоугольники — транзисторы доступа, а сама ячейка памяти — чуть выше/ниже их — в красном прямоугольнике видна овальная область с более тонким диэлектриком. Именно там и происходит пробой.
Именно там и происходит пробой.
Invensense MPU6050 — 6-осевой гироскоп+акселерометр, широко используется в квадкоптерах и телефонах. Состоит из 2 кристаллов, приваренных лицом к лицу. Механические элементы при движении микросхемы — также сдвигаются относительно друг друга, и этот сдвиг можно оценить по изменению емкости.
Первый кристалл:
Второй кристалл:
Под микромеханическими элементами — обычная цифровая логика:
Статическая память, технология производства порядка 250нм:
Microchip 24lcs52 — EEPROM на 2 килобита, используется как SPD-чип в модулях памяти:
Крупнее charge-pump: умножитель напряжения на переключаемых конденсаторах (т.к. для записи/стирания EEPROM нужно относительно высокое напряжение). Здесь конденсаторы — зеленые прямоугольники, а «силовые» транзисторы — между ними.
Еще одна EEPROM на 2 килобита — ST 34C02:
Ti TS5A3159 — 1.65-5В 2:1 аналоговый переключатель с подогнанным сопротивлением каждого канала ~1Ω и гарантией разрыва перед переключением. Транзисторы для обеспечения сопротивления канала 1Ω — занимают бОльшую часть кристалла.
Транзисторы для обеспечения сопротивления канала 1Ω — занимают бОльшую часть кристалла.
Размер кристалла — 1017×631 µm, технология 1µm.
TI LM393 — сдвоенный компаратор напряжения, одна из старых рабочих лошадок электроники.
Размер кристалла — 704×748 µm.
TI TL431 — шунт-регулятор напряжения, часто используемый в линейных источниках питания в сочетании с мощным внешним транзистором. Очень старая микросхема по старым техпроцессам — но до сих пор активно используемая в новых разработках. Конкретно эта микросхема была выпаяна из видеокарты AMD 4870.
Размер кристалла — 1011×1013 µm.
Ken Shirriff уже сделал полную аннотацию электрической схемы, более полный пост он опубликует в ближайшие дни-недели, а пока рисунок. Схему можно увидеть тут.
О SiTime я уже упоминал в статье про высокотехнологичное производство в России. SiTime — одна из компаний, в которую инвестировала деньги Роснано. SiTime SiT8008 — MEMS генератор, который должен заменить кварц с бОльшей надежностью и сравнимой ценой. Для обеспечения максимального Q-фактора механический резонатор запаян в вакууме _внутри_ кристалла.
Для обеспечения максимального Q-фактора механический резонатор запаян в вакууме _внутри_ кристалла.
Основной кристалл — бросается в глаза катушка индуктивности для PLL:
После травления металлизации:
Крупным планом стандартные ячейки — снова технология уровня 250нм.
NXP/Phillips PCF8574 — 8-битный I2C расширитель портов, технология производства 3мкм (!!!). До сих пор производится и продается. Как видим, дело тут не в технологии производства.
SkyWorks AAT4292 — 7-битный расширитель ввода-вывода, с 1.1Ω 100мА ключами в верхнем плече.
После травления металлизации видно, что 7 MOSFET-ов на ток 100мА заняли практически всю площадь кристалла:
Вкусное на последок: Vslav-ом была восстановлена схема серии микросхем из компьютера БК0010 — результаты
опубликованы тут. По результатом анализов — был даже
обнаружен багв реализации контроллера гибких дисков.
Как и в случае с PS1 — это нужно, чтобы делать абсолютно точные эмуляторы.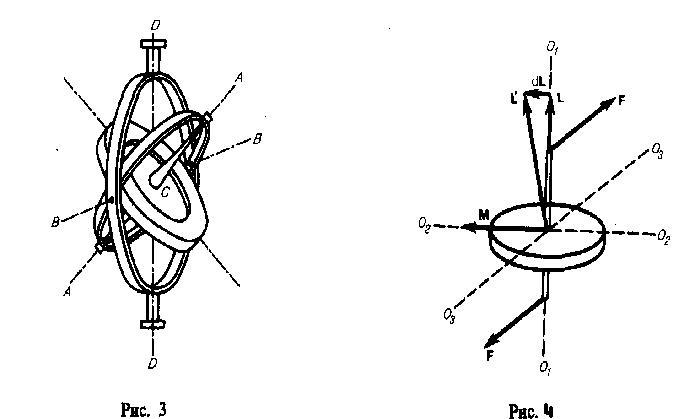
Вся серия КР1801ВП1* — это БМК, базовый матричный кристалл. В БМК все транзисторы / логические блоки уже готовые выходят с завода, остается лишь добавить слой металлизации, который их соединит нужным образом. Получается примерно как FPGA — только программирование раз и навсегда.
Кусочек БМК крупнее. Светлые линии — это металлизация, которой конфигурируется конкретная логическая схема. Подробнее про схему базовой ячейки можно почитать тут.
Все больше людей интересуются восстановлением схемы из микросхем как хобби — что не может не радовать. Следующие кандидаты на восстановление схемы — КР1818ВГ93, популярный в exСССР контроллер гибких дисков (2 микросхемы уже с трепетом ожидают кислотную ванну) и наконец — собственно КР580ВМ80А (заинтересованные люди
скапливаются тут).
Мне также интересно попробовать восстановить схему игры волк-заяц — в прошлую акцию сбора старого железа мне передали одну штуку, но качество вскрытия чипа оказалось неудовлетворительным. Не завалялось ли у кого еще одной игры на растерзание? Нужна именно волк-заяц, или аналогичная с микки-маусом (можно с разбитым экраном или другими повреждениями).
Не завалялось ли у кого еще одной игры на растерзание? Нужна именно волк-заяц, или аналогичная с микки-маусом (можно с разбитым экраном или другими повреждениями).
Надеюсь, эта очередная экскурсия в микромир была интересна.
Update: Добавлена аннотация схемы TL431
В рубрику “Спутниковая связь” | К списку рубрик | К списку авторов | К списку публикаций
Впоследнее время появились сразу несколько новых проектов всемирного спутникового Интернета – американский проект компаний Google и SpaceX, британский OneWeb и российский Yaliny. Каждая группировка представляет собой десятки малых спутников. Чтобы подобные коммерческие проекты могли эффективно работать, вышедшие из строя аппараты нужно будет оперативно заменять новыми. Это не смогут сделать традиционные большие ракеты, поскольку выводить лишь один малый спутник большой ракетой – это абсурдно дорого. Если же ждать попутного запуска на большой ракете, то цена станет очень привлекательной, но ни о какой оперативности уже говорить не придется. Поэтому множество стартапов в мире пытаются разработать сверхлегкую ракету, которая могла бы оперативно выводить в космос спутники массой ориентировочно от 1 до 200 кг. Одна из сложностей при создании маленькой ракеты – бюджетная система управления. Такую систему можно построить на основе MEMS-гироскопов. В статье исследованы источники систематических и случайных ошибок MEMS-гироскопов повышенной точности, смоделировано поведение датчика при выведении на орбиту, собрана модельная статистика точности выведения на орбиту с таким датчиком.
Поэтому множество стартапов в мире пытаются разработать сверхлегкую ракету, которая могла бы оперативно выводить в космос спутники массой ориентировочно от 1 до 200 кг. Одна из сложностей при создании маленькой ракеты – бюджетная система управления. Такую систему можно построить на основе MEMS-гироскопов. В статье исследованы источники систематических и случайных ошибок MEMS-гироскопов повышенной точности, смоделировано поведение датчика при выведении на орбиту, собрана модельная статистика точности выведения на орбиту с таким датчиком.
Recently several new worldwide satellite internet projects (American one of Google and SpaceX, British OneWeb and Russian Yaliny) have been started. Each project is based on network of dozens of small satellites.In order to run smoothly broken satellites must be promptly replaced with new ones. Replacing small satellites one by one by dedicated traditional large space launch vehicles will be absurdly expensive. Launching as secondary payload is a low priced option, but preparing the primary payload often leads to huge delays. That is why a lot of start-ups in the world are trying to develop ultralight rocket that could quickly launch into space a satellites weighing from about 1 to 200 kg. One of the difficulties of creating such rocket is to design and build cheap guidance system. Really cheap rocket control system could be based on MEMS-gyroscopes.
That is why a lot of start-ups in the world are trying to develop ultralight rocket that could quickly launch into space a satellites weighing from about 1 to 200 kg. One of the difficulties of creating such rocket is to design and build cheap guidance system. Really cheap rocket control system could be based on MEMS-gyroscopes.
This article is dedicated to the MEMS sensor errors, both systema- tic and stochastic, sensor behavior during simulated rocket launch and orbital insertion scattering using this sensor.
Главный конструктор по системам управления ООО “ЛИН Индастриал” Andrey Suvorov
Lead Designer for Control Systems, Lin Industrial LLC Ключевые слова:
MEMS, система управления, коррекция систематических ошибок, моделирование выведения на орбиту
Keywords:MEMS, guidance system, systematic errors compensation, orbital launch modeling
Введение
Создание сверхлегких ракет-носителей (с массой полезной нагрузки, выводимой на низкую околоземную орбиту, примерно до 100 кг) в последние годы стало актуальной задачей. Это вызвано бумом малых спутников. Множество стартапов в мире пытаются разработать сверхлегкую ракету. Ниже в таблице приводятся основные технико-экономические характеристики таких ракет от самых известных компаний (всего о планах разработки сверхлегких ракет заявляли десятки организаций).
Это вызвано бумом малых спутников. Множество стартапов в мире пытаются разработать сверхлегкую ракету. Ниже в таблице приводятся основные технико-экономические характеристики таких ракет от самых известных компаний (всего о планах разработки сверхлегких ракет заявляли десятки организаций).
Одна из сложностей при создании маленькой ракеты – бюджетная система управления.
Создание системы управления для ракеты-носителя размерности нанокласса (величина полезной нагрузки (ПН) от 1 до 10, возможно, до 100 кг) подразумевает необходимость использования современных электронных компонентов малой массы и стоимости при обеспечении заданных точности и надежности. Очевидно, что эти условия противоречат друг другу, поэтому поиск оптимального решения затрудняется.
Использование MEMS-технологий вместо механических гироскопов и акселерометров или волоконно-оптических лазерных датчиков угловой скорости требует специального исследования ввиду более сильного влияния на новые датчики факторов ракетного полета. В отличие от космического аппарата ракета-носитель подвергается воздействию специфических факторов космического полета единицы минут. Весь участок выведения на низкую околоземную орбиту занимает 5–15 минут, причем до того, как ракета поднимется выше 40 км, условия работы системы управления мало отличаются от работы на любом транспортном средстве.
В отличие от космического аппарата ракета-носитель подвергается воздействию специфических факторов космического полета единицы минут. Весь участок выведения на низкую околоземную орбиту занимает 5–15 минут, причем до того, как ракета поднимется выше 40 км, условия работы системы управления мало отличаются от работы на любом транспортном средстве.
Содержательной частью этой работы является исследование реально достижимой точности выведения на орбиту при использовании MEMS-датчиков повышенного класса точности. Математическое моделирование позволило определить разброс параметров орбиты выведения по реальным данным, собранным на экспериментальной установке (макете).
Задача настоящего исследования
Проведенное исследование включает в себя создание экспериментальной установки (далее – макета), включая программное обеспечение; набор статистики, анализ величин и причин ошибок и алгоритмов для их коррекции.
MEMS-гироскопы сейчас применяются очень широко ввиду их низкой стоимости, однако датчики низшей ценовой категории недостаточно точны для большинства применений в системах управления.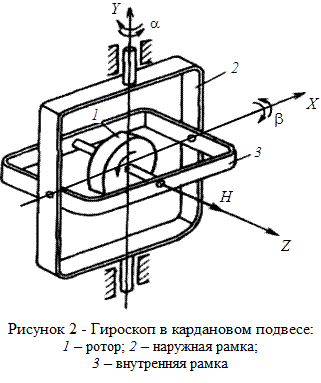
MEMS-гироскопы с ценой порядка $100 за ось имеют гораздо лучшие характеристики точности и стабильности, что позволяет, по крайней мере, попытаться построить на них систему управления (СУ) космической ракеты.
Хотя в космической технике предлагалось использовать такие гироскопы для быстрого восстановления ориентации по звездному датчику [1], никто не ставил целью использовать их как первичные датчики ориентации.
Строго говоря, полностью твердотопливная ракета с наклонным стартом, как ранние японские ракеты-носители Lamb-da-4S [2] и Mu-4S [3], может вывести на орбиту спутник, вообще не используя инерциальную СУ или радиотехническое дистанционное управление. В Lambda-4S использовалась одноосная ориентация, ее датчиком служил четырехрамочный механический гироскоп. Вместо этого можно использовать одноосную солнечную ориентацию. Если правильно выбрать момент запуска, чтобы направление на центр Солнца совпадало с желаемым положением оси ракеты, можно сориентировать ракету по солнечному датчику и, по определенному закону рассчитав вершину траектории, запустить РДТТ, то спутник выйдет на орбиту.
Однако начиная с некоторой размерности, жидкостные ступени оказываются дешевле твердотопливных, поэтому экономически целесообразно попытаться построить такую ракету, используя ЖРД на первой ступени. Но жидкостная ступень требует вертикального старта и ограничения угла атаки из-за малого запаса прочности конструкции и меньшей тяговооруженности. Следовательно, такой ракете понадобится дешевая и малогабаритная система управления. С использованием MEMS-датчиков можно создать СУ массой менее 1 кг (не считая кабельной сети и исполнительных органов).
Для определения применимости MEMS-гироскопов необходимо хотя бы частично смоделировать условия полета на ракете и воспроизвести, насколько это возможно, реакцию исполнительных органов на сигналы, поступающие с MEMS-датчиков.
Исходные данные для модельной установки
Для поисковых работ при большой степени неопределенности конечного результата была выбрана схема ракеты-носителя, обещавшая минимальную зависимость от точности используемого гироскопа. Некоторое “нулевое” приближение требовало снижения требований к гироскопам, поэтому было решено в модели использовать верхние ступени на РДТТ, стабилизируемые вращением.
Некоторое “нулевое” приближение требовало снижения требований к гироскопам, поэтому было решено в модели использовать верхние ступени на РДТТ, стабилизируемые вращением.
Система управления должна работать в составе гипотетической трехступенчатой ракеты, у которой первая ступень жидкостная со временем работы около 150 сек., а верхние две – твердотопливные с небольшим временем работы. Подразумевается, что во время баллистической паузы и прицеливания по Солнцу ориентация обеспечивается газовыми соплами, работающими на газе наддува 1-й ступени.
Модельная установка должна обеспечить отклонение измерительного элемента для имитации программы полета как минимум по двум углам – тангажа и рыскания. Управляющая программа должна обеспечивать передачу данных на персональный компьютер для регистрации и дальнейшей обработки.
Модельная установка
Установка состоит из головки с датчиками, двухкоординатного качающегося стола с электромеханическими приводами, платы управления, источника питания (см. рис. 1). К установке для управления подключается персональный компьютер через последовательный порт (RS-232).
рис. 1). К установке для управления подключается персональный компьютер через последовательный порт (RS-232).
Датчик ADIS16300 включает MEMS-гироскоп (датчик угловой скорости) по оси Z с цифровым представлением выходной информации, 3-осный MEMS-акселерометр по осям X, Y, Z, датчик температуры для коррекции нуля гироскопов и т.д. [4].
На рис. 2 приведен график квадратного корня из вариации Аллана, описывающий точность и стабильность гироскопа. Из этого графика следует, что стабильность гироскопа на временных интервалах более 100 сек. определяется фликер-шумом и не может обеспечить величину дрейфа лучше 25 град. в час. Помимо этого на стабильность нуля гироскопа влияет температура датчика, которую требуется контролировать. Наконец, третьим источником ошибок является паразитная чувствительность к линейному ускорению, которая неодинакова для разных осей.
За время от старта до коррекции по солнечному датчику (номинальное значение 300 сек. ) при хорошей компенсации паразитных эффектов уход может составить около 2 град.
) при хорошей компенсации паразитных эффектов уход может составить около 2 град.
Датчик ADIS16251, стоящий в канале рыскания, обладает похожим набором свойств, но относится к предыдущему поколению, из-за чего его заявленная стабильность примерно вдвое хуже.
Управляющая программа была написана на ассемблере AVR8, а выполнять сложные математические вычисления на ассемблере неудобно. Поэтому для внутренних вычислений используются упрощенные формулы и алгоритмы. В случае численного интегрирования это приводит к потере точности, однако точность самого датчика лимитирует точность получаемых результатов даже сильнее. Поэтому численное интегрирование реализовано в простейшем виде, методом прямоугольников [5], что позволяет обойтись без умножения благодаря удачно выбранному весу младшего разряда и временного кванта. Частота обновления ADIS16300 равна 819,2 Гц, вес единицы младшего разряда составляет 1/80 град. угла в сек.: 1/819,2*1/80=1/65536.
При таких частоте обновления и весе младшего разряда метод прямоугольников дает достаточную точность. Легко определить, что на развороте от 90 до 0 град. за 180 сек. максимальная ошибка не превысит 1,125 град.
Легко определить, что на развороте от 90 до 0 град. за 180 сек. максимальная ошибка не превысит 1,125 град.
Выбор представления ориентации и навигационной модели
Для предварительного анализа точности MEMS-датчиков целесообразно применить простейшую модель, которая не будет включать угол крена, а только углы рыскания и тангажа. Учет ошибки, вносимый дрейфом по крену, довольно сложен и на данном этапе нецелесообразен.
По аналогичным причинам пришлось отказаться и от моделирования терминального наведения, более целесообразным для “нулевого” приближения выглядит жесткий закон управления. Поскольку верхние ступени моделируемой ракеты используют РДТТ, пришлось отказаться и от управления кажущейся скоростью.
На исторических примерах [6] известно, что первые управляемые баллистические ракеты не использовали систему стабилизации центра масс и систему одновременного опорожнения баков. Это приводит к потерям в дальности и точности, однако сравнимые потери привносит использование простейшей программы угла тангажа.
Поэтому на данном этапе целесообразно ограничиться моделью “плоской” Земли (т.е. целевое значение угла тангажа в конце траектории принимается равным нулю), не учитывать нецентральность гравитационного поля. Для моделирования вывода на орбиту используется спредшит Launchmodel [7], написанный Кириллом Левиным для программы Microsoft Excel, как простой в использовании и достаточно точный расчетный инструмент.
Модельная программа угла тангажа и результаты прогонов
При проверке работы программы угла тангажа было обнаружено значительное систематическое расхождение между углом тангажа, измеренным с помощью акселерометра-инклинометра, входящего в состав ADIS16300, и вычисленного интегрированием по данным гироскопа, достигавшее 20 град. (см. рис. 3). По оси абсцисс – время в сек., по вертикальной оси – угол тангажа в град.
Ступеньки, показывающие, что головка двигалась рывками, возникли из-за мертвой зоны электроприводов. Для борьбы с мертвой зоной программа была модифицирована. Было введено слагаемое для компенсации мертвой зоны. Такое слагаемое привело к автоколебаниям амплитудой около 1/8–3/16 град. При их возникновении трение покоя не сказывается и не влияет на точность отработки. Интересно, что трение покоя в подшипниках создавало проблемы и при использовании традиционных механических гироскопов, одним из решений было вибрационное вращение сепаратора в шарикоподшипниках.
Для борьбы с мертвой зоной программа была модифицирована. Было введено слагаемое для компенсации мертвой зоны. Такое слагаемое привело к автоколебаниям амплитудой около 1/8–3/16 град. При их возникновении трение покоя не сказывается и не влияет на точность отработки. Интересно, что трение покоя в подшипниках создавало проблемы и при использовании традиционных механических гироскопов, одним из решений было вибрационное вращение сепаратора в шарикоподшипниках.
Температурная коррекция
MEMS-датчики угловой скорости демонстрируют дрейф нуля из-за колебаний температуры. При включении датчика начинается его разогрев из-за собственного тепловыделения, при этом происходит уход нуля угловой скорости. Для малых скоростей изменения температуры уход примерно пропорционален температуре, при резких изменениях температуры эта пропорциональность нарушается. Таким образом, при эксплуатации датчика необходимо избегать быстрых изменений температуры.
Постоянная времени прогрева гироскопа в спокойном воздухе была экспериментально определена и составила около 12 минут.![]() Обычно требовалось не менее 18 минут от первого включения до калибровки нуля.
Обычно требовалось не менее 18 минут от первого включения до калибровки нуля.
Коррекция медленных изменений температуры была реализована, но, поскольку при быстрых изменениях она не работает, все равно требуется подождать 15 минут до использования датчика. На приведенном графике (см. рис. 4) коррекция медленных изменений уже включена, но видно, что ее влияние в первые 5 минут работы недостаточно.
Коррекция линейного ускорения
Несмотря на то, что MEMS-гироскоп является датчиком угловой скорости, у него есть паразитная чувствительность к линейному ускорению. Ускорение, направленное вдоль определенной оси гироскопа, вызывает смещение нуля, а при интегрировании – фантомный поворот, что и было причиной расхождения, показанного на рис. 4. “Ступеньки” на графике затруднили правильную интерпретацию явления.
В фирменном справочном листе на микросхему ADIS16300[4] чувствительность к линейному ускорению указана одинаковой для всех осей, что не соответствует истине, поэтому пришлось экспериментально выяснить характер этой зависимости. Оказалось, что и у ADIS16300, и у ADIS16251 чувствительность датчика угловой скорости к линейному ускорению максимальна вдоль оси Y и практически отсутствует вдоль оси X. По оси Z, являющейся осью измерения угловой скорости, она промежуточная. Как следствие, если гироскоп установить в ракете так, чтобы продольное ускорение было направлено вдоль оси X, то нормальный полет ракеты не будет сказываться на показаниях гироскопа, и влияние паразитной чувствительности будет невелико. В модельной установке в начале разворота по тангажу гироскоп занимает наивыгоднейшее положение, при котором влияние ускорения свободного падения минимально. По мере поворота проекция вектора g на ось Y увеличивается, и по мере увеличения ноль угловой скорости гироскопа смещается. Это воспринимается как изменение угловой скорости. В результате при постоянной, по данным гироскопа, угловой скорости происходит фактическое замедление поворота.
Оказалось, что и у ADIS16300, и у ADIS16251 чувствительность датчика угловой скорости к линейному ускорению максимальна вдоль оси Y и практически отсутствует вдоль оси X. По оси Z, являющейся осью измерения угловой скорости, она промежуточная. Как следствие, если гироскоп установить в ракете так, чтобы продольное ускорение было направлено вдоль оси X, то нормальный полет ракеты не будет сказываться на показаниях гироскопа, и влияние паразитной чувствительности будет невелико. В модельной установке в начале разворота по тангажу гироскоп занимает наивыгоднейшее положение, при котором влияние ускорения свободного падения минимально. По мере поворота проекция вектора g на ось Y увеличивается, и по мере увеличения ноль угловой скорости гироскопа смещается. Это воспринимается как изменение угловой скорости. В результате при постоянной, по данным гироскопа, угловой скорости происходит фактическое замедление поворота.
Несмотря на то, что это явление не будет иметь места на борту ракеты, т. к. там отклонение вектора ускорения от продольной оси ракеты ничтожно, для оценки точностных характеристик в макете потребовалось ввести такую коррекцию. Для летной системы управления коррекция будет необходима для гироскопа, измеряющего угловую скорость по крену, т.к. он не может быть сориентирован “выгодной” осью X вдоль продольного ускорения. После использования процедур коррекции по температуре и по линейному ускорению данные прогонов стали соответствовать заявленным в даташите характеристикам гироскопа по повторяемости и вариации Аллана.
к. там отклонение вектора ускорения от продольной оси ракеты ничтожно, для оценки точностных характеристик в макете потребовалось ввести такую коррекцию. Для летной системы управления коррекция будет необходима для гироскопа, измеряющего угловую скорость по крену, т.к. он не может быть сориентирован “выгодной” осью X вдоль продольного ускорения. После использования процедур коррекции по температуре и по линейному ускорению данные прогонов стали соответствовать заявленным в даташите характеристикам гироскопа по повторяемости и вариации Аллана.
По результатам 100 прогонов определено среднеквадратичное значение ошибки на 190-й сек. программы в 1,5 град. со стандартным отклонением σ = 1,5 град. При этом 0,25 из 1,5 град. могут быть “списаны” на неперпендикулярность осей гироскопа и акселерометра Y.
На рис. 5 и 6 представлены типичные графики работы установки при включенных коррекциях.
Анализ влияния ошибок MEMS-гироскопа на параметры итоговой орбиты
Для моделирования фактические величины угла тангажа подставлялись в спредшит Launchmodel, и параметры получившейся орбиты сравнивались с идеальными. Целевые орбиты выбирались низкими, т.к. на них больше заметно влияние аэродинамических потерь, а грузоподъемность наноносителя увеличивалась.
Целевые орбиты выбирались низкими, т.к. на них больше заметно влияние аэродинамических потерь, а грузоподъемность наноносителя увеличивалась.
Прицеливание по Солнцу позволяет уменьшить в несколько раз угловую ошибку перед запуском верхних ступеней, но не погрешности в целом.
Оказывается выгодным поставить длительность баллистической паузы в зависимость от фактической скорости разворота по тангажу, которая может быть измерена по времени прихода Солнца в поле зрения солнечного датчика, тогда можно добиться, чтобы перигей был не ниже терминальной точки.
При этом высота апогея изменяется значительно больше, чем высота перигея, поскольку верхние ступени описываемой модели не имеют возможности отсечки и всегда работают до полной выработки топлива. Изменение высоты перигея на 1 км приводит к изменению высоты апогея на 10–12 км. На рис. 7 приведена зависимость высот перигея и апогея, а также оптимальной длительности баллистической паузы для рассматриваемой гипотетической ракеты.
Следует отметить, что вся отображаемая по оси абсцисс область (от 0,51 град./c до 0,56 град./c) – это отклонение ±2 LSB датчика ADIS16300, таким образом, даже с коррекцией по Солнцу выведение на орбиту с таким низким перигеем находится на пределе точностных возможностей этого гироскопа. Если, однако, уменьшить величину полезной нагрузки и выбрать орбиту с более высоким перигеем (240–300 км), то диапазон возможных ошибок, при которых выведение на стабильную орбиту (пусть и отличающуюся от целевой в некоторой степени), заметно увеличится.
Вибростенд и испытания на нем
Для оценки влияния вибраций на точность датчиков использовался самодельный вибростенд из сабвуфера и усилителя мощности звуковой частоты (УМЗЧ), обеспечивающий амплитуду вибрационного ускорения до 25 g на частоте 40 Гц. Ускорение контролировалось по внешнему акселерометру ADXL150, так как встроенный акселе роме т р ADIS16300 имеет диапазон только до 3,5 g.
Значимого влияния по оси X на выходной сигнал гироскопа не обнаружено. Влияние по осям Y и Z в диапазоне до 10 g линейно с точностью не хуже 1%, поэтому на значении интеграла обнаружимо не сказывается. Объем испытаний на вибростенде было решено сократить, так как было обнаружено, что вибрация величиной ~0,5 м/с2, возникающая в рабочем режиме, на точности не сказывается, а вхождение акселерометра в ограничение не влияет на точность показаний гироскопа вплоть до 10 g.
Заключение
Проведенные эксперименты показали, что для ракеты с очень коротким активным участком применение датчика со свойствами ADIS16300 по точности и устойчивости к вибрации и перегрузке позволяет создать систему управления, решающую задачу выхода на орбиту при вертикальном старте. При этом следует уделить внимание термостабилизации датчика в составе СУ, правильной его ориентации (осью Х по продольной оси ракеты), а также адекватной программной обработке данных.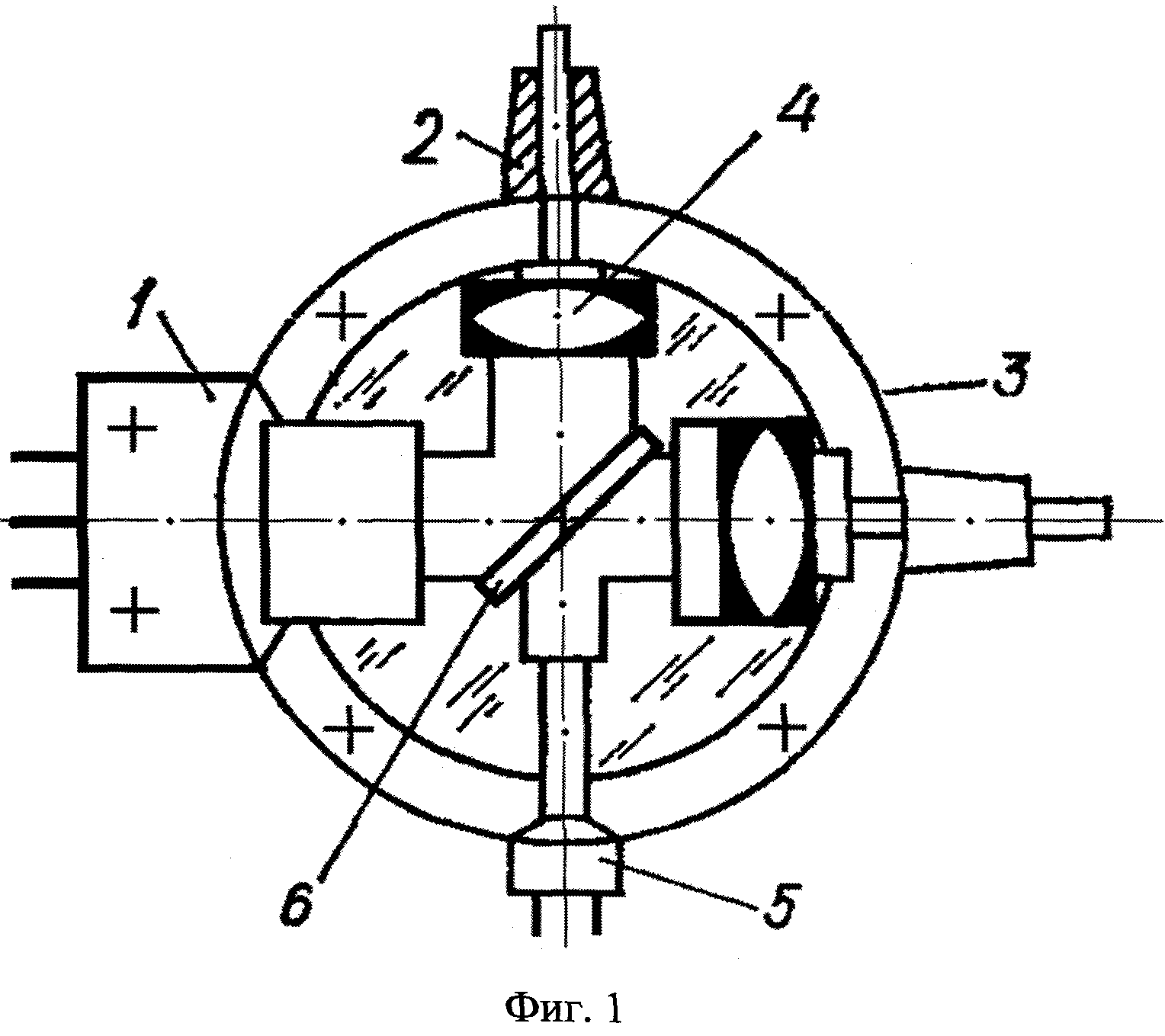 Желательно иметь меньшую дискретность выходных данных, что может облегчить калибровку нуля. Это достижимо в датчике следующего поколения ADIS16445 или при использовании датчика с аналоговым выходом, например ADXRS646-EP, совместно с 16-разрядным АЦП.
Желательно иметь меньшую дискретность выходных данных, что может облегчить калибровку нуля. Это достижимо в датчике следующего поколения ADIS16445 или при использовании датчика с аналоговым выходом, например ADXRS646-EP, совместно с 16-разрядным АЦП.
Для ракет с типичными параметрами активного участка, особенно – многоступенчатых жидкостных, точность ADIS16300 недостаточна и требует дополнительной коррекции, например с помощью одноосной солнечной ориентации. К сожалению, объем статьи не позволил включить в нее описание работы с датчиком солнца, хотя в составе установки датчик был.
Параметры точности, ограничиваемые датчиком:
- перигей, номинал: не ниже 240 км;
- перигей, разброс: ±40 км;
- наклонение, разброс: ±0,25 град.;
- апогей, разброс: ±250 км.
Результаты работы
- Поставлена задача доказательства возможности построения СУ на базе датчиков угловой скорости, построенных на MEMS-технологиях, при параметрах, доступных на начало 2014 г.

- Проведен анализ источников ошибок и возможностей их коррекции на основе датчика ADIS16300.
- Изготовлен макет устройства, моделирующего поведение системы управления в полете.
- Проведено статистическое исследование точности датчика в составе стендовой установки при имитации отработки ракетой с моделируемой СУ программы по углам тангажа и рыскания.
- Проведен анализ влияния получающихся ошибок по углам на параметры орбиты при помощи численного моделирования.
- Определены рекомендации для проектных параметров летной системы управления.
Литература
- Морозова Л.М., Нехамкин Л.И., Рябиков В.С. Об одном алгоритме повышения надежности системы ориентации космического аппарата при сбоях звездного датчика. Третья Всероссийская научно-техническая конференция “Современные проблемы ориентации и навигации космических аппаратов”. Сборник трудов под редакцией Г.
 А. Аванесова. Серия “Механика, управление и информатика”. Москва: ИКИ РАН, 2013. [online] Доступ через: http://ofo.ikiweb.ru/publ/conf_2012_st.pdf (дата обращения: 22.03.2016).
А. Аванесова. Серия “Механика, управление и информатика”. Москва: ИКИ РАН, 2013. [online] Доступ через: http://ofo.ikiweb.ru/publ/conf_2012_st.pdf (дата обращения: 22.03.2016). - L-4S Satellite Launch Vehicles. JAXA official Web-site. [online] Доступ через: http://www.isas.jaxa.jp/e/enterp/roc-kets/vehicles/l-4s/index.shtml (дата обращения: 22.03.2016).
- M-4S Satellite Launch Vehicles. JAXA official Web-site. . [online] Доступ через: http://www.isas.jaxa.jp/e/enterp/roc-kets/vehicles/mu/m4s.shtml (дата обращения: 22.03.2016).
- ADIS16300: Four Degrees of Freedom Inertial Sensor Data Sheet. Analog Devices official Web-site. [online]Доступ через: http://www.analog.com/media/en/technical-documentation/data-sheets/ADIS16300.pdf (дата обращения: 22.03.2016)/.
- Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа: приближение функций, дифференциальные и интегральные уравнения. – 3-е изд. – М.: Наука, Гл.
 ред. физ-мат литературы, 1967. – С. 368.
ред. физ-мат литературы, 1967. – С. 368. - Феодосьев В.И. Основы техники ракетного полета. М.: Наука, Гл. ред. физ-мат литературы, 1979.
- Официальный сайт программы Launchmodel (Авторский сайт Кирилл Левина). [online] Доступ через: http://www.geocities.ws/levinkirill/SpaceModel/rus/index.html (дата обращения: 22.03.2016).
Опубликовано: Журнал “Технологии и средства связи” #3, 2016
Посещений: 5003
Автор
| |||
В рубрику “Спутниковая связь” | К списку рубрик | К списку авторов | К списку публикаций
Как работают оптоволоконные гироскопы?
Сводка
В каждом гироскопе есть лазер, который используется для передачи двух отдельных лучей света через оптическое волокно. Лучи проходят в противоположных направлениях через замкнутый контур и возвращаются к световому датчику, где регистрируется время их прохождения. Если не было изменения вращения, два луча света вернутся одновременно. Любое вращение означает, что расстояние, на которое проходит каждый луч, будет изменяться, и лучи будут приходить в разное время.Угловое вращение можно измерить на основе того, какой луч пришел первым и как долго задерживался второй луч.
Лучи проходят в противоположных направлениях через замкнутый контур и возвращаются к световому датчику, где регистрируется время их прохождения. Если не было изменения вращения, два луча света вернутся одновременно. Любое вращение означает, что расстояние, на которое проходит каждый луч, будет изменяться, и лучи будут приходить в разное время.Угловое вращение можно измерить на основе того, какой луч пришел первым и как долго задерживался второй луч.
Использование технологии гироскопа
На протяжении более 100 лет гироскопическая технология помогает навигации в различных приложениях. Механические гироскопы использовались около 60 лет, пока в 1960-х годах не был изобретен кольцевой лазерный гироскоп . Однако только в 1970-х годах были разработаны, внедрены и реализованы оптоволоконные гироскопы , которые стали популярными в широком диапазоне приложений , от подводных лодок до космических кораблей .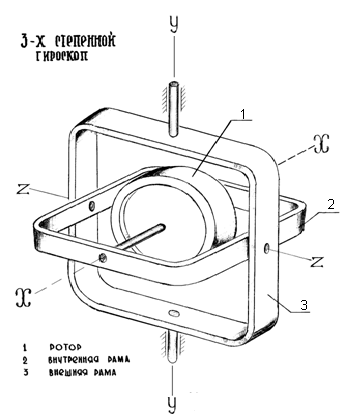
Механический гироскоп (Источник: Pinterest)
Цель любого гироскопа – измерить угловое вращение на любой отдельной оси . Это очень важно для определения углов тангажа, крена и рыскания в системе, которая требует надежной навигационной информации для правильного функционирования. Представьте взлетающий самолет, ракету НАСА, снижающую дальность тангажа, или ракету, обнаруживающую цель. Гироскопы, используемые для таких приложений, измеряют скорость углового вращения каждого транспортного средства.Эта критическая информация отправляется ниже по потоку в систему управления и стабилизирует транспортное средство . (Вельович, 2010)
Каждый гироскоп предоставляет эту информацию с разной степенью надежности и точности, так что же отличает волоконно-оптические гироскопы от других гироскопов?
Волоконно-оптическая технология
Как следует из названия, оптоволоконные гироскопы используют для своей работы оптоволокно .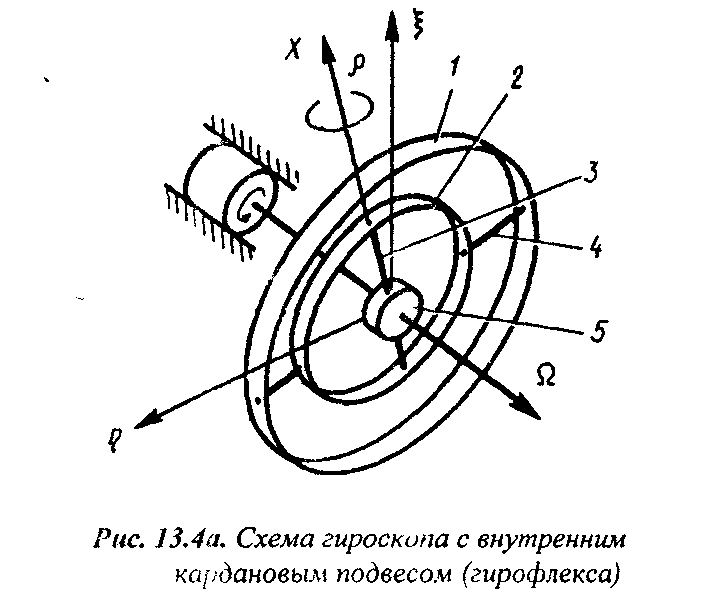 Сделанное из стекла, оптическое волокно используется во многих приложениях для передачи света из одной точки в другую .Часто используемый в телекоммуникациях, таких как телефон и Интернет, оптоволоконный кабель очень быстрый и надежный . (Circuit Digest, 2019)
Сделанное из стекла, оптическое волокно используется во многих приложениях для передачи света из одной точки в другую .Часто используемый в телекоммуникациях, таких как телефон и Интернет, оптоволоконный кабель очень быстрый и надежный . (Circuit Digest, 2019)
Волоконно-оптический кабель крупным планом (Источник: Fiverr Getty)
В волоконно-оптических гироскопах этот метод передачи света не используется для доставки информации где-либо еще, а, скорее, плотно намотан в автономном замкнутом контуре гироскопа . Это позволяет оптоволоконным гироскопам использовать «эффект Саньяка» .
Эффект Саньяка
Обнаруженный французским физиком Жорж Саньяк , это явление лежит в основе работы каждого оптоволоконного гироскопа.
Внутри гироскопа используется лазер для передачи двух отдельных световых лучей по оптическому волокну.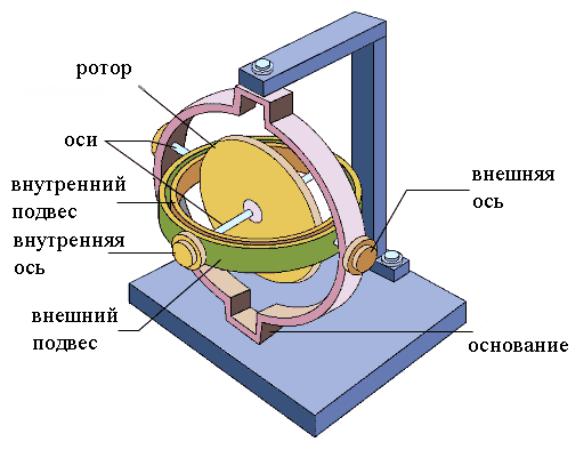 Каждый луч проходит в противоположных направлениях , проходя по всей длине оптического волокна, которое может достигать 5 км. Затем каждый луч возвращается к световому датчику, где записывается их времен прохождения .
Каждый луч проходит в противоположных направлениях , проходя по всей длине оптического волокна, которое может достигать 5 км. Затем каждый луч возвращается к световому датчику, где записывается их времен прохождения .
Возьмем, к примеру, международный полет на крейсерской высоте. Самолет устойчив, летит прямо и ровно без изменения угла поворота.
Самолет, летящий на крейсерской высоте (Источник: Pinterest)
Когда самолет испытывает без изменения вращения , лучей света возвращаются на детектор одновременно . В этом случае нет задержки или «фазового сдвига» между каждым лучом света. Самолет определяется как устойчивый и не вращается со скоростью относительно любой заданной оси.
Однако, когда самолет поворачивает, Саньяк действует в полную силу. Когда самолет поворачивает вправо, оптоволоконный гироскоп, предназначенный для оси крена, будет испытывать задержку прибытия между двумя лучами света .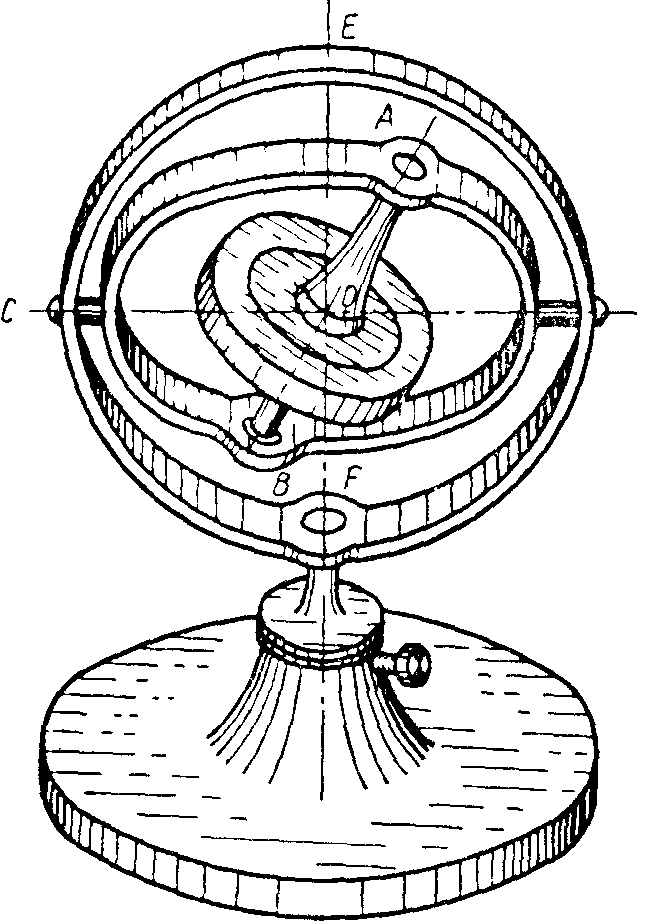 При этом – расстояние, которое должна пройти каждая балка, меняется на .
При этом – расстояние, которое должна пройти каждая балка, меняется на .
Внутренняя схема оптоволоконного гироскопа (Источник: PatentSwarm)
Свет , движущийся против направления вращения, вернется в первый , когда детектор немного приблизился к бегущему лучу.В этом примере луч света, идущий налево, вернется первым. Точно так же луч света, идущий вправо, займет больше времени. Этот фазовый сдвиг между каждым световым лучом определяется как вращательное изменение . Эта важная информация затем может быть отправлена вниз по потоку в самолете, космическом корабле, подводной лодке или ракете для ее стабилизации. Это происходит со скоростью 100 раз в секунду, дает очень точные измерения. (Pascoli, 2017)
Калибровка гироскопа Как и в случае с любым другим гироскопом, источники ошибки , смещения и шума должны быть тщательно учтены и исправлены. Во время производства оптоволоконные гироскопы калибруются для коррекции нескольких потенциальных источников ошибки , которые могут быть внесены самим гироскопом или окружающей средой . После исправления оптоволоконные гироскопы предлагают очень высокий уровень производительности .
Во время производства оптоволоконные гироскопы калибруются для коррекции нескольких потенциальных источников ошибки , которые могут быть внесены самим гироскопом или окружающей средой . После исправления оптоволоконные гироскопы предлагают очень высокий уровень производительности .
Зачем нужны оптоволоконные гироскопы?
Волоконно-оптические гироскопы стали повсеместными во многих приложениях, имея несколько привлекательных характеристик. Они надежны в суровых условиях со значительной вибрацией , не имеют движущихся частей , предлагают хороший баланс между ценой и высокой производительностью и служат в течение значительного времени в эксплуатации .
Источники
Вельович, 2010 г., доступно по адресу: http://www.vti.mod.gov.rs/ntp/rad2010/34-10/12/12.pdf
Circuit Digest, 2019 г., доступно по адресу: https : //circuitdigest.com/article/how-optical-fiber-communication-works-and-why-it-is-used-in-high-speed-communication
Пасколи, 2017 г. , Доступно по адресу: https: // www .sciencedirect.com / science / article / pii / S1631070517300907
, Доступно по адресу: https: // www .sciencedirect.com / science / article / pii / S1631070517300907
Исследования схемы обработки сигналов жидкостного гироскопа | Интернет-исследования в области здравоохранения и окружающей среды (HERO)
ID ГЕРОЯ
2187573
Тип ссылки
Журнальная статья
Заголовок
Исследование схемы обработки сигналов жидкостного гироскопа
Авторы)
Ван, Х; Piao, L; Ю, Q
Год
2012 г.
Проверяется коллегами?
да
Журнал
Расширенные исследования материалов
ISSN: 1022-6680
Заголовок книги
Расширенные исследования материалов
Объем
542-543
Номера страниц
924-927
DOI
10.4028 / www.scientific.net / AMR. 542-543.924
542-543.924Идентификатор Web of Science
WOS: 000317555500187Абстрактный
Исследована схема обработки сигналов жидкостного гироскопа. Эта статья нацелена на проблему схемы для множества электронных компонентов и нестабильности выходного сигнала, была использована схема регулируемого регулятора напряжения и реализован выход другого сигнала напряжения, были использованы стабилизатор напряжения и повторитель напряжения и реализована температурная компенсация сигнала напряжения.Результаты эксперимента показывают, что по сравнению с существующей схемой регулятора напряжения площадь печатной платы уменьшается на 16%, а температурный дрейф выходного сигнала уменьшается на 10% в улучшенной цепи напряжения. Эта схема обработки сигналов проста в применении и доступна для других гироскопов, точность повторяемости которых достаточно высока.
Ключевые слова
Гидравлический гироскоп; Схема обработки сигнала; Схема регулятора напряжения; Температурная компенсация
[PDF] Система и схема для емкостного гироскопа МЭМС
ПОКАЗЫВАЕТ 1-10 ИЗ 143 ССЫЛОК
СОРТИРОВАТЬ ПО РелевантностиСамые популярные статьи Недавность
Гироскоп с боковой осью КМОП-МЭМС
В этой статье сообщается о результатах экспериментов с первого конструкция КМОП-вибрационного гироскопа с поперечной осью, в котором используются гребенчатые пальцы как для срабатывания, так и для измерения.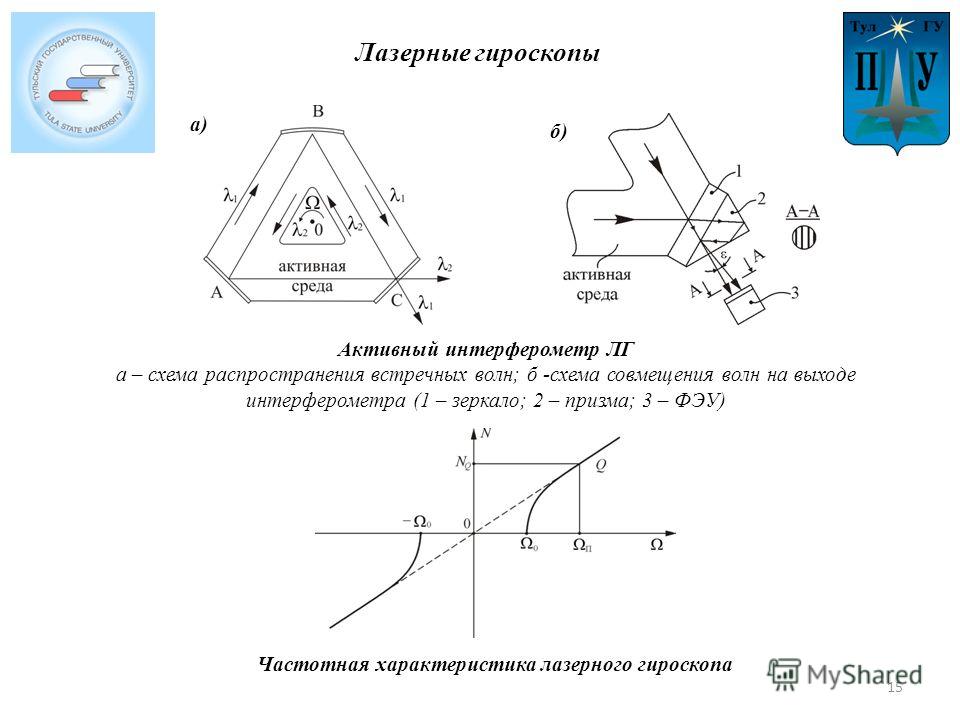 Производство… Развернуть
Производство… Развернуть
Прецизионные схемы считывания для емкостных микроакселерометров
В этой статье представлен обзор входных схем емкостного считывания для высокоточных акселерометров. Представлены основные параметры дизайна и компромиссы, влияющие на разрешение. … Развернуть
- Просмотреть 2 выдержки, справочная информация
Обработка гироскопов МЭМС на основе КМОП-микросхем
Интегрированные гироскопы из поли-SiGe толщиной 10 мкм / м обрабатываются поверх 8-дюймового стандартного 0.КМОП пластина 35 мкм / м с 5 уровнями металлов с использованием усовершенствованного плазменного химического осаждения из паровой фазы… Развернуть
- Просмотреть 5 выдержек, справочные методы и справочную информацию
Микрогироскоп 0,2 ° / час с автоматическим режимом КМОП Соответствие
- Аджит Шарма, FM Заман, Ф. Аязи
Инженерия, информатика
2007 Международная конференция по твердотельным схемам IEEE.
 Дайджест технических документов
Дайджест технических документов- 2007
- Просмотреть 1 отрывок, ссылки на методы
ASIC для емкостных микроакселерометров высокого разрешения
Аннотация Представлена ASIC (специализированная интегральная схема) для емкостных акселерометров с высоким разрешением, использующая методы переключаемых конденсаторов. Схема, реализованная в КМОП-матрице 3 мкм… Развернуть
- Посмотреть 3 выдержки, справочные сведения, фон и методы
Медный КМОП-МЭМС-гироскоп оси Z
В этой статье описывается первый тонкопленочный гироскоп оси Z, изготовленный в медный процесс CMOS-MEMS.Он работает при атмосферном давлении 1 атм и не зависит от повышения добротности. Датчик … Развернуть
Датчик … Развернуть
- Просмотреть 1 отрывок, ссылки на методы
A Микромощный входной модуль для емкостных микроакселерометров
В этой статье представлены результаты измерений микромощного внешнего интерфейса с переключаемым конденсатором, разработанного для емкостных микроакселерометров. Перед рассмотрением результатов измерения… Развернуть
- Просмотреть 2 выдержки, ссылки на методы
MVP Disc Sports и Circuit Events представляют ГИРОскоп №4: Matador
Open (7)
Коди Брэдшоу # 58007
Professional
Fredericksbrg, Вирджиния, США
Трэвис Форман # 32888
Professional
Мартинсбург, Западная Вирджиния, США
Конрад Павлоски # 29571
Professional
Александрия, Вирджиния, США
Tommy Donelson II # 18414
Professional
Burke, Вирджиния, США
Натан Хьюз # 78987
Professional
Стивенс-Сити, Вирджиния, США
Райан Джонс # 26497
Professional
Warrenton, Virginia, United States
Джесси Стоукс # 114842
Professional
Манассас, Вирджиния, США
Профессиональные мастера 60+ (2)
Рик Хонн # 25403
Professional
Silver Spring, Мэриленд, США
Марк Шервуд # 14279
Professional
Hyattsville, Мэриленд, США
| Место | Очки | Имя | PDGA # | Рейтинг | Пар. | Rd1 | Rd2 | Итого | Приз | 903 903Рик Хонн | 25403 | 914 | +5 | 53 | 905 | 52 | 916 | 105 | $ 150 |
|---|---|---|---|---|---|---|---|---|---|---|
| +5 | 52 | 916 | 53 | 905 | 105 |
Продвинутый (5)
Остин Келлехер # 100733
Professional
Mechanicsville, Вирджиния, США
Райан Хаттон # 96254
Любитель
Берк, Вирджиния, США.
Адам Салливан # 85442
Professional
Пасадена, Мэриленд, США
Коннор Галли # 73157
Professional
Fairfax Station, Вирджиния, США
Эван Фрейди # 97524
Amateur
Severna Park, Мэриленд, США
Женщины преклонного возраста (1)
Ingrid Parada # 75878
Amateur
Шантильи, Вирджиния, США
| Место | Очки | Имя | PDGA # | Рейтинг | Пар.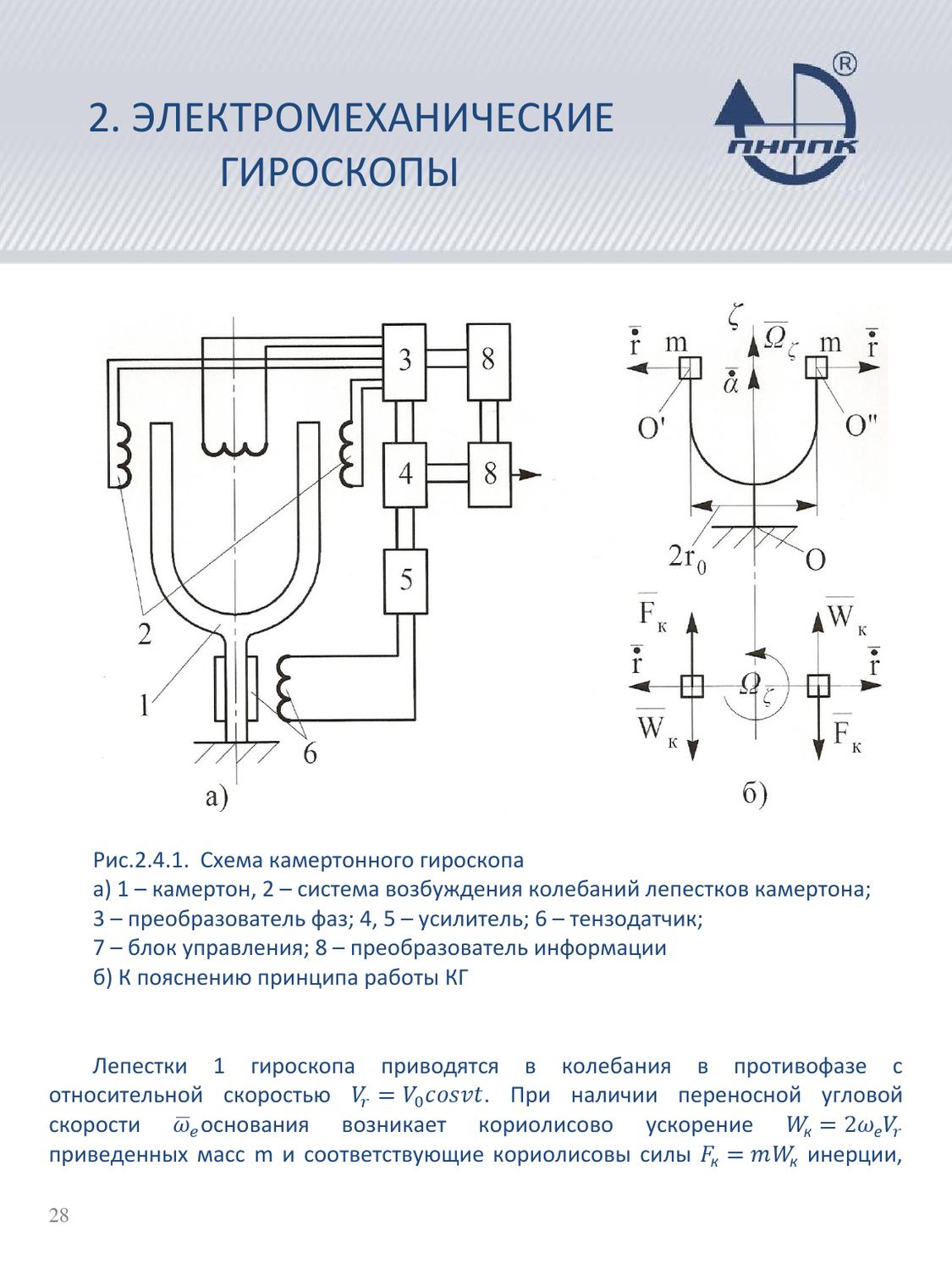 | Rd1 | Rd2 | Всего | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Ингрид Парада | 75878 | 755 | +40 | 69 | 723 | 71 | 700 | 140 |
Мастера-любители 4068 9 (4) 902 Фернандо Мелендес # 79601
Любитель
Сентервиль, Вирджиния, США.
Кевин Сильвер Вольф Джонсон # 7417
Любитель
Ланхэм, Мэриленд, США.
Майк МакКиттрик # 27268
Amateur
Fairfax, Virginia, United States
Мастерс, любители, женщины 40+ (1)
Линдси Салливан # 73389
Любитель
Спрингфилд, Вирджиния, США.
| Место | точек | Имя | PDGA # | Рейтинг | Пар. 00 00 | Линдси Салливан | 73389 | 708 | +29 | 64 | 780 | 65 | 768 | 129 |
|---|
4 9000 мастеров 902 Дэвид Веллборн # 46265
Amateur
Woodbridge, Virginia, United States.
Крис Капелл # 79102
Amateur
Fairfax, Virginia, United States
Джон Илифф # 73985
Amateur
Weirsdale, Florida, United States.
| Место | точек | Имя | PDGA # | Рейтинг | Пар.00 | Дэвид Веллборн | 46265 | 898 | +3 | 50 | 939 | 53 | 905 | 103 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 9.00 | Крис +1256 | 871 | 56 | 871 | 112 | ||||||||
| 3 | 6,00 | Джон Илифф | 73985 | 877 | 6 | 871 | 117 | |||||||
| 4 | 3.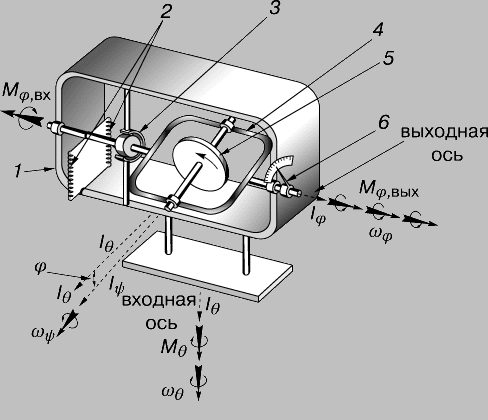 00 00 | Майкл Харт | +18 | 59 | 59 | 118 |
Промежуточный (20)
Энди Эндикотт # 100390
Amateur
Хеймаркет, Вирджиния, США
Brian Drop Zone Davidson # 93683
Amateur
Marshall, Virginia, United States.
Рид Мартинко # 100671
Amateur
Springfield, Virginia, United States
Крис Уоткинс # 88354
Любитель
Гейнсвилл, Вирджиния, США.
Кевин Кейт # 87984
Amateur
Charleston, South Carolina, United States
Trey Tucker # 114095
Amateur
Манассас, Вирджиния, США.
Джерри Манн #
Любитель
Смитфилд, Вирджиния, США.
Ian Servera #
Amateur
Estero, Флорида, США.
Джеймс Маклафлин # 95088
Любитель
Шарлоттсвль, Вирджиния, США.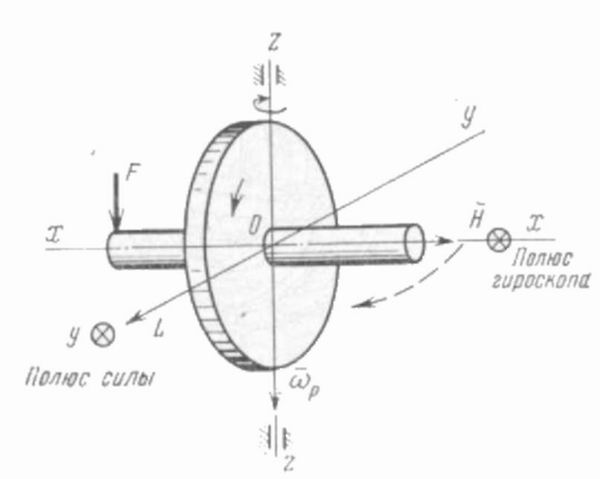
Джеймс Аллен # 99559
Любитель
Сентервиль, Вирджиния, США
Джошуа Салливан # 85443
Любитель
Пасадена, Мэриленд, США.
Тайлер Эби # 112568
Amateur
Poquoson, Virginia, United States
J Keagy # 112468
Professional
Ричмонд, Вирджиния, США
Крис Ханклер # 102497
Любитель
Манассас, Вирджиния, США
Марк Метц # 31220
Amateur
Fredericksburg, Virginia, United States
Аарон Харт # 101447
Amateur
Chester, Virginia, United States
Стивен Труонг # 96294
Amateur
Port Orchard, Вашингтон, США
Роберт Мишо # 45953
Любитель
Александрия, Вирджиния, США
Ричард Флориан # 100462
Amateur
Manassas Park, Virginia, United States
Джош Уилкинсон # 109343
Amateur
Manassas Park, Virginia, United States
Развлекательный (15)
Кевин Карр # 103426
Amateur
Burke, Virginia, United States
Уильям Лэнди # 105191
Любитель
Бристоу, Вирджиния, США.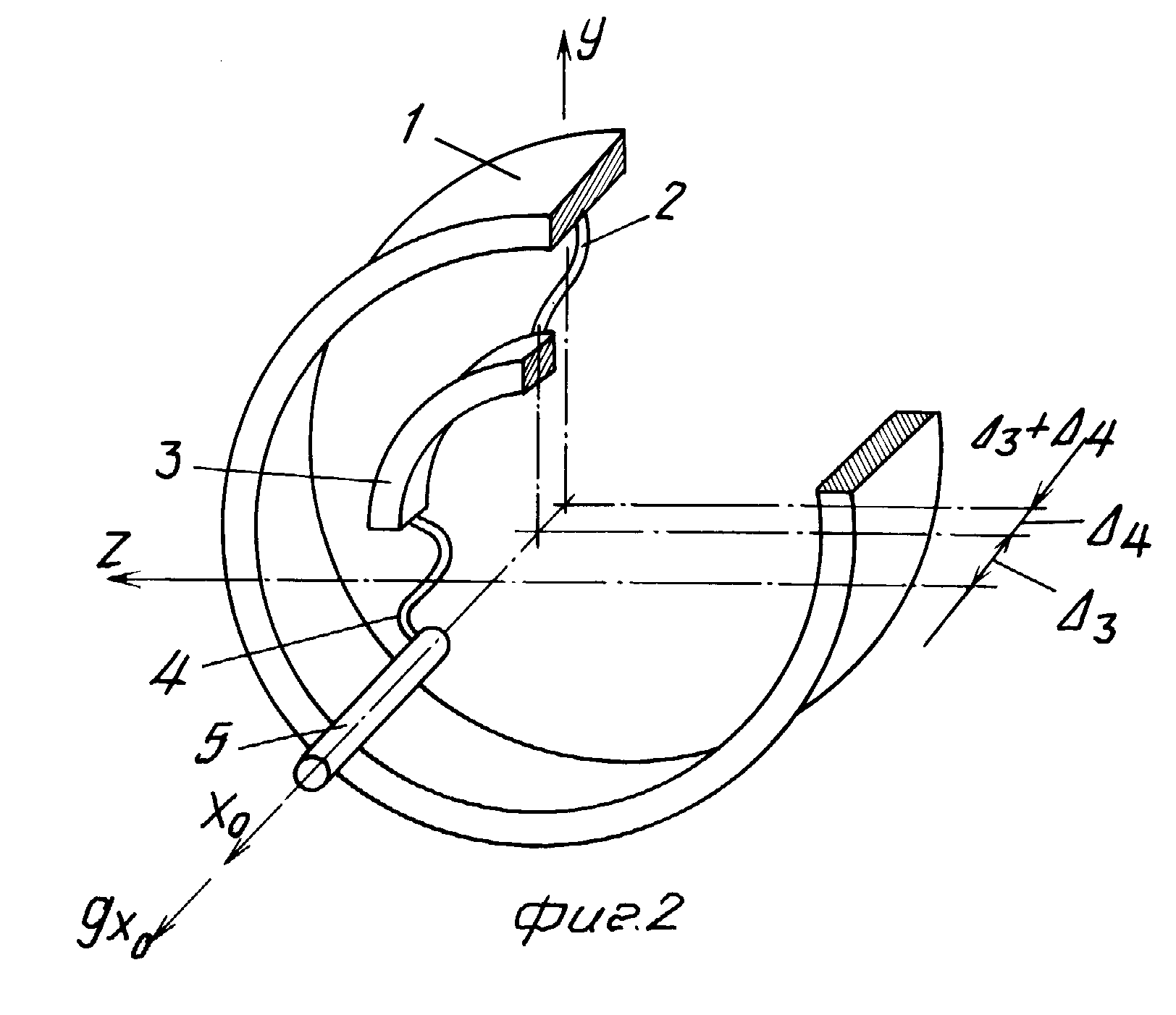
Кен Темплин # 50159
Amateur
Spencerville, Maryland, United States
Мэтт Нолан # 39914
Любитель
Катлетт, Вирджиния, США
Бретт Олингер # 99638
Amateur
Хеймаркет, Вирджиния, США
Уилл Дебесис # 30349
Amateur
Annandale, Virginia, United States
Грег Гарднер # 6524
Amateur
Centerville, Virginia, United States
Nikolas Huist # 62989
Amateur
Wake Forest, Северная Каролина, США
Ноэль Дюк # 80617
Amateur
Waldorf, Мэриленд, США.
Вэнс Уокер # 112532
Amateur
Goldvein, Virginia, United States
Riki Cusic # 113362
Amateur
Уолдорф, Мэриленд, США
Дэвид Сигафу # 107207
Amateur
Сентервиль, Вирджиния, США
Тони Родригес # 113026
Любитель
Банкер-Хилл, Западная Вирджиния, США.
Роб Вейк #
Amateur
Александрия, Вирджиния, США
новичок (4)
Роберт Старк # 98770
Amateur
Purcellville, Virginia, United States
Джесси Дюк # 101440
Любитель
Уолдорф, Мэриленд, США.
| Место | точек | Имя | PDGA # | Рейтинг | Пар.00 | Роберт Старк | 98770 | 813 | +17 | 60 | 825 | 57 | 859 | 117 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 6,00 | +2365 | 768 | 58 | 848 | 123 | ||||||||||||
| 3 | 4,00 | Джон Хассан | 66 | 66 | 71 | 42.00 | Энтони Демария | +41 | 74 | 67 | 141 |
Женщины-новички (1)
Габи Сигафу # 107188
Любитель
Сентервиль, Вирджиния, США.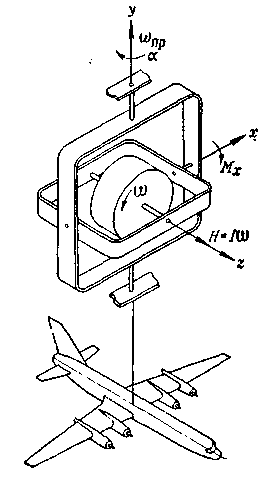
| Место | точек | Имя | PDGA # | Рейтинг | Пар. | Rd1 | Rd2 | Всего | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Габи Лунгу | 107188 | 570 | +43 | 74 | 666 | 69 | 723 | 143 |
MVP Disc Sports and Cirps Открытый (7)
Sam Shiley # 56072
Professional
White Post, Вирджиния, США
Стивен Миллер # 29922
Professional
Стаффорд, Вирджиния, США
Нил Бишоп # 104998
Professional
Винчестер, Вирджиния, США
Дуглас Маринович # 29536
Professional
Sulphur, Луизиана, США
Натан Хьюз # 78987
Professional
Стивенс-Сити, Вирджиния, США
Эндрю Слейтер # 44182
Professional
Вестминстер, Мэриленд, США
Дэвид Стоуэлл # 25674
Professional
Партлоу, Вирджиния, США
Профессиональные мастера 40+ (5)
Роберт Марр # 11617
Professional
Фредерик, Мэриленд, США
Джейкоб Кайзер # 69100
Professional
Мартинсбург, Западная Вирджиния, США
Дэниел Хэтфилд # 62717
Amateur
Arlington, Virginia, United States
Джон Бискоу # 9456
Professional
Спотсильвания, Вирджиния, США
Рон Смит # 22331
Professional
Спрингфилд, Вирджиния, США
Профессиональные мастера 60+ (5)
Боб Харрис # 39048
Professional
Ричмонд, Вирджиния, США
Рик Хонн # 25403
Professional
Silver Spring, Мэриленд, США
Марк Шервуд # 14279
Professional
Hyattsville, Мэриленд, США
Билли Боб Виджил # 7310
Professional
Спрингфилд, Вирджиния, США
Рори Уильямсон # 37268
Professional
Woodbridge, Virginia, United States
Продвинутый (9)
Сэм Ньюман # 77290
Professional
Дервуд, Мэриленд, США
Мэтью Макдэниел # 82802
Professional
Hagerstown, Мэриленд, США
Эндрю Киркнер # 40439
Professional
Ричмонд, Вирджиния, США
Блейк Хербольд # 41773
Любитель
Вашингтон, округ Колумбия, США.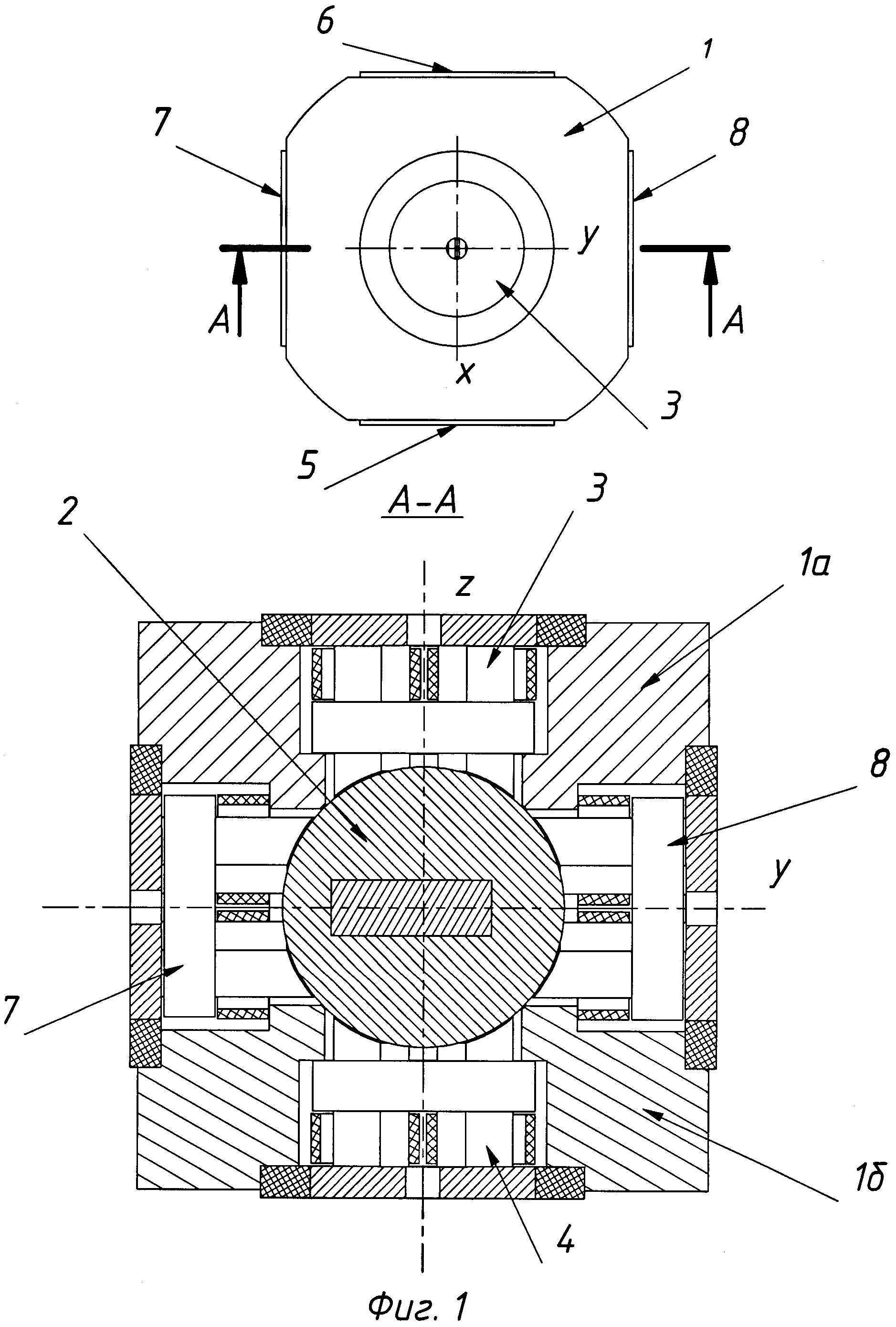
Коннор Галли # 73157
Professional
Fairfax Station, Вирджиния, США
Джошуа Доннер # 74654
Amateur
Brandywine, Мэриленд, США
Дуглас Феррио # 89662
Professional
Александрия, Вирджиния, США
Даррен Хопперт # 78353
Amateur
Laurel, Мэриленд, США.
Thomas Fletcher # 68040
Amateur
Эшберн, Вирджиния, США
Продвинутые женщины (3)
Девон Харрис # 94152
Professional
Virginia Bch, Virginia, United States
Jessica Geraci # 89663
Amateur
Александрия, Вирджиния, США
Adrienne Krauel # 83383
Amateur
Рестон, Вирджиния, США.
Мастера-любители 40+ (3)
Кевин Сильвер Вольф Джонсон # 7417
Любитель
Ланхэм, Мэриленд, США.
Эндрю Кассиоппи # 53327
Amateur
Huntsville, Alabama, United States
Мастера-любители 50+ (6)
Джефф Уотсон # 39846
Amateur
Ellicott City, Мэриленд, США.
Дж.W. Read # 69237
Amateur
Burke, Вирджиния, США
Chet Butler # 44168
Amateur
Александрия, Вирджиния, США
Ноэль Дюк # 80617
Amateur
Waldorf, Мэриленд, США.
Кевин Карр # 103426
Amateur
Burke, Virginia, United States
Джоэл Харроп # 102402
Professional
Fairfax, Virginia, United States
Средний (20)
Джонатан Хоксфорд # 95135
Любитель
Нью-Виндзор, Мэриленд, США.
Эдгар Мохика # 63886
Любитель
Линвуд, Вашингтон, США
Блейк Дюваль # 88723
Amateur
Leesburg, Virginia, United States
Рид Мартинко # 100671
Amateur
Springfield, Virginia, United States
Райан Хаттон # 96254
Любитель
Берк, Вирджиния, США.
Николас Марр # 87932
Любитель
Фредерик, Мэриленд, США
Джозеф Литтл # 84478
Любитель
Стонтон, Вирджиния, США
Эван Фрейди # 97524
Amateur
Severna Park, Мэриленд, США
Майкл Клементс # 88578
Amateur
Bethesda, Мэриленд, США.
Майкл Кавано # 87930
Любитель
Гленмур, Пенсильвания, США.
Кеннет Спайкер # 26310
Amateur
Fredericksburg, Virginia, United States
Джои Харрисон # 77077
Любитель
Спрингфилд, Вирджиния, США
Даррен Уоррингтон # 99849
Amateur
Virginia Bch, Virginia, United States
Тимоти Мэтт # 88842
Amateur
Мидлтаун, Мэриленд, США
Деннис Кавалларо # 60797
Любитель
Эшберн, Вирджиния, США.
Бен Людерс # 89783
Amateur
Woodbridge, Virginia, United States
Энди Хассан # 88627
Professional
Фэрфакс, Вирджиния, США
Джейсон Абернати # 97486
Professional
Virginia Bch, Virginia, United States
Роберт Мишо # 45953
Любитель
Александрия, Вирджиния, США
Ian Servera #
Amateur
Estero, Флорида, США.
Женщины среднего уровня (4)
Лили Марр # 94613
Любитель
Фредерик, Мэриленд, США
Линдси Салливан # 73389
Любитель
Спрингфилд, Вирджиния, США.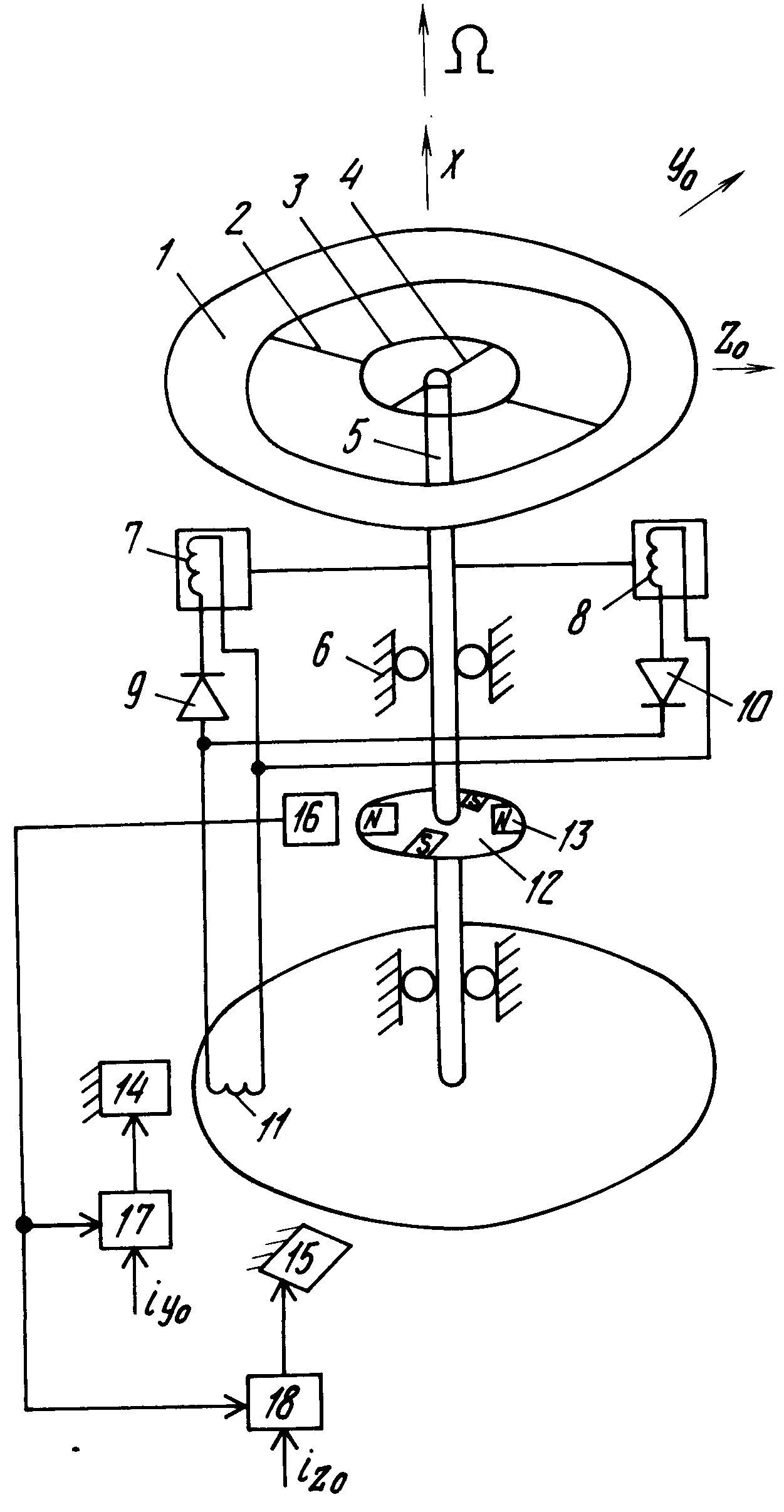
Эйлин Тоули # 77786
Любитель
Лортон, Вирджиния, США
Брианна Кейн # 101507
Amateur
Дамфрис, Вирджиния, США.
Развлекательный (12)
Стивен Труонг # 96294
Amateur
Port Orchard, Вашингтон, США
Джереми Баклер # 104033
Amateur
Вашингтон, округ Колумбия, США.
Крис Ханклер # 102497
Любитель
Манассас, Вирджиния, США
Уильям Лэнди # 105191
Любитель
Бристоу, Вирджиния, США.
Майк МакКиттрик # 27268
Amateur
Fairfax, Virginia, United States
Джимми Мостеллер # 98020
Amateur
Шрусбери, Массачусетс, США
Скотт Николс # 99762
Любитель
Бристоу, Вирджиния, США.
Филлип Накин # 100406
Amateur
Herndon, Virginia, United States
Роберт Старк # 98770
Amateur
Purcellville, Virginia, United States
Bryant Slimp # 102702
Amateur
Манассас, Вирджиния, США
Джесси Дюк # 101440
Любитель
Уолдорф, Мэриленд, США.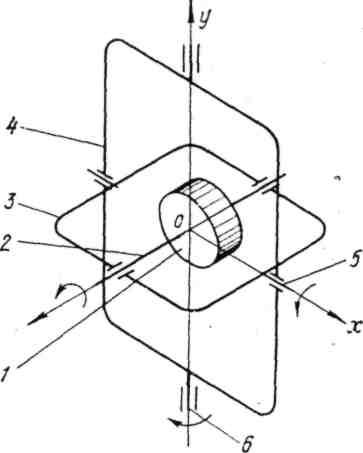
Высокочувствительный туннельный магниторезистивный микрогироскоп с устойчивостью к внешним магнитным помехам
Хорошо известно, что рабочие характеристики устройства зависят от допусков микропроизводства.В условиях используемой нами производственной системы мы проводим тест на гармонический отклик микрогироскопа. Блок-схема экспериментальной установки представлена на рис. 3а. Тестирование гармонического отклика используется для исследования согласования мод микрогироскопа. Сигнал переменного тока с качающейся частотой, генерируемый генератором сигналов, используемым для управления микрогироскопом, выходной сигнал направления возбуждения / считывания усиливается и фильтруется нижними частотами, а затем синхронно демодулируется с помощью синхронизирующего усилителя (AMETEK Model 7270). Усилитель синхронизации DSP).Результат теста гармонического отклика показан на рис. 3b. Резонансные частоты режимов движения и измерения протестированы как 7850 Гц и 7854 Гц. Это разделение частот на 4 Гц в основном вызвано асимметрией в процессе изготовления.
( a ) Экспериментальная установка для проверки производительности микрогироскопа. ( b ) Результат гармонического отклика микрогироскопа TMR. ( c ) Зависимость смещения в направлении измерения от угловой скорости в направлении оси Z .{2}}}} $$
(1)
где Q x , Q y \ ({\ mathrm {Q}} _ {\ mathrm {x}}, {\ mathrm {Q}} _ {\ mathrm {y} } \) – добротность режима управления и определения, ω x , ω y – собственная частота режима управления и определения, соответственно. Используя уравнение. По формуле (1) структурная чувствительность рассчитана равной 28.\ circ {\ text {/ s}} $$
(2)
, что согласуется с теоретическим значением структурной чувствительности.
Во время работы микрогироскопа чувствительность к магнитному полю определяется как отношение между изменением магнитного поля и диапазоном смещения микрогироскопа в направлении измерения.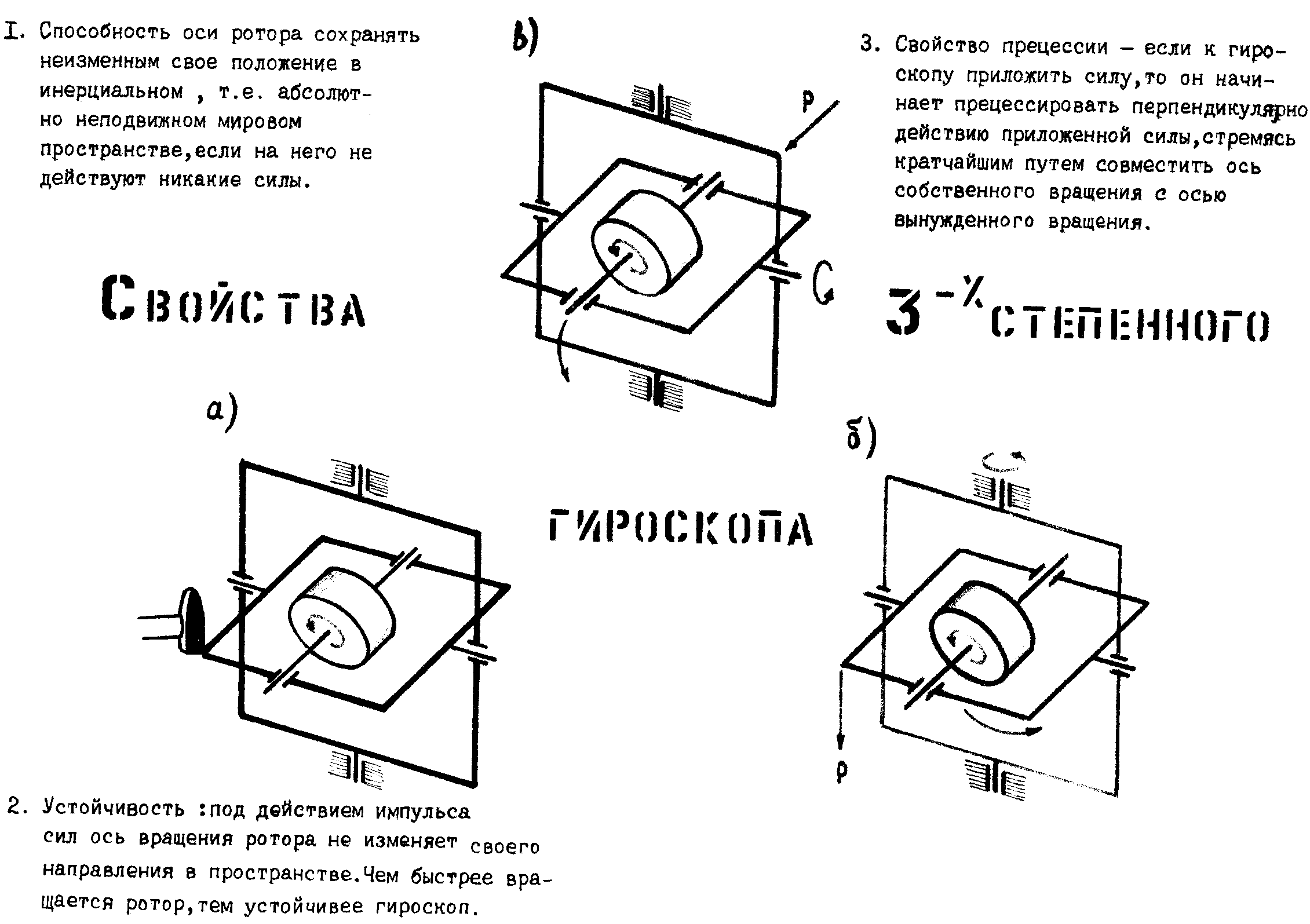 Устройство TMR требует не только высокочувствительного магнитного поля в направлении обнаружения, но также для предотвращения помех магнитного поля в направлении движения.По этим причинам магнитное поле должно иметь возможность поддерживать однородное магнитное поле той же высоты в направлении движения и быстро менять направление восприятия.
Устройство TMR требует не только высокочувствительного магнитного поля в направлении обнаружения, но также для предотвращения помех магнитного поля в направлении движения.По этим причинам магнитное поле должно иметь возможность поддерживать однородное магнитное поле той же высоты в направлении движения и быстро менять направление восприятия.
Для дальнейшей проверки осуществимости конструкции, модель распределения магнитного поля электронных катушек моделируется с помощью Ansoft Maxwell 13.0. Из моделирования и анализа чувствительности к магнитному полю гироскопа TMR мы получаем оптимальные размерные параметры с шириной 30 мкм, толщиной 15 мкм и расстоянием 30 мкм между соседними катушками.Пространственное распределение магнитного поля может быть измерено с помощью гауссметра с разрешением 0,1 мТл, мы в основном фокусируемся на пяти линиях с параллельным интервалом 5 мкм вдоль оси X и интервалом 10 мкм вдоль оси Y при высота 1 мкм над электронными катушками, как показано на рис.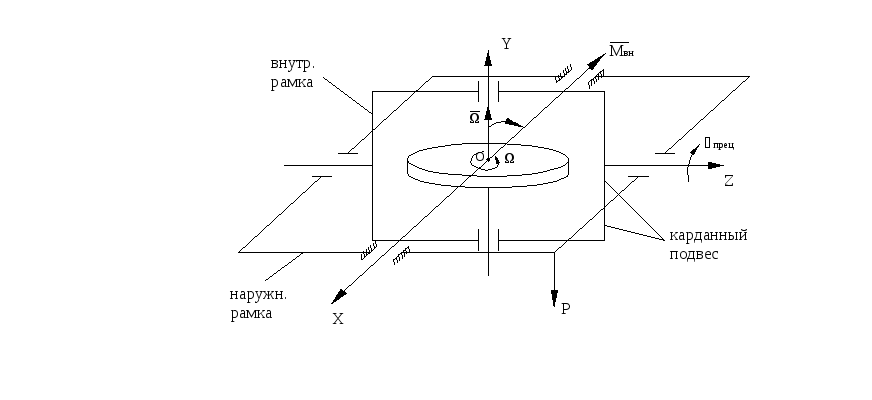 4a. Пространственное распределение магнитного поля в направлении движения и направлении измерения показано на рис. 4b, c соответственно. Результаты показывают, что величина магнитного поля остается постоянной вдоль направления движения (ось X), в то время как представляет собой квазисинусоидальное распределение магнитного поля в направлении измерения (ось Y) с быстрым изменением магнитного поля. и хорошая повторяемость в линейном диапазоне (рис.4г). Следовательно, чувствительность к магнитному полю записывается как:
4a. Пространственное распределение магнитного поля в направлении движения и направлении измерения показано на рис. 4b, c соответственно. Результаты показывают, что величина магнитного поля остается постоянной вдоль направления движения (ось X), в то время как представляет собой квазисинусоидальное распределение магнитного поля в направлении измерения (ось Y) с быстрым изменением магнитного поля. и хорошая повторяемость в линейном диапазоне (рис.4г). Следовательно, чувствительность к магнитному полю записывается как:
$$ S _ {{{\ text {mag}}}} = \ frac {\ Delta B} {{\ Delta d}} = 0.0023 {\ text {Oe / nm }} $$
(3)
Рисунок 4 Распределение магнитного поля электронных катушек. ( a ) Положение обнаружения по оси X и оси Y, ( b , c ) Распределение магнитного поля для направления движения (ось X) / направления обнаружения (ось Y) , ( d ) увеличенный вид ( c ).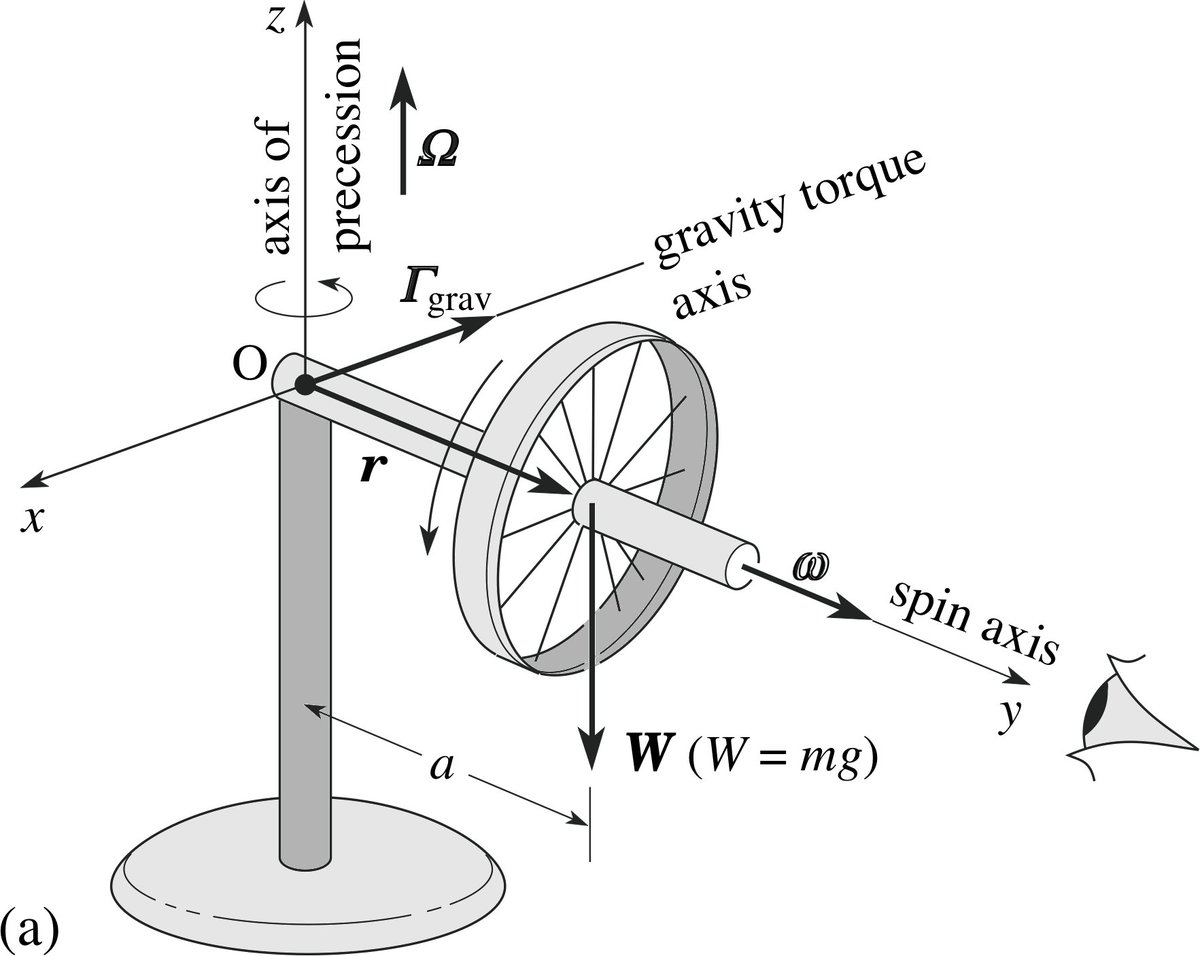
Чтобы обеспечить чувствительность измерения при работе устройства TMR, необходимо минимизировать влияние внешнего магнитного поля на работу устройства TMR, а затем повысить стабильность их обнаружения. Нами предложена многомостовая схема микрогироскопа TMR, которая является перспективным методом подавления воздействия внешних возмущений, как показано на рис. 5а.
Рисунок 5Схема многомостовой схемы и результаты тестирования устройства TMR.( a ) Схема многомостовых цепей в микрогироскопе TMR, ( b ) Смещение базовой линии дифференциального выходного напряжения близко к нулю при использовании схемы многомостовой схемы, ( c ) Экспериментальные результаты магнето -чувствительность к сопротивлению, красная линия представляет собой линейную аппроксимацию точек данных.
Распределение магнитного поля представляет собой кривую квазикосинусной функции в направленном направлении. Магнитное поле, воспринимаемое TMR в каждой мостовой схеме, может быть выражено как:
$$ {B_i} = {B_0} + A \ cdot \ cos \ left ({2 \ uppi \ frac {{x + \ left ({i – 1} \ right) d}} {{2D}}} \ right) $$
(4)
где B 0 – статическое магнитное поле, A – амплитуда магнитного поля, D – межстрочный интервал электрических катушек и d – расстояние между соседними мостовыми схемами. {j} \ cdot K \ cdot B_ {i} $$
{j} \ cdot K \ cdot B_ {i} $$
(5)
где i ( i = 1–4) – номер моста, j ( j = 1,2 ) – тип TMR мостовой схемы, K – чувствительность устройство TMR.
Объединенный уравнения. (4) с (5), два выходных сигнала напряжения для устройства TMR (рис. 5a) получаются следующим образом:
$$ V_ {a} = V _ {{0}} \ cdot \ frac {{R_ {11 }}} {{R_ {11} + R_ {12}}} $$
(6)
$$ V_ {b} = V _ {{0}} \ cdot \ frac {{R_ {21}}} {{R_ {21} + R_ {22}}} $$
(7)
Следовательно, дифференциальное напряжение на выходе любых двух соседних мостов в многомостовых схемах равно:
$$ V {= -} \ frac {{V _ {{0}} KA}} {{R _ {0} }}} \ sin \ frac {{{\ pi (} 2x {+} d {)}}} {{{2} D}} \ cdot \ sin \ frac {{{\ uppi} d}} {{{ 2} D}} $$
(8)
Обратите внимание, что в уравнении. (8) выходной сигнал не зависит от внешнего магнитного поля B 0 , следовательно, метод с несколькими мостами может использоваться для подавления влияния внешних магнитных помех, а также для предотвращения ошибки интеграции устройства TMR. Кроме того, это позволяет избежать снижения точности измерения из-за нестабильности внешнего магнитного поля. На рисунке 5b показано выходное дифференциальное напряжение как функция расстояния. Обратите внимание, что смещение базовой линии выходного дифференциального напряжения подавляется до нуля в схеме с несколькими мостами.
(8) выходной сигнал не зависит от внешнего магнитного поля B 0 , следовательно, метод с несколькими мостами может использоваться для подавления влияния внешних магнитных помех, а также для предотвращения ошибки интеграции устройства TMR. Кроме того, это позволяет избежать снижения точности измерения из-за нестабильности внешнего магнитного поля. На рисунке 5b показано выходное дифференциальное напряжение как функция расстояния. Обратите внимание, что смещение базовой линии выходного дифференциального напряжения подавляется до нуля в схеме с несколькими мостами.
Результаты экспериментальных испытаний устройства TMR показаны на рис. 5c. Магниторезистивная чувствительность определяется как отношение изменения напряжения устройства TMR к изменению пространственного магнитного поля. Согласно данным испытаний и линейной аппроксимации, чувствительность магниторезистивного устройства TMR получена:
$$ S _ {{{\ text {TMR}}}}} = \ frac {\ Delta V} {{\ Delta B }} = 29,5 {\ text {мВ / э}} $$
(9)
Общая чувствительность разработанного TMR-микрогироскопа складывается из структурной чувствительности, чувствительности к магнитному полю и чувствительности к магниторезистивному сопротивлению.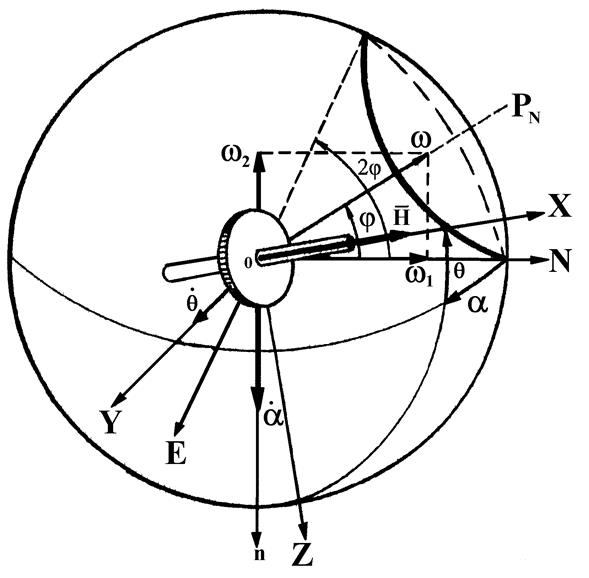 \ circ / {\ text {s}} $$
\ circ / {\ text {s}} $$
(10)
Для повышения общей чувствительности ПМР-гироскопа мы использовали магниторезистивное устройство с более высокой чувствительностью и одновременно гарантировали его работу в линейной области. Однако магниторезистивный прибор имеет более высокую чувствительность к слабому изменению магнитного поля за счет линейного рабочего диапазона. Поэтому диапазон измерения гироскопа TMR в основном ограничен диапазоном работы магниторезистивного устройства.В соответствии с соотношением между выходной мощностью магниторезистивного устройства и величиной обнаруженного магнитного поля рабочий диапазон составляет приблизительно ± 30 Э, что соответствует динамическому диапазону ± 600 ° / с.
Чтобы исследовать различные шумы, которые устанавливают ограничения чувствительности гироскопа TMR, мы проанализировали минимальный уровень шума гироскопа TMR и определили его пределы масштабирования. Броуновское движение контрольной массы, вызванное столкновениями молекул с окружающей средой, представляет собой фундаментальную ограничивающую составляющую шума гироскопа TMR 30 . Броуновский термомеханический шум определяется выражением:
Броуновский термомеханический шум определяется выражением:
$$ {\ Omega _B} = \ frac {1} {{{B_x} {\ omega _x}}} \ sqrt {\ frac {{{k_B} T {\ омега _y}}} {{{m_y} {Q_y}}}} $$
(11)
где k B – постоянная Больцмана, T – температура окружающей среды, ω x ( ω y ) – резонансная частота режима управления (чувствительность mode), B x – это управляемое смещение, м y – чувственная масса и Q y – добротность чувственного направления.Согласно выражению броуновского термомеханического шума, можно увидеть, что характеристики микрогироскопа могут быть улучшены путем увеличения амплитуды режима возбуждения или с высоким коэффициентом качества. Кроме того, электронный шум TMR-микрогироскопа в основном возникает из-за шума 1 / f относительной интенсивности шума лазера ( RIN ) и шума усилителя. Электронный шум микрогироскопа TMR может быть записан как: (где спектральная плотность шума ( PSD ) устройства TMR на уровне 10 –7 В / Гц).2} $$
Электронный шум микрогироскопа TMR может быть записан как: (где спектральная плотность шума ( PSD ) устройства TMR на уровне 10 –7 В / Гц).2} $$
(13)
Таким образом, малошумящие характеристики микрогироскопа TMR могут быть реализованы с общим минимальным уровнем шума 6,8 × 10 –5 º / с / Гц 1/2 , что превосходит некоторые современные типы микрогироскопы.
Что такое гироскоп – история, три степени свободы, основные свойства
Гироскоп – одно из обязательных навигационных устройств, необходимых любому плавучему судну для определения направления.Его важность знает каждый моряк. Не ограничиваясь этим, он также находит применение в смарт-часах, смартфонах, игровой индустрии и камерах. В этом посте будет обсуждаться, что такое гироскоп, его история, три степени свободы гироскопа и основные свойства «жесткость в пространстве» и «правило точности».
История гироскопа
Слово G yrocope было первоначально названо в 1852 году г-ном Фуко.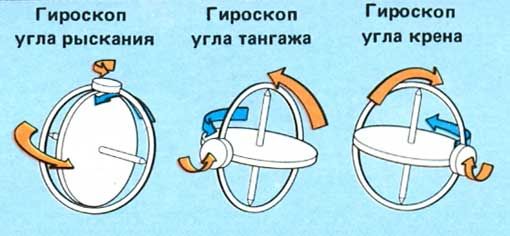 Мистер Фуко был французским ученым. «Гироскоп» – это сочетание двух греческих слов «Gyro» и «Scopien». Gyro по-гречески означает революция, а skopien означает взгляд. Он также широко известен как гироскоп.
Мистер Фуко был французским ученым. «Гироскоп» – это сочетание двух греческих слов «Gyro» и «Scopien». Gyro по-гречески означает революция, а skopien означает взгляд. Он также широко известен как гироскоп.
Рис. 1 – Знакомство с гироскопом
Гироскоп существует на этой Земле с того времени, когда первый в истории электрон начал вращаться вокруг своей оси. В реальном мире существует множество примеров естественных гироскопов. Электроны вокруг нас вращаются с очень высокой скоростью и обладают всеми свойствами гироскопа.
Наша Земля, по сути, также является примером естественного гироскопа.Почему ?? Это потому, что наша Земля имеет массу и вращается с чрезвычайно высокой скоростью (1000 миль / час). Именно это вращение обеспечивает стабилизацию Земли, и поэтому северный полюс нашей Земли всегда указывает на Полярную звезду.
Что такое гироскоп Любой сильно вращающийся объект, имеющий массу, в первую очередь является гироскопом. например – быстро вращающееся колесо, выпущенная пуля, пропеллер тягового двигателя самолета и т.д. скорость, масса и три степени свободы .
например – быстро вращающееся колесо, выпущенная пуля, пропеллер тягового двигателя самолета и т.д. скорость, масса и три степени свободы .
Рис. 2 – Три степени свободы гироскопа
Что такое три степени свободы гироскопа?
«Три степени свободы» означает, что гироскоп может принимать любое положение в пространстве. Однако, в частности, три степени свободы могут быть перечислены как: –
- Он должен иметь возможность вращаться вокруг своей оси. Как следует из названия, эту ось обычно называют осью вращения.
- Он должен иметь возможность дрейфа по вертикальной оси.
- Он должен иметь возможность наклоняться по горизонтальной оси.
Посмотрите видео ниже, чтобы лучше понять, что означают три степени свободы.
Основные свойства гироскопа
Когда мы обсуждаем основные свойства гироскопа, он должен следовать двум основным свойствам:
- Жесткость в пространстве
- Правило точности


 А. Аванесова. Серия “Механика, управление и информатика”. Москва: ИКИ РАН, 2013. [online] Доступ через: http://ofo.ikiweb.ru/publ/conf_2012_st.pdf (дата обращения: 22.03.2016).
А. Аванесова. Серия “Механика, управление и информатика”. Москва: ИКИ РАН, 2013. [online] Доступ через: http://ofo.ikiweb.ru/publ/conf_2012_st.pdf (дата обращения: 22.03.2016).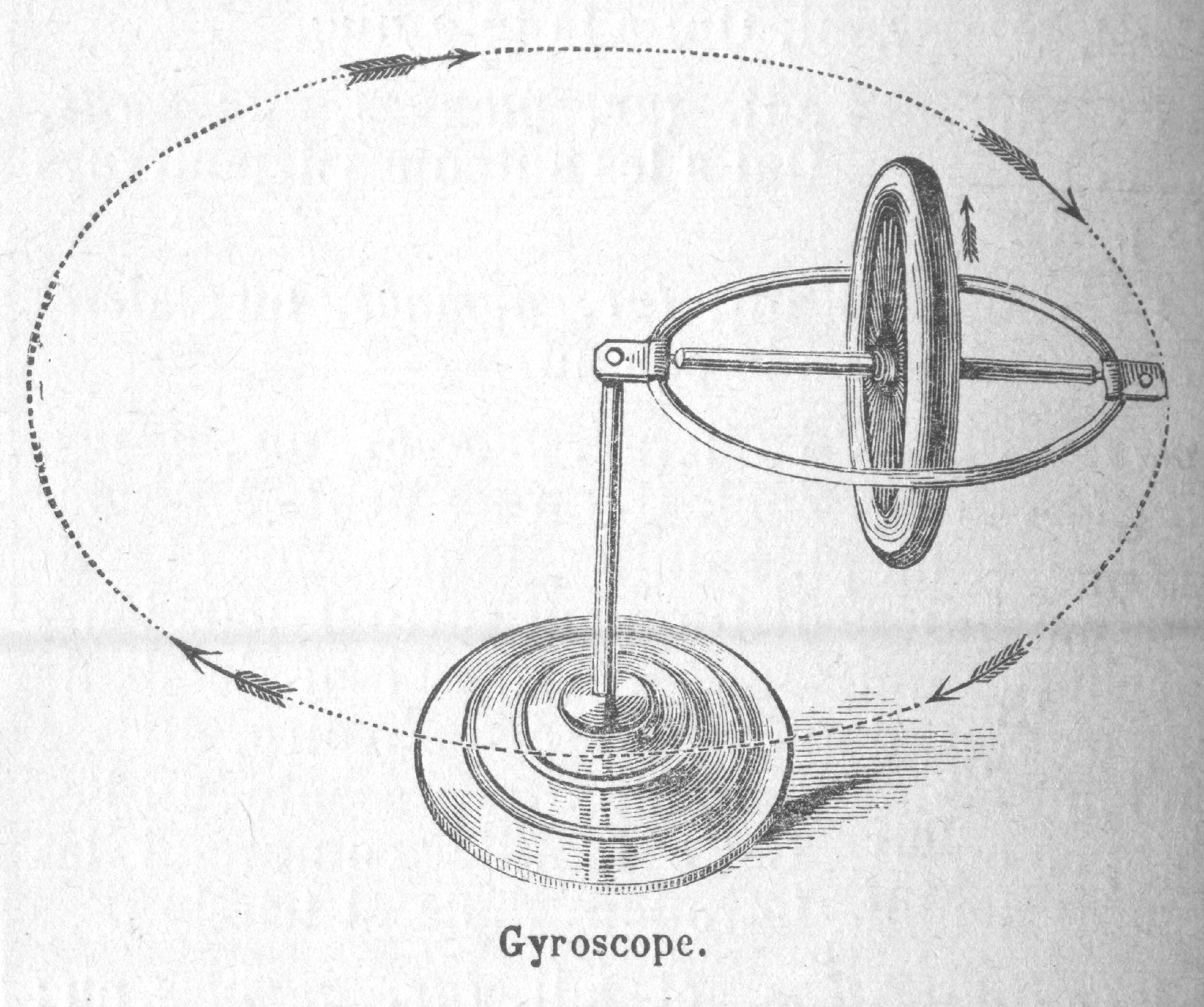 ред. физ-мат литературы, 1967. – С. 368.
ред. физ-мат литературы, 1967. – С. 368. Дайджест технических документов
Дайджест технических документов