Матрица – схема – Большая Энциклопедия Нефти и Газа, статья, страница 3
Матрица – схема
Cтраница 3
Как и для метода узловых напряжений, анализ и расчет методом контурных токов сводится к нахождению определителя матрицы схемы. Искомые расчетные соотношения между токами и напряжениями схемы определяются при помощи математических операций над параметрами элементов определителя матрицы сопротивления схемы. [31]
Члены элементов матрицы вида рдах заменяем элементами mlxau, где m и / – номера строк и столбцов матрицы схемы соответственно, х – степень оператора р элементов матрицы D ( p), а и и – номер параметров элемента и знак параметра ( 0 – плюс, 1 – минус), в результате чего осуществляется переход к матричному числу м ( mlxau) анализируемой схемы. [32]
При реализации изложенных процедур преобразования уравнений схемы операции суммирования и умножения матриц удобно свести к алгебраическому суммированию столбцов
Как видно из табл. 3.1 и 3.2, нахождение схемных функций сводится к вычислению или раскрытию определителя и алгебраических дополнений матрицы схемы W. Соотношения для схемных функций получены в предположении, что W является матрицей КК-уравнений. Аналогично соотношения для других типов уравнений будут отличаться только видом преобразующих векторов. [34]
Из выражений ( 1а) и ( 16) следует, что коэффициенты ок, & к представляют собой некоторые детерминантные функции элементов матрицы схемы. В связи с этим для дальнейшего изучения внутренней структуры приведенных формул целесообразно рассмотреть понятие определителя с позиций современной математики. [35]
Во второй колонке таблицы величины Ки, Ki, Увх и УВЫХ при соответствующих значениях Ун и Уг выражены в общем виде через определитель матрицы схемы и его алгебраические дополнения.
Индексы а и Ъ алгебраических дополнений означают номера входного и выходного узла схемы.
[36]
В табл. 11 приведены значения коэффициентов F, G и Н основных параметров для III варианта выбора системы координат схемы, выраженные непосредственно через определитель
Подставив значения соответствующих ( / – параметров четырехполюсника в формулы (3.28) – (3.35), получим выражения для схемных функций, которые приведены в табл. 3.1. В этих выражениях схемные функции представлены через суммарные алгебраические дополнения матрицы схемы W относительно векторов-столбцов явх и ЛЕЫХ матрицы сечений. [38]
В табл. 9 даны величины F, G и Я основных параметров схемы усилителя, приведенной к виду четырехполюсника для третьего варианта выбора системы координат ( d с 0), выраженные непосредственно через определитель А
Формулы основных параметров усилителя необходимо представить в таком виде, чтобы нужные расчетные соотношения можно было бы получить наиболее простым путем, а методика их нахождения была бы достаточно общей. Определитель матрицы схемы усилителя сравнительно просто найти на основании обобщенного метода узловых напряжений или контурных токов. [40]
Необходимо отметить, что формулы, приведенные в табл. 5 для определения относительного изменения основных параметров схем усилителей в зависимости от изменения ее п параметров, пригодны для любой по сложности схемы.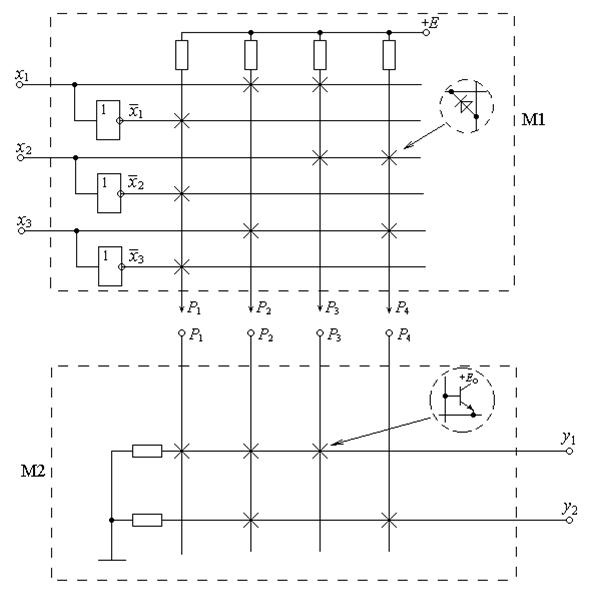
Зная матрицу схемы, при помощи этих формул сравнительно просто определить относительное изменение, а с помощью табл. 4 ( при условии, что приращения параметров равны нулю) и табл. 5-абсолютное изменение интересующей нас характеристики схемы.
[41]
Как уже указывалось, система координат может быть произвольная и ее выбор диктуется свойствами исходной схемы и стремлением к простоте. Наиболее простой вид матрица схемы и выражения для схемных функций принимают в канонических системах координат, но их применение связано с рядом ограничений. В общем случае для получения матрицы схемы может быть использован любой из алгоритмов формирования уравнений, изложенных в предыдущих главах. Следует заметить, что выбор системы координат в значительной мере связан и со способом вычисления или раскрытия определителей. [43]
Выразим определитель А в явном виде через х взаимных иммитан-сов ( усилительных параметров) управляемых элементов схемы. На основании этой формулы определитель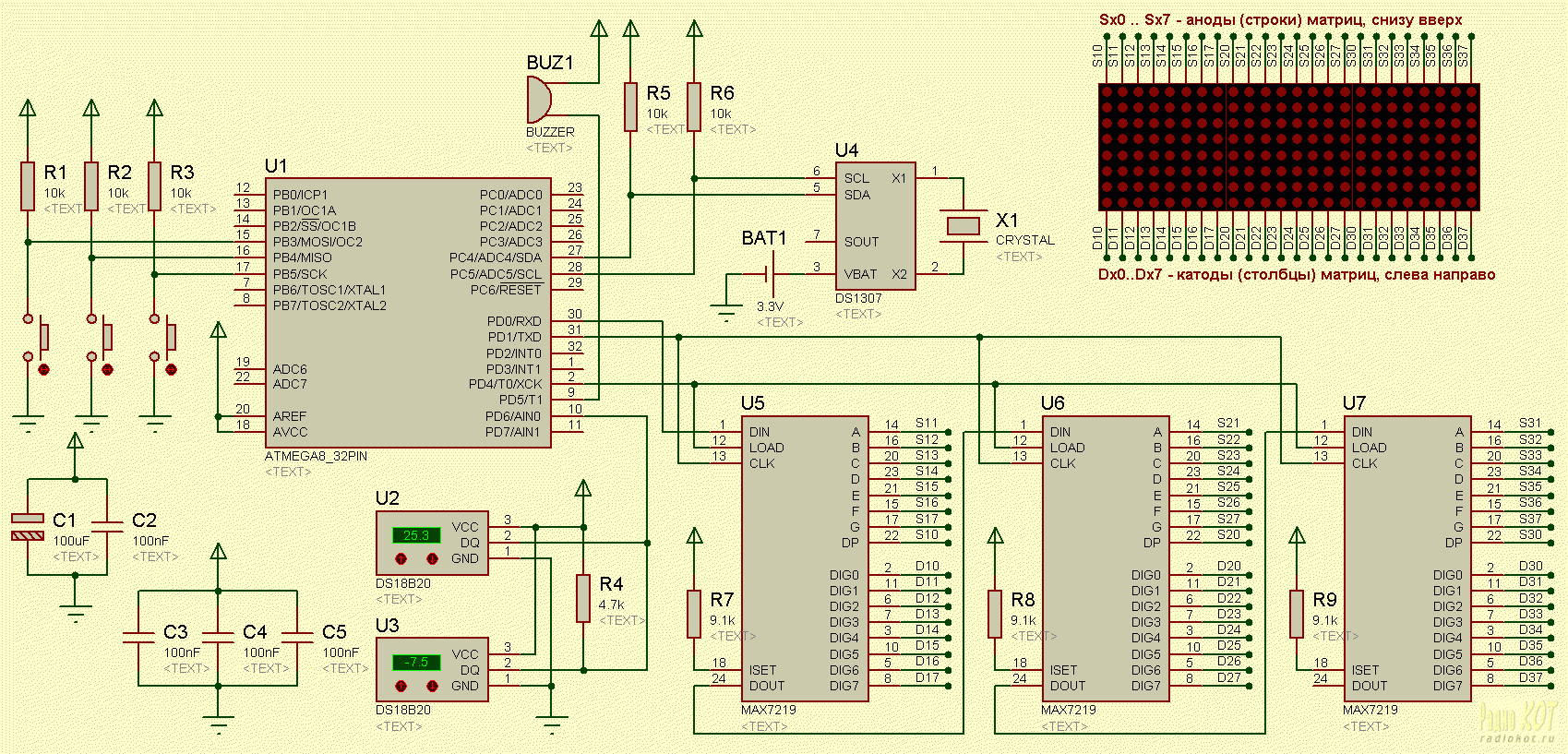
[44]
Если параметр Wj находится в определителе матрицы схемы, например, для первоначального ее состояния на пересечении только одной строки и одного столбца, то два других индекса, означающие строку и столбец матрицы, необходимо приравнять нулю. Так, когда параметр W, находится на пересечении только ау-й строки и Yrro столбца, то индексы ( J / и е / нужно приравнять нулю. [45]
Страницы: 1 2 3 4
Схема матрицы клавиатуры – Keyboard matrix circuit
Матрица клавиатуры схема является дизайном , используемым в большинстве электронных музыкальных клавиатур и компьютерных клавиатурах , в котором ключевые переключатели соединены сеткой проводов, похожих на диодную матрицу . Например, 16 проводов, расположенных в 8 рядов и 8 столбцов, могут соединить 64 клавиши – этого достаточно для полных пяти октав диапазона (61 нота). Сканируя эти пересечения, контроллер клавиатуры может определить, какие клавиши в данный момент нажаты.
Описание
Без матричной схемы 61-клавишная клавиатура для синтезатора , электронного органа или цифрового пианино потребовала бы 62 проводов для подключения (по одному на каждую ноту и заземление) – неудобно толстый пучок проводов. С помощью матричной схемы любая из 61 ноты может быть определена с помощью всего 16 проводов. Это схематично изображено в виде матрицы из 8 столбцов и 8 строк проводов с переключателем на каждом пересечении. Контроллер клавиатуры просматривает столбцы. Если была нажата клавиша, контроллер просматривает строки – и аналогично настольной игре « Морской бой» контроллер определяет комбинацию строка-столбец, в которой была нажата клавиша, и генерирует примечание, соответствующее этой клавише. Этот процесс происходит так быстро, что исполнитель не подозревает ни о какой задержке.
У этой системы есть как минимум два ограничения. Во-первых, он предоставляет только грубый двоичный сигнал включения / выключения для каждой клавиши. Лучшие электронные музыкальные клавиатуры используют два набора переключателей для каждой клавиши, которые слегка смещены. Путем определения времени между активацией первого и второго переключателей можно определить скорость нажатия клавиши, что значительно улучшает динамику производительности клавиатуры.
Во-вторых, инструменты с матричной схемой могут играть только в монофоническом режиме без добавления диода для каждого пересечения клавиш. В диодном предотвращает нежелательные ноты ( «фантомные ключи») от , которые инициированы или предназначены примечаний от маскируются ( «ключ фантом блокировки» ).
Монофонические инструменты и большинство недорогих компьютерных клавиатур сокращают расходы за счет исключения большинства или всех этих диодов. Чтобы избежать «фантомных клавиш», контроллер клавиатуры в современных недорогих компьютерных клавиатурах будет игнорировать дальнейшие нажатия клавиш после нажатия двух клавиш (кроме клавиш-модификаторов ), что называется заклиниванием .
Подход с матричной схемой также используется в немузыкальных клавиатурах, например, в клавиатурах для калькуляторов и буквенных и цифровых клавиатурах QWERTY, используемых для ввода информации в компьютеры. Такой же подход к матричной схеме используется во многих автоматах для игры в пинбол .
Часто в карманных калькуляторах мультиплексированные линии ввода цифр также используются для сканирования клавиатуры, что обеспечивает дополнительную экономию.
Смотрите также
Рекомендации
<img src=”https://en.
wikipedia.org//en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=”” title=””>ЖК-монитор. Технология LCD, принцип работы. Устройство TFT матрицы | Eco
08 Сентября 2019 г.
LCD-матрица. Принцип работы жидкокристаллической панели.
“Сердцем” любого жидкокристаллического монитора является LCD-матрица (Liquid Cristall Display). ЖК-панель представляет из себя сложную многослойную структуру. Упрощенная схема цветной TFT LCD-панели представлена на Рис.2.
Принцип работы любого жидкокристаллического экрана основан на свойстве жидких кристаллов изменять (поворачивать) плоскость поляризации проходящего через них света пропорционально приложенному к ним напряжению. Если на пути поляризованного света, прошедшего через жидкие кристаллы, поставить поляризационный светофильтр (поляризатор), то, изменяя величину приложенного к жидким кристаллам напряжения, можно управлять количеством света, пропускаемого поляризационным светофильтром. Если угол между плоскостями поляризации прошедшего сквозь жидкие кристаллы света и светофильтра составляет 0 градусов, то свет будет проходить сквозь поляризатор без потерь (максимальная прозрачность), если 90 градусов, то светофильтр будет пропускать минимальное количество света (минимальная прозрачность).
| Принцип работы LCD-панели |
Рис.1. ЖК-монитор. Принцип работы LCD-технологии.
Таким образом, используя жидкие кристаллы, можно изготавливать оптические элементы с изменяемой степенью прозрачности. При этом уровень светопропускания такого элемента зависит от приложенного к нему напряжения. Любой ЖК-экран у монитора компьютера, ноутбука, планшета или телевизора содержит от нескольких сотен тысяч до нескольких миллионов таких ячеек, размером долей миллиметра. Они объединены в LCD-матрицу и с их помощью мы можем формировать изображение на поверхности жидкокристаллического экрана.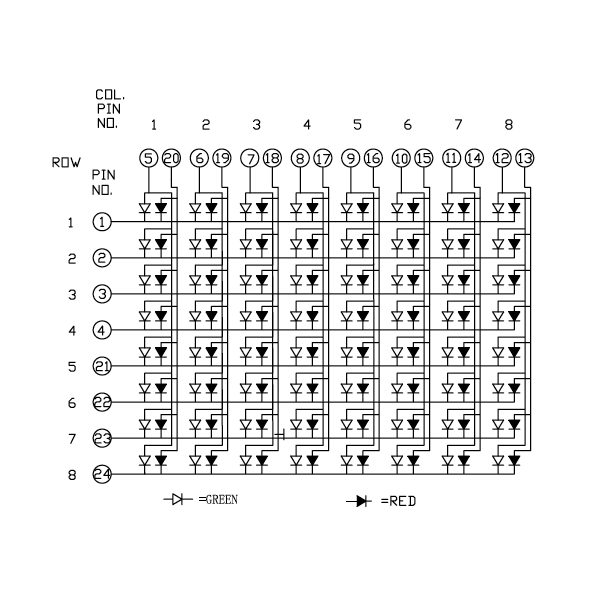
Жидкие кристаллы были открыты еще в конце XIX века. Однако первые устройства отображения на их основе появились только в конце 60-х годов XX века. Первые попытки применить LCD-экраны в компьютерах были предприняты в восьмидесятых годах прошлого века. Первые жидкокристаллические мониторы были монохромными и сильно уступали по качеству изображения дисплеям на электронно-лучевых (ЭЛТ) трубках. Главными недостатками LCD-мониторов первых поколений были:
- – низкое быстродействие и инерционность изображения;
- – «хвосты» и «тени» на изображении от элементов картинки;
- – плохое разрешение изображения;
- – черно-белое или цветное изображение с низкой цветовой глубиной;
- – и т.п.
Однако, прогресс не стоял на месте и, со временем, были разработаны новые материалы и технологии в изготовлении жидкокристаллических мониторов. Достижения в технологиях микроэлектроники и разработка новых веществ со свойствами жидких кристаллов позволило существенно улучшить характеристики ЖК-мониторов.
Устройство и работа TFT LCD матрицы.
Одними из главных достижений стало изобретение технологии LCD TFT-матрицы – жидкокристаллической матрицы с тонкопленочными транзисторами (Thin Film Transistors). У TFT-мониторов кардинально возросло быстродействие пикселей, выросла цветовая глубина изображения и удалось избавиться от «хвостов» и «теней».
Структура панели, изготовленной по TFT технологии, приведена на Рис.2
| Структура ЖК-панели |
Рис.2. Схема структуры TFT LCD матрицы.
Полноцветное изображение на ЖК-матрице формируется из отдельных точек (пикселей), каждая из которых состоит обычно из трех элементов (субпикселей), отвечающих за яркость каждой из основных составляющих цвета – обычно красной (R), зеленой (G) и синей (B) – RGB. Видеосистема монитора непрерывно сканирует все субпиксели матрицы, записывая в запоминающие конденсаторы уровень заряда, пропорциональный яркости каждого субпикселя.
Тонкопленочные транзисторы (Thin FilmTrasistor (TFT) – собственно, поэтому так и называется TFT-матрица) подключают запоминающие конденсаторы к шине с данными на момент записи информации в данный субпиксель и переключают запоминающий конденсатор в режим сохранения заряда на все остальное время.
Напряжение, сохраненное в запоминающем конденсаторе TFT- матрицы, действует на жидкие кристаллы данного субпикселя, поворачивая плоскость поляризации проходящего через них света от тыловой подсветки, на угол, пропорциональный этому напряжению. Пройдя через ячейку с жидкими кристаллами, свет попадает на матричный светофильтр, на котором для каждого субпикселя сформирован свой светофильтр одного из основных цветов (RGB). Рисунок взаиморасположения точек разных цветов для каждого типа ЖК-панели разный, но это отдельная тема. Далее, сформированный световой поток основных цветов поступает на внешний поляризационный фильтр, коэффициент пропускания света которого зависит от угла поляризации падающей на него световой волны. Поляризационный светофильтр прозрачен для тех световых волн, плоскость поляризации которых параллельна его собственной плоскости поляризации. С возрастанием этого угла, поляризационный фильтр начинает пропускать все меньше света, вплоть до максимального ослабления при угле 90 градусов. В идеале, поляризационный фильтр не должен пропускать свет, поляризованный ортогонально его собственной плоскости поляризации, но в реальной жизни, все-таки небольшая часть света проходит. Поэтому всем ЖК-дисплеям свойственна недостаточная глубина черного цвета, которая особенно ярко проявляется при высоких уровнях яркости тыловой подсветки.
В результате, в LCD-дисплее световой поток от одних субпикселей проходит через поляризационный светофильтр без потерь, от других субпикселей – ослабляется на определенную величину, а от какой-то части субпикселей практически полностью поглощается. Таким образом, регулируя уровень каждого основного цвета в отдельных субпикселях, можно получить из них пиксель любого цветового оттенка.
А из множества цветных пикселей составить полноэкранное цветное изображение.
ЖК-монитор позволил совершить серьезный прорыв в компьютерной технике, сделав ее доступной большому количеству людей. Более того, без LCD-экрана невозможно было бы создать портативные компьютеры типа ноутбуков и нетбуков, планшеты и сотовые телефоны. Но так ли все безоблачно с применением жидкокристаллических дисплеев?
Понравился материал? Поделитесь им в соцсетях:
Категория:Экраны (тесты)
Дата:08 Сентября 2019 г.
Понимание матрицы Эйзенхауэра – Dropbox Business
Что такое матрица Эйзенхауэра?
Никто не хочет быть непродуктивным, особенно на работе. Но на протяжении дня появляются срочные запросы, и, по мере того как ваш список задач растет, становится все сложнее поддерживать это стремление к продуктивности. Если вы не успеваете выполнять ключевые задачи в срок, или вам сложно придерживаться графика в долгосрочных проектах, эффективная расстановка приоритетов в выполнении задач может вывести вас из отстающих в лидеры. И здесь на сцену выходит матрица Эйзенхауэра.
Понимание матрицы Эйзенхауэра
Матрица Эйзенхауэра, также известная под названием «коробка Эйзенхауэра» или «матрица срочных/важных задач» — это простая схема определения приоритетности задач и регулирования рабочей нагрузки. Она названа в честь Дуайта Д. Эйзенхауэра, пятизвездочного генерала и 34-го президента США. Эйзенхауэр известен благодаря своей неимоверной продуктивности, поэтому его подход к постановке целей и управлению временем всесторонне изучался многими людьми, одним из которых был Стивен Кови. В своей книге «7 навыков высокоэффективных людей» Кови создал на основе идей Эйзенхауэра простой инструмент расстановки приоритетов в выполнении задач: матрицу Эйзенхауэра.
Что же представляет из себя матрица Эйзенхауэра? По сути, это стратегия, которая позволяет вам применить на практике следующую цитату, приписываемую Эйзенхауэру: «У меня есть два типа проблем: срочные и важные. Срочные не важны, а важные никогда не бывают срочными». Вам нужно просто оценить свои задачи по критериям срочности и важности.
Как работает коробка Эйзенхауэра?
Компании и частные лица могут использовать матрицу Эйзенхауэра для планирования, делегирования, определения приоритетности и включения задач в график работы на день или на неделю. Распределив задачи в один из четырех квадрантов ниже, вы сможете определить их срочность и решить, как с ними следует поступить:
- Первый Квадрант. Срочное и важное (задачи, которые необходимо выполнить немедленно). Это очень важные задачи, которые нужно сделать в первую очередь и как можно скорее. Как правило, это запросы, полученные в последний момент по причине непредвиденных обстоятельств. Обычно такие задачи нужно выполнять немедленно или в тот же день. Сюда можно отнести работу в проекте вместо заболевшего коллеги или реагирование на непредвиденную ситуацию, например сбои в цепи поставок.
- Второй квадрант. Важное, но не срочное (задачи, которые можно запланировать на более поздний срок). Это важные долгосрочные цели или задачи, не имеющие жесткого срока выполнения, поэтому их можно запланировать на более поздний срок. Сюда можно отнести получение профессиональной квалификации или планирование долгосрочных бизнес-целей, например сокращение бюджета.
- Третий квадрант. Срочное, но не важное (задачи, которые можно кому-то делегировать). Эти задачи нужно выполнить немедленно, но они могут быть не настолько важными, чтобы привлечь ваше внимание, а значит, их можно делегировать другим участникам рабочей группы. Сюда можно отнести повседневную работу, длительные встречи или телефонные звонки без четкой цели.
- Четвертый квадрант. Несрочное и неважное (задачи, которые можно убрать из плана).
Эти задачи только отвлекают вас, поэтому их нужно избегать по возможности. Во многих случаях можно просто игнорировать или отменить такие задачи. Сюда можно отнести общественные мероприятия или излишне длительные перерывы на чай или кофе.
Эти задачи только отвлекают вас, поэтому их нужно избегать по возможности. Во многих случаях можно просто игнорировать или отменить такие задачи. Сюда можно отнести общественные мероприятия или излишне длительные перерывы на чай или кофе.Проще говоря, применение коробки Эйзенхауэра может помочь вам визуализировать ваши задачи с точки зрения важности и срочности. Когда вы начнете рассматривать свой рабочий процесс с такой позиции, вам гораздо проще будет расставить приоритеты для самых важных задач и выполнить их как можно скорее.
Как различить срочность и важность?
Нет универсальной формулы для определения различия между срочностью и важностью при создании матрицы приоритетов, но это очень важно. Чаще всего различие между этими двумя категориями в реальности определить намного труднее, чем при составлении абстрактной коробки Эйзенхауэра. Если вкратце, срочные задачи неизбежны и требуют незамедлительного уделения им внимания, а важные задачи в большей степени требуют планирования и способствуют достижению долгосрочных целей. Например, отвечать на телефонные звонки крупного клиента — это срочная задача, а ознакомиться с последними исследованиями в своей сфере — важная.
Каковы преимущества матрицы Эйзенхауэра?
Одним из основных преимуществ матрицы Эйзенхауэра является простота ее реализации. Не нужно покупать дорогостоящий пакет программного обеспечения и уделять много времени составлению матрицы. В общем, матрица приоритетов позволяет вам оптимизировать управление временем, установив четкие и однозначные приоритеты. Этот инструмент очень полезен для сотрудников, занимающих руководящие должности, или собственников бизнеса, а также фрилансеров, которым нужно совмещать задачи из нескольких различных проектов или работу с несколькими клиентами одновременно.
Каковы недостатки матрицы Эйзенхауэра?
С матрицей приоритетов связаны некоторые недостатки. Особо следует отметить, что зачастую бывает сложно точно определить важность задачи.
Это означает, что в конечном итоге вы можете делегировать задачу не тому человеку, что приведет к снижению качества. Более того, важно помнить, что не всегда есть возможность действовать немедленно, когда вы имеете дело с событиями, требующими мгновенной реакции. Это может быть невозможным по причине недостатка знаний, времени, из-за существующих правил и бюрократических процедур или большого количества срочных/важных задач, что снижает эффективность матрицы приоритетов при принятии решений и управлении временем.
Как использовать коробку Эйзенхауэра для управления задачами и рабочей нагрузкой
Матрица срочных/важных задач может стать отличной отправной точкой для управления рабочими процессами и проектами. После того как вы разместите свои задачи по соответствующим квадрантам, можно приступать к настройке процессов управления временем, что поможет вам своевременно реагировать на важные события. Например, вы можете использовать Dropbox для более эффективного управления своим списком заданий. Можно использовать эти инструменты управления задачами для делегирования срочных, но не важных задач другим участникам вашей рабочей группы, а также установить сроки сдачи и напоминания для срочных, но не важных задач, которые можно запланировать на более поздний срок.
Также стоит подумать о внедрении средств автоматизации на рабочем месте. Автоматизация, где это возможно, является отличным способом работы с задачами, которые необходимо выполнить, но не требующими длительного планирования или анализа до начала их выполнения. С помощью средств автоматизации или интеграции в Dropbox вы можете делегировать задачи из квадранта Q3 (срочное, но не важное) таким образом, чтобы это было эффективно с точки зрения времени для вашего бизнеса. Вы можете назначать задачи участникам рабочей группы в Dropbox Paper с указанием сроков их выполнения или переносить их непосредственно в карточки Trello для участников вашей рабочей группы из файлов Dropbox. Инструменты автоматического создания контента помогут вам избежать трудоемких, не защищенных от ошибок задач, которые могут создавать помехи в работе, обеспечив таким образом более продуктивную работу вашей рабочей группы в будущем.
Более того, можно объединить коробку Эйзенхауэра с другими методиками управления временем для достижения лучших результатов. Например, можно использовать метод «Съешь лягушку». В основе этой техники лежит высказывание Марка Твена: «Если с утра первым делом съесть лягушку, остаток дня будет чудесным». В контексте бизнеса это означает, что сначала нужно выполнить самую большую или сложную задачу, а затем перейти к более мелким задачам, приоритетность которых вы можете определить на основании других факторов, например, сроков их выполнения. Также существует метод ABCDE, где вы присваиваете своим задачам буквенное значение в зависимости от их важности, и затем выполняете их в этом порядке.
Заключительные соображения
Коробка Эйзенхауэра — чрезвычайно эффективный инструмент управления временем и задачами. Узнав, как эффективно определять приоритетность задач, вы сможете повысить эффективность своей работы, избежать действий, занимающих много времени, и достичь долгосрочных целей в бизнесе.
Определитель матрицы 3 на 3. Калькулятор
Найти определитель матрицы 3*3 можно быстро по правилу треугольника
Определители обозначают следующими знаками
Примеры вычисления определителей
Пример 1. Найти определитель матрицы
Решение: Применяем правило треугольника для нахождения определителя
Определитель равен 11.
Приведенная схема пригодиться Вам для вычисления определителя матрицы 3 * 3. Все что Вам нужно – подставить свои значения.
Пример 2. Вычислить определитель матрицы
Решение: В целях научить Вас чему-то новому, найдем определитель матрицы по правилу Саррюса.
Схема вычислений приведена выше поэтому копировать ее не будем, а лишь распишем в деталях. Для этого дописываем к стандартному определителю два первых столбца и выполняем следующие расчеты.
В результате вычислений определитель равен нулю.
Пример 3. Найти определитель матрицы 3*3
Решение: Применяем правило треугольника для нахождения определителя
Определитель равен -161.
Пример 4. Вычислить определитель матрицы
Решение: Находим определитель матрицы 3*3 по правилу треугольников
Пример 5. Найти определитель матрицы
Решение: Матрица имеет несколько нулевых элементов. Такие матрицы называют разреженными. Для уменьшения количества операций вычислим определитель через алгебраические дополнения ко второму строки или столбца.
Проще уже не может быть.
Пример 6. Доказать что определитель матрицы А равен 3
Решение: Матрица содержит два нулевых элементы, поэтому можем найти определитель через алгебраические дополнения. Разложим определитель по элементам первого столбца.
Определитель равен 3 что и требовалось доказать.
Пример 7. Найти определитель матрицы
Решение:По предварительной схеме определитель матрицы вычисляем через алгебраические дополнения первой строки или третьего столбца. выполняем вычисления
Определитель равен 39.
Пример 8. При каких значениях параметра а определитель матрицы равен нулю
Решение: По правилу треугольников находим определитель
По условию приравниваем определитель к нулю и находим параметр
Параметры при которых определитель обращается в нуль уровне a=-3;a=3.
Пример 9. Найти определитель матрицы
Решение: Найдем определитель матрицы по правилу треугольников и через алгебраические дополнения. По первой схеме получим
Теперь разложим с помощью алгебраических дополнений, например, третьим столбцом. Он удобен тем, что содержит самые элементы матрицы. Находим определитель
Сравнением количества расчетов убеждаемся, что в таких случаях целесообразнее использовать правило треугольников.
Вычисления проще и меньше вероятность сделать ошибку.
Для разреженных матриц или большего порядка блочных стоит применять расписание определителя по строке или столбцу.
И напоследок бонус от нас – калькулятор YukhymCalc.
С его помощью Вы легко проверите правильность исчисления основных операций с матрицами, а также сможете найти определитель матрицы и обратную матрицу. Для матриц 3*3 используется правило треугольников, для 4*4 – расписание определителя через элементы первой строки. Меню довольно простое и интуитивно понятное.
Определитель 7 задачу через матричный калькулятор иметь следующий вид
Как видите преимущество матричного калькулятора перед другими, в том числе онлайн калькуляторами, в том, что Вы видите все промежуточные операции. А это важно для проверки и контроля ошибок.
Используйте приведенные схемы вычислений определителей в обучении. Если возникают трудности в вычислениях и есть возможность, то можете проверить найдены определители калькулятором. Скачать матричный калькулятор YukhymCalc Вы можете без регистрации по этой ссылке.
Нужна помощь в принципиальной схеме матрицы герконового выключателя 8*8
Я разрабатываю матрицу геркона 8*8, которая будет соединена с Arduino. Я использую Arduino Duemilanove. Я завершил часть Матрицы, но не знаю, как соединить и где соединить другие элементы. Моя матричная схема
Я решил использовать следующие пункты:
- Arduino (Duemilanove)
- 64х геркон
- 64x диод (1N4148)
- 20х резисторы (10К)
- 1x 74HC595
- 1x 74HC165
Я не знаю, где разместить резисторы и сдвиговые регистры, а также подключение от сдвиговых регистров к arduino. Мне нужна помощь в создании схемы. Пожалуйста, помогите мне с принципиальной схемой.
Ссылка: https://mtifall10.wordpress.com/2010/12/10/magnetic-sensing-chessboard/
arduino circuit-diagramПоделиться Источник Aman Sinha 02 декабря 2016 в 05:32
2 ответа
- Нужна помощь в развертывании приложения Windows 8 PhoneGap
Я разработал приложение, с помощью Windows 8 HTML, И.
пустой шаблон приложения. Я включил PhoneGap / Cordova JS ссылку на проект, как описано в документации PhoneGap по адресу http:/ / docs.phonegap.com/en / 2.3.0/guide_getting-started_windows-8_index.md.html Я могу запустить приложение в… - UTF-8 в jsPDF работает, нужна помощь в укладке
Я заставил UTF 8 работать в jsPDF, чтобы иметь возможность печатать любой символ в PDF из Javascript. Араб, китаец, Turkish все это работает. Проверить fiddle: http://jsfiddle.net/oscoweb/fqpgcap1/2 / То, что я делаю, это: Напишите в canvas Сделать изображение из canvas Встроить изображение в PDF…
пустой шаблон приложения. Я включил PhoneGap / Cordova JS ссылку на проект, как описано в документации PhoneGap по адресу http:/ / docs.phonegap.com/en / 2.3.0/guide_getting-started_windows-8_index.md.html Я могу запустить приложение в…
0
Я бы использовал что-то вроде этого:
Где LOAD должно быть в состоянии HIGH по умолчанию, LOW уровень загружает входы на 74HC165, а LOW – HIGH изменение загружает выходы.
Поэтому вы просто посылаете короткий импульс LOW в LOAD , а затем отправляете следующую строку для сканирования (будет загружена в следующем раунде) в SPI . Вы должны запомнить предыдущую строку или подключить выход QH* от 595 до SER на 165 и сдвинуть два байта, один фиктивный, а второй будет новой строкой для сканирования.
И сканирование матрицы активно LOW. Таким образом, вы должны отправить байт с одним очищенным битом (выбранная строка) и набором rest битов. И это похоже на чтение (но вы также можете использовать инвертированный вывод из 165, чтобы получить инвертированные значения напрямую).
Поделиться KIIV 03 декабря 2016 в 10:05
0
Я не специалист, но постараюсь сделать все, что в моих силах. Я не могу заверить вас, что это 100% правильно.
Из-за ограниченного количества цифровых портов вам также придется использовать аналоговые порты.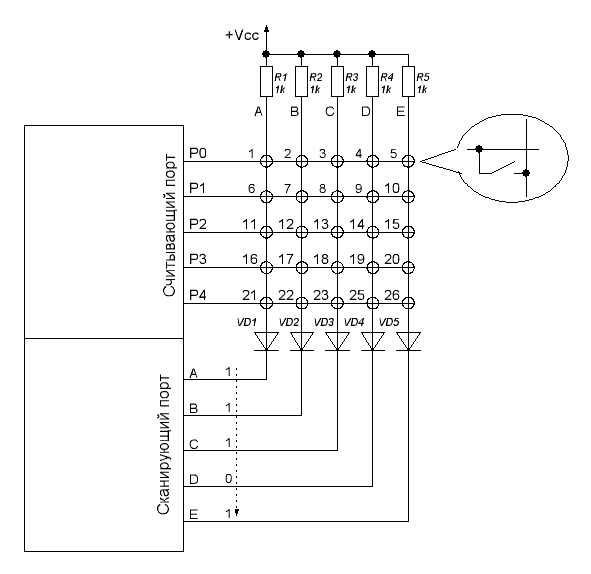
. В вашем случае контакты a, b, c, d… равны “positive”(ток идет от плюса к минусу). Булавки 1, 2, 3… это ваши основания/отрицательная сторона.
Резисторы должны быть подключены к каждому положительному контакту, в вашем случае к контакту a, b, c и так далее.
EDIT: Извините, я не учел сдвиговый регистр. Вам придется ознакомиться с таблицей данных. Вы, вероятно, будете использовать порт с широтно-импульсной модуляцией(PWM), GND порта и VoltageOut порта.
Поделиться Micropop 02 декабря 2016 в 08:18
Похожие вопросы:
Собственный вектор и собственное значение матрицы 8 X 8
У меня есть матрица чисел с плавающей запятой 8 х 8, и мне нужно вычислить из нее собственный вектор и собственное значение. Это делается для сокращения функций с использованием PCA (анализ главных…
Ищете способ считывания матрицы 8*8 из файла CSV и сохранения ее
Я новичок в программировании в C и ищу способ считывания матрицы 8*8 из файла CSV и хранения ее. Кто-нибудь может помочь?
Алгоритм существенной матрицы из 8 точек
В „ геометрии множественного вида в компьютерном зрении R.Hartley,A.зиссермана в главе 11-о вычислении фундаментальной матрицы можно прочитать: 11.7.3 калиброванный корпус В случае калиброванных…
Нужна помощь в развертывании приложения Windows 8 PhoneGap
Я разработал приложение, с помощью Windows 8 HTML, И. пустой шаблон приложения. Я включил PhoneGap / Cordova JS ссылку на проект, как описано в документации PhoneGap по адресу http:/ /…
UTF-8 в jsPDF работает, нужна помощь в укладке
Я заставил UTF 8 работать в jsPDF, чтобы иметь возможность печатать любой символ в PDF из Javascript. Араб, китаец, Turkish все это работает. Проверить fiddle: http://jsfiddle.net/oscoweb/fqpgcap1/2…
Размер матрицы всегда возвращает 8
в приведенном ниже коде я хочу найти размер массива 2d (матрицы), однако, когда я пытаюсь это сделать, несмотря на то, что я был объявлен размером матрицы непосредственно перед ее тестированием, она.
..
Как это происходит (+ (-(*))4 5) Оценка до 8
Я очень новичок в схеме и изучаю основы прямо сейчас. Я понимаю, что в (+ 1 2) + это как функция, принимающая два входа и возвращающая выход. В моей викторине был вопрос (+ (-(*))4 5) . Согласно…
Каким будет шаблон для UTF-8 в схеме Json?
Я пытаюсь сопоставить значение файла JSON, которое может содержать только UTF-8, иначе оно покажет ошибку. Я написал сценарий в python, чтобы проверить файл JSON с помощью схемы JSON. Я использовал…
8 точечный алгоритм оценки фундаментальной матрицы
Я смотрю лекцию об оценке фундаментальной матрицы для использования в стереовидении с использованием 8-точечного алгоритма. Я понимаю, что как только мы восстановим фундаментальную матрицу между…
Нужна помощь по логике потока Java 8
У меня есть список массивов, содержащий несколько строк. Мне нужно заменить один из элементов в этом списке обновленным значением, основанным на некотором условии, и сохранить другие строки. Мне…
Основные типы светочувствительной матрицы CCD (ПЗС) и CMOS (КМОП)
Основные типы светочувствительной матрицы CCD (ПЗС) и CMOS (КМОП)
Светочувствительные матрицы (сенсоры) бывают двух основных типов ― CCD (ПЗС) и CMOS (КМОП).
Рис. 1. Структурная схема матриц ПЗС и КМОП.
1) CCD (Charge-Coupled Device) матрица ― чип памяти, чувствительный к синему, красному и зелёному цветам. Используется в технологии сканирования в качестве оптических приемников. Изготовливается по технологии «приборов с зарядовой связью» (ПЗС).
2) CMOS (Complementary Metal-Oxide-Semiconductor) матрица ― светочувствительная матрица, изготовленная по технологии металл-оксид-полупроводник структура (КМОП), сенсорная технология – конвертирует свет в электронные сигналы.
Таблица 1. Основные отличия между матрицами CCD и CMOS.
|
CCD матрица |
CMOS матрица |
|
заряжается светом, значит, меньше проблем с темновыми токами |
разряжается светом, есть токи утечки |
|
считывается от строки к строке последовательно, энергопотребление системы большое |
строки и столбцы могут считываться произвольно, что позволяет строить более гибкие системы |
|
матрицы требуют специальных технологических процессов и материалов при производстве, что значительно ограничивает их производство и требует капиталовложений |
матрицы могут производиться на любом КМОП заводе, а значит, их массовый выпуск наладить просто и недорого |
|
имеют лучшую чувствительность, но требуют дополнительных микросхем для получения изображения, что увеличивает стоимость, размеры и энергопотребление системы |
содержат все устройства на одном кристалле, что делает систему экономичной, малогабаритной и дешевой; принцип “все в одной схеме” |
Из таблицы следует, что матрицы CMOS намного дешевле по сравнению с CCD-матрицами. На основе технологии CMOS можно делать сенсоры с большим количеством мегапикселей, и стоить они будут недорого (по сравнению с CCD). Но шумы CMOS-матрицы не дают изображение такого качества, которое имеют камеры с CDD-матрицами.
>> Назад
Каталог товаров
Нет товаров для сравнения
матричных диаграмм: что это такое и как их использовать
Руководители проектов управляют множеством процессов, программ и людей.
С таким количеством переменных, которые взаимодействуют и влияют на траекторию проекта, может быть трудно понять, как каждый элемент работает вместе и влияет на результаты.
Matrix помогают руководителям проектов визуализировать и оценивать эти сложные отношения, чтобы они могли принимать более обоснованные решения и отслеживать выполнение проектов.
Что такое матричная диаграмма?
Матричная диаграмма или диаграмма – это инструмент управления проектами и планирования, используемый для анализа и понимания взаимосвязей между наборами данных.
Матричные диаграммы сравнивают две или более групп элементов или элементов в одной группе. Они помогают руководителям проектов определить, как связана информация, а также насколько сильны эти отношения.
Типы информации, которую вы можете анализировать в матрице, включают:
- Данные
- Функции
- Концепции
- Люди
- Материалы
- Оборудование
- Действия
Отношения между элементами обозначаются числом или символом в ячейке, где пересекаются каждая пара элементов.
Форма матрицы, которую вы будете использовать, будет зависеть от количества элементов, которые вы хотите сравнить. Существует пять распространенных матричных диаграмм: L-образная, Y-образная, C-образная, T-образная и X-образная.
Зачем нужны матричные диаграммы?
Матричные диаграммы – это эффективный инструмент для визуализации сложных отношений (многие ко многим). Они помогают руководителям проектов определять различные способы взаимодействия элементов и зависимости друг от друга для принятия более эффективных решений, решения проблем и улучшения процессов.
Помещая группы элементов в матричную диаграмму из строк и столбцов, руководители проектов могут более легко визуализировать взаимосвязь между целями, факторами и причинами внутри организации, за которой они наблюдают.
Например, сравнивая два списка с помощью простой взаимно-однозначной связи, вы можете легко изобразить отношения в простой параллельной таблице. Однако, если некоторые элементы в списке связаны с более чем одним другим элементом, визуализация параллельной таблицы неадекватна.Связи между каждым элементом запутываются, и их трудно отследить.
Вот здесь и появляется матричная диаграмма.
Матричная диаграмма четко отображает эти сложные отношения, документируя два (или более) списка в виде строк и столбцов и отображая их отношения в ячейках.
Когда использовать матричные диаграммы
Вы можете использовать матричные диаграммы всякий раз, когда вам нужно определить и оценить отношения между двумя или более наборами данных.
Общие приложения матричного анализа включают:
- Выявление причин неисправностей
- Соответствие требованиям со спецификациями
- Распределение ресурсов в зависимости от потребностей или компетенции
- Сравнение возможных решений
- Определение возможностей для улучшения
- Проверка того, насколько хорошо выполняются требования
Матричные диаграммы особенно полезны при попытке понять причинно-следственные связи или провести анализ развертывания функции качества (QFD).
Виды матричных диаграмм
Существует пять основных типов матричных диаграмм. Ниже мы расскажем, что такое каждый тип и когда его использовать.
Г-образная матричная диаграмма
Что это: L-образная диаграмма – самая простая и наиболее распространенная матричная диаграмма. Он сравнивает два набора данных в двумерной таблице.
Один набор данных представлен в левом столбце, и он сравнивается со вторым набором данных в верхней строке таблицы. Цифры или символы обозначают отношения между парами в пересекающихся ячейках.
Вы также можете подсчитать баллы и записать итоги в конечных строках, чтобы помочь ранжировать или приоритизировать элементы на диаграмме.
Когда использовать: Используйте L-образную диаграмму, когда вам нужно сравнить две группы элементов или одну группу сама с собой.
Пример L-образной матрицы (щелкните изображение, чтобы изменить в Интернете)Y-образная матричная диаграмма
Что это такое: Y-образная диаграмма связывает три группы элементов, которые связаны друг с другом в круговом потоке (т.е.е., A ← → B ← → C ← → A). Эти отношения изображены на круговой диаграмме.
Когда использовать: Используйте Y-образную матрицу, когда вам нужно сравнить три тесно связанные группы. Его также можно использовать как практическое упрощение С-образной матрицы.
Пример Y-образной матрицы (щелкните изображение, чтобы изменить в Интернете)С-образная матричная диаграмма
Что это: C-образная диаграмма, похожая на Y-образную матрицу, сравнивает три набора данных. Однако С-образная матрица связывает три группы одновременно в трехмерной кубической диаграмме.
Когда использовать: Используйте C-образную матрицу, когда вам нужно сравнить три группы одновременно (например, людей, продукты и процессы на заводе).
Пример С-образной матрицы (Щелкните изображение, чтобы изменить в Интернете)Т-образная матричная схема
Что это такое: Т-образная диаграмма – это две L-образные матрицы, соединенные одним списком. Эта матрица позволяет сравнивать один список (центральный «полюс» буквы Т) с двумя другими группами. Это полезно, когда у вас есть два разных набора вопросов об основной группе.
Когда использовать: Используйте Т-образную матрицу, когда вам нужно сравнить две группы, которые связаны с одним основным списком (но не друг с другом).
Х-образная матричная диаграмма
Что это: X-образная матрица полезна для сравнения двух пар дополнительных списков. Он похож на Т-образную диаграмму, но расширяет Т-образную диаграмму, чтобы включить дополнительный набор данных.
Результатом является диаграмма с осями X и Y, образующими крест или форму «X», на которой сравниваются четыре полные группы данных.В этой матрице отношений каждая ось связана с группами, непосредственно примыкающими к ней, но не с группой напротив нее.
Когда использовать: Используйте X-образную диаграмму, когда вам нужно сравнить четыре группы предметов.
Пример X-образной матрицы (щелкните изображение, чтобы изменить в Интернете)Как строить матричные диаграммы
Выполните следующие действия, чтобы начать матричный анализ.
1. Определите свою цель
Прежде чем вы начнете строить диаграмму, вам нужно определить цель упражнения.Какую информацию или идеи вы пытаетесь почерпнуть из своего анализа?
Если вы просто изучаете отношения или хотите достичь чего-то более конкретного (например, принятия важного решения по проекту), четко определите эту цель с самого начала. Это поможет вам при сборе данных, выборе группы поддержки и выборе типа матрицы.
2. Наберите команду
Далее вам нужно выбрать, кого вы хотите в свою команду. Выберите членов команды, у которых есть время и опыт, наиболее подходящие для достижения поставленной цели.Эти люди должны понимать наборы данных и уметь связывать списки между собой.
Имейте в виду, что матричный анализ может занять много времени, поэтому важно, чтобы ваша команда смогла выполнить задание.
3. Определить и собрать наборы данных
После того, как вы собрали свою команду, вы можете приступить к идентификации и сбору данных, которые вы будете анализировать.
Ваша команда может помочь вам определить, какие данные следует сравнивать, и это наиболее важно для получения точных и значимых данных.
Будьте осторожны во время этого процесса, чтобы избежать предвзятости, которая может исказить ваши результаты.
4. Выберите соответствующий тип матрицы
Матрица, которую вы используете для анализа данных, зависит от вашей цели и типов данных, которые вы сравниваете. (См. Раздел выше, чтобы определить, какой тип матричной диаграммы лучше всего подходит для ваших наборов данных.)
5. Определите, как сравнивать ваши данные
Определите, как вы будете сравнивать данные и какие символы вы будете использовать для обозначения матрицы.
Например, будете ли вы сравнивать отношения на основе силы (например, сильная, средняя, слабая) или какого-либо другого фактора, такого как влияние или ответственность? Как вы отметите эти отношения в матрице?
6. Задокументируйте матричные отношения
Это основной этап матричного анализа. Не торопитесь и методично проработайте каждую ячейку, тщательно сравнивая каждый набор взаимосвязей на основе правил, изложенных вами на шаге 5.
Убедитесь, что по каждому решению существует консенсус, и задокументируйте все соответствующие обсуждения, связанные с анализом.Документация может помочь вам, когда вы пересмотрите свой выбор и доработаете диаграмму.
7. Просмотрите и сделайте выводы
После завершения анализа вы можете просмотреть матрицу, чтобы оценить и сделать выводы на основе результатов.
Хотя процесс матричного анализа может занять много времени, вложение того стоит. Матричные диаграммы помогают понять факторы, переменные и взаимосвязи, влияющие на ваш проект или бизнес, чтобы вы могли принимать более обоснованные решения.
Начните сегодня с простых в использовании шаблонов матричных диаграмм от Lucidchart.
Как понять матричную диаграмму
Справочник по качеству> Матричная диаграмма> Как это понять
Когда использовать | Как это понять | Пример | Как это сделать | Практичный вариации
<- Предыдущая | Далее ->
Как это понимать
При сравнении двух списков иногда возникает простая взаимно-однозначная взаимосвязь, которую можно легко задокументировать в соседней таблице.Однако, когда один элемент из одного списка может быть связан с несколькими элементами в другом списке, тогда параллельный формат не работает, так как на рис. 1.
Рис. 1. Отношения между списками
Матричная диаграмма позволяет сравнивать два списка, перевернув второй список на бок, чтобы сформировать матрицу.
На рис. 2 показано, как отношения между двумя элементами теперь могут быть обозначены в квадрате или ячейке , где пересекаются строка и столбец двух элементов.
Рис. 2. Отношения «многие ко многим» в матрице
Матрица может рассматриваться как особая форма таблицы, в которой ячейки содержат простой символ или число, полученное из определенного набора правила.
Распространенным расширением матриц является использование различных символов в ячейках матрицы, чтобы показать степень взаимосвязи между парами элементов. Общую силу взаимосвязи между отдельным элементом и всем другим списком также можно определить либо путем визуальной проверки диаграммы, либо путем присвоения числового значения каждому символу и суммирования строк и столбцов, как в Инжир.3.
Наиболее распространенные символы взаимосвязи и их соответствующие значения показаны ниже. Нелинейная взаимосвязь между значениями числовых символов показывает, насколько сильная взаимосвязь обычно намного сильнее , чем средняя или слабая взаимосвязь. Другой фактор, который может быть включен в это вычисление, – это относительный приоритет каждого элемента списка.
Рис. 3. Демонстрация и суммирование силы взаимоотношений
Базовая матрица, показанная выше, является наиболее часто используемой матрицей и называется L-Matrix из-за ее формы.Если требуется более чем простое сравнение двух списков, доступны другие матрицы, которые показаны
на рис. 4. Они также имеют описательные названия букв, указывающие на их форму.
Рис. 4. Различные типы матричной диаграммы
Типичное использование матричной диаграммы для сравнения двух списков – это когда список слева представляет проблему («что»), а список выше представляет решение этой проблемы («как»).Например, в первом списке подробно описаны требования заказчика к продукту, а во втором списке показано, как это преобразовано в проектные спецификации. Значения отношений теперь можно использовать для определения конкретных проблем и других интересных моментов, например:
- Строки с низкими итоговыми значениями указывают на неудовлетворительные требования клиентов.
- Столбцы с низкими итоговыми значениями могут указывать на чрезмерно сложные или ненужные элементы дизайна.
- Столбцы с высокими итоговыми значениями указывают на элементы дизайна, которые особенно важны для удовлетворения ряда требований клиентов.
Ограничение при использовании матричной диаграммы заключается в количестве сравнений, которые могут быть выполнены на практике. Матрица десять на десять требует 100 сравнений, для завершения которых требуются умеренные усилия. Однако сложный продукт может иметь сотни деталей требований и соответствующее количество элементов проектной спецификации, но матрица сто на сто требует выполнения непозволительно 10 000 сравнений!
Практическое использование матричной диаграммы в сложной ситуации заключается в том, чтобы сосредоточить внимание на деталях критических, подозрительных или сложных частей проблемы, а не пытаться использовать ее для всей ситуации.
<- Предыдущая | Далее ->
Матричная диаграмма| Лучшая оценка
Примеры
В этом примере мы сравниваем игроков (ось Y) с шестью переменными на оси X. Шрифт намеренно маленький, потому что в этом примере был применен цвет, чтобы увидеть, где выделяются отдельные игроки. Глядя на строки, можно увидеть, что переменные, в которых этот игрок выделяется, темнее по сравнению с другими, более слабыми характеристиками.
Глядя на столбцы, игроки, которые выделяются по определенной переменной, легко заметить по более темному цвету. Эта матричная диаграмма выполняется с помощью условного форматирования в MS Excel.
Источник: Дэйв Шеллард и Марк Фогельгесан
В этом примере матричная диаграмма по сути представляет собой расширенную столбчатую или гистограмму, где данные представлены пропорционально другим значениям. В этом примере требуется некоторая работа в MS Excel для правильного форматирования набора данных (см. Ссылку или руководство ниже).
Американское общество качества
На этой матричной диаграмме простые точки представляют высокие и низкие значения. В столбцах указаны основные производители и покупатели модели. Читая строки, выявляются тенденции развития и покупки моделей.
Источник: http: //asq.org/learn-about-quality/new-management-planning-tools/overvie …
Many Eyes: Руководство по матричным диаграммам
Более продвинутые программные инструменты могут позволить использовать другое измерение, например, этот пример из Many Eyes.Этот инструмент позволяет отображать два дополнительных элемента данных в формате круговой диаграммы с помощью матричной диаграммы.
Источник: www-958.ibm.com/software/analytics/manyeyes/page/Matrix_Chart.html
Совет
Советы по ВЫБОРУ этой опции (насадки и ловушки)
Матрицыполезны для визуального отображения кросс-таблиц, которые в противном случае было бы сложно читать. Если вы хотите опубликовать результат кросс-таблицы, подумайте о добавлении элемента цвета или символа, чтобы привлечь внимание читателя.С помощью дополнительного программного обеспечения вы можете сделать матричную диаграмму более сложной и показать дополнительные переменные в сравнительной форме.
Рекомендации по ИСПОЛЬЗОВАНИЮ этой опции (наконечники и ловушки)
Поскольку в матричной диаграмме представлено очень много данных, визуальное отображение самих графиков должно быть очень простым и лаконичным.
Если печатаются фактические элементы данных, уменьшите размер шрифта, чтобы цвет передавал сообщение.
ресурсов
Направляющие
Матричная диаграмма.Вычислительные решения Mouse Trax: различные наглядные примеры и пошаговые инструкции для создания различных видов матричных диаграмм от Джона Пелтье (2012)
Excel Panel Charts (в архиве): инструкции по созданию различных типов матричных диаграмм с помощью Excel
Пример
Matrix Chart Guide: Пример круговой матричной диаграммы из Many Eyes (2011)
Другие способы просмотра взаимосвязей между точками данных
Диаграмма рассеяния
Отображение взаимосвязи между двумя количественными переменными, нанесенными по двум осям.Ряд точек представляет положение наблюдений из набора данных.
Схема сети
Показывает, как люди (или другие элементы) в сети связаны.
Посмотреть все параметры визуализации данных можно здесь.
Источники
Многие глаза (2011). Руководство по матричным диаграммам . Получено с http://www-958.ibm.com/software/data/cognos/manyeyes/page/Matrix_Chart.html
.Полное руководство по диаграмме матрицы отношений
Руководство или учебное пособие по диаграмме матрицы отношений поможет вам лучше понять диаграмму матрицы отношений, чтобы вы могли в полной мере использовать ее для хороших целей.
Диаграмма матрицы отношений объединяет данные в наборы элементов для сравнения. Он также позволяет создавать, изменять и удалять отношения между элементами одним щелчком мыши – еще один быстрый способ установить сложные наборы взаимосвязей элементов с минимальными усилиями.
Определение матрицы отношений
Диаграмма матрицы отношений – это удобный метод быстрой и точной визуализации отношений. Диаграмма матрицы отношений графически показывает отношения и позволяет группе или отдельному лицу систематически выявлять, анализировать и оценивать наличие и силу отношений внутри набора элементов или между двумя или более наборами информации.
Диаграмма матрицы отношенийпредставляет собой компактный способ представления отношений «многие ко многим» различной силы.
Зачем нужна матричная диаграмма отношений?
Многим может быть интересно узнать, почему мы должны использовать диаграмму матрицы отношений, чтобы показать сложные отношения. Для меня большая честь ответить на ваши вопросы. Потому что отношения между вещами часто бывают сложными (многие ко многим) и требуют от нас мыслить более чем в одном измерении. Диаграмма матрицы отношений – это простой инструмент, который позволяет разрешать относительно сложные ситуации. проанализированы простым и понятным способом.Они помогают нам выявить взаимодействия и зависимости между вещами, которые помогают нам понять сложные причинно-следственные связи.
При сравнении двух списков иногда возникает простая взаимно-однозначная взаимосвязь, которую можно легко задокументировать в соседней таблице. Однако, когда один элемент из одного списка может быть связан с несколькими элементами в другом списке, то параллельный формат не работает.
Диаграмма матрицы отношений позволяет сравнивать два списка, перевернув второй список на бок, чтобы сформировать матрицу.Взаимосвязь на диаграмме матрицы отношений между двумя элементами теперь может быть указана в квадрате или ячейке, где пересекаются строка и столбец двух элементов.
Шаги, чтобы нарисовать диаграмму матрицы отношений
Существует пять основных типов диаграмм матриц отношений, которые позволяют исследовать разное количество списков. L-образный, T-образный, Y-образный, X-образный, C-образный, QFD-тип (развертывание качественной функции). Хотя для отображения взаимосвязей удобно использовать диаграмму матрицы взаимосвязей, рисовать диаграмму матрицы взаимосвязей вручную довольно сложно.Не беспокойтесь, вы можете использовать конструктор диаграмм матрицы отношений, чтобы нарисовать ее. Теперь позвольте мне показать вам, как шаг за шагом построить диаграмму матрицы отношений.
Перво-наперво, откройте Edraw Max, укажите на «Файл», затем укажите на «Создать», найдите «Матрицу отношений» и щелкните по ней.
Когда вы щелкнете по шаблонам диаграммы матрицы отношений, вы можете обнаружить, что в нижней части программного обеспечения есть примеры. Дважды щелкните пример, и вы откроете его. Вы можете настроить и отредактировать пример по своему усмотрению, что определенно сэкономит вам много времени.
Выберите нужную форму матрицы отношений в библиотеке слева от холста.
При использовании символа «флажок» вы можете обнаружить плавающую кнопку в правом верхнем углу фигуры. С помощью плавающей кнопки у вас есть три варианта, как показано на рисунке ниже.
Кроме того, при использовании цветных круглых флагов вы можете обнаружить, что плавающая кнопка имеет множество вариантов цвета.
При использовании символа нумерации вы можете найти стрелку поворота в верхней части символа.Кроме того, вы можете дважды щелкнуть фигуру, чтобы изменить число, как показано на рисунке ниже.
И последнее, но не менее важное: вы должны обратить внимание на плавающую кнопку с четырьмя направлениями и 6-значные символы флага.
Вы также можете отредактировать другие элементы диаграммы матрицы отношений, чтобы сделать ее более привлекательной.
Ознакомьтесь с другими примерами диаграмм матрицы отношений, чтобы получить готовые шаблоны.
Узнайте больше о том, как создать диаграмму матрицы отношений, прежде чем начать.
Диаграмма Матрица отношений | Руководство пользователя Enterprise Architect
Представление матрицы отношений диаграммы представляет содержимое текущей диаграммы в виде простой сетки, определяющей отношения между элементами на этой диаграмме.
Доступ
Дизайн> Схема> Просмотреть как> Представление матрицы отношений | |
Щелкните правой кнопкой мыши фон диаграммы | Переключить вид | Перейти к просмотру матрицы отношений или Щелкните правой кнопкой мыши вкладку диаграммы | Перейти к просмотру матрицы отношений В окне браузера щелкните правой кнопкой мыши имя открытой диаграммы | Переключить вид | Перейти к просмотру матрицы отношений |
Матрица отношений
Представление «Матрица отношений» похоже на «Матрицу отношений на уровне проекта», но представляет собой представление диаграммы и, как таковое, отображает только те элементы, которые содержатся в выбранной диаграмме, и имеет меньшее количество полей для определения того, где эти отношения обнаруживаются.
Каждая строка и каждый столбец представления «Матрица отношений» представляют элемент диаграммы. В верхнем левом углу каждой ячейки строки и столбца есть небольшой курсив, который является индексом строки / столбца. Ячейка на пересечении строки и столбца показывает подробности любых отношений между соответствующими элементами диаграммы.
Представление «Матрица отношений» предоставляет средства для быстрой идентификации элементов, которые еще не связаны с другими элементами, например элементов требований, которые еще не реализованы.Вы также можете создавать новые отношения или удалять существующие прямо в матрице.
При выборе ячейки в матрице отображаются дополнительные свойства отношений, если они существуют, например значения мощности и роли. Если между функциями исходного и целевого элементов существуют отношения, это также отображается в матрице.
Параметры просмотра
Вы можете улучшить отображение, чтобы отображать только:
- Взаимосвязь соединителей определенного типа
- Исходные элементы определенного типа и / или
- Целевые элементы определенного типа
Щелкните стрелку раскрывающегося списка для соответствующего поля в верхней части матрицы и выберите требуемый тип.Обратите внимание, что типы элементов и соединителей в списках предназначены только для тех объектов, которые уже присутствуют на схеме.
Вы можете дополнительно ограничить отображение, чтобы отображались только элементы, у которых уже есть соединители, установив флажок «Ограничить подключенными элементами».
Формат
По умолчанию в представлении матрицы отношений элементы отображаются в виде иерархии, как для требования A1 в предыдущем примере. Вы можете изменить это, чтобы отображать элементы в плоских списках, щелкнув правой кнопкой мыши в верхней левой ячейке и отменив выбор параметра «Показать иерархию элементов».
Перемещение по матрице отношений
Вы можете перемещаться по матрице отношений с помощью полос прокрутки или клавиш со стрелками.
Полосы прокрутки:
- Если матрица больше, чем область отображения экрана, и некоторые ячейки элемента / отношения не видны, отображается вертикальная и / или горизонтальная полоса прокрутки, чтобы вы могли прокручивать до скрытой области матрицы.
- Если вы прокрутите матрицу вверх, заголовки столбцов останутся видимыми, в то время как строки будут катиться под ними и будут скрыты; в этом случае верхний край первого видимого заголовка строки становится пунктирной линией, чтобы указать, что над ним есть скрытые строки (и вы заметите, что курсивом в верхнем левом углу ячейки будет число больше 1)
- Аналогичным образом, если вы прокрутите матрицу влево, заголовки строк останутся видимыми, а столбцы будут катиться под ними и будут скрыты; левый край первого видимого заголовка столбца становится пунктирной линией, чтобы указать, что слева от него есть скрытые столбцы (а курсивом в верхнем левом углу ячейки будет число больше 1)
Клавиши со стрелками:
- Из выбранной ячейки матрицы вы можете нажимать клавиши со стрелками для перехода к соседней ячейке того же типа (то есть от заголовка столбца к заголовку столбца, заголовка строки к заголовку строки или ячейки сетки к ячейке сетки)
- Для перемещения между ячейками разных типов, например, из ячейки сетки в ячейку заголовка столбца или наоборот, нажимайте Ctrl при нажатии клавиш со стрелками
- Если соседняя ячейка скрыта или находится за пределами области отображения, нажатие соответствующей клавиши со стрелкой прокрутит матрицу отношений, чтобы отобразить строку или столбец, содержащий эту ячейку
Добавить / удалить элемент
Вы можете добавлять элементы в матрицу отношений:
- Перетаскивание значка соответствующего элемента из панели инструментов на треугольник «Целевой» или «Исходный» (для добавления однорангового элемента) или на элемент в строке «Целевой объект» или в столбце «Источник» (для добавления нового элемента в качестве дочернего элемента выбранный элемент)
- Перетаскивание элемента из окна браузера в целевую строку или исходный столбец
- Щелкните правой кнопкой мыши имя элемента в строке «Цель» или в столбце «Источник» и выберите параметр «Новый дочерний элемент», чтобы добавить новый дочерний элемент типа, указанного в подменю.
- Щелкните правой кнопкой мыши имя элемента в строке «Цель» или в столбце «Источник» и выберите «Вставить связанные элементы»… ‘, чтобы вставить связанный элемент выбранного элемента, используя диалоговое окно «Вставить связанные элементы»
- Щелкните правой кнопкой мыши фон диаграммы за пределами матрицы отношений и выберите параметр «Вставить другой элемент …», чтобы вставить элемент из любого пакета, обнаруженного и выбранного с помощью браузера «Выбрать элемент»
Вы можете удалить элемент из матрицы отношений, выбрав ячейку с именем элемента и либо:
- Нажатие Ctrl + Delete удаляет элемент и его соединители из модели; Вам будет предложено подтвердить удаление, или
- Щелчок правой кнопкой мыши по ячейке и выбор опции «Удалить <имя элемента>» (элемент немедленно удаляется из матрицы и диаграммы), или
- Нажатие клавиши удаления
Добавить / удалить коннектор
Матрица отношений диаграммы значительно упрощает процесс создания и удаления соединителей отношений между элементами.
Чтобы добавить соединитель , щелкните ячейку на пересечении строки исходного элемента и столбца целевого элемента и:
- Щелкните правой кнопкой мыши и выберите параметр «Создать новую связь», а затем выберите тип соединителя в подменю или
- Если в настоящее время нет соединителя между исходным и целевым элементом, нажмите клавишу пробела и затем выберите тип соединителя в подменю, или
- Если есть соединитель, и вы хотите добавить еще один, нажмите клавишу пробела, выберите параметр «Создать новую связь», а затем выберите тип соединителя в подменю
К удалить соединитель :
Щелкните ячейку, содержащую соединитель, который необходимо удалить, и либо:
.- Нажмите Ctrl + Delete, при этом вам будет предложено подтвердить действие перед удалением соединителя из модели, или
- Щелкните правой кнопкой мыши и выберите опцию «Удалить соединитель», в которой вам будет предложено указать, следует ли просто скрыть соединитель или удалить соединитель из модели, или
- Нажмите клавишу «Удалить», которая снова предложит вам выбрать между скрытием и удалением соединителя.
Свойства отображаемого элемента / соединителя
Вы можете отобразить свойства любого элемента или соединителя в матрице либо в диалоговом окне «Свойства» объекта, либо в закрепленном окне «Свойства».
- Чтобы отобразить диалоговое окно «Свойства», дважды щелкните имя элемента или соединителя в ячейке
- Чтобы отобразить закрепленное окно «Свойства», щелкните имя элемента или соединителя в ячейке и нажмите Ctrl + Enter; если окно уже отображается, просто щелкните имя элемента или соединителя, чтобы сделать его фокусом окна
Редактирование имен элементов на месте
Если вам нужно исправить имя элемента в матрице отношений, вы можете легко сделать это с помощью локального редактора; щелкните ячейку элемента и либо нажмите F2, либо дважды щелкните имя элемента (не дважды щелкните).Введите правильный текст и нажмите клавишу Enter.
Скрыть / Показать отношения
Если вы хотите упростить диаграмму и ее различные представления, вы можете скрыть соединители, которые не имеют непосредственного отношения к представлению, и вызвать их, когда они потребуются для вашей цели. Скрытие или отображение соединителя в одном представлении схемы влияет на все остальные представления.
Прежде чем пытаться скрыть соединители, убедитесь, что на странице «Ссылки» диалогового окна «Настройки» («Пуск> Рабочий стол> Настройки> Настройки> Ссылки» установлен флажок «Запрашивать при удалении соединителя»).
Чтобы скрыть разъем:
Щелкните ячейку с соединителем, который вы хотите скрыть, затем выполните одно из следующих действий:
- Щелкните правой кнопкой мыши и выберите «Видимость | Вариант “Скрыть соединитель” или
- Щелкните правой кнопкой мыши и выберите опцию «Удалить соединитель», затем в диалоговом окне «Удалить соединитель» выберите переключатель «Скрыть соединитель» и нажмите кнопку «ОК», или
- Нажмите клавишу «Удалить» и снова в диалоговом окне «Удалить соединитель» выберите переключатель «Скрыть соединитель» и нажмите кнопку «ОК»,
Чтобы показать скрытый разъем:
Щелкните ячейку, содержащую соединитель, который вы хотите показать, затем:
- Щелкните правой кнопкой мыши и, если ячейка содержит какие-либо скрытые соединители, выберите опцию «Показать связь» (опция не предоставляется, если нет скрытых соединителей)
- В подменю, в котором перечислены все скрытые соединители по типу и (если задано) имени, выберите соединитель, чтобы отобразить
Перемещение между графическим представлением и представлением матрицы отношений
Вы можете легко переключиться с представления матрицы отношений на графическое представление или любое другое представление диаграмм, используя пункт контекстного меню «Переключить представление | Перейти к графическому представлению »(или« Перейти к <другому> виду »).
Если вы выберете опцию после нажатия на:
- Общая область матрицы, диаграмма отображается из верхнего левого угла, а другие виды отображаются из начальной точки
- Ячейка отношения, которая показывает конкретный соединитель, диаграмму или другое представление, отображающее этот соединитель или его информацию, видимую и выбранную
Если вы находитесь на диаграмме в ее графическом представлении, вы можете выбрать соединитель и сфокусироваться на нем в матрице отношений диаграммы, щелкнув правой кнопкой мыши выбранный соединитель и выбрав опцию «Перейти к просмотру матрицы отношений».Матрица отображается с ячейкой для этого разъема в центре дисплея.
Опубликовать матрицу отношений
Когда вы визуализируете диаграмму как матрицу отношений, вы можете зафиксировать внешний вид матрицы в:
- Печатная копия – «Опубликовать> Изображение схемы> Печать> Печать» Файл PDF
- – «Опубликовать> Изображение диаграммы> Печать> Печать в PDF ». Файл изображения
- – ‘Опубликовать> Изображение диаграммы> Сохранить> Сохранить в файл
- Захват буфера обмена – «Опубликовать> Изображение диаграммы> Сохранить> Сохранить в буфер обмена »
Узнать больше
Диаграмма анализа данных матрицы| Объяснено с помощью примера
Что такое диаграмма анализа матричных данных?→ Матричная диаграмма анализа данных (MDAC) используется для определения взаимосвязей. связанных элементов группы в большей группе наборов данных.
→ Иногда эта диаграмма называется MDAC.
→ Этот инструмент является одним из важнейших инструментов 7 Management and Planning Инструменты (новые 7 инструментов контроля качества).
→ MDAC в основном используется для проведения маркетинговых исследований и описания продуктов и Сервисы.
→ Matrix_Data организована для удобной визуализации и сравнения.
→ MDAC помогает классифицировать предметы, определяя две основные характеристики общий для всех элементов, а затем нанесение каждого элемента в виде точки на стандартном x-y Диаграмма.
→ Так легче увидеть, как отдельные элементы соотносятся с характеристики и друг к другу.
→ Базовая диаграмма анализа матричных данных приведена на рисунке ниже. Мы легко понять анализ матричной диаграммы.
→ Мы можем принять решение на основе оценки различных характеристик матрица попадает в какой квадрант.
➨ Квадрантный анализ, как указано ниже.
→ (1) 1-й квадрант известен как желательный квадрант
→ (2) 2-й квадрант известен как частично желательный Квадрант
→ (3) 3-й квадрант известен как нежелательный квадрант
→ (4) 4-й квадрант известен как частично желательный Квадрант
Когда использовать матричную диаграмму анализа данных→ Мы можем использовать этот инструмент при исследовании факторов, влияющих на количество разные предметы, чтобы определить общие отношения.
→ Этот инструмент используется для проверки того, что похожие предметы имеют одинаковый эффект. факторов или влияющих также на разные факторы.
→ Диаграмма анализа матричных данных также используется в качестве инструмента решения проблем .
→ При сравнении большого набора элементов сложность ситуации может затруднить определение того, как разные факторы соотносятся друг с другом, в данном случае мы можем использовать этот инструмент.
→ Этот инструмент полезен для поиска группы элементов, которые ведут себя одинаково или нет.
Как создать матричную диаграмму анализа данных (MDAC)?→ Четыре шага для создания диаграммы MDAC упомянуты ниже.
- Определите две характеристики для анализа
- Назначьте оценку характеристикам и подготовьте матрицу
- Поместите all_data в график типа X-Y.
- Дайте подходящее название графику и проанализируйте график на основе квадранта
→ Для лучшего понимания диаграммы анализа матричных данных (MDAC) мы взяв пример ниже.
Пример диаграммы анализа матричных данных→ Нам нужно проанализировать разные блюда в столовой колледжа. Так что мы будем для этого выполните вышеупомянутые шаги.
Шаг 01: Определите две характеристики для анализа→ Сравним разные блюда столовой колледжа по ниже двухпараметрический (Характеристики).
→ (1) Визуальная привлекательность блюд и
→ (2) Вкус блюд
→ Теперь возьмем эти блюда на анализ Chilly Potato, Masala Dosa, Papdi Чат, макароны, обед / ужин, сэндвич, жареный сэндвич и самоса.
Шаг 02: Присвойте баллы характеристикам и подготовьте Матрица→ Таким образом, мы будем считать оценку на основе оценки студентом всех блюд столовая колледжа по шкале от 1 до 10.
→ 1 балл означает очень плохо, а 10 баллов – очень хорошо.
→ Поэтому см. Таблицу ниже для выставления оценок учащимися.
Шаг 03: Поместите все данные в график типа X-Y→ Из приведенной выше таблицы точки all_data затем наносятся на простой x-y график.
→ Обе оси X и Y показаны от 0 до 10.
→ См. Рисунок ниже для размещения графика.
Шаг 04: Дайте подходящее название графику и проанализируйте график на основе квадранта→ Теперь, наконец, нам нужно проанализировать график на основе квадранта данных падение.
→ Итак, на основе квадранта и матрицы data_types мы можем получить следующие результаты для разных блюд путем сравнения и оценки двух разных параметров, таких как как (1) визуальная привлекательность блюд и (2) вкус блюд.
➨ Желательные блюда: макароны, папди чат, самоса, и чили картофель
➨ Частично желаемые блюда: масала доса, сэндвич и жареные на гриле. Бутерброд
➨ Нежелательные блюда: Обед / Ужин
Другие примеры анализа диаграмм MDAC→ Производственная компания стремится разработать альтернативные материалы для строительства более прочный редуктор, сравнивая стоимость материала и материал долговечность.
→ Производственное предприятие ищет альтернативного поставщика сырья. материал за меньшие деньги и своевременную доставку для того же материального имущества.
👉 Читайте также:👉 Для регулярного обновления:
👉 См. Также:
Матричная диаграмма Шаблоны презентаций PowerPoint | SketchBubble
Визуализация соединенийЛюди любят визуализировать связи. Он отлично подходит для передачи данных и того, как каждый набор данных связан друг с другом.Данные требуются для многих целей. Это может помочь компаниям отслеживать их рост, вероятный потенциал, сдерживать риски и многое другое. Конечно, существуют разные типы диаграмм. Однако рекомендуется, чтобы для отображения связей между наборами данных (в отношении управления) использовалась матричная диаграмма или диаграмма. Здесь вам может помочь наш профессионально разработанный шаблон PowerPoint «Матричная диаграмма». Эти готовые слайды не только визуально привлекательны, но и сэкономят время и силы.
Опыт не требуетсяВы раньше не пользовались профессионально разработанным готовым набором? Что ж, тебе не о чем беспокоиться. Наша команда была полна решимости создать шаблон, доступный для всех. Чтобы начать использовать наши слайды, вам не требуется никакого опыта. Будь вы преподавателем, студентом или бренд-менеджером, такой набор подойдет каждому. Доступен в двух разных цветовых темах, вы можете выбрать желаемую тему. Как только это будет сделано, вы можете щелкнуть и настроить.Да, это действительно так просто! Эти полностью настраиваемые слайды можно без проблем придать любой форме.
Привлекающий вниманиеПрезентации должны увлекать аудиторию. Именно в этом и помогает наша предварительно разработанная матричная диаграмма PPT. Эти слайды содержат векторные изображения высокой четкости. Это гарантирует, что размеры значков и изображений могут быть изменены без каких-либо проблем.