Штейнера закон: Теорема Штейнера

Теорема Штейнера.

В приведенных примерах оси проходят через центр инерции тела. Мо­мент инерции относительно других осей вращения определяется при по­мощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а – расстояние от центра инерции тела до выбранной оси вращения,т.е.

, где m – масса тела, а – расстояние от центра

инерции тела до выбранной оси вращения.

Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню.

Прямое вычисление сводится к тому же ин­тегралу (*),но взятому в других пределах:

Расстояние до оси, проходящей через центр масс, равно а = ℓ/2.По теореме Штейнера получаем тот же результат.

.

§22.Основной закон динамики вращательного движения.

Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е.

.

В проекциях на оси координат: .

Если вращение тела происходит относительно неподвижной оси, то основной закон динамики вращательного движения примет вид: . В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси:. Тогда основной закон динамики вращательного движения примет вид:. Если тело не рассыпается и не деформируется, то

, вследствие чего . Если ко всему, тои, оно равно:.

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*).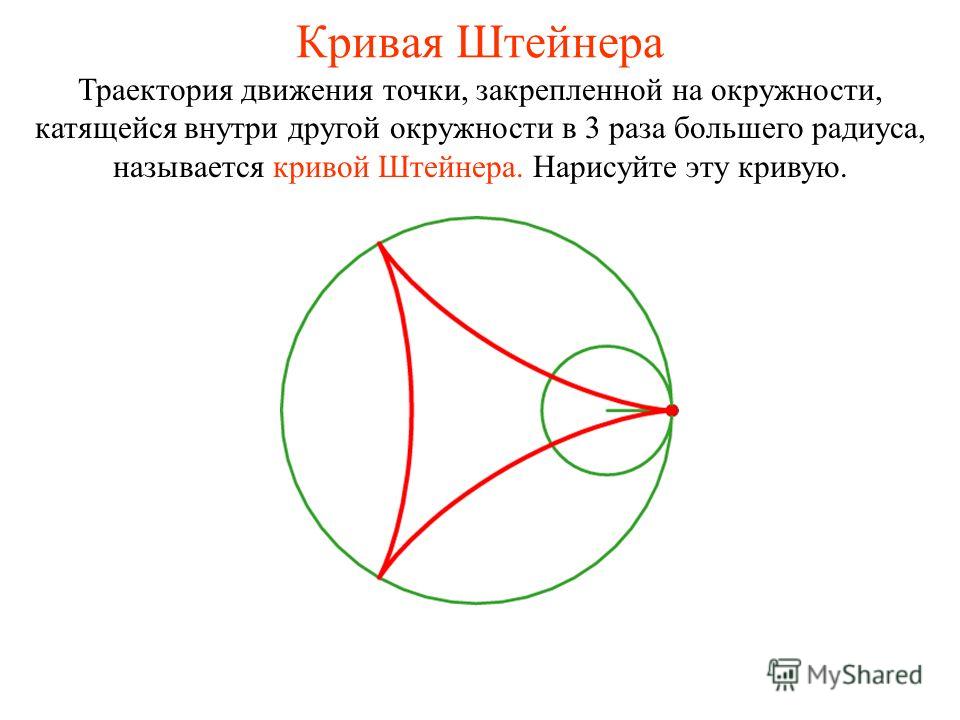 Полная работа. Если, то.

На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к. , то. После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси.

§23.Закон сохранения момента импульса.

Как уже указывалось, законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмер­ного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство само по себе изотропно,в нем нет выделен­ных направлений. С этой симметрией связанзакон сохранениямомента импульса.Эта связь проявляется в том, что момент количества движе­ния, является одной из основных величин, описывающих вращательное движение.

По определению момент импульса отдельной частицы равен .

Направление вектора Lопределяется по правилу буравчика (штопора), а его величина равна L = r p sin ,где

  угол между направлениями радиус-вектора частицы и ее импульса.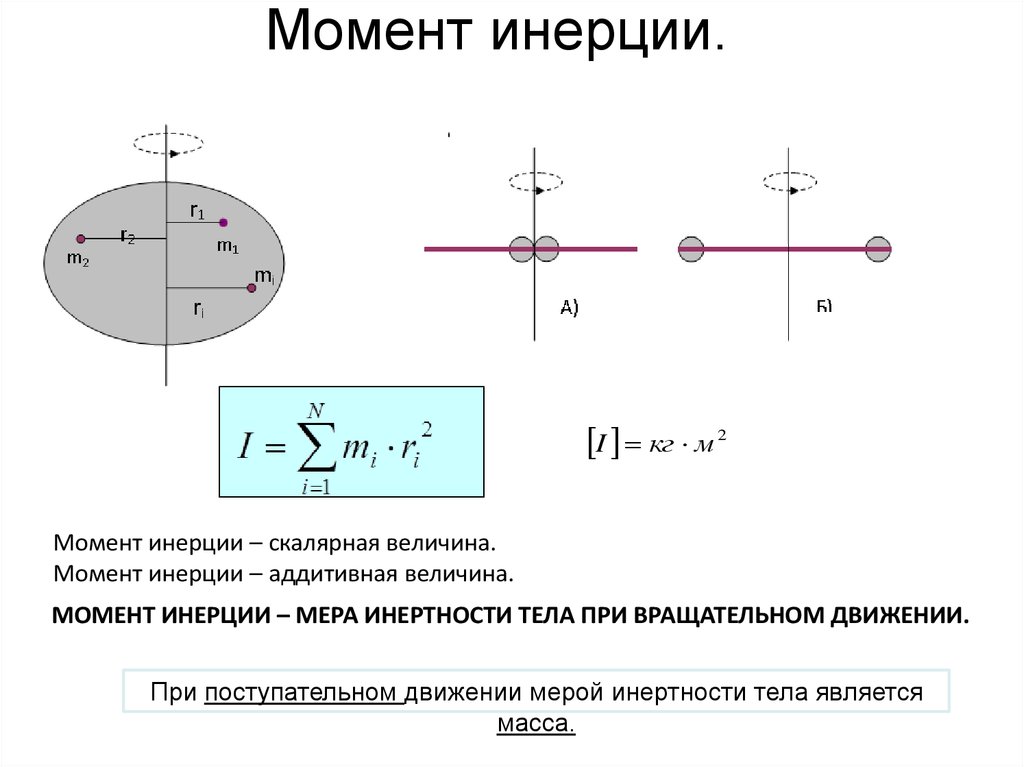 Величина ℓ = r sinравна рас­стоянию от начала координатОдо прямой, вдоль которой направлен импульс частицы. Эта величина называетсяплечом импульса.ВекторLзависит от выбора начала координат, поэтому говоря о нем, обычно указывают: “момент импульса относительно точки

О“.

Рассмотрим производную по времени от момента импульса:

.

Первое слагаемое равно нулю, т.к. . Во втором слагаемом, согласно второму закону Ньютона, производную по импульсу можно заменить на действующую на тело силу. Векторное произведение радиус-вектора на силу называетсямоментом силыотносительно точкиО: .

Направление момента силы определяется тем же правилом буравчика. Его величина М = r F sin ,где

ℓ = r sin — расстояние от точкиОдо линии действия силы.

В итоге получаем уравнение движения для момента импульса частицы:.

По форме уравнение аналогично второму закону Ньютона: вместо им­пульса частицы стоит момент импульса, а вместо силы —момент силы. Если,то,т.е. момент импульса постоянен в отсутствие внешних моментов сил.

Формулировка закона: Момент импульса замкнутой системы относительно полюса не изменяется с течением времени.

В частном случае вращения относительно неподвижной оси, имеем: , где

начальные момент инерции и угловая скорость тела относительно рассматриваемой оси, а

конечные момент инерции и угловая скорость тела относительно рассматриваемой оси.

Закон сохранения полной механической энергии с учётом вращательного движения: полная механическая энергия консервативной системы постоянна: .

Пример: Найти скорость системы при прохождении расстояния h.

Дано: m, M, h. Найти: V – ?

Теорема Штейнера.

А как вычислять момент инерции тела, если ось вращения не проходят через центр масс и симметрия распределение элементарных масс, составляющих тело, нарушена? В этом случае необходимо применять теорему Штейнера. Пусть ось вращения твердого тела не совпадает с центром масс и находятся на расстояние d от него. Тогда согласно теореме Штейнера:

Момент инерции твердого тела относительно произвольной оси О, не проходящей через центр масс, равен сумме момента инерции этого тела относительно оси, проходящей через центр масс и произведение массы тела на квадрат расстояние между осями:

I = I₀ +md² .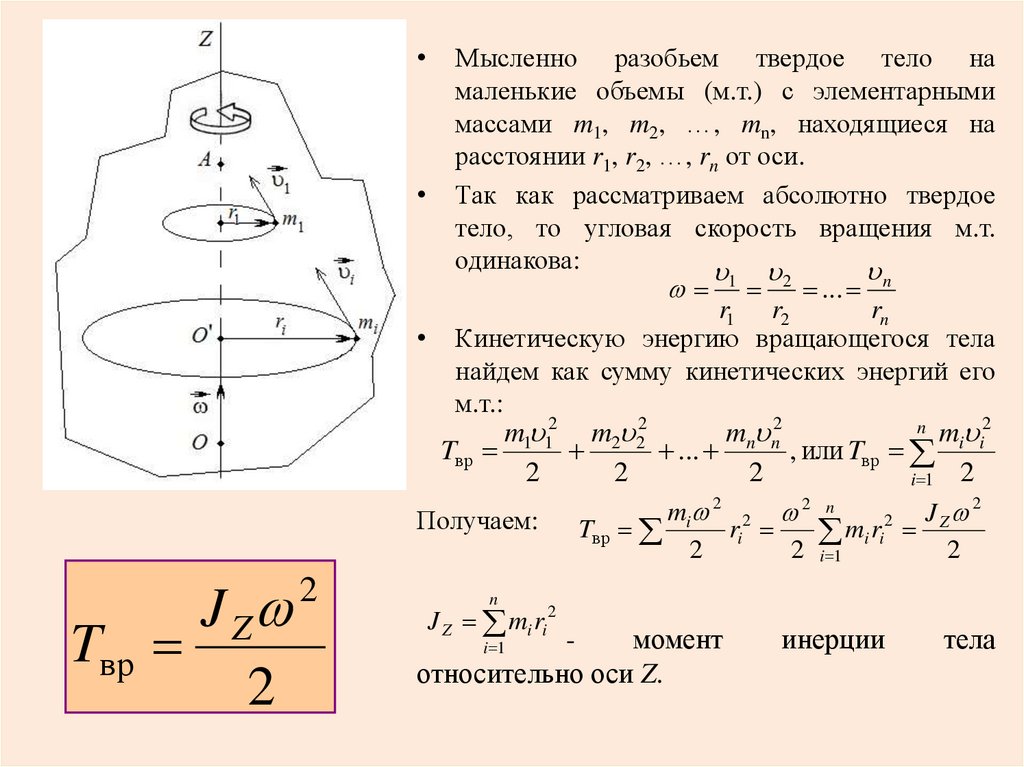 ( 6.9 )

Для иллюстрации применения теоремы Штейнера вычислим момент инерции однородного стержня относительно оси вращения, находящийся на краю стержня ( см. рис. 6.6 ).

Рис. 6.6. К вычислению момента инерции тела относительно оси, не проходящей через центр масс ( применение теоремы Штейнера )

Вычисляем искомый момент инерции двумя способами:

1)Используем формулу ( 6.5 ), учитывая, что интегрирование необходимо будет веста от 0 до l ( см. рис. 6.6 ). По стандартной методике:

. ( 6.10а )

2)Применим теорему Штейнера, учитывая полученный ранее результат для момента инерции стержня относительно оси, проходящей через центр масс: I₀ = ml² /12 и принимая d =

l/2 :

. ( 6.10б )

Видим, что результаты совпадают, но по теореме Штейнера вычисления существенно упрощаются.

При рассмотрении процесса вращения материального тела вокруг фиксированной оси, мы использовали понятие момента силы, вызывающего вращение тела, если этот момент ( или сумма моментов ) отличен от нуля. Также мы использовали понятие момента инерции как меры инертности тела при вращательном движении. Таким образом, прослеживается следующая аналогия поступательного и вращательного движения:

сила момент силы; масса – момент инерции. Но мы знаем, что при поступательном движении тело, движущее с какой либо скоростью, обладает кинетической энергией и количеством движения. Есть ли аналог количеству движения при поступательном движении для вращающегося тела? Да имеется. Применительно к вращательному движению используется понятие момента импульса ( момента количества движения ).

Пусть твердое тело вращается вокруг неподвижной оси О ( см. рис. 6.7 ). Выберем материальную точку А

, принадлежащую этому телу массой m_i , расположенную на расстоянии r_i от оси вращения. Поскольку тело вращается, эта материальная точка будет обладать окружной скоростью .

Введем определение момента импульса по аналогии с моментом силы:

Моментом импульса материальной точки относительно произвольно выбранной фиксированной в инерциальной системе отсчёта точки, называется величина, равная векторному произведению радиус-вектора этой точки на импульс этой материальной частицы.:

Рис.6.7. К определению момента импульса.

=  = , ( 6.11 )

или в скалярном виде:

, (6. 12)

где l_i = r_i Sin – плечо импульса.

Плечо импульса, как и плечо силы – это кратчайшее расстояние ( длина перпендикуляра ОВ, см. рис. 6.7 ) от оси вращения до линии действия импульса (или скорости ) DЕ. Вектор скорости при этом лежит на линии действия импульса DE.

Необходимо добавить, что компоненту момента импульса вдоль любой линии ( или оси, проходящей через фиксированную точку отсчёта ) часто называют моментом импульса частицы относительно этой оси.

Направление момента импульса определяется по правилу правого винта: если вращать правый винт от вектора к вектору по часовой стрелке, то направление перемещения винта жала винта будет задавать направление вектора . Вектор будет перпендикулярен плоскости, в которой лежат вектора и .

Для удобства пользования правилом правого винта необходимо переносить вектор параллельно самому себе так, чтобы его начало находилось в точки приложения импульса частицы ( или скорости ) ( на рис. 6.7 это точка А ).

Поскольку всякое материальное тело можно представить в виде совокупности материальных точек, то моментом количества движения материального тела относительно оси называется векторная сумма моментов количества движения всех материальных точек вращающегося материального тела :

. ( 6.13 ).

Если речь идет не о вращение тела вокруг фиксированной оси, а о движение материальной точки по произвольной траектории и её моменте импульса относительно произвольно выбранной фиксированной точки, то частица в общем смысле обладает моментом импульса при любой траектории своего движения.

Все-таки наибольший интерес представляет вращение твердого тела ( совокупности материальных точек ) вокруг какой – либо определённой оси. Для поступательного движения материальной точки имеет место соотношение (II закон Ньютона):

. ( 6.14 ).

Нет ли чего-нибудь похожего для вращательного движения? Рассмотрим еще раз движение материальной точки окружности ( см. рис. 6.8 ) относительно оси вращения, проходящей через точку О.

Рис. 6.8. Момент импульса частицы при вращательном движении.

Для движения по окружности  =90 , а Sin  =1, поэтому из формулы ( 6.12 ) следует, что:

L= mvr ; . ( 6.15 )

Продифференцируем уравнение ( 6.15 ) по времени:

. ( 6.16 )

Учтем, что , поскольку , то =0, поскольку = 0 Для второго слагаемого уравнение ( 6. 16 ) получим: выражение:

( 6.16 а )

( здесь мы использовали II закон Ньютона ). Таким образом, уравнение ( 6.16 ) принимает вид:

, ( 6.17 )

-скорость изменения момента импульса равна моменту силы, приложенной к материальной точке. Т.е. прослеживается аналогия с поступательным движением:

. ( 6.17а )

Если на каждую частицу твердого тела действуют внешние и внутренние силы, то уравнение ( 6.17 ) можно переписать в виде ( для одной i-ой частицы ):

. ( 6.18 )

Используя уравнение ( 6.13 ) и просуммировав по всему объёму твердого тела, получим выражение :

. ( 6.19 )

По III-му закону Ньютона каждой внутренней силе в системе материальных точек соответствует сила, равная ей по величине и направленная противоположно вдоль той же прямой, по которой действует первая сила. Моменты этих сил попарно равны по величине и противоположны по знаку. Поэтому очевидно, что алгебраическая сумма моментов всех внутренних сил будет равна нулю, следовательно:

. (6.20).

Алгебраическую сумму моментов всех внешних сил, действующих на тело, назовем полным моментом внешних сил и обозначим:

. (6.21).

Тогда из соотношения (6.19) получим, что :

. (6.22).

Скорость изменения полного момента количества движения твердого тела относительно оси вращения равна полному моменту внешних сил . , приложенных к телу.

или иначе:

Импульс момента внешних сил, действующих на вращательное тело, равен изменению его момента количества движения.

Если система материальных точек замкнута и внешние силы отсутствуют (суммарный момент внешних сил равен нулю .=0 ), то:

( 6.23 ).

Уравнение ( 6.23 ) представляет собой запись закона сохранения количества движения:

В замкнутой системе материальных тел момент количества движения есть величина постоянная.

областей практики | Steiner Law Offices

Мы можем помочь вам с юридическими потребностями вашего бизнеса. Наша область практики коммерческого права включает в себя выбор юридического лица, организационную структуру, первоначальные и текущие требования к подаче документов, переговоры по контракту и планирование преемственности бизнеса.

Подробнее

Закон о пожилых — это область права, в которой основное внимание уделяется вопросам, с которыми сталкиваются пожилые люди. Эти вопросы включают планирование имущества, Medicaid и квалификацию по инвалидности, а также другие вопросы долгосрочного ухода.

Подробнее

Планирование наследства означает план и документы, которые будут играть важную роль в определении вашего личного ухода, обращения с вашими активами и кто будет заботиться о ваших несовершеннолетних детях в случае вашей нетрудоспособности и/или смерти.​

Подробнее

Независимо от того, защищаете ли вы несовершеннолетних детей, что является вашим самым важным и самым важным приоритетом, или помогаете пожилым близким или всем, кто не может принимать решения самостоятельно, вам может понадобиться опекунство.

Подробнее

Деловые споры часто являются неизбежной реальностью. Ключ в том, чтобы работать с адвокатом, который может максимизировать ваше законное возмещение, если у вас есть иск против бизнеса, и свести к минимуму ваши юридические риски, если ваш бизнес защищается от иска, поданного другой стороной.

Читать далее

Оспаривать и оспаривать имущество, завещания, трасты и завещания при возникновении споров неприятно. Часто эти сложные ситуации связаны с разногласиями с семьей и близкими людьми. Вы должны работать с адвокатом с терпением и сочувствием, необходимыми для работы с членами семьи.

Читать дальше

Работа с адвокатами Steiner Law Offices для обеспечения вашего существования поможет вашим близким легче принимать важные решения и снимать стресс в трудные времена.

Подробнее

Помимо вашего медицинского обслуживания, вы, скорее всего, не можете дать кому-то больше полномочий, чем распоряжаться своими деньгами вместо вас. Steiner Law Offices оказывает профессиональную помощь с доверенностями, поэтому эти полномочия выдаются и используются должным образом.

Подробнее

Во Флориде завещание — это процесс в судебной системе, который определяет распределение определенных активов после смерти человека. Личному представителю (также известному как душеприказчик) поручено заниматься вопросами завещания, и адвокат из Флориды ведет этого личного представителя в течение всего процесса.

Подробнее

Планирование особых потребностей гарантирует, что люди с ограниченными возможностями или те, у кого нет возможности или финансовой ответственности позаботиться о себе, будут обеспечены в будущем. Планирование с особыми потребностями включает в себя закладку фундамента, чтобы противостоять вызовам бенефициара с особыми потребностями.

Подробнее

Траст — это место, где вы можете хранить активы для себя и других и, возможно, ими управляет другая сторона. Траст может оплачивать обучение ваших детей или внуков в колледже, служить первоначальным взносом за дом или обеспечивать безопасность члена семьи с ограниченными возможностями.

Читать дальше

Адвокаты Steiner Law Offices могут помочь вам составить завещание, которое воплотит в жизнь ваши последние пожелания для вас и ваших близких. Правильно составленное и оформленное завещание может обеспечить вам и вашей семье душевное спокойствие.

Подробнее

Ведущая юридическая фирма в Кливленде, штат Огайо = Solomon, Steiner & Peck, Ltd

Чем мы занимаемся

Просмотреть все направления практики

Планирование недвижимости

Закон Старейшины

Планирование особых потребностей

Коммерческое право

ЛГБТК + Планирование недвижимости

Управление наследства и доверительного управления

Судебные разбирательства по завещанию и доверительному управлению

Посвящается вашему успеху

Мы в Solomon, Steiner & Peck, Ltd. сосредоточены на том, чтобы помогать отдельным лицам, семьям и владельцам бизнеса решать проблемы, связанные с планированием имущества, престарелыми законами и коммерческим правом. Узкая направленность нашей юридической фирмы позволяет нам разрабатывать сложные решения некоторых из самых сложных юридических проблем. Мы рады отпраздновать более 27 лет службы в Северо-восточном Огайо.

Наши юристы и сотрудники понимают, что люди, которые обращаются за нашими услугами, часто сталкиваются с настоящим кризисом. Независимо от того, нужна ли вам или члену вашей семьи помощь в понимании льгот Medicaid, установлении доверительных отношений или рассмотрении деловой сделки, мы относимся к каждому клиенту с тем же терпением, состраданием, честностью и уважением, что и наши собственные семьи.

Что говорят наши клиенты

«Мы были большим облегчением как семья, получив руководство Лори Штайнер и прекрасное понимание ухода за престарелыми/семейного права, когда я перевезла своего отца и сестру с отставанием в развитии в северо-восточный штат Огайо. С этим привнесены слои решений от различных фракций льгот/законов/управлений. И в последние дни моего отца она и ее коллеги были удивительно проницательны и отзывчивы , поскольку мы рассматривали все варианты, если состояние моего отца затянется. А совсем недавно произошла необычная, часто неправильно понимаемая ситуация с льготами Medicare Premium моей сестры, когда только Лори могла принести любые ясность другим людям из лучших побуждений, чья работа заключается в том, чтобы понимать сложные нюансы, которые часто представляет система льгот Medicare/Medicaid».

– ДСВ | Chagrin Falls, OH

«Мы не можем в полной мере отблагодарить вас за ваше время, таланты и знания , объясняющие, что необходимо сделать для заявлений наших родителей в Medicaid. Вы были так дотошны , так терпеливы когда выслушивали нас всякий раз, когда мы начинали рассказывать истории о семейных проблемах, и так знающий . Большое спасибо за ваше компетентное направление ».

– ФС | Конкорд, Огайо

«Еще раз искренне благодарю вас за тщательную и эффективную манеру, с которой вы со всем справились и дали моим родителям полное душевное спокойствие. ”

– БД | Бедфорд, Огайо

«Моя сестра и я действительно оценили всю вашу помощь и помощь ваших фирм на протяжении всей этой ситуации с нашей мамой, так как все было улажено очень быстро.0105 профессиональный способ».

– ПК | Middleburg Hts., Ohio

«В очередной раз ваша фирма предоставила выдающиеся юридические услуги, которые я ожидал и ценю ».

– ДЛ | Солон, Огайо

«Ваш персонал был так услужлив , что я все понял. Вы сделали все это таким легким для меня – было прекрасным опытом ».

– Джей Би | Акрон, Огайо

«Все всегда вели себя крайне профессиональный. Дженнифер и Энн заслуживают особого признания, потому что они обе были понимающими , добрыми и очень полезными моей жене и мне».

– РЭК | Северный Олмстед, Огайо

«Лори Штайнер объяснила все превосходно ».

– ГС | Seven Hills, Ohio

«Все были очень дружелюбны и заставили нас чувствовать себя непринужденно . Мы впервые имели дело с адвокатами».

– PR | Ментор, Огайо

«Дженнифер Пек проделала отличную работу . Весь наш опыт был хорошим, и все были очень полезны ».

– КС | North Royalton, Ohio

«Лори и Жозефина заслуживают особого признания за их исключительный интерес».

– ЛЮТ | Strongsville, Ohio

«Я и наша семья хотели бы еще раз поблагодарить вас за доброту и профессионализм , которые вы проявили к нам в течение последних нескольких месяцев, которые были связаны с заботой о моей жене… Еще раз большое спасибо, и я будет больше рад порекомендовать ваши услуги любому заинтересованному лицу».

– РГ | Линдхерст, Огайо,

Душевное спокойствие

Когда вы имеете дело с такими вопросами планирования имущества, как траст и наследство, планирование особых потребностей в соответствии с Законом о старейшинах или коммерческое право, все может быстро запутаться и стать непосильным.