Сила архимеда равна: формула и суть закона силы Архимеда в жидкостях и газах, как действует сила Архимеда

Сила Архимеда, теория и онлайн калькуляторы

Сила Архимеда, теория и онлайн калькуляторы

Из опыта нам известно, что тело, находящееся в жидкости, весит меньше, чем, если оно находится в воздухе. Следовательно, на тело, погруженное в жидкость, действует выталкивающая сила. Величину этой силы определил ученый из древней Греции – Архимед.

Определение

Сила, с которой жидкость или газ действует на тело, погруженное в вещество, называют силой Архимеда (выталкивающей силой).

Данная сила появляется вследствие того, что давление жидкости (газа) увеличивается с ростом глубины. Получается, что сила давления, которая действует на тело со стороны жидкости (газа) снизу вверх больше, чем сила давления, направленная сверху вниз.

Закон Архимеда

Пусть тело в виде прямоугольного параллелепипеда полностью погрузили в жидкость рис.1. Будем считать, что верхнее и нижнее основания расположены горизонтально.

Силы, которые действуют на боковые грани параллелепипеда, уравновешиваются.

Они лишь сжимают параллелепипед. Силы, действующие на верхнюю и нижнюю грани тела не равны между собой. Сила ($F_1$), с которой столб жидкости действует на верхнюю грань, равна:

\[F_1=p_1S=\rho gh_1S\ \left(1\right),\]

где $\rho $ – плотность жидкости; $S$ – площадь основания; $h_1$ – высота столба жидкости над верхним основанием параллелепипеда. Отметим, что давление атмосферы на жидкость мы не учитываем.

Величина силы, с которой жидкость действует на нижнее основание параллелепипеда, равна:

\[F_2=p_2S=\rho gh_2S\ \left(2\right),\]

где $h_2$ – высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль равнодействующей силы, действующей на тело со стороны жидкости:

\[F_A=F_2-F_1=\rho g{S(h}_2-h_1)\ (3).\ \]

Если обозначить высоту параллелепипеда как $h=h_2-h_1$, тогда имеем:

\[F_A=\rho gSh=\rho gV\ \left(4\right),\]

где $V$ – объем параллелепипеда. Если тело находится в жидкости (газе) не целиком, то под V понимают объем находящийся в веществе (жидкости, газе). Правую часть выражения еще называют весом жидкости, которую вытесняет тело, погруженное в нее.

Сила Архимеда в жидкости и газе

На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещества (жидкости или газа) в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.

Данный закон выполняется для тел любой формы.

Сила Архимеда позволяет плавать лодкам и разного рода кораблям, несмотря на то, что плотность материала, из которого сделан корпус транспортного средства в несколько раз больше, чем плотность воды. Необходимо только чтобы вес воды, которую вытесняет подводная часть судна, был равен силе тяжести, которая действует на судно. Средняя же плотность корабля меньше плотности воды.

Сила Архимеда действует на тела находящиеся в воздухе. Но так как плотность воздуха мала, действием этой силы часто пренебрегают. В состоянии невесомости сила Архимеда равна нулю. В состоянии невесомости нет гидростатического давления.

Следует учесть, рассуждая о действии силы Архимеда, мы имеем в виду, что тело окружено жидкостью (газом), может быть за исключением своей верхней части. Если тело примыкаем ко дну сосуда или его стенке, то равнодействующая сил гидростатического давления станет прижимать тело ко дну или стенке. В этой связи, например, присасываются ко дну якоря кораблей, и если якорь лежит на большой глубине, то его крайне сложно оторвать от дна.

Примеры задач с силой Архимеда

Пример 1

Задание. Чему равно отношение силы трения ($F_{tr}$), которая действует на шарик, движущийся с постоянной скоростью вверх в жидкости, к силе тяжести ($mg$), если плотность жидкости (${\rho }_g$) в $n$ раз больше плотности материала шарика (${\rho }_{sh}$)?

Решение. Сделаем рисунок.

Запишем второй закон Ньютона для сил, действующих на шарик, учтем, что шарик всплывает равномерно, следовательно, его ускорение равно нулю:

\[m\overline{g}+{\overline{F}}_A+{\overline{F}}_{tr}=0\ \left(1.

1\right).\]

В проекции на ось Y выражение (1.1) предстанет в виде:

\[-mg-F_{tr}+F_A=0\ \left(1.2\right).\]

Модуль силы Архимеда найдем как:

\[F_A={\rho }_gVg\ \left(1.3\right).\]

Сила тяжести, действующая на шарик:

\[mg={\rho }_{sh}Vg\ \left(1.4\right).\]

Выразим из (1.2) силу трения, учтем выражения (1.3) и (1.4):

\[F_{tr}=F_A-mg={\rho }_gVg-{\rho }_{sh}V\ \left(1.5\right).\]

Найдем отношение $\frac{F_{tr}}{mg}$:

\[\frac{F_{tr}}{mg}=\frac{с_gVg-с_{sh}V}{с_{sh}Vg}=\frac{с_g}{с_{sh}}-1=n-1.\]

Ответ. $\frac{F_{tr}}{mg}=n-1$

Пример 2

Задание. Сформулируйте условия плавания тел в жидкости. Что происходит с телом, если оно полностью погружено в жидкость, а плотность вещества тела равна плотности жидкости? Чему равна сила Архимеда, если тело плавает на границе раздела двух жидкостей с разными плотностями?

Решение. Из закона Архимеда можно легко получить условия плавания тел. Так, если сила Архимеда больше веса тела, то тело всплывает на поверхность жидкости до тех пор, пока не наступит равенства этих сил. Если сила Архимеда равна весу тела, то тело находится в состоянии покоя (плавает) в той точке жидкости, куда его поместили. Если сила Архимеда меньше веса тела, то тело тонет.

Если тело находится целиком в жидкости и плотности тела и жидкости равны, то тело плавает.

В случае если мы имеем несколько видов жидкостей с разными плотностями (например, поверх воды налили масло) и тело плавает на границе сред, то сила Архимеда будет равна:

\[F_A=g\left[{\rho }_1V_1+{\rho }_2V_2\right]\ \left(2.1\right),\]

где ${\rho }_1$ – плотность первой жидкости; ${\rho }_2$ – плотность второй жидкости; $V_1$ – объем тела, находящийся в первой жидкости; $V_2$ – объем тела во второй жидкости.

Читать дальше: сила упругости.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

В каком случае сила архимеда.

Вычисление силы архимеда. то тело плавает

Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.

О чем говорит закон Архимеда?

Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.

Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:

• погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
• итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
• при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.

Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.

Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.

Закон записывается в виде следующей формулы:

Какое значение имеет закон Архимеда?

Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.

Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.

В интегральной форме

Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.

Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также

архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда

не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами

В формуле мы использовали:

Сила Архимеда

Плотность жидкости

Эмпирически еще в древней Греции было получено, что тело, погруженное в жидкость, весит меньше, чем находящееся в воздухе. На тело в жидкости со всех сторон она оказывает давление. Силы давления направлены перпендикулярно поверхности тела в каждой его точке.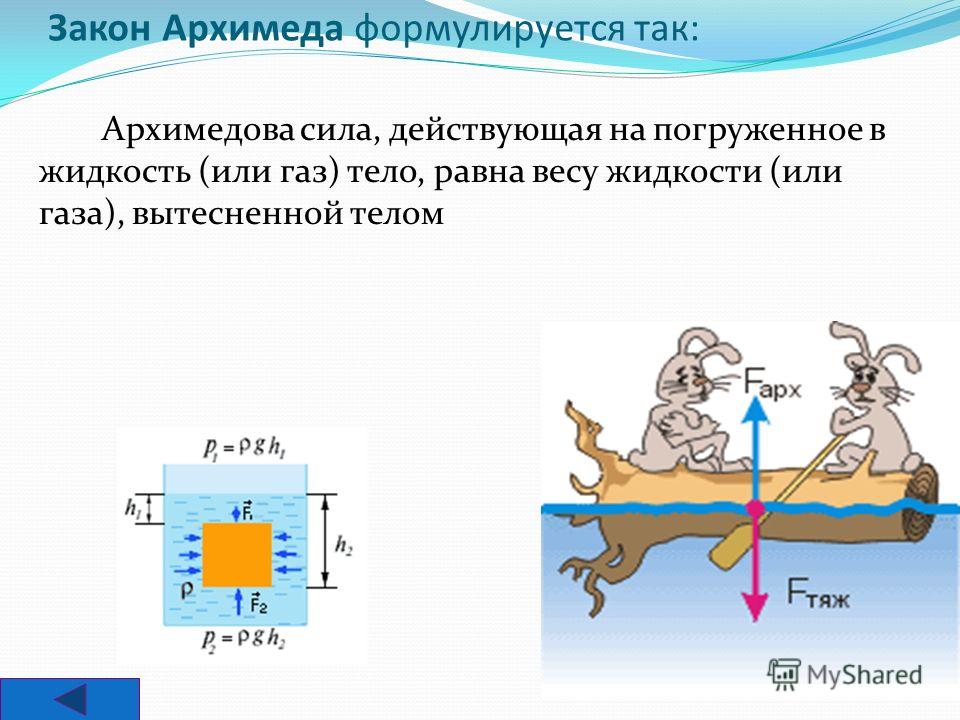 В том случае, если все силы, действующие на тело, были бы равны по модулю, то это тело испытывало только всестороннее сжатие. Мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.

Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.

Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.

Величина силы Архимеда

Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.

Рассмотрим тело в виде прямоугольного параллелепипеда полностью находящееся в жидкости рис.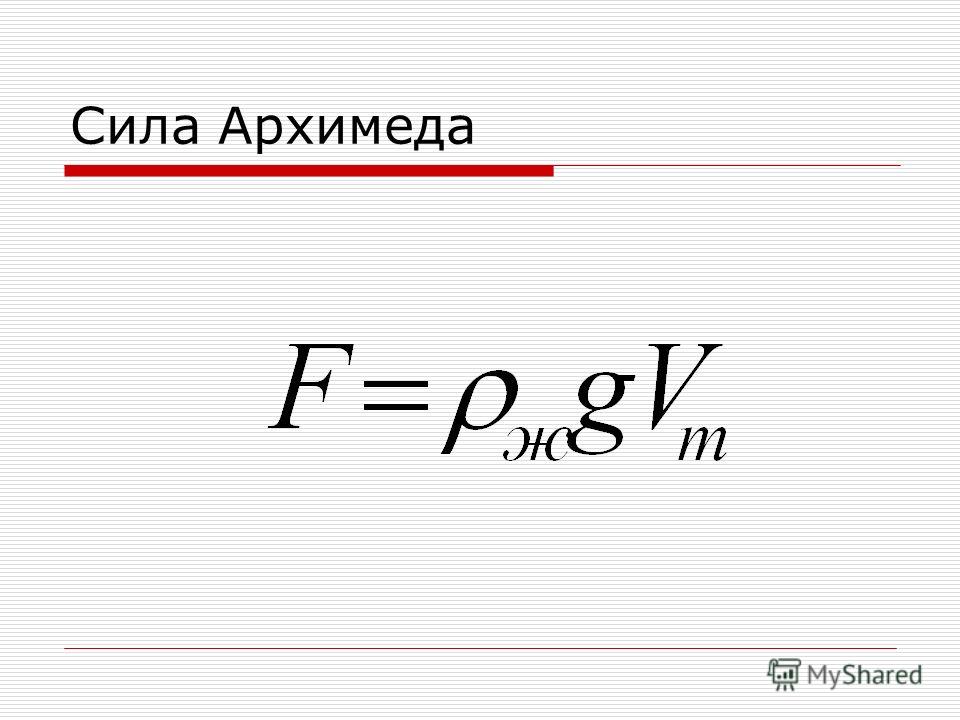 1. Предположим, что верхнее и нижнее основания располагаются параллельно горизонту.

Силы давления, действующие на боковые грани параллелепипеда, попарно уравновешены (например, ${\overline{F}}_{12}$=$-{\overline{F}}_{21}$). Они только сжимают параллелепипед. Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:

где $\rho $ – плотность жидкости; $S$ – площадь основания; $h_1$ – высота столба жидкости над верхним основанием параллелепипеда.$\ p_0-$ давление атмосферы на поверхность жидкости.

Сила давления жидкости на нижнее основание параллелепипеда:

где $h_2$ – высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль результирующей силы, действующей на тело со стороны жидкости:

Если обозначить высоту параллелепипеда как $h=h_2-h_1$, получим:

где $V$ – объем параллелепипеда. При нахождении тела в жидкости (газе) частично, то под V понимают объем погруженный в вещество (жидкость, газ). Правую часть выражения (4) еще называют весом жидкости, которую вытесняет тело, погруженное в нее.

На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещества (жидкости или газа) в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.

Закон Архимеда (4) выполняется для тел любой формы.

Сила Архимеда дает возможность плавать разного рода кораблям, несмотря на то, что плотность материала, из которого изготовлен корпус транспортного средства в несколько раз больше, чем плотность воды. Необходимо только чтобы вес воды, которую вытесняет подводная часть судна, был равен силе тяжести, которая действует на судно. Средняя же плотность корабля меньше плотности воды.

Сила Архимеда действует на тела находящиеся в воздухе. Но так как плотность воздуха мала, действием этой силы часто пренебрегают. В состоянии невесомости сила Архимеда равна нулю. В состоянии невесомости нет гидростатического давления.

Следует учесть, рассуждая о действии силы Архимеда, мы имеем в виду, что тело окружено жидкостью (газом), может быть за исключением своей верхней части. {-2}$Н

Пример 2

Задание. Чему равна сила натяжения каната (N), при помощи которого из пресного водоема равномерно двигая, поднимают тело плотностью $\rho $ и объемом V? Плотность воды считайте известной (${\rho }_g$). Движение рассмотрите в жидкости.

Решение. Рассмотрим силы, действующие на тело, поднимаемое из воды (рис.2).

В соответствии со вторым законом Ньютона равнодействующая всех сил, приложенных к телу равна нулю, так как тело поднимают равномерно:

\[\overline{N}+m\overline{g}+{\overline{F}}_A=0\ \left(2.1\right).\]

В проекции на ось Y инерциальной системы отсчета, которую мы связали с Землей, уравнение (2.1) даст нам следующее скалярное выражение:

Масса поднимаемого тела может быть найдена как:

Силу Архимеда определим как:

Подставим правые части выражений (2.3) и (2.4) в формулу (2.2) вместо соответствующих величин, выразим силу натяжения каната:

Ответ. $N=\left(\rho -{\rho }_g\right)Vg$

F A = ρ g V , {\displaystyle F_{A}=\rho gV,}

Описание

Выталкивающая или подъёмная сила по направлению противоположна силе тяжести , прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Обобщения

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) – на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление p {\displaystyle p} на глубине h {\displaystyle h} , оказываемое жидкостью плотностью ρ {\displaystyle \rho } на тело, есть p = ρ g h {\displaystyle p=\rho gh} . Пусть плотность жидкости ( ρ {\displaystyle \rho } ) и напряжённость гравитационного поля ( g {\displaystyle g} ) – постоянные величины, а h {\displaystyle h} – параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат O x y z {\displaystyle Oxyz} , причём выберем направление оси z совпадающим с направлением вектора g → {\displaystyle {\vec {g}}} . {**}grad(h)=\nabla h={\vec {e}}_{z}.}

Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Замечание . Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погруженного тела на жидкость, приводит к изменению ее потенциальной энергии:

A = F Δ h = m ж g Δ h = Δ E p {\displaystyle \ A=F\Delta h=m_{\text{ж}}g\Delta h=\Delta E_{p}}

где m ж − {\displaystyle m_{\text{ж}}-} масса вытесненной части жидкости, Δ h {\displaystyle \Delta h} – перемещение ее центра масс. Отсюда модуль вытесняющей силы:

F = m ж g {\displaystyle \ F=m_{\text{ж}}g}

Инструкция

Архимедова сила возникает из-за разности давлений воды на уровне верхнего и нижнего срезов тела. На верхнюю часть давит столб воды высотой h2 с силой, равной весу этого . На нижнюю часть действует сила, равная весу столба высотой h3. Эта высота определяется сложением h2 и высотой самого тела. Согласно закону Паскаля, давление в жидкости или газе распределяется равномерно во все стороны. В том числе и вверх.

Очевидно, что сила, действующая вверх, превышает силу, действующую вниз. Но, следует учесть, что принимается во внимание только воздействие столба жидкости. От собственного веса тела выталкивающая сила не зависит. Ни материал, из которого сделано тело, ни его иные качества, кроме размеров при вычислениях не используются. Расчет архимедовой силы базируется только на плотности жидкости и геометрических размерах погруженной части.

Существует два способа, архимедову силу, действующую на тело, погруженное в жидкость. Первый состоит в измерении объема тела и вычислении веса жидкости, занимающей аналогичный объем. Для этого необходимо, чтобы тело обладало правильной геометрической формой, то есть, было кубом, параллелепипедом, шаром, полусферой, конусом. Объем твердого тела более сложной формы рассчитать очень трудно, поэтому для определения силы Архимеда в этом случае существует более практичный способ № 2. Но о нем несколько позже.

Определив объем погружаемого тела, умножаем его на плотность жидкости и находим величину выталкивающей силы, действующей на это тело в однородной среде заданной плотности и на ускорение свободного падения g (9,8 м/с2). Формула для определения силы Архимеда выглядит так:
F=ρgV
ρ – удельная плотность жидкости;
g – ускорение свободного падения;
V – объем вытесненной жидкости.
Как и любая сила, она измеряется в Ньютонах (Н).

Второй способ базируется на измерении объема вытесненной жидкости. Он наиболее соответствует тому опыту, который и привел Архимеда к открытию своего закона. Этот способ очень удобен и при вычислении архимедовой силы при частичном погружении тела. Для получения необходимых данных исследуемое тело подвешивают на нитке и медленно опускают в жидкость.

Достаточно замерить уровень жидкости в сосуде до погружения тела и после, умножить разницу уровней на площадь поверхности и найти объем вытесненной жидкости. Как и в первом случае, умножаем этот объем на плотность жидкости и g. Полученная величина и является силой Архимеда. Чтобы единицей измерения силы стал Ньютон, следует объем измерять в м3, а плотность – в кг/м3.

Как найти сила архимеда. Как найти сила архимеда

Автор Historian Просмотров 40 Опубликовано 23.08.2022

Закон Архимеда формулируется следующим образом. К объекту, погруженному в жидкость (или газ), прикладывается сила тяги, равная весу жидкости (или газа), выдавливаемой из объекта. Эта сила называется архимедовой силой:.

Содержание

1. Сила Архимеда
2. Закон Архимеда
3. Сила Архимеда в жидкости и газе
4. Как найти сила архимеда
5. Тело тонет, если рПлавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.Конец.-Архимедовы силы — это pжПлавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.
6. Закон Архимеда
7. Погружение, равновесие, всплытие
8. Закон Архимеда
9. Обобщения
10. Воздухоплавание
11. Архимедова сила и законы Ньютона
12. Условия плавания тел
13. Варианты условий задач на условия плавания тел

Сила Архимеда

Опыт показывает, что предметы в жидкостях легче, чем в воздухе. В результате предметы, погруженные в жидкость, обладают силой релаксации. Значение этой силы было определено древнегреческим ученым Архимедом.

Сила, действующая со стороны жидкости или газа на объект, погруженный в вещество, называется архимедовой силой (исходящей силой).

Эта сила обусловлена тем, что давление жидкости (газа) увеличивается с глубиной. Видно, что давление, оказываемое на тело снизу вверх, больше, чем давление сверху вниз.

Закон Архимеда

Прямоугольное тело полностью погружено в жидкость Рис. 1. Предположим, что верхнее и нижнее основания расположены горизонтально.

Силы на гранях параллелепипеда уравновешены. Сжимается только параллелепипед. Силы, действующие на верхнюю и нижнюю стороны тела, не равны. Сила ($ F_1 $), действующая со стороны столба жидкости на верхнюю поверхность, равна

\ F_1 = p_1S = \ rho gh_1S \ слева (1 \ справа), 섹

где $

ho$ — плотность жидкости- $S$ — площадь дна- $h_1$ — высота столба жидкости от верхнего дна параллелепипеда. Обратите внимание, что атмосферное давление в жидкости не учитывается.

Величина силы, действующей со стороны жидкости на нижнее основание параллелепипеда, равна

\ F_2 = p_2S = \ rho gh_2S \ слева (2 \ справа), ⌘

Где $ h_2 $ — высота столба жидкости от нижнего основания. Если $ h_2> h_1 $, это означает, что $ F_2>F_1$. Мера чистой силы, действующей на тело под действием жидкости:.

Если высота параллелограмма равна $ h= h_2-h_1 $, это означает, что

\ F_A = \ rho gSh = \ rho gV \ слева (4 \ справа), \

Сила Архимеда в жидкости и газе

где $V$ — объем параллелограмма. Если все тело не находится в жидкости (газе), V$ — это объем, содержащийся в веществе (жидкости или газе). Правая часть уравнения, называемая также весом жидкости, отталкивается от объекта, погруженного в жидкость.

На тело действует сила Архимеда. Она соответствует весу вещества (жидкости или газа), содержащегося в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.

Этот закон применим к объектам любой формы.

Сила Архимеда позволяет лодкам и кораблям всех видов плавать, но плотность материалов, используемых для изготовления корпуса транспортного средства, в несколько раз превышает плотность воды. Пока вес воды, отталкивающейся от подводной части корабля, равен силе тяжести, действующей на корабль. С другой стороны, средняя плотность судна меньше плотности воды.

Сила Архимеда действует на тела в воздухе. Однако из-за низкой плотности воздуха влияние этой силы часто игнорируется. В условиях нулевой гравитации сила Архимеда равна нулю. В невесомости нет гидростатического давления.

Когда мы говорим о силе Архимеда, нужно иметь в виду, что она означает, что тело, вероятно, помимо верха, окружено жидкостью (газом). Если тело прижато ко дну сосуда или его стенкам, то равновесная сила гидростатического давления толкает тело ко дну или стенкам. Так, например, якорь корабля будет засасываться в дно, что очень затруднит его извлечение со дна, если он находится на большой глубине.

Как найти сила архимеда

На каждое тело, погруженное в жидкость или газ, действуют две противоположные силы: сила тяжести и Архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю.

Полное гидростатическое давление, оказываемое на тело, находящееся в жидкости, называется силой Бритвы. _{Местоположение: f}é _{-Архимедовы силы — это p}ж _{— плотность жидкости, g — ускорение силы тяжести.} ж _{— плотность жидкости, g — ускорение силы тяжести.} ж _{-Архимедовы силы — это p}ж

— Вес жидкости.

Тело тонет, если р

_{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.}Конец. _{-Архимедовы силы — это p}ж _{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.} -Архимедовы силы — это p.

ж_{Необходимое условие для движения тела по поверхности жидкости: тело, движущееся по поверхности жидкости, должно уравновешивать гравитацию силами разгрузки: f:f}В

= m — g _{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.}Конец. _{-Архимедовы силы — это p}ж. _{-Архимедовы силы — это p}ж

.

Закон Архимеда

Задание. Сформулируйте условия существования тела, плавающего в жидкости. Что произойдет с телом, если оно полностью погружено в жидкость, а плотность вещества тела равна плотности жидкости? Каковы силы Архимеда, если тело плавает на границе раздела двух жидкостей разной плотности?

Тяжелые предметы, которые очень трудно поднять с земли, можно легко поднять, находясь в воде. Если у вас есть пустая пластиковая бутылка с закрытой пробкой, оставьте ее полностью погруженной в воду. Бутылка будет плавать. Почему это происходит;

Чтобы объяснить эти явления, достаточно рассмотреть последний тип (4). Зависимость давления P на жидкость или газ от глубины h (высоты) приводит к воздействию вяжущей силы на каждое тело, погруженное в жидкость или газ. Эта сила называется силой Архимеда.

Рисунок 1.Портрет, фотография Архимеда.

Древнегреческий математик, инженер и физик Архимед (287-212 гг. до н.э.) не только открыл это явление, но и экспортировал тип, чтобы найти объяснение и рассчитать излучающую силу. В дополнение к законам Архимеда он открыл знаменитое правило рычага. Он первым нашел математическую формулу для расчета сложных геометрических поверхностей, открыл первую планету и изобрел множество полезных гаджетов.

Рис. 2.Действие внеземных сил на тело, погруженное в воду.₂Диаграмма, изображающая прямоугольник, установленный на жидкости (высота H и область S), помогает ответить на вопрос, как найти Архимеда. Силы давления на стороны взаимозависимы, и силы f₁ и ф₂ Согласно виду (4), верхнее и нижнее давление различны, поэтому h₁ > h

:._{Где: $ s*h = v $ — объем, а $ p*v = m $ — масса жидкости, вытесненной телом. Затем, поскольку $ m * g $ — это вес вытесненной жидкости, мы получаем окончательный вид архитектонической силы f} > h

:.

В зависимости от взятого типа можно сформулировать закон Архимеда.

Погружение, равновесие, всплытие

Сила, выталкивающая тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), вытесненной телом.

Теперь понятно, почему тяжелые камни можно легко поднять в воду. Сила Архимеда «помогает» нам, потому что она направлена против гравитации. По этой же причине вес предмета, взвешенного в жидкости, всегда меньше, чем его вес, измеренный в воздухе._{Где: $ s*h = v $ — объем, а $ p*v = m $ — масса жидкости, вытесненной телом. Затем, поскольку $ m * g $ — это вес вытесненной жидкости, мы получаем окончательный вид архитектонической силы f}A _{и гравитационная сила F}g

• Если FA > Fg, то тело будет выталкиваться наверх — “всплывать”;
• Если FA

возможны три положения тела в жидкости:.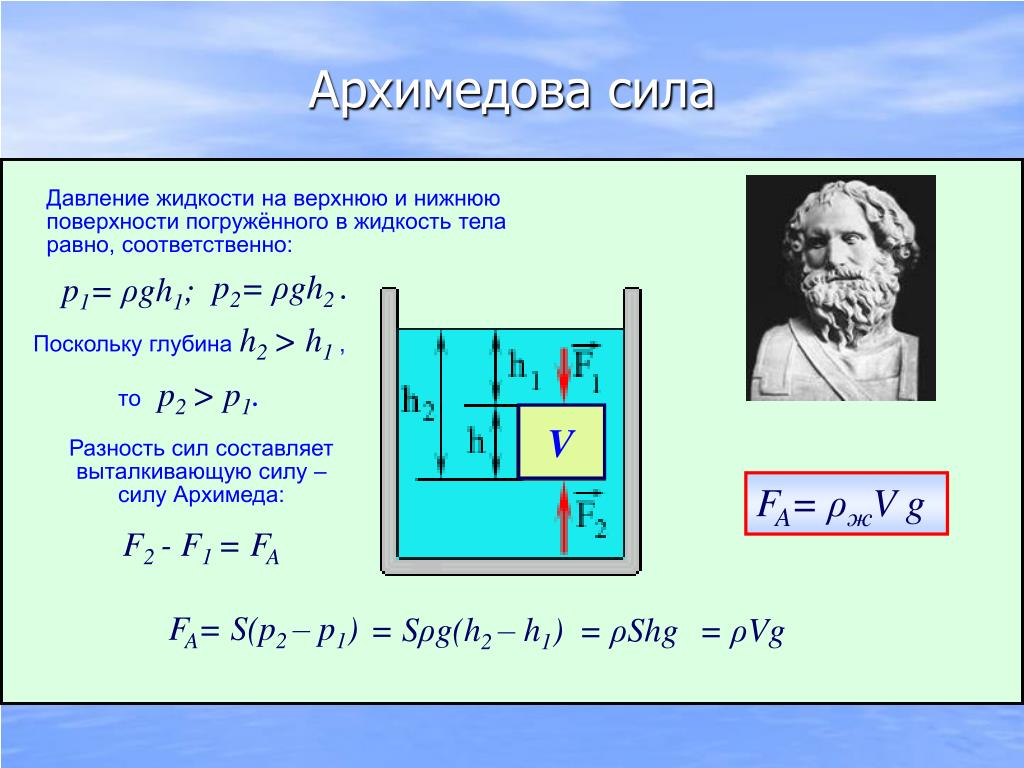

Закон Архимеда лежит в основе удельного гравиметра — прибора, используемого для измерения плотности жидкостей. Измеритель удельного веса представляет собой герметичную бутылку из стекла, взвешенную на нижнем конце с помощью гири. В верхней части находится длинный стержень, на котором нанесена шкала. При помещении в жидкость шкала удельного веса увеличивается или уменьшается по глубине в зависимости от плотности жидкости. Чем выше плотность жидкости, тем меньше опускается шкала удельного веса. Индикатор на шкале показывает плотность этой жидкости, когда измеритель удельного веса находится в равновесии.

где $V$ — объем параллелограмма. Если все тело не находится в жидкости (газе), V$ — это объем, содержащийся в веществе (жидкости или газе). Правая часть уравнения, называемая также весом жидкости, отталкивается от объекта, погруженного в жидкость.

Закон Архимеда

Когда объект погружен в жидкость или газ, на его величину действует сила Архимеда, равная весу вещества (жидкости или газа), содержащегося в объеме подводной части объекта. Сила Архимеда направлена вертикально вверх.

Закон Архимеда — один из основных законов гидростатического давления и статического движения газов.

Закон Архимеда формулируется следующим образом. На объект, погруженный в жидкость (или газ), действует движущая сила, равная весу жидкости (или газа), вытолкнутой из объекта. Эта сила называется силой Архимеда:.

где » width=»» height=»» /> — ускорение свободного падения, а

V, «width =»» «» height =»»/>.

Обратите внимание, что тело должно быть полностью окружено жидкостью (или пересекать ее поверхность). Так, например, закон Архимеда не может быть применен к кубу, находящемуся на дне резервуара и запечатанному на дне.

Для объектов, находящихся внутри газа, например, воздуха, плотность жидкости необходимо заменить на плотность газа, чтобы найти подъемную силу. Например, воздушный шар с гелием взлетит вверх, потому что плотность солнца меньше плотности воздуха.

Закон Архимеда можно проиллюстрировать на примере разницы статического давления в прямоугольном теле. _{Где: $ s*h = v $ — объем, а $ p*v = m $ — масса жидкости, вытесненной телом. Затем, поскольку $ m * g $ — это вес вытесненной жидкости, мы получаем окончательный вид архитектонической силы f}A_{, P}B

— давление в точках A и B, p — плотность жидкости, h — разница в уровне между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объем в воде части тела.

В теоретической физике закон Архимеда также используется в его полной форме.

> «width =» «height =» «/>

Где — когда давление прикладывается к произвольной точке, завершение происходит по всей поверхности тела.

Обобщения

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Астронавты знакомы с этим явлением. В частности, поскольку не существует (естественного) обоснования отсутствия гравитации, например, охлаждение воздуха и вентиляция пространства космического корабля осуществляется принудительно с помощью вентиляторов.

— \ rho g \ int \ limits_vvzdv> = — — — \ rho g \ vec_z \ int \ limits_v =(\ rho g v) (- \ vec_) «width =» «height =» «

При прохождении через поверхностные интегралы, приводящие к интегралам объема, используйте обобщенную теорему Остроградского-Гаусса.

Получаем, что модуль силы Архимеда равен

grad (h) = \ nabla h = \ vec_ «width =» «height =» » />

Воздухоплавание

На тело, погруженное в жидкость (газ), действует выталкивающая сила, равная весу жидкости (газа), вытесненной этим телом.

Подъемная сила воздушного шара — это архимедова сила, равная

В подъемных силах им противостоят сила тяжести и сила сопротивления воздуха.

• чтобы взлететь, шар заполняют нагретым воздухом или газом, плотность которого меньше плотности окружающего воздуха;
• чтобы увеличить высоту полета, с шара сбрасывают балласт;
• чтобы спуститься на землю, газ охлаждают.

Проверка воздушных шаров:.

Пример нет. 2. воздушный шар объемом 1000 м 3 наполнен солнцем. Плотность солнца составляет 0,18 кг/м 3, а плотность воздуха — 1,29 кг/м 3. Какие огромные силы действуют на воздушный шар?

Архимедова сила и законы Ньютона

Сила излучения зависит только от плотности среды и объема погруженного в нее тела. Поскольку воздушный шар полностью погружен в воздух:.

Если тело полностью погружено в жидкость (или газ):.

Особые случаи._{Определите минимальную массу груза, который необходимо разместить на уровне однородного участка плавающего льда, чтобы он был полностью погружен в воду. Айсберг имеет толщину H и плотность льда p}δ_{и плотность воды p}

В.

Второй закон Ньютона в векторной форме для полностью погруженного айсберга (не тонущего и не плавающего):.

Поскольку эти силы направлены в противоположные стороны:.

Архимедовы силы, действующие только на айсберг, равны:.

Сила тяжести равна сумме масс льда и груза.

Масса айсберга равна произведению площади его толщины на плотность его объема.

Пример №3. какую силу нужно затратить, чтобы поднять под водой камень весом 30 кг?

12 000 см3 = 0,012 куб.м.

Условия плавания тел

Когда мы говорим о силе Архимеда, нужно иметь в виду, что она означает, что тело, вероятно, помимо верха, окружено жидкостью (газом). Если тело прижато ко дну сосуда или его стенкам, то равновесная сила гидростатического давления толкает тело ко дну или стенкам. Так, например, якорь корабля будет засасываться в дно, что очень затруднит его извлечение со дна, если он находится на большой глубине.

На каждое тело, погруженное в жидкость или газ, действуют две противоположные силы. Это силы гравитации и Архимеда. Направление движения тела зависит от того, какая из этих сил больше по модулю.

Примечание: Тело, плотность которого меньше плотности жидкости, на которой оно плавает, находится на поверхности и частично погружено в жидкость.

• Архимедова сила и сила тяжести, действующие на него, равны: F_{Где: $ s*h = v $ — объем, а $ p*v = m $ — масса жидкости, вытесненной телом. Затем, поскольку $ m * g $ — это вес вытесненной жидкости, мы получаем окончательный вид архитектонической силы f}a_{= f}В
• Сила тяжести равна: F_{= f}провисать. _{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.}конец_vВ
• Архимедова сила равна: F_{Где: $ s*h = v $ — объем, а $ p*v = m $ — масса жидкости, вытесненной телом. Затем, поскольку $ m * g $ — это вес вытесненной жидкости, мы получаем окончательный вид архитектонической силы f}a _{-Архимедовы силы — это p}конец_vg .
• Взаимосвязь между объемом и высотой тела правильной формы: V = Sh.

Варианты условий задач на условия плавания тел

P.H. _{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости.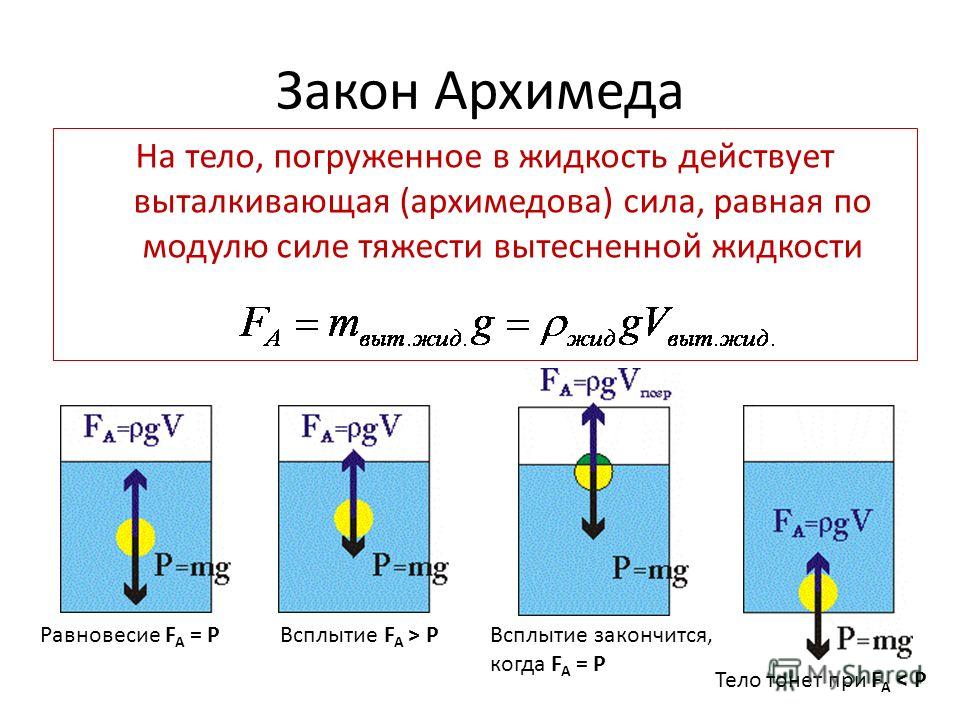 На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.}Конец._{Необходимое условие для движения тела по поверхности жидкости: тело, движущееся по поверхности жидкости, должно уравновешивать гравитацию силами разгрузки: f:f}В

.

Второй закон Ньютона в векторной форме:.

Поэтому (показана вертикальная ось):._{Определите минимальную массу груза, который необходимо разместить на уровне однородного участка плавающего льда, чтобы он был полностью погружен в воду. Айсберг имеет толщину H и плотность льда p}δ_{Необходимое условие для движения тела по поверхности жидкости: тело, движущееся по поверхности жидкости, должно уравновешивать гравитацию силами разгрузки: f:f}В

.

Второй закон Ньютона в векторной форме:.

Поэтому (показана вертикальная ось):.

Ускорение свободного падения является взаимным. Найдите погруженную часть айсберга в процентах.

Найденный процент по-прежнему умножается на 100 %. _{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.}Конец. _{Плавает в воде и тонет на 1/5 своего объема. Находит количество полостей}п _{Плавучесть — это способность тела плавать на поверхности жидкости или на определенном уровне внутри жидкости. На каждое тело внутри жидкости действуют две противоположные силы: сила тяжести и сила Архимеда. Гравитация равна весу тела и направлена вниз. Сила Архимеда зависит от плотности жидкости и направлена вверх.}конец_{и плотность воды p}

.

Второй закон Ньютона в векторной форме:.

Следовательно (отображается на вертикальной оси):.

Преобразуя уравнение, получаем.

V n = V t(5ρt-ρin)5ρt.

Пример 4. Куб массой 40 г и объемом 250 см3 плавает на поверхности воды. Найдите значение экспоненциальной функции, добавленной к кубу.

Если тело плавает, сила Архимеда равна силе тяжести. Это определяется следующим уравнением.

Деревянный шарик плавает в стакане с водой. Как изменяются сила тяжести и сила Архимеда на шарике, когда он плавает в подсолнечном масле?

Для каждого количества укажите характер соответствующего изменения.ПишитеНа борту.

Выбранное число для каждого физического размера. Числа в ответе могут повторяться.

1. Записать условие плавания тел.
2. На основании условия плавания тел сделать вывод о том, как изменятся указанные физические величины.

Алгоритм решения.

Согласно описанию задачи, деревянный шар плавает на поверхности воды. Однако это возможно только в том случае, если сила Архимеда равна силе тяжести.

Если шар плавает в подсолнечном масле, можно также применить условие плавания.

Гравитация зависит только от массы тела, которая не меняется. Поэтому гравитация также не изменяется. Однако из этого следует, что тело не плавает.

Принцип Архимеда | Подводное плавание с аквалангом — советы

Изучение физики подводного мира может помочь дайверам лучше понять свой вид спорта. Одной из основных концепций является принцип Архимеда, который гласит:

Любой объект, полностью или частично погруженный в жидкость, будет подниматься вверх под действием силы, равной весу вытесненной жидкости.

Принцип Архимеда на простом английском языке:

Когда объект помещается в воду (или любую другую жидкость), вода оказывает на объект восходящую силу. Сила восходящей силы равна весу воды, вытесненной телом.

Чтобы визуализировать эту концепцию, представьте, что вы бросаете шарик в полный стакан воды. Часть воды будет вытеснена мрамором и перельется через стекло. Если вытесненную воду взвесить, то вес воды будет равен восходящей силе.

Некоторые объекты, такие как мячи для пинг-понга, могут частично плавать над водой. В этом случае восходящая сила равна весу воды, вытесненной погруженной частью тела.

Как принцип Архимеда помогает определить плавучесть объекта?

Принцип Архимеда описывает восходящие силы, действующие на объект, погруженный в воду. Однако вес объекта (сила, направленная вниз) также влияет на его плавучесть. Чтобы понять плавучесть объекта, необходимо рассмотреть присутствующие как нисходящие, так и восходящие силы, и определить, равны ли они или одна больше другой.

Если сила, действующая вниз на объект, больше силы, направленной вверх, то он утонет, и говорят, что он имеет отрицательную плавучесть . Если восходящая сила, действующая на объект, больше, чем направленная вниз сила, объект будет плавать, и говорят, что он обладает положительной плавучестью . Наконец, если две силы равны, объект останется подвешенным в воде и, как говорят, имеет нейтральную плавучесть .

В случае падения шарика в стакан с водой, шарик утонет, потому что вес шарика (нисходящая сила) больше веса вытесненной им воды (восходящая сила). С другой стороны, шарик для пинг-понга будет плавать, если его поместить в воду.

Закон Архимеда объясняет, почему мячик для пинг-понга и другие предметы, наполненные воздухом, имеют тенденцию плавать. Наполненный воздухом объект мало весит, но вытесняет относительно большое количество воды. Одним из примеров является лодка, которая представляет собой наполненную воздухом оболочку. Даже металлическая лодка может плавать, если вытесняемая ею вода весит больше, чем она сама.

Какое отношение принцип Архимеда имеет к подводному плаванию с аквалангом?:

Принцип Архимеда объясняет, как различные факторы, включая рост, вес и снаряжение дайвера, влияют на его плавучесть. Вот несколько примеров действия принципа Архимеда:

Компенсаторы плавучести (КП):

В своей простейшей форме компенсатор плавучести представляет собой надувную воздушную камеру, которую дайвер носит с собой под водой. Он надувает и сдувает воздушную камеру во время погружения, чтобы отрегулировать свою плавучесть. Когда дайвер надувает компенсатор плавучести, воздушная камера расширяется, вытесняя больший объем воды и увеличивая восходящую силу, действующую на дайвера. Когда дайвер сдувает компенсатор плавучести, воздушная камера теряет объем, вытесняет меньше воды и ослабляет восходящую силу, действующую на дайвера. Под водой дайвер использует компенсатор плавучести для поддержания нейтральной плавучести. На поверхности дайвер почти полностью надувает компенсатор плавучести, чтобы он мог плавать на поверхности.

Гири:

Использование свинцовых гирь в подводном плавании также оправдано законом Архимеда. При полной экипировке большинство дайверов обладают положительной плавучестью на поверхности. Аквалангист вытесняет совсем немного воды! Чтобы противодействовать восходящей силе, ныряльщик носит свинцовые грузы, маленькие и тяжелые; они увеличивают вес водолаза, но едва увеличивают его водоизмещение.

Гидрокостюмы:

Гидрокостюм увеличивает водоизмещение дайвера без значительного увеличения его веса, что делает дайвера более плавучим. Даже тонкий гидрокостюм повысит плавучесть дайвера. Чем толще его гидрокостюм, тем больше водоизмещение дайвера и тем больше будет восходящая сила, действующая на его тело. Сухие костюмы более громоздкие и обладают большей положительной плавучестью, чем гидрокостюмы 9.0003

Баллоны:

Алюминиевые баллоны также оказывают интересное влияние на плавучесть дайвера. Полный стандартный алюминиевый бак объемом 80 кубических футов (Al 80) обладает отрицательной плавучестью. Однако форма и объем Al 80 таковы, что, когда бак пуст, его водоизмещение больше, чем его вес (алюминий очень легкий). По мере того, как сжатый воздух вдыхается из полного бака, бак становится все легче и легче, пока в конечном итоге не станет положительно плавучим. Дайвер должен утяжелить себя, чтобы противодействовать плавучести алюминиевого баллона в конце погружения, что означает, что он начнет погружение с небольшим перевесом. Он должен надуть свой компенсатор плавучести, чтобы компенсировать эту отрицательную плавучесть, когда он начинает погружение, а затем постепенно выпускать воздух из компенсатора плавучести на протяжении всего погружения, чтобы поддерживать нейтральную плавучесть.

Нравится:

Нравится Загрузка…

Насколько велика верхушка айсберга? – Математическое мышление

Фраза «верхушка айсберга» происходит от того факта, что большая часть айсберга, плавающего в океане, находится под поверхностью воды. С помощью расчетов обратной стороны конверта мы можем оценить, какая часть свободно плавающего айсберга находится над поверхностью.

Рассмотрим ситуацию, когда объект (айсберг) погружен в жидкость (соленую воду океана). Гравитация оказывает на объект направленную вниз силу. Поскольку не все объекты тонут, на объект действует противодействующая сила. Эта сила, которая достаточно сильна, чтобы заставить некоторые объекты плавать, называется выталкивающая сила .

Выталкивающая сила — это сила, действующая на погруженный объект со стороны жидкости в направлении, противоположном силе тяжести. На самом деле, эта сила тоже является следствием гравитации – действия гравитации на жидкость . Гравитация притягивает молекулы жидкости; молекулы глубоко в жидкости могут «чувствовать» вес молекул над ними. Как следствие, давление в жидкости увеличивается с глубиной. Вы можете почувствовать более высокое давление на уши, когда плывете на дно бассейна. Точно так же, поскольку воздух является жидкостью, ваши уши лопаются из-за меньшего давления на больших высотах, например, в самолете или в горах.

Каким образом увеличение давления с глубиной приводит к возникновению выталкивающей силы? Представьте себе, что мы привязываем зеленый шарик к нити и подвешиваем его в стакане с водой:

Жидкость будет воздействовать на шарик силой в каждой точке его поверхности в направлении, перпендикулярном поверхности (красные стрелки)– это давление жидкости при работе. Однако давление на дне жидкости на больше, чем на , чем давление наверху жидкости. Как следствие, жидкость оказывает результирующую восходящую силу на объект. Стрелки внизу толще стрелок вверху, чтобы представить величину силы на большей глубине, чтобы быть больше. Будет ли объект плавать или тонуть, зависит от того, как величина выталкивающей силы соотносится с направленной вниз гравитационной силой, действующей на объект.

Принцип Архимеда количественно определяет силу этой выталкивающей силы, и она зависит только от объема жидкости, которую вытесняет объект, когда он погружен (частично или полностью). В конце я вывожу принцип Архимеда.

Объект, полностью или частично погруженный в жидкость, испытывает восходящую силу жидкости, равную весу жидкости, которую он вытесняет.

— Принцип Архимеда

Назад к айсбергу.

Плотность льда составляет кг/м ³ , а плотность соленой морской воды составляет около кг/м ³ . Поскольку плотность морской воды выше, чем у льда, вес льда меньше веса эквивалентного объема морской воды; Принцип Архимеда говорит нам, что айсберг будет плавать, поскольку выталкивающая сила айсберга, когда он полностью погружен в воду, больше, чем вес айсберга.

Давайте, наконец, рассчитаем долю айсберга, которая будет погружена под воду, когда он будет плавать. Айсберг будет находиться в равновесии, когда выталкивающая сила морской воды будет равна силе тяжести самого айсберга. Позвольте быть объемом айсберга и быть частью айсберга, который находится под поверхностью, для которой мы будем решать. Как и объем айсберга, который находится под водой.

Сила тяжести, действующая на айсберг, равна , его масса умножается на ускорение силы тяжести м/с. Выталкивающая сила на айсберг равна , так как это вес морской воды, вытесненной айсбергом вместе с нашим погруженным объемом льда.

Приравняв эти две силы и найдя , мы получим долю айсберга, находящегося под водой, как отношение плотности льда к плотности морской воды.

Итак, 89% свободно плавающего айсберга погружено под поверхность океана; мы видим только 11% его над поверхностью океана. То, что верхушка айсберга составляет всего 11%, является результатом простого расчета.

В качестве проверки интуиции, если вместо этого мы рассмотрим объект с плотностью больше, чем у морской воды, мы получим , что указывает на то, что объект утонет, поскольку мы не можем погрузить объект более чем на 100%!

Рассмотрим гидростатическую жидкость с давлением и замкнутым объемом жидкости, нарисованные пунктирными линиями на рисунке выше. Давление увеличивается с глубиной согласно следующему уравнению:

Здесь – плотность жидкости.

Поскольку давление действует нормально к поверхности объема, результирующая выталкивающая сила, действующая на объем жидкости со стороны окружающей жидкости, представляет собой поверхностный интеграл по границе объема:

Здесь – внешний единичный вектор нормали к поверхности ; отрицательный знак должен учитывать давление, действующее в направлении, противоположном . Теорема Гаусса о расходимости связывает этот интеграл по поверхности с интегралом по объему:

Теперь мы интегрируем по всему объему . Используя уравнение выше, и интеграл по объему становится:

, если плотность жидкости пространственно однородна. Значение – это просто объем !

С точки зрения жидкости за пределами объема, который мы здесь рассмотрели, не имеет значения, находится ли объект внутри или это жидкость ¹ . Таким образом, это выталкивающая сила, действующая на объект, погруженный в жидкость с плотностью: направленная вверх сила, равная .

¹ Да, да, здесь мы игнорируем поверхностное натяжение, но я думаю, что на айсберге этой силой можно пренебречь.

Спасибо Аарону Брэдли за идею для этой записи в блоге!

Включите JavaScript для просмотра комментариев на базе Disqus.comments на основе Disqus

Принцип Архимеда (плавучесть): что это такое и почему это важно?

Круизные лайнеры и авианосцы построены из сотен тысяч тонн материала, в том числе большого количества стали, и они плавают. Но бросьте с палубы тяжелый металлический якорь, и он утонет на дне океана. Почему?

Принцип Архимеда описывает, как объекты плавают или тонут в жидкости. В ньютоновской физике это представлено выталкивающей силой.

Кем был Архимед Сиракузский?

Архимед был классическим греческим мыслителем и ремесленником, жившим примерно в 287 г. до н.э. до 212 г. до н.э. в Сиракузах, древнегреческом городе-государстве на острове Сицилия. В молодости Архимед путешествовал, чтобы учиться в крупнейшей в мире библиотеке того времени, Александрийской библиотеке в Египте.

Известный своими многочисленными математическими формулировками, в том числе расчетом числа пи до самого точного значения, пока не появились электронные калькуляторы, он также был одним из первых ученых, применивших свою математику к физике и наоборот. Открытие Архимедом принципа для описания плавучести, или как вещи плывут , находится в центре одной из самых известных историй в истории науки.

Король Гиеро II, сицилийский тиран той эпохи, как сообщается, получил новую корону, которая, как он подозревал, была сделана не из чистого золота. Опасаясь, что мастер короны украл у него часть сырья, заменив часть материала в короне серебром, Гиерон обратился за помощью к гению острова Архимеду.

Согласно легенде, Архимед размышлял над проблемой в ванне, когда заметил, что когда он входил и выходил из воды, уровень воды поднимался на предсказуемую величину. Говорят, что при этом он крикнул: «Эврика!» («Я нашел это!») — слово, которое теперь неизгладимо приклеилось к открытиям и озарениям.

Предположительно, купающийся ученый объединил две идеи: во-первых, из двух объектов одинакового объема более плотный объект имеет большую массу. Во-вторых, чем больше места занимает погруженный в воду объект, тем больше жидкости вытесняется при его опускании (взрослый, заходя в ванну, выплескивает больше воды, чем ребенок).

Итак, рассуждал Архимед, если бы он знал вес короны, он мог бы собрать равный вес чистого золота, опустить оба предмета в воду и сравнить, насколько вода движется или вытесняется. Если они были равны, корона была законной. Если золото переместило больше воды, погрузившись глубже, корона должна быть менее плотный , чем чистое золото, а это означает, что производитель короны действительно обманывал короля.

Как оказалось, корона не была чистой: победа Архимеда, но, вероятно, катастрофа для создателя короны.

Плотность жидкости

Как знал Архимед во втором веке до нашей эры, плотность жидкости является мерой ее массы на единицу объема. Математически это:

d = \frac {m}{V}

Чем больше массы втиснуто в тот же объем, тем плотнее объект. Если плотность объекта больше, чем плотность жидкости, в которой он находится, он утонет.

Между тем более плотные жидкости оказывают большую выталкивающую силу на объекты, находящиеся в них.

Вместе эти концепции помогают объяснить, почему люди могут почти без усилий плавать на вершине очень соленого озера или моря, такого как Большое Соленое озеро или Мертвое море, по сравнению с менее плотным водоемом.

Давление жидкости

Давление жидкости помогает более подробно описать выталкивающую силу.

Давление в целом равно силе на единицу площади . Все жидкости имеют внутреннее давление, которое давит на любые объекты, погруженные в жидкость. Эта сила на единицу площади, действующая на объект со стороны воды, возникает со всех сторон, где бы вода ни давила на него.

Кроме того, давление жидкости зависит от плотности жидкости и ее глубины. Чем глубже в жидкости находится объект, тем большее давление жидкости оказывает на него вода. Это означает, что для чего-то вроде лодки в воде дно лодки испытывает большее давление жидкости, толкающее ее вверх, чем бока лодки, которые толкают внутрь.

Принцип Архимеда

Как показывает анекдот с ванной Архимеда, удобным способом измерения силы жидкости, действующей на объект, или выталкивающей силы, является количественное определение воды, вытесняемой этим объектом при погружении.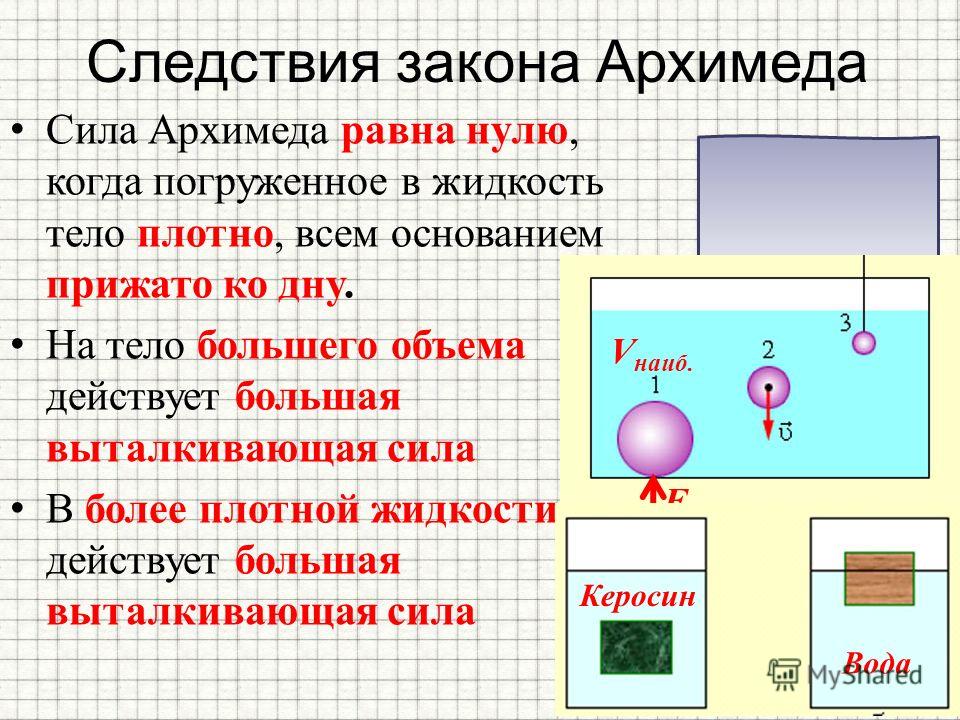

Это верно, потому что выталкивающая сила равна весу жидкости, которую вытесняет объект. Другими словами, для каноэ, плавающего по реке, количество речной воды, отталкиваемой при спуске на воду, равно количеству воды, которое заполнило бы погруженную часть каноэ (однако большая часть внутренней части лодки в настоящее время находится ниже уровня моря). поверхность воды).

Причина, по которой это происходит, заключается в том, что разность давлений между верхом и низом объекта вызывает чистую направленную вверх силу, равную разнице между весом объекта и весом вытесненной жидкости.

Например, рассмотрим погруженный в воду куб. Векторы силы от давления жидкости вокруг куба направлены внутрь, но векторы ниже в жидкости больше.

Следовательно, хотя давление в верхней части погруженного объекта приводит к направленной вниз силе, а давление в нижней части приводит к восходящей силе, поскольку векторы, направленные вверх, больше, будет иметь место результирующая выталкивающая сила, направленная вверх на кубе. Пока эта сила по крайней мере равна дополнительной направленной вниз силе тяжести или весу куба, он будет плавать.

Когда объект покоится в жидкости, вес объекта точно соответствует весу вытесненной жидкости. Однако, если объект весит больше, чем вытесненная жидкость, результирующая сила, действующая на него, направлена ​​вниз, и он утонет; если он весит меньше, чем вытесненная вода, он ускорится вверх.

Поскольку в любом случае объем объекта и объем вытесняемой им жидкости являются заданными величинами, единственная разница в их весе (сила гравитации, действующая на них) заключается в их соответствующих массах. Поскольку плотность — это масса на единицу объема, отсюда следует, что плотность объекта — это еще один способ определить, будет ли он тонуть или плавать: объекты, более плотные, чем жидкость, будут тонуть, и наоборот.

Применение принципа Архимеда

Объединив все эти концепции, физик теперь может объяснить, как невероятно тяжелый авианосец, транспортное судно или круизный лайнер может плавать, даже если он сделан из таких материалов, как сталь, плотность которых превышает плотность воды.