PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
III закон Ньютона – Физический факультет СПбГУ
III закон Ньютона
По III закону Ньютона сила  Для центрально-симметричных взаимодействий силы действия и противодействия всегда направлены по одной прямой. В общем случае эти силы направлены как показано на рис. A1
Для центрально-симметричных взаимодействий силы действия и противодействия всегда направлены по одной прямой. В общем случае эти силы направлены как показано на рис. A1
не по линии, соединяющей точки приложения этих сил, а по параллельным линиям. При этом оказывается, что суммарный момент сил в системе двух взаимодействующих тел A и B отличен от нуля!
Докажем, что отличный от нуля момент сил, действующих на некоторую систему из N тел, приводит к изменению ее момента количества движения.
Выпишем уравнения движения для каждого из N тел в следующем виде:
Введенные здесь обозначения очевидны:
Fi — суммарная сила, действующая на тело i;
vi и pi — скорость и импульс этого тела в данный момент;
Dt — промежуток времени, малый настолько, чтобы можно было пренебречь изменением любых параметров системы.
Умножим равенство (A1) слева векторно на радиус-вектор точки приложения силы Fi:
Правую часть этого равенства можно переписать в виде
так как имеет место тождество
Последнее слагаемое в правой части этого тождества обращается в ноль в виду того, что D ri||pi (векторное произведение параллельных векторов равно нулю).
Проведем в (A2) суммирование по i:
В левой части этого равенства стоит импульс суммарного момента сил
Из этого равенства следует, что отличный от нуля момент сил приводит к изменению вектора момента количества движения системы.
В системе двух тел, изображенной на рис. A1, суммарный момент сил отличен от нуля. Такая система должна, в соответствии с формулой (A3), ускоренно вращаться относительно общего центра масс, что противоречит, в частности, закону сохранения энергии. Могут ли существовать системы, подобные изображенной на рис. A1?
A1, суммарный момент сил отличен от нуля. Такая система должна, в соответствии с формулой (A3), ускоренно вращаться относительно общего центра масс, что противоречит, в частности, закону сохранения энергии. Могут ли существовать системы, подобные изображенной на рис. A1?
Сила, действующая на частицу в потенциальном поле, равна
где введен векторный оператор градиента
Для центрального-симметричного потенциального поля потенциал взаимодействия двух частиц зависит (по определению) только от расстояния между ними: U(r1, r2)=U(|r1- r2|). Следовательно, силы взаимодействия частиц F1 и F
Здесь
Обозначим |r1- r2|=r и заметим, что
Таким образом, для центрально-симметричных потенциалов силы действия и противодействия всегда направлены по одной линии в противоположенные стороны. В природе центрально-симметричные потенциалы описывают все дальнодействующие поля – гравитационное и электростатическое. Нецентральные поля (ядерные) имеют конечный радиус взаимодействия (-13см) и не проявляются в макроскопической физике.
В природе центрально-симметричные потенциалы описывают все дальнодействующие поля – гравитационное и электростатическое. Нецентральные поля (ядерные) имеют конечный радиус взаимодействия (-13см) и не проявляются в макроскопической физике.
Тем не менее центрально-симметричные потенциалы могут приводить к нецентральным взаимодействиям. Приведем конкретный пример такой системы. Заряд q расположим на расстоянии L от середины диполя, состоящего из зарядов +q и -q, как показано на рис. A2. Дл ина диполя dL.
Силы F1 и F2, действующие на заряд со стороны диполя, равны по величине. Их векторная сумма равна F. Силы, действующие на диполь со стороны заряда, равны –F1 и –F2 соответственно, а их сумма – Но заметим, что момент сил –F1 и –F2, п риложенных к диполю, тоже отличен от нуля, направлен против часовой стрелки и равен M’@ F1d. Из сравнения треугольника сил F1, F2, F с треугольником, в вершинах которого находятся заряды, видим, что F 1/F@ L/d. Отсюда получаем, что F1d @ FL и M=M’, а в векторной форме
Но заметим, что момент сил –F1 и –F2, п риложенных к диполю, тоже отличен от нуля, направлен против часовой стрелки и равен M’@ F1d. Из сравнения треугольника сил F1, F2, F с треугольником, в вершинах которого находятся заряды, видим, что F 1/F@ L/d. Отсюда получаем, что F1d @ FL и M=M’, а в векторной форме
Заряд, находящийся в точке B, действуя на диполь, расположенный в точке A, создает не только силу – F, но и момент сил – M’.
Покажем, что потенциальное поле, создаваемое диполем, нецентральное.
Для этого обратимся к рис. А3 и вычислим потенциал в произвольной точке на расстоянии R от центра диполя под углом q к вектору d, соединяющему заряды диполя:
Это выражение на расстояниях R>>d можно упростить, используя разложение по малой величине d/R:
С учетом этого приближения формула (A8) может быть переписана в виде
Для элементарного диполя d- 0, q стремится к бесконечности при фиксированном значении дипольного момента p=qd.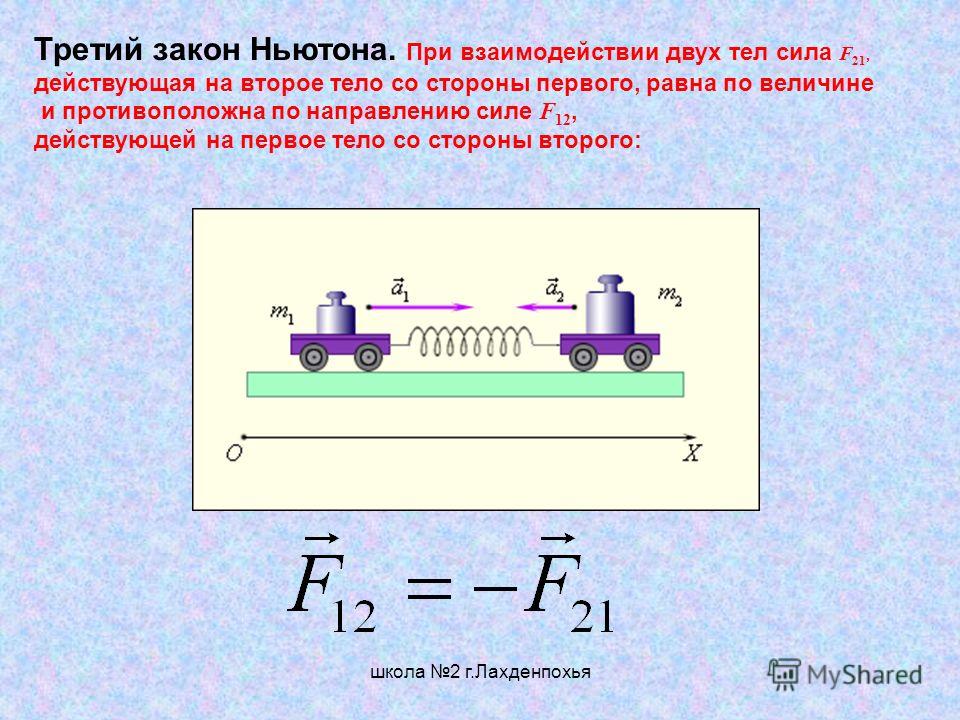 Потенциал поля такого диполя
Потенциал поля такого диполя
Видим, что потенциальное поле диполя не обладает сферической симметрией — потенциал явно зависит не только от расстояния R до диполя, но и от угла q между осью диполя и направлением в точку наблюдения.
Таким образом, даже в центрально-симметричных потенциальных полях взаимодействие элементарных объектов может иметь вид, характерный для нецентральных потенциалов. Силы действия и противодей ствия равны, направлены противоположно, но не по одной прямой, соединяющей точки приложения сил, а по параллельным линиям. При этом взаимодействие в целом описывается не только силами, но и моментами сил, т. е. имеет более сложный вид, чем обычно подразумевается при формулировке III закона.
4.Масса сила импульс. Второй закон ньютона
Физика вопросы и ответы:
3.Первый закон Ньютона и понятие инерциальной системы отчёта:
Первый
закон Ньютона постулирует существование
инерциальных систем отсчета. Поэтому
он также известен как Закон
инерции. Инерция —
это свойство тела сохранять свою скорость
движения неизменной (и по величине, и
по направлению), когда на тело не действуют
никакие силы. Чтобы изменить скорость
движения тела, на него необходимо
подействовать с некоторой силой.
Естественно, результат действия
одинаковых по величине сил на различные
тела будет различным. Таким образом,
говорят, что тела обладают разной
инертностью. Инертность — это свойство
тел сопротивляться изменению их скорости.
Величина инертности характеризуется массой тела
Поэтому
он также известен как Закон
инерции. Инерция —
это свойство тела сохранять свою скорость
движения неизменной (и по величине, и
по направлению), когда на тело не действуют
никакие силы. Чтобы изменить скорость
движения тела, на него необходимо
подействовать с некоторой силой.
Естественно, результат действия
одинаковых по величине сил на различные
тела будет различным. Таким образом,
говорят, что тела обладают разной
инертностью. Инертность — это свойство
тел сопротивляться изменению их скорости.
Величина инертности характеризуется массой тела
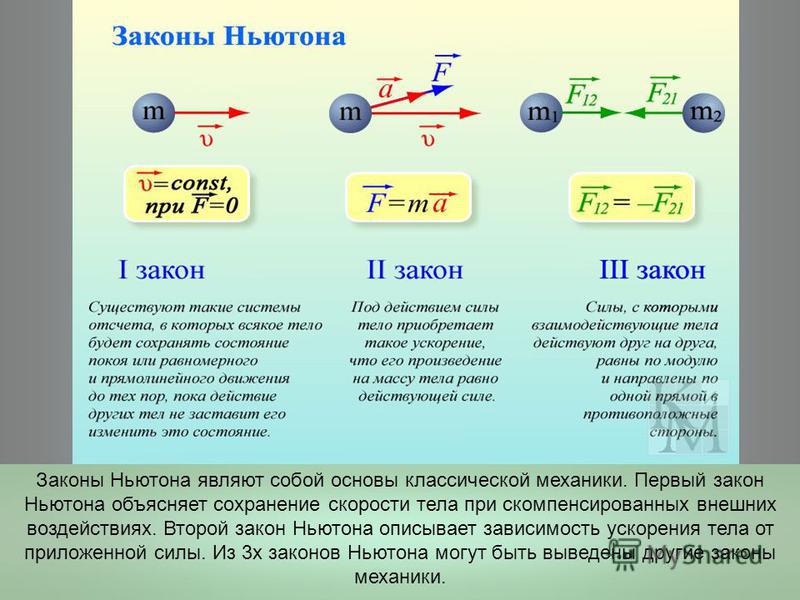
В современной физике первый закон Ньютона принято формулировать в следующем виде:
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Формула первого закона Ньютона: F=ma
Ма́сса (от греч. μάζα —
«кусок теста») — скалярная физическая
величина,
одна из важнейших величин в физике.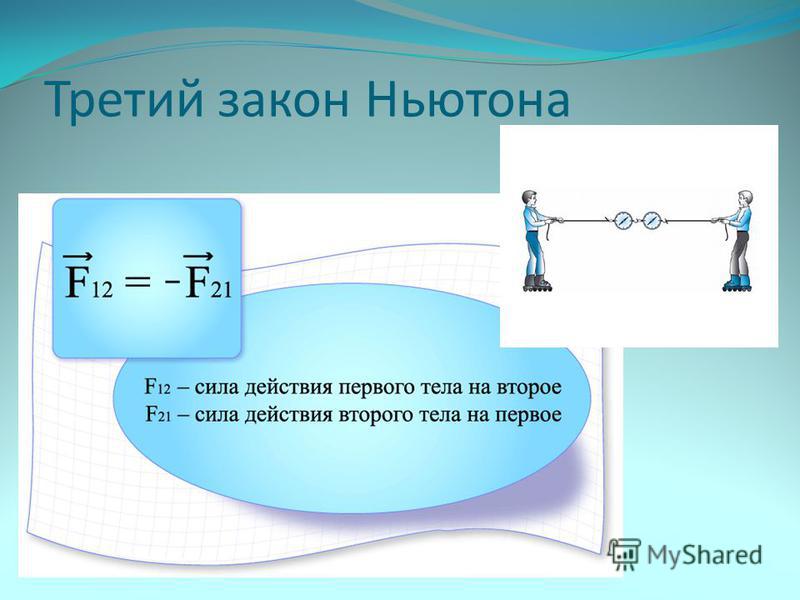 Первоначально (XVII—XIX
века)
она характеризовала «количество
вещества» в физическом объекте, от
которого, по представлениям того времени,
зависели как способность объекта
сопротивляться приложенной силе
(инертность),
так и гравитационные свойства — вес.
Первоначально (XVII—XIX
века)
она характеризовала «количество
вещества» в физическом объекте, от
которого, по представлениям того времени,
зависели как способность объекта
сопротивляться приложенной силе
(инертность),
так и гравитационные свойства — вес.
В современной физике понятие «количество вещества» имеет другой смысл, а масса тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). Масса проявляется в природе несколькими способами.
Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.
Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.
Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона.
 Если произвольная сила в инерциальной
системе отсчётаодинаково
ускоряет разные исходно неподвижные
тела, этим телам приписывают одинаковую
инертную массу.
Если произвольная сила в инерциальной
системе отсчётаодинаково
ускоряет разные исходно неподвижные
тела, этим телам приписывают одинаковую
инертную массу.
Си́ла(F) — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная кмассивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений.
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:.
Второй закон Ньютона — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона.
Современная
формулировка:
В инерциальных системах отсчёта
ускорение, приобретаемое материальной
точкой, прямо
пропорционально вызывающей
его силе, совпадает с ней по направлению
и обратно
пропорционально массе
материальной точки. Обычно
этот закон записывается в виде формулы:
Обычно
этот закон записывается в виде формулы:
где —ускорение тела, —сила, приложенная к телу, а —масса материальной точки.
Или, в ином виде:
Формулировка второго закона Ньютона с использованием понятия импульса:
Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой , а вторая — на первую с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия
Современная формулировка: атериальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Зако́н
сохране́ния и́мпульса (Зако́н
сохране́ния количества движения)
утверждает, что векторная сумма импульсов всех
тел (или частиц) системы есть величина
постоянная, если векторная сумма внешних
сил, действующих на систему, равна
нулю. В классической
механике закон
сохранения импульса обычно выводится
как следствие законов Ньютона. Из законов
Ньютона можно
показать, что при движении в пустом
пространстве импульс сохраняется во
времени, а при наличии взаимодействия
скорость его изменения определяется
суммой приложенных сил.
В классической
механике закон
сохранения импульса обычно выводится
как следствие законов Ньютона. Из законов
Ньютона можно
показать, что при движении в пустом
пространстве импульс сохраняется во
времени, а при наличии взаимодействия
скорость его изменения определяется
суммой приложенных сил.
Законы Ньютона и электрическая сила
Взаимодействие притяжения или отталкивания между любыми двумя заряженными объектами представляет собой электрическую силу . Как и всякая сила, ее действие на объекты описывается законами движения Ньютона. Электрическая сила — F Elect — присоединяется к длинному списку других сил, которые могут воздействовать на объекты. Законы Ньютона применяются для анализа движения (или отсутствия движения) объектов под действием такой силы или комбинации сил. Анализ обычно начинается с построения диаграммы свободного тела, на которой тип и направление отдельных сил представлены векторными стрелками и помечены в соответствии с типом. Затем величины сил складываются в виде векторов, чтобы определить результирующую сумму, также известную как результирующая сила. Затем результирующую силу можно использовать для определения ускорения объекта.
Затем величины сил складываются в виде векторов, чтобы определить результирующую сумму, также известную как результирующая сила. Затем результирующую силу можно использовать для определения ускорения объекта.
В некоторых случаях целью анализа не является определение ускорения объекта. Вместо этого диаграмма свободного тела используется для определения пространственного разделения или заряда двух объектов, находящихся в статическом равновесии. В этом случае диаграмма свободного тела сочетается с пониманием векторных принципов, чтобы определить некую неизвестную величину посреди головоломки, включающей геометрию, тригонометрию и закон Кулона. В этом последнем разделе Урока 3 мы исследуем оба типа применения законов Ньютона к явлению статического электричества.
Электрическая сила и ускорение Предположим, что резиновый воздушный шар и пластиковая трубка для гольфа заряжаются отрицательно, если их натереть шерстью животного. Предположим, что воздушный шар подброшен в воздух, а трубка для гольфа удерживается под ним, чтобы поднять воздушный шар в воздухе. Эта цель может быть достигнута, когда пространственное разделение между заряженными объектами отрегулировано таким образом, чтобы направленная вниз сила тяжести (F grav ) и направленная вверх электрическая сила (F избрать ) сбалансированы. Это представляло бы сложную задачу манипулирования, поскольку воздушный шар постоянно перемещался бы из стороны в сторону и вверх и вниз под влиянием как силы тяжести, так и электрической силы. Когда трубка для гольфа удерживается слишком далеко от воздушного шара, воздушный шар падает и ускоряется вниз. Это, в свою очередь, уменьшило бы разделяющее расстояние и привело бы к увеличению электрической силы. Поскольку F Elect увеличивается, он, вероятно, превысит F grav 9.0006, и воздушный шар внезапно ускорится вверх. И, наконец, если точка заряда на трубе для гольфа не находится непосредственно под точкой заряда воздушного шара (вероятный сценарий), электрическая сила будет действовать под углом к вертикали, и воздушный шар будет боковое ускорение.
Эта цель может быть достигнута, когда пространственное разделение между заряженными объектами отрегулировано таким образом, чтобы направленная вниз сила тяжести (F grav ) и направленная вверх электрическая сила (F избрать ) сбалансированы. Это представляло бы сложную задачу манипулирования, поскольку воздушный шар постоянно перемещался бы из стороны в сторону и вверх и вниз под влиянием как силы тяжести, так и электрической силы. Когда трубка для гольфа удерживается слишком далеко от воздушного шара, воздушный шар падает и ускоряется вниз. Это, в свою очередь, уменьшило бы разделяющее расстояние и привело бы к увеличению электрической силы. Поскольку F Elect увеличивается, он, вероятно, превысит F grav 9.0006, и воздушный шар внезапно ускорится вверх. И, наконец, если точка заряда на трубе для гольфа не находится непосредственно под точкой заряда воздушного шара (вероятный сценарий), электрическая сила будет действовать под углом к вертикали, и воздушный шар будет боковое ускорение.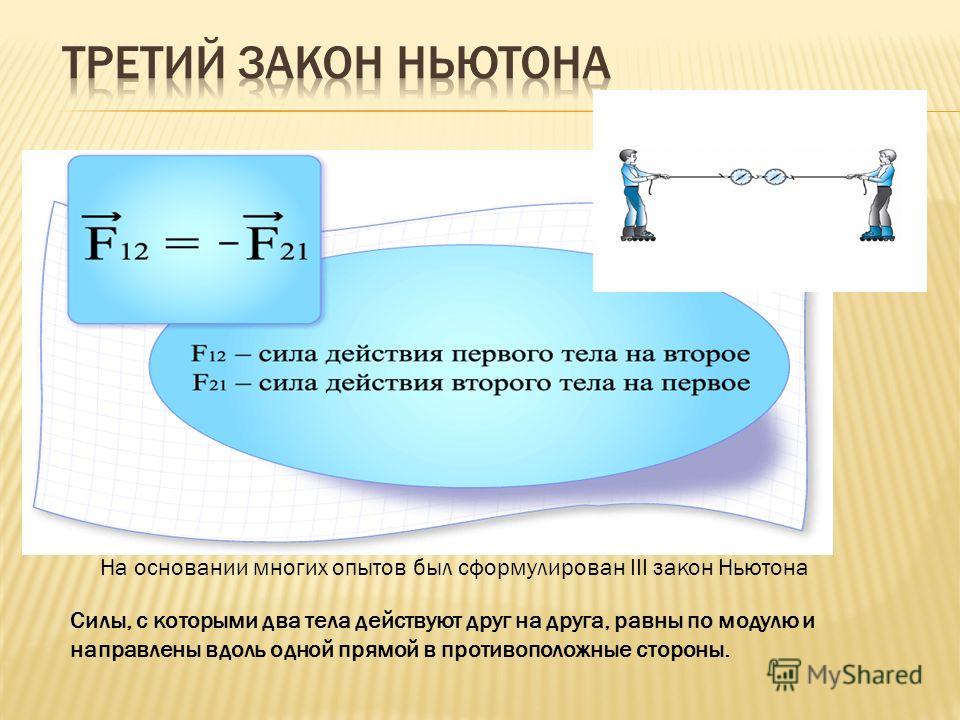 Вероятным результатом такой попытки поднять шар в воздух будет множество мгновенных ускорений в различных направлениях.
Вероятным результатом такой попытки поднять шар в воздух будет множество мгновенных ускорений в различных направлениях.
Предположим, что в какой-то момент в процессе попытки левитации воздушного шара возникли следующие условия:
0,90-граммовый воздушный шар с зарядом -75 нКл находится на расстоянии 12 см над пластиковой трубкой для гольфа, имеющей заряд -83 нКл.
Как можно применить законы Ньютона для определения ускорения воздушного шара в данный момент?
Как и любая задача, связанная с силой и ускорением, задача начинается с построения диаграммы свободного тела. На шарик действуют две силы. Сила тяжести на шаре направлена вниз. Электрическая сила воздействует на воздушный шар вверх, поскольку воздушный шар и трубка для гольфа заряжены одинаково, а трубка для гольфа удерживается ниже воздушного шара. Эти две силы показаны на диаграмме свободного тела справа. Второй шаг включает определение величины этих двух сил. Сила тяжести определяется путем умножения массы (в килограммах) на ускорение свободного падения.
Сила тяжести определяется путем умножения массы (в килограммах) на ускорение свободного падения.
F грав = 8,82 x 10 -3 N, вниз
Электрическая сила определяется по закону Кулона. Как показано ниже, соответствующей единицей измерения заряда является кулон (Кл), а соответствующей единицей расстояния — метр (м). Использование этих единиц приведет к единице силы Ньютона. Спрос на эти единицы вытекает из единиц постоянной Кулона.
F избранный = (9 x 10 9 Н•м 2 /C 2 900 -9 С) • (-83 x 10 -9 С) / (0,12) 2
F избранный = 3,89 x 10 -3 N, вверх
Чистая сила представляет собой векторную сумму этих двух сил. Восходящие и нисходящие силы складываются как векторы.
F нетто = 8,82 x 10 -3 Н, вниз + 3,89 x 10 -3 Н, вверх
F нетто = 4,93 x 10 -3 N, вниз
Последний шаг этой задачи включает использование второго закона Ньютона для определения ускорения объекта. Ускорение равно чистой силе, деленной на массу (в килограммах).
а = 5,5 м/с/с, вниз
Вышеприведенный анализ показывает, как можно применить закон Ньютона и закон Кулона для определения мгновенного ускорения. Следующий анализ включает случай, когда два объекта находятся в состоянии статического равновесия.
Электрическая сила и статическое равновесие
Предположим, что два резиновых шарика подвешены к потолку на двух длинных нитях так, что они висят вертикально. Затем предположим, что каждый шарик получает 10 трений средней силы о шерсть животных. Воздушные шары, обладающие большим притяжением для электронов, чем шерсть животных, приобретут отрицательный заряд. Воздушные шары будут иметь одинаковый тип заряда, и впоследствии они будут отталкиваться друг от друга. Результатом их отталкивания является то, что струны и подвешенные воздушные шары теперь образуют угол с вертикалью. Угол нити с вертикалью будет математически связан с количеством заряда на воздушных шарах. По мере того как воздушные шары приобретают большее количество заряда, сила отталкивания между ними будет увеличиваться, а также будет увеличиваться угол, который образует нить с вертикалью. Как и любую ситуацию, связанную с электростатической силой, эту ситуацию можно проанализировать, используя векторные принципы и законы Ньютона.
Затем предположим, что каждый шарик получает 10 трений средней силы о шерсть животных. Воздушные шары, обладающие большим притяжением для электронов, чем шерсть животных, приобретут отрицательный заряд. Воздушные шары будут иметь одинаковый тип заряда, и впоследствии они будут отталкиваться друг от друга. Результатом их отталкивания является то, что струны и подвешенные воздушные шары теперь образуют угол с вертикалью. Угол нити с вертикалью будет математически связан с количеством заряда на воздушных шарах. По мере того как воздушные шары приобретают большее количество заряда, сила отталкивания между ними будет увеличиваться, а также будет увеличиваться угол, который образует нить с вертикалью. Как и любую ситуацию, связанную с электростатической силой, эту ситуацию можно проанализировать, используя векторные принципы и законы Ньютона.
Предположим, что существуют следующие условия.
Два воздушных шара весом 1,1 грамма подвешены на двухметровых нитях к потолку.Затем их десять раз натирают шерстью животных, чтобы передать одинаковый заряд Q каждому шарику. Воздушные шары отталкиваются друг от друга, и наблюдается, что каждая нить составляет угол 15 градусов с вертикалью. Определить электрическую силу отталкивания, заряд каждого шарика (считается одинаковым) и количество электронов, переданных каждому шарику в результате 10 натираний мехом животного.
Из-за сложности физической ситуации было бы целесообразно изобразить ее с помощью диаграммы. Диаграмма будет служить средством идентификации известной информации для этой ситуации. На приведенной ниже диаграмме изображены два воздушных шара с длиной нити L и углом «тета». Масса ( м ) шаров известна; здесь он выражается в килограммах (стандартная единица массы). Расстояние между шариками (переменная в законе Кулона) отмечено на диаграмме и представлено переменной д . Рисуется вертикальная линия, идущая от точки поворота на потолке; эта вертикальная линия является одной стороной прямоугольного треугольника, образованного горизонтальной линией, соединяющей воздушные шары, и веревкой, идущей от воздушного шара к потолку. Этот прямоугольный треугольник будет полезен, когда мы будем анализировать ситуацию, используя векторные принципы. Обратите внимание, что вертикальная линия делит пополам отрезок, соединяющий воздушные шары; таким образом, одна сторона прямоугольного треугольника имеет расстояние d/2 .
Этот прямоугольный треугольник будет полезен, когда мы будем анализировать ситуацию, используя векторные принципы. Обратите внимание, что вертикальная линия делит пополам отрезок, соединяющий воздушные шары; таким образом, одна сторона прямоугольного треугольника имеет расстояние d/2 .
Применение законов Ньютона к этой ситуации начинается с построения диаграммы свободного тела для одного из воздушных шаров. На шары действуют три силы: сила натяжения, сила тяжести и электростатическая сила отталкивания. Эти три силы представлены для воздушного шара справа. (См. схему ниже.) Обратите внимание, что сила натяжения направлена под углом к вертикали. В физике такие ситуации рассматриваются путем разложения вектора силы на горизонтальную и вертикальную составляющие. Это показано ниже; компоненты обозначены как F x и F y . Эти компоненты связаны с углом, который струна образует с вертикалью, тригонометрическими функциями. Поскольку воздушный шар находится в равновесии, силы, действующие на воздушный шар, должны уравновешивать друг друга. Это означает, что вертикальная составляющая силы натяжения ( F y ) должна уравновешивать направленную вниз силу тяжести ( F грав ). А горизонтальная составляющая силы натяжения ( F x ) должны уравновешивать направленную вправо электростатическую силу ( F Elect ).
Поскольку воздушный шар находится в равновесии, силы, действующие на воздушный шар, должны уравновешивать друг друга. Это означает, что вертикальная составляющая силы натяжения ( F y ) должна уравновешивать направленную вниз силу тяжести ( F грав ). А горизонтальная составляющая силы натяжения ( F x ) должны уравновешивать направленную вправо электростатическую силу ( F Elect ).
Поскольку масса воздушного шара известна, можно определить действующую на него силу тяжести.
F грав = 0,01078 Н
Сила тяжести равна вертикальной составляющей силы натяжения ( F y = 0,0108 N ). Компонент F y связан с компонентой F x и углом тета функцией тангенса. Это соотношение можно использовать для определения горизонтальной составляющей силы натяжения. Работа представлена ниже.
Это соотношение можно использовать для определения горизонтальной составляющей силы натяжения. Работа представлена ниже.
Тангенс (тета) = F x / F y
Тангенс (15 градусов) = F x / (0,01078 Н)
F x = (0,01078 Н) • Тангенс (15 градусов)
F x = 0,00289 Н
Горизонтальная составляющая силы натяжения равна электростатической силе. Таким образом,
Теперь, когда электростатическая сила определена с использованием законов Ньютона и векторных принципов, теперь можно применить закон Кулона для определения заряда воздушного шара.
Предполагается, что баллоны имеют одинаковое количество заряда, так как они заряжаются одинаково с 10 трениями средней силы. Поскольку Q 1 равно Q 2 , уравнение можно переписать как
. Это уравнение можно алгебраически изменить, чтобы найти Q. Шаги показаны ниже.
Это уравнение можно алгебраически изменить, чтобы найти Q. Шаги показаны ниже.
Q 2 = F • d 2 / k
Q = SQRT(F • d 2 / k)
Для завершения решения необходимо знать значение d . Это требует анализа прямоугольного треугольника, чтобы определить длину стороны, противоположной углу в 15 градусов. Эта длина составляет половину расстояния d. Поскольку длина гипотенузы известна, используется функция синуса.
Синус (15 градусов) = противоположная сторона / (2,0 м)
противоположная сторона = (2,0 м) • Синус (15 градусов)
противоположная сторона = d /2 = 0,518 м
Удвоение этого расстояния дает значение d равное 1,035 м. Теперь можно произвести замены, чтобы определить значение Q.
Q = SQRT [(0,00289 Н) • (1,035 м) 2 / (9 x 10 9 Н•м 2 /C 2 )]
Q = 5,87 х 10 -7 С (отрицательный)
Заряд объекта связан с количеством избыточных (или недостаточных) электронов в объекте. Используя заряд одного электрона (-1,6 х 10 -19 Кл), можно определить количество электронов на этом объекте:
# избыточные электроны = 3,67 x 10 12 электронов
В процессе зарядки более трех триллионов электронов было передано от шерсти животных к каждому из воздушных шаров. Ух ты!
Конфигурации трех и более зарядов
В каждом из приведенных выше примеров мы исследовали взаимодействие двух заряженных объектов. Законы Ньютона и закон Кулона были объединены для анализа ситуаций. Но что, если зарядов три и более? Закон Кулона может учитывать только взаимодействие между Q 1 и Q 2 . Нужно ли переписывать закон для электрической силы, чтобы учесть Q 3 ? Нет!
Законы Ньютона и закон Кулона были объединены для анализа ситуаций. Но что, если зарядов три и более? Закон Кулона может учитывать только взаимодействие между Q 1 и Q 2 . Нужно ли переписывать закон для электрической силы, чтобы учесть Q 3 ? Нет!
Электрические силы возникают в результате взаимодействия двух зарядов. В ситуациях с участием трех или более зарядов электрическая сила, действующая на один заряд, является просто результатом комбинированных эффектов взаимодействия каждого отдельного заряда этого заряда со всеми другими зарядами. Если конкретный заряд сталкивается с двумя или более взаимодействиями, то результирующая электрическая сила представляет собой векторную сумму этих отдельных сил. В качестве примера этого подхода предположим, что присутствуют четыре заряда (A, B, C и D), которые расположены в пространстве так, что образуют квадрат. Заряды A и D заряжены отрицательно и занимают противоположные углы квадрата, а заряды B и C заряжены положительно и занимают оставшиеся два угла, как показано на рисунке. Если речь идет об общей электрической силе, действующей на заряд А, то необходимо рассчитать электрические силы между А и каждым из трех других зарядов. То есть Ф BA , F CA и F DA должны быть сначала определены применением закона Кулона к каждой из этих пар зарядов. Обозначение F BA используется для обозначения силы В на А .
Если речь идет об общей электрической силе, действующей на заряд А, то необходимо рассчитать электрические силы между А и каждым из трех других зарядов. То есть Ф BA , F CA и F DA должны быть сначала определены применением закона Кулона к каждой из этих пар зарядов. Обозначение F BA используется для обозначения силы В на А .
F BA = K • Q A • Q B / D BA 2
F CA = K • Q A • Q C / D CA 2
F DA = k • Q A • Q D / d DA 2
Направление каждой из этих трех сил можно определить, применяя основные правила взаимодействия зарядов: противоположно заряженные объекты притягиваются, а одноименно заряженные отталкиваются. Применительно к этому сценарию можно предположить, что силы F BA , F CA и F DA направлены, как показано на диаграмме ниже. Заряд B притягивает A, а заряд C притягивает A, так как это пары противоположно заряженных объектов. Но заряд D отталкивает A, поскольку они представляют собой пару объектов с одинаковым зарядом.
Заряд B притягивает A, а заряд C притягивает A, так как это пары противоположно заряженных объектов. Но заряд D отталкивает A, поскольку они представляют собой пару объектов с одинаковым зарядом.
Таким образом, величины отдельных сил определяются посредством расчетов по закону Кулона. Направление отдельных сил определяется применением правил взаимодействия зарядов. И как только величина и направление трех векторов силы известны, эти три вектора можно сложить, используя правила сложения векторов, чтобы определить результирующую электрическую силу. Это показано на диаграмме выше.
Используйте свое понимание заряда, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Положительно заряженный объект с зарядом +85 нКл используется для уравновешивания направленной вниз силы тяжести на 1,8-граммовом воздушном шаре с зарядом -63 нКл. На какой высоте над воздушным шаром нужно держать предмет, чтобы уравновесить воздушный шар? (ПРИМЕЧАНИЕ: 1 нКл = 1 x 10 -9 В)
На какой высоте над воздушным шаром нужно держать предмет, чтобы уравновесить воздушный шар? (ПРИМЕЧАНИЕ: 1 нКл = 1 x 10 -9 В)
2. Воздушный шар A и воздушный шар B заряжаются аналогичным образом путем натирания мехом животного. Каждый приобретает избыток 25 триллионов электронов. Если масса воздушных шаров равна 1 грамму, то насколько ниже воздушного шара B должен находиться воздушный шар A, чтобы поднять воздушный шар B? Предположим, что воздушные шары действуют как точечные заряды.
3. Два 1,2-граммовых шара подвешены на световых нитях, прикрепленных к потолку в одной точке. Чистый заряд на воздушных шарах составляет -540 нКл. Воздушные шары находятся на расстоянии 68,2 см друг от друга, когда находятся в равновесии. Определить длину строки.
4. ZINGER : Три заряда расположены по оси X. Заряд А представляет собой заряд +18 нКл, размещенный в начале координат. Заряд B представляет собой заряд -27 нКл, размещенный на расстоянии 60 см. Где вдоль оси (в какой координате x?) должен быть помещен положительно заряженный C, чтобы он находился в равновесии?
Заряд B представляет собой заряд -27 нКл, размещенный на расстоянии 60 см. Где вдоль оси (в какой координате x?) должен быть помещен положительно заряженный C, чтобы он находился в равновесии?
Перейти к следующему уроку:
Преобразователь случайных чисел | Перевести единицы: ньютон [Н] в фунт-сила [фунт-сила] Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. 1 newton [N] = 0.2248089431 pound-force [lbf] From: newtonexanewtonpetanewtonteranewtongiganewtonmeganewtonkilonewtonhectonewtondekanewtondecinewtoncentinewtonmillinewtonmicronewtonnanonewtonpiconewtonfemtonewtonattonewtondynejoule/meterjoule/centimetergram-forcekilogram-forceton-force (short)ton-force (long)ton-force (metric)kip- силакилофунт-силафунт-силаунция-силафунтфунт-фут/секунду²прудкилопрудстенегрейв-силамиллиграв-силаатомная единица силы To: newtonexanewtonpetanewtonteranewtongiganewtonmeganewtonkilonewtonhectonewtondekanewtondecinewtoncentinewtonmillinewtonmicronewtonnanonewtonpiconewtonfemtonewtonattonewtondynejoule/meterjoule/centimetergram-forcekilogram-forceton-force (short)ton-force (long)ton-force (metric)kip-forcekilopound-forcepound-forceounce-forcepoundalpound foot/second²pondkilopondsthenegrave-forcemilligrave-forceatomic единица силы Объем Плотность зарядаЗнаете ли вы, что на вашей кухне и в радарах используется одно и то же вакуумное устройство? Нажмите или коснитесь, чтобы узнать, что это за устройство! Три силы, находящиеся в динамическом равновесии, действуют на этого серфера: гравитация, подъемная сила и лобовое сопротивление Сила Приливы Неосновные силы Нормальная сила Трение Интересные факты о силах Обзор Физика определяет силу как влияние, которое изменяет движение тела, будь то внешнее движение или движение. Сила является вектором, то есть имеет направление. Когда несколько сил действуют на объект и тянут его в разные стороны, эти силы могут быть в равновесии, а это означает, что их векторная сумма равна нулю. В этом случае объект будет покоиться. Камень из предыдущего примера может катиться после удара о землю, но в конце концов он остановится. Сила тяжести по-прежнему тянет его вниз, но в то же время нормальная сила, или сила реакции земли, толкает камень вверх. Суммарная сумма этих сил равна нулю, они находятся в равновесии, и камень не движется. Единицей силы в системе СИ является ньютон. Один ньютон соответствует чистой силе, которая ускоряет объект массой один килограмм на один метр в секунду в квадрате. Равновесие Одним из первых ученых, исследовавших силы и создавших модель их взаимодействия с материей во Вселенной, был Аристотель. Фундаментальные силы во ВселеннойСилы в природе заставляют объекты двигаться или оставаться на месте. В природе существует четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. Все остальные силы являются подмножествами этих четырех. В отличие от электрических и гравитационных сил сильные и слабые силы воздействуют на материю только на ядерном уровне. Они не работают на больших расстояниях. Сильная сила Сильная сила — самая сильная из четырех сил. Он действует на элементы ядра атома, удерживая вместе нейтроны и протоны. Электромагнитная силаТрансформаторы полюсного типа в Киото, Япония Электромагнитная сила является второй по силе силой. Это взаимодействие между частицами с противоположными или одинаковыми электрическими зарядами. Когда две частицы имеют одинаковый заряд, то есть обе они положительны или обе отрицательны, они отталкиваются друг от друга. Если, с другой стороны, они имеют противоположный заряд, где один положительный, а другой отрицательный, они притягиваются друг к другу. Это движение частиц, которые отталкиваются или притягиваются к другим частицам, и есть электричество — физическое явление, которое мы используем в нашей повседневной жизни и в большинстве технологий. Электромагнитная сила может объяснить химические реакции, свет и электричество, а также взаимодействие между молекулами, атомами и электронами. Эти взаимодействия между частицами ответственны за форму, которую твердые объекты принимают в мире. Электромагнитная сила препятствует проникновению двух твердых тел друг в друга, поскольку электроны одного объекта отталкивают электроны того же заряда другого объекта. Исторически электрические и магнитные силы рассматривались как отдельные воздействия, но со временем было обнаружено, что они связаны. Большинство объектов имеют нейтральный заряд, но можно изменить заряд объекта, потирая два объекта друг о друга. Электроны будут перемещаться между двумя материалами, притягиваясь к противоположно заряженным электронам в другом материале. Это оставит больше электронов с одинаковым зарядом на поверхности каждого объекта, тем самым изменив доминирующий заряд объекта в целом. Например, если потереть волосы свитером, а затем снять свитер, волосы встанут и «последуют» за свитером. Слабое взаимодействиеСлабое взаимодействие слабее электромагнитного. Точно так же, как глюоны несут сильное взаимодействие, бозоны W и Z несут слабое взаимодействие. Это элементарные частицы, которые испускаются или поглощаются. Бозоны W облегчают процесс радиоактивного распада, в то время как бозоны Z не влияют на частицы, с которыми они вступают в контакт, кроме передачи импульса. Углеродное датирование, процесс определения возраста органического вещества, возможен из-за слабого взаимодействия. Он используется для установления возраста исторических артефактов и основан на оценке распада углерода, присутствующего в этом органическом веществе. Гравитационная сила Озеро Онтарио. Сила гравитации самая слабая из четырех. Он удерживает астрономические объекты на их местах во вселенной, отвечает за приливы и заставляет объекты падать на землю, когда их отпускают. Это сила, которая действует на объекты, притягивая их друг к другу. Сила этого притяжения увеличивается с увеличением массы объекта. Как и другие силы, считается, что она передается частицами, гравитонами, но эти частицы еще не обнаружены. Гравитация влияет на то, как движутся астрономические объекты, и это движение можно рассчитать на основе массы окружающих объектов. Эта зависимость позволила ученым предсказать существование Нептуна, наблюдая за движением Урана до того, как Нептун был замечен в телескоп. Это произошло потому, что движение Урана не соответствовало его предсказанному движению, основанному на астрономических объектах, известных в то время, поэтому ученые пришли к выводу, что другая планета, еще невидимая, должна влиять на его модели движения. Согласно теории относительности, гравитация также изменяет пространственно-временной континуум, четырехмерное пространство, в котором существует все, включая людей. Сила гравитации заставляет объекты ускоряться при падении на другой объект, и это заметно, когда разница в массе между ними велика. Это ускорение можно рассчитать на основе массы объектов. Для объектов, падающих на Землю, она составляет около 9,8 метра в секунду в квадрате. Приливы и отливыМорские скалы Приливы являются примерами гравитационной силы в действии. Приливы случаются с разной частотой в зависимости от географического региона. Поскольку гравитация Луны и Солнца притягивает как воду, так и всю планету Земля, в некоторых районах приливы возникают, когда сила гравитации тянет воду и Землю в одном или разных направлениях. Приливная сила, которая перемещает воду к берегу и от берега, иногда используется для выработки энергии. Приливные мельницы веками использовали эту силу. Неосновные силыСилы, производные от основных сил, называются неосновными силами. Нормальная силаРавновесие Одной из неосновных сил является нормальная сила, которая действует перпендикулярно поверхности объекта и выталкивает наружу, сопротивляясь давлению других объектов. Когда объект помещается на поверхность, величина нормальной силы равна результирующей силе, давящей на поверхность. На плоской поверхности, когда силы, отличные от силы тяжести, находятся в равновесии, нормальная сила равна силе тяжести по величине и противоположна по направлению. Более широкие шины обеспечивают лучшее трение Трение Трение — это сила, параллельная поверхности объекта и направленная против его движения. Это происходит, когда два объекта скользят друг относительно друга (кинетическое трение) или когда неподвижный объект помещается на наклонную поверхность (статическое трение). Эта сила используется при приведении объектов в движение, например, при сцеплении колес с землей за счет трения. Без него они не смогли бы приводить в движение транспортные средства. Трение между резиной шин и землей достаточно сильное, чтобы гарантировать, что шины не скользят по земле, и обеспечивает качение и лучший контроль направления движения. Интересные факты о силах Силы могут деформировать твердые объекты или изменять объем и давление в жидкостях и газах. Это происходит, когда силы приложены неодинаково к разным частям объекта или вещества. В некоторых случаях, когда к тяжелому объекту прикладывается достаточное усилие, его можно сжать в очень маленькую сферу. Если эта сфера достаточно мала, меньше определенного радиуса, то может образоваться черная дыра. Этот радиус называется радиусом Шварцшильда . Он варьируется в зависимости от массы объекта и может быть рассчитан по формуле. Ссылки Эта статья была написана Kateryna Yuri Перевести ньютоны в дин Перевести ньютоны в кип-силы Перевести джоули/метры в ньютоны сила Преобразовать фунт-фут/секунду² в ньютон Преобразовать фунт-силу в ньютон Преобразовать унцию-силу в ньютон Преобразовать килограмм-силу в дину Преобразовать дину в фунт-фут/секунду² Вас могут заинтересовать другие конвертеры из группы «Общие конвертеры единиц измерения»:Конвертер длины и расстояния Конвертер массы Объем сухого вещества и общепринятые измерения приготовления Преобразователь площади Преобразователь объема и измерения температуры приготовления Преобразователь давления, напряжения, модуля Юнга Преобразователь энергии и работы Преобразователь мощности Преобразователь времени Конвертер линейной скорости и скорости Конвертер угла Конвертер топливной эффективности, расхода топлива и экономии топлива Конвертер чисел Конвертер единиц информации и хранения данных Конвертер метрических префиксов Передача данных ТарифыРазмеры мужской одежды и обуви Размеры женской одежды и обуви Компактный калькулятор Полный калькулятор Определения единиц измерения Вам трудно перевести единицу измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков. |
Ньютон | Единицы измерения Wiki
| На этой странице используется контент из английской Википедии . Оригинальная статья была в Ньютоне (единица измерения). Список авторов можно увидеть на странице истории . Как и в случае с Вики по единицам измерения, текст Википедии доступен по лицензии Creative Commons, см. Викия:Лицензирование. |
ньютонов (обозначение: Н ) — производная единица силы в системе СИ. Он назван в честь Исаака Ньютона в знак признания его работ по классической механике, в частности, по второму закону движения Ньютона.
Содержание
- 1 Определение
- 2 примера
- 3 Обычное использование килоньютонов в строительстве
- 4 Переводные коэффициенты
- 5 См. также
- 6 Каталожные номера
Definition[]
Ньютон — единица силы в СИ; она равна сумме чистой силы, необходимой для ускорения массы в один килограмм со скоростью один метр в секунду в квадрате.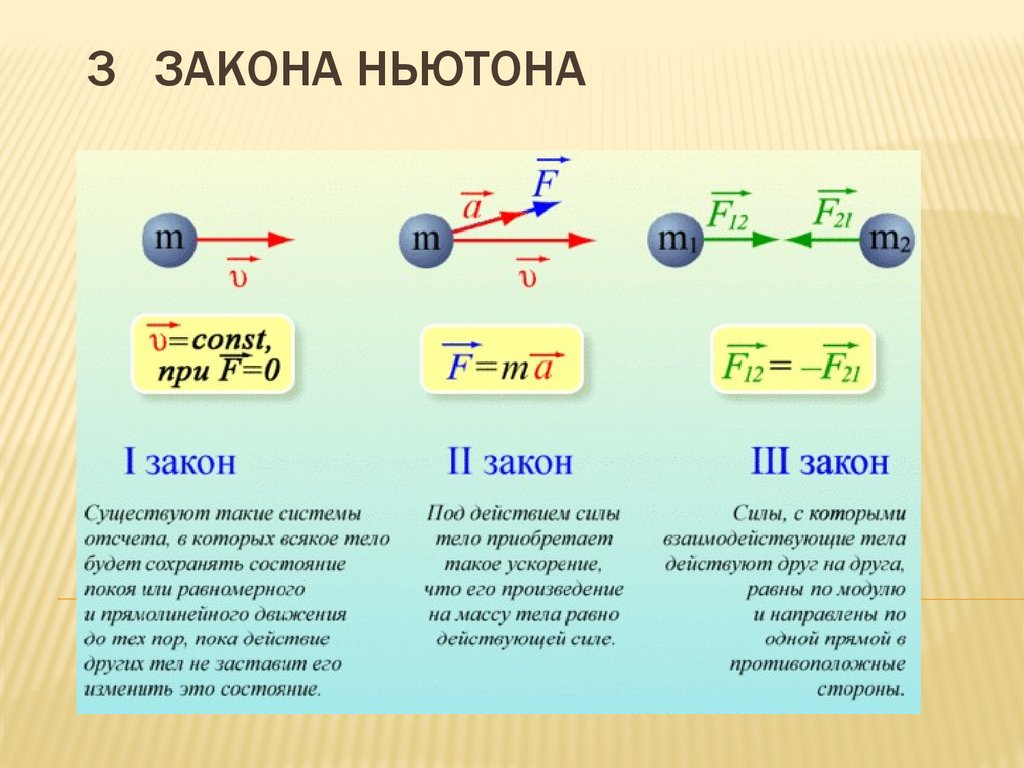 [1]
[1]
- Н = ньютон
- кг = килограммов
- м = метров
- с = секунда
В размерном анализе:
где
- М = Масса
- L = длина
- T = Время
Примеры[]
- 1 Н — сила земного притяжения, действующая на массу около 100 г = ( 1 ∕ 9,81 кг).
- На поверхности Земли масса в 1 кг действует с силой приблизительно 9,8 Н [вниз] (или 1,0 килограмм-сила; 1 кгс = 9,80665 Н по определению). Приближение 1 кгс, соответствующее 10 Н (1 деканьютон или даН), иногда используется в качестве эмпирического правила в повседневной жизни и в технике.
- Сила земного притяжения, действующая на (= вес) человека массой 70 кг, приблизительно равна 686 Н.
- Скалярное произведение силы на расстояние есть механическая работа. Таким образом, в единицах СИ сила в 1 Н, приложенная на расстоянии 1 м, составляет 1 Н·м работы.
 Теорема о работе и энергии утверждает, что работа, совершаемая над телом, равна изменению энергии тела. 1 Н·м = 1 Дж (джоуль), единица измерения энергии в системе СИ.
Теорема о работе и энергии утверждает, что работа, совершаемая над телом, равна изменению энергии тела. 1 Н·м = 1 Дж (джоуль), единица измерения энергии в системе СИ. - Обычно силы выражаются в килоньютонах или кН, где 1 кН = 1 000 Н.
Обычное использование килоньютонов в строительстве[]
Килоньютоны часто используются для определения безопасного удерживания крепежа, анкеров и многого другого в строительной отрасли. Они также часто используются в спецификациях для скалолазного снаряжения. Безопасные рабочие нагрузки как при растяжении, так и при сдвиге могут быть указаны в килоньютонах. Машины для литья под давлением, используемые для изготовления пластиковых деталей, классифицируются по килоньютону (т.е. по силе зажима, которую они прикладывают к пресс-форме).
На поверхности Земли 1 кН составляет примерно 101,97162 килограмма-силы нагрузки, но умножение значения в килоньютонах на 100 (т. е. с использованием слегка консервативного и легко подсчитываемого значения) является хорошим практическим правилом. [2] [3]
[2] [3]
Переводные коэффициенты[]
v · d · e | ньютон (единица СИ) | дин | килограмм-сил, килопондов | фунт-сила | фунтов стерлингов |
|---|---|---|---|---|---|
| 1 Н | ≡ 1 кг·м/с² | = 10 5 дин | ≈ 0,10197 кп | ≈ 0,22481 фунта F | ≈ 7,2330 пдл |
| 1 дин | = 10 −5 Н | ≡ 1 г·см/с² | ≈ 1,0197×10 −6 кп | ≈ 2,2481×10 −6 фунтов Ф | ≈ 7,2330×10 −5 пдл |
| 1 шт. | = 9,80665 Н | = 980665 дин | ≡ г n ·(1 кг) | ≈ 2,2046 фунта F | ≈ 70,932 пдл |
| 1 фунт F | ≈ 4,448222 Н | ≈ 444822 дин | ≈ 0,45359 кп | ≡ г n ·(1 фунт) | ≈ 32,174 пдл |
1 шт. | ≈ 0,138255 Н | ≈ 13825 дин | ≈ 0,014098 кп | ≈ 0,031081 фунта F | ≡ 1 фунт·фут/с² |
| Значение g n , используемое в официальном определении килограмм-силы, используется здесь для всех единиц гравитации. | |||||
v · d · e база | сила, длина, время | вес, длина, время | масса, длина, время | |||||
|---|---|---|---|---|---|---|---|---|
| Сила ( Ф ) | F = м·а = вт·а/г | F = м·а/г c = ва·а/г | F = м·а = вт·а/г | |||||
| Вес ( с ) | вес = м·г | w = м·г/г c ≈ m | вес = мг·г | |||||
| Система | БГ | ГМ | ЕЕ | М | АЕ | CGS | МТС | СИ |
| Ускорение ( a ) | фут/с 2 | м/с 2 | фут/с 2 | м/с 2 | фут/с 2 | галлонов | м/с 2 | м/с 2 |
| Масса ( м ) | пуля | hyl, также называемый «метрическим слагом» или «TME».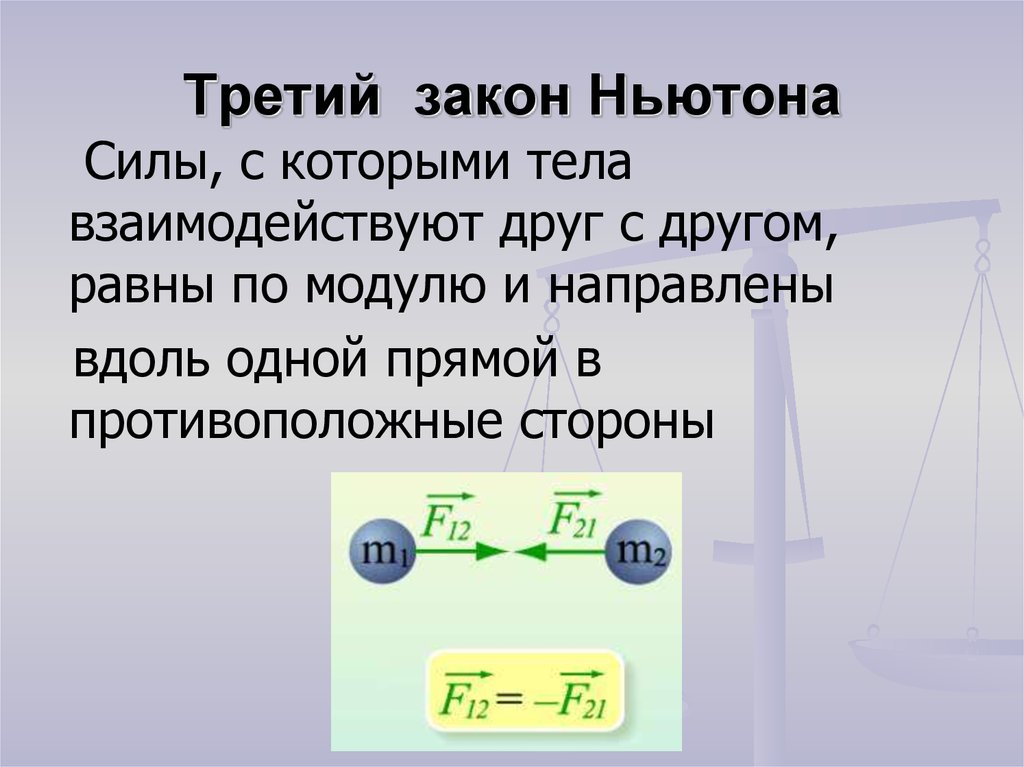 | фунтов м | кг | фунтов | г | т | кг |
| Сила ( Ф ) | фунтов | кп | фунтов F | кп | пдл | дин | серийный номер | с.ш. |
| Давление ( р ) | фунтов/дюйм 2 | в | фунт/кв. дюйм | атм | пдл/фут 2 | Ба | пз | Па |
См.

 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия
 Если произвольная сила в инерциальной
системе отсчётаодинаково
ускоряет разные исходно неподвижные
тела, этим телам приписывают одинаковую
инертную массу.
Если произвольная сила в инерциальной
системе отсчётаодинаково
ускоряет разные исходно неподвижные
тела, этим телам приписывают одинаковую
инертную массу. Затем их десять раз натирают шерстью животных, чтобы передать одинаковый заряд Q каждому шарику. Воздушные шары отталкиваются друг от друга, и наблюдается, что каждая нить составляет угол 15 градусов с вертикалью. Определить электрическую силу отталкивания, заряд каждого шарика (считается одинаковым) и количество электронов, переданных каждому шарику в результате 10 натираний мехом животного.
Затем их десять раз натирают шерстью животных, чтобы передать одинаковый заряд Q каждому шарику. Воздушные шары отталкиваются друг от друга, и наблюдается, что каждая нить составляет угол 15 градусов с вертикалью. Определить электрическую силу отталкивания, заряд каждого шарика (считается одинаковым) и количество электронов, переданных каждому шарику в результате 10 натираний мехом животного. Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица тела, например, изменение его формы. Например, когда камень отпускается, он падает, потому что его притягивает сила земного притяжения. Во время удара он сгибает травинки, на которые падает, — сила веса камня заставляет их двигаться и менять форму.
тела, например, изменение его формы. Например, когда камень отпускается, он падает, потому что его притягивает сила земного притяжения. Во время удара он сгибает травинки, на которые падает, — сила веса камня заставляет их двигаться и менять форму. Согласно его модели, если чистая векторная сумма сил, действующих на объект, равна нулю, силы находятся в состоянии равновесия, а объект неподвижен. Позже эта модель была исправлена, чтобы включить объекты, движущиеся с постоянной скоростью, когда силы находятся в равновесии. Этот тип равновесия называется динамическим равновесием, а тот, в котором объект находится в состоянии покоя, называется статическим равновесием.
Согласно его модели, если чистая векторная сумма сил, действующих на объект, равна нулю, силы находятся в состоянии равновесия, а объект неподвижен. Позже эта модель была исправлена, чтобы включить объекты, движущиеся с постоянной скоростью, когда силы находятся в равновесии. Этот тип равновесия называется динамическим равновесием, а тот, в котором объект находится в состоянии покоя, называется статическим равновесием. Эта сила переносится глюонами и связывает кварки вместе, образуя более крупные частицы. Кварки образуют нейтроны, протоны и другие более крупные частицы. Глюоны — это более мелкие элементарные частицы, не имеющие субструктуры и движущиеся между кварками как переносчики силы. Движение глюонов создает сильное взаимодействие между кварками. Это сила, из которой состоит материя во Вселенной.
Эта сила переносится глюонами и связывает кварки вместе, образуя более крупные частицы. Кварки образуют нейтроны, протоны и другие более крупные частицы. Глюоны — это более мелкие элементарные частицы, не имеющие субструктуры и движущиеся между кварками как переносчики силы. Движение глюонов создает сильное взаимодействие между кварками. Это сила, из которой состоит материя во Вселенной.
 Это связано с тем, что электроны на поверхности волос больше притягиваются к атомам на поверхности свитера, чем электроны на поверхности свитера притягиваются к атомам на поверхности волос. Волосы или другие объекты с аналогичным зарядом также будут притягиваться к нейтрально заряженным поверхностям.
Это связано с тем, что электроны на поверхности волос больше притягиваются к атомам на поверхности свитера, чем электроны на поверхности свитера притягиваются к атомам на поверхности волос. Волосы или другие объекты с аналогичным зарядом также будут притягиваться к нейтрально заряженным поверхностям. Миссиссога (Канада). Звездная ночь
Миссиссога (Канада). Звездная ночь Согласно этой теории, искривление пространства-времени увеличивается с увеличением массы, и поэтому его легче заметить на объектах размером с планету или больше по массе. Эта кривизна доказана экспериментально и видна при сравнении двух синхронизированных часов, из которых одни неподвижны, а другие движутся на значительное расстояние вдоль тела большой массы. Например, если часы перемещаются по орбите Земли, как в эксперименте Хафеле-Китинга, то время, которое они показывают, будет отставать от неподвижных часов, потому что искривление пространства-времени заставляет время двигаться медленнее для движущихся часов.
Согласно этой теории, искривление пространства-времени увеличивается с увеличением массы, и поэтому его легче заметить на объектах размером с планету или больше по массе. Эта кривизна доказана экспериментально и видна при сравнении двух синхронизированных часов, из которых одни неподвижны, а другие движутся на значительное расстояние вдоль тела большой массы. Например, если часы перемещаются по орбите Земли, как в эксперименте Хафеле-Китинга, то время, которое они показывают, будет отставать от неподвижных часов, потому что искривление пространства-времени заставляет время двигаться медленнее для движущихся часов.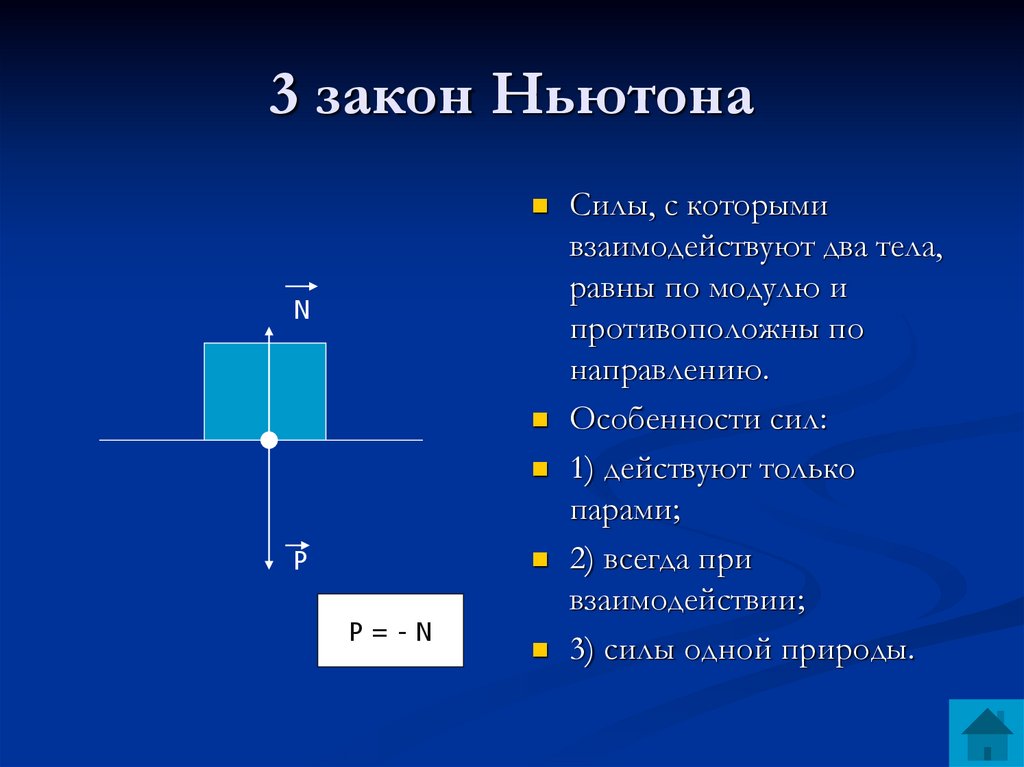 Они вызваны гравитационными силами Луны, Солнца и Земли. В отличие от твердых тел, вода может легко менять форму под действием сил. Поэтому, когда на Землю действуют гравитационные силы Луны и Солнца, земная поверхность не так притягивается этими силами, как вода. Луна и Солнце движутся по небу, а вода на Земле следует за ними, вызывая приливы. Силы, действующие на воду, называются приливными; они представляют собой различные гравитационные силы. Луна, будучи ближе к Земле, имеет более сильную приливную силу по сравнению с Солнцем. Когда приливные силы Солнца и Луны действуют в одном направлении, прилив является самым сильным и называется весенним приливом. Когда эти две силы находятся в оппозиции, прилив самый слабый и называется квадратным приливом.
Они вызваны гравитационными силами Луны, Солнца и Земли. В отличие от твердых тел, вода может легко менять форму под действием сил. Поэтому, когда на Землю действуют гравитационные силы Луны и Солнца, земная поверхность не так притягивается этими силами, как вода. Луна и Солнце движутся по небу, а вода на Земле следует за ними, вызывая приливы. Силы, действующие на воду, называются приливными; они представляют собой различные гравитационные силы. Луна, будучи ближе к Земле, имеет более сильную приливную силу по сравнению с Солнцем. Когда приливные силы Солнца и Луны действуют в одном направлении, прилив является самым сильным и называется весенним приливом. Когда эти две силы находятся в оппозиции, прилив самый слабый и называется квадратным приливом.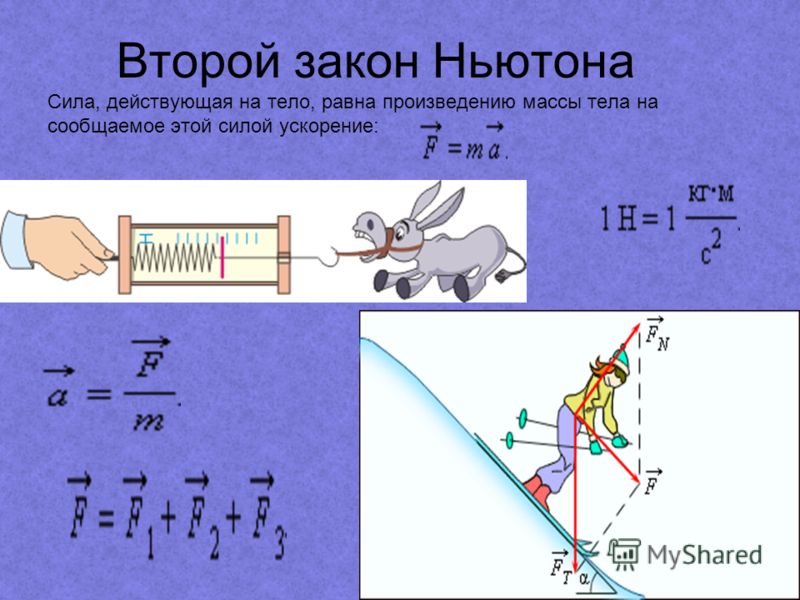 В этом случае пара приливов и отливов происходит дважды за один день. В некоторых районах это происходит только один раз в день. Модели приливов на побережье зависят от формы побережья, глубинных моделей приливов в океане и местоположения Луны и Солнца, а также от взаимодействия их гравитационных сил. В некоторых местах продолжительность времени между приливами может длиться до нескольких лет. В зависимости от береговой линии и глубины океана приливы могут вызывать течения, штормы, изменения характера ветра и колебания атмосферного давления. В некоторых местах используются специальные часы, чтобы рассчитать, когда произойдет следующий прилив. Они настраиваются на основе приливов и отливов в этом районе, и их необходимо перенастраивать при перемещении в другое место. В некоторых районах приливные часы неэффективны, потому что там трудно предсказать приливы.
В этом случае пара приливов и отливов происходит дважды за один день. В некоторых районах это происходит только один раз в день. Модели приливов на побережье зависят от формы побережья, глубинных моделей приливов в океане и местоположения Луны и Солнца, а также от взаимодействия их гравитационных сил. В некоторых местах продолжительность времени между приливами может длиться до нескольких лет. В зависимости от береговой линии и глубины океана приливы могут вызывать течения, штормы, изменения характера ветра и колебания атмосферного давления. В некоторых местах используются специальные часы, чтобы рассчитать, когда произойдет следующий прилив. Они настраиваются на основе приливов и отливов в этом районе, и их необходимо перенастраивать при перемещении в другое место. В некоторых районах приливные часы неэффективны, потому что там трудно предсказать приливы. Базовая конструкция имеет резервуар для воды, вода поступает во время прилива и выливается во время отлива. Кинетическая энергия протекающей воды приводит в движение колесо мельницы, а вырабатываемая мощность используется для выполнения работы, например, перемалывания зерна в муку. Хотя с этой системой связан ряд проблем, в том числе опасность для экосистемы, в которой построен этот завод, у этого метода производства энергии есть потенциал, поскольку он является возобновляемым и надежным источником энергии.
Базовая конструкция имеет резервуар для воды, вода поступает во время прилива и выливается во время отлива. Кинетическая энергия протекающей воды приводит в движение колесо мельницы, а вырабатываемая мощность используется для выполнения работы, например, перемалывания зерна в муку. Хотя с этой системой связан ряд проблем, в том числе опасность для экосистемы, в которой построен этот завод, у этого метода производства энергии есть потенциал, поскольку он является возобновляемым и надежным источником энергии. Тогда сумма векторов двух сил равна нулю, и объект неподвижен или движется с постоянной скоростью. Когда объект находится под наклоном и другие силы находятся в равновесии, сумма гравитационных и нормальных сил направлена вниз (но не прямо вниз, перпендикулярно горизонту), и объект скользит вниз по наклону.
Тогда сумма векторов двух сил равна нулю, и объект неподвижен или движется с постоянной скоростью. Когда объект находится под наклоном и другие силы находятся в равновесии, сумма гравитационных и нормальных сил направлена вниз (но не прямо вниз, перпендикулярно горизонту), и объект скользит вниз по наклону. Трение катящегося объекта, трение качения или сопротивление качению не так сильно, как сухое трение двух объектов, скользящих друг о друга. Трение используется при остановке с применением тормозов — колеса автомобиля затормаживаются за счет сухого трения в дисковых или барабанных тормозах. В некоторых случаях трение нежелательно, поскольку оно замедляет движение и изнашивает механические компоненты. Жидкости или гладкие поверхности используются для минимизации трения.
Трение катящегося объекта, трение качения или сопротивление качению не так сильно, как сухое трение двух объектов, скользящих друг о друга. Трение используется при остановке с применением тормозов — колеса автомобиля затормаживаются за счет сухого трения в дисковых или барабанных тормозах. В некоторых случаях трение нежелательно, поскольку оно замедляет движение и изнашивает механические компоненты. Жидкости или гладкие поверхности используются для минимизации трения. Объем этой сферы настолько мал, что по сравнению с массой объекта он почти равен нулю. Поскольку масса черных дыр так сильно сгущена, они обладают чрезвычайно сильным гравитационным притяжением, так что другие объекты не могут избежать его, и ни один из них не может светиться. Черные дыры не отражают свет, поэтому они кажутся абсолютно черными. Вот почему их называют черными дырами. Ученые считают, что большие звезды в конце своей жизни превращаются в черные дыры и могут увеличиваться в массе за счет поглощения других объектов, находящихся в заданном радиусе.
Объем этой сферы настолько мал, что по сравнению с массой объекта он почти равен нулю. Поскольку масса черных дыр так сильно сгущена, они обладают чрезвычайно сильным гравитационным притяжением, так что другие объекты не могут избежать его, и ни один из них не может светиться. Черные дыры не отражают свет, поэтому они кажутся абсолютно черными. Вот почему их называют черными дырами. Ученые считают, что большие звезды в конце своей жизни превращаются в черные дыры и могут увеличиваться в массе за счет поглощения других объектов, находящихся в заданном радиусе.
 Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах.
Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах. », то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами. com Конвертер единиц YouTube канал
com Конвертер единиц YouTube канал Теорема о работе и энергии утверждает, что работа, совершаемая над телом, равна изменению энергии тела. 1 Н·м = 1 Дж (джоуль), единица измерения энергии в системе СИ.
Теорема о работе и энергии утверждает, что работа, совершаемая над телом, равна изменению энергии тела. 1 Н·м = 1 Дж (джоуль), единица измерения энергии в системе СИ.