понятие и особенности применения формулы для их расчета
Не смотря на то, что гравитация – это слабейшее взаимодействие между объектами во Вселенной, ее значение в физике и астрономии огромно, так как она способна оказывать влияние на физические объекты на любом расстоянии в космосе.
Если вы увлекаетесь астрономией, вы наверняка задумывались над вопросом, что собой представляет такое понятие, как гравитация или закон всемирного тяготения. Гравитация – это универсальное фундаментальное взаимодействие между всеми объектами во Вселенной.
Открытие закона гравитации приписывают знаменитому английскому физику Исааку Ньютону. Наверное, многим из вас известна история с яблоком, упавшим на голову знаменитому ученому. Тем не менее, если заглянуть вглубь истории, можно увидеть, что о наличии гравитации задумывались еще задолго до его эпохи философы и ученые древности, например, Эпикур. Тем не менее, именно Ньютон впервые описал гравитационное взаимодействие между физическими телами в рамках классической механики.
Закон всемирного тяготения Ньютона говорит, что сила гравитационного притяжения между двумя точками массы, разделенными расстоянием обратно пропорциональна квадрату расстояния и прямо пропорциональна обеим массам. Сила гравитации является дальнодействующей. То есть, в независимости от того, как будет двигаться тело, обладающее массой, в классической механике его гравитационный потенциал будет зависеть сугубо от положения этого объекта в данный момент времени. Чем больше масса объекта, тем больше его гравитационное поле – тем более мощной гравитационной силой он обладает. Такие космически объекты, как галактики, звезды и планеты обладают наибольшей силой притяжения и соответственно достаточно сильными гравитационными полями.
Гравитационные поля
Гравитационное поле Земли
Гравитационное поле – это расстояние, в пределах которого осуществляется гравитационное взаимодействие между объектами во Вселенной. Чем больше масса объекта, тем сильнее его гравитационное поле – тем ощутимее его воздействие на другие физические тела в пределах определенного пространства. Гравитационное поле объекта потенциально. Суть предыдущего утверждения заключается в том, что если ввести потенциальную энергию притяжения между двумя телами, то она не изменится после перемещения последних по замкнутому контуру. Отсюда выплывает еще один знаменитый закон сохранения суммы потенциальной и кинетической энергии в замкнутом контуре.
Чем больше масса объекта, тем сильнее его гравитационное поле – тем ощутимее его воздействие на другие физические тела в пределах определенного пространства. Гравитационное поле объекта потенциально. Суть предыдущего утверждения заключается в том, что если ввести потенциальную энергию притяжения между двумя телами, то она не изменится после перемещения последних по замкнутому контуру. Отсюда выплывает еще один знаменитый закон сохранения суммы потенциальной и кинетической энергии в замкнутом контуре.
В материальном мире гравитационное поле имеет огромное значения. Им обладают все материальные объекты во Вселенной, у которых есть масса. Гравитационное поле способно влиять не только на материю, но и на энергию. Именно за счет влияния гравитационных полей таких крупных космических объектов, как черные дыры, квазары и сверхмассивные звезды, образуются солнечные системы, галактики и другие астрономические скопления, которым свойственна логическая структура.
Последние научные данные показывают, что знаменитый эффект расширения Вселенной так же основан на законах гравитационного взаимодействия. В частности расширению Вселенной способствуют мощные гравитационные поля, как небольших, так и самых крупных ее объектов.
В частности расширению Вселенной способствуют мощные гравитационные поля, как небольших, так и самых крупных ее объектов.
Гравитационное излучение в двойной системе
Гравитационное излучение или гравитационная волна – термин, впервые введенный в физику и космологии известным ученым Альбертом Эйнштейном. Гравитационное излучение в теории гравитации порождается движением материальных объектов с переменным ускорением. Во время ускорения объекта гравитационная волна как бы «отрывается» от него, что приводит к колебаниям гравитационного поля в окружающем пространстве. Это и называют эффектом гравитационной волны.
Хотя гравитационные волны предсказаны общей теорией относительности Эйнштейна, а также другими теориями гравитации, они еще ни разу не были обнаружены напрямую. Связано это в первую очередь с их чрезвычайной малостью. Однако в астрономии существуют косвенные свидетельства, способные подтвердить данный эффект. Так, эффект гравитационной волны можно наблюдать на примере сближения двойных звезд.
В современной физике существует два понятия механики: классическая и квантовая. Квантовая механика была выведена относительно недавно и принципиально отличается от механики классической. В квантовой механике у объектов (квантов) нет определенных положений и скоростей, все здесь базируется на вероятности. То есть, объект может занимать определенное место в пространстве в определенный момент времени. Куда переместиться он дальше, достоверно определить нельзя, а только с высокой долей вероятности.
Интересный эффект гравитации заключается в том, что она способна искривлять пространственно-временной континуум. Теория Эйнштейна гласит, что в пространстве вокруг сгустка энергии или любого материального вещества пространство-время искривляется. Соответственно меняется траектория частиц, которые попадают под воздействие гравитационного поля этого вещества, что позволяет с высокой долей вероятности предсказать траекторию их движения.
Соответственно меняется траектория частиц, которые попадают под воздействие гравитационного поля этого вещества, что позволяет с высокой долей вероятности предсказать траекторию их движения.
Теории гравитации
Сегодня ученым известно свыше десятка различных теорий гравитации. Их подразделяют на классические и альтернативные теории. Наиболее известными представителем первых является классическая теория гравитации Исаака Ньютона, которая была придумана известным британским физиком еще в 1666 году. Суть ее заключается в том, что массивное тело в механике порождает вокруг себя гравитационное поле, которое притягивает к себе менее крупные объекты. В свою очередь последние также обладают гравитационным полем, как и любые другие материальные объекты во Вселенной.
Следующая популярная теория гравитации была придумана всемирно известным германским ученым Альбертом Эйнштейном в начале XX века. Эйнштейну удалось более точно описать гравитацию, как явление, а также объяснить ее действие не только в классической механике, но и в квантовом мире.
Среди альтернативных теорий гравитации наибольшего внимания, пожалуй, заслуживает релятивистская теория, которая была придумана нашим соотечественником, знаменитым физиком А.А. Логуновым. В отличие от Эйнштейна, Логунов утверждал, что гравитация – это не геометрическое, а реальное, достаточно сильное физическое силовое поле. Среди альтернативных теорий гравитации известны также скалярная, биметрическая, квазилинейная и другие.
- Людям, побывавшим в космосе и возвратившимся на Землю, достаточно трудно на первых порах привыкнуть к силе гравитационного воздействия нашей планеты. Иногда на это уходит несколько недель.
- Доказано, что человеческое тело в состоянии невесомости может терять до 1% массы костного мозга в месяц.
- Наименьшей силой притяжения в Солнечной системе среди планет обладает Марс, а наибольшей – Юпитер.

- Известные бактерии сальмонеллы, которые являются причиной кишечных заболеваний, в состоянии невесомости ведут себя активнее и способны причинить человеческому организму намного больший вред.
- Среди всех известных астрономических объектов во Вселенной наибольшей силой гравитации обладают черные дыры. Черная дыра размером с мячик для гольфа, может обладать той же гравитационной силой, что и вся наша планета.
- Сила гравитации на Земле одинакова не во всех уголках нашей планеты. К примеру, в области Гудзонова залива в Канаде она ниже, чем в других регионах земного шара.
Самым главным явлением, постоянно изучаемым физиками, является движение. Электромагнитные явления, законы механики, термодинамические и квантовые процессы – все это широкий спектр изучаемых физикой фрагментов мироздания. И все эти процессы сводятся, так или иначе, к одному – к .
Вконтакте
Все во Вселенной движется. Гравитация – привычное явление для всех людей с самого детства, мы родились в гравитационном поле нашей планеты, это физическое явление воспринимается нами на самом глубоком интуитивном уровне и, казалось бы, даже не требует изучения.
Но, увы, вопрос, почему и каким образом все тела притягиваются друг к другу , остается и на сегодняшний день не до конца раскрытым, хотя и изучен вдоль и поперек.
В этой статье мы рассмотрим, что такое всемирное притяжение по Ньютону – классическую теорию гравитации. Однако прежде чем перейти к формулам и примерам, расскажем о сути проблемы притяжения и дадим ему определение.
Быть может, изучение гравитации стало началом натуральной философии (науки о понимании сути вещей), быть может, натуральная философия породила вопрос о сущности гравитации, но, так или иначе, вопросом тяготения тел заинтересовались еще в Древней Греции .
Движение понималось как суть чувственной характеристики тела, а точнее, тело двигалось, пока наблюдатель это видит. Если мы не можем явление измерить, взвесить, ощутить, значит ли это, что этого явления не существует? Естественно, не значит. И с тех пор, как Аристотель понял это, начались размышления о сути гравитации.
Как оказалось в наши дни, спустя многие десятки веков, гравитация является основой не только земного притяжения и притяжения нашей планеты к , но и основой зарождения Вселенной и почти всех имеющихся элементарных частиц.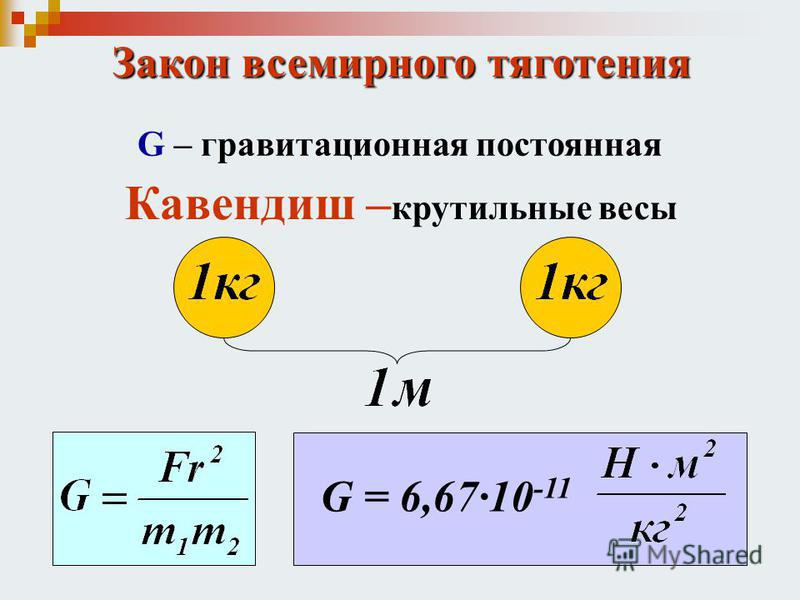
Задача движения
Проведем мысленный эксперимент. Возьмем в левую руку небольшой шарик. В правую возьмем такой же. Отпустим правый шарик, и он начнет падать вниз. Левый при этом остается в руке, он по-прежнему недвижим.
Остановим мысленно ход времени. Падающий правый шарик «зависает» в воздухе, левый все также остается в руке. Правый шарик наделен «энергией» движения, левый – нет. Но в чем глубокая, осмысленная разница между ними?
Где, в какой части падающего шарика прописано, что он должен двигаться? У него такая же масса, такой же объем. Он обладает такими же атомами, и они ничем не отличаются от атомов покоящегося шарика. Шарик обладает ? Да, это правильный ответ, но откуда шарику известно, что обладает потенциальной энергией, где это зафиксировано в нем?
Именно эту задачу ставили перед собой Аристотель, Ньютон и Альберт Эйнштейн. И все три гениальных мыслителя отчасти решили для себя эту проблему, но на сегодняшний день существует ряд вопросов, требующих разрешения.
Гравитация Ньютона
В 1666 году величайшим английским физиком и механиком И. Ньютоном открыт закон, способный количественно посчитать силу, благодаря которой вся материя во Вселенной стремится друг к другу. Это явление получило название всемирное тяготение. Когда вас просят: «Сформулируйте закон всемирного тяготения», ваш ответ должен звучать так:
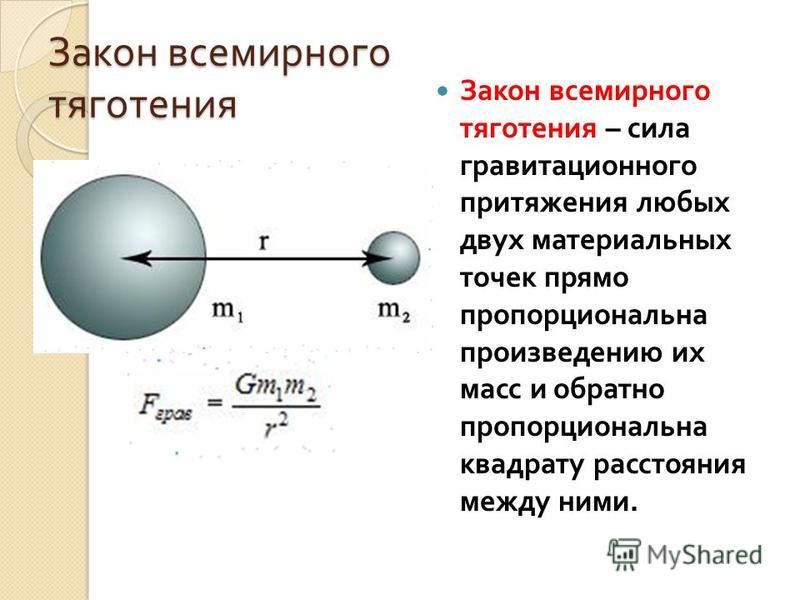
Сила гравитационного взаимодействия, способствующая притяжению двух тел, находится в прямой пропорциональной связи с массами этих тел и в обратной пропорциональной связи с расстоянием между ними.
Важно! В законе притяжения Ньютона используется термин «расстояние». Под этим термином следует понимать не дистанцию между поверхностями тел, а расстояние между их центрами тяжести. К примеру, если два шара радиусами r1 и r2 лежат друг на друге, то дистанция между их поверхностями равна нулю, однако сила притяжения есть. Все дело в том, что расстояние между их центрами r1+r2 отлично от нуля. В космических масштабах это уточнение не суть важно, но для спутника на орбите данная дистанция равна высоте над поверхностью плюс радиус нашей планеты. Расстояние между Землей и Луной также измеряется как расстояние между их центрами, а не поверхностями.
Расстояние между Землей и Луной также измеряется как расстояние между их центрами, а не поверхностями.
Для закона тяготения формула выглядит следующим образом:
,
- F – сила притяжения,
- – массы,
- r – расстояние,
- G – гравитационная постоянная, равная 6,67·10−11 м³/(кг·с²).
Что же представляет собой вес, если только что мы рассмотрели силу притяжения?
Сила является векторной величиной, однако в законе всемирного тяготения она традиционно записана как скаляр. В векторной картине закон будет выглядеть таким образом:
.
Но это не означает, что сила обратно пропорциональна кубу дистанции между центрами. Отношение следует воспринимать как единичный вектор, направленный от одного центра к другому:
.
Закон гравитационного взаимодействия
Вес и гравитация
Рассмотрев закон гравитации, можно понять, что нет ничего удивительного в том, что лично мы ощущаем притяжение Солнца намного слабее, чем земное . Массивное Солнце хоть и имеет большую массу, однако оно очень далеко от нас. тоже далеко от Солнца, однако она притягивается к нему, так как обладает большой массой. Каким образом найти силу притяжения двух тел, а именно как вычислить силу тяготения Солнца, Земли и нас с вами – с этим вопросом мы разберемся чуть позже.
Массивное Солнце хоть и имеет большую массу, однако оно очень далеко от нас. тоже далеко от Солнца, однако она притягивается к нему, так как обладает большой массой. Каким образом найти силу притяжения двух тел, а именно как вычислить силу тяготения Солнца, Земли и нас с вами – с этим вопросом мы разберемся чуть позже.
Насколько нам известно, сила тяжести равна:
где m – наша масса, а g – ускорение свободного падения Земли (9,81 м/с 2).
Важно! Не бывает двух, трех, десяти видов сил притяжения. Гравитация – единственная сила, дающая количественную характеристику притяжения. Вес (P = mg) и сила гравитации – одно и то же.
Если m – наша масса, M – масса земного шара, R – его радиус, то гравитационная сила, действующая на нас, равна:
Таким образом, поскольку F = mg:
.
Массы m сокращаются, и остается выражение для ускорения свободного падения:
Как видим, ускорение свободного падения – действительно постоянная величина, поскольку в ее формулу входят величины постоянные — радиус, масса Земли и гравитационная постоянная. Подставив значения этих констант, мы убедимся, что ускорение свободного падения равно 9,81 м/с 2 .
Подставив значения этих констант, мы убедимся, что ускорение свободного падения равно 9,81 м/с 2 .
На разных широтах радиус планеты несколько отличается, поскольку Земля все-таки не идеальный шар. Из-за этого ускорение свободного падения в отдельных точках земного шара разное.
Вернемся к притяжению Земли и Солнца. Постараемся на примере доказать, что земной шар притягивает нас с вами сильнее, чем Солнце.
Примем для удобства массу человека: m = 100 кг. Тогда:
- Расстояние между человеком и земным шаром равно радиусу планеты: R = 6,4∙10 6 м.
- Масса Земли равна: M ≈ 6∙10 24 кг.
- Масса Солнца равна: Mc ≈ 2∙10 30 кг.
- Дистанция между нашей планетой и Солнцем (между Солнцем и человеком): r=15∙10 10 м.
Гравитационное притяжение между человеком и Землей:
Данный результат довольно очевиден из более простого выражения для веса (P = mg).
Сила гравитационного притяжения между человеком и Солнцем:
Как видим, наша планета притягивает нас почти в 2000 раз сильнее.
Как найти силу притяжения между Землей и Солнцем? Следующим образом:
Теперь мы видим, что Солнце притягивает нашу планету более чем в миллиард миллиардов раз сильнее, чем планета притягивает нас с вами.
Первая космическая скорость
После того как Исаак Ньютон открыл закон всемирного тяготения, ему стало интересно, с какой скоростью нужно бросить тело, чтобы оно, преодолев гравитационное поле, навсегда покинуло земной шар.
Правда, он представлял себе это несколько иначе, в его понимании была не вертикально стоящая ракета, устремленная в небо, а тело, которое горизонтально совершает прыжок с вершины горы. Это была логичная иллюстрация, поскольку на вершине горы сила притяжения немного меньше .
Так, на вершине Эвереста ускорение свободного падения будет равно не привычные 9,8 м/с 2 , а почти м/с 2 . Именно по этой причине там настолько разряженный , частицы воздуха уже не так привязаны к гравитации, как те, которые «упали» к поверхности.
Постараемся узнать, что такое космическая скорость.
Первая космическая скорость v1 – это такая скорость, при которой тело покинет поверхность Земли (или другой планеты) и перейдет на круговую орбиту.
Постараемся узнать численной значение этой величины для нашей планеты.
Запишем второй закон Ньютона для тела, которое вращается вокруг планеты по круговой орбите:
,
где h — высота тела над поверхностью, R — радиус Земли.
На орбите на тело действует центробежное ускорение , таким образом:
.
Массы сокращаются, получаем:
,
Данная скорость называется первой космической скоростью:
Как можно заметить, космическая скорость абсолютно не зависит от массы тела. Таким образом, любой предмет, разогнанный до скорости 7,9 км/с, покинет нашу планету и перейдет на ее орбиту.
Первая космическая скорость
Вторая космическая скорость
Однако, даже разогнав тело до первой космической скорости, нам не удастся полностью разорвать его гравитационную связь с Землей. Для этого и нужна вторая космическая скорость. При достижении этой скорости тело покидает гравитационное поле планеты и все возможные замкнутые орбиты.
Для этого и нужна вторая космическая скорость. При достижении этой скорости тело покидает гравитационное поле планеты и все возможные замкнутые орбиты.
Важно! По ошибке часто считается, что для того чтобы попасть на Луну, космонавтам приходилось достигать второй космической скорости, ведь нужно было сперва «разъединиться» с гравитационным полем планеты. Это не так: пара «Земля — Луна» находятся в гравитационном поле Земли. Их общий центр тяжести находится внутри земного шара.
Для того чтобы найти эту скорость, поставим задачу немного иначе. Допустим, тело летит из бесконечности на планету. Вопрос: какая скорость будет достигнута на поверхности при приземлении (без учета атмосферы, разумеется)? Именно такая скорость и потребуется телу, чтобы покинуть планету.
Закон всемирного тяготения. Физика 9 класс
Закон Всемирного тяготения.
Вывод
Мы с вами узнали, что хотя гравитация является основной силой во Вселенной, многие причины этого явления до сих пор остались загадкой. Мы узнали, что такое сила всемирного тяготения Ньютона, научились считать ее для различных тел, а также изучили некоторые полезные следствия, которые вытекают из такого явления, как всемирный закон тяготения.
Мы узнали, что такое сила всемирного тяготения Ньютона, научились считать ее для различных тел, а также изучили некоторые полезные следствия, которые вытекают из такого явления, как всемирный закон тяготения.
Гравитация, она же притяжение или тяготение, – это универсальное свойство материи, которым обладают все предметы и тела во Вселенной. Суть гравитации залучается в том, что все материальные тела притягивают к себе все другие тела, находящиеся вокруг.
Земное притяжение
Если гравитация – это общее понятие и качество, которым обладают все предметы во Вселенной, то земное притяжение – это частный случай этого всеобъемлющего явления. Земля притягивает к себе все материальные объекты, находящиеся на ней. Благодаря этому люди и животные могут спокойно перемещаться по земле, реки, моря и океаны – оставаться в пределах своих берегов, а воздух – не летать по бескрайним просторам Космоса, а образовывать атмосферу нашей планеты.
Возникает справедливый вопрос: если все предметы обладают гравитацией, почему Земля притягивает к себе людей и животных, а не наоборот? Во-первых, мы тоже притягиваем к себе Землю, просто, по сравнению с ее силой притяжения наша гравитация ничтожно мала. Во-вторых, сила гравитации прямо пропорционально зависит от массы тела: чем меньше масса тела, тем ниже его гравитационные силы.
Во-вторых, сила гравитации прямо пропорционально зависит от массы тела: чем меньше масса тела, тем ниже его гравитационные силы.
Второй показатель, от которого зависит сила притяжения – это расстояние между предметами: чем больше расстояние, тем меньше действие гравитации. В том числе благодаря этому, планеты движутся на своих орбитах, а не падают друг на друга.
Примечательно, что своей сферической формой Земля, Луна, Солнце и другие планеты обязаны именно силе тяготения. Она действует в направлении центра, подтягивая к нему вещество, составляющее «тело» планеты.
Гравитационное поле Земли
Гравитационное поле Земли – это силовое энергетическое поле, которое образуется вокруг нашей планеты благодаря действию двух сил:
- гравитации;
- центробежной силе, которая своим появление обязана вращению Земли вокруг своей оси (суточное вращение).
Поскольку и гравитация, и центробежная сила действуют постоянно, то и гравитационное поле является постоянным явлением.
Незначительное воздействие на поле оказывают силы тяготения Солнца, Луны и некоторых других небесных тел, а также атмосферных масс Земли.
Закон всемирного тяготения и сэр Исаак Ньютон
Английский физик, сэр Исаак Ньютон, согласно известной легенде, однажды гуляя по саду днем, увидел на небе Луну. В это же время с ветки упало яблоко. Ньютон тогда занимался изучением закона движения и знал, что яблоко падает под воздействием гравитационного поля, а Луна вращается по орбите вокруг Земли.
И тут в голову гениальному ученому, озаренную инсайтом, пришла мысль, что, возможно, яблоко падает на землю, подчиняясь той же силе, благодаря которой Луна находится на своей орбите, а не носится беспорядочно по всей галактике. Так был открыт закон всемирного тяготения, он же Третий закон Ньютона.
На языке математических формул этот закон выглядит так:
F = GMm/D 2 ,
где F – сила взаимного тяготения между двумя телами;
M – масса первого тела;
m – масса второго тела;
D 2 – расстояние между двумя телами;
G – гравитационная постоянная, равная 6,67х10 -11 .
Высоты, на которых движутся искусственные спутники, уже сравнимы с радиусом Земли, так что для расчета их траектории учет изменения силы земного притяжения с увеличением расстояния совершенно необходим.
Итак, Галилей утверждал, что все тела, отпущенные с некоторой высоты вблизи поверхности Земли будут падать с одинаковым ускорением g (если пренебречь сопротивлением воздуха). Сила, вызывающая это ускорение называется силой тяжести. Применим к силе тяжести второй закон Ньютона, рассматривая в качестве ускорения a ускорение свободного падения g . Таким образом, действующую на тело силу тяжести можно записать как:
F g =mg
Эта сила направлена вниз, к центру Земли.
Т.к. в системе СИ g = 9,8 , то сила тяжести, действующая на тело массой 1кг, составляет.
Применим
формулу закона всемирного тяготения
для описания силы тяжести – силы тяготения
между землей и телом, находящимся на ее
поверхности. Тогда m 1
заменится
на массу Земли
m 3
, а
r –
на расстояние до центра Земли, т.е. на
радиус Земли r 3 .
Таким образом получим:
Тогда m 1
заменится
на массу Земли
m 3
, а
r –
на расстояние до центра Земли, т.е. на
радиус Земли r 3 .
Таким образом получим:
Где m – масса тела, находящегося на поверхности Земли. Из этого равенства следует, что:
Иными словами ускорение свободного падения на поверхности земли g определяется величинами m 3 и r 3 .
На Луне, на других планетах, или в космическом пространстве сила тяжести, действующая на тело одинаковой массы, будет различна. Например, на Луне величина g представляет всего лишь одну шестую g на Земле, и на тело массой 1 кг действует сила тяжести, равная всего лишь 1,7 Н.
До тех пор, пока не была измерена гравитационная постоянная G, масса Земли оставалась неизвестной. И только после того, как G была измерена, с помощью соотношения удалось вычислить массу земли. Это впервые проделал сам Генри Кавендиш. Подставляя в формулу ускорение свободного падения значение g=9,8м/с и радиуса земли r з =6,3810 6 получаем следующее значение массы Земли:
Для
силы тяготения, действующей на тела,
находящиеся вблизи поверхности Земли,
можно просто пользоваться выражением
mg. Если
же необходимо рассчитать силу притяжения,
действующую на тело, расположенное на
некотором отдалении от Земли, или силу,
вызываемую другим небесным телом(например
Луной или другой планетой), то следует
использовать значение величины g,
вычисленное с помощью известной формулы,
в которой r 3
и
m 3 должны
быть заменены на соответствующее
расстояние и массу, можно также
непосредственно воспользоваться
формулой закона всемирного тяготения.
Существует несколько методов очень
точного определения ускорения силы
тяжести. Можно найти g
просто
взвешиванием стандартного груза на
пружинных весах. Геологические весы
должны быть удивительны – их пружина
изменяет растяжение при добавлении
нагрузки меньше чем в миллионную долю
грамма. Превосходные результаты дают
крутильные кварцевые весы. Устройство
их в принципе несложно. К горизонтально
натянутой кварцевой нити приварен
рычаг, весом которого нить слегка
закручивается:
Если
же необходимо рассчитать силу притяжения,
действующую на тело, расположенное на
некотором отдалении от Земли, или силу,
вызываемую другим небесным телом(например
Луной или другой планетой), то следует
использовать значение величины g,
вычисленное с помощью известной формулы,
в которой r 3
и
m 3 должны
быть заменены на соответствующее
расстояние и массу, можно также
непосредственно воспользоваться
формулой закона всемирного тяготения.
Существует несколько методов очень
точного определения ускорения силы
тяжести. Можно найти g
просто
взвешиванием стандартного груза на
пружинных весах. Геологические весы
должны быть удивительны – их пружина
изменяет растяжение при добавлении
нагрузки меньше чем в миллионную долю
грамма. Превосходные результаты дают
крутильные кварцевые весы. Устройство
их в принципе несложно. К горизонтально
натянутой кварцевой нити приварен
рычаг, весом которого нить слегка
закручивается:
Для
тех же целей применяется и маятник. Еще
недавно маятниковые способы
измерения
g
были единственными, и лишь в 60-е – 70-е гг. Их стали вытеснять более удобные и
точные весовые методы. Во всяком случае,
измеряя период колебания математического
маятника, по формуле
можно
найти значение g
достаточно точно. Измеряя на одном
приборе значение g
в разных местах, можно судить об
относительных изменениях силы тяжести
с точностью до миллионных долей.
Их стали вытеснять более удобные и
точные весовые методы. Во всяком случае,
измеряя период колебания математического
маятника, по формуле
можно
найти значение g
достаточно точно. Измеряя на одном
приборе значение g
в разных местах, можно судить об
относительных изменениях силы тяжести
с точностью до миллионных долей.
Значения
ускорения свободного падения g
в
разных точках Земли несколько различаются.
Из формулы g
= Gm 3
можно
увидеть, что величина g
должна
быть меньше, например, на вершинах гор,
чем на уровне моря, поскольку расстояние
от центра Земли до вершины горы несколько
больше. Действительно, этот факт
установили экспериментально. Однако
формула g=Gm 3 /r 3 2 не
дает точного значения g
во
всех точках, так как поверхность земли
не является в точности сферической: на
ее поверхности не только существуют
горы и моря, но также имеет место изменение
радиуса Земли на экваторе;
кроме
того, масса земли распределена неоднородно;
вращение
Земли также влияет на изменение g.
Однако свойства ускорения свободного падения оказались сложнее, чем предполагал Галилей. Выяснить, что величина ускорения зависит от широты, на которой его измеряют:
Величина ускорения свободного падения меняется также с высотой над поверхностью Земли:
Вектор ускорения свободного падения всегда направлен по вертикали вниз, а вдоль отвесной линии в данном месте Земли.
Таким образом, на одной и той же широте и на одной и той же высоте над уровнем моря ускорение силы тяжести должно быть одинаковым. Точные измерения показывают, что весьма часто встречаются отклонения от этой нормы – аномалии тяготения. Причина аномалий состоит в неоднородном распределении массы вблизи места измерения.
Как
уже было сказано, сила тяготения со
стороны большого тела может быть,
представлена как сумма сил, действующих
со стороны отдельных частиц большого
тела. Притяжение маятника Землей есть
результат действия на него всех частиц
Земли. Но ясно, что близкие частицы
вносят наибольший вклад в суммарную
силу – ведь притяжение обратно
пропорционально квадрату расстояния.
Если вблизи места измерения сосредоточены тяжелые массы, g будет больше нормы, в обратном случае g меньше нормы.
Если, например, измерить g на горе или на самолете, летящем над морем на высоте горы, то в первом случае получится большая цифра. Также выше нормы величина g на уединенных океанских островах. Ясно, что в обоих случаях возрастание g объясняется сосредоточением дополнительных масс в месте измерения.
Не только величина g, но и направление силы тяжести может отклоняться от нормы. Если подвесить груз на нитке, то вытянутая нить покажет вертикаль для этого места. Эта вертикаль может отклониться от нормы. “Нормальное” направление вертикали известно геологам из специальных карт, на которых по данным о значениях g построена “идеальная” фигура Земли.
Произведем
опыт с отвесом у подножия большой горы.
Грузик отвеса притягивается Землей к
ее центру и горой – в сторону. Отвес
должен отклониться при таких условиях
от направления нормальной вертикали.
Так как масса Земли много больше массы
горы, то такие отклонения не превышают
нескольких угловых секунд.
“Нормальная” вертикаль определяется по звездам, так как для любой географической точки вычислено, в какое место неба в данный момент суток и года “упирается” вертикаль “идеальной” фигуры Земли.
Отклонения отвеса приводят иногда к странным результатам. Например, во Флоренции влияние Апеннин приводит не к притяжению, а к отталкиванию отвеса. Объяснение может быть одно: в горах есть огромные пустоты.
Замечательный результат дают измерения ускорения силы тяжести в масштабе материков и океанов. Материки значительно тяжелее океанов, поэтому, казалось бы, значения g над материками должны быть больше. Чем над океанами. В действительности же значения g, вдоль одной широты над океанами и материками, в среднем одинаковы.
Объяснение
опять -таки лишь одно: материки покоятся
на более легких породах, а океаны – на
более тяжелых. И действительно, там, где
возможны непосредственные изыскания,
геологи устанавливают, что океаны
покоятся на тяжелых базальтовых породах,
а материки- на легких гранитах.
Но сразу же возникает следующий вопрос: почему тяжелые и легкие породы точно компенсируют различие весов материков и океанов? Такая компенсация не может быть делом случая, причины ее должны коренится в устройстве оболочки Земли.
Геологи полагают, что верхние части земной коры как бы плавают на подстилающей пластичной, то есть легко деформируемой массе. Давление на глубинах около 100 км должно быть всюду одинаковым, так же как одинаково давление на дне сосуда с водой, в котором плавают куски дерева разного веса. Поэтому столб вещества площадью 1 м 2 от поверхности до глубины 100 км должен иметь и под океаном и под материками одинаковый вес.
Это
выравнивание давлений (его называют
изостазией) и приводит к тому, что над
океанами и материками вдоль одной
широтной линии значение ускорения силы
тяжести g
не
отличается существенно. Местные аномалии
силы тяжести служат геологической
разведке, цель которой- найти залежи
полезных ископаемых под землей, не роя
ям, не копая шахт.
Тяжелую руду нужно искать в тех местах, где g наибольшее. Напротив, залежи легкой соли обнаруживают по местным заниженным значениям величины g. Измерить g можно с точностью до миллионных долей от 1 м/сек 2 .
Методы разведки при помощи маятников и сверхточных весов называют гравитационными. Они имеют большое практическое значение, в частности для поисков нефти. Дело в том, что при гравитационных методах разведки легко обнаружить подземные соляные купола, а очень часто оказывается, что где есть соль, там и нефть. Причем нефть лежит в глубине, а соль ближе к земной поверхности. Методом гравитационной разведки была открыта нефть в Казахстане и в других местах.
Вместо
того, чтобы тянуть тележку с помощью
пружины, ей можно придать ускорение,
прикрепив перекинутый через блок шнур,
к противоположному концу которого
подвешивается груз. Тогда сила, сообщающая
ускорение, будет обусловлена весом этого
груза. Ускорение свободного падения
опять таки сообщается телу его весом.
В физике вес – это официальное наименование силы, которая обусловлена притяжением предметов к земной поверхности – “притяжением силы тяжести”. То обстоятельство, что тела притягиваются по направлению к центру Земли, делает такое объяснение разумным.
Как бы его не определили, вес – это сила. Он ничем не отличается от любой другой силы, если не считать двух особенностей: вес направлен вертикально и действует постоянно, его невозможно устранить.
Чтобы непосредственно измерить вес тела, мы должны воспользоваться пружинными весами, проградуированными в единицах силы. Поскольку это зачастую сделать неудобно, мы сравниваем один вес с другим при помощи рычажных весов, т.е. находим отношение:
ЗЕМНОЕ ПРИТЯЖЕНИЕ, ДЕЙСТВУЮЩЕЕ НА ТЕЛО Х ЗЕМНОЕ ПРИТЯЖ-Е, ДЕЙСТВУЮЩЕЕ НА ЭТАЛОН МАССЫ
Предположим,
что тело Х притягивается в 3 раза сильнее,
чем эталон массы. В этом случае мы
говорим, что земное притяжение, действующее
на тело Х равно 30 ньютонам силы, что
означает, что оно в 3 раза больше земного
притяжения, которое действует на
килограмм массы. Нередко путают понятие
массы и веса, между которыми имеется
существенное различие. Масса – это
свойство самого тела (она является мерой
инертности или его “количества
вещества”). Вес же – это сила, с которой
тело действует на опору или растягивает
подвес (вес численно равен силе тяжести,
если опора или подвес не имеют ускорения).
Нередко путают понятие
массы и веса, между которыми имеется
существенное различие. Масса – это
свойство самого тела (она является мерой
инертности или его “количества
вещества”). Вес же – это сила, с которой
тело действует на опору или растягивает
подвес (вес численно равен силе тяжести,
если опора или подвес не имеют ускорения).
Если мы при помощи пружинных весов измерим вес какого-нибудь предмета с очень большой точностью, а потом перенесем весы в другое место, то обнаружим, что вес предмета на поверхности Земли несколько меняется от места к месту. Мы знаем, что вдали от поверхности Земли, или в глубине земного шара, вес должен быть значительно меньше.
Меняется ли масса? Ученые, размышляя над этим вопросом, давно пришли к выводу, что масса должна оставаться неизменной. Даже в центре Земли, где тяготение, действуя во всех направлениях, должно давать нулевую результирующую силу, тело по-прежнему имело бы ту же самую массу.
Таким
образом, масса, оцениваемая по трудности,
которую мы встречаем при попытке ускорить
движение маленькой тележки, одна и та
же всюду: на поверхности Земли, в центре
Земли, на Луне. Вес, оцениваемый по
удлинению пружинных весов(и ощущению
Вес, оцениваемый по
удлинению пружинных весов(и ощущению
в мускулах руки человека, держащего весы), будет значительно меньше на Луне и практически равен нулю в центре Земли. (рис.7)
Как велико земное притяжение, действующее на разные массы? Как сравнить веса двух предметов? Возьмем два одинаковых куска свинца, скажем, по 1 кг каждый. Земля притягивает каждый из них с одинаковой силой, равной весу 10 Н. Если соединить оба куска в 2 кг, то вертикальные силы просто складываются: Земля притягивает 2 кг вдвое сильнее, чем 1 кг. Мы получим точно такое же удвоенное притяжение, если сплавим оба куска в один или поместим их один на другой. Гравитационные притяжения любого однородного материала просто складываются, и нет ни поглощения, ни экранирования одного куска вещества другим.
Для
любого однородного материала вес
пропорционален массе. Поэтому мы считаем,
что Земля является источником “поля
силы тяжести”, исходящего из ее центра
по вертикали и способного притягивать
любой кусок вещества. Поле силы тяжести
воздействует одинаково, скажем, на
каждый килограмм свинца. А как обстоит
дело с силами притяжения, действующими
на одинаковые массы разных материалов,
например 1 кг свинца и 1 кг алюминия?
Смысл этого вопроса зависит от того,
что нужно понимать под одинаковыми
массами. Наиболее простой способ
сравнения масс, которым пользуются в
научных исследованиях и в торговой
практике – это применение рычажных
весов. В них сравниваются силы, которые
тянут оба груза. Но получив таким путем
одинаковые массы, скажем свинца и
алюминия, можно предположить, что равные
веса имеют равные массы. Но фактически
здесь разговор идет о двух совершенно
разных видах массы – об инертной и о
гравитационной массе.
Поле силы тяжести
воздействует одинаково, скажем, на
каждый килограмм свинца. А как обстоит
дело с силами притяжения, действующими
на одинаковые массы разных материалов,
например 1 кг свинца и 1 кг алюминия?
Смысл этого вопроса зависит от того,
что нужно понимать под одинаковыми
массами. Наиболее простой способ
сравнения масс, которым пользуются в
научных исследованиях и в торговой
практике – это применение рычажных
весов. В них сравниваются силы, которые
тянут оба груза. Но получив таким путем
одинаковые массы, скажем свинца и
алюминия, можно предположить, что равные
веса имеют равные массы. Но фактически
здесь разговор идет о двух совершенно
разных видах массы – об инертной и о
гравитационной массе.
Величина
в формуле Представляет
собой инертную массу. В опытах с
тележками, которым придают ускорение
пружины, величина выступает как
характеристика “тяжеловесности
вещества” показывающая, насколько
трудно сообщить ускорение рассматриваемому
телу. Количественной характеристикой
служит отношение. Эта масса
представляет собой меру инертности,
тенденции механических систем
сопротивляться изменению состояния.
Масса – это свойство, которое должно
быть одним и тем же и вблизи поверхности
Земли, и на Луне, и в далеком космосе, и
в центре Земли. Какова ее связь с
тяготением и что на самом деле происходит
при взвешивании?
Эта масса
представляет собой меру инертности,
тенденции механических систем
сопротивляться изменению состояния.
Масса – это свойство, которое должно
быть одним и тем же и вблизи поверхности
Земли, и на Луне, и в далеком космосе, и
в центре Земли. Какова ее связь с
тяготением и что на самом деле происходит
при взвешивании?
Совершенно независимо от инертной массы можно ввести понятие гравитационной массы как количества вещества, притягиваемого Землей.
Мы считаем, что поле тяготения Земли одинаково для всех находящихся в нем предметов, но приписываем различным пред
метам
разные массы, которые пропорциональны
притяжению этих предметов полем. Это
гравитационная масса. Мы говорим, что
разные предметы имеют разный вес,
поскольку они обладают различными
гравитационными массами, которые
притягиваются полем тяготения. Таким
образом, гравитационные массы по
определению пропорциональны весам, а
также силе тяжести. Гравитационная
масса определяет, с какой силой тело
притягивается Землей. При этом тяготение
взаимно: если Земля притягивает камень,
то камень точно также притягивает Землю.
Значит, гравитационная масса тела
определяет
также, насколько сильно оно притягивает
другое тело, Землю. Таким образом,
гравитационная масса измеряет количество
вещества, на которое действует земное
притяжение, или количество вещества,
обуславливающее гравитационные
притяжения между телами.
При этом тяготение
взаимно: если Земля притягивает камень,
то камень точно также притягивает Землю.
Значит, гравитационная масса тела
определяет
также, насколько сильно оно притягивает
другое тело, Землю. Таким образом,
гравитационная масса измеряет количество
вещества, на которое действует земное
притяжение, или количество вещества,
обуславливающее гравитационные
притяжения между телами.
Гравитационное
притяжение действует на два одинаковых
куска свинца вдвое сильнее, чем на один.
Гравитационные массы кусков свинца
должны быть пропорциональны инертным
массам, поскольку массы того и другого
вида, очевидно, пропорциональны числу
атомов свинца. То же самое относится к
кускам любого другого материала, скажем,
воска, но как сравнить кусок свинца с
куском воска? Ответ на этот вопрос дает
символический эксперимент по изучению
падения тел всевозможных размеров с
вершины наклонной Пизанской башни, тот,
который по легенде производил Галилей.
Сбросим два куска любого материала
любых размеров. Они падают с одинаковым
ускорением g. Сила, действующая на тело
и сообщающая ему ускорение6 – это
притяжение Земли, приложенное к этому
телу. Сила притяжения тел Землей
пропорциональна гравитационной массе.
Но силы тяжести сообщают всем телам
одинаковое ускорение g. Поэтому сила
тяжести, как и вес, должна быть
пропорциональна инертной массе.
Следовательно, тела любой формы содержат
одинаковые пропорции обеих масс.
Они падают с одинаковым
ускорением g. Сила, действующая на тело
и сообщающая ему ускорение6 – это
притяжение Земли, приложенное к этому
телу. Сила притяжения тел Землей
пропорциональна гравитационной массе.
Но силы тяжести сообщают всем телам
одинаковое ускорение g. Поэтому сила
тяжести, как и вес, должна быть
пропорциональна инертной массе.
Следовательно, тела любой формы содержат
одинаковые пропорции обеих масс.
Если принять 1 кг в качестве единицы обеих масс, то гравитационная и инертная массы будут одинаковы у всех тел любых размеров из любого материала и в любом месте.
Вот
как это доказывается. Сравним эталон
килограмма, сделанный из платины6 с
камнем неизвестной массы. Сравним их
инертные массы, перемещая поочередно
каждое из тел в горизонтальном направлении
под действием некоторой силы и измеряя
ускорение. Предположим, что масса камня
равна 5,31 кг. Земное тяготение в этом
сравнении не участвует. Затем сравним
гравитационные массы обоих тел, измерив
гравитационное притяжение между каждым
из них и каким-нибудь третьим телом,
проще всего Землей. Это можно проделать
путем взвешивания обоих тел. Мы увидим,
что гравитационная
масса камня тоже равна 5,31 кг .
Это можно проделать
путем взвешивания обоих тел. Мы увидим,
что гравитационная
масса камня тоже равна 5,31 кг .
Более чем за полстолетия до того как Ньютон предложил свой закон всемирного тяготения, Иоганн Кеплер (1571-1630) обнаружил, что “запутанное движение планет Солнечной системы можно было бы описать с помощью трех простых законов. Законы Кеплера укрепили веру в гипотезу Коперника о том, что планеты вращаются вокруг Солнца, а.
Утверждать в начале XVII века, что планеты вокруг Солнца, а не вокруг Земли, было величайшей ересью. Джордано Бруно открыто защищавший систему Коперника, как еретик был осужден святой инквизицией и сожжен на костре. Даже великий Галлилей, несмотря на тесную дружбу с папой римским, был заточен в тюрьму, осужден инквизицией и вынужден был публично отречься от своих взглядов.
В
те времена священными и неприкосновенными
считались учения Аристотеля и Птолемея,
гласившие, что орбиты планет возникают
в результате сложных движений по системе
окружностей. Так для описания орбиты
Марса требовалась дюжина, или около
того, окружностей различного диаметра.
Иоганн Кеплер поставил задачу “доказать”,
что Марс и Земля должны обращаться
вокруг Солнца. Он пытался найти орбиту
простейшей геометрической формы, которая
точно бы соответствовала многочисленным
измерениям положения планеты. Прошли
годы утомительных вычислений, прежде
чем Кеплер смог сформулировать три
простых закона, очень точно описывающих
движение всех планет:
Так для описания орбиты
Марса требовалась дюжина, или около
того, окружностей различного диаметра.
Иоганн Кеплер поставил задачу “доказать”,
что Марс и Земля должны обращаться
вокруг Солнца. Он пытался найти орбиту
простейшей геометрической формы, которая
точно бы соответствовала многочисленным
измерениям положения планеты. Прошли
годы утомительных вычислений, прежде
чем Кеплер смог сформулировать три
простых закона, очень точно описывающих
движение всех планет:
Первый закон: Каждая планета движется по эллипсу, в
одном из фокусов которого находится
Второй закон: Радиус-вектор (линия, соединяющая Солнце
и планету) описывает за равные промежутки
времени равные площади
Третий закон: Квадраты периодов обращения планет
пропорциональны кубам их средних
расстояний от Солнца:
R 1 3 /T 1 2 = R 2 3 /T 2 2
Значение
трудов Кеплера огромно. Он открыл законы,
которые затем Ньютон связал с законом
всемирного тяготения Конечно, сам Кеплер
не отдавал себе отчета в том, к чему
приведут его открытия. “Он занимался
утомительными намеками эмпирических
правил, которые в будущем должен был
привести к рациональному виду Ньютон”.
Кеплер не мог объяснить, чем обусловлено
существование эллиптических орбит, но
восхищался тем, что они существуют.
“Он занимался
утомительными намеками эмпирических
правил, которые в будущем должен был
привести к рациональному виду Ньютон”.
Кеплер не мог объяснить, чем обусловлено
существование эллиптических орбит, но
восхищался тем, что они существуют.
На
основе третьего закона Кеплера Ньютон
сделал вывод, что силы притяжения должны
убывать с увеличением расстояния и что
притяжение должно изменяться как
(расстояние) -2 .
Открыв закон всемирного тяготения,
Ньютон перенес простое представление
о движении Луны на всю планетную систему.
Он показал, что притяжение по выведенным
им законам обусловливает движение
планет по эллиптическим орбитам, причем
в одном из фокусов эллипса должно
находится Солнце. Ему удалось легко
вывести два других закона Кеплера,
которые также вытекают из его гипотезы
всемирного тяготения. Эти законы
справедливы, если учитывается только
притяжение Солнцем. Но нужно учитывать
и действие на движущуюся планету других
планет, хотя в Солнечной системе эти
притяжения малы по сравнению с притяжением
Солнца.
Второй закон Кеплера следует из произвольной зависимости силы притяжения от расстояния, если эта сила действует по прямой, соединяющей центры планеты и Солнца. Но первому и третьему законам Кеплера удовлетворяет только закон обратной пропорциональности сил притяжения квадрату расстояния.
Чтобы получить третий закон Кеплера, Ньютон просто объединил законы движения с законом всемирного тяготения. Для случая круговых орбит можно рассуждать следующим образом: пусть планета, масса которой равна m, движется со скоростью v по окружности радиуса R вокруг Солнца, масса которого равна М. Это движение может осуществляться только в том случае, если на планету действует внешняя сила F = mv 2 /R, создающая центростремительное ускорение v 2 /R. Предположим, что притяжение между Солнцем и планетой как раз и создает необходимую силу. Тогда:
GMm/r 2 = mv 2 /R
и расстояние r между m и M равно радиусу орбиты R. Но скорость
где
Т – время, за которое планета совершает
один оборот. Тогда
Тогда
Чтобы получить третий закон Кеплера, нужно перенести все R и Т в одну сторону уравнения, а все остальные величины – в другую:
R 3 /T 2 = GM/4 2
Если перейти теперь к другой планете с другим радиусом орбиты и периодом обращения, то новое отношение опять будет равно GM/4 2 ; эта величина будет одинаковой для всех планет, так как G -универсальная постоянная, а масса М – одна и та же для всех планет, вращающихся вокруг Солнца. Таким образом, величина R 3 /T 2 будет одной и той же для всех планет в согласии с третьим законом Кеплера. Такое вычисление позволяет получить третий закон и для эллиптических орбит, но в этом случае R – средняя величина между наибольшим и наименьшим расстоянием планеты от Солнца.
Вооруженный
мощными математическими методами и
руководимый великолепной интуицией,
Ньютон применил свою теорию к большому
числу задач, вошедших в его ПРИНЦИПЫ, касающиеся
особенностей Луны, Земли других планет
и их движения, а также других небесных
тел: спутников, комет.
Луна
испытывает многочисленные возмущения,
отклоняющие ее от равномерного кругового
движения. Прежде всего, она движется по
кеплеровскому эллипсу, в одном из фокусов
которого находится Земля, как и любой
спутник. Но эта орбита испытывает
небольшие вариации за счет притяжения
Солнцем. При новолунии Луна находится
ближе к Солнцу, чем полная Луна,
появляющаяся на две недели позднее; эта
причина изменяет притяжение, что ведет
к замедлению и ускорению движения Луны
в течение месяца. Этот эффект увеличивается,
когда зимой Солнце ближе, так, что
наблюдаются и годовые вариации скорости
движения Луны. Кроме того, изменения
солнечного притяжения меняют эллиптичность
лунной орбиты; лунная орбита отклоняется
вверх и вниз, плоскость орбиты медленно
вращается. Таким образом, Ньютон показал,
что отмеченные нерегулярности в движении
Луны вызваны всемирным тяготением. Он
не разработал во всех деталях вопрос о
солнечном притяжении, движение Луны
осталось сложной проблемой, которая
разрабатывается со все возрастающими
подробностями и до наших дней.
Океанские
приливы и отливы долгое время оставались
загадкой, объяснить которую казалось
можно было бы, установив их связь с
движением Луны. Однако люди считали,
что такая связь реально существовать
не может, и даже Галилей осмеял эту идею.
Ньютон показал, что приливы и отливы
обусловлены неравномерным притяжением
воды в океане со стороны Луны. Центр
лунной орбиты не совпадает с центром
Земли. Луна и Земля вместе вращаются
вокруг их общего центра масс. Этот центр
масс находится на расстоянии примерно
4800 км от центра Земли, всего лишь в 1600
км от поверхности Земли. Когда Земля
притягивает Луну, луна притягивает
Землю с равной и противоположно
направленной силой, благодаря чему
возникает сила Mv 2 /r,
вызывающая движение Земли вокруг общего
центра масс с периодом, равным одному
месяцу. Ближайшая к Луне часть океана
притягивается сильнее (она ближе), вода
поднимается – и возникает прилив.
Находящаяся на большем от Луны расстоянии
часть океана притягивается слабее, чем
суша, и в этой части океана также
поднимается водяной горб. Поэтому, за
24 часа наблюдается два прилива. Солнце
тоже вызывает приливы, хотя и не столь
сильные, ибо большое расстояние от
Солнца сглаживает неодинаковость
притяжения.
Поэтому, за
24 часа наблюдается два прилива. Солнце
тоже вызывает приливы, хотя и не столь
сильные, ибо большое расстояние от
Солнца сглаживает неодинаковость
притяжения.
Ньютон раскрыл природу комет – этих гостей солнечной системы, которые всегда вызывали интерес и даже священный ужас. Ньютон показал, что кометы движутся по очень вытянутым эллиптическим орбитам, водном из фокусов которого находится Солнце. Их движение определяется, как и движение планет, гравитацией. Но они имеют очень малую величину, так что их можно увидеть только тогда, когда и они проходят вблизи Солнца. Эллиптическая орбита кометы может быть измерена, и время ее возвращения в нашу область точно предсказано. Их регулярное возвращение в предсказанные сроки позволяет проверить наши наблюдения и дает еще одно подтверждение закона всемирного тяготения.
В
некоторых случаях комета испытывает
сильное гравитационное возмущение,
проходя вблизи больших планет, и переходит
на новую орбиту с другим периодом. Вот
почему мы знаем, что у комет масса
невелика: планеты оказывают воздействие
на их движение, а кометы не влияют на
движение планет, хотя и действуют на
них с такой же силой.
Кометы движутся так быстро и приходят так редко, что еще до сих пор ученые ждут момента, когда можно применить современные средства к исследованию большой кометы.
Если вдуматься, какую роль играют силы тяготения в жизни нашей планеты, то открываются целые океаны явлений, и даже океаны в буквальном смысле этого слова: океаны воды, воздушный океан. Без тяготения они бы не существовали.
В природе существуют различные силы, которые характеризуют взаимодействие тел. Рассмотрим те силы, которые встречаются в механике.
Гравитационные силы. Вероятно, самой первой силой, существование которой осознал человек, являлась сила притяжения, действующая на тела со стороны Земли.
И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. Первым этот факт понял английский физик Ньютон. Анализируя законы, которым подчиняется движение планет (законы Кеплера), он пришёл к выводу, что наблюдаемые законы движения планет могут выполняться только в том случае, если между ними действует сила притяжения, прямо пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними.
Ньютон сформулировал закон всемирного тяготения . Любые два тела притягиваются друг к другу. Сила притяжения между точечными телами направлена по прямой, их соединяющей, прямо пропорциональна массам обоих и обратно пропорциональна квадрату расстояния между ними:
Под точечными телами в данном случае понимают тела, размеры которых во много раз меньше расстояния между ними.
Силы всемирного тяготения называют гравитационными силами. Коэффициент пропорциональности G называют гравитационной постоянной. Его значение было определено экспериментально: G = 6,7 10¯¹¹ Н м² / кг².
Сила тяготения действующая вблизи поверхности Земли, направлена к её центру и вычисляется по формуле:
где g – ускорение свободного падения (g = 9,8 м/с²).
Роль силы тяготения в живой природе очень значительна, так как от её величины во многом зависят размеры, формы и пропорции живых существ.
Вес тела. Рассмотрим, что происходит, когда некоторый груз кладут на горизонтальную плоскость (опору). В первый момент после того, как груз опустили, он начинает двигаться вниз под действием силы тяжести (рис. 8).
В первый момент после того, как груз опустили, он начинает двигаться вниз под действием силы тяжести (рис. 8).
Плоскость прогибается и возникает сила упругости (реакция опоры), направленная вверх. После того как сила упругости (Fу) уравновесит силу тяжести, опускание тела и прогиб опоры прекратятся.
Прогиб опоры возник под действием тела, следовательно, со стороны тела на опору действует некоторая сила (Р), которую называют весом тела (рис. 8, б). По третьему закону Ньютона вес тела равен по величине силе реакции опоры и направлен в противоположную сторону.
Р = – Fу = Fтяж.
Весом тела называют силу Р, с которой тело действует на неподвижную относительно него горизонтальную опору .
Поскольку сила тяжести (вес) приложены к опоре, она деформируется и за счёт упругости оказывает противодействие силе тяжести. Силы, развиваемые при этом со стороны опоры называются силами реакции опоры, а само явление развития противодействия – реакцией опоры. По третьему закону Ньютона сила реакции опоры равна по величине силе тяжести тела и противоположна ему по направлению.
По третьему закону Ньютона сила реакции опоры равна по величине силе тяжести тела и противоположна ему по направлению.
Если человек на опоре движется с ускорением звеньев его тела, направленных от опоры, то сила реакции опоры возрастает на величину ma, где m – масса человека, а – ускорения с которыми движутся звенья его тела. Эти динамические воздействия можно фиксировать с помощью тензометрических устройств (динамограммы).
Вес не следует путать с массой тела. Масса тела характеризует его инертные свойства и не зависит ни от силы тяготения, ни от ускорения, с которым оно движется.
Вес тела характеризует силу, с которой оно действует на опору и зависит как от силы тяготения, так и от ускорения движения.
Например, на Луне вес тела примерно в 6 раз меньше, чем вес тела на Земле, Масса же в обоих случаях одинакова и определяется количеством вещества в теле.
В быту, технике, спорте вес часто указывают не в ньютонах (Н), а в килограммах силы (кгс). Переход от одной единицы к другой осуществляется по формуле: 1 кгс = 9,8 Н.
Когда опора и тело неподвижны, то масса тела равна силе тяжести этого тела. Когда же опора и тело движутся с некоторым ускорением, то в зависимости от его направления тело может испытывать или невесомость или перегрузку. Когда ускорение совпадает по направлению и равно ускорению свободного падения, вес тела будет равен нулю, поэтому возникает состояние невесомости (МКС, скоростной лифт при опускании вниз). Когда же ускорение движения опоры противоположно ускорению свободного падения, человек испытывает перегрузку (старт с поверхности Земли пилотируемого космического корабля, Скоростной лифт, поднимающийся вверх).
Что такое гравитация и как она работает, простыми словами
Люди с древности задумывались о том, какая сила притягивает предметы к Земле. Явление гравитации пытались объяснить такие великие умы, как Ньютон и Эйнштейн, но до сих пор оно остается не до конца изученным
Гравитация (от лат. gravis, «тяжелый») — это сила, которая притягивает два тела друг к другу.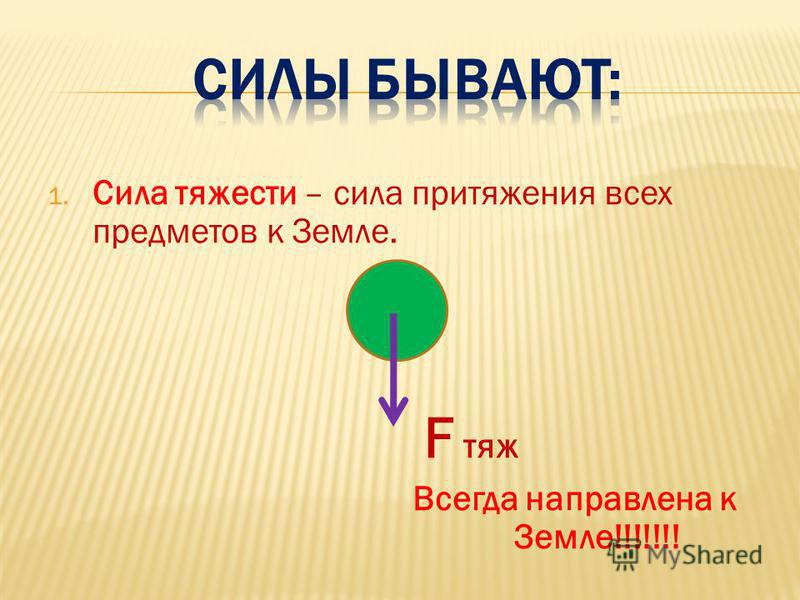 Все, что имеет материю, то есть все, к чему можно прикоснуться, имеет также гравитационное притяжение. Гравитация является одной из четырех фундаментальных сил во Вселенной наряду с электромагнетизмом, а также сильными и слабыми ядерными взаимодействиями. Хотя это самая слабая сила, она наиболее видима. Из-за работы гравитационной силы люди могут ходить по Земле, а планеты — вращаться по орбите вокруг Солнца.
Все, что имеет материю, то есть все, к чему можно прикоснуться, имеет также гравитационное притяжение. Гравитация является одной из четырех фундаментальных сил во Вселенной наряду с электромагнетизмом, а также сильными и слабыми ядерными взаимодействиями. Хотя это самая слабая сила, она наиболее видима. Из-за работы гравитационной силы люди могут ходить по Земле, а планеты — вращаться по орбите вокруг Солнца.
Степень гравитации любого объекта пропорциональна его массе. Таким образом, объекты с большей массой имеют большую гравитацию. Поскольку Земля является самым крупным и ближайшим объектом вокруг, то все предметы и объекты притягивается к ней. Например, яблоки падают на землю, а не притягиваются, к примеру, к голове человека.
Луна притягивается к Земле как к объекту с большей массой (Фото: Shutterstock)
Расстояние также влияет на гравитацию. Чем дальше объект, тем гравитационное притяжение слабее.
Древние ученые, пытавшиеся описать мир, придумали собственные объяснения того, почему предметы падают на землю. Древнегреческий философ Аристотель утверждал, что объекты имеют естественную тенденцию двигаться к центру Вселенной, который, по его мнению, находился в середине Земли.
Однако поляк Николай Коперник в XVI веке понял, что траектории планет на небе определяются положением Солнца, которое и является центром Солнечной системы. Век спустя британский математик и физик Исаак Ньютон расширил идеи Коперника и пришел к выводу, что, поскольку Солнце притягивает планеты, все объекты притягиваются друг к другу.
В наши дни действующей теорией, описывающей гравитацию, является общая теория относительности Эйнштейна.
Классическая теория тяготения Ньютона
Английский физик Исаак Ньютон рассказывал, что идея о всемирном тяготении пришла ему в голову на прогулке. Он шел по яблоневому саду в поместье своих родителей и вдруг увидел Луну в дневном небе, а затем — как с ветки оторвалось и упало на землю яблоко. Ньютон к тому моменту уже работал над законами движения и понимал, что яблоко упало под воздействием гравитационного поля Земли. Он также знал, что Луна не занимает статичную позицию в небе, а вращается по орбите вокруг Земли, то есть, на нее воздействует какая-то сила, которая не дает спутнику улететь в космос. Физик понял, что, возможно, на яблоко и Луну действует одна и та же сила.
Ньютон к тому моменту уже работал над законами движения и понимал, что яблоко упало под воздействием гравитационного поля Земли. Он также знал, что Луна не занимает статичную позицию в небе, а вращается по орбите вокруг Земли, то есть, на нее воздействует какая-то сила, которая не дает спутнику улететь в космос. Физик понял, что, возможно, на яблоко и Луну действует одна и та же сила.
Предшественники Ньютона рассуждали иначе. Итальянский физик Галилео Галилей считал, что на Земле действует природное притяжение. Немецкий астроном Иоганн Кеплер полагал, что в небесных сферах действуют совсем иные законы движения, чем на Земле. Ньютон же объединил эти два типа гравитации в своем сознании.
Закон всемирного тяготения Ньютона, сформулированный им в 1687 году, гласит, что между любой парой тел во Вселенной действует сила взаимного притяжения. Он выражен математическим уравнением: если M и m — массы двух тел, а r — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна F = GMm/r², где G — гравитационная постоянная, равная силе, с которой действуют друг на друга тела с массами в 1 кг каждое, находясь на расстоянии в 1 метр друг от друга. Уравнение гласит, что сила (F) пропорциональна массам двух объектов, разделенным на квадрат расстояния между ними. Из него следует, что чем массивнее объекты, тем больше сила притяжения между ними, но чем дальше они друг от друга, тем слабее притяжение.
Уравнение гласит, что сила (F) пропорциональна массам двух объектов, разделенным на квадрат расстояния между ними. Из него следует, что чем массивнее объекты, тем больше сила притяжения между ними, но чем дальше они друг от друга, тем слабее притяжение.
Закон гравитации Ньютона (Фото: praxilabs.com)
Действие закона распространяется на все без исключения физические материальные тела во Вселенной. Сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. На каждого человека действует сила земного притяжения, которая ощущается как вес.
Закон всемирного тяготения Ньютона говорит, что не только Земля притягивает яблоко, но и яблоко притягивает Землю. Но огромная масса Земли означает, что требуется гораздо больше силы, чтобы сдвинуть ее на ощутимую величину, поэтому яблоко падает, а Земля остается практически неподвижной.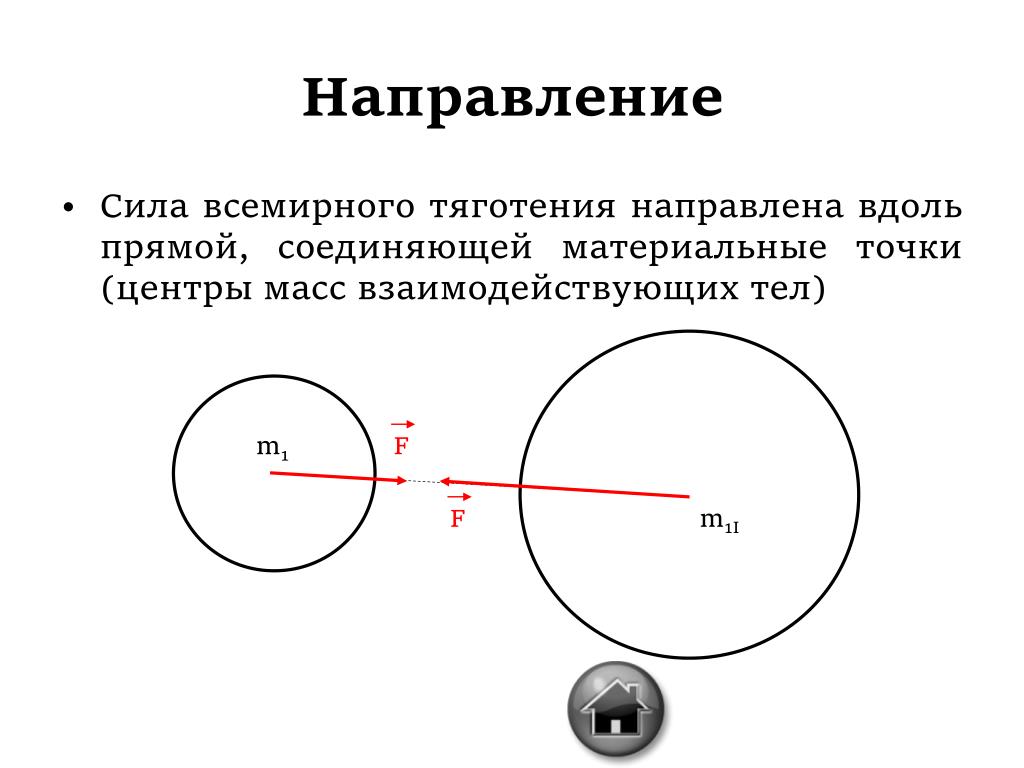 То же самое верно и в более широком контексте. Каждый объект во Вселенной притягивает любой другой объект, и чем он ближе и массивнее, тем больше его гравитационная сила.
То же самое верно и в более широком контексте. Каждый объект во Вселенной притягивает любой другой объект, и чем он ближе и массивнее, тем больше его гравитационная сила.
По Ньютону, сила притяжения действует на любых расстояниях и мгновенно. Однако самая большая скорость в мире — скорость света, а для преодоления больших расстояний свету нужно не мгновение, а несколько секунд и иногда даже лет.
Теория гравитации Эйнштейна
В 1798 году британский физик Генри Кавендиш провел один из первых в мире высокоточных экспериментов, чтобы попытаться точно определить значение G, гравитационной постоянной. Он построил так называемые крутильные весы, прикрепив два маленьких свинцовых шарика к концам балки, подвешенной горизонтально на тонкой проволоке. Рядом с каждым из шаров физик поместил большой сферический свинцовый груз. Маленькие свинцовые шарики гравитационно притягивались к тяжелым свинцовым гирям, в результате чего проволока слегка скручивалась. Это явление позволило ему рассчитать величину G. 2. Чтобы получить точное значение, ученые должны разработать невероятно чувствительное оборудование.
2. Чтобы получить точное значение, ученые должны разработать невероятно чувствительное оборудование.
Немецко-американский физик Альберт Эйнштейн произвел следующую революцию в нашем понимании гравитации. Его общая теория относительности показала, что гравитация возникает из-за искривления пространства-времени, а это означает, что даже лучи света, которые должны следовать этой кривизне, преломляются чрезвычайно массивными объектами. В рамках его теории гравитация рассматривается не как сила, которая действует на тела, но как искривление пространства и времени под действием массы и энергии.
Теории Эйнштейна использовались для предположений о существовании черных дыр — небесных объектов с такой большой массой, что даже свет не может выйти из-под их поверхности. Вблизи черной дыры закон всемирного тяготения Ньютона уже не может точно описать, как движутся объекты.
Теория, которую Эйнштейн опубликовал в 1915 году, расширила его специальную теорию относительности, которую ученый разработал за десятилетие до этого. Специальная теория относительности утверждала, что пространство и время неразрывно связаны, но эта теория не признавала существование гравитации.
Специальная теория относительности утверждала, что пространство и время неразрывно связаны, но эта теория не признавала существование гравитации.
В своей специальной теории относительности Эйнштейн определил, что законы физики одинаковы для всех наблюдателей, не движущихся с ускорением, и показал, что скорость света в вакууме одинакова независимо от скорости, с которой движется наблюдатель. В результате он обнаружил, что пространство и время переплетаются, и события, происходящие в одно и то же время для одного наблюдателя, могут происходить в разное время для другого.
Разрабатывая уравнения своей общей теории относительности, Эйнштейн понял, что массивные объекты вызывают искажение пространства-времени. Представьте, что вы устанавливаете большой объект в центре батута. Объект вдавливался в ткань, вызывая появление ямочек. Если затем попытаться катить шарик по краю батута, он будет двигаться по спирали внутрь к этому объекту.
Вращение тяжелого объекта, такого как Земля, должно скручивать и искажать пространство-время вокруг него.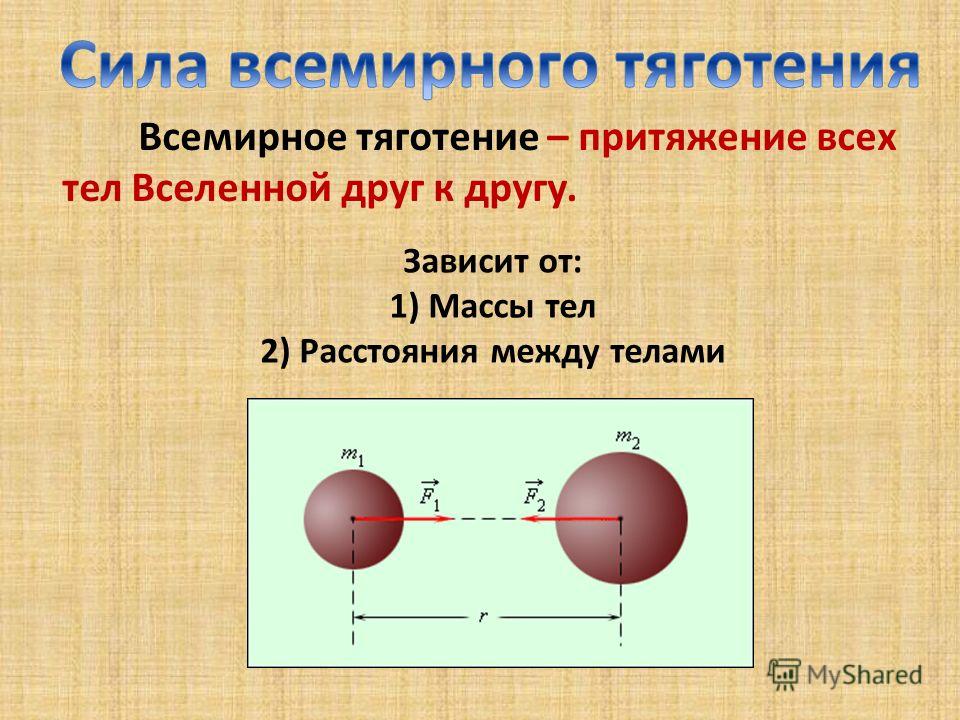 В 2004 году NASA запустило гравитационный зонд Gravity Probe B. По данным агентства, оси точно откалиброванных гироскопов спутника с течением времени очень незначительно дрейфовали, что соответствует теории Эйнштейна.
В 2004 году NASA запустило гравитационный зонд Gravity Probe B. По данным агентства, оси точно откалиброванных гироскопов спутника с течением времени очень незначительно дрейфовали, что соответствует теории Эйнштейна.
Эйнштейн предсказал, что такие события, как столкновение двух черных дыр, создают рябь в пространстве-времени, известную как гравитационные волны. А в 2016 году Лазерная интерферометрическая гравитационно-волновая обсерватория (LIGO) объявила, что впервые определила такой сигнал. Гравитационная волна была вызвана столкновением двух черных дыр массой в 29 и 36 раз больше массы Солнца. После этого они слились в одну большую черную дыру. Это произошло, предположительно, 1,3 млрд лет назад.
Гравитационные волны, создаваемые двумя сталкивающимися черными дырами (Фото: Р. Хёрт / Caltech-JPL)
С тех пор LIGO и ее европейский аналог Virgo обнаружили в общей сложности 50 гравитационно-волновых событий.
Чему равна сила гравитации
Гравитационное поле Земли — это поле силы тяжести, которое образуется из-за силы тяготения Земли и центробежной силы, вызванной ее суточным вращением.
Сила тяжести на поверхности Земли варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. В приблизительных расчетах значение обычно принимают равным 9,81; 9,8 или 10 м/с². Однако оно учитывает только силу тяжести и не учитывает центробежную силу, возникающую за счет вращения Земли. При подъеме тела над поверхностью Земли значение уменьшается.
NASA в рамках проекта GRACE создало визуализацию гравитационных аномалий на Земле. Красным цветом показаны области, где гравитация сильнее, а синим — где она слабее стандартных значений (Фото: NASA)
Французские ученые утверждают, что различие в гравитационной постоянной в различных регионах нашей планеты зависит от величины напряженности магнитного поля Земли. Они предположили, что такое влияние может объясняться наличием дополнительных и скрытых для непосредственного наблюдения измерений пространства. Ученые подсчитали, что земное тяготение будет сильнее в тех местах, где сильнее магнитное поле. Таким образом, своих максимальных значений оно достигает в районах северного и южного магнитных полюсов. Они не совпадают с географическими полюсами. Так, северный магнитный полюс располагается в границах нынешней канадской Арктики, а южный лежит на краю Антарктиды.
Они предположили, что такое влияние может объясняться наличием дополнительных и скрытых для непосредственного наблюдения измерений пространства. Ученые подсчитали, что земное тяготение будет сильнее в тех местах, где сильнее магнитное поле. Таким образом, своих максимальных значений оно достигает в районах северного и южного магнитных полюсов. Они не совпадают с географическими полюсами. Так, северный магнитный полюс располагается в границах нынешней канадской Арктики, а южный лежит на краю Антарктиды.
Если принимать значение гравитации на Земле за единицу, то на Солнце оно будет равно 27,9, на Меркурии — 0,37, на Венере — 0,9, на Луне — 0,16, на Марсе — 0,37, на Юпитере — 2,6. Таким образом, если человек, который на Земле весит 60 кг, взвесится на Юпитере, то весы покажут 142 кг.
Космонавты на орбите также испытывают микрогравитацию. Они как бы бесконечно падают вместе с кораблем, в котором находятся.
Современное представление о гравитации
Научные исследования в области гравитации продолжаются. Теория относительности Эйнштейна объясняет некоторые аномалии в ньютоновской гравитации; однако открытия в атомной, ядерной физике и физике элементарных частиц показали, что ее нельзя отнести к взаимодействиям в квантовой физике. Проще говоря, эйнштейновская теория не работает в микромире. В связи с этим получило развитие направление «квантовой гравитации» или квантового описания гравитационного взаимодействия.
Теория относительности Эйнштейна объясняет некоторые аномалии в ньютоновской гравитации; однако открытия в атомной, ядерной физике и физике элементарных частиц показали, что ее нельзя отнести к взаимодействиям в квантовой физике. Проще говоря, эйнштейновская теория не работает в микромире. В связи с этим получило развитие направление «квантовой гравитации» или квантового описания гравитационного взаимодействия.
Однако теория квантовой гравитации пока не построена. Основная трудность заключается в том, что две физические теории, которые она пытается связать воедино, — квантовая механика и общая теория относительности — опираются на разные наборы принципов. Первая описывает временну́ю эволюцию физических систем (например, атомов или элементарных частиц) на фоне внешнего пространства-времени. Во второй внешнего пространства-времени вообще нет — оно само является динамической переменной в теории.
В квантовой гравитации развиваются два основных направления — это теория струн и петлевая квантовая гравитация. В первой теории вместо частиц и фонового пространства-времени выступают струны и их многомерные аналоги — браны.
В первой теории вместо частиц и фонового пространства-времени выступают струны и их многомерные аналоги — браны.
Во второй делается попытка сформулировать квантовую теорию поля без привязки к пространственно-временному фону; пространство и время по этой теории состоят из дискретных частей. Это маленькие квантовые ячейки пространства, которые определенным способом соединены друг с другом, так что на малых масштабах времени и длины они создают дискретную структуру пространства, а в больших масштабах плавно переходят в непрерывное гладкое пространство-время. Предполагается, что именно петлевая квантовая гравитация может описать сам процесс взрыва, который предшествовал образованию Вселенной.
Сотрудники Университета штата Пенсильвания с 1980-х годов разрабатывают парадигму, основанную на представлении о петлевой квантовой гравитации. Она описывает все современные крупные структуры во Вселенной как квантовые флуктуации пространства-времени, имевшие место при рождении мира.
Существующая теория Большого взрыва, как уже говорилось, не объясняет, что было до зарождения Вселенной. Ученые из Пенсильвании придерживаются альтернативной гипотезы Большого отскока, согласно которой текущая расширяющаяся Вселенная возникла из распада предыдущей вселенной. Для описания этого состояния они объединили квантовую механику и теорию относительности. Авторы работы утверждают, что смогли описать космическое излучение, которое возникло непосредственно после зарождения Вселенной. Они заявили, что в эйнштейновскую ткань пространства-времени вплетены квантовые нити. Именно это в будущем может позволить объяснить, почему галактики и материя распространены во Вселенной неравномерно.
Ученые из Пенсильвании придерживаются альтернативной гипотезы Большого отскока, согласно которой текущая расширяющаяся Вселенная возникла из распада предыдущей вселенной. Для описания этого состояния они объединили квантовую механику и теорию относительности. Авторы работы утверждают, что смогли описать космическое излучение, которое возникло непосредственно после зарождения Вселенной. Они заявили, что в эйнштейновскую ткань пространства-времени вплетены квантовые нити. Именно это в будущем может позволить объяснить, почему галактики и материя распространены во Вселенной неравномерно.
В 1990-х годах астрономы обнаружили, что расширение Вселенной ускоряется. Это противоречит предсказаниям общей теории относительности, согласно которой гравитация должна замедлять расширение. Чтобы объяснить это явление, космологи начали ссылаться на «темную энергию», силу, которая составляет почти три четверти материи и энергии во Вселенной и поэтому раздвигает ее. Но происхождение темной энергии по сей день остается загадкой. Некоторые исследователи пытаются объяснить ускорение расширения Вселенной без темной энергии, предполагая, что если общая теория относительности неверна, а гравитация ослабевает в космических масштабах. Но до сих пор никто не придумал способ проверить данную теорию.
Некоторые исследователи пытаются объяснить ускорение расширения Вселенной без темной энергии, предполагая, что если общая теория относительности неверна, а гравитация ослабевает в космических масштабах. Но до сих пор никто не придумал способ проверить данную теорию.
Существует и такое понятие как антигравитация — предполагаемое противодействие, которое гасит или даже превышает гравитационное притяжение путем отталкивания.
Нынешний подход к антигравитации заключается в том, чтобы освободить объект от действия силы тяжести, чтобы он какое-то время не был подвержен гравитации. Например, полет человека в аэродинамической трубе обеспечивается за счет того, что силе тяжести противодействует поток воздуха.
Полет в аэротрубе (Фото: FlyStation)
Пока вопрос существования антигравитации как самостоятельного явления остается открытым, так как само явление гравитации только изучается.
Как преодолеть гравитацию
Чтобы преодолеть силу гравитации Земли, тело должно иметь скорость, равную 7,91 км/с. Это первая космическая скорость. Ее достаточно, чтобы объект двигался по орбите вокруг планеты. Чтобы вырваться из гравитационного поля Земли, космический корабль должен иметь скорость не менее 11,2 км/с. Это вторая космическая скорость. Чтобы выйти за границу сферы земного притяжения, которая заканчивается на расстоянии около 930 тыс. км от Земли, скорость объекта должна составлять около 16,6 км/с. Это третья космическая скорость.
Если бы не было гравитации
В соответствии с вышеприведенными законами физики на практике такая ситуация невозможна.
Бывший астронавт NASA, физик Джей Баки, отмечает, что наш организм адаптирован к силе земного притяжения. Когда сила тяжести почти исчезает (например, на борту МКС), организм начинает перестраиваться. За время миссий в космосе члены экипажей кораблей теряют костную массу и мышечный тонус, а также чувство равновесия.
Доктор Кевин Фонг добавляет, что количество эритроцитов в организме падает, что приводит к так называемой космической анемии. При этом раны заживают дольше, а также снижается иммунитет, наблюдаются проблемы со сном. Таким образом, в отсутствие гравитации мышцы, вестибулярный аппарат, сердце и кровеносные сосуды развивались бы иначе.
Астроном Карен Мастерс из Портсмутского университета в Великобритании предположил, что в отсутствие гравитации Земля начала бы вращаться с большой угловой скоростью как раскручиваемая над головой веревка. Таким образом, любые объекты на планете улетели бы прямо в космос, как и вода с атмосферой. Только укрепленные строения могли бы какое-то время держаться на поверхности Земли.
В конечном счете отсутствие гравитации разрушит саму планету. Земля развалится на части, которые разлетятся в разные стороны.
Похожий пример, но с Солнцем, приводит канал Discovery News в своем видео.
Что произойдет, если гравитации не станет
Без гравитации не осталось бы ни звезд, ни планет, а Вселенная стала бы смесью рассеянных атомов и молекул.
Возможна ли искусственная гравитация
Когда человек оказывается в космосе, далеко от гравитационных воздействий, испытываемых на поверхности Земли, он переживает невесомость. Хотя все массы Вселенной продолжат притягивать его, они продолжат притягивать и космический корабль, поэтому человек как бы «плавает» внутри него. В связи с этим возникает вопрос — как создать условия искусственной гравитации, при которых человек сможет не летать, а спокойно ходить по космическому кораблю?
Пока нужный эффект можно получить только через ускорение. В случае с космическим кораблем — заставить его вращаться. Тогда можно можно получить центробежную тягу, как на Земле. Но для путешествия в другую звездную систему придется ускорять корабль по пути туда и замедлять по прибытии обратно. Человеческий организм вряд ли сможет перенести такие нагрузки. Например, чтобы разогнаться до «импульсной скорости» как в фильме «Звездный путь», до нескольких процентов от скорости света, то пришлось бы выдержать ускорение в 4000 g (единиц ускорения, вызванного гравитацией) в течение часа. Это в 100 раз больше ускорения, которое предотвращает ток крови в теле человека. В Роскосмосе изучают идею встроенной центрифуги на борту корабля, в которую космонавты смогут периодически заходить, чтобы испытывать силу тяжести и снижать негативные последствия от пребывания в невесомости.
Это в 100 раз больше ускорения, которое предотвращает ток крови в теле человека. В Роскосмосе изучают идею встроенной центрифуги на борту корабля, в которую космонавты смогут периодически заходить, чтобы испытывать силу тяжести и снижать негативные последствия от пребывания в невесомости.
Кадр из фильма «Звездный путь» (Фото: YouTube)
Предполагалось, что искусственная гравитация возможна при отрицательной гравитационной массе, которая, как ожидалось, свойственна антиматерии. Однако Европейская организация по ядерным исследованиям (ЦЕРН) обнаружила, что инертная масса антипротона («зеркального отражения» протона, который отличается знаками всех характеристик физического взаимодействия) совпадает с массой протона. Если бы гравитация действовала на антипротоны как-то иначе, то физики заметили бы разницу. Получается, что действие гравитации на антипротоны и протоны совпадает. Кроме того, в ЦЕРН получили антиводород — первую стабильную форму антиматерии. Но ее изучают, и пока сдвигов в теории антиматерии нет.
Кроме того, в ЦЕРН получили антиводород — первую стабильную форму антиматерии. Но ее изучают, и пока сдвигов в теории антиматерии нет.
Направление и гравитация — анимация в приложениях Windows – Windows apps
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 2 мин
Направленные сигналы помогают закрепить ментальную модель пути, который пользователь проделывает в интерфейсе. Очень важно, чтобы направление любого движения поддерживало и непрерывность пространства, и целостность объектов в пространстве.
Очень важно, чтобы направление любого движения поддерживало и непрерывность пространства, и целостность объектов в пространстве.
Направленное движение подвергается таким силам, как гравитация. Применение сил к движению усиливает естественное чувство движения.
Примеры
Если у вас установлено приложение коллекции WinUI 2 , щелкните здесь, чтобы открыть приложение и увидеть движение в действии.
|
Направление движения
Направление движения соответствует физическому движению. Так же, как в природе, объекты могут перемещаться по любой оси — X, Y, Z. Так мы воспринимаем движение объектов на экране.
При перемещении объектов избегайте неестественных конфликтов. Имейте в виду, откуда приходят и переходят объекты, и всегда поддерживайте конструкции более высокого уровня, которые могут использоваться в сцене, например направление прокрутки или иерархия макета.
Направление навигации
Для направления навигации между сценами в приложении характерна концептуальность. Пользователи переходят вперед и назад. Сцены появляются в поле зрения и уходят из него. Эти концепции в сочетании с физическим перемещением помогают пользователю.
Когда навигация вызывает перемещение объекта из предыдущей сцены в новую, объект просто перемещается из точки A в точку B. Чтобы повысить реалистичность перемещения объекта, добавляется стандартная анимация, а также ощущение силы притяжения.
При переходе назад перемещение отображается в обратном порядке (из точки B в точку A). Когда пользователи переходят назад, они рассчитывают как можно быстрее вернуться к предыдущему состоянию. Движение происходит быстрее, более прямолинейно и с замедлением в анимации.
Здесь эти принципы применяются, так как выбранный элемент остается на экране во время навигации вперед и назад.
Когда навигация вызывает вымещение расположенных на экране элементов, важно показать, куда уходит старая сцена и откуда появляется новая.
Это имеет несколько преимуществ:
- Закрепление ментальной модели пространства у пользователя.
- Продолжительность выхода сцены обеспечивает больше времени для подготовки содержимого для анимации для входящей сцены.
- Это повышает воспринимаемую производительность приложения.
Существует 4 сдержанных направления навигации для рассмотрения.
Переадресация Празднуйте содержимое, которое вводит сцену таким образом, чтобы не сталкивались с исходящим содержимым. Содержимое замедляется в сцене.
Переадресация Содержимое завершается быстро. Объекты ускоряют работу с экрана.
Назад Аналогично переадресации, но обратно.
Назад То же, что и переадресация, но обратный.
Сила тяготения
Сила тяготения делает процессы более естественными. Объекты, которые перемещаются по оси Z и не привязываются к сцене с помощью возможностей на экране, могут повлиять на гравитацию. Как объект ломается от сцены и до того, как он достигает escape-скорости, гравитация тянет вниз на объект, создавая более естественную кривую траектории объекта по мере его перемещения.
Как объект ломается от сцены и до того, как он достигает escape-скорости, гравитация тянет вниз на объект, создавая более естественную кривую траектории объекта по мере его перемещения.
Гравитация обычно проявляется, когда объект должен переходить от одной сцены к другой. Из-за этого подключенная анимация использует концепцию гравитации.
Здесь на элемент в верхней строке сетки воздействует гравитация, что вызывает его небольшое падение по мере отрыва от своего места и перемещения на передний план.
- Обзор движения
- Согласование по времени и реалистичная анимация
определение, объяснение для чайников, формулы
Оби-Ван Кеноби сказал, что сила скрепляет галактику. То же самое можно сказать и о гравитации. Факт – гравитация позволяет нам ходить по Земле, Земле вращаться вокруг Солнца, а Солнцу двигаться вокруг сверхмассивной черной дыры в центре нашей галактики. Как понять гравитацию? Об этом – в нашей статье.
Сразу скажем, что вы не найдете здесь однозначно верного ответа на вопрос «Что такое гравитация». Потому что его просто нет! Гравитация – одно из самых таинственных явлений, над которым ученые ломают голову и до сих пор полностью не могут объяснить его природу.
Есть множество гипотез и мнений. Насчитывается более десятка теорий гравитации, альтернативных и классических. Мы рассмотрим самые интересные, актуальные и современные.
Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.
Гравитация – физическое фундаментальное взаимодействие
Всего в физике 4 фундаментальных взаимодействия. Благодаря им мир является именно таким, какой он есть. Гравитация – одно из этих взаимодействий.
Фундаментальные взаимодействия:
- гравитация;
- электромагнетизм;
- сильное взаимодействие;
- слабое взаимодействие.
Гравитация – самое слабое из четырех фундаментальных взаимодействий.
На текущий момент действующей теорией, описывающей гравитацию, является ОТО (общая теория относительности). Она была предложена Альбертом Эйнштейном в 1915-1916 годах.
Однако мы знаем, что об истине в последней инстанции говорить рано. Ведь несколько веков до появления ОТО в физике для описания гравитации главенствовала Ньютоновская теория, которая была существенно расширена.
В рамках ОТО на данный момент нельзя объяснить и описать все вопросы, связанные с гравитацией.
До Ньютона было широко распространено мнение, что гравитация на земле и небесная гравитация – разные вещи. Считалось, что планеты движутся по своим, отличным от земных, идеальным законам.
Закон всемирного тяготения
Ньютон открыл закон всемирного тяготения в 1667 году. Конечно, этот закон существовал еще при динозаврах и намного раньше.
Античные философы задумывались над существованием силы тяготения. Галилей экспериментально рассчитал ускорение свободного падения на Земле, открыв, что оно одинаково для тел любой массы. Кеплер изучал законы движения небесных тел.
Кеплер изучал законы движения небесных тел.
Ньютону удалось сформулировать и обобщить результаты наблюдений. Вот что у него получилось:
Два тела притягиваются друг к другу с силой, называемой гравитационной силой или силой тяготения.
Формула силы притяжения между телами:
G – гравитационная постоянная, m – массы тел, r – расстояние между центрами масс тел.
Каков физический смысл гравитационной постоянной? Она равна силе, с которой действуют друг на друга тела с массами в 1 килограмм каждое, находясь на расстоянии в 1 метр друг от друга.
Закон всемирного тяготенияПо теории Ньютона, каждый объект создает гравитационное поле. Точность закона Ньютона была проверена на расстояниях менее одного сантиметра. Конечно, для малых масс эти силы незначительны, и ими можно пренебречь .
Формула Ньютона применима как для расчету силы притяжения планет к солнцу, так и для маленьких объектов. Мы просто не замечаем, с какой силой притягиваются, скажем, шары на бильярдном столе. Тем не менее эта сила есть и ее можно рассчитать.
Тем не менее эта сила есть и ее можно рассчитать.
Сила притяжения действует между любыми телами во Вселенной. Ее действие распространяется на любые расстояния.
Закон всемирного тяготения Ньютона не объясняет природы силы притяжения, но устанавливает количественные закономерности. Теория Ньютона не противоречит ОТО. Ее вполне достаточно для решения практических задач в масштабах Земли и для расчета движения небесных тел.
Гравитация в ОТО
Несмотря на то, что теория Ньютона вполне применима на практике, она имеет ряд недостатков. Закон всемирного тяготения является математическим описанием, но не дает представления о фундаментальной физической природе вещей.
Согласно Ньютону, сила притяжения действует на любых расстояниях. Причем действует мгновенно. Учитывая, что самая большая скорость в мире – скорость света, выходит несоответствие. Как гравитация может мгновенно действовать на любые расстояниях, когда для их преодоления свету нужно не мгновение, а несколько секунд или даже лет?
В рамках ОТО гравитация рассматривается не как сила, которая действует на тела, но как искривление пространства и времени под действием массы.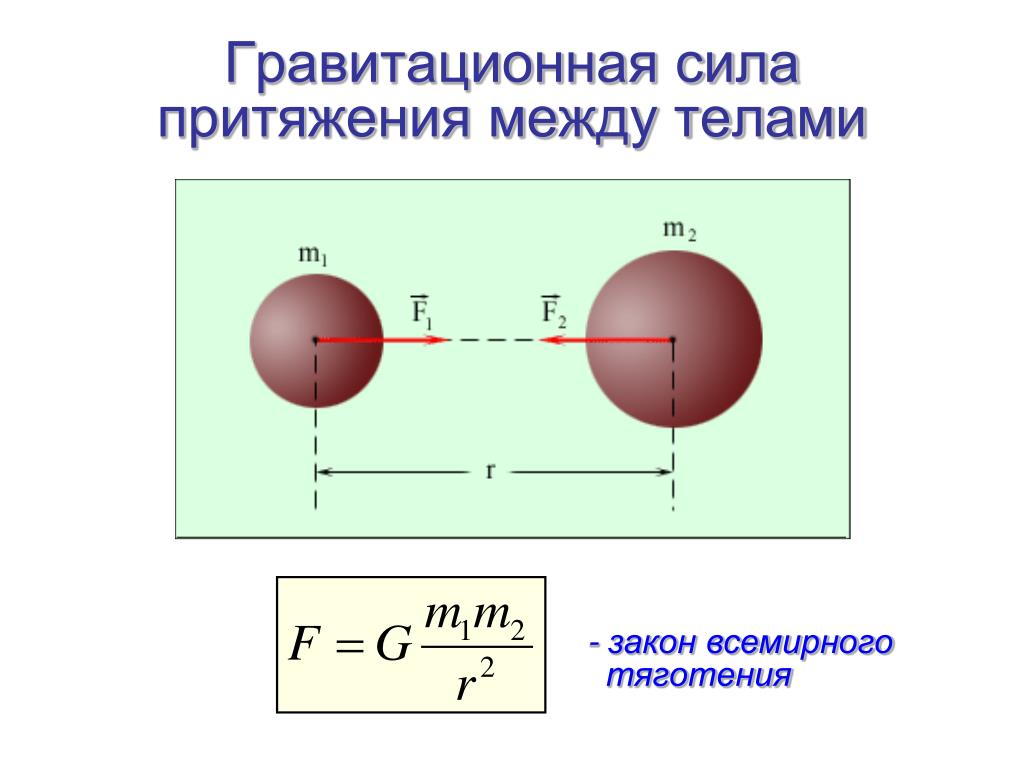 Таким образом гравитация – не силовое взаимодействие.
Таким образом гравитация – не силовое взаимодействие.
Каково действие гравитации? Попробуем описать его с использованием аналогии.
Представим пространство в виде упругого листа. Если положить на него легкий теннисный мячик, поверхность останется ровной. Но если рядом с мячиком положить тяжелую гирю, она продавит на поверхности ямку, и мячик начнет скатываться к большой и тяжелой гире. Это и есть «гравитация».
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Открытие гравитационных волн
Гравитационные волны были предсказаны Альбертом Эйнштейном еще в 1916 году, но открыли их только через сто лет, в 2015.
Что такое гравитационные волны? Снова проведем аналогию. Если бросить камень в спокойную воду, от места его падения по поверхности воды пойдут круги. Гравитационные волны – такая же рябь, возмущение. Только не на воде, а в мировом пространстве-времени.
Вместо воды – пространство-время, а вместо камня, скажем, черная дыра. Любое ускоренное передвижение массы порождает гравитационную волну. Если тела находятся в состоянии свободного падения, при прохождении гравитационной волны расстояние между ними изменится.
Моделирование гравитационных волн от слияния двух черных дырТак как гравитация – очень слабое взаимодействие, обнаружение гравитационных волн было связано с большими техническими трудностями. Современные технологии позволили обнаружить всплеск гравитационных волн только от сверхмассивных источников.
Подходящее событие для регистрации гравитационной волны – слияние черных дыр. К сожалению или к счастью, это происходит достаточно редко. Тем не менее ученым удалось зарегистрировать волну, которая буквально раскатилась по пространству Вселенной.
Для регистрации гравитационных волн был построен детектор диаметром 4 километра. При прохождении волны регистрировались колебания зеркал на подвесах в вакууме и интерференция света, отраженного от них.
Гравитационные волны подтвердили справедливость ОТО.
Гравитация и элементарные частицы
В стандартной модели за каждое взаимодействие отвечают определенные элементарные частицы. Можно сказать, что частицы являются переносчиками взаимодействий.
За гравитацию отвечает гравитон – гипотетическая безмассовая частица, обладающая энергией. Кстати, в нашем отдельном материале читайте подробнее о наделавшем много шума бозоне Хиггса и других элементарных частицах.
Напоследок приведем несколько любопытных фактов о гравитации.
10 фактов о гравитации
- Чтобы преодолеть силу гравитации Земли, тело должно иметь скорость, равную 7,91 км/с. Это первая космическая скорость. Ее достаточно, чтобы тело (например, космический зонд) двигалось по орбите вокруг планеты.
- Чтобы вырваться из гравитационного поля Земли, космический корабль должен иметь скорость не менее 11,2 км/с. Это вторая космическая скорость.
- Объекты с наиболее сильной гравитацией – черные дыры.
 Их гравитация настолько велика, что они притягивают даже свет (фотоны).
Их гравитация настолько велика, что они притягивают даже свет (фотоны). - Ни в одном уравнении квантовой механики вы не найдете силы гравитации. Дело в том, что при попытке включения гравитации в уравнения, они теряют свою актуальность. Это одна из самых важных проблем современной физики.
- Слово гравитация происходит от латинского “gravis”, что означает “тяжелый”.
- Чем массивнее объект, тем сильнее гравитация. Если человек, который на Земле весит 60 килограмм, взвесится на Юпитере, весы покажут 142 килограмма.
- Ученые NASA пытаются разработать гравитационный луч, который позволит перемещать предметы бесконтактно, преодолевая силу притяжения.
- Астронавты на орбите также испытывают гравитацию. Точнее, микрогравитацию. Они как бы бесконечно падают вместе с кораблем, в котором находятся.
- Гравитация всегда притягивает и никогда не отталкивает.
- Черная дыра, размером с теннисный мяч, притягивает объекты с той же силой, что и наша планета.

Теперь вы знаете определение гравитации и можете сказать, по какой формуле рассчитывается сила притяжения. Если гранит науки придавливает вас к земле сильнее, чем гравитация, обращайтесь в наш студенческий сервис. Мы поможем учиться легко при самых больших нагрузках!
Что такое гравитация и как она работает?
Латинское слово gravitas означает вес и дает нам слово “гравитация”, которое является силой, которая дает объектам их вес. Это также корень слова “гравитировать”, которое описывает то, что делает гравитация: заставляет объекты притягиваться друг к другу. Это то, что удерживает людей на Земле и держит Землю на своем месте в Солнечной системе. Хотя древние философы задавались вопросом, почему объекты падали столетия назад, у ученых до сих пор остаются вопросы о том, как действует гравитация и сегодня.
Что такое гравитация?
Проще говоря, гравитация – это сила, которая притягивает два тела друг к другу. Все, что имеет материю, то есть все, к чему можно прикоснуться, имеет гравитационное притяжение. Это включает в себя яблоки, людей и Землю. Несмотря на термин невесомость, невозможно избежать гравитационных сил. Космонавты все еще подвержены воздействию гравитации, но они движутся так быстро, что не приближаются к центру планеты и находятся в постоянном состоянии свободного падения.
Все, что имеет материю, то есть все, к чему можно прикоснуться, имеет гравитационное притяжение. Это включает в себя яблоки, людей и Землю. Несмотря на термин невесомость, невозможно избежать гравитационных сил. Космонавты все еще подвержены воздействию гравитации, но они движутся так быстро, что не приближаются к центру планеты и находятся в постоянном состоянии свободного падения.
Гравитация, масса и расстояние
Степень гравитации любого объекта пропорциональна массе объекта. Объекты с большей массой имеют большую гравитацию. Поскольку Земля является самым крупным и ближайшим объектом вокруг, все притягивается к ее гравитационному притяжению, а это означает, что яблоки падают на землю, а не притягиваются к голове человека.
Расстояние также влияет на гравитацию. Если объект находится далеко, то гравитационное притяжение слабее. Например, в космосе есть точка, где притяжение Марса становится сильнее притяжения Земли.
Фундаментальные силы во Вселенной
По мнению физиков, четыре фундаментальные силы Вселенной – это гравитация, электромагнитные, слабые и сильные взаимодействия. Силы изменяют движение объекта, и эти четыре фундаментальные силы определяют, как все во Вселенной взаимодействует. Гравитация – самая слабая сила, но она наиболее легко видима и оказывает наибольшее влияние на крупномасштабном уровне. Это не только причина, по которой люди могут ходить по Земле, но и удерживает планеты, вращающиеся по орбите вокруг Солнца, и Солнце на своем месте в галактике.
Силы изменяют движение объекта, и эти четыре фундаментальные силы определяют, как все во Вселенной взаимодействует. Гравитация – самая слабая сила, но она наиболее легко видима и оказывает наибольшее влияние на крупномасштабном уровне. Это не только причина, по которой люди могут ходить по Земле, но и удерживает планеты, вращающиеся по орбите вокруг Солнца, и Солнце на своем месте в галактике.
Древняя история гравитационной теории
Древние греки верили, что сила, притягивающая предметы к Земле, была внутренней тяжестью, а не внешней силой. Тяжелые люди естественным образом притягиваются к Земле, в то время как легкие языки пламени прыгают к небу. Напротив, индийские ученые, в частности Арьябхата, говорили, что некая сила удерживает объекты на Земле, хотя его теория помещает Землю в центр вселенной. В 600-х годах н. э. математик Брахмагупта был первым, кто описал гравитацию как силу притяжения.
Гравитационная теория эпохи Возрождения
Говорят, что Галилей бросал предметы со стороны падающей Пизанской башни, чтобы наблюдать, что происходит, когда они падают. Независимо от того, была ли задействована башня или нет, Галилей обнаружил, что все объекты имеют тенденцию ускоряться с одинаковой скоростью при падении. Другие ученые основывались на своей работе, а Гримальди и Риччоли вычислили гравитационную постоянную. Другие работы по гравитации сосредоточены вокруг астрономии и Иоганна Кеплера, построенного на этих теориях для расчета орбит известных планет.
Независимо от того, была ли задействована башня или нет, Галилей обнаружил, что все объекты имеют тенденцию ускоряться с одинаковой скоростью при падении. Другие ученые основывались на своей работе, а Гримальди и Риччоли вычислили гравитационную постоянную. Другие работы по гравитации сосредоточены вокруг астрономии и Иоганна Кеплера, построенного на этих теориях для расчета орбит известных планет.
Закон всемирного тяготения
Другая легенда о гравитации гласит, что Исаак Ньютон был поражен падающим яблоком и понял, что должна быть сила, заставляющая вещи падать на землю. Он написал уравнение, в котором описывается сила гравитации, показывающее, что чем массивнее объекты, тем больше сила притяжения между ними. Оно также показало, что чем дальше они находятся, тем слабее тяга. Некоторые планеты двигались так, что не могли объяснить это уравнение, но по большей части оно существовало веками.
Эйнштейн и общая теория относительности
Теория общей относительности Эйнштейна изменила взгляд физиков на гравитацию. Считается, что воздействие гравитации вызвано не силой, а кривой в пространстве-времени, которая возникает вокруг крупных объектов, а скорее похожа на шар для боулинга, сидящий на батуте. Эта теория объяснила странную орбиту Меркурия и установила ньютоновскую гравитацию на его голову, поскольку гравитация больше не была силой, а следствием геометрии.
Считается, что воздействие гравитации вызвано не силой, а кривой в пространстве-времени, которая возникает вокруг крупных объектов, а скорее похожа на шар для боулинга, сидящий на батуте. Эта теория объяснила странную орбиту Меркурия и установила ньютоновскую гравитацию на его голову, поскольку гравитация больше не была силой, а следствием геометрии.
Что делает гравитация?
Гравитация оказывает несколько воздействий на реальный мир. Помимо того, что гравитация не только удерживает предметы на земле, но и придает им вес. Объекты меньше весят на планетах с меньшей гравитационной тягой. Гравитация Луны – это сила, которая создает океанские приливы. Гравитация также удерживает Землю на комфортном расстоянии от Солнца и удерживает атмосферу на месте, давая всем живым существам воздух, пригодный для дыхания, и защищая их от солнечного излучения.
Гравитация и сотворение Вселенной.
Гравитация также является существенным элементом в создании Вселенной. Газы, существующие во Вселенной, притягиваются друг к другу под действием гравитации и объединяются в крупные объекты, в том числе звезды и планеты. Некоторые исследователи считают, что именно гравитация стабилизировала частицы после Большого взрыва, остановив коллапс Вселенной. Гравитация притягивает солнечные системы друг к другу, образуя галактики, и как таковая является основополагающим элементом в создании Вселенной.
Некоторые исследователи считают, что именно гравитация стабилизировала частицы после Большого взрыва, остановив коллапс Вселенной. Гравитация притягивает солнечные системы друг к другу, образуя галактики, и как таковая является основополагающим элементом в создании Вселенной.
Гравитация и научные исследования
Научные исследования в области гравитации будут продолжаться и в будущем. Теория относительности объясняет некоторые аномалии в ньютоновской гравитации; во Вселенной все еще есть тайны, которые ученые не могут объяснить. Гравитация не вписывается в теорию квантовых полей, и ученые до сих пор исследуют, как она соединяется с другими фундаментальными силами. Исследования гравитации также имеют более практическое применение. Космические аппараты НАСА отслеживают изменения гравитации Земли, что помогает ученым отслеживать изменения уровня моря и земной коры.
Значение, Определение, Предложения . Что такое сила притяжения
- Онлайн-переводчик
- Грамматика
- Видео уроки
- Учебники
- Лексика
- Специалистам
- Английский для туристов
- Рефераты
- Тесты
- Диалоги
- Английские словари
- Статьи
- Биографии
- Обратная связь
- О проекте
Примеры
Значение слова «СИЛА»
Способность живых существ напряжением мышц производить физические действия, движения; также вообще — физическая или моральная возможность активно действовать.
Смотреть все значения слова СИЛА
Значение слова «ПРИТЯЖЕНИЕ»
Физическое явление тяготения тел друг к другу.
Смотреть все значения слова ПРИТЯЖЕНИЕ
Предложения с «сила притяжения»
Мы пришли к согласию, что некая сила притяжения Солнца управляет движением планет. | |
Огромная сила притяжения влияет на космический корабль, иначе он бы просто потерялся в космосе. | |
Сила притяжения постоянно изменяется по некоей формуле, известной только инженерам. | |
Сила притяжения побеждает все известные силы. | |
У него есть определенная сила притяжения с женским населением. | |
Сила притяжения Юпитера была так велика, что комета распалась на мелкие части, летящие друг за другом. | |
Это говорит нам, что сила притяжения между двумя телами . | |
На нашей планете, – заметил Мин, – жуки остаются сравнительно небольшими, поскольку им не дает расти сила притяжения. | |
Однако сила притяжения победила. | |
Огромная сила притяжения влияет на космический корабль, иначе он бы просто потерялся в космосе. | |
Есть такая штука – сила притяжения… и из-за нее все падает. | |
Все станет настолько отдалено, что даже сила притяжения иссякнет. | |
Хорошо. Кстати, я собираюсь сказать, что сила притяжения сравнима с длинным луком не больше и не меньше, потому что широкий диапазон возможных чисел. | |
Мичелл постулировал, что если плотность звездного объекта станет достаточно большой, его сила притяжения станет настолько большой, что даже свет не сможет вырваться наружу. | |
Два противоположно заряженных Иона притягивают друг друга, и ионная связь-это электростатическая сила притяжения между ними. | |
Более сильная сила притяжения была постулирована, чтобы объяснить, как атомное ядро было связано, несмотря на взаимное электромагнитное отталкивание протонов. | |
Ответ заключается в том, что на таком расстоянии ядерная сила притяжения сильнее, чем их электрическое отталкивание. | |
Как правило, по мере увеличения расстояния между ионами сила притяжения и энергия связи приближаются к нулю, и ионная связь становится менее благоприятной. | |
Ньютон получил уникальное геометрическое доказательство и продолжал доказывать, что притягательная сила притяжения Солнца была причиной всех законов Кеплера. | |
Большая часть периодических гравитационных сил исходит от Луны, но также важна и сила притяжения Солнца. | |
Сила притяжения Земли может быть использована для вычисления ее массы. | |
И поэтому сила притяжения находится в обоих телах. | |
Флокуляция происходит тогда, когда между каплями возникает сила притяжения, поэтому они образуют хлопья, похожие на грозди винограда. | |
| Другие результаты | |
В конечном счете именно сила земного притяжения ограничивает размеры и подвижность всех сухопутных гигантов. | |
Чем больше масса планеты, тем выше сила её притяжения. | |
И сила эта отвечает за притяжение между объектами. | |
1. Сильное ядерное взаимодействие. Это сила, отвечающая за взаимное притяжение атомных ядер, протонов и нейтронов. | |
Значительно уменьшилась бы и сила земного притяжения. Обманчивое уменьшение веса тела живых существ позволило бы им развиться до гигантских размеров. | |
Это сила электромагнитного притяжения. | |
Чем больше масса животного, тем более важную роль играет в его жизни сила земного притяжения. | |
На данной странице приводится толкование (значение) фразы / выражения «сила притяжения», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных. Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «сила притяжения», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «сила притяжения», просим написать нам в разделе «Обратная связь».
Формула силы притяжения – заявление, уравнение и часто задаваемые вопросы
Сила притяжения — это сила, которая притягивает тело к себе из-за притяжения. В природе существует несколько сил притяжения. Это электрическая сила, магнитная сила, электростатическая сила, гравитационная сила и электромагнитная сила. Гравитационная сила — хорошо известная сила, которая притягивает к себе тело, несмотря на расстояние. Благодаря гравитационной силе Ньютона мы получаем много разъяснений относительно этой силы и того, как она действует. В нем говорится, что масса, существующая во Вселенной, притягивает к себе ту или иную массу, распространенную во Вселенной. Это подтверждает, что все, что выбрасывается вверх, в конечном итоге падает. Формула силы притяжения основана на этой теории. 92} \]
В нем говорится, что масса, существующая во Вселенной, притягивает к себе ту или иную массу, распространенную во Вселенной. Это подтверждает, что все, что выбрасывается вверх, в конечном итоге падает. Формула силы притяжения основана на этой теории. 92} \]
Где,
F = сила притяжения
G = гравитационная постоянная
M A = МАССА Первого объекта A
M B . = масса второго объекта b
d = расстояние между двумя объектами d
Эта формула силы притяжения помогает в расчете любых двух тел, имеющих большую массу, поскольку меньшая масса незначительна.
Даже когда предметы не находятся в непосредственной близости, сила притяжения притягивает их друг к другу. Узнайте о трех силах гравитационного, электрического и магнитного притяжения, а также об их формулах и концепциях.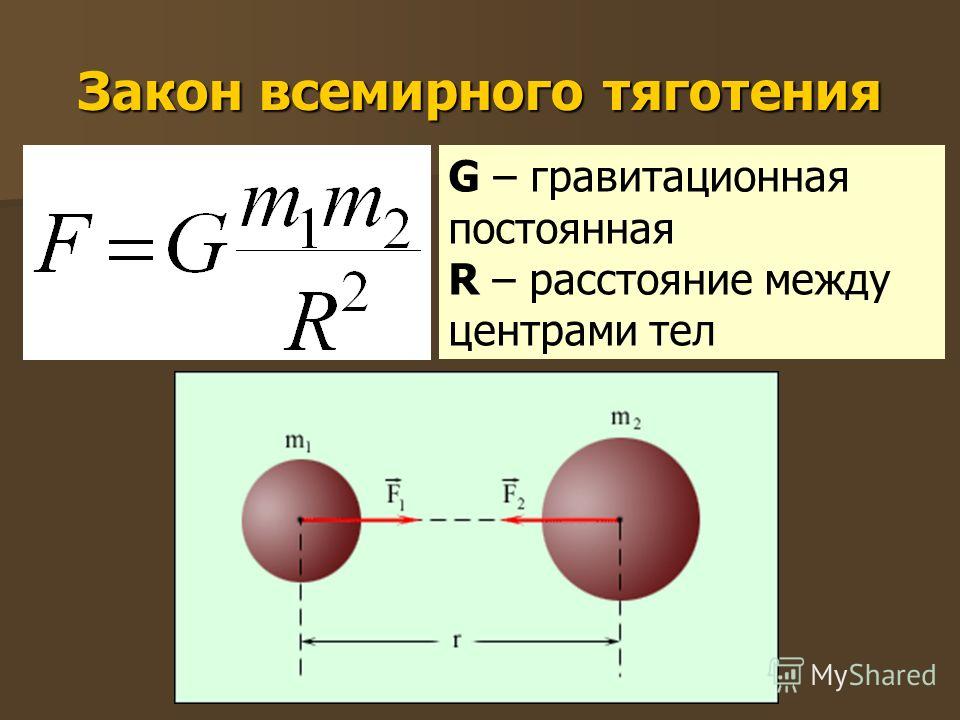
Что понимается под гравитацией?
Гравитация, наверное, самая известная сила из всех. Мы, люди на Земле, представляем гравитацию как яблоко, приземлившееся на голову Исаака Ньютона. Только из-за гравитации мы наблюдаем, как вещи падают на землю. Подобные случаи происходят и по всей Вселенной. Однако это всего лишь наше восприятие гравитации. В действительности, подобно тому, как земля притягивает к себе яблоко под действием гравитации, яблоко притягивает и землю. Проблема в том, что Земля настолько огромна, что гравитационные взаимодействия любого другого предмета на земном шаре подавляются.
Каждый предмет с массой имеет гравитационное притяжение ко всему остальному. Эта сила объясняет, среди прочего, почему планеты вращаются вокруг своей оси. Кроме того, все, включая вас, притягивает все остальные объекты в космосе, что известно как универсальный закон всемирного тяготения Ньютона. Ускорение Луны по сравнению с ускорением вещей на Земле Исаака Ньютона. Ньютон смог сделать важный вывод о зависимости гравитации от расстояния, полагая, что за каждую из них ответственны гравитационные силы. На основе этого сравнения он пришел к выводу, что гравитационное притяжение между Землей и другими объектами обратно пропорционально расстоянию между центром Земли и центром объекта. Однако расстояние — не единственный фактор, влияющий на амплитуду гравитационных сил.
Ньютон смог сделать важный вывод о зависимости гравитации от расстояния, полагая, что за каждую из них ответственны гравитационные силы. На основе этого сравнения он пришел к выводу, что гравитационное притяжение между Землей и другими объектами обратно пропорционально расстоянию между центром Земли и центром объекта. Однако расстояние — не единственный фактор, влияющий на амплитуду гравитационных сил.
Что вы подразумеваете под электрической силой?
Электрическая сила, также известная как электростатическая сила, является второй силой, которая может вызвать притяжение. В то время как гравитация влияет на массовые объекты, электростатические силы воздействуют на заряженные объекты. Количество электронов и протонов в веществе определяет его заряд. Большинство предметов электрически нейтральны, что означает, что они содержат равное количество электронов (имеющих отрицательный заряд) и протонов (имеющих положительный заряд). Однако объекты могут терять электроны и становиться положительно заряженными или поглощать электроны и становиться отрицательно заряженными. В результате положительные и отрицательные заряды будут притягиваться друг к другу. В результате поговорка «противоположности притягиваются» верна.
В результате положительные и отрицательные заряды будут притягиваться друг к другу. В результате поговорка «противоположности притягиваются» верна.
Что такое магнитная сила?
Магнитная сила — третья сила, которая может вызывать притяжение. Объекты с магнитными характеристиками притягиваются магнитной силой. Магнит притягивает богатые железом металлы, такие как сталь, а также никель и кобальт. Когда северный магнитный полюс расположен близко к южному магнитному полюсу, когда объект намагничен, магнитная сила притягивается. Электрические токи являются основным источником магнетизма. При движении зарядов возникает электрический ток. Электрическая сила действует на заряды, которые не движутся, а магнитная сила действует на заряды, которые движутся. Пословицу «Противоположности притягиваются» также можно объяснить магнитным притяжением.
Факторы, влияющие на три силы гравитационного, электрического и магнитного притяжения
Сила гравитации равна произведению масс m1 и m2 и обратно пропорциональна квадрату расстояния между двумя массами, обозначаемому r . Притяжение обратно пропорционально, что означает, что оно сильно, когда массы находятся близко друг к другу, и слабо, когда они далеко друг от друга.
Притяжение обратно пропорционально, что означает, что оно сильно, когда массы находятся близко друг к другу, и слабо, когда они далеко друг от друга.
Сила электрического притяжения пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между зарядами, точно так же, как гравитация. Существует притяжение между положительным и отрицательным зарядами, разделенными расстоянием r.
Сила сильнее, когда заряды находятся близко друг к другу, и слабее, когда заряды дальше друг от друга, как и гравитационная сила.
Атомы металлов отдают электроны атомам неметаллов, когда металлы и неметаллы объединяются в соединения. Из-за потери отрицательно заряженных электронов атомы металлов становятся положительными ионами, тогда как атомы неметаллов становятся отрицательными ионами. Ионы проявляют силы притяжения к ионам с противоположным зарядом, отсюда и поговорка «противоположности притягиваются». Закон Кулона регулирует силу притяжения между противоположно заряженными ионами: F = k * q1 * q2 / d2, где F — сила притяжения в ньютонах, q1 и q2 — заряды двух ионов в кулонах, d — расстояние между ядра двух ионов в метрах, а k – константа пропорциональности 8,9. 9 х 109 Ньютон квадратных метров на квадратный кулон.
9 х 109 Ньютон квадратных метров на квадратный кулон.
Заключение
Формула силы притяжения важна для понимания концепции гравитации, которая действует на Земле. Более того, когда мы вычисляем силу притяжения, это также объясняет явление гравитации, происходящее в космосе.
Формула силы притяжения – GeeksforGeeks
Сила притяжения определяется как сила, которая заставляет два или более объектов сближаться, даже если они не находятся рядом или не касаются друг друга. Это сила, которая притягивает тела ближе друг к другу. Согласно универсальному закону всемирного тяготения Ньютона, каждая масса, существующая в космосе, притягивает другую массу, и все, что брошено вверх, обязательно упадет обратно на землю. Магнитная сила, электрическая сила, электростатическая сила и гравитационная сила являются некоторыми силами притяжения.
Формула силы притяжения
Сила притяжения между любыми двумя телами прямо пропорциональна их массам и обратно пропорциональна расстоянию между ними. Обозначается символом F g . Его единицей измерения является Ньютон (Н), а размерная формула задается как [M 1 L 1 T -2 ]. Его формула равна произведению гравитационной постоянной на отношение произведения масс тел на квадрат расстояния между ними.
Обозначается символом F g . Его единицей измерения является Ньютон (Н), а размерная формула задается как [M 1 L 1 T -2 ]. Его формула равна произведению гравитационной постоянной на отношение произведения масс тел на квадрат расстояния между ними.
F G = GM 1 M 2 /R 2
, где,
- F G – это сила аттракции,
- G G – это сила аттракции,
- G. 6,67 × 10 −11 Н·м 2 /кг 2 ,
- м 1 — масса тела,
- м 2 — масса другого тела,
- м 2 — масса другого тела между двумя телами.
Вывод
Рассмотрим систему из двух тел с массами m 1 и m 2 , разделенных расстоянием r. Известно, что сила притяжения между этими двумя телами прямо пропорциональна произведению масс тел.
F ∝ м 1 м 2 ⇢ (1)
Кроме того, сила косвенно пропорциональна квадрату расстояния между двумя телами. Итак, мы получаем
F ∝ 1/r 2 ⇢ (2)
Из (1) и (2),
F ∝ m 1 m 2 /r 2
0 получаем константу 90,0080,
0 F g = Gm 1 m 2 /r 2
Здесь G известна как гравитационная постоянная.
Отсюда выводится формула силы притяжения между двумя телами.
Примеры задач
Задача 1. Вычислить силу притяжения между двумя телами массами 50 кг и 100 кг, находящимися на расстоянии 20 м друг от друга.
Solution:
m 1 = 50
m 2 = 100
r = 20
Using the formula we get,
F = Gm 1 m 2 / r 2
= (6,67 × 10 −11 × 50 × 100)/(20) 2
= 8,343 × 10 -10 N
Проблема 2: Вычисление. два тела массами 100 кг и 150 кг, находящиеся на расстоянии 80 м.
два тела массами 100 кг и 150 кг, находящиеся на расстоянии 80 м.
Решение:
M 1 = 100
M 2 = 150
R = 80
Используя формулу, которую мы получаем,
F = GM 1 M 2 11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 / R 2
= (6,67 × 10 −11 × 100 × 150)/(80) 2
= 1,5643 × 10 -10 N
Проблема 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: Расчет 3: расчет. два тела массами 200 кг и 170 кг, находящиеся на расстоянии 1000 м.
Solution:
m 1 = 200
m 2 = 170
r = 1000
Using the formula we get,
F = Gm 1 m 2 / r 2
= (6.
67 ×10 −11 × 200 × 170)/(1000) 2
= 2.26 × 10 -12 N
Problem 4: Calculate the mass of the тел, если сила тяжести между ними равна 2,8 × 10 -12 N так, что они имеют равные массы и находятся на расстоянии 120 м друг от друга.
Solution:
F = 2.8 × 10 -12
r = 120
Using the formula we get,
F = Gm 2 /r 2
=> m 2 = FR 2 /G
=> M 2 = (2,8 × 10 -12 × 120 × 120) /(6,67 × 10 -11 )
=> M 2 -11 )
=> M 2 – = 625
=> m = 25 кг
Задача 5. Вычислить массу тел, если сила притяжения между ними равна 1,89 × 10 -11 Н так, что они имеют равные массы и находятся на расстоянии 60 м друг от друга. .
Solution:
F = 1.
89 × 10 -11
r = 60
Using the formula we get,
F = Gm 2 /r 2
=> m 2 = Пт 2 /Г
=> м 2 = (1,89 × 10 -11 × 60 × 60)/(6,67 × 10 −11 )
=> м 2 > м 3 = 1023 900 = 1023 900
Задача 6. Вычислить расстояние между телами массами 16 и 32 кг, если сила тяжести между ними равна 4,2 × 10 -12 Н.
10 -12
м 1 = 16
м 2 = 32
Using the formula we get,
F = Gm 1 m 2 /r 2
=> r 2 = Gm 1 m 2 /F
= > r 2 = (6,67 × 10 −11 × 16 × 32)/(4,2 × 10 -12 )
=> R 2 = 8100
=> R = 90 М
5303080 => r = 90 М 9003
50 => r = 90 М . Задача 7. Вычислить расстояние между телами массами 40 кг и 34 кг, если сила тяжести между ними равна 2,6 × 10 -11 N.
Задача 7. Вычислить расстояние между телами массами 40 кг и 34 кг, если сила тяжести между ними равна 2,6 × 10 -11 N.
Решение:
. Формула мы получаем,
F = GM 1 M 2 /R 2
=> R 2 = GM 1 M 2 /F
=> R 2 = ((F
=> R 2 = ((F
=> R 2 = ( 6,67 × 10 −11 × 40 × 34)/(2,6 × 10 -11 )
=> r 2 = 3600
=> r = 60 м
Притяжение и отталкивание: значения и примеры
Притяжение и отталкивание имеют разные определения. Вы, возможно, уже слышали, что поход на пляж — привлекательная идея для людей летом или что тухлая еда имеет отталкивающий запах. Однако в физике мы используем эти термины для описания поведения неконтактных сил. Знаете ли вы, что пластиковая расческа может притягивать воду? Попробуйте сделать это: возьмите пластиковую расческу и несколько раз проведите ею по волосам. Теперь дайте воде из крана течь тонкой струйкой и попробуйте поднести к ней расческу.
Теперь дайте воде из крана течь тонкой струйкой и попробуйте поднести к ней расческу.
Расческа может притягивать воду после прохождения ею по волосам. StudySmarter Originals
Вы были удивлены? Это происходит потому, что два объекта могут взаимодействовать, не касаясь друг друга, что приводит к тенденции сближаться (притяжение) или удаляться друг от друга (отталкивание). Мы наблюдаем такое поведение в заряженных телах и магнитах. В этой статье мы более подробно рассмотрим, как это работает, чтобы понять, когда электрические и магнитные силы являются притягивающими или отталкивающими, и как мы можем рассчитать электрическую силу.
Значение притяжения и отталкивания в физике
Как мы упоминали ранее в физике, существует особый тип сил, называемых бесконтактными силами.
Бесконтактные силы — это взаимодействия, которые могут влиять на движение тела без необходимости касаться его.
Примеры бесконтактных сил включают гравитационные, электростатические и магнитные силы.
Бесконтактные силы могут быть притягивающими или отталкивающими.
Сила является притягивающей , если взаимодействующие объекты притягивают друг друга, создавая тенденцию сближаться. С другой стороны, сила равна отталкивающий если взаимодействующие объекты отталкивают друг друга.
Гравитация всегда привлекательна. Вот почему независимо от того, где мы находимся, мы чувствуем тягу «вниз» к центру земли. Однако электростатические и магнитные силы могут быть как притягивающими, так и отталкивающими в зависимости от заряда вовлеченных объектов или полюса магнитов.
Притяжение и отталкивание зарядов
Электростатическая сила представляет собой взаимодействие между заряженными частицами.
Есть два типа зарядов: положительный и отрицательный. Если два объекта имеют одинаковый тип заряда, электростатическая сила между ними будет равна отталкивания. Это означает, что если положительно заряженный объект приблизится к другому, они оба будут отталкивать друг друга. То же самое происходит с двумя отрицательно заряженными объектами.
То же самое происходит с двумя отрицательно заряженными объектами.
Объекты с одинаковыми зарядами чувствуют силу отталкивания, StudySmarter Originals
С другой стороны, противоположные заряды притягивают друг друга. Поэтому, когда один положительно заряженный объект находится рядом с отрицательно заряженным объектом, они притягиваются друг к другу, стремясь сблизиться.
Объекты с противоположными зарядами испытывают силу притяжения, StudySmarter Originals
Закон притяжения и отталкивания электростатических сил
В 1785 году Шарль-Огюстен де Кулон измерил величину электростатических сил между заряженными объектами с помощью крутильных весов , которые он изобрел. Он использовал иглу с латунным диском на одном конце и противовесом на другом. Игла была подвешена на волокне, чтобы она могла вращаться. Затем он зарядил металлическую сферу и латунный диск зарядом того же типа и измерил, насколько далеко они отталкивают друг друга, используя шкалу, прикрепленную к внешней части устройства.
.
Кулон использовал градуированные крутильные весы для измерения расстояния, на которое две заряженные частицы отталкивают друг друга, Ален Лериль CC BY-SA 3.0
сила электростатических сил. Эта формула теперь известна как закон Кулона и зависит от заряда объектов и расстояния между ними.
В этой формуле сила измеряется в ньютонах, заряд первого тела в кулонах, аналогично величина заряда второго тела, а расстояние между ними измеряется в метрах. Константа называется константой закона Кулона и зависит от среды, в которой находятся заряженные объекты. Например, если объекты находятся в вакууме, значение приблизительно равно.
Притяжение и отталкивание между магнитами
Магнит — это любой объект или материал, создающий магнитное поле.
Независимо от формы каждый магнит имеет два полюса, называемые северным (N) и южным (S) полюсами. Как и в случае с электрическими зарядами, разные магнитные полюса притягиваются.
Противоположные полюса двух магнитов испытывают силу притяжения, StudySmarter Originals
Кроме того, одинаковые магнитные полюса отталкивают друг друга.
Одинаковые полюса двух магнитов ощущают силу отталкивания, StudySmarter Originals
Земля сама по себе похожа на гигантский магнит, но ее географический северный полюс на самом деле является магнитным южным полюсом. Точно так же географический южный полюс является магнитным северным полюсом. Из-за этого свободно движущийся магнит — например, стрелка компаса — всегда будет выравнивать свой магнитный северный полюс с географическим северным полюсом Земли, а южный полюс магнита — с географическим южным полюсом Земли. Вот почему так называются полюса магнитов.
Магниты работают благодаря магнитным силам, возникающим в атомах, образующих магнитные зоны в материале, которые сами действуют как крошечные магниты. Обычно эти зоны располагаются случайным образом. Однако существует особый тип материала, который называется 9. 0098 ферромагнитный . Они обладают тем свойством, что их магнитные зоны легко выравниваются при воздействии внешнего магнитного поля, и они сохраняют это выравнивание после исчезновения магнитного поля, сами становясь магнитами! Объект, который генерирует магнитное поле благодаря своей внутренней структуре, называется постоянным магнитом .
0098 ферромагнитный . Они обладают тем свойством, что их магнитные зоны легко выравниваются при воздействии внешнего магнитного поля, и они сохраняют это выравнивание после исчезновения магнитного поля, сами становясь магнитами! Объект, который генерирует магнитное поле благодаря своей внутренней структуре, называется постоянным магнитом .
Ферромагнитные материалы сильно притягиваются к магнитам. Некоторыми примерами являются железо, кобальт и никель.
Примеры притяжения и отталкивания
Теперь, когда мы поняли, как работают электростатические и магнитные силы, мы рассмотрим несколько повседневных примеров, где мы можем наблюдать силы притяжения и отталкивания в действии.
Примеры притяжения и отталкивания: Электростатические силы
Отличный и очень распространенный пример включает статическое электричество. Воздушный шар можно зарядить отрицательно, если потереть им волосы. При трении большое количество электронов «перескакивает» с волос на шарик. Это приводит к тому, что волосы заряжаются положительно из-за нехватки электронов, а поскольку шарик получил эти электроны, он теперь заряжен отрицательно.
Это приводит к тому, что волосы заряжаются положительно из-за нехватки электронов, а поскольку шарик получил эти электроны, он теперь заряжен отрицательно.
Воздушный шарик может быть заряжен отрицательно, если потереть его о волосы. StudySmarter Originals
Теперь воздушный шарик притягивается к положительно заряженным волосам. Электрическую силу можно увидеть на расстоянии, когда воздушный шар приближается к волосам – волосы притягиваются к поверхности воздушного шара. И волосы, и воздушный шар притягиваются друг к другу.
Воздушный шар притягивает положительно заряженные волосы, StudySmarter Originals
Точно так же, если два воздушных шарика потереть о волосы, оба они приобретут отрицательный заряд. Если их поставить рядом друг с другом, они отталкивают друг друга.
Два отрицательно заряженных шарика отталкиваются друг от друга, StudySmarter Originals
Как вы могли догадаться, это та же самая причина, по которой расческа притягивает струю воды после того, как вы пропускаете ее через волосы, она получает электростатический заряд!
Примеры притяжения и отталкивания: Силы магнитного поля
Как мы объясняли ранее, вы можете наблюдать притяжение и отталкивание из-за магнитных сил, играя с двумя магнитами. Однако, если у вас есть только один магнит, вы все равно можете увидеть, как он будет притягивать некоторые металлы. В частности, железо, кобальт и никель сильно притягиваются к магнитам, поскольку они ферромагнитный .
Однако, если у вас есть только один магнит, вы все равно можете увидеть, как он будет притягивать некоторые металлы. В частности, железо, кобальт и никель сильно притягиваются к магнитам, поскольку они ферромагнитный .
Магнит притягивает маленькие кусочки ферромагнитного металла, StudySmarter Originals
Магнитное поле может создаваться током, протекающим по проводнику. Это заставит проводник вести себя как магнит. Намотав провод на металлический сердечник и подключив его к батарее, мы создаем электромагнит. Конец, подключенный к положительной клемме батареи, будет действовать как южный полюс магнита, а конец, подключенный к отрицательной клемме, будет вести себя как северный полюс.
Ток, протекающий по проводу, может превратить его в электромагнит. StudySmarter Originals
Притяжение и отталкивание — основные выводы
- Притяжение и отталкивание — это характеристики бесконтактных сил, таких как электростатические и магнитные силы.

- Бесконтактные силы — это взаимодействия, которые могут влиять на движение тела без необходимости касаться его. Примеры бесконтактных сил включают электрические и магнитные силы.
- Объекты, имеющие противоположные заряды, испытывают электростатическую силу притяжения, притягивая их друг к другу.
- На объекты с одинаковым зарядом действует отталкивающая электростатическая сила, отталкивающая их друг от друга.
- На одинаковые полюса двух магнитов действует магнитная сила притяжения, притягивающая их друг к другу.
- На противоположные полюса двух магнитов действует отталкивающая магнитная сила, отталкивающая их друг от друга.
- Закон Кулона гласит, что сила, действующая между двумя заряженными объектами, будь то сила притяжения или отталкивания, может определяться зарядом обоих объектов, расстоянием между ними и средой, в которой находятся заряды.
Силы притяжения
Электростатические силы притяжения
Электростатические силы притяжения ответственны за удерживание ионов с сильными силами, создающими
стабильная молекула. Линии сил притяжения можно увидеть между объединяющимися атомами.
Линии сил притяжения можно увидеть между объединяющимися атомами.
Молекулы и движение: Кредит косвенно наблюдение за существованием молекул впервые принадлежит Роберту Брауну, шотландский ботаник.
В 1827 году Браун наблюдал под микроскопом
что пыльцевые зерна размером 10,5 мкм в подвешенном состоянии
в воде, по-видимому, совершали беспорядочные движения. Этот тип случайного
движение частиц называется броуновским движением. Зигзагообразное движение
малых частиц можно увидеть в нашей повседневной жизни Эйнштейн разработал
теорию броуновского движения в 1905 году. Он объяснил, что случайное движение
пыльцевых зерен в воде было обусловлено движением самих частиц воды.
Далее, хотя было известно, что материя состоит из молекул,
открытие броуновского движения и его объяснение Эйнштейном
дал первое прямое свидетельство присутствия малых физических частиц,
молекулы, совершающие хаотическое движение.
Атомы объединяются в молекулы. Три атома водорода (H) объединяются
с одним атомом азота (N) для получения молекулы аммиака (NH 3 ).
Силы притяжения В природе существуют два типа сил. Внутримолекулярные силы сильны по сравнению с межмолекулярными силы из-за влияния нескольких сил, действующих между ними.
Силы притяжения:
При сближении двух атомов и расстоянии между ними
становится сравнимой с их размерностью, положительной и отрицательной
заряды каждого атома начинают влиять на заряды другого атома. Этот
вызывает межатомную силу и изменяет полную энергию пары.
Подобный механизм также приводит к межмолекулярному взаимодействию.
Зная размер и количество атомов и молекул, следующий естественный
любопытство заключается в том, как они взаимодействуют друг с другом.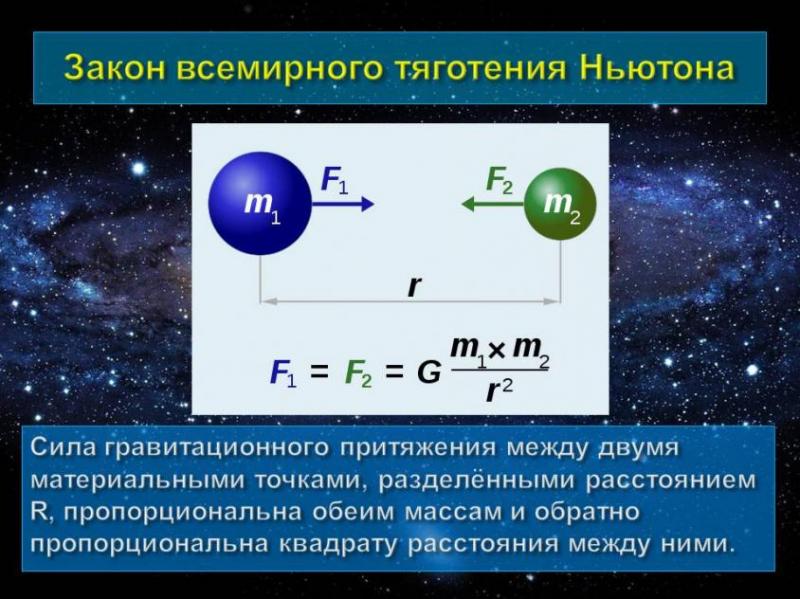 Ясно, что взаимодействие
между молекулами определяет свойства материи.
Ясно, что взаимодействие
между молекулами определяет свойства материи.
В молекуле NaCl атом Na отдает электрон к атому Cl с образованием ионной связи. Когда большие расстояния отдельные атомы Na и Cl переноса электрона нет. Когда Атомы Na и Cl находятся на расстоянии около 2,8 Å, перенос электрона происходит. Это расстояние является длиной связи атома NaCl.
Различные формы молекул из-за различий в валентных углах
Помимо того, что молекулы имеют конечные размеры, также имеют определенные формы.
- Молекула воды имеет такие валентные углы что молекула имеет атом кислорода в центре с двумя водородные связи под углом около 104,28°.
- Молекула аммиака (NH 3 ) имеет тетраэдрическую форму.

- CO или CO 2 молекула имеет линейную форму.
- Углеводороды, такие как молекула сахарозы или полиэтилен молекулы представляют собой молекулы с длинной цепью.
Форма определяется минимальной энергетическая конфигурация атомов, составляющих молекулу. Большие молекулы, такие как углеводороды, также проявляют что длины связей и направления связей определяют их форма. Таким образом, минимальная потенциальная энергия зависит от длина связи, ориентация связей и размер молекулы.
Межмолекулярные силы
Межмолекулярные силы между молекулами будут очень слабыми по сравнению с силами внутри
молекула. Связь между двумя молекулами кислорода разорвать легче, чем между двумя атомами кислорода, так как силы
притяжение прямо пропорционально 1/r 6 .
Связь между двумя молекулами кислорода разорвать легче, чем между двумя атомами кислорода, так как силы
притяжение прямо пропорционально 1/r 6 .
Молекулярные силы — силы притяжения или отталкивания, которые действуют между соседними частицами, т.е. атомы, молекулы или ионы. Эти силы слабы по сравнению внутриатомным силам, существующим в ядре, которые отвечают за сохранение молекулы вместе.
Эти силы можно разделить на 2 типа:
- Внутримолекулярные силы: Внутримолекулярные силы Сила притяжения – это силы притяжения, удерживающие молекула вместе.
- Межмолекулярные силы: Межмолекулярные силы
силы – это силы притяжения или отталкивания, действующие
между соседними частицами (атомами, молекулами или ионами).

ПОДРОБНЕЕ
Межмолекулярные силы – Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1228
- Уильям Ройш
- Университет штата Мичиган
Молекула — это наименьшая наблюдаемая группа атомов с уникальными связями, которые представляют собой состав, конфигурацию и характеристики чистого соединения. До сих пор наша главная цель заключалась в том, чтобы открыть и описать способы, которыми атомы соединяются друг с другом, образуя молекулы. Поскольку все наблюдаемые образцы соединений и смесей содержат очень большое число молекул (~10 20 ), мы должны также заняться взаимодействием между молекулами, а также их отдельными структурами. Действительно, многие физические характеристики соединений, которые используются для их идентификации (например, точки кипения, температуры плавления и растворимости), обусловлены межмолекулярными взаимодействиями.
Действительно, многие физические характеристики соединений, которые используются для их идентификации (например, точки кипения, температуры плавления и растворимости), обусловлены межмолекулярными взаимодействиями.
Все атомы и молекулы имеют слабое притяжение друг к другу, известное как притяжение Ван-дер-Ваальса . Эта сила притяжения берет свое начало в электростатическом притяжении электронов одной молекулы или атома к ядрам другой. Если бы не было сил Ван-дер-Ваальса, вся материя существовала бы в газообразном состоянии, и жизнь, какой мы ее знаем, была бы невозможна. Следует отметить, что существуют и меньшие силы отталкивания между молекулами, которые быстро возрастают на очень малых межмолекулярных расстояниях.
Точки кипения
Для общих целей полезно рассматривать температуру как меру кинетической энергии всех атомов и молекул в данной системе. С повышением температуры соответственно возрастает сила поступательных и вращательных движений всех молекул, а также колебаний атомов и групп атомов внутри молекул. Опыт показывает, что многие соединения обычно существуют в виде жидкостей и твердых веществ; и что даже газы с низкой плотностью, такие как водород и гелий, могут быть сжижены при достаточно низкой температуре и высоком давлении. Из этого следует четкий вывод, что силы межмолекулярного притяжения значительно различаются и что точка кипения соединения является мерой силы этих сил. Таким образом, чтобы разрушить межмолекулярные притяжения, удерживающие молекулы соединения в конденсированном жидком состоянии, необходимо увеличить их кинетическую энергию за счет повышения температуры образца до характерной температуры кипения соединения.
Опыт показывает, что многие соединения обычно существуют в виде жидкостей и твердых веществ; и что даже газы с низкой плотностью, такие как водород и гелий, могут быть сжижены при достаточно низкой температуре и высоком давлении. Из этого следует четкий вывод, что силы межмолекулярного притяжения значительно различаются и что точка кипения соединения является мерой силы этих сил. Таким образом, чтобы разрушить межмолекулярные притяжения, удерживающие молекулы соединения в конденсированном жидком состоянии, необходимо увеличить их кинетическую энергию за счет повышения температуры образца до характерной температуры кипения соединения.
В следующей таблице показаны некоторые факторы, влияющие на силу межмолекулярного притяжения. За формулой каждой записи следует ее формульный вес в скобках и температура кипения в градусах Цельсия. Во-первых, это молекулярный размер. Большие молекулы имеют больше электронов и ядер, которые создают силы притяжения Ван-дер-Ваальса, поэтому их соединения обычно имеют более высокие температуры кипения, чем подобных соединений, состоящих из более мелких молекул. Очень важно применять это правило только к однородным соединениям. Примеры, приведенные в первых двух строках, схожи тем, что молекулы или атомы имеют сферическую форму и не имеют постоянных диполей. Молекулярная форма также важна, как показывает вторая группа соединений. Верхний ряд состоит из молекул примерно сферической формы, тогда как изомеры в нижнем ряду имеют молекулы цилиндрической или линейной формы. Силы притяжения между последней группой обычно больше. Наконец, постоянные молекулярные диполи, образованные полярными ковалентными связями, приводят к еще большим силам притяжения между молекулами, при условии, что они обладают подвижностью для выстраивания в соответствующие ориентации. Последние записи в таблице сравнивают неполярные углеводороды с соединениями одинакового размера, имеющими полярные связи с кислородом и азотом. Галогены также образуют полярные связи с углеродом, но они также увеличивают молекулярную массу, что затрудняет различение этих факторов.
Очень важно применять это правило только к однородным соединениям. Примеры, приведенные в первых двух строках, схожи тем, что молекулы или атомы имеют сферическую форму и не имеют постоянных диполей. Молекулярная форма также важна, как показывает вторая группа соединений. Верхний ряд состоит из молекул примерно сферической формы, тогда как изомеры в нижнем ряду имеют молекулы цилиндрической или линейной формы. Силы притяжения между последней группой обычно больше. Наконец, постоянные молекулярные диполи, образованные полярными ковалентными связями, приводят к еще большим силам притяжения между молекулами, при условии, что они обладают подвижностью для выстраивания в соответствующие ориентации. Последние записи в таблице сравнивают неполярные углеводороды с соединениями одинакового размера, имеющими полярные связи с кислородом и азотом. Галогены также образуют полярные связи с углеродом, но они также увеличивают молекулярную массу, что затрудняет различение этих факторов.
Увеличение размера | ||||
| Атомный | Ар (40)-186 | Кр (83)-153 | Хе (131) -109 | |
| Молекулярный | СН 4 (16) -161 | (СН 3 ) 4 С (72) 9,5 | (CH 3 ) 4 Si (88) 27 | ККл 4 (154) 77 |
Молекулярная форма | ||||
| Сферический: | (СН 3 ) 4 С (72) 9,5 | (CH 3 ) 2 CCl 2 (113) 69 | (CH 3 ) 3 CC(CH 3 ) 3 (114) 106 | |
| Линейный: | CH 3 (CH 2 ) 3 CH 3 (72) 36 | Cl(CH 2 ) 3 Cl (113) 121 | CH 3 (CH 2 ) 6 CH 3 (114) 126 | |
Молекулярная полярность | ||||
| Неполярный: | H 2 C=CH 2 (28) -104 | Ф 2 (38) -188 | CH 3 C≡CCH 3 (54) -32 | ЦФ 4 (88) -130 |
| Полярный: | Н 2 С=О (30) -21 | CH 3 CH=O (44) 20 | (CH 3 ) 3 N (59) 3,5 | (СН 3 ) 2 С=О (58) 56 |
| HC≡N (27) 26 | CH 3 C≡N (41) 82 | (СН 2 ) 3 О (58) 50 | CH 3 NO 2 (61) 101 | |
Температуры плавления кристаллических твердых тел нельзя классифицировать так же просто, как точки кипения. Расстояние между молекулами в кристаллической решетке небольшое и регулярное, а межмолекулярные силы ограничивают движение молекул сильнее, чем в жидком состоянии. Молекулярный размер важен, но форма также имеет решающее значение, поскольку отдельные молекулы должны совместно подходить друг к другу, чтобы силы притяжения в решетке были большими. Молекулы сферической формы обычно имеют относительно высокие температуры плавления, которые в некоторых случаях приближаются к температуре кипения. Это отражает тот факт, что сферы могут собираться вместе более плотно, чем другие формы. Эта чувствительность к структуре или форме является одной из причин того, что точки плавления широко используются для идентификации конкретных соединений. Данные в следующей таблице служат для иллюстрации этих моментов.
Расстояние между молекулами в кристаллической решетке небольшое и регулярное, а межмолекулярные силы ограничивают движение молекул сильнее, чем в жидком состоянии. Молекулярный размер важен, но форма также имеет решающее значение, поскольку отдельные молекулы должны совместно подходить друг к другу, чтобы силы притяжения в решетке были большими. Молекулы сферической формы обычно имеют относительно высокие температуры плавления, которые в некоторых случаях приближаются к температуре кипения. Это отражает тот факт, что сферы могут собираться вместе более плотно, чем другие формы. Эта чувствительность к структуре или форме является одной из причин того, что точки плавления широко используются для идентификации конкретных соединений. Данные в следующей таблице служат для иллюстрации этих моментов.
| Соединение | Формула | Точка кипения | Точка плавления |
|---|---|---|---|
| пентан | CH 3 (CH 2 ) 3 CH 3 | 36ºC | –130ºC |
| гексан | CH 3 (CH 2 ) 4 CH 3 | 69ºC | –95ºC |
| гептан | CH 3 (CH 2 ) 5 CH 3 | 98ºC | –91ºC |
| октановое число | CH 3 (CH 2 ) 6 CH 3 | 126ºC | –57ºC |
| нонан | CH 3 (CH 2 ) 7 CH 3 | 151ºC | –54ºC |
| декан | CH 3 (CH 2 ) 8 CH 3 | 174ºC | –30ºC |
| тетраметилбутан | (CH 3 ) 3 C-C(CH 3 ) 3 | 106ºC | +100ºC |
Обратите внимание, что температуры кипения неразветвленных алканов (от пентана до декана) довольно плавно увеличиваются с увеличением молекулярной массы, но температуры плавления четных углеродных цепей увеличиваются больше, чем температуры плавления нечетных углеродных цепей. Цепи с четными звеньями упаковываются однородно более компактно, чем цепи с нечетными звеньями. Последнее соединение, изомер октана, имеет почти сферическую форму и исключительно высокую температуру плавления (всего на 6º ниже точки кипения).
Цепи с четными звеньями упаковываются однородно более компактно, чем цепи с нечетными звеньями. Последнее соединение, изомер октана, имеет почти сферическую форму и исключительно высокую температуру плавления (всего на 6º ниже точки кипения).
Водородная связь
Наиболее мощной межмолекулярной силой, влияющей на нейтральные (незаряженные) молекулы, является водородная связь . Если мы сравним точки кипения метана (CH 4 ) -161ºC, аммиака (NH 3 ) -33ºC, воды (H 2 O) 100ºC и фтористого водорода (HF) 19ºC, мы увидим больший разброс для эти молекулы аналогичного размера, чем ожидалось из данных, представленных выше для полярных соединений. Это показано графически на следующей диаграмме. Большинство простых гидридов элементов групп IV, V, VI и VII демонстрируют ожидаемое повышение температуры кипения с увеличением молекулярной массы, но гидриды наиболее электроотрицательных элементов (азота, кислорода и фтора) имеют аномально высокие температуры кипения для своей массы.
Исключительно сильное диполь-дипольное притяжение, вызывающее такое поведение, называется водородной связью . Водород образует полярные ковалентные связи с более электроотрицательными атомами, такими как кислород, и, поскольку атом водорода довольно мал, положительный конец диполя связи (водород) может приближаться к соседним нуклеофильным или основным центрам ближе, чем другие полярные связи. Кулоновские силы обратно пропорциональны шестой степени расстояния между диполями, что делает эти взаимодействия относительно сильными, хотя и слабыми (9).0764 ок. от 4 до 5 ккал на моль) по сравнению с большинством ковалентных связей. Уникальные свойства воды во многом обусловлены прочными водородными связями, возникающими между ее молекулами. На следующей диаграмме водородные связи изображены пурпурными пунктирными линиями.
Молекула, обеспечивающая полярный водород для водородной связи, называется донором . Молекула, которая обеспечивает богатый электронами участок, к которому притягивается водород, называется акцептором 9.0107 . Вода и спирты могут служить как донорами, так и акцепторами, тогда как простые эфиры, альдегиды, кетоны и сложные эфиры могут действовать только как акцепторы. Точно так же первичные и вторичные амины являются как донорами, так и акцепторами, а третичные амины функционируют только как акцепторы. Как только вы научитесь распознавать соединения, которые могут образовывать межмолекулярные водородные связи, станет понятным их относительно высокая температура кипения. Данные в следующей таблице иллюстрируют этот момент.
Молекула, которая обеспечивает богатый электронами участок, к которому притягивается водород, называется акцептором 9.0107 . Вода и спирты могут служить как донорами, так и акцепторами, тогда как простые эфиры, альдегиды, кетоны и сложные эфиры могут действовать только как акцепторы. Точно так же первичные и вторичные амины являются как донорами, так и акцепторами, а третичные амины функционируют только как акцепторы. Как только вы научитесь распознавать соединения, которые могут образовывать межмолекулярные водородные связи, станет понятным их относительно высокая температура кипения. Данные в следующей таблице иллюстрируют этот момент.
| Соединение | Формула | Мол. Вес. | Точка кипения | Точка плавления |
|---|---|---|---|---|
| диметиловый эфир | СН 3 ОСН 3 | Wt.”> 46 | –24ºC | –138ºC |
| этанол | CH 3 CH 2 ОН | 46 | 78ºC | –130ºC |
| пропанол | СН 3 (СН 2 ) 2 ОН | 60 | 98ºC | –127°С |
| диэтиловый эфир | (CH 3 CH 2 ) 2 О | 74 | 34ºC | –116ºC |
| пропиламин | CH 3 (CH 2 ) 2 NH 2 | Wt.”> 59 | 48ºC | –83ºC |
| метиламиноэтан | CH 3 CH 2 NHCH 3 | 59 | 37ºC | |
| триметиламин | (CH 3 ) 3 N | 59 | 3ºC | –117°С |
| этиленгликоль | HOCH 2 CH 2 OH | 62 | 197ºC | –13ºC |
| уксусная кислота | CH 3 CO 2 H | Wt.”> 60 | 118ºC | 17ºC |
| этилендиамин | H 2 NCH 2 CH 2 NH 2 | 60 | 118ºC | 8,5ºC |
Спирты кипят значительно выше, чем сравнимые по размеру простые эфиры (первые две позиции), а изомерные 1º, 2º и 3º-амины, соответственно, демонстрируют пониженные температуры кипения, причем два изомера с водородной связью имеют значительно более высокую температуру кипения, чем 3º- амин (записи с 5 по 7). Кроме того, водородные связи O-H—O явно прочнее, чем водородные связи N-H—N, как мы видим, сравнивая пропанол с аминами. Как и ожидалось, наличие двух функций водородной связи в соединении еще больше повышает температуру кипения.
Уксусная кислота (девятая запись) — интересный случай. Показанные выше димеры, удерживаемые вместе двумя водородными связями, являются основным компонентом жидкого состояния. Если это точное представление состава этого соединения, то можно ожидать, что его точка кипения будет эквивалентна температуре кипения соединения C 4 H 8 O 4 (масса формулы = 120). Подходящим приближением такого соединения является тетраметоксиметан (CH 3 O) 4 C, что на самом деле немного больше (масса формулы = 136) и имеет температуру кипения 114ºC. Таким образом, димерная структура с водородными связями, по-видимому, является хорошим представлением уксусной кислоты в конденсированном состоянии.
В этом месте стоит отметить родственный принцип. Хотя водородная связь относительно слабая ( ок. от 4 до 5 ккал на моль), когда существует несколько таких связей, результирующая структура может быть довольно прочной. Водородные связи между волокнами целлюлозы придают большую прочность древесине и связанным с ней материалам.
Свойства кристаллических твердых тел
Точки плавления
Большинство органических соединений имеют температуру плавления ниже 200 ºC. Некоторые разлагаются перед плавлением, некоторые возгоняются, но большинство подвергается многократному плавлению и кристаллизации без изменения молекулярной структуры. При нагревании чистого кристаллического соединения или охлаждении жидкости изменение температуры образца во времени примерно однородно. Однако, если твердое тело плавится или жидкость замерзает, возникает разрыв, и температура образца остается постоянной до тех пор, пока не завершится фазовый переход. Это поведение показано на диаграмме справа, где зеленый сегмент представляет твердую фазу, светло-синий – жидкость, а красный – температурно-инвариантное равновесие жидкость/твердое тело. Для данного соединения эта температура представляет его точку плавления (или точку замерзания) и является воспроизводимой константой до тех пор, пока внешнее давление не меняется. Длина горизонтального участка зависит от размера образца, так как количество тепла, пропорциональное теплоте плавления, должно быть добавлено (или удалено) до завершения фазового перехода
Длина горизонтального участка зависит от размера образца, так как количество тепла, пропорциональное теплоте плавления, должно быть добавлено (или удалено) до завершения фазового перехода
Теперь хорошо известно, что точка замерзания растворителя понижается растворенным веществом, т.е. рассола по сравнению с водой. Если два кристаллических соединения (А и В) тщательно смешать, температура плавления этой смеси обычно снижается и расширяется по сравнению с характерной резкой точкой плавления каждого чистого компонента. Это обеспечивает полезные средства для установления идентичности или неидентичности двух или более соединений, поскольку точки плавления многих твердых органических соединений задокументированы и обычно используются в качестве критерия чистоты.
На приведенной ниже фазовой диаграмме показано изменение температуры плавления смесей в диапазоне от чистого A слева до чистого B справа. Небольшое количество соединения B в образце соединения A снижает (и расширяет) его температуру плавления; и то же верно для образца В, содержащего немного А. Самая низкая точка плавления смеси, е, называется эвтектической точкой . Например, если А представляет собой коричную кислоту, т.пл. 137 ºC, B – бензойная кислота, т.пл. 122 ºC, точка эвтектики 82 ºC.
Самая низкая точка плавления смеси, е, называется эвтектической точкой . Например, если А представляет собой коричную кислоту, т.пл. 137 ºC, B – бензойная кислота, т.пл. 122 ºC, точка эвтектики 82 ºC.
Ниже температуры изотермической линии ced смесь полностью твердая, состоящая из конгломерата твердого вещества A и твердого вещества B. Выше этой температуры смесь представляет собой либо жидкость, либо жидкую твердую смесь, состав который варьируется. В некоторых редких случаях из неполярных соединений сходного размера и кристаллической структуры образуется не конгломерат, а настоящий твердый раствор одного в другом. Плавление или замерзание происходит в широком диапазоне температур, и истинной точки эвтектики не существует.
Интересная, но менее распространенная смешанная система включает молекулярные компоненты, образующие плотный комплекс или молекулярное соединение , способное существовать в виде дискретных частиц в равновесии с жидкостью того же состава. Такой вид обычно имеет резко конгруэнтную температуру плавления и дает фазовую диаграмму, имеющую вид двух соседних эвтектических диаграмм. Пример такой системы показан справа, молекулярное соединение представлено как 9.0098 A:B или C . Одна такая смесь состоит из α-нафтола, т.пл. 94 ºC, и п-толуидин, т.пл. 43 ºС. Комплекс A:B имеет температуру плавления 54 ºC, а на фазовой диаграмме показаны две точки эвтектики, первая при 50 ºC, вторая при 30 ºC. Как показано, молекулярные комплексы такого типа обычно имеют стехиометрию 50:50, но известны и другие интегральные соотношения.
Такой вид обычно имеет резко конгруэнтную температуру плавления и дает фазовую диаграмму, имеющую вид двух соседних эвтектических диаграмм. Пример такой системы показан справа, молекулярное соединение представлено как 9.0098 A:B или C . Одна такая смесь состоит из α-нафтола, т.пл. 94 ºC, и п-толуидин, т.пл. 43 ºС. Комплекс A:B имеет температуру плавления 54 ºC, а на фазовой диаграмме показаны две точки эвтектики, первая при 50 ºC, вторая при 30 ºC. Как показано, молекулярные комплексы такого типа обычно имеют стехиометрию 50:50, но известны и другие интегральные соотношения.
В дополнение к потенциальным осложнениям, отмеченным выше, на простой процесс определения точки плавления также могут влиять изменения в кристаллической структуре до или после первоначального плавления. Существование более чем одной кристаллической формы для данного соединения называется полиморфизмом.
Полиморфизм
Полиморфы соединения представляют собой различные кристаллические формы, в которых расположение молекул в решетке отличается. Эти различные твердые вещества обычно имеют разные температуры плавления, растворимости, плотности и оптические свойства. Многие полиморфные соединения имеют гибкие молекулы, которые могут принимать различные конформации, и рентгенологическое исследование этих твердых тел показывает, что их кристаллические решетки налагают определенные конформационные ограничения. В расплавленном состоянии или в растворе различные полиморфные кристаллы такого типа образуют одну и ту же быстро уравновешивающуюся смесь молекулярных частиц. Полиморфизм похож на гидратированные или сольватированные кристаллические формы, но отличается от них. Было подсчитано, что более 50% известных органических соединений способны к полиморфизму.
Эти различные твердые вещества обычно имеют разные температуры плавления, растворимости, плотности и оптические свойства. Многие полиморфные соединения имеют гибкие молекулы, которые могут принимать различные конформации, и рентгенологическое исследование этих твердых тел показывает, что их кристаллические решетки налагают определенные конформационные ограничения. В расплавленном состоянии или в растворе различные полиморфные кристаллы такого типа образуют одну и ту же быстро уравновешивающуюся смесь молекулярных частиц. Полиморфизм похож на гидратированные или сольватированные кристаллические формы, но отличается от них. Было подсчитано, что более 50% известных органических соединений способны к полиморфизму.
Тетраацетат рибофуранозы, показанный в верхнем левом углу ниже, был источником ранней загадки, связанной с полиморфизмом. Соединение было впервые получено в Англии в 1946 году и имело температуру плавления 58 ºC. Несколько лет спустя тот же материал, имеющий ту же температуру плавления, был получен независимо друг от друга в Германии и США. Затем американские химики обнаружили, что температура плавления их первых препаратов повысилась до 85 ºC. В конце концов, стало очевидно, что любая лаборатория, в которой была введена форма с более высокой температурой плавления, больше не могла производить форму с более низкой температурой плавления. Микроскопические зародыши стабильного полиморфа в окружающей среде неизбежно направляют кристаллизацию в эту сторону. Данные рентгеновской дифракции показали, что низкоплавкий полиморф является моноклинным, пространственная группа P2. Форма с более высокой температурой плавления была орторомбической, пространственная группа P2 1 2 1 2 1 .
Затем американские химики обнаружили, что температура плавления их первых препаратов повысилась до 85 ºC. В конце концов, стало очевидно, что любая лаборатория, в которой была введена форма с более высокой температурой плавления, больше не могла производить форму с более низкой температурой плавления. Микроскопические зародыши стабильного полиморфа в окружающей среде неизбежно направляют кристаллизацию в эту сторону. Данные рентгеновской дифракции показали, что низкоплавкий полиморф является моноклинным, пространственная группа P2. Форма с более высокой температурой плавления была орторомбической, пространственная группа P2 1 2 1 2 1 .
Полиморфизм оказался решающим фактором в производстве фармацевтических препаратов, твердых пигментов и полимеров. Некоторые примеры описаны ниже.
Пример 1: Ацетаминофен
Ацетаминофен — распространенный анальгетик (например, тайленол).
Обычно получают в виде моноклинных призм (справа)) при кристаллизации из воды. Слева показан менее стабильный орторомбический полиморф, обладающий лучшими физическими свойствами для прессования в таблетки.
Слева показан менее стабильный орторомбический полиморф, обладающий лучшими физическими свойствами для прессования в таблетки.
Два полиморфа ацетаминофена.
Пример 2: хинакридон
хинакридон является важным пигментом, используемым в красках и чернилах. Он имеет жесткую плоскую молекулярную структуру, а в разбавленном растворе имеет светло-желтый цвет. Были идентифицированы три полиморфа. Межмолекулярные водородные связи являются важной особенностью всего этого. Цвета кристаллов варьируются от ярко-красного до фиолетового.
Пример 3: Ранитидин
Противоязвенный препарат ранитидин (Зантак) был впервые запатентован компанией Glaxo-Wellcome в 1978. Спустя семь лет той же компанией был запатентован второй полиморф ранитидина. Это продлило срок действия лицензии до 2002 г., а усилия по маркетингу генерической формы были сорваны, поскольку было невозможно приготовить первый полиморф, не загрязненный вторым.
Пример 4: EL1
Относительно простой арилтиофен, обозначенный EL1, был получен и изучен химиками компании Eli Lilly. Он показал шесть полиморфных кристаллических форм.
Он показал шесть полиморфных кристаллических форм.
| Полиморф | Цвет/Форма | Космическая группа | Температура плавления |
| Я | желтые призмы | моноклинный P2 1 /n[14] | 110 °С |
| II | красноватые пластины | моноклинный P2 1 /n[14] | 113 °С |
| III | оранжевые иглы | моноклинный P2 1 /c[14] | 115 °С |
| IV | желтые иглы | триклинная P1[2] | переставляет в VI |
| В | оранжевые тарелки | орторомбическая Pbca[61] | переставляет в I |
| VI | красные призмы | триклинная P1[2] | 106 °С |
Типичным примером изменения полиморфизма является шоколад, подвергшийся нагреванию и/или длительному хранению. Со временем или когда он сбрасывается после размягчения, на нем могут появиться белые пятна, он больше не тает во рту и не имеет такого хорошего вкуса, как должен. Это связано с тем, что шоколад имеет более шести полиморфов, и только один из них идеален в качестве кондитерского изделия. Он создается в тщательно контролируемых заводских условиях. Неправильные условия хранения или транспортировки приводят к превращению шоколада в другие полиморфы.
Со временем или когда он сбрасывается после размягчения, на нем могут появиться белые пятна, он больше не тает во рту и не имеет такого хорошего вкуса, как должен. Это связано с тем, что шоколад имеет более шести полиморфов, и только один из них идеален в качестве кондитерского изделия. Он создается в тщательно контролируемых заводских условиях. Неправильные условия хранения или транспортировки приводят к превращению шоколада в другие полиморфы.
Шоколад по сути представляет собой какао-массу и частицы сахара, взвешенные в матрице какао-масла. Какао-масло представляет собой смесь триглицеридов, в которой преобладают стеароильные, олеоильные и пальмитоильные группы. Именно полиморфы этой матрицы влияют на качество шоколада. Полиморфы с низкой температурой плавления кажутся слишком липкими или густыми во рту. Форма V, полиморф какао-масла с лучшим вкусом, имеет температуру плавления от 34 до 36 ºC, что немного ниже, чем у внутренней части человеческого тела, что является одной из причин, по которой оно тает во рту. К сожалению, форма VI с более высокой температурой плавления более стабильна и образуется с течением времени.
К сожалению, форма VI с более высокой температурой плавления более стабильна и образуется с течением времени.
| Полиморф | Точка плавления | Комментарии |
|---|---|---|
| я | 17,4 °С | Производится путем быстрого охлаждения расплава. |
| II | 23,4 °С | Производится путем охлаждения расплава со скоростью 2 ºC/мин. |
| III | 26 ºC | Получают превращением формы II при 5-10 ºC. |
| IV | 27 ºC | Получают превращением формы III при хранении при 16-21 ºС. |
| В | 34 °С | Производится путем закалки (охлаждение с последующим легким нагревом при перемешивании). |
| VI | 36–37 °С | Производится из Ви после 4 месяцев хранения при комнатной температуре. |
Растворимость в воде
Воду называют «универсальным растворителем», и ее широкое распространение на этой планете и важная роль в жизни делают ее эталоном для дискуссий о растворимости. Вода растворяет многие ионные соли благодаря своей высокой диэлектрической проницаемости и способности сольватировать ионы. Первый уменьшает притяжение между противоположно заряженными ионами, а второй стабилизирует ионы, связываясь с ними и делокализуя плотность заряда. Многие органические соединения, особенно алканы и другие углеводороды, практически нерастворимы в воде. Органические соединения, растворимые в воде, такие как большинство перечисленных в таблице выше, обычно имеют акцепторные и донорные группы водородной связи. Наименее растворимым из перечисленных соединений является диэтиловый эфир, который может служить только акцептором водородной связи и на 75% состоит из углеводородов. Тем не менее, диэтиловый эфир примерно в двести раз более растворим в воде, чем пентан.
Органические соединения, растворимые в воде, такие как большинство перечисленных в таблице выше, обычно имеют акцепторные и донорные группы водородной связи. Наименее растворимым из перечисленных соединений является диэтиловый эфир, который может служить только акцептором водородной связи и на 75% состоит из углеводородов. Тем не менее, диэтиловый эфир примерно в двести раз более растворим в воде, чем пентан.
Главной характеристикой воды, которая влияет на эту растворимость, является обширная ассоциация ее молекул друг с другом посредством водородных связей. Эта сеть с водородными связями стабилизируется суммой всех энергий водородных связей, и если бы неполярные молекулы, такие как гексан, были вставлены в сеть, они разрушили бы локальную структуру, не внося никаких собственных водородных связей. Конечно, молекулы гексана испытывают значительное ван-дер-ваальсово притяжение к соседним молекулам, но эти силы притяжения гораздо слабее, чем водородная связь. Следовательно, когда гексан или другие неполярные соединения смешиваются с водой, сильные ассоциативные силы водной сети исключают неполярные молекулы, которые должны существовать в отдельной фазе. Это показано на следующем рисунке, и, поскольку гексан менее плотный, чем вода, гексановая фаза плавает на водной фазе.
Это показано на следующем рисунке, и, поскольку гексан менее плотный, чем вода, гексановая фаза плавает на водной фазе.
Важно помнить об этой тенденции воды исключать неполярные молекулы и группы, поскольку она является фактором структуры и поведения многих сложных молекулярных систем. Обычная номенклатура, используемая для описания молекул и областей внутри молекул, представляет собой гидрофильных для полярных групп с водородными связями и гидрофобных для неполярных частиц.
Межмолекулярные силы и физические свойства
Силы притяжения, существующие между молекулами, ответственны за многие объемные физические свойства, проявляемые веществами. Одни соединения представляют собой газы, другие – жидкости, третьи – твердые вещества. Температуры плавления и кипения чистых веществ отражают эти межмолекулярные силы и обычно используются для идентификации. Из этих двух точка кипения считается наиболее репрезентативной мерой общего межмолекулярного притяжения. Таким образом, точка плавления отражает тепловую энергию, необходимую для преобразования высокоупорядоченного набора молекул в кристаллической решетке в хаотичность жидкости. Расстояние между молекулами в кристаллической решетке небольшое и регулярное, а межмолекулярные силы ограничивают движение молекул сильнее, чем в жидком состоянии. Молекулярный размер важен, но форма также имеет решающее значение, поскольку отдельные молекулы должны совместно подходить друг к другу, чтобы силы притяжения в решетке были большими. Молекулы сферической формы обычно имеют относительно высокие температуры плавления, которые в некоторых случаях приближаются к температуре кипения, что отражает тот факт, что сферы могут упаковываться друг в друга более плотно, чем другие формы. Эта чувствительность к структуре или форме является одной из причин того, что точки плавления широко используются для идентификации конкретных соединений.
Таким образом, точка плавления отражает тепловую энергию, необходимую для преобразования высокоупорядоченного набора молекул в кристаллической решетке в хаотичность жидкости. Расстояние между молекулами в кристаллической решетке небольшое и регулярное, а межмолекулярные силы ограничивают движение молекул сильнее, чем в жидком состоянии. Молекулярный размер важен, но форма также имеет решающее значение, поскольку отдельные молекулы должны совместно подходить друг к другу, чтобы силы притяжения в решетке были большими. Молекулы сферической формы обычно имеют относительно высокие температуры плавления, которые в некоторых случаях приближаются к температуре кипения, что отражает тот факт, что сферы могут упаковываться друг в друга более плотно, чем другие формы. Эта чувствительность к структуре или форме является одной из причин того, что точки плавления широко используются для идентификации конкретных соединений.
Температуры кипения, с другой стороны, по существу отражают кинетическую энергию, необходимую для высвобождения молекулы из-под кооперативного притяжения жидкого состояния, чтобы она стала свободной и относительно независимой частицей в газообразном состоянии. Все атомы и молекулы имеют слабое притяжение друг к другу, известное как притяжение Ван-дер-Ваальса. Эта сила притяжения берет свое начало в электростатическом притяжении электронов одной молекулы или атома к ядрам другой и получила название лондонской дисперсионной силы.
Все атомы и молекулы имеют слабое притяжение друг к другу, известное как притяжение Ван-дер-Ваальса. Эта сила притяжения берет свое начало в электростатическом притяжении электронов одной молекулы или атома к ядрам другой и получила название лондонской дисперсионной силы.
Следующая анимация иллюстрирует, как близкое сближение двух атомов неона может нарушить распределение их электронов таким образом, что это вызовет дипольное притяжение. Индуцированные диполи являются временными, но их достаточно для сжижения неона при низкой температуре и высоком давлении.
Как правило, более крупные молекулы имеют более высокие температуры кипения, чем более мелкие молекулы того же типа, что указывает на то, что дисперсионные силы увеличиваются с увеличением массы, числа электронов, числа атомов или некоторой их комбинации. В следующей таблице перечислены температуры кипения ряда элементов и ковалентных соединений, состоящих из молекул, лишенных постоянного диполя. Количество электронов в каждом виде указано в первом столбце, а масса каждого дана в виде надстрочного числа перед формулой.
Количество электронов в каждом виде указано в первом столбце, а масса каждого дана в виде надстрочного числа перед формулой.
| # Электроны | Молекулы и температуры кипения ºC |
|---|---|
| 10 | 20 Ne –246 ; 16 CH 4 –162 |
| 18 | 40 Ar –186 ; 32 SiH 4 –112 ; 30 С 2 Н 6 –89 ; 38 F 2 –187 |
| 34-44 | 84 Кр –152 ; 58 С 4 Н 10 –0,5 ; 72 (СН 3 ) 4 С 10 ; 71 Кл 2 –35 ; 88 CF 4 –130 |
| 66-76 | 114 [(CH 3 ) 3 C] 2 106 ; 126 (CH 2 ) 9 174; 160 Бр 2 59 ; 154 CCl 4 77 ; 138 С 2 F 6 –78 |
Молекулы с двумя десятью электронами показаны в первом ряду. Неон тяжелее метана, но кипит на 84º ниже. Метан состоит из пяти атомов, и дополнительные ядра могут предоставить больше возможностей для индуцированного образования диполей по мере приближения других молекул. Легкость, с которой электроны молекулы, атома или иона вытесняются соседним зарядом, называется поляризуемость , поэтому мы можем заключить, что метан более поляризуем, чем неон. Во второй строке перечислены четыре восемнадцатиэлектронные молекулы. Большинство их температур кипения выше, чем у десятиэлектронных соединений неона и метана, но фтор является исключением, его температура кипения на 25° ниже, чем у метана. Остальные примеры в таблице соответствуют корреляции температуры кипения с общим количеством электронов и числом ядер, но фторсодержащие молекулы остаются исключением.
Неон тяжелее метана, но кипит на 84º ниже. Метан состоит из пяти атомов, и дополнительные ядра могут предоставить больше возможностей для индуцированного образования диполей по мере приближения других молекул. Легкость, с которой электроны молекулы, атома или иона вытесняются соседним зарядом, называется поляризуемость , поэтому мы можем заключить, что метан более поляризуем, чем неон. Во второй строке перечислены четыре восемнадцатиэлектронные молекулы. Большинство их температур кипения выше, чем у десятиэлектронных соединений неона и метана, но фтор является исключением, его температура кипения на 25° ниже, чем у метана. Остальные примеры в таблице соответствуют корреляции температуры кипения с общим количеством электронов и числом ядер, но фторсодержащие молекулы остаются исключением.
Аномальное поведение фтора можно объяснить его очень высокой электроотрицательностью. Ядро фтора так сильно притягивает свои электроны, что они гораздо менее поляризуемы, чем электроны большинства других атомов.
Конечно, в зависимости от температуры кипения могут доминировать еще более сильные силы притяжения, такие как электростатическое притяжение между противоположно заряженными ионами и между частичным разделением зарядов молекулярных диполей. Следовательно, молекулы, имеющие постоянный дипольный момент, должны иметь более высокие точки кипения, чем эквивалентные неполярные соединения, как показано в следующей таблице.
| # Электроны | Молекулы и температуры кипения ºC |
|---|---|
| 14-18 | 30 С 2 Н 6 –89 ; 28 H 2 C=CH 2 –104 ; 26 HC≡CH –84 30 H 2 C=O –21 27 HC≡N 26 34 CH 3 -F –78 |
| 22-26 | 42 СН 3 СН=СН 2 –48 ; 40 Ч 3 С≡СН –23 ; 44 CH 3 CH = O 21 41 CH 3 CENN 81 46 (CH 3 ) 2 O –24 50,5 CH 3 -CL –24 50,5 CH 3 – CH 2 F 2 –52 |
| 32-44 | 58 (CH 3 ) 3 CH –12 56 (CH 3 ) 2 C = CH 2 –7 58 (CH 3 ) –7 58 (Ch 3 ) 2 58 (Ch 3 ) 2 . О 56 59 (CH 3 ) 3 N 3 95 CH 3 -Br 45 85 CH 2 Cl 2 40 70 CHF 3 –84 О 56 59 (CH 3 ) 3 N 3 95 CH 3 -Br 45 85 CH 2 Cl 2 40 70 CHF 3 –84 |
В первом ряду соединений этан, этен и этин не имеют молекулярного диполя и служат полезными эталонами для производных с одинарной, двойной и тройной связью, у которых он есть. Формальдегид и цианистый водород ясно показывают усиленное межмолекулярное притяжение в результате постоянного диполя. Метилфторид является аномальным, как и большинство фторорганических соединений. Во втором и третьем рядах все соединения имеют постоянные диполи, но диполи, связанные с углеводородами (первые два соединения в каждом случае), очень малы. Большие молекулярные диполи возникают главным образом из-за связей с высокоэлектроотрицательными атомами (по отношению к углероду и водороду), особенно если они представляют собой двойные или тройные связи. Таким образом, альдегиды, кетоны и нитрилы, как правило, имеют более высокую температуру кипения, чем эквивалентные по размеру углеводороды и алкилгалогениды. Нетипичное поведение соединений фтора является неожиданным ввиду большой разницы электроотрицательностей между углеродом и фтором.
Нетипичное поведение соединений фтора является неожиданным ввиду большой разницы электроотрицательностей между углеродом и фтором.
Водородная связь
Большинство простых гидридов элементов групп IV, V, VI и VII демонстрируют ожидаемое повышение температуры кипения с увеличением числа электронов и молекулярной массы, но гидриды наиболее электроотрицательных элементов (азота, кислорода и фтора ) имеют аномально высокие температуры кипения (табл. 4).
| Группа | Молекулы и температуры кипения ºC |
|---|---|
| VII | ВЧ 19 ; HCl –85; HBr –67; Привет –36 |
| VI | Н 2 О 100 ; H 2 S –60 ; H 2 Se –41 ; Н 2 Те –2 |
| В | NH 3 –33 ; РН 3 –88 ; АШ 3 –62 ; СбХ 3 –18 |
Исключительно сильное диполь-дипольное притяжение, ответственное за такое поведение, называется водородные связи . Когда атом водорода является частью полярной ковалентной связи с более электроотрицательным атомом, таким как кислород, его малый размер позволяет положительному концу диполя связи (водороду) приближаться к соседним нуклеофильным или основным центрам ближе, чем компоненты других полярных атомов. облигации. Кулоновские силы обратно пропорциональны шестой степени расстояния между диполями, что делает эти взаимодействия относительно сильными, хотя они все еще слабые (примерно 4–5 ккал на моль) по сравнению с большинством ковалентных связей. Таблица данных справа дает убедительные доказательства существования водородных связей. В каждой строке первое перечисленное соединение имеет наименьшее общее количество электронов и самую низкую массу, но его температура кипения самая высокая из-за водородных связей. Другие соединения в каждом ряду имеют молекулярные диполи, взаимодействия которых можно было бы назвать водородными связями, но притяжение явно намного слабее. Первые два гидрида элементов группы IV, метан и силан, перечислены в первой таблице выше и не обнаруживают каких-либо значительных водородных связей.
Когда атом водорода является частью полярной ковалентной связи с более электроотрицательным атомом, таким как кислород, его малый размер позволяет положительному концу диполя связи (водороду) приближаться к соседним нуклеофильным или основным центрам ближе, чем компоненты других полярных атомов. облигации. Кулоновские силы обратно пропорциональны шестой степени расстояния между диполями, что делает эти взаимодействия относительно сильными, хотя они все еще слабые (примерно 4–5 ккал на моль) по сравнению с большинством ковалентных связей. Таблица данных справа дает убедительные доказательства существования водородных связей. В каждой строке первое перечисленное соединение имеет наименьшее общее количество электронов и самую низкую массу, но его температура кипения самая высокая из-за водородных связей. Другие соединения в каждом ряду имеют молекулярные диполи, взаимодействия которых можно было бы назвать водородными связями, но притяжение явно намного слабее. Первые два гидрида элементов группы IV, метан и силан, перечислены в первой таблице выше и не обнаруживают каких-либо значительных водородных связей.
Органические соединения, содержащие связи O-H и N-H, также проявляют повышенное межмолекулярное притяжение благодаря водородным связям. Некоторые примеры приведены ниже.
| Класс | Молекулы и температуры кипения ºC | |
|---|---|---|
| Кислород Соединения | С 2 Н 5 ОН 78 ; (СН 3 ) 2 О –24 ; (CH 2 ) 2 O 11 этанол диметиловый эфир этиленоксид | (CH 2 ) 3 CHOH 124 & (CH 2 ) 4 O 66 циклобутанол тетрагидрофуран |
| Азот Соединения | C 3 H 7 NH 2 50 ; C 2 H 5 NH(CH 3 ) 37 ; (СН 3 ) 3 N 3 пропиламин этилметиламин триметиламин | (CH 2 ) 4 CHNH 2 107 & (CH 2 ) 4 NCH 3 80 циклопентиламин 6-метилпирропентиламин |
| Комплекс Функции | C 2 H 5 CO 2 H 141 и CH 3 CO 2 CH 3 57 пропановая кислота метилацетат | C 3 H 7 CONH 2 218 & CH 3 CON(CH 3 ) 2 165 бутирамид N,N- |
Растворимость в воде
Вода является самой распространенной и важной жидкостью на этой планете. При выделении и очистке соединений необходимо учитывать смешиваемость других жидкостей с водой и растворимость твердых веществ в воде. С этой целью в следующей таблице указана смешиваемость с водой (или растворимость) ряда низкомолекулярных органических соединений. Сразу бросается в глаза влияние важных атомов водородной связи, кислорода и азота. В первой строке перечислены несколько углеводородных и хлорсодержащих растворителей. Все они без исключения не смешиваются с водой, хотя интересно отметить, что π-электроны бензола и несвязывающие валентные электроны хлора слегка увеличивают их растворимость по сравнению с насыщенными углеводородами. По сравнению с углеводородами соединения кислорода и азота, перечисленные во втором, третьем и четвертом рядах, более чем в сто раз более растворимы в воде, а многие полностью смешиваются с водой.
При выделении и очистке соединений необходимо учитывать смешиваемость других жидкостей с водой и растворимость твердых веществ в воде. С этой целью в следующей таблице указана смешиваемость с водой (или растворимость) ряда низкомолекулярных органических соединений. Сразу бросается в глаза влияние важных атомов водородной связи, кислорода и азота. В первой строке перечислены несколько углеводородных и хлорсодержащих растворителей. Все они без исключения не смешиваются с водой, хотя интересно отметить, что π-электроны бензола и несвязывающие валентные электроны хлора слегка увеличивают их растворимость по сравнению с насыщенными углеводородами. По сравнению с углеводородами соединения кислорода и азота, перечисленные во втором, третьем и четвертом рядах, более чем в сто раз более растворимы в воде, а многие полностью смешиваются с водой.
| Составной тип | Особые соединения | г/100 мл | Моль/литр | Особые соединения | г/100 мл | Моль/литр | |
|---|---|---|---|---|---|---|---|
| Углеводороды и Алкилгалогениды | бутан гексан циклогексан | 0,007 0,0009 0,006 | 0,0012 0,0001 0,0007 | бензол метиленхлорид хлороформ | 0,07 1,50 0,8 | 0,009 0,180 0,07 | |
| Соединения Имеющие Один кислород | 1-бутанол трет -бутанол циклогексанол фенол | 9,0 в сборе 3,6 8,7 | 1,2 в сборе 0,36 0,90 | этиловый эфир ТГФ фуран анизол | 6,0 в сборе 1,0 1,0 | 0,80 полный 0,15 0,09 | |
| Соединения Имеющие Два кислорода | 1,3-пропандиол 2-бутоксиэтанол бутановая кислота бензойная кислота | в сборе в сборе в сборе в сборе | в сборе в сборе в сборе в сборе | 1,2-диметоксиэтан 1,4-диоксан этилацетат γ-бутиролактон | в сборе в сборе 8,0 в сборе | полный в сборе 0,91 в сборе | |
| Азот Содержащие Соединения | 1-аминобутан циклогексиламин анилин пирролидин пиррол | в сборе в сборе 3,4 в сборе 6,0 | в сборе в сборе 0,37 в сборе 0,9 | триэтиламин пиридин пропионитрил 1-нитропропан ДМФА | 5,5 в сборе 10,3 1,5 в сборе | 0,54 в сборе 2,0 0,17 в сборе |
Из приведенных выше данных следует отметить некоторые общие тенденции. Во-первых, спирты (вторая строка, левая колонка) обычно более растворимы, чем простые эфиры того же размера (вторая строка, правая колонка). Это отражает тот факт, что гидроксильная группа может действовать как донор и акцептор водородной связи; тогда как эфирный кислород может служить только акцептором. Повышенная растворимость фенола по сравнению с циклогексанолом может быть связана с его большей кислотностью, а также с пи-электронным эффектом, отмеченным в первой строке.
Во-первых, спирты (вторая строка, левая колонка) обычно более растворимы, чем простые эфиры того же размера (вторая строка, правая колонка). Это отражает тот факт, что гидроксильная группа может действовать как донор и акцептор водородной связи; тогда как эфирный кислород может служить только акцептором. Повышенная растворимость фенола по сравнению с циклогексанолом может быть связана с его большей кислотностью, а также с пи-электронным эффектом, отмеченным в первой строке.
Циклический эфир ТГФ (тетрагидрофуран) более растворим, чем его аналог с открытой цепью, возможно, потому, что атом кислорода более доступен для водородных связей с молекулами воды. Из-за пониженной основности кислорода в фуране ароматического соединения он гораздо менее растворим. Атом кислорода в анизоле также дезактивируется сопряжением с бензольным кольцом (заметим, что он активирует кольцо в реакциях электрофильного замещения). Второй атом кислорода резко увеличивает растворимость в воде, что демонстрируют соединения, перечисленные в третьем ряду. Снова гидроксильные соединения перечислены слева.
Снова гидроксильные соединения перечислены слева.
Азот оказывает солюбилизирующее действие, сходное с кислородом, как показано соединениями в четвертом ряду. Первичные и вторичные амины, перечисленные в левой колонке, могут действовать как доноры и акцепторы водородных связей. Ароматичность снижает основность пиррола, но увеличивает его кислотность. Соединения в правом столбце способны выполнять только роль акцептора. Низкая растворимость нитросоединения удивительна.
Эта страница под названием «Интермолекулярные силы» распространяется по незаявленной лицензии, автором, ремиксом и/или куратором которой является Уильям Ройш.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Уильям Ройш
- Показать страницу TOC
- нет на странице
- Теги

Повышенное притяжение между каплями, несущими флуктуирующие распределения заряда
- Список журналов
- Proc Math Phys Eng Sci
- PMC87
Proc Math Phys Eng Sci. январь 2022 г.; 478(2257): 20210714.
Опубликовано в Интернете 26 января 2022 г. doi: 10.1098/rspa.2021.0714
, Концептуализация, Формальный анализ, Привлечение финансирования, Исследование, Методология, Управление проектом, Надзор, Визуализация, Написание – первоначальный проект, Письмо – рецензирование и редактирование, 1 , Концептуализация, Исследование, Программное обеспечение, Валидация, Визуализация, Написание – первоначальный проект, 1 , Программное обеспечение, Валидация, Визуализация, 2 и , Концептуализация, Привлечение финансирования, Исследование, Управление проектом, Ресурсы, Валидация, Написание – первоначальный проект, Написание – обзор и редактирование 1
Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности
- Заявление о доступности данных
Электростатическая сила между проводящими сферами всегда притягивается при малых расстояниях, независимо от их среднего заряда, когда заряд на сферах постоянен. Во многих ситуациях заряд не может быть фиксированным, например, для капель воды в естественной атмосфере, которые различаются по размеру и заряду. Мы показываем, что сила притяжения между заряженными проводящими сферами увеличивается с увеличением дисперсии заряда. Важность этого непризнанного электростатического эффекта между каплями воды оценивается с точки зрения его способности усиливать образование дождя.
Во многих ситуациях заряд не может быть фиксированным, например, для капель воды в естественной атмосфере, которые различаются по размеру и заряду. Мы показываем, что сила притяжения между заряженными проводящими сферами увеличивается с увеличением дисперсии заряда. Важность этого непризнанного электростатического эффекта между каплями воды оценивается с точки зрения его способности усиливать образование дождя.
Ключевые слова: капли, электростатика, образование дождя
Давно известно, что воздух содержит аэрозольные частицы и капли, которые могут приобретать электрический заряд, например, в тумане [1] или пыли [2]. Зарядка капель возникает, прежде всего, в результате обмена зарядом с кластерными ионами, непрерывно образующимися под действием радиоактивности и космических лучей (например, [3]). Эти ионы очень подвижны. Химические различия между положительными и отрицательными кластерными ионами вызывают естественную асимметрию их диффузионных свойств [4]. Эта асимметрия приводит к ненулевому заряду капель, в которые диффундируют ионы. Влияние заряда на поведение капель и многих аэрозолей (отныне называемых просто «каплями») можно исследовать, моделируя их электрически проводящими сферами.
Эта асимметрия приводит к ненулевому заряду капель, в которые диффундируют ионы. Влияние заряда на поведение капель и многих аэрозолей (отныне называемых просто «каплями») можно исследовать, моделируя их электрически проводящими сферами.
В этой статье мы покажем, что любая изменчивость заряда капель приводит к чистому среднему притяжению между каплями, независимо от средней полярности заряда капель. Что касается дисперсионных сил Лондона-Ван-дер-Ваальса, то эти силы притяжения действуют относительно на небольшом расстоянии, но будут доминировать над любыми силами отталкивания на достаточно близком расстоянии.
Это имеет значение для нашего понимания роли электрических эффектов в таких процессах, как образование теплого дождя или коагуляция аэрозоля.
Рассмотрение облачных капель как проводящих сфер является хорошим приближением к реальности и значительно упрощает задачу их электростатического взаимодействия по сравнению с взаимодействием между диэлектрическими сферами [5]. Во-первых, облачные капли, особенно в теплых облаках, могут образовываться только при наличии в них какого-либо растворенного вещества (обычно ионного характера из-за сильной полярности молекул воды), которое за счет эффекта Рауля подавляет необходимое для образования капель пересыщение [6]. ]. Это придает этим облачным каплям конечную проводимость, и для эффектов нулевой частоты, которые мы изучаем в этой статье, капли эффективно ведут себя как проводящая сфера. Вторым важным фактором, особенно для капель более чистой воды, является высокая диэлектрическая проницаемость (около 80) воды, которая существенно заставляет электрическое поле внутри сферы стать бездивергентным, а статическое электрическое поле становится эквивалентным полю в проводящей сфере. [7].
Во-первых, облачные капли, особенно в теплых облаках, могут образовываться только при наличии в них какого-либо растворенного вещества (обычно ионного характера из-за сильной полярности молекул воды), которое за счет эффекта Рауля подавляет необходимое для образования капель пересыщение [6]. ]. Это придает этим облачным каплям конечную проводимость, и для эффектов нулевой частоты, которые мы изучаем в этой статье, капли эффективно ведут себя как проводящая сфера. Вторым важным фактором, особенно для капель более чистой воды, является высокая диэлектрическая проницаемость (около 80) воды, которая существенно заставляет электрическое поле внутри сферы стать бездивергентным, а статическое электрическое поле становится эквивалентным полю в проводящей сфере. [7].
Электростатическая сила между двумя проводящими сферами на самом деле представляет собой чрезвычайно сложную задачу [8,9]. Конечно, если расстояние между каплями существенно больше радиуса любой капли, то электростатическая сила определяется законом обратных квадратов Кулона для зарядов, рассматриваемых в центре капель. Однако для капель проводящего или сильно поляризуемого вещества, такого как вода, в которой могут мигрировать заряды, детальная ситуация более сложная, и заряды в одной капле будут индуцировать заряды изображения в другой капле. Эти индуцированные заряды изображения будут индуцировать дополнительные заряды изображения в исходной капле, а затем снова во второй капле, повторяясь бесконечно, что приводит к силе притяжения, которая может преобладать, если капли расположены близко друг к другу.
Однако для капель проводящего или сильно поляризуемого вещества, такого как вода, в которой могут мигрировать заряды, детальная ситуация более сложная, и заряды в одной капле будут индуцировать заряды изображения в другой капле. Эти индуцированные заряды изображения будут индуцировать дополнительные заряды изображения в исходной капле, а затем снова во второй капле, повторяясь бесконечно, что приводит к силе притяжения, которая может преобладать, если капли расположены близко друг к другу.
Вычисление силы будет включать в себя размещение бесконечного сходящегося ряда взаимно индуцированных зарядов изображений с последующим суммированием сил между всеми парами зарядов изображений. Мы продемонстрируем детали этой процедуры в следующем разделе. Недавно было показано, что этот бесконечный ряд может быть выражен в замкнутой форме [10], что, тем не менее, на практике также потребует разложения ряда, требующего численной оценки.
Все эти расчеты силы основаны на том, что заряд капли является фиксированной величиной. В действительности заряд капли представляет собой переменную величину, определяемую тепловым равновесием диффузии ионов вблизи заряженной сферы, иногда с дополнительным влиянием миграции ионов, вызванной электрическими полями.
В действительности заряд капли представляет собой переменную величину, определяемую тепловым равновесием диффузии ионов вблизи заряженной сферы, иногда с дополнительным влиянием миграции ионов, вызванной электрическими полями.
В простейшем случае незначительного внешнего электрического поля, типичного для условий хорошей погоды при наличии слоистых облаков, временной масштаб диффузии ионов к каплям радиуса a пропорционален 1/aZ, где Z — число капель на единица объема [11]. Этот временной масштаб обычно составляет около 100 с для капель радиусом 10 мкм с Z=100 см-3. Когда присутствует электрическое поле, приводящее к упорядоченному движению ионов, время зарядки может быть более быстрым [12]. Это показывает, что капли, взаимодействующие в естественной среде, будут демонстрировать переменный заряд, который более точно моделируется как стохастическая переменная, а не фиксированная величина.
В следующем разделе изложено теоретическое развитие того, как замена фиксированного заряда стохастическим переменным изменяет силу взаимодействия между двумя каплями. В § 3 обсуждается стохастический характер заряда капли и демонстрируются последствия для фактически рассчитанных сил между каплями. В §4 мы обсуждаем, как наши результаты могут повлиять на процессы образования дождя, включая модифицированные ядра столкновений, а также моделирование ожидаемых эффектов на образование теплого дождя.
В § 3 обсуждается стохастический характер заряда капли и демонстрируются последствия для фактически рассчитанных сил между каплями. В §4 мы обсуждаем, как наши результаты могут повлиять на процессы образования дождя, включая модифицированные ядра столкновений, а также моделирование ожидаемых эффектов на образование теплого дождя.
Когда две капли с радиусами a1 и a2 и зарядами q1 и q2 расположены близко друг к другу, заряды будут индуцировать заряды изображения в другой капле, чтобы гарантировать, что поверхность капли является поверхностью постоянного потенциала. Заряд изображения, индуцированный зарядом q1 (), индуцирует заряд изображения q2′ во второй капле на расстоянии d2′ от центра капли, где
q2′=−q1a2randd2′=a22r.
2.1
Здесь r — расстояние между центрами капель. Эквивалентно, заряд q2 второй капли индуцирует заряд изображения q1′ в первой капле. Эти заряды изображения, в свою очередь, индуцируют вторичные заряды изображения в противоположных каплях q1″ и q2″, где расстояния между зарядами изображения и центрами противоположных капель должны использоваться для значения r в расчетах.
Открыть в отдельном окне
Расположение зарядов изображения в двух близко расположенных сферических каплях. Каждый заряд изображения индуцирует новый заряд изображения в другой капле, что приводит к бесконечному ряду взаимно индуцированных зарядов изображения. Обратите внимание, что расположение зарядов изображения быстро сходится к фиксированной точке.
Сохранение заряда требует, чтобы индуцированные заряды изображения компенсировались регулировкой центрального заряда до
q1(0)=q1−q1′−q1″−q1‴−…=q1−∑n=1∞q1(n),
2.2
и эквивалентно для q2(0).
В итоге мы получим бесконечный ряд зарядов изображений и скорректированных центральных зарядов, которые будут взаимодействовать через кулоновские силы попарно через капли. Таким образом, общая сила между двумя каплями равна
4πϵF=∑m,n=0∞q1(m)q2(n)(r−d1(m)−d2(n))2,
2,3
где ϵ — соответствующая диэлектрическая проницаемость среды, в которой находятся капли, а d1(m) и d2(n) — смещения от центров капель для зарядов изображения q1(m) и q2(n) соответственно. Силе отталкивания соответствует положительное значение F. Мы будем рассматривать только взаимодействия между двумя каплями, когда сила всегда направлена по вектору разности между центрами капель. Это означает, что все вычисления включают только скалярные величины.
Силе отталкивания соответствует положительное значение F. Мы будем рассматривать только взаимодействия между двумя каплями, когда сила всегда направлена по вектору разности между центрами капель. Это означает, что все вычисления включают только скалярные величины.
Эффективное приближение полной силы, которое дает хорошие результаты для широкого диапазона параметров, включает стандартную кулоновскую силу между q1 и q2 плюс силу притяжения между q1 и индуцированным диполем конечного размера q2′d2′ плюс силу притяжения между q2 и индуцированным диполем конечного размера q1′d1′, приближение, подобное использованному в [13]. Это приближение приводит к силе, равной
4πϵF=q1q2r2−q12a2r(1(r−a22/r)2−1r2)−q22a1r(1(r−a12/r)2−1r2).
2,4
Ключевым результатом является то, что сила, даже в более высоких приближениях, может быть записана как сумма трех компонентов, пропорциональных соответственно q1q2, -q12 и -q22. Последние два компонента всегда притягивающие и могут доминировать на достаточно близком расстоянии, за исключением некоторых симметричных случаев, когда притяжение возникает только при соприкосновении капель. Знак вклада нулевого порядка, конечно, зависит от знаков q1 и q2 и является отталкивающим для зарядов одного знака.
Знак вклада нулевого порядка, конечно, зависит от знаков q1 и q2 и является отталкивающим для зарядов одного знака.
Далее мы предположим, что заряд каждой капли на самом деле является стохастической переменной, устанавливаемой тепловым равновесием потока ионов окружающей среды любой полярности к каплям. В следующем разделе мы обсудим физическую основу такого предположения. Пока будем считать, что заряды являются независимыми стохастическими переменными со средними значениями q¯1 и q¯2 и стандартными отклонениями σ1 и σ2.
Мы можем видеть, что при этих стохастических предположениях кулоновская сила (первый член в уравнении (2.4)) не изменяется из-за того, что два стохастических заряда независимы. Однако величина сил притяжения (второе и третье слагаемые в уравнении (2.4)) увеличивается: слагаемое q1q2 заменяется на q¯1q¯2, а слагаемые q12 и q22 заменяются на q¯12+σ12 и q¯22+σ22 соответственно.
Интересный пример возникает для стохастической ситуации, когда средний заряд капли равен нулю. Тогда для точечных зарядов средняя сила между каплями будет равна нулю, но для капель конечного размера мы находим силу притяжения, примерно равную
Тогда для точечных зарядов средняя сила между каплями будет равна нулю, но для капель конечного размера мы находим силу притяжения, примерно равную
4πϵF=−2σ12a23+σ22a13r5,
2,5
где для простоты мы аппроксимировали уравнение (2.4) при r ≫ a1, a2. Какой бы уровень приближения ни использовался, мы находим силу притяжения, пропорциональную дисперсии зарядов. Отрицательная степень r в силе притяжения меньше и, следовательно, имеет больший диапазон, чем зависимость шестой степени в случае Лондона-Ван-дер-Ваальса, потому что здесь мы рассматриваем притяжение между двумя независимыми стохастическими зарядами и их индуцированными диполями.
Ожидается, что для близлежащих капель любая изменчивость заряда двух капель будет антикоррелированной, поскольку ионы, захваченные одной каплей, не могут быть захвачены другой каплей. В этом случае модифицированная кулоновская часть, пропорциональная q1q2, также будет содержать вклад, пропорциональный cov(q1,q2), который является отрицательным и, следовательно, способствует притяжению между каплями. Трудно количественно оценить, насколько большим будет этот вклад.
Трудно количественно оценить, насколько большим будет этот вклад.
Таким образом, рассмотрение зарядов как стохастических переменных приводит к силе взаимодействия, которая увеличивается на среднюю часть притяжения, пропорциональную дисперсии зарядов. В следующих разделах мы количественно определяем стохастическую природу заряда для мелких капель и приводим явные примеры стохастического эффекта на электростатическую силу между каплями и возможные эффекты на образование дождя в облаках.
Для простейшего случая диффузионного заряда монодисперсного аэрозоля радиусом a в присутствии равных концентраций положительных и отрицательных ионов, имеющих одинаковую подвижность, находится доля частиц, несущих j элементарных зарядов, Nj, экспериментально (например, для масляных капель [14]) дать
NjN0=exp(−j2e28πϵakT),
3,1
где k – постоянная Больцмана, а T – абсолютная температура. Для очень маленьких капель (a<10−8 m) наблюдается некоторое отклонение от этого соотношения [15, 16]): Шредингер указал, что это, вероятно, связано с нарушением предположения о континууме для заряда при таких малых размерах. [17].
[17].
Основная форма уравнения (3.1) обычно объясняется [18] как возникающая из фактора Больцмана e(−ε)/kT, где свободная энергия ε соответствует энергии изолированной сферы, несущей заряд Q. Если общее заряд Q на сфере состоит из j элементарных зарядов e, и если предположить, что емкость изолированной сферы равна C=4πϵa, соответствующая электрическая энергия равна
12CV2=12Q2C=j2 e28πϵa.
3,2
Следовательно, уравнение (3.1) иногда называют распределением заряда Больцмана. (Уравнение (3.1) также может быть получено с учетом подробного баланса [19,20] с использованием коэффициентов прилипания ионов к аэрозолям [21], из которых видно, что распределение заряда Больцмана является предельным случаем, когда и концентрации биполярных ионов, и подвижности ионов равны — Клемент и Харрисон [19] приводят доводы в пользу модифицированного больцмановского распределения заряда. распределение в более общем случае.) Среднее значение распределения заряда Больцмана равно нулю, поскольку распределение симметрично от отрицательного к положительному. Более важным соображением является доля присутствующих заряженных капель из-за последствий электростатического воздействия на капли и между ними. Путем интегрирования по распределению заряда Больцмана доля заряженных капель fc определяется выражением
Более важным соображением является доля присутствующих заряженных капель из-за последствий электростатического воздействия на капли и между ними. Путем интегрирования по распределению заряда Больцмана доля заряженных капель fc определяется выражением
fc=1−λπ,
3,3
где λ=e2/8πϵakT. Для монодисперсных наборов капель с радиусом от 0,1 до 20 мкм fc колеблется примерно от 0,7 до 0,98 при 5°C (хотя зависимость от температуры незначительна), что указывает на то, что большинство присутствующих капель будет заряжено. Если свойства положительных и отрицательных ионов различаются, доля капель, заряженных для любого монодисперсного размера капель, будет даже больше, чем указанная в уравнении (3.3) (например, см. коэффициент усиления асимметрии в уравнении (47) из [20]) .
Ширина распределения заряда может быть описана по аналогии между (симметричным) распределением Больцмана и распределением Гаусса с нулевым средним значением, т.е. стандартным отклонением в j
σj=12λ.
3,4
Пример расчета для капли радиусом 10 мкм при температуре 5∘C приводит к стандартному отклонению заряда, равному 13 элементарным зарядам.
Следовательно, принимая во внимание пропорцию присутствующих заряженных капель или изменчивость их заряда, становится ясно, что в естественных условиях всегда ожидается наличие диапазона зарядов капель. Если, кроме того, локальные концентрации ионов неодинаковы, то асимметрия от этого и различия их подвижности приведут к большему заряду с ненулевым средним зарядом в распределении заряда капель.
Мы завершаем этот раздел, показывая несколько примеров электростатической силы между заряженными каплями и дополнительные эффекты, связанные со стохастичностью заряда.
В , мы сопоставляем набор примеров сил между маленькими заряженными и незаряженными каплями. Не существует простого масштабирования уравнений силы с зарядом, расстоянием или размером капли, поэтому мы можем только попытаться дать представление о возможных эффектах. Расчеты сил с фиксированными зарядами, далее обозначенными детерминированный , используйте уравнение (2.3). В качестве альтернативы, рассматривая заряд как стохастическую переменную, мы предполагаем, что корректировка зарядов изображения происходит мгновенно, так что мы можем вычислить среднюю силу (далее обозначенную как стохастическая ) для двух зарядов, взятых независимо из нормального распределения заданного среднего и стандартное отклонение. В , мы использовали 4096 реализаций этой силы, чтобы вычислить ее среднее значение. Любую силу можно сравнить с кулоновской силой между соответствующими точечными зарядами, которая также входит в . Выбранные значения параметров указаны в подписи к рисунку.
Расчеты сил с фиксированными зарядами, далее обозначенными детерминированный , используйте уравнение (2.3). В качестве альтернативы, рассматривая заряд как стохастическую переменную, мы предполагаем, что корректировка зарядов изображения происходит мгновенно, так что мы можем вычислить среднюю силу (далее обозначенную как стохастическая ) для двух зарядов, взятых независимо из нормального распределения заданного среднего и стандартное отклонение. В , мы использовали 4096 реализаций этой силы, чтобы вычислить ее среднее значение. Любую силу можно сравнить с кулоновской силой между соответствующими точечными зарядами, которая также входит в . Выбранные значения параметров указаны в подписи к рисунку.
Открыть в отдельном окне
Сила между каплями (в 10−16 Н) как функция расстояния между центрами капель (в мкм). (а) Две капли радиусом 10 мкм, заряды 13e, стандартные отклонения 13e. (б) Две капли радиусом 10 мкм, заряды 0e и 13e, стандартные отклонения 13e. (в) Две капли радиусом 10 мкм, заряды 0e, стандартные отклонения 13e. (г) Две капли радиусом 5 мкм и 10 мкм, заряды 30e, стандартные отклонения 13e.
(в) Две капли радиусом 10 мкм, заряды 0e, стандартные отклонения 13e. (г) Две капли радиусом 5 мкм и 10 мкм, заряды 30e, стандартные отклонения 13e.
a показывает силу между двумя одинаково заряженными каплями одинакового размера. И кулоновская сила, и детерминированная сила являются отталкивающими, хотя в точке, где капли касаются, силы изображения создают особое притяжение, которое не видно на рисунке. Эта особенность является патологической, так как имеет место только для выбранных симметричных параметров.
На этом же рисунке показана сила, когда заряды рассматриваются как стохастические переменные. Хотя на больших расстояниях преобладает кулоновская сила отталкивания, на близком расстоянии (в данном случае, когда две капли находятся на расстоянии около 4 мкм друг от друга) сила становится притягивающей. Природа высокого порядка эффекта заряда изображения гарантирует, что, когда сила притягивает на близком расстоянии, сила быстро достигает очень большой величины.
b показывает силу, когда заряжена только одна капля. Кулоновская сила исчезает, как и ожидалось, но детерминированная сила всегда притягивает, особенно на близком расстоянии. Стохастическая сила еще более привлекательна, ее диапазон притяжения примерно в два раза больше, чем в детерминированном случае.
c показывает силу между двумя средними нейтральными каплями. И кулоновская, и детерминированная силы исчезают. Стохастическая сила сильно притягивается на близких расстояниях. Для справки, панель включает график силы притяжения, аппроксимированный уравнением (2.5), который хорошо аппроксимирует стохастическую силу на больших расстояниях, но, как и ожидалось, не работает на меньших расстояниях.
d показывает силу между двумя более заряженными маленькими каплями, где, как мы можем ожидать, преобладает кулоновское отталкивание. Действительно, сила отталкивания в этом случае существенно больше, но и здесь на близких расстояниях начинает преобладать сила притяжения. Стохастическая составляющая, имеющая те же стандартные отклонения заряда, что и в предыдущем случае, усиливает это притяжение, но в этом случае в меньшей степени, чем в детерминированном случае.
Стохастическая составляющая, имеющая те же стандартные отклонения заряда, что и в предыдущем случае, усиливает это притяжение, но в этом случае в меньшей степени, чем в детерминированном случае.
Абсолютные значения сил остаются относительно небольшими (за исключением очень близкого расстояния), например, по сравнению с ожидаемой гравитационной силой для капли радиусом 10 мкм. Однако сравнение с весом капли может быть не самым подходящим для облачных процессов, как указывалось ранее в [22], где также предполагалось, что близкое притяжение может оказывать существенное усиливающее влияние на скорость, с которой маленькие капли сливаются, образуя большие капли дождя (то есть скорость автоконверсии). Дополнительные аспекты, возникающие при рассмотрении заряда как стохастической переменной, позволяют предположить, что в действительности это улучшение может быть даже больше.
Формирование теплого дождя в атмосфере (то есть образование дождя, в котором замороженные гидрометеоры не играют роли) зависит от столкновения и слияния более мелких капель с образованием более крупных капель до тех пор, пока капли не станут достаточно большими, чтобы вырваться из облачного воздуха и упасть на землю. Принципы этих процессов хорошо понятны, и существует множество учебников по физике облаков, в которых подробно описываются эти процессы (например, [6,23]). Методы дистанционного зондирования можно использовать для наблюдения за процессами сбора теплых облачных капель, например, путем объединения профилей отражательной способности от CloudSat и спектрорадиометра визуализации со средним разрешением (MODIS) [24].
Принципы этих процессов хорошо понятны, и существует множество учебников по физике облаков, в которых подробно описываются эти процессы (например, [6,23]). Методы дистанционного зондирования можно использовать для наблюдения за процессами сбора теплых облачных капель, например, путем объединения профилей отражательной способности от CloudSat и спектрорадиометра визуализации со средним разрешением (MODIS) [24].
Ключевой переменной в формировании дождя является средняя скорость, с которой сталкиваются две капли разного размера, так называемое ядро столкновения. Это ядро задается несколькими системными параметрами и переменными, в первую очередь радиусами капель.
Ядро пропорционально сечению столкновения капель, средней относительной скорости двух капель и модифицируется гидродинамическими эффектами одной капли, движущейся вслед за другой каплей. Средняя относительная скорость часто принимается как разница между конечными скоростями двух капель, но в турбулентном поле она обычно увеличивается из-за турбулентной адвекции капель [25].
Когда капли заряжены, ожидается, что сила притяжения между каплями усилит ядро столкновения, хотя отдаленное кулоновское отталкивание между зарядами с одинаковым знаком может фактически уменьшить ядро.
Здесь мы показываем один результат модели, использующей АВС-поток [26] для моделирования турбулентной адвекции и столкновения капель под действием электростатического взаимодействия [27]. Мы выражаем эффект электростатических взаимодействий как коэффициент усиления, отношение ядра столкновений с электростатическими эффектами к ядру без электростатических эффектов.
показывает один пример случая, когда моделировалась популяция капель размером от 10 до 60 мкм. Капли размером 10 мкм имели заряд 10 000 е, и заряд линейно возрастал с радиусом. Это тот случай, когда можно ожидать достаточно сильного эффекта кулоновского отталкивания. Стохастический эффект на заряды моделировался с использованием полиномиальной аппроксимации ожидаемых электростатических сил.
Открыть в отдельном окне
Коэффициент электростатического усиления: соотношение между ядрами столкновений для заряженного корпуса по сравнению с незаряженным корпусом в зависимости от соотношения размеров капель. Ключи к символам представляют собой размер наибольшего падения во взаимодействии. Черная линия представляет собой гладкую аппроксимацию, используемую для изменения ядер в моделировании заряженного стохастического уравнения столкновения. (Онлайн-версия в цвете.)
Ключи к символам представляют собой размер наибольшего падения во взаимодействии. Черная линия представляет собой гладкую аппроксимацию, используемую для изменения ядер в моделировании заряженного стохастического уравнения столкновения. (Онлайн-версия в цвете.)
Как видно из , ядро столкновений в этом случае усиливается на несколько процентов в широком диапазоне соотношений размеров капель. Мы обнаружили, что это имеет место для нескольких наборов параметров. При отношении размеров капель, близком к 1, мы часто обнаруживаем уменьшение ядра столкновений. Особенно это касается капель меньшего размера (10 мкм и меньше) и сильно заряженных капель. Это можно понять по тому факту, что при отношении размеров капель, близком к 1, относительная скорость капель будет очень мала, обычно слишком мала для преодоления дальнодействующего кулоновского отталкивания зарядов одного знака [22]. На более крупные капли с их большей инерцией и сопротивлением это влияет меньше, чем на более мелкие капли. Мы также наблюдаем, что для малых соотношений размеров (≲0,25) усиление за счет заряда также невелико. Здесь естественная относительная скорость в большинстве случаев уже довольно велика, и любые зарядовые эффекты лишь незначительно изменят траектории капель.
Мы также наблюдаем, что для малых соотношений размеров (≲0,25) усиление за счет заряда также невелико. Здесь естественная относительная скорость в большинстве случаев уже довольно велика, и любые зарядовые эффекты лишь незначительно изменят траектории капель.
Несмотря на все эти конкурирующие эффекты, мы обнаружили, что обычно общая частота столкновений по всему спектру размеров капель в этом моделировании увеличивается до 5%, хотя общий результат получить трудно, поскольку он зависит от рассматриваемого распределения заряда и размера. .
Стандартный способ прогнозирования эволюции спектра размеров капель с течением времени использует так называемое стохастическое уравнение столкновения (SCE). SCE представляет собой уравнение Смолуховского, в котором ядра столкновений получены из конечной скорости падающих капель и включают эффекты гидродинамического следа за каплями. SCE использует ядра столкновений, чтобы предсказать скорость, с которой капли двух размеров сталкиваются, а затем образуют большую каплю с массой, равной сумме масс сталкивающихся капель. Используемая здесь численная реализация описана в [28].
Используемая здесь численная реализация описана в [28].
Мы аппроксимировали усиление ядра за счет заряда гладкой функцией отношения двух капель, как видно черной линией на , и модифицировали ядро, используемое в модели SCE Ботта, с этим усилением. Мы смоделировали плотное кучевое облако морского типа с начальным содержанием жидкой воды 2 г м−3 и средним радиусом капли 10 мкм.
Как видно из рисунка, эта популяция облачных капель быстро развивается, и через 25 мин большинство мелких капель коагулируют в капли радиусом более 500 мкм. Эти капли продолжают увеличиваться в размерах. b показывает видимость, рассчитанную по распределению размеров капель. Это показывает, как видимость продолжает улучшаться с течением времени после того, как первоначальные капли облаков в значительной степени сгустились. Продолжающееся увеличение видимости соответствует продолжающемуся удалению капель меньшего размера из распределения капель по размерам.
Открыть в отдельном окне
Результаты моделирования стохастического уравнения столкновений (SCE). Эволюция доли дождя (доля содержания жидкой воды в каплях радиусом более 500 мкм) и видимости в облаках (с использованием теории Кошмидера и минимального видимого контраста 2%) для контрольного прогона и прогона с модифицированными зарядом столкновениями .
Эволюция доли дождя (доля содержания жидкой воды в каплях радиусом более 500 мкм) и видимости в облаках (с использованием теории Кошмидера и минимального видимого контраста 2%) для контрольного прогона и прогона с модифицированными зарядом столкновениями .
Пунктирные кривые показывают, что зарядка действительно ускоряет эволюцию распределения капель облаков. Несмотря на очень скромное предполагаемое увеличение из-за заряда (максимум 5% при соотношении размеров капель около 0,75, что согласуется с ), конкурирующие эффекты при малых отношениях размеров капель и уменьшение ядер при отношении размеров около 1, мы обнаруживаем, что существует скромное чистое ускорение эволюции распределения капель по размерам, порядка минуты или около того, фактически согласующееся с увеличением частоты столкновений на 5%. Это указывает на то, что в быстрой эволюции спектра капель вблизи 20-минутной отметки преобладают столкновения капель с отношением размеров около 0,75.
Электростатическое взаимодействие между двумя заряженными сферами — чрезвычайно сложная задача, требующая суммирования по бесконечному ряду пар взаимодействий зарядов изображений. Чистое взаимодействие всегда притягивает на коротких расстояниях, независимо от среднего заряда сфер.
Чистое взаимодействие всегда притягивает на коротких расстояниях, независимо от среднего заряда сфер.
Обычно для атмосферных условий заряд капли считается фиксированным, как и заряд изолированной заряженной сферы. Однако естественнее считать заряд капли стохастической величиной, флуктуации которой являются следствием диффузионного переноса ионов окружающей среды к каплям.
Одним из важных следствий этого улучшенного представления заряда как стохастической переменной является то, что сила притяжения между каплями всегда увеличивается и действует в более широком диапазоне. В результате для капель в атмосфере электростатическое притяжение между ними будет больше, чем считалось ранее, и, соответственно, будет играть другую роль в процессах образования дождя.
Применяя эти результаты непосредственно к теплым облакам, моделирование показывает, что частота столкновений действительно увеличивается за счет электростатических взаимодействий. И это несмотря на то, что существует несколько конкурирующих эффектов. Один из этих эффектов заключается в том, что для капель одинакового размера относительная скорость ближайших капель очень одинакова, что дает кулоновскому отталкиванию зарядов капель с одинаковым знаком возможность удерживать капли на расстоянии друг от друга. Особенно это касается мелких капель. Если бы капли в среднем были нейтральными, то кулоновское отталкивание не происходило бы, а стохастическое притяжение фактически способствовало бы столкновению капель. Моделируя распределение капель по размерам во времени с помощью SCE, мы обнаруживаем, что электростатическая сила притяжения доминирует в эволюции распределения капель по размерам.
Один из этих эффектов заключается в том, что для капель одинакового размера относительная скорость ближайших капель очень одинакова, что дает кулоновскому отталкиванию зарядов капель с одинаковым знаком возможность удерживать капли на расстоянии друг от друга. Особенно это касается мелких капель. Если бы капли в среднем были нейтральными, то кулоновское отталкивание не происходило бы, а стохастическое притяжение фактически способствовало бы столкновению капель. Моделируя распределение капель по размерам во времени с помощью SCE, мы обнаруживаем, что электростатическая сила притяжения доминирует в эволюции распределения капель по размерам.
Таким образом, повсеместное присутствие захвата ионов каплями в атмосфере гарантирует, что капли притягиваются друг к другу на близких расстояниях, независимо от наличия какого-либо среднего заряда капли. Это связано с тем, что средний эффект флуктуаций заряда капли всегда приводит к взаимодействию притяжения. Следовательно, временные масштабы эволюции от облачных капель к дождевым каплям становятся более быстрыми, чем в нейтральном случае.
Описание и проверка используемой трехмерной модели DNS опубликованы как Auerswald & Ambaum [27]. Модель SCE описана в работе Bott [28].
M.H.P.A.: концептуализация, формальный анализ, получение финансирования, исследование, методология, управление проектом, надзор, визуализация, написание — первоначальный проект, написание — обзор и редактирование; Т.А.: концептуализация, исследование, программное обеспечение, проверка, визуализация, написание — первоначальный проект; Р.Э.: программное обеспечение, валидация, визуализация; RGH: концептуализация, получение финансирования, исследование, управление проектом, ресурсы, проверка, написание — первоначальный проект, написание — обзор и редактирование.
Мы заявляем, что у нас нет конкурирующих интересов.
М.Х.П.А. и Р.Г.Х. частично поддержали и Т.А. и Р.Э. были полностью поддержаны Программой увеличения количества осадков в ОАЭ.
1. Ронейн Т. 1772.
Письмо от Томаса Ронейна, эсквайра; Бенджамину Франклину, LL. Д. Ф.Р.С. включение отчета о некоторых наблюдениях за атмосферным электричеством; по поводу туманов, туманов и т. д. С некоторыми замечаниями. Фил. Транс. Р. Соц. 62 , 137–146. ( 10.1098/rstl.1772.0020) [Перекрестная ссылка]
Д. Ф.Р.С. включение отчета о некоторых наблюдениях за атмосферным электричеством; по поводу туманов, туманов и т. д. С некоторыми замечаниями. Фил. Транс. Р. Соц. 62 , 137–146. ( 10.1098/rstl.1772.0020) [Перекрестная ссылка]
2. Баддели ПФХ. 1860. Вихри и пыльные бури Индии. Лондон, Великобритания: Белл и Дэлди. [Google Scholar]
3. Nolan JJ, Boylan RK, DeSachy GP. 1925 г. Равновесие ионов в атмосфере. проц. Р. Ирландский академик. 37А , 1-12. [Google Scholar]
4. Horrak U, Salm J, Tammet H. 2000. Статистическая характеристика спектров подвижности аэроионов в обсерватории Тахкусе: классификация аэроионов. Дж. Геофиз. Рез. 105 , 9291-9302. ( 10.1029/1999JD7) [CrossRef] [Google Scholar]
5. Бичуцкая Е., Боутрайт А.Л., Хачатурян А., Стейс А.Дж. 2010.
Электростатический анализ взаимодействий между заряженными частицами диэлектрических материалов. J. Chem. физ. 133 , 024105. (10.1063/1.3457157) [PubMed] [CrossRef] [Google Scholar]
(10.1063/1.3457157) [PubMed] [CrossRef] [Google Scholar]
6. Ambaum MHP. 2020. Теплофизика атмосферы, 2-е изд., с. 257. Амстердам, Нидерланды: Elsevier. [Google Scholar]
7. Джексон Д.Д. 1999. Классическая электродинамика, 3-е изд., с. 808. Нью-Йорк, штат Нью-Йорк: Wiley. [Академия Google]
8. Хамакер Х.К. 1937 год. Притяжение Лондона-Ван-дер-Ваальса между сферическими частицами. Физика 4 , 1058-1072. ( 10.1016/S0031-8914(37)80203-7) [CrossRef] [Google Scholar]
9. Лекнер Дж. 2012. Электростатика двух заряженных проводящих сфер. проц. Р. Соц. А 468 , 2829-2848. ( 10.1098/rspa.2012.0133) [CrossRef] [Google Scholar]
10. Banerjee S, Peters T, Brown N, Song Y. 2021. Точные замкнутые и асимптотические выражения для электростатической силы между двумя проводящими сферами. проц. Р. Соц. А 477 , 20200866. (10.1098/rspa.2020.0866) [CrossRef] [Google Scholar]
11. Harrison RG, Carslaw KS. 2003. Ионно-аэрозольно-облачные процессы в нижних слоях атмосферы. Преподобный Геофиз. 41 , 1012. (10.1029/2002RG000114) [CrossRef] [Google Scholar]
Ионно-аэрозольно-облачные процессы в нижних слоях атмосферы. Преподобный Геофиз. 41 , 1012. (10.1029/2002RG000114) [CrossRef] [Google Scholar]
12. Pauthenier M, Cochet R, Dupuy J. 1956. Problème général de la charge acquise par une particule sphérique dans un champ électrique bi-ioinsé. Комптес Рендус 243B , 1606-1608. [Академия Google]
13. Хаин А, Архипов В, Пинский М, Фельдман Ю, Рябов Я. 2004. Усиление дождя и устранение тумана путем заполнения заряженными каплями. Часть I: теория и численное моделирование. Дж. Заявл. метеорол. 43 , 1513-1529. ( 10.1175/JAM2131.1) [CrossRef] [Google Scholar]
14. Lissowski P. 1940. Das Laden von Aerosolteilchen in einer bipolaren Ionenatmosphäre. Акта Физикохимика УРСС 13 , 157-192. [Google Scholar]
15. Liu BYH, Pui DYH. 1974.
Равновесное биполярное распределение заряда аэрозолей. Дж. Колл. Междунар. науч. 49 , 305-312. ( 10.1016/0021-9797(74)-X) [CrossRef] [Google Scholar]
( 10.1016/0021-9797(74)-X) [CrossRef] [Google Scholar]
16. Кодзима Х. 1978. Измерения равновесных распределений заряда в биполярной ионной атмосфере. Атмос. Окружающая среда. 12 , 2363-2368. ( 10.1016/0004-6981(78)
-9) [CrossRef] [Google Scholar]
17. Поллак Л., Метниекс А. 1962. О справедливости закона распределения Больцмана для зарядов аэрозольных частиц, находящихся в электрическом равновесии. Geofisica Pura e Applicata 53 , 111-132. ( 10.1007/BF02007116) [CrossRef] [Google Scholar]
18. Киф Д., Нолан П.Дж., Рич Т.А. 1959. Зарядовое равновесие в аэрозолях по закону Больцмана. проц. Р. Ирландский академик. 60А , 27-45. [Google Scholar]
19. Клемент С.Ф., Харрисон Р.Г. 1992. Распределение заряда на аэрозолях. Инст. физ. конф. сер. 118 , 275-280. [Google Scholar]
20. Клемент С.Ф., Харрисон Р.Г. 1992.
Зарядка радиоактивных аэрозолей. J. Aerosol Sci. 23 , 481-504. ( 10.1016/0021-8502(92)
( 10.1016/0021-8502(92)
21. Ганн Р. 1954. Диффузионная зарядка атмосферных капель ионами и результирующие коэффициенты сочетания. Дж. Метеорол. 11 , 339-347. (10.1175/1520-0469(1954)011<0339:DCOADB>2.0.CO;2) [CrossRef] [Google Scholar]
22. Harrison RG, Nicoll KA, Ambaum MHP. 2015. О микрофизических эффектах наблюдаемой зарядки края облака. кв. Дж. Р. Метеорол. соц. 141 , 2690-2699. ( 10.1002/qj.2554) [CrossRef] [Google Scholar]
23. Yau MK, Rogers RR. 1996. Краткий курс физики облаков, 3-е изд., с. 293. Амстердам, Нидерланды: Elsevier. [Google Scholar]
24. Suzuki K, Nakajima TY, Stephens GL. 2010. Рост частиц и эффективность сбора капель теплых облаков по результатам совместных наблюдений CloudSat и MODIS. Дж. Атмос. науч. 67 , 3019-3032. ( 10.1175/2010JAS3463.1) [CrossRef] [Google Scholar]
25. Grabowski WW, Wang LP. 2013.
Рост облачных капель в турбулентной среде.


 Их гравитация настолько велика, что они притягивают даже свет (фотоны).
Их гравитация настолько велика, что они притягивают даже свет (фотоны).
 .. находится в прямой пропорции к их массам … и в обратной пропорции к квадрату расстояния между ними.
.. находится в прямой пропорции к их массам … и в обратной пропорции к квадрату расстояния между ними.
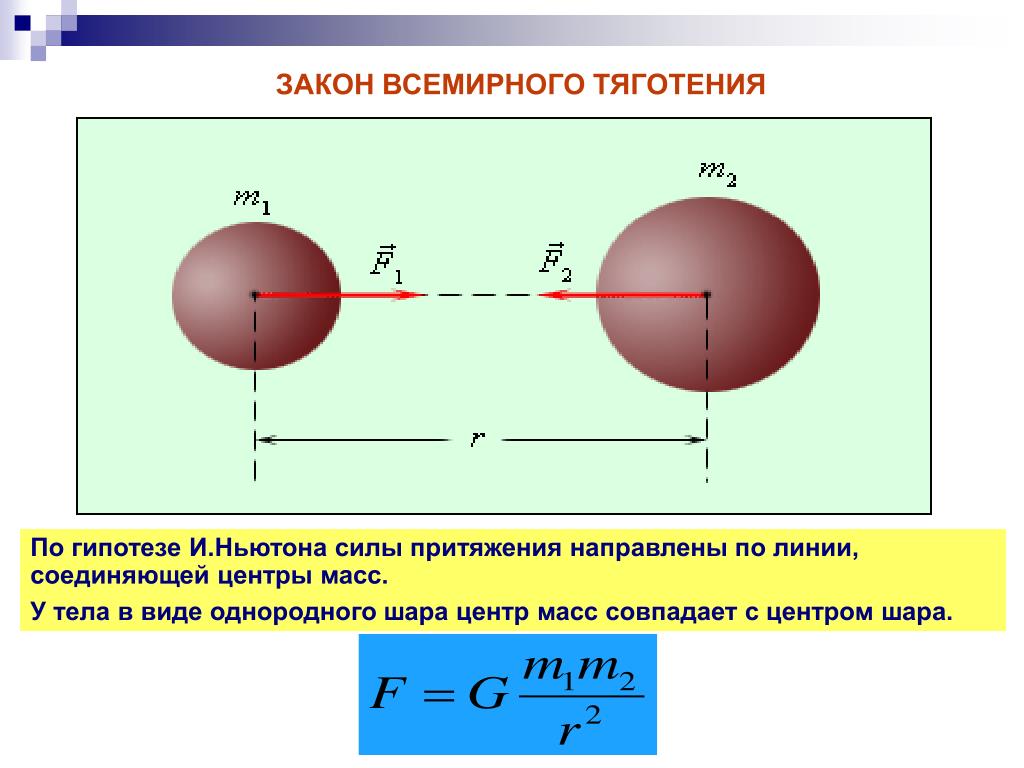


 67 ×10 −11 × 200 × 170)/(1000) 2
67 ×10 −11 × 200 × 170)/(1000) 2 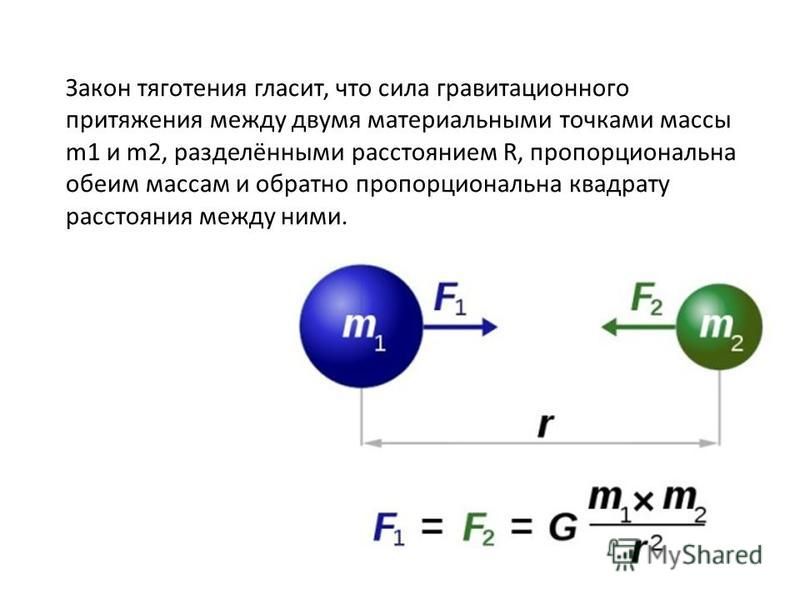 89 × 10 -11
89 × 10 -11