Как найти сопротивление силы тока
Здравствуйте. В интернете часто можно встретить вопросы как найти сопротивление тока или найти сопротивление силы тока, но на самом деле это сделать невозможно. Я уже писал в статье про мощность в цепи постоянного тока про закон Ома и три связанные им величины: напряжение, сопротивление и ток. Так вот, ток это — следствие приложенного напряжения к замкнутой цепи, имеющей сопротивление. Другими словами, у тока нет, и не может быть сопротивления. А вот как найти сопротивление цепи или участка цепи я вам сейчас расскажу.
Как найти сопротивление в цепях постоянного тока
В постоянном токе всё довольно просто. Как правило, сопротивление в таких цепях постоянно, то есть его можно принять за константу (дальше, когда будем рассматривать переменный ток, вы поймёте, про что я говорю). Следовательно, можно выделить два основных способа для вычисления сопротивления: аналитический и физический.
Как найти сопротивление с помощью омметра
Для этого вам потребуется любой прибор, способный измерить сопротивление.
Сейчас для этой цели гораздо удобнее использовать мультиметр.
Если значение сопротивления не известно, то надо начинать с самого большого предела мультиметра. Если прибор показывает значение «0», нужно уменьшить предел, пока не появится какое-нибудь сопротивление. В принципе, такие приборы довольно точны и для домашнего применения их более, чем хватает. Если же говорить о точных значениях, то для измерения сопротивления потребуется специальный измерительный мост.
Измерительный мост — это откалиброванное устройство, которое позволяет вычислить значение сопротивления очень точно. Зачастую такие мосты измеряют несколько различных величин.
Аналитический метод поиска сопротивления. Здесь потребуется уже два прибора: амперметр и вольтметр, и чем они будут точнее, тем меньше будет погрешность вычислений.
Какие здесь нюансы? Амперметр всегда включается последовательно в цепь, а вот вольтметр нужно подсоединять как можно ближе к сопротивлению параллельно. Дело в том, что провода тоже имеют сопротивление (об этом расскажу чуть позже).
Поэтому, если мы измерим напряжение в источнике питания, то мы получим сопротивление всей цепи, а именно: сопротивление проводов + сопротивление амперметра + само искомое сопротивление. Но даже это ещё не всё. Помните, мы говорили про параллельное и последовательное соединение сопротивлений. Так вот, вольтметр имеет сопротивление, поэтому после измерения напряжения нужно будет узнать сопротивление вольтметра и только тогда, можно точно высчитать номинал сопротивления с учётом места присоединения вольтметра.
Подведём итоги. В постоянном токе гораздо проще сделать вычисления с помощью омметра или функции измерения сопротивления в мультиметре. Если требуется высокая точность, то для вычисления номинала сопротивления нужно использовать измерительный мост.
Как вычислить сопротивление проводника
Как я уже говорил, провод тоже имеет сопротивление, а значит, его можно вычислить. Для этого используется формула:
p- удельное электрическое сопротивление при температуре 20°С, значение которого берётся из таблицы;
l- длина проводника в метрах
S – площадь поперечного сечения (школьный курс геометрии).
Если это круг, то , если квадрат или прямоугольник, то одна сторона умножается на другую и т.д. Значение подставляется в мм².
Перейдём к практике. Допустим, у нас есть стальной круглый прут длиной 5 метров и диаметром 5 мм. Посчитаем его сопротивление. p стали составляет 0,15 Ом·мм²/м, длина известна – 5 метров, площадь поперечного сечения
(обратите внимание, что диаметр делим пополам, чтобы получить радиус и только потом вычисляем площадь). Осталось всё это подставить в формулу:
Где можно применить этот расчёт? Например, для изготовления предохранителей, когда нужно из подручных материалов в срочном порядке сделать новый или сделать мощное сопротивление. Под мощным подразумевается способность сопротивления выдерживать большие токи, то есть успевать отдавать тепло в окружающую среду без физического разрушения, а не значение. Таким образом, сопротивление может быть номиналом 1 Ом и мощностью 2000 ватт. Но чаще всего этот расчёт применяют для вычисления потери мощности на линии, однако это тема отдельной статьи, и касаться её мы пока не будем.
Нужно так же обратить внимание, что при температурных условиях, отличных от 20°С необходимо применять поправочные коэффициенты, если требуется высокая точность.
Как найти сопротивление в цепях переменного тока
Вот здесь, товарищи, будет посложнее. Дело в том, что переменный ток вводит два понятия сопротивления: активное и реактивное. Активное сопротивление не зависит от частоты колебания напряжения, следовательно, и тока, а реактивное, наоборот, очень сильно зависит от этой частоты. Если очень просто, то к активному сопротивлению относят всё то, что не содержит индуктивности или емкости (отдельный провод, лампочка накаливания, спираль электрической плитки (хотя её нельзя назвать исключительно активным сопротивлением, однако реактивная составляющая там очень мала), лист железа и т.д.). Если вы заметили, то я указал отдельный провод, а не двух- и более жильный кабель. По сути, кабель или воздушная линия из нескольких проводов при большой длине превращается в конденсатор, где провода это обкладки конденсатора, а оболочка в кабеле или расстояние между проводами в воздушных линиях электропередачи выступают в роли диэлектрика между обкладками конденсатора.
Таким образом, методы вычисления активного сопротивления для переменного и постоянного напряжения одинаковы, в то время, как реактивное сопротивление ведёт себя абсолютно по другому.
В общем, когда мы говорим о сопротивлении в переменном токе или напряжении, то мы говорим о полном электрическом сопротивлении:
Где: R – активное сопротивление;
L – индуктивность в генри;
С – ёмкость в фарадах;
f – частота колебаний сети в герцах.
Давайте посмотрим, почему вычислить сопротивление омметром для индуктивности и ёмкости будет сложнее. Заострим внимание на том, что при измерении сопротивления омметром используется постоянный ток, то есть его частота равна нулю. Смотрим, как меняется сопротивление ёмкости и индуктивности в этом случае:
Почему нельзя делить на ноль? Правильно, потому что получаем бесконечно большое число, то есть бесконечно большое сопротивление. Другими словами, конденсатор в цепи постоянного тока это всё равно, что выключатель. Вроде бы конденсатор в цепи, но он как бы разрывает её.
Здесь ситуация другая. Индуктивность в постоянном токе становится просто проводником, а поскольку мы видим из формулы, что полное сопротивление индуктивности это сумма активной и индуктивной (которой, к слову, гораздо больше, чем активной) частей, то мы не учитываем львиную долю сопротивления индуктивности. Именно по этой причине, если включить трансформатор в сеть постоянного напряжения вместо переменного, трансформатор очень быстро нагреется и сгорит – его полное сопротивление уменьшится в разы, а уменьшение сопротивления ведёт к увеличению силы тока, на которую трансформатор не рассчитан.
Где можно использовать эти знания? В основном, эти знания применяются в звукотехнике, где нужно отсечь постоянное напряжение или отсечь определенный звуковой диапазон. Сопротивление конденсатора возрастает с понижением частоты, а сопротивление индуктивности наоборот, с повышением частоты.
Вывод: как найти сопротивление в переменном токе? Для активного сопротивления, так же, как и в постоянном: с помощью омметра или измерительного моста, или амперметра с вольтметром.
Для реактивного сопротивления использовать измерительные мосты для получения значений индуктивности или ёмкости, затем вычислять их сопротивления с учётом частоты, затем, если это конденсатор, то XC=R, а индуктивное сопротивление равно XL+R (то есть, у катушки есть еще активное сопротивление, хоть и небольшое), а затем, если требуется, вычислять полное сопротивление.
На этом можно закончить знакомство с темой, как найти сопротивление тока или как найти сопротивление и вы теперь знаете, что это неправильный вопрос и теперь знаете, что у тока нет сопротивления.
Напряжение, ток, сопротивление и закон Ома
Узнайте все о том, как измерять и манипулировать схемой в вашей электронной конструкции с помощью напряжения, тока, сопротивления и закона Ома.
Чтобы понять истинную сущность электричества, нужно понять, как манипулировать и измерять напряжение, ток и сопротивление. Мы взобрались на самые высокие вершины, чтобы найти правильную аналогию для объяснения природы того, как электричество работает в цепи: наши тела в движении.
Напряжение — все дело в потенциале
Представьте, что вы просыпаетесь утром. Вы лежите в постели, хотите еще несколько часов сна, но пришло время вашей ужасной утренней пробежки. Вы знаете, что это полезно для вас, и вы будете чувствовать себя прекрасно, как только начнете двигаться, но каждое утро вы должны делать выбор. Вы можете либо остаться в постели и поспать немного дольше, либо встать и начать двигаться.
Это сущность напряжения; все дело в разнице потенциалов. У всех нас есть потенциал, и когда дело доходит до бега, потенциал, о котором идет речь, делает выбор: бежать или спать. Если вы не решите бежать сегодня утром, ваш потенциал будет дремать, но если вы это сделаете, то этот потенциал вырвется наружу, заставив вас пробежать много миль и зарядив энергией весь оставшийся день.
Напряжение в электричестве
Как и способность двигаться или нет, напряжение представляет собой запасенную электрическую энергию с потенциалом движения.
Именно эта сила напряжения побуждает электроны течь по цепи и заставляет их работать час за часом.
В электрической цепи напряжение измеряется путем нахождения так называемой разности потенциалов между двумя точками с помощью мультиметра. Возьмите 9-вольтовую батарею, например, если вы измерите положительный и отрицательный полюсы, вы получите разность потенциалов 9 вольт (или близкую к этому). Положительный конец измеряет 9 В, а отрицательный конец измеряет 0 В. Минус два числа, и вы получите разность потенциалов.
(Источник изображения) Напряжение бывает двух видов:
- Напряжение постоянного тока (постоянный ток), обеспечивающее постоянный поток отрицательного электричества.
- Напряжение переменного тока (переменного тока), которое постоянно переключается с отрицательного на положительное.
Вот символы, которые вы должны искать на схеме для напряжения постоянного тока, напряжения переменного тока и батареи:
Вот некоторые из символов напряжения, на которые следует обратить внимание в вашей следующей схеме — батареи, постоянный и переменный ток.Отец напряжения — Алессандро Вольта
Человек дня, которому приписывают открытие напряжения – Алессандро Вольта (Источник изображения)Человек, первым открывший напряжение, был итальянский физик Алессандро Вольта. Он также обнаружил массу других интересных вещей, в том числе:
- Открытие того, что при смешивании метана с воздухом можно создать электрическую искру, что положило начало ныне известному двигателю внутреннего сгорания.
- Открытие того, что электрический потенциал, хранящийся в конденсаторе, пропорционален его электрическому заряду.
- Вольте также приписывают создание первой электрической батареи, называемой вольтовой батареей, которая позволила ученым того времени создать постоянный поток электронов.
Актуальность – Плывите по течению
Возвращаясь к нашей аналогии с бегом, представьте, что вы приняли решение совершить утреннюю пробежку. На вас надеты кроссовки и шорты для бега, и вы выходите из своей двери, чтобы отправиться в путь. В этот момент у вас есть какое-то движение, когда вы начинаете свой бег, поток.
Может быть, через час вы начнете бегать, готовые пробежать много миль. Когда вы бежите, ваши умные часы точно измеряют, как далеко вы пробежали и как быстро вы двигались. Этот процесс запуска и измерения процесса и есть суть тока.
Ток в электричестве
Подобно тому, как вы делаете шаги для завершения утренней пробежки, ток представляет собой постоянное движение или поток электричества в цепи. Электрический ток, протекающий через вашу цепь, всегда измеряется в амперах или амперах. Но что держит этот поток в движении?
Это напряжение, о котором мы говорили ранее. Точно так же, как вам нужно сказать себе продолжать бежать, как только вы устанете, напряжение является движущей силой тока, которая заставляет его двигаться. Есть две точки зрения на то, как ток течет в цепи; Обычный поток или электронный поток. Давайте посмотрим на оба.
Обычный поток
Обычный поток был первым в период научных открытий, когда люди не понимали, что такое электроны и как они текут в цепи. В рамках этой модели предполагалось, что электричество течет от плюса к минусу.
Обычный поток с электричеством, протекающим от положительной к отрицательной стороне батареи. Вы все еще увидите, что этот менталитет используется в схемах сегодня, и хотя он не совсем точен, его немного легче понять, чем электронный поток.
В конце концов, если мы вернемся к нашей аналогии с бегом, вы начинаете с положительного источника энергии и бежите, пока она не закончится. Это позитивно-негативные отношения, как и многие вещи в жизни.
Электронный поток
Electron Flow был продолжением обычного потока. Эта модель точно изображает электроны как движущиеся в противоположном направлении, от отрицательного к положительному. Поскольку электроны отрицательны по своей природе, они всегда будут вытекать из отрицательного и бесконечно пытаться найти свой путь к положительной, низковольтной стороне источника питания.
Имеет ли значение, каким образом вы отображаете ток, протекающий в цепи? Не совсем. Вы, вероятно, увидите, что это представлено в обоих направлениях, когда вы смотрите на различные схемы. Взгляните на диоды или транзисторы на следующей схеме, которую вы исследуете; все они будут указывать в направлении обычного потока.
Человек, стоящий за током – Андре-Мари Ампер
Андре-Мари Ампер совершил гораздо больше, чем просто открытие Amperes. (Источник изображения)Ампер был французским физиком и математиком. Он также был одним из основателей науки классического электромагнетизма. Вы можете поблагодарить Ampere за несколько замечательных вещей, в том числе:
- Его главное открытие, демонстрирующее, что провод, по которому течет электрический ток, может либо притягивать, либо отталкивать другой провод, по которому также протекает ток, без использования физических магнитов.
- Он также был первым, кто выдвинул идею существования частицы, которую мы все широко знаем как электрон.
- Он также организовал химические элементы по их свойствам в периодической таблице за полвека до того, как появилась современная современная таблица Менделеева.
Сопротивление — это материальный мир
Наша окончательная концепция: Сопротивление.
Представьте, что вы стоите спиной на беговой дорожке. По какой поверхности вы бегаете? Если вам повезет, то вы можете путешествовать по мягкой траве или грунтовой дорожке. Или, может быть, вы предпочитаете твердость улицы или тротуара.
Независимо от того, по какому пути вы бежите, ваши ноги встречают некоторое сопротивление, когда вы продолжаете двигаться вперед. Естественно, не все пути сопротивления одинаковы. Бег по грязи оказывает большее сопротивление вашей способности бежать по сравнению с бегом по грунтовой дорожке или улице. Вот что такое сопротивление — тяга и тяга материального мира.
Сопротивление в электричестве
Через какой бы материал ни проходило электричество, оно будет сталкиваться с некоторым трением, препятствующим его движению. Проще говоря, сопротивление замедляет ток. Хотя в электрической цепи есть определенные компоненты, такие как резистор, единственной задачей которого является сопротивление электричеству, любой физический материал будет оказывать некоторое сопротивление.
Сопротивление измеряется в Ом·Ом и имеет прямое отношение к току и напряжению. Например, чем больше у вас сопротивление, тем меньший ток может течь по цепи. Это как с бегом, чем гуще грязь, тем медленнее ты будешь бежать. Обратное также работает: если вы увеличиваете напряжение, чтобы ток двигался быстрее, ваше сопротивление будет меньше влиять на вашу цепь.
Мастер сопротивления — Георг Саймон Ом
Георг Ом – человек, который объединил напряжение, ток и сопротивление в ныне известный закон Ома. (Источник изображения) Г-н Ом был немецким физиком и математиком, и именно в дни работы школьным учителем он начал свои исследования с использованием новой электрической батареи, изобретенной Вольтой. С помощью своего собственного оборудования Ом обнаружил, что существует прямая зависимость между напряжением, приложенным к проводнику (например, к медному проводу), и результирующим электрическим током. Это стало известно как ныне известный закон Ома, на который мы все полагаемся сегодня.
Интересно отметить, что, когда Ом представил свои открытия в своей первой книге «Математическое исследование гальванической цепи», колледжу, в котором он работал в то время, это было безразлично. Так что же сделал Ом? Он ушел в отставку и получил новую работу в Нюрнбергской политехнической школе. Именно здесь его работа, к счастью, получила заслуженное внимание.
Собираем все вместе с законом Ома
Итак, пришло время собрать все наши концепции воедино. Вот с чем нам предстоит работать:
- Напряжение (В) — Сохраненное электричество, которое может двигаться. Когда этот потенциал активирован, напряжение действует как своего рода давление, толкая ток по цепи.
- Ток (I) – Поток электричества в цепи. Это можно измерить непосредственно в амперах, и есть две точки зрения на то, как течет ток — обычный поток и электронный поток.
- Сопротивление (R) – Сопротивление, с которым сталкивается электричество, просто протекая через какой-либо физический материал. Это измеряется в Омах.
Это измеряется в Омах.Собирая все это вместе, мы приходим к закону Ома:
В=ИК
В этом уравнении V = напряжение, I = ток и R = сопротивление. Гибкость закона Ома впечатляет, и его можно использовать для нахождения любого из этих трех значений, когда известны только два из них. Давайте рассмотрим пример, чтобы увидеть, как это работает.
Использование треугольника Ома
Ознакомьтесь с треугольником Ома ниже. Он обеспечивает простое визуальное представление того, как вы можете манипулировать законом Ома, чтобы получить нужные вам ответы. Чтобы использовать его, все, что вам нужно сделать, это закрыть букву значения, которое вам нужно выяснить, а оставшиеся буквы покажут вам, как туда добраться.
«Треугольник Ома» — удобный инструмент, позволяющий точно определить, какой именно вариант закона Ома необходимо использовать. Взгляните на схему ниже. У нас есть батарея 9В, подключенная к светодиоду и резистору. Единственная проблема заключается в том, что нам нужно выяснить, каково значение резистора.
Для этого давайте посмотрим на наш треугольник Ома. Закрыв R, мы можем увидеть, что V больше I, или V делится на I. Таким образом, разделив эти два числа, мы получим значение нашего резистора. Подставим эти числа в это уравнение: R = V/I.
- Начнем с самого очевидного, напряжение нашей батареи 9 вольт.
- Глядя на техническое описание нашего светодиода, мы видим рекомендуемый максимальный ток 16 мА (миллиампер), который преобразуется в 0,016 ампер.
- Подставив эти два числа в наше уравнение, мы получим R = 9 В/0,016 А, что равно 473,68. Это означает, что нам нужен резистор на 473 Ом, чтобы наш светодиод включился!
Сопротивление бесполезно
Понять, как работают вместе напряжение, ток и сопротивление, было не так уж сложно, не так ли? Мы надеемся, что в следующий раз, когда вы отправитесь на утреннюю пробежку, у вас появится новый взгляд на электричество.
Почувствуйте, как ваши ноги летят по тротуару или грязи, и помните, что это сопротивление. И когда вы проверяете, как далеко вы пробежали, вы наблюдаете ток в движении! И та сила, которая подняла тебя с постели и заставила бежать? Напряжение.
Готовы сделать свой первый круг сегодня? Попробуйте Autodesk Fusion 360 бесплатно!
Сопротивление и закон Ома | Ultimate Electronics Book
Ultimate Electronics: Практические схемы и анализ
≡ Оглавление
«
2,5
Земля»
2,7
МощностьКак решить задачи по закону Ома для резисторов. Микроскопические причины, по которым закон Ома является макроскопически линейным. 11 минут чтение
В разделе «Электроны в движении» мы обсуждали, как электрические поля вызывают силу →F=qe→E
на электрон. Как и в случае с любым объектом, на который действует результирующая сила, электрон будет ускоряться →Fnet=me→a
в ответ на эту силу.
Со временем это ускорение вызывает увеличение скорости: →a=d→vdt
. Скорость носителей заряда можно описать как электрический ток.
Для свободных электронов, летающих в вакууме, это конец истории.
Однако для электронов, путешествующих в материале – обычно, но не всегда в твердом теле – столкновения между электроном и самим веществом являются невероятно доминирующим фактором общего движения электрона.
Хотя электрон все еще ускоряется электрическим полем, он часто теряет энергию из-за столкновений с материалом. Каждое столкновение рассеивает кинетическую энергию , накопленную электроном в материале, который становится теплом.
В результате, чтобы электроны двигались через материал с постоянной средней скоростью (нулевое среднее ускорение), нам по-прежнему необходимо добавлять энергию для компенсации кинетической энергии, теряемой при столкновениях с неподвижным материалом. Это свойство называется сопротивление .
(Исходя из изучения механики и кинематики, существует спектр между упругими столкновениями, которые сохраняют полную кинетическую энергию, и неупругими столкновениями, которые не сохраняют полную кинетическую энергию, потому что часть этой энергии преобразуется в тепло, звук, деформацию материала и т.
д. В случае трения или омического сопротивления мы имеем в виду неупругие столкновения.)
Электрическое сопротивление из-за столкновений аналогично сопротивлению воздуха.
Представьте себе мячик для пинг-понга, упавший с башни. Под действием силы тяжести мяч летит к земле. Если бы не было сопротивления воздуха, скорость мяча продолжала бы увеличиваться и возрастать без ограничений. Но в воздухе между мячом и молекулами воздуха происходят столкновения, поэтому мяч достигает некоторой стационарной скорости, которую в этой ситуации часто называют «конечной скоростью». При этой установившейся скорости энергия, полученная при движении вниз в гравитационном поле потенциальной энергии, равна энергии, потерянной при столкновениях при отталкивании воздуха с пути. Когда мы усредняем многие из этих микроскопических столкновений, оказывается, что мяч не ускоряется и не замедляется, а вместо этого продолжает падать с постоянной скоростью.
Это действительно рассеивание кинетической энергии.
Если бы это было не так, то добавление энергии вызвало бы дальнейшее ускорение, а не просто поддержание постоянной скорости.
Аналогия с жидкостью тоже уместна. Проталкивание жидкости через трубу требует энергии (обычно определяемой как разность давлений) для поддержания постоянной скорости (обычно определяемой как расход), потому что поток постоянно теряет энергию из-за сопротивления внутренних стенок трубы, а также к вязким взаимодействиям между молекулами жидкости. Эти силы сопротивления действительно рассеиваются в виде тепла. (Однако из-за такой высокой удельной теплоемкости воды мы обычно не замечаем этого повышения температуры в повседневной жизни!)
Автомобиль, движущийся с постоянной скоростью по ровному шоссе, демонстрирует оба этих явления: для поддержания постоянной скорости необходимо добавлять энергию за счет сопротивления воздуха, а также сопротивления жидкостей внутри двигателя и трансмиссии, трения в колесные подшипники, неупругая деформация резиновых покрышек и т.
д. Если бы это было не так, мы могли бы просто поставить машину на нейтраль и заглушить двигатель, как только достигнем крейсерской скорости.
Когда мы движемся через что-либо, кроме вакуума без трения (или сверхпроводника!), материалы будут взаимодействовать, сталкиваться, деформироваться и вызывать потери кинетической энергии. Независимо от того, движется ли это автомобиль по шоссе или электрон в металле, результат один и тот же: нужно постоянно добавлять больше энергии просто для поддержания постоянной средней кинетической энергии.
Закон Ома обычно рассматривается как:
V=IR
где R – сопротивление резистора, В – падение напряжения на резисторе, а I это ток через резистор. (См. оставшуюся часть этой главы, в том числе Закон Кирхгофа о напряжении (KVL) и Закон Кирхгофа о токе (KCL), Обозначение напряжений, токов и узлов, а также Решение систем цепей для получения дополнительной информации о правильном указании напряжения и тока!)
Поскольку напряжение – это мера работы на единицу заряда, закон Ома означает, что для материалов с более высоким сопротивлением требуется больше работы, чтобы пропустить тот же поток тока.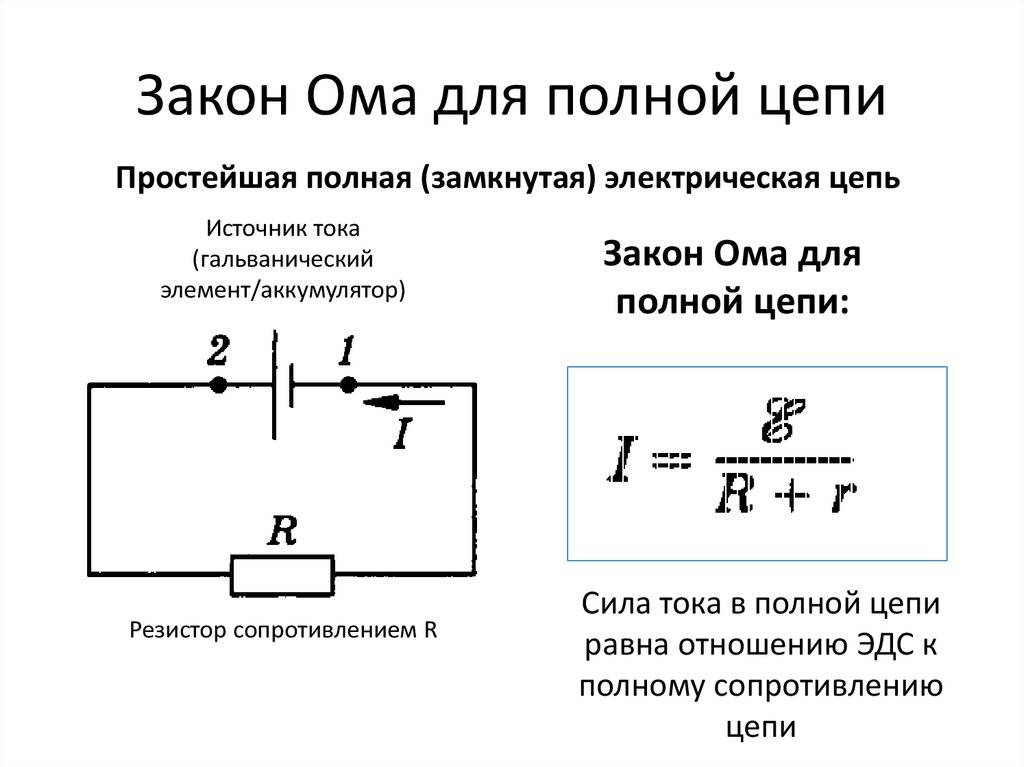
Закон Ома утверждает, что сопротивление является линейной функцией, но это правило не является универсальным ; на самом деле это эмпирических (основанных на наблюдениях, а не на теории). На самом деле это линеаризованная модель триллионов или более взаимодействий атомарного масштаба внутри материала, и оказывается, что в среднем , агрегированное поведение выглядит примерно линейным.
Если мы знаем любые два из V, I или R , мы можем решить для третьей переменной:
V=I⋅RI=VRR=VI
Это одно из самых основных практических уравнений в электронике, поэтому мы выделяем его во всех его формах.
Эти соотношения можно рассматривать с теоретической точки зрения при установлении связи между токами и напряжениями в цепи, но они также имеют практическое значение:
- два, чтобы получить напряжение: V=I⋅R .
- Если у нас есть известных напряжение на известном сопротивлении , мы можем разделить два, чтобы получить ток: I=VR
.
- Наконец, если у нас есть известное напряжение и известный ток , мы можем разделить их, чтобы получить сопротивление: R=VI .
В математическом смысле, когда мы используем слово известное , мы противопоставляем его неизвестной переменной, которую ищем. (См. Системы уравнений.)
Но в практическом смысле известно может означать две несколько разные вещи:
- «Известный» может означать внешне контролируемый или фиксированный . Например, если у нас есть источник тока, который всегда выдает 2 ампера, то этот ток известен, потому что он контролируется и устанавливается на определенное значение.
- «Известно» может означать измеренное . Например, мы можем измерить напряжение 6 вольт на выходе источника тока. Это напряжение известно, потому что оно измеряется, а не фиксируется каким-либо процессом.
В большинстве вопросов, связанных с законом Ома, мы комбинируем два типа «известных».
Чтобы объединить два приведенных выше примера, если наши 2 A
источник тока подключен к какому-то неизвестному сопротивлению, и мы измеряем 6 В
на выходе мы можем определить, что неизвестное сопротивление равно:
R=VI=62=3 Ом
Линейность закона Ома чрезвычайно полезна при проведении измерений. Резисторы — это компоненты, которые линейно преобразуют разность напряжений в ток и наоборот, и это полезный эффект во многих аналоговых схемах. Подробнее о вольтметрах, амперметрах и омметрах мы поговорим в разделе «Мультиметры и измерения».
Наш первый пример — одиночный 100 Ом резистор R1, подключенный к источнику напряжения:
Закон Ома — постоянный резистор с источником напряжения
Circuitlab.com/cu5584wxrenxw
Править – Имитация
Упражнение Нажмите на схему, затем нажмите «Симуляция» и нажмите «Запустить DC Solver». Это покажет рассчитанный ток:
I=VR=5 В100 Ом=0,05 А=50 мА
Затем нажмите «Запустить развертку постоянным током».
Это настроено для регулировки значения источника напряжения от -5 до +5. Симулятор мгновенно построит график с настройкой напряжения по оси x и результирующим током по оси y.
Вместо того, чтобы управлять сопротивлением с источником напряжения, мы можем вместо этого подключить его к фиксированному источнику тока:
Закон Ома — постоянный резистор с источником тока
Circuitlab.com/cd2yet2jf36x7
Править – Имитация
Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить DC Solver». Это покажет рассчитанное напряжение:
ВА=I⋅R=(1 А)⋅(100 Ом)=100 В
Затем нажмите «Запустить развертку постоянным током». Это настроено для настройки значения текущего источника. Симулятор мгновенно построит график с текущими настройками по оси x и результирующим напряжением по оси y.
Использование симулятора CircuitLab для изменения токов и напряжений и построения графика развертки постоянного тока является очень простой функцией.
Чуть более продвинутый случай – изменение сопротивления:
Закон Ома — Регулируемый резистор с источником напряжения
Circuitlab.com/cqa89rtgrxx86
Править – Имитация
Упражнение Щелкните цепь, нажмите «Симуляция» и «Запустить развертку постоянным током». Теперь симулятор подключает различные резисторы от 1 до 1000 Ом и строит результирующую кривую тока с сопротивлением в Омах по оси x и током по оси y.
Это работает, устанавливая развертку постоянного тока на изменение «R1.R», что означает «сопротивление резистора с именем R1». Просмотр параметров компонента — мощный инструмент моделирования цепей.
Сопротивление зависит от выбора материала (например, алюминия или меди) и его физических размеров. Для твердого тела постоянной площади поперечного сечения A и длина L , сопротивление равно:
R=ρLA
Размеры имеют смысл: если мы сделаем резистор в два раза длиннее, расстояние, на котором могут произойти столкновения и потеря энергии, будет в два раза больше, как при последовательном соединении резисторов.
Вместо этого, если мы увеличим площадь поперечного сечения, средняя скорость дрейфа будет ниже при той же величине тока, поэтому при каждом столкновении теряется меньше энергии.
Удельное сопротивление ρ является свойством материала, а также функцией температуры: см. Практические резисторы: температурный коэффициент для получения дополнительной информации.
Почему ток линейно пропорционален напряжению в резистивном материале?
Это часто считается само собой разумеющимся, но на самом деле это не очевидно. В свободном пространстве заряд в постоянном электрическом поле имел бы линейно возрастающую скорость , а не (в среднем) постоянную скорость в резистивном материале.
Вот одна из возможных моделей:
Даже при нулевом электрическом поле (то есть при нулевом напряжении) заряды не являются остатком. Из-за теплового движения они постоянно толкаются.
Теперь применим электрическое поле (то есть ненулевое напряжение). Это поле →E Поле воздействует на заряд силой:
→F=q→E=m→a
Эта сила немного ускоряет заряд в направлении поля.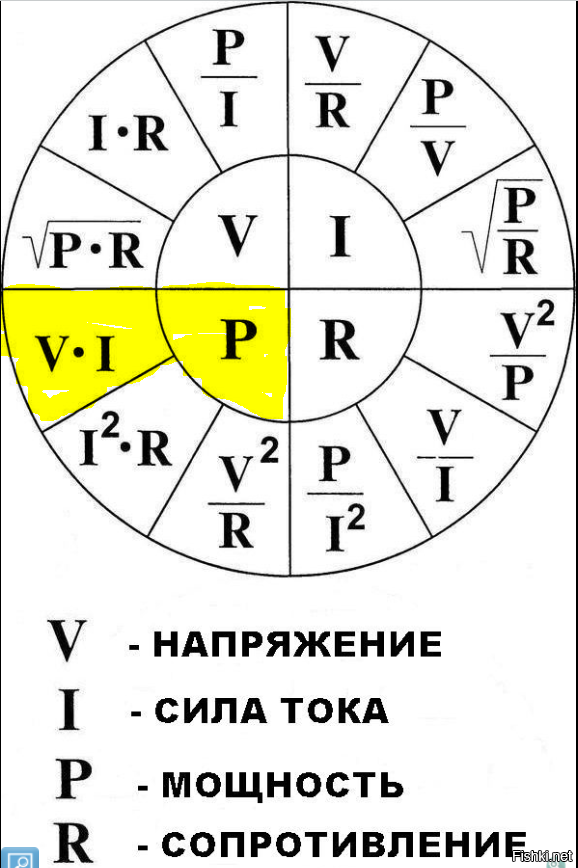
Однако, прежде чем он начнет двигаться особенно быстро, заряд сталкивается с другими зарядами внутри материала. Это столкновение вызывает потерю кинетической энергии (превращающейся в тепло в материале), и заряд должен снова стартовать с нулевой скоростью. Оттуда он начинает ускоряться за счет поля, и цикл ускорения и столкновения повторяется.
Предположим, что среднее время между столкновениями равно tcollision . В этом случае в промежутках между столкновениями →E поле может ускорить заряд от v=0 до некоторой скорости vmax до столкновения. В этом случае (с фиксированным tcollision ), средняя скорость частицы будет пропорциональна ускорению, обусловленному полем. (Если это неясно, нарисуйте график зависимости скорости заряда от времени. Это будет иметь вид пилообразной формы: увеличение от 0 до vmax во время tcollision , затем внезапно падает до 0 и повторяется снова. Средняя скорость ¯¯¯¯¯vd=vmax2 .)
Чтобы узнать больше о том, как все это работает со случайными тепловыми колебаниями в трех измерениях, посмотрите модель Drude .
Вы можете задаться вопросом, почему у нас есть среднее время между столкновениями, а не среднее расстояние между столкновениями. Это связано с тем, что тепловая скорость намного больше, чем скорость дрейфа, поэтому эти случайные тепловые скорости в основном определяют, когда происходит столкновение, а не скорость дрейфа, которая важна для определения частоты столкновений.
Для большинства материалов более высокая температура означает более высокие тепловые скорости и более короткое время tстолкновения , поэтому более высокое сопротивление. Дополнительные сведения о взаимосвязи между сопротивлением и температурой см. в разделе Практические резисторы: температурный коэффициент.
Резисторы обычно линейны на много порядков величины тока — в отличие от полупроводникового перехода, как мы увидим позже.
Резисторы обычно линейны, независимо от направления протекания тока — тоже в отличие от полупроводникового перехода.
Представьте себе механическую цилиндрическую пружину: сила линейна для маленьких толчков и для больших толчков, но в какой-то момент вы начинаете постоянно деформировать металл (пластическая деформация), и вы получаете нелинейное поведение.
Таким же образом, если вы превысите пределы резистора, вы можете безвозвратно заменить его, как правило, из-за перегрева. Дополнительные сведения см. в нескольких следующих разделах, посвященных мощности и практическим резисторам: номинальная мощность (мощность).
Сверхпроводники когда-то были экзотическими материалами, но становятся все более и более распространенными, поскольку их цена снижается, а диапазон рабочих температур растет. В настоящее время нет известных материалов, которые являются сверхпроводниками при комнатной температуре и давлении, но исследования в этой области находят материалы, которые работают при все более и более высоких температурах.
Сверхпроводники обладают не только низким сопротивлением, но и предлагают действительно нулевое сопротивление при протекании тока.
В сверхпроводнике нет внутренних неупругих столкновений между носителями заряда и веществом.
Существуют практические ограничения для сверхпроводников в нескольких измерениях:
- Ток. Сверхпроводник может поддерживать только определенную максимальную плотность тока, известную как критический ток .
- Магнитное поле. Сверхпроводящие материалы имеют ограничения по напряженности магнитного поля, в котором они могут работать.
- Рабочая температура. Сверхпроводящие материалы перестают быть сверхпроводящими при превышении некоторого максимального предела температуры.
В дополнение к этому, сверхпроводники и сверхпроводящие провода по-прежнему относительно сложны в производстве с точки зрения производства. Материалы часто хрупкие, их необходимо охлаждать до чрезвычайно низких температур, и их трудно соединять и соединять с другими компонентами.
В следующем разделе «Мощность» мы поговорим о том, куда уходит тепло от этих резистивных столкновений, и подумаем больше о потоке энергии и мощности в целом.