где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
Онлайн калькулятор – закон Ома (ток, напряжение, сопротивление) + Мощность :: АвтоМотоГараж
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая – мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
Вторая – метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.
сопротивления через силу тока и напряжение
Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.
Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.
Многообразие устройств электротехники
Электрический ток
Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде. Такими частицами могут быть свободные электроны или ионы, частицы вещества, в которых число протонов в ядре не равно количеству электронов, то есть имеющие определенный заряд, положительный или отрицательный. Электроток может быть постоянный или переменный.
Электрическое напряжение
Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.
Сопротивление
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Мощность
Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Закон Ома и его основатель
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Единицы измерения в формуле
Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:
- Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
- Сила тока – Ампер. Обозначается символом А;
- Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
- Электрическая мощность – Ватт. Обозначается как Вт или W.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Лампа накаливания
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Правило для запоминания расчетов
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Зависимость сопротивления воды от содержания солей
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
По какой формуле определяется напряжение
Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:
- Ток и сопротивление – U=I∙R;
- Ток и мощность – U=P/I;
- Мощность и сопротивление – U=√P∙R
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие.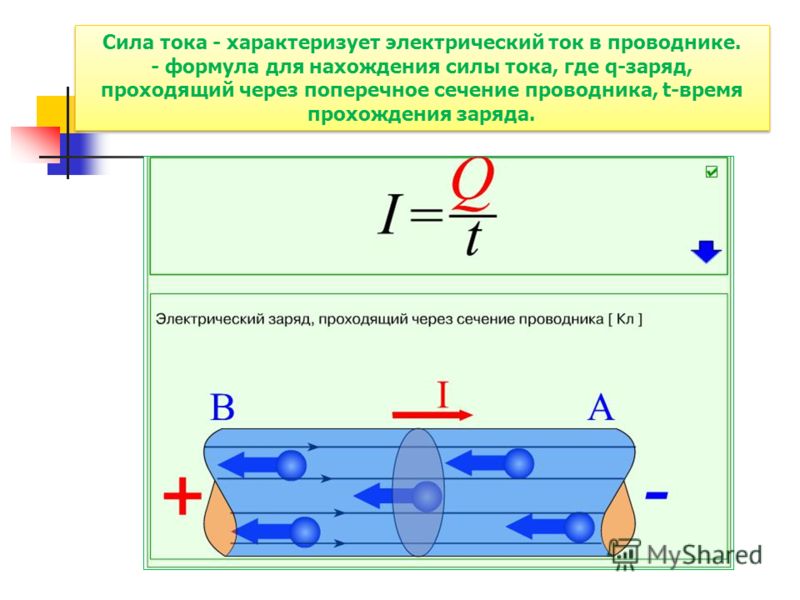 Для обозначений применяют соответствующие приставки:
Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Гидравлическая аналогия
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Один из самых распространенных авометров
Типичные напряжения
Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:
- Бытовая сеть –220В;
- Бортовая сеть автомобиля – 12 или 24В;
- Батареи и аккумуляторы – 1.5, 3 или 9В.
Потенциал Гальвани
В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.
Видео
Сила тока | Самое простое объяснение, формула, единица измерения
Сила тока с точки зрения гидравлики
Думаю, вы не раз слышали такое словосочетание, как “сила тока“. А для чего нужна сила? Ну как для чего? Чтобы совершать полезную или бесполезную работу. Главное, чтобы что-то делать. Каждый из нас обладает какой-либо силой. У кого-то сила такая, что он может одним ударом разбить кирпич в пух и в прах, а другой не сможет поднять даже соломинку. Так вот, дорогие мои читатели, электрический ток тоже обладает силой.
Представьте себе шланг, с помощью которого вы поливаете свой огород
Давайте теперь проведем аналогию. Пусть шланг – это провод, а вода в нем – электрический ток. Мы чуть-чуть приоткрыли краник и вода сразу же побежала по шлангу. Медленно, но все-таки побежала. Сила струи очень слабая.
А давайте теперь откроем краник на полную катушку. В результате струя хлынет с такой силой, что можно даже полить соседский огород.
В обоих случаях диаметр шланга одинаков.
А теперь представьте, что вы наполняете ведро. Напором воды из какого шланга вы его быстрее наполните? Разумеется из зеленого, где напор воды очень сильный. Но почему так происходит? Все дело в том, что объем воды за равный промежуток времени из желтого и зеленого шланга выйдет тоже разный. Или иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Напором воды из какого шланга вы его быстрее наполните? Разумеется из зеленого, где напор воды очень сильный. Но почему так происходит? Все дело в том, что объем воды за равный промежуток времени из желтого и зеленого шланга выйдет тоже разный. Или иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Разберем еще один интересный пример. Давайте допустим, что у нас есть большая труба, и к ней заварены две другие, но одна в два раза меньше диаметром, чем другая.
Из какой трубы объем воды будет выходить больше за секунду времени? Разумеется с той, которая толще в диаметре, потому что площадь поперечного сечения S2 большой трубы больше, чем площадь поперечного сечения S1 малой трубы. Следовательно, сила потока через большую трубу будет больше, чем через малую, так как объем воды, который протекает через поперечное сечение трубы S2, будет в два раза больше, чем через тонкую трубу.
Что такое сила тока?
Итак, теперь давайте все что мы тут пописали про водичку применим к электронике. Провод – это шланг. Тонкий провод – это тонкий в диаметре шланг, толстый провод – это толстый в диаметре шланг, можно сказать – труба. Молекулы воды – это электроны. Следовательно, толстый провод при одинаковом напряжении можно протащить больше электронов, чем тонкий. И вот здесь мы подходим вплотную к самой терминологии силы тока.
Сила тока – это количество электронов, прошедших через площадь поперечного сечения проводника за какое-либо определенное время.
Все это выглядит примерно вот так. Здесь я нарисовал круглый проводок, “разрезал” его и получил ту самую площадь поперечного сечения. Именно через нее и бегут электроны.
За период времени берут 1 секунду.
Формула силы тока
Формула для чайников будет выглядеть вот так:
где
I – собственно сила тока, Амперы
N – количество электронов
t – период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды
Более правильная (официальная) формула выглядит вот так:
где
Δq – это заряд за какой-то определенный промежуток времени, Кулон
Δt – тот самый промежуток времени, секунды
I – сила тока, Амперы
В чем прикол этих двух формул? Дело все в том, что электрон обладает зарядом приблизительно 1,6 · 10-19 Кулон. Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Итак, теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетят 6,24151⋅1018 электронов, то сила тока в таком проводнике будет равна 1 Ампер! Все! Ничего не надо больше придумывать! Так и скажите своему преподавателю по физике).
Если преподу не понравится ваш ответ, то скажите типа что-то этого:
Сила тока – это физическая величина, равная отношению количества заряда прошедшего через поверхность (читаем как через площадь поперечного сечения) за какое-то время. Измеряется как Кулон/секунда. Чтобы сэкономить время и по другим морально-эстетическим нормам, Кулон/секунду договорились называть Ампером, в честь французского ученого-физика.
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы. От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум – это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе – это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
Все те же самые умозаключения можно применить и к обыкновенному проводу. Чем он больше в диаметре, тем больше он сможет “протащить” через себя силу тока. Чем меньше в диаметре, то желательно меньше его нагружать, иначе его “порвет”, то есть он тупо сгорит. Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
Как только сила тока через тонкий проводок предохранителя превысит силу тока, на которую рассчитан предохранитель, то плавкий проводок перегорает и размыкает цепь. Через перегоревший предохранитель ток уже течь не может, так как проводок в предохранителе в обрыве.
сгоревший плавкий предохранительПоэтому, силовые кабели, через которые “бегут” сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.
Сила тока в проводнике
Очень часто можно увидеть задачки по физике с вопросом: какая сила тока в проводнике? Проводник, он же провод, может иметь различные параметры: диаметр, он же площадь поперечного сечения; материал, из которого сделан провод; длина, которая играет также важную роль.
Да и вообще, сопротивление проводника рассчитывается по формуле:
формула сопротивления проводникаТаблица с удельным сопротивлением из разных материалов выглядит вот так.
таблица с удельным сопротивлением веществДля того, чтобы найти силу тока в проводнике, мы должны воспользоваться законом Ома для участка цепи. Выглядит он вот так:
закон Ома
Задача
У нас есть медный провод длиной в 1 метр и его площадь поперечного сечения составляет 1 мм2 . Какая сила тока будет течь в этом проводнике (проводе), если на его концы подать напряжение в 1 Вольт?
задача на силу тока в проводникеРешение:
Как измерить силу тока?
Для того, чтобы измерить значение силы тока, мы должны использовать специальные приборы – амперметры. В настоящее время силу тока можно измерить с помощью цифрового мультиметра, который может измерять и силу тока, и напряжение и сопротивление и еще много чего. Для того, чтобы измерить силу тока, мы должны вставить наш прибор в разрыв цепи вот таким образом.
Более подробно как это сделать, можете прочитать в этой статье.
Также советую посмотреть обучающее видео, где очень умный преподаватель объясняет простым языком, что такое “сила тока”.
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
| |||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||
формулы и определения / Блог / Справочник :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
чему равно напряжение, как найти сопротивление нагрузки
В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.
Что такое напряжение в сети электричества.
Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.
Показатель напряжения на вольтметреЗа единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.
Общепринятой единицей измерения напряжения считается 1 В – Вольт.
Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.
Чему равно напряжение.
Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.
Изображение вольтметра и электрической цепиНапряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.
Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.
Электрическое полеФормула закона Ома
Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.
Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.
Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению в сети и обратно пропорционально силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока.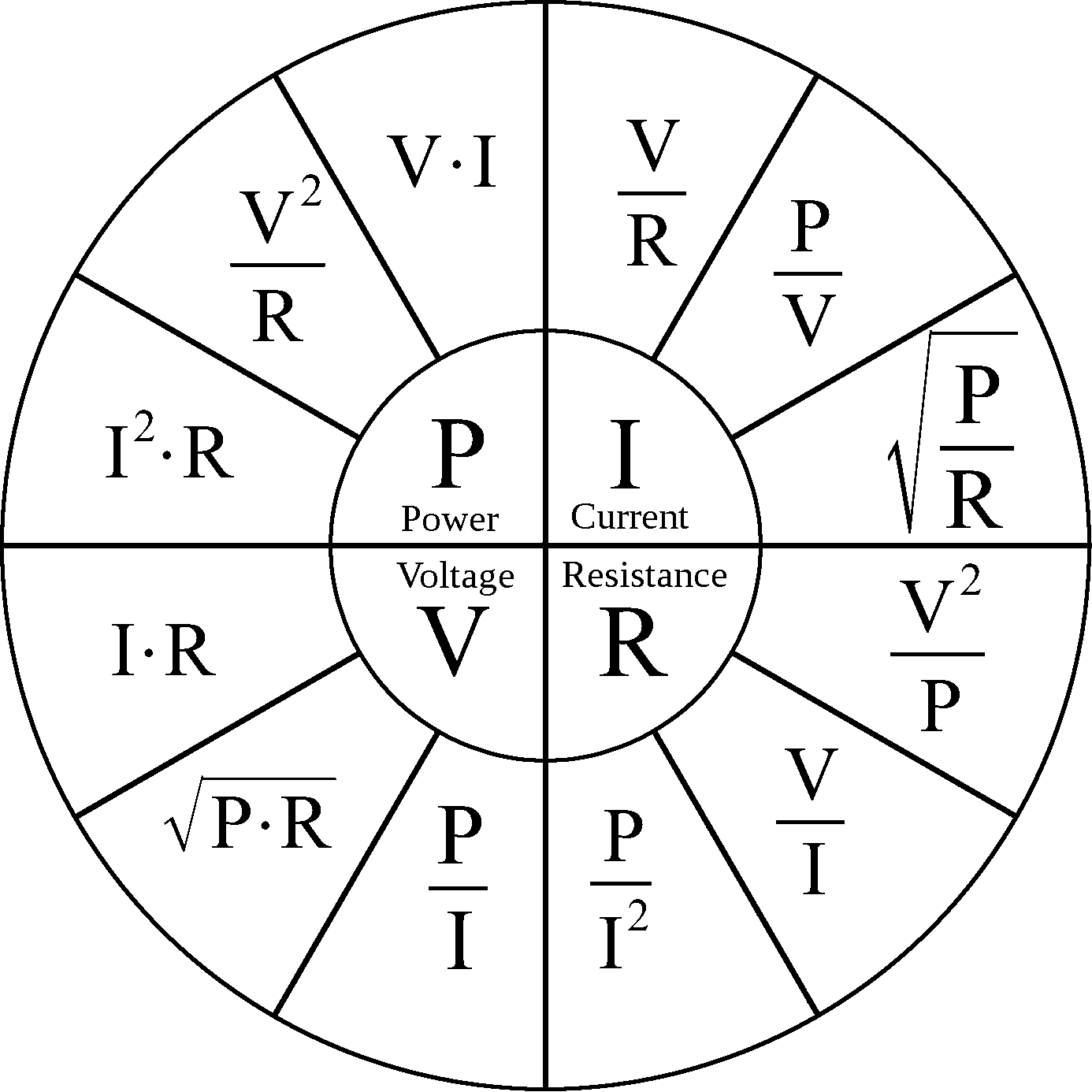 1 Ом равняется 1 Вольту, деленному на 1 Ампер.
1 Ом равняется 1 Вольту, деленному на 1 Ампер.
Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.
Ползунковый реостатИз формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.
Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.
Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].
Ом и формулаКак найти сопротивление нагрузки
Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.
Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.
Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.
Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.
Измерение напряженияПо каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Как найти силу тока через сопротивление и напряжение
Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т. е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.
е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.
Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.
При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.
Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.
ЗаконОма – Как соотносятся напряжение, ток и сопротивление | Закон Ома
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда через проводники цепи называется током , и его часто называют «потоком», как поток жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» в цепи, называется напряжением . Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками.
Когда мы говорим об определенном количестве напряжения, присутствующем в цепи, мы имеем в виду измерение того, сколько потенциальной энергии существует для перемещения носителей заряда из одной конкретной точки в этой цепи в другую конкретную точку. Без ссылки на две конкретные точки термин «напряжение» не имеет значения.
Без ссылки на две конкретные точки термин «напряжение» не имеет значения.
Ток имеет тенденцию проходить через проводники с некоторой степенью трения или сопротивления движению. Это противодействие движению правильнее называть сопротивлением . Сила тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующей прохождению тока.
Как и напряжение, сопротивление – это величина, относительная между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» или «поперек» двух точек в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, мы должны уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любой другой вид физической величины. Для массы мы можем использовать единицы «килограмм» или «грамм».
Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. Вот стандартные единицы измерения электрического тока, напряжения и сопротивления:
«Символ», присвоенный каждой величине, представляет собой стандартную буквенную букву, используемую для представления этой величины в алгебраическом уравнении.Подобные стандартизированные буквы распространены в физических и технических дисциплинах и признаны во всем мире.
«Аббревиатура единицы» для каждой величины представляет собой алфавитный символ, используемый в качестве сокращенного обозначения для конкретной единицы измерения. И, да, этот странно выглядящий символ «подкова» – это заглавная греческая буква Ω, просто символ иностранного алфавита (извинения перед читателями-греками).
Каждая единица измерения названа в честь известного экспериментатора в области электричества: amp в честь француза Андре М.Ампер, вольт после итальянского Алессандро Вольта и Ом после немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя, тогда как «I» для тока кажется немного странным. Считается, что буква «I» должна представлять «интенсивность» (потока заряда), а другой символ напряжения, «E», означает «электродвижущую силу». Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «Я».”
Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах зарезервировано «E» для обозначения напряжения на источнике (таком как батарея или генератор) и «V» для обозначения напряжения на чем-либо еще.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (называемого «мгновенным» значением). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», в то время как пик напряжения при ударе молнии в тот самый момент, когда он попадает в линию электропередачи, скорее всего, будет обозначается строчной буквой «е» (или строчной буквой «v»), чтобы обозначить это значение как имеющееся в один момент времени.
То же самое соглашение о нижнем регистре справедливо и для тока, строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.
Кулон и электрический заряд
Одна из основополагающих единиц электрического измерения, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это единица кулонов , которая представляет собой меру электрического заряда, пропорционального количеству электронов в несбалансированном состоянии.Один кулон заряда равен 6 250 000 000 000 000 000 электронов.
Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается заглавной буквой «C». Бывает так, что единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этих терминах ток – это скорость движения электрического заряда по проводнику.
Бывает так, что единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этих терминах ток – это скорость движения электрического заряда по проводнику.
Как указывалось ранее, напряжение является мерой потенциальной энергии на единицу заряда , доступной для стимулирования протекания тока из одной точки в другую.Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общая метрическая единица для энергии любого вида – джоулей , что равно количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении).
В британских подразделениях это чуть меньше 3/4 фунта силы, приложенной на расстоянии 1 фута. Проще говоря, требуется около 1 джоуля энергии, чтобы поднять гирю весом 3/4 фунта на 1 фут от земли или перетащить что-то на расстояние 1 фут, используя параллельную тяговую силу 3/4 фунта.В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленный на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Уравнение закона Ома
Основное открытиеОма заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, прямо пропорциональна напряжению, приложенному к нему при любой заданной температуре.Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя методы алгебры, мы можем преобразовать это уравнение в два варианта, решая для I и R соответственно:
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти уравнения могут работать, чтобы помочь нам анализировать простые схемы:
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа).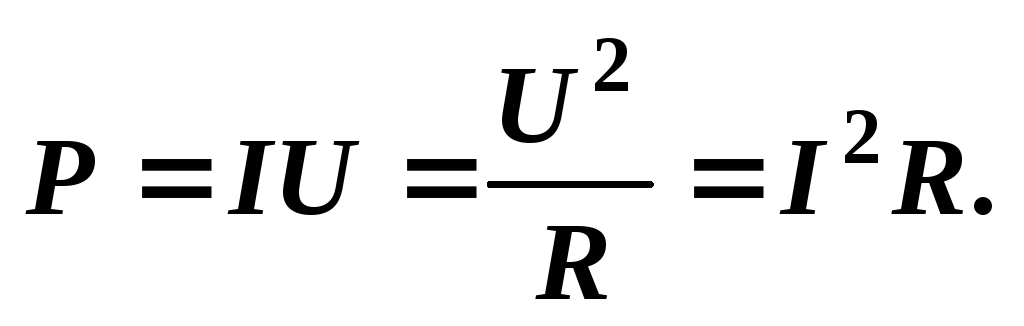 Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы рассчитаем величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Какой ток (I) в этой цепи?
В этом втором примере мы рассчитаем величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Какое сопротивление (R) дает лампа?
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Какое напряжение обеспечивает аккумулятор?
Техника треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей.Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, чтобы запомнить, как решить для любого количества, учитывая два других.
Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
В конце концов, вам придется быть знакомым с алгеброй, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений.Если вы знакомы с алгеброй, все, что вам нужно сделать, это зафиксировать E = IR в памяти и вывести из нее две другие формулы, когда они вам понадобятся!
ОБЗОР:
- Напряжение измеряется в вольт , обозначается буквами «E» или «V».

- Ток измеряется в ампер , обозначается буквой «I».
- Сопротивление измеряется в Ом. обозначается буквой «R».
- Закон Ома: E = IR; I = E / R; R = E / I
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Попробуйте наш калькулятор закона Ома в разделе «Инструменты».
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторы
(b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторысерии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке \ (\ PageIndex {2} \) ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается по формуле \ (V = IR \), где \ (I \) – ток в амперах (\ (A \)), а \ (R \) – сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. На рисунке \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V – V_1 – V_2 – V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \]
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов. N R_i.\ label {серия эквивалентных сопротивлений} \]
N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Раствор
- Эквивалентное сопротивление – это алгебраическая сумма сопротивлений (уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W.
 \ nonumber \]
\ nonumber \]
Значение
Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска провода через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды идут от батареи, некоторые проходят через резистор \ (R_1 \), а некоторые – через резистор \ (R_2 \).Сумма токов, протекающих в переходе, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. \ nonumber \]
Это уравнение называется правилом соединения Кирхгофа и будет подробно рассмотрено в следующем разделе. На рисунке \ (\ PageIndex {4} \) правило соединения дает \ (I = I_1 + I_2 \). В этой схеме есть два контура, которые приводят к уравнениям \ (V = I_1R_1 \) и \ (I_1R_1 = I_2R_2 \). Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (\ (V = V_1 = V_2 \)), а ток – аддитивный:
\ [\ begin {align *} I & = I_1 + I_2 \\ [4pt] & = \ frac {V_1} {R_1} + \ frac {V_2} {R_2} \\ [4pt] & = \ frac {V } {R_1} + \ frac {V} {R_2} \\ [4pt] & = V \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) = \ frac {V} {R_ {P}} \ end {align *} \]
Решение для \ (R_ {P} \)
\ [R_ {P} = \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) ^ {- 1}.
 {-1}. \ label {10.3} \]
{-1}. \ label {10.3} \]Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0.50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0.50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.
 00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток – это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.
 00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Решение
Река, текущая горизонтально с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение – это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается.
 В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, А \) от источника напряжения.Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса – включить резисторы в качестве индексов. Здесь эквивалентное сопротивление \ (R_3 \) и \ (R_4 \) равно
.\ [R_ {34} = R_3 + R_4 = 6 \, \ Omega + 4 \, \ Omega = 10 \, \ Omega. \ nonumber \]
Схема теперь сокращается до трех резисторов, как показано на рисунке \ (\ PageIndex {5c} \). Перерисовывая, мы теперь видим, что резисторы \ (R_2 \) и \ (R_ {34} \) составляют параллельную цепь. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V – 14 \, V = 10 \, V \) отбрасывать в параллельной комбинации \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти по закону Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.\ [I_3 = I_4 = I – I_2 = 2 \, A – 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какая мощность рассеивается \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаковое: \ [V_2 = V_3 = V – V_1 = 12.0 \, V – 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Решение
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, включенным последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой – для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Раствор
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
- Один из способов проверить соответствие ваших результатов – это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, обеспечиваемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и указание авторства
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
| Клуб электроники
Закон Ома | Клуб электроникиСледующая страница: Power and Energy
См. Также: Напряжение и ток | Сопротивление
Закон Ома показывает взаимосвязь между напряжением, током и сопротивлением
Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение.Закон Ома показывает взаимосвязь между тремя величинами: напряжением, током и сопротивлением.
Закон Ома можно записать в виде словесного уравнения :
напряжение = ток × сопротивление Или используя символы для обозначения величин напряжения (В), тока (I) и сопротивления (R):
На самом деле его можно записать тремя способами, и вы можете выбрать версию, которая лучше всего подходит для ваших целей:
Треугольник ВИР – способ запомнить закон Ома
Вы можете использовать треугольник VIR, чтобы помочь вам запомнить три версии закона Ома.
- Для расчета напряжения, В : поместите палец на V, это оставляет I R, поэтому уравнение V = I × R
- Чтобы рассчитать ток , I : положите палец на I, это оставляет V над R, поэтому уравнение I = V / R
- Чтобы рассчитать сопротивление , R : поместите палец на R, это оставляет V над I, поэтому уравнение R = V / I
Расчет по закону Ома
Используйте этот метод для проведения расчетов:
- Запишите значения , при необходимости конвертируя единицы.
- Выберите нужное Equation (используйте треугольник VIR).
- Подставьте чисел в уравнение и вычислите ответ.
Должно быть V ery E asy N ow! См. Примеры ниже:
Пример 3:
Резистор 1,2 кОм пропускает ток 0,2 А, какое напряжение на нем?
Пример 4:
9 В подается на резистор 15 кОм, какой ток?
- V alues: V = 9V, I =?, R = 15k
- E предложение: I = V / R
- N umbers: Ток, I = 9 / 15 = 0.6 мА
(использование k для сопротивления означает, что расчет дает ток в мА)
Следующая страница: Энергетика | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию. Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет используется только для ответа на ваше сообщение, оно не будет передано никому. На этом веб-сайте отображается реклама, если вы нажмете на рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.Рекламодателям не передается никакая личная информация. Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации. Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов. (включая этот), как объяснил Google. Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста, посетите AboutCookies.org.
клуб электроники.инфо © Джон Хьюс 2021
Ток и сопротивление
Электрические цепи с движущимися зарядами – обычное дело в нашем технологическом обществе. Ток, сопротивление и электродвижущая сила – понятия, необходимые для описания этих цепей.Текущий
Ток (I) – это количество заряда за время, которое проходит через область, перпендикулярную потоку:
Ток измеряется в единицах СИ – амперах (A) и
Это определение тока может применяться к зарядам, движущимся в проводе, в электролитической ячейке или даже в ионизированных газах.
При визуализации заряда, протекающего по цепи, неточно представляет , чтобы представить электроны, движущиеся очень быстро по цепи. Средняя скорость, или скорость дрейфа ( v b ), отдельных зарядов мала; электроны проводимости в медной проволоке движутся со скоростью 10 –4 м / с. Формула
, где q – заряд электрона, A – площадь поперечного сечения провода, а n – количество электронов проводимости на кубический метр.При такой скорости время прохождения 10 см составляет около 11 минут. Из опыта очевидно, что лампочка загорится не так долго после включения выключателя. Когда цепь замыкается, все распределение зарядов почти немедленно реагирует на электрическое поле и приводится в движение почти одновременно, даже если отдельные заряды движутся медленно.
Батарея обеспечивает напряжение (В) между своими выводами. Электрическое поле, созданное в проводе, подключенном к клеммам батареи, вызывает протекание тока, которое возникает, когда ток имеет полный проводящий путь от одного контакта батареи к другому – это называется схемой .По соглашению направление тока во внешней цепи (не в батарее) является направлением движения положительных зарядов. В металлах электроны являются движущимися зарядами, поэтому определение направления тока противоположно действительному течению отрицательных зарядов в проводе. (Примечание: электрические поля не обнаруживаются в проводниках со статическими зарядами, как показывает закон Гаусса, но электрические поля могут существовать в проводнике, когда заряды находятся в движении.)
Разность потенциалов между выводами батареи при отсутствии тока называется электродвижущей силой (ЭДС).Исторический термин ЭДС является неправильным, потому что он измеряется в вольтах, а не в единицах силы, но терминология все еще широко используется.
Сопротивление и удельное сопротивление
Экспериментальным путем было обнаружено, что ток в проводниках пропорционален напряжению. Константа пропорциональности – это сопротивление в цепи. Это соотношение называется законом Ома : V = IR . Сопротивление измеряется в омах ( Вт, ): ом равен 1 вольт / 1 ампер.
Сопротивление проводника зависит от его длины (l) , площади поперечного сечения (A) и его удельного сопротивления ( r ). Удельное сопротивление для конкретного проводника можно найти в таблице свойств материалов. Единица измерения удельного сопротивления – ом-метр. Сопротивление току в проводнике возникает из-за того, что потоку движущихся зарядов препятствует материал провода. Интуитивно понятно, что сопротивление должно увеличиваться с увеличением длины провода, быть обратно пропорциональным площади поперечного сечения (меньшее сопротивление для большей площади) и зависеть от материала провода.Соотношение между сопротивлением и удельным сопротивлением равно
.Примечание : Резистор – это особый электронный компонент, единственная функция которого – сопротивление току. Сопротивление генерируется любым препятствующим током, например, лампочкой или нагревательным элементом.
Электроэнергия и энергия
На рисунке 1 показана простая схема батареи с проводами, соединяющими ее с лампочкой. Нить накала лампы представляет собой сопротивление, обозначенное в цепи как R рядом с символом сопротивления.Обозначение напряжения батареи – ε. Предположим, что сопротивление в соединительных проводах незначительно, так что лампочка фактически является единственным сопротивлением в цепи. Аккумулятор обеспечивает постоянную разность потенциалов, например, 6 вольт. Когда ток проходит через лампочку, заряды переходят от более высокого потенциала к более низкому с разницей в 6 вольт. Энергия преобразуется в свет и тепло нитью накала лампы.
Рисунок 1
Простая схема с лампочкой в виде резистора R .
Норма расхода энергии равна мощности , задаваемой любым из трех выражений:
Мощность измеряется в ваттах (Вт):
Калькулятор закона Ома
Наш калькулятор закона Ома – это удобный небольшой инструмент, который поможет вам найти взаимосвязь между напряжением, током и сопротивлением в данном проводнике. Формула закона Ома и формула напряжения в основном используются в электротехнике и электронике.Кроме того, если вы знаете, как рассчитать мощность, вы можете найти его очень полезным при изучении электронных схем. Все эти расчеты вы производите с помощью нашего Калькулятора Ом.
В оставшейся части статьи вы найдете:
- Формула закона Ома
- Как использовать формулу напряжения
- Какое уравнение для мощности
- Как рассчитать мощность
- Закон Ома для анизотропных материалов
Формула закона Ома
Закон Ома – один из основных законов физики.Он описывает взаимосвязь между напряжением, силой тока (также известной как ток) и сопротивлением. Напряжение относится к разности потенциалов между двумя точками электрического поля. Сила тока связана с потоком носителей электрического заряда, обычно электронов или электронодефицитных атомов. Последний термин, сопротивление, – это сопротивление вещества потоку электрического тока.
ЗаконОма гласит, что ток течет по проводнику со скоростью, пропорциональной напряжению между концами этого проводника.Другими словами, соотношение между напряжением и током постоянно:
I / V = constФормулу закона Ома можно использовать для расчета сопротивления как отношения напряжения и тока. Это может быть записано как:
R = V / IГде:
- R – сопротивление
- В – напряжение
- I – Текущий
Сопротивление выражается в омах. И устройство, и правило названы в честь Георга Ома – физика и изобретателя закона Ома.
Помните, что формула закона Ома относится только к веществам, которые способны вызывать энергию. такие как металлы и керамика. Однако есть много других материалов, для которых нельзя использовать формулу закона Ома, например, полупроводники и изоляторы. Закон Ома также действует только при определенных условиях, например, при фиксированной температуре.
Ищете практическое применение закона Ома? Обязательно ознакомьтесь с калькулятором светодиодного резистора!
Формула напряжения
Формула напряжения – это одно из трех математических уравнений, связанных с законом Ома.Это формула, приведенная в предыдущем абзаце, но переписанная так, чтобы вы могли рассчитать напряжение на основе тока и сопротивления, то есть формула напряжения является произведением тока и сопротивления. Уравнение:
В = ИКЭто значение измеряется в вольтах.
Какое уравнение мощности?
Другая величина, которую вы можете вычислить на основании закона Ома, – это мощность. Мощность – это произведение напряжения и тока, поэтому уравнение выглядит следующим образом:
P = V x IС помощью этой формулы вы можете рассчитать, например, мощность лампочки.Если вы знаете, что напряжение батареи составляет
18V, а ток составляет6A, вы можете, что мощность будет 108, со следующим расчетом:P = 6A x 18V = 108 ВтКак рассчитать мощность?
Если вы все еще не знаете, как рассчитать мощность по приведенным формулам, или просто хотите сэкономить время, вы можете использовать наш калькулятор закона Ома. Структура этого инструмента не слишком сложна, просто введите любые два из четырех значений, чтобы получить два других.Калькулятор закона Ома основан на формуле мощности вместе с формулой закона Ома. Все, что вам нужно сделать, чтобы получить значение мощности, это набрать:
- Напряжение (выраженное в вольтах)
- Ток (выраженный в амперах)
Затем калькулятор закона Ома выдаст вам два значения – сопротивление, выраженное в омах, и мощность, выраженное в ваттах. Если вам нужен этот результат в другом устройстве, вы можете использовать наш калькулятор ватт в ампер.
Закон Ома для анизотропных материалов
Существует еще одна версия закона Ома, которая использует положение электрических свойств внутри проводника.Некоторые предпочитают его предыдущей формуле из-за его размерного вида. Электропроводящие материалы подчиняются закону Ома, когда удельное сопротивление материалов не зависит от величины и направления приложенного электрического поля.
Вы можете найти следующую формулу, если нажмете кнопку
Расширенный режим:ρ = E / J, гдеρ– удельное сопротивление проводящего материала.E– вектор электрического поля.J– вектор плотности тока.
Что касается изотропных материалов, лучше всего использовать первую формулу, поскольку она намного менее сложна. Изотропные материалы – это материалы с одинаковыми электрическими свойствами во всех направлениях, например металлы и стекло. Эта формула может пригодиться при работе с анизотропными материалами, такими как дерево или графит.
Закон Ома: определение и взаимосвязь между напряжением, током и сопротивлением – Видео и стенограмма урока
Закон Ома
Взаимосвязь между напряжением, током и сопротивлением описывается законом Ома .Это уравнение, i = v / r , говорит нам, что ток, i , протекающий по цепи, прямо пропорционален напряжению, v , и обратно пропорционален сопротивлению, r . . Другими словами, если мы увеличим напряжение, то увеличится и ток. Но, если мы увеличим сопротивление, то ток уменьшится. Мы увидели эти концепции в действии с садовым шлангом. Увеличение давления привело к увеличению потока, но изгиб шланга увеличил сопротивление, что привело к уменьшению потока.
Эта диаграмма – простой способ решать уравнения. Как написано здесь уравнение, было бы легко использовать закон Ома, чтобы вычислить ток, если бы мы знали напряжение и сопротивление. Но что, если бы мы вместо этого захотели вычислить напряжение или сопротивление? Один из способов сделать это – переставить члены уравнения для решения других параметров, но есть более простой способ. Приведенная выше диаграмма даст нам соответствующее уравнение для решения любого неизвестного параметра без использования алгебры.Чтобы использовать эту диаграмму, мы просто закрываем параметр, который пытаемся найти, чтобы получить правильное уравнение. Это станет более понятным, когда мы начнем его использовать, поэтому давайте рассмотрим несколько примеров.
Закон Ома в действии
Ниже представлена простая электрическая схема, которую мы будем использовать для выполнения наших примеров. Наш источник напряжения – это аккумулятор, подключенный к лампочке, которая обеспечивает сопротивление электрическому току. Для начала предположим, что наша батарея имеет напряжение 10 вольт, электрическая лампочка имеет сопротивление 20 Ом, и нам нужно вычислить ток, протекающий по цепи.Используя нашу диаграмму, мы закрываем параметр, который мы пытаемся найти, то есть ток, или i , и это оставляет нам напряжение v над сопротивлением r . Другими словами, чтобы найти ток, нам нужно разделить напряжение на сопротивление. Делая математические вычисления, 10 вольт, разделенные на 20 Ом, дают половину ампера тока, протекающего в цепи.
Чтобы найти ток, разделите напряжение (20 вольт) на сопротивление (20 Ом). Теперь давайте увеличим напряжение, чтобы увидеть, что происходит с током.Мы будем использовать ту же лампочку, но перейдем на 20-вольтовую батарею. Используя то же уравнение, что и раньше, мы разделим 20 вольт на 20 Ом, и мы получим 1 ампер тока. Как мы видим, удвоение напряжения привело к удвоению тока. Это имеет смысл, когда мы думаем о садовом шланге. Если бы мы увеличили давление в шланге, можно было бы ожидать, что поток воды также увеличится. Всегда полезно перепроверить свою работу, спросив, соответствуют ли результаты тому, что вы ожидали.
Если бы мы увеличили сопротивление лампочки, что бы вы ожидали, что произойдет с током? Чтобы выяснить это, давайте поменяем существующую лампочку на другую с сопротивлением 40 Ом.Поскольку мы все еще ищем ток, мы используем то же уравнение, что и раньше. Разделив 20 вольт на 40 Ом, мы получим половину ампера тока. Этот результат говорит нам, что удвоение сопротивления уменьшило ток вдвое. Вы этого ожидали? Если вернуться к нашему шлангу, логично предположить, что перегиб в шланге уменьшит поток воды, точно так же, как увеличение сопротивления в цепи уменьшит ток.
До сих пор мы только рассчитали ток в цепи, но что, если бы кто-то поменял нашу лампочку, когда мы не смотрели, и нам нужно было вычислить сопротивление новой? Что ж, мы знаем, что напряжение нашей батареи составляет 20 вольт, и мы можем измерить ток в цепи с помощью инструмента, называемого амперметром, поэтому все, что нам осталось, – это выполнить некоторые вычисления.Используя нашу диаграмму, мы закрываем параметр, который мы пытаемся найти, а именно сопротивление, r . Схема теперь показывает нам, что нам нужно разделить напряжение на ток. Если наш амперметр измерил ток в 5 ампер, протекающий по цепи, то сопротивление будет равно 20 вольт, разделенным на 5 ампер, что составляет 4 Ом
Чтобы определить напряжение, умножьте силу тока (3 ампера) на сопротивление (4 Ом). Наконец, представьте, что кто-то заменил нашу батарею, и нам нужно выяснить ее напряжение.Процесс почти такой же. Мы знаем, что наша новая лампочка имеет сопротивление 4 Ом, и мы можем измерить ток в цепи с помощью амперметра. Используя диаграмму, мы покрываем напряжение v , которое говорит нам, что нам нужно умножить ток на сопротивление. Если бы амперметр измерил ток в 3 ампера, тогда напряжение было бы 3 ампера, умноженным на 4 Ом, что составляет 12 вольт. Это все, что нужно сделать. Зная любые два из трех параметров, мы всегда можем вычислить третий, используя закон Ома.
Резюме урока
Закон Ома определяет соотношение между напряжением, током и сопротивлением в электрической цепи: i = v / r . Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Это означает, что увеличение напряжения вызовет увеличение тока, а увеличение сопротивления приведет к уменьшению тока. Зная любые два из трех параметров, мы можем вычислить третий, неизвестный параметр.Мы можем сделать это, переставив члены в уравнении закона Ома или используя диаграмму, приведенную выше в уроке. Скрытие параметра, который мы пытаемся найти, показывает нам соответствующее уравнение с использованием двух известных параметров.
Результаты обучения
По завершении этого урока вы сможете:
- Описывать взаимосвязь между напряжением, током и сопротивлением, используя закон Ома
- Напишите уравнение закона Ома
- Объясните, как можно найти любую из трех переменных в уравнении закона Ома, если вы знаете две другие.
- Рассчитайте любую из трех переменных, используя уравнение закона Ома
и электрические формулы
Используйте закон Ома для расчета напряжения, тока, сопротивления или мощности в электрической цепи.Введите любые два известных значения, чтобы найти два других.
Например, введите напряжение и мощность, чтобы найти ток и сопротивление.
Что такое закон Ома?
Закон Ома определяет соотношение между электрическим током, сопротивлением и напряжением. Более конкретно, в нем говорится, что ток через элемент схемы прямо пропорционален приложенной к нему разности потенциалов и обратно пропорционален сопротивлению . [1]
Закон Ома позволяет рассчитать напряжение, ток, мощность и сопротивление электрической цепи, если вы знаете хотя бы два других значения.
Например, если вы знаете напряжение и сопротивление, воспользуйтесь калькулятором выше, чтобы найти мощность и ток по закону Ома. Кроме того, вы можете использовать калькулятор для вычисления мощности и сопротивления, если вы знаете напряжение и ток.
Формула закона Ома
Формула закона Ома: I = E / R, где I – ток через проводник, измеренный в амперах, E – разность потенциалов на проводнике, измеренная в вольтах, а R – измеренное сопротивление проводника. в ом. [2]
I = ER
Формула утверждает, что ток I равен напряжению E , деленному на сопротивление R .
Треугольник закона Ома
Треугольник закона Ома показывает, как рассчитать напряжение, ток или сопротивление. Чтобы использовать его, накройте единицу, которую вы хотите вычислить, чтобы открыть формулу для ее решения.
Треугольник закона Ома, где E представляет напряжение, I представляет ток, а R представляет сопротивление.Например, чтобы найти вольты, прикройте E большим пальцем, и это покажет, что напряжение равно I × R.
Что означают буквы в формуле закона Ома?
В формуле закона Ома E представляет электродвижущую силу или напряжение, I представляет силу или ток, а R представляет сопротивление.
Георг Симон Ом создал закон Ома в статье, опубликованной в 1827 году, [3] задолго до того, как были определены единицы измерения напряжения, тока и сопротивления.
Вольт, ампер и ом были определены только в 1881 году, спустя более 50 лет после того, как был опубликован закон Ома. Это объясняет, почему буквы не относятся к современным единицам, используемым в формуле.
Формула силы
Формула мощности гласит, что электрическая мощность, измеренная в ваттах, равна току в цепи, умноженному на напряжение. Эта формула очень похожа на закон Ома и может помочь найти мощность или мощность.
Мы часто используем формулу мощности в сочетании с законом Ома для определения электрических свойств, когда мощность цепи известна.
P = I × E
Таким образом, формула мощности утверждает, что мощность P равна I , умноженному на напряжение E . [4]
Треугольник силы
Треугольник мощности иллюстрирует формулу для определения ватт, вольт или ампер. Как и в случае с другим треугольником, накройте единицу измерения, которую вы хотите решить, чтобы открыть формулу для ее решения.
Например, чтобы найти усилители, прикройте I большим пальцем, чтобы увидеть, что ток равен P / E.
Формула мощности, где P представляет мощность, I представляет ток, а E представляет напряжение.Наш калькулятор ватт в ампер использует эту формулу, например, для преобразования мощности в ток в электрических цепях.
Колесо закона Ома
Мы можем использовать закон Ома для вычисления вольт, ватт, ампер или ом, если известны как минимум два измерения. Формула позволяет нам вывести уравнения для расчета любого измерения с учетом двух других известных значений.
Колесо закона Ома показывает все формулы, которые вы можете использовать для определения вольт, ватт, ампер или ом. См. Все производные формулы ниже.
Колесо закона Ома со всеми формулами, которые можно использовать для расчета вольт, ампер, ом или ватт.Формулы напряжения
Найдите напряжение, используя следующие формулы:
Напряжение = ток × сопротивление
Напряжение = мощность ÷ ток
Напряжение = мощность × сопротивление
Формулы мощности
Найдите мощность по этим формулам:
Мощность = Напряжение × Ток
Мощность = Напряжение 2 ÷ Сопротивление
Мощность = Ток 2 × Сопротивление
Текущие формулы
Решите для тока, используя эти формулы:
Ток = Напряжение ÷ Сопротивление
Ток = Мощность ÷ Напряжение
Ток = мощность ÷ сопротивление
Формулы сопротивления
Найдите сопротивление, используя следующие формулы:
Сопротивление = Напряжение ÷ Ток
Сопротивление = Напряжение 2 ÷ Мощность
Сопротивление = мощность ÷ ток 2
Мы используем закон Ома для многих вещей, таких как определение максимального размера микроволн или максимального количества осветительных приборов, с которыми цепь может безопасно обращаться, не создавая опасности возгорания.
Наш калькулятор затрат на освещение может помочь определить потребление энергии на освещение, а наш калькулятор затрат на электроэнергию поможет определить затраты на питание электрических устройств.
Используйте закон Ома, чтобы определить размер электрической цепи или выяснить, какой размер нагревателя можно безопасно использовать в обычной розетке. Вы также можете найти наш калькулятор падения напряжения, чтобы определить падение напряжения, необходимый минимальный размер провода и максимальную длину провода для вашего следующего электрического проекта.

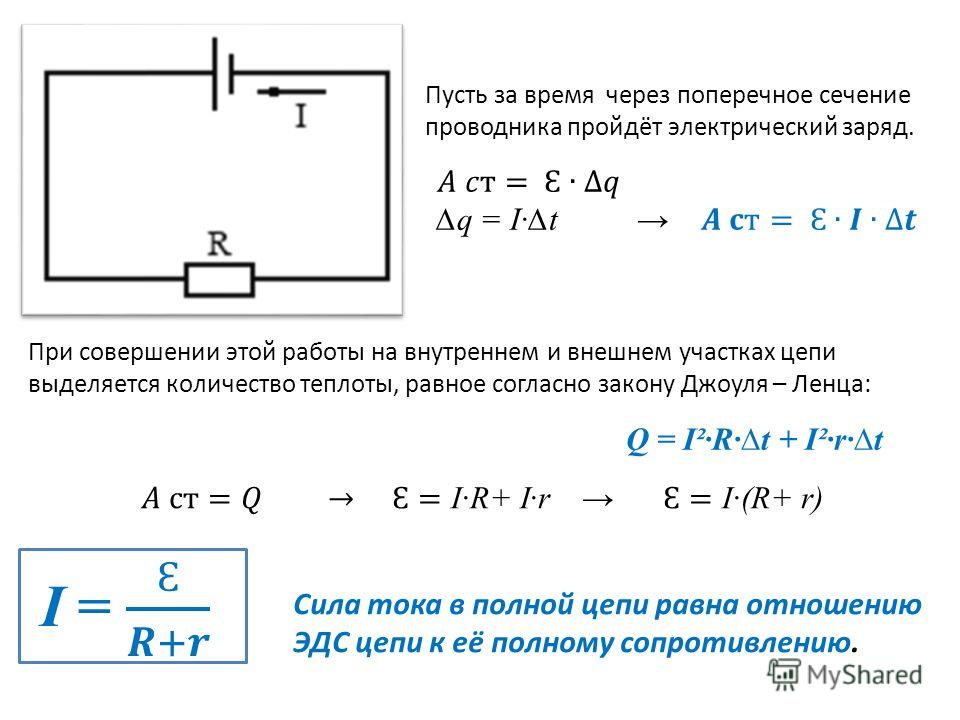

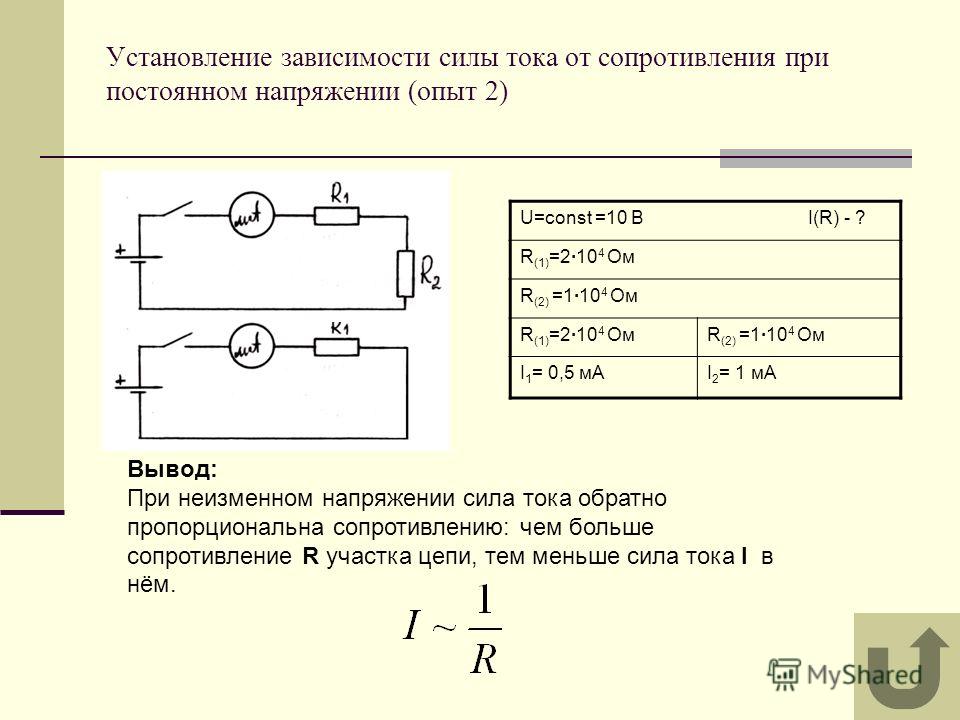 \ nonumber \]
\ nonumber \] Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании. {-1}. \ label {10.3} \]
{-1}. \ label {10.3} \] 00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.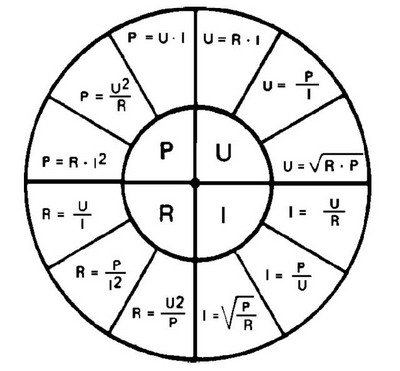 00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \). В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.