Сила тяжести — урок. Физика, 7 класс.
Силу гравитации, с которой Земля притягивает тело, находящееся на её поверхности или вблизи неё, называют силой тяжести. Эта сила направлена к центру Земли.
Сила гравитации Земли для нас является самой важной, поэтому ей и дано особое название.
Земля притягивает всё, что находится вокруг неё: твёрдые тела, жидкости, газы.
Из-за того, что есть сила тяжести, возможно существование атмосферы (молекулы газа не улетают в космос), воды морей и океанов удерживаются на своих местах, если какой-либо предмет приподнимают и роняют, этот предмет падает вниз — в направлении Земли.
Силу, с которой Земля притягивает тела, можно рассчитать по формуле F=m⋅g, где \(m\) — масса тела, а \(g\) — ускорение свободного падения.
Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно. Вблизи поверхности Земли значение \(g\) равно примерно \(9,81\) мс2, для приблизительных расчётов можно использовать значение \(10\) мс2.
Что означает эта единица измерения?
Скорость свободно падающего тела каждую секунду увеличивается на \(9,81\) метров в секунду (м/с).
Если предмет падает, например, в течение \(4\) секунд, то скорость его падения в самом начале равна \(0\) м/с;
за \(1\)-ю секунду он достигает скорости \(9,81\) м/с;
за \(2\)-ю секунду он достигает скорости: \(9,81\), умноженное на \(2\) м/с \(=\) \(19,62\) м/с;
за \(3\)-ю секунду он достигает скорости: \(9,81\), умноженное на \(3\) м/с \(=\) \(29,43\) м/с;
за \(4\)-ю секунду тело достигает скорости: \(9,81\), умноженное на \(4\) м/с \(=\) \(39,24\) м/с, что приблизительно составляет \(141\) км/ч.
Обрати внимание!
Интересно, что кирпич и яблоко падают с одинаковой скоростью. Только падение лёгких предметов сопротивление воздуха замедляет сильнее, например, птичье перо из-за сопротивления воздуха будет падать медленнее.
Ускорение свободного падения на поверхности Луны составляет только \(1,62\) мс2.
На Юпитере значение \(g\) приблизительно равно \(26,2\) мс2, это примерно так же, как если бы человек в дополнение к своим \(60\) кг веса взвалил бы на плечи ещё примерно \(102\) кг.
Формула силы тяжести в физике
Содержание:
Определение и формула силы тяжести
Определение
Под воздействием силы притяжения к Земле все тела падают с одинаковыми по отношению к ее поверхности ускорениями. Такое ускорение называют ускорением свободного падения и обозначают: g. Его величина в системе СИ считается равной g=9,80665 м/с2 – это так называемое, стандартное значение.
Вышесказанное обозначает то, что в системе отсчета, которая связывается с Землей, на любое тела обладающее массой m действует сила равная:
$$\bar{P}=m \bar{g}(1)$$которая называется силой тяжести.
Если тело находится в состоянии покоя на поверхности Земли, тогда сила тяжести уравновешивается реакцией подвеса или опоры, которая удерживает тело от падения (вес тела). {2} r$$
{2} r$$
где m – масса тела, r – расстояние от оси Земли. Если тело расположено не высоко от поверхности Земли ( в сравнении с радиусом Земли), то можно считать, что
где RZ – радиус земли, $\varphi$ – широта местности.
В таком случае ускорение свободного падения (g) по отношению к Земле будет определено действием сил: силы притяжения к Земле ( $\bar{F}_{g}$) и силы инерции ( $\bar{F}_{in}$). При этом сила тяжести – есть результирующая этих сил:
$$\bar{P}=\bar{F}_{g}+\bar{F}_{i n}(4)$$Так как сила тяжести сообщает телу, обладающему массой m ускорение равное $\bar{g}$, то соотношение (1) является справедливым.
Разница между силой тяжести $\bar{P}$ и силой притяжения к Земле $\bar{F}_{g}$ небольшая. Так как $F_{g} \gg F_{i n}$.
 Сила
$\bar{F}_{g}$ направлена к центру Земли. Значит, нить отвеса направлена
также только на полюсах и экваторе. На других широтах угол отклонения ($\alpha$)
от направления к центру Земли составляет величину, равную: $$\alpha \approx 0,0018 \sin (2 \varphi)(5)$$
Сила
$\bar{F}_{g}$ направлена к центру Земли. Значит, нить отвеса направлена
также только на полюсах и экваторе. На других широтах угол отклонения ($\alpha$)
от направления к центру Земли составляет величину, равную: $$\alpha \approx 0,0018 \sin (2 \varphi)(5)$$Разница между Fg-P максимальна на экваторе, она составляет 0,3% от величины силы Fg.
Так как земной шар является сплюснутым около полюсов, то F
По отношению к инерциальной системе отсчета (например, гелиоцентрической СО) тело в свободном падении будет перемещаться с ускорением (a) отличающимся от g, равным по модулю:
$$a=\frac{F_{g}}{m}(6)$$и совпадающим по направлению с направлением силы $\bar{F}_{g}$.
Единицы измерения силы тяжести
Основной единицей измерения силы тяжести в системе СИ является: [P]=H
В СГС: [P]=дин
Примеры решения задач
Пример
Задание.
Таким образом, для ответа на поставленный вопрос следует найти отношение:
$$\frac{P_{1}}{P_{2}}=\frac{9,8}{1,6} \approx 6,1$$Проведем вычисления:
Ответ. $\frac{P_{1}}{P_{2}} \approx 6,1$
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Получите выражение, которое связывает широту и угол, который образуют вектор силы тяжести и вектор силы притяжения к Земле.
Решение. Угол, который образуется между направлениями силы притяжения к Земле и направлением силы тяжести можно
оценить, если рассмотреть рис.1 и применить теорему синусов. На рис.1 изображены:
$\bar{F}_{in}$ – центробежная сила инерции, которая возникает за счет вращения
Земли вокруг оси, $\bar{P}$ – сила тяжести,
$\bar{F}_{g}$ – сила притяжения тела к Земле. {2} R_{Z}}{g}$ можно рассчитать, если учесть,
что радиус Земли равен Rz=6400 км. Угловая скорость вращения Земли есть:
{2} R_{Z}}{g}$ можно рассчитать, если учесть,
что радиус Земли равен Rz=6400 км. Угловая скорость вращения Земли есть:
Получаем, что:
$$\sin \alpha=0,0035 \cos \varphi \sin \varphi=0,0018 \sin (2 \varphi)$$Читать дальше: Формула ускорения.
Сила тяжести в физике – формулы и определения с примерами
Содержание:
Сила тяжести:
Почему все подброшенные вверх тела падают на Землю ? Почему на санках легко съезжать с горки, а вверх их нужно тянуть?
Подбросьте вверх мяч. Поднявшись на некоторую высоту, он начнёт двигаться вниз и упадёт на Землю. Парашютист, выпрыгнувший из самолёта, падает вниз и после раскрытия парашюта. С появлением дождевой тучи на Землю падает густой дождь. Как бы высоко мы не прыгали вверх, всегда опускаемся на Землю.
Все тела, находящиеся на Земле или вблизи неё, взаимодействуют с ней: Земля притягивает тела, а они притягивают Землю.
Поскольку масса у Земли очень большая, то в результате взаимодействия с нею заметно изменяют свои скорости и положения именно тела, а Земля практически остаётся на месте.
Силу, с которой Земля притягивает к себе любое тело, называют силой тяжести.
От чего зависит сила тяжести
Из опыта с яблоками, выполненного ранее, можем сделать вывод, что на два яблока, подвешенных на пружине, действует сила тяжести больше, чем на одно, так как масса двух яблок больше массы одного. Силу тяжести обозначают
Единицей силы тяжести, как и любой другой, в СИ является
Тогда на тело массой 1кг действует сила тяжести 9,81 Н, т. е.
Как, пользуясь единицей силы 1 Н, определить силу тяжести, которая действует на тело любой массы?
Поскольку на тело массой 1 кг действует сила тяжести 9,81 Н, то на тело массой т будет действовать сила тяжести, в т раз большая.
Чтобы определить силу тяжести , действующую на тело, нужно постоянную для данной местности величину = 9,81 умножить на массу тела , выраженную в килограммах:
Но притяжение существует не только между Землёй и телами на ней или вблизи неё. Все тела притягиваются друг к другу. Например, притягиваются между собой Земля и Луна, Солнце и Земля или другие планеты, корабли в море, предметы в комнате. Вследствие притяжения Земли к Луне на Земле возникают приливы и отливы (рис. 69).
Вода в океанах поднимается дважды в сутки на несколько метров.
Благодаря силе тяжести атмосфера удерживается возле Земли, реки текут сверху вниз, Луна удерживается возле Земли, планеты двигаются по орбитам вокруг Солнца.
Явление притяжения всех тел Вселенной друг к другу называют всемирным тяготением.
Исаак Ньютон доказал, что сила притяжения между телами тем больше, чем больше массы этих тел и чем меньше расстояние между телами. Если бы сила тяжести на Земле вдруг исчезла, то все незакреплённые на ее поверхности тела от любого небольшого толчка разлетелись бы во все стороны в космическом пространстве.
Каково направление силы тяжести
Опыт. Если взять отвес или привязанный к нити какой-либо предмет (рис. 70), то увидим, что нить с грузиком вследствие действия на него силы тяжести всегда направлена к Земли вдоль прямой, которую называют вертикалью.
Выполнив этот опыт во всех точках Земли, учёные убедились, что сила тяжести всегда направлена к центру Земли.
Силу тяжести изображают в виде вертикальной стрелки, направленной вниз и приложенной к определённой точке тела (рис. 71 а, б).
Кстати:
Кроме планет с их спутниками вокруг Солнца двигаются малые планеты, которые еще называют астероидами. Наибольшая из них – Церера – имеет статус карликовой планеты и радиусом почти в 20 раз, а по массе в 7500 раз меньше Земли. Сила тяжести на ней настолько мала, что человек, оттолкнувшись от поверхности планеты, мог бы улететь с нее.
Вот как описывает основатель теории космонавтики К,Э. Циолковский в рассказе “Путь к звездам” условия пребывания человека на этом астероиде: “На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны. Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона”.
На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны. Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона”.
Все тела возле Земли падают на ее поверхность, если их ничто не удерживает. В чем причина этого явления?
Рассмотрим фотографию падения шарика, на которой положение шарика фиксировалось на пленке через равные интервалы времени (рис. 45). Если линейкой отмерить расстояние между изображениями шарика в различные моменты времени, то можно заметить, что эти расстояния постепенно увеличиваются. Это свидетельствует о том, что скорость шарика при падении постепенно увеличивается.
Как увеличивается скорость падающего телаЕсли вспомнить определение силы, по которому сила изменяет скорость тела, то можно сделать вывод, что на шарик действует сила, направленная к Земле.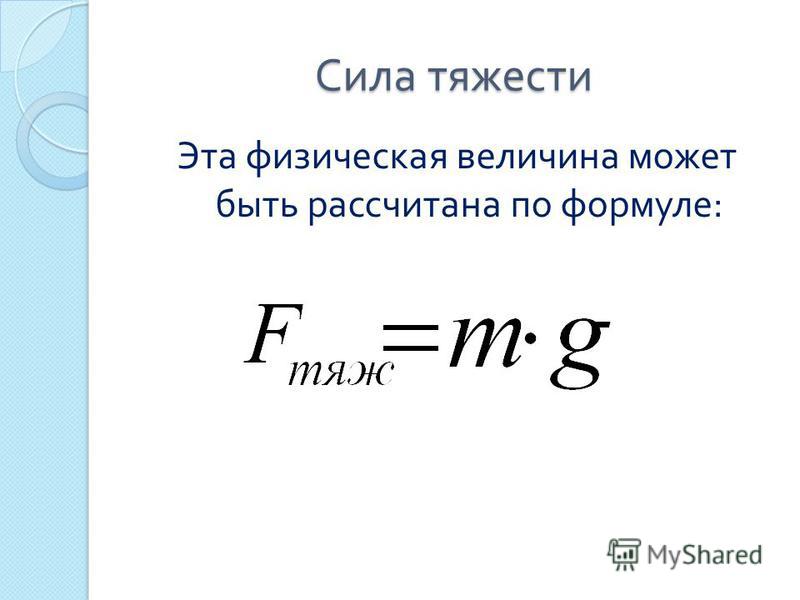
Силу, действующую на каждое тело со стороны Земли, называют силой тяготения.
Измерения показывают, что скорость тела, падающего на поверхность Земли при отсутствии сопротивления воздуха, каждую секунду увеличивается на 9,8 .
Как рассчитать силу тяготенияЕсли знать массу тела, то можно рассчитать силу тяготения. Способ таких расчетов подсказывают результаты опытов.
Возьмем динамометр и подвесим к нему гирьку массой 102 г, стрелка динамометра остановится на отметке 1 Н. Если подвесить два таких груза, то динамометр покажет силу 2 Н и т. д. С этого опыта можно сделать вывод, что сила тяжести пропорциональна массе тела.
Сила тяготения пропорциональна массе тела:
Коэффициент пропорциональности равен приблизительно
Для расчетов при решении задач иногда принимают, что
Если знать такую зависимость силы тяготения от массы, то можно заранее рассчитать ее значение.
Например, необходимо определить, что покажет динамометр, если на его крючок повесить гирю массой 500 г.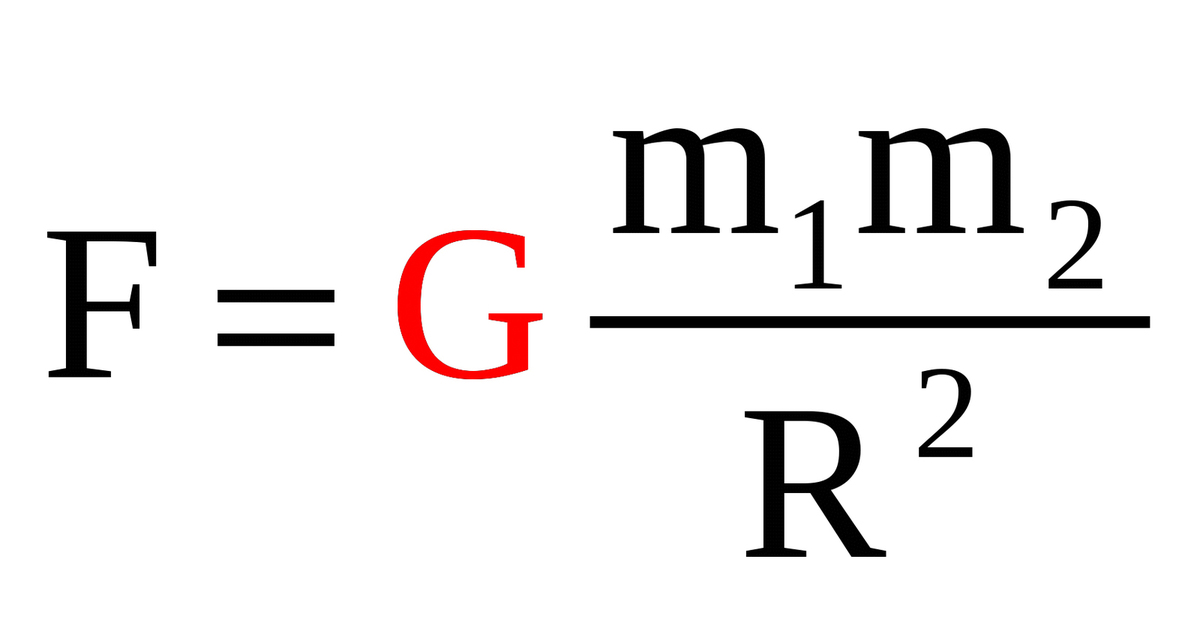
Дано:
Решение
Ответ. Стрелка динамометра покажет 4,9 Н.
Какая природа силы тяготенияСила тяготения является проявлением общего закона природы, действующего во всей Вселенной закона всемирного тяготения. Открытый и сформулированный в XVII в. английским физиком Ньютоном, он утверждает, что сила гравитационного притяжения во Вселенной пропорциональна массам взаимодействующих тел и зависит от расстояния между ними.
где R — расстояние между телами, m1 и m2 — массы взаимодействующих тел, — гравитационная постоянная.
Сила тяготения, как проявление гравитационного взаимодействия Земли, является следствием взаимодействия всех тел с Землей. Поэтому в расчетах силы тяготения пользуются только массой данного тела. Характеристики Земли отображены в обобщенной форме в коэффициенте
Работа силы тяжестиКаждая сила, действующая на движущееся тело, совершает работу. Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h1 до высоты h2 (рис. 132). Модуль перемещения равен при этом h1 –h2 . Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h1 до высоты h2 (рис. 132). Модуль перемещения равен при этом h1 –h2 . Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
(1)
Рис. 132
Высоты h1 и h2 можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола класса или поверхности стола и т. д. Высоту выбранного уровня принимают равной пулю. Поэтому этот уровень называют нулевым.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести:
(2)
Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости. Пусть тело массой m совершило перемещение , равное по модулю длине наклонной плоскости (рис. 133). Работа силы тяжести в этом случае равна: , где — угол между вектором перемещения и вектором силы тяжести. Из рисунка видно, что . Поэтому
Пусть тело массой m совершило перемещение , равное по модулю длине наклонной плоскости (рис. 133). Работа силы тяжести в этом случае равна: , где — угол между вектором перемещения и вектором силы тяжести. Из рисунка видно, что . Поэтому
Рис. 133
Мы получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали (см. формулу (2)). Отсюда следует, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. Работа силы тяжести определяется только изменением высоты относительно некоторого уровня.
Теперь докажем, что работа силы тяжести определяется формулой (2) при движении по любой траектории. Например, некоторое тело бросили горизонтально с высоты h (рис. 134). Как известно, траекторией такого движения является парабола. Мысленно разобьем траекторию на маленькие участки , такие, что их можно считать прямыми линиями. Каждый из них можно считать маленькой наклонной плоскостью, а движение по траектории AB рассматривать как движение по множеству наклонных плоскостей. Работа силы тяжести на каждой из них равна произведению силы тяжести на изменение высоты. Например, на участке А2А3 работа равна mg(h2-h3). Полную же работу силы тяжести на всем пути найдем, сложив работу на каждом участке:
Работа силы тяжести на каждой из них равна произведению силы тяжести на изменение высоты. Например, на участке А2А3 работа равна mg(h2-h3). Полную же работу силы тяжести на всем пути найдем, сложив работу на каждом участке:
Рис. 134
Таким образом, работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела, т. е. вычисляется но формуле (1). Отсюда следует, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными. Другое определение потенциальных сил: это такие силы, работа которых по замкнутой траектории равна нулю.
Для потенциальных сил можно ввести понятие потенциальной энергии. Действительно, формула (I) может быть переписана следующим образом:
A = mg(hl – h2)= -(mgh2– mgh1). (3)
Правая часть этого равенства представляет собой изменение величины mgh, взятое с противоположным знаком.
Понятие кинетической энергии, изменение которой равно работе сил, действующих на тело. Теперь мы встретились еще с одной величиной, изменение которой (но с противоположным знаком) тоже равно работе силы — в данном случае работе силы тяжести. Величину, равную mgh, называют потенциальной энергией П тела в гравитационном поле. Тогда формулу (3) можно записать в виде:
(4)
Говорят, что работа силы тяжести равна убыли потенциальной энергии тела в гравитационном поле Земли.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна его начальной потенциальной энергии:
Следовательно, потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты. Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.
Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.
Рис. 135
Потенциальная энергия зависит от положения тела относительно нулевого уровня и, следовательно, от координат тела. Так как пулевой уровень может быть выбран произвольно, то и потенциальная энергия определяется неоднозначно. Однако физический смысл имеет разность потенциальных энергий тела ΔП, а эта разность не зависит от выбора нулевого уровня.
Сила тяжести является силой, с которой Земля притягивает тело. Тело обладает потенциальной энергией, потому что оно взаимодействует с Землей. Не было бы Земли, не было бы и силы притяжения, а следовательно, и потенциальной энергии тела. Поэтому потенциальная энергия — это энергия взаимодействия, в данном случае тела и Земли.
Главные выводы:
- Работа силы тяжести не зависит от формы траектории, а определяется начальным и конечным положениями тела.

- Работа силы тяжести равна нулю, если тело возвращается в исходное положение.
- Сила тяжести является потенциальной силой.
- Потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты.
- Потенциальная энергия — это энергия взаимодействия тел.
Как вы знаете, по современным научным представлениям взаимное притяжение между телами осуществляется посредством особого вида материи – гравитационного поля. Каждое тело вокруг себя создает гравитационное поле. Как и другие физические поля, гравитационное поле имеет свою силовую характеристику – напряженность гравитационного поля.
Напряженность гравитационного поля – это векторная физическая величина, равная отношению силы притяжения, действующей на материальную точку (тело) в гравитационном поле, к его массе:
Где – напряженность гравитационного поля, – масса материальной точки (тела), – сила притяжения, действующая на материальную точку в гравитационном поле.
Чтобы ответить на этот вопрос, определим модуль напряженности гравитационного поля для произвольной точки на поверхности Земли и на высоте от поверхности Земли:
Здесь и — силы притяжения на поверхности Земли и на высоте h соответственно, — масса Земли, — радиус Земли.
Модуль напряженности гравитационного поля в некоторой точке прямо пропорционален массе источника данного поля и обратно пропорционален
квадрату расстояния до этой точки. Модуль напряженности гравитационного поля не зависит от массы тела, помещенного в это поле. Вектор напряженности гравитационного поля в произвольной точке поля направлен вдоль радиуса к центру источника поля (b). В данной точке гравитационного поля модуль и направление напряженности гравитационного поля совпадают с модулем и направлением ускорения свободного падения.
Являются ли напряженность гравитационного поля и ускорение свободного падения одной и той же величинойНа помещенное в гравитационное поле произвольное тело действует сила притяжения со стороны источника поля. В результате тело получает ускорение (ускорение свободного падения), направленное к центру источника поля (например, центру Земли). Это ускорение сообщается телу действующей на него силой тяжести гравитационного поля.
В результате тело получает ускорение (ускорение свободного падения), направленное к центру источника поля (например, центру Земли). Это ускорение сообщается телу действующей на него силой тяжести гравитационного поля.
Сила тяжести – это сила, с которой Земля (планета) притягивает тела. Сила тяжести равна произведению массы тела, помещенного в гравитационное поле Земли (планеты), на ускорение свободного падения:
Сила тяжести всегда приложена к центру массы тела и направлена вертикально вниз (перпендикулярно к горизонтальной поверхности) к центру Земли (планеты) (с).
Из вышесказанного ясно, что понятия “напряженность гравитационного поля” и “ускорение свободного падения” имеют разный физический смысл. Так, напряженность гравитационного поля появляется в случае возникновения поля, а ускорение свободного падения возникает в результате действия силы тяжести при помещении в это поле произвольного тела (пробное тело).
Если выпустить из рук карандаш, он обязательно упадет. Если поставить рюкзак на скамейку, она (хоть и незаметно для глаз) прогнется. Если подвесить к резиновому шнуру какое-нибудь тело, шнур растянется. Все это — следствия притяжения Земли. При этом репортажи с космических станций демонстрируют нам вроде бы «исчезновение» земного притяжения — космонавты и все вещи на борту находятся в состоянии невесомости.
Гравитационное взаимодействие:
Почему любой предмет, например выпущенный из руки карандаш, капля дождя, лист дерева и т. д., падает вниз? Почему стрела, выпущенная из лука, не летит все время прямо, а в конце концов падает на землю? Почему Луна движется вокруг Земли? Причина всех этих явлений в том, что Земля притягивает к себе все тела (рис. 20.1).
При этом все тела притягивают к себе Землю. Например, притяжение к Луне вызывает на Земле приливы и отливы (рис. 20.2). В результате притяжения к Солнцу наша планета и все другие планеты Солнечной системы движутся вокруг Солнца по определенным орбитам. В 1687 г. Исаак Ньютон сформулировал закон, согласно которому между всеми телами Вселенной существует взаимное притяжение. Такое взаимное притяжение объектов называют гравитационным взаимодействием или всемирным тяготением. Опираясь на опыты и математические расчеты, Ньютон доказал, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что всех нас притягивает Земля, и при этом мы совсем не ощущаем притяжение соседа по парте.
В 1687 г. Исаак Ньютон сформулировал закон, согласно которому между всеми телами Вселенной существует взаимное притяжение. Такое взаимное притяжение объектов называют гравитационным взаимодействием или всемирным тяготением. Опираясь на опыты и математические расчеты, Ньютон доказал, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что всех нас притягивает Земля, и при этом мы совсем не ощущаем притяжение соседа по парте.
В физике силу гравитационного притяжения Земли, действующую на тела вблизи ее поверхности*, называют силой тяжести.
Сила тяжести — это сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.
Сила тяжести приложена к телу, которое притягивается Землей, и направлена вертикально вниз, к центру Земли (рис. 20.3).
Многочисленными опытами доказано, что сила тяжести, действующая на тело, прямо пропорциональна массе этого тела: где — значение силы тяжести; m — масса тела; g — коэффициент пропорциональности, который называют ускорением свободного падения.
Будем считать, что, когда говорят «вблизи поверхности Земли», имеют в виду расстояние, не превышающее нескольких десятков километров.
Вблизи поверхности Земли ускорение свободного падения равно приблизительно 9,8 ньютона на килограмм: Значение ускорения свободного падения несущественно изменяется на экваторе и полюсах Земли (рис. 20.4), при подъеме над поверхностью Земли и при спуске в шахту. Используя рис. 20.4, определите, на сколько сила тяжести, действующая на вас, на экваторе меньше, чем на полюсе.
Что физики называют весом телаИз-за притяжения к Земле все тела сжимают или прогибают опору либо растягивают подвес. Сила, которая характеризует такое действие тел, называется весом тела (рис. 20.5).
Вес тела — это сила, с которой вследствие притяжения к Земле тело давит на горизонтальную опору или растягивает вертикальный подвес. Единица веса в СИ, как и любой другой силы,— ньютон Если тело находится в состоянии покоя или прямолинейного равномерного движения, то его вес совпадает по направлению с силой тяжести и равен ей по значению: P=mg. Однако в отличие от силы тяжести, которая приложена к телу, вес приложен к опоре или подвесу (рис. 20.6).
Однако в отличие от силы тяжести, которая приложена к телу, вес приложен к опоре или подвесу (рис. 20.6).
Для упрощения расчетов в случаях, когда большая точность не существенна, можно считать, что g= 10 Н/кг.
Состояние невесомостиВы наверняка хорошо знаете термин «невесомость», но его значение многие понимают неправильно. Например, считают, что невесомость — это состояние, которое наблюдается только в космосе, где нет воздуха, или там, где отсутствует гравитация. Но это не так! Отсутствие воздуха само по себе не вызывает невесомости, а от гравитации вообще не спрячешься — во Вселенной нет ни одного уголка, где бы не действовали силы всемирного тяготения*. На самом деле невесомость — это отсутствие веса. Уберите у тела опору или подвес — и оно окажется в состоянии невесомости. (Обратите внимание: сопротивление воздуха тоже является своего рода опорой!)
Невесомость — это такое состояние тела, при котором тело не действует на опору или подвес. Тело вблизи поверхности Земли находится в состоянии невесомости, если на него действует только одна сила — сила тяжести. На короткое время невесомость легко создать и дома. Можно, например, подпрыгнуть — и вы на мгновение окажетесь в состоянии невесомости: в данном случае, пока выдвигаетесь вниз, сопротивление воздуха пренебрежимо мало и можно считать, что на вас действует только сила тяжести. Постоянно в состоянии невесомости находятся космические орбитальные станции и все, что на них находится (рис. 20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).
Тело вблизи поверхности Земли находится в состоянии невесомости, если на него действует только одна сила — сила тяжести. На короткое время невесомость легко создать и дома. Можно, например, подпрыгнуть — и вы на мгновение окажетесь в состоянии невесомости: в данном случае, пока выдвигаетесь вниз, сопротивление воздуха пренебрежимо мало и можно считать, что на вас действует только сила тяжести. Постоянно в состоянии невесомости находятся космические орбитальные станции и все, что на них находится (рис. 20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).
Плотность материи в нашей Вселенной очень мала (2-3 атома Гидрогена на 1 м3), потому во Вселенной в среднем очень мала и гравитация. Ее называют микрогравитацией. Вестибулярный аппарат — орган чувств у людей и позвоночных животных, воспринимающий изменение положения тела в пространстве и направление движения. Этот орган отвечает, например, за способность человека различать в темноте, где верх, а где низ.
Ее называют микрогравитацией. Вестибулярный аппарат — орган чувств у людей и позвоночных животных, воспринимающий изменение положения тела в пространстве и направление движения. Этот орган отвечает, например, за способность человека различать в темноте, где верх, а где низ.
Итоги:
Во Вселенной все тела притягиваются друг к другу. Такое взаимное притяжение тел называют всемирным тяготением. Сила тяжести — сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее. Сила тяжести вычисляется по формуле и направлена вертикально вниз, к центру Земли. Вес тела — это сила, с которой вследствие притяжения к Земле тело действует на горизонтальную опору или вертикальный подвес. Следует различать силу тяжести и вес тела: сила тяжести приложена к самому телу, а вес — к опоре или подвесу; вес тела равен по значению силе тяжести (P=mg) только в состоянии покоя тела или его равномерного прямолинейного движения. Когда тело движется под действием только силы тяжести, то оно находится в состоянии невесомости (его вес равен нулю).
Закон всемирного тяготения :: Класс!ная физика
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Великий закон Всемирного тяготения был открыт Исааком Ньютоном.
Ученому было всего 23 года !
Два любых тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.
Силы тяготения или иначе гравитационные силы, действующие между двумя телами:
– дальнодействующие;
– для них не существует преград;
– направлены вдоль прямой, соединяющей тела;
– равны по величине;
– противоположны по направлению.
ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ
Физический смысл гравитационной постоянной:
гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга
УСЛОВИЯ ПРИМЕНИМОСТИ ЗАКОНА ВСЕМИРНОГО ТЯГОТЕНИЯ
1. если размеры тел много меньше, чем расстояния между ними;
если размеры тел много меньше, чем расстояния между ними;
2. если оба тела шары и они однородны;
;
3. если одно тело большой шар , а другое находится вблизи него
( планета Земля и тела у ее поверхности).
Гравитационное взаимодействие ощутимо проявляется при взаимодействии тел большой массы.
КАВЕРЗНАЯ ЗАДАЧКА НА ПРЕДЫДУЩУЮ ТЕМУ
Сумеешь решить?
Молодец!
(как всегда “5”)
За последние 0,5 секунд свободно падающее тело пролетает 30 метров.
Найдите скорость тела в момент приземления.
Устали? – Отдыхаем!
Что такое сила тяжести в физике.
 Физика — вспомнить всё
Физика — вспомнить всёВ данном параграфе мы напомним Вам о силе тяжести, центростримительном ускорение и весе тела
На каждое тело, находящееся на планете, действует гравитация Земли . Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз .
Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
F т =GMm/R 2
где М – масса Земли; R – радиус Земли.
Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле
F
т =GMm/R
2 модуль ускорения свободного падения g находят по формуле
g=F т /m=GM/R 2 .
Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т. е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде
е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде
F т =mg
В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы F т =GMm/R 2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.
Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют связями. Под действием силы тяжести связи деформируются и сила реакции деформированной связи по третьему закону Ньютона уравновешивает силу тяжести.
На ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета – Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.
Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.
Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с 2 .
Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле
g=GM/(R+h) 2.
Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2.
Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.
Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес – это упругая сила, приложенная к опоре или подвесу (т. е. к связи).
Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести F т только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае
Р=F т =mg.
Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.
Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести F т =mg и сила упругости F yп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил F т и F уп дает равнодействующую, вызывающую ускорение тела, т. е.
Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил F т и F уп дает равнодействующую, вызывающую ускорение тела, т. е.
F т + F уп =mа.
Согласно приведенному выше определению понятия “вес”, можно написать, что Р=-F yп. Из формулы: F т + F уп =mа. с учетом того, что F т =mg, следует, что mg-mа=-F yп . Следовательно, Р=m(g-а).
Силы F т и F уп направлены по одной вертикальной прямой. Поэтому если ускорение тела а направлено вниз (т.е. совпадает по направлению с ускорением свободного падения g), то по модулю
P=m(g-a)
Если же ускорение тела направлено вверх (т. е. противоположно направлению ускорения свободного падения), то
Р = m = m(g+а).
Следовательно, вес тела, ускорение которого совпадает по направлению с ускорением свободного падения, меньше веса покоящегося тела, а вес тела, ускорение которого противоположно направлению ускорения свободного падения, больше веса покоящегося тела. Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.
Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.
При свободном падении a=g. Из формулы: P=m(g-a)
следует, что в таком случае Р=0, т. е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости . Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.
Семнадцатый век недаром называют веком великих астрономических открытий. Многолетние наблюдения Галилея, Коперника, Тихо Браге дали возможность сформировать Иоганну Кеплеру законы движения небесных тел. Для того чтобы объяснить, почему планеты находятся в бесконечном движении, что заставляет их оставаться на своей орбите и что такое сила тяжести, понадобился гений – Исаак Ньютон.
Гипотезы гения
Свои законы о движении Исаак Ньютон сформулировал не для теории, а для практического применения. Обобщая данные многолетних астрономических наблюдений и благодаря своим законам о движении, этот великий ученый смог ответить на вопрос, который ставил в тупик не одно поколение ученых: «Что удерживает планеты на своих орбитах?» Ведь до Ньютона учеными выдвигались разные предположения – от хрустальных сфер до магнитных флюидов. Благодаря первому закону Ньютона стало ясно, что для равномерного прямолинейного движения сила не нужна. Сила необходима для того, чтобы заставить планеты двигаться по криволинейной орбите. Если применить формулу силы из второго закона Ньютона, то она будет равна произведению ускорения на массу. Ньютон пришел к выводу, что ускорение должно быть равным v 2 /R. Так более легкое небесное тело, Луна например, будет вращаться вокруг более тяжелого, но никогда не станет к нему приближаться. Это можно представить себе как падение с касательной к окружности на саму окружность. В точке соприкосновения скорость может быть постоянной или равной нулю, но ускорение присутствует всегда. Постоянное движение по заданной орбите без отсутствия видимого ускорения – вот ответ Ньютона на вопрос о движении планет.
В точке соприкосновения скорость может быть постоянной или равной нулю, но ускорение присутствует всегда. Постоянное движение по заданной орбите без отсутствия видимого ускорения – вот ответ Ньютона на вопрос о движении планет.
Притяжение
Так, Луна движется вокруг Земли, а Земля – вокруг Солнца, повинуясь некой силе. Гениальность Ньютона проявилась в том, что он объединил силу притяжения небесных тел с силой тяжести, которая известна каждому жителю Земли. Существует легенда, что к правильным выводам Ньютона подтолкнуло обычное яблоко, упавшее ему на голову. Притяжение яблока и Луны к Земле описывается по абсолютно одинаковым законам – сделал вывод исследователь. Свое второе название сила тяжести получила от слова «гравис», что означает «вес».
Гравитация
Обобщив законы движения планет, Ньютон выяснил, что сила их взаимодействия может быть вычислена по формуле:
Где m 1 m 2 – массы взаимодействующих тел, R – расстояние между ними, а G – некий коэффициент пропорциональности, получивший название гравитационной постоянной. Слово «гравитация» подобрано абсолютно правильно, ведь происходит оно от слова «вес». Точное число постоянной Ньютону известно не было, гораздо позже значение G установил Кавендиш. Можно видеть, что на действие силы притяжения влияют массы тел и учитывается расстояние между ними. Никакие другие факторы на силу притяжения влиять не могут.
Слово «гравитация» подобрано абсолютно правильно, ведь происходит оно от слова «вес». Точное число постоянной Ньютону известно не было, гораздо позже значение G установил Кавендиш. Можно видеть, что на действие силы притяжения влияют массы тел и учитывается расстояние между ними. Никакие другие факторы на силу притяжения влиять не могут.
Значение закона притяжения
Данный закон универсален и может применяться к любым двум телам, имеющим массу. В случае, когда масса одного взаимодействующего тела много больше массы другого, можно говорить о частном случае гравитационной силы, для которого имеется специальный термин “сила тяжести”. Это понятие применяется для задач, вычисляющих силу притяжения на Земле или других небесных телах. Если подставить значение силы тяжести в формулу второго закона Ньютона, то получим значение F=ma. Здесь а – ускорение силы тяжести, которое заставляет тела стремиться друг к другу. В задачах, связанных с использованием ускорения свободного падения, его обычно обозначают буквой g. С помощью разработанного им интегрального исчисления Ньютон математически доказал, что сила тяжести в шаре всегда сосредоточена в центре большего тела. В паре яблоко-Земля вектор ускорения направлен к центру земли, в паре Земля-Солнце направлен к Солнцу и так далее.
С помощью разработанного им интегрального исчисления Ньютон математически доказал, что сила тяжести в шаре всегда сосредоточена в центре большего тела. В паре яблоко-Земля вектор ускорения направлен к центру земли, в паре Земля-Солнце направлен к Солнцу и так далее.
Зависимости силы тяжести от широты
Сила тяжести на Земле зависит от высоты тела под поверхностью планеты и от широты, на которой проводится эксперимент. Высота тела влияет на значение R, как видно, чем дальше расстояние от поверхности Земли, тем величина g меньше. Связь силы тяжести с широтой объясняется тем, что Земля имеет форму не шара, а геоида. У полюсов она немного сплюснута. Поэтому расстояние от центра Земли до экватора и до полюса будет разным – до 10 %. Такое расхождение делает весьма неудобным расчеты, например расчеты грузов трансконтинентальных перевозок. Поэтому за основу принимают показатель силы притяжения на средних широтах 9,81 м/с 2 .
Вес тела
В быту широко применяется такое понятие, как вес тела. В физике он обозначается буквой P. Вес – это сила, с которой тело давит на опору. В бытовом понятии вес часто подменяется понятием «масса», хотя это совершенно разные величины. В зависимости от того, какое значение принимает сила тяжести, изменяется и вес тела. Например, вес свинцовой детали на Земле и Луне будет отличаться. А вот масса остается неизменной и на Земле, и на Луне. Кроме этого, в определенных случаях вес тела может быть нулевым. Вес – величина, имеющая направление, а масса – скаляр.
В физике он обозначается буквой P. Вес – это сила, с которой тело давит на опору. В бытовом понятии вес часто подменяется понятием «масса», хотя это совершенно разные величины. В зависимости от того, какое значение принимает сила тяжести, изменяется и вес тела. Например, вес свинцовой детали на Земле и Луне будет отличаться. А вот масса остается неизменной и на Земле, и на Луне. Кроме этого, в определенных случаях вес тела может быть нулевым. Вес – величина, имеющая направление, а масса – скаляр.
Но так как согласно третьему закону Ньютона действие равно противодействию, вес тела равен силе реакции опоры.
Так как силу реакции простой опоры измерить довольно трудно, то опыт можно «перевернуть», подвесив какое-либо тело на пружину и измеряя степень растяжения этой пружины. При этом сила, растягивающая пружину с грузом, будет иметь вполне логичное F=mg, где m – масса, а g – ускорение свободного падения.
Перегрузка
Если груз с пружинкой поднять вверх, то ускорение силы тяжести и ускорение подъема будут направлены в противоположные стороны. Представить это можно так: F = m(g+a). Сила тяжести, а соответственно, и его вес, возрастают.
Представить это можно так: F = m(g+a). Сила тяжести, а соответственно, и его вес, возрастают.
Для увеличения веса, связанного с дополнительным ускорением, существует специальный термин – перегрузка. Действие перегрузки испытывал каждый из нас, поднимаясь на лифте или взлетая на самолете. Особенно сильную перегрузку испытывают на себе космонавты и летчики сверхзвуковых самолетов при взлете своих летательных аппаратов.
Невесомость
Когда телу придается ускорение в направлении силы тяжести, то есть вниз в нашем случае, тогда F=m(g-a). Так, вес тела становится меньше. В предельном случае, когда a=g и направлены они в разные стороны, можно говорить о нулевом весе, то есть тело падает с постоянной скоростью. Состояние, при котором вес тела является нулевым, называют невесомостью. Человек испытывает состояние невесомости в космическом корабле, когда он движется с выключенными двигателями. Невесомость – обычное состояние для космонавтов и летчиков, летающих на сверхзвуковых самолетах.
Значение силы тяжести
Без силы тяжести не происходило бы многих, кажущихся нам естественными, вещей – не сходили бы лавины с гор, не шли бы дожди, не текли бы реки. Атмосфера Земли сохраняется благодаря силе тяжести. Для сравнения, планеты с меньшей массой, такие как Луна или Меркурий, растеряли свою атмосферу очень быстро и остались беззащитными перед потоком жесткого космического излучения. Атмосфера Земли играла решающую роль при возникновении жизни на Земле, ее видоизменении и сохранении.
Кроме силы тяжести, на Земле действует сила притяжения Луны. Благодаря ее близкому (в космических масштабах) соседству на Земле существуют приливы и отливы, сдвигаются континенты, а многие биологические ритмы совпадают с лунным календарем.
Таким образом, силу тяжести нужно рассматривать не как досадную помеху, а как полезный и необходимый закон природы.
Сила тяжести – это сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения:
\(~\vec F_T = m \vec g. 2}\) .
2}\) .
Из этой формулы видно, что ускорение свободного падения g не зависит от массы падающего тела, но зависит от высоты.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C. 39-40.
Определение
Под воздействием силы притяжения к Земле все тела падают с одинаковыми по отношению к ее поверхности ускорениями. Такое ускорение называют ускорением свободного падения и обозначают: g. Его величина в системе СИ считается равной g=9,80665 м/с 2 – это так называемое, стандартное значение.
Вышесказанное обозначает то, что в системе отсчета, которая связывается с Землей, на любое тела обладающее массой m действует сила равная:
которая называется силой тяжести.
Если тело находится в состоянии покоя на поверхности Земли, тогда сила тяжести уравновешивается реакцией подвеса или опоры, которая удерживает тело от падения (вес тела).
Различие между силой тяжести и силой притяжения к Земле
Если быть точным, то следует заметить, что в результате неинерциальности системы отсчета, которая связывается с Землей, сила тяжести отличается от силы притяжения к Земле. Ускорение, которое соответствует движению по орбите существенно меньше, чем ускорение, которое связывается с суточным вращением Земли. Система отсчета, связанная с Землей, осуществляет вращение по отношению к инерциальным системам с угловой скоростью =const. Поэтому в случае рассмотрения перемещения тел по отношению к Земле следует учитывать центробежную силу инерции (F in), равную:
где m – масса тела, r – расстояние от оси Земли. Если тело расположено не высоко от поверхности Земли (в сравнении с радиусом Земли), то можно считать, что
где R Z – радиус земли, – широта местности.
В таком случае ускорение свободного падения (g) по отношению к Земле будет определено действием сил: силы притяжения к Земле () и силы инерции (). При этом сила тяжести – есть результирующая этих сил:
Так как сила тяжести сообщает телу, обладающему массой m ускорение равное
, то соотношение (1) является справедливым.
Разница между силой тяжести и силой притяжения к Земле небольшая. Так как .
Как и всякая сила, сила тяжести – векторная величина. Направление силы , например, совпадает с направлением нити, натянутой грузом, которое называют направлением отвеса. Сила направлена к центру Земли. Значит, нить отвеса направлена также только на полюсах и экваторе. На других широтах угол отклонения () от направления к центру Земли составляет величину, равную:
Разница между F g -P максимальна на экваторе, она составляет 0,3% от величины силы F g . Так как земной шар является сплюснутым около полюсов, то F g имеет некоторые вариации по широте. Так она у экватора на 0,2% меньше, чем у полюсов. В результате ускорение g изменяется с широтой от 9,780 м/с 2 (экватор) до 9,832 м/с 2 (полюса).
По отношению к инерциальной системе отсчета (например, гелиоцентрической СО) тело в свободном падении будет перемещаться с ускорением (a) отличающимся от g, равным по модулю:
и совпадающим по направлению с направлением силы .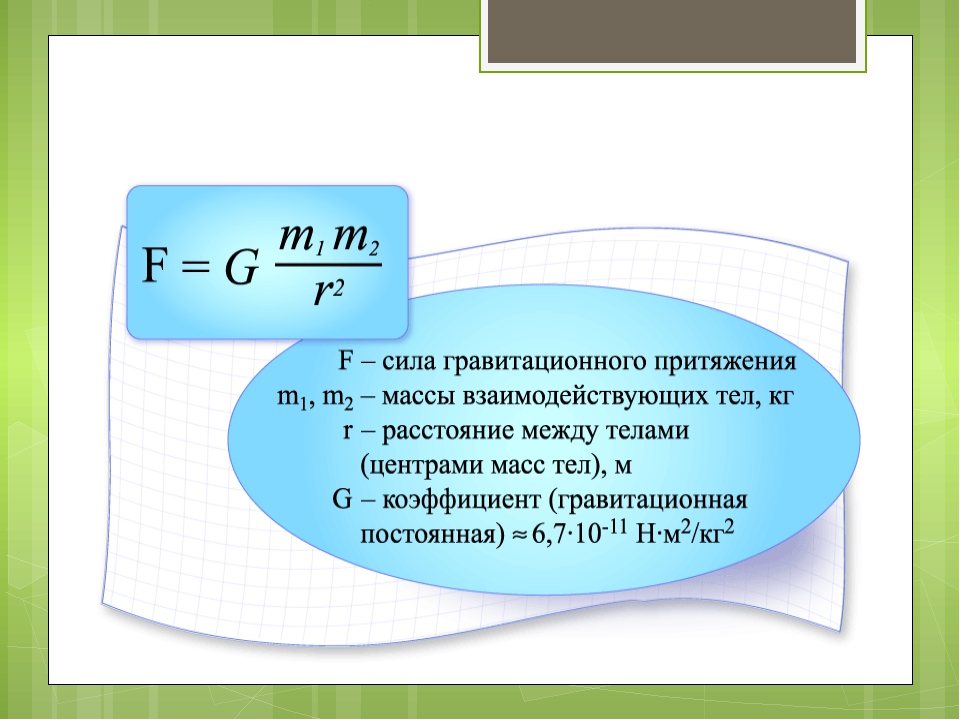 2 .
2 .
Таким образом, для ответа на поставленный вопрос следует найти отношение:
Проведем вычисления:
Ответ.
Пример
Задание. Получите выражение, которое связывает широту и угол, который образуют вектор силы тяжести и вектор силы притяжения к Земле.
Решение. Угол, который образуется между направлениями силы притяжения к Земле и направлением силы тяжести можно оценить, если рассмотреть рис.1 и применить теорему синусов. На рис.1 изображены: – центробежная сила инерции, которая возникает за счет вращения Земли вокруг оси, – сила тяжести, – сила притяжения тела к Земле. Угол – широта местности на Земле.
Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли . Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз .
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе.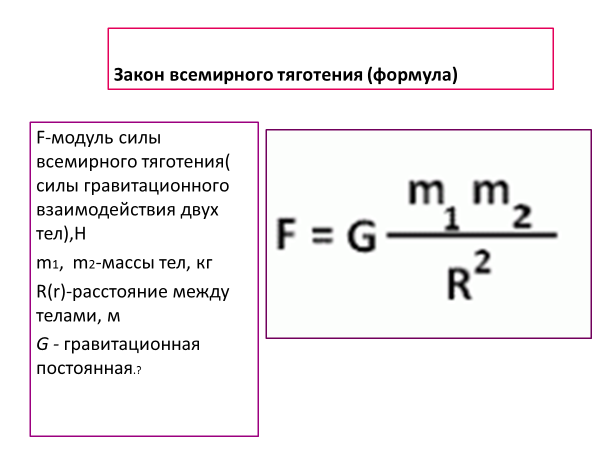 Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы “говорит” реагирует опора . Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, “сопротивляются”.
Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы “говорит” реагирует опора . Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, “сопротивляются”.
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину – уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации – сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел .
Вес тела
Вес тела – это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести – сила, которая возникает в результате взаимодействия с Землей. Вес – результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же – сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Сила реакции опоры и вес – силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес – это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью . Невесомость – состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес – сила, измеряется в Ньютонах. Как верно ответить на вопрос: “Сколько ты весишь”? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка – отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона , сила Ампера , сила Лоренца , подробно рассмотрены в разделе Электричество .
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой . Поэтому на схемах различные точки приложения переносят в одну точку – в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Различают внешнее (сухое) и внутреннее (вязкое) трение. Внешнее трение возникает между соприкасающимися твердыми поверхностями, внутреннее – между слоями жидкости или газа при их относительном движении. Существует три вида внешнего трения: трение покоя, трение скольжения и трение качения.
Трение качения определяется по формуле
Сила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела
При больших скоростях пропорциональна квадрату скорости
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила
А сейчас сравним закон гравитации и силу тяжести
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
Рекомендуем также
Закон Всемирного тяготения. Гравитационное поле – методическая разработка для учителей, Набиева Зарина Асановна
Проверка домашнего задания.
Беседа по пройденной теме.
На прошлом уроке мы говорили о весе тела. Давайте посмотрим, достигли ли мы целей?
Учащиеся обсуждают в парах случай на слайде №3, вспоминают формулы по каждому предложенному случаю. После того, как ребята вспомнили каждый случай, они приступают к решению задач по вариантам.
После того, как ребята вспомнили каждый случай, они приступают к решению задач по вариантам.
Решив каждый свою задачу, ребята приступают к объяснению решения соседу.
После проделанной работы учащиеся оценивают друг друга по предложенным критериям.
Учащиеся получают тест для выполнения.
Для того, чтобы настроить детей на объяснение новой темы, учащимся предлагается фильм «Что такое Солнечная система?»
Вопрос для ребят: Как вы думаете, почему в Солнечной системе планеты движутся вокруг Солнца?
Что вы можете сказать о движении Луны?
После беседы ребятам предлагается выполнить задание в парах.
Завершите текст.
Луна по своей орбите
В соответствии с __ законом Ньютона, силы происходят в парах. Таким образом, __ действует на Землю с силой той же величины и __ как сила, с которой Земля действует на Луну.
Вопрос: как зависит сила притяжения Земли и Луны от их масс и расстояния между ними?
Учащиеся выполняют виртуальную лабораторную работу в парах для выяснения зависимости силы тяготения.
После того, как учащиеся выведут зависимость самостоятельно, переходим к следующему разделу
Давайте рассмотрим, каким образом была выведена величина гравитационная постоянная.
Теперь мы с вами можем поговорить о взаимодействии не только планет, но и о гравитационном взаимодействии всех тел, например на Земле.
После беседы учащимся предлагается выполнить упражнение:
Упражнение 1
Вычислить силу притяжения между шаром массой 4 кг и кеглей для боулинга массой 1,5 кг. Расстояние между ними составляет 3м. Предположим, G=6,67∙10-11Нм2кг2.
FG=GMmR2
Используйте формулу силы тяготения, которая действует на два тел. FG=GMmR2
FG=GMmR2
Сила притяжения между мячом: F= • 10-11 Н.
Вопрос: Можем ли мы относиться к Земному притяжению таким же образом, как притяжение, оказываемое на точке массы с тем же самым значением, поскольку Земля находится в том же центре?
Вопрос: Как вы думаете, каковы границы применимости закона Всемирного тяготения?
Беседа о силовых линиях гравитационного поля и о напряженности гравитационного поля.
На следующем уроке мы с вами поговорим о движении искусственных спутниках Земли. Теперь мы с вами можем поговорить о движениях искусственных спутниках Земли. Учащимся предлагается просмотреть видеофильм по ссылке
Подумайте о движении Луны вокруг Земли и ответьте на вопрос: при каких условиях тело может облететь всю Землю, став искусственным спутником Земли?
Как рассчитать данную скорость?
Решаем задачи
№10. 28, 10.31
28, 10.31
определение, формула расчета, роль в природе и космосе
Абсолютно все тела, которые обладают конечной массой, взаимодействуют друг с другом благодаря так называемой силе притяжения или гравитации. Дадим в статье определение силы тяжести, а также рассмотрим, какую роль она играет в природе и космосе.
Что такое сила тяжести или гравитациия?
В физике определение силы тяжести или гравитации дают следующее: это сила, с которой два тела, имеющие массу, притягиваются друг к другу. Это означает, что каждый человек притягивается к любому предмету, который встречает в своей жизни. Однако эта сила является настолько маленькой, что она не ощущается.
Проявление гравитации заметно, когда среди взаимодействующих тел имеется объект с огромной массой, например, наша планета. Во многих задачах по физике определение силы тяжести сводят до понятия притяжения объектов к Земле. В последнем случае говорят о весе тела, который вычисляют по формуле P = m*g. Здесь m и g – масса тела и ускорение свободного падения, которое приблизительно равно 9,81 м/с2.
Сэр Исаак Ньютон и всемирное тяготение
Впервые исчерпывающее определение силы тяжести дал в конце XVII века великий английский ученый Исаак Ньютон. Он смог объединить существовавшие на то время разрозненные знания и эмпирические наблюдения (понятие Галилея об инерции тел и законы Кеплера) и оформить их в виде стройной теории, получившей название «Небесная механика».
Согласно Ньютону, все тела притягиваются друг к другу с силой, которая записывается следующей формулой
F = G*m1*m2/R2, где
m1 и m2 – массы тел,
R – расстояние между ними,
G=6,67 10-11 Н*м2/кг2 – универсальная гравитационная постоянная.
Сила тяжести (гравитации) F действует на абсолютно любых расстояниях, направлена к центру масс тел и быстро убывает с увеличением дистанции между ними.
Если в отмеченную формулу подставить значение для массы и радиуса Земли, то можно получить названное выше ускорение g.
Эффекты, обусловленные существованием гравитации
Выше было дано определение силы тяжести, но не было сказано, какую роль она играет в нашей жизни. Во-первых, благодаря ее существованию мы не парим в воздухе, а твердо стоим на поверхности, и сам воздух не улетает в космическое пространство. Во-вторых, любое подброшенное тело падает обратно на землю. В-третьих, при расчете траекторий полета свободных тел учет влияния этой силы является принципиальным. Наконец, сила всемирного тяготения является главным фактором, который определяет особенности движения нашей планеты вокруг Солнца, и вообще движение любых космических тел.
В настоящее время ученые всего мира пытаются объединить гравитацию с другими фундаментальными взаимодействиями, чтобы создать единую физическую теорию нашей Вселенной.
Центр тяжести
Центр тяжести является геометрическим свойством любого объекта.
Центр тяжести – это среднее положение
масса
объекта. Мы можем полностью описать
движение
любого объекта через пространство с точки зрения перевода центр тяжести объекта из одного места в другое, и поворот объекта вокруг его центра тяжести, если он
может свободно вращаться.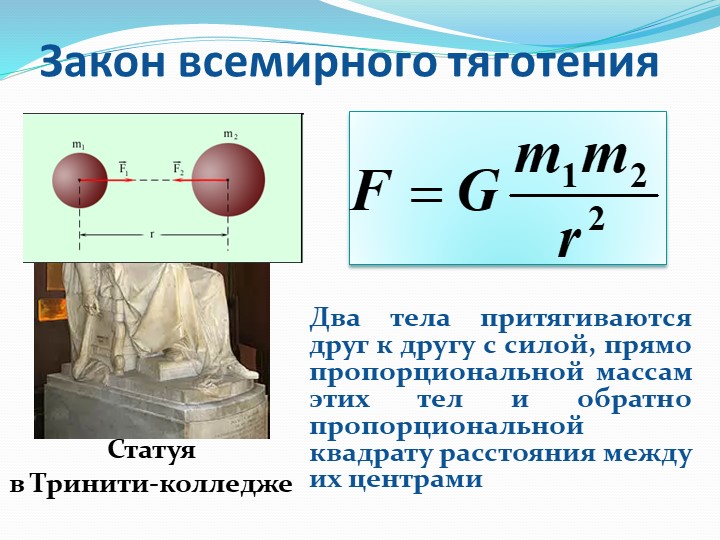 Если объект вынужден вращаться вокруг некоторого
другой точки, как шарнир, мы все еще можем описать его движение.В полете оба
самолеты
и
ракеты
вращаться вокруг своего центра тяжести.
Воздушный змей, с другой стороны, вращается вокруг
точка уздечки.
Но
подрезать
воздушного змея по-прежнему зависит от местоположения
центр гравитации
относительно точки уздечки, потому что на каждый объект вес всегда действует через
центр гравитации.
Если объект вынужден вращаться вокруг некоторого
другой точки, как шарнир, мы все еще можем описать его движение.В полете оба
самолеты
и
ракеты
вращаться вокруг своего центра тяжести.
Воздушный змей, с другой стороны, вращается вокруг
точка уздечки.
Но
подрезать
воздушного змея по-прежнему зависит от местоположения
центр гравитации
относительно точки уздечки, потому что на каждый объект вес всегда действует через
центр гравитации.
Определение центра тяжести очень важно для любого летающего объекта. Как инженеры определяют местонахождение центра сила тяжести для самолета, который они проектируют?
В общем, определение центра тяжести (cg) является сложной задачей.
процедура, потому что масса (и вес) могут быть неравномерно распределены
по всему объекту.Общий случай требует использования исчисления
которые мы обсудим внизу этой страницы.
Если масса распределена равномерно, задача значительно упрощается.
Если объект имеет линию (или плоскость) симметрии , центр тяжести лежит
на линии симметрии. Для
сплошной блок из однородного материала, центр тяжести просто
в среднем месте
физические размеры. (Для прямоугольного блока 50 х 20 х 10,
центр тяжести находится в точке (25,10,5) ).
Для треугольника высоты h центр тяжести равен h/3, а для полукруга радиуса
r, cg составляет (4 * r / (3 * pi)), где pi – это отношение длины окружности
круг по диаметру.Есть таблицы расположения центра тяжести
для многих простых фигур в учебниках по математике и естественным наукам. Таблицы были сгенерированы
с помощью уравнения из исчисления, показанного на слайде.
Для
сплошной блок из однородного материала, центр тяжести просто
в среднем месте
физические размеры. (Для прямоугольного блока 50 х 20 х 10,
центр тяжести находится в точке (25,10,5) ).
Для треугольника высоты h центр тяжести равен h/3, а для полукруга радиуса
r, cg составляет (4 * r / (3 * pi)), где pi – это отношение длины окружности
круг по диаметру.Есть таблицы расположения центра тяжести
для многих простых фигур в учебниках по математике и естественным наукам. Таблицы были сгенерированы
с помощью уравнения из исчисления, показанного на слайде.
Для объекта общей формы существует простой механический способ определить центр тяжести:
- Если мы просто сбалансируем объект, используя струна или ребро, точка, в которой объект уравновешен – это центр тяжести. (Точно так же, как уравновешивание карандаш на пальце!)
- Другой, более сложный способ — это двухэтапный метод, показанный на
слайд.На шаге 1 вы подвешиваете объект к любому
точка, и вы бросаете взвешенный
строка из той же точки.
 Нарисуйте линию на объекте вдоль
нить. Для шага 2 повторите процедуру с другой точки объекта.
Теперь у вас есть две линии, нарисованные на объекте, которые пересекаются.
Центр тяжести – это точка пересечения линий. Этот
процедура хорошо работает для объектов неправильной формы, которые являются твердыми
сбалансировать.
Нарисуйте линию на объекте вдоль
нить. Для шага 2 повторите процедуру с другой точки объекта.
Теперь у вас есть две линии, нарисованные на объекте, которые пересекаются.
Центр тяжести – это точка пересечения линий. Этот
процедура хорошо работает для объектов неправильной формы, которые являются твердыми
сбалансировать.
Если масса объекта распределена неравномерно, мы должны использовать исчисление для определения центра тяжести.Мы будем использовать символ S dw для обозначения интегрирования непрерывного функция по отношению к весу. Тогда центр тяжести можно определить из:
cg * W = S x dw
где x — расстояние от опорной линии, dw — увеличение веса и W — общий вес объекта. Чтобы оценить правую часть, мы должны определить, как меняется вес геометрически. От весовое уравнение, мы знаем, что:
ш = м * г
где м — масса объекта, а г — гравитационная
постоянный. В свою очередь, масса m любого объекта равна
плотность, ро ,
объекта, умноженное на
объем, В :
В свою очередь, масса m любого объекта равна
плотность, ро ,
объекта, умноженное на
объем, В :
м = ро * V
Мы можем объединить последние два уравнения:
ш = г * ро * V
тогда
dw = g * ро * dV
dw = g * rho(x, y, z) * dx dy dz
Если у нас есть функциональная форма для распределения массы, мы можем решить уравнение для центра тяжести:
cg * W = g * SSS x * rho(x,y,z) dx dy dz
где SSS указывает тройной интеграл по dx . dy . и дз .
Если мы не знаем функциональную форму распределения масс,
мы можем численно интегрировать уравнение, используя электронную таблицу.
Разделите расстояние на несколько небольших объемных сегментов и
определение среднего значения веса/объема (плотность, умноженная на силу тяжести) за
тот маленький сегмент. Взяв сумму среднего значения веса/объема
умножить на расстояние, умноженное на сегмент объема
разделить на вес и получится центр тяжести.
Вы можете просмотреть короткий кино из «Орвилл и Уилбур Райт», объясняя, как центр тяжести повлияло на полет их самолетов.Файл фильма может сохранять на свой компьютер и просматривать как подкаст на проигрывателе подкастов.
Виды деятельности:
Экскурсии с гидом
- Вес самолета:
- Фюзеляж:
Навигация ..
- Домашняя страница руководства для начинающих
Ускорение под действием силы тяжести | bartleby
Уравнения, формулы и объяснение ускорения свободного падения:
1.Круговое орбитальное движение радиуса R, вращающееся за период времени T, требует внутреннего ускорения A, равного произведению длины окружности 4π,2, уравнение ускорения A=4Π2RT2
2. Уравнение гравитационной силы Ньютона F12=GM1M2r122. Здесь F12 — величина гравитационной силы, M1 и M2 — массы двух тел, r12 — расстояние между двумя телами и G — постоянная всемирного тяготения.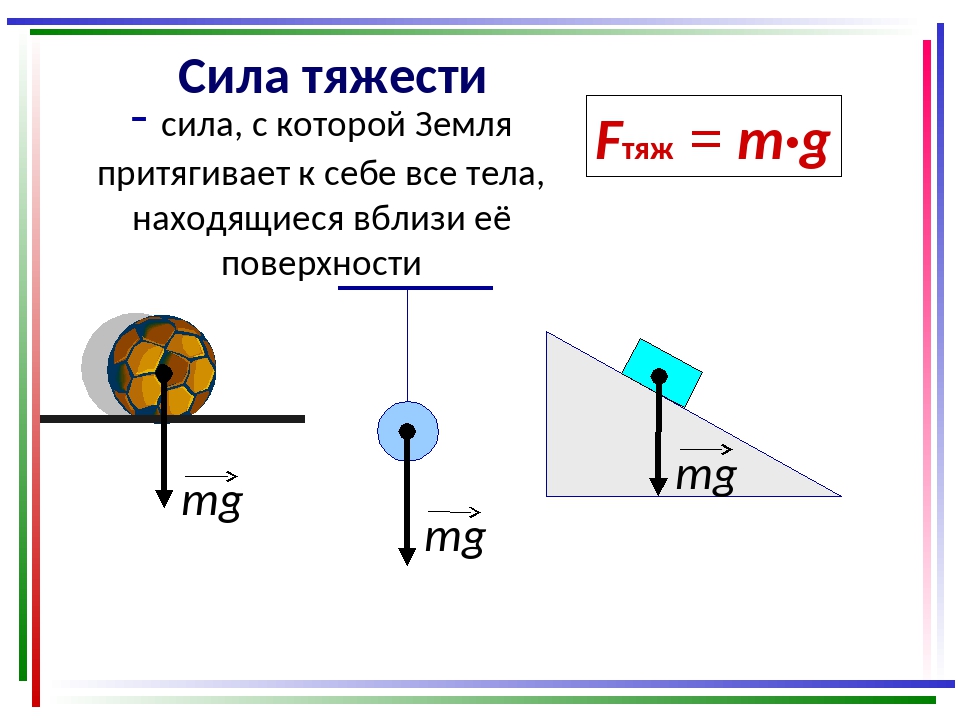 Уравнение можно изменить, чтобы найти массу одного из тел: M2=F2/F1 × M1.Согласно теории эквивалентности, гравитационная масса равна инертной массе тела. Универсальная гравитационная постоянная G имеет значение 6,67 × 10-11 кг -2 м2, которое зависит от физических величин, таких как длина, масса и время, необходимое для достижения земли.
Уравнение можно изменить, чтобы найти массу одного из тел: M2=F2/F1 × M1.Согласно теории эквивалентности, гравитационная масса равна инертной массе тела. Универсальная гравитационная постоянная G имеет значение 6,67 × 10-11 кг -2 м2, которое зависит от физических величин, таких как длина, масса и время, необходимое для достижения земли.
3. Гравитационная сила является векторной величиной, которая действует в направлении двух тел, поэтому пусть r будет векторной величиной расстояния разделения. Таким образом, формула гравитационной силы принимает вид F=GM1M2rr3, а упрощенное уравнение принимает вид F=GM1M2r2
4.Например, объект падает с высоты h над поверхностью земли, с учетом этой высоты формула принимает вид F=GM1M2r+h3, но эта высота очень мала и ею можно пренебречь. Таким образом, объект начинает падать вниз под действием силы тяжести с увеличением его скорости, когда он достигает поверхности земли, объект ускоряется и меняет скорость из-за силы, создаваемой гравитацией. та же самая формула универсального закона тяготения принимает вид Итак, обозначая ускорение свободного падения как «а», формула принимает вид a=GMErE2, где ME — масса Земли, а rE — радиус Земли.
та же самая формула универсального закона тяготения принимает вид Итак, обозначая ускорение свободного падения как «а», формула принимает вид a=GMErE2, где ME — масса Земли, а rE — радиус Земли.
5. Гравитационное ускорение тела обозначается как «g», а его упрощенное уравнение: g=масса силы объекта. Значение ускорения свободного падения на Земле составляет 9,81 м с-2, где единица СИ – м/с2
6. Равномерное круговое движение и сила тяжести. Первый закон, сформулированный Ньютоном, гласит, что объект, движущийся с постоянной скоростью, будет продолжать движение. двигаться до тех пор, пока не появится внешняя сила. Допустим, объект движется в идеальном круговом движении, мяч, связанный веревкой и вращающийся в непрерывном круговом движении, сила, которая заставляет его вращаться в этом движении, является центростремительной силой, и эта сила вызывает центростремительное ускорение.Центростремительный означает поиск центра. Другим распространенным примером является вращение Земли вокруг Солнца также из-за центростремительной силы, вызывающей движение, которое происходит из-за гравитационного притяжения между ними. Скорость объекта, преодолеваемого на расстояние, равное длине окружности Земли, за период времени T равна v=2πrT. Центростремительное ускорение равно a=v2r, где v — скорость, r — радиус. Таким образом, уравнение центростремительной силы имеет вид F=ma или F=mv2r. Центробежная сила – это сила, которая создается инерцией тела и распространяется по окружности и действует на тело, движущееся по окружности, направленной от центра, вокруг которого движется тело.
Скорость объекта, преодолеваемого на расстояние, равное длине окружности Земли, за период времени T равна v=2πrT. Центростремительное ускорение равно a=v2r, где v — скорость, r — радиус. Таким образом, уравнение центростремительной силы имеет вид F=ma или F=mv2r. Центробежная сила – это сила, которая создается инерцией тела и распространяется по окружности и действует на тело, движущееся по окружности, направленной от центра, вокруг которого движется тело.
Ньютон изучает силу гравитации — домашнее обучение для детей
Что такое гравитация? Согласно Ньютону, гравитация — это сила притяжения между двумя объектами, имеющими массу. Это означает, что два шара на диаграмме имеют гравитационную силу притяжения друг к другу, потому что они имеют массу.
Сила притяжения между двумя объектами зависит от их массы и расстояния между ними.
Если синий шар имеет массу 2 кг, а зеленый мяч имеет массу 1 кг и расстояние между ними 10 см, какова сила притяжения между ними?
УРА!! Посмотрите на уравнение, которое придумал Ньютон. G — это константа, используемая независимо от того, что и где находятся объекты.
G — это константа, используемая независимо от того, что и где находятся объекты.
Ньютон опубликовал работу, содержащую уравнение всемирного тяготения, в июле 1687 года. Это уравнение гравитации и многие другие идеи Ньютона используются до сих пор.
Вы можете узнать больше о работе Ньютона, а также других ученых в «Ученый сквозь века. ”
Используя формулу универсального тяготения Ньютона, я рассчитал, что сила притяжения между двумя шарами на диаграмме равна 13,4 x 10 -9 Н, что составляет 0,00000000030 фунтов. Эта сила слишком мала, чтобы притягивать шары друг к другу, потому что гравитация Земли, действующая на каждый шар, удерживает их на месте. Притяжение Земли к синему шару составляет 19,6 Н. Земное притяжение к зеленому шару составляет 9,8 Н.
Уравнение всемирного тяготения Ньютона необходимо для расчета силы притяжения между небесными телами, такими как Земля и Солнце.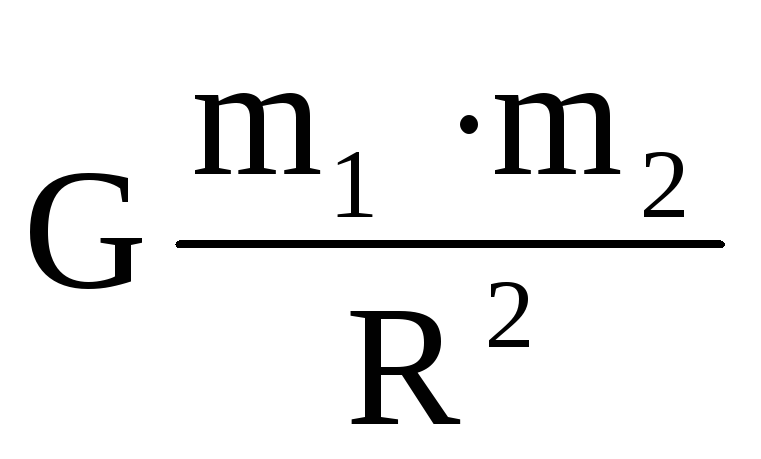 Но есть гораздо менее сложное уравнение, которое можно использовать для расчета силы притяжения между объектами на Земле. Это уравнение было получено из уравнения всемирного тяготения Ньютона. На схеме показано, как это было сделано. Ниже приводится разбивка уравнения, которое используется для расчета силы гравитации, действующей на все на Земле.
Но есть гораздо менее сложное уравнение, которое можно использовать для расчета силы притяжения между объектами на Земле. Это уравнение было получено из уравнения всемирного тяготения Ньютона. На схеме показано, как это было сделано. Ниже приводится разбивка уравнения, которое используется для расчета силы гравитации, действующей на все на Земле.
F = m x g
F= сила тяжести между землей и объектом, измеренная в ньютонах, N
m= масса объекта, измеренная в килограммах, кг
г = земная гравитационная постоянная равна 9.8 Н/кг
На иллюстрации изображены дети, мяч и пожилой мужчина, стоящий на земле. Диаграмма представляет собой модель, показывающую, что независимо от того, где находится объект на земле, он тянется вниз. Вниз — это направление относительно того места, где вы находитесь на земле. Направление «вниз» — это линия, перпендикулярная земной поверхности.
1. Какая сила земного притяжения действует на мальчика массой 30 кг?
Думаю:
- Уравнение для расчета силы земного притяжения F = m x g
- F — сила земного притяжения.

- м это масса мальчика
- г – константа, 9,8 Н/кг
- F = 30 кг x 9,8 Н/кг = 295 Н
При наборе легко написать дробь так: 9,8 Н/м.
Но когда единицы измерения являются частью уравнения, их необходимо учитывать. Я настоятельно рекомендую вам учить детей писать дроби с горизонтальной дробной чертой .
Обратите внимание, что дробная черта, отделяющая числитель 9,8 Н от знаменателя кг, расположена горизонтально.
Также обратите внимание, что я предлагаю расширить линейку дробей с коэффициентом 30 кг. Я делаю это, потому что это помогает мне систематизировать информацию. Когда я занимаюсь репетиторством по математике, я замечаю, что дети часто не очень аккуратно пишут. Таким образом, я призываю их расширить планку факторов.
Обратите внимание, что единица кг в числителе (над дробной чертой) отменяет единицу кг в знаменателе (под дробной чертой).
Обратите внимание, что единица измерения ньютонов, Н, слева. Это будет единица в ответе.
Это будет единица в ответе.
После того, как единицы рассмотрены, рассмотрите числа и решите задачу.
Произведение 30 x 9,8 равно 295.
Ответ: 295 Н.
Обратите внимание, что необходимо учитывать единицы измерения, и, как и числа, они сокращаются, как в приведенном выше примере. Когда единицы являются частью расчетов, это называется анализом измерений . Изучение размерного анализа в начальной и средней школе значительно упрощает понимание задач по химии и физике.
Большинству детей горизонтальная дробная черта помогает лучше понять проблемы.
Сила тяжести, действующая на мальчика, равна 295 Н, следовательно, вес мальчика равен 295 Н.
В Техасе мы обычно измеряем массу тела в фунтах, lb.
Ниже приведен еще один пример размерного анализа с использованием коэффициента преобразования фунтов в ньютоны.
Проблема:
Вес мальчика 295 Н, скольким фунтам он равен?
Думаю:
- Цель состоит в том, чтобы определить, скольким фунтам эквивалентны 295 Н.

- Перечислите факты, которые вам известны:
295 Н — вес, который необходимо преобразовать в вес в фунтах - Известные отношения между ньютонами и фунтами:
1 фунт = 4,5 Н и 4.5 N = 1 фунт
Коэффициенты пересчета записываются в виде дробей: 1 фунт/4.5 Н или 4,5 Н/1 фунт - У вас есть вся информация, необходимая для расчета веса мальчиков в фунтах.
- Каждый раз, когда требуется коэффициент преобразования, используйте то, что вы знаете об анализе размерностей.
1. Запишите количество, которое необходимо изменить.
2. Нарисуйте дробную черту
3. Умножьте на коэффициент преобразования. Обратите внимание, что единица ответа находится в числителе. Таким образом, используемый коэффициент пересчета составляет 1 фунт/4,5 Н.
4. Упростите уравнение. Единица ньютона в числителе отменяет единицу ньютона в знаменателе, оставляя в ответе только единицу фунта.
5. Посчитайте, разделите 295 на 4,5.
Гравитация — это сила между двумя массами. Это означает, что пока земля притягивает вас, в то же время вы притягиваете землю. Это похоже на перетягивание каната. Хотя сила одинакова, масса Земли намного больше вашей, поэтому Земля побеждает.
Родственные
Ускорение гравитации
Введение
Объект в свободном падении имеет нисходящее ускорение величиной 90 276 g 90 277 , где 90 002 g = 9.80 м/с 2 . Ускорение создается гравитационной силой, с которой Земля воздействует на объект. Применение второго закона Ньютона к объекту в свободном падении даетВт = мг,
уравнение, которое связывает массу и вес объекта. На рис. 1 показана диаграмма силы свободного тела для объекта, скользящего по наклонной поверхности без трения, расположенной под углом θ над горизонталью. Н — нормальная сила, действующая на объект со стороны поверхности наклона, а мг — сила тяжести, действующая на объект со стороны Земли, вес объекта.Нормальная сила направлена перпендикулярно поверхности склона, а сила тяжести направлена вертикально вниз, к центру Земли. Поскольку ускорение объекта параллельно наклону, удобно взять наши координатные оси x и y параллельными и перпендикулярными поверхности наклона. Если ось х направлена вниз по склону, то ускорение объекта находится в направлении + х и
Н — нормальная сила, действующая на объект со стороны поверхности наклона, а мг — сила тяжести, действующая на объект со стороны Земли, вес объекта.Нормальная сила направлена перпендикулярно поверхности склона, а сила тяжести направлена вертикально вниз, к центру Земли. Поскольку ускорение объекта параллельно наклону, удобно взять наши координатные оси x и y параллельными и перпендикулярными поверхности наклона. Если ось х направлена вниз по склону, то ускорение объекта находится в направлении + х иа х = а.
Составляющие силы тяжести по координатным направлениям показаны на рисунке 1. Применение| F x | |
мг SIN θ = MA и A = G SIN θ .
Объект скользит по склону с постоянным ускорением, g sin θ . Если объект выходит из состояния покоя и проходит расстояние 90 276 x 90 277 вниз по склону за время 90 276 t 90 277 , одно из кинематических уравнений с постоянным ускорением дает следующее выражение: Движение подобно свободному падению, но с уменьшенным значением ускорения.Уменьшенное ускорение означает более длительные интервалы времени для данного расстояния. Это позволяет более точно измерить 90 276 г 90 277, чем мы могли бы легко получить для свободного падения.
Если объект выходит из состояния покоя и проходит расстояние 90 276 x 90 277 вниз по склону за время 90 276 t 90 277 , одно из кинематических уравнений с постоянным ускорением дает следующее выражение: Движение подобно свободному падению, но с уменьшенным значением ускорения.Уменьшенное ускорение означает более длительные интервалы времени для данного расстояния. Это позволяет более точно измерить 90 276 г 90 277, чем мы могли бы легко получить для свободного падения.Цель
В этом эксперименте мы измеряем время, которое требуется тележке, чтобы пройти расстояние вниз по склону без трения, и используем это для определения ускорения свободного падения, 90 276 g 90 277 . Измеренное значение г будет сравниваться с принятым значениемг = 9,80 м/с 2 .
Аппарат
- Трек и тележка PASCO
- Секундомер
Обсуждение
Введение для этого эксперимента показывает, что для объекта, движущегося вниз по склону, который наклонен под углом 90 276 θ 90 277 по отношению к горизонтали, время, 90 276 t 90 277, требуется объекту, чтобы переместиться на расстояние, 90 276 x 90 277 , вдоль наклона задается уравнением Схема экспериментальной установки показана на рис. 2.Из рисунка видно, что Это дает Решая для г , мы получаем В этом эксперименте мы измерим L , x , h и t и используем эти измерения для вычисления г . Применение уравнения для стандартного отклонения из Приложения дает где Δ г — неопределенность расчетного значения г из-за неопределенностей измерения величин L , x , h и t , которые используются для расчета г .
2.Из рисунка видно, что Это дает Решая для г , мы получаем В этом эксперименте мы измерим L , x , h и t и используем эти измерения для вычисления г . Применение уравнения для стандартного отклонения из Приложения дает где Δ г — неопределенность расчетного значения г из-за неопределенностей измерения величин L , x , h и t , которые используются для расчета г .Процедура
Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных. Осторожно:
Будьте осторожны, чтобы не поцарапать поверхность гусеницы и не уронить на нее ничего! Когда тележка не используется, ставьте ее на лабораторный стол колесами вверх.
1
См. рис. 2. Расстояние x , пройденное тележкой, будет определяться двумя карандашными отметками на дорожке, которые служат начальной и конечной линиями для переднего конца тележки. Измерьте и запишите расстояние x между двумя карандашными отметками на дорожке. Расстояние L между опорами гусеницы было измерено и указано на боковой стороне гусеницы. Запишите значение L .
2. Расстояние x , пройденное тележкой, будет определяться двумя карандашными отметками на дорожке, которые служат начальной и конечной линиями для переднего конца тележки. Измерьте и запишите расстояние x между двумя карандашными отметками на дорожке. Расстояние L между опорами гусеницы было измерено и указано на боковой стороне гусеницы. Запишите значение L .2
Поместите тележку в середину гусеницы и посмотрите, катится ли она к любому концу, чтобы проверить, выровнена ли гусеница (при отсутствии прокладки). При необходимости отрегулируйте винт под одним концом направляющей, чтобы убедиться, что она выровнена.Также убедитесь, что автомобиль плавно движется по трассе. (Сообщите своему ТА, если это не так.)3
Можно поднять гусеницу, поместив металлический блок (прокладку) под регулировочный винт. Предусмотрены прокладки на 1 см и прокладки на 2 см. Поэтому дорожку можно поднять на высоту 1, 2 и 3 см. Это значение ч . Сначала используйте 1-сантиметровую прокладку. Поместите тележку на рельсы так, чтобы ее передний конец был выровнен с большей из двух карандашных отметок, определяющих x .Осторожно освободите тележку из состояния покоя и одновременно включите секундомер. Остановите секундомер, когда передняя часть тележки достигнет нижней карандашной отметки, и запишите время, t 1 , в Таблицу 1. Повторите эту процедуру еще три раза, один раз с тем же человеком, использующим секундомер, а затем дважды с другим партнером по лаборатории, производящим измерение времени. Запишите свои результаты как t 1 , t 2 , t 3 и t 4 в таблице 1.1.
Это значение ч . Сначала используйте 1-сантиметровую прокладку. Поместите тележку на рельсы так, чтобы ее передний конец был выровнен с большей из двух карандашных отметок, определяющих x .Осторожно освободите тележку из состояния покоя и одновременно включите секундомер. Остановите секундомер, когда передняя часть тележки достигнет нижней карандашной отметки, и запишите время, t 1 , в Таблицу 1. Повторите эту процедуру еще три раза, один раз с тем же человеком, использующим секундомер, а затем дважды с другим партнером по лаборатории, производящим измерение времени. Запишите свои результаты как t 1 , t 2 , t 3 и t 4 в таблице 1.1.4
Повторите шаг 3 для высот (значения h ) 2 см и 3 см. Запишите четыре измерения времени для каждого 90 276 ч 90 277 в таблице 1.5
Рассчитайте среднее значение 90 276 т 90 277 для каждых 90 276 ч 90 277 и внесите свои результаты в Таблицу 1. Затем используйте уравнение для расчета 90 276 г 90 277 для каждых 90 276 ч 90 277 и введите в Таблицу 1.
Затем используйте уравнение для расчета 90 276 г 90 277 для каждых 90 276 ч 90 277 и введите в Таблицу 1.6
Процентная неопределенность в каждой из величин x , L и h мала.Следовательно, неопределенность вашего измеренного значения г определяется в основном погрешностью измерения t и Δg = g( 4 )
Δt =
|
( 5 )
% неопределенности = = × 100% и занесите результаты в таблицу 2.
7
Для каждых ч рассчитайте процентную ошибку в измеренном вами значении г по сравнению с принятым значением 9.80 м/с 2 . Используйте уравнение где г — ваше значение в таблице 1. Внесите свои результаты в последний столбец таблицы 2. Для каждого ч сравните % неопределенности в таблице 2 с % ошибки. Ваша ошибка % меньше, чем неопределенность %? Дает ли одно значение ч более точные результаты для г ?Copyright © 2012-2013 Advanced Instructional Systems, Inc. и Техасский университет A&M. Фрагменты из Университета штата Северная Каролина.| Кредиты
Проблемы гравитации с решениями и пояснениями
Гравитация, задачи представлены вместе с подробными решениями.
Задача 1:
Объект падает без начальной скорости над поверхностью планеты Большая Альфа и падает с высоты 13,5 метров за 3 секунды. Радиус планеты Большая Альфа составляет 5,8210 6 метров.
Радиус планеты Большая Альфа составляет 5,8210 6 метров.
а) Каково ускорение падающего тела?
б) Какова масса планеты Большая Альфа?
Реклама Решение задачи 1:
а) Зная расстояние и время, мы можем рассчитать ускорение a , используя формулу расстояния для равноускоренного движения следующим образом:
d = (1/2) у 2
а = 2 д/т 2 = 2 13.5 / 3 2 = 3 м/с 2
б)
Пусть R — радиус, m b — масса планеты Большая Альфа, а m o — масса объекта. Ускорение обусловлено универсальной силой тяжести, поэтому универсальная сила тяжести и второй закон Ньютона дают
Ускорение обусловлено универсальной силой тяжести, поэтому универсальная сила тяжести и второй закон Ньютона дают
G m b m o / R 2 = m o a
Упростить, чтобы получить
м б = а Р 2 / G = 3 (5,8210 6 ) 2 / (6. 67410 -11 ) = 1,5210 24 кг
67410 -11 ) = 1,5210 24 кг
Задача 2:
Объект, брошенный без начальной скорости вблизи поверхности планеты Манта, достигает скорости 21 м/с за 3,0 секунды. Планета Манта имеет массу 2,3 10 23 кг.
а) Какое ускорение действует на объект?
б) Каков радиус планеты Манта?
Решение задачи 2:
а) Зная скорость и время, мы можем рассчитать ускорение a, используя формулу скорости равномерного ускоренного движения следующим образом:
v = at
a = v / t = 21 / 3 = 7 м/с 2
б)
Пусть R — радиус, m m — масса планеты Манта, а m o — масса объекта. Ускорение обусловлено универсальной силой тяжести, поэтому универсальная сила тяжести и второй закон Ньютона дают
Ускорение обусловлено универсальной силой тяжести, поэтому универсальная сила тяжести и второй закон Ньютона дают
G m m m o / R 2 = m o a
Упростить, чтобы получить
R 2 = G m m / a
R = √ ( G m m / a ) = √ [ ( 6,67410 -11 )(2,3 10 90 4 23 ] 6 м
Задача 3:
Спутник массой 1500 кг вращается вокруг Земли на высоте 2. 510 6 м.
510 6 м.
а) Какова орбитальная скорость спутника?
б) Каков период спутника?
в) Какова кинетическая энергия спутника?
Решение задачи 3:
а) Чтобы спутник находился и оставался на орбите, центростремительные силы F c и универсальные силы F u должны быть равны по величине.
F c = m v 2 / R , v орбитальная скорость спутника, m масса спутника и радиус орбиты R
R = радиус Земли + высота над уровнем моря = 6. 410 6 м + 2.510 6 м = 6,910 6 м
410 6 м + 2.510 6 м = 6,910 6 м
F U = GM M / R 2 , M Масса планеты Земля
GM M / R 2 = MV 2 / R
Упростите до получения
В = √ (GM / R) = √ [(6. 6710 -11 ) (5.9610 24 ) / (6.910 6 )] = 7590 м / с
6710 -11 ) (5.9610 24 ) / (6.910 6 )] = 7590 м / с
b ) Период Т — это время, за которое спутник совершает один оборот вокруг Земли. Отсюда
T = 2πR / v = 2π6.37110 6 / 7590 = 5274 с
в) Кинетическая энергия E k спутника равна
E k = (1 / 2) mv 2 = (1/2) 1500 7590 2 = 4,32 10 9 10 60 Задача 4: Сила тяжести, действующая на предмет на поверхности Марса, равна 20 Н. Решение задачи 4: Пусть напряженность гравитационного поля на Марсе равна g m , а на Земле g и m — масса объекта. Ускорение обусловлено универсальной силой тяжести, поэтому второй закон Ньютона и универсальная сила тяжести равны. мг м = Gm M / R = Gm M / R M 2 , на поверхности Марса Упрости для получения г м = GM / R M 2 , где m (= 6. На поверхности Марса F = мг м и F = 20 Н м = F/g м = 20/g м На поверхности Земли 9 F 9 9 = гм = 9,8 Ф/г м = 9,8 20 / (Г М / R м 2 ) = 9,820 R м 2 / (Г М) = 9,820 (3,39 10 6 6 )674 10 -11 6,39 10 23 ) = 53 N Задача 5: Спутник массой 500 кг первоначально был выведен на орбиту радиусом 24 000 км с периодом обращения 31 час вокруг планеты Баригу. а) Выразите массу этой планеты через Универсальную постоянную G, радиус R и период Т. б) Затем спутник был выведен на окончательную орбиту радиусом 10 000 км. Каким был его новый период? в) Как изменяется кинетическая энергия спутника при переходе с первой на вторую орбиты? Решение задачи 5: а)
Пусть M — масса планеты, а m (=500 кг) — масса спутника.Орбита спутника означает, что универсальная гравитационная сила и центростремительные силы равны. GM m / R 2 = mv 2 / R , v – орбитальная скорость спутника Упрощаем: M = R v 2 / G v = 2πR / T M R 90 (2πR / T) 2 / G = 4π 2 R 3 / (ГТ 2 ) б)
Пусть T 1 и T 2 — период спутника на R 1 = 24 000 000 и R 2 = 10 000 000 м соответственно. T 1 2 = 4π 2 R 1 3 / (мг) и T 2 2 = 4π 2 R 2 3 / (MG) Разделите левые стороны и правые стороны вышеуказанных уравнений и упрощают, чтобы получить T 2 2 / T 1 2 = R 2 3 / R 1 3 3 Отсюда T 2 = √ (T 1 2 R 2 3 / R 1 3 ) = T 1 (R 2 / R 1 ) 3/2 = 8. в)
Пусть E k1 и E k2 — кинетическая энергия спутника, а v 1 и v 2 — орбитальные скорости на первом и втором витках соответственно. E K1 = (1/2) MV = (1/2) MV 1 2 = (1/2) 500 (2πr 1 / T 1 ) 2 E K2 = (1 / 2) MV 2 2 2 = (1/2) 500 (2πr 2 / T 2 ) 2 E K2 – E K1 = 1000 π 2 [(R 2 / Т 2 ) 2 – (Р 1 / Т 1 ) 2 ] = 1000 π 2 [ (10710 6 9346060)) 2 – (2410 6 / (316060)) 2 ] = 2,30 10 12 Дж Задача 6: спутник Земли находится на асинхронной орбите кг. а) Каков радиус орбиты спутника? б) Какова высота спутника? в) Какова кинетика спутника? Решение задачи 6: а)
Пусть M — масса планеты, а m — масса стеллита.Движение спутника по орбите означает, что всеобщая гравитационная сила и центростремительные силы равны GM м / R 2 = mv 2 / R , v орбитальная скорость спутника и R радиус орбиты v = 2πR / T GM м / R 2 = M (2πR / T) 2 / R Решите для получения: R 3 = MGT 2 / (4π 2 ) R = [MGT 2 / (4π 2 ) ] 1/3 = [ 5,9610 24 6. б)
Радиус Земли равен 6371 км, высота спутника h равна h = 42 211 – 6371 = 35 840 км c)
Кинетическая энергия E k спутника определяется выражением E k = (1/2) mv 2 = (1/2) 1000 (2πR / T) 2 = (1/2) 1000 (2π 42 211 000 / (24 60 60)) 2 = 4,7 10 9 Дж 2 10 23 , is – 4,8 10 9 J. а) Каков радиус орбиты этого спутника? б) Какова кинетическая энергия этого спутника? в) Какова полная энергия этого спутника? г) Какова орбитальная скорость этого спутника? Решение задачи 7: а)
Воспользуйтесь формулой потенциальной еберги E p = – G M m / R. – 4,8 10 9 = – G M m / R или G M m / R = 4.8 10 9 Решить вышесказанный для R R = G M / 4.8 10 9 = 6 9 = 605710 -11 4. b)
Кинетическая энергия E k определяется выражением E k = (1/2) mv 2 , v орбитальная скорость спутника Равенство центростремительной и гравитационной сил дает mv 2 / R Приведенное выше уравнение можно записать в виде: mv 2 = GM m / R и E k = (1/2) mv 2 = (1/2) Гм м / R = (1/2) 4. в)
Totale Energy E T дается E T = E P = E K = – 4.8 10 9 + 2.4 10 9 J = – 2. D )
Используйте кинетическую энергию (1/2) MV 2 найдено выше (1/2) MV 2 = 2.4 10 9 J V 2 = 2 2.4 10 9 / м V = (2 2,4 10 9 / 500) 1/2 = 3098 м/с Задача 8: Каков период обращения спутника вокруг Луны на высоте 5. Решение задачи 8: Пусть M — масса Луны, а m — масса стеллита. Орбита спутника означает, что универсальная гравитационная сила и центростремительные силы равны. GM m / R 2 = mv 2 / R , v орбитальная скорость спутника и R радиус орбиты v = 2πR / T , T период GM m / R 2 = m (2πR / T) 2 / R Решив вышеприведенное для T, получим T = [ 4π 2 R 3 / GM] 1/2 T = [ 73 2 75 90 90 6  Какая сила тяжести будет действовать на тот же предмет на поверхности Земли? (используйте напряженность гравитационного поля g = 9,8 Н/кг на поверхности Земли).
Какая сила тяжести будет действовать на тот же предмет на поверхности Земли? (используйте напряженность гравитационного поля g = 9,8 Н/кг на поверхности Земли). 39 10 23 кг) — масса Марса, R м (= 3,39 10 6 м) — радиус Марса.
39 10 23 кг) — масса Марса, R м (= 3,39 10 6 м) — радиус Марса.
 От последнего уравнения выше, мы можем написать
От последнего уравнения выше, мы можем написать 34 часа
34 часа Период этой синхронной орбиты соответствует вращению Земли вокруг своей оси, принятому за 24 часа, так что спутник кажется неподвижным.
Период этой синхронной орбиты соответствует вращению Земли вокруг своей оси, принятому за 24 часа, так что спутник кажется неподвижным.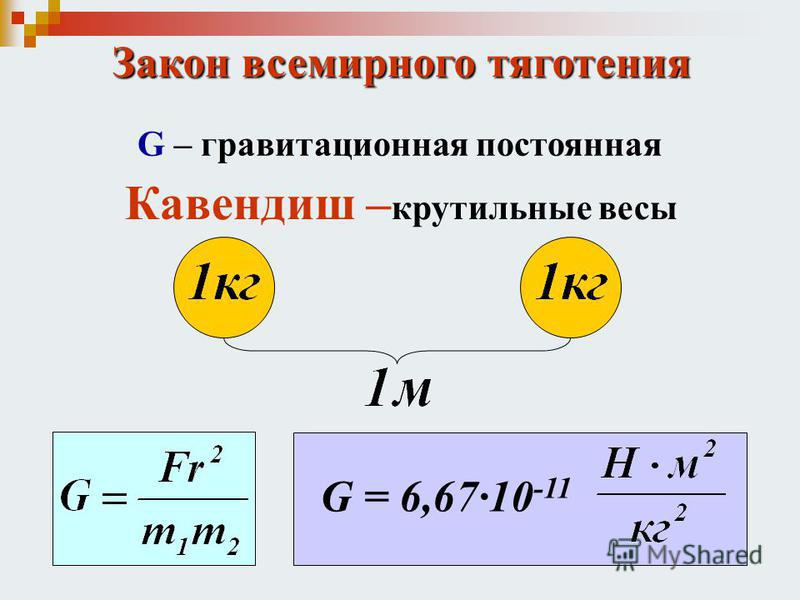 6710 -11 (246060) 2 / (4π 2 ) ] 1/3 = 42 211 км
6710 -11 (246060) 2 / (4π 2 ) ] 1/3 = 42 211 км
 2 10 23 500 / 4,8 10 9 = 2,919 км
2 10 23 500 / 4,8 10 9 = 2,919 км 8 10 9 = 2,4 10 9 Дж
8 10 9 = 2,4 10 9 Дж 4 10 9 J
4 10 9 J 0 10 3 км.
0 10 3 км. 6710 -11 7,3510 22 )] 1/2 = 8,81 часа
6710 -11 7,3510 22 )] 1/2 = 8,81 часа
Задача 9:
Каково ускорение на поверхности Луны?
Решение задачи 9:
Ускорение g м на поверхности Луны обусловлено универсальной силой тяжести, поэтому второй закон Ньютона и универсальная сила тяжести равны.
г м м = G M m / R 2 , m масса любого объекта на поверхности Луны, M масса Луны и R радиус Луны.
RELVE для G M
G M G M = GM / R 2 = 6.6710 -11 7. 3510 22 / 1,737000 2 = 1,62 м / с 2
3510 22 / 1,737000 2 = 1,62 м / с 2
Проблема 10:
Космический телескоп Хаббл вращается вокруг Земли на высоте 568 км.
а) Какова орбитальная скорость телескопа?
б) Каков период телескопа?
Решение задачи 10:
а) Пусть M — масса планеты, а m — масса телескопа.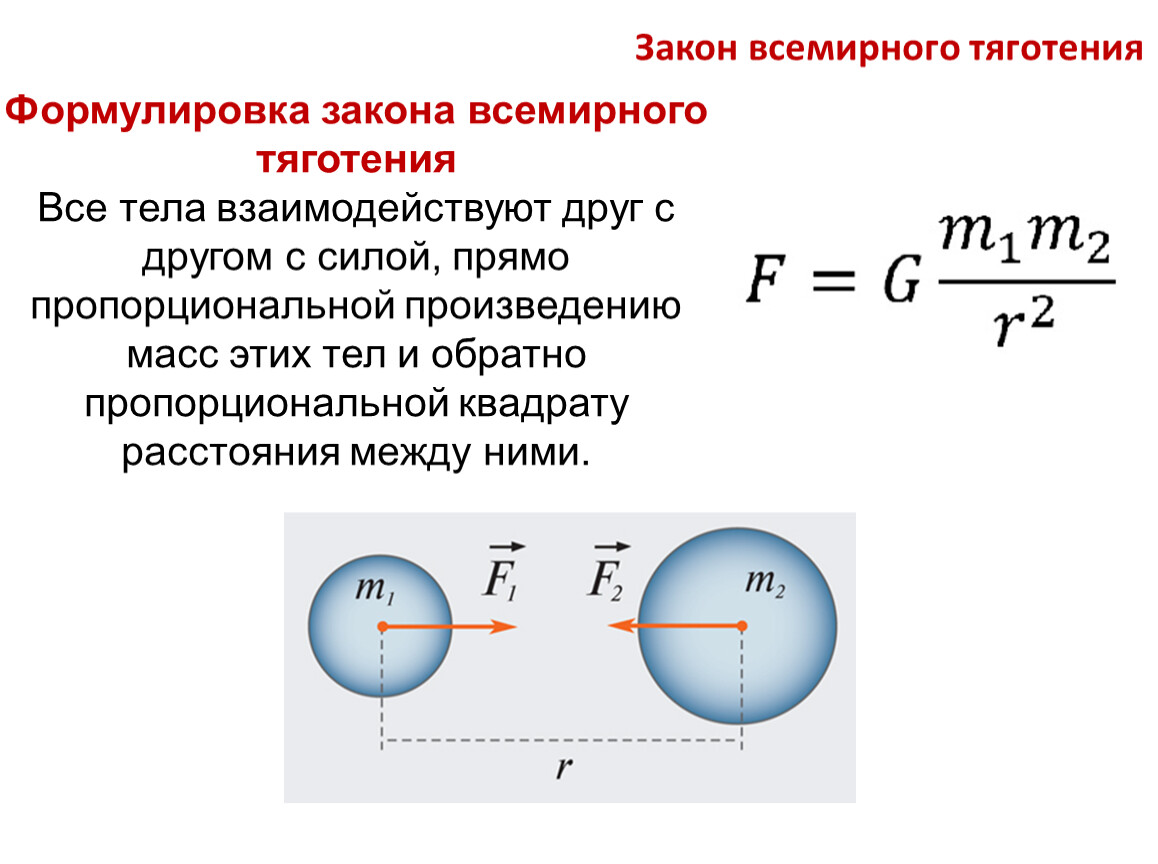 Движение телескопа по орбите означает, что универсальная гравитационная сила и центростремительные силы равны.
Движение телескопа по орбите означает, что универсальная гравитационная сила и центростремительные силы равны.
GM m / R 2 = mv 2 / R , v орбитальная скорость телескопа и R его орбитальный радиус -11 5.96 10 24 / (568 10 3 + 6 400 10 3 )) 1/2 = 7553 м / с
b) v = 2πr / t
t = 2πr / t = 2π(568 10 3 + 6400 10 3 ) / 7553 = 5796 с = 96. 6 мин
6 мин
Урок 25: Гравитация на наклонных плоскостях
Вы должны быть особенно осторожны, когда решаете задачи, связанные с гравитацией, которые тянут что-то вниз по склону.
- Задействованная физика значительно сложнее, чем может показаться на первый взгляд, в основном потому, что все наклонено.
- Давайте посмотрим на стандартный вопрос гравитации на наклонной плоскости ( наклон ), чтобы посмотреть, как мы его решим.
Пример 1: Определить ускорение коробки массой 15 кг вниз по склону 30°, если коэффициент трения равен 0.15.
Первое, что мы должны сделать, это набросать свободную диаграмму ситуации.
Рисунок 1
На этой диаграмме следует обратить внимание на несколько особенностей:
- Сила гравитации: F г указывает прямо вниз, хотя мы находимся на склоне.
Ничего не будет когда-либо изменить гравитацию от направления прямо вниз. Единственная причина для эта коробка, чтобы двигаться вниз по склону, будет компонентом силы тяжести.
- Нормальная сила: Помните, что нормальная сила F Н всегда перпендикулярно поверхности, на которой вы находитесь. Поскольку эта поверхность наклонена под небольшим углом, нормальная сила также будет указывать на немного угол. В этих вопросах F g ≠ F N
- Сила трения: F f будет всегда быть противоположным направлению движения чего-либо. В этом ситуация, когда объект движется вниз по склону, поэтому трение направлено назад вверх по склону.
- Нет приложенной силы, так как это означало бы, что что-то иное, чем гравитация, на самом деле пытающаяся столкнуть его вниз. склон.
Мы можем рассчитать силу гравитации…
F г = мг = 15 (9,81) = 147,15 N
(Держите это неокругленное число наготове, чтобы мы могли использовать его в расчетах позже.)
Нам нужно разбить F g вверх на составляющие, которые направлены вниз параллельно склону (F // ) и перпендикулярно склону (F ⊥ ).
Рисунок 2
Если вам интересно, как я понял, что угол 30° находится на вершине красного треугольника, взгляните на это…
Рисунок 3
- Я создал желтый треугольник, немного продлив линию F g вниз.
- Так как это хороший прямоугольный треугольник, я знаю, что угол при вершине желтого треугольника должен быть 60° (поскольку сумма углов должна составлять 180°).
- Поскольку F ⊥ перпендикулярна склону, угол в вершине красного треугольника должен составлять 30°, чтобы в сумме они составляли 90°.
Поскольку мы знаем F g и угол треугольника, мы можем использовать базовую триггерную схему для вычисления двух других сторон.
Округляйте число, только если оно конечное ответ, как если бы это было частью (а) кучи вопросов вместе.
В противном случае оставьте все как есть, чтобы не смотреть на округленное ответ округленного ответа и т. д. и т. д. и т. д.
Определить F // …
sinΘ = опп / hyp
sinΘ = F // / F g
F // = sinΘ F g
= sin30° (147.15 Н)
F // = 73,575 Н
(Опять же не будем округлять число. Это сила, тянущая его вниз по склону.)Определить F ⊥ …
cosθ = прил / гип
cosθ = f ⊥ / f g / f g / f g / f g
f ⊥ = cosθ f g
= cos30 ° (147.15 N)
F ⊥ = 127,436 N
(Угадай что , пока не округлять… или еще что-нибудь до конца.Да, и кстати, оглянитесь на Рисунок 2 ... F ⊥ равна нормальной силе, F Н !)
Определите силу трения, используя значение, которое вы только что получили для нормальной силы.
F f = мкФ N
= 0,15 (127,436)
F f = 19.115 НТеперь вы знаете силу, которая тянет его вниз по склону, и трение, которое его замедляет. Определить чистую силу F NET …
Я сделал F f отрицательным, потому что он работает против F // . Один из них должен быть отрицательным, если другой положительный.
F NET = F // + F f
= 73,575 + -19,115
F NET = 54.460 НТеперь, наконец, мы можем определить ускорение ящика…
F NET = ma
a = F NET / m
= 54.460 / 15
а = 3,6 м/с 2Наш окончательный ответ: 3,6 м/с 2 , и да, округляем.
Обратите внимание, что на каждом шаге я просил вас что-то набросать или определить.
- Бьюсь об заклад, вы видите, как каждый из них может быть частью многоэтапного вопроса, такого как (a), (b), (c) и т. д.
- На самом деле, на этот вопрос у меня может быть 7 или 8 частей.
- Если ты когда-нибудь задашь такой вопрос, то да, ты должен округлить ваш окончательный ответ для каждого шага к правильному количеству sig digs.
- Вы все равно должны писать неокругленное число как минимум где-то, так как вы должны использовать неокругленные числа для следующие вопросы.
- В противном случае вы получите окончательный ответ, прошедший примерно 7 округлений!
Перечитайте этот пример несколько раз. Это долго и запутанно в
некоторые части, но попробуйте посмотреть на каждый отдельный крошечный расчет. Взятый
в маленьких битах каждая часть не так сложна.
Это долго и запутанно в
некоторые части, но попробуйте посмотреть на каждый отдельный крошечный расчет. Взятый
в маленьких битах каждая часть не так сложна.
Закон всемирного тяготения Ньютона
Закон всемирного тяготения Ньютона Закон Вселенной Ньютона Гравитациянажмите здесь, чтобы скачать в более удобном для печати формате
Исаак Ньютон — один из величайших ученых, когда-либо жил.Среди прочего, он сформулировал Закон Всеобщего Гравитация, которая позволяет рассчитать гравитационное притяжение между двумя объектами. С участием немного подумав, вы можете понять, почему определенные переменные появляются в Закон Ньютона и почему они появляются либо в числителе (прямая пропорциональность), либо в знаменатель (обратная пропорциональность).
Вы, наверное, интуитивно понимаете, что гравитационное Привлечение между двумя объекты (М и м в цифры) зависит на расстоянии между объектами.гравитационное сила становится слабее, чем дальше друг от друга находятся два объекта.
 разное. Закон всемирного тяготения на самом деле обратный
квадратичный закон, гравитационное притяжение между двумя объектами
обратно пропорциональна квадрату расстояния между двумя
объекты.
разное. Закон всемирного тяготения на самом деле обратный
квадратичный закон, гравитационное притяжение между двумя объектами
обратно пропорциональна квадрату расстояния между двумя
объекты.Если мы думаем о М как о масса планеты и m массы его луны, мы можем видеть, что притяжение между двумя зависит от массы планеты. Юпитер оказывает более сильное гравитационное притяжение на своих спутниках, чем на Земле.М принадлежит в числителе уравнения Ньютона.
На рисунке ниже мы рассматриваем два объекта разной массы m на поверхности планеты. Человек с большей массой (правый рисунок ниже) весит больше, чем внизу человек с меньшей массой (левый рисунок). Так что нам нужно включить m в уравнение.
Полная формула приведена внизу страницы. выше. г является константой. На поверхности земли Г, М, а не изменять. Ускорение свободного падения g равно количество [Г раз М земля разделить на (R земля ) 2 ].К обозначить вес (на земной поверхности) предмета с массой m вы просто умножаете m х г.
 Кстати, g имеет значения 9,8 м/с 2 (метрические единицы) или 32 фута/сек 2 (английские единицы).
Кстати, g имеет значения 9,8 м/с 2 (метрические единицы) или 32 фута/сек 2 (английские единицы). На рисунке ниже показаны метрические и английские единицы
масса
а вес. Вы, наверное, слышали о фунтах, граммах и
килограммы. Возможно, вы не слышали о динах и ньютонах.
Если вы не посещали курс физики, вы, вероятно, никогда не слышали о
слизни.
Вы, наверное, слышали о теории Ньютона. 2-й закон движения: сила = масса x ускорение (часто сокращенно F = m а). Если к объекту приложить силу, он начнет двигаться (в направлении действия силы). Скорость объекта будет увеличиваться (ускоряться) до тех пор, пока действует сила. Ньютона Закон позволяет определить ускорение, вы просто делите Сила от массы объекта (среднее уравнение выше).

Гравитация заставляет предметы падать и ускоряться, когда они падать. Вы можете использовать 2-й закон Ньютона и уравнение веса, чтобы определить ускорение движения вниз под действием силы тяжести. Обратите внимание, что ускорение, вызванное силой тяжести, одинаково независимо от масса. Объект с большой массой будет ускоряться одновременно скорость как объект с меньшей массой. Это верно до тех пор, пока гравитация – единственная сила.
Ускорение свободного падения
значение 32 фут/сек в английской системе единиц (9.8 м/с). Мы
пусть объект на рисунке ниже начнет падать в нулевое время.
Через секунду он упадет на 16 футов и будет двигаться со скоростью
скорость 32 фута в секунду (ft/sec). В следующую секунду это
скорость увеличится на 32 фута/сек и теперь будет падать на 64
футов/сек. То же самое произойдет во второй после
тот. Через три секунды объект будет падать со скоростью 96 футов в секунду.
и упадет с высоты 144 фута.
.



 Нарисуйте линию на объекте вдоль
нить. Для шага 2 повторите процедуру с другой точки объекта.
Теперь у вас есть две линии, нарисованные на объекте, которые пересекаются.
Центр тяжести – это точка пересечения линий. Этот
процедура хорошо работает для объектов неправильной формы, которые являются твердыми
сбалансировать.
Нарисуйте линию на объекте вдоль
нить. Для шага 2 повторите процедуру с другой точки объекта.
Теперь у вас есть две линии, нарисованные на объекте, которые пересекаются.
Центр тяжести – это точка пересечения линий. Этот
процедура хорошо работает для объектов неправильной формы, которые являются твердыми
сбалансировать.


 Ничего не будет
когда-либо изменить гравитацию от направления прямо вниз. Единственная причина для
эта коробка, чтобы двигаться вниз по склону, будет компонентом силы тяжести.
Ничего не будет
когда-либо изменить гравитацию от направления прямо вниз. Единственная причина для
эта коробка, чтобы двигаться вниз по склону, будет компонентом силы тяжести. )
)  В противном случае оставьте все как есть, чтобы не смотреть на округленное
ответ округленного ответа и т. д. и т. д. и т. д.
В противном случае оставьте все как есть, чтобы не смотреть на округленное
ответ округленного ответа и т. д. и т. д. и т. д. .. F ⊥ равна нормальной силе, F Н !)
.. F ⊥ равна нормальной силе, F Н !) 