Понятие силы в физике, теория и онлайн калькуляторы
Понятие силы в физике, теория и онлайн калькуляторыВ инерциальной системе отсчета изменение скорости тела возможно только при взаимодействии его с другими телами. Для характеристики этого взаимодействия используют такую физическую величину как сила. Сила дает количественную меру взаимодействия тел.
Виды сил
По своей природе силы могут быть различными. Существуют гравитационные, электрические, магнитные и другие силы. При рассмотрении задач механики физическая природа сил, вызывающих ускорение тела, не является значимой и не рассматривается. При этом для всех видов взаимодействия количественная мера взаимодействия тел выбирается единым образом. Силы разной природы измеряют в одинаковых единицах, при помощи одних и тех же эталонов. В связи с такой универсальностью механика успешно описывает движение под воздействием сил любой природы.
Определение силы в механике отвечает на вопросы: как измерять силу, и какими свойствами она обладает?
Измерение сил
Результатом взаимодействия тел является деформация тела или его ускорение (или то и другое одновременно).
{-12}.$
Для измерения силы на основе явления упругой деформации выбирают, как эталон пружину, для которой известно, что при растяжении на заданную длину пружина действует на закрепленное на ней тело, силой$\ F_0$, которая направлена по оси пружины. Считаем, что две любые силы равны и имеют противоположные направления, если они действуют одновременно, а тело в инерциальной системе отсчета находится в покое или равномерно и прямолинейно движется. Тогда такой эталон можно дублировать в любом количестве. Имея описанную выше пружину можно установить наличие силы, но для ее измерения наш динамометр следует градуировать.
Сила – вектор
Сила имеет модуль (величину), направление и точку приложения. Если на тело действуют несколько сил, то их можно заменять равнодействующей силой, которая находится как векторная сумма всех сил, приложенных к телу. И наоборот, любую силу можно разложить на составляющие, векторная сумма которых равна рассматриваемой силе.
Равнодействующую можно найти по правилу треугольника, параллелограмма или многоугольника.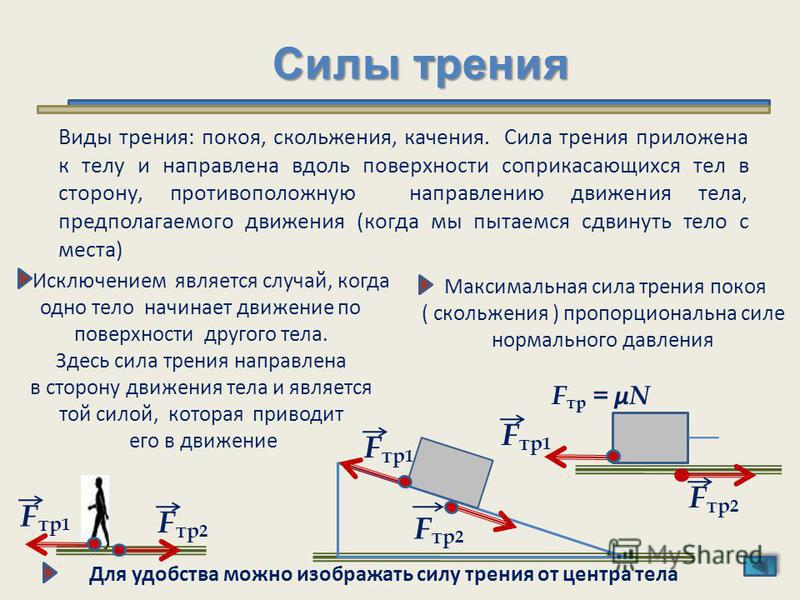
2}=Н.\]
Основная задача динамики
Основной задачей динамики является изучение и описание движения тел в разных системах отсчета, объяснение причин, определяющих характер их движения. Взаимодействие тел, характеризуемое силами, ведет к изменению характера их движения, следовательно, сила, является важной составляющей большинства законов динамики. Базой классической динамики служат законы Ньютона.
- Первый закон Ньютона: В инерциальной системе отсчета, если на тело не действуют с другие тела или действие их взаимно компенсировано, скорость тела не изменяется ни по модулю, ни по направлению. Тело движется равномерно и прямолинейно.
- Второй закон Ньютона: если тело массы $m$ движется с ускорением $\overline{a}$, по отношению к инерциальной системе отсчета, то на него действует сила: \[\overline{F}=m\overline{a}\left(1\right).\]
Направление ускорения совпадает с направлением, действующей силы.
Закон (1) можно записать в другом виде:
\[\overline{F}=\frac{d\left(m\overline{v}\right)}{dt}=\frac{d\left(\overline{p}\right)}{dt}\left(2\right),\]
где $\overline{p}=m\overline{v}$ – импульс тела.
Ответ. $\mu =\frac{m\left(v_0-v_1\right)}{{t_1v}_1v_0}$
Читать дальше: примеры продольных и поперечных волн.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Силы в физике
Каждый день нам приходится сталкиваться с действиями одних тел на другие. Для понимания процессов, происходящих в окружающем нас мире, физики приложили немало усилий, чтобы понять, что происходит с одним телом при воздействии на него другого. И ученые смогли доказать, что любое движение происходит под действием различных сил.
Что такое сила?
Сила — это воздействие одного тела на другое. Воздействие может быть разным: в результате приложения силы тело способно приводиться в движение, менять скорость или направление движения, останавливаться и т.
п. Например, толкая в магазине тележку для продуктов, ты приводишь ее в движение. При этом скорость тележки и направление ее движения меняются в зависимости от той силы, с которой ты действуешь на тележку. А твой папа может толкать такую тележку с гораздо большей скоростью, так как он сильнее тебя.
Под воздействием силы можно не только изменить скорость тела или его форму, но и направление его движения. Например, во время игры в теннис, бадминтон, бильярд при помощи ракетки или кия можно изменить направление движения шара. Шар или мяч может полететь в другом направлении не только после воздействия на него человека (при помощи ракетки, например), но и ударившись о любой предмет во время полета: стенку, забор, штангу и т.д. Приложение силы способно привести к изменению не только скорости, но и размеров или формы тела. Говоря другими словами, в результате приложения силы тело может деформироваться.
Пример: на рисунке ниже видно растяжение (удлинение) пружины после того, как на нее подвесили груз.
Причем чем тяжелее груз и, соответственно, большая сила прилагается, тем сильнее растягивается пружина.
Любая сила не может существовать сама по себе. Запомни: если речь идет о приложении силы, то это означает, что на тело действует другое тело. Как только действие сил прекращается, тело переходит в состояние покоя. Как правило, на тело одновременно действует не одна сила, а несколько.
Что такое сила тяжести?
Сила тяжести — это сила, с которой Земля притягивает к себе тело. Эта сила всегда направлена вертикально вниз. Запомни: чем больше масса тела, тем больше сила тяжести, действующая на это тело. Именно поэтому нам трудно поднять или сдвинуть с места очень тяжелые предметы. И чем тяжелее предмет, тем больше сила тяжести и тем сложнее нам преодолеть эту силу. Сила тяжести, действующая на тело, несколько отдаленное от поверхности Земли, зависит от массы тела и расстояния.
«Космические» факты
Каждый космонавт переживает так называемую космическую болезнь: при отсутствии силы тяготения он привыкает к тому, что все окружающие предметы, да и он сам, летают, а не падают.
Поэтому по возвращении на Землю космонавты в течение некоторого времени обращаются с вещами так, как привыкли это делать в космосе: просто отпускают их, при этом совершенно не задумываясь над тем, что они сразу упадут на землю или на пол.
В условиях невесомости в организме космонавта увеличивается объем циркулирующей крови, что, в свою очередь, может привести к повышению давления. Однако сердце космонавта очень интересно приспосабливается к данной ситуации: во избежание дополнительной нагрузки оно уменьшается в объеме и, соответственно, начинает перекачивать меньшее количество крови. Это своеобразная защитная реакция на увеличение объема крови.
Ученые выяснили, что в случае длительного пребывания в невесомости (состояние, при котором вес тела равен нулю) в организме человека происходят некоторые изменения. Например, рост космонавтов увеличивается почти на 5 см за счет расхождения позвоночных дисков. В течение 10 дней после возвращения на Землю рост становится прежним.
Что такое сила всемирного тяготения?
Притяжение существует не только между Землей и всеми телами, находящимися на ней, но и всеми телами между собой.
Такое притяжение всех тел в нашей Вселенной называется всемирным тяготением.
Ты когда-нибудь видел, как магнит притягивает к себе различные предметы? Так вот, всемирное тяготение можно сравнить с магнитом: тела притягиваются не только к Земле, но и друг к другу.
На какие тела действует сила всемирного тяготения?
Эта сила действует абсолютно на все тела, которые имеют какой-либо, пусть даже самый незначительный вес. Именно благодаря такому притяжению мы не улетаем в открытый космос вместе с другими окружающими нас предметами, а остаемся на Земле.
Если бы сила притяжения отсутствовала, то любое подброшенное тело никогда бы не вернулось на Землю.
Согласно легенде, английский ученый Исаак Ньютон открыл закон всемирного тяготения после того, как на его глазах с дерева оторвалось яблоко и упало на землю. Ньютон задумался над тем, почему оно упало вертикально вниз, перпендикулярно земле, а не в сторону. Позже гениальный ученый сумел доказать, что все тела притягиваются друг к другу.
Ускорение и сила всемирного тяготения
Ускорение — это изменение скорости в течение единицы времени. Представь, что с большой высоты на Землю падает какое-либо тело. Пока расстояние до Земли очень большое, ее сила притяжения не так велика. Но по мере приближения тела к поверхности Земли сила притяжения Земли возрастает, и ускорение движения тела становится равным 9,8 м/с2. Например, если ты бросишь яблоко с большой высоты, скажем, с пятого этажа, оно будет лететь со скоростью 9,8 м/с спустя 1 секунду падения и уже 19,6 м/с после второй секунды. То есть с каждой секундой падения его скорость будет увеличиваться почти на 10 м/с!
Ускорение и масса тела
Ускорение не зависит от массы падающего тела. Например, два тела, падающие с одинаковой высоты, достигнут земли одновременно, при этом не важно, что падает — яблоко или машина. Конечно, если ты бросишь листик бумаги и камешек, то камешек окажется на земле раньше, но только лишь потому, что листику мешает падать сопротивление воздуха.
Но если предположить, что листик бумаги и камешек будут падать вниз внутри высокого стеклянного цилиндра, из которого откачан воздух, то оба предмета достигнут дна одновременно.
Вес тела
Да, не удивляйся, вес тела — это тоже сила, с которой тело давит на опору или какой-либо подвес (если тело висит).
Ты уже знаешь, что все тела притягиваются к Земле, и эта сила называется силой тяжести. Посмотри внимательно на картинку. В данном случае лавочка не позволяет мальчику и коту упасть, и именно лавочка испытывает действие силы, возникающей из-за притяжения Земли.
Вес тела — это сила, с которой любое тело действует на опору или подвес благодаря земному притяжению
Какие есть сходства и различия между весом тела и силой тяжести?
Обе силы — и вес тела, и сила тяжести — возникают благодаря притяжению Земли.
Разница между весом тела и силой тяжести заключается в том, что вес действует на опору, которая находится под телом, а сила тяжести — на само тело.
Каким бы странным это ни показалось, но вес тела может быть равен нулю! Один из случаев, когда вес тела равен 0, — состояние невесомости. Например, в космическом корабле ни космонавт, ни тела, находящиеся на борту корабля, не оказывают никакого действия на опору. Они просто летают в пространстве.
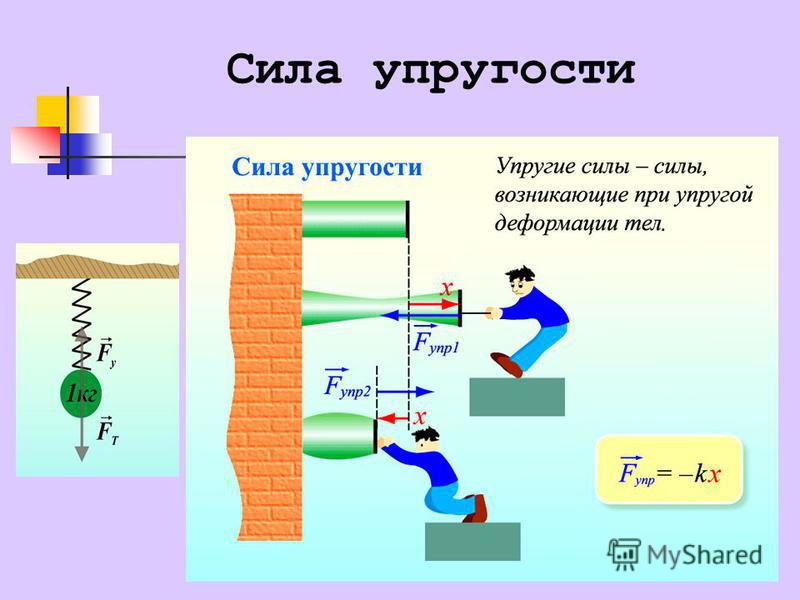
Сила упругости
Сила упругости — это сила, которая возникает в теле в результате его деформации и стремится вернуть тело в исходное положение.
Скорее всего, ты не задумывался над тем, где и в каких предметах проявляется сила упругости. На самом деле таких вещей довольно много. Это и самые простые пружинные весы (безмен), используемые для взвешивания продуктов, и резиночки для волос, различные эластичные резинки и пояса, специальные ленты для фитнеса и многое другое
Самый простой и доступный пример проявления силы упругости — это деформация обычной пружины!
Возьми пружину, сожми ее, а затем убери пальцы. После того как ты отпустил ее, пружина стремится принять первоначальную форму.
Так при деформации пружины возникла сила упругости, и ты можешь наблюдать ее проявление.
Давай рассмотрим интересный пример проявления силы упругости во время прыжка на тарзанке.
Какая сила растягивает канат во время прыжка?
Как только человек совершает прыжок, он начинает падать под действием силы тяжести. Под весом прыгуна канат растягивается, а затем стремится возвратиться в свое первоначальное положение, т.е. прыгун двигается вверх и вниз.
Сила трения
Тебе приходилось видеть, как кто-то нечаянно соскользнул со стула и упал на пол? Ты рассмеялся? А вот представь, что мы постоянно падаем со стульев и кроватей, а предметы не могут удержаться на месте и выскальзывают из рук… На самом деле не так и смешно, правда?
К счастью, благодаря силе трения этого не происходит. Если бы трение отсутствовало, то все предметы не могли бы держаться на поверхностях, а постоянно скатывались вниз, на землю.
Трение — это сила, возникающая при движении одного тела по поверхности другого.
На льду трение между подошвой обуви и льдом очень мало, поэтому мы не можем ходить по льду так, как ходим по земле: наши ноги скользят. Для того чтобы улучшить сцепление обуви с поверхностью, лед посыпают песком
Одной из причин, вызывающих трение, является шероховатость поверхностей соприкасающихся тел. Причем чем больше шероховатостей и неровностей, тем больше сила трения.
Различают несколько видов трения, из них основные: трение скольжения, качения и покоя.
Трение скольжения
В данном случае одно тело скользит по поверхности другого. Например: катание с горы на санках или лыжах, катание на коньках по льду.
Сила трения направлена в сторону, противоположную направлению движения. Более того, она направлена вдоль соприкасающихся поверхностей
Трение качения
Этот вид трения возникает, когда одно тело катится по поверхности другого. Это может быть любое колесо или тело в форме шара.
Трение покоя
В состоянии трения покоя тело может сдвинуться с места, но ему что-то мешает, и мешает ему именно сила трения.
Например, в комнате стоит диван, и сдвинуть его с места можно только в случае приложения другой силы, которая будет больше силы трения покоя.
К чему приводит уменьшение силы трения?
Снижением силы трения и плохим контактом шин с асфальтом объясняется повышение количества аварий на мокрой дороге.
На мокром полу мы можем легко упасть.
Это происходит потому, что жидкость создает барьер между полом и подошвой обуви, при котором сцепление подошвы с полом значительно уменьшается, и, соответственно, уменьшается сила трения.
Поделиться ссылкой
11 различных типов сил | New-Science.ru
В физике сила может быть определена как толчок или тяга на любой объект, который имеет массу. Это меняет движение объекта.
Другими словами, сила заставляет объект с массой изменить свое направление и скорость.
Два великих физика Исаак Ньютон и Галилео Галилей описали поведение сил математически. В 1638 году Галилей провел эксперимент на наклонной плоскости, который произвел революцию в способе измерения силы.
Пять десятилетий спустя Ньютон разработал законы движения, которые заложили основу классической механики.
Поскольку сила имеет и величину, и направление, она является векторной величиной. Она представлена символом F и измеряется в единице СИ Ньютона (N).
Силы можно разделить на две группы в зависимости от их применения:
- Контактная сила: действует на тело напрямую или через среду.
- Бесконтактная сила: действует через пространства без прямого контакта с телом.
Чтобы лучше объяснить это явление, мы описали все различные типы сил на примерах. Давайте начнем с четырех фундаментальных сил в природе.
1. Гравитационная сила
G – универсальная гравитационная постоянная, которая варьируется в зависимости от различных астрономических тел.Тип: бесконтактная сила
Гравитационная сила — это то, что притягивает два объекта с массой. Она действует на каждый объект, включая вас, во Вселенной.
Величина гравитационной силы, оказываемой объектами друг на друга, “прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними”.
Чем массивнее объекты и меньше расстояние между ними, тем выше сила.
Это самая слабая из четырех фундаментальных сил, обнаруженных в природе.
Хотя гравитационная сила не оказывает существенного влияния на субатомном масштабе, она является доминирующим взаимодействием на макроскопическом масштабе и существенно влияет на формирование, строение и траекторию небесных тел.
Пример: гравитация заставляет яблоко падать с дерева; она заставляет Луну вращаться вокруг Земли; она удерживает газы на Солнце.
2. Электромагнитная сила
Тип: Бесконтактная сила
Это вид взаимодействия, которое происходит между электрически заряженными частицами. Электромагнитные поля (создаваемые движущимися электрическими зарядами) несут в себе электромагнитную силу.
Электричество и магнетизм связаны друг с другом: текущие электроны создают магнетизм, а движущиеся магниты генерируют электричество. Отношения между ними очень хорошо объяснены Джеймсом Клерком Максвеллом и количественно определены в его уравнениях.
Пример: Наиболее распространенным примером электромагнетизма является свет, поскольку он распространяется (излучается) в пространстве, перенося энергию электромагнитного излучения.
Следующим наиболее распространенным примером могут быть силы, действующие между электрически заряженными атомными ядрами и электронами атомов.
3. Сильная ядерная сила
Протоны и нейтроны удерживаются сильным ядерным взаимодействиемТип: Бесконтактная сила
В ядерной физике и физике элементарных частиц сильное взаимодействие отвечает за структурную целостность атомных ядер. Поскольку все протоны имеют положительный заряд, они отталкиваются друг от друга. Сильное ядерное взаимодействие удерживает эти отталкивающие протоны вместе, так что они могут образовать атомное ядро.
Около 99% массы нейтрона или протона является результатом энергии сильного силового поля.
Это самая сильная сила в природе, действующая на расстоянии 1 фемтометра ( 10–15 м).
Он почти в 137 раз сильнее электромагнетизма и в 100 миллиардов (10 38) раз сильнее, чем сила гравитации.
Пример: Сильная ядерная сила связывает кварки с адронными частицами, такими как протон и нейтрон, для создания атомного ядра. Это сила, которая соединяет обычную материю.
В более широком масштабе она используется на атомных электростанциях для производства тепла с целью выработки электроэнергии. Она также ответственна за огромную разрушительную мощь ядерного оружия. Из-за этой силы ядерное оружие при взрыве высвобождает экстремальное количество энергии.
4. Слабая ядерная сила
Радиоактивный распад частицыТип: Бесконтактная сила
В ядерной физике слабое взаимодействие относится к взаимодействию между субатомными частицами, которое вызывает радиоактивный распад атомов. Более конкретно, он отвечает за распад некоторых нуклонов на лептоны и другие типы адронов.
Его напряженность поля примерно в 10 13 раз меньше, чем у сильной ядерной силы.
Тем не менее он значительно сильнее, чем гравитационная сила на коротких расстояниях.
Пример: Наиболее известным эффектом действия слабой силы является бета-распад (нейтронов) и связанная с ним радиоактивность. Она возникает в нескольких различных реакциях, включая сжигание Солнца и радиоуглеродное датирование.
Это четыре фундаментальные (бесконтактные) силы, из которых происходит все остальное. Они поддерживают горение звезд и вращение планет. Без них вселенная, которую мы знаем, не существовала бы, и даже если бы она существовала, это было бы совершенно другое место.
Теперь давайте перейдем к неосновным силам, которые возникают в результате прямого физического взаимодействия между двумя объектами.
5. Прикладная сила
Тип: Контактная силаТип: Контактная сила
Как следует из названия, это сила, которую вы применяете к объекту. Объект начинает двигаться, когда величина силы преодолевает инерцию объекта.
Тело остается в покое или в равномерном движении по прямой линии, если к ним не приложена внешняя сила, которая изменяет состояние движения и направление тела. Ускорение тела прямо пропорционально приложенной силе.
Пример: Сила, приложенная к ящику человеком.
6. Сила трения
Тип: Контактная сила
Поверхностная сила, противостоящая относительному движению тела, называется силой трения. Поскольку в реальном мире ни один объект не является абсолютно гладким, всегда существует некоторое трение между двумя поверхностями. Его величина пропорциональна коэффициенту трения материала поверхности.
Двумя основными типами сил трения являются статические (сила трения о неподвижный объект) и кинетические (сила трения о движущийся объект). Сопротивление воздуха также является силой трения, которая действует на объекты, когда они перемещаются по воздуху.
Оно всегда действует в направлении, противоположном движению, и преобразует кинетическую энергию в тепловую энергию (работа в тепло).
В целом, трение является критической и желательной силой, которая обеспечивает сцепление для облегчения движения по суше.
Пример: Примером трения является скольжение каботажа по столу, скольжение двух карт в колоде друг о друга и трение руки для получения тепла.
7. Нормальная сила
Тип: Контактная сила
Когда две поверхности находятся в контакте, они оказывают нормальное воздействие друг на друга. Термин «нормальный» относится к перпендикулярному. Это означает, что сила направлена перпендикулярно двум контактирующим поверхностям.
Пример: когда ноутбук стоит на столе, обычная сила удерживает его от падения через стол. Гравитационная сила Земли тянет ноутбук вниз, но поскольку он на самом деле не падает, должна быть сила, постоянно толкающая его вверх. Это то, что мы называем нормальной силой.
Она исходит от электромагнитной силы: электроны ноутбука толкают электроны стола. Поскольку все электроны отрицательно заряжены, они не становятся намного ближе друг к другу, и ноутбук опирается на верхнюю часть стола.
8. Сила натяжения
Тип: Контактная сила
Сила натяжения обычно передается через провод, кабель, струну или веревку, когда она плотно натягивается силами, действующими с противоположных концов. Усилие направлено вдоль длины кабеля.
Натяжение можно также определить как действие-реакция пары сил, действующих на каждом конце кабеля. Это противоположность сжатия.
Пример: веревка, тянущая коробку или коробку, висящую на веревке, будет отличным примером натяжения (в веревке).
9. Сила упругости
Тип: Контактная сила
Сила упругости — это сила, прилагаемая натянутой или сжатой струной к объекту, который к ней прикреплен.
Способность пружины противостоять искажающему воздействию и возвращаться в исходное состояние при снятии воздействия зависит от ее материала, количества витков и диаметра проволоки, образующей витки. Как правило, эти характеристики количественно выражаются в параметре, называемом постоянной пружины “k”.
Для всех пружин, подчиняющихся закону Гука, величина силы прямо пропорциональна постоянной пружины (k) и сжатой/растянутой длине (x).
Пример: Автомобильные амортизаторы изготовлены из пружин. Они предназначены для поглощения ударных импульсов путем преобразования кинетической энергии удара в другую форму энергии (например, тепло), которая затем рассеивается.
10. Центростремительная сила
Тип: Бесконтактная сила
Центростремительная сила действует на объекты, ускоряющиеся в круговом движении. Это сила, которая заставляет объект следовать по изогнутому пути.
Направление этой силы всегда направлено к фиксированной точке мгновенного центра кривизны траектории и ортогонально движению объекта.
Пример: Два наиболее распространенных примера центростремительной силы — это вращение автомобиля и Земля, вращающаяся вокруг Солнца. В первом случае центростремительная сила обеспечивается за счет трения между колесами и землей, а во втором — за счет силы тяжести.
11. Сила инерции
Тип: Бесконтактная сила
Сила инерции (также называемые инерционная сила) являются очевидными силами, действующими на массы, движение которых описывается с использованием неинерциальной системы отсчета, включая вращающуюся систему отсчета.
Это вступает в силу, когда система отсчета начала ускорение. Термин «инерционная сила» имеет точное значение для ньютоновской механики — фактически он всегда пропорционален массе объекта, на который он действует.
Пример: силы, которые вы испытываете в движущемся автомобиле, являются повседневными примерами сил инерции. Когда автомобиль разгоняется в переднем направлении, он толкает вас обратно на сиденье. Когда автомобиль делает резкие повороты, он бросает вас из стороны в сторону. Эти влияния возникают из-за того, что естественная система отсчета для данной ситуации сама ускоряется.
4.5 Нормальные, растягивающие и другие примеры сил — College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Определение нормальной силы и силы растяжения.
- Применяйте законы движения Ньютона для решения задач, связанных с различными силами.
- Используйте тригонометрические тождества для разложения веса на компоненты.
Силы имеют множество названий, например, толкание, тяга, тяга, подъемная сила, вес, трение и напряжение. Традиционно силы были сгруппированы в несколько категорий и получили имена, относящиеся к их источнику, способу их передачи или их воздействию. В этом разделе обсуждаются наиболее важные из этих категорий вместе с некоторыми интересными приложениями. Дальнейшие примеры сил обсуждаются далее в этом тексте.
Нормальная сила
Вес (также называемый силой тяжести) — это всепроникающая сила, действующая постоянно, и ей необходимо противодействовать, чтобы объект не упал. Вы определенно заметили, что должны поддерживать вес тяжелого объекта, отталкиваясь от него, когда держите его неподвижно, как показано на рис. 4.11 (а). Но как неодушевленные предметы, такие как стол, выдерживают вес размещенного на них груза, как показано на рис.
Рисунок
4.11
(a) Человек, держащий пакет с кормом для собак, должен приложить направленную вверх силу FhandFhand, равную по величине и противоположную по направлению весу корма ww.
(b) Карточный стол прогибается, когда на него кладут корм для собак, как жесткий батут. Упругие восстанавливающие силы в столе возрастают по мере его провисания, пока не создадут силу NN, равную по модулю и противоположную по направлению весу груза.
Мы должны заключить, что все, что поддерживает груз, одушевленное оно или нет, должно создавать направленную вверх силу, равную весу груза, как мы предполагали в нескольких предыдущих примерах. Если сила, поддерживающая груз, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь дается символ NN. (Это не единица силы Н.) Слово нормальное означает перпендикулярно поверхности. Нормальная сила может быть меньше веса объекта, если объект находится под наклоном, как вы увидите в следующем примере.
Распространенное заблуждение: нормальная сила (Н) против силы Ньютона (Н)
В этом разделе мы ввели величину нормальной силы, которая представлена переменной NN.
Его не следует путать с символом ньютона, который также обозначается буквой N. Эти символы особенно важно различать, поскольку единицами измерения нормальной силы (NN) являются ньютоны (Н). Например, нормальная сила NN, с которой пол действует на стул, может быть N=100 NN=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица измерения. Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях! По мере изучения физики вы обнаружите больше сходства между переменными и единицами. Другим примером этого является количество работы (WW) и единица мощности (Вт).
Пример 4,5
Вес на склоне, двумерная задача
Рассмотрим лыжника на склоне, показанном на рис. 4.12. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если известно, что трение равно 45,0 Н?
Рисунок
4.12
Поскольку движение и трение параллельны склону, удобнее всего спроецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника).
Стратегия
Это двумерная задача, поскольку силы, действующие на лыжника (система интересов), не параллельны. Подход, который мы использовали в двумерной кинематике, также очень хорошо работает здесь. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав два связаны один -мерные проблемы для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Помните, что движения вдоль взаимно перпендикулярных осей независимы.) Мы используем символы ⊥⊥ и ∥ ∥ для обозначения перпендикулярности и параллельности соответственно.
Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а трение между двумя объектами всегда параллельно поверхности. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и опора склона, соответственно обозначенные ww, ff и NN на рис. 4.12. NN всегда перпендикулярно склону, а ff параллельно ему. Но ww не направлена ни к одной из осей, поэтому первый шаг, который мы предпримем, — это спроецировать его на компоненты вдоль выбранных осей, определив w∥ w∥ как компонент веса, параллельный наклону, и w⊥w⊥ составляющая веса перпендикулярна склону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Решение
Величина составляющей веса, параллельной наклону, равна w∥ =wsin(25º)=mgsin(25º)w∥ =wsin(25º)=mgsin(25º), а величина составляющей веса, перпендикулярной к наклону w⊥=wcos(25°)=mgcos(25°)w⊥=wcos(25°)=mgcos(25°).
(a) Без учета трения. Поскольку ускорение параллельно наклону, нам нужно рассматривать только силы, параллельные наклону. (Силы, перпендикулярные склону, складываются в ноль, так как ускорение в этом направлении отсутствует.) Силы, параллельные склону, представляют собой массу веса лыжника, параллельного склону, w∥ w∥ и силы трения ff. Используя второй закон Ньютона с нижними индексами для обозначения величин, параллельных наклону,
a∥ =Fnet ∥ ma∥ =Fnet ∥ m
4,30
где Fnet ∥ =w∥ =mgsin(25°)Fnet ∥ =w∥ =mgsin(25°), в предположении отсутствия трения в этой части, так что
a∥ =Fnet ∥ m=mgsin(25°)m=gsin(25°)a∥ =Fnet ∥ m=mgsin(25°)m=gsin(25°)
4,31
(9,80 м/с2)(0,4226)= 4,14 м/с2(9,80 м/с2)(0,4226)=4,14 м/с2
4,32
— ускорение.
(b) Включая трение. Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно противодействует движению между соприкасающимися поверхностями.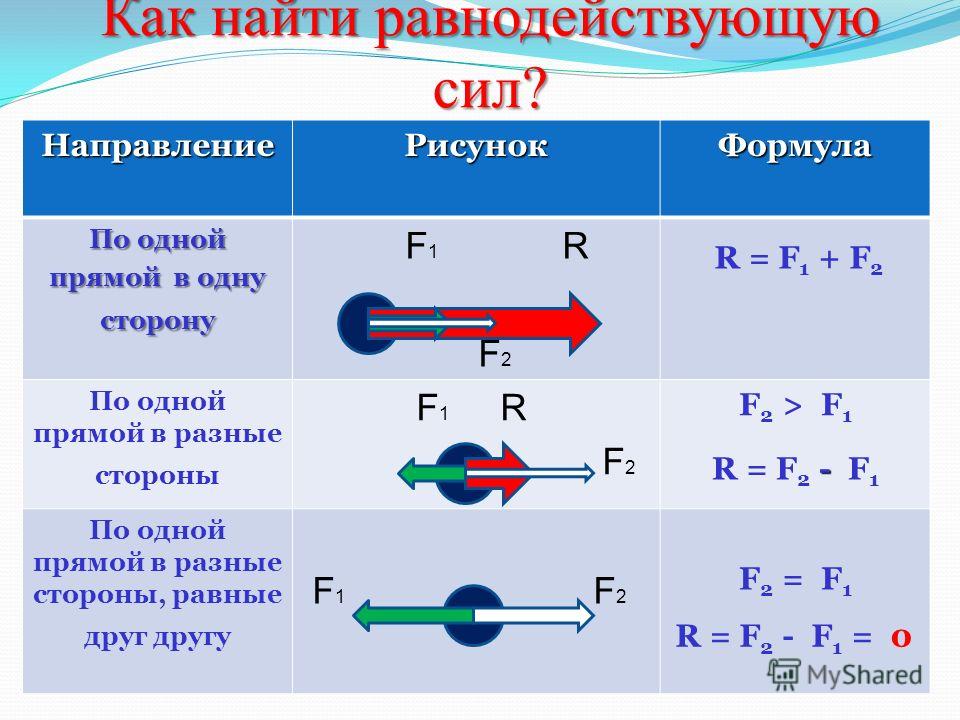
Таким образом, чистая внешняя сила теперь равна 9.0005
Fnet ∥ =w∥ −f,Fnet ∥ =w∥ −f,
4,33
и подставив это во второй закон Ньютона, a∥ =Fnet ∥ ma∥ =Fnet ∥ m, получим
a∥ =Fnet ∣∣m=w∥ −fm=mgsin(25°)−fm.a∥ =Fnet ∣∣m=w∥ −fm=mgsin(25°)−fm.
4,34
Подставляем известные значения, чтобы получить
0,4226)−45,0 N60,0 кг,
4,35
что дает
a∥ =3,39 м/с2, a∥ =3,39 м/с2,
4,36
, ускорение, параллельное наклону, при силе встречного трения 45,0 Н.
Обсуждение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии. На самом деле общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону составляет a=gsinθa=gsinθ, , независимо от массы .
Это связано с ранее обсуждавшимся фактом, что все тела падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
Разложение веса на компоненты
Рисунок 4.13 Объект лежит на склоне, который составляет угол θ с горизонтом.
Когда объект покоится на склоне, который составляет угол θθ с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости,
w⊥w⊥ , и сила, действующая параллельно плоскости,
ш∥ ш∥ . Перпендикулярная сила веса,
ж⊥ш⊥ , обычно равна по величине и противоположна по направлению нормальной силе,
НН. Сила, действующая параллельно плоскости,
w∥ w∥ , заставляет объект ускоряться вниз по склону. Сила трения,
ff, противодействует движению объекта, поэтому действует вверх по плоскости.
Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона составляет угол θθ к горизонту, то величины компонентов веса равны
w∥ =wsin(θ)=mgsin(θ)w∥ =wsin(θ)=mgsin(θ)
4,37
и
w⊥=wcos(θ)=mgcos(θ).w⊥= wcos(θ)=mgcos(θ).
4.38
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона θθ совпадает с углом, образованным между ww и w⊥w⊥ . Зная это свойство, можно с помощью тригонометрии определить величину составляющих веса:
cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)
4,39
sin(θ)= w∥ ww∥ =wsin(θ)=mgsin(θ)sin(θ)=w∥ ww∥ =wsin(θ)=mgsin(θ)
4,40
Захватывающий эксперимент: Force Parallel
Чтобы исследовать, как изменяется сила, параллельная наклонной плоскости, найдите резиновую ленту, несколько предметов, которые можно повесить на конец резинки, и доску, которую можно расположить под разными углами.
На сколько растянется резинка, если повесить предмет на конец доски? Теперь поместите доску под углом, чтобы объект соскальзывал при размещении на доске. На сколько растянется резинка, если ее выстроить параллельно доске и использовать для неподвижного удержания предмета на доске? Попробуйте еще два угла. Что это показывает?
Напряжение
Натяжение — это сила по длине среды, особенно сила, передаваемая гибкой средой, например веревкой или кабелем. Слово «натяжение » происходит от латинского слова, означающего «растягивать». Не случайно гибкие тяжи, передающие мышечные силы к другим частям тела, называются сухожилиями . Любой гибкий соединитель, такой как струна, веревка, цепь, проволока или кабель, может натягивать только параллельно своей длине; таким образом, сила, переносимая гибким соединителем, представляет собой натяжение с направлением, параллельным соединителю.
Важно понимать, что натяжение — это натяжение соединителя. В отличие от этого, рассмотрим фразу: «Вы не можете толкнуть веревку». Сила натяжения тянет наружу вдоль двух концов веревки.
Рассмотрим человека, держащего груз на веревке, как показано на рис. 4.14.
Рисунок
4.14
Когда совершенно гибкий соединитель (не требующий усилия для его изгиба), такой как эта веревка, передает силу TT, эта сила должна быть параллельна длине веревки, как показано на рисунке. Натяжение такого гибкого соединителя представляет собой натяжение. Обратите внимание, что веревка тянет с одинаковой силой, но в противоположных направлениях, на руку и поддерживаемую массу (без учета веса веревки). Это пример третьего закона Ньютона. Веревка — это среда, которая переносит равные и противоположные силы между двумя объектами. Натяжение в любом месте веревки между рукой и грузом одинаково. Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки.
Натяжение веревки должно равняться весу поддерживаемой массы, что можно доказать с помощью второго закона Ньютона. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю, и, следовательно, Fnet=0Fnet=0. Единственными внешними силами, действующими на массу, являются ее вес ww и натяжение TT, создаваемое веревкой. Таким образом,
Fnet=T−w=0,Fnet=T−w=0,
4,41
, где TT и ww — величины натяжения и веса, а их знаки указывают направление, причем up здесь положителен. Таким образом, как и следовало ожидать, натяжение равно весу поддерживаемой массы:
T=w=мг.T=w=мг.
4,42
Для массы 5,00 кг тогда (без учета массы веревки) получаем, что
T=mg=(5,00 кг)(9,80 м/с2)=49,0 N.T=mg=(5,00 кг)(9,80 м/с2)=49,0 Н.
4,43
Если разрезать веревку и вставить пружину, пружина растягивается на длину, соответствующую силе 49,0 Н, обеспечивая прямое наблюдение и измерение силы натяжения веревки.
Гибкие соединители часто используются для передачи усилий на поворотах, например, в больничной системе вытяжения, пальцевом шарнире или тормозном тросе велосипеда. Если трения нет, то напряжение передается без уменьшения. Меняется только его направление, и он всегда параллелен гибкому соединителю. Это показано на рис. 4.15 (а) и (б).
Рисунок 4.15 (а) Сухожилия в пальце передают силу TT от мышц к другим частям пальца, обычно изменяя направление силы, но не ее величину (сухожилия относительно свободны от трения). (b) Тормозной трос велосипеда передает натяжение TT от руля к тормозному механизму. Опять же, меняется направление, но не величина TT.
Пример 4.6
Что такое натяжение каната?
Рассчитайте натяжение троса, поддерживающего канатоходца массой 70,0 кг, показанного на рис. 4.16.
Рисунок
4.16
Вес канатоходца заставляет проволоку прогибаться на 5,0 градусов. Система, представляющая интерес, представляет собой точку на проволоке, в которой стоит канатоходец.
Стратегия
Как видно на рисунке, провод не идеально горизонтален (не может быть!), а прогибается под весом человека. Таким образом, напряжение с обеих сторон человека имеет направленный вверх компонент, способный выдержать его вес. Как обычно, силы представляют собой векторы, представленные графически стрелками, имеющими те же направления, что и силы, и длины, пропорциональные их величине. Система представляет собой канатоходца, и единственными внешними силами, действующими на него, являются его вес ww и два напряжения TLTL (слева натяжение) и TRTR (правое натяжение), как показано на рисунке. Весом самого провода разумно пренебречь. Суммарная внешняя сила равна нулю, так как система неподвижна. Теперь можно использовать небольшую тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из части (б) рисунка видно, что величины натяжений TLTL и TRTR должны быть равны. Это связано с тем, что веревка не имеет горизонтального ускорения, и единственными силами, действующими влево и вправо, являются TLTL и TRTR.
Таким образом, величина этих сил должна быть равна, чтобы они уравновешивали друг друга.
Всякий раз, когда у нас есть двумерные векторные задачи, в которых нет двух параллельных векторов, самый простой способ решения — выбрать удобную систему координат и спроецировать векторы на ее оси. В этом случае наилучшая система координат имеет одну ось горизонтальную, а другую вертикальную. Мы называем горизонтальную ось xx, а вертикальную ось yy.
Решение
Во-первых, нам нужно разложить векторы натяжения на их горизонтальную и вертикальную составляющие. Это помогает нарисовать новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему.
Рисунок
4.17
Когда векторы проецируются на вертикальную и горизонтальную оси, их компоненты вдоль этих осей должны в сумме равняться нулю, поскольку канатоходец неподвижен. Малый угол приводит к тому, что TT намного больше, чем ww.
Рассмотрим горизонтальные составляющие сил (обозначенные нижним индексом xx):
Fnet x=TLx−TRx.Fnet x=TLx−TRx.
4,44
Суммарная внешняя горизонтальная сила Fnet x=0Fnet x=0, поскольку человек неподвижен. Таким образом,
Fnet x=0=TLx-TRxTLx=TRx.Fnet x=0=TLx-TRxTLx=TRx.
4,45
Теперь обратите внимание на рисунок 4.17. Вы можете использовать тригонометрию, чтобы определить величину TLTL и TRTR. Обратите внимание, что:
cos(5,0°)=TLxTLTLx=TLcos(5,0°)cos(5,0°)=TRxTRTRx=TRcos(5,0°).cos(5,0°)=TLxTLTLx=TLcos(5,0°)cos(5,0°) =TRxTRTRx=TRcos(5,0º).
4,46
Приравнивание TLxTLx и TRxTRx:
TLcos(5,0°)=TRcos(5,0°).TLcos(5,0°)=TRcos(5,0°).
4,47
Таким образом,
TL=TR=T,TL=TR=T,
4,48
, как и предполагалось. Теперь, рассматривая вертикальные компоненты (обозначаемые индексом yy), мы можем найти TT.
Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что net Fy=0Fy=0. Таким образом, как показано на диаграмме свободного тела на рис. 4.17,
Fnet y=TLy+TRy-w=0.Fnet y=TLy+TRy-w=0.
4,49
Наблюдая за рисунком 4.17, мы можем использовать тригонометрию для определения соотношения между ТЛиТЛы, ПОПРОБУЙ, и ТТ. Как мы определили из анализа в горизонтальном направлении, TL=TR=TTL=TR=T:
sin(5.0º)=TLyTLTLy=TLsin(5.0º)=Tsin(5.0º)sin(5.0º)=TRyTRTRy=TRsin(5.0º)=Tsin(5.0º).sin(5.0º)=TLyTLTLy=TLsin (5,0°)=Tsin(5,0°)sin(5,0°)=TRyTRTRy=TRsin(5,0°)=Tsin(5,0°).
4,50
Теперь мы можем подставить значения TlyTLy и TRyTRy в уравнение результирующей силы в вертикальном направлении: º)−w=02Tsin(5,0°)−w=02Tsin(5,0°)=wFnet y=TLy+TRy−w=0Fnet y=Tsin(5,0°)+Tsin(5,0°)−w=02Tsin(5,0°) −w=02Tsin(5,0º)=w
4,51
и
T=w2sin(5,0º)=mg2sin(5,0º),T=w2sin(5,0º)=mg2sin(5,0º),
4,52
, так что
T=(70,0 кг м/с2)2(0,0872),T=(70,0 кг)(9,80 м/с2)2(0,0872),
4,53
и натяжение
T=3900 N.
T=3900 Н.
4,54
5 Обсуждение
Обратите внимание, что вертикальное натяжение троса действует как нормальная сила, поддерживающая вес канатоходца. Натяжение почти в шесть раз превышает вес 686-Н канатоходца. Поскольку проволока почти горизонтальна, вертикальная составляющая ее натяжения составляет лишь малую часть натяжения проволоки. Большие горизонтальные компоненты направлены в противоположные стороны и компенсируются, поэтому большая часть натяжения проволоки не используется для поддержки веса канатоходца.
Если мы хотим создать очень большое натяжение, все, что нам нужно сделать, это приложить усилие, перпендикулярное гибкому соединителю, как показано на рис. 4.18. Как мы видели в последнем примере, вес канатоходца действовал как сила, перпендикулярная веревке. Мы видели, что натяжение каната связано с весом канатоходца следующим образом:
T=w2sin(θ).
T=w2sin(θ).
4,55
Мы можем расширить это выражение для описания натяжения TT, создаваемого перпендикулярной силой (F⊥F⊥) к середине гибкого соединителя:
Т=F⊥2sin(θ).T=F⊥2sin(θ).
4,56
Обратите внимание, что θθ — это угол между горизонталью и изогнутым соединителем. В этом случае TT становится очень большим, когда θθ приближается к нулю. Даже относительно небольшой вес любого гибкого соединителя вызовет его провисание, поскольку в горизонтальном положении возникло бы бесконечное натяжение (т. θ=0θ=0 и sinθ=0sinθ=0). (См. рис. 4.18.)
Рисунок
4.18
Мы можем создать очень большое натяжение цепи, надавив на нее перпендикулярно ее длине, как показано на рисунке. Предположим, мы хотим вытащить машину из грязи, когда эвакуатора нет. Каждый раз, когда автомобиль движется вперед, цепь натягивается, чтобы он оставался как можно более прямым. Натяжение цепи определяется как T=F⊥2sin(θ)T=F⊥2sin(θ) ; поскольку θθ мало, TT очень велико.
Эта ситуация аналогична канатоходцу, показанному на рис. 4.16, за исключением того, что показанные здесь напряжения передаются на автомобиль и дерево, а не действуют в точке приложения F⊥F⊥.
Рисунок 4.19 Если не будет приложено бесконечное натяжение, любой гибкий соединитель, такой как цепь в нижней части рисунка, будет прогибаться под собственным весом, образуя характерную кривую, когда вес равномерно распределен по длине. Висячие мосты, такие как мост Золотые Ворота, показанный на этом изображении, по существу представляют собой очень тяжелые гибкие соединители. Вес моста равномерно распределяется по длине гибких соединителей, обычно тросов, которые принимают характерную форму. (кредит: Листовка, Викисклад)
Расширенная тема: Реальные силы и инерциальные системы отсчета
Существует еще одно различие между силами в дополнение к уже упомянутым типам. Одни силы реальны, другие нет. Реальные силы — это те, которые имеют какое-то физическое происхождение, например гравитационное притяжение.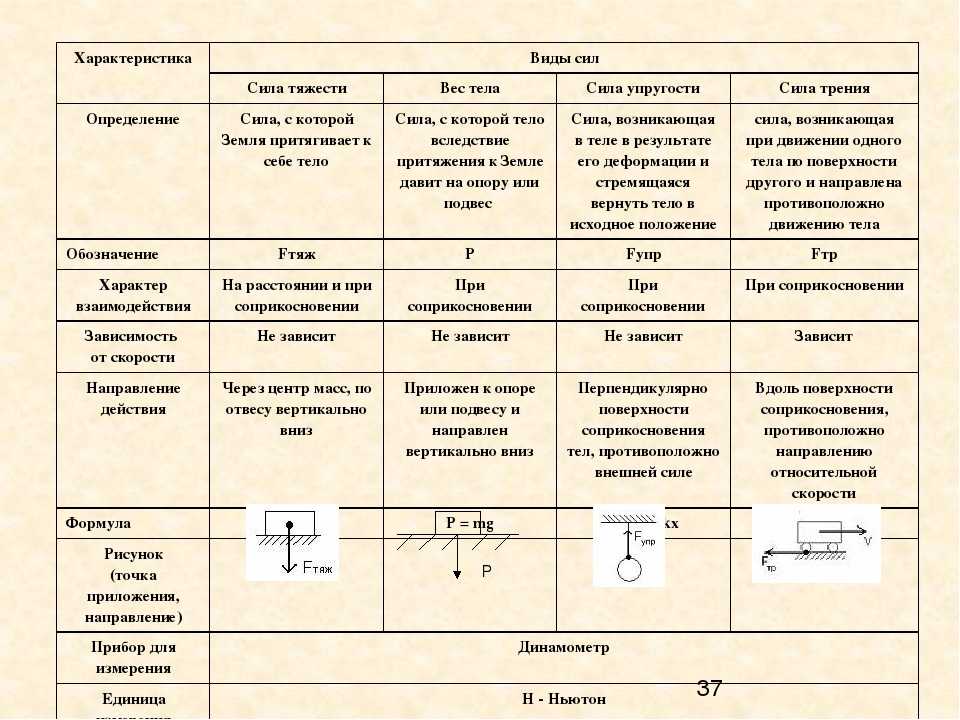
Напротив, фиктивных сил возникают просто потому, что наблюдатель находится в ускоряющейся системе отсчета, такой как та, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется). Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Конечно, здесь происходит то, что Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Инерциальная система отсчета — это система, в которой все силы реальны, и, что то же самое, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Вращение Земли настолько медленное, что Земля представляет собой почти инерциальную систему отсчета.
Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект. В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать.
Решающим фактором при определении того, является ли система отсчета инерциальной, является ее ускорение или вращение относительно известной инерциальной системы отсчета. Если не указано иное, все явления, обсуждаемые в этом тексте, рассматриваются в инерциальных системах отсчета.
Все силы, обсуждаемые в этом разделе, являются реальными силами, но есть ряд других реальных сил, таких как подъемная сила и тяга, которые в этом разделе не рассматриваются. Они более специализированы, и нет необходимости обсуждать каждый тип силы. Однако естественно задаться вопросом, где в длинном списке сил находится основная простота, которую мы стремимся найти в физике.
Являются ли некоторые более простыми, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как будет показано в следующем (расширенном) разделе и в трактовке современной физики далее в тексте.
Исследования ФЕТ
Силы в 1 измерении
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Просмотрите диаграмму всех сил свободного тела (включая гравитационные и нормальные силы).
Нажмите, чтобы просмотреть содержимое.
5.6 Общие силы – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определить нормальную силу и силу растяжения
- Различать реальные и фиктивные силы
- Применение законов движения Ньютона для решения задач, связанных с различными силами
Силы имеют множество названий, например, толкание, притяжение, тяга и вес.
Традиционно силы были сгруппированы в несколько категорий и получили имена, относящиеся к их источнику, способу их передачи или их воздействию. Некоторые из этих категорий обсуждаются в этом разделе вместе с некоторыми интересными приложениями. Дальнейшие примеры сил обсуждаются далее в этом тексте.
Каталог сил: нормальные, растягивающие и другие примеры сил
Каталог сил будет полезен для справки при решении различных задач, связанных с силой и движением. Эти силы включают в себя нормальную силу, натяжение, трение и силу пружины.
Нормальная сила
Вес (также называемый силой тяжести) — это всепроникающая сила, действующая постоянно, и ей необходимо противодействовать, чтобы объект не упал. Вы должны поддерживать вес тяжелого предмета, отталкиваясь от него, удерживая его неподвижно, как показано на рис. 5.21(а). Но как неодушевленные предметы, такие как стол, выдерживают вес размещенного на них груза, как показано на рис.
5.21(b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже крепкий дубовый стол деформируется при приложении к нему силы. Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину). Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока восстанавливающая сила не станет равной весу груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро и провисание незначительное, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.
Рисунок
5.21
(a) Человек, держащий пакет с собачьим кормом, должен приложить восходящую силу F→рукаF→рука, равная по величине и противоположная по направлению весу корма w→w→, чтобы он не упал на землю.
(b) Карточный стол прогибается, когда на него кладут корм для собак, как жесткий батут. Упругие восстанавливающие силы в столе возрастают по мере его провисания, пока не создадут силу N→N→, равную по величине и противоположную по направлению весу груза.
Мы должны заключить, что все, что поддерживает груз, одушевленное оно или нет, должно создавать направленную вверх силу, равную весу груза, как мы предполагали в нескольких предыдущих примерах. Если сила, поддерживающая вес объекта или груза, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь обозначается символом N→.N→. (Это не ньютон для силы или Н.) Слово нормальный означает перпендикулярно поверхности. Это означает, что нормальная сила, действующая на объект, покоящийся на горизонтальной поверхности, может быть выражена в векторной форме следующим образом:
N→=−мг→.N→=−мг→.
5.11
В скалярной форме это становится
N=мг.
N=мг.
5.12
Нормальная сила может быть меньше веса объекта, если объект находится под наклоном.
Пример 5.12
Груз на склоне
Рассмотрим лыжника на склоне на рис. 5.22. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если трение равно 45,0 Н?
Рисунок
5.22
Поскольку ускорение параллельно склону и действует вниз по склону, все силы удобнее всего спроецировать на систему координат, где одна ось параллельна склону, а другая перпендикулярна ему (оси показаны слева от лыжника). ). N→N→ перпендикулярно склону, а f→f→ параллельно склону, но w→w→ имеет компоненты по обеим осям, а именно, wywy и wxwx. Здесь w→w→ имеет волнистую линию, показывающую, что она была заменена этими компонентами. Сила N→N→ равна по модулю wywy, поэтому ускорение перпендикулярно склону отсутствует, а f меньше, чем wxwx, поэтому имеет место ускорение вниз по склону (вдоль оси, параллельной склону).
Стратегия
Это двумерная задача, поскольку не все силы, действующие на лыжника (исследуемую систему), параллельны. Здесь также хорошо работает подход, который мы использовали в двумерной кинематике. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав две одномерные задачи для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Движения вдоль взаимно перпендикулярных осей независимы.) Используем x и y для параллельного и перпендикулярного направлений соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а ускорение направлено вниз по склону. Что касается сил, то трение рисуется против движения (трение всегда препятствует движению вперед) и всегда параллельно склону, wxwx рисуется параллельно склону и вниз по склону (вызывает движение лыжника вниз по склону) и wywy изображается как составляющая веса, перпендикулярная уклону.
Затем мы можем рассмотреть отдельные задачи о силах, параллельных склону, и силах, перпендикулярных склону.
Решение
Величина составляющей веса, параллельной наклону, равна
wx=wsin25°=mgsin25°,wx=wsin25°=mgsin25°,
и величина составляющей веса перпендикулярно наклону
wy=wcos25°=mgcos25°.wy=wcos25°=mgcos25 °.
а. Трением пренебречь. Поскольку ускорение параллельно наклону, нам нужно рассматривать только силы, параллельные наклону. (Силы, перпендикулярные склону, складываются в ноль, так как ускорение в этом направлении отсутствует.) Силы, параллельные склону, представляют собой составляющую веса лыжника, параллельную склону, wxwx и силы трения 9.0025 ф . Используя второй закон Ньютона с нижними индексами для обозначения величин, параллельных наклону,
ax=Fnetxmax=Fnetxm
, где Fnetx=wx-mgsin25°, Fnetx=wx-mgsin25°, при условии отсутствия трения в этой части. Следовательно,
ax=Fnetxm=mgsin25°m=gsin25°(9,80 м/с2)(0,4226)=4,14 м/с2ax=Fnetxm=mgsin25°m=gsin25°(9,80 м/с2)(0,4226)=4,14 м/ s2
— ускорение.
б. Включите трение. У нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно препятствует движению между соприкасающимися поверхностями. Таким образом, чистая внешняя сила равна
Fnetx=wx-f.Fnetx=wx-f.
Подставив это во второй закон Ньютона, ax=Fnetx/m,ax=Fnetx/m, получим
ax=Fnetxm=wx-fm=mgsin25°-fm.ax=Fnetxm=wx-fm=mgsin25°-fm.
Подставим известные значения, чтобы получить 0кг.
Это дает нам
ax=3,39 м/с2, ax=3,39 м/с2,
, что является ускорением, параллельным наклону, когда существует 45,0 Н противодействующего трения.
Значение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии. Общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону равно a=gsinθa=gsinθ, независимо от массы. Как обсуждалось ранее, все объекты падают с одинаковым ускорением при отсутствии сопротивления воздуха.
Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
Когда объект покоится на наклонной плоскости, составляющей угол θθ с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: силу, действующую перпендикулярно плоскости, wywy, и силу, действующую параллельно плоскости, wxwx (рис. 5.23). Нормальная сила N→N→ обычно равна по величине и противоположна по направлению перпендикулярной составляющей веса wywy. Сила, действующая параллельно плоскости, wxwx, заставляет объект ускоряться вниз по склону.
Рисунок 5.23 Объект лежит на склоне, который составляет угол θθ с горизонтом.
Будьте осторожны при разложении веса объекта на составляющие. Если наклон составляет угол θθ к горизонту, то величины компонентов веса равны
wx=wsinθ=mgsinθwx=wsinθ=mgsinθ
и
wy=wcosθ=mgcosθ.wy=wcosθ=mgcosθ.
Воспользуемся вторым уравнением, чтобы записать нормальную силу, действующую на объект, покоящийся на наклонной плоскости:
N=мгcosθ.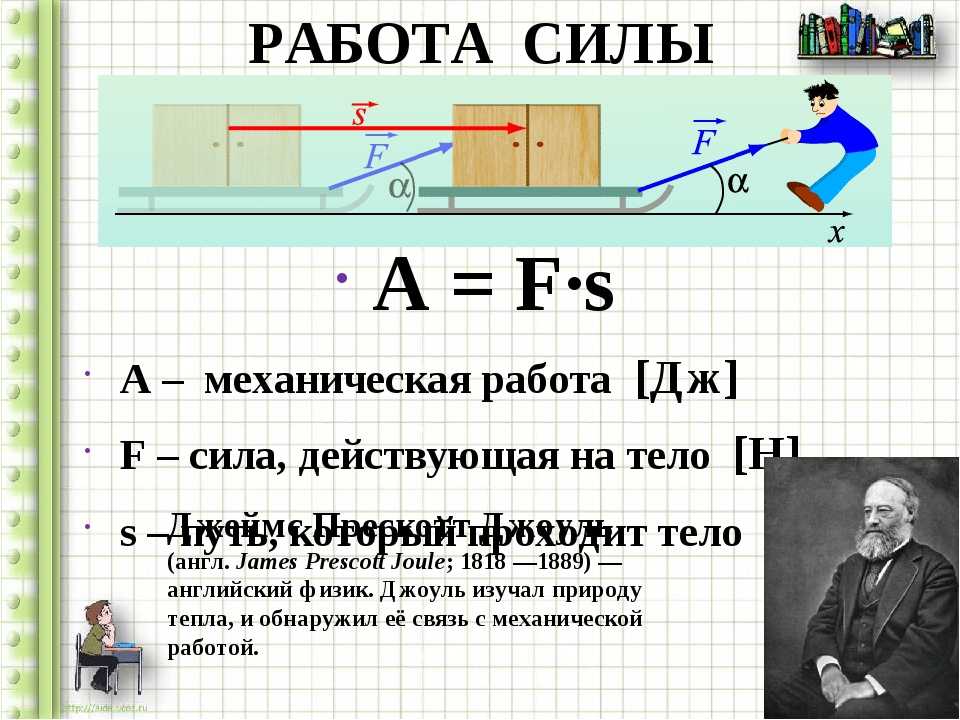
N=мгcosθ.
5.13
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого мы рисуем прямой угол, образованный тремя весовыми векторами. Угол наклона θθ такой же, как угол, образованный между w и wywy. Зная это свойство, мы можем с помощью тригонометрии определить величину составляющих веса:
cosθ=wyw,wy=wcosθ=mgcosθsinθ=wxw,wx=wsinθ=mgsinθ.cosθ=wyw,wy=wcosθ=mgcosθsinθ=wxw,wx=wsinθ=mgsinθ.
Проверьте свое понимание 5,8
Сила 1150 Н, действующая параллельно пандусу, вталкивает 250-килограммовый оружейный сейф в движущийся фургон. Пандус не имеет трения и наклонен под углом 17°.17°. а) Каково ускорение сейфа вверх по пандусу? б) Если в этой задаче рассмотреть трение при силе трения 120 Н, каково ускорение сейфа?
Напряжение
Натяжение — это сила по длине среды; в частности, это тяговое усилие, действующее вдоль натянутого гибкого соединителя, такого как канат или трос.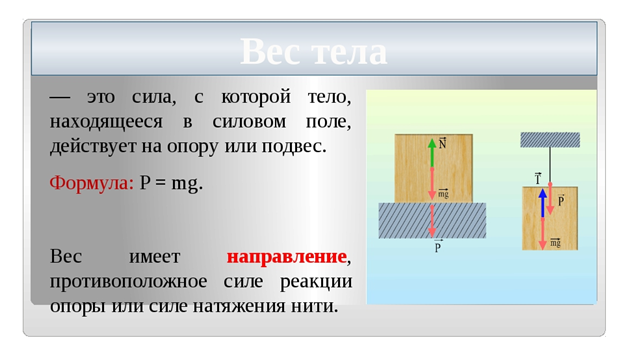
Слово «напряжение» происходит от латинского слова, означающего «растягивать». Не случайно гибкие шнуры, передающие мышечные силы к другим частям тела, называются 9.0025 сухожилия .
Любой гибкий соединитель, такой как веревка, веревка, цепь, проволока или кабель, может оказывать натяжение только параллельно своей длине; таким образом, сила, переносимая гибким соединителем, представляет собой натяжение с направлением, параллельным соединителю. Напряжение — это натяжение в соединителе. Рассмотрим фразу: «Вы не можете толкнуть веревку». Вместо этого сила натяжения тянет наружу вдоль двух концов веревки.
Рассмотрим человека, держащего груз на веревке, как показано на рис. 5.24. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю и результирующая сила равна нулю. Единственными внешними силами, действующими на массу, являются ее вес и натяжение веревки. Таким образом,
Fnet=T−w=0,Fnet=T−w=0,
, где T и w — величины натяжения и веса, соответственно, а их знаки указывают направление, причем значение up положительное.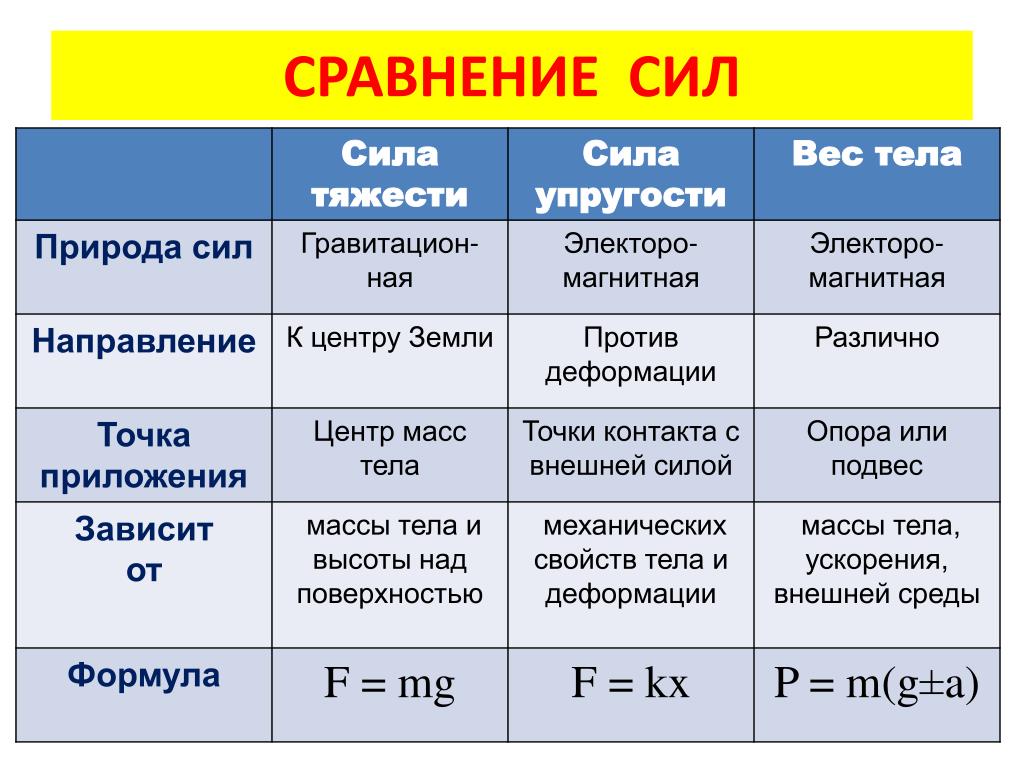
Как мы доказали с помощью второго закона Ньютона, натяжение равно весу поддерживаемой массы:
T=w=мг.T=w=мг.
5.14
Таким образом, для массы 5,00 кг (без учета массы веревки) получаем, что
T=мг=(5,00 кг)(9,80 м/с2)=49,0 Н.Т=мг=(5,00 кг)(9,80 м/с2)=49.0Н.
Если мы разрежем веревку и вставим пружину, пружина растянется на длину, соответствующую силе 49,0 Н, что обеспечит прямое наблюдение и измерение силы натяжения веревки.
Рисунок
5.24
Когда совершенно гибкий соединитель (не требующий усилия для его изгиба), такой как эта веревка, передает силу T→,T→, эта сила должна быть параллельна длине веревки, как показано на рисунке. По третьему закону Ньютона веревка тянет с одинаковой силой, но в противоположных направлениях, на руку и поддерживаемую массу (без учета веса веревки). Веревка — это среда, которая переносит равные и противоположные силы между двумя объектами. Натяжение в любом месте веревки между рукой и грузом одинаково.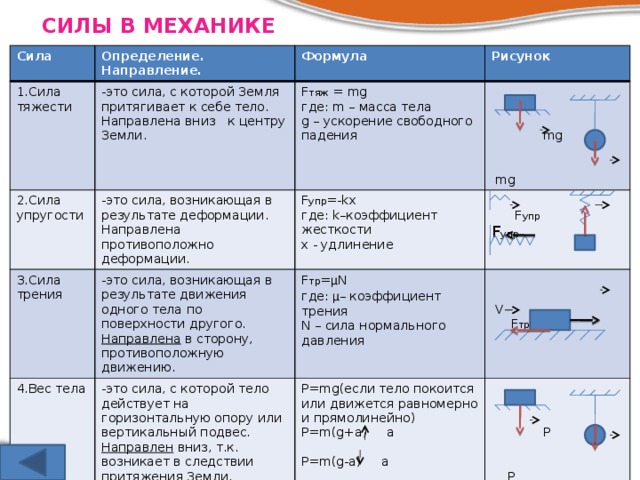
Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки.
Гибкие соединители часто используются для передачи усилий на поворотах, например, в больничной системе вытяжения, сухожилиях или велосипедном тормозном тросе. Если нет трения, передача натяжения не уменьшается; меняется только его направление, и он всегда параллелен гибкому соединителю, как показано на рис. 5.25.
Рисунок 5,25 (а) Сухожилия в пальце переносят силу T от мышц к другим частям пальца, обычно изменяя направление силы, но не ее величину (сухожилия относительно свободны от трения). (b) Тормозной трос на велосипеде выдерживает натяжение T от рычага тормоза на руле к тормозному механизму. Опять же, изменилось направление, но не величина T .
Пример 5.13
Что такое натяжение каната?
Рассчитайте натяжение троса, поддерживающего канатоходца массой 70,0 кг, показанного на рис.
5.26.
Рисунок 5.26 Вес канатоходца заставляет канат прогибаться на 5,0°5,0°. Исследуемая система представляет собой точку на проводе, в которой стоит канатоходец.
Стратегия
Как видно на рис. 5.26, проволока изгибается под весом человека. Таким образом, напряжение с обеих сторон человека имеет направленный вверх компонент, способный выдержать его вес. Как обычно, силы представляют собой векторы, представленные графически стрелками, которые имеют то же направление, что и силы, и длины, пропорциональные их величине. Система представляет собой канатоходца, и единственными внешними силами, действующими на него, являются его вес w→w→ и два напряжения T→LT→L (левое натяжение) и T→RT→R (правое натяжение). Весом провода разумно пренебречь. Чистая внешняя сила равна нулю, потому что система статична. Мы можем использовать тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из рис. 5.26(б) видно, что величины натяжений TLTL и TRTR должны быть равны.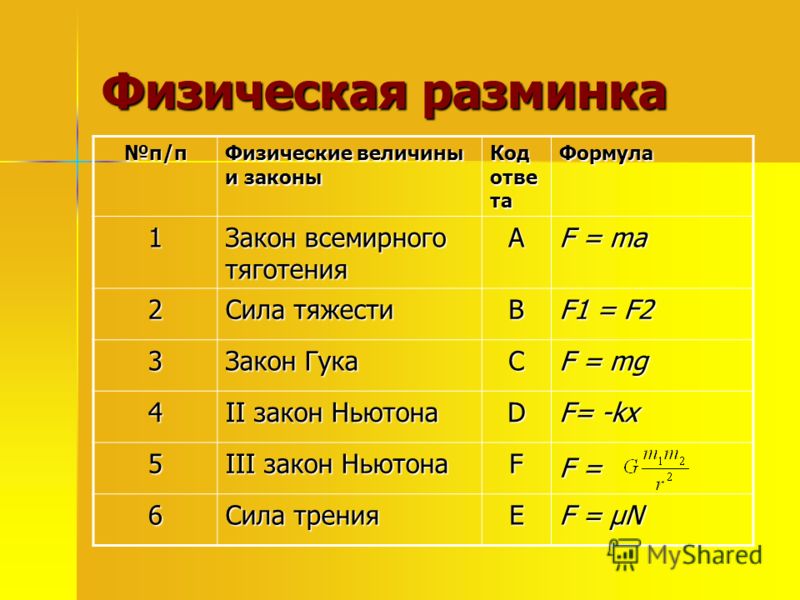
Мы знаем это, потому что в веревке нет горизонтального ускорения, и единственными силами, действующими влево и вправо, являются TLTL и TRTR. Таким образом, величина этих горизонтальных составляющих сил должна быть равна, чтобы они уравновешивали друг друга.
Всякий раз, когда у нас есть двумерные векторные задачи, в которых нет двух параллельных векторов, самый простой способ решения — выбрать удобную систему координат и спроецировать векторы на ее оси. В этом случае наилучшая система координат имеет одну горизонтальную ось ( x ) и одну вертикальную ось ( y ).
Раствор
Во-первых, нам нужно разложить векторы натяжения на их горизонтальную и вертикальную составляющие. Это помогает взглянуть на новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему (рис. 5.27).
Рисунок
5.
27
При проецировании векторов на вертикальную и горизонтальную оси их составляющие по этим осям должны в сумме равняться нулю, так как канатоходец неподвижен. Малый угол приводит к тому, что T намного больше, чем w .
Рассмотрим горизонтальные составляющие сил (обозначены нижним индексом x ):
Fnetx=TRx-TLx.Fnetx=TRx-TLx.
Суммарная внешняя горизонтальная сила Fnetx=0,Fnetx=0, так как человек неподвижен. Таким образом,
Fnetx=0=TRx-TLxTLx=TRx.Fnetx=0=TRx-TLxTLx=TRx.
Теперь обратите внимание на рисунок 5.27. Вы можете использовать тригонометрию для определения величины TLTL и TRTR:
cos5.0°=TLxTL,TLx=TLcos5.0°cos5.0°=TRxTR,TRx=TRcos5.0°.cos5.0°=TLxTL,TLx =TLcos5.0°cos5.0°=TRxTR,TRx=TRcos5.0°.
Эквивалент T L x и T R x :
TLcos5.
0°s.5.0°=TRcos5.0°.
Таким образом,
TL=TR=T,TL=TR=T,
как и предполагалось. Теперь, рассматривая вертикальные компоненты (обозначенные нижним индексом y ), мы можем найти T . Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что Fnety=0Fnety=0. Таким образом, как показано на диаграмме свободного тела,
Fnety=TLy+TRy-w=0.Fnety=TLy+TRy-w=0.
Мы можем использовать тригонометрию, чтобы определить отношения между TLy, TRy, TLy, TRy и T . Как мы определили из анализа в горизонтальном направлении, TL=TR=TTL=TR=T:
sin5.0°=TLyTL,TLy=TLsin5.0°=Tsin5.0°sin5.0°=TRyTR,TRy=TRsin5.0°=Tsin5.0°.sin5.0°=TLyTL,TLy=TLsin5. 0°=Tsin5.0°sin5.0°=TRyTR,TRy=TRsin5.0°=Tsin5.0°.
Теперь мы можем подставить значения для TlyTLy и TRyTRy в уравнение общей силы в вертикальном направлении:
Fnety=TLy+TRy−w=0Fnety=Tsin5.0°+Tsin5.0°−w=02Tsin5.
0 °−w=02Tsin5.0°=wFnety=TLy+TRy−w=0Fnety=Tsin5.0°+Tsin5.0°−w=02Tsin5.0°−w=02Tsin5.0°=w
и
T =w2sin5.0°=mg2sin5.0°,T=w2sin5.0°=mg2sin5.0°,
поэтому
T=(70.0кг)(9.80м/с2)2(0.0872),T=(70.0кг)(9.80м/с2)2(0.0872),
и натяжение
T=3930Н .Т=3930Н.
Значение
Вертикальное натяжение троса действует как сила, поддерживающая вес канатоходца. Натяжение почти в шесть раз превышает вес 686 Н канатоходца. Поскольку проволока почти горизонтальна, вертикальная составляющая ее натяжения составляет лишь часть натяжения проволоки. Большие горизонтальные компоненты направлены в противоположные стороны и компенсируются, поэтому большая часть натяжения проволоки не используется для поддержки веса канатоходца.
Если мы хотим создать большое натяжение, все, что нам нужно сделать, это приложить усилие, перпендикулярное натянутому гибкому соединителю, как показано на рис. 5.26. Как мы видели в примере 5.
13, вес канатоходца действует как сила, перпендикулярная веревке. Мы видели, что натяжение веревки связано с весом канатоходца следующим образом:
T=w2sinθ.T=w2sinθ.
Мы можем расширить это выражение, чтобы описать натяжение T , создаваемое перпендикулярной силой (F⊥)(F⊥) к середине гибкого соединителя:
Т=F⊥2sinθ.T=F⊥2sinθ.
Угол между горизонталью и изогнутым соединителем обозначается θθ. В этом случае T становится большим, когда θθ приближается к нулю. Даже относительно небольшой вес любого гибкого соединителя вызовет его провисание, так как если бы он был горизонтальным (т. е. θ=0θ=0 и sin θ=0θ=0), возникло бы бесконечное натяжение). Например, на рис. 5.28 показана ситуация, когда мы хотим вытащить автомобиль из грязи, когда эвакуатора нет. Каждый раз, когда автомобиль движется вперед, цепь натягивается, чтобы он оставался как можно более прямым. Натяжение в цепи определяется как T=F⊥2sinθ,T=F⊥2sinθ, а поскольку θθ мало, T большой.
Эта ситуация аналогична ситуации с канатоходцем, за исключением того, что показанные здесь напряжения передаются машине и дереву, а не действуют в точке приложения F⊥F⊥.
Рисунок 5,28 Мы можем создать сильное натяжение в цепи — и, возможно, большой беспорядок — надавив на нее перпендикулярно ее длине, как показано на рисунке.
Проверьте свое понимание 5,9
Один конец 3,0-метровой веревки привязан к дереву; другой конец привязан к застрявшей в грязи машине. Автомобилист тянет вбок за середину веревки, смещая ее на расстояние 0,25 м. Если он приложит в этих условиях силу 200,0 Н, определите силу, действующую на автомобиль.
В «Применении законов Ньютона» мы расширяем обсуждение натяжения троса, включив в него случаи, когда показанные углы не равны.
Трение
Трение – это сила сопротивления, противодействующая движению или его тенденции. Представьте себе объект, покоящийся на горизонтальной поверхности.
Суммарная сила, действующая на объект, должна быть равна нулю, что приводит к равенству веса и нормальной силы, действующих в противоположных направлениях. Если поверхность наклонена, нормальная сила уравновешивает составляющую веса, перпендикулярную поверхности. Если предмет не скользит вниз, то часть веса, параллельная наклонной плоскости, уравновешивается трением. Трение обсуждается более подробно в следующей главе.
Сила пружины
Пружина – это особая среда с определенной атомной структурой, обладающая способностью восстанавливать свою форму при деформации. Чтобы восстановить свою форму, пружина прикладывает восстанавливающую силу, которая пропорциональна и направлена в противоположном направлении, в котором она растягивается или сжимается. Это формулировка закона, известного как закон Гука, который имеет математическую форму
.F→=−kx→.F→=−kx→.
Константа пропорциональности k является мерой жесткости пружины.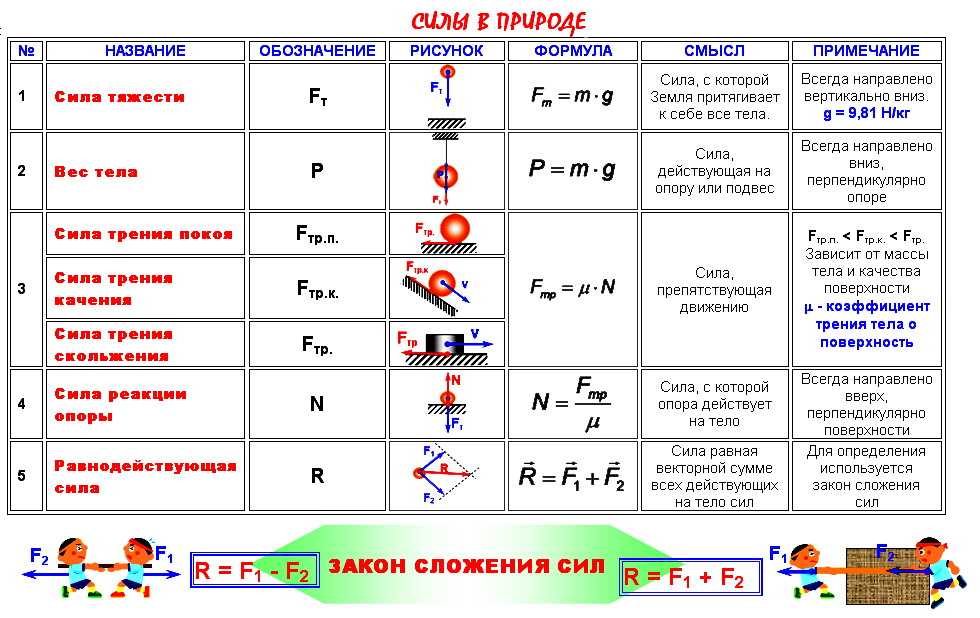
Линия действия этой силы параллельна оси пружины, а направление силы противоположно направлению вектора смещения (рис. 5.29).). Смещение должно быть измерено из расслабленного положения; x=0x=0, когда пружина ослаблена.
Рисунок 5.29 Сила пружины пропорциональна смещению независимо от того, сжата она или растянута. (а) Пружина находится в расслабленном состоянии и не оказывает никакого действия на блок. (b) Пружина сжимается перемещением Δx→1Δx→1 объекта и оказывает восстанавливающую силу −kΔx→1.−kΔx→1. (c) Пружина растягивается за счет смещения Δx→2Δx→2 объекта и оказывает восстанавливающую силу −kΔx→2.−kΔx→2.
Реальные силы и инерциальные системы отсчета
Существует еще одно различие между силами: одни силы реальны, а другие нет. Реальные силы имеют какое-то физическое происхождение, например гравитационное притяжение. Напротив, фиктивные силы возникают просто потому, что наблюдатель находится в ускоряющейся или неинерциальной системе отсчета, например, в системе, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется).
Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Вместо этого Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Мы можем идентифицировать фиктивную силу, задав вопрос: «Что такое сила реакции?» Если мы не можем назвать силу реакции, то рассматриваемая нами сила является фиктивной. В примере со спутником сила реакции должна быть направлена на восток на Земле. Напомним, что инерциальная система отсчета — это система, в которой все силы реальны, и, что эквивалентно, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Вращение Земли настолько медленное, что Земля представляет собой почти инерциальную систему отсчета. Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект.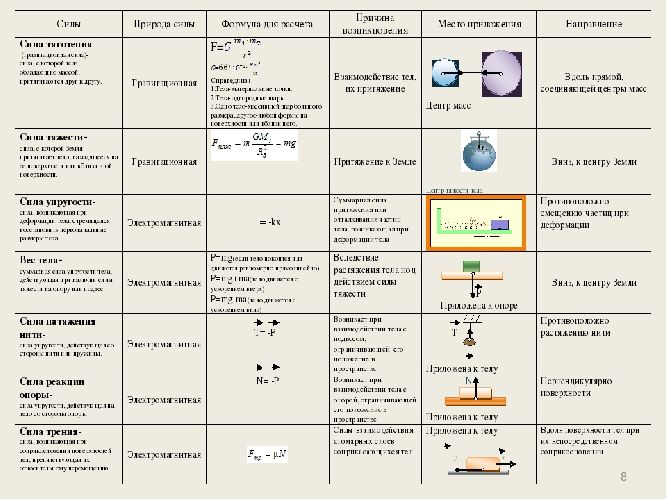
В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать (рис. 5.30).
Рисунок 5.30 Ураган Фрэн направляется к юго-восточному побережью США 19 сентября.96. Обратите внимание на характерную форму «глаза» урагана. Это результат эффекта Кориолиса, который представляет собой отклонение объектов (в данном случае воздуха) во вращающейся системе отсчета, подобно вращению Земли. Этот ураган показывает вращение против часовой стрелки, потому что это шторм низкого давления. (кредит “бегун”: модификация работы “Greenwich Photography”/Flickr)
Решающим фактором в определении того, является ли система отсчета инерциальной, является ее ускорение или вращение относительно известной инерциальной системы отсчета. Если не указано иное, все явления, обсуждаемые в этом тексте, находятся в инерциальных системах отсчета.
Силы, обсуждаемые в этом разделе, являются реальными силами, но не единственными реальными силами.
Подъемная сила и тяга, например, являются более специализированными реальными силами. Есть ли в длинном списке сил более основные, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как вы увидите в трактовке современной физики далее в тексте.
Интерактивный
Исследуйте силы и движение в этом интерактивном симуляторе, толкая предметы домашнего обихода вверх и вниз по пандусу. Опустите и поднимите рампу, чтобы увидеть, как угол наклона влияет на параллельные силы. Графики показывают силы, энергию и работу.
Интерактивный
Растягивание и сжатие пружин в этом упражнении для изучения взаимосвязи между силой, жесткостью пружины и смещением. Исследуйте, что произойдет, если две пружины соединить последовательно и параллельно.
Заметки по физике – Силы
| Силы |
|
|
| ||||||||||
 youtube.com/embed/bojmd5xQNK4?wmode=opaque” frameborder=”0″ allowfullscreen=””> |
|
|
|
| ||||||
|
|
|
| ||||||
 youtube.com/embed/jsiuReBJOl0?wmode=opaque” frameborder=”0″ allowfullscreen=””> |
|
|
|
| ||||||
|
|
|
| ||||||
 |