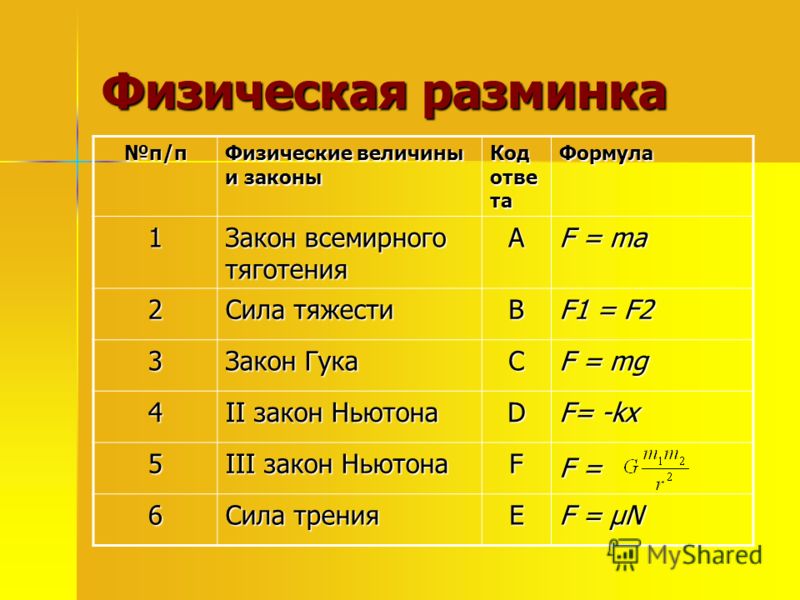
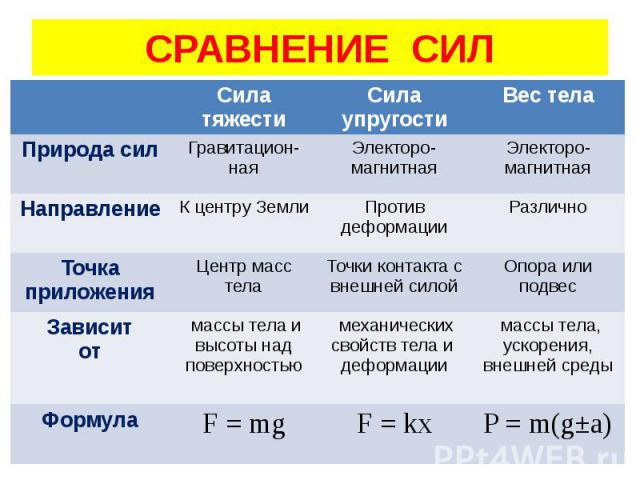
№ п/п | Название физ. величины | Буква | Ед. измер. в СИ | Другие ед. измер. | Формула | Определение | Свойства и особенности |
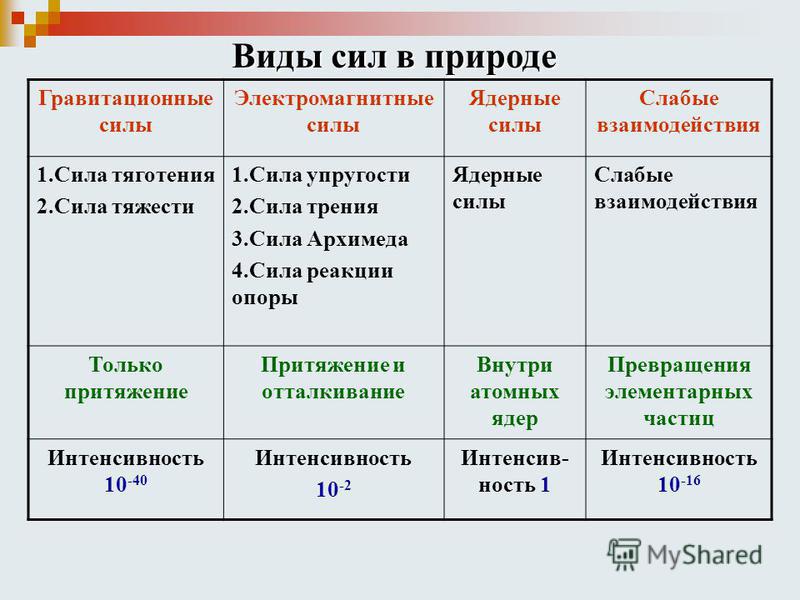
1 | Сила | F, P, N, T | Н | кН, мН | Зависит от вида силы | Векторная физ. величина, являющаяся причиной изменения скорости движения тела. | 1.Имеет числовое значение (модуль), точку приложения и направление действия. 2.Можно измерить с помощью динамометра. |
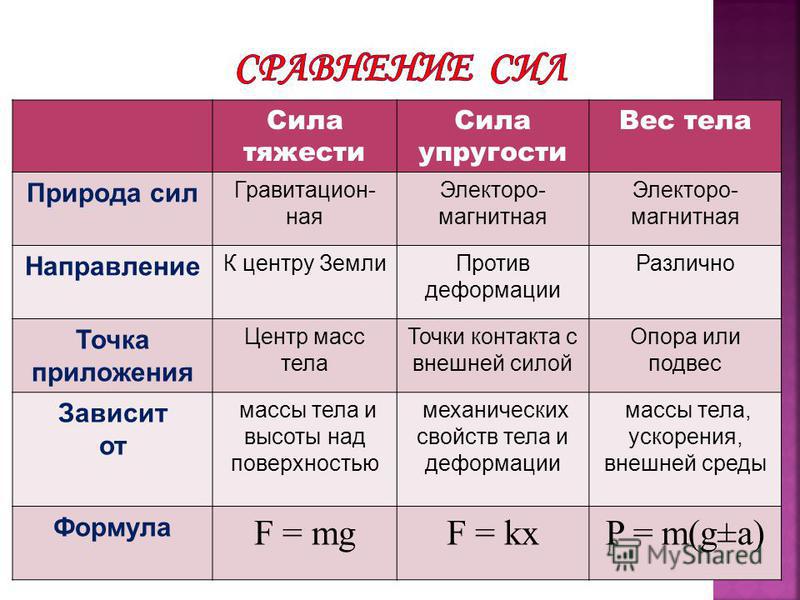
2 | Сила тяжести | FТ | Н | кН, мН | , | Сила, с которой Земля притягивает к себе тело. | 1.Всегда направлена вертикально вниз из центра тела. 3. Приложена к самому телу. |
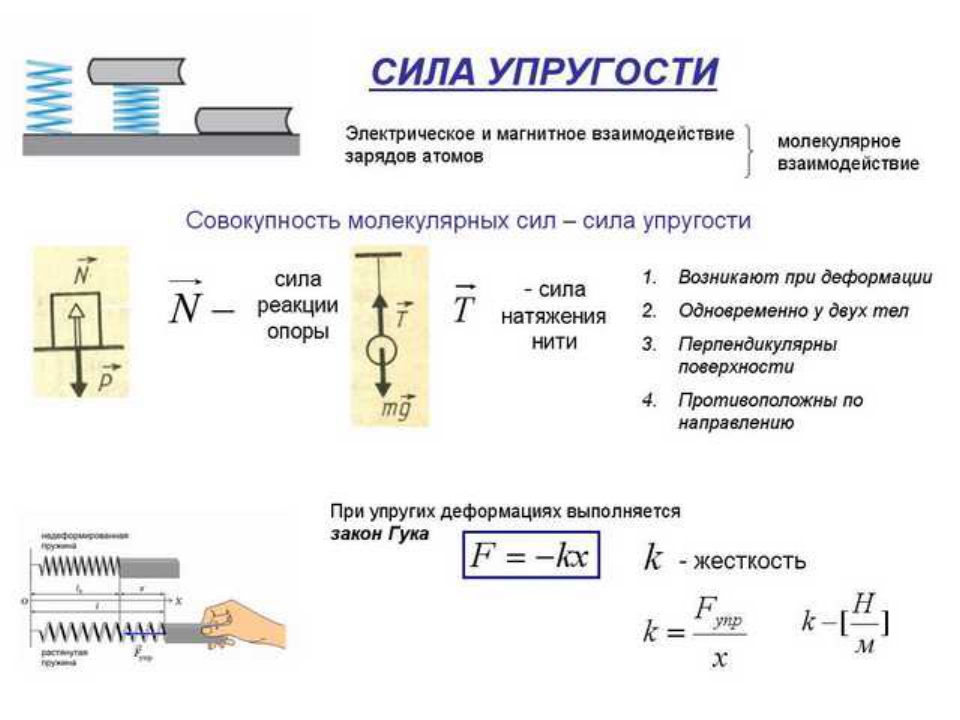
3 | Сила упругости | Fупр., N | Н | кН, мН | , (Н/м) – жёсткость материала, | Сила, с которой опора или подвес действуют на тело. | 1.Направлена перпендикулярно плоскости опоры противоположно силе, вызывающей деформацию тела, из середины соприкасающихся поверхностей. |
4 | Вес тела | P | Н | кН, мН | P = N или Fупр Если тело покоится или движется равномерно и прямолинейно, то | Сила, с которой тело действует на опору или растягивает подвес. | 1.Направлена перпендикулярно плоскости опоры противоположно силе упругости из середины соприкасающихся поверхностей. 2. Приложена к телу, которое давит на опору или растягивает подвес. |
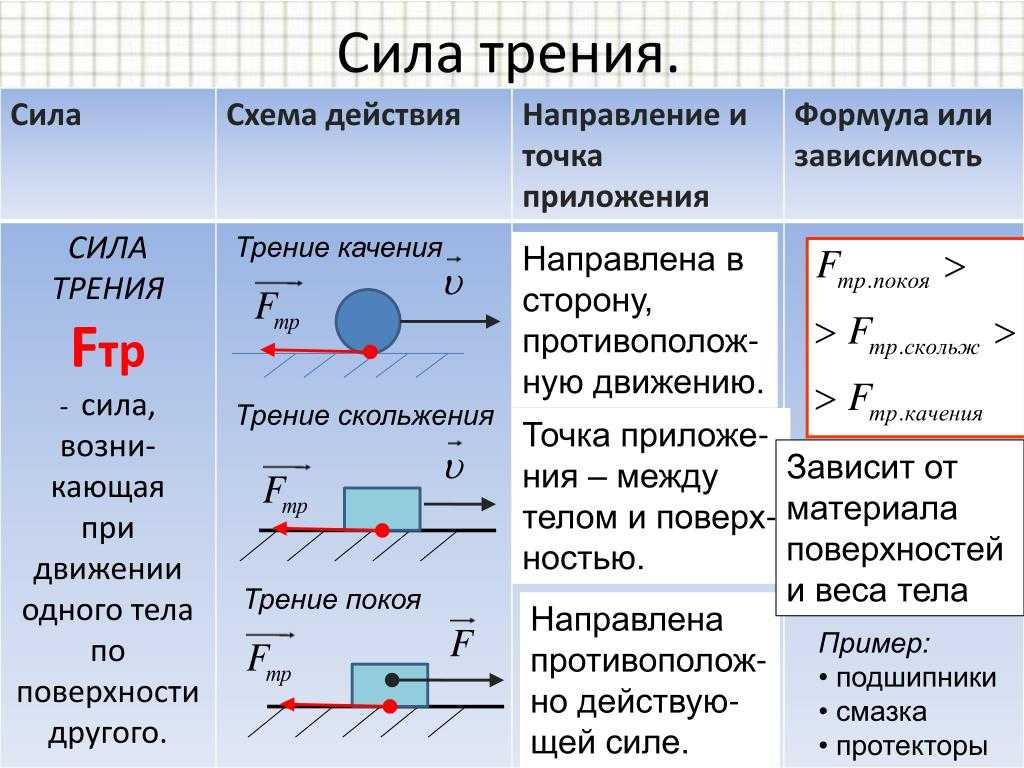
5 | Сила трения | FТР. | Н | кН, мН | , – коэффициент трения, – сила реакции опоры. Если тело покоится или движется равномерно и прямолинейно, то . | Сила, препятствующая движению тел. | 1. Направлена против движения тела из середины соприкасающихся поверхностей. 3. Виды трения: трение покоя, трение скольжения, трение качения. |
6 | Равнодействующая сил | F или R | Н | кН, мН | 1.Если силы, действующие на тело, направлены в одном направлении, то F = F1 + F2. 3. Если силы, действующие на тело, направлены в противоположных направлениях и равны по модулю, то F = 0. | Геометрическая сумма всех сил, действующих на тело. | 1.Чтобы тело изменило свою скорость относительно Земли надо, чтобы равнодействующая сил не равнялась нулю (F≠0). 2. Если равнодействующая сил равна 0, то тело либо покоится, либо движется равномерно и прямолинейно. |
Таблица характеристик физических величин по теме: «Виды сил». | Методическая разработка по физике (7 класс):
Таблица характеристик физических величин по теме: «Виды сил».
№ п/п | Название физ. величины | Буква | Ед. | Другие ед. измер. | Формула | Определение | Свойства и особенности |
1 | Сила | F, P, N, T | Н | кН, мН | Зависит от вида силы | Векторная физ. величина, являющаяся причиной изменения скорости движения тела. | 1.Имеет числовое значение (модуль), точку приложения и направление действия. 2.Можно измерить с помощью динамометра. |
2 | Сила тяжести | FТ | Н | кН, мН | , | Сила, с которой Земля притягивает к себе тело. | 1.Всегда направлена вертикально вниз из центра тела. 3. Приложена к самому телу. |
3 | Сила упругости | Fупр., N | Н | кН, мН | , (Н/м) – жёсткость материала, | Сила, с которой опора или подвес действуют на тело. | 1.Направлена перпендикулярно плоскости опоры противоположно силе, вызывающей деформацию тела, из середины соприкасающихся поверхностей. |
4 | Вес тела | P | Н | кН, мН | P = N или Fупр Если тело покоится или движется равномерно и прямолинейно, то | Сила, с которой тело действует на опору или растягивает подвес. | 1.Направлена перпендикулярно плоскости опоры противоположно силе упругости из середины соприкасающихся поверхностей. 2. Приложена к телу, которое давит на опору или растягивает подвес. |
5 | Сила трения | FТР. | Н | кН, мН | , – коэффициент трения, – сила реакции опоры. Если тело покоится или движется равномерно и прямолинейно, то . | Сила, препятствующая движению тел. | 1. Направлена против движения тела из середины соприкасающихся поверхностей. 3. Виды трения: трение покоя, трение скольжения, трение качения. |
6 | Равнодействующая сил | F или R | Н | кН, мН | 1.Если силы, действующие на тело, направлены в одном направлении, то F = F1 + F2. 3. Если силы, действующие на тело, направлены в противоположных направлениях и равны по модулю, то F = 0. | Геометрическая сумма всех сил, действующих на тело. | 1.Чтобы тело изменило свою скорость относительно Земли надо, чтобы равнодействующая сил не равнялась нулю (F≠0). 2. Если равнодействующая сил равна 0, то тело либо покоится, либо движется равномерно и прямолинейно. |
Таблица характеристик физических величин по теме: «Виды сил».
№ п/п | Название физ. величины | Буква | Ед. измер. в СИ | Другие ед. измер. | Формула | Определение | Свойства и особенности |
1 | Сила | ||||||
2 | Сила тяжести | ||||||
3 | Сила упругости | ||||||
4 | Вес тела | ||||||
5 | Сила трения | , . | |||||
6 | Равнодействующая сил |
Урок 09. Лабораторная работа № 01. Исследование движения тела под действием постоянной силы (отчет)
Лабораторная работа №1
Исследование зависимости силы трения скольжения от веса тела
Цель работы: 1. выяснить, зависит ли сила трения скольжения от силы нормального давления, если зависит, то как.
2. Определить коэффициент трения дерева по дереву.
Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.
Выполнение работы.
1. Определили цену деления шкалы динамометра.
Цена деления динамометра:
(2H-1H)/10 дел = 0,1Н/дел
2. Определили массу бруска. Сначала подвесив брусок к динамометру нашли вес бруска Pбруска=0,7Н
Зная, что P=mg и g=10м/с2 получим mбруска=P/g
mбруска=0,7Н/10м/с2=0,07кг
Определяем общий вес тела (силу нормального давления по формуле:
Р=N=(m1+m2)∙g
1.Р=N=(0,07кг+0,1кг)∙10м/с2=1,7Н
2.Р=N=(0,07кг+0,2кг)∙10м/с2=2,7Н
3.Р=N=(0,07кг+0,3кг)∙10м/с2=3,7Н
4.Р=N=(0,07кг+0,4кг)∙10м/с2=4,7Н
5.Р=N=(0,07кг+0,5кг)∙10м/с2=5,7Н
Провели измерения силы трения.
5. Подготовили таблицу для записи результатов измерений и вычислений:
|
№ опыта |
Масса бруска, |
Масса груза, |
Общий |
Сила трения, |
Коэффициент трения, |
Среднее значение |
|
1 |
0,07 |
0,1 |
1,7 |
0,4 |
|
|
|
2 |
0,2 |
2,7 |
0,6 |
|
||
|
3 |
0,3 |
3,7 |
0,8 |
|
||
|
4 |
0,4 |
4,7 |
1 |
|
||
|
5 |
0,5 |
5,7 |
1,2 |
|
6. Из опыта видим, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения)
Из опыта видим, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения)
7. В каждом опыте рассчитали коэффициент трения по формуле: .
μ=0,4Н/1,7Н=0,235
μ=0,8Н/3,7Н=0,216
μ=1,0Н/4,7Н=0,213
μ=1,2Н/5,7Н=0,211
Результаты расчётов занесли в таблицу.
8. По результатам измерений построили график зависимости силы трения от силы нормального давления:
Определили по графику средние значения силы трения и силы нормального давления:
N=3Н
Fтр=0,68Н
Вычислили среднее значение коэффициент трения:
μср=0,68Н/3Н=0,227
Вывод: мы определили, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения). Коэффициент трения дерева по дереву получился равен 0,227
Ответы на контрольные вопросы.
1. Что называется силой трения?
Что называется силой трения?
Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.
2. Какова природа сил трения?
Сила трения – это сила электромагнитной природы.
3. Назовите основные причины, от которых зависит сила трения?
Возникновение силы трения объясняется двумя причинами:
1) Шероховатостью поверхностей
2) Проявлением сил молекулярного взаимодействия.
4. Перечислите виды трения.
Силы трения подразделяются на силы трения покоя, скольжения, качения.
5. Можно ли считать явление трения вредным? Почему?
Силовые таблицы
Имена и тому подобное
Пожалуйста, введите ваши имена ниже.
Студент 1 = войдите в систему
Студент 2 = войдите в систему
Студент 3 = войдите в систему
И имя присутствующего лаборанта:
Инструктор лаборатории = пожалуйста, войдите в систему
Введение
Таблица Сил позволяет нам манипулировать и измерять влияние векторных величин.
Голы
Цель этой лабораторной работы — получить полное представление о сложении векторов. Это достигается за счет использования таблиц сил для установления равновесия для частицы и сопоставления этого состояния равновесия с математикой сложения векторов. Обсуждаются два метода сложения векторов: графический и аналитический.
Проверка оборудования
Убедитесь, что на вашей станции есть все перечисленные ниже элементы. Если нет, проверьте еще раз, а затем поговорите со своим лаборантом.
Знакомство с векторами
Физические величины, для описания которых требуется как величина, так и направление, являются векторными величинами. Отличным примером векторной величины является скорость ветра. Поскольку ветер может дуть в определенном направлении и с определенной скоростью, для описания этой физической величины нам потребуется использовать как величину, так и направление.
Interactive Task
На приведенной ниже карте Нью-Йорка манипулируйте вектором ветра (перетаскивая кончик стрелки), пока не получите скорость ветра 10 миль в час, направленную точно в северо-восточном направлении.
Задача выполнена
Добавление векторов
Векторы должны добавляться по специальным правилам, учитывающим обе части описания.
Ниже показаны два синих вектора и сумма векторов, показанная пунктирной черной линией. Попробуйте манипулировать синими векторами и посмотреть, что произойдет с суммой.
О таблице Force
Давайте разберемся, как именно работает таблица сил. Масса помещена в каждую сковорода (каждая сковорода имеет массу 50 г). На эту массу действует сила гравитации, равная ее массе, умноженной на $g$. Эта сила действует в вертикальном направлении. Чтобы перенаправить силу, чтобы она действовала в горизонтальном направлении (т.е. параллельно поверхности стола), используются хорды и шкивы. Таким образом, натяжения от хорд на кольце в центре равны по величине силе тяжести на поддоне + масса: $$T_1 = m_1 g$$ Прикрепление к столу нескольких систем поддон/шкив позволяет тянуть на кольце с разным натяжением в разные стороны.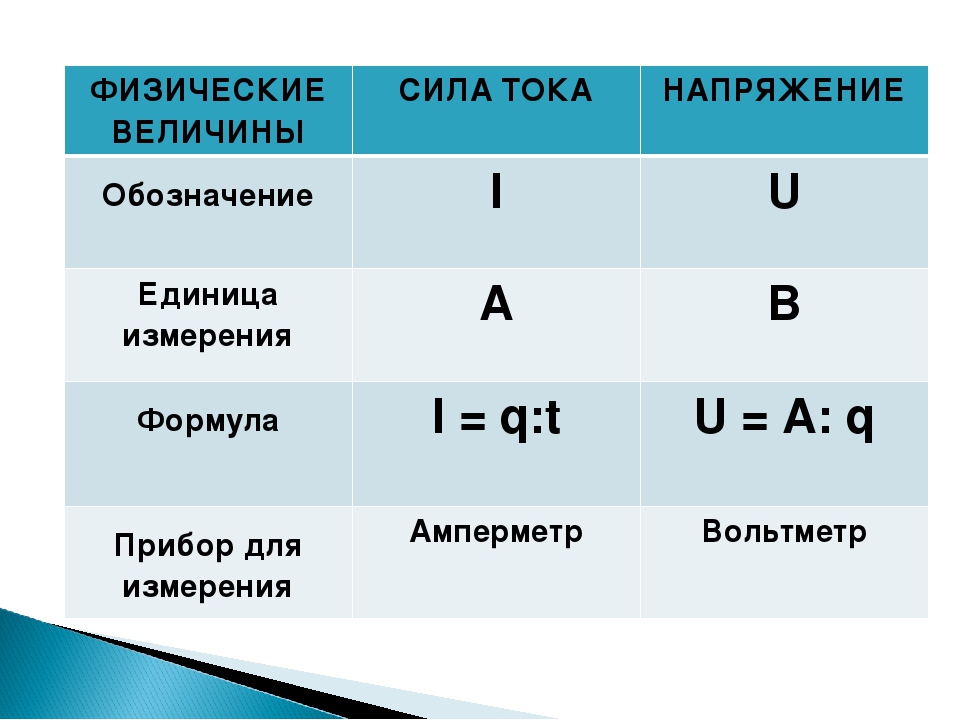
Чему будет равно натяжение в ньютонах, если к лотку массой 50 г прикрепить груз массой 20 г?
Натяжение [Н] = пожалуйста, войдите в систему
Инструкция по применению:
- Центральное кольцо имеет спицы, соединяющие внутренний и внешний края. При подсоединении шнуров следите за тем, чтобы крючки не зацепились за спицу. В этом случае шнур не будет радиальным. Также всякий раз, когда вы меняете положение шкива, проверяйте, чтобы шнур оставался радиальным.
- Убедитесь, что при установке шкива оба края зажима плотно прилегают к краю силового стола. Убедитесь, что шнур находится на шкиве.
- Есть два теста на равновесие.
- Первый тест — двигать штифт вверх и вниз и наблюдать за кольцом. Если он движется вместе со штифтом, система НЕ находится в равновесии, и силы необходимо отрегулировать.
- Второй тест – удалить штифт. Однако делать это следует в два этапа. Сначала просто поднимите его, но держите в кольце, чтобы предотвратить большие движения.
 Если движения нет, уберите его полностью. Если кольцо остается в центре, то система находится в равновесии.
Если движения нет, уберите его полностью. Если кольцо остается в центре, то система находится в равновесии.
Расшир. 1: Чувствительность прибора
Давайте измерим, насколько точны таблицы силы.
- Расположите две системы шкивов, поддон 1 под углом 0° и поддон 2 под углом 180°.
- В форму 1 поместите 50 граммов. В кастрюлю 2 также положите 50 гр.
- Теперь добавьте в чашу 2 1 грамм и проверьте равновесие. Скорее всего, он все еще находится в равновесии, верно?
- Найдите максимальную массу, которую вы можете поместить на чашу 2, сохраняя при этом экспериментальное равновесие.
Запишите это значение ниже. Это чувствительность к весу силового стола.
Чувствительность [g] = пожалуйста, войдите в систему
Какие факторы могут способствовать этой чувствительности?
Результат против. Эквилибрант
Следует помнить, что сила, необходимая для уравновешивания системы, равна не равнодействующей весов, а отрицательному вектору этого вектора, также называемого уравновешивающим.
Ответ:
Если равнодействующая двух систем масс/тарелок указывает в направлении 234°, измеренном против часовой стрелки (CCW) от линии 0°, в каком направлении должна указывать точка равновесия?
Направление равновесия [°] = пожалуйста, войдите в систему
Эксперимент 2: Симметричное расположение
- Используя приведенный ниже генератор чисел, выберите две начальные массы и направления.
- Установите две чаши и системы массы на основе этих значений.
- Экспериментально сбалансировать систему. (т. е. не выполняя никаких математических или аналитических операций, найдите третью систему панорамирования/массы, которая уравновесит первые две.)
Масса 1: Икс грамм
Направление 1: Икс °
Масса 2: Икс грамм
Направление 2: Икс °
Масса, необходимая для балансировки Системы [г] = пожалуйста, войдите в систему
Используйте приведенную ниже смоделированную таблицу сил, чтобы предсказать, какая масса вам потребуется, и сравните ее со значением, которое вы нашли экспериментально. 2$)
2$)
На сколько граммов ваш эксперимент отличался от этой симуляции?
Разницаграммов = пожалуйста, войдите в систему
Сообщите о разнице между тем, что вы измерили экспериментально, и тем, что предсказывало моделирование. Находятся ли они в пределах ожидаемой чувствительности прибора?
Экспл. 3: Найдите функцию
Установите таблицу, как показано. Поместите 50 грамм в формы 1 и 2. Сделайте оба угла $b$ равными 5 градусам.
- Экспериментально определить массу, необходимую для подвешивания к чаше 3, чтобы привести систему в равновесие
- Повторите измерение, каждый раз изменяя углы $b$ с шагом 5°, пока не достигнете 80°. (Каждый раз меняйте положение обеих чаш 1 и 2)
- Скомпилируйте результаты в таблицу, подобную этой.
| Уголок | Масса поддона 3 системы |
|---|---|
| 5° | $P_3$ mass |
| 10° | $P_3$ mass |
| ⋮ | ⋮ |
| 80° | $P_3$ mass |
We would expect there to be some математическое соотношение между углом $b$, массой $P_1$ и $P_2$ и массой $P_3$, необходимой для балансировки системы. Используя базовую тригонометрию, определите уравнение, которое можно использовать для предсказания массы $P_3$ в зависимости от угла $b$ и массы $P_1 + P_2$ (считается константой, равной 200 г). Это должно быть что-то вроде $P_3 = C \cos(b)$, где $C$ — константа.
Используя базовую тригонометрию, определите уравнение, которое можно использовать для предсказания массы $P_3$ в зависимости от угла $b$ и массы $P_1 + P_2$ (считается константой, равной 200 г). Это должно быть что-то вроде $P_3 = C \cos(b)$, где $C$ — константа.
В поле ниже введите найденную формулу, которая позволит предсказать массу сковороды 3.
Формула: = пожалуйста, войдите в систему
Нанесите на один график экспериментальные данные из вашей таблицы вместе с аналитическим прогнозом найденной вами функции. Следуют ли они той же тенденции?
Ваши графики должны быть частью функции косинуса. Мы можем немного упростить работу с данными, нанеся вместо этого массу как функцию $\cos(b)$. Нанесите результаты (как экспериментальные, так и аналитические) с массой $P_3$ по вертикальной оси и $\cos(b)$ по горизонтальной оси. Это должна быть линейная линия:
$$\textrm{if } h(x) = \cos(x) \; \textrm{и}\; f(x) = C \cos(x)$$ $$\Вниз$$ $$f(x) = C \times h(x) \; \textrm{линейная функция}$$
Найдите наклон ваших линейных данных и сравните его с наклоном, который должен быть из вашего аналитического уравнения. Отличается ли он от наклона, полученного аналитически, меньше, чем погрешность? Подробнее об этом процессе здесь.
Отличается ли он от наклона, полученного аналитически, меньше, чем погрешность? Подробнее об этом процессе здесь.
Компоненты вектора
Наша математическая структура для работы с несколькими векторами включает использование векторных компонентов. Если у нас есть координатная ось x-y, любой вектор на этой оси может быть разложен на его компоненты x и y. Моделирование ниже показывает один вектор, разложенный на его компоненты x и y.
В: Компоненты
Какой угол (отсчитываемый против часовой стрелки от оси x) должен иметь вектор $\overrightarrow{A}$, чтобы величина компонента x была в два раза больше величины компонента y?
угол для $A_x = 2A_y$ = пожалуйста, войдите в систему
Какой угол (отсчитываемый против часовой стрелки от оси x) должен иметь вектор $\overrightarrow{A}$, чтобы величина компонента y была равна половине величина исходного вектора?
угол для $A_y = 0,5 |A|$ = пожалуйста, войдите в систему
Нам понадобятся векторные компоненты для более сложных вычислений, как показано в следующем разделе.
Несколько сил
Interactive Task
На самолет в полете действует множество сил. В самой упрощенной модели мы можем рассмотреть четыре основных фактора: вес, подъемную силу, сопротивление и тягу. Ваша задача: Сбалансировать силы на этом самолете так, чтобы самолет летел с одинаковой скоростью. (т. е. $F_\textrm{net} = 0$.)
Задача выполнена
Экспл. 4: Вернуться к силовому столу
Теперь давайте применим эти концепции к таблице сил. Если у нас действуют 3 известные силы, мы должны быть в состоянии аналитически предсказать четвертую силу, которую нужно добавить, чтобы система находилась в равновесии, то есть $F_\textrm{net} = 0$.
Нажмите синюю кнопку ниже, чтобы сгенерировать 3 набора случайных масс и направлений
Вектор $\overrightarrow{A}$
Масса 1: Икс грамм
Направление 1: Икс °
Вектор $\overrightarrow{B}$
Масса 2: Икс грамм
Направление 2: Икс °
Вектор $\overrightarrow{C}$
Масса 3: Икс грамм
Направление 3: Икс °
Теперь используйте алгебру компонентов для вычисления четвертого вектора, $\overrightarrow{D}$, добавление которого в систему приведет к равновесию
Уравнение, которое вы, по сути, пытаетесь решить: $\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}+\overrightarrow{D}=0$
После получения ответа введите компоненты вектора в поля ниже
.
$|D_x| = $ = пожалуйста, авторизуйтесь
$|Д_у| = $ = пожалуйста, войдите
Используйте триггер, чтобы преобразовать ответ обратно в формат величин и градусов. Добавьте все четыре системы масса/чашка (3 из приведенных выше, четвертая из вашего прогноза) в таблицу и убедитесь, что прогноз действительно уравновешивает систему.
Расскажите подробности этого расчета и сравните результаты анализа с результатами эксперимента.
Нарисуйте векторную диаграмму, показывающую расположение стола.
Готово?
Сначала проверьте оборудование на своей станции. Пожалуйста, верните станцию в аккуратное и упорядоченное состояние, как показано на этом рисунке. Сделав это, установите флажок ниже.
Да, наша станция чистая, аккуратная и полная.
Теперь нажмите эту кнопку ниже, чтобы просмотреть заполненный рабочий лист. На следующей странице вы можете отправить его себе по электронной почте, чтобы вести учет выполнения лабораторной работы.
Как пользоваться таблицей сил
Таблица сил иллюстрирует векторное сложение сил.
Смотреть видео:
Обучаемые темы:
- Статическое равновесие
- Ускорение
- Бесплатные диаграммы тела
Теория:
Если объект находится в статическом равновесии, он находится в неизменном состоянии. Второй закон Ньютона говорит нам, что Ф = мА ; результирующая сила F , действующая на объект массой м , заставит объект ускориться с a . Если объект ускоряется, то он явно не находится в неизменном состоянии! Следовательно, одно из условий статического равновесия состоит в том, что на объект не может действовать результирующая сила, иначе он будет ускоряться. Конечно, это не означает, что на объект вообще не может воздействовать никакая сила — для статического равновесия требуется только, чтобы сумма векторов всех отдельных сил равнялась нулю ,
∑F = 0
Другими словами, результирующая сила должна быть равна нулю, когда на объект действуют несколько отдельных сил. Поскольку сила является вектором, мы должны рассматривать компоненты вектора x , y и z отдельно. Истинное условие статического равновесия состоит в том, что
Поскольку сила является вектором, мы должны рассматривать компоненты вектора x , y и z отдельно. Истинное условие статического равновесия состоит в том, что
∑F x = 0; ∑F y = 0; ∑F z = 0
Рассмотрим простой пример, показанный ниже. Две веревки тянут объект с одинаковой силой, но в противоположных направлениях. Из повседневного опыта мы знаем, что сила двух веревок компенсирует друг друга, и, следовательно, объект не будет двигаться — это пример статического равновесия.
Рисунок 1
Можно показать, что условие статического равновесия выполняется как для направлений x , так и для направлений y . Например, в направлении x
∑F x = (50 Н)(cos45°) – (50 Н)(cos45°) = 0
, где разница в + и – знаков, потому что сила справа тянет в +x направлении, а сила слева тянет в -x направление. Если вы сделаете то же самое для направления y, вы также обнаружите, что [SUM] F y = 0 . Поскольку здесь нет результирующей силы, выполняется условие статического равновесия.
Если вы сделаете то же самое для направления y, вы также обнаружите, что [SUM] F y = 0 . Поскольку здесь нет результирующей силы, выполняется условие статического равновесия.
Аппарат:
- Силовой стол
- Различные веса
- Массовый баланс
Процедура:
Силы прикладывают к маленькому кольцу на силовом столе с помощью веревок, к которым можно прикрепить различные грузы. Общая сила, действующая на струну, — это просто вес грузов, свисающих с конца, плюс вес самого подвеса. Следовательно,
F на струне = m подвеска g + m гири
где g = 9,81 м/с 2 ускорение силы тяжести на Земле. Обратите внимание, что величину силы, действующей на каждую струну, можно изменить, добавляя или удаляя разные грузы, а направление силы можно менять, перемещая рычаги силовой машины.
Штифт в центре служит точкой отсчета для центрирования кольца, а также предотвращает падение кольца со стола в ситуациях сильного дисбаланса.
Использование трех веревок вместо четырех — более простой способ провести этот эксперимент, поэтому снимите одну из четырех вешалок. Три струны изначально должны быть примерно симметричны. Убедитесь, что струны правильно отцентрованы на кольце (т. е. сдвиньте узлы так, чтобы струны не перекручивались вокруг кольца). Затем нагрузите три вешалки тремя разными весами (примечание: старайтесь использовать довольно тяжелые веса; тогда эксперимент пройдет лучше).
Скорее всего, вы обнаружите, что кольцо не будет отцентровано. Это означает, что оно не находится в статическом равновесии — если бы силы трех струн точно уравновешивались, то кольцо было бы идеально отцентровано на столе. Вместо этого его тянет то в одну, то в другую сторону, потому что он чувствует результирующую силу; если бы центрального штифта не было, кольцо ускорилось бы сразу же после конца таблицы сил в соответствии со вторым законом Ньютона
Рис. 1: Таблица силы с маркировкой
Перемещайте струны до тех пор, пока кольцо не освободится от штифта и не окажется почти в центре.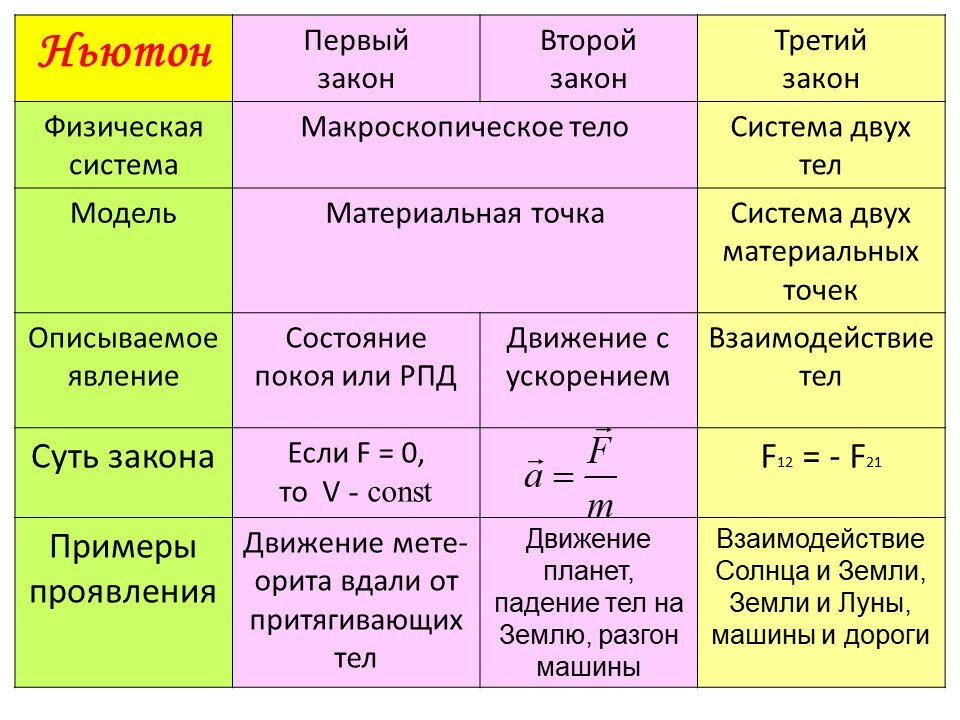 Аккуратно постучите по силовому столу, чтобы временно устранить трение, что позволит кольцу более свободно перемещаться в новое положение. Повторно отрегулируйте положение струн и повторяйте постукивание, пока кольцо не будет правильно отцентровано и останется там. Теперь кольцо находится в статическом равновесии, поскольку векторные компоненты всех трех сил компенсируют друг друга – на кольцо не действует результирующая сила.
Аккуратно постучите по силовому столу, чтобы временно устранить трение, что позволит кольцу более свободно перемещаться в новое положение. Повторно отрегулируйте положение струн и повторяйте постукивание, пока кольцо не будет правильно отцентровано и останется там. Теперь кольцо находится в статическом равновесии, поскольку векторные компоненты всех трех сил компенсируют друг друга – на кольцо не действует результирующая сила.
Запишите общий вес каждой подвески (включая саму подвеску) и направление каждой струны, которое соответствует углу, указанному в таблице сил. Обязательно пронумеруйте каждую струну и ее соответствующий вес и угол. Сделайте набросок вашей таблицы сил.
Лаборатория 1 — Таблица Force
Введение
Все измеримые величины могут быть классифицированы либо как скаляр, либо как вектор. У скаляра есть только величина, а у вектора есть и величина, и направление. Примерами скалярных величин являются количество учеников в классе, масса объекта или скорость объекта, и это лишь некоторые из них. Скорость, сила и ускорение являются примерами векторных величин. Утверждение «автомобиль движется со скоростью 60 миль в час» говорит нам о том, как быстро движется автомобиль, но не о том, в каком направлении он движется. В этом случае мы знаем, что скорость автомобиля равна 60 км/ч. С другой стороны, утверждение «автомобиль, движущийся со скоростью 60 миль в час строго на восток» дает нам не только скорость автомобиля, но и направление. В этом случае скорость автомобиля составляет 60 миль в час строго на восток, и это векторная величина. В отличие от скалярных величин, которые складываются арифметически, сложение векторных величин включает в себя как величину, так и направление. В этой лабораторной работе мы будем использовать таблицу сил для определения равнодействующей двух или более векторов сил и научимся складывать векторы, используя как графические, так и аналитические методы.
Скорость, сила и ускорение являются примерами векторных величин. Утверждение «автомобиль движется со скоростью 60 миль в час» говорит нам о том, как быстро движется автомобиль, но не о том, в каком направлении он движется. В этом случае мы знаем, что скорость автомобиля равна 60 км/ч. С другой стороны, утверждение «автомобиль, движущийся со скоростью 60 миль в час строго на восток» дает нам не только скорость автомобиля, но и направление. В этом случае скорость автомобиля составляет 60 миль в час строго на восток, и это векторная величина. В отличие от скалярных величин, которые складываются арифметически, сложение векторных величин включает в себя как величину, так и направление. В этой лабораторной работе мы будем использовать таблицу сил для определения равнодействующей двух или более векторов сил и научимся складывать векторы, используя как графические, так и аналитические методы.
Обсуждение принципов
Векторное представление
Как упоминалось выше, векторная величина имеет как величину, так и направление. Вектор обычно представляется стрелкой, где направление стрелки представляет собой направление вектора, а длина стрелки представляет величину вектора. В трехмерном пространстве вектор, направленный за пределы страницы (или вдоль положительной оси z ), представлен (кругом с точкой внутри него), а вектор, направленный внутрь страницы (или вдоль отрицательной оси 9).0425 z -ось) представлена (кружком с символом × внутри). В математических уравнениях вектор представляется как
Вектор обычно представляется стрелкой, где направление стрелки представляет собой направление вектора, а длина стрелки представляет величину вектора. В трехмерном пространстве вектор, направленный за пределы страницы (или вдоль положительной оси z ), представлен (кругом с точкой внутри него), а вектор, направленный внутрь страницы (или вдоль отрицательной оси 9).0425 z -ось) представлена (кружком с символом × внутри). В математических уравнениях вектор представляется как
A
. В некоторых учебниках вектор представлен жирной буквой A . Отрицательным вектором
A
является вектор той же длины, но с направлением, противоположным вектору
A
. См. рис. 1 ниже.
Рисунок 1 : Векторы в виде стрелок
Декартова система координат используется для графического представления векторов. Хвост вектора помещается в начало координат, а направление вектора определяется углом θ (тета) между положительной осью x и вектором, как показано на рис. 2.
Хвост вектора помещается в начало координат, а направление вектора определяется углом θ (тета) между положительной осью x и вектором, как показано на рис. 2.
Рисунок 2 : Графическое представление вектора
Компоненты векторов
Важным приемом математической работы с векторами является их разбиение на 9 частей.Компоненты 0425 x и и . В этом примере мы рассмотрим вектор положения
A
, направленный под углом 30° к оси + x и имеющий величину 8,0 миль. Из головы вектора проведите линию, перпендикулярную оси x , и вторую линию, перпендикулярную оси y . Мы называем эти линии проекциями вектора на оси x и y . Проекция вектора на 9Ось 0425 y дает величину компонента x вектора (зеленая линия на рис. 3 ниже), а проекция вектора на ось x дает величину компонента y (красная линия на рис. 3).
3).
Рисунок 3 : Разбиение вектора на компоненты x и y
Обратите внимание, что зеленые и красные линии на диаграмме выше образуют две стороны прямоугольника с вектором в качестве диагонали прямоугольника. Мы также можем посмотреть на описанную выше ситуацию двумя другими способами, как показано на рис. 4.
Рисунок 4 : Представление компонентов вектора
На рис. 4а у нас есть прямоугольный треугольник, в котором вектором является гипотенуза, сторона, параллельная оси х (зеленая стрелка), является х -компонентой вектора, а сторона параллельна y -ось (красная стрелка) – это y -компонент вектора. Рисунок 4b математически эквивалентен рис. 4a, но теперь
A y
рисуется вдоль оси y .
Нахождение компонентов по величине и направлению вектора
Мы знаем направления векторов
A x
и
A y
, но чтобы найти их величины, нам нужно использовать некоторые тригонометрические тождества.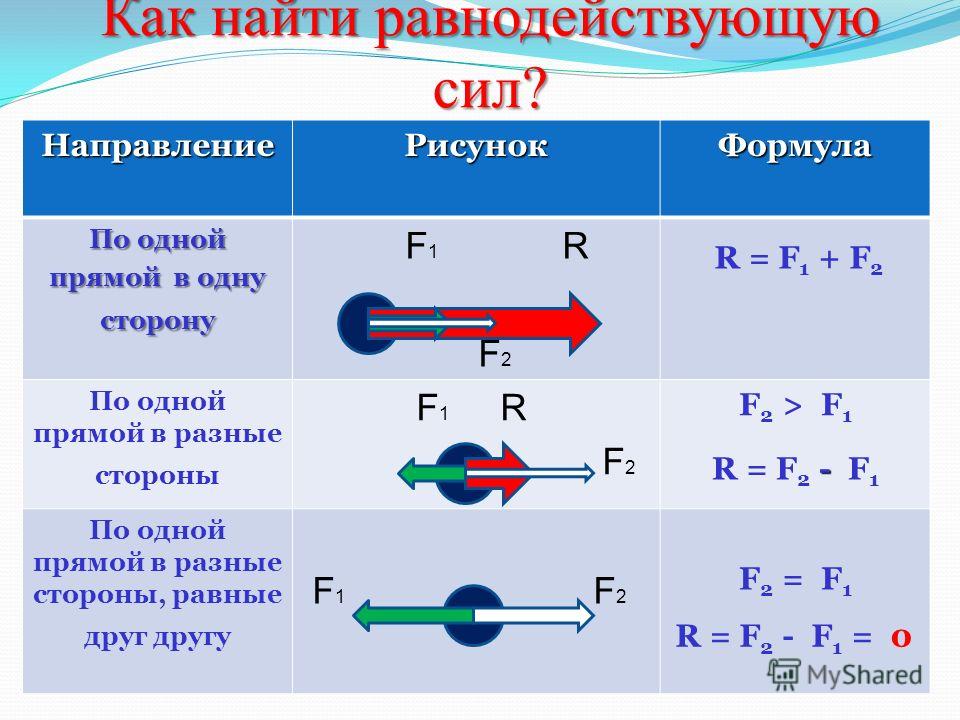 На рис. 5 гипотенуза представляет величину вектора
На рис. 5 гипотенуза представляет величину вектора
A
, а две другие стороны прямоугольного треугольника представляют x и y компоненты вектора
A
.
Рисунок 5 : Нахождение компонентов вектора
Для любого прямоугольного треугольника справедливы следующие тригонометрические тождества.
(1)
COS θ =
| Прилегающая сторона |
| Hypotenuse |
(2)
47.
(2)
47.
8
(2).0155
Здесь смежная сторона относится к стороне, примыкающей к углу θ , а противоположная сторона относится к стороне, противоположной углу θ . Рассмотрим установку на рис. 5а. Используя определения в уравнениях.
Рассмотрим установку на рис. 5а. Используя определения в уравнениях.
cos θ =
| соседняя сторона |
| гипотенуза |
и
θ 9004 =| противоположная сторона |
| гипотенуза |
, имеем
( 3 )
cos θ = or A x = A cos θ
( 4 )
sin θ = or A y = A sin θ
Однако на рис. 5b угол θ определяется иначе. В таком случае
( 5 )
sin θ = или A x = A sin θ
( 6 )
cos θ = или A y = A cos θ
Распространенной ошибкой является предположение, что
A x
всегда является компонентом косинуса, а
A y
всегда является компонентом синуса. Однако это будет зависеть от того, какой из двух углов прямоугольного треугольника определяется как θ . Обратите внимание, что
Однако это будет зависеть от того, какой из двух углов прямоугольного треугольника определяется как θ . Обратите внимание, что
A x
примыкает к углу θ на рис. 5а, а на рис. 5б
A y
примыкает к углу θ . На рис. 3 звездная величина
A
составляет 8,0 миль, а ее направление на 30° выше оси + x . Таким образом, вы находите величины
A x
и
A y
следующим образом:
( 7 )
A x = A cos θ = 8,0 миль * cos(30°) = 6,9 миль
( 8 )
A y = A sin θ = 8,0 миль * sin(30°) = 4 мили
Другими словами, если бы вы шли пешком, вы могли бы пройти 6,9 мили строго на восток (вдоль оси + x ), а затем 4 мили на север (вдоль оси + y ). Это привело бы вас к тому же месту назначения, если бы вы прошли 8 миль в направлении, которое составляет 30° от оси + x .
Это привело бы вас к тому же месту назначения, если бы вы прошли 8 миль в направлении, которое составляет 30° от оси + x .
Нахождение модуля и направления вектора по компонентам
Если вы не знаете величину или направление вектора, но знаете расстояния, пройденные в направлениях x и y , вы можете использовать теорему Пифагора, чтобы найти гипотенузу, то есть общее пройденное расстояние.
( 9 )
A 2 = A x 2 + A y 2 или A =
| А x 2 + А у 2 |
Направление вектора можно найти с помощью одного из следующих уравнений.
( 10 )
θ = sin −1
( 11 )
θ = cos −1
( 12 )
θ = tan −1
Some Basic Properties of Vectors
Два вектора равны, если они имеют одинаковую величину и направление.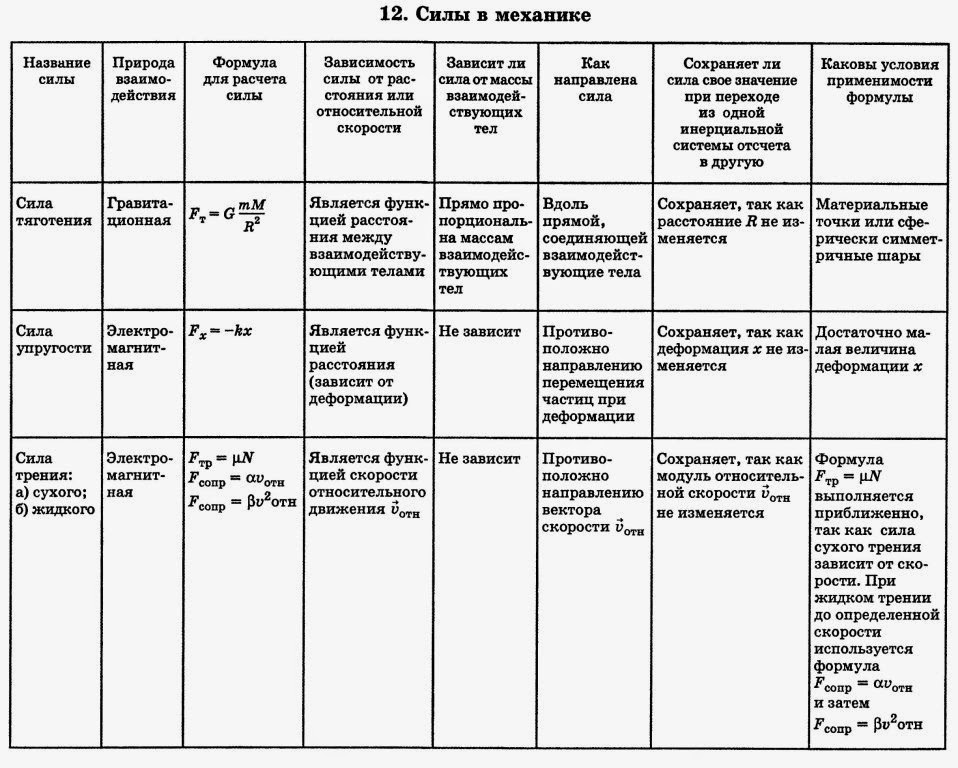 Итак, на бумаге вы можете переместить вектор в другое место, но пока вы сохраняете ту же длину и ориентацию стрелки, два вектора будут равны. На рис. 6а два вектора
Итак, на бумаге вы можете переместить вектор в другое место, но пока вы сохраняете ту же длину и ориентацию стрелки, два вектора будут равны. На рис. 6а два вектора
A
и
B
имеют одинаковую длину и ориентацию. Негатив вектора имеет ту же длину, но с обратным направлением, как показано на рис. 6b. Вектор, умноженный на скаляр, будет вектором того же направления, что и исходный вектор, но с другой величиной. На рис. 6с p — это скаляр. Вектор
B
имеет то же направление, что и
A
, но длиннее в 9 раз.0425 p с p больше 1. Если бы p было меньше 1, то
B
было бы короче, чем
A
.
Рисунок 6 : Свойства вектора
Графический метод сложения векторов
Рассмотрим два вектора
A
и
B
, ориентированные, как показано на рис. 7. Нам нужно найти сумму и разность двух векторов. В отличие от добавления скалярных величин, в этом случае нам нужно учитывать как величину, так и направление.
Рисунок 7 : Два вектора
Чтобы добавить два вектора, сдвиньте второй вектор так, чтобы его хвост оказался в начале первого вектора. Сумма двух векторов представляет собой вектор, проведенный из хвоста первого вектора в начало второго вектора. На рис. 8а
B
перемещен так, что его хвост находится в голове
A
. Обратите внимание, что направление
Обратите внимание, что направление
B
не меняется. Красная стрелка дает сумму
Р = А + В
. Сложение является коммутативным, поэтому вы получите тот же результат, переместив
A
в начало
B
. Чтобы найти разность двух векторов, мы можем взять отрицательное значение второго вектора и добавить его к первому вектору, выполнив шаги, описанные выше для сложения. Другими словами,
A − B = A + (−B)
. Это показано на рис. 8b.
Рисунок 8 : Сумма и разность двух векторов
Аналитический метод сложения векторов
Сложение или вычитание векторов включает в себя разбиение векторов на компоненты и последующее сложение или вычитание компонентов x и y по отдельности.
(13)
R x = A x + B x
(14)
R Y = A Y + B Y = A Y + B Y Y + B Y0005 Теперь, используя уравнения. A 2 = A x 2 + A y 2 or A = and θ = tan −1 we can find the magnitude and direction of the resultant vector Р . Этот процесс будет таким же, если вы добавляете более двух векторов или вычитаете векторы. A x = 1 and B x = 3 giving A x + B x = 4; A y = −3 и B y = 2 , что дает A y + B 3 y = 903. Эти значения согласуются с компонентами x и y красной стрелки на рис. 5а. В случае вычитания А х – В х = -2; А г – В г = -5 . Эти значения согласуются с компонентами x и y красной стрелки на рис. 5б. В этой лабораторной работе вы будете иметь дело с векторами силы. Цель этого эксперимента состоит в том, чтобы найти равновесие одной или нескольких известных сил с помощью таблицы сил и сравнить результаты с результатами, полученными аналитическим методом. Имея два вектора силы, вы определите третью силу, которая установит равновесие в системе. Рисунок 9 : Таблица сил Висячие массы будут создавать силу натяжения в каждой струне. Массы прямо пропорциональны гравитационной силе (о которой вы узнаете позже в курсе). Сила натяжения каждой струны равна силе тяжести. Рисунок 10 : Таблица сил с осями 1 Воспользуйтесь пузырьковым уровнем, чтобы проверить горизонтальность круглой платформы. При необходимости используйте регулировочные винты для выполнения необходимых регулировок. 2 Вам даны два груза массой 150 г, которые нужно расположить под углами 60° и 300°. Помните, что подвески для гирь имеют массу 50 г каждая, и это должно быть включено как часть массы для подвешивания. Вы определите величину (в ньютонах) и угол третьей силы, необходимые для уравновешивания сил этих двух масс. 3 Представьте эти силы в виде векторов на диаграмме в рабочем листе. Обязательно включите оси. Каждый вектор на диаграмме должен быть нарисован так, чтобы чем больше вектор, тем большую силу он представлял. 4 Вычислите компоненты x и y (с точностью до тысячной ньютона) и введите эти значения в Таблицу данных 1 на рабочем листе. 5 Найдите компоненты равнодействующей двух векторов x и y и введите эти значения в Таблицу данных 1 на рабочем листе. 6 Теперь вычислите компоненты равновесия этих двух векторов x и y и введите эти значения в рабочий лист. 7 Используя уравнения А 2 = А x 2 + А у 2 or A = and θ = tan −1 вычислить величину и угол равновесия. Введите эти значения в рабочий лист. Это расчетное значение третьей силы. 8 Добавьте этот вектор на диаграмму, чтобы представить третью силу. 9 Расположите третью струну под углом, который вы определили в шаге 6, и повесьте груз (включая подвесной груз), соответствующий расчетной третьей силе, представляющей третью силу. Отрегулируйте (при необходимости) массу и угол, пока кольцо не окажется в центре. Запишите это значение в рабочий лист. 10 Сравните рассчитанные и экспериментальные значения для третьей силы, вычислив разницу в процентах между двумя значениями. См. Приложение Б. 11 Сравните расчетные и экспериментальные значения угла для третьей силы, вычислив процентную разницу между двумя значениями угла. КПП 1: 12 Подвесьте груз массой 300 г (включая подвеску) на отметке угла 150°. 13 Выберите значения для величины и угла второй массы и введите это значение в Таблицу данных 2 на рабочем листе. Вы должны использовать грузы только с шагом 10 г. Значения для F 2 должны отличаться от значений, используемых в процедуре A. Подумайте о симметрии при выборе угла для F 2 . 15 Начертите силовую диаграмму для этой установки в отведенном для этого месте рабочего листа. 16 Заполните Таблицу данных 2 и определите величину и угол для F 3 , необходимые для достижения равновесия; т. е. привести кольцо к центру силового стола. 17 Теперь подвесьте два выбранных груза под выбранными углами. Отрегулируйте одну или обе эти массы, а также их углы, если необходимо, так, чтобы кольцо располагалось по центру силового стола. A x 2 + A y 2 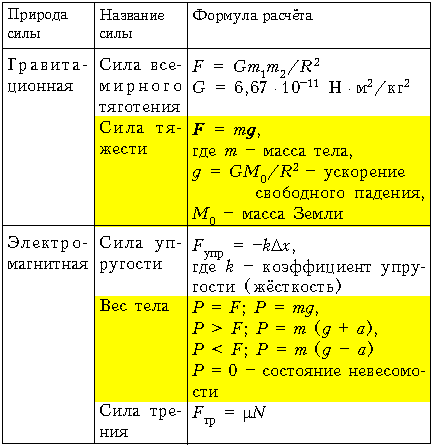 In Fig. 5a,
In Fig. 5a, Векторы силы
 В дополнение к общим свойствам векторов, обсуждавшимся до сих пор в этой лабораторной работе, следующие определения будут полезны при работе с этой лабораторной работой. Векторная сумма двух или более сил равна результат . Результирующий может, по сути, заменить отдельные векторы. уравновешивающая совокупность сил — это сила, необходимая для удержания системы в равновесии. Она равна и противоположна равнодействующей совокупности сил.
В дополнение к общим свойствам векторов, обсуждавшимся до сих пор в этой лабораторной работе, следующие определения будут полезны при работе с этой лабораторной работой. Векторная сумма двух или более сил равна результат . Результирующий может, по сути, заменить отдельные векторы. уравновешивающая совокупность сил — это сила, необходимая для удержания системы в равновесии. Она равна и противоположна равнодействующей совокупности сил. Объектив
Оборудование
Процедура
 Эта третья сила известна как уравновешивающая, и она будет равна и противоположна равнодействующей двух известных сил. Вы будете использовать таблицу сил, как показано на рис. 9., и работать с векторами силы. Силовой стол представляет собой круглую платформу, установленную на треноге. Три ножки штатива имеют регулируемые винты, которые можно использовать для выравнивания круглой платформы. Круглая платформа имеет маркировку угла в градусах на своей поверхности. Два или более шкива могут быть зажаты в любом месте вдоль края платформы. В этой лабораторной работе мы будем использовать три шкива. Три струны прикреплены к центральному кольцу, а затем каждая струна пропущена через шкив. К другому концу струн добавляются массы.
Эта третья сила известна как уравновешивающая, и она будет равна и противоположна равнодействующей двух известных сил. Вы будете использовать таблицу сил, как показано на рис. 9., и работать с векторами силы. Силовой стол представляет собой круглую платформу, установленную на треноге. Три ножки штатива имеют регулируемые винты, которые можно использовать для выравнивания круглой платформы. Круглая платформа имеет маркировку угла в градусах на своей поверхности. Два или более шкива могут быть зажаты в любом месте вдоль края платформы. В этой лабораторной работе мы будем использовать три шкива. Три струны прикреплены к центральному кольцу, а затем каждая струна пропущена через шкив. К другому концу струн добавляются массы. Например, удвоение массы удваивает силу и т. д. Когда силы уравновешены, кольцо будет расположено точно в центре стола. Когда силы не уравновешены, кольцо будет упираться в одну сторону центральной стойки. Примечание : Сила, создаваемая каждой подвешенной массой, будет равна мг , где г — ускорение свободного падения. Чтобы упростить чтение углов, предположим, что ось x проходит от отметки 180° до отметки 0°, где 0° является положительным направлением x , а ось y начинается от отметку 270° к отметке 90°, где 90° является положительным направлением y . См. рис. 10.
Например, удвоение массы удваивает силу и т. д. Когда силы уравновешены, кольцо будет расположено точно в центре стола. Когда силы не уравновешены, кольцо будет упираться в одну сторону центральной стойки. Примечание : Сила, создаваемая каждой подвешенной массой, будет равна мг , где г — ускорение свободного падения. Чтобы упростить чтение углов, предположим, что ось x проходит от отметки 180° до отметки 0°, где 0° является положительным направлением x , а ось y начинается от отметку 270° к отметке 90°, где 90° является положительным направлением y . См. рис. 10. Процедура A: Нахождение равновесия двух известных сил

A x 2 + A y 2 
Попросите вашего ассистента проверить вашу диаграмму, расчеты и настройку таблицы сил. Процедура B: Определение расположения двух неизвестных сил






 измер. в СИ
измер. в СИ

 Если движения нет, уберите его полностью. Если кольцо остается в центре, то система находится в равновесии.
Если движения нет, уберите его полностью. Если кольцо остается в центре, то система находится в равновесии.