Символ интеграл с кружком: Что означает интегральный символ с кружком? - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Что означает интегральный символ с кружком?

Это интеграл по замкнутому контуру (который топологически является кругом). Пример из Википедии:

∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>∮ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>С ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>1 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>Z ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>d ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>Z ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>= ∫ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>1 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>е ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>я т ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я е ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я т ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>d ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>т = я ∫ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>1 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>d ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>T ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>= [ т ] ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я = ( 2 π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>- 0 ) i = 2 π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>я , ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>, ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”> ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>∮ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>С ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>1 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>Z ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>d ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>Z ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>знак равно ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>∫ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>1 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>е ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>T ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>е ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>T ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>d ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>T ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>знак равно ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>∫ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>1 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>d ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>T ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>знак равно ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>[ ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>T ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>] ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>знак равно ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>( ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>- ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>0 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. ” role=”presentation”>) ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>знак равно ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>2 ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>π ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>я ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,. 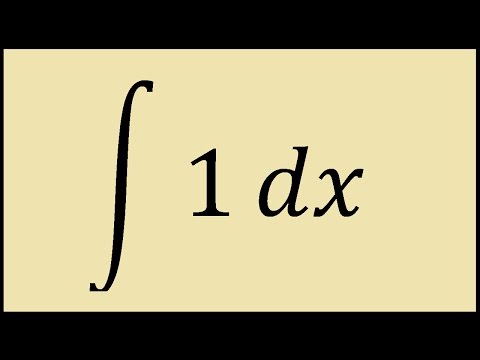” role=”presentation”>, ∮C1zdz=∫02π1eitieitdt=i∫02π1dt=[t]02πi=(2π−0)i=2πi,.” role=”presentation”>,

Перечень специальных символов — Документация Qucs Help 0.0.19

В компоненте “Текст” и в тексте меток осей диаграмм можно использовать специальные символы. Это делается с помощью тэгов LaTeX. В следующей таблице приводится перечень символов, имеющихся в настоящее время.

Примечание: Правильное отображение этих символов зависит от шрифта, используемого Qucs!

Строчные греческие буквы

Тэг LaTeX	Юникод	Описание
`\alpha`	0x03B1	alpha
`\beta`	0x03B2	beta
`\gamma`	0x03B3	gamma
`\delta`	0x03B4	delta
`\epsilon`	0x03B5	epsilon
`\zeta`	0x03B6	zeta
`\eta`	0x03B7	eta
`\theta`	0x03B8	theta
`\iota`	0x03B9	iota
`\kappa`	0x03BA	kappa
`\lambda`	0x03BB	lambda
`\mu`	0x03BC	mu
`\textmu`	0x00B5	mu
`\nu`	0x03BD	nu
`\xi`	0x03BE	xi
`\pi`	0x03C0	pi
`\varpi`	0x03D6	pi
`\rho`	0x03C1	rho
`\varrho`	0x03F1	rho
`\sigma`	0x03C3	sigma
`\tau`	0x03C4	tau
`\upsilon`	0x03C5	upsilon
`\phi`	0x03C6	phi
`\chi`	0x03C7	chi
`\psi`	0x03C8	psi
`\omega`	0x03C9	omega

Прописные греческие буквы

Тэг LaTeX	Юникод	Описание
`\Gamma`	0x0393	Gamma
`\Delta`	0x0394	Delta
`\Theta`	0x0398	Theta
`\Lambda`	0x039B	Lambda
`\Xi`	0x039E	Xi
`\Pi`	0x03A0	Pi
`\Sigma`	0x03A3	Sigma
`\Upsilon`	0x03A5	Upsilon
`\Phi`	0x03A6	Phi
`\Psi`	0x03A8	Psi
`\Omega`	0x03A9	Omega

Математические символы

Тэг LaTeX	Юникод	Описание
`\cdot`	0x00B7	знак умножения – точка (центрированная точка)
`\times`	0x00D7	знак умножения – крестик
`\pm`	0x00B1	знак плюс минус
`\mp`	0x2213	знак минус плюс
`\partial`	0x2202	знак частного дифференцирования
`\nabla`	0x2207	набла-оператор
`\infty`	0x221E	знак бесконечности
`\int`	0x222B	знак интеграла
`\approx`	0x2248	символ приближения (волнистый знак равенства)
`\neq`	0x2260	знак не равно
`\in`	0x220A	символ “содержится в”
`\leq`	0x2264	знак меньше-равно
`\geq`	0x2265	знак больше-равно
`\sim`	0x223C	(центрально-европейский) знак пропорциональности
`\propto`	0x221D	(американский) знак пропорциональности
`\diameter`	0x00F8	знак диаметра (также знак среднего)
`\onehalf`	0x00BD	половина
`\onequarter`	0x00BC	четверть
`\twosuperior`	0x00B2	квадрат (степень 2)
`\threesuperior`	0x00B3	степень 3
`\ohm`	0x03A9	единица для сопротивления (прописная греческая омега)

back to the top

Спецсимволы HTML + CSS (мнемоника и коды)

Мнемоника и коды специальных символов html в десятичной и шестнадцатиричной системе, а также инструкция как использовать спецсимволы html через CSS.

Инструкция вставки спецсимволов в HTML

Для вставки специальных символов в HTML код вы можете использовать любое из значений столбиков «Обозначение», «10-ный код» или «16-ный код». Ошибки не будет.

Пример добавления специальных символов:

<!DOCTYPE html> <html> <head> <title>Страница</title> </head> <body> &#x21D2;&#x21D2;&#x21D2;&#x21D2;&#x21D2; <!-- Шестнадцатиричный код --> &#8659;&#8659;&#8659;&#8659;&#8659; <!-- Десятичный код --> &hArr;&hArr;&hArr;&hArr;&hArr; <!-- Обозначение --> </body> </html>

Вот как это будет выглядеть на странице:

⇒⇒⇒⇒⇒ ⇓⇓⇓⇓⇓ ⇔⇔⇔⇔⇔

Инструкция вставки спецсимволов через CSS

Для вставки специальных символов через CSS код можно использовать только 16-ный код и не в том виде, что он дан в таблице.

Каждый 16-ный символ в таблице кодируется так – &#x“Шестнадцитиричный код”;

Если вы хотите добавить символ, то вам нужно скоппировать необходимый “Шестнадцитиричный код” из таблицы (без приставки &#x), поставить перед ним обратный слеш \ и добавить его при помощи свойства content. Чаше всего также для использования свойства content применяют псевдоклассы :before или :after.

Пример: «закрашенный телефон»: ☎

десятичный код:

&#9742;

шестнадцатиричный код:

&#x260E;

css код:

content: '\260E';

Пример добавления спец-символа через CSS:

<!DOCTYPE html> <html> <head> <title>Страница</title> </head> <body> <p>Двойная стрелка вправо</p>  </body> </html>

 p.str675:after { content: '\21D2'; }

Вот как это будет выглядеть на странице:

Двойная стрелка вправо ⇒

Таблица с кодами спецсимволов (мнемоник) HTML

Описание символа	Мнемоника	10-ный код	16-ный код	Вид
перевернутый восклицательный знак	¡	¡	¡	¡
цент	¢	¢	¢	¢
фунт стерлингов	£	£	£	£
знак денежной единицы	¤	¤	¤	¤
йена	¥	¥	¥	¥
вертикальная черта	¦	¦	¦	¦
параграф	§	§	§	§
диереза	¨	¨	¨	¨
знак авторского права	©	©	©	©
показатель женского рода	ª	ª	ª	ª
открывающая двойная угловая кавычка	«	«	«	«
знак отрицания	¬	¬	¬	¬
мягкий перенос
охраняемый знак	®	®	®	®
надчеркивание	¯	¯	¯	¯
градус	°	°	°	°
плюс-минус	±	±	±	±
вторая степень	²	²	²	²
третья степень	³	³	³	³
острое ударение	´	´	´	´
знак микро	µ	µ	µ	µ
конец абзаца	¶	¶	¶	¶
средняя точка	·	·	·	·
седиль	¸	¸	¸	¸
единица в верхнем индексе	¹	¹	¹	¹
показатель мужского рода	º	º	º	º
закрывающая двойная угловая кавычка	»	»	»	»
одна четвертая	¼	¼	¼	¼
одна вторая	½	½	½	½
три четверти	¾	¾	¾	¾
перевернутый вопросительный знак	¿	¿	¿	¿
A с тупым ударением	À	À	À	À
A с острым ударением	Á	Á	Á	Á
A с циркумфлексом	Â	Â	Â	Â
A с тильдой	Ã	Ã	Ã	Ã
A с диерезой	Ä	Ä	Ä	Ä
A с кружком	Å	Å	Å	Å
лигатура AE	Æ	Æ	Æ	Æ
C с седилем	Ç	Ç	Ç	Ç
E с тупым ударением	È	È	È	È
E с острым ударением	É	É	É	É
E с циркумфлексом	Ê	Ê	Ê	Ê
E с диерезой	Ë	Ë	Ë	Ë
I с тупым ударением	Ì	Ì	Ì	Ì
I с острым ударением	Í	Í	Í	Í
I с циркумфлексом	Î	Î	Î	Î
I с диерезой	Ï	Ï	Ï	Ï
ETH	Ð	Ð	Ð	Ð
N с тильдой	Ñ	Ñ	Ñ	Ñ
O с тупым ударением	Ò	Ò	Ò	Ò
O с острым ударением	Ó	Ó	Ó	Ó
O с циркумфлексом	Ô	Ô	Ô	Ô
O с тильдой	Õ	Õ	Õ	Õ
O с диерезой	Ö	Ö	Ö	Ö
знак умножения	×	×	×	×
O перечеркнутое	Ø	Ø	Ø	Ø
U с тупым ударением	Ù	Ù	Ù	Ù
U с острым ударением	Ú	Ú	Ú	Ú
U с циркумфлексом	Û	Û	Û	Û
U с диерезой	Ü	Ü	Ü	Ü
Y с острым ударением	Ý	Ý	Ý	Ý
THORN	Þ	Þ	Þ	Þ
двойное s	ß	ß	ß	ß
a с тупым ударением	à	à	à	à
a с острым ударением	á	á	á	á
a с циркумфлексом	â	â	â	â
a с тильдой	ã	ã	ã	ã
a с диерезой	ä	ä	ä	ä
a с кружком	å	å	å	å
лигатура ae	æ	æ	æ	æ
c с седилем	ç	ç	ç	ç
e с тупым ударением	è	è	è	è
e с острым ударением	é	é	é	é
e с циркумфлексом	ê	ê	ê	ê
e с диерезой	ë	ë	ë	ë
i с тупым ударением	ì	ì	ì	ì
i с острым ударением	í	í	í	í
i с циркумфлексом	î	î	î	î
i с диерезой	ï	ï	ï	ï
eth	ð	ð	ð	ð
n с тильдой	ñ	ñ	ñ	ñ
o с тупым ударением	ò	ò	ò	ò
o с острым ударением	ó	ó	ó	ó
o с циркумфлексом	ô	ô	ô	ô
o с тильдой	õ	õ	õ	õ
o с диерезой	ö	ö	ö	ö
знак деления	÷	÷	÷	÷
o перечеркнутое	ø	ø	ø	ø
u с тупым ударением	ù	ù	ù	ù
u с острым ударением	ú	ú	ú	ú
u с циркумфлексом	û	û	û	û
u с диерезой	ü	ü	ü	ü
y с острым ударением	ý	ý	ý	ý
thorn	þ	þ	þ	þ
y с диерезой	ÿ	ÿ	ÿ	ÿ
кавычка	"	"	"	“
амперсанд	&	&	&	&
меньше (левая угловая скобка)	<	<	<	<
больше (правая угловая скобка)	>	>	>	>
лигатура OE	&OElig;	Œ	Œ	Œ
лигатура oe	&oelig;	œ	œ	œ
S с птичкой	&Scaron;	Š	Š	Š
s с птичкой	&scaron;	š	š	š
Y с диерезой	&Yuml;	Ÿ	Ÿ	Ÿ
циркумфлекс	&circ;	ˆ	ˆ	ˆ
малая тильда	&tilde;	˜	˜	˜
неразрывный межсловный пробел
узкий пробел (тонкая шпация)
короткий пробел (полукруглая шпация)	&ensp;
длинный пробел (круглая шпация)	&emsp;
разделитель нулевой ширины	&zwnj;	‌	‌	‌
соединитель нулевой ширины	&zwj;	‍	‍	‍
указатель слева направо	&lrm;	‎	‎	‎
указатель справа налево	&rlm;	‏	‏	‏
короткое тире	–	–	–	–
длинное тире	—	—	—	—
открывающая одинарная кавычка	‘	‘	‘	‘
закрывающая одинарная кавычка	’	’	’	’
нижняя одинарная кавычка	&sbquo;	‚	‚	‚
открывающая двойная кавычка	“	“	“	“
закрывающая двойная кавычка	”	”	”	”
нижняя двойная кавычка	&bdquo;	„	„	„
кинжал (крест)	&dagger;	†	†	†
двойной кинжал (двойной крест)	&Dagger;	‡	‡	‡
знак промилле	&permil;	‰	‰	‰
открывающая угловая кавычка	&lsaquo;	‹	‹	‹
закрывающая угловая кавычка	&rsaquo;	›	›	›
евро	€	€	€	€
курсивное f	&fnof;	ƒ	ƒ	ƒ
прописная альфа	Α	Α	Α	Α
прописная бета	Β	Β	Β	Β
прописная гамма	Γ	Γ	Γ	Γ
прописная дельта	Δ	Δ	Δ	Δ
прописной эпсилон	Ε	Ε	Ε	Ε
прописная дзета	Ζ	Ζ	Ζ	Ζ
прописная эта	Η	Η	Η	Η
прописная тета	Θ	Θ	Θ	Θ
прописная иота	Ι	Ι	Ι	Ι
прописная каппа	Κ	Κ	Κ	Κ
прописная ламбда	Λ	Λ	Λ	Λ
прописная мю	Μ	Μ	Μ	Μ
прописная ню	Ν	Ν	Ν	Ν
прописная кси	Ξ	Ξ	Ξ	Ξ
прописной омикрон	Ο	Ο	Ο	Ο
прописная пи	Π	Π	Π	Π
прописная ро	Ρ	Ρ	Ρ	Ρ
прописная сигма	Σ	Σ	Σ	Σ
прописная тау	Τ	Τ	Τ	Τ
прописная ипсилон	Υ	Υ	Υ	Υ
прописная фи	Φ	Φ	Φ	Φ
прописная хи	Χ	Χ	Χ	Χ
прописная пси	Ψ	Ψ	Ψ	Ψ
прописная омега	Ω	Ω	Ω	Ω
строчная альфа	α	α	α	α
строчная бета	β	β	β	β
строчная гамма	γ	γ	γ	γ
строчная дельта	δ	δ	δ	δ
строчная эпсилон	ε	ε	ε	ε
строчная дзета	ζ	ζ	ζ	ζ
строчная эта	η	η	η	η
строчная тета	θ	θ	θ	θ
строчная иота	ι	ι	ι	ι
строчная каппа	κ	κ	κ	κ
строчная ламбда	λ	λ	λ	λ
строчная мю	μ	μ	μ	μ
строчная ню	ν	ν	ν	ν
строчная кси	ξ	ξ	ξ	ξ
строчный омикрон	ο	ο	ο	ο
строчная пи	π	π	π	π
строчная ро	ρ	ρ	ρ	ρ
строчная сигма конечная	&sigmaf;	ς	ς	ς
строчная сигма	σ	σ	σ	σ
строчная тау	τ	τ	τ	τ
строчная ипсилон	υ	υ	υ	υ
строчная фи	φ	φ	φ	φ
строчная хи	χ	χ	χ	χ
строчная пси	ψ	ψ	ψ	ψ
строчная омега	ω	ω	ω	ω
символ строчная тета	&thetasym;	ϑ	ϑ	ϑ
ипсилон с крючком	&upsih;	ϒ	ϒ	ϒ
символ пи	ϖ	ϖ	ϖ	ϖ
маркер списка	•	•	•	•
многоточие	…	…	…	…
знак прим	′	′	′	′
знак двойной прим	″	″	″	″
надчеркивание	&oline;	‾	‾	‾
дробная черта	&frasl;	⁄	⁄	⁄
рукописная P	&weierp;	℘	℘	℘
мнимая часть числа	&image;	ℑ	ℑ	ℑ
действительная часть числа	&real;	ℜ	ℜ	ℜ
торговая марка	™	™	™	™
алеф	&alefsym;	ℵ	ℵ	ℵ
стрелка влево	←	←	←	←
стрелка вверх	↑	↑	↑	↑
стрелка вправо	→	→	→	→
стрелка вниз	↓	↓	↓	↓
стрелка влево-вправо	↔	↔	↔	↔
возврат каретки	&crarr;	↵	↵	↵
двойная стрелка влево	⇐	⇐	⇐	⇐
двойная стрелка вверх	&uArr;	⇑	⇑	⇑
двойная стрелка вправо	⇒	⇒	⇒	⇒
двойная стрелка вниз	&dArr;	⇓	⇓	⇓
двойная стрелка влево-вправо	⇔	⇔	⇔	⇔
квантор всеобщности	∀	∀	∀	∀
знак дифференциала	∂	∂	∂	∂
квантор существования	∃	∃	∃	∃
пустое множество	∅	∅	∅	∅
набла	∇	∇	∇	∇
принадлежит множеству	∈	∈	∈	∈
не принадлежит множеству	∉	∉	∉	∉
является членом	&ni;	∋	∋	∋
n-арное произведение	∏	∏	∏	∏
n-арная сумма	∑	∑	∑	∑
знак минус	−	−	−	−
оператор звездочка	&lowast;	∗	∗	∗
радикал	√	√	√	√
пропорционально	&prop;	∝	∝	∝
бесконечность	∞	∞	∞	∞
угол	&ang;	∠	∠	∠
логическое И	&and;	∧	∧	∧
логическое ИЛИ	&or;	∨	∨	∨
пересечение	∩	∩	∩	∩
объединение	∪	∪	∪	∪
интеграл	∫	∫	∫	∫
следовательно	&there4;	∴	∴	∴
оператор тильда	&sim;	∼	∼	∼
приблизительно равно	&cong;	≅	≅	≅
асимптотически равно	≈	≈	≈	≈
не равно	≠	≠	≠	≠
тождественно равно	&equiv;	≡	≡	≡
меньше или равно	≤	≤	≤	≤
больше или равно	≥	≥	≥	≥
подмножество	⊂	⊂	⊂	⊂
надмножество	⊃	⊃	⊃	⊃
не подмножество	&nsub;	⊄	⊄	⊄
подмножество или равно	&sube;	⊆	⊆	⊆
надмножество или равно	&supe;	⊇	⊇	⊇
прямая сумма	&oplus;	⊕	⊕	⊕
векторное произведение	&otimes;	⊗	⊗	⊗
перпендикулярно	&perp;	⊥	⊥	⊥
оператор точка	⋅	⋅	⋅	⋅
левый верхний угол	&lceil;	⌈	⌈	⌈
правый верхний угол	&rceil;	⌉	⌉	⌉
левый нижний угол	&lfloor;	⌊	⌊	⌊
правый нижний угол	&rfloor;	⌋	⌋	⌋
левая угловая скобка	&lang;	〈	〈	(
правая угловая скобка	&rang;	〉	〉	)
ромб	&loz;	◊	◊
пики	&spades;	♠	♠	♠
трефы	&clubs;	♣	♣	♣
червы	&hearts;	♥	♥	♥
бубны	&diams;	♦	♦	♦

Дополнительные спецсимволы HTML

Описание символа	10-ный код	16-ный код	Вид
Паром, переправа, судно, корабль	⛴	⛴	⛴
триграмма	☰	☰	☰
карандаш	✏	✏	✏
карандаш	✎	✎	✎
карандаш	✐	✐	✐
перо	✑	✑	✑
перо	✒	✒	✒
треугольная стрелка вверх	▲	▲	▲
треугольная стрелка вниз	▼	▼	▼
треугольная стрелка вправо	►	►	►
треугольная стрелка влево	◄	◄	◄
галочка	✓	✓	✓
жирная галочка	✔	✔	✔
крест	☓	☓	☓
жирный крест	✖	✖	✖
крестик	✗	✗	✗
жирный крестик	✘	✘	✘
круг	○	○	○
круг закрашенный	●	●	●
квадрат	□	□	□
квадрат закрашенный	■	■	■
еврейская звезда	✡	✡	✡
звезда	✪	✪	✪
звезда	✫	✫	✫
звезда	&#10028	✬	✬
звезда рельефная	&#10031	✯	✯
3-d звезда	✰	✰	✰
звезда	★	★	★
звезда	☆	☆	☆
солнце	☀	☀	☀
солнце	☼	☼	☼
облако, туча	☁	☁	☁
снежинка	❄	❄	❄
снежинка	❅	❅	❅
снежинка	❆	❆	❆
зонт	☂	☂	☂
снеговик	☃	☃	☃
цветок	✿	✿	✿
цветок	✽	✽	✽
цветок разноцветный	✾	✾	✾
красивый цветок	❀	❀	❀
растущий месяц	☽	☽	☽
убывающий месяц	☾	☾	☾
закрашенный телефон	☎	☎	☎
незакрашенный телефон	☏	☏	☏
телефонная трубка	✆	✆	✆
многоугольник	✹	✹	✹
многоугольник	✸	✸	✸
многоугольник	✷	✷	✷
шестиугольник	✶	✶	✶
пункт	☐	☐	☐
активный пункт, галочка	☑	☑	☑
активный пункт, крест	☒	☒	☒
череп и кости	☠	☠	☠
мусульманский символ	☪	☪	☪
серп и молот	☭	☭	☭
письмо, конверт, адрес	✉	✉	✉
Конверт с молнией, электронное письмо	🖄	🖄	🖄
инь и янь	☯	☯	☯
пишущая рука	✍	✍	✍
грустный смайл	☹	☹	☹
веселый смайл	☺	☺	☺
веселый смайл	☻	☻	☻
незакрашенные ножницы	✄	✄	✄
закрашенные ножницы	✂	✂	✂
женщина	♀	♀	♀
мужчина	♂	♂	♂
сердце	❥	❥	❥
сердце-узор	❦	❦	❦
одиночная кавычка левая	❛	❛	❛
одиночная кавычка правая	❜	❜	❜
двойная кавычка левая	❝	❝	❝
двойная кавычка правая	❞	❞	❞
четвертная нота	♩	♩	♩
восьмая	♪	♪	♪
две восьмые	♫	♫	♫
шестнадцатая	♬	♬	♬
бемоль	♭	♭	♭
бекар	♮	♮	♮
диез	♯	♯	♯
шар	❍	❍	❍
куб	❒	❒	❒
астеризм	⁂	⁂	⁂
Жест хорошо (большой палец поднят)	👍	👍	👍
Жест плохо (большой палец вниз)	&#1F44E;	👎	👎
Развёрнутый жест с большим пальцем вверх	&#1F592;	👍	🖒
Развёрнутый жест с большим пальцем вниз	&#1F593;	🖓	🖓

Полная таблица символов Юникода – https://unicode-table. com/ru/

Обновление МойОфис 2021.02. Пишите формулы и математические выражения в текстовом редакторе / Хабр

Привет, Хабр! Недавно мы обновили МойОфис до версии 2021.02. Одним из важных улучшений стала возможность добавления формул в текстовом редакторе. Она может быть полезна всем, кто работает с текстами и хочет получить корректное отображение сложных математических выражений в документах, особенно при последующей печати.

Для работы с формулами мы применяем LaTeX. Эта система набора и вёрстки документов считается стандартом «де факто» в научной среде благодаря корректной работе даже с особо сложными математическими формулами. В его основе лежит TeX — язык разметки низкого уровня, созданный Д. Кнутом в 70-х годах прошлого века. В 1984 году Л. Лампорт выпустил пакет расширения (или макронадстройки) для TeX, который включал порядка 600 макрокоманд. На сегодняшний день для LaTeX доступно большое количество различных пакетов-дополнений, позволяющих эффективно работать с разнообразными данными, такими как формулы, графика, ноты и другие. Потенциальные возможности системы не ограничены.

Работа с формулами при использовании LaTeX заметно отличается от привычного многим визуального редактора. Тем не менее, даже в Microsoft Word 2019 реализована возможность ввода формул в формате LaTeX, да и в файлах документов формулы хранятся именно в таком виде.

После изучения основ и базовых тегов языка, ввод и последующее редактирование формул становится простым и понятным процессом. А результат всегда будет выглядеть качественно.

Как вводить формулы

Сейчас мы продемонстрируем, как работать с формулами в МойОфис Текст. В меню “Вставка” необходимо выбрать раздел “Формула” с символом π в кружке.

По нажатию появляется окно с двумя полями: “Выражение LaTeX” и “Предварительный просмотр”.

Попробуем ввести какую-нибудь формулу. Большинство математических функций и символов, а также скобки, матрицы и системы уравнений в синтаксисе LaTeX обозначаются тегами, начинающимися с символа \. Например, возьмём классический определённый интеграл функции f(x) на интервале [a, b]. b f(x) dx

В данном случае a и b являются параметрами тега \int. После вставки формулы в поле предпросмотра мы видим результат.

Остаётся только нажать “ОК”, и готовая формула появляется в указанном месте тестового документа. Работать с формулой можно так же, как и с любым другим объектом: после выделения её можно выровнять по центру, по правой или левой стороне, а также изменить размеры, потянув за одну из четырёх ключевых точек по углам объекта.

Также при выделении формулы на панели инструментов появляется блок кнопок “Формула” для изменения или удаления объекта. Удалить формулу можно и привычным способом, выделив её и нажав клавиши Backspace или Del — аналогично удалению других объектов.

Теперь давайте добавим более сложные формулы, чтобы продемонстрировать возможности текстового редактора “МойОфис Текст”. Например, используем некую абстрактную функцию с четырьмя переменными. Буквы греческого языка и лемниската, символ бесконечности, также вводятся в виде тегов.

{\infty} S_n \tan \left( \frac{104-2\delta \pi}{\mu} \right)+\gamma } { \mathcal{F} {g(a,b)} }

В результате ввода получаем следующее выражение:

Видим, что всё отображается хорошо и корректно.

Теперь попробуем добавить ошибку в формулу и посмотрим, как поведет себя редактор. Например, добавим лишний пробел в слове delta (верхняя зеленая стрелка на скриншоте ниже).
Видим, что при наличии ошибки синтаксиса в формуле, в окне результата место с ошибкой будет выделено красным (нижняя зеленая стрелка). Удобно.

Редактор формул поможет найти ошибки, однако всегда стоит дополнительно контролировать результат, так как нередко разделённое случайным пробелом имя функции может случайно совпасть с именем совершенно иной функции, также существующим в LaTeX.

Если у вас есть длинное выражение, которое занимает более одной строки, стоит использовать разделитель \\. Так, к примеру, для записи такого равенства

1+2+3+4+5+6+7+8+ . .. +97+98+99+100+101+102+103+...+146+147+148+149+150 = 11325

потребуется в редакторе формул ввести следующее выражение, в котором горизонтальное многоточие обозначено тегом \dots:

1+2+3+4+5+6+7+8+ \dots + \\ +97+98+99+100+101+102+103+ \dots + \\ +146+147+148+149+150 = 11325

В результате получаются аккуратно перенесённые строки.

Еще с помощью LaTeX удобно записывать матрицы и другие сложные выражения в несколько строк. Давайте для начала введём некую матрицу “А” произвольного размера с количеством столбцов и рядов, равным n. Для этого используем такой код:

A = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\ 
\vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & \ldots & a_{nn}
\end{array}
\right)

К слову, в этом коде присутствуют уже три варианта многоточия: горизонтальное, обозначенное \ldots, вертикальное \vdots и диагональное \ddots. Даже сама структура тегов языка LaTeX понятна и логична, что порой позволяет интуитивно догадаться о смысле и различиях родственных элементов. В результате ввода получаем следующее:

Также можно объединять различное количество выражений в систему или использовать структуру для наглядного представления вариантов выбора с последствиями. В качестве примера возьмём систему из трёх уравнений с тригонометрическими функциями.

 \begin{cases}
  x &=  \cos \alpha +2 \sqrt[3]{\cos 2 \alpha+3} + \cos \alpha + 4\\
  y &=2 \sin \alpha +3 \sqrt[4]{\sin  \alpha - 1} + \sin \alpha \\
  z &= 5 \sin \alpha + 4 \cos 2 \alpha
\end{cases}

Количество элементов-строк может быть произвольным, а отделяются они так же, как и обычные строки — с помощью \\. В результате получается такая конструкция:

Сравним как формулы отображаются в других редакторах

Теперь проверим, как документ с формулами, созданный в МойОфис, открывается и читается в других популярных текстовых редакторах. Для чистоты эксперимента используем сразу несколько формул из приведённых выше. Тестовый документ выглядит так:

Сохраним его в двух форматах — ODT и DOCX. После чего откроем его в LibreOffice и Microsoft Word 2019 и сравним полученное с исходным.

Как формулы из МойОфис отображаются в LibreOffice

В LibreOffice файл .odt прочитался нормально за исключением некоторых деталей. Так, во второй формуле не отобразился каллиграфический шрифт для обозначения “F”, вместо него добавился лишний оператор в знаменателе. В третьей формуле исчезла скобка и добавились красные перевёрнутые знаки вопроса в системе выражений, а также возникла проблема с диагональными точками в матрице.

При открытии файла .docx в первой формуле дополнительно появилось пустое поле между символом интеграла и функцией. Ещё одно отличие между двумя форматами — выравнивание: .odt выровнен по левому краю, а .docx — по центру.

Как формулы из МойОфис отображаются в Microsoft Office

Откроем те же документы в Microsoft Word 2019. В формате .odt формулы читаются, но снова проявилось пустое поле между интегралом и функцией. Также иначе отображаются пределы суммы, есть ошибка в отображении функции в знаменателе второй формулы, отсутствует скобка в системе выражений, а их форматирование внутри формулы сделано по центру.

В файле .docx ситуация аналогична, только все формулы выровнены по центру.

Как формулы из Microsoft Office отображаются в МойОфис

Многим пользователям важно и то, насколько успешно МойОфис открывает файлы c формулами, созданными в других редакторах. Для проверки этого создадим два документа в форматах .docx и .odt c полностью аналогичным набором выражений, используя для этого встроенные системы редактирования формул.

Начнём с Microsoft Office. Все формулы, которые мы создали во встроенном WYSIWYG-редакторе Word, без проблем открылись в МойОфис. Корректно отобразились все элементы, включая внутреннее форматирование (да, система из трёх уравнений и там расположена по центру). Разницы между форматами .docx и .odt не выявлено.

Как формулы из LibreOffice отображаются в МойОфис

А вот у файлов, созданных в LibreOffice, возникла небольшая проблема с изменением размера формул: при открытии в МойОфис все элементы оказались сжатыми по горизонтали. Самый очевидный момент — большая фигурная скобка в системе уравнений отобразилась в виде скобки обычного размера и к тому же располагается выше центра. Таким образом некоторые формулы после открытия в МойОфис, возможно, придётся подкорректировать. Но не более того.

В статье мы продемонстрировали лишь малую часть возможностей LaTeX для отображения формул в текстовом редакторе “МойОфис Текст”. Если вы захотите изучить систему верстки подробнее, то легко сможете найти инструкции и описания всех тегов в сети.

Наше исследование показало, что при работе с формулами в разных редакторах возможно возникновение небольших погрешностей при отображении математических выражений. В целом, “МойОфис Текст” корректно обрабатывает синтаксис LaTeX, благодаря чему вы можете писать формулы в полном соответствии с требованиями к оформлению инженерной документации. Пользователям доступна полноценная работа как с простыми функциями, так и сложными конструкциями из многих элементов, вы можете в реальном времени контролировать вид будущего выражения в окне предпросмотра и при необходимости сразу вносить изменения в код формулы. При этом критические ошибки в синтаксисе сразу будут заметны благодаря цветовому выделению.

Делитесь в комментариях впечатлениями о работе с формулами в “МойОфис Текст”: нашей команде важны ваши пожелания, предложения и замечания!

Спецсимволы HTML и мнемоники

Символ	Мнемоника	Код символа	Описание

	` `	` `	Неразрывный пробел
	`&ensp;`	` `	Узкий пробел
	`&emsp;`	` `	Широкий пробел
–	`–`	`–`	Узкое тире
—	`—`	`—`	Широкое тире
	``	``	Мягкий перенос
́		`́`	Ударение
©	`©`	`©`	Копирайт
®	`®`	`®`	Зарегистрированная торговая марка
™	`™`	`™`	Торговая марка
º	`º`	`º`	Копье Марса
ª	`ª`	`ª`	Зеркало Венеры
‰	`&permil;`	`‰`	Промилле
π	`π`	`π`	Пи
¦	`¦`	`¦`	Вертикальный пунктир
§	`§`	`§`	Параграф
°	`°`	`°`	Градус
µ	`µ`	`µ`	Знак «микро»
¶	`¶`	`¶`	Знак абзаца
…	`…`	`…`	Многоточие
‾	`&oline;`	`‾`	Надчеркивание
´	`´`	`´`	Ударение
№		`№`	Номер
🔍		`🔍`	Лупа (наклонённая влево)
🔎		`🔎`	Лупа (наклонённая вправо)
&	`&`	`&`	Амперсанд

Символ	Мнемоника	Код символа	Описание
“	`"`	`"`	Двойная кавычка
«	`«`	`«`	Левая кавычка-елочка
»	`»`	`»`	Правая кавычка-елочка
‹		`‹`	Одиночная угловая кавычка открывающая
›		`›`	Одиночная угловая кавычка закрывающая
′	`′`	`′`	Штрих (минуты, футы)
″	`″`	`″`	Двойной штрих (секунды, дюймы)
‘	`‘`	`‘`	Левая верхняя одиночная кавычка
’	`’`	`’`	Правая верхняя одиночная кавычка
‚	`&sbquo;`	`‚`	Правая нижняя одиночная кавычка
“	`“`	`“`	Кавычка-лапка левая
”	`”`	`”`	Кавычка-лапка правая верхняя
„	`&bdquo;`	`„`	Кавычка-лапка правая нижняя
❛		`❛`	Одиночная английская кавычка открывающая
❜		`❜`	Одиночная английская кавычка закрывающая
❝		`❝`	Двойная английская кавычка открывающая
❞		`❞`	Двойная английская кавычка закрывающая

Символ	Мнемоника	Код символа	Описание
¤	`&current;`	`¤`	Знак валюты
€	`€`	`€`	Евро
¢	`¢`	`¢`	Цент
£	`£`	`£`	Фунт
¥	`¥`	`¥`	Йена и Юань
ƒ	`&fnof;`	`ƒ`	Знак флорина

Символ	Мнемоника	Код символа	Описание
×	`×`	`×`	Умножить
÷	`÷`	`÷`	Разделить
<	`<`	`<`	Меньше
>	`>`	`>`	Больше
±	`±`	`±`	Плюс/минус
¹	`¹`	`¹`	Степень 1
²	`²`	`²`	Степень 2
³	`³`	`³`	Степень 3
¬	`¬`	`¬`	Отрицание
¼	`¼`	`¼`	Одна четвертая
½	`½`	`½`	Одна вторая
¾	`¾`	`¾`	Три четверти
⁄	`&frasl;`	`⁄`	Дробная черта
−	`−`	`−`	Минус
≤	`≤`	`≤`	Меньше или равно
≥	`≥`	`≥`	Больше или равно
≈	`≈`	`≈`	Приблизительно
≠	`≠`	`≠`	Не равно
≡	`&equiv;`	`≡`	Тождественно
√	`√`	`√`	Квадратный корень
∞	`∞`	`∞`	Бесконечность
∑	`∑`	`∑`	Сумма, сумма ряда
∏	`∏`	`∏`	Произведение
∂	`∂`	`∂`	Частичный дифференциал
∫	`∫`	`∫`	Интеграл
∀	`∀`	`∀`	Для всех
∃	`∃`	`∃`	Существует
∅	`∅`	`∅`	Пустое множество
Ø	`Ø`	`Ø`	Диаметр
∈	`∈`	`∈`	Принадлежит
∉	`∉`	`∉`	Не принадлежит
∋	`&ni;`	`∗`	Содержит
⊂	`⊂`	`⊂`	Является подмножеством
⊃	`⊃`	`⊃`	Является надмножеством
⊄	`&nsub;`	`⊄`	Не является подмножеством
⊆	`&sube;`	`⊆`	Является подмножеством либо равно
⊇	`&supe;`	`⊇`	Является надмножеством либо равно
⊕	`&oplus;`	`⊕`	Плюс в кружке
⊗	`&otimes;`	`⊗`	Знак умножения в кружке
⊥	`&perp;`	`⊥`	Перпендикулярно
∠	`&ang;`	`∠`	Угол
∧	`&and;`	`∧`	Логическое И
∨	`&or;`	`∨`	Логическое ИЛИ
∩	`∩`	`∩`	Пересечение
∪	`∪`	`∪`	Объединение

Символ	Мнемоника	Код символа	Описание
←	`←`	`←`	Стрелка влево
↑	`↑`	`↑`	Стрелка вверх
→	`→`	`→`	Стрелка вправо
↓	`↓`	`↓`	Стрелка вниз
↔	`↔`	`↔`	Стрелка влево и вправо
↕		`↕`	Стрелка вверх и вниз
↵	`&crarr;`	`↵`	Возврат каретки
⇐	`⇐`	`⇐`	Двойная стрелка влево
⇑	`&uArr;`	`⇑`	Двойная стрелка вверх
⇒	`⇒`	`⇒`	Двойная стрелка вправо
⇓	`&dArr;`	`⇓`	Двойная стрелка вниз
⇔	`⇔`	`⇔`	Двойная стрелка влево и вправо
⇕		`⇕`	Двойная стрелка вверх и вниз
▲		`▲`	Треугольная стрелка вверх
▼		`▼`	Треугольная стрелка вниз
►		`►`	Треугольная стрелка вправо
◄		`◄`	Треугольная стрелка влево

Символ	Мнемоника	Код символа	Описание
•	`•`	`•`	Простой маркер
○		`○`	Круг
·	`·`	`·`	Средняя точка
†		`†`	Крестик
‡		`‡`	Двойной крестик
♠	`&spades;`	`♠`	Пики
♣	`&clubs;`	`♣`	Трефы
♥	`&hearts;`	`♥`	Червы
♦	`&diams;`	`♦`	Бубны
◊	`&loz;`	`◊`	Ромб
✏		`✏`	Карандаш
✎		`✎`	Карандаш
✐		`✐`	Карандаш
✍		`✍`	Рука

Символ	Код символа	Описание
⏰	`⏰`	Часы
⌚	`⌚`	Часы
⌛	`⌛`	Песочные часы
⏳	`⏳`	Песочные часы

Символ	Код символа	Описание
☃	`☃`	Снеговик
❄	`❄`	Снежинка
❅	`❅`	Зажатая трилистниками снежинка
❆	`❆`	Жирная остроугольная снежинка
★	`★`	Закрашенная звезда
☆	`☆`	Незакрашенная звезда
✪	`✪`	Незакрашенная звезда в закрашенном круге
✫	`✫`	Закрашенная звезда с незакрашенным кругом внутри
✯	`✯`	Вращающаяся звезда
⚝	`⚝`	Начерченная белая звезда
⚪	`⚪`	Средний незакрашенный круг
⚫	`⚫`	Средний закрашенный круг
⚹	`⚹`	Секстиле (типа снежинка)
✵	`✵`	Восьмиконечная вращающаяся звезда
❉	`❉`	Звёздочка с шарообразными окончаниями
❋	`❋`	Жирная восьмиконечная каплеобразная звёздочка-пропеллер
✺	`✺`	Шестнадцатиконечная звёздочка
✹	`✹`	Двенадцатиконечная закрашенная звезда
✸	`✸`	Жирная восьмиконечная прямолинейная закрашенная звезда
✶	`✶`	Шестиконечная закрашенная звезда
✷	`✷`	Восьмиконечная прямолинейная закрашенная звезда
✴	`✴`	Восьмиконечная закрашенная звезда
✳	`✳`	Восьмиконечная звёздочка
✲	`✲`	Звёздочка с незакрашенным центром
✱	`✱`	Жирная звёздочка
✧	`✧`	Заострённая четырёхконечная незакрашенная звезда
✦	`✦`	Заострённая четырёхконечная закрашенная звезда
⍟	`⍟`	Звезда в круге
⊛	`⊛`	Снежинка в круге

Текстовые символы для ников и социальных сетей

Навигация

Популярные текстовые символы
Текстовые символы любви
Специальные текстовые символы
Символы людей
Символы звезд
Символы стрелок
Графические символы
Математические символы
Языковые символы
Текстовые символы валют

Текстовые символы стрелок

[adinserter block=”12″]

↕
Двойная стрелочка вверх-вниз
↖
стрелочка влево-вверх
↗
стрелочка вправо-вверх
↘
стрелочка вправо-вниз
↙
стрелочка влево-вниз
↚
стрелочка влево с чертой
↛
Перечёркнутая стрелочка вправо
↜
Волнистая стрелочка влево
↝
Волнистая стрелочка вправо
↞
Двуглавая стрелочка влево
↟
Двуглавая стрелочка вверх
↠
Двуглавая стрелочка вправо
↡
Двуглавая стрелочка вниз
↢
стрелочка влево с хвостиком
↣
стрелочка вправо с хвостиком
↤
стрелочка от планки влево
↥
стрелочка от планки вверх
↦
стрелочка от планки вправо
↧
стрелочка от планки вниз
↨
стрелочка вверх и вниз от планки внизу
↩
стрелочка влево с крючком
↪
↫
↬
↭
↮
↯
↰
↱
↲
↳
↴
↶
Полукруглая с наконечником против часовой стрелки
↷
Полукруглая с наконечником по часовой стрелке
↸
Влево вверх, упирающаяся в планку
↹
влево, упирающаяся в планку над стрелкой вправо, упирающейся в планку
↺
Круглая с наконечником против часовой стрелки
↻
Круглая с наконечником по часовой стрелке
↼
Гарпун влево с зубцом вверх
↽
Гарпун влево с зубцом вниз
↾
Гарпун вверх с зубцом вправо
↿
Гарпун вверх с зубцом влево
⇀
Гарпун вправо с зубцом вверх
⇁
Гарпун вправо с зубцом вниз
⇂
Гарпун вниз с зубцом вправо
⇃
Гарпун вниз с зубцом влево
⇄
вправо над стрелкой влево
⇅
вверх слева от стрелка вниз
⇆
влево над стрелкой вправо
⇇
Парные стрелки влево
⇈
Парные стрелки вверх
⇉
Парные стрелки вправо
⇊
Парные стрелки вниз
⇋
Гарпун влево над гарпуном вправо
⇌
Гарпун вправо над гарпуном влево
⇍
Перечёркнутая влево
⇎
Перечёркнутая влево-вправо
⇏
Перечёркнутая вправо
⇕
вверх-вниз
⇖
Двойная свлево-вверх
⇗
вправо-вверх
⇘
⇙
⇚
⇛
⇜
⇝
⇞
⇟
⇠
⇡
⇢
⇣
⇤
⇥
⇦
⇧
Толстая полая стрелка вверх
⇨
Толстая полая стрелка вправо
⇩
Толстая полая стрелка вниз
⇪
Толстая полая стрелка вверх на прямоугольнике
⌅
Проективный
⌆
Перспективный
⌤
Вверх до стрелки между двумя горизонтальными полосами
⏎
Символ возврата
▶
Черный треугольник с вершиной направо
☇
Молния
☈
Гроза
☊
Восходящий узел
☋
Нисходящий узел
☌
Связь
☍
Противник
➔
с широким углом правонаправленная стрелка
➘
стрелка, указывающая на юго-восток
➙
стрелка, указывающая направо
➚
стрелка, указывающая на северо-восток
➛
Короткая стрелка, указывающая вправо
➜
стрелка с закруглёнными концами, указывающая вправо
➝
Стрелка с треугольным наконечником, указывающая вправо
➞
стрелка с треугольным наконечником, указывающая вправо
➟
Летящая стрелка с треугольным наконечником, указывающая вправо
➠
летящая стрелка с треугольным наконечником, указывающая вправо
➡
Закрашенная стрелка, указывающая вправо
➢
Трёхмерный закрашенный сверху правонаправленный наконечник стрелы
➣
Трёхмерный закрашенный снизу правонаправленный наконечник стрелы
➤
Закрашенный правонаправленный наконечник стрелы
➥
закрашенная изогнутая стрелка, указывающая вниз и вправо
➦
закрашенная изогнутая стрелка, указывающая вверх и вправо
➧
Сплющенная закрашенная стрелка, направленная вправо
➨
закрашенная с вогнутым наконечником стрелка, направленная вправо
➩
Незакрашенная стрелка с отпадающей вправо тенью, направленная вправо
➪
Незакрашенная стрелка с отпадающей влево тенью, направленная вправо
➫
Наклонённая вниз оттенённая незакарашенная стрелка, указывающая вправо
➬
Повёрнутая вверх оттенённая незакарашенная стрелка, указывающая вправо
➭
незакрашенная с отпадающей вправо и вниз тенью стрелка, указывающая вправо
➮
незакрашенная с отпадающей вправо и вверх тенью стрелка, указывающая вправо
➯
Зубчатая незакрашенная с отпадающей вниз и вправо тенью стрелка, указывающая вправо
➱
Зубчатая незакрашенная с падающей вверх и вправо тенью стрелка, указывающая вправо
➲
Незакрашенная стрелка в закрашенном круге, указывающая вправо
➳
Незкарашенная перьевая стрелка, указывающая вправо
➴
Закрашенная перьевая стрелка, указывающая на юго-восток
➵
Закрашенная перьевая стрелка, указывающая вправо
➶
Закрашенная перьевая стрелка, указывающая на северо-восток
➷
закрашенная перьевая стрелка, указывающая на юго-восток
➸
закрашенная перьевая стрелка, указывающая вправо
➹
закрашенная перьевая стрелка, указывающая на северо-восток
➺
Стрелка с каплевидными окончаниями, указывающая вправо
➻
с каплевидным стержнем стрелка, направленная вправо
➼
Стрелка с клинообразным стержнем, указывающая вправо
➽
стрелка с клинообразным стержнем, указывающая вправо
➾
Стрелка из очертаний, направленная вправо
⤴
Стрелка, направленная вправо, затем изогнутая вверх
⤵
Стрелка, направленная вправо, затем изогнутая вниз
↵
Стрелка вниз с поворотом налево
↓
Стрелка вниз
↔
Двойная стрелка влево-вправо
←
Стрелка влево
→
Стрелка вправо
↑
Стрелка вверх

Графические символы

Квадратные, прямоугольные и алмазный

ˍ
Модификатор буквы нижний макрон
∎
Конец доказательства
⊞
Плюс в квадрате
⊟
Минус в квадрате
⊠
Умножение-крест в квадрате
⊡
Оператор точка в квадрате
⋄
Операция ромб
⎔
Программно-функциональный символ
⎚
Символ очистить экран
▀
Верхняя половина блока
▁
Нижняя одна восьмая блока
▂
Нижняя одна четверть блока
▃
Нижние три восьмых блока
▄
Нижняя половина блока
▅
Нижние пять восьмых блока
▆
Нижние три четверти блока
▇
Нижние семь восьмых блока
█
Полный блок
▉
Левые семь восьмых блока
▊
Левые три четверти блока
▋
Левые пять восьмых блока
▋
Левые пять восьмых блока
▌
Левая половина блока
▍
Левые три восьмых блока
▎
Левая одна четверть блока
▏
Левая одна восьмая блока
▐
Правая половина блока
░
Легкое затемнение
▒
Среднее затемнение
▓
Темное затемнение
▔
Верхняя одна восьмая блока
■
Черный квадрат
□
Белый квадрат
▢
Белый квадрат с закругленными углами
▣
Белый квадрат содержащий маленький черный квадрат
▤
Квадрат с горизонтальным заполнением
▥
Квадрат с вертикальным наполнением
▦
Квадрат с ортогональным штриховым заполнением
▧
Квадрат с верхним левым и нижним правым заполнением
▨
Квадрат с верхним правым и нижним левым заполнением
▩
Квадрат с диагональным штриховым заполнением
▪
Маленький черный квадрат
▫
Маленький белый квадрат
▬
Черный прямоугольник
▭
Белый прямоугольник
▮
Черный вертикальный прямоугольник
▯
Белый вертикальный прямоугольник
▰
Черный параллелограмм
▱
Белый параллелограмм
►
Черный указатель направо
◄
Черный указатель налево
◆
Черный алмаз
◇
Белый алмаз
◈
Белый алмаз содержащий маленький черный алмазик
◘
Инвертированный маркер списка
◙
Инвертированная окружность
◚
Верхняя половина инвертированной окружности
◛
Нижняя половина инвертированной окружности
◢
Черный треугольник снизу справа
◣
Черный треугольник снизу слева
◤
Черный треугольник сверху слева
◥
Черный треугольник сверху справа
◧
Квадрат с левой черной половиной
◨
Квадрат с правой черной половиной
◩
Квадрат с верхней левой черной половинной диагональю
◪
Квадрат с нижней правой черной половинной диагональю
◫
Белый квадрат с вертикальной биссектрисой
☖
Белая фигура сёги
☗
Черная фигура сёги
❏
Незакрашенный квадрат, отбрасывающий тень вниз вправо
❐
Незакрашенный квадрат, отбрасывающий тень вверх вправо
❑
Незакрашенный квадрат с правой нижней тенью
❒
Незакрашенный квадрат с правой верхней тенью
❖
Закрашенный ромб со вписанным внутрь внутрь незакрашенным крестом
❘
Тонкая вертикальная черта
❙
Средняя вертикальная черта
❚
вертикальная черта
◊
Ромб

Треугольники

∆
Конечная разность
⊿
Прямоугольный треугольник
▲
Черный треугольник с вершиной вверх
△
Белый треугольник с вершиной вверх
▴
Маленький черный треугольник с вершиной вверх
▵
Маленький белый треугольник с вершиной вверх
▶
Черный треугольник с вершиной направо
▷
Белый треугольник с вершиной направо
▸
Маленький черный треугольник с вершиной направо
▹
Маленький белый треугольник с вершиной направо
►
Черный указатель направо
▻
Белый указатель направо
▼
Черный треугольник с вершиной вниз
▽
Белый треугольник с вершиной вниз
▾
Маленький черный треугольник с вершиной вниз
▿
Маленький белый треугольник с вершиной вниз
◀
Черный треугольник с вершиной налево
◁
Белый треугольник с вершиной налево
◂
Маленький черный треугольник с вершиной налево
◃
Маленький белый треугольник с вершиной налево
◄
Черный указатель налево
◅
Белый указатель налево
◢
Черный треугольник снизу справа
◣
Черный треугольник снизу слева
◤
Черный треугольник сверху слева
◥
Черный треугольник сверху справа
◬
Белый треугольник с вершиной вверх и точкой
◭
Треугольник с вершиной вверх и черной левой половиной
◮
Треугольник с вершиной вверх с правой черной половиной
∇
Оператор набла

Строка

`
Апостроф
ˊ
Модификатор буквы акут ударение
ᐟ
Канадская слоговая письменность последний акут
‐
Дефис
‑
Неразрывный дефис
‒
Цифровое тире
―
Горизонтальная линия
⁃
Дефис маркер списка
≣
Строго эквивалентный
⋐
Двойное подмножество
⋑
Двойное супермножество
⋒
Двойное пересечение
⋓
Двойное объединение
⌒
Дуга
⌜
Верхний левый угол
⌝
Верхний правый угол
⌞
Нижний левый угол
⌟
Нижний правый угол
⎯
Горизонтальная линия вытянутая
─
легкая горизонтальная
━
горизонтальная
│
легкая вертикальная
┃
вертикальная
┄
легкое тройное тире горизонтальное
┅
жирное тройное тире горизонтальное
┆
легкое тройное тире вертикальное
┇
жирное тройное тире вертикальное
┈
легкое четверное тире горизонтальное
┉
жирное четверное тире горизонтальное
┊
легкое четверное тире вертикальное
┋
жирное четверное тире вертикальное
┌
легкая вниз в направо
┍
легкая вниз и направо
┎
вниз и легкая направо
┏
вниз и направо
┐
легкая вниз и налево
┑
легкая вниз и налево
┒
вниз и легкая налево
┓
вниз и налево
└
легкая вверх и направо
└
легкая вверх и направо
┕
легкая вверх и направо
┖
вверх и легкая направо
┗
вверх и направо
┘
легкая вверх и налево
┙
легкая вверх и налево
┚
вверх и легкая налево
┛
вверх и налево
├
легкая вертикальная и направо
├
легкая вертикальная и направо
┝
легкая вертикальная и направо
┞
вверх и легкая направо и вниз
┟
вниз и легкая направо и вверх
┠
вертикальная и легкая направо
┡
легкая вниз направо и вверх
┢
легкая вверх и направо и вниз
┣
вертикальная и направо
┤
легкая вертикальная и налево
┥
легкая вертикальная и налево
┦
вверх и легкая налево и вниз
┧
вниз и легкая вверх и налево
┨
вертикальная и легкая налево
┩
легкая вниз и вверх и налево
┪
легкая вверх и налево и вниз
┫
вертикальная и налево
┬
легкая вниз и горизонтально
┭
налево и легкая направо и вниз
┮
направо и легкая налево и вниз
┯
легкая вниз и горизонтально
┰
вниз и легкая горизонтально
┱
легкая направо и налево и вниз
┲
легкая налево и направо и вниз
┳
вниз и горизонтально
┴
легкая вверх и горизонтально
┵
налево легкая направо и вниз
┶
направо и легкая налево и вверх
┷
легкая вверх и горизонтально
┸
вверх и легкое горизонтально
┹
легкая направо и налево и вверх
┺
легкая налево и вверх и направо
┻
вверх и горизонтально
┼
легкая вертикальная и горизонтальная
┽
налево легкая вертикально и направо
┾
направо легкая вертикально и налево
┿
легкая вертикальная горизонтальная
╀
вверх легкая горизонтально и вниз
╁
вниз легкая горизонтально и вверх
╂
вертикально легкая горизонтально
╃
вверх и налево легкая вниз и направо
╄
вверх и направо легкая вниз и налево
╅
вниз и налево легкая вверх и направо
╆
вниз и направо легкая вверх и налево
╇
легкая вниз горизонтально и вверх
╈
легкая вверх вниз горизонтально
╉
легкая направо вертикально и налево
╊
легкая налево вертикально и направо
╋
вертикально и горизонтально
╌
легкое двойное горизонтальное тире
╍
жирное двойное горизонтально тире
╎
легкое двойное вертикальное тире
╏
жирное двойное вертикальное тире
═
двойная горизонтальная
═
двойная горизонтальная
║
вертикальная
╒
вниз одинарная и направо двойная
╓
вниз и одинарная направо
╔
вниз и направо
╔
вниз и направо
╔
вниз и направо
╕
одинарная вниз налево
╕
одинарная вниз налево
╖
вниз и одинарная налево
╖
вниз и одинарная налево
╗
вниз и налево
╗
вниз и налево
╘
одинарная вверх направо
╙
вверх и одинарная направо
╚
вверх и направо
╚
вверх и направо
╛
одинарная вверх налево
╛
одинарная вверх налево
╜
вверх и одинарная налево
╜
вверх и одинарная налево
╝
вверх и налево
╝
вверх и налево
╞
вертикальная одинарная и направо двойная
╟
вертикальная двойная и одинарная направо
╟
вертикальная двойная и одинарная направо
╠
вертикальная и направо
╡
вертикальная одинарная налево
╡
вертикальная одинарная налево
╢
вертикальная двойная и одинарная налево
╢
вертикальная двойная и одинарная налево
╣
вертикальная и налево
╣
вертикальная и налево
╤
одинарная вниз горизонтально
╤
одинарная вниз горизонтально
╥
вниз и одинарная горизонтально
╥
вниз и одинарная горизонтально
╦
вниз и горизонтально
╦
вниз и горизонтально
╧
одинарная вверх горизонтально
╧
одинарная вверх горизонтально
╨
вверх и одинарная горизонтально
╨
вверх и одинарная горизонтально
╩
вверх и горизонтально
╩
вверх и горизонтально
╪
одинарная вертикально горизонтально
╪
одинарная вертикально горизонтально
╫
вертикально и одинарная горизонтально
╬
вертикально и горизонтально
╬
вертикально и горизонтально
╭
легкая дуга вниз и направо
╮
легкая дуга вниз и налево
╯
легкая дуга вверх и вверх и налево
╰
легкая дуга вверх и направо
╱
легкая диагональ с верхнего правого в нижний левый
╲
легкая диагональ с верхнего левого в нижний правый
╳
легкий диагональный крест
╴
легкая слева
╵
легкая вверх
╶
легкая направо
╷
легкая вниз
╸
налево
╹
вверх
╺
направо
╻
вниз
╼
легкая налево и направо
╽
легкая вверх и вниз
╾
налево и легкая направо
╿
вверх и легкая вниз
▏
Левая одна восьмая блока
▕
Правая одна восьмая блока
◜
Дуга в верхнем левом квадранте
◝
Дуга в среднем правом квадранте
◞
Дуга в нижнем правом квадранте
◟
Дуга в нижнем левом квадранте
◠
Верхняя половина круга
◡
Нижняя половина круга
☰
Триграмма для небес
☱
Триграмма для озера
☲
Триграмма для огня
☳
Триграмма для гром
☴
Триграмма для ветра
☵
Триграмма для воды
☶
Триграмма для гор
☷
Триграмма для земли
✕
Знак умножения
≡
Идентичный, тождество
⌈
Потолок числа, левая скобка
⌊
Пол числа, левая скобка
—
Длинное тире
⌉
Потолок числа, правая скобка
⌋
Пол числа, правая скобка

Круги

⊖
Минус
⊘
Черта деления
⊙
Оператор точка
⊚
Оператор круг
⊛
Оператор звездочки
⊜
Равно
⊝
Тире
◉
рыбий глаз
○
Белый круг
◌
Пунктирный круг
◍
Круг с вертикальным заполнением
◎
Бычий глаз
●
Черный круг
◐
Круг с левой черной половиной
◑
Круг с черной правой половиной
◒
Круг с черной нижней половиной
◓
Круг с черной верхней половиной
◔
Круг с черным верхним правым квадрантом
◕
Черный круг с левым верхним белым квадрантом
◖
Левая половина черного круга
◗
Правая половина черного круга
◦
Прозрачный маркер списка
◯
Большой круг
❍
Незакрашенный оттенённый круг
⦿
Шайба
⊕
Плюс
⊗
Умножение-крест

Символы Брайля

⣿
Шрифт Брайля точки-12345678
⠿
Шрифт Брайля точки-123456
⠾
Шрифт Брайля точки-23456
⠽
Шрифт Брайля точки-13456
⠼
Шрифт Брайля точки-3456
⠻
Шрифт Брайля точки-12456
⠺
Шрифт Брайля точки-2456
⠹
Шрифт Брайля точки-1456
⠸
Шрифт Брайля точки-456
⠷
Шрифт Брайля точки-12356
⠶
Шрифт Брайля точки-2356
⠵
Шрифт Брайля точки-1356
⠴
Шрифт Брайля точки-356
⠳
Шрифт Брайля точки-1256
⠲
Шрифт Брайля точки-256
⠱
Шрифт Брайля точки-156
⠰
Шрифт Брайля точки-56
⠯
Шрифт Брайля точки-12346
⠮
Шрифт Брайля точки-2346
⠭
Шрифт Брайля точки-1346
⠬
Шрифт Брайля точки-346
⠫
Шрифт Брайля точки-1246
⠪
Шрифт Брайля точки-246
⠩
Шрифт Брайля точки-146
⠨
Шрифт Брайля точки-46
⠧
Шрифт Брайля точки-1236
⠦
Шрифт Брайля точки-236
⠥
Шрифт Брайля точки-136
⠤
Шрифт Брайля точки-36
⠣
Шрифт Брайля точки-126
⠢
Шрифт Брайля точки-26
⠡
Шрифт Брайля точки-16
⠠
Шрифт Брайля точки-6
⠟
Шрифт Брайля точки-12345
⠞
Шрифт Брайля точки-2345
⠝
Шрифт Брайля точки-1345
⠜
Шрифт Брайля точки-345
⠛
Шрифт Брайля точки-1245
⠚
Шрифт Брайля точки-245
⠙
Шрифт Брайля точки-145
⠘
Шрифт Брайля точки-45
⠗
Шрифт Брайля точки-1235
⠖
Шрифт Брайля точки-235
⠕
Шрифт Брайля точки-135
⠔
Шрифт Брайля точки-35
⠓
Шрифт Брайля точки-125
⠒
Шрифт Брайля точки-25
⠑
Шрифт Брайля точки-15
⠐
Шрифт Брайля точки-5
⠏
Шрифт Брайля точки-1234
⠎
Шрифт Брайля точки-234
⠍
Шрифт Брайля точки-134
⠌
Шрифт Брайля точки-34
⠋
Шрифт Брайля точки-124
⠊
Шрифт Брайля точки-24
⠉
Шрифт Брайля точки-14
⠈
Шрифт Брайля точки-4
⠇
Шрифт Брайля точки-123
⠆
Шрифт Брайля точки-23
⠅
Шрифт Брайля точки-13
⠄
Шрифт Брайля точки-3
⠃
Шрифт Брайля точки-12
⠂
Шрифт Брайля точки-2
⠁
Шрифт Брайля точки-1
⠀
Шрифт Брайля чистый

Математические символы

Символы счета

∟
Прямой угол
∬
Двойной интеграл
∭
Тройной интеграл
∮
Контурный интеграл
∵
Поскольку
∷
Пропорция
≦
Меньше чем над равно
≧
Больше, чем над равно
≋
Тройная тильда
╳
легкий диагональный крест
✕
Знак умножения
✖
Жирный знак умножения
✚
Жирный закрашенный греческий крест
﹢
Маленький знак плюс
﹣
Маленький дефис-минус
﹤
Маленький знак меньше чем
﹥
Маленький знак больше чем
％
Fullwidth Percent Sign
＋
Fullwidth Plus Sign
－
Fullwidth Hyphen-Minus
／
Fullwidth Solidus
＝
Fullwidth Equals Sign
∧
Логическое И
∠
Угол
∩
Пересечение
∪
Объединение
°
Знак градуса
÷
Знак деления
≡
Идентичный, тождество
≥
Больше чем или равно
∞
∫
Интеграл
≤
Меньше или равный
≠
Не равный
∨
Логическое ИЛИ
‰
Знак промилле
‱
Знак на десять тысяч
⊥
Кнопка вверх
π
Греческая пи
±
Знак плюс-минус
√
Квадратный корень
∑
N-ичное суммирование
∴
Следовательно
×
Знак умножения
¬
Знак отрицания

Символы дроби

½
Дробь – одна вторая
⅓
Простая дробь одна треть
⅔
Простая дробь две трети
¼
Дробь – одна четверть
¾
Дробь – три четверти
⅕
Простая дробь одна пятая
⅖
Простая дробь две пятые
⅗
Простая дробь три пятые
⅘
Простая дробь четыре пятые
⅙
Простая дробь одна шестая
⅚
Простая дробь пять шестых
⅐
Простая дробь одна седьмая
⅛
Простая дробь одна восьмая
⅜
Простая дробь три восьмые
⅝
Простая дробь пять восьмых
⅞
Простая дробь семь восьмых
⅑
Простая дробь одна девятая
⅒
Простая дробь одна десятая
↉
Простая дробь ноль третьих
⅟
Дробный числитель один

Группа символов

μ
Греческая мю
°
Знак градуса
℃
Градус по Цельсию
℉
Градус по Фаренгейту
㎍
Квадратный mu g
㎎
Квадратный mg
㎏
Квадратный kg
㏌
Квадратный in
㎚
Квадратный nm
㎛
Квадратный mu m
㎜
Квадратный mm
㎝
Квадратный cm
㎞
Квадратный km
²
Верхний индекс 2
³
Верхний индекс 3
㎖
Квадратный ml
㎗
Квадратный еl
㎘
Квадратный kl
㏄
Квадратный cc
㏖
Квадратный mol
㏒
Квадратный log
㎅
Квадратный kb
㎆
Квадратный mb
㎇
Квадратный gb
㎈
Квадратный cal
㎉
Квадратный kcal
㎐
Квадратный hz
㎑
Квадратный khz
㎒
Квадратный mhz
㎓
Квадратный ghz
㎾
Квадратный kw
Ω
Греческая омега
㏑
Квадратный ln
㏈
Квадратный еb
㏐
Квадратный lm
㏂
Квадратный am
㏘
Квадратный pm
㎳
Квадратный ms
㎭
Квадратный rad
㏅
Квадратный cd
㎪
Квадратный kpa
㏗
Квадратный ph

Нижний индекс и верхний индекс

⁰
Надстрочный нуль
¹
Верхний индекс 1
²
Верхний индекс 2
³
Верхний индекс 3
⁴
Верхний индекс четыре
⁵
Верхний индекс пять
⁶
Верхний индекс шесть
⁷
Верхний индекс семь
⁸
Верхний индекс восемь
⁹
Верхний индекс девять
⁺
Верхний индекс плюс
⁻
Верхний индекс минус
⁼
Верхний индекс равно
⁽
Верхний индекс левая скобка
⁾
Верхний индекс правая скобка
ⁿ
Верхний индекс n
₀
Нижний индекс ноль
₁
Нижний индекс один
₂
Нижний индекс два
₃
Нижний индекс три
₄
Нижний индекс четыре
₅
Нижний индекс пять
₆
Нижний индекс шесть
₇
Нижний индекс семь
₈
Нижний индекс восемь
₉
Нижний индекс девять
₊
Нижний индекс плюс
₋
Нижний индекс минус
₌
Нижний индекс равно
₍
Нижний индекс круглая скобка
₎
Нижний индекс круглая скобка
ₐ
подA
ₑ
подE
ₒ
подO
ₓ
подX
ₔ
подшва
°
Знак градуса
ⁱ
Надi
⁄
Дробная наклонная черта

Числа

Ⅰ
Римская цифра один
Ⅱ
Римская цифра два
Ⅲ
Римская цифра три
Ⅳ
Римская цифра четыре
Ⅴ
Римская цифра пять
Ⅵ
Римская цифра шесть
Ⅶ
Римская цифра семь
Ⅷ
Римская цифра восемь
Ⅸ
Римская цифра девять
Ⅹ
Римская цифра десять
Ⅺ
Римская цифра одиннадцать
Ⅻ
Римская цифра двенадцать
ⅰ
римская цифра один
ⅱ
римская цифра два
ⅲ
римская цифра три
ⅳ
римская цифра четыре
ⅴ
римская цифра пять
ⅵ
римская цифра шесть
ⅶ
римская цифра семь
ⅷ
римская цифра восемь
ⅸ
римская цифра девять
ⅹ
римская цифра десять
ⅺ
римская цифра одиннадцать
ⅻ
римская цифра двенадцать
⓪
Цифра ноль
①
Цифра один
②
Цифра два
③
Цифра три
④
Цифра четыре
⑤
Цифра пять
⑥
Цифра шесть
⑦
Цифра семь
⑧
Цифра восемь
⑨
Цифра девять
⑩
Цифра десять
⓵
Цифра один в двойном круге
⓶
Цифра два в двойном круге
⓷
Цифра три в двойном круге
⓸
Цифра четыре в двойном круге
⓹
Цифра пять в двойном круге
⓺
Цифра шесть в двойном круге
⓻
Цифра семь в двойном круге
⓼
Цифра восемь в двойном круге
⓽
Цифра девять в двойном круге
⓾
Цифра десять в двойном круге
⑴
Цифра один в скобках
⑵
Цифра два в скобках
⑶
Цифра три в скобах
⑷
Цифра четыре в скобах
⑸
Цифра пять в скобках
⑹
Цифра шесть в скобках
⑺
Цифра семь в скобках
⑻
Цифра восемь в скобках
⑼
Цифра девять в скобках
⑽
Цифра десять в скобках
⓿
Цифра ноль в черном круге
❶
Номер 1, заключённый в чёрный круг
❷
Номер 2, заключённый в чёрный круг
❸
Номер 3, заключённый в чёрный круг
❹
Номер 4, заключённый в чёрный круг
❺
Номер 5, заключённый в чёрный круг
❻
Номер 6, заключённый в чёрный круг
❼
Номер 7, заключённый в чёрный круг
❽
Номер 8, заключённый в чёрный круг
❾
Номер 9, заключённый в чёрный круг
❿
Номер 10, заключённый в чёрный круг
㈠
Заключенная в скобках идеограмма один
㈡
Заключенная в скобках идеограмма два
㈢
Заключенная в скобках идеограмма три
㈣
Заключенная в скобках идеограмма четыре
㈤
Заключенная в скобках идеограмма пять
㈥
Заключенная в скобках идеограмма шесть
㈦
Заключенная в скобках идеограмма семь
㈧
Заключенная в скобках идеограмма восемь
㈨
Заключенная в скобках идеограмма девять
㈩
Заключенная в скобках идеограмма десять
㊀
Обведенная кругом идеограмма один
㊁
Обведенная кругом идеограмма два
㊂
Обведенная кругом идеограмма три
㊃
Обведенная кругом идеограмма четыре
㊄
Обведенная кругом идеограмма пять
㊅
Обведенная кругом идеограмма шесть
㊆
Обведенная кругом идеограмма семь
㊇
Обведенная кругом идеограмма восемь
㊈
Обведенная кругом идеограмма девять
㊉
Обведенная кругом идеограмма десять
０
Fullwidth Digit Zero
１
Fullwidth Digit One
２
Fullwidth Digit Two
３
Fullwidth Digit Three
４
Fullwidth Digit Four
５
Fullwidth Digit Five
６
Fullwidth Digit Six
７
Fullwidth Digit Seven
８
Fullwidth Digit Eight
９
Fullwidth Digit Nine

Символ числа пи

Π
Греческая пи
π
Греческая пи
𝜫
курсивная пи
𝝅
курсивная пи
𝝥
без засечек пи
𝝿
без засечек пи
𝞟
без засечек курсивная пи
𝞹
без засечек курсивная пи
П
Кириллическая пэ
п
Кириллическая пэ
∏
N-арное произведение
ϖ
Греческий символ пи
∐
N-арное копроизведение
ℼ
Дважды начерченная пи
ㄇ
Чжуинь (бопомофо) m
兀
Идеограмма

Языковые символы

[adinserter block=”12″]

Греческие символы

Α
Греческая альфа
Β
Греческая бета
Γ
Греческая гамма
Δ
Греческая дельта
Ε
Греческая эпсилон
Ζ
Греческая дзета
Η
Греческая эта
Θ
Греческая тета
Ι
Греческая йота
Κ
Греческая каппа
Λ
Греческая лямбда
Μ
Греческая мю
Ν
Греческая ню
Ξ
Греческая кси
Ο
Греческая омикрон
Π
Греческая пи
Ρ
Греческая ро
Σ
Греческая сигма
Τ
Греческая тау
Υ
Греческая ипсилон
Φ
Греческая фи
Χ
Греческая хи
Ψ
Греческая пси
Ω
Греческая омега
α
Греческая альфа
β
Греческая бета
γ
Греческая гамма
δ
Греческая дельта
ε
Греческая эпсилон
ζ
Греческая дзета
η
Греческая эта
θ
Греческая тета
ι
Греческая йота
κ
Греческая каппа
λ
Греческая лямбда
μ
Греческая мю
ν
Греческая ню
ξ
Греческая кси
ο
Греческая омикрон
π
Греческая пи
ρ
Греческая ро
ς
Греческая окончательная сигма
σ
Греческая сигма
τ
Греческая тау
υ
Греческая ипсилон
φ
Греческая фи
χ
Греческая хи
ψ
Греческая пси
ω
Греческая омега

Латинские буквы

Æ
AE
Á
A с акутом
Â
A с циркумфлексом
Â
A с циркумфлексом
À
A с грависом
Å
A с кружочком сверху
Ã
A с тильдой
Ä
A с диэризисом
Ç
C с седилью
Ð
ETH
É
E с акутом
Ê
E с циркумфлексом
È
E с грависом
Ë
E с диэрезисом
Í
I с акутом
Î
I с циркумфлексом
Ì
I с грависом
Ï
I с диэрезисом
Ñ
N с тильдой
Ó
O с акутом
Ô
O с циркумфлексом
Ò
O с грависом
Ø
O со штрихом
Õ
O с тильдой
Ö
O с диэризисом
Þ
торн
Ú
U с акутом
Û
U с циркумфлексом
Ù
U с грависом
Ü
U с диэризисом
Ý
Y с акутом
á
a с акутом
â
a с циркумфлексом
æ
лигатура ae
à
a с грависом
å
a с кружочком сверху
ã
a с тильдой
ä
a с диэризисом
ç
c с седилью
é
e с акутом
ê
e с циркумфлексом
è
e с грависом
ð
eth
ë
e с диэризисом
í
i с акутом
î
i с циркумфлексом сверху
ì
i с грависом
ï
i с диэризисом (умляутом)
ñ
n с тильдой
ó
o с ударением
ô
o с циркумфлексом
ò
o с грависом
ø
o со штрихом
õ
o с тильдой
ö
o с диэризисом
ß
эсцет (S острое)
þ
торн
ú
u с акутом
û
u с циркумфлексом
ù
u с грависом
ü
u с диэризисом
ý
y с акутом
ÿ
y с диэризисом

пунктуация

¡
Перевернутый восклицательный знак
¿
Перевернутый вопросительный знак
¦
Изломанная вертикальная черта
¨
Диэрезис
ª
Женский порядковый индикатор
Мягкий перенос
¯
Макрон. Надчёркивание
´
Знак ударения
·
Точка по центру
¸
Седиль
º
Мужской порядковый индикатор
«
Открывающая левая кавычка «ёлочка»
»
Закрывающая правая кавычка «ёлочка»

Латинские расширенные символы

Ā
«A» с макроном
ā
«a» с макроном
Ă
«A» с бревисом
ă
«a» с бревисом
Ą
«A» с огонэком
ą
«a» с огонэком
Ć
«C» с акутом
ć
«c» с акутом
Ĉ
«C» с циркумфлексом
ĉ
«с» с циркумфлексом
Ċ
«С» с точкой сверху
ċ
«c» с точкой сверху
Č
«C» с гачеком
č
«c» с гачеком
Ď
«D» с гачеком
ď
«d» с гачеком
Đ
«D» со штрихом
đ
«d» со штрихом
Ē
«E» с макроном
ē
«e» с макроном
Ĕ
«E» с бревисом
ĕ
«e» с бревисом
Ė
«E» с точкой сверху
ė
«e» с точкой сверху
Ę
«E» с огонэком
ę
«e» с огонэком
Ě
«E» с гачеком
ě
«e» с гачеком
Ĝ
«G» с циркумфлексом
ĝ
«g» с циркумфлексом
Ğ
«G» с бревисом
ğ
«g» с бревисом
Ġ
«G» с точкой сверху
ġ
«g» с точкой сверху
Ģ
«G» с седилью
ģ
«g» с седилью
Ĥ
«H» с циркумфлексом
ĥ
«h» с циркумфлексом
Ħ
«H» со штрихом
ħ
«h» со штрихом
Ĩ
«I» с тильдой
ĩ
«i» с тильдой
Ī
«I» с макроном
ī
«i» с макроном
Ĭ
«I» с бревисом
ĭ
«i» с бревисом
Į
«I» с огонэком
į
«i» с огонэком
İ
«I» с точкой сверху
ı
«i» без точки
Ĳ
лигатура IJ
ĳ
лигатура ij
Ĵ
«J» с циркумфлексом
ĵ
«j» с циркумфлексом
Ķ
«K» с седилью
ķ
«k» с седилью
ĸ
кра
Ĺ
«L» с акутом
ĺ
«l» с акутом
Ļ
«L» с седилью
ļ
«l» с седилью
Ľ
«L» с гачеком
ľ
«l» с гачеком
Ŀ
«L» с внутристрочной точкой
ŀ
«l» с внутристрочной точкой
Ł
«L» со штрихом, символ Лайткоина
ł
«l» со штрихом
Ń
«N» с акутом
ń
«n» с акутом
Ņ
«N» с седилью
ņ
«n» с седилью
Ň
«N» с гачеком
ň
«n» с гачеком
Ŋ
энг
ŋ
энг
Ō
«O» с макроном
ō
«o» с макроном
Ŏ
«O» с бревисом
ŏ
«o» с бревисом
Ő
«O» с двойным акутом
ő
«o» с двойным акутом
Œ
лигатура OE
œ
лигатура oe
Ŕ
«R» с акутом
ŕ
«r» с акутом
Ŗ
«R» с седилью
ŗ
«r» с седилью
Ř
«R» с гачеком
ř
«r» с гачеком
Ś
«S» с акутом
ś
«s» с акутом
Ŝ
«S» с циркумфлексом
ŝ
«s» с циркумфлексом
Ş
«S» с седилью
ş
«s» с седилью
Š
«S» с гачеком
š
«s» с гачеком
Ţ
«T» с седилью
ţ
«t» с седилью
Ť
«T» с гачеком
ť
«t» с гачеком
Ŧ
«T» со штрихом
ŧ
«t» со штрихом
Ũ
«U» с тильдой
ũ
«u» с тильдой
Ū
«U» с макроном
ū
«u» с макроном
Ŭ
«U» с бревисом
ŭ
«u» с бревисом
Ů
«U» с кружком сверху
ů
«u» с кружком сверху
Ű
«U» с двойным акутом
ű
«u» с двойным акутом
Ų
«U» с огонэком
ų
«u» с огонэком
Ŵ
«W» с циркумфлексом
ŵ
«w» с циркумфлексом
Ŷ
«Y» с циркумфлексом
ŷ
«y» с циркумфлексом
Ÿ
«Y» с диэрезисом
Ź
«Z» с акутом
ź
«z» с акутом
Ż
«Z» с точкой сверху
ż
«z» с точкой сверху
Ž
«Z» с гачеком
ž
«z» с гачеком
ſ
длинная «s»
ŉ
«n» предшествующим апострофом

Буквенные шрифты

Ⓐ
A
Ⓑ
B
Ⓒ
C
Ⓓ
D
Ⓔ
E
Ⓕ
F
Ⓖ
G
Ⓗ
H
Ⓘ
I
Ⓙ
J
Ⓚ
K
Ⓛ
L
Ⓜ
M
Ⓝ
N
Ⓞ
O
Ⓟ
P
Ⓠ
Q
Ⓡ
R
Ⓢ
S
Ⓣ
T
Ⓤ
U
Ⓥ
V
Ⓦ
W
Ⓧ
X
Ⓨ
Y
Ⓩ
Z
ⓐ
a
ⓑ
b
ⓒ
c
ⓓ
d
ⓔ
e
ⓕ
f
ⓖ
g
ⓗ
h
ⓘ
i
ⓙ
j
ⓚ
k
ⓛ
l
ⓜ
m
ⓝ
n
ⓞ
o
ⓟ
p
ⓠ
q
ⓡ
r
ⓢ
s
ⓣ
t
ⓤ
u
ⓥ
v
ⓦ
w
ⓧ
x
ⓨ
y
ⓩ
z

ᴀ
a
ʙ
b
ᴄ
c
ᴅ
d
ᴇ
e
ғ
Кириллическая фрикативное «г»
ɢ
g
ʜ
h
ɪ
i
ᴊ
j
ᴋ
k
ʟ
l
ᴍ
m
ɴ
n
ᴏ
o
ᴏ
o
ᴘ
p
ǫ
«o» с огонэком
ʀ
R
s
s
ᴛ
t
ᴜ
u
ᴠ
v
ᴡ
w
x
x
ʏ
y
ᴢ
z

𝓐
рукописная A
𝓑
рукописная B
𝓒
рукописная C
𝓓
рукописная D
𝓔
рукописная E
𝓕
рукописная F
𝓖
рукописная G
𝓗
рукописная H
𝓘
рукописная I
𝓙
рукописная J
𝓚
рукописная K
𝓛
рукописная L
𝓜
рукописная M
𝓝
рукописная N
𝓞
рукописная O
𝓟
рукописная P
𝓠
рукописная Q
𝓡
рукописная R
𝓢
рукописная S
𝓣
рукописная T
𝓤
рукописная U
𝓥
рукописная V
𝓦
рукописная W
𝓧
рукописная X
𝓨
рукописная Y
𝓩
рукописная Z
𝓪
рукописная a
𝓫
рукописная b
𝓬
рукописная c
𝓭
рукописная d
𝓮
рукописная e
𝓯
рукописная f
𝓰
рукописная g
𝓱
рукописная h
𝓲
рукописная i
𝓳
рукописная j
𝓴
рукописная k
𝓵
рукописная l
𝓶
рукописная m
𝓷
рукописная n
𝓸
рукописная o
𝓹
рукописная p
𝓺
рукописная q
𝓻
рукописная r
𝓼
рукописная s
𝓽
рукописная t
𝓾
рукописная u
𝓿
рукописная v
𝔀
рукописная w
𝔁
рукописная x
𝔂
рукописная y
𝔃
рукописная z
𝒜
рукописная A
ℬ
Каллиграфическая B
𝒞
рукописная C
𝒟
рукописная D
ℰ
Каллиграфическая E
ℱ
Каллиграфическая F
𝒢
рукописная G
ℋ
Каллиграфическая H
ℐ
Каллиграфическая I
𝒥
рукописная J
𝒦
рукописная K
ℒ
Каллиграфическая L
ℳ
Каллиграфическая M
𝒩
рукописная N
𝒪
рукописная O
𝒫
рукописная P
𝒬
рукописная Q
ℛ
Каллиграфическая R
𝒮
рукописная S
𝒯
рукописная T
𝒰
рукописная U
𝒱
рукописная V
𝒲
рукописная W
𝒳
рукописная X
𝒴
рукописная Y
𝒵
рукописная Z
𝒶
рукописная a
𝒷
рукописная b
𝒸
рукописная c
𝒹
рукописная d
𝑒
курсивная e
𝒻
рукописная f
𝑔
курсивная g
𝒽
рукописная h
𝒾
рукописная i
𝒿
рукописная j
𝓀
рукописная k
𝓁
рукописная l
𝓂
рукописная m
𝓃
рукописная n
𝑜
курсивная o
𝓅
рукописная p
𝓆
рукописная q
𝓇
рукописная r
𝓈
рукописная s
𝓉
рукописная t
𝓊
рукописная u
𝓋
рукописная v
𝓌
рукописная w
𝓍
рукописная x
𝓎
рукописная y
𝓏
рукописная z

🅐
В чёрном круге A
🅑
В чёрном круге B
🅒
В чёрном круге C
🅓
В чёрном круге D
🅔
В чёрном круге E
🅕
В чёрном круге F
🅖
В чёрном круге G
🅗
В чёрном круге H
🅘
В чёрном круге I
🅙
В чёрном круге J
🅚
В чёрном круге K
🅛
В чёрном круге L
🅜
В чёрном круге M
🅝
В чёрном круге N
🅞
В чёрном круге O
🅟
В чёрном круге P
🅠
В чёрном круге Q
🅡
В чёрном круге R
🅢
В чёрном круге S
🅣
В чёрном круге T
🅤
В чёрном круге U
🅥
В чёрном круге V
🅦
В чёрном круге W
🅧
В чёрном круге X
🅨
В чёрном круге Y
🅩
В чёрном круге Z

𝔸
текстовый символ a
𝔹
текстовый символ b
ℂ
Дважды начерченная С
𝔻
текстовый символ d
𝔼
текстовый символ e
𝔽
текстовый символ f
𝔾
текстовый символ g
ℍ
Дважды начерченная H
𝕀
текстовый символ i
𝕁
текстовый символ j
𝕂
текстовый символ k
𝕃
текстовый символ l
𝕄
текстовый символ m
ℕ
Дважды начерченная N
𝕆
текстовый символ o
ℙ
Дважды начерченная P
ℚ
Дважды начерченная Q
ℝ
Дважды начерченная R
𝕊
текстовый символ s
𝕋
текстовый символ t
𝕌
текстовый символ u
𝕍
текстовый символ v
𝕎
текстовый символ w
𝕏
текстовый символ x
𝕐
текстовый символ y
ℤ
Дважды начерченная Z
𝕒
текстовый символ a
𝕓
текстовый символ b
𝕔
текстовый символ c
𝕕
двойная d
𝕖
двойная e
𝕗
двойная f
𝕘
двойная g
𝕙
двойная h
𝕚
двойная i
𝕛
двойная j
𝕜
двойная k
𝕝
двойная l
𝕞
двойная m
𝕟
двойная n
𝕠
двойная o
𝕡
двойная p
𝕢
двойная q
𝕣
двойная r
𝕤
двойная s
𝕥
двойная t
𝕦
двойная u
𝕧
двойная v
𝕨
двойная w
𝕩
двойная x
𝕪
двойная y
𝕫
двойная z

🄰
A заключённая в квадрат
🄱
B заключённая в квадрат
🄲
C заключённая в квадрат
🄳
D заключённая в квадрат
🄴
E заключённая в квадрат
🄵
F заключённая в квадрат
🄶
G заключённая в квадрат
🄷
H заключённая в квадрат
🄸
I заключённая в квадрат
🄹
J заключённая в квадрат
🄺
K заключённая в квадрат
🄻
L заключённая в квадрат
🄼
M заключённая в квадрат
🄽
N заключённая в квадрат
🄾
O заключённая в квадрат
🄿
P заключённая в квадрат
🅀
Q заключённая в квадрат
🅁
R заключённая в квадрат
🅂
S заключённая в квадрат
🅃
T заключённая в квадрат
🅄
U заключённая в квадрат
🅅
V заключённая в квадрат
🅆
W заключённая в квадрат
🅇
X заключённая в квадрат
🅈
Y заключённая в квадрат
🅉
Z заключённая в квадрат

🅰
В чёрном квадрате A
🅱
В чёрном квадрате B
🅲
В чёрном квадрате C
🅳
В чёрном квадрате D
🅴
В чёрном квадрате E
🅵
В чёрном квадрате F
🅶
В чёрном квадрате G
🅷
В чёрном квадрате H
🅸
В чёрном квадрате I
🅹
В чёрном квадрате j
🅺
В чёрном квадрате K
🅻
В чёрном квадрате L
🅼
В чёрном квадрате L
🅽
В чёрном квадрате N
🅾
В чёрном квадрате O
🅿
В чёрном квадрате P
🆀
В чёрном квадрате Q
🆁
В чёрном квадрате R
🆂
В чёрном квадрате S
🆃
В чёрном квадрате T
🆄
В чёрном квадрате U
🆅
В чёрном квадрате V
🆆
В чёрном квадрате W
🆇
В чёрном квадрате X
🆈
В чёрном квадрате Y
🆉
В чёрном квадрате Z

𝕬
a
𝕭
b
𝕮
c
𝕯
d
𝕰
e
𝕱
f
𝕲
g
𝕳
h
𝕴
i
𝕵
j
𝕶
k
𝕷
l
𝕸
m
𝕹
n
𝕺
o
𝕻
p
𝕼
q
𝕽
r
𝕾
s
𝕿
t
𝖀
u
𝖁
v
𝖂
w
𝖃
x
𝖄
y
𝖅
z
𝖆
a
𝖇
b
𝖈
c
𝖉
d
𝖊
e
𝖋
f
𝖌
g
𝖍
h
𝖎
i
𝖏
j
𝖐
k
𝖑
l
𝖒
m
𝖓
n
𝖔
o
𝖕
p
𝖖
q
𝖗
r
𝖘
s
𝖙
t
𝖚
u
𝖛
v
𝖜
w
𝖝
x
𝖞
y
𝖟
z
𝔄
a
𝔅
b
ℭ
Готическая C
𝔇
d
𝔈
e
𝔉
f
𝔊
g
ℌ
Готическая H
ℑ
Готическая I
𝔍
j
𝔎
k
𝔏
l
𝔐
m
𝔑
n
𝔒
o
𝔓
p
𝔔
q
ℜ
Готическая R
𝔖
s
𝔗
t
𝔘
u
𝔙
v
𝔚
w
𝔛
x
𝔜
y
ℨ
Готическая Z
𝔞
a
𝔟
b
𝔠
c
𝔡
d
𝔢
e
𝔣
f
𝔤
g
𝔥
h
𝔦
i
𝔧
j
𝔨
k
𝔩
l
𝔪
m
𝔫
n
𝔬
o
𝔭
p
𝔮
q
𝔯
r
𝔰
s
𝔱
t
𝔲
u
𝔳
v
𝔴
w
𝔵
x
𝔶
y
𝔷
z

𝐀
A
𝐁
B
𝐂
C
𝐃
D
𝐄
E
𝐅
F
𝐆
G
𝐇
H
𝐈
I
𝐉
J
𝐊
K
𝐋
L
𝐌
M
𝐍
N
𝐎
O
𝐏
P
𝐐
Q
𝐑
R
𝐒
S
𝐓
T
𝐔
U
𝐕
V
𝐖
W
𝐗
X
𝐘
Y
𝐙
Z
𝐚
a
𝐛
b
𝐜
c
𝐝
d
𝐞
e
𝐟
f
𝐠
g
𝐡
h
𝐢
i
𝐣
j
𝐤
k
𝐥
l
𝐦
m
𝐧
n
𝐨
o
𝐩
p
𝐪
q
𝐫
r
𝐬
s
𝐭
t
𝐮
u
𝐯
v
𝐰
w
𝐱
x
𝐲
y
𝐳
z

𝘈
𝘉
𝘊
𝘋
𝘌
𝘍
𝘎
𝘏
𝘐
𝘑
𝘒
𝘓
𝘔
𝘕
𝘖
𝘗
𝘘
𝘙
𝘚
𝘛
𝘜
𝘝
𝘞
𝘟
𝘠
𝘡
𝘢
𝘣
𝘤
𝘥
𝘦
𝘧
𝘨
𝘩
𝘪
𝘫
𝘬
𝘭
𝘮
𝘯
𝘰
𝘱
𝘲
𝘳
𝘴
𝘵
𝘶
𝘷
𝘸
𝘹
𝘺
𝘻
𝘼
𝘽
𝘾
𝘿
𝙀
𝙁
𝙂
𝙃
𝙄
𝙅
𝙆
𝙇
𝙈
𝙉
𝙊
𝙋
𝙌
𝙍
𝙎
𝙏
𝙐
𝙑
𝙒
𝙓
𝙔
𝙕
𝙖
𝙗
𝙘
𝙙
𝙚
𝙛
𝙜
𝙝
𝙞
𝙟
𝙠
𝙡
𝙢
𝙣
𝙤
𝙥
𝙦
𝙧
𝙨
𝙩
𝙪
𝙫
𝙬
𝙭
𝙮
𝙯

Китайские символы

㊊
Символ Обведенная кругом идеограмма луна
㊋
Символ Обведенная кругом идеограмма огонь
㊌
Символ Обведенная кругом идеограмма вода
㊍
Символ Обведенная кругом идеограмма дерево
㊎
Символ Обведенная кругом идеограмма металл
㊏
Символ Обведенная кругом идеограмма земля
㊐
Символ Обведенная кругом идеограмма солнце
㊑
Символ Обведенная кругом идеограмма запас
㊒
Символ Обведенная кругом идеограмма иметь
㊓
Символ Обведенная кругом идеограмма общество
㊔
Символ Обведенная кругом идеограмма имя
㊕
Символ Обведенная кругом идеограмма особый
㊖
Символ Обведенная кругом идеограмма денежный
㊗
Символ Обведенная кругом идеограмма поздравление
㊘
Символ Обведенная кругом идеограмма работа
㊙
Символ Обведенная кругом идеограмма секрет
㊚
Символ Обведенная кругом идеограмма мужчина
㊛
Символ Обведенная кругом идеограмма женщина
㊜
Символ Обведенная кругом идеограмма подходящий
㊝
Символ Обведенная кругом идеограмма превосходный
㊞
Символ Обведенная кругом идеограмма печать
㊟
Символ Обведенная кругом идеограмма внимание
㊠
Символ Обведенная кругом идеограмма предмет
㊡
Символ Обведенная кругом идеограмма отдых
㊢
Символ Обведенная кругом идеограмма копия
㊣
Символ Обведенная кругом идеограмма правильный
㊤
Символ Обведенная кругом идеограмма высокий
㊥
Символ Обведенная кругом идеограмма центр
㊦
Символ Обведенная кругом идеограмма низкий
㊧
Символ Обведенная кругом идеограмма лево
㊨
Символ Обведенная кругом идеограмма право
㊩
Символ Обведенная кругом идеограмма медицина
㊪
Символ Обведенная кругом идеограмма религия
㊫
Символ Обведенная кругом идеограмма учеба
㊬
Символ Обведенная кругом идеограмма смотреть
㊭
Символ Обведенная кругом идеограмма промышленное предприятие
㊮
Символ Обведенная кругом идеограмма средство
㊯
Символ Обведенная кругом идеограмма союз
㊰
Символ Обведенная кругом идеограмма ночь

Имена японской эпохи

㋿
Square Era Name Reiwa
㍻
Квадратный era имя heisei
㍼
Квадратный era имя syouwa
㍽
Квадратный era имя taisyou
㍾
Квадратный era имя meizi

Японские иероглифы

ぁ
Текстовый уменьшенная a
あ
Текстовый a
ぃ
Текстовый уменьшенная i
い
Текстовый i
ぅ
Текстовый уменьшенная u
う
Текстовый u
ぇ
Текстовый уменьшенная e
え
Текстовый e
ぉ
Текстовый уменьшенная o
お
Текстовый o
か
Текстовый ka
が
Текстовый ga
き
Текстовый ki
ぎ
Текстовый gi
く
Текстовый ku
ぐ
Текстовый gu
け
Текстовый ke
げ
Текстовый ge
こ
Текстовый ko
ご
Текстовый go
さ
Текстовый sa
ざ
Текстовый za
し
Текстовый si
じ
Текстовый zi
す
Текстовый su
ず
Текстовый zu
せ
Текстовый se
ぜ
Текстовый ze
そ
Текстовый so
ぞ
Текстовый zo
た
Текстовый ta
だ
Текстовый da
ち
Текстовый ti
ぢ
Текстовый di
っ
Текстовый уменьшенная tu
つ
Текстовый tu
づ
Текстовый du
て
Текстовый te
で
Текстовый de
と
Текстовый to
ど
Текстовый do
な
Текстовый na
に
Текстовый ni
ぬ
Текстовый nu
ね
Текстовый ne
の
Текстовый no
は
Текстовый ha
ば
Текстовый ba
ぱ
Текстовый pa
ひ
Текстовый hi
び
Текстовый bi
ぴ
Текстовый pi
ふ
Текстовый hu
ぶ
Текстовый bu
ぷ
Текстовый pu
へ
Текстовый he
べ
Текстовый be
ぺ
Текстовый pe
ほ
Текстовый ho
ぼ
Текстовый bo
ぽ
Текстовый po
ま
Текстовый ma
み
Текстовый mi
む
Текстовый mu
め
Текстовый me
も
Текстовый mo
ゃ
Текстовый уменьшенная ya
や
Текстовый ya
ゅ
Текстовый уменьшенная yu
ゆ
Текстовый yu
ょ
Текстовый уменьшенная yo
よ
Текстовый yo
ら
Текстовый ra
り
Текстовый ri
る
Текстовый ru
れ
Текстовый re
ろ
Текстовый ro
ゎ
Текстовый уменьшенная wa
わ
Текстовый wa
ゐ
Текстовый wi
ゑ
Текстовый we
を
Текстовый wo
ん
Текстовый n
ゔ
Текстовый vu
ゕ
Текстовый уменьшенная ka
ゖ
Текстовый уменьшенная ke
゚
゛
Текстовый знак звонкого звука
゜
Текстовый знак полузвонкого звука
ゝ
Текстовый знак повторения
ゞ
Текстовый звонкий знак повторения
ゟ
Текстовый диграф yori
゠
Текстовый двойной дефис
ァ
Катакана уменьшенная a
ア
Катакана a
ィ
Катакана уменьшенная i
イ
Катакана i
ゥ
Катакана уменьшенная u
ウ
Катакана u
ェ
Катакана уменьшенная e
エ
Катакана e
ォ
Катакана уменьшенная o
オ
Катакана o
カ
Катакана ka
ガ
Катакана ga
キ
Катакана ki
ギ
Катакана gi
ク
Катакана ku
グ
Катакана gu
ケ
Катакана ke
ゲ
Катакана ge
コ
Катакана ko
ゴ
Катакана go
サ
Катакана sa
ザ
Катакана za
シ
Катакана si
ジ
Катакана zi
ス
Катакана su
ズ
Катакана zu
セ
Катакана se
ゼ
Катакана ze
ソ
Катакана so
ゾ
Катакана zo
タ
Катакана ta
ダ
Катакана da
チ
Катакана ti
ヂ
Катакана di
ッ
Катакана уменьшенная tu
ツ
Катакана tu
ヅ
Катакана du
テ
Катакана te
デ
Катакана de
ト
Катакана to
ド
Катакана do
ナ
Катакана na
ニ
Катакана ni
ヌ
Катакана nu
ネ
Катакана ne
ノ
Катакана no
ハ
Катакана ha
バ
Катакана ba
パ
Катакана pa
ヒ
Катакана hi
ビ
Катакана bi
ピ
Катакана pi
フ
Катакана hu
ブ
Катакана bu
プ
Катакана pu
ヘ
Катакана he
ベ
Катакана be
ペ
Катакана pe
ホ
Катакана ho
ボ
Катакана bo
ポ
Катакана po
マ
Катакана ma
ミ
Катакана mi
ム
Катакана mu
メ
Катакана me
モ
Катакана mo
ャ
Катакана уменьшенная ya
ヤ
Катакана ya
ュ
Катакана уменьшенная yu
ユ
Катакана yu
ョ
Катакана уменьшенная yo
ヨ
Катакана yo
ラ
Катакана ra
リ
Катакана ri
ル
Катакана ru
レ
Катакана re
ロ
Катакана ro
ヮ
Катакана уменьшенная wa
ワ
Катакана wa
ヰ
Катакана wi
ヱ
Катакана we
ヲ
Катакана wo
ン
Катакана n
ヴ
Катакана vu
ヵ
Катакана уменьшенная ka
ヶ
Катакана уменьшенная ke
ヷ
Катакана va
ヸ
Катакана vi
ヹ
Катакана ve
ヺ
Катакана vo
・
Катакана средняя точка
ー
Текстовый знак протяжный звук
ヽ
Катакана знак повторения
ヾ
Катакана звонкий знак повторения
ヿ
Катакана орграфа koto
㍐
Квадратный юань
㍿
Квадратный корпорация

Корейские символы

ㄱ
хангыля kiyeok
ㄲ
хангыля ssangkiyeok
ㄳ
хангыля kiyeok-sios
ㄴ
хангыля nieun
ㄵ
хангыля nieun-cieuc
ㄶ
хангыля nieun-hieuh
ㄷ
хангыля tikeut
ㄸ
хангыля ssangtikeut
ㄹ
хангыля rieul
ㄺ
хангыля rieul-kiyeok
ㄻ
хангыля rieul-mieum
ㄼ
хангыля rieul-pieup
ㄽ
хангыля rieul-sios
ㄾ
хангыля rieul-thieuth
ㄿ
хангыля rieul-phieuph
ㅀ
хангыля rieul-hieuh
ㅁ
хангыля mieum
ㅂ
хангыля pieup
ㅃ
хангыля ssangpieup
ㅄ
хангыля pieup-sios
ㅅ
хангыля sios
ㅆ
хангыля ssangsios
ㅇ
хангыля ieung
ㅈ
хангыля cieuc
ㅉ
хангыля ssangcieuc
ㅊ
хангыля chieuch
ㅋ
хангыля khieukh
ㅌ
хангыля thieuth
ㅍ
хангыля phieuph
ㅎ
хангыля hieuh
ㅏ
хангыля a
ㅐ
хангыля ae
ㅑ
хангыля ya
ㅒ
хангыля yae
ㅓ
хангыля eo
ㅔ
хангыля e
ㅕ
хангыля yeo
ㅖ
хангыля ye
ㅗ
хангыля o
ㅘ
хангыля wa
ㅙ
хангыля wae
ㅚ
хангыля oe
ㅛ
хангыля yo
ㅜ
хангыля u
ㅝ
хангыля weo
ㅞ
хангыля we
ㅟ
хангыля wi
ㅠ
хангыля yu
ㅡ
хангыля eu
ㅢ
хангыля yi
ㅥ
хангыля ssangnieun
ㅦ
хангыля nieun-tikeut
ㅧ
хангыля nieun-sios
ㅨ
хангыля nieun-pansios
ㅩ
хангыля rieul-kiyeok-sios
ㅪ
хангыля rieul-tikeut
ㅫ
хангыля rieul-pieup-sios
ㅬ
хангыля rieul-pansios
ㅭ
хангыля rieul-yeorinhieuh
ㅮ
хангыля mieum-pieup
ㅯ
хангыля mieum-sios
ㅰ
хангыля mieum-pansios
ㅱ
хангыля kapyeounmieum
ㅲ
хангыля pieup-kiyeok
ㅳ
хангыля pieup-tikeut
ㅴ
хангыля pieup-sios-kiyeok
ㅵ
хангыля pieup-sios-tikeut
ㅶ
хангыля pieup-cieuc
ㅷ
хангыля pieup-thieuth
ㅸ
хангыля kapyeounpieup
ㅹ
хангыля kapyeounssangpieup
ㅺ
хангыля sios-kiyeok
ㅻ
хангыля sios-nieun
ㅼ
хангыля sios-tikeut
ㅽ
хангыля sios-pieup
ㅾ
хангыля sios-cieuc
ㅿ
хангыля pansios
ㆀ
хангыля ssangieung
ㆁ
хангыля yesieung
ㆂ
хангыля yesieung-sios
ㆃ
хангыля yesieung-pansios
ㆄ
хангыля kapyeounphieuph
ㆅ
хангыля ssanghieuh
ㆆ
хангыля yeorinhieuh
ㆇ
хангыля yo-ya
ㆈ
хангыля yo-yae
ㆉ
хангыля yo-i
ㆊ
хангыля yu-yeo

Знаки пунктуации

˙
Точкой сверху
‥
Двухточечный пунктир
‧
Точка переноса
‵
Обратный штрих
‵
Обратный штрих
❛
одинарная повёрнутая верхняя запятая
❜
одинарная верхняя запятая
❝
двойная повёрнутая верхняя запятая
❞
верхняя запятая
、
Символ ККЯ запятая
。
Символ ККЯ точка
〃
Символ повторения
「
Левосторонняя скобка
」
Правосторонняя скобка
『
Левосторонняя скобка белая
』
Правосторонняя скобка белая
〝
Обратные двойные кавычки
〞
Двойные кавычки
︰
форма представления для вертикальной многоточия
︰
форма представления для вертикальной многоточия
﹁
форма представления для вертикальной левой ломанной скобки
﹂
форма представления для вертикальной правой ломанной скобки
﹃
форма представления для вертикальной левой белой ломанной скобки
﹄
форма представления для вертикальной правой белой ломанной скобки
﹐
запятая
﹒
Маленькое полное окончание
﹔
точка с запятой
﹔
точка с запятой
﹕
Маленькое двоеточие
！
Fullwidth Exclamation Mark
＃
Fullwidth Number Sign
＄
Полноширинный знак доллара
％
Fullwidth Percent Sign
＆
Fullwidth Ampersand
＊
Fullwidth Asterisk
，
Fullwidth Comma
．
Fullwidth Full Stop
：
Fullwidth Colon
；
Fullwidth Semicolon
？
Fullwidth Question Mark
＠
Fullwidth Commercial At
～
Fullwidth Tilde
•
Точка маркер списка
…
Многоточие
¿
Перевернутый вопросительный знак
“
Закрывающая двойная кавычка
‘
Открывающая одинарная кавычка
·
Точка по центру
′
Знак штриха
”
Правая двойная кавычка
’
Закрывающая одинарная кавычка

Скобки

〈
Левая угловая скобка
〈
Левая угловая скобка
〉
Правая угловая скобка
《
Левая двойная угловая скобка
》
Правая двойная угловая скобка
「
Левосторонняя скобка
」
Правосторонняя скобка
『
Левосторонняя скобка белая
』
Правосторонняя скобка белая
【
Левосторонняя скобка черная двояковыпуклая
】
Правосторонняя скобка черная двояковыпуклая
〔
Левосторонняя скобка в виде панцыря черепахи
〕
Правосторонняя скобка в виде панцыря черепахи
︵
форма представления для вертикальной левой скобки
︶
форма представления для вертикальной правой скобки
︷
форма представления для вертикальной левой фигурной скобки
︸
форма представления для вертикальной правой фигурной скобки
︹
форма представления для вертикальной левой черепаховой скобки
︺
форма представления для вертикальной правой черепаховой скобки
︻
форма представления для вертикальной левой чёрной линзовидной скобки
︼
форма представления для вертикальной правой чёрной линзовидной скобки
︽
форма представления для вертикальной левой двойной угловой скобки
︽
форма представления для вертикальной левой двойной угловой скобки
︾
форма представления для вертикальной правой двойной угловой скобки
︿
форма представления для вертикальной левой угловой скобки
﹀
форма представления для вертикальной правой угловой скобки
﹁
форма представления для вертикальной левой ломанной скобки
﹁
форма представления для вертикальной левой ломанной скобки
﹂
форма представления для вертикальной правой ломанной скобки
﹃
форма представления для вертикальной левой белой ломанной скобки
﹄
форма представления для вертикальной правой белой ломанной скобки
﹙
левая скобка
﹙
левая скобка
﹚
правая скобка
﹛
левая фигурная скобка
﹜
правая фигурная скобка
﹝
левая черепашья скобка
﹞
правая черепашья скобка
﹤
Маленький знак меньше чем
﹥
Маленький знак больше чем
（
Fullwidth Left Parenthesis
）
Fullwidth Right Parenthesis
＜
Fullwidth Less-Than Sign
＞
Fullwidth Greater-Than Sign
｛
Fullwidth Left Curly Bracket
｝
Fullwidth Right Curly Bracket
❬
Средняя левая углообразная скобка
❭
Средняя правая углообразная скобка
❮
левая углообразная скобка цитирования
❯
правая углообразная скобка цитирования
❰
левая углообразная скобка
❱
правая углообразная скобка
〖
Левосторонняя белая двояковыпуклая скобка
〗
Правоосторонняя белая двояковыпуклая скобка
〘
Левосторонняя белая кобка в виде панцыря черепахи
〙
Правосторонняя белая кобка в виде панцыря черепахи
〚
Левосторонняя белая квадратная скобка
〛
Правосторонняя белая квадратная скобка
⟨
левая угловая скобка
⟩
правая угловая скобка
‹
Одинарная открывающая (левая) французская угловая кавычка
›
Одинарная закрывающая (правая) французская угловая кавычка
«
Открывающая левая кавычка «ёлочка»
»
Закрывающая правая кавычка «ёлочка»

Символы валют

[adinserter block=”12″]

$
Текстовый символ Доллар
¢
Текстовый символ Знак цента и сентаво
€
Текстовый символ Знак евро
£
Текстовый символ Знак фунта
¥
Текстовый символ Знак иены
₩
Текстовый символ Вулонг
₿
Текстовый символ Знак биткоина
₽
Текстовый символ Знак рубля
₹
Текстовый символ Индийская рупия
¤
Текстовый символ Знак валюты
₱
Текстовый символ Знак песо
₦
Текстовый символ Нигерийская найра
ƒ
Текстовый символ «f» с хвостиком или знак флорина
₮
Текстовый символ Монгольский тугрик
৲
Текстовый символ Бенгальская рупия
৳
Текстовый символ Бангладешская така
₨
Текстовый символ Знак рупии
௹
Текстовый символ Тамильский знак рупии
฿
Текстовый символ Тайский бат и символ биткоина
៛
Текстовый символ Камбоджийский риель
₪
Текстовый символ Знак нового шекеля
₫
Текстовый символ Вьетнамский донг
₭
Текстовый символ Лаоский кип
₲
Текстовый символ Парагвайский гуарани
₴
Текстовый символ Знак гривны
₵
Текстовый символ Ганский седи
≋
Текстовый символ Тройная тильда
﷼
Текстовый символ

Сегодня общение перешло в цифровой формат. Помимо привычного письма люди часто используют различные символы в сообщениях. Люди посещают различные сайты, соцсети, форумы, на которых обсуждают разный круг вопросов.

Мамочки доказывают какая система воспитания лучшая для детей, автомеханики — делятся секретами лучшей резины, а игроманы обсуждают стратегию войны с большим уничтожением военной техники соперника. От внешнего вида вашего ника в интернет-пространстве зависит восприятие нас другими людьми.

Одни хотят выделиться оригинальностью и уникальностью: ღ★ ТОПОВЫЙ_Т ОП★ღ Другие — отражают в никнейме личный зодиакальный знак или подчеркивают увлеченность, хобби для поиска единомышленников. Создать украшение для своего ника можно используя специальные символы Юникода, собранные в представленной коллекции.

В ней находятся крутые символы для ников —звездочки, короны 👑, геометрические фигуры, каллиграфические литеры и симпатичные буквы. Вам остается только собрать индивидуальный ник из тех, которые понравились. С этой целью выделяется выбранный символ правой кнопкой мыши, копируется и вставляется в текст.

Можно воспользоваться коллекцией в виде красивых букв, в котором также есть разнообразные варианты символов.

Существует множество способов для выражения нежных чувств онлайн-общения, среди которых применение символа сердечка❤. Отобразить символ сердечка с клавиатуры сложно, а наш сайт предлагает легкое копирование и использование.

Есть несколько цветов, имеющих особое значение. К примеру, красный цвет сердца обозначает открытое проявление любви. Зелёный цвет – предложение свидания. Если после романтического свидания вам вместо красных шлют желтый или оранжевый цвет символа, значит предлагается дружить. Также есть Эмоджи разбитого сердца: 💔.

Знак бесконечности — ∞ является математическим символом, представляющим теорию бесконечности. Впервые знак был применен математиком Джоном Валлисом в 17 веке для трактата «Конические сечения».

Данные знак используется в алгебре и геометрии. Знак, символизирующий упавшую восьмерку, принадлежит более поздней исторической эпохи. Его происхождение связывают со змеем уроборосом, проглотившем собственный хвост. Такой тип символов присутствовал в эпоху наскального письма, обнаруженного в Тибете. Данный символ оформлен частью Юникода версии 1.1 в 1993.

Знак копирайта выглядит как «с» обведенная кругом. Носит название знака, охраняющего авторское право. Используется одновременно с представлением имени или названия учреждения. Может указывать защищённость контента. Само слово копирайт является транскрипцией кириллицы английского copyright.

Первый слог Copy означает копирование, вторая right — права. Символ основывается на первой букве слова. Первая этого слова и составляет основу символа. «Знак авторского права» оформлен частью Юникода версии 1.1 в 1993 г.

Символ интеграла: с пояснениями — Eggradients.com

Символ интеграла ∫ — это математический символ интегрирования, опубликованный в 1655 году Исааком Ньютоном. Это был первый символ интеграции, который был задуман специально для этой цели и имел специальную систему обозначений.

Символ	Имя
∫	встроенный
∬	двойной интеграл
∮	замкнутый контур / линейный интеграл
∰	Интеграл замкнутого объема
∯	интегральная закрытая поверхность
∭	тройной интеграл

Исаак Ньютон был одним из самых влиятельных и известных ученых в современной истории. По сути, его можно считать гигантом в области науки.

Ему часто приписывают открытия и инновации во многих областях исследований со времени его пребывания в Кембридже; его работа оживила каждую отрасль натурфилософии, от телескопической астрономии до физики и даже алхимии.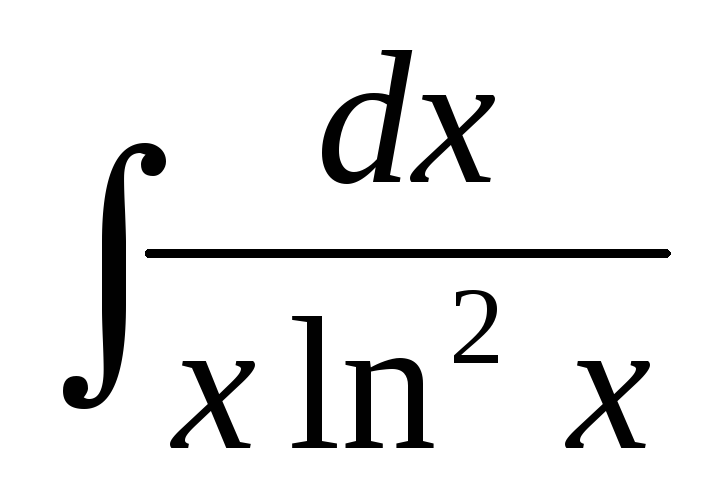 Есть много способов представить функцию в виде графика.

Вертикальную и горизонтальную оси графика обычно называют осью x и осью y соответственно.

Хотя большинство графиков не имеют осей, они могут содержать линии или другие метки, указывающие определенные значения функции. Как мы все знаем, интеграл — это часть высшей математики, которой не учат в большинстве школ или колледжей.

Некоторые называют это уровнем знаний исчисления, но где бы и где бы он ни был, интеграл можно четко определить как часть пределов, которые рассматриваются как введение в исчисление.

В 1675 году Лейбниц впервые ввел этот символ в свои личные сочинения. Он появился публично в 1686 году, когда он опубликовал статью о «скрытой геометрии». Он был основан на характере длинного s, и Лейбниц думал об интеграле как о бесконечной сумме бесконечно малых членов.

Символ был основан на длинном символе s, который был выбран потому, что Лейбниц представлял интеграл как бесконечную сумму бесконечно малых элементов. Символ и понятие были основаны на длинном символе s (ſ), который Лейбниц считал бесконечным сумма бесконечно малых слагаемых.

Двойной интеграл

Двойной интеграл. Представьте себе круг размером с Землю, а затем представьте еще один. Это пример двойного интеграла.

Быстрый поиск в Google двойного интеграла покажет вам, что это наиболее широко используемая часть математики, которую никто не понимает.

Тема двойного интеграла поставила в тупик даже некоторых из лучших математиков в истории, в том числе таких, как Гаусс и Риман с их тензорной теорией, а также Фурье, Лагранжа, Пуанкаре и Вейерштрасса, у которых были теории о том, как обращаться с этими интегралами.

Тройной интеграл

В математическом анализе тройной интеграл представляет собой трехмерное обобщение понятия двойного интеграла и определяется как определенный интеграл по трем взаимозависимым переменным.

Если областью интегрирования является n-мерное дифференцируемое многообразие, то тройной интеграл оценивает функцию трех переменных на этом многообразии.

Линейный интеграл

Линейный интеграл является обобщением идеи интегрирования. Это позволяет нам найти функцию, которая использовалась для получения данного выражения, из которого было получено исходное выражение.

Например, если мы рассматриваем объем под поверхностью $f(x, y)$, то линейный интеграл дает нам то же значение, что и при интегрировании этой функции по $x$, но без интегрирования по $y$.

Интеграл по замкнутой поверхности

Интеграл по замкнутой поверхности является наиболее полезным процессом для вычисления интеграла для квадратичной поверхности.

Этот метод позволяет нам вычислять интегралы по замкнутым формам и получать результаты, которые часто невозможно получить другим способом. 93.

Интеграл по замкнутому объему

Интеграл по замкнутому объему – это интеграл, независимая переменная которого не зависит от зависимой переменной.

Например, если у нас есть замкнутый объем “””V””” и функция f, описывающая ограничивающую его поверхность, то интегрирование функции f по этой замкнутой поверхности “””S””” даст постоянное значение функции f вдоль всей кривой, построенной путем трассировки «S» в пространстве.

Если вы хотите увидеть все математические символы, вот страница, которую вы должны проверить.

Что означает знак интеграла с кружком на нем?

Содержание:

Что означает знак интеграла с кружком на нем?
Кто изобрел интегральный символ?
Для чего используется интеграл?
Что такое символ для того же, что и?
Зачем мы изучаем интеграцию?
Почему в физике используется интегрирование?
Что такое интеграл в физике?
Что такое интеграция в 11 классе физики?
Как используется интеграция в биологии?
Используются ли исчисления в биологии?
Как исчисление используется в реальной жизни?
Как исчисление применяется в медицине?
Используют ли врачи исчисление?
Врачи изучают исчисление?
Используют ли фармацевты вычисления?
Трудно ли стать фармацевтом?
Есть ли математика в Pharm D?
Какую математику используют фармацевты?
Нужно ли хорошо разбираться в математике, чтобы стать фармацевтом?
Легко ли быть фармацевтом?
Какая квалификация нужна для помощника аптекаря?
Кто такой помощник аптекаря уровня 2?

Что означает знак интеграла с кружком на нем?

Знак интеграла с кружком является замкнутым интегралом и показывает, что вы интегрируете по замкнутому контуру или замкнутой поверхности, такой как круг или оболочка. Математически различий нет, действуют все те же правила.

Кто изобрел интегральный символ?

Готфрид Лейбниц

Для чего используется интеграл?

Как правило, интеграл присваивает числа функциям таким образом, что они могут описывать перемещение, площадь, объем и даже вероятность. Этот тип 9Интеграл 0180 относится к числовым значениям. Это используется в чистой математике, прикладной математике, статистике, естественных науках и многом другом.

Какой символ означает то же, что и?

Символы алгебры

Символ

Название символа

Значение / Определение

≡

Эк.0014

равны по определению

приблизительно равны

слабое приближение

8 Почему мы учимся интегрированию?

Часто мы знаем связь, включающую скорость изменения двух переменных, но нам может понадобиться знать прямую связь между двумя переменными. Чтобы найти эту прямую связь, мы необходимо использовать процесс, противоположный дифференциации. …

Почему в физике используется интегрирование?

Определенные интегралы можно использовать для определения массы объекта, если известна его функция плотности. Работу также можно рассчитать из 90 180, интегрируя 90 181 силовую функцию, или при противодействии силе тяжести, как в задаче о насосе.

Что такое интеграл в физике?

Интеграл можно назвать обратной производной. Предположим, что функция f(x) является производной от F(x) с ‘x’. В этом случае интегрирование f(x) дает ‘F(x) + C( целое постоянное)’.

Что такое интеграция в 11 классе физики?

Дифференциация и Интеграция — две основные концепции исчисления. Дифференцирование используется для изучения малого изменения одной величины по отношению к единичному изменению другой. … С другой стороны, интеграция используется для добавления небольших и дискретных данных, которые не могут быть добавлены по отдельности и представлены в одном значении.

Как интеграция используется в биологии?

Интеграция также используется в биологии и используется для нахождения изменения температуры за интервал времени от глобального потепления, чувствительности лекарств, напряжения нейронов головного мозга через заданный интервал времени, рассеивания семян во внешней среде и средней скорости кровотока в организме.

Используются ли вычисления в биологии?

Одно важное применение исчисления в биологии называется моделью хищник-жертва, которая определяет равновесное количество хищников и животных-жертв в экосистеме. На самом деле это приложение “дифференциальные уравнения”, но вам понадобится исчисление , чтобы “дойти”.

Как исчисление используется в реальной жизни?

К дисциплинам, использующим исчисление , относятся физика, инженерия, экономика, статистика и медицина. использовал для создания математических моделей, чтобы прийти к оптимальному решению. … В области химии исчисление может быть использовано для предсказания таких функций, как скорость реакции и радиоактивный распад.

Как исчисление применяется в медицине?

Концентрация лекарства рассчитывается с течением времени с помощью исчисления ! На самом деле курс приема лекарств с течением времени можно рассчитать с помощью дифференциального уравнения. … Следовательно, дифференциальное уравнение описывает взаимосвязь между этими физическими величинами и скоростью их изменения.

Используют ли врачи вычисления?

Нет, врачи не используют исчисление в клинической практике. НО расчет требуется очень многим школам (более 10-20), и на то есть веские причины. Не только помогает объяснить физику и химию по курсу , но, по сути, это курс мышления.

Врачи изучают исчисление?

Почему студенты-медики изучают исчисление ? Они не делают. Студент-медик может пройти его как часть учебы, но исчисление не имеет значения в медицинском вузе. … В общем, нет, Врачи не обязаны знать и использовать вычисления в повседневной практике, хотя это может быть частью учеба работа.

Используют ли фармацевты вычисления?

Использует ли фармацевт исчисление ? Да, Фармацевт использует исчисление , и вам нужно будет пройти этот класс, чтобы поступить в школу аптека , а также добиться успеха в своей карьере фармацевта .

Трудно ли стать фармацевтом?

Хотя путь к и становлению фармацевтом непрост — приготовьтесь к шести-восьми классам школы и государственному экзамену, чтобы получить степень PharmD — Рик Мосс, бывший практикующий розничный торговец и больница фармацевт , говорит, что это невероятно полезная профессия.

Есть ли математика в Pharm D?

PharmD Этап II – Интернатура или резидентура в течение шестого года с размещением в специализированных подразделениях…. PharmD Syllabus.

Pharmd Syllabus для первого года
Pharmaceutics	Pharmaceutical Inorganic Chemistry
Биохимия
.0014

Какую математику используют фармацевты?

базовая алгебра

Нужно ли хорошо разбираться в математике, чтобы стать фармацевтом?

Аптека Студенты нуждаются в прочных знаниях в области химии и физики, а могут нуждаться в для завершения курсовой работы по микробиологии, социологии и микроэкономике. Математика необходима для естественнонаучных курсов, поэтому для поступления в университет часто требуется два семестра изучения математики в колледже.0180 аптека программа.

Легко ли быть фармацевтом?

В то время как путь к становлению фармацевтом может быть довольно легким — вам нужен только аттестат о среднем образовании и опыт работы на месте — путь к становлению сертифицированным фармацевтом стоит того.

Какая квалификация требуется для помощника аптекаря?

Вступительных требований для того, чтобы стать провизором, не существует. Работодатели обычно ожидают хорошей грамотности, умения считать и ИТ-навыков . Они могут запросить GCSE или эквивалентную квалификацию. Работодатели часто запрашивают соответствующий опыт работы .

Кто такой помощник аптекаря уровня 2?

1 Помощники в аптеке помогают фармацевтам в предоставлении товаров и услуг населению. 19.

Раннее использование символов исчисления

Раннее использование символов исчисления Последняя редакция: 1 декабря 2004 г.

Производная. Символы dx, dy, и dx/dy были введены Готфрид Вильгельм Лейбниц (1646-1716) в рукописи от 11 ноября 1675 г. (Каджори, т. 2, стр. 204).

f'(x) для первой производной, f”(x) для второй производной и т.д. Жозеф Луи Лагранж (1736-1813). В 1797 году в Тори аналитических функций символы f’x и f”x найдено; в Произведения, Том. Х , “который претендует на то, чтобы быть репринтом издания 1806 года, на стр. 15, 17, можно найти соответствующие части дается как f(x), f'(x), f”(x), f”'(x) ” (Cajori vol. 2, page 207).

В 1770 году Жозеф Луи Лагранж (1736-1813) написал в своих мемуарах Nouvelle mthode pour rsoudre les quations littrales par le moyen des sries (Сочинения, Том III, стр. 5-76). Это обозначение также встречается в мемуарах Франсуа Давье де Фонсенекса в 1759 году.считается, что на самом деле она была написана Лагранжем (Cajori 1919, стр. 256).

В 1772 году Лагранж написал, что u’ = du / dx и du = u’dx in “Sur une nouvelle espce de calcul relatif” la diffrentiation et l’integration des Quantits Variables», Nouveaux Memoires de l’Academie royale des Sciences et Belles-Lettres de Berlin (Сочинения, Том III, стр. 451-478).

D _x у был представлен Луи Франсуа Антуан Арбогаст (1759-1803) в “De Calcul des drivations et ses обычаи dans la thorie des suites” et dans le calcul diffrentiel», Strasbourg, xxii, pp. 404, Impr. de Levrault, Фрес, VIII (1800 г.). (Эта информация исходит от Хулио Гонслеза Кабильна; Каджори указывает в своей Истории математики , что Арбогаст ввел этот символ, но кажется, что он не показывает этот символ в A History of Mathematical Обозначения. )

D использовался Арбогастом в той же работе, хотя этот символ ранее использовался Иоганном Бернулли (Каджори, т. 2, стр. 209). Бернулли использовал этот символ в неоперациональном смысле (Маор, стр. 97).

Частная производная. «Кривая d» использовалась в 1770 г. Антуан-Николя Карита, маркиз де Кондорсе (1743-1794) в «Memoire sur les Equations aux diffrence partielles» который был опубликован в История Королевской академии наук, стр. 151–178, Энни М. DCCLXXIII (1773 г.). На странице 152 Кондорсе говорит:

Dans toute la suite de ce Memoire, dz и z dsigneront ou deux Различия между частями z, , не одинаковые по отношению к x, l’autre par rapport a y, ou bien dz sera une diffrentielle totale, & z une diffrentielle partielle. [В этой статье как dz , так и z будут обозначать два частичные разности z, , где одна из них относится к х, и другие, в отношении у, или дз и z будет использоваться как символы полного дифференциала и частичного разница соответственно.]

Однако «кудрявая д» впервые использовалась в форме по Адриан Мари Лежандр в 1786 году в его «Memoire sur la manire de distinguer les maxima des minima dans le Calcul des Variations» История Королевской академии наук, Annee M. DCCLXXXVI (1786 г.), стр. 7–37, Париж, M. DCCXXXVIII (1788 г.). На странице 8 написано:

Pour viter toute ambiguit, je rpresentarie parle коэффициент де x данс ла разница u, и полная разница u дивизия пар dx.

Лежандр отказался от этого символа, и он был вновь введен Карл Густав Якоб Якоби в 1841 г. Якоби широко использовал его в своей замечательной статье «De determinantibus Functionalibus». Журнал Крелла, Band 22, стр. 319-352, 1841 г. ( С. 393-438 т. 1 из Собрания сочинений ).

Sed quia uncorum accumulatio et legenti et scribenti molestior fieri solet, характеристики praetuli д
дифференциалия вульгарная, дифференциальная аутем парциальная характеристика
денотар.

Символ «фигурная d» иногда называют «закругленной d» или «изогнутой d». или дельта Якоби. Соответствует скорописи “дей” (эквивалент нашего d ) на кириллице.

Интеграл. Прежде чем ввести целочисленный символ, Лейбниц написал омн. для «omnia» перед термином, который необходимо интегрировать.

Интегральный символ был впервые использован Готфридом Вильгельмом Лейбницем. (1646-1716) 29 октября 1675 г. , в неопубликованной рукописи. Несколько недель спустя, 21 ноября, он впервые поставил dx после того, как интегральный символ (Бертон, стр. 359). Позднее, в 1675 г., он предложил использование символа в письме Генри Ольденбургу, секретарю Королевское общество: «Utile erit scribi pro omnia, ut l = omn. l , id est summa ipsorum l ” [Полезно будет написать для омн. так что л = общий. l , или сумма всех l s.] Первое появление интегрального символа в печати был в статье Лейбница в Acta Eruditorum. Интеграл на самом деле это была длинная буква S, означающая «сумма».

В своей работе Quadratura curvarum 1704 года Ньютон написал небольшое вертикальная черта над x для обозначения интеграла от x. Он написал два рядом расположенные вертикальные черточки над x для обозначения интеграла от (x с одна полоса над ним). Еще одно обозначение, которое он использовал, заключалось в заключении член в прямоугольнике, чтобы указать его интеграл. Каджори пишет, что Символизм Ньютона для интегрирования был дефектным, потому что x с a bar может быть неверно истолкован как x-prime, а размещение прямоугольник вокруг термина было трудно для печатника, и что поэтому символизм Ньютона никогда не был популярен даже в Англии.

Пределы интегрирования. Пределы интегрирования были сначала указывается только словами. Эйлер был первым, кто использовал символ в Institutiones calculiintegris, , где он написал пределы в скобках и использовали латинские слова ab и ad (Каджори, т. 2, стр. 249).

Современный определенный интегральный символ был создан Жаном Батист Жозеф Фурье (1768-1830). В 1822 году в своем знаменитом номере The Analytical Теория тепла он писал:

Nous dsignons en gnral par le signe l’intgrale qui begin lorsque la variable quivaut a, et qui est complte lorsque переменная переменная quivaut b . . .

Цитата выше взята из “Аналитическая Тори де ла Шалёр” [Аналитическая теория тепла], Фирмин Дидо, Париж, 1822 г.

, стр. 252 (параграф 231).

Фурье использовал это обозначение несколько раньше в Mmoires Французской академии за 1819-20 гг., в статья, перепечаткой которой является ранняя часть его книги 1822 г. (Каджори, т. 2, стр. 250).

Обозначение бар для обозначения оценки первообразной на двух пределах интегрирования впервые использовал Пьер Фредерик Саррус (1798-1861) в 1823 году в Анналах Жергонна , Vol. XIV. Обозначение было использовано позже Мойньо и Коши (Cajori vol. 2, page 250).

Интеграция по замкнутому пути. Дэн Раттл, читатель этой страницы, нашел применение интегралу символ с кружком посередине Арнольд Зоммерфельд (1868–1951) в 1917 в Аннален дер Physik, “Die Drudesche Dispersiontheorie vom Standpunkte des Bohrschen Modelles und die Konstitution von h3, O2 и N2». раньше, чем использование в 1923 году, показанное Каджори. Раттл сообщает, что Дж. У. Гиббс использовал только стандартный знак интеграла в своих элементах. Vector Analysis (1881-1884), а тот и Э. Б. Уилсон использовали маленький кружок под стандартным интегральным символом для обозначения интеграции вокруг замкнутой кривой в его векторном анализе (1901, 1909) и в Advanced Calculus (1911, 1912).

Предел. лим. (с точкой) впервые был использован Симон-Антуан-Жан Л’Юилье (1750-1840). В 1786 году Л’Юилье получил большую популярность, выиграв приз, предлагаемый * l’Academie royale des Sciences et Belles-Lettres de Berlin*. Его очерк «Изложение lmentaire des principes des calculs superieurs», принял вызов, брошенный Академией, — ясный и четкий теории о природе бесконечности. На странице 31 этой замечательной статьи Л’Уилье утверждает:

Pour abreger & pour faciliter le calcul par une notation плюс комод, на est convenu de dsigner autrement que par
,
la limite du rapport des changes simultanes de P & de х, фаворит пар
;
en sorte que
ОУ
;
Дизайнерская лама выбрала

лим (без точки) был написан в 1841 г.

Карл Вейерштрасс (1815-1897) в одной из своих статей, опубликованной в 189 г.4 дюйма Mathematische Werke, Band I, стр. 60 (Cajori, т. 2, стр. 255).

Стрелочное обозначение пределов было введено Годфри Гарольд Харди (1877-1947) в своем замечательном “А. Курс чистой математики», Кембридж: At the University Press, xv, стр. 428, 1908. Проверьте предисловие к этому первому изданию (Julio Гонслез Кэбилн и Каджори, том. 2, стр. 257).

Бесконечность. Символ бесконечности был введен Джон Уоллис (1616-1703) в 1655 году в его De sectionibus conicis 9Бонавентура Каваллери Geometriam Indivisibilium ) Planum quodlibet Quasi ex Infinitis lineis parallelis conflari: Vel potiu\s (quod ego mallem) ex infinitis Prallelogrammis [так в оригинале] aeque\ altis; наличие кворума singulorum altitudo sit totius altitudinis 1/, sive alicuota pars infinity парва; (esto enim nota numeri infiniti;) adeo/q; всенаправленная одновременная высота aequalis altitudini figurae. Уоллис также использовал символ бесконечности в различных отрывках своего Арифметика бесконечности (Арифметика Бесконечности) (1655 или 1656 г.). Например, он писал (стр. 70):

Cum enim primus terminus in serie Primanorum sit 0, primus terminus in serie reciproca erit vel infinitus: (sicut, в Divisione, si diviso sit 0, quotiens erit infinitus)

В Zero to Lazy Eight, Александр Хьюмес, Николас Хьюмес и Джозеф Магуайр пишет: «Уоллис был ученым-классиком, и это возможно, что он произошел от древнеримского знака 1000, CD, также написано М — хотя также возможно, что он взял эту идею от строчная омега, омега – последняя буква греческого алфавита и, таким образом, давняя метафора верхнего предела, конец.”
Каджори (т. 2, стр. 44) говорит, что было сделано предположение, что Уоллис принял этот символ из позднеримского символа 1000. Он приписывает гипотеза Вильгельма Ваттенбаха (1819-1897), Anleitung zur lateinischen Palographie 2. Aufl., Лейпциг: С. Хирцель, 1872. Приложение: с. 41.
Это предположение подтверждается этикетками, начертанными на римском ручные счеты, хранящиеся в Национальной библиотеке в Париже. А гипсовый слепок этих счетов показан на фотографии на странице 305 Английский перевод Карла Меннингера Числовые слова и числа символы ; в то время актерский состав хранился в Кабинете де Мдаль в Париже. На фото видно, что колонка, посвященная до 1000 на этих счетах вписан символ, довольно близкий по форма к символу лемнискаты, и который, как показывает Меннингер, легко превратились в символ М, окончательный римский символ для 1000 [Рэнди К. Шварц].
[Хулио Гонслез Кабильн внес свой вклад в эту запись.]
Дельта для обозначения небольшого количества. В 1706 г. Иоганн Бернулли использовал δ для обозначения разности функций. Хулио Гонслез Кабильн считает, что вероятно, одно из первых, если не первое использование дельты в этом смысле.
Дельта и эпсилон. Огюстен-Луи Коши (1789-1857) использовали ε в 1821 году в Cours d’analyse (Творчество II.3), а иногда вместо этого использовал δ (Каджори, т. 2, стр. 256). Согласно Финнею и Томасу (стр. 113), «δ означало «различие» (по-французски разность а ε означает «ошибка» (по-французски ошибка )”.
Первая теорема о пределах, которую Коши намеревается доказать в Cours d’Analyse (Творчество II.3, стр. 54) имеет в качестве гипотезы, что
по возрастанию значений х, разность ф ( х + 1) – ф ( х ) сходится к некоторому пределу к .
Затем доказательство начинается со слов
обозначим через ε любое число, сколь угодно малое. Поскольку возрастающие значения x разница f ( x + 1) – f ( x ) сходятся к пределу k, можно задать достаточно существенное значение в число h , так что для x больше или равно h , рассматриваемая разница всегда находится между границами k – е, к + е.
[Уильям С. Уотерхаус]
Первое доказательство дельта-эпсилон — это доказательство Коши того, что по сути, теорема о среднем значении для производных. Это из его лекций на Исчислении бесконечно малых, 1823, Леон 7, в Произведения, сер. 2, том. 4, стр. 44-45. Доказательство переводит словесное определение Коши производной как предела (когда он существует) частное разностей на языке алгебраич. неравенства с использованием как дельта, так и эпсилон. В 1820-х годах Коши сделал не уточняйте, от чего, учитывая эпсилон, зависела его дельта или n, так что можно прочитать его доказательства как верные для всех значений переменной. Таким образом, он не делает различия между сходимостью к пределу поточечно и сходящимся к ней равномерно.
[Джудит В. Грабинер, автор книги «Истоки строгого исчисления Коши » (MIT, 1981)]
СИМВОЛЫ ВЕКТОРНОГО ВЫЧИСЛЕНИЯ
Для записей векторного анализа на страницах Words , см. здесь для списка.
Векторный дифференциальный оператор, теперь записанный и названный nabla или del , был введен Уильямом Роуэном Гамильтоном. (1805-1865). Гамильтон записал оператор как и именно П. Г. Тейт установил как общепринятый символ — см. его Элементарный трактат о кватернионах (1867 г.). Тейт также был ответственен за установление термина набла . Видеть НАБЛА на странице «Самые ранние употребления слов».
Дэвид Уилкинс предполагает, что Гамильтон мог использовать наблу. как символ общего назначения или аббревиатура для любого оператора, который он хотел представить в любое время. В 1837 году Гамильтон использовал наблу в ее современной ориентации. как символ любой произвольной функции в Trans. Р. Ирландский академик. XVII. 236. (OED.) Он использовал наблу для обозначения оператора перестановки в «На Аргумент Абеля относительно невозможности выразить Корень любого Общее уравнение выше четвертой степени для любой конечной комбинации радикалов и рациональные функции», Труды Королевской ирландской академии, 18 (1839), стр. 171-259.
Гамильтон использовал повернутую наблу, т.е. , для векторного дифференциального оператора в “Proceedings of the Royal Irish Academy” для встречи от 20 июля 1846 г. Эта статья появилась в томе 3 (1847 г.), стр. 273–29.2. Гамильтон также использовал повернутую наблу в качестве векторного дифференциального оператора в «On кватернионы; или о новой системе воображаемых в алгебре», которую он опубликовал частями в Philosophical Magazine между 1844 и 1850 годами. соответствующая часть статьи состоит из статей 49-50, в части которая появилась в октябре 1847 г. в томе 31 (3-я серия, 1847 г.) «Философского Журнал, стр. 278-283. Сноска в томе. 31, стр. 291, гласит:
В этой бумаге, предназначенной для Саутгемптона, была написана характеристика ; но этот более распространенный знак так часто употреблялся в других значениях, что кажется желательным воздержаться от присвоения его здесь новому значению предложенный.
Уилкинс пишет, что «эта бумага» относится к неопубликованному документу, который Гамильтон подготовил к встрече Британская ассоциация содействия развитию науки, но которая была направлена по ошибке на домашний адрес сэра Джона Гершеля, а не на саму встречу в Саутгемптон, и поэтому не было сообщено на этом собрании. сноска указывает на то, что Гамильтон изначально намеревался использовать символ набла, который используется сегодня, но затем решил повернуть его, чтобы не путать с другими вариантами использования. символа.
Повернутая форма появляется в великом произведении Гамильтона, Лекции о кватернионах (1853 г., стр. 610).
Каджори (том 2, стр. 135) и OED дают эту ссылку.
Согласно Штейну и Барселлосу (стр. 836), Гамильтон обозначал градиент с обыкновенной столичной дельтой в 1846 г. Однако эта информация может быть неверным, так как Дэвид Уилкинс пишет, что никогда не видел градиент обозначается обычной заглавной дельтой в любой статье Гамильтона, опубликованной в его продолжительность жизни.
Дэвид Уилкинс из Школы математики Тринити-колледжа в Дублине сделал доступные тексты математических статей, опубликованных Гамильтоном при его жизни в его Сайт истории математики.
град как символ градиента появляется в книге Х. Вебера Die partiellen Differential-gleichungen. der mathematischen physik nach Riemanns Vorlesungen 1900 г. (Cajori, том 2, стр. 135). Видеть ГРАДИЕНТ на странице «Самое раннее использование слов».
Уильям Кингдон Клиффорд (1845-1879 гг.)) использовали div u или dv u в качестве символов расхождения (Cajori vol. 2, page 135).
Символ ∆ для оператора Лапласа (также представленный ² ) был представлен Робертом Мерфи в 1833 г. в Элементарных принципах теории электричества. (Клайн, стр. 786). См. ОПЕРАТОР ЛАПЛАСА на странице «Самые ранние употребления слов».

Первая страница | Операция | Группировка | Отношение | Фракции | Константы | Переменные | Функции | Геометрия | Тригонометрия | Исчисление | Теория множеств и логика | Теория чисел | Статистика | Источники
Знаки интеграла (введите символ интеграла на клавиатуре)
Интегралы ∫ — это математические текстовые символы (об их значении мы поговорим позже), которые люди писали со времен, когда была разработана кодировка ASCII. И вы можете набирать их прямо с клавиатуры. Я покажу вам, как это сделать, используя различные методы в зависимости от вашей операционной системы и вкусов.
Математика ∫ ∬ ∭ ∯
∮ ∲ ∳ ∰
Текстовые символы

Математика интеграла
При заданной функции f действительной переменной x и интервале [a, b] действительной прямой определенный Интеграл неформально определяется как площадь области в плоскости xy ограничен графиком f, осью x и вертикальными линиями x = a и x = b, так что площадь над осью x добавляется к общему количеству, а площадь под осью x вычитается из общего.
Интеграция обычно обозначается как:
∫ f(x)dx
Знак интеграла ∫ представляет интегрирование. dx указывает, что мы интегрируем более x ; х называется переменной интегрирования. В правильной математической типографии dx отделяется от подынтегральной функции пробелом. Внутри ∫… dx находится выражение, которое нужно проинтегрировать, называемое подынтегральной функцией. В этом случае подынтегральной функцией является функция ф(х) . Поскольку не указана область, интеграл называется неопределенным интегралом.
Как вводить целочисленные символы
Выберите свою систему, чтобы узнать.
Окна
Состояния сдвига
Настройте раскладку клавиатуры в Windows, чтобы вы могли вводить все дополнительные символы так же просто, как и любой другой текст. Настройка занимает около 5-10 минут, но вы будете печатать как босс. С помощью этой техники вы можете назначить символ математического целого числа ∫ и любые другие текстовые символы на клавиатуру.
Карта символов
CharMap позволяет вам просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. С его помощью можно вводить целочисленные символы.
Мак
Emoji на iOS (iPhone, iPad и iPod touch)
Текстовые символы с клавиатурой iPhone Emoji 📲Простой и красивый способ узнать, как добавить виртуальную клавиатуру для символов Emoji, видимых в виде маленьких картинок. Сама клавиатура предустановлена на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.
Средство просмотра клавиатуры
Вы можете создавать часто используемые технические непричудливые символы, такие как «√ ∑ π ∞ ∆ ™ © æ £ ¢» и буквы с диакритическими знаками на Mac, используя клавишу [Option]. Я составил список горячих клавиш в своей статье и объяснил, как открыть программу просмотра клавиатуры. Вы также можете использовать средство просмотра клавиатуры в качестве альтернативы моему списку.
[Опция] + [B] дает знак интеграла ∫.

Палитра символов
Палитра символов позволяет просматривать и использовать все символы и знаки, включая интегральный знак, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.

линукс
С клавиатуры
Карта символов
Карта символов позволяет просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. Это также может помочь вам найти коды Unicode для ввода символов с клавиатуры.
HTML-код
Ниже приведен список объектов HTML и JavaScript для интегральных символов. В Javascript вы должны написать как = “это \ u2669символ”, если вы хотите включить в строку специальный символ.
HTML-объект JS-сущность Символ
∫ \ u222b ∫
∬ \u222c ∬
∭ = ∭
∮ > ∮
∲ \u2232 ∲
∳ \u2233 ∳
∯ \u222f ∯
∰ \u2230 ∰
2.
4: Второй закон термодинамики – Технические LibreTexts
Последнее обновление
Сохранить как PDF
Код страницы
639
Геник Бар-Меир
Potto Project
Существует несколько определений второго закона. Независимо от того, какое определение используется для описания второго закона, оно будет иметь математическую форму. Наиболее распространенной математической формой является неравенство Клаузиуса, которое утверждает, что
\[ \oint \dfrac {\delta Q} {T} \ge 0
\label{thermo:eq:clausius}
\]
Символ интегрирования с кружком представляет собой интеграл цикла (поэтому кружок) при возврате системы в то же состояние. Если потерь нет, то это называется обратимым процессом и неравенство меняется на равенство.
\[ \oint \dfrac {\delta Q} {T} = 0
\label{thermo:eq:clausiusE}
\]
Последний интеграл может проходить через несколько состояний. Эти состояния не зависят от пути, по которому проходит система. Следовательно, интеграл не зависит от пути. Это наблюдение приводит к определению энтропии и обозначается как $S$, а производная энтропии равна
.
\[ ds \equiv \left( \dfrac{ \delta Q}{T} \right)_{\hbox{rev}}
\label{thermo:eq:engropy}
\]
92_1 dS
\label{thremo:eq:deltaS}
\]
Один из выводов, который можно сделать из этого анализа, касается обратимого и адиабатического процесса $dS=0$. Таким образом, процесс, в котором носит обратимый и адиабатический характер, энтропия остается постоянной и называется изэнтропическим процессом. Можно отметить, что существует вероятность того, что процесс может быть необратимым, а правильное количество теплопередачи должно иметь нулевое изменение энтропии. Таким образом, обратный вывод о том, что нулевое изменение энтропии приводит к обратимому процессу, неверен. Для обратимого процесса уравнение (12) можно записать в виде
\[ \дельта Q = T\, dS
\label{thermo:eq:dQ}
\]
, а работа, которую система выполняет над окружением, равна
.
\[ \delta W = P\,dV
\label{thermo:eq:dW}
\]
Подстановка уравнений (15) (16) в (10) приводит к
\[ T\,dS = d\,E_U + P\, dV
\label{thermo:eq:Tds}
\]
Несмотря на то, что вывод приведенных выше уравнений был сделан в предположении, что нет изменения кинетической или потенциальной энергии, они по-прежнему остаются в силе для всех ситуаций. Кроме того, можно показать, что оно справедливо для обратимых и необратимых процессов.
Энтальпия
Обычной практикой является определение нового свойства, представляющего собой комбинацию уже определенных свойств, а именно энтальпии системы.
\[ H = E_U + P\,V
\label{thermo:eq:enthalpy}
\]
Удельная энтальпия представляет собой энтальпию на единицу массы и обозначается как $h$. Или в дифференциальной форме как
\[ dH = dE_U + dP\,V + P\,dV
\label{thermo:eq:dEnthalpy}
\]
Объединение уравнений (18) и (17) дает
(одна форма) Уравнение Гиббса
\[\label{thermo:eq:TdSH}T\,dS = dH -V\,dP \]
Для изоэнтропического процесса уравнение (17) сводится к $dH =VdP$. Уравнение (17) в единицах массы имеет вид
\[T\,ds = du + P\,dv = dh – \dfrac{dP}{\rho}\label{thermo:eq:Tdsh} \]
, когда плотность входит через отношение $\rho=1/v$.
Удельная теплоемкость
Изменение внутренней энергии и энтальпии требует новых определений. Первое изменение внутренней энергии и определяется следующим образом:
Удельная объемная теплота
\[\label{thermo:eq:cv}C_v \equiv \left( \dfrac {\partial E_u }{\partial T} \right) \]
А так как изменение энтальпии включают некоторую граничную работу, определяется как
Удельное давление Теплота
\[\label{thermo:eq:cp}C_p \equiv \left( \dfrac {\partial h}{\partial T} \right) \]
Отношение удельной теплоемкости под давлением к удельной объемной теплоемкости называется отношением удельной теплоемкости и обозначается $k$.
Отношение удельных их почти ноль. Обычно разница для твердых тел игнорируется, и оба считаются одинаковыми и поэтому называются $C$. Это приближение менее сильное для жидкости, но ненамного и в большинстве случаев применимо к расчетам. Отношение удельной теплоемкости газов больше единицы.
Уравнение состояния
Уравнение состояния представляет собой отношение между переменными состояния. Обычно соотношение температуры, давления и удельного объема определяют уравнение состояния газов. Простейшее уравнение состояния называют идеальным газом. И определяется как
\[P = \rho\, R\, T\label{thermo:eq:idealGas} \]
Применение закона Авогадро, согласно которому «все газы при одинаковых давлениях и температурах имеют одинаковые количество молекул на единицу объема», позволяет рассчитать «универсальную газовую постоянную». Эта константа, соответствующая стандартным единицам, дает
\[ \bar{R} = 8,3145 \dfrac{kj} {кмоль\; K }
\label{thermo:eq:Rbar}
\]
Таким образом, удельный газ можно рассчитать как
\[ R = \dfrac{\bar{R}} {M}
\label{thermo:eq:R}
\]
Конкретные константы для выбранного газа при 300K приведены в таблице 2. 1.
Таблица 2.1 Свойства различных идеальных газов [300K]
Газ Химическая формула Молекулярный вес $R\, \left[\dfrac{kj}{Kg K}\right]$ $C_p\, \left[\dfrac{kj}{Kg K}\right]$ $C_V\, \влево[\dfrac{kj}{Kg K}\вправо]$ $к$
Воздух – 28.970 0,28700 1.0035 0,7165 1. 400
Аргон $Арг$ 39,948 0,20813 0,5203 0,3122 1.400
Бутан $C_4H_{10}$ 58.124 0,14304 1.7164 1,5734 1.091
Двуокись углерода $СО_2$ 44. 01 0,18892 0,8418 0,6529 1,289
Окись углерода $СО$ 28.01 0,29683 1.0413 0,7445 1.400
Этан $C_2H_6$ 30.07 0,27650 1,7662 1. 4897 1,186
Этилен $C_2H_4$ 28.054 0,29637 1,5482 1.2518 1,237
Гелий $Не$ 4.003 2.07703 5.1926 3.1156 1,667
Водород $Н_2$ 2. 016 4.12418 14.2091 10.0849 1.409
Метан $СН_4$ 16.04 0,51835 2,2537 1.7354 1,299
Неон $Не$ 20.183 0,41195 1. 0299 0,6179 1,667
Азот $N_2$ 28.013 0,29680 1.0416 0,7448 1.400
Октан $C_8H_{18}$ 114.230 0,07279 1.7113 1.6385 1. 044
Кислород $О_2$ 31,999 0,25983 0,9216 0,6618 1,393
Пропан $C_3H_8$ 44.097 0,18855 1.6794 1.4909 1,327
Пар $Н_2О$ 18. 015 0,48152 1.8723 1.4108 1,327
Из уравнения (25) состояния идеального газа следует
\[ d\left(P\,v\right) = R\,dT
\label{thermo:eq:stateD}
\]
Для идеального газа
\[ dh = dE_u + d(Pv) = dE_u + d(R\,T) = f(T)\hbox{ (только)}
\label{thermo:eq:dhIdeal}
\]
Из определения энтальпии следует, что
\[ d(Pv) = dh – dE_u
\label{thermo:eq:defHd}
\]
Использование уравнения (28) и подстановка в уравнение (29) и деление на $dT$ дает
\[ C_p – C_v = R
\label{thermo:eq:CpCvR}
\]
Это соотношение справедливо только для идеальных/идеальных газов. Отношение удельных теплоемкостей может быть выражено в нескольких формах как
$C_v$ к коэффициенту удельных теплоемкостей
\[ \label{thermo:eq:Cv}
C_v = \dfrac{R}{k-1}
\]
$C_p$ к удельной теплоемкости
\[ \label{thermo:eq:Cp}
C_p = \dfrac{k\,R}{k-1}
\]
Коэффициент удельной теплоемкости $k$ колеблется от единицы до примерно 1,667. {\dfrac{k -1}}{k}} 9{k -1 }
\]
Модель идеального газа представляет собой упрощенную версию реального поведения реального газа. Реальный газ имеет поправочный коэффициент для учета отклонений от модели идеального газа. Этот поправочный коэффициент называется коэффициентом сжимаемости и определяется как отклонение
Z от модели идеального газа
\[\label{thermo:eq:Z}Z = \dfrac{P\,V}{R\,T} \ ]
Авторы и ссылки
Доктор Геник Бар-Меир. Разрешается копировать, распространять и/или изменять этот документ в соответствии с условиями лицензии GNU Free Documentation License версии 1.2 или более поздней или лицензии Potto.
Эта страница под названием 2.4: Второй закон термодинамики распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Эта страница под названием 2.4: Второй закон термодинамики распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Геником Бар-Меиром посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
Геник Бар-Меир
Лицензия
ГНУ ФДЛ
Версия лицензии
1,3
Показать оглавление
нет
Метки
источник@https://potto. org/fluidMech
Интегральный символ png скачать бесплатно – День числа Пи
Интегральный символ png скачать бесплатно – День числа Пи – математический символ
Главная > HD PNG >  Интегральный символ (61 совпадение)
День Пи – математический символ
Стол Мультфильм – составной символ png картинки
Мультфильм Мышь – неотъемлемый символ системы иконок ПНГ
School Line Art – неотъемлемый символ png cambio de
Логотип Круга – неотъемлемый символ png cambio de
интегральный символ png cambio de
3d Circle – неотъемлемый символ png системная интеграция
Маркетинг Фон – неотъемлемый символ png системная интеграция
Логотип Майкрософт – неотъемлемый символ png системная интеграция
Желтый фон – интегральный символ png на неопределенный срок
Круг Фон – интегральный символ png svg
Логотип Intel — интеграция Microsoft Dynamics gp
Деловой фон – неотъемлемый символ
Образование – неотъемлемый символ
Математика
Фон вопросительного знака – интегральный символ
Научный мультфильм – Бизнес
Фон дерева – энергия
Белая звезда – ребенок
символ
Силуэт круга – целостный символ
Туалет Мультфильм – туалет
Логотип социальных сетей – социальные сети
Значок “Поделиться” – интегральный символ
История бизнеса – Бизнес
Кровать Cartoon – целостный символ
Знак “Стоп” – интегральный символ
Домашний мультфильм – Линкольн
Круглый логотип – строчная буква
Символ авторского права — математический символ
Математика
Рисунок облака – целостный символ
интегральный символ
Мобильный мультфильм – Математика
Стрелка фона круга – символ
Круглый логотип – целостный символ
Математика
Черный круг – Математика
Математика
Математика
Математика
Математика
Фон Иисуса – символ
Математика
Cloud Symbol – облачные вычисления
Математика
Математика
встроенная карта
другие
Фон круга – символ
примечания к статье
исчисление математических функций
Треугольный фон — 3 корня
Современный фон – скрипка
пи математика
Современный фон – математика пи
Россия
Цвет фона – программное обеспечение
Образование – стратегия
скрипка
1
SubPNG предлагает бесплатные картинки Интегральный символ, прозрачные изображения Интегральный символ, векторные ресурсы Интегральный символ.
Оставить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Поиск:
Рубрики
2019 © Все права защищены. Карта сайта
Меню
Поиск:

Символ	Мнемоника	Код символа	Описание

	` `	` `	Неразрывный пробел
	`&ensp;`	` `	Узкий пробел
	`&emsp;`	` `	Широкий пробел
–	`–`	`–`	Узкое тире
—	`—`	`—`	Широкое тире
	``	``	Мягкий перенос
́		`́`	Ударение
©	`©`	`©`	Копирайт
®	`®`	`®`	Зарегистрированная торговая марка
™	`™`	`™`	Торговая марка
º	`º`	`º`	Копье Марса
ª	`ª`	`ª`	Зеркало Венеры
‰	`&permil;`	`‰`	Промилле
π	`π`	`π`	Пи
¦	`¦`	`¦`	Вертикальный пунктир
§	`§`	`§`	Параграф
°	`°`	`°`	Градус
µ	`µ`	`µ`	Знак «микро»
¶	`¶`	`¶`	Знак абзаца
…	`…`	`…`	Многоточие
‾	`&oline;`	`‾`	Надчеркивание
´	`´`	`´`	Ударение
№		`№`	Номер
🔍		`🔍`	Лупа (наклонённая влево)
🔎		`🔎`	Лупа (наклонённая вправо)
&	`&`	`&`	Амперсанд

Символ	Мнемоника	Код символа	Описание

	` `	` `	Неразрывный пробел
	`&ensp;`	` `	Узкий пробел
	`&emsp;`	` `	Широкий пробел
–	`–`	`–`	Узкое тире
—	`—`	`—`	Широкое тире
	``	``	Мягкий перенос
́		`́`	Ударение
©	`©`	`©`	Копирайт
®	`®`	`®`	Зарегистрированная торговая марка
™	`™`	`™`	Торговая марка
º	`º`	`º`	Копье Марса
ª	`ª`	`ª`	Зеркало Венеры
‰	`&permil;`	`‰`	Промилле
π	`π`	`π`	Пи
¦	`¦`	`¦`	Вертикальный пунктир
§	`§`	`§`	Параграф
°	`°`	`°`	Градус
µ	`µ`	`µ`	Знак «микро»
¶	`¶`	`¶`	Знак абзаца
…	`…`	`…`	Многоточие
‾	`&oline;`	`‾`	Надчеркивание
´	`´`	`´`	Ударение
№		`№`	Номер
🔍		`🔍`	Лупа (наклонённая влево)
🔎		`🔎`	Лупа (наклонённая вправо)
&	`&`	`&`	Амперсанд

Что означает интегральный символ с кружком?

Перечень специальных символов — Документация Qucs Help 0.0.19

Спецсимволы HTML + CSS (мнемоника и коды)

Инструкция вставки спецсимволов в HTML

Инструкция вставки спецсимволов через CSS

Пример добавления спец-символа через CSS:

Таблица с кодами спецсимволов (мнемоник) HTML

Дополнительные спецсимволы HTML

Обновление МойОфис 2021.02. Пишите формулы и математические выражения в текстовом редакторе / Хабр

Как вводить формулы

Сравним как формулы отображаются в других редакторах

Как формулы из МойОфис отображаются в LibreOffice

Как формулы из МойОфис отображаются в Microsoft Office

Как формулы из Microsoft Office отображаются в МойОфис

Как формулы из LibreOffice отображаются в МойОфис

Спецсимволы HTML и мнемоники

Текстовые символы для ников и социальных сетей

Символ интеграла: с пояснениями — Eggradients.com

Двойной интеграл

Тройной интеграл

Линейный интеграл

Интеграл по замкнутой поверхности

Интеграл по замкнутому объему

Что означает знак интеграла с кружком на нем?

Содержание:

Что означает знак интеграла с кружком на нем?

Кто изобрел интегральный символ?

Для чего используется интеграл?

Какой символ означает то же, что и?

Почему в физике используется интегрирование?

Что такое интеграл в физике?

Что такое интеграция в 11 классе физики?

Как интеграция используется в биологии?

Используются ли вычисления в биологии?

Как исчисление используется в реальной жизни?

Как исчисление применяется в медицине?

Используют ли врачи вычисления?

Врачи изучают исчисление?

Используют ли фармацевты вычисления?

Трудно ли стать фармацевтом?

Есть ли математика в Pharm D?

Какую математику используют фармацевты?

Нужно ли хорошо разбираться в математике, чтобы стать фармацевтом?

Легко ли быть фармацевтом?

Какая квалификация требуется для помощника аптекаря?

Кто такой помощник аптекаря уровня 2?

Раннее использование символов исчисления

СИМВОЛЫ ВЕКТОРНОГО ВЫЧИСЛЕНИЯ

Знаки интеграла (введите символ интеграла на клавиатуре)

Математика интеграла

Как вводить целочисленные символы

Состояния сдвига

Карта символов

Emoji на iOS (iPhone, iPad и iPod touch)

Средство просмотра клавиатуры

Палитра символов

С клавиатуры

Карта символов

2.

Энтальпия

(одна форма) Уравнение Гиббса

Удельная теплоемкость

Удельная объемная теплота

Удельное давление Теплота

Уравнение состояния

\(C_v\) к коэффициенту удельных теплоемкостей

\(C_p\) к удельной теплоемкости

Z от модели идеального газа

Авторы и ссылки

Интегральный символ png скачать бесплатно – День числа Пи

Оставить комментарий Отменить ответ

Символ	Мнемоника	Код символа	Описание

	` `	` `	Неразрывный пробел
	`&ensp;`	` `	Узкий пробел
	`&emsp;`	` `	Широкий пробел
–	`–`	`–`	Узкое тире
—	`—`	`—`	Широкое тире
	``	``	Мягкий перенос
́		`́`	Ударение
©	`©`	`©`	Копирайт
®	`®`	`®`	Зарегистрированная торговая марка
™	`™`	`™`	Торговая марка
º	`º`	`º`	Копье Марса
ª	`ª`	`ª`	Зеркало Венеры
‰	`&permil;`	`‰`	Промилле
π	`π`	`π`	Пи
¦	`¦`	`¦`	Вертикальный пунктир
§	`§`	`§`	Параграф
°	`°`	`°`	Градус
µ	`µ`	`µ`	Знак «микро»
¶	`¶`	`¶`	Знак абзаца
…	`…`	`…`	Многоточие
‾	`&oline;`	`‾`	Надчеркивание
´	`´`	`´`	Ударение
№		`№`	Номер
🔍		`🔍`	Лупа (наклонённая влево)
🔎		`🔎`	Лупа (наклонённая вправо)
&	`&`	`&`	Амперсанд