Метод Гаусса для решения систем линейных уравнений (стр. 1 из 2)
1. Система линейных алгебраических уравнений
1.1 Понятие системы линейных алгебраических уравнений
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:
где числа aij называются коэффициентами системы, числа bi – свободными членами, aij и bi (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x1,…, xn – неизвестные. В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа xn. Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;
Здесь А – матрица коэффициентов системы, называемая основной матрицей;
– вектор-столбец из неизвестных xj.
– вектор-столбец из свободных членов bi.
Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов
1.2 Решение системы линейных алгебраических уравнений
Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.
Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.
2. Метод исключения Гаусса
2.1 Сущность метода исключения Гаусса
Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.
1. Прямой ход.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид:
,
где
Коэффициенты aii называются главными (ведущими) элементами системы.
1-й шаг.
Будем считать, что элемент
(если a11=0, переставим строки матрицы так, чтобы a11 не был равен 0. Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).
Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).
Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы (или из второго уравнения почленно вычтем первое, умноженное на
). Затем умножим обе части первого уравнения на
и сложим с третьим уравнением системы (или из третьего почленно вычтем первое, помноженное на
). Таким образом, последовательно умножаем первую строку на число
и прибавляем к i-й строке, для i=2, 3, …, n.
Продолжая этот процесс, получим эквивалентную систему:
Здесь
– новые значения коэффициентов при неизвестных и свободные члены в последних m-1 уравнениях системы, которые определяются формулами:
Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a11
0, на втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а22(1) (если a22(1)
0) и т. д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.
д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.
Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида
то это свидетельствует о несовместности системы.
На этом прямой ход метода Гаусса заканчивается.
2. Обратный ход.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.
Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.
Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11).
2.2 Примеры решения СЛАУ методом Гаусса
В данном разделе на трех различных примерах покажем, как методом Гаусса можно решить СЛАУ.
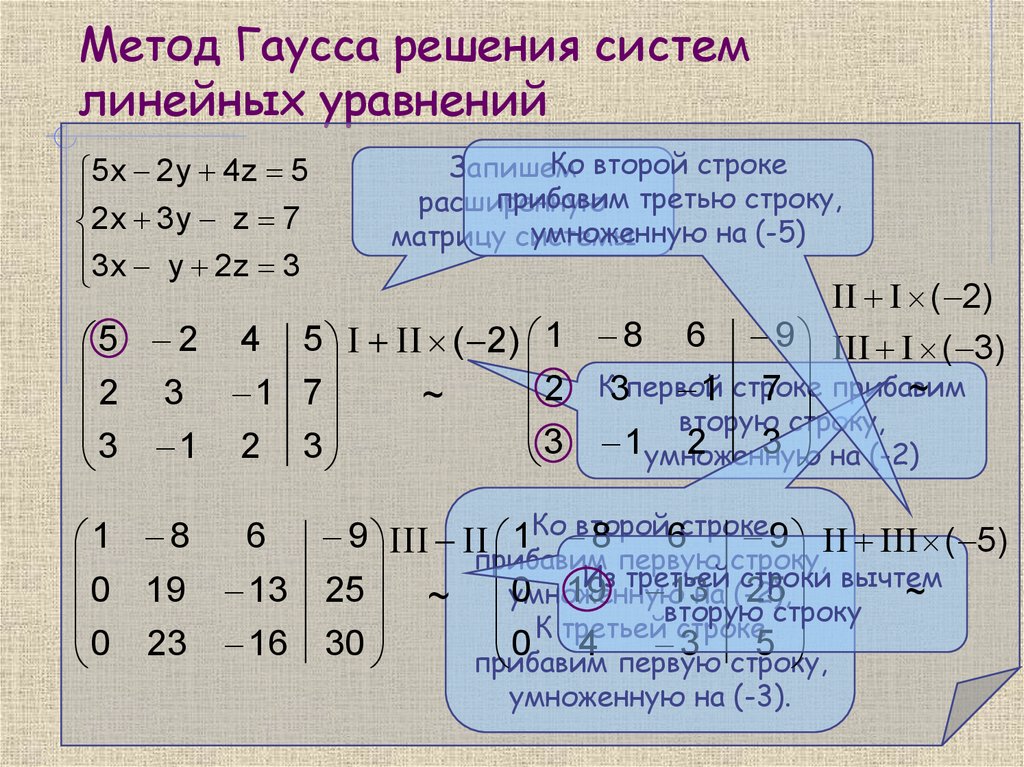
Пример 1. Решить СЛАУ 3-го порядка.
Обнулим коэффициенты при
во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:
Метод Гаусса решения систем линейных уравнений
Рассмотрим квадратную систему
. (1)
У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.
Проведем следующие преобразования системы:
1) поскольку a11¹0, первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1 – 4):
. (2)
Можно доказать, что замена любого уравнения системы новым, получающимся прибавлением к данному уравнению любого другого уравнения системы, умноженного на любое число, является эквивалентным преобразованием системы.
Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде таблицы
Исходную систему можно представить в виде таблицы
. (3)
Прямоугольную таблицу, состоящую из p строк и q столбцов, будем называть матрицей размера p´q:
.
Числа aij называются элементами матрицы. Первый индекс фиксирует номер строки, а второй – номер столбца, в которых стоит данный элемент. Если p = q, то есть число столбцов матрицы равно числу строк, то матрица называется квадратной. Элементы aii образуют главную диагональ матрицы.
Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.
Очевидно, что матрица коэффициентов квадратной системы является квадратной матрицей.
Каждую систему m линейных уравнений с n неизвестными можно представить в виде расширенной матрицы, содержащей m строк и n+1 столбцов. Каждую матрицу можно считать расширенной матрицей или матрицей коэффициентов некоторой системы линейных уравнений. Системе (2) соответствует расширенная матрица
.
Преобразуем эту матрицу следующим образом:
1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
.
Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:
Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a33 ¹ 0;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:
.
Полученная матрица соответствует системе
. (4)
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.).
Назовем элементарными преобразованиями матрицы следующие преобразования:
1) перемена местами двух строк;
2) умножение строки на число, отличное от нуля;
3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.
Если матрица A является расширенной матрицей некоторой системы, и путем ряда элементарных преобразований матрица A переводится в матрицу B, являющуюся расширенной матрицей некоторой другой системы, то эти системы эквивалентны.
Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей. Матрица коэффициентов системы (4) – треугольная матрица.
Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна.
Рассмотрим другой пример:
. (5)
Проведем следующие преобразования расширенной матрицы системы:
1) первую строку оставим без изменения;
2) вместо второй строки запишем разность между второй строкой и удвоенной первой;
3) вместо третьей строки запишем разность между третьей строкой и утроенной первой;
4) четвертую строку заменим разностью между четвертой и первой;
5) пятую строку заменим разностью пятой строки и удвоенной первой.
В результате преобразований получим матрицу
.
Оставив без изменения первые две строки этой матрицы, приведем ее элементарными преобразованиями к следующему виду:
.
Если теперь, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки привести к нулю коэффициенты при x3 в четвертой и пятой строках, то после деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получим матрицу
.
Каждая из двух последних строк этой матрицы соответствует уравнению 0x1+0x2+0x3+0x4+0x5 = 0. Это уравнение удовлетворяется любым набором чисел x1, x2, ¼, x5, и его следует удалить из системы. Таким образом, система с только что полученной расширенной матрицей эквивалентна системе с расширенной матрицей вида
. (6)
(6)
Последняя строка этой матрицы соответствует уравнению x3 – 2x4 + 3x5 = –4. Если неизвестным x4 и x5 придать произвольные значения: x4 = r; x5 = s, то из последнего уравнения системы, соответствующей матрице (6), получим x3 = –4 + 2r – 3s. Подставив выражения x3, x4, и x5 во второе уравнение той же системы, получим x2 = –3 + 2r – 2s. Теперь из первого уравнения можно получить x1 = 4 – r + s. Окончательно решение системы представляется в виде
.
Рассмотрим прямоугольную матрицу A, у которой число столбцов m больше, чем число строк n. Если матрицу A можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера m и стоящую справа прямоугольную матрицу, то матрицу A назовем трапециевидной или трапецеидальной. Очевидно, что матрица (6) — трапециевидная матрица.
Очевидно, что матрица (6) — трапециевидная матрица.
Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду
0x1+ 0x2+ ¼0xn = bj (bj ¹ 0),
то система несовместна или противоречива, так как ни один набор чисел x1, x2, ¼, xn не удовлетворяет этому уравнению.
Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к трапецеидальному виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений.
В последней системе можно получить все решения, придавая конкретные числовые значения параметрам r и s.
Те переменные, коэффициенты при которых стоят на главной диагонали трапецеидальной матрицы (это значит, что эти коэффициенты отличны от нуля), называются базисными. В рассмотренном выше примере это неизвестные x1, x2, x3. Остальные неизвестные называются свободными. В рассмотренном выше примере это неизвестные x4, и x5. Свободным неизвестным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.
В рассмотренном выше примере это неизвестные x1, x2, x3. Остальные неизвестные называются свободными. В рассмотренном выше примере это неизвестные x4, и x5. Свободным неизвестным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.
Базисные неизвестные единственным образом выражаются через свободные неизвестные.
Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением.
Если свободные неизвестные выражены через параметры, то получается решение, которое называется общим решением.
Все бесконечное множество решений системы можно получить, придавая свободным неизвестным любые числовые значения и находя соответствующие значения базисных неизвестных.
Если всем свободным неизвестным приданы нулевые значения, то полученное решение называется базисным.
Одну и ту же систему иногда можно привести к разным наборам базисных неизвестных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда базисными будут неизвестные x1, x2, x4, а свободными – x3 и x5. Рекомендуем читателю самостоятельно привести последнюю систему к такому виду, чтобы свободными неизвестными были x1 и x2, а базисными – x3, x4, x5.
Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы.
Рассмотрим еще одну систему, имеющую бесконечно много решений:
.
Проведем преобразование расширенной матрицы системы по методу Гаусса:
.
Как видно, мы не получили трапецеидальной матрицы, однако последнюю матрицу можно преобразовать, поменяв местами третий и четвертый столбцы:
.
Эта матрица уже является трапецеидальной. У соответствующей ей системы две свободных неизвестных – x3, x5 и три базисных – x1, x2, x4. Решение исходной системы представляется в следующем виде:
.
Приведем пример не имеющей решения системы:
.
Преобразуем матрицу системы по методу Гаусса:
.
Последняя строка последней матрицы соответствует не имеющему решения уравнению 0x1 + 0x2 + 0x3 = 1. Следовательно, исходная система несовместна.
Сформулируем теперь кратко суть метода Гаусса. Полагая, что в системе коэффициент a11 отличен от нуля ( если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1 и переобозначить коэффициенты), преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью эквивалентных преобразований описанным выше способом.
В полученной системе
,
считая, что (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений и переобозначив коэффициенты системы), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
15. Характеристика еженедельника «Эспрессо » – лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
при условии оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:
1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;
2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;
3) если получается система с трапецеидальной матрицей коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.
Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений
|
является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.
Из последнего уравнения выражаем
Из второго уравнения выражаем
Из первого уравнения выражаем
Выпишем общее решение системы:
Ответ: Система имеет множество решений, общее решение системы:
Решение однородных систем
Система линейных уравнений называется однородной, если правые части уравнений равны нулю:
Матричный вид однородной системы:

Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю. Линейная комбинация решений однородной системы также является решением этой системы.
Пример: Исследовать однородную систему на совместность, найти решения:
Решение: Расширенную матрицу системы приведем к ступенчатому виду:
восстановим систему:
Система имеет множество решений. и главные переменные, и свободные переменные. Перенесем свободные переменные в правые части уравнений.
Из второго уравнения находим подставляя это выражение в первое уравнение, получим:
Общее решение системы:
Для нахождения частных решений, свободным переменным даем произвольные значения:
Элементы векторной алгебры
Векторы
Величины, которые полностью определяются своим численным значением, называются скалярными. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными.
Вектор-это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А- начало вектора, а В- его конец, то вектор обозначается символом , или . Вектор ( у него начало в точке В , а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .
Длиной или модулем вектора называется длина отрезка AB и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .
Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы ║
Коллинеарные векторы могут быть направлены одинаково, т.е. быть сонаправленными ( ), или быть противоположно направленными ( ).
Нулевой вектор считается коллинеарным любому вектору.
Два вектора и называются равными ( ), если они коллинеарные, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора перемешать в любую точку пространства.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
©2015- 2022 pdnr.ru Все права принадлежат авторам размещенных материалов.
линейная алгебра — решение системы уравнений с использованием Гаусса/Гаусса-Жордана (матрица)
$\begingroup$
Система уравнений $$\begin{выравнивание*} х -2у +3г &= 2\\ 2x -3y +8z &= 7\\ 3x -4y +13z &= 8 \end{align*}$$
В расширенной матрице $3\times 4$ $$\left(\begin{массив}{crc|c} 1 &-2 &3 &2\\ 2&-3&8&7\\ 3 &-4 &13& 8\\ \end{array}\right).$$
Выше приведены уравнения/строки. Используя эти операции со строками: постоянное число, умноженное на строку, обмен/переключение уравнений/строки и, наконец, добавление двух уравнений/строк вместе после умножения одного из них на константу – я все еще не могу решить и в конечном итоге должен отменить часть диагонали матрицы при попытке добиться результата, аналогичного или равного единичной матрице.
Похоже, что аналогичная ситуация имеет место с двумя неизвестными и теми же тремя числами уравнений
$$\begin{align*} х + у &= 1\\ 9x -y &= 0\\ х -19у &= -17 \end{align*}$$
- линейная алгебра
- матрицы
- матричные уравнения
- джордан-нормальная форма
- исключение Гаусса
$\endgroup$
4
$\begingroup$
Система несовместима: второе уравнение минус удвоенное первое уравнение дает $y+2z=3$, а третье уравнение минус тройное второе уравнение дает $2y+4z=2$. Эти два уравнения несовместимы, поэтому система не имеет решений. Вы можете видеть это при выполнении исключения Гаусса:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 &-2 &3 &2\\
2&-3&8&7\\
3 &-4 &13& 8\\
\end{массив}\right) &\stackrel{R_2-2R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
3 и -4 и 13 и 8
\end{массив}\right) \stackrel{R_3-3R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 2
\конец{массив}\справа)\\
&\stackrel{R_3-2R_2}{\longrightarrow} \left(\begin{array}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и -4
\end{массив}\right) \stackrel{-\frac{1}{4}R_3}{\longrightarrow}
\left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
И коэффициент, и расширенная матрица теперь имеют эшелонированную форму строк: первый ненулевой элемент каждой строки — это $1$, и $1$ в каждой строке появляется справа от $1$ в предыдущей строке, и все строки $0$ находятся внизу.
Вы можете видеть это при выполнении исключения Гаусса:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 &-2 &3 &2\\
2&-3&8&7\\
3 &-4 &13& 8\\
\end{массив}\right) &\stackrel{R_2-2R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
3 и -4 и 13 и 8
\end{массив}\right) \stackrel{R_3-3R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 2
\конец{массив}\справа)\\
&\stackrel{R_3-2R_2}{\longrightarrow} \left(\begin{array}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и -4
\end{массив}\right) \stackrel{-\frac{1}{4}R_3}{\longrightarrow}
\left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
И коэффициент, и расширенная матрица теперь имеют эшелонированную форму строк: первый ненулевой элемент каждой строки — это $1$, и $1$ в каждой строке появляется справа от $1$ в предыдущей строке, и все строки $0$ находятся внизу.
Поскольку ранг уменьшенной матрицы коэффициентов равен $2$, а ранг расширенной матрицы равен $3$, система несовместна. Вы можете продолжить отсюда, чтобы получить форму эшелона с уменьшенной строкой, но это не «решит» проблему внезапно:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\end{массив}\right)&\stackrel{R_1-2R_3}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 0\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\end{массив}\right) \stackrel{R_2-3R_3}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 0\\
0 и 1 и 2 и 0 \\
0 и 0 и 0 и 1
\конец{массив}\справа)\\
&\stackrel{R_1+2R_2}{\longrightarrow}
\left(\begin{массив}{ccc|c}
1 и 0 и 7 и 0\\
0 и 1 и 2 и 0\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
Это в сокращенной эшелонированной форме строк (дополнительное условие состоит в том, что начальные $1$ в каждой строке являются единственными ненулевыми элементами в своих столбцах), но опять же вы видите, что это соответствует несогласованной системе.
Вы можете продолжить отсюда, чтобы получить форму эшелона с уменьшенной строкой, но это не «решит» проблему внезапно:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\end{массив}\right)&\stackrel{R_1-2R_3}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 0\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\end{массив}\right) \stackrel{R_2-3R_3}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 0\\
0 и 1 и 2 и 0 \\
0 и 0 и 0 и 1
\конец{массив}\справа)\\
&\stackrel{R_1+2R_2}{\longrightarrow}
\left(\begin{массив}{ccc|c}
1 и 0 и 7 и 0\\
0 и 1 и 2 и 0\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
Это в сокращенной эшелонированной форме строк (дополнительное условие состоит в том, что начальные $1$ в каждой строке являются единственными ненулевыми элементами в своих столбцах), но опять же вы видите, что это соответствует несогласованной системе.
Теперь предположим, что последнее уравнение было $3x-4y+13z=12$ вместо $8$. Тогда на третьем шаге приведения выше мы получили бы матрицу
$$\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 6
\end{массив}\right)\stackrel{R_3-2R_2}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 0
\конец{массив}\справа).$$
Это совершенно прекрасная матрица формы строки-эшелона; просто вы получите одну свободную переменную и бесконечно много решений. Затем вы можете перейти к уменьшенной форме эшелона строк, дважды добавив вторую строку к первой строке, и вы получите
$$\left(\begin{массив}{ccc|c}
1 и 0 и 7 и 8\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 0
\end{массив}\right)$$
который дает решения
$$\begin{выравнивание*}
х &= 8 – 7t\\
у &= 3 – 2t\\
г &= т
\end{align*},\qquad t\text{произвольный.}$$
Тогда на третьем шаге приведения выше мы получили бы матрицу
$$\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 6
\end{массив}\right)\stackrel{R_3-2R_2}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 0
\конец{массив}\справа).$$
Это совершенно прекрасная матрица формы строки-эшелона; просто вы получите одну свободную переменную и бесконечно много решений. Затем вы можете перейти к уменьшенной форме эшелона строк, дважды добавив вторую строку к первой строке, и вы получите
$$\left(\begin{массив}{ccc|c}
1 и 0 и 7 и 8\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 0
\end{массив}\right)$$
который дает решения
$$\begin{выравнивание*}
х &= 8 – 7t\\
у &= 3 – 2t\\
г &= т
\end{align*},\qquad t\text{произвольный.}$$
$\endgroup$
8
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
160 Линейные системы
160 Линейные системыМатрицы и линейные системы в Attaway
Следующие накладные лекции и сопроводительное чтение являются независимыми из МатЛаб. Attaway Глава 11.1 ссылки матрицы, как описано здесь, с их представлением и использованием в Матлаб. Аттавей 11.1 следует читать и понимать как дополнение к он-лайн лекции и чтению.
Аттавей 11.2, ведущий к 11.2.2.1, дает предысторию и алгоритм исключения Гаусса как метод решения линейного Уравнения. Полезно прочитать “как сделать” для задания.
Линейные системы
- А
линейное уравнение – это уравнение, содержащее только
скалярные кратные его переменных и констант. Например:
а 1 х 1 + а 2 х 2 + а 3 Х 3 = с
представляет собой линейное уравнение с тремя переменными .
Х 1 -Х 3 представлять переменные, а 1 -а 3 соответствующие коэффициенты , и с называется постоянным членом .5x + 7,5y – 10z = 30
является частным примером. - А система линейных уравнений представляет собой (конечный) набор такие уравнения, которые (обычно) связаны тем, что содержат (некоторые из) одних и тех же переменных.
- Линейные системы важны, потому что они полезны для моделирования
большое количество практических ситуаций и
математики знают о них чертовски много, в том числе:
- Именно тогда, когда существуют решения.
- Именно тогда, когда решение уникально.
- Эффективные алгоритмы поиска решений, если они существуют.
- Эффективные методы аппроксимации решений в случаях, когда
реальных решений не существует (метод наименьших квадратов).

- В общем, если у нас есть N переменных (или неизвестных), нам нужно N линейно независимые уравнения, чтобы найти единственное решение. Такая независимость означает, что мы не можем вывести ни одно из уравнения из других.
- Если у нас больше переменных, чем уравнений, говорят, что система быть недоопределенным . Уравнения обычно ограничивают решение линейное подпространство пространства возможных решения, но нет единственного, единственного решения. Например. с тремя переменными одно линейное уравнение описывает плоскость (подпространство 3-D), каждая из точек которого удовлетворяет уравнению.
- Если у нас больше уравнений, чем переменных, то система
вообще говоря, не будет иметь решения (если только некоторые из
уравнения линейно зависимы). Говорят, что такая система переопределено или несовместимо .
 Хотя фактического решения может и не быть, часто
точки в пространстве переменных, которые являются «почти решениями»
в том смысле, который можно сделать математически строгим.
Анализ методом наименьших квадратов является одним из распространенных подходов к
нахождение таких приближенных решений. (Подробнее в модели
Будет актуальная тема).
Хотя фактического решения может и не быть, часто
точки в пространстве переменных, которые являются «почти решениями»
в том смысле, который можно сделать математически строгим.
Анализ методом наименьших квадратов является одним из распространенных подходов к
нахождение таких приближенных решений. (Подробнее в модели
Будет актуальная тема).
Геометрическая интуиция
- Напомним, что точки, удовлетворяющие линейному уравнению
топор + по = с
в двух переменных x и y попадают на прямую в плоскости xy. - Если мы введем второе уравнение с (обычно) другим константы a, b и c, то у нас есть вторая строка. Есть четыре возможности:
- В общем вторая линия пересечет первую в одной точке. Это общий случай двух неизвестных, двух уравнений и единственного решения.
- Если две линии параллельны (например, если a и b одинаковы, а c
разные), то решения нет.
 Это пример несогласованная система . (Также, если есть три или более линий, которые не пересекаются
в одной точке. Этот случай часто называют сверхопределенный )
Это пример несогласованная система . (Также, если есть три или более линий, которые не пересекаются
в одной точке. Этот случай часто называют сверхопределенный ) - Если две строки идентичны (например, с a, b и c в второе уравнение все равно кратно их значениям в первое уравнение), то существует бесконечное множество решений (все точки на прямой). В этом случае уравнения линейно зависимым особенно простым образом. Это пример недоопределенная система .
- Если a, b и c равны 0 в обоих уравнениях, то система называется тривиальным , и все точки являются решениями. Это можно рассматривать как крайний пример недоопределенная система.
 Возможности недоопределенных систем
сложнее, чем совпадающие плоскости (например, три плоскости могут
пересекаются на прямой). Возможности для непоследовательного
системы также более сложны, чем параллельные плоскости (например,
три плоскости могут попарно пересекаться по трем параллельным прямым).
Возможности недоопределенных систем
сложнее, чем совпадающие плоскости (например, три плоскости могут
пересекаются на прямой). Возможности для непоследовательного
системы также более сложны, чем параллельные плоскости (например,
три плоскости могут попарно пересекаться по трем параллельным прямым).Матричное представление
- Систему линейных уравнений можно компактно представить с помощью
матрица коэффициентов и векторов (столбцов) для
переменные и постоянные члены.
Краткое введение в матрицы - Умножение вектора на матрицу определяется так, что выполнение манипуляции генерирует линейные уравнения.
- Например, предположим, что у нас есть следующая система уравнений:
а 1 х + б 1 у = с 1
а 2 х + Ь 2 у = с 2
Это можно записать в матричной форме как:
[а 1 б 1 ] [х] = [с 1 ] [а 2 б 2 ] [у] [с 2 ]

Таким образом, нижеследующее представляет общую систему 3×3.
[а 11 а 12 а 13 ] [х 1 ] [с 1 ] [a 21 a 22 a 23 ] [x 2 ] = [c 2 ] [а 31 а 32 а 33 ] [х 3 ] [с 3 ]
Ax = c
- Перестановка ERO: строки матрицы можно поменять местами или переставить без изменения представленной системы уравнений пока элементы константы c вектор переставлен таким же образом.
- Линейная комбинация ERO: кратное ряду (и его
соответствующий элемент в постоянном векторе) может быть
умножается на константу, или добавляется к другой строке, или и то, и другое, без
изменение базовой системы (ее решений).

Линейные системы случаются
- Анализ механических сил
- Анализ цепи LCR
- Оптика: (например, формализация трассировки лучей): 160 Ex.
- Химия и хим. Engg: Кинетика реакции
- Общее: Подгонка математических моделей к данным: 160 Ex.
- Общее: оптимизация методом наименьших квадратов
- Общие: Численное решение дифференциальных уравнений: 160 упр.

Исключение Гаусса
- Исключение Гаусса – это общий алгоритм решения систем линейных уравнений
- Кажется, был известен Древние китайцы до 100 г. до н.э.
- Европейское введение Карл Фридрих Гаусс (немецкий математик) около 1809 г. в контексте анализа методом наименьших квадратов.
- Базовая техника с небольшими вариациями все еще используется для общие системы до нескольких тысяч переменных.
- Для больших систем (т.е. миллионы переменных) итеративный используются методы аппроксимации.
- Для разреженных систем (в основном нули в матрице) разработаны различные специальные быстрые методы.
Базовый подход
- Вспомним линейную комбинацию ERO: добавление кратного одного уравнения к другому дает новое
уравнение, которое выполняется тогда и только тогда, когда выполняются исходные уравнения.

- Идея состоит в том, чтобы добавить кратное одного уравнения к другому так, чтобы коэффициент некоторой (выбранной) переменной равен 0,
- В результате на одну переменную меньше, чем в оригинале.
- Делая это постепенно для выбранных переменных, организованно, системы уравнений со все меньшим и меньшим количеством переменных можно составить до тех пор, пока уравнение только с одним получается переменная.
- Это последнее уравнение может быть решено непосредственно для последнего переменная, которую можно подставить в 2-уравнение система для получения значения второй переменной, и и так далее, пока не будут получены значения всех переменных.
Детали A: Ступень уменьшения
Примечание о внедрении: Хотя он смешивает семантику элементов и не является математически чистым
объект,
расширенная матрица системы N переменных AX = B
это матрица
N x N+1
[А | B] (это столбец
константы
B соединяется справа от A ). Этот
расширенная матрица
полезен, потому что все ERO включают как A, так и
B , которые теперь вместе в расширенной матрице
вместе ими можно манипулировать в два раза легче, чем порознь.
Этот
расширенная матрица
полезен, потому что все ERO включают как A, так и
B , которые теперь вместе в расширенной матрице
вместе ими можно манипулировать в два раза легче, чем порознь.
- Уравнения записываются в матричной форме Ax = c. Вектор x иногда выписывается не на каждом шагу поскольку он служит только для указания порядка неизвестных.
- Соответствующие кратные первой строки добавляются к остальные строки так, чтобы первый коэффициент был равен 0 в каждый последующий ряд. Это создает столбец 0 ниже элемент (1,1) матрицы. Постоянные элементы рассматриваются как часть строки.
- Соответствующие множители определяются путем деления первого коэффициента каждой нижней строки на первый коэффициент первая строка (элемент (1,1)). Этот делитель известен как стержень
- Аналогичным образом подбираются соответствующие множители второй строки.
 добавляется к строкам под ним, чтобы получить 0 во втором столбце ниже
элемент (2,2) (который теперь служит стержнем)
добавляется к строкам под ним, чтобы получить 0 во втором столбце ниже
элемент (2,2) (который теперь служит стержнем) - Процесс повторяется для последующих строк до тех пор, пока верхняя треугольная матрица который содержит 0s ниже главной диагонали. Эта матрица вместе с (модифицированным) постоянным вектором представляет система, имеющая точно такие же решения, как и начальная система. На этом стадия редукции завершается.
Детали B: Этап обратной замены
- Теперь алгоритм входит в стадию обратной замены . Обратите внимание, что последняя строка верхней треугольной матрицы представляет уравнение с одной переменной (та, которая связана с последний столбец), который может быть непосредственно решен для этой переменной.
- Предпоследняя строка представляет уравнение с двумя переменными,
одна из которых является переменной, для которой только что найдено решение.
 Подставляя значение, получаем уравнение, которое можно решить
непосредственно для переменной, связанной с предпоследним
столбец.
Подставляя значение, получаем уравнение, которое можно решить
непосредственно для переменной, связанной с предпоследним
столбец. - Процесс повторяется до тех пор, пока не будут получены значения для всех неизвестных переменных. были получены. На этом решение системы завершено.
- Рабочий пример
Вычислительная сложность
- Если мы подсчитаем задействованные операции, то окажется, что примерно N 3 /3 сложения и умножения необходимы для стадии восстановления, и примерно № 2 /2 сложения и умножения для шаг обратной замены, где N – размер системы.
- Как Н
становится большим, в подсчете операций преобладает
№ 3 /3
срок. Ученые-компьютерщики описывают ситуацию так:
что алгоритм порядка N 3 .

- Условно пишется O(N 3 ), именуемый Обозначение «большое О». Технический смысл заключается в том, что при достаточно больших N количество операций ограничено кН 3 для некоторой постоянной к.
- Таких асимптотических оценок являются важной областью изучения в область компьютерных наук, известная как теория вычислительной сложности.
- Довольно неожиданно, кН 3 не является нижней границей. Сложность аналогична умножению квадратных матриц, для которого (в основном непрактичные) алгоритмы меньшей асимптотической сложности известны, например, Алгоритм Штрассена, который примерно О(N 2,807 ).
Возможная проблема A: Zero Pivot
- Если диагональный элемент, который должен служить
пивот равен 0, никакое число, кратное строке, не может исключить эту переменную
в следующих рядах.

- Простое решение — использовать обмен ERO на поменять местами проблемное строку (и связанный с ней постоянный член) с нижней строкой, которая делает не иметь 0 в сокращаемой колонке.
- Если такой строки не существует, то в каком-то смысле столбец уже уменьшается, и мы можем перейти к следующему. Однако мы обнаружили линейная зависимость, что означает, что единственного решения не существует. Такая система называется единственное число .
- Подробнее о редукции в сингулярных системах
Возможная проблема B: Поворот около нуля
- Если поворотный элемент
очень мал по сравнению с одним или несколькими элементами
ниже него в столбце, то большое число, кратное сводной строке, должно
добавить, чтобы привести коэффициент столбца к нулю.
Это усилит любые ошибки, существующие из-за округления или
погрешность измерения и может привести к
неверное решение системы.

- Простой подход — поменять местами строки, чтобы использовать ту, которая в данный момент имеет наибольшее значение в сводном столбце. Это известно как частичный поворот .
- Более сложный подход — поменять местами строки и столбцы, чтобы чтобы получить максимально возможную опору. Это известно как полноповоротный , но обычно это не так. используется, так как поиск занимает много времени, а частичный поворот обычно достаточно.
Потенциальная проблема C: нестабильная система
- пивот мал по сравнению со значениями над ним (в строках, где редукция уже завершена) то большая умножения будут введены во время обратной замены этап, который также может усилить существующие ошибки.
- В этом случае система изначально чувствительна к ошибкам.
Такая система называется в плохом состоянии или иногда почти единственное число .

- Примером является пара уравнений в плоскости, представляющей почти параллельные линии. Явно небольшое изменение положения или ориентации одного линий может привести к большому изменению местоположения точку пересечения (или даже сделать их параллельными).
- Плохо обусловленная система, возникающая из реальных экспериментальных данных часто указывает на более глубокую проблему с экспериментальным дизайном, протоколы сбора данных или даже с базовой моделью. Обнаружение таких систем, таким образом, важно.
Вариации
- Вместо выполнения шага обратной замены после
получение верхней треугольной формы, стадия обжатия
можно продолжить. Повторяем идею, только вверх ногами и
назад, начиная с последнего ряда вверх и с последнего
столбец обратно влево. Таким образом, мы используем последнюю строку, чтобы исключить
коэффициенты последнего столбца, предпоследняя строка для исключения
коэффициенты предпоследнего столбца и так далее.
 Получается диагональная форма, представляющая собой
отдельное, легко решаемое уравнение для каждой переменной.
Это известно как Гаусс-Джордан устранение.
Получается диагональная форма, представляющая собой
отдельное, легко решаемое уравнение для каждой переменной.
Это известно как Гаусс-Джордан устранение. - Каждая строка и соответствующая константа диагональной формы могут быть разделить на значение диагонального элемента, что дает единичная матрица, из которой значения переменных можно просто прочитать.
- Если мы поместим единичную матрицу я рядом с исходной матрицей коэффициентов A вместо постоянного вектора в, и провести указанное выше сокращение А к личности, добавление кратных строк на всем протяжении, тождественная матрица преобразуется в А -1 . Это стандартный алгоритм для вычисления обратного.
запишите систему в виде матрицы и решите ее методом исключения Гаусса-Жордана. (если
10 007 результатов
trig gauss jordan
Запишите расширенную матрицу, а затем решите систему, используя исключение Гаусса Жордана на расширенной матрице.
 х + 2у – z = 4 -2х + у – 4z = -6 4х – 3у + 2z = -10
х + 2у – z = 4 -2х + у – 4z = -6 4х – 3у + 2z = -10- спросил Шон
- 956 просмотров
домашнее задание по математике
решить систему методом исключения Гаусса Джордана { 1/3x + 3/4 y – 2/3 z = -8 x + 1/2 y – z = -24 1/6 x – 1/8 y – г = -24 а. (-6, 8, -24) б. (-6, -8, -24) в. (0, 8, -24) д. (6, 8, 24) д. (6, -8, 24)
- спросила Лотти
- 367 просмотров
конечная математика
Решить систему линейных уравнений методом исключения Гаусса-Жордана. 3x−2y+ 4z = 22 2x+y− 2z = 3x+ 4y − 8z = −16
- спросил Броди
- 1 908 просмотров
МАТЕМАТИКА
решить систему линейных уравнений методом исключения Гаусса-Жордана x1- x2+ 4×3 = 15 x1+ x2 = X3 = 4 -3X1-X2 + X3 = -2
- спросил Глория
- 841 просмотров
математика
Мере, Сэм и Натан идут в книжный магазин, чтобы купить школьные принадлежности.
. Мере купил два ластика и четыре карандаша и заплатил за них 2,40 доллара. Сэм купил шесть ластиков, один карандаш и две ручки и заплатил 3,95 доллара, а Натан заплатил 4,15 доллара за ластик, карандаш и четыре
Мере купил два ластика и четыре карандаша и заплатил за них 2,40 доллара. Сэм купил шесть ластиков, один карандаш и две ручки и заплатил 3,95 доллара, а Натан заплатил 4,15 доллара за ластик, карандаш и четыре- спросил anjie
- 1 014 просмотров
Линейная алгебра
Используйте исключение Гаусса Жордана, чтобы записать решение системы уравнений: x1+4×2+2×3=17 3×1+x2-5×3=7 2×1-3×2-7×3=-10
- спросил Шэрон
- 647 просмотров
Конечная математика
Решите систему линейных уравнений, используя метод исключения Гаусса-Жордана. (Если решения нет, введите NO SOLUTION. Если существует бесконечно много решений, включающих один параметр, введите решение, используя t в качестве последней переменной. Если решение
- спросил Ди
- 1 605 просмотров
алгебра
решить систему линейных уравнений [2x+3y_z=5 [4x+4y_3z=3 [2x_3y_z=1] методом исключения Гаусса
- спросил olika
- 246 просмотров
Линейная алгебра
Рассмотрим следующую систему линейных уравнений: 2×1+2×2+4×3 = −12 x1+6×2−8×3 = −6 x1−2×2+9×3 = −8 Пусть A — матрица коэффициентов, а X — матрица решений система.
 Решите систему, сначала вычислив A−1, а затем используя его для нахождения X. I
Решите систему, сначала вычислив A−1, а затем используя его для нахождения X. I- спросил Сал
- 1 280 просмотров
Алгебра
2. Используйте расширенную матрицу для решения системы. x + y = 5 3x – y = –1 (1 балл) (1, 4) (1, 5) (3, –1)*** (5, –1) 3. При преобразовании системы линейных уравнений в расширенная матрица, какая форма уравнения нужна? (1 балл) Форма пересечения наклона
- спросил Студент
- 1 618 просмотров
Алгебра 2 (проверить пункт 4)
1)Правило Крамера используется для решения системы уравнений: 3m-5n=12,4m+7n=-5 Какой определитель представляет числитель для n? answer=[12 -5] [-5 7] 2)Правило Крамера используется для решения системы уравнений: 3x-y+2z=17,4x+2y-3z=10 и 2x+5y-9z=-6 Какой
- спросил Эрин
- 2 101 просмотр
Метод исключения Гаусса
Запишите систему уравнений в виде расширенной матрицы.
 Затем решить для х и у. 5x-4y=12 -5x+3y=9
Затем решить для х и у. 5x-4y=12 -5x+3y=9- спросил Джимми
- 8 388 просмотров
Исключение Гаусса-Жордана
Запишите систему уравнений в виде расширенной матрицы. Затем решить для х и у. -3x+3y=-21 3x+2y=-4
- спросил Аноним
- 795 просмотров
математика
1. Каково решение системы? −x+2y = 4 −4x+y = −5 2. Сколько решений имеет система? −2x+y = 3 4y−4 =x 3. Сколько решений имеет система? 3x+y= 5 −2y=6x − 10 4. Сколько решений имеет система? −x−2y=
- спросил не важно
- 748 просмотров
система уравнений
Запишите систему уравнений в виде расширенной матрицы. Затем решить для х и у.
 5x-3y=-34 10x-5y=-65
5x-3y=-34 10x-5y=-65- спросил Аноним
- 898 просмотров
Метод исключения Гаусса
Запишите систему уравнений в виде расширенной матрицы. Затем решить для х и у. -3x-y=11 -9x-2y=34 Решение =
- спросил Девин
- 431 просмотр
Math
Решите каждую систему методом исключения. Обязательно запишите свой ответ в форме (x,y). 0,2x – 0,5y = -27,8 0,3x + 0,4y = 68,7
- спросил Бренна
- 769 просмотров
Исчисление — линейная алгебра
Матрица коэффициентов линейной системы состоит из четырех строк и четырех столбцов. 1) Какие могут быть уравнения в этой линейной системе? 2) Сколько переменных может быть в этой линейной системе? 3) Если эта матрица коэффициентов имеет точку опоры в каждом столбце, сколько
- спросил неизвестное имя
- 472 просмотра
Математика
Используйте исключение для решения каждой системы уравнений.
 x+y-2z=10 8x-9y-z=5 3x+4y+2z=-10 Мне нужно выяснить, чему равны x,y и z. Я должен использовать метод исключения.
x+y-2z=10 8x-9y-z=5 3x+4y+2z=-10 Мне нужно выяснить, чему равны x,y и z. Я должен использовать метод исключения.- спросил Карли
- 981 просмотров
математика
Пожалуйста, решите систему методом исключения. Объясните каждый шаг по мере его выполнения. 5y = x 2x – 3y = 7 Был бы метод исключения вашим первым выбором для решения этой задачи?
- спросил Кэти
- 917 просмотров
Алгебра
3. Как проще всего решить систему? y=1/2x 2x + 3y = 28 A. Графики B. Замена***** МОЙ ОТВЕТ! C. Элиминационная D. Распределительная 4. Каково решение системы? y=-3x 2x + 3y = 6 A. (2,6) B. (-1,3) C. (-2,6)*****МОЙ ОТВЕТ! Д.
- спросил рад помочь
- 1 861 просмотров
Математика
1) Какова размерность AB, если A — матрица 5 × 6, а B — матрица 6 × 3? для вторых вопросов это заполнение пустого вопроса.
 2) Точкой пересечения графиков уравнений системы является ? системы. ? это где один
2) Точкой пересечения графиков уравнений системы является ? системы. ? это где один- спросил аноним
- 1 275 просмотров
Алгебра II
Решите систему подстановкой. {-x – y – z = -8 { -4x + 4y + 5z = 7 { 2x + 2z = 4 Решите систему методом исключения. {-2x + 2y + 3z = 0 {-2x – y + z = -3 {2x+ 3y+ 3z = 5
- спросил HELPME
- 2 329 просмотров
Алгебра 1
решить каждую систему методом исключения. 1.) 6x – 3y =15 7x + 14y =10 Укажите, имеет ли система одно решение, бесконечно много решений или нет решений. 1.) 9x +8y =15 9x +8y =30 2.) 5x – 3y =10 10x + 6y = 20
- спросил Линдси
- 789 просмотров
математика
решить систему методом исключения 4x-7y=3 x-7y=15
- спросил Венера
- 1 730 просмотров
Алгебра
Решите систему методом исключения -2x + 2y + 3z = 0 -2x – y + z = -3 2x + 3y + 3z = 5
- спросил TaylorBear
- 5 923 просмотра
Математика
Решите эту систему методом исключения: (3x-5y=4) (-2x+6y=18)
- спросил Джейкоб
- 507 просмотров
Math
Решите систему методом исключения.
 5x-5y=10 и x-5y=-14
5x-5y=10 и x-5y=-14- спросил Белль
- 753 просмотра
Math
1. Решить систему методом исключения. 3x+3y=27x-3y=-11 а. (8,1) б. (3,6) в. (6,3) д. (4,5)*** 2. Решить систему методом исключения. 4x-7y=3x-7y=-15 а. (-12/5,10/7) б. (-1,2) в. (6,3)*** д. (1,1/7) 3. Решить систему методом исключения. 2х+3у=9 х+5у=8
- спросил Kaai97
- 19 011 просмотров
Алгебра 1 (Рейни или Куай)
Решите каждую систему методом исключения. а. 2х + 3у = 33 у = 1/4х
- спросил Аноним
- 451 просмотр
Алгебра
Найдите количество решений каждой системы. а. 4x-y+1=0 4x-y+3=0 б. 2x-y+4=0 4x-2y+8=0 Напишите вопрос, который можно решить с помощью системы линейных уравнений.
 Решите графически следующую систему уравнений: y=x+3 и y=-2x-3
Решите графически следующую систему уравнений: y=x+3 и y=-2x-3- спросила LadyPhantomhive
- 1 510 просмотров
Алгебра 2
Решите каждую систему методом исключения x + 4y =6 3x + 12y = 18
- спросил Ларсон
- 436 просмотров
math
Используйте исключение для решения каждой системы уравнений. х+у=3 2х-3у=16
- спросил Лейлер
- 1 075 просмотров
math
решить систему методом исключения: 4x=5y+24 5x=4y+21
- спросил Тейлор
- 1 143 просмотра
алгебра
решить систему методом исключения 5x+5y=-7 7x-3y=19
- спросил akaray
- 635 просмотров
алгебра 1
Решите систему с помощью замены или исключения 3x-5y=21 2x+y=1 A (2,-3) B (2,3) C (-2,-1) D (-2,1) )
- спросила Нина
- 4 391 просмотров
алгебра
ПОЖАЛУЙСТА, помогите со следующим.
 Решите систему уравнений, сначала представив ее в матричной форме, а затем вычислив. а). 3x-2y=5 4x-y=-10 б). 3x -2y = -2 4x -y = 3
Решите систему уравнений, сначала представив ее в матричной форме, а затем вычислив. а). 3x-2y=5 4x-y=-10 б). 3x -2y = -2 4x -y = 3- спросил Ви
- 469 просмотров
Математика (просто нужна помощь)
Решите систему, используя расширенную матрицу. -x-3y=-17 2x-6y=-26 Может кто-нибудь объяснить, что я должен делать в этой задаче?
- спросил Оливия N J
- 1 574 просмотра
Предварительное исчисление
Решите систему уравнений с помощью матриц. Используйте исключение Гаусса с обратной заменой. x + y + z = -5 x – y + 3z = -1 4x + y + z = -2 Мне очень нужна помощь.. 1 1 1 -5 1 -1 3 -1 4 1 1 1 -2 Я сделал так много разных методов, чтобы решить эту проблему, и я получаю
- спросил Alexa
- 803 просмотра
math
Напишите матрицу, которая представляет систему уравнений ниже.
 7х – 3у = 21 5х – у = 85
7х – 3у = 21 5х – у = 85- спросила Алайна
- 1 094 просмотра
математика (количественный метод)
Запишите расширенную матрицу, соответствующую системе уравнений. 2a-3b+c=1 -a+b-4c=3 3a-b=2
- спросил Заин
- 886 просмотров
алгебра 2a решение систем с помощью матриц
напишите систему уравнений, представленную матрицей [0 1 2 4] [-2 3 6 9] [1 0 1 3] a: x+2y=4 -2x-3y+69 =0 x+y=3 b: x+2y=4 -2-3y+6=9 x+y=3 c: y+2z=4 -2x+3y+6z=9x+z=3 d: x+2z=4 -2x-3y+6=9 думаю, это A
- спросила Миа
- 5 595 просмотров
Алгебра
Я не получаю ни одного из опубликованных ответов: Решите систему методом исключения.
 2x + 6y = -12 и 5x – 5y = 10 (2, 1) (0, –2) (–2, 0) (1, 2)
2x + 6y = -12 и 5x – 5y = 10 (2, 1) (0, –2) (–2, 0) (1, 2)- спросила Сандра
- 1 156 просмотров
math 3
Решите следующую систему методом исключения: 10x – 6y = -16 5x + 2y = 22
- спросил охотник
- 1 883 просмотра
math
Решите следующую систему методом исключения: -3x + 4y = 6 9x – 12y = -18
92-2х-3- спросил Алекс
- 1 142 просмотра
математика
Как использовать стратегию исключения для решения линейной системы: 5/3x +1/4y = 10 1/3x + 1/2y = 5
- спросил Лин
- 507 просмотров
алгебра
решить методом исключения 7r-3s=0 3r+7s=58 каково решение системы
- спросил Джон
- 603 просмотра
Алгебра
Используйте метод исключения, чтобы решить следующую систему уравнений.
 х + 3у – z = 2 х – 2у + 3z = 7 х + 2у – 5z = –21
х + 3у – z = 2 х – 2у + 3z = 7 х + 2у – 5z = –21- спросил Дороти
- 914 просмотров
Алгебра 2
Решите систему методом исключения: -2x + 2y + 3z = 0 -2x – y + z = -3 2x + 3y + 3z = 5 Как мне это сделать? Мне нужны шаги, чтобы понять, пожалуйста….
- спросила Саманта Тейлор Грифилд
- 1 583 просмотра
математика
Запишите расширенную матрицу для системы линейных уравнений. 7х + 4у = 53 5х – 9у = -57
- спросил аноним
- 1 173 просмотра
math
Напишите систему уравнений, соответствующую расширенной матрице, используя переменные x, y и z. 0 10 6 –5 3 8 – 9 7 – 5 0 – 3 –4
- спросил Аноним
- 1100 просмотров
Алгебра
Напишите матричное уравнение, эквивалентное системе уравнений.
 7х – 8у = -9 -2х – 2у = -2
7х – 8у = -9 -2х – 2у = -2- спросил lue
- 1 152 просмотра
Алгебра
Используйте матричный инструмент для решения системы уравнений. Выберите правильную упорядоченную пару. -3х + 5у = 195х – 5у = -5
- спросил АА`
- 1 702 просмотра
Math
Решите систему уравнений с помощью инструмента матрицы и введите решение в виде упорядоченной пары. 3x + 4y = 18 2x + 5y = 19
- спросил Sandale
- 894 просмотра
Математика 10 класса
решить следующую систему или линейные уравнения методом исключения. проверьте свое решение 1. -4 – 9y = 9. 2.x – 3y = -6
- спросил Аноним
- 272 просмотра
Math
Решите следующую систему уравнений методом исключения.
 5х+у=24 ; -5x-4y=-56. Решите для X/Y. Помогите мне, пожалуйста-?
5х+у=24 ; -5x-4y=-56. Решите для X/Y. Помогите мне, пожалуйста-?- спросил Египет
- 646 просмотров
Математика
Какой метод будет самым простым для решения системы? у=1/2х 2х+3у=28 а. графическое б. замена*** в. устранение д. дистрибутив
- спросил Kaai97
- 1 931 просмотров
math
Решите систему уравнений методом исключения. Представьте решение в виде упорядоченной пары. −5x−2y=−12 3x+2y=8
- спросила Кейлин Джонсон
- 1 073 просмотра
math
Решите систему уравнений методом Исключения ИЛИ Подстановки. Объясните, почему вы выбрали один метод вместо другого. 3х – 2у = 8 2х + 5у = -1
- спросил Сью
- 722 просмотра
Математика
Какой метод будет самым простым для решения системы? 7x + 5y = 19 -7x – 2y = -16 а.
 График б. Замена в. Ликвидация*** д. Дистрибутив
График б. Замена в. Ликвидация*** д. Дистрибутив- спросил Kaai97
- 2 229 просмотров
Алгебра 1
Какой метод будет самым простым для решения системы? 7x +5y = 19 -7x-2y = -16 графическая замена замены или дистрибутив
- спросил Стив
- 21 851 просмотр
Математика: Алгебра
1. Какой метод будет самым простым для решения системы? 7х + 5у = 19–7x – 2y = –16 A.) график B.) замена C.) удаление D.) дистрибутив Думаю, что C.
- спросил Тимоти
- 7 645 просмотров
Математика: алгебра 1
3. Какой метод будет самым простым для решения системы? y =1/2 x 2x + 3y = 28 A.) график B.) замена C.
 ) исключение D.) дистрибутив Я думаю, что это B.
) исключение D.) дистрибутив Я думаю, что это B.- спросил Тимоти
- 1 185 просмотров
математика
решить следующую систему линейных уравнений матричным методом:- 12p+4q+17r+11s=5 14p+8q+9r+4s=8 3p+7q+2r+5s=12 5p+12q+9r+7s =7
- спросил салони
- 490 просмотров
Math
Напишите расширенную матрицу для системы линейных уравнений. (Не выполняйте никаких операций со строками.) 4x − y = 9 x + y = 4
- спросила Юлия
- 517 просмотров
math
Примечание. Введите свой ответ и покажите все шаги, которые вы используете для решения этой задачи, в отведенном для этого месте. Для каждого вопроса напишите алгебраическое уравнение и решите его.
 Запишите ответ в простейшей форме. У Джордана в 4,5 раза больше DVD, чем у Джозефа. Если у Джордана
Запишите ответ в простейшей форме. У Джордана в 4,5 раза больше DVD, чем у Джозефа. Если у Джордана- по запросу idc
- 927 просмотров
math
Если попытаться решить линейную систему методом подстановки и получить результат 0 = 8, что это значит? А. Система имеет одно решение (0,8). Б. Система имеет одно решение (8,0). C. Система не имеет решений. D. Система имеет бесконечное число
- задано по математике !!@@
- 3 352 просмотра
Справка по алгебре
1. Убедитесь, что (-4, 12) является решением системы. Покажите работу, чтобы обосновать свой ответ 2x+y=5 -5x-2y=-6 2. Решите систему с помощью графика. Укажите решение. x + y =2 2y – x = 10 3. Решить систему подстановкой. Укажите, есть ли в системе один
- спросила PicturesDon’tChangeThePeopleInsideOfThemDo
- 2 479 просмотров
math
Решите каждую систему графически.
 Обязательно проверьте свое решение. Если система имеет бесконечное количество решений, используйте нотацию построителя наборов для записи набора решений. Если система не имеет решений, укажите это. 6х – 2у = 2, 9х – 3у = 1
Обязательно проверьте свое решение. Если система имеет бесконечное количество решений, используйте нотацию построителя наборов для записи набора решений. Если система не имеет решений, укажите это. 6х – 2у = 2, 9х – 3у = 1- спросил Деб
- 643 просмотра
- спросил Рейни
- 645 просмотров
алгебра
Решить методом исключения. Показать свою работу. Если система не имеет решений или их бесконечное число, укажите это. -3x + 6y = -3 / -6x + 4y = -10
- спросил Джекстер
- 405 просмотров
Биология
Соедините термины с правильным описанием: a.
 регулирует подачу газов от производства АТФ b. обеспечивает сигналы отрицательной обратной связи c. защищает тело от внешних опасностей d. “быстрый транзит” для жидкостей и газов e. первичный “регулятор” сенсорики
регулирует подачу газов от производства АТФ b. обеспечивает сигналы отрицательной обратной связи c. защищает тело от внешних опасностей d. “быстрый транзит” для жидкостей и газов e. первичный “регулятор” сенсорики- спросила mymychicken
- 1 585 просмотров
Алгебра/метод исключения
Решить методом исключения. Если система не имеет решений или их бесконечное число, укажите это. -27x – 18y = -180 9x + 6y = 60
- спросил Келли
- 1 229 просмотров
MaTh = Algebra = help
Решите эту систему линейных уравнений алгебраическим методом. Итак, если бы мне пришлось решить эту проблему методом исключения, как бы я это сделал? х-2у = 10 3х-у = 0
- спросила Рианна
- 1 352 просмотра
math
Сколько решений имеет следующая система: 2x + 5y = 10 3x + 6y = 12 Объясните, как определить количество решений, не решая систему.
 Затем примените исключение и интерпретируйте полученное уравнение.
Затем примените исключение и интерпретируйте полученное уравнение.- спросил Кэти Камкат
- 1 012 просмотров
Math
Пожалуйста, помогите мне. Мне нужна помощь!!!! Для задач 1-4 решите данную систему уравнений, используя либо замену, либо исключение. 1. 2x + y = -8 y = 2x + 4 A. (-4, 0) B. (-3, -2) C. (1, 6) D. бесконечно много решений.
- спросил Медь
- 2 521 просмотров
Наука
На какую из следующих систем организма полагается иммунная система, чтобы обеспечить первую линию защиты от патогенов. A. Покровная система B. Нервная система C. Кровеносная система D. Эндокринная система Думаю, C
- спросил Джек
- 1 968 просмотров
Алгебра
Решите каждую систему графически.
. № 6. 4x – y = 9 x – 3y = 16 Мне нужно найти хотя бы одну пару подходящих точек. Я попробовал использовать метод исключения и получил (5 и 6/7, -22), что не работает даже для первого уравнения. Я также пытался построить график, но он
№ 6. 4x – y = 9 x – 3y = 16 Мне нужно найти хотя бы одну пару подходящих точек. Я попробовал использовать метод исключения и получил (5 и 6/7, -22), что не работает даже для первого уравнения. Я также пытался построить график, но он- спросил Сюзанна
- 1 405 просмотров
алгебра
Рассмотрим следующую систему уравнений. y = −2x − 3 y = −2x + 2 Являются ли графики двух линий пересекающимися линиями, одной и той же линией или параллельными линиями? Объясните свои рассуждения. Сколько решений имеет система? Объясните, как вы можете сказать
- спросил babbel
- 662 просмотра
Справка по линейным алгебраическим неравенствам
8. Приведенная ниже система имеет решение (1,3), где A, B, C, D, E и F — ненулевые действительные числа.
 Ax+By=C, Dx+Ey=F Решением какой из следующих систем не будет (1,3)? A- Ax+By=C & (2A-D)x+(2B+E)y=C-2F B- Ax+By=C & 7Dx+7Ey=7F C-
Ax+By=C, Dx+Ey=F Решением какой из следующих систем не будет (1,3)? A- Ax+By=C & (2A-D)x+(2B+E)y=C-2F B- Ax+By=C & 7Dx+7Ey=7F C-- спросил нуждающийся
- 1 379 просмотров
алгебра 2
Врачу требуется не менее 60 взрослых для медицинского исследования. Он не может использовать более 40 человек в исследовании. Напишите систему неравенств, чтобы смоделировать ситуацию и решить систему с помощью графика.
- спросил Кинзи
- 1 379 просмотров
Алгебра
Прямоугольник на 4 дюйма длиннее, чем его ширина. Его периметр составляет 28 дюймов. Напишите систему двух уравнений с двумя переменными, описывающую эту информацию. Затем решите систему графически.
- спросил Аноним
- 708 просмотров
Math
Решить методом исключения.
 Показать свою работу. Если система не имеет решений или их бесконечное число, укажите это. 8x + 11y = -50 -32x – 44y = -200
Показать свою работу. Если система не имеет решений или их бесконечное число, укажите это. 8x + 11y = -50 -32x – 44y = -200- спросил Donnice
- 653 просмотра
math
Решите следующую систему методом исключения. Если существует единственное решение, запишите решение в виде упорядоченной пары. Вашим ответом будет упорядоченная пара, отсутствие решения или бесконечное множество решений x-y=4 3x-5=2
- спросил ,алгебра
- 1 338 просмотров
биология
Кровь поступает в легкие, насыщается кислородом и возвращается в сердце, прежде чем прокачивается через тело. Какие кровеносные сосуды несут кровь от сердца? эластические капилляры вены артерии*** Кислород поступает в организм из окружающей среды,
- спросил Алексделл
- 11 149 просмотров
Математика
Метод исключения Гаусса 3x+4y+5z=18, 2x-y+8z=13, 5x-2y+7z=20
- спросил Тамил
- 1 014 просмотров
алгебра
Сумма двух чисел равна 82.
 Их разность равна 24. Выберите систему уравнений, описывающую данную ситуацию. Решите методом исключения, чтобы найти два числа.
Их разность равна 24. Выберите систему уравнений, описывающую данную ситуацию. Решите методом исключения, чтобы найти два числа.- спросил Лаура
- 1 137 просмотров
Алгебра
Проверка нескольких ответов на некоторые задачи по алгебре: 1. Найдите наклон прямой, проходящей через точки (-4,1) и (3,5). Я получил m = 5-1 / 3-(4) Ответ: m = 4/7 2. Найдите уравнение прямой, проходящей через точки
, в форме наклона и точки пересечения.- спросил Джон
- 777 просмотров
алгебра
решить систему методом исключения 2x-5y=8 x-3y=-1 объясните шаг за шагом
- спросила Сара
- 404 просмотра
Математика 116 алгебра пожалуйста проверьте
Решить методом исключения 2x + 3y =1 4x + 6y =2 Каково решение системы N решения нет
- спросил Джей Джей
- 1 339 просмотров
Алгебра 2
1.
 ) Напишите систему уравнений, у которой НЕТ решений. 2.) Если бы вы хотели исключить переменные y в приведенной ниже системе уравнений, на что бы вы умножили первое и второе уравнения? (Не решать уравнение) 2x-3y=8 7x-4y=11
) Напишите систему уравнений, у которой НЕТ решений. 2.) Если бы вы хотели исключить переменные y в приведенной ниже системе уравнений, на что бы вы умножили первое и второе уравнения? (Не решать уравнение) 2x-3y=8 7x-4y=11- спросил Одри
- 1 001 просмотр
обществознание
На какую систему правления больше всего похожа федеральная система? A – Унитарная система B – Конфедеративная система C – Унитарная система D – Конфедеральная система ******
- спросил Блейк
- 641 просмотр
Наука Помогите плз
5. Как взаимодействуют кровеносная и эндокринная системы в поддержании гомеостаза у человека? A. Эндокринная система вырабатывает гормоны, которые транспортируются системой кровообращения к клеткам-мишеням, когда необходимы изменения.
 Б.
Б.- спросил Мств
- 3 415 просмотров
math 209
Периметр прямоугольника равен 44 футам, длина на 4 фута больше ширины. Найдите размеры. Напишите систему линейных уравнений и решите полученную систему. Пусть x будет длиной, а y будет шириной.
- спросил Крис
- 494 просмотра
предварительное исчисление
пожалуйста, проверьте мои ответы 1.Используйте метод исключения Гаусса, чтобы записать систему уравнений, приведенную ниже, в форме строки-эшелона. 2x+4y+z=-4 2x-4y+6z=13 4x-2y+z=6 ответ: 2x+4y+z=-4 8y-5z=-17 z=1 2. Найдите решение системы уравнения, приведенные ниже. х+у+г=2
- спросил Аноним
- 1 042 просмотра
Университет Феникса
Решите систему уравнений с помощью графика.
 Затем классифицируйте систему. х+у=9x-y=3 Используйте графический инструмент для построения графика системы
Затем классифицируйте систему. х+у=9x-y=3 Используйте графический инструмент для построения графика системы- спросил Иветт
- 1 510 просмотров
Наука
Какое утверждение о выделительной системе верно? A: К ключевым органам системы относятся мочевой пузырь, кишечник и почки B: Она похожа на пищеварительную систему, и обе они избавляют организм от отходов*** C: Она избавляет организм от пищи, которую организм делал
- спросила LadyPhantomhive
- 6 706 просмотров
наука
Что из перечисленного отвечает за избавление организма от отходов? А) нервная система Б) выделительная система*** В) кровеносная система Г) половая система
- спросил 🐱Darkwolf 🐱
- 2 213 просмотров
9рт.



 д.
д.

 Хотя фактического решения может и не быть, часто
точки в пространстве переменных, которые являются «почти решениями»
в том смысле, который можно сделать математически строгим.
Анализ методом наименьших квадратов является одним из распространенных подходов к
нахождение таких приближенных решений. (Подробнее в модели
Будет актуальная тема).
Хотя фактического решения может и не быть, часто
точки в пространстве переменных, которые являются «почти решениями»
в том смысле, который можно сделать математически строгим.
Анализ методом наименьших квадратов является одним из распространенных подходов к
нахождение таких приближенных решений. (Подробнее в модели
Будет актуальная тема).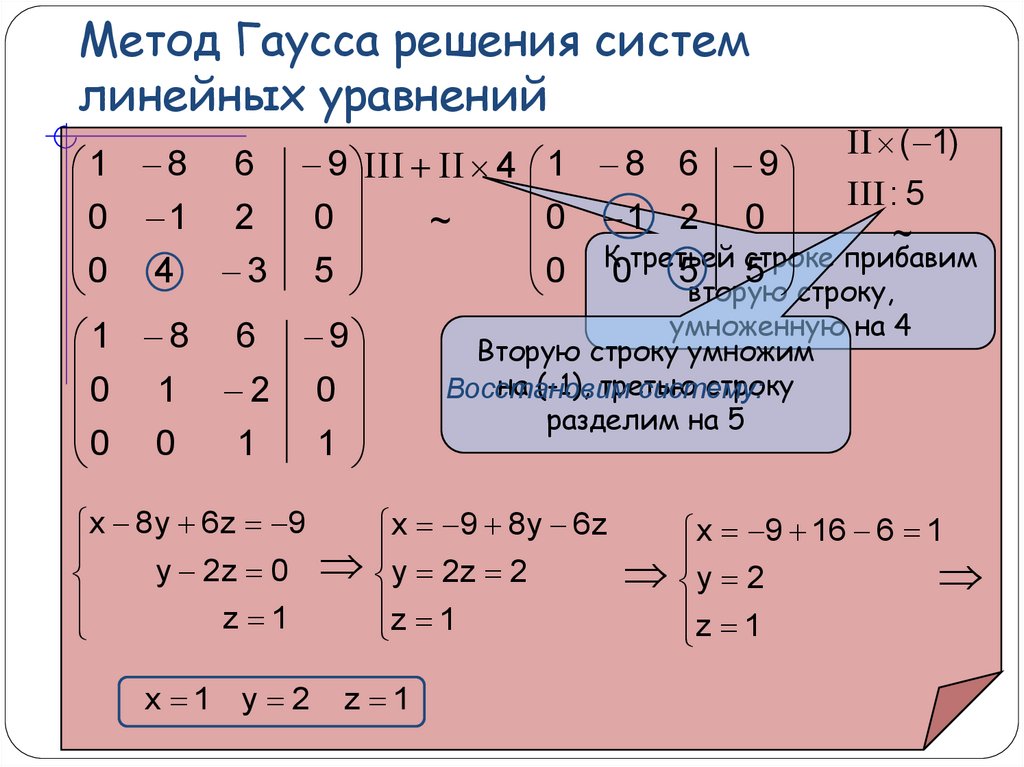 Это пример несогласованная система .
Это пример несогласованная система .


 добавляется к строкам под ним, чтобы получить 0 во втором столбце ниже
элемент (2,2) (который теперь служит стержнем)
добавляется к строкам под ним, чтобы получить 0 во втором столбце ниже
элемент (2,2) (который теперь служит стержнем) Подставляя значение, получаем уравнение, которое можно решить
непосредственно для переменной, связанной с предпоследним
столбец.
Подставляя значение, получаем уравнение, которое можно решить
непосредственно для переменной, связанной с предпоследним
столбец.



 Получается диагональная форма, представляющая собой
отдельное, легко решаемое уравнение для каждой переменной.
Это известно как Гаусс-Джордан устранение.
Получается диагональная форма, представляющая собой
отдельное, легко решаемое уравнение для каждой переменной.
Это известно как Гаусс-Джордан устранение. х + 2у – z = 4 -2х + у – 4z = -6 4х – 3у + 2z = -10
х + 2у – z = 4 -2х + у – 4z = -6 4х – 3у + 2z = -10 Мере купил два ластика и четыре карандаша и заплатил за них 2,40 доллара. Сэм купил шесть ластиков, один карандаш и две ручки и заплатил 3,95 доллара, а Натан заплатил 4,15 доллара за ластик, карандаш и четыре
Мере купил два ластика и четыре карандаша и заплатил за них 2,40 доллара. Сэм купил шесть ластиков, один карандаш и две ручки и заплатил 3,95 доллара, а Натан заплатил 4,15 доллара за ластик, карандаш и четыре Решите систему, сначала вычислив A−1, а затем используя его для нахождения X. I
Решите систему, сначала вычислив A−1, а затем используя его для нахождения X. I Затем решить для х и у. 5x-4y=12 -5x+3y=9
Затем решить для х и у. 5x-4y=12 -5x+3y=9 5x-3y=-34 10x-5y=-65
5x-3y=-34 10x-5y=-65 x+y-2z=10 8x-9y-z=5 3x+4y+2z=-10 Мне нужно выяснить, чему равны x,y и z. Я должен использовать метод исключения.
x+y-2z=10 8x-9y-z=5 3x+4y+2z=-10 Мне нужно выяснить, чему равны x,y и z. Я должен использовать метод исключения. 2) Точкой пересечения графиков уравнений системы является ? системы. ? это где один
2) Точкой пересечения графиков уравнений системы является ? системы. ? это где один 5x-5y=10 и x-5y=-14
5x-5y=10 и x-5y=-14 Решите графически следующую систему уравнений: y=x+3 и y=-2x-3
Решите графически следующую систему уравнений: y=x+3 и y=-2x-3 Решите систему уравнений, сначала представив ее в матричной форме, а затем вычислив. а). 3x-2y=5 4x-y=-10 б). 3x -2y = -2 4x -y = 3
Решите систему уравнений, сначала представив ее в матричной форме, а затем вычислив. а). 3x-2y=5 4x-y=-10 б). 3x -2y = -2 4x -y = 3 7х – 3у = 21 5х – у = 85
7х – 3у = 21 5х – у = 85 2x + 6y = -12 и 5x – 5y = 10 (2, 1) (0, –2) (–2, 0) (1, 2)
2x + 6y = -12 и 5x – 5y = 10 (2, 1) (0, –2) (–2, 0) (1, 2) х + 3у – z = 2 х – 2у + 3z = 7 х + 2у – 5z = –21
х + 3у – z = 2 х – 2у + 3z = 7 х + 2у – 5z = –21 7х – 8у = -9 -2х – 2у = -2
7х – 8у = -9 -2х – 2у = -2 5х+у=24 ; -5x-4y=-56. Решите для X/Y. Помогите мне, пожалуйста-?
5х+у=24 ; -5x-4y=-56. Решите для X/Y. Помогите мне, пожалуйста-? График б. Замена в. Ликвидация*** д. Дистрибутив
График б. Замена в. Ликвидация*** д. Дистрибутив ) исключение D.) дистрибутив Я думаю, что это B.
) исключение D.) дистрибутив Я думаю, что это B. Запишите ответ в простейшей форме. У Джордана в 4,5 раза больше DVD, чем у Джозефа. Если у Джордана
Запишите ответ в простейшей форме. У Джордана в 4,5 раза больше DVD, чем у Джозефа. Если у Джордана Обязательно проверьте свое решение. Если система имеет бесконечное количество решений, используйте нотацию построителя наборов для записи набора решений. Если система не имеет решений, укажите это. 6х – 2у = 2, 9х – 3у = 1
Обязательно проверьте свое решение. Если система имеет бесконечное количество решений, используйте нотацию построителя наборов для записи набора решений. Если система не имеет решений, укажите это. 6х – 2у = 2, 9х – 3у = 1 регулирует подачу газов от производства АТФ b. обеспечивает сигналы отрицательной обратной связи c. защищает тело от внешних опасностей d. “быстрый транзит” для жидкостей и газов e. первичный “регулятор” сенсорики
регулирует подачу газов от производства АТФ b. обеспечивает сигналы отрицательной обратной связи c. защищает тело от внешних опасностей d. “быстрый транзит” для жидкостей и газов e. первичный “регулятор” сенсорики Затем примените исключение и интерпретируйте полученное уравнение.
Затем примените исключение и интерпретируйте полученное уравнение. № 6. 4x – y = 9 x – 3y = 16 Мне нужно найти хотя бы одну пару подходящих точек. Я попробовал использовать метод исключения и получил (5 и 6/7, -22), что не работает даже для первого уравнения. Я также пытался построить график, но он
№ 6. 4x – y = 9 x – 3y = 16 Мне нужно найти хотя бы одну пару подходящих точек. Я попробовал использовать метод исключения и получил (5 и 6/7, -22), что не работает даже для первого уравнения. Я также пытался построить график, но он Ax+By=C, Dx+Ey=F Решением какой из следующих систем не будет (1,3)? A- Ax+By=C & (2A-D)x+(2B+E)y=C-2F B- Ax+By=C & 7Dx+7Ey=7F C-
Ax+By=C, Dx+Ey=F Решением какой из следующих систем не будет (1,3)? A- Ax+By=C & (2A-D)x+(2B+E)y=C-2F B- Ax+By=C & 7Dx+7Ey=7F C- Показать свою работу. Если система не имеет решений или их бесконечное число, укажите это. 8x + 11y = -50 -32x – 44y = -200
Показать свою работу. Если система не имеет решений или их бесконечное число, укажите это. 8x + 11y = -50 -32x – 44y = -200 Их разность равна 24. Выберите систему уравнений, описывающую данную ситуацию. Решите методом исключения, чтобы найти два числа.
Их разность равна 24. Выберите систему уравнений, описывающую данную ситуацию. Решите методом исключения, чтобы найти два числа. ) Напишите систему уравнений, у которой НЕТ решений. 2.) Если бы вы хотели исключить переменные y в приведенной ниже системе уравнений, на что бы вы умножили первое и второе уравнения? (Не решать уравнение) 2x-3y=8 7x-4y=11
) Напишите систему уравнений, у которой НЕТ решений. 2.) Если бы вы хотели исключить переменные y в приведенной ниже системе уравнений, на что бы вы умножили первое и второе уравнения? (Не решать уравнение) 2x-3y=8 7x-4y=11 Б.
Б. Затем классифицируйте систему. х+у=9x-y=3 Используйте графический инструмент для построения графика системы
Затем классифицируйте систему. х+у=9x-y=3 Используйте графический инструмент для построения графика системы