July 6th, 2011
1-ый закон говорит, что инерциальные системы отсчета (то есть системы, в которых, если сила =0, то скорость постоянна) существуют. Измерение силы так же, как и измерение любой другой аддитивной величины, делается с помощью сравнения с эталоном. Сколько раз нужно приложить эталон, чтобы получить данную силу, тому данная сила и равна. То есть здесь вообще нет проблемы. Аддитивность силы предполагается. 3-ий закон также был опровергнут (взаимодействие двух движущихся зарядов). То есть оказалось, что закон сохранения импульса более фундаментален, естественно, если учесть импульс поля. (Reply) (Thread)
Давайте разбираться. 1-ый закон говорит, что инерциальные системы отсчета (то есть системы, в которых, если сила =0, то скорость постоянна) существуют. 1 закон НИЧЕГО не говорит о связи силы с ускорением (то есть о 2-лм законе). Например, F=m*a*a*a не противоречит 1-му закону. Первый з-н является следствием второго (частным случаем при F=0). Потому сам по себе отдельного смысла не имеет. Потому его понимают, как утверждение о существовании инерциальных систем отсчета. Инерциальность выполняется с некоторой точностью и это можно экспериментально проверить: если в пределах наших погрешностей сила 0, а скорость меняется более, чем на соответствующую погрешность, то надо разбираться либо с погрешностями, либо с 1-ым законом . Не совсем. Вы можете утверждать, что сила – ноль, потому что ваша система изолирована. То есть к ней не привязаны веревки и т.п., гравитационное и др. взаимодействие вы тоже исключили. Это можно. Ускорение вы имеете право измерять только в инерциальных системах отсчета. То есть вы обязаны доказать, что ваша система – инерциальная, прежде чем браться за измерения. Как только вы это доказали, первый закон доказан, измерение уже ничего не опровергнет. Правда, вы можете подойти и иначе. Выбрать два тела, на которые не действуют силы, и измерить ускорение между ними. Логический закон или определение нельзя опровергнуть. Измерение силы так же, как и измерение любой другой аддитивной величины, делается с помощью сравнения с эталоном. Сколько раз нужно приложить эталон, чтобы получить данную силу, тому данная сила и равна. То есть здесь вообще нет проблемы. Аддитивность силы предполагается. Про аддитивность силы — отдельное утверждение. Дело в том, что силу трудно измерить непосредственно. 3-ий закон также был опровергнут (взаимодействие двух движущихся зарядов). То есть оказалось, что закон сохранения импульса более фундаментален, естественно, если учесть импульс поля. Если 3-ий закон опровергнут, это значит, что импульс не сохранярестя. Система из двух тел АБ станет самопроизвольно двигаться куда-то без преложенных внешних сил. Но тут две проблемы. Первая – наружение первого закона – и см. Логические законы не опровергнуть экпериментально. (Reply) (Parent) (Thread)
http://ru. (Reply) (Thread) |
Динамика. Законы Ньютона. Применение законов Ньютона при решении задач
Динамика.
Законы Ньютона.
Динамикой прежде всего рассматривается вопрос по причине того или иного характера движения. Основными законами динамика являются законы Ньютона.
1 ЗАКОН:
Формулировка:
Существуют такие инерциальные системы отсчета относительно которых тело двигается равномерно и прямолинейно или находится в состоянии покоя.
Если действие других тел на данное тело отсутствует или скомпенсировано, то
– равнодействующая это результат действия сразу нескольких сил, на какое либо тело.
Равнодействующая является геометрической (вектор) суммой всех сил действующих на тело.
(Особой формулы для данного закона НЕ СУЩЕСТВУЕТ)
Область применения:
Первый закон применяется в том случае, если в условии задачи указано, что:
1. Тело находится в покое;
2. Тело двигается равномерно и прямолинейно;
3. Тело находится в равновесии (то есть силы скомпенсированы).
2 ЗАКОН:
Формулировка:
Если на тело действует не скомпенсированная сила то, под действием этой силы тело будет двигаться ускоренно
Формула:
– равнодействующая это результат действия сразу нескольких сил, на какое либо тело.
Следствия:
1. всегда!!!
Для того, чтобы движение было равноускоренным необходимо чтобы действующая на тело сила сохранялась и по модулю и по направлению.
Область применения:
Если в задаче указано, что:
1. Указано ускорение или изменение скорости;
2. Действует не скомпенсированная сила;
3. Если тело движется по окружности.
Если тело движется по окружности.
3 ЗАКОН:
Формулировка:
Два тела действуют друг на друга силами равными по модулю, но противоположными по направлению (действие = противодействию).
Формула:
Внимание!
Силы F1 и F2 приложены к различным телам, поэтому их нельзя ни складывать, ни вычитать.
Следствие:
1. F1=F2 модули одинаковые;
2. направления противоположные.
Область применения:
1. Если идёт речь о взаимодействии двух тел.
Решение задач по теме: «Законы Ньютона»
9 класс
Задача № 1. Какое ускорение приобретет тело массой 500 г под действием силы 0,2 Н?
Задача № 2. Сила 30 Н сообщает телу ускорение 0,4 м/с. Какая сила сообщит тому же телу ускорение 2 м/с2 ?
Задача № 3. Какую скорость приобретает тело массой 3 кг под действием силы, равной 9 Н, по истечении 5 с?
Задача № 4. Сколько времени потребуется автомобилю массой 700 кг, чтобы разогнаться из состояния покоя до скорости 72 км/ч, если сила тяги двигателя 1,4 кН?
Сколько времени потребуется автомобилю массой 700 кг, чтобы разогнаться из состояния покоя до скорости 72 км/ч, если сила тяги двигателя 1,4 кН?
Задача № 5. Поезд массой 500 т, трогаясь с места, через 25 с набрал скорость 18 км/ч. Определите силу тяги.
Задача № 6. Под действием постоянной силы, равной 10 Н, тело движется прямолинейно так, что зависимость координаты тела от времени описывается уравнением х = 3 — 2t + t2. Определите массу тела.
Задача № 7. Скорость тела массой 2 кг изменяется со временем так, как представлено на графике рисунка.
Найдите силу, действующую на каждом этапе этого движения. Определите по графику, на каком этапе движения тело прошло наибольший путь.
Задача № 8. (повышенной сложности) Начальная скорость тела, находящегося в точке А, равна нулю. В течение 8 с на тело действует постоянная сила. Затем направление силы изменяется на противоположное, а модуль остается прежним. Через какое время от начала движения тело вернется в точку А?
Через какое время от начала движения тело вернется в точку А?
Задача № 9. (повышенной сложности) Самолет массой 14 т, пройдя по взлетной полосе путь 600 м, приобретает необходимую для отрыва от поверхности Земли скорость 144 км/ч. Считая движение равноускоренным, определите время разгона, ускорение и силу, сообщающую самолету это ускорение.
Задача № 10 на 1 закон Ньютона
Нахождение равнодействующей силы
Условие
На тело действуют три силы, равные по модулю. Величина каждой – 200 Н. Угол между первой и второй силами равен 60 градусов, как и угол между второй и третьей силами. Найти равнодействующую этих сил. Скомпенсировано ли действие сил?
Решение
Будем использовать теорему косинусов. Вычислим модуль суммы первой пары сил:
Угол между этим результирующим вектором и вектором третьей силы составляет 90 градусов (так как результирующая первых двух сил направлена по биссектрисе угла). Для нахождения равнодействующей можно воспользоваться теоремой Пифагора:
Для нахождения равнодействующей можно воспользоваться теоремой Пифагора:
Ответ: 400 Н. Действие сил не скомпенсировано, иначе их равнодействующая была бы равна нулю
Решение задач по теме: «Законы Ньютона»
10 класс
Задача № 1: Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с силой 15 Н вправо по столу. Массы брусков m1 = 1 кг и m2 = 4 кг, μ = 0,1.
С каким ускорением движутся бруски? Чему равна сила натяжения нити?
Условие невесомости и не растяжимости нити позволяет считать, что сила натяжения нити на всех участках одинакова и все тела движутся с одним и тем же ускорением, т.е. Т1 = Т2 = Т, .
Для того, чтобы решить задачу надо её проанализировать.
Рассмотрим все силы, действующие на каждое тело отдельно. Оба тела взаимодействуют с землёй, столом и нитью.
На первое тело действуют: m1g, Т1, Fтр1, N1
На второе тело действуют: m2g, N2, T2, Fтр2 и сила F
Системы отсчета свяжем со столом.
Анализ провели, теперь приступаем к решению задачи.
Дано:
Равноускоренное движение связанных тел
F= 15 Н
m1= 1 кг
m2 = 4 кг
μ = 0,1
_____________________
– ? (м/с2)
Т – ? (Н)
1. Изобразим все силы, действующие на тела.
Ускорение тела направлено вправо:
Из условия задачи = Т1 = Т2 = Т;
2. Запишем II закон Ньютона в общем виде ∑ = m и для каждого тела в векторной форме, для этого страницу разделим пополам:
3. Выберем координатные оси: ось ОУ направим по направлению, а ось ОХ по направлению системы тел.
4. Проецируем векторные уравнения II закона Ньютона для I и II тела на координатные оси:
OX: T – Fтр1 = m1 (1) | OX: F – T – Fтр2 = m2 * (1/) |
Мы получили два уравнения для 2-х тел, где учтены все силы, действующие на тело в отдельности.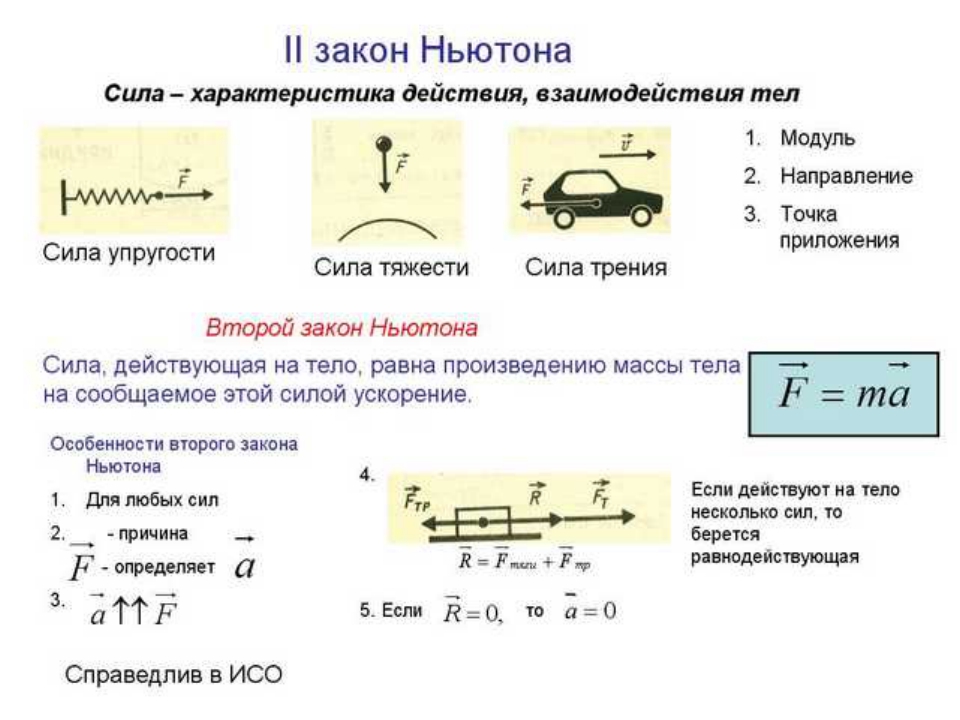
Далее решаем совместно систему уравнений (3) и (31) методом почленного сложения уравнений, получаем:
(4), в этом уравнении учтены все силы, действующие на систему 2-х тел, связанных невесомой нерастяжимой нитью.
Откуда =
Силу натяжения нити находим из уравнения (3) или (31)
Т= μ * m1 * g + m1 = m1 (μ * g + ) = 1 (0,1 * 10 + 2) = 3Н
или Т = F – m2 – μ * m2 g = F – m2 ( + μ * g) = 15 – 4 * (2 + 0,1* 10) = 3Н
Ответ: 2 м/с2, 3Н.
Задача №2. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок без трения в оси, подвешены грузы с массами m1= 1кг и m2= 2 кг. Каково ускорение, с которым движется второй груз?
Снова анализируем задачу.
Из условия невесомости и не растяжимости нити следует, что сила натяжения нити на всех участках одинакова: T1 = T2 = T и система тел движется как единое целое с одинаковым по модулю ускорением:
Рассмотрим все силы действующие на каждый груз отдельно:
на I груз действуют: m1g и T1,
на II груз действуют: m2g и T2
Систему отсчёта свяжем с Землёй.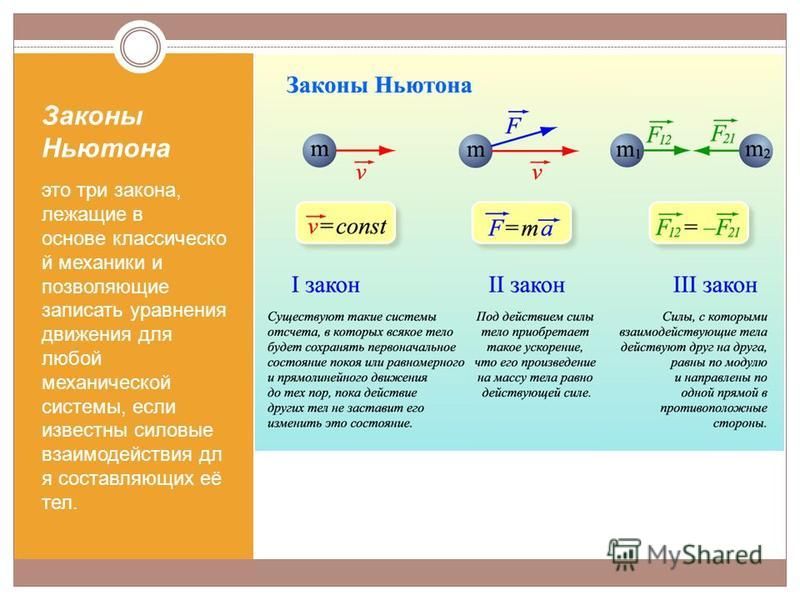
Задачу решаем по алгоритму:
Дано:
равноускоренное движение связанных грузов
m1 = 1 кг
m2 = 2 кг
– ? (м/с2 )
1. Изобразим рисунок и расставим все силы, действующие на тело. Ускорение тела направим в сторону большого тела.
1. Запишем II закон Ньютона в векторной форме для каждого тела
2. Выберем координатные оси, ось ОУ направлена по направлению ускорения, на рисунке изображаем ОУ1, ОУ2.
3. Проецируем векторные уравнения II закона Ньютона для I и II тела на координатные оси ОУ1 и ОУ2, учитывая, что T1 = T2 = T,
ОУ1: T- m1g = m1 * (1) | ОУ2: m2 g – T = m2 ( 11 ) |
Складываем почленно уравнения (1) и (11 ), получаем:
Ответ: 3,3 м/с2
Задача № 3. Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок.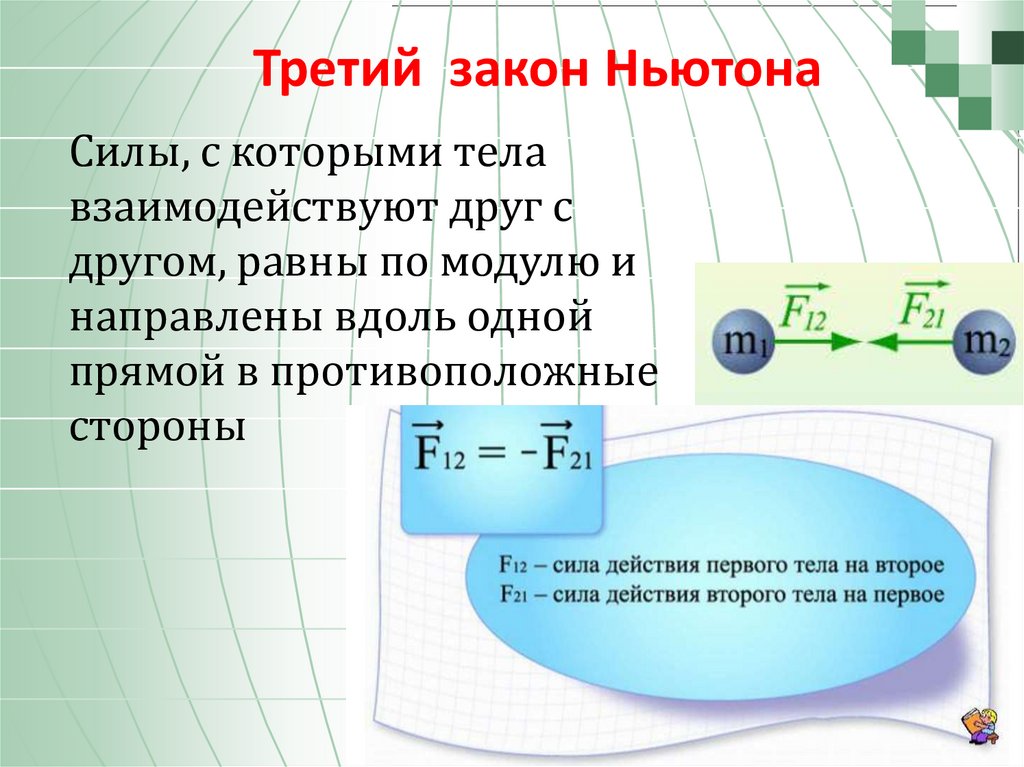 Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
Дано
m1= 2 кг
m2 = 0,5 кг
µ = 0,1
– ? м/с2
Т – ? (H)
Решение:
1. Изобразим рисунок и расставим все силы, действующие на тела. Ускорение первого тела направим вправо, второго – вниз.
2. Запишем II закон Ньютона в векторной форме для каждого тела, поделив страницу пополам
для I тела: | для II тела: |
3. Спроецируем полученные уравнения на выбранные направления осей X и Y, учитывая условие невесомости и нерастяжимости:.
OX: (1) | (31)
|
Решаем совместно систему уравнений (3) и (31) методом почленного сложения уравнений, получаем:
Т – µ * m1g + m2g – T = (m1+m2) *
откуда
Силу натяжения нити Т находим из уравнения (31).
Т = m2g – m2 =m2 (g – )
Т = 0,5 (10 – 1,2) = – 4,4 H. (знак « – » указывает, что сила натяжения направлена в противоположную сторону оси OY).
Т = 4,4 Н.
Ответ: 1,2 м/с2 ; 4,4 Н.
Задача № 4. (Слайд № 21) Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный блок, с другим грузом массой 2 кг движется вниз по наклонной плоскости. Найти натяжение нити и ускорение грузов, если коэффициент трения между первым грузом и плоскостью 0,1, угол наклона плоскости к горизонту 450. Массами нитей и блока, а также трением в блоке пренебречь.
Дано:
m1 = 5 кг
m2 = 2 кг
µ = 0,1
α = 450
– ? (м/с2)
Т–? ( Н)
Решение:
1. Изобразим рисунок и расставим все силы.
2. Запишем II закон Ньютона в векторной форме.
для I тела | для II тела |
3. Спроецируем полученные уравнения на выбранные направления осей X1 , Y1 , Y2, учитывая условие невесомости и нерастяжимости: Т1 = Т2 = Т, .
Спроецируем полученные уравнения на выбранные направления осей X1 , Y1 , Y2, учитывая условие невесомости и нерастяжимости: Т1 = Т2 = Т, .
|
|
OX1: m1g * sin α – T- Fтр= m1* | (1) OY2: – m2 * g +T = m2 * (11) |
складываем почленно (11) и (4), получаем
m1∙g∙sin α – T – µ∙m1∙g∙cos α – m2∙g + T= (m1+m2)
Силу натяжения нити Т находим из уравнения (11).
T = m2g + m2 = m2 (g+ )
T = 2∙ (10+1,7) = 2 ∙ 11,7= 23,4 Н.
Ответ: 1,7 м/с2; 23,4 Н.
Задачи для самостоятельного решения:
Вертолёт, масса которого 27,2 т, поднимает на тросах вертикально вверх груз массой 15,3 т с ускорением 0,6 м/с2. Найти силу тяги вертолёта и силу, действующую со стороны груза на прицепной механизм вертолёта.
Найти силу тяги вертолёта и силу, действующую со стороны груза на прицепной механизм вертолёта.
С каким ускорением движется система, изображенная на рисунке 43, если m = 1 кг и коэффициент трения μ = 0,2? Какова сила натяжения Fн1, связывающей тела I и II, и сила натяжения нити Fн2, связывающей тела II и III?
законов движения Ньютона | Определение, примеры и история
Исаак Ньютон: три закона движения
Смотреть все СМИ
- Ключевые люди:
- Исаак Ньютон
- Похожие темы:
- закон инерции уравнение движения движение закон действия и противодействия закон силы
Просмотреть весь связанный контент →
Популярные вопросы
Что такое законы движения Ньютона?
Законы движения Ньютона связывают движение объекта с действующими на него силами. Согласно первому закону, объект не изменит своего движения, если на него не действует сила.
Почему важны законы движения Ньютона?
Законы движения Ньютона важны, потому что они лежат в основе классической механики, одного из основных разделов физики. Механика — это наука о том, как объекты движутся или не движутся, когда на них действуют силы.
Сводка
Прочтите краткий обзор этой темы
Законы движения Ньютона , три утверждения, описывающие отношения между силами, действующими на тело, и движением тела, впервые сформулированные английским физиком и математиком Исааком Ньютоном, которые являются основой классической механики.
Первый закон Ньютона гласит, что если тело находится в состоянии покоя или движется с постоянной скоростью по прямой линии, оно останется в состоянии покоя или продолжит двигаться по прямой линии с постоянной скоростью, если на него не действует сила.
Закон инерции был впервые сформулирован Галилео Галилеем для горизонтального движения на Земле, а затем был обобщен Рене Декартом. Хотя принцип инерции является отправной точкой и фундаментальным допущением классической механики, он менее чем интуитивно очевиден для нетренированного глаза. В аристотелевской механике и в обычном опыте объекты, которые не толкают, имеют тенденцию останавливаться. Закон инерции был выведен Галилеем из его экспериментов с шарами, катящимися по наклонным плоскостям.
Для Галилея принцип инерции был фундаментальным для его центральной научной задачи: он должен был объяснить, как возможно, что если Земля действительно вращается вокруг своей оси и вращается вокруг Солнца, мы не ощущаем этого движения. Принцип инерции помогает дать ответ: поскольку мы находимся в движении вместе с Землей и наша естественная тенденция состоит в том, чтобы удерживать это движение, Земля кажется нам покоящейся. Таким образом, принцип инерции, далекий от того, чтобы быть констатацией очевидного, когда-то был центральным вопросом научных споров. К тому времени, когда Ньютон разобрался во всех деталях, удалось точно учесть небольшие отклонения от этой картины, вызванные тем, что движение земной поверхности не является равномерным прямолинейным движением (обсуждаются эффекты вращательного движения). ниже). В ньютоновской формулировке обычное наблюдение о том, что тела, которые не толкают, имеют тенденцию останавливаться, объясняется тем фактом, что на них действуют неуравновешенные силы, такие как трение и сопротивление воздуха.
Принцип инерции помогает дать ответ: поскольку мы находимся в движении вместе с Землей и наша естественная тенденция состоит в том, чтобы удерживать это движение, Земля кажется нам покоящейся. Таким образом, принцип инерции, далекий от того, чтобы быть констатацией очевидного, когда-то был центральным вопросом научных споров. К тому времени, когда Ньютон разобрался во всех деталях, удалось точно учесть небольшие отклонения от этой картины, вызванные тем, что движение земной поверхности не является равномерным прямолинейным движением (обсуждаются эффекты вращательного движения). ниже). В ньютоновской формулировке обычное наблюдение о том, что тела, которые не толкают, имеют тенденцию останавливаться, объясняется тем фактом, что на них действуют неуравновешенные силы, такие как трение и сопротивление воздуха.
Тест “Британника”
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.
Physics4Kids.com: Движение: законы движения
В Англии был парень по имени сэр Исаак Ньютон . Немного душный, с плохой прической, но вполне интеллигентный парень. Он работал над разработкой исчисления и физики одновременно. В ходе своей работы он выдвинул три основные идеи, применимые к физике большинства движений (НЕ к современной физике). Идеи проверялись и проверялись столько раз на протяжении многих лет, что ученые теперь называют их Три закона движения Ньютона .
Первый закон гласит, что объект, находящийся в состоянии покоя , имеет тенденцию оставаться в покое, а объект в состоянии движения стремится оставаться в движении с тем же направлением и скоростью. Движение (или отсутствие движения) не может измениться без действия неуравновешенной силы. Если с вами ничего не происходит и ничего не происходит, вы никогда никуда не пойдете. Если вы идете в определенном направлении, пока с вами ничего не случится, вы всегда будете идти в этом направлении. Навсегда.
Если вы идете в определенном направлении, пока с вами ничего не случится, вы всегда будете идти в этом направлении. Навсегда.
Вы можете увидеть хорошие примеры этой идеи, когда посмотрите видеозапись астронавтов . Вы когда-нибудь замечали, что их инструменты плавают? Их можно просто разместить в пространстве, и они останутся на одном месте. Нет никакой мешающей силы, которая могла бы изменить эту ситуацию. То же самое верно, когда они бросают предметы на камеру. Эти объекты движутся по прямой линии. Если бы они что-то бросили во время выхода в открытый космос, этот объект продолжал бы двигаться в том же направлении и с той же скоростью, если бы ему не мешали; например, если гравитация планеты притягивает ее (Примечание: это действительно очень простой способ описать большую идею. Вы узнаете все настоящие детали — и математику — когда начнете посещать более сложные занятия по физике).
Второй закон гласит, что ускорение объекта, создаваемое чистой (суммарной) приложенной силой, прямо связано с величиной силы, того же направления, что и сила, и обратно пропорционально массе объекта (обратно значение, которое больше другого числа. .. обратное 2 равно 1/2). Второй закон показывает, что если вы приложите одинаковую силу к двум объектам разной массы, вы получите разные ускорения (изменения в движении). Эффект (ускорение) на меньшей массе будет больше (заметнее). Влияние силы в 10 ньютонов на бейсбольный мяч будет намного больше, чем та же сила, действующая на грузовик. Разница в эффекте (ускорении) полностью обусловлена разницей в их массах.
.. обратное 2 равно 1/2). Второй закон показывает, что если вы приложите одинаковую силу к двум объектам разной массы, вы получите разные ускорения (изменения в движении). Эффект (ускорение) на меньшей массе будет больше (заметнее). Влияние силы в 10 ньютонов на бейсбольный мяч будет намного больше, чем та же сила, действующая на грузовик. Разница в эффекте (ускорении) полностью обусловлена разницей в их массах.
Третий закон гласит, что на каждое действие (силу) есть равное и противоположное противодействие (сила). Силы находятся парами. Подумайте о времени, когда вы сидите в кресле. Ваше тело прилагает силу вниз, и этот стул должен прилагать равную силу вверх, иначе стул рухнет. Это вопрос симметрии. Действующие силы встречают другие силы в противоположном направлении. Есть также пример стрельбы пушечным ядром. Когда пушечное ядро летит по воздуху (при взрыве), пушка отталкивается назад. Сила, выталкивающая шар, была равна силе, толкающей пушку назад, но влияние на пушку менее заметно, поскольку она имеет гораздо большую массу.


 Как его фальсифицировать? Казалось бы очень просто – измерять силу и ускорение, например, для какого-нибудь тела массой в килограмм. Как только ускорение окажется не пропорционально силе, второй закон опровергнут. Для простоты мы не рассматриваем понятие массы (иначе тут же придется разбирать закон сохранения массы), а полагаем, что имеем дело с одним и тем же телом постоянной массы (что, кстати, подразумевает использование аристотелева закона тождества объекта себе, относимый не к физике, а к метафизике). Итак, ускорения мы измерять yмеем, потому что первый з-н дал нам инерциальные системы. Осталось разобраться, что такое сила? Допустим, мы приложили к телу силу 9.81 ньютона и намерили ускорение 9.81 м/с
Как его фальсифицировать? Казалось бы очень просто – измерять силу и ускорение, например, для какого-нибудь тела массой в килограмм. Как только ускорение окажется не пропорционально силе, второй закон опровергнут. Для простоты мы не рассматриваем понятие массы (иначе тут же придется разбирать закон сохранения массы), а полагаем, что имеем дело с одним и тем же телом постоянной массы (что, кстати, подразумевает использование аристотелева закона тождества объекта себе, относимый не к физике, а к метафизике). Итак, ускорения мы измерять yмеем, потому что первый з-н дал нам инерциальные системы. Осталось разобраться, что такое сила? Допустим, мы приложили к телу силу 9.81 ньютона и намерили ускорение 9.81 м/с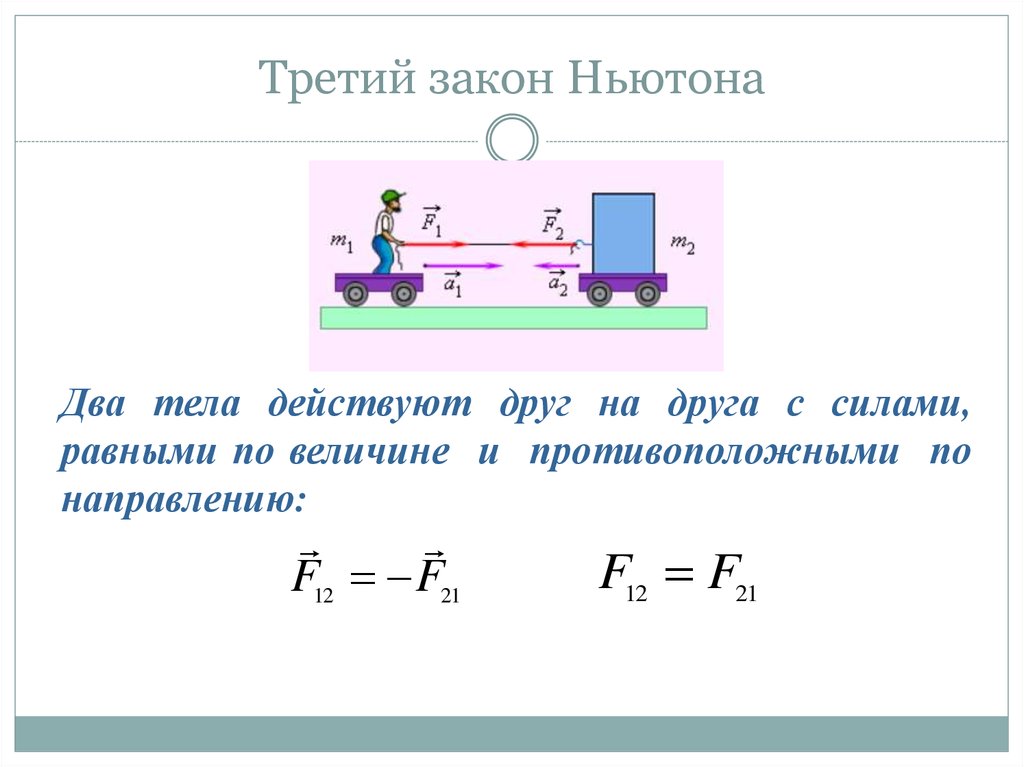

 Неинерциальные тоже существуют. Более того, предложить идеально инерциальную систему отсчета крайне сложно. Инерциальность выполняется с некоторой точностью и это можно экспериментально проверить: если в пределах наших погрешностей сила 0, а скорость меняется более, чем на соответствующую погрешность, то надо разбираться либо с погрешностями, либо с 1-ым законом .
Неинерциальные тоже существуют. Более того, предложить идеально инерциальную систему отсчета крайне сложно. Инерциальность выполняется с некоторой точностью и это можно экспериментально проверить: если в пределах наших погрешностей сила 0, а скорость меняется более, чем на соответствующую погрешность, то надо разбираться либо с погрешностями, либо с 1-ым законом .
 То есть таких систем, в которых все тела, на которые не действует сила (предполагается, что тела можно изолировать, и тогда на них не действует сила), имеют нулевое ускорение друг относительно друга.
То есть таких систем, в которых все тела, на которые не действует сила (предполагается, что тела можно изолировать, и тогда на них не действует сила), имеют нулевое ускорение друг относительно друга. Одно тело тут выступает в качестве системы отсчета, а второе в качестве собственно тела. Это можно. Но, допустим, вы обнаружили, что тела ускоряются друг относительно друга. На первый взгляд, это значит, что вы экспериментально опровергли 1-ый закон. А заодно второй (сила ноль, ускорение не пропорционально силе). Но на деле вы ничего не опровергли. Вам просто придется заключить, что ваша система не 100% изолирована, между вашими телами действует некая сила неизвестной природу, о которой до вашего опыта вы не знали. Вы открыли новую силу, а не опровергли Ньютона.
Одно тело тут выступает в качестве системы отсчета, а второе в качестве собственно тела. Это можно. Но, допустим, вы обнаружили, что тела ускоряются друг относительно друга. На первый взгляд, это значит, что вы экспериментально опровергли 1-ый закон. А заодно второй (сила ноль, ускорение не пропорционально силе). Но на деле вы ничего не опровергли. Вам просто придется заключить, что ваша система не 100% изолирована, между вашими телами действует некая сила неизвестной природу, о которой до вашего опыта вы не знали. Вы открыли новую силу, а не опровергли Ньютона. Физические величины вообще приходят парами (сопряженные величины – темперетура и энтропия, сила и перемещение, ток и напряжение) в которых часто возможно непосредтсвенно измерить только одну, а вторую опосредованно. Допустим, вы разрезали яблоко на две половины. На каждую будет действоват 1/2 исходной силы гравитации. Но это подразумавает заком сохранения массы (масса половинок равна массе целого яблока). Если в эксперименте аддитивность нарушается, то непонятно, это аддитивность силы или аддитивность массы. Можно пытаться аддитивность ввести иначе, но и там будут подобные проблемы.
Физические величины вообще приходят парами (сопряженные величины – темперетура и энтропия, сила и перемещение, ток и напряжение) в которых часто возможно непосредтсвенно измерить только одну, а вторую опосредованно. Допустим, вы разрезали яблоко на две половины. На каждую будет действоват 1/2 исходной силы гравитации. Но это подразумавает заком сохранения массы (масса половинок равна массе целого яблока). Если в эксперименте аддитивность нарушается, то непонятно, это аддитивность силы или аддитивность массы. Можно пытаться аддитивность ввести иначе, но и там будут подобные проблемы. выше. Как доказать, что нет внешних сил (а не появились новые силы неучтенной природы)? Второе – в наше время (теорема Нётер) считается, что сохранение импулься — результат однородности пространства. Пространство как мы его понимаем по определению не имеет выделенных направлений. Потому система тел АБ не может самопроизвольно начать ускорятся в неком направлении. Если же такое произойдет, то это изменит наши представления о пространстве, а не о законах Ньютона.
выше. Как доказать, что нет внешних сил (а не появились новые силы неучтенной природы)? Второе – в наше время (теорема Нётер) считается, что сохранение импулься — результат однородности пространства. Пространство как мы его понимаем по определению не имеет выделенных направлений. Потому система тел АБ не может самопроизвольно начать ускорятся в неком направлении. Если же такое произойдет, то это изменит наши представления о пространстве, а не о законах Ньютона. wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD%D1%8B_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0#.D0.A2.D1.80.D0.B5.D1.82.D0.B8.D0.B9_.D0.B7.D0.B0.D0.BA.D0.BE.D0.BD_.D0.9D.D1.8C.D1.8E.D1.82.D0.BE.D0.BD.D0.B0
wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD%D1%8B_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0#.D0.A2.D1.80.D0.B5.D1.82.D0.B8.D0.B9_.D0.B7.D0.B0.D0.BA.D0.BE.D0.BD_.D0.9D.D1.8C.D1.8E.D1.82.D0.BE.D0.BD.D0.B0