Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца | ЕГЭ по физике
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
2}$
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
То есть $1$ Кл$= 1А·с$.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т.
2$ – электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
$C={q}/{φ}$
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика.
2}/{2}$
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
$I={∆q}/{∆t}$
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц.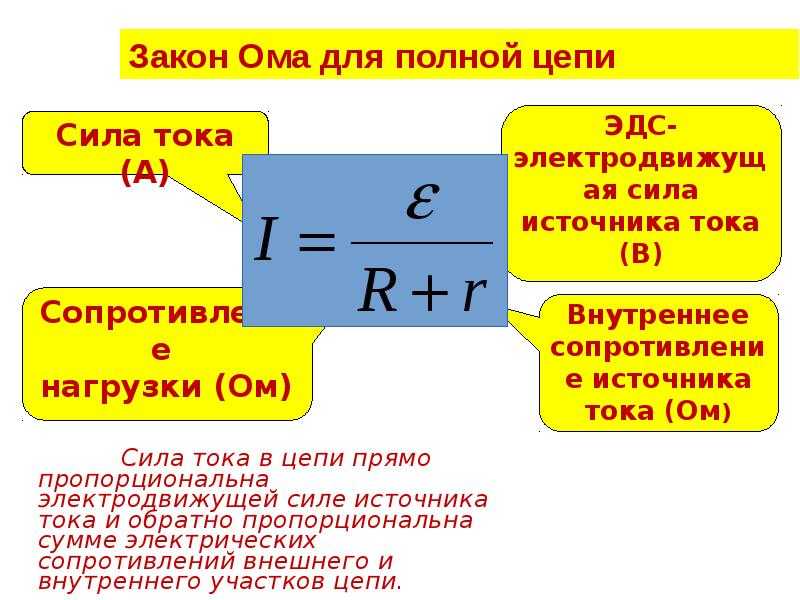
2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:
$I={U}/{R}$
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.
Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов.
Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:
- сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
- сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
$R=ρ{l}/{S}$
где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Из формулы $R=ρ{l}/{S}$ следует, что
$ρ={RS}/{l}$
Величина, обратная $ρ$, называется удельной проводимостью $σ$:
$σ={1}/{ρ}$
Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м.
{-1}$. Для растворов электролитов $α
Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.
Параллельное и последовательное соединение проводников
Для параллельного соединения проводников справедливы следующие соотношения:
1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:
$I=I_1+I_2;$
2) напряжение $U$ на концах проводников, соединенных параллельно, одно и то же:
$U=U_1=U_2;$
3) при параллельном соединении проводников складываются их обратные сопротивления:
${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$
4) сила тока и сопротивление в проводниках связаны соотношением:
${I_1}/{I_2}={R_2}/{R_1}$
Для последовательного соединения проводников в цепи справедливы следующие соотношения:
1) для общего тока $I$:
$I=I_1=I_2,$
где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т.
е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;
2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:
$U=U_1+U_2;$
3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:
$R=R_1+R_2;$
4) также справедливо соотношение:
${U_1}/{U_2}={R_1}/{R_2}$
Работа электрического тока. Закон Джоуля-Ленца
Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:
$A=qU$
где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:
$A=IUt$
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Закон Джоуля-Ленца
Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:
$Q=I^2Rt$
Закон был установлен в 1841 г.
2}/{R}$
Из соотношения для ЭДС легко получить мощность источника тока:
$P_ε=εI$
В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом
$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.
Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:
$Р=10А·220В=2200Вт=2.2кВт.$
Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.
В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению.
Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах ($кВт·ч$).
$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.
Закон Ома « Попаданцев.нет
Сколько времени надо чтобы разобраться с законом Ома для полной цепи? «I = U / ( R + r )» — четыре переменных, знак равенства и два арифметических действия. Возможно, где-нибудь во вселенной и живет разумный вид, способный сделать это быстро, но у Homo Sapiens на это ушло примерно столетие.
Эта история началась в лаборатории Генри Кавендиша в конце восемнадцатого века. Ученый исследовал процесс статического разряда. Напряжение он определял электроскопом, силу тока, за отсутствием еще не изобретенного амперметра, приходилось оценивать пропуская заряд через собственное тело. Кавендиш заметил, что сила электрического удара прямо пропорциональна напряжению, что и считается первой формулировкой закона Ома.
Великий затворник не утруждал себя публикациями в научных журналах, так что о его открытии узнали лишь в конце девятнадцатого века при разборе архивов.
Наука тем временем узнавала о электричестве все больше и больше — природа молний, вольтов столб, электромагнит. Последнее изобретение позволило создать гальванометр и исследовать электрические процессы основываясь на показаниях электрических приборов, а не ощущениях экспериментатора.
Тем не менее от изобретения гальванометра до публикации Омом закона для полной цепи прошло 7 лет и признание он получил давно не сразу. Чтобы понять причину такого промедления, надо взглянуть на доступные экспериментаторам источники электричества.
Статические генераторы генерировали высокие напряжения при высоком внутреннем напряжении. Сила тока была маленькой и очень мало менялась в зависимости от величины внешнего сопротивления. Точно определить связь напряжения и тока в таких условиях было непросто.
Вольтов столб — очень простой в устройстве источник электрического тока, но его характеристики удручают.
Он состоит из множества элементов — цинковых и медных пластин, разделенных прокладкой, пропитанной кислотой. Атом цинка отдает пару электронов, отделяется от цинковой пластины и в виде иона отправляется в плавание в кислоту. Электроны проходят по цепи и возвращаются в батарею, восстанавливая ионы водорода до газа. На медной пластине возникает множество мельчайших пузырьков водорода, быстро увеличивающих внутреннее сопротивление батареи в несколько раз, это явление было названо поляризацией батареи. То что водород восстанавливается у медной пластины, связано с разностью стандартных электродных потенциалов цинка и меди, детальное рассмотрение этого понятия выходит за рамки статьи.
Идеальная очистка цинка — недешевое удовольствие даже сейчас, а во времена изобретения вольтова столба она была банально невозможна. Мельчайшие частички примесей в цинке — железо, углерод, свинец, мышьяк и другие, действовали аналогично медному электроду, восстанавливая водород электролита. Между ними и пластиной цинка возникал электрический ток, который немедленно возвращался в цинковую пластину через электролит — на ничтожных расстояниях между пластиной цинка и частичкой примеси на его поверхности его электрическое сопротивление невелико.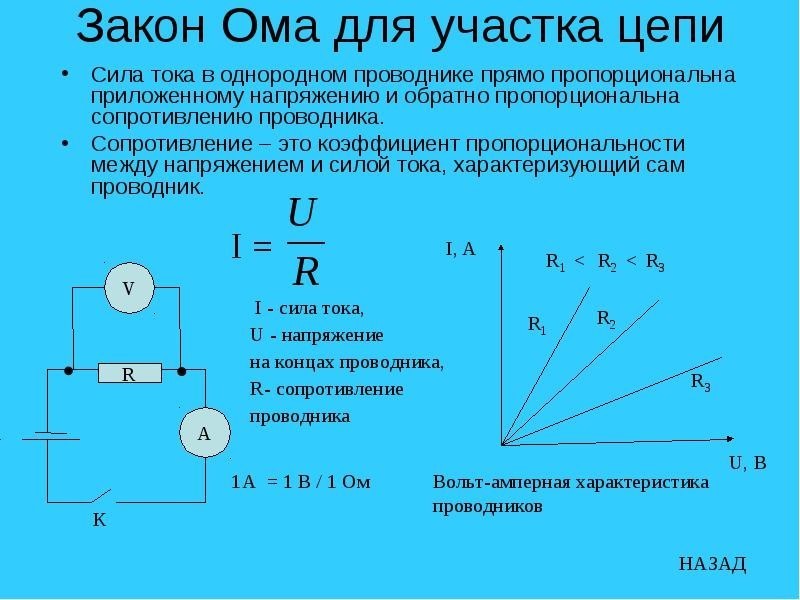
Эти процессы расходовали цинк без какого-либо полезного эффекта и были названы местным действием(local action).
Местное действие научились устранять лишь в 1835, много позже работ Ома, периодической очисткой цинкового электрода ртутью, а поляризация была устранена в 1836 Даниелем за счет использования гораздо более сложного устройства гальванического элемента.
Так что вольтов столб был неэкономичным и капризным электрическим источником. Из-за постоянно меняющегося внутреннего сопротивления, вывести закон Ома было очень непросто, и, несомненно, автору это удалось лишь благодаря огромному усердию и мастерству. Тем не менее, полученные результаты выглядели не слишком убедительно и Ому пришлось провести вторую серию экспериментов уже с термоэлементом из висмута и из меди, один из спаев которого находился в кипящей воде, а другой — в тающем снеге. Только так ему удалось добиться постоянства характеристик источника.
Признан закон Ома был далеко не сразу. Нам сейчас трудно даже представить дикую мешанину теорий о природе электричества в начале девятнадцатого века — теории одной и двух жидкостей, животное электричество, учения о разной природе гальванического и статического электричества и многие другие(см.
например The Electric Current in Early Nineteenth-Century French Physics by Theodore M. Brown, Resistance to Ohm’s Law by Morton L. Schagrin). Отдельно стоит упомянуть разве что закон Барлоу, задержавший развитие телеграфии на несколько лет.
Тем не менее в 1840-х, с началом развития телеграфии, правота Ома стала очевидной. Но главный факап безволосых обезьян еще ждал своего часа.
Якоби сделал свою электрическую моторную лодку еще в 1834, запитав двигатель от вольтового столба. В связи с дрянными характеристиками источника он был заинтересован в извлечении максимальной мощности, поэтому он сформулировал простое правило — максимальная мощность снимается в том случае, если внутреннее и внешнее сопротивления равны.
Улучшения в технологии гальванических батарей и первые генераторы на слабых постоянных магнитах из железа не слишком исправили положение — источники оставались маломощными. Электротехники были заинтересованы в первую очередь в высокой мощности и старались уравнивать внутреннее и внешнее сопротивление.
Шли годы и простое правило превратилось в догму.
В чем проблема такого решения? Мощность максимальна при равенстве сопротивления нагрузки и источника, но при этом половина энергии выделяется внутри источника в виде бесполезного тепла. Для эффективного использования нужно чтобы внутреннее сопротивление было как можно меньше внешнего.
Использование в генераторе электромагнитов резко увеличило их мощность. Промышленные динамо начинают выпускаться по крайней мере с 1867, но их конструкторы даже не пытаются минимизировать внутреннее сопротивление. Dynamo-Elecric Machines, The Jornal of Franklin Institute, 1878 — возможно первое в истории тестирование эффективности генераторов. В нем уже правило уравнивания сопротивления источника и нагрузки упоминается как данность. Исследованию подверглись 6 генераторов, КПД генератора-рекордсмена — 38%! Механические потери составили всего 7%, 21% ушел на вихревые токи, 33% потрачено на преодоление сопротивления обмоток. Остальные генераторы выдали на нагрузку 31%, 27%, 22%, 14% и 12%! При этом электротехническая проволока, с сопротивлением всего на 15% хуже современной производилась по крайней мере 8 лет, с 1870-го!
Внутреннее сопротивление эти генераторов составляло несколько Ом, при том что уменьшить его на порядок не составляло никакого труда, а о индуктивных потерях никто явно даже не думал.
В 1878 году над проблемой электрификации начинает работать Эдисон. Он быстро замечает допущенную профессионалами ошибку и создает собственную конструкцию генератора. Его прототип, прозванный «длинноногой Мери» из-за характерной формы магнитов, имеет внутреннее сопротивление всего пол-Ома, а его якорь сделан из дерева, для уменьшения индукционных потерь. Это позволяет Эдисону добиться КПД в 90% — мировой рекорд.
После публикации описания этого генератора в Scientific America, #41 1879: 242, поднялся настоящий shitstorm(см. например SA #41 1879: 276, SA #41 1879: 305). Профессионалы легко и непринужденно ссылались на учебники, подкрепляя эти ссылки пространными рассуждениями. Понадобилось вмешательство самого лорда Кельвина, для того чтобы разобраться в разности между максимальной мощностью и максимальной эффективностью. Ситуация живо напоминает реакцию некоторых специалистов-ракетчиков на схему спасения первой ступени Фалькона — псевдонаучная болтовня маскирующая незамысловатое «предки так не делали, а они не дураки были».
Эдисон построил первую в мире электростанцию на полмегаватта на Pearl Street в Манхеттане, начав победоносное шествие постоянного тока по планете. Которое было бесцеремонно прервано током переменным — благодаря трансформаторам тот легко передавался на сотни и тысячи километров по высоковольтным линиям, в то время как низковольтная Эдисоновская система несла неоправданно большие потери даже при передаче электричества из одного конца Манхеттана в другой. Опять таки банальный закон Ома — высокое напряжение позволяет уменьшить ток и потери.
Не правда ли, поучительный набор промедлений и заблуждений?
Закон Ома – Академия MEP
Узнайте, как работает закон Ома и как использовать его для решения проблем.
Чтобы посмотреть БЕСПЛАТНУЮ версию этой презентации на YouTube, прокрутите вниз.
Что такое закон Ома
Существует взаимосвязь между напряжением, током и сопротивлением, которую легко объяснить с помощью закона Ома. Немецкий физик по имени Георг Ом разработал теорию, которую мы собираемся объяснить здесь.
Мы можем вычислить любой из трех факторов, составляющих закон Ома, если у нас есть любые два фактора. Вот три варианта формулы.
Напряжение (В) = Ток (I) x Сопротивление (R).
Ток (I) = напряжение (В) / сопротивление (R).
Сопротивление (R) = напряжение (В) / ток (I).
КОЛЕСО ЗАКОНА ОМФормулы легко запоминаются с помощью колеса закона Ома. Вы также можете увидеть версию этого с использованием треугольника.
Колесо ОмаКаждая из трех формул представлена одним из трех колес, при этом продукт пытались решить, окрашенный в красный цвет. Все, что вам нужно сделать, это закрыть красную букву или букву, которую вы пытаетесь решить. Например, если вы закроете «V» для напряжения, вы увидите только ток (I) и сопротивление (R). Когда буквы стоят рядом, вы умножаете, когда напряжение «V» находится над любой буквой, вы делите на напряжение.
Колесо Ома — Простой метод определения формулы закона Ома Просто закройте букву, которую вы хотите решить, и формула откроется сама собой.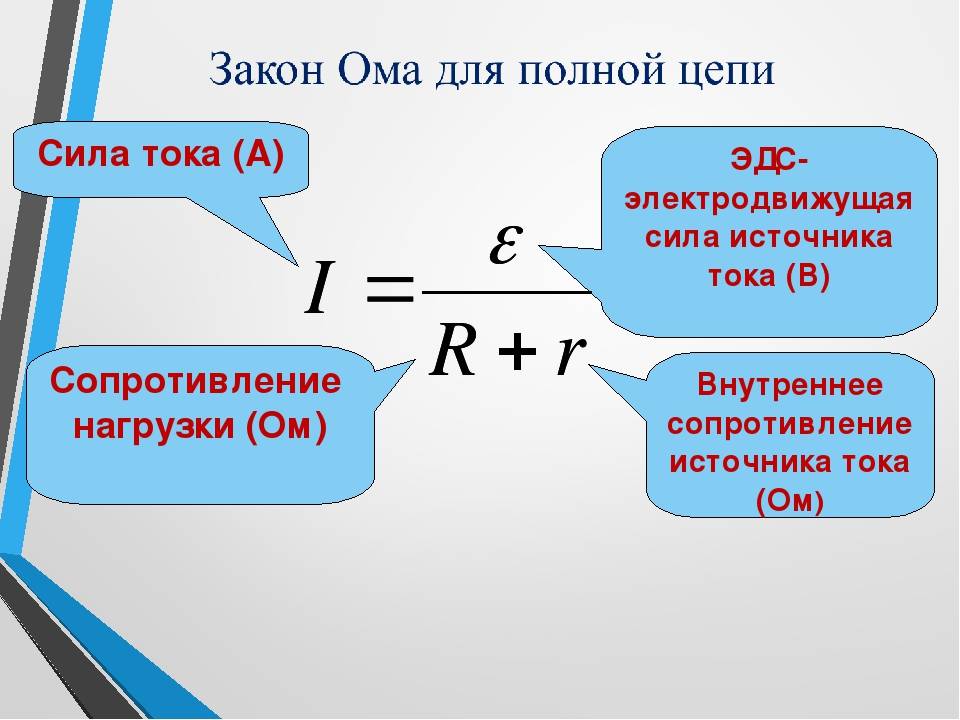
С помощью цифрового измерителя мы можем определить, сколько ампер проходит через цепь, подобную этой здесь.
Закон Ома для расчета амперЕсли мы закроем (I) колеса Ома, пытаясь найти ампер или ток, протекающий через систему, мы увидим, что два известных значения 6 вольт и 2 ома сопротивление отлично работает в рамках формулы. Это дает нам 6 вольт разделить на 2 ома = 3 ампера.
Удвоение напряженияСоединяя батареи последовательно, вы суммируете общее напряжение. Как показано в приведенном здесь примере, две последовательно соединенные 6-вольтовые батареи равны 12 вольтам.
Закон Ома для определения силы тока при удвоении напряженияУдвоив напряжение и сохранив сопротивление неизменным, мы эффективно удвоили силу тока. Теперь у нас есть 12 вольт, разделенных на те же 2 ома сопротивления, чтобы получить вдвое больше ампер, чем раньше, 6 ампер вместо 3.
Помните, поскольку напряжение всегда стоит в числителе, каждый раз, когда вы увеличиваете напряжение, будет увеличиваться сила тока, если сопротивление останется прежним.
Увеличив сопротивление вдвое и сохранив напряжение на том же уровне, мы фактически сократили силу тока вдвое.
Удвоение сопротивления в электрической цепи уменьшит силу тока вдвое.Ток или амперы обратно пропорциональны сопротивлению. При увеличении сопротивления ток уменьшается, и наоборот, при уменьшении сопротивления в Омах увеличивается сила тока в цепи.
Сопротивление в амперах в электрической цепи с фиксированным напряжением Нахождение сопротивления (Ом)Чтобы найти сопротивление (R) в цепи, закройте букву «R» на колесе Ом и введите два известных значения Напряжение (В) и Ампер (I).
Нахождение сопротивления по закону Ома Зная напряжение и измеряя ток, протекающий через цепь, мы можем определить сопротивление. Есть три 6-вольтовых батареи, которые эквивалентны 18-вольтовым, плюс цифровой счетчик показывает 3 ампера. С этими двумя значениями мы получаем 18 вольт, разделенных на 3 ампера, равно 6 Ом.
Решение для напряжения требует знания значения сопротивления и силы тока. Используя цифровой измеритель, можно определить амперы. При этом мы вводим сопротивление и амперы в формулу, чтобы определить напряжение.
Решение для напряжения с использованием закона ОмаНапряжение — это сила, которая толкает ампер через цепь, в то время как омы создают сопротивление протекающему току.
Другие способы измеренияПомните, что существуют и другие способы определения напряжения, тока и сопротивления в цепи, но эта презентация была предназначена для демонстрации использования закона Ома.
Напряжение можно определить напрямую, подключив к клеммам аккумуляторов с помощью мультиметра.
Мультиметр для измерения напряжения, силы тока и сопротивления. Измерение сопротивления можно выполнить с помощью того же цифрового измерителя, настроив его на чтение в омах и установив два щупа с каждой стороны резистора.
Мультиметр имеет внутреннюю батарею, которая пропускает ток через резистор.
Измерение силы тока или силы тока можно выполнить, как показано выше, или с помощью амперметра типа клещей, который изолирует провод. Вместо того, чтобы быть соединенным последовательно со схемой, пробник усилителя охватывает провод. Эти измерительные клещи могут измерять как переменный, так и постоянный ток.
Амперметр — клещи Узнайте, что такое закон Ома и как легко рассчитать напряжение, ток и сопротивлениеИнструменты и задачи по обслуживанию (интерактивные)
Перейти к содержимому
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению V.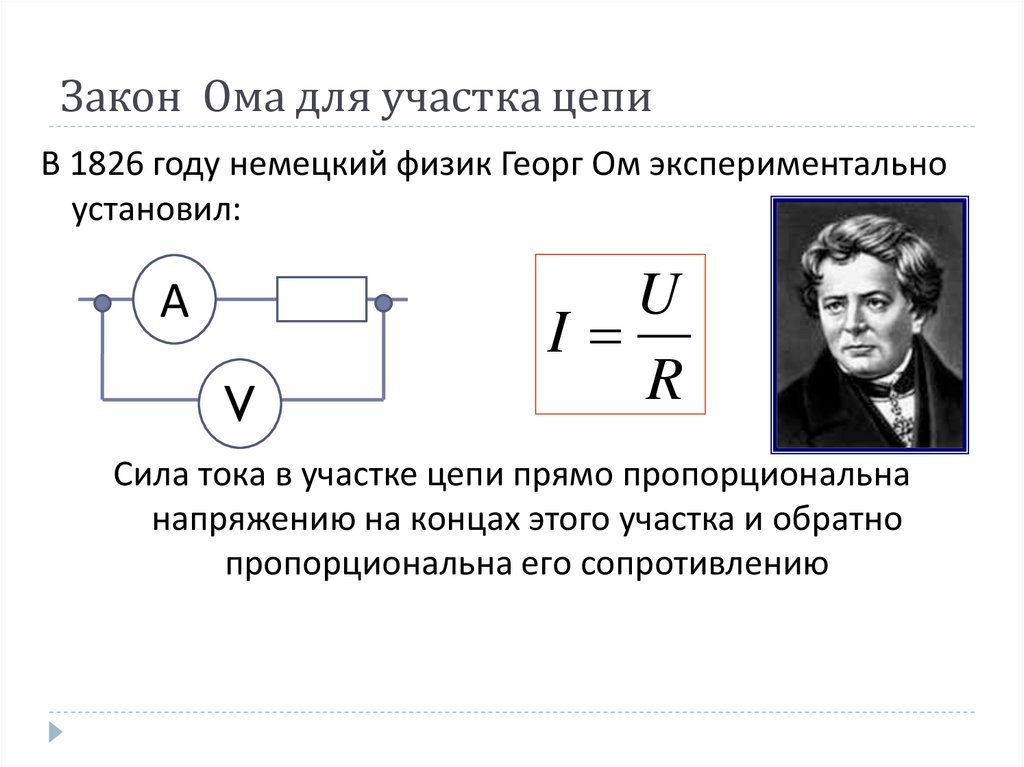
Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению : I ∝ V.
Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток – следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Сопротивление и простые схемы
Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением R. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или I ∝ .
Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает I = .
Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R, не зависящее от напряжения V и тока I. Объект, имеющий простое сопротивление, называется резистором .0099, даже если его сопротивление невелико. Единицей измерения сопротивления является ом, который обозначается символом Ω (греческая омега в верхнем регистре). Преобразование I = дает R = , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер: 1 Ом = 1.
На рисунке показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в R.
Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Установление связей: связи в реальном мире
Закон Ома (V=IR) представляет собой фундаментальное соотношение, которое может быть представлено линейной функцией, где наклон линии представляет собой сопротивление. Сопротивление представляет собой напряжение, которое необходимо приложить к резистору, чтобы создать ток силой 1 А в цепи. На графике (на рисунке ниже) показано это представление для двух простых цепей с резисторами, которые имеют разные сопротивления и, следовательно, разные наклоны.
На рисунке показано соотношение между током и напряжением для двух разных резисторов. Наклон графика представляет значение сопротивления, которое составляет 2 Ом и 4 Ом для двух показанных линий.
Материалы, которые следуют закону Ома, имея линейную зависимость между напряжением и током, известны как омические материалы. С другой стороны, некоторые материалы демонстрируют нелинейную зависимость напряжения от тока и поэтому известны как неомические материалы. На рисунке ниже показаны соотношения тока и напряжения для двух типов материалов.
Рисунок №. Показана зависимость между напряжением и током для омических и неомических материалов.
Очевидно, что сопротивление омического материала (показанного на (а)) остается постоянным и может быть рассчитано путем нахождения наклона графика, но это неверно для неомического материала (показанного на (б)).
Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 1012 Ом и более. У сухого человека сопротивление рук и ног может составлять 105 Ом, тогда как сопротивление человеческого сердца составляет около 103 Ом.
Метровый отрезок медного провода большого диаметра может иметь сопротивление 10-5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».
Дополнительное понимание достигается путем решения I = для V, что дает V = IR.
Это выражение для V можно интерпретировать как падение напряжения на резисторе, создаваемое током I. Фраза IR падение часто используется для этого напряжения. Например, фара в Примере имеет падение ИК-излучения 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления.
Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Установление связей: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
Резисторы последовательно и параллельно
Большинство цепей имеют более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением. Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рис. Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
На изображении показано (а) последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы соединены параллельно, от источника протекает больший ток, чем от каждого из них по отдельности, поэтому общее сопротивление меньше.
Закон Джоуля
Энергия у многих ассоциируется с электричеством. Зная, что мощность – это скорость использования или преобразования энергии, каково выражение для электрической мощности? На ум могут прийти линии электропередач. Мы также думаем о лампочках с точки зрения их номинальной мощности в ваттах.
Сравним 25-ваттную лампочку с 60-ваттной. (См. Рисунок (а).) Поскольку обе лампы работают при одинаковом напряжении, лампочка мощностью 60 Вт должна потреблять больший ток, чтобы иметь большую номинальную мощность. Таким образом, сопротивление лампочки мощностью 60 Вт должно быть меньше, чем у лампы мощностью 25 Вт. Если мы увеличиваем напряжение, мы также увеличиваем мощность. Например, когда лампочка мощностью 25 Вт, рассчитанная на работу от сети 120 В, подключается к сети 240 В, она короткое время очень ярко светится, а затем перегорает. Как именно напряжение, ток и сопротивление связаны с электроэнергией?
Электрическая энергия зависит как от задействованного напряжения, так и от перемещенного заряда. Проще всего это выражается как PE = qV , где q — пройденный заряд, а q — напряжение (или, точнее, разность потенциалов, через которую проходит заряд). Мощность — это скорость, с которой перемещается энергия, поэтому электрическая мощность равна 
Учитывая, что ток равен I = ( обратите внимание, что здесь Δt=t), выражение для мощности становится равным Р = IV.
Электроэнергия ( P ) — это просто произведение тока на напряжение. Мощность имеет привычные единицы измерения ватт. Поскольку единицей СИ для потенциальной энергии (PE) является джоуль, мощность измеряется в джоулях в секунду или ваттах. Таким образом, 1 А⋅В = 1 Вт. Например, в автомобилях часто есть одна или несколько дополнительных розеток, с помощью которых можно заряжать сотовый телефон или другие электронные устройства. Эти розетки могут быть рассчитаны на 20 А, чтобы цепь могла выдавать максимальную мощность
Чтобы увидеть зависимость мощности от сопротивления, соединим закон Ома с P = IV. Замена I = V/R дает P = ()V = V 2 /R .
Аналогично, замена V = IR дает P = I(IR) = I 2 R . Для удобства здесь перечислены вместе три выражения для электрической мощности:
П = IV
Р = В 2 /Р
П = И 2 Р.
Обратите внимание, что первое уравнение справедливо всегда, а два других можно использовать только для резисторов. В простой схеме с одним источником напряжения и одним резистором мощность, подаваемая источником напряжения, и мощность, рассеиваемая резистором, идентичны. (В более сложных схемах P может быть мощностью, рассеиваемой одним устройством, а не общей мощностью в цепи.)
Из трех разных выражений для электроэнергии можно получить разные выводы. Например, P = V 2 /R подразумевает, что чем ниже сопротивление, подключенное к данному источнику напряжения, тем больше выдаваемая мощность. Кроме того, поскольку напряжение возводится в квадрат в P = V 2 /R , эффект приложения более высокого напряжения, возможно, больше, чем ожидалось.