Скорость изменения магнитного потока: № 912. Найти скорость изменения магнитного потока в соленоиде из 2000 витков при возбуждении в нем ЭДС индукции 120 В.

явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца

9.5. Индукционный ток

9.5.1. Тепловое действие индукционного тока

Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока , сила которого определяется по формуле

I i = | ℰ i | R ,

где ℰ i – ЭДС индукции, возникающая в контуре; R – сопротивление контура.

При протекании индукционного тока в контуре выделяется теплота , количество которой определяется одним из выражений:

Q i = I i 2 R t , Q i = ℰ i 2 t R , Q i = I i | ℰ i | t ,

где I i – сила индукционного тока в контуре; R – сопротивление контура; t – время; ℰ i – ЭДС индукции, возникающая в контуре.

Мощность индукционного тока вычисляется по одной из формул:

P i = I i 2 R , P i = ℰ i 2 R , P i = I i | ℰ i | ,

где I i – сила индукционного тока в контуре; R – сопротивление контура; ℰ i – ЭДС индукции, возникающая в контуре.

При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд , величина которого вычисляется по формуле

q i = I i ∆t ,

где I i – сила индукционного тока в контуре; Δt – интервал времени, в течение которого по контуру течет индукционный ток.

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение . Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф 1 = B 1 S  cos α,

где B 1 – первоначальное значение модуля индукции магнитного поля, B 1 = 250 мТл; S – площадь кольца; α – угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф 2 = B 2 S  cos α = 0,

где B 2 – значение модуля индукции после выключения магнитного поля, B 2 = 0.

∆Ф = Ф 2 − Ф 1 = −Ф 1 ,

или, с учетом явного вида Ф 1 ,

∆Ф = −B 1 S  cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

| ℰ i | = | Δ Ф Δ t | = | − B 1 S cos α Δ t | = B 1 S | cos α | Δ t ,

где ∆t – интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = B 1 S | cos α | R Δ t ,

где R – сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

q i = I i Δ t = B 1 S | cos α | R .

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

q i max = I i Δ t = B 1 S R .

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.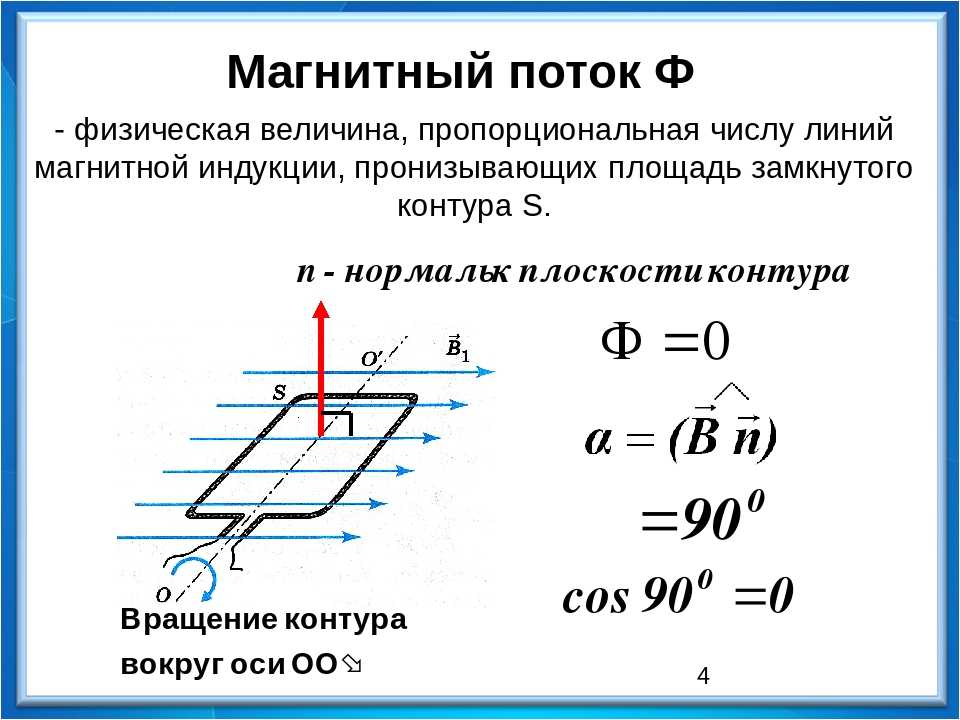

Площадь кольца – площадь круга радиусом r , периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

l = 2πr ,

где l – длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

r = l 2 π ,

а его площадь –

S = π r 2 = π l 2 4 π 2 = l 2 4 π .

Сопротивление кольца задается формулой

R = ρ l S 0 ,

где ρ – удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S 0 – площадь поперечного сечения проволоки, S 0 = = 0,100 мм 2 .

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

q i max = B 1 l 2 S 0 4 π ρ l = B 1 l S 0 4 π ρ .

Вычислим:

q i max = 250 ⋅ 10 − 3 ⋅ 1,57 ⋅ 0,100 ⋅ 10 − 6 4 ⋅ 3,14 ⋅ 50,0 ⋅ 10 − 10 = 0,625 Кл = 625 мКл.

При выключении поля по кольцу проходит заряд, равный 625 мКл.

Пример 22. Контур площадью 2,0 м 2 и сопротивлением 15 мОм находится в однородном магнитном поле, индукция которого возрастает на 0,30 мТл в секунду. Найти максимально возможную мощность индукционного тока в контуре.

Решение . Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.

Изменение потока вектора индукции магнитного поля определяется разностью

∆Ф = ∆BS  cos α,

где ∆B – изменение модуля индукции магнитного поля за выбранный интервал времени; S – площадь, ограниченная контуром, S = 2,0 м 2 ; α – угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура.

Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:

| ℰ i | = | Δ Ф Δ t | = | Δ B S cos α Δ t | = Δ B S | cos α | Δ t ,

где ∆B /∆t – скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆B /∆t = 0,30 мТл/с.

Появление ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = Δ B S | cos α | R Δ t ,

где R – сопротивление контура.

Мощность индукционного тока

P i = I i 2 R = (Δ B Δ t) 2 S 2 R cos 2 α R 2 = (Δ B Δ t) 2 S 2 cos 2 α R .

Максимальному значению мощности индукционного тока соответствует максимальное значение функции косинус (cos α = 1):

P i max = (Δ B Δ t) 2 S 2 R .

Вычислим:

P i max = (0,30 ⋅ 10 − 3) 2 (2,0) 2 15 ⋅ 10 − 3 = 24 ⋅ 10 − 6 Вт = 24 мкВт.

Максимальная мощность индукционного тока в данном контуре равна 24 мкВт.

Взаимосвязь электрических и магнитных полей замечена очень давно. Данную связь еще в 19 веке обнаружил английский ученый-физик Фарадей и дал ему название . Она появляется в тот момент, когда магнитный поток пронизывает поверхность замкнутого контура.

После того как происходит изменение магнитного потока в течение определенного времени, в этом контуре наблюдается появление электрического тока.

Взаимосвязь электромагнитной индукции и магнитного потока

Суть магнитного потока отображается известной формулой: Ф = BS cos α. В ней Ф является магнитным потоком, S – поверхность контура (площадь), В – вектор магнитной индукции. Угол α образуется за счет направления вектора магнитной индукции и нормали к поверхности контура. Отсюда следует, что максимального порога магнитный поток достигнет при cos α = 1, а минимального – при cos α = 0.

Во втором варианте вектор В будет перпендикулярен к нормали. Получается, что линии потока не пересекают контур, а лишь скользят по его плоскости. Следовательно, определять характеристики будут линии вектора В, пересекающие поверхность контура. Для расчета в качестве единицы измерения используется вебер: 1 вб = 1в х 1с (вольт-секунда). Еще одной, более мелкой единицей измерения служит максвелл (мкс). Он составляет: 1 вб = 108 мкс, то есть 1 мкс = 10-8 вб.

Для исследования Фарадеем были использованы две проволочные спирали, изолированные между собой и размещенные на катушке из дерева. Одна из них соединялась с источником энергии, а другая – с гальванометром, предназначенным для регистрации малых токов. В тот момент, когда цепь первоначальной спирали замыкалась и размыкалась, в другой цепи стрелка измерительного устройства отклонялась.

Проведение исследований явления индукции

В первой серии опытов Майкл Фарадей вставлял намагниченный металлический брусок в катушку, подключенную к току, а затем вынимал его наружу (рис. 1, 2).

1 2

В случае помещения магнита в катушку, подключенную к измерительному прибору, в цепи начинает протекать индукционный ток. Если магнитный брусок удаляется из катушки, индукционный ток все равно появляется, но его направление становится уже противоположным. Следовательно, параметры индукционного тока будут изменены по направлению движения бруска и в зависимости от полюса, которым он помещается в катушку. На силу тока оказывает влияние быстрота перемещения магнита.

Во второй серии опытов подтверждается явление, при котором изменяющийся ток в одной катушке, вызывает индукционный ток в другой катушке (рис. 3, 4, 5). Это происходит в моменты замыкания и размыкания цепи. От того, замыкается или размыкается электрическая цепь, будет зависеть и направление тока. Кроме того, эти действия есть ни что иное, как способы изменения магнитного потока. При замыкании цепи он будет увеличиваться, а при размыкании – уменьшаться, одновременно пронизывая первую катушку.

3 4

5

В результате опытов было установлено, что возникновение электрического тока внутри замкнутого проводящего контура возможно лишь в том случае, когда они помещаются в переменное магнитное поле. При этом, поток может изменяться во времени любыми способами.

Электрический ток, появляющийся под действием электромагнитной индукции, получил название индукционного, хотя это и не будет током в общепринятом понимании. Когда замкнутый контур оказывается в магнитном поле, происходит генерация ЭДС с точным значением, а не тока, зависящего от разных сопротивлений.

Данное явление получило название ЭДС индукции, которую отражает формула: Еинд = – ∆Ф/∆t. Ее значение совпадает с быстротой изменений магнитного потока, пронизывающего поверхность замкнутого контура, взятого с отрицательным значением. Минус, присутствующий в данном выражении, является отражением правила Ленца.

Правило Ленца в отношении магнитного потока

Известное правило было выведено после проведения цикла исследований в 30-х годах 19 века. Оно сформулировано в следующем виде:

Направление индукционного тока, возбуждаемого в замкнутом контуре изменяющимся магнитным потоком, оказывает влияние на создаваемое им магнитное поле таким образом, что оно в свою очередь создает препятствие магнитному потоку, вызывающему появление индукционного тока.

Когда магнитный поток увеличивается, то есть становится Ф > 0, а ЭДС индукции снижается и становится Еинд

Если поток снижается, то наступает обратный процесс, когда Ф 0, то есть действие магнитного поля индукционного тока, происходит увеличение магнитного потока, проходящего через контур.

Физический смысл правила Ленца заключается в отражении закона сохранения энергии, когда при уменьшении одной величины, другая увеличивается, и, наоборот, при увеличении одной величины другая будет уменьшаться. Различные факторы влияют и на ЭДС индукции. При вводе в катушку поочередно сильного и слабого магнита, прибор соответственно будет показывать в первом случае более высокое, а во втором – более низкое значение. То же самое происходит, когда изменяется скорость движения магнита.

На представленном рисунке видно, как определяется направление индукционного тока с применением правила Ленца. Синий цвет соответствует силовым линиям магнитных полей индукционного тока и постоянного магнита. Они расположены в направлении полюсов от севера к югу, которые имеются в каждом магните.

Изменяющийся магнитный поток приводит к возникновению индукционного электрического тока, направление которого вызывает противодействие со стороны его магнитного поля, препятствующее изменениям магнитного потока.

В связи с этим, силовые линии магнитного поля катушки направлены в сторону, противоположную силовым линиям постоянного магнита, поскольку его движение происходит в сторону этой катушки.

Для определения направления тока используется с правой резьбой. Он должен ввинчиваться таким образом, чтобы направление его поступательного движения совпадало с направлением индукционных линий катушки. В этом случае направления индукционного тока и вращения рукоятки буравчика будут совпадать.

На рисунке показано направление индукционного тока,возникающего в короткозамкнутой проволочной катушке,когда относительно нее перемещают

магнит.Отметьте,какие из следующих утверждений правильные,а какие- неправильные.
А.Магнит и катушка притягиваются друг к другу.
Б. Внутри катушки магнитное поле индукционного тока направленно вверх.
В. Внутри катушки линии магнитной индукции поля магнита направлены вверх.
Г. Магнит удаляют от катушки.

1. Первый закон Ньютона?

2. Какие системы отсчета являются инерциальными и неинерциальными? Приведите примеры.
3. В чем состоит свойство тел, называемое инертностью? Какой величиной характеризуется инертность?
4. Какова связь между массами тел и модулями ускорений, которые они получают при взаимодействии?
5. Что такое сила и чем она характеризуется?
6. Формулировка 2 закона Ньютона? Какова его математическая запись?
7. Как формулируется 2 закон Ньютона в импульсной форме? Его математическая запись?
8. Что такое 1 Ньютон?
9. Как движется тело, если к нему приложена сила постоянная по модулю и направлению? Как направлено ускорение, вызванное действующей на него силой?
10. Как определяется равнодействующая сил?
11. Как формулируется и записывается 3 закон Ньютона?
12. Как направлены ускорения, взаимодействующих между собой тел?
13. Приведите примеры проявления 3 закона Ньютона.
14. Каковы границы применимости всех законов Ньютона?
15. Почему мы можем считать Землю инерциальной системой отсчета, если она двигается с центростремительным ускорением?
16. Что такое деформация, какие виды деформации вы знаете?
17. Какая сила называется силой упругости? Какова природа этой силы?
18. Каковы особенности силы упругости?
19. Как направлена сила упругости (сила реакции опоры, сила натяжения нити?)
20. Как формулируется и записывается закон Гука? Каковы его границы применимости? Постройте график, иллюстрирующий закон Гука.
21. Как формулируется и записывается закон Всемирного тяготения, когда он применим?
22. Опишите опыты, по определению значения гравитационной постоянной?
23. Чему равна гравитационная постоянная, каков ее физический смысл?
24. Зависит ли работа силы тяготения от формы траектории? Чему равна работа силы тяжести по замкнутому контуру?
25. Зависит ли работа силы упругости от формы траектории?
26. Что вы знаете о силе тяжести?
27. Как вычисляется ускорение свободного падения на Земле и других планетах?
28. Что такое первая космическая скорость? Как ее вычисляют?
29. Что называют свободным падением? Зависит ли ускорение свободного падения от массы тела?
30. Опишите опыт Галилео Галилея, доказывающий, что все тела в вакууме падают с одинаковым ускорением.
31. Какая сила называется силой трения? Виды сил трения?
32. Как вычисляют силу трения скольжения и качения?
33. Когда возникает сила трения покоя? Чему она равна?
34. Зависит ли сила трения скольжения от площади соприкасающихся поверхностей?
35. От каких параметров зависит сила трения скольжения?
36. От чего зависит сила сопротивления движению тела в жидкостях и газах?
37. Что называют весом тела? В чем заключается различие между весом тела и силой тяжести, действующей на тело?
38. В каком случае вес тела численно равен модулю силы тяжести?
39. Что такое невесомость? Что такое перегрузка?
40. Как вычислить вес тела при его ускоренном движении? Изменяется ли вес тела, если оно движется по неподвижной горизонтальной плоскости с ускорением?
41. как изменяется вес тела при его движении по выпуклой и вогнутой части окружности?
42. Каков алгоритм решения задач при движении тела под действием нескольких сил?
43. Какая сила называется Силой Архимеда или выталкивающей силой? От каких параметров зависит эта сила?
44. По каким формулам можно вычислить силу Архимеда?
45. При каких условиях тело, находящееся в жидкости плавает, тонет, всплывает?
46. Как зависит глубина погружения в жидкость плавающего тела от его плотности?
47. Почему воздушные шары наполняют водородом, гелием или горячим воздухом?
48. Объясните влияние вращения Земли вокруг своей оси на значение ускорения свободного падения.
49. Как изменяется значение силы тяжести при: а) удалении тела от поверхности Земли, Б) при движении тела вдоль меридиана, параллели

электрической цепи?

3. Каков физический смысл ЭДС? Дать определение вольту.

4. Соединить на короткое время вольтметри источником электрической энергии, соблюдая полярность.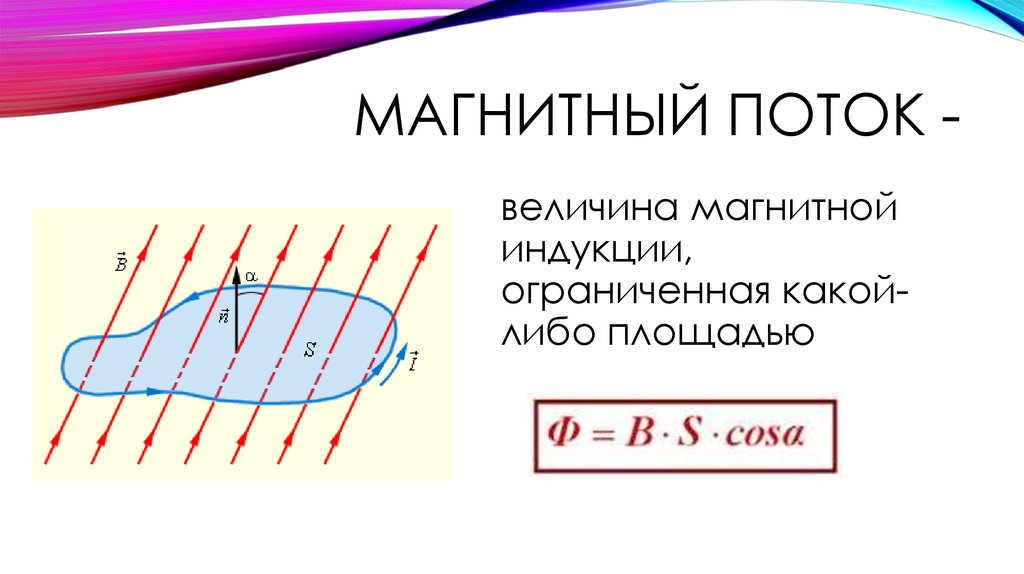 Сравнить его показания с вычислением по результатам опыта.

5. От чего зависит напряжение на зажимах источников тока?

6. Пользуясь результатами измерений, определить напряжение на внешней цепи (если работа выполнена I методом), сопротивление внешней цепи (если работа выполнена II методом).

6 вопрос во вложение вычисление

Помогите пожалуйста!

1. При каких условиях появляются силы трения?
2. От чего зависят модуль и направление силы трения покоя?
3. В каких пределах может изменяться сила трения покоя?
4. Какая сила сообщает ускорение автомобилю или тепловозу?
5. Может ли сила трения скольжения увеличить скорость тела?
6. В чем состоит главное отличие силы сопротивления в жидкостях и газах от силы трения между двумя твердыми телами?
7. Приведите примеры полезного и вредного действия сил трения всех видо

Как мы уже выяснили, электрический ток способен порождать магнитные поля. Возникает вопрос: может ли магнитное поле вызывать появление электрического тока? Эта задача была решена английским физиком Майклом Фарадеем, открывшим явление электромагнитной индукции в 1831 г. Свитый в катушку проводник замыкается на гальванометре (рис. 3.19). Если вдвигать в катушку постоянный магнит, то гальванометр покажет наличие тока в течение всего промежутка времени, пока магнит перемещается относительно катушки. При выдергивании магнита из катушки гальванометр показывает наличие тока противоположного направления. Изменения направления тока происходит при изменении вдвигаемого или выдвигаемого полюса магнита.

Аналогичные результаты наблюдались при замене постоянного магнита электромагнитом (катушкой с током). Если обе катушки закрепить неподвижно, но в одной из них менять значение тока, то в этот момент в другой катушке наблюдается индукционный ток.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ состоит в возникновении электродвижущей силы (э.д.с.) индукции в проводящем контуре, через который меняется поток вектора магнитной индукции. Если контур является замкнутым, то в нем возникает индукционный ток.

Открытие явления электромагнитной индукции:

1) показало взаимосвязь между электрическим и магнитным полем ;

2) предложило способ получения электрического тока с помощью магнитного поля.

Основные свойства индукционного тока :

1. Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.

2. Сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

Опытами Фарадея было установлено, что величина электродвижущей силы индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур проводника (закон электромагнитной индукции Фарадея)

Или , (3.46)

где (dF) – изменение потока в течении времени (dt).МАГНИТНЫМ ПОТОКОМ или ПОТОКОМ МАГНИТНОЙ ИНДУКЦИИ называется величина, которая определяется на основе следующего соотношения: (магнитный поток через поверхность площадью S ): Ф=ВScosα, (3.45), угол a – угол между нормалью к рассматриваемой поверхности и направлением вектора индукции магнитного поля

единица магнитного потока в системе СИ носит название вебер – [Вб=Тл×м 2 ].

Знак «–» в формуле означает, что э.д.с. индукции вызывает индукционный ток, магнитное поле которого противодействует всякому изменению магнитного потока, т.е. при >0 э.д.с. индукции e И

э.д.с. индукции измеряется в вольтах

Для нахождения направления индукционного тока существует правило Ленца (правило установлено в 1833 г.): индукционный ток имеет такое направление, что создаваемое им магнитное поле стремится компенсировать изменение магнитного потока, вызвавшее этот индукционный ток.

Например, если вдвигать северный полюс магнита в катушку, т. е. увеличивать магнитный поток через его витки, в катушке возникает индукционный ток такого направления, что на ближайшем к магниту конце катушки возникает северный полюс (рис.3.20). Итак, магнитное поле индукционного тока стремится нейтрализовать вызвавшее его изменение магнитного потока.

Не только переменное магнитное поле порождает индукционный ток в замкнутом проводнике, но и при движении замкнутого проводника длиной l в постоянном магнитном поле (В) со скоростью v в проводнике возникает эдс:

a (B Ùv) (3. 47)

Как вы уже знаете, электродвижущая сила в цепи– это результат действия сторонних сил. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца (которая действует со стороны магнитного поля на движущийся электрический заряд). Под действием этой силы происходит разделение зарядов и на концах проводника возникает разность потенциалов. Э.д.с. индукции в проводнике является работой по перемещению единичных зарядов вдоль проводника.

Направление индукционного тока можно определитьпо правилу правой руки: Вектор В входит в ладонь, отведенный большой палец совпадает с направлением скорости проводника, а 4 пальца укажут направление индукционного тока.

Таким образом переменное магнитное поле вызывает появление индуцированного электрического поля. Оно не потенциально (в отличие от электростатического), т.к. работа по перемещению единичного положительного заряда равна э.д.с. индукции , а не нулю.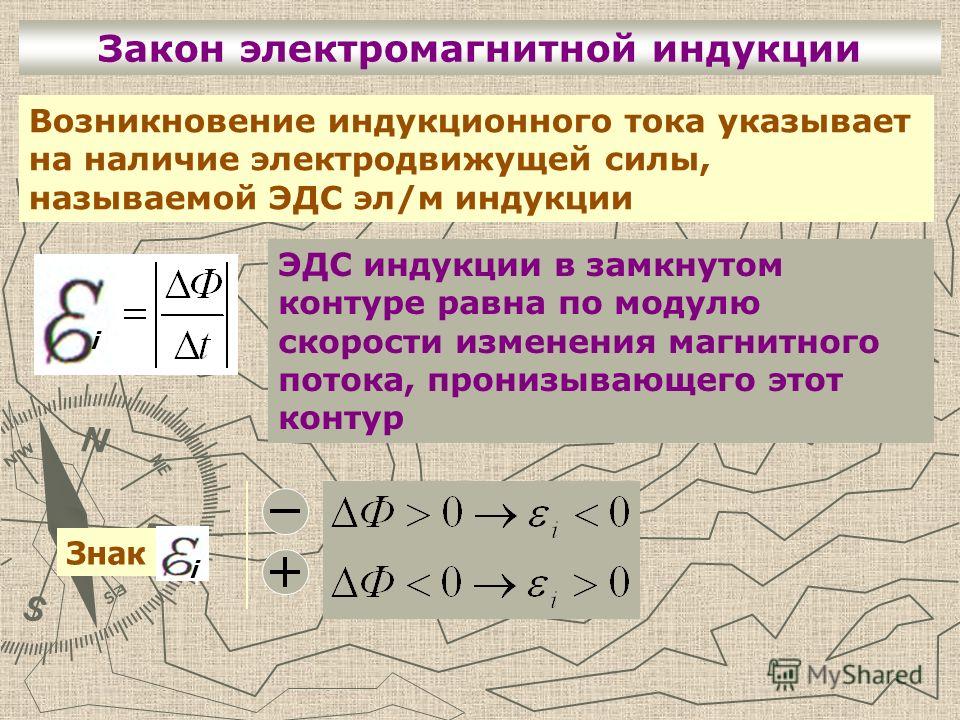

Такие поля называются вихревыми. Силовые линии вихревого электрического поля – замкнуты сами на себя, в отличие от линий напряженности электростатического поля.

Э.д.с. индукции возникает не только в соседних проводниках, но и в самом проводнике при изменении магнитного поля тока, идущего по проводнику. Возникновение э.д.с. в каком-либо проводнике при изменении в нем самом силы тока (следовательно, магнитного потока в проводнике) называется самоиндукцией, а ток, индуцируемый в этом проводнике, – током самоиндукции.

Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, напряженность которого пропорциональна силе тока I. Поэтому магнитный поток Ф, пронизывающий контур, пропорционален силе тока в контуре

Ф=L×I, (3.48).

L – коэффициент пропорциональности, который носит название коэффициента самоиндукции, или, просто, индуктивности. Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости среды, окружающей контур.

В этом смысле индуктивность контура – аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.

Единица индуктивности – генри (Гн) : 1Гн – индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1А равен 1Вб (1Гн=1Вб/А=1В·с/А).

Если L=const, то э.д.с. самоиндукции можно представить в следующем виде:

, или , (3.49)

где DI (dI) – изменение тока в цепи, содержащей катушку индуктивности (или контур) L, за время Dt (dt). Знак «–» в этом выражении означает, что э.д.с. самоиндукции препятствует изменению тока (т. е. если ток в замкнутом контуре уменьшается, то э.д.с. самоиндукции приводит к возникновению тока того же направления и наоборот).

Одним из проявлений электромагнитной индукции является возникновение замкнутых индукционных токов в сплошных проводящих средах: металлических телах, растворах электролитов, биологических органах и т. д. Такие токи носят название вихревых токов или токов Фуко. Эти токи возникают при перемещении проводящего тела в магнитном поле и/или при изменении со временем индукции поля, в которое помещены тела. Сила токов Фуко зависит от электрического сопротивления тел, а также от скорости изменения магнитного поля.

Токи Фуко также подчиняются правилу Ленца : их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему вихревые токи.

Поэтому массивные проводники тормозятся в магнитном поле. В электрических машинах, для того чтобы минимизировать влияние токов Фуко, сердечники трансформаторов и магнитные цепи электрических машин собирают из тонких пластин, изолированных друг от друга специальным лаком или окалиной.

Вихревые токи вызывают сильное нагревание проводников. Джоулево тепло, выделяемое токами Фуко , используется в индукционных металлургических печах для плавки металлов, согласно закону Джоуля-Ленца .

Вопрос: Что определяет скорость изменения магнитного потока через контур? Ответ на вопрос – iq2u

Точные науки Физика

Ответ:

ЭДС индукции

Проверь себя, пройди тесты онлайн

Физика. Сопротивления проводника. 8 класс

Статистика теста

0–25% 2120 человек
26–50% 1418 человек
51–75% 1065 человек
76–100% 1080 человек

0% Пройти тест

Физика. Тренировочный. Тест 1. 7 класс.

Статистика теста

0–25% 1418 человек
26–50% 6899 человек
51–75% 4546 человек
76–100% 2544 человека

0% Пройти тест

Архимедова сила.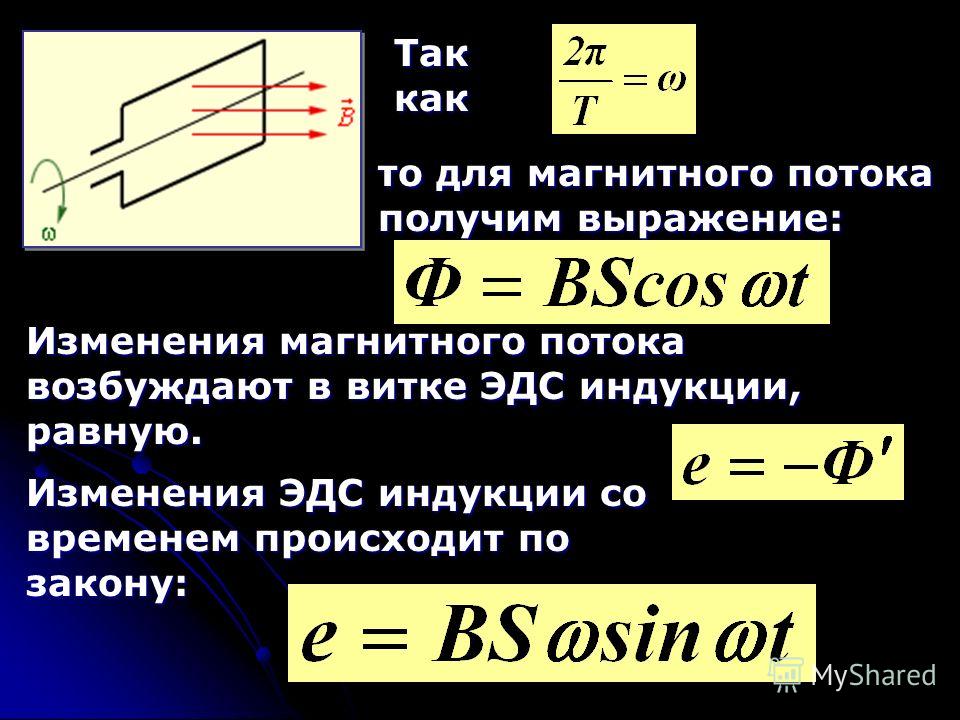 (Fa=pgV, p – плотность жидкости(газа), g – ускорение свободного падения, V – объем погруженного тела.). 7 класс.

Статистика теста

0–25% 5319 человек
26–50% 9159 человек
51–75% 3291 человек
76–100% 4027 человек

0% Пройти тест

Физика. 7 класс. Итоговый тест 1часть.

Статистика теста

0–25% 7753 человека
26–50% 5793 человека
51–75% 11825 человек
76–100% 8681 человек

0% Пройти тест

все тесты

Что? Где? Когда? Эрудит онлайн: ответы на вопросы:

• Сколько в этом атоме других частиц?”> Известно, что в ядре 7 частиц, из которых 3 – протоны. Сколько в этом атоме других частиц?
• Что такое олицетворение?
• Что является основной единицей массы в Международной системе единиц?
• Какой кинетической энергией будет обладать пуля, если её скорость при вылете из ружья равна 600 м/с, а масса 9 г?
• Что такое инверсия?
• Что из перечисленного является физической величиной?
• Что является особенностью географического положения Атлантического океана?
• Что можно сказать об инертности первого тела по сравнению со вторым?”> Масса первого тела больше массы второго. Что можно сказать об инертности первого тела по сравнению со вторым?
• Утром вы выходите из дома, а вечером снова возвращаетесь. Что больше: пройденный вами путь или модуль перемещения?
• Что стало причиной развития научных знаний в XVII в.?
• Через точку С(-2;-3) проведена прямая, параллельная оси абсцисс. Какая из точек лежит на этой прямой?
• Что из перечисленного характерно для обыденного (житейского) познания?
• Что в гальваническом элементе служит положительным электродом, что – отрицательным?
• Из какого металла – алюминия, меди или стали – нужно изготовить плавильный сосуд, чтобы расплавить в нем свинец?
• Чему равна средняя квадратичная скорость молекул водорода при температуре 27°С?

Закон электромагнитной индукции | СПАДИЛО

теория по физике 🧲 магнетизм

Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.

Если за малое время ∆t магнитный поток поменялся на ∆Ф, то скорость изменения магнитного потока равна ΔΦΔt… Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:

Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:

Ii~ΔΦΔt.

Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуров, появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции. Обозначают ее как εi.

Согласно закону Ома для замкнутой цепи:

Ii=εiR. .

Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

εi=∣∣∣ΔΦΔt..∣∣∣

Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.

Определение знака ЭДС индукции

На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль →n к контуру образует правый винт с направлением обхода.

Пусть магнитная индукция →B внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Φ>0 и ΔΦΔt..>0. Согласно правилу Ленца индукционный ток создает магнитный поток Φ‘<0. Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток I_i согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что εi и ΔΦΔt.. имеют разные знаки:

εi=−ΔΦΔt..

Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10^–2 Ом за 2 с изменился на 1,2∙10^–2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.

Известно, что:

Ii=εiR..

εi=∣∣∣ΔΦΔt..∣∣∣

Следовательно:

ЭДС индукции в движущихся проводниках

Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью →v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции →B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.

Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:

FL=|q|vBsin. α

Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:

A=FLl=|q|vBlsin.α

Внимание!

Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника →v. Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.

Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:

εi=A|q|..=vBlsin.α

Эта формула справедлива для любого проводника длиной l, движущегося со скоростью →v в однородном магнитном поле.

В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна εi и остается неизменной, если скорость движения →v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.

С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:

Φ=BScos.(90°−α)=BSsin.α

угол 90°−α представляет собой угол между векторами →B и нормалью →n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:

S=l(NC−vt)

За время ∆t площадь контура меняется на ΔS=−lvΔt. Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за это время равно:

ΔΦ=−BvlΔtsin.α

Следовательно:

εi=−ΔΦΔt..=Bvlsin.α

Если весь контур MNCD движется в однородном магнитном поле, сохраняя свою ориентацию по отношению к вектору →B, то ЭДС индукции в контуре будет равна нулю, так как поток Φ через поверхность, ограниченную контуром, не меняется. Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.

Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.

50 см = 0,5 м

8 мТл = 8∙10^–3 Тл

Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:

εi=Bvlsin.α=8·10−3·4·0,5·1=16·10−3 (В)

Задание EF17754

В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?

Ответ:

а) 1 мА

б) 5 мА

в) 10 мА

г) 20 мА

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Записать формулу для определения величины индукционного тока.

3.Записать закон электромагнитной индукции для движущихся проводников.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решения

Запишем исходные данные:

• Модуль вектора магнитной индукции однородного магнитного поля: B = 0,1 Тл.

• Сопротивление внутри квадратной проволочной рамки: R = 10 Ом.

• Сторона рамки: l = 10 см.

• Скорость перемещения рамки: v = 1 м/с.

10 см = 0,1 м

Индукционный ток, возникающий в рамке, определяется по формуле:

Ii=εiR..

Закон электромагнитной индукции для движущихся проводников:

εi=vBlsin. α

Отсюда индукционный ток равен:

Ii=vBlsin.αR..

На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:

Ii=vBlsin.90°R..=1·0,1·0,1·110..=0,001 (А)=1 (мА)

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17970

При вращении в однородном магнитном поле плоскости металлического кольца из тонкой проволоки вокруг оси, перпендикулярной линиям поля, максимальная сила индукционного тока, возникающего в кольце, равна I₁. Чему будет равна максимальная сила индукционного тока I₂ в этом кольце при уменьшении скорости вращения кольца в 2 раза?

Ответ:

а) I₂ = 2I₁

б) I₂ = I₁

в) I₂ = 0,5I₁

г) I₂ = 4I₁

---

Алгоритм решения

1. Записать закон электромагнитной индукции.

2.Установить зависимость между величиной индукционного тока и скоростью вращения рамки.

3.Определить, как изменится величина индукционного тока в кольце при уменьшении скорости ее вращения.

Решение

Запишем формулу закона электромагнитной индукции:

εi=∣∣∣ΔΦΔt..∣∣∣

Известно, что отношение изменения магнитного потока ко времени его изменения — это величина, характеризующая скорость этого изменения. Если кольцо в однородном магнитном поле вращать медленнее, то и магнитный поток начнет менять медленнее. Так как ЭДС индукции прямо пропорционально зависит от скорости изменения магнитного потока, то при уменьшении скорости вращения кольца в 2 раза она также уменьшится вдвое.

Также известно, что индукционный ток в рамке определяется формулой:

Ii=εiR..

Видно, что индукционный ток и ЭДС индукции — прямо пропорциональные величины. Следовательно, при уменьшении ЭДС индукции вдвое сила индукционного тока тоже уменьшится в 2 раза. Отсюда следует, что I₂ = 0,5I₁.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18860

По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1  Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать закон электромагнитной индукции для двигающихся стержней.

3.Выполнить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса стержней: m1=m2=m=100 г.

• Сопротивление стержней: R1=R2=R=0,1 Ом.

• Расстояние между рельсами: l = 10 см.

• Коэффициент трения между стержнями и рельсами: μ = 0,1.

• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.

• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).

100 г = 0,1 кг

10 см = 0,1 м

Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:

εi=vBlsin.α

Причем v — это разность скоростей стержней (v₂ – v₁), которая характеризует скорость изменения площади проводящего контура.

Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:

εi=IRк

где Rк — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:

Rк=2R

Отсюда закон Ома принимает вид:

εi=2IR

Тогда ток в контуре равен:

I=εi2R..=vBlsin.α2R..

С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):

Fтр=FА

μmg=BIlsin.α

Подставим сюда выражение, полученное для силы тока в контуре:

μmg=BvBlsin.α2R..lsin.α=vB2l2sin2.α2R..

Отсюда скорость равна:

v=2μmgRB2l2sin2.α..

Так как синус угла равен «1»:

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 4. 9k | Оценить:

электромагнетизм – Почему ЭДС равна скорости изменения магнитного потока?

$\begingroup$

Я не понимаю, как Фарадей вычислил, что ЭДС, возникающая при движении магнита в катушке, будет равна скорости изменения магнитного потока. Да, я, как и любой старшеклассник, вбил себе в голову эту формулу, но только вчера я задался вопросом, есть ли какая-то интуитивная причина того, почему ЭДС равна скорости изменения магнитного потока

$$\varepsilon = – \dfrac {d\phi}{dt}$$

На LHS вы получаете работу на единицу заряда в двух точках. На правой стороне вы получили производную магнитного потока по времени. Как они интуитивно связаны?

• электромагнетизм
• дифференцирование
• электромагнито-индукция

$\endgroup$

$\begingroup$

Я не понимаю, как Фарадей вычислил, что ЭДС, возникающая при перемещении магнита в катушке, будет равна скорости изменения магнитного потока.
Фарадей провел множество собственных экспериментов и рассмотрел эксперименты других, и на их основе он создал теорию, которую в ее современной форме мы называем Законом Фарадея .

Майкл Фарадей. Открытие электромагнитной индукции — статья, которая дает вам подробное объяснение того, что сделал Фарадей, и вот несколько выдержек, чтобы дать вам представление о событиях, которые породили теорию.

Открытие электромагнитной индукции произошло в результате серии экспериментов, которые он провел с 29 августадо 4 ноября 1831 года.

Изготовьте железное кольцо, круглое, толщиной 7/8 дюйма и внешним диаметром кольца 6 дюймов. Намотайте много витков медной проволоки вокруг одной половины, витки разделите бечевкой и бязью. Было 3 отрезка провода длиной около 24 футов каждый, и их можно было соединить как один отрезок или использовать как отдельные отрезки… Назовем эту сторону кольца А. На другой стороне, но разделенной промежутком, был намотан провод в две части вместе, составляющие около 60 футов в длина, направление такое же, как у предыдущих катушек; этот боковой звонок B

Соединил концы одной из частей на стороне А с батареей; сразу ощутимый эффект на игле. Он колебался и, наконец, сел в исходное положение. При разрыве соединения стороны А с аккумулятором снова нарушение стрелки… Продолжался контакт стороны А с аккумулятором, но попеременно разрывался и замыкался контакт стороны В. Никакого эффекта в такие моменты на стрелку – зависит от смены стороны батарейки. Следовательно, это не постоянное или особое состояние провода от В, а эффект, вызванный волной электричества, возникающей в моменты разрыва и замыкания контактов на стороне А.

[Математическая] теория нуждалась в концепции нового типа, вопрос о электромагнитное поле, а также вопрос о силовых линиях. Фарадей вводил эти концепции в разное время между 1822 и 1836 годами, но они оставались неприемлемыми для сообщества физиков во времена Фарадея.

Первая поддержка концепции поля Фарадея исходила от Уильяма Томсон, впоследствии лорд Кельвин. Томсон показал, что линии сила может быть использована для объяснения математической теории электростатическое действие. 2$, так что мы получим $\textrm{Nms/C}$. Дифференцируйте, чтобы получить $d\Phi/dt$, и единицы измерения станут $\textrm{Nm/C}$. Ньютон-метры — это единица работы, так что это работа на единицу заряда, что, конечно же, именно так мы определяем электрический потенциал.

$\endgroup$

$\begingroup$

Это следует непосредственно из уравнений Максвелла. Уравнение Фарадея-Максвелла утверждает, что изменяющееся магнитное поле приводит к электрическому полю:

$$\nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t} $$

Это электрическое поле вызывает разность потенциалов, которую мы называем электродвижущей силой. Интегрирование уравнения Фарадея-Максвелла и применение теоремы Стокса дает форму в вашем вопросе.

Трудно связать интуицию с этим уравнением, если вы спросите меня. Уравнения Максвелла, в конечном счете, эмпирические, и чтобы принять их, нужно совершить прыжок веры, но это должно быть одно из очень немногих предположений, которое вам нужно сделать в электромагнетизме.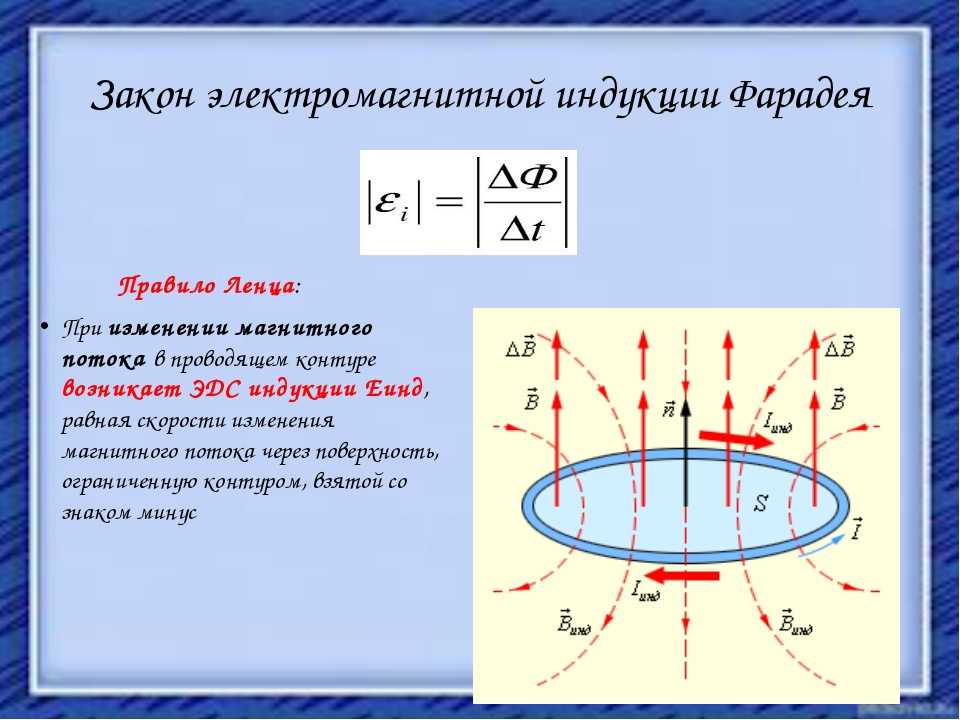

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

индукция – Скорость изменения магнитного потокосцепления с вращающейся катушкой

Спрашиваемый 5 лет, 4 месяца назад

Изменено 5 лет, 4 месяца назад

Просмотрено 7к раз

\$\начало группы\$

Когда скорость изменения магнитного потокосцепления с катушкой, вращающейся в однородном магнитном поле, равна нулю?

Думаю, ответ будет:

, когда катушка совершает один оборот.

так как изменение магнитного потока в первой половине оборота противоположно изменению магнитного потока во второй половине, или я ошибаюсь? Потому что кто-то сказал мне, что это будет, когда катушка будет параллельна силовым линиям магнитного поля, так что правильно?

• вводный инструктаж
• домашнее задание

\$\конечная группа\$

\$\начало группы\$

Ответ на картинке выше. Итак, почему максимальное напряжение должно возникать, когда катушка находится на одной линии с линиями магнитного поля (как показано на рисунке).

Помните, что формула для наведенного напряжения пропорциональна скорости изменения потока, “срезаемого” катушкой. Это мгновенная величина, а не то, что «накапливается» за один оборот.

Когда катушка находится в показанном положении, линии потока не “перерезаются”, но через мгновение она действительно “перерезает” линии потока. скорость изменения разреза линий потока значительна в этой переходной области. Его скорость возрастает от нуля до некоторого значения, зависящего от нового угла катушки и скорости вращения.

Теперь посмотрим, как изменится скорость перерезанных линий магнитного потока, когда катушка будет перемещена на 90 градусов (по вертикали к показанному рисунку). Максимальное количество линий потока проходит через катушку, но одинаковое количество линий потока обрезается немного раньше и немного позже, и, следовательно, скорость изменения фактически равна нулю.

---

Еще несколько мыслей.

Я понимаю, как это может сбивать с толку, потому что если бы магнитное поле (от N до S) создавалось открытым железным сердечником и катушкой, питаемой переменным напряжением, максимальное индуцированное напряжение на вращающейся катушке было бы, когда эта катушка в вертикальном положении. Это, возможно, кажется противоречащим вращающейся катушке и магниту, показанным на картинке.

\$\конечная группа\$

3

\$\начало группы\$

1. Запишите уравнение для зависимости потока через катушку от угла.

$$\Phi =BNA\sin \theta$$

где A — площадь катушки, N — количество витков в катушке, а theta — угол между полем B и плоскостью, в которой лежит катушка in.

2. Продифференцируйте уравнение один раз по углу. Результатом является скорость изменения потока через катушку при ее вращении.

$$\frac{d\Phi}{d\theta} =BNA\cos \theta $$

3. Приравняйте результат к нулю и найдите угол.

$$0=BNA\cos\theta $$

$$\theta = 90, 270$$

\$\конечная группа\$

6

\$\начало группы\$

«когда катушка совершает один оборот» — это когда общее изменение потока от начала до конца равно нулю. Это не то, что задавал вопрос.

Скорость изменения потокосцепления равна нулю, когда нет изменения потокосцепления при небольшом изменении угла катушки. Это происходит, когда плоскость катушки нормальна к полю, ось катушки параллельна полю, когда катушка охватывает максимально возможный поток.

\$\конечная группа\$

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Закон Фарадея

Закон Фарадея
Следующая: Закон Ленца Вверх: Магнитная индукция Предыдущий: Магнитная индукция Явление магнитной индукции играет решающую роль в три очень полезных электрических устройства: электрический генератор , электрический генератор двигатель и трансформатор . Без этих устройств современная жизнь была бы невозможным в его нынешнем виде. Магнитная индукция была открыта в 1830 г. английский физик Майкл Фарадей. Американский физик Джозеф Генри независимо сделал то же самое открытие примерно в одно и то же время. Оба физиков заинтриговал тот факт, что электрический ток, протекающий вокруг цепь может генерировать магнитное поле. Конечно, рассуждали они, если электрический ток может генерировать магнитное поле, тогда магнитное поле должно каким-то образом быть в состоянии генерировать электрический ток. Однако потребовались годы бесплодных экспериментов. прежде чем они смогли найти основной ингредиент, который позволяет магнитное поле для создания электрического тока. Этот ингредиент изменение времени .

Рассмотрим плоскую петлю из проводника площадью поперечного сечения . Поместим эту петлю в магнитное поле, напряженность которого приблизительно равна равномерный по всей длине петли. Предположим, что направление магнитное поле образует угол с направлением нормали к петля. Магнитный поток через контур равен определяется как произведение площади петли на составляющую магнитное поле перпендикулярно контуру. Таким образом,

(191)

Если цикл оборачивается вокруг самого себя раз ( т.е. , если цикл имеет витка ), тогда магнитный поток через петлю просто умножить на магнитный поток через один виток:

(192)

Наконец, если магнитное поле неоднородно по петле или петля не лежат в одной плоскости, то мы должны оценить магнитный поток как поверхностный интеграл

(193)

Здесь — некоторая поверхность, присоединенная к . Если петля имеет витки, то поток умножается на указанное выше значение. Единицей магнитного потока в системе СИ является вебер (Вб). Один тесла эквивалентен один вебер на квадратный метр:

(194)

Фарадей обнаружил, что если магнитное поле через проволочную петлю меняется во времени , то вокруг контура индуцируется ЭДС. Фарадей смог наблюдать этот эффект, потому что ЭДС вызывает ток, циркулирующий в контуре. Фарадей обнаружил, что величина ЭДС прямо пропорциональна скорости изменения магнитного поля во времени. Он также обнаружил, что ЭДС генерируется, когда петля провода перемещается из области с низкой напряженностью магнитного поля в область с высокой напряженностью магнитного поля, и наоборот . ЭДС прямо пропорциональна скорость, с которой петля перемещается между двумя областями. Окончательно, Фарадей обнаружил, что ЭДС генерируется вокруг петли, которая вращается в однородном магнитном поле постоянной напряженности. В этом случае ЭДС прямо пропорциональна скорости вращения петли. В конце концов Фарадей в состоянии предложить один закон, который мог объяснить все его многочисленные и разнообразные наблюдения. Этот закон, известный как Закон Фарадея о магнитной индукции выглядит следующим образом:

ЭДС, индуцированная в цепи, пропорциональна скорости изменения во времени магнитный поток, связывающий эту цепь.

Единицы СИ были зафиксированы таким образом, чтобы константа пропорциональности в этом закон единство . Таким образом, если магнитный поток через цепь изменяется на сумму во временном интервале тогда ЭДС, возникающая в цепи, равна

(195)

Существует много разных способов, которыми магнитный поток, связывающий электрическая цепь может сдача.