Скорость изменения магнитного потока формула: Страница не найдена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Формула ЭДС индукции, E

Закон Фарадея – Максвелла для электромагнитной индукции

Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:

где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.

В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:

Частные случаи формул ЭДС индукции

Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:

где – потокосцепление.

При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:

где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .

При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:

где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .

Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:

В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:

Примеры решения задач по теме «ЭДС индукции»

Репетитор-онлайн — подготовка к ЦТ

Пример 13. Проводящий контур, имеющий форму квадрата со стороной 20 см, помещен в однородное магнитное поле с индукцией 45 мТл. Плоскость контура составляет угол 30° с направлением силовых линий поля. За 0,15 с контур поворачивают таким образом, что его плоскость устанавливается перпендикулярно силовым линиям поля. Найти среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле.

Решение. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость квадрата, при повороте контура в магнитном поле.

Поток индукции магнитного поля через площадь квадрата определяется формулами:

в первом положении контура (до поворота)

Ф₁ = BS cos α₁,

где B — модуль индукции магнитного поля, B = 45 мТл; S — площадь квадрата, S = a ²; a — сторона квадрата, a = 20 см; α₁ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата в первом положении контура, α

1 = = 90° − 30° = 60°;

во втором положении контура (после поворота)

Ф₂ = BS cos α₂,

где α₂ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата во втором положении контура, α₂ = 0°.

Изменение потока вектора индукции магнитного поля определяется разностью

ΔФ=Ф2−Ф1=BScos0°−BScos60°=BS2.

Среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле:

〈ℰi〉=|ΔФΔt|=−BS2Δt=Ba22Δt,

где ∆t — интервал времени, за который происходит поворот контура, ∆t = 0,15 с.

Расчет дает значение:

〈ℰi〉=45⋅10−3⋅(20⋅10−2)22⋅0,15=6,0⋅10−3 В=6,0 мВ.

При повороте контура в нем возникает ЭДС индукции, среднее значение которой равно 6,0 мВ.

Величина равная скорости изменения магнитного потока. Изменение магнитного потока создает электрическое поле

Электрические и магнитные поля порождаются одними и теми же источниками – электрическими зарядами, поэтому можно предположить, что между этими полями существует определенная связь. Это предположение нашло экспериментальное подтверждение в 1831 г. в опытах выдающегося английского физика М.Фарадея. Он открыл явление электромагнитной индукции.

Явление электромагнитной индукции лежит в основе работы индукционных генераторов электрического тока, на которые приходится вся вырабатываемая в мире электроэнергия.

Магнитный поток

Замкнутый контур, помещенный в однородное магнитное поле

Количественной характеристикой процесса изменения магнитного поля через замкнутый контур является физическая величина называемая магнитным потоком . Магнитным потоком (Ф) через замкнутый контур площадью (S) называют физическую величину, равную произведению модуля вектора магнитной индукции (В) на площадь контура (S) и на косинус угла

между вектором В и нормалью к поверхности : Φ = BS cos α. Единица магнитного потока Ф – вебер (Вб): 1 Вб = 1 Тл · 1 м 2 .

перпендикулярен максимальный.

Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.

Закон электромагнитной индукции

Опытным путем был установлен закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром: Эта формула носит название закона Фарадея .

Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея. В нем, чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.

Правило Ленца

Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский физик Э.Х.Ленц. Согласно правилу Ленца , возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Более кратко это правило можно сформулировать следующим образом:

индукционный ток направлен так, чтобы препятствовать причине, его вызывающей. Правило Ленца отражает тот экспериментальный факт, что всегда имеют противоположные знаки (знак «минус» в формуле Фарадея ).

Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине. Они могли вращаться вокруг оси, как коромысло. При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца оно стремилось «догнать» магнит. При движении же магнита внутри разрезанного кольца никакого движения не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

> Изменение магнитного потока создает электрическое поле

Рассмотрите возникновение электрического поля при изменении магнитного потока : закон электромагнитной индукции Фарадея, уравнение Максвелла, теорема Стокса.

При перемене магнитного потока создается электрическое поле. Это утверждает закон индукции Фарадея:

Задача обучения

Охарактеризовать связь меняющегося магнитного поля и электрического.

Основные пункты

Термины

Уравнение Максвелла – набор формул, характеризующих электрические и магнитные поля и их взаимодействие.
Область вектора – величина рассматриваемого вектора, расположенная перпендикулярно плоскости.
Теорема Стокса – интегрирование дифференциальных форм на многообразие, упрощающее и обобщающее несколько теорем из векторных вычислений.

Закон индукции Фарадея говорит о том, что при перемене магнитного поля создается электрическое: (ε индуцируется ЭДС, а Φ B – магнитный поток). Это главный закон в электромагнетизме, предсказывающий принципы взаимодействия магнитного поля с электрической цепью, что приведет к ЭДС.

В этом эксперименте демонстрируется индукция между катушками провода: жидкая батарея (справа) создает ток, протекающий сквозь небольшую катушку (А), формируя магнитное поле. Если катушки лишены движения, ток не индуцируется. Если же катушка смещается из/в более крупную (B ), то магнитный поток изменится и создаст ток, который проявит себя в гальванометре

Дифференциальная форма закона Фарадея

Магнитный поток , где – векторная площадь над замкнутой поверхностью S.

Устройство, способное поддерживать разность потенциалов, несмотря на токовые потоки, выступает источником ЭДС. В математическом виде: , где интеграл характеризуется по замкнутой петле C.

Закон Фарадея теперь можно переписать: . Используя теорему Стокса в векторном исчислении, левая часть приравнивается к

В правой части . Поэтому мы получаем альтернативную форму закона индукции Фарадея: . Ее также именуют дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, контролирующих все электромагнитные явления.

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.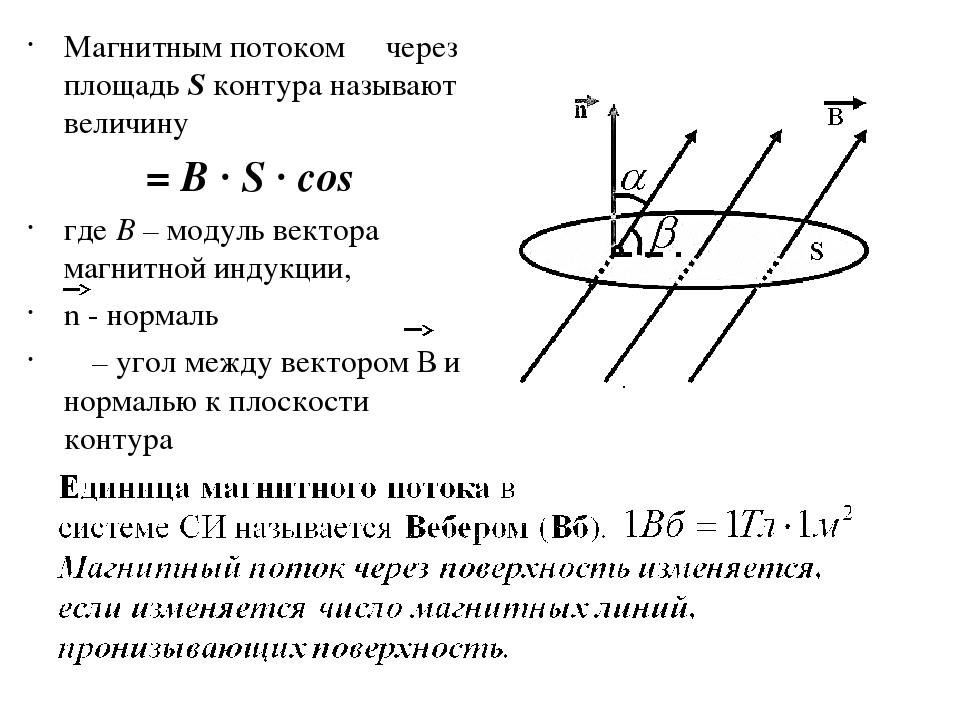

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

где – индукция поля, – площадь контура, – угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м 2 однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

Здесь – изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

где – сила тока в цепи, – коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

где – индуктивность контура, – сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции – появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3 ). Все остальное – результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2 ), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2 ).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3 ) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4 ).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1 ).

При вращении рамки 1 (задача 23.1.5 ) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота – будет равен , где – индукция, – площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2 ).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2 ). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7 ) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче – 2 .

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3 ).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4 ). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1 ).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1 ), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1 ). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 – ответ 3 ).

Используя формулу (23.3) находим в задаче 32. 2.3 Гн (ответ 4 ).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4 ) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) – ответ 3 .

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5 ) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2 ).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2 ).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7 ), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1 ).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8 ). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина – увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2 ). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина – приближение магнита, кольцо будет отталкиваться от него (ответ 2 ). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 – единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4 ).

На картинке показано однородное магнитное поле. Однородное означает одинаковое во всех точках в данном объеме. В поле помещена поверхность с площадью S. Линии поля пересекают поверхность.

Определение магнитного потока :

Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.

Формула магнитного потока:

здесь α – угол между направлением вектора магнитной индукции B и нормалью к поверхности S.

Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.

А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.

Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 10 8 мкс. Соответственно 1 мкс = 10 -8 вб.

Магнитный поток является скалярной величиной.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? – выделяется (при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Основные формулы

· Закон электромагнитной индукции (закон Фарадея):

, (39)

где – эдс индукции;– полный магнитный поток (потокосцепление).

· Магнитный поток, создаваемый током в контуре,

где – индуктивность контура;– сила тока.

· Закон Фарадея применительно к самоиндукции

· Эдс индукции, возникающая при вращении рамки с током в магнитном поле,

где – индукция магнитного поля;– площадь рамки;– угловая скорость вращения.

· Индуктивность соленоида

, (43)

где – магнитная постоянная;– магнитная проницаемость вещества;– число витков соленоида;– площадь сечения витка;– длина соленоида.

· Сила тока при размыкании цепи

где – установившаяся в цепи сила тока;– индуктивность контура,– сопротивление контура;– время размыкания.

· Сила тока при замыкании цепи

. (45)

· Время релаксации

Примеры решения задач

Пример 1.

Магнитное поле изменяется по закону , где= 15 мТл,. В магнитное поле помещен круговой проводящий виток радиусом = 20 см под угломк направлению поля (в начальный момент времени). Найти эдс индукции, возникающую в витке в момент времени= 5 с.

Решение

По закону электромагнитной индукции возникающая в витке эдс индукции , где– магнитный поток, сцепленный в витке.

где – площадь витка,;– угол между направлением вектора магнитной индукциии нормалью к контуру:.

Подставим числовые значения: = 15 мТл,,= 20 см = = 0,2 м,.

Вычисления дают .

Пример 2

В однородном магнитном поле с индукцией = 0,2 Тл расположена прямоугольная рамка, подвижная сторона которой длиной= 0,2 м перемещается со скоростью= 25 м/с перпендикулярно линиям индукции поля (рис. 42). Определить эдс индукции, возникающую в контуре.

Решение

При движении проводника АВ в магнитном поле площадь рамки увеличивается, следовательно, возрастает магнитный поток сквозь рамку и возникает эдс индукции.

По закону Фарадея , где, тогда, но, поэтому.

Знак «–» показывает, что эдс индукции и индукционный ток направлены против часовой стрелки.

САМОИНДУКЦИЯ

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции. Это явление называется самоиндукцией.Самоиндукция – явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

Замыкание цепи При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результатеЛ1 загорается позже, чем Л2.

Размыкание цепи При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает. Вывод в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции? Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике (B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью. Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:

где Ф – магнитный поток через контур, I – сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды (возможен сердечник).

ЭДС САМОИНДУКЦИИ

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

Для характеристики намагниченности вещества в магнитном поле используетсямагнитный момент (Р м ). Он численно равен механическому моменту, испытываемому веществом в магнитном поле с индукцией в 1 Тл.

Магнитный момент единицы объема вещества характеризует его намагниченность – I , определяется по формуле:

I = Р м /V , (2.4)

где V – объем вещества.

Намагниченность в системе СИ измеряется, как и напряженность, в А/м , величина векторная.

Магнитные свойства веществ характеризуются объемной магнитной восприимчивостью – c о , величина безразмерная.

Если какое-либо тело поместить в магнитное поле с индукцией В 0 , то происходит его намагничивание. Вследствие этого тело создает свое собственное магнитное поле с индукцией В ” , которое взаимодействует с намагничивающим полем.

В этом случае вектор индукции в среде (В) будет слагаться из векторов:

В = В 0 + В ” (знак вектора опущен), (2.5)

где В ” – индукция собственного магнитного поля намагнитившегося вещества.

Индукция собственного поля определяется магнитными свойствами вещества, которые характеризуются объемной магнитной восприимчивостью – c о , справедливо выражение:В ” = c о В 0 (2.6)

Разделим на m 0 выражение (2.6):

В ” / m о = c о В 0 /m 0

Получим: Н ” = c о Н 0 , (2.7)

но Н ” определяет намагниченность вещества I , т.е. Н ” = I , тогда из (2.7):

I = c о Н 0 . (2.8)

Таким образом, если вещество находится во внешнем магнитном поле с напряженностьюН 0 , то внутри него индукция определяется выражением:

В=В 0 + В ” = m 0 Н 0 +m 0 Н ” = m 0 (Н 0 + I) (2.9)

Последнее выражение строго справедливо, когда сердечник (вещество) находится полностью во внешнем однородном магнитном поле (замкнутый тор, бесконечно длинный соленоид и т.д.).

МАГНИТНОЕ ПОЛЕ

Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.

В – физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).

Магнитная индукция – векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:

Единица магнитной индукции . В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:

СИЛА ЛОРЕНЦА

Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F А = IBlsin a , а сила Лоренца действует на движущийся заряд:

где a – угол между векторами B и v .

Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила м, постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:

В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,

Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.

Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.

Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м:

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.

МАГНИТНЫЙ ПОТОК

Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S – величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:

Ф=BScos

В СИ единица магнитного потока 1 Вебер (Вб) – магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:

Электромагнитная индукция -явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.

Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Опыты Фарадея показали, что сила индукционного тока I i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.

Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:

Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε i .

По закону Ома для замкнутой цепи

Так как R не зависит от , то

ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:

САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ

Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:

Ф = L*I .

Индуктивность контура L – коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.

Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.

Самоиндукция – явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.

Самоиндукция – частный случай электромагнитной индукции.

Индуктивность – величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.

Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :

Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.

ЭДС самоиндукции имеет в этом случае постоянное значение:

где I – начальное значение тока, t – промежуток времени, за который сила тока убывает от I до 0.

За время t в цепи проходит электрический заряд q = I cp t . Так как I cp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:

Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:

Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?

Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1 . Следовательно,

Ответ: энергия поля равна 8,6 Дж; при уменьшении тока вдвое она уменьшится в 4 раза.

Явление электромагнитной индукции. Закон Фарадея

где – индуктивность контура, – сила тока в нем.

Рассмотрим теперь задачи.

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4 ).

В нашем мире все виды существующих сил, за исключением сил тяготения, представлены электромагнитными взаимодействиями. Во Вселенной, несмотря на удивительное разнообразие воздействий тел друг на друга, в любых веществах, живых организмах всегда встречается проявление электромагнитных сил . Как произошло открытие электромагнитной индукции (ЭИ), расскажем ниже.

Вконтакте

Открытие ЭИ

Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.

Так нельзя ли добиться его возникновения посредством магнитного поля — подобную задачу поставил Майкл Фарадей. В 1821 году он отметил это свойство в своем дневнике о превращении магнетизма в .

Успех к ученому пришел не сразу. Лишь глубокая уверенность в единстве природных сил и упорный труд привели его через десять лет к новому великому открытию.

Решение задачи долго не давалось Фарадею и другим его коллегам, потому как они пытались получить электричество в неподвижной катушке, используя действие постоянного магнитного поля. Между тем, впоследствии выяснилось: изменяется количество силовых линий, пронизывающих провода, и возникает электроэнергия.

Явление ЭИ

Процесс появления в катушке электричества в результате изменения магнитного поля характерен для электромагнитной индукции и определяет это понятие. Вполне закономерно, что разновидность , возникающего в ходе данного процесса, называется индукционным. Эффект сохранится, если саму катушку оставить без движения, но перемещать при этом магнит. С использованием второй катушки можно и вовсе обойтись без магнита.

Если пропустить электричество через одну из катушек, то при их взаимном перемещении во второй возникнет индукционный ток . Можно надеть одну катушку на другую и менять величину напряжения одной из них, замыкая и размыкая ключ. При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй.

Закон

Во время опытов легко обнаружить, что увеличивается число пронизывающих катушку силовых линий — стрелка используемого прибора (гальванометр) смещается в одну сторону, уменьшается – в иную. Более тщательное исследование показывает, что сила индукционного тока прямо пропорциональна скорости изменения числа силовых линий. В этом заключен основной закон электромагнитной индукции.

Данный закон выражает формула:

Она применяется, если за период времени t магнитный поток изменяется на одну и ту же величину, когда скорость изменения магнитного потока Ф/t постоянна.

Важно! Для индукционных токов справедлив закон Ома: I=/R, где — это ЭДС индукции, которую находят по закону ЭИ.

Замечательные опыты, проведенные когда-то знаменитым английским физиком и ставшие основой открытого им закона, сегодня без особого труда способен проделать любой школьник. Для этих целей используются:

магнит,
две проволочные катушки,
источник электроэнергии,
гальванометр.

Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.

Поворачивая, наклоняя и перемещая ее вверх и вниз, мы меняем число силовых линий магнитного поля, пронизывающих ее витки.

Гальванометр регистрирует возникновение электричества с постоянно меняющимися в ходе опыта величиной и направлением.

Находящиеся же относительно друг друга в покое катушка и магнит не создадут условий и для возникновения электричества.

Другие законы Фарадея

На основе проведенных исследований были сформированы еще два одноименных закона:

Суть первого состоит в такой закономерности: масса вещества m , выделяемая электрическим напряжением на электроде, пропорциональна количеству электричества Q, прошедшему через электролит.
Определение второго закона Фарадея, или зависимости электрохимического эквивалента от атомного веса элемента и его валентности формулируется так: электрохимический эквивалент вещества пропорционален его атомному весу, а также обратно пропорционален валентности.

Из всех существующих видов индукции огромное значение имеет обособленный вид данного явления – самоиндукция. Если мы возьмем катушку, которая имеет большое количество витков, то при замыкании цепи, лампочка загорается не сразу.

На этот процесс может уйти несколько секунд. Очень удивительный на первый взгляд факт. Чтобы понять, в чем здесь дело, необходимо разобраться, что же происходит в момент замыкания цепи . Замкнутая цепь словно «пробуждает» электроток, начинающий свое движение по виткам провода. Одновременно в пространстве вокруг нее мгновенно создается усиливающееся магнитное поле.

Катушечные витки оказываются пронизанными изменяющимся электромагнитным полем, концентрирующимся сердечником. Возбуждаемый же в витках катушки индукционный ток при нарастании магнитного поля (в момент замыкания цепи) противодействует основному. Мгновенное достижение им своего максимального значения в момент замыкания цепи невозможно, оно «растет» постепенно. Вот и объяснение, почему лампочка не вспыхивает сразу. Когда цепь размыкается, основной ток усиливается индукционным в результате явления самоиндукции, и лампочка ярко вспыхивает.

Важно! Суть явления, названного самоиндукцией, характеризуется зависимостью изменения, возбуждающего индукционный ток электромагнитного поля от изменения силы текущего по цепи электротока.

Направление тока самоиндукции определяет правило Ленца. Самоиндукция легко сравнима с инерцией в области механики, поскольку оба явления обладают схожими характеристиками. И действительно, в результате инерции под влиянием силы тело приобретает определенную скорость постепенно, а не сиюминутно. Не сразу – под действием самоиндукции — при включении батареи в цепь появляется и электричество. Продолжая сравнение со скоростью, заметим, он так же не способен мгновенно исчезнуть.

Вихревые токи

Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции.

Специалисты знают, что металлические трансформаторные сердечники, якоря генераторов и электродвигателей никогда не бывают сплошными. При их изготовлении на отдельные тонкие листы, из которых они состоят, накладывается слой лака, изолирующий один лист от другого.

Нетрудно понять, какая сила заставляет человека создавать именно такое устройство . Под действием электромагнитной индукции в переменном магнитном поле сердечник пронизывают силовые линии вихревого электрополя.

Представим, что сердечник изготовлен из сплошного металла. Поскольку его электрическое сопротивление невелико, возникновение индукционного напряжения большой величины было бы вполне объяснимым. Сердечник бы в итоге разогревался, и немалая часть электрической терялась бесполезно. Кроме того, возникла бы необходимость принятия специальных мер для охлаждения. А изолирующие слои не позволяют достигать больших величин .

Индукционные токи, присущие массивным проводникам, называются вихревыми не случайно – их линии замкнуты подобно силовым линиям электрополя, где они и возникают. Чаще всего вихревые токи применяются в работе индукционных металлургических печей для выплавки металлов. Взаимодействуя с породившим их магнитным полем, они иногда становятся причиной занимательных явлений.

Возьмем мощный электромагнит и поместим между вертикально расположенными его полюсами, к примеру, пятикопеечную монету. Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды.

Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.

Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды. Передвижение монеты напоминает перемещение тела в вязкой среде. Почему такое происходит.

По правилу Ленца направления возникающих при передвижении монеты вихревых токов в неоднородном магнитном поле таковы, что поле магнита выталкивает монету вверх. Эту особенность используют для «успокоения» стрелки в измерительных приборах. Алюминиевая пластина, находящаяся между магнитными полюсами, прикрепляется к стрелке, и вихревые токи, возникающие в ней, способствуют быстрому затуханию колебаний.

Демонстрацию явления электромагнитной индукции поразительной красоты предложил профессор Московского университета В.К. Аркадьев. Возьмем свинцовую чашу, обладающую сверхпроводящей способностью, и попробуем уронить над ней магнит. Он не упадет, а будет словно «парить» над чашей. Объяснение здесь простое: равное нулю электрическое сопротивление сверхпроводника способствует возникновению в нем электричества большой величины, способных сохраняться продолжительное время и «удерживать» магнит над чашей. По правилу Ленца, направление магнитного поля их таково, что отталкивает магнит и не дает ему упасть.

Изучаем физику — закон электро-магнитной индукции

Правильна формулировка закона Фарадея

Вывод

Электромагнитные силы – это силы, которые позволяют людям видеть окружающий мир и чаще других встречаются в природе, например, свет – тоже пример электромагнитных явлений. Жизнь человечества невозможно представить без данного явления.

На данном уроке, тема которого: «Правило Ленца. Закон электромагнитной индукции», мы узнаем общее правило, позволяющее определить направление индукционного тока в контуре, установленное в 1833 г. Э.X. Ленцем. Также рассмотрим опыт с алюминиевыми кольцами, наглядно демонстрирующий это правило, и сформулируем закон электромагнитной индукции

Приближением или удалением магнита от сплошного кольца мы меняем магнитный поток, который пронизывает площадь кольца. Согласно теории явления электромагнитной индукции, в кольце должен возникнуть индукционный электрический ток. Из опытов Ампера известно, что там, где проходит ток, возникает магнитное поле. Следовательно, замкнутое кольцо начинает вести себя как магнит. То есть происходит взаимодействие двух магнитов (постоянный магнит, который мы двигаем, и замкнутый контур с током).

Так как система не реагировала на приближение магнита к кольцу с разрезом, то можно сделать вывод, что индукционный ток в незамкнутом контуре не возникает.

Причины отталкивания или притягивания кольца к магниту

1. При приближении магнита

При приближении полюса магнита кольцо отталкивается от него. То есть оно ведет себя как магнит, у которого с нашей стороны такой же полюс, как у приближающегося магнита. Если мы приближаем северный полюс магнита, то вектор магнитной индукции кольца с индукционным током направлен в противоположную сторону относительно вектора магнитной индукции северного полюса магнита (см. Рис. 2).

Рис. 2. Приближение магнита к кольцу

2. При удалении магнита от кольца

При удалении магнита кольцо тянется за ним. Следовательно, со стороны удаляющегося магнита у кольца образовывается противоположный полюс. Вектор магнитной индукции кольца с током направлен в ту же сторону, что и вектор магнитной индукции удаляющегося магнита (см. Рис. 3).

Рис. 3. Удаление магнита от кольца

Из данного опыта можно сделать вывод, что при движении магнита кольцо ведет себя также подобно магниту, полярность которого зависит от того, увеличивается или уменьшается магнитный поток, пронизывающий площадь кольца. Если поток возрастает, то векторы магнитной индукции кольца и магнита противоположны по направлению. Если магнитный поток сквозь кольцо уменьшается со временем, то вектор индукции магнитного поля кольца совпадает по направлению с вектором индукции магнита.

Направление индукционного тока в кольце можно определить по правилу правой руки. Если направить большой палец правой руки по направлению вектора магнитной индукции, то четыре согнутых пальца укажут направление тока в кольце (см. Рис. 4).

Рис. 4. Правило правой руки

При изменении магнитного потока, пронизывающего контур, в контуре возникает индукционный ток такого направления, чтобы своим магнитным потоком компенсировать изменение внешнего магнитного потока.

Если внешний магнитный поток возрастает, то индукционный ток своим магнитным полем стремится замедлить это возрастание. Если магнитный поток убывает, то индукционный ток своим магнитным полем стремится замедлить это убывание.

Эта особенность электромагнитной индукции выражается знаком «минус» в формуле ЭДС индукции.

Закон электромагнитной индукции

При изменении внешнего магнитного потока, пронизывающего контур, в контуре возникает индукционный ток. При этом значение электродвижущей силы численно равно скорости изменения магнитного потока, взятой со знаком «-».

Правило Ленца является следствием закона сохранения энергии в электромагнитных явлениях.

Список литературы

Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.

Домашнее задание

Вопросы в конце параграфа 10 (стр. 33) – Мякишев Г.Я. Физика 11 (см. список рекомендованной литературы)
Как формулируется закон электромагнитной индукции?
Почему в формуле для закона электромагнитной индукции стоит знак «-»?

Интернет-портал Festival.1september.ru ().
Интернет-портал Physics.kgsu.ru ().
Интернет-портал Youtube.com ().

Мы достаточно подробно рассмотрели три различных, на первый взгляд, варианта явления электромагнитной индукции, возникновения электрического тока в проводящем контуре под действием магнитного поля: при движении проводника в постоянном магнитном поле; при движении источника магнитного поля; при изменении во времени магнитного поля. Во всех этих случаях закон электромагнитной индукции одинаков:
ЭДС электромагнитной индукции в контуре равна скорости изменения магнитного потока через контур, взятой с противоположным знаком

независимо от причин, приводящих к изменению этого потока.
Уточним некоторые детали приведенной формулировки.
Первое . Магнитный поток через контур может изменяться произвольным образом, то есть функция Ф(t) не обязана всегда быть линейной, а может быть любой. Если магнитный поток изменяется по линейному закону, то ЭДС индукции в контуре постоянна, в этом случае величина интервала времени Δt может быть произвольной, значение отношения (1) в этом случае не зависит от величины этого интервала. Если же поток изменяется более сложным образом, то величина ЭДС не является постоянной, а зависит от времени. В этом случае рассматриваемый интервал времени следует считать бесконечно малым, тогда отношение (1) с математической точки зрения превращается в производную от функции магнитного потока по времени. Математически этот переход полностью аналогичен переходу от средней к мгновенной скорости в кинематике.
Второе . Понятие потока векторного поля применимо только к поверхности, поэтому необходимо уточнять о какой поверхности идет речь в формулировке закона. Однако, поток магнитного поля через любую замкнутую поверхность равен нулю. Поэтому для двух различных поверхностей, опирающихся на контур магнитные потоки одинаковы. Представьте себе поток жидкости, вытекающий из отверстия. Какую бы вы не выбрали поверхность, границей которого являются границы отверстия, потоки через них будут одинаковы. Здесь уместна еще одна аналогия: если работа силы по замкнутому контуру равна нулю, то работа этой силы не зависит от формы траектории, а определяется только ее начальной и конечной точками.
Третье . Знак минус в формулировке закона имеет глубокий физический смысл, фактически он обеспечивает выполнение закона сохранения энергии в этих явлениях. Этот знак является выражением правила Ленца. Пожалуй, это единственный случай в физике, когда один знак удостоился собственного имени.
Как мы показали, во всех случаях физическая сущность явления электромагнитной индукции одинакова и кратко формулируется следующим образом: переменное магнитное поле порождает вихревое электрическое поле . С этой, полевой, точки зрения закон электромагнитной индукции выражается через характеристики электромагнитного поля:циркуляция вектора напряженности электрического поля по любому контуру равна скорости изменения магнитного потока через этот контур

В этой трактовке явления существенно, что вихревое электрическое поле возникает при изменении магнитного поля, независимо от того, имеется ли реальный замкнутый проводник (контур), в котором возникает ток или нет. Это реальный контур может играть роль прибора, для обнаружения индуцированного поля.
Наконец, еще раз подчеркнем − электрические и магнитные поля относительны, то есть их характеристики зависят выбора системы отсчета, в которой дается их описание. Однако, этот произвол в выборе системы отсчета, в выборе способа описания не приводит к каким-либо противоречиям. Измеряемые физические величины инвариантны, не зависят от выбора системы отсчета. Например, сила, действующая на заряженное тело со стороны электромагнитного поля, не зависит от выбора системы отсчета. Но при ее описании в одних системах она может трактоваться как сила Лоренца, в других к ней может «добавляться» электрическая сила. Аналогично (даже как следствие) ЭДС индукции в контуре (сила индуцированного тока, количество выделившейся теплоты, возможная деформация контура и т.д.) не зависят от выбора системы отсчета.
Как всегда предоставляемой свободой выбора можно и необходимо пользоваться − всегда есть возможность выбрать тот метод описания, который вам больше нравится − как наиболее простой, наиболее наглядный, наиболее привычный и т.д.

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока , пронизывающего контур.

Магнитным потоком Φ через площадь S контура называют величину

где B – модуль вектора магнитной индукции , α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называетсявебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м 2:

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Эта формула носит название закона Фарадея .

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца .

Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.

Правило Ленца отражает тот экспериментальный факт, что инд и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью по двум другим сторонам (рис. 1.20.3).

На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен

По определению ЭДС

Для того, чтобы установить знак в формуле, связывающей инд и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.

Если сопротивление всей цепи равно R , то по ней будет протекать индукционный ток, равный I инд = инд /R . За время Δt на сопротивлении R выделится джоулево тепло

Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен F A = I B l . Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа A мех равна

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение . Полная работа силы Лоренца равна нулю . Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не являетсяпотенциальным . Его называют вихревым электрическим полем . Представление о вихревом электрическом поле было введено в физику великим английским физикомДж. Максвеллом в 1861 г.

Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково , но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Вектор магнитной индукции \(~\vec B\) характеризует силовые свойства магнитного поля в данной точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величина называется магнитным потоком и обозначается греческой буквой Φ (фи).

Магнитный поток Φ однородного поля через плоскую поверхность – это скалярная физическая величина, численно равная произведению модуля индукции B магнитного поля, площади поверхности S и косинуса угла α между нормалью \(~\vec n\) к поверхности и вектором индукции \(~\vec B\) (рис. 1):

\(~\Phi = B \cdot S \cdot \cos \alpha .\) (1)

В СИ единицей магнитного потока является вебер (Вб):

1 Вб = 1 Тл ⋅ 1 м 2 .

Магнитный поток в 1 Вб – это магнитный поток однородного магнитного поля с индукцией 1 Тл через перпендикулярную ему плоскую поверхность площадью 1 м 2 .

Поток может быть как положительным, так и отрицательным в зависимости от значения угла α. Поток магнитной индукции наглядно может быть истолкован как величина, пропорциональная числу линий вектора индукции \(~\vec B\), пронизывающих данную площадку поверхности.

Из формулы (1) следует, что магнитные поток может изменяться:

или только за счет изменения модуля вектора индукции B магнитного поля, тогда \(~\Delta \Phi = (B_2 – B_1) \cdot S \cdot \cos \alpha\) ;
или только за счет изменения площади контура S , тогда \(~\Delta \Phi = B \cdot (S_2 – S_1) \cdot \cos \alpha\) ;
или только за счет поворота контура в магнитном поле, тогда \(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 – \cos \alpha_1)\) ;
или одновременно за счет изменения нескольких параметров, тогда \(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 – B_1 \cdot S_1 \cdot \cos \alpha_1\) .

Электромагнитная индукция (ЭМИ)

Открытие ЭМИ

Вам уже известно, что вокруг проводника с током всегда существует магнитное поле. А нельзя наоборот, с помощью магнитного поля создать ток в проводнике? Именно такой вопрос заинтересовал английского физика Майкла Фарадея, который в 1822 г. записал в своем дневнике: «Превратить магнетизм в электричество». И только через 9 лет эта задача была им решена.

Открытие электромагнитной индукции , как назвал Фарадей это явление, было сделано 29 августа 1831 г. Первоначально была открыта индукция в неподвижных друг относительно друга проводниках при замыкании и размыкании цепи. Затем, ясно понимая, что сближение или удаление проводников с током должно приводить к тому же результату, что и замыкание и размыкание цепи, Фарадей с помощью опытов доказал, что ток возникает при перемещении катушек относительно друг друга (рис. 2).

17 октября, как зарегистрировано в его лабораторном журнале, был обнаружен индукционный ток в катушке во время вдвигания (или выдвигания) магнита (рис. 3).

В течение одного месяца Фарадей опытным путем открыл, что в замкнутом контуре возникает электрический ток при любом изменении магнитного потока через него. Полученный таким способом ток называется индукционным током I i .

Известно, что в цепи возникает электрический ток в том случае, когда на свободные заряды действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы, действие которых характеризуется ЭДС, которую называют ЭДС индукции и обозначают E i .

Индукционный ток I i в контуре и ЭДС индукции E i связаны следующим соотношением (законом Ома):

\(~I_i = -\dfrac {E_i}{R},\)

где R – сопротивление контура.

Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции . Если контур замкнут, то вместе с ЭДС индукции возникает и индукционный ток. Джеймс Клерк Максвелл предложил такую гипотезу: изменяющееся магнитное поле создает в окружающем пространстве электрическое поле, которое и приводит свободные заряды в направленное движение, т.е. создает индукционный ток. Силовые линии такого поля замкнуты, т.е. электрическое поле вихревое . Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами .

История

Вот краткое описание первого опыта, данное самим Фарадеем.

«На широкую деревянную катушку была намотана медная проволока длиной в 203 фута (фут равен 304,8 мм), и между витками ее намотана проволока такой же длины, но изолированная от первой хлопчатобумажной нитью. Одна из этих спиралей была соединена с гальванометром, а другая – с сильной батареей, состоящей из 100 пар пластин… При замыкании цепи удалось заметить внезапное, но чрезвычайно слабое действие на гальванометр, и то же самое замечалось при прекращении тока. При непрерывном же прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого-либо индукционного действия на другую спираль, не смотря на то что нагревание всей спирали, соединенной с батареей, и яркость искры, проскакивающей между углями, свидетельствовали о мощности батареи».

См. так же

Васильев А. Вольта, Эрстед, Фарадей //Квант. – 2000. – № 5. – С. 16-17

Правило Ленца

Русский физик Эмилий Ленц в 1833 г. сформулировал правило (правило Ленца ), которое позволяет установить направление индукционного тока в контуре:

возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится препятствовать тому изменению внешнего магнитного потока, вызвавшее данный ток.

индукционный ток имеет такое направление, что препятствует причине его вызывающей.

Например, при увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки, т.е. вектор индукции \({\vec{B}}”\) этого поля направлен против вектора индукции \(\vec{B}\) внешнего магнитного поля. Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с индукцией \({\vec{B}}”\), увеличивающее магнитный поток через витки катушки.

См. так же

Закон ЭМИ

Опыты Фарадея показали, что ЭДС индукции (и сила индукционного тока) в проводящем контуре пропорциональна скорости изменения магнитного потока. Если за малое время Δt магнитный поток меняется на ΔΦ, то скорость изменения магнитного потока равна \(\dfrac{\Delta \Phi }{\Delta t}\). С учетом правила Ленца Д. Максвелл в 1873 г. дал следующую формулировку закона электромагнитной индукции:

ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, пронизывающего этот контур, взятой с противоположным знаком

\(~E_i = -\dfrac {\Delta \Phi}{\Delta t}.\)

Эту формулу можно применять только при равномерном изменении магнитного потока.

Знак «минус» в законе следует из закона Ленца. При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (E i i > 0) (рис. 4, б).

Рис. 4

В Международной системе единиц закон электромагнитной индукции используют для установления единицы магнитного потока. Так как ЭДС индукции E i выражают в вольтах, а время в секундах, то из закона ЭМИ вебер можно определить следующим образом:

магнитный поток через поверхность, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции равная 1 В:

1 Вб = 1 В ∙ 1 с.

ЭДС индукции в движущемся проводнике

При движении проводника длиной l со скоростью \(\vec{\upsilon}\) в постоянном магнитном поле с вектором индукции \(\vec{B}\) в нем возникает ЭДС индукции

\(~E_i = B \cdot \upsilon \cdot l \cdot \sin \alpha,\)

где α – угол между направлением скорости \(\vec{\upsilon}\) проводника и вектором магнитной индукции \(\vec{B}\).

Причиной появления этой ЭДС является сила Лоренца, действующая на свободные заряды в движущемся проводнике. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.

С учетом этого можно сформулировать следующее для определения направления индукционного тока в движущемся проводнике (правило левой руки ):

нужно расположить левую руку так, чтобы вектор магнитной индукции \(\vec{B}\) входил в ладонь, четыре пальца совпадали с направлением скорости \(\vec{\upsilon}\)проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 5).

Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C.344- 351.
Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учрежде-ний с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. – Мн.: Нар. асвета, 2008. – С. 170-182.
Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. – М.: Дрофа, 2005. – С. 399-408, 412-414.

Если через замкнутый проводник или контур будет изменяться магнитный поток Ф, а значит магнитное поле, то в нем будет возникать ЭДС индукции и электрический ток.
Источниками переменного магнитного поля являются:
а) движущийся постоянный магнит;
б)движущийся проводник с постоянным током;
в) неподвижный проводник с переменным током.
Причем, чем быстрее изменяется магнитный поток магнитного поля через контур, тем большая ЭДС индукции, а значит и сила тока возникает в нем, таким образом, величина ЭДС индукции зависит от скорости изменения магнитного потока через контур, т.е.
– это и будет законом электромагнитной индукции, для замкнутого проводника или контура:
“ЭДС индукции ?инд, возникающая в контуре прямо пропорциональна скорости изменения магнитного потока через него”.
Электромагнитная индукция – это создание ЭДС индукции в проводнике, а если он замкнут, то и электрического тока в нем, под действием переменного магнитного поля.
Закон электромагнитной индукции для катушки:
“ЭДС индукции возникающая в катушке прямо пропорциональна числу витков катушки и скорости изменения магнитного потока через нее”. Если прямолинейный проводник будет двигаться в однородном магнитном поле равномерно, то в нем будет возникать ЭДС индукции, величина которой будет определяться по формуле:
где l – длина проводника, – скорость его движения, – угол между направлением и .

“ЭДС индукции возникающая в прямолинейном проводнике равномерно движущимся в однородном магнитном поле с индукцией , прямо пропорциональна длине проводника, скорости его движения, синусу угла между направлениями магнитной индукции магнитного поля и скорости движения проводника в магнитном поле ”.
Знак «-» в законе электромагнитной индукции указывает на направление индукционного тока в замкнутом проводнике, определяемое по правилу Ленца: “Индукционный ток всегда имеет такое направление, что своим магнитным полем препятствует изменению магнитного поля, которое вызвало индукционный ток”. Если магнитное поле, вызвавшее индукционный ток нарастает или увеличивается через замкнутый проводник, то магнитное поле индукционного тока направлено ему противоположно и не будет давать ему нарастать, если же магнитное поле, вызвавшее индукционный ток убывает, то магнитное поле индукционного тока направленно также, как и убывающее магнитное поле и препятствует убыванию магнитного поля вызывающего индукционный ток.
Величина индукционного поля определяется по закону Ома: “Сила индукционного тока прямо пропорциональна ЭДС индукции возникающей в замкнутом проводнике и обратно пропорциональна сопротивлению замкнутого проводника”.
Индукционным током называется ток, полученный в замкнутом проводнике под действием переменного магнитного поля, т.е. благодаря электромагнитной индукции.
Проводник с переменным током в пространстве вокруг себя образует переменное магнитное поле, в котором будет находиться сам проводник с переменным током, поэтому в нем будет возникать ЭДС индукции, которую называют ЭДС самоиндукции, а явление электромагнитной индукции в проводнике с переменным током называют самоиндукцией.
Таким образом, самоиндукция – это частный случай электромагнитной индукции, который имеет место в проводнике с переменным током. Величина ЭДС самоиндукции, возникающая в проводнике с переменным током определяется по закону самоиндукции: “ЭДС самоиндукции, возникающая в проводнике с переменным током прямо пропорциональна скорости изменения силы тока, текущего в проводнике”.
где – скорость изменения силы тока в проводнике, характеризует быстроту изменения тока в проводнике, и показывает на сколько изменяется ток за единицу времени;
L – индуктивность проводника – это характеристика проводника по которому течет переменный ток зависит от размеров и формы проводника, и не зависит от его материала.
L показывает какая ЭДС самоиндукции возникает в проводнике при скорости изменения тока в нем равной единице или какая ?сам возникает в проводнике, если ток в нем изменяется на единицу за единицу времени.
СИ: – это индуктивность такого проводника, в котором возникает ЭДС самоиндукции равная 1 В при изменении тока на 1 А за 1 секунду.
Знак «-» в законе самоиндукции указывает на направление тока самоиндукции, определяемого по правилу Ленца. Например, при замыкании цепи ток увеличивается, возникает ЭДС самоиндукции, которая препятствует нарастанию тока; если же ток уменьшается, что происходит при размыкании цепи, то ЭДС самоиндукции будет поддерживать убывающий ток, не давая ему убывать, поэтому при размыкании цепи большой индуктивности искрит рубильник из-за большого тока самоиндукции, определяемого по закону Ома для тока самоиндукции: .
Вариант №1
1. В каком случае в катушке замкнутой на гальванометр возникает электрический ток?
2. Что определяет закон электромагнитной индукции?
3. От чего зависит ЭДС индукции, возникающая в катушке?

4. В замкнутую катушку вдвигают постоянный магнит: один раз быстро, второй медленно. В каком случае в ней возникнет больший индукционный ток?
5. Что определяют по правилу Ленца? по правилу левой руки? правого винта?
6. Из формул
а)силы Ампера выразить силу тока;
б)силы Лоренца выразить скорость движения частиц;
в) закона индукции электромагнитной индукции выразить изменение магнитного потока.
7. Что такое самоиндукция? Где она имеет место?
8. В каких единицах измеряются
а)магнитная индукция;
б)магнитный поток;
в)ЭДС индукции;
г)индуктивность проводника.
Вариант №2
1. В чем заключается явление электромагнитной индукции?
2. Какое поле создает ЭДС индукции в замкнутом проводнике? Разве может магнитное поле заставить двигаться неподвижные электрические заряды?
3. В каком случае может возникать, а в каком не возникать, ЭДС индукции в прямолинейном проводнике, движущимся в однородном магнитном поле?
4. Почему в проводнике с постоянным током не возникает ЭДС индукции, а в проводнике с переменным возникает?
5. За 3 секунды магнитный поток, пронизывающий проволочную рамку, равномерно увеличивается с 6 Вб до 9 Вб. Чему равно при этом значение ЭДС индукции в рамке?
6. Чему равна ЭДС самоиндукции в катушке индуктивностью L = 3 Гн, при равномерном уменьшении силы тока от 5 А до 1 А за 2 секунды?
Вариант №3
1. Как направлена сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле?
2. Как направлена магнитная индукция внешнего магнитного поля, в котором против часовой стрелки движется отрицательно заряженная частица?
3. Электрон влетел в магнитное поле со скоростью V перпендикулярно линиям магнитной индукции и стал двигаться по окружности радиуса R. Определите величину вектора магнитной индукции магнитного поля. (заряд электрона e, m – масса электрона)
4. Под каким углом расположен проводник с током 3 А длиной 0,1 м в однородном магнитном поле с индукцией 4 Тл, если на него действует сила Ампера равная 0,6 Н?
5. Что происходит с индукционным током в кольце, плоскость которого перпендикулярна линиям магнитной индукции, если ее величина равномерно увеличивается?
6. Чему равна индуктивность проволочной рамки, если при силе тока I = 3 А в рамке возникает магнитный поток Ф = 6 Вб?
7. Катушка сопротивлением 100 Ом, состоящая из 1000 витков площадью 5 см2, внесена в однородное магнитное поле. В течение некоторого времени индукция магнитного поля уменьшилась от 0,8 Тл до 0,3 Тл. Какой заряд будет индуцирован в проводнике за это время?

Модуль изменения магнитного потока

Автор На чтение 13 мин. Опубликовано 12.12.2019

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока , пронизывающего контур.

Магнитным потоком Φ через площадь контура называют величину

где – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).

Рисунок 1.20.1.

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный , создается магнитным полем с индукцией , пронизывающим по направлению нормали плоский контур площадью :

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции , равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Эта формула носит название закона Фарадея .

Рисунок 1.20.2.

Правило Ленца отражает тот экспериментальный факт, что и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.

Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной скользит со скоростью по двум другим сторонам (рис. 1.20.3).

Рисунок 1.20.3.

На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен

Работа силы _Л на пути равна

По определению ЭДС

В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для можно придать привычный вид. За время Δ площадь контура изменяется на Δ = υΔ. Изменение магнитного потока за это время равно ΔΦ = υΔ. Следовательно,

Для того, чтобы установить знак в формуле, связывающей _инд и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.

Если сопротивление всей цепи равно , то по ней будет протекать индукционный ток, равный _инд = _инд/. За время Δ на сопротивлении выделится джоулево тепло

Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен _A = . Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δ эта работа равна

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение . Полная работа силы Лоренца равна нулю . Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным . Его называют вихревым электрическим полем . Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.

Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково , но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

В однородном магнитном поле с индукцией 40 мТл находится плоский контур в виде кольца радиусом 5 см, изготовленный из тонкой проволоки. Сначала контур располагается так, что линии индукции магнитного поля перпендикулярны плоскости кольца. Затем кольцо поворачивают вокруг его диаметра на угол 120°. Найдите модуль изменения потока вектора магнитной индукции через кольцо при таком повороте. Ответ выразите в мкВб и округлите до целого числа.

Магнитный поток через рамку равен произведению площади рамки на величину вектора магнитной индукции и на косинус угла между перпендикуляром к рамке и направлением поля:

Найдём модуль изменения потока вектора магнитной индукции:

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

источник – переменное магнитное поле;
обнаруживается по действию на заряд;
не является потенциальным;
линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :

При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec ) и ( vec ) .

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

определить направление линий магнитной индукции внешнего магнитного поля;
выяснить, как изменяется магнитный поток;
определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

закона электромагнитной индукции;
ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

Эдс индукции в замкнутом контуре это

Электромагнитная индукция (индукция значит наведение) это явление, при котором в замкнутом контуре возникает электрический ток при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было обнаружено в 1831 г.

М. Фарадеем. Ток, возникающий при электромагнитной индукции называют индукционным.

Закон электромагнитной индукцииЭДС индукции в контуре равна скорости изменения магнитного поля сквозь поверхность, ограниченную контуром.

Электромагнитная индукция
1831 г. – М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, – появление, возникновение).
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи
Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или:явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией.
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): . e не зависит от свойств контура: . ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы.

Правило Ленца Возникновение индукционного тока – следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: , где – т.н. индукционное магнитное поле. В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: . Магнитный поток Ф → ΔФ 0). Ток в контуре имеет положительное направление ( ), если совпадает с , (т.е. ΔΦ

Не нашли то, что искали? Воспользуйтесь поиском:

Явление электромагнитной индукции

Явление электромагнитной индукции было открыто М. Фарадеем.

На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Объяснения возникновения индукционного тока

Свойства вихревого электрического поля:

источник – переменное магнитное поле;
обнаруживается по действию на заряд;
не является потенциальным;
линии поля замкнутые.

Магнитный поток

Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :

где ( alpha ) – угол между векторами ( vec ) и ( vec ) .

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Алгоритм решения задач с использованием правила Ленца:

определить направление линий магнитной индукции внешнего магнитного поля;
выяснить, как изменяется магнитный поток;
определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Энергия магнитного поля

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

2. Записать формулу:

закона электромагнитной индукции;
ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

5. Решить полученную систему уравнений относительно искомой величины.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность [1] , краем которой является этот контур. [2][3][4] .

— магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно – в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри [7] , сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10 9 см) [4] . Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz) [ источник не указан 1017 дней ] . Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry) [8] . Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года [ источник не указан 1017 дней ] .

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: (1) где коэффициент пропорциональности L называетсяиндуктивностью контура. При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией. Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ_{μ(N 2 I/l)S . Подставив в (1), найдем (2) т. е. индуктивность соленоида зависит от длиныl солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида. Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и(3) где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем увеличивается, то (dI/dt 0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξ_s >1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.}

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I₁, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда (1) где L₂₁ — коэффициент пропорциональности.

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй: Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый: Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е. (2) Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ_{(N₁I₁/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф₂ = BS = μμ_{(N₁I₁/l)S}}

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков, Поток Ψ создается током I₁, поэтому, используя (1), найдем (3) Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

Закон Фарадея

Концепция закона Фарадея состоит в том, что любое изменение магнитной среды катушки с проволокой вызывает «индуцирование» в катушке напряжения (ЭДС). Независимо от того, как производится изменение, напряжение будет генерироваться. Изменение может быть произведено изменением напряженности магнитного поля, перемещением магнита к катушке или от нее, перемещением катушки в магнитное поле или из него, вращением катушки относительно магнита и т. Д.

Слева вверху на иллюстрации две катушки пронизаны изменяющимся магнитным полем.Магнитный поток F определяется как F = BA, где B – магнитное поле или среднее магнитное поле, а A – площадь, перпендикулярная магнитному полю. Обратите внимание, что для данной скорости изменения потока через катушку генерируемое напряжение пропорционально количеству витков N, через которые проходит поток. Этот пример относится к работе трансформаторов, где магнитный поток обычно следует за железным сердечником от первичной катушки ко вторичной катушке и генерирует вторичное напряжение, пропорциональное количеству витков во вторичной катушке.

По часовой стрелке второй пример показывает напряжение, генерируемое при перемещении катушки в магнитное поле. Иногда это называют «ЭДС движения», и она пропорциональна скорости, с которой катушка перемещается в магнитное поле. Эта скорость может быть выражена через скорость изменения области, находящейся в магнитном поле.

Следующий пример – это стандартная геометрия генератора переменного тока, в которой катушка с проволокой вращается в магнитном поле. Вращение изменяет перпендикулярную площадь катушки по отношению к магнитному полю и генерирует напряжение, пропорциональное мгновенной скорости изменения магнитного потока.При постоянной скорости вращения генерируемое напряжение синусоидальное.

Последний пример показывает, что напряжение можно генерировать, перемещая магнит к катушке с проволокой или от нее. При постоянной площади изменяющееся магнитное поле вызывает генерируемое напряжение. Направление или «смысл» генерируемого напряжения таковы, что любой результирующий ток создает магнитное поле, противодействующее изменению магнитного поля, которое его создало. Это значение знака минус в законе Фарадея, и это называется законом Ленца.

Как мы можем изменить скорость изменения магнитного потока? Напишите любыми двумя способами.

Скорость изменения магнитного потока может быть изменена с помощью:

Очень быстрое вращение магнита
Использование магнита высокой прочности.

Магнитный поток F определяется как F = BA, где B – магнитное поле или среднее магнитное поле, а A – площадь, перпендикулярная магнитному полю. Обратите внимание, что для данной скорости изменения потока через катушку генерируемое напряжение пропорционально количеству витков N, через которые проходит поток.

Поскольку константа пропорциональности равна 1, для равномерной скорости изменения потокосцепления это можно записать как: величина наведенной ЭДС. N = ΔΦ / Δt, где ΔΦ – изменение потока во времени Δt. Чтобы создать высокое напряжение, необходимое для возникновения искры, магнитный поток должен быстро измениться.

Магнитный поток определяется как общее количество силовых линий магнитного поля, проходящих через данную катушку или область. … Магнитный поток обозначается как ΦB, где B – магнитное поле, а его единица – Вебер (Wb).Величина магнитного потока зависит от направления магнитного поля и является векторной величиной. Таким образом, изменение магнитного потока индуцирует ток и напряжение, которые пропорциональны скорости изменения магнитного потока. Это соответствует закону Ома (V = IR). Ток и напряжение в катушке индуцируют поток, который пропорционален току и напряжению.

Потоковая связь может быть рассчитана по магнитному потоку * количеству витков на катушке, и, согласно закону электромагнитной индукции Фарадея, изменение магнитной связи приводит к индукции эл.м.ф. через катушку, равную по величине скорости изменения потокосцепления. Формула электрического потока. Электрический поток через плоскую область определяется как электрическое поле, умноженное на компонент площади, перпендикулярной полю. Электрический поток = электрическое поле * Площадь * (угол между плоской площадью и электрическим потоком) Уравнение: Φ = E A cos (θ)

Читать все

Демонстрационное оборудование

Набор индукционной первичной вторичной обмотки (Science First item # 10-140)
4.Аккумулятор 5V
Гальвонометр
Переключатель
Зажимы Алигатора (4)
Скрепки

Студенты могут задаться вопросом, как работают трансформаторы и генераторы. Здесь описана потенциальная лаборатория или демонстрация принципа электромагнитной индукции Фарадея. Поскольку медные катушки (называемые петлей) содержат изменяющийся электрический заряд, объект, помещенный в электрическое поле, станет заряженным (намагниченным).Когда стержень вставляется и выходит из катушек, магнитное поле вокруг катушки заменены. Это, в свою очередь, заставляет электроны (ток) в катушка двигаться. Это можно наблюдать по чередующемуся (+) и (-) движениям. на гальванометре. Альтернативно или дополнительно устройство можно переконфигурировать так, чтобы электрический ток, генерируемый батареей, проходил через катушку. Стержень обеспечивает направление тока и стабилизирует его.Кроме того, стержень намагничивается, и его можно использовать для захвата небольших металлических предметов, например скрепок.

Справочная информация:

Закон индукции Фарадея

Прописью:

Индуцированная ЭДС (напряжение или разность потенциалов) вокруг замкнутого контура равна мгновенной скорости изменения (производной) магнитного потока через контур.

В форме уравнения:

Есть три способа изменить магнитный поток через петлю:

Изменение напряженности магнитного поля (увеличение, уменьшение) по площади поверхности
Изменить площадь петли (увеличить за счет расширения петли, уменьшить за счет сжатия петли)
Измените угол между поверхностью, определяемой петлей, и вектором магнитного поля.Помните, что поток – это интеграл скалярного произведения между B и dA .

Следовательно, изменение угла либо увеличивает, либо уменьшает поток, потому что скалярное произведение зависит от синуса угла между векторами B и dA . Так работает генератор. Генератор вращает петлю (фактически несколько витков) провода через фиксированное магнитное поле и индуцирует напряжение вокруг петли, быстро изменяя поток через петлю при ее вращении.Это индуцированное напряжение вокруг контуров заставляет ток течь через провод, и это выходной ток генератора.

Знак минус указывает, что индуцированное напряжение направлено в направлении, которое создает ток, противодействующий изменению магнитного потока в контуре. Это соотношение зафиксировано в Законе Ленца.

Закон Ленца :

Индуцированный ток в петле из проволоки будет иметь направление, противоположное изменению потока через петлю.Другими словами, если поток через контур увеличивается, то индуцированный ток создаст свой собственный поток, который будет пытаться компенсировать увеличение потока. Если поток через петлю уменьшается, то индуцированный ток будет в направлении, которое пытается увеличить поток через петлю.

Процедура :

Соберите материалы
Подключите первичную (большую) катушку к гальванометру с помощью алигатора. зажимы
Вводите стержень в катушку и вынимайте из нее и наблюдайте, как гальванометр движется в направлении движения
Измените конфигурацию проводов и зажимов так, чтобы батарея замыкала цепь с большой катушкой.
Продемонстрируйте, что стержень, помещенный в катушку, теперь намагничен и поднимает канцелярские скрепки, тактильные кнопки и скобы.
Используйте то же расположение с батареей, на этот раз используя катушку меньшего диаметра. Обратите внимание, что с большим количеством витков катушка меньшего диаметра будет производить более сильный магнатизм, чем катушка большего размера. Стержень в меньшей катушке захватит больше зажимов.
Записать результаты в таблицу данных
Попросите учащихся ответить на вопросы
Проведите мозговой штурм “реальных” приложений электромагнитных индукция

Физика для науки и техники II

из отдела академических технологий на Vimeo.

Пример – изменение магнитного потока

Мы видели, что если магнитный поток через область, окруженную проводящей петлей, изменяется, то, согласно закону Фарадея, мы получаем индуцированную электродвижущую силу вдоль этой петли. Закон Фарадея гласил, что эта наведенная ЭДС или электромагнитная сила равна отрицательной скорости изменения магнитного потока. Мы сказали, что отрицательный знак появляется из закона Ленца, и он просто утверждает, что связанный индуцированный ток появляется вдоль этой замкнутой проводящей петли, когда магнитный поток изменяется через область, окруженную этой петлей, таким образом, что он противодействует своей причине.

Если мы посмотрим на магнитный поток, который в основном представляет собой вектор магнитного поля, пунктирный с вектором площади из общего определения потока любого вектора величины, происходит изменение магнитного потока – назовем это изменение как Δ Φ B – если происходит изменение магнитного поля, то мы собираемся закончить с изменением потока или магнитное поле может оставаться постоянным, но область, с которой мы имеем дело, может измениться, что опять же приведет к изменению потока или обе эти величины могут измениться.В каждом из этих случаев происходит изменение потока. Следовательно, это приведет к индуцированной электродвижущей силе и соответствующему индуцированному току вдоль замкнутого проводящего контура.

Рассмотрим простой пример. Предположим, что в данной системе поток изменяется как функция времени, и это задано в явной форме как 8 т 3 плюс 6 т 2 плюс 7 веберов. Следовательно, поток, который изменяется относительно этой математической функции как функция времени таким образом, и, если мы заинтересованы в определении индуцированной электромагнитной силы, он будет равен – dΦ B более dt , который будет равен минусу, если вы возьмете производную этой функции по времени, у нас будет 24 t 2 плюс 12 t и производная последнего члена, поскольку это константа, будет равно 0.Таким образом, индуцированная электромагнитная сила также будет изменяться в зависимости от времени, заданного этой величиной.

Если нас интересует наведенная электродвижущая сила при t равна 2 секундам, то мы можем легко вычислить величину этой наведенной электродвижущей силы, подставив 24 t вместо первого члена. Следовательно, у нас будет квадрат 2, умноженный на 24, и плюс для второго члена у нас будет 12 умноженное на 2. Следовательно, индуцированная электродвижущая сила будет равна 2 умноженным на 24, что даст нам 96, плюс 2 умноженное на 12 равно 24, и если вы сложите эти количества, мы получим 120 вольт.

Электромагнитная индукция – Physics A-Level

Изучив этот раздел, вы должны уметь:

рассчитать потокосцепление через катушку с проводом в магнитном поле
объясните, как возникает электромагнитная индукция из-за изменений в потокосцеплении
применять закон Фарадея и закон Ленца

В этом разделе рассматриваются следующие темы

Флюсовая и флюсовая передача

Почти все, что мы делаем, кроме сна в темноте, основано на электромагнитной индукции .Индукция используется для выработки электроэнергии на электростанциях и для преобразования ее напряжения при прохождении через распределительную систему.

Эффекты индукции объясняются с помощью концепции потока . Хотя существование потока уже давно дискредитировано, осознание его значения полезно для понимания законов индукции, изложенных Фарадеем и Ленцем.

Flux представляет собой полезную модель для объяснения эффектов магнитных полей.

Магнитные поля действуют на расстоянии, как гравитационное и электрическое поля.Картины магнитного поля используются, чтобы показать силы, действующие вокруг магнита или электрического тока. Эти силы действуют без какой-либо физической связи между магнитом или током, который вызывает поле, и магнитным материалом или током, помещенным в поле. Во времена Фарадея и Ленца их приписывали эффектам потока.

В настоящее время считается, что эти силы можно отнести к «обмену частицами».

При рисовании диаграмм магнитного поля:

относительная напряженность в разных точках поля показана разделением силовых линий
чем ближе линии вместе, тем сильнее поле
эти силовые линии представляют магнитный поток , который, как представляется, занимает пространство вокруг магнита и отвечает за эффект магнитного поля.

Чтобы интегрировать модель потока с сегодняшним объяснением магнитных эффектов с точки зрения напряженности магнитного поля, это можно представить в терминах плотности потока, представленной концентрацией силовых линий магнитного поля. Плотность потока – это поток на единицу площади, поэтому поток теперь определяется в терминах напряженности магнитного поля и площади, через которую это поле проникает.

КЛЮЧЕВОЙ МОМЕНТ – Магнитный поток Φ, проходящий через область A, определяется как произведение напряженности магнитного поля и площади, перпендикулярной полю.
Φ = B × A
Магнитный поток измеряется в сетках (Wb), где 1 Wb – поток через площадь 1 м ², нормальный к однородному полю с напряженностью 1 T.

Это определение связывает эквивалентность современной концепции напряженности магнитного поля с более старой концепцией «магнитной индукции».

На схеме показан поток через прямоугольную катушку в однородном магнитном поле.

Когда катушка вращается, она «прорезает» магнитный поток или силовые линии и эл.м.ф. индуцируется.

Размер или величина наведенной ЭДС. зависит от:

количество потока через катушку
скорость вращения
количество витков на катушке.

Каждый виток катушки имеет потокосцепление, которое изменяется по мере вращения катушки. Потоковая связь катушки с Н и витками составляет НФ , где Ф – это поток, проходящий через катушку.

Движение катушки параллельно полю не вызывает эл.m.f., поскольку никакие силовые линии не «срезаются». Индуцированная э.д.с. имеет наибольшее значение, когда движение катушки перпендикулярно полю.

Закон Фарадея

Электромагнитная индукция возникает всякий раз, когда изменяется магнитное поле через проводник. Это может быть связано с тем, что проводник движется через магнитное поле, или проводник находится в фиксированном положении в изменяющемся магнитном поле, например, из-за переменного тока.Оба эти результата приводят к ЭДС. индуцируется в проводнике.

Примеры электромагнитной индукции:

перемещение магнита внутри проволочной катушки
генерирование высокого напряжения, необходимого для ионизации пара в люминесцентной лампе и возникновения искры, необходимой для воспламенения взрывоопасной смеси в бензиновом двигателе
изменение напряжения переменного тока с помощью трансформатора.

На электростанции электричество вырабатывается электромагнитом, вращающимся внутри медных катушек.

На диаграмме ниже показана разница в размере ЭДС. когда магнит движется в катушке с разной скоростью.

Закон Фарадея связывает величину наведенной ЭДС. к изменению потокосцепления.

КЛЮЧЕВЫЙ МОМЕНТ – Закон Фарадея гласит, что величина наведенной ЭДС. пропорциональна скорости изменения потокосцепления. Поскольку константа пропорциональности равна 1, для равномерной скорости изменения потокосцепления это можно записать как:

величина индуцированной эл.м.ф. N = ΔΦ / Δt, где ΔΦ – изменение потока во времени Δt.

Для создания высокого напряжения, необходимого для возникновения искры, магнитный поток должен быстро меняться. Это происходит, когда ток в электромагните отключен.

В каком направлении?

Закон Фарадея можно использовать для определения величины наведенной ЭДС. например, через концы крыльев самолета, летящего в магнитном поле Земли. В Британии поле Земли составляет 20 ° с вертикалью, см. Следующую диаграмму.

В отличие от стержневого магнита, магнитное поле Земли направлено с юга на север. Можно считать, что он состоит из двух компонентов: вертикального и горизонтального.

Самолет, летящий в направлении Север-Юг, пересекает только вертикальную составляющую, в то время как полет Восток-Запад включает в себя дополнительно пересечение горизонтальной составляющей.

Индуцированная э.д.с. возникает как следствие действия силы на свободные электроны в металле корпуса самолета.Когда самолет движется по воздуху, движение этих электронов образует ток, противоположный направлению полета. Правило левой руки Флеминга можно использовать для определения направления силы, действующей на электроны, и, следовательно, направления индуцированной ЭДС.

Все заряженные частицы испытывают силу из-за их движения через магнитное поле, но эта сила слишком мала, чтобы воздействовать на что-либо, кроме свободных электронов.

В случае полета самолета с севера на юг:

текущее – юг – север
“разрезаемое” магнитное поле направлено вертикально вниз
сила, действующая на свободные электроны, направлена на восток.

Это приводит к дисбалансу заряда и возникновению напряжения на законцовках крыла. Направление э.д.с. индуцируется в самолете и когда магнит движется в катушку с проволокой, можно рассчитать, используя закон Ленца .

КЛЮЧЕВЫЙ МОМЕНТ – Закон Ленца гласит, что направление индуцированной ЭДС. всегда противостоит изменению, которое его вызывает.

Если наведенная э.д.с. в самолете заставлял электроны течь с запада на восток, это создавало силу в северном направлении – противоположном движению самолета.Этого не происходит, потому что нет полной схемы.

На схеме ниже показано, что когда северный полюс магнита перемещается в один конец катушки, индуцированная ЭДС. вызывает индуцированный ток в направлении против часовой стрелки. Когда ток проходит в катушке, магнитное поле похоже на магнитное поле стержневого магнита, причем северный полюс является концом, где ток проходит против часовой стрелки.

Направление индуцированного тока меняется на противоположное путем изменения направления магнита или направления его движения.

Если бы индуцированный ток был в противоположном направлении, он притягивал бы магнит в катушку и генерировал электричество без подвода энергии.

Закон Ленца – это переформулировка принципа сохранения энергии; индуцированный ток противодействует движению магнита, поэтому необходимо выполнить работу по перемещению магнита против индуцированного магнитного поля. Эта работа представляет собой передачу энергии в цепь, необходимую для возникновения тока.

Объединение законов Фарадея и Ленца дает уравнение для индуцированной e.м.ф .:

КЛЮЧ – Где ε – наведенная ЭДС. Отрицательный знак показывает, что наведенная ЭДС. противостоит вызывающему его изменению потока.

Трансформатор

Трансформаторы используют изменяющиеся магнитные поля для изменения величины переменного напряжения. Переменный ток, протекающий в одной катушке (первичной), вызывает э.д.с. в соседней катушке (вторичной).

На диаграмме ниже показан поток, когда две катушки намотаны на железный сердечник.

Э.д.с. индуцируется независимо от наличия вторичной цепи. Если есть замкнутая цепь, есть также индуцированный ток.

В трансформаторе:

переменный ток в первичной обмотке создает переменное магнитное поле
это усилено железным сердечником с высокой проницаемостью
флюс концентрируется в чугуне
ЭДС индуцируется во вторичной обмотке из-за изменения магнитной связи.

Железо легко намагничивается; его магнитные домены вносят вклад в силу магнитного поля.

Из последнего пункта следует, что индуцированная ЭДС. пропорционально количеству витков вторичной обмотки.

КЛЮЧЕВЫЙ МОМЕНТ – Соотношение между напряжениями и количеством витков для идеального трансформатора составляет:

Трансформатор, построенный из катушек с низким сопротивлением на многослойном железном сердечнике, близок к идеалу.

Это означает, что напряжения находятся в том же соотношении, что и количество витков. В идеальном трансформаторе нет потерь энергии в проводах или сердечнике, поэтому выходная мощность вторичной обмотки равна мощности, потребляемой первичной обмоткой, а токи обратно пропорциональны напряжению.

ПРОВЕРКА ПРОГРЕССА

Страница не найдена | MIT

Перейти к содержанию ↓
Образование
Исследовательская работа
Инновации
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О Массачусетском технологическом институте
Подробнее ↓
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О Массачусетском технологическом институте
Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Напряженность электрического поля при циркуляции
Вторая предельная ситуация, типичные для рассматриваемых магнитоквазистатических систем, в первую очередь касается обращения E , и, следовательно, часть электрического поля, создаваемого изменяющимся во времени магнитным потоком плотность.Примечателен тот факт, что закон Фарадея справедлив для любого контур, будь то в свободном пространстве или в материале. Однако часто интересующий контур совпадает с токопроводящим проводом, состоящим из катушка, которая связывает плотность магнитного потока.
Иллюстрация. Терминальная ЭДС катушки
Катушка с одним витком представлена на рис. 1.6.3. Контур (1) есть внутри провода, а (2) соединяет клеммы по заданному пути. С этими контурами, составляющими C , интегральный закон Фарадея, заданный формулой (1) определяет конечную электродвижущую силу.Если электрическая сопротивление провода можно считать нулевым в том смысле, что Напряженность электрического поля внутри провода незначительна, контур интеграл сводится к интегрированию от (b) до (a).
⁵ С здесь цели ограничиваются приданием интуитивного значения Закон Фарадея, уделим особое внимание условиям требуется для выполнения этого терминального отношения в гл. 8, 9 и 10.
С учетом определения ЭДС, (2), эта интеграция дает отрицательную величину ЭДС.Таким образом, закон Фарадея дает терминальную ЭДС как
Рисунок 1.6.3. Отрезок (1) через идеально проводящий провод и (2) соединение клемм (a) и (b) образуют замкнутый контур.
где _f , полный поток магнитного поля, соединяющего катушку, равен определяется как потокосцепление. Обратите внимание, что закон Фарадея делает это возможно измерение _o H электрически (как сейчас показано).
Демонстрация 1.6.1. Показания вольтметра, индуцированные магнитной индукцией
Прямоугольная катушка, показанная на рис. 1.6.4, используется для измерения напряженность магнитного поля, связанная с током в проводе. Таким образом расположение и поле такие же, как в Демонстрации 1.4.1. В высота и длина змеевика составляют х и л , как показано, и потому катушка имеет Н виток, она связывает поток, заключенный на один виток Н раз. С верхними проводниками катушки на расстоянии R от провода, а напряженность магнитного поля принимается равной силе линейного тока, дается формулой (1.4.10) оценка (8) дает
Рисунок 1.6.4. Демонстрация показаний вольтметра индуцируется на выводах катушки в соответствии с законом Фарадея. К нанести данные на график, нормализовать напряжение до В _o , как определено в (11). Поскольку I – это пиковый ток, В, – это пиковое напряжение.
В эксперименте ток принимает вид
где = 2 (60) . ЭДС между клеммами тогда следует из (8) и (9) как
Вольтметр считывает электродвижущую силу между двумя точками, чтобы с которым он связан, при соблюдении определенных условий.Мы обсудим это в гл. 8.
В типичном эксперименте с использованием 20-витковой катушки с размерами h = 8 см, l = 20 см, I = 6 ампер пик, пиковое напряжение, измеренное при терминалы при шаге R = 8 см составляет v = 1,35 мВ. Чтобы поставить эту точку данных на на нормализованном графике рис. 1.6.4, обратите внимание, что R / h = 1 и измерено об / об _o = 0,7 .
Условие непрерывности Фарадея
Из интегрального закона Фарадея следует, что касательная электрическая поле непрерывно по поверхности неоднородности при условии, что напряженность магнитного поля конечна в окрестность поверхности разрыва.Это можно показать, применив интегральный закон к приращению поверхность, показанная на рис. 1.4.7, так же, как это было сделано в п. 1.4 для Закон Ампера. Если J установлено равным нулю, существует формальный аналогия между интегральным законом Ампера (1.4.1) и законом Фарадея интегральный закон, (1). Первое становится вторым, если H E , J 0 и _o E – _o H . Таким образом, условие непрерывности Ампера (1.4.16) становится непрерывностью условие, связанное с законом Фарадея.

Формула ЭДС индукции, E

Закон Фарадея – Максвелла для электромагнитной индукции

Частные случаи формул ЭДС индукции

Примеры решения задач по теме «ЭДС индукции»

Репетитор-онлайн — подготовка к ЦТ

Величина равная скорости изменения магнитного потока. Изменение магнитного потока создает электрическое поле

(adsbygoogle=window.adsbygoogle||[]).push({});Задача обучения

Основные пункты

Термины

Дифференциальная форма закона Фарадея

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Явление электромагнитной индукции. Закон Фарадея

Открытие ЭИ

Явление ЭИ

Закон

Другие законы Фарадея

Вихревые токи

Вывод

Электромагнитная индукция (ЭМИ)

Открытие ЭМИ

История

Правило Ленца

См. так же

Закон ЭМИ

ЭДС индукции в движущемся проводнике

Литература

Модуль изменения магнитного потока

Явление электромагнитной индукции

Магнитный поток

Закон электромагнитной индукции Фарадея

Правило Ленца

Самоиндукция

Индуктивность

Энергия магнитного поля

Основные формулы раздела «Электромагнитная индукция»

Эдс индукции в замкнутом контуре это

Явление электромагнитной индукции

Магнитный поток

Закон электромагнитной индукции Фарадея

Правило Ленца

Самоиндукция

Индуктивность

Энергия магнитного поля

Основные формулы раздела «Электромагнитная индукция»

Обозначение и единицы измерения

Закон Фарадея

Как мы можем изменить скорость изменения магнитного потока? Напишите любыми двумя способами.

Демонстрационное оборудование

Физика для науки и техники II

Электромагнитная индукция – Physics A-Level

Страница не найдена | MIT

Напряженность электрического поля при циркуляции

Иллюстрация. Терминальная ЭДС катушки

Демонстрация 1.6.1. Показания вольтметра, индуцированные магнитной индукцией

Условие непрерывности Фарадея

Оставить комментарий Отменить ответ

Задача обучения