Скорость материальной точки: Скорость материальной точки – формула - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

§2.1. Скорость материальной точки при равномерном движении по прямой

Пусть некоторое тело, которое можно считать материальной точкой, движется вдоль заданной прямой. Для описания его движения направим ось X декартовой системы координат вдоль этой прямой (которая является траекторией движения), выберем также на этой оси начало отсчета. Положение тела однозначно определяется одной координатой, поэтому закон движения в данном случае представляет собой одну функцию зависимость координаты x от времени t – x(t). Рассмотрим наиболее простой вид движения – равномерное.

Равномерным называется такое движение точки, при котором за любые равные промежутки времени она проходит равные пути.

При таком движении легко определить физическую характеристику быстроты движения – скорость.

Скоростью равномерного движения называется отношение пути, пройденного телом, к интервалу времени, за который этот путь пройден.

Эту величину также называют путевой скоростью.

При равномерном движении это отношение не зависит от рассматриваемого промежутка времени, так как пройденный путь пропорционален временному интервалу. Можно дать еще одно истолкование скорости – скорость тела равна пути, пройденному телом за единицу времени.

Скорость – есть физическая величина, имеющая в системе СИ размерность м/с (метр в секунду). Кроме этой единицы измерения скорости довольно часто используется внесистемная единица – км/час, а в некоторых странах миль/час.

Величина пройденного пути S показывает, на сколько сместилось тело, но не указывает направление этого смещения. Используя введенные координаты, можно определить смещение тела как изменение его координаты. Изменение координаты может быть как положительным (при увеличении значения координаты), так и отрицательным (при ее уменьшении). Таким образом, знак величины ?x просто указывает направление движения, в положительном, либо отрицательном направлении оси X.

Очевидно, что путь, пройденный материальной точкой при движении вдоль оси в одном направлении, связан с изменением координаты соотношением.

Соответствующим образом можно переопределить и скорость движения – скорость равномерного движения вдоль прямой равна отношению изменения координаты к промежутку времени, в течение которого это изменения произошло.

Заметьте, для величины интервала времени мы также используем обозначение t – разность между показаниями часов в конечный и начальный момент времени. В данном определении скорость может быть положительной (если тело движется в положительном направлении оси) и отрицательной (при движении в противоположном направлении). Таким образом, знак скорости указывает направление движения, а ее модуль сохраняет прежнее значение – путь, пройденный в единицу времени.

Коротко о главном:

Равномерным называется такое движение точки, при котором за любые равные промежутки времени она проходит равные пути. При таком движении легко определить физическую характеристику быстроты движения – скорость. Скоростью равномерного движения называется отношение пути, пройденного телом, к интервалу времени, за который этот путь пройден. Эту величину также называют путевой скоростью.

Контрольные вопросы:

1. Что такое равномерное движение?

2. На что указывает знак скорости?

3. Чем определяется скорость движения?

Скорость материальной точки – Энциклопедия по машиностроению XXL

Задачи, в которых рассматривается движение материальной точки под действием некоторой заданной силы (постоянной или переменной) в сопротивляющейся среде, причем сила сопротивления среды зависит от скорости материальной точки. [c.257]

Как уже указывалось р. предыдущих параграфах, сила —результат сложных физических процессов, обусловливающих взаимодействие материальных объектов. Механика не изучает физическую природу этих взаимодействий. Поэтому силы как функции положений и скоростей материальных точек или тел в каждой конкретной механической задаче считаются известными — их определяют в иных дисциплинах.

[c.62]

И (или) скорости материальных точек или тел, и треб> ется учесть эти ограничения. [c.66]

Несколько сложнее обстоит дело для внутренних точек плато С. Если отклонить материальную точку из С так, чтобы она еще осталась на плато , и не сообщать ей начальной скорости, то материальная точка останется в равновесии в новой точке плато но если сообщить ей начальную скорость, то, как бы ни была мала эта скорость, материальная точка, двигаясь вдоль плато , выйдет за пределы малой окрестности положения равновесия и сойдет с плато .

[c.217]

Это значит, что при определении ускорения материальной точки можно пользоваться методом суперпозиции (наложения).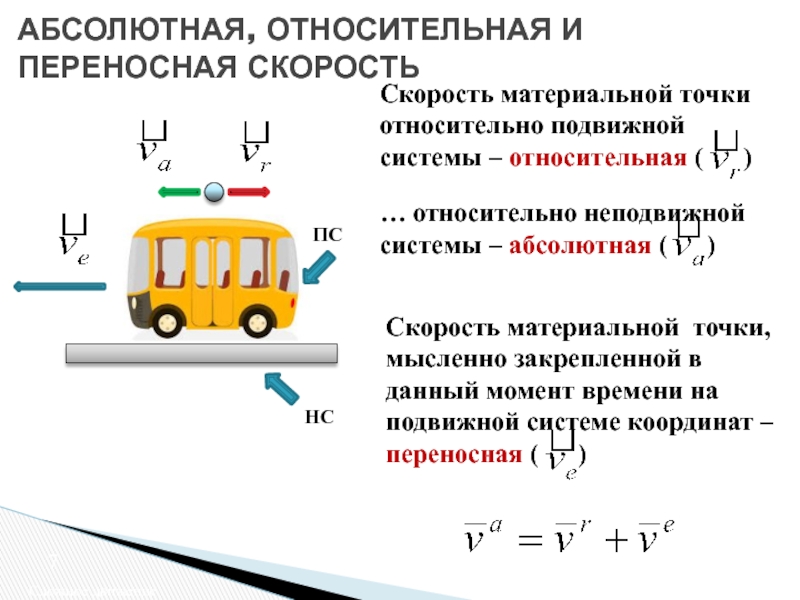 Следует иметь в виду, что при определении скорости материальной точки аналогичная суперпозиция не имеет места, т. е. скорость материальной точки не равна векторной сумме скоростей, которые имела бы эта точка при действии каждой из сил в отдельности. [c.11]

На рисунке кориолисова сила инерции не изображена. Мы не можем сейчас указать ее направление, так как 7 = —2/и(0 X л> а направление скорости материальной точки в относительном движении Ф,. нам пока неизвестно.)

[c.139]

Теорему об изменении количества движения материальной точки применяют в задачах, где силы постоянны, либо являются известными функциями времени, а в число данных и неизвестных величин входят масса (вес) материальной точки, силы, приложенные к точке, промежуток” времени действия сил, скорости материальной точки в начале и в конце этого промежутка времени. [c.538]

Здесь т — мгновенное значение массы материальной точки т — скорость материальной точки и — скорость присоединяющихся илй

[c. 576]

Поэтому, в отличие от скорости материальной точки или точки произвольно движущегося тела, которая есть вектор, приложенный к этой точке в данном ее положении, скорость твердого тела, движущегося поступательно, есть вектор свободный, ибо он может быть приложен к любой точке тела. Только в случае поступательного движения и можно говорить о скорости тела как целого. Траектории всех точек тела в этом случае суть конгруэнтные кривые, т. е. такие кривые, которые при наложении совпадают всеми своими точками. [c.95]

Скорость материальной точки, движущейся под действием центральной силы. Известно, что в полярных координатах г и ф скорость точки выражается формулой

[c.384]

Знание коэффициента восстановления позволяет замкнуть задачу о вычислении скачка скорости материальной точки при наложении связи, идеальной при ударе. Такой будет, например, любая связь, идеальная по отношению к конечным силам реакции. В самом деле, сила, с которой такая связь действует на материальную точку, всегда направлена по нормали к связи. Поэтому и удар из-за ее наложения, вычисляемый с помощью соответствующего предельного перехода, будет направлен по нормали. [c.293]

Другой пример периодического движения с соударениями можно построить, воспользовавшись решением примера 3.5.2. Пусть х = / /2 — длина горизонтальной хорды, находящейся ниже центра окружности, ограничивающей область свободного движения. Пусть VI — скорость материальной точки в пересечении хорды с окружностью. Обозначим Ь = у (/д максимальную горизонтальную дальность бросания и 3 начальный угол наклона скорости к горизонту. Если ж [c.297]

Может ли первый интеграл вообще не зависеть от скоростей материальных точек Как тогда найти его производную в силу уравнений движения [c.299]

Следовательно, скорость материальной точки может получить ко ечное изменение лишь в том случае, если будет конечным импульс мгновенной силы у. Обозначим этот импульс через

[c.127]

Уравнение (3) называют основным уравнением динамики точки при ударе. Из этого уравнения для скорости материальной точки в конце удара находим [c.481]

Момент начала фазы вос-становления совпадает с концом фазы деформации, поэтому в начале фазы восстановления скорость материальной точки равна й,, скорость в конце фазы й. Скорость й является и скоростью точки в конце всего удара. Материальная точка удаляется с поверхности благодаря ударному импульсу реакции поверхности за вторую фазу удара. Этот импульс обозначим а- Он направлен также, как и импульс т. е. 5а 1. Таким образом, за фазу восстановления с материальной точки снимается связь ударом, импульс которого перпендикулярен к скорости точки.

[c.488]

Скорости материальной точки относительно различных инерциальных систем отсчета разные, но нет возможности из наблюдений за движением материальной точки в различных системах отсчета сделать утверждение, какая из инерциальных систем отсчета является основной, неподвижной, а какая — подвижной. [c. 252]

Определить, модуль начальной скорости материальной точки, при которой ее свободные колебания будут соответствовать закону движения, заданному графиком функции у = = j(r). (-1,05) [c.207]

Материальная точка М массой т движется под действием силы тяжести по внутренней поверхности полуцилиндра радиуса г = 0,2 м. Определить скорость материальной точки в точке В поверхности, если ее скорость в точке А равна нулю. (1,98) [c.253]

Приведем некоторые физические эксперименты, позволяющие найти аналитическую зависимость между количеством движения, скоростью материальной точки и ее массой. [c.224]

Дифференцирование векторов. Скорость материальной точки V — вектор, ускорение а также является вектором. Скорость — это характеристика изменения положения материальной точки со временем. Положение материальной точки в любой момент времени t можно определить с помощью вектора г(/), который соединяет с данной точкой определенную неподвижную точку О,. называемую началом отсчета. С течением времени материальная точка движется, а вектор, характеризующий ее положение,, изменяется по направлению и по величине (рис. 2.6). Разность между г( г) и r(/i) — это разность двух векторов [c.42]

Абсолютное значение скорости v (или, что то же самое, модуль вектора скорости lv ) называется числовым значением скорости материальной точки. Числовое значение скорости — скаляр. [c.43]

Для того чтобы получить значение вектора скорости материальной точки, движущейся по окружности, мы используем формулу (10), но при этом dr/dt = Q, так как радиус г окружности постоянен. Тогда из (12) и (13) следует [c.45]

Здесь мы использовали тождество sin a + os a s 1. Таким образом, получен важный результат, согласно которому числовое значение скорости материальной точки при равномерном круговом движении равно [c.46]

Если скорость материальной точки имеет в некоторый момент времени разрыв, т. е. ее величина или направление резко изменяется, то говорят, что [c.191]

Дополняя динамику свободных тел Ньютона, Даламбер (1717—1783) рассматривает несвободные тела как окруженные действуюш,ими на них другими телами. Определяя движение тела как скорость тела с учетом ее направления , т. е. как вектор скорости материальной точки, Даламбер отличает передаваемое телу движение от действительно воспринимаемого телом движения и поясняет, что из-за действия на данное тело окружающих его тел часть движения, определяемая разностью между передаваемым и воспринимаемым, не может быть воспринята телом и является потерянной . [c.345]

ЧТО неизменной остается н относительная скорость этих двух точек. Вспоминая теперь, что силы F в механике Ньютона зависят только от относительных положений и относительных скоростей материальных точек (тел), найдем, что в результате преобразования Галилея не изменяется и правая часть (1).

Таким образом, это преобразование оставляет уравнение (1 инвариантным, т. е. сохраняющим свой вид в любой из возможных инерциальных систем отсчета. Иначе говоря, движение материальной точки (тела) в двух произвольных инерциальных системах происходит по одинаковым законам в одной — в переменных r,t), в другой — в переменных причем, но Ньютону, t — t, а г связан с г преобразованием Галилея. [c.445]

Из принципа относительности Галилея следует, что в рамках классической механики понятие скорости не может иметь абсолютного смысла. Однако, если существует мировой эфир как всепроникающая материальная среда, то система отсчета, связанная с эфиром, будет иметь преимущественное значение по сравнению со всеми инерциальными системами и скорость материальной точки в этой системе будет абсолютной скоростью точки в пространстве. Если это действительно так, то можно найти способы измерения абсолютной скорости или, как было принято говорить, обнаружения эфирного ветра . [c. 204]

Из определения векторного произведения следует, что вектор с —скользящий, если векторы а и Ь — связанные, и связанный, если один из векторов а пли Ь—скользящий. Так, например, вектор v линейной скорости материальной точки тела (связанный вектор) есть векторное произведение радиуса-вектора г (связанного вектора) и угловой скорости вращения тела м (скользящего вектора) [c.293]

Вектор V направлен по касательной к траектории (в точке 0 ) осевой линии. Отличие формулы (1.22) (скорости элемента стержня) от скорости материальной точки заключается в том, что в (1.22) и г и V есть функции двух независимых переменных х и /. Например, если координата х точки О, осевой линии стержня при его движении остается неизменной (от 1 не зависит), то из (1-12) получаем [c.16]

Скорости материальной точки отпостельпо различных инерциальных систем отсчета разные, но нет возможности из [c.248]

Пусть в начальный мом( нт 0 = 0о, ф = 0. Тогда ф = onst и 0 = 00, т. е. движение будет происходить по меридиану (например, по меридиану (рис. 8.1). Скорость материальной точки равна [c.224]

Из равенства, (45) видно, что при движении в консервативном поле скорость материальной точки является функцией только ее положения. В частности, точка, движущаяся в консервативном поле по замкнутому пути, будет, приходя в данное положение j (см. рис. 323) иметь в нем всегда одну и ту же скорость сколько бы циклов (оборотов) точка ни совершила. Отсюда вытекает невозможность построения вечного двигателя (perpetuum mobile), т. е. машины, которая могла бы передавать движение другому объекту (совершать работу) вечно, без притока энергии извне. [c.342]

Связи, уравнения которых содержал скорости материальных точек, называются дифференциальными. Ес.чи выполнено условие дФj/д1 = о, то соответствующие связи называются етационарными. [c.306]

Механика, конечно, не ограничивается изучением только систем с идеальными связями. Однако подчеркнем, что лишь для определения реакций идегильных связей достаточно задать уравнения этих связей. При исследовании систем с неидеальными связями кроме ограничений на значения координат и скоростей материальных точек необходимо сформулировать некоторые дополнительные сведения о реакциях. Примером могут служить задачи о движении или равновесии систем с трением. [c.339]

Очевидно, что эта сила зависит от величины и направления скорости материальной точки относительно Земли. Эта сила будет отсутствовать в двух случаях когда точка находится в покое (Vqth = = 0) и когда векторы и и v коллинеарны. [c.139]

Рис. 2,8. Материальная точка движется по окруж иостн единичного радиуса с угловой скорвстью (О. Скорость материальной точки определяется по формуле (19), а ее ускорение—по формуле (22).

Определить скорость материальной точки Л/ в тот момент времени, когда она достигнет точки В на цилнидричоской но-ьерхиости, если ф == 4.

°. [c.263]

Из Уравнения (1.136), представляющего собой выражение закона кинетической энергии для частного случая, когда начальная скорость материальной точки равна нулю, следует, что работа силы на некотором прти равна приращению кинетической энергии на том же пути. [c.170]

Задача С1. Начальная скорость материальной точки

Задача С1. Начальная скорость материальной точки 4 м/с. Вначале точка движется замедленно с модулем ускорения . Найти весь путь, который она проделает за 10 с, двигаясь с постоянным по модулю ускорением?

Обозначим начальную скорость точки, а — ускорение, t — все время движения, S — весь пройденный путь, v — скорость в конце движения с замедлением, — время движения с замедлением, — путь, пройденный точкой до остановки, — путь, пройденный точкой после остановки.

Решение:

На вид простая задачка. Применить формулу пути равноускоренного движения со знаком «минус» перед ускорением — и все решение. Что ж, давайте попробуем:

Но позвольте, путь не бывает отрицательным. Путь это длина траектории, а длина может быть только положительной величиной. Значит, наше решение неверно.

Тогда давайте думать дальше. Точка двигалась равнозамедленно, а такое движение оканчивается остановкой. Интересно, сколько времени она двигалась до остановки. Это время несложно определить из формулы скорости равноускоренного движения, если конечную скорость и приравнять нулю, а перед ускорением а поставить минус. Тогда получим:

Давайте вычислим, сколько времени точка двигалась до остановки:

Вот оно что: из 10 с движения точка двигалась с замедлением всего с, после чего она еще двигалась равноускоренно без начальной скорости и с прежним по модулю ускорением. Тогда весь путь S, проделанный точкой, можно представить как сумму пути , пройденного равнозамедленно в течение времени , в конце которого точка остановилась, и пути , пройденного равноускоренно без начальной скорости в течение времени :

Обратите внимание, что если при равнозамедленном движении тело в конце останавливается, то для определения его пути укороченная формула применима, несмотря на то, что начальная скорость здесь не равна нулю.

Мы решили задачу в общем виде. Подставим числа и вычислим:

Ответ: S = 26 м.

Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти задачи:

Задача В9. Частота вращения колеса увеличилась. Как изменились его угловая скорость, линейная скорость точек обода колеса и их центростремительное ускорение?

Задача В10. Винт самолета вращается с частотой 1800 об/мин. Посадочная скорость самолета 54 км/ч, длина посадочной линии 700 м. Сколько оборотов сделает винт за время торможения?

Задача C2. Ракета стартовала с земли вертикально вверх, двигаясь равноускоренно с ускорением . Через 10 с двигатель ракеты заглох. Через сколько времени она упадет на землю? Сопротивлением воздуха пренебречь.

Задача СЗ. Колонна солдат длиной 20 м движется по шоссе со скоростью 3,6 км/ч.

Командир, находящийся в хвосте колонны, посылает солдата с вопросом к сержанту, шагающему во главе колонны. Солдат бежит туда и обратно со скоростью, превышающей скорость колонны на 20%. Через сколько времени солдат доставит командиру ответ сержанта, если он слушал его в течение 0,5 мин?

1.5. Скорость – Лекции по физике

Для характеристики движения материальной точки вводят векторную физическую величину – скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.

Пусть материальная точка движется по криволинейной траектории МN так, что в момент времени t она находится в т.М, а в момент времени в т. N. Радиус-векторы точек М и N соответственно равны , а длина дуги МN равна (рис. 1.3).

Вектором средней скорости точки в интервале времени от t до t+Δt называют отношение приращения радиуса-вектора точки за этот промежуток времени к его величине :

(1.

Вектор средней скорости направлен также, как вектор перемещения т.е. вдоль хорды МN.

Мгновенная скорость или скорость в данный момент времени. Если в выражении (1.5) перейти к пределу, устремляя к нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.

(1.6)

В процессе уменьшения величины точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектор и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.

(1.7)

где – проекции вектора скорости на оси координат х, у, z.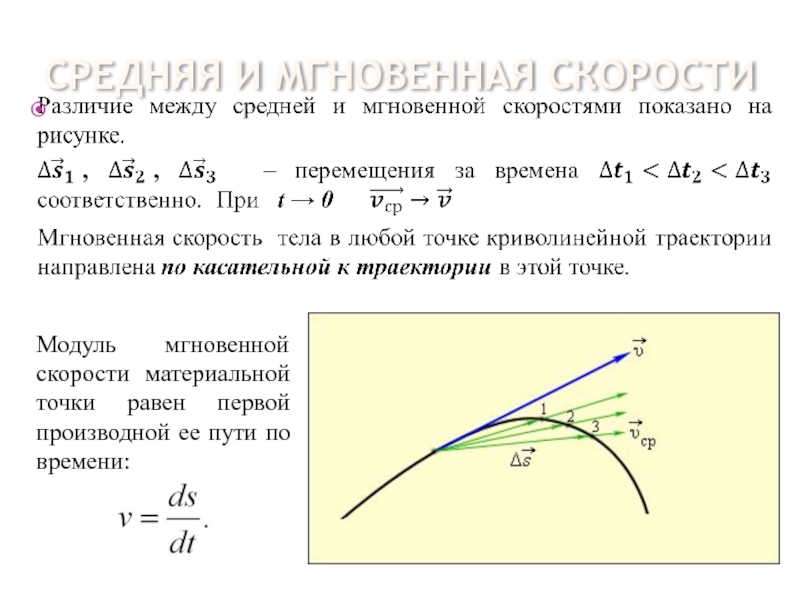

Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:

(1.8)

Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:

(1.9)

Поэтому численное значение скорости:

(1.10)

Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.

Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.

В этом случае часто пользуются скалярной величиной , называемой средней путевой скоростью неравномерного движения на данном участке траектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение пути затрачивается то же время , что и при заданном неравномерном движении:

(1.11)

Т.к. только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае:

Закон сложения скоростей. Если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещения в соответствии с законом независимости движения, равно векторной (геометрической) сумме элементарных перемещений, обусловленных каждым из этих движений в отдельности:

В соответствии с определением (1.6):

(1.

12)

Таким образом, скорость результирующего движения равна геометрической сумме скоростей всех движений, в которых участвует материальная точка, (это положение носит название закона сложения скоростей).

(PDF) Метод материальных точек: основы и приложения

7 ПРИМЕРЫ 7.3 Удар двух упругих тел

нм ome ntu m (id,:) + = N (i) ∗ Mp (pid) ∗ vp (pid,:) ;

n i f o r c e (id, 1) – = Vp (p i d) ∗ (s t r e s s (1) ∗ d NI dx + s t r e s s s (3) ∗ dNIdy);

n i f o r c e (id, 2) – = Vp (p i d) ∗ (s t r e s s (3) ∗ d NI dx + s t r e s s (2) ∗ dNIdy);

en d

Листинг 9: Двумерный MPM: узлы для частиц.

f o r e = 1: e le m C o u nt% l o o p o v e r e l e m e n t s

e s c t r = e l e m e n t (e,:);

e no d e = no d e (e s c t r,:);

m p ts = m p o i n t s {e};

% л о п о в е р п а р т и к л е с

для п = 1: л е н г т ч (м пт с)

п и д = м п тс (п);

p t (1) = (2 ∗ xp (p i d, 1) – (e n od e (1, 1) + e no d e (2, 1))) / d e l t a X;

p t (2) = (2 ∗ xp (p i d, 2) – (e n od e (2, 2) + e no d e (3, 2))) / d e l t a Y;

[N, d Nd xi] = l a g r a n g e _ b a s i s (’Q4’, p t);

J 0 = en o de ’∗ dN dxi;

i n v J 0 = i n v (J 0);

dNdx = d N dxi ∗ i n v J 0;

Lp = нули (2, 2);

f o r i = 1: l e n g t h (e s c t r)

i d = e s c t r (i); % номер ID

v I = [0 0];

i f n ma s s (i d)> t o l

v p (p i d,:) + = d t i m e ∗ N (i) ∗ n i f o r c e (id,:) / nmas s (i d);

x p (p i d,:) + = d t i m e ∗ N (i) ∗ nm ome ntu m (i d,:) / n m как s (i d);

v I = нм ome ntu m (i d,:) / нм as s (i d); % n o d a l v e l o c i t y

en d

Lp = L p + v I ’∗ d Ndx (i,:); % п а р т и к л е г р а д и е н т в е л о к и т у

F = ([1 0; 0 1] + Lp ∗ dt i m e) ∗ r e s h a p e (Fp (p i d,:), 2, 2);

Fp (p i d,:) = r e s h a p e (F, 1, 4);

Vp (p i d) = d e t (F) ∗ V p0 (p i d);

d Ep s = d t i m e ∗ 0. 5 * (L p + Lp ’);

ds i g ma = C ∗ [d Ep s (1, 1); dE ps (2, 2); 2 ∗ d Ep s (1, 2)];

s (p i d,:) = s (p i d,:) + d s ig m a ’;

ep s (p i d,:) = e ps (p id,:) + [d E ps (1, 1) dEp s (2, 2) 2 ∗ dE ps (1, 2)];

en d

Движение двух дисков показано на рис. 18. Столкновение происходит физически реалистичным образом

, хотя закон контакта не указан. На рис. 19 показана эволюция кинетической,

деформации и полной энергии.

Разработка метода неявной материальной точки для геотехнических приложений

https://doi.org/10.1016/j.compgeo.2015.08.008Получение прав и содержания

Аннотация

Метод неявной материальной точки (MPM), a Вариант метода конечных элементов (МКЭ) представлен в данной статье. Ключевой особенностью MPM является то, что пространственная дискретизация использует набор материальных точек, которым разрешено свободно перемещаться через фоновую сетку. Все зависящие от истории переменные отслеживаются в материальных точках, и эти материальные точки используются как точки интегрирования, аналогичные точкам Гаусса. Используется алгоритм сопоставления и повторного сопоставления, позволяющий отображать переменные состояния и другую информацию взад и вперед между материальными точками и узлами фоновой сетки во время анализа. В отличие от схемы явного интегрирования по времени, используемой большинством исследователей, здесь использовалась схема неявного интегрирования по времени. У такого подхода двоякие преимущества: во-первых, он решает проблему ограничения размера временного шага, присущего схемам явного интегрирования, тем самым потенциально экономя значительные вычислительные затраты для определенных типов задач; во-вторых, это позволяет повысить точность алгоритма, что важно для некоторых основных характеристик, таких как эластопластичность.Основная цель этой статьи – предоставить единую структуру MPM, в которой могут быть решены как квазистатический, так и динамический анализ, а также продемонстрировать поведение модели. Реализация близко следует стандартным подходам FEM, где это возможно, чтобы обеспечить легкое преобразование других кодов FEM. Метод Ньютона используется для решения уравнения движения для обоих случаев, в то время как формирование матрицы масс и требуемое обновление кинематических переменных являются уникальными для динамического анализа. Сравнения с обновленным лагранжевым FEM и явным кодом MPM сделаны в отношении алгоритмической точности и размера временного шага в нескольких репрезентативных примерах, что помогает проиллюстрировать относительную производительность и преимущества неявного MPM.Затем рассматривается геотехническое приложение, иллюстрирующее возможности предложенного метода при его применении в геотехнической области.

Ключевые слова

Динамика

Квазистатика

Метод конечных элементов

Неявные процедуры

Метод материальной точки

Обрушение склона

Рекомендуемые статьиЦитирующие статьи (0)

Цитирование статей

Что такое материальная точка в определении физики.

Материальная точка

Материальная точка – это бесконечно маленькое тело с массой, формой которой можно пренебречь. Это простейшее идеализированное тело, геометрические размеры которого невелики, и для его определения в пространстве нужны всего 3 координаты. Вращением материальной точки также пренебрегаем. Считается, что внутри материальной точки нет сил. Он не дает усадки, не растягивается, но абсолютно эластичен. Масса материальной точки не меняется во времени и не зависит от каких-либо других условий.

Рисунок 1 – замена тела материальной точкой.

Понятие материальной точки введено в механику для упрощения описания движения материальных тел. Тело произвольной формы, уже упругое и способное совершать как поступательное, так и вращательное движение. Он также может деформироваться. То есть отдельные точки тела, помимо движения вместе с телом, также перемещаются относительно него. В общем случае движение тела произвольной формы довольно сложно и трудно описать.

Для упрощения описания такого движения введено понятие материальной точки. Считается, что он имеет массу описываемого тела, но бесконечно мал по размеру. В этом случае он совершает только поступательное движение. Материальная точка используется для определения центра масс. Именно эта точка имеет массу, распределенную по объему тела.

Рисунок 2 – материальная точка.

Понятно, что нельзя просто взять и заменить корпус сложного гандикапа на предельно упрощенную модель.Для этого необходимо выполнение определенных условий. Главный из них: размер тела должен быть во много раз меньше пройденного им расстояния. Также важным фактором, влияющим на возможность замены реального тела на упрощенную модель, являются условия эксперимента и ожидаемый результат.

Предположим, что по условиям эксперимента необходимо определить время, за которое поезд преодолеет расстояние от точки A до точки B, зная его скорость.В данном случае нас не волнует, какой формы будет поезд и из какого количества вагонов он состоит. Поскольку мы знаем его скорость. Его можно представить как материальную точку. Но если нам нужно определить сопротивление воздуха, оказываемое поездом при движении с большой скоростью. Нет смысла представлять это как материальную точку. Так как результат этого эксперимента зависит от формы поезда.

А что делать в случае, когда тело нельзя представить как материальную точку. В связи с тем, что он имеет сложную форму.И отдельные его части движутся не только с линейной, но и с угловой скоростью. Тогда тело представляется как сумма отдельных материальных точек. Что будет только двигаться вперед.

ТОЧКА МАТЕРИАЛА ТОЧКА МАТЕРИАЛА – понятие, введенное в механике для обозначения тела, размером и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной точкой в тех случаях, когда оно поступательно движется на большие (по сравнению с его размерами) расстояния; например, Земля с радиусом около 6.

4 тыс. Км – материальная точка в его годовом движении вокруг Солнца (радиус орбиты – так называемой эклиптики – около 150 млн км). Точно так же понятие материальной точки применимо, если вращательную часть движения тела можно не учитывать в условиях рассматриваемой задачи (например, суточным вращением Земли можно пренебречь при изучении годового движения).

Современная энциклопедия. 2000.

Материальная точка

Основываясь на возможности локализации физических объектов во времени и пространстве, в классической механике изучение законов перемещения начинается с простейшего случая.Этот случай – движение материальной точки. Имея схематическое представление об элементарной частице, аналитическая механика создает предпосылки для представления основных законов динамики.

Материальная точка – это объект бесконечно малых размеров и конечной массы. Эта идея полностью соответствует представлению о дискретности материи. Раньше физики пытались определить его как совокупность элементарных частиц в состоянии движения. В связи с этим материальная точка в своей динамике стала именно тем инструментом, который необходим для теоретических построений.

В основе динамики рассматриваемого объекта лежит принцип инерции. По его словам, материальная точка, не находящаяся под воздействием внешних сил, с течением времени сохраняет состояние покоя (или движения). Это положение выполняется довольно строго.

В соответствии с принципом инерции материальная точка (свободная) движется равномерно и прямолинейно. Рассматривая частный случай, когда скорость равна нулю, мы можем сказать, что объект остается в покое. В связи с этим можно предположить, что влияние определенной силы на рассматриваемый объект сводится просто к изменению его скорости.Самая простая гипотеза – это предположение, что изменение скорости материальной точки прямо пропорционально показателю силы, действующей на нее. В этом случае коэффициент пропорциональности уменьшается с увеличением инерции.

Материальную точку естественно характеризовать с помощью значения коэффициента инерции – массы. В этом случае основной закон динамики объекта можно сформулировать следующим образом: сообщаемое ускорение в каждый момент времени равно отношению силы, действующей на объект, к его массе.Таким образом, представление кинематики предшествует представлению динамики. Масса, которая в динамике характеризует материальную точку, вводится апостериори (из опыта), а наличие траектории, положения, ускорения, скорости допускается априори.

В связи с этим уравнения динамики объекта утверждают, что произведение массы рассматриваемого объекта на любую из составляющих его ускорения равно соответствующей составляющей силы, действующей на объект.Предполагая, что сила является известной функцией времени и координат, определение координат материальной точки в соответствии со временем выполняется с помощью трех обыкновенных дифференциальных уравнений второго порядка по времени.

В соответствии с известной теоремой из курса математического анализа решение указанной системы уравнений однозначно определяется заданием координат, а также их первых производных в некотором начальном интервале времени. Другими словами, зная положение материальной точки и ее скорость в определенный момент, можно точно определить характер ее движения во все будущие периоды.

В результате становится ясно, что классическая динамика рассматриваемого объекта находится в абсолютном соответствии с принципом физического детерминизма. По его словам, предстоящее состояние (положение) материального мира может быть полностью предсказано при наличии параметров, определяющих его положение в определенный предыдущий момент.

Из-за того, что размер материальной точки бесконечно мал, ее траектория будет линией, занимающей только одномерный континуум в трехмерном пространстве. На каждом участке траектории имеет место определенное значение силы, задающее движение в следующий бесконечно малый промежуток времени.

/ ответы по физике, не все

Вопрос

Механика, кинематика, динамика (определение, область применения).

Ответ

Механика – наука об общих законах движения тел.

Тела вокруг нас движутся относительно медленно. Следовательно, их движения подчиняются законам Ньютона. Таким образом, область применения классической механики очень широка. И в этой области человечество всегда будет использовать законы Ньютона для описания любого движения тела.

Кинематика – это раздел механики, изучающий способы описания движений и взаимосвязь между величинами, которые характеризуют эти движения.

Описать движение тела – значит указать способ определения его положения в пространстве в любой момент времени.

Вопрос

Механическое движение, опорное тело, система отсчета, способы указания положения материальной точки на координатной плоскости, понятие кинематического уравнения материальной точки.

Ответ

Механическое движение называется перемещением тел или частей тел в пространстве относительно друг друга во времени.

Тело, относительно которого считается движение, называется опорным телом .

Набор опорного тела, связанной системы координат и часов называется системой отсчета .

Математически движение тела (или материальной точки) относительно выбранной системы отсчета описывается уравнениями, которые устанавливают, как координаты изменяются с течением времени t, которые определяют положение тела (точки) в этой системе отсчета. .Эти уравнения называются уравнениями движения. Например, в декартовых координатах x, y, z движение точки определяется уравнениями ,,.

Методы задания положения материальной точки на координатной плоскости

Указание положения точки с помощью координат. Из курса математики вы знаете, что положение точки на плоскости можно указать с помощью двух чисел, которые называются координатами этой точки. Для этого, как известно, можно провести на плоскости две пересекающиеся взаимно перпендикулярные оси, например оси OX и OY.Точка пересечения осей называется началом координат, а сами оси – осями координат.

Координаты точки M1 (рис. 1.2) равны Xj = 2, yx – 4; координаты точки M2: x2 = -2,5, y2 = -3,5.

Положение точки M в пространстве относительно опорного тела можно задать с помощью трех координат. Для этого необходимо провести три взаимно перпендикулярные оси OX, OY, OZ через выбранную точку опорного тела.В полученной системе координат положение точки будет определяться тремя координатами x, y, z.

Если число x положительное, то отрезок прокладывается в положительном направлении оси OX (рис. 1.3) (x – OA). Если число x отрицательное, то отрезок строится в отрицательном направлении оси OX. С конца этого отрезка проводится прямая линия, параллельная оси OY, и на этой прямой от оси OX прокладывается отрезок, соответствующий числу y (y = AB) – в положительном направлении оси OY оси, если M – число y положительно, и в отрицательном направлении оси OY, если число y отрицательно.

Далее, из точки B другого от-U резка выполняется по прямой, параллельной оси OZ. На этой прямой от координатной плоскости XOY прокладывается отрезок, соответствующий номеру 2. Направление, рис. 1.4, в котором проложен этот отрезок, определяется так же, как и в предыдущих случаях.

Конец третьего отрезка – точка, положение которой задается координатами x, y, z.

Для определения координат заданной точки необходимо в обратном порядке провести операции, которые мы выполняли, нахождение положения этой точки по ее координатам.

Задает положение точки с помощью радиус-вектора. Положение точки можно указать не только с помощью координат, но и с помощью радиус-вектора. Радиус-вектор – это линия направления, проведенная от начала координат до заданной точки. _

Радиус-вектор обычно обозначается буквой r. Длина радиус-вектора, или, что одно и то же, его модуль (рис. 1.4) – это расстояние от начала координат до точки М.

Положение точки будет определяться с помощью радиус-вектора, только если известны ее модуль (длина) и направление в пространстве. Только при этом условии мы узнаем, в каком направлении от начала координат следует отложить отрезок длины r, чтобы определить положение точки.

Итак, положение точки в пространстве определяется ее координатами или радиус-вектором.

Модуль и направление любого вектора находятся из его проекций на координатную ось. Чтобы понять, как это делается, сначала нужно ответить на вопрос: что подразумевается под проекцией вектора на ось?

Опустим перпендикуляры от начала A и конца B вектора a к оси OX.

Точки Aj и Bj являются проекциями соответственно начала и конца вектора a на эту ось.

Проекция вектора a на любую ось – это длина отрезка A1B1 между проекциями начала и конца вектора на эту ось, взятого со знаком «+» или «-».

Обозначим проекцию вектора той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор.Итак, ax и ay – проекции вектора a на оси координат OX и OY.

Согласно определению проекции вектора на ось можно записать: ax = ± I AjEJ.

Проекция вектора на ось – это алгебраическая величина. Он выражается в тех же единицах, что и модуль вектора.

Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца необходимо идти в положительном направлении оси проекции.В противном случае (см. Рис. 1.5) он считается отрицательным.

Из рисунков 1.5 и 1.6 легко увидеть, что проекция. вектор к оси будет положительным, когда вектор образует острый угол с направлением оси проекции, и отрицательным, когда вектор составляет тупой угол с направлением оси проекции.

Положение точки в пространстве можно указать с помощью координат или радиус-вектора, соединяющего начало координат и точку.

СПОСОБЫ ОПИСАНИЯ ДВИЖЕНИЯ.СИСТЕМА СЧЕТА

Если тело можно рассматривать как точку, то для описания его движения необходимо научиться вычислять положение точки в любой момент времени относительно выбранного опорного тела.

Есть несколько способов описания или, что одно и то же, присвоений движения точки. Давайте посмотрим на два из них, которые используются чаще всего.

Координатный путь. Положение точки зададим с помощью координат (рис.1.7). Если точка движется, то ее координаты со временем меняются.

Поскольку координаты точки зависят от времени, мы можем сказать, что они являются функциями времени. Математически это принято записывать в виде

(1,1)

Уравнения (1.1) называются кинематическими уравнениями движения точки, записанными в координатной форме. Если они известны, то для каждого момента времени мы можем вычислить координаты точки, а значит, и ее положение относительно выбранного эталонного тела.Вид уравнений (1.1) для каждого конкретного движения будет вполне определенным.

Линия, по которой точка движется в пространстве, называется траекторией.

В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траектория представляет собой прямую линию, движение точки называется прямолинейным, а если кривая – криволинейной.

Векторный путь. Положение точки можно задать, как известно, и с помощью радиус-вектора.Когда материальная точка перемещается, радиус-вектор, определяющий ее положение, изменяется со временем (он поворачивается и меняет свою длину; рис. 1.8), то есть это функция времени:

Последнее уравнение – это закон движения точки, записанный в векторной форме. Если он известен, то мы можем вычислить радиус-вектор точки для любого момента времени и, следовательно, определить ее положение. Таким образом, задание трех скалярных уравнений (1.1) эквивалентно заданию одного векторного уравнения (1.2).

Кинематические уравнения движения, записанные в координатной или векторной форме, позволяют определять положение точки в любое время.

Вопрос

Траектория, путь, движение.

Ответ

Траектория материальной точки – это линия в пространстве, которая представляет собой набор точек, в которых материальная точка находилась, находится или будет, когда она перемещается в пространстве относительно выбранной системы отсчета. Важно, чтобы понятие траектории имело физический смысл даже при отсутствии движения по ней. Идею траектории довольно наглядно иллюстрирует бобслейная трасса.(Если по условиям задачи ее шириной можно пренебречь). И это был трек, а не сам боб.

Принято описывать траекторию материальной точки в заданной системе координат с помощью радиус-вектора, направление, длина и начальная точка которого зависят от времени. В этом случае кривая, описываемая концом радиус-вектора в пространстве, может быть представлена в виде сопряженных дуг различной кривизны, которые обычно находятся в пересекающихся плоскостях.В этом случае кривизна каждой дуги определяется ее радиусом кривизны, направленным в сторону дуги от мгновенного центра вращения, который находится в той же плоскости, что и сама дуга. Причем прямая рассматривается как предельный случай кривой, радиус кривизны которой можно считать равным бесконечности. И поэтому траекторию в общем случае можно представить как набор сопряженных дуг.

Важно, что форма траектории зависит от системы отсчета, выбранной для описания движения материальной точки.Таким образом, прямолинейное равномерно ускоряющееся движение в одной инерциальной системе отсчета обычно будет параболическим в другой равномерно движущейся инерциальной системе отсчета.

Скорость материала точек всегда касаются дуги, используемой для описания траектории точки. В этом случае существует взаимосвязь между величиной скорости, нормальным ускорением и радиусом кривизны траектории в данной точке:

Однако не каждое движение с известной скоростью по кривой известного радиуса и нормального (центростремительного) ускорения, определяемого по приведенной выше формуле, связано с проявлением силы, направленной по нормали к траектории (центростремительной силы).Итак, ускорение любой из звезд, обнаруженное по фотографиям суточного движения звезд, вовсе не указывает на существование силы, вызывающей это ускорение, которое притягивает ее к Полярной звезде как центру вращения.

Путь – длина участка траектории материальной точки в физике.

Смещение (в кинематике) – изменение положения физического тела в пространстве относительно выбранной системы отсчета. Также называется смещением вектор, который характеризует это изменение.Обладает свойством аддитивности. Длина сегмента – это модуль движения, в Международной системе единиц (СИ) он измеряется в метрах.

Вы можете определить перемещение как изменение радиус-вектора точки :.

Модуль движения совпадает с пройденным расстоянием тогда и только тогда, когда направление скорости не изменяется во время движения. В этом случае траектория будет отрезком прямой. В любом другом случае, например при криволинейном движении, из неравенства треугольника следует, что путь строго длиннее.

Мгновенная скорость точки определяется как предел отношения смещения к небольшому периоду времени, в течение которого оно завершается. Более строго:

См. Википедию …………………………………………… ..

Вопрос

Скорость, средняя скорость, мгновенная скорость, кинематическое уравнение для равномерного прямолинейного движения.

Ответ

Скорость (часто обозначаемая от английского velocity или французского vitesse) – векторная физическая величина, которая характеризует скорость движения и направление движения материальной точки относительно выбранной системы отсчета; по определению равна производной по времени радиус-вектора точки.Этим же словом называется и скалярная величина – либо модуль вектора скорости, либо алгебраическая скорость точки, то есть проекция этого вектора на касательную к траектории точки

Средняя скорость – в кинематике некоторая усредненная характеристика скорости движущегося тела (или материальной точки). Существует два основных определения средней скорости, соответствующих рассмотрению скорости как скалярного или векторного значения: средняя путевая скорость (скалярное значение) и средняя скорость перемещения (векторное значение).При отсутствии дополнительных уточнений под средней скоростью обычно понимается средняя путевая скорость.

Вы также можете ввести среднюю скорость движения, которая будет вектором, равным отношению движения ко времени, которое потребовалось

Скорость равномерного прямолинейного движения тела – величина, равная отношению его движения к интервалу времени, в течение которого это движение произошло.

Мгновенная скорость – Мгновенная скорость – это отношение изменения координаты точки к временному интервалу, в течение которого это изменение произошло, с временным интервалом, стремящимся к нулю.

Геометрический смысл мгновенной скорости – это коэффициент наклона касательной к графику закона движения.

Таким образом, мы «привязали» значение мгновенной скорости к определенному моменту времени – мы установили значение скорости в данный момент времени, в данной точке пространства. Таким образом, у нас есть возможность рассматривать скорость тела как функцию времени или функцию координат.

Ускорение, среднее ускорение, мгновенное ускорение, нормальное ускорение, тангенциальное ускорение, кинематическое уравнение для равномерного движения.

Ответ

Вопрос

Свободное падение тел. Ускорение свободного падения.

Ответ

свободное падение – это движение, которое совершает тело только под действием силы тяжести, без учета сопротивления воздуха. При свободном падении тела с небольшой высоты h от поверхности Земли (h ≪Rz, где Rz – радиус Земли) оно движется с постоянным ускорением g, направленным вертикально вниз.

Ускорение g называется ускорением свободного падения. Он одинаков для всех тел и зависит только от высоты над уровнем моря и географической широты. Если в момент начала обратного отсчета (t0 = 0) тело имело скорость v0, то через произвольный интервал времени ∆t = t – t0 скорость тела при свободном падении будет: v = v0 + g · Т.

Путь h, пройденный телом в свободном падении, за время t:

Модуль скорости тела после прохождения пути h в свободном падении находится по формуле:

Поскольку vk2-v02 = 2 g h, то

Продолжительность свободного падения ∆t без начальной скорости (v0 = 0) с высоты h:

Пример 1.Тело падает вертикально вниз с высоты 20 м без начальной скорости. Определить:

1) путь h, пройденный телом за последнюю секунду падения,

2) средняя скорость падения vav,

3) средняя скорость на второй половине пути вав2.

Вопрос

Основные положения молекулярно-кинематической теории.

Ответ

Вопрос

Понятие о молекуле, единице атомной массы, относительной молекулярной массе атомов и молекул ( Mr ), количестве вещества, постоянном авогадро, молярной массе.

Ответ

Вопрос

Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа.

Ответ

Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона).

Вопрос

Изотермические, изохорные и изобарические процессы.

Ответ

Вопрос

Электрический заряд и его свойства.

Ответ

Вопрос

Закон Кулона.

Вопрос

Электрическое поле. Напряженность электрического поля.

Ответ

Вопрос

Работа сил поля при перемещении заряда. Потенциал и разность потенциалов.

Ответ

Вопрос

Законы геометрической оптики, абсолютный показатель преломления света.Относительный показатель преломления света.

Ответ

Вопрос

Тонкая линза, формула тонкой линзы.

Ответ

Линза – это стекловидное тело, ограниченное одной или двумя сферическими поверхностями.

Материальная точка ??

Валентин

Стандартное определение материальной точки в механике – это модель объекта, размерами которого можно пренебречь при решении задачи.Однако более четко можно сказать следующее: материальная точка – это модель механической системы, которая имеет только поступательные, но не внутренние степени свободы. Это автоматически означает неспособность материальной точки деформироваться и вращаться. Механическая энергия может храниться в материальной точке только в виде кинетической энергии поступательного движения или потенциальной энергии взаимодействия с полем, но не в виде энергии вращения или деформации. Другими словами, материальная точка – это простейшая механическая система с минимально возможным числом степеней свободы.Материальная точка может иметь массу, заряд, скорость, импульс, энергию.
Точность этого определения можно увидеть на следующем примере: в разреженном газе при высоких температурах размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, этим можно пренебречь и считать молекулу материальной точкой. Однако это не так: колебания и вращения молекулы являются важным резервуаром «внутренней энергии» молекулы, «емкость» которой определяется размером молекулы.

Материальная точка

Материальная точка (частица) – простейшая физическая модель в механике – идеальное тело, размеры которого равны нулю, размеры тела также можно считать бесконечно малыми по сравнению с другими измерениями или расстояния в пределах допущений изучаемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.

На практике под материальной точкой понимается тело с массой, размером и формой которой можно пренебречь при решении этой задачи.

При прямолинейном движении тела одной координатной оси достаточно для определения его положения.

Особенности

Масса, положение и скорость материальной точки в любой момент времени полностью определяют ее поведение и физические свойства.

Последствия

Механическая энергия может храниться материальной точкой только в виде кинетической энергии ее движения в пространстве и (или) потенциальной энергии взаимодействия с полем.Это автоматически означает неспособность материальной точки к деформациям (материальной точкой можно назвать только абсолютно твердое тело) и вращению вокруг собственной оси и изменению направления этой оси в пространстве. В то же время модель движения тела, описываемого материальной точкой, заключающаяся в изменении его расстояния от некоторого мгновенного центра вращения и двух углов Эйлера, задающих направление линии, соединяющей эту точку с центром. , чрезвычайно широко используется во многих отраслях механики.

Ограничения

Ограниченное применение концепции материальной точки видно из такого примера: в разреженном газе при высокой температуре размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, этим можно пренебречь и считать молекулу материальной точкой. Однако это не всегда так: колебания и вращения молекулы являются важным резервуаром «внутренней энергии» молекулы, «емкость» которой определяется размером молекулы, ее структурой и химическими свойствами.В хорошем приближении одноатомную молекулу (инертные газы, пары металлов и т. Д.) Иногда можно рассматривать как материальную точку, но даже в таких молекулах при достаточно высокой температуре наблюдается возбуждение электронных оболочек за счет столкновений молекул, с последующей эмиссией.

Заметки (править)

Фонд Викимедиа. 2010.

Механизм
Абсолютно прочный

Посмотреть, что такое “Материальная точка” в других словарях:

ТОЧКА МАТЕРИАЛА – точка с массой. В механике понятие материальной точки используется в тех случаях, когда размер и форма тела не играют роли в изучении его движения, а важна только масса. Материальной точкой можно считать практически любое тело, если … … Большой энциклопедический словарь

ТОЧКА МАТЕРИАЛА – понятие, введенное в механике для обозначения объекта, который рассматривается как точка с массой. Позиция М. т. Н. In pr ve определяется как положение геометрии. очков, что значительно упрощает решение задач по механике.На практике тело можно рассматривать … … Физическая энциклопедия

материальная точка – точка с массой. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет по научно-технической терминологии. 1984] Темы теоретическая механика EN Particle DE materialle Punkt FR point matériel … Пособие технического переводчика

МАТЕРИАЛЬНАЯ ТОЧКА Современная энциклопедия

ТОЧКА МАТЕРИАЛА – В механике: бесконечно маленькое тело. Словарь иностранных слов, входящих в русский язык. Чудинов А.Н., 1910 … Словарь иностранных слов русского языка

Материальная точка – Материальная точка – понятие, введенное в механике для обозначения тела, размером и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Кузов можно считать материальным … … Иллюстрированный энциклопедический словарь

материальная точка – понятие, введенное в механике для объекта бесконечно малых размеров с массой.Положение материальной точки в пространстве определяется как положение геометрической точки, что упрощает решение задач механики. Практически любой орган может … … энциклопедический словарь

Материальная точка – геометрическая точка с массой; материальная точка – это абстрактное изображение материального тела, имеющего массу и без размеров … Начало современного естествознания

материальная точка – materialusis taškas statusas T sritis fizika atitikmenys: angl. массовая точка; материальный пункт вок. Массенпункт, м; матчасть Пункт, м рус. материальная точка, f; точечная масса, f пранк. точечная масса, м; точечный материал, м … Fizikos terminų žodynas

материальная точка – Точка с массой … Политехнический терминологический толковый словарь

Книги

Набор столов. Физика. 9 класс (20 таблиц). Учебный альбом из 20 листов. Существенная точка. Координаты движущегося тела. Ускорение.Законы Ньютона. Закон всемирного тяготения. Прямое и изогнутое движение. Движение тела по …

Из курса физики седьмого класса мы помним, что механическое движение тела – это его движение во времени относительно других тел. Основываясь на такой информации, мы можем предположить необходимый набор инструментов для расчета движения тела.

Во-первых, нам нужно кое-что, о чем мы будем делать наши вычисления. Далее нам нужно договориться о том, как мы будем определять положение тела относительно этого «чего-то». И наконец, вам нужно будет как-то исправить время. Таким образом, чтобы рассчитать, где будет находиться тело в конкретный момент, нам нужна система отсчета.

Система отсчета в физике

Система отсчета в физике называется набором опорного тела, системы координат, связанной с опорным телом, и часов или другого устройства для измерения времени. Всегда следует помнить, что любая система отсчета условна и относительна. Вы всегда можете принять другую систему отсчета, относительно которой любое движение будет иметь совершенно другие характеристики.

Относительность обычно является важным аспектом, который следует принимать во внимание практически при любых вычислениях в физике. Например, во многих случаях мы далеко не в любой момент можем определить точные координаты движущегося тела.

В частности, мы не можем размещать наблюдателей с часами через каждые сто метров вдоль железнодорожной линии от Москвы до Владивостока. В этом случае мы рассчитываем скорость и положение тела приблизительно за определенный период времени.

Мы не заботимся о точности до одного метра при определении местоположения поезда на пути в несколько сотен или тысяч километров.Для этого есть приближения в физике. Одним из таких приближений является понятие «материальная точка».

Материальная точка в физике

Материальная точка в физике обозначает тело в тех случаях, когда его размером и формой можно пренебречь. В этом случае считается, что материальная точка имеет массу исходного тела.

Например, при расчете времени перелета самолета из Новосибирска в Новополоцк мы не обращаем внимания на размер и форму самолета.Достаточно знать, с какой скоростью он развивается и расстояние между городами. В том случае, когда нам нужно рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то без точного знания формы и размеров одного и того же самолета не обойтись.

Практически любое тело можно рассматривать как материальную точку, либо когда расстояние, которое оно преодолевает, велико по сравнению с его размерами, либо когда все точки тела движутся одинаково. Например, машина, проехавшая несколько метров от магазина до перекрестка, вполне сравнима с этим расстоянием.Но даже в такой ситуации это можно считать материальной точкой, потому что все части автомобиля двигались одинаково и на равном расстоянии.

Но в том случае, когда нам нужно поставить такую же машину в гараж, нельзя считать это материальным моментом. Придется учесть его размер и форму. Это также примеры, когда необходимо учитывать относительность, то есть по отношению к тому, что мы делаем конкретные вычисления.

Определение

Материальная точка – это макроскопическое тело, размером, формой, вращением и внутренней структурой которого можно пренебречь при описании его движения.

Вопрос о том, можно ли рассматривать данное тело как материальную точку, зависит не от размера этого тела, а от условий решаемой задачи. Например, радиус Земли намного меньше, чем расстояние от Земли до Солнца, и ее орбитальное движение можно хорошо описать как движение материальной точки с массой, равной массе Земли, и расположенной в ее центре. . Однако при рассмотрении суточного движения Земли вокруг собственной оси замена ее материальной точкой не имеет смысла.Применимость модели материальной точки к конкретному телу зависит не столько от размеров самого тела, сколько от условий его движения. В частности, в соответствии с теоремой о движении центра масс системы при поступательном движении любое твердое тело можно считать материальной точкой, положение которой совпадает с центром масс тела.

Масса, положение, скорость и некоторые другие физические свойства материальной точки в любой момент времени полностью определяют ее поведение.

Положение материальной точки в пространстве определяется как положение геометрической точки. В классической механике масса материальной точки считается постоянной во времени и не зависит от каких-либо особенностей ее движения и взаимодействия с другими телами. При аксиоматическом подходе к построению классической механики в качестве одной из аксиом принимается:

Аксиома

Материальная точка – геометрическая точка, которой присвоен скаляр, называемый массой: $ (r, m) $, где $ r $ – вектор в евклидовом пространстве, относящийся к любой декартовой системе координат. Считается, что масса постоянна, независимо от положения точки в пространстве или времени.

Механическая энергия может храниться материальной точкой только в виде кинетической энергии ее движения в пространстве и (или) потенциальной энергии взаимодействия с полем. Это автоматически означает неспособность материальной точки к деформациям (материальной точкой можно назвать только абсолютно твердое тело) и вращению вокруг собственной оси и изменению направления этой оси в пространстве.В то же время модель движения тела, описываемого материальной точкой, заключающаяся в изменении его расстояния от некоторого мгновенного центра вращения и двух углов Эйлера, задающих направление линии, соединяющей эту точку с центром, чрезвычайно широко используется во многих отраслях механики.

Метод изучения законов движения реальных тел путем изучения движения идеальной модели – материальной точки – является основным в механике. Любое макроскопическое тело можно представить как набор взаимодействующих материальных точек g, массы которых равны массам его частей. Изучение движения этих частей сводится к изучению движения материальных точек.

Упражнение 1

а) въезд автомобиля в гараж;

б) автомобиль по трассе Воронеж – Ростов?

а) въезд автомобиля в гараж нельзя принять за материальную точку, так как в этих условиях габариты автомобиля значительны;

б) за материальную точку можно принять автомобиль на трассе Воронеж-Ростов, так как размер автомобиля намного меньше расстояния между городами.

Можно ли принять за материальную точку:

а) мальчик, который проходит 1 км по дороге из школы домой;

б) мальчик делает зарядку.

а) Когда мальчик, возвращаясь из школы, проходит расстояние 1 км до своего дома, тогда мальчика в этом движении можно рассматривать как материальную точку, потому что его размеры малы по сравнению с расстоянием, которое он проходит.

б) когда тот же мальчик выполняет утреннюю зарядку, то его нельзя считать материальной точкой.

Материальный балл. Описание. Концепция. Определение. Материальная точка, твердое тело Определение материальной точки

Во-первых, нам нужно кое-что, о чем мы будем делать наши вычисления. Далее нам нужно договориться о том, как мы будем определять положение тела относительно этого «чего-то».И наконец, вам нужно будет как-то исправить время. Таким образом, чтобы рассчитать, где будет находиться тело в конкретный момент, нам нужна система отсчета.

Система отсчета в физике

Система отсчета в физике – это набор опорного тела, системы координат, связанной с опорным телом, и часов или другого устройства для измерения времени. Всегда следует помнить, что любая система отсчета условна и относительна. Вы всегда можете принять другую систему отсчета, относительно которой любое движение будет иметь совершенно другие характеристики.

В частности, мы не можем размещать наблюдателей с часами через каждые сто метров вдоль железнодорожной линии от Москвы до Владивостока. В этом случае мы рассчитываем скорость и местоположение тела приблизительно за определенный период времени.

Материальная точка в физике

Материальная точка в физике обозначает тело в тех случаях, когда его размером и формой можно пренебречь. Считается, что материальная точка имеет массу исходного тела.

Например, при расчете времени полета самолета из Новосибирска в Новополоцк нас не интересуют размер и форма самолета.Достаточно знать, с какой скоростью он развивается и расстояние между городами. В том случае, когда нам нужно рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то без точного знания формы и размеров одного и того же самолета не обойтись.

Практически любое тело можно считать материальной точкой, если расстояние, пройденное телом велико по сравнению с его размером, или когда все точки тела движутся одинаково. Например, машина, проехавшая несколько метров от магазина до перекрестка, вполне сравнима с этим расстоянием.Но даже в такой ситуации это можно считать материальной точкой, потому что все части автомобиля двигались одинаково и на одинаковое расстояние.

Материальная точка

Материальная точка (частица) – простейшая физическая модель в механике – идеальное тело, размеры которого равны нулю, размеры тела также можно считать бесконечно малыми по сравнению с другими измерениями или расстояния в пределах допущений изучаемой задачи.Положение материальной точки в пространстве определяется как положение геометрической точки.

При прямолинейном движении тела одной координатной оси достаточно для определения его положения.