Скорость мгновенная физика: Ошибка 403 — доступ запрещён

Неравномерное движение. Мгновенная скорость

Урок 6. Физика 10 класс

Легко заметить, что в большинстве жизненных ситуаций мы сталкиваемся с неравномерным движением. Для описания такого движения вводится понятие мгновенной скорости, то есть скорости, присущей тому или иному телу в данный момент времени. Об этом мы и поговорим.

Конспект урока “Неравномерное движение. Мгновенная скорость”

Ранее мы рассматривали равномерное прямолинейное движение. Строго говоря, такое движение — это идеализированный пример. На самом деле тела двигаются неравномерно. Например, автомобиль едет чуть быстрее или чуть медленнее в определённые промежутки времени.

Да и траектория его никогда не является прямой на достаточно длинных участках.

Существует также колебательное движение, примером которого может являться движение маятника. Кроме того, как вы знаете, тело, находящееся в свободном падении, двигается с ускорением. Наконец, тело, двигающееся по кривой, обладает центростремительным ускорением. Все эти примеры являются примерами неравномерного движения.

Неравномерным движением называется такое движение, при котором расстояния, пройденные за одинаковые промежутки времени, не равны.

Именно, с неравномерным движением связано понятие мгновенной скорости. Чтобы понять, что такое мгновенная скорость, рассмотрим простой пример. На рисунке вы видите траекторию, по которой перемещается точка.

Отметим три случайных положения этой точки на траектории. Тогда мы можем найти три разных вектора перемещения: ,  и . Соответственно, эти перемещения были совершены за промежутки времени , и . Тогда мы можем посчитать средние скорости на этих участках:

 Очевидно, что эти скорости будут неравны. Но по мере уменьшения промежутка времени, средние скорости всё меньше и меньше будут отличаться друг от друга. В конце концов, если мы возьмём бесконечно малый промежуток времени, выражение

будет стремиться к определённому значению. То есть, это скорость в данный момент времени или, точнее сказать, мгновенная скорость.

Заметим, что какой бы сложной ни была траектория движения, если мы возьмём бесконечно малый промежуток времени, то на нём перемещение будет казаться прямолинейным. В этом случае, мы можем подсчитать скорость по формуле для прямолинейного движения. Но в каждое последующее мгновение, скорость будет меняться. Именно поэтому, она и называется

мгновенной скоростью.

Мгновенная скорость — это величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Мгновенная скорость направлена по касательной к траектории. Например, если вы едете в машине и наехали на кочку, то вас подбрасывает вверх. Почему? Потому что в тот миг, когда машина переезжает через кочку, мгновенная скорость направлена вверх. Но в следующее же мгновение, она направлена вниз, а еще через мгновение, скорость снова направлена также, как и была направлена до кочки.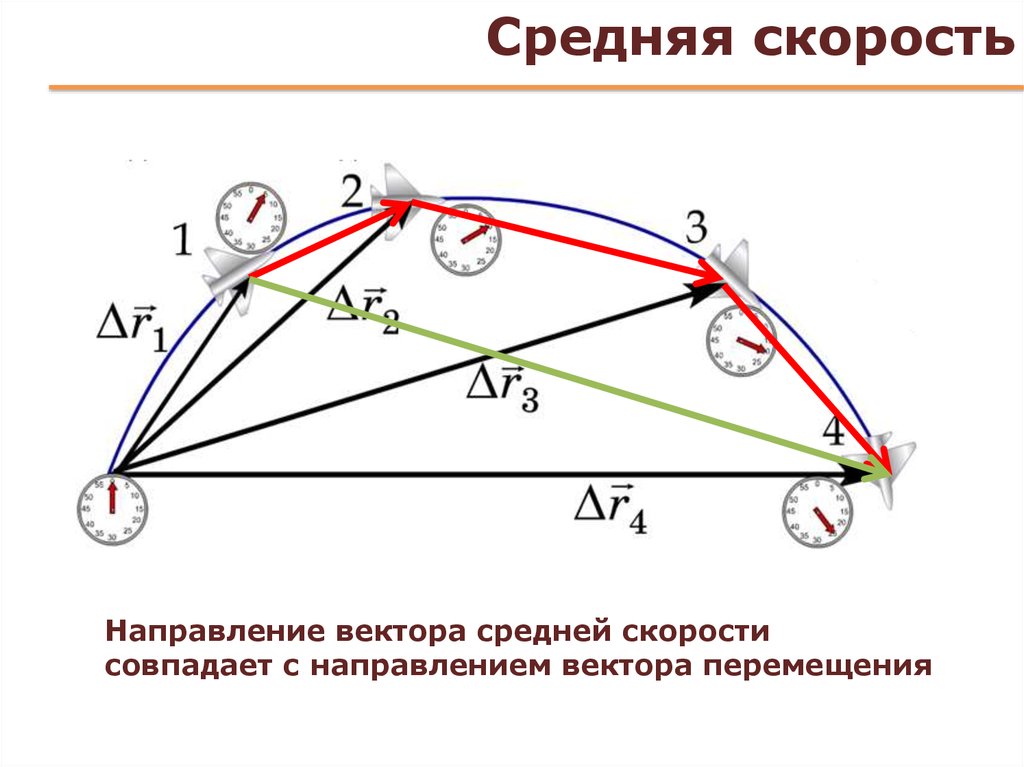

Рассмотрим конкретный пример. Вы видите график зависимости положения материальной точки от времени при равноускоренном движении.

График представляет собой параболу. Очевидно, что в каждой точке скорость разная. Если мы рассчитаем среднюю скорость в период от 2 до 5 секунд, то она будет равна 7 м/с. Рассмотрим теперь промежуток времени от 4 до 5 секунд. В этом случае, средняя скорость будет равна 9 м/с. Рассмотрим теперь участок от 4,796 секунд до 5 секунд. Этот промежуток времени довольно мал, поэтому если мы достаточно приблизим график, то траектория будет казаться почти прямой. Средняя скорость на этом участке равна 9,8 м/с.

Как видите, с уменьшением интервала времени, средняя скорость стремится к какому-то определённому значению. То есть, к значению мгновенной скорости в момент времени t = 5 с, которое в нашем случае равно 10 м/с. Если мы подсчитаем среднюю скорость на временном интервале, равным 0,01 с, то убедимся, что средняя скорость почти равна 10 м/с.

Заметим, что во всех упомянутых примерах мы рассматривали среднюю скорость перемещения. Существует также, такое понятие, как средняя путевая скорость. Именно путевая скорость чаще всего используется для описания движения.

Средняя путевая скорость определяется отношением пройденного пути к промежутку времени, за который этот путь пройден:

Мы уже говорили, что пройденный путь всегда больше либо равен модулю перемещения. Из этого можно сделать вывод, что средняя путевая скорость больше либо равна модулю средней скорости перемещения:

Предыдущий урок 5 Уравнение РПД

Следующий урок 7 Сложение скоростей

Получите полный комплект видеоуроков, тестов и презентаций Физика 10 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Кинематика.

Физика. 10 класс. – Скорость при неравномерном движении. Мгновенная скорость. Сложение скоростей.

Комментарии преподавателя

Нерав­но­мер­ным на­зы­ва­ет­ся дви­же­ние, при ко­то­ром тело за рав­ные про­ме­жут­ки вре­ме­ни про­хо­дит нерав­ные пути.

 

 

Ос­нов­ная за­да­ча ме­ха­ни­ки – опре­де­лить по­ло­же­ние тела в любой мо­мент вре­ме­ни. При нерав­но­мер­ном дви­же­нии ско­рость тела ме­ня­ет­ся, сле­до­ва­тель­но, необ­хо­ди­мо на­учить­ся опи­сы­вать из­ме­не­ние ско­ро­сти тела. Для этого вво­дят­ся два по­ня­тия: сред­няя ско­рость и мгно­вен­ная ско­рость.

Факт из­ме­не­ния ско­ро­сти тела при нерав­но­мер­ном дви­же­нии не все­гда необ­хо­ди­мо учи­ты­вать, при рас­смот­ре­нии дви­же­нии тела на боль­шом участ­ке пути в целом (нам не важна ско­рость в каж­дый мо­мент вре­ме­ни) удоб­но вве­сти по­ня­тие сред­ней ско­ро­сти.

Сред­ней ско­ро­стью на­зы­ва­ют от­но­ше­ние пол­но­го пе­ре­ме­ще­ния, ко­то­рое со­вер­ши­ло тело, ко вре­ме­ни, за ко­то­рое со­вер­ше­но это пе­ре­ме­ще­ние.

 

На прак­ти­ке чаще всего ис­поль­зу­ет­ся по­ня­тие сред­ней пу­те­вой ско­ро­сти.

Сред­няя пу­те­вая ско­рость – это от­но­ше­ние пол­но­го пути, прой­ден­но­го телом, ко вре­ме­ни, за ко­то­рое путь прой­ден.

 

Су­ще­ству­ет ещё одно опре­де­ле­ние сред­ней ско­ро­сти.

Сред­няя ско­рость – это та ско­рость, с ко­то­рой долж­но дви­гать­ся тело рав­но­мер­но, чтобы прой­ти дан­ное рас­сто­я­ние за то же время, за ко­то­рое оно его про­шло, дви­га­ясь нерав­но­мер­но.

Из курса ма­те­ма­ти­ки нам из­вест­но, что такое сред­нее ариф­ме­ти­че­ское. Для чисел 10 и 36 оно будет равно:

 

Для того чтобы узнать воз­мож­ность ис­поль­зо­ва­ния этой фор­му­лы для на­хож­де­ния сред­ней ско­ро­сти, решим сле­ду­ю­щую за­да­чу.

За­да­ча

Ве­ло­си­пе­дист под­ни­ма­ет­ся со ско­ро­стью 10 км/ч на склон, за­тра­чи­вая на это 0,5 часа. Далее со ско­ро­стью 36 км/ч спус­ка­ет­ся вниз за 10 минут. Най­ди­те сред­нюю ско­рость ве­ло­си­пе­ди­ста (см. Рис. 4).

Дано:; ; ;

Найти:

Ре­ше­ние:

Рис. 4. Ил­лю­стра­ция к за­да­че

Так как еди­ни­ца из­ме­ре­ния дан­ных ско­ро­стей – км/ч, то и сред­нюю ско­рость най­дём в км/ч. Сле­до­ва­тель­но, дан­ные за­да­чи не будем пе­ре­во­дить в СИ. Пе­ре­ве­дём в часы.

 

Сред­няя ско­рость равна:

 

Пол­ный путь () со­сто­ит из пути подъ­ёма на склон () и спус­ка со скло­на ():

 

Путь подъ­ёма на склон равен:

 

Путь спус­ка со скло­на равен:

 

Время, за ко­то­рое прой­ден пол­ный путь, равно:

 

 

Ответ:

Ис­хо­дя из от­ве­та за­да­чи, видим, что при­ме­нять фор­му­лу сред­не­го ариф­ме­ти­че­ско­го для вы­чис­ле­ния сред­ней ско­ро­сти нель­зя.

Сред­нюю ско­рость, из­ме­рен­ную за бес­ко­неч­но малый про­ме­жу­ток вре­ме­ни, на­зы­ва­ют мгно­вен­ной ско­ро­стью тела (для при­ме­ра, спи­до­метр ав­то­мо­би­ля по­ка­зы­ва­ет мгно­вен­ную ско­рость).

Су­ще­ству­ет ещё одно опре­де­ле­ние мгно­вен­ной ско­ро­сти.

Мгно­вен­ная ско­рость – ско­рость дви­же­ния тела в дан­ный мо­мент вре­ме­ни, ско­рость тела в дан­ной точке тра­ек­то­рии.

Для того чтобы лучше по­нять дан­ное опре­де­ле­ние, рас­смот­рим при­мер.

Пусть ав­то­мо­биль дви­жет­ся пря­мо­ли­ней­но по участ­ку шоссе. У нас есть гра­фик за­ви­си­мо­сти про­ек­ции пе­ре­ме­ще­ния от вре­ме­ни для дан­но­го дви­же­ния (см. Рис. 5), про­ана­ли­зи­ру­ем дан­ный гра­фик.

На гра­фи­ке видно, что ско­рость ав­то­мо­би­ля не по­сто­ян­ная. До­пу­стим, необ­хо­ди­мо найти мгно­вен­ную ско­рость ав­то­мо­би­ля через 30 се­кунд после на­ча­ла на­блю­де­ния (в точке

A). Поль­зу­ясь опре­де­ле­ни­ем мгно­вен­ной ско­ро­сти, най­дём мо­дуль сред­ней ско­ро­сти за про­ме­жу­ток вре­ме­ни от  до . Для этого рас­смот­рим фраг­мент дан­но­го гра­фи­ка (см. Рис. 6).

Рис. 5. Гра­фик за­ви­си­мо­сти про­ек­ции пе­ре­ме­ще­ния от вре­ме­ни

Рис. 6. Гра­фик за­ви­си­мо­сти про­ек­ции пе­ре­ме­ще­ния от вре­ме­ни

Рас­счи­ты­ва­ем сред­нюю ско­рость на дан­ном участ­ке вре­ме­ни:

 

Для того чтобы про­ве­рить пра­виль­ность на­хож­де­ния мгно­вен­ной ско­ро­сти, най­дём мо­дуль сред­ней ско­ро­сти за про­ме­жу­ток вре­ме­ни от  до , для этого рас­смот­рим фраг­мент гра­фи­ка (см. Рис. 7).

Рис. 7. Гра­фик за­ви­си­мо­сти про­ек­ции пе­ре­ме­ще­ния от вре­ме­ни

Рас­счи­ты­ва­ем сред­нюю ско­рость на дан­ном участ­ке вре­ме­ни:

 

По­лу­чи­ли два зна­че­ния мгно­вен­ной ско­ро­сти ав­то­мо­би­ля через 30 се­кунд после на­ча­ла на­блю­де­ния. Точ­нее будет то зна­че­ние, где ин­тер­вал вре­ме­ни мень­ше, то есть . Если умень­шать рас­смат­ри­ва­е­мый ин­тер­вал вре­ме­ни силь­нее, то мгно­вен­ная ско­рость ав­то­мо­би­ля в точке A будет опре­де­лять­ся более точно.

Мгно­вен­ная ско­рость – это век­тор­ная ве­ли­чи­на. По­это­му, кроме её на­хож­де­ния (на­хож­де­ния её мо­ду­ля), необ­хо­ди­мо знать, как она на­прав­ле­на.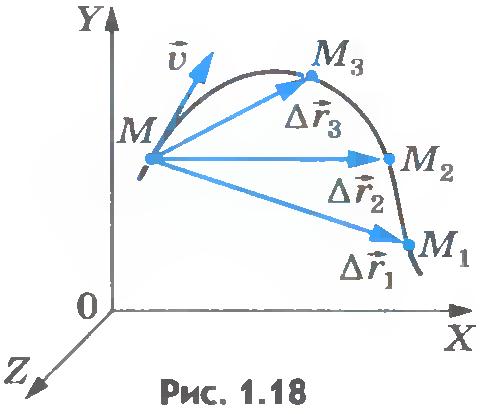

 (при ) – мгно­вен­ная ско­рость

 

На­прав­ле­ние мгно­вен­ной ско­ро­сти сов­па­да­ет с на­прав­ле­ни­ем пе­ре­ме­ще­ния тела.

Если тело дви­жет­ся кри­во­ли­ней­но, то мгно­вен­ная ско­рость на­прав­ле­на по ка­са­тель­ной к точке тра­ек­то­рии (см. Рис. 8).

Рис. 8. На­прав­ле­ние мгно­вен­ной ско­ро­сти

Если мы го­во­рим, что тра­ек­то­рия, путь, пе­ре­ме­ще­ние и ско­рость яв­ля­ют­ся от­но­си­тель­ны­ми, то есть за­ви­сят от вы­бо­ра си­сте­мы от­сче­та, то про время мы этого не го­во­рим. В рам­ках клас­си­че­ской, или Нью­то­но­вой, ме­ха­ни­ки время есть ве­ли­чи­на аб­со­лют­ная, то есть про­те­ка­ю­щее во всех си­сте­мах от­сче­та оди­на­ко­во.

Рас­смот­рим, как на­хо­дить пе­ре­ме­ще­ние и ско­рость в одной си­сте­ме от­сче­та, если они нам из­вест­ны в дру­гой си­сте­ме от­сче­та.

Че­ло­век идет по па­лу­бе па­ро­хо­да со ско­ро­стью  от­но­си­тель­но па­ро­хо­да. Па­ро­ход дви­жет­ся по­сту­па­тель­но со ско­ро­стью  от­но­си­тель­но бе­ре­га. Най­дем ско­рость  че­ло­ве­ка от­но­си­тель­но бе­ре­га (Рис. 9).

Свя­жем непо­движ­ную си­сте­му от­сче­та (хОу) с Зем­лей, а по­движ­ную (х’О’у) – с па­ро­хо­дом.

 

Рис. 9. При­мер за­да­чи

Из Рис. 9 видно, что пе­ре­ме­ще­ние:

 Δ = Δ + Δ ⇒ Δ ≠ Δ,

где Δ – пе­ре­ме­ще­ние че­ло­ве­ка от­но­си­тель­но па­ро­хо­да, Δ – пе­ре­ме­ще­ние па­ро­хо­да от­но­си­тель­но бе­ре­га, Δ – пе­ре­ме­ще­ние че­ло­ве­ка от­но­си­тель­но бе­ре­га.

Таким об­ра­зом, если тело од­но­вре­мен­но участ­ву­ет в несколь­ких дви­же­ни­ях, то ре­зуль­ти­ру­ю­щее пе­ре­ме­ще­ние точки равно век­тор­ной сумме пе­ре­ме­ще­ний, со­вер­ша­е­мых ею в каж­дом из дви­же­ний. В этом со­сто­ит уста­нов­лен­ный экс­пе­ри­мен­таль­но прин­цип неза­ви­си­мо­сти дви­же­ний.

Раз­де­лив это урав­не­ние на про­ме­жу­ток вре­ме­ни, за ко­то­рый про­изо­шли пе­ре­ме­ще­ния че­ло­ве­ка и па­ро­хо­да, по­лу­чим закон сло­же­ния ско­ро­стей:

  = +

Ско­рость  тела от­но­си­тель­но непо­движ­ной си­сте­мы от­сче­та равна гео­мет­ри­че­ской сумме ско­ро­сти  тела от­но­си­тель­но по­движ­ной си­сте­мы от­сче­та и ско­ро­сти  самой по­движ­ной си­сте­мы от­сче­та от­но­си­тель­но непо­движ­ной.

До­маш­нее за­да­ние

1. Можно ли, зная сред­нюю ско­рость за опре­де­лен­ный про­ме­жу­ток вре­ме­ни, найти пе­ре­ме­ще­ние, со­вер­шен­ное телом за любую часть этого про­ме­жут­ка?
2. Чем от­ли­ча­ет­ся мгно­вен­ная ско­рость при рав­но­мер­ном пря­мо­ли­ней­ном дви­же­нии от мгно­вен­ной ско­ро­сти при нерав­но­мер­ном дви­же­нии?
3. Во время езды на ав­то­мо­би­ле через каж­дую ми­ну­ту сни­ма­лись по­ка­за­ния спи­до­мет­ра. Можно ли по этим дан­ным опре­де­лить сред­нюю ско­рость дви­же­ния ав­то­мо­би­ля?
4. Первую треть трас­сы ве­ло­си­пе­дист ехал со ско­ро­стью 12 км в час, вто­рую треть – со ско­ро­стью 16 км в час, а по­след­нюю треть — со ско­ро­стью 24 км в час. Най­ди­те сред­нюю ско­рость ве­ло­си­пе­да на про­тя­же­нии всего пути. Ответ дайте в км в час.

К занятию прикреплен файл  «Ребусы по теме». Вы можете скачать файл  в любое удобное для вас время.

Использованные источники: 

• http://interneturok. ru/ru/school/physics/10-klass/
• http://www.youtube.com/watch?v=fLEtoof1l2c
• http://www.youtube.com/watch?v=pWStlFLGaqk
   

13 примеров мгновенной скорости –

Мгновенная скорость – это скорость, с которой тело движется в определенный момент времени. В этой статье вы узнаете о более примерах мгновенной скорости , с которыми мы сталкиваемся в повседневной жизни.

• Спидометр транспортного средства
• Бегущий гепард
• Скорость набора текста
• Движение монет в шахматной доске
• 3 004
• A Moving Apan
• Game Squash Ball Ball Game
• Индивидуальная ходьба с равномерной скоростью
• пробегает
• 999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999. 0000
• 9.9003
• 99999999999999999999999.nefore
• 99.com скорость поезда
• Уборка грязного места

Спидометр транспортного средства

Спидометр транспортного средства — это прибор, который показывает скорость этого транспортного средства в определенное время. Спидометр является идеальным примером мгновенной скорости . Если мы хотим узнать показатель скорости за определенное время, это четко показано на спидометре.

Изображение предоставлено: Animated_Aston_Martin_Speedometer.gif, DineshAdv на en.wikipedia, CC BY-SA 3.0

Бегущий гепард

В общем, мы наблюдали бегущего гепарда в каналах дикой природы. Cheetah, вообще, известен своими скорость и может рассматриваться как мгновенная скорость например ; по нашим оценкам, он движется со скоростью 76 миль/час. Это мгновенная скорость гепарда , потому что это в час.

Изображение предоставлено:
https://commons.wikimedia.org/wiki/Файл:FPClogogif.gif, автор Free Pascal, через Wikimedia Commons в минуту; это пример мгновенной скорости . Здесь мгновенная скорость рассчитывается в минуту, т. е. 30 слов в минуту, и это будет 60 слов за 2 минуты.

Перемещение монет в скоростных шахматах

Обычно мы можем определить победителя в шахматных соревнованиях даже по скорости хода игрока. Здесь скорость рассчитывается для каждого движения, чтобы дать точный результат. Таким образом, движение шахматных монет является примером мгновенной скорости .

Изображение предоставлено: Chess-american-krikor-2021-final.gif, Davidesouzarj, CC BY-SA 4.0, 9. Здесь скорость может варьироваться для каждой компоновки и может вычислять показатель скорости для другой компоновки.

A Транспортное средство в движении

Транспортное средство облегчает нашу транспортировку. Движение транспортного средства – мгновенная скорость пример . Предположим, вы ведете транспортное средство со средней скоростью , равной 40 км/ч, и настаиваете на расчете скорости транспортного средства в минуту. В этом случае вы пытаетесь найти мгновенную скорость этого транспортного средства за определенное время.

Игра в мяч для сквоша

Игра в мяч для сквоша — это своего рода игра со скоростью . Если мы пренебрежем направлением и сосредоточимся только на величине скорости в определенный момент времени удара по мячу, то мы вычислим его мгновенная скорость . Следовательно, скорость мяча для сквоша в определенное время является мгновенной скоростью пример .

Индивидуум, идущий с постоянной скоростью

Индивидуум продолжает идти по пути с постоянной скоростью и внезапно мчится к себе домой. Здесь мы можем наблюдать изменение скорости, и если мы хотим узнать скорость в момент его бега, то это мгновенная скорость пример .

Бег трусцой

Некоторые люди имеют привычку бегать трусцой, и это реальный пример мгновенной скорости . Во время пробежки они могут преодолевать 3 км за 30 минут, и их скорость может измениться в любое время. Здесь изменение скорости в конкретный момент вычисляется как мгновенной скорости.

Работающий вентилятор

Работающий вентилятор также является примером мгновенной скорости из повседневной жизни . В общем, меняем скорость вентилятора по нашему требованию. Здесь, если мы пренебрежем направлением и сосредоточимся только на величине скорости, можно вычислить мгновенную скорость вентилятора.

Изображение предоставлено: https://cdn.pixabay.com/photo/2014/12/17/11/17/ceiling-fan-571309_1280. jpg

Мгновенная скорость шара 2 9 Скорость мяча всегда зависит от материала, из которого он изготовлен. Сначала скорость будет максимальной, когда вы ударите по мячу, т. е. 124 мили в час, и постепенно уменьшится до 94 миль в час. Здесь изменение в степени скорости в любой момент времени, не учитывая направления, в котором движется мяч, можно узнать, вычислив мгновенная скорость .

Мгновенная скорость поезда

Поезд движется со скоростью 150 миль в час в течение определенного времени, но при пересечении или достижении пункта назначения скорость постепенно уменьшается до 120 миль в час относительно позиции и времени . Здесь скорость , рассчитанная во время убывания, является примером мгновенной скорости.

       Изображение предоставлено: https://cdn.pixabay.com/photo/2012/10/10/05/04/train-60539__340. jpg

Уборка грязного места

Скорость , с которой человек убирает место в определенное время, является примером мгновенной скорости . Человек может убрать комнату за 3 часа с постоянной скоростью , и тот же человек может убрать оставшееся место за 1 час , если он увеличит свою скорость . Здесь изменение скорости в тот момент, когда он увеличивает свою скорость , равно мгновенной скорости.

Часто задаваемые вопросы о мгновенной скорости | Часто задаваемые вопросы

Какой самый яркий пример мгновенной скорости?

Величайшим примером мгновенной скорости является нарушение ограничения скорости .

Когда человек превышает скорость до 10%, его останавливает полицейский за нарушение правил. Уменьшение скорости в тот момент, когда он останавливает транспортное средство, называется мгновенной скоростью.

Что такое мгновенная скорость?

В общем, мгновенная скорость определение следующее:

При движении, когда происходит изменение скорости тела в течение определенного интервала времени, скорость, рассчитанная для этого конкретного интервала, называется мгновенной скоростью. Это зависит от изменения смещения тела при изменении временного интервала.

Как мы можем измерить мгновенную скорость объекта?

Мы можем рассчитать мгновенную скорость ед в любой заданный интервал времени движения тела.

Мгновенная скорость — это величина мгновенной скорости, и она не может быть отрицательной. Когда велосипед движется по пути со средней скоростью 63 мили в час, мгновенная скорость измеряется с учетом пройденного расстояния и времени, необходимого для преодоления этого расстояния. Здесь направлением можно пренебречь.

Определить скорость объекта?

Скорость является скаляром и показывает только величину тела.

В общем случае скорость — это устойчивость тела и скорость, с которой тело проходит определенное расстояние по заданному пути за определенный промежуток времени. Мы указываем скорость обычно в виде числового значения вместе с единицей измерения метр/секунду или м/с.

Сравните мгновенную скорость и среднюю скорость?

Сравнение между средней скоростью и мгновенной скоростью показано ниже;

	Средняя скорость	Мгновенная скорость
Определение	Это общая скорость тела в пределах периода.	Это скорость тела в определенное время.
Количество	Скаляр        У него есть только величина.	Скаляр    Имеет только величину.
Formula
.	Спидометр.

Связь между мгновенной скоростью и мгновенной скоростью?

Типичная связь между мгновенной скоростью и мгновенной скоростью заключается в величине, в которой мы их измеряем.

• Мгновенная скорость дает направление и величину движения тела. Напротив, мгновенная скорость определяет только величину величины тела.
• Оба имеют единицу   в метре в секунду,
• Мгновенная скорость – это величина мгновенной скорости.
• Мгновенная скорость — вектор, а мгновенная скорость — скаляр.

По какой формуле рассчитать мгновенную скорость?

Формула для расчета мгновенной скорости приведена ниже:

Мгновенная скорость =  

Здесь V = это предел, когда изменение времени приближается к нулю. При равномерном движении мгновенная скорость всегда постоянна, а S _вместо не может быть на меньше или равно нулю.

Проблемы с мгновенной скоростью. Задача 1 Вычислите мгновенную скорость тела в момент времени t = 4 с?

Решение: заданная функция смещения s(t) = 5t ² – 10t +2 .

 Чтобы рассчитать мгновенную скорость, мы можем использовать формулу.

                      S _inst  = 10(4) – 10

               S _inst = 40 – 10

              S _inst = 30 м/с

Следовательно, мгновенная скорость данного объекта равна 30 м/с.

 

Скорость | механика | Британика

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, правительство, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.