| 1. |
Терминология
Сложность: лёгкое |
2 |
| 2. |
Единица ускорения в СИ
Сложность: среднее |
2 |
3.
|
Вычисление ускорения лифта
Сложность: среднее |
2 |
| 4. |
Равномерное торможение мотоцикла
Сложность: среднее |
2 |
5.
|
Графики равноускоренного движения
|
2 |
| 6. |
Ускорение
Сложность: среднее |
2 |
7.
|
Задача на прямолинейное равноускоренное движение
|
3 |
| 8. |
Средняя скорость
Сложность: сложное |
3 |
9.
|
Равноускоренное движение грузовика
Сложность: сложное |
3 |
| 10. |
Характер движения автомобиля
Сложность: сложное |
3 |
11.
|
Длина взлётной полосы
|
3 |
| 12. |
Полный пройденный путь
Сложность: сложное |
3 |
Скорость и ускорение.
 Методические материалы
Методические материалыПлан работы
- Введение. Постановка цели и задач моделирования (3 мин).
- Теоретическое обоснование работы. (12 мин).
- Моделирование. Описание окна модели и ее основных элементов. Выбор конкретного варианта работы. Выполнение моделирования и заполнение рабочих таблиц. Обработка и оформление результатов работы. Анализ полученных результатов (20 мин).
- Выводы из работы (5 мин).
Литература
1. Физика-10. О. Ф. Кабардин, В. А. Орлов, Э. Е. Эвенчик и др.; Под ред. А. А. Пинского.
Глава 1. Механика.
§ 1. Основные понятия и уравнения кинематики.
Способы описания движения тел.
Скорость. Ускорение.
Прямолинейное ускоренное движение (С. 5–7).
Основная задача кинематики (С. 8–9).
2. Физика. 10 класс. В. А. Касьянов.
Механика. Глава 2.
§ 11. Скорость.
§ 13. Ускорение.
§ 14. Прямолинейное движение с постоянным ускорением.
3. Физика. 9 класс. А. В. Перышкин, Е. М. Гутник.
Глава 1. Законы взаимодействия и движения тел.
§ 5. Прямолинейное равноускоренное движение. Ускорение.
§ 6. Скорость прямолинейного равноускоренного движения. График скорости.
§ 7. Перемещение при прямолинейном равноускоренном движении.
Методика и порядок выполнения работы
- Откройте модель «Скорость и ускорение».
Непосредственно внутри окна модели, в нижней части расположены кнопки «Старт» и «Сброс» (кнопка «Старт» при нажатии заменяется кнопкой «Стоп» и служит для кратковременной остановки происходящего процесса). При нажатии кнопки «Сброс» модель возвращается в первоначальное состояние. В верхней части окна расположено рабочее поле модели.
 На рабочем поле находятся шесть подвижных точек, обозначенных латинскими буквами (A, B, C, D, E, F). Сдвигая их вверх и вниз в пределах рабочего поля модели можно выбирать начальную и конечную скорость и ускорение. Под рабочим полем модели появляются значения перемещений и ускорений, для каждого участка модели (AB, BC, CD и т. д.). Ниже окна рабочего поля модели расположено окно, показывающее движение тела и векторы скорости и ускорения.
На рабочем поле находятся шесть подвижных точек, обозначенных латинскими буквами (A, B, C, D, E, F). Сдвигая их вверх и вниз в пределах рабочего поля модели можно выбирать начальную и конечную скорость и ускорение. Под рабочим полем модели появляются значения перемещений и ускорений, для каждого участка модели (AB, BC, CD и т. д.). Ниже окна рабочего поля модели расположено окно, показывающее движение тела и векторы скорости и ускорения. - Подведите курсор мышки к точкам A и B и установите начальное и конечное значения скорости согласно вашему варианту (см. Таблицу 1). Измерения будем проводить на участке AB, в течение первых 10 секунд движения тела. В Таблице 1 указаны максимальные разницы начальной и конечных скоростей. Нажмите кнопку «Старт» и пронаблюдайте движение тела.
Вариант 1 2 3 4 5 6 υAO, м/с (точка A) 15 –15 15 0 0 –15 υB, м/с (точка B) –15 15 0 15 –15 0 Таблица 1.

- Не трогая начальную скорость (точку A), изменяйте конечную скорость тела (просто сдвигая точку B на одинаковую величину вверх или вниз, в зависимости от вашего варианта). Проведите измерения и данные занесите в таблицу 2. Например, для первого варианта, таблица будет выглядеть следующим образом:
t = 10 с; υAO = 15 м/с υB, м/c 10 5 0 –5 –10 –15 a, м/с2 s, м Таблица 2.

По данным таблицы 2 постройте зависимость ускорения движущегося тела от перемещения a (s). Проведите анализ полученного графика, найдите особую точку (точка пересечения с осью абсцисс), объясните ход графика и сделайте вывод.
Выводы из работы
Сделайте выводы по проделанной работе (исходите из проведенного анализа графиков; выводы должны соответствовать поставленной цели работы).
На графике получается прямая линия, проходящая через ось абсцисс при ускорении, равном нулю (соответствует равномерному движению тела). Точка пересечения показывает, какое расстояние прошло бы тело, если бы двигалось с постоянной фиксированной скоростью.
Вопросы к работе
- Что такое средняя скорость?
- Что такое мгновенная скорость? Как направлен вектор мгновенной скорости?
- Чем отличается мгновенная скорость при равноускоренном прямолинейном движении от мгновенной скорости при неравномерном движении?
- Что такое ускорение?
- Чем отличается «замедленное» прямолинейное движение от «ускоренного»?
- Что именно изменяется при прямолинейном равноускоренном движении: направление вектора скорости или его модуль?
- Может ли скорость движения тела быть равной нулю, а ускорение не равно нулю?
- Чем отличаются зависимости перемещения от времени при равномерном и равноускоренном движении?
Домашняя работа
В качестве домашнего задания учащимся необходимо дать несколько вопросов и расчетную задачу. Примеры вопросов и задач, подходящих для домашней работы:
Примеры вопросов и задач, подходящих для домашней работы:
- Скорость тела, движущегося прямолинейно и равноускоренно, изменилась при перемещении из точки 1 в точку 2 так, как показано на рисунке. Какое направление имеет вектор ускорения на этом участке?
Рис. 1.
- По графику зависимости скорости от времени, представленному на рисунке, определите ускорение прямолинейно движущегося тела в момент времени t = 2 с.
Рис. 2.
- По графику зависимости скорости от времени, представленному на рисунке, определите перемещение тела за три секунды.
Рис.
 3.
3. - При торможении на прямолинейном участке дороги скорость автомобиля равномерно уменьшается от υ1 = 20 м/с до υ2 = 10 м/с за время t = 5 с. Определите модуль ускорения автомобиля.
Конспект урока прямолинейное равноускоренное движение мгновенная скорость. Прямолинейное равноускоренное движение. Ускорение. I. Организационный этап
Тема урока: « Прямолинейное равноускоренное движение.
Решение задач».
Цель урока: Систематизировать знания о способах решения задач при равноускоренном движении.
Задачи урока :
Сформировать умения выделять ускоренное движение и характеризовать его с помощью физических величин – ускорения, скорости.
Научиться строить график скорости.
Научиться составлять уравнение скорости по графику скорости.
Научиться составлять уравнение скорости.
Ход урока.
1. Организационный этап
Приветствие, проверка подготовленности учащихся к учебному занятию, раскрытие целей урока и плана его проведения.
Фронтальный опрос.
1)Что называется ускорением равноускоренного движения?
2) Что такое равноускоренное движение?
3)Что характеризует ускорение? По какой формуле вычисляется? (а х =
4) При каком условии модуль вектора скорости движущегося тела увеличивается? Уменьшается?
5) Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости
(V x = V 0 x + a x t)
На сегодняшнем уроке будем рассматривать следующие вопросы:
Как составить уравнение скорости;
Как по уравнению скорости определить направление скорости и ускорения;
Как по уравнению скорости построить график проекции скорости:
Как по графику проекции скорости составить уравнение скорости.
Задача 1. По данному рисунку составить уравнение проекции скорости:
3м/с 2 1м/с 2
1 тело : V x = 6 – 3 t , т.к вектор скорости сонаправлен с осью Х, то V 0 x =6 м/с, вектор ускорения противоположно направлен с осью Х, то а х = -3м/с 2 .
2 тело : V x = 2 + t , т.к вектор скорости сонаправлен с осью Х, то V 0 x =2 м/с, вектор ускорения тоже сонаправлен с осью Х, то а х = 1м/с 2 .
Задача 2 . (самостоятельно).
По данным уравнениям проекции скорости нарисовать положение тел на координатной прямой.
V x = -10 + 2 t 2) V x = -6 – 3 t
2м/с 2 3м/с 2
10м/с 6м/с X
Задача 3. По данным уравнениям проекции скорости построить графики проекции скорости.(Из условия первой задачи)
1)V x = 6 – 3 t 2) V x = 2 + t
Графиками данных функций являются прямые, которые строятся по точкам.
Вопросы учащимся:
1.Как движется первое тело? Второе тело?(первое тело – тормозит, второе- ускоряется)
2. Что означает точка пересечения графиков? (скорости тел через 1 сек после начала движения стали равны)
Задача4 . По данному графику проекции скорости написать уравнение проекции скорости. (рис А)
(рис.А)
Ответ: по графику определяем, что V 0х = 3м/с.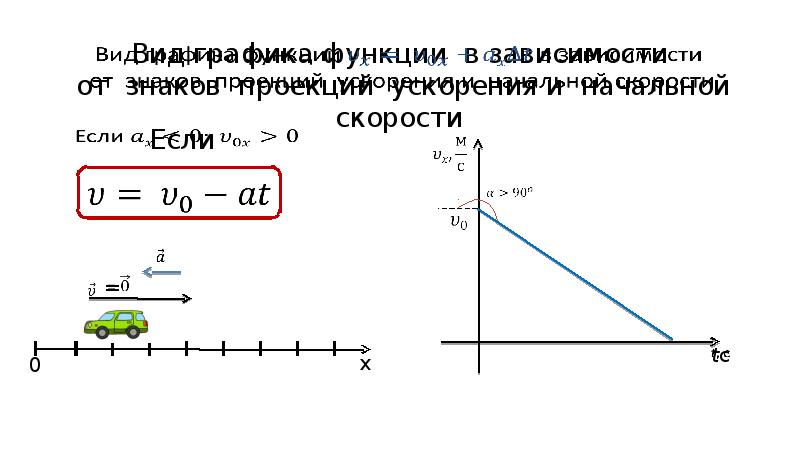 Чему равно ускорение? а х =
Чему равно ускорение? а х =
а х = = 2 м/с 2 . Подставляя числа в уравнение, имеем: V x = 3 +2 t .
Закрепление:
Какое из приведенных ниже уравнений описывает движение, при котором скорость тела увеличивается?
На рисунке 1 приведен график зависимости скорости движения тела от времени. Какое уравнение соответствует этому графику?
(рис.1)
Какой из графиков (рис.2) соответствует уравнению скорости V = 2-t?
(рис.2)
Какой из графиков (рис 3) соответствует равноускоренному движению тела, при котором вектор ускорения направлен противоположно вектору скорости?
(рис.3)
По графику зависимости скорости от времени (рис. 4) определите ускорение тела в момент времени t= 4с.
(рис. 4)
Итоги.Домашнее задание. §6.Упр.6 (3,4)
Список использованной литературы
1. Перышкин А.В., Гутник Е.М. Физика. 9 класс –М. Дрофа 2005.
2. Лукашик В. И., Иванова Е.В. Сборник задач по физике 7-9 класс – М.: Просвещение, 2008.
И., Иванова Е.В. Сборник задач по физике 7-9 класс – М.: Просвещение, 2008.
3. Марон А.Е., Марон Е.А. Физика. Дидактические материалы.9 класс. – М. Дрофа. 2008г.
Прямолинейное равноускоренное движение. Ускорение.
Ход урока
I. Организационный этап
II. Проверка домашнего задания.
1 слайд: Тест.
1.Среди предложенных ниже величин выберите только векторные.
А: пройденный путь
Б: перемещение
В: проекция перемещения
2.При прямолинейном движении тела проекция вектора перемещения на ось считается положительной, если. . . .
направление вектора перемещения совпадает с направлением оси
направление вектора перемещения противоположно направлению оси
направление вектора перемещения перпендикулярно направлению оси
длина вектора равна нулю
3.Автобус переместился из точки с координатой х 0 =200 м в точку с координатой х 1 =-200 м. Определите проекцию перемещения автобуса.
А) 0 м Б) -200 м С) -400 м Д) 400 м
4.Определите конечную координату мотоциклиста, если он выехал из точки х 0 =30 м, а проекция перемещения на ось ОХ равна S x =240 м.
А) 0 м Б) 30 м С) 210 м Д) 270 м
5.Спортсмен переместился из точки с координатой х 0 =-100 м в точку с координатой х 1 =500 м. Определите проекцию перемещения спортсмена.
А) 0 м Б) 400 м С) -400 м Д) 600 м
2 слайд: III. Изучение нового материала
Тема урока «Прямолинейное равноускоренное движение. Ускорение». Для описания такого движения мы введем важную величину – ускорение . Напомним, что на предыдущих занятиях мы обсуждали вопрос о прямолинейном равномерном движении, т.е. таком движении, когда скорость остается величиной постоянной.
3 слайд:
А если скорость изменяется, что тогда? В этом случае говорят о том, что движение неравномерное.
Из всех видов неравномерного движения мы будем изучать самое простое – прямолинейное равноускоренное, при котором тело движется вдоль прямой линии, а проекция вектора скорости тела за любые равные промежутки времени меняется одинаково (при этом модуль вектора скорости может как увеличиваться, так и уменьшаться).
4 слайд:
Для характеристики неравномерного движения вводится новая физическая величина – мгновенная скорость .
Определение: мгновенная скорость – это скорость тела в данный момент или в данной точке траектории.
Прибор, который показывает мгновенную скорость, есть на любом движущемся средстве: в автомобиле, поезде и т.д. Это прибор, который называется спидометр (от англ. – speed («скорость»)). Обращаем ваше внимание на то, что мгновенная скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло. Но ведь это определение ничем не отличается от данного нами ранее определения скорости при РПД. Для более точного определения необходимо отметить, что промежуток времени и соответствующее ему перемещение берутся очень маленькими, стремящимися к нулю. Тогда скорость не успевает поменяться сильно, и мы можем пользоваться формулой, которую вводили ранее: .
Обратите внимание на рис. . х 0 и х 1 – это координаты вектора перемещения. Если этот вектор будет очень маленьким, то и изменение скорости произойдет достаточно быстро. Это изменение в данном случае мы характеризуем изменением мгновенной скорости.
Таким образом, неравномерное движение имеет смысл характеризовать изменением скорости от точки к точке, тем, как быстро это происходит. Это изменение скорости характеризуется величиной, которая называется ускорение. Обозначается ускорение , это векторная величина.
Определение: ускорение определяется как отношение изменения скорости ко времени, в течение которого это изменение произошло.
Ускорение измеряется м/с 2 .
6 слайд: Вычислить ускорение тела, движущегося прямолинейно и равноускоренно, можно с помощью следующего уравнения, в которое входят проекции векторов ускорения и скорости:
Покажем на конкретных примерах, как находится ускорение. На рисунке а изображены санки, которые равноускоренно скатываются с горы.
На рисунке а изображены санки, которые равноускоренно скатываются с горы.
Известно, что участок пути АВ санки прошли за 4 с. При этом в точке А они имели скорость, равную 0,4 м/с, а в точке В – скорость, равную 2 м/с (санки приняты за материальную точку).
Определим, с каким ускорением двигались санки на участке АВ.
В данном случае за начало отсчёта времени следует принять момент прохождения санками точки А, поскольку согласно условию именно от этого момента отсчитывается промежуток времени, за который модуль вектора скорости изменился от 0,4 до 2 м/с.
Теперь проведём ось X, параллельную вектору скорости движения санок и направленную в ту же сторону. Спроецируем на неё начала и концы векторов v 0 и v. Образовавшиеся при этом отрезки v 0x и v x являются проекциями векторов v 0 и v на ось X. Обе эти проекции положительны и равны модулям соответствующих векторов: v 0x = 0,4 м/с, v x = 2 м/с.
Запишем условие задачи и решим её.
Проекция вектора ускорения на ось X получилась положительной, значит, вектор ускорения сонаправлен с осью X и со скоростью движения санок.
Если векторы скорости и ускорения направлены в одну сторону, то скорость растёт.
Теперь рассмотрим другой пример, в котором санки, скатившись с горы, движутся по горизонтальному участку CD (рис. б).
В результате действия на санки силы трения их скорость непрерывно уменьшается, и в точке D санки останавливаются, т. е. их скорость равна нулю. Известно, что в точке С санки имели скорость 1,2 м/с, а участок CD был пройден ими за 6 с.
Рассчитаем ускорение санок в этом случае, т. е. определим, на сколько менялась скорость санок за каждую единицу времени.
Проведём ось X параллельно отрезку CD и сонаправим её со скоростью движения санок, как показано на рисунке. При этом проекция вектора скорости санок на ось X в любой момент их движения будет положительна и равна модулю вектора скорости. В частности, при t 0 = 0 v 0x = 1,2 м/с, а при t = 6 с v x = 0.
Запишем данные и вычислим ускорение.
Проекция ускорения на ось X отрицательна. Это значит, что вектор ускорения а направлен противоположно оси X и соответственно противоположно скорости движения. При этом скорость санок уменьшалась.
При этом скорость санок уменьшалась.
Таким образом, если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости тела увеличивается, а если в противоположные – уменьшается.
7 слайд: IV. Домашняя работа.
п.5, вопросы, упр.5 (2,3)
\ Документы \ Для учителя физикиПри использовании материалов этого сайта – и размещение баннера -ОБЯЗАТЕЛЬНО!!!
Урок разработал и прислал: Калинин В.Н., студент ПГПУ им.Белинского
Конспект урока.
Тема урока: Прямолинейное равноускоренное движение. Ускорение.
Цели урока: Познакомить учащихся с равнопеременным видом движения. Ввести понятие ускорения, мгновенной скорости.
Ход урока.
Этапы урока:
- 1.Орг.момент
- 2.Повторение. Фронтальный опрос
- 3.Изучение новой темы. Беседа, рассказ
- 4.Закрепление изученного материала.
 Беседа
Беседа - 5.Д/З
1. Запись на доске
1.Повторение.Проверка домашнего задания.
Учитель: Прошлый урок мы закончили решением задачи, в которой с помощью графика зависимости координаты от времени мы находили место и время встречи автомобилей. Дома нужно было проверить полученные результаты аналитически.
Учитель: Ну что сошлись ответы?
Учитель: Хорошо! Давайте решим еще одну задачу.
Задача. Движения 2 велосипедистов заданы уравнениями
Найти время и место встречи велосипедистов. (вызываю к доске ученика)
Учитель: Давайте вначале запишем дано. Теперь вспомним, что является графиком зависимости координаты от времени.
Ученики: Прямая
Учитель: Хорошо. Тогда скажите, сколько точек достаточно для построения прямой?
9 класс физика Тема: Прямолинейное равноускоренное движение. Ускорение.Цели урока:
Образовательная: повторение, углубление и систематизация имеющихся у учащихся сведений о механических явлениях; сформировать новые знания и умения:
определение прямолинейного равнопеременного движение, ускорения, единица измерения ускорения, проекции ускорения.
Развивающая: развитие мышления, эмоционально-волевой и потребностно-мотивационной областей; умственной деятельности (выполнять операции анализа, синтеза, классификации, способность наблюдать, делать выводы,
Воспитательная: формирование системы взглядов на мир, способности следовать нормам поведения.
Тип урока: комбинированный.
Методы: словесные, наглядные, практические.
Оборудование:
План урока.
Организационный момент
Повторение (решение задач).
Изучение нового материала.
Домашнее задание
Подведение итогов урока.
Рефлексия
Ход урока.
Орг. Момент.
Повторение.
Решение задач упр.2 (1 – 3).
1. В начальный момент времени тело находилось в точке с координатами х 0 = – 2м и у 0 =4м. Тело переместилось в точку с координатами х =2м и у =1м. Найдите проекции вектора перемещения на осях х и у. Начертите вектор перемещения.
Начертите вектор перемещения.
2. Из начальной точки с координатами х 0 = – 3м и у 0 =1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5,2м, а на ось у – 3м. Найдите координаты конечного положения тела. Начертите вектор перемещения. Чему равен его модуль?
3. Путешественник прошел 5км в южном направлении, а затем еще 12км в восточном. Чему равен модуль совершенного им перемещения?
Изучение нового материала.
Презентация «Векторы и действия над ними». Повторим наглядно, что собой представляют векторы и какие действия можно совершать над ними.
Вопрос: Какое же движение называется равномерным?
Ответ: Движение, при котором тело, за любые равные промежутки времени проходит одинаковые расстояния.
Движение с постоянной скоростью.
Вопрос: Что называется скоростью прямолинейного равномерного движения?
Ответ: Постоянная векторная величина равная отношению перемещения к промежутку времени, за которое это изменение произошло.
V = s / t .
Вопрос: Тогда скажите, как вы понимаете: скорость автомобиля 60 км/ч?
Ответ: За каждый час автомобиль проезжает 60 км.
Вопрос: Скорость скалярная или векторная величина?
Ответ: Скалярная. Поэтому характеризуется направлением и модулем (численным значением).
Вопрос: В каких случаях проекция вектора скорости положительна, в каких отрицательна?
Ответ: Положительна, если проекция вектора скорости сонаправлена с осью.
Отрицательно, если проекция скорости и выбранная ось противоположно направлены.
Вопрос: Определите знак проекции вектора скорости
Ответ :1-положител.
2-положител.
3-отрицател.
4- равна 0
Вопрос: Вспомните формулу по которой можно найти положение тела в любой момент времени.
Ответ: x = x 0 + v х t
Основной материал.
До этого нам приходилось иметь дело с равномерным движением. Еще раз давайте повторим.
Равномерным называется движение, при котором тело за любые равные промежутки времени проходит одинаковые расстояния. По-другому, движение с постоянной скоростью, не очень часто встречается на практике. Гораздо чаще приходится иметь дело с таким движением, при котором скорость со временем изменяется. Такое движение называется равнопеременным.
С самым простым видом равнопеременного движения является равноускоренное. При котором тело движется вдоль прямой линии, а проекция вектора скорости тела за любые равные промежутки времени меняется одинаково. Допустим, по дороге движется автомобиль и из бака капает бензин через одинаковые промежутки времени оставляет следы.
Время, каждые 2сек.
Мы видим, что через одинаковые промежутки времени скорость меняется одинаково. Так вот такое движение называется равноускоренным.
Учитель: Давайте запишем в тетрадях определение равноускоренного движения.
Движение тела при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным.
При рассмотрении равноускоренного движения вводится понятие мгновенной скорости.
Мгновенная скорость- скорость в каждой конкретной точке траектории, в соответствующий момент времени.
Рассмотрим движение, при котором в начальный момент времени скорость тела была равно V 0 , а через промежуток времени t она оказалась равной V,
тогда отношение – быстрота изменения скорости.
Т.е. быстрота изменения скорости называется ускорением.
а =
V 0 – начальная скорость, скорость в момент времени t=0
V – скорость, которую тело имело к концу промежутка t.
Ускорение величина векторная.
– [а]=м/с 2
Из формулы можно найти значение скорости в определенный момент.
Сначала запишем значение скорости в векторном виде, а затем и скалярном.
V = V 0 + at
V = V 0 – at
Ускорением тела называется величина, характеризующая быстроту изменения скорости; она равна отношению изменения скорости к промежутку времени за которое это изменение произошло.
Равноускоренное движение это движение с постоянным ускорением.
Т.к. ускорение это векторная величина, значит она имеет направление.
Как определить, куда направлен вектор ускорения?
Допустим, прямолинейно движется тело и с течением времени его скорость увеличивается. Изобразим это на чертеже.
В этом случае вектор ускорения направлен в ту же скорость что и вектор скорости.
Если тело движется, и его скорость с течением времени уменьшается (тормозит) – вектор ускорения направлен противоположно вектору скорости.
Если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости увеличивается.
Если в противоположные стороны, то модуль вектора скорости уменьшается.
Домашнее задание
§4 упр. 3.
Подведение итогов.
1. Какое движение называют равноускоренным или равнопеременным?
2. Что называют ускорением?
3.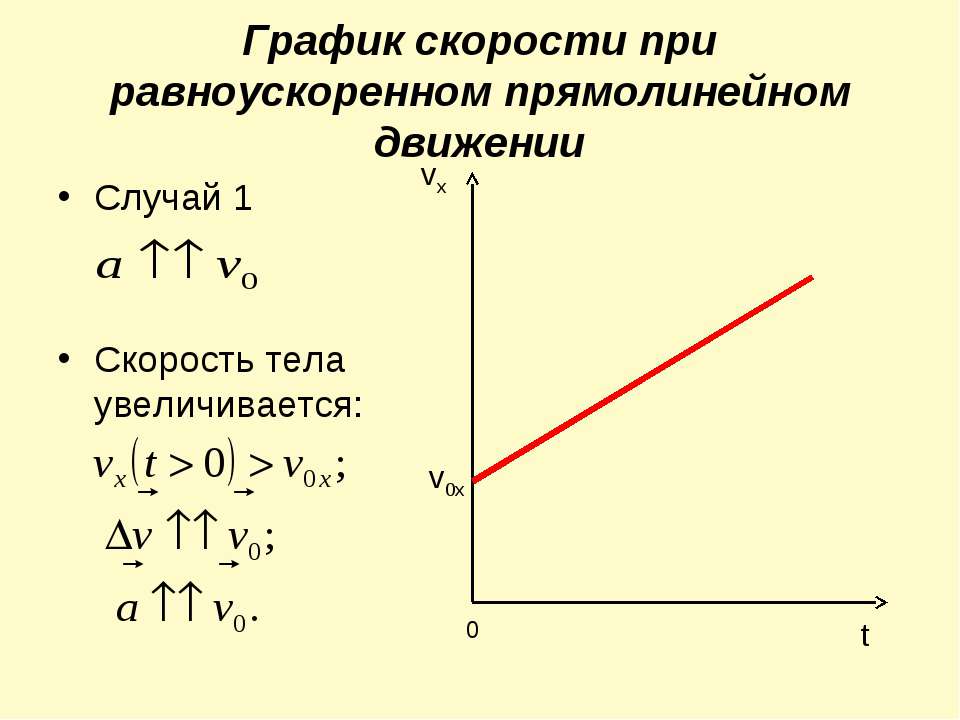 Какая формула выражает смысл ускорения?
Какая формула выражает смысл ускорения?
4. Чем отличается «ускоренное» прямолинейное движение от «замедленного»?
Таким образом, прямолинейное движение рассматривается двух видов: равномерное и равнопеременное (с ускорением). Равномерное с постоянной скоростью, равнопеременное с постоянным ускорением. Ускорение характеризует быстроту изменения скорости.
Рефлексия.
Урок полезен…
Мне было…
Я узнал…
На данном уроке по теме «Прямолинейное равноускоренное движение. Ускорение» мы рассмотрим неравномерное движение и его особенности. Будет изложено, что такое прямолинейное неравномерное движение и чем оно отличается от равномерного движения, рассмотрено определение ускорения.
Тема урока «Неравномерное прямолинейное движение, прямолинейное равноускоренное движение. Ускорение». Для описания такого движения мы введем важную величину – ускорение .
На предыдущих занятиях обсуждался вопрос о прямолинейном равномерном движении, т. е. таком движении, когда скорость остается величиной постоянной. А что, если скорость изменяется? В этом случае говорят в том, что движение неравномерное, то есть скорость от точки к точке меняется. Важно понимать, что скорость может увеличиваться, тогда движение будет ускоренным, или уменьшаться (рис. 1) (в этом случае мы будем говорить о движении замедленном).
е. таком движении, когда скорость остается величиной постоянной. А что, если скорость изменяется? В этом случае говорят в том, что движение неравномерное, то есть скорость от точки к точке меняется. Важно понимать, что скорость может увеличиваться, тогда движение будет ускоренным, или уменьшаться (рис. 1) (в этом случае мы будем говорить о движении замедленном).
Рис. 1. Движение с изменением скорости
В общем случае изменение скорости можно характеризовать величиной уменьшения или увеличения скорости.
Средняя скорость
Когда мы говорим о неравномерном движении, то, помимо понятия «мгновенная скорость», которым мы будем часто пользоваться, крайнюю важность приобретает и понятие «средняя скорость». Более того, именно это понятие позволит нам дать корректное определение мгновенной скорости.
Что же такое средняя скорость? Это можно понять на простом примере. Представьте себе, что вы едете на автомобиле из Москвы в Санкт-Петербург и проезжаете 700 км за 7 часов. Какова была ваша скорость во время этого перемещения? Если автомобиль проехал 700 км за 7 часов, то его скорость составляла 100 км/ч. Но это не значит, что спидометр в каждый момент времени показывал 100 км/ч, так как где-то автомобиль стоял в пробке, где-то он разгонялся, где-то он обгонял или вообще останавливался. В этом случае можно сказать, что мы искали не мгновенную скорость, а какую-то другую.
Какова была ваша скорость во время этого перемещения? Если автомобиль проехал 700 км за 7 часов, то его скорость составляла 100 км/ч. Но это не значит, что спидометр в каждый момент времени показывал 100 км/ч, так как где-то автомобиль стоял в пробке, где-то он разгонялся, где-то он обгонял или вообще останавливался. В этом случае можно сказать, что мы искали не мгновенную скорость, а какую-то другую.
Именно для таких ситуаций в физике и вводится понятие средней скорости (а также средней путевой скорости). Сегодня мы рассмотрим и одну, и другую и выясним, какой пользоваться удобнее и практичнее.
Средней скоростью называют отношение модуля полного перемещения тела ко времени, за которое это перемещение совершено: .
Представим пример: вы вышли в магазин за покупками и вернулись домой, модуль вашего перемещения равен нулю, но ведь скорость не была равна нулю, поэтому понятие средней скорости в данном случае неудобно.
Перейдем к более практичному понятию – средняя путевая скорость. Средняя путевая скорость – отношение полного пути, которое пройдено телом, к полному времени, за которое этот путь пройден: .
Средняя путевая скорость – отношение полного пути, которое пройдено телом, к полному времени, за которое этот путь пройден: .
Это понятие удобное, ведь путь – скалярная величина, он может только нарастать. Часто понятия средней скорости и средней путевой скорости путают, и мы также часто будем под средней скоростью иметь в виду среднюю путевую скорость.
Существует множество интересных задач на нахождение средней скорости, самые интересные из которых мы вскоре рассмотрим.
Определение мгновенной скорости через среднюю скорость движения
Для того чтобы описать неравномерное движение, мы вводим понятие мгновенной скорости, называя ее скоростью в данной точке траектории в данный момент времени. Но такое определение не будет корректным, потому что мы знаем всего два определения скорости: скорость равномерного прямолинейного движения и средняя скорость, которой мы пользуемся в случае, когда хотим найти отношение полного пути к полному времени. Эти определения в данном случае не подходят. Как же корректно найти мгновенную скорость? Здесь можно воспользоваться понятием средней скорости.
Как же корректно найти мгновенную скорость? Здесь можно воспользоваться понятием средней скорости.
Посмотрим на рисунок, на котором изображен произвольный участок криволинейной траектории с точкой А, в которой нам нужно найти мгновенную скорость (рис. 4). Для этого рассмотрим участок , который содержит точку А, и нарисуем вектор перемещения на этом участке. Средней скоростью на этом участке будет отношение перемещения ко времени . Будем уменьшать этот участок и найдем аналогичным образом среднюю скорость уже для меньшего участка. Совершая таким образом предельный переход от к и т. д., мы приходим к очень маленькому перемещению за очень маленький промежуток времени.
Рис. 3. Определение мгновенной скорости через среднюю скорость
Безусловно, сначала средние скорости будут сильно отличаться от мгновенной скорости в точке А, но, чем ближе мы будем приближаться к точке А, тем меньше за это время будут меняться условия движения, тем больше движение будет походить на равномерное движение, для которого мы знаем, что такое скорость.
Итак, при устремлении промежутка времени к нулю средняя скорость практически совпадает со скоростью в данной точке траектории, и мы переходим к мгновенной скорости. Мгновенная скорость в данной точке траектории – это отношение малого перемещения, которое совершает тело ко времени, за которое оно произошло.
Интересно, что в английском языке для понятия скорости существует два отдельных определения: speed (модуль скорости), отсюда спидометр; velocity, первая буква которого – v, отсюда обозначение вектора скорости.
Мгновенная скорость имеет направление. Вспомним, что когда мы говорили о мгновенной скорости, то рисовали перемещения , и т.тд. (рис. 4). По отношению к участку криволинейной траектории они являются секущими. Если ближе приближаться к точке А, они станут касательными (рис. 5). Мгновенная скорость на участке траектории всегда направлена по касательной к траектории.
Рис. 4. При уменьшении участка секущие приближаются к касательной
Например, в дождь, когда проезжающая мимо машина забрызгивает нас каплями, они летят именно по касательной к окружности, а данной окружностью является колесо автомобиля (рис. 6).
6).
Рис. 5. Движения капель
Другой пример: если к жгуту привязать камень и раскрутить, то, когда камень оторвется, он тоже полетит по касательной к траектории, по которой движется жгут.
Другие примеры мы рассмотрим при изучении равноускоренного движения.
Для характеристики неравномерного движения вводится новая физическая величина – мгновенная скорость . Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Прибор, который показывает мгновенную скорость, есть на любом транспортном средстве: в автомобиле, поезде и т. д. Это прибор, который называется спидометр (от англ. speed – «скорость»).
Обращаем ваше внимание на то, что мгновенная скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло. Если перемещение будет уменьшаться, стремиться к точке, то в этом случае можно говорить о мгновенной скорости: .
Обратите внимание, что и – это координаты тела (рис. 2). Если промежуток времени будет очень маленьким, то и изменение координаты произойдет очень быстро, а изменение скорости на малом промежутке будет незаметным. Скорость на данном промежутке мы характеризуем мгновенной скоростью.
2). Если промежуток времени будет очень маленьким, то и изменение координаты произойдет очень быстро, а изменение скорости на малом промежутке будет незаметным. Скорость на данном промежутке мы характеризуем мгновенной скоростью.
Рис. 2. К вопросу об определении мгновенной скорости
Таким образом, неравномерное движение имеет смысл характеризовать изменением скорости от точки к точке, тем, как быстро это происходит. Это изменение скорости характеризуется величиной, которая называется ускорением. Обозначается ускорение , это векторная величина.
Ускорение – физическая величина, которая характеризует быстроту изменения скорости. По сути скорость изменения скорости – это есть ускорение. Поскольку это вектор, значение проекции ускорения может быть отрицательным и положительным.
Ускорение измеряется в и находится по формуле: . Ускорение определяется как отношение изменения скорости ко времени , в течение которого это изменение произошло.
Важный момент – это разность векторов скоростей. Обратите внимание, что разность мы обозначим (рис. 3).
Обратите внимание, что разность мы обозначим (рис. 3).
Рис. 6. Вычитание векторов скорости
В заключение отметим, что проекция ускорения на ось точно так же, как любая векторная величина, может иметь отрицательные и положительные значения в зависимости от направления. Важно отметить, что, куда направлено изменение скорости, туда будет направлено ускорение (рис. 7). Особое значение это приобретает при криволинейном движении, когда изменяется не только значение скорости, но и направление.
Рис. 7. Проекция вектора ускорения на ось
Список литературы
- Кикоин И.К., Кикоин А.К. Физика: учебник для 9 класса средней школы. – М.: Просвещение.
- Слободянюк А.И. Физика 10. Часть 1. Механика. Электричество.
- Физика. Механика. 10 класс / Под ред. Мякишева Г.Я. – М.: Дрофа.
- Филатов Е.Н. Физика 9. Часть 1. Кинематика. – ВШМФ: Авангард.
Домашнее задание
- Чем отличается средняя скорость от мгновенной?
- Начальная скорость велосипедиста 36 км/ч, затем он замедлил движение до 18 км/ч.
 Он тормозил на протяжении 10 секунд. С каким ускорением двигался велосипедист и куда оно было направлено?
Он тормозил на протяжении 10 секунд. С каким ускорением двигался велосипедист и куда оно было направлено? - Мальчик вышел из пункта В и направился в пункт С, при этом пройдя 400 м, и оттуда вернулся в пункт А. Чему равна средняя путевая скорость, если расстояние от пункта А до пункта В равно 150 метров, а на всю дорогу мальчик потратил 12 минут?
Урок по физике на тему “Равномерное прямолинейное движение. Уравнения и графики. Мгновенная скорость и ускорение. Свободное падение тел. Движение по окружности.” (10 класс)
Тема: Равномерное прямолинейное движение. Уравнения и графики. Мгновенная скорость и ускорение. Свободное падение тел. Движение по окружности.
Цель: изучить характеристики прямолинейного равномерного движения; сформулировать понятие скорости и ускорения; движение точки по окружности.
План:
1. Характеристики прямолинейного равномерного движения, графики.
Характеристики прямолинейного равномерного движения, графики.
2. Скорость при прямолинейном равномерном движении, ускорение.
3. Движение точки по окружности.
Задание для самопроверки.
1. Материальная точка движется равномерно от центра вращающегося диска по его радиусу. В какой системе отсчета траектория точки будет прямой линией?
2. Автомобиль преодолел подъем длиной 200 м с углом наклона к горизонту 30°. Определите перемещение автомобиля в вертикальном и горизонтальном направлениях.
Изложение нового материала
Определение прямолинейного равномерного движения. С прямолинейным равномерным движением Вы уже знакомы из курсов физики и математики предыдущих классов: в большинстве задач на движение рассматривалось именно такое движение. Следует дать определение прямолинейного равномерного движения, привести примеры и подчеркнуть существенный признак такого движения: равенство перемещений в любые сколь угодно малые промежутки времени.

Можно пронаблюдать за равномерным движением воздушных пузырьков в двух стеклянных трубках разного сечения и выяснить, чем отличаются эти равномерные движения. Опыт позволяет получить понятие скорости.
Скорость при прямолинейном равномерном движении. Скорость — одна из основных кинематических характеристик движения материальной точки, определяемая отношением перемещения к интервалу времени, в течение которого оно произошло:
Из этой формулы следует, что
Удобно направить ось х вдоль прямой, по которой движется тело: тогда единственная отличная от нуля проекция скорости
Проекция скорости vx может быть как положительной, так и отрицательной — в зависимости от того, в каком направлении оси х движется тело.
Перемещение при прямолинейном равномерном движении.
 Формулы для зависимости проекции перемещения sx и координаты х от времени имеют вид:
Формулы для зависимости проекции перемещения sx и координаты х от времени имеют вид:
Sx= vxt,
X = Xo+vxt .
Вопросы для самопроверки.
Можно ли утверждать, что тело движется прямолинейно равномерно, если оно:
за каждую секунду проходит путь, равный 1 м;
движется вдоль прямой в одном направлении и за каждую секунду проходит путь 3 м?
Какая скорость больше: 15 м/с или 36 км/ч?
Можно ли, зная начальное положение тела и длину пройденного пути, определить его конечное положение?
Задачи для самопроверки
1. Какие из приведенных ниже формул описывают прямолинейное равномерное движение? Какие формулы вообще не могут описывать реальное движение: a) s = 5 – 2t; б) v = 5 – 2t; в) х = 5 – 2t; г) l = 5 – 2t?
Какие из приведенных ниже формул описывают прямолинейное равномерное движение? Какие формулы вообще не могут описывать реальное движение: a) s = 5 – 2t; б) v = 5 – 2t; в) х = 5 – 2t; г) l = 5 – 2t?
2. Тело движется прямолинейно равномерно. Обязательно ли являются линейными функциями времени: а) пройденный путь; б) модуль перемещения; в) модуль координаты?
3. При равномерном движении вдоль оси ОХ координата точки за первые 5с изменилась от значения х0 = 10 м до значения Х1 = -10 м. Найдите модуль скорости точки и проекцию вектора скорости на ось ОХ. Запишите формулу зависимости х(t). (Ответ: 4 м/с; -4 м/с; х = 10 – 4t.)
Для конспекта студента.
■ Прямолинейным равномерным движением называется движение, при котором тело за любые равные интервалы времени совершает одинаковые перемещения.
■Скорость прямолинейного равномерного движения равна отношению перемещения тела к интервалу времени, за который совершено это перемещение:
■Зависимость от времени перемещения, проекции перемещения и координаты тела:
Контрольное задание №1
1) Сколько времени потребуется поезду длиной 450 м, чтобы преодолеть мост длиной 750 м, если скорость поезда 72 км/ч?
2) Один автомобиль, двигаясь со скоростью 16 м/с, проехал туннель за 30 с, а другой автомобиль, двигаясь равномерно, проехал тот же туннель за 24 с. Какова скорость второго автомобиля?
3)Тело движется в отрицательном направлении оси ОХ со скоростью 36 км/ч. Начальная координата равна 20 м. Найдите координату тела через 4 с. Какой путь прошло тело?
4) Собака бежит за велосипедистом по прямолинейному участку шоссе. Движение велосипедиста описывается уравнением X1 = 25 + 10t, а движение собаки — уравнением х2 = -35 + 12t . Опишите оба движения (укажите тип каждого движения и значения характеризующих его величин), постройте графики X1(t) и X2(t) . Догонит ли собака велосипедиста? Если догонит, то когда и где это произойдет?
Опишите оба движения (укажите тип каждого движения и значения характеризующих его величин), постройте графики X1(t) и X2(t) . Догонит ли собака велосипедиста? Если догонит, то когда и где это произойдет?
Самостоятельная работа № 1
«Прямолинейное равномерное движение»
1. Сколько времени потребуется скорому поезду длиной 150 м, чтобы проехать мост длиной 850 м, если скорость поезда равна 72 км/ч?
2. Двигаясь равномерно прямолинейно, тело за 10 с преодолело 200 см. За сколько часов это тело, двигаясь с той же скоростью и в том же направлении, преодолеет путь 36 км?
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
В каждый данный момент времени движущаяся точка может находиться только в одном определенном положении на траектории. Поэтому ее удаление от начала координат есть некоторая функция времени t. Зависимость между переменными s и t выражается уравнением s = f(t). Траекторию движения точки можно задать аналитически, т. е. в виде уравнений: s = 2t + 3, s = 4t или графически.
Траекторию движения точки можно задать аналитически, т. е. в виде уравнений: s = 2t + 3, s = 4t или графически.
Графики — «международный язык». Овладение ими имеет большое образовательное значение. Поэтому необходимо научиться не только строить графики, но и анализировать их, читать, понимать, какую информацию о движении тела можно получить из графика.
Графики зависимости проекции перемещения от времени.
График функции sx = f (t) называется графиком движения.
Графиком sx(t) = vxt является прямая, проходящая через начало координат. Если vx > 0, то sx возрастает со временем, а если vx < 0, то sx убывает со временем (рис. 1).
1).
Наклон графика тем больше, чем больше модуль скорости.
Графики зависимости проекции скорости от времени. Наряду с графиками движения часто используются графики скорости vx = f (t). При изучении равномерного прямолинейного движения необходимо научиться строить графики скорости и пользоваться ими при решении задач.
График функции vx(t) — прямая, параллельная оси t. Если vx > О, эта прямая проходит выше оси t, а если vx < 0, то ниже (рис. 2).
Площадь фигуры, ограниченной графиком ux(t) и осью t, численно равна модулю перемещения (рис. 3).
Наряду с графиком скорости очень важны графики координаты движущегося тела, так как они дают возможность определить положение движущегося тела в любой момент времени.
Графики зависимости координаты от времени. График x(t) = = x0+sx(t) отличается от графика sx(t) только сдвигом на х0 по оси ординат. Точка пересечения двух графиков соответствует моменту, когда координаты тел равны, т. е. эта точка определяет момент времени и координату встречи двух тел (рис. 4).
По графикам x(t) видно, что велосипедист и автомобиль в течение первого часа двигались навстречу друг другу, а затем — удалялись друг от друга.
Графики пути. Полезно обратить внимание на отличие графика координаты (перемещения) от графика пути. Только при прямолинейном движении в одном направлении графики пути и координаты совпадают. Если направление движения изменяется, то эти графики уже не будут одинаковыми (рис.
 5).
5).
Рис. 4
Обратите внимание: хотя велосипедист и автомобиль движутся в противоположных направлениях, в обоих случаях путь возрастает со временем.
Вопросы для самопроверки студента
1. Графики х (t) для двух тел параллельны. Что можно сказать о скорости этих тел?
2. Графики l (t) для двух тел пересекаются. Обозначает ли точка пересечения графиков момент встречи этих тел?
Контрольные задания №2
Опишите движения, графики которых приведены на рис. 6. Запишите для каждого движения формулу зависимости x(f).
По графикам скорости (рис. 7) запишите формулы и постройте графики зависимости sx(t).
Рис. 7
По приведенным на рисунке графикам скорости (см. рис. 8) запишите формулы и постройте графики зависимости sx(t).

НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ. СКОРОСТЬ ПРИ НЕРАВНОМЕРНОМ ДВИЖЕНИИ. УСКОРЕНИЕ
1. Неравномерное движение. Из повседневной жизни известно, что равномерное движение встречается редко. Чаще приходится сталкиваться с движением, при котором скорость с течением времени меняется. Такое движение называют неравномерным.
2. Средняя скорость. Так как скорость при неравномерном движении изменяется во времени, то формулой для вычисления перемещения пользоваться нельзя, поскольку скорость является переменной величиной и неизвестно, какое именно ее значение нужно подставить в эту формулу. Однако в некоторых случаях можно рассчитывать перемещение, если ввести величину, называемую средней скоростью. Она показывает, какое перемещение совершает тело в среднем за единицу времени, т. е.
Средняя скорость vcp — векторная величина: ее направление совпадает с направлением s , а ее модуль vcp = s/t.
3. Средняя путевая скорость. Однако средняя скорость не всегда подходит для описания движения. Рассмотрим такой пример: автомобиль выехал из гаража и через 2 часа вернулся обратно. Спидометр показывает, что автомобиль проехал 100 км. Какова средняя скорость движения?
Правильный ответ: средняя скорость равна нулю, потому что тело вернулось в начальную точку, т. е. перемещение тела равно нулю. Возможен и другой ответ, если определять не среднюю скорость, а среднюю путевую скорость, равную отношению пути, пройденному телом, ко времени движения: . Поскольку путь — скалярная величина, то и средняя путевая скорость (в отличие от средней скорости) является скалярной величиной.
Знание средней скорости не дает возможности определять положение тела в любой момент времени, даже если известна траектория его движения. Однако это понятие удобно для выполнения некоторых расчетов, например, времени движения.
4. Примеры решения задач.
Примеры решения задач.
Задача. Человек выехал из поселка по прямой дороге на велосипеде со скоростью v1=15 км/ч . В дороге велосипед сломался, и дальше человеку пришлось идти пешком со скоростью v2 = 5 км/ч . Найдите среднюю скорость движения на всем пути, если: а) человек половину времени своего движения ехал и половину времени — шел; б) человек половину пути ехал и половину пути шел. Почему средняя скорость в случаях а и б не совпадает?
Решение. В обоих случаях движение происходит вдоль прямой в одном направлении, поэтому средняя скорость совпадает со средней путевой скоростью. Обозначим весь пройденный путь l, а все затраченное время t. Тогда
В случае «а» человек ехал в течение времени t1 и такое же время t2 шел пешком. Следовательно, он проехал путь l1= v1t1 и прошел путь l2= v2t2 .
Поскольку l=l1+l2, получаем
Подставляя численные данные, получаем v ср = 10 км/ч . При этом обращаем внимание: средняя скорость равна среднему арифметическому скоростей на различных участках, если движение на каждом участке занимало одинаковое время.
В случае «б» человек проехал путь l1 и такой же путь l2 прошел пешком. Следовательно ехал он в течение времени t1 , и шел в течение времени t2 .
Поскольку t = t1+ t2, получаем
Подставляя численные данные, получаем и v ср =7,5 км/ч . Как видим, в этом случае средняя скорость движения меньше, чем в первом. Это объясняется тем, что в случае «а» человек ехал и шел одинаковое время, а в случае «б» он проехал и прошел одинаковое расстояние, т.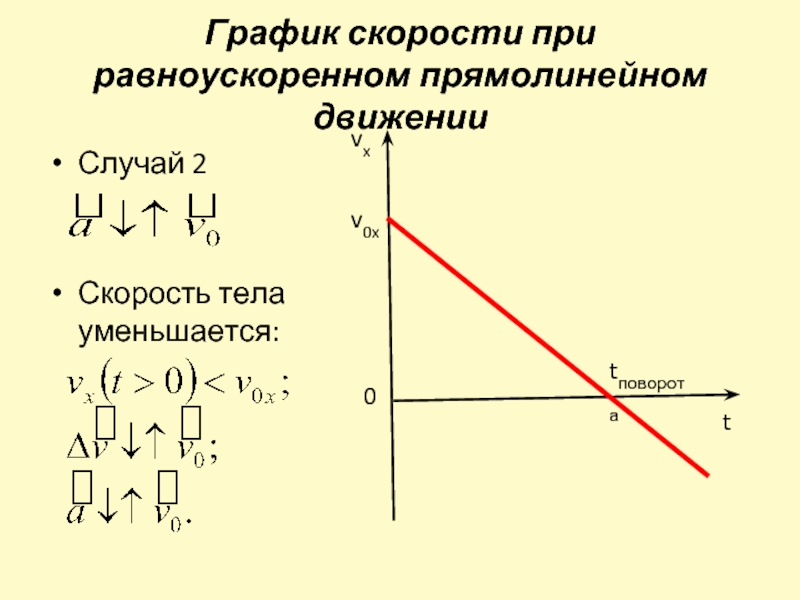 е. шел дольше, чем ехал.
е. шел дольше, чем ехал.
Вопросы для самопроверки студента
Почему нельзя говорить о средней скорости переменного движения вообще, а можно говорить только о средней скорости за данный промежуток времени или о средней скорости на данном участке пути?
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Автомобиль за час проехал по прямому шоссе 60 км, а за следующий час — 30 км назад. Какова средняя путевая скорость на всем пути? Средняя скорость?
Задачи для самопроверки
Человек прошел по прямой дороге 3 км за 1 ч, потом повернул под прямым углом и прошел еще 4 км за 1 ч. Найдите среднюю и среднюю путевую скорости движения на первом этапе движения, на втором этапе и за все время движения. (Ответ: средняя скорость — 3 км/ч; 4 км/ч; 2,5 км/ч; средняя путевая скорость 3 км/ч; 4 км/ч; 3,5 км/ч.
 )
)Человек проехал первую половину пути на автомобиле со скоростью 75 км/ч, а вторую половину — на велосипеде со скоростью 25 км/ч. Какова средняя путевая скорость на всем пути? (Ответ: 37,5 км/ч.)
Пешеход две трети времени своего движения шел со скоростью 3 км/ч. Оставшееся время — со скоростью 6 км/ч. Определите среднюю и среднюю путевую скорости движения пешехода. (Ответ: 4 км/ч.)
Для конспекта студента
■ Средняя скорость движения равна отношению перемещения тела ко времени t , в течение которого это перемещение произошло:
■ Средняя скорость — векторная величина.
■ Средняя путевая скорость равна отношению пути, пройденного телом, ко времени движения:
■ Средняя путевая скорость — скалярная величина.
Контрольные задания №3
1) Велосипедист проехал 80 км со скоростью 20 км/ч, а потом еще 60 км со скоростью 10 км/ч. Какова средняя путевая скорость его движения на всем пути?
Какова средняя путевая скорость его движения на всем пути?
2) Мотоциклист проехал 20 км за 30 мин, а затем ехал со скоростью 60 км/ч в течение 1,5 ч. какой была его средняя путевая скорость на всем пути?
3) Мотоциклист ехал сначала со скоростью 90 км/ч, а затем — со скоростью 30 км/ч. Какова средняя путевая скорость мотоциклиста на всем пути? Рассмотрите случаи, когда мотоциклист ехал со скоростью 90 км/ч: а) половину пути; б) половину времени.
ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ. УСКОРЕНИЕ
Мгновенная скорость. Если скорость тела изменяется со временем, для описания движения нужно знать, чему равна скорость тела в данный момент времени (или в данной точке траектории). Эта скорость называется мгновенной скоростью.
Можно также сказать, что мгновенная скорость — это средняя скорость за очень малый интервал времени. При движении с переменной скоростью средняя скорость, измеренная за различные интервалы времени, будет разной. Однако, если при измерении средней скорости брать все меньшие и меньшие интервалы времени, значение средней скорости будет стремиться к некоторому определенному значению. Это и есть мгновенная скорость в данный момент времени. В дальнейшем, говоря о скорости тела, мы будем иметь в виду его мгновенную скорость.
Однако, если при измерении средней скорости брать все меньшие и меньшие интервалы времени, значение средней скорости будет стремиться к некоторому определенному значению. Это и есть мгновенная скорость в данный момент времени. В дальнейшем, говоря о скорости тела, мы будем иметь в виду его мгновенную скорость.
Ускорение. При неравномерном движении мгновенная скорость тела — величина переменная; она различна по модулю и (или) по направлению в разные моменты времени и в разных точках траектории. Все спидометры автомобилей и мотоциклов показывают только модуль мгновенной скорости.
Если мгновенная скорость неравномерного движения изменяется неодинаково за одинаковые промежутки времени, то рассчитать ее очень трудно. Такие сложные неравномерные движения нами не изучаются, поэтому рассмотрим только самое простое неравномерное движение — равноускоренное прямолинейное.
Прямолинейное движение, при котором мгновенная скорость за любые равные интервалы времени изменяется одинаково, называется равноускоренным прямолинейным движением.
Если скорость тела при движении изменяется, возникает вопрос: какова скорость изменения скорости? Эта величина, называемая ускорением, играет важнейшую роль во всей механике: ускорение тела определяется действующими на это тело силами.
Ускорением называется отношение изменения скорости тела к интервалу времени, за который это изменение произошло:
Единица измерения ускорения в СИ: . Если тело движется в одном направлении с ускорением 1 м/с2 , его скорость изменяется каждую секунду на 1м/с.
Термин «ускорение» используется в физике, когда речь идет о любом изменении скорости,— в том числе и тогда, когда модуль скорости уменьшается или когда модуль скорости остается неизменным и скорость изменяется только по направлению.
Скорость при прямолинейном равноускоренном движении. Из определения ускорения следует, что .

Если направить ось Ох вдоль прямой, по которой движется тело, то в проекциях на ось Ох получим vx = v0x + axt.
Таким образом, при прямолинейном равноускоренном движении проекция скорости линейно зависит от времени. Это означает, что графиком зависимости vx(t) является отрезок прямой.
График скорости разгоняющегося автомобиля дан на рис. 1.
График скорости тормозящего автомобиля дан на рис. 2.
Рис. 2
Вопросы для самопроверки
Чему равна мгновенная скорость камня, брошенного вертикально вверх, в верхней точке траектории?
О какой скорости — средней или мгновенной — идет речь в следующих случаях:
поезд прошел путь между станциями со скоростью 70 км/ч;
скорость движения молотка при ударе равна 5 м/с;
скоростемер на электровозе показывает 60 км/ч;
пуля вылетает из винтовки со скоростью 600 м/с?
Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг.
 Как направлены ускорения поездов?
Как направлены ускорения поездов?
Контрольные задания №4
Ось Ох направлена вдоль траектории прямолинейного движения тела. Что вы можете сказать о движении, при котором: a) vx > 0, ах > 0; б) vx > 0, ах < 0; в) vx < 0, ах > 0; г) vx < 0, ах < 0; д) vx < 0, ах = 0?
Тело движется равноускоренно. При этом vOx = 20 м/с, ах = -4 м/с2. Сколько времени тело будет двигаться в том же направлении, что и в начальный момент? Начертите график vx (t).

Чему равна проекция ускорения, если в моменты времени t1= 10 с и t2 = 30 с проекции скорости v1x = 30 м/с и v2x =10 м/с? Начертите график vx (t).
Поезд через 10 с после начала движения прцобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равной 3 м/с?
Для конспекта студента
■ Мгновенной скоростью называется скорость тела в данный момент времени (или в данной точке траектории).
■ Ускорением тела называется отношение изменения скорости тела к интервалу времени, за который это изменение произошло:
■ Прямолинейным равноускоренным движением называется движение тела вдоль прямой с постоянным ускорением. При прямолинейном равноускоренном движении скорость тела за любые равные интервалы времени изменяется на одну и ту же величину.
При прямолинейном равноускоренном движении скорость тела за любые равные интервалы времени изменяется на одну и ту же величину.
ПЕРЕМЕЩЕНИЕ ПРИ ПРЯМОЛИНЕЙНОМ
РАВНОУСКОРЕННОМ ДВИЖЕНИИ
1. Перемещение при прямолинейном равноускоренном движении.
Для решения основной задачи механики нужно найти закон движения, определяющий положение тела в любой момент времени, т. е. s = f (t). Для этого нужно уметь находить вектор перемещения, а для нахождения перемещения, в свою очередь, удобно воспользоваться графическим методом.
Сначала следует всмнить, что при равномерном движении проекция перемещения sx численно равна площади фигуры, ограниченной графиком vx (t) и осью Ot.
Это справедливо и для неравномерного движения, потому что время движения можно разбить на такие малые интервалы времени, в течение каждого из которых движение тела можно считать практически равномерным (рис. 1).
1).
Воспользуемся этим, чтобы найти зависимость перемещения от времени при прямолинейном равноускоренном движении.
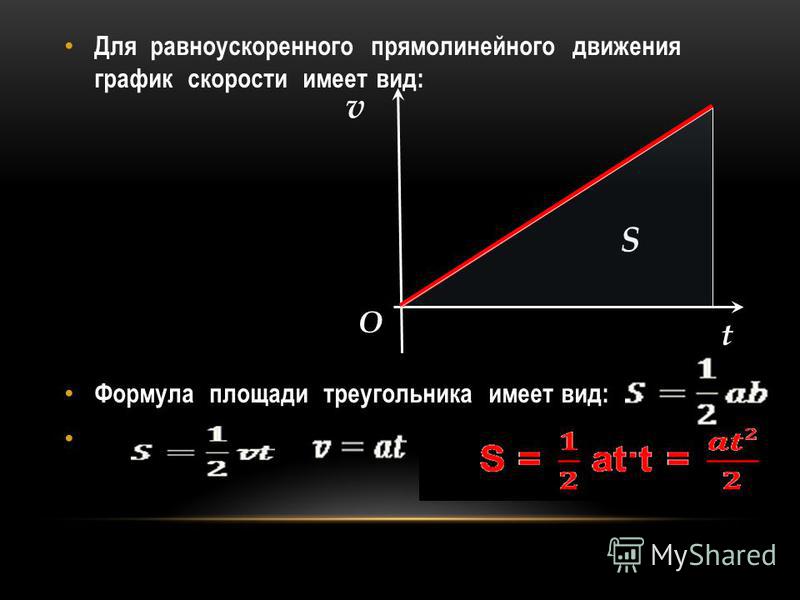
Если начальная скорость тела равна нулю, фигура, ограниченная графиком vx (t) и осью Ot,— треугольник площадью axt2/2 (рис. 2).
Следовательно, при прямолинейном равноускоренном движении без начальной скорости
Если начальная скорость тела не равна нулю, фигура, ограниченная графиком Vx(t) и осью Ot,— трапеция, состоящая из прямоугольника площадью vOxt и треугольника площадью axt2/2 (рис. 3).
Рис.3
Таким образом, при прямолинейном равноускоренном движении с начальной скоростью
2. Координата при прямолинейном равноускоренном движении. Поскольку х = х0 +sx , получаем:
Координата при прямолинейном равноускоренном движении. Поскольку х = х0 +sx , получаем:
Средняя скорость при прямолинейном равноускоренном движении. Пользуясь выведенными выше формулами можно доказать, что
Это соотношение упрощает решение многих задач.
Соотношение между перемещением и скоростью. Для решения задач, в условии которых не задано время движения, полезны формулы, связывающие перемещение с начальной и конечной скоростями. Из формул
Если начальная скорость равна нулю, эта формула принимает вид:
Вопросы для самоконтроля
Когда модуль перемещения и пройденный путь совпадают?
Как связаны между собой проекции перемещения, модуль перемещения и пройденный путь при прямолинейном движении в одном направлении?
Как по графику скорости определить проекцию перемещения?
Контрольные задания №5
Уравнения движения различных тел, движущихся вдоль оси Ох, имеют вид (все величины измеряются в единицах СИ):
х = 5 + 3t – 6t2; в) х = -2 – 4t + 3t2;
x = 4 + 3t; г) x = 3-7t-2t2.

Какие из этих тел движутся равноускоренно? Чему равны при этом проекция начальной скорости и проекция ускорения ах ? В каких случаях в начале движения тело движется в положительном направлении оси Ох ? В каких случаях скорость тела в начале движения увеличивается по модулю?
Автомобиль трогается с места и движется равноускоренно по прямому шоссе. За первую секунду автомобиль проходит 3 м. Какой путь пройдет автомобиль за первые 2 секунды? За первые 5 секунд?
Автомобиль начал движение с ускорением 0,5 м/с2 в тот момент, когда мимо него равноускоренно проезжал трамвай со скоростью 18 км/ч. Какую скорость будет иметь автомобиль, когда догонит трамвай? Ускорение трамвая 0,3 м/с2.
Для конспекта студента
■ Проекция перемещения при движении без начальной скорости:
■ Проекция перемещения при движении с начальной скоростью:
■ Зависимость координаты от времени при движении с начальной скоростью:
■ Уравнение средней скорости:
■ Соотношение между перемещением и скоростью:
без начальной скорости: .
с начальной скоростью:
Контрольные задания №6
За первую секунду равноускоренного движения без начальной скорости тело прошло 5 м. Какое расстояние оно прошло за первые 3 с? За первые 10 с?
При прямолинейном равноускоренном движении за 10 с скорость тела уменьшилась с 20 м/с до 10 м/с. Каково перемещение тела за это время? Какова скорость через 5 с после начала наблюдения?
Тележка скатывается с наклонной плоскости равноускоренно. Пройдя расстояние 2 м, она приобретает скорость 1 м/с. Какое расстояние должна преодолеть тележка, чтобы приобрести скорость 2 м/с?
Пуля, летевшая со скоростью 400 м/с, пробила стену толщиной 20 см, в результате чего скорость пули уменьшилась до 100 м/с. Сколько времени двигалась пуля в стене?
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
1.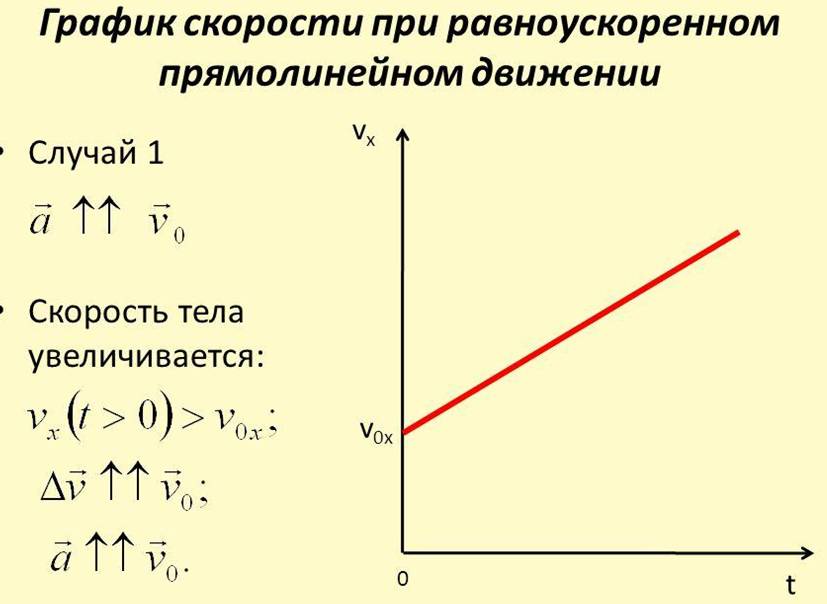 Свободное падение. Ускорение свободного падения. Великий ученый древности Аристотель на основе наблюдений построил теорию, согласно которой чем тяжелее тело, тем быстрее оно падает. Эта теория просуществовала две тысячи лет — ведь камень действительно падает быстрее, чем цветок!
Свободное падение. Ускорение свободного падения. Великий ученый древности Аристотель на основе наблюдений построил теорию, согласно которой чем тяжелее тело, тем быстрее оно падает. Эта теория просуществовала две тысячи лет — ведь камень действительно падает быстрее, чем цветок!
Возьмем два тела, легкое и тяжелое, свяжем их вместе и бросим с высоты. Если легкое тело всегда падает медленнее, чем тяжелое, оно должно «притормаживать» падение тяжелого тела, и поэтому связка двух тел должна падать медленнее, чем одно тяжелое тело. Но ведь связку можно считать одним телом, еще более тяжелым, и, значит, связка должна падать быстрее, чем одно тяжелое тело!
Обнаружив это противоречие, Галилей решил проверить на опыте, как же в действительности будут падать шары разного веса: пусть ответ на этот вопрос даст сама природа. Он изготовил два шара и сбросил их с Пизанской башни — оба шара упали почти одновременно!
Падение тела в условиях, когда сопротивлением воздуха можно пренебречь, называют свободным падением.
Тот факт, что свободное падение тел — ускоренное движение, не вызывает сомнений. В этом легко убеждиться, наблюдая за движением падающего шарика и других тел. Однако на вопрос, является ли свободное падение равноускоренным движением, трудно ответить. Ответ на этот вопрос может дать эксперимент. Если, например, сделать ряд моментальных снимков падающего шарика через равные промежутки времени (стробоскопические фотографии), то по расстояниям между последовательными положениями шарика можно определить, что движение действительно является равноускоренным.
Значит .
Понятие свободного падения имеет широкий смысл: тело совершает свободное падение не только, когда его начальная скорость равна нулю. Если тело брошено вниз с начальной скоростью v0 , то оно будет при этом тоже свободно падать. Более того, свободное падение не обязательно представляет собой движение вниз. Если начальная скорость тела направлена вверх, то тело при свободном падении некоторое время будет лететь вверх, уменьшая свою скорость, и лишь затем начинает падать вниз.
2. Зависимость скорости и координаты падающего тела от времени. Если совместить начало координат с начальным положением тела и направить ось Оу вниз, то графики vy (t) и y(t) будут иметь следующий вид (рис. 1).
Таким образом, при свободном падении скорость тела увеличивается за каждую секунду примерно на 10 м/с (рис. 2).
3. Зависимость скорости и координаты тела, брошенного вертикально вверх, от времени. Далее следует рассмотреть случай, когда тело брошено вверх. Если совместить начало координат с начальным положением тела и направить ось у вертикально вверх, то проекции скорости и перемещения в начале движения будут положительными.
На рисунках 3, 4 приведены графики vy(t) и y(t) для тела, брошенного вертикально вверх с начальной скоростью 30 м/с.
Рис.3 Рис. 4
4. Связь начальной скорости бросания и конечной скорости падения.
Далее можно сравнить уравнения для скоростей свободно падающего тела: vy = vOy + gt и тела, брошенного вертикально вверх, vy = vOy – gt.
Если начальная скорость свободно падающего тела равна нулю, то получим: vy = gt . При достижении максимальной высоты подъема тела, брошенного вертикально вверх, его конечная скорость равна нулю vy = 0 . Тогда — 0 = vOy – gt. Откуда vOy = gt.
Сравнивая полученные выражения vy = gt и vOy = gt, получим, что vOy = vy, т. е. начальная скорость бросания равна конечной скорости падения.
е. начальная скорость бросания равна конечной скорости падения.
Вопросы для самопроверки
Одинаковым ли будет время свободного падения различных тел с одной и той же высоты?
Чему равно ускорение тела, брошенного вертикально вверх, в верхней точке траектории?
Из одной точки падают без начальной скорости два тела с интервалом времени t секунд. Как движутся эти тела относительно друг друга в полете?
Контрольные задания №7
1. Тело свободно падает без начальной скорости. Какое расстояние оно • пролетает за первую секунду? За вторую секунду? За третью секунду?
Примите g = 10м/с2.
2. Камень падал с одной скалы 2 с, а с другой 6 с. Во сколько раз вторая скала выше первой?
Для конспекта студента
■ Свободным падением называется падение тела в условиях, когда сопротивлением воздуха можно пренебречь.
■ При свободном падении вблизи поверхности Земли все тела движутся с одинаковым ускорением, которое называется ускорением: свободного падения и обозначается g . Из опытов следует, что g = 9,8 м/с2.
■ Зависимость скорости от времени при движении с начальной скоростью:
.
РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Особенности криволинейного движения. Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любое криволинейное движение можно рассматривать как движение по дугам окружностей с различными радиусами. Изучение движения по окружности дает также ключ к рассмотрению произвольного криволинейного движения.
Далее перейдем непосредственно к рассмотрению равномерного движения по окружности, т. е. движения по окружности с постоянной по модулю скоростью.
Основные характеристики равномерного движения по окружности. Период обращения Т — это время одного полного оборота.
Чтобы совершить один полный оборот, тело должно пройти путь 2πr (длина окружности). Следовательно,
Т= 2πr
v
Частота обращения «ύ» равна числу полных оборотов за единицу времени.
1
ύ = — .
T
Единица измерения частоты [ύ]= .
Угловая скорость ώ =
где — угол поворота радиуса, проведенного к телу из центра окружности, по которой движется тело за время (рис. 1).
Угол измеряется в радианах (1 радиан (рад) — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности; 1 рад = 57°), т.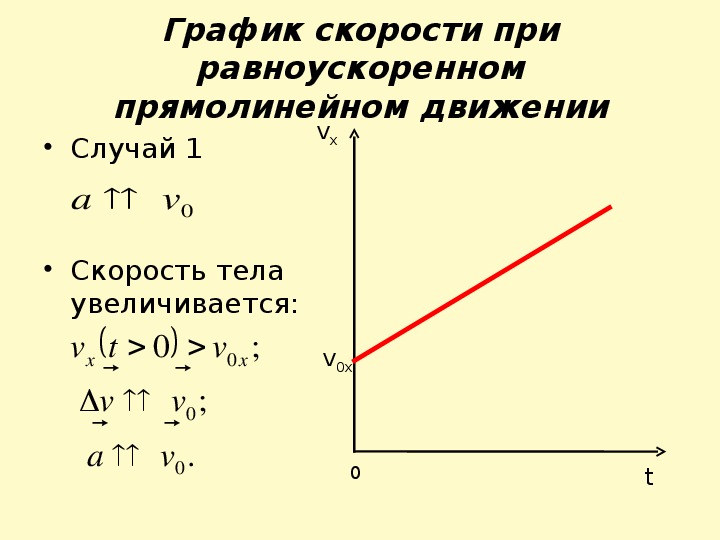 е. одному полному обороту соответствует угол 2π . Поскольку полный оборот тело совершает за время Т, получаем:
е. одному полному обороту соответствует угол 2π . Поскольку полный оборот тело совершает за время Т, получаем:
ώ=
Единицей измерения угловой скорости является радиан в секунду (рад/с). Сравнивая формулу ώ = 2π/Т с формулой ύ = 1/Т , получаем связь между угловой скоростью и частотой: ώ = 2πr.
При криволинейном движении мгновенная скорость в любой точке траектории направлена по касательной к траектории в этой точке. А поскольку касательная к окружности перпендикулярна радиусу, то мгновенная скорость при движении по окружности в каждой точке траектории направлена перпендикулярно радиусу (рис. 2).
Ускорение при равномерном движении по окружности. При движении по окружности, как и при любом криволинейном движении, направление скорости изменяется со временем. А раз скорость тела изменяется — хотя бы только по направлению,— значит, тело движется с ускорением.
 При равномерном движении изменение скорости обусловлено только изменением направления скорости. Нетрудно доказать, что изменение скорости направлено перпендикулярно скорости — по радиусу к центру окружности.
При равномерном движении изменение скорости обусловлено только изменением направления скорости. Нетрудно доказать, что изменение скорости направлено перпендикулярно скорости — по радиусу к центру окружности.
Ускорение направлено так же, как , поэтому при равномерном движении по окружности ускорение в каждый момент времени направлено по радиусу к центру окружности. По этой причине ускорение тела при равномерном движении по окружности называют центростремительным ускорением.
Рассмотрим равнобедренный треугольник, образованный векторами v1, v2 и (рис. 3), который подобен равнобедренному треугольнику, образованному двумя радиусами, проведенными из центра окружности в точки, где находилось тело в моменты времени t1, и t2, и перемещением за время . Из подобия этих треугольников следует, что
Контрольные вопросы №1
1. Как направлена мгновенная скорость при движении по окружности?
Как направлена мгновенная скорость при движении по окружности?
2. Как направлено ускорение при равномерном движении по окружности?
3. Можно ли равномерное движение по окружности считать равноускоренным движением?
При равномерном движении по прямой ускорение равно нулю. Можно ли равномерное движение по кривой считать движением без ускорения?
Два тела движутся по окружностям разных радиусов. Ускорение какого тела больше, если: а) скорости тел одинаковы; б) периоды обращения тел одинаковы?
Контрольные задания №9
1. Во сколько раз скорость конца минутной стрелки башенных часов больше скорости конца минутной стрелки наручных часов, если длина стрелки башенных часов 1,5 м, а длина стрелки наручных часов 1,5 см?
2. С каким ускорением движется автомобиль по кольцевой трассе, имеющей вид окружности радиусом 100 м, если скорость автомобиля 20 м/с? Во сколько раз это ускорение меньше ускорения свободного падения?
Для конспекта ученика
■ Равномерным движением по окружности называется движение по окружности с постоянной по модулю скоростью.
■ Основные характеристики равномерного движения по окружности: радиус окружности r , период обращения Т, частота обращения ύ, угловая скорость ώ. Соотношения между этими величинами:
■ Мгновенная скорость в данной точке траектории направлена по касательной к траектории в этой точке, т. е. перпендикулярно радиусу, проведенному из центра окружности в данную точку.
■ При равномерном движении по окружности ускорение в каждый момент времени направлено по радиусу к центру окружности. Модуль центростремительного ускорения можно найти по любой из формул:
ЗАДАНИЕ:
Составить конспект по лекции.
Ответить на контрольные вопросы.
Решить контрольные задачи.
ФОРМА ОТЧЕТНОСТИ:
Предоставить выполненные задания на электронный адрес:
4558bi@gmail. com
com
Срок выполнения задания до 21.10.2020 г.
Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение
Прямолинейное равноускоренноедвижение: мгновенная скорость,
ускорение, перемещение.
Что характеризует скорость?
Быстроту
движения
Быстроту
изменения
скорости
Скорость
характеризует
быстроту
движения
Длину
траектории
3. Основная единица измерения скорости
км/чм/с
см/с
4. Что такое равномерное движение?
это движение, при котором телоза любые равные промежутки
времени совершает одинаковые
перемещения.
Эксперимент
Что такое неравномерное движение?
– это движение с изменяющейся
скоростью
Равноускоренное движение
0
S1
1
2
S2
S3
Движение, при котором тело движется
воль прямой линии, а проекции
вектора скорости тела а любые
промежутки времени меняются
одинаково
Неравномерное движение
это такое движение, при котором тело, за любые равные
промежутки времени совершает разные перемещения, или,
говорят, меняется проекция вектора скорости.

Средняя скорость показывает, чему равно перемещение,
которое тело в среднем совершает за единицу времени.
ср
S
t
S ср t
Автомобиль, двигаясь по прямой, проходит 600 км за 10 ч, то это
значит, что в среднем она за каждый час проходит 60 км. Но
ясно, что какую-то часть времени автомобиль вовсе не двигался,
а стоял на остановке; трогаясь с нее, автомобиль увеличивал
свою скорость, приближаясь к ней — уменьшал ее. Все это не
принимается во внимание и считается, что автомобиль каждый
час проходит по 60 км.
Главная задача механики?
определять положение тела в любой момент времени.
Зная среднюю скорость, нельзя решать главную задачу
механики. Можно ли каким-нибудь другим способом
свести неравномерное движение к равномерному?
Этого сделать нельзя, потому что механическое
тела в каждой
движение — это скорость
процесс непрерывный:
ни координаты
конкретной
тела, ни его скорость
не могут изменятьсяточке
скачками.

траектории
Мгновенная
скорость
Мгновенная скорость – скорость тела в каждой
конкретной точке траектории в соответствующий
момент времени
Равноускоренное движение
а
0
S1
1
2
S2
S3
Ускорение величина, характеризующая быстроту
изменения скорости
Ускорение равно отношению изменения
скорости тела ко времени, в течение
которого это изменение произошло.
а
0
t
13. Ускорение показывает изменение модуля вектора скорости в единицу времени.
Основная единица ускорения:м
1
м
с
1 2
с
1с
Решите задачу
Тело начинает движение из состояния покоя
равноускоренно и за 2 с достигает скорости 12 м/с.
Определите ускорение тела.
Решите задачу
Тело, двигаясь со скоростью 20 м/с,
останавливается через 10 с.
Каково ускорение тела?
Решите задачу
Какую скорость разовьет автомобиль, который
трогается с места и движется с ускорением 0,2
м/с2 в течение 6 с? Какой путь он при этом
пройдет?
Кинематические уравнения
равнопеременного
прямолинейного движения
Домашнее задание
§5, упр.
 5
5Продолжи предложение
Я сегодня на уроке открыл для себя…
Мне понравилось на уроке то, что…
На уроке меня порадовало…
Я удовлетворён своей работой, потому что…
Мне хотелось бы порекомендовать…
Если бы я был учителем, то …
https://doc4web.ru/uploads/files/9/8597/hell
o_html_6b9914a2.jpg
https://png.pngtree.com/element_origin_mi
n_pic/16/07/10/165782044ce67df.jpg
23. Интернет – ресурсы
Слайд 1 http://bukashka.org/wp-content/2010/01/dvizenie.jpgлев 2 http://kladraz.ru/upload/blogs2/2016/10/11498_eb4b62630807cc85cee94864eab59eb8.jpg
Слайд 2 велосипедист https://ds04.infourok.ru/uploads/ex/0956/000d152d-818bab9f/hello_html_m2eb2e831.png
Лыжник http://clipart-library.com/img/1301143.png
Слайд 3 http://4.bp.blogspot.com/_tcYfuTKy2w/TgyBk2YtVOI/AAAAAAAAANo/EYSlAmgptN0/s1600/Soccer%2Bspeed%2Bpic.jpg
Слайд 3,4 шкала http://ekuzmenko.ru/wp-content/uploads/2016/03/speed_test_poster-682×350.jpg
Слайд 4
https://videouroki.
 net/videouroki/conspekty/fizika9/3-priamolinieinoie-ravnouskoriennoie-dvizhieniieuskorieniie.files/image001.png
net/videouroki/conspekty/fizika9/3-priamolinieinoie-ravnouskoriennoie-dvizhieniieuskorieniie.files/image001.pngСлайд 5
https://videouroki.net/videouroki/conspekty/fizika9/3-priamolinieinoie-ravnouskoriennoie-dvizhieniieuskorieniie.files/image002.png
Слайд 6 Человек http://filed8-1.my.mail.ru/pic?url=http%3A%2F%2Fimgfotki.yandex.ru%2Fget%2F5645%2F65387414.70%2F0_c17ca_12e43ac9_GIFL.gif&mw=&mh=&sig=a539b5d
3f1b2a782744f3987bad60136
Слайд 6, 10 часы http://cliparts.co/cliparts/qiB/Xr7/qiBXr7yoT.jpg
Слайд 7 https://media.istockphoto.com/vectors/racing-cyclist-red-vectorid96611533?k=6&m=96611533&s=612×612&w=0&h=4LkydaEoCaFdx4h3IGKk2w7up8hOgF1XSTVjuUjOh
Uc=
Слайд 8,9 https://www.iconspng.com/images/car-racing/car-racing.jpg
Слайд
9
траектория
https://videouroki.net/videouroki/conspekty/fizika9/3-priamolinieinoieravnouskoriennoie-dvizhieniie-uskorieniie.files/image006.png
Слайд 12 https://img3.stockfresh.
 com/files/u/urchenkojulia/m/65/4806376_stock-vectorkids-sledding.jpg
com/files/u/urchenkojulia/m/65/4806376_stock-vectorkids-sledding.jpgСлайд 13-15 http://ivanov-shkola-70.myjino.ru/informatika_06_fgos/par_17/ris_62.png
Слайд 16 https://t3.ftcdn.net/jpg/00/88/46/10/500_F_88461044_O4jZKFtfraJElxrteditW7uV6ih0vufA.jpg
Слайд 17 http://habazavr.ru/prez-uchit-u-dos/school-teacher-at-the-blackboard_075.png
Слайд 18 http://900igr.net/up/datai/97700/0014-036-.png
Автор: Ошлыкова Л.В.- учитель физики
МАОУ “Лянторская СОШ №7”
Технологическая карта урока «Равноускоренное движение»
1.Неравномерное движение. Мгновенная скорость.
Исследовательский метод.
Задание: Какой вид движения мы изучили? Как найти скорость при равномерном движении? Приведите примеры равномерного движения. Как часто мы можем наблюдать такое движение?
Вывод: в окружающем нас мире распространено другое движение.
Задание: Рассмотрите движение шарика по наклонной плоскости (демонстрация видеофильма).
– Что вы можете сказать о расстояниях, пройденным шариком за каждую секунду? ( они разные).
– Сформулируйте определение неравномерного движения. (Движение, при котором тело за равные промежутки времени проходит разные расстояния, называется неравномерным).
– А что вы можете сказать о скорости, которую имеет шарик на каждом участке пути? (если расстояние, пройденное телом за каждую секунду разное, то и скорость на каждом участке пути тоже будет неодинакова).
Вывод: При неравномерном движении скорость непрерывно изменяется: от точки к точке, от одного момента времени к другому.
Такая скорость называется мгновенной – скорость в данный момент времени в данной точке траектории.
2. Равноускоренное движение. Ускорение.
Эвристический метод.
-Как вы думаете, как должна меняться скорость тела, чтобы неравномерное движение выглядело более просто? (Для простоты мы будем рассматривать такое неравномерное движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково).
Вывод: Такое движение называется равнопеременным (или равноускоренным).
Задание: Запишите, чему равно изменение скорости () и разделите его на промежуток времени, в течение которого это изменение произошло. Как вы думаете, эта величина может служить характеристикой равноускоренного движения? (Да, так как она постоянна).
Вывод: Величина характеризует изменение скорости тела. Это ускорение. У этой величины есть обозначение, формула и единицы измерения.
Ускорением движущегося тела называют величину, равную отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло.
Задание: Вернемся к физическому диктанту, заданиям №8 и №9. Теперь мы можем их выполнить? Выполняйте.
Проверка. Самооценка (суммируйте все баллы физического диктанта).
– Если ускорение тела по абсолютному значению велико, что из этого следует? (что оно быстро меняет свою скорость).
– В системе единиц СИ скорость измеряется в метрах в секунду, а время — в секундах, тогда в чем измеряется ускорение? ( ускорение измеряется в метрах на секунду в квадрате м/с2).
Как найти ускорение при равноускоренном движении. Графическое представление равноускоренного прямолинейного движения
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой .Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.

Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.
По форме траектории движение делится на:
а) прямолинейное – траектория представляет собой отрезок прямой;
б) криволинейное – траектория представляет собой отрезок кривой.
Путь – это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение – это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение – это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь – это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение – это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x 0 + V x t , где x 0 – начальная координата тела, V x – скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с 2 , не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности.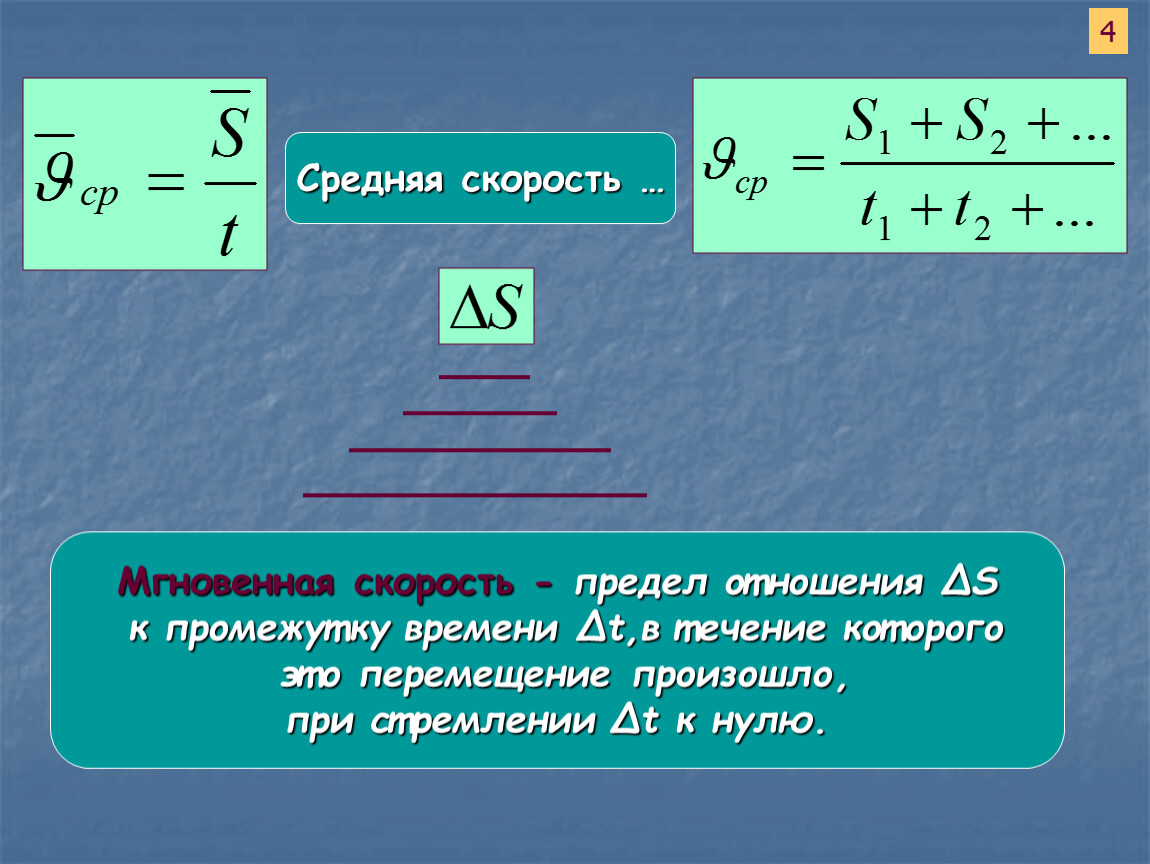 При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω :
При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω :
Угловая скорость связана с линейной скоростью соотношением
где r – радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду – частота обращения – ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением , оно направлено по радиусу к центру окружности:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса – это мера инертности тела
Сила – это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом – Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости .
Закон Гука записывают в виде
где k – жёсткость пружины, x – деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N – сила реакции опоры, µ – коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R – расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
Сила тяжести – это сила, с которой все тела притягиваются к Земле:
При неподвижной опоре вес тела равен по модулю силе тяжести:
Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес
Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес
В этом случае вес тела меньше веса покоящегося тела.
Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила – сила тяжести.
Искусственный спутник Земли – это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила – сила тяжести, направленная к центру Земли
Первая космическая скорость – это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.
где R – расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна
 Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение ; если никаких сил не возникает – безразличное (см. рис. 3).
Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение ; если никаких сил не возникает – безразличное (см. рис. 3).
Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.
Здесь d -плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.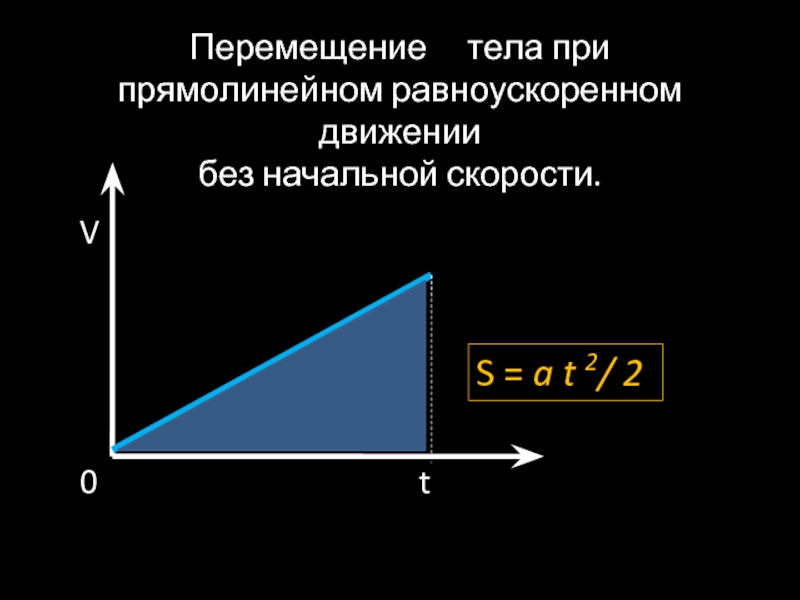
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей
где ρ – плотность жидкости, h – глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае
Высоты столбов жидкости обратно пропорциональны плотностям:
Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда : на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:
где ρ жидк – плотность жидкости, в которую погружено тело; V погр – объём погружённой части тела.
Условие плавания тела – тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохранения Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:Импульс – векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса : сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса : сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
Мощность – это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле
Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
где h – высота подъёма
Энергия сжатой пружины:
где k – коэффициент жёсткости пружины, x – абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии : если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
1.5. Механические колебания и волны Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.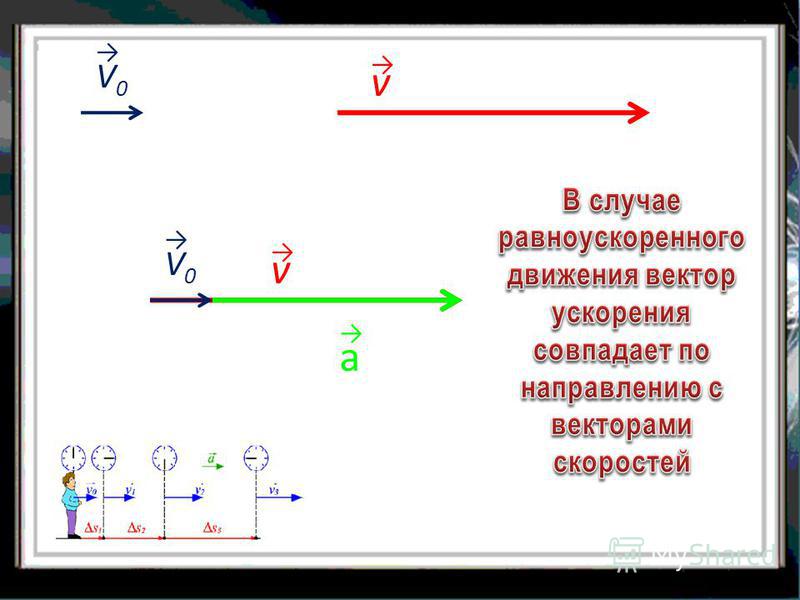
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.
Величина A, равная наибольшему абсолютному значению колеблющейся физической величины x, называется амплитудой колебаний . Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:
Частота измеряется в с -1 . Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле
где l – длина маятника.
Период колебаний груза на пружине определяется по формуле
где k – жёсткость пружины, m – масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной , если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной , если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:
где v – скорость распространения волны.
Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
Механическое движение
Механическое движение -это процесс изменения положения тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.
Тело, условное принятое за неподвижное- тело отсчета.
Тело отсчета -это тело, относительно которого определяется положение другого тела.
Система отсчета -это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.
Траектория движения
Траектория движения тела -это непрерывная линия, которую описывает движущееся тело(рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Пройденный путь
Пройденный путь -скалярная величина, равная длине дуги траектории, пройденной телом за некоторое время.
Перемещение
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением, векторная величина.
Средняя и мгновенная скорости движения.Направление и модуль скорости.
Скорость – физическая величина, которая характеризует быстроту изменения координаты.
Средняя скорость движения – это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за которое это перемещение произошло. Направление вектора средней скорости совпадает с направлением вектора перемещения ∆S
Мгновенная скорость -это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени ∆t. Вектор мгновенной скорости направлен по касательной к траектории. Модуль равен первой производной пути по времени.
Формула пути при равноускоренном движении.
Равноускоренное движение – это движение, при котором ускорение постоянно по модулю и направлению.
Ускорение движения
Ускорение движения – векторная физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.
Тангенциальное и нормальное ускорения.
Тангенциальное(касательное) ускорение -это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Направление вектора тангенциального ускорения a лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела.
Вектор перпендикулярен линейной скорости движения, направлен по радиусу кривизны траектории.
Формула скорости при равноускоренном движении
Первый закон Ньютона (или закон инерции )
Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.
Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т.е. с постоянной скоростью).
В природе существуют четыре вида взаимодействия
1. Гравитационное (сила тяготения) – это взаимодействие между телами, которые обладают массой.
2. Электромагнитное- справедливо для тел, обладающих электрическим зарядом, ответственно за такие механические силы, как сила трения и сила упругости.
3.Сильное- взаимодействие короткодействующее, то есть действует на расстоянии порядка размера ядра.
4. Слабое. Такое взаимодействие ответственно за некоторые виды взаимодействия среди элементарных частиц, за некоторые виды β-распада и за другие процессы, происходящие внутри атома, атомного ядра.
Масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие.
Сила – является количественной мерой действия одного тела на другое.
Второй закон Ньютона.
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: F=ma
Измеряется в
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения ). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с) .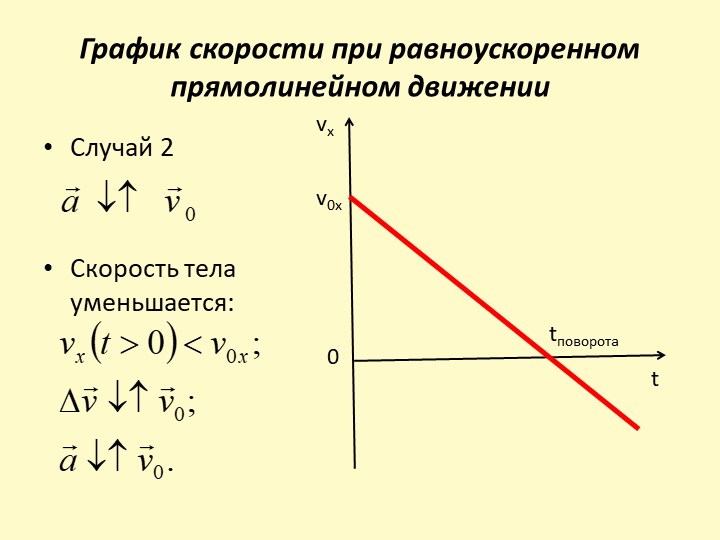
Выражение второго закона Ньютона через изменение импульса тела
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равноускоренное движение – движение, при котором ускорение постоянно по модулю и направлению.
Третий закон Ньютона. Примеры.
Плечо силы.
Плечо силы – это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести – это длина перпендикуляра (отрезок d) на рисунке
Тогда плечо силы тяжести – это длина перпендикуляра (отрезок d) на рисунке
Момент инерции тел.
Момент инерции J (кгм 2) – параметр, аналогичный по физическому смыслу массе при поступательном движении. Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения: .
Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. Он может быть выражен через массу тела и его размеры
Теорема Штейнера.
Момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
Jc – известный момент инерции относительно оси, проходящей через центр масс тела,
J – искомый момент инерции относительно параллельной оси,
m – масса тела,
d – расстояние между указанными осями.
Закон сохранения момента импульса. Примеры.
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса) :
.
Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы (рис. 6.9).
Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).
Работа силы.
Работа силы – мера действия силы при превращении механического движения в другую форму движения.
Примеры формул работы сил.
работа силы тяжести; работа силы тяжести наклонной пов-ти
работа силы упругости
Работа силы трения
Механическая энергия тела.
Механическая энергия – это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
Циклическая частота характеризует скорость изменения фазы колебаний.
Начальное состояние колебательной системы характеризует начальная фаза
Амплитуда колебаний A – это наибольшее смещение из положения равновесия
Период T – это промежуток времени, в течение которого точка выполняет одно полное колебание.
Частота колебаний – это число полных колебаний в единицу времени t.
Частота, циклическая частота и период колебаний соотносятся как
Физический маятник.
Физический маятник – твёрдое тело способное совершать колебания относительно оси, не совпадающей с центром масс.
Электрический заряд.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
· Существует два рода электрических зарядов, условно названных положительными и отрицательными.
· Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
· Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Закон Кулона.
Модуль силы взаимодействия двух точечных неподвижных электрических зарядов в вакууме прямо пропорционален произведению величин этих зарядов и обратно пропорционален квадрату расстояния между ними.
Г – расстояние между ними, k – коэффициент пропорциональности, зависящий от выбора системы единиц, в СИ
Величина, показывающая, во сколько раз сила взаимодействия зарядов в вакууме больше, чем в среде, называется диэлектрической проницаемостью среды Е. Для среды с диэлектрической проницаемостью е закон Кулона записывается следующим образом:
В СИ коэффициент k принято записывать следующим образом:
Электрическая постоянная, численно равная
Использованием электрической постоянной закон Кулона имеет вид:
Электростатическое поле.
Электростатическое поле – поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.
Основные характеристики электростатического поля:
· напряженность
· потенциал
Примеры формул напряженности поля заряженных тел.
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность заряда в любой точке сферы будет одинакова.
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
По теореме Гаусса
Следовательно
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г
2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью.
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда,расположенного в центре шара.
Тогда вне шара
а на его поверхности (r=R)
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
с другой стороны, в соответствии с теоремой Гаусса
Из сопоставления последних выражений следует
где – диэлектрическая проницаемость внутри шара.
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью .
Проведем коаксиальную цилиндрическую поверхность радиуса Поток вектора напряженности через эту поверхность
По теореме Гаусса
Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
Суммарный поток вектора; напряженности равен вектору , умноженному на площадь S первого основания, плюс поток вектора через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают.
Таким образом, с другой стороны по теореме Гаусса
Следовательно
Но тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов и , равны сумме напряженностей полей, создаваемых пластинами, т.е.
Таким образом,
Вне пластины векторы от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
Электрический ток.
Электри́ческий ток – направленное (упорядоченное) движение заряженных частиц
Сторонние силы.
Сторонние силы – силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил.
Э.д.с. Напряжение.
Электродвижущая сила (ЭДС) – физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил
Напряжение (U) равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.
Единица измерения напряжения в системе СИ:
Сила тока.
Сила тока (I)- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.
Плотность тока.
Плотность тока j – вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярно направлению тока, к величине этой площадки.
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).
Закон Ома.
Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Закон Джоуля-Ленца.
При прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.
Магнитное взаимодействие.
Магнитное взаимодействие – это взаимодействие упорядочение движущихся электрических зарядов.
Магнитное поле.
Магнитное поле – это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
Сила Лоренца и сила Ампера.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью положительный заряд (здесь – скорость упорядоченного движения носителей положительного заряда). Модуль лоренцевой силы:
Модуль лоренцевой силы:
Сила Ампера – это сила, с которой магнитное поле действует на проводник с током.
Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индукции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.
Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера определяется по правилу левой руки.
Закон Био-Савара-Лапласа.
Закон Био Савара Лапласа – Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
Формулировка
Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме, -точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)
Направление перпендикулярно и , то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление , еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора определяется выражением (в системе СИ)
Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление , еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора определяется выражением (в системе СИ)
Векторный потенциал даётся интегралом (в системе СИ)
Индуктивность контура.
Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф – магнитный поток через контур, I – сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Энергия магнитного поля.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
Электромагнитная индукция.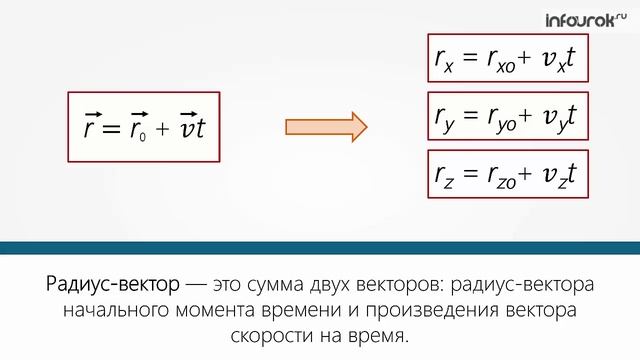
Электромагнитная индукция – явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Правило Ленца.
Правило Ленца
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым он вызван.
Первое уравнение Максвелла
2. Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).
Второе уравнение Максвелла:
Электромагнитное излучение.
Электромагни́тные во́лны, электромагни́тное излуче́ние – распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.
3.1. Волна – это колебания, распространяющиеся в пространстве в течение времени.
Механические волны могут распространяться только в какой-нибудь среде (веществе): в газе, в жидкости, в твердом теле.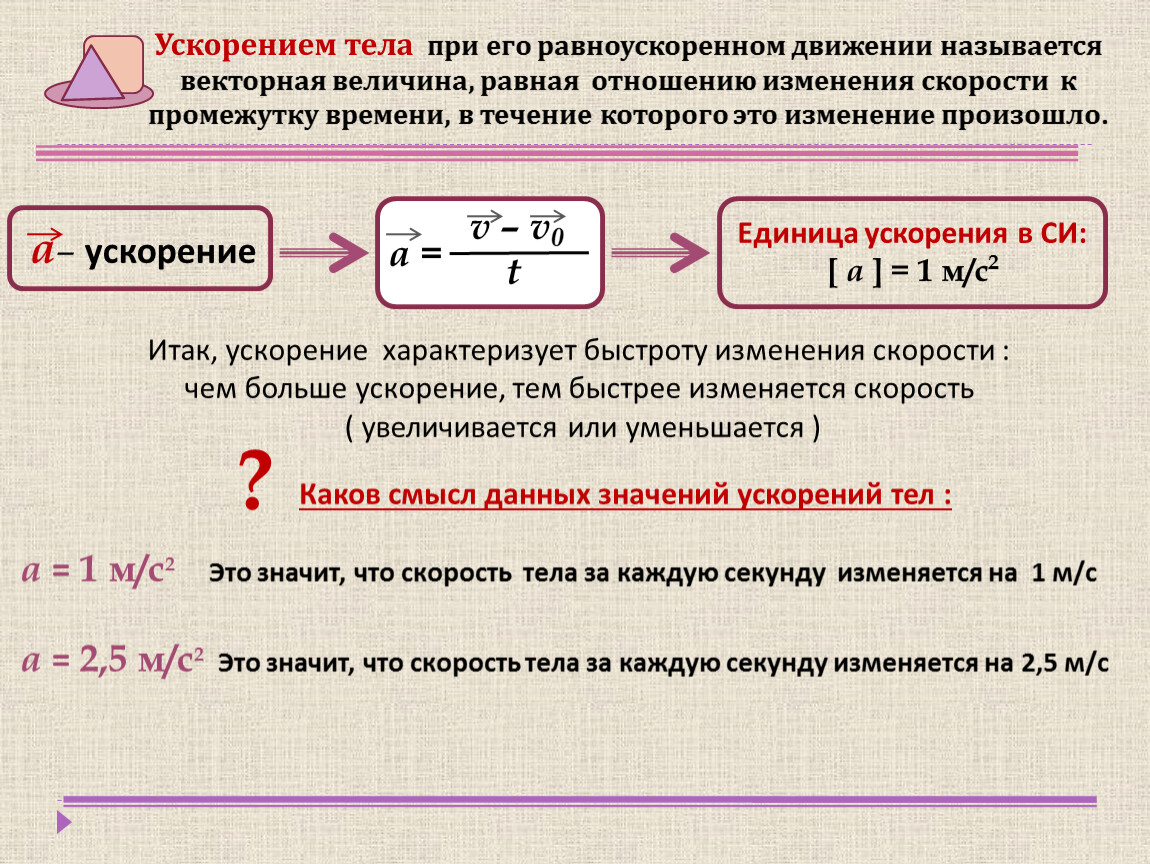 Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды. Необходимым условием для появления упругих волн является возникновение в момент возмущения среды препятствующих ему сил, в частности, упругости. Они стремятся сблизить соседние частицы, когда они расходятся, и оттолкнуть их друг от друга в момент сближения. Силы упругости, действуя на удаленные от источника возмущения частицы, начинают выводить их из равновесия. Продольные волны характерны только газообразным и жидким средам, а вот поперечные – также и твердым телам: причина этого заключается в том, что частицы, составляющие данные среды, могут свободно перемещаться, так как жестко не зафиксированы, в отличие от твердых тел. Соответственно, поперечные колебания принципиально невозможны.
Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды. Необходимым условием для появления упругих волн является возникновение в момент возмущения среды препятствующих ему сил, в частности, упругости. Они стремятся сблизить соседние частицы, когда они расходятся, и оттолкнуть их друг от друга в момент сближения. Силы упругости, действуя на удаленные от источника возмущения частицы, начинают выводить их из равновесия. Продольные волны характерны только газообразным и жидким средам, а вот поперечные – также и твердым телам: причина этого заключается в том, что частицы, составляющие данные среды, могут свободно перемещаться, так как жестко не зафиксированы, в отличие от твердых тел. Соответственно, поперечные колебания принципиально невозможны.
Продольные волны возникают тогда, когда частицы среды колеблются, ориентируясь вдоль вектора распространения возмущения. Поперечные волны распространяются в перпендикулярном вектору воздействия направлении.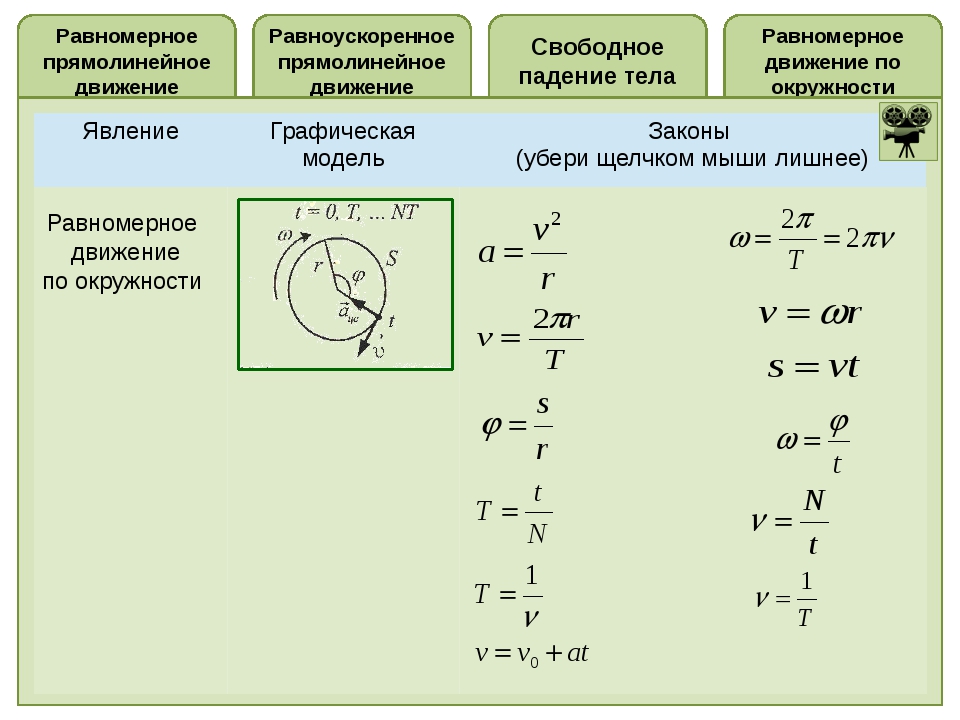 Короче: если в среде деформация, вызванная возмущением, проявляется в виде сдвига, растяжения и сжатия, то речь идет о твердом теле, для которого возможны как продольные, так и поперечные волны. Если же появление сдвига невозможно, то среда может быть любой.
Короче: если в среде деформация, вызванная возмущением, проявляется в виде сдвига, растяжения и сжатия, то речь идет о твердом теле, для которого возможны как продольные, так и поперечные волны. Если же появление сдвига невозможно, то среда может быть любой.
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
Длина́ волны́ – расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду колебаний, поэтому
Волновое число (также называемое пространственной частотой ) – это отношение 2π радиан к длине волны: пространственный аналог круговой частоты.
Определение : волновым числом k называется быстрота роста фазы волны φ по пространственной координате.
3.2. Плоская волна – волна, фронт которой имеет форму плоскости.
Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту. Плоская волна является частным решением волнового уравнения и удобной моделью: такая волна в природе не существует, так как фронт плоской волны начинается в и заканчивается в , чего, очевидно, быть не может.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции записывается в виде:
где
· – оператор Лапласа;
· – искомая функция;
· – радиус вектора искомой точки;
· – скорость волны;
· – время.
Волновая поверхность – геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Частный случай волновой поверхности – волновой фронт.
А) Плоская волна – это волна, волновые поверхности которой представляют собой совокупность параллельных друг другу плоскостей.
Б) Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических сфер.
Луч – линия, нормальной и волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причём, если волна плоская – параллельные прямые).
Понятием луч в физике обычно пользуются только в геометрической оптике и акустике, так как при проявлении эффектов, не изучаемых в данных направлениях, смысл понятия луч теряется.
3.3. Энергетические характеристики волны
Среда, в которой распространяется волна, обладает механической энергией, складывающейся из энергий колебательного движения всех ее частиц. Энергия одной частицы с массой m 0 находится по формуле: Е 0 = m 0 Α 2 ω 2 /2. В единице объема среды содержится n = p /m 0 частиц (ρ – плотность среды). Поэтому единица объема среды обладает энергией w р = nЕ 0 = ρ Α 2 ω 2 /2.
В единице объема среды содержится n = p /m 0 частиц (ρ – плотность среды). Поэтому единица объема среды обладает энергией w р = nЕ 0 = ρ Α 2 ω 2 /2.
Объемная плотность энергии (W р)- энергия колебательного движения частиц среды, содержащихся в единице ее объема:
Поток энергии (Ф) – величина, равная энергии, переносимой волной через данную поверхность за единицу времени:
Интенсивность волны или плотность потока энергии (I) – величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны:
3.4. Электромагнитная волна
Электромагнитная волна – процесс распространения электромагнитного поля в пространстве.
Условие возникновения электромагнитных волн. Изменения магнитного поля происходят при изменении силы тока в проводнике, а сила тока в проводнике изменяется при изменении скорости движения электрических зарядов в нем, т. е. при движении зарядов с ускорением. Следовательно, электромагнитные волны должны возникать при ускоренном движении электрических зарядов. При скорости заряда, равной нулю, существует только электрическое поле. При постоянной скорости заряда возникает электромагнитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, которая распространяется в пространстве с конечной скоростью.
е. при движении зарядов с ускорением. Следовательно, электромагнитные волны должны возникать при ускоренном движении электрических зарядов. При скорости заряда, равной нулю, существует только электрическое поле. При постоянной скорости заряда возникает электромагнитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, которая распространяется в пространстве с конечной скоростью.
Электромагнитные волны распространяются в веществе с конечной скоростью. Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε 0 и μ 0 – электрическая и магнитная постоянные: ε 0 = 8,85419·10 –12 Ф/м, μ 0 = 1,25664·10 –6 Гн/м.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше.
Электромагнитное излучение принято делить по частотам диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
Интерференция волн. Когерентные волны. Условия когерентности волн.
Оптическая длина пути (о.д.п.) света. Связь разности о.д.п. волн с разностью фаз колебаний, вызываемых волнами.
Амплитуда результирующего колебания при интерференции двух волн. Условия максимумов и минимумов амплитуды при интерференции двух волн.
Интерференционные полосы и интерференционная картина на плоском экране при освещении двух узких длинных параллельных щелей: а) красным светом, б) белым светом.
Теперь мы должны выяснить самое главное – как изменяется координата тела при его прямолинейном равноускоренном движении. Для этого, как мы знаем, нужно знать перемещение тела, потому что проекция вектора перемещения как раз и равна изменению координаты.
Формулу для вычисления перемещения проще всего получить графическим методом.
При равноускоренном движении тела вдоль оси X скорость изменяется со временем согласно формуле v x = v 0х + a x t Так как время в эту формулу входит в первой степени, то график для проекции скорости в зависимости от времени представляет собой прямую, как это показано на рисунке 39. Прямая 1 на этом рисунке соответствует движению с положительной проекцией ускорения (скорость растет), прямая 2 – движению с отрицательной проекцией ускорения (скорость убывает). Оба графика относятся к случаю, когда в момент времени t = О тело имеет некоторую начальную скорость v 0 .
Перемещение выражается площадью. Выделим на графике скорости равноускоренного движения (рис. 40) маленький участок ab и опустим из точек а и Ь перпендикуляры на ось t. Длина отрезка cd на оси t в выбранном масштабе равна тому малому промежутку времени, за который скорость изменилась от ее значения в точке а до ее значения в точке Ь. Под участком ab графика получилась узкая полоска abсd.
Под участком ab графика получилась узкая полоска abсd.
Если промежуток времени, соответствующий отрезку cd, достаточно мал, то в течение этого малого времени скорость не может заметно измениться – движение в течение этого малого промежутка времени можно считать равномерным. Полоска abсd поэтому мало отличается от прямоугольника, а ее площадь численно равна проекции перемещения за время, соответствующее отрезку cd (см. § 7).
Но на такие узкие полоски можно разбить всю площадь фигуры, расположенной под графиком скорости. Следовательно, перемещение за все время t численно равно площади трапеции ОАВС. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы ее оснований на высоту. В нашем случае длина одного из оснований численно равна v ox , другого-v x (см. рис. 40). Высота же трапеции численно равна t. Отсюда следует, что проекция s x перемещения выражается формулой
3с 15. 09
09
Если проекция v ox начальной скорости равна нулю (в начальный момент времени тело покоилось!), то формула (1) принимает вид:
График скорости такого движения показан на рисунке 41.
При пользовании формулами (1) и (2) НУЖНО ПОМНИТЬ, ЧТО S x , V ox и v x могут быть как положительным», так и отрицательными – ведь это проекции векторов s, v o и v на ось X.
Таким образом, мы видим, что при равноускоренном движении перемещение растет со временем не так, как при равномерном движении: теперь в формулу входит квадрат времени. Это значит, что перемещение со временем растет быстрее, чем при равномерном движении.
Как зависит от времени координата тела? Теперь легко получить и формулу для вычисления координаты х в любой момент времени для тела, движущегося равноускоренно.
проекция s x вектора перемещения равна изменению координаты х-х 0 .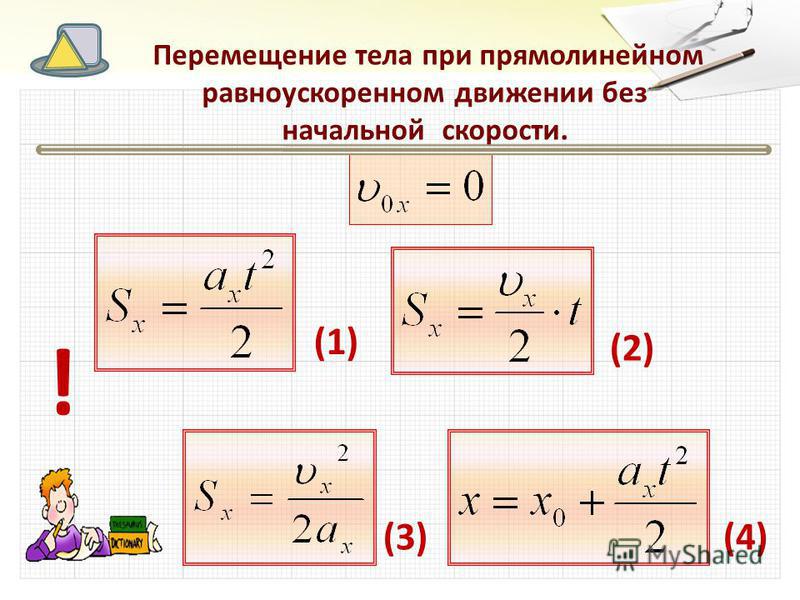 Поэтому можно записать
Поэтому можно записать
Из формулы (3) видно, что, для того чтобы вычислить координату х в любой момент времени t, нужно знать начальную координату, начальную скорость и ускорение.
Формула (3) описывает прямолинейное равноускоренное движение, подобно тому как формула (2) § 6 описывает прямолинейное равномерное движение.
Другая формула для перемещения. Для вычисления перемещения можно получить и другую полезную формулу, в которую время не входит.
Из выражения v x = v 0x + a x t. получим выражение для времени
t = (v x – v 0x): a x и подставим его в формулу для перемещения s x , приведенную выше. Тогда получаем:
Эти формулы позволяют найти перемещение тела, если известны ускорение, а также начальная и конечная скорости движения. Если начальная скорость v o равна нулю, формулы (4) принимают вид:
Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении»
При равноускоренном движении график имеет вид прямой линии, уходящей вверх, так как его проекция ускорения больше нуля.
При равномерном прямолинейном движении площадь численно будет равна модулю проекции перемещения тела. Оказывается, этот факт можно обобщить для случая не только равномерного движения, но и для любого движения, то есть показать, что площадь под графиком численно равна модулю проекции перемещения. Это делается строго математически, но мы воспользуемся графическим способом.
Рис. 2. График зависимости скорости от времени при равноускоренном движении ()
Разобьем график проекции скорости от времени для равноускоренного движения на небольшие промежутки времени Δt. Предположим, что они так малы, что на их протяжении скорость практически не менялась, то есть график линейной зависимости на рисунке мы условно превратим в лесенку. На каждой ее ступеньке мы считаем, что скорость практически не поменялась. Представим, что промежутки времени Δt мы сделаем бесконечно малыми. В математике говорят: совершаем предельный переход. В этом случае площадь такой лесенки будет неограниченно близко совпадать с площадью трапеции, которую ограничивает график V x (t). А это значит, что и для случая равноускоренного движения можно сказать, что модуль проекции перемещения численно равен площади, ограниченной графиком V x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площади трапеции ОАВС, которую мы видим на рисунке 2.
Задача из физической превращается в математическую задачу – поиск площади трапеции. Это стандартная ситуация, когда ученые физики составляют модель, которая описывает то или иное явление, а затем в дело вступает математика, которая обогащает эту модель уравнениями, законами – тем, что превращает модель в теорию.
Находим площадь трапеции: трапеция является прямоугольной, так как угол между осями – 90 0 , разобьем трапецию на две фигуры – прямоугольник и треугольник. Очевидно, что общая площадь будет равна сумме площадей этих фигур (рис. 3). Найдем их площади: площадь прямоугольника равна произведению сторон, то есть V 0x · t, площадь прямоугольного треугольника будет равна половине произведения катетов – 1/2АD·BD, подставив значения проекций, получим: 1/2t·(V x – V 0x), а, вспомнив закон изменения скорости от времени при равноускоренном движении: V x (t) = V 0x + а х t, совершенно очевидно, что разность проекций скоростей равна произведению проекции ускорения а х на время t, то есть V x – V 0x = а х t.
Рис. 3. Определение площади трапеции (Источник)
Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, получим:
S х(t) = V 0 x t + а х t 2 /2
Мы с вами получили закон зависимости проекции перемещения от времени при равноускоренном движении в скалярной форме, в векторной форме он будет выглядеть так:
(t) = t + t 2 / 2
Выведем еще одну формулу для проекции перемещения, в которую не будет входить в качестве переменной время. Решим систему уравнений, исключив из нее время:
S x (t) = V 0 x + а х t 2 /2
V x (t) = V 0 x + а х t
Представим, что время нам неизвестно, тогда выразим время из второго уравнения:
t = V x – V 0x / а х
Подставим полученное значение в первое уравнение:
Получим такое громоздкое выражение, возведем в квадрат и приведем подобные:
Мы получили очень удобное выражение проекции перемещения для случая, когда нам неизвестно время движения.
Пусть у нас начальная скорость автомобиля, когда началось торможение, составляет V 0 = 72 км/ч, конечная скорость V = 0, ускорение а = 4 м/с 2 . Узнаем длину тормозного пути. Переведя километры в метры и подставив значения в формулу, получим, что тормозной путь составит:
S x = 0 – 400(м/с) 2 / -2 · 4 м/с 2 = 50 м
Проанализируем следующую формулу:
S x = (V 0 x + V x) / 2 · t
Проекция перемещения- это полусумма проекций начальной и конечной скоростей, умноженная на время движения. Вспомним формулу перемещения для средней скорости
S x = V ср · t
В случае равноускоренного движения средняя скорость будет:
V ср = (V 0 + V к) / 2
Мы вплотную подошли к решению главной задачи механики равноускоренного движения, то есть получению закона, по которому меняется координата со временем:
х(t) = х 0 + V 0 x t + а х t 2 /2
Для того чтобы научиться пользоваться этим законом, разберем типичную задачу.
Автомобиль, двигаясь из состояния покоя, приобретает ускорение 2 м/с 2 . Найти путь, который прошел автомобиль за 3 секунды и за третью секунду.
Дано: V 0 x = 0
Запишем закон, по которому меняется перемещение со временем при
равноускоренном движении: S х = V 0 x t + а х t 2 /2. 2 c
Мы можем ответить на первый вопрос задачи, подставив данные:
t 1 = 3 c S 1х = а х t 2 /2 = 2· 3 2 / 2 = 9 (м) – это путь, который прошел
c автомобиль за 3 секунды.
Узнаем сколько он проехал за 2 секунды:
S х (2 с) = а х t 2 /2 = 2· 2 2 / 2 = 4 (м)
Итак, мы с вами знаем, что за две секунды автомобиль проехал 4 метра.
Теперь, зная два эти расстояния, мы можем найти путь, который он прошел за третью секунду:
S 2х = S 1х + S х (2 с) = 9 – 4 = 5 (м)
Страница 8 из 12
§ 7. Перемещение при равноускоренном
прямолинейном движении
1. Используя график зависимости скорости от времени, можно получить формулу перемещения тела при равномерном прямолинейном движении.
На рисунке 30 приведен график зависимости проекции скорости равномерного движения на ось X от времени. Если восставить перпендикуляр к оси времени в некоторой точке C , то получим прямоугольник OABC . Площадь этого прямоугольника равна произведению сторон OA и OC . Но длина стороны OA равна v x , а длина стороны OC – t , отсюда S = v x t . Произведение проекции скорости на ось X и времени равно проекции перемещения, т. е. s x = v x t .
Таким образом, проекция перемещения при равномерном прямолинейном движении численно равна площади прямоугольника, ограниченного осями координат, графиком скорости и перпендикуляром, восставленным к оси времени.
2. Получим аналогичным образом формулу проекции перемещения при прямолинейном равноускоренном движении. Для этого воспользуемся графиком зависимости проекции скорости на ось X от времени (рис. 31). Выделим на графике малый участок ab и опустим перпендикуляры из точек a и b на ось времени. Если промежуток времени Dt , соответствующий участку cd на оси времени, мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура cabd мало отличается от прямоугольника и ее площадь численно равна проекции перемещения тела за время, соответствующее отрезку cd .
На такие полоски можно разбить всю фигуру OABC , и ее площадь будет равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время t численно равна площади трапеции OABC . Из курса геометрии вы знаете, что площадь трапеции равна произведению полусуммы ее оснований и высоты:S = (OA + BC )OC .
Как видно из рисунка 31, OA = v 0x , BC = v x , OC = t . Отсюда следует, что проекция перемещения выражается формулой: s x = (v x + v 0x )t .
При равноускоренном прямолинейном движении скорость тела в любой момент времени равна v x = v 0x + a x t , следовательно,s x = (2v 0x + a x t )t .
Отсюда:
Чтобы получить уравнение движения тела, подставим в формулу проекции перемещения ее выражение через разность координат s x = x – x 0 .
Получим: x – x 0 = v 0x t + , или
По уравнению движения можно определить координату тела в любой момент времени, если известны начальная координата, начальная скорость и ускорение тела.
3. На практике часто встречаются задачи, в которых нужно найти перемещение тела при равноускоренном прямолинейном движении, но время движения при этом неизвестно. В этих случаях используют другую формулу проекции перемещения. Получим ее.
Из формулы проекции скорости равноускоренного прямолинейного движения v x = v 0x + a x t выразим время:
t = .
Подставив это выражение в формулу проекции перемещения, получим:
s x = v 0x + .
Отсюда:
s x = , или
–= 2a x s x .
Если начальная скорость тела равно нулю, то:
2a x s x .
4. Пример решения задачи
Лыжник съезжает со склона горы из состояния покоя с ускорением 0,5 м/с 2 за 20 с и дальше движется по горизонтальному участку, проехав до остановки 40 м. С каким ускорением двигался лыжник по горизонтальной поверхности? Какова длина склона горы?
Дано : | Решение |
v 01 = 0 a 1 = 0,5 м/с 2 t 1 = 20 с s 2 = 40 м v 2 = 0 | Движение лыжника состоит из двух этапов: на первом этапе, спускаясь со склона горы, лыжник движется с возрастающей по модулю скоростью; на втором этапе при движении по горизонтальной поверхности его скорость уменьшается. Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапус индексом 2. |
a 2? s 1? |
Систему отсчета свяжем с Землей, ось X направим по направлению скорости лыжника на каждом этапе его движения (рис. 32).
Запишем уравнение для скорости лыжника в конце спуска с горы:
v 1 = v 01 + a 1 t 1 .
В проекциях на ось X получим: v 1x = a 1x t . Поскольку проекции скоростии ускорения на ось X положительны, модуль скорости лыжника равен: v 1 = a 1 t 1 .
Запишем уравнение, связывающее проекции скорости, ускорения и перемещения лыжника на втором этапе движения:
–= 2a 2x s 2x .
Учитывая, что начальная скорость лыжника на этом этапе движения равна его конечной скорости на первом этапе
v 02 = v 1 , v 2x = 0 получим
– = –2a 2 s 2 ; (a 1 t 1) 2 = 2a 2 s 2 .
Отсюда a 2 = ;
a 2 == 0,125 м/с 2 .
Модуль перемещения лыжника на первом этапе движения равен длине склона горы. Запишем уравнение для перемещения:
s 1x = v 01x t + .
Отсюда длина склона горы равна s 1 = ;
s 1 == 100 м.
Ответ: a 2 = 0,125 м/с 2 ; s 1 = 100 м.
Вопросы для самопроверки
1. Как по графику зависимости проекции скорости равномерного прямолинейного движения на ось X
2. Как по графику зависимости проекции скорости равноускоренного прямолинейного движения на ось X от времени определить проекцию перемещения тела?
3. По какой формуле рассчитывается проекция перемещения тела при равноускоренном прямолинейном движении?
4. По какой формуле рассчитывается проекция перемещения тела, движущегося равноускоренно и прямолинейно, если начальная скорость тела равна нулю?
Задание 7
1. Чему равен модуль перемещения автомобиля за 2 мин, если за это время его скорость изменилась от 0 до 72 км/ч? Какова координата автомобиля в момент времени t = 2 мин? Начальную координату считать равной нулю.
2. Поезд движется с начальной скоростью 36 км/ч и ускорением0,5 м/с 2 . Чему равны перемещение поезда за 20 с и его координата в момент времени t = 20 с, если начальная координата поезда 20 м?
3. Каково перемещение велосипедиста за 5 с после начала торможения, если его начальная скорость при торможении равна 10 м/с,а ускорение составляет 1,2 м/с 2 ? Чему равна координата велосипедиста в момент времени t = 5 с, если в начальный момент времени он находился в начале координат?
4. Автомобиль, движущийся со скоростью 54 км/ч, останавливается при торможении в течение 15 с. Чему равен модуль перемещения автомобиля при торможении?
5. Два автомобиля движутся навстречу друг другу из двух населенных пунктов, находящихся на расстоянии 2 км друг от друга. Начальная скорость одного автомобиля 10 м/с и ускорение 0,2 м/с 2 , начальная скорость другого – 15 м/с и ускорение 0,2 м/с 2 . Определите время и координату места встречи автомобилей.
Лабораторная работа № 1
Исследование равноускоренного
прямолинейного движения
Цель работы:
научиться измерять ускорение при равноускоренном прямолинейном движении; экспериментально установить отношение путей, проходимых телом при равноускоренном прямолинейном движении за последовательные равные промежутки времени.
Приборы и материалы:
желоб, штатив, металлический шарик, секундомер, измерительная лента, цилиндр металлический.
Порядок выполнения работы
1. Укрепите в лапке штатива один конец желоба так, чтобы он составлял небольшой угол с поверхностью стола.У другого конца желоба положите в него цилиндр металлический.
2. Измерьте пути, проходимые шариком за 3 последовательных промежутка времени, равных 1 с каждый. Это можно сделать по‑разному. Можно поставить мелом на желобе метки, фиксирующие положения шарика в моменты времени, равные 1 с, 2 с, 3 с, и измерить расстояния s_ между этими метками. Можно, отпуская каждый раз шарик с одной и той же высоты, измерить путь s , пройденный им сначала за 1 с, затем за 2 с и за 3 с, а затем рассчитать путь, пройденный шариком за вторую и третью секунды. Результаты измерений запишите в таблицу 1.
3. Найдите отношения пути, пройденного за вторую секунду, к пути, пройденному за первую секунду, и пути, пройденного за третью секунду, к пути, пройденному за первую секунду. Сделайте вывод.
4. Измерьте время движения шарика по желобу и пройденныйим путь. Вычислите ускорение его движения, используя формулуs = .
5. Используя экспериментально полученное значение ускорения, вычислите пути, которые должен пройти шарик за первую, вторую и третью секунды своего движения. Сделайте вывод.
Таблица 1
№ опыта | Экспериментальные данные | Теоретические результаты | |||||
Время t, с | Путь s, см | Время t, с | Путь s, см | Ускорение a, см/с2 | Время t , с | Путь s, см | |
1 | 1 | 1 | |||||
Уравнения движения с постоянным ускорением
Равномерно ускоренное прямолинейное движение (u.a.r.m.) , также известное как движение с постоянным ускорением , представляет собой прямолинейное движение с постоянным ускорением, отличным от нуля. В этом разделе мы собираемся изучить:
Концепция движения с постоянным ускорением
Движение с постоянным ускорением довольно часто встречается в вашей повседневной жизни. Хорошими примерами этого являются объект, которому разрешено падать и который не встречает на своем пути никаких препятствий (свободное падение), или лыжник, который спускается по склону непосредственно перед тем, как прибыть в зону прыжка.Движение с постоянным ускорением или равноускоренное прямолинейное движение (u.a.r.m) имеет следующие свойства :
Тело движется с движением с постоянным ускорением или равноускоренным прямолинейным движением (u.a.r.m) , когда его траектория является прямой и его ускорение постоянно и отличается от 0 . Это означает, что скорость увеличивается или уменьшается равномерно .
Равномерно ускоренное прямолинейное движение
В нашем примере автомобиль описывает u.a.r.m, поскольку он движется по прямой с постоянным ускорением, эквивалентным 2 м / с 2 . [Обратите внимание, что каждую секунду скорость и расстояние, пройденное телом, увеличиваются в зависимости от значения ускорения за предыдущую секунду.]
Обратите внимание, что хотя в разговорной речи мы проводим различие между ускоряющимся и тормозящим телом, с точки зрения физики, оба являются равноускоренными прямолинейными движениями .Разница в том, что у одного ускорение положительное, а у другого – отрицательное.
Уравнения движения с постоянным ускорением
уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m.) :
Где:
- x , x 0 : положение тела в данный момент времени ( x ) и в начальный момент времени ( x 0 ).Его единица измерения в Международной системе (СИ) – метр (м) .
- v , v 0 : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v 0 ). Его единица измерения в Международной системе – метр в секунду (м / с) .
- a : Разгон кузова. Остается постоянным при значении, отличном от 0. Его единица измерения в Международной системе – метр в секунду (м / с 2 )
- t : Время изучается.Его единица измерения в Международной системе – вторая ( с )
Хотя первые являются основными уравнениями u.a.r.m. и единственные, необходимые для решения упражнений, иногда полезно знать следующее выражение:
v2 = v02 + 2 · a · ∆x
Приведенная выше формула позволяет связать скорость и пройденное расстояние, если ускорение известно и может быть выведено из предыдущих, как вы можете видеть ниже.
v = v0 + a · tx = x0 + v0 · t + 12 · a · t2⇒t = v-v0a∆x = v0 · t + 12 · a · t2⇒∆x = v0v-v0a + 12 · a · v-v0a2;
2 · a · ∆x = v2-v02
Вывод уравнений движения с постоянным ускорением
Для вывода уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m) , необходимо учитывать, что:
- Нормальное или центростремительное ускорение равно нулю: an = 0
- Среднее ускорение, мгновенное ускорение и тангенциальное ускорение имеют одинаковое значение: a = aa = at = cst
С этими ограничениями получаем:
aa = aaa = ΔvΔt = v-v0t-t0 = ⏟t0 = 0x-x0t → v-v0 = a⋅t → v = v0 + a⋅t
Это первое уравнение связывает скорость тела с его ускорением в любой момент времени и представляет собой прямую линию ( v ), наклон которой совпадает с величиной ускорения, а ее координата y в начале координат является начальной скоростью. ( против 0 ).Нам нужно получить уравнение, которое позволит нам получить позицию. Есть разные методы, чтобы вывести это. Мы будем использовать теорему о средней скорости или правило равномерного ускорения Мертона :
«Тело с равномерно ускоренным движением в любой момент времени преодолевает такое же расстояние, которое могло бы пройти тело, движущееся с постоянной скоростью, равной средней скорости первого тела».
Это означает, что
∆x = va⋅t
Значение средней скорости при постоянном ускорении четко видно на следующем рисунке:
ва = v + v02
Если мы разработаем уравнения, которые мы видели до сих пор, мы получим уравнение положения в равномерно ускоренном прямолинейном движении (u.а.р.м.) :
∆x = x-x0 = va⋅t = ⏞1v + v02t = ⏞2v0 + at + v02t = 2v0 + at2t = 22v0t + at22⇒x = x0 + v0t + 12at2
Куда мы обращались:
ва = v + v02
v = v0 + a⋅t
Наконец, обратите внимание, что в предыдущих уравнениях движение учитывалось по оси x . Если мы перемещаемся по оси ординат на , например, при свободном падении или вертикальном старте, просто замените положение x на y , в результате получится следующее уравнение:
Пример
Велосипедист начинает утреннюю поездку и через 10 секунд его скорость равна 7.2 км / ч. В этот момент он видит приближающуюся собаку и замедляет ход на 6 секунд, пока велосипед не остановится. Вычислить:
а) Ускорение до тех пор, пока он не начнет замедляться.
б) Тормозное ускорение велосипеда.
c) Общее пройденное расстояние.
Лаборатория физических измерений 2:
Равномерное и ускоренное движение
Введение :
Цель этого эксперимента заключается в изучении понятий средней скорости, ускорения, равномерное движение и неравномерное движение по прямой или в одном измерении.Вы также получите некоторый опыт в работа с данными.
Средняя скорость движущегося объекта за время т равно
(1)
В случае постоянного ускорения скорость (такая же, как скорость для линейного движения в одном направлении) изменяется на постоянную величину в равные промежутки времени.
разгон = (2)
и
(3)
Оборудование :
динамический тележка, таймер зажигания, гусеница тележки, шкив и груз.
ЭКСПЕРИМЕНТ:
A. Постоянная Скорость .
1. Отрежьте один метр длинную бегущую ленту и пропустите ее через искровой таймер. Прикрепите бегущую ленту к динамической тележке. Таймер и тележка должны быть правильно выровнены и должны быть на одном уровне. Лента бегущей строки должна быть параллельна столешнице.
2.Установите искру таймер в режиме 10 Гц. Установите тележку рядом с таймером и слегка толкните тележку сразу после таймера. включен. Вам следует практиковать пару раз, прежде чем включить таймер зажигания. Обратите внимание, что 10 Гц означает 10 циклов в секунду и время одного цикла. составляет 0,1 сек. Поэтому время Таким образом, интервал между последовательными точками на тикерной ленте составляет 0,1 с (D t в уравнении 1 составляет 0,1 с).
3. Измерьте и запись D x , длина каждого интервала между две последовательные искровые метки.Сделать в минимум 6-7 последовательных измерений. Делать не используйте первые несколько точек.
4. Рассчитайте скорость для каждого интервала, используя уравнение (1).
5. Запишите свой результаты D t , D x и v av in таблицу и вычислите общую среднюю скорость путем усреднения всех v av s.
Пример
D т (с) | D x (см) | v средн. (см / с) |
0.1 | 1,1 | 11 |
0,1 | 1,2 | 12 |
0,1 | 1,1 | 11 |
0.1 | 1,1 | 11 |
общий v пр. = 11.25
B. Постоянное ускорение .
1. Используйте то же самое настройку как в процедуре A. 1. Подключите тележка массой 50 грамм (только вешалка, вес добавлять не нужно) который проходит над шкивом, как показано ниже.
2.Осторожно отпустите тележка сразу после включения таймера зажигания и поймать тележку перед ним попадает в шкив.
3. Измерьте и запишите расстояние между последовательными искровыми метками как D x 1 , D x 2 , и т.д. Пренебрегайте первым интервалом.
Δx 2 Δx 4
Δx 1 Δx 3
4.Рассчитать скорость для каждого интервала: v i = D x i / D t i где i = 1, 2, 3 ….. и определите другие значения в таблице ниже
Пример , как подготовить таблицу данных:
1 | 2 | 3 | 4 | 5 | 6 | 7 |
D т (т) | т (т) | Δx i (см) | общее расстояние x (см) | v i (см / с) | D v (см / с) | a = (см / с 2 ) |
0.0 | 0,0 | |||||
0,1 | 0,1 | 0,5 | 0,5 | v 1 = 0.5 / 0,1 = 5,0 | ||
0,1 | 0,2 | 0,9 | 1,4 + 0,5 = 1,4 | v 2 = 0,9 / 0,1 = 9,0 | в 2 в 1 = 4.0 | |
0,1 | 0,3 | 1,2 | 1,2 + 1,4 = 2,6 | против 3 = 1,2 / 0,1 = 12,0 | v 3 -v 2 = 3,0 | 30. |
0,1 | 0,4 | 1,6 | 1,6 + 2,6 = 4,2 | против 4 = 1,6 / 0,1 = 16,0 | в 4 в 3 = 4,0 | 40. |
0,1 | 0,5 | 2 | 2 + 4,2 = 6,2 | v 5 = 2,0 / 0,1 = 20,0 | в 5 в 4 = 4,0 | 40. |
0,1 | 0,6 | 2,4 | 2,4 + 6,2 = 8,6 | v 6 = 2,4 / 0,1 = 24,0 | в 6 в 5 = 4,0 | 40. |
Пример готовой таблицы:
т (с) | Δ x (см) | x (см) | v (см / с) = Δ x / Δ t | Δ v (см / с) | a (см / с / с) = Δ v / Δ t |
0 | 0 | ||||
0.1 | 0,5 | 0,5 | 5 | ||
0,2 | 0,9 | 1,4 | 9 | 4.0 | 40 |
0,3 | 1,2 | 2,6 | 12 | 3,0 | 30 |
0,4 | 1.6 | 4,2 | 16 | 4,0 | 40 |
0,5 | 2 | 6,2 | 20 | 4.0 | 40 |
0,6 | 2,4 | 8,6 | 24 | 4,0 | 40 |
5.Постройте следующие графики на миллиметровой бумаге, используя значения из ваша таблица данных выше.
а) всего расстояние (столбец 4) от общего времени (2)
б) Мгновенная скорость в зависимости от график времени (это гистограмма, как показано ниже). Обратите внимание, что для постоянного ускоренного движения мгновенное значение
скорость посреди времени interval – средняя скорость для этого временного интервала . Чтобы получить мгновенную скорость график зависимости от времени, просто отметьте среднюю точку вверху каждой полосы и соедините их лучшей прямой линией возможный. Используйте миллиметровую бумагу (спросите инструктор копию), или компьютер для создания графика.
в) ускорение (7) от общего времени (2)
6. Определите ускорение a, найдя крутизну вашего графика скорость-время (b).
7. Сравните это со средним значением ускорения, определенным в Ваш стол для раздела Б.
8. Рассчитайте теоретическое значение (см. Свои конспекты лекций, мы прорабатывали это на примере) разгона и сравниваем с крутизной графа v-t. Какой из них меньше? Почему?
Click and Learn – графический анализ линейного движения
Графический анализ линейного движения
А.Равномерное движение – постоянная скорость – без ускорения
Это типичный график зависимости между положением и временем для объекта, движущегося с постоянной скоростью.
Наклон m графика «положение-время» дает скорость объекта, даже если соотношение между положением (d) и временем (t) не является прямой линией.
Отметим, что «m», наклон линии (вида y = mx + b) постоянен и может быть вычислен несколькими способами.
1. Наклон = подъем / спуск
2.
Б. Равномерно ускоренное движение – переменная скорость
Этот график иллюстрирует взаимосвязь между положением и временем для объекта, скорость которого изменяется со временем.
Мы знаем, что скорость меняется с течением времени, потому что наклон этой линии непостоянен, а функция (вида y = ax 2 + bx + c) является возрастающей.
Чтобы правильно проанализировать эту функцию, нужно взять первую производную функции с помощью исчисления.
Однако достаточно сказать, что мы все еще можем получить некоторую полезную информацию, полагаясь на методы графического анализа.
1. Средняя скорость
Чтобы получить среднюю скорость между двумя точками времени (скажем, t 1 и t 2 ), мы можем провести секущую линию между этими двумя точками и вычислить наклон секущей линии.
Наклон секущей линии (линия, которая пересекает кривую в двух точках пересечения (d 1 , t 1 и d 2 , t 2 ) может быть рассчитана обычным методом наклона:
наклон (секущей линии) = Delta d / Delta t
Это дает нам среднюю скорость между временным интервалом от t 1 до 2
. Следовательно: vav = v = наклон или,
2.Мгновенная скорость
Чтобы получить мгновенную скорость, то есть скорость в один момент (в один момент времени – скажем, точно в t 1 ), нужно взять наклон касательной, которая только касается кривой в этом месте. точка.
т.е. V inst = наклон касательной
V inst = v или, используя уравнение наклона, мы вычисляем наклон касательной (красная линия):
С.Разгон
1. Неравномерное ускорение
Используя метод, аналогичный получению скорости из графиков расстояние-время, мы можем получить значения ускорения из графиков скорость-время.
Наклон касательной к графику v-t в один момент времени даст мгновенного ускорения [ inst ] в случае, когда имеется неравномерное (изменяющееся) ускорение .
2.Равномерное ускорение
Если ускорение постоянное, график v-t будет прямой.
Наклон этой линии даст нам ускорение.
Ускорение: определение, формула, типы, проблемы и примеры
HelpYouBetter »Физика» Одномерное движение »Ускорение: определение, формула, типы, проблемы и примеры
Неравномерное движение – это движение, в котором скорость частицы изменения.Скорость может измениться из-за изменения величины (скорости), изменения направления движения или и того, и другого. В одномерном движении движение происходит в заданном направлении, и изменение скорости происходит только за счет изменения величины скорости.
Ускорение – Определение
Когда скорость объекта изменяется со временем, считается, что он имеет ускорение. Таким образом, ускорение определяется как скорость изменения скорости тела.
Единица ускорения в системе СИ – мс -2 , а ее размерная формула – [M 0 L 1 T -2 ].
Ускорение является векторной величиной, поскольку скорость является векторной величиной. Однако направление движения тела определяется направлением скорости, а не направлением ускорения. Например, в случае движения тела вверх, скорость направлена вверх, а его ускорение – вниз.
Ускорение может быть положительным, отрицательным или нулевым. Когда скорость тела увеличивается со временем, ускорение имеет положительное значение, и говорят, что тело находится в ускоренном движении.С другой стороны, если скорость тела уменьшается со временем, ускорение отрицательное, и говорят, что тело находится в замедленном или замедленном движении. Отрицательное ускорение называется замедлением или замедлением. Если тело движется с постоянной скоростью, его ускорение равно нулю.
Пример: скорость падающего тела не меняет своего направления, но его величина изменяется равномерно со временем. Следовательно, у тела есть ускорение.
Ускорение – Формула
Если ускорение в каждый момент движения одинаково, считается, что объект движется с равномерным или постоянным ускорением.
Рассмотрим объект, движущийся с равномерным ускорением «a». Если v 1 и v 2 – его скорости в моменты времени t 1 и t 2 соответственно (где t 2 > t 1 ), то ускорение объекта определяется выражением,
Если скорость v 2 > v 1 , т. Е. В течение данного интервала вязкость увеличивается, ускорение считается положительным.
Если скорость v 2
То есть в общих чертах можно сказать, что ускорение означает ускорение, а замедление означает замедление.
Аналогично, для частицы, имеющей скорость v 0 при t = 0 и скорость v t через время t, ускорение определяется как:
Типы ускорения
В целом мы можем классифицировать ускорение как равномерное ускорение, среднее ускорение и мгновенное ускорение.
Равномерное ускорение:
Как было сказано ранее, тело движется с равномерным ускорением, если равные изменения скорости происходят в равные промежутки времени, какими бы малыми эти промежутки ни были.
Пример: движение свободно падающего тела
Среднее ускорение:
Если ускорение частицы неоднородно во временном интервале, считается, что частица движется с неравномерным ускорением. Отношение изменения скорости ко времени называется средним ускорением.
Пусть (v 2 – v 1 ) будет изменение скорости в интервале времени (t 2 – t 1 ). Тогда среднее ускорение определяется как:
Мгновенное ускорение:
Ускорение объекта в любой момент называется мгновенным ускорением.
Пусть Δv – это изменение скорости в бесконечно малом интервале времени Δt, около t, тогда мгновенное ускорение a t в момент t определяется выражением,
То есть мгновенное ускорение является вторым производная положения по времени.
Ускорение свободного падения
Земля притягивает все тела к своему центру. Следовательно, если объект падает с высоты, он свободно падает вниз с равномерным ускорением.Это равномерное ускорение называется ускорением свободного падения и обозначается буквой «g». Значение «g» составляет около 9,8 мс -2 для всех свободно падающих тел у поверхности земли.
Значение «g» варьируется от места к месту на поверхности земли. Его значение максимально на полюсах и минимально на экваторе. Над и под поверхностью земли его значение меньше, чем на поверхности земли. В центре Земли значение g равно нулю.
Общие отношения, связывающие положение, скорость и ускорение
Общие отношения, связывающие координату положения и скорость в одномерном движении, задаются выражением,
Таким образом, скорость объекта является производной от положения по времени.
Аналогично, соотношение, связывающее скорость объекта в момент t и ускорение объекта, определяется выражением
Таким образом, ускорение объекта является второй производной от положения по времени.
Применение дифференцирования и интегрирования в равномерно ускоренном движении
Зависимость скорости от времени
Мгновенное ускорение объекта при равномерно ускоренном движении определяется выражением,
Пусть u будет скоростью объекта в момент времени t = 0 и v – скорость в момент времени t.
Интегрируя обе части уравнения (1) в пределах начальной скорости u и конечной вязкости v и времени t = 0 и t = t,
Соотношение смещение – время
Мгновенная скорость объекта при его перемещении через ds определяется выражением,
Как было получено в предыдущем разделе {уравнение (2)}, если начальная скорость объекта в момент времени t = 0 равна u, а скорость в момент времени t = t равна v, то
Интегрируя обе части вышеприведенного уравнения между пределами от s = 0 до s и временем t = 0 до t, мы получаем:
Проблемы ускорения и решения
Проблема 1:
Смещение движущейся частицы вдоль прямой x = k 0 + k 1 t + k 2 t 2 , где k 0 , k 1 и k 2 – постоянные.Найдите ускорение.
Ответ:
Задача 2:
Положение объекта в любой момент времени t определяется соотношением x = mt + nt 2 + pt 3 , где m, n и p – константы. Найдите мгновенное ускорение объекта при t = 8 секунд.
Ответ:
Задача 3:
Расстояние x частицы, движущейся в одном измерении под действием постоянной силы, связано со временем t уравнением, где x выражается в метрах и секундах.Найдите смещение частицы, когда (а) ее скорость равна нулю (б) ее скорость равна 4 м / с.
Решение:
Задача 4:
Ускорение объекта определяется выражением a = α + βt, где α и β – константы. В момент времени t = 0 пусть x 0 и v 0 – это положение и скорость объекта. Найдите выражение для положения и скорости объекта в любой момент времени t.
Решение:
Задача 5:
Положение объекта, движущегося вдоль оси x, определяется как x = a + bt 2 , где a = 8.5 м, b = 2,5 мс -2 и t измеряется в секундах. Какова его скорость при t = 0 с и t = 2 с? Какова средняя скорость между t = 2 с и t = 4 с?
Ответ:
Задача 6:
Смещение частицы вдоль оси x определяется как x = 3 + 8t + 7t 2 . Получите его скорость и ускорение при t = 2 с.
Решение:
Я надеюсь, что информация в этой статье поможет вам получить краткое представление о концепции ускорения.Если вы считаете, что я что-то пропустил, или у вас есть предложения, дайте мне знать в комментариях.
Следите за обновлениями HelpYouBetter, чтобы узнать больше об уравнениях движения с постоянным ускорением, концепции относительной скорости и других связанных темах.
Глава 17: Среднее и мгновенное движение
Глава 17: Среднее и мгновенное движение
- Расстояние и смещение – это одинаковые величины.
- Мы имеем дело с величиной, если мы рассматриваем фактическое расстояние, пройденное объектом по пути.
- Поскольку направления указаны, это число.
- Средняя скорость – это отношение общего пройденного расстояния к общему затраченному времени.
- Единицы измерения скорости – метры в секунду.
- Если мы хотим узнать мгновенную скорость в любой момент времени, мы можем определить ее как v, определенную в любой точный момент времени.
- Если принять во внимание направление движения, мгновенная скорость может стать скоростью.
- Скорость – это количество, а скорость – это количество.
- График мог бы выглядеть следующим образом, если бы мы построили график зависимости скорости от времени для этого движения.
- Для любого временного интервала площадь под графиком равна смещению.
- При изменении направления или скорости автомобиль изменится.
- Мы говорим, что объект ускоряется, если скорость изменяется.
- Объект имеет равномерное ускорение, если скорость изменяется равномерно.
- График зависимости скорости от времени будет выглядеть так.
- Наклон графика равен нулю.
- Если скорость постоянна, ускорение равно нулю.
- Скорость изменения скорости равна величине ускорения.
- Площадь треугольника равна смещению от t к любому другому моменту времени.
- Между двумя точками фигура представляет собой трапецию.
- График смещения в зависимости от времени для равноускоренного движения представляет собой параболу, если мы зададим начальные условия t, x и v.
- Среднее ускорение в метрах в секунду в квадрате известно как наклон графика зависимости скорости от времени.
- Объект с нулевым ускорением не находится в состоянии покоя в системе отсчета.
- Объект может быстро перемещаться.
- Если ускорение постоянно во времени, наше выражение для среднего ускорения может быть записано таким образом, чтобы мы могли вычислить мгновенную конечную скорость после того, как период ускорения имел место.
- Мы получим график, который выглядит следующим образом, если построить график зависимости скорости от времени для равноускоренного движения.
- Общая площадь под графиком будет равна смещению за любой период времени.
- Общая площадь будет суммой двух площадей, одна из которых представляет собой треугольник, а другая – прямоугольник.
- Площадь прямоугольника какое-то время была просто витой.
- Площадь треугольника составляет половину высоты.
- Период времени – основание, а высота – изменение скорости.
- Площадь треугольника 1/2 D vt.
- На основе этого анализа предлагается альтернативный метод определения средней скорости объекта.
- Область на полпути между vi и vf будет такой же.
- Иногда в проблеме кинематики не упоминается затраченное время.
- Было бы неплохо иметь формулу, не учитывающую фактор времени.
- Все остальные формулы можно использовать для получения одной.
- Поскольку vf + vi, мы можем выразить время как t.
- Движение можно увидеть графически.
- Каждая область графика имеет отрицательное, положительное или нулевое среднее ускорение.
- Мгновенные наклоны на временном графике такие же, как мгновенные наклоны на позиции.
- Нам нужно посмотреть, как меняются наклоны на интервале.
- Все мгновенные уклоны имеют одинаковое значение.
- Нет изменения скорости.
- Мгновенные наклоны уменьшаются от большого положительного значения до нуля в течение этого интервала.
- Положительное ускорение увеличивается от малых положительных значений до больших.
- Нам необходимо принять во внимание соглашение, принятое для работы с разными направлениями, поскольку скорость и ускорение являются векторными величинами.
- Обычно мы соглашаемся рассматривать движение вверх или вниз как положительное или отрицательное.
- Отрицательная скорость означает движение влево и не означает, что объект замедляется.
- Объект не замедляется, если используется отрицательное ускорение.
- Объект замедляется, когда люди говорят, что он замедляется.
- Это может произойти двумя разными способами.
- Объект с положительной скоростью может замедляться.
- Объект с отрицательной скоростью может замедляться.
- Общее правило состоит в том, что если двое указывают в одном направлении, объект будет ускоряться.
- Объект замедляется, если они находятся в противоположных направлениях.
- Направление ускорения можно найти, выполнив быстрое прямое графическое решение v f – v i.
- Ускорение вниз обеспечивается силой тяжести.
- Символ g используется для обозначения силы тяжести на Земле.
- Объект, движущийся вверх, будет замедлен силой тяжести, а объект, движущийся вниз, будет ускорен.
- Даже если объект движется вертикально вверх или вниз, это все равно верно.
- Если объект движется вбок под действием силы тяжести, это называется свободным падением.
- В свободном падении вектор ускорения не меняется.
- Если объект падает, vi равен 0.
- Все последующие смещения и скорости отрицательны.
- vi положительно, если объект брошен вверх.
- vi отрицательно, если объект брошен вниз.
- Снаряд выстреливается с большой скоростью.
- Графический анализ движения может дать нам много информации.
- Если в движении происходят сложные изменения, визуализация может помочь лучше понять физику.
- Техники графического анализа просты в использовании.
- Для равноускоренного движения график зависимости расстояния от времени представляет собой параболу.
- Мгновенную скорость можно приблизительно определить, найдя наклон линии, проведенной к точке на кривой.
- Мы можем использовать графики скорости и ускорения смещения в зависимости от времени, чтобы представить движение.
- К графикам можно применить множество примеров движения.
- График зависимости скорости от времени для объекта, подброшенного вверх в воздух, достижения своей наивысшей точки, изменения направления, а затем замедления, используется в случае изменения скорости.
- Сначала это движение замедляет объект, но позже ускоряет его.
- Есть график этого движения.
- Мяч подброшен в воздух и пойман человеком на высоте 5 м над землей.
- Поскольку мяч подбрасывается вверх, начальная скорость положительна, а ускорение свободного падения всегда направлено вниз.
- Мы можем использовать приведенное выше уравнение, чтобы найти начальную скорость, когда y равно 5 м, а t равно 9 с.
- Скорость мяча становится нулевой, когда он поднимается на максимальную высоту.
- Максимальная высота равна значению y, когда конечная скорость равна нулю.
- Мы находим, что y max составляет 101,7 м, используя наш ответ и известное значение g.
- Все измерения относительны.
- Все измерения, включая скорость, производятся относительно объекта.
- Все скорости относятся к определенной системе координат.
- Когда мы говорим, что автомобиль движется со скоростью 55 миль в час, мы имеем в виду, что это 55 миль в час относительно поверхности Земли.
- Средства для перевода одной относительной скорости в другую обеспечиваются правилами сложения векторов.
- Пример такого движения можно увидеть, когда лодка пытается пересечь реку или самолет пытается пересечь боковой ветер.
- Скорость лодки определяется характеристиками двигателя и измеряется бортовым спидометром.
- Относительная скорость человека на берегу отличается от скорости лодки.
- Река движется вправо со скоростью 4 метра в секунду, а лодка движется со скоростью 10 метров в секунду.
- Результат дается теоремой Пифагора.
- Направление находится путем соединения головы с хвостом простым эскизом.
- Мы можем использовать это численно.
- Под углом 22 градуса к востоку от севера скорость составляет 10,5 метров в секунду.
- Если вы скатываете мяч со стола, вы увидите, что он не падает прямо вниз.
- Вы можете наблюдать, как далеко он упадет, методом проб и ошибок.
- Мяч не имеет вертикальной скорости.
- Способность «падать» определяется силой тяжести, и для падения требуется 9,8 метра в секунду.
- Два движения независимы, поскольку сила тяжести действует вертикально, а начальная скорость горизонтальна.
- Траектория, характеризующаяся постоянной горизонтальной скоростью и постоянным вертикальным ускорением, Галилей назвал параболой.
- Поскольку время одинаково для обоих движений, мы можем сначала решить для времени, используя уравнение x, а затем заменить его на уравнение y.
- Уравнение y через x называется траекторией снаряда, а два отдельных уравнения для x и y как функций времени называются параметрическими уравнениями.
- Два движения компонентов не зависят друг от друга.
- Горизонтальная скорость постоянна на протяжении всего движения снаряда.
- Время падения можно рассчитать по формуле, если известна высота снаряда.
- Время падения 3,16 с при высоте 49 м.
- Снаряд запускается с высоты 25 м, и видно, что он приземлился в 50 м от базы.
- Вертикальное движение не зависит от горизонтального движения.
Если бы ракета запускалась с некоторой начальной скоростью под углом, как бы это выглядело?
- Поскольку каждое движение является независимым, мы можем учитывать тот факт, что горизонтальная скорость будет постоянной, в то время как скорость y будет уменьшаться по мере взлета ракеты.
- Вертикальная скорость ракеты будет равна нулю, когда она достигнет максимальной высоты.
- С постоянной скоростью он будет двигаться вперед.
- На этот раз общее время полета будет вдвое больше.
- Диапазон зависит от начальной горизонтальной скорости и общего времени.
- На максимальной высоте вертикальная составляющая скорости равна нулю.
- При запуске и посадке на одной высоте максимальная дальность достигается, когда угол запуска равен 45 градусам.
- Если мы хотим узнать максимальную достигнутую высоту, мы просто используем время, чтобы достичь наивысшей точки.
- Максимальная дальность будет равна 883,7 м, если снаряд запущен с начальной скоростью 100 м / с под углом 30 градусов.
- Максимальная достигнутая высота 127,55 м.
- Мы знаем, что viy является v 0 sin th.
- Avector – это название вещи.
- Изменение направления – это изменение вектора, поэтому для изменения направления скорости требуется ускорение.
- Направление скорости будет изменено направлением ускорения.
- Равномерное круговое движение достигается, когда изменяется только направление.
- Объект совершает периодическое равномерное круговое движение.
- Мы имеем в виду, что объект поддерживает постоянную скорость, когда он вращается по кругу в течение определенного периода времени.
- Число оборотов в секунду называется Частотой.
- Центростремительное ускорение – это направление ускорения.
- Движение удобнее описывать в радианах.
- Скорость изменения положения тела также известна как скорость вращения.
- Масса движется с постоянной скоростью 10 м / с по кругу длиной 2 м.
- Все три смещения, скорости и ускорения связаны.
- Расстояние, скорость и время – все переменные.
- Есть описание движения.
- Скорость изменения смещения равна частному.
- Скорость изменения скорости определяется как ускорение.
- Наклон графика зависимости смещения от времени называется автомобилем.
- Наклон графика называется ускорением.
- Область под графиком можно использовать для получения смещения.
- Ускорение вызвано силой тяжести у поверхности Земли и направлено вниз.
- Это единственный способ избавиться от проблем со свободным падением и движением снарядов.
- Относительную скорость можно найти, сложив отдельные скорости.
- При отсутствии сопротивления воздуха горизонтальное движение не зависит от вертикального движения.
- Скорость запуска может быть получена с использованием вертикальной и горизонтальной составляющих.
- Для каждого направления можно использовать обычные уравнения.
- Центростремительное ускорение – это когда объект движется по кругу.
- Решая физическую задачу, обязательно учитывайте допущения, сделанные относительно движущегося объекта.
- Таким образом вы сможете отслеживать, что важно для вашего пути решения.
- Цели могут быть явными или неявными.
- Если вопрос основан на решении или прогнозе, вам необходимо понять требования, чтобы получить ответ.
- Обдумайте смысл вашего решения.
- Помните о знаках для обработки векторных величин при выборе системы координат.
- Убедитесь, что вы понимаете природу обсуждаемых концепций.
- Убедитесь, что в ваш окончательный ответ включены правильные единицы, используя правильные единицы СИ в ваших расчетах.
- Попробуйте понять, имеет ли ответ смысл.
- Может быть, он выглядит слишком большим или маленьким, потому что выражен в неправильных единицах измерения.
- Если эскиз не предоставлен, сделайте его.
- Если вы интерпретируете график, вам необходимо понимать взаимосвязь всех переменных.
- Если вы хотите построить график, вам нужно пометить обе оси, выбрать масштаб для каждой оси и четко нарисовать.
- Если вы застряли на сложной проблеме, попробуйте разные приемы решения проблемы.
- Если проблема двумерная, сначала разбейте векторы на компоненты.
- Мяч с начальной скоростью 20 м / с подбрасывается вверх.
- Самолет приземляется на взлетно-посадочной полосе со скоростью 150 м / с.
- Мяч сбрасывается с крыши со скоростью 25 м / с.
- После 25 м / с 2 в течение 5 с двигатель выключается, и ракета продолжает движение вверх.
- График зависимости скорости от времени показан ниже.
- Объект имеет скорость 15 м / с.
- Снаряд запускается со скоростью 250 м / с.
- Снаряд запускается с высоты 75 м.
- Выпущен снаряд.
- На расстоянии 500 м попадает в верхнюю часть здания.
- Водитель лодки хочет пересечь реку шириной 5 км, текущую на восток со скоростью 10 м / с.
- Он хочет достичь точной точки на противоположном берегу через 15 минут.
- График зависимости скорости от времени можно построить, если частица начинает свое движение в момент t.
- Камень упал.
- Второй камень бросается вниз одновременно с первым ударом о землю.
- Частица движется в одном направлении.
- Камень падает с высоты и падает за 4 секунды.
- Девушка, стоящая на крыше, бросает в воздух камень.
- Она бросает камень с такой же скоростью.
- Когда камни достигают земли, сравните их скорость.
- Масса, прикрепленная к струне, вращается над головой по горизонтальному кругу.
- Масса приземляется на расстоянии 2,6 м.
- Футбольный квотербек передает пас принимающему под углом 25 градусов к горизонтали и с начальной скоростью 25 м / с.
- Квотербек находится в 30 м от ресивера.
- Принимающий бежит в постоянном темпе, чтобы поймать мяч.
- Автомобиль движется по прямой.
- Капли дождя падают с постоянной конечной скоростью.
- Нам нужно знать, сколько времени потребуется, чтобы замедлить мяч.
- Ответ: 2,04 с, если разделить 20 м / с на 9,8 м / с 2.
- Ракета развивает скорость 125 м / с после 5 с ускорения.
- Ракета замедляется под действием силы тяжести, поскольку она продолжает двигаться вверх после остановки двигателя.
- Время до нуля определяется делением 125 м / с на силу тяжести.
- Первое ускоренное расстояние добавляется к расстоянию, пройденному за это время.
- Общее пройденное расстояние равно 1100 м.
- Суммарная площадь треугольников и прямоугольников составляет 62,5 м.
- 35 – 2,5 – 20 – 5 – окончательное смещение.
- Изменение смещения из вопроса 6 составляет 7.5 м за 14 с, а средняя скорость составляет 0,53 м / с.
- Если средняя скорость составляет 30 м / с, конечная скорость должна быть 45 м / с.
- Подразумевается изменение на 30 м / с со скоростью 3 м / с 2 в течение 10 с.
- Получаем vx с известными числами, то есть 175 м / с.
- Если подставить известные числа, мы получим 3,81 с для времени.
- Следовательно, vi cos th составляет 125, vi sin составляет 32,1, а tan – 0,2568.
- Теорема Пифагора утверждает, что скорость лодки должна быть не менее 11 м / с.
- Угол задается функцией.
- Ширина северной широты 60,9 град.
- На графике показано постоянное ускорение от t до t. Область имеет постоянное изменение скорости от 0 до 9 м / с.
- Объект замедляется и разворачивается во второй области.
- Площадь -12 м / с.
- График изменился с 9 до 3 м / с.
- Последняя область имеет изменение 3 м / с.
- Первый камень упадет с высоты 75 м и упадет свободно под действием силы тяжести.
- Поскольку первый камень должен упасть на 15 м раньше второго, мы можем определить, что t составляет 1,75 с, чтобы упасть на это расстояние.
- Второй камень должен достичь земли после того, как первый пройдет 3,8 с.
- Второй камень имеет начальную скорость вниз 24,34 м / с.
- Средняя скорость равна 15 м / с для D x и D t. Новая средняя скорость равна 13,5 м / с.
- Продолжаем эту процедуру.
- Среднее значение составляет 12,6 м / с.
- Среднее значение 12,3 м / с.
- Среднее значение 12,03 м / с.
- Средняя скорость 12,003 м / с.
- Мгновенная скорость равна 12 м / с за 2 с.
- T – полное время до падения.
- Камень падает за 4 секунды.
- h – количество метров, а T – количество секунд.
- Средняя скорость – это отношение изменения смещения к изменению во времени.
- Возможно, что объект остановится и продолжит работу.
- Можно иметь нулевую мгновенную скорость.
- Когда камни достигают земли, они будут иметь одинаковую скорость.
- Когда первый камень поднимается, сила тяжести замедляет его до упора, а затем он падает обратно вниз.
- Он имеет ту же скорость, но в другом направлении, когда он проходит свою начальную точку.
- Стартовая скорость такая же, как у второго камня.
- Оба камня ускоряются за счет одинакового смещения, что придает им одинаковые конечные скорости.
- Общее смещение делится на общее время, необходимое для достижения средней скорости.
- Средняя скорость равна общему расстоянию, разделенному на время.
- Объект может иметь нулевое смещение за один период, если он возвращается в свою начальную точку.
- Имеет нулевую среднюю скорость.
- Так как проехал большой путь, скорость у него средняя.
- Масса движется по прямой.
- Имеет постоянную скорость.
- Высота массы и горизонтальный диапазон могут использоваться для определения скорости при выпуске.
- Мы находим, что r составляет 0,288 м.
- Принимающий должен отойти на 18,85 м от защитника, чтобы поймать мяч.
- Чтобы определить, с какой скоростью должен бежать приемник, нам нужно знать, сколько времени требуется мячу, чтобы пройти.
- Чтобы пройти 18,85 м за 2,16 с, приемник должен двигаться со скоростью 8,73 м / с.
- Водитель может видеть это на диаграмме ниже.
Ускоряется ли объект при равномерном круговом движении?
Чтобы избежать путаницы, давайте посмотрим на определение ускорения: скорость изменения скорости во времени. Всякий раз, когда изменяется скорость, должно быть соответствующее ускорение.
Автомобиль в равномерном круговом движении по тупику.
Путаница возникает из-за разницы между скоростью в одном измерении и скоростью в нескольких измерениях. В одном измерении скорость имеет величину (например, 5 м / с \ SI [per-mode = symbol] {5} {\ meter \ per \ second} 5 м / с) и направление (например, на северо-восток). Однако, поскольку направление может быть только влево или вправо, не может плавно изменять направление скорости – как в случае с круговым движением – мы можем иметь только дискретные сдвиги. Такое движение обычно не встречается, за исключением столкновений, когда мало кто сомневается в существовании значительного ускорения.
В измерениях d> 1d \ gt 1d> 1 скорость является полноценной векторной величиной, и ее направление может изменяться естественным образом. Одним из таких случаев является равномерное круговое движение, при котором направление скорости плавно меняется по мере того, как мы движемся по кругу. Несмотря на постоянство скорости, направление движения меняется, и поэтому скорость изменения скорости во времени отлична от нуля, что составляет ускорение.
В каком направлении ускоряет объект? Поскольку его скорость неизменна, ускорение должно быть перпендикулярно направлению движения и, следовательно, к центру круга.2 / R, acent = v2 / R, где RRR – радиус окружности.
См. Общие опровержения
Опровержение : В случае равномерного кругового движения, каков угол между скоростью и ускорением?
Ответ : Если скорость остается постоянной, то составляющая ускорения, параллельная скорости, равна нулю. Эта составляющая называется тангенциальным ускорением. Направление меняется из-за центростремительного ускорения, направленного радиально внутрь.Таким образом, чистое ускорение в случае равномерного кругового движения перпендикулярно скорости.Опровержение : Можно ли в случае равномерного кругового движения записать величину ускорения равной скорости изменения скорости?
Ответ : Нет, скорость изменения скорости полностью отличается от скорости изменения скорости. Ускорение определяется как скорость изменения скорости.
Только (a) и (b) верны Только (a), (b) и (c) верны Только (c) и (d) верны Все варианты верны
Частица движется по круговой дорожке с постоянной ненулевой скоростью.\ circ 90∘.
См. Также
Motion в одном измерении | MIT OpenCourseWare
Разгон
Определение среднего ускорения; определение мгновенного ускорения с примерами; равноускоренное движение, с примерами.
Материалы курса, относящиеся к этой теме:
Определение ускорения как функции времени из уравнений положения.
Материалы курса, относящиеся к этой теме:
В начало
Скорость
Идеальное упрощение частиц; определение средней скорости с примерами; определение мгновенной скорости с примерами; равномерное поступательное движение; Пример скорости винтовочной пули.
Материалы курса, относящиеся к этой теме:
В начало
Ускорение свободного падения
Определение, включая уравнение движения под действием силы тяжести, с примерами.
Материалы курса, относящиеся к этой теме:
В начало
Одномерная кинематика
Материалы курса, относящиеся к этой теме:
Определены относительная скорость и ускорение; частный случай постоянного ускорения.
Смещение, скорость и ускорение объектов, движущихся в одном измерении. Решение не включено.
Материалы курса, относящиеся к этой теме:
Задача из 4 частей; определение положения, ускорения и средней скорости из v vs.т. Ниже приведены решения проблем.
В начало
Постоянное ускорение
График зависимости площади ускорения от времени; площадь под графиком зависимости скорости от времени; скорость как интеграл ускорения; положение как интеграл скорости, с примером.
Материалы курса, относящиеся к этой теме:
В начало
Габаритные размеры
Отображение согласованности размеров и поиск новых измерений для увеличенного уравнения.
Материалы курса, относящиеся к этой теме:
В начало
Тайм против половины
5-компонентная 1D кинематика; один человек ходит половину времени, а другой бежит; другой человек проходит половину расстояния и бежит за другим.
Материалы курса, относящиеся к этой теме:
В начало
Кривые ускорения
Построение кривых скоростей в параметрах смещения и ускорения.
Материалы курса, относящиеся к этой теме:
В начало
Столкновение упавших шаров
Задача из 3 частей; построение графиков и определение времени до столкновения для шаров, выпавших последовательно.
Материалы курса, относящиеся к этой теме:
В начало
Автомобиль и мотоцикл
Одномерное движение двух транспортных средств.
Материалы курса, относящиеся к этой теме:
В начало
Рабочий объем
Сравнение перемещения объекта и пройденного расстояния.Решение не включено.
Материалы курса, относящиеся к этой теме:
В начало
Вертикальное перемещение
Движение мяча, брошенного вертикально. Решение не включено.
Материалы курса, относящиеся к этой теме:
В начало
Положение и скорость
Определение скорости по графику зависимости положения от времени. Решение не включено.
Материалы курса, относящиеся к этой теме:
В начало
Относительная скорость
Разница в скорости между двумя падающими камнями.Решение не включено.
Материалы курса, относящиеся к этой теме:
В начало
Относительное положение
Разница в положении двух падающих камней. Решение не включено.
Материалы курса, относящиеся к этой теме:
В начало
Падающие камни
Интервал времени между падением двух камней на землю. Решение не включено
Материалы курса, относящиеся к этой теме:
В начало
Падающие шары
Скорость двух вертикально брошенных шаров.Решение не включено.
Материалы курса, относящиеся к этой теме:
В начало
Кинематика
Относительное движение двух падающих камней.
Материалы курса, относящиеся к этой теме:
В начало
Измерение g
Измерение ускорения свободного падения по падающему мячу.
Материалы курса, относящиеся к этой теме:
В начало
Одномерная кинематика: отслеживание события
Движение двух бегунов в гонке.
Материалы курса, относящиеся к этой теме:
В начало
Относительные инерционные кадры
Материалы курса, относящиеся к этой теме:
Движение падающего объекта в лифте, вид из нескольких опорных кадров.
В начало
Самолет против ветра
Задача из 3 частей; вычисление времени для поездки туда и обратно, средней скорости и средней скорости. Ниже приведены решения проблем.
Материалы курса, относящиеся к этой теме:
В начало
Движение в одном измерении
Материалы курса, относящиеся к этой теме:
Положение, скорость и ускорение бегуна.
Материалы курса, относящиеся к этой теме:
Определение кинематики; система координат в одном измерении; определения положения, смещения, средней скорости, мгновенной скорости, среднего ускорения, мгновенного ускорения.
Моделирование движения человека, ловящего трамвай.
В начало
Замедление мчащегося автомобиля
Движение двух автомобилей, одна с постоянной скоростью, а другая замедляющаяся.
Материалы курса, относящиеся к этой теме:
В начало
Полет на ракете
Вертикальное движение ракеты.
Материалы курса, относящиеся к этой теме:
В начало
Прыгающий мужчина
Движение и силы, действующие на прыгающего баскетболиста.
Материалы курса, относящиеся к этой теме:
В начало
Спейс шаттл
Средняя скорость космического челнока при расходе топлива.
Материалы курса, относящиеся к этой теме:
В начало
.
 На рабочем поле находятся шесть подвижных точек, обозначенных латинскими буквами (A, B, C, D, E, F). Сдвигая их вверх и вниз в пределах рабочего поля модели можно выбирать начальную и конечную скорость и ускорение. Под рабочим полем модели появляются значения перемещений и ускорений, для каждого участка модели (AB, BC, CD и т. д.). Ниже окна рабочего поля модели расположено окно, показывающее движение тела и векторы скорости и ускорения.
На рабочем поле находятся шесть подвижных точек, обозначенных латинскими буквами (A, B, C, D, E, F). Сдвигая их вверх и вниз в пределах рабочего поля модели можно выбирать начальную и конечную скорость и ускорение. Под рабочим полем модели появляются значения перемещений и ускорений, для каждого участка модели (AB, BC, CD и т. д.). Ниже окна рабочего поля модели расположено окно, показывающее движение тела и векторы скорости и ускорения.

 3.
3.  Беседа
Беседа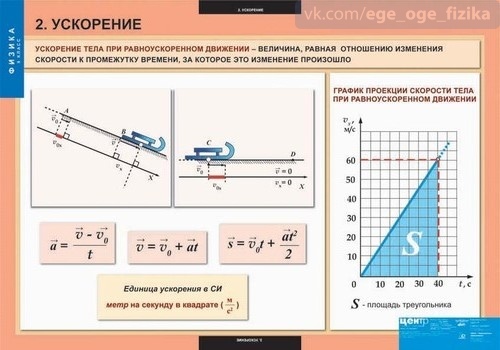 Он тормозил на протяжении 10 секунд. С каким ускорением двигался велосипедист и куда оно было направлено?
Он тормозил на протяжении 10 секунд. С каким ускорением двигался велосипедист и куда оно было направлено?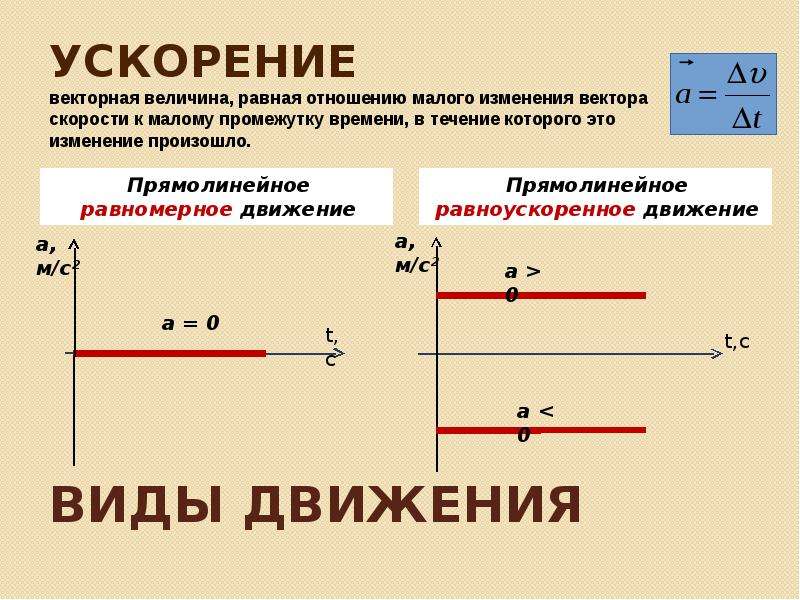
 Формулы для зависимости проекции перемещения sx и координаты х от времени имеют вид:
Формулы для зависимости проекции перемещения sx и координаты х от времени имеют вид: 5).
5).
 )
)
 Как направлены ускорения поездов?
Как направлены ускорения поездов?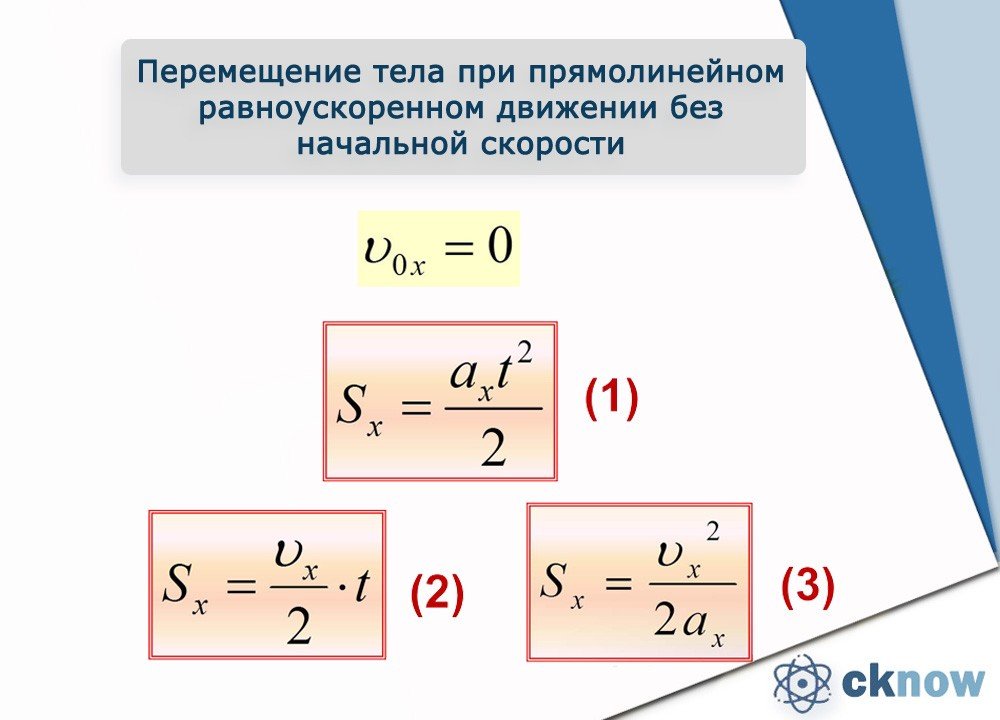
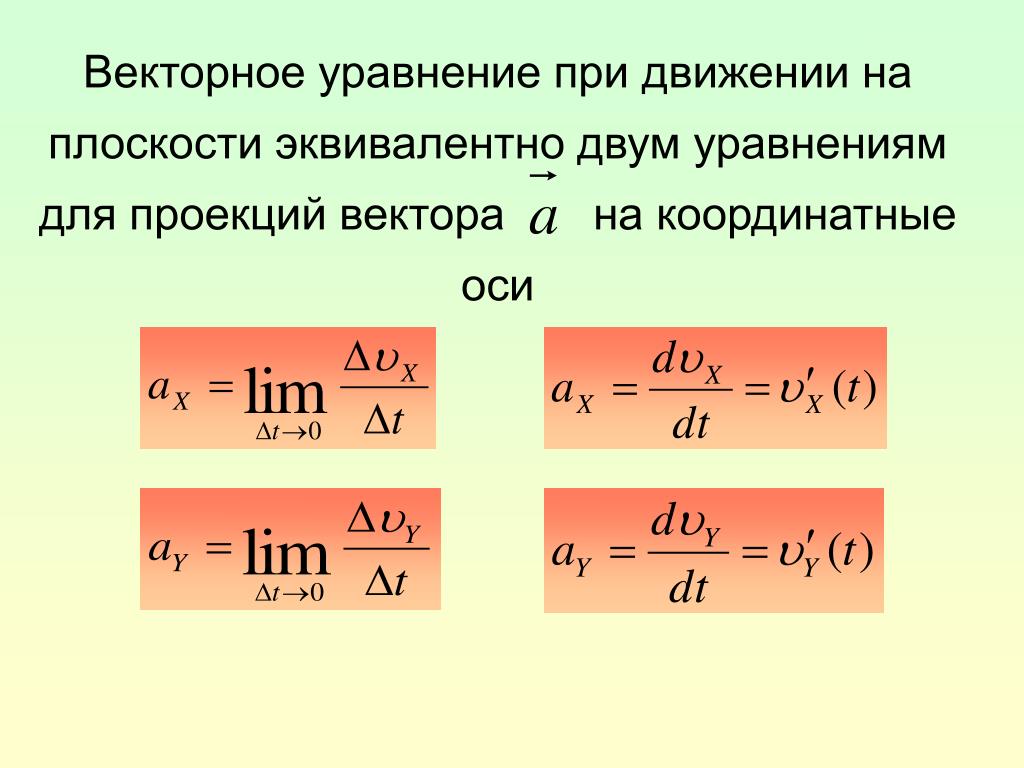
 При равномерном движении изменение скорости обусловлено только изменением направления скорости. Нетрудно доказать, что изменение скорости направлено перпендикулярно скорости — по радиусу к центру окружности.
При равномерном движении изменение скорости обусловлено только изменением направления скорости. Нетрудно доказать, что изменение скорости направлено перпендикулярно скорости — по радиусу к центру окружности.