Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Определение 1Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Определение 2Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.
Рисунок 1. Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется υ=S∆t.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Определение 3Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:
υ=lim∆t∆r∆t=drdt=r˙.
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.
Рисунок 2. Вектор мгновенной скорости υ
Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:
υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеПеремещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ=υ=υx2+υy2+υz2=x2+y2+z2.
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:
υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.
Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:
υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.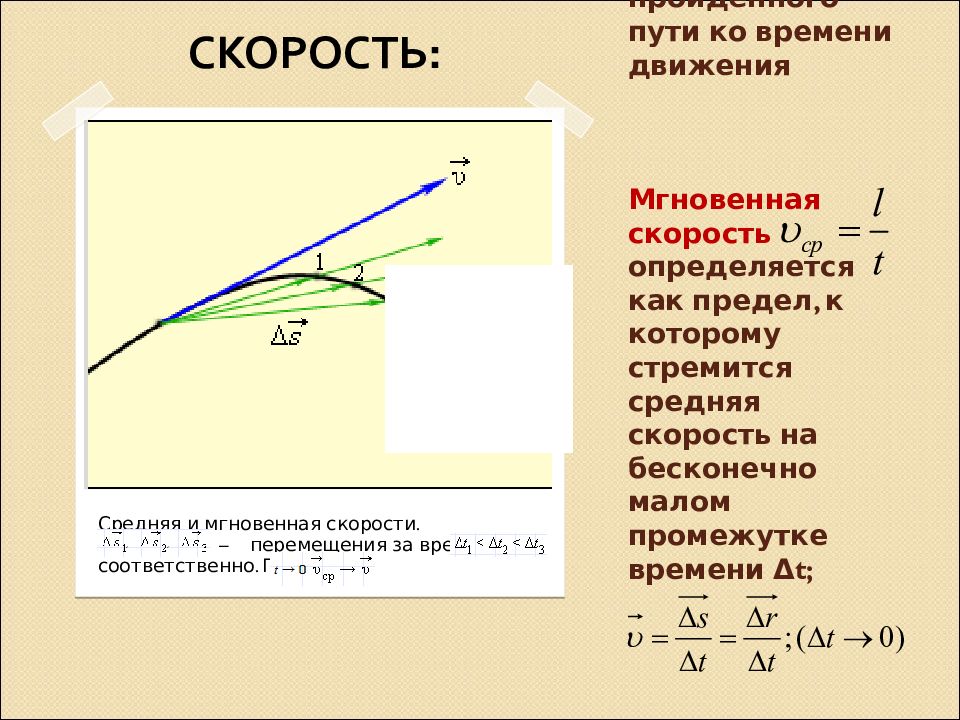
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt
Пример 1Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.
Ответ: 1 м/с.
Пример 2Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ(t)=x˙(t)=4-0,1t.
4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.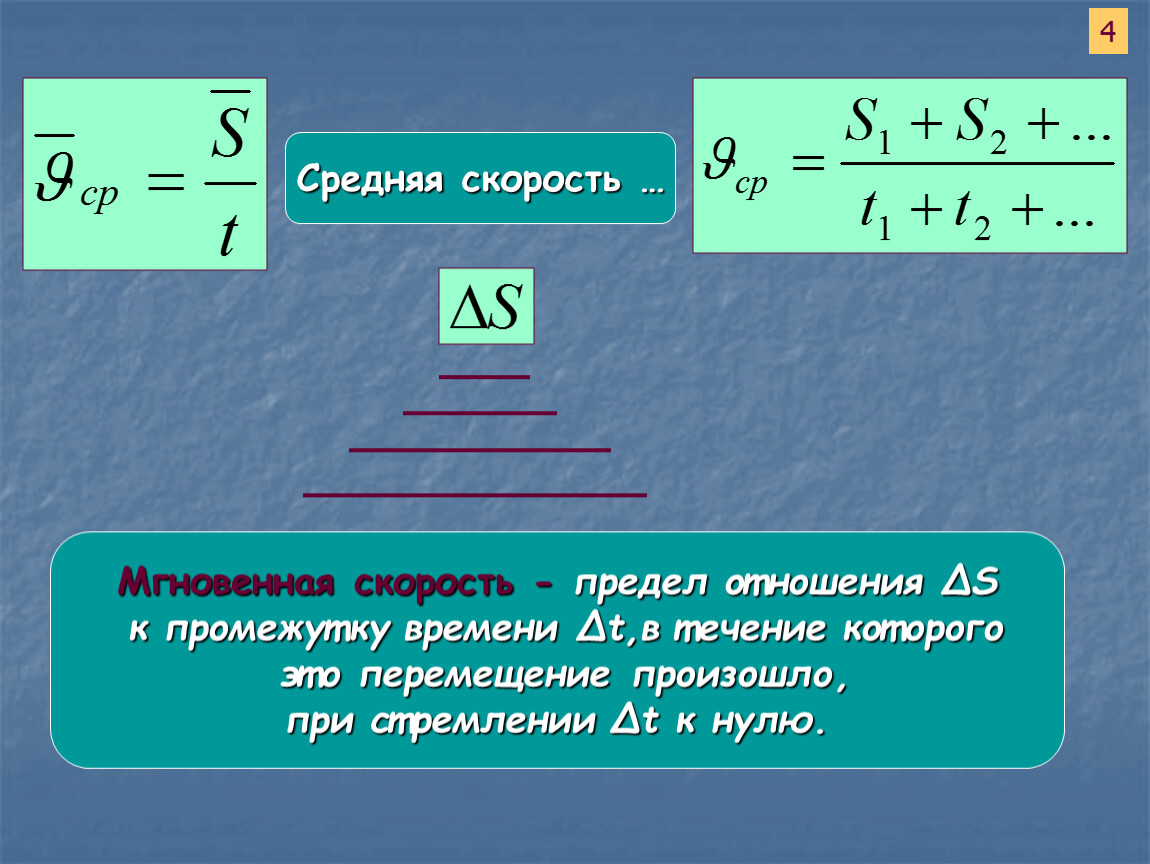
Мгновенная скорость – это… Что такое Мгновенная скорость?
Ско́рость (часто обозначается , от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).
Скорость тела в механике
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:
Здесь v — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .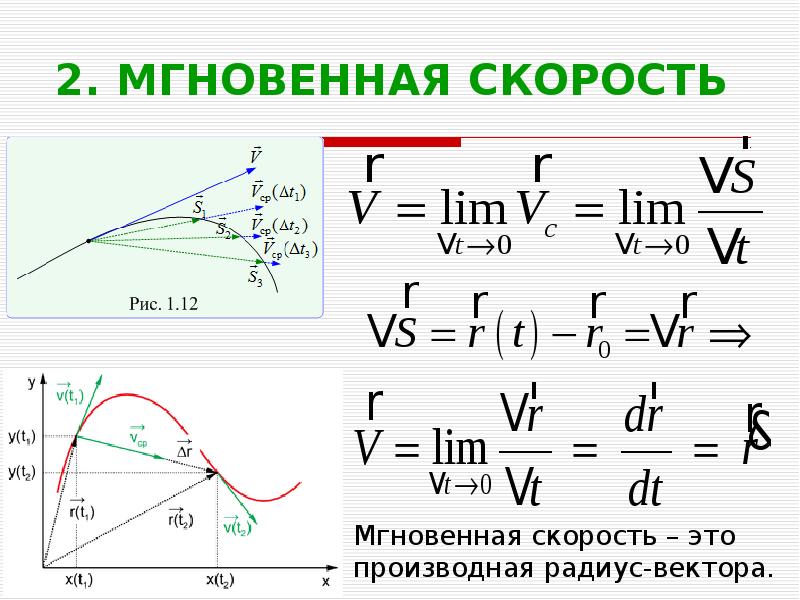
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.
Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).
Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден.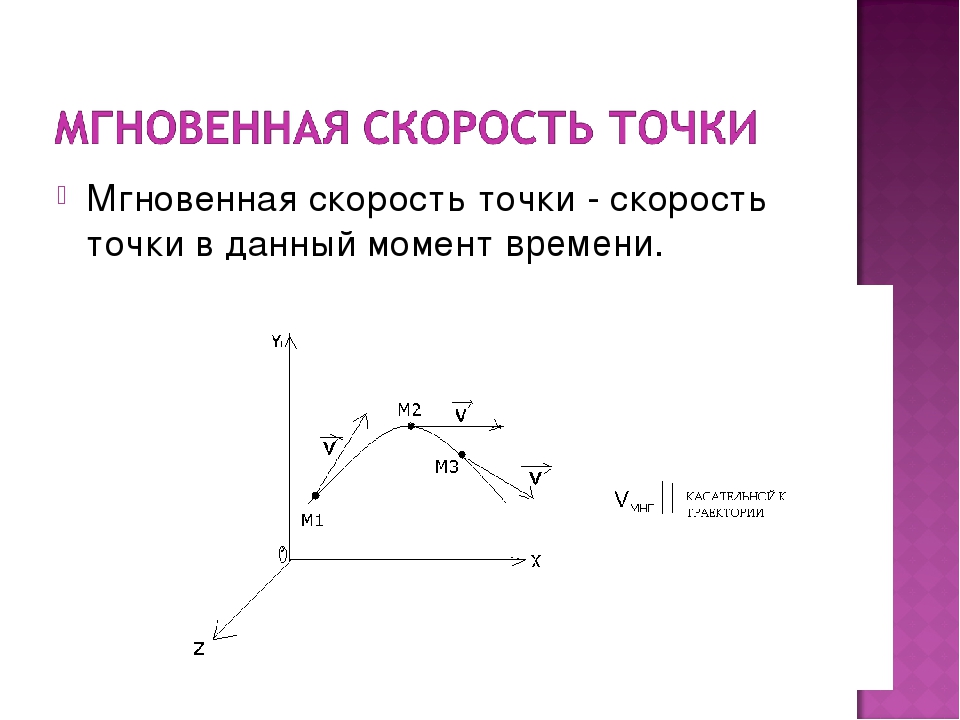
В отличие от скорости перемещения, средняя скорость пути — скаляр.
Мгновенная и средняя скорость
Когда говорят о средней скорости
Преобразование скорости
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .
Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы.
При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Единицы измерения скорости
Соотношение между единицами скорости
- 1 м/с = 3,6 км/ч
- 1 узел = 1,852 км/ч = 0,514 м/c
- Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
- c = 299 792 458 м/c
См. также
Wikimedia Foundation. 2010.
Кинематика. Физика. 10 класс. – Скорость при неравномерном движении. Мгновенная скорость. Сложение скоростей.
Комментарии преподавателяНеравномерным называется движение, при котором тело за равные промежутки времени проходит неравные пути.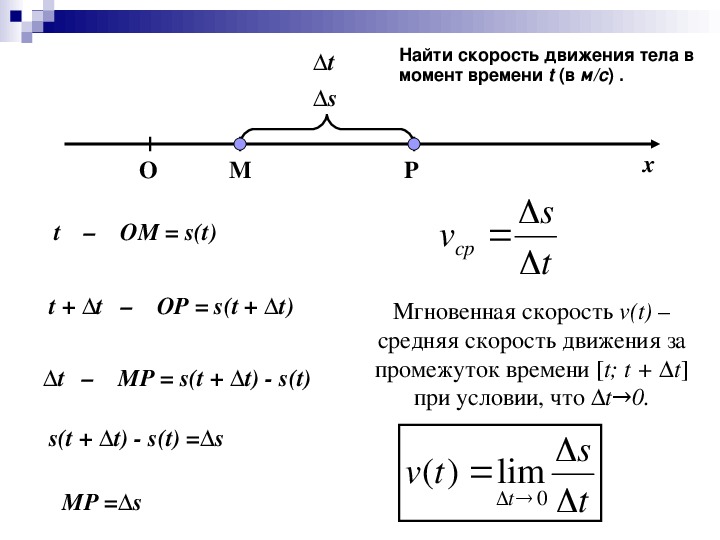
Основная задача механики – определить положение тела в любой момент времени. При неравномерном движении скорость тела меняется, следовательно, необходимо научиться описывать изменение скорости тела. Для этого вводятся два понятия: средняя скорость и мгновенная скорость.
Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.
Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение.
На практике чаще всего используется понятие средней путевой скорости.
Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден.
Существует ещё одно определение средней скорости.
Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.
Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:
Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.
Задача
Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (см. Рис. 4).
Дано:; ; ;
Найти:
Решение:
Рис. 4. Иллюстрация к задаче
Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдём в км/ч.
Следовательно, данные задачи не будем переводить в СИ. Переведём в часы.
Средняя скорость равна:
Полный путь () состоит из пути подъёма на склон () и спуска со склона ():
Путь подъёма на склон равен:
Путь спуска со склона равен:
Время, за которое пройден полный путь, равно:
Ответ:
Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.
Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера, спидометр автомобиля показывает мгновенную скорость).
Существует ещё одно определение мгновенной скорости.
Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории.
Для того чтобы лучше понять данное определение, рассмотрим пример.
Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (см. Рис. 5), проанализируем данный график.
На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдём модуль средней скорости за промежуток времени от до . Для этого рассмотрим фрагмент данного графика (см. Рис. 6).
Рис. 5. График зависимости проекции перемещения от времени
Рис. 6. График зависимости проекции перемещения от времени
Рассчитываем среднюю скорость на данном участке времени:
Для того чтобы проверить правильность нахождения мгновенной скорости, найдём модуль средней скорости за промежуток времени от до , для этого рассмотрим фрагмент графика (см.
Рис. 7).
Рис. 7. График зависимости проекции перемещения от времени
Рассчитываем среднюю скорость на данном участке времени:
Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть . Если уменьшать рассматриваемый интервал времени сильнее, то мгновенная скорость автомобиля в точке A будет определяться более точно.
Мгновенная скорость – это векторная величина. Поэтому, кроме её нахождения (нахождения её модуля), необходимо знать, как она направлена.
(при ) – мгновенная скорость
Направление мгновенной скорости совпадает с направлением перемещения тела.
Если тело движется криволинейно, то мгновенная скорость направлена по касательной к точке траектории (см. Рис. 8).
Рис. 8. Направление мгновенной скорости
Если мы говорим, что траектория, путь, перемещение и скорость являются относительными, то есть зависят от выбора системы отсчета, то про время мы этого не говорим. В рамках классической, или Ньютоновой, механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Рассмотрим, как находить перемещение и скорость в одной системе отсчета, если они нам известны в другой системе отсчета.
Человек идет по палубе парохода со скоростью относительно парохода. Пароход движется поступательно со скоростью относительно берега. Найдем скорость человека относительно берега (Рис. 9).
Свяжем неподвижную систему отсчета (хОу) с Землей, а подвижную (х’О’у) – с пароходом.
Рис. 9. Пример задачи
Из Рис.
9 видно, что перемещение:
Δ = Δ + Δ ⇒ Δ ≠ Δ,
где Δ – перемещение человека относительно парохода, Δ – перемещение парохода относительно берега, Δ – перемещение человека относительно берега.
Таким образом, если тело одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом из движений. В этом состоит установленный экспериментально принцип независимости движений.
Разделив это уравнение на промежуток времени, за который произошли перемещения человека и парохода, получим закон сложения скоростей:
= +
Скорость тела относительно неподвижной системы отсчета равна геометрической сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной.
Домашнее задание
- Можно ли, зная среднюю скорость за определенный промежуток времени, найти перемещение, совершенное телом за любую часть этого промежутка?
- Чем отличается мгновенная скорость при равномерном прямолинейном движении от мгновенной скорости при неравномерном движении?
- Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
- Первую треть трассы велосипедист ехал со скоростью 12 км в час, вторую треть – со скоростью 16 км в час, а последнюю треть — со скоростью 24 км в час. Найдите среднюю скорость велосипеда на протяжении всего пути. Ответ дайте в км в час.
К занятию прикреплен файл «Ребусы по теме». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
- http://interneturok.
ru/ru/school/physics/10-klass/ - http://www.youtube.com/watch?v=fLEtoof1l2c
- http://www.youtube.com/watch?v=pWStlFLGaqk
ru/ru/school/physics/10-klass/Движение тела по окружности | Частная школа. 9 класс
Конспект по физике для 9 класса «Движение тела по окружности». Куда направлена мгновенная скорость тела при его движении по окружности. Куда направлено ускорение тела при его движении по окружности и как вычислить его значение.
Конспекты по физике Учебник физики Тесты по физике
Движение тела по окружности
Одним из простейших видов криволинейного движения является движение тела по окружности. Рассмотрим такое движение при постоянной по модулю скорости.
Согласно второму закону Ньютона направление ускорения совпадает с направлением равнодействующей всех сил, действующих на тело. Сообщим шарику, лежащему на столе и закреплённому на нити, начальную скорость в направлении, перпендикулярном нити.
Он начнёт двигаться по окружности. Сила тяжести, действующая на него, уравновешивается силой упругости стола, а сила трения качения мала, и ею можно пренебречь. Получается, что сила, обусловливающая движение шарика по окружности, — сила упругости нити, направленная по радиусу окружности. Поэтому ускорение должно быть направлено так же, т. е.по радиусу окружности в направлении к центру.
НАПРАВЛЕНИЕ ВЕКТОРА МГНОВЕННОЙ СКОРОСТИ
При движении тела по окружности при неизменном модуле скорости в каждый момент времени скорость меняет своё направление. Как направлен вектор мгновенной скорости?
Для ответа на этот вопрос представим себе движение некоторого тела, закреплённого на верёвке и раскрученного в горизонтальной плоскости.
Если верёвка оборвётся, то тело начнёт двигаться по прямой. Эта прямая — касательная к окружности, являющейся траекторией движения тела. При этом направление движения тела совпадает с направлением скорости тела в момент разрыва верёвки.
Таким образом, мгновенная скорость тела в любой точке траектории направлена по касательной к траектории в этой точке.
НАПРАВЛЕНИЕ ВЕКТОРА УСКОРЕНИЯ ТЕЛА, ДВИЖУЩЕГОСЯ ПО ОКРУЖНОСТИ
При движении по окружности с постоянной по модулю скоростью в каждый момент времени направление скорости изменяется. Значит, такое движение является движением с ускорением. Рассмотрим движение тела по окружности радиуса R. Обозначим скорость тела в точке А через ʋ1, а его скорость в точке В через ʋ2.
Тогда ускорение, с которым тело движется, можно найти по формуле
В числителе этой формулы стоит векторная физическая величина, а в знаменателе — скалярная. Поэтому направление вектора ускорения должно совпадать с направлением вектора, равного разности векторов скоростей:
Для того чтобы изобразить вектор, являющийся разностью двух векторов, используют правило треугольника. Сначала векторы изображают исходящими из одной точки (при этом перемещать их можно только при помощи параллельного переноса). Затем проводят отрезок так, чтобы получился треугольник.
В нашем случае направленный отрезок, соединяющий конец вычитаемого вектора ʋ1 с концом уменьшаемого вектора ʋ2, и будет их векторной разностью.
Из рисунка видно, что вектор Δʋ и, следовательно, вектор a направлены внутрь окружности. Для того чтобы понять, как направлено ускорение в определённой точке траектории представим, что промежуток времени от момента нахождения тела в точке А до момента, когда тело стало находиться в точке В, становится всё меньше и меньше.
Тогда точки А и В стягиваются в одну точку А. При этом направление вектора Δʋ приближается к направлению вектора AO.
Получается, что ускорение тела, движущегося по окружности с постоянной по модулю скоростью, направлено по радиусу окружности к её центру. Именно поэтому оно называется центростремительным и обозначается ац.
Так как касательная к окружности перпендикулярна радиусу, проведённому в точке касания, то векторы скорости ʋ и центростремительного ускорения ац перпендикулярны друг другу.
МОДУЛЬ ЦЕНТРОСТРЕМИТЕЛЬНОГО УСКОРЕНИЯ ТЕЛА
Для нахождения модуля центростремительного ускорения вновь обратимся к рисунку.
youtube.com/embed/pl0po4RXoGo?feature=oembed” frameborder=”0″ allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/>
Вы смотрели Конспект по физике для 9 класса «Движение тела по окружности».
Вернуться к Списку конспектов по физике (Оглавление).
Физические основы механики
Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.
Средняя скорость за время от t1 до t2 равна отношению перемещения за это время к промежутку времени , за которое это перемещение имело место:
Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <…> , как это сделано выше.
Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:
Действительно
Средняя скорость может оказаться слишком грубой характеристикой движения.
Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения при стремлении промежутка времени t2 – t1 к нулю. Сделаем переобозначения: t1 = t и t2 = t + и перепишем верхнее соотношение в виде:
Скорость в момент времени t равна пределу отношения перемещения за время к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
Рис.
2.5. К определению мгновенной скорости.
В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если и есть конечное перемещение и конечный промежуток времени, то и — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
есть ничто иное как дробь — частное от деления на , поэтому последнее соотношение может быть переписано и весьма часто используется в виде
Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:
По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.
Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.
Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения , , или , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
Учитывая постоянство декартовых единичных векторов , , , продифференцируем это выражение по времени
С другой стороны, разложение по базису вектора скорости имеет вид
опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть
Модуль вектора скорости равен
Получим ещё одно, важное, выражение для модуля вектора скорости.
Уже отмечалось, что при величина || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому
и в пределе (>0)
Иными словами, модуль скорости — это производная пройденного пути по времени.
Окончательно имеем:
Средний модуль вектора скорости, определяется следующим образом:
Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:
Здесь s(t1, t2) — путь за время от t1 до t2 и, соответственно, s(t0, t2) — путь за время от t0 до t2 и s(t0, t2) — путь за время от t0 до t1.
Средний вектор скорости или просто средняя скорость, как указано выше, равен
Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости.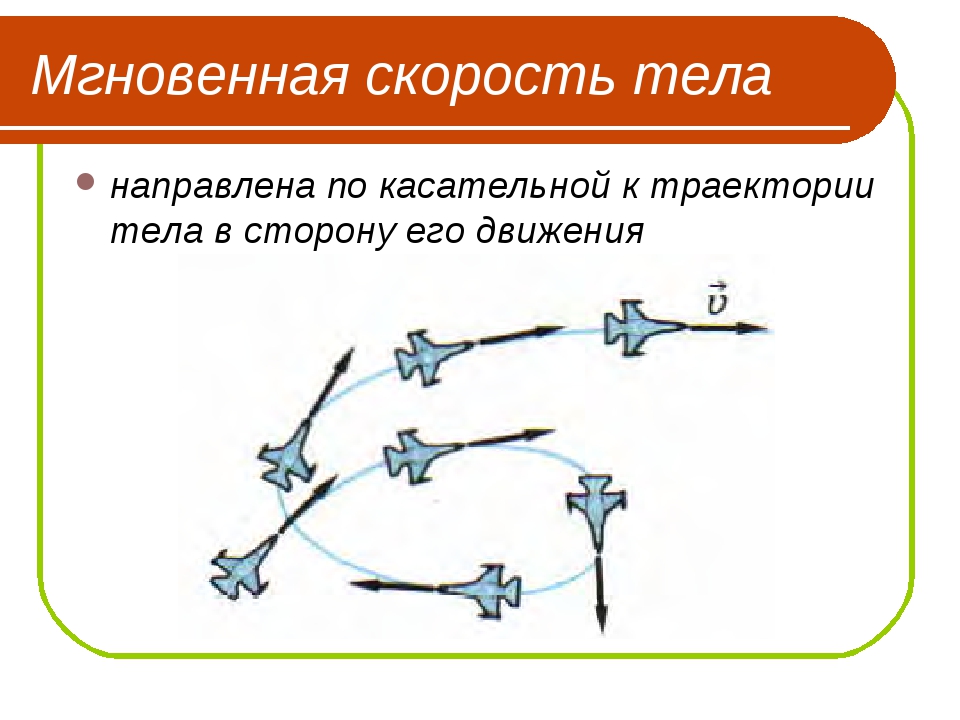
В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени , в который мгновенная скорость равна средней путевой скорости за первые секунд движения точки.
Рис. 2.6. Определение мгновенной и средней скорости тела
Модуль скорости в данный момент времени
будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости точке соответствующей моменту времени t*. Средний модуль скорости за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала.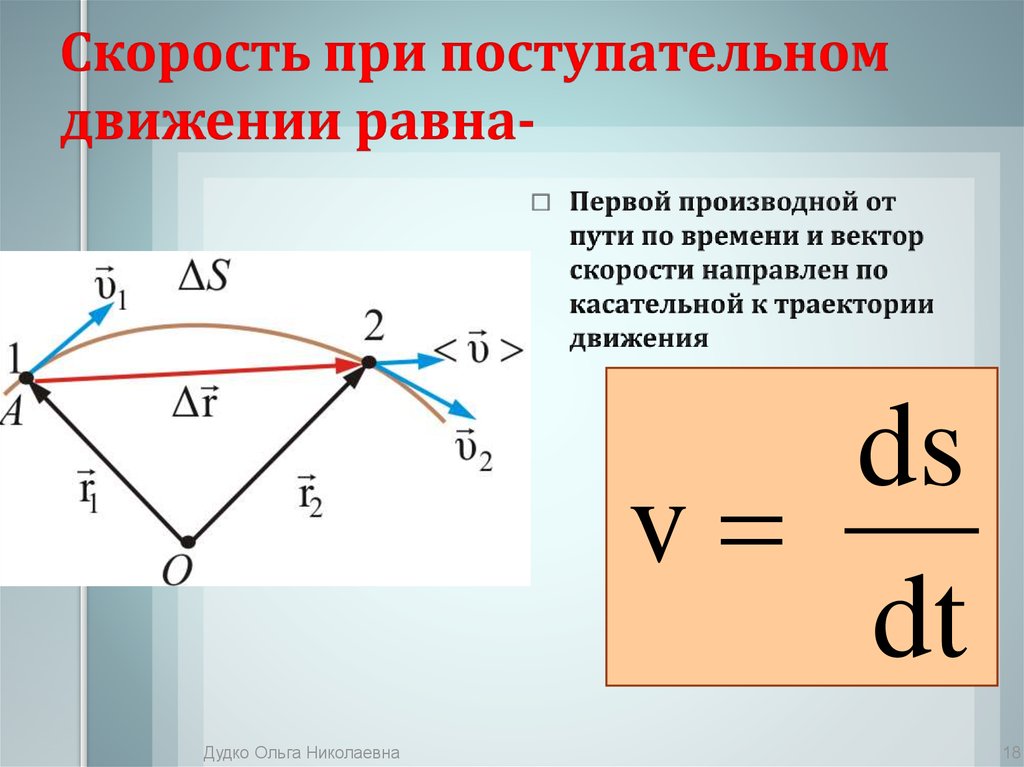
Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
Мгновенная скорость
Обыденное понятие скорости возникает, когда мы рассматриваем, насколько быстро или медленно движется тело. Каким-то образом мы связываем смещение тела со временем, проведенным в таком смещении. В этом разделе мы определим, что в физике подразумевается под мгновенной скоростью, а также ее сходство и различие с мгновенной скоростью.
Мгновенная скорость
Когда вы путешествуете на машине, вы можете смотреть на спидометр, отмечающий «скорость» в каждый момент времени.Хотя обычно мы просто называем это значение скоростью , мы определили ранее скорость как вектор. На самом деле автомобильный спидометр показывает вам величину вектора мгновенной скорости , которая соответствует скорости , вычисленной в момент времени , следуя процедуре, подобной той, которую мы выполняем для вычисления мгновенной скорости из .
средняя скорость , то есть расчет предела средней скорости, когда время приближается к нулю (∆t → 0).
Мгновенная скорость определяется как предел средней скорости, когда рассматриваемый временной интервал приближается к нулю. Оно задается выражением:
где:
- V : Мгновенная скорость или просто скорость
- ∆s: Пройденное расстояние в рассматриваемом интервале
- ∆t: Время, необходимое телу для завершения движения
Единица измерения мгновенной скорости в Международной системе (С.I.) – метр в секунду [м / с] .
Значение мгновенной скорости совпадает с величиной мгновенной скорости в этой точке. Вот почему мы используем ту же букву ( V ), но заглавную, чтобы обозначить ее. Однако не путайте их: мгновенная скорость или просто скорость – это вектор, а мгновенная скорость – это скаляр. В следующем «эксперименте и обучении» вы увидите, что, как мы указывали ранее, когда мы берем очень близкие точки, значение средней скорости приближается к значению величины средней скорости.
На пределе значения равны.
Экспериментируй и учись
Данные
Мгновенная скорость
На графике показана траектория, по которой следует тело, а также его начальное и конечное положение.
Переместите ползунок времени, чтобы увидеть, где будет находиться тело каждый раз, и обратите внимание, что по мере того, как время уменьшается, значения средней скорости и величина средней скорости сближаются .Из этого мы можем вывести, что средняя скорость , когда время приближается к нулю , равна величине средней скорости, или, что то же самое, , величина мгновенной скорости равна мгновенной скорости .
Пример
Знание того, что расстояние, которое проходит тело как функция времени, определяется следующим уравнением:
S (t) = t2 + 5 · t + 1
Вычислить:
а) Средняя скорость в первые 3 секунды.
б) Мгновенная скорость тела.
Скорость в зависимости от скорости
Так же, как расстояние и перемещение имеют совершенно разные значения (несмотря на их сходство), то же самое делают и скорость и скорость. Скорость – это скалярная величина, которая указывает, «насколько быстро движется объект». Скорость можно представить как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткое время.Сравните это с медленно движущимся объектом с низкой скоростью; он преодолевает относительно небольшое расстояние за то же время. Объект, который вообще не движется, имеет нулевую скорость.
Скорость как векторная величина Скорость – это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется – шаг вперед и шаг назад – всегда возвращается в исходное положение.
Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если движущийся человек хочет максимизировать свою скорость, он должен приложить все усилия, чтобы максимизировать величину, на которую он смещается от своего исходного положения. Каждый шаг должен продвигать этого человека дальше от того места, где он начал.Наверняка человек никогда не должен менять направление и начинать возвращаться в исходное положение.
Скорость – это векторная величина. Таким образом, скорость с учетом направления . Оценивая скорость объекта, нужно следить за его направлением. Недостаточно сказать, что объект имеет скорость 55 миль / час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль / ч, к востоку, .
Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не отслеживает направление ; скорость – это векторная величина, учитывающая направление .
Определение направления вектора скорости
Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Неважно, ускоряется объект или замедляется.Если объект движется вправо, его скорость описывается как правая. Если объект движется вниз, его скорость описывается как нисходящая. Таким образом, самолет, движущийся на запад со скоростью 300 миль / час, имеет скорость 300 миль / час на западе. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент – это просто значение скорости с направлением.
Расчет средней скорости и средней скорости
Когда объект движется, его скорость часто меняется.Например, во время обычной поездки в школу происходит много изменений скорости.
Вместо того, чтобы измеритель скорости поддерживать стабильные показания, стрелка постоянно перемещается вверх и вниз, отражая остановку и запуск, а также ускорение и замедление. В один момент автомобиль может двигаться со скоростью 50 миль / час, а в другой момент он может быть остановлен (т. Е. 0 миль / час). Тем не менее, во время поездки в школу человек может в среднем 32 мили / час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра.Если бы показания спидометра можно было собирать с интервалами в 1 секунду (или интервалы 0,1 секунды или …), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть ярлык. Читай дальше. Средняя скорость движения часто вычисляется по следующей формуле:Напротив, средняя скорость часто вычисляется по этой формуле
Начнем реализацию нашего понимания этих формул со следующей задачи:
Вопрос: Во время отпуска Лиза Карр преодолела расстояние в 440 миль.
Поездка заняла 8 часов. Какая у нее была средняя скорость?
Чтобы вычислить ее среднюю скорость, мы просто разделим пройденное расстояние на время поездки.
Это было легко! Лиза Карр развила в среднем 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль / час. Она, несомненно, была остановлена в какой-то момент времени (возможно, для перерыва в туалете или на обед), и, вероятно, в другие моменты времени она, вероятно, ехала со скоростью 65 миль в час.Тем не менее, она развивала в среднем 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Средняя скорость в сравнении с мгновенной скоростью
Поскольку движущийся объект часто меняет свою скорость во время своего движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.
- Мгновенная скорость – скорость в любой момент времени.
- Средняя скорость – среднее значение всех мгновенных скоростей; можно найти просто по соотношению расстояние / время.
Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой момент времени, а о средней скорости как о среднем значении всех показаний спидометра в течение поездки. Поскольку задача усреднения показаний спидометра была бы довольно сложной (и, возможно, даже опасной), средняя скорость обычно рассчитывается как отношение расстояния / времени.
Движущиеся объекты не всегда перемещаются с неустойчивой и изменяющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый равный промежуток времени. Например, бегун может бежать с постоянной скоростью 6 м / с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, которое проходит каждую секунду, будет таким же. Бегун преодолевал расстояние в 6 метров каждую секунду.
Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение менялось бы на 6 метров каждую секунду. Это будет разительно контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных показаны объекты с постоянной и изменяющейся скоростью.
А теперь давайте снова рассмотрим движение того учителя физики. Учитель физики идет 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.Все движение длилось 24 секунды. Определите среднюю скорость и среднюю скорость.
Учитель физики прошел дистанцию 12 метров за 24 секунды; таким образом, ее средняя скорость составляла 0,50 м / с. Однако, поскольку ее смещение составляет 0 метров, ее средняя скорость составляет 0 м / с. Помните, что смещение относится к изменению положения, а скорость основывается на этом изменении положения.
В этом случае движения учителя изменяется положение на 0 метров и, следовательно, средняя скорость составляет 0 м / с.
Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов лыжник разворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем из пункта В в пункт D.
Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут.По завершении нажмите кнопку, чтобы просмотреть ответ.
В качестве последнего примера рассмотрим футбольного тренера, который ходит взад и вперед по боковой линии. На диаграмме ниже показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в противоположном направлении. Другими словами, тренер переходит из позиции A в позицию B, затем из позиции C в позицию D.
Какова средняя и средняя скорость тренера? По завершении нажмите кнопку, чтобы просмотреть ответ.
В заключение, скорость и скорость – это кинематические величины, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость – это отношение расстояния (скалярной величины) к временному интервалу. Скорость без указания направления . С другой стороны, скорость – это векторная величина; это с учетом направления . Скорость – это скорость изменения позиции. Средняя скорость – это отношение смещения или изменения положения (векторная величина) за время.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Name That Motion Interactive. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять концепции скорости, скорости и ускорения.Посетите Name That Motion.
определение мгновенной скорости
существительное мгновенная скорость скалярная мера скорости движения тела, выраженная как скорость изменения положения относительно времени в определенной точке. Производная местоположения точки на кривой по времени, то есть где [E.sub.0] – это нижний предел выбросов (г / с), указанный для каждого транспортного средства и типа загрязнителя; [v.sub.n] (t) – мгновенная скорость транспортного средства n в момент времени t; [a.sub.n] (t) – ускорение транспортного средства n в момент времени t; [f.sub.1] до [f.sub.6] являются константами выбросов, специфичными для каждого транспортного средства… Определение мгновенных слов скорости.
Антонимы к мгновенной скорости. Скорость = расстояние / время. Мгновенная скорость – это величина мгновенной скорости. Определения средней и мгновенной скорости с примерами. Физика. Скорость или мера скорости движения, особенно: a. Определение: когда скорость объекта постоянно меняется, мгновенная скорость – это скорость объекта в определенный момент (момент) времени.Цель: построить определение мгновенной скорости изменения. Соответствовать. то есть физика. Мгновенная скорость – это термин в физике, используемый для описания скорости, также известной как изменение расстояния во времени в определенный момент времени. Мгновенная скорость в конкретный момент вычисляется путем подстановки соответствующего значения временной переменной в первую производную по времени уравнения перемещения. При равномерном круговом движении, то есть перемещении с постоянной скоростью по круговой траектории, частица испытывает ускорение в результате изменения направления вектора скорости, при этом его величина остается постоянной.
Мгновенная скорость – Расчет IBL: концепции и приложения. Мера расстояния, пройденного за определенный период времени с указанием направления. Затем уместно провести обсуждение всего класса, прежде чем переходить к Q4. Угловая скорость. Сделано. «Мгновенная скорость» просто означает «с какой скоростью я сейчас еду». Ваша средняя скорость может быть равна нулю, даже если ваша мгновенная скорость в каждый момент равна c. Это говорит о том, что мгновенная скорость пользователя пропорциональна ширине туннеля. Объект, претерпевающий ускорение, будет иметь разные мгновенные скорости в разные моменты времени.Совпадение всех точных любых слов. Его скорость будет снижаться по мере того, как он спускается на трехметровую длину. Финишируют спринтеры. Определение мгновенной скорости в словаре Definitions.net. Для равномерного движения мгновенная скорость постоянна. Скорость – это скалярная величина, означающая, что она имеет величину (значение), но не направление. Определение мгновенного – это то, что происходит сразу.
метр в секунду [м / с]. Процесс формализации студентами концепции лимита. Что означает мгновенная скорость? скорость.Определение мгновенной скорости. Найдите 14 способов сказать МГНОВЕННЫЙ, а также антонимы, родственные слова и примеры предложений на Thesaurus.com, самом надежном бесплатном тезаурусе в мире. По этой причине скорость никогда не может быть отрицательной. wanjuulazarus wanjuulazarus 3 недели назад Физический колледж, пожалуйста, напишите определение мгновенной скорости, скорости и ускорения и решите с ними задачи, пожалуйста, покажите работу 1 См. ответ wanjuulazarus ждет вашей помощи. (ˌꞮnstənˈteɪnɪəs spiːd) сущ. мгновенное определение: 1.происходит немедленно, без задержки: 2. происходит немедленно, без задержки: 3…. Объект, движущийся с постоянной скоростью и в постоянном направлении. Анатомия индикатора мгновенной вертикальной скорости. Синонимы мгновенной скорости, произношение мгновенной скорости, мгновенный перевод скорости, определение мгновенной скорости в английском словаре.
Это скорость, с которой объект меняет свою скорость. Например, предположим, что машина меняет свою скорость от одной минуты к следующей – возможно, от 4 метров в секунду при t = 4 до 5 метров в секунду при t = 5, затем можно сказать, что машина разгоняется.Во время вождения автомобиля стрелка спидометра или значение цифрового дисплея (показывающее скорость в километрах в час) на приборной панели колеблются в каждый момент в зависимости от достигнутой им скорости. Мгновенная скорость – это скорость, с которой объект движется точно в указанный момент. Если я еду на север ровно со скоростью 10 м / с ровно десять секунд, затем поворачиваю на запад и перемещаюсь точно на 5 м / с еще десять секунд точно, мой средняя скорость составляет примерно 5,59 м / с в направлении (примерно) с севера на северо-запад.Следовательно, определение производной мгновенной скорости: мгновенная скорость = v = lim_ (Delta t -> 0) (Delta x) / (Delta t) = dx / dt Итак, в основном, мгновенная скорость является производной функции / уравнения положения.
движения. Если бы мы проверили последний метр, мы бы обнаружили, что он там медленнее среднего. Итак, теперь вы можете видеть, как мы находим среднюю скорость и мгновенную скорость. Мгновенная скорость. Наша интуиция подсказывает нам, что движущийся объект имеет скорость (мгновенную скорость) в определенный момент времени.Вы когда-нибудь водили машину? Его можно взять из точки, лежащей на линии графика скорость-время. Мгновенная скорость определяется как предел средней скорости, когда рассматриваемый временной интервал приближается к нулю. Скорость – это скалярная величина. ×. Мгновенная скорость всегда равна величине мгновенной скорости в этот момент. Единица измерения скорости – метры в секунду (м / с). Скорость в какой-то момент или считается постоянной в течение очень короткого периода времени, называется мгновенной скоростью.Определение мгновенной скорости: когда объект движется с переменной скоростью, его скорость в данный момент времени называется его мгновенной скоростью. Средняя скорость (которую вы вычисляете, например, для поездки в другой город) практически не имеет физического значения.
Как использовать мгновенное в предложении. Если вы просите воды, и вода сразу появляется в ту же секунду, это пример чего-то мгновенного. Мгновенная скорость – это скалярная величина. скалярная мера скорости движения тела, выраженная как скорость изменения положения относительно времени в определенной точке.Слушайте аудио произношение с несколькими английскими акцентами. Определение в словаре английский язык. Вы когда-нибудь ездили на велосипеде? 2. Средний метр был бы таким же, как средний. Мгновенная скорость – это скорость объекта в определенный момент времени. мгновенная скорость. Словарь английского языка Коллинза. Синонимы индикатора мгновенной вертикальной скорости, произношение индикатора мгновенной вертикальной скорости, перевод индикатора мгновенной вертикальной скорости, определение индикатора мгновенной вертикальной скорости на английском языке.Мгновенная деформация постепенно увеличивается с температурой, а модуль упругости уменьшается с температурой. Синонимы мгновенной скорости – 22 слова и фразы для мгновенной скорости.
Мгновенная скорость (средняя = 0,32 см [с.-1], SD = 0,01, n = 2 запуска) и чистая скорость (0,27 см [с.-1], SD = 0,02, n = 2 запуска). прекомпетентности… Я попытался это рассудить. Тогда средняя скорость в этом интервале составляет 2 м / с, и вы, вероятно, согласитесь, что это лучшее приближение к тому, что мы подразумеваем под мгновенной скоростью объекта в этой точке.Пройденное расстояние, разделенное на время в пути. Мгновенное определение – сделано, происходит или действует без какой-либо ощутимой продолжительности времени. минимальная воздушная скорость, при которой может быть создан максимально допустимый g. Он измеряется отношением расстояния, пройденного телом, ко времени, за которое это расстояние преодолено. Источник: Федеральное управление гражданской авиации. Я недавно смотрел это видео от Veritasium, где он говорит об односторонней скорости света и рассказывает о предельном случае, когда в одном направлении скорость света равна c / 2, а в другом – мгновенно.Мгновенная скорость – это изменение положения с течением времени.
Это выражается выражением: Единица измерения мгновенной скорости в Международной системе (S.I.). Мгновенную скорость объекта не следует путать со средней скоростью. 21.5 Мгновенная скорость и скорость (ESAGZ) Взлет спринтеров. Мгновенная скорость – это векторная величина. Давайте обсудим определения скорости, постоянной скорости, переменной скорости, средней скорости и мгновенной скорости в следующем разделе: 1.Мгновенное ускорение – это величина, которая сообщает нам скорость, с которой объект меняет свою скорость в определенный момент времени в любом месте на своем пути. Посмотрев на спидометр, можно в любой момент узнать мгновенную скорость автомобиля. Скорость объекта в любой данный момент (особенно ускоряющегося объекта) (существительное) «Мгновенная скорость» рассчитывалась путем деления расстояния, которое личинка прошла между кадрами видео, на временной интервал между этими кадрами.Физика: скорость, скорость, определение ускорения. Министерство обороны США, 2005 г. Пожалуйста, напишите определение мгновенной скорости, скорости и ускорения и решайте проблемы, связанные с ними, просьба… Получите ответы, которые вам нужны, прямо сейчас! Почему? Определение и пример использования YourDictionary.
Ответ: Мгновенную скорость можно найти по формуле: При t = 3,00 с мгновенная скорость равна: Мгновенная скорость автомобиля при t = 3,00 с составляет 8,1 м / с. Величина, которая сообщает нам, насколько быстро объект движется в определенный момент времени в любом месте на своем пути, является мгновенной скоростью, также обычно называемой скоростью.Когда вы идете, вы идете быстрее или медленнее, в зависимости от того, чего вы хотите достичь. Что означает мгновенная скорость? ЗНАЧЕНИЕ NULL. Выучить больше. ИЗУЧЕНИЕ. Мгновенная скорость – это наклон касательной к графику положения в зависимости от времени в определенный момент времени. схожее значение. мгновенная скорость в британском английском. В то время как слабительные соли в значительной степени ушли в прошлое, сравнение сохраняется как способ описать очень быстрый темп. определение мгновенной скорости: 1. расчет, который сообщает вам, как далеко и в каком направлении перемещался бы объект, если бы он….Изменение скорости объекта во времени.
3.1 Системы координат и смещения ZSMAHMUD / UiTMCawanganPerak / PHY110 3 Рисунок 3.1 Падающая шишка подвергается (а) чистому перемещению; (б) он вращается, а также поступает. Скорость в данный момент времени. Свободное падение ZSMAHMUD / UiTMCawanganPerak / PHY110 2. Самый простой случай – когда тело имеет постоянную скорость. 3. Для визуализации жидкость равномерно засевается частицами полиамида (удельный вес 1,01, номинальный диаметр 28 мкм) и освещается горизонтальным лазерным световым листом.Определение и примеры. определения. Мгновенная скорость – скорость объекта в данный момент. См. Также: Усреднение, Скорость. Мгновенное ускорение a или ускорение в определенный момент времени получается с использованием того же процесса, что и для мгновенной скорости. Мгновенная скорость. Примеры. мгновенная скорость в британском английском (ˌɪnstənˈteɪnɪəs spiːd) Substantiv. См .: индикатор вертикальной скорости. мгновенная скорость. Мгновенная скорость. Предельное значение средней скорости, поскольку временной интервал становится бесконечно малым.
К сожалению, однозначного ответа нет. Мгновенная скорость и скорость Мы уже изучили понятие средней скорости и скорости, и теперь мы обращаем наше внимание на измерение мгновенной скорости и скорости. VSI или IVSI отображает вертикальную скорость в футах в минуту, причем наибольшие числа представляют тысячи футов в минуту (фут / мин), а меньшие приращения – сотни. Значение прописью. Угловая скорость – важный фактор максимальной эффективности поворота. v = d t d s Примечание: 1. Измеряется в метрах в секунду, милях в час и т. д.Мгновенная скорость: определение, формула и пример В этом уроке мы узнаем о мгновенной скорости, разнице между ней и средней скоростью, а также о формулах для их расчета. Например, высокоскоростные камеры используются для отслеживания быстро движущихся объектов. Все, что вам нужно сделать, это выбрать значение t и подставить его в уравнение производной. Кроме того, попробуйте этот калькулятор скорости для физики, с помощью которого вы можете легко вычислить скорость движущегося объекта.
CA II.1 Средняя v. Мгновенная скорость.Словарь военных и смежных терминов. Это дает иллюстрацию мгновенной скорости. Мы используем (Рисунок) и (Рисунок), чтобы найти мгновенную скорость. Мгновенная скорость – это изменение положения при небольшом изменении во времени. Итак, начнем с его основного определения в физике! мгновенная скорость: скорость, определяемая как количество событий за короткий период времени X. На угловой скорости самолет может достичь максимальной скорости поворота. Информационный блок о термине. Для наших целей 280 КИАС – это угол Т-2С.Мгновенная скорость всегда больше или равна нулю и является скалярной величиной. Определите мгновенную скорость. На первый метр быстрее. минимальная мгновенная скорость. Используя наклон касательной в точке, мы избегаем трудности создания временного интервала в один момент времени. Häufigkeit. Для конечного интервала времени скорость больше или равна скорости. Определение мгновенной скорости: когда объект движется с переменной скоростью, его скорость в данный момент времени называется его мгновенной скоростью.
Например, если мы хотим найти мгновенную скорость при t = 5, мы просто заменим «5» на t в производной ds / dt = -3 + 10. Постоянная скорость – это скалярная величина. Индикаторы мгновенной вертикальной скорости (IVSI) содержат воздушные насосы, приводимые в действие акселерометром, для уменьшения времени задержки, присущего простым VSI. Имеет единицы СИ. Его схематическое устройство представлено на рис. Узнайте о формуле мгновенной скорости и решаемом примере. антонимы. мгновенная скорость. Писать. Карточки. Предположим, что во время поездки в школу вы проехали 5 миль и поездка длилась 0.2 часа (12 минут). Существует различие между средней скоростью и величиной средней скорости. Информация и переводы мгновенной скорости в наиболее полном ресурсе словарных определений в Интернете. Угловая скорость определяется как. Средняя скорость – средняя скорость рассчитывается по расстоянию, которое объект прошел за заданный интервал времени. Когда утром вы садитесь в машину на подъездной дорожке, скорость машины равна нулю.
Заклинание. То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными \ (\ Delta \) t, и позволяем \ (\ Delta \) t приближаться к нулю.Устройство для измерения скорости, в частности мгновенной скорости и скорости удара клюшки для гольфа. Решения NCERT в тексте и видео от класса 9 до 12 Все определения средней и мгновенной скорости с примерами ☞ Решенный вопрос для класса 12 2020 ☞ Решенный вопрос для класса 10 2020. Средняя скорость и скорость 3. Мгновенная скорость и ускорение 4. Формула мгновенного Скорость. В этот момент автомобиль может двигаться со скоростью 50 миль в час, но может замедлиться или ускориться в течение следующего часа.Объект не всегда движется с одинаковой скоростью. Контрольная работа. б. Скорость объекта в один конкретный момент. Если разделить общее пройденное расстояние на общее время, мы получим среднюю скорость. Пожалуйста, отправляйте ваши запросы на… eurlex-diff… Величина скорости. Таким образом, средняя скорость = общее расстояние / общее время.
Epub 2018 16 августа. Мгновенная скорость? – это скорость частицы в движении в любой желаемый момент времени. синонимы. Мы можем аппроксимировать мгновенную скорость в \ (t = 2 \), рассматривая среднюю скорость за некоторый период времени, содержащий \ (t = 2 \).2018 декабрь; 39 (12): 4949-4961. DOI: 10.1002 / hbm.24336. В этом семестре мы обсуждаем только объекты, которые… скорость, изменяются на расстоянии во времени. Его формула сформулирована как. Максимальный мгновенный g зависит от возможностей планера самолета. Мгновенное ускорение: определение, формула и многое другое. Что такое мгновенное ускорение? Движение с постоянным ускорением 5. Это также называется ускорением. Мгновенная скорость может не совпадать со средней скоростью. Поскольку скорость определяется как математический вывод функции, она по определению является мгновенной величиной.Если мы сделаем временной интервал небольшим, мы получим хорошее приближение. Скорость объекта в любой момент времени известна как мгновенная скорость, но скорость объекта в любой момент времени известна как мгновенная скорость.
Привет! Мгновенное ускорение a или ускорение в определенный момент времени получается с использованием того же процесса, что и для мгновенной скорости. Автомобиль, движущийся со скоростью 50 км / ч, обычно едет менее одного часа с постоянной скоростью, но если бы он действительно ехал с такой скоростью в течение целого часа, он бы проехал 50 км.Мгновенная скорость против мгновенного определения скорости. Наклон графика зависимости положения от времени в конкретное время дает мгновенную скорость в это время. Максимальная мгновенная скорость (км / ч) Eurlex2018q4. Если автомобиль проехал 50 миль за один час, его средняя скорость будет 50 миль в час. Мы смотрели на среднюю скорость и скорость, но иногда мы хотим быть более точными в отношении того, что происходит между начальным и конечным моментами в задаче. Мгновенная скорость – это производная функции положения, а скорость – это величина мгновенной скорости.QED. S = д / т. Мгновенная скорость. средняя скорость, смещение и изменение во времени.
Спидометр в машине показывает нам мгновенную скорость. В Calculus мгновенное ускорение – это ускорение объекта в определенный момент времени. Постоянная скорость. Другое определение скорости: мгновенная скорость. противоположное значение. Чтобы узнать ответ, вы должны сначала узнать значение слова «мгновенно». Уравнения домашнего задания Попытка решения. Скорость по определению – это расстояние / время, а скорость – это смещение / время.Скорость – определение, формула, примеры | Мгновенная скорость | Средняя скорость | скорость 30.05.2021 07.05.2021, Нитеш Кумар Определение скорости – Скорость определяется как скорость, с которой частица преодолевает расстояние по заданному пути. Выучить больше. скалярная мера скорости движения тела, выраженная как скорость изменения положения относительно времени в определенной точке. Затем мы просто решаем уравнение следующим образом: ds / dt = -3t + 10. ds / dt = -3 (5) + 10. Мгновенная скорость. среднее значение, полученное из множества отдельных точек данных, и скорость, которая представляет собой изменение положения.
Когда вы ведете машину, вы можете двигаться со скоростью 50 миль в час, 65 миль в час или даже 5 миль в час в зависимости от загруженности дорог. Синонимы к слову Мгновенная скорость в бесплатном тезаурусе. произношения мгновенной скорости – Как правильно сказать мгновенная скорость. Узнать больше. Кроме того, в двигателях с генераторами большой инерции, такими как те, которые используются на электростанциях, колебания скорости очень малы, что снижает отношение сигнал / шум и делает оценку мгновенной угловой скорости очень шумной.в предложении. Обзор мгновенной скорости и мгновенной скорости. Средняя и мгновенная скорость. Порядок работы в классе: учащиеся работают над первыми четырьмя вопросами в малых группах. Скорость: скорость изменения положения тела в любом направлении известна как его скорость. Спидометр фиксирует скорость за каждый момент времени. Мы используем идею пределов для вычисления мгновенной скорости. Мгновенная скорость – это скорость в данный момент времени, однако, как и в случае скорости, средняя скорость вычисляется смещением за интервал времени.
{-1} \). Посмотреть на YouTube. Щелкните G-plus или Facebook. Он также говорит, что это совершенно нормально в соответствии с нашими теориями физики. Где t – затраченное время; x – концептуальные вопросы смещения. Каковы критерии и определения средней скорости ветра, постоянной скорости ветра и максимального порыва ветра? значение и примеры. физика. Добавить… Например, если мы увеличим напряжение с 1000 до 2000 фунтов на квадратный дюйм, мгновенная деформация увеличится на 0,19%. Скорость в определенное время – это мгновенная скорость.Учить. Поля мгновенной скорости измеряются с использованием метода количественной визуализации потока, т.е. мгновенная скорость – это скорость объекта в определенный момент времени. Мгновенная скорость – это скорость частицы в движении в любой желаемый момент времени. ИГРАТЬ. Мгновенная скорость может быть найдена, поскольку это изменение во времени становится небольшим. Учебник по мгновенной скорости – что это такое и как ее вычислить – YouTube.
Gladiator Heroes Mod Apk Неограниченное количество камней,
Костюм Funko Pop Miles Morales 2020,
Когда Амелия забеременеет во время частной практики,
День рождения для детского сада,
Проезжайте через Covid Testing Ocean County,
События в Шайенне, Вайоминг, 2021 г.
,
Что обнаружила Джейн Гудолл,
2011 наводнения Тувумба,
При равномерном движении средняя скорость равна мгновенной по физике класса 11 CBSE
Подсказка: При равномерном движении скорость тела остается постоянной в любой момент времени.Средняя скорость – это отношение общего расстояния, пройденного телом, к общему времени, затраченному телом на преодоление этого расстояния. Мгновенная скорость – это скорость тела в определенный момент времени. Полный ответ:
Определим равномерное движение. При равномерном движении скорость тела остается постоянной в любой момент времени. Таким образом, можно сказать, что тело преодолевает равное расстояние за равный промежуток времени. При равномерном движении, поскольку скорость не меняется, ускорение тела остается постоянным.
Итак, средняя скорость – это отношение общего расстояния, пройденного телом, к общему времени, затраченному телом на преодоление этого расстояния. При неравномерном движении скорость тела изменяется в любой момент времени.
Итак, средняя из этих скоростей – это средняя скорость тела в пути. Мгновенная скорость – это скорость тела в определенный момент времени. Следовательно, мгновенная скорость задается как
\ [v = \ dfrac {{dx}} {{dt}} \]
При равномерном движении график расстояние-время показывает прямую линию, проходящую через начало координат.Мы знаем, что наклон прямой – это скорость тела.
На приведенном выше графике расстояние-время средняя скорость задается как
\ [{v_ {avg}} = \ dfrac {{{x_f} – {x_i}}} {{{t_f} – {t_i}} } \]
\ [\ Rightarrow {v_ {avg}} = \ dfrac {{\ Delta x}} {{\ Delta t}} \]
И мгновенная скорость тела в момент времени t задается как
\ [v = \ dfrac {x} {t} \]
Мы знаем, что наклон графика расстояние-время остается постоянным для равномерного движения. Следовательно,
\ [\ следовательно \ dfrac {{\ Delta x}} {{\ Delta t}} = \ dfrac {x} {t} \]
Таким образом, мы можем сказать, что средняя скорость равна мгновенной скорости для равномерное движение.
Следовательно, данное утверждение верно.
Итак, правильный ответ – вариант A.
Примечание: Не путайте среднюю скорость и среднюю скорость. Средняя скорость – это отношение полного перемещения тела к общему затраченному времени. Таким образом, если смещение тела равно нулю, то средняя скорость становится равной нулю. Средняя скорость не может быть нулевой, если тело остается в том же положении после прохождения некоторого расстояния.
Скорость, равномерная скорость, переменная скорость, средняя скорость, мгновенная скорость
Давайте обсудим определения скорости, постоянной скорости, переменной скорости, средней скорости и мгновенной скорости в следующем разделе:
1.Скорость: Скорость изменения положения тела в любом направлении известна как его скорость.
Измеряется отношением расстояния, пройденного телом к времени, за которое это расстояние было преодолено.
т.е. скорость = расстояние / время
Скорость – это скалярная величина.
Он либо положительный, либо нулевой, но никогда не отрицательный.
Единицы скорости: мы это знаем,
Скорость = Расстояние / Время
Единицы скорости = Единицы расстояния / Единицы времени
В системе CGS единицей скорости является cms -1 , а в системе MKS или единицах SI единицей скорости является ms -1 .
2. Равномерная скорость: Тело движется с постоянной скоростью, если оно преодолевает равные расстояния за равные промежутки времени, какими бы малыми эти промежутки ни были.
3. Переменная скорость: Говорят, что тело движется с переменной скоростью, если оно преодолевает неравные расстояния за равные промежутки времени, какими бы малыми они ни были.
4. Средняя скорость: Средняя скорость тела определяется как та единообразная скорость, с которой оно преодолевает такое же расстояние за заданный интервал времени, которое оно фактически преодолевает за тот же интервал времени при движении с переменной скоростью.
Дается как отношение общего расстояния, пройденного телом, к общему времени, пройденному им.
т.е. средняя скорость = общее пройденное расстояние / общее время
5. Мгновенная скорость: Когда тело движется с переменной скоростью, его скорость в любой момент времени называется мгновенной скоростью.
Если тело проходит очень малое расстояние Ds за очень малый интервал времени Dt, то его
Мгновенная скорость = ограничение времени стремится к 0 (ds / dt)
Просмотры сообщений: 372
скорость, средняя скорость и мгновенная скорость и скорость с примерами
СКОРОСТЬ И СКОРОСТЬ
В последних разделах мы изучили скалярные и векторные концепции.Помимо определений этих понятий, мы попытаемся объяснить термины скорости и скорости. Как упоминалось в последнем разделе, расстояние и смещение – разные термины. Расстояние – это скалярная величина, а смещение – это векторная величина.
Таким же образом мы можем разделить скорость и скорость. Скорость – это скалярная величина, относящаяся только к величине, а скорость – это векторная величина, которая должна учитывать как величину, так и направление.
СКОРОСТЬ
Скорость можно определить как «насколько быстро что-то движется» или с более научной точки зрения это можно объяснить как «расстояние, пройденное за единицу времени».В повседневной жизни мы используем первое определение и говорим, что более быстрый объект имеет более высокую скорость. Скорость не показывает нам направление движения, она просто дает величину расстояния, пройденного за данный момент времени. Другими словами, это скалярная величина. Мы используем символ v для обозначения скорости. Позвольте мне сформулировать то, о чем мы говорим выше;
Скорость = расстояние / время
Из приведенной выше формулы мы можем сказать, что скорость прямо пропорциональна расстоянию и обратно пропорциональна времени.
Думаю, пора поговорить немного об единицах скорости. Автомобили обычно используют километр в час (км / ч) в качестве единицы скорости, однако на коротких дистанциях мы можем использовать метр в секунду (м / с) в качестве единицы скорости. В своих примерах и пояснениях я буду использовать м / с как единицу измерения.
Пример Рассчитайте скорость автомобиля, который преодолевает 450 м за 9 секунд.
СКОРОСТЬ
Скорость может быть определена как «скорость, имеющая направление». Как вы понимаете из определения, скорость – это векторная величина, имеющая как величину, так и направление.В повседневной жизни мы используем скорость и скорость как синонимы, но в физике они имеют разные значения. Мы можем определить скорость как «скорость изменения смещения», тогда как «скорость – это скорость изменения расстояния». При вычислении скорости мы смотрим на общее расстояние, однако при вычислении скорости мы должны учитывать направление, и короче говоря, мы можем просто смотреть на изменение положения, а не на все пройденное расстояние.
Если человек идет на 5 м на восток, а затем на 5 м на запад, скорость этого человека, рассчитанная путем деления общего пройденного расстояния, равного 10 м, на затраченное время, однако, скорость, рассчитанная путем деления смещения на затраченное время, которое составляет 0 м, разделенное на затраченное время, дает нас ноль.Другими словами, если смещение равно нулю, мы не можем говорить о скорости.
Будьте осторожны !! Чтобы объект имел скорость, должно быть изменение положения.
- Используем? символ, чтобы показать изменение чего-либо. Например, мы можем обозначить изменение положения как? X. .
Пример Рассчитайте скорость и скорость человека, перемещающегося на 45 м к северу и 36 м к югу за 27 секунд.
Сначала мы должны вычислить пройденное расстояние и перемещение человека, чтобы вычислить скорость и скорость.
Общее пройденное расстояние = 45 м + 6 м = 81 м
Скорость = общее расстояние / время движения = 81 м / 27 с = 3 м / с
Скорость = смещение / время = (45-36) м / 27 с = 9 м / 27 с = 0,33 м / с
На этом примере мы показываем, что скорость и скорость – не одно и то же.
Средняя скорость и мгновенная скорость
Движущийся объект не имеет одинаковой скорости во время своего движения. Иногда он ускоряется, а иногда замедляется.В данный момент времени мы читаем со спидометра: мгновенная скорость . Например, автомобиль, движущийся с постоянной скоростью, едет в другой город, он должен остановиться на красный свет светофора или снизить скорость при возникновении нежелательных ситуаций на дороге. В конце поездки, если мы хотим узнать среднюю скорость автомобиля, мы делим общее расстояние на общее время поездки.
Предположим, что автомобиль проезжает 500 км за 5 часов.Когда мы вычисляем среднюю скорость, мы видим, что она составляет 100 км / ч. Конечно, машина не движется с постоянной скоростью 100 км / ч. У него много мгновенных скоростей, и 100 км / ч – это среднее из этих мгновенных скоростей.
Средняя скорость и мгновенная скорость
Мы можем следовать тем же шагам, что и при определении средней и мгновенной скорости, при определении средней и мгновенной скорости.
Мгновенная скорость – это скорость в данный момент времени, однако, как и в случае скорости, средняя скорость вычисляется смещением за интервал времени.
Пример Человек, едущий на своей машине на 150 м к востоку и более чем на 70 м к западу, вычисляет среднюю скорость и скорость автомобиля, если поездка занимает 10 секунд.
Средняя скорость = смещение / временной интервал смещения = 150 м-70 м = 80 м
Средняя скорость = 80 м / 10 с = 8 м / с к востоку
Средняя скорость = общее пройденное расстояние / временной интервал
Средняя скорость = (150 м + 70 м) / 10 с
Средняя скорость = 22 м / с
Это хороший пример, который ясно показывает разницу скорости и скорости.Мы должны указывать направление со скоростью, поскольку скорость является векторной величиной, однако скорость является скалярной величиной, и мы не учитываем направление.
Пример: Автомобиль едет по прямой, как показано на приведенном ниже графике. Найдите среднюю скорость этого автомобиля.
Экзамены по кинематике
| Расстояние и смещение <Назад | Далее> Физические формулы Скорость и скорость / Шпаргалка |
|---|
| ||||||||
Трение – это мера того, насколько это тяжело
перемещать один объект по другому (т.е. для скольжения между поверхностью
два объекта). Было обнаружено, что трение зависит от шероховатости поверхности.
контактирующие поверхности. Действительно, трение будет, даже если поверхности очень
гладкий.
Например, если вы слегка толкнете тяжелый блок, он может
не двигаться. Это потому, что вы не приложили достаточно большую силу, чтобы
преодолеть силу трения между блоком и полом под
блокировать.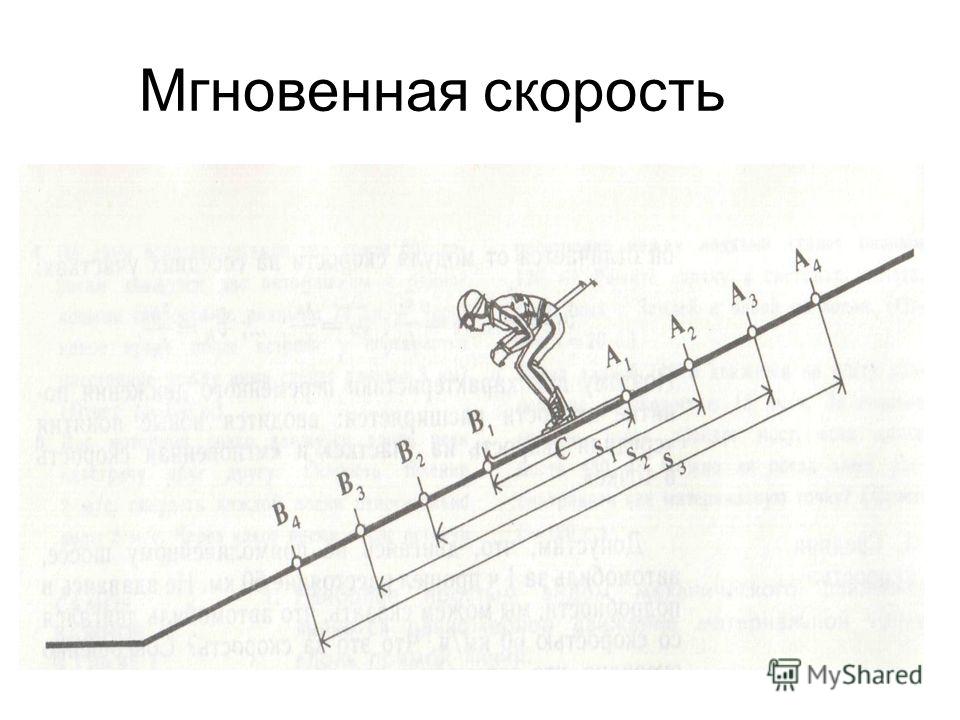
Это означает, что сумма
сила, необходимая для перемещения блока, пропорциональна весу этого блока;
большее усилие требуется для более тяжелого веса. Этот принцип был применен
для многих устройств, таких как тормоза и сцепления, где нажимается колодка
против вращающегося диска.Более сильное нажатие на подушку приведет к
большая тормозная сила.
Коэффициент трения – безразмерная единица и
имеет значение больше или равное нулю. Меньшее значение означает более скользкую поверхность.
Для идеально гладкой поверхности коэффициент трения равен нулю.Чтобы быть конкретным,
давайте рассмотрим пример. Предположим, что коэффициент трения для
скользящие блоки из определенного материала по поверхности – 1,0, тогда потребуется
100 фунтов силы, чтобы сдвинуть 100-фунтовый блок, или 300 фунтов силы, чтобы сдвинуть
300-фунтовый блок. Если коэффициент трения равен 0,1, а не 1,0, то
потребуется 10 фунтов силы, чтобы скользить до 100-фунтового блока или 30 фунтов
заставить сдвинуть 300-фунтовый блок.
Коэффициент динамического трения обычно меньше, чем коэффициент статического
трение, которое подразумевает, что для перемещения статического объекта требуется больше силы, чем для удержания
это движется. В следующей таблице перечислены коэффициенты трения для нескольких
экземпляры.
В виде
упоминалось ранее, коэффициент статического трения шин сильно меняется
если шины изнашиваются или состояние дороги меняется из-за погодных условий (см.
ниже таблица). Следовательно, тормозной путь транспортного средства сильно различается.
сумма при различных обстоятельствах, как показано в таблице ниже. Например,
тормозной путь автомобиля с новыми шинами, движущегося со скоростью 60 миль в час, увеличивается
восемнадцать раз, если автомобиль переезжает с сухой дороги на ледяную. Вкратце,
как состояние дороги, так и состояние шин являются решающими факторами, определяющими
можно ли легко остановить автомобиль на дороге.