Глава 2. Ускорение. Равноускоренное движение
Характеристикой изменения скорости является ускорение. Эта величина определяется как отношение изменения скорости тела к тому интервалу времени, за который это изменение произошло
(2.1) |
где и — скорости тела в конце и начале интервала времени . Из определения (2.1) следует, что вектор ускорения тела отличен от нуля только в том в случае, когда изменяется вектор скорости. При этом направление вектора определяется направлением разности , и может не совпадать с направлениями векторов и . Поэтому в задаче 2.1.1 ситуации, перечисленные в ответах 1, 3 и 4, возможны в следующих случаях. В 1 — когда тело, поворачивая на восток, в некоторый момент времени имеет вектор скорости, направленный на север. В 3 — при равноускоренном движении. В 4 — например, в такой ситуации: тело бросили вертикально вверх и в верхней точке траектории оно имеет нулевую скорость и ускорение, равное ускорению свободного падения. Ситуация, сформулированная в ответе
В задаче 2.1.2 вектор скорости в конце любого интервала времени меньше вектора скорости в начале этого интервала. Поэтому при направлении вектора скорости на юг вектор изменения скорости, а, следовательно, и вектор ускорения направлены на север (ответ 3).
Если тело движется с постоянной скоростью, координата линейно зависит от времени, причем наклон графика определяется скоростью. Поэтому скорость тела уменьшается, если уменьшается угол наклона графика зависимости координаты от времени к оси времени (задача
Движение тела, при котором его ускорение (как величина, так и направление) не изменяется, называется равноускоренным (задача 2. 1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
При равноускоренном движении зависимости радиус-вектора тела по отношению к произвольной системе координат и скорости тела от времени даются соотношениями
(2.2) |
(2.3) |
где и — радиус-вектор и скорость тела в момент времени , — ускорение тела. После проецирования на оси координат зависимости (2.2) и (2.3) позволяют находить координаты тела и проекции его скорости на оси в любые моменты времени.
Поскольку тело движется из начала координат и только в одну сторону, то, очевидно, координата тела совпадает с пройденным путем. Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ 1).
В задаче 2.1.8 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось , направленную вдоль вектора ускорения, имеет вид
где – проекция вектора скорости тела на ось . Так как в момент времени , находим (правильный ответ – 2).
Так как в момент времени , находим (правильный ответ – 2).
Сравнивая данную в задаче 2.1.9 зависимость координаты от времени с законом (2.2), заключаем, что начальная скорость тела , проекция ускорения тела на ось – . Поэтому из (2.3) получаем зависимость скорости тела от времени .
Из этой зависимости следует, что скорость тела равна нулю при (правильный ответЗависимость проекции скорости от времени на ось, направленную вертикально вверх, для тела из задачи 2.1.10 имеет вид
где — начальная скорость тела. Подставляя в эту формулу время , находим скорость тела через 0,5 с после броска (ответ 3). Знак «плюс» для проекции скорости на рассматриваемую ось показывает, что через 0,5 c после броска вектор скорости тела все еще направлен вверх.
Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту (
где — начальная скорость тела. Отсюда получаем для времени подъема (ответ 4). А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени
Подстановка в эту формулу числовых значений дает (ответ 1).
Пусть время, затраченное телом на прохождение участка пути длиной , отсчитанного от начальной точки, равно , а время, затраченное телом на прохождение участка пути длиной , отсчитанного от этой же точки, равно (
 2.3). Тогда из уравнения движения (2.2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем
2.3). Тогда из уравнения движения (2.2) в проекции на ось, направленную вдоль вектора ускорения тела, имеемТест №5 «Путь. Перемещение. Скорость. Ускорение», ФГОС
Материал опубликовала| Вытоптова Татьяна Александровна400 Работаю в КГКОУ “Вечерняя (сменная) общеобразовательная школа №2” с 2005 г. Общий стаж работы в образовательном учреждении 18 лет. С 2013 прошла переподготовку по курсу ОРКСЭ, модуль “Основы православной культуры”. Россия, Алтайский край, Шипуново |
Вытоптова Татьяна Александровна, КГКОУ «Вечерняя (сменная) общеобразовательная школа №2», с. Шипуново Алтайского края, учитель физики.
Тематический контроль по теме «Путь. Перемещение. Скорость. Ускорение». Физика 9 класс.
Аннотация к тесту
Тематический тест по физике для текущего контроля. Тест состоит из 10 вопросов, на каждый вопрос предлагается 5-6 ответов, из которых учащемуся нужно выбрать один правильный. Для этого учащемуся необходимо щелкнуть левой кнопкой мыши на желтый квадрат выбранного ответа, справа появится слово «да» или «нет».
На выполнение теста отводится 15-20 минут.
Критерий оценивания:
Число правильных ответов: Оценка в баллах:
0-2 1
3-4 2
5-6 3
7-8 4
9-10 5
При составлении теста использовалась литература: Кабардин О.Ф., Орлов В.А. Физика. Тесты 7-9 классы: Учебно-методическое пособие.
Тест состоит из 10 вопросов, на каждый вопрос предлагается 5-6 ответов, из которых учащемуся нужно выбрать один правильный. Для этого учащемуся необходимо щелкнуть левой кнопкой мыши на желтый квадрат выбранного ответа, справа появится слово «да» или «нет».
На выполнение теста отводится 15-20 минут.
Критерий оценивания:
Число правильных ответов: Оценка в баллах:
0-2 1
3-4 2
5-6 3
7-8 4
9-10 5
При составлении теста использовалась литература: Кабардин О.Ф., Орлов В.А. Физика. Тесты 7-9 классы: Учебно-методическое пособие.
Тест 5 Физика 9 класс Путь. Перемещение. Скорость. Ускорение.
1. Искусственный спутник обращается вокруг Земли по круговой орбите радиусом R с периодом обращения 1 сут. Каковы путь и перемещение спутника за 1 сут? Путь и перемещение одинаковы и равны нулю. Путь и перемещение одинаковы равны 2πR. Путь и перемещение одинаковы равны 2R. Путь 2πR, перемещение 0. Путь πR, перемещение 0. Путь πR, перемещение 2R. Следующий вопрос Нет Да
На рисунке 1 даны векторы а и b. Какой из векторов с на рисунке 2 равен сумме этих векторов c=a+b? А Г Б Д В Е Следующий вопрос Нет Да
Даны векторы a и b (см. рис. 1). Какой из векторов с равен разности этих векторов с = а-b?
А
Г
Б
Д
В
Е
Следующий вопрос
Нет
Да
рис. 1). Какой из векторов с равен разности этих векторов с = а-b?
А
Г
Б
Д
В
Е
Следующий вопрос
Нет
Да
4. Если ∆S есть перемещение тела за сколько угодно малый интервал времени ∆t, то какая величина определяется отношением ∆S/∆t? Путь. Перемещение. Скорость только равномерного прямолинейного движения. Мгновенная скорость любого движения. Ускорение. Следующий вопрос Нет Да
5. Если обозначить ∆ϑ изменение скорости за сколько угодно малый интервал времени ∆t, то какая величина определяется отношением ∆ϑ∕∆t? Увеличение скорости. Уменьшение скорости. Ускорение только равноускоренного прямолинейного движения. Ускорение только равномерного движения по окружности. Ускорение любого движения. Следующий вопрос Нет Да
По графику зависимости пути ℓ от времени t на рисунке определите скорость движения тела в момент времени
t = 3 с. 1 м/с.
3 м/с.
2 м/с.
0 м/с.
2/3 м/с.
3/5 м/с.
Следующий вопрос
Нет
Да
1 м/с.
3 м/с.
2 м/с.
0 м/с.
2/3 м/с.
3/5 м/с.
Следующий вопрос
Нет
Да
7. По графику на рисунке зависимости модуля скорости ϑ от времени t прямолинейного движения тела определите модуль его ускорения а в момент времени t =3с. 6 м/с². 0 м/с². 3м/с². 1.5 м/с². 1 м/с². Следующий вопрос Нет Да
8. Автомобиль начинает прямолинейное равноускоренное движение из состояния покоя. Какой путь ℓ будет пройден за 1 мин при движении с ускорение 2 м/с²? 1 м. 2 м. 120 м. 1800 м. 3600 м. 7200 м. Следующий вопрос Нет Да
9. Какой путь пройден самолетом до остановки, если его ускорение в процессе торможения было равно 6 м/с², а скорость в момент начала торможения 60 м/с²?
600 м. 300 м.
360 м.
180 м.
Следующий вопрос
Нет
Да
300 м.
360 м.
180 м.
Следующий вопрос
Нет
Да
Средняя скорость. Ускорение | 7 класс Онлайн
Конспект по физике для 7 класса «Средняя скорость. Ускорение». ВЫ УЗНАЕТЕ: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. ВСПОМНИТЕ: В каком случае тело движется неравномерно? Что такое путь? Что такое скорость? Каковы единицы скорости? Как определить скорость тела при равномерном движении?
Средняя скорость. Ускорение
В окружающем нас мире мы крайне редко сталкиваемся с равномерным движением. Обычно скорость тела изменяется с течением времени, и за одинаковые промежутки времени тетю проходит неодинаковые пути. Такое движение является неравномерным. Однако никого не удивляет, когда мы говорим, что ехали на автомобиле со скоростью 60 км/ч, хотя при этом подразумевается, что мы и тормозили, и останавливались перед светофорами, и вновь ускорялись. О какой же скорости тогда идёт речь?
СРЕДНЯЯ СКОРОСТЬ
Для характеристики неравномерного движения вводят понятие средней скорости. Средняя скорость тела при неравномерном движении находится так же, как и скорость при равномерном движении, т. е. весь пройденный телом путь необходимо разделить на полное время движения тела, включая остановки.
путь
———— = средняя скорость
время
Полученное значение показывает среднюю скорость движения тела на всём пути, и оно может не совпадать со значением скорости в различные моменты времени движения.
Предположим, что автомобиль проехал путь s, состоящий из участков s1, s2, и s3, причём прохождение каждого из них заняло соответственно время t1, t2и t3.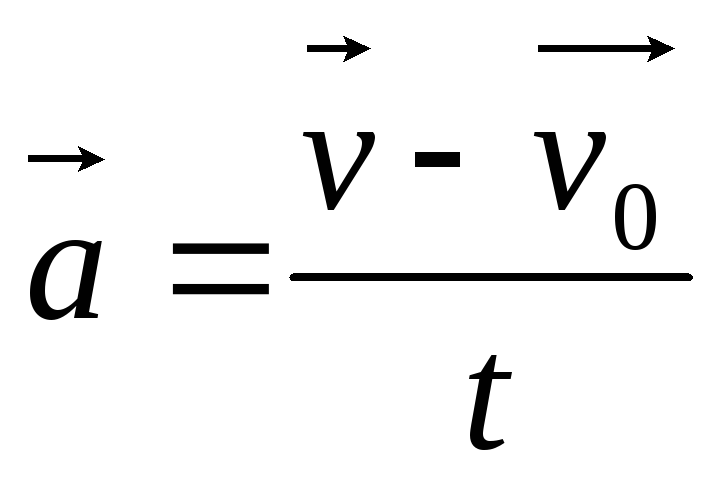 Для определения средней скорости движения автомобиля надо весь пройденный путь разделить на общее время движения:
Для определения средней скорости движения автомобиля надо весь пройденный путь разделить на общее время движения:
ʋср = (s1 + s2 + s3) / (t1 + t2 + t3)
Зная среднюю скорость движения тела и время движения, можно найти пройденный за это время путь по формуле s = t ʋср.
Если нам известны средняя скорость движения и пройденный путь, мы можем определить время движения по формуле t = s ʋср.
ГРАФИКИ ЗАВИСИМОСТИ ПУТИ И СКОРОСТИ ОТ ВРЕМЕНИ
В отличие от графиков прямолинейного равномерного движения при неравномерном движении графики зависимости скорости и пути от времени могут выглядеть совершенно по-разному в зависимости от конкретной задачи.
Рассмотрим пример. Пусть велосипедист при движении из одного города в другой сначала проехал 8 км за 20 мин. Затем, отдохнув 10 мин, проехал ещё 6 км за 30 мин, а оставшиеся 2,5 км прошёл пешком за 30 мин. Как будут выглядеть соответствующие графики, если в пределах каждого временного интервала велосипедист двигался с постоянными скоростями?
РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ
Предположим, в начале определённого отрезка времени мы движемся в автомобиле со скоростью ʋ0. Автомобиль начинает увеличивать скорость, и через время t его скорость становится равной ʋ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.
Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.
Прямолинейным равнопеременным движением называется движение, при котором траекторией тела является прямая линия и за любые равные промежутки времени скорость тела изменяется (увеличивается или уменьшается) на одно и то же значение.
УСКОРЕНИЕ
В физике существует величина, характеризующая изменение скорости тела при равнопеременном движении. Она называется ускорением и обозначается латинской буквой а. Для того чтобы вычислить ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло, т. е. от значения его конечной скорости нужно отнять значение начальной скорости и полученный результат разделить на рассматриваемое время движения.
В Международной системе единиц (СИ) за единицу ускорения принимают ускорение такого равнопеременного движения, при котором скорость движущегося тела за время 1 с изменяется на 1 м/с.
Эту единицу называют 1 метр на секунду в квадрате и обозначают 1 м/с2.
Ускорение может принимать как положительное, так и отрицательное значение. Действительно, если скорость тела в начале движения (ʋ0) меньше скорости тела в конце движения (ʋ), то при нахождении ускорения положительное число (ʋ — ʋ0) мы делим на положительное число (t) и получаем положительное значение ускорения. Если же тело замедляется, то значение начальной скорости оказывается больше значения скорости в конце движения, разность ʋ — ʋ0 становится отрицательной и значение ускорения тоже оказывается меньше нуля.
Вы смотрели Конспект по физике для 7 класса «Средняя скорость. Ускорение»: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).
Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).
Движение | Физика
Равномерное движение
Величина скорости показывает, какое расстояние s может преодолеть тело за определенное время t. Если машина ехала со скоростью 100 километров в час, это значит, что расстояние в 100 километров машина проехала за один час. Если эта скорость является постоянной, то мы имеем дело с равномерным движением тела.
Таким образом, скорость тела определяет отношение между расстоянием s и временем t. Зная эти величины, можно легко вычислить скорость тела V. Скорость равна расстоянию, деленному на время: v = s/t.
Средняя и мгновенная скорость
Так как любая машина вряд ли будет ехать весь путь с одинаковой скоростью, то часто речь идет о средней скорости движения. Скорость машины может меняться каждую секунду, но это не помешает машине преодолеть 100 километров за 1 час.
Движение с ускорением
При равноускоренном движении, то есть при постоянном ускорении, машина за равные отрезки времени будет проходить все большее расстояние. Если мы рассмотрим такое движение, то моментальная скорость Vм в конце пути будет в два раза больше, чем средняя скорость Vср. В любом случае среднюю скорость тела можно вычислить таким образом: скорость тела в начале пути, обозначенная как V0, плюс моментальная скорость в конце пути Vм, деленная на 2.
Машина, которая только начинает движение и набирает желаемую скорость 100 км/ч или 27,8 м/с за 10 секунд, имеет постоянное ускорение 2,78 м/с2. Ускорение тела показывает, как быстро машина набирает определенную скорость, и обозначается a.
Если машина в течение 5 секунд после начала пути развила скорость от 0 до 100 км/ч, то ее ускорение было в два раза больше, чем в предыдущем примере.
Если машина в начале пути находилась в состоянии покоя, то, зная ускорение, можно вычислить путь, который она пройдет за определенное время. Обратимся к известным нам формулам: S = Vср * t, где Vср = Vм/2, а моментальная скорость измеряется следующим образом: Vм = a * t. Отсюда мы можем вывести формулу для пройденного пути: s = (a * t2) / 2.
Обратимся к известным нам формулам: S = Vср * t, где Vср = Vм/2, а моментальная скорость измеряется следующим образом: Vм = a * t. Отсюда мы можем вывести формулу для пройденного пути: s = (a * t2) / 2.
При торможении движение машины замедляется, что означает движение с отрицательным ускорением.
Сила и ускорение
Если мы хотим, чтобы машина массой 1 тонна за 10 секунд развила скорость от нуля до 100 км/ч, то необходимо приложить силу F.
Если машина массой 2 тонны будет набирать скорость 100 км/ч за 20 секунд, то понадобится сила 1F.
Если машина массой 1 тонна разгонится от 0 до 100 км/ч, но уже за 5 секунд, то есть в два раза быстрее, то для этого понадобится приложить силу, равную 2F. При постоянной массе m сила F будет пропорциональна ускорению a: m = F/a.
Если необходимо сохранить прежнее ускорение машины, а масса составляет уже 2 тонны, то в этом случае к машине нужно приложить силу в 2F. Отсюда следует, что при постоянном ускорении сила пропорциональна массе тела: a = F/m (чем больше масса, тем больше силы надо приложить).
Отсюда следует вывод, который лег в основу закона Ньютона: F = m * a. Таким образом, сила F – это произведение массы тела m на его ускорение a.
Свободное падение
К большому удивлению своих современников Галилео Галилей утверждал, что тяжелые и легкие тела падают на Землю с одинаковой скоростью. Когда тело находится в состоянии свободного падения, то в качестве тормозящей силы будет выступать сопротивление воздуха, поэтому тела различной формы и веса будут падать с разной скоростью. Доказательством этого, может служить пример, когда мы поместим тело в вакуум, где сила сопротивления воздуха будет “выключена”. Ты можешь убедиться в этом сам!
При свободном падении речь идет о равномерно ускоренном движении, которое возникает посредством действия силы гравитации Земли.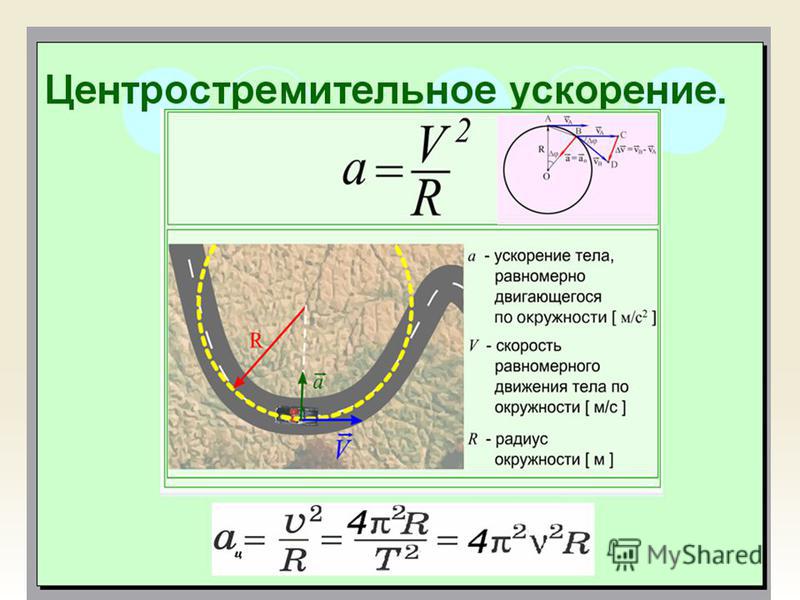 Сила гравитации влияет на то, что в безвоздушном пространстве все тела за одинаковое время достигают одинаковой скорости. Ускорение при свободном падении можно вывести из формулы равномерного ускоренного движения. Исходя из того, что
Сила гравитации влияет на то, что в безвоздушном пространстве все тела за одинаковое время достигают одинаковой скорости. Ускорение при свободном падении можно вывести из формулы равномерного ускоренного движения. Исходя из того, что
Движение по окружности
Линейную скорость тела, которое двигается по окружности, в принципе можно вычислить таким же образом, как и скорость прямолинейно двигающегося тела.
Линейная скорость вращения — это отношение расстояния S, в данном случае длины окружности, и времени, затраченного на прохождение этого пути. Таким образом, мы получаем, что
Время, затраченное двумя машинками карусели, для того чтобы сделать полный круг, будет одинаково. А вот проделанный путь у крайней машинки будет значительно больше, так как она находится на большем расстоянии от центра окружности.
Чем больше расстояние от центра окружности, тем больше должна быть линейная скорость вращения крайней машинки.
Так как внутренняя и внешняя машинка совершают полный оборот за одинаковое время, то их угловая скорость будет одинаковой. Угловой скоростью называется отношение угла поворота к интервалу времени, за который этот поворот произошел.
Сила, которая удерживает машины на треке, называется центробежной силой.
Ускорение. Равноускоренное движение | LAMPA
Что такое ускоренное движение
Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.
“Движение” — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.
“Ускоренное” — значит “убыстренное”, с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее… То есть скорость все время увеличивается.
Это может прозвучать странно, но случай, когда скорость уменьшается и уменьшается, а тело двигается все медленнее, медленнее и медленнее, – это тоже “ускоренное” движение. В это трудно поверить (и это трудно понять) прямо сейчас, но позже вам станет понятнее. Иногда такое движение с уменьшением скорости называют равнозамедленным движением.
Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 555 км/ч, потом 101010 км/ч, потом 151515 км/ч, 202020 км/ч, 252525 км/ч, 303030 км/ч и т.д. — насколько у него хватит сил.
Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 101010 км/ч, потом 555 км/ч, а потом 000 км/ч. То есть скорость все время уменьшается на 555 км/ч.
Следуя этой логике, через мгновение после скорости в 000 км/ч скорость должна вновь уменьшиться на 555 км/ч, и тогда скорость будет равна −5-5−5 км/ч, а потом еще уменьшиться на 555 км/ч и стать уже −10-10−10 км/ч, а потом и −15-15−15 км/ч и т.д. Ведь уменьшение скорости должно происходить и дальше. Кому-то отрицательная скорость может показаться странной. Тем, кому она кажется странной, хочу напомнить, что когда мы говорим о скорости не как о векторе (не как о “стрелочке”), то чаще всего мы имеем в виду проекцию скорости на некоторую ось. Если направление вектора совпадает с направлением этой оси, то проекция получается положительной. Если скорость противоположна направлению оси — то проекция получается отрицательной. Тем, кому приведенные объяснения кажутся непонятными, мы рекомендуем прочитать темы “Два вида физических величин: скалярные величины и векторные величины” и “Проектирование векторов на оси”. В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.
В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.
Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.
В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме “Равноускоренное движение”, а второй случай — с поворотом — в теме “Движение по окружности”, когда тело поворачивает, а значит — изменяет направление скорости.
Урок 02. Механическое движение, его характеристики
Механика – раздел физики, в котором изучают механическое движение.
Механику подразделяют на кинематику, динамику и статику.
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения. Кинематика изучает способы описания движения и связь между величинами, характеризующими эти движения.
Задача кинематики: определение кинематических характеристик движения (траектории движения, перемещения, пройденного пути, координаты, скорости и ускорения тела), а также получение уравнений зависимости этих характеристик от времени.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно, выражение «тело движется» лишено всякого смысла, пока не определено, относительно чего рассматривается движение. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен (примеры: пассажир в покоящемся поезде смотрит на проходящий мимо поезд)
Главная задача механики – уметь вычислять координаты точек тела в любой момент времени.
Чтобы решить эту надо иметь тело, от которого ведется отсчет координат, связать с ним систему координат и иметь прибор для измерения промежутков времени.
Система координат, тело отсчета, с которым она связана, и прибор для отсчета времени образуют систему отсчета, относительно которой и рассматривается движение тела.
Системы координат бывают:
1. одномерная – положение тела на прямой определяется одной координатой x.
2. двумерная – положение точки на плоскости определяется двумя координатами x и y.
3. трехмерная – положение точки в пространстве определяется тремя координатами x, y и z.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным.
Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
д. При поступательном движении тела его также можно рассматривать как материальную точку.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.
Понятие материальной точки играет важную роль в механике. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстоянием от него до других тел.
Пример. Размеры орбитальной станции, находящейся на орбите около Земли, можно не учитывать, а рассчитывая траекторию движения космического корабля при стыковке со станцией, без учета ее размеров не обойтись.
Характеристики механического движения: перемещение, скорость, ускорение.
Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Линия, по которой движется точка тела, называется траекторией движения.
Длина траектории называется пройденным путем.
Обозначается l, измеряется в метрах. (траектория – след, путь – расстояние)
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.
Обозначается S, измеряется в метрах.(перемещение – вектор, модуль перемещения – скаляр)
Скорость – векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка.
Обозначается v
Формула скорости: или
Единица измерения в СИ – м/с.
На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с).
Измеряют скорость спидометром.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Ускорение измеряют акселерометром
Единица измерения в СИ м/с2
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение , скорость и ускорение . Путь l является скалярной величиной. Перемещение , скорость и ускорение – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Проверить свои знания (тест по теме “Механическое движение, его характеристики”)
Последовательный многошаговый синтез управления позиционным электроприводом
%PDF-1.3 % 1 0 obj > endobj 4 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > stream
 0 842.0]
/Annots [16 0 R]
>>
endobj
6 0 obj
>
/Contents 19 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
7 0 obj
>
/Contents 22 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
8 0 obj
>
/Contents 27 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
9 0 obj
>
/Contents 30 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
10 0 obj
>
endobj
11 0 obj
>
endobj
12 0 obj
>
stream
x
0 842.0]
/Annots [16 0 R]
>>
endobj
6 0 obj
>
/Contents 19 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
7 0 obj
>
/Contents 22 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
8 0 obj
>
/Contents 27 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
9 0 obj
>
/Contents 30 0 R
/CropBox [0 0 595.0 842.0]
>>
endobj
10 0 obj
>
endobj
11 0 obj
>
endobj
12 0 obj
>
stream
xУравнения для скорости, скорости и ускорения
Обновлено 15 декабря 2020 г.
Карен Дж. Блаттлер
Проблемы, связанные с вычислением скорости, скорости и ускорения, обычно возникают в физике. Часто эти задачи требуют расчета относительного движения поездов, самолетов и автомобилей. Эти уравнения также могут применяться к более сложным задачам, таким как скорости звука и света, скорость планетарных объектов и ускорение ракет.
Формула скорости
Скорость означает расстояние, пройденное за определенный период времени.Обычно используемая формула для скорости вычисляет среднюю скорость, а не мгновенную скорость. Расчет средней скорости показывает среднюю скорость всего путешествия, а мгновенная скорость показывает скорость в любой данный момент поездки. Спидометр автомобиля показывает мгновенную скорость.
Среднюю скорость можно найти, используя общее пройденное расстояние, обычно обозначаемое как d, разделенное на общее время, необходимое для прохождения этого расстояния, обычно обозначаемое как t. Итак, если автомобилю требуется 3 часа, чтобы преодолеть общее расстояние в 150 миль, средняя скорость равна 150 миль, разделенным на 3 часа, что равняется средней скорости 50 миль в час:
\ frac {150} {3} = 50
Мгновенная скорость – это расчет скорости, который будет обсуждаться в разделе скорости.
Единицы скорости показывают длину или расстояние во времени. Мили в час (миль / час или миль в час), километры в час (км / час или км / ч), футы в секунду (фут / с или фут / сек) и метры в секунду (м / с) – все указывают на скорость.
Формула скорости
Скорость – это векторное значение, означающее, что скорость включает направление. Скорость равна пройденному расстоянию, деленному на время движения (скорость) плюс направление движения. Например, скорость поезда, идущего на 1500 километров к востоку от Сан-Франциско за 12 часов, составит 1500 км, разделенных на 12 часов к востоку, или 125 км / ч к востоку.
Возвращаясь к проблеме скорости автомобиля, представьте, что две машины начинают движение из одной и той же точки и едут с одинаковой средней скоростью 50 миль в час. Если одна машина едет на север, а другая на запад, машины не останутся в одном месте. Скорость машины, идущей на север, будет 50 миль в час на север, а скорость машины, идущей на запад, будет 50 миль в час на запад. Их скорости разные, хотя их скорости одинаковы.
Мгновенная скорость, чтобы быть полностью точной, требует вычисления для оценки, потому что для приближения к «мгновенной» требуется сокращение времени до нуля.Однако можно сделать приближение, используя уравнение: мгновенная скорость (v i ) равна изменению расстояния (Δd), деленному на изменение во времени (Δt), или:
v_i = \ frac {\ Delta d} {\ Delta t}
Установив изменение времени как очень короткий период времени, можно рассчитать почти мгновенную скорость. Греческий символ дельты, треугольник (Δ), означает изменение.
Например, если движущийся поезд прошел 55 км на восток в 5:00 и достиг 65 км на восток в 6:00, изменение расстояния составит 10 км на восток с изменением времени на 1 час.Вставка этих значений в формулу дает:
v_i = \ frac {10} {1} = 10
или 10 км / ч на восток (по общему признанию, медленная скорость для поезда). Мгновенная скорость будет 10 км / ч на восток, по спидометру двигателя – 10 км / ч. Конечно, час не «мгновенный», но он служит для примера.
Вместо этого предположим, что ученый измеряет изменение положения (Δd) объекта на 8 метров за интервал времени (Δt) в 2 секунды. Используя формулу, мгновенная скорость равна 4 метрам в секунду (м / с) на основе расчета:
Используя формулу, мгновенная скорость равна 4 метрам в секунду (м / с) на основе расчета:
v_i = \ frac {8} {2} = 4
В качестве векторной величины мгновенная скорость должна включать направление.Однако многие проблемы предполагают, что объект продолжает двигаться в том же направлении в течение этого короткого промежутка времени. Тогда направленность объекта игнорируется, что объясняет, почему это значение часто называют мгновенной скоростью.
Уравнение ускорения
Какая формула ускорения? Исследования показывают два явно разных уравнения. Одна формула из второго закона Ньютона связывает силу, массу и ускорение в уравнении: сила (F) равна массе (м), умноженной на ускорение (а), записывается как F = ma.Другая формула, ускорение (a) равняется изменению скорости (Δv), деленному на изменение во времени (Δt), вычисляет скорость изменения скорости во времени. Эту формулу можно записать:
a = \ frac {\ Delta v} {\ Delta t}
Так как скорость включает в себя как скорость, так и направление, изменения ускорения могут быть результатом изменений скорости или направления, либо обоих. В науке единицами измерения ускорения обычно являются метры в секунду в секунду (м / с / с) или метры в секунду в квадрате (м / с 2 ).
Эти два уравнения не противоречат друг другу. Первый показывает соотношение силы, массы и ускорения. Второй рассчитывает ускорение на основе изменения скорости за определенный период времени.
Ученые и инженеры называют увеличение скорости положительным ускорением, а уменьшение скорости – отрицательным ускорением. Однако большинство людей используют термин замедление вместо отрицательного ускорения.
Ускорение свободного падения
Вблизи поверхности Земли ускорение свободного падения является постоянной величиной: a = -9.8 м / с 2 (метры в секунду в секунду или метры в секунду в квадрате). Как предположил Галилей, объекты с разной массой испытывают одинаковое ускорение силы тяжести и будут падать с одинаковой скоростью.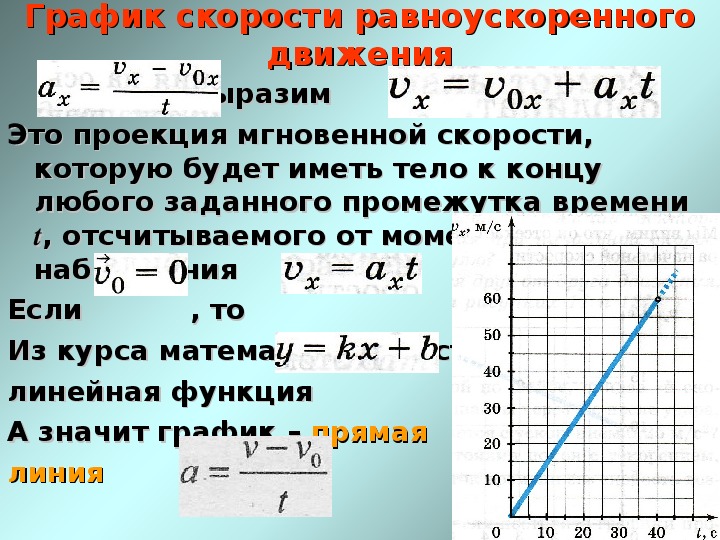
Онлайн-калькуляторы
Введя данные в онлайн-калькулятор скорости, можно рассчитать ускорение. Онлайн-калькуляторы можно использовать для вычисления уравнения скорости, ускорения и силы. Использование калькулятора ускорения и расстояния требует знания скорости и времени.
Калькулятор ускорения | Определение | Формула
Калькулятор ускорения – это инструмент, который поможет вам определить , насколько быстро изменяется скорость объекта . Он работает тремя разными способами, в зависимости от:
- разница между скоростями в два разных момента времени,
- расстояние, пройденное при разгоне,
- масса ускоряющегося объекта и сила, действующая на него.
Если вы спрашиваете себя, что такое ускорение, какова формула ускорения или каковы единицы ускорения, продолжайте читать, и вы узнаете, как найти ускорение.Ускорение строго связано с движением объекта, и каждый движущийся объект обладает определенной энергией. Если вам нужно это оценить, посетите другие наши калькуляторы, где вы можете найти формулу кинетической энергии и ее угловую версию – формулу кинетической энергии вращения.
Чтобы все было понятно, мы также подготовили несколько примеров ускорения, которые распространены в физике. Вы можете найти там:
- центростремительное ускорение и тангенциальное ускорение,
- угловое ускорение,
- ускорение свободного падения,
- ускоритель частиц.
Ускорение всегда происходит всякий раз, когда на объект действует ненулевая чистая сила. Вы можете почувствовать это в лифте, когда вы станете немного тяжелее (ускорение) или легче (замедление), или когда вы едете по крутому склону на санях по снегу. Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже ускоряется! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что каждый масштаб в мире тоже расширяется.
Что такое ускорение? – определение ускорения
Ускорение – это скорость изменения скорости объекта; другими словами, насколько быстро изменяется скорость. Согласно второму закону Ньютона, ускорение прямо пропорционально сумме всех сил, действующих на объект, и обратно пропорционально его массе. Это все здравый смысл – если несколько разных сил толкают объект, вам нужно выяснить, к чему они складываются (они могут действовать в разных направлениях), а затем разделить результирующую чистую силу на массу вашего объекта.
Это определение ускорения гласит, что ускорение и сила, по сути, одно и то же. При изменении силы изменяется и ускорение, но величина его изменения зависит от массы объекта. Это неверно в ситуации, когда масса также изменяется, например, при ракетной тяге, когда сгоревшее топливо выходит из сопла ракеты. Если вы когда-нибудь задумывались, какова физика космических путешествий, взгляните на это уравнение ракеты Циолковского.
Мы можем измерить ускорение объекта напрямую с помощью акселерометра .Если повесить объект на акселерометр, он покажет ненулевое значение. Это почему? Ну, это из-за гравитационных сил, которые действуют на каждую частицу, имеющую массу. А где чистая сила, там и ускорение. Таким образом, акселерометр в состоянии покоя измеряет ускорение свободного падения, которое на поверхности Земли составляет около 31,17405 фут / с² (9,80665 м / с²). Другими словами, это ускорение свободного падения, которое любой объект получает при свободном падении в вакууме.
Кстати о пылесосах, вы когда-нибудь смотрели «Звездные войны» или другой фильм, действие которого происходит в космосе? Эпические сражения космических кораблей, звуки бластеров, двигателей и взрывов.Что ж, это ложь. Космос – это вакуум, и в нем нельзя услышать звук (для распространения звуковых волн требуется материя). Эти битвы должны быть беззвучными! В космосе никто не услышит твой крик. Чтобы проверить скорость звука в воздухе или воде, воспользуйтесь нашим калькулятором скорости звука. Учитывается даже температура!
Учитывается даже температура!
Как найти ускорение? – счетчик ускорения
Калькулятор ускорения на этом сайте учитывает только ситуацию, в которой объект имеет равномерное (постоянное) ускорение.В этом случае уравнение ускорения по определению представляет собой отношение изменения скорости за конкретное время. Однако здесь вы можете узнать, как найти ускорение еще двумя способами. Давайте посмотрим, как пользоваться нашим калькулятором (уравнения ускорения вы можете найти в разделе после):
- В зависимости от имеющихся данных вы можете рассчитать ускорение тремя разными способами. Во-первых, выберите соответствующее окно (# 1, # 2 или # 3),
- [при выборе # 1] – Введите начальную скорость
v_iи конечнуюv_fскорости объекта и сколько времениΔtпотребовалось для изменения скорости. - [при выборе # 2] – Введите начальную скорость
v_i, пройденное расстояниеΔdи времяΔt, пройденное во время ускорения. Здесь вам не нужно знать конечную скорость. - [при выборе # 3] – Введите массу
мобъекта и чистую силуF, действующую на этот объект. Это совершенно другой набор переменных, который возникает из второго закона движения Ньютона (другое определение ускорения). - Считайте результирующее ускорение из последнего поля. Вы также можете выполнить вычисления другим способом, если знаете, что такое ускорение, например, чтобы оценить расстояние
Δd. Просто укажите остальные параметры в этом окне.
Знание того, что такое ускорение, необходимо для анализа движения объектов. Например, вы можете определить изменение импульса за определенный период времени с помощью этой формулы для импульса. Это одна из физических величин, которые мы используем в нашем калькуляторе автокатастроф, где мы объясняем и визуализируем важность ремней безопасности с помощью чисел и определяем, с какой скоростью вы можете погибнуть в автокатастрофе. Повышение скорости и содержание алкоголя в крови – главные причины автомобильных аварий. Пожалуйста, водите осторожно!
Повышение скорости и содержание алкоголя в крови – главные причины автомобильных аварий. Пожалуйста, водите осторожно!
Формула ускорения – три уравнения ускорения
В 17 веке сэр Исаак Ньютон , один из самых влиятельных ученых всех времен, опубликовал свою знаменитую книгу Principia . В нем он сформулировал закон всемирного тяготения, согласно которому любые два объекта с массой будут притягиваться друг к другу с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния).Чем тяжелее объекты, тем больше сила тяжести. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
В Principia Ньютон также включает три закона движения, которые являются центральными для понимания физики нашего мира. Калькулятор ускорения основан на трех различных уравнениях ускорения, третье из которых получено из работы Ньютона:
-
a = (v_f - v_i) / Δt, -
a = 2 * (Δd - v_i * Δt) / Δt², -
a = Ф / м,
где:
-
a– ускорение, -
v_iиv_f– соответственно начальная и конечная скорости, -
Δt– время разгона, -
Δd– расстояние, пройденное при ускорении, -
F– чистая сила, действующая на объект, который ускоряется, -
м– масса этого объекта.
Теперь вы знаете, как рассчитать ускорение! В следующем абзаце мы обсудим единицы ускорения (СИ и британские). Вы уже видели наши калькуляторы конвертации? Они могут сэкономить вам много времени при работе с различными юнитами. В случае расстояния вас может заинтересовать конвертер длины, который включает в себя таблицу преобразования длины. Если вы хотите переключаться между разными единицами массы, вот наш конвертер веса. Оба калькулятора позволяют быстро выполнять вычисления с любым набором единиц измерения. Попробуйте!
Попробуйте!
Блоки ускорения
Если вы уже умеете рассчитывать ускорение, давайте сосредоточимся на единицах ускорения. Вы можете вывести их из приведенных выше уравнений. Все, что вам нужно знать, это то, что скорость выражается в футах в секунду (британская / американская система) или в метрах в секунду (система СИ), а время – в секундах. Следовательно, если вы разделите скорость на время (как мы делаем в первой формуле ускорения), вы получите единицу ускорения фут / с² или м / с² в зависимости от того, какую систему вы используете.
В качестве альтернативы можно использовать третье уравнение. В этом случае вам нужно разделить силу (фунты в США и ньютоны в СИ) на массу (фунты в США и килограммы в СИ), получив пдл / фунт или Н / кг . Они оба представляют одно и то же, поскольку фунт составляет фунтов на кв. Дюйм = фунт * фут / с² , а ньютон составляет Н = кг * м / с² . Если вы замените его и уменьшите единицы, вы получите (фунт * фут / с²) / фунт = фут / с² или (кг * м / с²) / кг = м / с² .
Существует также третий вариант, который фактически широко используется.Вы можете выразить ускорение как стандартное ускорение , вызванное силой тяжести у поверхности Земли, которое определяется как g = 31,17405 фут / с² = 9,80665 м / с² . Например, если вы говорите, что лифт движется вверх с ускорением 0,2 g , это означает, что он ускоряется примерно со скоростью 6,2 фут / с² или 2 м / с² (т. Е. 0,2 * g ) . Мы округлили приведенные выше выражения до двух значащих цифр с помощью правил значащих цифр, которые вы можете найти в нашей математической категории.
Примеры разгона
Центростремительное ускорение и тангенциальное ускорение
Ускорение – это обычно вектор, поэтому его всегда можно разложить на составляющие. Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму следа, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения.Он изменяет только значение скорости , но не ее направление.
Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму следа, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения.Он изменяет только значение скорости , но не ее направление.
В круговом движении (крайний левый рисунок ниже), когда объект движется по окружности круга, присутствует только центростремительная составляющая. Объект будет поддерживать постоянную скорость; подумайте о Земле, которая имеет центростремительное ускорение из-за силы тяжести Солнца (на самом деле ее скорость немного меняется в течение года – см. калькулятор орбитальной скорости и калькулятор орбитального периода для получения дополнительной информации).
Когда присутствуют оба компонента, траектория объекта выглядит как на правом изображении. Что будет, если есть только тангенциальное ускорение? Затем происходит линейное движение. Это похоже на нажатие педали газа в автомобиле на прямом участке автострады. А если вы водитель, наш счетчик бензина может вас заинтересовать; оценивает стоимость проезда на автомобиле. Вы указываете экономию топлива, расстояние и цену на бензин, и вы быстро получаете стоимость поездки. Есть даже возможность разделить его на несколько человек, ведь вместе путешествовать весело и выгодно! Группа разговорчивых друзей в вашей машине будет: e.g., не дать вам заснуть.
Угловое ускорение
Угловое ускорение играет важную роль в описании вращательного движения. Однако не путайте это с ранее упомянутыми центростремительными или тангенциальными ускорениями. Эта физическая величина соответствует скорости изменения угловой скорости. Другими словами, он сообщает вам, насколько быстро ускоряется вращение объекта – объект вращается все быстрее и быстрее (или все медленнее и медленнее, если угловое ускорение меньше нуля).
Знаете ли вы, что мы можем найти аналогию между этим и законом динамики Ньютона во вращательном движении? Согласно его второму закону, если вы можете переключить ускорение на угловое ускорение, силу на крутящий момент и массу на момент инерции, вы получите уравнение углового ускорения. Вы могли заметить, что некоторые физические законы, подобные этому, универсальны, что делает их действительно важными для физики.
Ускорение свободного падения
Мы несколько раз упоминали ускорение свободного падения.Он возникает из-за гравитационной силы, которая существует между каждыми двумя объектами, имеющими массу (обратите внимание, что уравнение гравитации не зависит от объема объекта – здесь важна только масса). Сначала это может показаться странным, но согласно третьему закону движения Ньютона, вы действуете на Землю с той же силой, что и Земля на вас . Однако масса Земли намного больше, чем масса человека (в ~ 10 ² раз больше), поэтому наше воздействие на Землю практически равно нулю. Это аналогично всем бактериям (в ~ 10¹⁸ раз легче человека), живущим на вашей руке; вы их даже не заметите! С другой стороны, мы чувствуем влияние нашей планеты, и это ускорение силы тяжести.
Стандартная сила тяжести по определению составляет 31,17405 фут / с² (9,80665 м / с²), поэтому, если человек весит 220 фунтов (около 100 кг), на него действует сила тяжести около 7000 фунтов на квадратный дюйм (1000 Н). Давайте введем это значение в окно №3 нашего калькулятора вместе с массой Земли (1,317 × 10²⁵ фунта или 5,972 × 10²⁴ кг в экспоненциальном представлении). Что такое расчетное ускорение? Это настолько мало , что наш калькулятор считает, что это ноль . Мы ничего не значим по сравнению с планетой!
Ускоритель частиц
Поговорив об огромных объектах в космосе, перейдем к микроскопическому миру частиц.Хотя мы не можем видеть их глазами, мы использовали частицы высоких энергий, такие как электроны и протоны, и регулярно используем их в ускорителях частиц; распространены в физике, химии и медицине. Мы используем их для уничтожения раковых клеток, сохраняя при этом окружающую здоровую ткань, или исследуем структуру материала в атомном масштабе. В последнее время рак – одна из болезней достатка, которая, вероятно, является следствием роста благосостояния в обществе. Даже неправильное питание может увеличить риск рака! С помощью этого ежедневного калькулятора протеина вы можете проверить, сколько протеина вам нужно в день, а если вы также хотите улучшить свою физическую форму, наш макро калькулятор здесь, чтобы помочь вам.
Мы используем их для уничтожения раковых клеток, сохраняя при этом окружающую здоровую ткань, или исследуем структуру материала в атомном масштабе. В последнее время рак – одна из болезней достатка, которая, вероятно, является следствием роста благосостояния в обществе. Даже неправильное питание может увеличить риск рака! С помощью этого ежедневного калькулятора протеина вы можете проверить, сколько протеина вам нужно в день, а если вы также хотите улучшить свою физическую форму, наш макро калькулятор здесь, чтобы помочь вам.
Вы, наверное, знаете о Большом адронном коллайдере (ЦЕРН), самом мощном ускорителе элементарных частиц в мире. Это позволяет нам сделать шаг вперед, чтобы понять, как устроена Вселенная, и разработать технологии, которые могут найти множество важных приложений в будущем. Однако, чтобы достичь таких высоких энергий, мы должны разогнать частицы до скоростей, близких к скорости света. Вкратце, мы можем сделать это с помощью магнитных или электрических полей. Чтобы увидеть, насколько быстро частицы ускоряются по сравнению со стандартной силой тяжести, посмотрите наше ускорение в калькуляторе электрического поля, где мы объяснили, как рассчитать ускорение заряженных частиц.
Мир микроскопических частиц управляется статистической физикой, которая уделяет особое внимание концепции вероятности. У нас есть много калькуляторов, связанных с этой темой. Взгляните на калькулятор вероятности, чтобы узнать, как найти вероятность, или попробуйте калькулятор перестановок, чтобы определить количество способов, которыми вы можете упорядочить определенное количество элементов. Физики используют перестановку для предсказания теоретических свойств материала, которые затем можно наблюдать в повседневной жизни. Например, вы можете узнать, какова средняя скорость частиц газа.
FAQ
Ускорение – это вектор?
Да , ускорение является вектором, так как имеет как величину, так и направление . Величина – это скорость ускорения объекта, а направление – это ускорение в том направлении, в котором движется объект, или против него. Это соответственно ускорение и замедление.
Величина – это скорость ускорения объекта, а направление – это ускорение в том направлении, в котором движется объект, или против него. Это соответственно ускорение и замедление.
Как масса влияет на ускорение?
Если сила, с которой объект толкает, остается прежней, ускорение будет уменьшаться по мере увеличения массы .Это потому, что F / m = a, поэтому с увеличением массы фракция становится все меньше и меньше.
Может ли ускорение быть отрицательным?
Да , ускорение может быть отрицательным, , которое известно как замедление . Два объекта с равным, но противоположным ускорением будут ускоряться на одинаковую величину, только в двух противоположных направлениях.
Как определить среднее ускорение?
- Рассчитайте изменение скорости для заданного времени.
- Вычислите изменение времени за рассматриваемый период.
- Разделите изменение скорости на изменение во времени.
- Результат – среднее ускорение за этот период.
Как узнать величину ускорения?
- Преобразуйте величину силы в Ньютоны.
- Измените массу объекта на килограммы.
- Умножьте оба значения на вместе, чтобы найти ускорение в м / с 2 .
В чем разница между ускорением и скоростью?
Скорость – это скорость, с которой объект движется в определенном направлении, а ускорение – это то, как скорость этого объекта на изменяется со временем. Оба имеют величину и направление, но их единицы – м / с и 2 м / с соответственно.
Как найти угловое ускорение?
- Используйте уравнения углового ускорения:
a = Δv / Δt. - Найдите начальную и конечную угловую скорость в радианах / с.
- Вычтите начальную угловую скорость из конечной угловой скорости, чтобы получить изменение угловой скорости .

- Найдите начальное и конечное время для рассматриваемого периода.
- Вычтите начальное время из последнего, чтобы получить изменение времени .
- Разделите изменение угловой скорости на изменение во времени, чтобы получить угловое ускорение в радианах / с. 2 .
Сила и ускорение при круговом движении
Введение
Ускорение – это скорость изменения скорости во времени. Поскольку скорость является вектором, она может изменяться двумя способами: ее величина может изменяться и ее направление может изменяться. Любое изменение вызывает ускорение. Для кругового движения с постоянной скоростью скорость всегда тангенциальна к круговой траектории, и поэтому ее направление постоянно меняется, даже если ее величина постоянна.Следовательно, у объекта есть ускорение. Можно показать, что величина ускорения a c для равномерного кругового движения со скоростью v по траектории радиуса R равна, а направление ускорения – внутрь к центру круговой траектории. . Это показано на рисунке 1. Второй закон Ньютона требует, чтобы на объект действовала результирующая сила, равная по величине мА c и в направлении a c .Круговое движение со скоростью v по траектории радиуса R имеет период (время на один оборот) T и частоту (оборотов / с)f = 1 / T.
Поскольку объект проходит расстояние 2 π R (длина окружности его кругового пути) за время T , скорость v равна иa c = 4 π 2 f 2 р.
Схема эксперимента показана на рис. 2. Когда пластиковая трубка перемещается по небольшому кругу над вашей головой, ракетка перемещается по горизонтальному кругу на конце струны, которая проходит через трубку и имеет подвес для массы с на его нижнем конце подвешены щелевые массы. Применение
ПрименениеΣF = ma
к стационарной подвеске масс даетF струна = Mg,
, где F струна – натяжение струны, а M – это сумма масс подвески масс и на нем размещаются щелевые массы. Из-за направленной вниз силы тяжести на мяч, когда мяч движется по горизонтальному кругу, струна находится под углом θ ниже горизонтали, как показано на рисунке 3. На рисунке L – длина струна, измеренная от центра трубки до центра шара.Радиус R круговой траектории шара равенR = L cos θ .
Силы, действующие на мяч, – это сила тяжести и натяжение струны. Натяжение струны направлено вдоль струны, а сила тяжести направлена прямо вниз. Схема свободного тела движущегося шара приведена на рисунке 4. Поскольку мяч движется по горизонтальной окружности, его ускорение является горизонтальным. Поэтому удобно использовать горизонтальные и вертикальные координаты, и на диаграмме сил F струна была разделена на ее горизонтальную и вертикальную составляющие.ΣF x = ma x
даетF строка cos θ = ma c = m4 π 2 f 2 R.
R = L cos θ
поэтомуF строка = m4 π 2 f 2 L.
А, посколькуF строка = Mg,
, тогдаMg = m4 π 2 f 2 L.
Перестановка дает следующее уравнение. f 2 =Цель
В этом эксперименте мы проверим выражение для ускорения объекта, движущегося равномерно по кругу.Аппарат
- Ракетбол с прикрепленной веревкой и зажимом из кожи аллигатора
- Пластиковая трубка
- Набор масс с прорезями и подвеска
- Остаток средств
- Секундомер
- Метрическая палочка
Обсуждение
Как обсуждалось во введении к этому эксперименту, применение второго закона Ньютона в экспериментальной установке дает следующее.
(1)
f 2 =ΣF = ma.
Мы сделаем это, построив график f 2 и проверив, хорошо ли представлены наши данные прямой линией с нулевыми интерцепциями y . Мы также будем использовать наклон линии и измерение массы м вращающегося объекта, чтобы вычислить г и посмотреть, насколько хорошо полученное таким образом значение согласуется с фактическим значением г .Процедура
Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.1
Для практики поместите гирю в 100 грамм с прорезью на подвеску для массы на нижнем конце струны и покрутите ракетку над головой, удерживая струну под трубкой. Практикуйтесь, вращая мяч над головой, сохраняя при этом полностью горизонтальную траекторию движения мяча, пока вы не сможете отпустить струну под трубкой и поддерживать такое же движение, пока масса не поднимается и не опускается. Это упражнение должен выполнять каждый партнер по лаборатории.2
Протяните струну через трубку так, чтобы длина L составляла 50.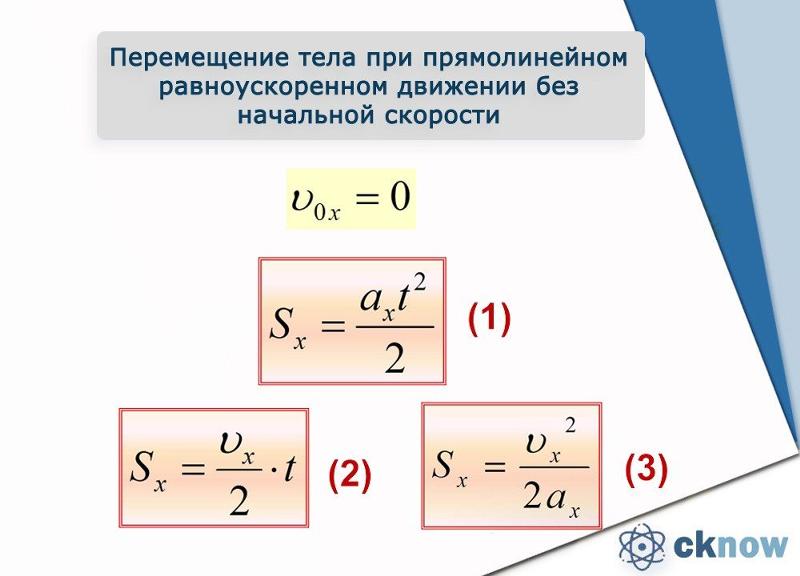 0 см. Напомним, что L – это расстояние от центра верхней части трубки до центра шара. Прикрепите зажим из крокодила к веревке примерно на 1 см ниже пластиковой трубки, чтобы он служил маркером, чтобы вы могли поддерживать постоянство L при вращении мяча. Вращая мяч по горизонтальному кругу, убедитесь, что веревка или зажим из крокодиловой кожи не соприкасаются с вашей рукой или рукой. Перед измерением времени убедитесь, что мяч вращается по горизонтальной окружности .Затем попросите вашего партнера по лаборатории измерить время t 20 (1) , которое требуется, чтобы мяч совершил 20 оборотов. Поменяйте местами завихритель и таймер и повторите измерение, чтобы получить время t 20 (2) . Повторяйте измерения, пока не получите пару раз, которые отличаются менее чем на 2,0 секунды.
0 см. Напомним, что L – это расстояние от центра верхней части трубки до центра шара. Прикрепите зажим из крокодила к веревке примерно на 1 см ниже пластиковой трубки, чтобы он служил маркером, чтобы вы могли поддерживать постоянство L при вращении мяча. Вращая мяч по горизонтальному кругу, убедитесь, что веревка или зажим из крокодиловой кожи не соприкасаются с вашей рукой или рукой. Перед измерением времени убедитесь, что мяч вращается по горизонтальной окружности .Затем попросите вашего партнера по лаборатории измерить время t 20 (1) , которое требуется, чтобы мяч совершил 20 оборотов. Поменяйте местами завихритель и таймер и повторите измерение, чтобы получить время t 20 (2) . Повторяйте измерения, пока не получите пару раз, которые отличаются менее чем на 2,0 секунды.3
Введите свои значения t 20 (1) и t 20 (2) в столбец дляM = 150 граммов
в таблице 1.Обратите внимание на это и позвольте заполнить оставшуюся часть столбца. Повторите процедуру для других наборов значений M и L . Помните, что M – это общая масса подвешенного к струне, масса подвески плюс масса продольных масс, размещенных на подвеске.4
Откройте Excel и постройте график f 2 (для f в об / с) в зависимости от кг / м. Используйте Excel, чтобы найти уравнение прямой линии, которое лучше всего соответствует вашим данным.Все ваши точки данных должны находиться близко к этой линии, а пересечение линии и должно быть близко к нулю. Если один или оба из них не соответствуют действительности, вы допустили ошибку при сборе, записи или графическом отображении ваших данных. Если вы и ваш партнер по лаборатории не можете найти, что не так, обратитесь за помощью к своему техническому специалисту.5
Запишите наклон линии, который лучше всего соответствует вашим данным.
6
Используйте весы, чтобы измерить массу мяча. Запишите свои результаты.7
Используйте уравнение.(1) f 2 =8
Если фактическое значение г принято равным 9,80 м / с 2 , какова разница в процентах между вашим экспериментальным результатом и фактическим значением г ? В расчетах оставьте достаточно значащих цифр, чтобы избежать ошибки округления.Авторские права © 2012-2013 Advanced Instructional Systems, Inc.и Техасский университет A&M. Части из Университета штата Северная Каролина. | Кредиты
Разгон
Разгон Разгон :Ускорение – это скорость изменения скорости. Поскольку скорость имеет как величину, так и направление, она называется векторная величина; ускорение также является векторной величиной и должно учитывать изменения как в величине, так и в направлении скорость. Скорость точки или объекта, движущегося по прямой. путь может изменяться только по величине; на изогнутом пути, это может или может не меняется по величине, но всегда будет меняться по направлению.Этот условие означает, что ускорение точки, движущейся по криволинейной путь никогда не может быть нулевым.
Если скорость точки, движущейся по прямому пути, увеличивается (т.е. если скорость, которая является величиной скорости, равна возрастает), вектор ускорения будет иметь то же направление, что и вектор скорости. Если скорость уменьшается (то есть точка или объект замедляется), вектор ускорения будет указывать в обратном направлении. Среднее ускорение за время интервал равен полному изменению скорости за время интервал, деленный на временной интервал.Ускорение при любом момент равен пределу отношения изменения скорости к длина временного интервала, по мере приближения временного интервала нуль.
Когда точка движется по изогнутой траектории, компонент
ускорение, возникающее в результате изменения направления движения
Вектор скорости перпендикулярен вектору скорости и равен
направлен внутрь, на вогнутую сторону дорожки; его величина
дается квадратом скорости, деленной на радиус
кривизна r пути: v 2 / r. Изменение величины
of v может быть представлен другим вектором (то есть вторым
компонент ускорения) коллинеарны v и в том же
направление, если v увеличивается, и противоположное направление, если v равно
уменьшается. Если скорость указана в метрах в секунду, ускорение
будут указаны в метрах в секунду в секунду.
Изменение величины
of v может быть представлен другим вектором (то есть вторым
компонент ускорения) коллинеарны v и в том же
направление, если v увеличивается, и противоположное направление, если v равно
уменьшается. Если скорость указана в метрах в секунду, ускорение
будут указаны в метрах в секунду в секунду.
Выдержка из Британской энциклопедии без разрешения.
Выдержка из Британской энциклопедии без разрешения.
Равномерное круговое движение
Центростремительное ускорение
Движение объекта по круговой траектории с постоянной скоростью известно как равномерное круговое движение (UCM).Объект в UCM постоянно меняет направление, и поскольку скорость является вектором и имеет направление, можно сказать, что объект, подвергающийся UCM, имеет постоянно меняющуюся скорость, даже если его скорость остается постоянной. И если скорость объекта меняется, он должен ускоряться. Следовательно, объект, подвергающийся UCM, постоянно ускоряется. Этот тип ускорения известен как центростремительное ускорение .
Вопрос : Если автомобиль ускоряется, увеличивается ли его скорость?
Ответ : Это зависит от обстоятельств.Его скорость может увеличиваться, или он может ускоряться в направлении, противоположном его скорости (замедление). Или его скорость может оставаться постоянной, но при этом ускоряться, если он движется равномерно по кругу.
Не менее важно, что нам нужно выяснить направление ускорения объекта, поскольку ускорение – это вектор. Для этого нарисуем объект, движущийся против часовой стрелки по круговой траектории, и покажем его вектор скорости в двух разных точках времени.Поскольку мы знаем, что ускорение – это скорость изменения скорости объекта во времени, мы можем определить направление ускорения объекта, найдя направление его изменения скорости Δv.
Чтобы найти его изменение скорости Δv, мы должны это вспомнить.
Следовательно, нам необходимо графически найти разность векторов v f и v i , которую можно переписать как.
Напомним, что для графического сложения векторов мы выстраиваем их кончик к хвосту, а затем рисуем результирующий вектор от начальной точки (хвоста) нашего первого вектора до конечной точки (кончика) нашего последнего вектора.
Итак, вектор ускорения должен указывать в указанном выше направлении. Если я снова покажу этот вектор на нашем исходном круге, выстроив его прямо между нашим начальным и конечным векторами скорости, легко увидеть, что вектор ускорения указывает на центр круга.
Вы можете повторить эту процедуру из любой точки окружности … куда бы вы ни пошли, вектор ускорения всегда направлен к центру окружности. Фактически, слово центростремительный в словосочетании «центростремительное ускорение» означает «центростремительный»!
Итак, теперь мы знаем направление ускорения объекта (к центру круга), но как насчет его величины? Величина центростремительного ускорения объекта может быть найдена в справочной таблице и определяется по формуле:
Круговая скорость
Так как же определить скорость объекта, движущегося по круговой траектории? Формула скорости, которую мы изучили в кинематике, все еще применима.
Однако мы должны быть осторожны при использовании этого уравнения, чтобы понять, что объект, движущийся по круговой траектории, движется по окружности круга. Следовательно, если объект совершит один полный оборот по окружности, расстояние, которое он преодолеет, будет равно длине окружности круга.
Давайте посмотрим на пример задачи:
Вопрос : Миранда едет на своей машине по часовой стрелке по круговой колее радиусом 30 метров.
Она делает 10 кругов по трассе за 2 минуты. Найдите общее пройденное расстояние, среднюю скорость и центростремительное ускорение Миранды.
Ответ :
Центростремительная сила
Если объект, движущийся по круговой траектории, имеет внутреннее ускорение, второй закон Ньютона говорит нам, что чистая сила также должна быть направлена к центру круга.Этот тип силы, известный как центростремительная сила, может быть гравитационной силой, натяжением, приложенной силой или даже силой трения.
ПРИМЕЧАНИЕ: Имея дело с проблемами кругового движения, важно понимать, что центростремительная сила на самом деле не новая сила, центростремительная сила – это просто ярлык или группировка, которые мы применяем к силе, чтобы указать ее направление к центру круг. Это означает, что вы никогда не захотите обозначать силу на диаграмме свободного тела как центростремительную силу, F c .Вместо этого обозначьте силу, направленную к центру, как можно точнее. Если усилие вызывает натяжение, обозначьте его F T . Если сила трения вызывает силу, направленную к центру, обозначьте ее F f и так далее.
Мы можем объединить уравнение центростремительного ускорения со 2-м законом Ньютона, чтобы получить 2-й закон Ньютона для кругового движения. Напомним, что 2-й закон Ньютона гласит:
Для объекта, движущегося по круговой траектории, должна существовать чистая (центростремительная) сила, направленная к центру круговой траектории, чтобы вызвать (центростремительное) ускорение, направленное к центру круговой траектории. В таком случае мы можем пересмотреть 2-й закон Ньютона для этого конкретного случая следующим образом:
В таком случае мы можем пересмотреть 2-й закон Ньютона для этого конкретного случая следующим образом:
Затем, вспомнив нашу формулу центростремительного ускорения как:
Мы можем сложить их вместе, заменив c в нашем уравнении, чтобы получить комбинированную форму 2-го закона Ньютона для равномерного кругового движения:
Конечно, если объект движется по круговой траектории и центростремительная сила устранена, объект продолжит движение по прямой в любом направлении, в котором он двигался в момент снятия силы.
Вопрос : Бегущий назад 800N поворачивает угол по круговой траектории r = 1 м со скоростью 8 м / с. Найдите массу бегущего спина, центростремительное ускорение и центростремительную силу.
Ответ : Дано mg = 800N, r = 1m, v = 8m / s; Найдите m, ac, Fc
Попробуем еще:
Еще одна примерная задача, на этот раз включающая только алгебраические манипуляции:
Частота и период
Для объектов, движущихся по круговой траектории, мы можем охарактеризовать их движение по кругу, используя термины частота (f) и период (T).Частота объекта – это количество оборотов, которые объект совершает за полную секунду. Он измеряется в единицах [1 / с] или Герцах (Гц). Точно так же период объекта – это время, необходимое для совершения одного полного оборота. Поскольку период – это временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:
Вопрос : Игрушечный поезд весом 500 г проходит 10 кругов по круговой колее за 1 мин 40 сек.Если диаметр пути составляет 1 м, найдите центростремительное ускорение поезда (a c ), центростремительную силу (F c ), период (T) и частоту (f).
Ответ :
Давайте посмотрим на другой пример:
Вертикальное круговое движение
Объекты движутся по кругу как по вертикали, так и по горизонтали.Поскольку скорость этих объектов обычно не является постоянной, технически это не равномерное круговое движение , но наши навыки анализа UCM по-прежнему применимы.
Представьте американские горки, движущиеся по вертикальной петле радиусом 10 м. Вы путешествуете по петле вверх ногами, но не падаете с американских горок. Как это возможно? Мы можем использовать наше понимание UCM и динамики, чтобы выяснить это!
Нижняя граница круга
Для начала давайте сначала посмотрим на каботажное судно, когда машина находится в нижней части петли.Нарисуя диаграмму свободного тела, сила тяжести на подставке, также известная как его вес, тянет его вниз, поэтому мы рисуем направленный вниз вектор с надписью «mg». Этой силе противодействует нормальная сила, с которой рельсы каботажного судна толкают вверх, которую мы обозначили как F N .
Поскольку каботажное судно движется по круговой траектории, мы можем проанализировать его с помощью инструментов, которые мы разработали для равномерного кругового движения. 2-й закон Ньютона все еще применяется, поэтому мы можем написать:
Обратите внимание: поскольку мы говорим о круговом движении, мы примем соглашение, согласно которому силы, направленные к центру круга, положительны, а силы, направленные от центра круга, отрицательны.На этом этапе вспомните, что сила, которую вы «чувствуете», когда вы находитесь в движении, на самом деле является нормальной силой. Итак, вычисляя нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что
Поскольку мы знаем, что чистая сила всегда равна массе, умноженной на ускорение, поэтому чистая центростремительная сила равна массе, умноженной на центростремительное ускорение, мы можем заменить F NET c следующим образом:
Из полученного уравнения видно, что нормальная сила теперь равна весу плюс дополнительный член центростремительной силы кругового движения. Когда мы движемся по круговой траектории в нижней части петли, мы чувствуем себя тяжелее своего веса. В общем, мы чувствуем дополнительные «перегрузки». Сколько g, по нашему мнению, можно получить, приложив немного больше усилий. Если мы перепишем наше уравнение для нормальной силы, вытягивая массу, применяя распределительное свойство умножения, мы получим:
Когда мы движемся по круговой траектории в нижней части петли, мы чувствуем себя тяжелее своего веса. В общем, мы чувствуем дополнительные «перегрузки». Сколько g, по нашему мнению, можно получить, приложив немного больше усилий. Если мы перепишем наше уравнение для нормальной силы, вытягивая массу, применяя распределительное свойство умножения, мы получим:
Обратите внимание, что внутри скобок у нас есть стандартное ускорение свободного падения, g, плюс член центростремительного ускорения ().
Этот дополнительный термин – дополнительная перегрузочная сила, которую ощущает человек. Например, если c равно g (9,81 м / с 2 ), можно сказать, что человек в тележке испытывает две g (1 g от центростремительного ускорения и 1 g от гравитационного поля Земли). Если бы c было равно 3 * g (29,4 м / с 2 ), человек испытал бы в общей сложности четыре g.
Расширяя этот анализ до аналогичной ситуации в другом контексте, попробуйте представить вместо американских горок массу, вращающуюся по вертикальному кругу на веревке.В нашем анализе вы можете заменить нормальную силу натяжением струны. Поскольку сила больше в нижней части круга, вероятность разрыва струны наиболее высока, когда масса находится в нижней части круга!
Вершина круга
В верхней части цикла мы видим существенно другую картину. Теперь нормальная сила от рельсов подстаканника должна давить вниз на тележку, хотя все еще в положительном направлении, так как теперь вниз направлено к центру круговой траектории.В этом случае, однако, вес объекта также указывает на центр круга, поскольку гравитационное поле Земли всегда тянется к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко 2-му закону Ньютона для кругового движения также значительно отличается.
Поскольку сила, которую вы чувствуете, на самом деле является нормальной силой, мы можем найти нормальную силу и расширить чистую центростремительную силу, как показано:
Из уравнения видно, что нормальная сила теперь равна центростремительной силе за вычетом вашего веса. Если бы центростремительная сила была равна вашему весу, вы бы почувствовали себя невесомым. Обратите внимание, что это также точка, в которой нормальная сила в точности равна 0. Это означает, что рельсы гусеницы больше не давят на тележку американских горок … если бы центростремительная сила была хоть чуть-чуть меньше (скорость автомобиля было немного меньше), нормальная сила FN будет меньше 0. Поскольку рельсы не могут физически тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает с рельса. и у пассажира телеги вот-вот будет очень, очень плохой день.Только поддерживая высокую скорость, тележка может успешно преодолеть петлю … идти слишком медленно, и тележка падает.
Если бы центростремительная сила была равна вашему весу, вы бы почувствовали себя невесомым. Обратите внимание, что это также точка, в которой нормальная сила в точности равна 0. Это означает, что рельсы гусеницы больше не давят на тележку американских горок … если бы центростремительная сила была хоть чуть-чуть меньше (скорость автомобиля было немного меньше), нормальная сила FN будет меньше 0. Поскольку рельсы не могут физически тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает с рельса. и у пассажира телеги вот-вот будет очень, очень плохой день.Только поддерживая высокую скорость, тележка может успешно преодолеть петлю … идти слишком медленно, и тележка падает.
В целях безопасности настоящие американские горки на самом деле имеют колеса по обеим сторонам рельсов, чтобы тележка не упала, если она когда-либо замедлялась на вершине петли, хотя горки спроектированы так, что на самом деле такая ситуация никогда не возникает.
Планирование оптимальной траектории с ограничением скорости и ускорения в динамическом моделировании толпы
Создание сложных и реалистичных моделей поведения толпы, таких как пешеходная навигация с динамическими препятствиями, является сложной и трудоемкой задачей.В этой статье мы изучаем один особый тип толпы, который состоит из неотложных людей, нормальных людей и нормальных групп. Мы используем три шага для построения симуляции толпы в динамической среде. Во-первых, срочные индивиды движутся вперед по заданному пути, обходя динамические препятствия и других членов толпы. Оптимальный метод планирования траектории с ограничением скорости и ускорения используется для моделирования их поведения, который гарантирует, что длительность сгенерированных траекторий минимальна, а срочные лица не столкнутся с динамическими препятствиями (например,г. , динамические автомобили). На втором этапе принимается выталкивающая модель для моделирования взаимодействий между неотложными и нормальными элементами, что гарантирует приемлемость вычислительных затрат на планирование оптимальной траектории. Третий шаг обязан имитировать взаимодействия между обычными членами, используя поведение избегания столкновений и поведение стая. Различные результаты моделирования демонстрируют, что эти три шага дают реалистичное явление толпы, как и в реальном мире.
, динамические автомобили). На втором этапе принимается выталкивающая модель для моделирования взаимодействий между неотложными и нормальными элементами, что гарантирует приемлемость вычислительных затрат на планирование оптимальной траектории. Третий шаг обязан имитировать взаимодействия между обычными членами, используя поведение избегания столкновений и поведение стая. Различные результаты моделирования демонстрируют, что эти три шага дают реалистичное явление толпы, как и в реальном мире.
1.Введение
Толпы, вездесущие в реальном мире, от групп людей до стай насекомых, являются жизненно важными функциями для моделирования в виртуальной среде. Моделирование пешеходов – сложная задача, которая начинает привлекать внимание исследователей и практиков в области моделирования эвакуации и городского планирования. Область компьютерной графики, в которой виртуальная человеческая анимация была важным исследовательским интересом на протяжении десятилетий, внесла вклад в технологии, фундаментальные для компьютерной визуализации, включая автоматическую анимацию пешеходов [1–3].До сих пор были разработаны различные имитационные модели и архитектуры. Реалистичность поведения толпы во многом зависит от методов, используемых при построении моделей толпы. В этой статье основное внимание уделяется одному особому феномену толпы, который имеет большое значение в реальном мире. Толпа, состоящая из срочных членов и нормальных, имеет следующие характеристики: срочные члены – это люди, которые движутся вперед по фиксированному, заданному пути, чтобы сделать что-то срочное. Нормальные – это люди, которые двигаются нормально, как и большинство людей в своей повседневной жизни.В реальном мире срочные люди не позволяют другим встать у них на пути. Следовательно, если нормальные члены находятся в заранее определенном диапазоне срочных, последний оттолкнет их. Тем не менее, мы должны гарантировать, что срочные члены не столкнутся с динамическими препятствиями в окружающей среде.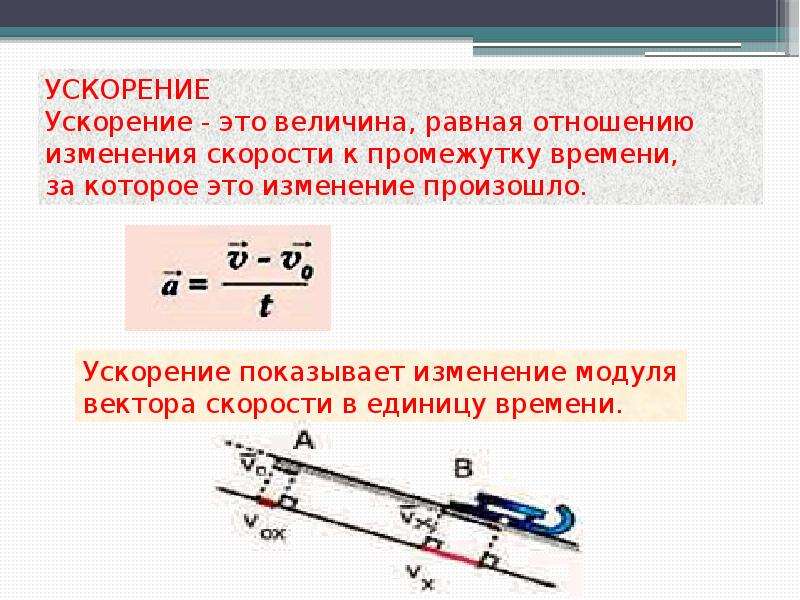 Более того, взаимодействие между обычными членами является важным фактором для повышения достоверности поведения толпы. Для этой особой толпы все это требует изучения ее поведения.
Более того, взаимодействие между обычными членами является важным фактором для повышения достоверности поведения толпы. Для этой особой толпы все это требует изучения ее поведения.
Принимая во внимание наблюдения в реальном мире, как возможно, что срочные люди могут безопасно перемещаться через толпы и динамические препятствия по заранее определенному пути? Ключевой вывод заключается в том, что срочные люди обычно участвуют в движении вперед, просто учитывая динамическое препятствие: они отталкивают нормальных членов от своих траекторий, чтобы освободить место для их навигации.
В своей работе мы разрабатывали автономную самоанимирующуюся модель пешеходной толпы, способную выполнять широкий спектр естественных действий в динамичной городской среде.Поскольку ускорение и скорость реального человека ограничены, мы приняли оптимальный метод планирования траектории с ограничением ускорения в области планирования и комплексный подход с искусственной жизнью (например, метод предотвращения столкновений и метод стайкинга) для решения проблемы поведения пешеходов. . Наш подход в большей степени вдохновлен работой Джонсона и Хаузера [4] по оптимальному планированию траектории и Фудила и Нуреддина [5] по моделированию предотвращения столкновений в моделировании толпы с правилами приоритета.Также для справки используется работа Олфати-Сабера по модели флокирования [6].
Таким образом, наш основной вклад состоит в трех аспектах: (1) Построение поведения неотложных элементов с помощью оптимального метода планирования траектории с ограничением скорости и ускорения. Этот новый метод гарантирует, что срочные участники дойдут до места назначения как можно скорее и не столкнутся с динамическими препятствиями. (2) Имитация взаимодействия между срочными и нормальными участниками. Принята новая модель толкания, чтобы гарантировать, что нормальные члены не будут мешать срочным.Таким образом, нормальные элементы не будут рассматриваться как динамические препятствия, что способствует тому, что вычислительные затраты на планирование траектории приемлемы для приложений в реальном времени. (3) Имитируйте взаимодействия между нормальными элементами. Эти взаимодействия играют важную роль в синтезе анимации толпы. Ключевой вывод заключается в том, что обычные члены обычно участвуют в совместном предотвращении столкновений: они адаптируют свои движения друг к другу, чтобы освободить место для навигации. Таким образом, используются поведение предотвращения столкновений и поведение скопления.
(3) Имитируйте взаимодействия между нормальными элементами. Эти взаимодействия играют важную роль в синтезе анимации толпы. Ключевой вывод заключается в том, что обычные члены обычно участвуют в совместном предотвращении столкновений: они адаптируют свои движения друг к другу, чтобы освободить место для навигации. Таким образом, используются поведение предотвращения столкновений и поведение скопления.
Вышеупомянутые три аспекта объединены вместе, чтобы создать реалистичное поведение для нашей особой толпы. Компоненты толпы представлены на рисунке 1.
Как показано на рисунке 1, поведение толпы состоит из четырех частей: оптимального планирования траектории, модели толкания, поведения предотвращения столкновений и поведения скопления, каждая из которых отвечает за имея дело с различными взаимодействиями. Путем разработки и комбинирования соответствующих поведений этих четырех частей достигаются реалистичные и сложные поведенческие явления.
Остальная часть этого документа организована следующим образом. Вначале в разделе 2 описываются предыстория и связанные с этим работы по планированию траектории, модели предотвращения столкновений и поведению стай. В разделе 3 мы подробно описываем процесс планирования оптимальной траектории с ограничением скорости и ускорения и модели толкания. В разделе 4 кратко представлены модель предотвращения столкновений и поведение стай для моделирования толпы. Результаты моделирования и выводы после проведения экспериментов с трехмерными виртуальными средами приведены в конце статьи.
2. Связанные работы
В этой статье поведение срочных элементов представляет собой проблему планирования траектории, которая имеет большое отличие от планирования пути. Что касается задачи планирования оптимальной траектории с динамическими ограничениями в динамических средах, Фрайхард сначала обратился к планированию оптимальной траектории в динамических средах, то есть к планированию движения для робота, подверженного динамическим ограничениям и перемещающегося в рабочем пространстве с движущимися препятствиями [7]. Была введена новая концепция пространства состояний и времени, и была получена траектория, близкая к оптимальной по быстродействию, путем поиска набора канонических траекторий.Пространство состояния-времени для планирования в динамической среде – это декартово произведение пространства и времени конфигурации, то есть. Фрейхард определил канонические траектории как траектории, которые имеют кусочно-постоянное ускорение и изменяют свое значение в дискретные моменты времени [7]. Фиорини и Шиллер также представили двухэтапный подход к планированию локальной оптимальной по времени траектории для руки манипулятора в динамических средах [8]. Планирование на основе оптимизации было использовано Park et al. для решения задачи планирования в произвольных динамических средах [9].Однако в их работе динамические ограничения не учитывались [9]. Фиорини и Шиллер представили глобальное оптимальное планирование движения марсохода с учетом проходимости и динамической устойчивости [10]. Недавно Maček et al. приняла быстрое исследование случайных деревьев и B-сплайнов для разработки метода планирования траектории без столкновений в динамических городских сценариях. Этот метод может выполняться автоматически с естественными фазами ускорения / замедления в соответствии с динамическими препятствиями на заданном пути.Преимущество этого метода заключается в том, что скорость движения транспортного средства может быть найдена за минимальное время. Maček et al. использовали методы кинодинамического планирования для исследования пространства действия транспортного средства [11]. Хотя эти вышеупомянутые алгоритмы могут находить пути, а также профили скорости, они имеют недостаток, заключающийся в игнорировании ограничения ускорения или получении траекторий, близких к оптимальным.
Была введена новая концепция пространства состояний и времени, и была получена траектория, близкая к оптимальной по быстродействию, путем поиска набора канонических траекторий.Пространство состояния-времени для планирования в динамической среде – это декартово произведение пространства и времени конфигурации, то есть. Фрейхард определил канонические траектории как траектории, которые имеют кусочно-постоянное ускорение и изменяют свое значение в дискретные моменты времени [7]. Фиорини и Шиллер также представили двухэтапный подход к планированию локальной оптимальной по времени траектории для руки манипулятора в динамических средах [8]. Планирование на основе оптимизации было использовано Park et al. для решения задачи планирования в произвольных динамических средах [9].Однако в их работе динамические ограничения не учитывались [9]. Фиорини и Шиллер представили глобальное оптимальное планирование движения марсохода с учетом проходимости и динамической устойчивости [10]. Недавно Maček et al. приняла быстрое исследование случайных деревьев и B-сплайнов для разработки метода планирования траектории без столкновений в динамических городских сценариях. Этот метод может выполняться автоматически с естественными фазами ускорения / замедления в соответствии с динамическими препятствиями на заданном пути.Преимущество этого метода заключается в том, что скорость движения транспортного средства может быть найдена за минимальное время. Maček et al. использовали методы кинодинамического планирования для исследования пространства действия транспортного средства [11]. Хотя эти вышеупомянутые алгоритмы могут находить пути, а также профили скорости, они имеют недостаток, заключающийся в игнорировании ограничения ускорения или получении траекторий, близких к оптимальным.
Совсем недавно Джонсон и Хаузер представили оптимальный, точный, полиномиальный планировщик для оптимальных траекторий с ограниченным ускорением вдоль фиксированного заданного пути с динамическими препятствиями [4]. В своем методе планировщик использует технику распространения интервалов скоростей для вычисления достижимых наборов скоростей в вершинах препятствий в пространстве времени пути. В этом процессе ограничения ускорения и скорости рассматриваются в плоскости траектории-скорости. Такой подход дает нам большие возможности для выполнения этой статьи по созданию оптимальных траекторий срочных членов. Однако в этом методе целевая скорость представляет собой интервал, а не фиксированное значение. В реальной жизни это не так; например, скорость цели виртуального человека в позиции цели равна нулю.Таким образом, планирование оптимальной траектории в этой статье более сложное и труднопреодолимое.
В своем методе планировщик использует технику распространения интервалов скоростей для вычисления достижимых наборов скоростей в вершинах препятствий в пространстве времени пути. В этом процессе ограничения ускорения и скорости рассматриваются в плоскости траектории-скорости. Такой подход дает нам большие возможности для выполнения этой статьи по созданию оптимальных траекторий срочных членов. Однако в этом методе целевая скорость представляет собой интервал, а не фиксированное значение. В реальной жизни это не так; например, скорость цели виртуального человека в позиции цели равна нулю.Таким образом, планирование оптимальной траектории в этой статье более сложное и труднопреодолимое.
Что касается поведения по предотвращению столкновений для отдельных лиц и групп, были предложены методы моделирования толпы как единого объекта, а также методы, которые рассматривают каждого человека в толпе отдельно. Предотвращение столкновений – одна из важнейших проблем симуляции толпы. Без предотвращения столкновений симуляция толпы не выглядит реалистичной. В симуляции толпы статические и динамические объекты – это два типа препятствий, которые должны нас беспокоить.Неподвижные объекты можно рассматривать как статические препятствия, в то время как динамические объекты относятся к людям, животным и транспортным средствам в городской среде [12]. Однако разработать поведение для предотвращения столкновения для нескольких человек сложнее, чем для двух человек. Morini et al. представили алгоритм краткосрочного избегания [13]. Ориентируясь на применение в густонаселенной городской среде, Tecchia и Chrysanthou предложили простой и быстрый метод обнаружения столкновений.В их методе использовались два разных подхода для обнаружения и предотвращения столкновения движущихся объектов. Ферти предложил алгоритм предотвращения столкновений, который планировался от их текущего положения до цели на основе прогнозирования и изменения траекторий. Таким образом, в своем методе агенты могли предсказывать свой путь, используя информацию о местоположении и скорости препятствий [13]. Musse и Thalmann разработали поведение избегания столкновений с несколькими разрешениями для групповых взаимоотношений с несколькими разрешениями [14].Фудил и Нуреддин предложили новое поведение предотвращения столкновений для моделирования толпы с правилами приоритета. Этот метод также вдохновляет нас на создание различных стратегий предотвращения столкновений для нормальных членов [5].
Musse и Thalmann разработали поведение избегания столкновений с несколькими разрешениями для групповых взаимоотношений с несколькими разрешениями [14].Фудил и Нуреддин предложили новое поведение предотвращения столкновений для моделирования толпы с правилами приоритета. Этот метод также вдохновляет нас на создание различных стратегий предотвращения столкновений для нормальных членов [5].
Что касается поведения стай в группах, многие исследователи использовали алгоритм стай для моделирования стада, стада и больших скоплений людей. Флокирование – одна из первых техник, используемых для моделирования толпы животных или людей. Флокирование в основном состоит из трех правил: разделение – держаться подальше от соседей и препятствий, сплоченность – держаться к центру ближайших сущностей и выравнивание – держаться по средней скорости и направлению с соседями.В последние годы были предложены различные алгоритмы распределенного управления движением нескольких динамических агентов и многоагентных систем. Например, проблема стайки с одним виртуальным лидером рассматривалась Shi et al. [15]. Su et al. исследовал проблему управления группой автономных агентов для отслеживания нескольких виртуальных лидеров. Они доказали, что агенты с одним и тем же виртуальным лидером достигли одинаковой скорости, а центр и средняя скорость всей группы сходились к взвешенному центру и средней скорости всех лидеров [16].Олфати-Сабер предложил новаторскую работу по флокированию для многоагентных динамических систем. Он предложил три типа алгоритма флокирования. Первый – это базовый алгоритм флокирования, включающий только разделение, сцепление и выравнивание. Затем был добавлен один агент-лидер, чтобы получить второй алгоритм. Его третий алгоритм был обязан иметь дело с проблемой флокирования при наличии множества препятствий. Также предоставляется систематический метод анализа маневра разделения / воссоединения при флокировании [6].
Все вышеперечисленные методы можно рассматривать как источник света для наших исследований по созданию реалистичного поведения толпы в этой статье.
3. Планирование оптимальной траектории с ограничением скорости и ускорения
3.1. Предварительные сведения
Предположим, виртуальные люди упрощены в цилиндр с единым радиусом. Предполагается, что они перемещаются в рабочем пространстве. Конфигурация виртуального человека однозначно определяется тройкой, где обозначает конфигурационное пространство. Предположим, одному срочному человеку дан фиксированный параметризованный геометрический путь, который представляет собой непрерывную последовательность конфигураций, то есть прямую линию или кривую в конфигурационном пространстве.В этой статье мы предполагаем, что кривая должна быть кусочно-классной (кривая является классной, если она дифференцируема раз и ее -я производная непрерывна). Поскольку срочный индивидуум движется вперед, мы можем свести его конфигурацию к единственной переменной, которая удовлетворяет. – это функция масштабирования времени, которая присваивает значение каждому времени. представляет собой пройденное расстояние, которое представляет собой общую длину. Причем масштабирование по времени должно быть дважды дифференцируемым и монотонным (для всех).Двойная дифференцируемость гарантирует, что ускорение экстренного индивидуума четко определено и ограничено [17].
Проблема динамического планирования возникает в пространстве состояний путь-скорость-время, то есть в пространстве, которое обозначается как PVT [4]. Итак, состояние одного экстренного человека состоит из переменной, скорости и времени. Для данного имеет место следующее: Динамические ограничения срочных лиц должны удовлетворять ограничениям скорости и ускорения: Подставляя (2) в (1), мы получаем следующие динамические ограничения на переменную: с и.Траектория, определенная над в пространстве состояний, является динамически допустимой тогда и только тогда, когда (3) и (4) выполняются одновременно. Затем мы говорим, что целевое состояние динамически достижимо из начального состояния, если существует динамически допустимая траектория на интервале, такая, что и существует. Обратите внимание, что существует взаимно однозначное соответствие между траекторией и ее функцией масштабирования по времени.
Обратите внимание, что существует взаимно однозначное соответствие между траекторией и ее функцией масштабирования по времени.
Позвольте быть набор движущихся препятствий. Позвольте обозначить область, занятую в момент времени, и область, занимаемую в позиции по.Тогда область препятствий в пространстве состояний определяется как
Очевидно, соответствует точкам в пространстве. Траектория является бесстолкновительной, если для.
Прежде всего, мы можем формально сформулировать проблему, которую необходимо решить. Позвольте быть начальным состоянием и его целевым состоянием.
Траектория является решением проблемы тогда и только тогда, когда (1),, и, (2) динамически допустимы и свободны от столкновений для и. – максимальное время, указанное планировщику, (3) – конкретное значение (например,g.,), а не интервал скоростей.
Мы заинтересованы в нахождении точной траектории, оптимальной по быстродействию, то есть такой траектории, которая должна быть минимальной. Более того, в методе Джонсона это интервал, а не конкретное значение. Таким образом, планирование оптимальной траектории в этой статье более сложное и труднопреодолимое.
3.2. Оптимальное планирование траектории с ограничением скорости и ускорения
Метод, который мы разработали для решения вышеупомянутой проблемы, изначально мотивирован работой, описанной в [4].Мы улучшаем метод Джонсона, чтобы найти точную оптимальную по времени траекторию между начальным и конкретным целевым состоянием. Блок-схема нашего метода проиллюстрирована на рисунке 2.
Далее мы подробно опишем каждую часть рисунка 2.
3.2.1. Вычислить наборы достижимой скорости
(I) Вычислить наборы достижимой скорости из одного заданного начального состояния. Цель этого раздела – облегчить вычисление достижимых интервалов скорости из одного заданного начального состояния.Без ограничения общности, мы предполагаем, что указанное начальное состояние – это любое состояние, в котором может быть. Набор динамически достижимых скоростей в любой момент времени – это набор скоростей, достижимых в точке с помощью динамически возможных траекторий. Его можно вычислить в космосе. Чтобы упростить вычисления, мы предполагаем, что это прямая линия. Тогда (3) и (4) можно упростить до Джонсон показал, что это ограничено не более чем шестью кривыми [4], которые обозначены на рисунке 3 в нашей статье.
Набор динамически достижимых скоростей в любой момент времени – это набор скоростей, достижимых в точке с помощью динамически возможных траекторий. Его можно вычислить в космосе. Чтобы упростить вычисления, мы предполагаем, что это прямая линия. Тогда (3) и (4) можно упростить до Джонсон показал, что это ограничено не более чем шестью кривыми [4], которые обозначены на рисунке 3 в нашей статье.
На рисунке 3 параболический сегмент (a) соответствует процессу, в котором сначала происходит минимальное ускорение в течение времени, а затем происходит переключение на максимальное ускорение в течение времени. Следует отметить, что конечная скорость процесса торможения и скорость процесса ускорения должны удовлетворять формуле (6). Состояния на (а) можно сформулировать следующим образом: Точно так же параболический сегмент (d) соответствует процессу, принимает максимальное ускорение в течение времени, а затем переключается на минимальное ускорение в течение времени.Состояния на (d) можно сформулировать как Параболический сегмент (c) соответствует процессу, принимает максимальное ускорение до достижения момента времени, прогрессирует до тех пор, пока не истечет время, а затем замедляется на время. Состояния на (c) можно сформулировать как Точно так же параболический сегмент (f) соответствует процессу, принимает минимальное ускорение до достижения, прогрессирует до истечения времени, а затем ускоряется в течение времени. Состояния на (f) можно сформулировать как Отрезок линии (b) соответствует процессу, принимает минимальное ускорение в течение времени, а затем переключается на максимальное ускорение до достижения и, наконец, прогрессирует до тех пор, пока не истечет время.Состояния на (b) можно сформулировать как Точно так же отрезок линии (e) соответствует процессу, принимает максимальное ускорение в течение времени, а затем переключается на минимальное ускорение до достижения и, наконец, прогрессирует до тех пор, пока не истечет время. Состояния на (e) можно сформулировать как
Все эти шесть кривых охватывают набор достижимой скорости из одного начального состояния, которое графически показано как область тени на рисунке 3.
(II) Вычислить интервал достижимой скорости в точке в пространстве из . После получения набора достижимой скорости в пространстве, мы можем затем вычислить интервал достижимой скорости в точке в пространстве из начального состояния. Мы используем для представления достижимого интервала скоростей при. Мы используем для вычисления в следующей формулировке: где и представляют собой верхнюю и нижнюю границы интервала скоростей соответственно. определяется как пересечение граничной кривой с.
Нам нужно рассмотреть только три граничных решения в вычислениях (кривые (a), (b) и (f)) и (кривые (c), (d) и (e)), как показано на рисунке 4.
В этом процессе мы определяем время переключения, подставляя в (8), (11) и (12) для и (9), (10) и (13) для соответственно, и решая полученный квадратное уровненеие. В то же время ограничения в (8) ~ (13) проверяются, чтобы определить, существуют ли какие-то траектории от до.
(III) Алгоритм VIP, вычисляющий достижимый интервал скорости из начального интервала скорости. После вычисления достижимого интервала скоростей из начальной заданной скорости, мы можем расширить его, чтобы вычислить достижимый интервал скоростей из начального интервала скоростей, который составляет основу оптимального планировщика траектории.В качестве входных данных он принимает и целевую точку в пространстве. Он выводит диапазон достижимых скоростей цели. вычисляется в следующих шагах.
Шаг 1. Вычислить достижимый интервал скорости для начальной скорости из.
Шаг 2. Вычислить достижимый интервал скорости для начальной скорости из.
Шаг 3. Цель этого шага – максимизировать конечную скорость при. Это достигается путем построения параболической траектории с ускорением, которое интерполирует и.Если начальная скорость этой интерполирующей параболической траектории принадлежит, то.
Шаг 4. Целью этого шага является минимизация конечной скорости на. Это также достигается путем построения параболической траектории с ускорением, которое интерполирует и. Если начальная скорость этой интерполирующей параболической траектории принадлежит, то.
Это также достигается путем построения параболической траектории с ускорением, которое интерполирует и. Если начальная скорость этой интерполирующей параболической траектории принадлежит, то.
Шаг 5. Наконец, интервал выходной скорости. Обратите внимание, что либо,,, либо может быть пустым.
Поскольку целью метода в этом разделе является распространение интервалов скорости от одного интервала скорости к другому, пока мы знаем начальную и конечную точки в пространстве, мы называем этот метод распространением интервалов скорости (алгоритм VIP).Шаги 1 ~ 4 можно представить как краткие.
3.2.2. Вычисление оптимальной траектории
Предположим, что в окружающей среде есть динамические препятствия; тогда для нашего оптимального планирования важны только вершины, которые соответствуют левой верхней и правой нижней вершине препятствия [4]. Позвольте быть последовательность верхних левых и нижних правых вершин препятствия такая, что для всех. Затем сортируем эти вершины по возрастанию координаты и обозначаем и. Наш планировщик состоит из четырех этапов.
На первом этапе, используя алгоритм VIP, мы можем получить интервал скоростей от любой вершины одного динамического препятствия до любой вершины другого; то есть выполняем для всех.
На втором этапе мы получаем каналы и интервалы конечных скоростей этих каналов. Эти конечные интервалы скорости могут быть объединены в интервалы скоростей, соответствующие вершинам с помощью операции объединения.
На третьем этапе мы используем алгоритм VIP для соединения, принимая эти интервалы скорости в качестве входных данных для определения конечного интервала скорости в заданное конечное время.Мы используем дискретное значение для представления заданного конечного времени:
Затем мы можем получить интервал предельной скорости в каждое заданное конечное время, позвонив.
На четвертом этапе мы судим, находится ли скорость в этих предельных интервалах скорости или нет. Если true, мы возвращаем траекторию с минимальным конечным временем, которая является оптимальной траекторией и ее конечная скорость равна. В противном случае планировщик возвращает отказ. Это означает, что не существует траектории между начальным состоянием и целевым состоянием, которое удовлетворяет динамическим ограничениям и не имеет столкновений с динамическими препятствиями.
Если true, мы возвращаем траекторию с минимальным конечным временем, которая является оптимальной траекторией и ее конечная скорость равна. В противном случае планировщик возвращает отказ. Это означает, что не существует траектории между начальным состоянием и целевым состоянием, которое удовлетворяет динамическим ограничениям и не имеет столкновений с динамическими препятствиями.
Анализ сложности . Вычислительные затраты планировщика в основном связаны с первым и третьим этапами. На первом этапе мы должны вызвать алгоритм VIP несколько раз. На третьем этапе алгоритм VIP называется временем. Тогда сложность нашего планировщика эквивалентна. Эти вычислительные затраты огромны для больших значений. Однако в нашей среде есть только несколько динамических препятствий, и поэтому мы применяем толкающее поведение, чтобы иметь дело с взаимодействием между срочными и нормальными участниками.
3.3. Модель выталкивания
Модель выталкивания используется для моделирования взаимодействий между срочными и нормальными элементами; то есть нормальные члены будут оттеснены, когда они попадут в заранее определенный диапазон срочных. Мы используем четыре следующих правила для моделирования поведения толчка между любым нормальным индивидуумом и срочным: в котором обозначает расстояние между и. представляет собой порог расстояния взаимодействия. представляет скорость в направлении вектора.представляет скорость в перпендикулярном направлении вектора. указывает максимальную скорость, с которой движется нормальный человек. И представляет собой скорость до того, как произойдет взаимодействие между и.
Эта новая модель выталкивания гарантирует, что срочные элементы никогда не столкнутся с нормальными. Таким образом, нам не нужно учитывать нормальные элементы в процессе планирования оптимальной траектории, затраты времени на которые значительно уменьшатся благодаря учету только динамических препятствий.
4. Поведение по предотвращению столкновений и поведение флокирования
4.
 1. Поведение по предотвращению столкновений
1. Поведение по предотвращению столкновенийВ этом разделе мы представляем поведение по предотвращению столкновений на основе работы Фудила и Нуреддина. Как общий подход, этот метод можно комбинировать с различными алгоритмами массового и многоагентного моделирования. На каждом временном шаге моделирования нам нужно предсказать, столкнется ли каждый агент с другими агентами в толпе. Затем мы должны определить тип столкновения, которое может произойти.В реальной жизни существует три возможных типа столкновений [5]. Первый тип – в отношении поведения столкновения . Это происходит, когда два агента идут навстречу друг другу. Второй – от столкновения . Это происходит, когда один агент, находящийся позади другого, движется с большей скоростью и направление движения соответствует линии от заднего агента к переднему. Третье поведение при столкновении – это скользящее столкновение , которое происходит, когда два агента идут примерно в одном направлении.
Эти три типа поведения при столкновении показаны на рисунке 5.
Мы используем ряд правил, чтобы реализовать эти три поведения по предотвращению столкновений по отдельности. В в отношении поведения столкновения мы используем следующую стратегию, чтобы избежать предстоящего столкновения: агент с низким приоритетом может выбрать ожидание или изменить направление своего движения, а агент с более высоким приоритетом выбирает сохранение своего движения в неизменном направлении и скорость. Что касается столкновения на расстоянии , задний агент может выбрать замедление скорости или изменение направления движения в любую сторону.Мы справляемся со скользящим столкновением таким же образом, как и при столкновении.
В частности, когда эти три поведения по предотвращению столкновений конфликтуют друг с другом, мы решаем эту проблему, предварительно определяя их порядок приоритета. В этой статье порядок приоритета этих трех типов поведения по предотвращению столкновений следующий: столкновение, столкновение вдалеке и скользящее столкновение от высокого к низкому.
4.2. Поведение стада
Поведение стайки используется для моделирования поведения коллективного скопления нормальных групп.Ориентируясь на группу агентов, состоящую из одного агента-лидера и подчиненных, мы используем метод распределенного управления для моделирования поведения группировки [15, 16]. Движение каждого виртуального агента описывается двумя интеграторами как где, и обозначают положение, скорость и ускорение агента соответственно. Аналогично виртуальный лидер имеет следующую динамику движения: где, и представляют положение, скорость и ускорение агента-лидера, соответственно.Алгоритм управления методом флокирования представлен в виде где – множество пространственных соседей агента. представляет диапазон взаимодействия. – евклидова норма и для вектора. является искусственной неотрицательной гладкой попарной потенциальной функцией, характеристики которой зависят от относительных расстояний между агентом и его соседями: достигает своего максимального значения as и приобретает свое уникальное минимальное значение на заранее определенном расстоянии. Когда, агент достигает силы отталкивания от праха.Когда, сила отталкивания и сила притяжения между и становятся балансом. Когда, агент достигает силы притяжения от. И когда, становится постоянным; тогда нет силы между и. и являются положительными константами, которые отражают степень влияния позиции и скорости лидера. – смежный весовой коэффициент.
5. Экспериментальные результаты и обсуждение
В нашем моделировании мы используем пакет программного обеспечения для анимации людей под названием DI-Guy, который коммерчески доступен от Boston Dynamics Inc.Мы контролируем перемещение срочных и обычных участников с помощью интерфейса SDK с помощью программ на C ++. Сценарий можно изобразить следующим образом: в городе с большинством мирных жителей и двумя движущимися автомобилями. Гражданские лица состоят из трех неотложных лиц и 50 обычных членов, включая 30 обычных людей и 2 обычные группы по 10 человек, соответственно. Ходовые качества автомобилей известны заранее. Значения приоритета 50 обычных агентов выбираются случайным образом из интервала.Диапазон взаимодействия и заданное расстояние. Значения и устанавливаются такими же, как в [6], и,, и. Динамическая среда экспериментов изображена на рисунке 6.
Ходовые качества автомобилей известны заранее. Значения приоритета 50 обычных агентов выбираются случайным образом из интервала.Диапазон взаимодействия и заданное расстояние. Значения и устанавливаются такими же, как в [6], и,, и. Динамическая среда экспериментов изображена на рисунке 6.
На рисунке 6 мы установили и. Длина указанных дорожек неотложных лиц есть и и. Первое динамическое препятствие (движущиеся автомобили) движется с постоянной скоростью (Car1), а второе движется с постоянной скоростью (Car2). Пространства трех неотложных людей в динамической среде изображены на рисунке 7.
На рис. 8 показаны множества достижимости и оптимальная траектория для каждого пациента, нуждающегося в срочной помощи.
Результаты моделирования поведения толпы в трехмерном пространстве показаны на рисунке 9.
Из рисунка 8 мы можем видеть, что градиент в пространстве равен нулю, что означает, что конечная скорость экстренного человека равна нулю, и это удовлетворяет требование постановки задачи в разделе 3.1; например, на рис. 8 (b) срочное лицо 2 набирает максимальное ускорение до достижения точки A до того, как Car1 прибывает на его путь, а затем переключается на замедление для пути A-B в случае столкновения с Car2.После этого он продолжает набирать максимальное ускорение для пути B-C, а затем сбрасывает скорость до нуля от точки C до конечной точки всего пути. На рисунке 9 показано реалистичное и правдоподобное поведение толпы в городской среде: человек, срочно требующий срочной помощи, может добраться до места назначения по заданному пути за минимальное время и избежать столкновений с динамичными автомобилями. Одновременно агенты двух нормальных групп демонстрируют реальное собирательное поведение в соответствии с методом стайки, а нормальные особи стараются держаться подальше от срочных и избегать столкновений друг с другом.
Стоимость вычислений нашего подхода проиллюстрирована на рисунке 10, когда мы меняем количество динамических препятствий. Точно так же на рисунке 11 показано время затрат на наш подход в зависимости от количества нормальных членов в толпе.
Точно так же на рисунке 11 показано время затрат на наш подход в зависимости от количества нормальных членов в толпе.
Из рисунка 10 мы можем видеть, что время затрат нашего подхода в значительной степени зависит от количества динамических препятствий в окружающей среде. Однако результаты эксперимента на рисунке 11 показывают, что стоимость времени нашего подхода немного меняется в зависимости от количества нормальных членов.Это означает, что увеличение числа обычных членов не требует больших вычислительных затрат. И все вышеперечисленные результаты соответствуют предыдущим исследованиям.
6. Выводы
Хотя было проведено несколько исследований по оптимальному планированию траектории для различных целей, было предпринято мало усилий для моделирования реалистичного поведения толпы с ее помощью, например поведения пешеходов при навигации в динамической среде. В этой статье мы сначала представляем оптимальный метод планирования траектории с ограничением скорости и ускорения вдоль фиксированной заданной траектории с динамическими препятствиями.Мы используем его, чтобы генерировать оптимальную траекторию срочных элементов при динамических ограничениях. Этот планировщик гарантирует, что время движения срочных элементов будет минимальным за счет использования алгоритма распространения интервалов скоростей для вычисления достижимых наборов скоростей в вершинах препятствий в пространстве. Более того, затраты времени на этот метод планирования оптимальной траектории приемлемы за счет применения новой модели толкания. Наконец, в сочетании с поведением избегания столкновений и поведением скопления реализовано моделирование толпы с динамическими транспортными средствами.Таким образом, потенциал нашего подхода к планированию оптимальных траекторий и моделированию социального поведения толпы является многообещающим.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Благодарность
Эта статья поддержана Национальным фондом естественных наук Китая (гранты № 61170160 и 61374185).
| Рассмотрим небольшую массу на конце легкого жесткого стержня, движущуюся по кругу. путь с постоянной скоростью . | ||
| Величина скорости тела постоянна, но направление постоянно меняется . | ||
| Это означает, что, хотя скорость не меняется на , скорость меняется . | ||
| Мы заключаем, что тело, движущееся по круговой (или, фактически, любой криволинейной траектории) ускоряется . | ||
| В любой момент направление скорости – касательная к круговой дорожке. | ||
| В момент времени t = 0 тело находится в A (произвольно выбранной точке), а Величина составляющей его скорости в направлении A-O составляет ноль . | ||
| (По определению касательная проходит под углом 90 к радиусу.) | ||
| Через время Δt тело переместилось в B и угловое смещение Δθ. | ||
| Когда в B, величина составляющей скорости в направлении B-O (который параллелен A-O) больше не равен нулю. | ||
| Сейчас выдается | ||
Итак, произошло изменение скорости вдоль
направление A-O (или B-O), что означает, что там
было ускорение в направлении A-O (или B-O). | ||
| Величина ускорения равна изменение скорости, деленное на время, необходимое для изменения. | ||
| Следовательно | ||
| Для малый углов, синус угла очень почти равен угол в радианах . Смотрите здесь для доказательства. | ||
| Чтобы чтобы найти мгновенное значение ускорения , рассмотрим, как B получает все ближе и ближе к А. | ||
| Это эквивалентно рассмотрению меньшего и меньшие временные интервалы. | ||
| As Δt 0 (Δθ 0) затем sinΔθ Δθ (в радианах), и поэтому ускорение дается | ||
| что, конечно, дает | ||
| также, как Δt 0 (Δθ 0) прямая B-O приближается к линии A-O, поэтому направление ускорение направлено к центру круговой траектории . | ||
| Вспоминая что v = rω, это дает нам два полезных уравнения чтобы вычислить величину этого ускорения: | ||
| Выводы | ||
| Кузов движение с постоянной скоростью по круговой траектории испытывает ускорение , направленное в сторону центр круговой траектории . | ||
| Это ускорение называется центростремительным . ускорение и обеспечивается центростремительным приводом сила . | ||
Сила может быть вызвана гравитацией или электростатическим зарядом.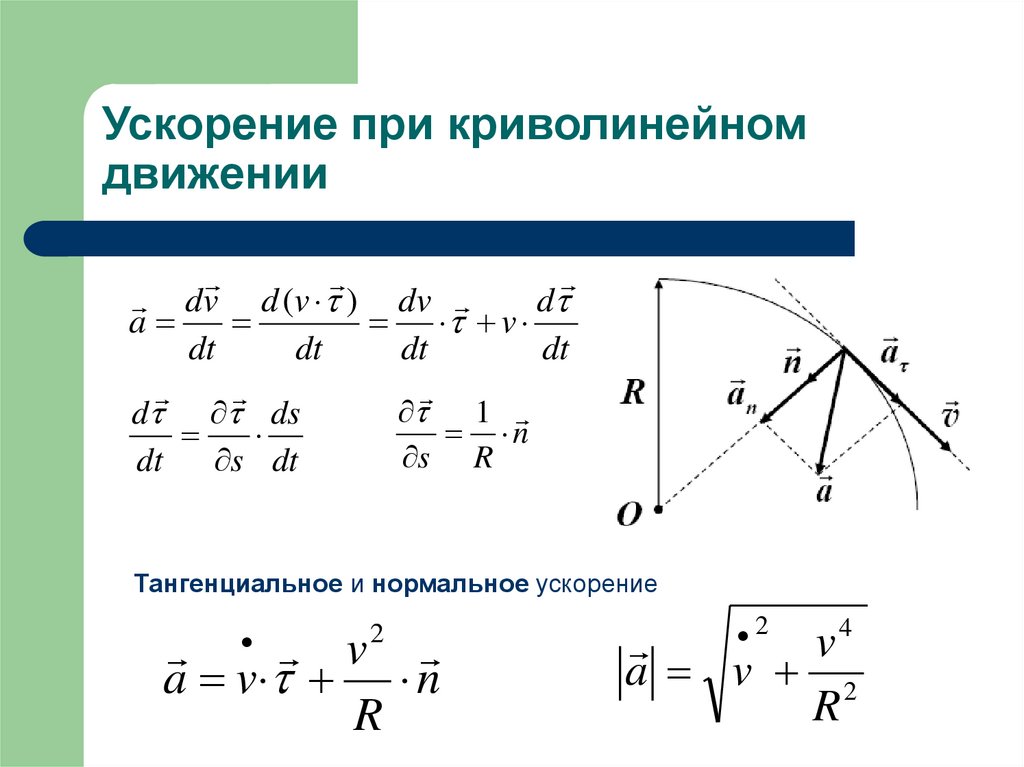 | ||

 Поэтому за третью секунду движения автомобиль пройдет путь 5 м — ответ 3.
Поэтому за третью секунду движения автомобиль пройдет путь 5 м — ответ 3.
 А она по условию больше у тела 1, которое, таким образом, и улетит дальше (ответ 1).
А она по условию больше у тела 1, которое, таким образом, и улетит дальше (ответ 1).
 Она делает 10 кругов по трассе за 2 минуты. Найдите общее пройденное расстояние, среднюю скорость и центростремительное ускорение Миранды.
Она делает 10 кругов по трассе за 2 минуты. Найдите общее пройденное расстояние, среднюю скорость и центростремительное ускорение Миранды.