Скорость в любой момент времени формула: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Скорость движения в физике, теория и онлайн калькуляторы

Скорость движения в физике, теория и онлайн калькуляторы

Мгновенная скорость движения материальной точки

Пусть положение материальной точки в пространстве задано радиус-вектором $\overline{r}$. При движении этой точки этот радиус-вектор изменяется по величине и направлению. Допустим, что положение материальной точки в момент времени $t_1$ задано при помощи вектора ${\overline{r}}_1$, в момент времени $t_2$ положение этой же точки определяет вектор ${\overline{r}}_2$.

Тогда за время $\Delta t=t_2-t_1$, рассматриваемая нами материальная точка совершает перемещение, равное:

\[\Delta \overline{r}={\overline{r}}_2-{\overline{r}}_1\left(1\right).\]

Тогда предел отношения $\frac{\Delta \overline{r}}{\Delta t}$ при $\Delta t\to 0$ называют мгновенной скоростью ($\overline{v}$):

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}\ }\left(2\right). 2_z}\left(5\right).\]

Элементарный путь ($\Delta s$) в общем случае не равен модулю элементарного перемещения ($\left|\Delta \overline{r}\right|$), но если рассматривать отрезки пути и перемещения при $\Delta t\to 0$, то различие между этими параметрами будет тем меньше, чем ближе $\Delta t$ к нулю, поэтому можно считать, что:

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\ }\left(6\right).\]

Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:

\[\left[v\right]=\frac{\left[s\right]}{\left[t\right]}.\]

В Международной системе единиц (СИ) единицей измерения скорости (в том числе и средней скорости) является метр в секунду:

\[\left[v\right]=\frac{м}{с}.\]

Средняя скорость движения тела

Физическая величина, равная отношению перемещения, которое совершило тело к этому промежутку времени движения называют средней скоростью ($\left\langle v\right\rangle $) материальной точки:

\[\overline{\left\langle v\right\rangle }=\frac{\Delta \overline{r}}{\Delta t}\left(7\right). \]

Иногда при вычислении средней скорости используют другое ее определение: среднюю скорость считают равной отношению всего пройдённого пути (s) ко времени (t) движения тела:

\[\left\langle v\right\rangle =\frac{s}{t}\left(8\right).\]

При таком определении средняя скорость – это скалярная величина.

Формулы для вычисления скорости при движении разных видов

Если тело движется равномерно, то его скорость постоянна. Ее вычисляют при помощи выражения:

\[v=\frac{s}{t}\left(9\right),\]

где $s$ – путь; $t$ – время движения. При равномерном прямолинейном движении у скорости постоянным является не только величина, но и направление, то есть можно записать:

\[\overline{v}=const.\]

Если известно ускорение точки как функция от времени ($\overline{a}(t)$) и начальная скорость движения тела (при $t=0$) (${\overline{v}}_0$), то скорость можно найти в любой момент времени применяя формулу:

\[\overline{v}={\overline{v}}_0+\int\limits^{t’}_0{\overline{a}(t)}dt\ \left(10\right). 2+Bt\ \right)=2At+B\ \left(2.3\right).\]

При $t=0$ мгновенная скорость рассматриваемого нами движения равна:

\[v\left(t=0\right)=B\ \left(2.4\right).\]

Конечная скорость при $t=t’$:

\[v\left(t=t’\right)=2At’+B\left(2.5\right).\]

Найдем среднее арифметическое начальной и конечной скоростей на заданном отрезке времени:

\[\frac{v\left(t=0\right)+v\left(t=t’\right)}{2}=\frac{2At’+B+B}{2}=At’+B.\ \]

Ответ: При данном в условии задачи законе движения материальной точки средняя скорость может быть найдена как среднее арифметическое начальной скорости и конечной ($\left\langle v\right\rangle =\frac{v\left(t=0\right)+v\left(t=t’\right)}{2}$).

   

Читать дальше: тело, брошенное под углом к горизонту.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Движение — что это, определение и ответ

Движением тела называется изменение его положения в пространстве относительно других.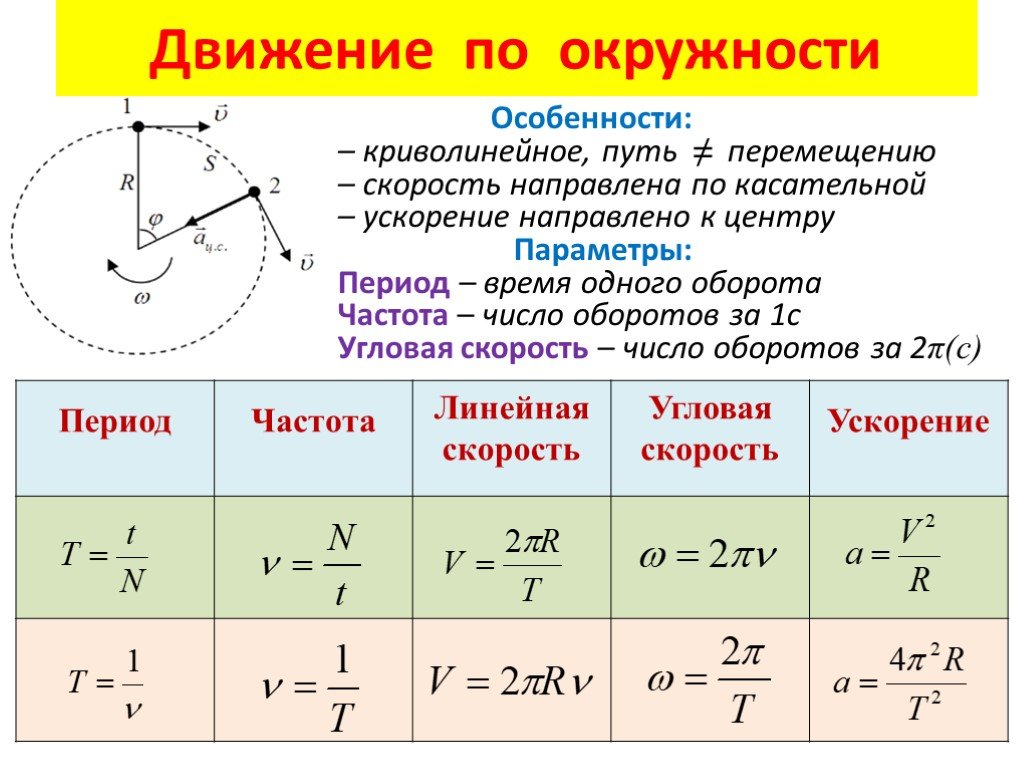

Координата — величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.

Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.

Траектория — это линия, вдоль которой движется тело.

Путь — это длина траектории, вдоль которой движется тело.

Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела \(\overrightarrow{S}\) к времени t, за которое это перемещение произошло:

\(\overrightarrow{v} = \frac{\overrightarrow{S}}{t}\)

Скорость ― это векторная величина!

В заданиях, где дана зависимость скорости тела от времени.

Пройденный путь можно вычислить как площадь под графиком. {2}}{2}\)

Где x₀ ― начальная координата тела;

v₀ ― проекция начальная скорость на ось x;

a ― проекция ускорения на ось x;

t ― время движения.

Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получив взяв производную по времени от этой зависимости.

Скорость ― это производная координаты тела по времени v_x(t) = x^‘(t). Например, если зависимость координаты тела при равноускоренном движении имеет вид x(t) = 6 – 2t + 12t², то, взяв первую производную от координаты мы получим зависимость скорости тела от времени v_x(t) = –2 + 12 ∙ 2t = –2 + 24t.

Точно так же, ускорение ― это производная от скорости тела. a_x(t) = v_x^‘(t). {2}}{2}\),

Где:

H(t) — высота тела над нулевым уровнем в момент времени t [м],

h — начальная высота тела над нулевым уровнем [м],

v₀ — начальная скорость тела [м/с]

α — угол, под которым бросили тело [°],

t — время движения тела [c],

g — ускорении свободного падения [м/с²].

Зависимость горизонтальной координаты от времени при движении под углом к горизонту:

S(t) = v₀ ‧ cos a ‧ t, где:

S(t) — путь, пройденный телом за время t [м]

Угол между вектором скорости тела и горизонтом в любой момент времени может быть выражен из геометрических соображений как:

\(\alpha\left( t \right) = arctg(\frac{v_{y}}{v_{x}})\),

Где:

α(t) — угол между скоростью и горизонтом в момент времени t [°],

v_y = v₀ ∙ sin α – gt — вертикальная проекция скорости тела в момент времени t [м/с],

v_х = v₀ ∙ cos α — горизонтальная проекция скорости тела [м/с].

Работа силы тяжести при падении тела на тот же уровень, с которого тело взлетело (с Земли на Землю, с балкона на балкон и т.д.) равна нулю.

В этом случае выполняется симметрия полета:

• угол, под которым тело упадет, равен углу, под которым тело бросили;

• скорость, с которой тело упадет, равна скорости, с которой тело бросили;

• время взлета тела до максимальной высоты равно времени падания с неё обратно.

Если работа силы тяжести не равна нулю (бросок с Земли на балкон, с балкона на Землю и так далее), симметрия полета не выполняется.

Время взлета на максимальную высоту:

\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\). {2}\sin{2\alpha}}{g}\).

Выводится с помощью подставления прошлой формулы в уравнения равномерного движения вдоль горизонтальной оси:

S = v₀ ‧ cos a ‧ t _полета

Здесь используются формула синуса двойного угла и свойство симметрии полета: время взлета равно времени падения, или полное время движения равно удвоенному времени взлета: t_полета = 2t_взлета

Очевидно, что формула применима только при падении тела на тот же уровень, с которого оно взлетело.

Время падения тела с балкона (без начальной скорости) или при броске горизонтально:

\(t_{падения} = \sqrt{\frac{2H}{g}}\)

Формула выводится при проецировании уравнения координаты при равноускоренном движении на ось OY:

\(H\left( t \right) = h + v_{0}\sin a \cdot t – \frac{gt^{2}}{2}\)

с учетом, что проекция начальной скорости на эту ось равна нулю, а конечная координата — тоже ноль:

\(0 = h – \frac{gt_{падения}^{2}}{2}\)

Максимальная высота подъема тела над Землей:

\(\ h = \frac{v_{0}^{2}\sin^{2}\alpha}{2g}\)

Формулу легко получить объединением уравнения координаты при равноускоренном движении на ось OY с поверхности Земли:

\(\left( t \right) = h + v_{0} \cdot \sin a \cdot t – \frac{gt^{2}}{2}\)

с формулой времени подъема тела на максимальную высоту:

\(t_{взлета} = \frac{v_{0}\sin\alpha}{g}\)

Все представленные выше формулы могут быть использованы без вывода в задачах первой части, но в задачах второй части за это будут снимать баллы.

При движении по окружности часто удобно использовать не обычную скорость, а угловую скорость.

Угловая скорость численно равна углу поворота радиуса за единицу времени.

Угловая скорость для тела, двигающегося из точки 1 в точку 2, будет равна:

\(\omega = \frac{\mathrm{\Delta}\varphi}{\mathrm{\Delta}t}\), где

∆φ ― угол поворота [рад],

∆t ― промежуток времени [с],

ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).

Линейную скорость точки на определенном расстоянии (радиусе) R от оси вращения можно считать как: v = ωR.

Соответственно, чем больше будет радиус окружности, тем больше будет линейная скорость, при постоянной угловой скорости.

Период — время, за которое тело делает полный оборот по окружности.

\(T = \frac{2\pi R}{v}\), где

T ― период [с],

R ― радиус окружности [м],

v ― скорость [м/с]. {2}R\), где

R ― радиус окружности [м],

a_n ― нормальное ускорение [м/с²],

v ― скорость [м/с],

ω ― угловая скорость \(\lbrack\frac{рад}{с}\rbrack\).

Как найти среднюю скорость (формула и примеры)

, написанный

Малкольм Маккинси

11 января 2023

Проверка по фактам

Пол Маззола

Средняя скорость. Средняя скорость

Средняя скорость. два слова: среднее значение, означающее среднее значение, полученное из множества отдельных точек данных, и скорость, означающая изменение положения. Вы можете рассчитать среднюю скорость для любого типа движения, если можете рассчитать время движения и измерить расстояние.

Формула средней скорости

Средняя скорость  это общее расстояние, пройденное для рассматриваемого объекта, деленное на общее время, затраченное на преодоление расстояния, общий период времени. Формула средней скорости:

Определение средней скорости и формула

Средняя скорость отличается от мгновенной скорости.

Мгновенная скорость

Средняя скорость учитывает совокупность событий, таких как ускорение автомобиля с места, ускорение, движение некоторое время, затем замедление на желтый сигнал светофора и, наконец, остановка.

Автомобиль движется с разной скоростью. В любой момент автомобиль не едет со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час, затем 53 мили в час, затем 61 миля в час и, наконец, 3 мили в час, прежде чем вернуться к 0 милям в час.

Чтобы упростить измерения и добиться прогресса в решении задачи по физике или математике, вы берете среднюю скорость всех дискретных событий, говоря, что автомобиль проехал 5,5 миль  за 6 минут :

Все эти другие измерения в определенные моменты времени в путешествии мгновенные скорости . В большинстве случаев вам нужно , а не знать формулу мгновенной скорости, v , нахождение предела по мере того, как изменение во времени («момент») приближается к 0:

Мгновенные скорости колеблются в течение хронометрируемого события. Найти среднюю скорость far проще и, как правило, гораздо полезнее, чем вычислить мгновенную скорость.

Скалярные и векторные величины

Скорость есть скалярная величина . У него нет направления. Он имеет только размер, то есть величину или масштаб. Скалярные величины могут изменяться от 0 (без скорости) до бесконечно быстрой.

Векторная величина имеет размер и направление, как и движение самолета в небе. Скорость является векторной величиной.

Скорость, будучи скалярной величиной, никогда не может быть меньше 0. Средняя и мгновенная скорости всегда являются скалярными величинами, что означает, что вы всегда можете измерить их числом. Расстояние и время также являются скалярными величинами и также могут быть измерены числами.

Как рассчитать среднюю скорость

Чтобы рассчитать среднюю скорость объекта, вы должны знать общее расстояние, которое проходит объект, и общее время, затраченное на весь его путь.

Треугольник расстояние/скорость/время удобен для расчета этой и двух других скалярных величин (расстояние и время):

Скорость расстояние время треугольник и формулы

Три части треугольника математически расставлены в правильном положении:

1. Чтобы получить среднюю скорость, s , разделите общее расстояние на прошедшее время: Dt\frac{D}{t}tD​

2. Чтобы получить пройденное время, t , разделите общее расстояние на скорость: Ds\frac{D }{s}sD​

3. Чтобы получить расстояние, D , умножьте скорость на количество времени: s×ts\times ts×t

Допустим, вы хотите найти среднюю скорость Тихоокеанская афалина. Вам говорят, что он может пройти расстояние 89,7 км за 3 часа.

Подставьте эти два заданных числа в треугольник в их двух углах, чтобы получить:

Как рассчитать среднюю скорость

Если вы знаете две из трех переменных, расстояние, время и скорость, то вы можете использовать алгебру, чтобы найти то, что вы повторно отсутствует.

Если вам нужно общее время, вы должны иметь расстояние и скорость. Вы подставляете эти две скалярные величины в соответствующие части треугольника, чтобы получить:

Вычисление общего времени по средней скорости и расстоянию

Если вам нужно общее расстояние, вы должны знать скорость и время:

Расчет общего расстояния по средней скорости и времени

Средняя скорость особенно полезна, поскольку она учитывает реальность события, а не предполагает, что что-то или кто-то движется с постоянной скоростью.

Морская свинья могла начать медленно, ускориться, сделать паузу, чтобы поиграть, и продолжить. Этот трехпалый ленивец, возможно, остановился на мгновение, чтобы отдышаться, прежде чем поспешить дальше.

Возможно, вам придется делать многочисленные остановки при выгуле собаки, но во всех трех случаях вы можете легко рассчитать среднюю скорость, разделив общее пройденное расстояние на общее затраченное время.

Предостережение

Средняя скорость часто выводится из единиц расстояния или времени, которые должны быть преобразованы в другие единицы для окончательного ответа. Соблюдайте осторожность при этом.

Обычными преобразованиями являются умножение единиц в секунду на 60 или 3600, чтобы получить единицы в минуту и ​​единицы в час. Просто убедитесь, что ваш ответ дан в правильной единице времени.

Преобразование единиц измерения средней скорости

Если изменяется только одна единица измерения, вам нужно будет выполнить только одну математическую операцию (например, умножить секунды, чтобы получить минуты или часы). Если изменить две единицы (футы в секунду на мили в час), вы должны умножить и разделить (или умножить на десятичное значение).

Проблемы средней скорости

1. Тарпон (разновидность рыбы) может путешествовать 105 миль за 3 часа . Какова его средняя скорость?

2. Синий тунец может проплыть и преодолеть  286 миль за обычный учебный день 6,5 часов . Какова его средняя скорость, пока вы проводите свой день в классе?

3. Мировой рекорд по скорости бега назад (во время жонглирования!) принадлежит Джо Солтеру, который проехал 5280 футов дюйма 457 секунд . Какова была его средняя скорость в милях за час ? (умножить на 3600 и затем разделить на 5280 ; или умножить на 0,681818 )

4. Гепард может пройти 0,6 мили за 3 секунд. Какова средняя скорость гепарда в милях за секунду ? Как насчет скорости в милях за час ? (умножить на 3600 )

5. Косатка может двигаться со средней крейсерской скоростью 8 миль в час. Большая белая акула может преодолеть расстояние 35 миль за семь часов. Какова скорость большой белой акулы и какое животное плывет быстрее?

6. Самый быстрый человек в воде преодолел 22,9 метра за 10 секунд. Кальмар Гумбольдта может пройти 399,6 метра за 60 секунд . Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольдта, чтобы узнать, кто кого может обогнать.

Мы знаем, что вы сначала сделаете работу, прежде чем проверять эти ответы, верно?

1. Рассчитайте среднюю скорость тарпона следующим образом: s=105miles3hourss=\frac{105miles}{3hours}s=3hours105miles​, что означает, что рыба может двигаться со средней скоростью 35 миль в час .

2. Формула голубого тунца будет выглядеть так: s = 286 миль 6,5 часов = \ frac {286 миль {6,5 часов} s = 6,5 часов 286 миль​, поэтому средняя скорость рыбы составляет 44 мили в час.

3. Joe Salter’s Cover 5,280 футов в 457 секунд , S = 5,280FEET457Seconds = \ frac {\ mathrm {5,280} футов} {457S {\ sepecond weeeled weeeled weeelds {\ sethrm {5,280} фута} {457S ateels ateeled weeelet {457s weeeled weeeled weeel {\ sethrm {5 280}}} aeeet steels {\ per {5,280}}}. . Мы умножаем это на 3600 (количество секунд в часе), а затем делим на 5280 (футы в миле), чтобы получить среднюю скорость 7,87745 миль в час .

4. Формула для средней скорости гепарда будет:0021 0,01666 (повторяющееся десятичное число, поэтому мы аппроксимируем 0,01666 ) в милях за секунду , которые можно умножить на 3600 , чтобы получить среднюю скорость 60 миль/ч .

5. Косатка может двигаться со средней крейсерской скоростью 8 миль/ч , в то время как средняя скорость большой белой акулы s=35mi. 7hours=5mph=\frac{35mi.}{7hours}=5mph=7hours35mi.​ =5 миль в час. Косатка плавает быстрее.

6. Самый быстрый человек в воде плавал 22,9 метра в 10 секунд , поэтому средняя скорость s=22,9м10секунд=2,29метра/секунды=\frac{22,9м}{10секунд}=2,29метра/секунды=10секунд22,9м​=2,29метра/секунду. Кальмар Гумбольдта может пройти 399,6 метров за 60 секунд , поэтому s=399,6м60секунд=6,67м/сс=\frac{399,6м}{60секунд}=6,67м/сс=60секунд399,6м​=6,67м/с , значительно быстрее, чем самый быстрый пловец-человек. Будем надеяться, что вас никогда не преследовал кальмар Гумбольдта!

Формула скорости и скорости с решенными примерами

Физические формулы

Скорость : Определяется как скорость изменения расстояния по отношению ко времени.

Это скалярная величина.

Его единица СИ — м/с, а размеры — [LT ^–1 ]

• . Мгновенная скорость частицы – это скорость в конкретный момент времени. △S – расстояние, пройденное частицей за интервал времени △t, тогда мгновенная скорость – это предельное значение △S/△t при приближении △t к нулю.

В математических обозначениях этот предел называется производной s по времени и записывается как ds/dt

. Мгновенная скорость (v) = ds/dt.

• Средняя скорость : Средняя скорость частицы определяется как отношение общего пройденного расстояния к общему затраченному времени

Если частица проходит расстояния S ₁ , S ₂ , S ₃ ….и т.д. во времени t ₁ , t ₂ , t ₃ …и т.д. соответственно.

• Если часть пробега равна интервалу расстояния скоростей v ₁ , v ₂ , v ₃ …..v _n соответственно, то

Средняя скорость представляет собой гармоническое среднее отдельных скоростей.

Формула скорости

Он определяется как скорость изменения смещения во времени.

Это векторная величина. Его единица СИ — м/с, а размеры — [LT ^–1 ]

• . Instantaneous Velocity : Мгновенная скорость частицы — это скорость в конкретный момент времени. Он определяется как скорость изменения положения частицы во времени. Если положение частицы изменяется на △r за небольшой промежуток времени △t, предельное значение △r/△t 

когда △t приближается к нулю, дает мгновенную скорость.

В математических обозначениях этот предел называется производной r по времени и записывается как dr/dt

.

• Средняя скорость : Средняя скорость частицы за данный интервал времени определяется как отношение ее смещения к затраченному времени.

Средняя скорость не зависит от пути, пройденного между любыми двумя точками. Оно зависит только от начального и конечного положения частицы, так как зависит от смещения. Если частица стартует из какой-то точки и возвращается в ту же точку по любому пути, то средняя скорость в этом путешествии будет равна нулю.

Примеры для скорости и скорости

Пример 1: Расстояние, пройденное частицей за время t, определяется выражением S = 3t ² + 2,

а) Найдите мгновенную скорость в момент времени t = 3 с.

(б) Средняя скорость частицы от 0 до 3 с

Решение: (a) Мгновенная скорость = ds/dt

Здесь S = 3t ² + 2

ds/dt= 6t

= 6 × 3 = 18 м/с

(b) Расстояние, пройденное за время от 0 до 3 с, равно

. S = 3(3 ² ) + 2 = 29 м

Пример 2:  Бегун бежит по прямоугольной дорожке длиной = 50 метров и шириной = 20 метров. Он дважды проходит по прямоугольной дорожке и, наконец, возвращается к исходной точке. Если общее время, затрачиваемое им на бег по дорожке, равно 100 секундам, определите среднюю скорость и среднюю скорость.

Решение: Окружность прямоугольника, равная расстоянию, пройденному за один круг = 2(50 метров) + 2(20 метров) = 100 метров + 40 метров = 140 метров.