Решение уравнений методом Гаусса онлайн калькулятор
Карл Фридрих Гаусс – немецкий математик, механик, физик, астроном и геодезист. Он считается одним из
величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом
Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и
прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры,
теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии
и многих разделов астрономии. Метод Гаусса позволяет максимально легко и быстро решить систему линейных
алгебраических уравнений (СЛАУ). Успех данного метода заключается в последовательном исключении неизвестных
из уравнений. Сегодня решить систему алгебраических уравнений онлайн методом Гаусса можно с помощью
специальных решательов, но ниже мы разберем решение системы линейных уравнений, чтобы наглядно на примере
увидеть все его достоинства.
Так же читайте нашу статью “Решить уравнение матричным способом онлайн решателем”
Допустим, дана система линейных уравнений:
\[\left\{\begin{matrix} 2\cdot x_1+4\cdot x_2+1\cdot x_3 = 36\\ 5\cdot x_1 + 2 \cdot x_2 +1 \cdot x_3 =47\\ 2\cdot x_1 + 3\cdot x_2 + 4 \cdot x_3 = 37 \end{matrix}\right.\]
Представим ее в матричной форме:
\[\begin{bmatrix} 2 & 4 & 1\\ 5 & 2 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 36\\ 47\\ 37 \end{bmatrix}\]
Выберем строку с максимальным коэффициентом \[a_i1\] и меняем ее с первой.
\[\begin{bmatrix} 5 & 2 & 1\\ 2 & 4 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 47\\ 36\\ 37 \end{bmatrix}\]
Нормируем уравнения относительно коэффициента при \[x_1\]:
\[\begin{bmatrix} 1 & \frac{2}{5} & \frac{1}{5}\\ 2 & \frac{4}{2} & \frac{1}{2}\\ 2 & \frac{3}{2} & \frac{4}{2} \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} \frac{47}{5}\\ \frac{36}{2}\\ \frac{37}{2} \end{bmatrix} \]
\[\begin{bmatrix} 1 & 0.
Вычитаем 1 уравнение из 2 и 3:
\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]
Выбираем строку с наибольшим коэффициентом при \[a_i2\] (уравнение 1 не рассматривается) и перемещаем ее на место 2.
\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]
Нормируем 2 и 3 уравнения относительно коэффициента при \[x_2\]
\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 1 & 1.636 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\
x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9. 4\\ 5.375\\ 8.272 \end{bmatrix}\]
4\\ 5.375\\ 8.272 \end{bmatrix}\]
Вычитаем уравнение 2 из 3
\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 0 & 1.4489 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 2.897 \end{bmatrix}\]
Нормируем уравнение 3 относительно коэффициента при \[x_3\]
\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.166\\ 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.333\\ 2 \end{bmatrix}\]
Откуда получаем \[x_3=2\]. Подставляем полученное значение в уравнения 2 и 1 получаем
\[x_2 = 5.333 – 0.1666 \cdot 2 = 5.333 – 0.333 =5\]
\[x_1+0.4 \cdot x_2 = 9.4 – 0.2 \cdot 2 = 9.4 – 0.4=9\]
Подставляя полученное значение \[x_2=5\] в уравнение 1, найдем
\[x_1 = 9 – 0.4 \cdot 5 = 9 – 2 = 7\]
Таким образом, решением системы уравнений будет вектор
\[x =\begin{bmatrix} 7 & 5 & 2 \end{bmatrix}^T\].
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
3. Система линейных алгебраических уравнений (слау). Метод Гаусса. Пример.
Система м линейных уравнений с н переменными имеет вид:
а11х1+ а12х2+ …+а1jхj+..+a1nxn=b1
а21х1+ а22х2+…+ а2jхj+..+a2nxn=b2
аi1х1+ аi2х2+…+ аijхj+..+ainxn=bi
аm1х1+ аm2х2+…+ аmjхj+..+amnxn=bm
где аij, bi (i=1,n
j=1,m) – произвольные числа при переменных,
называемые коэффициентами при переменных
и свободныи членами уравнений.
В более краткой записи с помощью знаков суммирования систему можно записать:
n
∑aijxj =bi
j=1
Решение такой системы – это набор чисел, при подстановке которых в эту систему каждое уравнение превращается в тождество. Совместной СЛАУ называется такая система, которая имеет хотя бы одно решение. Если система решений не имеет, то она называется несовместной.
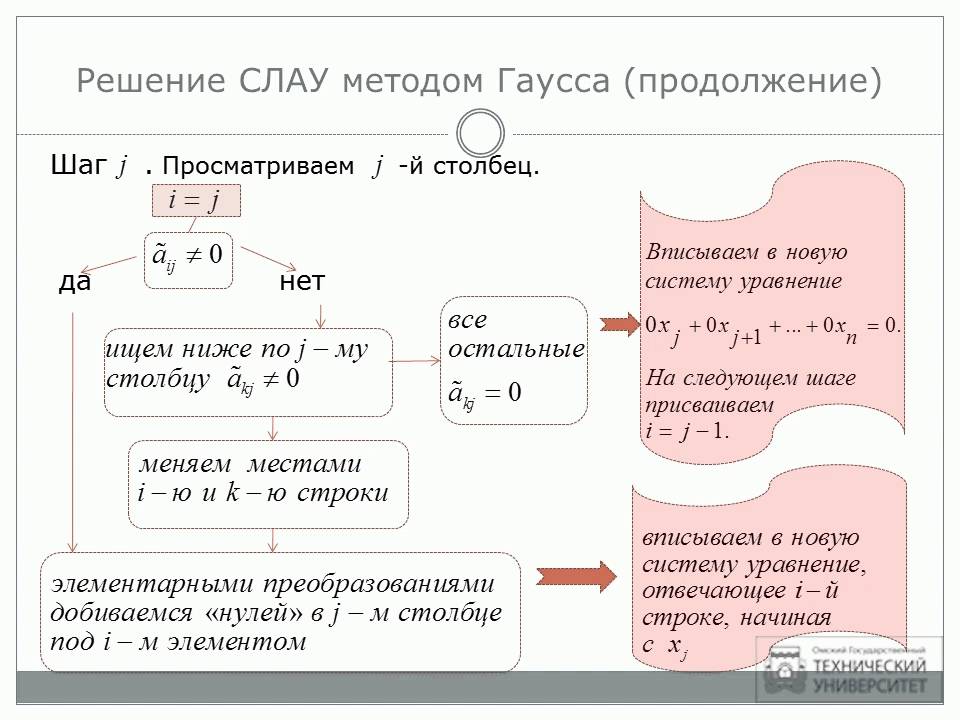
Метод Гаусса.
Метод последовательного исключения переменных заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Ход решения
умножая 1-ое уравнение на подходящие числа и прбавляя полученные уравнения соответственно ко второму, третьему ,… m-му уравнению системы, исключим переменную х1 из всех последующих уравнений, начиная со второго.
Предположим
что а22 <>0 умножая второе уравнение на
подходящие числа и прибавляя полученные
уравнения соответственно к третьему,
четвертому,…, m-му уравнению системы,
исключим переменную х2 из всех последующих уравнений, начиная
с третьего.
Матрицей размера м*н называется прямоугольная таблица чисел, содержащая м строк и н столбцов. Числа составляющие матрицу называются ее элементами.
Матрица состоящая из одной строки, называется матрицей (вектором) – строк, а из одного столбца – матрицей –столбцом
Матрица называется квадратной, если число ее строк = числу ее столбцов. Элементы матрицы, у которых номера столбца = номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Если все недиоганальные элементы квадратной матрицы =0, то матрица назыв диагональной. Если у диагональной матрицы все диагональные элементы = 1, то матрица назыв единичной матрицей. Матрица любого порядка назыв нулевой, если все ее эл-ты = 0
Операции над матрицами.
Умножение матрицы на число. Все эл-ты матрицы умножаем на это число. Произведением матрицы А на число № назыв матрица В=№А.
Сложение матриц.
 Сумма 2х матриц одинакового размера
назыв матрица С=А+В, эл-ты которой
cij=aij+bij
Сумма 2х матриц одинакового размера
назыв матрица С=А+В, эл-ты которой
cij=aij+bijВычитание. А-В=А+(-1)*В
Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов 1ой матрицы =числу строк второй. Тогда произведением матриц А*В назыв такая матрица С, каждый элемент которой сij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Транспонирование. Переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка.
Возведение в степень. Целой положительной степенью А в степени м (м>1)квадратной матрицы А называется произведение м матриц, равных А.
В матрице А размера
m x n вычеркиванием каких-либо строк и
столбцов можно вычленить квадратные
подматрицы k-го порядка, где k≤min(m;n). Определители таких подматриц называются
минорами k-го порядка матрицы А.
Определители таких подматриц называются
минорами k-го порядка матрицы А.
Ранг матрицы – наивысший порядок отличных от нуля миноров матрицы.
2.1. Гауссовые смешанные модели — документация scikit-learn 1.2.2
sklearn.mixture — это пакет, который позволяет изучать
Модели гауссовой смеси (диагональная, сферическая, связанная и полная ковариация).
поддерживаемых матриц), отберите их и оцените по
данные. Средства, помогающие определить необходимое количество
компоненты также предоставляются.
Модель двухкомпонентной смеси Гаусса: точек данных и равновероятность поверхности модели.
Смешанная модель Гаусса — это вероятностная модель, которая предполагает все
точки данных генерируются из смеси конечного числа
Распределения Гаусса с неизвестными параметрами. Можно подумать о
смешанные модели как обобщающие кластеризацию k-средних для включения
информацию о ковариационной структуре данных, а также
центры латентных гауссианов.
Scikit-learn реализует различные классы для оценки гауссова смешанные модели, соответствующие разным стратегиям оценивания, подробно ниже.
2.1.1. Гауссовская смесь
Объект GaussianMixture реализует
максимизация ожидания (EM)
алгоритм подбора смешанных гауссовых моделей. Он также может рисовать
эллипсоиды доверия для многомерных моделей и вычислить
Байесовский информационный критерий для оценки количества кластеров в
данные. Предоставляется метод GaussianMixture.fit , который изучает гауссову
Модель смеси из данных поезда. Учитывая тестовые данные, он может назначить каждому
образец Гаусса, скорее всего, принадлежит использованию Метод GaussianMixture.predict .
GaussianMixture поставляется с различными опциями для ограничения
оценивается ковариация разностных классов: сферическая, диагональная, связанная или
полная ковариация.
Примеры:
2.1.1.1. Плюсы и минусы класса
GaussianMixture 2.
 1.1.1.1. Плюсы
1.1.1.1. Плюсы- Скорость:
Самый быстрый алгоритм обучения смешанных моделей
- Агностик:
Поскольку этот алгоритм максимизирует только вероятность, он не будет смещать средние значения к нулю или смещать размеры кластеров к имеют определенные структуры, которые могут применяться, а могут и не применяться.
2.1.1.1.2. Минусы
- Особенности:
При недостаточном количестве очков за смеси, оценка ковариационных матриц становится затруднительной, известно, что алгоритм расходится и находит решения с бесконечная вероятность, если только искусственно не упорядочить ковариации.
- Количество компонентов:
Этот алгоритм всегда будет использовать все компоненты, к которым у него есть доступ, нуждающиеся в удерживаемых данных или информационные теоретические критерии, чтобы решить, сколько компонентов использовать при отсутствии внешних сигналов.
2.
 1.1.2. Выбор количества компонентов в классической гауссовской модели смеси
1.1.2. Выбор количества компонентов в классической гауссовской модели смесиКритерий BIC можно использовать для выбора количества компонентов в гауссовой Смешивание эффективным способом. Теоретически он восстанавливает истинное количество компоненты только в асимптотическом режиме (т.е. если имеется много данных и предполагая, что данные были фактически сгенерированы i.i.d. из смеси гауссовых распределение). Обратите внимание, что использование вариационной байесовской гауссовой смеси избегает указания количества компонентов для гауссовской смеси модель.
Примеры:
2.1.1.3. Алгоритм оценки Максимизация ожидания
Основная трудность в изучении смешанных моделей Гаусса из немаркированных
данных заключается в том, что обычно не известно, из каких точек
какой скрытый компонент (если кто-то имеет доступ к этой информации, он получает
очень легко подогнать отдельное распределение Гаусса к каждому набору
точки). Ожидание-максимизация
является хорошо обоснованным статистическим
алгоритм, чтобы обойти эту проблему с помощью итеративного процесса. Первый
один предполагает случайные компоненты (случайно сосредоточенные на точках данных,
полученные из k-средних, или даже просто нормально распределенные по
происхождения) и вычисляет для каждой точки вероятность того, что она будет сгенерирована
каждого компонента модели. Затем человек настраивает
параметры, чтобы максимизировать вероятность данных, учитывая те
задания. Повторение этого процесса всегда гарантирует сходимость
к локальному оптимуму.
Первый
один предполагает случайные компоненты (случайно сосредоточенные на точках данных,
полученные из k-средних, или даже просто нормально распределенные по
происхождения) и вычисляет для каждой точки вероятность того, что она будет сгенерирована
каждого компонента модели. Затем человек настраивает
параметры, чтобы максимизировать вероятность данных, учитывая те
задания. Повторение этого процесса всегда гарантирует сходимость
к локальному оптимуму.
2.1.1.4. Выбор метода инициализации
Существует выбор из четырех методов инициализации (а также ввод определяемых пользователем начальные средства) для создания начальных центров для компонентов модели:
- k-средних (по умолчанию)
Применяет традиционный алгоритм кластеризации k-средних. Это может быть дорогостоящим в вычислительном отношении по сравнению с другими методами инициализации.
- k-means++
Здесь используется метод инициализации кластеризации k-средних: k-means++.
 Это выберет первый центр случайным образом из данных. Последующие центры будут
выбран из взвешенного распределения данных в пользу точек, находящихся дальше от
действующие центры. k-means++ — это инициализация по умолчанию для k-means, поэтому будет
быстрее, чем выполнение полного k-средних, но все же может занять значительное количество времени.
время для больших наборов данных со многими компонентами.
Это выберет первый центр случайным образом из данных. Последующие центры будут
выбран из взвешенного распределения данных в пользу точек, находящихся дальше от
действующие центры. k-means++ — это инициализация по умолчанию для k-means, поэтому будет
быстрее, чем выполнение полного k-средних, но все же может занять значительное количество времени.
время для больших наборов данных со многими компонентами.- random_from_data
Это выберет случайные точки данных из входных данных в качестве исходных центры. Это очень быстрый метод инициализации, но он может привести к неконвергентным результатам. результаты, если выбранные точки находятся слишком близко друг к другу.
- random
Центры выбираются как небольшое отклонение от среднего значения всех данных. Этот метод прост, но может привести к увеличению времени сходимости модели.
Примеров:
2.1.2. Вариационная байесовская гауссовская смесь
Объект BayesianGaussianMixture реализует вариант
Модель смеси Гаусса с вариационными алгоритмами вывода.
GaussianMixture .2.1.2.1. Алгоритм оценки: вариационный вывод
Вариационный вывод — это расширение максимизации ожидания, которое максимизирует нижнюю границу модельных доказательств (включая априорные) вместо вероятности данных. Принцип, лежащий в основе вариационные методы аналогичны методу максимизации ожидания (т. оба являются итеративными алгоритмами, которые чередуются между поиском вероятности образования каждой точки каждой смесью и подгонка смеси к этим назначенным точкам), но вариационная методы добавляют регуляризацию, интегрируя информацию из предыдущих дистрибутивы. Это позволяет избежать сингулярностей, часто встречающихся в решения для максимизации ожиданий, но вносит некоторые тонкие предубеждения к модели. Вывод часто заметно медленнее, но обычно не так быстро, как настолько, чтобы сделать использование непрактичным.
Из-за своей байесовской природы вариационный алгоритм нуждается в большем количестве гиперпараметров. чем максимизация ожидания, наиболее важным из которых является
параметр концентрации
чем максимизация ожидания, наиболее важным из которых является
параметр концентрации weight_concentration_prior . Указание низкого значения
для предварительной концентрации модель придаст большую часть веса нескольким
компонентов и установите веса остальных компонентов очень близко к нулю. Высокий
Предварительные значения концентрации позволят большему количеству компонентов
быть активным в смеси.
Параметры реализации класса BayesianGaussianMixture предлагает два типа априорного распределения весов: модель конечной смеси
с распределением Дирихле и модель бесконечной смеси с распределением Дирихле
Процесс. На практике алгоритм вывода процесса Дирихле аппроксимируется и
использует усеченный дистрибутив с фиксированным максимальным числом компонентов (называемым
представление ломания палки). Количество компонентов, которые фактически используются
почти всегда зависит от данных.
На следующем рисунке сравниваются результаты, полученные для разных типов
предыдущая концентрация веса (параметр weight_concentration_prior_type )
для разных значений weight_concentration_prior . Здесь мы видим значение параметра
Здесь мы видим значение параметра weight_concentration_prior .
оказывает сильное влияние на эффективное количество полученных активных компонентов. Мы
можно также заметить, что большие значения массы концентрации ранее приводили к
более однородные веса, когда тип априорного распределения — «dirichlet_distribution», а
это не обязательно относится к типу «dirichlet_process» (используется
по умолчанию).
В приведенных ниже примерах сравниваются смешанные модели Гаусса с фиксированным числом
компонентов, к вариационным гауссовским моделям смеси с процессом Дирихле
прежний. Здесь классическая гауссовская смесь снабжена 5 компонентами на
набор данных, состоящий из 2 кластеров. Мы видим, что вариационная гауссовская смесь
с предварительным процессом Дирихле может ограничиться только двумя компонентами
тогда как смесь Гаусса соответствует данным с фиксированным количеством компонентов
который должен быть установлен пользователем заранее. В этом случае пользователь выбрал n_components=5 , что не соответствует истинному генеративному распределению этого
игрушечный набор данных. Обратите внимание, что при очень небольшом количестве наблюдений вариационный гауссовский
смешанные модели с априорным процессом Дирихле могут занять консервативную позицию, и
подходит только один компонент.
Обратите внимание, что при очень небольшом количестве наблюдений вариационный гауссовский
смешанные модели с априорным процессом Дирихле могут занять консервативную позицию, и
подходит только один компонент.
На следующем рисунке мы аппроксимируем набор данных, плохо представленный
Гауссова смесь. Настройка параметра weight_concentration_prior BayesianGaussianMixture контролирует количество компонентов, используемых для
эти данные. Мы также представляем на последних двух графиках случайную выборку, сгенерированную
из двух полученных смесей.
Примеры:
См. эллипсоид модели смеси Гаусса для примера на построение доверительных эллипсоидов для обоих
GaussianMixtureиBayesianGaussianMixture.Гауссова модель смеси Синусоидальная кривая показывает использование
GaussianMixtureиBayesianGaussianMixtureдля синусоидальная волна.См.
 Концентрация предшествующего анализа вариации байесовской гауссовой смеси
для примера построения эллипсоидов доверия для
Концентрация предшествующего анализа вариации байесовской гауссовой смеси
для примера построения эллипсоидов доверия для BayesianGaussianСмесьс разнымиweight_concentration_prior_typeдля разных значений параметраweight_concentration_prior.
2.1.2.2. Плюсы и минусы вариационного вывода с
BayesianGaussianMixture 2.1.2.2.1. Плюсы
- Автоматический выбор:
, когда
weight_concentration_priorдостаточно мал иn_componentsбольше, чем требуется моделью, Модель вариационной байесовской смеси имеет естественную тенденцию задавать некоторую смесь. значения весов близки к нулю. Это позволяет модели выбирать подходящее количество эффективных компонентов автоматически. Только верхняя граница необходимо указать это количество. Обратите внимание, однако, что «идеальное» количество активные компоненты очень специфичны для приложения и обычно плохо определены в настройках исследования данных.
- Меньшая чувствительность к количеству параметров:
в отличие от конечных моделей, которые почти всегда используют все компоненты настолько, насколько это возможно, и, следовательно, производят совершенно разные решения для разного количества компонентов, вариационный вывод с предварительным процессом Дирихле (
weight_concentration_prior_type='dirichlet_process') мало что изменится с изменениями параметров, что приводит к большей стабильности и меньшему количеству настроек.- Регуляризация:
в связи с включением предварительной информации, вариационные решения имеют меньше патологических частных случаев, чем решения, максимизирующие ожидания.
2.1.2.2.2. Минусы
- Скорость:
дополнительная параметризация, необходимая для вариационного вывода, делает вывод медленнее, хотя и ненамного.
- Гиперпараметры:
этому алгоритму нужен дополнительный гиперпараметр для этого может потребоваться экспериментальная настройка с помощью перекрестной проверки.

- Смещение:
в алгоритмах вывода (а также в процесс Дирихле, если он используется), и всякий раз, когда возникает несоответствие между эти предубеждения и данные, возможно, можно было бы подобрать лучшие модели, используя конечная смесь.
2.1.2.3. Процесс Дирихле
Здесь мы описываем алгоритмы вариационного вывода по процессу Дирихле. смесь. Процесс Дирихле представляет собой априорное распределение вероятностей на кластеризаций с бесконечным, неограниченным числом разделов . Вариационные методы позволяют нам включить эту предыдущую структуру в Смешанные модели Гаусса почти без потерь во времени вывода, сравнивая с моделью конечной гауссовой смеси.
Важный вопрос заключается в том, как процесс Дирихле может использовать бесконечное,
неограниченное количество кластеров и при этом быть непротиворечивым. Пока полное объяснение
не подходит к этому руководству, можно подумать о процессе ломания палки
аналогия, чтобы помочь понять это. Процесс ломания палки является генеративным
рассказ о процессе Дирихле. Начнем с палочки единичной длины и в каждой
шаг мы обламываем часть оставшейся палочки. Каждый раз мы связываем
длина куска палки к доле точек, попадающих в
группа смеси. В конце концов, чтобы представить бесконечную смесь, мы
связать последний оставшийся кусок палки с долей очков
которые не попадают во все остальные группы. Длина каждой части является случайной
переменная с вероятностью, пропорциональной параметру концентрации. Меньше
значения концентрации будут делить единицу длины на более крупные части
палочка (определяющая более концентрированное распределение). Большая концентрация
значения будут создавать меньшие части палки (увеличение количества
компоненты с ненулевыми весами).
Процесс ломания палки является генеративным
рассказ о процессе Дирихле. Начнем с палочки единичной длины и в каждой
шаг мы обламываем часть оставшейся палочки. Каждый раз мы связываем
длина куска палки к доле точек, попадающих в
группа смеси. В конце концов, чтобы представить бесконечную смесь, мы
связать последний оставшийся кусок палки с долей очков
которые не попадают во все остальные группы. Длина каждой части является случайной
переменная с вероятностью, пропорциональной параметру концентрации. Меньше
значения концентрации будут делить единицу длины на более крупные части
палочка (определяющая более концентрированное распределение). Большая концентрация
значения будут создавать меньшие части палки (увеличение количества
компоненты с ненулевыми весами).
Методы вариационного вывода для процесса Дирихле все еще работают
с конечным приближением к этой модели бесконечной смеси, но
вместо того, чтобы указывать априори, сколько компонентов нужно
использования, достаточно указать параметр концентрации и верхнюю границу
от числа компонентов смеси (эта верхняя граница, если предположить, что
больше, чем «истинное» количество компонентов, влияет только на алгоритмические
сложность, а не фактическое количество используемых компонентов).
Inderscience Publishers — связь академических кругов, бизнеса и промышленности посредством исследований
- Судоходство Турецкий талант
Согласно исследованию, опубликованному в Международном журнале судоходства и транспортной логистики , управление кадрами имеет решающее значение для успеха турецкой индустрии контейнерных перевозок. Исследование, проведенное Рамазаном Озканом Йилдизом, Седатом Бастугом и Сонером Эсмером из Технического университета Искендерун в Искендеруне, Хатай, Турция, открывает иллюминатор практики и предлагает новые идеи как для практиков, так и для исследователей. В работе предполагается, что понимание местного контекста и адаптация методов управления талантами могут помочь привлечь, удержать и развить хороших людей в отрасли с жесткой конкуренцией.
Команда провела обширный обзор литературы, собрала данные и провела интервью, чтобы помочь им определить функции управления талантами. По сути, их работа отходит от традиционного западного подхода и открывает новые каналы для понимания судоходной отрасли в контексте страны, расположенной на важной оси между востоком и западом.
 Исследование показывает, что управление талантами с точки зрения найма и обучения, оценки эффективности и развития карьеры заметно отличается от их аналогов в других местах. Различия возникают из-за культурных норм, динамики рынка труда и нормативных требований.
Исследование показывает, что управление талантами с точки зрения найма и обучения, оценки эффективности и развития карьеры заметно отличается от их аналогов в других местах. Различия возникают из-за культурных норм, динамики рынка труда и нормативных требований.Стратегии привлечения и удержания талантов должны быть тщательно разработаны, чтобы обеспечить наличие квалифицированной рабочей силы, способной справиться со сложностями мировой торговли и удовлетворить постоянно меняющиеся потребности клиентов по всему миру. Они должны сосредоточиться на развитии специальных навыков и знаний в области обработки контейнеров, логистических операций и управления цепочками поставок, которые имеют решающее значение для успеха бизнеса контейнерных перевозок.
Полученные данные могут иметь значение для компаний, не занимающихся контейнерными перевозками в Турции, поскольку они позволят компаниям увидеть, как они могут адаптироваться к местным условиям и идти полным ходом в своих предприятиях.

Йилдиз, Р.О., Бастуг, С. и Эсмер, С. (2023) «Функции управления талантами: качественное исследование в отрасли контейнерных перевозок», Int. J. Судоходство и транспортная логистика, Vol. 16, №№ 3/4, стр. 320–359.
DOI: 10.1504/IJSTL.2023.10049269 - Преодолеть ловушку бедности
Перед лицом климатического кризиса, который приносит с собой повторяющиеся экстремальные погодные условия по всему миру, новая работа в International Journal of Economics and Business Research своевременно. Исследование, проведенное Мулатом Гошу Гебейеху с факультета экономики Университета Дебре-Маркос в городе Дебре-Маркос, регион Амхара, Эфиопия, показывает, что политики и эксперты в области сельского хозяйства должны стремиться повысить эффективность методов адаптации и внедрять новые варианты, инфраструктуру и образование, чтобы помочь защитить сельские домохозяйства от разрушительных последствий изменчивости погоды, чтобы предотвратить попадание этих домохозяйств в хроническую бедность.

В настоящее время хорошо известно, что климатические потрясения, такие как засухи, могут иметь серьезные, пагубные, а иногда и длительные последствия для бедных или близких к бедности людей в развивающихся странах. Эфиопия является особенно уязвимой страной в этом отношении, особенно с учетом того, что экономика страны почти полностью поддерживается сельским хозяйством, которое, конечно же, проходит циклы подъема и спада вслед за экстремальными погодными условиями. Те хозяйства, в которых есть работники вне сельского хозяйства, в какой-то степени защищены от капризов погоды, но даже для них остается потребность в воспитании, поддержке и защите от бедности.
Гебейеху изучил взаимосвязь между экологическим стрессом, вариантами адаптации и динамикой бедности в Эфиопии. Он проанализировал данные за три года, собранные из 825 сельских домохозяйств в бассейне Нила в Эфиопии Центром исследований окружающей среды и климата Эфиопского научно-исследовательского института развития.
 Используя линейную модель с фиксированными эффектами, он обнаружил, что изменчивость погоды значительно влияет на благосостояние этих домохозяйств.
Используя линейную модель с фиксированными эффектами, он обнаружил, что изменчивость погоды значительно влияет на благосостояние этих домохозяйств.В частности, его анализ показал, что увеличение среднего количества осадков изначально оказывает положительное влияние на расходы домохозяйства на душу населения. Однако резкое увеличение среднего количества осадков, измеряемое квадратом среднего количества осадков, отрицательно сказывается на расходах. Он также показал, что аномалии осадков и температуры отрицательно сказываются на общих расходах на душу населения и расходах на продукты питания.
Интересно, что увеличение среднего количества осадков снижает вероятность того, что домохозяйства впадут в временную бедность. Напротив, повышение температуры увеличивает вероятность того, что домохозяйство попадет в состояние временной бедности, а затем и в хроническую бедность.
Гебейеху, М.Г. (2023) «Кто спасается от бедности? Понимание связи между экологическим стрессом, вариантами адаптации и динамикой бедности в Эфиопии», Int.
 J. Экономика и бизнес-исследования, Vol. 25, № 3, с. 309–329.
J. Экономика и бизнес-исследования, Vol. 25, № 3, с. 309–329.
DOI: 10.1504/IJEBR.2022.10038358 - Exergy Boost для энергетических напитков
ценность кисломолочного напитка кефир.
Считается, что кефир возник на Кавказе в Восточной Европе. Он производится путем сбраживания молока с помощью кефирных грибков, небольших желеобразных скоплений бактерий и дрожжей. Напиток острый и слегка шипучий, кремовой консистенции похож на йогурт, но с отчетливым вкусом. Польза кефира для здоровья обсуждается уже много лет. Это источник так называемых пробиотиков, полезных бактерий, которые, как считается, поддерживают здоровье пищеварительной системы. Он также содержит белок, кальций и другие питательные вещества.
Мустафа Озилген из отдела пищевой инженерии Университета Йедитепе в Стамбуле, Турция, обратился к концепции эксергии для изучения эффективности и культивирования в этом организме с целью оптимизации среды для выращивания и снабжения дрожжей пищей для получения максимального рост и кратчайшие сроки.

Эксергия — термин из термодинамики, связанный с энергией, энтальпией и энтропией. Он представляет собой максимальную полезную работу, которую система может выполнить при достижении равновесия с окружающей средой, принимая во внимание тепловые и механические компоненты. Обычно его описывают как меру способности энергии системы выполнять полезную работу и обычно обсуждают в контексте управления энергопотреблением, эффективности и устойчивости.
В этой работе Озилген оценил эффективность выращивания Kluyveromyces fragilis на различных типах систем, содержащих один из сахаров — глюкозу или лактозу, на органической или минимально неорганической среде. Он обнаружил, что, хотя наибольшее количество клеточной массы производилось на сложных органических средах, культивирование K. fragilis было более эксергетически эффективным на минимальной неорганической среде. Это различие можно объяснить явлением, известным как эффект Крэбтри. Эффект Крэбтри наблюдается у различных видов дрожжей и других микроорганизмов, у которых снижено дыхание и увеличена скорость брожения в присутствии высоких уровней глюкозы или других ферментируемых сахаров.
 Это приводит к предпочтительному использованию ферментации в качестве метаболического пути для производства энергии, даже в присутствии кислорода, который в противном случае использовался бы для дыхания, а не для производства клеточной массы.
Это приводит к предпочтительному использованию ферментации в качестве метаболического пути для производства энергии, даже в присутствии кислорода, который в противном случае использовался бы для дыхания, а не для производства клеточной массы.В работе Озилгена эффект Крэбтри снижает эффективность эксергии в присутствии глюкозы в органических средах, но не в минимальном количестве неорганических сред. Действительно, самая высокая эксергетическая эффективность, мера того, насколько эффективно используется энергия, составила 61,2% в минимальной неорганической среде с глюкозой, тогда как самая низкая эффективность 24% наблюдалась в минимальной органической среде с глюкозой. Это предполагает, что культивирование K. fragilis для использования в производстве кефира выиграет от использования глюкозы и минимального неорганического материала в культуральной среде для снижения общих затрат энергии. Стремление к устойчивости производства продуктов питания имеет важное значение в контексте загрязнения и изменения климата.
 Можно предположить, что это особенно касается пищевых продуктов, направленных на улучшение здоровья.
Можно предположить, что это особенно касается пищевых продуктов, направленных на улучшение здоровья.Özilgen, M. (2023) «Экзергетическая эффективность роста Kluyveromyces fragilis на сложных органических и минимальных неорганических средах», Int. Дж. Эксергия, Том. 40, № 3, стр. 336–346.
DOI: 10.1504/IJEX.2023.10055055 - Улучшение судоходства с помощью машинного обучения
Исследование, опубликованное в International Journal of Shipping and Transport Logistics , использовало новый подход машинного обучения, известный как MGGP, для ранжирования и определения приоритетов критериев эффективности при оценке страны. эффективность логистики с использованием Индекса эффективности логистики Всемирного банка (LPI). Сам LPI состоит из шести различных компонентов, которые измеряют и ранжируют эффективность международной логистики. Рассматриваемые компоненты: таможня, инфраструктура, простота организации поставок, качество логистических услуг, отслеживание и отслеживание, своевременность.

Команда из Турции в статье с открытым доступом в IJSTL объясняет, как подход MGGP может строить модели линейного или нелинейного прогнозирования. Команда использовала выборку наборов данных LPI с 2010 по 2018 год, состоящую из примерно 790 записей, для обучения своих моделей и проверки прогнозов, которые они могут делать, по сравнению с другими, не обучающими наборами данных.
Билал Бабайигит и Фейза Гюрбюз из Университета Эрджиес и Беррин Денижан из Университета Сакарья показали, что подход MGGP превосходит другие методы в прогнозировании показателя LPI. Более того, в то время как в предыдущих инструментах не изучалось относительное влияние каждого компонента LPI, этот новый подход позволяет выявить наиболее важные компоненты.
Команда обсуждает шесть компонентов в следующем контексте:
Таможня: Эффективность пограничного контроля. Инфраструктура необходима для таможенного оформления и перемещения товаров. Международные перевозки в отношении простоты организации поставок по конкурентоспособным ценам.
 Качество логистических услуг, которое позволяет выполнять поставщикам логистических услуг. Отслеживание и отслеживание для обеспечения бесперебойного движения товаров от источника до места назначения. Своевременность, мера графика и ожидаемого времени доставки.
Качество логистических услуг, которое позволяет выполнять поставщикам логистических услуг. Отслеживание и отслеживание для обеспечения бесперебойного движения товаров от источника до места назначения. Своевременность, мера графика и ожидаемого времени доставки.Команда предполагает, что прогнозы, созданные MGGP, могут стать бесценным инструментом для политиков и исследователей в области логистики, занимающихся разработкой более эффективных планов логистики. Таким образом, эта работа может иметь важные последствия для мировой торговли и экономического развития, позволяя принимать более обоснованные решения в области логистической политики и планирования. Это может привести к повышению эффективности логистики на международном уровне и, возможно, даже к сокращению энергопотребления и выбросов.
Бабайигит, Б., Гюрбюз, Ф. и Денижан, Б. (2023) «Оценка индекса эффективности логистики с помощью искусственного интеллекта», Int. J. Судоходство и транспортная логистика, Vol.
 16, №№ 3/4, стр. 360–371.
16, №№ 3/4, стр. 360–371.
DOI: 10.1504/IJSTL.2022.10044449 - Сжатие энергии в промышленности
Промышленный Интернет вещей (IIoT) относится к множеству подключенных устройств и датчиков, используемых в промышленных условиях, таких как производственные предприятия, транспортные системы и энергетические сети. Эти устройства могут собирать данные и обмениваться ими с целью повышения эффективности, производительности и безопасности систем, в которых они используются, а иногда и за их пределами.
Устройства IIoT обычно предназначены для мониторинга и контроля различных аспектов производственных процессов, таких как производительность машин, уровни запасов, энергопотребление и условия окружающей среды. Собранные данные можно обрабатывать с помощью обычных статистических инструментов или анализировать с помощью искусственного интеллекта для выявления тенденций и закономерностей и прогнозирования того, как изменения различных параметров могут повлиять на результаты с целью оптимизации различных производственных процессов.

В целом мы видим, что IIoT является важной частью оцифровки и автоматизации промышленности, которая оказывает все большее влияние на экономику и общество.
Но есть проблема.
Несмотря на то, что IIoT будет иметь решающее значение для повышения эффективности и устойчивости производства в различных отраслях, в настоящее время он использует Wi-Fi для подключения (стандарт IEEE 802.11), а Wi-Fi может потреблять много энергии из-за размера устройства. пакеты данных, отправленные туда и обратно, и максимальная единица передачи (MTU).
Исследователи из Бразилии исследовали сжатие данных как возможное решение этой проблемы. Статья в International Journal of Embedded Systems команда описывает два новых метода, которые, по их мнению, могут значительно сократить объем данных, отправляемых устройствами IIoT. Их методы используют сжатие данных для минимизации размера передаваемых пакетов и MTU. Первый метод предполагает использование настроенного бинарного дерева Хаффмана.
 Этот подход анализирует частоту символов в потоке данных и назначает каждому код переменной длины таким образом, чтобы минимизировать общее количество битов, необходимых для представления данных. Второй метод использует алгоритм Лемпеля-Зива-Велча с гибким словарем. Этот алгоритм сжатия данных без потерь работает, идентифицируя повторяющиеся шаблоны или последовательности данных в заданном потоке данных и заменяя эти последовательности более короткими кодами.
Этот подход анализирует частоту символов в потоке данных и назначает каждому код переменной длины таким образом, чтобы минимизировать общее количество битов, необходимых для представления данных. Второй метод использует алгоритм Лемпеля-Зива-Велча с гибким словарем. Этот алгоритм сжатия данных без потерь работает, идентифицируя повторяющиеся шаблоны или последовательности данных в заданном потоке данных и заменяя эти последовательности более короткими кодами.Эксперименты группы с этими методами сжатия показывают, что они могут снизить потребление энергии на 8% по сравнению с существующими решениями для IIoT. Производственное предприятие, использующее в настоящее время систему IIoT, может ежемесячно потреблять 1000 киловатт-часов (кВтч) энергии. При использовании предлагаемых методов сжатия данных потребление энергии снижается на 8%, что может привести к ежемесячной экономии около 1 мегаватт-часа в год, что эквивалентно потреблению энергии сотнями типичных домов в развитых странах.

Сильва, М. В., Моска, Э. Э. и Гомеш, Р. Л. (2022) «Зеленый промышленный интернет вещей посредством сжатия данных», Int. J. Встроенные системы, Vol. 15, № 6, стр. 457–466.
DOI: 10.1504/IJES.2022.10055057 - Машинное обучение прогнозирует качество воды
Исследование, опубликованное в Международном журнале устойчивого управления сельским хозяйством и информатики , продемонстрировало, как машинное обучение можно использовать для прогнозирования индекса качества воды. Эта работа может иметь последствия для будущего управления водными ресурсами при питьевом водоснабжении и сельскохозяйственном использовании.
В последние годы вызывает беспокойство ухудшение качества воды, поскольку его влияние на здоровье человека и сельскохозяйственное производство привлекает повышенное внимание. Действительно, на момент написания статьи загрязнение рек и прибрежных вод, вызванное ненадлежащим сбросом неочищенных сточных вод, занимало важное место в экологической повестке дня, в то время как сельскохозяйственные вопросы, связанные с водной безопасностью, всегда были на повестке дня.

Для определения качества воды используются различные факторы, такие как кислотность и щелочность, уровень pH, мутность, растворенный кислород, содержание нитратов, температура и наличие фекальных микробов. Поэтому крайне важно разработать эффективные методы прогнозирования качества воды для мониторинга и контроля загрязнения.
Ахмад Дебоу, Самаа Швейкани и Кадан Алджумаа из Высшего института прикладных наук и технологий (HIAST) в Дамаске, Сирия, разработали модели LSTM с четырьмя стопками для прогнозирования WQI. LSTM с 4 стеками (длинная кратковременная память) — это тип рекуррентной нейронной сети, которая может находить долгосрочные закономерности в данных, которые меняются с течением времени. Такие модели, проанализировав данные, могут затем делать прогнозы о том, как эти данные могут измениться в будущем. Накладывая четыре слоя LSTM друг на друга, модель лучше находит нюансы в данных.
Чтобы подготовить данные и выбрать объекты для анализа, команда использовала различные алгоритмы, в том числе K-NN (K ближайших соседей) и среднегодовое значение.
 K-NN — это хорошо известный алгоритм, используемый в машинном обучении для задач классификации и регрессии. Это непараметрический алгоритм, который не делает никаких предположений о базовом распределении данных. Основная идея, лежащая в основе K-NN, состоит в том, чтобы классифицировать новые точки данных на основе сходства между ближайшими соседями в обучающем наборе данных.
K-NN — это хорошо известный алгоритм, используемый в машинном обучении для задач классификации и регрессии. Это непараметрический алгоритм, который не делает никаких предположений о базовом распределении данных. Основная идея, лежащая в основе K-NN, состоит в том, чтобы классифицировать новые точки данных на основе сходства между ближайшими соседями в обучающем наборе данных.Успех команды с этими моделями в воспроизведении известных данных служит хорошим предзнаменованием для реальных прогнозов и может внести важный вклад в усилия по управлению водными ресурсами. Это должно позволить принимать более активные меры для минимизации загрязнения воды как для потребления человеком, так и для сельскохозяйственных нужд на основе прогнозов, сделанных моделями.
Дебоу А., Швейкани С. и Алджумаа К. (2023) «Прогнозирование и прогнозирование качества воды с использованием глубокого обучения», Int. J. Устойчивое управление сельским хозяйством и информатика, Vol. 9, № 2, стр.
 114–135.
114–135.
DOI: 10.1504/IJSAMI.2022.10051380 - ИИ разоблачает неисправности СИЗ
Медицинские средства индивидуальной защиты (СИЗ) необходимы для борьбы с инфекционными заболеваниями, что стало очевидным во время пандемии. Правительства и организации в пострадавших районах обычно рекомендуют носить медицинские СИЗ, включая хирургические маски, перчатки и лицевые щитки, особенно в людных местах. Однако для обеспечения того, чтобы медицинский персонал в сильно пострадавших районах соблюдал рекомендации, необходимы средства для мониторинга в режиме реального времени использования СИЗ.
В статье International Journal of Sensor Networks группа из Китая разработала систему, основанную на машинном обучении, которая может определять, носит ли персонал необходимые СИЗ. Этот подход использует глубокие нейронные сети (DNN) для обнаружения объектов в реальных сценариях.
Jianlou Lou, Xiangyu Li, Guang Huo, Feng Liang, Zhaoyang Qu и Ndagijimana Kwihangano Soleil из Северо-восточного электроэнергетического университета в Цзилине и Tianrui Lou из Университета Гуанчжоу использовали два новых модуля: Deformable и Attention Residual с 50 слоями ( DAR50) и модуль объединения функций Criss-Cross Feature Pyramid Network (CCFPN), чтобы решить две ключевые проблемы, которые до сих пор ограничивали производительность при обнаружении PPE.
 Таким образом, они преодолели проблемы помех от фоновой информации и масштабов целей обнаружения, которые различаются по размеру.
Таким образом, они преодолели проблемы помех от фоновой информации и масштабов целей обнаружения, которые различаются по размеру.Объединив два модуля, исследователи смогли создать сеть обнаружения объектов, регионы на основе внимания и многомасштабного слияния со сверточной нейронной сетью (AMS R-CNN). Их тесты с медицинскими СИЗ и наборами данных Visual Object Classes Challenge 2007 (VOC 2007) показали, что их система работает лучше, чем различные современные методы.
Разработка AMS R-CNN может принести пользу тем, кто управляет медицинскими работниками, и помочь обеспечить соблюдение правил СИЗ с целью сведения к минимуму риска передачи инфекционных заболеваний. Медицинский персонал, работающий в условиях повышенного риска, например, в больницах и лабораториях, сам выиграет от усиленной защиты со стороны коллег, что повысит общую безопасность, а также снизит риск для пациентов.
В работе подчеркивается потенциал глубоких нейронных сетей, которые революционизируют способы обнаружения объектов.
 Точность можно повысить только за счет дальнейшего совершенствования этой технологии.
Точность можно повысить только за счет дальнейшего совершенствования этой технологии.Лу, Дж., Ли, X., Хо, Г., Лян, Ф., Цюй, З., Лу, Т. и Солей, Н.К. (2023) «Обнаружение медицинских средств индивидуальной защиты на основе механизма внимания и многомасштабного слияния», Int. J. Сенсорные сети, Vol. 41, № 3, стр. 189–203.
DOI: 10.1504/IJSNET.2022.10052844 - Шаг в сторону лечения фантомной боли в конечностях
Исследование, опубликованное в Международном журнале биомедицинской инженерии и технологии , выявило многообещающую область исследований для лечения фантомной боли в конечностях, часто встречающейся у людей с ампутированными конечностями, лечение которой может быть сложным. Исследование сосредоточено на людях с трансгуморальной ампутацией, у которых отсутствует значительная часть одной или обеих рук.
Фантомная боль в конечностях — это явление, возникающее у людей, которым была частично или полностью ампутирована конечность. Несмотря на потерю конечности, люди могут испытывать такие ощущения, как боль, зуд и покалывание, как будто отсутствующая конечность все еще является частью их тела.
 Это может быть стойкое и мучительное состояние, которое оказывает значительное и пагубное влияние на качество жизни.
Это может быть стойкое и мучительное состояние, которое оказывает значительное и пагубное влияние на качество жизни.В исследовании, проведенном группой исследователей из Соединенного Королевства, использовалась теория управления моторикой человека и гомункулус Пенфилда, чтобы предоставить всесторонний обзор и новый взгляд на фантомные ощущения и боль в конечностях, а также потенциал для терапии и протезирования. Контрольные эксперименты были проведены в клинике с интактными людьми с использованием ультразвукового изображения вдоль кости плеча, плечевой кости, в то время как участников проинструктировали производить различные движения руками.
Теория управления моторикой человека фокусируется на том, как мозг и нервная система контролируют движение тела. Он направлен на понимание процессов и механизмов, связанных с планированием, выполнением и контролем движения, начиная от простых действий, таких как потягивание объекта, до сложных действий, таких как игра на музыкальном инструменте.
 Знаменитый гомункул Пенфилда представляет собой неврологическую «карту» человеческого тела, разработанную в 1930-х годах. Он представляет области мозга, которые контролируют движения и ощущения различных частей тела, при этом руки и лицо представлены более подробно и в большем масштабе.
Знаменитый гомункул Пенфилда представляет собой неврологическую «карту» человеческого тела, разработанную в 1930-х годах. Он представляет области мозга, которые контролируют движения и ощущения различных частей тела, при этом руки и лицо представлены более подробно и в большем масштабе.Эджай Нсугбе из Исследовательской лаборатории Нсугбе в Суиндоне и радиолог Кэрол Филлипс из Университетской больницы Бристоля, Великобритания, обнаружили, что вдоль плечевой кости можно обнаружить сложные движения жестов, которые включают в себя массовое задействование мышц. Это открытие может иметь большое значение для протезистов клинической реабилитации, которые могут использовать эти жесты для изучения подвижности и ощущения фантомных конечностей. Работа может иметь значение для людей, борющихся с фантомной болью в конечностях, и может предоставить новый путь для терапии, а также привести к улучшению конструкции протезов, чтобы сделать их более чувствительными к потребностям пользователя.
Существуют предпосылки для разработки более эффективных методов лечения фантомных болей в конечностях, таких как физиотерапия или медикаментозное лечение, которые могут улучшить качество жизни людей с ампутированными конечностями.
 Кроме того, получив лучшее понимание основных механизмов фантомной боли в конечностях, исследователи смогут определить новые цели для разработки лекарств, что в конечном итоге приведет к лучшему обезболиванию у тех, кто испытывает это состояние.
Кроме того, получив лучшее понимание основных механизмов фантомной боли в конечностях, исследователи смогут определить новые цели для разработки лекарств, что в конечном итоге приведет к лучшему обезболиванию у тех, кто испытывает это состояние.Nsugbe, E. and Philips, C. (2023) «Понимание фантомных ощущений и применение ультразвуковой визуализации для изучения движений жестов для трансгумерального протеза», Int. J. Биомедицинская инженерия и технология, Vol. 41, № 3, стр. 258–271.
DOI: 10.1504/IJBET.2023.10055089 - Разумное сельское хозяйство в развивающихся странах с помощью Интернета вещей
Интернет вещей (IoT) можно описать как свободную сеть физических устройств, в которые могут быть встроены датчики, программное обеспечение и подключение. Хотя целостный подход рассматривает IoT как все устройства в мире с подключением к Интернету, часто бывает так, что эти портативные или удаленные устройства доступны в кластерах или вокруг концентраторов со специализированным доступом и приложениями.
 Тем не менее, устройства в IoT могут собирать и обмениваться данными с другими устройствами или системами через Интернет.
Тем не менее, устройства в IoT могут собирать и обмениваться данными с другими устройствами или системами через Интернет.Устройства IoT могут варьироваться от повседневных потребительских устройств, таких как смартфоны, бытовая техника, такая как холодильники, камеры видеонаблюдения и носимые мониторы, и устройства для фитнеса, до промышленного оборудования и инфраструктуры в умных городах, заводах и транспортных системах. Данные, генерируемые этими объектами, можно анализировать и использовать для получения информации, автоматизации процессов и улучшения процесса принятия решений в различных отраслях и областях.
Исследование в International Journal of Cloud Computing рассмотрел необходимость улучшения технологий, связанных с управлением базами данных, чтобы иметь возможность лучше обрабатывать большие объемы данных, генерируемых Интернетом вещей. В статье основное внимание уделяется использованию технологии IoT в социальной и сельскохозяйственной сферах в сельских секторах.
 В этом контексте необходимы улучшения, которые могли бы принести пользу мониторингу, условиям и методам ведения сельского хозяйства. Если бы можно было обеспечить и реализовать адаптивные, эффективные удаленные и логистические операции с использованием устройств IoT, таких как приводы и клапаны, то динамическая интеграция могла бы улучшить различные процессы в сельском хозяйстве, такие как своевременное орошение. Это позволит, например, сэкономить на воде, а также оптимизировать ирригацию для повышения урожайности в зависимости от меняющихся погодных и других условий.
В этом контексте необходимы улучшения, которые могли бы принести пользу мониторингу, условиям и методам ведения сельского хозяйства. Если бы можно было обеспечить и реализовать адаптивные, эффективные удаленные и логистические операции с использованием устройств IoT, таких как приводы и клапаны, то динамическая интеграция могла бы улучшить различные процессы в сельском хозяйстве, такие как своевременное орошение. Это позволит, например, сэкономить на воде, а также оптимизировать ирригацию для повышения урожайности в зависимости от меняющихся погодных и других условий.Тот же анализ данных IoT может позволить контролировать активность вредителей и рост сорняков и, таким образом, позволить более разумно применять пестициды и гербициды или даже позволить фермеру вообще избежать их использования, своевременно используя альтернативы.
Здзислав Полковски из Университета Яна Выжиковского в Польковицах, Польша, и его коллеги в Индии отмечают, что фермеры в развивающихся странах сталкиваются с множеством ограничений и проблем.
 Однако там, где технологии могут помочь тем, кто живет в развитом мире, они также могут улучшить практику и условия в развивающемся мире.
Однако там, где технологии могут помочь тем, кто живет в развитом мире, они также могут улучшить практику и условия в развивающемся мире.Полковски З., Мишра С.К., Мишра Б.К., Бора С. и Моханти А. (2023) «Влияние Интернета вещей на социальные и сельскохозяйственные сферы в сельском секторе: тематическое исследование», Int. . J. Облачные вычисления, Vol. 12, № 1, стр. 90–105.
DOI: 10.1504/IJCC.2023.10054989 - Нанотехнологии дают импульс сельскому хозяйству0253 Международный журнал нанотехнологий .
Наночастицы — это крошечные частицы, диаметр которых может варьироваться от 1 до 100 нанометров, иногда немного больше. Металлические наночастицы размером менее 1 нанометра считаются атомными кластерами. Частицы размером более 500 нанометров обычно рассматриваются как микрочастицы, если только они не являются нанотрубками или волокнами, которые могут быть длиннее, но имеют наноскопическое поперечное сечение. Наноскопичность придает частице уникальные свойства по сравнению с атомными кластерами или более крупными частицами.
 Как таковые, они широко исследовались во многих различных секторах, включая материаловедение, инженерию, медицину и сельское хозяйство.
Как таковые, они широко исследовались во многих различных секторах, включая материаловедение, инженерию, медицину и сельское хозяйство.Учитывая, что медь является важным питательным веществом для роста растений, обсуждалась идея о том, что наночастицы меди или, точнее, оксида меди (НЧ CuO) могут обладать полезными свойствами, помогающими растениям легко усваивать минерал и, таким образом, лучше расти. Физик Али Раза из Сельскохозяйственного университета в Фейсалабаде, Пенджаб, Пакистан, и его коллеги исследовали влияние дозирования среды для выращивания проростков кукурузы Cuo NPS. Исследователи хотели увидеть, насколько хорошо НЧ CuO могут проникать в растения и перемещаться по ним, и повлияют ли они на рост проростков кукурузы. Им также нужно было знать, будут ли наночастицы этого типа токсичными. Наночастицы металлической меди, в отличие от НЧ CuO, могут оказывать положительное влияние на прорастание семян, но фитотоксичны для растущей пшеницы, Triticum aestivum, проростков.


 Сумма 2х матриц одинакового размера
назыв матрица С=А+В, эл-ты которой
cij=aij+bij
Сумма 2х матриц одинакового размера
назыв матрица С=А+В, эл-ты которой
cij=aij+bij Это выберет первый центр случайным образом из данных. Последующие центры будут
выбран из взвешенного распределения данных в пользу точек, находящихся дальше от
действующие центры. k-means++ — это инициализация по умолчанию для k-means, поэтому будет
быстрее, чем выполнение полного k-средних, но все же может занять значительное количество времени.
время для больших наборов данных со многими компонентами.
Это выберет первый центр случайным образом из данных. Последующие центры будут
выбран из взвешенного распределения данных в пользу точек, находящихся дальше от
действующие центры. k-means++ — это инициализация по умолчанию для k-means, поэтому будет
быстрее, чем выполнение полного k-средних, но все же может занять значительное количество времени.
время для больших наборов данных со многими компонентами. Концентрация предшествующего анализа вариации байесовской гауссовой смеси
для примера построения эллипсоидов доверия для
Концентрация предшествующего анализа вариации байесовской гауссовой смеси
для примера построения эллипсоидов доверия для 

 Исследование показывает, что управление талантами с точки зрения найма и обучения, оценки эффективности и развития карьеры заметно отличается от их аналогов в других местах. Различия возникают из-за культурных норм, динамики рынка труда и нормативных требований.
Исследование показывает, что управление талантами с точки зрения найма и обучения, оценки эффективности и развития карьеры заметно отличается от их аналогов в других местах. Различия возникают из-за культурных норм, динамики рынка труда и нормативных требований.

 Используя линейную модель с фиксированными эффектами, он обнаружил, что изменчивость погоды значительно влияет на благосостояние этих домохозяйств.
Используя линейную модель с фиксированными эффектами, он обнаружил, что изменчивость погоды значительно влияет на благосостояние этих домохозяйств. J. Экономика и бизнес-исследования, Vol. 25, № 3, с. 309–329.
J. Экономика и бизнес-исследования, Vol. 25, № 3, с. 309–329. 
 Это приводит к предпочтительному использованию ферментации в качестве метаболического пути для производства энергии, даже в присутствии кислорода, который в противном случае использовался бы для дыхания, а не для производства клеточной массы.
Это приводит к предпочтительному использованию ферментации в качестве метаболического пути для производства энергии, даже в присутствии кислорода, который в противном случае использовался бы для дыхания, а не для производства клеточной массы. Можно предположить, что это особенно касается пищевых продуктов, направленных на улучшение здоровья.
Можно предположить, что это особенно касается пищевых продуктов, направленных на улучшение здоровья.
 Качество логистических услуг, которое позволяет выполнять поставщикам логистических услуг. Отслеживание и отслеживание для обеспечения бесперебойного движения товаров от источника до места назначения. Своевременность, мера графика и ожидаемого времени доставки.
Качество логистических услуг, которое позволяет выполнять поставщикам логистических услуг. Отслеживание и отслеживание для обеспечения бесперебойного движения товаров от источника до места назначения. Своевременность, мера графика и ожидаемого времени доставки. 16, №№ 3/4, стр. 360–371.
16, №№ 3/4, стр. 360–371. 
 Этот подход анализирует частоту символов в потоке данных и назначает каждому код переменной длины таким образом, чтобы минимизировать общее количество битов, необходимых для представления данных. Второй метод использует алгоритм Лемпеля-Зива-Велча с гибким словарем. Этот алгоритм сжатия данных без потерь работает, идентифицируя повторяющиеся шаблоны или последовательности данных в заданном потоке данных и заменяя эти последовательности более короткими кодами.
Этот подход анализирует частоту символов в потоке данных и назначает каждому код переменной длины таким образом, чтобы минимизировать общее количество битов, необходимых для представления данных. Второй метод использует алгоритм Лемпеля-Зива-Велча с гибким словарем. Этот алгоритм сжатия данных без потерь работает, идентифицируя повторяющиеся шаблоны или последовательности данных в заданном потоке данных и заменяя эти последовательности более короткими кодами.

 K-NN — это хорошо известный алгоритм, используемый в машинном обучении для задач классификации и регрессии. Это непараметрический алгоритм, который не делает никаких предположений о базовом распределении данных. Основная идея, лежащая в основе K-NN, состоит в том, чтобы классифицировать новые точки данных на основе сходства между ближайшими соседями в обучающем наборе данных.
K-NN — это хорошо известный алгоритм, используемый в машинном обучении для задач классификации и регрессии. Это непараметрический алгоритм, который не делает никаких предположений о базовом распределении данных. Основная идея, лежащая в основе K-NN, состоит в том, чтобы классифицировать новые точки данных на основе сходства между ближайшими соседями в обучающем наборе данных. 114–135.
114–135.  Таким образом, они преодолели проблемы помех от фоновой информации и масштабов целей обнаружения, которые различаются по размеру.
Таким образом, они преодолели проблемы помех от фоновой информации и масштабов целей обнаружения, которые различаются по размеру. Точность можно повысить только за счет дальнейшего совершенствования этой технологии.
Точность можно повысить только за счет дальнейшего совершенствования этой технологии. Это может быть стойкое и мучительное состояние, которое оказывает значительное и пагубное влияние на качество жизни.
Это может быть стойкое и мучительное состояние, которое оказывает значительное и пагубное влияние на качество жизни. Знаменитый гомункул Пенфилда представляет собой неврологическую «карту» человеческого тела, разработанную в 1930-х годах. Он представляет области мозга, которые контролируют движения и ощущения различных частей тела, при этом руки и лицо представлены более подробно и в большем масштабе.
Знаменитый гомункул Пенфилда представляет собой неврологическую «карту» человеческого тела, разработанную в 1930-х годах. Он представляет области мозга, которые контролируют движения и ощущения различных частей тела, при этом руки и лицо представлены более подробно и в большем масштабе. Кроме того, получив лучшее понимание основных механизмов фантомной боли в конечностях, исследователи смогут определить новые цели для разработки лекарств, что в конечном итоге приведет к лучшему обезболиванию у тех, кто испытывает это состояние.
Кроме того, получив лучшее понимание основных механизмов фантомной боли в конечностях, исследователи смогут определить новые цели для разработки лекарств, что в конечном итоге приведет к лучшему обезболиванию у тех, кто испытывает это состояние. Тем не менее, устройства в IoT могут собирать и обмениваться данными с другими устройствами или системами через Интернет.
Тем не менее, устройства в IoT могут собирать и обмениваться данными с другими устройствами или системами через Интернет.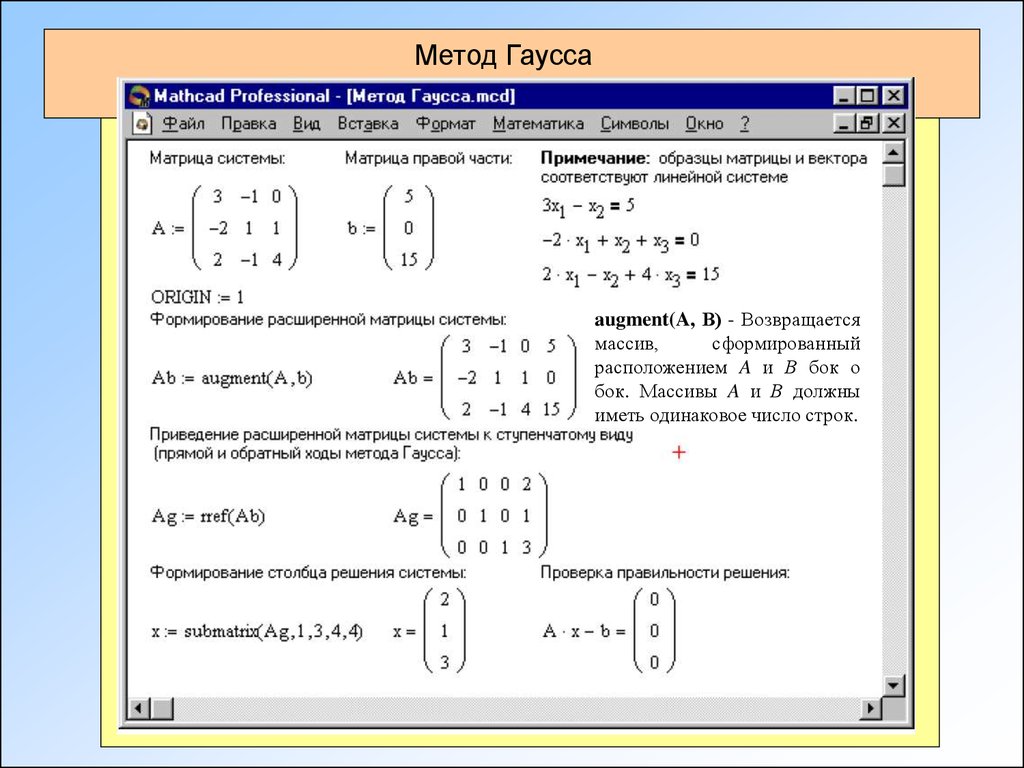 В этом контексте необходимы улучшения, которые могли бы принести пользу мониторингу, условиям и методам ведения сельского хозяйства. Если бы можно было обеспечить и реализовать адаптивные, эффективные удаленные и логистические операции с использованием устройств IoT, таких как приводы и клапаны, то динамическая интеграция могла бы улучшить различные процессы в сельском хозяйстве, такие как своевременное орошение. Это позволит, например, сэкономить на воде, а также оптимизировать ирригацию для повышения урожайности в зависимости от меняющихся погодных и других условий.
В этом контексте необходимы улучшения, которые могли бы принести пользу мониторингу, условиям и методам ведения сельского хозяйства. Если бы можно было обеспечить и реализовать адаптивные, эффективные удаленные и логистические операции с использованием устройств IoT, таких как приводы и клапаны, то динамическая интеграция могла бы улучшить различные процессы в сельском хозяйстве, такие как своевременное орошение. Это позволит, например, сэкономить на воде, а также оптимизировать ирригацию для повышения урожайности в зависимости от меняющихся погодных и других условий. Однако там, где технологии могут помочь тем, кто живет в развитом мире, они также могут улучшить практику и условия в развивающемся мире.
Однако там, где технологии могут помочь тем, кто живет в развитом мире, они также могут улучшить практику и условия в развивающемся мире. Как таковые, они широко исследовались во многих различных секторах, включая материаловедение, инженерию, медицину и сельское хозяйство.
Как таковые, они широко исследовались во многих различных секторах, включая материаловедение, инженерию, медицину и сельское хозяйство.