Сложение и вычитание матриц.
Навигация по странице:
- Сложение матриц
- Вычитание матриц
- Свойства сложения и вычитания матриц
- Примеры сложения и вычитания матриц
Онлайн калькулятор. Сложение и вычитание матриц.
Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.
Определение.
Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:
сij = aij + bij
Определение.
Вычитание матриц (разность матриц) A – B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц
сij = aij – bij
Свойства сложения и вычитания матриц
- Ассоциативность: (A + B) + C = A + (B + C)
- A + Θ = Θ + A = A, где Θ – нулевая матрица
- A – A = Θ
- Коммутативность: A + B = B + A
Примеры задач на сложение и вычитание матриц
Пример 1.
| Найти сумму матриц A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 |
| A + B = | 4 | 2 | + | 3 | 1 | = | 4 + 3 | 2 + 1 | = | 7 | 3 | ||||||||
| 9 | 0 | -3 | 4 | 9 + (-3) | 0 + 4 | 6 | 4 |
Пример 2
| Найти разность матриц A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 |
Решение:
| A – B = | 4 | 2 | – | 3 | 1 | = | 4 – 3 | 2 – 1 | = | 1 | 1 | ||||||||
| 9 | 0 | -3 | 4 | 9 – (-3) | 0 – 4 | 12 | -4 |
Пример 3
| Найти значение матрицы С = 2A + 3B, если A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 | |||||||
| 4 | -6 | 9 | 1 |
Решение:
| C = 2A + 3B = 2 | 4 | 2 | + 3 | 3 | 1 | = | 2·4 + 3·3 | 2·2 + 3·1 | = | 17 | 7 | ||||||||
| 9 | 0 | -3 | 4 | 2·9 + 3·(-3) | 2·0 + 3·4 | 9 | 12 | ||||||||||||
| 4 | -6 | 9 | 1 | 2·4 + 3·9 | 2·(-6) + 3·1 | 35 | -9 |
Онлайн калькуляторы с матрицами.
Упражнения с матрицами.
Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Сложение матриц в Python | Сложение двух матриц
Здравствуйте программисты, сегодняшняя статья посвящена matrix addition в python. Мы обсудим различные способы добавления двух матриц в python. Сложение матриц в python означает сложение элементов одной матрицы с другой. Затем суммированные элементы сохраняются в третьей матрице.
Matrix addition в Python-это метод, с помощью которого вы можете добавить две матрицы одинаковой формы. Если матрицы не имеют одинаковой формы, сложение будет невозможно. Более того, сложение в матрицах работает одним способом, а это означает, что элемент (1,1) будет добавляться только к элементу (1, 1) другой матрицы.
Если матрицы не имеют одинаковой формы, сложение будет невозможно. Более того, сложение в матрицах работает одним способом, а это означает, что элемент (1,1) будет добавляться только к элементу (1, 1) другой матрицы.
Прежде чем мы начнем с различных способов сложения матриц, позвольте мне просто привести пример сложения матриц для вас.
Пусть A и B-две матрицы, которые добавляются, и результат сохраняется в новой матрице C.
A = [ [1, 2, 3],
[4, 5, 6] ]
B = [ [6, 5, 4],
[3, 2, 1] ]
C = [ [7, 7, 7],
[7, 7, 7] ]Элементы матрицы C являются суммой элементов матриц A и B, т. е.,
е.,
[ [1+6, 2+5, 3+4], [4+3, 5+2, 6+1] ]
Различные способы сложения матриц в python:
- Использование вложенного цикла for
- Использование понимания вложенных списков
- С помощью функции sum и zip()
- Использование NumPy
Добавление матрицы с использованием вложенного цикла for
ПРИМЕР:
A = [[1,2,3], [4,5,6], [7 ,8,9]] B = [[9,8,7], [6,5,4], [3,2,1]] result = [[0,0,0], [0,0,0], [0,0,0]] # iterate through rows for i in range(len(A)): # iterate through columns for j in range(len(A[0])): [i][j] + B[i][j] for x in result: print(x)
ВЫХОД:
[10,10,10] [10,10,10] [10,10,10]
ОБЪЯСНЕНИЕ:
В этом примере вложенные циклы for используются для итерации по каждой строке и столбцам заданных матриц. После каждой итерации мы добавляем соответствующие элементы матрицы A и B . И сохраните сумму в третьей матрице, называемой result.
После каждой итерации мы добавляем соответствующие элементы матрицы A и B . И сохраните сумму в третьей матрице, называемой result.
Использование метода понимания вложенного списка
ПРИМЕР:
A = [[1,2,3],
[4 ,5,6],
[7 ,8,9]]
B = [[9,8,7],
[6,5,4],
[3,2,1]]
result = [[A[i][j] + B[i][j] for j in range
(len(A[0]))] for i in range(len(A))]
for r in result:
print(r)ВЫХОД:
[10,10,10] [10,10,10] [10,10,10]
ОБЪЯСНЕНИЕ:
Понимание списка означает вложенный список, то есть список внутри списка. Этот метод используется для реализации матрицы в виде вложенного списка. В этом примере понимание списка используется для href=”https://www.w3schools.com/python/python_iterators.asp”>итерация через каждый элемент заданных матриц. Метод понимания списка сложения матриц в python помогает писать краткие и точечные коды. Таким образом, это делает коды сложения матриц более простыми и полезными. href=”https://www.w3schools.com/python/python_iterators.asp”>итерация через каждый элемент заданных матриц. Метод понимания списка сложения матриц в python помогает писать краткие и точечные коды. Таким образом, это делает коды сложения матриц более простыми и полезными.
Этот метод используется для реализации матрицы в виде вложенного списка. В этом примере понимание списка используется для href=”https://www.w3schools.com/python/python_iterators.asp”>итерация через каждый элемент заданных матриц. Метод понимания списка сложения матриц в python помогает писать краткие и точечные коды. Таким образом, это делает коды сложения матриц более простыми и полезными. href=”https://www.w3schools.com/python/python_iterators.asp”>итерация через каждый элемент заданных матриц. Метод понимания списка сложения матриц в python помогает писать краткие и точечные коды. Таким образом, это делает коды сложения матриц более простыми и полезными.
Сложение матриц с помощью функции Sum и zip()
ПРИМЕР:
A = [[1,2,3], [4 ,5,6], [7 ,8,9]] B = [[9,8,7], [6,5,4], [3,2,1]] result = [map(sum, zip(*i)) for i in zip(X, Y)] print(result)
ВЫХОД:
[[10, 10, 10], [10, 10, 10], [10, 10, 10]]
ОБЪЯСНЕНИЕ:
Функция zip() состоит в том, чтобы принять итератор каждого элемента матрицы, сопоставить их и добавить с помощью функции sum (). Он возвращает и сохраняет результат в форме отображения.
Он возвращает и сохраняет результат в форме отображения.
Сложение матриц с помощью NumPy
ПРИМЕР:
import numpy as np
import random
# Routine for printing a 2x2 matrix
def PrintMatrix(matrix_in):
for x in range(0, matrix_in.shape[0]):
for y in range(0, matrix_in.shape[1]):
print("%d \t"%(matrix_in[x][y]),
if(y%3>1):
print("\n")
# Function to populate a 2x2 matrix with random data
def FillMatrix(matrix_in):
for x in range(0, matrix_in.shape[0]):
for y in range(0, matrix_in.shape[1]):.randrange(2, 10) + 2
# Create matrices using ndarray
.ndarray((3,3)).ndarray((3,3))
# Fill the matrices i.e., the two dimensional arrays created using ndarray objects
FillMatrix(matrix1)
FillMatrix(matrix2)
# Add two matrices - two nd arrays
. __add__(matrix2)
# Print Matrix1
print("Matrix1:")
PrintMatrix(matrix1)
# Print Matrix2
print("Matrix2:")
PrintMatrix(matrix2)
# Print the results of adding two matrices
print("Result of adding Matrix1 and Matrix2:")
PrintMatrix(add_results)
__add__(matrix2)
# Print Matrix1
print("Matrix1:")
PrintMatrix(matrix1)
# Print Matrix2
print("Matrix2:")
PrintMatrix(matrix2)
# Print the results of adding two matrices
print("Result of adding Matrix1 and Matrix2:")
PrintMatrix(add_results)ВЫХОД:
Matrix1: [1 2 3 4 5 6 7 8 9] Matrix2: [9 8 7 6 5 4 3 2 1] Result of adding Matrix1 and Matrix2: [10 10 10 10 10 10 10 10 10]
ОБЪЯСНЕНИЕ:
Первое условие для добавления двух матриц состоит в том, что обе матрицы должны иметь одинаковое количество строк и столбцов. Полученный таким образом результат также имеет такое же количество строк и столбцов. ndarray модуля NumPy помогает создать матрицу. Метод __add__ (), предоставляемый ndarray модуля NumPy, выполняет сложение матрицы . Функция __add__ () добавляет два объекта ndarray одинаковой формы и возвращает сумму в виде другого объекта ndarrayobject.
Метод __add__ (), предоставляемый ndarray модуля NumPy, выполняет сложение матрицы . Функция __add__ () добавляет два объекта ndarray одинаковой формы и возвращает сумму в виде другого объекта ndarrayobject.
Должен Читать
- Введение в Python Super С примерами
- Функция Справки Python
- Почему Python sys.exit лучше других функций выхода?
- Python Bitstring: Классы и другие примеры | Модуль
Вывод:
Эта статья дает представление о различных способах сложения матриц в python. Вы можете использовать любой из вышеперечисленных способов в соответствии с вашими потребностями и удобством. Использование понимания списка-один из самых простых и лаконичных методов сложения матриц. Этот метод полезен и должен довольно часто включаться в программы python.
Если у вас все еще есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.
Счастливого Пифонирования!
ЛЕКЦИЯ 13.
 ОПЕРАЦИИ НАД МАТРИЦАМИ — презентация на Slide-Share.ru 🎓
ОПЕРАЦИИ НАД МАТРИЦАМИ — презентация на Slide-Share.ru 🎓1
Первый слайд презентации: ЛЕКЦИЯ 13. ОПЕРАЦИИ НАД МАТРИЦАМИ
Основными задачами лекции являются следующие : Определить операции умножения и сложения матриц, а также операцию умножения матриц на число. Сформулировать и обосновать основные свойства операций над матрицами.
Изображение слайда
2
Слайд 2: Сложение матриц
Опр. 1. Суммой двух -матриц A и B называется такая -матрица, каждый элемент которой равен сумме соответствующих элементов матриц A и B.
Изображение слайда
3
Слайд 3: Умножение матриц на число
Опр. 2. Произведением -матрицы A на число называется такая -матрица,,,, каждый элемент которой равен произведению соответственного элемента матрицы на число.
2. Произведением -матрицы A на число называется такая -матрица,,,, каждый элемент которой равен произведению соответственного элемента матрицы на число.
Изображение слайда
4
Слайд 4: Примеры
1)
Изображение слайда
5
Слайд 5: Примеры
1) 2)
Изображение слайда
6
Слайд 6: I. Свойства сложения матриц:
1. – сложение матриц коммутативно;
Изображение слайда
7
Слайд 7: I.
 Свойства сложения матриц :
Свойства сложения матриц :
1. – сложение матриц коммутативно; 2. – сложение матриц ассоциативно;
Изображение слайда
8
Слайд 8: I. Свойства сложения матриц :
1. – сложение матриц коммутативно; 2. – сложение матриц ассоциативно; 3., где O – нулевая матрица;
Изображение слайда
9
Слайд 9: Свойства сложения матриц :
1. – сложение матриц коммутативно; 2. – сложение матриц ассоциативно; 3., где O – нулевая матрица; 4., где – противоположная к A матрица.
Изображение слайда
10
Слайд 10: II.
 Свойства умножения матриц на число:
Свойства умножения матриц на число:
; 5..
Изображение слайда
11
Слайд 11: III. Свойства, связывающие сложение и умножение матриц на число:
7. ; 8..
Изображение слайда
12
Слайд 12: Свойства операций сложения матриц и умножения их на число:
1. 2. 3 4 5 6 7 8
Изображение слайда
13
Слайд 13: Умножение матриц
Опр. 3. Произведением квадратных матриц и порядка n называется квадратная матрица того же порядка n, каждый элемент ( ) которой, находящийся в i -ой строке и k -ом столбце матрицы, равен сумме произведений элементов i -ой строки матрицы A на соответственные элементы k -го столбца матрицы B.
Изображение слайда
14
Слайд 14: Умножение матриц
(1)
Изображение слайда
15
Слайд 15: Умножение матриц
(1) (1’)
Изображение слайда
16
Слайд 16: Пример на умножение матриц
3)
Изображение слайда
17
Слайд 17: Пример на умножение матриц
3)
Изображение слайда
18
Слайд 18: Пример 3 на умножение матриц
3)
Изображение слайда
19
Слайд 19: Умножение матричных единиц
3)
Изображение слайда
20
Слайд 20: Некоммутативность умножения матриц порядка n >1
Изображение слайда
21
Слайд 21: Свойства умножения матриц :
– умножение матриц ассоциативно;
Изображение слайда
22
Слайд 22: Доказательство ассоциативности умножения матриц :
– умножение матриц ассоциативно;
Изображение слайда
23
Слайд 23: Доказательство ассоциативности умножения матриц :
Изображение слайда
24
Слайд 24: Доказательство ассоциативности умножения матриц :
Изображение слайда
25
Слайд 25: Доказательство ассоциативности умножения матриц :
Изображение слайда
26
Слайд 26: Доказательство ассоциативности умножения матриц :
Изображение слайда
27
Слайд 27: Доказательство ассоциативности умножения матриц :
= =
Изображение слайда
28
Слайд 28: Доказательство ассоциативности умножения матриц :
= = =
Изображение слайда
29
Слайд 29: Доказательство ассоциативности умножения матриц :
= = = =
Изображение слайда
30
Слайд 30: Доказательство ассоциативности умножения матриц :
= = = =
Изображение слайда
31
Слайд 31: Свойства умножения матриц :
– умножение матриц ассоциативно; – умножение матриц дистрибутивно относительно сложения;
Изображение слайда
32
Слайд 32: Свойства умножения матриц :
9. – умножение матриц ассоциативно;
– умножение матриц
дистрибутивно относительно сложения;
11.
– умножение матриц ассоциативно;
– умножение матриц
дистрибутивно относительно сложения;
11.
Изображение слайда
33
Слайд 33: Свойства умножения матриц :
9. – умножение матриц ассоциативно; – умножение матриц дистрибутивно относительно сложения; 11. 12., где E – единичная матрица;
Изображение слайда
34
Слайд 34: Обратная матрица
Изображение слайда
35
Слайд 35: Произведение обратимых матриц обратимо
Изображение слайда
36
Слайд 36: Произведение обратимых матриц обратимо
Изображение слайда
37
Слайд 37: Произведение обратимых матриц обратимо
Изображение слайда
38
Слайд 38: Пример 4 на произведение прямоугольных матриц
Изображение слайда
39
Слайд 39: Матричная запись систем линейных уравнений
(1)
Изображение слайда
40
Слайд 40: Матричная запись систем линейных уравнений
( 2 )
Изображение слайда
41
Слайд 41: Матричная запись систем линейных уравнений
(2) (2 ’ )
Изображение слайда
42
Слайд 42: Матричная запись систем линейных уравнений
(2 ’ )
Изображение слайда
43
Слайд 43: Матричная запись систем линейных уравнений
(2)
Изображение слайда
44
Слайд 44: Матричная запись систем линейных уравнений
Изображение слайда
45
Слайд 45: Пример на решение систем в матричном виде
Изображение слайда
46
Слайд 46: Нахождение обратной матрицы
Изображение слайда
47
Слайд 47: Пример на решение систем в матричном виде
Изображение слайда
48
Слайд 48: Пример на решение систем в матричном виде
Изображение слайда
49
Последний слайд презентации: ЛЕКЦИЯ 13.
 ОПЕРАЦИИ НАД МАТРИЦАМИ: Окончание решения системы
ОПЕРАЦИИ НАД МАТРИЦАМИ: Окончание решения системы
– единственное решение системы
Изображение слайда
Онлайн калькулятор сложения и вычитания матриц
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | – | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор дает детальное решение с объяснением сложение и вычитание двух матриц.
 Сложить или вычесть две матрицы возможно только в том случае, если матрицы одинакового размера
Сложить или вычесть две матрицы возможно только в том случае, если матрицы одинакового размераМатрица размерности m × n – это таблица чисел у которой m строк и n столбцов. Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Суммой матриц А и В, размеры которых одинаковы, называется матрица С такой же размерности как матрицы А и В, элементы которой равны суммам элементов матриц А и В.
Как складывать и вычитать матрицы
Складывать и вычитать можно только матрицы одинакового размера.
При сложении (вычитании) матриц A и B, размерности (m × n), получаем матрицу C такой же размерности (m × n).
Чтобы сложить две матрицы, необходимо попарно сложить их элементы.
Например, сложим две матрицы A и B размерности 3 × 3.
| A = |
|
| B = |
|
| C = |
|
+ |
|
= |
|
= |
|
= |
|
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Операции (действия) над матрицами – Vmatematika.ru
Сами по себе матрицы, как таблицы чисел, не представляли бы никакого интереса, если бы с ними не возможно было производить действия. В этой статье мы познакомимся с основными действиями (операциями) над матрицами: сложением и вычитанием матриц, умножением матрицы на число, умножением матриц, транспонированием матриц.
Содержание Сложение матриц Сумма матриц Пример нахождения суммы матриц Вычитание матриц Разность матриц Пример нахождения разности матриц Умножение матрицы на число (скаляр) Произведение матрицы на число Пример нахождения произведения матрицы на число (скаляр) Противоположная матрица Теорема о единственности противоположной матрицы Свойства операций сложения, вычитания и умножения матриц на число Умножение матриц Произведение матриц Пример нахождения произведения матриц Перестановочные матрицы Свойства операции умножения матриц Транспонирование матриц Пример транспонирования матрицы Элементарные преобразования над матрицами Каноническая форма матрицы
На множестве матриц одного и того же размера можно ввести внутреннюю бинарную операцию сложение матриц, при такой операции двум матрицам и одинакового размера ставится в соответствие матрица того же размера, матрицу-результат будем называть суммой матриц и обозначать
Определение 1.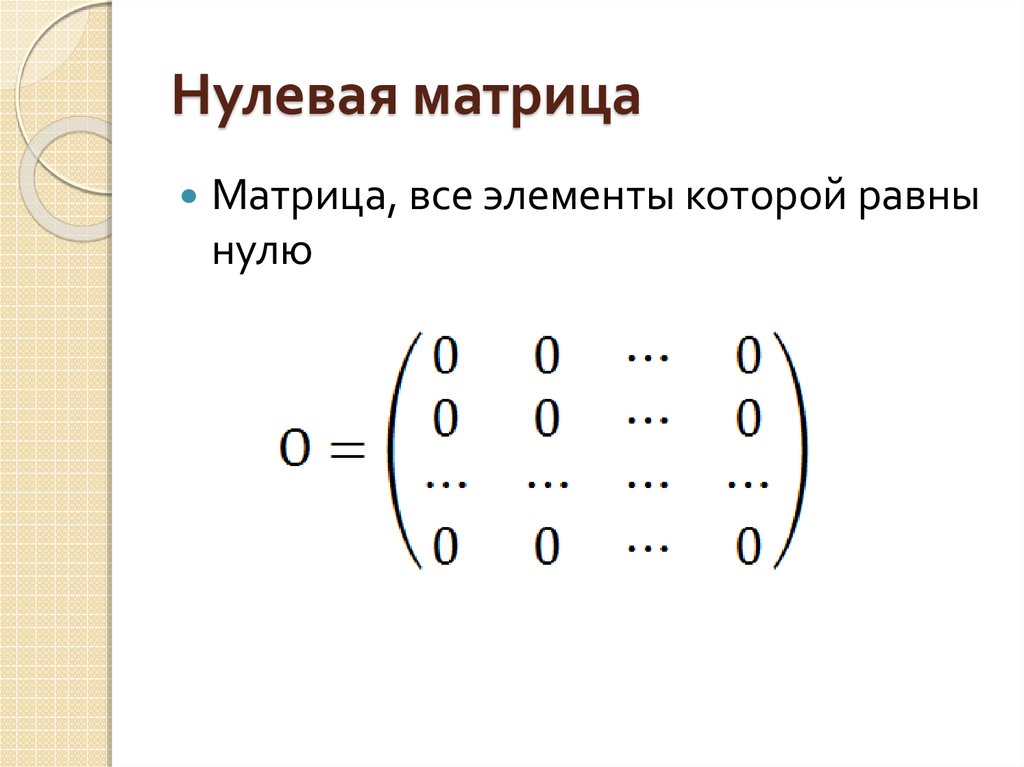 Суммой матриц и называется матрица где каждый элемент т.е.
Суммой матриц и называется матрица где каждый элемент т.е.
Таким образом, для нахождения суммы матриц надо сложить их соответствующие элементы.
Например,
Аналогичным образом на множестве матриц одного и того же размера вводится внутренняя бинарная операция вычитание матриц, при такой операции двум матрицам и одинакового размера ставится в соответствие матрица того же размера, матрицу-результат будем называть разностью матриц и и для обозначения использовать запись
Определение 2. Разностью матриц и называется матрица где т.е.
Таким образом, для нахождения разности двух матриц надо от элементов первой матрицы вычесть соответствующие элементы второй матрицы.
Например,
На множестве матриц введем внешнюю бинарную операцию умножение матрицы на число, при такой операции матрице и числу ставится в соответствие матрица того же размера, что и матрица Матрицу-результат будем называть произведением матрицы на число и обозначать
Определение 3. Произведением матрицы на число называется матрица где т.е.
Произведением матрицы на число называется матрица где т.е.
Таким образом, для нахождения произведения матрицы на число надо каждый элемент матрицы умножить на число
Например,
Противоположная матрица
Определение 4. Противоположной матрицей к матрице называется матрица, обозначаемая такая, что где — нулевая матрица того же размера, что и матрица
Теорема 1. Каждая матрица имеет единственную противоположную матрицу, причем
Доказательство. Пусть произвольная матрица. Тогда из задания операций сложения матриц и умножения матрицы на число, следует, что для матрицы существует противоположная матрица
Докажем единственность противоположной матрицы. Предположим, что матрица имеет противоположную матрицу отличную от матрицы Тогда
Мы получили, что каждый элемент матрицы равен соответствующему элементу матрицы а значит, матрицы и равны. Полученное противоречие (по предположению матрицы и не равны) доказывает то, что у матрицы не существует противоположной матрицы отличной от
Полученное противоречие (по предположению матрицы и не равны) доказывает то, что у матрицы не существует противоположной матрицы отличной от
Разность матриц и можно определить через сумму матрицы и противоположной матрицы
Пусть и произвольные матрицы размера а и любые действительные числа, тогда справедливы следующие утверждения.
На множестве матриц вводится операция (действие) умножение матриц. При умножении матрицы размера и матрицы размера им ставится в соответствие матрица размера называемая произведением матрицы на матрицу Для обозначения матрицы произведения используется запись или
Определение 5. Произведением матрицы на матрицу называется матрица где
Таким образом, для того чтобы найти матрицу-произведение надо вычислить все ее элементы. При этом, для элемента находящегося в -ой строке и -ом столбце матрицы-произведения (матрицы ), надо взять элементы -ой строки первой матрицы (матрицы ) и умножить их на соответствующие элементы -го столбца второй матрицы (матрицы ), полученные произведения следует сложить (рис. 1). Произведение можно найти лишь в том случае, когда количество столбцов матрицы совпадает с количеством строк матрицы У матрицы-произведения количество строк совпадает с количеством строк первой матрицы (матрицы ), а количество столбцов совпадает с количеством столбцов второй матрицы (матрицы ).
1). Произведение можно найти лишь в том случае, когда количество столбцов матрицы совпадает с количеством строк матрицы У матрицы-произведения количество строк совпадает с количеством строк первой матрицы (матрицы ), а количество столбцов совпадает с количеством столбцов второй матрицы (матрицы ).
Рис. 1
Заметим, что произведение в общем случае не совпадает с произведением более того, иногда одно из этих произведений может и не существовать.
Например, для матриц
произведение
В этом примере произведение не определено, так как у матрицы число столбцов — 3, а у матрицы две строки.
Определение 6. Если то матрицы и называются перестановочными матрицами.
Свойства операции умножения матриц
Каждой матрице размера можно поставить в соответствие транспонированную матрицу размера у которой каждая строка с номером будет состоять из элементов (в порядке их следования) столбца с номером матрицы Такая операция называется транспонированием матрицы.
Например,
Выделим преобразования матрицы, которые принято называть элементарными:
- Перестановка местами строк (столбцов) матрицы;
- Умножение или деление на ненулевое число всех элементов строки (столбца) матрицы;
- Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца) умноженных на один и тот же скаляр (число).
Определение 7. Если матрица получается из матрицы с помощью элементарных преобразований, то матрицы и называются эквивалентными матрицами.
Если матрицы и эквивалентны, то это будем записывать следующим образом:
Элементарные преобразования над матрицами обычно применяются для перехода от матрицы к эквивалентной ей матрице в канонической форме (матрице у которой в начале главной диагонали находятся подряд несколько единиц), что позволяет определить ранг матрицы. Так же проведение таких преобразований над строками матриц позволяет перейти от матрицы к эквивалентной ей ступенчатой матрице, что широко применяется в методе Гаусса решения систем линейных уравнений.
Линейные операции над матрицами: сложение и умножение матриц
О чем статья
Сложение матриц
Сумма двух матриц и размером x называется матрица того же размера, каждый элемент которой равняется сумме соответствующих элементов матриц-слагаемых, то есть и обозначается .
Если же , тогда – разница матриц.
Любые действия: вычитание, сложение или умножение матриц называются линейными действиями над матрицами.
У матриц есть такие свойства:
- .
- .
- .
- .
- x = – в случае, если число , то есть коэффициент 1 можно отпустить, как в алгебре.
- .
- .
- .
Здесь обозначено – – нулевая матрица, а – противоположная матрице .
Нужна помощь в написании работы?
Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Умножение матриц
Иногда в работе с таблицами (матрицами) приходится совершать определённые действия. Сложение мы рассмотрели, а теперь рассмотрим умножение матриц..
Сложение мы рассмотрели, а теперь рассмотрим умножение матриц..
Произведением числа на матрицу размера x называется новая матрица того же размера, каждый элемент которой равняется соответствующему элементу матрицы умноженному на число , то есть:
Матрица (-1) – противоположна матрице , и обозначается . Действие сложения применяется только для тех матриц, которые одного и того же размера.
Умножение матриц имеет такие свойства:
- – произведение матриц ассоциативно;
- , где – число;
- x = – произведение матриц дистрибутивно;
- .
Произведение матрицы размером x на матрицу размером x называется матрица размером x, элементы которой равняются сумме произведений элементов -той строки матрицы на соответствующие элементы -того столбца матрицы , то есть:
.
Из структуры элементов понятна необходимость согласованности матриц и : каждому элементу в -той строке матрицы (первого сомножителя) и в -том столбце матрицы (второго сомножителя). Число строк и матрицы равняется числу строк первого сомножителя, а число столбцов – числу второго сомножителя.
Число строк и матрицы равняется числу строк первого сомножителя, а число столбцов – числу второго сомножителя.
Примеры на сложение и умножение матриц
Как уже описывалось ранее, сложение матриц производится тогда, когда матрицы одинаковые по размерам. Рассмотрим несколько примеров.
Примеры на сложение матриц
Пример 1
Даны матрицы:
Найти: 1); 2) – x
Решение:
Теперь находим – x и получим результат:
Рассмотрим ещё один пример, но более большой. Будьте внимательны и не спешите, так как очень часто можно ошибиться в знаках:
Пример 2
Даны матрицы:
Примеры на умножение матриц
Приведём первый пример, на котором рассмотрим умножение матриц, где становится понятно, как составлять матрицы и какие операции с ними проводятся:
Пример 1
Шахтёры выполняют два вида работ: выемка пород и крепление. Эти работы при постоянной площади поперечного сечения могут измеряться в погонных метрах. Допустим, что в течение суток каждая из трёх смен добились таких результатов:
Эти работы при постоянной площади поперечного сечения могут измеряться в погонных метрах. Допустим, что в течение суток каждая из трёх смен добились таких результатов:
| Смены | Выемка (в м.) | Крепление (в м.) |
| первая смена | ||
| вторая смена | ||
| третья смена |
Эти результаты можно записать в виде матрицы размером :
Возьмём этот пример при подсчёте денежных затрат на выполнение робот в шахте. В матрице, которая у нас уже есть, записаны результаты работы за сутки каждой смены. Как уже упоминалось выше, результат работ измеряется в погонных метрах.
Заказчику необходимо знать, какую сумму придётся выделить на зарплату работникам, а какую на капитальные затраты. Это представим с виде матрицы расценок:
где первый столбец , – нормы зарплаты трудящихся: за 1 погонный метр по выемке породы, и, соответственно, за 1 погонный метр по креплению.
Второй столбец: , – капитальные затраты за 1 погонный метр выемки и за 1 погонный метр крепления.
Общие затраты на зарплату для каждой смены равняются произведению пройденного количества метров для каждого вида работ на определённые нормы расценок. Обозначим через сумму средств, которую заработала смена (). Аналогично подсчитываются капитальные затраты для смены по выемке и креплению.
Получим таблицу затрат:
| Смены | Затраты на зарплату по выемке и креплению | Капитальные затраты по выемке и креплению |
| первая смена | ||
| вторая смена | ||
| третья смена |
Эти данные запишем в виде новой матрицы затрат x, что получена из матриц и при помощи действий, которые называются умножение матриц, и обозначают:
Для умножения матрицы размером x на матрицу размером x необходима её согласованность, то есть, чтобы число столбцов матрицы (первого сомножителя) совпадало с числом строк матрицы (второго сомножителя). В приведенном примере матрица согласована с матрицей (для каждого вида работ – нормы расценок). Однако, в примере, который представлен выше, матрица не согласована с матрицей .
В приведенном примере матрица согласована с матрицей (для каждого вида работ – нормы расценок). Однако, в примере, который представлен выше, матрица не согласована с матрицей .
Пример 2
Найти произведение матриц и , если:
Решение:
У матрицы размер x, а размер матрицы – x. У матрицы 2 столбца, а у матрицы 2 строки, а это значит, что матрицы согласованы, так как можно умножать матрицу на матрицу . В результате получим матрицу размером x, то есть:
Пример 3
Убедитесь, что для данных матриц:
,
.
Обратите внимание, что в данном случае
Пример 4
Посмотрите, что получается, когда даны матрицы:
Видите, какие иногда получаются матрицы после решения? В нашем случае произведение двух ненулевых матриц дал нулевую матрицу, и, кроме этого,
Средняя оценка 1 / 5. Количество оценок: 2
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
4669
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Сложение матриц – объяснение и примеры
Операции стоимостью $4$, которые мы можем выполнять с матрицами, — это сложение, вычитание, скалярное умножение и матричное умножение. Матричное дополнение является одним из них.
Матричное дополнение является одним из них.
Примечание. Деление матрицы не является определенной операцией. Мы можем разделить матрицу только на скалярное число.
Итак, как определить сложение матриц? Давайте взглянем на приведенное ниже определение:
Сложение матриц — это операция сложения двух матриц одного размера путем добавления соответствующих записей друг к другу.
В этой статье будут показаны условия, при которых возможно сложение матриц, способы сложения матриц, а также несколько примеров, показывающих сложение матриц.
Когда можно добавлять матрицы?
Как и в случае с числами, можем ли мы добавить какие-либо матрицы?
Ответ НЕТ!
Мы можем складывать матрицы размером $2$ только в том случае, если они имеют одинаковую размерность. То есть, если матрицы $2$ имеют одинаковое количество строк и столбцов, то, и только тогда, мы можем складывать матрицы $2$ вместе.
Напомним, что измерение матрицы — это количество строк и количество столбцов. Если в матрице $m$ строк и $n$ столбцов, то можно сказать, что матрица имеет размеры $m\times n$. Чтобы узнать больше о размерах матрицы, ознакомьтесь с этой статьей!
Помните, матрица, полученная в результате операции сложения матриц, будет той же размерности, что и матрицы, из которых она получена.
Как добавить матрицы?
Сделав вывод, что матрицы имеют одинаковые размеры, добавить матрицы $ 2 $ , добавив соответствующие элементы . Рассмотрим Матрицу $ A $ и Матрицу $ B $, показанные ниже:
$ A = \begin{bmatrix} { – 2 } & { – 4 } \\ 9 & { – 3 } \end {bmatrix} $
$ B = \begin{bmatrix} { – 3 } & 0 \\ 6 & { – 1 } \end {bmatrix} $
Обе матрицы $ A $ и $ B $ имеют $ 2 $ строк и $ 2 $ столбцов. Следовательно, размерность матриц равна $ 2 \times 2 $. Поскольку они равны, мы можем сложить матрицы $2$, добавляя каждую соответствующую запись друг к другу. Процесс показан ниже:
Процесс показан ниже:
$ A + B = \begin{bmatrix} { – 2 + – 3 } & { – 4 + 0 } \\ { 9 + 6 } & { – 3 + – 1 } \ end {bmatrix} $
$ A + B = \begin{bmatrix} { – 5 } & { – 4 } \\ { 15 } & { – 4 } \end {bmatrix} $
Теперь рассмотрим две матрицы, показанные ниже:
$ A = \begin{bmatrix} { 0 } & { – 5 } \\ 1 & 4 \end {bmatrix} $
$ B = \begin{bmatrix} { – 5 } & 0 \\ 6 & 0 \\ 3 & 7 \end {bmatrix} $
Определены ли $ A + B $?
Нет! Матрица $A$ имеет размерность $2\times 2$. Матрица $B$ имеет размерность $3\times 2$. Поскольку размеры обеих матриц не равны, добавление матриц не определено! Мы не можем добавить Матрицы $A$ и $B$, потому что не будет соответствующей записи для каждого элемента Матрицы $A$ и Матрицы $B$.
Правила сложения матриц
Мы можем написать $ 4 $ правила для сложения матриц.
- Вы можете добавлять матрицы только с одинаковыми размерами ( означает, что количество строк и столбцов первой матрицы должно равняться количеству строк и столбцов второй матрицы.
 )
) - Матрица, полученная в результате сложения матриц, будет иметь ту же размерность, что и исходные матрицы, из которых она получена.
- Сложение матриц является коммутативным (т. е. $ A + B = B + A $). Вы можете изменить порядок матриц при сложении матриц $2$ вместе.
- Сложение матриц является ассоциативным (т. е. $ ( A + B ) + C = A + ( B + C ) $). При добавлении $3$-матриц можно сначала добавить любые $2$-матрицы, затем добавить третью матрицу с результатом сложения первых двух.
Давайте рассмотрим несколько примеров Добавление матрицы .
Пример 1Проверить, определено ли сложение матриц между матрицей $A$ и матрицей $B$. Если да, добавьте их.
$ A = \begin{bmatrix} { 3 } & { – 3 } \\ 0 & 3 \end {bmatrix} $
$ B = \begin{bmatrix} { 6 } & { 4 } \\ { – 2 } & 1 \end {bmatrix} $
Решение
Для определения сложения матриц размерность каждой матрицы должна быть одинаковой. Матрица $A$ является матрицей размера $2\times 2$. Матрица $B$ также является матрицей $2\times 2$. Таким образом, сложение матриц между Matrix $A$ и $B$ определено.
Матрица $A$ является матрицей размера $2\times 2$. Матрица $B$ также является матрицей $2\times 2$. Таким образом, сложение матриц между Matrix $A$ и $B$ определено.
Теперь давайте сложим матрицы $2$ вместе, добавляя соответствующие записи друг к другу. Ниже показано:
$ A + B = \begin{bmatrix} { 3 + 6 } & { – 3 + 4 } \\ { 0 + – 2 } & { 3 + 1 } \ end {bmatrix} $
$ A + B = \begin{bmatrix} { 9 } & { 1 } \\ { – 2 } & { 4 } \end{bmatrix} $
Пример 2Для матриц $ 2 $, показанных ниже , найти $C+D$.
$ C = \begin{bmatrix} { 1 } & { – 8 } \\ 0 & 3 \\ 0 & { – 4 } \ end {bmatrix} $
$ D = \begin{bmatrix} { 5 } & { – 8 } & { – 1 } \\ 0 & 6 & 0 \end {bmatrix} $
Решение
Размер матрицы $ C $ равен $ 3\раз 2$. Размерность матрицы $D$ равна $2\times 3$. Несмотря на то, что размеры эквивалентны, мы не можем сложить матрицу $C$ с матрицей $D$. Порядок размеров также важен. Матрица $3\times 2$ не равна матрице $2\times 3$. Таким образом, мы не можем сложить Matrix$C$ и Matrix$D$.
Матрица $3\times 2$ не равна матрице $2\times 3$. Таким образом, мы не можем сложить Matrix$C$ и Matrix$D$.
Мы можем решать основные алгебраические уравнения сложением матриц. Рассмотрим пример, показанный ниже.
Пример 3Найдите значения $ a $ и $ b $ по следующему уравнению:
$ \begin{pmatrix} { 5 } & { 2 } \\ b & { – 2 } \ end {pmatrix} + \begin{pmatrix} { a } & { 2 } \\ 1 & { – 2 } \ end {pmatrix} = \begin{pmatrix} { – 15 } & { 4 } \\ { – 2 } & { – 4 } \end {pmatrix} $
Решение
Мы можем добавить соответствующие записи для решения $ a $ и $ b $. Сначала сложим соответствующие элементы для $a$ и решим для переменной:
$5 + a = – 15$
$a = – 15 – 5$
$a = – 20$
Теперь найдем значение $b$ путем добавления соответствующих записей для $b$:
$b + 1 = – 2 $
$b = – 2 – 1 $
$b = – 3 $
Ваша очередь. Попробуйте эти практические вопросы.
Практические вопросы- Рассмотрим следующие матрицы $ 3 $:
$ P = \begin{pmatrix} { – 1 } & { 3 } \\ 6 & { 0 } \end {pmatrix} $
$ Q = \begin{ pmatrix} { 5 } & { -1 } \\ { – 2 } & 1 \end {pmatrix} $
$ R = \begin{pmatrix} 3 & 1 \\ 1 & 3 \\ -1 & -3 \end {pmatrix} $
Найти:- $ P + Q $
- $ Q + R $
- $ Q – Q $
- Найти значения $ a $, $ b $ и $ c $, заданные следующее уравнение:
$ \begin{pmatrix} { 3 } & { 2 } & 0 \\ b & { – 2 } & 3 \\ 11 & a & -2 \end {pmatrix} + \begin{pmatrix} { 3 } & { 2 } & c \\ 5 & { – 2 } & 3 \\ 11 & -1 & -2 \end {pmatrix} = \begin{pmatrix} { 6 } & { 4 } & -9 \\ 20 & { – 4 } & 6 \\ 22 & -3 & -4 \end {pmatrix} $
- Первые две задачи на сложение.
 Мы будем следовать правилам сложения матриц. Третья проблема — вычитание. Но помните, вычитание — это просто еще одна форма сложения. Ответы показаны ниже.
Мы будем следовать правилам сложения матриц. Третья проблема — вычитание. Но помните, вычитание — это просто еще одна форма сложения. Ответы показаны ниже. - Обе матрицы $P$ и $Q$ являются матрицами размера $2\times 2$. Таким образом, мы складываем матрицы $2$, добавляя соответствующие записи. Показано ниже:
$ P + Q = \begin{pmatrix} {-1 +5} & {3+ – 1} \\ {6 + – 2} & {0 + 1} \end {pmatrix} $
$ P + Q = \begin{pmatrix} { 4 } & { 2 } \\ 4 & 1 \end {pmatrix} $ - Мы не можем сложить матрицу $Q$ и матрицу $R$, поскольку их размеры не совпадают . Матрица $Q$ является матрицей размера $ 2 \times 2$, а матрица $R$ является матрицей размера $3 x 2$.
- Инвертируем (меняем знак каждого элемента) вторую матрицу $Q$ и складываем обе.
$ Q + (-Q) = \begin{pmatrix} { 5 } & {- 1 } \\ {- 2} & {1} \end {pmatrix} + \begin{pmatrix} {-5 } & {1 } \\ {2} & {-1} \end {pmatrix} $
$ Q – Q = \begin{pmatrix} { 0 } & 0 \\ 0 & 0 \end {pmatrix} $Результатом является $ 2 \times 2 $ матрица с всеми элементами $ 0 $.
 Это известно как нулевая матрица или нулевая матрица .
Это известно как нулевая матрица или нулевая матрица .
- Обе матрицы $P$ и $Q$ являются матрицами размера $2\times 2$. Таким образом, мы складываем матрицы $2$, добавляя соответствующие записи. Показано ниже:
- Мы можем добавить соответствующие записи для решения $ a $, $ b $ и $ c $. Сначала сложим соответствующие элементы для $a$ и решим для переменной:
$a+-1=-3$
$a=-3+1$
$a=-2$Теперь найдем значение $b$ путем добавления соответствующих записей для $b$:
$b + 5 = 20 $
$b = 20 – 5 $
$b = 15 $Наконец, давайте найдем значение $ c $, добавив соответствующие записи для $c$:
$ 0 + c = -9 $
$ c = -9 $
Добавление матрицы — обзор
ScienceDirectРегистрацияВход
Добавление матриц определяется как A+B=(a11a12a21a22)+(b11b12b21b22)=(a11+b11a12+b12a21+b22a).
Из: The Nuts and Bolts of Proofs (Fourth Edition), 2013 г.
PlusAdd to Mendeley Дж. Дуглас Кэрролл, Пол Э. Грин, в Mathematical Tools for Applied Multivariate Analysis, 1997
Дуглас Кэрролл, Пол Э. Грин, в Mathematical Tools for Applied Multivariate Analysis, 1997
2.5.7 Проблема деления матриц
До сих пор мы обсуждали сложение, вычитание и умножение матриц, но деление бросалось в глаза своим отсутствием. И не зря: деление, известное нам в скалярной арифметике, не определено в матричной алгебре .
То, что определяется, больше похоже на умножение на обратное. Например, в обычной арифметике вместо деления некоторого числа на 5 мы могли бы умножить число на обратную величину 5:9.0005
1/5=(5)−1
при условии, что делитель не равен нулю.
Аналогичная операция в матричной алгебре называется обращением матрицы . Эта операция настолько особенная (и значительно более сложная), что мы отложим ее обсуждение до главы 4. Пока можно сказать, что обратная матрица A , если такая обратная существует, аналогична умножению A обратной величиной в обычной алгебре. Таким образом, в матричной алгебре есть аналогия скалярному соотношению:
Таким образом, в матричной алгебре есть аналогия скалярному соотношению:
a×a−1=1
Излишне говорить, что мы потратим значительное количество времени на тему обращения матриц в последующих главах.
Просмотр книги Глава Чика
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/b9780121609542500032
Seifedine Kadry, в математическом уровне. Пусть 9Если заданы матрицы 0007 A , B и C , то основные свойства сложения матриц, скалярного умножения, умножения матриц и транспонирования матриц изложены ниже без доказательства. Эти свойства легко проверяются на примерах. Свойства сложения матриц и скалярного умножения : A+B=B+A (коммутативность) (А+В)+С=А+(В+С) (ассоциативность) A+O=O+A=A, где O — соответствующая нулевая матрица k(A+B)=kA+kB, где k — скаляр (дистрибутивность). Свойства умножения матриц : AB≠BA, вообще A(BC)=(AB)C (ассоциативность) AI=IA=A, где I — соответствующая единичная матрица A(B+C)=AB+AC (распределимость). Свойства перестановки матриц : (AT)T=A (A+B)T=AT+BT (кА)Т=кАТ (АВ)Т=БТАТ. Имея матрицы [12−34] и [4123], проверьте, что AB≠BA. Путем умножения имеем: AB=[12−34].[4123]=[1×4+2×21×1+2×3(−3)×4+4×2( −3)×1+4×3]=(87−49) BA=[4123]. Итак, AB≠BA. Данная матрица имеет вид A=(12−3−405). Убедитесь, что (AT)T=A. Здесь A=(12−3−405)⇒AT=(1−420−35)⇒(AT)T=(12−3−405) ∴ (AT)T=A. Значит, проверено. Предположим, что компания ставит перед вами проблему: Определите, какой из трех методов M 1 , M 2 и M 3 производства. . Количество каждого товара, произведенного каждым методом, показано ниже в виде матрицы: ABCM1M2M3(463595347) Матрица строк (304542) представляет прибыль на единицу товаров A , B и C , соответственно. Используйте матричное умножение, чтобы решить, какой метод максимизирует общую прибыль. Пусть P=(463595347) и Q=(304542). Тогда Q′=(304542). Теперь общая прибыль от трех методов определяется как R=PQ’=(463595347)(304542)=(120+270+126150+405+21090+180+294)=(516765564) Итак , прибыль, полученная методами M 1 , M 2 и M 3 , составляет рупий. Просмотр книги Глава Черта Читать полную главу URL: https://www.sciendirect.com/science/article/pii/b9780124201316000038 Valerio Magnasco, в Elebrecular Mehiefular Mehail 2.2.2 Свойства матриц Две матрицы A и B равны, если они имеют одинаковый порядок и Aij = B ij 7 я, к. Сложение и вычитание матриц (тот же порядок): (3)A±B=CCij=Aij±Bij. Сложение и вычитание матриц коммутативны и ассоциативны: (4)A±B=±B+A (5)A+B+C=(A+B)+C=A+(B+C) Произведение матрицы на (комплексное) число c : (6)cA=CCij=cAij. Каждый элемент матрицы умножается на c. Произведение строк матриц на столбцы: (7)Am×nBn×p=Cm×pCij=∑α=1nAiαBαj. Количество столбцов A должно быть равно количеству строк B (матрицы тогда называются созвучными). В общем, умножение матриц равно , а не коммутативно: (8)AB≠BA. Если: (9)AB=BA A и B считаются коммутирующими. Разница: (10)AB−BA=[A,B] называется коммутатором A и B . Произведение более двух матриц ассоциативно: (11)ABC=(AB)C=A(BC). Доказательство: (ABC)ij=∑α∑βAiαBαβCβj=∑β(AB)iβCβj=∑αAiα(BC)αj. Иногда удобно рассматривать матрицу как состоящую из элементов, которые сами являются матрицами. Другими словами, матрицы можно разбить на подматриц , для которых выполняются правила матричной алгебры. В заключение напомним, что матрица имеет ранг r тогда и только тогда, когда она имеет хотя бы одну невырожденную квадратную подматрицу, наибольший порядок которой равен r. Просмотреть главуКнига покупок Прочитать всю главу URL: https://www.sciencedirect.com/science/article/pii/B9780444527783500190 , 2013 Если это ваша первая встреча с группами перестановок, вы можете задаться вопросом, почему они используются. Это правда, что они дают интересные примеры некоммутативных групп, но они быстро становятся очень большими. Например, ( P 3 , ∘) = S 3 имеет шесть элементов. Группа перестановок из четырех элементов ( P 4 , ∘) = S 4 будет иметь двадцать четыре элемента. Просто изготовление операционного стола будет трудоемкой задачей. Есть несколько сокращений для работы с перестановками на больших множествах (которые мы не включили), но должно быть что-то, что делает их математически «ценными», а не просто любопытством. Пусть G = ( A , *) — группа. Если S является подмножеством A таким, что ( S , *) является группой, то ( S , *) называется подгруппой G = ( Пример 4.4.31 Рассмотрим группу ( M 2 ,+) всех матриц с двумя строками и двумя столбцами с вещественными элементами и обычным сложением матриц. Рассмотрим пару ( S ,+), определяемую той же операцией, и множество S={A=(n000) with n∈ℤ}. Докажите, что эта пара является подгруппой ( M 2 ,+). Доказательство Набор S является подмножеством набора M 2 . Таким образом, нам достаточно доказать, что пара ( S ,+) — это группа. Тогда это будет подгруппа ( M 2 ,+). Операция ассоциативная и закрывается на S . Это означает, что если A , C ∈ S , то A + C ∈ S . Докажем это утверждение. Так как A , C ∈ S , A=(n000) и C=(m000) с n , m ∈ Z. Тогда A+C=(n+m000) и n + м ∈ Z. Это означает, что А + С ∈ S . Элемент идентичности представляет собой матрицу 02=(0000), которая является элементом S . Дана матрица A=(n000) в S , ее обратной является матрица B=(−n000), поскольку A + B = 0 2 . Поскольку n ∈ ℤ, − n ∈ ℤ. Следовательно, B ∈ S . Итак, пара ( S ,+) является подгруппой ( M 2 ,+). 3.4 Свойства матричных операций

Пример 1
Решение
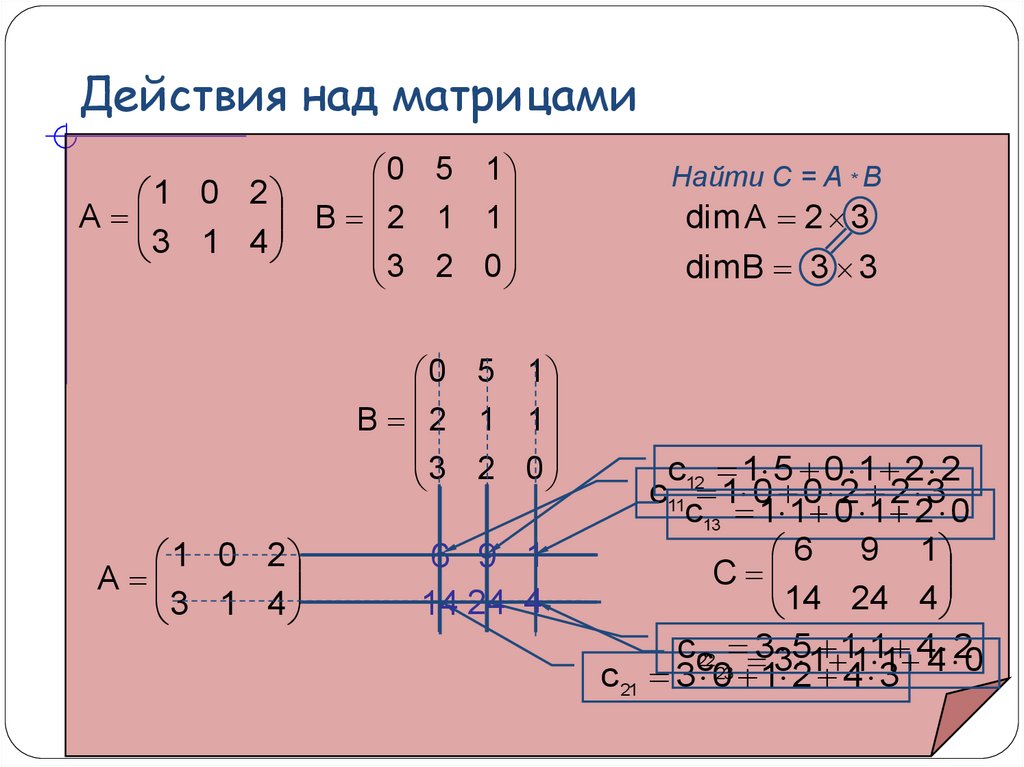 [12−34]=[112−414]
[12−34]=[112−414] Пример 2
Решение
Пример
Решение
 516, рупий. 765 и рупий. 564 соответственно. Следовательно, второй метод максимизирует прибыль.
516, рупий. 765 и рупий. 564 соответственно. Следовательно, второй метод максимизирует прибыль.
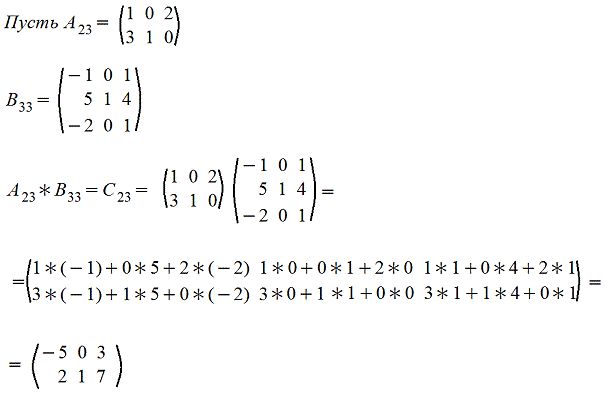
Важная теорема
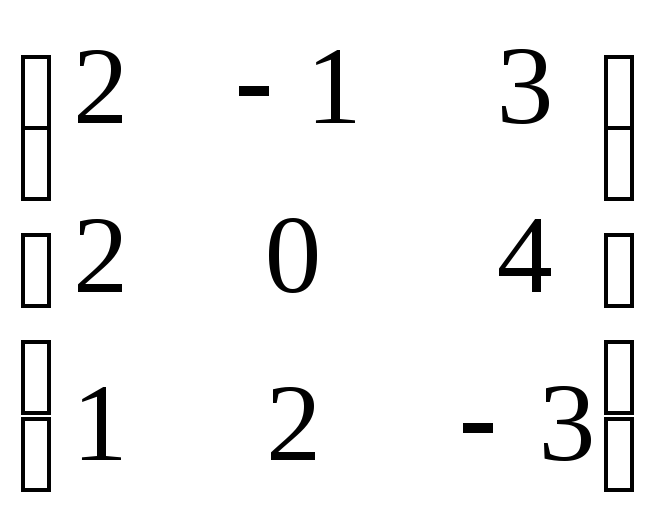 Действительно, группы перестановок являются основными объектами фундаментальной теоремы абстрактной алгебры, теоремы Кэли. Чтобы понять формулировку и важность этой теоремы, нам нужно исследовать еще одно понятие — идею подгрупп.
Действительно, группы перестановок являются основными объектами фундаментальной теоремы абстрактной алгебры, теоремы Кэли. Чтобы понять формулировку и важность этой теоремы, нам нужно исследовать еще одно понятие — идею подгрупп.7 A,
*). Это определение означает, что подгруппа сама по себе является группой, и ее множество содержится в множестве большей группы. Обе группы должны иметь одинаковые операции.

Пример 4.4.32
Рассмотрим группу ( P 3 ,∘) = S 3 . Докажите, что пара ( S ,∘), где S = { ι , h , y } является подгруппой S 3 .
Доказательство
Известно, что операция является ассоциативной, так как является композицией функций. Также
ι=(123123) h=(123231) y=(123312).
Рабочий стол для элементов S is
∘ ι hy¯ι|ιhyh|hyιy|yιh
Таблица показывает, что операция закрыта на S , а элемент идентификации принадлежит S . Более того, каждый элемент в S имеет обратный в S . Таким образом, ( S ,∘) является подгруппой S 3 . Обратите внимание, что ( S ,∘) является абелевой группой (также h и y обратны друг другу), а S 3 не является абелевой группой.
Этот последний пример уже показывает нам нечто особенное в отношениях между группами и их подгруппами. Все подгруппы абелевой группы также абелевы (простое доказательство этого утверждения оставлено в качестве упражнения), но неабелева группа может иметь абелевы подгруппы. В общем, подгруппы могут иметь больше свойств, чем вся группа, потому что они состоят только из некоторых элементов большей группы, а меньшему набору элементов легче удовлетворить заданное свойство.
Пример 4.4.33
Группа (ℤ 3 ,+ 3 ) является изоморфной подгруппе S 3 . , ч , у }.
Доказательство
Самый простой способ доказать это утверждение состоит в построении изоморфизма между двумя группами. Нам нужна биективная функция μ : ℤ 3 → S , совместимая по операциям. Более того, в силу свойств групповых изоморфизмов относительно единичных элементов μ ([0]) = ι . Таким образом, у нас есть два варианта назначения двух других элементов. Попробуем μ ([1]) = h и μ ([2]) = y . Чтобы проверить совместимость этой функции, нам нужно доказать, что
Таким образом, у нас есть два варианта назначения двух других элементов. Попробуем μ ([1]) = h и μ ([2]) = y . Чтобы проверить совместимость этой функции, нам нужно доказать, что
µ([a]+3[b])=µ([a])∘µ([b]) для всех [a],[b]∈ ℤ3.
Равенство тривиально верно, когда любой из двух классов равен [0]. Таким образом, мы будем рассматривать случаи, не связанные с тождеством. Остается проверить только четыре случая:
- 1.
Является ли µ([1]+3[1])=µ([1])∘µ([1])?
µ([1]+3[1])=µ([2])=y µ([1]∘µ[1])=h∘h=y
Таким образом, равенство верно.
- 2.
Является ли µ([1]+3[2])=µ([1])∘µ([2])?
µ([1]+3[2])=µ([0])=ι µ([1]∘µ([2]=h∘y=ι
Таким образом, равенство выполняется.
- 3.
Является ли µ([2]+3[1])=µ([2])∘µ([1])?
µ([2]+3[1])=µ([ 0])=ι µ([2]∘µ([1])=y∘h=ι
Таким образом, справедливо равенство.
- 4.
Является ли µ([2]+3[2])=µ([2])∘µ([2])?
µ([2]+3[2])=µ([1])=h µ([2])∘µ([2])=y∘y=h
Таким образом, равенство выполняется.

Таким образом, функция µ является групповым изоморфизмом.
Результат этого последнего примера позволяет нам думать об (ℤ 3 ,+ 3 ), абелевой группе, как о подгруппе S 3 , неабелевой группы. Это пример формулировки теоремы Кэли, очень важного результата в теории групп. Теорема утверждает, что каждая группа изоморфна подгруппе группы перестановок на соответствующем множестве. Группы перестановок могут быть очень большими, они обладают множеством свойств (не включенных сюда) и имеют большое количество (и разнообразие) подгрупп, некоторые из которых абелевы.
Теорема Кэли : Каждая конечная группа изоморфна группе перестановок.
Мы не будем включать доказательство этой теоремы, поскольку оно требует более глубоких знаний в области теории групп, и мы будем использовать эту теорему как завершающий результат краткого обзора теории групп, представленного в этой книге.
Упражнения
- 41.
Рассмотрим группу ( P 3 ,∘) = S 3 . Докажите, что пара ( H ,∘), где H = { ι , f } является подгруппой S 3 .
- 42.
Рассмотрим группу ( P 3 ,∘) = S 3 . Докажите, что пара ( T ,∘), где T = { ι , g } является подгруппой S 3 .
- 43.
Пусть G = ( A , ∗) — абелева группа и ( S , ∗) — одна из его подгрупп. Докажите, что ( S , ∗) также абелев.
- 44.
. { ι , f } (см. упражнение 41).
- 45.
Предположим, что функция в примере 4.4.33 была определена как μ ([0]) = ι , µ ([1]) = y и µ ([ 2 ]) = ч .
 Будет ли это по-прежнему изоморфизмом групп? Объяснять.
Будет ли это по-прежнему изоморфизмом групп? Объяснять.- 46.
Докажите, что пара ( T ,×) с T = {1, −1, i , − i }) является подгруппой (ℂ*,×) ℂ* — набор ненулевых комплексных чисел. Докажите, что пара ( S ,∘) является подгруппой S 4 , где S = { ι , f , h , y } и ι=(12341234), f=(12342134),h=(12341243) и y=(12342143). Является ли ( T ,×) изоморфным ( S ,∘)?
Просмотреть главуКнига покупок
Прочитать всю главу
URL: https://www.sciencedirect.com/science/article/pii/B978012382217800004X
Метод Коста Махирд Брон. издание), 2009 г.
Определение 2
Если A = [ A IJ ] и B = [ B IJ ] Оба порядка P × N , затем A + B is P, A + B . × N Matrix C = [ C IJ ] где C IJ = A IJ + B IJ ( I = , IJ ( I = = = = = = = = = = = = , IJ . , p ; j = 1, 2, 3,…, n ). Таким образом,
× N Matrix C = [ C IJ ] где C IJ = A IJ + B IJ ( I = , IJ ( I = = = = = = = = = = = = , IJ . , p ; j = 1, 2, 3,…, n ). Таким образом,
[5173−2−1]+[−632−141]=[5+(−6)1+37+23+(−1)(−2)+4(−1)+1]=[− 149220]
и
[t253t0]+[1−6t−t]=[t2+1−14t−t];
, но матрицы
[50−1021] и [−6211]
не могут быть добавлены, так как они имеют разный порядок.
Нетрудно показать, что сложение матриц является как коммутативным, так и ассоциативным: то есть, если А, В, С представляют собой матрицы одного порядка, то
(А1) А + В = B + A,
(A2) A + ( B + C ) = ( A + B ) + C.
Мы определяем аро 0 — матрица, состоящая только из нулевых элементов. Нулевые матрицы любого порядка существуют, и когда одна из матриц имеет тот же порядок, что и другая матрица A, , мы получаем дополнительное свойство
(A3) A + 0 = A.
Вычитание матриц определяется следующим образом: аналогично сложению: порядки задействованных матриц должны быть одинаковыми, а операция выполняется поэлементно.
Таким образом,
[51−32]−[6−14−1]=[−12−73].
Еще одна простая операция — умножение скаляра на матрицу. Интуиция подсказывает выполнение операции поэлементно, и снова интуиция верна. Так, например,
7[12−34]=[714−2128] и t[1032]=[t03t2t].
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B97800806500073
8.
 4 Структура векторного пространства
4 Структура векторного пространстваОпределить
Mµ:={A∈Mm×n|m/n=µ}.
Тогда у нас есть разбиение как
(8.18)M=⋃µ∈Q+Mµ,
, где Q+ — множество положительных рациональных чисел. Соответственно положим также
Ξμ:=Mμ/≈.
Тогда мы также имеем разбиение фактор-пространства как
(8.19)Ξ=⋃µ∈Q+Ξµ.
Наша цель состоит в том, чтобы представить правильную структуру векторного пространства на каждом Mµ и Ξµ, используя {Jk|k=1,2,⋯}.
Определение 8.5
[3]
Пусть X — множество и x,y∈X. Предположим, что существует отображение (x,y)↦x+y числа X×X в X , называемое сложением, и отображение (a,x)↦ax числа R×X в X , называемое скалярным умножением, такое что выполняются следующие аксиомы ( x , y , z , обозначающие произвольные элементы X , и a , b произвольные элементы R):
1)901
(x+y)+z=z+(y+z).
х+у=у+х.
Существует единственный элемент 0∈X, такой что x+0=x для всех x∈X.
Для каждого x∈X существует уникальное z=−x∈X такое, что x+z=0.
а(х+у)=ах+ау.
(a+b)x=ax+bx.
а(бх)=(аб)х.
1x=x,
Определение 8.6
Предположим, что X с добавлением + и скалярным произведением ⋅ удовлетворяет всем требованиям для векторного пространства, за исключением того, что ноль является множеством, следовательно, для каждого x ∈ X обратное значение − x может быть не уникальным . Тогда X называется псевдовекторным пространством.
Определение 8.7
Пусть A,B∈Mµ. А именно, A∈Mm×n, B∈Mp×q и m/n=p/q=µ. Установите t=m∨p. Затем
Затем
- 1.
левое сложение матрицы M-II A и B , обозначенное +ℓ, определяется как
(8.20)A+ℓB:=(A⊗Jt/m)+ (B⊗Jt/p).
Соответственно, левое вычитание матрицы M-II определяется как(8.21)A−ℓB:=A+ℓ(−B).
- 2.
Сложение правой матрицы M-II A и B , обозначенное +ℓ, определяется как (Jt/p⊗B).
Соответственно, правильное вычитание матрицы M-II определяется как(8.23)A−rB:=A+r(−B).
Замечание 8.4
Если в вышеприведенном определении все Jk заменить соответствующими Ik, то сложение и вычитание матриц M-II становятся соответственно сложением и вычитанием матриц M-I, которые обсуждались в главе 4.
Замечание 8.5
Пусть σ∈{+ℓ,−ℓ,+r,−r} — один из четырех бинарных операторов. Тогда легко проверить, что
- 1.
если A,B∈Mµ, то AσB∈Mµ;
- 2.
Если A и B такие же, как в определении 8.
 7, то AσB∈Mt×ntm;
7, то AσB∈Mt×ntm;- 3.
Установите s=n∨q, тогда s/n=t/m и s/q=t/p. Таким образом, σ также можно определить, используя номера столбцов соответственно, например,
A+ℓB:=(A⊗Is/n)+(B⊗Is/q),
и т. д.
Легко проверить следующий вывод.
Предложение 8.7
Mμ с добавлением ( +ℓ или +r ), а обычное скалярное произведение представляет собой псевдовекторное пространство, где для каждого A его обратное значение определяется как
(8.24)−A:={B|A+ℓB=0},
, что не равно уникальный.На самом деле легко проверить, что A+ℓB=0 тогда и только тогда, когда A≈ℓB (или A+rB=0 тогда и только тогда, когда A≈rB). Тогда, когда рассматривается факторпространство, мы имеем векторное пространство.
Определение 8.8
Пусть <>,<>∈Ξ. Тогда
(8.25)<>+ℓ<>:=<
(8.26)<>+r<>:=<
(8. 27)<>−ℓ<>:=<
27)<>−ℓ<>:=<
(8.28)<>-r<>:=<
Легко проверить, что (8.25) (или (8.26)) и (8.27) (или (8.28)) определены правильно. То есть они не зависят от выбора представителей A∈<> и B∈<>. Кроме того, скалярное произведение может быть правильно определено
(8.29)c<>=<
Наконец, у нас есть следующий результат:
Предложение 8.8
ξμ с добавлением, определенным (8,25) (или (8,26) ) и скалярной продукт, определенный (8,298 ) и скалярный продукт, определенный (8,298 ) и скалярный продукт (8,26) ) и скалярный продукт. ) — векторное пространство.
Просмотреть главуКнига покупок
Прочитать всю главу
URL: https://www.sciencedirect.com/science/article/pii/B9780128178010000144
Petros Maragos, в достижениях в области визуализации и физики электронов, 2013
2.
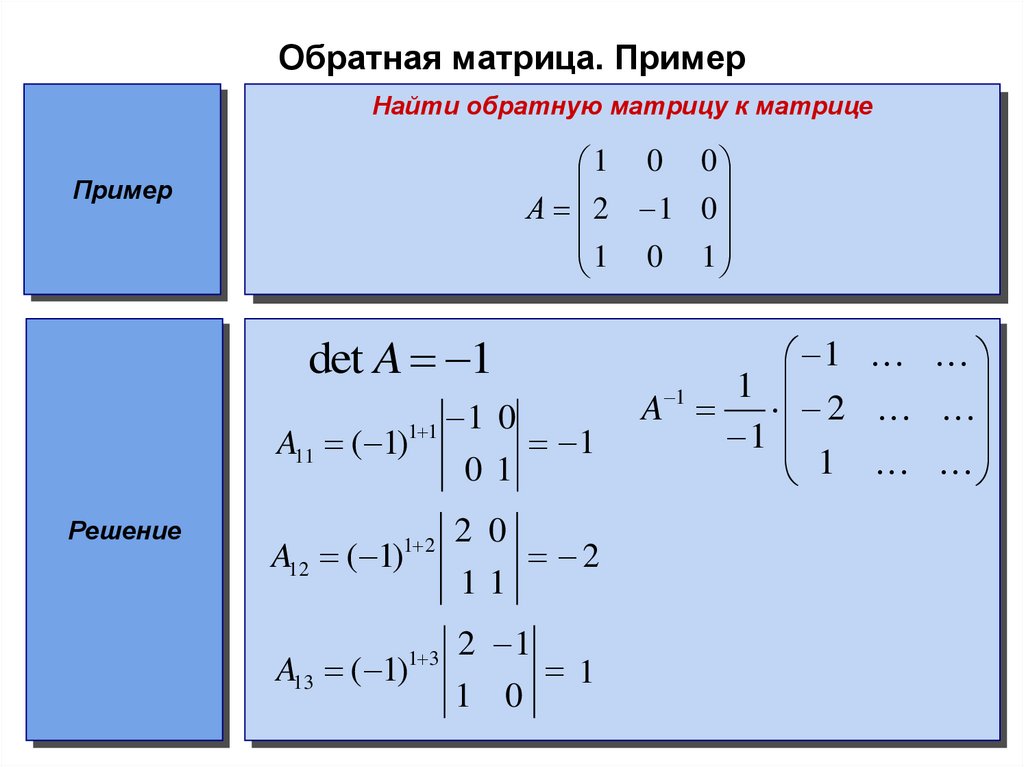 4 линейный оператор между двумя конечномерными линейными пространствами X и Y , гамелевскими базами которых являются соответственно множества B1={x1,…,xn} и B2={y1,…,ym}. Поскольку каждая точка x в X имеет единственное представление в виде линейной комбинации базисных элементов
4 линейный оператор между двумя конечномерными линейными пространствами X и Y , гамелевскими базами которых являются соответственно множества B1={x1,…,xn} и B2={y1,…,ym}. Поскольку каждая точка x в X имеет единственное представление в виде линейной комбинации базисных элементовx=c1x1+⋯+cnxn,
его образом будет
L(x)=c1L(x1)+⋯+cnL(xn).
Поскольку L(x) является точкой в Y , ее можно выразить как уникальную линейную комбинацию базовых элементов Y :
L(x)=d1y1+⋯+dmym.
Кроме того, L(x1),…,L(xn) также являются точками в Y и могут быть выражены соответствующими уникальными линейными комбинациями базисных элементов Y следующим образом:
L(x1)=a11y1+⋯+am1ym⋮⋮⋮L(xn)=a1ny1+⋯+amnym.
Следовательно, два вектора коэффициентов разложений x и L(x) по соответствующим основаниям связаны умножением матрицы на вектор:
[L][c1c2⋮cn]=[d1d2⋮dm] ,[L]=[a11a12⋯a1na21a22⋯a2n⋮⋮⋮⋮am1am2⋯amn].
Таким образом, существует взаимно однозначное соответствие между линейным оператором L и матрицей m×n [L] над полем F .
Аналогично, если мы рассмотрим линейный оператор из X самому себе, то это соответствует квадратной матрице n×n с элементами из F . Пусть Fn×n обозначает множество всех таких матриц; снабженный сложением и умножением матриц, он становится кольцом . Поэтому, если мы рассмотрим множество всех линейных операторов из X в себя, снабженное добавлением композиции операторов, эта алгебраическая структура представляет собой кольцо линейных операторов, изоморфное кольцу матриц Fn×n.
92.4.2 Теорема Рисса о представлении и линейная свертка F — , то есть любой линейный оператор ℓ:V→F, который отображает точки (например, векторы, сигналы) пространства в скалярные числа.Теорема 7
(Теорема Рисса о представлении). Пусть ϕ — ограниченный линейный функционал в гильбертовом пространстве H. Тогда существует единственная точка k∈H такое, что ϕ(x)=〈x,k〉 для всех x∈H . Далее , ‖ϕ‖=‖k‖.
Тогда существует единственная точка k∈H такое, что ϕ(x)=〈x,k〉 для всех x∈H . Далее , ‖ϕ‖=‖k‖.
«Вектор» k называется представлением функционала ϕ ; таким образом, сигнал представляет собой линейную систему. Эта фундаментальная теорема лежит в основе сверточных представлений линейных систем. Пусть H будет гильбертовым пространством L2(R,C) комплекснозначных сигналов с непрерывным временем. Рассмотрим ограниченный линейный оператор L на H , то есть ‖L‖<∞. Это действует как линейная система, которая отображает входной сигнал конечной нормы f(t) в выходной сигнал конечной нормы
g(t)=L[f(t)].
Если мы рассмотрим выходное значение в любой момент времени t=to, то отображение f(t)↦g(to)=ϕ(f) является ограниченным линейным функционалом на H . По теореме Рисса о представлении существует уникальный сигнал kto∈H такой, что
g(to)=L[f(t)]|t=to=〈f,kto〉=∫f(τ)kto∗(τ )dτ,∀to∈R.
Ясно, что функция kto(t) является комплексно-сопряженной системой Карта импульсной характеристики в момент времени t=to, то есть выход системы
(18)hto(t)≜L[δ(t−to)]
, когда вход представляет собой импульсную функцию δ(t−to ), расположенный в точке t=to. Обратите внимание, что приведенная выше функция представляет собой карту, которая назначает, возможно, другой сигнал в каждый момент времени, потому что система может меняться во времени.
Однако, если линейная система L также инвариантна во времени , то существует единственная функция h(t)=L[δ(t)], называемая импульсной характеристикой системы, такое что
hto(t)=h(t−to),∀to∈R.
В этом случае из теоремы Рисса о представлении следует, что выходной сигнал системы g является непрерывной линейной сверткой входного сигнала f и импульсной характеристики h :
(19)g( t)=L[f(t)]=∫f(τ)h(t−τ)dτ.
Приведенные выше идеи легко переносятся на линейные системы, обрабатывающие дискретных во времени сигналов, т. е. ограниченные линейные операторы L в гильбертовом пространстве H=ℓ2(Z,C). Если f[n] — входная последовательность, а g[n]=L(f[n]) — соответствующий выход, то для каждого n=no существует уникальная конечноэнергетическая последовательность hno=L(δ[n−no] ), определяемый как реакция системы на входной импульс в точке n=no, такая, что
е. ограниченные линейные операторы L в гильбертовом пространстве H=ℓ2(Z,C). Если f[n] — входная последовательность, а g[n]=L(f[n]) — соответствующий выход, то для каждого n=no существует уникальная конечноэнергетическая последовательность hno=L(δ[n−no] ), определяемый как реакция системы на входной импульс в точке n=no, такая, что
g[n]=L[f[n]]=∑mf[m]hno[n−m].
Если система также не зависит от времени, существует уникальная последовательность h[n]=L(δ[n]), называемая импульсной характеристикой , такая, что hno[n]=h[n−no] для всех нет, и, следовательно, отношение ввода-вывода системы задается линейная свертка с дискретным временем :
(20)g[n]=L[f[n]]=∑mf[m]h[n−m].
Наконец, теорема о представлении Рисса и ее следствия (например, сверточная формула в случае инвариантности к сдвигу) напрямую применимы к ограниченным линейным операторам на пространствах многомерных сигналов.
2.4.3 Спектральное представление линейных операторов в конечномерных векторных пространствах
Основная идея здесь заключается в проведении геометрического анализа комплексного гильбертова пространства H путем разложения его на сумму более простых подпространств (например, образованных диапазонами проекций), а линейный оператор L на H выражается в виде соответствующей суперпозиции более простых операций (например, проекций на эти подпространства ). Это также приводит к спектральному анализу оператора через его собственные значения и собственные векторы. Мы приведем из Нейлора и Селла (1982) некоторые основные результаты для случая, когда разложение выполняется с конечным числом проекций.
Это также приводит к спектральному анализу оператора через его собственные значения и собственные векторы. Мы приведем из Нейлора и Селла (1982) некоторые основные результаты для случая, когда разложение выполняется с конечным числом проекций.
Набор {P1,P2,…,Pm} непрерывных проекций на H называется -разложением тождества , если (1) они ортогональны, (2) PiPj=0, если i≠j, и ( 3) I=P1+⋯Pm. Без ограничения общности в дальнейшем будем считать, что Pi≠O для всех i . Тогда пространство можно разложить как
(21)H=Ran(P1)⊕⋯⊕Ran(Pm),
, где Ran(Pi)⊥Ran(Pj), если i≠j. Пусть {λ1,…,λm} — множество различных скаляров, и рассмотрим линейный оператор
(22)L=λ1P1+⋯+λmPm.
Тогда L непрерывный и нормальный. Далее, оно самосопряжено тогда и только тогда, когда все λi действительны. Обратите внимание, что L согласуется с λiI на Ran(Pi). Таким образом, поскольку любой «вектор» x∈H однозначно разлагается как
(23)x=x1+⋯+xm,xi∈Ran(Pi),
, действие L на x также можно разложить как
(24)L(x)=λ1×1+⋯+λmxm.
{λi} называются собственными значениями L , потому что они являются единственными скалярными решениями уравнения
L(x)=λx.
Для каждого λi соответствующий собственный вектор должен лежать в Ran(Pi). На самом деле существует ортонормированный базис из собственных векторов {ei} из L . Используя его, мы можем выразить любую точку x∈H (вход в оператор) как
(25)x=∑i=1m〈x,ei〉ei
, а соответствующий вывод оператора как
(26 )L(x)=∑i=1mλi〈x,ei〉ei.
Норма оператора также может быть выражена через его собственные значения:
(27)‖L‖=maxi|λi|.
Приведенный выше анализ был относительно простым, поскольку мы начали с синтеза линейного оператора как конечной линейной комбинации известных ортогональных проекций, которые могут полностью заполнить все пространство. Более сложная проблема состоит в том, чтобы начать с линейного оператора, а затем найти набор таких ортогональных проекций. За дальнейшими подробностями читатели могут обратиться к Naylor and Sell (1982).
Просмотреть главуКнига покупок
Прочитать всю главу
URL: https://www.sciencedirect.com/science/article/pii/B9780124077027000024
С.Дж. Гарретт, Введение в актуарные и финансовые математические методы, 2015 г. вещественные числа. Например, (10.1)A=5−21728,B=1−2875−1,C=−112,D=79−10 — все это примеры матриц (множественное число единственного числа «матрица» ). Матрицы можно классифицировать по размерности массива, то есть по количеству строки и столбцы указаны в таком порядке. Например, матрица A в уравнении. (10.1) представляет собой матрицу 3 × 2, тогда как B представляет собой матрицу 2 × 3. В общем, говорят о матрице м × n , которая относится к м строк и n столбцов. Матрицы C и D в формуле. Таким образом, (10.1) являются матрицами 1 × 3 и 3 × 1 соответственно. Отдельные числа, составляющие матрицу, называются ее элементами . Конкретная запись идентифицируется по ее местоположению в матрице, то есть по положению строки и столбца, в котором она появляется, нумерация начинается с левого верхнего угла. Например, ссылаясь на уравнение (10.1), (3,2)-запись A равна 8, а (2,1)-запись B равна 7. Матрицы обычно обозначаются прописными буквами, а их записи строчными буквами. Общая нотация A = [ A IJ ] для матрицы M × N особенно полезен для определения Matrix A с его конкретными записями A IJ . . Квадратные скобки следует интерпретировать как означающие, что матрица A сформирована из упорядоченного набора отдельных элементов a ij , каждый в строке i и столбце 9. A = A11A12 ⋯ A1NA21A22 ⋯ A2N ⋮⋮⋮⋮ AM1AM2 ⋯ AMN . Сформировано из G 11 = 1, G 12 = 3 и G 13 = 13 IS G = [GIJ] = 1313 Пример 10.1 G = 1313 Пример 10.1 G = [GIJ] = 1313 .0005 Укажите размеры следующих матриц в формате м × n . В каждом случае укажите любые три отдельные записи, используя обозначения « a ij ». А=142536 B=-2-4-3124321 С=-2-1382 D=132231312021007 Матрица 3 × 2 с определенными элементами, включая a 11 = 1, a 12 = 4 и a 21 90 = 0,5 0,2. 3 × 3 Матрица с конкретными записями, включая B 22 = 2, B 23 = 4, и B 32 = 2. Матрица 1 × 5 с определенными элементами, включая c 12 = −1, c 13 = 3 и c 15 = 2. 5 × 3 Матрица с конкретными записями, включая D 42 = 2, D 22 = 3 и D 53 = 7. для двух MATIRIERS BE BE BE BAIF BE BAIF BE BAIF BE BAIF BE BAIF BE BAIF BE BAIS BE BAIS BIT должно быть ясно, что все их соответствующие записи должны быть равны; это обязательно означает, что их размеры также идентичны. То есть, если A – это M × N Матрица и B A P × Q MATRIX, заявление A = B обязательно среднее, что M = P , N = Q = P , N = Q = P , N = Q = P , N = Q и A IJ = B IJ для всех I = 1,…, M и J = 1,…, N . Пример 10.2 Укажите с указанием причин, равны ли следующие пары матриц: А=44311-1,В=44311-1 C=121234,D=122314 E=121254,F=121264 Эти матрицы имеют одинаковые размеры и a ij = b ij для всех По понятным причинам C также является примером матрица строк и D пример матрицы столбцов .
По понятным причинам C также является примером матрица строк и D пример матрицы столбцов . 0007 j , где i = 1,…, m и j = 1,…, n . Нотация A = [ A IJ ] затем понимается как значение
0007 j , где i = 1,…, m и j = 1,…, n . Нотация A = [ A IJ ] затем понимается как значение Раствор


Раствор
i 8 j
7 , Следовательно, A = B .
Эти матрицы имеют разные размеры, C имеет размер 2 × 3, а D равен 3 × 2. Следовательно, C ≠ D .
Эти матрицы имеют одинаковые размеры. Однако e 22 ≠ f 22 и, следовательно, E ≠ D .
Как и в случае с отдельными числами, которые мы теперь называем скалярами , чтобы отличить их от матриц, можно добавить две или более матриц. Однако сложение матриц определено только для матриц одинаковой размерности. Например, если A , B и C являются матрицами 2 × 3, 2 × 3 и 2 × 2 соответственно, можно определить A + B , но не A 0 0+ или B + C . Матрица, полученная в результате добавления A и B , фактически определяется как
Однако сложение матриц определено только для матриц одинаковой размерности. Например, если A , B и C являются матрицами 2 × 3, 2 × 3 и 2 × 2 соответственно, можно определить A + B , но не A 0 0+ или B + C . Матрица, полученная в результате добавления A и B , фактически определяется как
(10.2)A+B=[aij+bij]
То есть просто добавляются соответствующие элементы. Это определение распространяется на сумму трех или более матриц одинакового размера очевидным образом.
Теперь пусть A , B и C обозначают матрицы одинаковой размерности, такие что сложение любых двух или всех трех определено. Уравнение (10.2) показывает, что общие свойства сложения матриц напрямую следуют из известных свойств скалярного сложения. В частности, сложение матриц коммутативно и ассоциативно . Эти два свойства символически представлены как
(10. 3)A+B=B+A
3)A+B=B+A
(10.4)A+B+C=A+B+C
Точно так же верно и очевидное определение вычитания матриц. То есть
(10.5)A−B=A+(−B)
Пример 10.3
Вам даны следующие матрицы:
(10.6)D=1−2010212,E=144422123,F=22111−33 −1
По возможности добудьте следующее:
- a.
D + E
- б.
D + F
- c.
E + F
- d.
D – F
Раствор
- а.
D и E имеют разные размеры, поэтому вычисление D + E невозможно.
- б.
D и F имеют одинаковые размеры и можно вычислить D + F . Используя уравнение (10.2), это
D+F=1−2010212+22111−33−1=1+2−2+20+11+10+12−31+32−1=30121−141
- c.

E и F имеют разные размеры, поэтому вычисление E + F невозможно.
- д.
D и F имеют одинаковые размеры и можно вычислить D − F . Используя уравнение (10.5), это
D−F=1−2010212−22111−33−1=1−2−2−20−11−10−12+31−32+1=−1−4−10−15 −23
Член − B в уравнении (10.5), конечно, интерпретируется как — 1 × B , и это поднимает важную концепцию скалярного умножения матриц.
Скалярное умножение следует очевидным образом и отличается от матричного умножения , которое мы рассматриваем в разделе 10.2. В частности, для любого скаляра k∈R (или даже C) мы определяем скалярное умножение матрицы A на k как
кА=[kaij]
Например,
2E=2144422123=2×12×42×42×42×22×22×12×22×3=288844246
Также можно определить скалярное деление матрицы любым ненулевым скаляром. Отсюда очевидным образом следует:
Отсюда очевидным образом следует:
1kA=aijk
Ясно, что результатом умножения (или деления) матрицы размером m × n на скаляр k является другая матрица m × 8 9000.
Идея скалярного умножения легко расширяется для доказательства очевидных результатов для двух скаляров k и l ,
(10,7)k(A+B)=kA+kB
(10,8)(k+l)A=kA+lA
Пример 10.4
Использовать “
7 a
ij », чтобы доказать результаты, данные в уравнениях. (10.3), (10.4) и (10.7).Решение
Это легко доказать, используя нотацию « a ij » и используя свойства скалярного сложения и умножения на уровне элементов. В частности,
A+B=[aij+bij]=[bij+aij]=B+AA+B+C=[(aij+bij)+cij]=[aij+(bij+cij)]=A+ B+Ck(A+B)=k[aij+bij]=[kaij+kbij]=kA+kB
по мере необходимости. Аналогичные рассуждения можно использовать для доказательства уравнения (10. 8).
8).Пример 10.5
Если k = 2, l = 3, A=1221 и B=0132, вычислите следующие выражения:
- a.
( к + л ) А
- б.
кА + фунтов
- c.
1кА
- д.
2 lA − 4 кБ
Раствор
- а.
(2+3)×1221=510105
- б.
2×1221+3×0132=2442+0396=27138
- в.
12×1221=121112
- д.
2×3×1221−4×2×0132=612126+0−8−24−16=64−12−10
Понятие матричного вычитания приводит к понятию нулевой матрицы . Так же, как скалярное вычисление 2 − 2, например, требует наличия нулевого скаляра, матричное вычисление E − E , например, требует нулевой матрицы. В частности,
E−E=144422123−144422123=000000000
Таким образом, нулевая матрица — это матрица любой размерности, в которой все элементы равны нулю. Должно быть ясно, что нулевая матрица также возникает в результате скалярного умножения любой матрицы на нулевой скаляр, k = 0,
Должно быть ясно, что нулевая матрица также возникает в результате скалярного умножения любой матрицы на нулевой скаляр, k = 0,
До сих пор наше обсуждение ограничивалось манипулированием матрицами, хранящимися в фиксированном массиве. Например, и скалярное умножение, и сложение матриц начинаются и приводят к m × n матриц. Однако существует фундаментальная операция, которая позволяет преобразовать m × n матрицу в конкретную n × m матрицу; эта операция называется транспозицией . Транспонирование матрицы A приводит к транспонированию из A , обозначенному как A T . Точнее,
ifA=[aij]thenAT=[aij′]=[aji]
То есть строки и столбцы числа A становятся столбцами и строками соответственно A T . Например,
A=10256⇒AT=10256B=123456⇒BT=135246C=10102−41−43⇒CT=10102−41−43
Последний пример интересен тем, что C T 0 C , что указывает на особую симметрию матрицы C . Действительно, симметричная -матрица определяется как матрица, равная своей транспонированной. Ясно, что все симметричные матрицы должны быть квадратных , то есть они должны иметь размерность м × м . Свойства транспонированных матриц исследуются в следующих примерах, а квадратные матрицы мы обсудим в разделе 10.3.
Действительно, симметричная -матрица определяется как матрица, равная своей транспонированной. Ясно, что все симметричные матрицы должны быть квадратных , то есть они должны иметь размерность м × м . Свойства транспонированных матриц исследуются в следующих примерах, а квадратные матрицы мы обсудим в разделе 10.3.
Пример 10.6
Используйте обозначения « a ij » для доказательства следующих свойств транспонирования. В каждом случае проверьте свойство на простом примере с использованием матриц 2 × 3.
- а.
( А Т ) Т = А
- б.
( кА ) T = кА T
- c.
( A + B ) T = A T + B T , with A and B having identical dimensions
Solution
- a .

Начиная с A = a ij , A T = [ A IJ ′ ] = [ A JI ] и SO ( A T ) 0 T a T ) T a
0 T ) . ′ ] = [ a ij ] = A , если требуется.Например, если A=123456, (AT)T=142536T=123456=A.
- б.
( кА ) T = [ ка ij ′ ] = [ Ka Ji ] = K [ A JI ] = Ka T .
Например, если k = 2,
(2A)T=24681012T=28410612=2142536=2123456T=2AT
- c.
( A + B ) T = [ A IJ + B IJ ] T = [9 ] T = [ ] T = [ ] T .
 0008 ij ′ + b ij ′ ] = [ a ji + b ji ] = [ a ji ] + [ b ji ] = A T + B T .
0008 ij ′ + b ij ′ ] = [ a ji + b ji ] = [ a ji ] + [ b ji ] = A T + B T .Например, если B=2011-23 и A взято из части a,
(A+B)T=324539T=352349=142536+210-213=123456T+2011-23T=AT+BT
Пример 10.7
Докажите, что если C и D — симметричные матрицы одинаковой размерности, то C + D также симметрична. Продемонстрируйте это свойство на простом примере с использованием матриц 4 × 4.
Решение
Свойство симметрии для одной матрицы равно C T = C . Поэтому нам необходимо доказать, что ( C + D ) T = C + D , и это следует ниже.
(C+D)T=CT+DT (из свойства c в примере 10.6)=C+D(поскольку C и D индивидуально симметричны)
Например, при работе с C=1101123−103−171−173 и D=02142− 3−2−11−2104−105, каждый из которых симметричен по отдельности,(C+D)T=13153−11−211075−278T=13153−11−211075−278=C+D
Посмотреть главуКнига покупок
Читать полная глава
URL: https://www.sciencedirect.com/science/article/pii/B9780128001561000108
Стивен Андрилли, Дэвид Хеккер, в элементарной линейной алгебре (пятое издание), 2016
Примеры векторных пространств
Пример 1
Let V = RN, с добавлением и скаляцией умноженной мастеры 777777777777777777777777777777 года
Let V = RN, с добавлением и скаляцией. -векторы, как определено в разделе 1.1. Поскольку эти операции всегда производят векторы в Rn, свойства замыкания, безусловно, выполняются для Rn. По теореме 1.3 остальные восемь свойств также выполняются. Таким образом, V=Rn — векторное пространство с этими операциями.
По теореме 1.3 остальные восемь свойств также выполняются. Таким образом, V=Rn — векторное пространство с этими операциями.
Аналогично, рассмотрим Mmn, набор из m × n матриц. Обычные операции матричного сложения и скалярного умножения на Mmn всегда дают 90 007 m 90 008 × 90 007 n 90 008 матриц, поэтому свойства замыкания определенно выполняются для Mmn. По теореме 1.12 остальные восемь свойств также выполняются. Следовательно, Mmn — векторное пространство с этими операциями.
Держите в уме Rn и Mmn (с обычными операциями сложения и скалярного умножения) в качестве примеров, так как они представляют большинство векторных пространств, которые мы рассматриваем в этой главе.
Обратите внимание, что определенные векторные пространства могут иметь дополнительные операции. Например, Rn имеет скалярное произведение, а Mmn — умножение матриц и транспонирование. Но они не являются общими для всех векторных пространств, потому что они не включены в определение. В абстрактном векторном пространстве мы не можем предположить существование каких-либо дополнительных операций, таких как умножение или деление одного вектора на другой. Единственной общей операцией векторного пространства, которая объединяет два векторов , является сложение векторов.
В абстрактном векторном пространстве мы не можем предположить существование каких-либо дополнительных операций, таких как умножение или деление одного вектора на другой. Единственной общей операцией векторного пространства, которая объединяет два векторов , является сложение векторов.
Пример 2
Множество V={0} представляет собой векторное пространство с правилами сложения и умножения, заданными как 0 + 0 = 0 и a 0 = 0 для каждого скаляра (действительного числа) a . Поскольку 0 – единственный возможный результат любой операции, V должно быть замкнуто как при сложении, так и при скалярном умножении. Быстрая проверка подтверждает, что оставшиеся восемь свойств также выполняются для V. Это векторное пространство называется тривиальным векторным пространством , и меньшее векторное пространство невозможно (почему?).
Пример 3
Плоскость в R3, содержащая начало координат, может рассматриваться как множество всех 3-векторов с начальными точками в начале координат, которые полностью лежат в этой плоскости при отображении на графике. Например, плоскость W, показанная на рис. 4.1, содержит векторы u и v в качестве элементов, а q не является элементом W. Докажем, что любая плоскость W в R3, содержащая начало координат, является векторным пространством .
Например, плоскость W, показанная на рис. 4.1, содержит векторы u и v в качестве элементов, а q не является элементом W. Докажем, что любая плоскость W в R3, содержащая начало координат, является векторным пространством .
Чтобы проверить свойства замыкания, мы должны показать, что сумма любых двух векторов из W является вектором из W и что любой скаляр, кратный вектору из W, также лежит в W.
Замыкание при сложении: Пусть х и y — любые два вектора из W. Тогда параллелограмм, который они образуют, полностью лежит в плоскости, поскольку х и y лежат в одной плоскости. Следовательно, диагональ x + y этого параллелограмма также лежит в плоскости, а значит, x + y лежит в W. Это доказывает, что W замкнуто относительно сложения (т. е. свойство замыкания выполняется для сложения ). (Обратите внимание, что недостаточно знать, что сумма x + y — еще один 3-вектор. Мы должны показать, что x + y на самом деле лежат в плоскости W. x , либо параллелен x , либо равен 0 . Следовательно, a x лежит в любой плоскости, проходящей через начало координат, содержащее x (в частности, W). Следовательно, a x находится в W, и W замыкается при скалярном умножении.
(Обратите внимание, что недостаточно знать, что сумма x + y — еще один 3-вектор. Мы должны показать, что x + y на самом деле лежат в плоскости W. x , либо параллелен x , либо равен 0 . Следовательно, a x лежит в любой плоскости, проходящей через начало координат, содержащее x (в частности, W). Следовательно, a x находится в W, и W замыкается при скалярном умножении.
Свойства (1)–(8): Свойства (1), (2), (5), (6), (7) и (8) верны для всех векторов из W по теореме 1.3, поскольку W⊆R3. Однако свойства (3) и (4) должны проверяться отдельно для W, поскольку они являются свойствами существования . Мы знаем, что нулевой вектор и аддитивные обратные существуют в R3, но существуют ли они в W? Теперь 0 = [0,0,0] находится в W, потому что плоскость W проходит через начало координат, что доказывает свойство (3). Кроме того, противоположный (аддитивный обратный) любому вектору, лежащему в плоскости W, также лежит в W, что доказывает свойство (4).
Кроме того, противоположный (аддитивный обратный) любому вектору, лежащему в плоскости W, также лежит в W, что доказывает свойство (4).
Рисунок 4.1. Плоскость W в R3, содержащая начало координат
. Поскольку свойства замыкания и все свойства с (1) по (8) выполняются, W является векторным пространством.Пример 4
Пусть Pn — множество многочленов степени ≤ n с вещественными коэффициентами. Векторы INPN имеют форму P = A N x N + ⋯ + A 1 x + A 1 x + A0008 0 для некоторых действительных чисел a 0 , a 1 ,…, a n . Мы показываем, что Pn является векторным пространством при обычных операциях сложения и скалярного умножения.
Замыкание при сложении: Поскольку сложение многочленов здесь производится обычным образом — т. е. добавлением соответствующих коэффициентов, — сумма любых двух многочленов степени ≤ n также имеет степень ≤ n и так в Пн. Таким образом, свойство замыкания сложения выполняется.
е. добавлением соответствующих коэффициентов, — сумма любых двух многочленов степени ≤ n также имеет степень ≤ n и так в Пн. Таким образом, свойство замыкания сложения выполняется.
Закрытие под скалярным умножением: Let B – реальное число и P = A N x N + ⋯ A 9367
77777777777777777777777777777777777777777777777777777777. 3777777777777777777777777774441 + + ⋯ + ⋯ . + a 0 — вектор в Pn. Определим b p обычным образом как многочлен ( ba n ) x n + ⋯ + ( ba 1 ) x + ba 7n, 3 0 0 0 Следовательно, свойство замыкания скалярного умножения выполняется.
Таким образом, если выполняются оставшиеся восемь свойств векторного пространства, Pn является векторным пространством относительно этих операций. Мы проверяем свойства (1), (3) и (4) определения, а остальные оставляем вам для проверки.
Мы проверяем свойства (1), (3) и (4) определения, а остальные оставляем вам для проверки.
Свойство (1) (переместительный закон сложения): Мы должны показать, что порядок сложения двух векторов (многочленов) не имеет значения. Теперь по коммутативному закону сложения для действительных чисел (bn+an)xn+⋯+(b1+a1)x+(b0+a0)=(bnxn+⋯+b1x+b0)+(anxn+⋯+a1x+a0).
Свойство (3) (Существование аддитивного элемента идентичности): Полином нулевой степени z = 0 x n + ⋯ + 0 x + элемент 0 действует как добавочный элемент 0 . То есть добавление Z к любому вектору P = A N X N + ⋯ + A 1 x + A 1 x + A 1 x + A 1 + A 1 + A 1 + A 1 . не менять вектор:
не менять вектор:z+p=(0+an)xn+⋯+(0+a1)x+(0+a0)=p.
Свойство (4) (существование аддитивной обратной): Мы должны показать, что каждый вектор0007 n + ⋯ + a 1 x + a 0 inPn имеет аддитивную инверсию в Pn. But, the vector − p = −( a n x n + ⋯ + a 1 x + a 0 ) = (− a n ) x n + ⋯ + (− a 1 ) + x7 a
0 ) обладает тем свойством, что p + [− p ] = z , нулевой вектор, и поэтому − p действует как аддитивная обратная величина p . Поскольку − p также находится в Pn, мы закончили. Векторное пространство в примере 4 похоже на наш прототип Rn. Для любого полинома из Pn рассмотрим последовательность его n + 1 коэффициентов. Эта последовательность полностью описывает этот многочлен и может рассматриваться как ( n +1)-вектор. Например, полиномиальная A 2 x 2 + A 1 x + A 0 в P2 можно описать 3-векером [ A 0 в P2. , и 1 , и 0 ]. Таким образом, векторное пространство P2 «похоже» на векторное пространство R3, и вообще Pn «похоже» на Rn+1. Мы будем часто использовать это «сходство» неформальным образом на протяжении всей главы. Мы формализуем эту связь между Pn и Rn+1 в разделе 5.5.
Для любого полинома из Pn рассмотрим последовательность его n + 1 коэффициентов. Эта последовательность полностью описывает этот многочлен и может рассматриваться как ( n +1)-вектор. Например, полиномиальная A 2 x 2 + A 1 x + A 0 в P2 можно описать 3-векером [ A 0 в P2. , и 1 , и 0 ]. Таким образом, векторное пространство P2 «похоже» на векторное пространство R3, и вообще Pn «похоже» на Rn+1. Мы будем часто использовать это «сходство» неформальным образом на протяжении всей главы. Мы формализуем эту связь между Pn и Rn+1 в разделе 5.5.
Пример 5
Множество P всех полиномов (всех степеней) является векторным пространством при обычных (почленных) операциях сложения и скалярного умножения (см. упражнение 14).
Пример 6
Пусть V — множество всех вещественных функций, определенных на R. Например, f(x)=arctan(x) находится в V. Определим сложение функций как обычно: h = f + g функция такая, что ч ( х ) = f ( х ) + г ( х ), для каждого x∈R. Точно так же, если a ∈ R и f находится в V, мы определяем скалярное кратное h = a f как функцию, такую, что h ( x ) = a ( x ) для каждого x∈R.
Например, f(x)=arctan(x) находится в V. Определим сложение функций как обычно: h = f + g функция такая, что ч ( х ) = f ( х ) + г ( х ), для каждого x∈R. Точно так же, если a ∈ R и f находится в V, мы определяем скалярное кратное h = a f как функцию, такую, что h ( x ) = a ( x ) для каждого x∈R.
Свойства замыкания: Эти свойства сохраняются для V, потому что суммы и скалярные множители функций с действительными значениями производят функции с действительными значениями.
Чтобы завершить проверку того, что V является векторным пространством, мы должны проверить выполнение оставшихся восьми свойств векторного пространства. Мы проверяем свойство (2) и свойства (5)–(8), а остальные оставляем вам для проверки.
Предположим, что f , g и h находятся в V, а a и b — действительные числа.
Свойство (2): Для каждого x∈R, f(x)+g(x)+h(x)=f(x)+g(x)+h(x), по ассоциативному закону сложение для действительных чисел. Таким образом, ф + ( г + ч ) = ( ф + г ) + ч .
Свойства (5) и (6) X
) + A G ( x ) и ( A + B ) F ( x ) = A F ( x ) + B ( x ) + B ( x ) + B 0003 f ( x ) по распределительным законам для действительных чисел умножения над сложением. Следовательно, A ( F + G ) = A F + A G и ( A + B ) F = A F + + б ф .
Свойство (7)0004 ( x )) следует из ассоциативного закона умножения действительных чисел. Следовательно, ( ab ) f = a ( b f ).
Свойство (8): С 1 ⋅ F ( x ) = F ( x ) для каждого реального числа x , мы имеем 1 ⋅ F = F в V.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B978012800853
49
Сложение матриц – Свойства
Сложение матриц представляет собой математическую операцию сложения двух или более матриц. Матрица представляет собой прямоугольный массив чисел, символов, выражений, букв и т. д., расположенных в строках и столбцах. Сложение матриц можно выполнять разными способами, но в этой статье мы в основном обсудим поэлементное сложение матриц и прямую сумму матриц. Матрицы можно складывать, вычитать или умножать. Здесь мы в основном сосредоточимся на операции сложения матриц.
Матрицы можно складывать, вычитать или умножать. Здесь мы в основном сосредоточимся на операции сложения матриц.
Сложение матриц — это операция сложения соответствующих элементов двух или более матриц. Добавление матриц определяется только для матриц одинакового размера (размерности). Давайте рассмотрим концепцию подробно на примерах.
| 1. | Что такое сложение матриц? |
| 2. | Типы сложения матриц |
| 3. | Сложение матриц 2 × 2 |
| 4. | Сложение матриц 3 × 3 |
| 5. | Свойства сложения матриц |
| 6. | Советы и рекомендации по добавлению матриц |
| 7. | Часто задаваемые вопросы о добавлении матриц |
Что такое сложение матриц?
Сложение матриц — это операция над матрицами, при которой добавляются соответствующие элементы двух или более матриц. Матрицы можно добавлять, только если они одного размера, то есть имеют одинаковую размерность или порядок. Матрица представляет собой прямоугольный массив чисел, выражений, символов и т. д., расположенных в строках и столбцах. Если количество горизонтальных строк в матрице равно «m», а количество вертикальных столбцов равно «n», то говорят, что матрица имеет размерность «m × n».
Матрицы можно добавлять, только если они одного размера, то есть имеют одинаковую размерность или порядок. Матрица представляет собой прямоугольный массив чисел, выражений, символов и т. д., расположенных в строках и столбцах. Если количество горизонтальных строк в матрице равно «m», а количество вертикальных столбцов равно «n», то говорят, что матрица имеет размерность «m × n».
Добавление матриц Определение
Добавление матриц — одна из основных операций, выполняемых над матрицами. Две или более матриц одного порядка могут быть добавлены путем добавления соответствующих элементов матриц. Если A = [a ij ] и B = [b ij ] — две матрицы одинаковой размерности, то есть они имеют одинаковое количество строк и столбцов, то сложение матриц A и B равно: A +B = [a ij ] + [b ij ] = [a ij + б и ]
Типы добавления матриц
Теперь мы обсудим два типа методов добавления матриц. Одним из них является простой метод добавления соответствующих элементов двух или более матриц. Другой метод сложения матриц — вычисление прямой суммы матриц. Давайте сначала обсудим предыдущий метод:
Одним из них является простой метод добавления соответствующих элементов двух или более матриц. Другой метод сложения матриц — вычисление прямой суммы матриц. Давайте сначала обсудим предыдущий метод:
Поэлементное сложение матриц
Сложение матриц или сложение матриц возможно только в том случае, если количество строк и столбцов обеих матриц одинаково. При добавлении двух матриц мы добавляем элементы в каждой строке и столбце к соответствующим элементам в строке и столбце следующей матрицы. Рассмотрим две матрицы A и B одного и того же порядка m × n, где m — количество строк, а n — количество столбцов двух матриц, обозначаемых как A = [a ij ] и B = [b ij ]. Теперь сумма двух матриц A и B определяется как: A+B = [a ij ] + [b ij ] = [a ij + b ij ], где ij обозначает положение каждого элемента в i -й -й строке и j -м -м столбце. Размер матрицы суммы, то есть A + B, также равен «m × n».
Прямая сумма — сложение матриц
Прямая сумма матриц — операция над матрицами, которая используется реже. Для обозначения прямой суммы матриц используется символ ⊕. При вычислении прямой суммы двух матриц порядок матриц не обязательно должен быть одинаковым. Предположим, у нас есть две матрицы X и Y порядков m × n и p × q соответственно, то есть X имеет m строк и n столбцов, а Y имеет p строк и q столбцов. Тогда размерность матрицы X ⊕ Y равна (m + p) × (n + q). Прямая сумма X и Y, то есть X ⊕ Y, дана на изображении ниже:
Как мы видим на изображении, в прямую сумму матриц мы не складываем соответствующие элементы матриц. Прямая сумма — это особый тип блочной матрицы. Прямая сумма матриц ассоциативна, т. е. (X⊕Y)⊕Z = X⊕(Y⊕Z).
Добавление матриц 2 × 2
Теперь разберемся в частных случаях сложения матриц. Наиболее часто используемые матрицы имеют порядок 2 × 2 или 3 × 3. Рассмотрим две матрицы A и B размерности 2 × 2. Добавим соответствующие элементы матриц.
Добавим соответствующие элементы матриц.
Теперь давайте рассмотрим пример двух матриц 2 × 2 A и B, добавим их, чтобы изучить сложение матриц 2 × 2.
Сложение матриц 3 × 3
Теперь разберем сложение матриц порядка 3 × 3 на примере. Как обсуждалось ранее, для сложения матриц порядок матриц должен быть одинаковым, чтобы можно было добавить все соответствующие элементы. Общая форма добавления матриц 3 × 3:
Теперь давайте рассмотрим пример матричного сложения двух матриц 3 × 3 A и B.
Обратите внимание, что для матричного сложения или сложения матриц матрицы не обязательно должны быть квадратными матрицами. Добавление прямоугольных матриц также определено, если порядок матриц одинаков.
Свойства добавления матриц
Точно так же, как сложение чисел, сложение матриц также имеет сходные свойства, такие как коммутативный закон, ассоциативный закон, аддитивная инверсия, аддитивная идентичность и т. д. Наиболее важной необходимостью сложения матриц для сохранения всех этих свойств является то, что добавление матрицы определены только в том случае, если порядок матриц одинаков.
д. Наиболее важной необходимостью сложения матриц для сохранения всех этих свойств является то, что добавление матрицы определены только в том случае, если порядок матриц одинаков.
- Коммутативное свойство – Если A = [a ij ] и B = [b ij ] две матрицы порядка m × n, то сложение матриц A + B = B + A, то есть сложение матриц коммутативно.
- Ассоциативное свойство — Если A = [a ij ], B = [b ij ] и C = [c ij ] — три матрицы порядка m × n, то (A+B)+C = A+(B+C), т. е. сложение матриц ассоциативно.
- Существование аддитивной идентичности – Если A = [a ij ] является матрицей порядка m × n, то аддитивной единицей A является нулевая матрица O порядка m × n такая, что A + O = O + A = A, то есть , матрица O является аддитивной идентичностью для сложения матриц.
- Существование аддитивной обратной матрицы – Если A = [a ij ] является матрицей порядка m × n, то аддитивной обратной матрицей A является -A = [-a ij ] порядка m × n такая, что A + (-A) = O = A + (-A), то есть матрица (-A) является аддитивной, обратной матрице сложения.

- Свойство транспонирования – Транспонирование суммы двух матриц равно сумме транспонирования соответствующих матриц, то есть (A + B) T = A T + B T
- Определяющее свойство – Определитель суммы двух матриц равен сумме определителей соответствующих матриц, то есть |A + B| = |А| + |Б|
Советы и рекомендации по сложению матриц
- Добавление матриц определяется только в том случае, если добавляемые матрицы имеют одинаковые размеры.
- Соответствующие элементы двух или более матриц добавляются для сложения матриц в сложении матриц.
- Сложение матриц замкнуто по коммутативным, ассоциативным законам и имеет аддитивное тождество и аддитивную обратную.
Похожие темы
- Матрицы
- Типы матриц
- Умножение матриц
- Калькулятор сложения матриц
Часто задаваемые вопросы о добавлении матриц
Что такое сложение матриц в математике?
Сложение матриц — это сложение соответствующих элементов двух или более матриц одного порядка. Матрицы можно добавлять только в том случае, если они имеют одинаковый размер, то есть имеют одинаковое количество строк и столбцов. Если A = [a ij ] и B = [b ij ], сумма двух матриц A и B определяется как: A+B = [a ij ] + [b ij ] = [a ij + b ij ], где ij обозначает позицию каждого элемента в i -й -й строке и j -м -м столбце.
Матрицы можно добавлять только в том случае, если они имеют одинаковый размер, то есть имеют одинаковое количество строк и столбцов. Если A = [a ij ] и B = [b ij ], сумма двух матриц A и B определяется как: A+B = [a ij ] + [b ij ] = [a ij + b ij ], где ij обозначает позицию каждого элемента в i -й -й строке и j -м -м столбце.
Как сделать
Добавление матриц ?Соответствующие элементы матриц A и B одинаковой размерности добавляются для определения матрицы суммы A + B. Если A = [a ij ] и B = [b ij ], сумма двух матриц A а B определяется как: A+B = [a ij ] + [b ij ] = [a ij + b ij ], где ij обозначает положение каждого элемента в i -й -й строке и j -м -м столбце.
Какое необходимое условие для сложения матриц?
Для сложения матриц необходимо условие, чтобы они имели одинаковое количество строк и столбцов. Добавляемые матрицы должны иметь одинаковую размерность.
Добавляемые матрицы должны иметь одинаковую размерность.
Является ли сложение матриц коммутативным?
Сложение матриц коммутативно, как если бы две матрицы A = [a ij ] и B = [b ij ] того же порядка, то A + B = [a ij + b ij ] = [b ij + a ij ]= B + A.
Возможно ли сложение матриц для матриц разных размеров?
Нет, добавление матриц возможно только в том случае, если добавляемые матрицы имеют одинаковые размеры. Когда добавляются две или более матриц, мы добавляем все соответствующие элементы матриц, но если порядок другой, то добавление всех соответствующих элементов невозможно.
Как сложить матрицы 3 x 3?
Матрицы порядка 3 x 3 могут быть добавлены путем сложения соответствующих элементов каждой матрицы.
Каково правило сложения матриц?
Правило добавления матриц состоит в том, что добавляемые матрицы должны иметь одинаковую размерность, т. е. иметь одинаковое количество строк и столбцов.
е. иметь одинаковое количество строк и столбцов.
Свойства сложения матриц и скалярного умножения | Класс 12 Математика
Матрица — это просто прямоугольный массив или набор элементов. Матрица может быть определена как элемент m * n в виде m горизонтальных линий (строк), n вертикальных линий (столбцов), известных как матрица порядка m * n. Элементы могут быть действительными, комплексными или неизвестными числами. Матрица m*n явно выглядит так:
На приведенном выше рисунке нарисована матрица порядка m*n, где I и j представляют точное положение элемента (i,j).
Типы матрицДоступно множество типов матриц, некоторые из них перечислены ниже.
Матрица строкМатрица, имеющая только одну строку, называется матрицей строк.
Пример:
Матрица столбцов Матрица, имеющая только один столбец, называется матрицей столбцов.
Пример:
Нулевая или нулевая матрицаМатрица, в которой все элементы равны 0, называется нулевой или нулевой матрицей.
Пример:
Квадратная матрицаМатрица с одинаковым количеством столбцов и строк называется квадратной матрицей.
Пример:
Диагональная матрицаМатрица, в которой все элементы равны нулю, кроме диагональных, называется диагональной матрицей.
Пример:
Скалярная матрицаОсобый вид диагональной матрицы, в которой все диагональные элементы одинаковы, называется скалярной матрицей.
Пример:
Матрица идентификации Матрица идентификации – это скалярная матрица, в которой все диагональные элементы – 1.
Пример:
2
2
Z.0004Когда мы добавляем или вычитаем матрицу 0 порядка m*n из любой другой матрицы, она возвращает ту же матрицу. Простыми словами, «А+0 = А» и «А – 0 = А».
Пример:
Точно так же вы можете видеть, что вычитание нулевой матрицы из любой другой матрицы даст в результате саму другую матрицу.
Среди всех типов матриц только нулевая матрица имеет ранг всегда нулевой во всех случаях умножения.
Свойства матрицы ДополнениеМатрица может быть дополнена другой матрицей тогда и только тогда, когда порядок матриц одинаков. Сложение будет происходить между элементами матриц. Полученная матрица также будет того же порядка. То есть [A]m×n + [B]m×n = [C]m×n
Например:
Существуют различные уникальные свойства сложения матриц. Мы обсудим следующие свойства:
Мы обсудим следующие свойства:
- Переместительное свойство сложения, т. е. A + B = B+ A
- Ассоциативное свойство сложения, т. е. A+ (B + C) = (A + B) + C
- Аддитивное свойство идентичности. Для любой матрицы A существует уникальная матрица O такая, что A+O = A
- Аддитивное обратное свойство. Когда мы добавляем уникальную матрицу –A к A, мы получаем матрицу O, A+ (-A) = O.
- Замыкание Свойство сложения A + B = C, , где C — матрица тех же размеров, что и A и B.
A, B и C являются матрицами одного порядка m*n. Чтобы добавить две матрицы одинакового порядка, просто добавьте соответствующий элемент каждой матрицы. Давайте подробно обсудим свойство сложения Matrix.
Коммутативное свойство сложения матриц
Это свойство сообщает, что любые две матрицы одного порядка могут быть сложены любым способом. Предположим, что имеются две матрицы A и B одного и того же порядка m*n, тогда коммутативное свойство сложения матриц утверждает, что: A + B = B + A
Пример:
Из приведенного выше примера вы можете видеть, что сложение матриц подчиняется коммутативному закону.
Ассоциативное свойство матрицы Дополнение
Аналогично, если три матрицы имеют одинаковый порядок, то их положение не имеет значения. Предположим, что имеются три матрицы A, B и C порядка m*n, тогда ассоциативное свойство сложения матриц утверждает, что: A + (B + C) = (A + B) + C
Пример:
Из приведенного выше примера видно, что сложение матриц следует ассоциативному закону.
Аддитивное свойство идентичности сложения матриц
Мы обсудили нулевую матрицу, которую можно добавить к любой матрице для получения того же результата. Согласно свойству аддитивной идентичности сложения матриц, для данной матрицы A порядка m*n существует матрица m*n O такая, что: A + O = A
Здесь O — матрица нулевого порядка m*n.
Итак, если к нулевой матрице добавить матрицу, то получится исходная Матрица.
Аддитивное обратное свойство сложения матриц
В Matrix существует правило, согласно которому обратным для любой матрицы A является -A того же порядка. Проще говоря, для данной матрицы A порядка m*n существует уникальная матрица B такая, что: A + B = O
Проще говоря, для данной матрицы A порядка m*n существует уникальная матрица B такая, что: A + B = O
Примечание: Эта матрица B равна –A, т.е. B = – А
Следовательно, A + (-A) = O
Пример:
Мы обсудили различные свойства сложения матриц. Теперь мы обсудим некоторые уникальные свойства матричного скалярного умножения.
Свойства матричного скалярного умножения
Термин скалярное умножение относится к произведению матрицы и действительного числа. Каждая запись умножается на заданный скаляр в скалярном умножении. Скаляр – это действительное число в скалярном умножении.
Пример:
Отсюда ясно, что Matrix можно умножать на любые скалярные величины.
Умножение матриц обладает некоторыми уникальными свойствами; некоторые из них перечислены ниже:
- Ассоциативное свойство умножения, т.
 е. (cd)A = c(dA)
е. (cd)A = c(dA) - Распределительное свойство, т. е. c[A + B] = c[A] + c[B ]
- Мультипликативное свойство тождества, т. е. 1.A = A
- Мультипликативное свойство нуля, т. е. 0.A = 0 c.0 = 0
- Замыкающее свойство умножения cA — матрица той же размерности, что и A
Примечание: A — матрица порядка m*n, c и d скаляры, а O — нулевая матрица.
Ассоциативное свойство матричного скалярного умножения:
В соответствии с ассоциативным свойством умножения, если матрица умножается на два скаляра, сначала можно перемножить скаляры, а затем результат можно умножить на матрицу или матрицу можно умножить сначала к одному скаляру, а затем к полученной матрице другим скаляром, т.е. (cd)A = c(dA)
Например:
Здесь мы берем два скаляра как 2 и 3.
что результат одинаков в обоих случаях.
Распределительное свойство матричного скалярного умножения
Распределительное свойство ясно доказывает, что скалярная величина может быть распределена по сложению матриц или матрица распределена по скалярному сложению.
1. C (A + B) = CA + CB
Например:
2. (C + D) A = CA + DA
Много Свойство идентичности матричного скалярного умножения
Если любую матрицу A умножить на скалярную единицу, результатом будет просто исходная матрица A. мультипликативное тождество в скалярном умножении.
Мультипликативное свойство нуля
Согласно мультипликативному свойству нуля, если любую матрицу A порядка m*n умножить на скаляр 0, то результатом будет m*n нулевая матрица O. Это следует мультипликативным свойствам нуля в реальная система счисления. Если любое действительное число x умножить на 0, результатом всегда будет 0. Если любое скалярное число умножить на нулевую матрицу, результат будет таким же, как и нулевая матрица.
Если любое скалярное число умножить на нулевую матрицу, результат будет таким же, как и нулевая матрица.
0.А = 0
c.0 = 0
Свойство замыкания матричного скалярного умножения
Свойство замыкания просто утверждает, что если у вас есть скалярная величина X и матрица A одного и того же порядка m*n, то каждый элемент будет умножен на X. Это свойство утверждает, что если любая матрица A порядка m * n умножается на любой скаляр, то порядок матрицы остается таким же, как m * n.
Матрицы сложения и вычитания
Матрицы складывать и вычитать легко. Если вы знаете, как складывать и вычитать целые числа, этот урок будет проще простого. Во-первых, внимательно изучите рисунок ниже, чтобы увидеть, как это делается для матрицы 2×2.
Важно знать следующее правило: при сложении и вычитании матриц сначала убедитесь, что матрицы имеют одинаковые размеры.
По порядку слов вы можете добавить или вычесть 2×3 с 2×3 или 3×3 с 3×3. Однако вы не можете добавить 3×2 к 2×3 или 2×2 к 3×3.
Однако вы не можете добавить 3×2 к 2×3 или 2×2 к 3×3.
Другие примеры, показывающие, как складывать и вычитать матрицы
Сложение матриц
Добавьте две матрицы, показанные ниже:
| + |
|
Добавление матрицы
Добавьте две матрицы, показанные ниже:
| + |
|
Правило для сложения и вычитания матриц
Вы можете добавлять элементы в одну и ту же позицию или элементы в одну строку и один столбец. Мы показываем эти элементы одним цветом, чтобы сделать их кристально четкими.
Мы показываем эти элементы одним цветом, чтобы сделать их кристально четкими.
| + |
|
| 1 + 9 | -4 + 3 | 0 + 7 |
| 8 + -8 | -1 + 0 | 6 + 5 |
| 0 + -3 | 3 + 2 | 2 + 9 |
| 10 | -1 | 7 |
| 0 | -1 | 11 |
| -3 | 5 | 11 |
| + |
|
| 1 + 9 | -4 + 3 | 0 + 7 |
| 8 + -8 | -1 + 0 | 6 + 5 |
| 0 + -3 | 3 + 2 | 2 + 9 |
| 10 | -1 | 7 |
| 0 | -1 | 11 |
| -3 | 5 | 11 |
Вычитание матриц
Вычитание матриц аналогично сложению матриц, за исключением того, что вы вычитаете элементы из одной строки и одного столбца.
Вычтите две следующие матрицы:
| – |
|
| 9 – 6 | 7 – 1 | 1 – 8 |
| -2 – -3 | 0 – 0 | 4 – 9 |
| 8 – -1 | -5 – 2 | 3 – 1 |
| 3 | 6 | -7 |
| 1 | 0 | -5 |
| 9 | -7 | 2 |
Вычитание матриц аналогично сложению матриц, за исключением того, что вы вычитаете элементы из одной и той же строки и одного столбца.
Вычтите две следующие матрицы:
| – |
|
| 9 – 6 | 7 – 1 | 1 – 8 |
| -2 – -3 | 0 – 0 | 4 – 9 |
| 8 – -1 | -5 – 2 | 3 – 1 |
| 3 | 6 | -7 |
| 1 | 0 | -5 |
| 9 | -7 | 2 |
Связь с реальным миром
У вас есть бизнес по продаже рубашек и брюк. Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1 , а матрица справа — неделя №2.
Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1 , а матрица справа — неделя №2.
В строке №1 указано количество брюк, проданных вами, а в строке №2 — количество рубашек, проданных с понедельника по пятницу.
Например, вы продали 40 штанов в среду (неделя 1).
Вы продали 28 рубашек в пятницу (2-я неделя)
Сколько штанов и рубашек вы продали за две недели?
Просто выполните сложение матриц!
| + |
|
| 50 + 20 | 25 + 30 | 40 + 70 | 80 + 65 | 10 + 80 |
| 30 + 55 | 90 + 35 | 60 + 75 | 12 + 14 | 45 + 28 |
| 70 | 55 | 110 | 145 | 90 |
| 85 | 125 | 135 | 26 | 73 |
Связь с реальным миром
У вас есть бизнес по продаже рубашек и брюк. Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1, матрица справа — неделя №2.
Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1, матрица справа — неделя №2.
В строке №1 указано количество брюк, проданных вами, а в строке №2 — количество рубашек, проданных с понедельника по пятницу.
Например, вы продали 40 штанов в среду (неделя 1).
Вы продали 28 рубашек в пятницу (2-я неделя)
Сколько штанов и рубашек вы продали за две недели?
Просто выполните сложение матриц!
| + |
|
| 50 + 20 | 25 + 30 | 40 + 70 | 80 + 65 | 10 + 80 |
| 30 + 55 | 90 + 35 | 60 + 75 | 12 + 14 | 45 + 28 |
| 70 | 55 | 110 | 145 | 90 |
| 85 | 125 | 135 | 26 | 73 |
Тест на сложение и вычитание матриц.
 Проверьте, насколько хорошо вы поняли этот урок.
Проверьте, насколько хорошо вы поняли этот урок.Сложение матриц — свойства и типы матриц
Прежде чем обсуждать операции с матрицами, давайте обсудим, что такое матрица.
Матрица представляет собой прямоугольный (двумерный) массив чисел или символов, которые обычно расположены в строках и столбцах. Можно думать об этом как о таблице чисел.
Порядок матрицы определяется количеством строк и столбцов.
Элементы — это числа в матрице, и каждое число известно как элемент.
Матрицы во множественном числе.
Размер матрицы называется матрицей «n на m» и записывается как m×n, где n — количество строк, а m — количество столбцов.

Например, у нас есть матрица 3×2, потому что количество строк здесь равно 3, а количество столбцов равно 2.
(Изображение будет загружено в ближайшее время)
Размерность матрицы можно определить как количество строк и столбцов матрицы в указанном порядке. Поскольку приведенная выше матрица А имеет 2 строки и 3 столбца, она известна как матрица 2 × 3.
Какие существуют типы матриц?
Существуют различные типы матриц. Вот они –
1) Матрица строк
2) Матрица столбцов
3) Матрица нулей
4) Матрица квадратов
5) Диагональная матрица
6) Верхняя треугольная матрица
7) Нижняя треугольная матрица
8) Симметричная матрица
9) Антисимметричная матрица
Сложение матриц
Две матрицы должны иметь одинаковое количество столбцов и строк чтобы добавить. Предположим, что сумма любых двух матриц A и B будет матрицей, имеющей то же количество строк и столбцов, что и матрицы A и B. Сумма A и B, которую можно обозначить как A + B, вычисляется путем сложения соответствующие элементы A и B.
Предположим, что сумма любых двух матриц A и B будет матрицей, имеющей то же количество строк и столбцов, что и матрицы A и B. Сумма A и B, которую можно обозначить как A + B, вычисляется путем сложения соответствующие элементы A и B.
A + B = \[\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\ \ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn} \end {bmatrix}\] + \[\begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1n}\\ b_{21} & b_{22} & \cdots & b_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ b_{m1 } & b_{m2} & \cdots & b_{mn} \end {bmatrix}\]
= \[\begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n}\\ a_{21} +b_{ 21} & a_{22} + b_{21}& \cdots & a_{2n} + b_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn} \end {bmatrix}\]
Матричные суммы и ответы
Предположим, что у нас есть две матрицы A и B.
Обе матрицы A и B имеют одинаковое количество строк и столбцов (то есть количество строк равно 2, а количество столбцов равно 3), поэтому их можно сложить. Другими словами, вы можете добавить матрицу 2 x 3 к матрице 2 x 3 или матрицу 2 x 2 к матрице 2 x 2. Однако нельзя добавить матрицу 3 x 2 к матрице 2 x 3 или матрицу 2 x 2 к матрице 3 x 3.
A = \[\begin{bmatrix} 1 & 2 & 3\\ 7 & 8 & 9\end {bmatrix}\] B = \[\begin{bmatrix} 5 & 6 & 7\\ 3 & 4 & 5\end {bmatrix}\]
A + B = \[\begin{bmatrix} 1 + 5 & 2 + 6 & 3+ 7\\ 7 + 3& 8 + 4 & 9 + 5\end {bmatrix }\]
A + B = \[\begin{bmatrix} 6 & 8 & 10\\ 10 & 12 & 14\end {bmatrix}\]
Примечание: Имейте в виду, что порядок, в котором матрицы добавляются не важно; таким образом, мы можем сказать, что A + B = B + A.
Свойства сложения матриц
1. | m × n, то A + B будет равно B + A. |
2. Ассоциативный закон | B = [bij] и C = [cij] того же порядка, допустим, m × n, тогда мы можем написать (A + B) + C равно A + (B + C). |
3. Существование аддитивного тождества | Допустим, у нас есть матрица A = [aij] — матрица размера m × n, а O — нулевая матрица размера m × n, тогда A + O равно O + A = A. Проще говоря, мы можем сказать, что O является аддитивным тождеством для сложения матриц. |
4. Существование аддитивной обратной A + (–A) равно (–A) + A= O. Таким образом, – A можно назвать аддитивной инверсией A или минусом A. |
Применение матриц
Матрица используется во многих разделах математики, например, для вычислений, связанных с векторами, таких как нахождение производной, интегрирование, интеграл матрицы и т.
 д.
д.Матрица также используется при решении задач на собственные значения, симметричных и собственных векторов, линейной регрессии, задач оптимизации и т. д.
Матрицы широко используются в матричной и линейной алгебре, в частности, для представления и решения линейных систем уравнений.
Решенные примеры задач
Вопрос 1. Добавьте следующие матрицы:
\[A = \begin{bmatrix}1 & 2&3 \\7 & 8&9 \end{bmatrix}\] \[B =\begin{ bmatrix}5 & 6&7 \\3& 4&5 \end{bmatrix} \]
Решение: у нас есть две матрицы A и B.
Обе матрицы A и B имеют одинаковое количество строк и столбцов (то есть количество строк — 2, а количество столбцов — 3), поэтому их можно добавить. Другими словами, вы можете добавить матрицу 2 x 3 к матрице 2 x 3 или матрицу 2 x 2 к матрице 2 x 2. Однако нельзя добавить матрицу 3 x 2 к матрице 2 x 3 или матрицу 2 x 2 к матрице 3 x 3.
Однако нельзя добавить матрицу 3 x 2 к матрице 2 x 3 или матрицу 2 x 2 к матрице 3 x 3.
\[A = \begin{bmatrix}1 & 2&3 \\7 & 8&9 \end{bmatrix}\] \[B =\begin{bmatrix}5 & 6&7 \\3& 4&5 \end{bmatrix} \]
\[ A + B =\begin{bmatrix}1+5 & 2+6&3+7 \\7+3& 8+4&9+5 \end{bmatrix} \]
\[ A+B = \begin{bmatrix }6 & 8&10 \\10 & 12&14 \end{bmatrix} \]
Вопрос 2. Добавьте следующие матрицы.
\[ A = \begin{bmatrix}3 & 4&9 \\12& 11&35 \end{bmatrix}\] \[ B = \begin{bmatrix}6 & 2 \\5 & 8 \end{bmatrix} \]
Решение: Добавим следующие две матрицы A и B. Поскольку мы знаем, что матрицы складываются по элементам, мы должны сложить 3 и 6, 12 и 5, 4 и 6, а также 11 и 8. Но что мне добавить к записям 9 и 35? Во второй матрице нет соответствующих элементов, которые можно добавить к этим элементам в первой матрице. Итак, вот ответ:
Мы не можем сложить эти матрицы A и B, потому что эти матрицы разного размера.
